Spaghettification of the Magic School Bus#
Prepared by: Logan Hennes (lhennes@nd.edu) and Joseph Emery (jemery@nd.edu)
Reference: This is an original problem created by the authors. With inspiration from Dr. Brian Olson’s Problem Solving class.
Intended Audience: This problem is intended for sophomores or juniors from the University of Notre Dame who are taking an introductory physics course.
Learning Objectives#
After studying this notebook, completing the activities, and asking questions in class, you should be able to:
Perform a degrees of freedom analysis
Solve a nonlinear system of equations using Newton’s Method and Python tools
Properly visualize data using matplotlib
Resources#
Relevant Modules in Class Website:
1.5. Functions and Scope
6.1. Modeling Systems of Nonlinear Equations: Flash Calculation Example
Import Libraries#
import numpy as np
from scipy import optimize
import matplotlib.pyplot as plt
from matplotlib import ticker, cm
Problem Statement#
Homework Problem
Complete the following problem outside of class to practice the concepts discussed.
Ms. Frizzle and her students have boarded the Magic School Bus for an adventure in space. However, while exploring the Milky Way galaxy, an asteroid collided with the bus, hurtling the bus toward a black hole. Write a python script to find at what distance away the Magic School Bus needs to be to experience a certain amount of stretching by a black hole.
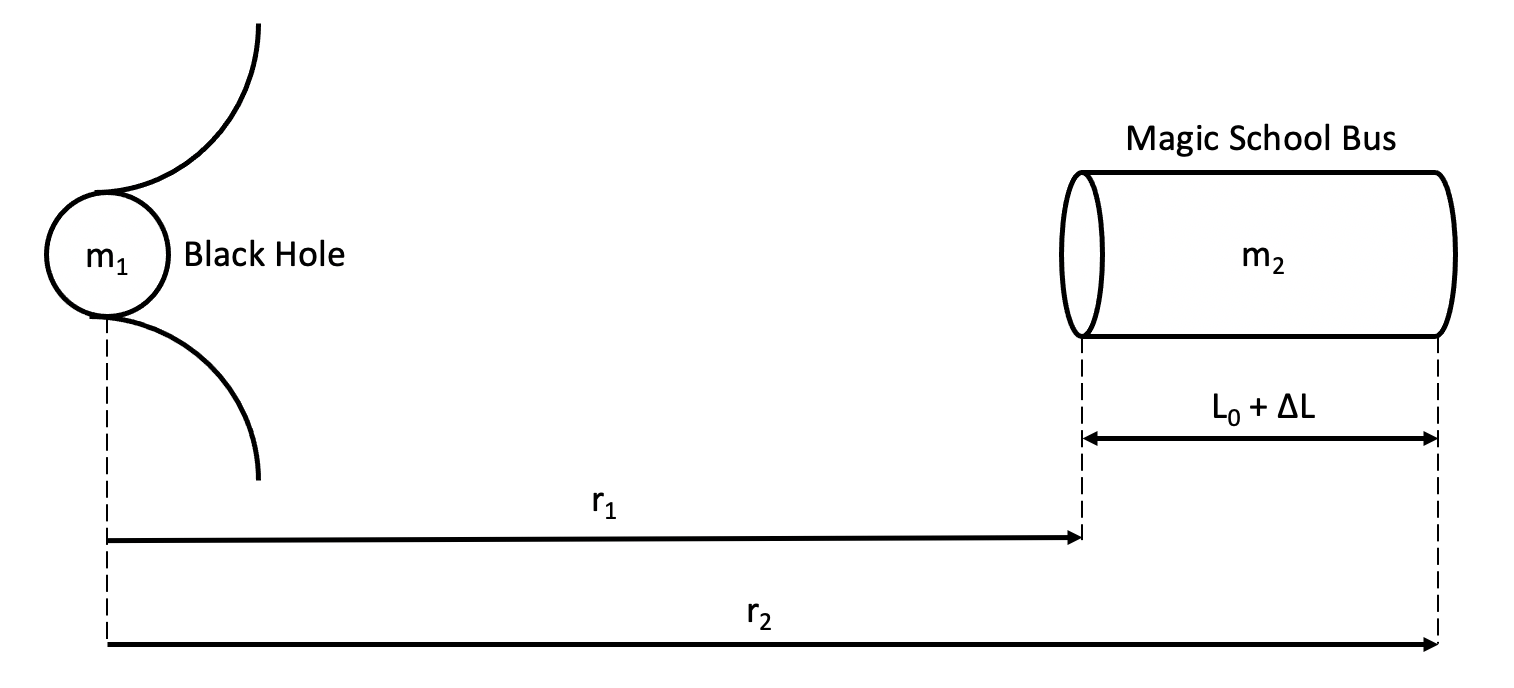
You will need to use Newton’s Law of Universal Gravitation and Youngs modulus.
\(F\) = the force exerted on an object by gravity
\(G\) = the gravitational constant
\(m_1\) = the mass of the black hole
\(m_2\) = the mass of the magic school bus
\(r_1\) = the distance between the black hole and the front of the bus
\(r_2\) = the distance between the black hole and the back of the bus
\(\Delta L\) = the change in length of the bus
\(Y\) = a measure of a solid’s resistance to elastic deformation under a load (Young’s Modulus)
\(F\) = the force exerted on the object causing stretching
\(A\) = cross-sectional area of the bus
\(L_0\) = the length of the bus before stretching
1. Degree of Freedom Analysis#
1.1. Setup#
Define the constants used in this problem. Use scholarly sources such as NASA to determine the mass of the sun. Use the height of the bus as the diameter of your cylinder.
# Constants
Y = 69e9 # Youngs modulus for aluminum
m_2 = 15000 # Mass of school bus in kg
L_0 = 0.01 # length of school bus in km
# Add your solution here
# Add your solution here
1.2. Analysis#
Perform a degree of freedom analysis using the equations provided and the unknown variables. What does this analysis tell you? How should you approach the problem moving forward?
Discuss in 2-4 sentences
Answer:
Submit your written work via Gradescope.
2. Nonlinear Equation#
2.1. Define a nonlinear equation#
Using substitution, define one nonlinear equation \(f(r_1, \Delta L)\).
Hint: The definition of the function above suggests what the variables are.
Submit your answer and written work via Gradescope.
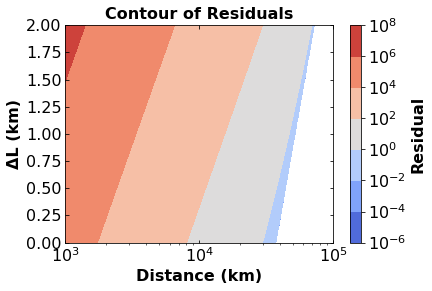
2.2. Create a plot and analyze#
Using the nonlinear equation you derived in part a, write a function that calculates the residual of that function given some value of \(r_1\) and some value of \(\Delta L\). Then define an array of \(r_1\) values labeled as r_1 and an array of \(\Delta L\) values labeled Delta_L. Then use these arrays to calculate the residual for each pair of values.
Use the 3-D plot function in matplotlib to analyze the results.
# Function for Nonlinear Equation Residual
def Residual_Function(r_1,ΔL):
''' Find residual using one Nonlinear equation
Args:
r_1, ΔL
Returns:
Residual
'''
# Add your solution here
Residual =
return Residual
File "<ipython-input-3-0e08dbf484a5>", line 12
Residual =
^
SyntaxError: invalid syntax
# Add your solution here
Plot Residual:
# Create array
# Add your solution here
# Initialize Matrix
# Add your solution here
for i in range(len(r_1)):
for j in range(len(ΔL)):
r_grid[i, j] = r_1[i]
# Add your solution here
# Plot Figure
fig, ax = plt.subplots()
plt.xscale("log")
cs = ax.contourf(
np.exp(r_grid),
ΔL_grid,
f_grid,
locator=ticker.LogLocator(),
cmap=cm.coolwarm,
levels=100,
)
cbar = fig.colorbar(cs)
cbar.ax.set_ylabel("Residual", fontsize=16, fontweight="bold")
cbar.ax.tick_params(labelsize=16)
cs2 = plt.contour(
cs, levels=cs.levels[::15], colors="k", alpha=0.7, linestyles="dashed", linewidths=3
)
# plot heatmap label
plt.clabel(cs2, fmt="%2.2f", colors="k", fontsize=16)
# define tick size
plt.xticks(fontsize=16)
plt.yticks(fontsize=16)
plt.tick_params(direction="in", top=True, right=True)
# plot titile and x,y label
plt.xlabel("Distance (km)", fontsize=16, fontweight="bold")
plt.ylabel("ΔL (km)", fontsize=16, fontweight="bold")
plt.title("Contour of Residuals", fontsize=16, fontweight="bold")
plt.show()
### END SOLUTION
<ipython-input-13-a0fea10ee60f>:16: UserWarning: Log scale: values of z <= 0 have been masked
cs = ax.contourf(np.exp(r_grid), ΔL_grid, f_grid, locator=ticker.LogLocator(), cmap=cm.coolwarm, levels=100)
# Add your solution here
<ipython-input-14-08db34fb24a9>:22: UserWarning: Log scale: values of z <= 0 have been masked
cs = ax.contourf(np.exp(r_grid), ΔL_grid, f_grid, locator=ticker.LogLocator(), cmap=cm.coolwarm, levels=100)

2.3. Discussion#
What does the 3-D plot tell you about the solution? Are there multiple solutions?
Discuss in 1-3 sentences
3. Inexact Newton’s Method#
Typically, a body of aluminum can be subjected to 10% to 25% elongation before deformation becomes permanent (plastic deformation). For simplicity, we will define our maximum tolerance for stretching to be one meter. Solve for the distance when the bus experiences this stretching using the inexact Newton’s Method.
You will need to write a new function for your nonlinear equation, \(f(r_1)\), so that the only variable is \(r_1\).
For more information on how to use the inexact Newton’s Method, click here
def inexact_newton(f, x0, delta=1.0e-7, epsilon=1.0e-6, LOUD=False, max_iter=50):
"""Find the root of the function f via Newton-Raphson method
Args:
f: function to find root of [function]
x0: initial guess [float]
delta: finite difference parameter [float]
epsilon: tolerance [float]
LOUD: toggle on/off print statements [boolean]
max_iter: maximum number of iterations [int]
Returns:
estimate of root [float]
"""
assert callable(f), "Warning: 'f' should be a Python function"
assert (
type(x0) is float or type(x0) is int
), "Warning: 'x0' should be a float or integer"
assert type(delta) is float, "Warning: 'delta' should be a float"
assert type(epsilon) is float, "Warning: 'eps' should be a float"
assert type(max_iter) is int, "Warning: 'max_iter' should be an integer"
assert max_iter >= 0, "Warning: 'max_iter' should be non-negative"
x = x0
# print intial guess
# if (LOUD):
# print("x0 =",x0)
iterations = 0
converged = False
# Check if the residual is close enough to zero
while not converged and iterations < max_iter:
# evaluate function 'f' at new 'x'
fx = f(x)
# calculate 'slope'
slope = (f(x + delta) - f(x)) / delta
# print every iteration
# if (LOUD):
# print("x_",iterations+1,"=",x,"-",fx,"/",slope,"=",x - fx/slope)
x = x - fx / slope
iterations += 1
# check if converged
if np.fabs(f(x)) < epsilon:
converged = True
if LOUD:
print("It took", iterations, "iterations")
if not converged:
print("Warning: Not a solution. Maximum number of iterations exceeded.")
return x # return estimate of root
# Set Value of ΔL
ΔL = 1
guess = 1000
# Add your solution here
# Use inexact newton method
# Add your solution here
# Add your solution here
# Add your solution here
It took 15 iterations
The result of the inexact newton function is 37407.4751508785
4. Newton’s Method using Scipy#
Now we have a working estimate for the correct result. Let’s use one of the functions in scipy to solve for the distance at which the bus experiences one meter of stretching.
4.1. Setup equations#
When using Newton’s Method in Scipy, the derivative of \(f(r_1)\) is required to determine the solution. Calculate the derivative of \(f(r_1)\) and define it as a function.
Submit your written work via Gradescope
# Set Value of ΔL
ΔL = 1
guess = 1000
def derivative_form(r_1):
"""Find max distance using canonical derivative
Args:
r_1
Returns:
derivative
"""
# Add your solution here
return derivative
4.2. Use Scipy to determine \(r_1\)#
# use scipy method
# Add your solution here
The result of the scipy optimize newton function is
(37406.02418060243, converged: True
flag: 'converged'
function_calls: 36
iterations: 18
root: 37406.02418060243)
5. Analysis and Comparison of Each Method#
5.1. Test the inexact Newton’s Method#
Test the inexact Newton’s Method function with guesses of different orders of magnitude. Find a guess that gives you a solution and a guess that doesn’t give you a solution. You should continue adjusting your initial guess until you get an error.
# Initial Guess
# Add your solution here
newton_sln1 = inexact_newton(canonical_form, guess1, epsilon=1.0e-2, LOUD=True)
print("The root using the inexact newton function for guess2 is found at", newton_sln1)
Try Newtons inexact with a very large guess to see if the function fails.
# Higher Guess
# Add your solution here
newton_sln2 = inexact_newton(canonical_form, guess2, epsilon=1.0e-2, LOUD=True)
print("The root using the inexact newton function for guess2 is found at", newton_sln2)
# Add your solution here
newton_sln3 = inexact_newton(canonical_form, guess3, epsilon=1.0e-2, LOUD=True)
print("The root using the inexact newton function for guess3 is found at", newton_sln3)
It took 23 iterations
The root using the inexact newton function for guess1 is found at 37459.136814048645
It took 15 iterations
The root using the inexact newton function for guess2 is found at 37407.4751508785
It took 7 iterations
The root using the inexact newton function for guess3 is found at 37424.27645628167
5.1.1 Discussion#
How do different orders of magnitude change result from guess? How do the number of iterations change?
Discuss in 2-4 sentences
Answer:
5.2. Finding the limits of inexact Newton’s Method#
Determine the upper and lower limit for your guess where the inexact Newton’s Method function gives you a usable solution. Continue making your guess larger until you get an error. The error is your upper limit. Then do the same for the lower limit.
# Find the upper limit using inexact newton method
# Add your solution here
inexact_newton(canonical_form, upper_limit_inexact, epsilon=1.0e-2)
# Find the lower limit using inexact newton method
### BEGIN SOLUTION
lower_limit_inexact = 7.7240e-3
### END SOLTUON
inexact_newton(canonical_form, lower_limit_inexact, epsilon=1.0e-2)
print(
"The range of guesses that you can use for the inexact newton method is",
lower_limit_inexact,
"km < guess <",
upper_limit_inexact,
"km",
)
The range of guesses that you can use for the inexact newton method is 0.007724 km < guess < 59326.0 km
5.3. Test Newton’s Method with Scipy#
Now do similar tests using the same numbers for the optimize.newton function in scipy. Find a guess that gives you a solution and a guess that doesn’t give you a solution. For the incorrect guess, you should get an error.
# Initial Guess
# Add your solution here
scipy_sln1 = optimize.newton(
func=canonical_form, x0=guess1, fprime=derivative_form, tol=1e-2, full_output=True
)
Try scipy with a very large guess to see if the function fails.
# higher Guess
### BEGIN SOLUTION
guess2 = 1e3
### END SOLTUION
scipy_sln2 = optimize.newton(
func=canonical_form, x0=guess2, fprime=derivative_form, tol=1e-2, full_output=True
)
# even larger guess
# Add your solution here
scipy_sln3 = optimize.newton(
func=canonical_form, x0=guess3, fprime=derivative_form, tol=1e-2, full_output=True
)
The result of guess1 is
(37406.024180626926, converged: True
flag: 'converged'
function_calls: 52
iterations: 26
root: 37406.024180626926)
The result of guess2 is
(37406.02418060243, converged: True
flag: 'converged'
function_calls: 36
iterations: 18
root: 37406.02418060243)
The result of guess3 is
(37406.02418060992, converged: True
flag: 'converged'
function_calls: 20
iterations: 10
root: 37406.02418060992)
print("The result of guess1 is \n", scipy_sln1, "\n")
print("The result of guess2 is \n", scipy_sln2, "\n")
print("The result of guess3 is \n", scipy_sln3)
# Initial Guess
guess = 1e6
scipy_sln = optimize.newton(
func=canonical_form, x0=guess, fprime=derivative_form, tol=1e-2
)
print("The root is found at", scipy_sln)
---------------------------------------------------------------------------
RuntimeError Traceback (most recent call last)
<ipython-input-140-7238afa42cc3> in <module>
5 # Use Scipy method
6 # Add your solution here
----> 7 scipy_sln = optimize.newton(func=canonical_form, x0 = guess, fprime=derivative_form, tol=1e-2)
8 print("The root is found at",scipy_sln)
9 ### END SOLUTION
/usr/local/lib/python3.8/dist-packages/scipy/optimize/zeros.py in newton(func, x0, fprime, args, tol, maxiter, fprime2, x1, rtol, full_output, disp)
292 " Failed to converge after %d iterations, value is %s."
293 % (itr + 1, p0))
--> 294 raise RuntimeError(msg)
295 warnings.warn(msg, RuntimeWarning)
296 return _results_select(
RuntimeError: Derivative was zero. Failed to converge after 3 iterations, value is -1.0466994161548342e+25.
5.3.1 Discussion#
How do different orders of magnitude change the result from guess? How do the number of iterations change?
Discuss in 2-4 sentences
Answer:
5.4. Finding the limits of Newton’s Method with Scipy#
Determine the upper and lower limit for your guess where the optimize.newton function in scipy gives you a useable solution.
# Find the upper limit using scipy method
upper_limit_scipy = 2.9e5
while True:
try:
upper_limit_scipy += 1
optimize.newton(
func=canonical_form, x0=upper_limit_scipy, fprime=derivative_form, tol=1e-2
)
except:
print(upper_limit_scipy)
break
# Find the lower limit using scipy method
lower_limit_scipy = 1e3
while True:
try:
lower_limit_scipy -= 1
optimize.newton(
func=canonical_form, x0=lower_limit_scipy, fprime=derivative_form, tol=1e-2
)
except:
print(lower_limit_scipy)
break
print(
"optimize.newton function from scipy works over",
lower_limit_scipy,
"km < guess <",
upper_limit_scipy,
"km",
)
optimize.newton function from scipy works over 0.0 km < guess < 290001.0 km
5.5. Discussion#
Over what range of guesses will the inexact newton function give you a result? Over what range of guesses will the optimize.newton function from scipy gives you a result? Which of the ranges is bigger? Which method uses fewer iterations?
Discuss in 2-4 sentences
Answer:

