1.15. Preparing Publication Quality Figures in Python#
1.15.1. Learning Objectives#
After studying this notebook, completing the activities, and asking questions in class, you should be able to:
Recognize features that make a scientific figure worthy of publication.
Understand how to add various features to scientific figures and be familiar with where to find syntax for reference.
1.15.2. What makes a scientific figure look great?#
Graphical Excellence
The following short article describes what makes a great scientific data visualization:
P. Kamat, G. V. Hartland, and G. C. Schatz (2014). Graphical Excellence, J. Phys. Chem. Lett., 5(12), 2118–2120.
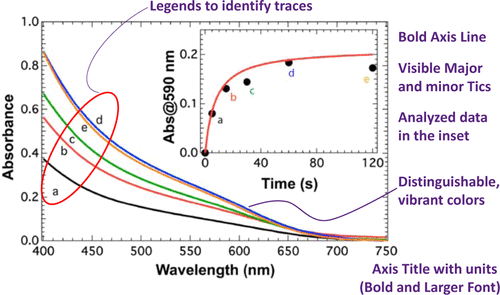
Python Format Recommandations
Based on this paper, we developed the following guidelines to use with matplotlib.
Figure
Figure size: 4x4, 4x6.4
Dpi: 300
Plot
Line width: 3
Marker size: 8
Axes
Ticks font size: 15
Major ticks direction: in
Minor ticks direction: in
Axis Label
Font size: 16
Font weight: bold
All of these examples (below) use these guidelines.
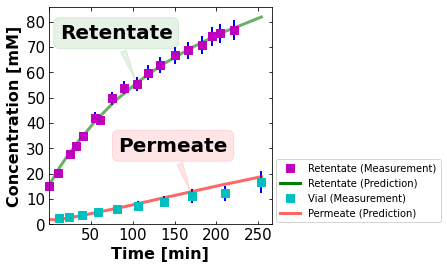
1.15.3. Example: Data and Model Predictions#
In this first example prepared by Xinhong Liu, we will create a plot in the graphical abstract from:
J. A. Ouimet, X. L., D. J. Brown, E. A. Eugene, T. Popps, Z. W. Muetzel, A. W. Dowling, W. A. Phillip (2022). DATA: Diafiltration Apparatus for high-Throughput Analysis, J. Membrane Science, 641(1), p. 119743.
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.lines import Line2D
For simplicity, we “hard coded” the data into this notebook. In our actually research code, these data are generated automaically, stored in csv files, and read into Python with pandas.
# Experiment data stored in dict
data_stru = {'time': [0, 10, 630, 715, 1445, 1480, 1930, 2395, 2430, 3330, 3540, 3665, 4530, 4875, 5360, 6280, 6415, 7085, 7940, 8240, 9030, 9930, 10235, 10930, 11680, 12280, 12575, 13230, 15215],
'cF_exp': [15.20517956, 15.20517956, 20.17925714, np.nan, np.nan, 27.74228235, 31.0364, np.nan, 34.73451321, 42.10616744, np.nan, 41.21821818, 49.70306667, np.nan, 53.94549091, 55.5364, np.nan, 59.79315676, 63.0364, np.nan, 66.67276364, 68.6614, np.nan, 70.77833548, 74.22284068, 75.4501931, np.nan, 76.72061053, np.nan],
'cV_avg': [np.nan, np.nan, np.nan, 2.371375951, 2.971221924, np.nan, np.nan, 3.608081644, np.nan, np.nan, 4.863598959, np.nan, np.nan, 6.184805962, np.nan, np.nan, 7.398282511, np.nan, np.nan, 8.986931928, np.nan, np.nan, 11.26145154, np.nan, np.nan, np.nan, 12.20494634, np.nan, 16.70175135]}
# Model predictions stored in dict
fit_stru = {'time': [0, 10, 630, 715, 1445, 1480, 1930, 2395, 2430, 3330, 3540, 3665, 4530, 4875, 5360, 6280, 6415, 7085, 7940, 8240, 9030, 9930, 10235, 10930, 11680, 12280, 12575, 13230, 15215],
'cF': [15.20517956, 15.30581000885246, 21.186911048158944, 21.94776258720176, 27.935712649713867, 27.935712649713867, 31.41957200691469, 34.79231254607359, 34.79231254607359, 40.737212176615486, 42.024440019753044, 42.62511080503662, 47.51297790337563, 49.32034465832626, 51.47034529371476, 55.72406395078971, 56.31185664451917, 59.00364601757129, 62.300546660870005, 63.39102918275215, 65.91456478110173, 68.79648688113936, 69.72116826647738, 71.66837157084154, 73.72202692048653, 75.27787416192324, 76.01654487095536, 77.42158102079782, 81.81060107249392],
'cH': [1.8971007608000001, 1.857468593269977, 1.7651071567700096, 1.844767802680894, 2.5666499819216466, 2.5666499819216466, 3.045470174932628, 3.5529667541583545, 3.5529667541583545, 4.568847236522133, 4.811750292853133, 4.92814180996477, 5.952827220990674, 6.369556241211926, 6.894439305225153, 8.034207387259743, 8.203010953189972, 9.013552663552899, 10.094858239741818, 10.475147439508877, 11.40039115341059, 12.537180598977393, 12.920607805042627, 13.758398327314904, 14.687274225493889, 15.422320387044207, 15.780811354585317, 16.479645784135432, 18.805287502530643]}
We define a function to create the plot. The optional arguements are toggles to turn certain aspects of the figure on or off. Sometimes, we add extra information to the figure (e.g., title with timestamp of experiment ID) that is useful when organizing results. But for a final publication, we want to remove that aspect of the figure. These toggles make sure customization easy (and clean).
Show code cell source
def plot_sim_comparison(data_stru,fit_stru,plot_pred=True,lg=False):
"""
Plot simulation results comparing model predictions (lines) and data
(symbols) with box annotations
Arguments:
data_stru: dictionary containing "time", "cF_exp", and "cV_avg" keys with
lists of floats as values
fit_stru: dictionary containing "time", "cF", and "cH" keys with lists
as floats as values
plot_pred: boolean. If true, plot the prediction
lg: boolean. If true, add the legend
Returns:
nothing
"""
fig = plt.figure(figsize=(4,4))
# plot ghost points for legend
plt.plot([],[],'ms',markersize=8,label='Retentate (Measurement)')
if plot_pred:
plt.plot([],[],'g',linewidth=3,label='Retentate (Prediction)')
plt.plot([],[],'cs',markersize=8,label='Vial (Measurement)')
if plot_pred:
plt.plot([],[],'r-',linewidth=3,alpha=.6,label='Permeate (Prediction)')
# add errorbars (arbitrary for this example)
cV_avg_err = [0.25*cv for cv in data_stru['cV_avg']] # 25 %
cF_exp_err = [0.05*cf for cf in data_stru['cF_exp']] # 5 %
# plot concentration data (with errorbars)/prediction comparison
plt.errorbar([t/60 for t in data_stru['time']], data_stru['cV_avg'],
yerr = cV_avg_err,
fmt='s', ms=8, color='c', # marker settings
ecolor = 'b', elinewidth = 2)
plt.errorbar([t/60 for t in data_stru['time']], data_stru['cF_exp'],
yerr = cF_exp_err,
fmt='s', ms=8, color='m',clip_on=False, # marker settings
ecolor = 'b', elinewidth = 2)
# code for plotting without error bars
"""
plt.plot([t/60 for t in data_stru['time']],
data_stru['cV_avg'], 'cs',markersize=8)
plt.plot([t/60 for t in data_stru['time']],
data_stru['cF_exp'],'ms',markersize=8,clip_on=False)
"""
if plot_pred:
plt.plot([t/60 for t in fit_stru['time']],
fit_stru['cF'],
'g',linewidth=3,alpha=.6)
plt.plot([t/60 for t in fit_stru['time']],
fit_stru['cH'],
'r-',linewidth=3,alpha=.6)
# add annotation
plt.annotate('Retentate', xy=((fit_stru['time'][15])/60,
fit_stru['cF'][15]), xycoords='data',
xytext=(36, 50), weight='bold', textcoords='offset points',
size=20, ha='right', va="center",
bbox=dict(boxstyle="round", color = "green", alpha=0.1),
arrowprops=dict(arrowstyle="wedge,tail_width=0.3",color = "green",alpha=0.1))
plt.annotate('Permeate', xy=((data_stru['time'][22])/60,
data_stru['cV_avg'][22]), xycoords='data',
xytext=(36, 50), weight='bold', textcoords='offset points',
size=20, ha='right', va="center",
bbox=dict(boxstyle="round", color = "red", alpha=0.1),
arrowprops=dict(arrowstyle="wedge,tail_width=0.3",color = "red",alpha=0.1))
plt.xlabel('Time [min]',fontsize=16,fontweight='bold')
plt.ylabel('Concentration [mM]',fontsize=16,fontweight='bold')
#plt.xticks(fontsize=15,rotation=45) # rotate ticks (optional)
plt.xticks(fontsize=15)
plt.yticks(fontsize=15)
plt.tick_params(direction="in",top=True, right=True)
# This commented out code turns on minor ticks
#plt.minorticks_on() # turn on minor ticks
#plt.tick_params(which="minor",direction="in",top=True, right=True)
#plt.gca().axes.xaxis.set_ticklabels([]) # remove tick labels
#plt.gca().axes.yaxis.set_ticklabels([])
plt.xlim(left=0)
plt.ylim(bottom=0)
# invisible overlaped ticks
ax = plt.gca()
xticks = ax.xaxis.get_major_ticks()
xticks[0].label1.set_visible(False)
if lg:
# Add legend
plt.legend(fontsize=10,bbox_to_anchor=(1.02, 0.3),borderaxespad=0)
plt.show()
# Save to file (for including in manuscript)
fname = 'concentration'
fig.savefig(fname+'.png',dpi=300,bbox_inches='tight')
plot_sim_comparison(data_stru,fit_stru,plot_pred=True,lg=True)
C:\Users\ebrea\anaconda3\envs\jbook\lib\site-packages\numpy\core\_methods.py:44: RuntimeWarning: invalid value encountered in reduce
return umr_minimum(a, axis, None, out, keepdims, initial, where)
C:\Users\ebrea\anaconda3\envs\jbook\lib\site-packages\numpy\core\_methods.py:40: RuntimeWarning: invalid value encountered in reduce
return umr_maximum(a, axis, None, out, keepdims, initial, where)
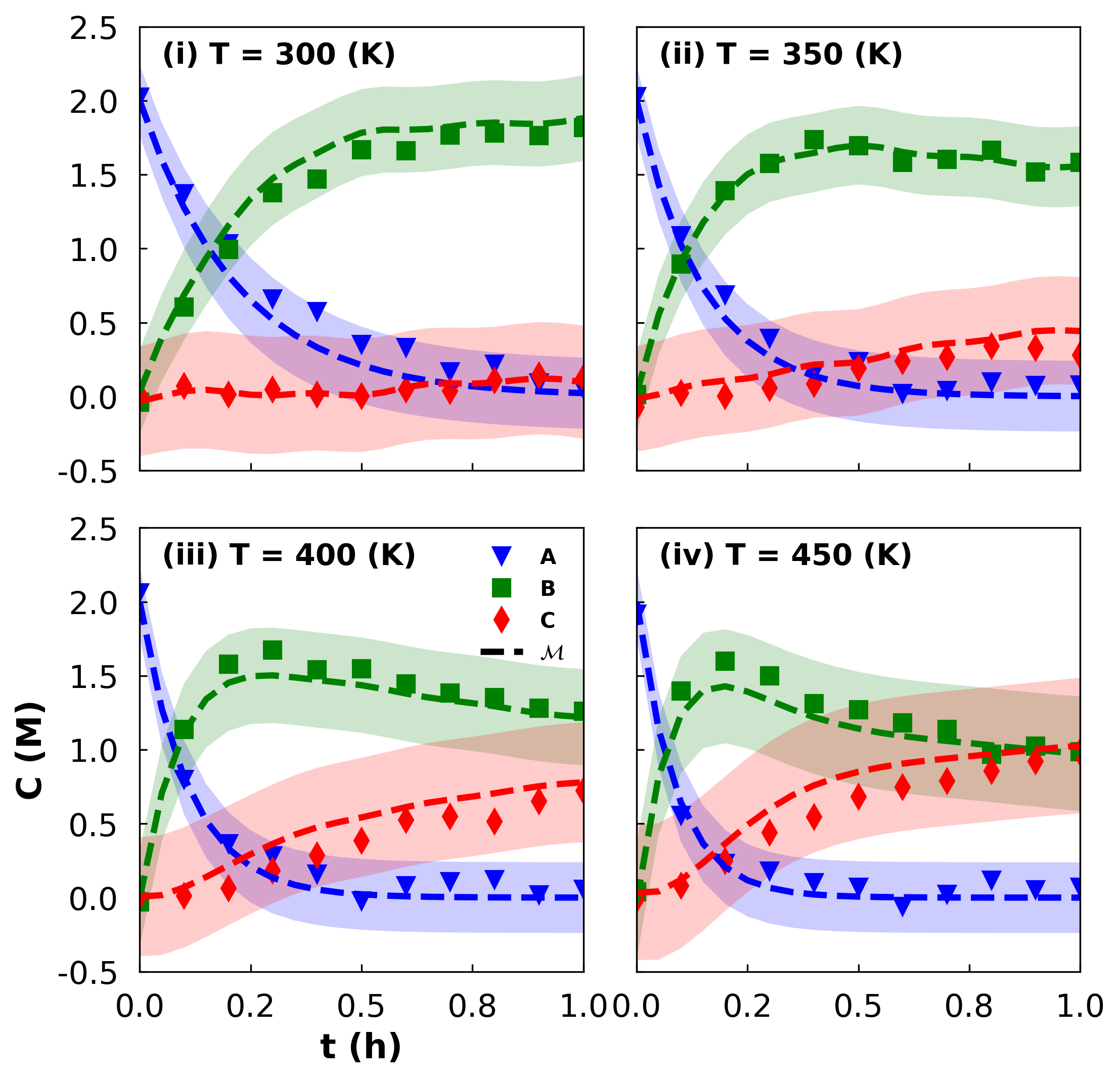
1.15.4. Example: Predictions with Uncertainty Bands#
In this next example, prepared by Kyla Jones, we will plot (synthetic) observed data, model predictions, and prediction uncertainty bands.
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import FormatStrFormatter
from matplotlib.patches import Patch
from matplotlib.lines import Line2D
For simplicity, we define all of the data in this notebook. In actuality, involved calculations we performed to obtain the model predictions and uncertainty estimates.
### Hardcode all data
## y observed
Nobs = 11
Ntemp = 4
empty_obs = np.zeros([Ntemp, Nobs])
# species A
y_a = empty_obs.copy()
y_a[0] = np.array([2.02344425, 1.36860251, 1.03096299, 0.65740269, 0.57241884, 0.34985885, 0.33058912, 0.1681872, 0.21952612, 0.09226589, 0.04931872])
y_a[1] = np.array([2.02586019, 1.08716909, 0.68781963, 0.39403194, 0.16032257, 0.23428204, 0.02076534, 0.04033475, 0.0978981, 0.07540423, 0.07714833])
y_a[2] = np.array([2.06153694, 0.79796719, 0.36428256, 0.28103432, 0.15975079, -0.02254134, 0.07891708, 0.10685296, 0.12181174, 0.02014969, 0.05518219])
y_a[3] = np.array([1.91735135, 0.55511856, 0.23183268, 0.17951325, 0.10104957, 0.07111516, -0.06139098, 0.02229231, 0.11901155, 0.05373958, 0.06958662])
# species B
y_b = empty_obs.copy()
y_b[0] = np.array([-0.03752427, 0.60530102, 0.9955825, 1.37850256, 1.46935982, 1.66645002, 1.66070452, 1.76850223, 1.77915875, 1.76184489, 1.81672473])
y_b[1] = np.array([0.01296338, 0.89639214, 1.39186189, 1.57595299, 1.73540578, 1.69419998, 1.5826509, 1.60318491, 1.66460086, 1.51776157, 1.58146774])
y_b[2] = np.array([-0.02792897, 1.13569095, 1.57844183, 1.67418324, 1.5395483, 1.54537824, 1.44573124, 1.38463391, 1.35080703, 1.28076757, 1.25975991])
y_b[3] = np.array([0.0379667, 1.39594316, 1.59870984, 1.50034396, 1.31129013, 1.27005324, 1.18085389, 1.13550051, 0.96852283, 1.02524932, 0.98662983])
# species C
y_c = empty_obs
y_c[0] = np.array([0.01385988, 0.07233084, 0.0138011, 0.04580091, 0.01139069, 0.00281789, 0.04759571, 0.03531502, 0.10974563, 0.14194261, 0.12514075])
y_c[1] = np.array([-0.07376425, 0.0243219, 0.00364111, 0.05713541, 0.08313851, 0.18909311, 0.23693068, 0.26420506, 0.3413782, 0.32597304, 0.27979896])
y_c[2] = np.array([0.00943458, 0.01096848, 0.06149562, 0.18328175, 0.285206, 0.38444738, 0.52486223, 0.55009396, 0.51287361, 0.65236054, 0.72341975])
y_c[3] = np.array([-0.01221299, 0.07851271, 0.24902781, 0.44011205, 0.54449372, 0.68277854, 0.74685861, 0.78954617, 0.85525827, 0.92077101, 0.98371899])
## y predicted
Npred = 21
empty_pred = np.zeros([Ntemp, Npred])
# species A
y_a_star = empty_pred.copy()
y_a_star[0] = np.array([2, 1.59768464, 1.2762981, 1.01956093, 0.81446842, 0.65063184, 0.51975225, 0.41520009, 0.3316794, 0.26495954, 0.21166089,
0.16908368, 0.1350712, 0.10790059, 0.08619556, 0.06885666, 0.05500561, 0.04394081, 0.03510178, 0.02804079, 0.02240017])
y_a_star[1] = np.array([2, 1.43192894, 1.02521025, 0.73401411, 0.52552803, 0.3762594, 0.26938836, 0.1928725, 0.13808985, 0.09886743, 0.07078557,
0.05067995, 0.03628504, 0.0259788, 0.0185999, 0.01331687, 0.0095344, 0.00682629, 0.00488738, 0.00349919, 0.0025053])
y_a_star[2] = np.array([2.00000000e+00, 1.27514755e+00, 8.13000633e-01, 5.18347881e-01, 3.30485014e-01, 2.10708578e-01, 1.34342263e-01, 8.56531035e-02,
5.46101724e-02, 3.48180137e-02, 2.21990524e-02, 1.41535336e-02, 9.02392180e-03, 5.75341587e-03, 3.66822707e-03, 2.33876537e-03,
1.49113546e-03, 9.50708864e-04, 6.06147038e-04, 3.86463454e-04, 2.46398963e-04])
y_a_star[3] = np.array([2.00000000e+00, 1.13393738e+00, 6.42906988e-01, 3.64508132e-01, 2.06664698e-01, 1.17172413e-01, 6.64330892e-02, 3.76654815e-02,
2.13551486e-02, 1.21077006e-02, 6.86468715e-03, 3.89206267e-03, 2.20667767e-03, 1.25111715e-03, 7.09344247e-04, 4.02175978e-04,
2.28021187e-04, 1.29280873e-04, 7.32982072e-05, 4.15577884e-05, 2.35619648e-05])
# species B
y_b_star = empty_pred.copy()
y_b_star[0] = np.array([0.03270519, 0.39926139, 0.68731271, 0.9354765, 1.15467428, 1.33761972, 1.47392424, 1.56736103, 1.64477813, 1.72322029, 1.78283252,
1.80362121, 1.80259763, 1.80761942, 1.82500871, 1.84425379, 1.85162638, 1.84487036, 1.84124298, 1.85587223, 1.88118926])
y_b_star[1] = np.array([0.01671025, 0.55383436, 0.91650889, 1.17570006, 1.36693187, 1.5015587, 1.5820901, 1.62015396, 1.64645615, 1.67929046, 1.69878894,
1.68435974, 1.65219138, 1.629514, 1.62213033, 1.6187281, 1.60468673, 1.57720045, 1.55336206, 1.54843504, 1.55513168])
y_b_star[2] = np.array([-0.00610998, 0.70773819, 1.11833386, 1.3416306, 1.4524385, 1.49667326, 1.50216811, 1.48843442, 1.4704685, 1.45434913, 1.43575602,
1.40975002, 1.37968974, 1.3530836, 1.3326319, 1.31447336, 1.29341394, 1.2690736, 1.24668352, 1.23083234, 1.21997388])
y_b_star[3] = np.array([-0.03278059, 0.82392828, 1.23715807, 1.40009353, 1.42839638, 1.39244126, 1.33332529, 1.2726671, 1.21982743, 1.17694373,
1.14258333, 1.11470584, 1.0921472, 1.07408545, 1.05895914, 1.04463014, 1.02965292, 1.01413203, 0.99917604, 0.98542831, 0.97209606])
# species C
y_c_star = empty_pred
y_c_star[0] = np.array([-0.03270519, 0.00305397, 0.03638919, 0.04496257, 0.0308573, 0.01174844, 0.00632351, 0.01743888, 0.02354247, 0.01182017,
0.00550658, 0.02729511, 0.06233117, 0.08447999, 0.08879573, 0.08688955, 0.09336801, 0.11118882, 0.12365524, 0.11608698, 0.09641057])
y_c_star[1] = np.array([-0.01671025, 0.0142367, 0.05828086, 0.09028582, 0.10754011, 0.12218191, 0.14852154, 0.18697355, 0.21545399, 0.22184211, 0.2304255,
0.26496031, 0.31152357, 0.3445072, 0.35926977, 0.36795504, 0.38577887, 0.41597325, 0.44175055, 0.44806577, 0.44236302])
y_c_star[2] = np.array([0.00610998, 0.01711426, 0.0686655, 0.14002152, 0.21707649, 0.29261817, 0.36348962, 0.42591248, 0.47492132, 0.51083286, 0.54204493,
0.57609645, 0.61128634, 0.64116298, 0.66369988, 0.68318787, 0.70509493, 0.72997569, 0.75271033, 0.76878119, 0.77977973])
y_c_star[3] = np.array([0.03278059, 0.04213434, 0.11993494, 0.23539834, 0.36493892, 0.49038633, 0.60024162, 0.68966742, 0.75881742, 0.81094857,
0.85055198, 0.88140209, 0.90564613, 0.92466343, 0.94033152, 0.95496768, 0.97011906, 0.98573869, 1.00075066, 1.01453013, 1.02788038])
## variance of predictions
# species A
var_a = np.array([[0.05719945, 0.06328314, 0.07272865, 0.07949682, 0.08249553, 0.08242237, 0.08037767, 0.07733186, 0.07397983, 0.07075224, 0.06787686,
0.06544412, 0.06346087, 0.06188887, 0.0606701, 0.05974194, 0.05904548, 0.05852935, 0.0581509, 0.05787595, 0.0576778],
[0.05719945, 0.05976117, 0.06245206, 0.06325761, 0.06272024, 0.0616213, 0.06046344, 0.05947678, 0.05872418, 0.05818864, 0.05782545,
0.05758773, 0.05743631, 0.05734195, 0.05728416, 0.0572493, 0.05722852, 0.05721627, 0.05720911, 0.05720497, 0.05720258],
[0.05719945, 0.06055497, 0.06265554, 0.06218973, 0.06080576, 0.05949002, 0.05854026, 0.05794131, 0.05759333, 0.05740209, 0.05730114,
0.05724947, 0.05722364, 0.05721099, 0.05720489, 0.05720199, 0.05720062, 0.05719998, 0.05719969, 0.05719956, 0.0571995],
[0.05719945, 0.06748288, 0.07042203, 0.06676295, 0.06266473, 0.0599445, 0.05847011, 0.0577554, 0.05743287, 0.05729441, 0.05723713,
0.0572141, 0.05720505, 0.05720156, 0.05720023, 0.05719974, 0.05719955, 0.05719948, 0.05719946, 0.05719945, 0.05719945]])
# species B
var_b = np.array([[0.08041407, 0.08548342, 0.0942853, 0.10031488, 0.10237395, 0.10161885, 0.09899488, 0.09577745, 0.09238062, 0.08946731,
0.08694899, 0.08513801, 0.08373001, 0.08292177, 0.08236026, 0.08223461, 0.08220564, 0.08247615, 0.0827256, 0.0832465, 0.08456729],
[0.06996611, 0.07250687, 0.07466939, 0.07500611, 0.07410654, 0.07300714, 0.07191716, 0.07126404, 0.07080229, 0.07072385, 0.07069991,
0.07091747, 0.07107363, 0.07138765, 0.07158516, 0.07190796, 0.07210113, 0.07243694, 0.07272244, 0.07309388, 0.07318622],
[0.10459769, 0.10714292, 0.10847073, 0.10738268, 0.10580067, 0.10463459, 0.10399859, 0.10375836, 0.10374181, 0.10383653, 0.10396538,
0.10410001, 0.10421888, 0.10432586, 0.10441817, 0.10451517, 0.10463752, 0.10483768, 0.10511517, 0.10537128, 0.10597695],
[0.14939687, 0.15640947, 0.15673244, 0.15218987, 0.14859712, 0.14695313, 0.1465719, 0.14673995, 0.14705303, 0.14734157, 0.14755549,
0.1476938, 0.14777069, 0.1478045, 0.14781535, 0.14782897, 0.14787997, 0.14801416, 0.14831035, 0.1490566, 0.15126877]])
# species C
var_c = np.array([[0.13761351, 0.14268368, 0.151495, 0.1575553, 0.15967659, 0.15902096, 0.15653546, 0.15349447, 0.15030938, 0.14763968, 0.14539309,
0.14387839, 0.14278781, 0.14231509, 0.1421044, 0.14234241, 0.14268768, 0.14334096, 0.14397984, 0.14489511, 0.14661361],
[0.12716556, 0.12970804, 0.13188809, 0.13227501, 0.13146534, 0.13049419, 0.12956507, 0.12909831, 0.1288415, 0.12898045, 0.1291812,
0.12962646, 0.1300098, 0.13054754, 0.13096292, 0.13149577, 0.13188955, 0.13241524, 0.1328789, 0.13341603, 0.13366104],
[0.16179714, 0.16434671, 0.16571033, 0.16470349, 0.16323702, 0.16220358, 0.16170392, 0.16159574, 0.16170286, 0.16191099, 0.16214216,
0.16236761, 0.1625656, 0.16273996, 0.16288795, 0.1630292, 0.16318473, 0.16340753, 0.16369774, 0.16395741, 0.16455827],
[0.20659632, 0.21363847, 0.21416268, 0.20998773, 0.20681539, 0.2055619, 0.20550853, 0.20593768, 0.2064511, 0.20688658, 0.20720041,
0.20739674, 0.20749437, 0.20751608, 0.20748645, 0.20743568, 0.2074028, 0.20743782, 0.20762347, 0.20825134, 0.21034041]])
# set controls for predictions:
t_star = np.linspace(0,1.0,Npred) # range of times we wish to predict over
T_star = np.array([300.00,350.00,400.00,450.00]) # range of temperatures we wish to predict over
assert len(T_star) == Ntemp, "Dimension mismatch"
t = np.linspace(0,1.0,Nobs) # time-series used to generate ζ
Next, we create the four subplots.
Show code cell source
# create a figure of 2x2 subplots
fig, axs = plt.subplots(2, 2, dpi = 300, figsize =(8,8))
for j in np.arange(0,Ntemp):
## some conditional formatting:
# determine the location of each subplot [a,b] and its subplot title (i-iv+temperature)
# to be displayed in subplot corner of choice (anch = 'NW,SW,..etc.')
if j == 0: # T = 300 K
a = 0
b = 0
anch = 'SE' # South East
tit = r'(i) '
elif j == 1: # T = 350 K
a = 0
b = 1
anch = 'SW' # Soutwest
tit = r'(ii) '
elif j == 2: # T = 400 K
a = 1
b = 0
anch = 'SE' # South East
tit = r'(iii) '
elif j == 3: # T= 450 K
a = 1
b = 1
anch = 'SW' # South West
tit = r'(iv) '
# set plot properties once so they can be easily changed later
lin_styl = '--' # set linestyle
mrk_siz = 8 # set markersize
lin_wdth = 3 # set linewidth
shade_intensity = 0.2 # set shade intensity
# plot observations on subplot axes[a,b]
axs[a,b].plot(t, y_a[j,:],'bv', markersize = mrk_siz)
axs[a,b].plot(t, y_b[j,:],'gs', markersize = mrk_siz)
axs[a,b].plot(t, y_c[j,:],'rd', markersize = mrk_siz)
# plot hybrid model predictions
axs[a,b].plot(t_star, y_a_star[j,:],'b'+str(lin_styl), label = r'$C_A$', linewidth = lin_wdth, markersize = mrk_siz)
axs[a,b].plot(t_star, y_b_star[j,:],'g'+str(lin_styl), label = r'$C_B$', linewidth = lin_wdth, markersize = mrk_siz)
axs[a,b].plot(t_star, y_c_star[j,:],'r'+str(lin_styl), label = r'$C_A$', linewidth = lin_wdth, markersize = mrk_siz)
# shade +/- one standard deviation from prediction
axs[a,b].fill_between(t_star, y_a_star[j,:] - var_a[j,:]**0.5,
y_a_star[j,:] + var_a[j,:]**0.5, facecolor='b', alpha = shade_intensity)
axs[a,b].fill_between(t_star, y_b_star[j,:] - var_b[j,:]**0.5,
y_b_star[j,:] + var_b[j,:]**0.5, facecolor='g', alpha = shade_intensity)
axs[a,b].fill_between(t_star, y_c_star[j,:] - var_c[j,:]**0.5,
y_c_star[j,:] + var_c[j,:]**0.5, facecolor='r', alpha = shade_intensity)
# set no. of decimal places for axes labels
axs[a,b].yaxis.set_major_formatter(FormatStrFormatter('%.1f'))
axs[a,b].xaxis.set_major_formatter(FormatStrFormatter('%.1f'))
# set tick marks insize plot, re-size axis labels
axs[a,b].tick_params(axis='both', which='major', direction='in', pad = 10, labelsize = 15)
# create subplot label for temperature
axs[a,b].text(0.05, 2.25, str(tit)+'T = '+str(int(T_star[j]))+' (K)', fontsize = 14, fontweight = 'bold')
# set bounds for plotting
axs[a,b].set_ylim([-0.5,2.5])
axs[a,b].set_xlim([0,1])
## make the plots square-shaped:
# define y-unit to x-unit ratio
ratio = 1.0
# get x and y limits
x_left, x_right = axs[a,b].get_xlim()
y_low, y_high = axs[a,b].get_ylim()
#set aspect ratio
axs[a,b].set_aspect(abs((x_right-x_left)/(y_low-y_high))*ratio, anchor = anch)
# for the entire plot:
# optional : include a figure title
# fig.suptitle('Hybrid model predictions with epistemic and aleatoric uncertainty', fontsize = 16, fontweight = 'bold')
# remove repitive axis and tick labels
for ax in fig.get_axes():
ax.label_outer()
# set axis labels
axs[1,0].set_xlabel(r't (h)', fontsize = 16, fontweight = 'bold')
axs[1,0].set_ylabel(r'C (M)', fontsize = 16, fontweight = 'bold')
# optional: manually tune spacing between plots
plt.subplots_adjust(top = 0.92, wspace = 0.12, hspace = 0.08)
# create a custom legend for plot
legend_elements = [Line2D([0], [0], marker = 'v', color = 'b', label = r'$\bf{A}$', markersize = mrk_siz, lw = 0),
Line2D([0], [0], marker = 's', color = 'g', label = r'$\bf{B}$', markersize = mrk_siz, lw = 0),
Line2D([0], [0], marker = 'd', color = 'r', label = r'$\bf{C}$', markersize = mrk_siz, lw = 0),
Line2D([0], [0], color = 'k', linestyle = lin_styl, label = r'$\mathcal{M}$', lw = lin_wdth)]
# place legend
axs[1,0].legend(handles = legend_elements, loc = 'upper right', fontsize = 10, frameon = False)
# optional: save in desired format
path_to_fig = 'example_fig'
fmt = '.pdf'
fig.savefig(path_to_fig + fmt, dpi = 1200, bbox_inches = 'tight')
1.15.5. Example: Bar Charts for Sensitivity Analysis#
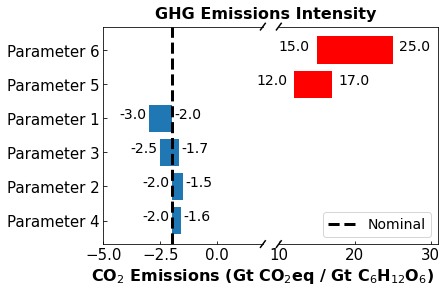
In this example, prepared by Maddie Watson, we plot results from a techneconomic sensitivity analysis. This plot is adapted from:
C. O’Brien, M. Watson, A. Dowling (2022). Challenges and Opportunities in Converting CO2 to Carbohydrates. under review code
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Organize Data into Pandas Dataframe
# Values are put into a pandas data frame so they can be sorted
# params is the parameter name of each bar
# values is the difference between the max and min of the parameter variation (bar width)
# start is the minimum point of the parameter variation and defines the starting value of each bar
df = pd.DataFrame(
dict(
params = ['Parameter 1','Parameter 2','Parameter 3','Parameter 4','Parameter 5','Parameter 6'],
values = [1 ,0.5,0.8,0.4,5,10],
start = [-3,-2,-2.5,-2,12,15]
)
)
print(df)
params values start
0 Parameter 1 1.0 -3.0
1 Parameter 2 0.5 -2.0
2 Parameter 3 0.8 -2.5
3 Parameter 4 0.4 -2.0
4 Parameter 5 5.0 12.0
5 Parameter 6 10.0 15.0
#Sort Data Frame
# The command below sorts the 'values' (barwidth) so they are displayed in the diagram as highest to lowest
# This ensures the tornado-like appearence
df_sorted = df.sort_values('values')
# re-index the dataframe to go 0-5 after sorting
df_sorted['index'] = np.arange(0,len(df['params']),1)
df_sorted.set_index('index',inplace=True)
print(df_sorted)
params values start
index
0 Parameter 4 0.4 -2.0
1 Parameter 2 0.5 -2.0
2 Parameter 3 0.8 -2.5
3 Parameter 1 1.0 -3.0
4 Parameter 5 5.0 12.0
5 Parameter 6 10.0 15.0
Show code cell source
# Plot Generation
# Broken axis example
# To create the broken axis create 2 subplots and merge together
fig, (ax,ax2) = plt.subplots(1,2,sharey=True)
p = ax.barh('params','values', data=df_sorted,left='start')
h = ax2.barh('params','values', data=df_sorted,left='start',color='red')
# Formatting
plt.suptitle('GHG Emissions Intensity',y=0.95, fontsize=16, fontweight = 'bold')
ax.set_xlabel('CO$_2$ Emissions (Gt CO$_2$eq / Gt C$_6$H$_{12}$O$_6$)',fontsize=16, fontweight='bold')
ax.xaxis.set_tick_params(labelsize=15)
ax2.xaxis.set_tick_params(labelsize=15)
ax.yaxis.set_tick_params(labelsize=15)
# Add a Nominal line for comparisons
ax2.axvline(-2, color='black', linewidth=3, linestyle='--',label='Nominal')
ax.axvline(-2, color='black', linewidth=3, linestyle='--',label='Nominal')
ax2.legend(loc='lower right', fontsize=14)
# Limits for left and right of x axis
ax.set_xlim(left=-5,right=2)
ax2.set_xlim(left=10,right=31)
# Formatting the axis
fig.subplots_adjust(wspace=0.1)
ax.xaxis.set_label_coords(1,-0.1)
ax.spines['right'].set_visible(False)
ax2.spines['left'].set_visible(False)
ax2.yaxis.set_ticks_position('none')
ax.yaxis.tick_left()
# Adding the diagonal lines between broken axis
d = .015 # how big to make the diagonal lines in axes coordinates
kwargs = dict(transform=ax.transAxes, color='k', clip_on=False)
ax.plot((1-d,1+d), (-d,+d), **kwargs)
ax.plot((1-d,1+d),(1-d,1+d), **kwargs)
kwargs.update(transform=ax2.transAxes) # switch to the bottom axes
ax2.plot((-d,+d), (1-d,1+d), **kwargs)
ax2.plot((-d,+d), (-d,+d), **kwargs)
ax.tick_params(direction="in")
ax2.tick_params(direction="in")
# Setting bar labels
# Broke into 2 sections beacuse we are using 2 axis
# This can be simplified to just loop through the dictionary if you don't have to specify which axis holds the label
# left side labels (red bars)
shift_l = 5
for i in [4,5]:
ax2.text(df_sorted['start'][i] - shift_l,i,np.round(df_sorted['start'][i],2),fontsize=14)
# Right side labels (red bars)
shift_r = 0.8
for i in [4,5]:
ax2.text(df_sorted['start'][i] + df_sorted['values'][i] + shift_r,i,np.round(df_sorted['start'][i] + df_sorted['values'][i],2),fontsize=14)
# Left side labels (blue bars)
shift_l = 1.3
for i in [0,1,2,3]:
ax.text(df_sorted['start'][i] - shift_l,i,np.round(df_sorted['start'][i],2),fontsize=14)
# Right side labels (blue bars)
shift_r = 0.1
for i in [0,1,2,3]:
ax.text(df_sorted['start'][i] + df_sorted['values'][i] + shift_r,i,np.round(df_sorted['start'][i] + df_sorted['values'][i],2),fontsize=14)
# Save plots to PNG and PDF to publication
fname = 'GHG_emissions_intensity'
fig.savefig(fname+'.png',dpi=300,bbox_inches='tight')
fig.savefig(fname+'.pdf',dpi=300,bbox_inches='tight')
plt.show()
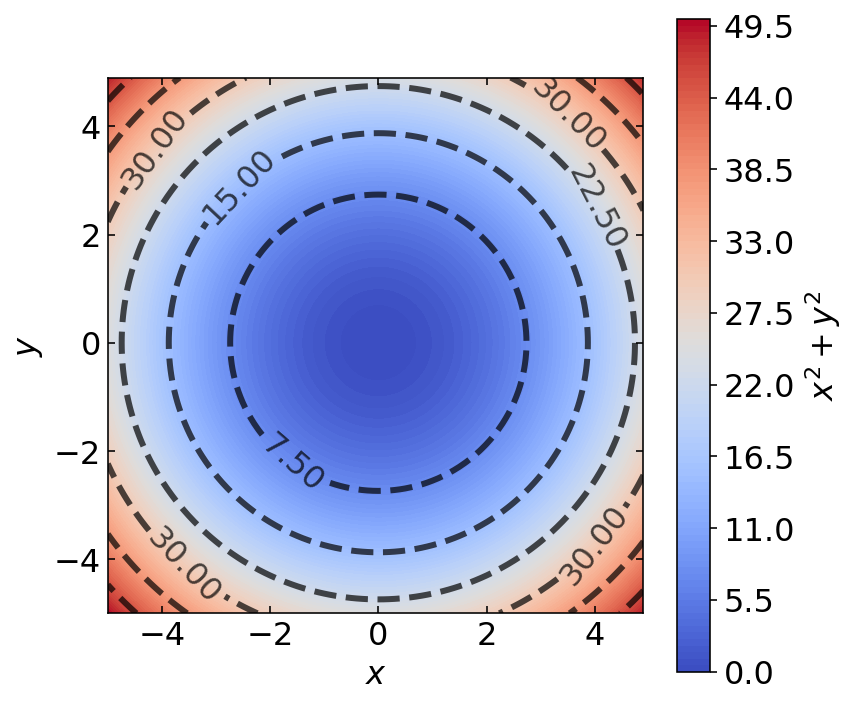
1.15.6. Example : Colored Contour Plots#
Finally, in this example prepared by Ke Wang, we prepare a colored contour plot.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
%matplotlib inline
%config InlineBackend.figure_format='retina'
We plot the function
\[z = x^2 + y^2\]
over the domain \(x \in [-5, 5]\) and \(y \in [-5, 5]\)
# enumerate samples
x = np.arange(-5, 5, 0.1)
y = np.arange(-5, 5, 0.1)
x, y = np.meshgrid(x, y)
# extract x-axis and y-axis size
m, n = x.shape
# define function for z
z = lambda x,y: x**2 + y**2
Show code cell source
# draw figure, using (6,6) because the plot is small otherwise
plt.figure(figsize=(6,6))
# plot heatmap
# cmap defines the overall color within the heatmap
# levels: determines the number and positions of the contour lines / regions.
cs = plt.contourf(x, y, z(x,y).reshape(m, n),cmap=cm.coolwarm, levels=100)
# plot color bar
cbar = plt.colorbar(cs)
# plot title in color bar
cbar.ax.set_ylabel(r'$x^2 + y^2$', fontsize=16, fontweight='bold')
# set font size in color bar
cbar.ax.tick_params(labelsize=16)
# plot equipotential line
# [::10] means sampling 1 in every 10 samples
# colors define the color want to use, 'k' for black
# alpha is blending value, between 0 (transparent) and 1 (opaque).
# linestyle defines the linestyle.
# linewidth defines the width of line
cs2 = plt.contour(cs, levels=cs.levels[::15], colors='k', alpha=0.7, linestyles='dashed', linewidths=3)
# plot the heatmap label
# %2.2f means keep to 2 digit
# fontsize defines the size of the text in figure
plt.clabel(cs2, fmt='%2.2f', colors='k', fontsize=16)
# define tick size
plt.xticks(fontsize=16)
plt.yticks(fontsize=16)
plt.tick_params(direction="in",top=True, right=True)
# set squared figure
plt.axis('square')
# plot titile and x,y label
plt.xlabel(r'$x$', fontsize=16, fontweight='bold')
plt.ylabel(r'$y$', fontsize=16, fontweight='bold')
plt.show()
# save figure (important for publications)
# plt.savefig('heatmap.png',bbox_inches='tight')
