11.3. Poisson Probability Distributions

Further Reading: §4.3 in Navidi (2015)

11.3.1. Learning Objectives

After studying this notebook, completing the activities, engaging in class, and reading the book, you should be able to:

• Model scientific and engineering problems using the Poisson distribution.

import numpy as np
import math
import matplotlib.pyplot as plt

11.3.2. Definition

The Poisson distribution is important for modeling rare events including failures and radioactive decay.

If \(X \sim\) Poisson(\(\lambda\)), then:

• \(X\) is a discrete random variable whose possible values are the non-negative integers (\(x\) is unbounded)

• The parameter \(\lambda\) is a positive constant

• The probability mass function is

\[\begin{split}p(x) = P(X = x) = \begin{cases} e^{-\lambda} \frac{\lambda^x}{x!} & \text{if } x \text{ is a non-negative integer} \\ 0 & \mathrm{otherwise} \end{cases}\end{split}\]

• The Poisson probability mass function is very close to the binomial probability mass function when \(n\) is large, \(p\) is small, and \(\lambda = n p\).

• The mean is \(\mu_X = \lambda\)

• The variance is \(\sigma_X^2 = \lambda\).

Alright, those are nice properties, but how do you specify \(\lambda\)? Often the Poisson distribution is used to model the number of rare events during a fixed duration. In this context, \(\lambda\) is the expected number of rare events. Let’s look at an example.

11.3.3. Example: Failure Rates

Consider a flood occurs on a specific river once every 100 years. Calculate the probability 0, 1, 2, …, 6 floods occur in the next 100 years. Assume the Poisson distribution accurately models flooding on this river.

Step 0: Identify \(\lambda\)

We are modeling floods, which are a rare event. The fixed duration is 100 years. We expect 1 flood every 100 years, so \(\lambda = 1\).

Step 1: Write a function to evaluate the PDF

def poisson(k,lmb):
    ''' PMF for Poisson distribution
    Args:
        k: number of events
        lmb: average number of events per interval
    Return:
        probability of k events occuring during interval
    '''
    
    assert k >= 0
    assert lmb >= 0
    
    return np.exp(-lmb) * lmb**k / math.factorial(k)

Step 2: Test out function for 10 floods

poisson(10,1)

1.0137771196302975e-07

Step 3: Answer the question asked

Home Activity

Evaluate the probabilities of 0 to 6 floods during the next 100 years. Store your answer as a numpy array p_floods such that p_floods[3] is the probability of 3 floods.

n_floods = range(0,7)
p_floods = np.zeros(7)

# Add your solution here

# Removed autograder test. You may delete this cell.

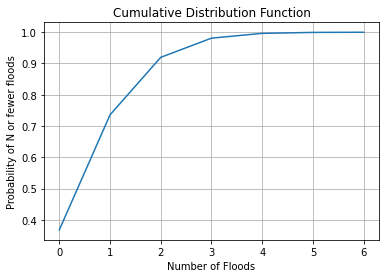
Using our results, we can plot the probability mass function and cumulative density function:

plt.bar(n_floods,p_floods)
plt.xlabel("Number of Floods")
plt.ylabel("Probability")
plt.title("Probability Mass Function")
plt.show()

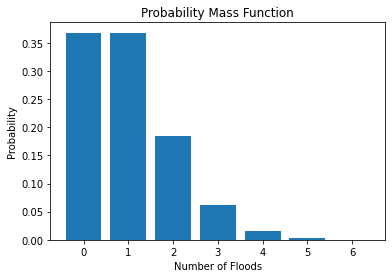
# calculate cumulative sum
cum_p_floods = np.cumsum(p_floods)

# Create the plot
plt.plot(n_floods,cum_p_floods)
plt.xlabel("Number of Floods")
plt.ylabel("Probability of N or fewer floods")
plt.grid(True)
plt.title("Cumulative Distribution Function")
plt.show()