Stochastic Gradient Descent Tutorial 1#
Prepared by: Reza Farzad (rfarzad@nd.edu, 2023)
1. Introduction#
In optimization, the goal is to find the argument corresponding to the minimum loss function. A loss function with two arguments is a surface in 3d space and the objective is to find the lowest point of this surface. One way is to use gradient descent (GD or Batch Gradient Descent or BGD) and go toward the lowest point by detecting the sharpest slope using the entire dataset to compute the loss function. Another method is the pure Stochastic Gradient Descent (SGD) that is another iterative optimization method through which the algorithm uses only a single sample for loss function computation to speed up the process. This algorithm starts from a random point on a function and travels down its slope in steps until it reaches the lowest point of that function. The third method which is called mini-Batch Gradient Descent (mBGD) is a cross-over between BGD and SGD. This method which is widely used in training deep neural network is a balance between BGD and pure SGD. This method is widely used, especially in machine learning since it is efficient (less memory, fast computation) and easy to apply (most of the time the second and third methods both are called SGD). The final goal of this project is to create a notebook that helps students know these methods, their differences, and how to use them for possible problems through simple examples and step-by-step algorithms.
1-1. Objective#
The goal is to compare three different kinds of Gradient Descent & how to compute the following loss function (using least square error) based on them: $\(l(\theta) = \sum_{i=1}^{k} (y_i - f(x_i, \theta))^2\)$
Batch Gradient Descent (BGD or GD): The algorithm uses the entire dataset to compute the loss function, i.e., k = N is the total number of data (population).
Stochastic Gradient Descent (SGD): The algorithm uses only one sample for loss computation to speed up the process, i.e., k = 1.
Mini-Batch Gradient Descent (mBGD): The cross-over between GD and SGD, i.e., 1 < k < N is a sample of dataset.
1-2. Formulation & Algorithm#
1-2-1. Formulation:
Typically, the problem is formulated as an optimization problem: $$
$$
1-2-2. Algorithm (PseudoCode) for BGD, SGD, & mBGD:
Initialize the vector of model parameters \(\boldsymbol\theta = (\theta_1, \cdots, \theta_n)\)
Define the learning rate \(\gamma_t\), grad threshold, maximum number of iterations, and the batch size (k):
If SGD, then k = 1, (only one data)
If BGD, then k = N, (total number of data)
If mBGD, then 1 < k < N, (a sample of dataset)
Initialize a vector to save updated parameters \(\boldsymbol\theta_t\) and their corresponding loss value
for t=1:max_iter do
4.1. Choose the k data and call it d
4-2. Use the parameters to compute the loss function $$
$\( 4-5. Save the \)\boldsymbol\theta_t$ and its loss value in the vector initialized in step 3
4-6. If \(\lVert \frac{\partial l(\boldsymbol\theta_{t-1}, d)}{\partial \theta} \rVert ≤ grad\_threshold\), then break the loop
end for loop of step 4
1-3. Functions#
# Import libraries
import matplotlib.pyplot as plt
from matplotlib import cm
import numpy as np
from scipy import linalg
import time
import sys
## Calculate gradient with central finite difference
def grad_approx(x,f,eps1,verbose=False):
'''
Calculate gradient of function f using central difference formula
Inputs:
x - point for which to evaluate gradient
f - function to consider
eps1 - perturbation size
Outputs:
grad - gradient (vector)
'''
n = len(x)
grad = np.zeros(n)
if(verbose):
print("***** my_grad_approx at x = ",x,"*****")
for i in range(0,n):
# Create vector of zeros except eps in position i
e = np.zeros(n)
e[i] = eps1
# Finite difference formula
my_f_plus = f(x + e)
my_f_minus = f(x - e)
# Diagnostics
if(verbose):
print("e[",i,"] = ",e)
print("f(x + e[",i,"]) = ",my_f_plus)
print("f(x - e[",i,"]) = ",my_f_minus)
grad[i] = (my_f_plus - my_f_minus)/(2*eps1)
if(verbose):
print("***** Done. ***** \n")
return grad
## Function for contout_plot of f(x, y)
def contour_plot(f, x_min, x_max, n_x, y_min, y_max, n_y):
# fig = plt.figure(figsize=(4,4))
xpts = np.linspace(x_min, x_max, n_x)
ypts = np.linspace(y_min, y_max, n_y)
[X, Y] = np.meshgrid(xpts, ypts)
Z = np.zeros([len(X), len(Y)])
for i in range(0, len(X)):
for j in range(0, len(Y)):
Z[i, j] = f([X[0, i], Y[j, 0]])
plt.xlabel('$\\theta_0$', fontsize=16, fontweight='bold')
plt.ylabel('$\\theta_1$', fontsize=16, fontweight='bold')
plt.title('Loss Function', fontsize = 16, fontweight = 'bold')
plt.xticks(fontsize=15)
plt.yticks(fontsize=15)
plt.tick_params(direction="in",top=True, right=True)
plt.contourf(X, Y, Z)
plt.show()
## Function for contout_plot of f(x, y)
def contour_surface_plot(f, x_min, x_max, n_x, y_min, y_max, n_y):
fig, ax = plt.subplots(subplot_kw={"projection": "3d"},figsize=(4,4))
# Make the data
xpts = np.linspace(x_min, x_max, n_x)
ypts = np.linspace(y_min, y_max, n_y)
[X, Y] = np.meshgrid(xpts, ypts)
Z = np.zeros([len(X), len(Y)])
for i in range(0, len(X)):
for j in range(0, len(Y)):
Z[i, j] = f([X[0, i], Y[j, 0]])
# Plot the surface
surf = ax.plot_surface(X, Y, Z, cmap=cm.coolwarm,
linewidth=0, antialiased=False)
# Add a color bar which maps values to colors.
fig.colorbar(surf, shrink=0.5, aspect=5, location = 'left')
plt.xlabel('$\\theta_0$', fontsize=16, fontweight='bold')
plt.ylabel('$\\theta_1$', fontsize=16, fontweight='bold')
plt.title('Loss Function Surface', fontsize=16, fontweight='bold')
plt.xticks(fontsize=15)
plt.yticks(fontsize=15)
plt.tick_params(direction="in",top=True, right=True)
plt.show()
## Loss function based on least squares:
# Given Xi = [x1i, x2i, x3i, ..., xni] and yi = f(Xi, theta)
# where, f: R^n -> R, i = 1,2,..,m, and theta are the parameters in f,
# the loss function is given by:
# LF = Sum((yi - f(Xi))^2, i=1,2,...,n)
# Inputs: data - numpy array [x1i, x2i, ..., xni, yi]
# f - function to which the data needs to be fit
# theta - parameters in the function f
# index_list - indices in data that will be considered
# to compute the loss function
# Output: Value of the loss function
def least_squares_loss_function(data, f, theta, index_list):
sum = 0
if len(data[0]) == 2:
for i in index_list:
sum = sum + (data[i, -1] - f(theta, data[i, 0]))**2
else:
for i in index_list:
sum = sum + (data[i, -1] - f(theta, data[i, 0:-2]))**2
return sum
## Do SGD, mBGD or BGD based on the data and hyperparameters
## to return loss value and updated parameters
def SGD_mBGD_BGD(data_samples, function, initial_parameters,
loss_function, gradient_function,
learning_rate=0.1,
batch_size=1,
max_iterations=1000,
verbose=True,
eps=1e-7,
gradient_threshold=1e-7):
####################
##### Step 3 #####
####################
# Initialize a vector to save updated vector of parameters
parameter_values = [initial_parameters]
# Initialize a list to save the loss values
loss_values = []
if verbose:
print("Iter. \tloss_func(x) \t\t||grad(x)|| \t||p||\n")
####################
##### Step 4 #####
####################
for iteration in range(max_iterations):
###########################
##### Steps 4-1 & 4-2 #####
###########################
if batch_size < len(data_samples): # If SGD or mBGD:
# Choose random indices of data for computing loss function ##### Step 4-1 ####
index_list = np.random.choice(range(len(data_samples)), size=batch_size, replace = False)
# Compute loss function ##### Step 4-2 #####
loss_func = lambda parameters: loss_function(data_samples, function, parameters, index_list)
elif iteration == 0: # If BGD:
# Compute loss function ##### Step 4-2 #####
loss_func = lambda parameters: loss_function(data_samples, function, parameters, range(0, len(data_samples)))
#####################
##### Steps 4-3 #####
#####################
# Compute the gradient of the loss function wrt the latest parameters
gradient = gradient_function(parameter_values[iteration], loss_func, eps)
#####################
##### Steps 4-4 #####
#####################
# Calculate the step using learning rate
step = learning_rate * gradient
# Update parameters
new_parameter_value = parameter_values[iteration] - step
#####################
##### Steps 4-5 #####
#####################
# Save the updated parameters and their loss value in the vectors defined in step 3
parameter_values.append(new_parameter_value.tolist())
loss_values.append(loss_func(new_parameter_value))
if verbose:
print(iteration, ' \t{0: 1.4e} \t{1:1.4e} \t{2:1.4e}'.format( \
loss_values[iteration],linalg.norm(gradient),linalg.norm(step)), end='\n')
#####################
##### Steps 4-6 #####
#####################
# Check if the norm of gradient is below the threshold, announce the 'Success' and break the loop
if linalg.norm(gradient) <= gradient_threshold:
print("SUCCESS")
print("Gradient below the specified tolerance\n")
break
if iteration == max_iterations - 1:
print("Max iterations reached\n")
return np.array(parameter_values), np.array(loss_values)
2. SGD vs BGD vs mBGD#
2-1. Problem 1 - Small Dataset (100 Data)#
2-1-1. Generate Dataset
Problem 1 - Nonconvex Input with Convex Loss
Lets consider a nonconvex cubic function.
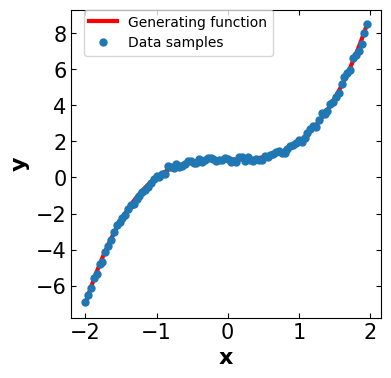
Let \(D = \{(x_i, y_i), i=1,2,...,t\}\) be the data set generated from the following function: $\( y_i = x_i^3 + 1 + \delta,\)\( where, \)\delta$ is a random variable with standard normal probability distribution.
This data set is generated in the following code snippets.
def f3(theta, x):
return theta[0]*x**3 + theta[1]
def generate_data_f3(x, start_value, end_value, n, sigma_noise):
step = (end_value - start_value)/n;
fvals = np.zeros([n, 2])
fvals_pure = np.zeros([n, 2])
rands = np.random.normal(0, sigma_noise, n)
for i in range(0, n):
value = start_value + step*i
fvals_pure[i] = [value, f3(x, value)]
fvals[i] = [value, f3(x, value)+rands[i]]
return [fvals, fvals_pure]
[data, fx] = generate_data_f3([1, 1], -2, 2, 100, 0.1)
fig = plt.figure(figsize=(4,4))
plt.xticks(fontsize=15)
plt.yticks(fontsize=15)
plt.tick_params(direction="in",top=True, right=True)
plt.plot(fx[:, 0], fx[:, 1], 'r', markersize=3, linewidth=3)
plt.plot(data[:, 0], data[:, 1], 'o', markersize=5, linewidth=3)
plt.legend(["Generating function", "Data samples"],fontsize=10,bbox_to_anchor=(0.65, 1.0),borderaxespad=0)
plt.xlabel('x',fontsize=16,fontweight='bold')
plt.ylabel('y',fontsize=16,fontweight='bold')
plt.show()
# # Save to file (for including in manuscript)
# fname = 'Small Dataset Samples'
# fig.savefig(fname+'.png',dpi=300,bbox_inches='tight')
2-1-2. Plot the loss function contours
Let us consider only the data samples and fit the data set to the following function: $\(y = f(x, \theta) = \theta_0 x^3 + \theta_1.\)\( In other words, the task is to estimate \)\theta = [\theta_0, \theta_1]\( that fits the function \)f(x)$ with minimum least square error.
The least square error can be defined as: $\(l(\theta) = \sum_{i=1}^t (y_i - f(x_i, \theta))^2.\)\( The least square error \)l(\theta)\( is considered as the loss function that needs to be minimized with \)\theta\( as the decision variables to fit the data set to \)f(x, \theta)$.
The following code snippets define and visualize the least square error loss function
# Loss function with theta = [theta1, theta2] as input
LFx = lambda theta : least_squares_loss_function(data, f3, theta, range(0, len(data)))
# Plot of the loss function
fig = plt.figure(figsize=(4,4))
contour_plot(LFx, -10., 10., 50, -10., 10., 50)
contour_surface_plot(LFx, -10., 10., 50, -10., 10., 50)
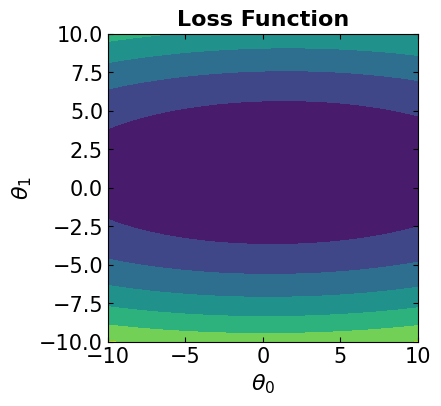
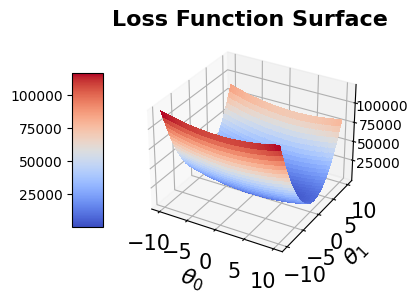
Let’s apply the three different types of “Gradient Descent” to minimize the loss function above:
2-1-3. BGD: (Batch size = t or length of data)
In this case, all the data samples are considered for computing the loss function. The algorithm is the same as steepest gradient descent. We should note that if we see jagged convergence to the solution for Gradient Descent method, it means that the learning rate is quite high and must be reduced to prevent overshooting.
### If learning rate = 0.00001 ###
####################
##### Step 1 #####
####################
# Initialize the vector of model parameters
theta_0 = [5, 5]
####################
##### Step 2 #####
####################
# Set the learning rate:
gamma_t = 0.00001
# Set the gradient threshold:
grad_thres = 1e-7
# Set the maximum number of iterations:
maxIter = 500
# Set the batch size:
# (select "len(data)"" for BGD, "one" for SGD, a "mini-batch size" for mBGD)
k = len(data)
#####################
##### Steps 3-4 #####
#####################
# Call the following function to do the steps 3 & 4
# (returns the theta vectors and loss values for all iterations)
start = time.time()
theta,loss = SGD_mBGD_BGD(data, f3, theta_0, least_squares_loss_function, grad_approx, \
learning_rate = gamma_t, max_iterations = maxIter, batch_size=k, gradient_threshold=grad_thres)
end = time.time()
print('Total time is: ', end - start)
# Visualize the convergence track on loss function
fig = plt.figure(figsize=(4,4))
plt.plot(theta[:, 0], theta[:, 1], '-r', markersize=5, linewidth=3)
contour_plot(LFx, -6., 6., 50, -6, 6., 50)
# Print the optimal solution
print("The optimal solution is: theta0 = ", str(theta[-1, 0]), ", theta1 = ", str(theta[-1, 1]))
print("The corresponding loss function is: ", str(loss[-1]))
Iter. loss_func(x) ||grad(x)|| ||p||
0 1.5465e+04 7.2953e+03 7.2953e-02
1 1.4956e+04 7.1632e+03 7.1632e-02
2 1.4466e+04 7.0335e+03 7.0335e-02
3 1.3993e+04 6.9062e+03 6.9062e-02
4 1.3538e+04 6.7813e+03 6.7813e-02
5 1.3098e+04 6.6587e+03 6.6587e-02
6 1.2675e+04 6.5383e+03 6.5383e-02
7 1.2266e+04 6.4202e+03 6.4202e-02
8 1.1872e+04 6.3043e+03 6.3043e-02
9 1.1493e+04 6.1905e+03 6.1905e-02
10 1.1126e+04 6.0788e+03 6.0788e-02
11 1.0773e+04 5.9692e+03 5.9692e-02
12 1.0433e+04 5.8616e+03 5.8616e-02
13 1.0104e+04 5.7560e+03 5.7560e-02
14 9.7878e+03 5.6523e+03 5.6523e-02
15 9.4825e+03 5.5506e+03 5.5506e-02
16 9.1881e+03 5.4508e+03 5.4508e-02
17 8.9041e+03 5.3529e+03 5.3529e-02
18 8.6303e+03 5.2567e+03 5.2567e-02
19 8.3662e+03 5.1623e+03 5.1623e-02
20 8.1114e+03 5.0697e+03 5.0697e-02
21 7.8658e+03 4.9789e+03 4.9789e-02
22 7.6288e+03 4.8897e+03 4.8897e-02
23 7.4003e+03 4.8021e+03 4.8021e-02
24 7.1798e+03 4.7163e+03 4.7163e-02
25 6.9672e+03 4.6320e+03 4.6320e-02
26 6.7621e+03 4.5492e+03 4.5492e-02
27 6.5642e+03 4.4681e+03 4.4681e-02
28 6.3734e+03 4.3884e+03 4.3884e-02
29 6.1892e+03 4.3102e+03 4.3102e-02
30 6.0116e+03 4.2335e+03 4.2335e-02
31 5.8402e+03 4.1583e+03 4.1583e-02
32 5.6749e+03 4.0844e+03 4.0844e-02
33 5.5154e+03 4.0119e+03 4.0119e-02
34 5.3614e+03 3.9408e+03 3.9408e-02
35 5.2129e+03 3.8710e+03 3.8710e-02
36 5.0696e+03 3.8025e+03 3.8025e-02
37 4.9313e+03 3.7354e+03 3.7354e-02
38 4.7978e+03 3.6694e+03 3.6694e-02
39 4.6690e+03 3.6048e+03 3.6048e-02
40 4.5447e+03 3.5413e+03 3.5413e-02
41 4.4248e+03 3.4790e+03 3.4790e-02
42 4.3090e+03 3.4180e+03 3.4180e-02
43 4.1972e+03 3.3580e+03 3.3580e-02
44 4.0893e+03 3.2992e+03 3.2992e-02
45 3.9851e+03 3.2416e+03 3.2416e-02
46 3.8846e+03 3.1850e+03 3.1850e-02
47 3.7875e+03 3.1295e+03 3.1295e-02
48 3.6938e+03 3.0750e+03 3.0750e-02
49 3.6032e+03 3.0216e+03 3.0216e-02
50 3.5159e+03 2.9692e+03 2.9692e-02
51 3.4315e+03 2.9178e+03 2.9178e-02
52 3.3499e+03 2.8673e+03 2.8673e-02
53 3.2712e+03 2.8179e+03 2.8179e-02
54 3.1952e+03 2.7694e+03 2.7694e-02
55 3.1217e+03 2.7218e+03 2.7218e-02
56 3.0508e+03 2.6751e+03 2.6751e-02
57 2.9822e+03 2.6293e+03 2.6293e-02
58 2.9160e+03 2.5845e+03 2.5845e-02
59 2.8520e+03 2.5404e+03 2.5404e-02
60 2.7902e+03 2.4973e+03 2.4973e-02
61 2.7304e+03 2.4549e+03 2.4549e-02
62 2.6727e+03 2.4134e+03 2.4134e-02
63 2.6169e+03 2.3727e+03 2.3727e-02
64 2.5629e+03 2.3328e+03 2.3328e-02
65 2.5107e+03 2.2936e+03 2.2936e-02
66 2.4603e+03 2.2552e+03 2.2552e-02
67 2.4115e+03 2.2176e+03 2.2176e-02
68 2.3644e+03 2.1807e+03 2.1807e-02
69 2.3188e+03 2.1445e+03 2.1445e-02
70 2.2747e+03 2.1091e+03 2.1091e-02
71 2.2320e+03 2.0743e+03 2.0743e-02
72 2.1907e+03 2.0402e+03 2.0402e-02
73 2.1508e+03 2.0068e+03 2.0068e-02
74 2.1121e+03 1.9741e+03 1.9741e-02
75 2.0747e+03 1.9420e+03 1.9420e-02
76 2.0385e+03 1.9105e+03 1.9105e-02
77 2.0034e+03 1.8797e+03 1.8797e-02
78 1.9695e+03 1.8495e+03 1.8495e-02
79 1.9367e+03 1.8198e+03 1.8198e-02
80 1.9048e+03 1.7908e+03 1.7908e-02
81 1.8740e+03 1.7624e+03 1.7624e-02
82 1.8442e+03 1.7345e+03 1.7345e-02
83 1.8153e+03 1.7072e+03 1.7072e-02
84 1.7872e+03 1.6805e+03 1.6805e-02
85 1.7601e+03 1.6543e+03 1.6543e-02
86 1.7338e+03 1.6286e+03 1.6286e-02
87 1.7083e+03 1.6035e+03 1.6035e-02
88 1.6835e+03 1.5789e+03 1.5789e-02
89 1.6595e+03 1.5547e+03 1.5547e-02
90 1.6363e+03 1.5311e+03 1.5311e-02
91 1.6137e+03 1.5080e+03 1.5080e-02
92 1.5918e+03 1.4853e+03 1.4853e-02
93 1.5705e+03 1.4631e+03 1.4631e-02
94 1.5499e+03 1.4414e+03 1.4414e-02
95 1.5299e+03 1.4201e+03 1.4201e-02
96 1.5105e+03 1.3993e+03 1.3993e-02
97 1.4916e+03 1.3789e+03 1.3789e-02
98 1.4733e+03 1.3589e+03 1.3589e-02
99 1.4554e+03 1.3394e+03 1.3394e-02
100 1.4381e+03 1.3203e+03 1.3203e-02
101 1.4213e+03 1.3016e+03 1.3016e-02
102 1.4050e+03 1.2832e+03 1.2832e-02
103 1.3891e+03 1.2653e+03 1.2653e-02
104 1.3736e+03 1.2478e+03 1.2478e-02
105 1.3586e+03 1.2306e+03 1.2306e-02
106 1.3439e+03 1.2138e+03 1.2138e-02
107 1.3297e+03 1.1974e+03 1.1974e-02
108 1.3158e+03 1.1813e+03 1.1813e-02
109 1.3023e+03 1.1656e+03 1.1656e-02
110 1.2892e+03 1.1502e+03 1.1502e-02
111 1.2764e+03 1.1351e+03 1.1351e-02
112 1.2639e+03 1.1204e+03 1.1204e-02
113 1.2518e+03 1.1060e+03 1.1060e-02
114 1.2399e+03 1.0919e+03 1.0919e-02
115 1.2284e+03 1.0782e+03 1.0782e-02
116 1.2171e+03 1.0647e+03 1.0647e-02
117 1.2061e+03 1.0516e+03 1.0516e-02
118 1.1954e+03 1.0387e+03 1.0387e-02
119 1.1849e+03 1.0261e+03 1.0261e-02
120 1.1747e+03 1.0138e+03 1.0138e-02
121 1.1647e+03 1.0018e+03 1.0018e-02
122 1.1550e+03 9.9009e+02 9.9009e-03
123 1.1455e+03 9.7862e+02 9.7862e-03
124 1.1362e+03 9.6740e+02 9.6740e-03
125 1.1271e+03 9.5644e+02 9.5644e-03
126 1.1182e+03 9.4573e+02 9.4573e-03
127 1.1095e+03 9.3527e+02 9.3527e-03
128 1.1010e+03 9.2505e+02 9.2505e-03
129 1.0926e+03 9.1506e+02 9.1506e-03
130 1.0845e+03 9.0530e+02 9.0530e-03
131 1.0765e+03 8.9577e+02 8.9577e-03
132 1.0687e+03 8.8646e+02 8.8646e-03
133 1.0610e+03 8.7736e+02 8.7736e-03
134 1.0535e+03 8.6848e+02 8.6848e-03
135 1.0462e+03 8.5980e+02 8.5980e-03
136 1.0389e+03 8.5132e+02 8.5132e-03
137 1.0319e+03 8.4305e+02 8.4305e-03
138 1.0249e+03 8.3496e+02 8.3496e-03
139 1.0181e+03 8.2707e+02 8.2707e-03
140 1.0114e+03 8.1936e+02 8.1936e-03
141 1.0049e+03 8.1183e+02 8.1183e-03
142 9.9843e+02 8.0447e+02 8.0447e-03
143 9.9210e+02 7.9729e+02 7.9729e-03
144 9.8588e+02 7.9028e+02 7.9028e-03
145 9.7977e+02 7.8343e+02 7.8343e-03
146 9.7377e+02 7.7675e+02 7.7675e-03
147 9.6786e+02 7.7022e+02 7.7022e-03
148 9.6205e+02 7.6384e+02 7.6384e-03
149 9.5633e+02 7.5762e+02 7.5762e-03
150 9.5070e+02 7.5154e+02 7.5154e-03
151 9.4517e+02 7.4560e+02 7.4560e-03
152 9.3972e+02 7.3980e+02 7.3980e-03
153 9.3435e+02 7.3414e+02 7.3414e-03
154 9.2906e+02 7.2861e+02 7.2861e-03
155 9.2385e+02 7.2320e+02 7.2320e-03
156 9.1871e+02 7.1793e+02 7.1793e-03
157 9.1365e+02 7.1277e+02 7.1277e-03
158 9.0866e+02 7.0774e+02 7.0774e-03
159 9.0373e+02 7.0282e+02 7.0282e-03
160 8.9888e+02 6.9802e+02 6.9802e-03
161 8.9409e+02 6.9333e+02 6.9333e-03
162 8.8936e+02 6.8874e+02 6.8874e-03
163 8.8469e+02 6.8426e+02 6.8426e-03
164 8.8008e+02 6.7988e+02 6.7988e-03
165 8.7553e+02 6.7560e+02 6.7560e-03
166 8.7104e+02 6.7142e+02 6.7142e-03
167 8.6660e+02 6.6733e+02 6.6733e-03
168 8.6221e+02 6.6334e+02 6.6334e-03
169 8.5788e+02 6.5943e+02 6.5943e-03
170 8.5359e+02 6.5561e+02 6.5561e-03
171 8.4935e+02 6.5188e+02 6.5188e-03
172 8.4516e+02 6.4822e+02 6.4822e-03
173 8.4102e+02 6.4465e+02 6.4465e-03
174 8.3692e+02 6.4116e+02 6.4116e-03
175 8.3286e+02 6.3774e+02 6.3774e-03
176 8.2885e+02 6.3439e+02 6.3439e-03
177 8.2487e+02 6.3111e+02 6.3111e-03
178 8.2094e+02 6.2791e+02 6.2791e-03
179 8.1705e+02 6.2477e+02 6.2477e-03
180 8.1319e+02 6.2170e+02 6.2170e-03
181 8.0937e+02 6.1869e+02 6.1869e-03
182 8.0559e+02 6.1574e+02 6.1574e-03
183 8.0184e+02 6.1286e+02 6.1286e-03
184 7.9813e+02 6.1003e+02 6.1003e-03
185 7.9445e+02 6.0726e+02 6.0726e-03
186 7.9081e+02 6.0454e+02 6.0454e-03
187 7.8719e+02 6.0188e+02 6.0188e-03
188 7.8361e+02 5.9927e+02 5.9927e-03
189 7.8005e+02 5.9671e+02 5.9671e-03
190 7.7653e+02 5.9419e+02 5.9419e-03
191 7.7304e+02 5.9173e+02 5.9173e-03
192 7.6957e+02 5.8931e+02 5.8931e-03
193 7.6613e+02 5.8694e+02 5.8694e-03
194 7.6272e+02 5.8461e+02 5.8461e-03
195 7.5934e+02 5.8232e+02 5.8232e-03
196 7.5598e+02 5.8008e+02 5.8008e-03
197 7.5265e+02 5.7787e+02 5.7787e-03
198 7.4934e+02 5.7570e+02 5.7570e-03
199 7.4605e+02 5.7357e+02 5.7357e-03
200 7.4279e+02 5.7148e+02 5.7148e-03
201 7.3956e+02 5.6942e+02 5.6942e-03
202 7.3634e+02 5.6739e+02 5.6739e-03
203 7.3315e+02 5.6540e+02 5.6540e-03
204 7.2998e+02 5.6344e+02 5.6344e-03
205 7.2684e+02 5.6151e+02 5.6151e-03
206 7.2371e+02 5.5962e+02 5.5962e-03
207 7.2060e+02 5.5775e+02 5.5775e-03
208 7.1752e+02 5.5591e+02 5.5591e-03
209 7.1445e+02 5.5410e+02 5.5410e-03
210 7.1141e+02 5.5231e+02 5.5231e-03
211 7.0838e+02 5.5055e+02 5.5055e-03
212 7.0537e+02 5.4882e+02 5.4882e-03
213 7.0239e+02 5.4711e+02 5.4711e-03
214 6.9941e+02 5.4542e+02 5.4542e-03
215 6.9646e+02 5.4376e+02 5.4376e-03
216 6.9353e+02 5.4212e+02 5.4212e-03
217 6.9061e+02 5.4050e+02 5.4050e-03
218 6.8771e+02 5.3891e+02 5.3891e-03
219 6.8483e+02 5.3733e+02 5.3733e-03
220 6.8196e+02 5.3577e+02 5.3577e-03
221 6.7911e+02 5.3423e+02 5.3423e-03
222 6.7628e+02 5.3272e+02 5.3272e-03
223 6.7346e+02 5.3122e+02 5.3122e-03
224 6.7066e+02 5.2973e+02 5.2973e-03
225 6.6787e+02 5.2827e+02 5.2827e-03
226 6.6510e+02 5.2682e+02 5.2682e-03
227 6.6234e+02 5.2538e+02 5.2538e-03
228 6.5960e+02 5.2397e+02 5.2397e-03
229 6.5687e+02 5.2256e+02 5.2256e-03
230 6.5416e+02 5.2118e+02 5.2118e-03
231 6.5146e+02 5.1980e+02 5.1980e-03
232 6.4878e+02 5.1845e+02 5.1845e-03
233 6.4611e+02 5.1710e+02 5.1710e-03
234 6.4345e+02 5.1577e+02 5.1577e-03
235 6.4081e+02 5.1445e+02 5.1445e-03
236 6.3818e+02 5.1314e+02 5.1314e-03
237 6.3556e+02 5.1185e+02 5.1185e-03
238 6.3296e+02 5.1056e+02 5.1056e-03
239 6.3037e+02 5.0929e+02 5.0929e-03
240 6.2779e+02 5.0803e+02 5.0803e-03
241 6.2522e+02 5.0678e+02 5.0678e-03
242 6.2267e+02 5.0554e+02 5.0554e-03
243 6.2013e+02 5.0431e+02 5.0431e-03
244 6.1760e+02 5.0309e+02 5.0309e-03
245 6.1509e+02 5.0188e+02 5.0188e-03
246 6.1258e+02 5.0068e+02 5.0068e-03
247 6.1009e+02 4.9949e+02 4.9949e-03
248 6.0761e+02 4.9830e+02 4.9830e-03
249 6.0514e+02 4.9713e+02 4.9713e-03
250 6.0269e+02 4.9596e+02 4.9596e-03
251 6.0024e+02 4.9481e+02 4.9481e-03
252 5.9781e+02 4.9366e+02 4.9366e-03
253 5.9538e+02 4.9252e+02 4.9252e-03
254 5.9297e+02 4.9138e+02 4.9138e-03
255 5.9057e+02 4.9026e+02 4.9026e-03
256 5.8818e+02 4.8914e+02 4.8914e-03
257 5.8580e+02 4.8802e+02 4.8802e-03
258 5.8343e+02 4.8692e+02 4.8692e-03
259 5.8108e+02 4.8582e+02 4.8582e-03
260 5.7873e+02 4.8473e+02 4.8473e-03
261 5.7639e+02 4.8364e+02 4.8364e-03
262 5.7407e+02 4.8256e+02 4.8256e-03
263 5.7175e+02 4.8149e+02 4.8149e-03
264 5.6945e+02 4.8042e+02 4.8042e-03
265 5.6715e+02 4.7935e+02 4.7935e-03
266 5.6487e+02 4.7830e+02 4.7830e-03
267 5.6259e+02 4.7725e+02 4.7725e-03
268 5.6033e+02 4.7620e+02 4.7620e-03
269 5.5807e+02 4.7516e+02 4.7516e-03
270 5.5582e+02 4.7412e+02 4.7412e-03
271 5.5359e+02 4.7309e+02 4.7309e-03
272 5.5136e+02 4.7207e+02 4.7207e-03
273 5.4915e+02 4.7105e+02 4.7105e-03
274 5.4694e+02 4.7003e+02 4.7003e-03
275 5.4474e+02 4.6902e+02 4.6902e-03
276 5.4255e+02 4.6801e+02 4.6801e-03
277 5.4038e+02 4.6701e+02 4.6701e-03
278 5.3821e+02 4.6601e+02 4.6601e-03
279 5.3605e+02 4.6502e+02 4.6502e-03
280 5.3390e+02 4.6403e+02 4.6403e-03
281 5.3175e+02 4.6304e+02 4.6304e-03
282 5.2962e+02 4.6206e+02 4.6206e-03
283 5.2750e+02 4.6108e+02 4.6108e-03
284 5.2538e+02 4.6011e+02 4.6011e-03
285 5.2328e+02 4.5914e+02 4.5914e-03
286 5.2118e+02 4.5817e+02 4.5817e-03
287 5.1909e+02 4.5721e+02 4.5721e-03
288 5.1701e+02 4.5625e+02 4.5625e-03
289 5.1494e+02 4.5529e+02 4.5529e-03
290 5.1288e+02 4.5434e+02 4.5434e-03
291 5.1083e+02 4.5339e+02 4.5339e-03
292 5.0878e+02 4.5244e+02 4.5244e-03
293 5.0674e+02 4.5150e+02 4.5150e-03
294 5.0472e+02 4.5056e+02 4.5056e-03
295 5.0270e+02 4.4962e+02 4.4962e-03
296 5.0069e+02 4.4869e+02 4.4869e-03
297 4.9868e+02 4.4776e+02 4.4776e-03
298 4.9669e+02 4.4683e+02 4.4683e-03
299 4.9470e+02 4.4591e+02 4.4591e-03
300 4.9272e+02 4.4499e+02 4.4499e-03
301 4.9075e+02 4.4407e+02 4.4407e-03
302 4.8879e+02 4.4315e+02 4.4315e-03
303 4.8684e+02 4.4224e+02 4.4224e-03
304 4.8489e+02 4.4133e+02 4.4133e-03
305 4.8295e+02 4.4042e+02 4.4042e-03
306 4.8102e+02 4.3952e+02 4.3952e-03
307 4.7910e+02 4.3862e+02 4.3862e-03
308 4.7719e+02 4.3772e+02 4.3772e-03
309 4.7528e+02 4.3682e+02 4.3682e-03
310 4.7338e+02 4.3593e+02 4.3593e-03
311 4.7149e+02 4.3503e+02 4.3503e-03
312 4.6961e+02 4.3415e+02 4.3415e-03
313 4.6774e+02 4.3326e+02 4.3326e-03
314 4.6587e+02 4.3237e+02 4.3237e-03
315 4.6401e+02 4.3149e+02 4.3149e-03
316 4.6216e+02 4.3061e+02 4.3061e-03
317 4.6031e+02 4.2974e+02 4.2974e-03
318 4.5847e+02 4.2886e+02 4.2886e-03
319 4.5664e+02 4.2799e+02 4.2799e-03
320 4.5482e+02 4.2712e+02 4.2712e-03
321 4.5301e+02 4.2625e+02 4.2625e-03
322 4.5120e+02 4.2538e+02 4.2538e-03
323 4.4940e+02 4.2452e+02 4.2452e-03
324 4.4761e+02 4.2366e+02 4.2366e-03
325 4.4582e+02 4.2280e+02 4.2280e-03
326 4.4404e+02 4.2194e+02 4.2194e-03
327 4.4227e+02 4.2109e+02 4.2109e-03
328 4.4051e+02 4.2023e+02 4.2023e-03
329 4.3875e+02 4.1938e+02 4.1938e-03
330 4.3700e+02 4.1853e+02 4.1853e-03
331 4.3526e+02 4.1769e+02 4.1769e-03
332 4.3352e+02 4.1684e+02 4.1684e-03
333 4.3179e+02 4.1600e+02 4.1600e-03
334 4.3007e+02 4.1516e+02 4.1516e-03
335 4.2835e+02 4.1432e+02 4.1432e-03
336 4.2665e+02 4.1348e+02 4.1348e-03
337 4.2495e+02 4.1265e+02 4.1265e-03
338 4.2325e+02 4.1182e+02 4.1182e-03
339 4.2156e+02 4.1099e+02 4.1099e-03
340 4.1988e+02 4.1016e+02 4.1016e-03
341 4.1821e+02 4.0933e+02 4.0933e-03
342 4.1654e+02 4.0851e+02 4.0851e-03
343 4.1488e+02 4.0768e+02 4.0768e-03
344 4.1323e+02 4.0686e+02 4.0686e-03
345 4.1158e+02 4.0604e+02 4.0604e-03
346 4.0994e+02 4.0522e+02 4.0522e-03
347 4.0831e+02 4.0441e+02 4.0441e-03
348 4.0668e+02 4.0360e+02 4.0360e-03
349 4.0506e+02 4.0278e+02 4.0278e-03
350 4.0344e+02 4.0197e+02 4.0197e-03
351 4.0184e+02 4.0116e+02 4.0116e-03
352 4.0024e+02 4.0036e+02 4.0036e-03
353 3.9864e+02 3.9955e+02 3.9955e-03
354 3.9705e+02 3.9875e+02 3.9875e-03
355 3.9547e+02 3.9795e+02 3.9795e-03
356 3.9389e+02 3.9715e+02 3.9715e-03
357 3.9233e+02 3.9635e+02 3.9635e-03
358 3.9076e+02 3.9556e+02 3.9556e-03
359 3.8921e+02 3.9476e+02 3.9476e-03
360 3.8765e+02 3.9397e+02 3.9397e-03
361 3.8611e+02 3.9318e+02 3.9318e-03
362 3.8457e+02 3.9239e+02 3.9239e-03
363 3.8304e+02 3.9160e+02 3.9160e-03
364 3.8151e+02 3.9082e+02 3.9082e-03
365 3.7999e+02 3.9003e+02 3.9003e-03
366 3.7848e+02 3.8925e+02 3.8925e-03
367 3.7697e+02 3.8847e+02 3.8847e-03
368 3.7547e+02 3.8769e+02 3.8769e-03
369 3.7398e+02 3.8691e+02 3.8691e-03
370 3.7249e+02 3.8614e+02 3.8614e-03
371 3.7100e+02 3.8536e+02 3.8536e-03
372 3.6953e+02 3.8459e+02 3.8459e-03
373 3.6805e+02 3.8382e+02 3.8382e-03
374 3.6659e+02 3.8305e+02 3.8305e-03
375 3.6513e+02 3.8228e+02 3.8228e-03
376 3.6367e+02 3.8151e+02 3.8151e-03
377 3.6223e+02 3.8075e+02 3.8075e-03
378 3.6078e+02 3.7999e+02 3.7999e-03
379 3.5935e+02 3.7923e+02 3.7923e-03
380 3.5792e+02 3.7847e+02 3.7847e-03
381 3.5649e+02 3.7771e+02 3.7771e-03
382 3.5507e+02 3.7695e+02 3.7695e-03
383 3.5366e+02 3.7620e+02 3.7620e-03
384 3.5225e+02 3.7544e+02 3.7544e-03
385 3.5085e+02 3.7469e+02 3.7469e-03
386 3.4945e+02 3.7394e+02 3.7394e-03
387 3.4806e+02 3.7319e+02 3.7319e-03
388 3.4667e+02 3.7245e+02 3.7245e-03
389 3.4529e+02 3.7170e+02 3.7170e-03
390 3.4392e+02 3.7096e+02 3.7096e-03
391 3.4255e+02 3.7021e+02 3.7021e-03
392 3.4119e+02 3.6947e+02 3.6947e-03
393 3.3983e+02 3.6873e+02 3.6873e-03
394 3.3847e+02 3.6799e+02 3.6799e-03
395 3.3713e+02 3.6726e+02 3.6726e-03
396 3.3578e+02 3.6652e+02 3.6652e-03
397 3.3445e+02 3.6579e+02 3.6579e-03
398 3.3312e+02 3.6506e+02 3.6506e-03
399 3.3179e+02 3.6433e+02 3.6433e-03
400 3.3047e+02 3.6360e+02 3.6360e-03
401 3.2915e+02 3.6287e+02 3.6287e-03
402 3.2784e+02 3.6214e+02 3.6214e-03
403 3.2654e+02 3.6142e+02 3.6142e-03
404 3.2524e+02 3.6070e+02 3.6070e-03
405 3.2395e+02 3.5997e+02 3.5997e-03
406 3.2266e+02 3.5925e+02 3.5925e-03
407 3.2137e+02 3.5854e+02 3.5854e-03
408 3.2009e+02 3.5782e+02 3.5782e-03
409 3.1882e+02 3.5710e+02 3.5710e-03
410 3.1755e+02 3.5639e+02 3.5639e-03
411 3.1629e+02 3.5568e+02 3.5568e-03
412 3.1503e+02 3.5496e+02 3.5496e-03
413 3.1377e+02 3.5425e+02 3.5425e-03
414 3.1252e+02 3.5355e+02 3.5355e-03
415 3.1128e+02 3.5284e+02 3.5284e-03
416 3.1004e+02 3.5213e+02 3.5213e-03
417 3.0881e+02 3.5143e+02 3.5143e-03
418 3.0758e+02 3.5073e+02 3.5073e-03
419 3.0636e+02 3.5002e+02 3.5002e-03
420 3.0514e+02 3.4933e+02 3.4933e-03
421 3.0392e+02 3.4863e+02 3.4863e-03
422 3.0271e+02 3.4793e+02 3.4793e-03
423 3.0151e+02 3.4723e+02 3.4723e-03
424 3.0031e+02 3.4654e+02 3.4654e-03
425 2.9911e+02 3.4585e+02 3.4585e-03
426 2.9792e+02 3.4515e+02 3.4515e-03
427 2.9674e+02 3.4446e+02 3.4446e-03
428 2.9556e+02 3.4378e+02 3.4378e-03
429 2.9438e+02 3.4309e+02 3.4309e-03
430 2.9321e+02 3.4240e+02 3.4240e-03
431 2.9204e+02 3.4172e+02 3.4172e-03
432 2.9088e+02 3.4103e+02 3.4103e-03
433 2.8972e+02 3.4035e+02 3.4035e-03
434 2.8857e+02 3.3967e+02 3.3967e-03
435 2.8742e+02 3.3899e+02 3.3899e-03
436 2.8628e+02 3.3832e+02 3.3832e-03
437 2.8514e+02 3.3764e+02 3.3764e-03
438 2.8401e+02 3.3696e+02 3.3696e-03
439 2.8288e+02 3.3629e+02 3.3629e-03
440 2.8175e+02 3.3562e+02 3.3562e-03
441 2.8063e+02 3.3495e+02 3.3495e-03
442 2.7952e+02 3.3428e+02 3.3428e-03
443 2.7840e+02 3.3361e+02 3.3361e-03
444 2.7730e+02 3.3294e+02 3.3294e-03
445 2.7619e+02 3.3228e+02 3.3228e-03
446 2.7509e+02 3.3161e+02 3.3161e-03
447 2.7400e+02 3.3095e+02 3.3095e-03
448 2.7291e+02 3.3029e+02 3.3029e-03
449 2.7183e+02 3.2963e+02 3.2963e-03
450 2.7074e+02 3.2897e+02 3.2897e-03
451 2.6967e+02 3.2831e+02 3.2831e-03
452 2.6859e+02 3.2766e+02 3.2766e-03
453 2.6753e+02 3.2700e+02 3.2700e-03
454 2.6646e+02 3.2635e+02 3.2635e-03
455 2.6540e+02 3.2569e+02 3.2569e-03
456 2.6435e+02 3.2504e+02 3.2504e-03
457 2.6330e+02 3.2439e+02 3.2439e-03
458 2.6225e+02 3.2375e+02 3.2375e-03
459 2.6121e+02 3.2310e+02 3.2310e-03
460 2.6017e+02 3.2245e+02 3.2245e-03
461 2.5913e+02 3.2181e+02 3.2181e-03
462 2.5810e+02 3.2117e+02 3.2117e-03
463 2.5708e+02 3.2052e+02 3.2052e-03
464 2.5605e+02 3.1988e+02 3.1988e-03
465 2.5504e+02 3.1924e+02 3.1924e-03
466 2.5402e+02 3.1861e+02 3.1861e-03
467 2.5301e+02 3.1797e+02 3.1797e-03
468 2.5201e+02 3.1733e+02 3.1733e-03
469 2.5100e+02 3.1670e+02 3.1670e-03
470 2.5001e+02 3.1607e+02 3.1607e-03
471 2.4901e+02 3.1543e+02 3.1543e-03
472 2.4802e+02 3.1480e+02 3.1480e-03
473 2.4704e+02 3.1417e+02 3.1417e-03
474 2.4605e+02 3.1355e+02 3.1355e-03
475 2.4508e+02 3.1292e+02 3.1292e-03
476 2.4410e+02 3.1229e+02 3.1229e-03
477 2.4313e+02 3.1167e+02 3.1167e-03
478 2.4216e+02 3.1105e+02 3.1105e-03
479 2.4120e+02 3.1043e+02 3.1043e-03
480 2.4024e+02 3.0981e+02 3.0981e-03
481 2.3929e+02 3.0919e+02 3.0919e-03
482 2.3834e+02 3.0857e+02 3.0857e-03
483 2.3739e+02 3.0795e+02 3.0795e-03
484 2.3645e+02 3.0734e+02 3.0734e-03
485 2.3551e+02 3.0672e+02 3.0672e-03
486 2.3457e+02 3.0611e+02 3.0611e-03
487 2.3364e+02 3.0550e+02 3.0550e-03
488 2.3271e+02 3.0489e+02 3.0489e-03
489 2.3178e+02 3.0428e+02 3.0428e-03
490 2.3086e+02 3.0367e+02 3.0367e-03
491 2.2994e+02 3.0306e+02 3.0306e-03
492 2.2903e+02 3.0246e+02 3.0246e-03
493 2.2812e+02 3.0185e+02 3.0185e-03
494 2.2721e+02 3.0125e+02 3.0125e-03
495 2.2631e+02 3.0065e+02 3.0065e-03
496 2.2541e+02 3.0005e+02 3.0005e-03
497 2.2452e+02 2.9945e+02 2.9945e-03
498 2.2362e+02 2.9885e+02 2.9885e-03
499 2.2274e+02 2.9825e+02 2.9825e-03
Max iterations reached
Total time is: 0.7796146869659424
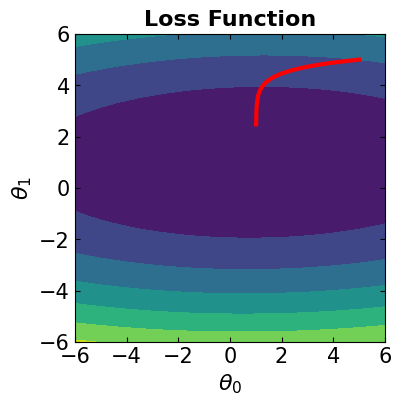
The optimal solution is: theta0 = 1.0163458431736672 , theta1 = 2.478808831685626
The corresponding loss function is: 222.73511700400618
### If learning rate = 0.0001 ###
####################
##### Step 1 #####
####################
# Initialize the vector of model parameters
theta_0 = [5, 5]
####################
##### Step 2 #####
####################
# Set the learning rate:
gamma_t = 0.0001
# Set the gradient threshold:
grad_thres = 1e-7
# Set the maximum number of iterations:
maxIter = 500
# Set the batch size:
# (select "len(data)"" for BGD, "one" for SGD, a "mini-batch size" for mBGD)
k = len(data)
#####################
##### Steps 3-4 #####
#####################
# Call the following function to do the steps 3 & 4
# (returns the theta vectors and loss values for all iterations)
start = time.time()
theta,loss = SGD_mBGD_BGD(data, f3, theta_0, least_squares_loss_function, grad_approx, \
learning_rate = gamma_t, max_iterations = maxIter, batch_size=k, gradient_threshold=grad_thres)
end = time.time()
print('Total time is: ', end - start)
# Visualize the convergence track on loss function
fig = plt.figure(figsize=(4,4))
plt.plot(theta[:, 0], theta[:, 1], '-r', markersize=5, linewidth=3)
contour_plot(LFx, -6., 6., 50, -6, 6., 50)
# Print the optimal solution
print("The optimal solution is: theta0 = ", str(theta[-1, 0]), ", theta1 = ", str(theta[-1, 1]))
print("The corresponding loss function is: ", str(loss[-1]))
Iter. loss_func(x) ||grad(x)|| ||p||
0 1.1152e+04 7.2953e+03 7.2953e-01
1 7.9031e+03 5.9754e+03 5.9754e-01
2 5.7170e+03 4.9000e+03 4.9000e-01
3 4.2408e+03 4.0247e+03 4.0247e-01
4 3.2389e+03 3.3135e+03 3.3135e-01
5 2.5541e+03 2.7367e+03 2.7367e-01
6 2.0817e+03 2.2703e+03 2.2703e-01
7 1.7515e+03 1.8948e+03 1.8948e-01
8 1.5169e+03 1.5938e+03 1.5938e-01
9 1.3466e+03 1.3543e+03 1.3543e-01
10 1.2197e+03 1.1651e+03 1.1651e-01
11 1.1223e+03 1.0168e+03 1.0168e-01
12 1.0452e+03 9.0171e+02 9.0171e-02
13 9.8198e+02 8.1291e+02 8.1291e-02
14 9.2857e+02 7.4468e+02 7.4468e-02
15 8.8213e+02 6.9220e+02 6.9220e-02
16 8.4076e+02 6.5153e+02 6.5153e-02
17 8.0320e+02 6.1959e+02 6.1959e-02
18 7.6857e+02 5.9398e+02 5.9398e-02
19 7.3626e+02 5.7294e+02 5.7294e-02
20 7.0588e+02 5.5515e+02 5.5515e-02
21 6.7714e+02 5.3970e+02 5.3970e-02
22 6.4981e+02 5.2593e+02 5.2593e-02
23 6.2376e+02 5.1338e+02 5.1338e-02
24 5.9886e+02 5.0172e+02 5.0172e-02
25 5.7504e+02 4.9074e+02 4.9074e-02
26 5.5221e+02 4.8029e+02 4.8029e-02
27 5.3033e+02 4.7024e+02 4.7024e-02
28 5.0933e+02 4.6055e+02 4.6055e-02
29 4.8919e+02 4.5114e+02 4.5114e-02
30 4.6985e+02 4.4198e+02 4.4198e-02
31 4.5129e+02 4.3305e+02 4.3305e-02
32 4.3346e+02 4.2433e+02 4.2433e-02
33 4.1635e+02 4.1581e+02 4.1581e-02
34 3.9991e+02 4.0747e+02 4.0747e-02
35 3.8412e+02 3.9931e+02 3.9931e-02
36 3.6897e+02 3.9131e+02 3.9131e-02
37 3.5441e+02 3.8348e+02 3.8348e-02
38 3.4042e+02 3.7581e+02 3.7581e-02
39 3.2700e+02 3.6830e+02 3.6830e-02
40 3.1410e+02 3.6093e+02 3.6093e-02
41 3.0171e+02 3.5372e+02 3.5372e-02
42 2.8982e+02 3.4665e+02 3.4665e-02
43 2.7839e+02 3.3972e+02 3.3972e-02
44 2.6742e+02 3.3293e+02 3.3293e-02
45 2.5688e+02 3.2628e+02 3.2628e-02
46 2.4675e+02 3.1976e+02 3.1976e-02
47 2.3703e+02 3.1337e+02 3.1337e-02
48 2.2770e+02 3.0710e+02 3.0710e-02
49 2.1873e+02 3.0097e+02 3.0097e-02
50 2.1012e+02 2.9495e+02 2.9495e-02
51 2.0184e+02 2.8906e+02 2.8906e-02
52 1.9390e+02 2.8328e+02 2.8328e-02
53 1.8627e+02 2.7762e+02 2.7762e-02
54 1.7894e+02 2.7207e+02 2.7207e-02
55 1.7190e+02 2.6663e+02 2.6663e-02
56 1.6514e+02 2.6131e+02 2.6131e-02
57 1.5865e+02 2.5608e+02 2.5608e-02
58 1.5241e+02 2.5097e+02 2.5097e-02
59 1.4643e+02 2.4595e+02 2.4595e-02
60 1.4067e+02 2.4104e+02 2.4104e-02
61 1.3515e+02 2.3622e+02 2.3622e-02
62 1.2984e+02 2.3150e+02 2.3150e-02
63 1.2475e+02 2.2687e+02 2.2687e-02
64 1.1986e+02 2.2234e+02 2.2234e-02
65 1.1515e+02 2.1789e+02 2.1789e-02
66 1.1064e+02 2.1354e+02 2.1354e-02
67 1.0630e+02 2.0927e+02 2.0927e-02
68 1.0214e+02 2.0509e+02 2.0509e-02
69 9.8141e+01 2.0099e+02 2.0099e-02
70 9.4300e+01 1.9697e+02 1.9697e-02
71 9.0611e+01 1.9304e+02 1.9304e-02
72 8.7068e+01 1.8918e+02 1.8918e-02
73 8.3665e+01 1.8540e+02 1.8540e-02
74 8.0396e+01 1.8169e+02 1.8169e-02
75 7.7257e+01 1.7806e+02 1.7806e-02
76 7.4243e+01 1.7451e+02 1.7451e-02
77 7.1347e+01 1.7102e+02 1.7102e-02
78 6.8566e+01 1.6760e+02 1.6760e-02
79 6.5895e+01 1.6425e+02 1.6425e-02
80 6.3330e+01 1.6097e+02 1.6097e-02
81 6.0866e+01 1.5775e+02 1.5775e-02
82 5.8500e+01 1.5460e+02 1.5460e-02
83 5.6228e+01 1.5151e+02 1.5151e-02
84 5.4045e+01 1.4848e+02 1.4848e-02
85 5.1949e+01 1.4551e+02 1.4551e-02
86 4.9935e+01 1.4261e+02 1.4261e-02
87 4.8002e+01 1.3976e+02 1.3976e-02
88 4.6145e+01 1.3696e+02 1.3696e-02
89 4.4361e+01 1.3423e+02 1.3423e-02
90 4.2648e+01 1.3154e+02 1.3154e-02
91 4.1003e+01 1.2892e+02 1.2892e-02
92 3.9422e+01 1.2634e+02 1.2634e-02
93 3.7905e+01 1.2381e+02 1.2381e-02
94 3.6447e+01 1.2134e+02 1.2134e-02
95 3.5047e+01 1.1891e+02 1.1891e-02
96 3.3702e+01 1.1654e+02 1.1654e-02
97 3.2411e+01 1.1421e+02 1.1421e-02
98 3.1171e+01 1.1193e+02 1.1193e-02
99 2.9980e+01 1.0969e+02 1.0969e-02
100 2.8836e+01 1.0750e+02 1.0750e-02
101 2.7737e+01 1.0535e+02 1.0535e-02
102 2.6682e+01 1.0324e+02 1.0324e-02
103 2.5668e+01 1.0118e+02 1.0118e-02
104 2.4695e+01 9.9159e+01 9.9159e-03
105 2.3760e+01 9.7178e+01 9.7178e-03
106 2.2862e+01 9.5236e+01 9.5236e-03
107 2.1999e+01 9.3332e+01 9.3332e-03
108 2.1171e+01 9.1467e+01 9.1467e-03
109 2.0376e+01 8.9639e+01 8.9639e-03
110 1.9612e+01 8.7848e+01 8.7848e-03
111 1.8878e+01 8.6092e+01 8.6092e-03
112 1.8173e+01 8.4372e+01 8.4372e-03
113 1.7496e+01 8.2686e+01 8.2686e-03
114 1.6846e+01 8.1033e+01 8.1033e-03
115 1.6222e+01 7.9414e+01 7.9414e-03
116 1.5622e+01 7.7827e+01 7.7827e-03
117 1.5046e+01 7.6272e+01 7.6272e-03
118 1.4493e+01 7.4747e+01 7.4747e-03
119 1.3962e+01 7.3254e+01 7.3254e-03
120 1.3452e+01 7.1790e+01 7.1790e-03
121 1.2962e+01 7.0355e+01 7.0355e-03
122 1.2491e+01 6.8949e+01 6.8949e-03
123 1.2039e+01 6.7571e+01 6.7571e-03
124 1.1605e+01 6.6221e+01 6.6221e-03
125 1.1188e+01 6.4897e+01 6.4897e-03
126 1.0787e+01 6.3600e+01 6.3600e-03
127 1.0403e+01 6.2329e+01 6.2329e-03
128 1.0033e+01 6.1084e+01 6.1084e-03
129 9.6786e+00 5.9863e+01 5.9863e-03
130 9.3378e+00 5.8667e+01 5.8667e-03
131 9.0106e+00 5.7494e+01 5.7494e-03
132 8.6963e+00 5.6345e+01 5.6345e-03
133 8.3944e+00 5.5219e+01 5.5219e-03
134 8.1045e+00 5.4116e+01 5.4116e-03
135 7.8260e+00 5.3034e+01 5.3034e-03
136 7.5586e+00 5.1975e+01 5.1975e-03
137 7.3017e+00 5.0936e+01 5.0936e-03
138 7.0550e+00 4.9918e+01 4.9918e-03
139 6.8181e+00 4.8920e+01 4.8920e-03
140 6.5905e+00 4.7943e+01 4.7943e-03
141 6.3720e+00 4.6985e+01 4.6985e-03
142 6.1621e+00 4.6046e+01 4.6046e-03
143 5.9605e+00 4.5125e+01 4.5125e-03
144 5.7669e+00 4.4224e+01 4.4224e-03
145 5.5809e+00 4.3340e+01 4.3340e-03
146 5.4023e+00 4.2474e+01 4.2474e-03
147 5.2308e+00 4.1625e+01 4.1625e-03
148 5.0660e+00 4.0793e+01 4.0793e-03
149 4.9078e+00 3.9978e+01 3.9978e-03
150 4.7558e+00 3.9179e+01 3.9179e-03
151 4.6099e+00 3.8396e+01 3.8396e-03
152 4.4697e+00 3.7629e+01 3.7629e-03
153 4.3351e+00 3.6877e+01 3.6877e-03
154 4.2058e+00 3.6140e+01 3.6140e-03
155 4.0816e+00 3.5418e+01 3.5418e-03
156 3.9623e+00 3.4710e+01 3.4710e-03
157 3.8478e+00 3.4016e+01 3.4016e-03
158 3.7378e+00 3.3336e+01 3.3336e-03
159 3.6321e+00 3.2670e+01 3.2670e-03
160 3.5306e+00 3.2017e+01 3.2017e-03
161 3.4331e+00 3.1377e+01 3.1377e-03
162 3.3395e+00 3.0750e+01 3.0750e-03
163 3.2496e+00 3.0136e+01 3.0136e-03
164 3.1633e+00 2.9534e+01 2.9534e-03
165 3.0803e+00 2.8943e+01 2.8943e-03
166 3.0007e+00 2.8365e+01 2.8365e-03
167 2.9242e+00 2.7798e+01 2.7798e-03
168 2.8507e+00 2.7243e+01 2.7243e-03
169 2.7801e+00 2.6698e+01 2.6698e-03
170 2.7124e+00 2.6165e+01 2.6165e-03
171 2.6473e+00 2.5642e+01 2.5642e-03
172 2.5847e+00 2.5129e+01 2.5129e-03
173 2.5247e+00 2.4627e+01 2.4627e-03
174 2.4670e+00 2.4135e+01 2.4135e-03
175 2.4116e+00 2.3653e+01 2.3653e-03
176 2.3585e+00 2.3180e+01 2.3180e-03
177 2.3074e+00 2.2717e+01 2.2717e-03
178 2.2583e+00 2.2263e+01 2.2263e-03
179 2.2112e+00 2.1818e+01 2.1818e-03
180 2.1659e+00 2.1382e+01 2.1382e-03
181 2.1224e+00 2.0954e+01 2.0954e-03
182 2.0807e+00 2.0536e+01 2.0536e-03
183 2.0406e+00 2.0125e+01 2.0125e-03
184 2.0021e+00 1.9723e+01 1.9723e-03
185 1.9651e+00 1.9329e+01 1.9329e-03
186 1.9296e+00 1.8943e+01 1.8943e-03
187 1.8954e+00 1.8564e+01 1.8564e-03
188 1.8627e+00 1.8193e+01 1.8193e-03
189 1.8312e+00 1.7830e+01 1.7830e-03
190 1.8010e+00 1.7473e+01 1.7473e-03
191 1.7719e+00 1.7124e+01 1.7124e-03
192 1.7441e+00 1.6782e+01 1.6782e-03
193 1.7173e+00 1.6446e+01 1.6446e-03
194 1.6916e+00 1.6118e+01 1.6118e-03
195 1.6669e+00 1.5796e+01 1.5796e-03
196 1.6431e+00 1.5480e+01 1.5480e-03
197 1.6204e+00 1.5171e+01 1.5171e-03
198 1.5985e+00 1.4868e+01 1.4868e-03
199 1.5775e+00 1.4570e+01 1.4570e-03
200 1.5573e+00 1.4279e+01 1.4279e-03
201 1.5379e+00 1.3994e+01 1.3994e-03
202 1.5193e+00 1.3714e+01 1.3714e-03
203 1.5014e+00 1.3440e+01 1.3440e-03
204 1.4842e+00 1.3172e+01 1.3172e-03
205 1.4677e+00 1.2908e+01 1.2908e-03
206 1.4519e+00 1.2650e+01 1.2650e-03
207 1.4367e+00 1.2398e+01 1.2398e-03
208 1.4220e+00 1.2150e+01 1.2150e-03
209 1.4080e+00 1.1907e+01 1.1907e-03
210 1.3945e+00 1.1669e+01 1.1669e-03
211 1.3816e+00 1.1436e+01 1.1436e-03
212 1.3691e+00 1.1207e+01 1.1207e-03
213 1.3572e+00 1.0983e+01 1.0983e-03
214 1.3457e+00 1.0764e+01 1.0764e-03
215 1.3347e+00 1.0549e+01 1.0549e-03
216 1.3241e+00 1.0338e+01 1.0338e-03
217 1.3140e+00 1.0131e+01 1.0131e-03
218 1.3042e+00 9.9289e+00 9.9289e-04
219 1.2948e+00 9.7304e+00 9.7304e-04
220 1.2858e+00 9.5360e+00 9.5360e-04
221 1.2772e+00 9.3454e+00 9.3454e-04
222 1.2689e+00 9.1586e+00 9.1586e-04
223 1.2609e+00 8.9756e+00 8.9756e-04
224 1.2532e+00 8.7962e+00 8.7962e-04
225 1.2459e+00 8.6205e+00 8.6205e-04
226 1.2388e+00 8.4482e+00 8.4482e-04
227 1.2320e+00 8.2794e+00 8.2794e-04
228 1.2255e+00 8.1139e+00 8.1139e-04
229 1.2193e+00 7.9517e+00 7.9517e-04
230 1.2132e+00 7.7928e+00 7.7928e-04
231 1.2075e+00 7.6371e+00 7.6371e-04
232 1.2019e+00 7.4845e+00 7.4845e-04
233 1.1966e+00 7.3349e+00 7.3349e-04
234 1.1915e+00 7.1883e+00 7.1883e-04
235 1.1866e+00 7.0447e+00 7.0447e-04
236 1.1819e+00 6.9039e+00 6.9039e-04
237 1.1773e+00 6.7659e+00 6.7659e-04
238 1.1730e+00 6.6307e+00 6.6307e-04
239 1.1688e+00 6.4982e+00 6.4982e-04
240 1.1648e+00 6.3683e+00 6.3683e-04
241 1.1609e+00 6.2411e+00 6.2411e-04
242 1.1572e+00 6.1163e+00 6.1163e-04
243 1.1537e+00 5.9941e+00 5.9941e-04
244 1.1502e+00 5.8743e+00 5.8743e-04
245 1.1470e+00 5.7569e+00 5.7569e-04
246 1.1438e+00 5.6419e+00 5.6419e-04
247 1.1408e+00 5.5291e+00 5.5291e-04
248 1.1379e+00 5.4186e+00 5.4186e-04
249 1.1351e+00 5.3103e+00 5.3103e-04
250 1.1324e+00 5.2042e+00 5.2042e-04
251 1.1298e+00 5.1002e+00 5.1002e-04
252 1.1274e+00 4.9983e+00 4.9983e-04
253 1.1250e+00 4.8984e+00 4.8984e-04
254 1.1227e+00 4.8005e+00 4.8005e-04
255 1.1205e+00 4.7046e+00 4.7046e-04
256 1.1184e+00 4.6106e+00 4.6106e-04
257 1.1164e+00 4.5184e+00 4.5184e-04
258 1.1144e+00 4.4281e+00 4.4281e-04
259 1.1126e+00 4.3396e+00 4.3396e-04
260 1.1108e+00 4.2529e+00 4.2529e-04
261 1.1091e+00 4.1679e+00 4.1679e-04
262 1.1074e+00 4.0846e+00 4.0846e-04
263 1.1058e+00 4.0030e+00 4.0030e-04
264 1.1043e+00 3.9230e+00 3.9230e-04
265 1.1028e+00 3.8446e+00 3.8446e-04
266 1.1014e+00 3.7678e+00 3.7678e-04
267 1.1001e+00 3.6925e+00 3.6925e-04
268 1.0988e+00 3.6187e+00 3.6187e-04
269 1.0975e+00 3.5464e+00 3.5464e-04
270 1.0963e+00 3.4755e+00 3.4755e-04
271 1.0952e+00 3.4060e+00 3.4060e-04
272 1.0941e+00 3.3380e+00 3.3380e-04
273 1.0930e+00 3.2713e+00 3.2713e-04
274 1.0920e+00 3.2059e+00 3.2059e-04
275 1.0910e+00 3.1418e+00 3.1418e-04
276 1.0901e+00 3.0790e+00 3.0790e-04
277 1.0892e+00 3.0175e+00 3.0175e-04
278 1.0883e+00 2.9572e+00 2.9572e-04
279 1.0875e+00 2.8981e+00 2.8981e-04
280 1.0867e+00 2.8402e+00 2.8402e-04
281 1.0859e+00 2.7834e+00 2.7834e-04
282 1.0852e+00 2.7278e+00 2.7278e-04
283 1.0845e+00 2.6733e+00 2.6733e-04
284 1.0838e+00 2.6199e+00 2.6199e-04
285 1.0832e+00 2.5675e+00 2.5675e-04
286 1.0825e+00 2.5162e+00 2.5162e-04
287 1.0819e+00 2.4659e+00 2.4659e-04
288 1.0814e+00 2.4166e+00 2.4166e-04
289 1.0808e+00 2.3683e+00 2.3683e-04
290 1.0803e+00 2.3210e+00 2.3210e-04
291 1.0798e+00 2.2746e+00 2.2746e-04
292 1.0793e+00 2.2292e+00 2.2292e-04
293 1.0788e+00 2.1846e+00 2.1846e-04
294 1.0783e+00 2.1410e+00 2.1410e-04
295 1.0779e+00 2.0982e+00 2.0982e-04
296 1.0775e+00 2.0562e+00 2.0562e-04
297 1.0771e+00 2.0152e+00 2.0152e-04
298 1.0767e+00 1.9749e+00 1.9749e-04
299 1.0763e+00 1.9354e+00 1.9354e-04
300 1.0760e+00 1.8967e+00 1.8967e-04
301 1.0756e+00 1.8588e+00 1.8588e-04
302 1.0753e+00 1.8217e+00 1.8217e-04
303 1.0750e+00 1.7853e+00 1.7853e-04
304 1.0747e+00 1.7496e+00 1.7496e-04
305 1.0744e+00 1.7146e+00 1.7146e-04
306 1.0741e+00 1.6804e+00 1.6804e-04
307 1.0738e+00 1.6468e+00 1.6468e-04
308 1.0736e+00 1.6139e+00 1.6139e-04
309 1.0733e+00 1.5816e+00 1.5816e-04
310 1.0731e+00 1.5500e+00 1.5500e-04
311 1.0729e+00 1.5190e+00 1.5190e-04
312 1.0726e+00 1.4887e+00 1.4887e-04
313 1.0724e+00 1.4589e+00 1.4589e-04
314 1.0722e+00 1.4298e+00 1.4298e-04
315 1.0720e+00 1.4012e+00 1.4012e-04
316 1.0718e+00 1.3732e+00 1.3732e-04
317 1.0717e+00 1.3458e+00 1.3458e-04
318 1.0715e+00 1.3189e+00 1.3189e-04
319 1.0713e+00 1.2925e+00 1.2925e-04
320 1.0712e+00 1.2667e+00 1.2667e-04
321 1.0710e+00 1.2414e+00 1.2414e-04
322 1.0709e+00 1.2166e+00 1.2166e-04
323 1.0707e+00 1.1923e+00 1.1923e-04
324 1.0706e+00 1.1684e+00 1.1684e-04
325 1.0705e+00 1.1451e+00 1.1451e-04
326 1.0703e+00 1.1222e+00 1.1222e-04
327 1.0702e+00 1.0998e+00 1.0998e-04
328 1.0701e+00 1.0778e+00 1.0778e-04
329 1.0700e+00 1.0562e+00 1.0562e-04
330 1.0699e+00 1.0351e+00 1.0351e-04
331 1.0698e+00 1.0145e+00 1.0145e-04
332 1.0697e+00 9.9418e-01 9.9418e-05
333 1.0696e+00 9.7431e-01 9.7431e-05
334 1.0695e+00 9.5484e-01 9.5484e-05
335 1.0694e+00 9.3576e-01 9.3576e-05
336 1.0693e+00 9.1706e-01 9.1706e-05
337 1.0693e+00 8.9873e-01 8.9873e-05
338 1.0692e+00 8.8077e-01 8.8077e-05
339 1.0691e+00 8.6317e-01 8.6317e-05
340 1.0690e+00 8.4592e-01 8.4592e-05
341 1.0690e+00 8.2901e-01 8.2901e-05
342 1.0689e+00 8.1245e-01 8.1245e-05
343 1.0688e+00 7.9621e-01 7.9621e-05
344 1.0688e+00 7.8030e-01 7.8030e-05
345 1.0687e+00 7.6471e-01 7.6471e-05
346 1.0687e+00 7.4942e-01 7.4942e-05
347 1.0686e+00 7.3445e-01 7.3445e-05
348 1.0686e+00 7.1977e-01 7.1977e-05
349 1.0685e+00 7.0538e-01 7.0538e-05
350 1.0685e+00 6.9129e-01 6.9129e-05
351 1.0684e+00 6.7747e-01 6.7747e-05
352 1.0684e+00 6.6393e-01 6.6393e-05
353 1.0683e+00 6.5067e-01 6.5067e-05
354 1.0683e+00 6.3766e-01 6.3766e-05
355 1.0683e+00 6.2492e-01 6.2492e-05
356 1.0682e+00 6.1243e-01 6.1243e-05
357 1.0682e+00 6.0019e-01 6.0019e-05
358 1.0681e+00 5.8820e-01 5.8820e-05
359 1.0681e+00 5.7644e-01 5.7644e-05
360 1.0681e+00 5.6492e-01 5.6492e-05
361 1.0681e+00 5.5363e-01 5.5363e-05
362 1.0680e+00 5.4257e-01 5.4257e-05
363 1.0680e+00 5.3173e-01 5.3173e-05
364 1.0680e+00 5.2110e-01 5.2110e-05
365 1.0679e+00 5.1069e-01 5.1069e-05
366 1.0679e+00 5.0048e-01 5.0048e-05
367 1.0679e+00 4.9048e-01 4.9048e-05
368 1.0679e+00 4.8068e-01 4.8068e-05
369 1.0679e+00 4.7107e-01 4.7107e-05
370 1.0678e+00 4.6166e-01 4.6166e-05
371 1.0678e+00 4.5243e-01 4.5243e-05
372 1.0678e+00 4.4339e-01 4.4339e-05
373 1.0678e+00 4.3453e-01 4.3453e-05
374 1.0678e+00 4.2585e-01 4.2585e-05
375 1.0677e+00 4.1734e-01 4.1734e-05
376 1.0677e+00 4.0899e-01 4.0899e-05
377 1.0677e+00 4.0082e-01 4.0082e-05
378 1.0677e+00 3.9281e-01 3.9281e-05
379 1.0677e+00 3.8496e-01 3.8496e-05
380 1.0677e+00 3.7727e-01 3.7727e-05
381 1.0676e+00 3.6973e-01 3.6973e-05
382 1.0676e+00 3.6234e-01 3.6234e-05
383 1.0676e+00 3.5510e-01 3.5510e-05
384 1.0676e+00 3.4800e-01 3.4800e-05
385 1.0676e+00 3.4105e-01 3.4105e-05
386 1.0676e+00 3.3423e-01 3.3423e-05
387 1.0676e+00 3.2755e-01 3.2755e-05
388 1.0676e+00 3.2101e-01 3.2101e-05
389 1.0676e+00 3.1459e-01 3.1459e-05
390 1.0675e+00 3.0830e-01 3.0830e-05
391 1.0675e+00 3.0214e-01 3.0214e-05
392 1.0675e+00 2.9611e-01 2.9611e-05
393 1.0675e+00 2.9019e-01 2.9019e-05
394 1.0675e+00 2.8439e-01 2.8439e-05
395 1.0675e+00 2.7871e-01 2.7871e-05
396 1.0675e+00 2.7314e-01 2.7314e-05
397 1.0675e+00 2.6768e-01 2.6768e-05
398 1.0675e+00 2.6233e-01 2.6233e-05
399 1.0675e+00 2.5709e-01 2.5709e-05
400 1.0675e+00 2.5195e-01 2.5195e-05
401 1.0675e+00 2.4691e-01 2.4691e-05
402 1.0675e+00 2.4198e-01 2.4198e-05
403 1.0675e+00 2.3714e-01 2.3714e-05
404 1.0674e+00 2.3240e-01 2.3240e-05
405 1.0674e+00 2.2776e-01 2.2776e-05
406 1.0674e+00 2.2321e-01 2.2321e-05
407 1.0674e+00 2.1875e-01 2.1875e-05
408 1.0674e+00 2.1438e-01 2.1438e-05
409 1.0674e+00 2.1009e-01 2.1009e-05
410 1.0674e+00 2.0589e-01 2.0589e-05
411 1.0674e+00 2.0178e-01 2.0178e-05
412 1.0674e+00 1.9775e-01 1.9775e-05
413 1.0674e+00 1.9379e-01 1.9379e-05
414 1.0674e+00 1.8992e-01 1.8992e-05
415 1.0674e+00 1.8613e-01 1.8613e-05
416 1.0674e+00 1.8241e-01 1.8241e-05
417 1.0674e+00 1.7876e-01 1.7876e-05
418 1.0674e+00 1.7519e-01 1.7519e-05
419 1.0674e+00 1.7169e-01 1.7169e-05
420 1.0674e+00 1.6826e-01 1.6826e-05
421 1.0674e+00 1.6489e-01 1.6489e-05
422 1.0674e+00 1.6160e-01 1.6160e-05
423 1.0674e+00 1.5837e-01 1.5837e-05
424 1.0674e+00 1.5520e-01 1.5520e-05
425 1.0674e+00 1.5210e-01 1.5210e-05
426 1.0674e+00 1.4906e-01 1.4906e-05
427 1.0674e+00 1.4608e-01 1.4608e-05
428 1.0674e+00 1.4316e-01 1.4316e-05
429 1.0674e+00 1.4030e-01 1.4030e-05
430 1.0674e+00 1.3750e-01 1.3750e-05
431 1.0674e+00 1.3475e-01 1.3475e-05
432 1.0674e+00 1.3206e-01 1.3206e-05
433 1.0674e+00 1.2942e-01 1.2942e-05
434 1.0674e+00 1.2683e-01 1.2683e-05
435 1.0674e+00 1.2430e-01 1.2430e-05
436 1.0674e+00 1.2181e-01 1.2181e-05
437 1.0674e+00 1.1938e-01 1.1938e-05
438 1.0674e+00 1.1699e-01 1.1699e-05
439 1.0673e+00 1.1466e-01 1.1466e-05
440 1.0673e+00 1.1237e-01 1.1237e-05
441 1.0673e+00 1.1012e-01 1.1012e-05
442 1.0673e+00 1.0792e-01 1.0792e-05
443 1.0673e+00 1.0576e-01 1.0576e-05
444 1.0673e+00 1.0365e-01 1.0365e-05
445 1.0673e+00 1.0158e-01 1.0158e-05
446 1.0673e+00 9.9547e-02 9.9547e-06
447 1.0673e+00 9.7558e-02 9.7558e-06
448 1.0673e+00 9.5608e-02 9.5608e-06
449 1.0673e+00 9.3698e-02 9.3698e-06
450 1.0673e+00 9.1825e-02 9.1825e-06
451 1.0673e+00 8.9990e-02 8.9990e-06
452 1.0673e+00 8.8192e-02 8.8192e-06
453 1.0673e+00 8.6429e-02 8.6429e-06
454 1.0673e+00 8.4702e-02 8.4702e-06
455 1.0673e+00 8.3009e-02 8.3009e-06
456 1.0673e+00 8.1351e-02 8.1351e-06
457 1.0673e+00 7.9725e-02 7.9725e-06
458 1.0673e+00 7.8132e-02 7.8132e-06
459 1.0673e+00 7.6570e-02 7.6570e-06
460 1.0673e+00 7.5040e-02 7.5040e-06
461 1.0673e+00 7.3540e-02 7.3540e-06
462 1.0673e+00 7.2071e-02 7.2071e-06
463 1.0673e+00 7.0630e-02 7.0630e-06
464 1.0673e+00 6.9219e-02 6.9219e-06
465 1.0673e+00 6.7836e-02 6.7836e-06
466 1.0673e+00 6.6480e-02 6.6480e-06
467 1.0673e+00 6.5151e-02 6.5151e-06
468 1.0673e+00 6.3849e-02 6.3849e-06
469 1.0673e+00 6.2573e-02 6.2573e-06
470 1.0673e+00 6.1323e-02 6.1323e-06
471 1.0673e+00 6.0097e-02 6.0097e-06
472 1.0673e+00 5.8896e-02 5.8896e-06
473 1.0673e+00 5.7719e-02 5.7719e-06
474 1.0673e+00 5.6566e-02 5.6566e-06
475 1.0673e+00 5.5435e-02 5.5435e-06
476 1.0673e+00 5.4328e-02 5.4328e-06
477 1.0673e+00 5.3242e-02 5.3242e-06
478 1.0673e+00 5.2178e-02 5.2178e-06
479 1.0673e+00 5.1135e-02 5.1135e-06
480 1.0673e+00 5.0113e-02 5.0113e-06
481 1.0673e+00 4.9112e-02 4.9112e-06
482 1.0673e+00 4.8130e-02 4.8130e-06
483 1.0673e+00 4.7169e-02 4.7169e-06
484 1.0673e+00 4.6226e-02 4.6226e-06
485 1.0673e+00 4.5302e-02 4.5302e-06
486 1.0673e+00 4.4397e-02 4.4397e-06
487 1.0673e+00 4.3510e-02 4.3510e-06
488 1.0673e+00 4.2640e-02 4.2640e-06
489 1.0673e+00 4.1788e-02 4.1788e-06
490 1.0673e+00 4.0953e-02 4.0953e-06
491 1.0673e+00 4.0134e-02 4.0134e-06
492 1.0673e+00 3.9332e-02 3.9332e-06
493 1.0673e+00 3.8546e-02 3.8546e-06
494 1.0673e+00 3.7776e-02 3.7776e-06
495 1.0673e+00 3.7021e-02 3.7021e-06
496 1.0673e+00 3.6281e-02 3.6281e-06
497 1.0673e+00 3.5556e-02 3.5556e-06
498 1.0673e+00 3.4846e-02 3.4846e-06
499 1.0673e+00 3.4149e-02 3.4149e-06
Max iterations reached
Total time is: 2.1641643047332764
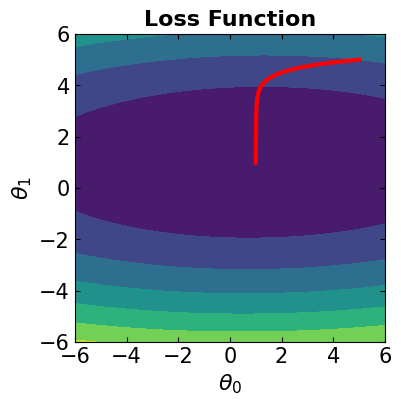
The optimal solution is: theta0 = 1.00135569186099 , theta1 = 0.989616451044002
The corresponding loss function is: 1.067321064779166
### If learning rate = 0.001 ###
####################
##### Step 1 #####
####################
# Initialize the vector of model parameters
theta_0 = [5, 5]
####################
##### Step 2 #####
####################
# Set the learning rate:
gamma_t = 0.001
# Set the gradient threshold:
grad_thres = 1e-7
# Set the maximum number of iterations:
maxIter = 500
# Set the batch size:
# (select "len(data)"" for BGD, "one" for SGD, a "mini-batch size" for mBGD)
k = len(data)
#####################
##### Steps 3-4 #####
#####################
# Call the following function to do the steps 3 & 4
# (returns the theta vectors and loss values for all iterations)
start = time.time()
theta,loss = SGD_mBGD_BGD(data, f3, theta_0, least_squares_loss_function, grad_approx, \
learning_rate = gamma_t, max_iterations = maxIter, batch_size=k, gradient_threshold=grad_thres)
end = time.time()
print('Total time is: ', end - start)
# Visualize the convergence track on loss function
fig = plt.figure(figsize=(4,4))
plt.plot(theta[:, 0], theta[:, 1], '-r', markersize=5, linewidth=3)
contour_plot(LFx, -6., 6., 50, -6, 6., 50)
# Print the optimal solution
print("The optimal solution is: theta0 = ", str(theta[-1, 0]), ", theta1 = ", str(theta[-1, 1]))
print("The corresponding loss function is: ", str(loss[-1]))
Iter. loss_func(x) ||grad(x)|| ||p||
0 1.0968e+04 7.2953e+03 7.2953e+00
1 7.5265e+03 6.0618e+03 6.0618e+00
2 5.1674e+03 5.0370e+03 5.0370e+00
3 3.5493e+03 4.1855e+03 4.1855e+00
4 2.4391e+03 3.4781e+03 3.4781e+00
5 1.6769e+03 2.8904e+03 2.8904e+00
6 1.1534e+03 2.4020e+03 2.4020e+00
7 7.9370e+02 1.9962e+03 1.9962e+00
8 5.4645e+02 1.6589e+03 1.6589e+00
9 3.7645e+02 1.3787e+03 1.3787e+00
10 2.5951e+02 1.1459e+03 1.1459e+00
11 1.7904e+02 9.5233e+02 9.5233e-01
12 1.2366e+02 7.9150e+02 7.9150e-01
13 8.5531e+01 6.5785e+02 6.5785e-01
14 5.9273e+01 5.4677e+02 5.4677e-01
15 4.1186e+01 4.5445e+02 4.5445e-01
16 2.8725e+01 3.7773e+02 3.7773e-01
17 2.0137e+01 3.1396e+02 3.1396e-01
18 1.4218e+01 2.6096e+02 2.6096e-01
19 1.0138e+01 2.1690e+02 2.1690e-01
20 7.3242e+00 1.8029e+02 1.8029e-01
21 5.3839e+00 1.4986e+02 1.4986e-01
22 4.0457e+00 1.2456e+02 1.2456e-01
23 3.1226e+00 1.0354e+02 1.0354e-01
24 2.4857e+00 8.6065e+01 8.6065e-02
25 2.0463e+00 7.1539e+01 7.1539e-02
26 1.7430e+00 5.9466e+01 5.9466e-02
27 1.5338e+00 4.9430e+01 4.9430e-02
28 1.3893e+00 4.1088e+01 4.1088e-02
29 1.2897e+00 3.4154e+01 3.4154e-02
30 1.2208e+00 2.8391e+01 2.8391e-02
31 1.1733e+00 2.3600e+01 2.3600e-02
32 1.1405e+00 1.9617e+01 1.9617e-02
33 1.1179e+00 1.6307e+01 1.6307e-02
34 1.1022e+00 1.3555e+01 1.3555e-02
35 1.0914e+00 1.1268e+01 1.1268e-02
36 1.0840e+00 9.3666e+00 9.3666e-03
37 1.0788e+00 7.7861e+00 7.7861e-03
38 1.0753e+00 6.4723e+00 6.4723e-03
39 1.0728e+00 5.3802e+00 5.3802e-03
40 1.0711e+00 4.4724e+00 4.4724e-03
41 1.0699e+00 3.7178e+00 3.7178e-03
42 1.0691e+00 3.0905e+00 3.0905e-03
43 1.0686e+00 2.5690e+00 2.5690e-03
44 1.0682e+00 2.1356e+00 2.1356e-03
45 1.0679e+00 1.7753e+00 1.7753e-03
46 1.0677e+00 1.4757e+00 1.4757e-03
47 1.0676e+00 1.2267e+00 1.2267e-03
48 1.0675e+00 1.0198e+00 1.0198e-03
49 1.0675e+00 8.4770e-01 8.4770e-04
50 1.0674e+00 7.0468e-01 7.0468e-04
51 1.0674e+00 5.8578e-01 5.8578e-04
52 1.0674e+00 4.8695e-01 4.8695e-04
53 1.0673e+00 4.0479e-01 4.0479e-04
54 1.0673e+00 3.3650e-01 3.3650e-04
55 1.0673e+00 2.7972e-01 2.7972e-04
56 1.0673e+00 2.3253e-01 2.3253e-04
57 1.0673e+00 1.9330e-01 1.9330e-04
58 1.0673e+00 1.6069e-01 1.6069e-04
59 1.0673e+00 1.3357e-01 1.3357e-04
60 1.0673e+00 1.1104e-01 1.1104e-04
61 1.0673e+00 9.2305e-02 9.2305e-05
62 1.0673e+00 7.6731e-02 7.6731e-05
63 1.0673e+00 6.3786e-02 6.3786e-05
64 1.0673e+00 5.3024e-02 5.3024e-05
65 1.0673e+00 4.4078e-02 4.4078e-05
66 1.0673e+00 3.6641e-02 3.6641e-05
67 1.0673e+00 3.0460e-02 3.0460e-05
68 1.0673e+00 2.5321e-02 2.5321e-05
69 1.0673e+00 2.1049e-02 2.1049e-05
70 1.0673e+00 1.7497e-02 1.7497e-05
71 1.0673e+00 1.4545e-02 1.4545e-05
72 1.0673e+00 1.2091e-02 1.2091e-05
73 1.0673e+00 1.0051e-02 1.0051e-05
74 1.0673e+00 8.3556e-03 8.3556e-06
75 1.0673e+00 6.9459e-03 6.9459e-06
76 1.0673e+00 5.7740e-03 5.7740e-06
77 1.0673e+00 4.7999e-03 4.7999e-06
78 1.0673e+00 3.9901e-03 3.9901e-06
79 1.0673e+00 3.3169e-03 3.3169e-06
80 1.0673e+00 2.7573e-03 2.7573e-06
81 1.0673e+00 2.2921e-03 2.2921e-06
82 1.0673e+00 1.9054e-03 1.9054e-06
83 1.0673e+00 1.5839e-03 1.5839e-06
84 1.0673e+00 1.3167e-03 1.3167e-06
85 1.0673e+00 1.0945e-03 1.0945e-06
86 1.0673e+00 9.0989e-04 9.0989e-07
87 1.0673e+00 7.5639e-04 7.5639e-07
88 1.0673e+00 6.2878e-04 6.2878e-07
89 1.0673e+00 5.2270e-04 5.2270e-07
90 1.0673e+00 4.3451e-04 4.3451e-07
91 1.0673e+00 3.6121e-04 3.6121e-07
92 1.0673e+00 3.0027e-04 3.0027e-07
93 1.0673e+00 2.4961e-04 2.4961e-07
94 1.0673e+00 2.0750e-04 2.0750e-07
95 1.0673e+00 1.7249e-04 1.7249e-07
96 1.0673e+00 1.4340e-04 1.4340e-07
97 1.0673e+00 1.1921e-04 1.1921e-07
98 1.0673e+00 9.9089e-05 9.9089e-08
99 1.0673e+00 8.2367e-05 8.2367e-08
100 1.0673e+00 6.8468e-05 6.8468e-08
101 1.0673e+00 5.6919e-05 5.6919e-08
102 1.0673e+00 4.7317e-05 4.7317e-08
103 1.0673e+00 3.9329e-05 3.9329e-08
104 1.0673e+00 3.2691e-05 3.2691e-08
105 1.0673e+00 2.7176e-05 2.7176e-08
106 1.0673e+00 2.2592e-05 2.2592e-08
107 1.0673e+00 1.8783e-05 1.8783e-08
108 1.0673e+00 1.5615e-05 1.5615e-08
109 1.0673e+00 1.2983e-05 1.2983e-08
110 1.0673e+00 1.0801e-05 1.0801e-08
111 1.0673e+00 8.9834e-06 8.9834e-09
112 1.0673e+00 7.4676e-06 7.4676e-09
113 1.0673e+00 6.2065e-06 6.2065e-09
114 1.0673e+00 5.1583e-06 5.1583e-09
115 1.0673e+00 4.2857e-06 4.2857e-09
116 1.0673e+00 3.5551e-06 3.5551e-09
117 1.0673e+00 2.9545e-06 2.9545e-09
118 1.0673e+00 2.4603e-06 2.4603e-09
119 1.0673e+00 2.0385e-06 2.0385e-09
120 1.0673e+00 1.6942e-06 1.6942e-09
121 1.0673e+00 1.4190e-06 1.4190e-09
122 1.0673e+00 1.1836e-06 1.1836e-09
123 1.0673e+00 9.7706e-07 9.7706e-10
124 1.0673e+00 8.0386e-07 8.0386e-10
125 1.0673e+00 6.7172e-07 6.7172e-10
126 1.0673e+00 5.6516e-07 5.6516e-10
127 1.0673e+00 4.6855e-07 4.6855e-10
128 1.0673e+00 3.8642e-07 3.8642e-10
129 1.0673e+00 3.1981e-07 3.1981e-10
130 1.0673e+00 2.6646e-07 2.6646e-10
131 1.0673e+00 2.2427e-07 2.2427e-10
132 1.0673e+00 1.8882e-07 1.8882e-10
133 1.0673e+00 1.5989e-07 1.5989e-10
134 1.0673e+00 1.3656e-07 1.3656e-10
135 1.0673e+00 1.1437e-07 1.1437e-10
136 1.0673e+00 9.3318e-08 9.3318e-11
SUCCESS
Gradient below the specified tolerance
Total time is: 0.36979031562805176
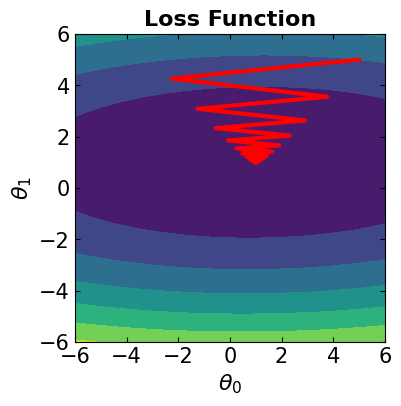
The optimal solution is: theta0 = 1.001354049365295 , theta1 = 0.9894489938894147
The corresponding loss function is: 1.0673182625203745
### Sensitivity Analysis for the learning rate (BGD): ###
# Initialize the vector of model parameters
theta_0 = [5, 5]
# Set the gradient threshold:
grad_thres = 1e-7
# Set the maximum number of iterations:
maxIter = 500
# Set the batch size:
# (select "len(data)"" for BGD, "one" for SGD, a "mini-batch size" for mBGD)
k = len(data)
# Define min, max & inc of learning rates
min_lr = 0.00001
max_lr = 0.001
inc_lr = 0.00001
nlr = int((max_lr+inc_lr-min_lr)/inc_lr)
# Initialize a vector for saving learning rate, its loss, and time:
lr_loss_time = np.zeros((nlr,3))
# Define the loop:
count = 0
for lr in np.arange(min_lr,max_lr+inc_lr,inc_lr):
print('The learning rate is: ', lr)
start = time.time()
theta,loss = SGD_mBGD_BGD(data, f3, theta_0, least_squares_loss_function, grad_approx, \
learning_rate = lr, max_iterations = maxIter, batch_size=k, gradient_threshold=grad_thres, verbose=False)
end = time.time()
lr_loss_time[count,:] = lr, loss[-1], end - start
count += 1
x = lr_loss_time[:,0]
y = lr_loss_time[:,1]
z = lr_loss_time[:,2]
print(' learning rate loss time')
print(lr_loss_time)
# Initialize layout
fig, ax1 = plt.subplots(figsize = (4,4))
fig, ax2 = plt.subplots(figsize = (4,4))
plt.xticks(fontsize=15)
plt.yticks(fontsize=15)
plt.tick_params(direction="in",top=True, right=True)
# Add scatterplot
ax1.scatter(x,y, s=8);
ax2.scatter(x,z, s=8);
# Set logarithmic scale on the x variable
ax1.set_xscale("log");
ax2.set_xscale("log");
ax1.set_title("BGD - max iter: 500",fontsize=16,fontweight='bold')
ax1.set_ylabel('Final Loss Value',fontsize=16,fontweight='bold')
ax1.set_xlabel('Learning Rate',fontsize=16,fontweight='bold')
ax2.set_title("BGD - max iter: 500",fontsize=16,fontweight='bold')
ax2.set_ylabel('Time (s)',fontsize=16,fontweight='bold')
ax2.set_xlabel('Learning Rate',fontsize=16,fontweight='bold')
plt.show()
The learning rate is: 1e-05
Max iterations reached
The learning rate is: 2e-05
Max iterations reached
The learning rate is: 3.0000000000000004e-05
Max iterations reached
The learning rate is: 4e-05
Max iterations reached
The learning rate is: 5e-05
Max iterations reached
The learning rate is: 6e-05
Max iterations reached
The learning rate is: 7.000000000000001e-05
Max iterations reached
The learning rate is: 8e-05
Max iterations reached
The learning rate is: 9e-05
Max iterations reached
The learning rate is: 0.0001
Max iterations reached
The learning rate is: 0.00011
Max iterations reached
The learning rate is: 0.00012
Max iterations reached
The learning rate is: 0.00013000000000000002
Max iterations reached
The learning rate is: 0.00014000000000000001
Max iterations reached
The learning rate is: 0.00015000000000000001
Max iterations reached
The learning rate is: 0.00016
Max iterations reached
The learning rate is: 0.00017
Max iterations reached
The learning rate is: 0.00018
Max iterations reached
The learning rate is: 0.00019
Max iterations reached
The learning rate is: 0.0002
Max iterations reached
The learning rate is: 0.00021
Max iterations reached
The learning rate is: 0.00022
Max iterations reached
The learning rate is: 0.00023
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00024
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00025000000000000006
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00026000000000000003
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00027000000000000006
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00028000000000000003
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00029000000000000006
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00030000000000000003
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00031000000000000005
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00032
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00033000000000000005
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0003400000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00035000000000000005
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0003600000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00037000000000000005
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0003800000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00039000000000000005
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0004000000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00041000000000000005
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00042000000000000007
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00043000000000000004
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00044000000000000007
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00045000000000000004
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00046000000000000007
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00047000000000000004
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00048000000000000007
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0004900000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0005000000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00051
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0005200000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0005300000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0005400000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00055
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0005600000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0005700000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0005800000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00059
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0006000000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0006100000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0006200000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00063
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00064
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0006500000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0006600000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0006700000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00068
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0006900000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0007000000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0007100000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00072
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0007300000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0007400000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0007500000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00076
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0007700000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0007800000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0007900000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0008
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0008100000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0008200000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0008300000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0008400000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0008500000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0008600000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0008700000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0008800000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0008900000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0009000000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0009100000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0009200000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00093
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0009400000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0009500000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0009600000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0009700000000000002
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.00098
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0009900000000000002
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.001
SUCCESS
Gradient below the specified tolerance
learning rate loss time
[[1.00000000e-05 2.22735117e+02 8.41719151e-01]
[2.00000000e-05 3.09338732e+01 3.84694815e-01]
[3.00000000e-05 5.07524258e+00 3.57868195e-01]
[4.00000000e-05 1.60298965e+00 3.57358217e-01]
[5.00000000e-05 1.13862242e+00 3.53100777e-01]
[6.00000000e-05 1.07677109e+00 3.45477343e-01]
[7.00000000e-05 1.06856631e+00 3.49965811e-01]
[8.00000000e-05 1.06748237e+00 3.60450268e-01]
[9.00000000e-05 1.06733975e+00 3.44614983e-01]
[1.00000000e-04 1.06732106e+00 3.48502874e-01]
[1.10000000e-04 1.06731863e+00 3.65819454e-01]
[1.20000000e-04 1.06731831e+00 3.36865902e-01]
[1.30000000e-04 1.06731827e+00 3.56440544e-01]
[1.40000000e-04 1.06731826e+00 3.50474119e-01]
[1.50000000e-04 1.06731826e+00 3.61862659e-01]
[1.60000000e-04 1.06731826e+00 3.41451406e-01]
[1.70000000e-04 1.06731826e+00 3.57663155e-01]
[1.80000000e-04 1.06731826e+00 3.49097013e-01]
[1.90000000e-04 1.06731826e+00 3.54200840e-01]
[2.00000000e-04 1.06731826e+00 3.58914614e-01]
[2.10000000e-04 1.06731826e+00 3.51370573e-01]
[2.20000000e-04 1.06731826e+00 3.62102509e-01]
[2.30000000e-04 1.06731826e+00 3.34707737e-01]
[2.40000000e-04 1.06731826e+00 3.34600925e-01]
[2.50000000e-04 1.06731826e+00 3.17473173e-01]
[2.60000000e-04 1.06731826e+00 2.94335127e-01]
[2.70000000e-04 1.06731826e+00 2.89124966e-01]
[2.80000000e-04 1.06731826e+00 2.79100895e-01]
[2.90000000e-04 1.06731826e+00 3.76189470e-01]
[3.00000000e-04 1.06731826e+00 5.35871983e-01]
[3.10000000e-04 1.06731826e+00 5.20030260e-01]
[3.20000000e-04 1.06731826e+00 4.96631861e-01]
[3.30000000e-04 1.06731826e+00 4.88309383e-01]
[3.40000000e-04 1.06731826e+00 4.57581997e-01]
[3.50000000e-04 1.06731826e+00 3.43142271e-01]
[3.60000000e-04 1.06731826e+00 2.18163252e-01]
[3.70000000e-04 1.06731826e+00 2.04155207e-01]
[3.80000000e-04 1.06731826e+00 2.22836971e-01]
[3.90000000e-04 1.06731826e+00 1.97869778e-01]
[4.00000000e-04 1.06731826e+00 2.06901789e-01]
[4.10000000e-04 1.06731826e+00 1.82152987e-01]
[4.20000000e-04 1.06731826e+00 1.87295914e-01]
[4.30000000e-04 1.06731826e+00 1.82845116e-01]
[4.40000000e-04 1.06731826e+00 1.72985077e-01]
[4.50000000e-04 1.06731826e+00 1.68145180e-01]
[4.60000000e-04 1.06731826e+00 1.76874876e-01]
[4.70000000e-04 1.06731826e+00 1.65036678e-01]
[4.80000000e-04 1.06731826e+00 1.66949987e-01]
[4.90000000e-04 1.06731826e+00 1.48567677e-01]
[5.00000000e-04 1.06731826e+00 1.56455517e-01]
[5.10000000e-04 1.06731826e+00 1.42461777e-01]
[5.20000000e-04 1.06731826e+00 1.56286716e-01]
[5.30000000e-04 1.06731826e+00 1.45114183e-01]
[5.40000000e-04 1.06731826e+00 1.45147800e-01]
[5.50000000e-04 1.06731826e+00 1.42008305e-01]
[5.60000000e-04 1.06731826e+00 1.38487816e-01]
[5.70000000e-04 1.06731826e+00 1.31688356e-01]
[5.80000000e-04 1.06731826e+00 1.29422665e-01]
[5.90000000e-04 1.06731826e+00 1.28806353e-01]
[6.00000000e-04 1.06731826e+00 1.35652542e-01]
[6.10000000e-04 1.06731826e+00 1.26837969e-01]
[6.20000000e-04 1.06731826e+00 1.40613079e-01]
[6.30000000e-04 1.06731826e+00 1.24771357e-01]
[6.40000000e-04 1.06731826e+00 1.29327536e-01]
[6.50000000e-04 1.06731826e+00 1.18362665e-01]
[6.60000000e-04 1.06731826e+00 1.15717649e-01]
[6.70000000e-04 1.06731826e+00 1.10393763e-01]
[6.80000000e-04 1.06731826e+00 1.24653339e-01]
[6.90000000e-04 1.06731826e+00 1.04698181e-01]
[7.00000000e-04 1.06731826e+00 1.15858316e-01]
[7.10000000e-04 1.06731826e+00 1.12066507e-01]
[7.20000000e-04 1.06731826e+00 1.03969097e-01]
[7.30000000e-04 1.06731826e+00 1.03758812e-01]
[7.40000000e-04 1.06731826e+00 1.02908373e-01]
[7.50000000e-04 1.06731826e+00 1.03696823e-01]
[7.60000000e-04 1.06731826e+00 1.01448774e-01]
[7.70000000e-04 1.06731826e+00 1.03541374e-01]
[7.80000000e-04 1.06731826e+00 1.07713699e-01]
[7.90000000e-04 1.06731826e+00 9.45022106e-02]
[8.00000000e-04 1.06731826e+00 9.37747955e-02]
[8.10000000e-04 1.06731826e+00 1.03118658e-01]
[8.20000000e-04 1.06731826e+00 8.93428326e-02]
[8.30000000e-04 1.06731826e+00 8.86723995e-02]
[8.40000000e-04 1.06731826e+00 9.75677967e-02]
[8.50000000e-04 1.06731826e+00 8.45749378e-02]
[8.60000000e-04 1.06731826e+00 9.13074017e-02]
[8.70000000e-04 1.06731826e+00 9.43768024e-02]
[8.80000000e-04 1.06731826e+00 9.43448544e-02]
[8.90000000e-04 1.06731826e+00 8.21163654e-02]
[9.00000000e-04 1.06731826e+00 9.14309025e-02]
[9.10000000e-04 1.06731826e+00 8.03017616e-02]
[9.20000000e-04 1.06731826e+00 7.89654255e-02]
[9.30000000e-04 1.06731826e+00 9.16364193e-02]
[9.40000000e-04 1.06731826e+00 8.42082500e-02]
[9.50000000e-04 1.06731826e+00 7.77211189e-02]
[9.60000000e-04 1.06731826e+00 8.01162720e-02]
[9.70000000e-04 1.06731826e+00 8.04557800e-02]
[9.80000000e-04 1.06731826e+00 7.69472122e-02]
[9.90000000e-04 1.06731826e+00 8.94436836e-02]
[1.00000000e-03 1.06731826e+00 1.05773211e-01]]
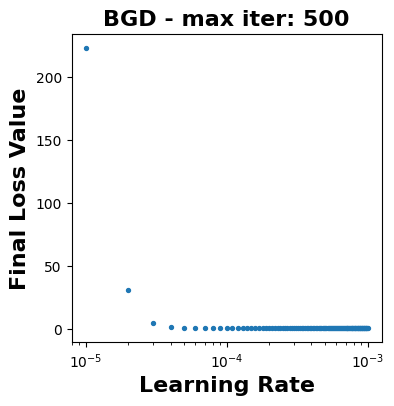
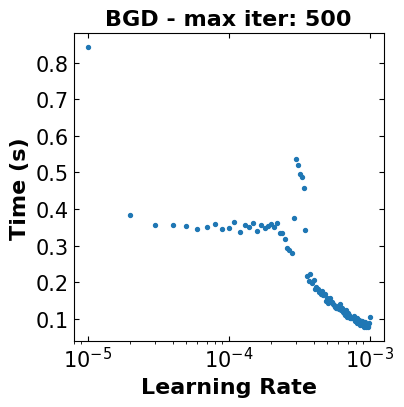
2-1-4. SGD: (Batch size = 1)
Only one data sample chosen randomly from the data set is considered to compute the loss function.
### If learning rate = 0.0001 ###
####################
##### Step 1 #####
####################
# Initialize the vector of model parameters
theta_0 = [5, 5]
####################
##### Step 2 #####
####################
# Set the learning rate:
gamma_t = 0.0001
# Set the gradient threshold:
grad_thres = 1e-5
# Set the maximum number of iterations:
maxIter = 10000
# Set the batch size:
# (select "len(data)"" for BGD, "one" for SGD, a "mini-batch size" for mBGD)
k = 1
#####################
##### Steps 3-4 #####
#####################
# Call the following function to do the steps 3 & 4
# (returns the theta vectors and loss values for all iterations)
start = time.time()
theta,loss = SGD_mBGD_BGD(data, f3, theta_0, least_squares_loss_function, grad_approx, \
learning_rate = gamma_t, max_iterations = maxIter, batch_size=k, gradient_threshold=grad_thres, verbose = False)
end = time.time()
print('Total time is: ', end - start)
# Visualize the convergence track on loss function
fig = plt.figure(figsize=(4,4))
plt.plot(theta[:, 0], theta[:, 1], '-r', markersize=5, linewidth=3)
contour_plot(LFx, 0., 6., 50, 0, 6., 50)
# Print the optimal solution
print("The optimal solution is: theta0 = ", str(theta[-1, 0]), ", theta1 = ", str(theta[-1, 1]))
print("The corresponding loss function is: ", str(loss[-1]))
Max iterations reached
Total time is: 1.7021312713623047
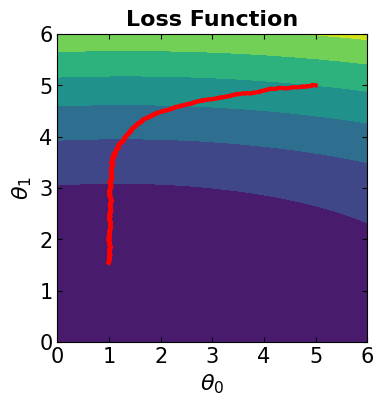
The optimal solution is: theta0 = 0.9952854353527355 , theta1 = 1.5439522770210523
The corresponding loss function is: 0.32792942437403655
### If learning rate = 0.001 ###
####################
##### Step 1 #####
####################
# Initialize the vector of model parameters
theta_0 = [5, 5]
####################
##### Step 2 #####
####################
# Set the learning rate:
gamma_t = 0.001
# Set the gradient threshold:
grad_thres = 1e-5
# Set the maximum number of iterations:
maxIter = 10000
# Set the batch size:
# (select "len(data)"" for BGD, "one" for SGD, a "mini-batch size" for mBGD)
k = 1
#####################
##### Steps 3-4 #####
#####################
# Call the following function to do the steps 3 & 4
# (returns the theta vectors and loss values for all iterations)
start = time.time()
theta,loss = SGD_mBGD_BGD(data, f3, theta_0, least_squares_loss_function, grad_approx, \
learning_rate = gamma_t, max_iterations = maxIter, batch_size=k, gradient_threshold=grad_thres, verbose = False)
end = time.time()
print('Total time is: ', end - start)
# Visualize the convergence track on loss function
fig = plt.figure(figsize=(4,4))
plt.plot(theta[:, 0], theta[:, 1], '-r', markersize=5, linewidth=3)
contour_plot(LFx, 0., 6., 50, 0, 6., 50)
# Print the optimal solution
print("The optimal solution is: theta0 = ", str(theta[-1, 0]), ", theta1 = ", str(theta[-1, 1]))
print("The corresponding loss function is: ", str(loss[-1]))
Max iterations reached
Total time is: 1.4233925342559814
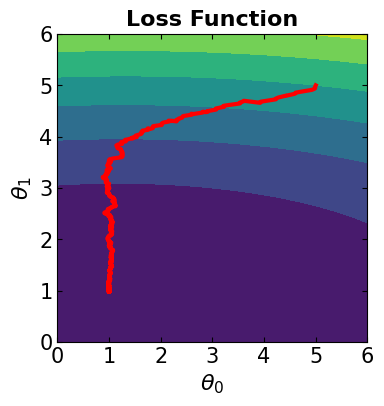
The optimal solution is: theta0 = 1.0096783451667168 , theta1 = 0.9828158198993225
The corresponding loss function is: 0.016145483538611397
### If learning rate = 0.01 ###
####################
##### Step 1 #####
####################
# Initialize the vector of model parameters
theta_0 = [5, 5]
####################
##### Step 2 #####
####################
# Set the learning rate:
gamma_t = 0.01
# Set the gradient threshold:
grad_thres = 1e-5
# Set the maximum number of iterations:
maxIter = 10000
# Set the batch size:
# (select "len(data)"" for BGD, "one" for SGD, a "mini-batch size" for mBGD)
k = 1
#####################
##### Steps 3-4 #####
#####################
# Call the following function to do the steps 3 & 4
# (returns the theta vectors and loss values for all iterations)
start = time.time()
theta,loss = SGD_mBGD_BGD(data, f3, theta_0, least_squares_loss_function, grad_approx, \
learning_rate = gamma_t, max_iterations = maxIter, batch_size=k, gradient_threshold=grad_thres, verbose = False)
end = time.time()
print('Total time is: ', end - start)
# Visualize the convergence track on loss function
fig = plt.figure(figsize=(4,4))
plt.plot(theta[:, 0], theta[:, 1], '-r', markersize=5, linewidth=3)
contour_plot(LFx, 0., 6., 50, 0, 6., 50)
# Print the optimal solution
print("The optimal solution is: theta0 = ", str(theta[-1, 0]), ", theta1 = ", str(theta[-1, 1]))
print("The corresponding loss function is: ", str(loss[-1]))
SUCCESS
Gradient below the specified tolerance
Total time is: 0.6045074462890625
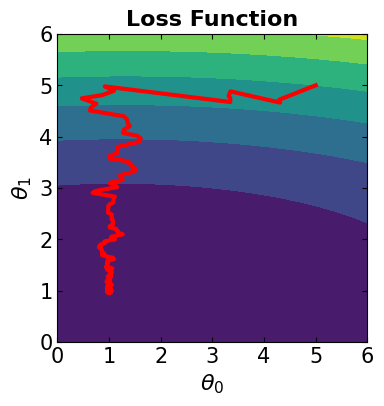
The optimal solution is: theta0 = 1.0063936241085758 , theta1 = 1.0052836030338979
The corresponding loss function is: 2.1453765736611015e-12
### Sensitivity Analysis for the learning rate (SGD): ###
# Initialize the vector of model parameters
theta_0 = [5, 5]
# Set the gradient threshold:
grad_thres = 1e-5
# Set the maximum number of iterations:
maxIter = 10000
# Set the batch size:
# (select "len(data)"" for BGD, "one" for SGD, a "mini-batch size" for mBGD)
k = 1
# Define min, max & inc of learning rates
min_lr = 0.0001
max_lr = 0.01
inc_lr = 0.0001
nlr = int((max_lr+inc_lr-min_lr)/inc_lr)
# Initialize a vector for saving learning rate, its loss, and time:
lr_loss_time = np.zeros((nlr,3))
# Define the loop:
count = 0
for lr in np.arange(min_lr,max_lr+inc_lr,inc_lr):
print('The learning rate is: ', lr)
start = time.time()
theta,loss = SGD_mBGD_BGD(data, f3, theta_0, least_squares_loss_function, grad_approx, \
learning_rate = lr, max_iterations = maxIter, batch_size=k, gradient_threshold=grad_thres, verbose=False)
end = time.time()
lr_loss_time[count,:] = lr, loss[-1], end - start
count += 1
x = lr_loss_time[:,0]
y = lr_loss_time[:,1]
z = lr_loss_time[:,2]
print(' learning rate loss time')
print(lr_loss_time)
# Initialize layout
fig, ax1 = plt.subplots(figsize = (4,4))
fig, ax2 = plt.subplots(figsize = (4,4))
plt.xticks(fontsize=15)
plt.yticks(fontsize=15)
plt.tick_params(direction="in",top=True, right=True)
# Add scatterplot
ax1.scatter(x,y, s=8);
ax2.scatter(x,z, s=8);
# Set logarithmic scale on the x variable
ax1.set_xscale("log");
ax2.set_xscale("log");
ax1.set_title("SGD (one data) - max iter: 10000",fontsize=16,fontweight='bold')
ax1.set_ylabel('Final Loss Value',fontsize=16,fontweight='bold')
ax1.set_xlabel('Learning Rate',fontsize=16,fontweight='bold')
ax2.set_title("SGD (one data) - max iter: 10000",fontsize=16,fontweight='bold')
ax2.set_ylabel('Time (s)',fontsize=16,fontweight='bold')
ax2.set_xlabel('Learning Rate',fontsize=16,fontweight='bold')
plt.show()
The learning rate is: 0.0001
Max iterations reached
The learning rate is: 0.0002
Max iterations reached
The learning rate is: 0.00030000000000000003
Max iterations reached
The learning rate is: 0.0004
Max iterations reached
The learning rate is: 0.0005
Max iterations reached
The learning rate is: 0.0006000000000000001
Max iterations reached
The learning rate is: 0.0007000000000000001
Max iterations reached
The learning rate is: 0.0008
Max iterations reached
The learning rate is: 0.0009000000000000001
Max iterations reached
The learning rate is: 0.001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0011
Max iterations reached
The learning rate is: 0.0012000000000000001
Max iterations reached
The learning rate is: 0.0013000000000000002
Max iterations reached
The learning rate is: 0.0014000000000000002
Max iterations reached
The learning rate is: 0.0015
Max iterations reached
The learning rate is: 0.0016
Max iterations reached
The learning rate is: 0.0017000000000000001
Max iterations reached
The learning rate is: 0.0018000000000000002
Max iterations reached
The learning rate is: 0.0019000000000000002
Max iterations reached
The learning rate is: 0.002
Max iterations reached
The learning rate is: 0.0021
Max iterations reached
The learning rate is: 0.0022
Max iterations reached
The learning rate is: 0.0023
Max iterations reached
The learning rate is: 0.0024
Max iterations reached
The learning rate is: 0.0025
Max iterations reached
The learning rate is: 0.0026
Max iterations reached
The learning rate is: 0.0027
Max iterations reached
The learning rate is: 0.0028
Max iterations reached
The learning rate is: 0.0029
Max iterations reached
The learning rate is: 0.003
Max iterations reached
The learning rate is: 0.0031
Max iterations reached
The learning rate is: 0.0032
Max iterations reached
The learning rate is: 0.0033
Max iterations reached
The learning rate is: 0.0034
Max iterations reached
The learning rate is: 0.0035
Max iterations reached
The learning rate is: 0.0036
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0037
Max iterations reached
The learning rate is: 0.0038
Max iterations reached
The learning rate is: 0.0039
Max iterations reached
The learning rate is: 0.004
Max iterations reached
The learning rate is: 0.0041
Max iterations reached
The learning rate is: 0.004200000000000001
Max iterations reached
The learning rate is: 0.004300000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0044
Max iterations reached
The learning rate is: 0.0045000000000000005
Max iterations reached
The learning rate is: 0.004600000000000001
Max iterations reached
The learning rate is: 0.0047
Max iterations reached
The learning rate is: 0.0048000000000000004
Max iterations reached
The learning rate is: 0.004900000000000001
Max iterations reached
The learning rate is: 0.005
Max iterations reached
The learning rate is: 0.0051
Max iterations reached
The learning rate is: 0.005200000000000001
Max iterations reached
The learning rate is: 0.005300000000000001
Max iterations reached
The learning rate is: 0.0054
Max iterations reached
The learning rate is: 0.0055000000000000005
Max iterations reached
The learning rate is: 0.005600000000000001
Max iterations reached
The learning rate is: 0.0057
Max iterations reached
The learning rate is: 0.0058000000000000005
Max iterations reached
The learning rate is: 0.005900000000000001
Max iterations reached
The learning rate is: 0.006
Max iterations reached
The learning rate is: 0.0061
Max iterations reached
The learning rate is: 0.006200000000000001
Max iterations reached
The learning rate is: 0.006300000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0064
Max iterations reached
The learning rate is: 0.006500000000000001
Max iterations reached
The learning rate is: 0.006600000000000001
Max iterations reached
The learning rate is: 0.0067
Max iterations reached
The learning rate is: 0.0068000000000000005
Max iterations reached
The learning rate is: 0.006900000000000001
Max iterations reached
The learning rate is: 0.007000000000000001
Max iterations reached
The learning rate is: 0.0071
Max iterations reached
The learning rate is: 0.007200000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.007300000000000001
Max iterations reached
The learning rate is: 0.0074
Max iterations reached
The learning rate is: 0.007500000000000001
Max iterations reached
The learning rate is: 0.007600000000000001
SUCCESS
Gradient below the specified tolerance
The learning rate is: 0.0077
Max iterations reached
The learning rate is: 0.0078000000000000005
Max iterations reached
The learning rate is: 0.0079
Max iterations reached
The learning rate is: 0.008
Max iterations reached
The learning rate is: 0.0081
Max iterations reached
The learning rate is: 0.008199999999999999
Max iterations reached
The learning rate is: 0.0083
Max iterations reached
The learning rate is: 0.0084
Max iterations reached
The learning rate is: 0.0085
Max iterations reached
The learning rate is: 0.0086
Max iterations reached
The learning rate is: 0.0087
Max iterations reached
The learning rate is: 0.0088
Max iterations reached
The learning rate is: 0.0089
Max iterations reached
The learning rate is: 0.009
Max iterations reached
The learning rate is: 0.0091
Max iterations reached
The learning rate is: 0.0092
Max iterations reached
The learning rate is: 0.0093
Max iterations reached
The learning rate is: 0.0094
Max iterations reached
The learning rate is: 0.0095
Max iterations reached
The learning rate is: 0.0096
Max iterations reached
The learning rate is: 0.0097
Max iterations reached
The learning rate is: 0.0098
Max iterations reached
The learning rate is: 0.009899999999999999
Max iterations reached
The learning rate is: 0.01
Max iterations reached
learning rate loss time
[[1.00000000e-04 3.04387387e-01 1.17973900e+00]
[2.00000000e-04 5.52556299e-03 1.31473827e+00]
[3.00000000e-04 2.42232113e-03 1.17332935e+00]
[4.00000000e-04 4.53630084e-03 1.32951951e+00]
[5.00000000e-04 2.08437686e-03 1.36329055e+00]
[6.00000000e-04 3.35520638e-03 1.41679478e+00]
[7.00000000e-04 3.68047147e-09 1.32982135e+00]
[8.00000000e-04 1.25901643e-02 1.34249783e+00]
[9.00000000e-04 6.38281276e-03 1.22189212e+00]
[1.00000000e-03 1.13739698e-11 8.08105469e-01]
[1.10000000e-03 4.56607295e-02 1.26644778e+00]
[1.20000000e-03 2.47561610e-02 1.29353309e+00]
[1.30000000e-03 6.30453691e-04 1.27230668e+00]
[1.40000000e-03 4.62670083e-04 1.33346415e+00]
[1.50000000e-03 1.70543739e-02 1.44003105e+00]
[1.60000000e-03 6.44325201e-03 1.43444800e+00]
[1.70000000e-03 3.90021555e-04 1.33889604e+00]
[1.80000000e-03 1.40259368e-03 1.36282325e+00]
[1.90000000e-03 1.04846395e-02 1.19138575e+00]
[2.00000000e-03 8.18915674e-04 1.25900698e+00]
[2.10000000e-03 1.15745503e-02 1.27594042e+00]
[2.20000000e-03 1.22883241e-02 1.15586972e+00]
[2.30000000e-03 1.31826165e-02 1.21243382e+00]
[2.40000000e-03 7.22696417e-03 1.18207645e+00]
[2.50000000e-03 7.54444168e-03 1.38539648e+00]
[2.60000000e-03 7.92725722e-03 1.44364476e+00]
[2.70000000e-03 1.27228084e-02 1.22922635e+00]
[2.80000000e-03 1.08822079e-02 1.19363952e+00]
[2.90000000e-03 1.66253429e-04 1.07091451e+00]
[3.00000000e-03 4.02377280e-03 1.24563432e+00]
[3.10000000e-03 1.01402641e-02 1.26750088e+00]
[3.20000000e-03 3.53696914e-03 1.22403383e+00]
[3.30000000e-03 7.44187453e-02 1.12843823e+00]
[3.40000000e-03 5.08275577e-03 1.22433949e+00]
[3.50000000e-03 2.22415244e-02 1.39064312e+00]
[3.60000000e-03 2.26907355e-12 8.77607584e-01]
[3.70000000e-03 5.90501554e-04 1.52207875e+00]
[3.80000000e-03 4.22419153e-05 1.12847042e+00]
[3.90000000e-03 5.97494210e-03 1.22120214e+00]
[4.00000000e-03 9.91578006e-03 1.15723157e+00]
[4.10000000e-03 9.62350015e-06 1.13314319e+00]
[4.20000000e-03 1.05315742e-02 1.06049418e+00]
[4.30000000e-03 1.40558508e-12 1.18237281e+00]
[4.40000000e-03 7.62684269e-03 1.22650528e+00]
[4.50000000e-03 5.58467506e-04 1.31393576e+00]
[4.60000000e-03 4.26609375e-05 1.47451448e+00]
[4.70000000e-03 2.72507701e-03 1.94648385e+00]
[4.80000000e-03 7.24260073e-03 1.63512874e+00]
[4.90000000e-03 4.11517461e-06 1.03107786e+00]
[5.00000000e-03 1.89560842e-03 1.13662505e+00]
[5.10000000e-03 1.62558246e-04 1.19529939e+00]
[5.20000000e-03 6.38723416e-03 1.13157558e+00]
[5.30000000e-03 3.93563509e-03 1.08976483e+00]
[5.40000000e-03 1.06300278e-02 1.24414062e+00]
[5.50000000e-03 7.42953348e-03 1.10393453e+00]
[5.60000000e-03 2.11276498e-02 1.49179769e+00]
[5.70000000e-03 7.99893333e-03 1.53460121e+00]
[5.80000000e-03 1.12834949e-02 1.23747826e+00]
[5.90000000e-03 1.16545371e-02 1.26339459e+00]
[6.00000000e-03 2.61645429e-03 1.29441404e+00]
[6.10000000e-03 7.94984809e-03 1.17760491e+00]
[6.20000000e-03 1.73284748e-02 1.20992708e+00]
[6.30000000e-03 1.68730464e-12 8.91552687e-01]
[6.40000000e-03 1.04321626e-04 1.27122092e+00]
[6.50000000e-03 9.65399839e-03 1.22233891e+00]
[6.60000000e-03 1.58349976e-02 1.48878455e+00]
[6.70000000e-03 6.73934650e-03 1.40924716e+00]
[6.80000000e-03 6.87790160e-04 1.17912817e+00]
[6.90000000e-03 3.43283421e-03 1.31773686e+00]
[7.00000000e-03 4.68724759e-03 1.13431382e+00]
[7.10000000e-03 1.77373832e-02 1.18350458e+00]
[7.20000000e-03 1.39409793e-11 3.98954391e-01]
[7.30000000e-03 5.92507737e-04 1.20102477e+00]
[7.40000000e-03 1.54093668e-02 1.06344271e+00]
[7.50000000e-03 2.93824441e-02 1.31338143e+00]
[7.60000000e-03 8.12590312e-14 4.80441570e-01]
[7.70000000e-03 2.51018119e-02 1.46316051e+00]
[7.80000000e-03 1.09465676e-03 1.52414560e+00]
[7.90000000e-03 3.70335613e-03 1.16869235e+00]
[8.00000000e-03 7.88580975e-04 1.00434756e+00]
[8.10000000e-03 1.99607645e-03 1.22339725e+00]
[8.20000000e-03 3.34233761e-05 1.27589011e+00]
[8.30000000e-03 9.93830861e-03 1.25398612e+00]
[8.40000000e-03 1.23250140e-03 1.10254383e+00]
[8.50000000e-03 9.49273938e-03 1.22728896e+00]
[8.60000000e-03 5.20754897e-05 1.18239975e+00]
[8.70000000e-03 4.89684713e-03 1.36572456e+00]
[8.80000000e-03 1.29018861e-02 1.45254540e+00]
[8.90000000e-03 1.77676058e-02 1.41105485e+00]
[9.00000000e-03 2.47601320e-04 1.23800802e+00]
[9.10000000e-03 3.58634768e-03 1.29460073e+00]
[9.20000000e-03 4.02013498e-02 1.20260406e+00]
[9.30000000e-03 6.80716860e-06 1.18968964e+00]
[9.40000000e-03 1.94731944e-06 1.27657819e+00]
[9.50000000e-03 5.72868233e-03 1.32410097e+00]
[9.60000000e-03 1.14005789e-03 1.27390146e+00]
[9.70000000e-03 7.90209942e-03 1.16976166e+00]
[9.80000000e-03 3.81353400e-03 1.43136668e+00]
[9.90000000e-03 1.05835646e-02 1.36834049e+00]
[1.00000000e-02 1.33058920e-02 1.21860695e+00]]
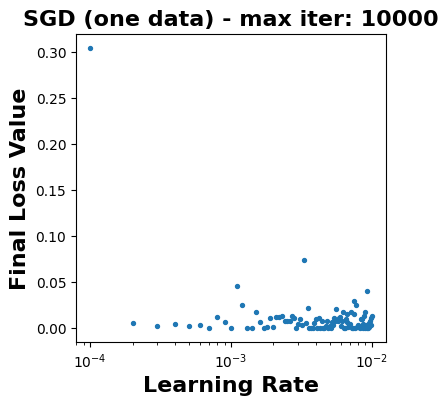
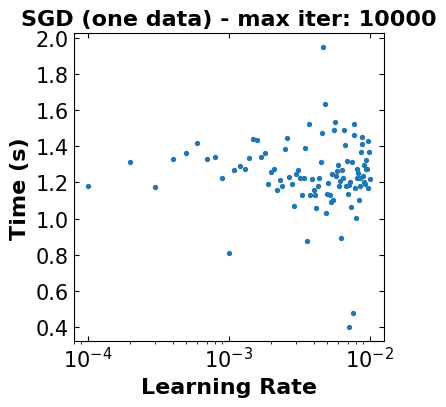
2-1-5. mBGD: (Batch size = 10)
10 data samples chosen randomly from the data set are considered to compute the loss function.
### If learning rate = 0.00001 ###
####################
##### Step 1 #####
####################
# Initialize the vector of model parameters
theta_0 = [5, 5]
####################
##### Step 2 #####
####################
# Set the learning rate:
gamma_t = 0.00001
# Set the gradient threshold:
grad_thres = 1e-6
# Set the maximum number of iterations:
maxIter = 10000
# Set the batch size:
# (select "len(data)"" for BGD, "one" for SGD, a "mini-batch size" for mBGD)
k = 10
#####################
##### Steps 3-4 #####
#####################
# Call the following function to do the steps 3 & 4
# (returns the theta vectors and loss values for all iterations)
start = time.time()
theta,loss = SGD_mBGD_BGD(data, f3, theta_0, least_squares_loss_function, grad_approx, \
learning_rate = gamma_t, max_iterations = maxIter, batch_size=k, gradient_threshold=grad_thres, verbose = False)
end = time.time()
print('Total time is: ', end - start)
# Visualize the convergence track on loss function
fig = plt.figure(figsize=(4,4))
plt.plot(theta[:, 0], theta[:, 1], '-r', markersize=5, linewidth=3)
contour_plot(LFx, 0., 6., 50, 0, 6., 50)
# Print the optimal solution
print("The optimal solution is: theta0 = ", str(theta[-1, 0]), ", theta1 = ", str(theta[-1, 1]))
print("The corresponding loss function is: ", str(loss[-1]))
Max iterations reached
Total time is: 2.0553228855133057
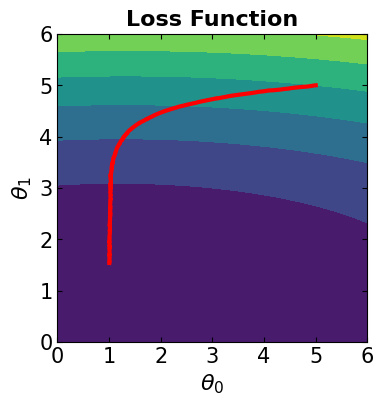
The optimal solution is: theta0 = 1.0058133346703757 , theta1 = 1.5385310507014482
The corresponding loss function is: 3.112445726025017
### If learning rate = 0.0001 ###
####################
##### Step 1 #####
####################
# Initialize the vector of model parameters
theta_0 = [5, 5]
####################
##### Step 2 #####
####################
# Set the learning rate:
gamma_t = 0.0001
# Set the gradient threshold:
grad_thres = 1e-6
# Set the maximum number of iterations:
maxIter = 10000
# Set the batch size:
# (select "len(data)"" for BGD, "one" for SGD, a "mini-batch size" for mBGD)
k = 10
#####################
##### Steps 3-4 #####
#####################
# Call the following function to do the steps 3 & 4
# (returns the theta vectors and loss values for all iterations)
start = time.time()
theta,loss = SGD_mBGD_BGD(data, f3, theta_0, least_squares_loss_function, grad_approx, \
learning_rate = gamma_t, max_iterations = maxIter, batch_size=k, gradient_threshold=grad_thres, verbose = False)
end = time.time()
print('Total time is: ', end - start)
# Visualize the convergence track on loss function
fig = plt.figure(figsize=(4,4))
plt.plot(theta[:, 0], theta[:, 1], '-r', markersize=5, linewidth=3)
contour_plot(LFx, 0., 6., 50, 0, 6., 50)
# Print the optimal solution
print("The optimal solution is: theta0 = ", str(theta[-1, 0]), ", theta1 = ", str(theta[-1, 1]))
print("The corresponding loss function is: ", str(loss[-1]))
Max iterations reached
Total time is: 2.451550006866455
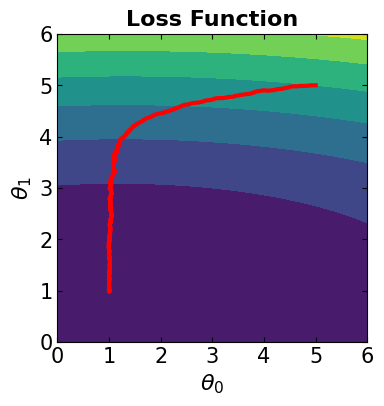
The optimal solution is: theta0 = 1.0004705293680973 , theta1 = 0.9906660383845045
The corresponding loss function is: 0.09409211018801161
### If learning rate = 0.001 ###
####################
##### Step 1 #####
####################
# Initialize the vector of model parameters
theta_0 = [5, 5]
####################
##### Step 2 #####
####################
# Set the learning rate:
gamma_t = 0.001
# Set the gradient threshold:
grad_thres = 1e-6
# Set the maximum number of iterations:
maxIter = 10000
# Set the batch size:
# (select "len(data)"" for BGD, "one" for SGD, a "mini-batch size" for mBGD)
k = 10
#####################
##### Steps 3-4 #####
#####################
# Call the following function to do the steps 3 & 4
# (returns the theta vectors and loss values for all iterations)
start = time.time()
theta,loss = SGD_mBGD_BGD(data, f3, theta_0, least_squares_loss_function, grad_approx, \
learning_rate = gamma_t, max_iterations = maxIter, batch_size=k, gradient_threshold=grad_thres, verbose = False)
end = time.time()
print('Total time is: ', end - start)
# Visualize the convergence track on loss function
fig = plt.figure(figsize=(4,4))
plt.plot(theta[:, 0], theta[:, 1], '-r', markersize=5, linewidth=3)
contour_plot(LFx, 0., 6., 50, 0, 6., 50)
# Print the optimal solution
print("The optimal solution is: theta0 = ", str(theta[-1, 0]), ", theta1 = ", str(theta[-1, 1]))
print("The corresponding loss function is: ", str(loss[-1]))
Max iterations reached
Total time is: 1.9722893238067627
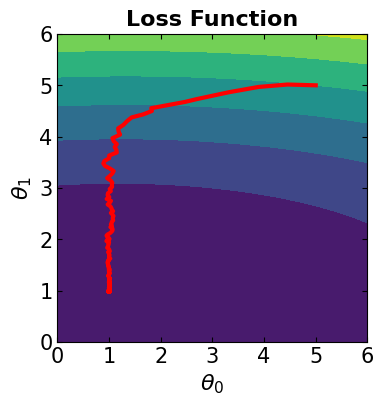
The optimal solution is: theta0 = 1.0019643156955036 , theta1 = 0.9858846261043579
The corresponding loss function is: 0.07547499200241083
### Sensitivity Analysis for the learning rate (mBGD): ###
# Initialize the vector of model parameters
theta_0 = [5, 5]
# Set the gradient threshold:
grad_thres = 1e-6
# Set the maximum number of iterations:
maxIter = 10000
# Set the batch size:
# (select "len(data)"" for BGD, "one" for SGD, a "mini-batch size" for mBGD)
k = 10
# Define min, max & inc of learning rates
min_lr = 0.00001
max_lr = 0.001
inc_lr = 0.00001
nlr = int((max_lr+inc_lr-min_lr)/inc_lr)
# Initialize a vector for saving learning rate, its loss, and time:
lr_loss_time = np.zeros((nlr,3))
# Define the loop:
count = 0
for lr in np.arange(min_lr,max_lr+inc_lr,inc_lr):
print('The learning rate is: ', lr)
start = time.time()
theta,loss = SGD_mBGD_BGD(data, f3, theta_0, least_squares_loss_function, grad_approx, \
learning_rate = lr, max_iterations = maxIter, batch_size=k, gradient_threshold=grad_thres, verbose=False)
end = time.time()
lr_loss_time[count,:] = lr, loss[-1], end - start
count += 1
x = lr_loss_time[:,0]
y = lr_loss_time[:,1]
z = lr_loss_time[:,2]
print(' learning rate loss time')
print(lr_loss_time)
# Initialize layout
fig, ax1 = plt.subplots(figsize = (4,4))
fig, ax2 = plt.subplots(figsize = (4,4))
plt.xticks(fontsize=15)
plt.yticks(fontsize=15)
plt.tick_params(direction="in",top=True, right=True)
# Add scatterplot
ax1.scatter(x,y, s=8);
ax2.scatter(x,z, s=8);
# Set logarithmic scale on the x variable
ax1.set_xscale("log");
ax2.set_xscale("log");
ax1.set_title("mBGD (10 data) - max iter: 10000",fontsize=16,fontweight='bold')
ax1.set_ylabel('Final Loss Value',fontsize=16,fontweight='bold')
ax1.set_xlabel('Learning Rate',fontsize=16,fontweight='bold')
ax2.set_title("mBGD (10 data) - max iter: 10000",fontsize=16,fontweight='bold')
ax2.set_ylabel('Time (s)',fontsize=16,fontweight='bold')
ax2.set_xlabel('Learning Rate',fontsize=16,fontweight='bold')
plt.show()
The learning rate is: 1e-05
Max iterations reached
The learning rate is: 2e-05
Max iterations reached
The learning rate is: 3.0000000000000004e-05
Max iterations reached
The learning rate is: 4e-05
Max iterations reached
The learning rate is: 5e-05
Max iterations reached
The learning rate is: 6e-05
Max iterations reached
The learning rate is: 7.000000000000001e-05
Max iterations reached
The learning rate is: 8e-05
Max iterations reached
The learning rate is: 9e-05
Max iterations reached
The learning rate is: 0.0001
Max iterations reached
The learning rate is: 0.00011
Max iterations reached
The learning rate is: 0.00012
Max iterations reached
The learning rate is: 0.00013000000000000002
Max iterations reached
The learning rate is: 0.00014000000000000001
Max iterations reached
The learning rate is: 0.00015000000000000001
Max iterations reached
The learning rate is: 0.00016
Max iterations reached
The learning rate is: 0.00017
Max iterations reached
The learning rate is: 0.00018
Max iterations reached
The learning rate is: 0.00019
Max iterations reached
The learning rate is: 0.0002
Max iterations reached
The learning rate is: 0.00021
Max iterations reached
The learning rate is: 0.00022
Max iterations reached
The learning rate is: 0.00023
Max iterations reached
The learning rate is: 0.00024
Max iterations reached
The learning rate is: 0.00025000000000000006
Max iterations reached
The learning rate is: 0.00026000000000000003
Max iterations reached
The learning rate is: 0.00027000000000000006
Max iterations reached
The learning rate is: 0.00028000000000000003
Max iterations reached
The learning rate is: 0.00029000000000000006
Max iterations reached
The learning rate is: 0.00030000000000000003
Max iterations reached
The learning rate is: 0.00031000000000000005
Max iterations reached
The learning rate is: 0.00032
Max iterations reached
The learning rate is: 0.00033000000000000005
Max iterations reached
The learning rate is: 0.0003400000000000001
Max iterations reached
The learning rate is: 0.00035000000000000005
Max iterations reached
The learning rate is: 0.0003600000000000001
Max iterations reached
The learning rate is: 0.00037000000000000005
Max iterations reached
The learning rate is: 0.0003800000000000001
Max iterations reached
The learning rate is: 0.00039000000000000005
Max iterations reached
The learning rate is: 0.0004000000000000001
Max iterations reached
The learning rate is: 0.00041000000000000005
Max iterations reached
The learning rate is: 0.00042000000000000007
Max iterations reached
The learning rate is: 0.00043000000000000004
Max iterations reached
The learning rate is: 0.00044000000000000007
Max iterations reached
The learning rate is: 0.00045000000000000004
Max iterations reached
The learning rate is: 0.00046000000000000007
Max iterations reached
The learning rate is: 0.00047000000000000004
Max iterations reached
The learning rate is: 0.00048000000000000007
Max iterations reached
The learning rate is: 0.0004900000000000001
Max iterations reached
The learning rate is: 0.0005000000000000001
Max iterations reached
The learning rate is: 0.00051
Max iterations reached
The learning rate is: 0.0005200000000000001
Max iterations reached
The learning rate is: 0.0005300000000000001
Max iterations reached
The learning rate is: 0.0005400000000000001
Max iterations reached
The learning rate is: 0.00055
Max iterations reached
The learning rate is: 0.0005600000000000001
Max iterations reached
The learning rate is: 0.0005700000000000001
Max iterations reached
The learning rate is: 0.0005800000000000001
Max iterations reached
The learning rate is: 0.00059
Max iterations reached
The learning rate is: 0.0006000000000000001
Max iterations reached
The learning rate is: 0.0006100000000000001
Max iterations reached
The learning rate is: 0.0006200000000000001
Max iterations reached
The learning rate is: 0.00063
Max iterations reached
The learning rate is: 0.00064
Max iterations reached
The learning rate is: 0.0006500000000000001
Max iterations reached
The learning rate is: 0.0006600000000000001
Max iterations reached
The learning rate is: 0.0006700000000000001
Max iterations reached
The learning rate is: 0.00068
Max iterations reached
The learning rate is: 0.0006900000000000001
Max iterations reached
The learning rate is: 0.0007000000000000001
Max iterations reached
The learning rate is: 0.0007100000000000001
Max iterations reached
The learning rate is: 0.00072
Max iterations reached
The learning rate is: 0.0007300000000000001
Max iterations reached
The learning rate is: 0.0007400000000000001
Max iterations reached
The learning rate is: 0.0007500000000000001
Max iterations reached
The learning rate is: 0.00076
Max iterations reached
The learning rate is: 0.0007700000000000001
Max iterations reached
The learning rate is: 0.0007800000000000001
Max iterations reached
The learning rate is: 0.0007900000000000001
Max iterations reached
The learning rate is: 0.0008
Max iterations reached
The learning rate is: 0.0008100000000000001
Max iterations reached
The learning rate is: 0.0008200000000000001
Max iterations reached
The learning rate is: 0.0008300000000000001
Max iterations reached
The learning rate is: 0.0008400000000000001
Max iterations reached
The learning rate is: 0.0008500000000000001
Max iterations reached
The learning rate is: 0.0008600000000000001
Max iterations reached
The learning rate is: 0.0008700000000000001
Max iterations reached
The learning rate is: 0.0008800000000000001
Max iterations reached
The learning rate is: 0.0008900000000000001
Max iterations reached
The learning rate is: 0.0009000000000000001
Max iterations reached
The learning rate is: 0.0009100000000000001
Max iterations reached
The learning rate is: 0.0009200000000000001
Max iterations reached
The learning rate is: 0.00093
Max iterations reached
The learning rate is: 0.0009400000000000001
Max iterations reached
The learning rate is: 0.0009500000000000001
Max iterations reached
The learning rate is: 0.0009600000000000001
Max iterations reached
The learning rate is: 0.0009700000000000002
Max iterations reached
The learning rate is: 0.00098
Max iterations reached
The learning rate is: 0.0009900000000000002
Max iterations reached
The learning rate is: 0.001
Max iterations reached
learning rate loss time
[[1.00000000e-05 3.13031600e+00 2.50332165e+00]
[2.00000000e-05 1.44498946e-01 1.86828947e+00]
[3.00000000e-05 1.03803310e-01 2.72794271e+00]
[4.00000000e-05 9.18421880e-02 1.83746171e+00]
[5.00000000e-05 1.13204694e-01 2.08306074e+00]
[6.00000000e-05 8.35751393e-02 1.88659978e+00]
[7.00000000e-05 9.53253459e-02 1.91185927e+00]
[8.00000000e-05 1.39527268e-01 1.88259888e+00]
[9.00000000e-05 1.10112764e-01 2.57301307e+00]
[1.00000000e-04 9.32240161e-02 1.94522357e+00]
[1.10000000e-04 1.66139646e-01 1.77367759e+00]
[1.20000000e-04 9.69246742e-02 1.94511962e+00]
[1.30000000e-04 1.23641907e-01 1.80034184e+00]
[1.40000000e-04 8.08565950e-02 1.89891815e+00]
[1.50000000e-04 1.55881947e-01 2.46921825e+00]
[1.60000000e-04 1.27577540e-01 2.27434707e+00]
[1.70000000e-04 1.07729676e-01 1.80439734e+00]
[1.80000000e-04 1.60929677e-01 1.89721942e+00]
[1.90000000e-04 1.01046550e-01 1.93339443e+00]
[2.00000000e-04 1.27985173e-01 1.87200999e+00]
[2.10000000e-04 1.25758725e-01 2.14135098e+00]
[2.20000000e-04 1.12751774e-01 2.64403629e+00]
[2.30000000e-04 9.36427293e-02 1.97082400e+00]
[2.40000000e-04 1.17594346e-01 1.96006203e+00]
[2.50000000e-04 7.81570761e-02 2.00782132e+00]
[2.60000000e-04 7.33031328e-02 1.91664839e+00]
[2.70000000e-04 1.16549705e-01 1.98457909e+00]
[2.80000000e-04 1.17225890e-01 2.79203629e+00]
[2.90000000e-04 6.86967466e-02 1.87015963e+00]
[3.00000000e-04 8.04436918e-02 1.92475462e+00]
[3.10000000e-04 7.36728467e-02 1.97397661e+00]
[3.20000000e-04 8.96050018e-02 1.92548943e+00]
[3.30000000e-04 1.09012259e-01 1.90870643e+00]
[3.40000000e-04 6.76444278e-02 2.77664781e+00]
[3.50000000e-04 8.37441072e-02 1.95403028e+00]
[3.60000000e-04 1.61525465e-01 1.94777369e+00]
[3.70000000e-04 1.00903445e-01 1.95278692e+00]
[3.80000000e-04 1.54609904e-01 1.90163445e+00]
[3.90000000e-04 7.45841243e-02 1.93007803e+00]
[4.00000000e-04 1.28591083e-01 2.53531456e+00]
[4.10000000e-04 7.57354687e-02 2.19810486e+00]
[4.20000000e-04 1.14078419e-01 2.52314115e+00]
[4.30000000e-04 7.34728175e-02 2.32045031e+00]
[4.40000000e-04 1.47259693e-01 1.89388752e+00]
[4.50000000e-04 6.88193540e-02 1.99121761e+00]
[4.60000000e-04 1.07297592e-01 2.78597331e+00]
[4.70000000e-04 9.95204808e-02 1.96611762e+00]
[4.80000000e-04 1.12333267e-01 1.96566892e+00]
[4.90000000e-04 1.26473712e-01 1.98645735e+00]
[5.00000000e-04 1.25528035e-01 2.01977634e+00]
[5.10000000e-04 1.08909317e-01 2.04917026e+00]
[5.20000000e-04 9.58557357e-02 2.78099918e+00]
[5.30000000e-04 1.10502302e-01 2.05057859e+00]
[5.40000000e-04 7.55158622e-02 2.01837707e+00]
[5.50000000e-04 7.04113784e-02 1.73176765e+00]
[5.60000000e-04 8.89513025e-02 1.88531876e+00]
[5.70000000e-04 1.24326307e-01 1.89303541e+00]
[5.80000000e-04 1.33064181e-01 2.49986744e+00]
[5.90000000e-04 1.04700288e-01 2.16874623e+00]
[6.00000000e-04 7.00824303e-02 1.87491632e+00]
[6.10000000e-04 4.91528354e-02 1.89034319e+00]
[6.20000000e-04 8.65491924e-02 2.00634146e+00]
[6.30000000e-04 8.37832560e-02 1.99865937e+00]
[6.40000000e-04 8.02611064e-02 2.30526853e+00]
[6.50000000e-04 4.28761791e-02 2.34055710e+00]
[6.60000000e-04 8.44573167e-02 1.98130631e+00]
[6.70000000e-04 6.23599927e-02 1.95872760e+00]
[6.80000000e-04 1.76275326e-01 1.89059114e+00]
[6.90000000e-04 6.08602992e-02 1.89441323e+00]
[7.00000000e-04 1.18830432e-01 2.16239548e+00]
[7.10000000e-04 7.84379737e-02 2.64601254e+00]
[7.20000000e-04 1.85422798e-01 1.98039985e+00]
[7.30000000e-04 5.88577140e-02 1.88733935e+00]
[7.40000000e-04 1.05810152e-01 2.03937244e+00]
[7.50000000e-04 8.12301835e-02 1.94903803e+00]
[7.60000000e-04 8.13879734e-02 2.04691577e+00]
[7.70000000e-04 8.35359935e-02 2.62532616e+00]
[7.80000000e-04 6.26119282e-02 1.97902536e+00]
[7.90000000e-04 1.02886634e-01 1.97674584e+00]
[8.00000000e-04 1.72715553e-01 1.96430826e+00]
[8.10000000e-04 1.00864957e-01 2.04551244e+00]
[8.20000000e-04 9.11340544e-02 1.98721409e+00]
[8.30000000e-04 1.58015003e-01 2.75005889e+00]
[8.40000000e-04 1.39594601e-01 1.81370902e+00]
[8.50000000e-04 1.16093786e-01 1.74368024e+00]
[8.60000000e-04 1.17008846e-01 1.88039327e+00]
[8.70000000e-04 1.11009516e-01 1.91391993e+00]
[8.80000000e-04 1.52267446e-01 1.98782229e+00]
[8.90000000e-04 9.81578002e-02 2.62534404e+00]
[9.00000000e-04 1.04916001e-01 2.08889341e+00]
[9.10000000e-04 6.50341382e-02 2.13695765e+00]
[9.20000000e-04 7.23255782e-02 1.98640323e+00]
[9.30000000e-04 8.16294490e-02 1.93920541e+00]
[9.40000000e-04 8.30859998e-02 2.03505635e+00]
[9.50000000e-04 8.48197418e-02 2.54369545e+00]
[9.60000000e-04 7.97123071e-02 2.06997275e+00]
[9.70000000e-04 6.61430695e-02 2.05721331e+00]
[9.80000000e-04 1.41012256e-01 2.05516362e+00]
[9.90000000e-04 7.36740025e-02 1.93002486e+00]
[1.00000000e-03 7.01111728e-02 1.98596048e+00]]
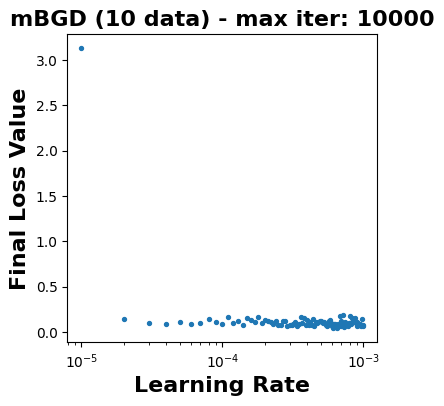
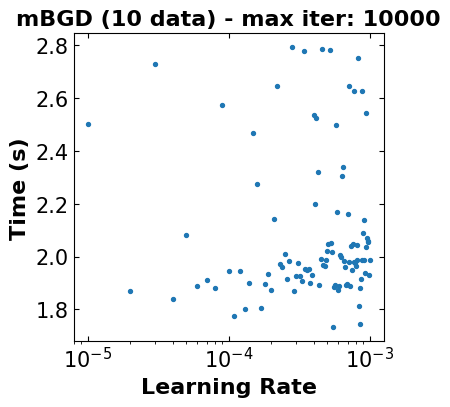
2-1-6. Conclusions:
1. BGD:
For BGD, one must find the optimal learning rate (the largest lr showing a stable behavior) to converge fast.
Although it converges fast to a global min if the problem is convex with small dataset, it is not applicable for huge dataset like Big Data (millions of data)
BGD is applicable only for small datasets and when the problem has a convex cost function like regression.
2. SGD:
SGD is slower than BGD for small datasets but it has no pattern showing runtime reduction due to stochasticity.
It converges to the solution in noisier steps and requires bigger threshold than BGD to prevent bouncing around the global min.
If the problem is not convex, it can also escape local minima provided that we use an adjusted learning rate. (If the lr is too high, it may jump over the global minimum! If it is too low, it cannot come out of a local minimum!)
SGD is only a basis of advanced stochastic algorithms for Deep NN.
3. mBGD:
mBGD is a good balance between BGD & SGD with one more hyper parameter called batch size.
If the problem is not convex, it can escape local minima.
The same as SGD, it requires bigger threshold than BGD to prevent bouncing around the global min.
mBGD is widely used in training deep NN since it is fast and accurate enough.
2-2. Problem 1 - Bigger Dataset (10000 Data)#
2-2-1. Generating Data:
[data2, fx2] = generate_data_f3([1, 1], -2, 2, 10000, 0.1)
fig = plt.figure(figsize=(4,4))
plt.xticks(fontsize=15)
plt.yticks(fontsize=15)
plt.tick_params(direction="in",top=True, right=True)
plt.plot(fx2[:, 0], fx2[:, 1], 'r', markersize=5, linewidth=3)
plt.plot(data2[:, 0], data2[:, 1], 'o', markersize=5, linewidth=3)
plt.legend(["Generating function", "Data samples"],fontsize=10,bbox_to_anchor=(0.65, 1.0),borderaxespad=0)
plt.xlabel('x',fontsize=16,fontweight='bold')
plt.ylabel('y',fontsize=16,fontweight='bold')
plt.show()
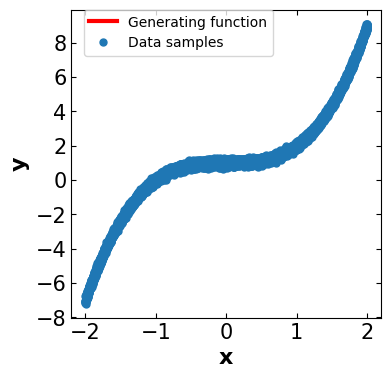
2-2-2. Plot the Loss Function
# Loss function with theta = [theta1, theta2] as input
LFx = lambda theta : least_squares_loss_function(data2, f3, theta, range(0, len(data2)))
# Plot of the loss function
fig = plt.figure(figsize=(4,4))
contour_plot(LFx, -10., 10., 50, -10., 10., 50)
contour_surface_plot(LFx, -10., 10., 50, -10., 10., 50)
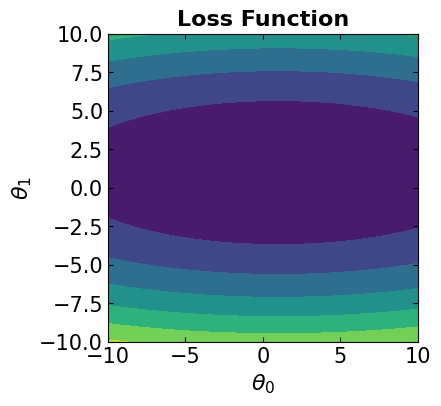
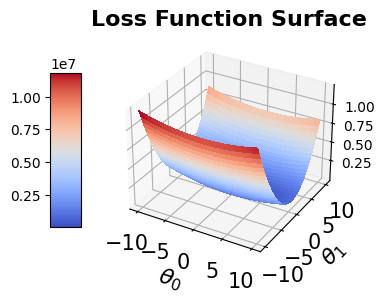
2-2-3. Compare the Run-Time:
# Initialize the vector of model parameters
theta_0 = [5, 5]
# Set the gradient threshold:
grad_thres = 1e-5
# Set the maximum number of iterations:
maxIter = 10000
# Set a loop for different batch sizes:
k_values = [1,5,10,20,50,100,200,500,1000,2000,5000,len(data2)]
time_values = []
for k in k_values:
print('\n---Batch Size = ', k)
if k <= 100:
gamma_t = 0.001
elif k > 100 and k <= 1000:
gamma_t = 0.0001
elif k > 1000 and k <= 10000:
gamma_t = 0.00001
# Call the following function to do the steps 3 & 4
# (returns the theta vectors and loss values for all iterations)
start = time.time()
theta, loss = SGD_mBGD_BGD(data2, f3, theta_0, least_squares_loss_function, grad_approx, \
learning_rate = gamma_t, max_iterations = maxIter, batch_size=k, gradient_threshold=grad_thres,verbose = False)
end = time.time()
time_values.append(end - start)
# Visualize the convergence track on loss function
fig = plt.figure(figsize=(4,4))
plt.plot(theta[:, 0], theta[:, 1], '-r', markersize=5, linewidth=3)
contour_plot(LFx, -6., 6., 50, -6, 6., 50)
# Print the optimal solution
print("The optimal solution is: theta0 = ", str(theta[-1, 0]), ", theta1 = ", str(theta[-1, 1]))
print("The corresponding loss function is: ", str(loss[-1]))
# Initialize layout
fig, ax1 = plt.subplots(figsize = (4,4))
plt.xticks(fontsize=15)
plt.yticks(fontsize=15)
plt.tick_params(direction="in",top=True, right=True)
# Add scatterplot
ax1.scatter(k_values, time_values, s=8);
ax1.set_title("Learning Rate: Varying - max_iter: 10000)",fontsize=16,fontweight='bold')
ax1.set_ylabel('Time (s)',fontsize=16,fontweight='bold')
ax1.set_xlabel('Batch Size',fontsize=16,fontweight='bold')
plt.show()
---Batch Size = 1
Max iterations reached
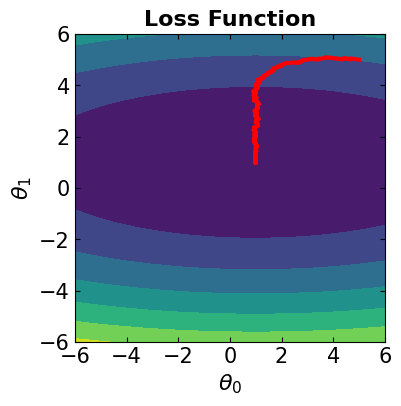
The optimal solution is: theta0 = 1.00396105716062 , theta1 = 1.00335836273951
The corresponding loss function is: 0.001189718845737115
---Batch Size = 5
Max iterations reached
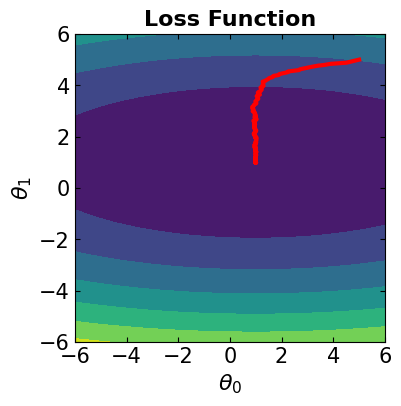
The optimal solution is: theta0 = 0.9923310195398389 , theta1 = 1.0010685523229677
The corresponding loss function is: 0.03479247571873773
---Batch Size = 10
Max iterations reached
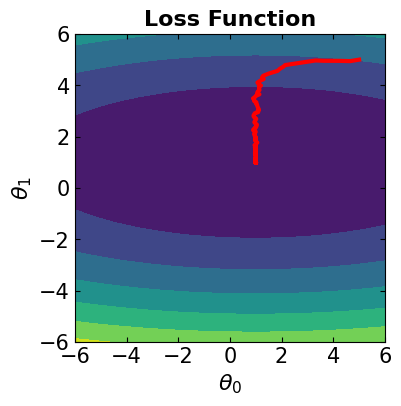
The optimal solution is: theta0 = 1.000882219575753 , theta1 = 0.9988203154713484
The corresponding loss function is: 0.07767044430355274
---Batch Size = 20
Max iterations reached
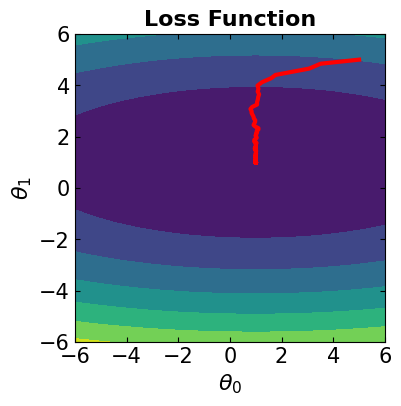
The optimal solution is: theta0 = 1.0026248380782692 , theta1 = 0.9988697821729882
The corresponding loss function is: 0.2253242245914549
---Batch Size = 50
Max iterations reached
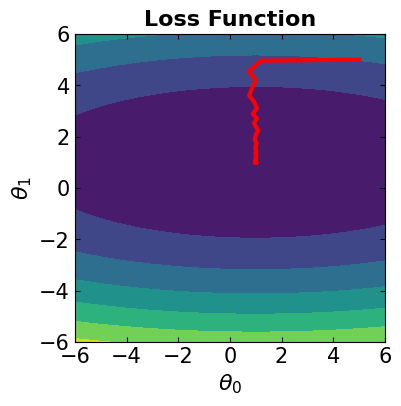
The optimal solution is: theta0 = 1.0015970758783754 , theta1 = 0.9979817161957738
The corresponding loss function is: 0.42437606855768406
---Batch Size = 100
Max iterations reached
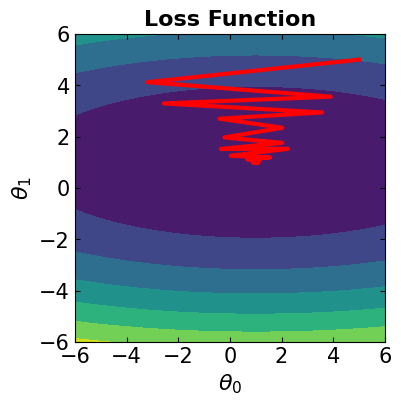
The optimal solution is: theta0 = 1.0052849541769504 , theta1 = 0.9991328571129454
The corresponding loss function is: 1.0379534182570722
---Batch Size = 200
Max iterations reached
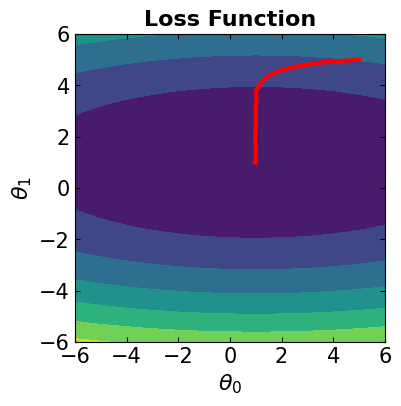
The optimal solution is: theta0 = 0.9997118035038843 , theta1 = 0.9984465924052177
The corresponding loss function is: 1.7084133552247633
---Batch Size = 500
Max iterations reached
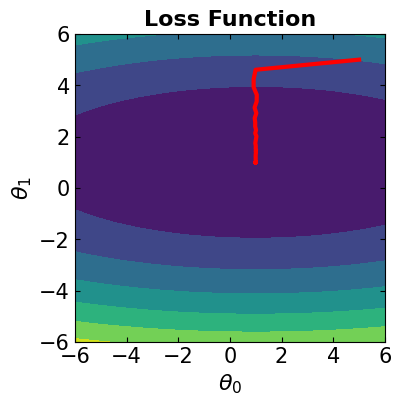
The optimal solution is: theta0 = 1.000286807090962 , theta1 = 0.9991798753291548
The corresponding loss function is: 5.4794432712666765
---Batch Size = 1000
Max iterations reached
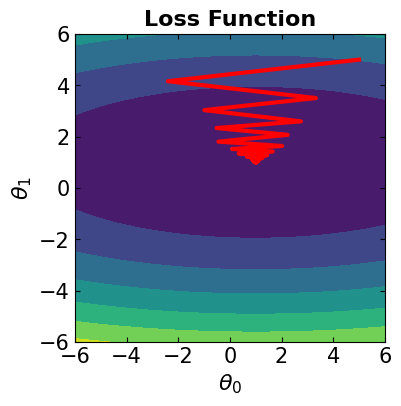
The optimal solution is: theta0 = 1.0029735926578809 , theta1 = 1.000578189031316
The corresponding loss function is: 9.551803887619446
---Batch Size = 2000
Max iterations reached
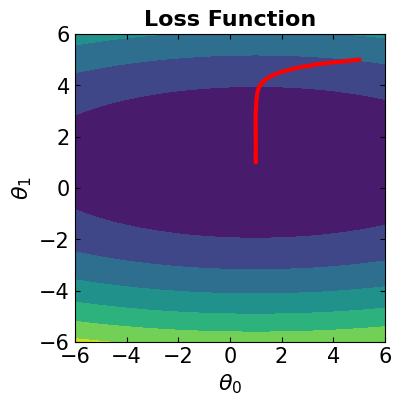
The optimal solution is: theta0 = 1.0001280895331988 , theta1 = 0.9987308184681254
The corresponding loss function is: 20.325235470022463
---Batch Size = 5000
Max iterations reached
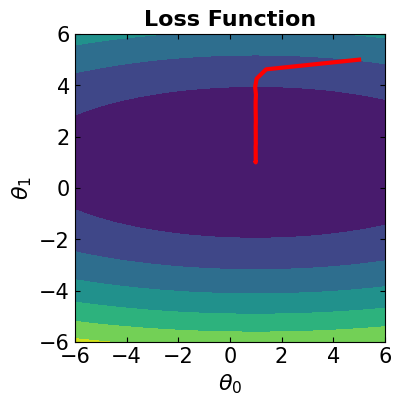
The optimal solution is: theta0 = 0.9996794926738057 , theta1 = 0.9993794331325034
The corresponding loss function is: 50.257707688524796
---Batch Size = 10000
SUCCESS
Gradient below the specified tolerance
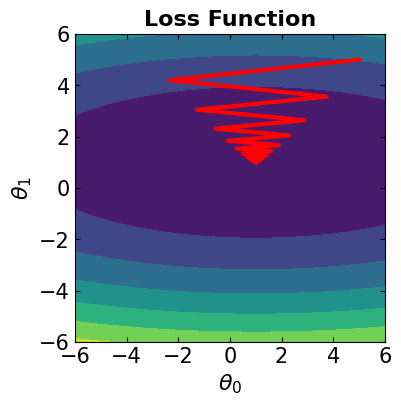
The optimal solution is: theta0 = 0.9998087560478552 , theta1 = 0.9992893193110319
The corresponding loss function is: 99.90911449942031
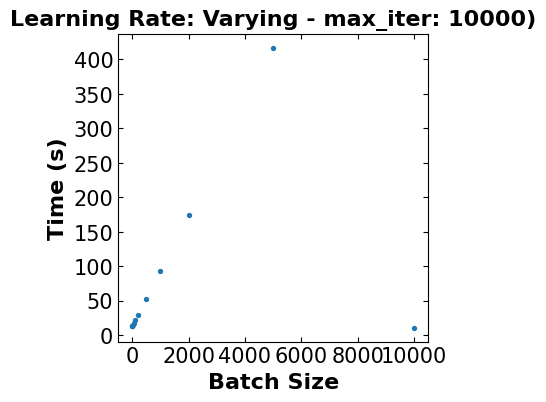
2-2-4. Conclusions:
The fastest convergence for large datasets is to use:
mBGD with a batch size smaller than 10% of dataset size.
BGD with the adequately large learning rate.
In SGD & mBGD, when the learning rate is high enough, the function fluctuates to converge. In this case, there is a chance to escape from local minima and go to the global minimum. Hence, SGD and mBGD are good options for a black box optimization.
3. References#
Wu, Wei, et al. “Learning dynamics of gradient descent optimization in deep neural networks.” Science China Information Sciences 64 (2021): 1-15.
Kwiatkowski, Robert. “Batch, Mini-Batch and Stochastic Gradient Descent for Linear Regression.” towardsdatascience, Jun 15. 2021, https://towardsdatascience.com/batch-mini-batch-and-stochastic-gradient-descent-for-linear-regression-9fe4eefa637c.

