7.3. Analysis of KKT Conditions#
Reference: Section 4.3 in Biegler (2010)
7.3.1. Active Sets#

7.3.2. Sensitivity Analysis#

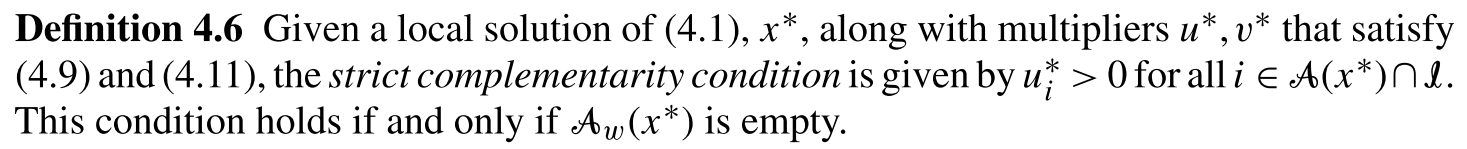
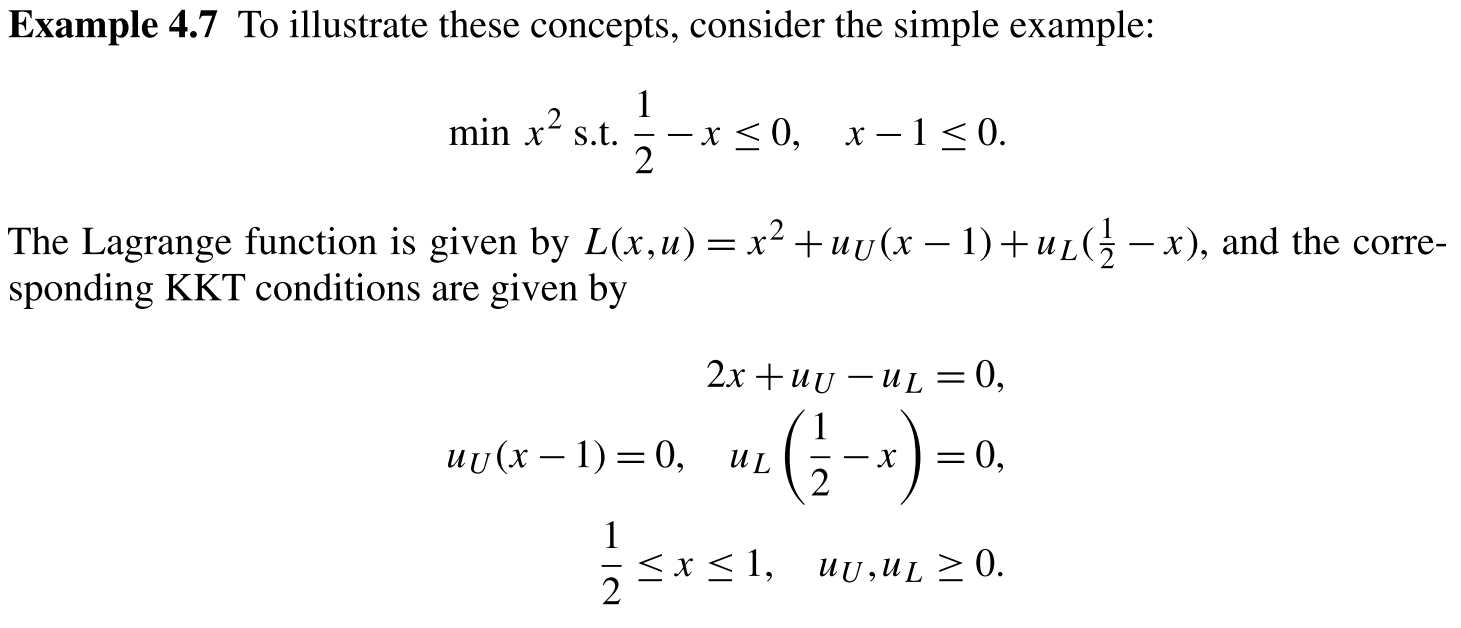

7.3.3. Multipliers in Pyomo#
Reference: https://pyomo.readthedocs.io/en/stable/pyomo_modeling_components/Suffixes.html
\[\begin{split}
\begin{align} \min_{x_1,...,x_4} \quad & x_1 \cdot x_4 \cdot (x_1 + x_2 + x_3) + x_3 \\
\mathrm{s.t.} \quad & x_1 \cdot x_2 \cdot x_3 \cdot x_4 \geq 25 \\
& x_1 + x_2 + x_3 + x_4 = 40
\end{align}
\end{split}\]
import pyomo.environ as pyo
# Example from
# https://pyomo.readthedocs.io/en/stable/pyomo_modeling_components/Suffixes.html#exporting-suffix-data
model = pyo.ConcreteModel()
model.x1 = pyo.Var(bounds=(1,5),initialize=1.0)
model.x2 = pyo.Var(bounds=(1,5),initialize=5.0)
model.x3 = pyo.Var(bounds=(1,5),initialize=5.0)
model.x4 = pyo.Var(bounds=(1,5),initialize=1.0)
model.obj = pyo.Objective(
expr=model.x1*model.x4*(model.x1 + model.x2 + model.x3) + model.x3)
model.inequality = pyo.Constraint(
expr=model.x1*model.x2*model.x3*model.x4 >= 25.0)
model.equality = pyo.Constraint(
expr=model.x1**2 + model.x2**2 + model.x3**2 + model.x4**2 == 40.0)
### Declare all suffixes
# Ipopt bound multipliers (obtained from solution)
model.ipopt_zL_out = pyo.Suffix(direction=pyo.Suffix.IMPORT)
model.ipopt_zU_out = pyo.Suffix(direction=pyo.Suffix.IMPORT)
# Ipopt bound multipliers (sent to solver)
model.ipopt_zL_in = pyo.Suffix(direction=pyo.Suffix.EXPORT)
model.ipopt_zU_in = pyo.Suffix(direction=pyo.Suffix.EXPORT)
# Obtain dual solutions from first solve and send to warm start
model.dual = pyo.Suffix(direction=pyo.Suffix.IMPORT_EXPORT)
ipopt = pyo.SolverFactory('ipopt')
7.3.3.1. Solve without warm starting#
ipopt.solve(model, tee=True)
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 4
Number of nonzeros in inequality constraint Jacobian.: 4
Number of nonzeros in Lagrangian Hessian.............: 10
Total number of variables............................: 4
variables with only lower bounds: 0
variables with lower and upper bounds: 4
variables with only upper bounds: 0
Total number of equality constraints.................: 1
Total number of inequality constraints...............: 1
inequality constraints with only lower bounds: 1
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 1.6109693e+01 1.12e+01 5.28e-01 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 1.6982239e+01 7.30e-01 1.02e+01 -1.0 6.11e-01 - 7.19e-02 1.00e+00f 1
2 1.7318411e+01 3.60e-02 5.05e-01 -1.0 1.61e-01 - 1.00e+00 1.00e+00h 1
3 1.6849424e+01 2.78e-01 6.68e-02 -1.7 2.85e-01 - 7.94e-01 1.00e+00h 1
4 1.7051199e+01 4.71e-03 2.78e-03 -1.7 6.06e-02 - 1.00e+00 1.00e+00h 1
5 1.7011979e+01 7.19e-03 8.50e-03 -3.8 3.66e-02 - 9.45e-01 9.98e-01h 1
6 1.7014271e+01 1.74e-05 9.78e-06 -3.8 3.33e-03 - 1.00e+00 1.00e+00h 1
7 1.7014021e+01 1.23e-07 1.82e-07 -5.7 2.69e-04 - 1.00e+00 1.00e+00h 1
8 1.7014017e+01 1.77e-11 2.52e-11 -8.6 3.32e-06 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 8
(scaled) (unscaled)
Objective...............: 1.7014017145179160e+01 1.7014017145179160e+01
Dual infeasibility......: 2.5166710821230136e-11 2.5166710821230136e-11
Constraint violation....: 1.7706724975141697e-11 1.7706724975141697e-11
Complementarity.........: 2.5277100427932999e-09 2.5277100427932999e-09
Overall NLP error.......: 2.5277100427932999e-09 2.5277100427932999e-09
Number of objective function evaluations = 9
Number of objective gradient evaluations = 9
Number of equality constraint evaluations = 9
Number of inequality constraint evaluations = 9
Number of equality constraint Jacobian evaluations = 9
Number of inequality constraint Jacobian evaluations = 9
Number of Lagrangian Hessian evaluations = 8
Total CPU secs in IPOPT (w/o function evaluations) = 0.002
Total CPU secs in NLP function evaluations = 0.000
EXIT: Optimal Solution Found.
{'Problem': [{'Lower bound': -inf, 'Upper bound': inf, 'Number of objectives': 1, 'Number of constraints': 2, 'Number of variables': 4, 'Sense': 'unknown'}], 'Solver': [{'Status': 'ok', 'Message': 'Ipopt 3.13.2\\x3a Optimal Solution Found', 'Termination condition': 'optimal', 'Id': 0, 'Error rc': 0, 'Time': 0.05761003494262695}], 'Solution': [OrderedDict([('number of solutions', 0), ('number of solutions displayed', 0)])]}
Inspect dual variables for lower bound
model.ipopt_zL_out.display()
ipopt_zL_out : Direction=Suffix.IMPORT, Datatype=Suffix.FLOAT
Key : Value
x1 : 1.087871225865903
x2 : 6.693166200639301e-10
x3 : 8.887657145296478e-10
x4 : 6.570872591662968e-09
Inspect dual variables for upper bound
model.ipopt_zU_out.display()
ipopt_zU_out : Direction=Suffix.IMPORT, Datatype=Suffix.FLOAT
Key : Value
x1 : -6.262653086171725e-10
x2 : -9.788835007044501e-09
x3 : -2.12284925206338e-09
x4 : -6.925197858855533e-10
7.3.3.2. Solve with warm starting#
### Set Ipopt options for warm-start
# The current values on the ipopt_zU_out and ipopt_zL_out suffixes will
# be used as initial conditions for the bound multipliers to solve the
# new problem
model.ipopt_zL_in.update(model.ipopt_zL_out)
model.ipopt_zU_in.update(model.ipopt_zU_out)
ipopt.options['warm_start_init_point'] = 'yes'
ipopt.options['warm_start_bound_push'] = 1e-6
ipopt.options['warm_start_mult_bound_push'] = 1e-6
ipopt.options['mu_init'] = 1e-6
ipopt.solve(model, tee=True)

