3.6. Pyomo.DAE: Racing Example Revisited#
Prepared by: Prof. Alexander Dowling, Molly Dougher (mdoughe6@nd.edu, 2023)
# Install Pyomo and solvers for Google Colab
import sys
if "google.colab" in sys.modules:
!wget "https://raw.githubusercontent.com/ndcbe/optimization/main/notebooks/helper.py"
import helper
helper.easy_install()
else:
sys.path.insert(0, '../')
import helper
helper.set_plotting_style()
# import Pyomo library
import pyomo.environ as pyo
import pyomo.dae as dae
import matplotlib.pyplot as plt
3.6.1. Car Example#
Adapted from Pyomo/pyomo
You are a race car driver with a simple goal. Drive distance \(L\) in the minimal amount of time but come to a complete stop at the finish line.
3.6.1.1. Optimal Control Problem Formulation#
Mathematically, you want to solve the following optimal control problem:
\[\begin{split}\begin{align*}
\min_{u} \quad & t_f \\
\mathrm{s.t.} \quad & \frac{dx}{dt} = v \\
& \frac{dv}{dt} = u - R v^2 \\
& x(t=0) = 0, ~~ x(t=t_f) = L \\
& v(t=0) = 0, ~~ v(t=t_f) = 0 \\
& -3 \leq u \leq 1
\end{align*}\end{split}\]
where \(a\) is the acceleration/braking (your control variable) and \(R\) is the drag coefficient (parameter).
3.6.1.2. Scale Time#
Let \(t = \tau \cdot t_f\) where \(\tau \in [0,1]\). Thus \(dt = t_f d\tau\). The optimal control problem becomes:
\[\begin{split}\begin{align*}
\min_{u} \quad & t_f \\
\mathrm{s.t.} \quad & \frac{dx}{d\tau} = t_f v \\
& \frac{dv}{d\tau} = t_f (u - R v^2) \\
& x(\tau = 0) = 0, ~~ x(\tau = 1) = L \\
& v(\tau = 0) = 0, ~~ v(\tau = 1) = 0 \\
& -3 \leq u \leq 1
\end{align*}\end{split}\]
3.6.1.3. Orthogonal Collocation on Finite Elements: Manual Approach#
Here is the “classical”/”old school” way of manually implementing collocation on finite elements with sets.
Indices and Sets
Finite elements: \(i \in \mathcal{I} = \{1,2,...,N_{FE}\}\)
Finite elements (except first): \(\mathcal{I} \setminus 1\)
Internal collocation points: \(j,k \in \mathcal{J} = \{1,2,...,N_{C}\}\)
Parameters
Coefficients in collocation/Runge-Kutta formula: \(a_{j,j}\)
Drag coefficient: \(R\)
Race length: \(L\)
Scaled time for each finite element: \(h_i = \frac{1}{N_{FE}}\)
Variables
Position (internal collocation points): \(x_{i,j}\)
Position (beginning of each finite element): \(\bar{x}_{i}\)
Position derivative (internal collocation points): \(\dot{x}_{i,j}\)
Velocity (internal collocation points): \(v_{i,j}\)
Velocity (beginning of each finite element): \(\bar{v}_{i}\)
Velocity derivative (internal collocation points): \(\dot{v}_{i,j}\)
Time (internal collocation points): \(t_{i,j}\)
Time (beginning of each finite element): \(\bar{t}_{i}\)
Acceleration (control degrees of freedom): \(u_i\)
Objective and Constraints
\[\begin{split}\begin{align*}
\min \quad & t_f \\
\mathrm{s.t.} \quad & \mathrm{Differential~equation~for~x:} \\
& x_{i,j} = \bar{x}_{i} + h_i \sum_{k \in \mathcal{J}} a_{k,j} \dot{x}_{i,k},\quad \forall i \in \mathcal{I},~j \in \mathcal{J} \\
& \bar{x}_{i} = \bar{x}_{i-1} + h_{i-1} \sum_{k \in \mathcal{J}} a_{k,N_C} \dot{x}_{i-1,k},\quad \forall i \in \mathcal{I} \setminus 1\\
& \dot{x}_{i,j} = t_f v_{i,j}, \quad \forall i \in \mathcal{I} \setminus 1,~j \in \mathcal{J} \\ \\
& \mathrm{Differential~equation~for~v:} \\
& v_{i,j} = \bar{v}_{i} + h_i \sum_{k \in \mathcal{J}} a_{k,j} \dot{v}_{i,k},\quad \forall i \in \mathcal{I},~j \in \mathcal{J} \\
& \bar{v}_{i} = \bar{v}_{i-1} + h_{i-1} \sum_{k \in \mathcal{J}} a_{k,N_C} \dot{v}_{i-1,k},\quad \forall i \in \mathcal{I} \setminus 1\\
& \dot{v}_{i,j} = t_f (u_{i} - R v_{i,j}^2), \quad \forall i \in \mathcal{I} \setminus 1,~j \in \mathcal{J} \\ \\
& \mathrm{Differential~equation~for~time:} \\
& t_{i,j} = \bar{t}_{i} + h_i \sum_{k \in \mathcal{J}} a_{k,j} t_f,\quad \forall i \in \mathcal{I},~j \in \mathcal{J} \\
& \bar{t}_{i} = \bar{t}_{i-1} + h_{i-1} \sum_{k \in \mathcal{J}} a_{k,N_C} t_f,\quad \forall i \in \mathcal{I} \setminus 1\\ \\
& \mathrm{Initial~conditions:} \\
& \bar{x}_{1} = 0, \quad \bar{v}_{1} = 0, \quad \bar{t}_1 = 0\\ \\
& \mathrm{Boundary~conditions:} \\
& L = \bar{x}_{N_{FE}} + h_{N_{FE}} \sum_{k \in \mathcal{J}} a_{k,N_C} \dot{x}_{N_{FE},k}, \\
& 0 = \bar{v}_{N_{FE}} + h_{N_{FE}} \sum_{k \in \mathcal{J}} a_{k,N_C} \dot{v}_{N_{FE},k}, \\ \\
& \mathrm{Bounds~on~acceleration:} \\
& -3 \leq a_i \leq 1, \quad \forall i \in \mathcal{I}
\end{align*}\end{split}\]
import pyomo.environ as pyo
import matplotlib.pyplot as plt
import pyomo.dae as dae
# Define the model
m2 = pyo.ConcreteModel()
# Define model parameters
m2.R = pyo.Param(initialize=0.001) # Friction factor
m2.L = pyo.Param(initialize=100.0) # Final position
# Define finite elements and collocation points
NFE = 15 # Number of finite elements
NC = 3 # Number of collocation points
m2.I = pyo.Set(initialize=pyo.RangeSet(1,NFE)) # Set of finite elements
m2.J = pyo.Set(initialize=pyo.RangeSet(1,NC)) # Set of internal collocation points
# Define first order derivative collocation matrix
A = {}
A[1,1] = 0.19681547722366
A[1,2] = 0.39442431473909
A[1,3] = 0.37640306270047
A[2,1] = -0.06553542585020
A[2,2] = 0.29207341166523
A[2,3] = 0.51248582618842
A[3,1] = 0.02377097434822
A[3,2] = -0.04154875212600
A[3,3] = 0.11111111111111
# Define A matrix as a model parameter
m2.a = pyo.Param(m2.J, m2.J, initialize=A)
# Define step for each finite element
m2.h = pyo.Param(m2.I,initialize=1/NFE)
# Define objective (final time)
m2.tf = pyo.Var(domain=pyo.NonNegativeReals)
# Variables for x (position)
m2.x0 = pyo.Var(m2.I) # Internal collocation points
m2.x = pyo.Var(m2.I,m2.J) # Beginning of each finite element
m2.xdot = pyo.Var(m2.I,m2.J) # Derivative, beginning of each finite element
# Variables for v (velocity)
m2.v0 = pyo.Var(m2.I) # Internal collocation points
m2.v = pyo.Var(m2.I,m2.J) # Beginning of each finite element
m2.vdot = pyo.Var(m2.I,m2.J) # Derivative, beginning of each finite element
# Variables for t
m2.t0 = pyo.Var(m2.I) # Internal collocation points
m2.t = pyo.Var(m2.I,m2.J) # Beginning of each finite element
# Acceleration
m2.u = pyo.Var(m2.I, bounds=(-3,1)) # Control DOF
### Finite Element Collocation Equations
# position
def FECOLx_(m2,i,j):
return m2.x[i,j] == m2.x0[i] + m2.h[i]*sum(m2.a[k,j]*m2.xdot[i,k] for k in m2.J)
m2.FECOLx = pyo.Constraint(m2.I,m2.J,rule=FECOLx_)
# velocity
def FECOLv_(m2,i,j):
return m2.v[i,j] == m2.v0[i] + m2.h[i]*sum(m2.a[k,j]*m2.vdot[i,k] for k in m2.J)
m2.FECOLv = pyo.Constraint(m2.I,m2.J,rule=FECOLv_)
# time
def FECOLt_(m2,i,j):
return m2.t[i,j] == m2.t0[i] + m2.h[i]*sum(m2.a[k,j]*m2.tf for k in m2.J)
m2.FECOLt = pyo.Constraint(m2.I,m2.J,rule=FECOLt_)
### Continuity Equations
# position
def CONx_(m2,i):
if i == 1:
return pyo.Constraint.Skip
else:
return m2.x0[i] == m2.x0[i-1] + m2.h[i-1]*sum(m2.a[k,NC]*m2.xdot[i,k] for k in m2.J)
m2.CONx = pyo.Constraint(m2.I, rule=CONx_)
# velocity
def CONv_(m2,i):
if i == 1:
return pyo.Constraint.Skip
else:
return m2.v0[i] == m2.v0[i-1] + m2.h[i-1]*sum(m2.a[k,NC]*m2.vdot[i,k] for k in m2.J)
m2.CONv = pyo.Constraint(m2.I, rule=CONv_)
# time
def CONt_(m2,i):
if i == 1:
return pyo.Constraint.Skip
else:
return m2.t0[i] == m2.t0[i-1] + m2.h[i-1]*sum(m2.a[k,NC]*m2.tf for k in m2.J)
m2.CONt = pyo.Constraint(m2.I, rule=CONt_)
### Differential equations
# position
def ODEx_(m2,i,j):
return m2.xdot[i,j] == m2.tf*m2.v[i,j]
m2.ODEx = pyo.Constraint(m2.I,m2.J,rule=ODEx_)
# velocity
def ODEv_(m2,i,j):
return m2.vdot[i,j] == m2.tf*(m2.u[i] - m2.R*m2.v[i,j]**2)
m2.ODEv = pyo.Constraint(m2.I,m2.J,rule=ODEv_)
### Initial conditions
m2.xIC = pyo.Constraint(expr=m2.x0[1] == 0)
m2.vIC = pyo.Constraint(expr=m2.v0[1] == 0)
m2.tIC = pyo.Constraint(expr=m2.t0[1] == 0)
### Boundary conditions
m2.xBC = pyo.Constraint(expr=m2.L == m2.x0[NFE] + m2.h[NFE]*sum(m2.a[k,NC]*m2.xdot[NFE,k] for k in m2.J))
m2.vBC = pyo.Constraint(expr=0 == m2.v0[NFE] + m2.h[NFE]*sum(m2.a[k,NC]*m2.vdot[NFE,k] for k in m2.J))
### Set objective
m2.obj = pyo.Objective(expr=m2.tf)
# Solve the model
solver = pyo.SolverFactory('ipopt')
solver.solve(m2,tee=True)
print("final time = %6.2f" %(pyo.value(m2.tf)))
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
This version of Ipopt was compiled from source code available at
https://github.com/IDAES/Ipopt as part of the Institute for the Design of
Advanced Energy Systems Process Systems Engineering Framework (IDAES PSE
Framework) Copyright (c) 2018-2019. See https://github.com/IDAES/idaes-pse.
This version of Ipopt was compiled using HSL, a collection of Fortran codes
for large-scale scientific computation. All technical papers, sales and
publicity material resulting from use of the HSL codes within IPOPT must
contain the following acknowledgement:
HSL, a collection of Fortran codes for large-scale scientific
computation. See http://www.hsl.rl.ac.uk.
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 1093
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 105
Total number of variables............................: 286
variables with only lower bounds: 1
variables with lower and upper bounds: 15
variables with only upper bounds: 0
Total number of equality constraints.................: 272
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 9.9999900e-03 1.00e+02 0.00e+00 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1r 9.9999900e-03 1.00e+02 9.99e+02 2.0 0.00e+00 - 0.00e+00 1.05e-07R 2
2r 3.0578540e+00 9.99e+01 9.31e+02 2.0 4.49e+01 - 1.35e-01 6.80e-02f 2
3r 2.2146807e+00 9.91e+01 5.68e+02 1.3 2.16e+00 - 1.00e+00 3.91e-01f 1
4r 2.0626784e+00 9.87e+01 4.21e+02 0.6 2.94e+00 - 6.36e-01 2.59e-01f 1
5r 2.7501672e+00 9.77e+01 2.42e+02 0.6 8.74e+00 - 5.56e-01 4.24e-01f 1
6r 5.8696920e+00 9.43e+01 1.91e+02 -0.1 8.62e+00 - 4.13e-01 7.57e-01f 1
7r 8.6536528e+00 8.80e+01 1.65e+02 -0.1 1.29e+01 - 2.98e-01 7.27e-01f 1
8r 9.0137628e+00 8.55e+01 1.09e+02 -0.1 3.77e+00 - 5.42e-01 1.00e+00f 1
9 9.4134225e+00 8.42e+01 9.84e-01 -1.0 1.13e+02 - 3.63e-01 1.56e-02h 7
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
10 9.7719760e+00 8.29e+01 9.61e-01 -1.0 1.13e+02 - 6.94e-01 1.56e-02h 7
11 1.0069154e+01 8.16e+01 1.10e+00 -1.0 1.20e+02 - 6.26e-01 1.52e-02h 7
12 1.0350049e+01 8.04e+01 1.27e+00 -1.0 1.24e+02 - 1.00e+00 1.56e-02h 7
13 1.0613260e+01 7.91e+01 1.29e+00 -1.0 1.25e+02 - 6.03e-01 1.56e-02h 7
14 1.0858870e+01 7.79e+01 1.31e+00 -1.0 1.25e+02 - 1.00e+00 1.56e-02h 7
15 1.1089714e+01 7.66e+01 1.31e+00 -1.0 1.23e+02 - 7.24e-01 1.56e-02h 7
16 1.1306240e+01 7.55e+01 1.31e+00 -1.0 1.24e+02 - 1.00e+00 1.56e-02h 7
17 1.1714847e+01 7.31e+01 1.28e+00 -1.0 1.22e+02 - 8.51e-01 3.12e-02h 6
18 1.2077191e+01 7.08e+01 1.24e+00 -1.0 1.23e+02 - 1.00e+00 3.12e-02h 6
19 2.2531170e+01 7.10e+01 8.96e-01 -1.0 1.19e+02 - 1.00e+00 1.00e+00w 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
20 1.7706786e+01 4.49e+00 1.75e-01 -1.0 2.28e+01 - 1.00e+00 1.00e+00w 1
21 1.7349863e+01 1.01e-01 7.40e-04 -1.0 8.28e+00 - 1.00e+00 1.00e+00h 1
22 1.6478946e+01 1.06e+00 3.16e-02 -2.5 1.68e+01 - 8.21e-01 1.00e+00h 1
23 1.6333670e+01 1.11e-01 9.02e-04 -2.5 1.27e+01 - 9.80e-01 1.00e+00h 1
24 1.6324255e+01 5.10e-04 4.40e-06 -2.5 6.64e-01 - 1.00e+00 1.00e+00h 1
25 1.6289923e+01 3.05e-03 1.05e-05 -3.8 1.03e+00 - 1.00e+00 1.00e+00h 1
26 1.6289753e+01 1.16e-07 1.47e-09 -3.8 5.97e-03 - 1.00e+00 1.00e+00h 1
27 1.6287822e+01 9.84e-06 3.34e-08 -5.7 5.95e-02 - 1.00e+00 1.00e+00f 1
28 1.6287798e+01 1.59e-09 5.42e-12 -8.6 7.53e-04 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 28
(scaled) (unscaled)
Objective...............: 1.6287797665173553e+01 1.6287797665173553e+01
Dual infeasibility......: 5.4235099871736237e-12 5.4235099871736237e-12
Constraint violation....: 1.5949126463965513e-09 1.5949126463965513e-09
Complementarity.........: 2.5440456242841860e-09 2.5440456242841860e-09
Overall NLP error.......: 2.5440456242841860e-09 2.5440456242841860e-09
Number of objective function evaluations = 106
Number of objective gradient evaluations = 23
Number of equality constraint evaluations = 106
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 30
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 28
Total CPU secs in IPOPT (w/o function evaluations) = 0.013
Total CPU secs in NLP function evaluations = 0.001
EXIT: Optimal Solution Found.
final time = 16.29
3.6.1.4. Orthogonal Collocation on Finite Elements: Pyomo.dae#
There is a better way! We can use Pyomo.dae to automatically formulate the collocation equations.
3.6.1.4.1. Declare Model#
# Define the model
m = pyo.ConcreteModel()
# Deine the model parameters
m.R = pyo.Param(initialize=0.001) # Friction factor
m.L = pyo.Param(initialize=100.0) # Final position
# Define time
m.tau = dae.ContinuousSet(bounds=(0,1)) # Unscaled time
m.time = pyo.Var(m.tau) # Scaled time
m.tf = pyo.Var() # Final time
# Define remaining algebraic variables
m.x = pyo.Var(m.tau,bounds=(0,m.L+50)) # Position
m.v = pyo.Var(m.tau,bounds=(0,None)) # Velocity
m.u = pyo.Var(m.tau, bounds=(-3.0,1.0),initialize=0) # Acceleration
# Define derivative variables
m.dtime = dae.DerivativeVar(m.time)
m.dx = dae.DerivativeVar(m.x)
m.dv = dae.DerivativeVar(m.v)
# Declare the objective (minimize final time)
m.obj = pyo.Objective(expr=m.tf)
# Define the constraints
# position
def _ode1(m,i):
if i == 0 :
return pyo.Constraint.Skip
return m.dx[i] == m.tf * m.v[i]
m.ode1 = pyo.Constraint(m.tau, rule=_ode1)
# velocity
def _ode2(m,i):
if i == 0 :
return pyo.Constraint.Skip
return m.dv[i] == m.tf*(m.u[i] - m.R*m.v[i]**2)
m.ode2 = pyo.Constraint(m.tau, rule=_ode2)
# time
def _ode3(m,i):
if i == 0:
return pyo.Constraint.Skip
return m.dtime[i] == m.tf
m.ode3 = pyo.Constraint(m.tau, rule=_ode3)
# Define the inital/boundary conditions
def _init(m):
yield m.x[0] == 0
yield m.x[1] == m.L
yield m.v[0] == 0
yield m.v[1] == 0
yield m.time[0] == 0
m.initcon = pyo.ConstraintList(rule=_init)
3.6.1.4.2. Discretize/Transcribe and Solve#
#discretizer = TransformationFactory('dae.finite_difference')
#discretizer.apply_to(m,nfe=15,scheme='BACKWARD')
# Declare the discretizer
discretizer = pyo.TransformationFactory('dae.collocation')
discretizer.apply_to(m,nfe=15,scheme='LAGRANGE-RADAU',ncp=3)
#discretizer.apply_to(m,nfe=15,scheme='LAGRANGE-LEGENDRE',ncp=3)
# force piecewise constant controls (acceleration) over each finite element
m = discretizer.reduce_collocation_points(m,var=m.u,ncp=1,contset=m.tau)
# Solve
solver = pyo.SolverFactory('ipopt')
solver.solve(m,tee=True)
print("final time = %6.2f" %(pyo.value(m.tf)))
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
This version of Ipopt was compiled from source code available at
https://github.com/IDAES/Ipopt as part of the Institute for the Design of
Advanced Energy Systems Process Systems Engineering Framework (IDAES PSE
Framework) Copyright (c) 2018-2019. See https://github.com/IDAES/idaes-pse.
This version of Ipopt was compiled using HSL, a collection of Fortran codes
for large-scale scientific computation. All technical papers, sales and
publicity material resulting from use of the HSL codes within IPOPT must
contain the following acknowledgement:
HSL, a collection of Fortran codes for large-scale scientific
computation. See http://www.hsl.rl.ac.uk.
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 1145
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 135
Total number of variables............................: 319
variables with only lower bounds: 46
variables with lower and upper bounds: 91
variables with only upper bounds: 0
Total number of equality constraints.................: 305
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 0.0000000e+00 1.00e+02 1.00e+00 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 3.4627510e+01 9.96e+01 6.56e+12 -1.0 1.00e+04 - 9.91e-05 3.46e-03h 9
2 3.5266628e+01 9.94e+01 6.54e+12 -1.0 2.48e+02 6.0 2.78e-03 2.57e-03f 9
3 4.7357993e+01 3.13e+01 5.50e+11 -1.0 1.27e+02 6.4 6.25e-03 7.20e-01f 1
4 4.7456731e+01 3.38e-01 4.35e+09 -1.0 4.34e+01 5.9 6.08e-02 9.90e-01h 1
5 4.7455597e+01 3.25e-03 4.21e+07 -1.0 4.15e-01 5.5 9.91e-01 9.90e-01h 1
6 4.7455608e+01 2.03e-10 3.96e+02 -1.0 4.01e-03 5.0 1.00e+00 1.00e+00h 1
7 4.7455607e+01 1.24e-12 1.63e-02 -1.0 4.94e-07 4.5 1.00e+00 1.00e+00h 1
8 4.7455606e+01 1.86e-12 1.54e-02 -5.7 1.40e-06 4.0 1.00e+00 1.00e+00h 1
9 4.7455602e+01 9.89e-13 1.54e-02 -5.7 4.20e-06 3.6 1.00e+00 1.00e+00h 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
10 4.7455589e+01 8.55e-12 1.54e-02 -5.7 1.26e-05 3.1 1.00e+00 1.00e+00f 1
11 4.7455551e+01 7.71e-11 1.54e-02 -5.7 3.78e-05 2.6 1.00e+00 1.00e+00f 1
12 4.7455438e+01 6.93e-10 1.54e-02 -5.7 1.13e-04 2.1 1.00e+00 1.00e+00f 1
13 4.7455097e+01 6.24e-09 1.54e-02 -5.7 3.40e-04 1.7 1.00e+00 1.00e+00f 1
14 4.7454077e+01 5.62e-08 1.54e-02 -5.7 1.02e-03 1.2 1.00e+00 1.00e+00f 1
15 4.7451014e+01 5.05e-07 1.54e-02 -5.7 3.06e-03 0.7 1.00e+00 1.00e+00f 1
16 4.7441826e+01 4.55e-06 1.54e-02 -5.7 9.19e-03 0.2 1.00e+00 1.00e+00f 1
17 4.7414266e+01 4.10e-05 1.54e-02 -5.7 2.76e-02 -0.3 1.00e+00 1.00e+00f 1
18 4.7331605e+01 3.69e-04 1.54e-02 -5.7 8.27e-02 -0.7 1.00e+00 1.00e+00f 1
19 4.7083808e+01 3.32e-03 1.54e-02 -5.7 2.48e-01 -1.2 1.00e+00 1.00e+00f 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
20 4.6342119e+01 3.01e-02 1.53e-02 -5.7 7.42e-01 -1.7 1.00e+00 1.00e+00f 1
21 4.4133048e+01 2.74e-01 1.52e-02 -5.7 2.21e+00 -2.2 1.00e+00 1.00e+00f 1
22 3.9837199e+01 1.24e+00 1.50e-02 -5.7 6.46e+00 -2.6 1.00e+00 6.65e-01f 1
23 3.1994651e+01 5.48e+00 1.10e+00 -5.7 4.73e+01 -3.1 1.00e+00 1.00e+00f 1
24 2.3766836e+01 1.30e+01 2.27e+00 -5.7 1.45e+02 -3.6 5.95e-01 2.28e-01f 1
25 2.3554919e+01 1.24e+01 2.17e+00 -5.7 3.14e+01 -3.2 1.00e+00 4.76e-02h 1
26 2.2326003e+01 1.16e+01 1.96e+00 -5.7 1.10e+02 -3.6 1.00e+00 9.28e-02h 1
27 2.0535816e+01 1.19e+01 1.68e+00 -5.7 2.71e+02 -4.1 3.56e-03 6.94e-02h 1
28 2.0510626e+01 1.18e+01 1.67e+00 -5.7 4.60e+01 -3.7 1.00e+00 8.17e-03h 1
29 1.9232236e+01 1.23e+01 1.63e+00 -5.7 9.64e+02 -4.2 7.35e-04 1.98e-02h 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
30 1.8511271e+01 8.58e+00 1.09e+00 -5.7 3.63e+01 -3.7 1.00e+00 3.37e-01h 1
31 1.8028490e+01 8.33e+00 1.03e+00 -5.7 1.22e+02 -4.2 5.15e-04 4.70e-02h 1
32 1.7998896e+01 8.24e+00 1.02e+00 -5.7 3.07e+01 -3.8 5.44e-01 1.14e-02h 1
33 1.7193419e+01 7.81e+00 7.77e-01 -5.7 9.19e+01 -4.3 7.84e-01 1.25e-01h 1
34 1.6633972e+01 7.89e+00 8.66e-01 -5.7 2.72e+02 -4.8 2.03e-01 3.50e-02h 1
35 1.6625432e+01 7.87e+00 8.63e-01 -5.7 6.05e+01 -4.3 6.95e-01 2.77e-03h 1
36 1.6516801e+01 7.78e+00 1.35e+00 -5.7 1.92e+02 -4.8 8.33e-06 1.34e-02h 1
37 1.6208884e+01 7.89e+00 1.32e+00 -5.7 1.17e+03 -5.3 1.94e-04 6.85e-03h 1
38 1.6202825e+01 7.88e+00 1.31e+00 -5.7 1.22e+02 -4.9 4.29e-01 1.53e-03h 1
39 1.5956287e+01 7.93e+00 9.08e+00 -5.7 6.74e+02 -5.3 3.67e-06 1.34e-02h 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
40 1.5780450e+01 8.01e+00 9.04e+00 -5.7 2.33e+03 -5.8 4.42e-04 4.18e-03h 1
41 1.5779681e+01 8.01e+00 9.07e+00 -5.7 2.51e+02 -5.4 1.93e-01 2.41e-04h 1
42 1.5698253e+01 7.98e+00 7.02e+01 -5.7 9.64e+02 -5.9 4.23e-06 8.56e-03h 1
43 1.5667002e+01 7.97e+00 7.00e+01 -5.7 2.15e+03 -6.3 1.22e-02 2.60e-03h 1
44 1.5837843e+01 6.36e+00 5.60e+01 -5.7 5.46e+00 - 2.33e-02 2.02e-01h 1
45 1.5853269e+01 6.20e+00 5.47e+01 -5.7 8.01e+00 - 1.00e+00 2.41e-02h 1
46 1.6518208e+01 6.75e-02 2.24e-01 -5.7 4.29e+00 - 1.00e+00 9.96e-01h 1
47 1.6520269e+01 2.30e-06 2.11e-06 -5.7 7.60e-02 - 1.00e+00 1.00e+00h 1
48 1.6520192e+01 9.74e-09 1.62e-10 -8.6 1.19e-03 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 48
(scaled) (unscaled)
Objective...............: 1.6520191521006133e+01 1.6520191521006133e+01
Dual infeasibility......: 1.6221173243000771e-10 1.6221173243000771e-10
Constraint violation....: 9.7371355423092609e-09 9.7371355423092609e-09
Complementarity.........: 2.7044350486443075e-09 2.7044350486443075e-09
Overall NLP error.......: 9.7371355423092609e-09 9.7371355423092609e-09
Number of objective function evaluations = 69
Number of objective gradient evaluations = 49
Number of equality constraint evaluations = 69
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 49
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 48
Total CPU secs in IPOPT (w/o function evaluations) = 0.042
Total CPU secs in NLP function evaluations = 0.001
EXIT: Optimal Solution Found.
final time = 16.52
3.6.1.4.3. Plot Results#
# Define empty lists
x = [] # position, units of length
v = [] # velocity, units of length per time
u = [] # acceleration, units of length per time squared
time=[] # time
# Loop over time and append the solution values for each variable to their respective lists
for i in m.tau:
time.append(pyo.value(m.time[i]))
x.append(pyo.value(m.x[i]))
v.append(pyo.value(m.v[i]))
u.append(pyo.value(m.u[i]))
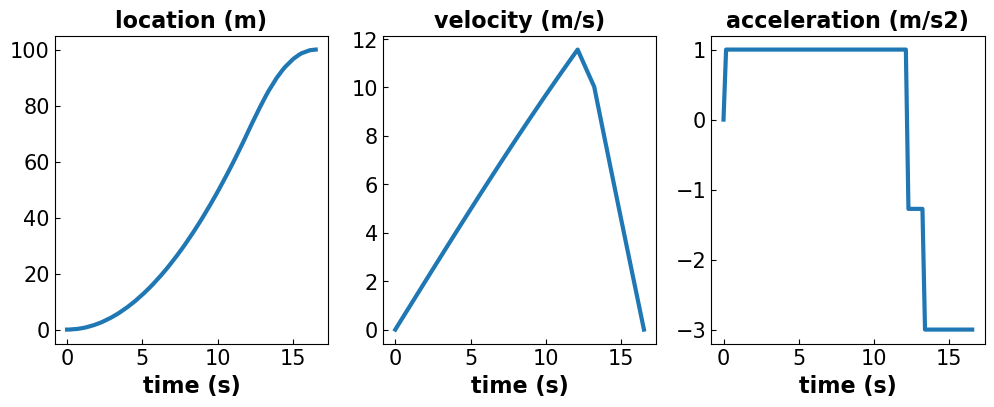
# Make a figure
plt.figure(figsize=(12,4))
# Format subplot 1 (position)
plt.subplot(131)
plt.plot(time,x,linewidth=3,label='x')
plt.title('location (m)',fontsize=16, fontweight='bold')
plt.xlabel('time (s)',fontsize=16, fontweight='bold')
plt.tick_params(direction="in",labelsize=15)
# Format subplot 2 (velocity)
plt.subplot(132)
plt.plot(time,v,linewidth=3,label='v')
plt.xlabel('time (s)',fontsize=16, fontweight='bold')
plt.title('velocity (m/s)',fontsize=16, fontweight='bold')
plt.tick_params(direction="in",labelsize=15)
# Format subplot 3 (acceleration)
plt.subplot(133)
plt.plot(time,u,linewidth=3,label='a')
plt.xlabel('time (s)',fontsize=16, fontweight='bold')
plt.title('acceleration (m/s2)',fontsize=16, fontweight='bold')
plt.tick_params(direction="in",labelsize=15)
plt.show()
Discussion Questions
How does the time/number of evaluations that IPOPT needs to solve the problem change for a discretized versus non-discretized model?
Why might the two solutions differ?
Check to make sure that these results make sense. Based on the known derivative relationships between position, velocity, and acceleration, do the 3 plots make sense? Hint: Match up the trends in each graph.