6.5. Quasi-Newton Methods for Unconstrained Optimization#
Reference: Sections 3.1 - 3.3 in Biegler (2010)
# Load required Python libraries.
import matplotlib.pyplot as plt
import numpy as np
from scipy import linalg
6.5.1. Unconstrained Optimization with Approximate Hessian#
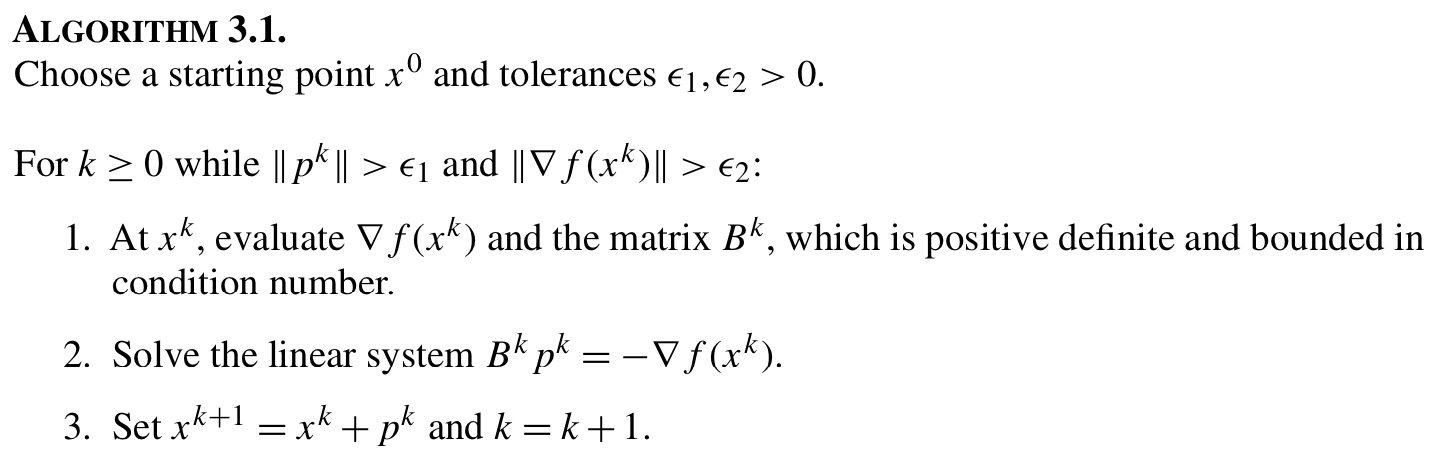
SR1 update is one way to approximate \(B^k\).
6.5.1.1. Library of helper functions#
## Check is element of array is NaN
def check_nan(A):
return np.sum(np.isnan(A))
## Calculate gradient with central finite difference
def my_grad_approx(x,f,eps1,verbose=False):
'''
Calculate gradient of function my_f using central difference formula
Inputs:
x - point for which to evaluate gradient
f - function to consider
eps1 - perturbation size
Outputs:
grad - gradient (vector)
'''
n = len(x)
grad = np.zeros(n)
if(verbose):
print("***** my_grad_approx at x = ",x,"*****")
for i in range(0,n):
# Create vector of zeros except eps in position i
e = np.zeros(n)
e[i] = eps1
# Finite difference formula
my_f_plus = f(x + e)
my_f_minus = f(x - e)
# Diagnostics
if(verbose):
print("e[",i,"] = ",e)
print("f(x + e[",i,"]) = ",my_f_plus)
print("f(x - e[",i,"]) = ",my_f_minus)
grad[i] = (my_f_plus - my_f_minus)/(2*eps1)
if(verbose):
print("***** Done. ***** \n")
return grad
## Calculate Hessian using cental finite difference
def my_hes_approx(x,grad,eps2):
'''
Calculate gradient of function my_f using central difference formula and my_grad
Inputs:
x - point for which to evaluate gradient
grad - function to calculate the gradient
eps2 - perturbation size (for Hessian NOT gradient approximation)
Outputs:
H - Hessian (matrix)
'''
n = len(x)
H = np.zeros([n,n])
for i in range(0,n):
# Create vector of zeros except eps in position i
e = np.zeros(n)
e[i] = eps2
# Evaluate gradient twice
grad_plus = grad(x + e)
grad_minus = grad(x - e)
# Notice we are building the Hessian by column (or row)
H[:,i] = (grad_plus - grad_minus)/(2*eps2)
return H
## Linear algebra calculation
def xxT(u):
'''
Calculates u*u.T to circumvent limitation with SciPy
Arguments:
u - numpy 1D array
Returns:
u*u.T
Assume u is a nx1 vector.
Recall: NumPy does not distinguish between row or column vectors
u.dot(u) returns a scalar. This functon returns an nxn matrix.
'''
n = len(u)
A = np.zeros([n,n])
for i in range(0,n):
for j in range(0,n):
A[i,j] = u[i]*u[j]
return A
## Analyze Hessian
def analyze_hes(B):
print(B,"\n")
l = linalg.eigvals(B)
print("Eigenvalues: ",l,"\n")
6.5.1.2. Symmetric Rank 1 (SR1) Update#
def alg1_sr1(x0,calc_f,calc_grad,eps1,eps2,verbose=False,max_iter=1000):
'''
Arguments:
x0 - starting point
calc_f - funcation that calculates f(x)
calc_grad - function that calculates gradient(x)
Outputs:
x - iteration history of x (decision variables)
f - iteration history of f(x) (objective value)
p - iteration history of p (steps)
B - Hessian approximation
'''
# Allocate outputs as empty lists
x = []
f = []
p = []
grad = []
B = []
# Store starting point
x.append(x0)
k = 0
flag = True
print("Iter. \tf(x) \t\t||grad(x)|| \t||p|| \t\tmin(lambda)")
while flag and k < max_iter:
# Evaluate f(x) at current iteration
f.append(calc_f(x[k]))
# Evaluate gradient
grad.append(calc_grad(x[k]))
if(check_nan(grad[k])):
print("WARNING: gradiant calculation returned NaN")
break
if verbose:
print("\n")
print("k = ",k)
print("x = ",x[k])
print("grad = ",grad[k])
# Update Hessian approximation
if k == 0:
# Initialize with identity
B.append(np.eye(len(x0)))
else:
# Change in x
s = x[k] - x[k-1]
# Change in gradient
y = grad[k] - grad[k-1]
# SR1 formulation
u = y - B[k-1].dot(s)
denom = (u).dot(s)
# Formula: dB = u * u.T / (u.T * s) if u is a column vector.
dB = xxT(u)/denom
if(verbose):
print("s = ",s)
print("y = ",y)
print("SR1 update denominator, (y-B[k-1]*s).T*s = ",denom)
print("SR1 update u = ",u)
print("SR1 update u.T*u/(u.T*s) = \n",dB)
B.append(B[k-1] + dB)
if verbose:
print("B = \n",B[k])
if(check_nan(B[k])):
print("WARNING: Hessian update returned NaN")
break
c = np.linalg.cond(B[k])
if c > 1E12:
flag = False
print("Warning: Hessian approximation is near singular.")
print("B[k] = \n",B[k])
else:
# Calculate step
p.append(linalg.solve(B[k],-grad[k]))
if verbose:
print("p = ",p[k])
# Take step
x.append(x[k] + p[k])
# Calculate norms
norm_p = linalg.norm(p[k])
norm_g = linalg.norm(grad[k])
# Calculate eigenvalues of Hessian (for display only)
ev = np.real(linalg.eigvals(B[k]))
# print("k = ",k,"\t"f[k],"\t",norm_g,"\t",norm_p)
print(k,' \t{0: 1.4e} \t{1:1.4e} \t{2:1.4e} \t{3: 1.4e}'.format(f[k],norm_g,norm_p,np.min(ev)))
# Check convergence criteria
flag = (norm_p > eps1) and (norm_g > eps2)
# Update iteration counter
k = k + 1
print("Done.")
print("x* = ",x[-1])
return x,f,p,B
print("Done.")
Done.
6.5.2. Test Case: Simple quadratic program#
def my_f_simple(x):
return x[0]**2 + (x[1]-1)**2
def my_grad_exact(x):
return np.array([2*x[0], 2*(x[1] - 1) ])
6.5.2.1. Near solution#
Consider \(x_0 = [-0.1, 0.5]^T\)
# Specify convergence criteria
eps1 = 1E-8
eps2 = 1E-4
# Create a Lambda (anonymous) function for gradient calculation
# calc_grad = lambda x : my_grad_approx(x,my_f_simple,1E-6,verbose=False)
calc_grad = lambda x : my_grad_exact(x)
# Specify starting point
x0 = np.array([-0.1, 0.2])
# Call optimization routine
x,f,p,B = alg1_sr1(x0,my_f_simple,calc_grad,eps1,eps2,verbose=False,max_iter=50);
# SR1 Hessian approximation
print("\nSR1 Hessian approximation. B[k] =")
analyze_hes(B[-1])
# Actual Hessian
print("True Hessian at x*. B =")
analyze_hes(my_hes_approx(x[-1],calc_grad,1E-6))
Iter. f(x) ||grad(x)|| ||p|| min(lambda)
0 6.5000e-01 1.6125e+00 1.6125e+00 1.0000e+00
1 6.5000e-01 1.6125e+00 8.0623e-01 1.0000e+00
2 1.9259e-34 2.7756e-17 2.7595e-17 1.0000e+00
Done.
x* = [1.36642834e-17 1.00000000e+00]
SR1 Hessian approximation. B[k] =
[[1.01538462 0.12307692]
[0.12307692 1.98461538]]
Eigenvalues: [1.+0.j 2.+0.j]
True Hessian at x*. B =
[[2. 0.]
[0. 2.]]
Eigenvalues: [2.+0.j 2.+0.j]
6.5.2.2. Far from solution#
Consider \(x_0 = [-100, 500]^T\)
# Specify starting point
x0 = np.array([-100, 500])
# Call optimization routine
x,f,p,B = alg1_sr1(x0,my_f_simple,calc_grad,eps1,eps2,verbose=False,max_iter=50);
# SR1 Hessian approximation
print("\nSR1 Hessian approximation. B[k] =")
analyze_hes(B[-1])
# Actual Hessian
print("True Hessian at x*. B =")
analyze_hes(my_hes_approx(x[-1],calc_grad,1E-6))
Iter. f(x) ||grad(x)|| ||p|| min(lambda)
0 2.5900e+05 1.0178e+03 1.0178e+03 1.0000e+00
1 2.5900e+05 1.0178e+03 5.0892e+02 1.0000e+00
2 3.4331e-27 1.1719e-13 7.2963e-14 1.0000e+00
Done.
x* = [2.46138186e-14 1.00000000e+00]
SR1 Hessian approximation. B[k] =
[[ 1.03860989 -0.19266335]
[-0.19266335 1.96139011]]
Eigenvalues: [1.+0.j 2.+0.j]
True Hessian at x*. B =
[[2. 0.]
[0. 2.]]
Eigenvalues: [2.+0.j 2.+0.j]
6.5.2.3. Activity/Discussion#
Does the number of iterations depend on the starting point for this problem?
How many iterations are needed for Newton’s method to converge for a positive definite quadratic program using exact second derivative information?
Why does the SR1 update not converge to the true Hessian?
6.5.3. Test Case: Example 2.19#

## Define Python function to calculate objective
def my_f_ex_2_19(x,verbose=False):
''' Evaluate function given above at point x
Inputs:
x - vector with 2 elements
Outputs:
f - function value (scalar)
'''
# Constants
a = np.array([0.3, 0.6, 0.2])
b = np.array([5, 26, 3])
c = np.array([40, 1, 10])
# Intermediates. Recall Python indicies start at 0
u = x[0] - 0.8
s = np.sqrt(1-u)
s2 = np.sqrt(1+u)
v = x[1] -(a[0] + a[1]*u**2*s-a[2]*u)
alpha = -b[0] + b[1]*u**2*s2+ b[2]*u # September 5, 2018: changed 's' to 's2'
beta = c[0]*v**2*(1-c[1]*v)/(1+c[2]*u**2)
f = alpha*np.exp(-beta)
if verbose:
print("##### my_f at x = ",x, "#####")
print("u = ",u)
print("sqrt(1-u) = ",s)
print("sqrt(1+u) = ",s2)
print("v = ",v)
print("alpha = ",alpha)
print("beta = ",beta)
print("f(x) = ",f)
print("##### Done. #####\n")
return f
6.5.3.1. \(x_0\) somewhat near solution#
Consider: $\(x_0 = [0.3, 0.1]^T\)$
# Create a Lambda (anonymous) function for gradient calculation
calc_grad = lambda x : my_grad_approx(x,my_f_ex_2_19,1E-6,verbose=False)
# Specify starting point
x0 = np.array([0.3, 0.1])
# Call optimization routine
x,f,p,B = alg1_sr1(x0,my_f_ex_2_19,calc_grad,eps1,eps2,verbose=False,max_iter=250);
# SR1 Hessian approximation
print("\nSR1 Hessian approximation. B[k] =")
analyze_hes(B[-1])
# Actual Hessian
print("True Hessian at x*. B =")
analyze_hes(my_hes_approx(x[-1],calc_grad,1E-6))
Iter. f(x) ||grad(x)|| ||p|| min(lambda)
0 -3.6022e-02 8.3847e-01 8.3847e-01 1.0000e+00
1 -4.1276e-02 4.7785e-01 3.0223e-01 1.0000e+00
2 -2.2301e+00 2.1236e+01 3.0865e-01 -6.8856e+01
3 -4.1260e-02 4.4645e-01 1.3053e-01 -6.7478e+01
4 -1.0354e-01 1.1855e+00 1.5062e-01 -7.1805e+01
5 -3.7115e-02 3.9982e-01 1.3096e-02 -5.8783e+01
6 -3.4039e-02 3.6164e-01 5.9865e-02 -1.4365e+01
7 -2.2398e-02 2.0377e-01 4.2988e-02 -9.5209e+00
8 -1.7133e-02 1.1914e-01 4.2522e-02 -6.4394e+00
9 -1.4292e-02 5.7282e-02 2.4810e-02 -4.8015e+00
10 -1.3542e-02 2.5813e-02 1.0353e-02 -2.8612e+00
11 -1.3373e-02 1.0933e-02 8.4091e-03 -1.6117e+00
12 -1.3325e-02 7.7765e-04 7.5906e-04 -1.6030e+00
13 -1.3324e-02 1.7106e-05 1.4129e-05 -1.5761e+00
Done.
x* = [0.80557705 0.96556999]
SR1 Hessian approximation. B[k] =
[[-1.48333926 -0.21589307]
[-0.21589307 -1.07333656]]
Eigenvalues: [-1.57605484+0.j -0.98062097+0.j]
True Hessian at x*. B =
[[-1.47002939 -0.20602227]
[-0.20602227 -1.06561938]]
Eigenvalues: [-1.55649728+0.j -0.9791515 +0.j]
6.5.3.2. \(x_0\) far from solution#
Consider: $\(x_0 = [-0.1, 0.2]^T\)$
# Specify starting point
x0 = np.array([-0.1, 0.2])
# Call optimization routine
x,f,p,B = alg1_sr1(x0,my_f_ex_2_19,calc_grad,eps1,eps2,verbose=False,max_iter=250);
# SR1 Hessian approximation
print("\nSR1 Hessian approximation. B[k] =")
analyze_hes(B[-1])
# Actual Hessian
print("True Hessian at x*. B =")
analyze_hes(my_hes_approx(x[-1],calc_grad,1E-6))
Iter. f(x) ||grad(x)|| ||p|| min(lambda)
0 -4.5540e-04 9.2580e-03 9.2580e-03 1.0000e+00
1 -5.4879e-04 1.0959e-02 5.9578e-02 -1.8395e-01
2 -1.5604e-04 3.4877e-03 2.7627e-02 -1.2568e-01
3 -8.3235e-05 1.9563e-03 3.5000e-02 -5.5390e-02
4 -3.6006e-05 9.0023e-04 2.9559e-02 -3.0011e-02
5 -1.7097e-05 4.4964e-04 2.9246e-02 -1.5078e-02
6 -7.9092e-06 2.1835e-04 2.7389e-02 -7.7836e-03
7 -3.7242e-06 1.0745e-04 2.6349e-02 -3.9664e-03
8 -1.7531e-06 5.2702e-05 2.5208e-02 -2.0268e-03
Done.
x* = [-0.11328951 -0.05033867]
SR1 Hessian approximation. B[k] =
[[ 1.00141633e+00 -4.82365647e-02]
[-4.82365647e-02 2.91945446e-04]]
Eigenvalues: [ 1.00373512+0.j -0.00202684+0.j]
True Hessian at x*. B =
[[ 6.99115848e-05 -2.18301460e-04]
[-2.18301460e-04 -7.02712139e-04]]
Eigenvalues: [ 0.00012733+0.j -0.00076013+0.j]
6.5.3.3. Activity/Discussion#
Classify each candidate solution.
Is the SR1 approximation always positive definite?
6.5.4. Broyden update with Cholesky factorization#
As part of Algorithms Homework 3, you will adapt this example and implement the BFGS (Broyden-Fletcher-Goldfarb-Shanno) update formula.
You may decide to use the Cholesky factorization of \(B^{k}\),
to make your BFGS update more efficient. (This is not required). Let’s see how to do Cholseky factorization with SciPy.
## Create random P.D. and symmetric matrix
B_ = np.eye(3) + xxT(np.random.normal(0,1,3))
print("B = \n",B_,"\n")
## Perform Cholesky factorization.
# By default, lower=False and L is upper triangular. Either works here,
# but we prefer L to be lower triangular for convention.
L = linalg.cholesky(B_,lower=True)
print("L = \n",L,"\n")
## Reconstruct B
print("L*L.T = \n",L.dot(L.T),"\n")
B =
[[ 1.00098448 0.00242031 -0.01329946]
[ 0.00242031 1.00595022 -0.03269612]
[-0.01329946 -0.03269612 1.17966326]]
L =
[[ 1.00049212 0. 0. ]
[ 0.00241912 1.00296778 0. ]
[-0.01329292 -0.03256731 1.08555328]]
L*L.T =
[[ 1.00098448 0.00242031 -0.01329946]
[ 0.00242031 1.00595022 -0.03269612]
[-0.01329946 -0.03269612 1.17966326]]

