7.5. Second Order Optimality Conditions#
# This code cell installs packages on Colab
import sys
if "google.colab" in sys.modules:
!wget "https://raw.githubusercontent.com/ndcbe/CBE60499/main/notebooks/helper.py"
import helper
helper.install_idaes()
helper.install_ipopt()
helper.download_figures(['cone1.png','cone2.png'])
7.5.1. Helpful Cones#
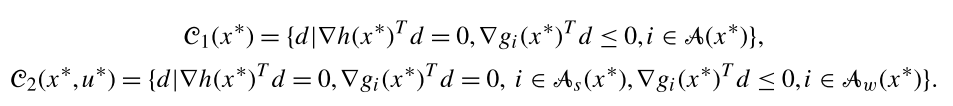

7.5.2. Second Order Necessary Conditions#
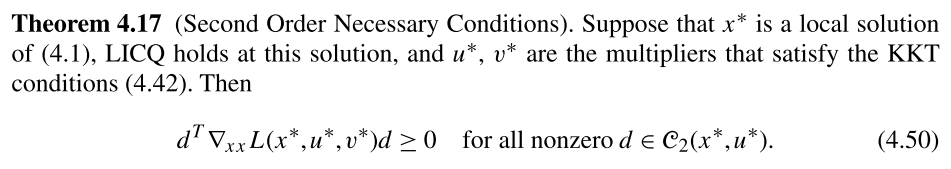
7.5.3. Second Order Sufficient Conditions#

7.5.4. Reduced Hessian#



7.5.5. Example#

See errata here: http://numero.cheme.cmu.edu/content/errata2.pdf
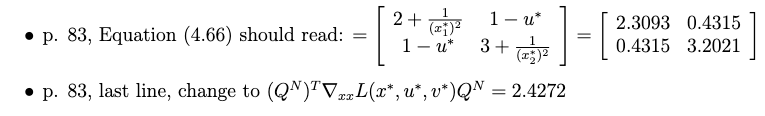
7.5.5.1. Calculation with numpy#
import numpy as np
# Define the Hessian of the Lagrange function
hessian_L = np.array([[2.3093, 0.4315], [0.4315, 3.2021]])
print(hessian_L)
[[2.3093 0.4315]
[0.4315 3.2021]]
# Define the gradiant of the constraints
A = np.reshape(np.array([-2.2245, -1.7981]),(2,1))
print(A)
[[-2.2245]
[-1.7981]]
Calculate the complete QR factorization.
\[
A = Q \times R
\]
# Calculate the COMPLETE QR factorization
Q, R = np.linalg.qr(A, mode='complete')
print(Q)
[[-0.77770385 -0.62863083]
[-0.62863083 0.77770385]]
print(R)
[[2.86034331]
[0. ]]
print(Q @ R)
[[-2.2245]
[-1.7981]]
The second column of \(Q\) is the null space of \(A\). How do we know it is the null space? It corresponds to the second element of \(R\) which is 0.
Finally, we can calculate the reduced Hessian:
# Calculate the reduced Hessian
print("Reduced Hessian w.r.t. null space of constraints:")
Q[:,1].T @ hessian_L @ Q[:,1]
Reduced Hessian w.r.t. null space of constraints:
2.4273753426093774
7.5.5.2. Calculate with Pyomo#
7.5.5.2.1. Define and solve the model#
import pyomo.environ as pyo
m = pyo.ConcreteModel()
# Define variables
m.x1 = pyo.Var(initialize=1)
m.x2 = pyo.Var(initialize=1)
# Define constraints
# Note: changing this to an equality constraint
# changes the reduced_hessian
m.con1 = pyo.Constraint(expr=4 - m.x1*m.x2 <= 0 )
# Define objective
m.obj = pyo.Objective(expr=m.x1**2 - 4*m.x1 + 1.5*m.x2**2 - 7*m.x2 + m.x1*m.x2 + 9 - pyo.log(m.x1) - pyo.log(m.x2))
# Obtain dual solutions from first solve and send to warm start
m.dual = pyo.Suffix(direction=pyo.Suffix.IMPORT)
# Specify Ipopt as the solver and solve
opt = pyo.SolverFactory('ipopt')
opt.solve(m, tee=True)
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 0
Number of nonzeros in inequality constraint Jacobian.: 2
Number of nonzeros in Lagrangian Hessian.............: 3
Total number of variables............................: 2
variables with only lower bounds: 0
variables with lower and upper bounds: 0
variables with only upper bounds: 0
Total number of equality constraints.................: 0
Total number of inequality constraints...............: 1
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 1.5000000e+00 3.00e+00 2.67e+00 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 -3.3886674e-01 2.05e+00 5.62e+00 -1.0 1.78e+00 - 1.00e+00 2.75e-01f 1
2 -1.1897000e-01 0.00e+00 5.69e-01 -1.0 8.27e-01 - 1.00e+00 1.00e+00f 1
3 -4.7085742e-01 0.00e+00 6.15e-02 -1.7 1.54e-01 - 1.00e+00 1.00e+00h 1
4 -4.9093265e-01 0.00e+00 5.84e-04 -2.5 2.04e-02 - 1.00e+00 1.00e+00h 1
5 -4.9428887e-01 0.00e+00 4.51e-06 -3.8 5.92e-03 - 1.00e+00 1.00e+00h 1
6 -4.9445149e-01 0.00e+00 9.87e-09 -5.7 2.84e-04 - 1.00e+00 1.00e+00h 1
7 -4.9445337e-01 0.00e+00 1.29e-12 -8.6 3.29e-06 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 7
(scaled) (unscaled)
Objective...............: -4.9445336916038940e-01 -4.9445336916038940e-01
Dual infeasibility......: 1.2920775560587572e-12 1.2920775560587572e-12
Constraint violation....: 0.0000000000000000e+00 0.0000000000000000e+00
Complementarity.........: 2.5098574967664475e-09 2.5098574967664475e-09
Overall NLP error.......: 2.5098574967664475e-09 2.5098574967664475e-09
Number of objective function evaluations = 8
Number of objective gradient evaluations = 8
Number of equality constraint evaluations = 0
Number of inequality constraint evaluations = 8
Number of equality constraint Jacobian evaluations = 0
Number of inequality constraint Jacobian evaluations = 8
Number of Lagrangian Hessian evaluations = 7
Total CPU secs in IPOPT (w/o function evaluations) = 0.002
Total CPU secs in NLP function evaluations = 0.000
EXIT: Optimal Solution Found.
{'Problem': [{'Lower bound': -inf, 'Upper bound': inf, 'Number of objectives': 1, 'Number of constraints': 1, 'Number of variables': 2, 'Sense': 'unknown'}], 'Solver': [{'Status': 'ok', 'Message': 'Ipopt 3.13.2\\x3a Optimal Solution Found', 'Termination condition': 'optimal', 'Id': 0, 'Error rc': 0, 'Time': 0.04768204689025879}], 'Solution': [OrderedDict([('number of solutions', 0), ('number of solutions displayed', 0)])]}
7.5.5.2.2. Extract the dual variable for the constraint#
m.dual[m.con1]
-0.5684977067847848
This is negative because of a sign convention in Pyomo. Notice it matches the book (expect the sign).
7.5.5.2.3. Extract the reduced Hessian#
# Warning: this Pyomo feature is experimental
from pyomo.contrib.interior_point.inverse_reduced_hessian import inv_reduced_hessian_barrier
# https://github.com/Pyomo/pyomo/blob/main/pyomo/contrib/interior_point/inverse_reduced_hessian.py
Compute the reduced Hessian with respect to \(x_1\)
solve_result, inv_red_hes = inv_reduced_hessian_barrier(
m,
independent_variables= [m.x1], # Warning: these variables cannot be at their bounds
tee=True)
print("\nReduced Hessian w.r.t. x1:")
print(np.linalg.inv(inv_red_hes))
Ipopt 3.13.2: bound_relax_factor=0
honor_original_bounds=no
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 0
Number of nonzeros in inequality constraint Jacobian.: 2
Number of nonzeros in Lagrangian Hessian.............: 3
Total number of variables............................: 2
variables with only lower bounds: 0
variables with lower and upper bounds: 0
variables with only upper bounds: 0
Total number of equality constraints.................: 0
Total number of inequality constraints...............: 1
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 -4.9445337e-01 3.56e-08 3.85e-01 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 -4.7328569e-01 0.00e+00 3.92e-04 -1.7 1.17e-02 - 1.00e+00 1.00e+00h 1
2 -4.9381301e-01 0.00e+00 1.46e-04 -3.8 3.57e-02 - 1.00e+00 1.00e+00f 1
3 -4.9445098e-01 0.00e+00 1.74e-07 -5.7 1.06e-03 - 1.00e+00 1.00e+00h 1
4 -4.9445335e-01 0.00e+00 2.15e-12 -8.6 4.10e-06 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 4
(scaled) (unscaled)
Objective...............: -4.9445334641782601e-01 -4.9445334641782601e-01
Dual infeasibility......: 2.1520563109334034e-12 2.1520563109334034e-12
Constraint violation....: 0.0000000000000000e+00 0.0000000000000000e+00
Complementarity.........: 2.5123319576325299e-09 2.5123319576325299e-09
Overall NLP error.......: 2.5123319576325299e-09 2.5123319576325299e-09
Number of objective function evaluations = 5
Number of objective gradient evaluations = 5
Number of equality constraint evaluations = 0
Number of inequality constraint evaluations = 5
Number of equality constraint Jacobian evaluations = 0
Number of inequality constraint Jacobian evaluations = 5
Number of Lagrangian Hessian evaluations = 4
Total CPU secs in IPOPT (w/o function evaluations) = 0.001
Total CPU secs in NLP function evaluations = 0.000
EXIT: Optimal Solution Found.
Reduced Hessian w.r.t. x1:
[[1.99699045]]
Compute the reduced Hessian with respect to \(x_2\)
solve_result, inv_red_hes = inv_reduced_hessian_barrier(
m,
independent_variables= [m.x2], # Warning: these variables cannot be at their bounds
tee=True)
print("\nReduced Hessian w.r.t. x2:")
print(np.linalg.inv(inv_red_hes))
Ipopt 3.13.2: bound_relax_factor=0
honor_original_bounds=no
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 0
Number of nonzeros in inequality constraint Jacobian.: 2
Number of nonzeros in Lagrangian Hessian.............: 3
Total number of variables............................: 2
variables with only lower bounds: 0
variables with lower and upper bounds: 0
variables with only upper bounds: 0
Total number of equality constraints.................: 0
Total number of inequality constraints...............: 1
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 -4.9445335e-01 0.00e+00 3.85e-01 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 -4.7328569e-01 0.00e+00 3.92e-04 -1.7 1.17e-02 - 1.00e+00 1.00e+00h 1
2 -4.9381301e-01 0.00e+00 1.46e-04 -3.8 3.57e-02 - 1.00e+00 1.00e+00f 1
3 -4.9445098e-01 0.00e+00 1.74e-07 -5.7 1.06e-03 - 1.00e+00 1.00e+00h 1
4 -4.9445335e-01 0.00e+00 2.15e-12 -8.6 4.10e-06 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 4
(scaled) (unscaled)
Objective...............: -4.9445334641782779e-01 -4.9445334641782779e-01
Dual infeasibility......: 2.1527224447481785e-12 2.1527224447481785e-12
Constraint violation....: 0.0000000000000000e+00 0.0000000000000000e+00
Complementarity.........: 2.5123319576325299e-09 2.5123319576325299e-09
Overall NLP error.......: 2.5123319576325299e-09 2.5123319576325299e-09
Number of objective function evaluations = 5
Number of objective gradient evaluations = 5
Number of equality constraint evaluations = 0
Number of inequality constraint evaluations = 5
Number of equality constraint Jacobian evaluations = 0
Number of inequality constraint Jacobian evaluations = 5
Number of Lagrangian Hessian evaluations = 4
Total CPU secs in IPOPT (w/o function evaluations) = 0.001
Total CPU secs in NLP function evaluations = 0.000
EXIT: Optimal Solution Found.
Reduced Hessian w.r.t. x2:
[[2.76904325]]
Take away message: The reduced Hessian relative to all three bases (null space, \([1, 0]\), and \([0, 1]\)) is positive definite.

