1.7. 60 Minutes to Pyomo: An Energy Storage Model Predictive Control Example#
# This code cell installs packages on Colab
import sys
if "google.colab" in sys.modules:
!wget "https://raw.githubusercontent.com/ndcbe/optimization/main/notebooks/helper.py"
import helper
helper.easy_install()
else:
sys.path.insert(0, '../')
import helper
helper.set_plotting_style()
import pandas as pd
import pyomo.environ as pyo
import numpy as np
import matplotlib.pyplot as plt
1.7.1. Problem Setup#
1.7.1.1. Background#
In many regions of the world, including the US, electricity generation is scheduled through wholesale electricity markets. Individual generators (resources) transmit information about their operating costs and constraints to the market via a bid. The market operator then solves an optimization problem (e.g., the unit commitment problem) to minimize the total electricity generator cost. The market operator decides which generators to dispatch during each hour to satisfy the forecasted demand while honoring limitations for each generator (e.g., maximum ramp rate, the required time for start-up/shutdown, etc.).
Read more information here:
1.7.1.2. Pandas and Energy Prices#
The CSV (comma separated value) file Prices_DAM_ALTA2G_7_B1.csv contains price data for a single location in California for an entire year. The prices are set every hour and have units $/MWh. We will use the package pandas to import and analyze the data.
# Load the data file
ca_data = pd.read_csv('https://raw.githubusercontent.com/ndcbe/optimization/main/notebooks/data/Prices_DAM_ALTA2G_7_B1.csv',names=['price'])
# Print the first 10 rows
ca_data.head()
| price | |
|---|---|
| 0 | 36.757 |
| 1 | 34.924 |
| 2 | 33.389 |
| 3 | 32.035 |
| 4 | 33.694 |
Next we can calculate summary statistics:
ca_data.describe()
| price | |
|---|---|
| count | 8760.000000 |
| mean | 32.516994 |
| std | 9.723477 |
| min | -2.128700 |
| 25% | 26.510000 |
| 50% | 30.797500 |
| 75% | 37.544750 |
| max | 116.340000 |
Activity
What are 2 or 3 interesting observations from these summary statistics?
Next, let’s visualize the data in a histogram:
plt.hist(ca_data["price"])
plt.xlabel('Day-Ahead Market Energy Price [$/MWh]',fontsize=18)
plt.ylabel('Count',fontsize=18)
plt.grid(True)
plt.show()
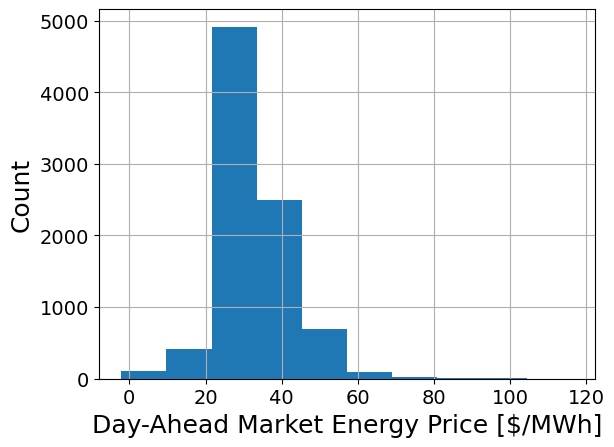
Finaly, let’s visualize the prices during the first full calendar week. The data are for calendar year 2015. For reference, January 1, 2015 was a Thursday.
offset = 4 # days
number_of_days = 7
first_week = ca_data["price"].to_numpy()[(0 + offset)*24: (0 + offset + number_of_days)*24]
# Customize the major and minor ticks on the plots
from matplotlib.ticker import MultipleLocator
fig, ax = plt.subplots()
# Plot data
ax.plot(range(0,number_of_days*24), first_week)
# Set major ticks every 24 hours (1 day)
ax.xaxis.set_major_locator(MultipleLocator(24))
# Set minor ticks every 6 hours
ax.xaxis.set_minor_locator(MultipleLocator(6))
# Set labels, add grid
plt.xlabel('Hour',fontsize=18)
plt.ylabel('DAM Energy Price [$/MWh]',fontsize=18)
plt.grid(True)
plt.show()
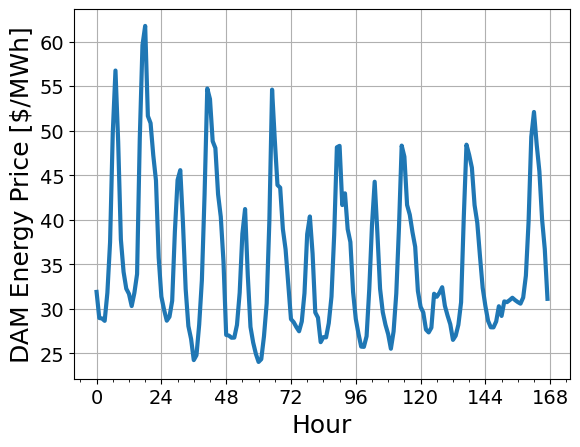
Activity
What are 1 or 2 interesting observations from these plots?
1.7.1.3. Optimization Mathematical Model#
Energy (price) arbitrage is the idea of using energy storage (e.g., a battery) to take advantage of the significant daily energy price swings. This gives rise to many analysis questions including:
If a battery energy storage system perfectly timed it’s energy purchases and sales (i.e., it could perfectly forecast the market price), how much money could it make from energy arbitrage?
We can answer this question using mathematical/computational optimization!
Let’s start by drawing a picture.

1.7.1.3.1. Sets#
Let’s say we want to define our optimization problem over a 24 hour window. The day-ahead market sets the energy prices in 1-hour intervals. We’ll define the set
for time where \(N = 24\) for a 24-hour planning horizon. For convienence, we’ll also define \(\mathcal{T}' := \mathcal{T} / \{0\}\), which is the original set \(\mathcal{T}\) substract subset \(\{0\}\).
1.7.1.3.2. Variables#
Next, let’s identify the variables in the optimization problem:
\(E_t\), energy stored in battery at time \(t\), units: MWh
\(d_t\), battery discharge power (sold to market) during time interval [t-1, t), units: MW
\(c_t\), battery charge power (purchased from the market) during time interval [t-1, t), units: MW
Notice how all of these variables are indexed by the timestep \(t\). We’ll write in the model \(t \in \mathcal{T}'\)
1.7.1.3.3. Parameters#
Parameters are data that are constant during the optimization problem. Here we have:
\(\pi_t\): Energy price during time interval [t-1, t), units: $/MW
\(\eta\): Round trip efficiency, units: dimensionless
\(c_{max}\) Maximum charge power, units: MW
\(d_{max}\) Maximum discharge power, units: MW
\(E_{max}\) Maximum storage energy, units: MWh
\(E_{0}\) Energy in storage at time \(t=0\), units: MWh
\(\Delta t = 1\) hour, Timestep for grid decisions and prices (fixed)
1.7.1.3.4. Objective and Constraints#
Finally, we’ll identify the objective, which is the function to improve, and the mathematical constraints. Below is the full mathematical model for the problem:
Activity
Write on paper a 1-sentence description for each equation.
1.7.1.4. Degree of Freedom Analysis#
Before we program our model in Pyomo, it is very important to first perform a degree of freedom analysis. Here are the steps:
Count the number of variables
Count the number of equality constraints
Degrees of freedom = number of variables subtract number of equality constraints
The degrees of freedom are the number of decisions variables that be freely manipulated by the optimizer. If there are no degrees of freedom, we ofter say the problem is square or it is a simulation problem.
For now, we will ignore inequality constraints and bounds. Later in the semester we will revisit degree of freedom analysis using some optimization theory concepts (e.g., active sets).
Activity
Perform degree of freedom analysis.
1.7.2. Pyomo Modeling Components#
Note
Important: Do NOT implement an optimization model in Pyomo (or any other software) until you have written it on paper and performed degree of freedom analysis, as done above. Be sure to resolve any doubts, questions, or concerns while your model is still on paper. When applying optimization to a problem, a majority of the mistakes happen at the problem formulation step. So do not rush it!
1.7.2.1. Create ConcreteModel#
We will start by creating a concrete Pyomo model. Recall, Pyomo is an object-oriented algebriac modeling language. The line below creates an instance of the ConcreteModel class.
m = pyo.ConcreteModel()
For those unfamilar with object-oriented programming, m is a container to define an optimization model. It includes a bunch of functionality to interface with different optimization solvers, perform diagnostics, and inspect the solution.
Pyomo also supports abstract models, but we will stick with concrete models this semester. See the Pyomo textbook for more details if you are curious.
1.7.2.2. Sets#
We start by declaring a set for time. From above, recall we want to index all of the variables and constraints over the set
# Save the number of timesteps
m.N = 24
# Define the horizon set
m.HORIZON = pyo.Set(initialize=range(1,m.N+1))
Some Pyomo modelers prefer to use all capital names for sets; this is a personal preference.
1.7.2.3. Variables#
Next, we can declare our three variables: \(E_t\), \(c_t\), \(d_t\)
# Charging rate [MW]
m.c = pyo.Var(m.HORIZON, initialize = 0.0, bounds=(0, 1), domain=pyo.NonNegativeReals)
# Discharging rate [MW]
m.d = pyo.Var(m.HORIZON, initialize = 0.0, bounds=(0, 1), domain=pyo.NonNegativeReals)
# Energy (state-of-charge) [MWh]
m.E = pyo.Var(m.HORIZON, initialize = 0.0, bounds=(0, 4), domain=pyo.NonNegativeReals)
See the table below (Hart et al., 2017) for an explanation of the arguments for Var:
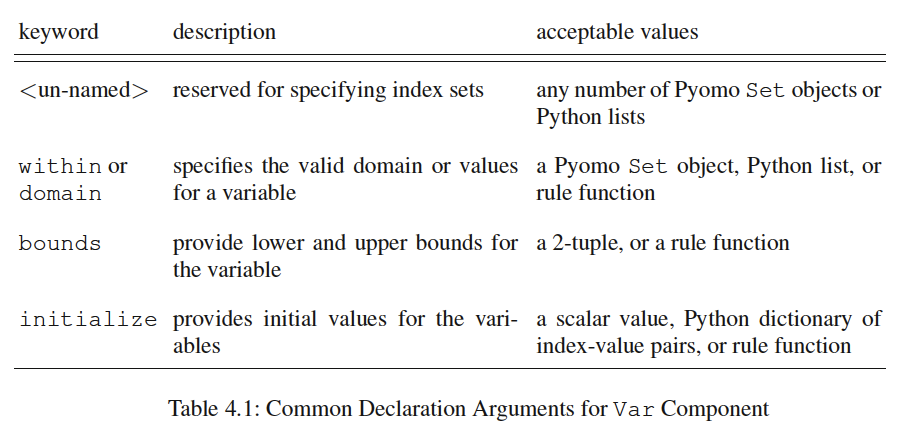
Pyomo also supports units. Even though we are not explicitly using the feature, the units for all variables are clearly marked in the comments.
The following table (Hart et al., 2017) shows the options for the within/domain variable keyword:
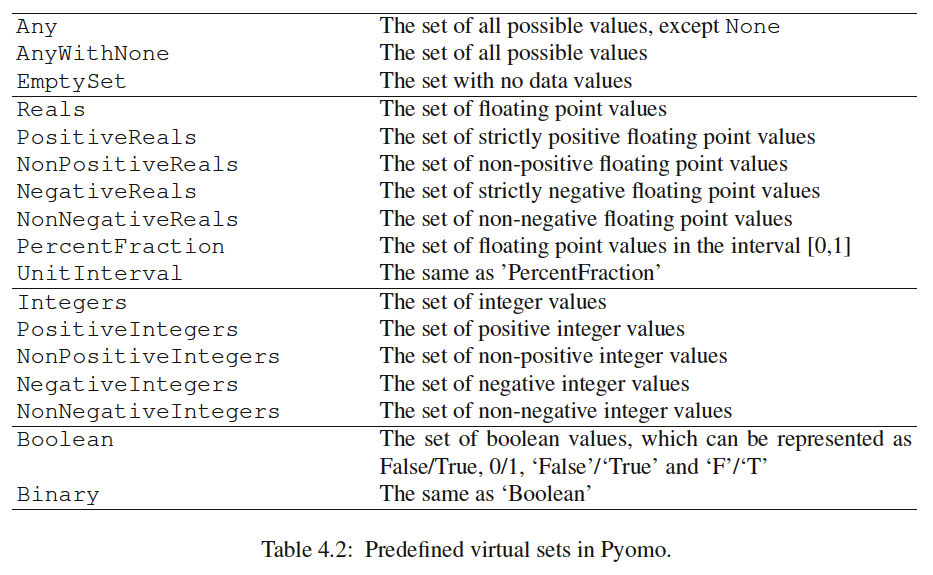
In the example above, domain=pyo.NonNegativeReals is not needs, as we are specifying stricker bounds. It is included above to show the syntax.
1.7.2.4. Parameters (Constants / Data)#
The next step is to define the parameter data: \(\pi_t\) (energy prices), \(\eta\) (round trip efficiency) and \(E_0\) (intial energy storage level).
# Square root of round trip efficiency
m.sqrteta = pyo.Param(initialize = pyo.sqrt(0.88))
# Energy in battery at t=0
m.E0 = pyo.Param(initialize = 2.0, mutable=True)
m.pprint()
1 Set Declarations
HORIZON : Size=1, Index=None, Ordered=Insertion
Key : Dimen : Domain : Size : Members
None : 1 : Any : 24 : {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24}
2 Param Declarations
E0 : Size=1, Index=None, Domain=Any, Default=None, Mutable=True
Key : Value
None : 2.0
sqrteta : Size=1, Index=None, Domain=Any, Default=None, Mutable=False
Key : Value
None : 0.938083151964686
3 Var Declarations
E : Size=24, Index=HORIZON
Key : Lower : Value : Upper : Fixed : Stale : Domain
1 : 0 : 0.0 : 4 : False : False : NonNegativeReals
2 : 0 : 0.0 : 4 : False : False : NonNegativeReals
3 : 0 : 0.0 : 4 : False : False : NonNegativeReals
4 : 0 : 0.0 : 4 : False : False : NonNegativeReals
5 : 0 : 0.0 : 4 : False : False : NonNegativeReals
6 : 0 : 0.0 : 4 : False : False : NonNegativeReals
7 : 0 : 0.0 : 4 : False : False : NonNegativeReals
8 : 0 : 0.0 : 4 : False : False : NonNegativeReals
9 : 0 : 0.0 : 4 : False : False : NonNegativeReals
10 : 0 : 0.0 : 4 : False : False : NonNegativeReals
11 : 0 : 0.0 : 4 : False : False : NonNegativeReals
12 : 0 : 0.0 : 4 : False : False : NonNegativeReals
13 : 0 : 0.0 : 4 : False : False : NonNegativeReals
14 : 0 : 0.0 : 4 : False : False : NonNegativeReals
15 : 0 : 0.0 : 4 : False : False : NonNegativeReals
16 : 0 : 0.0 : 4 : False : False : NonNegativeReals
17 : 0 : 0.0 : 4 : False : False : NonNegativeReals
18 : 0 : 0.0 : 4 : False : False : NonNegativeReals
19 : 0 : 0.0 : 4 : False : False : NonNegativeReals
20 : 0 : 0.0 : 4 : False : False : NonNegativeReals
21 : 0 : 0.0 : 4 : False : False : NonNegativeReals
22 : 0 : 0.0 : 4 : False : False : NonNegativeReals
23 : 0 : 0.0 : 4 : False : False : NonNegativeReals
24 : 0 : 0.0 : 4 : False : False : NonNegativeReals
c : Size=24, Index=HORIZON
Key : Lower : Value : Upper : Fixed : Stale : Domain
1 : 0 : 0.0 : 1 : False : False : NonNegativeReals
2 : 0 : 0.0 : 1 : False : False : NonNegativeReals
3 : 0 : 0.0 : 1 : False : False : NonNegativeReals
4 : 0 : 0.0 : 1 : False : False : NonNegativeReals
5 : 0 : 0.0 : 1 : False : False : NonNegativeReals
6 : 0 : 0.0 : 1 : False : False : NonNegativeReals
7 : 0 : 0.0 : 1 : False : False : NonNegativeReals
8 : 0 : 0.0 : 1 : False : False : NonNegativeReals
9 : 0 : 0.0 : 1 : False : False : NonNegativeReals
10 : 0 : 0.0 : 1 : False : False : NonNegativeReals
11 : 0 : 0.0 : 1 : False : False : NonNegativeReals
12 : 0 : 0.0 : 1 : False : False : NonNegativeReals
13 : 0 : 0.0 : 1 : False : False : NonNegativeReals
14 : 0 : 0.0 : 1 : False : False : NonNegativeReals
15 : 0 : 0.0 : 1 : False : False : NonNegativeReals
16 : 0 : 0.0 : 1 : False : False : NonNegativeReals
17 : 0 : 0.0 : 1 : False : False : NonNegativeReals
18 : 0 : 0.0 : 1 : False : False : NonNegativeReals
19 : 0 : 0.0 : 1 : False : False : NonNegativeReals
20 : 0 : 0.0 : 1 : False : False : NonNegativeReals
21 : 0 : 0.0 : 1 : False : False : NonNegativeReals
22 : 0 : 0.0 : 1 : False : False : NonNegativeReals
23 : 0 : 0.0 : 1 : False : False : NonNegativeReals
24 : 0 : 0.0 : 1 : False : False : NonNegativeReals
d : Size=24, Index=HORIZON
Key : Lower : Value : Upper : Fixed : Stale : Domain
1 : 0 : 0.0 : 1 : False : False : NonNegativeReals
2 : 0 : 0.0 : 1 : False : False : NonNegativeReals
3 : 0 : 0.0 : 1 : False : False : NonNegativeReals
4 : 0 : 0.0 : 1 : False : False : NonNegativeReals
5 : 0 : 0.0 : 1 : False : False : NonNegativeReals
6 : 0 : 0.0 : 1 : False : False : NonNegativeReals
7 : 0 : 0.0 : 1 : False : False : NonNegativeReals
8 : 0 : 0.0 : 1 : False : False : NonNegativeReals
9 : 0 : 0.0 : 1 : False : False : NonNegativeReals
10 : 0 : 0.0 : 1 : False : False : NonNegativeReals
11 : 0 : 0.0 : 1 : False : False : NonNegativeReals
12 : 0 : 0.0 : 1 : False : False : NonNegativeReals
13 : 0 : 0.0 : 1 : False : False : NonNegativeReals
14 : 0 : 0.0 : 1 : False : False : NonNegativeReals
15 : 0 : 0.0 : 1 : False : False : NonNegativeReals
16 : 0 : 0.0 : 1 : False : False : NonNegativeReals
17 : 0 : 0.0 : 1 : False : False : NonNegativeReals
18 : 0 : 0.0 : 1 : False : False : NonNegativeReals
19 : 0 : 0.0 : 1 : False : False : NonNegativeReals
20 : 0 : 0.0 : 1 : False : False : NonNegativeReals
21 : 0 : 0.0 : 1 : False : False : NonNegativeReals
22 : 0 : 0.0 : 1 : False : False : NonNegativeReals
23 : 0 : 0.0 : 1 : False : False : NonNegativeReals
24 : 0 : 0.0 : 1 : False : False : NonNegativeReals
6 Declarations: HORIZON c d E sqrteta E0
We see the initialize keyword is used to set the parameter value. When mutable=True, Pyomo builds the model such that we can easily update the parameter and resolved. Later in the notebook, we will see how this is helpful.
Below is a table (Hart et al., 2017) of options for Param:
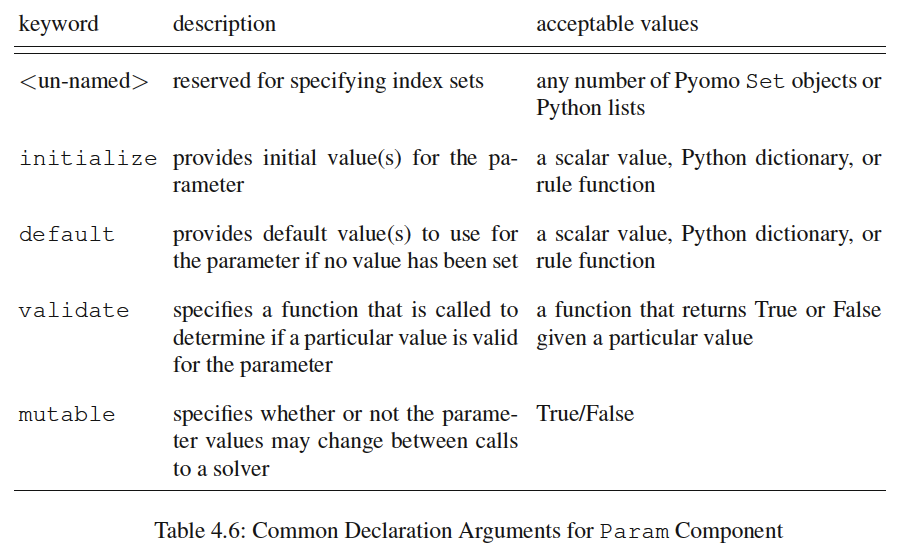
Let’s dig in more to the initialize syntax. First, let’s convert the price data from pandas into a numpy array:
my_np_array = ca_data["price"].to_numpy()
# get the length
print("len(my_np_array) =",len(my_np_array))
len(my_np_array) = 8760
Recall, our dataset constains an entire year (which has 8760 hours). To access the first 24 hours, we use the following slice:
my_np_array[0:24]
array([36.757, 34.924, 33.389, 32.035, 33.694, 36.88 , 38.662, 38.975,
35.08 , 29.979, 27.546, 25.944, 24.587, 23.788, 25.236, 30.145,
44.622, 50.957, 59.345, 52.564, 52.819, 48.816, 46.685, 38.575])
len(my_np_array[0:24])
24
Initializing parameters in Pyomo can be precarious. The most fool proof strategy is to prepare a dictionary where the keys match the elements of the sets that index the parameter of interest. In our example, m.HORIZON contains 1, …, 24, so we need a dictionary with the keys 1, …, 24.
ca_data["price"][0:24].to_dict()
{0: 36.757,
1: 34.924,
2: 33.389,
3: 32.035,
4: 33.694,
5: 36.88,
6: 38.662,
7: 38.975,
8: 35.08,
9: 29.979,
10: 27.546,
11: 25.944,
12: 24.587,
13: 23.788,
14: 25.236,
15: 30.145,
16: 44.622,
17: 50.957,
18: 59.345,
19: 52.564,
20: 52.819,
21: 48.816,
22: 46.685,
23: 38.575}
That was easy. But what if we wanted to build the optimization model using the second day of data? Let’s give it a try:
ca_data["price"][24:48].to_dict()
{24: 37.239,
25: 34.766,
26: 34.645,
27: 33.21,
28: 35.524,
29: 44.143,
30: 39.231,
31: 41.251,
32: 36.406,
33: 31.194,
34: 29.695,
35: 27.034,
36: 26.009,
37: 24.829,
38: 26.168,
39: 29.921,
40: 44.137,
41: 51.751,
42: 51.652,
43: 46.675,
44: 45.274,
45: 44.053,
46: 46.779,
47: 37.307}
Activity
Uncomment the line below and look at the error message and read below. Then comment the line out again and rerun the notebook up to this cell.
# m.price = pyo.Param(m.HORIZON, initialize = ca_data["price"][24:48].to_dict(), domain=pyo.Reals)
You should get the following error:
ERROR: Constructing component 'price' from data=None failed: KeyError: "Index
'25' is not valid for indexed component 'price'"
Why did this happen? Our dictionary started with key 25 but we tried to create a Param indexed over 1 through 24.
Let’s say we want to build the optimization model starting for an arbitrary day. We need to extract the correct data from the pandas DataFrame and convert it to a dictionary with the correct keys. The function below does this using a simple, easy to follow approach. There is more compact “Pythonic” syntax to do this, but we will skip it for this getting started tutorial.
def prepare_price_data(day):
''' Prepare dictionary of price data
Arugments:
day: int, day to start. day = 0 is the first day
Returns:
data_dict: dictionary of price data with keys 1 to 24
Notes:
This function assumes the pandas DataFrame ca_data is in scope.
'''
# Create empty dictionary
data_dict = {}
# Extract data as numpy array
data_np_array = ca_data["price"][(day)*24:24*(day+1)].to_numpy()
# Loop over elements of numpy array
for i in range(0,24):
# Add element to data_dict
data_dict[i + 1] = data_np_array[i]
return data_dict
# Create input data for day 1 (i.e., January 2, 2015)
my_data_dict = prepare_price_data(1)
print(my_data_dict)
{1: 37.239, 2: 34.766, 3: 34.645, 4: 33.21, 5: 35.524, 6: 44.143, 7: 39.231, 8: 41.251, 9: 36.406, 10: 31.194, 11: 29.695, 12: 27.034, 13: 26.009, 14: 24.829, 15: 26.168, 16: 29.921, 17: 44.137, 18: 51.751, 19: 51.652, 20: 46.675, 21: 45.274, 22: 44.053, 23: 46.779, 24: 37.307}
Activity
Confirm my_data_dict contains the correct prices for the January 2, 2015.
# Add your solution here
array([37.239, 34.766, 34.645, 33.21 , 35.524, 44.143, 39.231, 41.251,
36.406, 31.194, 29.695, 27.034, 26.009, 24.829, 26.168, 29.921,
44.137, 51.751, 51.652, 46.675, 45.274, 44.053, 46.779, 37.307])
Now we are ready to define the price data parameter:
m.price = pyo.Param(m.HORIZON, initialize = my_data_dict, domain=pyo.Reals, mutable=True)
Note
Tip: When initializing variables and parameters with a pandas DataFrame, always convert to dictionary and check the keys. Often incorrectly loaded data is the root cause of unexpected errors or strange results. Checking the keys while building the model helps prevent these mistakes.
1.7.2.5. Objectives#
Next, we will declare the objective function in Pyomo. Below are two equally valid syntax optimizations.
# Approach 1: Define a function and use *rule=*
def objfun(model):
return sum((-model.c[t] + model.d[t]) * model.price[t] for t in model.HORIZON)
m.OBJ = pyo.Objective(rule = objfun, sense = pyo.maximize)
# Approach 2: Use *expr=*
# m.OBJ = pyo.Objective(expr = sum((-m.c[t] + m.d[t]) * m.price[t] for t in model.HORIZON),
# sense = pyo.maximize)
Activity
Comment out Approach 2 above and rerun the notebook. You’ll get a warning message if you do not comment out Approach 1. The answer should not change.
The following table (Hart et al., 2017) summarizes the keyword arguments for Objective:

1.7.2.6. Constraints#
Now let’s add the last model component: the constraints.
# Define Energy Balance constraints. [MWh] = [MW]*[1 hr]
# Note: this model assumes 1-hour timestep in price data and control actions.
def EnergyBalance(model,t):
# First timestep
if t == 1 :
return model.E[t] == model.E0 + model.c[t]*model.sqrteta-model.d[t]/model.sqrteta
# Subsequent timesteps
else :
return model.E[t] == model.E[t-1]+model.c[t]*model.sqrteta-model.d[t]/model.sqrteta
m.EnergyBalance_Con = pyo.Constraint(m.HORIZON, rule = EnergyBalance)
# Enforce the amount of energy is the storage at the final time must equal
# the initial time.
# [MWh] = [MWh]
m.PeriodicBoundaryCondition = pyo.Constraint(expr=m.E0 == m.E[m.N])
Notice the above model includes detailed comments with the units for the left-hand side and right-hand side of each equation. This is strongly recommend; it is easy for units mistakes to go undetected in a complicated Pyomo model. Alternately, you can also use the units feature in Pyomo.
We see in this example a big advantage of the rule= approach for defininng a constraint. Inside the function EnergyBalance we incorporate a logical statement for how to handle the first timestep (which uses parameter E0).
Below is a table of keyword arguments for Constraint:

Activity
Compare the two model equations above to the optimization formulation below. Notice the one-to-one corespondance between the equality constraints in the mathematical formulation (below) and calls to pyo.Constraint. Also notice the sets used to create the Pyomo model are listed next to each constraint in the mathematical model. Once you learn the Pyomo syntax, translated a mathematical model into code is easy!
1.7.2.7. Printing the Model#
Here is the optimization model, reproduced from above for convenience:
Now let’s see if our Pyomo model matches the optimization formulation. We will use the pprint() command (pretty print) to inspect the full model.
m.pprint()
1 Set Declarations
HORIZON : Size=1, Index=None, Ordered=Insertion
Key : Dimen : Domain : Size : Members
None : 1 : Any : 24 : {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24}
3 Param Declarations
E0 : Size=1, Index=None, Domain=Any, Default=None, Mutable=True
Key : Value
None : 2.0
price : Size=24, Index=HORIZON, Domain=Reals, Default=None, Mutable=True
Key : Value
1 : 37.239
2 : 34.766
3 : 34.645
4 : 33.21
5 : 35.524
6 : 44.143
7 : 39.231
8 : 41.251
9 : 36.406
10 : 31.194
11 : 29.695
12 : 27.034
13 : 26.009
14 : 24.829
15 : 26.168
16 : 29.921
17 : 44.137
18 : 51.751
19 : 51.652
20 : 46.675
21 : 45.274
22 : 44.053
23 : 46.779
24 : 37.307
sqrteta : Size=1, Index=None, Domain=Any, Default=None, Mutable=False
Key : Value
None : 0.938083151964686
3 Var Declarations
E : Size=24, Index=HORIZON
Key : Lower : Value : Upper : Fixed : Stale : Domain
1 : 0 : 0.0 : 4 : False : False : NonNegativeReals
2 : 0 : 0.0 : 4 : False : False : NonNegativeReals
3 : 0 : 0.0 : 4 : False : False : NonNegativeReals
4 : 0 : 0.0 : 4 : False : False : NonNegativeReals
5 : 0 : 0.0 : 4 : False : False : NonNegativeReals
6 : 0 : 0.0 : 4 : False : False : NonNegativeReals
7 : 0 : 0.0 : 4 : False : False : NonNegativeReals
8 : 0 : 0.0 : 4 : False : False : NonNegativeReals
9 : 0 : 0.0 : 4 : False : False : NonNegativeReals
10 : 0 : 0.0 : 4 : False : False : NonNegativeReals
11 : 0 : 0.0 : 4 : False : False : NonNegativeReals
12 : 0 : 0.0 : 4 : False : False : NonNegativeReals
13 : 0 : 0.0 : 4 : False : False : NonNegativeReals
14 : 0 : 0.0 : 4 : False : False : NonNegativeReals
15 : 0 : 0.0 : 4 : False : False : NonNegativeReals
16 : 0 : 0.0 : 4 : False : False : NonNegativeReals
17 : 0 : 0.0 : 4 : False : False : NonNegativeReals
18 : 0 : 0.0 : 4 : False : False : NonNegativeReals
19 : 0 : 0.0 : 4 : False : False : NonNegativeReals
20 : 0 : 0.0 : 4 : False : False : NonNegativeReals
21 : 0 : 0.0 : 4 : False : False : NonNegativeReals
22 : 0 : 0.0 : 4 : False : False : NonNegativeReals
23 : 0 : 0.0 : 4 : False : False : NonNegativeReals
24 : 0 : 0.0 : 4 : False : False : NonNegativeReals
c : Size=24, Index=HORIZON
Key : Lower : Value : Upper : Fixed : Stale : Domain
1 : 0 : 0.0 : 1 : False : False : NonNegativeReals
2 : 0 : 0.0 : 1 : False : False : NonNegativeReals
3 : 0 : 0.0 : 1 : False : False : NonNegativeReals
4 : 0 : 0.0 : 1 : False : False : NonNegativeReals
5 : 0 : 0.0 : 1 : False : False : NonNegativeReals
6 : 0 : 0.0 : 1 : False : False : NonNegativeReals
7 : 0 : 0.0 : 1 : False : False : NonNegativeReals
8 : 0 : 0.0 : 1 : False : False : NonNegativeReals
9 : 0 : 0.0 : 1 : False : False : NonNegativeReals
10 : 0 : 0.0 : 1 : False : False : NonNegativeReals
11 : 0 : 0.0 : 1 : False : False : NonNegativeReals
12 : 0 : 0.0 : 1 : False : False : NonNegativeReals
13 : 0 : 0.0 : 1 : False : False : NonNegativeReals
14 : 0 : 0.0 : 1 : False : False : NonNegativeReals
15 : 0 : 0.0 : 1 : False : False : NonNegativeReals
16 : 0 : 0.0 : 1 : False : False : NonNegativeReals
17 : 0 : 0.0 : 1 : False : False : NonNegativeReals
18 : 0 : 0.0 : 1 : False : False : NonNegativeReals
19 : 0 : 0.0 : 1 : False : False : NonNegativeReals
20 : 0 : 0.0 : 1 : False : False : NonNegativeReals
21 : 0 : 0.0 : 1 : False : False : NonNegativeReals
22 : 0 : 0.0 : 1 : False : False : NonNegativeReals
23 : 0 : 0.0 : 1 : False : False : NonNegativeReals
24 : 0 : 0.0 : 1 : False : False : NonNegativeReals
d : Size=24, Index=HORIZON
Key : Lower : Value : Upper : Fixed : Stale : Domain
1 : 0 : 0.0 : 1 : False : False : NonNegativeReals
2 : 0 : 0.0 : 1 : False : False : NonNegativeReals
3 : 0 : 0.0 : 1 : False : False : NonNegativeReals
4 : 0 : 0.0 : 1 : False : False : NonNegativeReals
5 : 0 : 0.0 : 1 : False : False : NonNegativeReals
6 : 0 : 0.0 : 1 : False : False : NonNegativeReals
7 : 0 : 0.0 : 1 : False : False : NonNegativeReals
8 : 0 : 0.0 : 1 : False : False : NonNegativeReals
9 : 0 : 0.0 : 1 : False : False : NonNegativeReals
10 : 0 : 0.0 : 1 : False : False : NonNegativeReals
11 : 0 : 0.0 : 1 : False : False : NonNegativeReals
12 : 0 : 0.0 : 1 : False : False : NonNegativeReals
13 : 0 : 0.0 : 1 : False : False : NonNegativeReals
14 : 0 : 0.0 : 1 : False : False : NonNegativeReals
15 : 0 : 0.0 : 1 : False : False : NonNegativeReals
16 : 0 : 0.0 : 1 : False : False : NonNegativeReals
17 : 0 : 0.0 : 1 : False : False : NonNegativeReals
18 : 0 : 0.0 : 1 : False : False : NonNegativeReals
19 : 0 : 0.0 : 1 : False : False : NonNegativeReals
20 : 0 : 0.0 : 1 : False : False : NonNegativeReals
21 : 0 : 0.0 : 1 : False : False : NonNegativeReals
22 : 0 : 0.0 : 1 : False : False : NonNegativeReals
23 : 0 : 0.0 : 1 : False : False : NonNegativeReals
24 : 0 : 0.0 : 1 : False : False : NonNegativeReals
1 Objective Declarations
OBJ : Size=1, Index=None, Active=True
Key : Active : Sense : Expression
None : True : maximize : (- c[1] + d[1])*price[1] + (- c[2] + d[2])*price[2] + (- c[3] + d[3])*price[3] + (- c[4] + d[4])*price[4] + (- c[5] + d[5])*price[5] + (- c[6] + d[6])*price[6] + (- c[7] + d[7])*price[7] + (- c[8] + d[8])*price[8] + (- c[9] + d[9])*price[9] + (- c[10] + d[10])*price[10] + (- c[11] + d[11])*price[11] + (- c[12] + d[12])*price[12] + (- c[13] + d[13])*price[13] + (- c[14] + d[14])*price[14] + (- c[15] + d[15])*price[15] + (- c[16] + d[16])*price[16] + (- c[17] + d[17])*price[17] + (- c[18] + d[18])*price[18] + (- c[19] + d[19])*price[19] + (- c[20] + d[20])*price[20] + (- c[21] + d[21])*price[21] + (- c[22] + d[22])*price[22] + (- c[23] + d[23])*price[23] + (- c[24] + d[24])*price[24]
2 Constraint Declarations
EnergyBalance_Con : Size=24, Index=HORIZON, Active=True
Key : Lower : Body : Upper : Active
1 : 0.0 : E[1] - (E0 + 0.938083151964686*c[1] - 1.0660035817780522*d[1]) : 0.0 : True
2 : 0.0 : E[2] - (E[1] + 0.938083151964686*c[2] - 1.0660035817780522*d[2]) : 0.0 : True
3 : 0.0 : E[3] - (E[2] + 0.938083151964686*c[3] - 1.0660035817780522*d[3]) : 0.0 : True
4 : 0.0 : E[4] - (E[3] + 0.938083151964686*c[4] - 1.0660035817780522*d[4]) : 0.0 : True
5 : 0.0 : E[5] - (E[4] + 0.938083151964686*c[5] - 1.0660035817780522*d[5]) : 0.0 : True
6 : 0.0 : E[6] - (E[5] + 0.938083151964686*c[6] - 1.0660035817780522*d[6]) : 0.0 : True
7 : 0.0 : E[7] - (E[6] + 0.938083151964686*c[7] - 1.0660035817780522*d[7]) : 0.0 : True
8 : 0.0 : E[8] - (E[7] + 0.938083151964686*c[8] - 1.0660035817780522*d[8]) : 0.0 : True
9 : 0.0 : E[9] - (E[8] + 0.938083151964686*c[9] - 1.0660035817780522*d[9]) : 0.0 : True
10 : 0.0 : E[10] - (E[9] + 0.938083151964686*c[10] - 1.0660035817780522*d[10]) : 0.0 : True
11 : 0.0 : E[11] - (E[10] + 0.938083151964686*c[11] - 1.0660035817780522*d[11]) : 0.0 : True
12 : 0.0 : E[12] - (E[11] + 0.938083151964686*c[12] - 1.0660035817780522*d[12]) : 0.0 : True
13 : 0.0 : E[13] - (E[12] + 0.938083151964686*c[13] - 1.0660035817780522*d[13]) : 0.0 : True
14 : 0.0 : E[14] - (E[13] + 0.938083151964686*c[14] - 1.0660035817780522*d[14]) : 0.0 : True
15 : 0.0 : E[15] - (E[14] + 0.938083151964686*c[15] - 1.0660035817780522*d[15]) : 0.0 : True
16 : 0.0 : E[16] - (E[15] + 0.938083151964686*c[16] - 1.0660035817780522*d[16]) : 0.0 : True
17 : 0.0 : E[17] - (E[16] + 0.938083151964686*c[17] - 1.0660035817780522*d[17]) : 0.0 : True
18 : 0.0 : E[18] - (E[17] + 0.938083151964686*c[18] - 1.0660035817780522*d[18]) : 0.0 : True
19 : 0.0 : E[19] - (E[18] + 0.938083151964686*c[19] - 1.0660035817780522*d[19]) : 0.0 : True
20 : 0.0 : E[20] - (E[19] + 0.938083151964686*c[20] - 1.0660035817780522*d[20]) : 0.0 : True
21 : 0.0 : E[21] - (E[20] + 0.938083151964686*c[21] - 1.0660035817780522*d[21]) : 0.0 : True
22 : 0.0 : E[22] - (E[21] + 0.938083151964686*c[22] - 1.0660035817780522*d[22]) : 0.0 : True
23 : 0.0 : E[23] - (E[22] + 0.938083151964686*c[23] - 1.0660035817780522*d[23]) : 0.0 : True
24 : 0.0 : E[24] - (E[23] + 0.938083151964686*c[24] - 1.0660035817780522*d[24]) : 0.0 : True
PeriodicBoundaryCondition : Size=1, Index=None, Active=True
Key : Lower : Body : Upper : Active
None : E0 : E[24] : E0 : True
10 Declarations: HORIZON c d E sqrteta E0 price OBJ EnergyBalance_Con PeriodicBoundaryCondition
Activity
Does our Pyomo model match the optimization mathematical model (equations above)? How did we incorporate the inequality constraints into the Pyomo model?
1.7.2.8. Another Approach: Build the Model in a Function#
To emphasize the tutorial nature of this example, we build the model on piece at a time above. An often preferred approach is to define a Python function that builds the model, such as the one below.
Activity
The function below uses elements of price directly. Update the function to add the price data as a parameter in the Pyomo model. Make this parameter mutable as shown above.
Activity
Fix any syntax errors with the function below.
# define a function to build model
def build_model(price,e0 = 0):
'''
Create optimization model for MPC
Arguments (inputs):
price: NumPy array with energy price timeseries
e0: initial value for energy storage level
Returns (outputs):
my_model: Pyomo optimization model
'''
# Create a concrete Pyomo model. We'll learn more about this in a few weeks
my_model = pyo.ConcreteModel()
## Define Sets
# Number of timesteps in planning horizon
my_model.HORIZON = pyo.Set(initialize = range(len(price)))
## Define Parameters
# Square root of round trip efficiency
my_model.sqrteta = pyo.Param(initialize = sqrt(0.88))
# Energy in battery at t=0
my_model.E0 = pyo.Param(initialize = e0, mutable=True)
## Define variables
# Charging rate [MW]
my_model.c = pyo.Var(my_model.HORIZON, initialize = 0.0, bounds=(0, 1))
# Discharging rate [MW]
my_model.d = pyo.Var(my_model.HORIZON, initialize = 0.0, bounds=(0, 1))
# Energy (state-of-charge) [MWh]
my_model.E = pyo.Var(my_model.HORIZON, initialize = 0.0, bounds=(0, 4))
## Define constraints
# Define Energy Balance constraints. [MWh] = [MW]*[1 hr]
# Note: this model assumes 1-hour timestep in price data and control actions.
def EnergyBalance(model,t):
# First timestep
if t == 0 :
return model.E[t] == model.E0 + model.c[t]*model.sqrteta-model.d[t]/model.sqrteta
# Subsequent timesteps
else :
return model.E[t] == model.E[t-1]+model.c[t]*model.sqrteta-model.d[t]/model.sqrteta
my_model.EnergyBalance_Con = pyo.Constraint(my_model.HORIZON, rule = EnergyBalance)
# Enforce the amount of energy is the storage at the final time must equal
# the initial time.
# [MWh] = [MWh]
my_model.PeriodicBoundaryCondition = pyo.Constraint(expr=my_model.E0 == my_model.E[len(price)-1])
## Define the objective function (profit)
# Receding horizon
def objfun(model):
return sum((-model.c[t] + model.d[t]) * price[t] for t in model.HORIZON)
my_model.OBJ = Objective(rule = objfun, sense = maximize)
return my_model
1.7.3. Calling Optimization Solver#
Now that our Pyomo model is complete, we can numerically solve the model!
1.7.3.1. SolverFactory and Solver Options#
Algebraic Modeling Languages, including Pyomo, allow us to define optimization problems is a general, solver agnostic way. This means we can quickly swap between solvers.
We will start by using Ipopt. First, we will create an instance of the SolverFactory:
# Specify the solver
solver = pyo.SolverFactory('ipopt')
Next we can specify options for ipopt such as setting the maximum number of iterations to 50:
solver.options['max_iter'] = 50
Above solver is a SolverFactory objection which includes the dictionary options used to set solver specific options.
Finally, we are ready to solve our model!
results = solver.solve(m, tee=True)
Ipopt 3.13.2: max_iter=50
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
This version of Ipopt was compiled from source code available at
https://github.com/IDAES/Ipopt as part of the Institute for the Design of
Advanced Energy Systems Process Systems Engineering Framework (IDAES PSE
Framework) Copyright (c) 2018-2019. See https://github.com/IDAES/idaes-pse.
This version of Ipopt was compiled using HSL, a collection of Fortran codes
for large-scale scientific computation. All technical papers, sales and
publicity material resulting from use of the HSL codes within IPOPT must
contain the following acknowledgement:
HSL, a collection of Fortran codes for large-scale scientific
computation. See http://www.hsl.rl.ac.uk.
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 96
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 0
Total number of variables............................: 72
variables with only lower bounds: 0
variables with lower and upper bounds: 72
variables with only upper bounds: 0
Total number of equality constraints.................: 25
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 4.9960036e-16 1.99e+00 9.90e+00 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 1.6802497e-01 1.96e+00 9.85e+00 -1.0 1.99e+00 - 5.21e-03 1.44e-02f 1
2 2.1332988e+00 1.75e+00 9.89e+00 -1.0 1.96e+00 - 1.53e-02 1.09e-01f 1
3 2.8652446e+00 1.35e+00 8.39e+00 -1.0 2.08e+00 - 1.09e-01 2.30e-01f 1
4 -4.0482581e+00 1.01e+00 7.83e+00 -1.0 1.86e+00 - 6.95e-02 2.48e-01f 1
5 -1.9676532e+01 8.93e-01 8.09e+00 -1.0 7.32e+00 - 6.32e-02 1.17e-01f 1
6 -3.4249188e+01 7.76e-01 7.89e+00 -1.0 6.21e+00 - 7.33e-02 1.32e-01f 1
7 -4.6657256e+01 6.62e-01 6.69e+00 -1.0 4.81e+00 - 1.52e-01 1.47e-01f 1
8 -5.7915679e+01 5.23e-01 5.29e+00 -1.0 3.16e+00 - 2.06e-01 2.09e-01f 1
9 -6.3119259e+01 3.85e-01 3.92e+00 -1.0 1.34e+00 - 2.30e-01 2.65e-01f 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
10 -6.3706910e+01 3.12e-02 6.94e+00 -1.0 1.08e+00 - 2.85e-01 9.19e-01f 1
11 -6.5994667e+01 7.15e-03 3.17e+00 -1.0 6.93e-01 - 4.40e-01 7.71e-01f 1
12 -6.6628205e+01 3.78e-03 7.49e-01 -1.0 9.35e-01 - 1.00e+00 4.72e-01f 1
13 -6.9888933e+01 5.35e-04 1.10e-01 -1.7 2.22e-01 - 8.88e-01 8.58e-01f 1
14 -7.1043057e+01 8.75e-05 1.55e-02 -2.5 2.18e-01 - 7.83e-01 8.36e-01f 1
15 -7.1364922e+01 1.18e-05 3.85e-02 -3.8 2.82e-01 - 6.56e-01 8.65e-01f 1
16 -7.1428935e+01 4.44e-16 7.22e-03 -3.8 5.71e-02 - 8.66e-01 1.00e+00f 1
17 -7.1430287e+01 4.44e-16 7.11e-15 -3.8 8.19e-03 - 1.00e+00 1.00e+00f 1
18 -7.1437864e+01 4.44e-16 6.15e-15 -5.7 1.65e-03 - 1.00e+00 1.00e+00f 1
19 -7.1437961e+01 8.88e-16 8.30e-15 -8.6 2.85e-05 - 1.00e+00 1.00e+00f 1
Number of Iterations....: 19
(scaled) (unscaled)
Objective...............: -7.1437960657726151e+01 -7.1437960657726151e+01
Dual infeasibility......: 8.2967961385731204e-15 8.2967961385731204e-15
Constraint violation....: 8.8817841970012523e-16 8.8817841970012523e-16
Complementarity.........: 3.2570997913605615e-09 3.2570997913605615e-09
Overall NLP error.......: 3.2570997913605615e-09 3.2570997913605615e-09
Number of objective function evaluations = 20
Number of objective gradient evaluations = 20
Number of equality constraint evaluations = 20
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 20
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 19
Total CPU secs in IPOPT (w/o function evaluations) = 0.007
Total CPU secs in NLP function evaluations = 0.000
EXIT: Optimal Solution Found.
The keyword argument tee=True tells the solve to dispaly its output to the screen.
1.7.3.2. Interpreting Ipopt Output - Verifying Degree of Freedom Analysis#
Your Ipopt output should include the following:
Number of nonzeros in equality constraint Jacobian...: 96
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 0
Total number of variables............................: 72
variables with only lower bounds: 0
variables with lower and upper bounds: 72
variables with only upper bounds: 0
Total number of equality constraints.................: 25
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
Activity
Compare this output to your degree of freedom analysis.
1.7.4. Inspecting the Solution#
We can inspect the entire model solution using pprint().
m.pprint()
1 Set Declarations
HORIZON : Size=1, Index=None, Ordered=Insertion
Key : Dimen : Domain : Size : Members
None : 1 : Any : 24 : {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24}
3 Param Declarations
E0 : Size=1, Index=None, Domain=Any, Default=None, Mutable=True
Key : Value
None : 2.0
price : Size=24, Index=HORIZON, Domain=Reals, Default=None, Mutable=True
Key : Value
1 : 37.239
2 : 34.766
3 : 34.645
4 : 33.21
5 : 35.524
6 : 44.143
7 : 39.231
8 : 41.251
9 : 36.406
10 : 31.194
11 : 29.695
12 : 27.034
13 : 26.009
14 : 24.829
15 : 26.168
16 : 29.921
17 : 44.137
18 : 51.751
19 : 51.652
20 : 46.675
21 : 45.274
22 : 44.053
23 : 46.779
24 : 37.307
sqrteta : Size=1, Index=None, Domain=Any, Default=None, Mutable=False
Key : Value
None : 0.938083151964686
3 Var Declarations
E : Size=24, Index=HORIZON
Key : Lower : Value : Upper : Fixed : Stale : Domain
1 : 0 : 2.000000000804785 : 4 : False : False : NonNegativeReals
2 : 0 : 2.0000000112993037 : 4 : False : False : NonNegativeReals
3 : 0 : 2.0000000319069975 : 4 : False : False : NonNegativeReals
4 : 0 : 2.938083201679067 : 4 : False : False : NonNegativeReals
5 : 0 : 2.9380832045919867 : 4 : False : False : NonNegativeReals
6 : 0 : 1.8720796035614873 : 4 : False : False : NonNegativeReals
7 : 0 : 1.0660035914895196 : 4 : False : False : NonNegativeReals
8 : 0 : 0.0 : 4 : False : False : NonNegativeReals
9 : 0 : 0.0 : 4 : False : False : NonNegativeReals
10 : 0 : 0.0 : 4 : False : False : NonNegativeReals
11 : 0 : 0.24766733414144584 : 4 : False : False : NonNegativeReals
12 : 0 : 1.1857505048666763 : 4 : False : False : NonNegativeReals
13 : 0 : 2.12383367588992 : 4 : False : False : NonNegativeReals
14 : 0 : 3.061916847113209 : 4 : False : False : NonNegativeReals
15 : 0 : 4.0 : 4 : False : False : NonNegativeReals
16 : 0 : 4.0 : 4 : False : False : NonNegativeReals
17 : 0 : 4.0 : 4 : False : False : NonNegativeReals
18 : 0 : 2.9339964375769454 : 4 : False : False : NonNegativeReals
19 : 0 : 1.8679928365314515 : 4 : False : False : NonNegativeReals
20 : 0 : 1.8679928136956354 : 4 : False : False : NonNegativeReals
21 : 0 : 1.8679928137794752 : 4 : False : False : NonNegativeReals
22 : 0 : 1.8679928148969211 : 4 : False : False : NonNegativeReals
23 : 0 : 1.061916828884662 : 4 : False : False : NonNegativeReals
24 : 0 : 2.0 : 4 : False : False : NonNegativeReals
c : Size=24, Index=HORIZON
Key : Lower : Value : Upper : Fixed : Stale : Domain
1 : 0 : 0.0 : 1 : False : False : NonNegativeReals
2 : 0 : 4.6129851843523947e-10 : 1 : False : False : NonNegativeReals
3 : 0 : 1.1225149449049072e-08 : 1 : False : False : NonNegativeReals
4 : 0 : 1.0 : 1 : False : False : NonNegativeReals
5 : 0 : 0.0 : 1 : False : False : NonNegativeReals
6 : 0 : 0.0 : 1 : False : False : NonNegativeReals
7 : 0 : 0.0 : 1 : False : False : NonNegativeReals
8 : 0 : 0.0 : 1 : False : False : NonNegativeReals
9 : 0 : 0.0 : 1 : False : False : NonNegativeReals
10 : 0 : 0.0 : 1 : False : False : NonNegativeReals
11 : 0 : 0.26401426121322585 : 1 : False : False : NonNegativeReals
12 : 0 : 1.0 : 1 : False : False : NonNegativeReals
13 : 0 : 1.0 : 1 : False : False : NonNegativeReals
14 : 0 : 1.0 : 1 : False : False : NonNegativeReals
15 : 0 : 1.0 : 1 : False : False : NonNegativeReals
16 : 0 : 1.2446343201608404e-08 : 1 : False : False : NonNegativeReals
17 : 0 : 0.0 : 1 : False : False : NonNegativeReals
18 : 0 : 0.0 : 1 : False : False : NonNegativeReals
19 : 0 : 0.0 : 1 : False : False : NonNegativeReals
20 : 0 : 0.0 : 1 : False : False : NonNegativeReals
21 : 0 : 0.0 : 1 : False : False : NonNegativeReals
22 : 0 : 0.0 : 1 : False : False : NonNegativeReals
23 : 0 : 0.0 : 1 : False : False : NonNegativeReals
24 : 0 : 1.0 : 1 : False : False : NonNegativeReals
d : Size=24, Index=HORIZON
Key : Lower : Value : Upper : Fixed : Stale : Domain
1 : 0 : 0.0 : 1 : False : False : NonNegativeReals
2 : 0 : 0.0 : 1 : False : False : NonNegativeReals
3 : 0 : 0.0 : 1 : False : False : NonNegativeReals
4 : 0 : 0.0 : 1 : False : False : NonNegativeReals
5 : 0 : 0.0 : 1 : False : False : NonNegativeReals
6 : 0 : 1.0 : 1 : False : False : NonNegativeReals
7 : 0 : 0.7561663177961923 : 1 : False : False : NonNegativeReals
8 : 0 : 1.0 : 1 : False : False : NonNegativeReals
9 : 0 : 0.0 : 1 : False : False : NonNegativeReals
10 : 0 : 0.0 : 1 : False : False : NonNegativeReals
11 : 0 : 0.0 : 1 : False : False : NonNegativeReals
12 : 0 : 0.0 : 1 : False : False : NonNegativeReals
13 : 0 : 0.0 : 1 : False : False : NonNegativeReals
14 : 0 : 0.0 : 1 : False : False : NonNegativeReals
15 : 0 : 0.0 : 1 : False : False : NonNegativeReals
16 : 0 : 0.0 : 1 : False : False : NonNegativeReals
17 : 0 : 0.0 : 1 : False : False : NonNegativeReals
18 : 0 : 1.0 : 1 : False : False : NonNegativeReals
19 : 0 : 1.0 : 1 : False : False : NonNegativeReals
20 : 0 : 1.3022687125349388e-08 : 1 : False : False : NonNegativeReals
21 : 0 : 0.0 : 1 : False : False : NonNegativeReals
22 : 0 : 0.0 : 1 : False : False : NonNegativeReals
23 : 0 : 0.7561662932747802 : 1 : False : False : NonNegativeReals
24 : 0 : 0.0 : 1 : False : False : NonNegativeReals
1 Objective Declarations
OBJ : Size=1, Index=None, Active=True
Key : Active : Sense : Expression
None : True : maximize : (- c[1] + d[1])*price[1] + (- c[2] + d[2])*price[2] + (- c[3] + d[3])*price[3] + (- c[4] + d[4])*price[4] + (- c[5] + d[5])*price[5] + (- c[6] + d[6])*price[6] + (- c[7] + d[7])*price[7] + (- c[8] + d[8])*price[8] + (- c[9] + d[9])*price[9] + (- c[10] + d[10])*price[10] + (- c[11] + d[11])*price[11] + (- c[12] + d[12])*price[12] + (- c[13] + d[13])*price[13] + (- c[14] + d[14])*price[14] + (- c[15] + d[15])*price[15] + (- c[16] + d[16])*price[16] + (- c[17] + d[17])*price[17] + (- c[18] + d[18])*price[18] + (- c[19] + d[19])*price[19] + (- c[20] + d[20])*price[20] + (- c[21] + d[21])*price[21] + (- c[22] + d[22])*price[22] + (- c[23] + d[23])*price[23] + (- c[24] + d[24])*price[24]
2 Constraint Declarations
EnergyBalance_Con : Size=24, Index=HORIZON, Active=True
Key : Lower : Body : Upper : Active
1 : 0.0 : E[1] - (E0 + 0.938083151964686*c[1] - 1.0660035817780522*d[1]) : 0.0 : True
2 : 0.0 : E[2] - (E[1] + 0.938083151964686*c[2] - 1.0660035817780522*d[2]) : 0.0 : True
3 : 0.0 : E[3] - (E[2] + 0.938083151964686*c[3] - 1.0660035817780522*d[3]) : 0.0 : True
4 : 0.0 : E[4] - (E[3] + 0.938083151964686*c[4] - 1.0660035817780522*d[4]) : 0.0 : True
5 : 0.0 : E[5] - (E[4] + 0.938083151964686*c[5] - 1.0660035817780522*d[5]) : 0.0 : True
6 : 0.0 : E[6] - (E[5] + 0.938083151964686*c[6] - 1.0660035817780522*d[6]) : 0.0 : True
7 : 0.0 : E[7] - (E[6] + 0.938083151964686*c[7] - 1.0660035817780522*d[7]) : 0.0 : True
8 : 0.0 : E[8] - (E[7] + 0.938083151964686*c[8] - 1.0660035817780522*d[8]) : 0.0 : True
9 : 0.0 : E[9] - (E[8] + 0.938083151964686*c[9] - 1.0660035817780522*d[9]) : 0.0 : True
10 : 0.0 : E[10] - (E[9] + 0.938083151964686*c[10] - 1.0660035817780522*d[10]) : 0.0 : True
11 : 0.0 : E[11] - (E[10] + 0.938083151964686*c[11] - 1.0660035817780522*d[11]) : 0.0 : True
12 : 0.0 : E[12] - (E[11] + 0.938083151964686*c[12] - 1.0660035817780522*d[12]) : 0.0 : True
13 : 0.0 : E[13] - (E[12] + 0.938083151964686*c[13] - 1.0660035817780522*d[13]) : 0.0 : True
14 : 0.0 : E[14] - (E[13] + 0.938083151964686*c[14] - 1.0660035817780522*d[14]) : 0.0 : True
15 : 0.0 : E[15] - (E[14] + 0.938083151964686*c[15] - 1.0660035817780522*d[15]) : 0.0 : True
16 : 0.0 : E[16] - (E[15] + 0.938083151964686*c[16] - 1.0660035817780522*d[16]) : 0.0 : True
17 : 0.0 : E[17] - (E[16] + 0.938083151964686*c[17] - 1.0660035817780522*d[17]) : 0.0 : True
18 : 0.0 : E[18] - (E[17] + 0.938083151964686*c[18] - 1.0660035817780522*d[18]) : 0.0 : True
19 : 0.0 : E[19] - (E[18] + 0.938083151964686*c[19] - 1.0660035817780522*d[19]) : 0.0 : True
20 : 0.0 : E[20] - (E[19] + 0.938083151964686*c[20] - 1.0660035817780522*d[20]) : 0.0 : True
21 : 0.0 : E[21] - (E[20] + 0.938083151964686*c[21] - 1.0660035817780522*d[21]) : 0.0 : True
22 : 0.0 : E[22] - (E[21] + 0.938083151964686*c[22] - 1.0660035817780522*d[22]) : 0.0 : True
23 : 0.0 : E[23] - (E[22] + 0.938083151964686*c[23] - 1.0660035817780522*d[23]) : 0.0 : True
24 : 0.0 : E[24] - (E[23] + 0.938083151964686*c[24] - 1.0660035817780522*d[24]) : 0.0 : True
PeriodicBoundaryCondition : Size=1, Index=None, Active=True
Key : Lower : Body : Upper : Active
None : E0 : E[24] : E0 : True
10 Declarations: HORIZON c d E sqrteta E0 price OBJ EnergyBalance_Con PeriodicBoundaryCondition
The solution is stored in the value column. This is helpful for debugging small models but tendious overwise.
1.7.4.1. Extracting Solution from Pyomo#
A key advantage of Pyomo is that it is an Algebriac Modeling Language in Python. So let’s use Python to analyze the solution! The code below extracts the values of the variables into three lists.
# Declare empty lists
c_control = []
d_control = []
E_control = []
t = []
# Loop over elements of HORIZON set.
for i in m.HORIZON:
t.append(pyo.value(i))
# Use value( ) function to extract the solution for each varliable and append to the results lists
c_control.append(pyo.value(m.c[i]))
# Adding negative sign to discharge for plotting
d_control.append(-pyo.value(m.d[i]))
E_control.append(pyo.value(m.E[i]))
print(c_control)
[0.0, 4.6129851843523947e-10, 1.1225149449049072e-08, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.26401426121322585, 1.0, 1.0, 1.0, 1.0, 1.2446343201608404e-08, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0]
print(d_control)
[-0.0, -0.0, -0.0, -0.0, -0.0, -1.0, -0.7561663177961923, -1.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -1.0, -1.0, -1.3022687125349388e-08, -0.0, -0.0, -0.7561662932747802, -0.0]
print(E_control)
[2.000000000804785, 2.0000000112993037, 2.0000000319069975, 2.938083201679067, 2.9380832045919867, 1.8720796035614873, 1.0660035914895196, 0.0, 0.0, 0.0, 0.24766733414144584, 1.1857505048666763, 2.12383367588992, 3.061916847113209, 4.0, 4.0, 4.0, 2.9339964375769454, 1.8679928365314515, 1.8679928136956354, 1.8679928137794752, 1.8679928148969211, 1.061916828884662, 2.0]
1.7.4.2. Visualizing the Solution#
# Plot the state of charge (E)
plt.figure()
# add E0
t_ = [0] + t
E_control_ = [pyo.value(m.E0)] + E_control
plt.plot(t,E_control,'b.-')
plt.xlabel('Time (hr)')
plt.ylabel('Energy in Storage (MWh)')
plt.xticks(range(0,25,3))
plt.grid(True)
plt.show()
# This should NOT be a stair plot as energy is the integral of power. The graph below is reasonable.
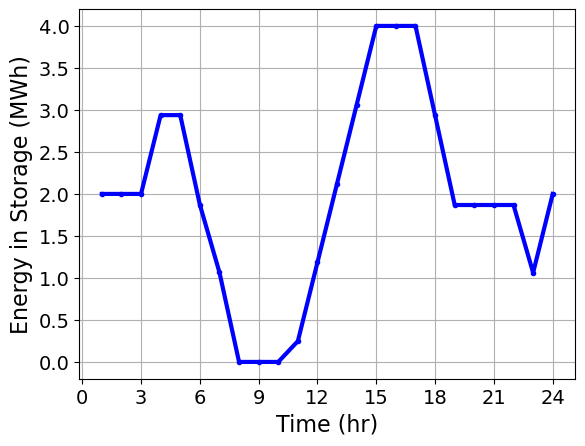
# Plot the charging and discharging rates
plt.figure()
# double up first data point to make the step plot
c_control_ = [c_control[0]] + c_control
d_control_ = [d_control[0]] + d_control
plt.step(t_,c_control_,'r.-',where='pre')
plt.step(t_,d_control_,'g.-',where='pre')
plt.xlabel('Time (hr)')
plt.ylabel('Power from Grid (MW)')
plt.xticks(range(0,25,3))
plt.grid(True)
plt.show()
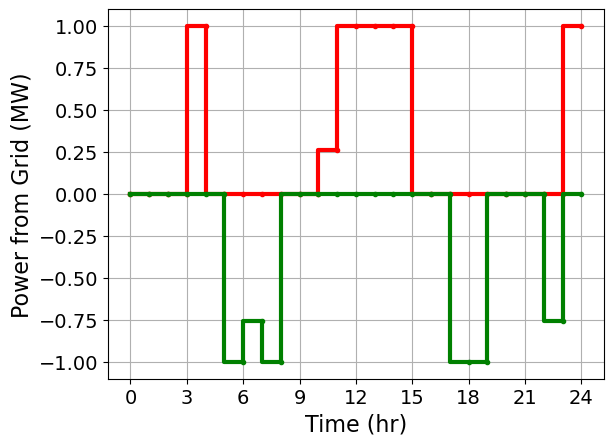
1.7.4.3. Accessing Dual Variables#
### Declare all suffixes
# https://pyomo.readthedocs.io/en/stable/pyomo_modeling_components/Suffixes.html#exporting-suffix-data
# Ipopt bound multipliers
m.ipopt_zL_out = pyo.Suffix(direction=pyo.Suffix.IMPORT)
m.ipopt_zU_out = pyo.Suffix(direction=pyo.Suffix.IMPORT)
# Ipopt constraint multipliers
m.dual = pyo.Suffix(direction=pyo.Suffix.IMPORT_EXPORT)
# Resolve the model
results = solver.solve(m, tee=True)
Ipopt 3.13.2: max_iter=50
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
This version of Ipopt was compiled from source code available at
https://github.com/IDAES/Ipopt as part of the Institute for the Design of
Advanced Energy Systems Process Systems Engineering Framework (IDAES PSE
Framework) Copyright (c) 2018-2019. See https://github.com/IDAES/idaes-pse.
This version of Ipopt was compiled using HSL, a collection of Fortran codes
for large-scale scientific computation. All technical papers, sales and
publicity material resulting from use of the HSL codes within IPOPT must
contain the following acknowledgement:
HSL, a collection of Fortran codes for large-scale scientific
computation. See http://www.hsl.rl.ac.uk.
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 96
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 0
Total number of variables............................: 72
variables with only lower bounds: 0
variables with lower and upper bounds: 72
variables with only upper bounds: 0
Total number of equality constraints.................: 25
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 -7.0590011e+01 2.00e-02 9.90e+00 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 -6.7757766e+01 1.19e-02 6.76e+00 -1.0 2.29e-01 - 2.29e-01 4.04e-01f 1
2 -6.6680579e+01 4.44e-16 2.66e+00 -1.0 1.52e-01 - 7.71e-01 1.00e+00h 1
3 -6.6663394e+01 4.44e-16 8.69e-15 -1.0 8.79e-02 - 1.00e+00 1.00e+00f 1
4 -7.0905011e+01 4.44e-16 8.57e-03 -2.5 1.20e-01 - 9.06e-01 9.26e-01f 1
5 -7.1259816e+01 4.44e-16 8.80e-02 -2.5 1.57e-01 - 8.04e-01 1.00e+00f 1
6 -7.1294102e+01 4.44e-16 6.75e-15 -2.5 8.18e-02 - 1.00e+00 1.00e+00f 1
7 -7.1429428e+01 4.44e-16 8.69e-04 -3.8 2.94e-02 - 9.56e-01 1.00e+00f 1
8 -7.1437868e+01 4.44e-16 7.55e-15 -5.7 4.53e-03 - 1.00e+00 1.00e+00f 1
9 -7.1437961e+01 8.88e-16 7.48e-15 -8.6 2.04e-05 - 1.00e+00 1.00e+00f 1
Number of Iterations....: 9
(scaled) (unscaled)
Objective...............: -7.1437960657845480e+01 -7.1437960657845480e+01
Dual infeasibility......: 7.4779217428591052e-15 7.4779217428591052e-15
Constraint violation....: 8.8817841970012523e-16 8.8817841970012523e-16
Complementarity.........: 3.3122665115371958e-09 3.3122665115371958e-09
Overall NLP error.......: 3.3122665115371958e-09 3.3122665115371958e-09
Number of objective function evaluations = 10
Number of objective gradient evaluations = 10
Number of equality constraint evaluations = 10
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 10
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 9
Total CPU secs in IPOPT (w/o function evaluations) = 0.005
Total CPU secs in NLP function evaluations = 0.000
EXIT: Optimal Solution Found.
# Inspect dual variables for lower bound
m.ipopt_zL_out.display()
ipopt_zL_out : Direction=IMPORT, Datatype=FLOAT
Key : Value
E[10] : -0.7942416193160723
E[11] : -9.959159559151526e-09
E[12] : -2.1026271696618103e-09
E[13] : -1.17578290872777e-09
E[14] : -8.162117659812082e-10
E[15] : -6.2506885965562e-10
E[16] : -6.264563243789251e-10
E[17] : -6.263268931807182e-10
E[18] : -8.539379352204578e-10
E[19] : -1.341422206806913e-09
E[1] : -1.2527829785585504e-09
E[20] : -1.341350289904925e-09
E[21] : -1.3409814411365547e-09
E[22] : -1.3409540074979394e-09
E[23] : -2.3608437770291847e-09
E[24] : -1.2529517735752844e-09
E[2] : -1.2561427947617305e-09
E[3] : -1.2655652532927255e-09
E[4] : -8.577658488883345e-10
E[5] : -8.581114250869248e-10
E[6] : -1.3533628470959604e-09
E[7] : -2.351074627003377e-09
E[8] : -1.2933647690071215
E[9] : -3.059357386103291
c[10] : -0.7539353271121385
c[11] : -9.178573911941868e-09
c[12] : -2.5046223507521217e-09
c[13] : -2.504981145674995e-09
c[14] : -2.505204613811326e-09
c[15] : -2.5049335000765823e-09
c[16] : -0.09378257453389889
c[17] : -4.225625753905217
c[18] : -10.585480009504597
c[19] : -10.486480008099354
c[1] : -2.7157200105877193
c[20] : -5.509480008254767
c[21] : -4.1084800084101225
c[22] : -2.8874800085646593
c[23] : -5.613480008720141
c[24] : -2.505054971752294e-09
c[2] : -0.24272001057702478
c[3] : -0.1217200105783847
c[4] : -2.5032939579251872e-09
c[5] : -1.0007200092145052
c[6] : -9.619720007824004
c[7] : -4.707720007994102
c[8] : -6.7277200093986425
c[9] : -3.0960037079608056
d[10] : -3.396982588174682
d[11] : -4.049318177854258
d[12] : -6.71031816795165
d[13] : -7.7353181666628466
d[14] : -8.915318166841939
d[15] : -7.576318168864481
d[16] : -3.973565261544163
d[17] : -1.2168343759122178
d[18] : -2.505198045055362e-09
d[19] : -2.5051853989409155e-09
d[1] : -1.9919999933188999
d[20] : -0.10399999597165342
d[21] : -1.50499999579355
d[22] : -2.7259999956183774
d[23] : -3.3102305950212514e-09
d[24] : -9.471999993835604
d[2] : -4.464999993320209
d[3] : -4.585999993313965
d[4] : -6.020999993293633
d[5] : -3.706999994877842
d[6] : -2.5052181084524623e-09
d[7] : -3.4362028761256405e-09
d[8] : -2.504243095823582e-09
d[9] : -1.446268519030817
# Inspect dual variables for upper bound
m.ipopt_zU_out.display()
ipopt_zU_out : Direction=IMPORT, Datatype=FLOAT
Key : Value
E[10] : 6.262126510435488e-10
E[11] : 6.693766261750669e-10
E[12] : 8.935597457148858e-10
E[13] : 1.343726742911317e-09
E[14] : 2.713588361024654e-09
E[15] : 0.14094426689994455
E[16] : 10.749747290646074
E[17] : 1.3369238562296126
E[18] : 2.3519283633282947e-09
E[19] : 1.1754291485432184e-09
E[1] : 1.253120766471938e-09
E[20] : 1.175503900129797e-09
E[21] : 1.1758414697720055e-09
E[22] : 1.1758669537675693e-09
E[23] : 8.52768230140698e-10
E[24] : 1.2529517547809998e-09
E[2] : 1.250266561351604e-09
E[3] : 1.24632281279438e-09
E[4] : 2.344219446630373e-09
E[5] : 2.343514697416166e-09
E[6] : 1.1716539589773153e-09
E[7] : 8.540487163434175e-10
E[8] : 6.263114689358477e-10
E[9] : 6.264067093301249e-10
c[10] : 2.501551046300082e-09
c[11] : 3.4858656539940548e-09
c[12] : 2.660999988097329
c[13] : 3.685999986963479
c[14] : 4.865999987121249
c[15] : 3.526999988900875
c[16] : 2.4883267841538603e-09
c[17] : 2.505087869933442e-09
c[18] : 2.5055784824939886e-09
c[19] : 2.505575764231218e-09
c[1] : 2.504663438587999e-09
c[20] : 2.5052724774879727e-09
c[21] : 2.5050505672851535e-09
c[22] : 2.5046738348391535e-09
c[23] : 2.5052848589351162e-09
c[24] : 3.8585199948754973
c[2] : 2.4942907974796294e-09
c[3] : 2.490129444629679e-09
c[4] : 1.313279994396989
c[5] : 2.502622398305555e-09
c[6] : 2.50555189696077e-09
c[7] : 2.5051873502835386e-09
c[8] : 2.505400368423204e-09
c[9] : 2.504812685816175e-09
d[10] : 2.5048969816613713e-09
d[11] : 2.5050580104567345e-09
d[12] : 2.5053966054632424e-09
d[13] : 2.5054642903322925e-09
d[14] : 2.5055223105939546e-09
d[15] : 2.5054535422253457e-09
d[16] : 2.505042743787309e-09
d[17] : 2.5032764345715254e-09
d[18] : 4.9720000104586255
d[19] : 4.873000008861757
d[1] : 2.5041842546629036e-09
d[20] : 2.50516925924289e-09
d[21] : 2.5038623791222157e-09
d[22] : 2.5047237561292218e-09
d[23] : 1.037256495247578e-08
d[24] : 2.5055510834792215e-09
d[2] : 2.5051398884588765e-09
d[3] : 2.5051602334378925e-09
d[4] : 2.505338096268117e-09
d[5] : 2.504981431387043e-09
d[6] : 4.912000008548914
d[7] : 9.673606290951011e-09
d[8] : 2.0200000103374722
d[9] : 2.503532249406393e-09
# Inspect duals for constraints
m.dual.display()
dual : Direction=IMPORT_EXPORT, Datatype=FLOAT
Key : Value
EnergyBalance_Con[10] : 32.449217973520675
EnergyBalance_Con[11] : 31.65497635483081
EnergyBalance_Con[12] : 31.65497634554103
EnergyBalance_Con[13] : 31.654976344331963
EnergyBalance_Con[14] : 31.654976344499907
EnergyBalance_Con[15] : 31.654976346397284
EnergyBalance_Con[16] : 31.79592061267216
EnergyBalance_Con[17] : 42.545667902691775
EnergyBalance_Con[18] : 43.882591758295064
EnergyBalance_Con[19] : 43.88259175979305
EnergyBalance_Con[1] : 36.801940126110026
EnergyBalance_Con[20] : 43.88259175962706
EnergyBalance_Con[21] : 43.882591759461214
EnergyBalance_Con[22] : 43.88259175929607
EnergyBalance_Con[23] : 43.88259175913098
EnergyBalance_Con[24] : 43.88259175762291
EnergyBalance_Con[2] : 36.80194012611037
EnergyBalance_Con[3] : 36.80194012610449
EnergyBalance_Con[4] : 36.80194012608524
EnergyBalance_Con[5] : 36.8019401275717
EnergyBalance_Con[6] : 36.8019401290571
EnergyBalance_Con[7] : 36.801940128875394
EnergyBalance_Con[8] : 36.801940127378366
EnergyBalance_Con[9] : 35.508575358997554
PeriodicBoundaryCondition : -43.88259175762291
1.7.5. Try Another Solver#
Let’s see how easy it is to switch to another solver with Pyomo.
Activity
Create a new instance of SolverFactory by specifying ’glpk’ or ’cbc’ as the solver name. Then solve the Pyomo model m and store the results in results2.
# Specify another solver
# Add your solution here
# Regenerate model without suffixes
# Note: CBC does not have the same suffix interface as Ipopt to get the dual variables
# Note: This requires you finished implementing build_model
m = build_model(price = ca_data["price"][24:48].to_numpy(),
e0 = 0
)
# Resolve the model
results2 = solver2.solve(m, tee=True)
Notice we used solver2, which is an instance of SolverFactory for the solver glpk. But we reused model m. This means the solver glpk used the solution from ipopt as its initial point.
1.7.6. References#
All tables are from Chapter 4 of Hart, W. E., Laird, C. D., Watson, J. P., Woodruff, D. L., Hackebeil, G. A., Nicholson, B. L., & Siirola, J. D. (2017). Pyomo-Optimization Modeling in Python (Vol. 67). Berlin: Springer. https://www.springer.com/gp/book/9783319588193

