5.1. Parameter estimation with parmest#
Created by Kanishka Ghosh, Jialu Wang, Prof. Alex Dowling, and Stephen Cini at the University of Notre Dame. Last updated December 2024.
# This code cell installs packages on Colab
import sys
if "google.colab" in sys.modules:
!wget "https://raw.githubusercontent.com/ndcbe/optimization/main/notebooks/helper.py"
import helper
helper.install_idaes()
helper.install_ipopt()
else:
sys.path.insert(0, '../')
import helper
helper.set_plotting_style()
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import pyomo.environ as pyo
import pyomo.dae as dae
import pyomo
import idaes
# Define the directory to save/read the data files
data_dir = 'https://raw.githubusercontent.com/ndcbe/optimization/main/notebooks/data/'
5.1.1. What is parameter estimation?#
Given a function \(f(x,\theta)\) where \(x\) is the input or array of inputs, \(\theta\) is the vector of unknown model parameters, and \(y\) is the array of observed output, parameter estimation is performed to determine the values of \(\theta\) to minimize the error between \(f(x,\theta)\) and \(y\). Commonly, parameter estimation is set up as a least squares objective problem:
where \(i\) is used to index the datapoints in a dataset and \(\hat{\theta}\) is the optimal set of parameter values that minimizes the prediction error.
5.1.2. What is parmest?#
parmest is a Python package built on the Pyomo optimization modeling language to support parameter estimation using experimental data along with confidence regions and subsequent creation of scenarios for PySP. parmest supports scenario generation for multiple ‘experiments’ and can be used to characterize estimate uncertainties through, for example, confidence region generations. parmest requires the following positional arguments in order solve the optimization problem:
Experimentclass with the following functions:init - Loads data into class, and initializes model to contain no information.
create_model - Define the model in a generic form with needed variables and parameters.
finalize_model - Initialize and/or discretize the model from create_model for use with specified data.
label_model - Add required labels.
parmestrequires the model contains labeled unknown_parameters and model_outputs.pyomo.DoEadditionally requires model_inputs and measurement_error.get_labeled_model - Calls previous functions to generate complete model for each
Experiment.Optional keyword argument to define the verbosity of solver output. Default: False
More information about the parmest package can be found here.
Detailed explanation of the various methods in parmest can be found here.
5.1.3. Example: Reaction Kinetics#
Consider two chemical reactions that convert molecule \(A\) to desired product \(B\) and a less valuable side-product \(C\).
Our ultimate goals is to design a large-scale continous reactor that maximizes the production of \(B\). This general sequential reactions problem is widely applicable to CO\(_2\) capture and industry more broadly (petrochemicals, pharmasuticals, etc.).
The rate laws for these two chemical reactions are:
Here, \(C_A\), \(C_B\), and \(C_C\) are the concentrations of each species. The rate constants \(k_1\) and \(k_2\) depend on temperature as follows:
\(A_1, A_2, E_1\), and \(E_2\) are fitted model parameters. \(R\) is the ideal-gas constant and \(T\) is absolute temperature.
5.1.3.1. Batch Reactor#
The concentrations in a batch reactor evolve with time per the following differential equations:
This is a linear system of differential equations. Assuming the feed is only species \(A\), i.e.,
leads to the following analytic solution:
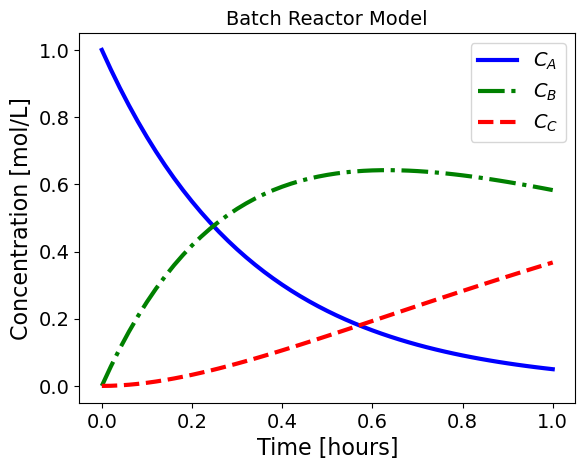
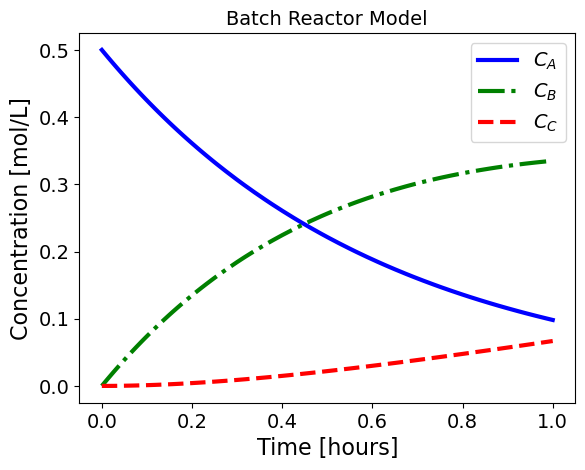
The following Python code simulates and plots this model.
def kinetics(A, E, T):
''' Computes kinetics from Arrhenius equation
Arguments:
A: pre-exponential factor, [1 / hr]
E: activation energy, [kJ / mol]
T: temperature, [K]
Returns:
k: reaction rate coefficient, [1 / hr]
'''
R = 8.31446261815324 # J / K / mole
return A * np.exp(-E*1000/(R*T))
def concentrations(t,k,CA0):
'''
Returns concentrations at time t
Arguments:
t: time, [hr]
k: reaction rate coefficient, [1 / hr]
CA0: initial concentration of A, [mol / L]
Returns:
CA, CB, CC: concentrations of A, B, and C at time t, [mol / L]
'''
CA = CA0 * np.exp(-k[0]*t);
CB = k[0]*CA0/(k[1]-k[0]) * (np.exp(-k[0]*t) - np.exp(-k[1]*t));
CC = CA0 - CA - CB;
return CA, CB, CC
CA0 = 1 # Moles/L
k = [3, 0.7] # 1/hr
t = np.linspace(0,1,51)
CA, CB, CC = concentrations(t,k,CA0)
plt.plot(t, CA, label="$C_{A}$",linestyle="-",color="blue")
plt.plot(t, CB, label="$C_{B}$",linestyle="-.",color="green")
plt.plot(t, CC, label="$C_{C}$",linestyle="--",color="red")
plt.xlabel("Time [hours]")
plt.ylabel("Concentration [mol/L]")
plt.title("Batch Reactor Model")
plt.legend()
plt.show()
plt.close()
5.1.3.2. Experimental Data#
See the notebook Supplementary material: data for parmest tutorial for details on how these experimental data were generated (via simulation).
Experimental data consists of the concentration of species A, B, and C in \(\mathrm{mol/L}\) with respect to time \(t\) in \(\mathrm{hours}\) inside the batch reactor. The experimental data is stored in csv files where the first column records the time \(t\) in the reactor. Next, the temperature \(T\) in \(\mathrm{K}\) at which the reaction was simulated is recorded followed by the initial concentration of species A, \(C_{A,0}\), in \(\mathrm{mol/L}\). Finally, the time-varying species concentrations (\(C_A\)), (\(C_B\)), and (\(C_C\)) are recorded in \(\mathrm{mol/L}\). Following is how the pandas dataframe of a single experiment looks like:
# define function to plot
def plot_exp(k, CA0, data, text):
'''
Plot concentration profiles
Arguments:
k: kinetic parameters
CA0: initial concentration
data: Pandas data frame
text: plot title
'''
# evaluate models
t = np.linspace(0,1,51)
CA, CB, CC = concentrations(t,k,CA0)
# plot model-generated and 'experimental' data
# symbols for 'experimental' data
# solid and dashed lines for model-generated data
plt.plot(t, CA,label="$C_{A}$",linestyle="-",color="blue")
plt.plot(data.time, data.CA, marker='o',linestyle="",color="blue",label=str())
plt.plot(t, CB, label="$C_{B}$",linestyle="-.",color="green")
plt.plot(data.time, data.CB, marker='s',linestyle="",color="green",label=str())
plt.plot(t, CC, label="$C_{C}$",linestyle="--",color="red")
plt.plot(data.time, data.CC, marker='^',linestyle="",color="red",label=str())
plt.xlabel("Time [hours]")
plt.ylabel("Concentration [mol/L]")
plt.title(text)
plt.legend()
plt.show()
plt.close()
5.1.3.3. Pyomo model#
In the following cell, we define a function to define and return the Pyomo model for the kinetic model to be used for parameter estimation.
import pyomo.contrib.parmest.parmest as parmest
from pyomo.contrib.parmest.experiment import Experiment
def reaction_kinetics_model(data):
# define Pyomo model
m = pyo.ConcreteModel()
m.T = data['T'][0] # K
m.CA0 = data['CA0'][0] # mol/L
m.R = 8.31446261815324 # J / K / mol
# # define 'experimental' data timesteps as Pyomo set
m.t = pyo.Set(initialize = data['time'].tolist())
# Kinetic parameters to be fitted defined as Pyomo variables
# Initialized by 'true' values
m.A1 = pyo.Var(initialize=200, bounds=(100,300)) # 1/hr
m.A2 = pyo.Var(initialize=400, bounds=(300,500)) # 1/hr
m.E1 = pyo.Var(initialize=10, bounds=(1,20)) # kJ/mol
m.E2 = pyo.Var(initialize=15, bounds=(1,30)) # kJ/mol
# Concentration variables indexed by time
m.CA = pyo.Var(m.t, initialize = m.CA0) # mol/L
m.CB = pyo.Var(m.t, initialize = 0) # mol/L
m.CC = pyo.Var(m.t, initialize = 0) # mol/L
# kinetic rate constants from Arrhenius equation
m.k1 = pyo.Expression(rule = m.A1 * pyo.exp(-m.E1*1000/(m.R*m.T))) # 1/hr
m.k2 = pyo.Expression(rule = m.A2 * pyo.exp(-m.E2*1000/(m.R*m.T))) # 1/hr
# Constraints to change concentrations based on kinetics
def conc_A(m,i):
if i == 0:
return pyo.Constraint.Skip
else:
return m.CA[i] == m.CA0 * pyo.exp(-m.k1*i)
m.CA_rate = pyo.Constraint(m.t,rule=conc_A)
def conc_B(m,i):
if i == 0:
return pyo.Constraint.Skip
else:
return m.CB[i] == m.k1*m.CA0/(m.k2-m.k1) * (pyo.exp(-m.k1*i) - pyo.exp(-m.k2*i))
m.CB_rate = pyo.Constraint(m.t,rule=conc_B)
def conc_C(m,i):
if i == 0:
return pyo.Constraint.Skip
else:
return m.CC[i] == m.CA0 - m.CA[i] - m.CB[i]
m.CC_rate = pyo.Constraint(m.t,rule=conc_C)
return m
class ReactionKineticsExperiment(Experiment):
def __init__(self, data):
self.data = data
self.model = None
def create_model(self):
self.model = m = reaction_kinetics_model(self.data)
return m
def finalize_model(self):
m = self.model
# Initial Conditions
m.CA[0].fix(m.CA0)
m.CB[0].fix(0.0)
m.CC[0].fix(0.0)
return m
def label_model(self):
m = self.model
m.experiment_outputs = pyo.Suffix(direction=pyo.Suffix.LOCAL)
m.experiment_outputs.update(
(m.CA[t], self.data['CA'][ind]) for ind, t in enumerate(self.data['time']))
m.experiment_outputs.update(
(m.CB[t], self.data['CB'][ind]) for ind, t in enumerate(self.data['time']))
m.experiment_outputs.update(
(m.CC[t], self.data['CC'][ind]) for ind, t in enumerate(self.data['time']))
m.unknown_parameters = pyo.Suffix(direction=pyo.Suffix.LOCAL)
m.unknown_parameters.update(
(k, pyo.ComponentUID(k)) for k in [m.A1, m.A2, m.E1, m.E2]
)
return m
def get_labeled_model(self):
m = self.create_model()
m = self.finalize_model()
m = self.label_model()
# m.pprint()
return m
# Test model
data = pd.read_csv(data_dir + 'parmest_20210609_data_exp1.csv', index_col=0)
print(data)
m = reaction_kinetics_model(data)
m.CA[0].fix(m.CA0)
m.CB[0].fix(0.0)
m.CC[0].fix(0.0)
# solve model
solver = pyo.SolverFactory('ipopt')
# solve model
solver.solve(m,tee=True)
# m.pprint()
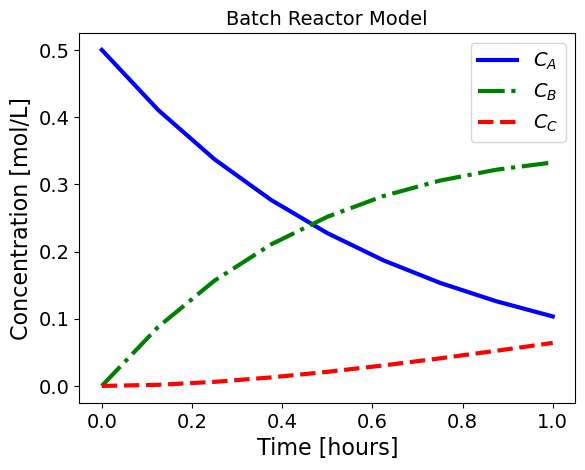
# plot results
CA = [pyo.value(m.CA[i]) for i in m.t]
CB = [pyo.value(m.CB[i]) for i in m.t]
CC = [pyo.value(m.CC[i]) for i in m.t]
plt.plot(m.t, CA, label="$C_{A}$",linestyle="-",color="blue")
plt.plot(m.t, CB, label="$C_{B}$",linestyle="-.",color="green")
plt.plot(m.t, CC, label="$C_{C}$",linestyle="--",color="red")
plt.xlabel("Time [hours]")
plt.ylabel("Concentration [mol/L]")
plt.title("Batch Reactor Model")
plt.legend()
time T CA0 CA CB CC
0 0.000 250 0.5 0.476266 0.000000 0.000000
1 0.125 250 0.5 0.332309 0.133593 0.000000
2 0.250 250 0.5 0.295725 0.362016 0.092655
3 0.375 250 0.5 0.394806 0.131512 0.004404
4 0.500 250 0.5 0.167992 0.271682 0.031808
5 0.625 250 0.5 0.117872 0.313196 0.009108
6 0.750 250 0.5 0.117052 0.582722 0.000000
7 0.875 250 0.5 0.175373 0.224904 0.043844
8 1.000 250 0.5 0.130619 0.360287 0.194820
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
This version of Ipopt was compiled from source code available at
https://github.com/IDAES/Ipopt as part of the Institute for the Design of
Advanced Energy Systems Process Systems Engineering Framework (IDAES PSE
Framework) Copyright (c) 2018-2019. See https://github.com/IDAES/idaes-pse.
This version of Ipopt was compiled using HSL, a collection of Fortran codes
for large-scale scientific computation. All technical papers, sales and
publicity material resulting from use of the HSL codes within IPOPT must
contain the following acknowledgement:
HSL, a collection of Fortran codes for large-scale scientific
computation. See http://www.hsl.rl.ac.uk.
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 88
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 10
Total number of variables............................: 28
variables with only lower bounds: 0
variables with lower and upper bounds: 4
variables with only upper bounds: 0
Total number of equality constraints.................: 24
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 0.0000000e+00 4.02e-01 0.00e+00 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 0.0000000e+00 5.34e-07 0.00e+00 -1.0 4.01e-01 - 9.91e-01 1.00e+00h 1
2 0.0000000e+00 6.14e-05 0.00e+00 -1.7 5.36e-02 - 1.00e+00 1.00e+00h 1
3 0.0000000e+00 2.72e-07 0.00e+00 -3.8 3.41e-03 - 1.00e+00 1.00e+00h 1
4 0.0000000e+00 7.12e-07 0.00e+00 -5.7 5.52e-03 - 1.00e+00 1.00e+00h 1
5 0.0000000e+00 8.50e-09 0.00e+00 -8.6 6.04e-04 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 5
(scaled) (unscaled)
Objective...............: 0.0000000000000000e+00 0.0000000000000000e+00
Dual infeasibility......: 0.0000000000000000e+00 0.0000000000000000e+00
Constraint violation....: 8.4954715484641952e-09 8.4954715484641952e-09
Complementarity.........: 2.6198259016630073e-09 2.6198259016630073e-09
Overall NLP error.......: 8.4954715484641952e-09 8.4954715484641952e-09
Number of objective function evaluations = 6
Number of objective gradient evaluations = 6
Number of equality constraint evaluations = 6
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 6
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 5
Total CPU secs in IPOPT (w/o function evaluations) = 0.001
Total CPU secs in NLP function evaluations = 0.000
EXIT: Optimal Solution Found.
<matplotlib.legend.Legend at 0x1fcda72da60>
5.1.4. Parameter estimation with a single dataset#
Here, we will estimate parameters \(A_1\), \(A_2\), \(E_1\), and \(E_2\) using data generated for a batch ‘experiment’ at 250 C with an inlet concentration of 0.5 mol/L of A.
The parameter estimation problem is solved with the least squares optimization scheme
The parameter estimation problem is solved with the least squares optimization scheme $$
$\( where \)i\( is used to index the datapoints in a dataset and \)\hat{\theta}$ is the optimal set of parameter values that minimizes the prediction error.
# # read-in data from csv file
data = pd.read_csv(data_dir + 'parmest_20210609_data_exp1.csv',index_col=0)
# # run parmest
exp_list = []
df = data
exp_list.append(ReactionKineticsExperiment(df))
pest = parmest.Estimator(exp_list, obj_function='SSE', tee = True)
obj, theta = pest.theta_est()
model = pest.ef_instance
print("=== Parameter values ===")
print("A1 = {:0.3f} 1/hr".format(pyo.value(model.A1)))
print("A2 = {:0.3f} 1/hr".format(pyo.value(model.A2)))
print("E1 = {:0.3f} kJ/mol".format(pyo.value(model.E1)))
print("E2 = {:0.3f} kJ/mol".format(pyo.value(model.E2)))
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
This version of Ipopt was compiled from source code available at
https://github.com/IDAES/Ipopt as part of the Institute for the Design of
Advanced Energy Systems Process Systems Engineering Framework (IDAES PSE
Framework) Copyright (c) 2018-2019. See https://github.com/IDAES/idaes-pse.
This version of Ipopt was compiled using HSL, a collection of Fortran codes
for large-scale scientific computation. All technical papers, sales and
publicity material resulting from use of the HSL codes within IPOPT must
contain the following acknowledgement:
HSL, a collection of Fortran codes for large-scale scientific
computation. See http://www.hsl.rl.ac.uk.
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 88
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 34
Total number of variables............................: 28
variables with only lower bounds: 0
variables with lower and upper bounds: 4
variables with only upper bounds: 0
Total number of equality constraints.................: 24
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 1.6338341e+00 4.02e-01 6.37e-01 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 1.9026209e-01 2.34e-04 4.98e-03 -1.0 4.13e-01 - 9.86e-01 1.00e+00f 1
2 1.8657853e-01 5.60e-04 2.39e-04 -1.0 1.99e-01 - 1.00e+00 1.00e+00h 1
3 1.8638673e-01 4.98e-05 1.92e-05 -2.5 7.10e-02 - 1.00e+00 1.00e+00h 1
4 1.8638598e-01 2.10e-07 1.36e-07 -3.8 4.52e-02 - 1.00e+00 1.00e+00h 1
5 1.8638599e-01 2.23e-10 3.93e-11 -5.7 9.66e-03 - 1.00e+00 1.00e+00h 1
6 1.8638599e-01 2.55e-12 2.09e-13 -8.6 1.05e-03 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 6
(scaled) (unscaled)
Objective...............: 1.8638598612196305e-01 1.8638598612196305e-01
Dual infeasibility......: 2.0863213371387894e-13 2.0863213371387894e-13
Constraint violation....: 2.5491830868418219e-12 2.5491830868418219e-12
Complementarity.........: 2.5255218792855822e-09 2.5255218792855822e-09
Overall NLP error.......: 2.5255218792855822e-09 2.5255218792855822e-09
Number of objective function evaluations = 7
Number of objective gradient evaluations = 7
Number of equality constraint evaluations = 7
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 7
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 6
Total CPU secs in IPOPT (w/o function evaluations) = 0.001
Total CPU secs in NLP function evaluations = 0.000
EXIT: Optimal Solution Found.
=== Parameter values ===
A1 = 200.209 1/hr
A2 = 400.037 1/hr
E1 = 9.640 kJ/mol
E2 = 14.939 kJ/mol
5.1.5. Parameter estimation with multiple datasets#
Here, we will estimate parameters \(A_1\), \(A_2\), \(E_1\), and \(E_2\) using data generated for a batch ‘experiment’ at 250 C with an inlet concentration of 0.5 mol/L of A.
The parameter estimation problem is now defined to solve optimization problem where the objective function is the mean of the least square error between observed and calculated data for multiple experiments.
where \(i\) is used to index the datapoints in a dataset, \(j\) is an index on the dataset such that \(j \in [1,N]\) and \(N\) is the number of experiments conducted.
5.1.5.1. Generate Experiment list#
In the following cell, we define a function to generate a list of Experiments using the Experiment class. For this, we read-in the list of file names generated earlier.
# Make empty experiment list
exp_list = []
# Set generic file name to fill with data 1-16
file_name_generic = data_dir + 'parmest_20210609_data_exp{}.csv'
for i in range(16): #making a list of different experiments, each exp has corresponding data
df = pd.read_csv(file_name_generic.format(i+1),index_col=0)
# print(df.head())
exp_list.append(ReactionKineticsExperiment(df))
5.1.5.2. Parameter estimation with parmest#
In the following cell, we perform parameter estimation using parmest to solve the least squares problem defined in the Pyomo model.
In Google Colab, an error appears: ‘_PyDrive2ImportHook’ object has no attribute ‘find_spec’. This is being fixed by a recent patch to Pyomo: Pyomo/pyomo#3444. Results generated using local run of software.
# run parmest
pest = parmest.Estimator(exp_list, obj_function='SSE')
obj, theta = pest.theta_est()
# print(theta)
#model = pest.ef_instance
model = pest.ef_instance.Scenario0
print("=== Parameter values ===")
print("A1 = {:0.3f} 1/hr".format(pyo.value(model.A1)))
print("A2 = {:0.3f} 1/hr".format(pyo.value(model.A2)))
print("E1 = {:0.3f} kJ/mol".format(pyo.value(model.E1)))
print("E2 = {:0.3f} kJ/mol".format(pyo.value(model.E2)))
=== Parameter values ===
A1 = 185.609 1/hr
A2 = 401.170 1/hr
E1 = 9.867 kJ/mol
E2 = 14.866 kJ/mol
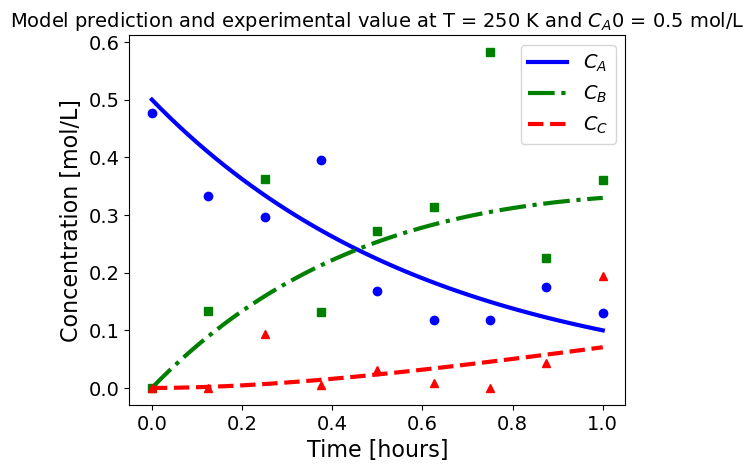
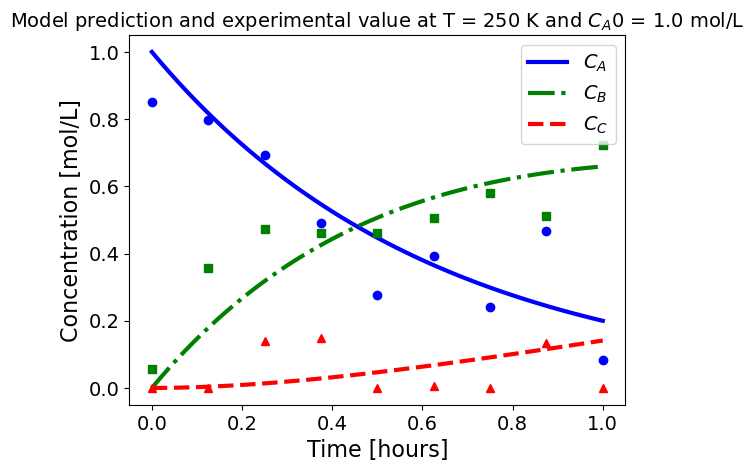
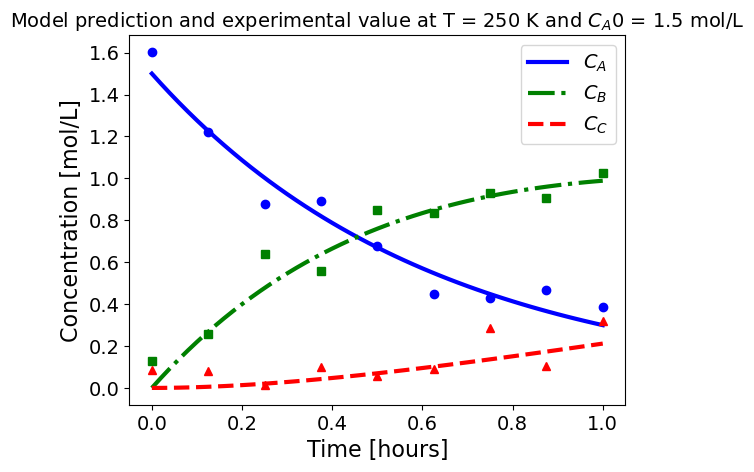
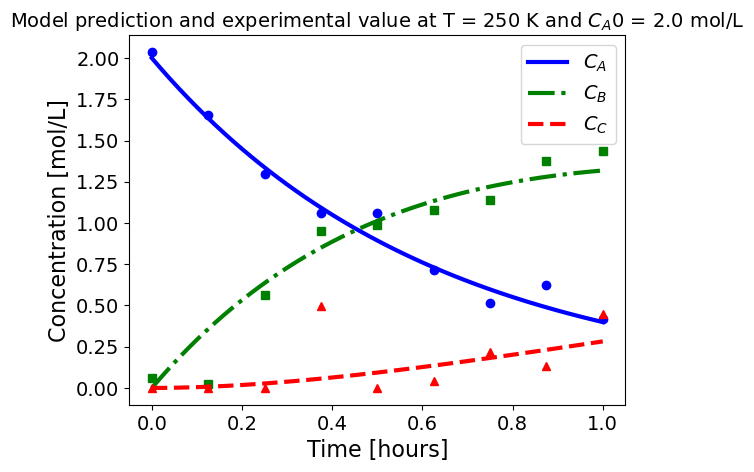
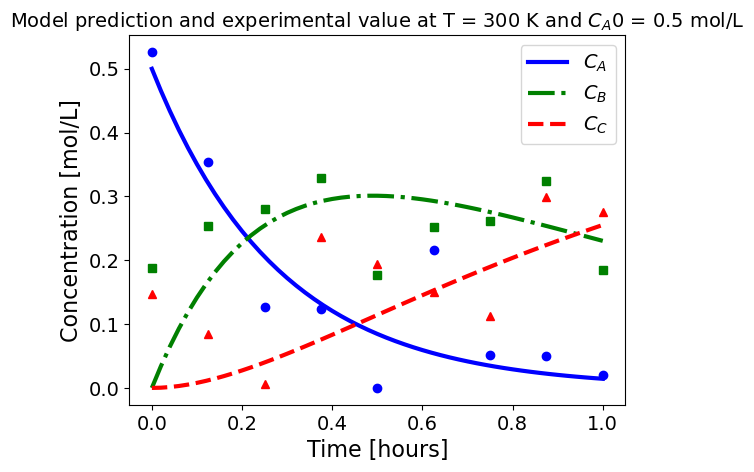
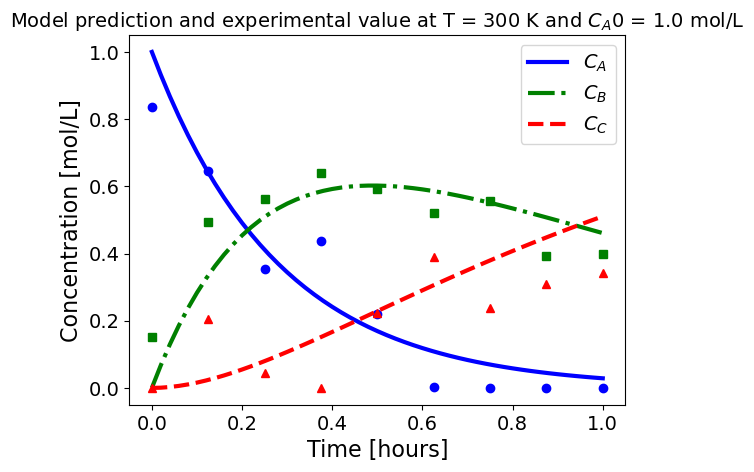
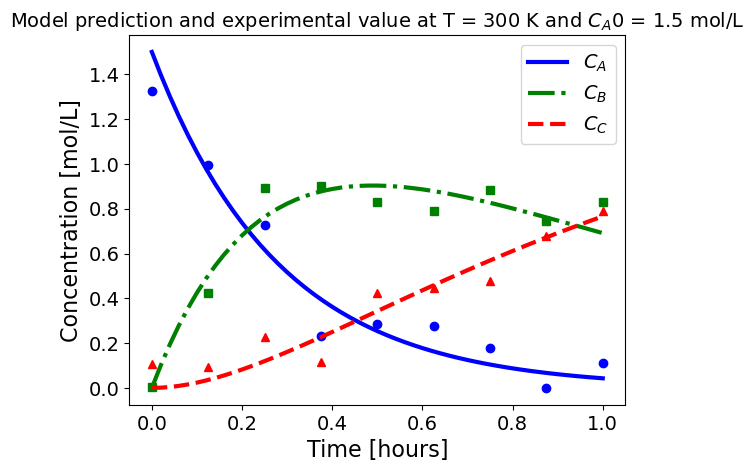
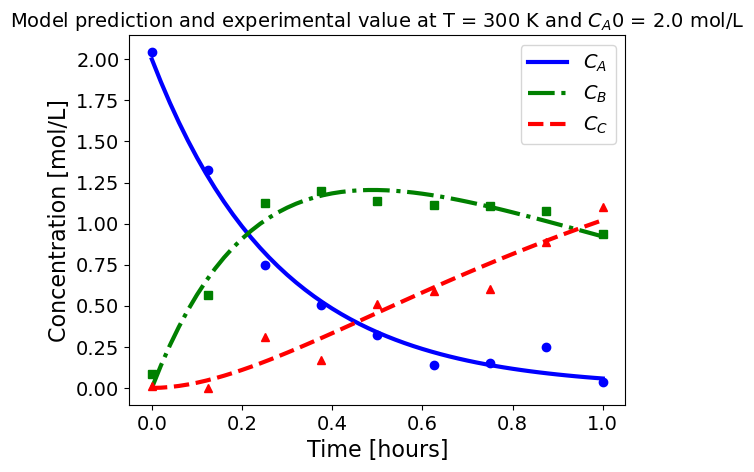
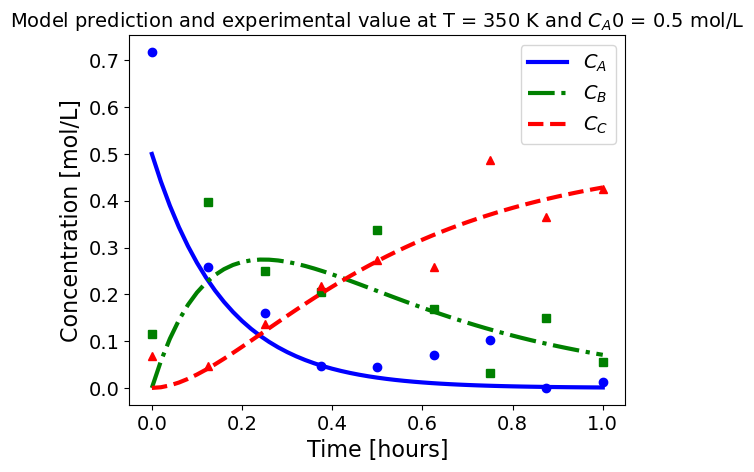
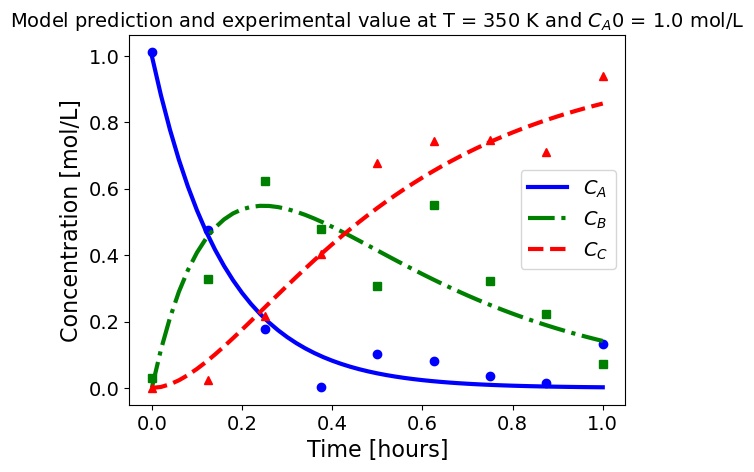
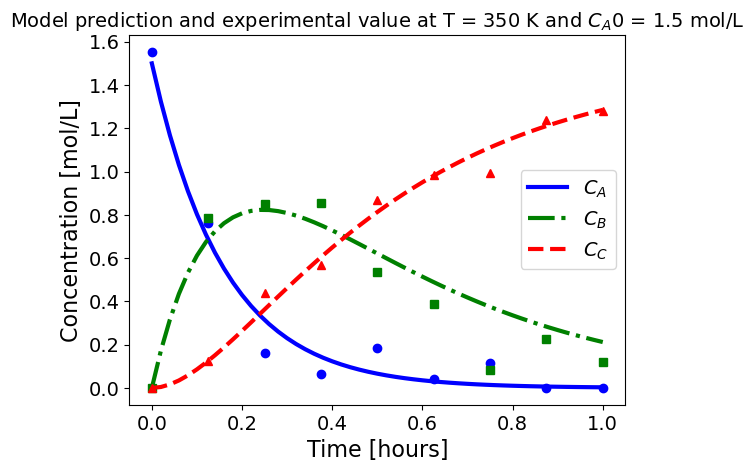
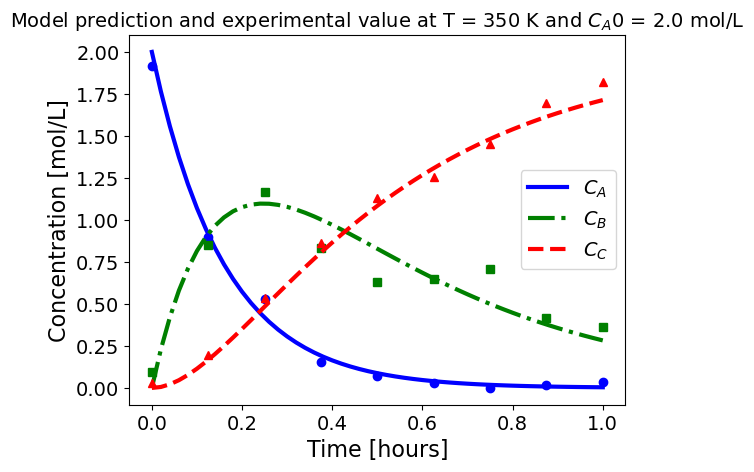
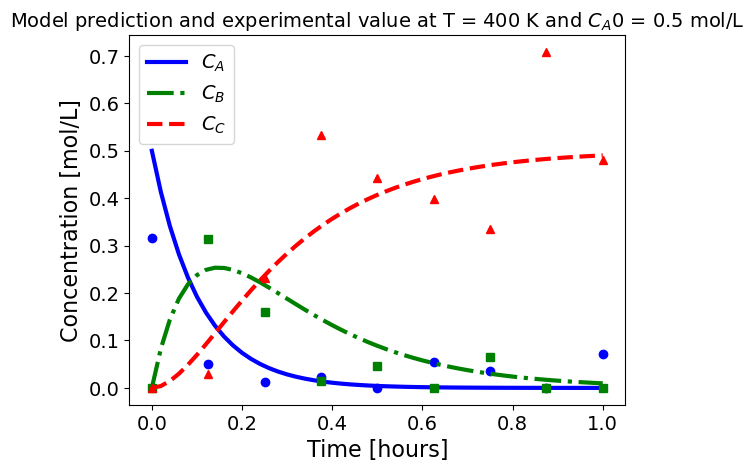
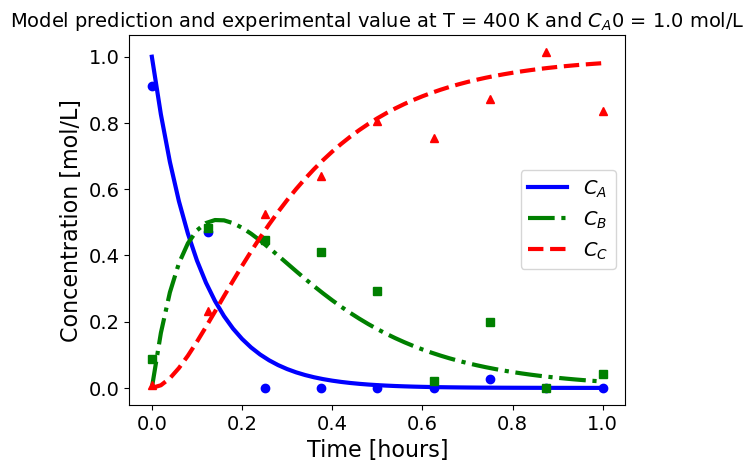
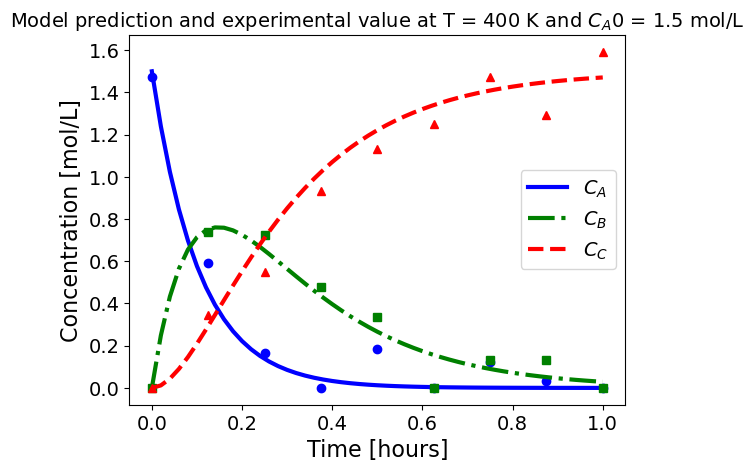
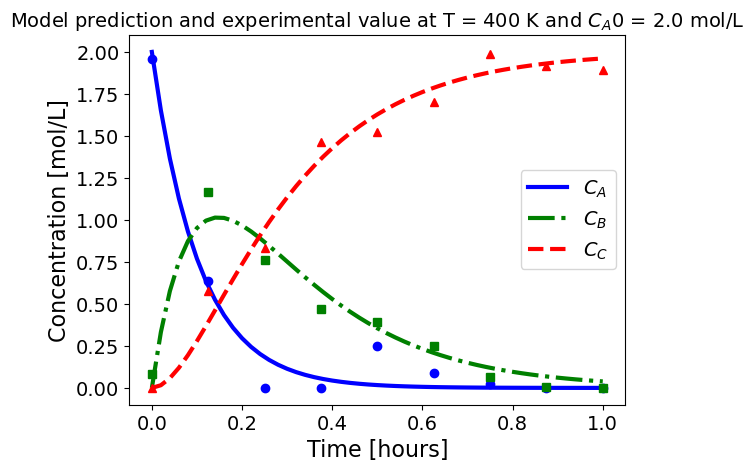
5.1.5.3. Plotting fitted model simulation with ‘experimental’ data#
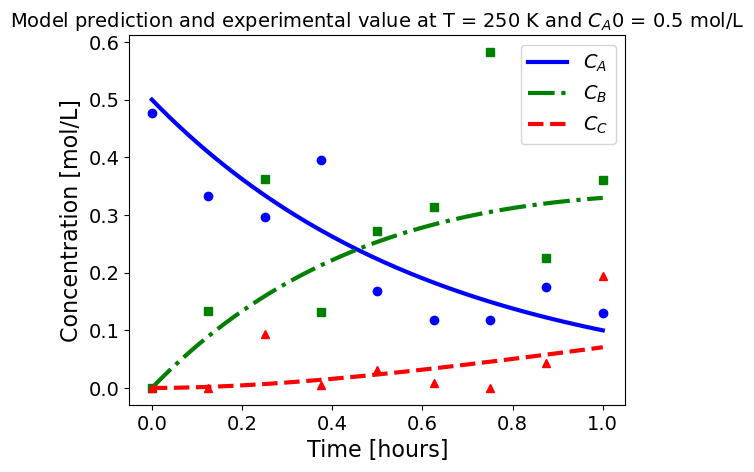
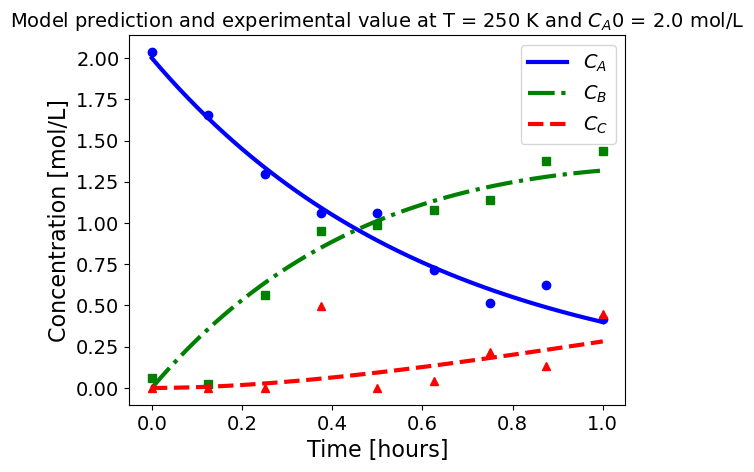
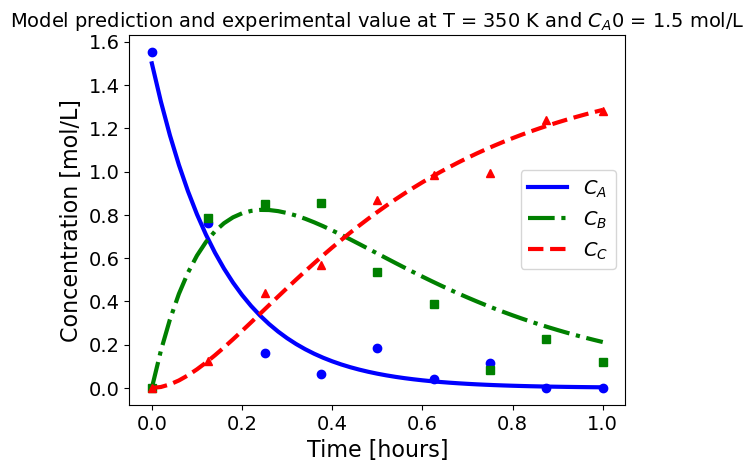
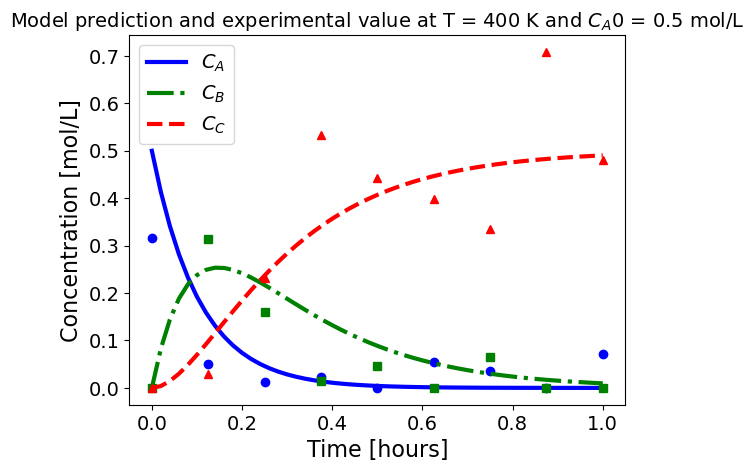
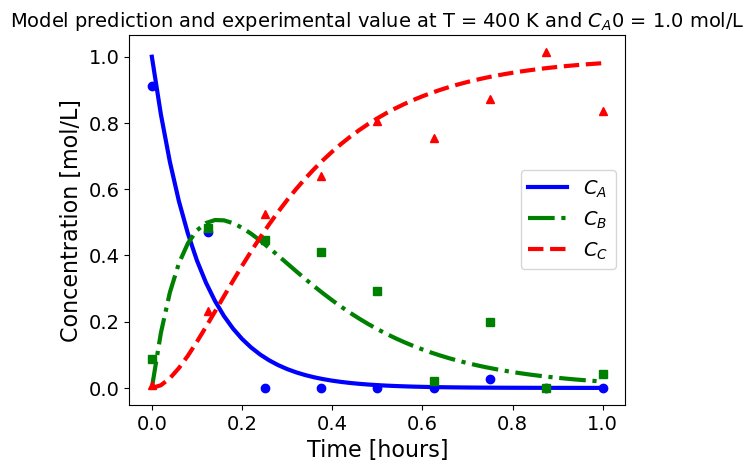
Next, we plot the ‘experimental’ data along with the profiles generated using the fitted kinetic model. The symbols represent the ‘experimental’ data and the solid and dashed lines are the profiles generated using the fitted model.
# list of temperatures
T_vals = [250,300,350,400] # K
# list of initial concentrations of A
CA0_vals = [0.5,1.0,1.5,2.0] # mol/L
# Parameter values from parameter estimation using parmest
A1 = theta['A1']
E1 = theta['E1']
A2 = theta['A2']
E2 = theta['E2']
A_est1 = [A1, A2]
A_est = np.asarray(A_est1)
E_est1 = [E1, E2]
E_est = np.asarray(E_est1)
ctr = 0
for T in T_vals:
for CA0 in CA0_vals:
# generate concentration profiles using estimated parameter values
k = kinetics(A_est, E_est, T)
# plot model-generated and 'experimental' data
# symbols for 'experimental' data
# solid and dashed lines for model-generated data
df = pd.read_csv(file_name_generic.format(ctr+1),index_col=0)
plot_exp(k, CA0, df, 'Model prediction and experimental value at T = {} K and $C_{}$ = {} mol/L'.format(T,'A0',CA0))
ctr+=1
5.1.6. Using parmest with pyomo.dae#
In contrast to the approach above, we will now try to solve the model without the analytic solution for the concentrations using Pyomo.DAE. To recap, the concentrations in a batch reactor evolve with time per the following differential equations:
This is a linear system of differential equations. Assuming the feed is only species \(A\), i.e.,
In the following cell, we define a function to define and return the Pyomo DAE model (dynamic mode) for the kinetic model to be used for parameter estimation. In this model, the rate equations are presented in terms of linear differential equations.
import pyomo.contrib.parmest.parmest as parmest
from pyomo.contrib.parmest.experiment import Experiment
def reaction_kinetics_model_dae(data):
# define Pyomo model
m = pyo.ConcreteModel()
m.T = data['T'][0] # K
m.CA0 = data['CA0'][0] # mol/L
m.R = 8.31446261815324 # J / K / mol
# # define 'experimental' data timesteps as Pyomo set
m.t = dae.ContinuousSet(initialize = data['time'].tolist(), bounds = (0,1))
# Kinetic parameters to be fitted defined as Pyomo variables
# Initialized by 'true' values
m.A1 = pyo.Var(initialize=200, bounds=(100,300)) # 1/hr
m.A2 = pyo.Var(initialize=400, bounds=(300,500)) # 1/hr
m.E1 = pyo.Var(initialize=10, bounds=(1,20)) # kJ/mol
m.E2 = pyo.Var(initialize=15, bounds=(1,30)) # kJ/mol
# Concentration variables indexed by time
m.CA = pyo.Var(m.t, initialize = m.CA0) # mol/L
m.CB = pyo.Var(m.t, initialize = 0) # mol/L
m.CC = pyo.Var(m.t, initialize = 0) # mol/L
# Derivatives of concentration
m.dCA = dae.DerivativeVar(m.CA, wrt = m.t)
m.dCB = dae.DerivativeVar(m.CB, wrt = m.t)
m.dCC = dae.DerivativeVar(m.CC, wrt = m.t)
# kinetic rate constants from Arrhenius equation
m.k1 = pyo.Expression(rule = m.A1 * pyo.exp(-m.E1*1000/(m.R*m.T))) # 1/hr
m.k2 = pyo.Expression(rule = m.A2 * pyo.exp(-m.E2*1000/(m.R*m.T))) # 1/hr
# Constraints to change concentrations based on kinetics
def conc_A(m,i):
return m.dCA[i] == - m.k1 * m.CA[i]
m.CA_rate = pyo.Constraint(m.t,rule=conc_A)
def conc_B(m,i):
return m.dCB[i] == m.k1 * m.CA[i] - m.k2 * m.CB[i]
m.CB_rate = pyo.Constraint(m.t,rule=conc_B)
def conc_C(m,i):
return m.dCC[i] == m.k2 * m.CB[i]
m.CC_rate = pyo.Constraint(m.t,rule=conc_C)
return m
class ReactionKineticsExperiment_dae(Experiment):
def __init__(self, data): # , experiment_number):
self.data = data
self.model = None
def create_model(self):
self.model = m = reaction_kinetics_model_dae(self.data)
return m
def finalize_model(self):
m = self.model
# Initial Conditions
m.CA0 = self.data['CA0'][0]
m.T = self.data['T'][0]
m.CA[0].fix(m.CA0)
m.CB[0].fix(0.0)
m.CC[0].fix(0.0)
# Initialize the model with simulator
sim = dae.Simulator(m, package='casadi')
tsim, profiles = sim.simulate(numpoints=100, integrator='idas')
sim.initialize_model()
# Discretize model using collocation
discretizer = pyo.TransformationFactory('dae.collocation')
discretizer.apply_to(m, wrt=m.t, nfe = 20, ncp = 4, scheme='LAGRANGE-RADAU')
return m
def label_model(self):
m = self.model
m.experiment_outputs = pyo.Suffix(direction=pyo.Suffix.LOCAL)
m.experiment_outputs.update(
(m.CA[t], self.data['CA'][ind]) for ind, t in enumerate(self.data['time']))
m.experiment_outputs.update(
(m.CB[t], self.data['CB'][ind]) for ind, t in enumerate(self.data['time']))
m.experiment_outputs.update(
(m.CC[t], self.data['CC'][ind]) for ind, t in enumerate(self.data['time']))
m.unknown_parameters = pyo.Suffix(direction=pyo.Suffix.LOCAL)
m.unknown_parameters.update(
(k, pyo.ComponentUID(k)) for k in [m.A1, m.A2, m.E1, m.E2]
)
return m
def get_labeled_model(self):
m = self.create_model()
m = self.finalize_model()
m = self.label_model()
return m
# Test model
data = pd.read_csv(data_dir + 'parmest_20210609_data_exp1.csv', index_col=0)
print(data)
m = reaction_kinetics_model_dae(data)
# discretize
discretizer = pyo.TransformationFactory('dae.collocation')
discretizer.apply_to(m, wrt=m.t, nfe = 20, ncp = 4, scheme='LAGRANGE-RADAU')
# Fix initial conditions in OG model
m.A1.fix(200) # 1/hr
m.A2.fix(400) # 1/hr
m.E1.fix(10) # kJ/mol
m.E2.fix(15) # kJ/mol
m.CA[0].fix(m.CA0)
m.CB[0].fix(0.0)
m.CC[0].fix(0.0)
# # solve model
solver = pyo.SolverFactory('ipopt')
# solve model
solver.solve(m,tee=True)
# m.pprint()
# plot results
CA = [pyo.value(m.CA[i]) for i in m.t]
CB = [pyo.value(m.CB[i]) for i in m.t]
CC = [pyo.value(m.CC[i]) for i in m.t]
plt.plot(m.t, CA, label="$C_{A}$",linestyle="-",color="blue")
plt.plot(m.t, CB, label="$C_{B}$",linestyle="-.",color="green")
plt.plot(m.t, CC, label="$C_{C}$",linestyle="--",color="red")
plt.xlabel("Time [hours]")
plt.ylabel("Concentration [mol/L]")
plt.title("Batch Reactor Model")
plt.legend()
time T CA0 CA CB CC
0 0.000 250 0.5 0.476266 0.000000 0.000000
1 0.125 250 0.5 0.332309 0.133593 0.000000
2 0.250 250 0.5 0.295725 0.362016 0.092655
3 0.375 250 0.5 0.394806 0.131512 0.004404
4 0.500 250 0.5 0.167992 0.271682 0.031808
5 0.625 250 0.5 0.117872 0.313196 0.009108
6 0.750 250 0.5 0.117052 0.582722 0.000000
7 0.875 250 0.5 0.175373 0.224904 0.043844
8 1.000 250 0.5 0.130619 0.360287 0.194820
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
This version of Ipopt was compiled from source code available at
https://github.com/IDAES/Ipopt as part of the Institute for the Design of
Advanced Energy Systems Process Systems Engineering Framework (IDAES PSE
Framework) Copyright (c) 2018-2019. See https://github.com/IDAES/idaes-pse.
This version of Ipopt was compiled using HSL, a collection of Fortran codes
for large-scale scientific computation. All technical papers, sales and
publicity material resulting from use of the HSL codes within IPOPT must
contain the following acknowledgement:
HSL, a collection of Fortran codes for large-scale scientific
computation. See http://www.hsl.rl.ac.uk.
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 1991
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 0
Total number of variables............................: 483
variables with only lower bounds: 0
variables with lower and upper bounds: 0
variables with only upper bounds: 0
Total number of equality constraints.................: 483
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 0.0000000e+00 8.14e-01 0.00e+00 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 0.0000000e+00 2.84e-14 0.00e+00 -1.7 8.14e-01 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 1
(scaled) (unscaled)
Objective...............: 0.0000000000000000e+00 0.0000000000000000e+00
Dual infeasibility......: 0.0000000000000000e+00 0.0000000000000000e+00
Constraint violation....: 1.0945572278273075e-14 2.8421709430404007e-14
Complementarity.........: 0.0000000000000000e+00 0.0000000000000000e+00
Overall NLP error.......: 1.0945572278273075e-14 2.8421709430404007e-14
Number of objective function evaluations = 2
Number of objective gradient evaluations = 2
Number of equality constraint evaluations = 2
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 2
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 1
Total CPU secs in IPOPT (w/o function evaluations) = 0.003
Total CPU secs in NLP function evaluations = 0.000
EXIT: Optimal Solution Found.
<matplotlib.legend.Legend at 0x1fcd99d1f70>
5.1.6.1. Parameter estimation with parmest#
In the following cell, we perform parameter estimation using parmest to solve the least squares problem defined in the Pyomo dynamic model.
# list of temperatures
T_vals = [250,300,350,400] # K
# list of initial concentrations of A
CA0_vals = [0.5,1.0,1.5,2.0] # mol/L
# run parmest
exp_list = []
for i in range(16): #making a list of different experiments, each exp has corresponding data
df = pd.read_csv(file_name_generic.format(i+1),index_col=0)
# print(df.head())
exp_list.append(ReactionKineticsExperiment_dae(df))
pest = parmest.Estimator(exp_list, obj_function='SSE') #, tee = True)
obj, theta = pest.theta_est()
# print(theta)
#model = pest.ef_instance
model = pest.ef_instance.Scenario0 # For multiple experiments, Scenarios are generated
print("=== Parameter values ===")
print("A1 = {:0.3f} 1/hr".format(pyo.value(model.A1)))
print("A2 = {:0.3f} 1/hr".format(pyo.value(model.A2)))
print("E1 = {:0.3f} kJ/mol".format(pyo.value(model.E1)))
print("E2 = {:0.3f} kJ/mol".format(pyo.value(model.E2)))
=== Parameter values ===
A1 = 185.609 1/hr
A2 = 401.170 1/hr
E1 = 9.867 kJ/mol
E2 = 14.866 kJ/mol
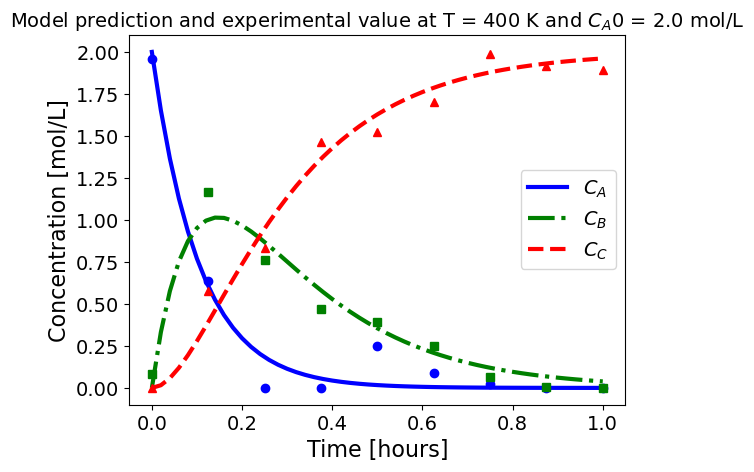
5.1.6.2. Plotting fitted model simulation with ‘experimental’ data#
Next, we plot the ‘experimental’ data along with the profiles generated using the fitted kinetic model. The symbols represent the ‘experimental’ data and the solid and dashed lines are the profiles generated using the fitted model.
# Parameter values from parameter estimation using parmest
A1 = theta['A1']
E1 = theta['E1']
A2 = theta['A2']
E2 = theta['E2']
A_est1 = [A1, A2]
A_est = np.asarray(A_est1)
E_est1 = [E1, E2]
E_est = np.asarray(E_est1)
ctr = 0
for T in T_vals:
for CA0 in CA0_vals:
# generate concentration profiles using estimated parameter values
k = kinetics(A_est, E_est, T)
# plot model-generated and 'experimental' data
# symbols for 'experimental' data
# solid and dashed lines for model-generated data
df = pd.read_csv(file_name_generic.format(ctr+1),index_col=0)
plot_exp(k, CA0, df, 'Model prediction and experimental value at T = {} K and $C_{}$ = {} mol/L'.format(T,'A0',CA0))
ctr+=1










5.1.7. Local uncertainty analysis#
5.1.7.1. Covariance matrix#
The parameter covariance matrix is calculated using the reduced Hessian approach. Using parmest, the covariance matrix can be calculated by setting optional argument calc_cov to True. More information on this approach can be found here: https://doi.org/10.1002/aic.16242
# run parmest
exp_list = []
for i in range(16): #making a list of different experiments, each exp has corresponding data
df = pd.read_csv(file_name_generic.format(i+1),index_col=0)
# print(df.head())
exp_list.append(ReactionKineticsExperiment(df))
pest = parmest.Estimator(exp_list, obj_function='SSE')
obj, theta, cov = pest.theta_est(calc_cov=True, cov_n = len(df))
# print(cov)
# print(theta)
model = pest.ef_instance.Scenario0
print("=== Parameter values ===")
print("A1 = {:0.3f} 1/hr".format(pyo.value(model.A1)))
print("A2 = {:0.3f} 1/hr".format(pyo.value(model.A2)))
print("E1 = {:0.3f} kJ/mol".format(pyo.value(model.E1)))
print("E2 = {:0.3f} kJ/mol".format(pyo.value(model.E2)))
=== Parameter values ===
A1 = 185.609 1/hr
A2 = 401.170 1/hr
E1 = 9.867 kJ/mol
E2 = 14.866 kJ/mol
5.1.7.2. Parameter identifiability#
The Fisher information matrix, \(FIM\), is calculated as the inverse of the parameter covariance matrix: \(FIM = {(Cov.)}^{-1}\)
Eigen decomposition of \(FIM\) following \(FIM = v \lambda {v}^{-1}\) gives eigenvector matrix \(v\) and \(\lambda\) is the diagonal matrix of eigenvalues. Column \(i\) in \(v\) is the eigenvector corresponding to the \(i\)-th eigenvalue. Further, each element of the eigenvector corresponds to the fitted parameters in order in which they appear in in theta_names. The magnitude of each element of an eigenvector denotes the contribution of the parameters on the direciton of the unit vector.
The eigenvector corresponding to the smallest eigenvalue denotes the direction of least variance in the parameter space. The parameter that corresponds to the major contributor in the eigenvector, then, has the lowest impact on model fit quality. Thus, this parameter is considered sloppy and fixing it’s value will not affect overall model behavior.
# Fisher information matrix can be computed using the inverse of the reduced Hessian
# defining the names of the parameters in a list
theta_names = ['A1','A2','E1','E2']
fim = np.linalg.inv(cov)
# Eigen decomposition of the Fisher information matrix
eig_values, eig_vectors = np.linalg.eig(fim)
for i,eig in enumerate(eig_values):
print('***************************************************************')
print('\nEigen value: {:0.3e}\n'.format(eig))
print('=== Eigen vector elements with correspondng parameter names ===\n')
print('------------------------------')
print('| Vector element | Parameter |')
print('------------------------------')
for j,theta_name in enumerate(theta_names):
if eig_vectors[i,j] < 0.0:
print('| {:0.3e} | {} |'.format(eig_vectors[i,j],theta_name))
else:
print('| {:0.3e} | {} |'.format(eig_vectors[i,j],theta_name))
print('\n')
***************************************************************
Eigen value: 6.495e+00
=== Eigen vector elements with correspondng parameter names ===
------------------------------
| Vector element | Parameter |
------------------------------
| 2.017e-01 | A1 |
| 9.794e-01 | A2 |
| 6.919e-03 | E1 |
| -1.150e-03 | E2 |
***************************************************************
Eigen value: 3.670e+00
=== Eigen vector elements with correspondng parameter names ===
------------------------------
| Vector element | Parameter |
------------------------------
| 9.794e-01 | A1 |
| -2.017e-01 | A2 |
| -5.644e-04 | E1 |
| -1.263e-02 | E2 |
***************************************************************
Eigen value: 2.688e-06
=== Eigen vector elements with correspondng parameter names ===
------------------------------
| Vector element | Parameter |
------------------------------
| -1.519e-03 | A1 |
| -6.805e-03 | A2 |
| 9.985e-01 | E1 |
| -5.373e-02 | E2 |
***************************************************************
Eigen value: 2.394e-05
=== Eigen vector elements with correspondng parameter names ===
------------------------------
| Vector element | Parameter |
------------------------------
| -1.254e-02 | A1 |
| 1.789e-03 | A2 |
| -5.373e-02 | E1 |
| -9.985e-01 | E2 |
Looking at the eigenvalues and corresponding eigenvectors, we can see that parameters A2 and A1 (in order) have the largest contributions to the direction of the eigenvector corresponding to the smallest eigenvalue. Therefore, as discussed above, we can conclude from this analysis that parameter A2 is the least identifiable parameter in this kinetic model, followed by parameter A1.
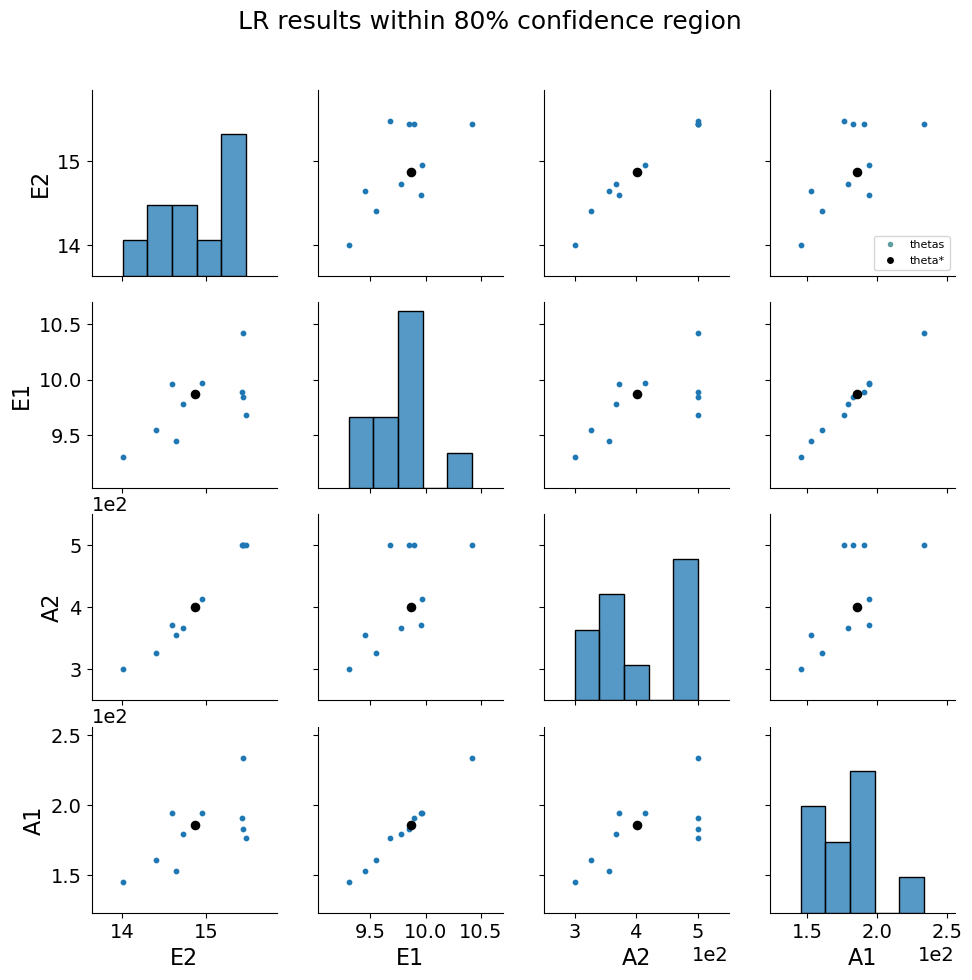
5.1.8. Bootstrap resampling#
Bootstrapping is a resampling method by independently sampling with replacement from an existing sample data with same sample size n, and performing inference among these resampled data (link). Bootstrap resampling is often used in parameter estimation problems to determine parameter confidence intervals. More information about bootstrap resampling and confidence interval calculation can be found here.
theta_est_bootstrap() is used to perform resampling with parmest. More information can be found here.
parmest also provides functions to plot bootstrap parameter estimates along with various confidence intervals link.
# create Estimator object
pest = parmest.Estimator(exp_list, obj_function='SSE', tee = True)
### Parameter estimation with bootstrap resampling
bootstrap_theta = pest.theta_est_bootstrap(10)
print(bootstrap_theta.head())
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
This version of Ipopt was compiled from source code available at
https://github.com/IDAES/Ipopt as part of the Institute for the Design of
Advanced Energy Systems Process Systems Engineering Framework (IDAES PSE
Framework) Copyright (c) 2018-2019. See https://github.com/IDAES/idaes-pse.
This version of Ipopt was compiled using HSL, a collection of Fortran codes
for large-scale scientific computation. All technical papers, sales and
publicity material resulting from use of the HSL codes within IPOPT must
contain the following acknowledgement:
HSL, a collection of Fortran codes for large-scale scientific
computation. See http://www.hsl.rl.ac.uk.
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 1528
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 544
Total number of variables............................: 448
variables with only lower bounds: 0
variables with lower and upper bounds: 64
variables with only upper bounds: 0
Total number of equality constraints.................: 444
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 1.2592126e+01 2.00e+00 1.36e-01 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 2.4281208e-01 3.25e-06 5.33e-04 -1.0 2.00e+00 - 9.91e-01 1.00e+00f 1
2 2.4273091e-01 1.82e-05 1.48e-06 -1.7 1.98e-02 - 1.00e+00 1.00e+00h 1
3 2.4270069e-01 4.90e-06 4.61e-07 -3.8 4.66e-01 - 1.00e+00 1.00e+00h 1
4 2.4226897e-01 3.52e-03 3.05e-05 -5.7 1.88e+01 - 8.66e-01 1.00e+00h 1
5 2.4219416e-01 6.40e-04 6.27e-06 -5.7 1.68e+01 - 1.00e+00 1.00e+00h 1
6 2.4218813e-01 3.23e-05 2.82e-07 -5.7 3.66e+00 - 1.00e+00 1.00e+00h 1
7 2.4218802e-01 6.28e-08 5.47e-10 -5.7 1.60e-01 - 1.00e+00 1.00e+00h 1
8 2.4218793e-01 1.43e-06 1.47e-08 -8.6 7.64e-01 - 9.96e-01 1.00e+00h 1
9 2.4218793e-01 1.06e-09 1.04e-11 -8.6 2.07e-02 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 9
(scaled) (unscaled)
Objective...............: 2.4218792850427115e-01 2.4218792850427115e-01
Dual infeasibility......: 1.0427097078251914e-11 1.0427097078251914e-11
Constraint violation....: 1.0560190499830924e-09 1.0560190499830924e-09
Complementarity.........: 2.5148073430467801e-09 2.5148073430467801e-09
Overall NLP error.......: 2.5148073430467801e-09 2.5148073430467801e-09
Number of objective function evaluations = 10
Number of objective gradient evaluations = 10
Number of equality constraint evaluations = 10
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 10
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 9
Total CPU secs in IPOPT (w/o function evaluations) = 0.005
Total CPU secs in NLP function evaluations = 0.003
EXIT: Optimal Solution Found.
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
This version of Ipopt was compiled from source code available at
https://github.com/IDAES/Ipopt as part of the Institute for the Design of
Advanced Energy Systems Process Systems Engineering Framework (IDAES PSE
Framework) Copyright (c) 2018-2019. See https://github.com/IDAES/idaes-pse.
This version of Ipopt was compiled using HSL, a collection of Fortran codes
for large-scale scientific computation. All technical papers, sales and
publicity material resulting from use of the HSL codes within IPOPT must
contain the following acknowledgement:
HSL, a collection of Fortran codes for large-scale scientific
computation. See http://www.hsl.rl.ac.uk.
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 1528
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 544
Total number of variables............................: 448
variables with only lower bounds: 0
variables with lower and upper bounds: 64
variables with only upper bounds: 0
Total number of equality constraints.................: 444
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 1.1130021e+01 2.00e+00 1.29e-01 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 2.1450418e-01 2.48e-06 7.94e-04 -1.0 2.00e+00 - 9.91e-01 1.00e+00f 1
2 2.1329569e-01 2.41e-04 4.14e-05 -1.7 9.15e-02 - 1.00e+00 1.00e+00h 1
3 2.1309689e-01 3.25e-05 4.15e-06 -3.8 1.24e+00 - 9.95e-01 1.00e+00h 1
4 2.1004486e-01 3.13e-02 2.89e-04 -5.7 5.25e+01 - 8.27e-01 1.00e+00h 1
5 2.0935359e-01 5.58e-03 5.37e-05 -5.7 4.70e+01 - 1.00e+00 1.00e+00h 1
6 2.0919143e-01 5.35e-04 6.67e-06 -5.7 1.30e+01 - 1.00e+00 1.00e+00h 1
7 2.0916259e-01 1.39e-04 7.48e-07 -5.7 6.43e+00 - 1.00e+00 1.00e+00h 1
8 2.0915651e-01 1.10e-05 5.93e-08 -5.7 1.78e+00 - 1.00e+00 1.00e+00h 1
9 2.0914468e-01 8.54e-05 4.88e-07 -8.6 4.91e+00 - 9.76e-01 1.00e+00h 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
10 2.0914141e-01 2.14e-05 1.18e-07 -8.6 2.43e+00 - 1.00e+00 1.00e+00h 1
11 2.0914047e-01 5.24e-06 2.91e-08 -8.6 1.19e+00 - 1.00e+00 1.00e+00h 1
12 2.0914020e-01 9.84e-07 5.48e-09 -8.6 5.15e-01 - 1.00e+00 1.00e+00h 1
13 2.0914014e-01 8.78e-08 4.90e-10 -8.6 1.54e-01 - 1.00e+00 1.00e+00h 1
14 2.0914013e-01 1.03e-09 5.75e-12 -8.6 1.66e-02 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 14
(scaled) (unscaled)
Objective...............: 2.0914012909343274e-01 2.0914012909343274e-01
Dual infeasibility......: 5.7510498247306951e-12 5.7510498247306951e-12
Constraint violation....: 1.0297200869757717e-09 1.0297200869757717e-09
Complementarity.........: 2.5112796767814955e-09 2.5112796767814955e-09
Overall NLP error.......: 2.5112796767814955e-09 2.5112796767814955e-09
Number of objective function evaluations = 15
Number of objective gradient evaluations = 15
Number of equality constraint evaluations = 15
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 15
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 14
Total CPU secs in IPOPT (w/o function evaluations) = 0.008
Total CPU secs in NLP function evaluations = 0.002
EXIT: Optimal Solution Found.
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
This version of Ipopt was compiled from source code available at
https://github.com/IDAES/Ipopt as part of the Institute for the Design of
Advanced Energy Systems Process Systems Engineering Framework (IDAES PSE
Framework) Copyright (c) 2018-2019. See https://github.com/IDAES/idaes-pse.
This version of Ipopt was compiled using HSL, a collection of Fortran codes
for large-scale scientific computation. All technical papers, sales and
publicity material resulting from use of the HSL codes within IPOPT must
contain the following acknowledgement:
HSL, a collection of Fortran codes for large-scale scientific
computation. See http://www.hsl.rl.ac.uk.
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 1528
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 544
Total number of variables............................: 448
variables with only lower bounds: 0
variables with lower and upper bounds: 64
variables with only upper bounds: 0
Total number of equality constraints.................: 444
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 1.5701740e+01 2.00e+00 1.30e-01 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 2.4396072e-01 6.04e-06 7.08e-04 -1.0 2.00e+00 - 9.91e-01 1.00e+00f 1
2 2.4147315e-01 3.07e-04 1.12e-04 -1.7 9.89e-02 - 1.00e+00 1.00e+00h 1
3 2.4141069e-01 8.59e-06 2.44e-06 -3.8 4.44e-01 - 1.00e+00 1.00e+00h 1
4 2.4012797e-01 3.74e-03 3.57e-05 -5.7 3.93e+01 - 7.34e-01 1.00e+00h 1
5 2.3949135e-01 2.29e-03 1.71e-05 -5.7 3.68e+01 - 1.00e+00 1.00e+00h 1
6 2.3927705e-01 4.63e-04 3.44e-06 -5.7 1.78e+01 - 1.00e+00 1.00e+00h 1
7 2.3924687e-01 1.19e-05 8.80e-08 -5.7 2.93e+00 - 1.00e+00 1.00e+00h 1
8 2.3921871e-01 8.80e-06 6.61e-08 -8.6 2.53e+00 - 9.89e-01 1.00e+00h 1
9 2.3921756e-01 1.69e-08 1.27e-10 -8.6 1.12e-01 - 1.00e+00 1.00e+00h 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
10 2.3921753e-01 8.47e-12 6.36e-14 -9.0 2.50e-03 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 10
(scaled) (unscaled)
Objective...............: 2.3921753224215234e-01 2.3921753224215234e-01
Dual infeasibility......: 6.3623990926121881e-14 6.3623990926121881e-14
Constraint violation....: 8.4734441685441197e-12 8.4734441685441197e-12
Complementarity.........: 9.0916085845819665e-10 9.0916085845819665e-10
Overall NLP error.......: 9.0916085845819665e-10 9.0916085845819665e-10
Number of objective function evaluations = 11
Number of objective gradient evaluations = 11
Number of equality constraint evaluations = 11
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 11
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 10
Total CPU secs in IPOPT (w/o function evaluations) = 0.008
Total CPU secs in NLP function evaluations = 0.001
EXIT: Optimal Solution Found.
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
This version of Ipopt was compiled from source code available at
https://github.com/IDAES/Ipopt as part of the Institute for the Design of
Advanced Energy Systems Process Systems Engineering Framework (IDAES PSE
Framework) Copyright (c) 2018-2019. See https://github.com/IDAES/idaes-pse.
This version of Ipopt was compiled using HSL, a collection of Fortran codes
for large-scale scientific computation. All technical papers, sales and
publicity material resulting from use of the HSL codes within IPOPT must
contain the following acknowledgement:
HSL, a collection of Fortran codes for large-scale scientific
computation. See http://www.hsl.rl.ac.uk.
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 1528
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 544
Total number of variables............................: 448
variables with only lower bounds: 0
variables with lower and upper bounds: 64
variables with only upper bounds: 0
Total number of equality constraints.................: 444
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 1.2439722e+01 1.95e+00 1.21e-01 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 2.2305711e-01 8.15e-06 1.93e-03 -1.0 1.95e+00 - 9.91e-01 1.00e+00f 1
2 2.2209585e-01 1.99e-04 4.28e-05 -1.7 6.31e-02 - 1.00e+00 1.00e+00h 1
3 2.2199626e-01 1.01e-05 7.07e-07 -3.8 1.04e+00 - 9.97e-01 1.00e+00h 1
4 2.2006688e-01 2.12e-02 1.82e-04 -5.7 4.40e+01 - 8.98e-01 1.00e+00h 1
5 2.1986930e-01 1.18e-03 1.85e-05 -5.7 2.42e+01 - 1.00e+00 1.00e+00h 1
6 2.1984720e-01 7.16e-05 6.50e-07 -5.7 5.39e+00 - 1.00e+00 1.00e+00h 1
7 2.1984699e-01 9.24e-07 6.07e-09 -5.7 6.03e-01 - 1.00e+00 1.00e+00h 1
8 2.1984679e-01 3.08e-06 1.58e-08 -8.6 1.10e+00 - 9.94e-01 1.00e+00h 1
9 2.1984679e-01 3.92e-09 2.35e-11 -8.6 3.91e-02 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 9
(scaled) (unscaled)
Objective...............: 2.1984678947461242e-01 2.1984678947461242e-01
Dual infeasibility......: 2.3529802826964871e-11 2.3529802826964871e-11
Constraint violation....: 3.9191224709966832e-09 3.9191224709966832e-09
Complementarity.........: 2.5381135858585810e-09 2.5381135858585810e-09
Overall NLP error.......: 3.9191224709966832e-09 3.9191224709966832e-09
Number of objective function evaluations = 10
Number of objective gradient evaluations = 10
Number of equality constraint evaluations = 10
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 10
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 9
Total CPU secs in IPOPT (w/o function evaluations) = 0.005
Total CPU secs in NLP function evaluations = 0.004
EXIT: Optimal Solution Found.
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
This version of Ipopt was compiled from source code available at
https://github.com/IDAES/Ipopt as part of the Institute for the Design of
Advanced Energy Systems Process Systems Engineering Framework (IDAES PSE
Framework) Copyright (c) 2018-2019. See https://github.com/IDAES/idaes-pse.
This version of Ipopt was compiled using HSL, a collection of Fortran codes
for large-scale scientific computation. All technical papers, sales and
publicity material resulting from use of the HSL codes within IPOPT must
contain the following acknowledgement:
HSL, a collection of Fortran codes for large-scale scientific
computation. See http://www.hsl.rl.ac.uk.
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 1528
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 544
Total number of variables............................: 448
variables with only lower bounds: 0
variables with lower and upper bounds: 64
variables with only upper bounds: 0
Total number of equality constraints.................: 444
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 2.1842207e+01 2.00e+00 1.67e-01 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 2.2084391e-01 8.29e-06 9.38e-04 -1.0 2.00e+00 - 9.91e-01 1.00e+00f 1
2 2.1772329e-01 3.39e-04 8.99e-05 -1.7 1.09e-01 - 1.00e+00 1.00e+00h 1
3 2.1765730e-01 5.37e-06 1.80e-06 -3.8 1.62e-01 - 1.00e+00 1.00e+00h 1
4 2.1761599e-01 1.74e-04 1.52e-06 -5.7 4.79e+00 - 9.67e-01 1.00e+00h 1
5 2.1760509e-01 1.15e-04 8.26e-07 -5.7 7.44e+00 - 1.00e+00 1.00e+00h 1
6 2.1760479e-01 9.97e-07 6.70e-09 -5.7 7.07e-01 - 1.00e+00 1.00e+00h 1
7 2.1760478e-01 1.60e-07 1.13e-09 -8.6 2.83e-01 - 9.99e-01 1.00e+00h 1
8 2.1760478e-01 8.87e-11 6.14e-13 -8.6 6.69e-03 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 8
(scaled) (unscaled)
Objective...............: 2.1760477732920155e-01 2.1760477732920155e-01
Dual infeasibility......: 6.1432087617157113e-13 6.1432087617157113e-13
Constraint violation....: 8.8729690261857286e-11 8.8729690261857286e-11
Complementarity.........: 2.5065269692916554e-09 2.5065269692916554e-09
Overall NLP error.......: 2.5065269692916554e-09 2.5065269692916554e-09
Number of objective function evaluations = 9
Number of objective gradient evaluations = 9
Number of equality constraint evaluations = 9
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 9
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 8
Total CPU secs in IPOPT (w/o function evaluations) = 0.006
Total CPU secs in NLP function evaluations = 0.002
EXIT: Optimal Solution Found.
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
This version of Ipopt was compiled from source code available at
https://github.com/IDAES/Ipopt as part of the Institute for the Design of
Advanced Energy Systems Process Systems Engineering Framework (IDAES PSE
Framework) Copyright (c) 2018-2019. See https://github.com/IDAES/idaes-pse.
This version of Ipopt was compiled using HSL, a collection of Fortran codes
for large-scale scientific computation. All technical papers, sales and
publicity material resulting from use of the HSL codes within IPOPT must
contain the following acknowledgement:
HSL, a collection of Fortran codes for large-scale scientific
computation. See http://www.hsl.rl.ac.uk.
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 1528
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 544
Total number of variables............................: 448
variables with only lower bounds: 0
variables with lower and upper bounds: 64
variables with only upper bounds: 0
Total number of equality constraints.................: 444
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 1.5082369e+01 2.00e+00 1.32e-01 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 2.1512438e-01 8.80e-06 1.05e-03 -1.0 2.00e+00 - 9.91e-01 1.00e+00f 1
2 2.1443321e-01 1.64e-04 1.16e-05 -1.7 4.68e-02 - 1.00e+00 1.00e+00h 1
3 2.1428685e-01 1.58e-05 2.61e-07 -3.8 1.31e+00 - 9.94e-01 1.00e+00h 1
4 2.1189138e-01 1.62e-02 1.35e-04 -5.7 3.86e+01 - 8.32e-01 1.00e+00h 1
5 2.1146420e-01 2.83e-03 3.20e-05 -5.7 3.42e+01 - 1.00e+00 1.00e+00h 1
6 2.1138745e-01 3.51e-04 3.98e-06 -5.7 1.11e+01 - 1.00e+00 1.00e+00h 1
7 2.1138066e-01 3.81e-05 4.32e-07 -5.7 3.57e+00 - 1.00e+00 1.00e+00h 1
8 2.1138025e-01 4.77e-07 5.41e-09 -5.7 3.97e-01 - 1.00e+00 1.00e+00h 1
9 2.1137939e-01 1.12e-05 1.34e-07 -8.6 1.92e+00 - 9.90e-01 1.00e+00h 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
10 2.1137937e-01 6.95e-08 8.04e-10 -8.6 1.50e-01 - 1.00e+00 1.00e+00h 1
11 2.1137937e-01 2.59e-12 3.00e-14 -8.6 9.17e-04 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 11
(scaled) (unscaled)
Objective...............: 2.1137936724570658e-01 2.1137936724570658e-01
Dual infeasibility......: 2.9971892143540737e-14 2.9971892143540737e-14
Constraint violation....: 2.5907054279628028e-12 2.5907054279628028e-12
Complementarity.........: 2.5059279484415384e-09 2.5059279484415384e-09
Overall NLP error.......: 2.5059279484415384e-09 2.5059279484415384e-09
Number of objective function evaluations = 12
Number of objective gradient evaluations = 12
Number of equality constraint evaluations = 12
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 12
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 11
Total CPU secs in IPOPT (w/o function evaluations) = 0.007
Total CPU secs in NLP function evaluations = 0.001
EXIT: Optimal Solution Found.
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
This version of Ipopt was compiled from source code available at
https://github.com/IDAES/Ipopt as part of the Institute for the Design of
Advanced Energy Systems Process Systems Engineering Framework (IDAES PSE
Framework) Copyright (c) 2018-2019. See https://github.com/IDAES/idaes-pse.
This version of Ipopt was compiled using HSL, a collection of Fortran codes
for large-scale scientific computation. All technical papers, sales and
publicity material resulting from use of the HSL codes within IPOPT must
contain the following acknowledgement:
HSL, a collection of Fortran codes for large-scale scientific
computation. See http://www.hsl.rl.ac.uk.
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 1528
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 544
Total number of variables............................: 448
variables with only lower bounds: 0
variables with lower and upper bounds: 64
variables with only upper bounds: 0
Total number of equality constraints.................: 444
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 1.3935145e+01 2.00e+00 1.30e-01 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 2.4203118e-01 8.64e-06 9.78e-04 -1.0 2.00e+00 - 9.91e-01 1.00e+00f 1
2 2.3739268e-01 6.74e-04 1.30e-04 -1.7 1.53e-01 - 1.00e+00 1.00e+00h 1
3 2.3728281e-01 1.99e-05 3.14e-06 -3.8 7.61e-01 - 1.00e+00 1.00e+00h 1
4 2.3601478e-01 3.93e-03 3.39e-05 -5.7 2.89e+01 - 7.91e-01 1.00e+00h 1
5 2.3553513e-01 2.15e-03 2.16e-05 -5.7 3.39e+01 - 1.00e+00 1.00e+00h 1
6 2.3538642e-01 6.89e-04 6.27e-06 -5.7 2.11e+01 - 1.00e+00 1.00e+00h 1
7 2.3534837e-01 9.01e-05 8.07e-07 -5.7 7.94e+00 - 1.00e+00 1.00e+00h 1
8 2.3534321e-01 2.05e-06 1.85e-08 -5.7 1.21e+00 - 1.00e+00 1.00e+00h 1
9 2.3532146e-01 3.88e-05 3.65e-07 -8.6 5.31e+00 - 9.75e-01 1.00e+00h 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
10 2.3531737e-01 1.75e-06 1.61e-08 -8.6 1.13e+00 - 1.00e+00 1.00e+00h 1
11 2.3531722e-01 2.68e-09 2.47e-11 -8.6 4.45e-02 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 11
(scaled) (unscaled)
Objective...............: 2.3531721677772968e-01 2.3531721677772968e-01
Dual infeasibility......: 2.4664363499299724e-11 2.4664363499299724e-11
Constraint violation....: 2.6836806110708267e-09 2.6836806110708267e-09
Complementarity.........: 2.5193272931833644e-09 2.5193272931833644e-09
Overall NLP error.......: 2.6836806110708267e-09 2.6836806110708267e-09
Number of objective function evaluations = 12
Number of objective gradient evaluations = 12
Number of equality constraint evaluations = 12
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 12
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 11
Total CPU secs in IPOPT (w/o function evaluations) = 0.005
Total CPU secs in NLP function evaluations = 0.002
EXIT: Optimal Solution Found.
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
This version of Ipopt was compiled from source code available at
https://github.com/IDAES/Ipopt as part of the Institute for the Design of
Advanced Energy Systems Process Systems Engineering Framework (IDAES PSE
Framework) Copyright (c) 2018-2019. See https://github.com/IDAES/idaes-pse.
This version of Ipopt was compiled using HSL, a collection of Fortran codes
for large-scale scientific computation. All technical papers, sales and
publicity material resulting from use of the HSL codes within IPOPT must
contain the following acknowledgement:
HSL, a collection of Fortran codes for large-scale scientific
computation. See http://www.hsl.rl.ac.uk.
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 1528
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 544
Total number of variables............................: 448
variables with only lower bounds: 0
variables with lower and upper bounds: 64
variables with only upper bounds: 0
Total number of equality constraints.................: 444
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 1.6333230e+01 1.95e+00 1.54e-01 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 2.4590917e-01 8.68e-06 7.89e-04 -1.0 1.95e+00 - 9.91e-01 1.00e+00f 1
2 2.4103269e-01 5.06e-04 2.00e-04 -1.7 1.52e-01 - 1.00e+00 1.00e+00h 1
3 2.4101218e-01 1.17e-05 4.85e-06 -3.8 1.74e-01 - 1.00e+00 1.00e+00h 1
4 2.4092607e-01 2.42e-04 2.78e-06 -5.7 9.44e+00 - 9.26e-01 1.00e+00h 1
5 2.4088107e-01 6.18e-04 4.54e-06 -5.7 1.66e+01 - 1.00e+00 1.00e+00h 1
6 2.4088053e-01 7.26e-06 8.37e-08 -5.7 1.76e+00 - 1.00e+00 1.00e+00h 1
7 2.4088049e-01 1.38e-06 1.01e-08 -8.6 7.58e-01 - 9.95e-01 1.00e+00h 1
8 2.4088049e-01 1.04e-09 7.68e-12 -8.6 2.08e-02 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 8
(scaled) (unscaled)
Objective...............: 2.4088049315145352e-01 2.4088049315145352e-01
Dual infeasibility......: 7.6810857901397675e-12 7.6810857901397675e-12
Constraint violation....: 1.0401730587972224e-09 1.0401730587972224e-09
Complementarity.........: 2.5142603482557913e-09 2.5142603482557913e-09
Overall NLP error.......: 2.5142603482557913e-09 2.5142603482557913e-09
Number of objective function evaluations = 9
Number of objective gradient evaluations = 9
Number of equality constraint evaluations = 9
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 9
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 8
Total CPU secs in IPOPT (w/o function evaluations) = 0.005
Total CPU secs in NLP function evaluations = 0.002
EXIT: Optimal Solution Found.
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
This version of Ipopt was compiled from source code available at
https://github.com/IDAES/Ipopt as part of the Institute for the Design of
Advanced Energy Systems Process Systems Engineering Framework (IDAES PSE
Framework) Copyright (c) 2018-2019. See https://github.com/IDAES/idaes-pse.
This version of Ipopt was compiled using HSL, a collection of Fortran codes
for large-scale scientific computation. All technical papers, sales and
publicity material resulting from use of the HSL codes within IPOPT must
contain the following acknowledgement:
HSL, a collection of Fortran codes for large-scale scientific
computation. See http://www.hsl.rl.ac.uk.
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 1528
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 544
Total number of variables............................: 448
variables with only lower bounds: 0
variables with lower and upper bounds: 64
variables with only upper bounds: 0
Total number of equality constraints.................: 444
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 1.6415199e+01 2.00e+00 1.43e-01 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 2.3519676e-01 1.75e-05 5.83e-04 -1.0 2.00e+00 - 9.91e-01 1.00e+00f 1
2 2.3027811e-01 5.59e-04 1.84e-04 -1.7 1.36e-01 - 1.00e+00 1.00e+00h 1
3 2.3025823e-01 6.82e-06 2.45e-06 -3.8 4.38e-01 - 1.00e+00 1.00e+00h 1
4 2.2919775e-01 3.31e-03 2.87e-05 -5.7 4.04e+01 - 7.28e-01 1.00e+00h 1
5 2.2850890e-01 2.52e-03 2.09e-05 -5.7 3.91e+01 - 1.00e+00 1.00e+00h 1
6 2.2829639e-01 3.82e-04 3.08e-06 -5.7 1.63e+01 - 1.00e+00 1.00e+00h 1
7 2.2827869e-01 3.50e-06 2.70e-08 -5.7 1.59e+00 - 1.00e+00 1.00e+00h 1
8 2.2825045e-01 6.13e-06 5.39e-08 -8.6 2.13e+00 - 9.91e-01 1.00e+00h 1
9 2.2824970e-01 5.07e-09 4.22e-11 -8.6 6.12e-02 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 9
(scaled) (unscaled)
Objective...............: 2.2824970226527747e-01 2.2824970226527747e-01
Dual infeasibility......: 4.2170372619787979e-11 4.2170372619787979e-11
Constraint violation....: 5.0666827400291936e-09 5.0666827400291936e-09
Complementarity.........: 2.5326953143394347e-09 2.5326953143394347e-09
Overall NLP error.......: 5.0666827400291936e-09 5.0666827400291936e-09
Number of objective function evaluations = 10
Number of objective gradient evaluations = 10
Number of equality constraint evaluations = 10
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 10
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 9
Total CPU secs in IPOPT (w/o function evaluations) = 0.006
Total CPU secs in NLP function evaluations = 0.001
EXIT: Optimal Solution Found.
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
This version of Ipopt was compiled from source code available at
https://github.com/IDAES/Ipopt as part of the Institute for the Design of
Advanced Energy Systems Process Systems Engineering Framework (IDAES PSE
Framework) Copyright (c) 2018-2019. See https://github.com/IDAES/idaes-pse.
This version of Ipopt was compiled using HSL, a collection of Fortran codes
for large-scale scientific computation. All technical papers, sales and
publicity material resulting from use of the HSL codes within IPOPT must
contain the following acknowledgement:
HSL, a collection of Fortran codes for large-scale scientific
computation. See http://www.hsl.rl.ac.uk.
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 1528
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 544
Total number of variables............................: 448
variables with only lower bounds: 0
variables with lower and upper bounds: 64
variables with only upper bounds: 0
Total number of equality constraints.................: 444
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 2.5739535e+01 2.00e+00 1.79e-01 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 2.0661280e-01 2.50e-05 1.38e-03 -1.0 2.00e+00 - 9.91e-01 1.00e+00f 1
2 2.0073777e-01 4.50e-04 9.34e-05 -1.7 1.25e-01 - 1.00e+00 1.00e+00h 1
3 2.0065697e-01 3.77e-06 7.82e-07 -3.8 3.66e-01 - 1.00e+00 1.00e+00h 1
4 1.9996926e-01 2.02e-03 1.75e-05 -5.7 3.02e+01 - 7.83e-01 1.00e+00h 1
5 1.9958166e-01 1.84e-03 1.38e-05 -5.7 3.22e+01 - 1.00e+00 1.00e+00h 1
6 1.9945710e-01 5.72e-04 4.31e-06 -5.7 1.93e+01 - 1.00e+00 1.00e+00h 1
7 1.9942351e-01 8.85e-05 6.69e-07 -5.7 7.84e+00 - 1.00e+00 1.00e+00h 1
8 1.9941745e-01 4.15e-06 3.14e-08 -5.7 1.72e+00 - 1.00e+00 1.00e+00h 1
9 1.9940051e-01 4.66e-05 3.57e-07 -8.6 5.79e+00 - 9.72e-01 1.00e+00h 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
10 1.9939542e-01 6.90e-06 5.23e-08 -8.6 2.25e+00 - 1.00e+00 1.00e+00h 1
11 1.9939462e-01 2.00e-07 1.52e-09 -8.6 3.85e-01 - 1.00e+00 1.00e+00h 1
12 1.9939460e-01 1.62e-10 1.23e-12 -8.6 1.10e-02 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 12
(scaled) (unscaled)
Objective...............: 1.9939459765620607e-01 1.9939459765620607e-01
Dual infeasibility......: 1.2301984165340900e-12 1.2301984165340900e-12
Constraint violation....: 1.6208756559166204e-10 1.6208756559166204e-10
Complementarity.........: 2.5070327221401204e-09 2.5070327221401204e-09
Overall NLP error.......: 2.5070327221401204e-09 2.5070327221401204e-09
Number of objective function evaluations = 13
Number of objective gradient evaluations = 13
Number of equality constraint evaluations = 13
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 13
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 12
Total CPU secs in IPOPT (w/o function evaluations) = 0.007
Total CPU secs in NLP function evaluations = 0.001
EXIT: Optimal Solution Found.
E2 E1 A2 A1
0 14.728451 9.777382 366.382668 179.167485
1 14.008765 9.304571 300.100481 145.197585
2 15.477783 9.680324 499.998675 176.293973
3 14.647181 9.450998 355.859651 152.982091
4 14.948308 9.971654 413.297037 194.342527
Once the parameter estimates are generated through bootstrap resampling, we can visualize the estimates using the pairwise_plot() function as follows:
pyomo.contrib.parmest.graphics.pairwise_plot(bootstrap_theta, title='Bootstrap theta estimates')
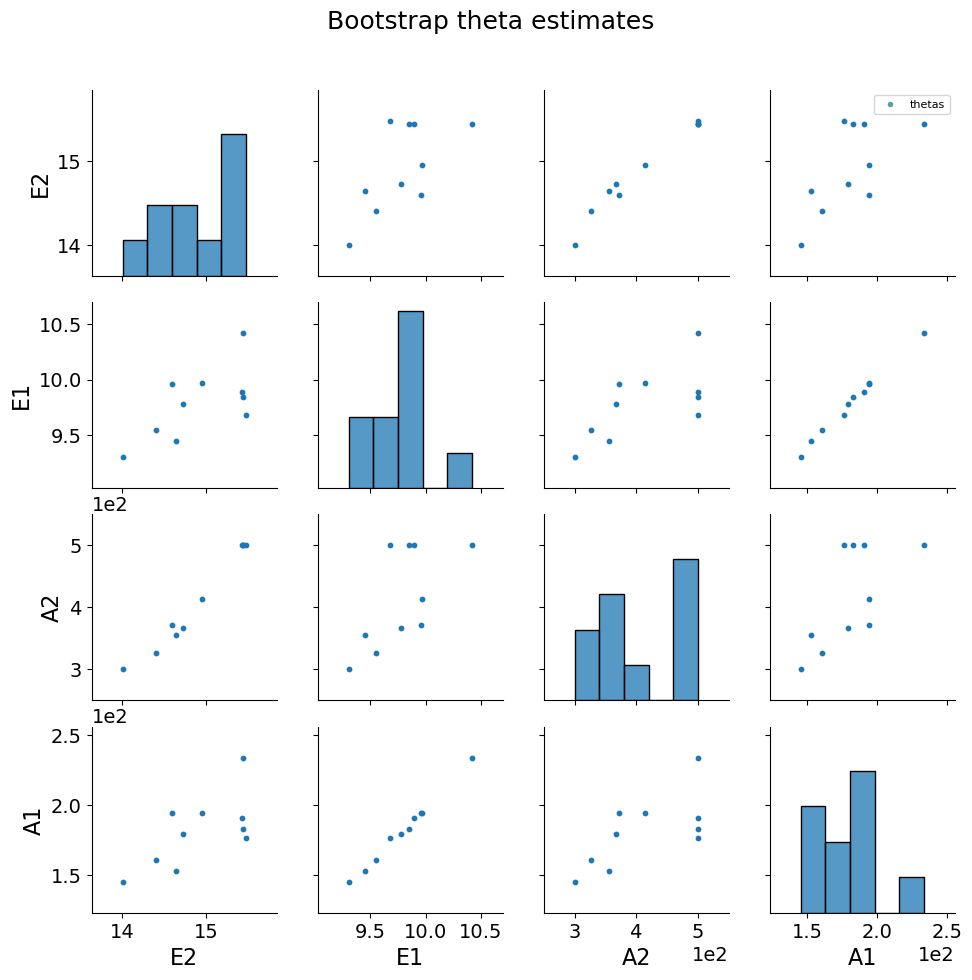
Confidence regions can be plotted around the bootstrap estimates for various distributions with confidence \(\alpha\).
# plot bootstrap parameter estimates with confidence intervals
pyomo.contrib.parmest.graphics.pairwise_plot(bootstrap_theta, theta, 0.8, ['MVN', 'KDE', 'Rect'],
title='Bootstrap theta with confidence regions')
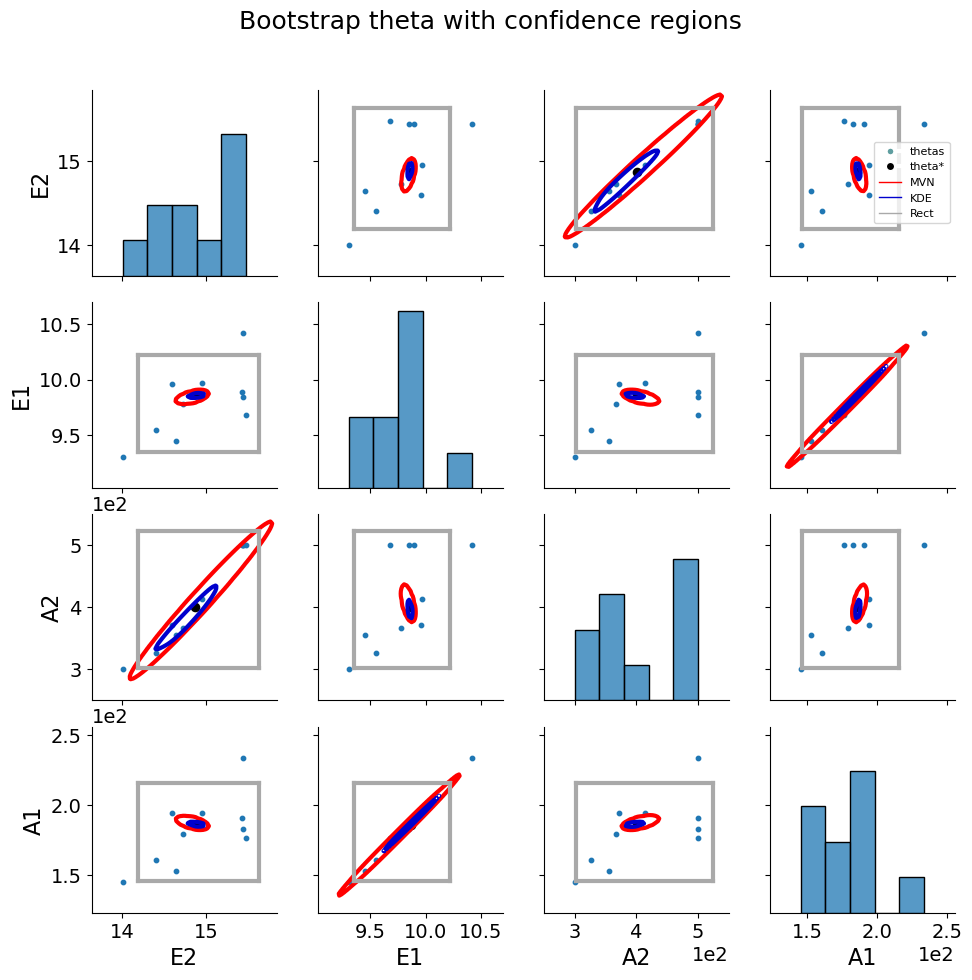
5.1.9. Nonlinear confidence regions#
The likelihood-ratio test (sometimes called the likelihood-ratio \(\chi^2\) test) is a hypothesis test that helps one choose the “best” model between two modelslink. Basically, the test compares the fit of two models. The null hypothesis is that the first model is the “best” model; It is rejected when the test statistic is large. In other words, if the null hypothesis is rejected, then the second model is a significant improvement over the first model.
In the last part of this notebook, we use the bootstrap parameter estimates to determine the goodness of fit using the likelihood-ratio \(\chi^2\) test. More information can be found here.
from itertools import product
### Likelihood ratio test
# generate arrays of parameter values
A1 = np.arange(180.0, 190.0, 1.0)
A2 = np.arange(395.0, 405.0, 1.0)
E1 = np.arange(5.0, 15.0, 1.0)
E2 = np.arange(10.0, 20.0, 1.0)
# format parameter values into a pandas dataframe to be provided as input to calculate
# corresponding objective function values
# theta_vals = pd.DataFrame(list(product(A1, A2, E1, E2)), columns=theta_names)
theta_vals = bootstrap_theta
obj_at_theta = pest.objective_at_theta(theta_vals)
print(obj_at_theta.head())
E2 E1 A2 A1 obj
0 14.728451 9.777382 366.382668 179.167485 0.224777
1 14.008765 9.304571 300.100481 145.197585 0.226707
2 15.477783 9.680324 499.998675 176.293973 0.224614
3 14.647181 9.450998 355.859651 152.982091 0.228158
4 14.948308 9.971654 413.297037 194.342527 0.222223
LR = pest.likelihood_ratio_test(obj_at_theta, obj, [0.8, 0.85, 0.9, 0.95])
print(LR.head())
E2 E1 A2 A1 obj 0.8 0.85 0.9 \
0 14.728451 9.777382 366.382668 179.167485 0.224777 True True True
1 14.008765 9.304571 300.100481 145.197585 0.226707 True True True
2 15.477783 9.680324 499.998675 176.293973 0.224614 True True True
3 14.647181 9.450998 355.859651 152.982091 0.228158 True True True
4 14.948308 9.971654 413.297037 194.342527 0.222223 True True True
0.95
0 True
1 True
2 True
3 True
4 True
The likelihood ratio test results with confidence \(\alpha\) can be visualized as follows:
pyomo.contrib.parmest.graphics.pairwise_plot(LR, theta, 0.8,
title='LR results within 80% confidence region')
Objective contour plot for E2 E1 slice failed
Objective contour plot for E2 A2 slice failed
Objective contour plot for E1 A2 slice failed
Objective contour plot for E2 A1 slice failed
Objective contour plot for E1 A1 slice failed
Objective contour plot for A2 A1 slice failed
Objective contour plot for E1 E2 slice failed
Objective contour plot for A2 E2 slice failed
Objective contour plot for A1 E2 slice failed
Objective contour plot for A2 E1 slice failed
Objective contour plot for A1 E1 slice failed
Objective contour plot for A1 A2 slice failed