1.5. Continuous Optimization: Nonlinear Programming#
# This code cell installs packages on Colab
import sys
if "google.colab" in sys.modules:
!wget "https://raw.githubusercontent.com/ndcbe/optimization/main/notebooks/helper.py"
import helper
helper.easy_install()
else:
sys.path.insert(0, '../')
import helper
helper.set_plotting_style()
import pandas as pd
import pyomo.environ as pyo
1.5.1. Nonlinear Programs: Circle Packing Example#
What is the smallest rectangle you can use to enclose three given circles? Reference: Example 4.4 in Biegler (2010).
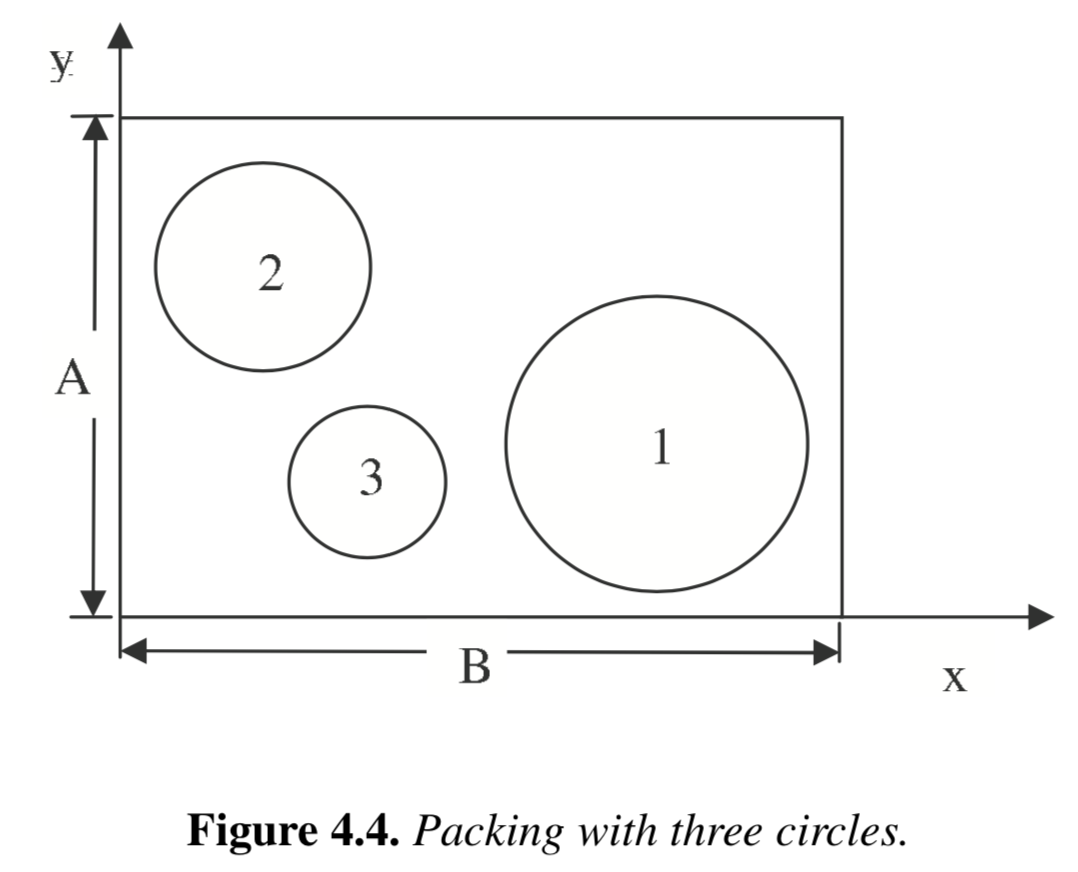
1.5.1.1. Propose an Optimization Model#
The following optimization model is given in Biegler (2010):
\[\begin{split}
\begin{align}
\text{min} \quad & 2(A + B) \\
\text{s.t.} \quad & A \geq 0, \quad B \geq 0, \\
& x_1, y_1, \geq R_1, \quad x_1 \leq B - R_1, \quad y_1 \leq A - R_1, \\
& x_2, y_2, \geq R_2, \quad x_2 \leq B - R_2, \quad y_2 \leq A - R_2, \\
& x_3, y_3, \geq R_3, \quad x_3 \leq B - R_3, \quad y_3 \leq A - R_3, \\
& (x_1 - x_2)^2 + (y_1 - y_2)^2 \geq (R_1 + R_2)^2, \\
& (x_1 - x_3)^2 + (y_1 - y_3)^2 \geq (R_1 + R_3)^2, \\
& (x_2 - x_3)^2 + (y_2 - y_3)^2 \geq (R_2 + R_3)^2,
\end{align}
\end{split}\]
How can we more compactly represent this using sets?
Activity
Identify the sets, parameters, variables, and constraints.
Sets
Click to expand
\(\mathcal{C} = \{1, 2, 3\}\): circles
Parameters
Click to expand
\(R_i\): radius of circle \(i\)
Variables
Click to expand
\(x_i\), \(y_i\): coordinates for circle \(i\)
\(A\), \(B\): dimensions of the bounding rectangle
Objective
Click to expand
\(2(A + B)\): perimeter of the bounding rectangle
Constraints
Click to expand
circle \(i\) cannot overlap with sides of bounding rectangle:
\(x_i, y_i, \geq R_i, \quad x_i \leq B - R_i, \quad y_i \leq A - R_i, \forall i \in \mathcal{C}\)
no overlap between circles \(i\) and \(j\):
\((x_i - x_j)^2 + (y_i - y_j)^2 \geq (R_i + R_j)^2, \forall i,j \in \{i \in \mathcal{C}, j \in \mathcal{C}: i < j\}\)
non-negative rectangle lengths:
\(A, B \geq 0\)
Complete Optimization Formulation
Click to see the solution to the activity
\[\begin{split}
\begin{align*}
\text{min}_{x,y,A,B} \quad & 2(A + B) & \text{perimeter} \\
\text{s.t.} \quad & A \geq 0, \quad B \geq 0 & \text{non-negative bounds}, \\
& x_i, y_i, \geq R_i, \quad x_i \leq B - R_i, \quad y_i \leq A - R_i, \forall i \in \mathcal{C} & \text{circles cannot overlap with perimeter} \\
& (x_i - x_j)^2 + (y_i - y_j)^2 \geq (R_i + R_j)^2, \forall i,j \in \{i \in \mathcal{C}, j \in \mathcal{C}: i < j\} & \text{circles cannot overlap with each other}
\end{align*}
\end{split}\]
Activity
Perform degree of freedom analysis.
Degree of Freedom Analysis
Click to expand
Continous variables: \(2 + | \mathcal{C} |\)
Inequality constraints: \(2 + 4 | \mathcal{C} | + {| \mathcal{C} | \choose 2}\)
1.5.1.2. Implement in Pyomo#
First, we will define functions to create and intialize the model.
import random
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
def create_circle_model(circle_radii):
''' Create circle optimization model in Pyomo
Arguments:
circle_radii: dictionary with keys=circle name and value=radius (float)
Returns:
model: Pyomo model
'''
# Number of circles to consider
n = len(circle_radii)
# Create a concrete Pyomo model.
model = pyo.ConcreteModel()
# Initialize index for circles
model.CIRCLES = pyo.Set(initialize = circle_radii.keys())
# Create parameter
model.R = pyo.Param(model.CIRCLES, domain=pyo.PositiveReals, initialize=circle_radii)
# Create variables for box
model.a = pyo.Var(domain=pyo.PositiveReals)
model.b = pyo.Var(domain=pyo.PositiveReals)
# Set objective
model.obj = pyo.Objective(expr=2*(model.a + model.b), sense = pyo.minimize)
# Create variables for circle centers
model.x = pyo.Var(model.CIRCLES, domain=pyo.PositiveReals)
model.y = pyo.Var(model.CIRCLES, domain=pyo.PositiveReals)
# "In the box" constraints
def left_x(m,c):
return m.x[c] >= model.R[c]
model.left_x_con = pyo.Constraint(model.CIRCLES, rule=left_x)
def left_y(m,c):
return m.y[c] >= model.R[c]
model.left_y_con = pyo.Constraint(model.CIRCLES, rule=left_y)
def right_x(m,c):
return m.x[c] <= m.b - model.R[c]
model.right_x_con = pyo.Constraint(model.CIRCLES, rule=right_x)
def right_y(m,c):
return m.y[c] <= m.a - model.R[c]
model.right_y_con = pyo.Constraint(model.CIRCLES, rule=right_y)
# No overlap constraints
def no_overlap(m,c1,c2):
if c1 < c2:
return (m.x[c1] - m.x[c2])**2 + (m.y[c1] - m.y[c2])**2 >= (model.R[c1] + model.R[c2])**2
else:
return pyo.Constraint.Skip
model.no_overlap_con = pyo.Constraint(model.CIRCLES, model.CIRCLES, rule=no_overlap)
return model
def initialize_circle_model(model, a_init=25, b_init=25):
''' Initialize the x and y coordinates using uniform distribution
Arguments:
a_init: initial value for a (default=25)
b_init: initial value for b (default=25)
Returns:
Nothing. But per Pyomo scoping rules, the input argument `model`
can be modified in this function.
'''
# Initialize
model.a = 25
model.b = 25
for i in model.CIRCLES:
# Adding circle radii ensures the remains in the >0, >0 quadrant
model.x[i] = random.uniform(0,10) + model.R[i]
model.y[i] = random.uniform(0,10) + model.R[i]
Next, we will create a dictionary containing the circle names and radii values.
# Create dictionary with circle data
circle_data = {'A':10.0, 'B':5.0, 'C':3.0}
circle_data
{'A': 10.0, 'B': 5.0, 'C': 3.0}
# Access the keys
circle_data.keys()
dict_keys(['A', 'B', 'C'])
Now let’s create the model.
# Create model
model = create_circle_model(circle_data)
model.pprint()
1 Set Declarations
CIRCLES : Size=1, Index=None, Ordered=Insertion
Key : Dimen : Domain : Size : Members
None : 1 : Any : 3 : {'A', 'B', 'C'}
1 Param Declarations
R : Size=3, Index=CIRCLES, Domain=PositiveReals, Default=None, Mutable=False
Key : Value
A : 10.0
B : 5.0
C : 3.0
4 Var Declarations
a : Size=1, Index=None
Key : Lower : Value : Upper : Fixed : Stale : Domain
None : 0 : None : None : False : True : PositiveReals
b : Size=1, Index=None
Key : Lower : Value : Upper : Fixed : Stale : Domain
None : 0 : None : None : False : True : PositiveReals
x : Size=3, Index=CIRCLES
Key : Lower : Value : Upper : Fixed : Stale : Domain
A : 0 : None : None : False : True : PositiveReals
B : 0 : None : None : False : True : PositiveReals
C : 0 : None : None : False : True : PositiveReals
y : Size=3, Index=CIRCLES
Key : Lower : Value : Upper : Fixed : Stale : Domain
A : 0 : None : None : False : True : PositiveReals
B : 0 : None : None : False : True : PositiveReals
C : 0 : None : None : False : True : PositiveReals
1 Objective Declarations
obj : Size=1, Index=None, Active=True
Key : Active : Sense : Expression
None : True : minimize : 2*(a + b)
5 Constraint Declarations
left_x_con : Size=3, Index=CIRCLES, Active=True
Key : Lower : Body : Upper : Active
A : 10.0 : x[A] : +Inf : True
B : 5.0 : x[B] : +Inf : True
C : 3.0 : x[C] : +Inf : True
left_y_con : Size=3, Index=CIRCLES, Active=True
Key : Lower : Body : Upper : Active
A : 10.0 : y[A] : +Inf : True
B : 5.0 : y[B] : +Inf : True
C : 3.0 : y[C] : +Inf : True
no_overlap_con : Size=3, Index=CIRCLES*CIRCLES, Active=True
Key : Lower : Body : Upper : Active
('A', 'B') : 225.0 : (x[A] - x[B])**2 + (y[A] - y[B])**2 : +Inf : True
('A', 'C') : 169.0 : (x[A] - x[C])**2 + (y[A] - y[C])**2 : +Inf : True
('B', 'C') : 64.0 : (x[B] - x[C])**2 + (y[B] - y[C])**2 : +Inf : True
right_x_con : Size=3, Index=CIRCLES, Active=True
Key : Lower : Body : Upper : Active
A : -Inf : x[A] - (b - 10.0) : 0.0 : True
B : -Inf : x[B] - (b - 5.0) : 0.0 : True
C : -Inf : x[C] - (b - 3.0) : 0.0 : True
right_y_con : Size=3, Index=CIRCLES, Active=True
Key : Lower : Body : Upper : Active
A : -Inf : y[A] - (a - 10.0) : 0.0 : True
B : -Inf : y[B] - (a - 5.0) : 0.0 : True
C : -Inf : y[C] - (a - 3.0) : 0.0 : True
12 Declarations: CIRCLES R a b obj x y left_x_con left_y_con right_x_con right_y_con no_overlap_con
And let’s initialize the model.
# Initialize model
initialize_circle_model(model)
model.pprint()
1 Set Declarations
CIRCLES : Size=1, Index=None, Ordered=Insertion
Key : Dimen : Domain : Size : Members
None : 1 : Any : 3 : {'A', 'B', 'C'}
1 Param Declarations
R : Size=3, Index=CIRCLES, Domain=PositiveReals, Default=None, Mutable=False
Key : Value
A : 10.0
B : 5.0
C : 3.0
4 Var Declarations
a : Size=1, Index=None
Key : Lower : Value : Upper : Fixed : Stale : Domain
None : 0 : 25 : None : False : False : PositiveReals
b : Size=1, Index=None
Key : Lower : Value : Upper : Fixed : Stale : Domain
None : 0 : 25 : None : False : False : PositiveReals
x : Size=3, Index=CIRCLES
Key : Lower : Value : Upper : Fixed : Stale : Domain
A : 0 : 19.721128404129697 : None : False : False : PositiveReals
B : 0 : 7.08632115423932 : None : False : False : PositiveReals
C : 0 : 4.18185123759586 : None : False : False : PositiveReals
y : Size=3, Index=CIRCLES
Key : Lower : Value : Upper : Fixed : Stale : Domain
A : 0 : 11.110078446910464 : None : False : False : PositiveReals
B : 0 : 11.995904930678053 : None : False : False : PositiveReals
C : 0 : 9.263055250683019 : None : False : False : PositiveReals
1 Objective Declarations
obj : Size=1, Index=None, Active=True
Key : Active : Sense : Expression
None : True : minimize : 2*(a + b)
5 Constraint Declarations
left_x_con : Size=3, Index=CIRCLES, Active=True
Key : Lower : Body : Upper : Active
A : 10.0 : x[A] : +Inf : True
B : 5.0 : x[B] : +Inf : True
C : 3.0 : x[C] : +Inf : True
left_y_con : Size=3, Index=CIRCLES, Active=True
Key : Lower : Body : Upper : Active
A : 10.0 : y[A] : +Inf : True
B : 5.0 : y[B] : +Inf : True
C : 3.0 : y[C] : +Inf : True
no_overlap_con : Size=3, Index=CIRCLES*CIRCLES, Active=True
Key : Lower : Body : Upper : Active
('A', 'B') : 225.0 : (x[A] - x[B])**2 + (y[A] - y[B])**2 : +Inf : True
('A', 'C') : 169.0 : (x[A] - x[C])**2 + (y[A] - y[C])**2 : +Inf : True
('B', 'C') : 64.0 : (x[B] - x[C])**2 + (y[B] - y[C])**2 : +Inf : True
right_x_con : Size=3, Index=CIRCLES, Active=True
Key : Lower : Body : Upper : Active
A : -Inf : x[A] - (b - 10.0) : 0.0 : True
B : -Inf : x[B] - (b - 5.0) : 0.0 : True
C : -Inf : x[C] - (b - 3.0) : 0.0 : True
right_y_con : Size=3, Index=CIRCLES, Active=True
Key : Lower : Body : Upper : Active
A : -Inf : y[A] - (a - 10.0) : 0.0 : True
B : -Inf : y[B] - (a - 5.0) : 0.0 : True
C : -Inf : y[C] - (a - 3.0) : 0.0 : True
12 Declarations: CIRCLES R a b obj x y left_x_con left_y_con right_x_con right_y_con no_overlap_con
Activity
Compare the initial values for x and y with and without initialization. What is the default initial value in Pyomo?
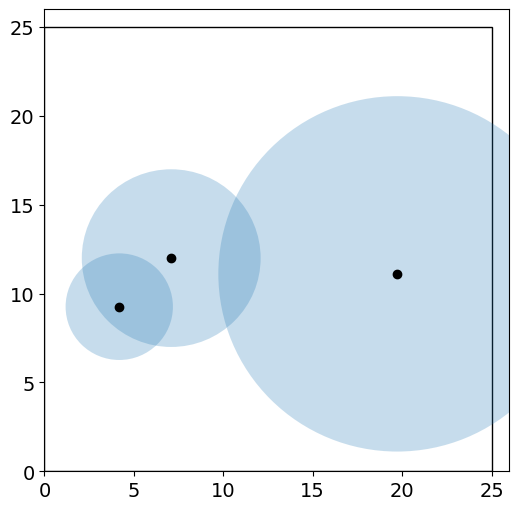
1.5.1.3. Visualize Initial Point#
Next, we’ll define a function to plot the solution (or initial point)
# Plot initial point
def plot_circles(m):
''' Plot circles using data in Pyomo model
Arguments:
m: Pyomo concrete model
Returns:
Nothing (but makes a figure)
'''
# Create figure
fig, ax = plt.subplots(1,figsize=(6,6))
# Adjust axes
l = max(m.a.value,m.b.value) + 1
ax.set_xlim(0,l)
ax.set_ylim(0,l)
# Draw box
art = mpatches.Rectangle((0,0), width=m.b.value, height=m.a.value,fill=False)
ax.add_patch(art)
# Draw circles and mark center
for i in m.CIRCLES:
art2 = mpatches.Circle( (m.x[i].value,m.y[i].value), radius=m.R[i],fill=True,alpha=0.25)
ax.add_patch(art2)
plt.scatter(m.x[i].value,m.y[i].value,color='black')
# Show plot
plt.show()
plot_circles(model)
1.5.1.4. Solve and Inspect the Solution#
# Specify the solver
solver = pyo.SolverFactory('ipopt')
# Solve the model
results = solver.solve(model, tee = True)
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
This version of Ipopt was compiled from source code available at
https://github.com/IDAES/Ipopt as part of the Institute for the Design of
Advanced Energy Systems Process Systems Engineering Framework (IDAES PSE
Framework) Copyright (c) 2018-2019. See https://github.com/IDAES/idaes-pse.
This version of Ipopt was compiled using HSL, a collection of Fortran codes
for large-scale scientific computation. All technical papers, sales and
publicity material resulting from use of the HSL codes within IPOPT must
contain the following acknowledgement:
HSL, a collection of Fortran codes for large-scale scientific
computation. See http://www.hsl.rl.ac.uk.
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 0
Number of nonzeros in inequality constraint Jacobian.: 30
Number of nonzeros in Lagrangian Hessian.............: 12
Total number of variables............................: 8
variables with only lower bounds: 8
variables with lower and upper bounds: 0
variables with only upper bounds: 0
Total number of equality constraints.................: 0
Total number of inequality constraints...............: 15
inequality constraints with only lower bounds: 9
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 6
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 1.0000000e+02 6.46e+01 1.01e+00 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 9.9770305e+01 1.64e+01 1.36e+00 -1.0 9.59e+00 - 5.62e-01 5.23e-01h 1
2 9.8534198e+01 3.26e+00 4.71e-01 -1.0 3.33e+00 - 8.55e-01 6.73e-01h 1
3 9.8964504e+01 1.03e-01 1.10e-01 -1.0 2.40e+00 - 9.11e-01 8.02e-01h 1
4 9.8759130e+01 0.00e+00 5.88e-02 -1.0 1.71e+01 - 1.00e+00 7.35e-01f 1
5 9.8391035e+01 0.00e+00 1.55e-02 -1.7 3.38e+01 - 9.89e-01 1.00e+00h 1
6 9.8394873e+01 0.00e+00 1.41e-02 -1.7 1.22e+02 - 1.00e+00 2.76e-01h 2
7 9.8404876e+01 0.00e+00 2.13e-04 -1.7 9.78e+00 - 1.00e+00 1.00e+00h 1
8 9.8404875e+01 0.00e+00 6.22e-06 -1.7 4.23e+00 - 1.00e+00 1.00e+00h 1
9 9.8285022e+01 0.00e+00 8.24e-05 -3.8 2.89e-01 - 1.00e+00 9.96e-01h 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
10 9.8284281e+01 0.00e+00 7.98e-09 -5.7 7.15e-03 - 1.00e+00 1.00e+00h 1
11 9.8284270e+01 0.00e+00 1.10e-12 -8.6 2.09e-04 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 11
(scaled) (unscaled)
Objective...............: 9.8284270438748507e+01 9.8284270438748507e+01
Dual infeasibility......: 1.1009340361698271e-12 1.1009340361698271e-12
Constraint violation....: 0.0000000000000000e+00 0.0000000000000000e+00
Complementarity.........: 2.5139755386181626e-09 2.5139755386181626e-09
Overall NLP error.......: 2.5139755386181626e-09 2.5139755386181626e-09
Number of objective function evaluations = 16
Number of objective gradient evaluations = 12
Number of equality constraint evaluations = 0
Number of inequality constraint evaluations = 16
Number of equality constraint Jacobian evaluations = 0
Number of inequality constraint Jacobian evaluations = 12
Number of Lagrangian Hessian evaluations = 11
Total CPU secs in IPOPT (w/o function evaluations) = 0.004
Total CPU secs in NLP function evaluations = 0.000
EXIT: Optimal Solution Found.
Next, we can inspect the solution. Because Pyomo is a Python extension, we can use Pyoth (for loops, etc.) to programmatically inspect the solution.
# Print variable values
print("Name\tValue")
for c in model.component_data_objects(pyo.Var):
print(c.name,"\t", pyo.value(c))
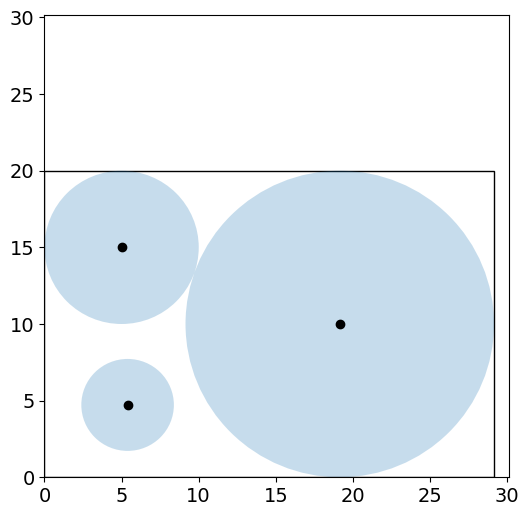
# Plot solution
plot_circles(model)
Name Value
a 19.999999803189517
b 29.142135416184733
x[A] 19.142135514931894
x[B] 4.999999951252102
x[C] 5.388458700112411
y[A] 9.999999901252012
y[B] 14.999999849644189
y[C] 4.720856828961742
# Print constraints
for c in model.component_data_objects(pyo.Constraint):
print(c.name,"\t", pyo.value(c.lower),"\t", pyo.value(c.body),"\t", pyo.value(c.upper))
left_x_con[A] 10.0 19.142135514931894 None
left_x_con[B] 5.0 4.999999951252102 None
left_x_con[C] 3.0 5.388458700112411 None
left_y_con[A] 10.0 9.999999901252012 None
left_y_con[B] 5.0 14.999999849644189 None
left_y_con[C] 3.0 4.720856828961742 None
right_x_con[A] None 9.87471615587765e-08 0.0
right_x_con[B] None -19.14213546493263 0.0
right_x_con[C] None -20.75367671607232 0.0
right_y_con[A] None 9.806249501309594e-08 0.0
right_y_con[B] None 4.645467122088576e-08 0.0
right_y_con[C] None -12.279142974227774 0.0
no_overlap_con[A,B] 225.0 224.99999778541851 None
no_overlap_con[A,C] 169.0 217.03297750421336 None
no_overlap_con[B,C] 64.0 105.81168143921077 None
1.5.1.5. Reinitialize and Resolve#
Activity
Reinitialize the model, plot the initial point, resolve, and plot the solution. Is there more than one solution?
# Initialize and print the model
# Add your solution here
1 Set Declarations
CIRCLES : Size=1, Index=None, Ordered=Insertion
Key : Dimen : Domain : Size : Members
None : 1 : Any : 3 : {'A', 'B', 'C'}
1 Param Declarations
R : Size=3, Index=CIRCLES, Domain=PositiveReals, Default=None, Mutable=False
Key : Value
A : 10.0
B : 5.0
C : 3.0
4 Var Declarations
a : Size=1, Index=None
Key : Lower : Value : Upper : Fixed : Stale : Domain
None : 0 : 25 : None : False : False : PositiveReals
b : Size=1, Index=None
Key : Lower : Value : Upper : Fixed : Stale : Domain
None : 0 : 25 : None : False : False : PositiveReals
x : Size=3, Index=CIRCLES
Key : Lower : Value : Upper : Fixed : Stale : Domain
A : 0 : 10.850147023982599 : None : False : False : PositiveReals
B : 0 : 9.780923462544251 : None : False : False : PositiveReals
C : 0 : 10.61608289663573 : None : False : False : PositiveReals
y : Size=3, Index=CIRCLES
Key : Lower : Value : Upper : Fixed : Stale : Domain
A : 0 : 13.134484970950401 : None : False : False : PositiveReals
B : 0 : 9.781300035681124 : None : False : False : PositiveReals
C : 0 : 7.155057832701888 : None : False : False : PositiveReals
1 Objective Declarations
obj : Size=1, Index=None, Active=True
Key : Active : Sense : Expression
None : True : minimize : 2*(a + b)
5 Constraint Declarations
left_x_con : Size=3, Index=CIRCLES, Active=True
Key : Lower : Body : Upper : Active
A : 10.0 : x[A] : +Inf : True
B : 5.0 : x[B] : +Inf : True
C : 3.0 : x[C] : +Inf : True
left_y_con : Size=3, Index=CIRCLES, Active=True
Key : Lower : Body : Upper : Active
A : 10.0 : y[A] : +Inf : True
B : 5.0 : y[B] : +Inf : True
C : 3.0 : y[C] : +Inf : True
no_overlap_con : Size=3, Index=CIRCLES*CIRCLES, Active=True
Key : Lower : Body : Upper : Active
('A', 'B') : 225.0 : (x[A] - x[B])**2 + (y[A] - y[B])**2 : +Inf : True
('A', 'C') : 169.0 : (x[A] - x[C])**2 + (y[A] - y[C])**2 : +Inf : True
('B', 'C') : 64.0 : (x[B] - x[C])**2 + (y[B] - y[C])**2 : +Inf : True
right_x_con : Size=3, Index=CIRCLES, Active=True
Key : Lower : Body : Upper : Active
A : -Inf : x[A] - (b - 10.0) : 0.0 : True
B : -Inf : x[B] - (b - 5.0) : 0.0 : True
C : -Inf : x[C] - (b - 3.0) : 0.0 : True
right_y_con : Size=3, Index=CIRCLES, Active=True
Key : Lower : Body : Upper : Active
A : -Inf : y[A] - (a - 10.0) : 0.0 : True
B : -Inf : y[B] - (a - 5.0) : 0.0 : True
C : -Inf : y[C] - (a - 3.0) : 0.0 : True
12 Declarations: CIRCLES R a b obj x y left_x_con left_y_con right_x_con right_y_con no_overlap_con
# Plot initial point
# Add your solution here
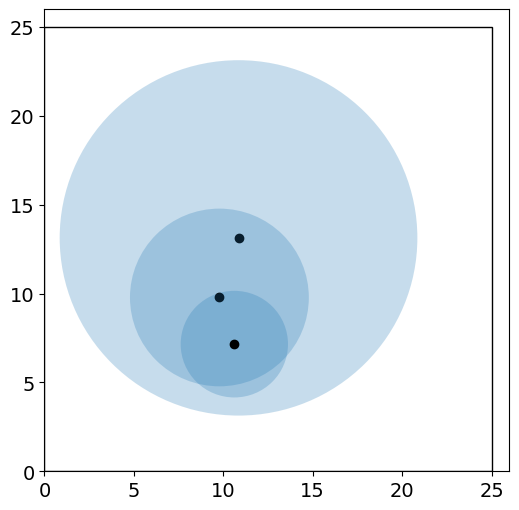
# Solve the model
# Add your solution here
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
This version of Ipopt was compiled from source code available at
https://github.com/IDAES/Ipopt as part of the Institute for the Design of
Advanced Energy Systems Process Systems Engineering Framework (IDAES PSE
Framework) Copyright (c) 2018-2019. See https://github.com/IDAES/idaes-pse.
This version of Ipopt was compiled using HSL, a collection of Fortran codes
for large-scale scientific computation. All technical papers, sales and
publicity material resulting from use of the HSL codes within IPOPT must
contain the following acknowledgement:
HSL, a collection of Fortran codes for large-scale scientific
computation. See http://www.hsl.rl.ac.uk.
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 0
Number of nonzeros in inequality constraint Jacobian.: 30
Number of nonzeros in Lagrangian Hessian.............: 12
Total number of variables............................: 8
variables with only lower bounds: 8
variables with lower and upper bounds: 0
variables with only upper bounds: 0
Total number of equality constraints.................: 0
Total number of inequality constraints...............: 15
inequality constraints with only lower bounds: 9
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 6
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 1.0000000e+02 2.13e+02 1.07e+00 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 9.9065790e+01 1.50e+02 2.01e+01 -1.0 3.69e+01 - 1.46e-01 1.28e-01h 1
2 1.0014388e+02 1.14e+02 1.52e+01 -1.0 1.21e+01 - 1.96e-01 2.33e-01h 1
3 1.0308715e+02 3.79e+01 5.20e+00 -1.0 4.21e+00 - 7.46e-01 5.77e-01h 1
4 1.0176992e+02 7.27e+00 1.84e+00 -1.0 3.15e+00 - 8.30e-01 6.57e-01h 1
5 1.0069191e+02 0.00e+00 1.52e+00 -1.0 1.64e+02 - 1.57e-01 4.63e-01f 1
6 9.9571913e+01 0.00e+00 3.42e-01 -1.0 3.58e+00 -2.0 8.94e-01 1.00e+00h 1
7 9.8844540e+01 0.00e+00 2.89e-01 -1.0 1.55e+01 -2.5 1.00e+00 2.71e-01h 1
8 9.8856677e+01 0.00e+00 2.53e-01 -1.0 6.71e+00 - 1.00e+00 7.65e-01h 1
9 9.8394858e+01 0.00e+00 7.40e-02 -1.7 6.91e+01 - 2.76e-01 1.00e+00h 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
10 9.8405222e+01 0.00e+00 1.81e-03 -1.7 8.69e+00 - 1.00e+00 1.00e+00h 1
11 9.8405014e+01 0.00e+00 5.25e-04 -1.7 3.15e+01 - 1.00e+00 1.00e+00h 1
12 9.8405027e+01 0.00e+00 1.15e-05 -1.7 9.13e+00 - 1.00e+00 1.00e+00h 1
13 9.8300696e+01 0.00e+00 1.30e-05 -2.5 2.98e-01 - 1.00e+00 1.00e+00h 1
14 9.8285160e+01 0.00e+00 3.22e-07 -3.8 5.72e-02 - 1.00e+00 1.00e+00h 1
15 9.8284281e+01 0.00e+00 1.84e-09 -5.7 6.42e-03 - 1.00e+00 1.00e+00h 1
16 9.8284270e+01 0.00e+00 2.50e-12 -8.6 5.00e-04 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 16
(scaled) (unscaled)
Objective...............: 9.8284270438747257e+01 9.8284270438747257e+01
Dual infeasibility......: 2.5044774225155953e-12 2.5044774225155953e-12
Constraint violation....: 0.0000000000000000e+00 0.0000000000000000e+00
Complementarity.........: 2.5245587089450044e-09 2.5245587089450044e-09
Overall NLP error.......: 2.5245587089450044e-09 2.5245587089450044e-09
Number of objective function evaluations = 17
Number of objective gradient evaluations = 17
Number of equality constraint evaluations = 0
Number of inequality constraint evaluations = 17
Number of equality constraint Jacobian evaluations = 0
Number of inequality constraint Jacobian evaluations = 17
Number of Lagrangian Hessian evaluations = 16
Total CPU secs in IPOPT (w/o function evaluations) = 0.006
Total CPU secs in NLP function evaluations = 0.000
EXIT: Optimal Solution Found.
# Plot solution
# Add your solution here
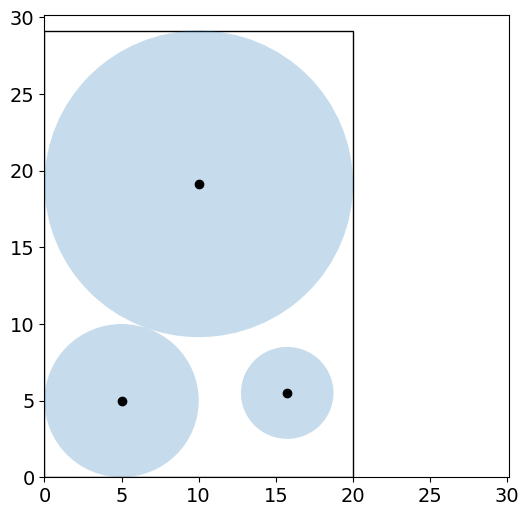
1.5.2. Take Away Messages#
Nonlinear programs may be nonconvex. For nonconvex problems, there often existings many local optima that are not also global optima.
We will learn how to mathematically define convexity and analyze this property.
Initialization is really important in optimization problems with nonlinear objectives or constraints!
There are specialize solves for linear programs, quadratic programs, and convex programs. In this class, we will focus on more general algorithms for (non)convex nonlinear programs including the algorithms used by the
ipoptsolver.