3.1. Pyomo.DAE Example: Race Car#
Adapted from Pyomo.DAE: Racing Example Revisited and Pyomo/pyomo
3.1.1. Learning Objectives#
Introduces syntax for Pyomo.DAE
Shows time-scaling modeling trick
Pratice using units feature in Pyomo
3.1.2. Install Packages and Load Modules#
# Imports
import sys
if "google.colab" in sys.modules:
!wget "https://raw.githubusercontent.com/ndcbe/optimization/main/notebooks/helper.py"
import helper
helper.easy_install()
else:
sys.path.insert(0, '../')
import helper
helper.set_plotting_style()
import pyomo.environ as pyo
import matplotlib.pyplot as plt
import pyomo.dae as dae
from pyomo.environ import units
3.1.3. Problem Statement and Optimal Control Formulation#
You are a race car driver with a simple goal. Drive distance \(L\) in the minimal amount of time but come to a complete stop at the finish line.
Mathematically, you want to solve the following optimal control problem:
where \(u\) is the acceleration/braking (your control variable) and \(R\) is the drag coefficient (parameter).
3.1.3.1. Scale Time#
Let \(t = \tau \cdot t_f\) where \(\tau \in [0,1]\). Thus \(dt = t_f d\tau\). The optimal control problem becomes:
3.1.3.2. Declaring our Model with Pyomo.DAE#
We can use Pyomo.dae to automatically formulate the collocation equations (i.e., add constraints that numerically integrate the ODE model).
def create_model1():
# Define the model
m = pyo.ConcreteModel()
# Deine the model parameters
m.R = pyo.Param(initialize=0.001, units=1/units.m) # Friction factor
m.L = pyo.Param(initialize=100.0, units=units.m) # Final position
# Define time
m.tau = dae.ContinuousSet(bounds=(0,1)) # Dimensionless time set
m.tf = pyo.Var(initialize=1, units=units.s) # Final time
# Define remaining algebraic variables
m.x = pyo.Var(m.tau, bounds=(0,m.L+50*units.m), units=units.m) # Position
m.v = pyo.Var(m.tau, bounds=(0,None), units=units.m/units.s) # Velocity
m.u = pyo.Var(m.tau, bounds=(-3.0,1.0),initialize=0, units=units.m/units.s/units.s) # Acceleration
# Define derivative variables
m.dx = dae.DerivativeVar(m.x)
m.dv = dae.DerivativeVar(m.v)
# Declare the objective (minimize final time)
m.obj = pyo.Objective(expr=m.tf)
# Define the constraints
# position
def _ode1(m,i):
if i == 0 :
return pyo.Constraint.Skip
return m.dx[i] == m.tf * m.v[i]
m.ode1 = pyo.Constraint(m.tau, rule=_ode1)
# velocity
def _ode2(m,i):
if i == 0 :
return pyo.Constraint.Skip
return m.dv[i] == m.tf*(m.u[i] - m.R*m.v[i]**2)
m.ode2 = pyo.Constraint(m.tau, rule=_ode2)
# Define the inital/boundary conditions
def _init(m):
yield m.x[0] == 0
yield m.x[1] == m.L
yield m.v[0] == 0
yield m.v[1] == 0
m.initcon = pyo.ConstraintList(rule=_init)
return m
m = create_model1()
Now let’s inspect the model.
m.pprint()
2 Param Declarations
L : Size=1, Index=None, Domain=Any, Default=None, Mutable=True, Units=m
Key : Value
None : 100.0
R : Size=1, Index=None, Domain=Any, Default=None, Mutable=True, Units=1/m
Key : Value
None : 0.001
4 Var Declarations
tf : Size=1, Index=None, Units=s
Key : Lower : Value : Upper : Fixed : Stale : Domain
None : None : 1 : None : False : False : Reals
u : Size=2, Index=tau, Units=m/s**2
Key : Lower : Value : Upper : Fixed : Stale : Domain
0 : -3.0 : 0 : 1.0 : False : False : Reals
1 : -3.0 : 0 : 1.0 : False : False : Reals
v : Size=2, Index=tau, Units=m/s
Key : Lower : Value : Upper : Fixed : Stale : Domain
0 : 0 : None : None : False : True : Reals
1 : 0 : None : None : False : True : Reals
x : Size=2, Index=tau, Units=m
Key : Lower : Value : Upper : Fixed : Stale : Domain
0 : 0 : None : 150.0 : False : True : Reals
1 : 0 : None : 150.0 : False : True : Reals
1 Objective Declarations
obj : Size=1, Index=None, Active=True
Key : Active : Sense : Expression
None : True : minimize : tf
3 Constraint Declarations
initcon : Size=4, Index={1, 2, 3, 4}, Active=True
Key : Lower : Body : Upper : Active
1 : 0.0 : x[0] : 0.0 : True
2 : L : x[1] : L : True
3 : 0.0 : v[0] : 0.0 : True
4 : 0.0 : v[1] : 0.0 : True
ode1 : Size=1, Index=tau, Active=True
Key : Lower : Body : Upper : Active
1 : 0.0 : dx[1] - tf*v[1] : 0.0 : True
ode2 : Size=1, Index=tau, Active=True
Key : Lower : Body : Upper : Active
1 : 0.0 : dv[1] - tf*(u[1] - R*v[1]**2) : 0.0 : True
1 ContinuousSet Declarations
tau : Size=1, Index=None, Ordered=Sorted
Key : Dimen : Domain : Size : Members
None : 1 : [0..1] : 2 : {0, 1}
2 DerivativeVar Declarations
dv : Size=2, Index=tau
Key : Lower : Value : Upper : Fixed : Stale : Domain
0 : None : None : None : False : True : Reals
1 : None : None : None : False : True : Reals
dx : Size=2, Index=tau
Key : Lower : Value : Upper : Fixed : Stale : Domain
0 : None : None : None : False : True : Reals
1 : None : None : None : False : True : Reals
13 Declarations: R L tau tf x v u dx dv obj ode1 ode2 initcon
3.1.3.3. Discretize/Transcribe and Solve#
#discretizer = TransformationFactory('dae.finite_difference')
#discretizer.apply_to(m,nfe=15,scheme='BACKWARD')
# Declare the discretizer
discretizer = pyo.TransformationFactory('dae.collocation')
discretizer.apply_to(m,nfe=15,scheme='LAGRANGE-RADAU',ncp=3)
#discretizer.apply_to(m,nfe=15,scheme='LAGRANGE-LEGENDRE',ncp=3)
# force piecewise constant controls (acceleration) over each finite element
m = discretizer.reduce_collocation_points(m,var=m.u,ncp=1,contset=m.tau)
# Solve
solver = pyo.SolverFactory('ipopt')
solver.solve(m,tee=True)
print("final time = %6.2f seconds" %(pyo.value(m.tf)))
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
This version of Ipopt was compiled from source code available at
https://github.com/IDAES/Ipopt as part of the Institute for the Design of
Advanced Energy Systems Process Systems Engineering Framework (IDAES PSE
Framework) Copyright (c) 2018-2019. See https://github.com/IDAES/idaes-pse.
This version of Ipopt was compiled using HSL, a collection of Fortran codes
for large-scale scientific computation. All technical papers, sales and
publicity material resulting from use of the HSL codes within IPOPT must
contain the following acknowledgement:
HSL, a collection of Fortran codes for large-scale scientific
computation. See http://www.hsl.rl.ac.uk.
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 829
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 135
Total number of variables............................: 228
variables with only lower bounds: 46
variables with lower and upper bounds: 91
variables with only upper bounds: 0
Total number of equality constraints.................: 214
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 1.0000000e+00 1.00e+02 1.30e+00 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1r 1.0000000e+00 1.00e+02 9.99e+02 2.0 0.00e+00 - 0.00e+00 3.26e-07R 8
2r 1.2449252e+00 9.95e+01 9.93e+02 2.0 1.26e+02 - 5.63e-03 6.22e-03f 1
3r 2.6155110e+00 9.91e+01 1.22e+02 0.6 1.56e+00 - 7.62e-01 8.77e-01f 1
4r 5.7407161e+00 9.81e+01 1.16e+02 -0.1 4.77e+01 0.0 2.43e-02 6.55e-02f 1
5r 6.9131266e+00 9.76e+01 1.19e+02 -0.1 4.77e+01 - 7.69e-02 2.46e-02f 1
6r 1.8926907e+01 9.25e+01 4.60e+02 -0.1 8.87e+01 - 2.39e-02 1.35e-01f 1
7r 1.9252497e+01 8.70e+01 3.95e+02 -0.1 1.08e+01 - 2.88e-02 8.03e-01f 1
8 2.0135727e+01 8.62e+01 6.54e+00 -1.0 2.64e+02 - 1.14e-01 9.09e-03h 5
9 2.0857378e+01 8.51e+01 1.12e+01 -1.0 3.10e+02 - 1.01e-01 1.20e-02h 6
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
10 2.1432701e+01 8.41e+01 1.85e+01 -1.0 3.11e+02 - 1.50e-01 1.20e-02h 6
11 2.2030985e+01 8.29e+01 3.02e+01 -1.0 2.93e+02 - 2.34e-01 1.41e-02h 6
12 2.2781040e+01 8.14e+01 4.72e+01 -1.0 2.74e+02 - 3.37e-01 1.87e-02h 6
13 1.4199237e+01 1.24e+02 3.11e+01 -1.0 2.62e+02 - 5.20e-01 4.38e-01H 1
14 2.1365014e+01 8.49e+01 1.03e+01 -1.0 9.32e+01 - 5.48e-02 2.34e-01h 2
15 2.2706495e+01 7.92e+01 8.10e+01 -1.0 1.15e+02 - 6.41e-01 6.36e-02h 4
16 2.3519561e+01 7.41e+01 1.19e+02 -1.0 8.53e+01 - 3.68e-01 6.19e-02h 5
17 2.3548373e+01 7.38e+01 2.26e+02 -1.0 6.83e+01 - 7.29e-01 3.34e-03h 9
18 2.0378731e+01 6.54e+01 1.94e+02 -1.0 2.92e+02 - 1.04e-01 1.28e-01h 1
19 1.9424173e+01 4.16e+01 7.83e+01 -1.0 1.12e+02 - 1.16e-01 3.70e-01h 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
20 1.7710108e+01 1.68e+01 3.14e+01 -1.0 9.79e+01 - 3.38e-01 5.75e-01f 1
21 1.7993344e+01 8.23e+00 2.96e+02 -1.0 2.83e+01 - 1.00e+00 5.14e-01h 1
22 1.9147366e+01 4.90e-01 1.61e+01 -1.0 9.69e+00 - 1.00e+00 9.90e-01h 1
23 1.9205734e+01 1.67e-02 1.26e+03 -1.0 4.50e+00 - 1.00e+00 9.90e-01h 1
24 1.9211008e+01 4.04e-05 1.02e-06 -1.0 1.18e-01 - 1.00e+00 1.00e+00h 1
25 1.7317872e+01 3.20e+00 1.46e+06 -5.7 1.68e+01 - 7.50e-01 1.00e+00f 1
26 1.6683635e+01 7.56e-01 1.79e+05 -5.7 1.22e+01 - 8.77e-01 9.88e-01h 1
27 1.6527179e+01 7.58e-02 3.73e+04 -5.7 7.89e+00 - 7.92e-01 9.92e-01h 1
28 1.6520375e+01 6.03e-05 5.38e-07 -5.7 8.83e-02 - 1.00e+00 1.00e+00h 1
29 1.6520269e+01 6.27e-09 8.71e-11 -5.7 9.10e-04 - 1.00e+00 1.00e+00h 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
30 1.6520192e+01 9.76e-09 1.62e-10 -8.6 1.19e-03 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 30
(scaled) (unscaled)
Objective...............: 1.6520191521080950e+01 1.6520191521080950e+01
Dual infeasibility......: 1.6219122342334269e-10 1.6219122342334269e-10
Constraint violation....: 9.7603276572044706e-09 9.7603276572044706e-09
Complementarity.........: 2.5852522114913472e-09 2.5852522114913472e-09
Overall NLP error.......: 9.7603276572044706e-09 9.7603276572044706e-09
Number of objective function evaluations = 96
Number of objective gradient evaluations = 26
Number of equality constraint evaluations = 96
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 32
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 30
Total CPU secs in IPOPT (w/o function evaluations) = 0.012
Total CPU secs in NLP function evaluations = 0.001
EXIT: Optimal Solution Found.
final time = 16.52 seconds
3.1.3.4. Plot Results#
def extract_plot_model1_results(m):
# Define empty lists
x = [] # position, units of length
v = [] # velocity, units of length per time
u = [] # acceleration, units of length per time squared
time=[] # time
tf = pyo.value(m.tf)
# Loop over time and append the solution values for each variable to their respective lists
for i in m.tau:
time.append(i*tf)
x.append(pyo.value(m.x[i]))
v.append(pyo.value(m.v[i]))
u.append(pyo.value(m.u[i]))
# Make a figure
plt.figure(figsize=(12,4))
# Format subplot 1 (position)
plt.subplot(131)
plt.plot(time,x,linewidth=3,label='x')
plt.title('location (m)',fontsize=16, fontweight='bold')
plt.xlabel('time (s)',fontsize=16, fontweight='bold')
plt.tick_params(direction="in",labelsize=15)
# Format subplot 2 (velocity)
plt.subplot(132)
plt.plot(time,v,linewidth=3,label='v')
plt.xlabel('time (s)',fontsize=16, fontweight='bold')
plt.title('velocity (m/s)',fontsize=16, fontweight='bold')
plt.tick_params(direction="in",labelsize=15)
# Format subplot 3 (acceleration)
plt.subplot(133)
plt.plot(time,u,linewidth=3,label='a')
plt.xlabel('time (s)',fontsize=16, fontweight='bold')
plt.title('acceleration (m/s$^2$)',fontsize=16, fontweight='bold')
plt.tick_params(direction="in",labelsize=15)
plt.show()
extract_plot_model1_results(m)
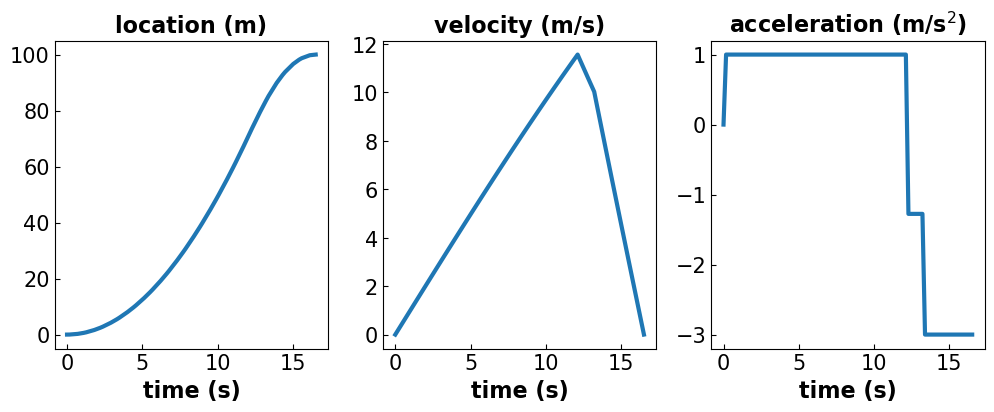
Discussion Questions
Do the results make sense?
What do you know about the relationships between position, velocity, and acceleration? Do you see this relationship in the plots?
3.1.4. Finer Time Discretization#
Does the intermediate braking force (see \(u \approx -1.2\) m/s/s around \(t=12\) s above) go away if we consider a finer time discretization?
m = create_model1()
# Declare the discretizer
discretizer = pyo.TransformationFactory('dae.collocation')
discretizer.apply_to(m,nfe=200,scheme='LAGRANGE-RADAU',ncp=3)
# force piecewise constant controls (acceleration) over each finite element
m = discretizer.reduce_collocation_points(m,var=m.u,ncp=1,contset=m.tau)
# Solve
solver = pyo.SolverFactory('ipopt')
solver.solve(m,tee=True)
print("final time = %6.2f seconds" %(pyo.value(m.tf)))
extract_plot_model1_results(m)
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
This version of Ipopt was compiled from source code available at
https://github.com/IDAES/Ipopt as part of the Institute for the Design of
Advanced Energy Systems Process Systems Engineering Framework (IDAES PSE
Framework) Copyright (c) 2018-2019. See https://github.com/IDAES/idaes-pse.
This version of Ipopt was compiled using HSL, a collection of Fortran codes
for large-scale scientific computation. All technical papers, sales and
publicity material resulting from use of the HSL codes within IPOPT must
contain the following acknowledgement:
HSL, a collection of Fortran codes for large-scale scientific
computation. See http://www.hsl.rl.ac.uk.
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 11004
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 1800
Total number of variables............................: 3003
variables with only lower bounds: 601
variables with lower and upper bounds: 1201
variables with only upper bounds: 0
Total number of equality constraints.................: 2804
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 1.0000000e+00 1.00e+02 2.77e+00 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 1.5275277e+01 9.98e+01 1.02e+02 -1.0 9.82e+03 - 9.91e-05 1.45e-03f 1
2 3.5437364e+01 8.51e+01 1.14e+05 -1.0 1.38e+02 2.0 1.74e-05 1.48e-01f 1
3 4.1813834e+01 7.61e+01 9.88e+04 -1.0 1.33e+02 1.5 7.52e-02 1.06e-01f 1
4 4.1825565e+01 7.61e+01 9.88e+04 -1.0 2.21e+02 1.0 1.39e-01 1.68e-04h 1
5 9.1089621e+01 6.96e+01 1.38e+05 -1.0 1.17e+02 1.5 2.29e-01 9.90e-01f 1
6 9.1067800e+01 6.95e+01 1.10e+06 -1.0 2.87e+01 2.8 6.30e-01 7.61e-04h 1
7 6.4034186e+01 2.10e+01 6.40e+05 -1.0 3.84e+01 2.3 9.56e-01 7.05e-01h 1
8 6.3919314e+01 2.09e+01 6.20e+05 -1.0 2.32e+01 1.8 9.51e-01 4.95e-03h 1
9 6.3915285e+01 2.09e+01 5.98e+05 -1.0 1.79e+01 2.3 1.00e+00 7.54e-04h 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
10 5.7448459e+01 9.02e+00 2.38e+05 -1.0 2.62e+01 1.8 6.91e-01 6.45e-01h 1
11 5.7388561e+01 8.94e+00 2.36e+05 -1.0 1.23e+01 1.3 2.73e-02 9.11e-03h 1
12 5.7388118e+01 8.93e+00 2.31e+05 -1.0 6.72e+00 1.7 1.00e+00 4.37e-04h 1
13 5.5324660e+01 6.00e-01 9.44e+03 -1.0 1.07e+01 1.3 6.60e-01 9.91e-01h 1
14 5.5306134e+01 2.06e-04 1.27e+04 -1.0 1.54e-01 0.8 9.90e-01 1.00e+00f 1
15 5.5324754e+01 5.39e-05 2.90e-01 -1.0 1.41e-01 0.3 1.00e+00 1.00e+00f 1
16 5.5308157e+01 2.00e-05 1.72e-02 -3.8 2.51e-02 -0.2 1.00e+00 1.00e+00h 1
17 5.5251447e+01 2.33e-04 1.90e-02 -3.8 8.30e-02 -0.6 1.00e+00 1.00e+00h 1
18 5.5158417e+01 7.15e-04 1.51e-01 -3.8 2.40e-01 -1.1 1.00e+00 6.41e-01h 1
19 5.4800274e+01 9.41e-03 1.85e-02 -3.8 7.30e-01 -1.6 1.00e+00 1.00e+00f 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
20 5.4630079e+01 1.00e-02 3.70e-01 -3.8 2.01e+00 -2.1 1.00e+00 1.63e-01h 1
21 5.2283571e+01 4.13e-01 6.29e-02 -3.8 5.59e+00 -2.5 1.00e+00 1.00e+00f 1
22 5.0371547e+01 6.00e-01 3.68e-01 -3.8 1.48e+01 -3.0 1.00e+00 2.94e-01h 1
23 4.9652461e+01 6.13e-01 9.27e-01 -3.8 3.52e+01 -3.5 1.00e+00 5.20e-02h 1
24 4.5660379e+01 1.88e+00 1.28e+00 -3.8 8.65e+01 -4.0 5.55e-01 1.40e-01f 1
25 4.1365798e+01 3.19e+00 1.27e+00 -3.8 2.25e+02 -4.5 3.44e-03 5.73e-02f 1
26 3.9993870e+01 2.96e+00 1.16e+00 -3.8 6.64e+01 -4.0 9.24e-03 6.86e-02h 1
27 3.9864312e+01 2.91e+00 1.13e+00 -3.8 2.41e+01 -3.6 1.00e+00 1.78e-02h 1
28 3.8005102e+01 2.98e+00 1.03e+00 -3.8 6.37e+01 -4.1 3.89e-02 9.19e-02h 1
29 3.6991133e+01 2.72e+00 8.72e-01 -3.8 2.35e+01 -3.7 1.00e+00 1.51e-01h 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
30 3.5743998e+01 2.49e+00 7.98e-01 -3.8 5.73e+01 -4.1 3.41e-02 8.17e-02h 1
31 3.5334903e+01 2.30e+00 7.33e-01 -3.8 2.40e+01 -3.7 1.00e+00 7.66e-02h 1
32 3.3879585e+01 2.38e+00 6.60e-01 -3.8 5.39e+01 -4.2 4.84e-02 9.84e-02h 1
33 3.2520352e+01 2.42e+00 6.20e-01 -3.8 3.40e+02 -4.7 9.16e-04 1.98e-02h 1
34 3.2175744e+01 2.35e+00 6.02e-01 -3.8 5.52e+01 -4.2 7.20e-01 2.71e-02h 1
35 3.2114696e+01 2.32e+00 5.92e-01 -3.8 2.16e+01 -3.8 1.00e+00 1.43e-02h 1
36 3.0152408e+01 2.46e+00 5.01e-01 -3.8 5.53e+01 -4.3 2.74e-01 1.61e-01h 1
37 2.9614879e+01 2.11e+00 4.26e-01 -3.8 2.08e+01 -3.9 1.00e+00 1.51e-01h 1
38 2.8390912e+01 2.15e+00 3.73e-01 -3.8 4.73e+01 -4.3 1.00e+00 1.27e-01h 1
39 2.6781248e+01 2.47e+00 3.56e-01 -3.8 4.96e+02 -4.8 9.48e-03 3.57e-02h 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
40 2.6438503e+01 2.38e+00 1.02e+00 -3.8 4.19e+01 -4.4 1.00e+00 4.51e-02h 1
41 2.6056663e+01 2.39e+00 9.94e+00 -3.8 3.78e+02 -4.9 5.12e-02 1.13e-02h 1
42 2.4740408e+01 2.33e+00 1.59e+01 -3.8 3.97e+01 -4.4 7.77e-02 1.99e-01h 1
43 2.4542619e+01 2.32e+00 4.35e+01 -3.8 1.30e+02 -4.9 3.95e-02 1.01e-02h 1
44 2.4296444e+01 2.23e+00 6.40e+03 -3.8 3.80e+01 -4.5 3.11e-04 4.33e-02h 1
45 2.3385415e+01 2.40e+00 6.18e+03 -3.8 3.73e+02 -5.0 3.08e-04 3.40e-02f 1
46 2.3139353e+01 2.31e+00 5.90e+03 -3.8 3.73e+01 -4.5 8.78e-02 4.59e-02h 1
47 2.2596855e+01 2.35e+00 5.77e+03 -3.8 3.77e+02 -5.0 3.87e-02 2.30e-02h 1
48 2.2248895e+01 2.22e+00 5.33e+03 -3.8 3.58e+01 -4.6 1.17e-01 7.50e-02h 1
49 2.1868855e+01 2.22e+00 5.23e+03 -3.8 2.45e+02 -5.1 7.91e-02 2.16e-02h 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
50 2.1305050e+01 2.04e+00 4.56e+03 -3.8 5.28e+01 -4.6 5.36e-03 1.36e-01h 1
51 2.0839022e+01 2.07e+00 4.40e+03 -3.8 1.28e+02 -5.1 1.44e-02 3.58e-02h 1
52 2.0594153e+01 1.95e+00 4.09e+03 -3.8 3.60e+01 -4.7 1.85e-01 6.83e-02h 1
53 2.0051011e+01 2.00e+00 3.88e+03 -3.8 1.08e+02 -5.2 3.66e-02 5.19e-02h 1
54 1.9902895e+01 1.92e+00 3.69e+03 -3.8 3.88e+01 -4.7 1.54e-01 4.83e-02h 1
55 1.9352610e+01 1.97e+00 3.45e+03 -3.8 9.04e+01 -5.2 1.73e-01 6.53e-02h 1
56 1.9300727e+01 1.93e+00 3.38e+03 -3.8 3.84e+01 -4.8 8.31e-02 2.03e-02h 1
57 1.8663238e+01 2.04e+00 3.05e+03 -3.8 8.07e+01 -5.3 4.28e-01 9.56e-02h 1
58 1.8436607e+01 2.07e+00 3.02e+03 -3.8 7.14e+02 -5.8 2.28e-02 9.08e-03h 1
59 1.8278142e+01 2.02e+00 2.91e+03 -3.8 6.26e+01 -5.3 3.26e-02 3.66e-02h 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
60 1.8266892e+01 2.02e+00 2.91e+03 -3.8 2.45e+02 -5.8 1.26e-02 7.95e-04h 1
61 1.8262333e+01 2.00e+00 2.88e+03 -3.8 2.05e+03 -5.4 2.27e-04 8.92e-03h 1
62 1.7396198e+01 2.75e+00 2.69e+03 -3.8 1.96e+02 -5.9 2.69e-02 6.77e-02h 1
63 1.7044192e+01 2.93e+00 2.63e+03 -3.8 4.05e+02 -6.3 7.45e-03 2.31e-02h 1
64 1.6857375e+01 2.84e+00 2.47e+03 -3.8 1.04e+02 -5.9 1.07e-01 5.96e-02h 1
65 1.6780263e+01 2.81e+00 2.43e+03 -3.8 4.94e+02 - 9.31e-03 1.69e-02h 1
66 1.6605425e+01 2.69e+00 2.24e+03 -3.8 2.44e+02 - 2.21e-02 7.62e-02h 1
67 1.6550140e+01 2.54e+00 2.12e+03 -3.8 2.46e+02 - 3.52e-02 5.54e-02h 1
68 1.6535445e+01 2.50e+00 2.08e+03 -3.8 1.71e+02 - 2.81e-02 1.74e-02h 1
69 1.6465224e+01 2.32e+00 1.93e+03 -3.8 3.02e+02 - 2.12e-02 7.04e-02h 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
70 1.6460090e+01 2.24e+00 1.86e+03 -3.8 8.66e+01 - 1.75e-02 3.77e-02h 1
71 1.6416854e+01 2.13e+00 1.77e+03 -3.8 1.66e+02 - 4.10e-02 4.91e-02h 1
72 1.6405953e+01 2.08e+00 1.74e+03 -3.8 1.37e+02 - 1.58e-01 2.03e-02h 1
73 1.6453958e+01 1.19e+00 9.91e+02 -3.8 2.67e+01 - 1.00e+00 4.30e-01h 1
74 1.6558852e+01 1.75e-02 9.09e-02 -3.8 2.75e+00 - 1.00e+00 1.00e+00h 1
75 1.6558690e+01 2.70e-06 7.66e-08 -3.8 2.63e-01 - 1.00e+00 1.00e+00h 1
76 1.6473396e+01 5.75e-02 2.41e+03 -5.7 1.11e+01 - 8.38e-01 1.00e+00f 1
77 1.6471743e+01 6.26e-04 6.35e+01 -5.7 6.23e+00 - 9.74e-01 1.00e+00h 1
78 1.6471737e+01 2.18e-08 2.02e-11 -5.7 6.29e-02 - 1.00e+00 1.00e+00h 1
79 1.6470638e+01 1.22e-05 6.67e-01 -8.6 1.83e-01 - 9.96e-01 1.00e+00f 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
80 1.6470638e+01 2.51e-11 2.54e-14 -8.6 5.63e-04 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 80
(scaled) (unscaled)
Objective...............: 1.6470637653941068e+01 1.6470637653941068e+01
Dual infeasibility......: 2.5424107263916085e-14 2.5424107263916085e-14
Constraint violation....: 8.8391516328556463e-12 2.5050600753258665e-11
Complementarity.........: 2.5063203280067963e-09 2.5063203280067963e-09
Overall NLP error.......: 2.5063203280067963e-09 2.5063203280067963e-09
Number of objective function evaluations = 81
Number of objective gradient evaluations = 81
Number of equality constraint evaluations = 81
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 81
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 80
Total CPU secs in IPOPT (w/o function evaluations) = 0.483
Total CPU secs in NLP function evaluations = 0.019
EXIT: Optimal Solution Found.
final time = 16.47 seconds
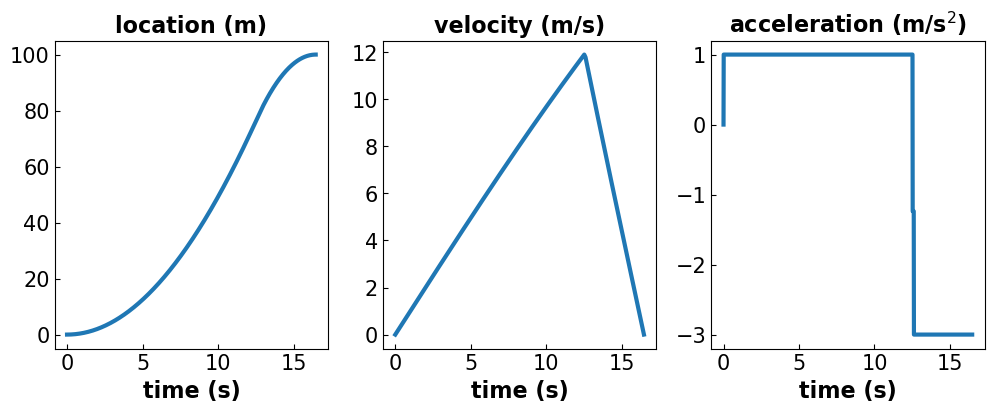
Yes, the intermediate braking amount gets smaller. The car also reaches the finish line slightly faster.
3.1.5. Another Version#
Antoher modeling option to to define an extra differential equation to compute time.
def create_model2():
# Define the model
m = pyo.ConcreteModel()
# Define the model
m = pyo.ConcreteModel()
# Deine the model parameters
m.R = pyo.Param(initialize=0.001, units=1/units.m) # Friction factor
m.L = pyo.Param(initialize=100.0, units=units.m) # Final position
# Define time
m.tau = dae.ContinuousSet(bounds=(0,1)) # Dimensionless time set
m.time = pyo.Var(m.tau, bounds=(0,None), units=units.s) # Time
m.tf = pyo.Var(initialize=1, units=units.s) # Final time
# Define remaining algebraic variables
m.x = pyo.Var(m.tau, bounds=(0,m.L + 50*units.m), units=units.m) # Position
m.v = pyo.Var(m.tau, bounds=(0,None), units=units.m/units.s) # Velocity
m.u = pyo.Var(m.tau, bounds=(-3.0,1.0),initialize=0, units=units.m/units.s/units.s) # Acceleration
# Define derivative variables
m.dtime = dae.DerivativeVar(m.time)
m.dx = dae.DerivativeVar(m.x)
m.dv = dae.DerivativeVar(m.v)
# Declare the objective (minimize final time)
m.obj = pyo.Objective(expr=m.tf)
# Define the constraints
# position
def _ode1(m,i):
if i == 0 :
return pyo.Constraint.Skip
return m.dx[i] == m.tf * m.v[i]
m.ode1 = pyo.Constraint(m.tau, rule=_ode1)
# velocity
def _ode2(m,i):
if i == 0 :
return pyo.Constraint.Skip
return m.dv[i] == m.tf*(m.u[i] - m.R*m.v[i]**2)
m.ode2 = pyo.Constraint(m.tau, rule=_ode2)
# time
def _ode3(m,i):
if i == 0:
return pyo.Constraint.Skip
return m.dtime[i] == m.tf
m.ode3 = pyo.Constraint(m.tau, rule=_ode3)
# Define the inital/boundary conditions
def _init(m):
yield m.x[0] == 0
yield m.x[1] == m.L
yield m.v[0] == 0
yield m.v[1] == 0
yield m.time[0] == 0
m.initcon = pyo.ConstraintList(rule=_init)
return m
m = create_model2()
# Declare the discretizer
discretizer = pyo.TransformationFactory('dae.collocation')
discretizer.apply_to(m,nfe=15,scheme='LAGRANGE-RADAU',ncp=3)
# force piecewise constant controls (acceleration) over each finite element
m = discretizer.reduce_collocation_points(m,var=m.u,ncp=1,contset=m.tau)
# Solve
solver = pyo.SolverFactory('ipopt')
solver.solve(m,tee=True)
print("final time = %6.2f seconds" %(pyo.value(m.tf)))
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
This version of Ipopt was compiled from source code available at
https://github.com/IDAES/Ipopt as part of the Institute for the Design of
Advanced Energy Systems Process Systems Engineering Framework (IDAES PSE
Framework) Copyright (c) 2018-2019. See https://github.com/IDAES/idaes-pse.
This version of Ipopt was compiled using HSL, a collection of Fortran codes
for large-scale scientific computation. All technical papers, sales and
publicity material resulting from use of the HSL codes within IPOPT must
contain the following acknowledgement:
HSL, a collection of Fortran codes for large-scale scientific
computation. See http://www.hsl.rl.ac.uk.
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 1145
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 135
Total number of variables............................: 319
variables with only lower bounds: 92
variables with lower and upper bounds: 91
variables with only upper bounds: 0
Total number of equality constraints.................: 305
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 1.0000000e+00 1.00e+02 3.48e-01 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 9.9965381e-01 9.99e+01 1.09e+02 -1.0 1.00e+03 - 7.69e-05 1.26e-03f 1
2 1.0672606e+00 9.98e+01 1.21e+02 -1.0 8.13e+02 - 1.78e-04 1.13e-03f 1
3 1.6627950e+00 9.94e+01 3.76e+01 -1.0 6.32e+02 - 4.66e-04 3.48e-03f 1
4 2.1580706e+00 9.89e+01 2.13e+01 -1.0 3.70e+02 - 5.94e-03 4.73e-03f 1
5 3.3740442e+00 9.75e+01 2.13e+01 -1.0 2.83e+02 - 6.48e-03 1.47e-02f 1
6 3.4568065e+00 9.75e+01 2.12e+01 -1.0 3.65e+03 -2.0 9.05e-05 2.25e-04f 4
7 3.5166768e+00 9.75e+01 2.12e+01 -1.0 1.45e+05 -1.6 3.05e-07 2.70e-06f 4
8 3.6179009e+00 9.74e+01 2.11e+01 -1.0 4.56e+02 -1.1 6.90e-03 7.57e-04h 4
9 3.7394769e+00 9.74e+01 2.10e+01 -1.0 2.14e+03 -1.6 4.01e-04 2.70e-04h 3
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
10 3.9133700e+00 9.72e+01 2.10e+01 -1.0 3.70e+02 -1.2 1.66e-02 1.41e-03h 3
11 4.4185485e+00 9.71e+01 1.98e+01 -1.0 1.58e+03 - 2.59e-03 1.55e-03h 1
12 4.5952693e+00 9.69e+01 1.98e+01 -1.0 4.16e+02 - 5.05e-03 1.57e-03h 1
13 4.9840028e+00 9.66e+01 1.97e+01 -1.0 4.67e+02 - 7.60e-03 3.38e-03h 1
14 5.3631837e+00 9.61e+01 1.98e+01 -1.0 2.80e+02 - 6.53e-03 5.27e-03h 1
15 5.8588385e+00 9.55e+01 1.96e+01 -1.0 3.63e+02 - 7.97e-03 5.72e-03h 2
16 6.2740527e+00 9.51e+01 1.96e+01 -1.0 4.21e+02 - 1.56e-02 4.53e-03h 1
17 6.6359047e+00 9.45e+01 2.20e+01 -1.0 2.85e+02 - 1.32e-02 6.28e-03h 1
18 7.1860006e+00 9.36e+01 2.75e+01 -1.0 3.17e+02 - 1.47e-02 9.08e-03h 4
19 7.8876904e+00 9.27e+01 2.76e+01 -1.0 4.06e+02 - 1.29e-02 9.78e-03h 2
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
20 8.3302999e+00 9.20e+01 2.73e+01 -1.0 3.73e+02 - 7.91e-03 7.33e-03h 2
21 8.7005071e+00 9.15e+01 3.38e+01 -1.0 3.73e+02 - 1.67e-03 5.55e-03h 1
22 8.8614541e+00 9.12e+01 3.54e+01 -1.0 3.10e+02 - 1.44e-02 3.62e-03h 1
23 9.3754873e+00 9.01e+01 3.94e+01 -1.0 3.09e+02 - 1.59e-02 1.18e-02h 1
24 1.0173832e+01 8.84e+01 3.85e+01 -1.0 3.05e+02 - 4.92e-02 1.97e-02h 3
25 1.1806583e+01 8.59e+01 5.17e+01 -1.0 3.68e+02 -1.7 4.14e-03 2.80e-02h 2
26 1.3077594e+01 8.20e+01 3.75e+01 -1.0 2.75e+02 -1.3 6.22e-02 4.47e-02h 3
27 1.3909957e+01 8.03e+01 2.75e+01 -1.0 3.28e+02 -1.7 6.11e-02 2.12e-02h 3
28 1.4861686e+01 7.65e+01 3.46e+01 -1.0 2.40e+02 -1.3 2.30e-02 4.78e-02f 3
29 1.5847144e+01 7.35e+01 3.03e+01 -1.0 2.70e+02 -1.8 9.50e-02 3.85e-02h 5
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
30 1.7199412e+01 7.22e+01 2.99e+01 -1.0 5.15e+02 -2.3 2.07e-02 1.84e-02h 1
31 1.7264467e+01 7.20e+01 4.19e+01 -1.0 2.86e+02 - 1.06e-01 2.56e-03h 1
32 3.3947489e+01 5.88e+00 1.98e+02 -1.0 2.70e+02 - 7.07e-02 9.22e-01H 1
33 3.3892282e+01 7.53e-02 7.75e+01 -1.0 1.50e+01 -1.8 5.55e-01 9.90e-01h 1
34 3.1099781e+01 3.25e+00 4.34e+02 -1.0 2.09e+02 - 1.62e-01 1.83e-01f 1
35 3.3257932e+01 1.99e+00 9.45e+03 -1.0 2.87e+01 - 5.56e-01 9.92e-01f 1
36 3.0676688e+01 3.10e+00 1.40e+06 -1.0 3.75e+01 - 2.66e-01 9.12e-01f 1
37 2.8971974e+01 1.94e+00 5.27e+06 -1.0 3.39e+01 - 2.61e-01 1.00e+00f 1
38 2.7979354e+01 1.41e+00 9.55e+05 -1.0 2.59e+01 - 7.48e-01 5.84e-01h 1
39 2.5272864e+01 5.18e+00 1.26e+06 -1.0 1.17e+02 - 1.27e-01 5.83e-01f 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
40 2.5693827e+01 3.44e-01 1.27e+06 -1.0 2.11e+01 - 2.36e-01 1.00e+00f 1
41 2.2982818e+01 4.74e+00 7.78e+05 -1.0 9.26e+01 - 3.86e-01 6.26e-01f 1
42 2.0165927e+01 6.73e+00 5.59e+05 -1.0 6.11e+01 - 2.81e-01 8.52e-01f 1
43 1.8548643e+01 5.04e+00 3.42e+05 -1.0 6.52e+01 - 3.89e-01 5.46e-01f 1
44 1.9691536e+01 1.01e+00 4.17e-02 -1.0 1.57e+01 - 1.00e+00 1.00e+00f 1
45 1.9758985e+01 5.69e-02 3.33e-03 -1.0 1.62e+01 - 1.00e+00 1.00e+00h 1
46 1.7116764e+01 5.67e+00 2.62e+06 -2.5 2.17e+01 - 7.30e-01 1.00e+00f 1
47 1.6751093e+01 3.80e-01 9.60e+04 -2.5 1.33e+01 - 9.63e-01 1.00e+00h 1
48 1.6637572e+01 4.98e-02 8.50e-05 -2.5 7.31e+00 - 1.00e+00 1.00e+00h 1
49 1.6637598e+01 7.09e-07 2.95e-08 -2.5 1.37e-01 - 1.00e+00 1.00e+00h 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
50 1.6521647e+01 2.19e-02 1.17e+04 -5.7 1.83e+00 - 9.59e-01 1.00e+00f 1
51 1.6520272e+01 3.39e-06 4.17e-08 -5.7 2.75e-02 - 1.00e+00 1.00e+00h 1
52 1.6520192e+01 9.39e-09 1.64e-10 -8.6 1.01e-03 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 52
(scaled) (unscaled)
Objective...............: 1.6520191520761482e+01 1.6520191520761482e+01
Dual infeasibility......: 1.6444812999846882e-10 1.6444812999846882e-10
Constraint violation....: 9.3907885911903577e-09 9.3907885911903577e-09
Complementarity.........: 2.5872224352029850e-09 2.5872224352029850e-09
Overall NLP error.......: 9.3907885911903577e-09 9.3907885911903577e-09
Number of objective function evaluations = 110
Number of objective gradient evaluations = 53
Number of equality constraint evaluations = 110
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 53
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 52
Total CPU secs in IPOPT (w/o function evaluations) = 0.024
Total CPU secs in NLP function evaluations = 0.001
EXIT: Optimal Solution Found.
final time = 16.52 seconds

