Testing Your Software Environment and TCLab

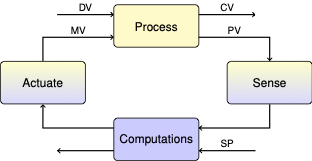
1.4. Testing Your Software Environment and TCLab#

We will use this notebook in the first tutorial to test your software environment and TCLab work.

1.4.1. Connect to TCLab and Turn On LED#

from tclab import TCLab

with TCLab() as lab:
    lab.LED(100) # Set LED to full brightness

TCLab version 1.0.0
Arduino Leonardo connected on port /dev/cu.usbmodemWUART1 at 115200 baud.
TCLab Firmware 1.3.0 Arduino Leonardo/Micro.
TCLab disconnected successfully.

1.4.2. Connect to TCLab and Measure Ambient Temperature#

from tclab import TCLab, clock, Historian, Plotter, setup

# experimental parameters
tfinal = 10 # seconds

# perform experiment
with TCLab() as lab:
    lab.U1 = 0
    lab.U2 = 0
    h = Historian(lab.sources)
    p = Plotter(h, tfinal)
    for t in clock(tfinal):
        p.update(t)
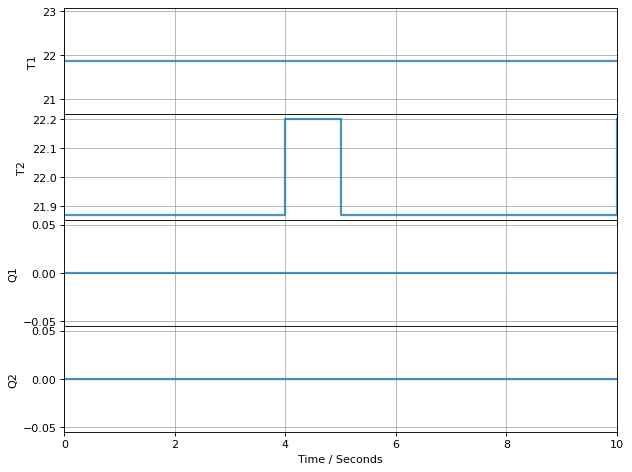
../_images/c806ce75203f98cfa86097c8843ada5039d3d395274ebede43dab29bffef8cb2.png 
TCLab disconnected successfully.
../_images/c806ce75203f98cfa86097c8843ada5039d3d395274ebede43dab29bffef8cb2.png

1.4.3. Solve Optimiation Problem in Pyomo#

import pyomo.environ as pyo
import idaes

# Create empty Pyomo model
m = pyo.ConcreteModel()

## Declare variables with initial values with bounds
m.x1 = pyo.Var(initialize=1, bounds=(-10, 10))
m.x2 = pyo.Var(initialize=1, bounds=(-10, 10))
m.x3 = pyo.Var(initialize=1, bounds=(-10, 10))

## Declare objective
m.OBJ = pyo.Objective(expr=m.x1**2 + 2*m.x2**2 - m.x3, sense = pyo.minimize)

## Declare equality constraints
m.h1 = pyo.Constraint(expr= m.x1 + m.x2 == 1)
m.h2 = pyo.Constraint(expr= m.x1 + 2*m.x2 - m.x3 == 5)

# Solve with Ipopt
opt1 = pyo.SolverFactory('ipopt')
status1 = opt1.solve(m, tee=True)

Ipopt 3.13.2: 

******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
 Ipopt is released as open source code under the Eclipse Public License (EPL).
         For more information visit http://projects.coin-or.org/Ipopt

This version of Ipopt was compiled from source code available at
    https://github.com/IDAES/Ipopt as part of the Institute for the Design of
    Advanced Energy Systems Process Systems Engineering Framework (IDAES PSE
    Framework) Copyright (c) 2018-2019. See https://github.com/IDAES/idaes-pse.

This version of Ipopt was compiled using HSL, a collection of Fortran codes
    for large-scale scientific computation.  All technical papers, sales and
    publicity material resulting from use of the HSL codes within IPOPT must
    contain the following acknowledgement:
        HSL, a collection of Fortran codes for large-scale scientific
        computation. See http://www.hsl.rl.ac.uk.
******************************************************************************

This is Ipopt version 3.13.2, running with linear solver ma27.

Number of nonzeros in equality constraint Jacobian...:        5
Number of nonzeros in inequality constraint Jacobian.:        0
Number of nonzeros in Lagrangian Hessian.............:        2

Total number of variables............................:        3
                     variables with only lower bounds:        0
                variables with lower and upper bounds:        3
                     variables with only upper bounds:        0
Total number of equality constraints.................:        2
Total number of inequality constraints...............:        0
        inequality constraints with only lower bounds:        0
   inequality constraints with lower and upper bounds:        0
        inequality constraints with only upper bounds:        0

iter    objective    inf_pr   inf_du lg(mu)  ||d||  lg(rg) alpha_du alpha_pr  ls
   0  2.0000000e+00 3.00e+00 3.33e-01  -1.0 0.00e+00    -  0.00e+00 0.00e+00   0
   1  4.3065612e+00 1.11e-16 2.89e-01  -1.0 4.36e+00    -  6.72e-01 1.00e+00h  1
   2  4.2501103e+00 0.00e+00 5.55e-17  -1.0 1.31e-01    -  1.00e+00 1.00e+00f  1
   3  4.2500000e+00 0.00e+00 4.32e-16  -2.5 6.02e-03    -  1.00e+00 1.00e+00f  1
   4  4.2500000e+00 8.88e-16 1.14e-16  -3.8 4.41e-05    -  1.00e+00 1.00e+00f  1
   5  4.2500000e+00 0.00e+00 3.13e-16  -5.7 1.98e-06    -  1.00e+00 1.00e+00h  1
   6  4.2500000e+00 0.00e+00 1.55e-16  -8.6 2.45e-08    -  1.00e+00 1.00e+00f  1

Number of Iterations....: 6

                                   (scaled)                 (unscaled)
Objective...............:   4.2500000000000000e+00    4.2500000000000000e+00
Dual infeasibility......:   1.5452628521041094e-16    1.5452628521041094e-16
Constraint violation....:   0.0000000000000000e+00    0.0000000000000000e+00
Complementarity.........:   2.5059105039901454e-09    2.5059105039901454e-09
Overall NLP error.......:   2.5059105039901454e-09    2.5059105039901454e-09


Number of objective function evaluations             = 7
Number of objective gradient evaluations             = 7
Number of equality constraint evaluations            = 7
Number of inequality constraint evaluations          = 0
Number of equality constraint Jacobian evaluations   = 7
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations             = 6
Total CPU secs in IPOPT (w/o function evaluations)   =      0.003
Total CPU secs in NLP function evaluations           =      0.000

EXIT: Optimal Solution Found.

1.4.4. Export Notebook as PDF#

Contents