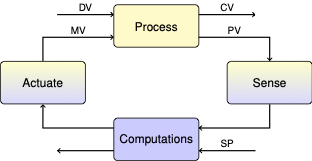
6.3. Predictive Control#
# Install Pyomo and solvers for Google Colab
import sys
if 'google.colab' in sys.modules:
!pip install idaes-pse --pre >/dev/null 2>/dev/null
!idaes get-extensions --to ./bin
os.environ['PATH'] += ':bin'
import numpy as np
import matplotlib.pyplot as plt
6.3.1. Feedforward Optimal Control#
An optimal control policy minimizes the differences
subject to constraints
Note that pyomo.dae has an Integral object to help with these situations.
# parameter estimates.
alpha = 0.00016 # watts / (units P * percent U1)
P = 200 # P units
Ua = 0.050 # heat transfer coefficient from heater to environment
CpH = 2.2 # heat capacity of the heater (J/deg C)
CpS = 1.9 # heat capacity of the sensor (J/deg C)
Ub = 0.021 # heat transfer coefficient from heater to sensor
Tamb = 21.0 # ambient temperature
6.3.2. Controlling to a Reference Trajectory#
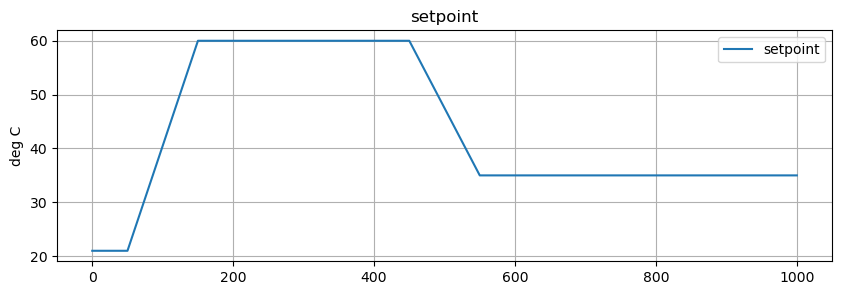
The reference trajectory is a sequence of ramp/soak intervals. Python function r(t) uses numpy.interp to compute values of the reference trajectory at any point in time.
# time grid
tf = 1000
dt = 2
n = round(tf/dt)
t_grid = np.linspace(0, 1000, n+1)
# ambient temperature
Tamb = 21
# setpoint/reference
def SP(t):
return np.interp(t, [0, 50, 150, 450, 550], [Tamb, Tamb, 60, 60, 35])
# plot function
fig, ax = plt.subplots(1, 1, figsize=(10, 3))
ax.plot(t_grid, SP(t_grid), label="setpoint")
ax.set_title('setpoint')
ax.set_ylabel('deg C')
ax.legend()
ax.grid(True)
import pyomo.environ as pyo
import pyomo.dae as dae
def optimal_control(Th, Ts, SP=lambda t: 60, tf=300):
m = pyo.ConcreteModel('TCLab Heater/Sensor')
m.t = dae.ContinuousSet(bounds=(0, tf))
m.Th = pyo.Var(m.t)
m.Ts = pyo.Var(m.t)
m.u = pyo.Var(m.t, bounds=(0, 100))
m.dTh = dae.DerivativeVar(m.Th)
m.dTs = dae.DerivativeVar(m.Ts)
@m.Integral(m.t)
def ise(m, t):
return (SP(t) - m.Th[t])**2
@m.Constraint(m.t)
def heater(m, t):
return CpH * m.dTh[t] == Ua *(Tamb - m.Th[t]) + Ub*(m.Ts[t] - m.Th[t]) + alpha*P*m.u[t]
@m.Constraint(m.t)
def sensor(m, t):
return CpS * m.dTs[t] == Ub *(m.Th[t] - m.Ts[t])
m.Th[0].fix(Th)
m.Ts[0].fix(Ts)
@m.Objective(sense=pyo.minimize)
def objective(m):
return m.ise
pyo.TransformationFactory('dae.finite_difference').apply_to(m, nfe=60, wrt=m.t, scheme="FORWARD")
pyo.SolverFactory('ipopt').solve(m)
return m, m.u[0]()
Th = 30
Ts = 30
m, u = optimal_control(Th, Ts, SP, 1000)
print(u)
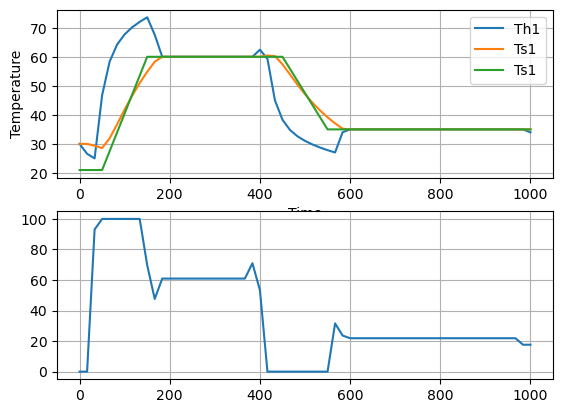
fig, ax = plt.subplots(2, 1)
ax[0].plot(m.t, [m.Th[t]() for t in m.t], label="Th1")
ax[0].plot(m.t, [m.Ts[t]() for t in m.t], label="Ts1")
ax[0].plot(m.t, [SP(t) for t in m.t], label="Ts1")
ax[0].legend()
ax[0].set_xlabel("Time")
ax[0].set_ylabel("Temperature")
ax[0].grid()
ax[1].plot(m.t, [m.u[t]() for t in m.t], label="U1")
ax[0].legend()
ax[1].grid()
0.0
6.3.3. Assumptions for Feedforward Optimal Control#
Future values of the setpoint are equal to the current setpoint.
Future values of the disturbance are known.
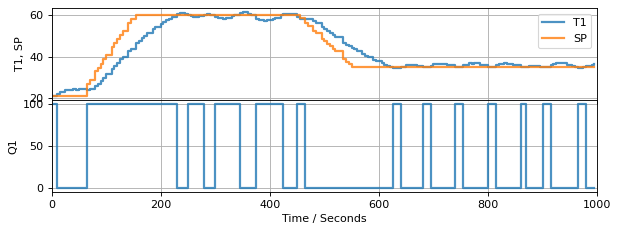
6.3.4. TCLab Event Loop with Relay Control#
Borrowing from notebook 4.6.
!pip install tclab
Requirement already satisfied: tclab in /Users/jeff/opt/anaconda3/lib/python3.9/site-packages (0.4.9)
Requirement already satisfied: pyserial in /Users/jeff/opt/anaconda3/lib/python3.9/site-packages (from tclab) (3.5)
t_step = 5
tf = 1000
import numpy as np
from tclab import setup, clock, Historian, Plotter
# Relay Control
def relay(MV_min, MV_max):
MV = MV_min
while True:
SP, PV = yield MV
MV = MV_max if PV < SP else MV_min
# create a controller instance
controller = relay(0, 100)
U1 = next(controller)
# execute the event loop
TCLab = setup(connected=False, speedup=20)
with TCLab() as lab:
h = Historian([('SP', lambda: SP(t)),
('T1', lambda: lab.T1),
('Q1', lab.Q1)])
p = Plotter(h, tf, layout=[['T1', 'SP'], ['Q1']])
for t in clock(tf, t_step):
T1 = lab.T1
U1 = controller.send([SP(t), T1])
lab.Q1(U1)
p.update(t)
TCLab Model disconnected successfully.

t_step = 5
tf = 300
import numpy as np
from tclab import setup, clock, Historian, Plotter
# Relay Control
def relay(MV_min, MV_max):
MV = MV_min
while True:
SP, PV = yield MV
MV = MV_max if PV < SP else MV_min
# Observer
def tclab_model():
# initialize variables
t_now = 0
x_now = x_initial
while True:
# yield current state, get MV for next period
t_next, Q = yield x_now
# compute next state
u = [Q]
x_next = x_now + (t_next - t_now)*(np.dot(A, x_now) + np.dot(Bu, u) + np.dot(Bd, d))
# update time and state
t_now = t_next
x_now = x_next
# create a controller instance
controller = relay(0, 100)
U1 = next(controller)
# execute the event loop
TCLab = setup(connected=False, speedup=20)
with TCLab() as lab:
h = Historian([('SP', lambda: SP),
('T1', lambda: lab.T1),
('Q1', lab.Q1)])
p = Plotter(h, tf, layout=[['T1', 'SP'], ['Q1']])
for t in clock(tf, t_step):
T1 = lab.T1
U1 = controller.send([SP, T1])
lab.Q1(U1)
p.update(t)
6.3.5. What we need our predictive controller to do …#
Compute given current values of Th, Ts, d, and SP
Compute control policy
def predictive_control(t_horizon=600, dt=2):
n = round(t_horizon/dt)
t_grid = np.linspace(0, t_horizon, n+1)
u = {t: cp.Variable(1, nonneg=True) for t in t_grid}
x = {t: cp.Variable(2) for t in t_grid}
y = {t: cp.Variable(1) for t in t_grid}
output = [y[t] == C@x[t] for t in t_grid]
inputs = [u[t] <= 100 for t in t_grid]
model = [x[t] == x[t-dt] + dt*(A@x[t-dt] + Bu@u[t-dt] + Bd@[Tamb]) for t in t_grid[1:]]
MV = 0
while True:
print(MV)
SP, Th, Ts = yield MV
objective = cp.Minimize(sum((y[t]-SP)**2 for t in t_grid))
IC = [x[0] == np.array([Th, Ts])]
problem = cp.Problem(objective, model + IC + output + inputs)
problem.solve()
MV = u[0].value[0]
t_final = 300
t_step = 2
# create a controller instance
controller = predictive_control()
U1 = next(controller)
# create estimator instance
L = np.array([[0.4], [0.2]])
observer = tclab_observer(L)
Th, Ts = next(observer)
# execute the event loop
TCLab = setup(connected=False, speedup=20)
with TCLab() as lab:
h = Historian([('SP', lambda: SP),
('T1', lambda: lab.T1),
('Q1', lab.Q1),
('Th', lambda: Th),
('Ts', lambda: Ts)])
p = Plotter(h, t_final, layout=[['T1','Ts','Th', 'SP'], ['Q1']])
for t in clock(t_final, t_step):
T1 = lab.T1
Th, Ts = observer.send([t, U1, T1])
U1 = controller.send([SP, Th, Ts])
lab.Q1(U1)
p.update(t)
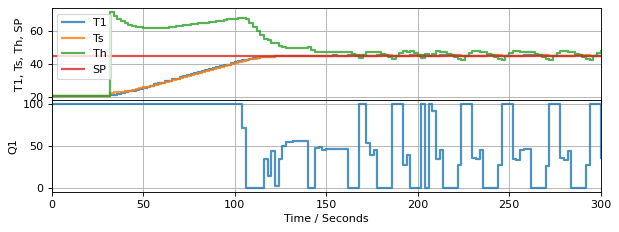
TCLab Model disconnected successfully.

What information do you need to compute the control policy \(u(t)\)?
Modify model for constant d
Demonstrate effect of lack of future information about setpoint
Demonstrate effect of initial condition
Now write a function that computes a control policy given tstep, d, x, and SP
Encapsulate code as a generator
Set up event loop for tclab
add observer