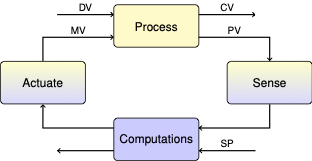
2.7. Characteristics of Second Order Systems#
2.7.1. Car Suspension: Spring-Mass-Damper System#
A car suspension (shock absorbers) includes a spring and damper. The spring absorbs bumps in the road and the damper keeps the spring from oscillating too much.

We will use this classic example to understand the characteristics of second order linear systems. These ideas generalize to higher-order linear and nonlinear systems. Figure source: How a Car Works
2.7.1.1. Mathematical Model#
We will start with a free body diagram (figure source: Wikipedia) and sum of forces acting on mass \(m\):

We can rewrite this as a coupled system of linear ODEs:
Let’s assume the mass of the car is 450 kg per wheel. Furthermore, let’s assume the spring constant \(k\) is 100,000 N/m and the dampening constant \(c\) is 2,000 Ns/m. Of course, this is a simplified model for a car suspection. See this example of a more sophisticate model of a bus’ suspension.
2.7.1.2. Numeric Simulation#
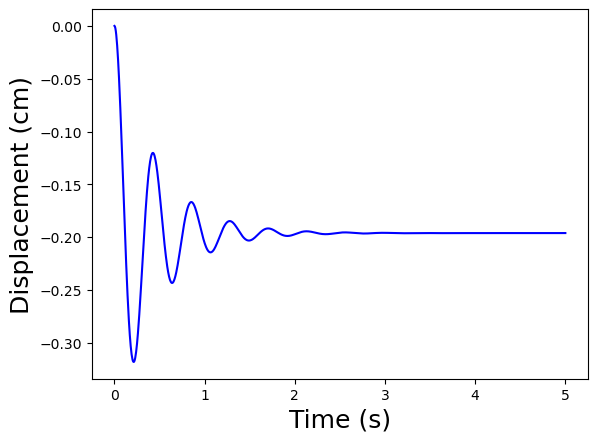
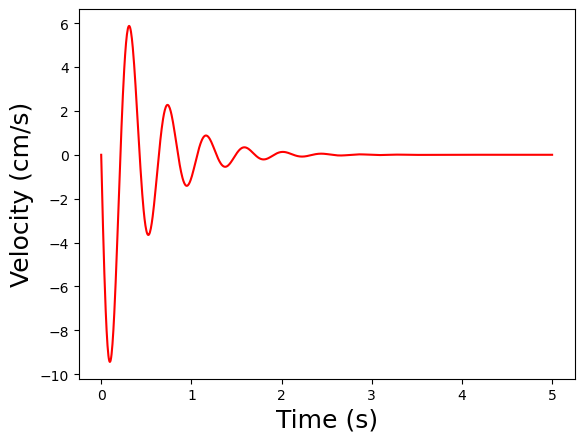
Let’s consider the empty car starts at rest. Then at time zero, the driver, who weighs 80 kg, gets into the car. The external forcing function is \(-80~\text{kg} \times 9.81~\text{m}~\text{s}^{-2} \times 1/4 = 196~\text{N}\) per tire.
import scipy.integrate
import numpy as np
import matplotlib.pyplot as plt
def suspension(t, y, f= lambda t: 0.0, k=1E5, c=2E3, m=450):
''' Linear model of a car suspension system
Arguments:
t: time (s)
y: array of the state variables [x, v]
where x is the displacement (m) and v is the velocity (m/s)
f: extenal forcing function (N)
k: spring constant (N/m)
c: damping constant (Ns/m)
m: mass per wheel (kg)
'''
# unpack state variables
x, v = y
# derivative of velocity
vdot = (-k*x - c*v + f(t))/m
# derivative of displacement
xdot = v
return np.array([xdot, vdot])
def simulate_driver_getting_in(driver_mass=80, k=1E5, c=2E3):
''' Simulate the suspension system with a step input (driver getting in)
Arguments:
driver_mass: mass of the driver (kg)
k: spring constant (N/m)
c: damping constant (Ns/m)
'''
initial_conditions = [0.0, 0.0]
t_span = [0, 5]
t_eval = np.linspace(*t_span, 1000)
g = 9.81 # m/s^2
driver_gets_in = lambda t,y: suspension(t, y, lambda t_: -driver_mass*g/4, k, c)
solution = scipy.integrate.solve_ivp(driver_gets_in, t_span, initial_conditions, t_eval=t_eval)
plt.plot(solution.t, solution.y[0]*100,color='b')
plt.xlabel('Time (s)',fontsize=18)
plt.ylabel('Displacement (cm)',fontsize=18)
plt.show()
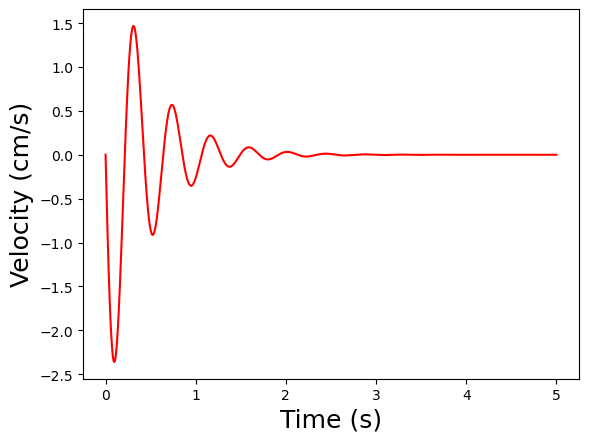
plt.plot(solution.t, solution.y[1]*100,color='r')
plt.xlabel('Time (s)',fontsize=18)
plt.ylabel('Velocity (cm/s)',fontsize=18)
plt.show()
simulate_driver_getting_in()
2.7.1.3. Activity#
Simulate the following what if scenarios:
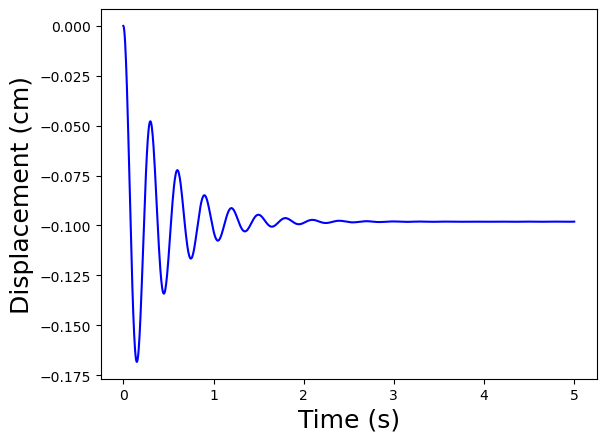
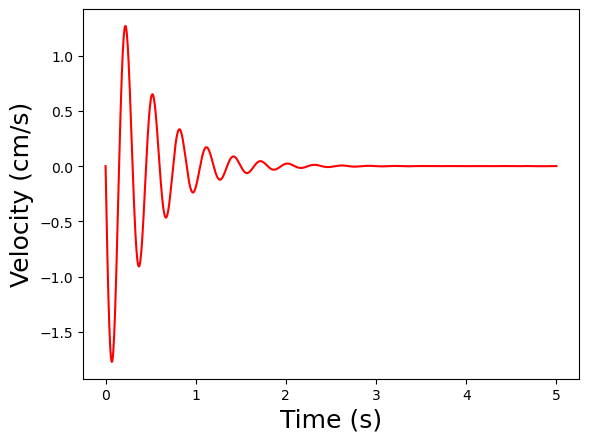
Double the spring stiffness
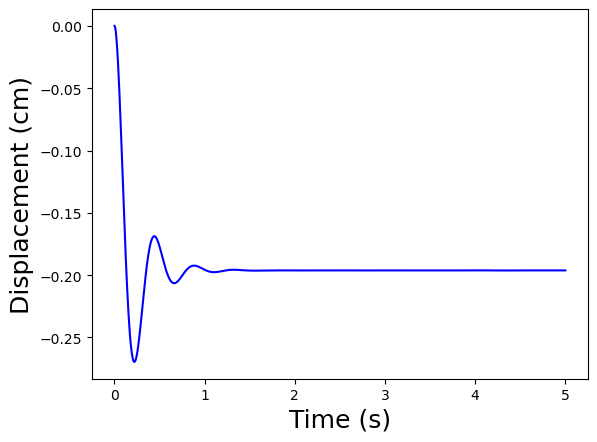
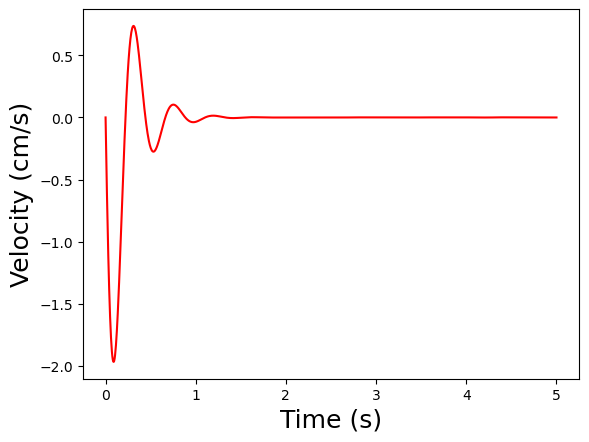
Double the strength of the dampers
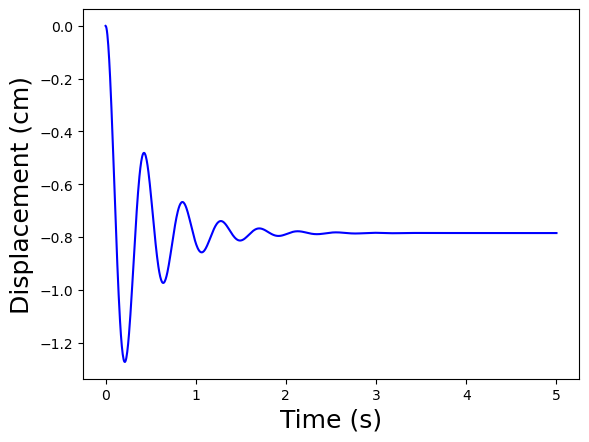
Four people instead of one person gets in the car
Do the results make sense?
# Double the spring constant
simulate_driver_getting_in(k=2E5)
# Double the damping constant
simulate_driver_getting_in(c=4E3)
# Four people get in the car
simulate_driver_getting_in(driver_mass=4*80)
2.7.2. Second Order Linear ODE Systems#
2.7.2.1. Generalized Model#
More generally, the second order linear system with a single state is:
Where:
\(\omega_n\) is the natural frequency, i.e., frequency of oscillations with no forcing \(u(t) = 0\),
\(\zeta\) is the damping coefficient, and
\(K_p\) is the gain.
This can be also written using the second order characteristic time \(\tau_s = \omega_n^{-1}\):
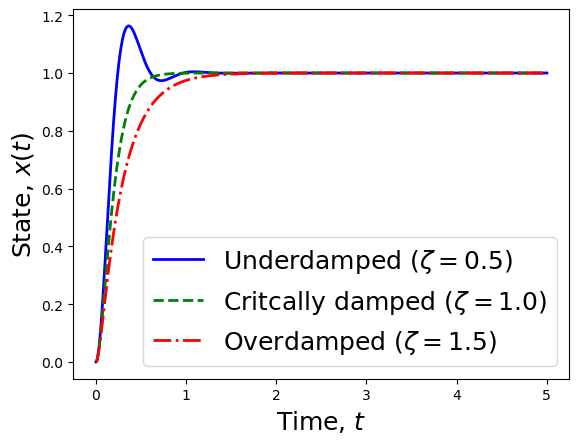
These general forms are convienent because there are three “modes” of the analytic solution, depending on the value of \(\zeta\). Here \(\bar{x}\) is the steady-state after a step change in the input.
2.7.2.2. Overdamped (\(\zeta > 1\))#
2.7.2.3. Critically Damped (\(\zeta = 1\))#
2.7.2.4. Underdamped (\(\zeta < 1\))#
2.7.2.5. Comparison of Modes#
def second_order(t, xbar=1.0, zeta=1.0, omega=10):
''' Analytic solution of second order system
Arguments:
t: times to evaluate solution
xbar: steady-state after step response
zeta: damping coefficient
omega: natural frequency
Note: t and omega need to have consistent units (time and inverse time)
Returns:
x(t), states x evaluated at times t
'''
if np.abs(zeta - 1) < 1E-6:
# Critically damped, zeta approx 1
# Hint: need the tolerance 1E-6 because of float point errors
return xbar*(1 - (1+t*omega)*np.exp(-t*omega))
elif zeta > 1:
# Overdamped, zeta > 1
return xbar*(1-np.exp(-zeta*t*omega)*(np.cosh(t*omega*np.sqrt(zeta**2-1)) + (zeta/np.sqrt(zeta**2-1))*np.sinh(t*omega*np.sqrt(zeta**2 - 1))))
else:
# Underdampled (oscillates), zeta < 1
return xbar*(1-np.exp(-zeta*t*omega)*(np.cos(t*omega*np.sqrt(1-zeta**2)) + (zeta/np.sqrt(1-zeta**2))*np.sin(t*omega*np.sqrt(1-zeta**2))))
teval = np.linspace(0,5,1001)
x_over = second_order(teval, zeta=1.5)
x_crit = second_order(teval, zeta=1.0)
x_under = second_order(teval, zeta=0.5)
plt.plot(teval,x_under,color="blue",linestyle="-",label="Underdamped ($\zeta = 0.5$)",linewidth=2)
plt.plot(teval,x_crit, color="green",linestyle="--",label="Critcally damped ($\zeta = 1.0$)",linewidth=2)
plt.plot(teval,x_over,color="red",linestyle="-.",label="Overdamped ($\zeta=1.5$)",linewidth=2)
plt.xlabel("Time, $t$",fontsize=18)
plt.ylabel("State, $x(t)$",fontsize=18)
plt.legend(fontsize=18)
<matplotlib.legend.Legend at 0x127ddabd0>
2.7.2.6. Spring-Mass-Damper Example#
Now let’s convert the spring-mass-damper systems into the general form. Recall,
which is equivalent to:
Comparing this to the general form,
we see that
Let’s revist our example and run some calculations.
def suspension(t, y, f= lambda t: 0.0, k=1E5, c=2E3, m=450):
''' Linear model of a car suspension system
Arguments:
t: time (s)
y: array of the state variables [x, v]
where x is the displacement (m) and v is the velocity (m/s)
f: extenal forcing function (N)
k: spring constant (N/m)
c: damping constant (Ns/m)
m: mass per wheel (kg)
'''
# unpack state variables
x, v = y
# derivative of velocity
vdot = (-k*x - c*v + f(t))/m
# derivative of displacement
xdot = v
return np.array([xdot, vdot])
def simulate_driver_getting_in(driver_mass=80, k=1E5, c=2E3):
''' Simulate the suspension system with a step input (driver getting in)
Arguments:
driver_mass: mass of the driver (kg)
k: spring constant (N/m)
c: damping constant (Ns/m)
'''
initial_conditions = [0.0, 0.0]
t_span = [0, 5]
t_eval = np.linspace(*t_span, 1000)
g = 9.81 # m/s^2
driver_gets_in = lambda t,y: suspension(t, y, lambda t_: -driver_mass*g/4, k, c)
solution = scipy.integrate.solve_ivp(driver_gets_in, t_span, initial_conditions, t_eval=t_eval)
plt.plot(solution.t, solution.y[0]*100,color='b')
plt.xlabel('Time (s)',fontsize=18)
plt.ylabel('Displacement (cm)',fontsize=18)
plt.show()
plt.plot(solution.t, solution.y[1]*100,color='r')
plt.xlabel('Time (s)',fontsize=18)
plt.ylabel('Velocity (cm/s)',fontsize=18)
plt.show()
def car_revisited(car_mass = 4*450, driver_mass=80, k=1E5, c=2E3, verbose=True):
''' Convert car suspension example into 2nd order system general form
Arguments:
car_mass: total mass of the vehicle without driver (kg)
driver_mass: total mass of the driver (kg)
k: spring constant (N/m)
c: damping constant (Ns/m)
Returns:
omega_n: natural frequency (1/s)
zeta: critical coefficient (dimensionless)
Notes:
All masses are divided by 4 within the calculations to convert from total to per wheel.
User should input total masses.
This function returns omega and zeta for the loaded car
'''
if verbose:
print("Spring constant, k =",round(k,0),"N/m")
print("Damping constant, c =",round(c,0),"Ns/m")
m = car_mass/4
omega_n = np.sqrt(k/m)
zeta = np.sqrt(c/(2*omega_n*m))
if verbose:
print("\nEmpty car, m =", round(m,1),"kg per wheel")
print("omega_n =",round(omega_n,2), "rad/s")
print("zeta =",round(zeta,2), "dimensionless")
m = (car_mass + driver_mass)/4
omega_n = np.sqrt(k/m)
zeta = np.sqrt(c/(2*omega_n*m))
if verbose:
print("\nLoaded car, m =", round(m,1),"kg per wheel")
print("omega_n =",round(omega_n,2), "rad/s")
print("zeta =",round(zeta,2), "dimensionless")
return omega_n, zeta
car_revisited()
Spring constant, k = 100000.0 N/m
Damping constant, c = 2000.0 Ns/m
Empty car, m = 450.0 kg per wheel
omega_n = 14.91 rad/s
zeta = 0.39 dimensionless
Loaded car, m = 470.0 kg per wheel
omega_n = 14.59 rad/s
zeta = 0.38 dimensionless
(14.586499149789455, 0.3819227559309533)
Discussion Questions:
Is it okay to ignore how the change in mass \(m\) impacts \(\omega_n\) and \(\zeta\) when analyzes the dynamic response of the suspension?
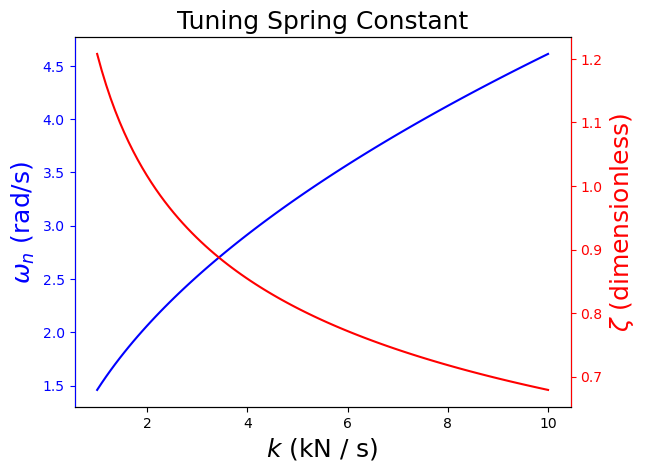
How would you tune the suspension, i.e., change \(k\) or \(c\), to make it critically damped or overdamped?
Is it better to have an overdamped, underdamped, or critically damped suspension?
k_adjust = np.linspace(1E3,1E4,101)
omega, zeta = car_revisited(k=k_adjust,verbose=False)
fig, ax1 = plt.subplots()
ax1.plot(k_adjust/1E3,omega,color="blue")
ax1.set_ylabel('$\omega_n$ (rad/s)', color='blue',fontsize=18)
ax1.set_xlabel('$k$ (kN / s)',fontsize=18)
ax1.tick_params(axis='y', color='blue', labelcolor='blue')
ax1.set_title('Tuning Spring Constant',fontsize=18)
ax2 = ax1.twinx()
ax2.plot(k_adjust/1E3,zeta,color='red')
ax2.set_ylabel('$\zeta$ (dimensionless)', color='red',fontsize=18)
ax2.tick_params(axis='y', color='red', labelcolor='red')
ax2.spines['right'].set_color('red')
ax2.spines['left'].set_color('blue')
plt.show()
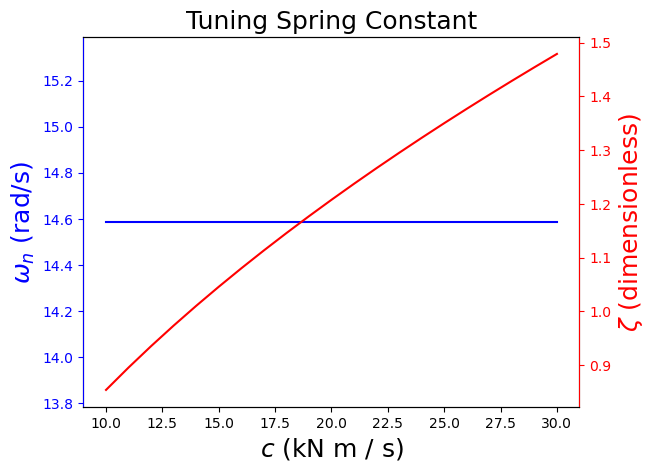
c_adjust = np.linspace(1E4,3E4,21)
omega, zeta = car_revisited(c=c_adjust,verbose=False)
# Convert from scalar to vector
omega = omega*np.ones(len(c_adjust))
fig, ax1 = plt.subplots()
ax1.plot(c_adjust/1E3,omega,color="blue")
ax1.set_ylabel('$\omega_n$ (rad/s)', color='blue',fontsize=18)
ax1.set_xlabel('$c$ (kN m / s)',fontsize=18)
ax1.tick_params(axis='y', color='blue', labelcolor='blue')
ax1.set_title('Tuning Spring Constant',fontsize=18)
ax2 = ax1.twinx()
ax2.plot(c_adjust/1E3,zeta,color='red')
ax2.set_ylabel('$\zeta$ (dimensionless)', color='red',fontsize=18)
ax2.tick_params(axis='y', color='red', labelcolor='red')
ax2.spines['right'].set_color('red')
ax2.spines['left'].set_color('blue')
plt.show()
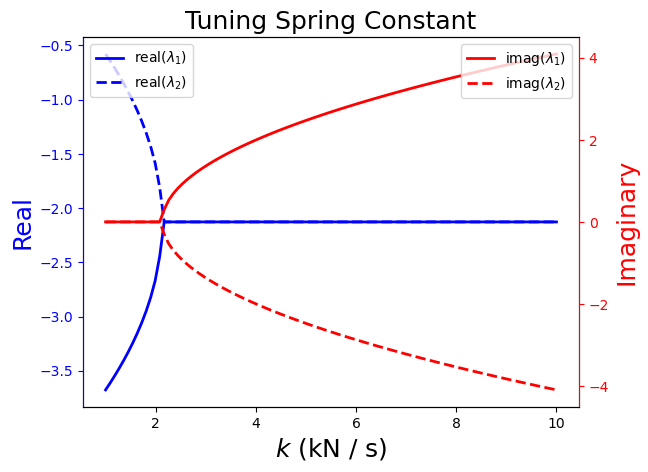
2.7.2.7. Sensitivity of Eigenvalues#
The dynamic response of the system depends on the eigenvalues of the (linear) differential equations.
The real componenent of the eigenvalues tell us…
One or more positive real components of the eigenvalues –> system is unstable and one of the states will diverge to positive or negative infinity
All negative real components of the eigenvalues –> system is stable and will approach steady-state
One or more zero real components of the eigenvalues –> some of the states will neither decay or grow, often coincides with oscillations
The imaginary components of the eigenvalues tell us…
Non-zero imaginary components of two of more eigenvales –> system response will oscillate
All imaginary components of eigenvalues are zero –> system response will not oscillate
Remember that imaginary eigenvalues come in conjugate pairs
Let’s see these properties in action with our spring-mass-damper example. We start by writing the linear system in cannonical state-space form:
Next, we will calculate the eigenvalues of \(\mathbf{A}\).
import sympy
c, m, k = sympy.symbols('c m k')
A = sympy.Matrix([[-c/m, -k/m],[1, 0]])
print("A =\n",A)
print("Eigenvalues(A) =",)
print(A.eigenvals())
A =
Matrix([[-c/m, -k/m], [1, 0]])
Eigenvalues(A) =
{-c/(2*m) - sqrt(c**2 - 4*k*m)/(2*m): 1, -c/(2*m) + sqrt(c**2 - 4*k*m)/(2*m): 1}
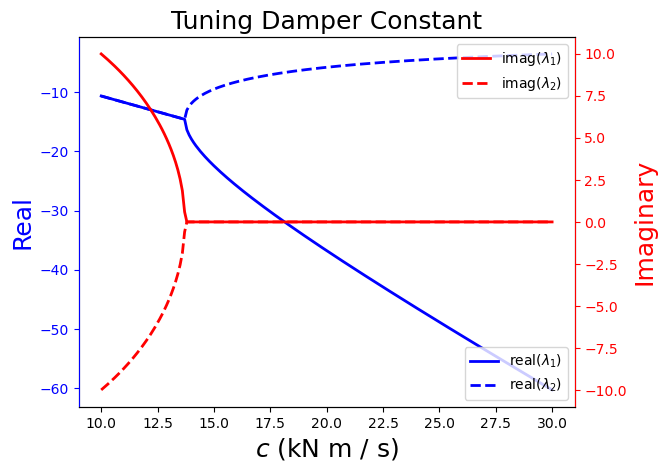
We see these eigenvalues are imaginary when
The real components of both eigenvalues are positive when
This would require \(km < 0\), which is not possible because \(k > 0\), \(c > 0\), and \(m > 0\) for the model to be physically realistic. Therefore, the real components must be negative.
This analysis explains the behavior of our simulations for this system so far!
def eigenvalues_car_revisited(car_mass = 4*450, driver_mass=80, k=1E5, c=2E3, verbose=True):
''' Convert car suspension example into 2nd order system general form
Arguments:
car_mass: total mass of the vehicle without driver (kg)
driver_mass: total mass of the driver (kg)
k: spring constant (N/m)
c: damping constant (Ns/m)
Returns:
eigenvalues
Notes:
All masses are divided by 4 within the calculations to convert from total to per wheel.
User should input total masses.
This function assumes k and c are scalars!
'''
if verbose:
print("Spring constant, k =",round(k,0),"N/m")
print("Damping constant, c =",round(c,0),"Ns/m")
m = car_mass/4
omega_n = np.sqrt(k/m)
zeta = np.sqrt(c/(2*omega_n*m))
A = np.array([[-c/m, -k/m],[1.,0]])
evals, evec = np.linalg.eig(A)
if verbose:
print("\nEmpty car, m =", round(m,1),"kg per wheel")
print("omega_n =",round(omega_n,2), "1/s")
print("zeta =",round(zeta,2), "dimensionless")
print("eignvalues=",evals)
m = (car_mass + driver_mass)/4
omega_n = np.sqrt(k/m)
zeta = np.sqrt(c/(2*omega_n*m))
A = np.array([[-c/m, -k/m],[1.,0]])
evals, evec = np.linalg.eig(A)
if verbose:
print("\nLoaded car, m =", round(m,1),"kg per wheel")
print("omega_n =",round(omega_n,2), "1/s")
print("zeta =",round(zeta,2), "dimensionless")
print("eignvalues=",evals)
return evals
eigenvalues_car_revisited()
Spring constant, k = 100000.0 N/m
Damping constant, c = 2000.0 Ns/m
Empty car, m = 450.0 kg per wheel
omega_n = 14.91 1/s
zeta = 0.39 dimensionless
eignvalues= [-2.22222222+14.74055462j -2.22222222-14.74055462j]
Loaded car, m = 470.0 kg per wheel
omega_n = 14.59 1/s
zeta = 0.38 dimensionless
eignvalues= [-2.12765957+14.43048933j -2.12765957-14.43048933j]
array([-2.12765957+14.43048933j, -2.12765957-14.43048933j])
# Perform sensitivity analysis of eigenvalues to k
k_adjust = np.linspace(1E3,1E4,101)
evals = np.zeros((len(k_adjust),2),dtype = complex)
for i in range(len(k_adjust)):
evals[i,:] = eigenvalues_car_revisited(k=k_adjust[i],verbose=False)
fig, ax1 = plt.subplots()
ax1.plot(k_adjust/1E3,np.real(evals[:,0]),label="real($\lambda_1$)",color="blue",linestyle="-",linewidth=2)
ax1.plot(k_adjust/1E3,np.real(evals[:,1]),label="real($\lambda_2$)",color="blue",linestyle="--",linewidth=2)
ax1.set_ylabel('Real', color='blue',fontsize=18)
ax1.set_xlabel('$k$ (kN / s)',fontsize=18)
ax1.tick_params(axis='y', color='blue', labelcolor='blue')
ax1.set_title('Tuning Spring Constant',fontsize=18)
plt.legend(loc='upper left')
ax2 = ax1.twinx()
ax2.plot(k_adjust/1E3,np.imag(evals[:,0]),label="imag($\lambda_1$)",color='red',linestyle="-",linewidth=2)
ax2.plot(k_adjust/1E3,np.imag(evals[:,1]),label="imag($\lambda_2$)",color='red',linestyle="--",linewidth=2)
ax2.set_ylabel('Imaginary', color='red',fontsize=18)
ax2.tick_params(axis='y', color='red', labelcolor='red')
ax2.spines['right'].set_color('red')
ax2.spines['left'].set_color('blue')
plt.legend(loc='upper right')
plt.show()
# Perform sensitivity analysis of eigenvalues to c
c_adjust = np.linspace(1E4,3E4,201)
evals = np.zeros((len(c_adjust),2),dtype = complex)
for i in range(len(c_adjust)):
evals[i,:] = eigenvalues_car_revisited(c=c_adjust[i],verbose=False)
fig, ax1 = plt.subplots()
ax1.plot(c_adjust/1E3,np.real(evals[:,0]),label="real($\lambda_1$)",color="blue",linestyle="-",linewidth=2)
ax1.plot(c_adjust/1E3,np.real(evals[:,1]),label="real($\lambda_2$)",color="blue",linestyle="--",linewidth=2)
ax1.set_ylabel('Real', color='blue',fontsize=18)
ax1.set_xlabel('$c$ (kN m / s)',fontsize=18)
ax1.tick_params(axis='y', color='blue', labelcolor='blue')
ax1.set_title('Tuning Damper Constant',fontsize=18)
plt.legend(loc='lower right')
ax2 = ax1.twinx()
ax2.plot(c_adjust/1E3,np.imag(evals[:,0]),label="imag($\lambda_1$)",color='red',linestyle="-",linewidth=2)
ax2.plot(c_adjust/1E3,np.imag(evals[:,1]),label="imag($\lambda_2$)",color='red',linestyle="--",linewidth=2)
ax2.set_ylabel('Imaginary', color='red',fontsize=18)
ax2.tick_params(axis='y', color='red', labelcolor='red')
ax2.spines['right'].set_color('red')
ax2.spines['left'].set_color('blue')
plt.legend(loc='upper right')
plt.show()
2.7.3. General Linear ODE Systems#
Second order systems (e.g., mass-spring-damper) are excellent to understand the types of dynamic system responses. But we will need to analyze higher order systems in practice.
Recall the general state-space of a linear ODE system:
where \(\mathbf{x}\) are the state variables and \(\mathbf{y}\) are the measured/observed variables. This is called a time-invarient linear system because the ODE system is linear with respect to the states \(\mathbf{x}\) and the matrices \(\mathbf{A}\) and \(\mathbf{B}\) are constants and do not depend on time.
Many chemical engineering examples are more complicated, which means matrices \(\mathbf{A}\), \(\mathbf{B}\), \(\mathbf{C}\), or \(\mathbf{D}\) depend on time \(t\) or states \(\mathbf{x}\) or both. But to analyze stability, we can construct linear approximations of the form above around the steady-states of interest. Hence building up our toolbox of techniques to analyze LTI systems is important!
2.7.3.1. Analytic Solution#
The LTI analytic solution is
where
There are many ways to compute \(\mathbf{\Phi}(t)\). For the case where \(\mathbf{u}(t) = \mathbf{0}\), i.e., no external input, the analytic solution of \(\dot{x} = \mathbf{A} \mathbf{x}\) is
where the columns of \(\mathbf{M}\) and the eigenvectors (\(\mathbf{v}_1\), …, \(\mathbf{v}_n\)) of \(\mathbf{A}\) and the diagonal of \(\Lambda\) are the eigenvalues (\(\lambda_1\), …, \(\lambda_n\)) of \(\mathbf{A}\):
Because \(\Lambda\) is a diagnol matrix, the matrix exponential simplies:
The situation is more nuanced if the eigenvalues are not distinct. Nevertheless, this gives the general idea and we will press on.
How does this related to our interpretation of the eigenvalues in the spring-mass-damper example above?
Recall Euluer’s formula:
Using Euler’s formula, we can express cosine, sine, hyperbolic cosine, and hyperbolic sine as:
If the eigenvalues are real and the imaginary component is zero, i.e., \(y = 0\) in Euler’s formula, then the solution does not oscillate and constains a hyperbolic cosine and hyperbolic sine. Take a minute to review the analytic solution for the overdamped system (\(\zeta > 1\)).
If the eigenvalues include a non-zero imaginary component, then the solution includes a sine or cosine and oscillates. Take a minute to review the analytic solution for the underdamped system \(\zeta < 1\).
It is possible for a large system (\(n > 2\)) to have some eigenvalues that are overdamped and some that are underdamped. Recall our second order system has two eigenvalues and imaginary eigenvalues come in conjugate pairs. This means for a second order system, both eigenvalues have either a non-zero or zero imaginary component.
2.7.3.2. Simulation with scipy.signal#
The good news is that scipy has a functions to model and simulate LTI systems. This means you do not need to explicitly code up the analytic solution of eigendecomposition above.
Let’s define the spring-mass-damper system as a state-space model. We will use the StateSpace function in scipy.signal, which takes the matrices \(\mathbf{A}\), \(\mathbf{B}\), \(\mathbf{C}\), and \(\mathbf{D}\) as arguments.
from scipy.signal import StateSpace, lsim, bode
# Define constants
car_mass = 4*450 # kg
driver_mass=80 # kg
k=1E5 # N/m
c=2E3 # Nm/s
m = (car_mass)/4 # kg
g = 9.81 # m/s^2
# Define the state space model
A = np.array([[-c/m, -k/m],[1.,0]])
B = np.array([[1/m],[0]])
C = np.array([[0,1]])
D = np.array([[0]])
# Print state space model
sys = StateSpace(A,B,C,D)
print(sys)
StateSpaceContinuous(
array([[ -4.44444444, -222.22222222],
[ 1. , 0. ]]),
array([[0.00222222],
[0. ]]),
array([[0, 1]]),
array([[0]]),
dt: None
)
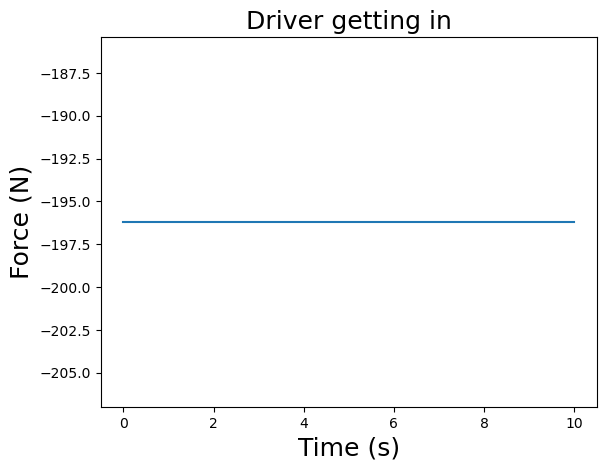
Next, let’s simulate the step response of a driver getting into the car. We will use the lsim function from scipy.signal which takes as arguments:
syswhich is a LTI system, e.g., created usingStateSpaceTwhich is the time point, which must be evenly spaced. We usenumpy.linspaceto create this time grid.Uwhich is the control grid defined for the time gridT. By default,lsimwith linearly interpolateU. Another option is zero-order hold, which means a piecewise constant signal forU, i.e., a sequence of steps.X0which are the initial conditions for the states.
# Define initial conditions
x0 = [0, # m/s
0] # m
# Define the time vector
t = np.linspace(0,10,1000)
# Calculate the input signal on the time grid
u = (-driver_mass*g/4)*np.ones(len(t)) # N
# Plot the input signal
plt.plot(t,u)
plt.xlabel('Time (s)',fontsize=18)
plt.ylabel('Force (N)',fontsize=18)
plt.title('Driver getting in',fontsize=18)
plt.show()
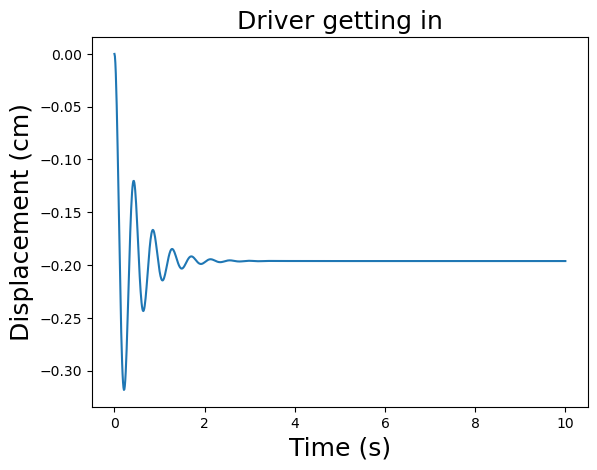
# Simulate the system using scipy.signal.lsim
t_, yout, xout = lsim(sys, U=u, T=t, X0=x0)
# Plot the output signal
plt.plot(t_,yout*100)
plt.xlabel('Time (s)',fontsize=18)
plt.ylabel('Displacement (cm)',fontsize=18)
plt.title('Driver getting in',fontsize=18)
plt.show()
2.7.4. Frequency Response#
What is our system experiences period excitement, such as driving over a series of speed bumps at constant speed?
Let’s say the external force \(f(t) = u(t)\) experienced by our spring-mass-damper system is a sine wave:
\(u(t) = A \sin(\omega t)\) where \(A\) is the amplitude, \(\omega\) is the frequency, and \(\phi\) is the phase shift.
What is the response of the system subject to this dynamic response?
2.7.4.1. Simulate Driving Over Speed Bumps#
def simulate_bumps(t, A=100, omega=4, title=None):
''' Simulate driving over bumps
Arguments:
A: amplitude (N)
omega: frequency (rad/s)
phi: phase angle (rad)
Returns:
Nothing
Action:
Creates plot
'''
# Time domain, s
t = np.linspace(0,5,1000)
# External forcing function, N
u = A*np.sin(omega*t)
# Initial conditions
x0 = [0, # m/s
0] # m
# Simulate linear system with scipy.signal.lsim
t_, yout, xout = lsim(sys, U=u, T=t, X0=x0)
# Create plot
fig, ax1 = plt.subplots()
# Plot forcing function of left y axis
ax1.plot(t,u,label="u(t)",color="blue",linestyle="-",linewidth=2)
ax1.set_ylabel('Force (N)', color='blue',fontsize=18)
ax1.set_xlabel('Time (s)',fontsize=18)
ax1.tick_params(axis='y', color='blue', labelcolor='blue')
if title is not None:
ax1.set_title(title,fontsize=18)
# Plot suspension displacement on right y axis
ax2 = ax1.twinx()
ax2.plot(t_,yout*100,label="x(t)",color='red',linestyle="-",linewidth=2)
ax2.set_ylabel('Suspension Displacement (cm)', color='red',fontsize=18)
ax2.tick_params(axis='y', color='red', labelcolor='red')
# Update colors and show plot
ax2.spines['right'].set_color('red')
ax2.spines['left'].set_color('blue')
plt.show()
simulate_bumps(t, A=100, omega=4, title="Speed Bumps")
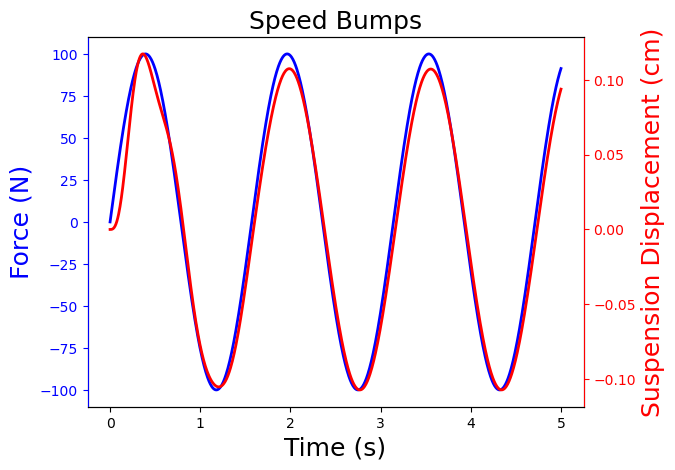
2.7.4.2. Bode Analysis#
We can see in this example the input \(u(t)\) is a sine wave,
and the output response is a shifted sine wave with a different amplitude:
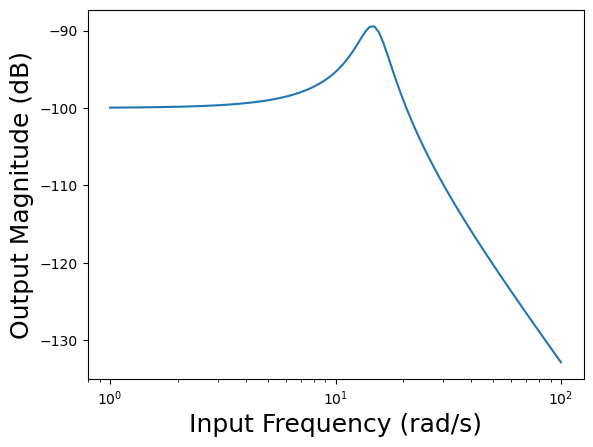
A Bode plot relates the gain of the system \(K\) and the phase shift \(\psi\) to the input frequency \(\omega\).
We will use scipy.signal to construct Bode plots. In a “classical controls class”, students often learn how to draw Bode plots by hand!
# Perform Bode analysis using the StateSpace model stored in `sy`
w, mag, phase = bode(sys)
# Plot the magnitude of the output signal as a function of input signal frequency
plt.figure()
plt.semilogx(w, mag) # Bode magnitude plot
plt.xlabel('Input Frequency (rad/s)',fontsize=18)
plt.ylabel('Output Magnitude (dB)',fontsize=18)
plt.show()
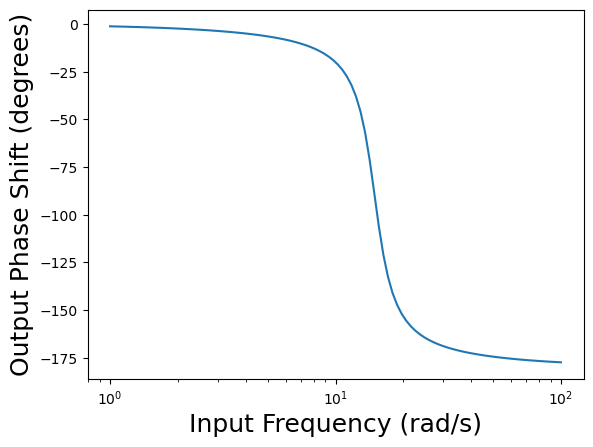
# Plot the phase shift of the output signal as a function of input signal frequency
plt.figure()
plt.semilogx(w, phase)
plt.xlabel('Input Frequency (rad/s)',fontsize=18)
plt.ylabel('Output Phase Shift (degrees)',fontsize=18)
plt.show()
/opt/anaconda3/lib/python3.11/site-packages/scipy/signal/_filter_design.py:1746: BadCoefficients: Badly conditioned filter coefficients (numerator): the results may be meaningless
warnings.warn("Badly conditioned filter coefficients (numerator): the "
2.7.4.3. Simulate Driving Over a Rumble Strip#
Based on the analysis above, let’s consider a higher frequency oscillation, such as driving over a rumple strip at high speed.
simulate_bumps(t, A=30, omega=20, title="Rumble Strip")
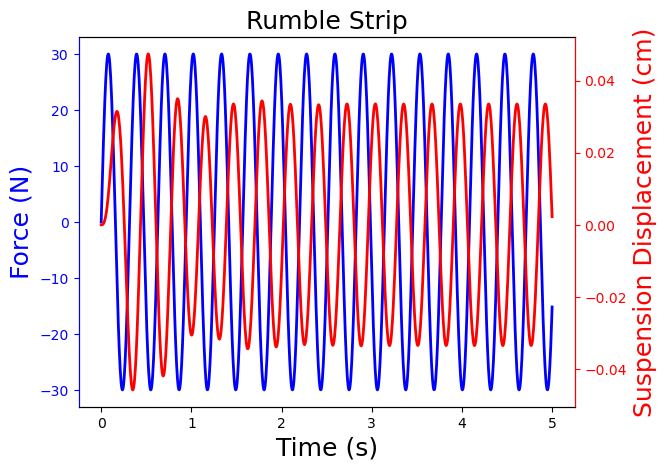
We see the higher frequency forcing function results in a larger phase shift, which is expected based on the Bode plot.
2.7.5. Take Away Messages#
State-space form with matrices \(\mathbf{A}\), \(\mathbf{B}\), \(\mathbf{C}\), and \(\mathbf{D}\) is convenient to model dynamical systems
The characteristics of the response depends on the eigenvalues of \(\mathbf{A}\)
Looking forward a few weeks, we will design control laws, i.e., formulas to calculate \(\mathbf{u}\), that shape the eigenvalues of the closed loop dynamics