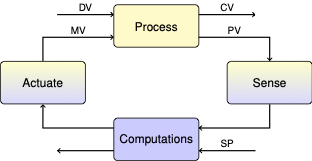
Lab 4: PI Control

Lab 4: PI Control#

This lab assignment introduces the use of proportional-integral (PI) control for the temperature control laboratory. In this assignment, you will:

use your mathematical model to tune a PI controller
test a few variants of the PI controller
compare your PI (this lab) and relay (Lab 3) controllers
analyze your data and answer discussion questions

# Set default parameters for publication quality plots
import matplotlib.pyplot as plt

SMALL_SIZE = 14
MEDIUM_SIZE = 16
BIGGER_SIZE = 18

plt.rc("font", size=SMALL_SIZE)  # controls default text sizes
plt.rc("axes", titlesize=SMALL_SIZE)  # fontsize of the axes title
plt.rc("axes", labelsize=MEDIUM_SIZE)  # fontsize of the x and y labels
plt.rc("xtick", labelsize=SMALL_SIZE)  # fontsize of the tick labels
plt.rc("ytick", labelsize=SMALL_SIZE)  # fontsize of the tick labels
plt.rc("legend", fontsize=SMALL_SIZE)  # legend fontsize
plt.rc("figure", titlesize=BIGGER_SIZE)  # fontsize of the figure title
plt.rc("lines", linewidth=3)

Exercise 0. Model-based Controller Tuning#

In this pre-lab exercise, you will use your mathematical model from Lab 2 to design and compare PI controllers. Specifically, you should:

Read this entire assignment.
Review your notes on PI controllers including advanced features
Review your notes on stability analysis
Review your notes on numerically simulating LTI systems with a controller

Mathematical Modeling for PI Controller#

On paper, write the mathematical model, e.g., system of differential and algebraic equations, for either the position-form or velocity-form PI controller. Next, transform your equations into a state-space linear time-invariant (LTI) systems model using the matrices \(\mathbf{A}\), \(\mathbf{B}\), \(\mathbf{C}\), and \(\mathbf{D}\). You will turn in this work as a PDF. Please bring it to the lab sessions and office hours.

Analyze Stability of PI Controller#

Next, write Python code to analyze the sensitivity of the eigenvalues of your system as a function of \(K_P\) and \(K_I\). Please consult the linked class notes above. You should use the model parameters \(U_a\), \(U_b\), \(C_p^H\), and \(C_p^S\) from Lab 2 in your analysis.

import matplotlib.pyplot as plt
import numpy as np
from scipy.linalg import eig

# parameters
T_amb = 21  # deg C
alpha = 0.00016  # watts / (units P1 * percent U1)
P1 = 100  # P1 units
U1 = 50  # steady state value of u1 (percent)

# fitted model parameters
# adjust using your values from Lab 2
Ua = 0.050  # watts/deg C
Ub = 0.097  # watts/deg C
CpH = 2.274  # joules/deg C
CpS = 5.046  # joules/deg C


# Add your solution here

Next, interpret your plots by identifying controller gains that are (a) stable and oscillatory and (b) stable and non-oscillatory. Fill in the table below to record your answer.

Answer:

	\(K_P\)	\(K_I\)
Stable and Oscillatory
Stable and Non-oscillatory

Plot Control Profiles#

Complete the functions below to generate the simple and chocolate temperature setpoints for channel 1 (T1) from Lab 3.

def SP1_simple(t):
    """Set point definition for T1
    Arguments:
        t: time (s)
    Returns:
        set point of T1
    """
    # Add your solution here


def SP1_chocolate(t):
    """Set point definition for T1
    Arguments:
        t: time (s)
    Returns:
        set point of T1
    """
    # Add your solution here


# Note: we will not use this function until Exercise 5
def SP2_chocolate(t):
    """Set point definition for T2
    Arguments:
        t: time (s)
    Returns:
        set point of T2
    """
    return 30


# Define time
dt = 1
t = np.arange(0, 600, dt)

# Evaluate set points
T_simple = [SP1_simple(ti) for ti in t]
T_chocolate = [SP1_chocolate(ti) for ti in t]

# Plot set points
plt.figure()
plt.plot(t, T_simple, label="Simple")
plt.plot(t, T_chocolate, label="Chocolate")
plt.xlabel("Time (s)")
plt.ylabel("Set Point (deg C)")
plt.legend()
plt.show()

Simulate PI Controllers#

Complete the following function to simulate the PI controller. Again, use the model parameters for your TCLab.

import pandas as pd
from scipy.signal import cont2discrete


def plot_tclab_results(data, title=None,SP1=None, SP2=None):
    ''' Plot results from TCLab simulation or experiment (saved to csv then loaded)
    Arguments:
        data: DataFrame with columns for Time, T1, T2, Q1, Q2
        title: plot title (default: "")
        SP1: function for channel 1 setpoint (default: None)
        SP2: function for channel 2 setpoint (default: None)
        
    Returns:
        nothing

    '''

    time = data["Time"]
    n = len(time)

    if "SP1" in data.columns:
        setpoint_1 = data["SP1"]
    elif SP1 is not None:
        setpoint_1 = SP1(data["Time"])
    else:
        setpoint_1 = [None] * n

    if "T1H" in data.columns:
        t1h = data["T1H"]
    else:
        t1h = [None] * n

    if "T1S" in data.columns:
        t1s = data["T1S"]
    elif "T1" in data.columns:
        t1s = data["T1"]
    else:
        t1s = [None] * n

    if title is not None:
        plt.title("Channel 1: " + title)
    plt.step(data["Time"], t1h, label="T1H", color='red', linestyle="--")
    plt.step(data["Time"], t1s, label="T1S", color='blue', linestyle="-")
    plt.step(
        data["Time"],
        setpoint_1,
        label="SP1",
        linestyle="-.",
        color="black",
        alpha=0.5,
    )
    plt.ylabel("Temperature (C)")
    plt.xlabel("Time (s)")
    plt.legend()
    plt.grid()
    plt.show()

    if "SP2" in data.columns:
        setpoint_2 = data["SP2"]
    elif SP2 is not None:
        setpoint_2 = SP2(data["Time"])
    else:
        setpoint_2 = [None] * n

    if "T2H" in data.columns:
        t2h = data["T2H"]
    else:
        t2h = [None] * n

    if "T2S" in data.columns:
        t2s = data["T2S"]
    elif "T2" in data.columns:
        t2s = data["T2"]
    else:
        t2s = [None] * n


    if t2s[0] is not None:
        # Skip the channel 2 plot if there are no data

        if title is not None:
            plt.title("Channel 2: " + title)
        plt.step(data["Time"], t2h, label="T2H", linestyle="--", color='purple')
        plt.step(data["Time"], t2s, label="T2S", linestyle="-", color='green')
        plt.step(
            data["Time"],
            setpoint_2,
            label="SP2",
            linestyle="-.",
            color="black",
            alpha=0.5,
        )
        plt.ylabel("Temperature (C)")
        plt.xlabel("Time (s)")
        plt.legend()
        plt.grid()
        plt.show()

    if "Q1" in data.columns:
        q1 = data["Q1"]
    else:
        q1 = [None] * n

    if "Q2" in data.columns:
        q2 = data["Q2"]
    else:
        q2 = [None] * n

    if title is not None:
        plt.title("Heaters: " + title)
    plt.step(data["Time"], q1, label="Q1", color='red')
    plt.step(data["Time"], q2, label="Q2", color='purple')
    plt.xlabel("Time (s)")
    plt.ylabel("Power Level (%)")
    plt.legend()
    plt.grid()
    plt.show()

def tclab_simulate_PI(
    t, setpoint, Kp=1.0, Ki=0.05, U_start=0, mode="position", verbose=False, plot=True
):
    """Simulate the TCLab system with PI control
    Arguments:
        Kp: the proportional control gain
        Ki: the integral control gain
        U_start: the initial heater value (same as MV_bar in class notes)
        mode: 'position' or 'velocity' form of PI control
        verbose: print matrices, default is False
        plot: create plots, default is True

    Returns:
        data: DataFrame with columns for Time, T1, T2, Q1, Q2
    """

    n = len(t)
    T_set = np.array([setpoint(ti) - T_amb for ti in t])

    # Original open loop state space model
    A = np.array([[-(Ua + Ub) / CpH, Ub / CpH], [Ub / CpS, -Ub / CpS]])
    B = np.array([[alpha * P1 / CpH], [0]])
    C = np.array([[0, 1]])
    D = np.array([[0]])

    Ad, Bd, Cd, Dd, dt = cont2discrete((A, B, C, D), dt=1, method="zoh")

    # Initialize state matrix
    # Recall that temperatures are in deviation variables, i.e., T - T_amb
    X = np.zeros((n, 2))

    # Initialize input matrix
    U = np.zeros((n, 1))
    U[0, 0] = U_start

    # Initialize previous error (for velocity form)
    prev_error = 0

    # Initialize integral of error (for position form)
    integral_error = 0

    # Loop over time steps
    for i in range(n):

        # Current state
        x = X[i, :]

        # Unpack into individual states
        T1H, T1S = x

        error = T_set[i] - T1S

        if i > 0:
            dt = t[i] - t[i - 1]

            if mode == "position":
                # Add your solution here

            elif mode == "velocity":
                # Add your solution here

        # Limit the power levels
        U[i, 0] = max(0, min(100, U[i, 0]))

        # Update state
        if i < n - 1:
            # Do not update the state for the last time step
            # We want to update U and SP for plotting
            X[i + 1, :] = Ad @ x + Bd @ U[i, :]

        # Store the previous error
        # (needed for velocity form)
        prev_error = error

    # Shift states from deviation variables to absolute values
    X += T_amb

    # Create DataFrame
    data = pd.DataFrame(X, columns=["T1H", "T1S"])
    data["Time"] = t
    data["Q1"] = U[:, 0]
    data["SP1"] = T_set + T_amb

    if plot:
        plot_tclab_results(data, title="Simulated PI Control with Kp={}, Ki={}".format(Kp, Ki))

    return data

Stable and Non-Oscillatory (Less Aggressive)#

Analyze your stability analysis plot to choose a value of \(K_P\) and \(K_I\) that is stable and should NOT oscillate. Record your answer below.

\(K_P = \)

\(K_I = \)

Using your function, simulate the position-form controller for the simple temperature setpoint.

# Position form simulation (keep U_start = 0)
# Hint: store the results in p1 (dataframe)
# Add your solution here

Copy your code from Lab 3 to compute the tracking error and run it on your simulation data.

def compute_tracking_error(data, SP1, SP2=None):
    """Compute the tracking error between the set point and the data

    Arguments:
        data: dataframe with columns for T1 and T2
        SP1: function that returns setpoint for T1
        SP2: function that returns setpoint for T2, default None

    Returns:
        rmse1: root mean square error for T1
        rmse2: root mean square error for T2
        ame1: absolute mean error for T1
        ame2: absolute mean error for T2
    """

    # Add your solution here

compute_tracking_error(p1, SP1_simple)

Next, simulate the velocity-form controller for the simple temperature profile using the same values of \(K_I\) and \(K_P\). Keep U_start = 0.

# Velocity form simulation (keep U_start = 0)
# Add your solution here
compute_tracking_error(p2, SP1_simple)

Now, repeat the simulation, but choose U_start greater than zero.

# Add your solution here
compute_tracking_error(p3, SP1_simple)

Next, simulate the position-form PI controller (using the same \(K_P\) and \(K_I\)) for the chocolate temperature profile.

# Position-form
# Add your solution here
compute_tracking_error(p4, SP1_chocolate)

Finally, simulate the velocity-form PI controller for the chocolate temperature setpoint. You can adjust U_start.

# Velocity form
# Add your solution here
compute_tracking_error(p5, SP1_chocolate)

Stable and Oscillatory (More Aggressive)#

Analyze your stability analysis plot to choose a value of \(K_P\) and \(K_I\) that is stable and oscillates. Record your answer below. You will likely choose larger controller gains (more aggressive).

\(K_P = \)

\(K_I = \)

Simulate the position-form controller for the simple temperature profile using the newly selected \(K_P\) and \(K_I\).

# Position form
# Add your solution here
compute_tracking_error(p6, SP1_simple)

Next, simulate the velocity-form controller for the simple temperature profile. You may adjust U_start.

# Add your solution here
compute_tracking_error(p7, SP1_simple)

Next, simulate the position-form PI controller for the chocolate tempering profile.

# Position form
# Add your solution here
compute_tracking_error(p8, SP1_chocolate)

Finally, simulate the velocity-form PI controller for the chocolate temperature profile. You may adjust U_start.

# Velocity form
# Add your solution here
compute_tracking_error(p9, SP1_chocolate)

Discussion#

Analyze the nine simulations above. First, fill in the following table.

Controller	Profile	Notes
Position	Simple	Original Gains
Velocity	Simple	Original Gains (`U_start` = 0)
Velocity	Simple	Original Gains (`U_start` > 0)
Position	Chocolate	Original Gains
Velocity	Chocolate	Original Gains
Position	Simple	Aggressive Gains
Velocity	Simple	Aggressive Gains (`U_start` > 0)
Position	Chocolate	Aggressive Gains
Velocity	Chocolate	Aggressive Gains

Next, distill this table and the above simulation results into three to five key observations. For each observation, write a bullet point that is at least one sentence. Be quantitative, i.e., use numbers and supporting calculations to justify your observations.

Answer:

Controller Tuning#

Based on your observations above, choose either a position-form or velocity-form PI controller. Next, using simulations, fine-tune the controller gains (and optionally U_start) to minimize the tracking error for the chocolate temperature profile.

You may do this by trial and error. If you are adventurous, consider trying to use scipy.optimize.minimize with bounds. Recall that in Lab 3, you already wrote code to calculate the tracking error.

# Add your solution here

Exercise 1. Position-Form PI Control with the Digital Twin#

Implement position-form PI control with the TCLab using connected=False (simulation/digital twin mode) for the chocolate temperature profile. You can find almost complete code in the class assigments. Using trial and error, adjust \(K_P\) and \(K_I\).

Note: In Exercise 0, you analyzed your own TCLab using \(U_a\), \(U_b\), \(C_p^S\), and \(C_p^H\) you fit in Lab 2. The digital twin mode does NOT use the same model parameters. Thus, do not be surprised if you find different \(K_P\) and \(K_I\) parameters.

from tclab import setup, clock, Historian, Plotter

def PI_position(Kp=1, Ki=0, MV_bar=0, antiwindup=True):
    """Position-form proportion-integral

    Arguments:
        Kp: proportional gain
        Ki: integral gain
        MV_bar: bias

    """

    # Minimum and maximum bounds for manipulated variables
    MV_min = 0
    MV_max = 100

    # Initialize with MV_bar
    MV = MV_bar

    # Initialize integral
    I = 0

    # Set limits for integral windup protection
    I_max = 100
    I_min = -100

    while True:
        t_step, SP, PV, MV = yield MV

        # Add your solution here


def PI_velocity(Kp=1, Ki=0, MV_bar=0, bumpless=True):
    """Velocity-form proportion-integral controller

    Arguments:
        Kp: proportional gain
        Ki: integral gain
        MV_bar: bias

    Note: This implements:
    - Type 1 anti-windup (velocity form) with MV limits
    - Type 2 anti-windup (using MV)
    - Bumpless transfer

    """

    # Initialize previous error as zero
    e_prev = 0
    PV_prev = None

    # Define upper and lower bounds for MV
    MV_min = 0
    MV_max = 100

    # Initialize MV with MV_bar
    MV = MV_bar

    first_pass = True

    # Infinite loop for the controller
    while True:
        # Yield MV and wait for new t_step, SP, and PV
        t_step, SP, PV, MV = yield MV

        if first_pass:
            # Initialize MV with MV_bar
            MV = MV_bar
            first_pass = False

        # Calculate error
        e = SP - PV

        # Apply the velocity form of the PI controller
        if bumpless and PV_prev is not None:
            # Bumpless transfer
            # Add your solution here
        else:
            # Standard form
            # Add your solution here

        # Apply upper and lower bounds
        # ** disabled for this simple controller, important later **
        MV = max(MV_min, min(MV_max, MV))  # Apply upper and lower bounds

        # Store the current error for the next iteration
        e_prev = e

        # Store the current PV for bumpless transfer
        PV_prev = PV

# Create and initialize the PI controller
# Add your solution here
controller1.send(None)


def run_tclab(
    control1,
    filename,
    control2=None,
    connected=False,
    disturbance=None,
    tfinal=600,
    t_step=1,
):
    """Run the PI controller with the TCLab

    Arguments:
        control1: PI controller for channel 1
        filename: name of the csv file to save the results
        control2: PI controller for channel 2 (default, None)
        connected: if True, connect to the real device, otherwise simulate (default)
        disturbance: function that returns a disturbance value
        tfinal: final time, seconds
        t_step: time step, seconds

    """

    assert (
        control2 is None or disturbance is None
    ), "Cannot have both control2 and disturbance"

    # Connect to the TCLab
    if connected:
        TCLab = setup(connected=True)
    else:
        TCLab = setup(connected=False, speedup=500)

    with TCLab() as lab:
        # Create the historian and plotter

        if control2 is None:
            sources = [
                ("T1", lambda: lab.T1),
                ("T2", lambda: lab.T2),
                ("SP1", lambda: SP1_chocolate(t)),
                ("Q1", lab.Q1),
                ("Q2", lab.Q2),
            ]

        else:
            sources = [
                ("T1", lambda: lab.T1),
                ("T2", lambda: lab.T2),
                ("SP1", lambda: SP1_chocolate(t)),
                ("SP2", lambda: SP2_chocolate(t)),
                ("Q1", lab.Q1),
                ("Q2", lab.Q2),
            ]

        h = Historian(sources)

        if control2 is None:
            p = Plotter(h, tfinal, layout=(("T1", "SP1", "T2"), ("Q1", "Q2")))
        else:
            p = Plotter(h, tfinal, layout=(("T1", "SP1"), ("T2", "SP2"), ("Q1", "Q2")))

        # Loop over time
        for t in clock(tfinal, t_step):

            # get the set point
            SP1 = SP1_chocolate(t)

            # measure the the process variable
            PV1 = lab.T1

            # measure the manipulated variable
            # this negates MV_bar in the controller (velocity form)
            MV1 = lab.Q1()

            # send the current time, set point, and process variable to the controller
            # compute the control action
            MV1 = control1.send([t_step, SP1, PV1, MV1])

            # set the heat power (actuate)
            lab.Q1(MV1)

            if control2 is not None:
                SP2 = SP2_chocolate(t)
                PV2 = lab.T2
                MV2 = lab.Q2()
                MV2 = control2.send([t_step, SP2, PV2, MV2])
                lab.Q2(MV2)

            elif disturbance is not None:
                lab.Q2(disturbance(t))

            # Log the data
            p.update()

        # This saves the results in case you accidentally overwrite the experiment
        # After running this exercise, please find and save this csv file
        h.to_csv(filename)

    plt.show()

    # It appears there is not an easy way to convert the historian to a dataframe
    df = pd.read_csv(filename)

    return df


# Note: in our function run_tclab, we set connected=False and speedup=500
# This makes the code run 500x faster than real time.
# However, with such a large value of speedup, you may notice the digital twin
# simulation does not start until time ~50 seconds to ~200 seconds and the simulation
# runs longer for a total run time of 600 seconds.
# We suspect this is due to a small lag in starting the digital twin simulation,
# which is amplified with a really large speedup factor.
# This is okay.
exp1 = run_tclab(controller1, "lab4-digital-twin-PI-position.csv", tfinal=600, t_step=1)

# Replot the results and compute the tracking error
plot_tclab_results(exp1, title="PI Position Digital Twin", SP1=SP1_chocolate)
compute_tracking_error(exp1, SP1_chocolate)

Complete the following table to document your trial and error fine tuning. For each experiment you conduct, record the value of \(K_P\), \(K_I\), and your notes. Each note should be at least one complete sentence.

\(K_P\)	\(K_I\)	Notes
Fill in	Fill in	Fill in
Fill in	Fill in	Fill in

Which experiment is your final choice of \(K_I\) and \(K_P\). Why did you choose those values? Please write a few sentences.

Answer:

Exercise 2. Velocity-Form Control with Digital Twin#

Repeat Exercise 1, but using the velocity-form controller. Use the same values of \(K_P\) and \(K_I\) as Exercise 1. You may adjust MV_bar (which is the same as U_start in Exercise 0). Run this with bumpless=False (without bumpless).

# Create and initialize the PI controller
# Add your solution here

exp2 = run_tclab(controller2, "lab4-digital-twin-PI-velocity.csv", tfinal=600, t_step=1)

# Replot results and compute the tracking error
plot_tclab_results(exp2, title="PI Velocity Digital Twin", SP1=SP1_chocolate)

compute_tracking_error(exp2, SP1_chocolate)

Next, run the velocity-form controlled with the same values of \(K_P\) and \(K_I\) using bumpless=True.

# Create and initialize the PI controller
# Add your solution here

exp3 = run_tclab(
    controller3, "lab4-digital-twin-PI-velocity-bumpless.csv", tfinal=600, t_step=1
)

# Replot results and compute the tracking error
plot_tclab_results(exp3, title="PI Velocity Digital Twin with Bumpless Transfer", SP1=SP1_chocolate)
compute_tracking_error(exp3, SP1_chocolate)

Write a few bullet points to describe the difference between the two results between the standard and bumpless implementations.

Answer:

Please write a few bullet points comparing your position-form and velocity-form simulation. What are the similarities and differences? Which controller do you prefer and why? Each bullet point should be one (and only one) thought.

Answer:

Exercise 3. PI Controller on Hardware#

Verify Device is at Ambient Temperature#

# Check that the device is at steady state
# length of check
tfinal = 30  # seconds

# Suggestion: set to False after you have completed this
# exercise to prevent yourself from accidentally overwriting your results.
# Students: you need to set this to True to run your code
run_exercise_3 = False

if run_exercise_3:

    # Make sure this is connected=True
    TCLab = setup(connected=True)

    # perform experiment
    with TCLab() as lab:
        # No power to either heater
        lab.U1 = 0
        lab.U2 = 0

        # Initialize plotter and historian
        h = Historian(lab.sources)
        p = Plotter(h, tfinal)

        # Loop over time
        for t in clock(tfinal):

            # Take measurements and update plots
            p.update(t)

Run Experiment with TCLab Hardware#

Implement a PI controller on your TCLab hardware. Choose the value of gains \(K_P\) and \(K_I\) you identified in Exercise 0.

if run_exercise_3:
    # Add your solution here

    # Make sure this is connected=True
    exp4 = run_tclab(
        my_controller, "lab4-exercise3.csv", connected=True, tfinal=600, t_step=1
    )

    compute_tracking_error(exp4, SP1_chocolate)

# Load results from csv file
exp4 = pd.read_csv("lab4-exercise3.csv")

# Replot results
plot_tclab_results(exp4, title="PI Controller on Hardware", SP1=SP1_chocolate)

# Compute tracking error
compute_tracking_error(exp4, SP1_chocolate)

Discussion#

For each of the following questions/prompts, write a few sentences. Your answers should be supported by your quantitative data.

How does the controller performance compare to the simulations using the model for your TCLab (Exercise 0)?

Answer:

Describe and explain the shape of the control signal, i.e., \(Q_1(t)\). Do you see the effects of the proportional and integral terms in the control signal?

Answer:

When is the tracking error the greatest? Why does this make sense?

Answer:

Quantitatively compare the performance of the PI controller (this assignment) and your relay controller (Lab 3) for the chocolate tempering experiment.

Answer:

How can you improve the performance of the controller? Be creative.

Answer:

Exercise 4. Comparison with Relay Control#

Next, we will compare our PI controller to your relay controller results from Lab 3. Recall, in Lab 3, we controlled both channels. We will want to do the same here.

Be sure to wait until your TCLab cools to room temperature before starting.

Verify Device is at Ambient Temperature#

# Check that the device is at steady state
# length of check
tfinal = 30  # seconds

# Suggestion: set to False after you have completed this
# exercise to prevent yourself from accidentally overwriting your results.
run_exercise_4 = False

if run_exercise_4:
    # Check this says connected=True
    TCLab = setup(connected=True)

    # perform experiment
    with TCLab() as lab:
        # No power to either heater
        lab.U1 = 0
        lab.U2 = 0

        # Initialize plotter and historian
        h = Historian(lab.sources)
        p = Plotter(h, tfinal)

        # Loop over time
        for t in clock(tfinal):

            # Take measurements and update plots
            p.update(t)
        plt.show()

Run Experiment for Dual Channel PI Control#

You will define a separate controller for each channel.

You do not need to use the same control structure (position versus velocity form) or gains for both channels. Experiment with connected=False! Once you are happy, switch to connected=True and run the experiment on your TCLab hardware.

# Add your solution here

if run_exercise_4:
    if False:
        # First experiment with connected=False
        # Then, switch to connected=True
        exp5 = run_tclab(
            control1, 
            "lab4-exercise4.csv", 
            control2, 
            connected=True, 
            tfinal=600, 
            t_step=1
        )

# Load results from csv file
exp5 = pd.read_csv("lab4-exercise4.csv")

# Replot results
plot_tclab_results(exp5, title="Two-Input PI Controller on Hardware", SP1=SP1_chocolate, SP2=SP2_chocolate)

# Compute tracking error
compute_tracking_error(exp5, SP1_chocolate, SP2_chocolate)

Load and Visualize Your Relay Control Data (Lab 3)#

# Load csv file
lab3 = pd.read_csv("lab3-chocolate-relay.csv")

# Replot results
plot_tclab_results(lab3, title="Relay Control (Lab 3)", SP1=SP1_chocolate, SP2=SP2_chocolate)

# Compute tracking error
compute_tracking_error(lab3, SP1_chocolate, SP2_chocolate)

Discussion#

For each of the following questions/prompts, write a few sentences. Your answers should be supported by your quantitative data.

Compare your PI controller results from Exercises 3 and 4. What is the impact of also controlling channel 2? Why do these results make sense?

Answer:

Compare your controller results from Exercise 4 and Lab 3. How are the results for the PI and relay controllers similar? How are they different?

Answer:

Which control strategy – relay or PI – do you recommend and why?

Answer:

Exercise 5. Disturbance#

Next, we will use heater 2 to simulate a disturbance. Be sure to wait until your TCLab cools to room temperature before starting.

Verify Device is at Ambient Temperature#

# Check that the device is at steady state
# length of check
tfinal = 30  # seconds

# Suggestion: set to False after you have completed this
# exercise to prevent yourself from accidentally overwriting your results.
# Students: you need to set this to True to run your code
run_exercise_5 = False


if run_exercise_5:

    # Check this is connected=True
    TCLab = setup(connected=False)

    # perform experiment
    with TCLab() as lab:
        # No power to either heater
        lab.U1 = 0
        lab.U2 = 0

        # Initialize plotter and historian
        h = Historian(lab.sources)
        p = Plotter(h, tfinal)

        # Loop over time
        for t in clock(tfinal):

            # Take measurements and update plots
            p.update(t)
        plt.show()

Perform Experiment with TCLab#

# Finish this function
def my_disturb(t):
    """Disturbance function for the TCLab
    Arguments:
        t: time
    Returns:
        disturbance value

    This function uses heat 2 as a disturbance:
        DV is 0% for t <= 50 seconds
        DV is 100% for 50 < t <= 300 seconds
        DV is 10% for t > 300 seconds
    """

    # Add your solution here


if run_exercise_5:
    # Add your solution here

    # TODO: Update from connected=False to connected=True
    exp6 = run_tclab(
        my_controller,
        "lab4-exercise5.csv",
        connected=False,
        disturbance=my_disturb,
        tfinal=600,
        t_step=1,
    )

    plt.show()

    

plot_tclab_results(exp6, title="PI Controller with Disturbance", SP1=SP1_chocolate)

compute_tracking_error(exp5, SP1_chocolate)

Discussion#

For each of the following questions/prompts, write a few sentences. Your answers should be supported by your quantitative data.

Compare the temperature profiles from Exercises 3 and 5. What is the impact of the disturbance? Why do these results physically make sense?

Answer:

How much does the disturbance impact the performance, e.g., tracking error, of the controller?

Answer:

Exercise 6. P&ID Discussion#

Please post your P&ID discussion on Canvas. This was previously Exercise 0.

Exercise 7. Feed-Forward Control (Extra Credit)#

We can use our mathematical model for our TCLab to incorporate a feed-forward component to further improve our PI controller. Specifically, we can adjust the offset, \(\bar{u}\) or \(\bar{MV}\) in our notes, based on the steady-state value for the control variable needed to reach the setpoint.

Steady-State Calculation#

Type the formula to calculate the steady-state power \(\bar{u}\) that corresponds to a setpoint \(T_{set}\).

(4)#\[\begin{equation} \bar{u} = \end{equation}\]

Hint: review your notes on steady-state gain and step tests. What value of \(\bar{u}\) should we apply in a step test to get the heater to reach \(T_{set}\) as the steady-state temperature?

Simulation#

Copy the simulation code from above here. Then modify the copied code to calculate the offset (\(\bar{u}\)) using your mathematical model. Each time step, you will update the offset \(\bar{u}(t)\) based on the \(T_{set}(t)\).

Hint: Is this easier to implement with a position-form or velocity-form controller?

Next, simulate the chocolate temperature profile and calculate the tracking error.

TCLab Experiment#

Finally, repeat this experiment with your TCLab hardware. Hint: use connected=False to debug your code. Once you are happy with it, switch to connected=True. Do not forget to verify your device is at ambient temperature.

Discussion#

Write a few bullet points comparing your PI controller with feed-forward to your PI controller with a constant (and likely zero) bias.

Answer:

Submission Instructions#

Please submit BOTH the .pdf and .ipynb files via Gradescope. There are separate assignments in Gradescope for each submission. There are separate submissions for Exercise 0 and the entire lab. Please ensure you are using the correct assignment in Gradescope.

To recap:

(First Deadline) Submit the Python portion of Exercise 0 as a .ipnyb file via Gradescope.
(First Deadline) Create a PDF that merges your handwritten work and Python code (print your notebook to PDF) for Exercise 0. Submit via Gradescope as a .pdf file.
(Second Deadline) Submit your entire notebook as a .ipynb file via Gradescope.
(Second Deadline) Print/convert your entire notebook to a .pdf file and submit via Gradescope.
(Second Deadline) Post your response about P&IDs (Exercise 6) to the Canvas Discussion.

Declarations#

TCLab Hardware: Did you use the same TCLab device for this and previous labs? If not, please provide details here. These labs are designed to use the same hardware throughout the semester. Please keep this in mind as you answer the discussion questions, especially when comparing the simulated to actual performance.

Collaboration: If you worked with any classmates, please give their names here. Describe the nature of the collaboration.

Generative AI: If you used any Generative AI tools, please elaborate here.

Reminder: The written discussions responses must be in your own words. Many of these questions ask about your specific results or are open-ended questions with many reasonable answers. Thus we expect unique responses, analyses, and ideas.

We may use writing analysis software to check for overly similar written responses. You are responsible for reviewing the collaboration policy outlined in the class syllabus to avoid violations of the honor code.

Lab 4: PI Control

Contents

Lab 4: PI Control#

Exercise 0. Model-based Controller Tuning#

Mathematical Modeling for PI Controller#

Analyze Stability of PI Controller#

Plot Control Profiles#

Simulate PI Controllers#

Stable and Non-Oscillatory (Less Aggressive)#

Stable and Oscillatory (More Aggressive)#

Discussion#

Controller Tuning#

Exercise 1. Position-Form PI Control with the Digital Twin#

Exercise 2. Velocity-Form Control with Digital Twin#

Exercise 3. PI Controller on Hardware#

Verify Device is at Ambient Temperature#

Run Experiment with TCLab Hardware#

Discussion#

Exercise 4. Comparison with Relay Control#

Verify Device is at Ambient Temperature#

Run Experiment for Dual Channel PI Control#

Load and Visualize Your Relay Control Data (Lab 3)#

Discussion#

Exercise 5. Disturbance#

Verify Device is at Ambient Temperature#

Perform Experiment with TCLab#

Discussion#

Exercise 6. P&ID Discussion#

Exercise 7. Feed-Forward Control (Extra Credit)#

Steady-State Calculation#

Simulation#

TCLab Experiment#

Discussion#

Submission Instructions#

Declarations#