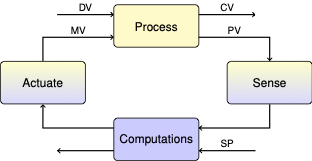
Lab 6: Model Predictive Control (MPC)

Lab 6: Model Predictive Control (MPC)#

Your Name:

Learning Objectives#

Compute optimal heater strategy using physics-based model
Demonstrate MPC (closed-loop optimization) workflow
Verify MPC performance with TC Lab hardware

Installation and Setup#

This notebook is using Pyomo and Ipopt. Be sure to follow the installation instructions on the class website.

Before beginning this lab, connect your TCLab device and run the following cell to estimate your ambient temperature.

# experimental parameters
tfinal = 30

# To complete the experiment, change this to True
# After completing the experiment, be sure to change it back to False
# This will prevent you from overwriting your data
run_tamb_tclab = True

from tclab import TCLab, clock, Historian, Plotter, setup
import numpy as np

if run_tamb_tclab:

    TCLab = setup(connected=True)

    # initialize list to store temperature
    T_list = []

    # perform experiment
    with TCLab() as lab:
        lab.U1 = 0
        lab.U2 = 0
        h = Historian(lab.sources)
        p = Plotter(h, tfinal)
        
        # save temperatures to access later
        T_list.append(lab.T1)
        T_list.append(lab.T2)

        for t in clock(tfinal):
            p.update(t)

    # estimate ambient temperature
    Tamb = np.mean(T_list) # deg C
    print(f"The ambient temperature is {Tamb} degrees C")

Exercise 0: Develop the Mathematical Model and Pyomo Simulation#

Recall the two-state model for a single heater/sensor assembly:

\[\begin{align*} C_p^H \frac{dT_H}{dt} & = U_a (T_{amb} - T_H) + U_b (T_S - T_H) + \alpha P u(t) + d(t)\\ C_p^S \frac{dT_S}{dt} & = - U_c (T_S - T_H) \end{align*}\]

Pyomo Model#

The code provides a library for performing several analysis tasks with our model. This is a class, which is a more sophisticated way to modularize our code. Briefly, classes store both data and methods to manipualte the data (as demonstrated in Lab 5).

Take a few minutes to study this code. A few features:

It supports four modes:
- simulate solve the model with all of the inputs specified (zero degrees of freedom)
- control determine the best \(u(t)\) to track the desired \(T_{set}(t)\)
- observe estimate the unmeasured state \(T_{H}(t)\) and disturbance \(d(t)\) from experimental data
The __init__ method is called automatically when you create an instance of the object. The initial method is how you pass in data
The solve method call the numerical optimization algorithm
The plot method plots the Pyomo results
The get_Ts, get_Th, get_U, and get_D methods return data stored in the Pyomo model after it is solved

# update value from code cell and run above if returning to notebook with reset kernel
# Tamb = 23.32 # deg C

import matplotlib.pyplot as plt
from scipy import interpolate
import numpy as np

# ensure that IDEAS is imported if there is an error calling Ipopt
import idaes

# Protip: only import the functions you need for each library.
# This tells other programs exactly where each function is defined.
# Avoid using from pyomo.environ import * as this imports everything
from pyomo.environ import ConcreteModel, Var, Param, Constraint, TransformationFactory, SolverFactory, Objective, minimize, value, Suffix
from pyomo.dae import DerivativeVar, ContinuousSet, Simulator

##### IMPORTANT #####
# Update the default values for Ua, Ub, CpH, and CpS with results from lab 3 or 5
# The values used below were taken from the open-loop optimization 
# lecture notebook ("Take Two" section)
#####################

P1_GLOBAL = 200

class TCLabPyomo:
    '''
    This class contains the methods used for simulating the TCLab model, optimizing u(t) per a 
    given set point for T, and estimating state variables in the TCLab.
    '''

    def __init__(self, mode, t_data, u_data, d_data, Tset_data, 
                 TS_data, Tamb = Tamb, alpha = 0.00016, P1 = P1_GLOBAL,
                 Ua = 0.0535, Ub = 0.0148, CpH = 6.911, CpS = 0.318,
                 obj_weight_observe=1.0, obj_weight_optimize=0.01, 
                 verbose = True, time_finite_difference = 'BACKWARD'
    ):
        '''
        This method is called automatically when instantiating class.
        It stores input data in the class and creates the pyomo model.
        
        Arguments:
            mode: specify mode
            t_data: time data
            u_data: input control data
            d_data: disturbance data
            Tset_data: set point data
            TS_data: experimental data
            Tamb: ambient temperature, deg C
            alpha: watts / (units P1 * percent U1)
            P1: max power, P1 units
            Ua: heat transfer coefficient from heater to environment, watts/deg C
            Ub: heat transfer coefficient from heater to sensor, watts/deg C
            CpH: heat capacity of the heater, joules/deg C
            CpS: heat capacity of the, joules/deg C
            obj_weight_observe: weight for disturbance in objective function, default is 0.1
            obj_weight_optimize: weight for heater temperature in objective function, default is 0.01
            verbose: Boolean to control ipopt output, default = True returns the ipopt output
            time_finite_difference: method for finite difference, 'BACKWARD' or 'FORWARD'
            
        Returns:
            None 
        '''
        
        # establish the valid operating modes
        valid_modes = ['simulate','optimize','observe']

        # raise an error if the user feeds in invalid operating mode
        if mode not in valid_modes:
            raise ValueError("'mode' must be one of the following:"+valid_modes)

        # define mode and data
        self.mode = mode
        self.t_data = t_data
        self.u_data = u_data
        self.d_data = d_data
        self.Tset_data = Tset_data
        self.TS_data = TS_data

        # set parameter values
        self.Tamb = Tamb
        self.Ua = Ua
        self.Ub = Ub
        self.CpH = CpH
        self.CpS = CpS
        self.alphaP = alpha*P1
        self.obj_weight_observe = obj_weight_observe
        self.obj_weight_optimize = obj_weight_optimize
        self.verbose = verbose
        
        if time_finite_difference not in ['BACKWARD', 'FORWARD']:
            raise ValueError("'time_finite_difference' must be either 'BACKWARD' or 'FORWARD'")

        self.time_finite_difference = time_finite_difference

        # create the pyomo model
        self._create_pyomo_model()

        return None


    def _create_pyomo_model(self):
        '''
        Method that creates and defines the pyomo model for each mode.
        Arguments:
            None
        Returns:
            m: the pyomo model
        '''
        
        # create the pyomo model
        m = ConcreteModel()

        # create the time set
        m.t = ContinuousSet(initialize = self.t_data)  # make sure the experimental time grid are discretization points
        # define the heater and sensor temperatures as variables
        m.Th = Var(m.t, bounds=[0, 80], initialize=self.Tamb)
        m.Ts = Var(m.t, bounds=[0, 80], initialize=self.Tamb)

        def helper(my_array):
            '''
            Method that builds a dictionary to help initialization.
            Arguments:
                my_array: an array
            Returns:
                data: a dict {time: array_value}
            '''
            # ensure that the dimensions of array and time data match
            assert len(my_array) == len(self.t_data), "Dimension mismatch."
            data = {}
            for k,t in enumerate(self.t_data):
                data[t] = my_array[k]
            return data

        # for the simulate and observe modes
        if self.mode in ['simulate', 'observe']:
            # control decision is a parameter initialized with the input control data dict
            m.U = Param(m.t, initialize=helper(self.u_data), default = 0)
        else:
            # otherwise (optimize) control decision is a variable
            m.U = Var(m.t, bounds=(0, 100))

        # for the simulate and optimize modes
        if self.mode in ['simulate', 'optimize']:
            # if no distrubance data exists, initialize parameter at 0
            if self.d_data is None:
                 m.D = Param(m.t, default = 0)
            # otherwise initialize parameter with disturbance data dict
            else:
                m.D = Param(m.t, initialize=helper(self.d_data))
        # otherwise (observe) the disturbance is a variable
        else:
            m.D = Var(m.t)

        # define parameters that do not depend on mode
        m.Tamb = Param(initialize=self.Tamb)
        m.alphaP = Param(initialize=self.alphaP)
        # Ua, Ub, CpH, and CpS are parameters
        m.Ua = Param(initialize=self.Ua)
        m.Ub = Param(initialize=self.Ub)
        # 1/CpH and 1/CpS parameters
        m.inv_CpH = Param(initialize=1/self.CpH)
        m.inv_CpS = Param(initialize=1/self.CpS)
        
        # define variables for change in temperature wrt to time
        m.Thdot = DerivativeVar(m.Th, wrt = m.t)
        m.Tsdot = DerivativeVar(m.Ts, wrt = m.t)

        # define differential equations (model) as contraints
        # moved Cps to the right hand side to diagnose integrator
        m.Th_ode = Constraint(m.t, rule = lambda m, t: 
                            m.Thdot[t] == (m.Ua*(m.Tamb - m.Th[t]) + m.Ub*(m.Ts[t] - m.Th[t]) + m.alphaP*m.U[t] + m.D[t])*m.inv_CpH)
        m.Ts_ode = Constraint(m.t, rule = lambda m, t: 
                            m.Tsdot[t] == (m.Ub*(m.Th[t] - m.Ts[t]) )*m.inv_CpS)


        # for the optimize mode
        if self.mode == 'optimize':
            # Add requested constraints on U ramping here
            m.Udot = DerivativeVar(m.U, wrt = m.t)

            m.U_rate1 = Constraint(m.t, rule = lambda m, t: m.Udot[t] <= 0.25)
            m.U_rate2 = Constraint(m.t, rule = lambda m, t: m.Udot[t] >= -0.25)

        # for the optimize mode, set point data is a parameter
        if self.mode == 'optimize':
            m.Tset = Param(m.t, initialize=helper(self.Tset_data))
            # otherwise, we are not using it

        # for the observe mode, experimental data is a parameter
        if self.mode == 'observe':
            m.Ts_measure = Param(m.t, initialize=helper(self.TS_data))
            # otherwise, we are not using it

        # apply backward finite difference to the model
        TransformationFactory('dae.finite_difference').apply_to(m, scheme=self.time_finite_difference, nfe=len(self.t_data)-1)

        if self.mode == 'optimize':
            # defining the tracking objective function
            m.obj = Objective(expr=sum( (m.Ts[t] - m.Tset[t])**2 + self.obj_weight_optimize*(m.Th[t] - m.Tset[t])**2 for t in m.t), sense=minimize)

        if self.mode == 'observe':
            # define observation (state estimation)
            m.obj = Objective(expr=sum((m.Ts[t] - m.Ts_measure[t])**2 + self.obj_weight_observe*m.D[t]**2 for t in m.t), sense=minimize)

        # initial conditions
        #For moving horizion we check if t=0 is in the horizon t data and fix initial conditions
        if self.t_data[0] == 0:
            if self.TS_data is not None:
                # Initilize with first temperature measurement
                m.Th[0].fix(self.TS_data[0])
                m.Ts[0].fix(self.TS_data[0])
            else:
                #Initialize with ambient temperature
                m.Th[0].fix(m.Tamb)
                m.Ts[0].fix(m.Tamb)
          

        if self.mode == 'optimize':
            
            if self.time_finite_difference == 'BACKWARD':
                # Remember that Pyomo is 1-indexed, which means '1' is the first element of the time set
                m.first_u = Constraint(expr=m.U[m.t.at(1)] == m.U[m.t.at(2)])

            if self.time_finite_difference == 'FORWARD':
                m.last_u = Constraint(expr=m.U[m.t.at(-1)] == m.U[m.t.at(-2)])
                
        # same idea also applies to disturbance estimates in 'observe' mode
        if self.mode == 'observe':

            if self.time_finite_difference == 'BACKWARD':
                m.first_d = Constraint(expr=m.D[m.t.at(1)] == m.D[m.t.at(2)])

            if self.time_finite_difference == 'FORWARD':
                m.last_d = Constraint(expr=m.D[m.t.at(-1)] == m.D[m.t.at(-2)])

        # store the model
        self.m = m
        
    def set_initial_conditions(self, Th0, Ts0):
        t0 = self.t_data[0]
        self.m.Th[t0].fix(Th0)
        self.m.Ts[t0].fix(Ts0)

    def solve(self):
        '''
        Solves the pyomo model using ipopt.
        '''
        solver = SolverFactory('ipopt')
        #solver.options['linear_solver'] = 'ma57'
        solver.solve(self.m, tee=self.verbose)


    def get_time(self):
        '''
        Returns time data from solved pyomo model.
        '''
        return self.t_data


    def get_Th(self):
        '''
        Returns heater temperature data from solved pyomo model.
        '''
        return np.array([value(self.m.Th[t]) for t in self.t_data])
    
    def get_Ts(self):
        '''
        Returns sensor temperature data from solved pyomo model.
        '''
        return np.array([value(self.m.Ts[t]) for t in self.t_data])
    

    def get_U(self):
        '''
        Returns control decision data from solved pyomo model.
        '''
        return np.array([value(self.m.U[t]) for t in self.t_data])
    

    def get_D(self):
        '''
        Returns disturbance data from solved pyomo model.
        '''
        return np.array([value(self.m.D[t]) for t in self.t_data])
    

    def get_parameters(self):
        '''
        Returns model parameters from solved pyomo model.
        '''
        return value(self.m.Ua), value(self.m.Ub), 1/value(self.m.inv_CpH), 1/value(self.m.inv_CpS)


    def print_parameters(self):
        '''
        Prints out the model parameters from solved pyomo model.
        '''
        Ua, Ub, CpH, CpS = self.get_parameters()

        print("The value of Ua is", round(Ua,4), "Watts/degC.")
        print("The value of Ub is", round(Ub,4), "Watts/degC.")
        print("The value of CpH is", round(CpH,3), "Joules/degC.")
        print("The value of CpS is", round(CpS,3),"Joules/degC.")
        
        
    def plot(self):
        '''
        Method to plot the results from the pyomo model.
        '''

        # extract predictions
        Th = self.get_Th()
        Ts = self.get_Ts()
        U = self.get_U()
        D = self.get_D()

        # create figure
        plt.figure(figsize=(10,6))

        # subplot 1: temperatures
        plt.subplot(3, 1, 1)
        if self.TS_data is not None:
            plt.scatter(self.t_data, self.TS_data, marker='.', label="$T_{S}$ measured", alpha=0.5,color='green')
        plt.plot(self.t_data, Th, label='$T_{H}$ predicted')
        plt.plot(self.t_data, Ts, label='$T_{S}$ predicted')
        if self.Tset_data is not None:
            plt.plot(self.t_data, self.Tset_data, label='$T_{set}$')

        plt.title('temperatures')
        plt.ylabel('deg C')
        plt.legend()
        plt.grid(True)

        # subplot 2: control decision
        plt.subplot(3, 1, 2)
        plt.plot(self.t_data, U)
        plt.title('heater power')
        plt.ylabel('percent of max')
        plt.grid(True)

        # subplot 3: disturbance
        plt.subplot(3, 1, 3)
        plt.plot(self.t_data, D)
        plt.title('disturbance')
        plt.ylabel('watts')
        plt.xlabel('time (s)')
        plt.grid(True)

        plt.tight_layout()
        plt.show()
    

Process Inputs#

The next cell defines some process inputs (from lab 5) that will be used throughout the notebook to demonstrate aspects of process simulation, control, and estimation. These are gathered in one place to make it easier to modify the notebook to test the response under different conditions. These functions are implemented using the interp1d from the scipy library.

%matplotlib inline

tclab_disturbance = interpolate.interp1d(
    [ 0, 300, 400, 9999],   # time
    [ 0, 0, -.5, -.5],      # disturbance value
    fill_value="extrapolate")   # tolerates slight exptrapolation

tclab_input = interpolate.interp1d(
    [ 0, 50, 51, 450, 451, 9999],   # time
    [ 0,  0, 80,  80,   25,   25],  # input value
    fill_value="extrapolate")   # tolerates slight exptrapolation

tclab_setpoint = interpolate.interp1d(
    [0, 50, 150, 450, 550, 9999],   # time 
    [Tamb, Tamb, 60, 60, 35, 35],   # set point value
    fill_value="extrapolate")   # tolerates slight exptrapolation`

t_sim = np.linspace(0, 1000, 201)       # create 201 time points between 0 and 1000 seconds
u_sim = tclab_input(t_sim)              # calculate input signal at time points
d_sim = tclab_disturbance(t_sim)        # calculate disturbance at time points
setpoint_sim = tclab_setpoint(t_sim)    # calculate set point at time points

plt.figure(figsize=(10,6))
plt.subplot(3, 1, 1)
plt.plot(t_sim, setpoint_sim)
plt.title('setpoint')
plt.ylabel('deg C')
plt.grid(True)

plt.subplot(3, 1, 2)
plt.plot(t_sim, u_sim)
plt.title('heat power input')
plt.ylabel('percent of max')
plt.grid(True)

plt.subplot(3, 1, 3)
plt.plot(t_sim, d_sim)
plt.title('unmeasured disturbance')
plt.ylabel('watts')
plt.xlabel('time (s)')
plt.grid(True)

plt.tight_layout()

Simulate#

Like we did in Lab 5, let’s see how well our initial guess at a control strategy will work for us by using simulate.

\[\begin{align*} C_p^H \frac{dT_H}{dt} & = U_a (T_{amb} - T_H) + U_b (T_S - T_H) + \alpha P u(t) + d(t)\\ C_p^S \frac{dT_S}{dt} & = - U_b (T_S - T_H) \end{align*}\]

subject to initial conditions

\[\begin{align*} T_H(t_0) & = T_{amb} \\ T_S(t_0) & = T_{amb} \end{align*}\]

and prior specification of inputs \(u(t)\) and \(d(t)\).

#Create the model in simulate mode with process inputs above
sim = TCLabPyomo('simulate',
                t_sim,
                u_sim,
                d_sim,
                setpoint_sim,
                None,
)

#Solve the model
sim.solve()

#Save Ts and Th data from the simulation for next steps
Ts_sim = sim.get_Ts()
Th_sim = sim.get_Th()
  
#Plot the simulation results
sim.plot()

Exercise 1: Coding the Observer as a Python Generator#

In this exercise we create a function using a python generator to estimate state variables from a previous time horizon (h).

from dataclasses import dataclass

@dataclass
class ObserverResult:
    """Class for keeping track of observer results for a single iteration"""

    t: float
    Th: float
    Ts: float
    d: float
        
def tclab_observer(h=2, history = None):
    '''
    Function that estimates the state varibles from time horizon (h)
    using a python generator:
        h: Time horize (default 2 seconds)
    Returns:
        t_est: time of state estimation
        Th_est: estimated heater temperature
        Ts_est: estimated sensor temperature
        d_est: estimated disturbance
    '''
    
    #Initialize the observer (_hist to store expeirmental data and _est to store state estimations)
    t_hist = [-1] 
    u_hist = [0]
    Ts_hist = [Tamb]
    
    t_est = -1
    Th_est = []
    Ts_est = []
    d_est = []
    
    #Create the generator: Use expeirmental data (meas) to estimate state variables (est)
    while True:
        t_meas, u_meas, Ts_meas = yield t_est, Th_est, Ts_est, d_est
  
        #Save expeirmental data to _hist arrays
        t_hist.append(t_meas)
        u_hist.append(u_meas)
        Ts_hist.append(Ts_meas)
        
        #Extract the last h elements of each array (default 2)
        t_hist = t_hist[-h:]
        u_hist = u_hist[-h:]
        Ts_hist = Ts_hist[-h:]
        
        #Create the model in observe mode with measured data
        #in the specified time horizon (h)
        #verbose = False supresses the ipopt output
        obsv = TCLabPyomo('observe',
                 t_hist,
                 u_hist,
                 d_sim,
                 None,
                 Ts_hist,
                 verbose = False)
        
        #Solve the model
        obsv.solve()
    
        #store model results
        t_est = t_hist[-1]
        Th_est = obsv.get_Th()
        Ts_est = obsv.get_Ts()
        d_est = obsv.get_D()
        
        if history is not None:
            history.append(ObserverResult(t_hist.copy(), Th_est.copy(), Ts_est.copy(), d_est.copy()))
        
        
        

Test the Observer#

Test the observer using simulated data from Exercise 0 as the expeirmental data input

#Create empty arrays to store estimated state variables
t_est = []
Th_est = []
Ts_est = []
d_est = []

# Create empty array to store observer results
obs_results = []

#Create the oberver with the observer function above (set the time horizon to 5)
observer = tclab_observer(5, history = obs_results)
observer.send(None)

#Loop through simulation data (Exercise 0) and record the estimated state variables calculated by the observer
for k in range(0, len(t_sim)):
    t, Th, Ts, d = observer.send([t_sim[k], u_sim[k], Ts_sim[k]])
    t_est.append(t)
    Th_est.append(Th[-1])
    Ts_est.append(Ts[-1])
    d_est.append(d[-1])
    

print("number of iterations:", len(obs_results))
    
# create figure
plt.figure(figsize=(10,6))

# subplot 1: temperatures
plt.subplot(3, 1, 1)
plt.scatter(t_sim, Ts_sim, marker='.', label="$T_{S}$ simulated", alpha=0.5,color='green')
plt.plot(t_est, Th_est, label='$T_{H}$ predicted')
plt.plot(t_est, Ts_est, label='$T_{S}$ predicted')
# plt.plot(, self.Tset_data, label='$T_{set}$')

plt.title('temperatures')
plt.ylabel('deg C')
plt.legend()
plt.grid(True)

# subplot 2: control decision
plt.subplot(3, 1, 2)
plt.plot(t_est, u_sim)
plt.title('heater power')
plt.ylabel('percent of max')
plt.grid(True)

# subplot 3: disturbance
plt.subplot(3, 1, 3)
plt.plot(t_est, d_est)
plt.title('disturbance')
plt.ylabel('watts')
plt.xlabel('time (s)')
plt.grid(True)

plt.tight_layout()
plt.show()

Discussion#

In your own words, explain how the observer function works. How does the value of h impact the observer output? (2 to 4 sentences)

Answer:

Qualitatively and quantitatively interpret your estimates for the heater temperature and disturbance. Compare these closed-loop results to your open-loop results from Exercise 3 in Lab 5 (‘observe’ mode). (3 to 5 sentences)

Answer:

Exercise 2: Coding the Controller as a Python Generator#

In this exercise we create a function using a python generator to optimize the heater output given state estimates from the obsrver.

#Controller: at time step 100 (default h controller), the observer looks back 2 secs (default h observer)
#at state estimates (Th and Ts) and propegates forward to determine u

@dataclass
class MPCResult:
    """Class for keeping track of observer results for a single iteration"""

    t: float
    Th: float
    Ts: float
    u: float
    d: float

def tclab_control(set_point_func, h=100, history = None): 
    '''
    Function that at time step 100 (default h controller), the observer looks back 2 secs (default h observer)
    at state estimates (Th and Ts) and propegates forward to determine u:
        set_point_func: Function of the temperature setpoint as a function of time
        h: Time horizon (default 100 seconds)
    Returns:
        u: heater output
    '''
    
    #Initialize the heater output to 0
    u = 0
    while True:
        # state estimations from the observer are used to determine the optimal heater output
        # t_est (float), Th_est (float), Ts_est (float), d_est (float) = yield u 
        t_est, Th_est, Ts_est, d_est = yield u
        
        #The optimization time horizon is the point of state estimation (t_est) + h (default 100)
        tf = t_est + h #Final time
        time = np.linspace(t_est, tf, h+1) #create an array for time 
        disturbance = np.ones(h+1) * d_est[-1] #use the last value of d_est (from the observer) to create an array for d_data
#         T_sensor = np.ones(h+1) * Ts_est[-1] #use the last value of Ts_est (from the observer) to create an array for Ts_data
        
        #Create the model in optimize mode with estimated data from the observer
        #in the specified time horizon (h)
        #verbose = False supresses the ipopt output
        opt = TCLabPyomo('optimize',
                 time,
                 None,
                 disturbance,  
                 set_point_func(time), 
                 None,
                 verbose = False) 
        
        # Set the initial conditions for the optimization model
        opt.set_initial_conditions(Th_est[-1], Ts_est[-1])

        #Solve the model
        opt.solve()

        #Store the optimal u value for t_est (first value of u output from the optimization model)
        umpc = opt.get_U()
        time = opt.get_time()
        u = umpc[0]
        
        # Optional: store results for animation
        if history is not None:
            history.append(MPCResult(opt.get_time(), opt.get_Th(), opt.get_Ts(), opt.get_U(), opt.get_D()))

Test the Controller#

Test the controller using output from the obserever using simulated data from Exercise 0 as the expeirmental data input

#Create the oberver with the observer function (set the time horizon to 3)
observer = tclab_observer(3)
observer.send(None)

#Create the controller with the controller function above, pass the set point function from Exercise 0
controller = tclab_control(tclab_setpoint,100)
controller.send(None)

#Create empty arrays to store MPC results
t_mpc = []
u_mpc = []
Th_mpc = []
Ts_mpc = []

#Loop through simulation data (Exercise 0) 
for k in range(0, len(t_sim)):
    #Estimate the state variables from the observer using simulation data
    t, Th, Ts, d = observer.send([t_sim[k], u_sim[k], Ts_sim[k]])
    #Optimize the heater ouput using the state estimations from the observer
    u = controller.send([t, Th, Ts, d])
    #Store optimization results
    u_mpc.append(u)
    Th_mpc.append(Th[-1])
    Ts_mpc.append(Ts[-1])

#Plot results
# create figure
plt.figure(figsize=(10,6))

# subplot 1: temperatures
plt.subplot(3, 1, 1)
plt.scatter(t_sim, Ts_sim, marker='.', label="$T_{S}$ simulated", alpha=0.5,color='green')
plt.plot(t_sim, Th_mpc, label='$T_{H}$ predicted')
plt.plot(t_sim, Ts_mpc, label='$T_{S}$ predicted')
plt.plot(t_sim, setpoint_sim, label='$T_{set}$', color='red')

plt.title('temperatures')
plt.ylabel('deg C')
plt.legend()
plt.grid(True)

# subplot 2: control decision
plt.subplot(3, 1, 2)
plt.step(t_sim, u_mpc, where = 'post')
plt.title('heater power')
plt.ylabel('percent of max')
plt.grid(True)

# subplot 3: disturbance
plt.subplot(3, 1, 3)
plt.plot(t_est, d_est)
plt.title('disturbance')
plt.ylabel('watts')
plt.xlabel('time (s)')
plt.grid(True)

plt.tight_layout()
plt.show()

Discussion#

In your own words, explain how the controller function works. How does the value of h impact the controller output? (2 to 4 sentences)

Answer:

Exercise 3: MPC Demonstration#

Now we demonstrate MPC on the tclab hardware.

from tclab import setup, clock, Historian, Plotter
TCLab = setup(connected=True)
     
# create a controller instance (setpoint from Exercise 0, with time horizon 600)
controller = tclab_control(tclab_setpoint,600)
controller.send(None)

# create an model estimator (time horizon 5 seconds)
observer = tclab_observer(5)
observer.send(None)

# execute the event loop
tf = 800  # run time, seconds
with TCLab() as lab:
    h = Historian([('T1', lambda: lab.T1), ('Q1', lab.Q1),
                   ('Th', lambda: Th), ('Ts', lambda: Ts),
                  ("SP1", lambda: tclab_setpoint(t))])
    p = Plotter(h, tf, layout=(("T1", "SP1", "Ts", "Th"),('Q1',)))
    U1 = 0
    lab.P1 = P1_GLOBAL
    for t in clock(tf, 5):                    # allow time for more calculations
        T1 = lab.T1                           # measure the sensor temperature
        t, Th, Ts, d = observer.send([t, U1, T1])  # estimate the heater temperature                 
        U1 = controller.send([t, Th, Ts, d])        # compute control action
        lab.U1 = U1                           # set manipulated variable  
        p.update(t)                           # log data

Discussion#

In your own words explain the MPC workflow. How does MPC compare to open loop optimization (Lab 5)? What makes MPC “closed-loop”? (3 to 6 sentences)

Answer:

In Class Notebook 6.10, you were shown a similar MPC demo on the same setpoint. In the class we see oscillations around the setpoint. Does your answer oscillate? If not, speculate about the reason for this. (2 to 4 sentences)

Answer:

In a short paragraph, describe another real-world application for model predictive control. For your example, which states can you measure, and which will you need to estimate? What are the control decisions? What is the system’s time constant, and how fast do you need to reoptimize (e.g., milliseconds, seconds, minutes, hours)? Please answer this question individually. Everyone in the class should have a unique answer.

Answer:

Exercise 4: Apply MPC to dark chocolate tempering#

Repeat the MPC demonstration from this lab for the dark chocolate tempering profile. Ensure your TCLab has cooled back to Tamb.

# experimental parameters
tfinal = 30

# To complete the experiment, change this to True
# After completing the experiment, be sure to change it back to False
# This will prevent you from overwriting your data
run_tamb_tclab = True

from tclab import TCLab, clock, Historian, Plotter, setup
import numpy as np

if run_tamb_tclab:

    TCLab = setup(connected=True)

    # initialize list to store temperature
    T_list = []

    # perform experiment
    with TCLab() as lab:
        lab.U1 = 0
        lab.U2 = 0
        h = Historian(lab.sources)
        p = Plotter(h, tfinal)
        
        # save temperatures to access later
        T_list.append(lab.T1)
        T_list.append(lab.T2)

        for t in clock(tfinal):
            p.update(t)

# Be sure to check and update the ambient temperature!

# Determine the optimal control scheme
# Hint: the correct implementation of the set point can be found in Lab 2 solutions
# Add your solution here

Discussion#

Review your results to Lab 2 (relay control), Lab 4 (PI control), and Lab 5 (open-loop optimal control) for the chocalate tempering experience. In a short paragraph or a few bullet points, quantitatively and qualitatively compare the performance of MPC (this lab) to the control strategies from Labs 2, 4, and 5.

Answer:

Reflecting on the labs this semester, what control strategy do you recommend for dark chocolate tempering? Briefly justify your answer. Your answer should be unique and distinct from your classmates. (2 to 4 sentences)

Answer:

Submission Instructions#

You will submit two files:

This notebook as a .ipynb file to Gradescope
This notebook converted to a PDF to Canvas.

Remember, the written discussions responses must be in your own words. Many of these questions ask about your specific results or are open-ended questions with many reasonable answers. Thus we expect unique responses, analyses, and ideas.

We may use writing analysis software to check for overly similar written responses. You are responsible for reviewing the colaboration policy outlined in the class syllabus to avoid violations of the honor code.

Lab 6: Model Predictive Control (MPC)

Contents

Lab 6: Model Predictive Control (MPC)#

Learning Objectives#

Installation and Setup#

Exercise 0: Develop the Mathematical Model and Pyomo Simulation#

Pyomo Model#

Process Inputs#

Simulate#

Exercise 1: Coding the Observer as a Python Generator#

Test the Observer#

Discussion#

Exercise 2: Coding the Controller as a Python Generator#

Test the Controller#

Discussion#

Exercise 3: MPC Demonstration#

Discussion#

Exercise 4: Apply MPC to dark chocolate tempering#

Discussion#

Submission Instructions#