# This code cell installs packages on Colab
import sys
if "google.colab" in sys.modules:
!wget "https://raw.githubusercontent.com/ndcbe/CBE60499/main/notebooks/helper.py"
import helper
helper.install_idaes()
helper.install_ipopt()
helper.install_glpk()
helper.download_figures(['pack1.png','pack2.png','pack3.png'])
import pandas as pd
import pyomo.environ as pyo
Reference: Beginning of Chapter 4 in Biegler (2010)

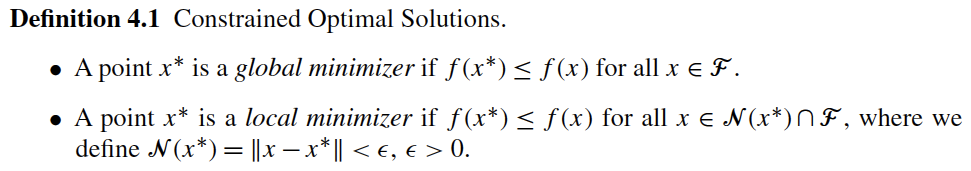
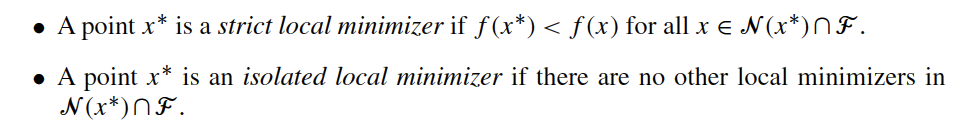

Reference: Section 4.1 in Biegler (2010)
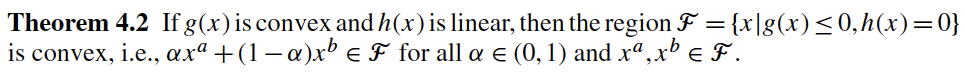
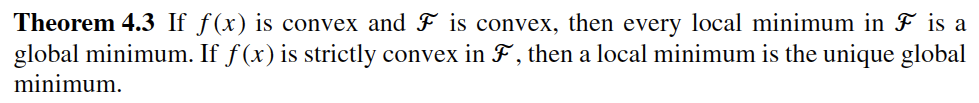
Reference: Section 4.1 in Biegler (2010)
Motivating Question: Is this problem convex?
What is the smallest rectangle you can use to enclose three given circles? Reference: Example 4.4 in Biegler (2010).
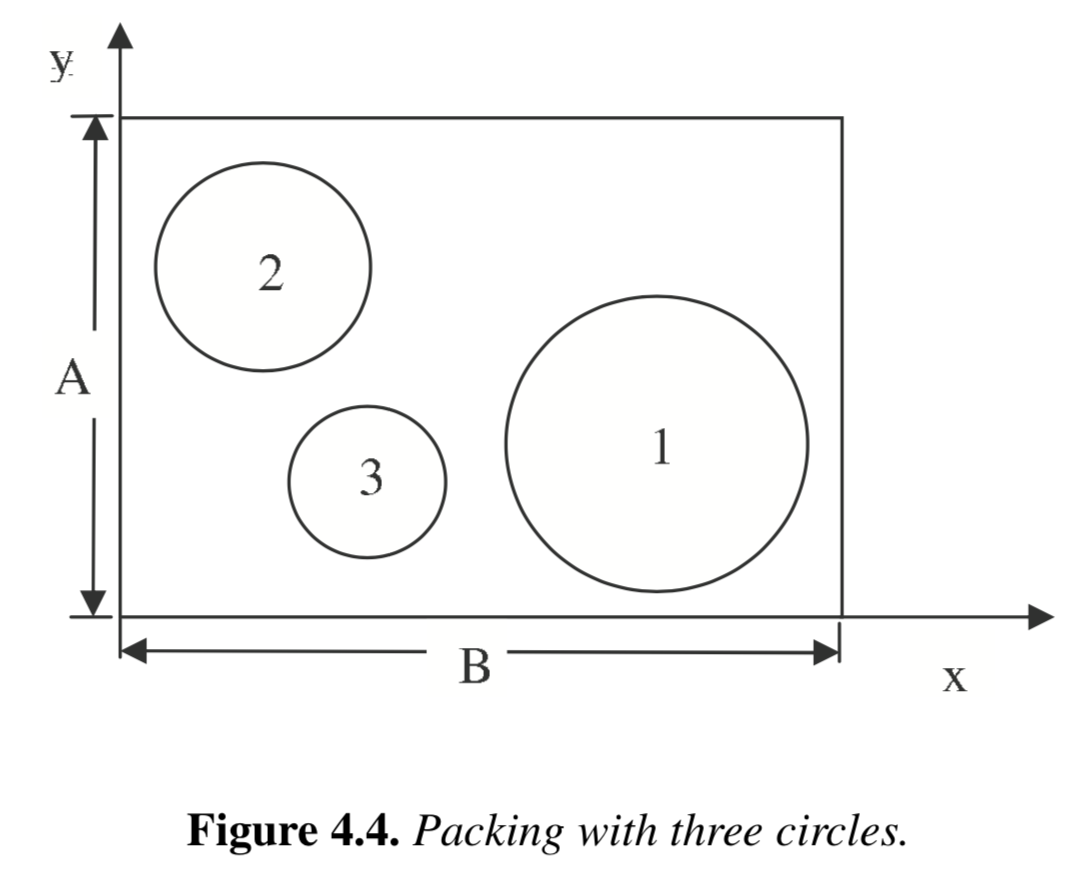
The following optimization model is given in Biegler (2010):
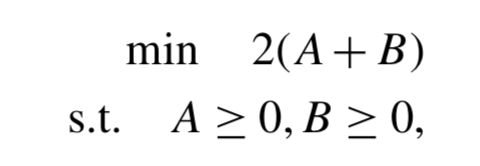
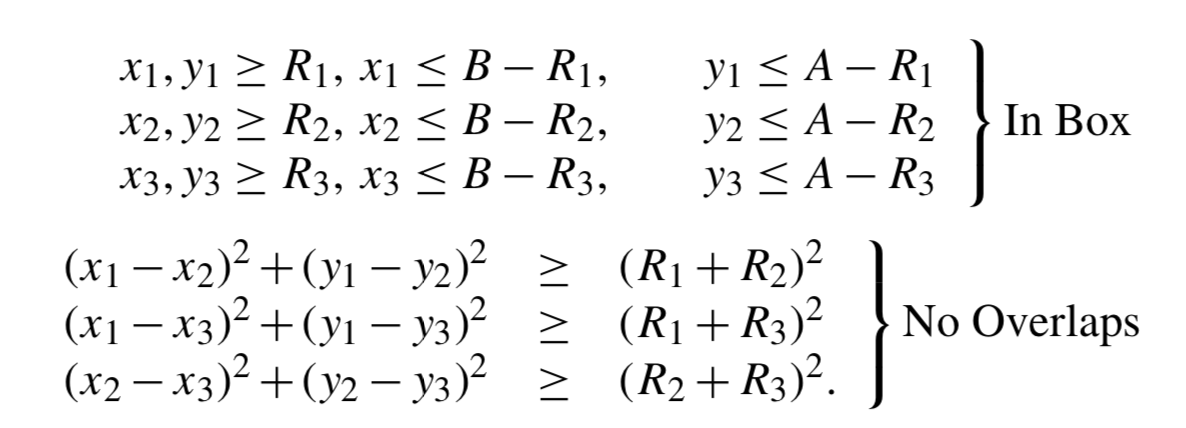
import random
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
def create_circle_model(circle_radii):
''' Create circle optimization model in Pyomo
Arguments:
circle_radii: dictionary with keys=circle name and value=radius (float)
Returns:
model: Pyomo model
'''
# Number of circles to consider
n = len(circle_radii)
# Create a concrete Pyomo model.
model = pyo.ConcreteModel()
# Initialize index for circles
model.CIRCLES = pyo.Set(initialize = circle_radii.keys())
# Create parameter
model.R = pyo.Param(model.CIRCLES, domain=pyo.PositiveReals, initialize=circle_radii)
# Create variables for box
model.a = pyo.Var(domain=pyo.PositiveReals)
model.b = pyo.Var(domain=pyo.PositiveReals)
# Set objective
model.obj = pyo.Objective(expr=2*(model.a + model.b), sense = pyo.minimize)
# Create variables for circle centers
model.x = pyo.Var(model.CIRCLES, domain=pyo.PositiveReals)
model.y = pyo.Var(model.CIRCLES, domain=pyo.PositiveReals)
# "In the box" constraints
def left_x(m,c):
return m.x[c] >= model.R[c]
model.left_x_con = pyo.Constraint(model.CIRCLES, rule=left_x)
def left_y(m,c):
return m.y[c] >= model.R[c]
model.left_y_con = pyo.Constraint(model.CIRCLES, rule=left_y)
def right_x(m,c):
return m.x[c] <= m.b - model.R[c]
model.right_x_con = pyo.Constraint(model.CIRCLES, rule=right_x)
def right_y(m,c):
return m.y[c] <= m.a - model.R[c]
model.right_y_con = pyo.Constraint(model.CIRCLES, rule=right_y)
# No overlap constraints
def no_overlap(m,c1,c2):
if c1 < c2:
return (m.x[c1] - m.x[c2])**2 + (m.y[c1] - m.y[c2])**2 >= (model.R[c1] + model.R[c2])**2
else:
return pyo.Constraint.Skip
model.no_overlap_con = pyo.Constraint(model.CIRCLES, model.CIRCLES, rule=no_overlap)
return model
def initialize_circle_model(model, a_init=25, b_init=25):
''' Initialize the x and y coordinates using uniform distribution
Arguments:
a_init: initial value for a (default=25)
b_init: initial value for b (default=25)
Returns:
Nothing. But per Pyomo scoping rules, the input argument `model`
can be modified in this function.
'''
# Initialize
model.a = 25
model.b = 25
for i in model.CIRCLES:
# Adding circle radii ensures the remains in the >0, >0 quadrant
model.x[i] = random.uniform(0,10) + model.R[i]
model.y[i] = random.uniform(0,10) + model.R[i]
Next, we will create a dictionary containing the circle names and radii values.
# Create dictionary with circle data
circle_data = {'A':10.0, 'B':5.0, 'C':3.0}
circle_data
{'A': 10.0, 'B': 5.0, 'C': 3.0}
# Access the keys
circle_data.keys()
dict_keys(['A', 'B', 'C'])
Now let's create the model.
# Create model
model = create_circle_model(circle_data)
And let's initialize the model.
# Initialize model
initialize_circle_model(model)
model.pprint()
2 Set Declarations
CIRCLES : Size=1, Index=None, Ordered=Insertion
Key : Dimen : Domain : Size : Members
None : 1 : Any : 3 : {'A', 'B', 'C'}
no_overlap_con_index : Size=1, Index=None, Ordered=True
Key : Dimen : Domain : Size : Members
None : 2 : CIRCLES*CIRCLES : 9 : {('A', 'A'), ('A', 'B'), ('A', 'C'), ('B', 'A'), ('B', 'B'), ('B', 'C'), ('C', 'A'), ('C', 'B'), ('C', 'C')}
1 Param Declarations
R : Size=3, Index=CIRCLES, Domain=PositiveReals, Default=None, Mutable=False
Key : Value
A : 10.0
B : 5.0
C : 3.0
4 Var Declarations
a : Size=1, Index=None
Key : Lower : Value : Upper : Fixed : Stale : Domain
None : 0 : 25 : None : False : False : PositiveReals
b : Size=1, Index=None
Key : Lower : Value : Upper : Fixed : Stale : Domain
None : 0 : 25 : None : False : False : PositiveReals
x : Size=3, Index=CIRCLES
Key : Lower : Value : Upper : Fixed : Stale : Domain
A : 0 : 12.841552708011381 : None : False : False : PositiveReals
B : 0 : 5.317917334950976 : None : False : False : PositiveReals
C : 0 : 7.92668839728193 : None : False : False : PositiveReals
y : Size=3, Index=CIRCLES
Key : Lower : Value : Upper : Fixed : Stale : Domain
A : 0 : 15.93994957385218 : None : False : False : PositiveReals
B : 0 : 5.402476587728794 : None : False : False : PositiveReals
C : 0 : 7.556772365151705 : None : False : False : PositiveReals
1 Objective Declarations
obj : Size=1, Index=None, Active=True
Key : Active : Sense : Expression
None : True : minimize : 2*(a + b)
5 Constraint Declarations
left_x_con : Size=3, Index=CIRCLES, Active=True
Key : Lower : Body : Upper : Active
A : 10.0 : x[A] : +Inf : True
B : 5.0 : x[B] : +Inf : True
C : 3.0 : x[C] : +Inf : True
left_y_con : Size=3, Index=CIRCLES, Active=True
Key : Lower : Body : Upper : Active
A : 10.0 : y[A] : +Inf : True
B : 5.0 : y[B] : +Inf : True
C : 3.0 : y[C] : +Inf : True
no_overlap_con : Size=3, Index=no_overlap_con_index, Active=True
Key : Lower : Body : Upper : Active
('A', 'B') : 225.0 : (x[A] - x[B])**2 + (y[A] - y[B])**2 : +Inf : True
('A', 'C') : 169.0 : (x[A] - x[C])**2 + (y[A] - y[C])**2 : +Inf : True
('B', 'C') : 64.0 : (x[B] - x[C])**2 + (y[B] - y[C])**2 : +Inf : True
right_x_con : Size=3, Index=CIRCLES, Active=True
Key : Lower : Body : Upper : Active
A : -Inf : x[A] - (b - 10.0) : 0.0 : True
B : -Inf : x[B] - (b - 5.0) : 0.0 : True
C : -Inf : x[C] - (b - 3.0) : 0.0 : True
right_y_con : Size=3, Index=CIRCLES, Active=True
Key : Lower : Body : Upper : Active
A : -Inf : y[A] - (a - 10.0) : 0.0 : True
B : -Inf : y[B] - (a - 5.0) : 0.0 : True
C : -Inf : y[C] - (a - 3.0) : 0.0 : True
13 Declarations: CIRCLES R a b obj x y left_x_con left_y_con right_x_con right_y_con no_overlap_con_index no_overlap_con
Next, we'll define a function to plot the solution (or initial point)
# Plot initial point
def plot_circles(m):
''' Plot circles using data in Pyomo model
Arguments:
m: Pyomo concrete model
Returns:
Nothing (but makes a figure)
'''
# Create figure
fig, ax = plt.subplots(1,figsize=(6,6))
# Adjust axes
l = max(m.a.value,m.b.value) + 1
ax.set_xlim(0,l)
ax.set_ylim(0,l)
# Draw box
art = mpatches.Rectangle((0,0), width=m.b.value, height=m.a.value,fill=False)
ax.add_patch(art)
# Draw circles and mark center
for i in m.CIRCLES:
art2 = mpatches.Circle( (m.x[i].value,m.y[i].value), radius=m.R[i],fill=True,alpha=0.25)
ax.add_patch(art2)
plt.scatter(m.x[i].value,m.y[i].value,color='black')
# Show plot
plt.show()
plot_circles(model)
# Specify the solver
solver = pyo.SolverFactory('ipopt')
# Solve the model
results = solver.solve(model, tee = True)
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 0
Number of nonzeros in inequality constraint Jacobian.: 30
Number of nonzeros in Lagrangian Hessian.............: 12
Total number of variables............................: 8
variables with only lower bounds: 8
variables with lower and upper bounds: 0
variables with only upper bounds: 0
Total number of equality constraints.................: 0
Total number of inequality constraints...............: 15
inequality constraints with only lower bounds: 9
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 6
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 1.0000000e+02 7.46e+01 1.06e+00 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 1.0050650e+02 4.98e+01 4.22e+00 -1.0 2.36e+01 - 1.84e-01 1.30e-01h 1
2 1.0015862e+02 3.01e+01 2.32e+00 -1.0 5.24e+00 - 8.18e-01 3.67e-01h 1
3 9.9730828e+01 1.33e+01 1.16e+00 -1.0 4.96e+00 - 7.51e-01 4.53e-01h 1
4 9.8213893e+01 8.23e+00 1.08e+00 -1.0 2.46e+01 - 2.93e-01 7.07e-02f 1
5 9.8307816e+01 1.84e+00 3.42e-01 -1.0 7.81e+00 - 1.00e+00 6.57e-01h 1
6 9.8901802e+01 0.00e+00 1.06e-02 -1.0 1.80e+01 - 1.00e+00 1.00e+00h 1
7 9.8393352e+01 0.00e+00 3.30e-03 -1.7 9.37e+00 - 1.00e+00 1.00e+00h 1
8 9.8405011e+01 0.00e+00 1.08e-03 -1.7 4.38e+01 - 1.00e+00 1.00e+00h 1
9 9.8405025e+01 0.00e+00 1.17e-04 -1.7 7.44e+00 - 1.00e+00 1.00e+00h 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
10 9.8405027e+01 0.00e+00 5.74e-07 -1.7 1.52e+00 - 1.00e+00 1.00e+00h 1
11 9.8284703e+01 0.00e+00 4.42e-05 -3.8 2.93e-01 - 1.00e+00 9.98e-01h 1
12 9.8284281e+01 0.00e+00 2.33e-09 -5.7 2.63e-03 - 1.00e+00 1.00e+00h 1
13 9.8284270e+01 0.00e+00 1.33e-13 -8.6 2.80e-05 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 13
(scaled) (unscaled)
Objective...............: 9.8284270438747228e+01 9.8284270438747228e+01
Dual infeasibility......: 1.3347017888941731e-13 1.3347017888941731e-13
Constraint violation....: 0.0000000000000000e+00 0.0000000000000000e+00
Complementarity.........: 2.5071615765896930e-09 2.5071615765896930e-09
Overall NLP error.......: 2.5071615765896930e-09 2.5071615765896930e-09
Number of objective function evaluations = 14
Number of objective gradient evaluations = 14
Number of equality constraint evaluations = 0
Number of inequality constraint evaluations = 14
Number of equality constraint Jacobian evaluations = 0
Number of inequality constraint Jacobian evaluations = 14
Number of Lagrangian Hessian evaluations = 13
Total CPU secs in IPOPT (w/o function evaluations) = 0.004
Total CPU secs in NLP function evaluations = 0.000
EXIT: Optimal Solution Found.
Next, we can inspect the solution. Because Pyomo is a Python extension, we can use Pyoth (for loops, etc.) to programmatically inspect the solution.
# Print variable values
print("Name\tValue")
for c in model.component_data_objects(pyo.Var):
print(c.name,"\t", pyo.value(c))
# Plot solution
plot_circles(model)
Name Value a 29.142135416184022 b 19.999999803189596 x[A] 9.99999990193744 x[B] 4.999999953543133 x[C] 15.734851787229463 y[A] 19.142135514931184 y[B] 4.999999951252124 y[C] 5.517617033892999
# Print constraints
for c in model.component_data_objects(pyo.Constraint):
print(c.name,"\t", pyo.value(c.lower),"\t", pyo.value(c.body),"\t", pyo.value(c.upper))
left_x_con[A] 10.0 9.99999990193744 None left_x_con[B] 5.0 4.999999953543133 None left_x_con[C] 3.0 15.734851787229463 None left_y_con[A] 10.0 19.142135514931184 None left_y_con[B] 5.0 4.999999951252124 None left_y_con[C] 3.0 5.517617033892999 None right_x_con[A] None 9.874784367980283e-08 0.0 right_x_con[B] None -9.999999849646462 0.0 right_x_con[C] None -1.2651480159601327 0.0 right_y_con[A] None 9.87471615587765e-08 0.0 right_y_con[B] None -19.142135464931897 0.0 right_y_con[C] None -20.624518382291022 0.0 no_overlap_con[A,B] 225.0 224.99999778541908 None no_overlap_con[A,C] 169.0 218.51602998638847 None no_overlap_con[B,C] 64.0 115.5049713354404 None
Reinitialize the model, plot the initial point, resolve, and plot the solution. Is there more than one solution?
# Initialize and print the model
initialize_circle_model(model)
# Plot initial point
plot_circles(model)
# Solve the model
results = solver.solve(model, tee = True)
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 0
Number of nonzeros in inequality constraint Jacobian.: 30
Number of nonzeros in Lagrangian Hessian.............: 12
Total number of variables............................: 8
variables with only lower bounds: 8
variables with lower and upper bounds: 0
variables with only upper bounds: 0
Total number of equality constraints.................: 0
Total number of inequality constraints...............: 15
inequality constraints with only lower bounds: 9
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 6
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 1.0000000e+02 1.37e+02 1.00e+00 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 1.0276645e+02 6.44e+01 6.62e-01 -1.0 7.31e+00 - 6.14e-01 4.44e-01h 1
2 1.0566116e+02 1.85e+01 1.63e+00 -1.0 2.55e+00 0.0 8.96e-01 6.48e-01h 1
3 1.0612677e+02 0.00e+00 5.99e-01 -1.0 1.46e+00 -0.5 1.00e+00 1.00e+00h 1
4 1.0329539e+02 0.00e+00 3.22e-01 -1.0 2.52e+00 -1.0 1.00e+00 6.55e-01f 1
5 1.0326145e+02 0.00e+00 3.12e-01 -1.0 1.93e+00 - 8.26e-01 1.00e+00h 1
6 1.0237284e+02 0.00e+00 1.44e-01 -1.7 4.25e+00 -1.4 6.57e-01 7.24e-01f 1
7 9.9794889e+01 0.00e+00 1.92e-01 -1.7 1.94e+00 -1.0 9.54e-01 1.00e+00h 1
8 9.8743606e+01 0.00e+00 9.11e-01 -1.7 3.49e+01 -1.5 2.76e-01 2.60e-02f 1
9 9.8483796e+01 0.00e+00 1.74e-01 -1.7 4.32e+00 - 9.92e-01 8.22e-01h 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
10 9.8455971e+01 0.00e+00 9.38e-02 -1.7 1.73e+02 - 9.38e-01 3.53e-01f 1
11 9.8404443e+01 0.00e+00 2.67e-03 -1.7 9.65e+00 - 1.00e+00 1.00e+00h 1
12 9.8405024e+01 0.00e+00 2.10e-05 -1.7 4.30e+00 - 1.00e+00 1.00e+00h 1
13 9.8300696e+01 0.00e+00 1.14e-05 -2.5 2.47e-01 - 1.00e+00 1.00e+00h 1
14 9.8285160e+01 0.00e+00 2.64e-07 -3.8 3.60e-02 - 1.00e+00 1.00e+00h 1
15 9.8284281e+01 0.00e+00 1.27e-09 -5.7 3.07e-03 - 1.00e+00 1.00e+00h 1
16 9.8284270e+01 0.00e+00 1.75e-12 -8.6 2.76e-04 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 16
(scaled) (unscaled)
Objective...............: 9.8284270438747257e+01 9.8284270438747257e+01
Dual infeasibility......: 1.7491657667044265e-12 1.7491657667044265e-12
Constraint violation....: 0.0000000000000000e+00 0.0000000000000000e+00
Complementarity.........: 2.5240899380720466e-09 2.5240899380720466e-09
Overall NLP error.......: 2.5240899380720466e-09 2.5240899380720466e-09
Number of objective function evaluations = 17
Number of objective gradient evaluations = 17
Number of equality constraint evaluations = 0
Number of inequality constraint evaluations = 17
Number of equality constraint Jacobian evaluations = 0
Number of inequality constraint Jacobian evaluations = 17
Number of Lagrangian Hessian evaluations = 16
Total CPU secs in IPOPT (w/o function evaluations) = 0.004
Total CPU secs in NLP function evaluations = 0.000
EXIT: Optimal Solution Found.
# Plot solution
plot_circles(model)