{
"cells": [
{
"cell_type": "markdown",
"id": "7c1856dd",
"metadata": {},
"source": [
"\n",
"*This notebook contains material from [CBE60499](https://ndcbe.github.io/CBE60499);\n",
"content is available [on Github](git@github.com:ndcbe/CBE60499.git).*\n"
]
},
{
"cell_type": "markdown",
"id": "373fb0a8",
"metadata": {},
"source": [
"\n",
"< [4.0 Constrained Nonlinear Optimization: Theory and Applications](https://ndcbe.github.io/CBE60499/04.00-Constrained.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [4.2 Local Optimality Conditions](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html) > 
 "
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 1,
"link": "[4.1 Convexity Revisited](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1-Convexity-Revisited)",
"section": "4.1 Convexity Revisited"
}
},
"source": [
"# 4.1 Convexity Revisited"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"nbpages": {
"level": 1,
"link": "[4.1 Convexity Revisited](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1-Convexity-Revisited)",
"section": "4.1 Convexity Revisited"
}
},
"outputs": [],
"source": [
"# This code cell installs packages on Colab\n",
"\n",
"import sys\n",
"if \"google.colab\" in sys.modules:\n",
" !wget \"https://raw.githubusercontent.com/ndcbe/CBE60499/main/notebooks/helper.py\"\n",
" import helper\n",
" helper.install_idaes()\n",
" helper.install_ipopt()\n",
" helper.install_glpk()\n",
" helper.download_figures(['pack1.png','pack2.png','pack3.png'])"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"nbpages": {
"level": 1,
"link": "[4.1 Convexity Revisited](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1-Convexity-Revisited)",
"section": "4.1 Convexity Revisited"
}
},
"outputs": [],
"source": [
"import pandas as pd\n",
"import pyomo.environ as pyo"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.1.1 Background](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.1-Background)",
"section": "4.1.1 Background"
}
},
"source": [
"## 4.1.1 Background"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.1.1 Background](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.1-Background)",
"section": "4.1.1 Background"
}
},
"source": [
"**Reference**: Beginning of Chapter 4 in Biegler (2010)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.1.1 Canonical Nonlinear Program](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.1.1-Canonical-Nonlinear-Program)",
"section": "4.1.1.1 Canonical Nonlinear Program"
}
},
"source": [
"### 4.1.1.1 Canonical Nonlinear Program"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.1.1 Canonical Nonlinear Program](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.1.1-Canonical-Nonlinear-Program)",
"section": "4.1.1.1 Canonical Nonlinear Program"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.1.2 Types of Constrained Optimal Solutions](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.1.2-Types-of-Constrained-Optimal-Solutions)",
"section": "4.1.1.2 Types of Constrained Optimal Solutions"
}
},
"source": [
"### 4.1.1.2 Types of Constrained Optimal Solutions"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.1.2 Types of Constrained Optimal Solutions](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.1.2-Types-of-Constrained-Optimal-Solutions)",
"section": "4.1.1.2 Types of Constrained Optimal Solutions"
}
},
"source": [
"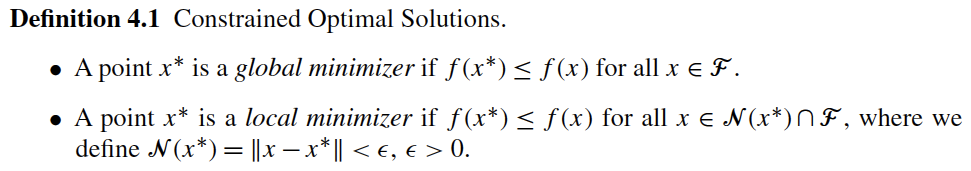"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.1.2 Types of Constrained Optimal Solutions](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.1.2-Types-of-Constrained-Optimal-Solutions)",
"section": "4.1.1.2 Types of Constrained Optimal Solutions"
}
},
"source": [
"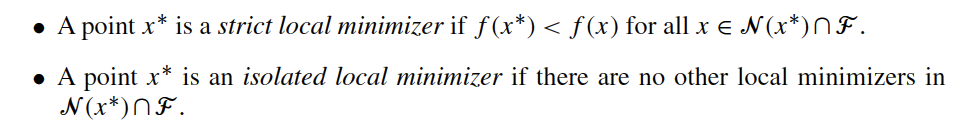"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.1.3 Key Questions](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.1.3-Key-Questions)",
"section": "4.1.1.3 Key Questions"
}
},
"source": [
"### 4.1.1.3 Key Questions"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.1.3 Key Questions](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.1.3-Key-Questions)",
"section": "4.1.1.3 Key Questions"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.1.2 Convexity for Constrained Optimization](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.2-Convexity-for-Constrained-Optimization)",
"section": "4.1.2 Convexity for Constrained Optimization"
}
},
"source": [
"## 4.1.2 Convexity for Constrained Optimization"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.1.2 Convexity for Constrained Optimization](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.2-Convexity-for-Constrained-Optimization)",
"section": "4.1.2 Convexity for Constrained Optimization"
}
},
"source": [
"**Reference**: Section 4.1 in Biegler (2010)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.1.2 Convexity for Constrained Optimization](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.2-Convexity-for-Constrained-Optimization)",
"section": "4.1.2 Convexity for Constrained Optimization"
}
},
"source": [
"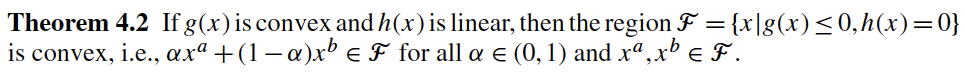"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.1.2 Convexity for Constrained Optimization](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.2-Convexity-for-Constrained-Optimization)",
"section": "4.1.2 Convexity for Constrained Optimization"
}
},
"source": [
"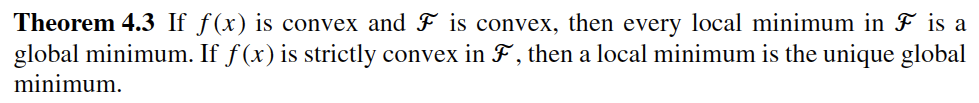"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.1.3 Circle Packing Example](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3-Circle-Packing-Example)",
"section": "4.1.3 Circle Packing Example"
}
},
"source": [
"## 4.1.3 Circle Packing Example"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.1.3 Circle Packing Example](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3-Circle-Packing-Example)",
"section": "4.1.3 Circle Packing Example"
}
},
"source": [
"**Reference**: Section 4.1 in Biegler (2010)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.1.3 Circle Packing Example](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3-Circle-Packing-Example)",
"section": "4.1.3 Circle Packing Example"
}
},
"source": [
"**Motivating Question**: Is this problem convex?"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.1.3 Circle Packing Example](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3-Circle-Packing-Example)",
"section": "4.1.3 Circle Packing Example"
}
},
"source": [
"What is the smallest rectangle you can use to enclose three given circles? Reference: Example 4.4 in Biegler (2010).\n",
"\n",
"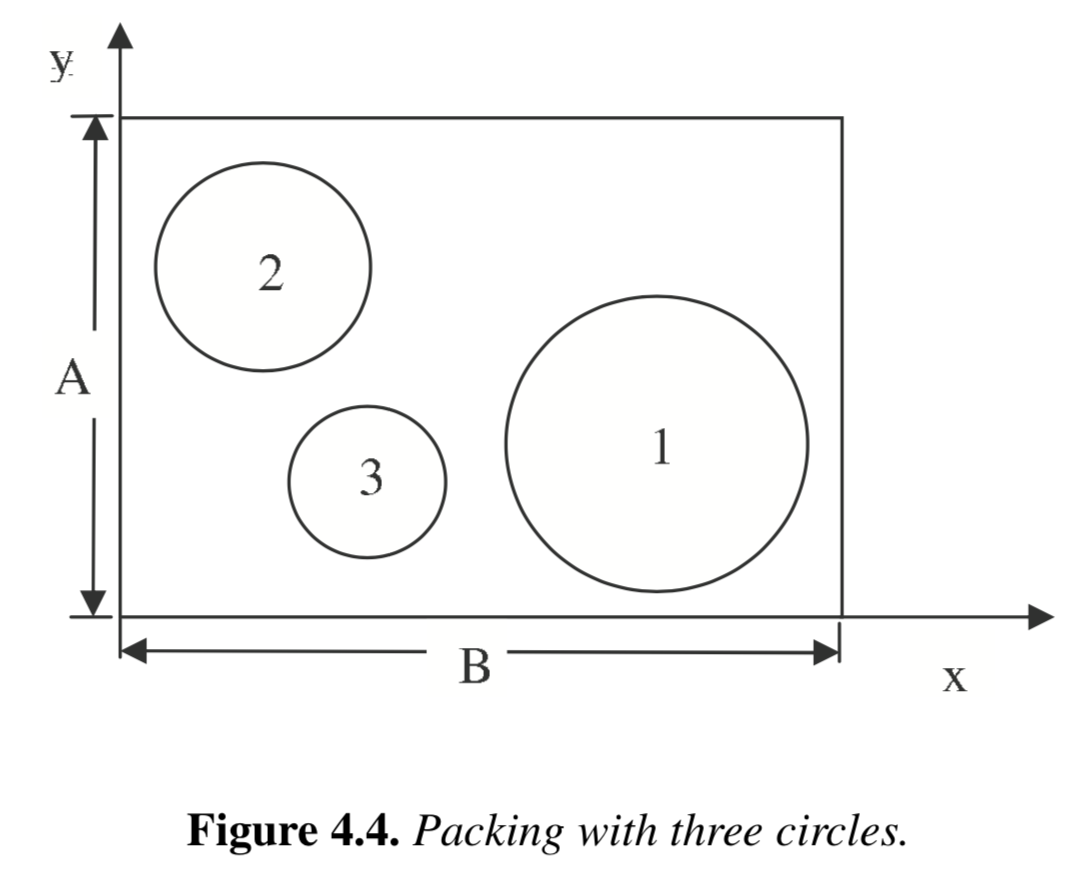"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.1 Optimization Model and Pyomo Implementation](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.1-Optimization-Model-and-Pyomo-Implementation)",
"section": "4.1.3.1 Optimization Model and Pyomo Implementation"
}
},
"source": [
"### 4.1.3.1 Optimization Model and Pyomo Implementation\n",
"\n",
"The following optimization model is given in Biegler (2010):"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.1 Optimization Model and Pyomo Implementation](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.1-Optimization-Model-and-Pyomo-Implementation)",
"section": "4.1.3.1 Optimization Model and Pyomo Implementation"
}
},
"source": [
"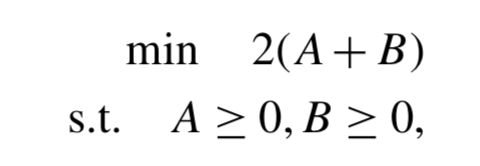\n",
"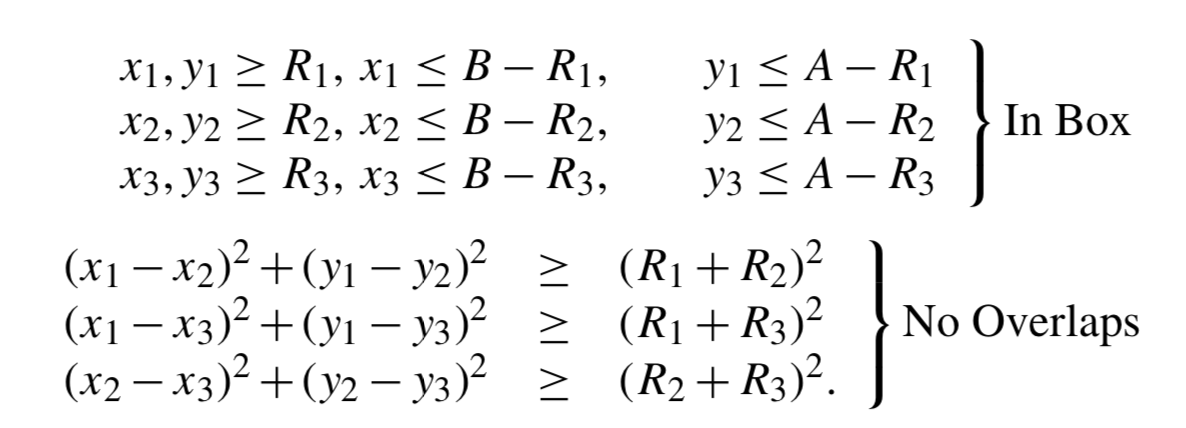"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.1 Optimization Model and Pyomo Implementation](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.1-Optimization-Model-and-Pyomo-Implementation)",
"section": "4.1.3.1 Optimization Model and Pyomo Implementation"
}
},
"outputs": [],
"source": [
"import random\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"import matplotlib.patches as mpatches\n",
"\n",
"def create_circle_model(circle_radii):\n",
" ''' Create circle optimization model in Pyomo\n",
" \n",
" Arguments:\n",
" circle_radii: dictionary with keys=circle name and value=radius (float)\n",
" \n",
" Returns:\n",
" model: Pyomo model\n",
" '''\n",
"\n",
" # Number of circles to consider\n",
" n = len(circle_radii)\n",
"\n",
" # Create a concrete Pyomo model.\n",
" model = pyo.ConcreteModel()\n",
"\n",
" # Initialize index for circles\n",
" model.CIRCLES = pyo.Set(initialize = circle_radii.keys())\n",
" \n",
" # Create parameter\n",
" model.R = pyo.Param(model.CIRCLES, domain=pyo.PositiveReals, initialize=circle_radii)\n",
"\n",
" # Create variables for box\n",
" model.a = pyo.Var(domain=pyo.PositiveReals)\n",
" model.b = pyo.Var(domain=pyo.PositiveReals)\n",
"\n",
" # Set objective\n",
" model.obj = pyo.Objective(expr=2*(model.a + model.b), sense = pyo.minimize)\n",
"\n",
" # Create variables for circle centers\n",
" model.x = pyo.Var(model.CIRCLES, domain=pyo.PositiveReals)\n",
" model.y = pyo.Var(model.CIRCLES, domain=pyo.PositiveReals)\n",
"\n",
" # \"In the box\" constraints\n",
" def left_x(m,c):\n",
" return m.x[c] >= model.R[c]\n",
" model.left_x_con = pyo.Constraint(model.CIRCLES, rule=left_x)\n",
"\n",
" def left_y(m,c):\n",
" return m.y[c] >= model.R[c]\n",
" model.left_y_con = pyo.Constraint(model.CIRCLES, rule=left_y)\n",
"\n",
" def right_x(m,c):\n",
" return m.x[c] <= m.b - model.R[c]\n",
" model.right_x_con = pyo.Constraint(model.CIRCLES, rule=right_x)\n",
"\n",
" def right_y(m,c):\n",
" return m.y[c] <= m.a - model.R[c]\n",
" model.right_y_con = pyo.Constraint(model.CIRCLES, rule=right_y)\n",
"\n",
" # No overlap constraints\n",
" def no_overlap(m,c1,c2):\n",
" if c1 < c2:\n",
" return (m.x[c1] - m.x[c2])**2 + (m.y[c1] - m.y[c2])**2 >= (model.R[c1] + model.R[c2])**2\n",
" else:\n",
" return pyo.Constraint.Skip\n",
" model.no_overlap_con = pyo.Constraint(model.CIRCLES, model.CIRCLES, rule=no_overlap)\n",
" \n",
" return model\n",
"\n",
"def initialize_circle_model(model, a_init=25, b_init=25):\n",
" ''' Initialize the x and y coordinates using uniform distribution\n",
" \n",
" Arguments:\n",
" a_init: initial value for a (default=25)\n",
" b_init: initial value for b (default=25)\n",
" \n",
" Returns:\n",
" Nothing. But per Pyomo scoping rules, the input argument `model`\n",
" can be modified in this function.\n",
" \n",
" '''\n",
" # Initialize \n",
" model.a = 25\n",
" model.b = 25\n",
"\n",
" for i in model.CIRCLES:\n",
" # Adding circle radii ensures the remains in the >0, >0 quadrant\n",
" model.x[i] = random.uniform(0,10) + model.R[i]\n",
" model.y[i] = random.uniform(0,10) + model.R[i]\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.1 Optimization Model and Pyomo Implementation](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.1-Optimization-Model-and-Pyomo-Implementation)",
"section": "4.1.3.1 Optimization Model and Pyomo Implementation"
}
},
"source": [
"Next, we will create a dictionary containing the circle names and radii values."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.1 Optimization Model and Pyomo Implementation](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.1-Optimization-Model-and-Pyomo-Implementation)",
"section": "4.1.3.1 Optimization Model and Pyomo Implementation"
}
},
"outputs": [
{
"data": {
"text/plain": [
"{'A': 10.0, 'B': 5.0, 'C': 3.0}"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Create dictionary with circle data\n",
"circle_data = {'A':10.0, 'B':5.0, 'C':3.0}\n",
"circle_data"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.1 Optimization Model and Pyomo Implementation](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.1-Optimization-Model-and-Pyomo-Implementation)",
"section": "4.1.3.1 Optimization Model and Pyomo Implementation"
}
},
"outputs": [
{
"data": {
"text/plain": [
"dict_keys(['A', 'B', 'C'])"
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Access the keys\n",
"circle_data.keys()"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.1 Optimization Model and Pyomo Implementation](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.1-Optimization-Model-and-Pyomo-Implementation)",
"section": "4.1.3.1 Optimization Model and Pyomo Implementation"
}
},
"source": [
"Now let's create the model."
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.1 Optimization Model and Pyomo Implementation](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.1-Optimization-Model-and-Pyomo-Implementation)",
"section": "4.1.3.1 Optimization Model and Pyomo Implementation"
}
},
"outputs": [],
"source": [
"# Create model\n",
"model = create_circle_model(circle_data)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.1 Optimization Model and Pyomo Implementation](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.1-Optimization-Model-and-Pyomo-Implementation)",
"section": "4.1.3.1 Optimization Model and Pyomo Implementation"
}
},
"source": [
"And let's initialize the model."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.1 Optimization Model and Pyomo Implementation](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.1-Optimization-Model-and-Pyomo-Implementation)",
"section": "4.1.3.1 Optimization Model and Pyomo Implementation"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"2 Set Declarations\n",
" CIRCLES : Size=1, Index=None, Ordered=Insertion\n",
" Key : Dimen : Domain : Size : Members\n",
" None : 1 : Any : 3 : {'A', 'B', 'C'}\n",
" no_overlap_con_index : Size=1, Index=None, Ordered=True\n",
" Key : Dimen : Domain : Size : Members\n",
" None : 2 : CIRCLES*CIRCLES : 9 : {('A', 'A'), ('A', 'B'), ('A', 'C'), ('B', 'A'), ('B', 'B'), ('B', 'C'), ('C', 'A'), ('C', 'B'), ('C', 'C')}\n",
"\n",
"1 Param Declarations\n",
" R : Size=3, Index=CIRCLES, Domain=PositiveReals, Default=None, Mutable=False\n",
" Key : Value\n",
" A : 10.0\n",
" B : 5.0\n",
" C : 3.0\n",
"\n",
"4 Var Declarations\n",
" a : Size=1, Index=None\n",
" Key : Lower : Value : Upper : Fixed : Stale : Domain\n",
" None : 0 : 25 : None : False : False : PositiveReals\n",
" b : Size=1, Index=None\n",
" Key : Lower : Value : Upper : Fixed : Stale : Domain\n",
" None : 0 : 25 : None : False : False : PositiveReals\n",
" x : Size=3, Index=CIRCLES\n",
" Key : Lower : Value : Upper : Fixed : Stale : Domain\n",
" A : 0 : 12.841552708011381 : None : False : False : PositiveReals\n",
" B : 0 : 5.317917334950976 : None : False : False : PositiveReals\n",
" C : 0 : 7.92668839728193 : None : False : False : PositiveReals\n",
" y : Size=3, Index=CIRCLES\n",
" Key : Lower : Value : Upper : Fixed : Stale : Domain\n",
" A : 0 : 15.93994957385218 : None : False : False : PositiveReals\n",
" B : 0 : 5.402476587728794 : None : False : False : PositiveReals\n",
" C : 0 : 7.556772365151705 : None : False : False : PositiveReals\n",
"\n",
"1 Objective Declarations\n",
" obj : Size=1, Index=None, Active=True\n",
" Key : Active : Sense : Expression\n",
" None : True : minimize : 2*(a + b)\n",
"\n",
"5 Constraint Declarations\n",
" left_x_con : Size=3, Index=CIRCLES, Active=True\n",
" Key : Lower : Body : Upper : Active\n",
" A : 10.0 : x[A] : +Inf : True\n",
" B : 5.0 : x[B] : +Inf : True\n",
" C : 3.0 : x[C] : +Inf : True\n",
" left_y_con : Size=3, Index=CIRCLES, Active=True\n",
" Key : Lower : Body : Upper : Active\n",
" A : 10.0 : y[A] : +Inf : True\n",
" B : 5.0 : y[B] : +Inf : True\n",
" C : 3.0 : y[C] : +Inf : True\n",
" no_overlap_con : Size=3, Index=no_overlap_con_index, Active=True\n",
" Key : Lower : Body : Upper : Active\n",
" ('A', 'B') : 225.0 : (x[A] - x[B])**2 + (y[A] - y[B])**2 : +Inf : True\n",
" ('A', 'C') : 169.0 : (x[A] - x[C])**2 + (y[A] - y[C])**2 : +Inf : True\n",
" ('B', 'C') : 64.0 : (x[B] - x[C])**2 + (y[B] - y[C])**2 : +Inf : True\n",
" right_x_con : Size=3, Index=CIRCLES, Active=True\n",
" Key : Lower : Body : Upper : Active\n",
" A : -Inf : x[A] - (b - 10.0) : 0.0 : True\n",
" B : -Inf : x[B] - (b - 5.0) : 0.0 : True\n",
" C : -Inf : x[C] - (b - 3.0) : 0.0 : True\n",
" right_y_con : Size=3, Index=CIRCLES, Active=True\n",
" Key : Lower : Body : Upper : Active\n",
" A : -Inf : y[A] - (a - 10.0) : 0.0 : True\n",
" B : -Inf : y[B] - (a - 5.0) : 0.0 : True\n",
" C : -Inf : y[C] - (a - 3.0) : 0.0 : True\n",
"\n",
"13 Declarations: CIRCLES R a b obj x y left_x_con left_y_con right_x_con right_y_con no_overlap_con_index no_overlap_con\n"
]
}
],
"source": [
"# Initialize model\n",
"initialize_circle_model(model)\n",
"model.pprint()"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.2 Visualize Initial Point](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.2-Visualize-Initial-Point)",
"section": "4.1.3.2 Visualize Initial Point"
}
},
"source": [
"### 4.1.3.2 Visualize Initial Point"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.2 Visualize Initial Point](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.2-Visualize-Initial-Point)",
"section": "4.1.3.2 Visualize Initial Point"
}
},
"source": [
"Next, we'll define a function to plot the solution (or initial point)"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.2 Visualize Initial Point](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.2-Visualize-Initial-Point)",
"section": "4.1.3.2 Visualize Initial Point"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXAAAAFlCAYAAADyArMXAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAAAtnElEQVR4nO3dW4yk6V0e8Of/Hetcfe7pmZ3d2VnvLl5MYqyV7cQI2cYggiIBFyDvReIo6ywXWAKJCxA3WImQEPJCchEhLR4rRgISJDBYyAp4kB3DBSt2HQevvd6jZ2dn+nys83d8c1HV456ePlRXfVXf6flJre6pqe566/TU+/2/9yBKKRARUfpocTeAiIhGwwAnIkopBjgRUUoxwImIUooBTkSUUgxwIqKUMqZ5YwsLC+ratWvTvEnKIQVAKQWl7v/5+HWOk+P/FoEIIAJo6P9MFIeXX355Wym1ePzyqQb4tWvX8NJLL03zJiljel6ArhvADUK4fggvCOEFCl4QwvFD+EGIcIJTGwxdYOoaTF1g6Vr/Z0ODpWuwDA1lS4eh88CWoiUi75x0+VQDnGhYSin0vBAtx0fH9QffA/hBvBPP/EDBDwJ0z7hOwdRQto3+l6WjbBswGeo0AQxwip1SCh03QNv10XYCtAdhHUyyKz1BPS9Ez3Ox03LvXWYZGiq2gdIg0Mu2DtvQY2wlZQEDnGLRdQPsdVzsdVy0ev5Eyx5J4Pohdn0Xu+0fXGYZgnrRxEzJwkzRZOmFLowBTlMRhgqNnof9joe9joueF8bdpNi5vsJW08VW04UIUC0YmC1ZmC1ZKFrsndP5GOA0Ma4fYr/jYq/j4aDrpbYkMg1KAY2uj0bXxzs7HRRM7V6YVwsGNI1DYOhBDHCKVNcNsN1ysN/x0HL8uJuTWj0vxNpBD2sHPehav9QyWzYxX7ahM8xpgAFOYwtDhZ22i81mD40uQztqQaiw23ax23ZxS+tgvmJhuVZAxebbN+/OfQWIyFUAfwTgEoAQwAtKqf8mIp8F8J8AbA2u+ptKqa9MqqGUPD0vwEajh62mAy/m4X15EYQKmw0Hmw0HFdvAcs3GfIW98rwa5iPcB/BrSqlvikgVwMsi8tXB//2+Uupzk2seJY1Sg952w8FB14u7ObnWcny0tny8s9vBQsXGUtVGmb3yXDn32VZKrQFYG/zcFJFXAVyZdMMoWXpegM2Gg61WD67P3naS+IHC+kEP6wc9VAsGlmo2Fso2T3zmwIU+rkXkGoAfBfAigI8A+IyI/HsAL6HfS9874XeeA/AcAOi6DuGCEqkiVglGfQlaoRp3U+giwgBBexd+YwsIg7hbQ0c88sgjuHXrViR/S4bdE1NEKgD+D4DfVkr9hYgsA9hGf12g/wJgRSn1H8/5G4p7cKZD2/Hx7l4He22WSdJM1wQr9QJW6gVOFEoIEcFFc1BEXlZKPf3A5cP8IRExAfw1gL9RSv3eCf9/DcBfK6Xed87fYYAnXNcN8O5e575p4JR+pi5YmSniUq3AE54xizLAhxmFIgBuAHj1aHiLyMqgPg4APw/glQu1iBKl5wW4s9fFdst5YOlVSj8vULi908H6QReXZ4pYrhZYI8+Ac3vgIvJjAP4ewLfRH0YIAL8J4BkA70e/hHILwC8dCfTT/hZ74Anj+AHu7nWx2WRw54ltanhopojFqs3zUlM29RJKVBjgyeEFIVb3u1g/6GV+ISk6XcHUcHWuhIWKHXdTcmOqJRTKnvWDHm7vdrg2CaHnhXhjo4W1/R6uL5Y5jjxl+GzlSNcN8NZWC80ep7vT/VqOj2/fPcDlehEPzRZZH08JBngOKKWwetDDnd0OyyV0KqWAu/td7HZcXF8so1Yw424SnYMBnnFtx8fbW22uDEhD67oBvrvawHKtgIfnShx2mGAM8IwKQ4U7e12sHnQ5uoQuTKn+uZK9jovrC2XMlKy4m0QnYIBnUKPn4e2tNroup1DTeBwvxKtrTSxWbVybL3E2Z8IwwDMkCBVu73aw0eix102R2mo6OOi6uDZfxjyHHCYGAzwjum6A1zaa7HXTxLi+wusbLSx3PTy6UOYEoARggGfAbtvFW1st+NxUgaZgo+Gg4wZ4YrkKy2BJJU589FPu3d0OXltvMrxpqpq9/rjxZo+rVcaJAZ5SfhDie+sN3Nnrxt0UyinXD/Hd1QY2Gr24m5JbLKGkEOvdlBShwr15Bo/OlzmDc8oY4Cmz23bx5maL65hQomw2HHTdAI8vV2AbetzNyQ2WUFJCKXWv3s3wpiRq9ny8cvcADdbFp4YBngJ+EOK1jSbr3ZR4rq9YF58illASzgtCvLrWQNthvZvSQQ3q4q4f4upcKe7mZBoDPMEcP8CrazxZSel0Z6+LIFS4tlCOuymZxQBPqJ4X4LtrDTheeP6ViRJq7aCHQClc58zNiWCAJ1DH9fHqWgOuz5OVlH6bDQdhqPCepQpDPGI8iZkwbcfHd1cZ3pQt2y0Xr200EXIEVaQY4Aly2PP2OC2eMmiv7eGNzdaFN/Sl0zHAE6Lj9nveDG/Kst22i9c3GOJRYYAnAMOb8oQhHh0GeMy6bsCyCeXObttlOSUCDPAYeYMVBXnCkvJop+Xi9m4n7makGgM8JkopvL7RRI/jvCnHVvd72OS0+5ExwGPy9nYbja4fdzOIYvf2dhsHXS6ANQoGeAxW97vYbDhxN4MoEZTC4GiUS0ZcFAN8ynbbrPsRHecHCt9bb8IPWFK8CAb4FLUdH29utsAT70QP6roBhxdeEAN8Slw/xPe4GQPRmQ66Hr6/3Y67GanBAJ+CMOyPOHF9Hh4SnWej4WDtgJuXDIMBPgVvbbXQ7HHECdGw3tnpYK/txt2MxGOAT9jqfhfbLb4QiS5CKeDNrRZHppyDAT5BHdfHuxxxQjQSP1B4a6sVdzMSjQE+IUopvLnZAs9ZEo2u0fVZDz8DA3xC7ux1uRExUQRu73S4L+wpGOAT0Ox5uLvPXgNRFEKFwfwJHs4exwCPWBgqvLXV5mQdogi1HB939tgpOo4BHrHbuzzcI5qEu/tdtBwOxz2KAR6hg66HtQMujUk0CUoBb222uDHyEQzwiPhByCFPRBPWcQO8u8ehuYcY4BG5tdOBw80ZiCZu7aDH9cMHGOAR2O+42GpyfW+iaVAKeHuLpRSAAT42pRTe2eEhHdE09bwQ69yKjQE+rq2mgw5HnRBN3d39bu43gGCAjyEIFd7l2FSiWPiByv2EOQb4GNYOulzjmyhG6we9XK9YyAAfkReEWN1nDY4oTqEC7uR4WCEDfER39rrcHo0oAbaabm5naDLAR9DzAmzwDDhRYtzO6UgwBvgIbu92uFgVUYIcdD3sd/K38xUD/IKaPQ873CKNKHHe2enkbsnZcwNcRK6KyNdE5FUR+Y6I/Mrg8jkR+aqIvDH4Pjv55saPk3aIkqnjBrmbET1MD9wH8GtKqfcC+DCAXxaRpwD8BoC/U0o9DuDvBv/OtP2Oy93liRLszn43V73wcwNcKbWmlPrm4OcmgFcBXAHwswC+OLjaFwH83ITamBicukuUbI4XYrednxLnhWrgInINwI8CeBHAslJqDeiHPIClyFuXID0vwH6HK6ARJV2eOlpDB7iIVAD8OYBfVUo1LvB7z4nISyLy0igNTIr1gx5HnhClQKPro+Pmo9Q5VICLiIl+eP+xUuovBhdviMjK4P9XAGye9LtKqReUUk8rpZ6OosFxCEKFrVa+To4Qpdl6TnbGGmYUigC4AeBVpdTvHfmvLwP41ODnTwH4q+iblwzbLQd+wO43UVpst9xcrFQ4TA/8IwD+HYCPi8i3Bl8/A+B3APykiLwB4CcH/86kvHyaE2VFECps5mBIoXHeFZRS/wBATvnvn4i2Oclz0PW43jdRCm00elipF9AvImQTZ2Keg71vonTqeWHmR44xwM/Q8wLs5XB9BaKsyPqQQgb4GTYbDocOEqXYfsdDN8MlUAb4KZRS2Gxm+9ObKA+yvPQzA/wUja4Pj0MHiVJvJ8NT6xngp9hl7ZsoE1w/zOyOPQzwU+RpQRyirNvL6PuZAX6CluNzt3miDMlqh4wBfoKsfloT5VXHDdDzsjcahQF+gqx+WhPlWRbf1wzwY3pewKnzRBnEAM+BLD7JRNQ/t+VlbIVCBvgxDHCibFIqe+e3GOBHZHm8KBFlb34HA/yI/Y7LtU+IMuyg4yEIs/MmZ4Afsd/N9tKTRHkXKqCRofc5A/yIZo/lE6Ksy1KZlAE+4PohZ18S5UA7QzvWM8AH2hn6VCai02Xpvc4AH8jSYRURnc71FRw/G5P1GOADWTqsIqKztTJyvosBPpClwyoiOlvbYQ88Mxw/gOtnZ2woEZ0tKyVTBjiy82lMRMPJSsmUAY7s1MOIaDh+oDKxPjgDHNk5nCKi4WXhfc8AR3YOp4hoeFkYuJD7AHf8AH7AE5hEeZOFc1+5D3BOnyfKJzcDmzswwBngRLmUhd15ch/gHssnRLnkByr1a4PnPsDZAyfKr7T3whngKX8CiWh0Tso7cAzwlD+BRDQ69sBTjj1wovxKewcu9wGe9k9gIhpd2t//uQ7wIFScxEOUY+yBp1jaP32JaDxpL6HmOsDTfgaaiMbDHniKsQdOlG9pn8iX6wAPVbqfPCIaT9ozINcBjnQ/d0Q0ppTnd74DPOXPHRFFQKU4xfMd4Ol93mhMN2/exDPPfBIf//jH8Mwzn8TNmzfjbhLFJM05YMTdgDgp9sFz6ebNm3j++c+h13MAAOvrG3j++c8BAD7xiU/E2TSKQagUNEjczRgJe+CUOzdufP5eeB/q9RzcuPH5mFpEcUpzDOQ6wCmfNjY2LnQ5ZVs6+959uQ5wSfMzRyNbXl6+0OWUbZLiIMh3gKf6s5dG9eyzn0ahYN93WaFg49lnPx1TiyhOaU6BXJ/ETPEHL43h8ETljRufx8bGBpaXl/Hss5/mCcycSnMOyDTHQIqIStKYy81GD29tteNuBhHF6F89Nj/V2xORC489F5GXlVJPH7881yWUVB87EdHY0tz7BnIe4IaW67tPlHuGlu4Ez3WCmXq6nzwiGo+ppzsCz229iHxBRDZF5JUjl31WRO6KyLcGXz8z2WZOhmWk+8kjovGkPQOGaf3/APDTJ1z++0qp9w++vhJts6bD0rXU18CIaHSZ74Erpb4BYHcKbZk6EWEZhSjH7Bz0wE/zGRH550GJZTayFk2ZpetxN4GIYpL5Hvgp/gDAYwDeD2ANwPOnXVFEnhORl0TkpRFva6JMgz1worzKQw38AUqpDaVUoJQKAfwhgA+ecd0XlFJPnzQIPQmslH8CE9Ho0l5CHSm9RGTlyD9/HsArp1036dJ+CEVEo0t7D/zctVBE5E8BfBTAgojcAfBbAD4qIu9HfyndWwB+aXJNnKy0n8QgotGIpP8I/NwAV0o9c8LFNybQlliwB06UT6YuqV5KFsj5TEwg/YdQRDSaLHTe0n8PxsQSClE+2Ub6hxDnPr0MXYNt5v5hIMqdss0Az4SKnet9LYhyKQvvewY4svFEEtHFlDPwvmeAIxtPJBENzzY1nsTMirKV/loYEQ0vK0fdDHD0T2QWGeJEuZGVo24G+EAlA2ekiWg47IFnTFY+kYnofFkpmzLABxjgRPlQtHQYGTiBCTDA76lYBrdXI8qBLJVLGeADmiYoZeSwiohOl6WjbQb4EVk5sUFEp8vS+5wBfsRsyYq7CUQ0QZYhqBbMuJsRGQb4EfWiCV1jIZwoq7LWSWOAH6FpgplSdj6dieh+c2UGeKZl7ROaiPp0TVDLUPkEYIA/YLZkcjghUQbNlkxoGSuRMsCPMXQtc5/SRATMZqx8AjDAT5S1OhlR3mkCzBSz1zFjgJ9gtpy9J5ooz2pFMzPT54/K3j2KgG3omRrsT5R3WT2qZoCfgr1wouzI6vBgBvgpsvqJTZQ3FduAbWRznSMG+ClKloFyhlYtI8qrhWp2O2MM8DNcqhXibgIRjUHXBIsVO+5mTAwD/AzzFRuGnq2B/0R5slCxMjn65FB271kEdE2wVM3upzdR1l2qZ/somgF+juVagVPriVKoXjRRsrI9HJgBfo6CqXOBK6IUynrvG2CAD4UnM4nSxTY1zGZ07PdRDPAh1Esmitwvkyg1LtUKkBzUPhngQ2IvnCgdNAEWczL4gAE+pMUqhxQSpcFC1YaZ4aGDR+XjXkZA1wQLGZ4QQJQVeTpaZoBfwEqdQwqJkqxWNFDO0UqiDPALKJg6J/YQJdgj8+W4mzBVDPALemi2BD1j++oRZcFCxcrdOv4M8AuyDA0rOZggQJQmmgBX50pxN2PqGOAjuDxThGWwF06UFMu1Agpm/uZqMMBHoGuCh2bz92lPlESGLrgyW4y7GbFggI9oqWpzdiZRAlyeKeZm3Pdx+bzXERARPJzDmhtRkliGhpUcjfs+jgE+hrmyhVoxX2e9iZLk6lwRWo5HhTHAx8ReOFE8yrae6e3ShsEAH1O1YGKhwvXCiabt4blSLlYcPAsDPAJX5zi5h2ia5soWZrjRCgM8CgVTx7V5llKIpsHUBY8u5GvK/GkY4BFZqhUwW87+DiBEcXt0oQzLYHQBAIdQROj6QgX/3NuHF6i4m/IApRQcP0TPC+D6IRSAUCmoQVNFAE0EAsA0NBRNHbah5b7GSMmyWLUwn/MTl0cxwCNkGRquLZTxxkYr1naESsHxQnS9AI4X9L/7IZS62AeLiMA2NBRMffDV/1ljqFMMLEPDtZytNngeBnjEFio29tou1g968EMFP1DwwxDe4HsY9gP2OE0EuiYwdIGhCQxdG3wXGNpwh4uOH2Cv7eGg6yEIw7Hvi1IKPS9Azwt+0E5NUC+amC1ZuVx7guLz2GIZRk5nXJ6GAT4mpRS6XoCW46Pj9L83eh7e3m7Bj6iUomvavd5vwdRRNPV7NcBQKTR7PvY6LjqOH8ntnSUMFfbaLvbaLoqWgdmSiVrRZK+cJmq5ZnPUyQnODXAR+QKAfwtgUyn1vsFlcwD+F4BrAG4B+EWl1N7kmpksHdfHXsfDfsdFq+cjPJbTAsHlehG3dzuR3F4Qhmg7IdpHAjpUCm6gEIYKpq7BjGG/zq7ro+v62Gg4mCn1e+U8uURRK5ha7jZqGJacVxcVkR8H0ALwR0cC/HcB7CqlfkdEfgPArFLq18+9MRF10TpsEoShQqPnYa/jYa/jwvGGK0+sHnSx33Yjb09z0JajpRhT11C0dJQsHbaux7L1myaCxaqNubLFk58UCRHgqcs11ArZGeElIqOcj3pZKfX0A5cP84dE5BqAvz4S4K8B+KhSak1EVgB8XSn15BB/J1UB3nUDbDR62G45I40sCZXCW1steP749WgA8IIQOy0XPT8483q6pqFq66gUTBgxTDAqWgYuzxRgG6yR03iuzBTxcMbmWEQZ4KPWwJeVUmsAMAjxpTNu+DkAz414O1MXhgq7HRcbjR4a3fFqypoIrswUcWunDYzxuaWUQqPnY7/jQQ3xh4IwxH43xH7XR8nSUbENFM3p9cq7ro+3t9pYqNhYqLA3TqMp2zoeyuk638Oa+ElMpdQLAF4A+j3wSd/eqIJQYXW/i41GL9Jx3CXLwOV6Eav73ZF+3/VD7LQdOCP14hU6ro+O68PQNNSKJiq2gWl0ypVS2Gr20Oh5uDJT5IgVuhDLEDx5qZrrlQaHMWqAb4jIypESymaUjZqmMFRYb/Swut+d2AScmZIFxw+w07pYPbzrBdhqOicOO7woPwyx23bQ6HqYKZkoW8ZUeuSOF+D72208NFtENUN1TJocTYAnL9VYghvCqEMGvgzgU4OfPwXgr6JpzvQopbB+0MP/fXcf7+x0Jj57crlWQKUw/Odl2/Gx2YgmvI/ywxDbLQerB120nLNr6VFRSuHdvS72O9Gf0KXsec9SJXe7y49qmFEofwrgowAWAGwA+C0AfwngzwA8DOA2gF9QSu2ee2MJOYl50OmP0+4NOZokKqFSuLXdvm9izEmaPQ+7bXecsvnQLF3DQsWe2vC/5VqBU6HpVFfnipnfb3bqo1CiEneA+0GIWzsdbDWd2NrgBgFubbdPneTT6vnYbk+7fYJ60UC9aE2lPn6pXsRcmZMy6H6LVQvvWarG3YyJizLAczPrYrft4v/d2Y81vAHA0nVcnS2dWH9uOz52ph7eAKBw0PWwdtA9d4hiFNYPWE6h+1ULBq4vVOJuRupkPsD9IMTrG028tt6E68dfvgEOx0nfPzzK8QNst5yplE1O4wUh1g8c7LbdB2aXRm31oIeOO/mp/5R8tqnhiWWOOBlFpgO84/r49t2DC4/+mIZ60cJitV8LVkphpzWdmvf5+rNONxr9xbgmdzP9YZvhpD8pKNF0TfBDl6pcgmFEmX3UdloOXrnbmPqJyotYrBZQL5rY63hwg2S10/EDrB30JlpScf0QG83exP4+JZsI8PhSBSWLI05GlbkAV0rh9k4Hr2+0EKSgdzdTMuFHsPTrJARhv6TS6E2u1LHXdtGawiqKlDzXF8uY5cnssWQqwINQ4XvrTdwdcdbjtIWhwup+D4uVQoJnKirsth1st1xMagDR6n43FR+2FJ3HFstYqhbibkbqZSbA/SDEq2sN7He8uJsytP60/RAiwHI1ySEOtBwPWy1nIic3/SDE+gFLKXnx2GIZSzWGdxQyEeCuH+I7qw00J3ioH7X+muI/OLmahhDvuD42m72JhPhB171vvXPKpusM70ilPsBdv9/z7rjTmRYelb32g0cKIsBSwkO85wUTC/HdCaydTslxfbGMZYZ3pFId4F6QzvD2gxCN3smlHm3QEy9a+QvxpuPDjWjtdEoOkf76Jgzv6KU2wMNQ4bX1ZurCGwD2Ou6ZU2kPyynlBA+v6nkBdloRzxpV6r6yEqWfJsATy9V7cx4oWqkN8Le2WqmqeR9SSmFvyBOti1U70Uuwtl0/8inx+8e2iqP06k/SqXHdmwlKZYC/u9vBdgJnVw6j0fPhX2DSznzZQq2Y3BDf73qRjuMOwhAH3fSMJKKTGbrgh1aqqJeS+9rNgtQF+HbLwZ29dIzzPskoJ+rmShYWKjaSulLEMPt0XgRPZqZbydLxI1fqmdqIOKlSFeAtx8dbm624mzEyPwjRHXEBp4pt4FK9AF1L3lOmoLDVdCNbO8XxAp7MTKm5soX3XakneiRVliQvDU4RhApvbDQnvkreJI17wtU2dFyuF2AncOGfYLDTT1S4UmG6iPQ3Y3jyUhU6VxWcmuQlwSlu73YSvTDVMLrn7MQzDF0TrNSLiTw87XlBZPXrKB4rmg5D768omPWddJIoFQF+0PEyMdU6yiGPc+Vk1sX3I1pZMY3DQ/PosN49U+JIkzgkPsD9IMSbW+mtex8KlTp3L8yL6tfFi4mqiysM1jYfs9Tl+CHXCk+4+Qrr3XFLzjv/FLd2Opk4oeV44YX3wRuGbWi4XC+gYCbnqXT8CEopSk1leze6OBHg4fkSnlhmvTtuyXnXn6DZ82LfwzIq3gTX/NY1waVasuriB11v7FEp3ikbP1N8zEG9+8qxLQEpHsmdqw3gnZ1O3E2IzGm70EdprmyhaOvYbbnwYt7hR6E/43SxMnpt9CITnmjyFioWri2UYeqJ7vflSmIDfLftpnKq/GmmFUZFQ8flehF7XReNc8oYr7/2Bl588R/RaDZQq9bwoQ99GE88+XhkbWk7PuoFY+T9DtkDTwbL0HB9gbvnJFEiA1wphdu72el9A0AwxfU9RPqzN8uWge2Wc2Jv/PXX3sDXv/41eH4/5BvNBr7+9a8BQIQhrrDbcXFpxFXopvmY0cmWazYenivBYK87kRL5rGw0HHQzNowsjiyyDQ1XZoqYKZoPDDd88cV/vBfehzzfw4sv/mOkbeh5wehjupnfsSmYGp66XMP1xQrDO8ES1wNXSuHufrZ633GbKVko2QZ2Wg6cwYieRrNx4nVPu3wc+x0PxTqHmqWBCLBSL+DqbAkaR5gkXuI+WrdbLlw/e10vifm9YOkaVupFzJYsaCKoVWsnXu+0y8fh+MG9D44LYX5MVcnS8b4rdTwyX2Z4p0TiAnyjkf4ZlyfR407wgXrRxMpMAT/2rz8I07h/2KFpmPjQhz48kdttjHBCOimPWdbpmuDqXBH/4qE6KnbiDsrpDIl6tlqOn6mRJ0clqY5oaho+9qEPoKgDX/36P6DR6U1kFMpRHcdHUDYvFMqmzgCfJE2AS/UCLs8UOTQwpRIV4FlY7+Q0RgLD6MNPfwAffvoD6HoB9jvuaGWOISkoNLs+Zi6wwH+SPvSyRBNgqVbAlZniyEM8KRkSE+BeEEa/x2KCmAlar+S4oqmjWC+i6wbY67iRLEZ1kqbjo140hz4fwB54tESAhYqNh2aLXL8kIxIT4LttN9VrfZ/HNjWIyETWQ4lK0dJRtIpoOT4Oul7kszmDMETPD1AcJjxEUDAYMlFZqFh4aLaEosXHNEsSFeBZpomgYOoj78gzTRXbQMU20HJ87He9SGeRdtzhAtw2NI6EiMBs2cTV2RLKPDmZSYl4Vv0gPHfadxaUrHQE+KGKbaBsGWi7PppdD04EQd51A6B8/vVKPMQfmSb9pV6XawVUE7TAGUUvEQG+3/UyXT45NFTpIGFEftAjd/wQTcdHx/ERjlgK8sMQjh+euy0cD/UvrmjpWKraWKzaHFWSE4kI8L2Ml08OpT2UbEODbVgISiY6boBmd7TddzquD9s4e2GkkpWIl2biadJfhXKpVkC9yN523sT+LlFKYT8H5RMAMHUNRctIVRnlJLoIqraBqm3A8QM0egE6jjf00iUdN8BZ2yfaps7hbecomBqWagUsVmw+VjkWe4C33WAqa2UnxVzZwt2UB/hRtqFjsaIjKJtoOwGavfNHr3hBiEABp40SnOOypSeSw9521eYelAQgCQHuZCfMhlErGNjQtcxtVqCLoFYwUCsYcIMQXTdAx/VPnRzknjKcUNc0lgKOMHTBTNHETMnCbMnk5Ca6T+wB3spZgIsIZktmZraKO4mla7CK/SAOlELXDfpfXnDv5KfrhycG+EzJhJbzNVBKlo7ZkoWZsomqbUBy/njQ6WIP8Lz1wAFgtmRhq+XGs0j4lOki90axAEDX74f5iXddBLM5LA1oAtSKZj+0SyZnSdLQYg3wMFToZGzjhmEYuoZ6wcRBNx+jb44qGjqKhg7T0PDIfAmtXr/U0vMC2EY+Tl5qApRtAyVLx0zJQr1ocnd3GkmsAd52/Tx0Qk80W85ngB/y/BC6CObK1r2Tlk8uV6DrGjquj7bjo+30yy5pfo3omqBk6ajYBkp2/3vR1FkWoUjEGuA9L1sn8i6iZBmYKVnY7+Q3xN1AoTjocC9WLcxVbAC47yRmEKpBoAdoD4K96waJnPhl6oKSZaBs6ygPZrGmfew/JVusAR71Yklpc6lWQNvxc/s4+EEIDMZ8X5s/eX69rgmqBfOBKeFeEPa/fAUnCOAFCp7fv8wNQniBguuHCMZMepF+MJu6du/L0jVYhta/3Oj/29Q1lkFo6mINcHeC60+ngaYJLs8U8c5uJxcnNI/zB+H62GL5wsPjDsMUFgCcPuwwCFV/3HmooNCfONb/DkD11ykXCCD9sBb0RwoJ+kP4LF1juYMSiz3wmJVtA/NlK9NroZ/GD0Is1yY7KUXXBLrGMgZlU6yn/Ce5A0yaLFZt2DkcOqZpgkdOKZ0Q0fliDXD2wPs0EVyuF+Pfun6aRHCpVmDdmGgMsQb4uCeY0urmzZt45plP4uMf/xieeeaTuHnzJoqWjisz+Qnxy/UCJ6wQjSnWGnge4/vmzZt4/vnPodfr17zX1zfw/POfAwB84hOfgFIKq/vdOJs4cZfqRS7GRBSBWHvgORx4gRs3Pn8vvA/1eg5u3Pg8AGCmZOFSvRhH06ZiuVa4N3Enj88/UZRiXwslbzY2Ns69fK5sQdcEq/vdRG+CfCEiuFwvsOdNFKFYe+A5KffeZ3l5eajL60UTV+dKmViZT0RwdfbBskkG7hpRrMYKcBG5JSLfFpFvichLF/79cW48pZ599tMoFOz7LisUbDz77KcfuG7FNnBtoZzqk322qePafJmb6xJNQBQllI8ppbZH+UVdE3g52o0H6J+oBPq18I2NDSwvL+PZZz997/LjCqaORxfK2Gm72Go6qSmpiAgWKjYWKtapMxk5hJBoPDJOIIjILQBPDxvgIqKO3t4rdw/Q7OVvPfBRuX6I1YMuOglfQ71oGbg8U4BtnH3ksFi18Z6lypRaRZQMInLhjpiIvKyUevr45ePWwBWAvxWRl0XkuVNu+DkReemkEkse1n6O0uGiT5fqxUTWxjURLNcKuDZfOje8gf4u90Q0unFLKB9RSq2KyBKAr4rI95RS3zh6BaXUCwBeAPo98KP/Z3F/v5HMlS1UCwZ22y72Ox6CMN4ZrbqmYabU31HmIh/KJp9/orGMFeBKqdXB900R+RKADwL4xtm/9QMme2AjM3UNy7UCFqs2mj0fex136qWVomVgtmSiVhxtH0segRGNZ+QAF5EyAE0p1Rz8/FMA/vNF/gZ74OPTRFAvmqgXTTh+gL22h4Pu5Hrlmta/vdmSNfboGFNPXhmIKE3G6YEvA/jSYISBAeBPlFL/+yJ/wDYZ4FGyDR2X6jqWajYcL0TXC+B4/W3JHD8c5cQJbENDwdQHX/2fo6q/D1MnJ6LTjRzgSqm3AfzLcW68bBkQ4ZTqqGkiKFr6fdt5KaXg+CF6XgDXD6HQ31T6sJ+uoR/YmvRLW0VTh21MbjMDy9BYQiEaU6xT6XVNUDT1XO5MP20icq8nnQTVAldxIBpX7F2gss03ch7xeScaX+wBXuEbOZcqFp93onHFHuBlOxmH9DRdfN6Jxhd/gFsG18TImZKlX3gXeiJ6UOzvIk0TzJS4Ul2ezHJNcKJIxB7gAN/QeTNb5gc2URQSEuAmF/fPCcvQuDY4UUQSEeCGrqHGN3UuzLJcRhSZRAQ4gHsb3VK28Xkmik6iApxllGyzjP5CWEQUjcQEuGVomGfvLNOWqoWJra1ClEeJCXAAWK4X4m4CTYgIsFzj80sUpUQFeK1gcmp9Rs2XL7ZbDxGdL3HvqOW6HXcTaAJ4dEUUvcQF+ELZ5k4tGVO2dQ4TJZqAxAW4pgkuzxTjbgZF6OpsKe4mEGVS4gIcAC7VCtxuLSNqRQOzHF1ENBGJTElNEzw8x15bFjwyX467CUSZlcgAB4CFis0RKSm3ULH4HBJNUGIDHAAenmcvPK00Aa7yKIpoohId4PWiifkK66dpdHmmmJgNlImyKtEBDgCPLpRhGRxWmCZlW8cVjiQimrjEB7ipa7i+UIm7GTQkTYD3LFWgcZs8oolLfIADwGzZwmKVMzTT4KG5EkrccZ5oKlIR4ABwbb7EseEJVy0YuMwp80RTk5pENHQN71mqcM3whDJ0GTw/fIKIpiU1AQ70Vyu8vsCJIUkjAjyxXOWoE6IpS1WAA8BSrYDLMzxMT5LrC2XutEMUg9QFOAA8PFfi3ooJsVIvYIkbNRDFIpUBLtKvt5ZtHrLHabZs4hHOliWKTSoDHAB0TfDkpSoKHJkSi2rBwONLVZ60JIpRqtPPNnQ8dbnGEJ+yasHAe1dq0DlZhyhWqU8+hvh0VQsGfuhSleFNlACZSD3b0PHDl+usiU/YTMnEe1dqMPRMvGyIUi8z70TL0PDUSg3VAqdxT8JCxcKTy+x5EyVJZgIc6M/W/OHLNVzidO7IiPTXZX98ucoFqogSJnPdVRHBowtllC0d399uI1Rxtyi9zMH0+JkSx9wTJVHmAvzQUq2Akm3gtfUmXD+MuzmpU7Z1To8nSrhMlVCOq9gGfuRKHTMlTvO+iMWqjR++XGd4EyVcZnvghyxDw3tXaths9nB7pwMvYE3lNLap4fpCmSUTopTIfIAfWqoWMFO0cGunjZ2WG3dzEkUEWK4V8PBciaNMiFIkNwEO9HvjTyxXsVtx8f3tNmvjAIqWjuuLZdQKLDMRpU2uAvzQXNlCvWhivdHD2n43l2UV29Tw0EwRi1Wb65kQpVQuAxzoL4Z1ZaaI5aqNtYMe1g56CHIw5tAyBFdmSliq2hzXTZRyuQ3wQ4au4epcCZfqBazud7HRcDIZ5KYuWJkp4lKtwDo3UUbkPsAPmbqGR+bLeGi2hO2Wg82Gg5bjx92ssdWKBpZrBcyVLPa4iTKGAX6MrgmWawUs1wpoOT42Gj3stNxU9cpNXbBYtbFULaBocSw3UVYxwM9QsQ1UFiu4Nq+w33Gx1/Gw33ETedLTNjXMFE3MlvonaNnbJso+BvgQdE0wX7ExX7GhlELL8bHf8bDXcdFxA6gY8lyk/wEzW7YwUzRRtvlUEuUN3/UXJCKoFkxUCyauzpUQhApt10fHCdByfHRcP/JQ1wQo2wZKlo6KbaBkGyiZOnvZRDnHAB+TrglqBfO+iTBhqOAGYf/LD+EFITy/f5kfhlAK/S8oCAQigCYCQxdYugZT12DqAtPQYOkabEPjWG0iegADfAI0TVDQdC4GRUQTNdZqhCLy0yLymoi8KSK/EVWjiIjofCMHuIjoAP47gH8D4CkAz4jIU1E1jIiIzjZOD/yDAN5USr2tlHIB/E8APxtNs4iI6DzjBPgVAO8e+fedwWVERDQF45zEPGlYxAOD50TkOQDPDf7piMgrY9xm2i0A2I67ETHL+2PA+5/v+w8ACyJy0cfgkZMuHCfA7wC4euTfDwFYPX4lpdQLAF4AABF5SSn19Bi3mWp5v/8AHwPe/3zffyDax2CcEso/AXhcRB4VEQvAJwF8OYpGERHR+UbugSulfBH5DIC/AaAD+IJS6juRtYyIiM401kQepdRXAHzlAr/ywji3lwF5v/8AHwPef4rsMRAVx0pMREQ0trFmYhIRUXymEuCccg+IyC0R+baIfEtEXoq7PZMmIl8Qkc2jw0ZFZE5Evioibwy+z8bZxkk75TH4rIjcHbwOviUiPxNnGydJRK6KyNdE5FUR+Y6I/Mrg8ly8Ds64/5G9BiZeQhlMuX8dwE+iP/TwnwA8o5T67kRvOGFE5BaAp5VSuRgDKyI/DqAF4I+UUu8bXPa7AHaVUr8z+CCfVUr9epztnKRTHoPPAmgppT4XZ9umQURWAKwopb4pIlUALwP4OQD/ATl4HZxx/38REb0GptED55T7HFJKfQPA7rGLfxbAFwc/fxH9F3NmnfIY5IZSak0p9c3Bz00Ar6I/WzsXr4Mz7n9kphHgnHLfpwD8rYi8PJidmkfLSqk1oP/iBrAUc3vi8hkR+edBiSWT5YPjROQagB8F8CJy+Do4dv+BiF4D0wjwoabc58BHlFIfQH/1xl8eHF5T/vwBgMcAvB/AGoDnY23NFIhIBcCfA/hVpVQj7vZM2wn3P7LXwDQCfKgp91mnlFodfN8E8CX0S0t5szGoCx7WBzdjbs/UKaU2lFKBUioE8IfI+OtAREz0w+uPlVJ/Mbg4N6+Dk+5/lK+BaQR47qfci0h5cBIDIlIG8FMA8rio15cBfGrw86cA/FWMbYnFYXAN/Dwy/DqQ/j6ANwC8qpT6vSP/lYvXwWn3P8rXwFQm8gyGyfxX/GDK/W9P/EYTRESuo9/rBvqzX/8k64+BiPwpgI+iv/rcBoDfAvCXAP4MwMMAbgP4BaVUZk/ynfIYfBT9Q2cF4BaAXzqsB2eNiPwYgL8H8G0A4eDi30S/Dpz518EZ9/8ZRPQa4ExMIqKU4kxMIqKUYoATEaUUA5yIKKUY4EREKcUAJyJKKQY4EVFKMcCJiFKKAU5ElFL/H1ATOwmwNjCFAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# Plot initial point\n",
"\n",
"def plot_circles(m):\n",
" ''' Plot circles using data in Pyomo model\n",
" \n",
" Arguments:\n",
" m: Pyomo concrete model\n",
" \n",
" Returns:\n",
" Nothing (but makes a figure)\n",
" \n",
" '''\n",
" \n",
" # Create figure\n",
" fig, ax = plt.subplots(1,figsize=(6,6))\n",
" \n",
" # Adjust axes\n",
" l = max(m.a.value,m.b.value) + 1\n",
" ax.set_xlim(0,l)\n",
" ax.set_ylim(0,l)\n",
" \n",
" # Draw box\n",
" art = mpatches.Rectangle((0,0), width=m.b.value, height=m.a.value,fill=False)\n",
" ax.add_patch(art)\n",
"\n",
" # Draw circles and mark center\n",
" for i in m.CIRCLES:\n",
" art2 = mpatches.Circle( (m.x[i].value,m.y[i].value), radius=m.R[i],fill=True,alpha=0.25)\n",
" ax.add_patch(art2)\n",
" \n",
" plt.scatter(m.x[i].value,m.y[i].value,color='black')\n",
" \n",
" # Show plot\n",
" plt.show()\n",
" \n",
"plot_circles(model)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.3 Solve and Inspect the Solution](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.3-Solve-and-Inspect-the-Solution)",
"section": "4.1.3.3 Solve and Inspect the Solution"
}
},
"source": [
"### 4.1.3.3 Solve and Inspect the Solution"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.3 Solve and Inspect the Solution](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.3-Solve-and-Inspect-the-Solution)",
"section": "4.1.3.3 Solve and Inspect the Solution"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Ipopt 3.13.2: \n",
"\n",
"******************************************************************************\n",
"This program contains Ipopt, a library for large-scale nonlinear optimization.\n",
" Ipopt is released as open source code under the Eclipse Public License (EPL).\n",
" For more information visit http://projects.coin-or.org/Ipopt\n",
"******************************************************************************\n",
"\n",
"This is Ipopt version 3.13.2, running with linear solver ma27.\n",
"\n",
"Number of nonzeros in equality constraint Jacobian...: 0\n",
"Number of nonzeros in inequality constraint Jacobian.: 30\n",
"Number of nonzeros in Lagrangian Hessian.............: 12\n",
"\n",
"Total number of variables............................: 8\n",
" variables with only lower bounds: 8\n",
" variables with lower and upper bounds: 0\n",
" variables with only upper bounds: 0\n",
"Total number of equality constraints.................: 0\n",
"Total number of inequality constraints...............: 15\n",
" inequality constraints with only lower bounds: 9\n",
" inequality constraints with lower and upper bounds: 0\n",
" inequality constraints with only upper bounds: 6\n",
"\n",
"iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls\n",
" 0 1.0000000e+02 7.46e+01 1.06e+00 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0\n",
" 1 1.0050650e+02 4.98e+01 4.22e+00 -1.0 2.36e+01 - 1.84e-01 1.30e-01h 1\n",
" 2 1.0015862e+02 3.01e+01 2.32e+00 -1.0 5.24e+00 - 8.18e-01 3.67e-01h 1\n",
" 3 9.9730828e+01 1.33e+01 1.16e+00 -1.0 4.96e+00 - 7.51e-01 4.53e-01h 1\n",
" 4 9.8213893e+01 8.23e+00 1.08e+00 -1.0 2.46e+01 - 2.93e-01 7.07e-02f 1\n",
" 5 9.8307816e+01 1.84e+00 3.42e-01 -1.0 7.81e+00 - 1.00e+00 6.57e-01h 1\n",
" 6 9.8901802e+01 0.00e+00 1.06e-02 -1.0 1.80e+01 - 1.00e+00 1.00e+00h 1\n",
" 7 9.8393352e+01 0.00e+00 3.30e-03 -1.7 9.37e+00 - 1.00e+00 1.00e+00h 1\n",
" 8 9.8405011e+01 0.00e+00 1.08e-03 -1.7 4.38e+01 - 1.00e+00 1.00e+00h 1\n",
" 9 9.8405025e+01 0.00e+00 1.17e-04 -1.7 7.44e+00 - 1.00e+00 1.00e+00h 1\n",
"iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls\n",
" 10 9.8405027e+01 0.00e+00 5.74e-07 -1.7 1.52e+00 - 1.00e+00 1.00e+00h 1\n",
" 11 9.8284703e+01 0.00e+00 4.42e-05 -3.8 2.93e-01 - 1.00e+00 9.98e-01h 1\n",
" 12 9.8284281e+01 0.00e+00 2.33e-09 -5.7 2.63e-03 - 1.00e+00 1.00e+00h 1\n",
" 13 9.8284270e+01 0.00e+00 1.33e-13 -8.6 2.80e-05 - 1.00e+00 1.00e+00h 1\n",
"\n",
"Number of Iterations....: 13\n",
"\n",
" (scaled) (unscaled)\n",
"Objective...............: 9.8284270438747228e+01 9.8284270438747228e+01\n",
"Dual infeasibility......: 1.3347017888941731e-13 1.3347017888941731e-13\n",
"Constraint violation....: 0.0000000000000000e+00 0.0000000000000000e+00\n",
"Complementarity.........: 2.5071615765896930e-09 2.5071615765896930e-09\n",
"Overall NLP error.......: 2.5071615765896930e-09 2.5071615765896930e-09\n",
"\n",
"\n",
"Number of objective function evaluations = 14\n",
"Number of objective gradient evaluations = 14\n",
"Number of equality constraint evaluations = 0\n",
"Number of inequality constraint evaluations = 14\n",
"Number of equality constraint Jacobian evaluations = 0\n",
"Number of inequality constraint Jacobian evaluations = 14\n",
"Number of Lagrangian Hessian evaluations = 13\n",
"Total CPU secs in IPOPT (w/o function evaluations) = 0.004\n",
"Total CPU secs in NLP function evaluations = 0.000\n",
"\n",
"EXIT: Optimal Solution Found.\n"
]
}
],
"source": [
"# Specify the solver\n",
"solver = pyo.SolverFactory('ipopt')\n",
"\n",
"# Solve the model\n",
"results = solver.solve(model, tee = True)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.3 Solve and Inspect the Solution](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.3-Solve-and-Inspect-the-Solution)",
"section": "4.1.3.3 Solve and Inspect the Solution"
}
},
"source": [
"Next, we can inspect the solution. Because Pyomo is a Python extension, we can use Pyoth (for loops, etc.) to programmatically inspect the solution."
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.3 Solve and Inspect the Solution](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.3-Solve-and-Inspect-the-Solution)",
"section": "4.1.3.3 Solve and Inspect the Solution"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Name\tValue\n",
"a \t 29.142135416184022\n",
"b \t 19.999999803189596\n",
"x[A] \t 9.99999990193744\n",
"x[B] \t 4.999999953543133\n",
"x[C] \t 15.734851787229463\n",
"y[A] \t 19.142135514931184\n",
"y[B] \t 4.999999951252124\n",
"y[C] \t 5.517617033892999\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXUAAAFoCAYAAACotWuNAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAAAq5ElEQVR4nO3dW6xc13kf8P+3r3M/93N4SEqkdbEkS07kgnCLuigcRw3coICTAA6sh0AFaCgPMeAAeYiRlzgFChiFlbQPRQBFNOICSVoDjmvDCJqYRoI0QeFENGRLNiVLoinxcq48l7nvPXvP14cZSpTMwzNzzsy+/n8wTXI058wa7pn/WbPWt9YSVQUREWWDEXcDiIhochjqREQZwlAnIsoQhjoRUYYw1ImIMoShTkSUIYeGuogUROSfROQHIvIjEfmD4e3zIvIdEXl9+Pvc9JtLRET3IofVqYuIACiralNEbAD/AODzAH4NwI6qfklEvgBgTlV/d+otJiKiAx3aU9eB5vCv9vCXAvgUgK8Ob/8qgF+ZRgOJiGh01ih3EhETwCUADwH476r6PRFZUdU1AFDVNRFZPuz7LC4u6tmzZ4/TXiKi3Ll06dK2qi6Nct+RQl1VQwBPisgsgG+IyBOjNkZEngXwLADcf//9ePHFF0f9UiIiAiAib41637GqX1R1D8DfAfgkgA0RWR0+4CqAzQO+5nlVPaeq55aWRvpBQ0RERzRK9cvSsIcOESkCeArAqwC+BeCZ4d2eAfDNKbWRiIhGNMrwyyqArw7H1Q0AX1PVb4vI/wPwNRE5D+BtAJ+eYjuJiGgEh4a6qv4QwEfucvstAL84jUYREdHRcEUpEVGGMNSJiDKEoU5ElCEMdSKiDBlp8dGkvPzyyxhsJUOJIQbEtAHTgpg2xBwWOQkAyM9cr8FeQTrYKAJ9aBgCYQ/aD6BBD9B+5E+B7u3MmTO4evVq3M2giEQa6r7vgwddR0dV0fZDtP0QXhCiFyp6YR9+0Icf9tEL+uhP+HIYAtiWAcc0YJsGHMuAbQocy0DZsVByTP5gjxj/vfMl0lCn6en3Fe1eiJYXDH+FaPvBxEP70HYo4PX68Hp377EbApQcCyXXRMUdhHzZsWAYDB6iSWCop1TLC9DoBmh6Adp+gLYfIg0fgvoKNL1BuzfhAQBEgKJtouxaKLsmqgUbFZcvTaKj4DsnJfp9xX6nh922j912D36QnbFrVbwzTLTVGNzmWILZkoO5koOZog2TPXmikTDUE6zbC98J8v12L/KhlDj5gWKz7mGz7sEQoFa0MVdyMFuyUbDNuJtHlFgM9YRpegF2mj522z7afhh3cxKhr8Beu4e9dg8AUHJMzJUczJVtVAt2zK0jShaGegIEYR/bTR+bjS5aHoP8MIOhmg5u7HVQckws11wsVVxYJpddEB16RulEH0xEWdL4rqYXYKPexa2mjzBPYytTYAiwUHGxUnPZe38fEWEpccqJyCVVPTfKfdlTj1jYV9xqetioe2h6QdzNyYy+AlsND1sND2XXxHK1gMWKw9475Q5DPSJtP8D6fhfb7JVPXcsL8VOvhbd32lioODhRK6DMEknKCb7Sp6zjh7i+28Z204+7KbkT9t+toJkvO7hvvoiSw5c8ZRtf4VPS7YW4vtvBdtNLxaKgrNtpDSqKFisOTs+VWBZJmcVQnzA/6OPGXgeb9W6u6srTQBXYavjYbvpYqro4PVeEazHcKVsY6hPSC/u4udfB+j7DPOlUgc26h+2Gh5VaASdni3AsTqhSNjDUjynsK27udbC23+UEaMr0FVjb72Kz4eFErYCTswVWy1DqMdSPYa/t48p268AdCSkdwr7ixl4HW00PDyyWMVd24m4S0ZEx1I8gCPu4equNrYYXd1Nogvygj1fXG1isODi7WIbNXjulEEN9TLeaHq7easEPONSSVdtNH/udHs4slLFUdeNuDtFYGOoj8oM+rt5q4RbrzXOhFyre2GziVsvDBxbLrJKh1GCoj2Cz0cVbt9oIQvbO82a31UOju4/750tYqRXibg7RoRjq9+AFIa5std7Z8pXyKQgVV7Za2G56eHCpwoVLlGicCTpAvdvDKzf2Gej0jnonwCs39rHP1wQlGEP9Ltb3u/jxzTonQ+ln9ELF5fU6bu514m4K0V1x+OUO/b7ip7da2KyzVJEOpgq8dauNlhfggaUKz0+lRGGoD3lBiJ+sN7nHOY1su+mj09vHB1eqHGenxODwC4D9zmD8nIFO42p5IcfZKVFyH+rr+11cXuP4OR3d7XH2GxxnpwTI7fCLquLKNsfPaTJUgbdvtdH2Ajy0XIEIx9kpHrnsqff7itc3mwx0mrjtpo9X1xvoc8dOiknuQj3sK17baHC5P03NXruHy+t1bsVMschVqAdhH5fX6lxQRFNX7wT48c06eiG3ZaZo5SbUB4HeQKPLCheKRtNjsFP0chHqtwOdJYsUtbYfMtgpUpkP9SAcHHzAQKe4tP0Ql9cY7BSNTIf67UDnkAvFreUx2CkamQ11VcVPNpoMdEqMlhfiNZY70pRlNtSvbLew32GVCyVLoxvgynYz7mZQhmUy1Nf2O1xYRIm11fBxfbcddzMoozIX6rstH2/d4huGku3aTge3mux40ORlKtTbfoDXN5tQDllSCryxya2eafIODXURuU9E/lZELovIj0Tk88PbvygiN0TkpeGvX55+cw/mB4NKFy7NprToK/Daeh1eEMbdFMqQUXZpDAD8jqp+X0SqAC6JyHeG/+2PVPXL02veaPp9xU82GvB6LBejdPEDxWvrDTx+coYnKNFEHNpTV9U1Vf3+8M8NAJcBnJp2w8ZxZZuli5ReLS/EG5usiKHJGGtMXUTOAvgIgO8Nb/qciPxQRL4iInOTbtwobu51sNXgjouUbjstH9d2OMFPxzdyqItIBcDXAfy2qtYB/DGABwE8CWANwHMHfN2zIvKiiLx4/Oa+V9sP+EagzLix1+HEKR2b6AilIiJiA/g2gL9W1T+8y38/C+DbqvrEId9HR3m8UagqXrlR55uAMqXkmPjwqRkYExxfFxFM6n1H8RCRS6p6bpT7jlL9IgAuALh8Z6CLyOodd/tVAK+M29DjuL7LXg1lT9sPcY0Lk+gYRql++RiA3wDwsoi8NLzt9wA8LSJPAlAAVwH85hTad1dNL+Ahv5RZa/tdzJYczBTtuJtCKTTS8MvEHmwCwy/9vuKHN/bR8VnbS9nl2gZ+/vTsRMocOfySfhMdfkmat3faDHTKPK/Xx9VbrbibQSmUqlDf7/Swtt+NuxlEkdise9htsVyXxpOaUA/CPt7c4gINypcr200erEFjSU2oX9/tcBsAyh0/ULzNtRg0hlSEercXYqPOYRfKp62Gx3kkGlkqQv3aThvcfJHyShV4a4eTpjSaxId60wuw3eRkEeXbbqvH4xlpJIkP9bdY1kUEAHibJ3rRCBId6rstH/UOtwIgAm5/auUReHRviQ11Vc76E73ftZ02+pxgontIbKhvNTy0OeNP9B7dXh8bDVaC0cESGephX7lTHdEBbux2EHBBEh0gkaG+Xu/CD/gRk+hueqFyuww6UOJCXVWxzhcs0T1t1LscW6e7Slyo77R8+AE/WhLdSy9UbLdYCUM/K3Ghvs7tAIhGsrHPUKeflahQb3kB69KJRtT0AjS6XGVK75WoUGcvnWg83OiO3i8xoR6EfdziHi9EY9lucg6K3isxob7Z8BByNp9oLKrsrdN7JSLUVZVDL0RHtNno8mBpekciQn2v3eOpRkRH5AeKWzzLlIYSEeqbDZZmER3HZp3vIRqIPdTDvmKvzV4G0XHUuz3uB0MAEhDq+50ej6ojOiZVYLfNmnVKQKjvcCyQaCJ2+YmXEHOoq3LohWhS9to9bvJF8YZ6vRugF/JFSDQJYV95ODXFG+q7HHohmqgdfvLNvVhDnS9Aosnaa/tciJRzsYV6ywu44IhowvxA0fC402mexRbqrHohmg4Oa+ZbbKHOCR2i6dhjvXquxRLqqooWPyISTUWnF3LH0xyLJdRbfshVpERTojo4FYnyKZ5Q5wuOaKr4HsuvWEKdvQii6WKo5xd76kQZxI5TfkUe6v2+ou2HUT8sUa50e31uxZtTkYd6yw/ABW9E09fy2HnKo8hDnR8LiaLR8FivnkfR99QZ6kSRYE89n2IIdb7QiKLAT8X5FHmoewEnb4ii0Av73LExhyIPdS5fJoqGKuCzAiZ3Dg11EblPRP5WRC6LyI9E5PPD2+dF5Dsi8vrw97lDH01kAk0molH5/GScO6P01AMAv6OqjwH4VwB+S0Q+BOALAL6rqg8D+O7w74dgqBNFicdF5s+hoa6qa6r6/eGfGwAuAzgF4FMAvjq821cB/Mqhj8aeOlGk2FPPn7HG1EXkLICPAPgegBVVXQMGwQ9geYTvMHYDiejoehxTzx1r1DuKSAXA1wH8tqrWZcRet4g8C+BZAIBhHqGJRHRUrDbLn5F66iJiYxDof6aqfzm8eUNEVof/fRXA5t2+VlWfV9VzqnpOGOpEkWJPPX9GqX4RABcAXFbVP7zjP30LwDPDPz8D4JuHPxyHX4iixDH1/Bll+OVjAH4DwMsi8tLwtt8D8CUAXxOR8wDeBvDpQ78TM50oUuyp58+hoa6q/4CD4/gXx3s4pjpRlFjSmD+xHJJBRFFiZypPIg51vriIIsf1IbnCnjrd08WLF/H005/BJz7xC3j66c/g4sWLcTeJiO5h5Dp1yp+LFy/iuee+jG7XAwCsr2/guee+DAB46qmn4mwajYM99VxhT50OdOHCC+8E+m3drocLF16IqUV0NAz1PGGo04E2NjbGup2SihUwecJQpwOtrKyMdTslFA/KyBWGOh3o/PnPolBw33NboeDi/PnPxtQiIjpMxBOl7DGkye3J0AsXXsDGxgZWVlZw/vxnOUmaNuyp54pEeYah4RT1Hy9fj+zxiAj41w8t8qzSlBORS6p6bpT7cviFKMNMg5UveRNtqLO3QBQp22So503EPXWGOlGUHIsfxvMm0ivOcT2iaDkmQz1vOPxClGHsqecPh1+IMsxmTz132FMnyjD21POHPXWiDGNPPX/YUyfKMJc99dyJ/Ipza2ei6LCnnj+RX3G+yIiiYZnCFaU5FHnCll0z6ockyqWSw/daHkUf6g5P0COKQsXley2PIg91vtCIolHmey2XYhh+4QuNKArsQOVT5KHuWAYXRBBNmW0KCjbH1PMolnStFtiDIJomfiLOr1hCnS84ouni0Et+xRLqFVbAEE0VO075FVNPnWN9RNPE91h+xRLqlmmgYHOylGgaHEvgWgz1vIotWWtFO66HJsq0WoHvrTyLLdTnS05cD02UaXNlvrfyLLZQnyna3GyIaMIMAebYYcq12ELdMASzJX5MJJqkGjtLuRfrbCV7FESTNc+hl9yLOdRtHppBNCHCoRdCzKFumQZn6okmpOJa3FeJ4g11gB8XiSaFVS8EJCDU58rsqRNNAsuECUhAqLuWyc2HiI6p6Jgo8vg6QgJCHQAWq+xhEB3HYoXvIRpIRKgvVVzW1hIdkSHAcrUQdzMoIRIR6pZpsKdBdEQLFYdVL/SOxLwSTsywp0F0FCs1vnfoXYkJ9ZJjoVbkhCnROCquhSrXetAdDg11EfmKiGyKyCt33PZFEbkhIi8Nf/3yJBpzgj0OorHwEy693yg99T8F8Mm73P5Hqvrk8NdfTaIx82UHLg/PIBqJYwkWuOCI3ufQBFXVvwewE0FbICIcHyQa0XK1AINVY/Q+x+kWf05Efjgcnpk76E4i8qyIvCgiL47yTZerLvg6Jbo3EWC55sbdDEqgo4b6HwN4EMCTANYAPHfQHVX1eVU9p6rnRvnGtmlgocIXK9G9zJcdnkNKd3WkUFfVDVUNVbUP4E8AfHSSjTo9V+SWvEQHEBm8R4ju5kihLiKrd/z1VwG8ctB9j6JgmxxbJzrAYsVFyWH5L93doa8MEfkLAB8HsCgi1wH8PoCPi8iTABTAVQC/OemGnZ4rYqvhIezrpL81UWoZAtw3z146HUxUowtNEdFxHu/6bhvXdjpTbBFRupyaLeL+hdJYXyMiiPJ9TpMnIpdGnZdMdFH4yZki97QgGrJNwclZDkvSvSU6MQ1DcB8nhIgAAKfmirDMRL9lKQES/wpZqroocfN/yrmCbXAbDRpJ4kNdRHD//HhjiERZc/98CcI6XxpB4kMdGByoO1PkTnSUT9WCxQV5NLJUhDoAnF0scfsAyh0R4MyY1S6Ub6kJ9ZJj4TSHYShnTs0WuV86jSU1oQ4AJ2cKqBa4ko7yoeya3A6AxpaqUBcRPLRc4SHVlHmGAA8tVzg5SmNLVagDg31hWA1DWXd6vsT9XehIUhfqwOAIL1bDUFZVCxZO8pg6OqJUhjoAPLhchmXyoylli2kIh13oWFIb6q5lstSLMufMQgkFmyuo6ehSG+rA4IzGeR68SxkxW7J5jgAdW6pDHQAeWCqjYKf+aVDOubaBB5cqcTeDMiD1aWibBh49UeP4OqWWaQgeWalym2maiEy8ioqOiQ8uV3muKaWOCPDwcgVll+WLNBmZCHUAmCnZ+MBiOe5mEI3l/vkS5jgvRBOUmVAHgJVaAaus76WUWK65ODnLbQBosjIV6sCgJGy2xIVJlGy1ooUH+MmSpiBzoS4ieHi5wtOSKLEKtoEPrlS5wIimInOhDgCWaeCRE1XYrIihhLFMwaMnarB51ihNSWZfWQXbxCMnqtzRkRLDEOCDK1UU+SmSpiizoQ4A1YKNR1cZ7BQ/Q4BHT9S4ER1NXaZDHQBqDHaK2TuBzgl8ikDmQx1gsFN8DAEeOVFloFNkchHqwLvBzu0EKCqmMZgUnS1xcRFFJzehDgyC/bHVGqtiaOosU/DoKnvoFL1chToAVFwLj5+c4eZJNDW2KfjQag21AgOdopfLZCs6Jh4/WeOWvTRxjmXg8ZMz3KCLYpPbVCvYJp44NYNakW8+moxqwcKHT82wDp1ildtQBwZ7sX9otcZNwOjYVmouHj9Z47AexS733VQRwdnFMsquhStbTfQ17hZRmhgCfGCxjGUeQ0cJkftQv22p6qLkmHhtowGv14+7OZQCjmXggysVVDkhSgnCz4p3KLuDMVEu5abD3B4/Z6BT0jDU38c2DTy2WsXJWX6cprs7MVPg+DklFodf7kJEcGZhMM7+0+0WgpAD7TRYIXp2sYTlKn/gU3Ix1O9hseKiWhgE+26rF3dzKEYzRRsPLJVRsFmuSMnGUD+Ea5l49EQNWw0Pb91qocdee65YpuDMfInVLZQaDPURLVVdzJZsXN1uYbvpx90cisB82cEHFsscO6dUYaiPwTYNPLxSxULFx0+3W/ADlj5mkWMJzi6UsVBx424K0dgY6kcwX3ZQK1h4a6eNzboXd3NogpaqDs4slHmGKKUWQ/2ILNPAg0sVLJZdXL3VQtsP424SHUPRMXF2ocS9zyn1GOrHNFOy8XPFGWw3fVzfbaPL1aip4toGTs8VsVRxIcJ99in9GOoTICJYqrpYrDjYani4ttvheHvCOZbg1GwJy1UXBo85pAw5NNRF5CsA/gOATVV9YnjbPID/BeAsgKsAfl1Vd6fXzHQQESzXClisuNhodHFzrwM/YAlkktim4ORsESdqBYY5ZdIos0F/CuCT77vtCwC+q6oPA/ju8O80ZBiC1ZkinrxvDvcvlHguagJYpuD0XBFP3jeLk7NFBjpllqge3pMUkbMAvn1HT/01AB9X1TURWQXwd6r6yAjfR0d5vKwJwj7W9rvYbHTZc4+YbQqWqwWszhZyW9EiIsjj+y5LROSSqp4b5b5HHVNfUdU1ABgG+/IRv0/qhH2FH/Thh330wj76qsDgfxAM/s8QgW0acC0DtmnAMg3cN1/C6bkidlo+Nuoe9jvcdmCaakULK7UC5ksOe+WUK1OfKBWRZwE8O+3HmTQvCNH2QjS9AG0/RNsP0AsV4RFO0TANgWMZKNomyq6J1ZkCTs8VsdfuYbPR5dYDE2Kbgwnr5WqBR8pRbh011DdEZPWO4ZfNg+6oqs8DeB4YDL8c8fGmrhf2sdv2sdfuodHtTXSYJOwrOn6Ijh9ip/Xu7Y4lqLoWIEC3F6Lts2LmKKqFQa98ocxeOdFRQ/1bAJ4B8KXh79+cWIsi1PFD3Gp52Gv30PQCRD3s6AeKnWAwDCMyOEkn7A+GdFQZTvfi2gbmSw6Way5KDitziW4bpaTxLwB8HMCiiFwH8PsYhPnXROQ8gLcBfHqajZykfl9xq+Vjs9FFvRPE3Zx3qOKO2naBaxnDjaQUTS+M/AdO0ogAFdfCXNnBXMlmkBMdYKTql4k9WIzVL91eiI16F1sNL1Vj2I4lmCs5cG0DHT/EXruXqvYfh20KZks2ZksOZos2rJxWrxwXq1/SL4rql9TwghA3djvYbHip7O36gWKj7sEQYLlWwIdPzcAP+9hr97Df6aHth0eavE0i0xCUHBO1go3Zso2qa3HpPtGYMttT74V93NzrYH2/i4xkHoBB8J2ovbfuuuOHaPkBWl6AlvdupU6SWeYgwCuuhZJjoeJaKNgGQ3wK2FNPv3F66pkLdVXF2n4X13c7menB3s3tFZInaoW7BuGgmiYcBL0fwA8GdfVRL36yzUE5p2MZKDsWSo6JsmvxWLgIMdTTL7eh3vYDvLnZQtNLzgTotFULFh5cqoxcl62qw4VTit4w6L3h771Q0Qv7GKyn0uHveCcQRASCwaSlQCAyODjENgeLrRzLgGMasK3BbY7JnncSMNTTL3eh3u8rbux1cGOvk8px8+MyBDg1V8Sp2SJDlH4GQz39cjVR2u2F+MlGAy0vv4dU9BW4ttPBbquHh1cqHNogyrFU14jttX28fGM/14F+p6YX4JUb+9hvc18ZorxKbajf2Ovg1fUGgoRXeUStFyour9dxc68Td1OIKAapG37p9xVvbDVxq+nH3ZTEUgXeutVG2w/wwGKF+6EQ5UiqeuphX/HqeoOBPqKtho/XNhqZLu0kovdKTU89CPt4db2BRjc/5YqTsNfu4fJaHY+t1mCyxz6SXthH2w/R7yv6qujroIzTEIEx3HitaJusNKJESkWoM9CPp9ENGOwH8IIQLe/dRVotLxzp0HBDgLJrvbsq1rVQsk0OdVHsEl+n3u8rfrxWZ6BPQK1o4bETtdwHT9hXbDc9bNS7E62cskzBYsXFSsK2A2adevplavHR6xsNbHMMfWKWqi4eWq7E3YxYtLwAG/Uutpv+1OcZqgULyzUXi2U39h+iDPX0y8zio2s7bQb6hG01PBQdE6dmi3E3JTL77R7e3mlHun1Eoxug0Q3wltnGSnVwfGHc4U75kNhQ3256uL7LWutpuLbTRtE2MV924m7KVAVhH2/ttLFZ92Jsw2ALi1stDw8sVTBTtGNrC+VDIksaW16ANzebcTcjs1SBNzabaPvZnafYafn4wfW9WAP9Tt1eHz++WcebW00EIc+ipelJXKj3+4o3NpuZ2gM9icLhv3PWxlr9oI/XNxp4bb0R+TbDo9ise/jB9X3stjisSNORuFC/tttG2+deLlFoeWGmhrg6foiXb+wnfh7GDwYlutd323E3hTIoUaFe7/awtt+Nuxm5cmOvg0Y3/RuANbo9/Ojm/kg15klxbaeDn2634m4GZUxiQj3sK97cbOZyP/Q4qQJvbrXQT/F4V73bw+W1RuKP8Lub9f0u3uD8EU1QYkL95l4H3V56ellZ0vFD3NxP5zBM0wvw2nq697fZani4ssVgp8lIRKh7QcitYmN2c6+bqqELYHBAyqtr9Uxsv7xR93Bth2PsdHyJCPXrux1Wu8QsHB4JmBaqg+qdNA65HOTGXgf7nfTPb1C8Yg/1th9gq5GMWuK826h30UlJ5dHN/W7m9gMazG80Uz2URPGLPdTf3mlzcjQhVAclpUnX8gJcz+hQhdfr4+otVsTQ0cUa6h0/xG6LHzeTZKflo9tLbm89D4vTNuseFyfRkcUa6ht11qQnjSoSs7T+bm7sdXKxOO3KNrcToKOJLdTDvmKrmdzwyLPNRjeRdetB2M/N4jQ/UGxwromOILZQ32p4mShFy6JeODhEImk2G16uJhE36t3M7c1D0xdbqHPoJdk2EjYEo6pYz9lrxuv1scOxdRpTLKHe8cNcjIumWdMLEjVhutfuwcvhiuO8/SCj44sl1Hfa7H2kwW6CrlNextLfr94JMr3vPU1eLKHOcq10SMpH/24vzPVKy6QNhVGyRR7qftCP9KxIOrpGN0AvAWV19RwHOsDnT+OJPNT3Oj5XkKaE6mAsO2557wR0emGuqn7oeCIP9azt15F1SQjUlpecCds4qAItjqvTiCIP9VYCQoJGF/f16veVE4UAmuwM0YgiD3WWMqZLywtiXQDT7oWZ3udlVHH/cKX0iDbURTienjJ9jfcHMcNsIAnDYJQOEYd67Dv90hHEGaxxn8Z08eJFPP30Z/CJT/wCnn76M7h48WIs7cjSYSA0XVakjyYS6cPRZHgxBms/xo92Fy9exHPPfRnd7qBOfH19A88992UAwFNPPRVpW+L8d6B0ibTrLGCop1G8oR7bQ+PChRfeCfTbul0PFy68EHlbVJHInTMpeSIfU6f0ScICpDhsbGyMdTtREjDU6VBxjmsbMb5kVlZWxrp9mkQAI85/DEqNY4W6iFwVkZdF5CUReXGErzjOw1FM4uypGzF2BM6f/ywKBfc9txUKLs6f/2zkbYnz34HSZRITpb+gqtuj3TV7L8yLFy/iwoUXsLGxgZWVFZw//9nIJ9GmLYhxLNcy43vN3L6OSbi+JnvpNKJoq18yJknVEdMUZ+FFyYn3JfrUU08l4lpWXL5VaTTHHVNXAH8jIpdE5NlJNChNklQdMW1xrSqtuBanYgCUXTPuJlBKHPfH/8dU9aaILAP4joi8qqp/f+cdhmE/CHzTPubDJQurI6bPNAQF20Qn59tLsKdOozpWT11Vbw5/3wTwDQAfvct9nlfVc6p6ToxsvTCTVB0xTSKAxNhdrrCXijJDnUZ05FAXkbKIVG//GcAvAXjl3l+VrcUTSaqOmKa4Ky8qbrY+4Y3LtQ3YJrfYoNEc58f/CoBvDHtwFoA/V9X/M5FWpUSSqiOmyY6xAgUAKoV891JrOX/+NB6JcgLMsAv6j6/eiOzxaDKqBQtPnJqJtQ0/vL6X28MyPnSyhpni0T+tiEis2yfT8YnIJVU9N8p9I/5MxxdWGrlW/B/9T9QKcTchFiXHPFagU/5E+m5lbyGdkjCeu1hxYx8GisOJmXz+MKOji/bdylBPJScBPXXDECxX8xVwlilYrLiH35HoDhGHej53+0u7csyrOm9brrm5Woi0XHW5PQCNjaFOh0rKasaCbWKx4sTdjEiYhmAlp/MIdDyRf65Owkd5Gl3BNmAlYEz9tjMLZThW9nuv98+XULCT8cOU0iXydyuXO6dL0q6XbRp4YLESdzOmaqZoc4KUjiz6UOdCilRJ4vL0ubKD5Vo2JxAtU/DgcjnuZlCKRR7qrLlNl6Rer7MLZbh2coaFJuXsQhmuxWEXOrpYhl84rp4OBdtIZE8dGEwkPrRcyVQ1zELFwVI1m59AKDqxpOt8OR8VDGk3V0r2daoV7MwE+0zRxkNL2Z4roGjEEupzpWR+pKf3mkvBD9/FiosHltI9Bl0tWHjkRJUHS9NExBLqM0U71rMn6XC2KanZHXC5Wkhtj32maOOx1RoXGdHExBLqIoKFFPQC82yx4sZ6MMa4lqouHlmppiocFyoOHj2RrjZT8sU2Y8k63OQSSef1mSs7+NDJGkpOsqtHDAHumy/i4eUKh1xo4mIL9ZJjJbZcLu9mS3ZqVzNWXAsfPjWD03NFJDEvqwULHz49g9NzpVR9EqL0iHXQ9MRMAfudXpxNoLtI+97lhiG4b76EhYqDK1stNLpB3E2CaQjumy/iRK3AMKepijXU50o2XNuA1+NGX0lRdEzMJryUcVQlx8LjJ2tY2+/ixl4HQRjP1s+zJRsfWCyn9tMPpUusoS4iOD1XxJubrTibQXc4PVeMuwkTJSI4OTvoIW+3PGzWvUh67vZwL/SVWgHFhI/xU7bEXrO2VHGxvt/N7fmTSVJxrcweynD7kI3lagEtL8BGvYvtpo+wP9nee7VgYaVWwELZ4SQoxSL2UBcR3D9fwuW1RtxNyb37F0pxNyESZdfCA0sVnFlQ1Ds9tPwALS9Eyw/GGgo0DUHJMVF2LZQdE9WCzV45xS72UAeA2ZKDmaLNSdMYzZXt3FUjmYZgruy8Z+VsL+yj7YVo9wKEfYUq0FeFQCAy6PE7poGKa6FgG5z0pMRJRKgDwJmFEl6+sc9jTGNgCHBmPt1L7SfFNg3MlAzMIF8/4Cg7ErNdYtm1cGo2W5N0aXF6vsRhA6KMSEyoA4PKi6SdtJN11YKFkylcPUpEd5eoUBcZ7JHNooFovLsnOf/BibIiUaEODBa/5KUKI2483JgoexIX6gCwOlPEYiUbqxqTaqnqpHLTLiK6t0SGOgA8uFTh+PqUVAsWHljkKTtEWZTYUDcMwSMnqjzPdMJc2+ApO0QZlujEdCyDhwhMkGUKHj1RhW0m+rIT0TEk/t1ddi08slJlRcwxmYbggytVlBwOaRFlWeJDHQBmSjYePVFjsB+RORzKyts2AER5lIpQB4bBzgN6x2aZgkdXGehEeZGaUAdun7xehW0y2Edhm4LHVmuoFRjoRHmRqlAHgGrBxhOnZlB2uWjmXiquhSdOzbAslChnUhfqAFCwTTx+coYLlA6wVHXw+MkaV4sS5VBqu3GmIXh4pYqy28HbO21u2QtAZLCF8eoMd7skyqvUhvptJ2eLKLsWrmw10c3xAdZFx8QDS2WOnxPlXOpDHRhMoP786Vlc221jbb+bq167CHBypojTc0WuEiWibIQ6MNhW4MxCGQsVF29uNtH2s3+Qddk18eBSBWVOhhLRUObSoOJa+LnTM9ioe7ix14YfZK/b7lgGTs8VsVx1uRc6Eb1H5kIdGBy2cWKmgKWqi/V6F2t7HfTC9Ie7bQpOzhZxolbgUAsR3VUmQ/020xCcmi1ipepibb+LzUY3lT13xxKs1ApYnSlyRS0R3VOmQ/02yzRw33wJp2aL2Gn72Kh3Ue8EcTfrUDNFGys1F/Nlh8MsRDSSY4W6iHwSwH8DYAJ4QVW/NJFWTYlhCBYrLhYrLjp+iM1GF7daPrwElUIWbAMLZRfLNZeLh4hobKJHrP8TERPATwD8OwDXAfwzgKdV9cf3+Bo96uNNU9sPsNvuYbflo+kFkZZEigxOIporOZgrOSg6DHKaLBFBEt93NDoRuaSq50a573F66h8F8IaqXhk+6P8E8CkAB4Z6UpUcCyXHwqnZIoKwj0Y3QMsP0PJCtPxgoj151zZQcS2UHBNlx0K1YMHioRVENCHHCfVTAK7d8ffrAP7l8ZoTP8s0MFd2MFd+d1+ZXthH2w/RC/uDX4HCD0P4gaI/7AGpDnrdwGCC1jYNOKYB2xr+2TJQsk0GOBFN1XFC/W4zdz/zGU9EngXw7PCvnoi8cozHTLJFANtxN2KK+PzSa1FEsvrcgIxfOwye25lRv+A4oX4dwH13/P00gJvvv5OqPg/geQAQkRdHHRdKmyw/N4DPL82y/NyAbD+/ozy344wF/DOAh0XkAyLiAPgMgG8d4/sREdExHbmnrqqBiHwOwF9jUNL4FVX90cRaRkREYztWnbqq/hWAvxrjS54/zuMlXJafG8Dnl2ZZfm5Atp/f2M/tyHXqRESUPKyvIyLKkEhCXUQ+KSKvicgbIvKFKB4zSiJyVUReFpGXROTFuNtzXCLyFRHZvLP8VETmReQ7IvL68Pe5ONt4VAc8ty+KyI3h9XtJRH45zjYelYjcJyJ/KyKXReRHIvL54e1ZuXYHPb+sXL+CiPyTiPxg+Pz+YHj7WNdv6sMvR9lOIG1E5CqAc6qaiVpZEfm3AJoA/oeqPjG87b8A2FHVLw1/MM+p6u/G2c6jOOC5fRFAU1W/HGfbjktEVgGsqur3RaQK4BKAXwHwH5GNa3fQ8/t1ZOP6CYCyqjZFxAbwDwA+D+DXMMb1i6Kn/s52AqrqA7i9nQAllKr+PYCd9938KQBfHf75qxi8mVLngOeWCaq6pqrfH/65AeAyBiu/s3LtDnp+maADzeFf7eEvxZjXL4pQv9t2Apm5EEMK4G9E5NJwBW0WrajqGjB4cwFYjrk9k/Y5EfnhcHgmlcMTdxKRswA+AuB7yOC1e9/zAzJy/UTEFJGXAGwC+I6qjn39ogj1kbYTSLmPqeq/APDvAfzW8CM+pccfA3gQwJMA1gA8F2trjklEKgC+DuC3VbUed3sm7S7PLzPXT1VDVX0SgxX6HxWRJ8b9HlGE+kjbCaSZqt4c/r4J4BsYDDllzcZwTPP22OZmzO2ZGFXdGL6Z+gD+BCm+fsOx2K8D+DNV/cvhzZm5dnd7flm6frep6h6AvwPwSYx5/aII9UxvJyAi5eGkDUSkDOCXAGRx07JvAXhm+OdnAHwzxrZM1O03zNCvIqXXbzjRdgHAZVX9wzv+Uyau3UHPL0PXb0lEZod/LgJ4CsCrGPP6RbL4aFhi9F/x7nYC/3nqDxoREXkAg945MFih++dpf34i8hcAPo7BDnEbAH4fwP8G8DUA9wN4G8CnVTV1E44HPLePY/DRXQFcBfCbt8cw00RE/g2A/wvgZQC3DwH4PQzGnbNw7Q56fk8jG9fv5zCYCDUx6HB/TVX/k4gsYIzrxxWlREQZwhWlREQZwlAnIsoQhjoRUYYw1ImIMoShTkSUIQx1IqIMYagTEWUIQ52IKEP+P/AR+xGWHSWzAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# Print variable values\n",
"print(\"Name\\tValue\")\n",
"for c in model.component_data_objects(pyo.Var):\n",
" print(c.name,\"\\t\", pyo.value(c))\n",
"\n",
"# Plot solution\n",
"plot_circles(model)"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.3 Solve and Inspect the Solution](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.3-Solve-and-Inspect-the-Solution)",
"section": "4.1.3.3 Solve and Inspect the Solution"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"left_x_con[A] \t 10.0 \t 9.99999990193744 \t None\n",
"left_x_con[B] \t 5.0 \t 4.999999953543133 \t None\n",
"left_x_con[C] \t 3.0 \t 15.734851787229463 \t None\n",
"left_y_con[A] \t 10.0 \t 19.142135514931184 \t None\n",
"left_y_con[B] \t 5.0 \t 4.999999951252124 \t None\n",
"left_y_con[C] \t 3.0 \t 5.517617033892999 \t None\n",
"right_x_con[A] \t None \t 9.874784367980283e-08 \t 0.0\n",
"right_x_con[B] \t None \t -9.999999849646462 \t 0.0\n",
"right_x_con[C] \t None \t -1.2651480159601327 \t 0.0\n",
"right_y_con[A] \t None \t 9.87471615587765e-08 \t 0.0\n",
"right_y_con[B] \t None \t -19.142135464931897 \t 0.0\n",
"right_y_con[C] \t None \t -20.624518382291022 \t 0.0\n",
"no_overlap_con[A,B] \t 225.0 \t 224.99999778541908 \t None\n",
"no_overlap_con[A,C] \t 169.0 \t 218.51602998638847 \t None\n",
"no_overlap_con[B,C] \t 64.0 \t 115.5049713354404 \t None\n"
]
}
],
"source": [
"# Print constraints\n",
"for c in model.component_data_objects(pyo.Constraint):\n",
" print(c.name,\"\\t\", pyo.value(c.lower),\"\\t\", pyo.value(c.body),\"\\t\", pyo.value(c.upper))"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.4 Reinitialize and Resolve](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.4-Reinitialize-and-Resolve)",
"section": "4.1.3.4 Reinitialize and Resolve"
}
},
"source": [
"### 4.1.3.4 Reinitialize and Resolve"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.4 Reinitialize and Resolve](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.4-Reinitialize-and-Resolve)",
"section": "4.1.3.4 Reinitialize and Resolve"
}
},
"source": [
"Reinitialize the model, plot the initial point, resolve, and plot the solution. Is there more than one solution?"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.4 Reinitialize and Resolve](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.4-Reinitialize-and-Resolve)",
"section": "4.1.3.4 Reinitialize and Resolve"
}
},
"outputs": [],
"source": [
"# Initialize and print the model\n",
"initialize_circle_model(model)"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.4 Reinitialize and Resolve](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.4-Reinitialize-and-Resolve)",
"section": "4.1.3.4 Reinitialize and Resolve"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXAAAAFlCAYAAADyArMXAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAAAs7ElEQVR4nO3dWYxk130e8O9/t9p7n+nZSA5FkLRlJZFFwhKgIKAdOXDoB9kPls0HR0Fo0A9WYAN+iOEXCwkMGIFo5yUwQpuCFcB2LMByLMREElGQouTBhElB0EZxn+EsvU0vtd79njxU9UxPs7tru1V3+35Ao3uqq7tO9VR9dep/NlFKgYiIskdLugFERDQZBjgRUUYxwImIMooBTkSUUQxwIqKMYoATEWWUMc8bW1tbU1evXp3nTRIRZd5rr712Ryl17vjlcw3wq1ev4tVXX53nTRIRZZ6IXD/pcpZQiIgyigFORJRRDHAiooxigBMRZRQDnIgooxjgREQZxQAnIsqooQEuIg+IyDdE5HUR+YGI/Obg8s+LyC0R+c7g4+nZN5eIiA6NspAnAPDbSqlvi0gDwGsi8rXB9/5IKfWF2TWPiIhOMzTAlVIbADYGX7dF5HUAl2fdMCIiOttYS+lF5CqAnwTwCoBPAviciPwrAK+i30vfP+FnngPwHADoug4RmbbNRESZ9dBDD+HatWux/C4Z9UxMEakD+D8Afl8p9RURWQdwB4AC8B8AXFRK/Zshv0PxDE4iKjIRwbg5KCKvKaWePH75SD1wETEB/DWAP1dKfQUAlFJbR77/JwD+x1gtIiowpRT8UMEPIwShQqQU1ODy/meg/xUgEIgAgv6TXwBomsDSNZi6wNA5mayohga49GseLwJ4XSn1h0cuvziojwPALwL4/myaSJQdSim4QQQ/jOCHCt7gay8cXBYoeGEIP1SI682orglMXWDqGixDgzkIdsvQBiGv3f0e5csoPfBPAvhVAN8Tke8MLvtdAM+IyEfRL6FcA/DrM2gfUWqFkULPC9B1Q3S9AF03gO2FiOZcJQwjhTBScPzozOuZuqBqGaiVdNRKBmqWgYqlz6mVNAsj18BjuTHWwCmjgjBC1wsHgd0PbdsPY+tFJ0XXBFVLR71koFrqf66YnGwwS3OvgRMVjRdEOLA9NHs+Om4wtHebVWGk0HYCtJ3g7mWaALWSgXrJwHLVwkLFYKCnFAOcaKDrBtjveTgYhHbWe9eTihTuhvpG04GhCxYrJpaqJpYqFmvpKcIAp8KKIoWm7WO/52G/58ML8tnLnlYQKux2POx2PIh0US8ZWKqaWK5aqJUYIUniX58KxQ1C7Hf9u+WReQ84Zp060ju/sWfDMjQsD8J8sWJC01hqmScGOOWeUgp7XQ9bLRdN20+6ObniBRG2Wi62Wi4MXbBWL2F9oYSqxWiZB/6VKbccP8RO28V224EXsKs9a0GosNl0sNl00CgbWF8oY7VmsVc+QwxwyhWlFPZ7PrbbDg56fmEHIpPWL7N0cP1ur7zMOeczwACnXHCDENstF9ttl4ORKeKHChtNBxtNBwuVfq98pcpeeVwY4JRpTdvHZtPBfs9jbzvlWnaAlt2BqQvON8q4sFjmlMQpMcApk9qOjxt7NgclM8gPFW4d2Nho2riwWMalpQpMbsg1EQY4ZUrXDXBjv4f9LoM76yIF3D5wsN12cWGhjIuLZe6sOCYGOGWC7YW4ud/DnY6XdFMoZkGocHPfxlbLwcWlCi4ulFkjHxEDnFLN8UPcOrCx03ZZ4845P1R4f7eHzaaNy0tVnG+UGORDMMAplbwgwq0DG9sth6slC8YLFN6708Xtpo0ryxWcq5e4mdYpGOCUKlF0OMDlIGRyF5rrR3hnu4vbBw4eXq1hsWom3aTUYYBTarQdH+/sdGF7YdJNoRSxvRA/3GjhXKOEq6tVDnQewQCnxIWRwo29HjZbDuvcdKqdtoum7eHqag2r9VLSzUkFBjglqtnz8c6dDtycHphA8fIChTe3Oljt9oO86AuBGOCUiCCMcG23h522m3RTKIN2Ox5ato8HV6s43ygn3ZzEMMBp7va6Ht670+EOgTQVP1R4Z7uL3Y6Hh9dqKJvF2yyLAU5z4wURru32n3BEcTno+fjuzSYeXKniwmKxeuMMcJqLg56Ht7c78EP2uil+YdSfO77bdfHYeqMwe6sU415Som4d2PjRZpvhTTPXsgN892YTHTdIuilzwQCnmQkjhTe32nh/t8fpgTQ3XhDhB7ea2G47STdl5lhCoZlw/BBvbLbR46IcSkCkgHe2u+i6Ia6uVnO7FJ8BTrE76Hl4a7uDgCUTSthm00HPC/Do+UYu54zn7x5Rom7u9/CjzTbDm1KjZQf43q0m2k7+9pBngFMsDuvdN/Zs1rspdbwgwg9vt7DdylddnCUUmhrr3ZQFkQLe2emi4wZ4eK2Wi7o4A5ym0nZ8vMEpgpQhWy0Xjh/h8QsN6Bk/MIIlFJpY0/bx+gbDm7Kn/9htIQizvYkaA5wmst/18KONFg9doMxqOwF+uNGCn+EQZ4DT2O50XLyx1eZRZ5R5XTfED2634AbZHL9hgNNYttsO3t7ucKYJ5Ybt9UPc8bMX4gxwGtl228G7O12GN+WO60f44Ub2QpwBTiNheFPeZTHEGeA01E7bZXhTIbh+hNc3slMTZ4DTmXbaLt7ZYc2bisPx+6s2sxDiDHA6VbPnM7ypkBw/whub7dRPk2WA04lsL8Sb222GNxVW1w3x1nYbKsVPAgY4fYAfRvjRZos7ClLh7Xd9vL/XS7oZp2KA032U6u8q6PjZXZ1GFKfbB05qdzFkgNN93r3TRcsuxnmCRKN6904XTTt9+4kzwOmu2wc2tltu0s0gSh2lgLe22qmbI84AJwD9zanSXOsjSpofqsFpU+kpLzLACV03wFvc34RoKNsL8eZWJzUzUxjgBecFEd7YSv98V6K0aNo+3rvTTboZABjghXY448TljBOisWy1XGylYGYKA7zAbh3YaDuccUI0ieu7vcQHNRngBdV1A9zct5NuBlFmhZEa7I2fXPmRAV5A0d0HXtItIcq2thPgdjO5UgoDvIBu7tvoeemaz0qUVTf3eui6yZQiGeAF03J83G6ydEIUl0gB7+x0ECUwk2togIvIAyLyDRF5XUR+ICK/Obh8RUS+JiJvDT4vz765NI0wUniHpROi2HXdMJExpVF64AGA31ZK/TiATwD4DRH5MIDfAfB1pdSjAL4++Del2PXdLjepIpqR200bbWe++6UMDXCl1IZS6tuDr9sAXgdwGcCnAXxpcLUvAfiFGbWRYnDQ87DFfU6IZkYp4O3tzlwXxY1VAxeRqwB+EsArANaVUhtAP+QBnI+9dRSLIIzwzk46Vo4R5ZnjR3PdU2jkABeROoC/BvBbSqnWGD/3nIi8KiKvTtJAmt613R68gKUTonnYbDpo9uZTShkpwEXERD+8/1wp9ZXBxVsicnHw/YsAtk/6WaXUC0qpJ5VST8bRYBpPxw2w02bphGieru1257LAZ5RZKALgRQCvK6X+8Mi3vgrgs4OvPwvgb+NvHk3r+i5LJ0Tz1vNC7HRm33EapQf+SQC/CuBnROQ7g4+nAfwBgJ8VkbcA/Ozg35Qi+12Pp+sQJeTGnj3zueHGsCsopf4fADnl2/883uZQXJRSPKCBKEFeEOF208aV5erMboMrMXNqp+1yuTxRwjaaDvwZnuDDAM+hMFK4sc/eN1HSglDNdIUmAzyHbh/Y8AKulydKg62WM7N9wxngOeMFETYS3N6SiO6nFGY2HsUAz5mb+z2eb0mUMrsdbyb7pDDAc8T2Qmxz0Q5RKl3fjb8XzgDPkRv7PW4VS5RSbSfAfteL9XcywHPC8UPsxfzgIKJ4xT0+xQDPie2Wy943Uco1bR9ilGL7fQzwHIgihe02Z54QZYHeWI3tdzHAc+BO14UfsvtNlAV6bRlBTKszGeA5sNXkzBOizBAttp0KGeAZ13J8dFzuOEiUJXEdb8gAz7gtrrokyhzbC3HQm37WGAM8w7wgwi6nDhJl0mZr+s4XAzzDtloOpw4SZdRBz596kysGeEZx6iBRtinVPwB5GgzwjNrredwylijjdjruVJvPMcAz6s4cDkwlotkKQjXVYCYDPIPCSKHZi39rSiKav30GeLEc9Dxwy2+ifDjo+VATzkZggGfQNK/YRJQufqjQsidbjMcAzxilFA5YPiHKlb0JO2UM8Ixp2QE3riLKmUnfVTPAM2bSV2oiSi/Xjyba04gBnjGsfxPl0yTHrTHAM6TjBnD9ePYRJqJ0meRIRAZ4hsR9ICoRpUfPC8feG4UBniEsnxDl27jPcQZ4RrhBiK473c5lRJRu+93xpggzwDOi4/DUHaK867jBWKsyGeAZwd43Uf6FkYIzxkQFBnhGtF2uviQqgnGe6wzwjOh57IETFcE477YZ4BlgeyECLp8nKoTuGCsyGeAZMMkSWyLKpu4YA5kM8AwY5xWZiLItUqOXTBngGcAeOFGxjNppY4CnnFKKA5hEBTNqp40BnnI9L5zq1Goiyh4GeE6w/k1UPD0vRDRCx40BnnJdlk+ICkcpoDfCzoQM8JRzAwY4URG5DPDs8wPWv4mKaJSzbxngKeeF7IETFZEXDN/UigGeYkopnkBPVFBeyADPNC+MMMbWwESUI+yBZxx730TF5bMHnm2jvAITUT6xhJJxo7wCE1E+BaEaupiHAZ5i7IETFduwXjgDPMVGeQtFRPnFAM8w9sCJim1YBjDAU4w1cKJiG5YBQwNcRL4oItsi8v0jl31eRG6JyHcGH0/H0FY6htvIEhXbsAwYpQf+ZwB+7oTL/0gp9dHBx0sTtI2GYHwTFduwhXxDA1wp9S0AezG1h8bAVZhEdJZpauCfE5HvDkosy7G1iI5gghfVyy+/jGee+RX8zM/8NJ555lfw8ssvJ90kSkA0pBc3aYD/MYBHAHwUwAaA50+7oog8JyKvisirE95WYbEEXkwvv/wynn/+C9jc3IJSwObmFp5//gsM8QKauoRy8i9VW0qpUCkVAfgTAD91xnVfUEo9qZR6cpLbKjKWUIrpxRf/FI7j3neZ47h48cU/TahFlJRhETBRgIvIxSP//EUA3z/tukQ0nq2trbEup+Iyhl1BRP4SwFMA1kTkJoDfA/CUiHwU/ReIawB+fXZNLC6RpFtASVhfX8fm5gfDen19PYHWUJKGRcDQAFdKPXPCxS9O1hwaB/O7mJ599tfw/PNfuK+MUi6X8Oyzv5ZgqygJwzpxQwOckiMi4EyU4vnUpz4FoF8L39rawvr6Op599tfuXk7FIUO6cQzwFIu7hBJFCn4UIQgVgkghCKP+50hBKfWBQVMRQBeBoQt0TYOpCwxNg6ELDE0GLzA0C5/61KcY2MQeeJZNE49+GMHxw8FHBNsPEcS4t4qIoGRoKJv64KP/tcZQJ4oNAzzDxgnDIIrQcQJ03AA9L96wPolS6u4LxF2DUK+XDDTKBiqmzl460RSGZQADPMVMXQMQnvp9xw/RcQO0nQC2HyY/cVwpuH4I1w+x23Gha/0wr5cN1EsGdI1hTjSOfgacjgGeYpbxwf+8MFJo2j72ex5c//RwT4MwitC0PTRtDyKChbKJ5ZqJqsWHHdEoTsqAo/hMSjHryKuv7YXY73lo2f7Q/RHSSCl1N8xLpo6liomlqsVeOdEZLPbAs8syNLQcH3fa7v215oxz/RBbfojttouliom1RmnoW0WiImIPPKOaPR9vb7dxc6+XdFNmRimF/Z6HA9vHctXCWsOCoTHIiQBA12ToO1QGeMq0HB839npo2UFhzsRUSmGv6+Kg52GlZmG1XmJphQpvWO8bYICnhhdEuLbbxW7Hu3uZrhcrxCKlcKfjYq/nYX2hjOWqlXSTiBJjjvD8Z4CnwHbLwfW9HoLw/sHJYQMYeRVFChsHNlq2j4uLlZF6IkR5U2IPPN0cP8S7O100bf+Ua/SXsR8P9qLougHe3engXKOElZrFRUFUKJauD70OAzwhm00H7+/1hp46bWgagjA/M1DGFSmFrZaDlhPg8hJ741QcpjG8w8Jnw5xFkcLb2228d6c7NLwBwChYHfw0thfg3TsdtJ3T3q0Q5csoJVQG+Bw5fojv325ip+0Nv/IA50ffE0UKN/Z62Gm7w69MlHGchZIizZ6Pt7bb8MesZ5fN4XWwotlpO3D8EJeXKtA43ZBySAQjbTnB7t0cbDRtvL7ZGju8AQb4adqOj3fvdAszV56KpWLqI62FYIDP2I29Hq7d6U28UWDZ0Hg25im8IMS13S7coLiDvJRPtdJoxREG+Axdu9PFzX17qt8hIigb7IWfJggjXLvTy9VeMUR1Bniyrt3pYqPpxPK7yhYD/Cxh1F/FyhCnvKiVRnvOM8BnIM7wBvr1MDpbFClc32VPnLJPBKiNuGc+Azxmtw7sWMMb4EDmqMIowvt7PfgzPk6OaJaqlj7y7CoGeIz2uh7e341/+9eyqXG63IiCsB/i0QiLpIjSaNT6N8AAj03XDfD2dmdGv11G2tiG+lw/xK0DGyqDJxcRMcDnzAsi/GizPdLS+EmxDj6etuNjmys2KYNGnUIIMMCnFkUKb2y2Z76gpMKZKGPb7fQPiSDKCk36NfCRrz/DthTCjf0eOm4w89thgE9ms+lwtSZlRq1kjLVtMgN8Ci3Hj33GyWksXedWqhOIlGI9nDJjqWqOdX0mwoTCSOHt7c7ES+Qn0Shz77FJ2F6A3S5LKZR+K7XxjhFkgE/o+m4Xrj/ft+aN8nivznTPTtvlIh9KtbKpjbQD4VEM8Akc9DxsteY/w6Fq6TzgYUKKpRRKuXF73wADfGxKKbx3p5vQrQvq7IVPzPVD7Pd4og+l0zIDfPa2Wi6cOZdOjloYY44ofdBO253pfH2iSZi6oDHBc5sBPoYwUri5H/9S+XHUSgaX1U8hjCLsdrjAh9JluWaNNX3wEAN8DLcP7IlO1YmTiIy11JY+aLfrccMrSpWV6vjlE4ABPjI3CHH7YLrDGeLC6YTTUUpxmT2lhq4JFiuTjW0xwEd0+8BBWkqn9ZIBsIoylabtc4UmpcJS1Zy4LMoAH0EQRthJUY9N17SRN3ynUyiFPS7uoRRYnrB8AjDAR3Kn46Vu5sLChG+56J4D2+O+4ZQoTYDlMZfP3/fzMbYltzZb89nvZByLFRM6Z6NMJYoUDmzOC6fkrDVKMPTJY5gBPsRBz4PtpW8JtiaTD3zQPfvcbpYSdGGhPNXPM8CHSGPv+9BKffLaGfW5fjiX7YCJjmuUjbEObzgJA/wMfhjhIMVLry1dR51TCqfWYhmFEnBhcbreN8AAP9N+z5vrdrGTmGQDHLpfxw24yRXNlWVoWI3hucsAP8N+N/09s3rJ5EEPUwrCCDa3mqU5Wl8oTbR0/jg+808RRQrNjLy1Zi98em2HdXCaExXhfGP68gnAAD/Vge2nbu73aRYrk6/kor62k40Xa8q+0G7G9q6ZAX6KLE0v0zUNS5xSOBUviHhiD81F2N6N7XcxwE+RtbfULKNMr5fC+f6UL42yAeXFtykeA/wEQRilcvHOWSxDn3pOaZYopRBFCuHgI4rU1DNJ2AOnWVufcuHOccV5xo+h62bziXy+UcJ7OVuUEkUKbhjBCwYfYYQgjHBWVBuaBsvQYOkaSkb/61G2HeBMFJqlqqVjLebFdwzwE3S8bIZgxTKwWDEzM3vmJFGk0PUC2H4/sINo/C1fgyhC4EU4enaSoQlMXUPZ1FEvGScGuhtEiJSCFsP0LqLjHlypxjJ18CgG+Am6Ge7FnlsooeX4qV+AdJwbhGg7AXpeiGgGjQ8ihSAKYfshDno+qpaORtlA2dTvXUkpOH6IKrfqpZgtVsyJDi0eZmgNXES+KCLbIvL9I5etiMjXROStwefl2FuWoCzvjWHp+lT7C89TpBTajo/bBzY2mg46bjCT8D5Ood/L32w5uHVgo3lkymiSB1ZTfj24Wp3J7x1lEPPPAPzcsct+B8DXlVKPAvj64N+5oJTK/Ekt5xqlVG81q5TCQc/DzX0bu10PXoLnU/phhP0jbXEyNnhN6XeuYc3sHNuhAa6U+haAvWMXfxrAlwZffwnAL8TbrOR4YZS58sNxuqZhtV5Kuhkncv0QG00HB7Y/l972qBT67wbe2+2gk7EppJRemgBXlmfT+wYmn0a4rpTaAIDB5/OnXVFEnhORV0Xk1Qlva66SPnU+Lqs1a6qN4uMWDY4w22w5ifa4h3H8CO/vdXFr355oAJXoqAuL5fvHWWI282e4UuoFpdSTSqknZ31bcch6+eSQiOD8Qjp64bYf4vaB0x9cTboxQxy+K2jaHt7d6WZ6Rg8ly9AFl5cqM72NSQN8S0QuAsDg83Z8TUqWn+Le4biWKuZMX/2HUUpht+thq+VkpjcbHHkHFoQRbu33cHO/l6pyD2XD5aXKzN8FT/rbvwrgs4OvPwvgb+NpTvLy0gPvS64XrpTCTsfN3CZRCgrHq2gt28f13V5mNjej5JVMberj0kYxdGhURP4SwFMA1kTkJoDfA/AHAL4sIs8CeB/AL82ykfOUtydpvWSiXjZGGph77bVv46WX/g57+3tYWV7B00//PJ544mNj32YUKWy3XThBNmd0RJGCrt8/i8f2Alzb7eKhlWqqxhYonR5cqc5lh9ChAa6UeuaUb/3zmNuSCvmK776Li2W863XPfHF67bVv48tf/it4Xn8Xxr29PXz5y38FAGOFeKQUttoO3Fy9k+lz/RDXdnu4usoQp9Ot1i2szWkWGB+Fx+TxaC1T14eev/fSS393N7wPeZ6Hl176u5FvRymF7Zab+fBWZ7yMe0GI63u9zNT0ab4sQ/DwWm1ut8cAL4jFioWFM/YM39s/PtX/7MuPUyrbZZNxuH6I93d7iHJWbqPpfWitDnOO784Y4MfEvdlMmlxcLMPQT75/K8srY11+XMsJcrObn2D4Y8DxQ2y1nTm0hrLiXKM0k/1OzsIAPya/8d1foXlx8eR5qU8//fOwrPsffJZl4emnf37o7/WCCAe9bM02icN+18v0vjkUn5Kp4eqM9js5CwP8mDTvIRKHRtnE4gmbXT3xxMfwmc/8MlZWVgABVlZW8JnP/PLQAUylFO503DPrxlmjjfGsuH1g527mEo3vkXP1RAa2uW/mMfOsXyXlwkIJPS+Af2yw8YknPjb2tMED20/10vhxCQT6GGW0IIyw2XRweXm2K+4ovS4ulrGY0Jm0+U+rMcV1WnSa6ZqGS6eUUsbh+iFaOVtqPsk7sKbtoZWxBUsUj4ql48GV+ZdODuU/rcZknjLIlze1kjHVQcj90omXo8JJ36QltI2D7GwXQPEQAR45V5vLgp3TMMCPKUIP/ND6QhnWhHuldNwAfg4Da9IAD6MI+11v+BUpNy4vVdAoJ1M6OVSctBqRpWvI8UzC+4gIHlyuTBRa7ZzumW1M0Zva7/m5XAhGH7RcM3ElBeMeDPBjRKRQvXDL0Psbzo+RW44f5mrg8qhpZiEFYYRWTl/Y6J5aScej5xupWDNSnKQaQ61gh9rWSsap88NPktfeN9CfzzuNPZZRcs0yBI+tN1Iz3ZgBfoJ6uVgBDgDLVWukQc0gjNDz8hrgAkufbv902wtg81zNXNIEeGy9kege+8cxwE9QL1gP/NCFxfLQF6+2G+Ru5skhUxfE0bHa67EXnkePnK8nPmh5HAP8BLVSel5h50twZbmK0ik9DKVUrg/8tYx4/t9bts/VmTlzZbkyty1ix8EAP4GhayhPWQvNKk0ED6xUTtz0yg8VwhzPsijFNHitlGIZJUfW6hYeSHCxzlmKmVIjSNtbpXmydB0PLFc/MJ3SzflWseUYZx/ld5ygWBplA4+cqyfdjFMxwE+xXC1ugANAxTJw6diJ2lk/qOEshqbFOn00L1vrFpllaHhsvZHoSsthGOCnWKpasQxoZdlixcL5Iwez5jnAq1a84x62F3JRT4aZuuDHLzZSvyYk3a1LkK4JFgveCweAtXoJ5xZKiCIFP6eLd4D+pkRxipTK9QtenvXDewHVDMxGY4CfYeWEfbOL6Fy9jIUcv5hpoqEc0wyUozwGeOYchnetlP7wBhjgZ1quWYXZF2WYpYqFpYT2PJ61iqXP5P85z+9Y8sjIWHgDDPAzmbqW2EbtaRNECkvVfIZ4PebyyaGAc8EzI4vhDfBEnqEuLJQLed7jccGgN7lUtSAi2E/BasM333gLr7zy92i1W1hoLODjH/8EHnv80bF+h6lrsde/DwUhAzwLLEPwYxeyF94AA3yopaqJkqnB9Yv9dvhoZ3KxYkLTBLsdN7H2vPnGW/jmN78BP+i/uLbaLXzzm98AgLFCvD7DJ23EWSipVzI1fPjiQqr2NxkHSyhDiAguHJlKV1THDy1ulIxElxa/8srf3w3vQ37g45VX/n7k36FBUC/wgq2iK2c8vAEG+EjON0qp2T4yKXLChuH1koHzjfI4W4nHptVujXX5SWplAwU5QY+OqZV0/MSlxUyHN8AAH4mha1irF3tK4WmzNKqWjvXF8txf4BYaC2NdfpLGjLcN1jiFKZWWayY+fHEh9Yt0RpH9ezAnl5YqhV6ZedZRY2VDx8XFcmybQY3i4x//BEzj/vKHaZj4+Mc/MdLP1ywDlj7b9p60IRgl68pyBY+vN2DM+P9+XvJxL+agbOq4sFjcWrg55AFvaBouLFTmVlN+7PFH8dRTP323x73QWMBTT/30SAOYAsHSHBZpTXO+JsVL1wSPX2jggZVqKo5CiwtnoYzh8lIF2223kNPDRulNigBrNQslQ5vLDJXHHn907GmDANCoGDDn0DvOSy8v6yqWjsfXGzObLpokPsLGYOgaLi8lfxJ1EsapFzZKBi4kUBcfhSaCxcp8xjPmWVKiky3XTHzk0kIuwxtggI/twkJ56oNvs6i/3eroT4Ik6uKjWKyYc5l5oomk7r4XzZXlCn7swkKu3wnl957NiKYJrq7Wkm5GIsbtxcy7Lj6MqWtzO6ijv79K+t6BFIGh36t35x0DfAIrNQvnGsWbVliZYM7sYV18tV5KZL74kZZgrV6a20yiSf5WNL2KpeMjlxaxUivG85ODmBO6ulpD0w4KtWXoNIceNEpGf3Cz7cJNYJe+pYox15JGXmuuaSXSL28+sFJN5djLrLAHPiFD1/DIuWKVUkqGBl2b/CFj6RouLlWwXLXm2hu3dG1uA5cAABEG+BxVLR0/cWkBV9dqhQpvgAE+laWqhfWF5PYDmTcRwVIMBzssVkxcWq6gPIfBYBmUTuZZjl4smzCmeKGj0Yj0Byr/0eXFwh5CzkfZlB5arcV+nmKaLVet09fVj8EcDHCu1kszXXK+XLPmvmR6uVbMMJmnesnAP76yiAdWqqk+dHjWGOBTOlzhZRnFeBBZhoZGjFuwNkoGLi2VZ1JyaJRMLMx4v5PjyqaeibMUs0oT4KHVKj5yORtnVs4aAzwGZVPHo+uNwuyVshzzCL+haVhvlAezROL5I5ZNPZGZCEWZ/ZCEhYqBf/LAEi4tVThFc4ABHpOFsokPnasn3Yy5qJcMlGYwTa5eMnB5uTL1ySimruFcozz380x1TcNCDo+cS5qhCz50rpaL7V/jxvcgMTrXKMHxQ9zct5NuyswtVy1sNuO/n7oIztVLWCyb2Lc92F441s9rouF8o5zIPt/LVZNbyMZI1wQXF8u4uFjO9WrKaTDAY/bAShVeGGG7ldxxY/OwVDGx23FndvK6ZfTLKk4Q4qDnwRnhSDsNgvML1lw2qvrAbWvC8klMNAEuLJZxaakydBfMomOAz8CH1mpQCthp5zfENU1waamC67vdmd5O2dBxYaEC2+8HuXvKwikNgvOLJZTH2K8lThcXK+wlTkmkf/rV5eUKSgn9P2YNA3wGRASPnKtBBLnuiddKBlZqJex1Z38fK6aOymIFPS/Efs+7r+evieD8QnLh3SibWGTte2IiwFrdwpXlKmvcY2KAz0g/xOvQRbDRdJJuzsycXyih6wVw/fFq1ZOqWjqqVgUdN0DT9hFGwPpCKbGd/wxdw8Wl4h70Ma3VuoUryxVOCZwQ/2ozdnWtBkMX3NjL58CmJoJLixW8t9sF1PwOuqiXDCxX+z3fthvO7QXkuIuLZa66HJNIf7rlpaUK6jGuKSgi/vXm4MpyFVXLwNvbHYRR/k7zqVg6ztWtudb8ayUDV5Yr0DUN5wH0vAD7PR8t25vb68hS1SrsEu5JlEwN5xslnG+Uc3GgcBqImmOvSUTUPG8vbWwvxBtb7bGnxmWBUgrX93roucHMb2u1bmF9oQycsCVWGEVo2j72ej68GfbKS6aOh1drhV7GPQqR/pTT9YUSFismF+CgX14dNwdF5DWl1JMfuJwBPl9BGOHtnQ72u37STYldFPVD3PZmE+LaYF7wqDsLdr0AB10PLcePtVduGTqurlY56+QMljHobS+UOKPkGAZ4Dtzc7+HWvo28VVTCSOH6bhdOzL3fkqnj8lJlolkKYRThoOdjv+dNvX+7qWu4ulbj/OQTiABLVRPnG2UsV9nbPg0DPCd6XoB3d7poO7MvO8xTEEW4sWfH0hPvTzErDbaEnT4Qul6AjuOj7YZjl1gsQ8eDK1XWb4/QpD+NcrlmYrlqcRrgCBjgOaKUwmbLwY09O1cDnFGkcGO/h+4UNfGKpePS0uwWdXhhiI4ToO0E6HnBmWWWsqnjwdUqZ5wAsAzBYsXCctXEUtUq3CEK00pNgIvINQBtACGA4KQbOHZ9BvgpHD/EuztdNO381MaVUrjddNDseWP9nKb190NZrVs4aaByFiKl7vbMu66PILz3OK2XTVxZqhR6wLJeMrBUNbFUNTnzZkppC/AnlVJ3Rrw+A3yIg56HG3s2OnOYzTEvLcfHZtNBMGTflMMZC2v1UuIDhLYfwvYCLJRNWIaWu7GKYUxd+qWRqonFqsmByBjFGeCcB54yS1ULS1ULux0XN/dt9HIw5XChbKJmGdhqOTg4qTcu/fu9Vrdg6ekIistLFTy8VoNlaFBKoeeF6HoBum6Irhug54W5KXlZhoZ6yUDV0lErGaiVdAZ2RkzbA38PwD4ABeC/KKVeOOE6zwF4bvDPJ9gDH51SCnc6Hm4d2LmZO95xA2w27f5sEOmfH3muUYKVksCwDMHV1RpW62efdaqUguNH6Lj9+nnX7Qf80dJLGpVNbRDSBmqDwOaMmvlKUwnlklLqtoicB/A1AP9WKfWtM67PEsqEmj0fW20He935rTScFUMXRJFCEKrU1JUPZ7s8tFqdKtAcP4QbRPCCCH5478MLVP9zGM0k5EX6UxwtXYNpyN2vLUODqWswdUHF1BMvTVGKSihKqduDz9si8jcAfgrAqQFOk1sc1CK9IMJOx8VWy4E7wh7ZaXFY3z7fKGFpMEfYDyPstF1st93E3mFYhob1hRLONeJZcFI29aFT6aJIwbsb7v1gVwpQUIPP/R7+4XNcpP+kl8OvIdA09MNavxfQnHddPBP3wEWkBkBTSrUHX38NwL9XSv3PM36GPfAYtRwfB93+ApU01sp1TbBYMe9ONztr/nTT9rHd6r/DmHVp+XDByXqjfPfFhGhe0tIDXwfwN4MHvwHgL84Kb4rfQtnEQtnEg6tVOH54d7Vh2wkSG2ArmxqWqv05wgtlc+QSyWKlv7PgYa+8afvougH8mMoNhi6oWjoWyiaXd1NucCFPDh0fYOsMZk3EXXstm4PZCyUDdctAtaTHPiDmBuHdmR+Hs0CGLYc3dRkM0vVnVNRKBlcIUmqkpQdOKSUiqFg6KpYO4N5sCjcI+zXXoD+Ydm+gTSFS6m4dViCDuitgaHKkznpvkKxk6HNZgVcy+lPajp43GUb99kbH6sSaCDQRrgykwmCAF0g/DHE00zNJ1wT6nFZoEqUZ5xQREWUUA5yIKKMY4EREGcUAJyLKKAY4EVFGMcCJiDKKAU5ElFEMcCKijGKAExFlFAOciCijGOBERBnFACciyigGOBFRRjHAiYgyigFORJRRDHAiooxigBMRZRQDnIgooxjgREQZxQAnIsooBjgRUUYxwImIMooBTkSUUQxwIqKMYoATEWUUA5yIKKMY4EREGcUAJyLKKAY4EVFGMcCJiDKKAU5ElFEMcCKijGKAExFlFAOciCijGOBERBnFACciyigGOBFRRjHAiYgyigFORJRRDHAiooxigBMRZRQDnIgooxjgREQZxQAnIsooBjgRUUYxwImIMooBTkSUUQxwIqKMYoATEWUUA5yIKKMY4EREGTVVgIvIz4nIGyLytoj8TlyNIiKi4SYOcBHRAfxnAP8SwIcBPCMiH46rYUREdLZpeuA/BeBtpdS7SikPwH8D8Ol4mkVERMNME+CXAdw48u+bg8uIiGgOjCl+Vk64TH3gSiLPAXhu8E9XRL4/xW1m3RqAO0k3ImFF/xvw/hf7/gPAmoiM+zd46KQLpwnwmwAeOPLvKwBuH7+SUuoFAC8AgIi8qpR6corbzLSi33+AfwPe/2LffyDev8E0JZR/APCoiDwsIhaAXwHw1TgaRUREw03cA1dKBSLyOQD/C4AO4ItKqR/E1jIiIjrTNCUUKKVeAvDSGD/ywjS3lwNFv/8A/wa8/xTb30CU+sC4IxERZQCX0hMRZdRcApxL7gERuSYi3xOR74jIq0m3Z9ZE5Isisn102qiIrIjI10TkrcHn5STbOGun/A0+LyK3Bo+D74jI00m2cZZE5AER+YaIvC4iPxCR3xxcXojHwRn3P7bHwMxLKIMl928C+Fn0px7+A4BnlFI/nOkNp4yIXAPwpFKqEHNgReSfAegA+K9KqY8MLvuPAPaUUn8weCFfVkr9uyTbOUun/A0+D6CjlPpCkm2bBxG5COCiUurbItIA8BqAXwDwr1GAx8EZ9/8ziOkxMI8eOJfcF5BS6lsA9o5d/GkAXxp8/SX0H8y5dcrfoDCUUhtKqW8Pvm4DeB391dqFeByccf9jM48A55L7PgXgf4vIa4PVqUW0rpTaAPoPbgDnE25PUj4nIt8dlFhyWT44TkSuAvhJAK+ggI+DY/cfiOkxMI8AH2nJfQF8Uin1MfR3b/yNwdtrKp4/BvAIgI8C2ADwfKKtmQMRqQP4awC/pZRqJd2eeTvh/sf2GJhHgI+05D7vlFK3B5+3AfwN+qWlotka1AUP64PbCbdn7pRSW0qpUCkVAfgT5PxxICIm+uH150qprwwuLszj4KT7H+djYB4BXvgl9yJSGwxiQERqAP4FgCJu6vVVAJ8dfP1ZAH+bYFsScRhcA7+IHD8OREQAvAjgdaXUHx75ViEeB6fd/zgfA3NZyDOYJvOfcG/J/e/P/EZTREQ+hH6vG+ivfv2LvP8NROQvATyF/u5zWwB+D8B/B/BlAA8CeB/ALymlcjvId8rf4Cn03zorANcA/PphPThvROSfAvi/AL4HIBpc/Lvo14Fz/zg44/4/g5geA1yJSUSUUVyJSUSUUQxwIqKMYoATEWUUA5yIKKMY4EREGcUAJyLKKAY4EVFGMcCJiDLq/wP1VWYEbYxwpwAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# Plot initial point\n",
"plot_circles(model)"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.4 Reinitialize and Resolve](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.4-Reinitialize-and-Resolve)",
"section": "4.1.3.4 Reinitialize and Resolve"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Ipopt 3.13.2: \n",
"\n",
"******************************************************************************\n",
"This program contains Ipopt, a library for large-scale nonlinear optimization.\n",
" Ipopt is released as open source code under the Eclipse Public License (EPL).\n",
" For more information visit http://projects.coin-or.org/Ipopt\n",
"******************************************************************************\n",
"\n",
"This is Ipopt version 3.13.2, running with linear solver ma27.\n",
"\n",
"Number of nonzeros in equality constraint Jacobian...: 0\n",
"Number of nonzeros in inequality constraint Jacobian.: 30\n",
"Number of nonzeros in Lagrangian Hessian.............: 12\n",
"\n",
"Total number of variables............................: 8\n",
" variables with only lower bounds: 8\n",
" variables with lower and upper bounds: 0\n",
" variables with only upper bounds: 0\n",
"Total number of equality constraints.................: 0\n",
"Total number of inequality constraints...............: 15\n",
" inequality constraints with only lower bounds: 9\n",
" inequality constraints with lower and upper bounds: 0\n",
" inequality constraints with only upper bounds: 6\n",
"\n",
"iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls\n",
" 0 1.0000000e+02 1.37e+02 1.00e+00 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0\n",
" 1 1.0276645e+02 6.44e+01 6.62e-01 -1.0 7.31e+00 - 6.14e-01 4.44e-01h 1\n",
" 2 1.0566116e+02 1.85e+01 1.63e+00 -1.0 2.55e+00 0.0 8.96e-01 6.48e-01h 1\n",
" 3 1.0612677e+02 0.00e+00 5.99e-01 -1.0 1.46e+00 -0.5 1.00e+00 1.00e+00h 1\n",
" 4 1.0329539e+02 0.00e+00 3.22e-01 -1.0 2.52e+00 -1.0 1.00e+00 6.55e-01f 1\n",
" 5 1.0326145e+02 0.00e+00 3.12e-01 -1.0 1.93e+00 - 8.26e-01 1.00e+00h 1\n",
" 6 1.0237284e+02 0.00e+00 1.44e-01 -1.7 4.25e+00 -1.4 6.57e-01 7.24e-01f 1\n",
" 7 9.9794889e+01 0.00e+00 1.92e-01 -1.7 1.94e+00 -1.0 9.54e-01 1.00e+00h 1\n",
" 8 9.8743606e+01 0.00e+00 9.11e-01 -1.7 3.49e+01 -1.5 2.76e-01 2.60e-02f 1\n",
" 9 9.8483796e+01 0.00e+00 1.74e-01 -1.7 4.32e+00 - 9.92e-01 8.22e-01h 1\n",
"iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls\n",
" 10 9.8455971e+01 0.00e+00 9.38e-02 -1.7 1.73e+02 - 9.38e-01 3.53e-01f 1\n",
" 11 9.8404443e+01 0.00e+00 2.67e-03 -1.7 9.65e+00 - 1.00e+00 1.00e+00h 1\n",
" 12 9.8405024e+01 0.00e+00 2.10e-05 -1.7 4.30e+00 - 1.00e+00 1.00e+00h 1\n",
" 13 9.8300696e+01 0.00e+00 1.14e-05 -2.5 2.47e-01 - 1.00e+00 1.00e+00h 1\n",
" 14 9.8285160e+01 0.00e+00 2.64e-07 -3.8 3.60e-02 - 1.00e+00 1.00e+00h 1\n",
" 15 9.8284281e+01 0.00e+00 1.27e-09 -5.7 3.07e-03 - 1.00e+00 1.00e+00h 1\n",
" 16 9.8284270e+01 0.00e+00 1.75e-12 -8.6 2.76e-04 - 1.00e+00 1.00e+00h 1\n",
"\n",
"Number of Iterations....: 16\n",
"\n",
" (scaled) (unscaled)\n",
"Objective...............: 9.8284270438747257e+01 9.8284270438747257e+01\n",
"Dual infeasibility......: 1.7491657667044265e-12 1.7491657667044265e-12\n",
"Constraint violation....: 0.0000000000000000e+00 0.0000000000000000e+00\n",
"Complementarity.........: 2.5240899380720466e-09 2.5240899380720466e-09\n",
"Overall NLP error.......: 2.5240899380720466e-09 2.5240899380720466e-09\n",
"\n",
"\n",
"Number of objective function evaluations = 17\n",
"Number of objective gradient evaluations = 17\n",
"Number of equality constraint evaluations = 0\n",
"Number of inequality constraint evaluations = 17\n",
"Number of equality constraint Jacobian evaluations = 0\n",
"Number of inequality constraint Jacobian evaluations = 17\n",
"Number of Lagrangian Hessian evaluations = 16\n",
"Total CPU secs in IPOPT (w/o function evaluations) = 0.004\n",
"Total CPU secs in NLP function evaluations = 0.000\n",
"\n",
"EXIT: Optimal Solution Found.\n"
]
}
],
"source": [
"# Solve the model\n",
"results = solver.solve(model, tee = True)"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.4 Reinitialize and Resolve](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.4-Reinitialize-and-Resolve)",
"section": "4.1.3.4 Reinitialize and Resolve"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXUAAAFoCAYAAACotWuNAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAAAqx0lEQVR4nO3dWYxk13kf8P93t9qr920WzpDD1aQlKhgoQRQEsswYihFAtgEZ4oPBACPQDxYgA36w4BfLAQIIgWgnD4EBmiNYAWwnAmRFgiDE1gg2HBuBbI5Ai5SGFBcNOUvvW+331r315aGqySE1PV3VXXXX/w8azUyxuuvU3Fv/Pvfc75wjqgoiIkoHI+oGEBHR+DDUiYhShKFORJQiDHUiohRhqBMRpQhDnYgoRY4MdRHJi8g/isg/i8iPROQPBo/Pish3ReT1we8zk28uERHdixxVpy4iAqCkqg0RsQH8PYDPA/g1ADuq+iUR+QKAGVX93Ym3mIiIDnVkT137GoO/2oNfCuBTAL46ePyrAH5lEg0kIqLhWcM8SURMAFcBPAjgv6vq90VkSVVXAUBVV0Vk8ajvMz8/r+fPnz9Je4mIMufq1atbqrowzHOHCnVVDQA8KSLTAL4hIk8M2xgReRbAswBw33334cUXXxz2S4mICICIvD3sc0eqflHVPQB/C+CTANZFZGXwgisANg75mudV9aKqXlxYGOoHDRERHdMw1S8Lgx46RKQA4CkArwL4FoBnBk97BsA3J9RGIiIa0jDDLysAvjoYVzcAfE1Vvy0i/w/A10TkEoB3AHx6gu0kIqIhHBnqqvpDAB+5y+PbAH5xEo0iIqLj4YxSIqIUYagTEaUIQ52IKEUY6kREKTLU5KNxefnll9FfSoZiQwyIaQOmBTFtiDkochIAkJ85Xv21grS/UAR60CAAgi6050P9LqC90N8C3du5c+dw/fr1qJtBIQk11D3PAze6Do+qouUFaHkBXD9AN1B0gx48vwcv6KHr99Ab8+EwBLAtA45pwDYNOJYB2xQ4loGSY6HomPzBHjL+e2dLqKFOk9PrKVrdAE3XH/wK0PL8sYf2ke1QwO324Hbv3mM3BCg6Foo5E+VcP+RLjgXDYPAQjQNDPaGaro96x0fD9dHyfLS8AEm4COop0HD77d6ACwAQAQq2iVLOQilnopK3Uc7x1CQ6Dn5yEqLXU+y3u9htedhtdeH56Rm7VsW7w0Sb9f5jjiWYLjqYKTqYKtgw2ZMnGgpDPcY63eDdIN9vdUMfSomS5ys2ai42ai4MAaoFGzNFB9NFG3nbjLp5RLHFUI+Zhutjp+Fht+Wh5QVRNycWegrstbrYa3UBAEXHxEzRwUzJRiVvR9w6onhhqMeAH/Sw1fCwUe+g6TLIj9Ifqmnj1l4bRcfEYjWHhXIOlslpF0RH7lE61hcTUZY0vqfh+livdbDd8BBkaWxlAgwB5so5LFVz7L1/gIiwlDjhROSqql4c5rnsqYcs6Cm2Gy7Way4arh91c1Kjp8Bm3cVm3UUpZ2Kxksd82WHvnTKHoR6Sludjbb+DLfbKJ67pBvip28Q7Oy3MlR0sV/MosUSSMoJn+oS1vQA3d1vYanhRNyVzgt57FTSzJQdnZwsoOjzlKd14hk9Ipxvg5m4bWw03EZOC0m6n2a8omi87ODNTZFkkpRZDfcw8v4dbe21s1DqZqitPAlVgs+5hq+FhoZLDmZkCchbDndKFoT4m3aCH23ttrO0zzONOFdioudiqu1iq5nFqugDH4g1VSgeG+gkFPcXtvTZW9zu8AZowPQVW9zvYqLtYruZxajrPahlKPIb6Cey1PLy11Tx0RUJKhqCnuLXXxmbDxQPzJcyUnKibRHRsDPVj8IMerm+3sFl3o24KjZHn9/DqWh3zZQfn50uw2WunBGKoj2i74eL6dhOez6GWtNpqeNhvd3FuroSFSi7q5hCNhKE+JM/v4fp2E9usN8+EbqB4Y6OB7aaL++dLrJKhxGCoD2Gj3sHb2y34AXvnWbPb7KLe2cd9s0UsVfNRN4foSAz1e3D9AG9tNt9d8pWyyQ8Ub202sdVwcWGhzIlLFGu8E3SIWqeLV27tM9DpXbW2j1du7WOf5wTFGEP9Ltb2O/jx7RpvhtLP6AaKa2s13N5rR90Uorvi8Msdej3FT7eb2KixVJEOpwq8vd1C0/XxwEKZ+6dSrDDUB1w/wE/WGlzjnIa21fDQ7u7j4aUKx9kpNjj8AmC/3R8/Z6DTqJpuwHF2ipXMh/rafgfXVjl+Tsd3MM5+i+PsFAOZHX5RVby1xfFzGg9V4J3tFlqujwcXyxDhODtFI5M99V5P8fpGg4FOY7fV8PDqWh09rthJEclcqAc9xWvrdU73p4nZa3Vxba3GpZgpEpkKdT/o4dpqjROKaOJqbR8/vl1DN+CyzBSuzIR6P9DrqHdY4ULhaLgMdgpfJkL9INBZskhha3kBg51ClfpQ94P+xgcMdIpKywtwbZXBTuFIdagfBDqHXChqTZfBTuFIbairKn6y3mCgU2w03QCvsdyRJiy1of7WVhP7bVa5ULzUOz7e2mpE3QxKsVSG+up+mxOLKLY26x5u7raibgalVOpCfbfp4e1tfmAo3m7stLHdYMeDxi9Vod7yfLy+0YByyJIS4I0NLvVM43dkqIvIWRH5GxG5JiI/EpHPDx7/oojcEpGXBr9+efLNPZzn9ytdODWbkqKnwGtrNbh+EHVTKEWGWaXRB/A7qvoDEakAuCoi3x38tz9S1S9PrnnD6fUUP1mvw+2yXIySxfMVr63V8fipKe6gRGNxZE9dVVdV9QeDP9cBXANwetING8VbWyxdpORqugHe2GBFDI3HSGPqInIewEcAfH/w0OdE5Ici8hURmRl344Zxe6+NzTpXXKRk22l6uLHDG/x0ckOHuoiUAXwdwG+rag3AHwO4AOBJAKsAnjvk654VkRdF5MWTN/f9Wp7PDwKlxq29Nm+c0omJDlEqIiI2gG8D+CtV/cO7/PfzAL6tqk8c8X10mNcbhqrilVs1fggoVYqOiZ8/PQVjjOPrIoJxfe4oGiJyVVUvDvPcYapfBMBlANfuDHQRWbnjab8K4JVRG3oSN3fZq6H0aXkBbnBiEp3AMNUvHwPwGwBeFpGXBo/9HoCnReRJAArgOoDfnED77qrh+tzkl1Jrdb+D6aKDqYIddVMogYYafhnbi41h+KXXU/zw1j7aHmt7Kb1ytoEPn5keS5kjh1+Sb6zDL3Hzzk6LgU6p53Z7uL7djLoZlECJCvX9dher+52om0EUio2ai90my3VpNIkJdT/o4c1NTtCgbHlrq8GNNWgkiQn1m7ttLgNAmeP5inc4F4NGkIhQ73QDrNc47ELZtFl3eR+JhpaIUL+x0wIXX6SsUgXe3uFNUxpO7EO94frYavBmEWXbbrPL7RlpKLEP9bdZ1kUEAHiHO3rREGId6rtND7U2lwIgAg6uWrkFHt1bbENdlXf9iT7oxk4LPd5gonuIbahv1l20eMef6H063R7W66wEo8PFMtSDnnKlOqJD3Nptw+eEJDpELEN9rdaB5/MSk+huuoFyuQw6VOxCXVWxxhOW6J7Wax2OrdNdxS7Ud5oePJ+XlkT30g0UW01WwtDPil2or3E5AKKhrO8z1OlnxSrUm67PunSiITVcH/UOZ5nS+8Uq1NlLJxoNF7qjD4pNqPtBD9tc44VoJFsN3oOi94tNqG/UXQS8m080ElX21un9YhHqqsqhF6Jj2qh3uLE0vSsWob7X6nJXI6Jj8nzFNvcypYFYhPpGnaVZRCexUeNniPoiD/Wgp9hrsZdBdBK1TpfrwRCAGIT6frvLreqITkgV2G2xZp1iEOo7HAskGotdXvESIg51VQ69EI3LXqvLRb4o2lCvdXx0A56EROMQ9JSbU1O0ob7LoReisdrhlW/mRRrqPAGJxmuv5XEiUsZFFupN1+eEI6Ix83xF3eVKp1kWWaiz6oVoMjismW2RhTpv6BBNxh7r1TMtklBXVTR5iUg0Ee1uwBVPMyySUG96AWeREk2Ian9XJMqmaEKdJxzRRPEzll2RhDp7EUSTxVDPLvbUiVKIHafsCj3Uez1FywvCflmiTOl0e1yKN6NCD/Wm54MT3ogmr+my85RFoYc6LwuJwlF3Wa+eReH31BnqRKFgTz2bIgh1nmhEYeBVcTaFHuquz5s3RGHoBj2u2JhBoYc6py8ThUMV8FgBkzlHhrqInBWRvxGRayLyIxH5/ODxWRH5roi8Pvh95shXExlDk4loWB6vjDNnmJ66D+B3VPUxAP8KwG+JyM8B+AKA76nqQwC+N/j7ERjqRGHidpHZc2Soq+qqqv5g8Oc6gGsATgP4FICvDp72VQC/cuSrsadOFCr21LNnpDF1ETkP4CMAvg9gSVVXgX7wA1gc4juM3EAiOr4ux9Qzxxr2iSJSBvB1AL+tqjUZstctIs8CeBYAYJjHaCIRHRerzbJnqJ66iNjoB/qfqepfDh5eF5GVwX9fAbBxt69V1edV9aKqXhSGOlGo2FPPnmGqXwTAZQDXVPUP7/hP3wLwzODPzwD45tEvx+EXojBxTD17hhl++RiA3wDwsoi8NHjs9wB8CcDXROQSgHcAfPrI78RMJwoVe+rZc2Soq+rf4/A4/sXRXo6pThQmljRmTySbZBBRmNiZypKQQ50nF1HoOD8kU9hTp3u6cuUKnn76M/jEJ34BTz/9GVy5ciXqJhHRPQxdp07Zc+XKFTz33JfR6bgAgLW1dTz33JcBAE899VSUTaNRsKeeKeyp06EuX37h3UA/0Om4uHz5hYhaRMfDUM8Shjodan19faTHKa5YAZMlDHU61NLS0kiPU0xxo4xMYajToS5d+izy+dz7Hsvnc7h06bMRtYiIjhLyjVL2GJLk4Gbo5csvYH19HUtLS7h06bO8SZo07KlnioS5h6HhFPQfrt0M7fWICPjXD85zr9KEE5GrqnpxmOdy+IUoxUyDlS9ZE26os7dAFCrbZKhnTcg9dYY6UZgcixfjWRPqEee4HlG4HJOhnjUcfiFKMfbUs4fDL0QpZrOnnjnsqROlGHvq2cOeOlGKsaeePeypE6VYjj31zAn9iHNpZ6LwsKeePaEfcZ5kROGwTOGM0gwKPWFLOTPslyTKpKLDz1oWhR/qDnfQIwpDOcfPWhaFHuo80YjCUeJnLZMiGH7hiUYUBnagsin0UHcsgxMiiCbMNgV5m2PqWRRJulby7EEQTRKviLMrklDnCUc0WRx6ya5IQr3MChiiiWLHKbsi6qlzrI9okvgZy65IQt0yDeRt3iwlmgTHEuQshnpWRZas1YId1UsTpVo1z89WlkUW6rNFJ6qXJkq1mRI/W1kWWahPFWwuNkQ0ZoYAM+wwZVpkoW4YgukiLxOJxqnKzlLmRXq3kj0KovGa5dBL5kUc6jY3zSAaE+HQCyHiULdMg3fqicaknLO4rhJFG+oALxeJxoVVLwTEINRnSuypE40Dy4QJiEGo5yyTiw8RnVDBMVHg9nWEGIQ6AMxX2MMgOon5Mj9D1BeLUF8o51hbS3RMhgCLlXzUzaCYiEWoW6bBngbRMc2VHVa90LticyYsT7GnQXQcS1V+dug9sQn1omOhWuANU6JRlHMWKpzrQXc4MtRF5CsisiEir9zx2BdF5JaIvDT49cvjaMwyexxEI+EVLn3QMD31PwXwybs8/keq+uTg13fG0ZjZkoMcN88gGopjCeY44Yg+4MgEVdW/A7ATQlsgIhwfJBrSYiUPg1Vj9AEn6RZ/TkR+OBiemTnsSSLyrIi8KCIvDvNNFys58DwlujcRYLGai7oZFEPHDfU/BnABwJMAVgE8d9gTVfV5Vb2oqheH+ca2aWCuzJOV6F5mSw73IaW7Olaoq+q6qgaq2gPwJwA+Os5GnZkpcEleokOI9D8jRHdzrFAXkZU7/vqrAF457LnHkbdNjq0THWK+nEPRYfkv3d2RZ4aI/AWAjwOYF5GbAH4fwMdF5EkACuA6gN8cd8POzBSwWXcR9HTc35oosQwBzs6yl06HE9XwQlNEdJTXu7nbwo2d9gRbRJQsp6cLuG+uONLXiAjC/JzT+InI1WHvS8a6KPzUVIFrWhAN2Kbg1DSHJeneYp2YhiE4yxtCRACA0zMFWGasP7IUA7E/QxYqORS5+D9lXN42uIwGDSX2oS4iuG92tDFEorS5b7YIYZ0vDSH2oQ70N9SdKnAlOsqmSt7ihDwaWiJCHQDOzxe5fABljghwbsRqF8q2xIR60bFwhsMwlDGnpwtcL51GkphQB4BTU3lU8pxJR9lQyplcDoBGlqhQFxE8uFjmJtWUeoYADy6WeXOURpaoUAf668KwGobS7sxskeu70LEkLtSB/hZerIahtKrkLZziNnV0TIkMdQC4sFiCZfLSlNLFNITDLnQiiQ31nGWy1ItS59xcEXmbM6jp+BIb6kB/j8ZZbrxLKTFdtLmPAJ1YokMdAB5YKCFvJ/5tUMblbAMXFspRN4NSIPFpaJsGHl2ucnydEss0BI8sVbjMNI1FKs6igmPi4cUK9zWlxBEBHloso5Rj+SKNRypCHQCmijbuny9F3Qyikdw3W8QM7wvRGKUm1AFgqZrHCut7KSEWqzmcmuYyADReqQp1oF8SNl3kxCSKt2rBwgO8sqQJSF2oiwgeWixztySKrbxt4OGlCicY0USkLtQBwDINPLJcgc2KGIoZyxQ8ulyFzb1GaUJSe2blbROPLFe4oiPFhiHAw0sVFHgVSROU2lAHgErexqMrDHaKniHAo8tVLkRHE5fqUAeAKoOdIvZuoPMGPoUg9aEOMNgpOoYAjyxXGOgUmkyEOvBesHM5AQqLafRvik4XObmIwpOZUAf6wf7YSpVVMTRxlil4dIU9dApfpkIdAMo5C4+fmuLiSTQxtin4uZUqqnkGOoUvk8lWcEw8fqrKJXtp7BzLwOOnprhAF0Ums6mWt008cXoK1QI/fDQelbyFnz89xTp0ilRmQx3or8X+cytVLgJGJ7ZUzeHxU1UO61HkMt9NFRGcny+hlLPw1mYDPY26RZQkhgD3z5ewyG3oKCYyH+oHFio5FB0Tr63X4XZ7UTeHEsCxDDy8VEaFN0QpRniteIdSrj8myqncdJSD8XMGOsUNQ/0DbNPAYysVnJrm5TTd3fJUnuPnFFscfrkLEcG5uf44+0+3mvADDrRTf4bo+fkiFiv8gU/xxVC/h/lyDpV8P9h3m92om0MRmirYeGChhLzNckWKN4b6EXKWiUeXq9isu3h7u4kue+2ZYpmCc7NFVrdQYjDUh7RQyWG6aOP6VhNbDS/q5lAIZksO7p8vceycEoWhPgLbNPDQUgVzZQ8/3WrC81n6mEaOJTg/V8JcORd1U4hGxlA/htmSg2rewts7LWzU3KibQ2O0UHFwbq7EPUQpsRjqx2SZBi4slDFfyuH6dhMtL4i6SXQCBcfE+bki1z6nxGOon9BU0caHClPYani4udtCh7NREyVnGzgzU8BCOQcRrrNPycdQHwMRwUIlh/myg826ixu7bY63x5xjCU5PF7FYycHgNoeUIkeGuoh8BcB/ALChqk8MHpsF8L8AnAdwHcCvq+ru5JqZDCKCxWoe8+Uc1usd3N5rw/NZAhkntik4NV3AcjXPMKdUGuZu0J8C+OQHHvsCgO+p6kMAvjf4Ow0YhmBlqoAnz87gvrki90WNAcsUnJkp4Mmz0zg1XWCgU2qJ6tE9SRE5D+Dbd/TUXwPwcVVdFZEVAH+rqo8M8X10mNdLGz/oYXW/g416hz33kNmmYLGSx8p0PrMVLSKCLH7u0kRErqrqxWGee9wx9SVVXQWAQbAvHvP7JE7QU3h+D17QQzfooacK9P8HQf//DBHYpoGcZcA2DVimgbOzRZyZKWCn6WG95mK/zWUHJqlasLBUzWO26LBXTpky8RulIvIsgGcn/Trj5voBWm6Ahuuj5QVoeT66gSI4xi4apiFwLAMF20QpZ2JlKo8zMwXstbrYqHe49MCY2Gb/hvViJc8t5Sizjhvq6yKycsfwy8ZhT1TV5wE8D/SHX475ehPXDXrYbXnYa3VR73THOkwS9BRtL0DbC7DTfO9xxxJUchYgQKcboOWxYuY4Kvl+r3yuxF450XFD/VsAngHwpcHv3xxbi0LU9gJsN13stbpouD7CHnb0fMWO3x+GEenvpBP0+kM6qgyne8nZBmaLDharORQdVuYSHRimpPEvAHwcwLyI3ATw++iH+ddE5BKAdwB8epKNHKdeT7Hd9LBR76DW9qNuzrtUcUdtuyBnGYOFpBQNNwj9B07ciADlnIWZkoOZos0gJzrEUNUvY3uxCKtfOt0A67UONutuosawHUswU3SQsw20vQB7rW6i2n8StimYLtqYLjqYLtiwMlq9clKsfkm+MKpfEsP1A9zabWOj7iayt+v5ivWaC0OAxWoeP396Cl7Qw16ri/12Fy0vONbN2zgyDUHRMVHN25gu2ajkLE7dJxpRanvq3aCH23ttrO13kJLMA9APvuXq++uu216Apuej6fpouu9V6sSZZfYDvJyzUHQslHMW8rbBEJ8A9tSTb5SeeupCXVWxut/Bzd12anqwd3MwQ3K5mr9rEParaYJ+0Hs+PL9fVx/25Cfb7JdzOpaBkmOh6Jgo5SxuCxcihnryZTbUW56PNzeaaLjxuQE6aZW8hQsL5aHrslV1MHFK0R0EvTv4vRsoukEP/flUOvgd7waCiEDQv2kpEIj0Nw6xzf5kK8cy4JgGbKv/mGOy5x0HDPXky1yo93qKW3tt3NprJ3Lc/KQMAU7PFHB6usAQpZ/BUE++TN0o7XQD/GS9jqab3U0qegrc2Gljt9nFQ0tlDm0QZViia8T2Wh5evrWf6UC/U8P18cqtfey3uK4MUVYlNtRv7bXx6lodfsyrPMLWDRTX1mq4vdeOuilEFIHEDb/0eoo3NhvYbnhRNyW2VIG3t1toeT4emC9zPRSiDElUTz3oKV5dqzPQh7RZ9/Daej3VpZ1E9H6J6an7QQ+vrtVR72SnXHEc9lpdXFut4bGVKkz22IfSDXpodwNoD+ipoqcKEYEh/UqSnGXwZjTFViJCnYF+MvWOz2A/xMG6+f0Zuf3f3e7RSyDbprw7E7aYM1FyLK7hTrEQ+zr1Xk/x49UaA30MqgULjy1XMz/G7gc9bDX6K3WOs3LKsQwsVnJYqORi1ZNnnXrypWry0evrdWxxDH1sFio5PLhYjroZkWi4PtZrHWw3vIneZxABpos2lip5TBftyCeEMdSTLzWTj27stBjoY7ZZd1FwTJyeLkTdlNDsNj3c3G2HtnyEKrDb7GK32YVjGTg1nT90jR6icYttqG81XNzcZa31JNzYaaFgm5gtOVE3ZaK6QQ/Xt5qRdgw8v4frWy1sNzw8sFDi5h40cbEsaWy6Pt7caETdjNRSBd7YaKDlpfc+xVbDxT/f2IvNlV694+OHN/dxY6eFHktMaYJiF+q9nuKNjUaq1kCPo2Dw75y2sVbXD/DqWg2vrzdit6a8KnBzt42Xb+2j3uFSDjQZsQv1G7sttDyu5RKGphukaojrYO2b3Wa8A7PlBfjR7Ro2627UTaEUilWo1zpdrO53om5Gptzaa6ei17jf6uLHt2uhbwJyXAdDYFyjh8YtNqEe9BRvbjQyuR56lFSBNzebiR7n3Wt5eHWtlsjlEN7ebuHmbivqZlCKxCbUb++10RliJh+NX9sLcHs/mT3G/VYXr63VE30P5sZOmz12GptYhLrrBzypI3Z7rwPPT9YP1Ybr47X1ZAf6gbe3W9ioceiRTi4WoX5zt52KD2aSBYMtAZPioEoqiUMuh7m+3UKnyyIBOpnIQ73l+awCiIn1WgfthFQevbPTSkxbh5XWMlMKV+Sh/s5OizdHY0K1X1Iad/vt9FZJ1Ts+bqf0vVE4Ig31thfEvqY4a3aaXqyHAIKe4s3NdM82vrnTQjOkdWoofSIN9XXeGIodVWCjFt/hsOvbzaHWO0+yngJvbnIYho4nslAPeorNRnzDI8s26p1Y1q13ukFm7r803QDbzXisW0PJElmob9Zd+DFbm4P6uoFiK4Y/cNdrnUzdf1nj2DodQ2ShzqGXeFuP2RBMr6eZ6aUfqHf80NaAp/SIJNTbXsBFu2Ku4fqxumG61XBjt+piGNhbp1FFEuo7LY4VJsFujI7TWkav7LYbLrpBum8M03hFEuq7vAGUCDsxOU61TnesG0QnSU+BjYwNO9HJhB7qnt/jOGFC1Dt+LHqJtXa25zJk/f3TaEIP9b22l6kKhiRTBfZa0QdKVnvpBzgRiUYReqjXOzxBkyQOV1VxaEOUuoHG6qY1xVvooc5eR7JEfbxcP0jcksCTkPUfbDS80EOdpYzJ0nT9SKerZ33o5UDUP1wpOcINdRGOpydMT6P9Qcww62NPnYYVcqhHvtIvHUOUwepFXH1z5coVPP30Z/CJT/wCnn76M7hy5Uok7cjixCs6HivUVxMJ9eVoPNwIx7SjXFjsypUreO65L6PT6deJr62t47nnvgwAeOqpp0JtS5p2eKLJCrXrLGCoJ1GkoR5hll2+/MK7gX6g03Fx+fILobeFy/DSsEIfU6fkicMEpCisr6+P9DhRHDDU6UhRlhQaEZ4yS0tLIz0+ScLPDg3pRKEuItdF5GUReUlEXhziK07ychSRKHvqUYbZpUufRT6fe99j+XwOly59NvS2RPnDjZJlHDdKf0FVt4Z7avrOzCtXruDy5Rewvr6OpaUlXLr02dBvok2aH+HAtm1Gd84cHMc4HF/bZOUYDSfc6peUiVN1xCRFeY+u6ER7ij711FOxOJZFx4y6CZQQJ/3xrwD+WkSuisiz42hQksSpOmLSoqq+KOfY7wD470DDO+mZ8jFVvS0iiwC+KyKvqurf3fmEQdj3A9+0T/hy8cLqiMkrOCYsUzK/n22JoU5DOlFPXVVvD37fAPANAB+9y3OeV9WLqnpRjHSdmHGqjpgkkWhvWGZ96MEQ/hvQ8I4d6iJSEpHKwZ8B/BKAV+79VenqbcWpOmKSjIjL6Sq5dF3hjaqUs1jSSEM7Sdd5CcA3BiebBeDPVfX/jKVVCRGn6ohJirICBQDK+XRd4Y2qkvH3T6ORMG+AGXZe/+HVW6G9Ho1HJW/hidNTkb2+quIH7+zC89N1pTesJ89Oo3CC4RcR4TIDCSciV1X14jDPDbn4lSdWEuWsaGukRQSLlXykbYjKVME+UaBT9oT6aWVvIZniMPFlqZrP5CoTy1PZ/GFGxxfup5WhnkhOxD31gzbMlZyomxGqnG1gppjtm8Q0upBDPZur/SVdKeJZnQey1mtdruZZ9UIjY6jTkUq5eIzpVvI2qoV4/ICZNNsULFZyRz+R6ANCv66Ow6U8DS9vG7BiMKZ+4MJCGWYGliy8f74Uq393So7QzxquYZEscTteedvEubli1M2YqIWKg7kye+l0POGHOidSJEoc1xxZquYxndIbiI5l4PxcKepmUIKFHupThXR+GNMqrsfrgYUSrIhnuk7ChQUOu9DJRDL8wnH1ZMjbRix76gCQs0zcP5+uHu3yVB7TxWyVbdL4RZKusxmrN06qmZgHzHw5l5rx9bmyg/MpeS8UrUhCnRMqkmEmAT98T00XcGamEHUzTmSmZOOhxTJr0mksIgn1qYKdyvHQNLFNQTUhN7XPzhZxdjaZwT5bcvDwYoWBTmMTSaiLSOamfCfNfDmXqKA5M1PEhYVSotaHWazm8PBSGUYG6u4pPJHdsczalO8kEUnm8Vms5vHociX2N+INAc7PF3FhgUMuNH6Rnf1Fx4ptuVzWTRdt5O14LA0wqumigw+fmcJSNZ6Td6oFCx8+O42VqWQOF1H8RTpoujyVx367G2UT6C6Wq8nrpd/JMg08sFDGXDmHtzYb6HSjX3PIMgXnZotYTPi/LcVfpNepM0UbOTvel8pZU3DM1NRKTxVsfPjMNE5N5xHlsPVsycGHzkwx0CkUkfbURQRnZgp4c6MZZTPoDkkvD/wgwxCcmyvh1HQBm3UX67VOKD132xQsVHJYquYTO5RFyRR5zdpCOYe1/Q6abhB1UzKvnLMwn9KFpGzTwKnpAk5NF7Df6mK93sFO0xv7vi2VvIWlah5zJYdVLRSJyENdRHDfbBHXVutRNyXz7svIjMapoo2pog3P76HW6aLp+mi6AVqej24wfMob0l/wrOiYKOcsVPLcT5SiF3moA/2KhamCzZumEZop2ZmrRnIsA/Pl3PuuTjrdAE3XR7sbQBXoqaKngAAwRCDS32aunLNQsE2WJFLsxCLUAeDcXBEv39rnNqYRMAQ4N5uuxbGOK2+bHAOnRItN6UkpZ+H0dLpu0iXFmdkihw2IUiI2oQ70Ky/ittNO2lXyFk4lcPYoEd1drEJdRPDgYjnSmuIsMY3+vzfHhYnSI1ahDvQnv2SlCiNq980WOX5MlDKxC3UAWJkqYL6cjlmNcbVQcRK5aBcR3VssQx0ALiyUOb4+IZW8hQfmy1E3g4gmILahbhiCRxKwjGrS5GwDjyxXONuRKKVinZiOZeDR5QpMBtBYWKbg0eUKbO5WT5Rasf90l3IWHlmqsCLmhExD8PBSBUWHQ1pEaRb7UAf6a3U8ulxlsB+TORjKytoyAERZlIhQBwbBvlLlUMyILFPw6AoDnSgrEhPqQH/Tg8dWKrBNBvswbFPw2EoV1TwDnSgrEhXqAFDJ23ji9BRKOU6auZdyzsITp6dYFkqUMYkLdaC/kt7jp6Y4QekQCxUHj5+qcrYoUQYlthtnGoKHlioo5dp4Z6fFJXsBiPSXMOZO9UTZldhQP3BquoBSzorNrvFRKTgmHlgocfycKOMSH+rAe7vG39htYXW/k6leuwhwaqqAMzMFzhIlonSEOvDervFz5Rze3Gig5aV/I+tSzsSFhTJKvBlKRAOpS4NyzsKHzkxhvebi1l4Lnp++brtjGTgzU8BiJce10InofVIX6kB/s43lqTwWKjms1TpY3WuPtEt8XNmm4NR0AcvVPIdaiOiuUhnqB0xDcHq6gKVKDqv7HWzUO4nsuTuWYKmax8pUgTNqieieUh3qByzTwNnZIk5PF7DT8rBe66DW9qNu1pGmCjaWqjnMlhwOsxDRUE4U6iLySQD/DYAJ4AVV/dJYWjUhhiGYL+cwX86h7QXYqHew3fTgxqgUMm8bmCvlsFjNcfIQEY1M9Jj1fyJiAvgJgH8H4CaAfwLwtKr++B5fo8d9vUlqeT52W13sNj00XD/UkkiR/k5EM0UHM0UHBYdBTuMlIojj546GJyJXVfXiMM89SU/9owDeUNW3Bi/6PwF8CsChoR5XRcdC0bFweroAP+ih3vHR9Hw03QBNzx9rTz5nGyjnLBQdEyXHQiVvweKmFUQ0JicJ9dMAbtzx95sA/uXJmhM9yzQwU3IwU3pvXZlu0EPLC9ANev1fvsILAni+ojfoAan2e91A/watbRpwTAO2NfizZaBomwxwIpqok4T63e7c/cw1nog8C+DZwV9dEXnlBK8ZZ/MAtqJuxATx/SXXvIik9b0BKT926L+3c8N+wUlC/SaAs3f8/QyA2x98kqo+D+B5ABCRF4cdF0qaNL83gO8vydL83oB0v7/jvLeTjAX8E4CHROR+EXEAfAbAt07w/YiI6ISO3VNXVV9EPgfgr9AvafyKqv5obC0jIqKRnahOXVW/A+A7I3zJ8yd5vZhL83sD+P6SLM3vDUj3+xv5vR27Tp2IiOKH9XVERCkSSqiLyCdF5DUReUNEvhDGa4ZJRK6LyMsi8pKIvBh1e05KRL4iIht3lp+KyKyIfFdEXh/8PhNlG4/rkPf2RRG5NTh+L4nIL0fZxuMSkbMi8jcick1EfiQinx88npZjd9j7S8vxy4vIP4rIPw/e3x8MHh/p+E18+OU4ywkkjYhcB3BRVVNRKysi/xZAA8D/UNUnBo/9FwA7qvqlwQ/mGVX93SjbeRyHvLcvAmio6pejbNtJicgKgBVV/YGIVABcBfArAP4j0nHsDnt/v450HD8BUFLVhojYAP4ewOcB/BpGOH5h9NTfXU5AVT0AB8sJUEyp6t8B2PnAw58C8NXBn7+K/ocpcQ55b6mgqquq+oPBn+sArqE/8zstx+6w95cK2tcY/NUe/FKMePzCCPW7LSeQmgMxoAD+WkSuDmbQptGSqq4C/Q8XgMWI2zNunxORHw6GZxI5PHEnETkP4CMAvo8UHrsPvD8gJcdPREwReQnABoDvqurIxy+MUB9qOYGE+5iq/gsA/x7Abw0u8Sk5/hjABQBPAlgF8FykrTkhESkD+DqA31bVWtTtGbe7vL/UHD9VDVT1SfRn6H9URJ4Y9XuEEepDLSeQZKp6e/D7BoBvoD/klDbrgzHNg7HNjYjbMzaquj74MPUA/AkSfPwGY7FfB/BnqvqXg4dTc+zu9v7SdPwOqOoegL8F8EmMePzCCPVULycgIqXBTRuISAnALwFI46Jl3wLwzODPzwD4ZoRtGauDD8zAryKhx29wo+0ygGuq+od3/KdUHLvD3l+Kjt+CiEwP/lwA8BSAVzHi8Qtl8tGgxOi/4r3lBP7zxF80JCLyAPq9c6A/Q/fPk/7+ROQvAHwc/RXi1gH8PoD/DeBrAO4D8A6AT6tq4m44HvLePo7+pbsCuA7gNw/GMJNERP4NgP8L4GUAB5sA/B76485pOHaHvb+nkY7j9yH0b4Sa6He4v6aq/0lE5jDC8eOMUiKiFOGMUiKiFGGoExGlCEOdiChFGOpERCnCUCciShGGOhFRijDUiYhShKFORJQi/x8uru3kWAIZhQAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# Plot solution\n",
"plot_circles(model)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.1.4 Take Away Messages](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.4-Take-Away-Messages)",
"section": "4.1.4 Take Away Messages"
}
},
"source": [
"## 4.1.4 Take Away Messages\n",
"* Nonlinear programs may be nonconvex. For nonconvex problems, there often exists many local optima that are not also global optima.\n",
"* Initialization is really important in optimization problems with nonlinear objectives or constraints!"
]
},
{
"cell_type": "markdown",
"id": "3a37f678",
"metadata": {},
"source": [
"\n",
"< [4.0 Constrained Nonlinear Optimization: Theory and Applications](https://ndcbe.github.io/CBE60499/04.00-Constrained.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [4.2 Local Optimality Conditions](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html) >
"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 1,
"link": "[4.1 Convexity Revisited](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1-Convexity-Revisited)",
"section": "4.1 Convexity Revisited"
}
},
"source": [
"# 4.1 Convexity Revisited"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"nbpages": {
"level": 1,
"link": "[4.1 Convexity Revisited](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1-Convexity-Revisited)",
"section": "4.1 Convexity Revisited"
}
},
"outputs": [],
"source": [
"# This code cell installs packages on Colab\n",
"\n",
"import sys\n",
"if \"google.colab\" in sys.modules:\n",
" !wget \"https://raw.githubusercontent.com/ndcbe/CBE60499/main/notebooks/helper.py\"\n",
" import helper\n",
" helper.install_idaes()\n",
" helper.install_ipopt()\n",
" helper.install_glpk()\n",
" helper.download_figures(['pack1.png','pack2.png','pack3.png'])"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"nbpages": {
"level": 1,
"link": "[4.1 Convexity Revisited](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1-Convexity-Revisited)",
"section": "4.1 Convexity Revisited"
}
},
"outputs": [],
"source": [
"import pandas as pd\n",
"import pyomo.environ as pyo"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.1.1 Background](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.1-Background)",
"section": "4.1.1 Background"
}
},
"source": [
"## 4.1.1 Background"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.1.1 Background](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.1-Background)",
"section": "4.1.1 Background"
}
},
"source": [
"**Reference**: Beginning of Chapter 4 in Biegler (2010)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.1.1 Canonical Nonlinear Program](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.1.1-Canonical-Nonlinear-Program)",
"section": "4.1.1.1 Canonical Nonlinear Program"
}
},
"source": [
"### 4.1.1.1 Canonical Nonlinear Program"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.1.1 Canonical Nonlinear Program](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.1.1-Canonical-Nonlinear-Program)",
"section": "4.1.1.1 Canonical Nonlinear Program"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.1.2 Types of Constrained Optimal Solutions](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.1.2-Types-of-Constrained-Optimal-Solutions)",
"section": "4.1.1.2 Types of Constrained Optimal Solutions"
}
},
"source": [
"### 4.1.1.2 Types of Constrained Optimal Solutions"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.1.2 Types of Constrained Optimal Solutions](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.1.2-Types-of-Constrained-Optimal-Solutions)",
"section": "4.1.1.2 Types of Constrained Optimal Solutions"
}
},
"source": [
"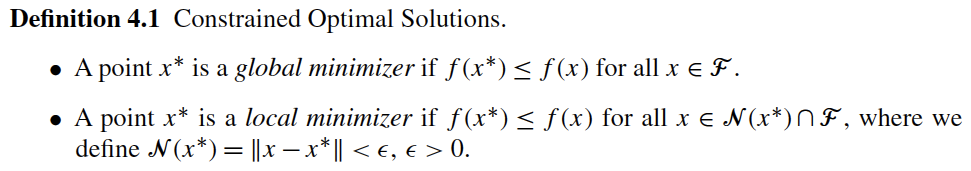"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.1.2 Types of Constrained Optimal Solutions](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.1.2-Types-of-Constrained-Optimal-Solutions)",
"section": "4.1.1.2 Types of Constrained Optimal Solutions"
}
},
"source": [
"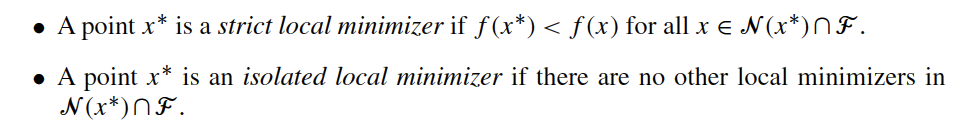"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.1.3 Key Questions](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.1.3-Key-Questions)",
"section": "4.1.1.3 Key Questions"
}
},
"source": [
"### 4.1.1.3 Key Questions"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.1.3 Key Questions](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.1.3-Key-Questions)",
"section": "4.1.1.3 Key Questions"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.1.2 Convexity for Constrained Optimization](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.2-Convexity-for-Constrained-Optimization)",
"section": "4.1.2 Convexity for Constrained Optimization"
}
},
"source": [
"## 4.1.2 Convexity for Constrained Optimization"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.1.2 Convexity for Constrained Optimization](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.2-Convexity-for-Constrained-Optimization)",
"section": "4.1.2 Convexity for Constrained Optimization"
}
},
"source": [
"**Reference**: Section 4.1 in Biegler (2010)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.1.2 Convexity for Constrained Optimization](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.2-Convexity-for-Constrained-Optimization)",
"section": "4.1.2 Convexity for Constrained Optimization"
}
},
"source": [
"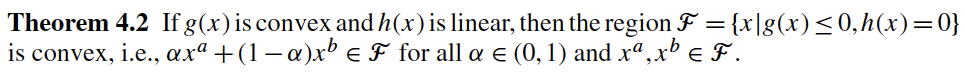"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.1.2 Convexity for Constrained Optimization](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.2-Convexity-for-Constrained-Optimization)",
"section": "4.1.2 Convexity for Constrained Optimization"
}
},
"source": [
"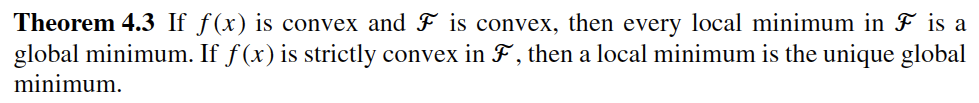"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.1.3 Circle Packing Example](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3-Circle-Packing-Example)",
"section": "4.1.3 Circle Packing Example"
}
},
"source": [
"## 4.1.3 Circle Packing Example"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.1.3 Circle Packing Example](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3-Circle-Packing-Example)",
"section": "4.1.3 Circle Packing Example"
}
},
"source": [
"**Reference**: Section 4.1 in Biegler (2010)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.1.3 Circle Packing Example](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3-Circle-Packing-Example)",
"section": "4.1.3 Circle Packing Example"
}
},
"source": [
"**Motivating Question**: Is this problem convex?"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.1.3 Circle Packing Example](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3-Circle-Packing-Example)",
"section": "4.1.3 Circle Packing Example"
}
},
"source": [
"What is the smallest rectangle you can use to enclose three given circles? Reference: Example 4.4 in Biegler (2010).\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.1 Optimization Model and Pyomo Implementation](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.1-Optimization-Model-and-Pyomo-Implementation)",
"section": "4.1.3.1 Optimization Model and Pyomo Implementation"
}
},
"source": [
"### 4.1.3.1 Optimization Model and Pyomo Implementation\n",
"\n",
"The following optimization model is given in Biegler (2010):"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.1 Optimization Model and Pyomo Implementation](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.1-Optimization-Model-and-Pyomo-Implementation)",
"section": "4.1.3.1 Optimization Model and Pyomo Implementation"
}
},
"source": [
"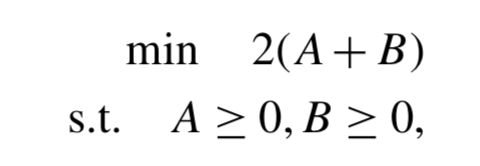\n",
"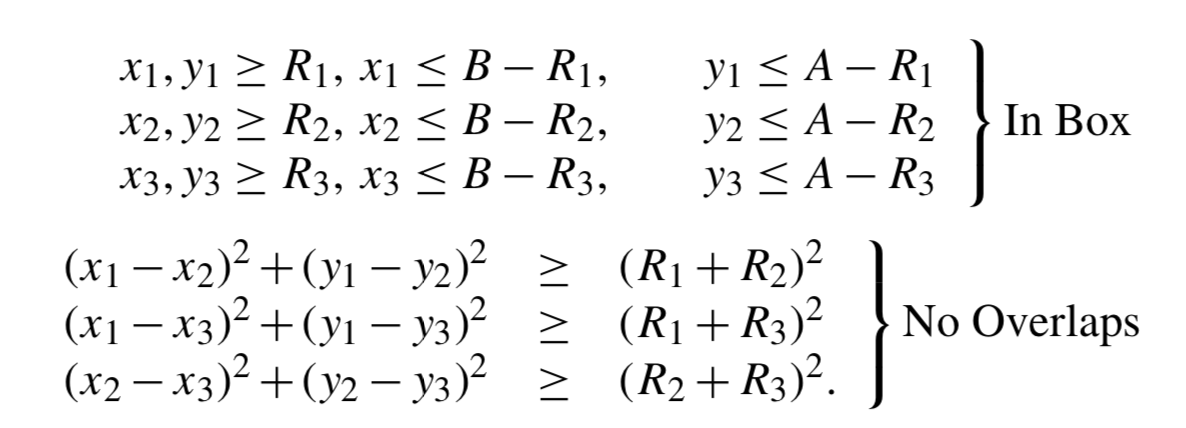"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.1 Optimization Model and Pyomo Implementation](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.1-Optimization-Model-and-Pyomo-Implementation)",
"section": "4.1.3.1 Optimization Model and Pyomo Implementation"
}
},
"outputs": [],
"source": [
"import random\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"import matplotlib.patches as mpatches\n",
"\n",
"def create_circle_model(circle_radii):\n",
" ''' Create circle optimization model in Pyomo\n",
" \n",
" Arguments:\n",
" circle_radii: dictionary with keys=circle name and value=radius (float)\n",
" \n",
" Returns:\n",
" model: Pyomo model\n",
" '''\n",
"\n",
" # Number of circles to consider\n",
" n = len(circle_radii)\n",
"\n",
" # Create a concrete Pyomo model.\n",
" model = pyo.ConcreteModel()\n",
"\n",
" # Initialize index for circles\n",
" model.CIRCLES = pyo.Set(initialize = circle_radii.keys())\n",
" \n",
" # Create parameter\n",
" model.R = pyo.Param(model.CIRCLES, domain=pyo.PositiveReals, initialize=circle_radii)\n",
"\n",
" # Create variables for box\n",
" model.a = pyo.Var(domain=pyo.PositiveReals)\n",
" model.b = pyo.Var(domain=pyo.PositiveReals)\n",
"\n",
" # Set objective\n",
" model.obj = pyo.Objective(expr=2*(model.a + model.b), sense = pyo.minimize)\n",
"\n",
" # Create variables for circle centers\n",
" model.x = pyo.Var(model.CIRCLES, domain=pyo.PositiveReals)\n",
" model.y = pyo.Var(model.CIRCLES, domain=pyo.PositiveReals)\n",
"\n",
" # \"In the box\" constraints\n",
" def left_x(m,c):\n",
" return m.x[c] >= model.R[c]\n",
" model.left_x_con = pyo.Constraint(model.CIRCLES, rule=left_x)\n",
"\n",
" def left_y(m,c):\n",
" return m.y[c] >= model.R[c]\n",
" model.left_y_con = pyo.Constraint(model.CIRCLES, rule=left_y)\n",
"\n",
" def right_x(m,c):\n",
" return m.x[c] <= m.b - model.R[c]\n",
" model.right_x_con = pyo.Constraint(model.CIRCLES, rule=right_x)\n",
"\n",
" def right_y(m,c):\n",
" return m.y[c] <= m.a - model.R[c]\n",
" model.right_y_con = pyo.Constraint(model.CIRCLES, rule=right_y)\n",
"\n",
" # No overlap constraints\n",
" def no_overlap(m,c1,c2):\n",
" if c1 < c2:\n",
" return (m.x[c1] - m.x[c2])**2 + (m.y[c1] - m.y[c2])**2 >= (model.R[c1] + model.R[c2])**2\n",
" else:\n",
" return pyo.Constraint.Skip\n",
" model.no_overlap_con = pyo.Constraint(model.CIRCLES, model.CIRCLES, rule=no_overlap)\n",
" \n",
" return model\n",
"\n",
"def initialize_circle_model(model, a_init=25, b_init=25):\n",
" ''' Initialize the x and y coordinates using uniform distribution\n",
" \n",
" Arguments:\n",
" a_init: initial value for a (default=25)\n",
" b_init: initial value for b (default=25)\n",
" \n",
" Returns:\n",
" Nothing. But per Pyomo scoping rules, the input argument `model`\n",
" can be modified in this function.\n",
" \n",
" '''\n",
" # Initialize \n",
" model.a = 25\n",
" model.b = 25\n",
"\n",
" for i in model.CIRCLES:\n",
" # Adding circle radii ensures the remains in the >0, >0 quadrant\n",
" model.x[i] = random.uniform(0,10) + model.R[i]\n",
" model.y[i] = random.uniform(0,10) + model.R[i]\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.1 Optimization Model and Pyomo Implementation](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.1-Optimization-Model-and-Pyomo-Implementation)",
"section": "4.1.3.1 Optimization Model and Pyomo Implementation"
}
},
"source": [
"Next, we will create a dictionary containing the circle names and radii values."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.1 Optimization Model and Pyomo Implementation](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.1-Optimization-Model-and-Pyomo-Implementation)",
"section": "4.1.3.1 Optimization Model and Pyomo Implementation"
}
},
"outputs": [
{
"data": {
"text/plain": [
"{'A': 10.0, 'B': 5.0, 'C': 3.0}"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Create dictionary with circle data\n",
"circle_data = {'A':10.0, 'B':5.0, 'C':3.0}\n",
"circle_data"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.1 Optimization Model and Pyomo Implementation](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.1-Optimization-Model-and-Pyomo-Implementation)",
"section": "4.1.3.1 Optimization Model and Pyomo Implementation"
}
},
"outputs": [
{
"data": {
"text/plain": [
"dict_keys(['A', 'B', 'C'])"
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"# Access the keys\n",
"circle_data.keys()"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.1 Optimization Model and Pyomo Implementation](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.1-Optimization-Model-and-Pyomo-Implementation)",
"section": "4.1.3.1 Optimization Model and Pyomo Implementation"
}
},
"source": [
"Now let's create the model."
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.1 Optimization Model and Pyomo Implementation](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.1-Optimization-Model-and-Pyomo-Implementation)",
"section": "4.1.3.1 Optimization Model and Pyomo Implementation"
}
},
"outputs": [],
"source": [
"# Create model\n",
"model = create_circle_model(circle_data)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.1 Optimization Model and Pyomo Implementation](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.1-Optimization-Model-and-Pyomo-Implementation)",
"section": "4.1.3.1 Optimization Model and Pyomo Implementation"
}
},
"source": [
"And let's initialize the model."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.1 Optimization Model and Pyomo Implementation](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.1-Optimization-Model-and-Pyomo-Implementation)",
"section": "4.1.3.1 Optimization Model and Pyomo Implementation"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"2 Set Declarations\n",
" CIRCLES : Size=1, Index=None, Ordered=Insertion\n",
" Key : Dimen : Domain : Size : Members\n",
" None : 1 : Any : 3 : {'A', 'B', 'C'}\n",
" no_overlap_con_index : Size=1, Index=None, Ordered=True\n",
" Key : Dimen : Domain : Size : Members\n",
" None : 2 : CIRCLES*CIRCLES : 9 : {('A', 'A'), ('A', 'B'), ('A', 'C'), ('B', 'A'), ('B', 'B'), ('B', 'C'), ('C', 'A'), ('C', 'B'), ('C', 'C')}\n",
"\n",
"1 Param Declarations\n",
" R : Size=3, Index=CIRCLES, Domain=PositiveReals, Default=None, Mutable=False\n",
" Key : Value\n",
" A : 10.0\n",
" B : 5.0\n",
" C : 3.0\n",
"\n",
"4 Var Declarations\n",
" a : Size=1, Index=None\n",
" Key : Lower : Value : Upper : Fixed : Stale : Domain\n",
" None : 0 : 25 : None : False : False : PositiveReals\n",
" b : Size=1, Index=None\n",
" Key : Lower : Value : Upper : Fixed : Stale : Domain\n",
" None : 0 : 25 : None : False : False : PositiveReals\n",
" x : Size=3, Index=CIRCLES\n",
" Key : Lower : Value : Upper : Fixed : Stale : Domain\n",
" A : 0 : 12.841552708011381 : None : False : False : PositiveReals\n",
" B : 0 : 5.317917334950976 : None : False : False : PositiveReals\n",
" C : 0 : 7.92668839728193 : None : False : False : PositiveReals\n",
" y : Size=3, Index=CIRCLES\n",
" Key : Lower : Value : Upper : Fixed : Stale : Domain\n",
" A : 0 : 15.93994957385218 : None : False : False : PositiveReals\n",
" B : 0 : 5.402476587728794 : None : False : False : PositiveReals\n",
" C : 0 : 7.556772365151705 : None : False : False : PositiveReals\n",
"\n",
"1 Objective Declarations\n",
" obj : Size=1, Index=None, Active=True\n",
" Key : Active : Sense : Expression\n",
" None : True : minimize : 2*(a + b)\n",
"\n",
"5 Constraint Declarations\n",
" left_x_con : Size=3, Index=CIRCLES, Active=True\n",
" Key : Lower : Body : Upper : Active\n",
" A : 10.0 : x[A] : +Inf : True\n",
" B : 5.0 : x[B] : +Inf : True\n",
" C : 3.0 : x[C] : +Inf : True\n",
" left_y_con : Size=3, Index=CIRCLES, Active=True\n",
" Key : Lower : Body : Upper : Active\n",
" A : 10.0 : y[A] : +Inf : True\n",
" B : 5.0 : y[B] : +Inf : True\n",
" C : 3.0 : y[C] : +Inf : True\n",
" no_overlap_con : Size=3, Index=no_overlap_con_index, Active=True\n",
" Key : Lower : Body : Upper : Active\n",
" ('A', 'B') : 225.0 : (x[A] - x[B])**2 + (y[A] - y[B])**2 : +Inf : True\n",
" ('A', 'C') : 169.0 : (x[A] - x[C])**2 + (y[A] - y[C])**2 : +Inf : True\n",
" ('B', 'C') : 64.0 : (x[B] - x[C])**2 + (y[B] - y[C])**2 : +Inf : True\n",
" right_x_con : Size=3, Index=CIRCLES, Active=True\n",
" Key : Lower : Body : Upper : Active\n",
" A : -Inf : x[A] - (b - 10.0) : 0.0 : True\n",
" B : -Inf : x[B] - (b - 5.0) : 0.0 : True\n",
" C : -Inf : x[C] - (b - 3.0) : 0.0 : True\n",
" right_y_con : Size=3, Index=CIRCLES, Active=True\n",
" Key : Lower : Body : Upper : Active\n",
" A : -Inf : y[A] - (a - 10.0) : 0.0 : True\n",
" B : -Inf : y[B] - (a - 5.0) : 0.0 : True\n",
" C : -Inf : y[C] - (a - 3.0) : 0.0 : True\n",
"\n",
"13 Declarations: CIRCLES R a b obj x y left_x_con left_y_con right_x_con right_y_con no_overlap_con_index no_overlap_con\n"
]
}
],
"source": [
"# Initialize model\n",
"initialize_circle_model(model)\n",
"model.pprint()"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.2 Visualize Initial Point](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.2-Visualize-Initial-Point)",
"section": "4.1.3.2 Visualize Initial Point"
}
},
"source": [
"### 4.1.3.2 Visualize Initial Point"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.2 Visualize Initial Point](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.2-Visualize-Initial-Point)",
"section": "4.1.3.2 Visualize Initial Point"
}
},
"source": [
"Next, we'll define a function to plot the solution (or initial point)"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.2 Visualize Initial Point](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.2-Visualize-Initial-Point)",
"section": "4.1.3.2 Visualize Initial Point"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXAAAAFlCAYAAADyArMXAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAAAtnElEQVR4nO3dW4yk6V0e8Of/Hetcfe7pmZ3d2VnvLl5MYqyV7cQI2cYggiIBFyDvReIo6ywXWAKJCxA3WImQEPJCchEhLR4rRgISJDBYyAp4kB3DBSt2HQevvd6jZ2dn+nys83d8c1HV456ePlRXfVXf6flJre6pqe566/TU+/2/9yBKKRARUfpocTeAiIhGwwAnIkopBjgRUUoxwImIUooBTkSUUgxwIqKUMqZ5YwsLC+ratWvTvEnKIQVAKQWl7v/5+HWOk+P/FoEIIAJo6P9MFIeXX355Wym1ePzyqQb4tWvX8NJLL03zJiljel6ArhvADUK4fggvCOEFCl4QwvFD+EGIcIJTGwxdYOoaTF1g6Vr/Z0ODpWuwDA1lS4eh88CWoiUi75x0+VQDnGhYSin0vBAtx0fH9QffA/hBvBPP/EDBDwJ0z7hOwdRQto3+l6WjbBswGeo0AQxwip1SCh03QNv10XYCtAdhHUyyKz1BPS9Ez3Ox03LvXWYZGiq2gdIg0Mu2DtvQY2wlZQEDnGLRdQPsdVzsdVy0ev5Eyx5J4Pohdn0Xu+0fXGYZgnrRxEzJwkzRZOmFLowBTlMRhgqNnof9joe9joueF8bdpNi5vsJW08VW04UIUC0YmC1ZmC1ZKFrsndP5GOA0Ma4fYr/jYq/j4aDrpbYkMg1KAY2uj0bXxzs7HRRM7V6YVwsGNI1DYOhBDHCKVNcNsN1ysN/x0HL8uJuTWj0vxNpBD2sHPehav9QyWzYxX7ahM8xpgAFOYwtDhZ22i81mD40uQztqQaiw23ax23ZxS+tgvmJhuVZAxebbN+/OfQWIyFUAfwTgEoAQwAtKqf8mIp8F8J8AbA2u+ptKqa9MqqGUPD0vwEajh62mAy/m4X15EYQKmw0Hmw0HFdvAcs3GfIW98rwa5iPcB/BrSqlvikgVwMsi8tXB//2+Uupzk2seJY1Sg952w8FB14u7ObnWcny0tny8s9vBQsXGUtVGmb3yXDn32VZKrQFYG/zcFJFXAVyZdMMoWXpegM2Gg61WD67P3naS+IHC+kEP6wc9VAsGlmo2Fso2T3zmwIU+rkXkGoAfBfAigI8A+IyI/HsAL6HfS9874XeeA/AcAOi6DuGCEqkiVglGfQlaoRp3U+giwgBBexd+YwsIg7hbQ0c88sgjuHXrViR/S4bdE1NEKgD+D4DfVkr9hYgsA9hGf12g/wJgRSn1H8/5G4p7cKZD2/Hx7l4He22WSdJM1wQr9QJW6gVOFEoIEcFFc1BEXlZKPf3A5cP8IRExAfw1gL9RSv3eCf9/DcBfK6Xed87fYYAnXNcN8O5e575p4JR+pi5YmSniUq3AE54xizLAhxmFIgBuAHj1aHiLyMqgPg4APw/glQu1iBKl5wW4s9fFdst5YOlVSj8vULi908H6QReXZ4pYrhZYI8+Ac3vgIvJjAP4ewLfRH0YIAL8J4BkA70e/hHILwC8dCfTT/hZ74Anj+AHu7nWx2WRw54ltanhopojFqs3zUlM29RJKVBjgyeEFIVb3u1g/6GV+ISk6XcHUcHWuhIWKHXdTcmOqJRTKnvWDHm7vdrg2CaHnhXhjo4W1/R6uL5Y5jjxl+GzlSNcN8NZWC80ep7vT/VqOj2/fPcDlehEPzRZZH08JBngOKKWwetDDnd0OyyV0KqWAu/td7HZcXF8so1Yw424SnYMBnnFtx8fbW22uDEhD67oBvrvawHKtgIfnShx2mGAM8IwKQ4U7e12sHnQ5uoQuTKn+uZK9jovrC2XMlKy4m0QnYIBnUKPn4e2tNroup1DTeBwvxKtrTSxWbVybL3E2Z8IwwDMkCBVu73aw0eix102R2mo6OOi6uDZfxjyHHCYGAzwjum6A1zaa7HXTxLi+wusbLSx3PTy6UOYEoARggGfAbtvFW1st+NxUgaZgo+Gg4wZ4YrkKy2BJJU589FPu3d0OXltvMrxpqpq9/rjxZo+rVcaJAZ5SfhDie+sN3Nnrxt0UyinXD/Hd1QY2Gr24m5JbLKGkEOvdlBShwr15Bo/OlzmDc8oY4Cmz23bx5maL65hQomw2HHTdAI8vV2AbetzNyQ2WUFJCKXWv3s3wpiRq9ny8cvcADdbFp4YBngJ+EOK1jSbr3ZR4rq9YF58illASzgtCvLrWQNthvZvSQQ3q4q4f4upcKe7mZBoDPMEcP8CrazxZSel0Z6+LIFS4tlCOuymZxQBPqJ4X4LtrDTheeP6ViRJq7aCHQClc58zNiWCAJ1DH9fHqWgOuz5OVlH6bDQdhqPCepQpDPGI8iZkwbcfHd1cZ3pQt2y0Xr200EXIEVaQY4Aly2PP2OC2eMmiv7eGNzdaFN/Sl0zHAE6Lj9nveDG/Kst22i9c3GOJRYYAnAMOb8oQhHh0GeMy6bsCyCeXObttlOSUCDPAYeYMVBXnCkvJop+Xi9m4n7makGgM8JkopvL7RRI/jvCnHVvd72OS0+5ExwGPy9nYbja4fdzOIYvf2dhsHXS6ANQoGeAxW97vYbDhxN4MoEZTC4GiUS0ZcFAN8ynbbrPsRHecHCt9bb8IPWFK8CAb4FLUdH29utsAT70QP6roBhxdeEAN8Slw/xPe4GQPRmQ66Hr6/3Y67GanBAJ+CMOyPOHF9Hh4SnWej4WDtgJuXDIMBPgVvbbXQ7HHECdGw3tnpYK/txt2MxGOAT9jqfhfbLb4QiS5CKeDNrRZHppyDAT5BHdfHuxxxQjQSP1B4a6sVdzMSjQE+IUopvLnZAs9ZEo2u0fVZDz8DA3xC7ux1uRExUQRu73S4L+wpGOAT0Ox5uLvPXgNRFEKFwfwJHs4exwCPWBgqvLXV5mQdogi1HB939tgpOo4BHrHbuzzcI5qEu/tdtBwOxz2KAR6hg66HtQMujUk0CUoBb222uDHyEQzwiPhByCFPRBPWcQO8u8ehuYcY4BG5tdOBw80ZiCZu7aDH9cMHGOAR2O+42GpyfW+iaVAKeHuLpRSAAT42pRTe2eEhHdE09bwQ69yKjQE+rq2mgw5HnRBN3d39bu43gGCAjyEIFd7l2FSiWPiByv2EOQb4GNYOulzjmyhG6we9XK9YyAAfkReEWN1nDY4oTqEC7uR4WCEDfER39rrcHo0oAbaabm5naDLAR9DzAmzwDDhRYtzO6UgwBvgIbu92uFgVUYIcdD3sd/K38xUD/IKaPQ873CKNKHHe2enkbsnZcwNcRK6KyNdE5FUR+Y6I/Mrg8jkR+aqIvDH4Pjv55saPk3aIkqnjBrmbET1MD9wH8GtKqfcC+DCAXxaRpwD8BoC/U0o9DuDvBv/OtP2Oy93liRLszn43V73wcwNcKbWmlPrm4OcmgFcBXAHwswC+OLjaFwH83ITamBicukuUbI4XYrednxLnhWrgInINwI8CeBHAslJqDeiHPIClyFuXID0vwH6HK6ARJV2eOlpDB7iIVAD8OYBfVUo1LvB7z4nISyLy0igNTIr1gx5HnhClQKPro+Pmo9Q5VICLiIl+eP+xUuovBhdviMjK4P9XAGye9LtKqReUUk8rpZ6OosFxCEKFrVa+To4Qpdl6TnbGGmYUigC4AeBVpdTvHfmvLwP41ODnTwH4q+iblwzbLQd+wO43UVpst9xcrFQ4TA/8IwD+HYCPi8i3Bl8/A+B3APykiLwB4CcH/86kvHyaE2VFECps5mBIoXHeFZRS/wBATvnvn4i2Oclz0PW43jdRCm00elipF9AvImQTZ2Keg71vonTqeWHmR44xwM/Q8wLs5XB9BaKsyPqQQgb4GTYbDocOEqXYfsdDN8MlUAb4KZRS2Gxm+9ObKA+yvPQzA/wUja4Pj0MHiVJvJ8NT6xngp9hl7ZsoE1w/zOyOPQzwU+RpQRyirNvL6PuZAX6CluNzt3miDMlqh4wBfoKsfloT5VXHDdDzsjcahQF+gqx+WhPlWRbf1wzwY3pewKnzRBnEAM+BLD7JRNQ/t+VlbIVCBvgxDHCibFIqe+e3GOBHZHm8KBFlb34HA/yI/Y7LtU+IMuyg4yEIs/MmZ4Afsd/N9tKTRHkXKqCRofc5A/yIZo/lE6Ksy1KZlAE+4PohZ18S5UA7QzvWM8AH2hn6VCai02Xpvc4AH8jSYRURnc71FRw/G5P1GOADWTqsIqKztTJyvosBPpClwyoiOlvbYQ88Mxw/gOtnZ2woEZ0tKyVTBjiy82lMRMPJSsmUAY7s1MOIaDh+oDKxPjgDHNk5nCKi4WXhfc8AR3YOp4hoeFkYuJD7AHf8AH7AE5hEeZOFc1+5D3BOnyfKJzcDmzswwBngRLmUhd15ch/gHssnRLnkByr1a4PnPsDZAyfKr7T3whngKX8CiWh0Tso7cAzwlD+BRDQ69sBTjj1wovxKewcu9wGe9k9gIhpd2t//uQ7wIFScxEOUY+yBp1jaP32JaDxpL6HmOsDTfgaaiMbDHniKsQdOlG9pn8iX6wAPVbqfPCIaT9ozINcBjnQ/d0Q0ppTnd74DPOXPHRFFQKU4xfMd4Ol93mhMN2/exDPPfBIf//jH8Mwzn8TNmzfjbhLFJM05YMTdgDgp9sFz6ebNm3j++c+h13MAAOvrG3j++c8BAD7xiU/E2TSKQagUNEjczRgJe+CUOzdufP5eeB/q9RzcuPH5mFpEcUpzDOQ6wCmfNjY2LnQ5ZVs6+959uQ5wSfMzRyNbXl6+0OWUbZLiIMh3gKf6s5dG9eyzn0ahYN93WaFg49lnPx1TiyhOaU6BXJ/ETPEHL43h8ETljRufx8bGBpaXl/Hss5/mCcycSnMOyDTHQIqIStKYy81GD29tteNuBhHF6F89Nj/V2xORC489F5GXlVJPH7881yWUVB87EdHY0tz7BnIe4IaW67tPlHuGlu4Ez3WCmXq6nzwiGo+ppzsCz229iHxBRDZF5JUjl31WRO6KyLcGXz8z2WZOhmWk+8kjovGkPQOGaf3/APDTJ1z++0qp9w++vhJts6bD0rXU18CIaHSZ74Erpb4BYHcKbZk6EWEZhSjH7Bz0wE/zGRH550GJZTayFk2ZpetxN4GIYpL5Hvgp/gDAYwDeD2ANwPOnXVFEnhORl0TkpRFva6JMgz1worzKQw38AUqpDaVUoJQKAfwhgA+ecd0XlFJPnzQIPQmslH8CE9Ho0l5CHSm9RGTlyD9/HsArp1036dJ+CEVEo0t7D/zctVBE5E8BfBTAgojcAfBbAD4qIu9HfyndWwB+aXJNnKy0n8QgotGIpP8I/NwAV0o9c8LFNybQlliwB06UT6YuqV5KFsj5TEwg/YdQRDSaLHTe0n8PxsQSClE+2Ub6hxDnPr0MXYNt5v5hIMqdss0Az4SKnet9LYhyKQvvewY4svFEEtHFlDPwvmeAIxtPJBENzzY1nsTMirKV/loYEQ0vK0fdDHD0T2QWGeJEuZGVo24G+EAlA2ekiWg47IFnTFY+kYnofFkpmzLABxjgRPlQtHQYGTiBCTDA76lYBrdXI8qBLJVLGeADmiYoZeSwiohOl6WjbQb4EVk5sUFEp8vS+5wBfsRsyYq7CUQ0QZYhqBbMuJsRGQb4EfWiCV1jIZwoq7LWSWOAH6FpgplSdj6dieh+c2UGeKZl7ROaiPp0TVDLUPkEYIA/YLZkcjghUQbNlkxoGSuRMsCPMXQtc5/SRATMZqx8AjDAT5S1OhlR3mkCzBSz1zFjgJ9gtpy9J5ooz2pFMzPT54/K3j2KgG3omRrsT5R3WT2qZoCfgr1wouzI6vBgBvgpsvqJTZQ3FduAbWRznSMG+ClKloFyhlYtI8qrhWp2O2MM8DNcqhXibgIRjUHXBIsVO+5mTAwD/AzzFRuGnq2B/0R5slCxMjn65FB271kEdE2wVM3upzdR1l2qZ/somgF+juVagVPriVKoXjRRsrI9HJgBfo6CqXOBK6IUynrvG2CAD4UnM4nSxTY1zGZ07PdRDPAh1Esmitwvkyg1LtUKkBzUPhngQ2IvnCgdNAEWczL4gAE+pMUqhxQSpcFC1YaZ4aGDR+XjXkZA1wQLGZ4QQJQVeTpaZoBfwEqdQwqJkqxWNFDO0UqiDPALKJg6J/YQJdgj8+W4mzBVDPALemi2BD1j++oRZcFCxcrdOv4M8AuyDA0rOZggQJQmmgBX50pxN2PqGOAjuDxThGWwF06UFMu1Agpm/uZqMMBHoGuCh2bz92lPlESGLrgyW4y7GbFggI9oqWpzdiZRAlyeKeZm3Pdx+bzXERARPJzDmhtRkliGhpUcjfs+jgE+hrmyhVoxX2e9iZLk6lwRWo5HhTHAx8ReOFE8yrae6e3ShsEAH1O1YGKhwvXCiabt4blSLlYcPAsDPAJX5zi5h2ia5soWZrjRCgM8CgVTx7V5llKIpsHUBY8u5GvK/GkY4BFZqhUwW87+DiBEcXt0oQzLYHQBAIdQROj6QgX/3NuHF6i4m/IApRQcP0TPC+D6IRSAUCmoQVNFAE0EAsA0NBRNHbah5b7GSMmyWLUwn/MTl0cxwCNkGRquLZTxxkYr1naESsHxQnS9AI4X9L/7IZS62AeLiMA2NBRMffDV/1ljqFMMLEPDtZytNngeBnjEFio29tou1g968EMFP1DwwxDe4HsY9gP2OE0EuiYwdIGhCQxdG3wXGNpwh4uOH2Cv7eGg6yEIw7Hvi1IKPS9Azwt+0E5NUC+amC1ZuVx7guLz2GIZRk5nXJ6GAT4mpRS6XoCW46Pj9L83eh7e3m7Bj6iUomvavd5vwdRRNPV7NcBQKTR7PvY6LjqOH8ntnSUMFfbaLvbaLoqWgdmSiVrRZK+cJmq5ZnPUyQnODXAR+QKAfwtgUyn1vsFlcwD+F4BrAG4B+EWl1N7kmpksHdfHXsfDfsdFq+cjPJbTAsHlehG3dzuR3F4Qhmg7IdpHAjpUCm6gEIYKpq7BjGG/zq7ro+v62Gg4mCn1e+U8uURRK5ha7jZqGJacVxcVkR8H0ALwR0cC/HcB7CqlfkdEfgPArFLq18+9MRF10TpsEoShQqPnYa/jYa/jwvGGK0+sHnSx33Yjb09z0JajpRhT11C0dJQsHbaux7L1myaCxaqNubLFk58UCRHgqcs11ArZGeElIqOcj3pZKfX0A5cP84dE5BqAvz4S4K8B+KhSak1EVgB8XSn15BB/J1UB3nUDbDR62G45I40sCZXCW1steP749WgA8IIQOy0XPT8483q6pqFq66gUTBgxTDAqWgYuzxRgG6yR03iuzBTxcMbmWEQZ4KPWwJeVUmsAMAjxpTNu+DkAz414O1MXhgq7HRcbjR4a3fFqypoIrswUcWunDYzxuaWUQqPnY7/jQQ3xh4IwxH43xH7XR8nSUbENFM3p9cq7ro+3t9pYqNhYqLA3TqMp2zoeyuk638Oa+ElMpdQLAF4A+j3wSd/eqIJQYXW/i41GL9Jx3CXLwOV6Eav73ZF+3/VD7LQdOCP14hU6ro+O68PQNNSKJiq2gWl0ypVS2Gr20Oh5uDJT5IgVuhDLEDx5qZrrlQaHMWqAb4jIypESymaUjZqmMFRYb/Swut+d2AScmZIFxw+w07pYPbzrBdhqOicOO7woPwyx23bQ6HqYKZkoW8ZUeuSOF+D72208NFtENUN1TJocTYAnL9VYghvCqEMGvgzgU4OfPwXgr6JpzvQopbB+0MP/fXcf7+x0Jj57crlWQKUw/Odl2/Gx2YgmvI/ywxDbLQerB120nLNr6VFRSuHdvS72O9Gf0KXsec9SJXe7y49qmFEofwrgowAWAGwA+C0AfwngzwA8DOA2gF9QSu2ee2MJOYl50OmP0+4NOZokKqFSuLXdvm9izEmaPQ+7bXecsvnQLF3DQsWe2vC/5VqBU6HpVFfnipnfb3bqo1CiEneA+0GIWzsdbDWd2NrgBgFubbdPneTT6vnYbk+7fYJ60UC9aE2lPn6pXsRcmZMy6H6LVQvvWarG3YyJizLAczPrYrft4v/d2Y81vAHA0nVcnS2dWH9uOz52ph7eAKBw0PWwdtA9d4hiFNYPWE6h+1ULBq4vVOJuRupkPsD9IMTrG028tt6E68dfvgEOx0nfPzzK8QNst5yplE1O4wUh1g8c7LbdB2aXRm31oIeOO/mp/5R8tqnhiWWOOBlFpgO84/r49t2DC4/+mIZ60cJitV8LVkphpzWdmvf5+rNONxr9xbgmdzP9YZvhpD8pKNF0TfBDl6pcgmFEmX3UdloOXrnbmPqJyotYrBZQL5rY63hwg2S10/EDrB30JlpScf0QG83exP4+JZsI8PhSBSWLI05GlbkAV0rh9k4Hr2+0EKSgdzdTMuFHsPTrJARhv6TS6E2u1LHXdtGawiqKlDzXF8uY5cnssWQqwINQ4XvrTdwdcdbjtIWhwup+D4uVQoJnKirsth1st1xMagDR6n43FR+2FJ3HFstYqhbibkbqZSbA/SDEq2sN7He8uJsytP60/RAiwHI1ySEOtBwPWy1nIic3/SDE+gFLKXnx2GIZSzWGdxQyEeCuH+I7qw00J3ioH7X+muI/OLmahhDvuD42m72JhPhB171vvXPKpusM70ilPsBdv9/z7rjTmRYelb32g0cKIsBSwkO85wUTC/HdCaydTslxfbGMZYZ3pFId4F6QzvD2gxCN3smlHm3QEy9a+QvxpuPDjWjtdEoOkf76Jgzv6KU2wMNQ4bX1ZurCGwD2Ou6ZU2kPyynlBA+v6nkBdloRzxpV6r6yEqWfJsATy9V7cx4oWqkN8Le2WqmqeR9SSmFvyBOti1U70Uuwtl0/8inx+8e2iqP06k/SqXHdmwlKZYC/u9vBdgJnVw6j0fPhX2DSznzZQq2Y3BDf73qRjuMOwhAH3fSMJKKTGbrgh1aqqJeS+9rNgtQF+HbLwZ29dIzzPskoJ+rmShYWKjaSulLEMPt0XgRPZqZbydLxI1fqmdqIOKlSFeAtx8dbm624mzEyPwjRHXEBp4pt4FK9AF1L3lOmoLDVdCNbO8XxAp7MTKm5soX3XakneiRVliQvDU4RhApvbDQnvkreJI17wtU2dFyuF2AncOGfYLDTT1S4UmG6iPQ3Y3jyUhU6VxWcmuQlwSlu73YSvTDVMLrn7MQzDF0TrNSLiTw87XlBZPXrKB4rmg5D768omPWddJIoFQF+0PEyMdU6yiGPc+Vk1sX3I1pZMY3DQ/PosN49U+JIkzgkPsD9IMSbW+mtex8KlTp3L8yL6tfFi4mqiysM1jYfs9Tl+CHXCk+4+Qrr3XFLzjv/FLd2Opk4oeV44YX3wRuGbWi4XC+gYCbnqXT8CEopSk1leze6OBHg4fkSnlhmvTtuyXnXn6DZ82LfwzIq3gTX/NY1waVasuriB11v7FEp3ikbP1N8zEG9+8qxLQEpHsmdqw3gnZ1O3E2IzGm70EdprmyhaOvYbbnwYt7hR6E/43SxMnpt9CITnmjyFioWri2UYeqJ7vflSmIDfLftpnKq/GmmFUZFQ8flehF7XReNc8oYr7/2Bl588R/RaDZQq9bwoQ99GE88+XhkbWk7PuoFY+T9DtkDTwbL0HB9gbvnJFEiA1wphdu72el9A0AwxfU9RPqzN8uWge2Wc2Jv/PXX3sDXv/41eH4/5BvNBr7+9a8BQIQhrrDbcXFpxFXopvmY0cmWazYenivBYK87kRL5rGw0HHQzNowsjiyyDQ1XZoqYKZoPDDd88cV/vBfehzzfw4sv/mOkbeh5wehjupnfsSmYGp66XMP1xQrDO8ES1wNXSuHufrZ633GbKVko2QZ2Wg6cwYieRrNx4nVPu3wc+x0PxTqHmqWBCLBSL+DqbAkaR5gkXuI+WrdbLlw/e10vifm9YOkaVupFzJYsaCKoVWsnXu+0y8fh+MG9D44LYX5MVcnS8b4rdTwyX2Z4p0TiAnyjkf4ZlyfR407wgXrRxMpMAT/2rz8I07h/2KFpmPjQhz48kdttjHBCOimPWdbpmuDqXBH/4qE6KnbiDsrpDIl6tlqOn6mRJ0clqY5oaho+9qEPoKgDX/36P6DR6U1kFMpRHcdHUDYvFMqmzgCfJE2AS/UCLs8UOTQwpRIV4FlY7+Q0RgLD6MNPfwAffvoD6HoB9jvuaGWOISkoNLs+Zi6wwH+SPvSyRBNgqVbAlZniyEM8KRkSE+BeEEa/x2KCmAlar+S4oqmjWC+i6wbY67iRLEZ1kqbjo140hz4fwB54tESAhYqNh2aLXL8kIxIT4LttN9VrfZ/HNjWIyETWQ4lK0dJRtIpoOT4Oul7kszmDMETPD1AcJjxEUDAYMlFZqFh4aLaEosXHNEsSFeBZpomgYOoj78gzTRXbQMU20HJ87He9SGeRdtzhAtw2NI6EiMBs2cTV2RLKPDmZSYl4Vv0gPHfadxaUrHQE+KGKbaBsGWi7PppdD04EQd51A6B8/vVKPMQfmSb9pV6XawVUE7TAGUUvEQG+3/UyXT45NFTpIGFEftAjd/wQTcdHx/ERjlgK8sMQjh+euy0cD/UvrmjpWKraWKzaHFWSE4kI8L2Ml08OpT2UbEODbVgISiY6boBmd7TddzquD9s4e2GkkpWIl2biadJfhXKpVkC9yN523sT+LlFKYT8H5RMAMHUNRctIVRnlJLoIqraBqm3A8QM0egE6jjf00iUdN8BZ2yfaps7hbecomBqWagUsVmw+VjkWe4C33WAqa2UnxVzZwt2UB/hRtqFjsaIjKJtoOwGavfNHr3hBiEABp40SnOOypSeSw9521eYelAQgCQHuZCfMhlErGNjQtcxtVqCLoFYwUCsYcIMQXTdAx/VPnRzknjKcUNc0lgKOMHTBTNHETMnCbMnk5Ca6T+wB3spZgIsIZktmZraKO4mla7CK/SAOlELXDfpfXnDv5KfrhycG+EzJhJbzNVBKlo7ZkoWZsomqbUBy/njQ6WIP8Lz1wAFgtmRhq+XGs0j4lOki90axAEDX74f5iXddBLM5LA1oAtSKZj+0SyZnSdLQYg3wMFToZGzjhmEYuoZ6wcRBNx+jb44qGjqKhg7T0PDIfAmtXr/U0vMC2EY+Tl5qApRtAyVLx0zJQr1ocnd3GkmsAd52/Tx0Qk80W85ngB/y/BC6CObK1r2Tlk8uV6DrGjquj7bjo+30yy5pfo3omqBk6ajYBkp2/3vR1FkWoUjEGuA9L1sn8i6iZBmYKVnY7+Q3xN1AoTjocC9WLcxVbAC47yRmEKpBoAdoD4K96waJnPhl6oKSZaBs6ygPZrGmfew/JVusAR71Yklpc6lWQNvxc/s4+EEIDMZ8X5s/eX69rgmqBfOBKeFeEPa/fAUnCOAFCp7fv8wNQniBguuHCMZMepF+MJu6du/L0jVYhta/3Oj/29Q1lkFo6mINcHeC60+ngaYJLs8U8c5uJxcnNI/zB+H62GL5wsPjDsMUFgCcPuwwCFV/3HmooNCfONb/DkD11ykXCCD9sBb0RwoJ+kP4LF1juYMSiz3wmJVtA/NlK9NroZ/GD0Is1yY7KUXXBLrGMgZlU6yn/Ce5A0yaLFZt2DkcOqZpgkdOKZ0Q0fliDXD2wPs0EVyuF+Pfun6aRHCpVmDdmGgMsQb4uCeY0urmzZt45plP4uMf/xieeeaTuHnzJoqWjisz+Qnxy/UCJ6wQjSnWGnge4/vmzZt4/vnPodfr17zX1zfw/POfAwB84hOfgFIKq/vdOJs4cZfqRS7GRBSBWHvgORx4gRs3Pn8vvA/1eg5u3Pg8AGCmZOFSvRhH06ZiuVa4N3Enj88/UZRiXwslbzY2Ns69fK5sQdcEq/vdRG+CfCEiuFwvsOdNFKFYe+A5KffeZ3l5eajL60UTV+dKmViZT0RwdfbBskkG7hpRrMYKcBG5JSLfFpFvichLF/79cW48pZ599tMoFOz7LisUbDz77KcfuG7FNnBtoZzqk322qePafJmb6xJNQBQllI8ppbZH+UVdE3g52o0H6J+oBPq18I2NDSwvL+PZZz997/LjCqaORxfK2Gm72Go6qSmpiAgWKjYWKtapMxk5hJBoPDJOIIjILQBPDxvgIqKO3t4rdw/Q7OVvPfBRuX6I1YMuOglfQ71oGbg8U4BtnH3ksFi18Z6lypRaRZQMInLhjpiIvKyUevr45ePWwBWAvxWRl0XkuVNu+DkReemkEkse1n6O0uGiT5fqxUTWxjURLNcKuDZfOje8gf4u90Q0unFLKB9RSq2KyBKAr4rI95RS3zh6BaXUCwBeAPo98KP/Z3F/v5HMlS1UCwZ22y72Ox6CMN4ZrbqmYabU31HmIh/KJp9/orGMFeBKqdXB900R+RKADwL4xtm/9QMme2AjM3UNy7UCFqs2mj0fex136qWVomVgtmSiVhxtH0segRGNZ+QAF5EyAE0p1Rz8/FMA/vNF/gZ74OPTRFAvmqgXTTh+gL22h4Pu5Hrlmta/vdmSNfboGFNPXhmIKE3G6YEvA/jSYISBAeBPlFL/+yJ/wDYZ4FGyDR2X6jqWajYcL0TXC+B4/W3JHD8c5cQJbENDwdQHX/2fo6q/D1MnJ6LTjRzgSqm3AfzLcW68bBkQ4ZTqqGkiKFr6fdt5KaXg+CF6XgDXD6HQ31T6sJ+uoR/YmvRLW0VTh21MbjMDy9BYQiEaU6xT6XVNUDT1XO5MP20icq8nnQTVAldxIBpX7F2gss03ch7xeScaX+wBXuEbOZcqFp93onHFHuBlOxmH9DRdfN6Jxhd/gFsG18TImZKlX3gXeiJ6UOzvIk0TzJS4Ul2ezHJNcKJIxB7gAN/QeTNb5gc2URQSEuAmF/fPCcvQuDY4UUQSEeCGrqHGN3UuzLJcRhSZRAQ4gHsb3VK28Xkmik6iApxllGyzjP5CWEQUjcQEuGVomGfvLNOWqoWJra1ClEeJCXAAWK4X4m4CTYgIsFzj80sUpUQFeK1gcmp9Rs2XL7ZbDxGdL3HvqOW6HXcTaAJ4dEUUvcQF+ELZ5k4tGVO2dQ4TJZqAxAW4pgkuzxTjbgZF6OpsKe4mEGVS4gIcAC7VCtxuLSNqRQOzHF1ENBGJTElNEzw8x15bFjwyX467CUSZlcgAB4CFis0RKSm3ULH4HBJNUGIDHAAenmcvPK00Aa7yKIpoohId4PWiifkK66dpdHmmmJgNlImyKtEBDgCPLpRhGRxWmCZlW8cVjiQimrjEB7ipa7i+UIm7GTQkTYD3LFWgcZs8oolLfIADwGzZwmKVMzTT4KG5EkrccZ5oKlIR4ABwbb7EseEJVy0YuMwp80RTk5pENHQN71mqcM3whDJ0GTw/fIKIpiU1AQ70Vyu8vsCJIUkjAjyxXOWoE6IpS1WAA8BSrYDLMzxMT5LrC2XutEMUg9QFOAA8PFfi3ooJsVIvYIkbNRDFIpUBLtKvt5ZtHrLHabZs4hHOliWKTSoDHAB0TfDkpSoKHJkSi2rBwONLVZ60JIpRqtPPNnQ8dbnGEJ+yasHAe1dq0DlZhyhWqU8+hvh0VQsGfuhSleFNlACZSD3b0PHDl+usiU/YTMnEe1dqMPRMvGyIUi8z70TL0PDUSg3VAqdxT8JCxcKTy+x5EyVJZgIc6M/W/OHLNVzidO7IiPTXZX98ucoFqogSJnPdVRHBowtllC0d399uI1Rxtyi9zMH0+JkSx9wTJVHmAvzQUq2Akm3gtfUmXD+MuzmpU7Z1To8nSrhMlVCOq9gGfuRKHTMlTvO+iMWqjR++XGd4EyVcZnvghyxDw3tXaths9nB7pwMvYE3lNLap4fpCmSUTopTIfIAfWqoWMFO0cGunjZ2WG3dzEkUEWK4V8PBciaNMiFIkNwEO9HvjTyxXsVtx8f3tNmvjAIqWjuuLZdQKLDMRpU2uAvzQXNlCvWhivdHD2n43l2UV29Tw0EwRi1Wb65kQpVQuAxzoL4Z1ZaaI5aqNtYMe1g56CHIw5tAyBFdmSliq2hzXTZRyuQ3wQ4au4epcCZfqBazud7HRcDIZ5KYuWJkp4lKtwDo3UUbkPsAPmbqGR+bLeGi2hO2Wg82Gg5bjx92ssdWKBpZrBcyVLPa4iTKGAX6MrgmWawUs1wpoOT42Gj3stNxU9cpNXbBYtbFULaBocSw3UVYxwM9QsQ1UFiu4Nq+w33Gx1/Gw33ETedLTNjXMFE3MlvonaNnbJso+BvgQdE0wX7ExX7GhlELL8bHf8bDXcdFxA6gY8lyk/wEzW7YwUzRRtvlUEuUN3/UXJCKoFkxUCyauzpUQhApt10fHCdByfHRcP/JQ1wQo2wZKlo6KbaBkGyiZOnvZRDnHAB+TrglqBfO+iTBhqOAGYf/LD+EFITy/f5kfhlAK/S8oCAQigCYCQxdYugZT12DqAtPQYOkabEPjWG0iegADfAI0TVDQdC4GRUQTNdZqhCLy0yLymoi8KSK/EVWjiIjofCMHuIjoAP47gH8D4CkAz4jIU1E1jIiIzjZOD/yDAN5USr2tlHIB/E8APxtNs4iI6DzjBPgVAO8e+fedwWVERDQF45zEPGlYxAOD50TkOQDPDf7piMgrY9xm2i0A2I67ETHL+2PA+5/v+w8ACyJy0cfgkZMuHCfA7wC4euTfDwFYPX4lpdQLAF4AABF5SSn19Bi3mWp5v/8AHwPe/3zffyDax2CcEso/AXhcRB4VEQvAJwF8OYpGERHR+UbugSulfBH5DIC/AaAD+IJS6juRtYyIiM401kQepdRXAHzlAr/ywji3lwF5v/8AHwPef4rsMRAVx0pMREQ0trFmYhIRUXymEuCccg+IyC0R+baIfEtEXoq7PZMmIl8Qkc2jw0ZFZE5Evioibwy+z8bZxkk75TH4rIjcHbwOviUiPxNnGydJRK6KyNdE5FUR+Y6I/Mrg8ly8Ds64/5G9BiZeQhlMuX8dwE+iP/TwnwA8o5T67kRvOGFE5BaAp5VSuRgDKyI/DqAF4I+UUu8bXPa7AHaVUr8z+CCfVUr9epztnKRTHoPPAmgppT4XZ9umQURWAKwopb4pIlUALwP4OQD/ATl4HZxx/38REb0GptED55T7HFJKfQPA7rGLfxbAFwc/fxH9F3NmnfIY5IZSak0p9c3Bz00Ar6I/WzsXr4Mz7n9kphHgnHLfpwD8rYi8PJidmkfLSqk1oP/iBrAUc3vi8hkR+edBiSWT5YPjROQagB8F8CJy+Do4dv+BiF4D0wjwoabc58BHlFIfQH/1xl8eHF5T/vwBgMcAvB/AGoDnY23NFIhIBcCfA/hVpVQj7vZM2wn3P7LXwDQCfKgp91mnlFodfN8E8CX0S0t5szGoCx7WBzdjbs/UKaU2lFKBUioE8IfI+OtAREz0w+uPlVJ/Mbg4N6+Dk+5/lK+BaQR47qfci0h5cBIDIlIG8FMA8rio15cBfGrw86cA/FWMbYnFYXAN/Dwy/DqQ/j6ANwC8qpT6vSP/lYvXwWn3P8rXwFQm8gyGyfxX/GDK/W9P/EYTRESuo9/rBvqzX/8k64+BiPwpgI+iv/rcBoDfAvCXAP4MwMMAbgP4BaVUZk/ynfIYfBT9Q2cF4BaAXzqsB2eNiPwYgL8H8G0A4eDi30S/Dpz518EZ9/8ZRPQa4ExMIqKU4kxMIqKUYoATEaUUA5yIKKUY4EREKcUAJyJKKQY4EVFKMcCJiFKKAU5ElFL/H1ATOwmwNjCFAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# Plot initial point\n",
"\n",
"def plot_circles(m):\n",
" ''' Plot circles using data in Pyomo model\n",
" \n",
" Arguments:\n",
" m: Pyomo concrete model\n",
" \n",
" Returns:\n",
" Nothing (but makes a figure)\n",
" \n",
" '''\n",
" \n",
" # Create figure\n",
" fig, ax = plt.subplots(1,figsize=(6,6))\n",
" \n",
" # Adjust axes\n",
" l = max(m.a.value,m.b.value) + 1\n",
" ax.set_xlim(0,l)\n",
" ax.set_ylim(0,l)\n",
" \n",
" # Draw box\n",
" art = mpatches.Rectangle((0,0), width=m.b.value, height=m.a.value,fill=False)\n",
" ax.add_patch(art)\n",
"\n",
" # Draw circles and mark center\n",
" for i in m.CIRCLES:\n",
" art2 = mpatches.Circle( (m.x[i].value,m.y[i].value), radius=m.R[i],fill=True,alpha=0.25)\n",
" ax.add_patch(art2)\n",
" \n",
" plt.scatter(m.x[i].value,m.y[i].value,color='black')\n",
" \n",
" # Show plot\n",
" plt.show()\n",
" \n",
"plot_circles(model)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.3 Solve and Inspect the Solution](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.3-Solve-and-Inspect-the-Solution)",
"section": "4.1.3.3 Solve and Inspect the Solution"
}
},
"source": [
"### 4.1.3.3 Solve and Inspect the Solution"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.3 Solve and Inspect the Solution](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.3-Solve-and-Inspect-the-Solution)",
"section": "4.1.3.3 Solve and Inspect the Solution"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Ipopt 3.13.2: \n",
"\n",
"******************************************************************************\n",
"This program contains Ipopt, a library for large-scale nonlinear optimization.\n",
" Ipopt is released as open source code under the Eclipse Public License (EPL).\n",
" For more information visit http://projects.coin-or.org/Ipopt\n",
"******************************************************************************\n",
"\n",
"This is Ipopt version 3.13.2, running with linear solver ma27.\n",
"\n",
"Number of nonzeros in equality constraint Jacobian...: 0\n",
"Number of nonzeros in inequality constraint Jacobian.: 30\n",
"Number of nonzeros in Lagrangian Hessian.............: 12\n",
"\n",
"Total number of variables............................: 8\n",
" variables with only lower bounds: 8\n",
" variables with lower and upper bounds: 0\n",
" variables with only upper bounds: 0\n",
"Total number of equality constraints.................: 0\n",
"Total number of inequality constraints...............: 15\n",
" inequality constraints with only lower bounds: 9\n",
" inequality constraints with lower and upper bounds: 0\n",
" inequality constraints with only upper bounds: 6\n",
"\n",
"iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls\n",
" 0 1.0000000e+02 7.46e+01 1.06e+00 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0\n",
" 1 1.0050650e+02 4.98e+01 4.22e+00 -1.0 2.36e+01 - 1.84e-01 1.30e-01h 1\n",
" 2 1.0015862e+02 3.01e+01 2.32e+00 -1.0 5.24e+00 - 8.18e-01 3.67e-01h 1\n",
" 3 9.9730828e+01 1.33e+01 1.16e+00 -1.0 4.96e+00 - 7.51e-01 4.53e-01h 1\n",
" 4 9.8213893e+01 8.23e+00 1.08e+00 -1.0 2.46e+01 - 2.93e-01 7.07e-02f 1\n",
" 5 9.8307816e+01 1.84e+00 3.42e-01 -1.0 7.81e+00 - 1.00e+00 6.57e-01h 1\n",
" 6 9.8901802e+01 0.00e+00 1.06e-02 -1.0 1.80e+01 - 1.00e+00 1.00e+00h 1\n",
" 7 9.8393352e+01 0.00e+00 3.30e-03 -1.7 9.37e+00 - 1.00e+00 1.00e+00h 1\n",
" 8 9.8405011e+01 0.00e+00 1.08e-03 -1.7 4.38e+01 - 1.00e+00 1.00e+00h 1\n",
" 9 9.8405025e+01 0.00e+00 1.17e-04 -1.7 7.44e+00 - 1.00e+00 1.00e+00h 1\n",
"iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls\n",
" 10 9.8405027e+01 0.00e+00 5.74e-07 -1.7 1.52e+00 - 1.00e+00 1.00e+00h 1\n",
" 11 9.8284703e+01 0.00e+00 4.42e-05 -3.8 2.93e-01 - 1.00e+00 9.98e-01h 1\n",
" 12 9.8284281e+01 0.00e+00 2.33e-09 -5.7 2.63e-03 - 1.00e+00 1.00e+00h 1\n",
" 13 9.8284270e+01 0.00e+00 1.33e-13 -8.6 2.80e-05 - 1.00e+00 1.00e+00h 1\n",
"\n",
"Number of Iterations....: 13\n",
"\n",
" (scaled) (unscaled)\n",
"Objective...............: 9.8284270438747228e+01 9.8284270438747228e+01\n",
"Dual infeasibility......: 1.3347017888941731e-13 1.3347017888941731e-13\n",
"Constraint violation....: 0.0000000000000000e+00 0.0000000000000000e+00\n",
"Complementarity.........: 2.5071615765896930e-09 2.5071615765896930e-09\n",
"Overall NLP error.......: 2.5071615765896930e-09 2.5071615765896930e-09\n",
"\n",
"\n",
"Number of objective function evaluations = 14\n",
"Number of objective gradient evaluations = 14\n",
"Number of equality constraint evaluations = 0\n",
"Number of inequality constraint evaluations = 14\n",
"Number of equality constraint Jacobian evaluations = 0\n",
"Number of inequality constraint Jacobian evaluations = 14\n",
"Number of Lagrangian Hessian evaluations = 13\n",
"Total CPU secs in IPOPT (w/o function evaluations) = 0.004\n",
"Total CPU secs in NLP function evaluations = 0.000\n",
"\n",
"EXIT: Optimal Solution Found.\n"
]
}
],
"source": [
"# Specify the solver\n",
"solver = pyo.SolverFactory('ipopt')\n",
"\n",
"# Solve the model\n",
"results = solver.solve(model, tee = True)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.3 Solve and Inspect the Solution](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.3-Solve-and-Inspect-the-Solution)",
"section": "4.1.3.3 Solve and Inspect the Solution"
}
},
"source": [
"Next, we can inspect the solution. Because Pyomo is a Python extension, we can use Pyoth (for loops, etc.) to programmatically inspect the solution."
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.3 Solve and Inspect the Solution](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.3-Solve-and-Inspect-the-Solution)",
"section": "4.1.3.3 Solve and Inspect the Solution"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Name\tValue\n",
"a \t 29.142135416184022\n",
"b \t 19.999999803189596\n",
"x[A] \t 9.99999990193744\n",
"x[B] \t 4.999999953543133\n",
"x[C] \t 15.734851787229463\n",
"y[A] \t 19.142135514931184\n",
"y[B] \t 4.999999951252124\n",
"y[C] \t 5.517617033892999\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXUAAAFoCAYAAACotWuNAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAAAq5ElEQVR4nO3dW6xc13kf8P+3r3M/93N4SEqkdbEkS07kgnCLuigcRw3coICTAA6sh0AFaCgPMeAAeYiRlzgFChiFlbQPRQBFNOICSVoDjmvDCJqYRoI0QeFENGRLNiVLoinxcq48l7nvPXvP14cZSpTMwzNzzsy+/n8wTXI058wa7pn/WbPWt9YSVQUREWWDEXcDiIhochjqREQZwlAnIsoQhjoRUYYw1ImIMoShTkSUIYeGuogUROSfROQHIvIjEfmD4e3zIvIdEXl9+Pvc9JtLRET3IofVqYuIACiralNEbAD/AODzAH4NwI6qfklEvgBgTlV/d+otJiKiAx3aU9eB5vCv9vCXAvgUgK8Ob/8qgF+ZRgOJiGh01ih3EhETwCUADwH476r6PRFZUdU1AFDVNRFZPuz7LC4u6tmzZ4/TXiKi3Ll06dK2qi6Nct+RQl1VQwBPisgsgG+IyBOjNkZEngXwLADcf//9ePHFF0f9UiIiAiAib41637GqX1R1D8DfAfgkgA0RWR0+4CqAzQO+5nlVPaeq55aWRvpBQ0RERzRK9cvSsIcOESkCeArAqwC+BeCZ4d2eAfDNKbWRiIhGNMrwyyqArw7H1Q0AX1PVb4vI/wPwNRE5D+BtAJ+eYjuJiGgEh4a6qv4QwEfucvstAL84jUYREdHRcEUpEVGGMNSJiDKEoU5ElCEMdSKiDBlp8dGkvPzyyxhsJUOJIQbEtAHTgpg2xBwWOQkAyM9cr8FeQTrYKAJ9aBgCYQ/aD6BBD9B+5E+B7u3MmTO4evVq3M2giEQa6r7vgwddR0dV0fZDtP0QXhCiFyp6YR9+0Icf9tEL+uhP+HIYAtiWAcc0YJsGHMuAbQocy0DZsVByTP5gjxj/vfMl0lCn6en3Fe1eiJYXDH+FaPvBxEP70HYo4PX68Hp377EbApQcCyXXRMUdhHzZsWAYDB6iSWCop1TLC9DoBmh6Adp+gLYfIg0fgvoKNL1BuzfhAQBEgKJtouxaKLsmqgUbFZcvTaKj4DsnJfp9xX6nh922j912D36QnbFrVbwzTLTVGNzmWILZkoO5koOZog2TPXmikTDUE6zbC98J8v12L/KhlDj5gWKz7mGz7sEQoFa0MVdyMFuyUbDNuJtHlFgM9YRpegF2mj522z7afhh3cxKhr8Beu4e9dg8AUHJMzJUczJVtVAt2zK0jShaGegIEYR/bTR+bjS5aHoP8MIOhmg5u7HVQckws11wsVVxYJpddEB16RulEH0xEWdL4rqYXYKPexa2mjzBPYytTYAiwUHGxUnPZe38fEWEpccqJyCVVPTfKfdlTj1jYV9xqetioe2h6QdzNyYy+AlsND1sND2XXxHK1gMWKw9475Q5DPSJtP8D6fhfb7JVPXcsL8VOvhbd32lioODhRK6DMEknKCb7Sp6zjh7i+28Z204+7KbkT9t+toJkvO7hvvoiSw5c8ZRtf4VPS7YW4vtvBdtNLxaKgrNtpDSqKFisOTs+VWBZJmcVQnzA/6OPGXgeb9W6u6srTQBXYavjYbvpYqro4PVeEazHcKVsY6hPSC/u4udfB+j7DPOlUgc26h+2Gh5VaASdni3AsTqhSNjDUjynsK27udbC23+UEaMr0FVjb72Kz4eFErYCTswVWy1DqMdSPYa/t48p268AdCSkdwr7ixl4HW00PDyyWMVd24m4S0ZEx1I8gCPu4equNrYYXd1Nogvygj1fXG1isODi7WIbNXjulEEN9TLeaHq7easEPONSSVdtNH/udHs4slLFUdeNuDtFYGOoj8oM+rt5q4RbrzXOhFyre2GziVsvDBxbLrJKh1GCoj2Cz0cVbt9oIQvbO82a31UOju4/750tYqRXibg7RoRjq9+AFIa5std7Z8pXyKQgVV7Za2G56eHCpwoVLlGicCTpAvdvDKzf2Gej0jnonwCs39rHP1wQlGEP9Ltb3u/jxzTonQ+ln9ELF5fU6bu514m4K0V1x+OUO/b7ip7da2KyzVJEOpgq8dauNlhfggaUKz0+lRGGoD3lBiJ+sN7nHOY1su+mj09vHB1eqHGenxODwC4D9zmD8nIFO42p5IcfZKVFyH+rr+11cXuP4OR3d7XH2GxxnpwTI7fCLquLKNsfPaTJUgbdvtdH2Ajy0XIEIx9kpHrnsqff7itc3mwx0mrjtpo9X1xvoc8dOiknuQj3sK17baHC5P03NXruHy+t1bsVMschVqAdhH5fX6lxQRFNX7wT48c06eiG3ZaZo5SbUB4HeQKPLCheKRtNjsFP0chHqtwOdJYsUtbYfMtgpUpkP9SAcHHzAQKe4tP0Ql9cY7BSNTIf67UDnkAvFreUx2CkamQ11VcVPNpoMdEqMlhfiNZY70pRlNtSvbLew32GVCyVLoxvgynYz7mZQhmUy1Nf2O1xYRIm11fBxfbcddzMoozIX6rstH2/d4huGku3aTge3mux40ORlKtTbfoDXN5tQDllSCryxya2eafIODXURuU9E/lZELovIj0Tk88PbvygiN0TkpeGvX55+cw/mB4NKFy7NprToK/Daeh1eEMbdFMqQUXZpDAD8jqp+X0SqAC6JyHeG/+2PVPXL02veaPp9xU82GvB6LBejdPEDxWvrDTx+coYnKNFEHNpTV9U1Vf3+8M8NAJcBnJp2w8ZxZZuli5ReLS/EG5usiKHJGGtMXUTOAvgIgO8Nb/qciPxQRL4iInOTbtwobu51sNXgjouUbjstH9d2OMFPxzdyqItIBcDXAfy2qtYB/DGABwE8CWANwHMHfN2zIvKiiLx4/Oa+V9sP+EagzLix1+HEKR2b6AilIiJiA/g2gL9W1T+8y38/C+DbqvrEId9HR3m8UagqXrlR55uAMqXkmPjwqRkYExxfFxFM6n1H8RCRS6p6bpT7jlL9IgAuALh8Z6CLyOodd/tVAK+M29DjuL7LXg1lT9sPcY0Lk+gYRql++RiA3wDwsoi8NLzt9wA8LSJPAlAAVwH85hTad1dNL+Ahv5RZa/tdzJYczBTtuJtCKTTS8MvEHmwCwy/9vuKHN/bR8VnbS9nl2gZ+/vTsRMocOfySfhMdfkmat3faDHTKPK/Xx9VbrbibQSmUqlDf7/Swtt+NuxlEkdise9htsVyXxpOaUA/CPt7c4gINypcr200erEFjSU2oX9/tcBsAyh0/ULzNtRg0hlSEercXYqPOYRfKp62Gx3kkGlkqQv3aThvcfJHyShV4a4eTpjSaxId60wuw3eRkEeXbbqvH4xlpJIkP9bdY1kUEAHibJ3rRCBId6rstH/UOtwIgAm5/auUReHRviQ11Vc76E73ftZ02+pxgontIbKhvNTy0OeNP9B7dXh8bDVaC0cESGephX7lTHdEBbux2EHBBEh0gkaG+Xu/CD/gRk+hueqFyuww6UOJCXVWxzhcs0T1t1LscW6e7Slyo77R8+AE/WhLdSy9UbLdYCUM/K3Ghvs7tAIhGsrHPUKeflahQb3kB69KJRtT0AjS6XGVK75WoUGcvnWg83OiO3i8xoR6EfdziHi9EY9lucg6K3isxob7Z8BByNp9oLKrsrdN7JSLUVZVDL0RHtNno8mBpekciQn2v3eOpRkRH5AeKWzzLlIYSEeqbDZZmER3HZp3vIRqIPdTDvmKvzV4G0XHUuz3uB0MAEhDq+50ej6ojOiZVYLfNmnVKQKjvcCyQaCJ2+YmXEHOoq3LohWhS9to9bvJF8YZ6vRugF/JFSDQJYV95ODXFG+q7HHohmqgdfvLNvVhDnS9Aosnaa/tciJRzsYV6ywu44IhowvxA0fC402mexRbqrHohmg4Oa+ZbbKHOCR2i6dhjvXquxRLqqooWPyISTUWnF3LH0xyLJdRbfshVpERTojo4FYnyKZ5Q5wuOaKr4HsuvWEKdvQii6WKo5xd76kQZxI5TfkUe6v2+ou2HUT8sUa50e31uxZtTkYd6yw/ABW9E09fy2HnKo8hDnR8LiaLR8FivnkfR99QZ6kSRYE89n2IIdb7QiKLAT8X5FHmoewEnb4ii0Av73LExhyIPdS5fJoqGKuCzAiZ3Dg11EblPRP5WRC6LyI9E5PPD2+dF5Dsi8vrw97lDH01kAk0molH5/GScO6P01AMAv6OqjwH4VwB+S0Q+BOALAL6rqg8D+O7w74dgqBNFicdF5s+hoa6qa6r6/eGfGwAuAzgF4FMAvjq821cB/Mqhj8aeOlGk2FPPn7HG1EXkLICPAPgegBVVXQMGwQ9geYTvMHYDiejoehxTzx1r1DuKSAXA1wH8tqrWZcRet4g8C+BZAIBhHqGJRHRUrDbLn5F66iJiYxDof6aqfzm8eUNEVof/fRXA5t2+VlWfV9VzqnpOGOpEkWJPPX9GqX4RABcAXFbVP7zjP30LwDPDPz8D4JuHPxyHX4iixDH1/Bll+OVjAH4DwMsi8tLwtt8D8CUAXxOR8wDeBvDpQ78TM50oUuyp58+hoa6q/4CD4/gXx3s4pjpRlFjSmD+xHJJBRFFiZypPIg51vriIIsf1IbnCnjrd08WLF/H005/BJz7xC3j66c/g4sWLcTeJiO5h5Dp1yp+LFy/iuee+jG7XAwCsr2/guee+DAB46qmn4mwajYM99VxhT50OdOHCC+8E+m3drocLF16IqUV0NAz1PGGo04E2NjbGup2SihUwecJQpwOtrKyMdTslFA/KyBWGOh3o/PnPolBw33NboeDi/PnPxtQiIjpMxBOl7DGkye3J0AsXXsDGxgZWVlZw/vxnOUmaNuyp54pEeYah4RT1Hy9fj+zxiAj41w8t8qzSlBORS6p6bpT7cviFKMNMg5UveRNtqLO3QBQp22So503EPXWGOlGUHIsfxvMm0ivOcT2iaDkmQz1vOPxClGHsqecPh1+IMsxmTz132FMnyjD21POHPXWiDGNPPX/YUyfKMJc99dyJ/Ipza2ei6LCnnj+RX3G+yIiiYZnCFaU5FHnCll0z6ockyqWSw/daHkUf6g5P0COKQsXley2PIg91vtCIolHmey2XYhh+4QuNKArsQOVT5KHuWAYXRBBNmW0KCjbH1PMolnStFtiDIJomfiLOr1hCnS84ouni0Et+xRLqFVbAEE0VO075FVNPnWN9RNPE91h+xRLqlmmgYHOylGgaHEvgWgz1vIotWWtFO66HJsq0WoHvrTyLLdTnS05cD02UaXNlvrfyLLZQnyna3GyIaMIMAebYYcq12ELdMASzJX5MJJqkGjtLuRfrbCV7FESTNc+hl9yLOdRtHppBNCHCoRdCzKFumQZn6okmpOJa3FeJ4g11gB8XiSaFVS8EJCDU58rsqRNNAsuECUhAqLuWyc2HiI6p6Jgo8vg6QgJCHQAWq+xhEB3HYoXvIRpIRKgvVVzW1hIdkSHAcrUQdzMoIRIR6pZpsKdBdEQLFYdVL/SOxLwSTsywp0F0FCs1vnfoXYkJ9ZJjoVbkhCnROCquhSrXetAdDg11EfmKiGyKyCt33PZFEbkhIi8Nf/3yJBpzgj0OorHwEy693yg99T8F8Mm73P5Hqvrk8NdfTaIx82UHLg/PIBqJYwkWuOCI3ufQBFXVvwewE0FbICIcHyQa0XK1AINVY/Q+x+kWf05Efjgcnpk76E4i8qyIvCgiL47yTZerLvg6Jbo3EWC55sbdDEqgo4b6HwN4EMCTANYAPHfQHVX1eVU9p6rnRvnGtmlgocIXK9G9zJcdnkNKd3WkUFfVDVUNVbUP4E8AfHSSjTo9V+SWvEQHEBm8R4ju5kihLiKrd/z1VwG8ctB9j6JgmxxbJzrAYsVFyWH5L93doa8MEfkLAB8HsCgi1wH8PoCPi8iTABTAVQC/OemGnZ4rYqvhIezrpL81UWoZAtw3z146HUxUowtNEdFxHu/6bhvXdjpTbBFRupyaLeL+hdJYXyMiiPJ9TpMnIpdGnZdMdFH4yZki97QgGrJNwclZDkvSvSU6MQ1DcB8nhIgAAKfmirDMRL9lKQES/wpZqroocfN/yrmCbXAbDRpJ4kNdRHD//HhjiERZc/98CcI6XxpB4kMdGByoO1PkTnSUT9WCxQV5NLJUhDoAnF0scfsAyh0R4MyY1S6Ub6kJ9ZJj4TSHYShnTs0WuV86jSU1oQ4AJ2cKqBa4ko7yoeya3A6AxpaqUBcRPLRc4SHVlHmGAA8tVzg5SmNLVagDg31hWA1DWXd6vsT9XehIUhfqwOAIL1bDUFZVCxZO8pg6OqJUhjoAPLhchmXyoylli2kIh13oWFIb6q5lstSLMufMQgkFmyuo6ehSG+rA4IzGeR68SxkxW7J5jgAdW6pDHQAeWCqjYKf+aVDOubaBB5cqcTeDMiD1aWibBh49UeP4OqWWaQgeWalym2maiEy8ioqOiQ8uV3muKaWOCPDwcgVll+WLNBmZCHUAmCnZ+MBiOe5mEI3l/vkS5jgvRBOUmVAHgJVaAaus76WUWK65ODnLbQBosjIV6sCgJGy2xIVJlGy1ooUH+MmSpiBzoS4ieHi5wtOSKLEKtoEPrlS5wIimInOhDgCWaeCRE1XYrIihhLFMwaMnarB51ihNSWZfWQXbxCMnqtzRkRLDEOCDK1UU+SmSpiizoQ4A1YKNR1cZ7BQ/Q4BHT9S4ER1NXaZDHQBqDHaK2TuBzgl8ikDmQx1gsFN8DAEeOVFloFNkchHqwLvBzu0EKCqmMZgUnS1xcRFFJzehDgyC/bHVGqtiaOosU/DoKnvoFL1chToAVFwLj5+c4eZJNDW2KfjQag21AgOdopfLZCs6Jh4/WeOWvTRxjmXg8ZMz3KCLYpPbVCvYJp44NYNakW8+moxqwcKHT82wDp1ildtQBwZ7sX9otcZNwOjYVmouHj9Z47AexS733VQRwdnFMsquhStbTfQ17hZRmhgCfGCxjGUeQ0cJkftQv22p6qLkmHhtowGv14+7OZQCjmXggysVVDkhSgnCz4p3KLuDMVEu5abD3B4/Z6BT0jDU38c2DTy2WsXJWX6cprs7MVPg+DklFodf7kJEcGZhMM7+0+0WgpAD7TRYIXp2sYTlKn/gU3Ix1O9hseKiWhgE+26rF3dzKEYzRRsPLJVRsFmuSMnGUD+Ea5l49EQNWw0Pb91qocdee65YpuDMfInVLZQaDPURLVVdzJZsXN1uYbvpx90cisB82cEHFsscO6dUYaiPwTYNPLxSxULFx0+3W/ADlj5mkWMJzi6UsVBx424K0dgY6kcwX3ZQK1h4a6eNzboXd3NogpaqDs4slHmGKKUWQ/2ILNPAg0sVLJZdXL3VQtsP424SHUPRMXF2ocS9zyn1GOrHNFOy8XPFGWw3fVzfbaPL1aip4toGTs8VsVRxIcJ99in9GOoTICJYqrpYrDjYani4ttvheHvCOZbg1GwJy1UXBo85pAw5NNRF5CsA/gOATVV9YnjbPID/BeAsgKsAfl1Vd6fXzHQQESzXClisuNhodHFzrwM/YAlkktim4ORsESdqBYY5ZdIos0F/CuCT77vtCwC+q6oPA/ju8O80ZBiC1ZkinrxvDvcvlHguagJYpuD0XBFP3jeLk7NFBjpllqge3pMUkbMAvn1HT/01AB9X1TURWQXwd6r6yAjfR0d5vKwJwj7W9rvYbHTZc4+YbQqWqwWszhZyW9EiIsjj+y5LROSSqp4b5b5HHVNfUdU1ABgG+/IRv0/qhH2FH/Thh330wj76qsDgfxAM/s8QgW0acC0DtmnAMg3cN1/C6bkidlo+Nuoe9jvcdmCaakULK7UC5ksOe+WUK1OfKBWRZwE8O+3HmTQvCNH2QjS9AG0/RNsP0AsV4RFO0TANgWMZKNomyq6J1ZkCTs8VsdfuYbPR5dYDE2Kbgwnr5WqBR8pRbh011DdEZPWO4ZfNg+6oqs8DeB4YDL8c8fGmrhf2sdv2sdfuodHtTXSYJOwrOn6Ijh9ip/Xu7Y4lqLoWIEC3F6Lts2LmKKqFQa98ocxeOdFRQ/1bAJ4B8KXh79+cWIsi1PFD3Gp52Gv30PQCRD3s6AeKnWAwDCMyOEkn7A+GdFQZTvfi2gbmSw6Way5KDitziW4bpaTxLwB8HMCiiFwH8PsYhPnXROQ8gLcBfHqajZykfl9xq+Vjs9FFvRPE3Zx3qOKO2naBaxnDjaQUTS+M/AdO0ogAFdfCXNnBXMlmkBMdYKTql4k9WIzVL91eiI16F1sNL1Vj2I4lmCs5cG0DHT/EXruXqvYfh20KZks2ZksOZos2rJxWrxwXq1/SL4rql9TwghA3djvYbHip7O36gWKj7sEQYLlWwIdPzcAP+9hr97Df6aHth0eavE0i0xCUHBO1go3Zso2qa3HpPtGYMttT74V93NzrYH2/i4xkHoBB8J2ovbfuuuOHaPkBWl6AlvdupU6SWeYgwCuuhZJjoeJaKNgGQ3wK2FNPv3F66pkLdVXF2n4X13c7menB3s3tFZInaoW7BuGgmiYcBL0fwA8GdfVRL36yzUE5p2MZKDsWSo6JsmvxWLgIMdTTL7eh3vYDvLnZQtNLzgTotFULFh5cqoxcl62qw4VTit4w6L3h771Q0Qv7GKyn0uHveCcQRASCwaSlQCAyODjENgeLrRzLgGMasK3BbY7JnncSMNTTL3eh3u8rbux1cGOvk8px8+MyBDg1V8Sp2SJDlH4GQz39cjVR2u2F+MlGAy0vv4dU9BW4ttPBbquHh1cqHNogyrFU14jttX28fGM/14F+p6YX4JUb+9hvc18ZorxKbajf2Ovg1fUGgoRXeUStFyour9dxc68Td1OIKAapG37p9xVvbDVxq+nH3ZTEUgXeutVG2w/wwGKF+6EQ5UiqeuphX/HqeoOBPqKtho/XNhqZLu0kovdKTU89CPt4db2BRjc/5YqTsNfu4fJaHY+t1mCyxz6SXthH2w/R7yv6qujroIzTEIEx3HitaJusNKJESkWoM9CPp9ENGOwH8IIQLe/dRVotLxzp0HBDgLJrvbsq1rVQsk0OdVHsEl+n3u8rfrxWZ6BPQK1o4bETtdwHT9hXbDc9bNS7E62cskzBYsXFSsK2A2adevplavHR6xsNbHMMfWKWqi4eWq7E3YxYtLwAG/Uutpv+1OcZqgULyzUXi2U39h+iDPX0y8zio2s7bQb6hG01PBQdE6dmi3E3JTL77R7e3mlHun1Eoxug0Q3wltnGSnVwfGHc4U75kNhQ3256uL7LWutpuLbTRtE2MV924m7KVAVhH2/ttLFZ92Jsw2ALi1stDw8sVTBTtGNrC+VDIksaW16ANzebcTcjs1SBNzabaPvZnafYafn4wfW9WAP9Tt1eHz++WcebW00EIc+ipelJXKj3+4o3NpuZ2gM9icLhv3PWxlr9oI/XNxp4bb0R+TbDo9ise/jB9X3stjisSNORuFC/tttG2+deLlFoeWGmhrg6foiXb+wnfh7GDwYlutd323E3hTIoUaFe7/awtt+Nuxm5cmOvg0Y3/RuANbo9/Ojm/kg15klxbaeDn2634m4GZUxiQj3sK97cbOZyP/Q4qQJvbrXQT/F4V73bw+W1RuKP8Lub9f0u3uD8EU1QYkL95l4H3V56ellZ0vFD3NxP5zBM0wvw2nq697fZani4ssVgp8lIRKh7QcitYmN2c6+bqqELYHBAyqtr9Uxsv7xR93Bth2PsdHyJCPXrux1Wu8QsHB4JmBaqg+qdNA65HOTGXgf7nfTPb1C8Yg/1th9gq5GMWuK826h30UlJ5dHN/W7m9gMazG80Uz2URPGLPdTf3mlzcjQhVAclpUnX8gJcz+hQhdfr4+otVsTQ0cUa6h0/xG6LHzeTZKflo9tLbm89D4vTNuseFyfRkcUa6ht11qQnjSoSs7T+bm7sdXKxOO3KNrcToKOJLdTDvmKrmdzwyLPNRjeRdetB2M/N4jQ/UGxwromOILZQ32p4mShFy6JeODhEImk2G16uJhE36t3M7c1D0xdbqHPoJdk2EjYEo6pYz9lrxuv1scOxdRpTLKHe8cNcjIumWdMLEjVhutfuwcvhiuO8/SCj44sl1Hfa7H2kwW6CrlNextLfr94JMr3vPU1eLKHOcq10SMpH/24vzPVKy6QNhVGyRR7qftCP9KxIOrpGN0AvAWV19RwHOsDnT+OJPNT3Oj5XkKaE6mAsO2557wR0emGuqn7oeCIP9azt15F1SQjUlpecCds4qAItjqvTiCIP9VYCQoJGF/f16veVE4UAmuwM0YgiD3WWMqZLywtiXQDT7oWZ3udlVHH/cKX0iDbURTienjJ9jfcHMcNsIAnDYJQOEYd67Dv90hHEGaxxn8Z08eJFPP30Z/CJT/wCnn76M7h48WIs7cjSYSA0XVakjyYS6cPRZHgxBms/xo92Fy9exHPPfRnd7qBOfH19A88992UAwFNPPRVpW+L8d6B0ibTrLGCop1G8oR7bQ+PChRfeCfTbul0PFy68EHlbVJHInTMpeSIfU6f0ScICpDhsbGyMdTtREjDU6VBxjmsbMb5kVlZWxrp9mkQAI85/DEqNY4W6iFwVkZdF5CUReXGErzjOw1FM4uypGzF2BM6f/ywKBfc9txUKLs6f/2zkbYnz34HSZRITpb+gqtuj3TV7L8yLFy/iwoUXsLGxgZWVFZw//9nIJ9GmLYhxLNcy43vN3L6OSbi+JnvpNKJoq18yJknVEdMUZ+FFyYn3JfrUU08l4lpWXL5VaTTHHVNXAH8jIpdE5NlJNChNklQdMW1xrSqtuBanYgCUXTPuJlBKHPfH/8dU9aaILAP4joi8qqp/f+cdhmE/CHzTPubDJQurI6bPNAQF20Qn59tLsKdOozpWT11Vbw5/3wTwDQAfvct9nlfVc6p6ToxsvTCTVB0xTSKAxNhdrrCXijJDnUZ05FAXkbKIVG//GcAvAXjl3l+VrcUTSaqOmKa4Ky8qbrY+4Y3LtQ3YJrfYoNEc58f/CoBvDHtwFoA/V9X/M5FWpUSSqiOmyY6xAgUAKoV891JrOX/+NB6JcgLMsAv6j6/eiOzxaDKqBQtPnJqJtQ0/vL6X28MyPnSyhpni0T+tiEis2yfT8YnIJVU9N8p9I/5MxxdWGrlW/B/9T9QKcTchFiXHPFagU/5E+m5lbyGdkjCeu1hxYx8GisOJmXz+MKOji/bdylBPJScBPXXDECxX8xVwlilYrLiH35HoDhGHej53+0u7csyrOm9brrm5Woi0XHW5PQCNjaFOh0rKasaCbWKx4sTdjEiYhmAlp/MIdDyRf65Owkd5Gl3BNmAlYEz9tjMLZThW9nuv98+XULCT8cOU0iXydyuXO6dL0q6XbRp4YLESdzOmaqZoc4KUjiz6UOdCilRJ4vL0ubKD5Vo2JxAtU/DgcjnuZlCKRR7qrLlNl6Rer7MLZbh2coaFJuXsQhmuxWEXOrpYhl84rp4OBdtIZE8dGEwkPrRcyVQ1zELFwVI1m59AKDqxpOt8OR8VDGk3V0r2daoV7MwE+0zRxkNL2Z4roGjEEupzpWR+pKf3mkvBD9/FiosHltI9Bl0tWHjkRJUHS9NExBLqM0U71rMn6XC2KanZHXC5Wkhtj32maOOx1RoXGdHExBLqIoKFFPQC82yx4sZ6MMa4lqouHlmppiocFyoOHj2RrjZT8sU2Y8k63OQSSef1mSs7+NDJGkpOsqtHDAHumy/i4eUKh1xo4mIL9ZJjJbZcLu9mS3ZqVzNWXAsfPjWD03NFJDEvqwULHz49g9NzpVR9EqL0iHXQ9MRMAfudXpxNoLtI+97lhiG4b76EhYqDK1stNLpB3E2CaQjumy/iRK3AMKepijXU50o2XNuA1+NGX0lRdEzMJryUcVQlx8LjJ2tY2+/ixl4HQRjP1s+zJRsfWCyn9tMPpUusoS4iOD1XxJubrTibQXc4PVeMuwkTJSI4OTvoIW+3PGzWvUh67vZwL/SVWgHFhI/xU7bEXrO2VHGxvt/N7fmTSVJxrcweynD7kI3lagEtL8BGvYvtpo+wP9nee7VgYaVWwELZ4SQoxSL2UBcR3D9fwuW1RtxNyb37F0pxNyESZdfCA0sVnFlQ1Ds9tPwALS9Eyw/GGgo0DUHJMVF2LZQdE9WCzV45xS72UAeA2ZKDmaLNSdMYzZXt3FUjmYZgruy8Z+VsL+yj7YVo9wKEfYUq0FeFQCAy6PE7poGKa6FgG5z0pMRJRKgDwJmFEl6+sc9jTGNgCHBmPt1L7SfFNg3MlAzMIF8/4Cg7ErNdYtm1cGo2W5N0aXF6vsRhA6KMSEyoA4PKi6SdtJN11YKFkylcPUpEd5eoUBcZ7JHNooFovLsnOf/BibIiUaEODBa/5KUKI2483JgoexIX6gCwOlPEYiUbqxqTaqnqpHLTLiK6t0SGOgA8uFTh+PqUVAsWHljkKTtEWZTYUDcMwSMnqjzPdMJc2+ApO0QZlujEdCyDhwhMkGUKHj1RhW0m+rIT0TEk/t1ddi08slJlRcwxmYbggytVlBwOaRFlWeJDHQBmSjYePVFjsB+RORzKyts2AER5lIpQB4bBzgN6x2aZgkdXGehEeZGaUAdun7xehW0y2Edhm4LHVmuoFRjoRHmRqlAHgGrBxhOnZlB2uWjmXiquhSdOzbAslChnUhfqAFCwTTx+coYLlA6wVHXw+MkaV4sS5VBqu3GmIXh4pYqy28HbO21u2QtAZLCF8eoMd7skyqvUhvptJ2eLKLsWrmw10c3xAdZFx8QDS2WOnxPlXOpDHRhMoP786Vlc221jbb+bq167CHBypojTc0WuEiWibIQ6MNhW4MxCGQsVF29uNtH2s3+Qddk18eBSBWVOhhLRUObSoOJa+LnTM9ioe7ix14YfZK/b7lgGTs8VsVx1uRc6Eb1H5kIdGBy2cWKmgKWqi/V6F2t7HfTC9Ie7bQpOzhZxolbgUAsR3VUmQ/020xCcmi1ipepibb+LzUY3lT13xxKs1ApYnSlyRS0R3VOmQ/02yzRw33wJp2aL2Gn72Kh3Ue8EcTfrUDNFGys1F/Nlh8MsRDSSY4W6iHwSwH8DYAJ4QVW/NJFWTYlhCBYrLhYrLjp+iM1GF7daPrwElUIWbAMLZRfLNZeLh4hobKJHrP8TERPATwD8OwDXAfwzgKdV9cf3+Bo96uNNU9sPsNvuYbflo+kFkZZEigxOIporOZgrOSg6DHKaLBFBEt93NDoRuaSq50a573F66h8F8IaqXhk+6P8E8CkAB4Z6UpUcCyXHwqnZIoKwj0Y3QMsP0PJCtPxgoj151zZQcS2UHBNlx0K1YMHioRVENCHHCfVTAK7d8ffrAP7l8ZoTP8s0MFd2MFd+d1+ZXthH2w/RC/uDX4HCD0P4gaI/7AGpDnrdwGCC1jYNOKYB2xr+2TJQsk0GOBFN1XFC/W4zdz/zGU9EngXw7PCvnoi8cozHTLJFANtxN2KK+PzSa1FEsvrcgIxfOwye25lRv+A4oX4dwH13/P00gJvvv5OqPg/geQAQkRdHHRdKmyw/N4DPL82y/NyAbD+/ozy344wF/DOAh0XkAyLiAPgMgG8d4/sREdExHbmnrqqBiHwOwF9jUNL4FVX90cRaRkREYztWnbqq/hWAvxrjS54/zuMlXJafG8Dnl2ZZfm5Atp/f2M/tyHXqRESUPKyvIyLKkEhCXUQ+KSKvicgbIvKFKB4zSiJyVUReFpGXROTFuNtzXCLyFRHZvLP8VETmReQ7IvL68Pe5ONt4VAc8ty+KyI3h9XtJRH45zjYelYjcJyJ/KyKXReRHIvL54e1ZuXYHPb+sXL+CiPyTiPxg+Pz+YHj7WNdv6sMvR9lOIG1E5CqAc6qaiVpZEfm3AJoA/oeqPjG87b8A2FHVLw1/MM+p6u/G2c6jOOC5fRFAU1W/HGfbjktEVgGsqur3RaQK4BKAXwHwH5GNa3fQ8/t1ZOP6CYCyqjZFxAbwDwA+D+DXMMb1i6Kn/s52AqrqA7i9nQAllKr+PYCd9938KQBfHf75qxi8mVLngOeWCaq6pqrfH/65AeAyBiu/s3LtDnp+maADzeFf7eEvxZjXL4pQv9t2Apm5EEMK4G9E5NJwBW0WrajqGjB4cwFYjrk9k/Y5EfnhcHgmlcMTdxKRswA+AuB7yOC1e9/zAzJy/UTEFJGXAGwC+I6qjn39ogj1kbYTSLmPqeq/APDvAfzW8CM+pccfA3gQwJMA1gA8F2trjklEKgC+DuC3VbUed3sm7S7PLzPXT1VDVX0SgxX6HxWRJ8b9HlGE+kjbCaSZqt4c/r4J4BsYDDllzcZwTPP22OZmzO2ZGFXdGL6Z+gD+BCm+fsOx2K8D+DNV/cvhzZm5dnd7flm6frep6h6AvwPwSYx5/aII9UxvJyAi5eGkDUSkDOCXAGRx07JvAXhm+OdnAHwzxrZM1O03zNCvIqXXbzjRdgHAZVX9wzv+Uyau3UHPL0PXb0lEZod/LgJ4CsCrGPP6RbL4aFhi9F/x7nYC/3nqDxoREXkAg945MFih++dpf34i8hcAPo7BDnEbAH4fwP8G8DUA9wN4G8CnVTV1E44HPLePY/DRXQFcBfCbt8cw00RE/g2A/wvgZQC3DwH4PQzGnbNw7Q56fk8jG9fv5zCYCDUx6HB/TVX/k4gsYIzrxxWlREQZwhWlREQZwlAnIsoQhjoRUYYw1ImIMoShTkSUIQx1IqIMYagTEWUIQ52IKEP+P/AR+xGWHSWzAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# Print variable values\n",
"print(\"Name\\tValue\")\n",
"for c in model.component_data_objects(pyo.Var):\n",
" print(c.name,\"\\t\", pyo.value(c))\n",
"\n",
"# Plot solution\n",
"plot_circles(model)"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.3 Solve and Inspect the Solution](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.3-Solve-and-Inspect-the-Solution)",
"section": "4.1.3.3 Solve and Inspect the Solution"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"left_x_con[A] \t 10.0 \t 9.99999990193744 \t None\n",
"left_x_con[B] \t 5.0 \t 4.999999953543133 \t None\n",
"left_x_con[C] \t 3.0 \t 15.734851787229463 \t None\n",
"left_y_con[A] \t 10.0 \t 19.142135514931184 \t None\n",
"left_y_con[B] \t 5.0 \t 4.999999951252124 \t None\n",
"left_y_con[C] \t 3.0 \t 5.517617033892999 \t None\n",
"right_x_con[A] \t None \t 9.874784367980283e-08 \t 0.0\n",
"right_x_con[B] \t None \t -9.999999849646462 \t 0.0\n",
"right_x_con[C] \t None \t -1.2651480159601327 \t 0.0\n",
"right_y_con[A] \t None \t 9.87471615587765e-08 \t 0.0\n",
"right_y_con[B] \t None \t -19.142135464931897 \t 0.0\n",
"right_y_con[C] \t None \t -20.624518382291022 \t 0.0\n",
"no_overlap_con[A,B] \t 225.0 \t 224.99999778541908 \t None\n",
"no_overlap_con[A,C] \t 169.0 \t 218.51602998638847 \t None\n",
"no_overlap_con[B,C] \t 64.0 \t 115.5049713354404 \t None\n"
]
}
],
"source": [
"# Print constraints\n",
"for c in model.component_data_objects(pyo.Constraint):\n",
" print(c.name,\"\\t\", pyo.value(c.lower),\"\\t\", pyo.value(c.body),\"\\t\", pyo.value(c.upper))"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.4 Reinitialize and Resolve](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.4-Reinitialize-and-Resolve)",
"section": "4.1.3.4 Reinitialize and Resolve"
}
},
"source": [
"### 4.1.3.4 Reinitialize and Resolve"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.4 Reinitialize and Resolve](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.4-Reinitialize-and-Resolve)",
"section": "4.1.3.4 Reinitialize and Resolve"
}
},
"source": [
"Reinitialize the model, plot the initial point, resolve, and plot the solution. Is there more than one solution?"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.4 Reinitialize and Resolve](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.4-Reinitialize-and-Resolve)",
"section": "4.1.3.4 Reinitialize and Resolve"
}
},
"outputs": [],
"source": [
"# Initialize and print the model\n",
"initialize_circle_model(model)"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.4 Reinitialize and Resolve](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.4-Reinitialize-and-Resolve)",
"section": "4.1.3.4 Reinitialize and Resolve"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXAAAAFlCAYAAADyArMXAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAAAs7ElEQVR4nO3dWYxk130e8O9/t9p7n+nZSA5FkLRlJZFFwhKgIKAdOXDoB9kPls0HR0Fo0A9WYAN+iOEXCwkMGIFo5yUwQpuCFcB2LMByLMREElGQouTBhElB0EZxn+EsvU0vtd79njxU9UxPs7tru1V3+35Ao3uqq7tO9VR9dep/NlFKgYiIskdLugFERDQZBjgRUUYxwImIMooBTkSUUQxwIqKMYoATEWWUMc8bW1tbU1evXp3nTRIRZd5rr712Ryl17vjlcw3wq1ev4tVXX53nTRIRZZ6IXD/pcpZQiIgyigFORJRRDHAiooxigBMRZRQDnIgooxjgREQZxQAnIsqooQEuIg+IyDdE5HUR+YGI/Obg8s+LyC0R+c7g4+nZN5eIiA6NspAnAPDbSqlvi0gDwGsi8rXB9/5IKfWF2TWPiIhOMzTAlVIbADYGX7dF5HUAl2fdMCIiOttYS+lF5CqAnwTwCoBPAviciPwrAK+i30vfP+FnngPwHADoug4RmbbNRESZ9dBDD+HatWux/C4Z9UxMEakD+D8Afl8p9RURWQdwB4AC8B8AXFRK/Zshv0PxDE4iKjIRwbg5KCKvKaWePH75SD1wETEB/DWAP1dKfQUAlFJbR77/JwD+x1gtIiowpRT8UMEPIwShQqQU1ODy/meg/xUgEIgAgv6TXwBomsDSNZi6wNA5mayohga49GseLwJ4XSn1h0cuvziojwPALwL4/myaSJQdSim4QQQ/jOCHCt7gay8cXBYoeGEIP1SI682orglMXWDqGixDgzkIdsvQBiGv3f0e5csoPfBPAvhVAN8Tke8MLvtdAM+IyEfRL6FcA/DrM2gfUWqFkULPC9B1Q3S9AF03gO2FiOZcJQwjhTBScPzozOuZuqBqGaiVdNRKBmqWgYqlz6mVNAsj18BjuTHWwCmjgjBC1wsHgd0PbdsPY+tFJ0XXBFVLR71koFrqf66YnGwwS3OvgRMVjRdEOLA9NHs+Om4wtHebVWGk0HYCtJ3g7mWaALWSgXrJwHLVwkLFYKCnFAOcaKDrBtjveTgYhHbWe9eTihTuhvpG04GhCxYrJpaqJpYqFmvpKcIAp8KKIoWm7WO/52G/58ML8tnLnlYQKux2POx2PIh0US8ZWKqaWK5aqJUYIUniX58KxQ1C7Hf9u+WReQ84Zp060ju/sWfDMjQsD8J8sWJC01hqmScGOOWeUgp7XQ9bLRdN20+6ObniBRG2Wi62Wi4MXbBWL2F9oYSqxWiZB/6VKbccP8RO28V224EXsKs9a0GosNl0sNl00CgbWF8oY7VmsVc+QwxwyhWlFPZ7PrbbDg56fmEHIpPWL7N0cP1ur7zMOeczwACnXHCDENstF9ttl4ORKeKHChtNBxtNBwuVfq98pcpeeVwY4JRpTdvHZtPBfs9jbzvlWnaAlt2BqQvON8q4sFjmlMQpMcApk9qOjxt7NgclM8gPFW4d2Nho2riwWMalpQpMbsg1EQY4ZUrXDXBjv4f9LoM76yIF3D5wsN12cWGhjIuLZe6sOCYGOGWC7YW4ud/DnY6XdFMoZkGocHPfxlbLwcWlCi4ulFkjHxEDnFLN8UPcOrCx03ZZ4845P1R4f7eHzaaNy0tVnG+UGORDMMAplbwgwq0DG9sth6slC8YLFN6708Xtpo0ryxWcq5e4mdYpGOCUKlF0OMDlIGRyF5rrR3hnu4vbBw4eXq1hsWom3aTUYYBTarQdH+/sdGF7YdJNoRSxvRA/3GjhXKOEq6tVDnQewQCnxIWRwo29HjZbDuvcdKqdtoum7eHqag2r9VLSzUkFBjglqtnz8c6dDtycHphA8fIChTe3Oljt9oO86AuBGOCUiCCMcG23h522m3RTKIN2Ox5ato8HV6s43ygn3ZzEMMBp7va6Ht670+EOgTQVP1R4Z7uL3Y6Hh9dqKJvF2yyLAU5z4wURru32n3BEcTno+fjuzSYeXKniwmKxeuMMcJqLg56Ht7c78EP2uil+YdSfO77bdfHYeqMwe6sU415Som4d2PjRZpvhTTPXsgN892YTHTdIuilzwQCnmQkjhTe32nh/t8fpgTQ3XhDhB7ea2G47STdl5lhCoZlw/BBvbLbR46IcSkCkgHe2u+i6Ia6uVnO7FJ8BTrE76Hl4a7uDgCUTSthm00HPC/Do+UYu54zn7x5Rom7u9/CjzTbDm1KjZQf43q0m2k7+9pBngFMsDuvdN/Zs1rspdbwgwg9vt7DdylddnCUUmhrr3ZQFkQLe2emi4wZ4eK2Wi7o4A5ym0nZ8vMEpgpQhWy0Xjh/h8QsN6Bk/MIIlFJpY0/bx+gbDm7Kn/9htIQizvYkaA5wmst/18KONFg9doMxqOwF+uNGCn+EQZ4DT2O50XLyx1eZRZ5R5XTfED2634AbZHL9hgNNYttsO3t7ucKYJ5Ybt9UPc8bMX4gxwGtl228G7O12GN+WO60f44Ub2QpwBTiNheFPeZTHEGeA01E7bZXhTIbh+hNc3slMTZ4DTmXbaLt7ZYc2bisPx+6s2sxDiDHA6VbPnM7ypkBw/whub7dRPk2WA04lsL8Sb222GNxVW1w3x1nYbKsVPAgY4fYAfRvjRZos7ClLh7Xd9vL/XS7oZp2KA032U6u8q6PjZXZ1GFKfbB05qdzFkgNN93r3TRcsuxnmCRKN6904XTTt9+4kzwOmu2wc2tltu0s0gSh2lgLe22qmbI84AJwD9zanSXOsjSpofqsFpU+kpLzLACV03wFvc34RoKNsL8eZWJzUzUxjgBecFEd7YSv98V6K0aNo+3rvTTboZABjghXY448TljBOisWy1XGylYGYKA7zAbh3YaDuccUI0ieu7vcQHNRngBdV1A9zct5NuBlFmhZEa7I2fXPmRAV5A0d0HXtItIcq2thPgdjO5UgoDvIBu7tvoeemaz0qUVTf3eui6yZQiGeAF03J83G6ydEIUl0gB7+x0ECUwk2togIvIAyLyDRF5XUR+ICK/Obh8RUS+JiJvDT4vz765NI0wUniHpROi2HXdMJExpVF64AGA31ZK/TiATwD4DRH5MIDfAfB1pdSjAL4++Del2PXdLjepIpqR200bbWe++6UMDXCl1IZS6tuDr9sAXgdwGcCnAXxpcLUvAfiFGbWRYnDQ87DFfU6IZkYp4O3tzlwXxY1VAxeRqwB+EsArANaVUhtAP+QBnI+9dRSLIIzwzk46Vo4R5ZnjR3PdU2jkABeROoC/BvBbSqnWGD/3nIi8KiKvTtJAmt613R68gKUTonnYbDpo9uZTShkpwEXERD+8/1wp9ZXBxVsicnHw/YsAtk/6WaXUC0qpJ5VST8bRYBpPxw2w02bphGieru1257LAZ5RZKALgRQCvK6X+8Mi3vgrgs4OvPwvgb+NvHk3r+i5LJ0Tz1vNC7HRm33EapQf+SQC/CuBnROQ7g4+nAfwBgJ8VkbcA/Ozg35Qi+12Pp+sQJeTGnj3zueHGsCsopf4fADnl2/883uZQXJRSPKCBKEFeEOF208aV5erMboMrMXNqp+1yuTxRwjaaDvwZnuDDAM+hMFK4sc/eN1HSglDNdIUmAzyHbh/Y8AKulydKg62WM7N9wxngOeMFETYS3N6SiO6nFGY2HsUAz5mb+z2eb0mUMrsdbyb7pDDAc8T2Qmxz0Q5RKl3fjb8XzgDPkRv7PW4VS5RSbSfAfteL9XcywHPC8UPsxfzgIKJ4xT0+xQDPie2Wy943Uco1bR9ilGL7fQzwHIgihe02Z54QZYHeWI3tdzHAc+BO14UfsvtNlAV6bRlBTKszGeA5sNXkzBOizBAttp0KGeAZ13J8dFzuOEiUJXEdb8gAz7gtrrokyhzbC3HQm37WGAM8w7wgwi6nDhJl0mZr+s4XAzzDtloOpw4SZdRBz596kysGeEZx6iBRtinVPwB5GgzwjNrredwylijjdjruVJvPMcAz6s4cDkwlotkKQjXVYCYDPIPCSKHZi39rSiKav30GeLEc9Dxwy2+ifDjo+VATzkZggGfQNK/YRJQufqjQsidbjMcAzxilFA5YPiHKlb0JO2UM8Ixp2QE3riLKmUnfVTPAM2bSV2oiSi/Xjyba04gBnjGsfxPl0yTHrTHAM6TjBnD9ePYRJqJ0meRIRAZ4hsR9ICoRpUfPC8feG4UBniEsnxDl27jPcQZ4RrhBiK473c5lRJRu+93xpggzwDOi4/DUHaK867jBWKsyGeAZwd43Uf6FkYIzxkQFBnhGtF2uviQqgnGe6wzwjOh57IETFcE477YZ4BlgeyECLp8nKoTuGCsyGeAZMMkSWyLKpu4YA5kM8AwY5xWZiLItUqOXTBngGcAeOFGxjNppY4CnnFKKA5hEBTNqp40BnnI9L5zq1Goiyh4GeE6w/k1UPD0vRDRCx40BnnJdlk+ICkcpoDfCzoQM8JRzAwY4URG5DPDs8wPWv4mKaJSzbxngKeeF7IETFZEXDN/UigGeYkopnkBPVFBeyADPNC+MMMbWwESUI+yBZxx730TF5bMHnm2jvAITUT6xhJJxo7wCE1E+BaEaupiHAZ5i7IETFduwXjgDPMVGeQtFRPnFAM8w9sCJim1YBjDAU4w1cKJiG5YBQwNcRL4oItsi8v0jl31eRG6JyHcGH0/H0FY6htvIEhXbsAwYpQf+ZwB+7oTL/0gp9dHBx0sTtI2GYHwTFduwhXxDA1wp9S0AezG1h8bAVZhEdJZpauCfE5HvDkosy7G1iI5gghfVyy+/jGee+RX8zM/8NJ555lfw8ssvJ90kSkA0pBc3aYD/MYBHAHwUwAaA50+7oog8JyKvisirE95WYbEEXkwvv/wynn/+C9jc3IJSwObmFp5//gsM8QKauoRy8i9VW0qpUCkVAfgTAD91xnVfUEo9qZR6cpLbKjKWUIrpxRf/FI7j3neZ47h48cU/TahFlJRhETBRgIvIxSP//EUA3z/tukQ0nq2trbEup+Iyhl1BRP4SwFMA1kTkJoDfA/CUiHwU/ReIawB+fXZNLC6RpFtASVhfX8fm5gfDen19PYHWUJKGRcDQAFdKPXPCxS9O1hwaB/O7mJ599tfw/PNfuK+MUi6X8Oyzv5ZgqygJwzpxQwOckiMi4EyU4vnUpz4FoF8L39rawvr6Op599tfuXk7FIUO6cQzwFIu7hBJFCn4UIQgVgkghCKP+50hBKfWBQVMRQBeBoQt0TYOpCwxNg6ELDE0GLzA0C5/61KcY2MQeeJZNE49+GMHxw8FHBNsPEcS4t4qIoGRoKJv64KP/tcZQJ4oNAzzDxgnDIIrQcQJ03AA9L96wPolS6u4LxF2DUK+XDDTKBiqmzl460RSGZQADPMVMXQMQnvp9xw/RcQO0nQC2HyY/cVwpuH4I1w+x23Gha/0wr5cN1EsGdI1hTjSOfgacjgGeYpbxwf+8MFJo2j72ex5c//RwT4MwitC0PTRtDyKChbKJ5ZqJqsWHHdEoTsqAo/hMSjHryKuv7YXY73lo2f7Q/RHSSCl1N8xLpo6liomlqsVeOdEZLPbAs8syNLQcH3fa7v215oxz/RBbfojttouliom1RmnoW0WiImIPPKOaPR9vb7dxc6+XdFNmRimF/Z6HA9vHctXCWsOCoTHIiQBA12ToO1QGeMq0HB839npo2UFhzsRUSmGv6+Kg52GlZmG1XmJphQpvWO8bYICnhhdEuLbbxW7Hu3uZrhcrxCKlcKfjYq/nYX2hjOWqlXSTiBJjjvD8Z4CnwHbLwfW9HoLw/sHJYQMYeRVFChsHNlq2j4uLlZF6IkR5U2IPPN0cP8S7O100bf+Ua/SXsR8P9qLougHe3engXKOElZrFRUFUKJauD70OAzwhm00H7+/1hp46bWgagjA/M1DGFSmFrZaDlhPg8hJ741QcpjG8w8Jnw5xFkcLb2228d6c7NLwBwChYHfw0thfg3TsdtJ3T3q0Q5csoJVQG+Bw5fojv325ip+0Nv/IA50ffE0UKN/Z62Gm7w69MlHGchZIizZ6Pt7bb8MesZ5fN4XWwotlpO3D8EJeXKtA43ZBySAQjbTnB7t0cbDRtvL7ZGju8AQb4adqOj3fvdAszV56KpWLqI62FYIDP2I29Hq7d6U28UWDZ0Hg25im8IMS13S7coLiDvJRPtdJoxREG+Axdu9PFzX17qt8hIigb7IWfJggjXLvTy9VeMUR1Bniyrt3pYqPpxPK7yhYD/Cxh1F/FyhCnvKiVRnvOM8BnIM7wBvr1MDpbFClc32VPnLJPBKiNuGc+Azxmtw7sWMMb4EDmqMIowvt7PfgzPk6OaJaqlj7y7CoGeIz2uh7e341/+9eyqXG63IiCsB/i0QiLpIjSaNT6N8AAj03XDfD2dmdGv11G2tiG+lw/xK0DGyqDJxcRMcDnzAsi/GizPdLS+EmxDj6etuNjmys2KYNGnUIIMMCnFkUKb2y2Z76gpMKZKGPb7fQPiSDKCk36NfCRrz/DthTCjf0eOm4w89thgE9ms+lwtSZlRq1kjLVtMgN8Ci3Hj33GyWksXedWqhOIlGI9nDJjqWqOdX0mwoTCSOHt7c7ES+Qn0Shz77FJ2F6A3S5LKZR+K7XxjhFkgE/o+m4Xrj/ft+aN8nivznTPTtvlIh9KtbKpjbQD4VEM8Akc9DxsteY/w6Fq6TzgYUKKpRRKuXF73wADfGxKKbx3p5vQrQvq7IVPzPVD7Pd4og+l0zIDfPa2Wi6cOZdOjloYY44ofdBO253pfH2iSZi6oDHBc5sBPoYwUri5H/9S+XHUSgaX1U8hjCLsdrjAh9JluWaNNX3wEAN8DLcP7IlO1YmTiIy11JY+aLfrccMrSpWV6vjlE4ABPjI3CHH7YLrDGeLC6YTTUUpxmT2lhq4JFiuTjW0xwEd0+8BBWkqn9ZIBsIoylabtc4UmpcJS1Zy4LMoAH0EQRthJUY9N17SRN3ynUyiFPS7uoRRYnrB8AjDAR3Kn46Vu5sLChG+56J4D2+O+4ZQoTYDlMZfP3/fzMbYltzZb89nvZByLFRM6Z6NMJYoUDmzOC6fkrDVKMPTJY5gBPsRBz4PtpW8JtiaTD3zQPfvcbpYSdGGhPNXPM8CHSGPv+9BKffLaGfW5fjiX7YCJjmuUjbEObzgJA/wMfhjhIMVLry1dR51TCqfWYhmFEnBhcbreN8AAP9N+z5vrdrGTmGQDHLpfxw24yRXNlWVoWI3hucsAP8N+N/09s3rJ5EEPUwrCCDa3mqU5Wl8oTbR0/jg+808RRQrNjLy1Zi98em2HdXCaExXhfGP68gnAAD/Vge2nbu73aRYrk6/kor62k40Xa8q+0G7G9q6ZAX6KLE0v0zUNS5xSOBUviHhiD81F2N6N7XcxwE+RtbfULKNMr5fC+f6UL42yAeXFtykeA/wEQRilcvHOWSxDn3pOaZYopRBFCuHgI4rU1DNJ2AOnWVufcuHOccV5xo+h62bziXy+UcJ7OVuUEkUKbhjBCwYfYYQgjHBWVBuaBsvQYOkaSkb/61G2HeBMFJqlqqVjLebFdwzwE3S8bIZgxTKwWDEzM3vmJFGk0PUC2H4/sINo/C1fgyhC4EU4enaSoQlMXUPZ1FEvGScGuhtEiJSCFsP0LqLjHlypxjJ18CgG+Am6Ge7FnlsooeX4qV+AdJwbhGg7AXpeiGgGjQ8ihSAKYfshDno+qpaORtlA2dTvXUkpOH6IKrfqpZgtVsyJDi0eZmgNXES+KCLbIvL9I5etiMjXROStwefl2FuWoCzvjWHp+lT7C89TpBTajo/bBzY2mg46bjCT8D5Ood/L32w5uHVgo3lkymiSB1ZTfj24Wp3J7x1lEPPPAPzcsct+B8DXlVKPAvj64N+5oJTK/Ekt5xqlVG81q5TCQc/DzX0bu10PXoLnU/phhP0jbXEyNnhN6XeuYc3sHNuhAa6U+haAvWMXfxrAlwZffwnAL8TbrOR4YZS58sNxuqZhtV5Kuhkncv0QG00HB7Y/l972qBT67wbe2+2gk7EppJRemgBXlmfT+wYmn0a4rpTaAIDB5/OnXVFEnhORV0Xk1Qlva66SPnU+Lqs1a6qN4uMWDY4w22w5ifa4h3H8CO/vdXFr355oAJXoqAuL5fvHWWI282e4UuoFpdSTSqknZ31bcch6+eSQiOD8Qjp64bYf4vaB0x9cTboxQxy+K2jaHt7d6WZ6Rg8ly9AFl5cqM72NSQN8S0QuAsDg83Z8TUqWn+Le4biWKuZMX/2HUUpht+thq+VkpjcbHHkHFoQRbu33cHO/l6pyD2XD5aXKzN8FT/rbvwrgs4OvPwvgb+NpTvLy0gPvS64XrpTCTsfN3CZRCgrHq2gt28f13V5mNjej5JVMberj0kYxdGhURP4SwFMA1kTkJoDfA/AHAL4sIs8CeB/AL82ykfOUtydpvWSiXjZGGph77bVv46WX/g57+3tYWV7B00//PJ544mNj32YUKWy3XThBNmd0RJGCrt8/i8f2Alzb7eKhlWqqxhYonR5cqc5lh9ChAa6UeuaUb/3zmNuSCvmK776Li2W863XPfHF67bVv48tf/it4Xn8Xxr29PXz5y38FAGOFeKQUttoO3Fy9k+lz/RDXdnu4usoQp9Ot1i2szWkWGB+Fx+TxaC1T14eev/fSS393N7wPeZ6Hl176u5FvRymF7Zab+fBWZ7yMe0GI63u9zNT0ab4sQ/DwWm1ut8cAL4jFioWFM/YM39s/PtX/7MuPUyrbZZNxuH6I93d7iHJWbqPpfWitDnOO784Y4MfEvdlMmlxcLMPQT75/K8srY11+XMsJcrObn2D4Y8DxQ2y1nTm0hrLiXKM0k/1OzsIAPya/8d1foXlx8eR5qU8//fOwrPsffJZl4emnf37o7/WCCAe9bM02icN+18v0vjkUn5Kp4eqM9js5CwP8mDTvIRKHRtnE4gmbXT3xxMfwmc/8MlZWVgABVlZW8JnP/PLQAUylFO503DPrxlmjjfGsuH1g527mEo3vkXP1RAa2uW/mMfOsXyXlwkIJPS+Af2yw8YknPjb2tMED20/10vhxCQT6GGW0IIyw2XRweXm2K+4ovS4ulrGY0Jm0+U+rMcV1WnSa6ZqGS6eUUsbh+iFaOVtqPsk7sKbtoZWxBUsUj4ql48GV+ZdODuU/rcZknjLIlze1kjHVQcj90omXo8JJ36QltI2D7GwXQPEQAR45V5vLgp3TMMCPKUIP/ND6QhnWhHuldNwAfg4Da9IAD6MI+11v+BUpNy4vVdAoJ1M6OVSctBqRpWvI8UzC+4gIHlyuTBRa7ZzumW1M0Zva7/m5XAhGH7RcM3ElBeMeDPBjRKRQvXDL0Psbzo+RW44f5mrg8qhpZiEFYYRWTl/Y6J5aScej5xupWDNSnKQaQ61gh9rWSsap88NPktfeN9CfzzuNPZZRcs0yBI+tN1Iz3ZgBfoJ6uVgBDgDLVWukQc0gjNDz8hrgAkufbv902wtg81zNXNIEeGy9kege+8cxwE9QL1gP/NCFxfLQF6+2G+Ru5skhUxfE0bHa67EXnkePnK8nPmh5HAP8BLVSel5h50twZbmK0ik9DKVUrg/8tYx4/t9bts/VmTlzZbkyty1ix8EAP4GhayhPWQvNKk0ED6xUTtz0yg8VwhzPsijFNHitlGIZJUfW6hYeSHCxzlmKmVIjSNtbpXmydB0PLFc/MJ3SzflWseUYZx/ld5ygWBplA4+cqyfdjFMxwE+xXC1ugANAxTJw6diJ2lk/qOEshqbFOn00L1vrFpllaHhsvZHoSsthGOCnWKpasQxoZdlixcL5Iwez5jnAq1a84x62F3JRT4aZuuDHLzZSvyYk3a1LkK4JFgveCweAtXoJ5xZKiCIFP6eLd4D+pkRxipTK9QtenvXDewHVDMxGY4CfYeWEfbOL6Fy9jIUcv5hpoqEc0wyUozwGeOYchnetlP7wBhjgZ1quWYXZF2WYpYqFpYT2PJ61iqXP5P85z+9Y8sjIWHgDDPAzmbqW2EbtaRNECkvVfIZ4PebyyaGAc8EzI4vhDfBEnqEuLJQLed7jccGgN7lUtSAi2E/BasM333gLr7zy92i1W1hoLODjH/8EHnv80bF+h6lrsde/DwUhAzwLLEPwYxeyF94AA3yopaqJkqnB9Yv9dvhoZ3KxYkLTBLsdN7H2vPnGW/jmN78BP+i/uLbaLXzzm98AgLFCvD7DJ23EWSipVzI1fPjiQqr2NxkHSyhDiAguHJlKV1THDy1ulIxElxa/8srf3w3vQ37g45VX/n7k36FBUC/wgq2iK2c8vAEG+EjON0qp2T4yKXLChuH1koHzjfI4W4nHptVujXX5SWplAwU5QY+OqZV0/MSlxUyHN8AAH4mha1irF3tK4WmzNKqWjvXF8txf4BYaC2NdfpLGjLcN1jiFKZWWayY+fHEh9Yt0RpH9ezAnl5YqhV6ZedZRY2VDx8XFcmybQY3i4x//BEzj/vKHaZj4+Mc/MdLP1ywDlj7b9p60IRgl68pyBY+vN2DM+P9+XvJxL+agbOq4sFjcWrg55AFvaBouLFTmVlN+7PFH8dRTP323x73QWMBTT/30SAOYAsHSHBZpTXO+JsVL1wSPX2jggZVqKo5CiwtnoYzh8lIF2223kNPDRulNigBrNQslQ5vLDJXHHn907GmDANCoGDDn0DvOSy8v6yqWjsfXGzObLpokPsLGYOgaLi8lfxJ1EsapFzZKBi4kUBcfhSaCxcp8xjPmWVKiky3XTHzk0kIuwxtggI/twkJ56oNvs6i/3eroT4Ik6uKjWKyYc5l5oomk7r4XzZXlCn7swkKu3wnl957NiKYJrq7Wkm5GIsbtxcy7Lj6MqWtzO6ijv79K+t6BFIGh36t35x0DfAIrNQvnGsWbVliZYM7sYV18tV5KZL74kZZgrV6a20yiSf5WNL2KpeMjlxaxUivG85ODmBO6ulpD0w4KtWXoNIceNEpGf3Cz7cJNYJe+pYox15JGXmuuaSXSL28+sFJN5djLrLAHPiFD1/DIuWKVUkqGBl2b/CFj6RouLlWwXLXm2hu3dG1uA5cAABEG+BxVLR0/cWkBV9dqhQpvgAE+laWqhfWF5PYDmTcRwVIMBzssVkxcWq6gPIfBYBmUTuZZjl4smzCmeKGj0Yj0Byr/0eXFwh5CzkfZlB5arcV+nmKaLVet09fVj8EcDHCu1kszXXK+XLPmvmR6uVbMMJmnesnAP76yiAdWqqk+dHjWGOBTOlzhZRnFeBBZhoZGjFuwNkoGLi2VZ1JyaJRMLMx4v5PjyqaeibMUs0oT4KHVKj5yORtnVs4aAzwGZVPHo+uNwuyVshzzCL+haVhvlAezROL5I5ZNPZGZCEWZ/ZCEhYqBf/LAEi4tVThFc4ABHpOFsokPnasn3Yy5qJcMlGYwTa5eMnB5uTL1ySimruFcozz380x1TcNCDo+cS5qhCz50rpaL7V/jxvcgMTrXKMHxQ9zct5NuyswtVy1sNuO/n7oIztVLWCyb2Lc92F441s9rouF8o5zIPt/LVZNbyMZI1wQXF8u4uFjO9WrKaTDAY/bAShVeGGG7ldxxY/OwVDGx23FndvK6ZfTLKk4Q4qDnwRnhSDsNgvML1lw2qvrAbWvC8klMNAEuLJZxaakydBfMomOAz8CH1mpQCthp5zfENU1waamC67vdmd5O2dBxYaEC2+8HuXvKwikNgvOLJZTH2K8lThcXK+wlTkmkf/rV5eUKSgn9P2YNA3wGRASPnKtBBLnuiddKBlZqJex1Z38fK6aOymIFPS/Efs+7r+evieD8QnLh3SibWGTte2IiwFrdwpXlKmvcY2KAz0g/xOvQRbDRdJJuzsycXyih6wVw/fFq1ZOqWjqqVgUdN0DT9hFGwPpCKbGd/wxdw8Wl4h70Ma3VuoUryxVOCZwQ/2ozdnWtBkMX3NjL58CmJoJLixW8t9sF1PwOuqiXDCxX+z3fthvO7QXkuIuLZa66HJNIf7rlpaUK6jGuKSgi/vXm4MpyFVXLwNvbHYRR/k7zqVg6ztWtudb8ayUDV5Yr0DUN5wH0vAD7PR8t25vb68hS1SrsEu5JlEwN5xslnG+Uc3GgcBqImmOvSUTUPG8vbWwvxBtb7bGnxmWBUgrX93roucHMb2u1bmF9oQycsCVWGEVo2j72ej68GfbKS6aOh1drhV7GPQqR/pTT9YUSFismF+CgX14dNwdF5DWl1JMfuJwBPl9BGOHtnQ72u37STYldFPVD3PZmE+LaYF7wqDsLdr0AB10PLcePtVduGTqurlY56+QMljHobS+UOKPkGAZ4Dtzc7+HWvo28VVTCSOH6bhdOzL3fkqnj8lJlolkKYRThoOdjv+dNvX+7qWu4ulbj/OQTiABLVRPnG2UsV9nbPg0DPCd6XoB3d7poO7MvO8xTEEW4sWfH0hPvTzErDbaEnT4Qul6AjuOj7YZjl1gsQ8eDK1XWb4/QpD+NcrlmYrlqcRrgCBjgOaKUwmbLwY09O1cDnFGkcGO/h+4UNfGKpePS0uwWdXhhiI4ToO0E6HnBmWWWsqnjwdUqZ5wAsAzBYsXCctXEUtUq3CEK00pNgIvINQBtACGA4KQbOHZ9BvgpHD/EuztdNO381MaVUrjddNDseWP9nKb190NZrVs4aaByFiKl7vbMu66PILz3OK2XTVxZqhR6wLJeMrBUNbFUNTnzZkppC/AnlVJ3Rrw+A3yIg56HG3s2OnOYzTEvLcfHZtNBMGTflMMZC2v1UuIDhLYfwvYCLJRNWIaWu7GKYUxd+qWRqonFqsmByBjFGeCcB54yS1ULS1ULux0XN/dt9HIw5XChbKJmGdhqOTg4qTcu/fu9Vrdg6ekIistLFTy8VoNlaFBKoeeF6HoBum6Irhug54W5KXlZhoZ6yUDV0lErGaiVdAZ2RkzbA38PwD4ABeC/KKVeOOE6zwF4bvDPJ9gDH51SCnc6Hm4d2LmZO95xA2w27f5sEOmfH3muUYKVksCwDMHV1RpW62efdaqUguNH6Lj9+nnX7Qf80dJLGpVNbRDSBmqDwOaMmvlKUwnlklLqtoicB/A1AP9WKfWtM67PEsqEmj0fW20He935rTScFUMXRJFCEKrU1JUPZ7s8tFqdKtAcP4QbRPCCCH5478MLVP9zGM0k5EX6UxwtXYNpyN2vLUODqWswdUHF1BMvTVGKSihKqduDz9si8jcAfgrAqQFOk1sc1CK9IMJOx8VWy4E7wh7ZaXFY3z7fKGFpMEfYDyPstF1st93E3mFYhob1hRLONeJZcFI29aFT6aJIwbsb7v1gVwpQUIPP/R7+4XNcpP+kl8OvIdA09MNavxfQnHddPBP3wEWkBkBTSrUHX38NwL9XSv3PM36GPfAYtRwfB93+ApU01sp1TbBYMe9ONztr/nTT9rHd6r/DmHVp+XDByXqjfPfFhGhe0tIDXwfwN4MHvwHgL84Kb4rfQtnEQtnEg6tVOH54d7Vh2wkSG2ArmxqWqv05wgtlc+QSyWKlv7PgYa+8afvougH8mMoNhi6oWjoWyiaXd1NucCFPDh0fYOsMZk3EXXstm4PZCyUDdctAtaTHPiDmBuHdmR+Hs0CGLYc3dRkM0vVnVNRKBlcIUmqkpQdOKSUiqFg6KpYO4N5sCjcI+zXXoD+Ydm+gTSFS6m4dViCDuitgaHKkznpvkKxk6HNZgVcy+lPajp43GUb99kbH6sSaCDQRrgykwmCAF0g/DHE00zNJ1wT6nFZoEqUZ5xQREWUUA5yIKKMY4EREGcUAJyLKKAY4EVFGMcCJiDKKAU5ElFEMcCKijGKAExFlFAOciCijGOBERBnFACciyigGOBFRRjHAiYgyigFORJRRDHAiooxigBMRZRQDnIgooxjgREQZxQAnIsooBjgRUUYxwImIMooBTkSUUQxwIqKMYoATEWUUA5yIKKMY4EREGcUAJyLKKAY4EVFGMcCJiDKKAU5ElFEMcCKijGKAExFlFAOciCijGOBERBnFACciyigGOBFRRjHAiYgyigFORJRRDHAiooxigBMRZRQDnIgooxjgREQZxQAnIsooBjgRUUYxwImIMooBTkSUUQxwIqKMYoATEWUUA5yIKKMY4EREGTVVgIvIz4nIGyLytoj8TlyNIiKi4SYOcBHRAfxnAP8SwIcBPCMiH46rYUREdLZpeuA/BeBtpdS7SikPwH8D8Ol4mkVERMNME+CXAdw48u+bg8uIiGgOjCl+Vk64TH3gSiLPAXhu8E9XRL4/xW1m3RqAO0k3ImFF/xvw/hf7/gPAmoiM+zd46KQLpwnwmwAeOPLvKwBuH7+SUuoFAC8AgIi8qpR6corbzLSi33+AfwPe/2LffyDev8E0JZR/APCoiDwsIhaAXwHw1TgaRUREw03cA1dKBSLyOQD/C4AO4ItKqR/E1jIiIjrTNCUUKKVeAvDSGD/ywjS3lwNFv/8A/wa8/xTb30CU+sC4IxERZQCX0hMRZdRcApxL7gERuSYi3xOR74jIq0m3Z9ZE5Isisn102qiIrIjI10TkrcHn5STbOGun/A0+LyK3Bo+D74jI00m2cZZE5AER+YaIvC4iPxCR3xxcXojHwRn3P7bHwMxLKIMl928C+Fn0px7+A4BnlFI/nOkNp4yIXAPwpFKqEHNgReSfAegA+K9KqY8MLvuPAPaUUn8weCFfVkr9uyTbOUun/A0+D6CjlPpCkm2bBxG5COCiUurbItIA8BqAXwDwr1GAx8EZ9/8ziOkxMI8eOJfcF5BS6lsA9o5d/GkAXxp8/SX0H8y5dcrfoDCUUhtKqW8Pvm4DeB391dqFeByccf9jM48A55L7PgXgf4vIa4PVqUW0rpTaAPoPbgDnE25PUj4nIt8dlFhyWT44TkSuAvhJAK+ggI+DY/cfiOkxMI8AH2nJfQF8Uin1MfR3b/yNwdtrKp4/BvAIgI8C2ADwfKKtmQMRqQP4awC/pZRqJd2eeTvh/sf2GJhHgI+05D7vlFK3B5+3AfwN+qWlotka1AUP64PbCbdn7pRSW0qpUCkVAfgT5PxxICIm+uH150qprwwuLszj4KT7H+djYB4BXvgl9yJSGwxiQERqAP4FgCJu6vVVAJ8dfP1ZAH+bYFsScRhcA7+IHD8OREQAvAjgdaXUHx75ViEeB6fd/zgfA3NZyDOYJvOfcG/J/e/P/EZTREQ+hH6vG+ivfv2LvP8NROQvATyF/u5zWwB+D8B/B/BlAA8CeB/ALymlcjvId8rf4Cn03zorANcA/PphPThvROSfAvi/AL4HIBpc/Lvo14Fz/zg44/4/g5geA1yJSUSUUVyJSUSUUQxwIqKMYoATEWUUA5yIKKMY4EREGcUAJyLKKAY4EVFGMcCJiDLq/wP1VWYEbYxwpwAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# Plot initial point\n",
"plot_circles(model)"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.4 Reinitialize and Resolve](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.4-Reinitialize-and-Resolve)",
"section": "4.1.3.4 Reinitialize and Resolve"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Ipopt 3.13.2: \n",
"\n",
"******************************************************************************\n",
"This program contains Ipopt, a library for large-scale nonlinear optimization.\n",
" Ipopt is released as open source code under the Eclipse Public License (EPL).\n",
" For more information visit http://projects.coin-or.org/Ipopt\n",
"******************************************************************************\n",
"\n",
"This is Ipopt version 3.13.2, running with linear solver ma27.\n",
"\n",
"Number of nonzeros in equality constraint Jacobian...: 0\n",
"Number of nonzeros in inequality constraint Jacobian.: 30\n",
"Number of nonzeros in Lagrangian Hessian.............: 12\n",
"\n",
"Total number of variables............................: 8\n",
" variables with only lower bounds: 8\n",
" variables with lower and upper bounds: 0\n",
" variables with only upper bounds: 0\n",
"Total number of equality constraints.................: 0\n",
"Total number of inequality constraints...............: 15\n",
" inequality constraints with only lower bounds: 9\n",
" inequality constraints with lower and upper bounds: 0\n",
" inequality constraints with only upper bounds: 6\n",
"\n",
"iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls\n",
" 0 1.0000000e+02 1.37e+02 1.00e+00 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0\n",
" 1 1.0276645e+02 6.44e+01 6.62e-01 -1.0 7.31e+00 - 6.14e-01 4.44e-01h 1\n",
" 2 1.0566116e+02 1.85e+01 1.63e+00 -1.0 2.55e+00 0.0 8.96e-01 6.48e-01h 1\n",
" 3 1.0612677e+02 0.00e+00 5.99e-01 -1.0 1.46e+00 -0.5 1.00e+00 1.00e+00h 1\n",
" 4 1.0329539e+02 0.00e+00 3.22e-01 -1.0 2.52e+00 -1.0 1.00e+00 6.55e-01f 1\n",
" 5 1.0326145e+02 0.00e+00 3.12e-01 -1.0 1.93e+00 - 8.26e-01 1.00e+00h 1\n",
" 6 1.0237284e+02 0.00e+00 1.44e-01 -1.7 4.25e+00 -1.4 6.57e-01 7.24e-01f 1\n",
" 7 9.9794889e+01 0.00e+00 1.92e-01 -1.7 1.94e+00 -1.0 9.54e-01 1.00e+00h 1\n",
" 8 9.8743606e+01 0.00e+00 9.11e-01 -1.7 3.49e+01 -1.5 2.76e-01 2.60e-02f 1\n",
" 9 9.8483796e+01 0.00e+00 1.74e-01 -1.7 4.32e+00 - 9.92e-01 8.22e-01h 1\n",
"iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls\n",
" 10 9.8455971e+01 0.00e+00 9.38e-02 -1.7 1.73e+02 - 9.38e-01 3.53e-01f 1\n",
" 11 9.8404443e+01 0.00e+00 2.67e-03 -1.7 9.65e+00 - 1.00e+00 1.00e+00h 1\n",
" 12 9.8405024e+01 0.00e+00 2.10e-05 -1.7 4.30e+00 - 1.00e+00 1.00e+00h 1\n",
" 13 9.8300696e+01 0.00e+00 1.14e-05 -2.5 2.47e-01 - 1.00e+00 1.00e+00h 1\n",
" 14 9.8285160e+01 0.00e+00 2.64e-07 -3.8 3.60e-02 - 1.00e+00 1.00e+00h 1\n",
" 15 9.8284281e+01 0.00e+00 1.27e-09 -5.7 3.07e-03 - 1.00e+00 1.00e+00h 1\n",
" 16 9.8284270e+01 0.00e+00 1.75e-12 -8.6 2.76e-04 - 1.00e+00 1.00e+00h 1\n",
"\n",
"Number of Iterations....: 16\n",
"\n",
" (scaled) (unscaled)\n",
"Objective...............: 9.8284270438747257e+01 9.8284270438747257e+01\n",
"Dual infeasibility......: 1.7491657667044265e-12 1.7491657667044265e-12\n",
"Constraint violation....: 0.0000000000000000e+00 0.0000000000000000e+00\n",
"Complementarity.........: 2.5240899380720466e-09 2.5240899380720466e-09\n",
"Overall NLP error.......: 2.5240899380720466e-09 2.5240899380720466e-09\n",
"\n",
"\n",
"Number of objective function evaluations = 17\n",
"Number of objective gradient evaluations = 17\n",
"Number of equality constraint evaluations = 0\n",
"Number of inequality constraint evaluations = 17\n",
"Number of equality constraint Jacobian evaluations = 0\n",
"Number of inequality constraint Jacobian evaluations = 17\n",
"Number of Lagrangian Hessian evaluations = 16\n",
"Total CPU secs in IPOPT (w/o function evaluations) = 0.004\n",
"Total CPU secs in NLP function evaluations = 0.000\n",
"\n",
"EXIT: Optimal Solution Found.\n"
]
}
],
"source": [
"# Solve the model\n",
"results = solver.solve(model, tee = True)"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.1.3.4 Reinitialize and Resolve](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.3.4-Reinitialize-and-Resolve)",
"section": "4.1.3.4 Reinitialize and Resolve"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXUAAAFoCAYAAACotWuNAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAAAqx0lEQVR4nO3dWYxk13kf8P93t9qr920WzpDD1aQlKhgoQRQEsswYihFAtgEZ4oPBACPQDxYgA36w4BfLAQIIgWgnD4EBmiNYAWwnAmRFgiDE1gg2HBuBbI5Ai5SGFBcNOUvvW+331r315aGqySE1PV3VXXXX/w8azUyxuuvU3Fv/Pvfc75wjqgoiIkoHI+oGEBHR+DDUiYhShKFORJQiDHUiohRhqBMRpQhDnYgoRY4MdRHJi8g/isg/i8iPROQPBo/Pish3ReT1we8zk28uERHdixxVpy4iAqCkqg0RsQH8PYDPA/g1ADuq+iUR+QKAGVX93Ym3mIiIDnVkT137GoO/2oNfCuBTAL46ePyrAH5lEg0kIqLhWcM8SURMAFcBPAjgv6vq90VkSVVXAUBVV0Vk8ajvMz8/r+fPnz9Je4mIMufq1atbqrowzHOHCnVVDQA8KSLTAL4hIk8M2xgReRbAswBw33334cUXXxz2S4mICICIvD3sc0eqflHVPQB/C+CTANZFZGXwgisANg75mudV9aKqXlxYGOoHDRERHdMw1S8Lgx46RKQA4CkArwL4FoBnBk97BsA3J9RGIiIa0jDDLysAvjoYVzcAfE1Vvy0i/w/A10TkEoB3AHx6gu0kIqIhHBnqqvpDAB+5y+PbAH5xEo0iIqLj4YxSIqIUYagTEaUIQ52IKEUY6kREKTLU5KNxefnll9FfSoZiQwyIaQOmBTFtiDkochIAkJ85Xv21grS/UAR60CAAgi6050P9LqC90N8C3du5c+dw/fr1qJtBIQk11D3PAze6Do+qouUFaHkBXD9AN1B0gx48vwcv6KHr99Ab8+EwBLAtA45pwDYNOJYB2xQ4loGSY6HomPzBHjL+e2dLqKFOk9PrKVrdAE3XH/wK0PL8sYf2ke1QwO324Hbv3mM3BCg6Foo5E+VcP+RLjgXDYPAQjQNDPaGaro96x0fD9dHyfLS8AEm4COop0HD77d6ACwAQAQq2iVLOQilnopK3Uc7x1CQ6Dn5yEqLXU+y3u9htedhtdeH56Rm7VsW7w0Sb9f5jjiWYLjqYKTqYKtgw2ZMnGgpDPcY63eDdIN9vdUMfSomS5ys2ai42ai4MAaoFGzNFB9NFG3nbjLp5RLHFUI+Zhutjp+Fht+Wh5QVRNycWegrstbrYa3UBAEXHxEzRwUzJRiVvR9w6onhhqMeAH/Sw1fCwUe+g6TLIj9Ifqmnj1l4bRcfEYjWHhXIOlslpF0RH7lE61hcTUZY0vqfh+livdbDd8BBkaWxlAgwB5so5LFVz7L1/gIiwlDjhROSqql4c5rnsqYcs6Cm2Gy7Way4arh91c1Kjp8Bm3cVm3UUpZ2Kxksd82WHvnTKHoR6Sludjbb+DLfbKJ67pBvip28Q7Oy3MlR0sV/MosUSSMoJn+oS1vQA3d1vYanhRNyVzgt57FTSzJQdnZwsoOjzlKd14hk9Ipxvg5m4bWw03EZOC0m6n2a8omi87ODNTZFkkpRZDfcw8v4dbe21s1DqZqitPAlVgs+5hq+FhoZLDmZkCchbDndKFoT4m3aCH23ttrO0zzONOFdioudiqu1iq5nFqugDH4g1VSgeG+gkFPcXtvTZW9zu8AZowPQVW9zvYqLtYruZxajrPahlKPIb6Cey1PLy11Tx0RUJKhqCnuLXXxmbDxQPzJcyUnKibRHRsDPVj8IMerm+3sFl3o24KjZHn9/DqWh3zZQfn50uw2WunBGKoj2i74eL6dhOez6GWtNpqeNhvd3FuroSFSi7q5hCNhKE+JM/v4fp2E9usN8+EbqB4Y6OB7aaL++dLrJKhxGCoD2Gj3sHb2y34AXvnWbPb7KLe2cd9s0UsVfNRN4foSAz1e3D9AG9tNt9d8pWyyQ8Ub202sdVwcWGhzIlLFGu8E3SIWqeLV27tM9DpXbW2j1du7WOf5wTFGEP9Ltb2O/jx7RpvhtLP6AaKa2s13N5rR90Uorvi8Msdej3FT7eb2KixVJEOpwq8vd1C0/XxwEKZ+6dSrDDUB1w/wE/WGlzjnIa21fDQ7u7j4aUKx9kpNjj8AmC/3R8/Z6DTqJpuwHF2ipXMh/rafgfXVjl+Tsd3MM5+i+PsFAOZHX5RVby1xfFzGg9V4J3tFlqujwcXyxDhODtFI5M99V5P8fpGg4FOY7fV8PDqWh09rthJEclcqAc9xWvrdU73p4nZa3Vxba3GpZgpEpkKdT/o4dpqjROKaOJqbR8/vl1DN+CyzBSuzIR6P9DrqHdY4ULhaLgMdgpfJkL9INBZskhha3kBg51ClfpQ94P+xgcMdIpKywtwbZXBTuFIdagfBDqHXChqTZfBTuFIbairKn6y3mCgU2w03QCvsdyRJiy1of7WVhP7bVa5ULzUOz7e2mpE3QxKsVSG+up+mxOLKLY26x5u7raibgalVOpCfbfp4e1tfmAo3m7stLHdYMeDxi9Vod7yfLy+0YByyJIS4I0NLvVM43dkqIvIWRH5GxG5JiI/EpHPDx7/oojcEpGXBr9+efLNPZzn9ytdODWbkqKnwGtrNbh+EHVTKEWGWaXRB/A7qvoDEakAuCoi3x38tz9S1S9PrnnD6fUUP1mvw+2yXIySxfMVr63V8fipKe6gRGNxZE9dVVdV9QeDP9cBXANwetING8VbWyxdpORqugHe2GBFDI3HSGPqInIewEcAfH/w0OdE5Ici8hURmRl344Zxe6+NzTpXXKRk22l6uLHDG/x0ckOHuoiUAXwdwG+rag3AHwO4AOBJAKsAnjvk654VkRdF5MWTN/f9Wp7PDwKlxq29Nm+c0omJDlEqIiI2gG8D+CtV/cO7/PfzAL6tqk8c8X10mNcbhqrilVs1fggoVYqOiZ8/PQVjjOPrIoJxfe4oGiJyVVUvDvPcYapfBMBlANfuDHQRWbnjab8K4JVRG3oSN3fZq6H0aXkBbnBiEp3AMNUvHwPwGwBeFpGXBo/9HoCnReRJAArgOoDfnED77qrh+tzkl1Jrdb+D6aKDqYIddVMogYYafhnbi41h+KXXU/zw1j7aHmt7Kb1ytoEPn5keS5kjh1+Sb6zDL3Hzzk6LgU6p53Z7uL7djLoZlECJCvX9dher+52om0EUio2ai90my3VpNIkJdT/o4c1NTtCgbHlrq8GNNWgkiQn1m7ttLgNAmeP5inc4F4NGkIhQ73QDrNc47ELZtFl3eR+JhpaIUL+x0wIXX6SsUgXe3uFNUxpO7EO94frYavBmEWXbbrPL7RlpKLEP9bdZ1kUEAHiHO3rREGId6rtND7U2lwIgAg6uWrkFHt1bbENdlXf9iT7oxk4LPd5gonuIbahv1l20eMef6H063R7W66wEo8PFMtSDnnKlOqJD3Nptw+eEJDpELEN9rdaB5/MSk+huuoFyuQw6VOxCXVWxxhOW6J7Wax2OrdNdxS7Ud5oePJ+XlkT30g0UW01WwtDPil2or3E5AKKhrO8z1OlnxSrUm67PunSiITVcH/UOZ5nS+8Uq1NlLJxoNF7qjD4pNqPtBD9tc44VoJFsN3oOi94tNqG/UXQS8m080ElX21un9YhHqqsqhF6Jj2qh3uLE0vSsWob7X6nJXI6Jj8nzFNvcypYFYhPpGnaVZRCexUeNniPoiD/Wgp9hrsZdBdBK1TpfrwRCAGIT6frvLreqITkgV2G2xZp1iEOo7HAskGotdXvESIg51VQ69EI3LXqvLRb4o2lCvdXx0A56EROMQ9JSbU1O0ob7LoReisdrhlW/mRRrqPAGJxmuv5XEiUsZFFupN1+eEI6Ix83xF3eVKp1kWWaiz6oVoMjismW2RhTpv6BBNxh7r1TMtklBXVTR5iUg0Ee1uwBVPMyySUG96AWeREk2Ian9XJMqmaEKdJxzRRPEzll2RhDp7EUSTxVDPLvbUiVKIHafsCj3Uez1FywvCflmiTOl0e1yKN6NCD/Wm54MT3ogmr+my85RFoYc6LwuJwlF3Wa+eReH31BnqRKFgTz2bIgh1nmhEYeBVcTaFHuquz5s3RGHoBj2u2JhBoYc6py8ThUMV8FgBkzlHhrqInBWRvxGRayLyIxH5/ODxWRH5roi8Pvh95shXExlDk4loWB6vjDNnmJ66D+B3VPUxAP8KwG+JyM8B+AKA76nqQwC+N/j7ERjqRGHidpHZc2Soq+qqqv5g8Oc6gGsATgP4FICvDp72VQC/cuSrsadOFCr21LNnpDF1ETkP4CMAvg9gSVVXgX7wA1gc4juM3EAiOr4ux9Qzxxr2iSJSBvB1AL+tqjUZstctIs8CeBYAYJjHaCIRHRerzbJnqJ66iNjoB/qfqepfDh5eF5GVwX9fAbBxt69V1edV9aKqXhSGOlGo2FPPnmGqXwTAZQDXVPUP7/hP3wLwzODPzwD45tEvx+EXojBxTD17hhl++RiA3wDwsoi8NHjs9wB8CcDXROQSgHcAfPrI78RMJwoVe+rZc2Soq+rf4/A4/sXRXo6pThQmljRmTySbZBBRmNiZypKQQ50nF1HoOD8kU9hTp3u6cuUKnn76M/jEJ34BTz/9GVy5ciXqJhHRPQxdp07Zc+XKFTz33JfR6bgAgLW1dTz33JcBAE899VSUTaNRsKeeKeyp06EuX37h3UA/0Om4uHz5hYhaRMfDUM8Shjodan19faTHKa5YAZMlDHU61NLS0kiPU0xxo4xMYajToS5d+izy+dz7Hsvnc7h06bMRtYiIjhLyjVL2GJLk4Gbo5csvYH19HUtLS7h06bO8SZo07KlnioS5h6HhFPQfrt0M7fWICPjXD85zr9KEE5GrqnpxmOdy+IUoxUyDlS9ZE26os7dAFCrbZKhnTcg9dYY6UZgcixfjWRPqEee4HlG4HJOhnjUcfiFKMfbUs4fDL0QpZrOnnjnsqROlGHvq2cOeOlGKsaeePeypE6VYjj31zAn9iHNpZ6LwsKeePaEfcZ5kROGwTOGM0gwKPWFLOTPslyTKpKLDz1oWhR/qDnfQIwpDOcfPWhaFHuo80YjCUeJnLZMiGH7hiUYUBnagsin0UHcsgxMiiCbMNgV5m2PqWRRJulby7EEQTRKviLMrklDnCUc0WRx6ya5IQr3MChiiiWLHKbsi6qlzrI9okvgZy65IQt0yDeRt3iwlmgTHEuQshnpWRZas1YId1UsTpVo1z89WlkUW6rNFJ6qXJkq1mRI/W1kWWahPFWwuNkQ0ZoYAM+wwZVpkoW4YgukiLxOJxqnKzlLmRXq3kj0KovGa5dBL5kUc6jY3zSAaE+HQCyHiULdMg3fqicaknLO4rhJFG+oALxeJxoVVLwTEINRnSuypE40Dy4QJiEGo5yyTiw8RnVDBMVHg9nWEGIQ6AMxX2MMgOon5Mj9D1BeLUF8o51hbS3RMhgCLlXzUzaCYiEWoW6bBngbRMc2VHVa90LticyYsT7GnQXQcS1V+dug9sQn1omOhWuANU6JRlHMWKpzrQXc4MtRF5CsisiEir9zx2BdF5JaIvDT49cvjaMwyexxEI+EVLn3QMD31PwXwybs8/keq+uTg13fG0ZjZkoMcN88gGopjCeY44Yg+4MgEVdW/A7ATQlsgIhwfJBrSYiUPg1Vj9AEn6RZ/TkR+OBiemTnsSSLyrIi8KCIvDvNNFys58DwlujcRYLGai7oZFEPHDfU/BnABwJMAVgE8d9gTVfV5Vb2oqheH+ca2aWCuzJOV6F5mSw73IaW7Olaoq+q6qgaq2gPwJwA+Os5GnZkpcEleokOI9D8jRHdzrFAXkZU7/vqrAF457LnHkbdNjq0THWK+nEPRYfkv3d2RZ4aI/AWAjwOYF5GbAH4fwMdF5EkACuA6gN8cd8POzBSwWXcR9HTc35oosQwBzs6yl06HE9XwQlNEdJTXu7nbwo2d9gRbRJQsp6cLuG+uONLXiAjC/JzT+InI1WHvS8a6KPzUVIFrWhAN2Kbg1DSHJeneYp2YhiE4yxtCRACA0zMFWGasP7IUA7E/QxYqORS5+D9lXN42uIwGDSX2oS4iuG92tDFEorS5b7YIYZ0vDSH2oQ70N9SdKnAlOsqmSt7ihDwaWiJCHQDOzxe5fABljghwbsRqF8q2xIR60bFwhsMwlDGnpwtcL51GkphQB4BTU3lU8pxJR9lQyplcDoBGlqhQFxE8uFjmJtWUeoYADy6WeXOURpaoUAf668KwGobS7sxskeu70LEkLtSB/hZerIahtKrkLZziNnV0TIkMdQC4sFiCZfLSlNLFNITDLnQiiQ31nGWy1ItS59xcEXmbM6jp+BIb6kB/j8ZZbrxLKTFdtLmPAJ1YokMdAB5YKCFvJ/5tUMblbAMXFspRN4NSIPFpaJsGHl2ucnydEss0BI8sVbjMNI1FKs6igmPi4cUK9zWlxBEBHloso5Rj+SKNRypCHQCmijbuny9F3Qyikdw3W8QM7wvRGKUm1AFgqZrHCut7KSEWqzmcmuYyADReqQp1oF8SNl3kxCSKt2rBwgO8sqQJSF2oiwgeWixztySKrbxt4OGlCicY0USkLtQBwDINPLJcgc2KGIoZyxQ8ulyFzb1GaUJSe2blbROPLFe4oiPFhiHAw0sVFHgVSROU2lAHgErexqMrDHaKniHAo8tVLkRHE5fqUAeAKoOdIvZuoPMGPoUg9aEOMNgpOoYAjyxXGOgUmkyEOvBesHM5AQqLafRvik4XObmIwpOZUAf6wf7YSpVVMTRxlil4dIU9dApfpkIdAMo5C4+fmuLiSTQxtin4uZUqqnkGOoUvk8lWcEw8fqrKJXtp7BzLwOOnprhAF0Ums6mWt008cXoK1QI/fDQelbyFnz89xTp0ilRmQx3or8X+cytVLgJGJ7ZUzeHxU1UO61HkMt9NFRGcny+hlLPw1mYDPY26RZQkhgD3z5ewyG3oKCYyH+oHFio5FB0Tr63X4XZ7UTeHEsCxDDy8VEaFN0QpRniteIdSrj8myqncdJSD8XMGOsUNQ/0DbNPAYysVnJrm5TTd3fJUnuPnFFscfrkLEcG5uf44+0+3mvADDrRTf4bo+fkiFiv8gU/xxVC/h/lyDpV8P9h3m92om0MRmirYeGChhLzNckWKN4b6EXKWiUeXq9isu3h7u4kue+2ZYpmCc7NFVrdQYjDUh7RQyWG6aOP6VhNbDS/q5lAIZksO7p8vceycEoWhPgLbNPDQUgVzZQ8/3WrC81n6mEaOJTg/V8JcORd1U4hGxlA/htmSg2rewts7LWzU3KibQ2O0UHFwbq7EPUQpsRjqx2SZBi4slDFfyuH6dhMtL4i6SXQCBcfE+bki1z6nxGOon9BU0caHClPYani4udtCh7NREyVnGzgzU8BCOQcRrrNPycdQHwMRwUIlh/myg826ixu7bY63x5xjCU5PF7FYycHgNoeUIkeGuoh8BcB/ALChqk8MHpsF8L8AnAdwHcCvq+ru5JqZDCKCxWoe8+Uc1usd3N5rw/NZAhkntik4NV3AcjXPMKdUGuZu0J8C+OQHHvsCgO+p6kMAvjf4Ow0YhmBlqoAnz87gvrki90WNAcsUnJkp4Mmz0zg1XWCgU2qJ6tE9SRE5D+Dbd/TUXwPwcVVdFZEVAH+rqo8M8X10mNdLGz/oYXW/g416hz33kNmmYLGSx8p0PrMVLSKCLH7u0kRErqrqxWGee9wx9SVVXQWAQbAvHvP7JE7QU3h+D17QQzfooacK9P8HQf//DBHYpoGcZcA2DVimgbOzRZyZKWCn6WG95mK/zWUHJqlasLBUzWO26LBXTpky8RulIvIsgGcn/Trj5voBWm6Ahuuj5QVoeT66gSI4xi4apiFwLAMF20QpZ2JlKo8zMwXstbrYqHe49MCY2Gb/hvViJc8t5Sizjhvq6yKycsfwy8ZhT1TV5wE8D/SHX475ehPXDXrYbXnYa3VR73THOkwS9BRtL0DbC7DTfO9xxxJUchYgQKcboOWxYuY4Kvl+r3yuxF450XFD/VsAngHwpcHv3xxbi0LU9gJsN13stbpouD7CHnb0fMWO3x+GEenvpBP0+kM6qgyne8nZBmaLDharORQdVuYSHRimpPEvAHwcwLyI3ATw++iH+ddE5BKAdwB8epKNHKdeT7Hd9LBR76DW9qNuzrtUcUdtuyBnGYOFpBQNNwj9B07ciADlnIWZkoOZos0gJzrEUNUvY3uxCKtfOt0A67UONutuosawHUswU3SQsw20vQB7rW6i2n8StimYLtqYLjqYLtiwMlq9clKsfkm+MKpfEsP1A9zabWOj7iayt+v5ivWaC0OAxWoeP396Cl7Qw16ri/12Fy0vONbN2zgyDUHRMVHN25gu2ajkLE7dJxpRanvq3aCH23ttrO13kJLMA9APvuXq++uu216Apuej6fpouu9V6sSZZfYDvJyzUHQslHMW8rbBEJ8A9tSTb5SeeupCXVWxut/Bzd12anqwd3MwQ3K5mr9rEParaYJ+0Hs+PL9fVx/25Cfb7JdzOpaBkmOh6Jgo5SxuCxcihnryZTbUW56PNzeaaLjxuQE6aZW8hQsL5aHrslV1MHFK0R0EvTv4vRsoukEP/flUOvgd7waCiEDQv2kpEIj0Nw6xzf5kK8cy4JgGbKv/mGOy5x0HDPXky1yo93qKW3tt3NprJ3Lc/KQMAU7PFHB6usAQpZ/BUE++TN0o7XQD/GS9jqab3U0qegrc2Gljt9nFQ0tlDm0QZViia8T2Wh5evrWf6UC/U8P18cqtfey3uK4MUVYlNtRv7bXx6lodfsyrPMLWDRTX1mq4vdeOuilEFIHEDb/0eoo3NhvYbnhRNyW2VIG3t1toeT4emC9zPRSiDElUTz3oKV5dqzPQh7RZ9/Daej3VpZ1E9H6J6an7QQ+vrtVR72SnXHEc9lpdXFut4bGVKkz22IfSDXpodwNoD+ipoqcKEYEh/UqSnGXwZjTFViJCnYF+MvWOz2A/xMG6+f0Zuf3f3e7RSyDbprw7E7aYM1FyLK7hTrEQ+zr1Xk/x49UaA30MqgULjy1XMz/G7gc9bDX6K3WOs3LKsQwsVnJYqORi1ZNnnXrypWry0evrdWxxDH1sFio5PLhYjroZkWi4PtZrHWw3vIneZxABpos2lip5TBftyCeEMdSTLzWTj27stBjoY7ZZd1FwTJyeLkTdlNDsNj3c3G2HtnyEKrDb7GK32YVjGTg1nT90jR6icYttqG81XNzcZa31JNzYaaFgm5gtOVE3ZaK6QQ/Xt5qRdgw8v4frWy1sNzw8sFDi5h40cbEsaWy6Pt7caETdjNRSBd7YaKDlpfc+xVbDxT/f2IvNlV694+OHN/dxY6eFHktMaYJiF+q9nuKNjUaq1kCPo2Dw75y2sVbXD/DqWg2vrzdit6a8KnBzt42Xb+2j3uFSDjQZsQv1G7sttDyu5RKGphukaojrYO2b3Wa8A7PlBfjR7Ro2627UTaEUilWo1zpdrO53om5Gptzaa6ei17jf6uLHt2uhbwJyXAdDYFyjh8YtNqEe9BRvbjQyuR56lFSBNzebiR7n3Wt5eHWtlsjlEN7ebuHmbivqZlCKxCbUb++10RliJh+NX9sLcHs/mT3G/VYXr63VE30P5sZOmz12GptYhLrrBzypI3Z7rwPPT9YP1Ybr47X1ZAf6gbe3W9ioceiRTi4WoX5zt52KD2aSBYMtAZPioEoqiUMuh7m+3UKnyyIBOpnIQ73l+awCiIn1WgfthFQevbPTSkxbh5XWMlMKV+Sh/s5OizdHY0K1X1Iad/vt9FZJ1Ts+bqf0vVE4Ig31thfEvqY4a3aaXqyHAIKe4s3NdM82vrnTQjOkdWoofSIN9XXeGIodVWCjFt/hsOvbzaHWO0+yngJvbnIYho4nslAPeorNRnzDI8s26p1Y1q13ukFm7r803QDbzXisW0PJElmob9Zd+DFbm4P6uoFiK4Y/cNdrnUzdf1nj2DodQ2ShzqGXeFuP2RBMr6eZ6aUfqHf80NaAp/SIJNTbXsBFu2Ku4fqxumG61XBjt+piGNhbp1FFEuo7LY4VJsFujI7TWkav7LYbLrpBum8M03hFEuq7vAGUCDsxOU61TnesG0QnSU+BjYwNO9HJhB7qnt/jOGFC1Dt+LHqJtXa25zJk/f3TaEIP9b22l6kKhiRTBfZa0QdKVnvpBzgRiUYReqjXOzxBkyQOV1VxaEOUuoHG6qY1xVvooc5eR7JEfbxcP0jcksCTkPUfbDS80EOdpYzJ0nT9SKerZ33o5UDUP1wpOcINdRGOpydMT6P9Qcww62NPnYYVcqhHvtIvHUOUwepFXH1z5coVPP30Z/CJT/wCnn76M7hy5Uok7cjixCs6HivUVxMJ9eVoPNwIx7SjXFjsypUreO65L6PT6deJr62t47nnvgwAeOqpp0JtS5p2eKLJCrXrLGCoJ1GkoR5hll2+/MK7gX6g03Fx+fILobeFy/DSsEIfU6fkicMEpCisr6+P9DhRHDDU6UhRlhQaEZ4yS0tLIz0+ScLPDg3pRKEuItdF5GUReUlEXhziK07ychSRKHvqUYbZpUufRT6fe99j+XwOly59NvS2RPnDjZJlHDdKf0FVt4Z7avrOzCtXruDy5Rewvr6OpaUlXLr02dBvok2aH+HAtm1Gd84cHMc4HF/bZOUYDSfc6peUiVN1xCRFeY+u6ER7ij711FOxOJZFx4y6CZQQJ/3xrwD+WkSuisiz42hQksSpOmLSoqq+KOfY7wD470DDO+mZ8jFVvS0iiwC+KyKvqurf3fmEQdj3A9+0T/hy8cLqiMkrOCYsUzK/n22JoU5DOlFPXVVvD37fAPANAB+9y3OeV9WLqnpRjHSdmHGqjpgkkWhvWGZ96MEQ/hvQ8I4d6iJSEpHKwZ8B/BKAV+79VenqbcWpOmKSjIjL6Sq5dF3hjaqUs1jSSEM7Sdd5CcA3BiebBeDPVfX/jKVVCRGn6ohJirICBQDK+XRd4Y2qkvH3T6ORMG+AGXZe/+HVW6G9Ho1HJW/hidNTkb2+quIH7+zC89N1pTesJ89Oo3CC4RcR4TIDCSciV1X14jDPDbn4lSdWEuWsaGukRQSLlXykbYjKVME+UaBT9oT6aWVvIZniMPFlqZrP5CoTy1PZ/GFGxxfup5WhnkhOxD31gzbMlZyomxGqnG1gppjtm8Q0upBDPZur/SVdKeJZnQey1mtdruZZ9UIjY6jTkUq5eIzpVvI2qoV4/ICZNNsULFZyRz+R6ANCv66Ow6U8DS9vG7BiMKZ+4MJCGWYGliy8f74Uq393So7QzxquYZEscTteedvEubli1M2YqIWKg7kye+l0POGHOidSJEoc1xxZquYxndIbiI5l4PxcKepmUIKFHupThXR+GNMqrsfrgYUSrIhnuk7ChQUOu9DJRDL8wnH1ZMjbRix76gCQs0zcP5+uHu3yVB7TxWyVbdL4RZKusxmrN06qmZgHzHw5l5rx9bmyg/MpeS8UrUhCnRMqkmEmAT98T00XcGamEHUzTmSmZOOhxTJr0mksIgn1qYKdyvHQNLFNQTUhN7XPzhZxdjaZwT5bcvDwYoWBTmMTSaiLSOamfCfNfDmXqKA5M1PEhYVSotaHWazm8PBSGUYG6u4pPJHdsczalO8kEUnm8Vms5vHociX2N+INAc7PF3FhgUMuNH6Rnf1Fx4ptuVzWTRdt5O14LA0wqumigw+fmcJSNZ6Td6oFCx8+O42VqWQOF1H8RTpoujyVx367G2UT6C6Wq8nrpd/JMg08sFDGXDmHtzYb6HSjX3PIMgXnZotYTPi/LcVfpNepM0UbOTvel8pZU3DM1NRKTxVsfPjMNE5N5xHlsPVsycGHzkwx0CkUkfbURQRnZgp4c6MZZTPoDkkvD/wgwxCcmyvh1HQBm3UX67VOKD132xQsVHJYquYTO5RFyRR5zdpCOYe1/Q6abhB1UzKvnLMwn9KFpGzTwKnpAk5NF7Df6mK93sFO0xv7vi2VvIWlah5zJYdVLRSJyENdRHDfbBHXVutRNyXz7svIjMapoo2pog3P76HW6aLp+mi6AVqej24wfMob0l/wrOiYKOcsVPLcT5SiF3moA/2KhamCzZumEZop2ZmrRnIsA/Pl3PuuTjrdAE3XR7sbQBXoqaKngAAwRCDS32aunLNQsE2WJFLsxCLUAeDcXBEv39rnNqYRMAQ4N5uuxbGOK2+bHAOnRItN6UkpZ+H0dLpu0iXFmdkihw2IUiI2oQ70Ky/ittNO2lXyFk4lcPYoEd1drEJdRPDgYjnSmuIsMY3+vzfHhYnSI1ahDvQnv2SlCiNq980WOX5MlDKxC3UAWJkqYL6cjlmNcbVQcRK5aBcR3VssQx0ALiyUOb4+IZW8hQfmy1E3g4gmILahbhiCRxKwjGrS5GwDjyxXONuRKKVinZiOZeDR5QpMBtBYWKbg0eUKbO5WT5Rasf90l3IWHlmqsCLmhExD8PBSBUWHQ1pEaRb7UAf6a3U8ulxlsB+TORjKytoyAERZlIhQBwbBvlLlUMyILFPw6AoDnSgrEhPqQH/Tg8dWKrBNBvswbFPw2EoV1TwDnSgrEhXqAFDJ23ji9BRKOU6auZdyzsITp6dYFkqUMYkLdaC/kt7jp6Y4QekQCxUHj5+qcrYoUQYlthtnGoKHlioo5dp4Z6fFJXsBiPSXMOZO9UTZldhQP3BquoBSzorNrvFRKTgmHlgocfycKOMSH+rAe7vG39htYXW/k6leuwhwaqqAMzMFzhIlonSEOvDervFz5Rze3Gig5aV/I+tSzsSFhTJKvBlKRAOpS4NyzsKHzkxhvebi1l4Lnp++brtjGTgzU8BiJce10InofVIX6kB/s43lqTwWKjms1TpY3WuPtEt8XNmm4NR0AcvVPIdaiOiuUhnqB0xDcHq6gKVKDqv7HWzUO4nsuTuWYKmax8pUgTNqieieUh3qByzTwNnZIk5PF7DT8rBe66DW9qNu1pGmCjaWqjnMlhwOsxDRUE4U6iLySQD/DYAJ4AVV/dJYWjUhhiGYL+cwX86h7QXYqHew3fTgxqgUMm8bmCvlsFjNcfIQEY1M9Jj1fyJiAvgJgH8H4CaAfwLwtKr++B5fo8d9vUlqeT52W13sNj00XD/UkkiR/k5EM0UHM0UHBYdBTuMlIojj546GJyJXVfXiMM89SU/9owDeUNW3Bi/6PwF8CsChoR5XRcdC0bFweroAP+ih3vHR9Hw03QBNzx9rTz5nGyjnLBQdEyXHQiVvweKmFUQ0JicJ9dMAbtzx95sA/uXJmhM9yzQwU3IwU3pvXZlu0EPLC9ANev1fvsILAni+ojfoAan2e91A/watbRpwTAO2NfizZaBomwxwIpqok4T63e7c/cw1nog8C+DZwV9dEXnlBK8ZZ/MAtqJuxATx/SXXvIik9b0BKT926L+3c8N+wUlC/SaAs3f8/QyA2x98kqo+D+B5ABCRF4cdF0qaNL83gO8vydL83oB0v7/jvLeTjAX8E4CHROR+EXEAfAbAt07w/YiI6ISO3VNXVV9EPgfgr9AvafyKqv5obC0jIqKRnahOXVW/A+A7I3zJ8yd5vZhL83sD+P6SLM3vDUj3+xv5vR27Tp2IiOKH9XVERCkSSqiLyCdF5DUReUNEvhDGa4ZJRK6LyMsi8pKIvBh1e05KRL4iIht3lp+KyKyIfFdEXh/8PhNlG4/rkPf2RRG5NTh+L4nIL0fZxuMSkbMi8jcick1EfiQinx88npZjd9j7S8vxy4vIP4rIPw/e3x8MHh/p+E18+OU4ywkkjYhcB3BRVVNRKysi/xZAA8D/UNUnBo/9FwA7qvqlwQ/mGVX93SjbeRyHvLcvAmio6pejbNtJicgKgBVV/YGIVABcBfArAP4j0nHsDnt/v450HD8BUFLVhojYAP4ewOcB/BpGOH5h9NTfXU5AVT0AB8sJUEyp6t8B2PnAw58C8NXBn7+K/ocpcQ55b6mgqquq+oPBn+sArqE/8zstx+6w95cK2tcY/NUe/FKMePzCCPW7LSeQmgMxoAD+WkSuDmbQptGSqq4C/Q8XgMWI2zNunxORHw6GZxI5PHEnETkP4CMAvo8UHrsPvD8gJcdPREwReQnABoDvqurIxy+MUB9qOYGE+5iq/gsA/x7Abw0u8Sk5/hjABQBPAlgF8FykrTkhESkD+DqA31bVWtTtGbe7vL/UHD9VDVT1SfRn6H9URJ4Y9XuEEepDLSeQZKp6e/D7BoBvoD/klDbrgzHNg7HNjYjbMzaquj74MPUA/AkSfPwGY7FfB/BnqvqXg4dTc+zu9v7SdPwOqOoegL8F8EmMePzCCPVULycgIqXBTRuISAnALwFI46Jl3wLwzODPzwD4ZoRtGauDD8zAryKhx29wo+0ygGuq+od3/KdUHLvD3l+Kjt+CiEwP/lwA8BSAVzHi8Qtl8tGgxOi/4r3lBP7zxF80JCLyAPq9c6A/Q/fPk/7+ROQvAHwc/RXi1gH8PoD/DeBrAO4D8A6AT6tq4m44HvLePo7+pbsCuA7gNw/GMJNERP4NgP8L4GUAB5sA/B76485pOHaHvb+nkY7j9yH0b4Sa6He4v6aq/0lE5jDC8eOMUiKiFOGMUiKiFGGoExGlCEOdiChFGOpERCnCUCciShGGOhFRijDUiYhShKFORJQi/x8uru3kWAIZhQAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# Plot solution\n",
"plot_circles(model)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.1.4 Take Away Messages](https://ndcbe.github.io/CBE60499/04.01-Convexity.html#4.1.4-Take-Away-Messages)",
"section": "4.1.4 Take Away Messages"
}
},
"source": [
"## 4.1.4 Take Away Messages\n",
"* Nonlinear programs may be nonconvex. For nonconvex problems, there often exists many local optima that are not also global optima.\n",
"* Initialization is really important in optimization problems with nonlinear objectives or constraints!"
]
},
{
"cell_type": "markdown",
"id": "3a37f678",
"metadata": {},
"source": [
"\n",
"< [4.0 Constrained Nonlinear Optimization: Theory and Applications](https://ndcbe.github.io/CBE60499/04.00-Constrained.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [4.2 Local Optimality Conditions](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html) > 
 "
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.6"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.6"
}
},
"nbformat": 4,
"nbformat_minor": 2
}

