5.3. Transient Heat Conduction in Various Geometries#
Keywords: ipopt usage, dae, differential-algebraic equations, pde, partial differential equations
5.3.1. Imports#
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D
import shutil
import sys
import os.path
if "google.colab" in sys.modules:
!wget 'https://raw.githubusercontent.com/IDAES/idaes-pse/main/scripts/colab_helper.py'
import colab_helper
colab_helper.install_idaes()
colab_helper.install_ipopt()
assert shutil.which("ipopt") or os.path.isfile("ipopt")
from pyomo.environ import (
ConcreteModel,
Var,
Constraint,
Objective,
TransformationFactory,
SolverFactory,
)
from pyomo.dae import ContinuousSet, DerivativeVar
# Uncomment the following line if you installed Ipopt via IDAES on your local machine
# but cannot find the Ipopt executable. Our Colab helper script takes care of the
# # environmental variables if you are on Colab. Otherwise, you need to either import
# idaes or set the path environmental variable yourself.
#
# import idaes
5.3.2. Rescaling the heat equation#
Transport of heat in a solid is described by the familiar thermal diffusion model
\[
\begin{align*}
\rho C_p\frac{\partial T}{\partial t} & = \nabla\cdot(k\nabla T)
\end{align*}
\]
We’ll assume the thermal conductivity \(k\) is a constant, and define thermal diffusivity in the conventional way
\[
\begin{align*}
\alpha & = \frac{k}{\rho C_p}
\end{align*}
\]
We will further assume symmetry with respect to all spatial coordinates except \(r\) where \(r\) extends from \(-R\) to \(+R\). The boundary conditions are
\[\begin{split}
\begin{align*}
T(t,R) & = T_{\infty} & \forall t > 0 \\
\nabla T(t,0) & = 0 & \forall t \geq 0
\end{align*}
\end{split}\]
where we have assumed symmetry with respect to \(r\) and uniform initial conditions \(T(0, r) = T_0\) for all \(0 \leq r \leq R\). Following standard scaling procedures, we introduce the dimensionless variables
\[\begin{split}
\begin{align*}
T' & = \frac{T - T_0}{T_\infty - T_0} \\
r' & = \frac{r}{R} \\
t' & = t \frac{\alpha}{R^2}
\end{align*}
\end{split}\]
5.3.3. Dimensionless model#
Under these conditions the problem reduces to
\[
\begin{align*}
\frac{\partial T'}{\partial t'} & = \nabla^2 T'
\end{align*}
\]
with auxiliary conditions
\[\begin{split}
\begin{align*}
T'(0, r') & = 0 & \forall 0 \leq r' \leq 1\\
T'(t', 1) & = 1 & \forall t' > 0\\
\nabla T'(t', 0) & = 0 & \forall t' \geq 0 \\
\end{align*}
\end{split}\]
which we can specialize to specific geometries.
5.3.4. Preliminary code#
def model_plot(m):
r = sorted(m.r)
t = sorted(m.t)
rgrid = np.zeros((len(t), len(r)))
tgrid = np.zeros((len(t), len(r)))
Tgrid = np.zeros((len(t), len(r)))
for i in range(0, len(t)):
for j in range(0, len(r)):
rgrid[i, j] = r[j]
tgrid[i, j] = t[i]
Tgrid[i, j] = m.T[t[i], r[j]].value
fig = plt.figure(figsize=(10, 6))
ax = fig.add_subplot(1, 1, 1, projection="3d")
ax.set_xlabel("Distance r")
ax.set_ylabel("Time t")
ax.set_zlabel("Temperature T")
p = ax.plot_wireframe(rgrid, tgrid, Tgrid)
plt.show()
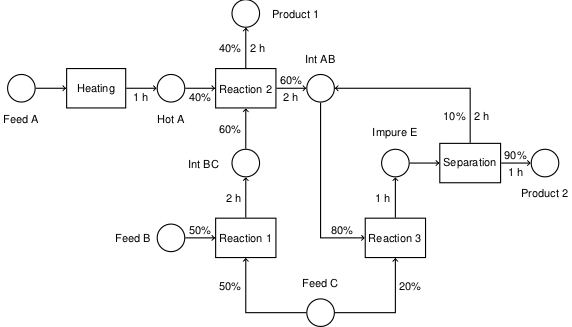
5.3.5. Planar coordinates#
Suppressing the prime notation, for a slab geometry the model specializes to
\[
\begin{align*}
\frac{\partial T}{\partial t} & = \frac{\partial^2 T}{\partial r^2}
\end{align*}
\]
with auxiliary conditions
\[\begin{split}
\begin{align*}
T(0, r) & = 0 & \forall 0 \leq r \leq 1 \\
T(t, 1) & = 1 & \forall t > 0\\
\frac{\partial T}{\partial r} (t, 0) & = 0 & \forall t \geq 0 \\
\end{align*}
\end{split}\]
m = ConcreteModel()
m.r = ContinuousSet(bounds=(0, 1))
m.t = ContinuousSet(bounds=(0, 2))
m.T = Var(m.t, m.r)
m.dTdt = DerivativeVar(m.T, wrt=m.t)
m.dTdr = DerivativeVar(m.T, wrt=m.r)
# This will not work because Pyomo.DAE does not know to use the boundary condition on the derivative
# m.d2Tdr2 = DerivativeVar(m.T, wrt=(m.r, m.r), bounds=(-100,100))
# This way Pyomo.DAE knows to use the boundary condition on the derivative at r=0
m.d2Tdr2 = DerivativeVar(m.dTdr, wrt=m.r, initialize=0.0)
@m.Constraint(m.t, m.r)
def pde(m, t, r):
if t == 0:
return Constraint.Skip
if r == 0:
return Constraint.Skip
return m.dTdt[t, r] == m.d2Tdr2[t, r]
m.obj = Objective(expr=1)
# Initial condition
m.ic = Constraint(m.r, rule=lambda m, r: m.T[0, r] == 0 if r < 1 else Constraint.Skip)
# Boundary conditions on temperature
m.bc1 = Constraint(m.t, rule=lambda m, t: m.T[t, 1] == 1)
# Boundary conditions on temperature gradient
# End is insulated
m.bc2 = Constraint(m.t, rule=lambda m, t: m.dTdr[t, 0] == 0)
# This needs to be backwards in time because:
# 1. The initial condition is at t=0
# 2. The insulated boundary condition is at r=0
TransformationFactory("dae.finite_difference").apply_to(
m, nfe=50, scheme="BACKWARD", wrt=m.r
)
TransformationFactory("dae.finite_difference").apply_to(
m, nfe=50, scheme="BACKWARD", wrt=m.t
)
# If we do not use BACKWARDS AND BACKWARDS, we have extra degrees of freedom
import idaes
from idaes.core.util.model_diagnostics import degrees_of_freedom
print("Degrees of Freedom:", degrees_of_freedom(m))
Degrees of Freedom: 0
SolverFactory("ipopt").solve(m, tee=True).write()
model_plot(m)
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
This version of Ipopt was compiled from source code available at
https://github.com/IDAES/Ipopt as part of the Institute for the Design of
Advanced Energy Systems Process Systems Engineering Framework (IDAES PSE
Framework) Copyright (c) 2018-2019. See https://github.com/IDAES/idaes-pse.
This version of Ipopt was compiled using HSL, a collection of Fortran codes
for large-scale scientific computation. All technical papers, sales and
publicity material resulting from use of the HSL codes within IPOPT must
contain the following acknowledgement:
HSL, a collection of Fortran codes for large-scale scientific
computation. See http://www.hsl.rl.ac.uk.
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 28102
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 0
Total number of variables............................: 10302
variables with only lower bounds: 0
variables with lower and upper bounds: 0
variables with only upper bounds: 0
Total number of equality constraints.................: 10302
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 1.0000000e+00 1.00e+00 0.00e+00 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 1.0000000e+00 7.62e-08 0.00e+00 -1.7 2.50e+03 - 1.00e+00 1.00e+00h 1
2 1.0000000e+00 1.71e-13 0.00e+00 -8.6 1.28e-09 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 2
(scaled) (unscaled)
Objective...............: 1.0000000000000000e+00 1.0000000000000000e+00
Dual infeasibility......: 0.0000000000000000e+00 0.0000000000000000e+00
Constraint violation....: 1.7053025658242223e-13 1.7053025658242223e-13
Complementarity.........: 0.0000000000000000e+00 0.0000000000000000e+00
Overall NLP error.......: 1.7053025658242223e-13 1.7053025658242223e-13
Number of objective function evaluations = 3
Number of objective gradient evaluations = 3
Number of equality constraint evaluations = 3
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 3
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 2
Total CPU secs in IPOPT (w/o function evaluations) = 0.060
Total CPU secs in NLP function evaluations = 0.000
EXIT: Optimal Solution Found.
# ==========================================================
# = Solver Results =
# ==========================================================
# ----------------------------------------------------------
# Problem Information
# ----------------------------------------------------------
Problem:
- Lower bound: -inf
Upper bound: inf
Number of objectives: 1
Number of constraints: 10302
Number of variables: 10302
Sense: unknown
# ----------------------------------------------------------
# Solver Information
# ----------------------------------------------------------
Solver:
- Status: ok
Message: Ipopt 3.13.2\x3a Optimal Solution Found
Termination condition: optimal
Id: 0
Error rc: 0
Time: 0.11686086654663086
# ----------------------------------------------------------
# Solution Information
# ----------------------------------------------------------
Solution:
- number of solutions: 0
number of solutions displayed: 0
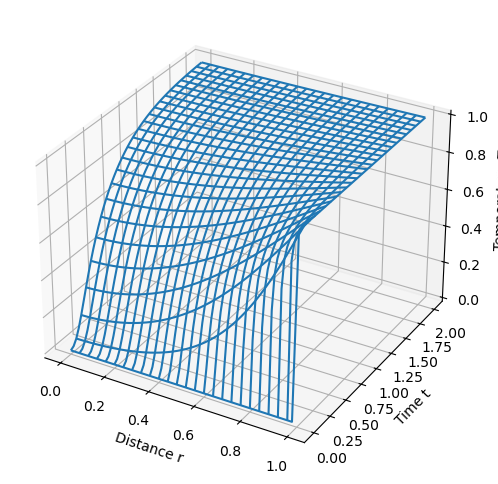
5.3.6. Cylindrical coordinates#
Suppressing the prime notation, for a cylindrical geometry the model specializes to
\[
\begin{align*}
\frac{\partial T}{\partial t} & = \frac{1}{r}\frac{\partial}{\partial r}\left(r\frac{\partial T}{\partial r}\right)
\end{align*}
\]
Expanding,
\[
\begin{align*}
\frac{\partial T}{\partial t} & = \frac{\partial^2 T}{\partial r^2} + \frac{1}{r}\frac{\partial T}{\partial r}
\end{align*}
\]
with auxiliary conditions
\[\begin{split}
\begin{align*}
T(0, r) & = 0 & \forall 0 \leq r \leq 1\\
T(t, 1) & = 1 & \forall t > 0\\
\frac{\partial T}{\partial r} (t, 0) & = 0 & \forall t \geq 0 \\
\end{align*}
\end{split}\]
m = ConcreteModel()
m.r = ContinuousSet(bounds=(0, 1))
m.t = ContinuousSet(bounds=(0, 2))
m.T = Var(m.t, m.r)
m.dTdt = DerivativeVar(m.T, wrt=m.t)
m.dTdr = DerivativeVar(m.T, wrt=m.r)
# This will give too many degrees of freedom
# m.d2Tdr2 = DerivativeVar(m.T, wrt=(m.r, m.r))
m.d2Tdr2 = DerivativeVar(m.dTdr, wrt=m.r)
@m.Constraint(m.t, m.r)
def pde(m, t, r):
if t == 0:
return Constraint.Skip
if r == 0:
return Constraint.Skip
return m.dTdt[t, r] == m.d2Tdr2[t, r] + (1 / r) * m.dTdr[t, r]
m.ic = Constraint(m.r, rule=lambda m, r: m.T[0, r] == 0)
m.bc1 = Constraint(m.t, rule=lambda m, t: m.T[t, 1] == 1 if t > 0 else Constraint.Skip)
m.bc2 = Constraint(m.t, rule=lambda m, t: m.dTdr[t, 0] == 0)
TransformationFactory("dae.finite_difference").apply_to(
m, nfe=20, wrt=m.r, scheme="BACKWARD"
)
TransformationFactory("dae.finite_difference").apply_to(
m, nfe=50, wrt=m.t, scheme="BACKWARD"
)
SolverFactory("ipopt").solve(m, tee=True).write()
model_plot(m)
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
This version of Ipopt was compiled from source code available at
https://github.com/IDAES/Ipopt as part of the Institute for the Design of
Advanced Energy Systems Process Systems Engineering Framework (IDAES PSE
Framework) Copyright (c) 2018-2019. See https://github.com/IDAES/idaes-pse.
This version of Ipopt was compiled using HSL, a collection of Fortran codes
for large-scale scientific computation. All technical papers, sales and
publicity material resulting from use of the HSL codes within IPOPT must
contain the following acknowledgement:
HSL, a collection of Fortran codes for large-scale scientific
computation. See http://www.hsl.rl.ac.uk.
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 12392
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 0
Total number of variables............................: 4212
variables with only lower bounds: 0
variables with lower and upper bounds: 0
variables with only upper bounds: 0
Total number of equality constraints.................: 4212
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 0.0000000e+00 1.00e+00 0.00e+00 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 0.0000000e+00 2.63e-11 0.00e+00 -1.7 2.50e+01 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 1
(scaled) (unscaled)
Objective...............: 0.0000000000000000e+00 0.0000000000000000e+00
Dual infeasibility......: 0.0000000000000000e+00 0.0000000000000000e+00
Constraint violation....: 2.6252197116669678e-11 2.6252197116669678e-11
Complementarity.........: 0.0000000000000000e+00 0.0000000000000000e+00
Overall NLP error.......: 2.6252197116669678e-11 2.6252197116669678e-11
Number of objective function evaluations = 2
Number of objective gradient evaluations = 2
Number of equality constraint evaluations = 2
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 2
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 1
Total CPU secs in IPOPT (w/o function evaluations) = 0.019
Total CPU secs in NLP function evaluations = 0.000
EXIT: Optimal Solution Found.
# ==========================================================
# = Solver Results =
# ==========================================================
# ----------------------------------------------------------
# Problem Information
# ----------------------------------------------------------
Problem:
- Lower bound: -inf
Upper bound: inf
Number of objectives: 1
Number of constraints: 4212
Number of variables: 4212
Sense: unknown
# ----------------------------------------------------------
# Solver Information
# ----------------------------------------------------------
Solver:
- Status: ok
Message: Ipopt 3.13.2\x3a Optimal Solution Found
Termination condition: optimal
Id: 0
Error rc: 0
Time: 0.04596400260925293
# ----------------------------------------------------------
# Solution Information
# ----------------------------------------------------------
Solution:
- number of solutions: 0
number of solutions displayed: 0
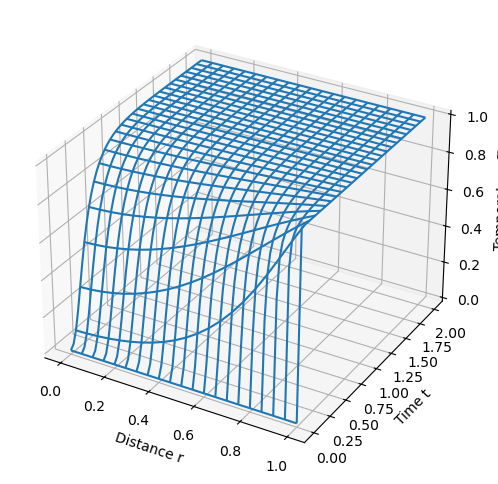
5.3.6.1. Central Finite Difference#
5.3.7. Spherical coordinates#
Suppressing the prime notation, for a cylindrical geometry the model specializes to
\[
\begin{align*}
\frac{\partial T}{\partial t} & = \frac{1}{r^2}\frac{\partial}{\partial r}\left(r^2\frac{\partial T}{\partial r}\right)
\end{align*}
\]
Expanding,
\[
\begin{align*}
\frac{\partial T}{\partial t} & = \frac{\partial^2 T}{\partial r^2} + \frac{2}{r}\frac{\partial T}{\partial r}
\end{align*}
\]
with auxiliary conditions
\[\begin{split}
\begin{align*}
T(0, r) & = 0 & \forall 0 \leq r \leq 1\\
T(t, 1) & = 1 & \forall t > 0\\
\frac{\partial T}{\partial r} (t, 0) & = 0 & \forall t \geq 0 \\
\end{align*}
\end{split}\]
m = ConcreteModel()
m.r = ContinuousSet(bounds=(0, 1))
m.t = ContinuousSet(bounds=(0, 2))
m.T = Var(m.t, m.r)
m.dTdt = DerivativeVar(m.T, wrt=m.t)
m.dTdr = DerivativeVar(m.T, wrt=m.r)
# m.d2Tdr2 = DerivativeVar(m.T, wrt=(m.r, m.r))
m.d2Tdr2 = DerivativeVar(m.dTdr, wrt=m.r)
@m.Constraint(m.t, m.r)
def pde(m, t, r):
if r == 0 or t == 0:
return Constraint.Skip
else:
return m.dTdt[t, r] == m.d2Tdr2[t, r] + (2 / r) * m.dTdr[t, r]
m.ic = Constraint(m.r, rule=lambda m, r: m.T[0, r] == 0)
m.bc1 = Constraint(m.t, rule=lambda m, t: m.T[t, 1] == 1 if t > 0 else Constraint.Skip)
m.bc2 = Constraint(m.t, rule=lambda m, t: m.dTdr[t, 0] == 0)
TransformationFactory("dae.finite_difference").apply_to(
m, nfe=20, wrt=m.r, scheme="BACKWARD"
)
TransformationFactory("dae.finite_difference").apply_to(
m, nfe=50, wrt=m.t, scheme="BACKWARD"
)
SolverFactory("ipopt", tee=True).solve(m, tee=True).write()
model_plot(m)
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
This version of Ipopt was compiled from source code available at
https://github.com/IDAES/Ipopt as part of the Institute for the Design of
Advanced Energy Systems Process Systems Engineering Framework (IDAES PSE
Framework) Copyright (c) 2018-2019. See https://github.com/IDAES/idaes-pse.
This version of Ipopt was compiled using HSL, a collection of Fortran codes
for large-scale scientific computation. All technical papers, sales and
publicity material resulting from use of the HSL codes within IPOPT must
contain the following acknowledgement:
HSL, a collection of Fortran codes for large-scale scientific
computation. See http://www.hsl.rl.ac.uk.
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 12392
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 0
Total number of variables............................: 4212
variables with only lower bounds: 0
variables with lower and upper bounds: 0
variables with only upper bounds: 0
Total number of equality constraints.................: 4212
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 0.0000000e+00 1.00e+00 0.00e+00 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 0.0000000e+00 1.23e-09 0.00e+00 -1.7 2.50e+01 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 1
(scaled) (unscaled)
Objective...............: 0.0000000000000000e+00 0.0000000000000000e+00
Dual infeasibility......: 0.0000000000000000e+00 0.0000000000000000e+00
Constraint violation....: 1.2267631052098105e-09 1.2267631052098105e-09
Complementarity.........: 0.0000000000000000e+00 0.0000000000000000e+00
Overall NLP error.......: 1.2267631052098105e-09 1.2267631052098105e-09
Number of objective function evaluations = 2
Number of objective gradient evaluations = 2
Number of equality constraint evaluations = 2
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 2
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 1
Total CPU secs in IPOPT (w/o function evaluations) = 0.018
Total CPU secs in NLP function evaluations = 0.000
EXIT: Optimal Solution Found.
# ==========================================================
# = Solver Results =
# ==========================================================
# ----------------------------------------------------------
# Problem Information
# ----------------------------------------------------------
Problem:
- Lower bound: -inf
Upper bound: inf
Number of objectives: 1
Number of constraints: 4212
Number of variables: 4212
Sense: unknown
# ----------------------------------------------------------
# Solver Information
# ----------------------------------------------------------
Solver:
- Status: ok
Message: Ipopt 3.13.2\x3a Optimal Solution Found
Termination condition: optimal
Id: 0
Error rc: 0
Time: 0.04324674606323242
# ----------------------------------------------------------
# Solution Information
# ----------------------------------------------------------
Solution:
- number of solutions: 0
number of solutions displayed: 0
5.3.8. Debuging Degrees of Freedom#
PDEs are tricky to solve because we need to choose the space and time discretization schemes to match the initial and boundary conditions.
Let’s consider a backward formula:
\[
\begin{equation*}
\frac{\partial T}{\partial r} \approx \frac{T_{i} - T_{i-1}}{\Delta r}
\end{equation*}
\]
This means that for the first cell, \(i=0\), which occurs at the edge of the object (\(r=0\) in our problem), we cannot easily estimate the derivate. Thus, we need a boundary condition and to skip the PDE equation for \(r=0\).
We can make a similar argument for the time derivative. We need an initial condition and to skip the PDE equation for \(t=0\).
For these heat transfer problems, we need to estimate \(\frac{\partial^2 T}{\partial r^2}\) using finite difference. Let’s consider a backward formula:
\[
\begin{equation*}
\frac{\partial^2 T}{\partial r^2} \approx \frac{\frac{\partial T}{\partial r}_{i} - \frac{\partial T}{\partial r}_{i-1}}{\Delta r} \approx \frac{T_{i-2} - T_{i-1} - T_{i-1} + T+i}{\Delta r^2}
\end{equation*}
\]
This might suggest that we need to skip the PDE for the first two cells, \(i=0\) and \(i=1\) in space to estimate the second derivative. But we have a boundary condition for the first derivative at \(r=0\), so we are okay if the just skip the first cell in space (\(i=0\)).
For these reasons, we want to choose backwards finite difference for both space and time in this problem. An early version of this notebook used forward and central, but had extra degrees of freedom.
Finally, below are some codes that are extra helpful for debugging degrees of freedom for PDE discretization.
# Check the degrees of freedom
import idaes
from idaes.core.util.model_diagnostics import degrees_of_freedom
print("Degrees of Freedom:", degrees_of_freedom(m))
Degrees of Freedom: 0
# Use the IDAES diagnostics toolbox to check for structural issues
from idaes.core.util import DiagnosticsToolbox
dt = DiagnosticsToolbox(m)
dt.report_structural_issues()
dt.display_underconstrained_set()
dt.display_overconstrained_set()
====================================================================================
Model Statistics
Activated Blocks: 1 (Deactivated: 0)
Free Variables in Activated Constraints: 4212 (External: 0)
Free Variables with only lower bounds: 0
Free Variables with only upper bounds: 0
Free Variables with upper and lower bounds: 0
Fixed Variables in Activated Constraints: 0 (External: 0)
Activated Equality Constraints: 4212 (Deactivated: 0)
Activated Inequality Constraints: 0 (Deactivated: 0)
Activated Objectives: 0 (Deactivated: 0)
------------------------------------------------------------------------------------
0 WARNINGS
No warnings found!
------------------------------------------------------------------------------------
1 Cautions
Caution: 72 unused variables (0 fixed)
------------------------------------------------------------------------------------
Suggested next steps:
Try to initialize/solve your model and then call report_numerical_issues()
====================================================================================
====================================================================================
Dulmage-Mendelsohn Under-Constrained Set
====================================================================================
====================================================================================
Dulmage-Mendelsohn Over-Constrained Set
====================================================================================
Finally, if you are still stuck after using the diagnostics toolbox (and m.pprint()), you can add temporary objective to the model to maximize the sum of one of the derivatives. Then plot the PDE solution and look for strange anomalies, which can help you hone in on the misspecification. This gives similar information as the under constrained set, but is graphical.