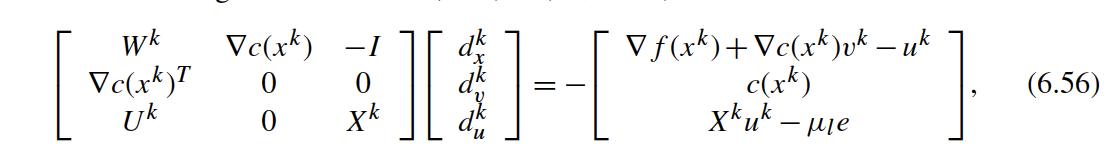
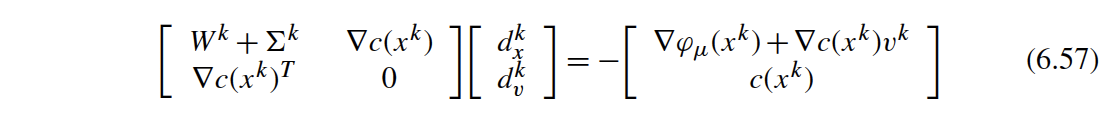
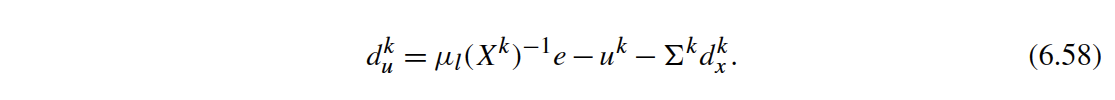
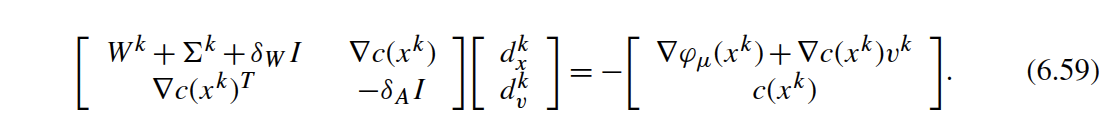
Consider the following nonlinear program:
$$ \begin{align} \min_{x} \quad & f(x) \\ \mathrm{s.t.} \quad & c(x) = 0 \\ & x_i \geq 0, \quad i \in \mathcal{I} \end{align} $$where $x \in \mathbb{R}^{n}$, $f(x): \mathbb{R}^{n} \rightarrow \mathbb{R}$, $c(x): \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$ and $|\mathcal{I} |$ = $r$ (i.e., there are $r$ variables with a lower bound and $r \leq n$). This is an extension of (6.48) in Biegler (2010).
This has the corresponding log-barrier approximation:
$$ \begin{align} \min_{x} \quad & \phi_{\mu_l}(x) := f(x) - \mu_l \sum_{i \in \mathcal{I}} \log(x_i) \\ \mathrm{s.t.} \quad & c(x) = 0 \end{align} $$which is an extension of (6.49) in Biegler (2010).
Let the $n \times r$ matrix $G$ encode which variables are bounded. If variable $i$ corresponds to the $j$th bound, then $G_{i,j} = 1$ and otherwise $G_{i,j} = 0$. $G$ is assembled as follows:
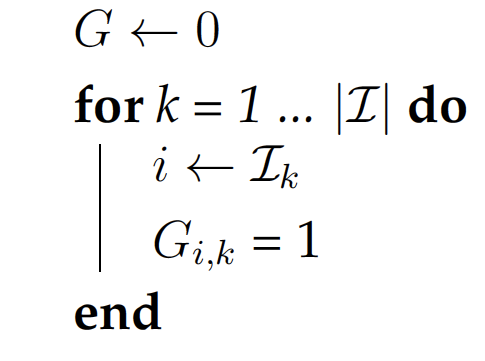
Notice that $G$ is the gradient of $x \geq 0$. $G^T G = I$ but the converse does not hold unless $r = n$.
Start with:
$$ \begin{align} \min_{x} \quad & x_1^2 + x_2 \\ \mathrm{s.t.} \quad & x_1 + x_2 = 1 \\ & x_1 + 1 \geq 0 \end{align} $$Add slack variable $x_3$ and convert the inequality constraint to an equality constraint and bound:
$$ \begin{align} \min_{x} \quad & x_1^2 + x_2 \\ \mathrm{s.t.} \quad & x_1 + x_2 = 1 \\ & x_1 + 1 - x_3 = 0 \\ & x_3 \geq 0 \end{align} $$Now assemble $G$:
$$ G = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} $$Next we extend (6.51) in Biegler (2010):
$$ \begin{gather} \dfx ~+~ \dcx \vk ~-~ \G \uk = \dims{0}{n}{1} \\ \X \uk = \mu \e \\ \cx = \dims{0}{m}{1} \end{gather} $$We now extend (6.56) in Biegler (2010):
$$ \begin{bmatrix} \W & \dcx & \G \\ \dcxT & \dims{0}{m}{m} & \dims{0}{m}{r} \\ \Uk \GT & \dims{0}{r}{m} & \X \end{bmatrix} \begin{bmatrix} \dx \\ \dv \\ \du \end{bmatrix} = - \begin{bmatrix} \dfx ~+~ \dcx \vk ~-~ \G \uk \\ \cx \\ \X \uk ~-~ \mu_l \e \end{bmatrix} $$where $U^k = \mathrm{diag}\{u^k\}$ and $W^k = \nabla_{xx} L(x^k,v^k)$. Notice that $W^k$ does NOT include a contribution from the barrier term:
$$ \begin{equation} \W = \dims{\nabla^2 f(x^k)}{n}{n} + \sum_{j=1}^{m} \left( \dims{\nabla^2 c_{j}(x^k)}{n}{n} \underbrace{v^k_{j}}_{\mathrm{scalar}} \right) \end{equation} $$We can verify that $W^k$ does not include $\hat{X}$ by showing that the KKT system above is a Newton step to solve the nonlinear system for the primal dual conditions.
The Newton step can be simplified, similar to (6.57) and (6.58) in Biegler (2010):
$$ \begin{equation} \begin{bmatrix} \W + \Sk & \dcx \\ \dcxT & 0 \end{bmatrix} \begin{bmatrix} \dx \\ \dv \end{bmatrix} = - \begin{bmatrix} \dphi ~+~ \dcx \vk \\ \cx \end{bmatrix} \end{equation} $$and
$$ \begin{equation} \label{eq:du} \du = \mu_l \Xinv \e ~-~ \uk ~-~ \GT \Sk \dx \end{equation} $$where $$ \begin{equation} \label{eq:Sk} \Sk = \G \Xinv \Uk \GT \end{equation} $$
and
$$ \begin{equation} \dphi = \dfx - \mu_l \G \Xinv \dims{e}{r}{1} \end{equation} $$Notice that the equation for $\du$ simplifies by substituting $G^T G = I$:
$$ \du = \mu_l \Xinv \e ~-~ \uk ~-~ \Xinv \Uk \GT \dx $$Finally, inertia correction can be applied to simplified KKT step similar to (6.59) in Biegler (2010).
Implement a basic interior point method for inequality and equality constrained nonlinear programs. See pg. 154 – 155 in Biegler (2010). You may skip the line search, i.e., always take a full step.
Write detailed pseudocode on paper or a whiteboard. Scan/take a photo and turn in.
Implement in Python. Hints: Reuse code from Algorithm 5.2 example.
### Load Python libraries
import numpy as np
from scipy import linalg
### Define helper functions
## Check is element of array is NaN
def check_nan(A):
return np.sum(np.isnan(A))
## Calculate gradient with central finite difference
def my_grad_approx(x,f,eps1,verbose=False):
'''
Calculate gradient of function f using central difference formula
Inputs:
x - point for which to evaluate gradient
f - function to consider
eps1 - perturbation size
Outputs:
grad - gradient (vector)
'''
n = len(x)
grad = np.zeros(n)
if(verbose):
print("***** my_grad_approx at x = ",x,"*****")
for i in range(0,n):
# Create vector of zeros except eps in position i
e = np.zeros(n)
e[i] = eps1
# Finite difference formula
my_f_plus = f(x + e)
my_f_minus = f(x - e)
# Diagnostics
if(verbose):
print("e[",i,"] = ",e)
print("f(x + e[",i,"]) = ",my_f_plus)
print("f(x - e[",i,"]) = ",my_f_minus)
grad[i] = (my_f_plus - my_f_minus)/(2*eps1)
if(verbose):
print("***** Done. ***** \n")
return grad
## Calculate gradient with central finite difference
def my_jac_approx(x,h,eps1,verbose=False):
'''
Calculate Jacobian of function h(x) using central difference formula
Inputs:
x - point for which to evaluate gradient
h - vector-valued function to consider. h(x): R^n --> R^m
eps1 - perturbation size
Outputs:
A - Jacobian (n x m matrix)
'''
# Check h(x) at x
h_x0 = h(x)
# Extract dimensions
n = len(x)
m = len(h_x0)
# Initialize Jacobian matrix
A = np.zeros((n,m))
# Calculate Jacobian by row
for i in range(0,n):
# Create vector of zeros except eps in position i
e = np.zeros(n)
e[i] = eps1
# Finite difference formula
my_h_plus = h(x + e)
my_h_minus = h(x - e)
# Diagnostics
if(verbose):
print("e[",i,"] = ",e)
print("h(x + e[",i,"]) = ",my_h_plus)
print("h(x - e[",i,"]) = ",my_h_minus)
A[i,:] = (my_h_plus - my_h_minus)/(2*eps1)
if(verbose):
print("***** Done. ***** \n")
return A
## Calculate Hessian using central finite difference
def my_hes_approx(x,grad,eps2):
'''
Calculate gradient of function my_f using central difference formula and my_grad
Inputs:
x - point for which to evaluate gradient
grad - function to calculate the gradient
eps2 - perturbation size (for Hessian NOT gradient approximation)
Outputs:
H - Hessian (matrix)
'''
n = len(x)
H = np.zeros([n,n])
for i in range(0,n):
# Create vector of zeros except eps in position i
e = np.zeros(n)
e[i] = eps2
# Evaluate gradient twice
grad_plus = grad(x + e)
grad_minus = grad(x - e)
# Notice we are building the Hessian by column (or row)
H[:,i] = (grad_plus - grad_minus)/(2*eps2)
return H
## Linear algebra calculation
def xxT(u):
'''
Calculates u*u.T to circumvent limitation with SciPy
Arguments:
u - numpy 1D array
Returns:
u*u.T
Assume u is a nx1 vector.
Recall: NumPy does not distinguish between row or column vectors
u.dot(u) returns a scalar. This functon returns an nxn matrix.
'''
n = len(u)
A = np.zeros([n,n])
for i in range(0,n):
for j in range(0,n):
A[i,j] = u[i]*u[j]
return A
## Analyze Hessian
def analyze_hes(B):
print(B,"\n")
l = linalg.eigvals(B)
print("Eigenvalues: ",l,"\n")
## Assemble KKT matrix (equality constrained only)
def assemble_check_KKT(W,Sk,A,deltaA,deltaW,verbose):
# YOUR SOLUTION HERE
return KKT,inertia_correct,pos_ev,neg_ev,zero_ev
def barrier_subproblem(x0,v0,u0,calc_f,calc_c,var_bounds,mu,eps,max_iter=100,verbose=False):
'''
Basic Full Space Newton Method for Solving Barrier Subproblem Constrained NLP
Input:
x0 - starting point (vector)
calc_f - function to calculate objective (returns scalar)
calc_c - function to calculate constraints (returns vector)
var_bounds - list of indicies for variables with lower bound
mu - barrier penalty
eps - tolerance for termination
Histories (stored for debugging):
x - history of steps (primal variables)
v - history of steps (duals for constraints)
u - history of steps (duals for bounds)
f - history of objective evaluations
c - history of constraint evaluations
df - history of objective gradients
dL - history of Lagrange function gradients
A - history of constraint Jacobians
W - history of Lagrange Hessians
S - history of sigma matrix
Outputs:
x - final value for primal variable
v - final value for constraint duals
u - final value for bound duals
Notes:
1. For simplicity, central finite difference is used
for all gradient calculations.
'''
### Specifics for Algorithm 5.2
# Tuning parameters
delta_bar_W_min = 1E-20
delta_bar_W_0 = 1E-4
delta_bar_W_max = 1E40
delta_bar_A = 1E-8
kappa_u = 8
kappa_l = 1/3
# Declare iteration histories as empty lists
x = []
v = []
u = []
f = []
L = []
c = []
df = []
dL = []
A = []
W = []
# YOUR SOLUTION HERE
def interior_point(x0,calc_f,calc_c,var_bounds,max_iter=20):
# YOUR SOLUTION HERE
return x, v, u, mu, E
f = lambda x: x[0] + 2*x[1]
c = lambda x: (x[0] + x[1] - 1)*np.ones(1)
# Indices of variables with lower bound of zero
vb = [1]
x0 = np.ones(2)
u0 = np.ones(1)
v0 = np.ones(1)
x_, v_, u_, E_ = barrier_subproblem(x0,v0,u0,f,c,vb,1E-1,1E-10,verbose=False)
Iter. f(x) ||c(x)|| E ||dx|| ||dv|| ||du|| delta_A delta_W 0 3.0000e+00 1.0000e+00 2.00e+00 9.06e-01 2.00e+00 3.56e-04 0.00e+00 0.00e+00 1 1.0996e+00 1.3978e-10 3.20e-04 5.03e-04 1.78e-04 3.56e-04 0.00e+00 0.00e+00 2 1.1000e+00 3.9524e-14 1.26e-07 1.70e-07 3.94e-08 5.91e-08 0.00e+00 0.00e+00 3 1.1000e+00 0.0000e+00 6.87e-11 1.48e-11 1.11e-10 1.04e-10 0.00e+00 0.00e+00
f = lambda x: x[0] + 2*x[1]
c = lambda x: (x[0] + x[1] - 1)*np.ones(1)
# Indices of variables with lower bound of zero
vb = [1]
x0 = np.ones(2)
#u0 = np.ones(1)
#v0 = np.ones(1)
# x_, v_, u_, E_ = barrier_subproblem(x0,v0,u0,f,c,vb,1E-1,1E-10,verbose=False)
x, v, u, mu, E = interior_point(x0,f,c,vb)
*** Barrier Subproblem 0 *** mu = 10.0 Iter. f(x) ||c(x)|| E ||dx|| ||dv|| ||du|| delta_A delta_W 0 3.0000e+00 1.0000e+00 9.00e+00 1.35e+01 2.00e+00 8.45e-03 0.00e+00 0.00e+00 *** Barrier Subproblem 1 *** mu = 2.0 Iter. f(x) ||c(x)|| E ||dx|| ||dv|| ||du|| delta_A delta_W 0 1.1008e+01 1.3978e-10 7.92e+00 1.14e+01 4.22e-03 8.45e-03 0.00e+00 0.00e+00 *** Barrier Subproblem 2 *** mu = 0.4 Iter. f(x) ||c(x)|| E ||dx|| ||dv|| ||du|| delta_A delta_W 0 2.9318e+00 0.0000e+00 1.53e+00 2.17e+00 1.70e-04 3.40e-04 0.00e+00 0.00e+00 *** Barrier Subproblem 3 *** mu = 0.08000000000000002 Iter. f(x) ||c(x)|| E ||dx|| ||dv|| ||du|| delta_A delta_W 0 1.3993e+00 2.5520e-10 3.19e-01 4.51e-01 1.70e-04 3.40e-04 0.00e+00 0.00e+00 *** Barrier Subproblem 4 *** mu = 0.016000000000000004 Iter. f(x) ||c(x)|| E ||dx|| ||dv|| ||du|| delta_A delta_W 0 1.0801e+00 5.3163e-11 6.41e-02 9.07e-02 1.07e-05 1.78e-05 0.00e+00 0.00e+00 *** Barrier Subproblem 5 *** mu = 0.0020238577025077633 Iter. f(x) ||c(x)|| E ||dx|| ||dv|| ||du|| delta_A delta_W 0 1.0160e+00 0.0000e+00 1.40e-02 1.98e-02 1.15e-05 1.86e-05 0.00e+00 0.00e+00 *** Barrier Subproblem 6 *** mu = 9.104790579399288e-05 Iter. f(x) ||c(x)|| E ||dx|| ||dv|| ||du|| delta_A delta_W 0 1.0020e+00 7.7571e-13 1.93e-03 2.73e-03 7.76e-07 8.83e-07 0.00e+00 0.00e+00 1 1.0001e+00 0.0000e+00 1.07e-07 2.43e-09 0.00e+00 1.07e-07 0.00e+00 0.00e+00 *** Barrier Subproblem 7 *** mu = 8.687702517211205e-07 Iter. f(x) ||c(x)|| E ||dx|| ||dv|| ||du|| delta_A delta_W 0 1.0001e+00 0.0000e+00 9.02e-05 1.28e-04 1.11e-10 5.12e-09 0.00e+00 0.00e+00 1 1.0000e+00 9.9920e-15 4.95e-09 6.52e-13 3.88e-17 4.95e-09 0.00e+00 0.00e+00
import matplotlib.pyplot as plt
# number of iterations
N = len(x)
# iteration
iters = range(0,N)
plt.figure
for i in range(0,len(x0)):
plt.plot(iters,[x[j][i] for j in range(0,N)],label="x"+str(i))
plt.xlabel("Iteration")
plt.ylabel("Primal Variables")
plt.legend()
plt.show()
plt.figure
for i in range(0,len(u[0])):
plt.plot(iters,[u[j][i] for j in range(0,N)],label="u"+str(i))
for i in range(0,len(v[0])):
plt.plot(iters,[v[j][i] for j in range(0,N)],label="v"+str(i))
plt.xlabel("Iteration")
plt.ylabel("Dual Variables")
plt.legend()
plt.show()
plt.figure
plt.semilogy(iters,mu)
plt.xlabel("Iteration")
plt.ylabel("Barrier Penalty")
plt.show()
plt.figure
plt.semilogy(range(1,N),E)
plt.xlabel("Iteration")
plt.ylabel("Error")
plt.show()
f = lambda x: x[0] + 2*x[1] + x[2]**2
def c(x):
rhs = np.zeros(2)
rhs[0] = x[0] + x[1] - 1
rhs[1] = x[2] - x[1] - 3
return rhs
# Indices of variables with lower bound of zero
vb = [1,2]
x0 = np.ones(3)
u0 = np.ones(2)
v0 = np.ones(2)
## Test barrier subproblem
# xtest, vtest, utest, Etest = barrier_subproblem(x0,v0,u0,f,c,vb,1E-1,1E-10,max_iter=10,verbose=True)
##
x, v, u, mu, E = interior_point(x0,f,c,vb)
*** Barrier Subproblem 0 *** mu = 10.0 Iter. f(x) ||c(x)|| E ||dx|| ||dv|| ||du|| delta_A delta_W 0 4.0000e+00 3.1623e+00 9.00e+00 6.17e+00 8.25e+00 8.06e+00 0.00e+00 0.00e+00 *** Barrier Subproblem 1 *** mu = 2.0 Iter. f(x) ||c(x)|| E ||dx|| ||dv|| ||du|| delta_A delta_W 0 4.0013e+01 4.4202e-10 2.80e+01 3.79e+00 1.52e+00 3.22e+00 0.00e+00 0.00e+00 1 1.6354e+01 1.3323e-15 6.22e+00 9.26e-01 2.49e-01 1.35e+00 0.00e+00 0.00e+00 *** Barrier Subproblem 2 *** mu = 0.4 Iter. f(x) ||c(x)|| E ||dx|| ||dv|| ||du|| delta_A delta_W 0 1.2029e+01 5.9350e-11 2.31e+00 3.94e-01 1.93e-01 6.76e-01 0.00e+00 0.00e+00 *** Barrier Subproblem 3 *** mu = 0.08000000000000002 Iter. f(x) ||c(x)|| E ||dx|| ||dv|| ||du|| delta_A delta_W 0 1.0363e+01 5.0465e-11 4.67e-01 7.00e-02 6.98e-02 1.66e-01 0.00e+00 0.00e+00 *** Barrier Subproblem 4 *** mu = 0.016000000000000004 Iter. f(x) ||c(x)|| E ||dx|| ||dv|| ||du|| delta_A delta_W 0 1.0077e+01 8.9693e-12 7.01e-02 1.52e-02 5.71e-03 2.39e-02 0.00e+00 0.00e+00 *** Barrier Subproblem 5 *** mu = 0.0020238577025077633 Iter. f(x) ||c(x)|| E ||dx|| ||dv|| ||du|| delta_A delta_W 0 1.0016e+01 4.8606e-13 1.42e-02 3.45e-03 7.38e-04 4.77e-03 0.00e+00 0.00e+00 *** Barrier Subproblem 6 *** mu = 9.104790579399288e-05 Iter. f(x) ||c(x)|| E ||dx|| ||dv|| ||du|| delta_A delta_W 0 1.0002e+01 4.5590e-13 1.94e-03 4.78e-04 9.46e-05 6.54e-04 0.00e+00 0.00e+00 1 1.0000e+01 6.1284e-14 2.94e-07 6.48e-09 4.36e-07 8.52e-07 0.00e+00 0.00e+00 *** Barrier Subproblem 7 *** mu = 8.687702517211205e-07 Iter. f(x) ||c(x)|| E ||dx|| ||dv|| ||du|| delta_A delta_W 0 1.0000e+01 4.4409e-16 9.02e-05 2.23e-05 4.29e-06 3.04e-05 0.00e+00 0.00e+00 1 1.0000e+01 2.6645e-15 1.67e-08 1.36e-11 1.69e-08 2.21e-08 0.00e+00 0.00e+00 *** Barrier Subproblem 8 *** mu = 1e-09 Iter. f(x) ||c(x)|| E ||dx|| ||dv|| ||du|| delta_A delta_W 0 1.0000e+01 1.1102e-16 8.68e-07 2.15e-07 4.23e-08 2.92e-07 0.00e+00 0.00e+00 1 1.0000e+01 0.0000e+00 1.36e-09 1.33e-15 3.33e-10 1.60e-09 0.00e+00 0.00e+00
import matplotlib.pyplot as plt
# number of iterations
N = len(x)
# iteration
iters = range(0,N)
plt.figure
for i in range(0,len(x0)):
plt.plot(iters,[x[j][i] for j in range(0,N)],label="x"+str(i))
plt.xlabel("Iteration")
plt.ylabel("Primal Variables")
plt.legend()
plt.show()
plt.figure
for i in range(0,len(u[0])):
plt.plot(iters,[u[j][i] for j in range(0,N)],label="u"+str(i))
for i in range(0,len(v[0])):
plt.plot(iters,[v[j][i] for j in range(0,N)],label="v"+str(i))
plt.xlabel("Iteration")
plt.ylabel("Dual Variables")
plt.legend()
plt.show()
plt.figure
plt.semilogy(iters,mu)
plt.xlabel("Iteration")
plt.ylabel("Barrier Penalty")
plt.show()
plt.figure
plt.semilogy(range(1,N),E)
plt.xlabel("Iteration")
plt.ylabel("Error")
plt.show()