{
"cells": [
{
"cell_type": "markdown",
"id": "648ea9f4",
"metadata": {},
"source": [
"\n",
"*This notebook contains material from [CBE60499](https://ndcbe.github.io/CBE60499);\n",
"content is available [on Github](git@github.com:ndcbe/CBE60499.git).*\n"
]
},
{
"cell_type": "markdown",
"id": "03d22611",
"metadata": {},
"source": [
"\n",
"< [4.8 Inertia-Corrected Netwon Method for Equality Constrained NLPs](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [5.0 Special Topics](https://ndcbe.github.io/CBE60499/05.00-Special-Topics.html) > 
 "
]
},
{
"cell_type": "markdown",
"id": "f3e9a52a",
"metadata": {
"nbpages": {
"level": 1,
"link": "[4.9 Algorithms Homework 4: Interior Point Methods](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9-Algorithms-Homework-4:-Interior-Point-Methods)",
"section": "4.9 Algorithms Homework 4: Interior Point Methods"
}
},
"source": [
"# 4.9 Algorithms Homework 4: Interior Point Methods"
]
},
{
"cell_type": "markdown",
"id": "ba74c034",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.9.1 Tips and Tricks](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.1-Tips-and-Tricks)",
"section": "4.9.1 Tips and Tricks"
}
},
"source": [
"## 4.9.1 Tips and Tricks"
]
},
{
"cell_type": "markdown",
"id": "a8715f98",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.1.1 Background](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.1.1-Background)",
"section": "4.9.1.1 Background"
}
},
"source": [
"### 4.9.1.1 Background"
]
},
{
"cell_type": "markdown",
"id": "4844e9f9",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.1.1 Background](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.1.1-Background)",
"section": "4.9.1.1 Background"
}
},
"source": [
"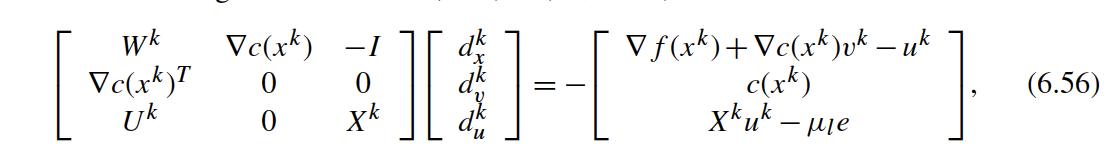\n",
"\n",
"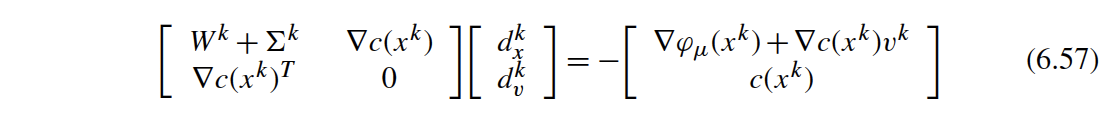\n",
"\n",
"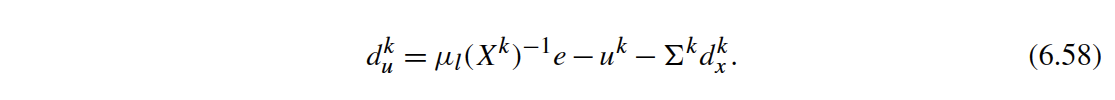\n",
"\n",
"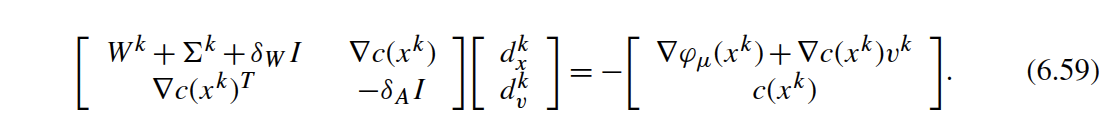"
]
},
{
"cell_type": "markdown",
"id": "11a91e88",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.1.2 Problem Formulation](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.1.2-Problem-Formulation)",
"section": "4.9.1.2 Problem Formulation"
}
},
"source": [
"### 4.9.1.2 Problem Formulation"
]
},
{
"cell_type": "markdown",
"id": "164bb509",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.1.2 Problem Formulation](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.1.2-Problem-Formulation)",
"section": "4.9.1.2 Problem Formulation"
}
},
"source": [
"Consider the following nonlinear program:\n",
"\n",
"$$\n",
"\\begin{align}\n",
"\t\\min_{x} \\quad & f(x) \\\\\n",
"\t\\mathrm{s.t.} \\quad & c(x) = 0 \\\\\n",
"\t& x_i \\geq 0, \\quad i \\in \\mathcal{I}\n",
"\\end{align}\n",
"$$\n",
"\n",
"where $x \\in \\mathbb{R}^{n}$, $f(x): \\mathbb{R}^{n} \\rightarrow \\mathbb{R}$, $c(x): \\mathbb{R}^{n} \\rightarrow \\mathbb{R}^{m}$ and $|\\mathcal{I} |$ = $r$ (i.e., there are $r$ variables with a lower bound and $r \\leq n$). This is an extension of (6.48) in Biegler (2010).\n",
"\n",
"This has the corresponding log-barrier approximation:\n",
"\n",
"$$\n",
"\\begin{align}\n",
"\t\\min_{x} \\quad & \\phi_{\\mu_l}(x) := f(x) - \\mu_l \\sum_{i \\in \\mathcal{I}} \\log(x_i) \\\\\n",
"\t\\mathrm{s.t.} \\quad & c(x) = 0\n",
"\\end{align}\n",
"$$\n",
"\n",
"which is an extension of (6.49) in Biegler (2010).\n",
"\n",
"Let the $n \\times r$ matrix $G$ encode which variables are bounded. If variable $i$ corresponds to the $j$th bound, then $G_{i,j} = 1$ and otherwise $G_{i,j} = 0$. $G$ is assembled as follows:\n",
"\n",
"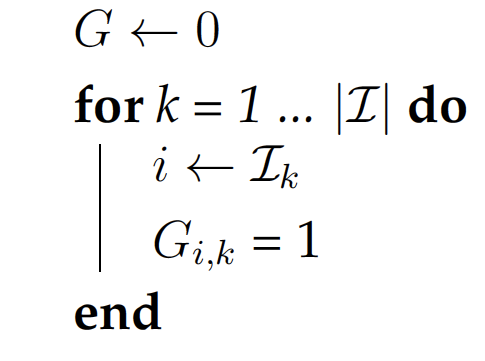\n",
"\n",
"Notice that $G$ is the gradient of $x \\geq 0$. $G^T G = I$ but the converse does not hold unless $r = n$."
]
},
{
"cell_type": "markdown",
"id": "c2fed8b8",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.1.3 Reformulation Example](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.1.3-Reformulation-Example)",
"section": "4.9.1.3 Reformulation Example"
}
},
"source": [
"### 4.9.1.3 Reformulation Example"
]
},
{
"cell_type": "markdown",
"id": "fae61884",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.1.3 Reformulation Example](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.1.3-Reformulation-Example)",
"section": "4.9.1.3 Reformulation Example"
}
},
"source": [
"Start with:\n",
"\n",
"$$\n",
"\t\\begin{align}\n",
"\t\t\\min_{x} \\quad & x_1^2 + x_2 \\\\\n",
"\t\t\\mathrm{s.t.} \\quad & x_1 + x_2 = 1 \\\\\n",
"\t\t& x_1 + 1 \\geq 0\n",
"\t\\end{align}\n",
"$$\n",
"\n",
"Add slack variable $x_3$ and convert the inequality constraint to an equality constraint and bound:\n",
"\n",
"$$\n",
"\t\\begin{align}\n",
"\t\t\\min_{x} \\quad & x_1^2 + x_2 \\\\\n",
"\t\t\\mathrm{s.t.} \\quad & x_1 + x_2 = 1 \\\\\n",
"\t\t& x_1 + 1 - x_3 = 0 \\\\\n",
"\t\t& x_3 \\geq 0\n",
"\t\\end{align}\n",
"$$\n",
"\n",
"Now assemble $G$:\n",
"\n",
"$$\n",
"\tG = \\begin{bmatrix}\n",
"\t\t0 \\\\\n",
"\t\t0 \\\\\n",
"\t\t1\n",
"\t\\end{bmatrix}\n",
"$$"
]
},
{
"cell_type": "markdown",
"id": "00e568fa",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.1.4 Primal Dual Optimality Conditions](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.1.4-Primal-Dual-Optimality-Conditions)",
"section": "4.9.1.4 Primal Dual Optimality Conditions"
}
},
"source": [
"### 4.9.1.4 Primal Dual Optimality Conditions"
]
},
{
"cell_type": "markdown",
"id": "b923aa13",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.1.4 Primal Dual Optimality Conditions](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.1.4-Primal-Dual-Optimality-Conditions)",
"section": "4.9.1.4 Primal Dual Optimality Conditions"
}
},
"source": [
"$$\n",
"\\newcommand{\\dims}[3]{\\underbrace{#1}_{#2 \\times #3}}\n",
"\\newcommand{\\I}[0]{\\mathcal{I}}\n",
"\\newcommand{\\dfx}[0]{\\dims{\\nabla f(x^k)}{n}{1}}\n",
"\\newcommand{\\cx}[0]{\\dims{c(x^k)}{m}{1}}\n",
"\\newcommand{\\dcx}[0]{\\dims{\\nabla c(x^k)}{n}{m}}\n",
"\\newcommand{\\dcxT}[0]{\\dims{\\nabla_x c(x^k)^T}{m}{n}}\n",
"\\newcommand{\\W}[0]{\\dims{W^k}{n}{n}}\n",
"\\newcommand{\\G}[0]{\\dims{G}{n}{r}}\n",
"\\newcommand{\\GT}[0]{\\dims{G^T}{r}{n}}\n",
"\\newcommand{\\vk}[0]{\\dims{v^k}{m}{1}}\n",
"\\newcommand{\\Xinv}[0]{\\dims{(\\hat{X}^k)^{-1}}{r}{r}}\n",
"\\newcommand{\\X}[0]{\\dims{\\hat{X}^k}{r}{r}}\n",
"\\newcommand{\\e}[0]{\\dims{e}{r}{1}}\n",
"\\newcommand{\\uk}[0]{\\dims{u^k}{r}{1}}\n",
"\\newcommand{\\dx}[0]{\\dims{d_x^k}{n}{1}}\n",
"\\newcommand{\\dv}[0]{\\dims{d_v^k}{m}{1}}\n",
"\\newcommand{\\du}[0]{\\dims{d_u^k}{r}{1}}\n",
"\\newcommand{\\Uk}[0]{\\dims{U^k}{r}{r}}\n",
"\\newcommand{\\Sk}[0]{\\dims{\\Sigma^k}{n}{n}}\n",
"\\newcommand{\\dphi}[0]{\\dims{\\nabla \\phi_{\\mu_l}}{n}{1}}\n",
"$$\n",
"\n",
"Next we extend (6.51) in Biegler (2010):\n",
" \n",
"$$\n",
"\\begin{gather}\n",
"\t\\dfx ~+~ \\dcx \\vk ~-~ \\G \\uk = \\dims{0}{n}{1} \\\\\n",
"\t\\X \\uk = \\mu \\e \\\\\n",
"\t\\cx = \\dims{0}{m}{1}\n",
"\\end{gather}\n",
"$$\n",
"\n",
"We now extend (6.56) in Biegler (2010):\n",
"\n",
"$$\n",
"\t\\begin{bmatrix}\n",
"\t\t\\W & \\dcx & \\G \\\\\n",
"\t\t\\dcxT & \\dims{0}{m}{m} & \\dims{0}{m}{r} \\\\\n",
"\t\t\\Uk \\GT & \\dims{0}{r}{m} & \\X\n",
"\t\\end{bmatrix} \n",
"\t\\begin{bmatrix}\n",
"\t\t\\dx \\\\\n",
"\t\t\\dv \\\\\n",
"\t\t\\du\n",
"\t\\end{bmatrix} = -\n",
"\t\\begin{bmatrix}\n",
"\t\\dfx ~+~ \\dcx \\vk ~-~ \\G \\uk \\\\\n",
"\t\\cx \\\\\n",
"\t\\X \\uk ~-~ \\mu_l \\e\n",
"\t\\end{bmatrix}\n",
"$$\n",
"\n",
"where $U^k = \\mathrm{diag}\\{u^k\\}$ and $W^k = \\nabla_{xx} L(x^k,v^k)$. Notice that $W^k$ does NOT include a contribution from the barrier term:\n",
"\n",
"$$\n",
"\\begin{equation}\n",
"\t\\W = \\dims{\\nabla^2 f(x^k)}{n}{n} + \\sum_{j=1}^{m} \\left( \\dims{\\nabla^2 c_{j}(x^k)}{n}{n} \\underbrace{v^k_{j}}_{\\mathrm{scalar}} \\right)\n",
"\\end{equation}\n",
"$$\n",
"\n",
"We can verify that $W^k$ does not include $\\hat{X}$ by showing that the KKT system above is a Newton step to solve the nonlinear system for the primal dual conditions.\n",
"\n",
"\n",
"The Newton step can be simplified, similar to (6.57) and (6.58) in Biegler (2010):\n",
"\n",
"$$\n",
"\\begin{equation}\n",
"\t\\begin{bmatrix}\n",
"\t\t\\W + \\Sk & \\dcx \\\\\n",
"\t\t\\dcxT & 0\n",
"\t\\end{bmatrix} \n",
"\t\\begin{bmatrix}\n",
"\t\t\\dx \\\\\n",
"\t\t\\dv\n",
"\t\\end{bmatrix} = -\n",
"\t\\begin{bmatrix}\n",
"\t\\dphi ~+~ \\dcx \\vk \\\\\n",
"\t\\cx\n",
"\t\\end{bmatrix}\n",
"\\end{equation}\n",
"$$\n",
"\n",
"and\n",
"\n",
"$$\n",
"\\begin{equation} \\label{eq:du}\n",
"\t\\du = \\mu_l \\Xinv \\e ~-~ \\uk ~-~ \\GT \\Sk \\dx\n",
"\\end{equation}\n",
"$$\n",
"\n",
"where\n",
"$$\n",
"\\begin{equation} \\label{eq:Sk}\n",
"\t\\Sk = \\G \\Xinv \\Uk \\GT\n",
"\\end{equation}\n",
"$$\n",
"\n",
"and \n",
"\n",
"$$\n",
"\\begin{equation}\n",
"\t\\dphi = \\dfx - \\mu_l \\G \\Xinv \\dims{e}{r}{1}\n",
"\\end{equation}\n",
"$$\n",
"\n",
"Notice that the equation for $\\du$ simplifies by substituting $G^T G = I$:\n",
"\n",
"$$\n",
"\t\\du = \\mu_l \\Xinv \\e ~-~ \\uk ~-~ \\Xinv \\Uk \\GT \\dx\n",
"$$\n",
"\n",
"Finally, inertia correction can be applied to simplified KKT step similar to (6.59) in Biegler (2010). "
]
},
{
"cell_type": "markdown",
"id": "1ca1ed21",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.9.2 Basic Interior Point Method for Inequality and Equality Constraint NLPs](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.2-Basic-Interior-Point-Method-for-Inequality-and-Equality-Constraint-NLPs)",
"section": "4.9.2 Basic Interior Point Method for Inequality and Equality Constraint NLPs"
}
},
"source": [
"## 4.9.2 Basic Interior Point Method for Inequality and Equality Constraint NLPs"
]
},
{
"cell_type": "markdown",
"id": "3fd841f9",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.9.2 Basic Interior Point Method for Inequality and Equality Constraint NLPs](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.2-Basic-Interior-Point-Method-for-Inequality-and-Equality-Constraint-NLPs)",
"section": "4.9.2 Basic Interior Point Method for Inequality and Equality Constraint NLPs"
}
},
"source": [
"Implement a basic interior point method for inequality and equality constrained nonlinear programs. See pg. 154 – 155 in Biegler (2010). You may skip the line search, i.e., always take a full step."
]
},
{
"cell_type": "markdown",
"id": "a7a244c5",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.2.1 Pseudocode](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.2.1-Pseudocode)",
"section": "4.9.2.1 Pseudocode"
}
},
"source": [
"### 4.9.2.1 Pseudocode"
]
},
{
"cell_type": "markdown",
"id": "23e86ba7",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.2.1 Pseudocode](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.2.1-Pseudocode)",
"section": "4.9.2.1 Pseudocode"
}
},
"source": [
"Write detailed pseudocode on paper or a whiteboard. Scan/take a photo and turn in."
]
},
{
"cell_type": "markdown",
"id": "d1ec363f",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.2.2 Python Implementation](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.2.2-Python-Implementation)",
"section": "4.9.2.2 Python Implementation"
}
},
"source": [
"### 4.9.2.2 Python Implementation"
]
},
{
"cell_type": "markdown",
"id": "2ad37a24",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.2.2 Python Implementation](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.2.2-Python-Implementation)",
"section": "4.9.2.2 Python Implementation"
}
},
"source": [
"Implement in Python. Hints: Reuse code from Algorithm 5.2 example."
]
},
{
"cell_type": "code",
"execution_count": 1,
"id": "ec182a38",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.2.2 Python Implementation](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.2.2-Python-Implementation)",
"section": "4.9.2.2 Python Implementation"
}
},
"outputs": [],
"source": [
"### Load Python libraries\n",
"import numpy as np\n",
"from scipy import linalg\n",
"\n",
"### Define helper functions\n",
"## Check is element of array is NaN\n",
"def check_nan(A):\n",
" return np.sum(np.isnan(A))\n",
"\n",
"## Calculate gradient with central finite difference\n",
"def my_grad_approx(x,f,eps1,verbose=False):\n",
" '''\n",
" Calculate gradient of function f using central difference formula\n",
" \n",
" Inputs:\n",
" x - point for which to evaluate gradient\n",
" f - function to consider\n",
" eps1 - perturbation size\n",
" \n",
" Outputs:\n",
" grad - gradient (vector)\n",
" '''\n",
" \n",
" n = len(x)\n",
" grad = np.zeros(n)\n",
" \n",
" if(verbose):\n",
" print(\"***** my_grad_approx at x = \",x,\"*****\")\n",
" \n",
" for i in range(0,n):\n",
" \n",
" # Create vector of zeros except eps in position i\n",
" e = np.zeros(n)\n",
" e[i] = eps1\n",
" \n",
" # Finite difference formula\n",
" my_f_plus = f(x + e)\n",
" my_f_minus = f(x - e)\n",
" \n",
" # Diagnostics\n",
" if(verbose):\n",
" print(\"e[\",i,\"] = \",e)\n",
" print(\"f(x + e[\",i,\"]) = \",my_f_plus)\n",
" print(\"f(x - e[\",i,\"]) = \",my_f_minus)\n",
" \n",
" \n",
" grad[i] = (my_f_plus - my_f_minus)/(2*eps1)\n",
" \n",
" if(verbose):\n",
" print(\"***** Done. ***** \\n\")\n",
" \n",
" return grad\n",
"\n",
"## Calculate gradient with central finite difference\n",
"def my_jac_approx(x,h,eps1,verbose=False):\n",
" '''\n",
" Calculate Jacobian of function h(x) using central difference formula\n",
" \n",
" Inputs:\n",
" x - point for which to evaluate gradient\n",
" h - vector-valued function to consider. h(x): R^n --> R^m\n",
" eps1 - perturbation size\n",
" \n",
" Outputs:\n",
" A - Jacobian (n x m matrix)\n",
" '''\n",
" \n",
" # Check h(x) at x\n",
" h_x0 = h(x)\n",
" \n",
" # Extract dimensions\n",
" n = len(x)\n",
" m = len(h_x0)\n",
" \n",
" # Initialize Jacobian matrix\n",
" A = np.zeros((n,m))\n",
" \n",
" # Calculate Jacobian by row\n",
" for i in range(0,n):\n",
" \n",
" # Create vector of zeros except eps in position i\n",
" e = np.zeros(n)\n",
" e[i] = eps1\n",
" \n",
" # Finite difference formula\n",
" my_h_plus = h(x + e)\n",
" my_h_minus = h(x - e)\n",
" \n",
" # Diagnostics\n",
" if(verbose):\n",
" print(\"e[\",i,\"] = \",e)\n",
" print(\"h(x + e[\",i,\"]) = \",my_h_plus)\n",
" print(\"h(x - e[\",i,\"]) = \",my_h_minus)\n",
" \n",
" \n",
" A[i,:] = (my_h_plus - my_h_minus)/(2*eps1)\n",
" \n",
" if(verbose):\n",
" print(\"***** Done. ***** \\n\")\n",
" \n",
" return A\n",
" \n",
"## Calculate Hessian using central finite difference\n",
"def my_hes_approx(x,grad,eps2):\n",
" '''\n",
" Calculate gradient of function my_f using central difference formula and my_grad\n",
" \n",
" Inputs:\n",
" x - point for which to evaluate gradient\n",
" grad - function to calculate the gradient\n",
" eps2 - perturbation size (for Hessian NOT gradient approximation)\n",
" \n",
" Outputs:\n",
" H - Hessian (matrix)\n",
" '''\n",
" \n",
" n = len(x)\n",
" H = np.zeros([n,n])\n",
" \n",
" for i in range(0,n):\n",
" # Create vector of zeros except eps in position i\n",
" e = np.zeros(n)\n",
" e[i] = eps2\n",
" \n",
" # Evaluate gradient twice\n",
" grad_plus = grad(x + e)\n",
" grad_minus = grad(x - e)\n",
" \n",
" # Notice we are building the Hessian by column (or row)\n",
" H[:,i] = (grad_plus - grad_minus)/(2*eps2)\n",
"\n",
" return H\n",
"\n",
"## Linear algebra calculation\n",
"def xxT(u):\n",
" '''\n",
" Calculates u*u.T to circumvent limitation with SciPy\n",
" \n",
" Arguments:\n",
" u - numpy 1D array\n",
" \n",
" Returns:\n",
" u*u.T\n",
" \n",
" Assume u is a nx1 vector.\n",
" Recall: NumPy does not distinguish between row or column vectors\n",
" \n",
" u.dot(u) returns a scalar. This functon returns an nxn matrix.\n",
" '''\n",
" \n",
" n = len(u)\n",
" A = np.zeros([n,n])\n",
" for i in range(0,n):\n",
" for j in range(0,n):\n",
" A[i,j] = u[i]*u[j]\n",
" \n",
" return A\n",
"\n",
"## Analyze Hessian\n",
"def analyze_hes(B):\n",
" print(B,\"\\n\")\n",
" \n",
" l = linalg.eigvals(B)\n",
" print(\"Eigenvalues: \",l,\"\\n\")\n"
]
},
{
"cell_type": "code",
"execution_count": 2,
"id": "f51b5c25",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.2.2 Python Implementation](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.2.2-Python-Implementation)",
"section": "4.9.2.2 Python Implementation"
}
},
"outputs": [],
"source": [
"## Assemble KKT matrix (equality constrained only)\n",
"def assemble_check_KKT(W,Sk,A,deltaA,deltaW,verbose):\n",
" \n",
" # YOUR SOLUTION HERE\n",
" \n",
" return KKT,inertia_correct,pos_ev,neg_ev,zero_ev"
]
},
{
"cell_type": "code",
"execution_count": 3,
"id": "ae9be074",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.2.2 Python Implementation](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.2.2-Python-Implementation)",
"section": "4.9.2.2 Python Implementation"
}
},
"outputs": [],
"source": [
"def barrier_subproblem(x0,v0,u0,calc_f,calc_c,var_bounds,mu,eps,max_iter=100,verbose=False):\n",
" '''\n",
" Basic Full Space Newton Method for Solving Barrier Subproblem Constrained NLP\n",
" \n",
" Input:\n",
" x0 - starting point (vector)\n",
" calc_f - function to calculate objective (returns scalar)\n",
" calc_c - function to calculate constraints (returns vector)\n",
" var_bounds - list of indicies for variables with lower bound\n",
" mu - barrier penalty\n",
" eps - tolerance for termination\n",
" \n",
" Histories (stored for debugging):\n",
" x - history of steps (primal variables)\n",
" v - history of steps (duals for constraints)\n",
" u - history of steps (duals for bounds)\n",
" f - history of objective evaluations\n",
" c - history of constraint evaluations\n",
" df - history of objective gradients\n",
" dL - history of Lagrange function gradients\n",
" A - history of constraint Jacobians\n",
" W - history of Lagrange Hessians\n",
" S - history of sigma matrix\n",
" \n",
" Outputs:\n",
" x - final value for primal variable\n",
" v - final value for constraint duals\n",
" u - final value for bound duals\n",
" \n",
" Notes:\n",
" 1. For simplicity, central finite difference is used \n",
" for all gradient calculations.\n",
" ''' \n",
" \n",
" ### Specifics for Algorithm 5.2\n",
" # Tuning parameters\n",
" delta_bar_W_min = 1E-20\n",
" delta_bar_W_0 = 1E-4\n",
" delta_bar_W_max = 1E40\n",
" delta_bar_A = 1E-8\n",
" kappa_u = 8\n",
" kappa_l = 1/3\n",
" \n",
" # Declare iteration histories as empty lists\n",
" x = []\n",
" v = []\n",
" u = []\n",
" f = []\n",
" L = []\n",
" c = []\n",
" df = []\n",
" dL = []\n",
" A = []\n",
" W = []\n",
"\n",
" # YOUR SOLUTION HERE"
]
},
{
"cell_type": "code",
"execution_count": 4,
"id": "6549fabb",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.2.2 Python Implementation](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.2.2-Python-Implementation)",
"section": "4.9.2.2 Python Implementation"
}
},
"outputs": [],
"source": [
"def interior_point(x0,calc_f,calc_c,var_bounds,max_iter=20):\n",
" \n",
" \n",
" # YOUR SOLUTION HERE\n",
" \n",
" return x, v, u, mu, E"
]
},
{
"cell_type": "markdown",
"id": "4fb21995",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.9.3 Test Problems](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.3-Test-Problems)",
"section": "4.9.3 Test Problems"
}
},
"source": [
"## 4.9.3 Test Problems"
]
},
{
"cell_type": "markdown",
"id": "2e7ab8ef",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.3.1 Problem 1: Convex](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.3.1-Problem-1:-Convex)",
"section": "4.9.3.1 Problem 1: Convex"
}
},
"source": [
"### 4.9.3.1 Problem 1: Convex"
]
},
{
"cell_type": "code",
"execution_count": 5,
"id": "4c290f53",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.3.1 Problem 1: Convex](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.3.1-Problem-1:-Convex)",
"section": "4.9.3.1 Problem 1: Convex"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 3.0000e+00 \t1.0000e+00 \t 2.00e+00 \t 9.06e-01 \t 2.00e+00 \t 3.56e-04 \t 0.00e+00 \t 0.00e+00\n",
"1 \t 1.0996e+00 \t1.3978e-10 \t 3.20e-04 \t 5.03e-04 \t 1.78e-04 \t 3.56e-04 \t 0.00e+00 \t 0.00e+00\n",
"2 \t 1.1000e+00 \t3.9524e-14 \t 1.26e-07 \t 1.70e-07 \t 3.94e-08 \t 5.91e-08 \t 0.00e+00 \t 0.00e+00\n",
"3 \t 1.1000e+00 \t0.0000e+00 \t 6.87e-11 \t 1.48e-11 \t 1.11e-10 \t 1.04e-10 \t 0.00e+00 \t 0.00e+00\n"
]
}
],
"source": [
"f = lambda x: x[0] + 2*x[1]\n",
"c = lambda x: (x[0] + x[1] - 1)*np.ones(1)\n",
"\n",
"# Indices of variables with lower bound of zero\n",
"vb = [1]\n",
"\n",
"x0 = np.ones(2)\n",
"u0 = np.ones(1)\n",
"v0 = np.ones(1)\n",
"\n",
"x_, v_, u_, E_ = barrier_subproblem(x0,v0,u0,f,c,vb,1E-1,1E-10,verbose=False)"
]
},
{
"cell_type": "markdown",
"id": "1f44a1a9",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.3.2 Problem 2: Convex](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.3.2-Problem-2:-Convex)",
"section": "4.9.3.2 Problem 2: Convex"
}
},
"source": [
"### 4.9.3.2 Problem 2: Convex"
]
},
{
"cell_type": "code",
"execution_count": 6,
"id": "08e17352",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.3.2 Problem 2: Convex](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.3.2-Problem-2:-Convex)",
"section": "4.9.3.2 Problem 2: Convex"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"\n",
"*** Barrier Subproblem 0 ***\n",
"mu = 10.0\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 3.0000e+00 \t1.0000e+00 \t 9.00e+00 \t 1.35e+01 \t 2.00e+00 \t 8.45e-03 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 1 ***\n",
"mu = 2.0\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 1.1008e+01 \t1.3978e-10 \t 7.92e+00 \t 1.14e+01 \t 4.22e-03 \t 8.45e-03 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 2 ***\n",
"mu = 0.4\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 2.9318e+00 \t0.0000e+00 \t 1.53e+00 \t 2.17e+00 \t 1.70e-04 \t 3.40e-04 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 3 ***\n",
"mu = 0.08000000000000002\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 1.3993e+00 \t2.5520e-10 \t 3.19e-01 \t 4.51e-01 \t 1.70e-04 \t 3.40e-04 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 4 ***\n",
"mu = 0.016000000000000004\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 1.0801e+00 \t5.3163e-11 \t 6.41e-02 \t 9.07e-02 \t 1.07e-05 \t 1.78e-05 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 5 ***\n",
"mu = 0.0020238577025077633\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 1.0160e+00 \t0.0000e+00 \t 1.40e-02 \t 1.98e-02 \t 1.15e-05 \t 1.86e-05 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 6 ***\n",
"mu = 9.104790579399288e-05\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 1.0020e+00 \t7.7571e-13 \t 1.93e-03 \t 2.73e-03 \t 7.76e-07 \t 8.83e-07 \t 0.00e+00 \t 0.00e+00\n",
"1 \t 1.0001e+00 \t0.0000e+00 \t 1.07e-07 \t 2.43e-09 \t 0.00e+00 \t 1.07e-07 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 7 ***\n",
"mu = 8.687702517211205e-07\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 1.0001e+00 \t0.0000e+00 \t 9.02e-05 \t 1.28e-04 \t 1.11e-10 \t 5.12e-09 \t 0.00e+00 \t 0.00e+00\n",
"1 \t 1.0000e+00 \t9.9920e-15 \t 4.95e-09 \t 6.52e-13 \t 3.88e-17 \t 4.95e-09 \t 0.00e+00 \t 0.00e+00\n"
]
}
],
"source": [
"f = lambda x: x[0] + 2*x[1]\n",
"c = lambda x: (x[0] + x[1] - 1)*np.ones(1)\n",
"\n",
"# Indices of variables with lower bound of zero\n",
"vb = [1]\n",
"\n",
"x0 = np.ones(2)\n",
"#u0 = np.ones(1)\n",
"#v0 = np.ones(1)\n",
"\n",
"# x_, v_, u_, E_ = barrier_subproblem(x0,v0,u0,f,c,vb,1E-1,1E-10,verbose=False)\n",
"\n",
"x, v, u, mu, E = interior_point(x0,f,c,vb)"
]
},
{
"cell_type": "code",
"execution_count": 7,
"id": "2efe01ca",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.3.2 Problem 2: Convex](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.3.2-Problem-2:-Convex)",
"section": "4.9.3.2 Problem 2: Convex"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEGCAYAAAB7DNKzAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAAAy70lEQVR4nO3deXxU9b3/8dcnO1nYsgBJWGXfEwMIiHVDQREktnXHrVLvFdvb3ntb79L2ent/9/bXX3t7b6tdEFGw1KUKFisq1qqgsoWwb4JAICFA2AmQ/fP740xkDJPJkMzMmSSf5+Mxj5kz58w5bxTmM+ec7yKqijHGGNOYKLcDGGOMiWxWKIwxxvhlhcIYY4xfViiMMcb4ZYXCGGOMXzFuBwiFtLQ07dOnj9sxjDGm1Vi/fv0xVU33ta5NFoo+ffpQUFDgdgxjjGk1RKSosXV26ckYY4xfViiMMcb4ZYXCGGOMX23yHoUxxoRSdXU1xcXFVFRUuB3lsiUkJJCdnU1sbGzAn7FCYYwxl6m4uJiUlBT69OmDiLgdJ2CqyvHjxykuLqZv374Bfy7kl55EZL6IHBWRrV7vdRWR90Rkt+e5SyOfnSIiu0Rkj4g8GeqsxhgTiIqKClJTU1tVkQAQEVJTUy/7TCgc9yheAKY0eO9J4H1VHQC871n+EhGJBp4BpgJDgbtFZGhooxpjTGBaW5Go15zcIS8UqroCONHg7RnAAs/rBcDtPj46FtijqntVtQp42fO59mfnMijb5XYKY0w75Varp26qWgrgec7wsU0WcNBrudjznk8iMltECkSkoKysLKhhXXWmFF65D974W7C5Q4wxfixYsIABAwYwYMAAFixY0PQHAhTJzWN9nR81+k2pqnNVNU9V89LTffZCb502/B60FkoK4OAat9MYYyLUiRMneOqpp1izZg1r167lqaee4uTJk0HZt1uF4oiI9ADwPB/1sU0x0NNrORs4FIZskaOuFta/AL3GQ4cu8Omv3E5kjIkA69atY+TIkVRUVHDu3DmGDRvGM888w+TJk+natStdunRh8uTJvPPOO0E5nlvNY5cCDwA/8Tz/ycc264ABItIXKAHuAu4JW8JIsPs9OFMMU/4TDm+BFT+DY3sgrb/byYwxHk+9uY3th84EdZ9DMzvyo9uGNbp+zJgxTJ8+nX/913/lwoUL3HfffcTGxtKz58Xf1tnZ2ZSUlAQlTziax74ErAIGiUixiDyCUyAmi8huYLJnGRHJFJFlAKpaA8wB3gV2AK+q6rZQ540oBfMhuRsMugXGzoboWFj9jNupjDER4Ic//CHvvfceBQUFfO9730N93MMMVsuskJ9RqOrdjay6wce2h4BbvJaXActCFC2ynToAu5fDNf/gFIjkDBh1F2z8A1z3L5CU5nZCYwz4/eUfSidOnKC8vJzq6moqKirIzs7mww8//GJ9cXEx1157bVCOFck3s9u39QtABHIfuPje+DlQUwHr5rmXyxgTEWbPns2Pf/xj7r33Xr7//e9z8803s3z5ck6ePMnJkydZvnw5N998c1COZUN4RKLaaihcCANuhs5e9/PTB8HAKbB2Lkz8NsR2cC+jMcY1CxcuJCYmhnvuuYfa2lomTJjAxo0b+cEPfsCYMWMA59JU165dg3I8KxSRaOdbcO4o5D186boJT8ALt8Kml3yvN8a0ebNmzWLWrFkAREdHs2bNxabzDz8c/O8Fu/QUiQrmQ6de0P+S2zjQeyJk5sCnT0NdXfizGWPaHSsUkebYHtj3EVz5AERFX7pexDmrOPE5fPZ2+PMZY9odKxSRZv3zEBUDOfc3vs2QGc4Zh3XAM8aEgRWKSFJdARsXweBpkNKt8e2iY2D838KBVXBwXfjyGWPaJSsUkWT7n+DCycBuUufcBwmdYJWdVRhjQssKRSQpmA+p/aHvNU1vG5/iFJQdb8KJvaHPZoxpt6xQRIoj2+DgarjyIeeGdSDGfhMkGlb/JrTZjDGtwpQpU+jcuTPTpk0L6n6tUESKguchOh5GX8a4hx17wMivO0ORn284N5Qxpr35x3/8R1588cWg79cKRSSoLIdNL8OwmZB4mT0px8+B6vNQ8FxoshljIo6vYca3bt3KDTfcQEpKStCPZz2zI8HW16HqbPN6WncbCv1vhDVzYfwTEJsQ/HzGmMa9/aQzDUAwdR8BU3/S6Gpfw4wPHz48uBm82BlFJCiYDxnDoOfY5n1+whPOkB9bXg1uLmNMxGo4zHgo2RmF20oKoXQj3PKzwG9iN9T3K84vkE+fhtH3QZTVf2PCxs8v/1BqOMx4UlJSyI5l3yhuK5gPsUkw8s7m70MEJnwLju2CPe8FL5sxJmI1HGY8lKxQuOnCKef+xIivQkLHlu1r2EzomGXDehjTDngPM/7kk0+ybt06/vrXvzJp0iS+9rWv8f7775Odnc27774blOO5dulJRAYBr3i91Q/4oar+j9c21+LMp73P89ZiVf33MEUMvc2vOi2W8h5q+b6iY+Gqv4Hl/+pczsrKbfk+jTERqbFhxq+//vqQHM+1MwpV3aWqo1V1NHAlcB5Y4mPTlfXbtakioepcdsrMdYYND4bcByC+I6x6Ojj7M8YYIufS0w3A56pa5HaQsDmwGsp2BHfyoYSOzvDk296Ak+3nP6UxJrQipVDcBbzUyLrxIrJJRN4WkUZnMReR2SJSICIFZWVloUkZTAXzIb4TDM8P7n7HPebc3F7z2+Du1xjzJarqdoRmaU5u1wuFiMQB04E/+lhdCPRW1VHAr4A3GtuPqs5V1TxVzUtPTw9J1qA5dxy2vwGj7oK4IDdp65QNw++A9QuckWiNMUGXkJDA8ePHW12xUFWOHz9OQsLldcyNhH4UU4FCVT3ScIWqnvF6vUxEfi0iaap6LKwJg23jIqitCs5NbF/Gz4HNr8D6F+Dq74TmGMa0Y9nZ2RQXF9Mqrl40kJCQQHZ29mV9JhIKxd00ctlJRLoDR1RVRWQszhnQ8XCGC7q6OmcWu14TIGNIaI7RYyT0uxZW/xauehxi4kJzHGPaqdjYWPr27et2jLBx9dKTiCQCk4HFXu89JiKPeRa/CmwVkU3AL4G7tLWd6zW07yNn/ohg3sT2ZcITUH4Ytr4W2uMYY9o8V88oVPU8kNrgvd96vX4aaFttPQvmQ2IqDJ0e2uNccQNkDHU64I26u/nDgxhj2j3Xb2a3K2dKYedbMPpeiIkP7bFEnLOKo9vh8/dDeyxjTJtmhSKcNvwetBaufDA8xxv+VUjpYcN6GGNaxApFuNTVOq2Q+l0HqVeE55gxcTDum7D3QyjdHJ5jGmPaHCsU4bL7PThTHPqb2A1d+RDEJdtZhTGm2axQhEvBfEjuDoOmhve4HTpD7ixnlNrTxeE9tjGmTbBCEQ6nDsDu5c4XdnRs+I8/ztPaePVvwn9sY0yrZ4UiHNYvcFoh5c5y5/hdesOw250cFafdyWCMabWsUIRabTUULoQBN0Pnnu7lGD8Hqs46xcIYYy6DFYpQ2/kWnDsa/pvYDWXlQp9JzuWnmip3sxhjWhUrFKFWMB869YL+N7idxOmAd/YQbPM1P5QxxvhmhSKUju1xxna68gGIinY7DfSfDGmDnKayrXzILGNM+FihCKX1z0NUDOTc73YSR1QUTJgDR7Y4nfCMMSYAVihCpbrCmXdi8DRI6eZ2motGfB2SMqwDnjEmYFYoQmX7n5wZ5ty+id1QbAKMm+0MFHh4q9tpjDGtgBWKUCmYD6n9oe81bie5VN4jEJsIq55xO4kxphWwQhEKR7bBwdXOOEuROA9EYlfIuQ+2/BHOHHI7jTEmwlmhCIWC5yE6Hkbf43aSxl31N86Q52t+53YSY0yEc3sq1P0iskVENopIgY/1IiK/FJE9IrJZRHLdyHlZKsth08swbKbzyz1Sde0HQ25zilrlWbfTGGMiWCScUVynqqNVNc/HuqnAAM9jNhD5o9ptfd0ZKiPSbmL7MuFbUHkaCl90O4kxJoJFQqHwZwawUB2rgc4i0sPtUH4VzIeMYdBzrNtJmpadB73Gw+pfQ22N22mMMRHK7UKhwHIRWS8is32szwIOei0Xe967hIjMFpECESkoKysLQdQAlBRC6UbIi9Cb2L5MeAJOH4Ttb7idxBgTodwuFBNVNRfnEtPjItKwLamvb1ufY0+o6lxVzVPVvPT09GDnDEzBfIhNgpF3unP85hg4FbpeAZ/+0ob1MMb45GqhUNVDnuejwBKg4fWaYsB7bO5sIDLbc1445dyfGPFVSOjodprA1Q/rUboJ9n/sdhpjTARyrVCISJKIpNS/Bm4CGnYVXgrM8rR+ugo4raqlYY4amM2vQvV557JTazPqbkhMtWE9jDE+uXlG0Q34WEQ2AWuBt1T1HRF5TEQ8c3eyDNgL7AGeBf7WnahNUHUuO2XmQmaO22kuX2wHGDsbdr8LR3e6ncYYE2Fi3Dqwqu4FRvl4/7derxV4PJy5muXAaijbAdOfdjtJ8435Bnz8C1j1NMxoxX8OY0zQuX0zu20omA/xnWB4vttJmi8pzelJvvkVOHvE7TTGmAhihaKlzh13mpaOugviktxO0zJXPe7M8b12rttJjDERxApFS21cBLVVrfMmdkNp/WHwrbBuHlSdczuNMSZCNFkoROSnItJRRGJF5H0ROSYi94UjXMSrq3Nmses1ATKGuJ0mOCY8ARWnYMMit5MYYyJEIGcUN6nqGWAaTr+GgcA/hjRVa7HvIzixt3WM6xSonuMge4xzU7uu1u00xpgIEEihiPU83wK8pKonQpindSmY7/Q/GDrd7STBI+KcVZwqgh1vup3GGBMBAikUb4rITiAPeF9E0oGK0MZqBc6Uws63YPS9EBPvdprgGjwNuvSxYT2MMUAAhUJVnwTGA3mqWg2cxxnVtX3b8Htn4p8rH3Q7SfBFRcP4OVCy3ukjYoxp1wK5mZ2I0+mtfi6ITJyzi/arrhbWvwD9roPUK9xOExqj74EOXWxYD2NMQJeengeqgAme5WLgP0KWqDXY/R6cKW5bN7EbiktyemvvWgbHdrudxhjjokAKxRWq+lOgGkBVL+B7+O/2o2A+JHeHQVPdThJaY2dDdCysesbtJMYYFwVSKKpEpAOeeSBE5AqgMqSpItmpA7B7OeTOcr5E27LkDKfH+aaXoNylyaCMMa4LpFD8CHgH6Ckii4D3ge+FNFUkW7/AaUKaO8vtJOExfg7UVDi9tY0x7VIgrZ7eA/KBB4GXcFo/fRjaWBGqthoKF8KAm6Fzz6a3bwvSB8HAKbDuWag673YaY4wLGi0UIpJb/wB6A6U4s8v18rzX/ux8C84dbds3sX2Z8AScP+5cgjLGtDv+5qP4uZ91Clwf5CyRr2A+dOoF/W9wO0l49Z7oTMi06hmn30hUtNuJjDFh1GihUNXrwhkk4h3b44ztdP0P2t8XZf2wHq89DLvehiHT3E5kjAmjQDrcJYjId0VksYi8LiJ/JyIJLT2wiPQUkQ9EZIeIbBORb/vY5loROS0iGz2PH7b0uM22/nmIioGc+12L4KohM6BzL+uAZ0w7FEirp4XAMOBXwNPAUODFIBy7Bvh7VR0CXAU8LiJDfWy3UlVHex7/HoTjXr7qCmfeicHTIKWbKxFcFx3jTGx0cDUcXOt2GmNMGAVSKAap6iOq+oHnMRtnqPEWUdVSVS30vD4L7ACyWrrfkNj+J7hwsv3dxG4o5z5I6GRnFca0M4EUig0iclX9goiMAz4JZggR6QPkAGt8rB4vIptE5G0RGeZnH7NFpEBECsrKgtw5rGA+pPaHvtcEd7+tTXwy5D3iDD9+Yq/baYwxYeKveewWEdkMjAM+FZH9IrIPWAUE7RtTRJKB14G/80yQ5K0Q6K2qo3Aufb3R2H5Uda6q5qlqXnp6erDiwZFtzuWWKx9ybuq2d+O+6dyrWfVrt5MYY8LEX/PYkDdtEZFYnCKxSFUXN1zvXThUdZmI/FpE0lT1WKizfaHgeYiOd0ZTNZDSHUbe6Qyzft0/Q2JXtxMZY0Ks0TMKVS3yfgAXcPpP1D9aREQEeA7Yoar/3cg23T3bISJjPXmPt/TYAassh00vw7CZ9oXobcIcqLkA655zO4kxJgwCaR47XUR2A/uAj4D9wNtBOPZE4H7geq/mr7eIyGMi8phnm68CW0VkE/BL4C7VME65tvV1qDprN7EbyhgC/SfD2t85LcKMMW2av0tP9X6M03z1L6qaIyLXAXe39MCq+jFNDFeuqk/jNMkNP1UoeA4yhkHPsa5EiGgTnoCF02Hlz2HS30Nsi7vWGGMiVCCtnqpV9TgQJSJRqvoBMDq0sSLAoUIo3QR5dhPbp77XODP8rfgp/GIo/OXfnCHYjTFtTiBnFKc8LZNWAItE5ChOZ7m2rWA+xCY5N27NpUTgvsWw70NYOw8++V/nMXAqjP2GU0SswBrTJgRSKGYAFcB3gHuBToA7PaTD5cIp2PI6jPw6JHR0O03kioqCK653HqcOOMW1cCHsegtSBzhTqY6+2+mkZ4xptSSc94bDJS8vTwsKCpq/gzW/g7e/B7M/dEZNNYGrroDtb8DaZ6GkwHNW9nUY+yh0a7S/pDHGZSKyXlXzfK1r9IxCRD5W1atF5Cxfbg4rgKpq2/yprer8Ms7MtSLRHLEJzvSpo+6CQxucy1KbXnIGVew1wSkYQ25r+9PIGtOG+OtHcbXnOUVVO3o9UtpskQA4sArKdlqT2GDIzIHbn4Hv7oDJ/w5nSuC1h+AXw+GD/4IzpW4nNMYEwG+rJxGJEpGt4QoTEQrmQ3wnGJ7vdpK2I7ErTPw2fGsD3PMqdB8BH/0E/mc4/PFB2P+JcyZnjIlIfm9mq2qdZ0C+Xqra9ts+njvmjBR75UMQl+R2mrYnKhoG3uw8jn/uFOUNL8K2JU5/lTGPOK3M4pPdTmqM8RJIP4oewDYReV9EltY/Qh3MFRsXQW2V03fChFbqFXDz/4Hv7oTpv3KKyFvfhf8eAm9/H47tdjuhMcYjkOaxT4U8RQQ4V1HF6fd/g3TKoUfGELfjtB9xiZA7y5k5sHid01pq3XOw5rfQ71oY8ygMnOJMnNTK1dYpFdW11NQqNXV11NSp86h1XtfWKdW1dZ5nZ7l+XU1dnedzX/5MTa1SW3fxdU3Dz3yxTcN911Fdp9R6PlOniqo6A7mpZ0A3z+VAZ1mdZ+/XAA2WG+6DLy1776OR/XvtA8XvoHJNtdj0/1n//6+05cPZuaJrYhx/mnN10Pfb5L8+Vf0o6EeNQElSxYdxeRTWjOAHbodpj0ScoVJ6jnXONAoXOCP3vnIvdOrpnOXlPgBJaW4n/ZILVbUcK6/kWHklx8urnOdzVZ73qjju9f6J81VhvRUTHSXE1D+iozzPQkxUlLMuun59FFFRIAginnF1RBDnyfPsvey8KYBEgRDlvC8X98Eln/nyMl7H8v7cJfv3fKYxTfXp9P9Z/x9ujd1FUxJC84OqyX4UnkmLfgUMAeKAaOBcJLd8am4/ioWr9vPDP21j2bcmMTQzYv947UdtDXz2tnOWse8jiI5zRvId8yhk54Wk53ddnXLyfFWjX/bHyqs4fu5iYThfVetzP8nxMaQlx5GaHE9qUhxpKfGkJcWRFB/T4Evb+aL2/gKPjRbPs/fypZ+5dJuLyzFR0uQXoTHemtWPwsvTwF3AH4E8YBYwIHjxIse0kZn8+M/bWbKhmKGZvqbvNmEVHeP0uRhyG5TtgnXzYONLsPkV6DHa6ZMx/A6I7eB3NxXVtZd86Zd5no+f+3IROHGukjofv52io4SuSXHOl35yPL17JTpFINlZTkuOIzUpnrQUpzAkxEaH5r+JMS4I5IyiQFXzRGSzqo70vPepqk4IS8JmaEnP7NkLC9hw8BSrnryemOhA7vWbsKo86xSKtfOgbAd06OLM5Z33CHTty/ZDZ1i0pogdpWecs4KzlZxr5Fd/Ulw0qfVf8p7nNM8ZQH0RSE+OJzU5ns4dYomKsl/opu1q6RnFeRGJAzaKyE+BUqDNth3Nz81i+fYjfPL5cb4yMIhTqprgiE9xxpDKewSKPoG1z6Krfg2fPk1h3Bh+VX4ta6JHk9MrlVHZnZ0v/uS4i0Wg/lJQcjwd4uxXvzGB8DeER56qFuBMLhQFzMEZGLAncEd44oXfdYMz6NQhlsWFxVYoIpkIh7vk8YfO6SyPupUplW9zv3zAC3Frqe3cl+jMGyApA5LTIcn70QHiO9jItsZcBn9nFM96hhd/CXhZVbfTDprKxsdEM21kD14vLKa8sobk+NbfLLMtUVVW7T3Oi6uKWL79CHWqXD+oL6PH/1+69OsEu/5MdMHzsOU1qDjleycxCZ6ikeZ5zrj4Ojnjy+8npraJprnGtESj/wI8s9kNwrmR/ZqIVHGxaBQF4+AiMgX4X5yWVPNU9ScN1otn/S3AeeBBVS0MxrH9yc/NZtGaA7y9pZSv5fUM9eFMAMora1hSWMzCVUXsPlpOl8RYvjGpL/eN603ProkXNxx+h/MAqKmC88fgXJnzKC+7+PqL947AkW1QfhTqqn0fvENX30XEV3GJS7azFdPmNDWExy6cs4inRGQUTtH4q4gcVtWJLTmwiEQDzwCTgWJgnYgs9Zy51JuK08JqADAO+I3nOaRye3WmT2oiSzaUWKFw2e4jZ3lxdRGLC0sor6xhZHYnfva1UUwb2aPplkUxcdAx03k0RRUqTjvDuJw72nhxObzFea443cgxO1w8W7mksKQ7w5NExTo90aNjISrGx7Ln4W/ZipEJo4DOqUUkCsgAuuHcyC4LwrHHAntUda/nGC/jTJLkXShmAAvVaZq1WkQ6i0gPVQ3psKMiwsycbP7n/c8oOXWBrM7+m1+a4KqpreO97UdYuKqIVXuPExcTxbSRPZg1vg+je3YOzUFFoENn55HWP4CQlZ6i0vAM5ejF98+UONPpniuDuiBPCinRXsUj2lNsfC3HeBUj7+UGBUqicHq5SSPPNLE+kGea//lG/zs0VTD9fbaJjza1QSQW69gkuOqxoO/Wb6EQkUnA3cDtwFbgZeA7qtrIz6nLkgUc9Fou5tKzBV/bZOG0vGqYdTYwG6BXr14tDjczJ4tf/OUz3thQwuPXBfDFYVqs7GwlL689wB/WHqD0dAVZnTvw/SmDuXNMT7omxbkd78ti4qFTlvNoiipcOOkUjKpzTtGoq4Ha6ouvv/RerXMZzOdy/bYNl+vfq/Xab8Nlz/6qzl963LpanDEzlItjZ3gvX+5zCz9vmicpI7yFQkQOAgdwisNTqnokyMf2VY4b/g0JZBvnTdW5wFxw+lG0LBr0Sk1kbJ+uLNlQwt9ee4X1cg0RVWV90UkWriri7a2lVNcqkwak8e8zhnP94Ayi20LfBRFnqPXErm4naV3qB4ZqfIOmPx+Szwbw+TbG3xnF1cG6ad2IYpymtvWygUPN2CZkZuZm8U+Lt7Cl5DQjszuH67DtwvmqGv608RALVzmd41ISYrj/qj7cd1Uv+qXbMOMGvhj8ybjOX6unUBYJgHXAABHpC5Tg3Ci/p8E2S4E5nvsX44DTob4/4e2WET340dJtLC4ssUIRJPuOneP3q4v4Y8FBzlTUMLh7Cv85cwS352SSGGfNUI2JRK79y1TVGhGZA7yL0zx2vqpuE5HHPOt/CyzDaRq7B6d5bFgniujUIZbJQ7qxdNMh/uXWIcTakB7NUlunfLDzKAtXF7HiszJiooSpI3owa3xv8np3sct6xkQ4V3/CqeoynGLg/d5vvV4r8Hi4c3nLz83irS2lfLSrjBuHdnMzSqtz4lwVrxYc5Periyg+eYFuHeP5zo0DuXtsTzI6JrgdzxgTIH83s3+Fnzs2qvqtkCSKMNcMTCc1KY4lG0qsUARo08FTLFxVxJubD1FVU8dV/bryz7cMYfLQbnZWZkwr5O+MonnDr7YxsdFR3DYqkz+sPcDp89V0Sox1O1JEqqiu5c+bS3lx1X42FZ8mKS6aO/N6cv/43gzsluJ2PGNMC/i7mb0gnEEi2R252bzw6X7e2lLKPeNa3kejLTl44jyL1hzglXUHOHm+mivSk3hq+jDyc7NISbCiakxb0OQ9ChFJB74PDAW+uLCsqteHMFdEGZ7Vkf4ZySzZUGyFwsuP/rSVhauLEGDy0G48ML4P469ItZvTxrQxgdzMXgS8AtwKPAY8QHCG8Gg1RIT83Cx++s4uio6fo3dqm52OI2BbS06zYFUR+TlZ/MPNg8i0YU6MabMCubOYqqrPAdWq+pGqPgxcFeJcEef20VmIwJINJW5HiQjzVu4lKS6aH00fZkXCmDYukEJRP/ZyqYjcKiI5OD2k25XMzh0Y3y+VJRtKaGr62Lbu0KkLvLm5lLvG9qJTB7sPYUxbF0ih+A8R6QT8PfAPwDycme7anfzcbIqOn6fwwEm3o7jq+U/2AfDQxD7uBjHGhEWThUJV/6yqp1V1q6pep6pXqurScISLNFOGd6dDbDSLC9vv5aczFdW8tPYgt47oQXaXxKY/YIxp9ZosFCLSV0T+W0QWi8jS+kc4wkWa5PgYbh7WjTc3HaKyptbtOK54ee0ByitreHRSP7ejGGPCJJBWT28AzwFvAnUhTdMK5Odm88bGQ/x1x1GmjujhdpywqqqpY/7H+xnfL5UR2Z3cjmOMCZNACkWFqv4y5ElaiYn908hIiWfxhpJ2Vyje2nKIw2cq+K/8EW5HMcaEUSA3s/9XRH4kIuNFJLf+EfJkESo6Srg9J4sPdh7lxLkqt+OEjaoyd8U+BmQk85WB6W7HMcaEUSCFYgTwKPAT4Oeex89CGSrS5edmUVOnvLkpbHMoue6TPcfZUXqGRyf1I6otzDpnjAlYIJeeZgL9VLX9/HxuwuDuHRnSoyOLN5TwwIQ+bscJi7kr95KWHM+MnEy3oxhjwiyQM4pNQOcQ52h17sjNYtPBU3xeVu52lJDbUXqGFZ+V8dDEPsTHRLsdxxgTZoEUim7AThF5t703j/U2fVQmUQJL2kGfinkr99EhNpp7bUBEY9qlQC49/SjYBxWR/wfcBlQBnwMPqeopH9vtB84CtUCNquYFO0tzZXRMYNKAdJZsKOG7kwe22ev2h09XsHRTCfeO603nxDi34xhjXBBIz+yPfD1aeNz3gOGqOhL4DPgnP9tep6qjI6lI1MvPzaLk1AXW7DvhdpSQeeHT/dTWKQ9P7Ot2FGOMSxotFCLysef5rIic8XqcFZEzLTmoqi5X1RrP4mpa6SCDNw3tTnJ8DEs2FLsdJSTKK2tYtKaIqcN70CvVhuswpr1qtFCo6tWe5xRV7ej1SFHVjkHM8DDwdmMxgOUisl5EZvvbiYjMFpECESkoKwvPdBkd4qKZOrw7y7Yc5kJV2xvS45V1BzlbUcM3JtnZhDHtmd9LTyISJSJbm7NjEfmLiGz18Zjhtc2/ADU4kyP5MlFVc4GpwOMick1jx1PVuaqap6p56enh6xCWn5tNeWUNy7cfDtsxw6Gmto75H+9jbJ+u5PTq4nYcY4yL/N7MVtU6EdkkIr1U9cDl7FhVb/S3XkQeAKYBN2gjEzyo6iHP81ERWQKMBVZcTo5QG9e3K1mdO7BkQwkzRme5HSdolm09TMmpC/zb9GFuRzHGuCyQ5rE9gG0i8n6wmseKyBScebinq+r5RrZJEpGU+tfATUCzzm5CKSpKuD0nkxWflXH0bIXbcYLCGa7jc/qlJXHD4Ay34xhjXBZI89inQnDcp4F44D0RAVitqo+JSCYwT1Vvwem/scSzPgb4g6q+E4IsLTYzJ5tnPvicpRsP8Y02MPz26r0n2Fpyhv+cOaLNNvs1xgSu0UIhIgnAY0B/YAvwnFdLpRZR1f6NvH8IuMXzei8wKhjHC7X+GcmMyu7E4sKSNlEonl25l9SkOPJz286lNGNM8/m79LQAyMMpElNxBgM0jcjPzWZ76Rl2Hm5Ry2HX7T5ylr/uPMqs8X1IiLXhOowx/gvFUFW9T1V/B3wVmBSmTK3SbaMyiYmSVj+kx7yV+4iPieL+8b3djmKMiRD+CkV1/YtgXXJqy7omxXHtoAyWbCihts5nI66Id/RsBUs2lPC1vGy6JtlwHcYYh79CMcq7NzYwMlg9s9uq/Nwsjp6t5JM9x9yO0iwLPy2iuq6OR65u/fdZjDHB469ndnSD3tgxIeqZ3WZcPziDjgkxLNnQ+i4/na+q4cXVRdw0tBt905LcjmOMiSCB9KMwAUqIjWbaqEze2XqY8srWdbXujwXFnL5Qzexr7GzCGPNlViiCLD8niwvVtbyztfUM6VFbp8z7eC+5vTpzZe+ubscxxkQYKxRBdmXvLvTqmtiqRpR9d9thDp64YGcTxhifrFAEmYgwMyeLTz8/TunpC27HaZKq8rsVe+mdmsjkod3djmOMiUBWKEIgPzcLVXhjwyG3ozSpoOgkmw6e4htX9yXahuswxvhghSIEeqcmkde7C4sLi2lkYNyIMXfFXrokxvLVK3u6HcUYE6GsUITIzNwsdh8tZ2tJ5HY5+bysnL/sOML9V/WmQ5wN12GM8c0KRYhMG5FJXHQUiyP4pvZzH+8jNjqK+8f3cTuKMSaCWaEIkU6Jsdw4NIOlGw9RXVvndpxLHCuv5PX1xdyRm0V6SrzbcYwxEcwKRQjNzMnm+LkqVnwWnjm8L8eLq4qorLHhOowxTbNCEUJfGZhO16Q4FkfYkB4Xqmp5cXURNw7JoH9GsttxjDERzgpFCMXFRHHbyB68t/0Ipy9UN/2BMHm9sJgT56p4tA1MsmSMCT1XCoWI/JuIlIjIRs/jlka2myIiu0Rkj4g8Ge6cwZCfm01VTR1vbyl1OwrgDNfx3Mf7GJXdibF9bbgOY0zT3Dyj+IWqjvY8ljVcKSLRwDM4s+sNBe4WkaHhDtlSI7M7cUV6EosjZEKjv+w4wr5j53j0mn545iM3xhi/IvnS01hgj6ruVdUq4GVghsuZLpuIkJ+bzdr9Jzh44rzbcXh2xV6yu3RgyjAbrsMYExg3C8UcEdksIvNFpIuP9VnAQa/lYs97PonIbBEpEJGCsrLIamV0e44T2+15KtYXnaSg6CSPXN2XmOhI/o1gjIkkIfu2EJG/iMhWH48ZwG+AK4DRQCnwc1+78PFeo+NhqOpcVc1T1bz09PRg/BGCJqtzB67q19X1IT3mrdxLx4QYvp5nw3UYYwIXE6odq+qNgWwnIs8Cf/axqhjw/kbLBiJ/lL1G5Odm873XNlN44BRX9vZ1AhVaRcfP8c62w/zNV64gKT5k/9uNMW2QW62eengtzgS2+thsHTBARPqKSBxwF7A0HPlCYerw7iTERrk2T8VzH+8jJkp4cEIfV45vjGm93LpQ/VMR2SIim4HrgO8AiEimiCwDUNUaYA7wLrADeFVVt7mUt8VSEmK5aWh33txUSmVNbViPffJcFa8WHOT20VlkdEwI67GNMa2fK9cgVPX+Rt4/BNzitbwMuKTpbGuVn5vF0k2H+GBnGVOGh6/V0e9XF1FRXcejNoOdMaYZrOlLGF3dP430lHgWF4bv8lNFdS0LVu3n2kHpDOyWErbjGmPaDisUYRQTHcWMUZl8sOsoJ89VheWYb2wo4Vh5FbNtuA5jTDNZoQiz/NxsqmuVP28OfQOuujrl2ZV7GZbZkfFXpIb8eMaYtskKRZgNzezI4O4pvB6GIT0+2HWUz8vOMduG6zDGtIAVChfk52ax8eApPi8rD+lx5q7YS2anBG4Z0aPpjY0xphFWKFwwY3QWUeLcPwiVTQdPsWbfCR6+ui+xNlyHMaYF7BvEBd06JjCxfxqLC0uoqwvNkB7PrtxLSnwMd46x4TqMMS1jhcIld+RmU3LqAuv2nwj6vg+eOM+yLaXcM64XKQmxQd+/MaZ9sULhkpuGdSMxLjok81TM/2QfUSI8OLFP0PdtjGl/rFC4JDEuhqnDe7BsSykV1cEb0uP0+WpeWXeQ6aMy6dGpQ9D2a4xpv6xQuOiO3CzOVtbw3vYjQdvnorVFnK+q5RvWwc4YEyRWKFx0Vb9UenRKCNqQHpU1tbzwyX4mDUhjaGbHoOzTGGOsULgoKkq4PSeLFbuPUXa2ssX7W7rxEEfPVvKonU0YY4LICoXL8nOyqK1Tlm5q2ZAeqs5wHYO7pzBpQFqQ0hljjBUK1w3olsKIrE4tvvz00WdlfHaknEcn2XAdxpjgskIRAfJzs9h26Ay7Dp9t9j6eXbmXbh3juW1UZhCTGWOMFYqIcNuoTKKjhMXNnCZ1a8lpPtlznIcm9iUuxv6XGmOCy605s18RkY2ex34R2djIdvs9U6ZuFJGCMMcMm7TkeK4dmM4bG0qobcaQHvNW7iUpLpq7x/YKQTpjTHvn1lSod9a/FpGfA6f9bH6dqh4LfSp35edm8/7Oo6z6/DhXX8bN6EOnLvDm5lIenNCHTh1suA5jTPC5ep1CnLuuXwdecjNHJLhhSAYpCTGXfVP7+U/2AfCQDddhjAkRty9oTwKOqOruRtYrsFxE1ovIbH87EpHZIlIgIgVlZWVBDxpqCbHRTBvZg7e3HuZcZU1AnzlTUc1Law9y64geZHdJDHFCY0x7FbJCISJ/EZGtPh4zvDa7G/9nExNVNReYCjwuItc0tqGqzlXVPFXNS09PD9KfIrxm5mRzobqWd7cdDmj7l9ceoLyyxjrYGWNCKmT3KFT1Rn/rRSQGyAeu9LOPQ57noyKyBBgLrAhmzkiS17sLPbt2YHFhCfm52X63raqpY/7H+xnfL5UR2Z3ClNAY0x65eenpRmCnqvq8KC8iSSKSUv8auAnYGsZ8YRcVJczMyeaTz49x+HSF323f2nKIw2cqmH2NnU0YY0LLzUJxFw0uO4lIpogs8yx2Az4WkU3AWuAtVX0nzBnDbmZOFqrwxsbG56lQVeau2MeAjGS+MrB1XmYzxrQerjSPBVDVB328dwi4xfN6LzAqzLFc1zctidxenVlcWMw3r/E9HMcne46zo/QMP71jJFFRNlyHMSa03G71ZHzIz83msyPlbDt0xuf6uSv3kpYcz4wcG67DGBN6Vigi0LSRPYiLjvI5TeqO0jOs+KyMhyb2IT4m2oV0xpj2xgpFBOqcGMf1gzNYuqmEmtq6L62bt3IfHWKjuXecDddhjAkPKxQRamZuFsfKq1i5++LoJYdPV7B0Uwl3julJ58Q4F9MZY9oTKxQR6rpBGXROjOV1ryE9Xvh0P7V1ysMT+7qYzBjT3lihiFBxMVFMH5XJe9uPcKaimvLKGhatKWLq8B70SrXhOowx4WOFIoLNzMmisqaOt7eU8sq6g5ytqOEbk+xswhgTXq71ozBNG92zM/3Skni1oJjDpysY26crOb26uB3LGNPO2BlFBBMRZuZksb7oJCWnLvCoDddhjHGBFYoId3tOFgD90pK4YXCGy2mMMe2RXXqKcD27JvIvtwxhWFZHG67DGOMKKxStgF1yMsa4yS49GWOM8csKhTHGGL+sUBhjjPHLCoUxxhi/rFAYY4zxywqFMcYYv6xQGGOM8csKhTHGGL9EVd3OEHQiUgYUNfPjacCxJrcKP8t1eSzX5bFcl6ct5uqtqum+VrTJQtESIlKgqnlu52jIcl0ey3V5LNflaW+57NKTMcYYv6xQGGOM8csKxaXmuh2gEZbr8liuy2O5Lk+7ymX3KIwxxvhlZxTGGGP8skJhjDHGLysUHiIyRUR2icgeEXnS7Tz1RGS+iBwVka1uZ6knIj1F5AMR2SEi20Tk225nAhCRBBFZKyKbPLmecjuTNxGJFpENIvJnt7N4E5H9IrJFRDaKSIHbeeqJSGcReU1Ednr+ro2PgEyDPP+d6h9nROTv3M4FICLf8fy93yoiL4lIQtD2bfconH/AwGfAZKAYWAfcrarbXQ0GiMg1QDmwUFWHu50HQER6AD1UtVBEUoD1wO1u//cSEQGSVLVcRGKBj4Fvq+pqN3PVE5HvAnlAR1Wd5naeeiKyH8hT1YjqQCYiC4CVqjpPROKARFU95XKsL3i+N0qAcara3A6+wcqShfP3faiqXhCRV4FlqvpCMPZvZxSOscAeVd2rqlXAy8AMlzMBoKorgBNu5/CmqqWqWuh5fRbYAWS5mwrUUe5ZjPU8IuKXkIhkA7cC89zO0hqISEfgGuA5AFWtiqQi4XED8LnbRcJLDNBBRGKAROBQsHZshcKRBRz0Wi4mAr74WgMR6QPkAGtcjgJ8cXlnI3AUeE9VIyIX8D/A94A6l3P4osByEVkvIrPdDuPRDygDnvdcrpsnIkluh2rgLuAlt0MAqGoJ8DPgAFAKnFbV5cHavxUKh/h4LyJ+iUYyEUkGXgf+TlXPuJ0HQFVrVXU0kA2MFRHXL9eJyDTgqKqudztLIyaqai4wFXjcc7nTbTFALvAbVc0BzgGRdO8wDpgO/NHtLAAi0gXnKkhfIBNIEpH7grV/KxSOYqCn13I2QTxta4s89wBeBxap6mK38zTkuUzxITDF3SQATASme+4FvAxcLyK/dzfSRap6yPN8FFiCcynWbcVAsdcZ4Ws4hSNSTAUKVfWI20E8bgT2qWqZqlYDi4EJwdq5FQrHOmCAiPT1/FK4C1jqcqaI5blp/BywQ1X/2+089UQkXUQ6e153wPnHs9PVUICq/pOqZqtqH5y/W39V1aD92msJEUnyNEjAc2nnJsD1Fnaqehg4KCKDPG/dALjeuMTL3UTIZSePA8BVIpLo+fd5A869w6CICdaOWjNVrRGROcC7QDQwX1W3uRwLABF5CbgWSBORYuBHqvqcu6mYCNwPbPHcDwD4Z1Vd5l4kAHoACzytUaKAV1U1opqiRqBuwBLnu4UY4A+q+o67kb7wBLDI8+NtL/CQy3kAEJFEnBaS33Q7Sz1VXSMirwGFQA2wgSAO52HNY40xxvhll56MMcb4ZYXCGGOMX1YojDHG+GWFwhhjjF9WKIwxxvhlhcIYP0Sk3PPcR0TuCfK+/7nB8qfB3L8xwWKFwpjA9AEuq1B4+nP486VCoapB60lrTDBZoTAmMD8BJnnmIPiOZ/DB/yci60Rks4h8E0BErvXM1fEHYIvnvTc8A+5tqx90T0R+gjPS50YRWeR5r/7sRTz73uqZJ+JOr31/6DVHwyJPL1xjQsp6ZhsTmCeBf6ifR8LzhX9aVceISDzwiYjUj9Y5Fhiuqvs8yw+r6gnPsCLrROR1VX1SROZ4BjBsKB8YDYwC0jyfWeFZlwMMwxmL7BOcXvIfB/sPa4w3O6MwpnluAmZ5hjBZA6QCAzzr1noVCYBvicgmYDXO4JMD8O9q4CXPSLhHgI+AMV77LlbVOmAjziUxY0LKziiMaR4BnlDVd7/0psi1OENiey/fCIxX1fMi8iHQ1BSV/i4nVXq9rsX+DZswsDMKYwJzFkjxWn4X+BvPcOuIyMBGJtbpBJz0FInBwFVe66rrP9/ACuBOz32QdJyZ3tYG5U9hTDPYrxFjArMZqPFcQnoB+F+cyz6FnhvKZcDtPj73DvCYiGwGduFcfqo3F9gsIoWqeq/X+0uA8cAmnAm0vqeqhz2Fxpiws9FjjTHG+GWXnowxxvhlhcIYY4xfViiMMcb4ZYXCGGOMX1YojDHG+GWFwhhjjF9WKIwxxvj1/wHGkZAa0gZrKgAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZAAAAEGCAYAAABLgMOSAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAAAkoElEQVR4nO3de5hddX3v8fdnLiEkBMh9NgkhUSOYwEzA4VbOsVCMB6gl6rE1VDGPtEYrFLE9aqRHhNPznPJY255ePNAo1HiqcJBrqpGLtEDVh0tASAgXSSPKkNsk4RJuSWbme/5Ya8edyVz27MusvWd/Xs+zn7XWb92+gWR/9/r9fuv3U0RgZmY2Uk1ZB2BmZvXJCcTMzEriBGJmZiVxAjEzs5I4gZiZWUlasg5gNE2bNi3mzp2bdRhmZnXl0Ucf3RER0/uXN1QCmTt3LmvXrs06DDOzuiLplwOVuwrLzMxK4gRiZmYlcQIxM7OSOIGYmVlJnEDMzKwkmSYQSddL2i7pyUH2S9LfSdooaZ2kkwr2nSPp2XTfitGL2szMIPsnkG8B5wyx/1xgfvpZDlwDIKkZ+Hq6fwFwgaQFVY3UzMwOkOl7IBHxgKS5QxyyBPh2JGPOPyjpSEk5YC6wMSI2AUi6MT32qWrEue7+23j1V+t5Zu7HaGkSrS1NtDY30dosWpubaGlqYlzLgestTckx+9dbmmhtSo5pbWmipUmMa26iqUnVCLloEcG+3qCnr499PcG+vj729R643tMb7O3tY19PHz19yXpPbyTH9faxL13v6e1jb7re2xcH3efA7X5xDBhb/2NGfo2DDhqIDvx/0P//iAb4X6R+R/U/pqhrDFRoViXvb89xzNSJFb1mrb9IOAt4oWC7Ky0bqPzUgS4gaTnJ0wtz5swpKYjd69fw7u7b+fiGE+mr8ENbk0gSTXMTLWlCOiA5NTcxrlm0FJTl97c0N9Ek0VPwJX7AF37hF30+QRR86ff0JcuxbqjvaU+HY41i4VGHN1wCGeiffgxRfnBhxEpgJUBnZ2dJXxen/6ffoun2m1h/yTz2TH7ngV/CvX3pl/Wv1wf+dZ7/5Z6U7R3ky72nr4+9Pfkv9wPX9/UGr+3pOeB6ESRPRc0HPuVMam1hXJpsWpo1bII6OFkdmLDy1xjoegdcu6mJ1hbR3KQSfqUf/L91uF/y1f4VP9CEa8M9+Rz0tDXgdftfw5nMqqu1qfItFrWeQLqAowu2ZwObgXGDlFdFU64DgIk7NzBx9vHVuo3VoAGT2rA5y1VT1hiybkQfzmrg42lvrNOAVyJiC/AIMF/SPEnjgKXpsdUx7Z3QMh62rqvaLczM6k2mTyCSbgDOBKZJ6gK+ArQCRMS1wBrgPGAj8AbwiXRfj6RLgLuAZuD6iNhQtUCbW2DGAtjyRNVuYWZWb7LuhXXBMPsDuHiQfWtIEszoyHXAhluTymv3njEzq/kqrNqRa4e3XoGXBxzV2Mys4TiBFKstaUhni9tBzMzACaR4MxeAmt2QbmaWcgIpVuuhMP1YN6SbmaWcQEaird1VWGZmKSeQkci1w2tbYfe2rCMxM8ucE8hIpG+kux3EzMwJZGTaTkiWbgcxM3MCGZHxR8DkuX4CMTPDCWTkch1uSDczwwlk5Nra4aVfJG+lm5k1MCeQkdrfkL4+2zjMzDLmBDJSbe3J0tVYZtbgnEBGatJMOKzNDelm1vCcQEqRa3dXXjNreE4gpWhrh+5nYd+bWUdiZpaZTBOIpHMkPStpo6QVA+z/vKTH08+TknolTUn3PS9pfbpv7agGnuuA6IXtT43qbc3MaklmCURSM/B14FxgAXCBpAWFx0TEX0bEoohYBHwJuD8idhUccla6v3O04gaSKixwNZaZNbQsn0BOATZGxKaI2AvcCCwZ4vgLgBtGJbLhHHlM8la6e2KZWQPLMoHMAl4o2O5Kyw4iaQJwDnBLQXEAd0t6VNLywW4iabmktZLWdnd3VyBskjnR29rdE8vMGlqWCUQDlMUgx/4O8JN+1VdnRMRJJFVgF0t6z0AnRsTKiOiMiM7p06eXF3GhXAds2wC9PZW7pplZHckygXQBRxdszwY2D3LsUvpVX0XE5nS5HbiNpEps9LS1Q89bsOPno3pbM7NakWUCeQSYL2mepHEkSWJ1/4MkHQH8JnBHQdlESZPy68D7gCdHJeq8fEO6q7HMrEFllkAioge4BLgLeBq4KSI2SPq0pE8XHPpB4O6IeL2gbCbwY0lPAA8DP4iIO0crdgCmzoeWQ92QbmYNqyXLm0fEGmBNv7Jr+21/C/hWv7JNQEeVwxtacwvMXOiuvGbWsPwmejly7cmovDFY27+Z2djlBFKOtnbY8wq89HzWkZiZjTonkHLsnxvE7SBm1nicQMoxYwGo2e0gZtaQnEDK0Toeph/nnlhm1pCcQMqV85AmZtaYnEDKleuA17bB7q1ZR2JmNqqcQMrlOdLNrEE5gZSr7YRkudUN6WbWWJxAyjX+cJjyNj+BmFnDcQKphLZ2d+U1s4bjBFIJuXZ4+Zfw5stZR2JmNmqcQCqhLf9G+vps4zAzG0VOIJWQnxvE1Vhm1kCcQCrhsBkwKecXCs2soWSaQCSdI+lZSRslrRhg/5mSXpH0ePq5othzR11bu3timVlDyWxCKUnNwNeBxSTzoz8iaXVEPNXv0H+PiPeXeO7oyXXAxntg7xswbkJmYZiZjZYsn0BOATZGxKaI2AvcCCwZhXOrI9cO0Qfbs8thZmajKcsEMgt4oWC7Ky3r73RJT0j6oaSFIzx39LS5Id3MGkuWc6JrgLL+c8M+BhwTEa9JOg+4HZhf5LnJTaTlwHKAOXPmlBzssI6cA+OPdEO6mTWMLJ9AuoCjC7ZnA5sLD4iIVyPitXR9DdAqaVox5xZcY2VEdEZE5/Tp0ysZ/4GkpBrLTyBm1iCyTCCPAPMlzZM0DlgKrC48QFKbJKXrp5DEu7OYczPR1g7bnoLefVlHYmZWdZlVYUVEj6RLgLuAZuD6iNgg6dPp/muBDwN/JKkHeBNYGhEBDHhuJn+QQrkO6N0DO34OMxcOf7yZWR3Lsg0kXy21pl/ZtQXr/wD8Q7HnZi6XDmmyZZ0TiJmNeX4TvZKmvgNaJ7gdxMwaghNIJTU1J08e7ollZg3ACaTS2tqTUXn7+rKOxMysqpxAKi3XAXtehZefzzoSM7OqcgKpNA/tbmYNwgmk0mYsgKYWj8xrZmOeE0iltRwC049zQ7qZjXlOINWQ60iqsGLA4bnMzMYEJ5BqaGuH17th99asIzEzqxonkGrIN6S7GsvMxrBhE4ikMyRNTNc/JumvJR1T/dDqWNsJydIN6WY2hhXzBHIN8IakDuALwC+Bb1c1qnp3yCSY8nbY8njWkZiZVU0xCaQnHQF3CfC3EfG3wKTqhjUG5NpdhWVmY1oxCWS3pC8BFwI/kNQMtFY3rDGgrR1e/hW8+VLWkZiZVUUxCeQjwB7goojYSjL3+F9WNaqxoHBodzOzMWjYBJImjVuAQ9KiHcBt1QxqTMgnEFdjmdkYVUwvrE8CNwP/mBbNAm6vxM0lnSPpWUkbJa0YYP9HJa1LPz9NG/Lz+56XtF7S45LWViKeipo4DSYd5ScQMxuzipmR8GLgFOAhgIh4TtKMcm+ctqV8HVgMdAGPSFodEU8VHPYL4Dcj4iVJ5wIrgVML9p8VETvKjaVqch1+AjGzMauYNpA9EbE3vyGpBajEGB2nABsjYlN6/RtJenrtFxE/jYh8K/SDwOwK3Hf05NqT+dH3vpF1JGZmFVdMArlf0uXAoZIWA98D/qUC954FvFCw3ZWWDeYPgB8WbAdwt6RHJS0f7CRJyyWtlbS2u7u7rIBHrK0dog+2bRjd+5qZjYJiEsgKoBtYD3wKWAP89wrcWwOUDfhkI+kskgTyxYLiMyLiJOBc4GJJ7xno3IhYGRGdEdE5ffr0cmMemf1DmnhuEDMbe4ZtA4mIPuAb6aeSuoCjC7ZnA5v7HySpHfgmcG5E7CyIa3O63C7pNpIqsQcqHGN5jjgaDp3syaXMbEwaNIFIWs8QbR0R0V7mvR8B5kuaB7wILAV+v18Mc4BbgQsj4ucF5ROBpojYna6/D/gfZcZTeVJSjeWeWGY2Bg31BPL+at44InokXQLcBTQD10fEBkmfTvdfC1wBTAX+jyRIhlXpBGYCt6VlLcB3I+LOasZbslw7PPSP0LsPmv0Cv5mNHYMmkIj4ZX5dUhtJFVEAj6QvF5YtItaQtKkUll1bsP6HwB8OcN4moKN/eU3KLYLevdD9LLQdn3U0ZmYVU8yLhH8IPAx8CPgw8KCki6od2JjRltb0uR3EzMaYYl4k/DxwYr4BW9JU4KfA9dUMbMyY+nZonZC+UPjRrKMxM6uYYrrxdgG7C7Z3c+D7GzaUpmaYebwb0s1szBmqF9afpKsvAg9JuoOkDWQJSZWWFSvXAU/cAH190ORZhM3Gqn379tHV1cVbb72VdSglGT9+PLNnz6a1tbgOP0NVYeUnjfqP9JN3R4mxNa5cOzzyDXjpF0mVlpmNSV1dXUyaNIm5c+eS9hKtGxHBzp076erqYt68eUWdM1QvrKsqFlmjK2xIdwIxG7PeeuutukweAJKYOnUqIxnyadhGdEnTSeZCXwiMz5dHxG+VEmRDmvEuaGpJGtKP/1DW0ZhZFdVj8sgbaezFVMh/B3gGmAdcBTxP8ha5FavlkCSJuCuvmWVk165dLF68mPnz57N48WJeeqn86baLSSBTI+I6YF9E3B8RFwGnlX3nRtPWkfTEikqMhG9mNjJXX301Z599Ns899xxnn302V199ddnXLCaB7EuXWyT9tqQTqbd5OWpBrh3e2AG7t2QdiZmNYc8//zzHH//rUS++9rWvceWVV3LHHXewbNkyAJYtW8btt99e9r2KeZHwf0o6AvhT4O+Bw4HPlX3nRpOfI33LOjj8qGxjMbOqu+pfNvDU5lcres0FRx3OV35nYUnnbtu2jVwuB0Aul2P79u1lx1PMcO7fT1dfAc4q+46NaubxgJJ2kGPPyToaM7OyDfUi4Rci4quS/p4BhnWPiEurGtlYc8hhSRdez5Fu1hBKfVIoV0tLC319ffu38y81zpw5ky1btpDL5diyZQszZswo+15DtYE8nS7XAo8O8LGR8twgZlZlM2fOZPv27ezcuZM9e/bw/e8nlUjnn38+q1atAmDVqlUsWbKk7HsN9SLhv0hqBo6PiM+XfSdL2kE23Apv7IIJU7KOxszGoNbWVq644gpOPfVU5s2bx3HHHQfAihUr+L3f+z2uu+465syZw/e+972y7zVkG0hE9Ep6d9l3scT+OdLXwdvOzDQUMxu7Lr30Ui699OBWhnvvvbei9ymmG+/PJK2WdKGkD+U/lbi5pHMkPStpo6QVA+yXpL9L96+TdFKx59aktoKeWGZmda6YbrxTgJ1A4dAlQTJXecnS6rGvA4tJhox/RNLqiHiq4LBzgfnp51TgGuDUIs+tPROnwuGz3ZBuZmNCMd14P1Gle58CbEynp0XSjSRDxRcmgSXAtyMiSGZCPFJSDphbxLm1KdfuIU3MbEwoZjDF8cAfcPBgiuVOazuLAyem6iJ5yhjumFlFnguApOXAcoA5c+aUF3EltLXDsz+Eva/DuIlZR2NmVrJi2kD+L9AG/BfgfpJhTHYPeUZxBhr2sf/7JoMdU8y5SWHEyojojIjO6dOnjzDEKsi1AwHbNmQdiZlZWYpJIO+IiC8Dr0fEKuC3gRMqcO8u4OiC7dnA5iKPKebc2rR/SBNXY5lZfRvJYIovSzoeOIKkDaJcjwDzJc2TNA5YCqzud8xq4ONpb6zTgFciYkuR59amw2fBoVOcQMxs1KxatYr58+czf/78/S8TVkIxvbBWSpoMfJnkS/qwdL0sEdEj6RLgLqAZuD4iNkj6dLr/WmANcB6wEXgD+MRQ55Yb06iQkmos98Qys1Gwa9currrqKtauXYsk3v3ud3P++eczefLksq891FhYT5FMJnVjRLxE0v7xtrLvWCAi1pAkicKyawvWA7i42HPrRq4DHrwGevZCy7isozGzMeKLX/wixxxzDJ/5zGcAuPLKK2ltbWXx4sVMmZKMfrF48WLuvPNOLrjggrLvN9QTyAUkVUN3S9oB3AD8v7QKycrR1g69e6H7mV+/nW5mY8sPV8DW9ZW9ZtsJcO7gE0EtXbqUyy67bH8Cuemmm1i6dClHH/3rJuPZs2fz4osvViScQdtAIuKJiPhSRLwd+CxwDPCQpH+V9MmK3L1R5RvSXY1lZhV04oknsn37djZv3swTTzzB5MmTOfTQQw86rlLzthfTBkJEPEjyIt8dwN8A/wB8oyIRNKIpb4fWicmQJidmHYyZVcUQTwrV9OEPf5ibb76ZrVu3snTpUqZNm8Z99923f39XVxdnnnlmRe5VzIuEJ5NUZ/1X4HlgJVD+MI6NrKkpeRR1Tywzq7ClS5fyyU9+kh07dnD//fdzyCGHcPnll/PSSy8BcPfdd/MXf/EXFbnXUI3o/wv4CPAScCNwRkR0VeSulrR9PP5d6OtLEoqZWQUsXLiQ3bt3M2vWrP1T2H75y1/m5JNPBuCKK67Y36BerqGeQPYA50bEzytyJztQWzvsXQm7NsG0d2QdjZmNIevXH9h4f9FFF3HRReWOPnWwoRrRr3LyqKL9c4O4GsvM6pPrTrIy/V3Q1Op2EDOrW04gWWkZBzPe5cmlzKxuDdWIftJg+wAi4rHKh9NgcunQ7hHJECdmVvciomLvWYy2ZPCP4g3ViP5XQ92HA2cotFLkFsHP/hlefRGOmJ11NGZWpvHjx7Nz506mTp1ad0kkIti5cyfjx48f/uDUoAkkIs6qSFQ2uLa0IX3LOicQszFg9uzZdHV10d3dnXUoJRk/fjyzZxf/XVTUm+jpMO4LOHBGwm+PODo70MyFgJIhTY47L+tozKxMra2tzJs3L+swRk0xb6J/BTiTJIGsAc4Ffgw4gZTrkMNg6jvckG5mdamYXlgfBs4GtkbEJ4AO4JCqRtVIch3uymtmdamYBPJmRPQBPZIOB7ZT5rwgkqZIukfSc+nyoJlNJB0t6d8kPS1pg6TPFuy7UtKLkh5PP/Vb/5Nrh1e74I1dWUdiZjYixSSQtZKOJBl991HgMeDhMu+7Arg3IuYD96bb/fUAfxoR7wJOAy6WtKBg/99ExKL0U58TS0FBQ7qfQsysvgybQCLiMxHxcjpT4GJgWVqVVY4lQH5i3lXABwa475b8uyYRsRt4GphV5n1rj+cGMbM6NWwCkfSe/AeYAxyZrpdjZn5mw3Q5Y5gY5pLMnPFQQfElktZJun6gKrC6MWEKHHG0n0DMrO4U04338wXr44FTSKqyhnyRUNKPgLYBdv1Z0dEl1zkMuAW4LCJeTYuvAf6c5IXGPyd56XHAoSYlLQeWA8yZM2cktx49be3uiWVmdWfYBBIRv1O4Lelo4KtFnPfewfZJ2iYpFxFbJOVIGuYHOq6VJHl8JyJuLbj2toJjvgF8f4g4VpJMgkVnZ+fI3tMfLbl2eHYN7Hkt6dprZlYHShlMsQs4vsz7rgaWpevLgDv6H6BkHIDrgKcj4q/77csVbH4QeLLMeLKV6wACttX3H8PMGksxLxL+PUlVESQJZxFQboX91cBNkv4A+BXwu+m9jgK+GRHnAWcAFwLrJT2ennd52uPqq5IWpXE9D3yqzHiyVTikyZzTso3FzKxIxbSBrC1Y7wFuiIiflHPTiNhJ8nJi//LNwHnp+o+BAUcji4gLy7l/zTn8KJgw1ZNLmVldKaYNZJWk6el6fY4QVuuk9I10N6SbWf0YtA1EiSsl7QCeAX4uqVvSFaMXXgNpa4ftT0PP3qwjMTMrylCN6JeRtEOcHBFTI2IycCpwhqTPjUZwDSXXDn37oPvprCMxMyvKUAnk48AFEfGLfEFEbAI+lu6zSmpL30h3NZaZ1YmhEkhrROzoX5i2g7RWL6QGNeVtMO4wv5FuZnVjqAQyVGW8K+orrakJ2k7wmFhmVjeG6oXVIenVAcpFwcyEVkFt7ckc6X290NScdTRmZkMa9AkkIpoj4vABPpMiwlVY1ZDrgH2vw65NWUdiZjasUoYysWrJeW4QM6sfTiC1ZPpx0DzOCcTM6oITSC1pboUZ73JDupnVBSeQWpPrSJ5AojZHnjczy3MCqTVt7fDmS/BKV9aRmJkNyQmk1niOdDOrE04gtWbmQkAe0sTMap4TSK0ZNxGmvdM9scys5mWSQCRNkXSPpOfS5eRBjnte0npJj0taO9Lz61au3VVYZlbzsnoCWQHcGxHzgXvT7cGcFRGLIqKzxPPrT1s7vPoivH7QWJZmZjUjqwSyBFiVrq8CPjDK59e2fEO6q7HMrIZllUBmRsQWgHQ5Y5DjArhb0qOSlpdwPpKWS1oraW13d53MyNt2QrJ0NZaZ1bBh50QvlaQfAW0D7PqzEVzmjIjYLGkGcI+kZyLigZHEERErgZUAnZ2d9fF23oQpcMQc98Qys5pWtQQSEe8dbJ+kbZJyEbFFUg7YPsg1NqfL7ZJuA04BHgCKOr+uuSHdzGpcVlVYq4Fl6foy4I7+B0iaKGlSfh14H/BksefXvVwH7NwIe3ZnHYmZ2YCySiBXA4slPQcsTreRdJSkNekxM4EfS3oCeBj4QUTcOdT5Y0pbOrT71ieHPs7MLCNVq8IaSkTsBM4eoHwzcF66vgnoGMn5Y0p+bpCt6+CY07ONxcxsAH4TvVZNysHE6e7Ka2Y1ywmkVklJNZZ7YplZjXICqWW5duh+Gnr2ZB2JmdlBnEBqWVs79PXA9qezjsTM7CBOILXMQ5qYWQ1zAqllk+fBuEl+odDMapITSC1rakrGxXJDupnVICeQWpfrgG1PQl9v1pGYmR3ACaTW5dph3xvJsCZmZjXECaTW5Yc0cTWWmdUYJ5BaN/1YaD4EtronlpnVFieQWtfcCjMXuCuvmdUcJ5B6kB/SJOpjPiwzawxOIPUg1w5vvQyvvJB1JGZm+zmB1IO2/Bvpbkg3s9rhBFIPZi4ENbkdxMxqSiYJRNIUSfdIei5dTh7gmGMlPV7weVXSZem+KyW9WLDvvFH/Q4ymcRNg2js9pImZ1ZSsnkBWAPdGxHzg3nT7ABHxbEQsiohFwLuBN4DbCg75m/z+iFjT//wxx3ODmFmNySqBLAFWpeurgA8Mc/zZwH9ExC+rGVRNy3XA7s3wWnfWkZiZAdklkJkRsQUgXc4Y5vilwA39yi6RtE7S9QNVgeVJWi5praS13d11/OW7f450t4OYWW2oWgKR9CNJTw7wWTLC64wDzge+V1B8DfB2YBGwBfirwc6PiJUR0RkRndOnTx/5H6RWtJ2QLF2NZWY1oqVaF46I9w62T9I2SbmI2CIpB2wf4lLnAo9FxLaCa+9fl/QN4PuViLmmHToZjpzjhnQzqxlZVWGtBpal68uAO4Y49gL6VV+lSSfvg8CTFY2uVuU63JXXzGpGVgnkamCxpOeAxek2ko6StL9HlaQJ6f5b+53/VUnrJa0DzgI+NzphZ6ytA3ZtgrdezToSM7PqVWENJSJ2kvSs6l++GTivYPsNYOoAx11Y1QBrVb4hfduTcMxvZBuLmTU8v4leT3L5IU1cjWVm2XMCqSeT2mDiDPfEMrOa4ARSb3Lt7ollZjXBCaTetLVD9zOw762sIzGzBucEUm9yHdDXA9ufyjoSM2twTiD1Zv+QJq7GMrNsOYHUmyPnwiGHuyHdzDLnBFJvmprSod3dldfMsuUEUo9y7bBtA/T1Zh2JmTUwJ5B61NYOPW/CjueyjsTMGpgTSD1yQ7qZ1QAnkHo07VhoGe92EDPLlBNIPWpugRkLnEDMLFNOIPUqP6RJRNaRmFmDcgKpV23t8NYr8PKvso7EzBpUJglE0u9K2iCpT1LnEMedI+lZSRslrSgonyLpHknPpcvJoxN5DcktSpauxjKzjGT1BPIk8CHggcEOkNQMfJ1kTvQFwAWSFqS7VwD3RsR84N50u7HMXABqdk8sM8tMVjMSPg0gaajDTgE2RsSm9NgbgSXAU+nyzPS4VcB9wBerE22Naj0Upr2zvCFNIpKXEaMXou/X632F230FZb3Q1zdAWW9yrcKy6Cvu/sUFWsFrFWnov5uFB47utcxKNXMhTJhS0UtmkkCKNAt4oWC7Czg1XZ8ZEVsAImKLpBmDXUTScmA5wJw5c6oUakZyHbDhVvi7kwqSQN/BX+QDlvVS1BezmY0NH70F5r+3opesWgKR9COgbYBdfxYRdxRziQHKRvyNFxErgZUAnZ2dY+sb85RPQu/e5BeumpIqrabmZL2pOdkuXG9qGqCscLvwGvnj+5flj+t/jfx1Cu5R1C/vIn91V/Jawyryr0lRTz2VvJZZGWYurPglq5ZAIqLcVNcFHF2wPRvYnK5vk5RLnz5ywPYy71WfZnfC7/5T1lGYWYOq5W68jwDzJc2TNA5YCqxO960GlqXry4BinmjMzKyCsurG+0FJXcDpwA8k3ZWWHyVpDUBE9ACXAHcBTwM3RcSG9BJXA4slPQcsTrfNzGwUKRqo7rWzszPWrl2bdRhmZnVF0qMRcdA7e7VchWVmZjXMCcTMzEriBGJmZiVxAjEzs5I4gZiZWUkaqheWpG7glyWePg3YUcFwKsVxjYzjGhnHNTK1GheUF9sxETG9f2FDJZBySFo7UDe2rDmukXFcI+O4RqZW44LqxOYqLDMzK4kTiJmZlcQJpHgrsw5gEI5rZBzXyDiukanVuKAKsbkNxMzMSuInEDMzK4kTiJmZlcQJpAiSzpH0rKSNklZkHQ+ApOslbZf0ZNaxFJJ0tKR/k/S0pA2SPpt1TACSxkt6WNITaVxXZR1TIUnNkn4m6ftZx5In6XlJ6yU9LqlmhrGWdKSkmyU9k/49O70GYjo2/e+U/7wq6bKs4wKQ9Ln07/yTkm6QNL5i13YbyNAkNQM/J5l3pItkoqsLIuKpjON6D/Aa8O2IOD7LWAqlM0TmIuIxSZOAR4EP1MB/LwETI+I1Sa3Aj4HPRsSDWcaVJ+lPgE7g8Ih4f9bxQJJAgM6IqKkX4yStAv49Ir6ZTjY3ISJezjis/dLvjBeBUyOi1BeXKxXLLJK/6wsi4k1JNwFrIuJblbi+n0CGdwqwMSI2RcRe4EZgScYxEREPALuyjqO/iNgSEY+l67tJJgOblW1UEInX0s3W9FMTv54kzQZ+G/hm1rHUOkmHA+8BrgOIiL21lDxSZwP/kXXyKNACHCqpBZjAr6cGL5sTyPBmAS8UbHdRA1+I9UDSXOBE4KGMQwH2VxM9DmwH7omImogL+N/AF4C+jOPoL4C7JT0qaXnWwaTeBnQD/5RW+X1T0sSsg+pnKXBD1kEARMSLwNeAXwFbgFci4u5KXd8JZHgaoKwmfrnWMkmHAbcAl0XEq1nHAxARvRGxCJgNnCIp86o/Se8HtkfEo1nHMoAzIuIk4Fzg4rTaNGstwEnANRFxIvA6UBPtkgBpldr5wPeyjgVA0mSSGpN5wFHAREkfq9T1nUCG1wUcXbA9mwo+Ao5FaRvDLcB3IuLWrOPpL63yuA84J9tIADgDOD9tb7gR+C1J/5xtSImI2JwutwO3kVTnZq0L6Cp4eryZJKHUinOBxyJiW9aBpN4L/CIiuiNiH3Ar8BuVurgTyPAeAeZLmpf+ulgKrM44ppqVNlZfBzwdEX+ddTx5kqZLOjJdP5TkH9YzmQYFRMSXImJ2RMwl+bv1rxFRsV+IpZI0Me0EQVpF9D4g8x5/EbEVeEHSsWnR2UCmHTT6uYAaqb5K/Qo4TdKE9N/m2STtkhXRUqkLjVUR0SPpEuAuoBm4PiI2ZBwWkm4AzgSmSeoCvhIR12UbFZD8or4QWJ+2NwBcHhFrsgsJgBywKu0h0wTcFBE102W2Bs0Ebku+c2gBvhsRd2Yb0n5/DHwn/UG3CfhExvEAIGkCSW/NT2UdS15EPCTpZuAxoAf4GRUc0sTdeM3MrCSuwjIzs5I4gZiZWUmcQMzMrCROIGZmVhInEDMzK4kTiFkJJL2WLudK+v0KX/vyfts/reT1zSrFCcSsPHOBESWQ9F2UoRyQQCKiYm8Om1WSE4hZea4G/nM6B8Tn0gEb/1LSI5LWSfoUgKQz03lSvgusT8tuTwcq3JAfrFDS1SQjpz4u6TtpWf5pR+m1n0zn6fhIwbXvK5gj4zvpW8dmVeU30c3KswL4b/k5PNJE8EpEnCzpEOAnkvKjn54CHB8Rv0i3L4qIXenQKo9IuiUiVki6JB30sb8PAYuADmBaes4D6b4TgYUk47T9hGREgB9X+g9rVshPIGaV9T7g4+kwLg8BU4H56b6HC5IHwKWSngAeJBmwcz5D+0/ADemowtuA+4GTC67dFRF9wOMkVWtmVeUnELPKEvDHEXHXAYXSmSRDjxduvxc4PSLekHQfMNxUo0NVS+0pWO/F/7ZtFPgJxKw8u4FJBdt3AX+UDmmPpHcOMuHREcBLafI4DjitYN++/Pn9PAB8JG1nmU4yM9/DFflTmJXAv1LMyrMO6Emror4F/C1J9dFjaUN2N/CBAc67E/i0pHXAsyTVWHkrgXWSHouIjxaU3wacDjxBMqnZFyJia5qAzEadR+M1M7OSuArLzMxK4gRiZmYlcQIxM7OSOIGYmVlJnEDMzKwkTiBmZlYSJxAzMyvJ/wfN8Cgk0bvA/gAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEGCAYAAAB7DNKzAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAAAmoElEQVR4nO3dd3yV9d3/8dcnC0jYGxIw7D2CDHFvsaIQauto1Tqq3j/tsHe11t53rd631rv2rva+XQ8HjluLdQQHoqhVXHUACXuJDEkChD0DWZ/fH+dE0xQOIZyT65zk/Xw88oBzSK7zxgfmnXN9ruv7NXdHRETkUJKCDiAiIvFNRSEiIhGpKEREJCIVhYiIRKSiEBGRiFKCDhALHTt29Ozs7KBjiIgklHnz5m1x9061n2+URZGdnc3cuXODjiEiklDMbN3BntepJxERiUhFISIiEakoREQkIhWFiIhEpKIQEZGIVBQiIhKRikJERCJSUdTw9pKNPPXJGrbuORB0FBGRuNEob7irr3eWbuLFeYX85xvLOKV/J3JHZXLmoC40T00OOpqISGCsMW5cNHr0aK/vndnLN+5ien4Rr8wvYtOuA7RqlsJ3hnUjd1QmY7Pbk5RkUU4rIhIfzGyeu4/+p+dVFAdXWeV8+tVW8goKeWvxRvaVVZLZtgWTc7qTm5NF384to5RWRCQ+qCiOwr6yCt5esom8giI+/nIzVQ7Ds9qQm5PJ+SO607Fls6i9lohIUFQUUVKyaz+vLSgmL7+IpRt2kZxkoXlGTiZnDdY8Q0QSl4oiBlZs3E1eQSGvFhSzcdd+WjVL4dxhXcnNyWJcL80zRCSxqChiqLLK+Wz1VvLyi3hr8Qb2hucZk0Z2Z8qoTPp2btVgWURE6ktF0UBKyyp5e+lG8vKL+Cg8zxiWGZpnXDBS8wwRiV8qigCU7N7Pa/OLmV5QxJLi0Dzj5H4dyR2VxdmaZ4hInFFRBGzlpt1MLyjilYIiNuzcT8tmKZw7tCu5ozI5rlcHzTNEJHAqijhRVeV8tiY0z3hzUWie0b1NcyblZDIlJ5N+XTTPEJFgqCjiUPU8Y3pBER99uYXKKmdoZmtyc7K4YER3OrXSPENEGo6KIs5t3n2A1xeE5hmLinaSnGSc1K8juTmZnD24Ky3SNM8QkdhSUSSQL2vMM4rD84wJQ7syJSeT43prniEisaGiSEBVVc7na7YxvaCQmYs2sudABd3aNGfSyEymjMqkv+YZIhJFKooEt7+8kneWbmJ6QREfrNxMZZUzuFtrpowK3Z/RuVXzoCOKSIJTUTQiW/Z8O89YWLiTJIMT+3ViSk4mZw/pQnqathkRkSOXsEVhZhnAQ0AZMNvdnzvc1zT2oqhpVckephcU8kpBMUU7SslIS+acoV2ZkpPF+D4dSNY8Q0TqKK6KwsymAhOBEncfWuP5CcCfgWTgcXe/x8wuA3a4++tm9ld3v+hwx29KRVGtqsr5Yu02pucXMXPRBnYfqKBr6+ZMGtmd3FGZDOzaOuiIIhLn4q0oTgb2AM9UF4WZJQMrgbOAQmAOcAkwCXjT3eeb2V/c/dLDHb8pFkVN+8sreXfZJqbnh+YZFVXOoG6tmZKTyaSR3encWvMMEflncVUUAGaWDcyoURTjgd+5+znhx78Of2ohsN3dZ5jZ8+5+8SGOdy1wLUDPnj2PXbduXaz/Cglha415xoLwPOOEvh2ZMiqTc4Z01TxDRL6RCEVxITDB3a8JP74MGAf8CngA2A98rBlF/a0q2cMrBUVMLyiiaEcp6WnJTBgSWm/q+D4dNc8QaeIOVRTx9OPkwb5LubvvBa5s6DCNUd/OLfnlOQP4xVn9mbN2G9MLinhj0QbyCoro0roZk0ZmkpuTyaBummeIyLfiqSgKgR41HmcBxQFladSSkoxxvTswrncHfnfBEP62rITpBYVM/XgNj364moFdWzFlVCaTRmbSRfMMkSYvnk49pRAaZp8BFBEaZl/q7kuO9Ng69VQ/W/ccCL3DyC9i/vod38wzcnNC84yMZvH0c4WIRFtczSjMbBpwKtAR2ATc7u5PmNl3gPsJXR471d3vqs/xVRRHb/Xm8DxjfhHrt5XSIjWZCUO7kpuTyQl9Nc8QaYziqihiTUURPe7O3HXbycsv4o2FxezaX0HnVs1C92fkZDG4u+YZIo2FikKO2v7ySt5fXkJeQRGzV5RQXukM7NqKyTmZTB6ZSdc2mmeIJDIVhUTV9r1lzFhYTF5BEQVf78AMju/TgdycLCYM7UpLzTNEEo6KQmJmzZa93+yf8fW2fbRITebsIV3IzcnkxL4dSUlOCjqiiNSBikJizt2Zt247eQVFvLFwAztLy+nUqhkXjOhObk4mQ7q3xkxDcJF4paKQBnWgIjzPyC/i/fA8o3+XluTmZDE5pzvd2rQIOqKI1KKikMBs31vGjEUbmJ5fSH54njG+dwdyczI5d1g3zTNE4oSKQuLCuq2hecb0giLWbd1H89Qkzh4cWm/qJM0zRAKlopC44u7kf72DvPxCZoTnGR1bhuYZU0ZpniESBBWFxK3QPGMz0wsKeW95aJ7Rr3NLckeF7s/o3lbzDJGGoKKQhLBjXxlvLNrA9Pwi5q7bjhkc16sDuaMyOXdoV1o1Tw06okijpaKQhPP11n3heUYha7fuo1lKEmcP6cqUnExO6qd5hki0qSgkYbk7Bet3MD2/iNcXFrNjXzkdW6Zx/ojuTMnJYmim5hki0aCikEahrKKK2StKmF5QxN+WlVBWWUXfzi3Jzclkck4mmZpniNSbikIanZ37ykPzjIJC5qzdDsC4Xu2ZMip0f0ZrzTNEjoiKQhq19dv2fXN/xpote2mWksSZg7swJSeTk/t3IlXzDJHDUlFIk+DuzF+/g+kFRby+oJjt+8rpkBGaZ+TmZDI8q43mGSKHoKKQJqesoooPVobuz3h3WQllFVX07pTBlPA8I6tdetARReKKikKatJ2l5cwM35/xxdptAIzt1Z4p4fWm2rTQPENERSEStn7bPl6dX0ReQRGrN+8lLSWJswaF9s84ZYDmGdJ0qShEanF3FhbuZHpBEa8tKGbb3jLaZ6Rx/vBu5I7KYoTmGdLEqChEIiivrOLDlZvJKyjinaWbQvOMjhnf3J/Ro73mGdL4qShE6mhnaTlvLd5AXn4Rn68JzzOy25M7KpPvaJ4hjZiKQqQeCrfv49X5xeTlF/JVeJ5x5qDO5OZkcUr/TqSlaJ4hjYeKQuQouDuLinaSlx+6P2Pr3jLapad+c3/GyB5tNc+QhKeiEImS8soqPvpyM3n5oXnGgYoqenXMYPLITHJzMunZQfMMSUwqCpEY2LW/nLcWbSSvoJDPVofmGaOPaUfuqEwmDutOm3TNMyRxqChEYqxoRymvhNebWlWyh7TkJE4f2JncUZmcNqCz5hkS91QUIg3E3VlctIu8gkJeX1DMlj1ltE1PZeLwbnx3VBY5PdsFHVHkoFQUIgGoqKzioy+3kFdQxNtLNnKgoorRx7TjX07tw2kDOpOUpAG4xI+ELgozmwycB3QGHnT3tyN9vopC4tHu/eW8PK+Qxz5aQ9GOUvp3acl1J/fhgpHdtWyIxIXAisLMpgITgRJ3H1rj+QnAn4Fk4HF3v6cOx2oH/NHdr470eSoKiWfllVXMWFjMI7NXs2LTbjLbtuCak3px0ZgepKelBB1PmrAgi+JkYA/wTHVRmFkysBI4CygE5gCXECqN39c6xFXuXhL+uv8GnnP3/EivqaKQRODuvL+ihEdmr+aLtdtol57K5eOzueL4bNpnpAUdT5qgQE89mVk2MKNGUYwHfufu54Qf/xrA3WuXRPXXG3AP8I67v3u411NRSKKZt24bD89ezbvLNtEiNZmLxvTgxyf31h7g0qAOVRRBvc/NBNbXeFwIjIvw+T8BzgTamFlfd3+k9ieY2bXAtQA9e/aMYlSR2Dv2mPY8fkV7vty0m0c+WM2zn63j2c/WccGI7lx3Sh8GdG0VdERpwoJ6R/E94Bx3vyb8+DJgrLv/JBqvp3cUkuiKdpTyxEdreH7O1+wrq+SMgZ25/tQ+jMluH3Q0acQO9Y4iqEstCoEeNR5nAcUBZRGJO5ltW/Db8wfzya9O56Yz+5P/9Xa+98inXPjw3/nbsk1UVcX/1YrSeARVFHOAfmbWy8zSgIuB1wLKIhK32mWk8bMz+/HJrafzu/MHs2Hnfq5+ei4T/vwhL88rpLyyKuiI0gQctijMbK6Z3RC+NPWImdk04FNggJkVmtnV7l4B3AjMApYBL7j7kvocX6QpSE9L4Ucn9GL2zady30UjMIx/fXEBp947m6kfr2FfWUXQEaURO+yMwsz6AlcCFwFzgSeBtz2O79TTjEIaO3dn9orNPDz7K75Yu4226alcoUtr5Sgd9eWxZpZE6Ma5h4EqYCrwZ3ffFs2g0aCikKbkYJfWXnNSL7LaablzOTJHVRRmNpzQu4rvEDpd9BxwInCZu4+MbtSjp6KQpqj60tpX5xfhwCRdWitHqN5FYWbzgB3AE8DL7n6gxp/lufuUKGc9aioKacqKd5TyuC6tlXo4mqLo7e6raz3Xy93XRDlj1KgoRGD73jKe+XQdT/19Ddv3lTP6mHZcf0ofTh+oVWvl4I6mKPLdfdRBDnZslDNGjYpC5FulZZW8MHc9j364WqvWSkRHXBRmNhAYAvwBuLnGH7UGbnb3IbEIGg0qCpF/Vl5ZxRsLN/Dw7K9YsWk33ds055qTenPxWK1aKyH1KYpJwGTgAv7xZrjdwPPu/vcY5IwKFYXIoR3s0torj+/Fdaf0pnlqctDxJEBHc+ppvLt/GrNkMaCiEKmbmpfW9u/SkvsvymFw99ZBx5KA1Ocdxf8Ch2wRd/9p9OJFl4pC5MjMXlHCzS8tZOe+cv717P5cc1JvkjXwbnLqs8y4vtOKNBGnDujMrJ+fzG15i/j9m8t5b3kJ//39EbppT4AE2TP7SOkdhUj9uDsvzivkjteWkGTGnZOHMHlkJqG9w6Sxq/cy42bWycz+aGYzzey96o/YxBSRIJkZ3x/dgzd/djIDurbipr8u4MZpBezYVxZ0NAlQXS6ifo7QCq+9gDuAtYSWCReRRqpnh3T+et14bj5nALMWb2TC/R/x8Zdbgo4lAalLUXRw9yeAcnf/wN2vAo6LcS4RCVhyknHDaX2Z/v9OIKNZMj984nPufH0p+8srg44mDawuRVEe/nWDmZ1nZjmEdqQTkSZgWFYbZvzkJC4ffwxTP1nDBQ98zNLiXUHHkgZUl6L4TzNrA/wr8EvgceCmmKYSkbjSIi2ZOycN5akrx7B9XzmTHvyYRz74ikptydok6KonETki2/aWcVveIt5aspGxvdrzJ11G22gczZ3ZnYAfA9nUuO8iPKuISyoKkdhyd16aV8jvwpfR3jFpCLk5uow20dXnhrtqrwIfAe8CmmKJCGbG90b3YFyvDvzihfn84oUF/G15CXdNHkrbdG3F2tjUpSjS3f1XMU8iIgmn+jLaRz74ivveWcm8tdv54/dGcGK/jkFHkyiqyzB7hpl9J+ZJRCQhHewy2jteX6LLaBuRuhTFzwiVxX4z22Vmu81M18aJyD+ovoz2ivHH8OQnazn/fz9mSfHOoGNJFBy2KNy9lbsnuXtzd28dfqx1iEXkn7RIS+aO8GW0O0rLmfzgJ7qMthGoy1pPZmY/NLN/Dz/uYWZjYx9NRBJV9Wq0Zwzswj1vLueSxz6jcPu+oGNJPdXl1NNDwHjg0vDjPcCDMUskIo1C+4w0Hv7hKO69cDhLi3dx7v0fkZdfSGO8d6uxq0tRjHP3G4D9AO6+HdD1byJyWNWX0b75s5MY0LUVv3hhATf+RavRJpo6rfVkZsmEd7sL34BXFdNUItKo9GhfYzXaJRs55/4PtRptAqlLUfwPMB3obGZ3AR8Dd8c0lYg0OtWX0b5ywwm0bJaiy2gTSJ3WejKzgcAZgAF/c/dlsQ52NLSEh0h8Ky2r5J43l/H0p+vo17kl9188kiHd2wQdq8k74h3uzGycmS0wsz3Ak8D77v5AvJeEiMS/6ston75qLDvDl9E+PFuX0carSKeeHiS0rHgH4E/AfQ2S6CDMLMPM5pnZxKAyiEj0ndK/E7N+fjJnDurCf72ly2jjVaSiSHL3d9z9gLu/CHQ60oOb2VQzKzGzxbWen2BmK8xslZndWodD/Qp44UhfX0TiX7uMNB76wSj++L0Ruow2TkVaFLCtmU051GN3z6vD8Z8CHgCeqX4ifAXVg8BZQCEwx8xeA5KB39f6+quA4cBSoHkdXk9EEpCZceGxWYzr1Z6b/hpejXZZCXflajXaeHDIYbaZPRnh67yu+1GYWTYww92Hhh+PB37n7ueEH/86fMDaJVH99XcBGcBgoBTIdfd/ujzXzK4FrgXo2bPnsevWratLPBGJM5VV/s1qtB1bNuPZa8bSt3OroGM1CfXeuCgKL5zNPxbFhcAEd78m/PgyQjf13XiY4/wI2OLuMw73mrrqSSTxLS7ayY+enENyErx43fH07KBd9GLtiK96imWWgzx32LZy96fqUhIi0jgMzWzDs9eM5UBFFZc+/hkbdpYGHanJCqIoCoEeNR5nAcUB5BCRODewa2ueuWosO/aV84PHP2fLngNBR2qSIhaFmSWZ2fFRfs05QD8z62VmacDFwGtRfg0RaSSGZ7XlySvHULyjlB8+/rnWiQpAxKIID43/u74HN7NpwKfAADMrNLOr3b0CuBGYBSwDXnD3JfV9DRFp/MZkt+exy0ezevNernhyDnsOVAQdqUmpy6mnt83su2Z2sNlCRO5+ibt3c/dUd89y9yfCz8909/7u3sfd7zri1CLS5JzUrxMPXJrD4qKdXPXUHErLtEZUQ6lLUfwCeBEo01aoIhKks4d05U/fH8Gctdu4/tl5HKhQWTSEI9kKNVVboYpI0CaNzOSeKcP4YOVmfjqtgIpK7XoQa9oKVUQSzkVjevLbiYOZtWQTv3xxAVVaTDCmIi3hUe0hQhsVnQ78B99uhTomhrlERCK66sRelJZXcu+sFaQ3S+GuyUOpxyhV6qAuRTHO3UeZWQGEtkINX9YqIhKoG07ry94DFTw0+yvSU5P5zXmDVBYxUJei0FaoIhK3bj5nAPvKKnn84zVkNEvhprP6Bx2p0alLUdTeCvVC4N9imkpEpI7MjN9OHMzeAxX8+W9fkp6WzHWn9Ak6VqNy2KJw9+fMbB7fboU6WbvciUg8SUoy7vnucErLK/n9m8tJT0vmsvHZQcdqNA5ZFGbW2t13mVl7oASYVuPP2rv7toYIKCJSF8lJxn0XjWR/eSX//uoSWqSlcOGxWUHHahQiXR77l/Cv84C5NT6qH4uIxJXU5CQeuHQUJ/TtwC0vLWDmog1BR2oUDlkU7j4xvGzHKe7eu8ZHL3fv3YAZRUTqrHlqMo9dPppRPdvx02kFvL+8JOhICe9wiwI6oUG2iEjCSE9LYeqVYxjYrRXXPzuPv3+1JehICa0uaz19Zma6uU5EEkrr5qk8c9U4jumQzjVPz2Xeuu1BR0pYdSmK04BPzewrM1toZovMbGGsg4mIHK32GWk8e/U4Ordqxo+e/ILFRTuDjpSQDrdxkQHXA30ILeFxPjAx/KuISNzr3Lo5z14zjlbNUrh86hesKtkddKSEU5cZxX3uvq72RwPlExE5alnt0nnux8eRZMalj33Ouq17g46UUDSjEJEmoVfHDJ67ZhxllVVc+tjnFO8oDTpSwtCMQkSajAFdW/F/V41jV2k5P3z8czbvPhB0pIRQl6I4F80oRKSRGJbVhqlXjmHDzv1c9sTn7NhXFnSkuFeXHe6qZxKlhFaQrf4QEUlIY7Lb89jlo1m9eS9XPDmH3fvLg44U1+qyw90FZvYlsAb4AFgLvBnjXCIiMXViv4489INRLCnaydVPz6W0TPtvH0pdTj39B3AcsNLdexFaRfaTmKYSEWkAZw7uwn0XjWTO2m1c9+w8DlSoLA6mLkVR7u5bgSQzS3L394GRsY0lItIwzh/Rnf+aMpwPV27mJ38poLxS+7LVVpei2GFmLYEPgefM7M9ARWxjiYg0nO+P6cHt5w/m7aWbuPnFBVRVaQxbU112uJtEaJB9E/ADoA1wZyxDiYg0tCtP6MW+skrunbWCFmkp3J07VPtvh9Vlh7vqWxirzOwNYGv4jm0RkUblhtP6sq+sggff/4r0tGT+7bxBKgsinHoys+PMbLaZ5ZlZjpktBhYDm8xsQsNFFBFpOL88ewA/Oj6bJz5ew33vfhl0nLgQ6R3FA8BthE41vQec6+6fmdlAQtuivtUA+UREGpSZ8duJgyktq+R//vYl6WnJXH9Kn6BjBSpSUaS4+9sAZnanu38G4O7L9VZMRBqzpCTj7inD2FdeyT1vLicjLZnLxmcHHSswkYqi5jVitVfParAZhZklEbqXozUw192fbqjXFpGmKznJ+NP3R1BaVsm/v7qEFmkpXHhsVtCxAhHp8tgRZrbLzHYDw8O/r348rC4HN7OpZlYSnm/UfH6Cma0ws1VmduthDjMJyATKgcK6vK6ISDSkJifxwKU5nNi3I7e8tIA3Fm4IOlIgDlkU7p7s7q3dvZW7p4R/X/04tY7Hfwr4h8G3mSUDDxJabHAwcImZDTazYWY2o9ZHZ2AA8Km7/wL4l/r8JUVE6qt5ajKPXn4so3q242fPF/De8k1BR2pwdbnhrt7c/UNgW62nxwKr3H21u5cBzwOT3H2Ru0+s9VFC6F1E9Wa3ur9eRBpceloKU68cw6Burbn+2Xz+vmpL0JEaVEyL4hAygfU1HheGnzuUPOAcM/tfQneHH5SZXWtmc81s7ubNm6OTVEQkrHXzVJ65aiy9OmRwzTNzm9SWqkEUxcEumTrkcNzd97n71e7+E3d/MMLnPeruo919dKdOnaISVESkpnYZaTxz9ViapSRx80sLqWwiS30EURSFQI8aj7OA4gByiIgcsS6tm3P7+UMo+HoHT36yJug4DSKIopgD9DOzXmaWBlwMvBZADhGRepk0sjtnDOzMH99ewdotew//BQkupkVhZtOAT4EBZlZoZle7ewVwIzALWAa84O5LYplDRCSazIy7coeRmpTErXkLG/1qs7G+6ukSd+/m7qnunuXuT4Sfn+nu/d29j7vfFcsMIiKx0LVNc35z3iA+W72Nv3zxddBxYiqIU08iIo3CRWN6cELfDvx+5jKKdtRewKLxUFGIiNSTmXHPlOE4cFveIhrrDgwqChGRo9CjfTq3nDOAD1Zu5uX8oqDjxISKQkTkKF0+PpvRx7TjzteXULJrf9Bxok5FISJylJKSjD9cOJwDFVX82yuLG90pKBWFiEgU9O7UkpvO6s/bSzfxxqLGtcqsikJEJEquObEXw7PacPurS9i2tyzoOFGjohARiZKU5CT+cOFwdu0v547XG899xCoKEZEoGti1NTec1pdX5xfzztLGsXeFikJEJMr+36l9Gdi1Fb+ZvoidpeVBxzlqKgoRkShLS0ni3gtHsHVvGXe/sSzoOEdNRSEiEgPDstrw45N689e56/noy8TeTE1FISISIz8/sx+9O2Vw68uL2HugIug49aaiEBGJkeapyfzhu8Mp3lnKH95aHnScelNRiIjE0Ojs9lwxPpunP13HF2u2BR2nXlQUIiIxdsuEAfRo34JfvbyQ/eWVQcc5YioKEZEYS09L4Z4pw1mzZS/3vbMy6DhHTEUhItIATujbkUvG9uCxj1azYP2OoOMcERWFiEgD+fV3BtG5VXNufmkBByoS5xSUikJEpIG0bp7K3VOGsnLTHh58/6ug49SZikJEpAGdPrALuTmZPPT+KpYW7wo6Tp2oKEREGthvJw6mbXoqt7y8gIrKqqDjHJaKQkSkgbXLSOM/Jg1lcdEuHv1oddBxDktFISISgHOHdePcoV25/90vWVWyJ+g4EakoREQCcsekIaSnJXPLSwuorIrffbZVFCIiAencqjm3nz+Y/K938PTf1wYd55BUFCIiAZo8MpPTBnTi3lkr+HrrvqDjHJSKQkQkQGbG3VOGkZJk/OrlhbjH3ykoFYWISMC6tWnBbecN4tPVW5n2xfqg4/wTFYWISBy4eEwPju/TgbtnLqN4R2nQcf5B3BeFmfU0s9fMbKqZ3Rp0HhGRWDAz7pkynMoq5zfTF8XVKaiYFkX4m3uJmS2u9fwEM1thZqvq8M2/P/CGu18FDI5ZWBGRgPXskM4tEwbw/orNTC8oCjrON2L9juIpYELNJ8wsGXgQOJfQN/5LzGywmQ0zsxm1PjoDBcDFZvYe8H6M84qIBOqK8dkce0w77nh9KSW79wcdB4hxUbj7h0Dtvf/GAqvcfbW7lwHPA5PcfZG7T6z1UQJcCdzu7qcD5x3qtczsWjOba2ZzN2/eHKu/kohITCUlGf/13eGUlldy+6tLgo4DBDOjyARqjvULw88dylvAT83sEWDtoT7J3R9199HuPrpTp05RCSoiEoS+nVty05n9eXPxRmYu2hB0HFICeE07yHOHnNq4+2LgwtjFERGJPz8+qRczF23gt68uZnzvDrTLSAssSxDvKAqBHjUeZwHFAeQQEYlbKclJ/OHC4ezYV86dM5YGmiWIopgD9DOzXmaWBlwMvBZADhGRuDaoW2tuOK0v0wuKeG/5psByxPry2GnAp8AAMys0s6vdvQK4EZgFLANecPf4mNiIiMSZG07ry4AurbgtbzG79pcHkiHWVz1d4u7d3D3V3bPc/Ynw8zPdvb+793H3u2KZQUQkkaWlhE5Blezez+9nLgskQ9zfmS0i0tSN6NGWH5/cm2lfrOeTVVsa/PVVFCIiCeCmM/vTq2MGt+YtZO+BigZ9bRWFiEgCaJ6azB8uHE7h9lLunbWiQV9bRSEikiDGZLfnivHZPP3pWuaurb3oReyoKEREEsjN5wwgs20LbnlpIfvLKxvkNVUUIiIJJKNZCvdMGc7qLXu5/90vG+Q1VRQiIgnmxH4duXhMDx798CsWFu6I+eupKEREEtBt5w2iU6tm3PLSQsoqqmL6WioKEZEE1Lp5KnfnDmP5xt08NHtVTF9LRSEikqDOGNSFySO788B7q1i+cVfMXkdFISKSwH57/hDatEjllpcWUlEZm1NQKgoRkQTWPiONOycNZWHhTh7/eE1MXkNFISKS4L4zrCsThnTlT++s5KvNe6J+/CB2uBMRkSgyM+6cPIS9L1Tgh9wvtP5UFCIijUDnVs35v6vHxeTYOvUkIiIRqShERCQiFYWIiESkohARkYhUFCIiEpGKQkREIlJRiIhIRCoKERGJyDwWt/EFzMw2A+vq+eUdgS1RjBMtynVklOvIKNeRaay5jnH3TrWfbJRFcTTMbK67jw46R23KdWSU68go15Fparl06klERCJSUYiISEQqin/2aNABDkG5joxyHRnlOjJNKpdmFCIiEpHeUYiISEQqChERiUhFUYOZTTCzFWa2ysxuDToPgJlNNbMSM1scdJaazKyHmb1vZsvMbImZ/SzoTABm1tzMvjCzBeFcdwSdqSYzSzazAjObEXSWama21swWmdl8M5sbdJ5qZtbWzF4ys+Xhf2fj4yDTgPB/p+qPXWb286BzAZjZTeF/84vNbJqZNY/asTWjCDGzZGAlcBZQCMwBLnH3pQHnOhnYAzzj7kODzFKTmXUDurl7vpm1AuYBk+Pgv5cBGe6+x8xSgY+Bn7n7Z0HmqmZmvwBGA63dfWLQeSBUFMBod4+rG8jM7GngI3d/3MzSgHR33xFwrG+Ev2cUAePcvb43+EYrSyahf+uD3b3UzF4AZrr7U9E4vt5RfGsssMrdV7t7GfA8MCngTLj7h8C2oHPU5u4b3D0//PvdwDIgM9hU4CHVu8unhj/i4qchM8sCzgMeDzpLvDOz1sDJwBMA7l4WTyURdgbwVdAlUUMK0MLMUoB0oDhaB1ZRfCsTWF/jcSFx8I0vEZhZNpADfB5wFOCb0zvzgRLgHXePi1zA/cAtQFXAOWpz4G0zm2dm1wYdJqw3sBl4Mnyq7nEzywg6VC0XA9OCDgHg7kXAH4GvgQ3ATnd/O1rHV1F8yw7yXFz8JBrPzKwl8DLwc3ffFXQeAHevdPeRQBYw1swCP2VnZhOBEnefF3SWgzjB3UcB5wI3hE93Bi0FGAU87O45wF4gLuaGAOFTYRcALwadBcDM2hE6A9IL6A5kmNkPo3V8FcW3CoEeNR5nEcW3bo1ReAbwMvCcu+cFnae28KmK2cCEYJMAcAJwQXge8Dxwupk9G2ykEHcvDv9aAkwndBo2aIVAYY13gy8RKo54cS6Q7+6bgg4Sdiawxt03u3s5kAccH62Dqyi+NQfoZ2a9wj8tXAy8FnCmuBUeGj8BLHP3PwWdp5qZdTKztuHftyD0P9DyQEMB7v5rd89y92xC/7bec/eo/cRXX2aWEb4YgfCpnbOBwK+wc/eNwHozGxB+6gwg0AslarmEODntFPY1cJyZpYf/3zyD0NwwKlKidaBE5+4VZnYjMAtIBqa6+5KAY2Fm04BTgY5mVgjc7u5PBJsKCP2EfBmwKDwPALjN3WcGFwmAbsDT4StSkoAX3D1uLkWNQ12A6aHvLaQAf3H3t4KN9I2fAM+Ff3BbDVwZcB4AzCyd0NWR1wWdpZq7f25mLwH5QAVQQBSX89DlsSIiEpFOPYmISEQqChERiUhFISIiEakoREQkIhWFiIhEpKIQicDM9oR/zTazS6N87NtqPf57NI8vEi0qCpG6yQaOqCjC93JE8g9F4e5Ru5NWJJpUFCJ1cw9wUngPgpvCCw/ea2ZzzGyhmV0HYGanhvfp+AuwKPzcK+EF95ZUL7pnZvcQWulzvpk9F36u+t2LhY+9OLxPxEU1jj27xh4Nz4XvwhWJKd2ZLVI3twK/rN5DIvwNf6e7jzGzZsAnZla9WudYYKi7rwk/vsrdt4WXFJljZi+7+61mdmN48cLapgAjgRFAx/DXfBj+sxxgCKF1yD4hdIf8x9H+y4rUpHcUIvVzNnB5ePmSz4EOQL/wn31RoyQAfmpmC4DPCC082Y/ITgSmhVfB3QR8AIypcexCd68C5hM6JSYSU3pHIVI/BvzE3Wf9w5NmpxJaErvm4zOB8e6+z8xmA4fbojLS6aQDNX5fif4flgagdxQidbMbaFXj8SzgX8JLrWNm/Q+xsU4bYHu4JAYCx9X4s/Lqr6/lQ+Ci8BykE6Gd3r6Iyt9CpB7004hI3SwEKsKnkJ4C/kzotE9+eKC8GZh8kK97C7jezBYCKwidfqr2KLDQzPLd/Qc1np8OjAcWENo86xZ33xguGpEGp9VjRUQkIp16EhGRiFQUIiISkYpCREQiUlGIiEhEKgoREYlIRSEiIhGpKEREJKL/D0v9ilie0TVJAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEGCAYAAAB7DNKzAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAAAiN0lEQVR4nO3deXjVhZ3v8fc3O1vYErJHUBQIYRFDcCu1KkJk62irxM7M09t2rHPrjFPv3F57Z+7TznMfp7135jptp860jlrrjMVadcoim3UD3NhkCQKKKBCSkLCHJfv3/nEONqbkJISc/E6Sz+t5zsM5v5Pzywce4JPf7/tbzN0RERFpT1zQAUREJLapKEREJCIVhYiIRKSiEBGRiFQUIiISUULQAaIhLS3NR48eHXQMEZFeZfPmzUfcPb3t8j5ZFKNHj2bTpk1BxxAR6VXMbP+FlmvXk4iIRKSiEBGRiFQUIiISkYpCREQiivmiMLPLzewJM3s+6CwiIv1RIEVhZk+aWbWZlbVZPsfM9pjZXjN7CMDd97n714PIKSIiwW1RPAXMab3AzOKBR4ESoAAoNbOCno8mIiKtBXIehbuvNbPRbRYXA3vdfR+AmT0LLATe78w6zexe4F6A/Pz8LuV6YXM5B46dJSkhjuSEOJIS4kiKD//a5nlyQhxJ8fG/f6/V+8nh53Fx1qUcIiKxJJZOuMsBDrZ6XQ7MMLORwMPA1Wb2XXf/wYU+7O6PAY8BFBUVdekmG8u2V/D6npqufPSCEuLsD0umneL5wxJq/d5nCyk5/N7ApHiuvWIkqSmJ3ZZZRKStWCqKC/347e5+FLivJwI89V+KaWlxGppbqG9qobG5hYam8CP8vL7N69Dz5k+f17d9r83r+lbPz6//dH1T+59vbqG5pf3eS0qI4+Zxo1gwNZubx48iJTG+J/6oRKQfiaWiKAfyWr3OBSp6OkRcnJESFx9T/+E2t3irovl9KR053cDKskqWbatk1c4qBicnMHtiJgumZnPDFSNJiI/5g9pEpBeIpaLYCFxpZmOAQ8Ai4J5gI8WG+DhjQFI8A5Ligd/vZro8HYrHjOBvbp/AO/uOsWTrIVbtrOKFLeWkDU5i7qQsFkzNYVr+MMw0LxGRrrEg7pltZouBm4A04DDwPXd/wsxuB34ExANPuvvDXVl/UVGR99eLAtY1NvP6nhqWbjvEK7uqqW9qIXf4ABZMyWbh1BzGZQ4JOqKIxCgz2+zuRX+wPIiiiLb+XBSt1dY1smbnYZZsq+DNvUdobnHGZw5h/pRsFkzJJm/EwKAjikgMUVH0c0dO17NiRyVLtlawef9xAK65bDgLpmQzd3IWaYOTA04oIkFTUcinDh47y7LtFSzdWsHuqlri44wbxqaxYEo2sydmMESH24r0SyoKuaA9VbUs3XaIJVsrKD9+juSEOG6ZMIoFU3K4aVx6TB39JSLRpaKQiNydLQdOsHTrIV7aUcmR0w0MSUlgzsRMFk7N4borRhKvM81F+jQVhXRaU3MLb310lCVbK1i9s4rT9U2kD0lm7qQsFk7NZmqeDrcV6YtUFNIldY3NvLa7miVbK3h1TzUNTS3kjxjIwqmhI6euzNDhtiJ9hYpCLtmpukZWl1WxNHy4bYvDhKxUFk7NZv6UbHKGDQg6oohcAhWFdKvq2jpWbK9kybYK3jtwAoDpo4ezYGoOcydlMWJQUrABReSiqSgkag4cDR1u+9v3DvFh9WkS4owbr0xj4dRsZhVkMjg5lq4UIyLtUVFI1Lk7u6tqWbK1gmXbKjh04hwpiXHcOiGDBVOy+fy4dJITdLitSKxSUUiPamlxthw4zpKtFby0o5JjZ0KH295WkMncyZncODadpARd3VYklqgoJDCNzS28ufcIy7dXsmZnFafqmkhNSWBWQSbzJmdxw9g0lYZIDFBRSExoaAqVxks7Klm9s4racGncNjGTuZNUGiJBUlFIzGloamH93hpe2l7Fmvd/XxqzJ2Zy++QsbrhCpSHSk1QUEtPqm5o/3T318vuHqa1rYuiARG4ryGBuePdUou7YJxJV7RWFjluUmJCcEM/N4zO4eXwG9U3NrP8wtHtqVVkVv9lcztABicyemMHtk1QaIj1NWxQS0+qbmln3wRFW7AhvadQ3MWxgIrMLQrunrr9ipEpDpJto15P0eudL46VwaZxuVRpzJ2dxnUpD5JKoKKRPqWtsZt2Hv9/SOF8acyZmcvsklYZIV6gopM+qa2xm7Qc1n5bGmYZmhg9MZE5huDQuH0mCSkOkQyoK6RfOl8ZLOyr5Xbg0RgxKYvbEDOZOyubay0eoNETaoaKQfqeusZk3wlsany2N0Ml9Kg2Rz1JRSL9W19jM63vCpbHrMGfDpTGnMFQaM8aoNERUFCJh50vjpR2VvBIujZGDkphdmMm8SVkUqzSkn1JRiFxAqDSqeWlH1WdKY05hJvMmZ1M8ZgTxcbo/uPQPKgqRDpxrOF8albyyq5pzjc2MGpLM7ZOymD8lm2n5wzBTaUjfpaIQuQhnG5p4dXc1y7ZV8NqeGhqaWsgZNoB5k0OlMTE7VaUhfY6KQqSLausaefn9wyzbVsG6D4/Q1OKMSRv0aWlclTEk6Igi3UJFIdINjp9pYPXOKpZtr+Dtj47S4nBVxmDmT85m3pRsxqQNCjqiSJepKES6WU1tPSvLKlm2rYKNnxwHoDAnlfmTs5k7OYvc4QMDTihycVQUIlFUceIcK3aESmNb+UkArrlsOPMmZzF3UhajUlMCTijSMRWFSA/Zf/QMy7eHSmN3VS1mMGPMCOZPyaakMIsRg5KCjihyQSoKkQDsra5l2bZKlm2vYF/NGeLjjBvGpjF/cha3Tcxk6IDEoCOKfKrXFoWZXQ78DTDU3b/Umc+oKCTWuDvvV576dEuj/Pg5kuLjmHlVOvOnZHHrhAwGJeuGkxKsQIrCzJ4E5gHV7l7Yavkc4MdAPPC4u/+wE+t6XkUhfYG7s638JMu2VbB8ewWHT9WTkhjHLeMzmD8li5vGjSIlMT7omNIPBVUUM4HTwNPni8LM4oEPgFlAObARKCVUGj9os4qvuXt1+HMqCulzWlqcjZ8cY/n2SlbsqOTomQYGJycwqyBUGjeOTScpQdedkp4R2K4nMxsNLG9VFNcB33f32eHX3wVw97Yl0XY9EYvCzO4F7gXIz8+/Zv/+/d3zGxDpIU3NLby97yjLt1WysqySU3VNDB0Qumvf/Cm6l4ZEXywVxZeAOe7+jfDrPwFmuPv97Xx+JPAwoS2QxzsqFNAWhfR+DU0trPuwhuXbK1mzs4ozDc2kDU6ipDB0NnjRZcOJ08UKpZu1VxRBTM8u9Le73bZy96PAfdGLIxJ7khLiuGVCBrdMyKCusZnXdlezfHslz206yL+/s5/M1BTmhi8hMiV3qK47JVEVRFGUA3mtXucCFQHkEOkVUhLjKZmURcmkLE7XN/HKrsMs21bJ029/whPrPyZvxADmTsqmpDCTySoNiYIgdj0lEBpm3wIcIjTMvsfdd3bX99SuJ+kPTp5tZPX7VSzbVsFbHx2lucXJGTaA2RMzKZmUyTX52j0lFyeoo54WAzcBacBh4Hvu/oSZ3Q78iNCRTk+6+8Pd+X1VFNLfnDjbwMvvH2ZVWRXrPjxCQ3ML6UOSmTMxk5LCTN21Tzql155w1xUqCunPausaeXV3NSt3VPH6B9XUNbYwYlASsyZkMGdSJjdckaZDbuWCVBQi/dDZhibe2FPDyrIqXt1dzen6JoakJHDrhAxKCjOZeVW6Tu6TT6koRPq5usZm1n94hJVlVfxu12FOnmtkYFI8Xxg/ipLCTL4wbpQuI9LPxdLhsSISgJTEeG4tyODWggwam1t4+6OjrCyrYs3OKl7aXklyQujaUyWFmdwyIUMXLJRPaYtCpJ9rDl9GZFVZFSvLKjl8qp7E+NBVbksKM5lVkKlLo/cT2vUkIh1qaXHeO3iCVWWVrCyrovz4OeLjjBljRlBSmMnsiZm6CVMfpqIQkYvi7uysOMXKskpW7qhi35EzmEHRZcOZU5jFnMJMcoYNCDqmdCMVhYh0mbvzweHTrCyrZFVZFburagGYkjuUOYVZlBRmMjptUMAp5VKpKESk2+yrOc2qnVWsKqtie/ge4ROyUikpDJ3gd2XGkIATSleoKEQkKg4eO8vqnVWsLKti8/7jAFyRPoiSwixKJmVSkJWq60/1EioKEYm6w6fqQqWxo4p3Pz5Ki0P+iIGUFGYypzCTqXnDVBoxTEUhIj3q6Ol61rx/mJVlVby19whNLU7W0BQWTs3hv912FYm69lTM0Ql3ItKjRg5OprQ4n9LifE6ebeR3uw6zfHsFP3vjI8ZlDuaPrs4NOqJ0kipdRKJu6MBE7rwmlye/Op3RIwey+N2DQUeSi6CiEJEeY2aUFuez4ZNj7K2uDTqOdJKKQkR61J3X5JIYbyzeoK2K3kJFISI9Km1wMrcVZPLilnLqGpuDjiOdoKIQkR5XWpzP8bONrN5ZFXQU6QQVhYj0uOuvGEn+iIEs3nAg6CjSCSoKEelxcXHGouI83tl3jH01p4OOIx1QUYhIIL50TS4JccazGzXUjnUqChEJxKghKcwqyOD5zeXUN2moHctUFCISmNLifI6daWDNzsNBR5EIVBQiEpgbx6aRO3yAhtoxTkUhIoGJiwudqf3WR0f5+MiZoONIO1QUIhKoL1+TS3yc8exGbVXEKhWFiARqVGoKt04YxfObymloagk6jlyAikJEAldanM/RMw28/L6G2rFIRSEigfvclenkDNNQO1apKEQkcPFxxqLpeazfe4T9RzXUjjUqChGJCV8uygsPtXWmdqxRUYhITMgcmsLN40fxm00HNdSOMSoKEYkZ9xTnc+R0A6/s0lA7lsR8UZjZBDP7mZk9b2Z/HnQeEYmemVelkz00hV9pqB1ToloUZvakmVWbWVmb5XPMbI+Z7TWzhyKtw913uft9wF1AUTTzikiw4uOMu6fns+7DIxw8djboOBIW7S2Kp4A5rReYWTzwKFACFAClZlZgZpPMbHmbx6jwZxYA64FXopxXRAJ21/Rc4gydqR1DoloU7r4WONZmcTGw1933uXsD8Cyw0N13uPu8No/q8HqWuvv1wFeimVdEgpc1dAA3jx/Fc5vKaWzWUDsWBDGjyAFaH/9WHl52QWZ2k5n9xMx+DqyI8HX3mtkmM9tUU1PTfWlFpMeVFudTU1vPK7uqg44iQEIA39MusMzb+2J3fx14vaOVuvtjwGMARUVF7a5PRGLf569KJ2toCos3HGBOYWbQcfq9ILYoyoG8Vq9zgYoAcohIjEqIj+OuojzWflijoXYMCKIoNgJXmtkYM0sCFgFLA8ghIjHsrumhnyd/s0lnagetw6Iwszgzu74rKzezxcDbwDgzKzezr7t7E3A/sBrYBTzn7ju7sn4R6btyhg3gpqvS+fWmgzRpqB2oDovC3VuA/9eVlbt7qbtnuXuiu+e6+xPh5Svc/Sp3v8LdH+7KukWk7ystzufwqXpe26MDVILU2V1Pa8zsTjO70CBaRCQqbh4/ilFDknX58YB1tigeBH4DNJjZKTOrNbNTUcwlIkJCfBx3T8/j9T3VHDpxLug4/VanisLdh7h7XHgXUmr4dWq0w4mI3FWUhwPP6fLjgen0UU9mtsDM/jH8mBfNUCIi5+WNGMjMK9N5TkPtwHSqKMzsh8ADwPvhxwPhZSIiUVdanE/lyTre+EBD7SB0dovidmCWuz/p7k8SutDf7dGLJSLye7dMGEW6htqBuZgT7oa1ej60m3OIiLQrMT6Ou4pyeXV3NZUnNdTuaZ0tir8H3jOzp8zsl8Dm8DIRkR6xaHo+LQ7PbSwPOkq/06kzs4EW4FrgxfDjOnd/NsrZREQ+lTdiIJ+7Mo1fbzxAc4uu+9mTOntm9v3uXhm+L8QSd6/qgWwiIp9xT3E+FSfrWKuhdo/q7K6nl83sr80sz8xGnH9ENZmISBu3FmSQNjhZ99TuYZ29H8XXwr9+q9UyBy7v3jgiIu1LjI/jy0W5PLZ2H1Un68gcmhJ0pH6hszOKh9x9TJuHSkJEetyi6Xk0t7guP96DOjuj+FZHXyci0hMuGzmIG8em8ezGgxpq9xDNKESk1yktzufQiXOs+1BD7Z6gGYWI9DqzCjIYOSiJxRsOcNO4UUHH6fM6VRTuPibaQUREOispIY4vFeXy+LqPqT5Vx6hUDbWjKeKuJzP7TqvnX27zns7MFpHALJqeHxpqb9aZ2tHW0YxiUavn323z3pxuziIi0mlj0gZx/RUjWbzhAC0aakdVR0Vh7Ty/0GsRkR5VWpxP+fFzrN97JOgofVpHReHtPL/QaxGRHnXbxAxGhIfaEj0dDbOnhO+NbcCAVvfJNkDTIxEJVHJCPHdOy+EXb35CTW096UOSg47UJ0XconD3+Fb3yE4IPz//OrGnQoqItGdRcT5NLc7zGmpHzcXcuEhEJOZckT6YGWNG8OxGDbWjRUUhIr3ePTPy2X/0LG/vOxp0lD5JRSEivd7siZkMG5ioy49HiYpCRHq9lMR47pyWy5qdVRw5XR90nD5HRSEifUJpcR6Nzc4LGmp3OxWFiPQJY0cNoXj0CBZvOIC7htrdSUUhIn1G6Yw8PtFQu9upKESkzygpzGLogEQWb9Dd77qTikJE+oyUxHjumJbD6rIqjmqo3W1UFCLSp5QW59PQ3MKLWw4FHaXPiPmiMLObzGydmf3MzG4KOo+IxLarMoZQdNlwDbW7UVSLwsyeNLNqMytrs3yOme0xs71m9lAHq3HgNKGLEOq4NxHpUGlxPvuOnOHdj48FHaVPiPYWxVO0ucGRmcUDjwIlQAFQamYFZjbJzJa3eYwC1rl7CfA/gL+Lcl4R6QPmTs4iNSVBlx/vJlEtCndfC7St9GJgr7vvc/cG4FlgobvvcPd5bR7V7t4S/txxoN1rCJvZvWa2ycw21dTUROX3IyK9Q2ioncvKHVUcP9MQdJxeL4gZRQ7Q+ti18vCyCzKzO8zs58C/Az9t7+vc/TF3L3L3ovT09G4LKyK906LiPBqaW3hhi/ZYX6ogiuJCt1Btd+Lk7i+6+zfd/W53fz16sUSkLxmfmcq0/GEaaneDIIqiHMhr9ToXqAggh4j0caXF+XxUc4aNnxwPOkqvFkRRbASuNLMxZpYELAKWBpBDRPq4eZOzGaKh9iWL9uGxi4G3gXFmVm5mX3f3JuB+YDWwC3jO3XdGM4eI9E8DkuL5o6tzeGlHJSfOaqjdVdE+6qnU3bPcPdHdc939ifDyFe5+lbtf4e4PRzODiPRvi6bn09CkM7UvRcyfmS0icikKslOZmqeh9qVQUYhIn3dPcT4fVp9mywENtbtCRSEifd68KVkMTk7gV+/q8uNdoaIQkT5vYFICC6dms3x7BSfPNgYdp9dRUYhIv1BanE99Uwu/3aqh9sVSUYhIv1CYM5TJuUM11O4CFYWI9BulxfnsrqrlvYMngo7Sq6goRKTfmD8lm0FJ8Sx+V2dqXwwVhYj0G4OTE1gwNYdl2ys4VaehdmepKESkX7mnOJ+6xhaWvKehdmepKESkX5mUO5TCnFSeeVdD7c5SUYhIv3N+qL2t/GTQUXoFFYWI9DsLpmQzUEPtTlNRiEi/MyQlkQVTslm6rYJaDbU7pKIQkX6ptDifc43NLNmqG2x2REUhIv3S5NyhFGSl8isNtTukohCRfsnMKJ2Rz/uVp9hxSEPtSFQUItJvLZyazYDEeN1TuwMqChHpt1JTEpk/JYslWys4Xd8UdJyYpaIQkX6ttDifsw3NLNVQu10qChHp16bmDWN85hDtfopARSEi/ZqZcc+MfHYcOskOnal9QSoKEen3Fk7NISUxjsUbtVVxISoKEen3hg5IZN7kbJa8d4gzGmr/ARWFiAihofaZhmaWbdNQuy0VhYgIMC1/GOMyhrB448Ggo8QcFYWICOEztYvz2HbwBDsrNNRuTUUhIhL2R1fnkpwQx7MbtFXRmopCRCRs6MBE5k7K4rfvHeJsg4ba56koRERaKZ2RT219E8u3VwYdJWaoKEREWim6bDhjRw3WmdqtqChERFoJDbXzee/ACXZVngo6TkxQUYiItHHH1TkkJcTxrLYqgF5QFGb2OTP7mZk9bmZvBZ1HRPq+4YOSuL0wkxffO8S5huag4wQuqkVhZk+aWbWZlbVZPsfM9pjZXjN7KNI63H2du98HLAd+Gc28IiLnlRbnU1vXpDO1if4WxVPAnNYLzCweeBQoAQqAUjMrMLNJZra8zWNUq4/eAyyOcl4REQCKx4xgfOYQ/va3ZTz62l4am1uCjhSYqBaFu68FjrVZXAzsdfd97t4APAssdPcd7j6vzaMawMzygZPu3u5kyczuNbNNZrappqYmWr8lEeknzIz/+MYMZhVk8A+r9/DFR9/st2dsBzGjyAFan/ZYHl4WydeBX0T6And/zN2L3L0oPT39EiOKiEDa4GQe/co0/vUr0zh8qp6FP32TR9bsob6pf80tgigKu8Ayj/QBd/+eu2uQLSKBKJmUxcvfnsmCKdn85NW9zP/n9Ww9eCLoWD0miKIoB/Javc4FNC0SkZg2fFASj9w9lSe/WsSpc03c8S9v8oMVu6hr7PtbF0EUxUbgSjMbY2ZJwCJgaQA5REQu2s3jM1jz4Ezunp7Hz9fuo+TH69j4SdtRbN8S7cNjFwNvA+PMrNzMvu7uTcD9wGpgF/Ccu++MZg4Rke6UmpLID+6YzDPfmEFjcwt3/fxtvr90Z5+9O565RxwP9EpFRUW+adOmoGOISD9wpr6Jf1i9h1++/Qk5wwbwf+6czA1j04KO1SVmttndi9ouj/kzs0VEYtmg5AS+v2Aiz33zOpLi4/jK4+/y3Re3c6quMeho3UZFISLSDaaPHsGKBz7HNz9/Ob/eeJDbHlnLq7sPBx2rW6goRES6SUpiPN8tmcB//tcbSB2QwNee2sSDv97KibMNQUe7JCoKEZFuNiVvGMv+4kb+8pYrWbqtglsfWcuqst57IyQVhYhIFCQnxPPgrKtYev+NZKQmc99/bOFbz2yhprY+6GgXTUUhIhJFBdmp/PZbN/DfZ4/j5fcPc9s/vcGSrYfoTUecqihERKIsMT6Ob31hLCseuJHRaYN44Nmt/NnTm6g6WRd0tE5RUYiI9JCxo4bw/H3X87dzJ7B+7xFm/dMbPLfxYMxvXagoRER6UHyc8Y3PXc6qB2ZSkJXKd17Yzp8+uYHy42eDjtYuFYWISABGpw1i8Z9dy//+YiFb9h9n9j+t5d/f/oSWltjbulBRiIgEJC7O+JNrL2P1t2cy7bLh/K8lO1n0b+/wyZEzQUf7DBWFiEjAcocP5OmvFfN/vzSZXZWnmPPjtfzb2n00x8jWhYpCRCQGmBl3FeXxuwc/z41j03h4xS7u/Ne3+PBwbdDRVBQiIrEkIzWFf/vTIn68aCr7j55h7k/W89NXP6SxuSWwTCoKEZEYY2YsnJrDyw9+nlkTM/jHNR+w8KdvsrPiZCB5VBQiIjEqbXAyj94zjZ/98TSqa+tZ+NM3eWTNHuqbevb2qyoKEZEYN6cwi989OJMFU7P5yat7mf/P69l68ESPfX8VhYhILzBsYBKP3DWVX3x1OrV1TdzxL2/ygxW7qGuM/taFikJEpBf5wvhRrP72TO6ens/P1+6j5Mfr2PDxsah+TxWFiEgvk5qSyA/umMQz35hBU0sLd/38bb63pIwz9U1R+X4qChGRXuqGsWmsemAmX71+NE+/s5/ZP1rLB1E470JFISLSiw1KTuD7Cyby3Dev4/L0weQMG9Dt3yOh29coIiI9bvroETz9teKorFtbFCIiEpGKQkREIlJRiIhIRCoKERGJSEUhIiIRqShERCQiFYWIiESkohARkYjMPTbuydqdzKwG2N/Fj6cBR7oxTrT1przKGj29KW9vygq9K++lZr3M3dPbLuyTRXEpzGyTuxcFnaOzelNeZY2e3pS3N2WF3pU3Wlm160lERCJSUYiISEQqij/0WNABLlJvyqus0dOb8vamrNC78kYlq2YUIiISkbYoREQkIhWFiIhEpKIIM7MnzazazMqCztIRM8szs9fMbJeZ7TSzB4LOFImZpZjZBjPbFs77d0Fn6oiZxZvZe2a2POgsHTGzT8xsh5ltNbNNQeeJxMyGmdnzZrY7/Pf3uqAztcfMxoX/TM8/TpnZXwWdqz1m9u3wv68yM1tsZindtm7NKELMbCZwGnja3QuDzhOJmWUBWe6+xcyGAJuBL7r7+wFHuyAzM2CQu582s0RgPfCAu78TcLR2mdmDQBGQ6u7zgs4TiZl9AhS5e8yfFGZmvwTWufvjZpYEDHT3EwHH6pCZxQOHgBnu3tWTeaPGzHII/bsqcPdzZvYcsMLdn+qO9WuLIszd1wLHgs7RGe5e6e5bws9rgV1ATrCp2uchp8MvE8OPmP0JxcxygbnA40Fn6UvMLBWYCTwB4O4NvaEkwm4BPorFkmglARhgZgnAQKCiu1asoujlzGw0cDXwbsBRIgrvytkKVAMvu3ss5/0R8B2gJeAcneXAGjPbbGb3Bh0mgsuBGuAX4d16j5vZoKBDddIiYHHQIdrj7oeAfwQOAJXASXdf013rV1H0YmY2GHgB+Ct3PxV0nkjcvdndpwK5QLGZxeTuPTObB1S7++ags1yEG9x9GlACfCu8GzUWJQDTgH9196uBM8BDwUbqWHgX2QLgN0FnaY+ZDQcWAmOAbGCQmf1xd61fRdFLhff1vwA84+4vBp2ns8K7Gl4H5gSbpF03AAvC+/2fBW42s/8INlJk7l4R/rUa+E+gONhE7SoHylttTT5PqDhiXQmwxd0PBx0kgluBj929xt0bgReB67tr5SqKXig8HH4C2OXujwSdpyNmlm5mw8LPBxD6S7070FDtcPfvunuuu48mtLvhVXfvtp/MupuZDQof0EB4N85tQEweuefuVcBBMxsXXnQLEJMHYLRRSgzvdgo7AFxrZgPD/z/cQmh22S1UFGFmthh4GxhnZuVm9vWgM0VwA/AnhH7aPX/o3u1Bh4ogC3jNzLYDGwnNKGL+sNNeIgNYb2bbgA3AS+6+KuBMkfwF8Ez478JU4O+DjROZmQ0EZhH6CT1mhbfSnge2ADsI/d/ebZfz0OGxIiISkbYoREQkIhWFiIhEpKIQEZGIVBQiIhKRikJERCJSUYhEYGanw7+ONrN7unnd/7PN67e6c/0i3UVFIdI5o4GLKorwFUcj+UxRuHu3nUkr0p1UFCKd80Pgc+GTG78dvsjhP5jZRjPbbmbfBDCzm8L3CvkVoROfMLPfhi/Yt/P8RfvM7IeErvS51cyeCS87v/Vi4XWXhe8zcXerdb/e6n4Oz4TPwhWJqoSgA4j0Eg8Bf33+3hTh//BPuvt0M0sG3jSz81frLAYK3f3j8Ouvufux8OVLNprZC+7+kJndH75QYlt3EDpreQqQFv7M2vB7VwMTCV1C+k1CZ+mv7+7frEhr2qIQ6ZrbgD8NXzr9XWAkcGX4vQ2tSgLgL8OX2HgHyGv1de25EVgcvuLuYeANYHqrdZe7ewuwldAuMZGo0haFSNcY8BfuvvozC81uInT57NavbwWuc/ezZvY60NEtKiPtTqpv9bwZ/RuWHqAtCpHOqQWGtHq9Gvjz8OXeMbOr2rkJz1DgeLgkxgPXtnqv8fzn21gL3B2eg6QTuivchm75XYh0gX4aEemc7UBTeBfSU8CPCe322RIeKNcAX7zA51YB94WvlrqH0O6n8x4DtpvZFnf/Sqvl/wlcB2wjdPe677h7VbhoRHqcrh4rIiIRadeTiIhEpKIQEZGIVBQiIhKRikJERCJSUYiISEQqChERiUhFISIiEf1/KX8ND8g2b18AAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"import matplotlib.pyplot as plt\n",
"\n",
"# number of iterations\n",
"N = len(x)\n",
"\n",
"# iteration\n",
"iters = range(0,N)\n",
"\n",
"plt.figure\n",
"for i in range(0,len(x0)):\n",
" plt.plot(iters,[x[j][i] for j in range(0,N)],label=\"x\"+str(i))\n",
"plt.xlabel(\"Iteration\")\n",
"plt.ylabel(\"Primal Variables\")\n",
"plt.legend()\n",
"plt.show()\n",
"\n",
"plt.figure\n",
"for i in range(0,len(u[0])):\n",
" plt.plot(iters,[u[j][i] for j in range(0,N)],label=\"u\"+str(i))\n",
"for i in range(0,len(v[0])):\n",
" plt.plot(iters,[v[j][i] for j in range(0,N)],label=\"v\"+str(i))\n",
"plt.xlabel(\"Iteration\")\n",
"plt.ylabel(\"Dual Variables\")\n",
"plt.legend()\n",
"plt.show()\n",
"\n",
"plt.figure\n",
"plt.semilogy(iters,mu)\n",
"plt.xlabel(\"Iteration\")\n",
"plt.ylabel(\"Barrier Penalty\")\n",
"plt.show()\n",
"\n",
"plt.figure\n",
"plt.semilogy(range(1,N),E)\n",
"plt.xlabel(\"Iteration\")\n",
"plt.ylabel(\"Error\")\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"id": "ce1653ce",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.3.3 Problem 3: Nonconvex](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.3.3-Problem-3:-Nonconvex)",
"section": "4.9.3.3 Problem 3: Nonconvex"
}
},
"source": [
"### 4.9.3.3 Problem 3: Nonconvex"
]
},
{
"cell_type": "code",
"execution_count": 8,
"id": "adaa8455",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.3.3 Problem 3: Nonconvex](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.3.3-Problem-3:-Nonconvex)",
"section": "4.9.3.3 Problem 3: Nonconvex"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"\n",
"*** Barrier Subproblem 0 ***\n",
"mu = 10.0\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 4.0000e+00 \t3.1623e+00 \t 9.00e+00 \t 6.17e+00 \t 8.25e+00 \t 8.06e+00 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 1 ***\n",
"mu = 2.0\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 4.0013e+01 \t4.4202e-10 \t 2.80e+01 \t 3.79e+00 \t 1.52e+00 \t 3.22e+00 \t 0.00e+00 \t 0.00e+00\n",
"1 \t 1.6354e+01 \t1.3323e-15 \t 6.22e+00 \t 9.26e-01 \t 2.49e-01 \t 1.35e+00 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 2 ***\n",
"mu = 0.4\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 1.2029e+01 \t5.9350e-11 \t 2.31e+00 \t 3.94e-01 \t 1.93e-01 \t 6.76e-01 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 3 ***\n",
"mu = 0.08000000000000002\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 1.0363e+01 \t5.0465e-11 \t 4.67e-01 \t 7.00e-02 \t 6.98e-02 \t 1.66e-01 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 4 ***\n",
"mu = 0.016000000000000004\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 1.0077e+01 \t8.9693e-12 \t 7.01e-02 \t 1.52e-02 \t 5.71e-03 \t 2.39e-02 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 5 ***\n",
"mu = 0.0020238577025077633\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 1.0016e+01 \t4.8606e-13 \t 1.42e-02 \t 3.45e-03 \t 7.38e-04 \t 4.77e-03 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 6 ***\n",
"mu = 9.104790579399288e-05\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 1.0002e+01 \t4.5590e-13 \t 1.94e-03 \t 4.78e-04 \t 9.46e-05 \t 6.54e-04 \t 0.00e+00 \t 0.00e+00\n",
"1 \t 1.0000e+01 \t6.1284e-14 \t 2.94e-07 \t 6.48e-09 \t 4.36e-07 \t 8.52e-07 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 7 ***\n",
"mu = 8.687702517211205e-07\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 1.0000e+01 \t4.4409e-16 \t 9.02e-05 \t 2.23e-05 \t 4.29e-06 \t 3.04e-05 \t 0.00e+00 \t 0.00e+00\n",
"1 \t 1.0000e+01 \t2.6645e-15 \t 1.67e-08 \t 1.36e-11 \t 1.69e-08 \t 2.21e-08 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 8 ***\n",
"mu = 1e-09\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 1.0000e+01 \t1.1102e-16 \t 8.68e-07 \t 2.15e-07 \t 4.23e-08 \t 2.92e-07 \t 0.00e+00 \t 0.00e+00\n",
"1 \t 1.0000e+01 \t0.0000e+00 \t 1.36e-09 \t 1.33e-15 \t 3.33e-10 \t 1.60e-09 \t 0.00e+00 \t 0.00e+00\n"
]
}
],
"source": [
"f = lambda x: x[0] + 2*x[1] + x[2]**2\n",
"\n",
"def c(x):\n",
" rhs = np.zeros(2)\n",
" rhs[0] = x[0] + x[1] - 1\n",
" rhs[1] = x[2] - x[1] - 3\n",
" return rhs\n",
"\n",
"# Indices of variables with lower bound of zero\n",
"vb = [1,2]\n",
"\n",
"x0 = np.ones(3)\n",
"u0 = np.ones(2)\n",
"v0 = np.ones(2)\n",
"\n",
"## Test barrier subproblem\n",
"# xtest, vtest, utest, Etest = barrier_subproblem(x0,v0,u0,f,c,vb,1E-1,1E-10,max_iter=10,verbose=True)\n",
"\n",
"##\n",
"x, v, u, mu, E = interior_point(x0,f,c,vb)"
]
},
{
"cell_type": "code",
"execution_count": 9,
"id": "5b06a941",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.3.3 Problem 3: Nonconvex](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.3.3-Problem-3:-Nonconvex)",
"section": "4.9.3.3 Problem 3: Nonconvex"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYAAAAEGCAYAAABsLkJ6AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAAAzFElEQVR4nO3dd3xU55Xw8d8ZFQRINCGqJCTRe7HAYAzG3Y4dt8SJ47ZeF7kktpM3iUuyu1m/ye6b3c1m0xzHuIG74xanOC7rhmFEkTGmGLCxECCLIpok1KU57x8zQhKojDR35o405/v5zGdm7tx57mGAe+7z3HvPI6qKMcaY2ONxOwBjjDHusARgjDExyhKAMcbEKEsAxhgToywBGGNMjIp3O4CuGDp0qGZlZbkdhjHG9CgfffTRQVVNO3F5j0oAWVlZFBQUuB2GMcb0KCKyq63lNgRkjDExyhKAMcbEKEsAxhgTo3rUOQBjjAm3+vp6iouLqampcTuULktKSiI9PZ2EhISg1rcEYIwxLRQXF5OSkkJWVhYi4nY4QVNVDh06RHFxMdnZ2UF9x9UhIBEZJCIvicg2EdkqIgvcjMcYY2pqakhNTe1RO38AESE1NbVLPRe3ewC/Bt5Q1a+LSCLQz+V4jDGmx+38m3Q1btcSgIgMABYDNwCoah1Q51Y8kbB+/3o84mHWsFluh2KMMa4OAeUApcATIvKxiDwqIv1PXElE8kSkQEQKSktLIx+lg3688sfc/d7dVNVXuR2KMaaHWb58OePHj2f8+PEsX77ckTbdTADxwBzgIVWdDVQC9524kqouVdVcVc1NSzvpTuYeY0/5HoqPFXO45jAvbH/B7XCMMT3I4cOHeeCBB1izZg1r167lgQce4MiRIyG362YCKAaKVXVN4P1L+BNCr+Qt8QIwbtA4ntj8hPUCjDFtWrduHTNmzKCmpobKykqmTp3Kgw8+yLnnnsuQIUMYPHgw5557Lm+88UbI23LtHICq7hORPSIyUVW3A2cDn7oVT7itKlnF6OTR/Otp/8q1r1/Lc9ue46bpN7kdljGmAw/8ZQuflpQ72uaUUQP4yVentvv53LlzueSSS/inf/onqqurufbaa0lISCAjI+P4Ounp6Xz55Zchx+L2ncB3As+IyEZgFvDv7oYTHvW+etbuW8uCUQuYmTaThaMXsmzLMusFGGPa9C//8i+8/fbbFBQUcM8999DW3O1OXKnk6mWgqroByHUzhkjYVLqJyvpKTht1GgDfnvltrn79ap7d9iw3T7/Z5eiMMe3p6Eg9nA4fPsyxY8eor6+npqaG9PR03n///eOfFxcXs2TJkpC343YPICZ4S7x4xMO8EfMAmJ42nUWjF7FsyzIq6ytdjs4YE23y8vL46U9/yjXXXMO9997L+eefz1tvvcWRI0c4cuQIb731Fueff37I23H7RrCYkF+Sz7Sh0xjYZ+DxZbfPvJ2rX7+a57Y9Z70AY8xxTz75JPHx8Vx99dU0NjZy2mmnsWHDBv75n/+ZuXPnAv4hoiFDhoS8LUsAYVZWW8bmQ5vJm5HXavn0tOksTl/Msi3LuGriVSQnJrsUoTEmmlx//fVcf/31AMTFxbFmzZrjn914442ObsuGgMJszd41+NR3fPy/pTtm3kFZbRnPbnvWhciMMbHOEkCYeUu8JCckM23otJM+mzp0KkvSl7B8y3Iq6ipciM4YE8ssAYSRqpJfks+8EfNI8LRdn/u2WbdRXlfOs1utF2CMiSxLAGG0q3wXJZUlLBy9sN11pqZOZUnGEpZ/ar0AY0xkWQIIo6byDwtGdTzNwR0z76CiroKntz4dibCMMQawBBBW+SX5ZKRkkJGS0eF6k1Mnc2bGmTy15SnK65y97dwYY9pjCSBM6hv95R/auvqnLXfMuoOK+gqe+fSZMEdmjOmJLrjgAgYNGsTFF1/sWJuWAMJkQ+kGqhqqOh3+aTJpyCTOzjybpz61XoAx5mQ//OEPeeqppxxt0xJAmOSX5BMnccfLPwTj9pm3U1FfwVOfOvuXbIzpOdoqB71582bOPvtsUlJSHN2W3QkcJt4SLzPSZpCSGPxf2MQhEzkn8xye/vRprp18bavSEcYYF/z9Pti3ydk2R0yHC3/e7sdtlYOeNu3k+4icYD2AMDhSc4RPD30a9PBPS7fNvI1j9cesF2BMDDuxHHS4WA8gDNbsXYOiQZ8AbmnikImcO+Zcnt76NNdNuc56Aca4qYMj9XA6sRx0//4nTZfuCOsBhIG3xEtKYgpTU7tXS/z2mbdTWV/J8i3OTPxsjOlZTiwHHS6uJgARKRKRTSKyQUQK3IzFKaqKt8TL/JHzifd0r4M1fvB4zhtzHs9sfYajNUedDdAYE9ValoO+7777WLduHe+++y6LFi3iyiuv5J133iE9PZ0333wz5G1FwxDQmap60O0gnLKzbCf7q/Z3a/y/pdtn3s7bu97myU+f5K45dzkUnTEm2rVXDvqss85yfFs2BOSwpvIP3Rn/b2nc4HGcn3U+z2x9hiM1R5wIzRhjWnE7ASjwloh8JCJ5ba0gInkiUiAiBaWlpREOr+u8JV6yBmQxOnl0yG3dNvM2qhuq7VyAMSYs3E4AC1V1DnAh8G0RWXziCqq6VFVzVTU3LS0t8hF2QV1jHQX7C0Ie/mkydtBYLsi6gGe3PcvhmsOOtGmMMU1cTQCqWhJ4PgC8CgR/22wU2nBgA9UN1SEP/7R028zbqGmosV6AMcZxriUAEekvIilNr4HzgM1uxeMEb4mXeIln7oi5jrWZMyiHC7Mv5Lltz1kvwBjjKDd7AMOBlSLyCbAW+JuqvuFiPCHzlniZOWwm/ROcvWnj1pm3UttYy7LNyxxt1xgT21xLAKpaqKozA4+pqvpvbsXihEPVh9h6eKujwz9Ncgb6ewHPb3+eQ9WHHG/fGBPdNmzYwIIFC5g6dSozZszghRdecKRdt08C9xqr964GQr/8sz23zbjN3wvYsiws7Rtjole/fv148skn2bJlC2+88Qbf/e53OXr0aMjtWgJwiLfEy8A+A5k8ZHJY2s8amMVF2Rfx/LbnOVjda+6bM8acoK1y0HV1dYwfPx6AUaNGMWzYMJy4LD4a7gTu8VSV/JJ85o+cT5wnLmzbyZuRx992/o0nNj/BD+f+MGzbMcb4/cfa/2Db4W2OtjlpyCTundd+fZ/OykGvXbuWuro6xo4dG3Is1gNwwI6jOyitLg3b8E+TrIFZXJxzMX/c/kfrBRjTi7VXDnrv3r1cd911PPHEE3g8oe++rQfggKbyDwtGOnMDWEdunXErfyv8G49vfpx75oavTrgxhg6P1MOprXLQ5eXlXHTRRfzsZz9j/vz5jmzHegAOyC/JJ3tgNiOTR4Z9W5kDMrko5yL+uP2PlFZFf2kMY0zXnVgOuq6ujssvv5zrr7+eK6+80rHtWAIIUW1jLQX7C8I+/NPSbTNuo8HXwOObH4/YNo0xkdFWOejnn3+eFStWsGzZMmbNmsWsWbPYsGFDyNuyIaAQrd+/ntrG2ogmgIwBGXx17Fd58bMXuXHajaT1i+4aScaY4LVXDrppmZOsBxCi/JJ84j3x5A7Pjeh282bk0eBr4LHNj0V0u8aY3sMSQIi8JV7mDJtDv4R+Ed1uRkoGl4y9hBe3v8j+yv0R3bYxpnewBBCCg9UH2X5ku2Pln7sqb0YePvVZL8AYh6mq2yF0S1fjtgQQgvySfCB85R86k56SzqXjLuWlz16yXoAxDklKSuLQoUM9LgmoKocOHSIpKSno79hJ4BB4S7wM7jOYSUMmuRbDLTNu4bUdr/Hopkf58fwfuxaHMb1Feno6xcXFjpRaiLSkpCTS09ODXt8SQDf51Ocv/zBqPh5xryM1Onk0l467lJc/f5mbpt/EiP4jXIvFmN4gISGB7Oxst8OICBsC6qbPj3zOoZpDrg3/tJQ3Iw9FeXTTo26HYozpQSwBdFMkyz90ZlTyKC4fdzkvf/4y+yr3uR2OMaaHcD0BiEiciHwsIn91O5au8JZ4GTdoHMP7D3c7FABumX4LAI9sfMTlSIwxPYXrCQC4G9jqdhBdUd1Qzfr96127/LMtI5NHcsW4K3hlxyuUHCtxOxxjTA/gagIQkXTgIqBHDV6v37+eOl9dVIz/t3TLjFsQhEc2WS/AGNM5t3sAvwLuAXztrSAieSJSICIF0XJZlrfES6InkVOGn+J2KK2M6D+CK8ZfwZ8+/5P1AowxnXItAYjIxcABVf2oo/VUdamq5qpqblpadBQ985Z4mTN8Dn3j+7odyklunn4zIsLSjUvdDsUYE+Xc7AEsBC4RkSLgeeAsEXnaxXiCcqDqADuO7oi64Z8mI/qP4Gvjv8ZrO16juKLY7XCMMVHMtQSgqverarqqZgFXAe+q6rVuxRMst8s/BKOpF2DnAowxHXH7HECP4y3xkpqUyvjB490OpV3D+w/n6xO+zp93/Jk9FXvcDscYE6WiIgGo6vuqerHbcXSmqfzDglELXC3/EIybp9+MRzx2X4Axpl3RvReLMtsOb+NI7ZGoHv5pMqzfMK6ceCV//uLP7Cm3XoAx5mSWALqgqfzD/JHzXY4kODdNu4l4TzxLN9kVQcaYk1kC6IL8knwmDJ7QY+bgTeuXxpUTruQvX/yF3eW73Q7HGBNlLAEEqaq+ivUH1veI4Z+Wbpx2I/GeeB7e+LDboRhjoowlgCAV7C+gwdcQVfV/gpHWL41vTPwGfy38K7vKd7kdjjEminSaAETkP0VkgIgkiMg7InJQRKL+en2n5Zfk0yeuD3OGzXE7lC67cdqNJHoS7e5gY0wrwfQAzlPVcuBioBiYAPwwrFFFIW+Jl1OGn0JSfPDzbUaLoX2HHu8FFJUVuR2OMSZKBJMAEgLPXwGeU9XDYYwnKu2r3EdhWWGPG/9v6R+n/SOJnkQ7F2CMOS6YBPAXEdkG5ALviEgaUBPesKJLTyj/0JmhfYdy1aSreH3n6+ws2+l2OMaYKNBpAlDV+4AFQK6q1gNVwKXhDiyaeEu8pPVNY9ygcW6HEpIbpt5An7g+1gswxgDBnQTuB3wbeCiwaBT+3kBMaPQ1kr/XX/5BRNwOJySpfVO5auJV/H3n3/lo/0c0+BrcDskY46L4INZ5AvgIaBr/KAZeBHrUHL7dtfXwVspqy3r08E9LN0y7gRc/e5Eb3riBBE8CWQOzGDtwLGMHNT8yUjJI8CR03pgxpkcLJgGMVdVvisi3AFS1Wnr6oXAX9LTyD50ZkjSEly95mYL9BXxx9Au+OPoFmw9u5s2iN1EUgHhPPFkDspqTwsCxjBs0jowBlhiM6U2CSQB1ItIX/HsHERkL1IY1qijiLfEyechkUvumuh2KY0Ylj+KS5EtaLatuqGZn2c7jSeGLo1/w6aFPeavorZMSQ87AHMYNGkfOIP9zZkomCXGWGIzpaYJJAD8B3gAyROQZ/DN53RDOoKJFZX0lnxz4hOunXu92KGHXN74vU1KnMCV1Sqvl1Q3VFJUVsePoDgrLCtlxdAfbDm/j7V1vNycGiWfMgDHHE0LOoBzGDRzHmAFjLDEYE8U6TQCq+raIrAfmAwLcraoHQ92wiCQBK4A+gTheUtWfhNquk9btW0eDNvSa8f/u6Bvfl8mpk5mcOrnV8pqGGorKA4nhqD8xbD+8nXd2v4NPfYA/MWQOyGw1lDR20FjGDBhDYlyiG38cY0wL7SYAETmx5sHewHOmiGSq6voQt10LnKWqx0QkAVgpIn9X1dUhtusYb4mXpLgkZg+b7XYoUScpPolJQyYxacikVsubEkPLoaTPjnzWKjHESRyZAzLJHpBNSmIKfeL6kBiXSGJcYvNrT/P7hLgE/3LPCesE1mu1TmBZDJ2mMqbbOuoB/HcHnylwVigbVlUFjgXeJgQeGkqbTssvySd3RK5zR6uHvgDxwJBsZ9qLQu0lhtrGWorK/ImhaTipqKyIyoZK6hrrmh++OkfiaEoWLRNLgifh5GTjSSQhLgGPePDgQUQQBI80vxaRkz5rmhHOI56T1j/pdVMbbbw+sZ22EpfQvKzp81bLAq/bS3rBfqfl59HAknhrC0YuYHj/4Y622W4CUNUzHd1SG0QkDv8lpuOAB1V1TRvr5AF5AJmZmeEO6bgvj31JUXkR35j4DWcaLN8Lj5wFfVLgzvUQH1tDIH3i+jBxyEQmDpnY4XqqSr2vntrGWmoba6lv9L+u8zUnidrG2rbXCSSQpnVart/y+3WNddQ21FJRV3H8vaL41Ieqtv0aRVXxEVje8nXTZ+rDhw8UfPiO93iMccJD5zwUuQTQJDBWfwdwOv4j9A+BP6hqyOUgVLURmCUig4BXRWSaqm4+YZ2lwFKA3NzciPUQHC3/oAp/vhNqK6DmKGx4GnJvDL3dXkhEjh+hp5Didjgha5Ug6DzBNH3n+Pc5+XV7n7fcphPfcVM0xBBtUpOcvxIxmKuAngQqgN8G3n8LeAq40qkgVPWoiLwPXABs7mT1iPCWeBnebzg5A3NCb2z9ctjxNlz4n7DpRVjx3zDrGojvE3rbJqo1DQUhEEec2+EY00owxeAmqupNqvpe4JGHvyR0SEQkLXDkT+A+g3OAbaG264RGXyOr967mtFGnhT4OeaQI3vwxZJ8Bc2+BJfdDeTF8/LQjsRpjTHcFkwA+FpHjt8GKyKnAKge2PRJ4T0Q2AuuAt1U1KspLbDm0hYq6itCHf3yN8Ort/hO/l/0ePB4YexZknAof/jc0xMz9dMaYKNTRZaCb8I/5JwDXi8juwPsxwKehblhVNwJReX2lt8SLIJw68tTQGlr9e9jthcsegoHp/mUisOQ+eOpyWP8kzLsl9ICNMaYbOjoHcHHEoogy3hIvU1KnMDhpcPcbObAV3vkpTLwIZn6r9Wc5Z0LGfPjwlzD7OkjoebOMGWN6vnaHgFR1V8sHUI2/B9D06JUq6irYWLoxtOGfxnp49Vbokwxf/bX/qL8lETjzfqgogY+fCi1gY4zppmDmA7hERD4HdgIfAEXA38Mcl2vW7ltLozayYNSC7jey4hew9xO4+FeQnNb2OtlnQOZp/nMB9TE1wZoxJkoEcxL4p/jrAH2mqtnA2ThzEjgq5Zfk0ze+L7PSZnWvgS/Xw4r/ghnfhCmXtL9e07mAir3+y0SNMSbCgkkA9ap6CPCIiEdV3wNmhTcs93hLvMwbMa97VSzrq+HV2yB5uP+a/85kL4YxC/3nAuqru749Y4wJQTAJ4KiIJOOv3PmMiPwa6JVzCe4p38Oeij3dH/5592dwcDtc9iD0HdT5+iL++wKO7YOPrBdgjImsYBLApfhPAH8P/7wAXwBfDWdQbsnfG0L5h6KVkP8gzL3Zf61/sLIXwZjTYaX1AowxkdVpAlDVSlVtVNUGVV2uqr8JDAn1Ot4SLyP7jyRrQFbXvlhbAX+63V/l89z/2/UNn3k/HNsPBU90/bvGGNNN7SYAEVkZeK4QkfIWjwoRKY9ciJHR4Gtgzd413Sv/8OaPoKwYLvsDJPbv+sazToesRbDyf6CuquvfN8aYbujoPoDTA88pqjqgxSNFVQdELsTI2HxwM8fqj3V9+OezN/139J52F2SGcOfwkvuh8gB8ZL0AY0xkdDgEJCIeEYmK6pzh5i3x4hFP18o/VB32l3keNhXO/FFoAWQt9F8VtPJX1gswxkREhwlAVX3AJyISuZlYXOIt8TItdRoD+wwM/kt/+74/CVz+B2dKOy/5kb8XUPBY6G0ZY0wngrkKaCSwRUTeEZE/Nz3CHVgkldeVs+ngpq5d/rnpJdjyiv9mrpEznAlkzALIWRLoBVQ606YxxrQjmAlhHgh7FC5bs3cNPvUFP/5fvtd/9J8+FxZ+19lgltwPj58P6x6DhXc527YxxrTQaQJQ1Q8iEYibvCVe+if0Z3ra9M5XbpresaHWf9VPXDA5tAsy5/urha76Ncy9qXtXFRljTBCCKQY3X0TWicgxEakTkcbedBmoquL9MlD+wRNE+Yem6R3PfQCGjgtPUGf+CKoOwtpHwtO+McYQ3DmA3+GfB/hzoC9wc2BZSEQkQ0TeE5GtIrJFRO4Otc3u2F2xm5LKkuCGf45P77jYP71juGTMg7Fng/c3UHssfNsxxsS0YBIAqroDiAvcEfwEsMSBbTcA31fVyfirjX5bRKY40G6XeEu8QBDlH3w++NMd/ukdLw1M7xhOS+6HqkOwznoBxpjwCGYvViUiicAGEflPEfkeEPLAtKruVdX1gdcVwFZgdKjtdpW3xMvo5NFkpGR0vOLq38OuVXDhf8CgTtZ1QsZcGHcOrPqNv9SEMcY4rKNSELmBl9cF1vsOUAlkAF9zMggRycI/P/CaNj7LE5ECESkoLS11crPU++pZu3dt5+UfDmyDd/5v29M7htOSH0H1YVi7NHLbNMbEjI56AI8EZgK7CchR1XJVfUBV/09gSMgRgVLTLwPfVdWTTi6r6lJVzVXV3LS0dmbX6qaNpRupaqjqePinsR5ezWt/esdwSj8Fxp8H3t9aL8AY47iOagHNxj8xfCPwkohsEJF7RWSMUxsXkQT8O/9nVPUVp9oNlrfES5zEMW/kvPZXCmZ6x3A64z6oPgJrHo78to0xvVpnpSC2B476pwD/AAwC3hWRkKeEFP+Yy2PAVlX9ZajtdUd+ST7Th05nQGI7te2Cnd4xnNJPgfHn+3sBNb3m6ltjTBQI6lIWEfEAw4Dh+E8AOzEYvxD/+YWzAr2LDSLyFQfaDUpZbRmbD25uf/inq9M7htOS+6DmqPUCjDGO6vA2VhFZhP8egMuAzcDzwPdUtSzUDavqSiCCA+qtrd67GkXbr//TNL3jta8EN71jOI2eAxMuhPzfwal5kNSFgnXGGNOOjq4C2gP8HP/lmbNV9TxVfdyJnX80yC/JJyUhhWlDp538YcvpHcedHfng2rLkXusFGGMc1VEP4HRV3RWxSCJIVVlVsopTR55KvOeEnyDU6R3DZdRsmPgVfy9gXp77vRJjTI/X0VVAvXLnD7CzfCf7Kve1PfwT6vSO4bTkPqgpgzV/cDsSY0wvEOZ6BtEpvyQfaKP8g1PTO4bLyJkw6WLI/z1UH3U7GmNMDxeTCcBb4iUzJZP0lPTmhU5O7xhOZ9wLtWWw+iG3IzHG9HDtngMQkd8C2t7nqtojZyupa6xj3b51XDL2hOv6m6Z3vOYlZ6Z3DJeRM/y9gNW/h/m3Qd/BbkdkjOmhOjoJXBCxKCLok9JPqG6obj38s/ll//SOZ/2Tc9M7htOS+2HbX/1DQWf92O1ojDE9VLsJQFWXRzKQSDle/mFEoPxDxT7/0f/oXFj4PXeDC9aIaTD5Ev/J4Pm3Q78hbkdkjOmBgpkRLE1EfiEir4vIu02PSAQXDt4SLzPTZpKcmNw8vWN9DVz+sPPTO4bTGfdCbbl/KMgYY7ohmJPAz+C/GSwb/wTxRcC6MMYUNodrDrP10Nbmyz/XPwmfvxXe6R3DZcQ0mHIprP6D/9yFMcZ0UTAJIFVVHwPqVfUDVb0R/wxePc6avWtQlIWjFgamd/xR+Kd3DKcz7oO6Cv/NYcYY00XBJID6wPNeEblIRGYD6R19IVp5S7wMSBzAlMGTIju9Y7gMnwJTLvOXh7BegDGmi4LZ8/1MRAYC3wd+ADwK9JCzpc1UFW+Jl/kj5xO39mH/9I4X/Dwy0zuG05L7oK7SXy7aGGO6oNOznqr618DLMuDM8IYTPoVlhRyoOsBpKTnw+gP+ujqzrnY7rNANmwxTL/dPG7ngO9A/1e2IjDE9RDBXAWWLyC9F5BUR+XPTIxLBOWnVl/45bBYUPOfO9I7hdMa9gV7Ab9yOxBjTgwRz3eOf8M/c9RfAF9Zowsi710tW/ABG7d0E33gKkoe5HZJzhk2CaVfA2kfgtDuh/1C3IzLG9ADBnAOoUdXfqOp7gauAPlDVD5zYuIg8LiIHRGSzE+21p7axlo/2ruO0wyXuTu8YTmfcC/VV1gswxgQtmATwaxH5iYgsEJE5TQ+Htr8MuMChttr1cclqanx1nKZ93Z/eMVzSJsL0r/t7AcecmLHTGNPbBTMENJ3A3L00DwFp4H1IVHWFiGSF2k5nXnzj34lPUOac94vePZHK4nv8dY28v4Hzfup2NI5RVRp8Sm2Dj7oGH7UNjYFnH7X1PuoaG6mt91Hb2PTeR219Y4v12/hei9f1jT58Cj5VfOrfngbeH38OxNH0+fH1aLle6+82f6/5O03rHm+Dprb8y6B1BcamZS2Xt1jU5ndavtET1mu3nRZf0laNuSMKQog6j16fy+IJaY62GUwCuBzIUdU6R7ccJBHJA/IAMjMzu9XGhJFncWD7e6xqmB3+7oab0ibAtK/Dukf9cxokO/uPJVQ19Y3sOHCMzw9U8Pn+YxSWVlJZ1xDYIbe1c2/078wbfI7slOI9Qp94D4nxHvrEx9EnwUNinIeEOA9xHsEjgPifPSII/mcE/zKPB2n67PjnIIHvSIvveDwgCNLi86Y2m9dvaqv5u03XJUiL6bJbXqsgx5edfAFD6/VO/r60sW7Ldlq1GAXXR0g0BBFFRg/u63ibop38zxKRF4A7VfWA41v3t58F/FVV25ict7Xc3FwtKOh6kdJGn3LmL95naHIir9yxsBtR9iAHd8CDc2H+HXD+v7kSQnVdI1+UHuOz/RV8fuAYnweedx+uOr4jj/cIY1L7MaBvQmCnHEefeE/rHXSr962XN71O7GCdPi3WSYz37+SNiUUi8pGq5p64PJgewHBgm4isA2qbFqpqjzmTGucRbl6Uzb+8toWCosPkZvXi6plDx8H0b8C6x/y9gJThYdtUdV3zEf1n+5t39HuONO/oE+KE7KH9mTZ6IJfPHs2E4SmMH5ZM1tD+JMT10DuwjeklgkkAPwl7FBFw5SkZ/M/bn/HwisLenQAAzrgHNv3Rfy7AgV5AVV2Df0e//xifHahgR+C5+Eh1qx19ztBkZqQP5Gtz0pkwPJnxw5MZk2o7emOiVTB3AjtyyWdbROQ5YAkwVESKgZ8ECs85rm9iHNfNH8Nv39vBF6XHGJuWHI7NRIfUsf7LXbvYC6isDezoWwzbfLbfv6NvkhjnISetP7MyBnPlKRlMGJ7MuGEpjEntZzt6Y3qYds8BiMhKVT1dRCpofVJeAFXVAZEIsKXungNocvBYLQt//i5XzBnN/7uiB8z8FYpDX8Dv5sKpt8IF/6/VRzX1jWzbV3F8J//5fv8QzpdHT97RNw3ZjB+e4j+iH9KPeNvRG9OjdPkcgKqeHnhOCWdgkTQ0uQ9fOyWdlz4q5v+cO5G0lCie+zdUqWNh5lVQ8DgsvBtSRgD+4Zzzf7WCPYf9O/vEeA9j05LJzRrMt4Zl+Hf0w5LJtB29Mb1eh0NAIuIBNgZzhU5PccuiHJ5bu5sn84v4/nkT3Q4nvBb/AD55Hlb+Ci78OQBP5e9iz+Fq/v3y6SwYm0rmkH52dYwxMarDQzxV9QGfiEj3LsCPQtlD+3PelOE8tXoXVXUNbocTXkNyYOa3/L2A8r1U1jbw8IpCFo0fytWnZpI9tL/t/I2JYcH08UcCW0TknZ5cDbSlvMU5HK2q54/r9rgdSvgt/gFoI6z8H57M38Xhyjq+e84Et6MyxkSBYC4DfSDsUUTYKWOGcMqYwTy6cifXzh/Tu8e6h2TDzG+hHy3jVd9sFk8YyyljBrsdlTEmCrS75xORJBH5LnAlMAlY5XQ1UDflLc6h+Eg1b2zZ53Yo4bf4B/h8DVxd/wrfO2e829EYY6JER4e+y4FcYBNwIfDfEYkoQs6dPJycof1ZuqKQzsph9HTH+qXzmi7hmvj3mD2wyu1wjDFRoqMEMEVVr1XVh4GvA4siFFNEeDzCzYty2FhcxurC3j2h+nJvEb+svYR4UVj5S7fDMcZEiY4SQH3TC1XtlZfLXDFnNKn9E1m64gu3Qwmbipp6HvmwkPETpiBzroX1T0JZsdthGWOiQEcJYKaIlAceFcCMptciUh6pAMMpKSGOfzgti/e2l/LZ/gq3wwmL5d4ijlbV+6/8WfR9f7H3D60XYIzpIAGoapyqDgg8UlQ1vsXriJeBCJfr5o+hb0Icj6wodDsUx5XX1PPIhzs5e9IwZmYMgkGZMDvQCzi80+3wjDEuC+Yy0F5tcP9EvpGbzrNrd/OD8ycyfECS2yE5ZtmqIsqq61tf97/o+7DhGfjNLBiYAWmT/NNJDpvc/LpPr6n+YYzpQMwnAICbTs/hqdW7eGJVEfddOMntcBxRXlPPox8Wcs7kYUxPH9j8waAMuOlt2PG/ULodSrdC0YfQUNO8zoB0GDYpkBAmNSeGpF7T8TPGYAkAgMzUflw4bSTPrNnFd84aR3Kfnv+zPLGyiPKahrbv+h01y/9o4muEI0XNCaF0OxzYCkUrT0gMo5sTwrCWiWEgxpiep+fv6RyStziHv23ay/Nrd3Pzohy3wwlJWXU9j64s5Nwpw5k2OoidsyfOXz00dSxM+krzcl8jHN3VnBCaEkTB49DQXDqalFFt9xj6DnL8z2aMcY6rCUBELgB+DcQBj6rqz92KZWbGIE7NHsLjK3fyD6dl9ejJTR5fuZOKmgbuPjvEu349cf6CckNyYOKFzct9vkBi2OZ/HAg8f7QM6lvcaJYysu0eQ18rRWFMNHAtAYhIHPAgcC5QDKwTkT+r6qduxXTrGTncuKyAv23cy2WzR7sVRkjKqut5fNVOzgv26L87PB5/jaEh2ScnhrLdzQmh6bF+eevEkDzCnwiaho/i+0BcH4hP8r9uesS1eB2fBHGJ7a/jiQvPn9WYXszNHsA8YIeqFgKIyPPApYBrCWDJhGGMG5bMwysKuXTWKER6XqnkxwJH/65U/PR4YHCW/zHxgublPh+U7Tm5x/DJ81B74oRz3d12fOdJor1EEpcI4gk8pPk10mKZnLDM08GyE5e31WaLdVuuR+DfXKt/ey1eH18e7LIWy9tcxsnLTlrXLdEQQxQZMQP6pzrapJsJYDTQsh5zMXDqiSuJSB6QB5CZGd5pCTweIW9RDve8vJGVOw6yaHxaWLfntLKqep5YuZMLpo5gyqgoumLH44HBY/yPCee3/kwVfA3+k80Ndf7nxlpoqD1hWeC5IfBZMOu0WlYHVYfbWCfQliqoz/8g8NqYaHLNyzD+HEebdDMBtJXeTzoUVNWlwFLwzwkc7qAunT2KX7y1naUrCntcAnhsZSEVtQ3c3ZMqfopAXIL/EW0zdKo2JwZaJIi2kkVn65607MTlLZOOto6h+U3XlrV62VabnWzHTb28QGO3DHP+EnU3E0AxkNHifTpQ4lIsx/WJj+OGhVn85xvb+bSkPLqOpDtwtKqOx1cVceG0EUwe2TNijnrHh2h67gUBxnTEzX/Z64DxIpItIonAVUBUzDR2zbwx9EuM45EPe055iEc/3Mmxnnb0b4xxlWsJIFBh9DvAm8BW4I+qusWteFoa2C+Bq+Zm8pdPSig5Wt35F1x2pLKOJ1bt5KLpI5k0wo7+jTHBcbVvq6qvq+oEVR2rqv/mZiwnuvH0LBT/NfXR7tGVhVTVN3JXqNf9G2Niig1utiN9cD8unjGS59bupqy6vvMvuORwZR3LVhXxlekjmTjCirgZY4JnCaADtyzKobKukefW7nY7lHY98qH/6P+7dvRvjOkiSwAdmDZ6IAvHpfLEqp3UNUTfdeGHjtWy3FvExTNGMX64Hf0bY7rGEkAn8haPZX95La9t+NLtUE7yyIc7qa5v5K6zxrkdijGmB7IE0InF44cyaUQKj3xYiEbRzSmHjtXyZH4RX7Wjf2NMN1kC6ISIkLc4h8/2H+P9z0rdDue4pSsKqbErf4wxIbAEEISLZ4xixIAkln4QHTeGHTxWy5P5u7hk5ijGDUt2OxxjTA9lCSAIifEebjw9i/zCQ2wqLnM7HJauKKS2oZE77ejfGBMCSwBB+ta8TFL6xPPwii9cjaO0wj/2f+ms0YxNs6N/Y0z3WQIIUkpSAlefmsnrm/ay53BV518Ik4c/+IK6Bh932pU/xpgQWQLogn9cmI1HhMdcKg9xoKKGp9fs4rLZo8mxo39jTIgsAXTBiIFJXDJrFC+s28PRqrqIb//hDwqpb1TuPMvG/o0xobME0EV5i3Oorm/k6dW7IrrdA+U1PL16F5fNGk320P4R3bYxpneyBNBFk0YM4IwJaSzz7qKmvjFi233ogy9o8Cl3nW1j/8YYZ1gC6IZbF+dw8Fgtf/o4MuUhDpTX8Oya3VwxezRjUu3o3xjjDEsA3bBgbCpTRw1g6YeF+HzhLw/x+/f9R//fsSt/jDEOciUBiMiVIrJFRHwikutGDKFoKg9RWFrJO9sOhHVb+8pqeHbtbr42x47+jTHOcqsHsBm4Aljh0vZDdtH0kYwe1JelYb4x7KH3d+Dz2ZU/xhjnuZIAVHWrqm53Y9tOiY/zcNPp2awrOsL63UfCso19ZTU8t3YPXz8lnYwh/cKyDWNM7Ir6cwAikiciBSJSUFoaPdU4Ab45N4MBSfE8siI8ReJ+//4OfKp8+0wb+zfGOC9sCUBE/ldENrfxuLQr7ajqUlXNVdXctLS0cIXbLf37xHPt/DG8sWUfRQcrHW275Gg1z6/dw5W5dvRvjAmPsCUAVT1HVae18XgtXNt0ww2nZZHg8fDoSmd7Ab9/fweKHf0bY8In6oeAot2wAUlcPns0LxYUc+hYrSNtlhyt5oV1e7gyN4P0wXb0b4wJD7cuA71cRIqBBcDfRORNN+Jwyi2Ls6lt8PGUQ+UhHnxvB4Ad/Rtjwsqtq4BeVdV0Ve2jqsNV9Xw34nDKuGEpnD1pGE/m76K6LrTyEMVHqvhjwR6+kZvB6EF9HYrQGGNOZkNADslbnMPhyjpeWl8cUjsPvue/r8CO/o0x4WYJwCHzsocwM2MQj35YSGM3y0MUH6nixYI9fHNuBqPs6N8YE2aWABwiIty6OIddh6p4a8u+brXx4Hs78IjY0b8xJiIsATjo/KkjyBzSj4dXFKLatV7AnsNVvFhQzFXzMhg50I7+jTHhZwnAQXEe4eZF2WzYc5SCXV0rD/G7d/1H/3cssaN/Y0xkWAJw2JWnZDC4XwIPfxD8jWG7D1Xx8vpivjUvgxEDk8IYnTHGNLME4LC+iXFctyCL/926nx0HjgX1nd+99zkej3CHjf0bYyLIEkAYXL9gDH3iPTwWRHmIXYcqeXn9l1w9L5PhA+zo3xgTOZYAwmBoch++dko6L6//ktKKjstD/O7dHcR7hDuWjI1QdMYY42cJIExuWZRDfaOP5d6idtcpOljJKx9/ydWnZjLMjv6NMRFmCSBMsof257wpw3lq9S4qaxvaXOe3gaP/28+wo39jTORZAgijvMVjKauu548Fe076bOfBSl79uJhr54+xo39jjCssAYTRKWMGkztmMI+t3ElDo6/VZ79993MS4z3cekaOS9EZY2KdJYAwu2VxDsVHqvn75ubyEIWlx/jTx19y7aljGJZiR//GGHdYAgizcycPJ2dof5a2KA/x23d3BI7+bezfGOMeSwBh5vEINy/KYdOXZeQXHuKL0mO8tuFLrl+QRVpKH7fDM8bEMLdmBPsvEdkmIhtF5FURGeRGHJFyxZzRDE1OZOmKQn77zuf0iY8jb7GN/Rtj3OVWD+BtYJqqzgA+A+53KY6ISEqI4/oFWby/vZTXPinh+gVjGJpsR//GGHe5NSXkW6radHH8aiDdjTgi6br5Y+ibEEffBDv6N8ZEh3i3AwBuBF5o70MRyQPyADIzMyMVk+MG90/k3y6fRpxHSLWjf2NMFJCuTlwSdMMi/wuMaOOjH6vqa4F1fgzkAldoEIHk5uZqQUGBs4EaY0wvJyIfqWruicvD1gNQ1XM6CegfgIuBs4PZ+RtjjHGWK0NAInIBcC9whqpWuRGDMcbEOreuAvodkAK8LSIbROQPLsVhjDExy5UegKra1FfGGOMyuxPYGGNilCUAY4yJUZYAjDEmRlkCMMaYGBW2G8HCQURKgV3d/PpQ4KCD4fR09ns0s9+iNfs9WusNv8cYVU07cWGPSgChEJGCtu6Ei1X2ezSz36I1+z1a682/hw0BGWNMjLIEYIwxMSqWEsBStwOIMvZ7NLPfojX7PVrrtb9HzJwDMMYY01os9QCMMca0YAnAGGNiVEwkABG5QES2i8gOEbnP7XjcIiIZIvKeiGwVkS0icrfbMUUDEYkTkY9F5K9ux+I2ERkkIi+JyLbAv5MFbsfkFhH5XuD/yWYReU5EktyOyWm9PgGISBzwIHAhMAX4lohMcTcq1zQA31fVycB84Nsx/Fu0dDew1e0gosSvgTdUdRIwkxj9XURkNHAXkKuq04A44Cp3o3Jer08AwDxgh6oWqmod8DxwqcsxuUJV96rq+sDrCvz/uUe7G5W7RCQduAh41O1Y3CYiA4DFwGMAqlqnqkddDcpd8UBfEYkH+gElLsfjuFhIAKOBPS3eFxPjOz0AEckCZgNrXA7Fbb8C7gF8LscRDXKAUuCJwJDYoyLS3+2g3KCqXwK/AHYDe4EyVX3L3aicFwsJQNpYFtPXvopIMvAy8F1VLXc7HreIyMXAAVX9yO1YokQ8MAd4SFVnA5VATJ4zE5HB+EcKsoFRQH8RudbdqJwXCwmgGMho8T6dXtiVC5aIJODf+T+jqq+4HY/LFgKXiEgR/qHBs0TkaXdDclUxUKyqTb3Cl/AnhFh0DrBTVUtVtR54BTjN5ZgcFwsJYB0wXkSyRSQR/4mcP7sckytERPCP725V1V+6HY/bVPV+VU1X1Sz8/y7eVdVed5QXLFXdB+wRkYmBRWcDn7oYkpt2A/NFpF/g/83Z9MIT4q7MCRxJqtogIt8B3sR/Jv9xVd3iclhuWQhcB2wSkQ2BZT9S1dfdC8lEmTuBZwIHS4XAP7ocjytUdY2IvASsx3/13Mf0wpIQVgrCGGNiVCwMARljjGmDJQBjjIlRlgCMMSZGWQIwxpgYZQnAGGNilCUAE5NE5FjgOUtErna47R+d8N7rZPvGOMUSgIl1WUCXEkCgwmxHWiUAVe11d5Ca3sESgIl1PwcWiciGQP33OBH5LxFZJyIbReRWABFZEphL4VlgU2DZn0Tko0DN+LzAsp/jryC5QUSeCSxr6m1IoO3NIrJJRL7Zou33W9ThfyZw96kxYdXr7wQ2phP3AT9Q1YsBAjvyMlWdKyJ9gFUi0lQFch4wTVV3Bt7fqKqHRaQvsE5EXlbV+0TkO6o6q41tXQHMwl9nf2jgOysCn80GpuKvU7UK/13bK53+wxrTkvUAjGntPOD6QKmMNUAqMD7w2doWO3+Au0TkE2A1/oKD4+nY6cBzqtqoqvuBD4C5LdouVlUfsAH/0JQxYWU9AGNaE+BOVX2z1UKRJfjLI7d8fw6wQFWrROR9oLMpAzsa1qlt8boR+79pIsB6ACbWVQApLd6/CdweKJuNiExoZ1KUgcCRwM5/Ev4pNpvUN33/BCuAbwbOM6Thn31rrSN/CmO6wY4yTKzbCDQEhnKW4Z8TNwtYHzgRWwpc1sb33gBuE5GNwHb8w0BNlgIbRWS9ql7TYvmrwALgE/yTEt2jqvsCCcSYiLNqoMYYE6NsCMgYY2KUJQBjjIlRlgCMMSZGWQIwxpgYZQnAGGNilCUAY4yJUZYAjDEmRv1/ZPmyyuwxTGMAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYAAAAEGCAYAAABsLkJ6AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAAAxf0lEQVR4nO3deXxU5fX48c+ZyR4yLGEnQEBRKgiCKCCioEZFECt1wbp9tS51b7UqdrHqr7UurV1tFbX96rfWHRQRkUVxoW4YNgUURYSEQAIkJBCyzZzfH3cCScgySWbmJpnzfr3mNTN3ee7JKHPmPvc+5xFVxRhjTOzxuB2AMcYYd1gCMMaYGGUJwBhjYpQlAGOMiVGWAIwxJkbFuR1Ac3Tv3l0zMzPdDsMYY9qVzz77bKeq9qi7vF0lgMzMTFasWOF2GMYY066IyHf1LbcuIGOMiVGWAIwxJkZZAjDGmBhlCcAYY2KUJQBjjIlRriYAEfmpiHwhIp+LyHMikuRmPMYYE0tcSwAi0g+4GRijqsMBLzDTrXiMMSbWuN0FFAcki0gckAJsczmeiPp0824Wfp6HP2AluI0x7nNtIJiq5orI74EtwH5gkaouqrudiFwDXAMwYMCA6AYZRlX+ANc/m01BSTmH9UjlplOGcPbIvng94nZoxpgY5WYXUFfgHGAQ0BdIFZFL6m6nqrNVdYyqjunR45CRzO3G8m92UVBSzv+ckEmcx8NPXlhF1iPvMic7hyp/wO3wjDExyM0uoNOAb1W1QFUrgTnACS7GE1FzsnPonBzPXWcN5c1bJvKPi0eTEOfh1hdXc9oj7/LSiq1UWiIwxkSRmwlgCzBORFJERIBTgfUuxhMxe8ureOuL7Uwb0YfEOC8ejzDl6D4suHkij196LKmJcdz+8hpO/cO7vPDpFksExpiocC0BqOrHwMtANrA2GMtst+KJpDfX5lFWGWDG6Ixayz0e4YxhvZl/04k8edkYuqTEc+cra5n08DL+8/EWKqosERhjIkfa06TwY8aM0fZYDfSi2R+Rt2c/7/xsEs7JTv1UlWVfFvCnpRtZvbWIvp2TuG7y4VwwJoPEOG8UIzbGdCQi8pmqjqm73O3bQDu8nMJSPty0ixmjMxr98gcQESYP7cmr15/A01ceT+/OSfzq1c+Z9PAynvlwM2WV/ihFbYyJBZYAIuy1Vc7QhnNH9Qt5HxHh5CN68Mp1J/DvH40lo2syd7/2BSc//A7/Wv6tJQJjTFhYAoggVeWV7ByOH9SN/t1Smr2/iHDikO68eO14/nP1WDLTU7n39XVMfOgdnnx/E/srLBEYY1rOEkAErc7Zw6aCfcxoxq//+ogIJxzWnReuHc/z14xjSM9O/OaN9Ux86G1mv/cNpRVVYYrYGBNL2tWUkO3NnOwcEuI8nDWiT9jaHDc4nXGD0/l0827+vGQj9y/YwOPvbuLqkwZz6biBpCbaf1JjTGjsDCBCKqoCvL56G6cf1QtfUnzY2z8usxv/vmosr1w3nmH9OvPAmxs48cG3efSdrykpqwz78YwxHY/9XIyQZV/mU1hayQ/q3PsfbscO7MYzVx7Pyi2F/GXpRh5+60tmv7eJq04cxOUTMiOSfNqTKn+ACn+AiirnUV5V+32FP+AMvFNQoPquaMV5cfB98Fn1wGsa2lZrb197/4PvDm079L+rRhRNb9t+7vQ2jRg7qBs9feGtmG8JIELmZOfSvVMCE4d0j8rxRg3oyr+uOJ41OUX8ZelG/rD4K554fxNXnjiIKyYMonOy+4mgvMpPUWklu/dVUFhawZ7SSsqq/A1/Odd5X97IuurX5VUBKqr8B95b4VXTUfzvFcdZAmgPikorWLphB5eNzyTOG91ethEZXXjy8uP4PHcPf1m6kT8t2chT73/LFRMyufLEQXRJSWj1MVSV0go/haUVFO6rdJ5LKyjcV0FhaSVFpRXsDj7X3Ka0GXctxXmEhDiP8/B6ar1ODL5OivfgS4oLrvMe2C6xxrbxNfeN85BYp62EOGeb6qKs1WM1RKB61MbB4Rv1rZMaaw5uKwh1h33Ut67mstrHalpz6sg2p13TNvXpnBz2Ni0BRMDra/Ko9CszRrfu7p/WGN6vM7MvG8MX2/bwt7e/5i9vf80/l2/m8hMGctWJg+ma6iSCQEApKatid/DLuqi0gt37anx5l1YGv9grDvx6LyqtpKKRekW+pDi6pibQNSWBHp0SOaJnWvB9PF1SnOVdU+PpkpxAcoK31pdxYvAL2cpkGxN5VgoiAs79+3L2V/h585aJTY7+jZYN24v569tfs2BtHinxXnp3Tjrwa72hbhKvR+iSHF/ry7tbSgJdUuOdL/GU4HPqwdedk+OjftZjjGlcQ6Ug7AwgzL7duY+VW4q4a8rQNvPlDzC0t49Hfziar3aU8NT737K3vIouwS/tLinxdAv+Yq9+3SUlgbTEODz2S9yYDssSQJjNzc7BI/D9Vg7+ipQjeqXx4Hkj3A7DGNMG2Ll6GAUCypyVuUw4vDu9wny13hhjws0SQBh9unk3OYX7I37vvzHGhIMlgDCak51LaoKX04f1cjsUY4xpkiWAMCmr9PPG2jymHN2HlAS7tGKMaftcTQAi0kVEXhaRDSKyXkTGuxlPayxat4O95VWu3vtvjDHN4fZP1T8DC1X1PBFJAJpfNL+NmJudQ9/OSYwblO52KMYYExLXzgBExAecBDwFoKoVqlrkVjytkV9Sxnsbd/L9Uf3svnljTLvhZhfQYKAA+JeIrBSRJ0Uk1cV4Wmzeqm34A+6WfjDGmOZyMwHEAaOBf6jqKGAfMKvuRiJyjYisEJEVBQUF0Y4xJHOycxmZ0ZnDe6a5HYoxxoTMzQSQA+So6sfB9y/jJIRaVHW2qo5R1TE9evSIaoChWJ9XzLq8YmbYvf/GmHbGtQSgqtuBrSJyZHDRqcA6t+Jpqbkrc4nzCGeP7Ot2KMYY0yxu3wV0E/Bs8A6gTcAVLsfTLP6A8urKXCYP7Um31NbX2TfGmGhyNQGo6irgkBKl7cXyr3eSX1LOjDZa+M0YYxpjI4FbYU52Dr6kOE75Xk+3QzHGmGazBNBCe8urWPjFds4e2ZfEOK/b4RhjTLNZAmihN9fmUVYZsLt/jDHtliWAFpqTnUtmegqjB3RxOxRjjGkRSwAtkFNYyoebdjFjdEabmvbRGGOawxJAC7y2ahsA59rdP8aYdswSQDOpKnOyczh+UDf6d2u3xUuNMcYSQHOtydnDNwX7mn/vvyq8cjW8dmNkAjPGmGZyeyRwuzMnO4eEOA9njejTvB1XPw9rX3ReHzkFhk4Nf3DGGNMMdgbQDBVVAeat3sbpR/XClxQf+o57C+Ctu6D/WOg5DBbcAeV7IxeoMcaEwBJAMyz7Mp/C0kp+0Nx7/xfeCRX7YPpfYdojUJwD7z4YmSCNMSZElgCaYU52Lt07JTBxSPfQd/pyIXz+Cpx0O/Q4EgaMg1GXwkd/hx1fRC5YY4xpgiWAEBWVVrB0ww7OOaYfcd4QP7ayYnjjVuh5FEz4ycHlWfdBog/m3wqBQETiNcaYplgCCNH8NXlU+ps57ePS+6B4m9P1E1ejXHRKNzj9/8HWj2DVs+EP1hhjQmAJIERzsnM4slcaR/XxhbbDlo/g0ydh7I8ho56K1yN/CANOgMW/gn27whusMcaEwBJACL7duY/sLUXMGN0vtNIPVeUw72bo3B9O+WX923g8zgXh8hJYcnd4AzbGmBBYAgjB3OwcPALfD3Xw1/t/gJ1fwrQ/QmKnhrfr+T0YfyOs/Dd892F4gjXGmBBZAmhCIKDMWZnLhMO708uX1PQOO9bB+4/AiAthyGlNb3/yHdB5AMz/KfgrWx+wMcaEyPUEICJeEVkpIvPdjqU+n27eTU7h/tDu/Q/4Yd5NkOSDM34X2gESUmHKg1CwHj58tHXBGmNMM7ieAIBbgPVuB9GQOdm5pCZ4OX1Yr6Y3/vRJyF0BZz4AqemhH2ToWXDkVGdwWNGWlgdrjDHN4GoCEJEMYCrwpJtxNKSs0s+CtXlMOboPKQlNlE0q2gJL7oXDs+Do85t/sCnBkcFv3tn8fY0xpgXcPgP4E3AH0OBoKBG5RkRWiMiKgoKCqAUGsHjdDkrKq5qu/KnqDOoC586elkwS06U/TJoFXy6ADQuav78xxjSTawlARKYB+ar6WWPbqepsVR2jqmN69OgRpegcc7Jz6Ns5iXGDm+jOWfsyfL0YTr0bugxo+QHHXe+MGn7zDqd2kDHGRJCbZwATgOkishl4HjhFRP7tYjy15JeU8d7GnXx/VD88nkZ+0e/b5RR76zcGjr+6dQf1xsPUR2DPVisWZ4yJONcSgKrepaoZqpoJzATeVtVL3IqnrnmrtuEPhFD64a27nJo/5/wNPN7WH3jgeBh1iXNH0I51rW/PGGMa4PY1gDZrTnYuIzM6c3jPtIY32rgE1rwAE291BnWFy2nBYnFvWLE4Y0zktIkEoKrLVHWa23FU27C9mHV5xcxo7N7/8r3O4K3uR8LE28IbQGq6UzF0y4ew+j/hbdsYY4LaRAJoa+Zm5xLnEc4e2bfhjd7+jdNXP/2vEJcY/iCOuRj6j4NFv4LS3eFv3xgT8ywB1OEPKHNX5jLpyJ50S02of6OcFfDxY3DcVTBgbGQCOVAsrhgWW7E4Y0z4WQKoY/nXO8kvKecHDV38rapwyj34+jq3fUZSr2HOraEr/88pL22MMWFkCaCOOdk5+JLiOOV7PevfYPmfIX+dc7tmUohzA7TGpFlOWWkrFmeMCTNLADXsLa9i4RfbOXtkXxLj6rmls+BLeO8hGP4DOPLM6ARVXSwuf50zj7AxxoSJJYAa3lybR1lloP67fwIBZ5KXhFQ4M8qDtIZOhSPPgmUPQNHW6B7bGNNhNZkARGSCiKQGX18iIo+IyMDIhxZ9c7JzyUxPYfSALoeu/Oyfzhy+Z9wPnaJbkgI4WCxu4azoH9sY0yGFcgbwD6BUREbiFG77DngmolG5ILdoPx99u4sZozMOnfZxTy4svgcGT4aRF7kSH10GOJPHbJgPX77pTgzGmA4llARQpaoKnAP8WVX/DDQyPLZ9enVlLqpwbt3Kn6rOiFz1w9l/almlz3AZfyP0+B4ssGJxxpjWCyUBlIjIXcClwBsi4gXiIxtWdKkqc7JzOD6zG/27pdRe+cVc+GohTP4FdM10Jb4DvPHO2IA9W+Ddh9yNxRjT7oWSAC4EyoErVXU70A94OKJRRdmanD18U7Dv0MJvpbud0sx9R8HYH7sTXF0DT4BjLoEP/wb5bXYiNWNMO9BkAgh+6b8CVNc72AnMjWRQ0TYnO4eEOA9njehTe8WiX8L+Qqfcg7eJGcGiKes+SExzJqFRdTsaY0w7FcpdQFcDLwOPBxf1A16NYExRVVEVYN7qbZx+VC98STV6tr55B1Y9CxNugd5HuxdgfQ4Ui/svrLJiccaYlgmlC+gGnMlbigFUdSPQwDDZ9mfZl/kUllbyg5r3/leUwuu3QPrhcNId7gXXmGMugf5jnbMUKxZnjGmBUBJAuapWVL8RkTigw/Q7zF2ZS/dOCUwc0v3gwmX3Q9F3cPZfID7JveAa4/HAtD9C2R5Y8mu3ozHGtEOhJIB3ReTnQLKIZAEvAa9HNqzoKCqtYOn6fM45ph9x3uBHkZvtzMZ17BWQOcHdAJvSaxiMvx6yn7FiccaYZgslAcwCCoC1wLXAAuCXkQwqWuavyaPCHzh477+/0in3kNoTsu51N7hQnTwLfBnOBWErFmeMaYZQ7gIKqOoTqnq+qp4XfN3qLiAR6S8i74jIehH5QkRuaW2bzTUnO4cje6UxrG+wqud//wo71sLUP0BS52iH0zKJnYLF4r5w5igwxpgQNXhvo4ispZG+flUd0cpjVwG3qWq2iKQBn4nIYlWNykzo3+7cR/aWIu6aMtQp/bDza6fY2vemw/fazOyUoRk6FY44E975HQw7Fzo3MpWlMcYENXZze0S/BVU1D8gLvi4RkfU4t5hGJQHMzc7BI/D9Uf2cSp+v3+Jc8D3r99E4fHiJwJSH4NGx8OadMPNZtyMyxrQDDXYBqep31Q+ckcAjgRE4dwV9F84gRCQTGAV8XM+6a0RkhYisKCgoCMvxAgFlzspcJhzenV6+JFj5DHz3AZz+G0jrFZZjRF3XgTWKxS10OxpjTDsQykCwq4BPgBnAecBHInJluAIQkU44I41/oqrFdder6mxVHaOqY3r0CE8Z5hXfFZJTuN+59784DxbdDZkTYdSlYWnfNeNvhB5DYcHtzlgGY4xpRCh3Ad0OjFLV/1HVy4FjgTvDcXARicf58n9WVeeEo81QzMnOITXBy+nDesGCn4G/HM7+s7uVPsMhLsGZqnLPFmfmMmOMaUQoCSAHKKnxvgRo9bRU4hTdfwpYr6qPtLa9UJVV+nljTR5nDu9DytcLnC6TSXdB+mHRCiGyMifAMRc7dzRZsThjTCMaTAAicquI3ArkAh+LyD0i8mvgI+DrMBx7Ak6J6VNEZFXwcVYY2m3U4nU7KCmv4oLhac6v/94jnK6TjiTrPkjoBG/cZsXijDENauwuoOpJX74JPqq9Fo4Dq+oHQNT7XOZk59C3cxLHf/0n2LcTfvhi26r0GQ6p3Z2BbK/fAqufg2N+6HZExpg2qMFvPlVtJ0NhQ1dQUs57G3fym5GFSPbTTqXPvse4HVZkjLoMVj7rFIs74kxI6eZ2RMaYNiaUu4B6iMjDIrJARN6ufkQjuHCbt3obcYFyfrDtIeg6yCmj0FFVF4vbXwRL7nE7GmNMGxTKReBngQ3AIOBeYDPwaQRjipg52Tn8tusbJOzZ7Nz1k5DS5D7tWu/hMO46yH4athwyxMIYE+NCSQDpqvoUUKmq76rqlcC4CMcVdhu2F0PeGmaUzYFRl8Dgk90OKTom3QW+fs7E9v4qt6MxxrQhoSSA6hKTeSIyVURGAe2u2Myrn33Hg/FPQHI3Z8RvrKguFrfjcysWZ4ypJZQE8BsR6QzcBvwMeBL4aUSjCjN/QEn+bDbDPd/imfp7SO7qdkjRNXQaDDkD3rkf9uS4HY0xpo0IpRz0fFXdo6qfq+pkVT1WVedFI7hwefutl5mQ/xo7+pwKR53jdjjRJwJnPQQagIUd+MK3MaZZGisHfYeqPiQif6WestCqenNEIwujoid/Q9evU1l4yUlchguDD9qCrplw8u2w9D746i044gy3IzLGuKyxM4DqOgIrgM/qebQbx132S1LLYfGCJ7jzvTsprYzRQmnjb4LuRzojoK1YnDExTxqb3EtEvMADqnp79EJq2JgxY3TFihXN3i9QXs7GEyawbdxgfjL2Swb5BvHHyX9kUOdBEYiyjdv8AfzvVOh2GBw2GTJPdCqhpnZ3OzJjTISIyGeqOqbu8kavAaiqH6f6Z7vmSUyk08kn029lLo+f8g92l+3mojcuYul3S90OLfoyT4RzH4dug2DVc/DS/8DDh8Gj45wy0uteg3273I7SGBMFjZ4BAIjIH4AhwEvAvurl0SzfXK2lZwAAxQsXkvuTnzLw/56h+Kj+3LrsVtbuXMsVw6/g5lE3E+fpYPWAQuGvhG2rYPP7zmPLR1DdPdZr+MGzg4EnWCkJY9qxhs4AQkkA/6pnsQYHhEVVaxJAYN8+vhp/Al1mXkjvn/+cCn8FD336EC98+QLH9z6eh056iPTk9DBH3M5UVcC2lbD5PaeraMvHULUfEGdUceZJTlIYeAIkd3E7WmNMiFqcANqS1iQAgK3X30DZ+vUc/vZSZyJ4YN4387jvw/vonNiZRyY9wsgeI8MVbvtXVQ65nznJ4Nv3YOsnzuQ5CPQZ4ZwdDDoJBoyDpM5uR2uMaUBrzgCSgB8Bw4Ck6uXt7QwAoOjVV8mbdReZL71E8tHDDyzfsHsDP33np2wv3c4dx93BzCNnHkgQpobKMshdEUwI70POJ+CvAPFAn2Ocs4PqhJCY1mRzxpjoaE0CeAmnGNwPgfuAi3Fm8bolEoE2prUJwF9UxFcnTiT9yivpeWvtwcx7yvfwiw9+wbs57zJt8DTuHn83yXHJrQ25Y6vcDzmfOslg8wfO60AliBf6joJBE52k0H+cU5LCGOOK1iSAlao6SkTWqOqI4Dy+b6nqKZEKtiGtTQAAW678EZXbtjH4zQWH/MoPaIAn1jzBo6se5fCuh/OnSX9igG9Aq44XUypKYevHTjLY/L7TfRSoAk8c9B1dOyF09EqsxrQhrUkAn6jq8SLyHnA9sB34RFUHhyGoM4E/A17gSVV9oLHtw5EACp9/nu333Mvg1+eROGRIvdssz13One/fSSAQ4Lcn/pbJAya36pgxq2Kfc2fRgYSQDeoHTzz0O9aZv9jXF5K6QKIPkny1nxM6OfMaGGNapTUJ4CrgFWAE8C+gE/ArVX28lQF5ga+ALJyJ5z8FLlLVdQ3tE44EUJmfz9cnT6L7TTfS4/rrG9wud28uty67lXW71nH10VdzwzE34PV4W3XsmFde4txZVH2X0baVTn2iBkn9iaHe5871L09IsyRiYl6zE4CIrMOZDOZ5Vf2m3o1aF9B44B5VPSP4/i4AVf1dQ/uEIwEAbP7hxQT272fw3MaHMpT7y/ndx7/jlY2vML7PeB486UG6JsVYJdFIqiyDsiIoK4byYijbE3wubuC57vo9ThdTo8S5IN1Q4kjqHDzTiHMuZosHPN6Dr2s+ai33OkX26l3ucZJO3WW1tpVDlyPO8uq4ocb7hpY1tU0o7TSyTSiadcNEpNqNAUmdIS6xRbs2lAAaG/10ETATWCQiO4HngBdUNa9FERyqH7C1xvscYGyY2m5UWlYW+Q8+SMXWrST079/gdoneRO454R5G9BjBbz/6LRfMv4BHTn6Eo3scHY0wO774JIjvDWm9W7a/qnMhutEkUU8S2bsDdm48uDxQ2fSxjHHbxa/AkNPC2mRjk8KvBlYDd4nIOOBC4GMR+Rp4TlWfaOWx60vvh5yOiMg1wDUAAwaE54JsWtZp5D/4ICWLl5B+5RVNbj9jyAyO7HYkty27jcsXXs6s42dx/hHn262ibhNxLiYnpLQuifgrIOB3uqO0+llrLKu5PBBcriGsq7l/oEZ7Ws8+gRrdYXowtrqxNri+7rIWvq/vuI1/gM3YNELtxooeR4a9yWYNBBORScAfgaNUtWXnIgfbcq0LCGDTjBl4EpPIfO4/Ie9TVFbErA9msTx3Oeccdg6/HPdLkuKSmt7RGGNc1KJicMEdjxORR0TkO5xJ4WfjdN+01qfAEBEZJCIJON1NUZtoxnf66exfuZLK/PyQ9+mS1IVHT3mU60Zex7xv5nHpm5eytWRr0zsaY0wb1GACEJH7ReQb4B/ANmCCqp6sqv9Q1Z2tPbCqVgE3Am/hzD3woqp+0dp2Q5WWlQXA3qXNqwjq9Xi5/pjr+dupfyN3by4Xzr+Q93Lei0SIxhgTUY2dAZQDU1R1jKr+XlXDPpmsqi5Q1SNU9TBV/W24229M4mGHkTB4MCWLF7do/5MyTuKFaS/Qr1M/blh6A4+uehR/wB/mKI0xJnIaTACqeq+qfhXNYKItLSuLfR9/QlVhYYv275/Wn/+b8n+cc9g5PLb6MW54+wb2lO8Jc5TGGBMZMT1CJi0rC/x+9r6zrMVtJMUl8f8m/D/uHn83n+R9woXzL2TdrgbHshljTJsR0wkgadhRxPXt0+JuoGoiwvlHnM8zU57Br34uXXApczfODVOUxhgTGY1dBB7d2COaQUaKiODLymLf8uX49+5reocmDO8+nBenvcjoXqO5+793c89/76HcXx6GSI0xJvwaGwn8h0bWKRD1aqCRkJaVxe6nn2Hf++/hmzKl1e11TerKY6c9xqOrHuWJtU+wfvd6/jjpj/Tt1DcM0RpjTPg0dhF4ciOPDvHlD5A8ahTe9PRWdwPV5PV4uXn0zfxl8l/YUryFC+ZfwPLc5WFr3xhjwiGkawAiMlxELhCRy6ofkQ4sWsTrJe2009i77F0C5eHtrpk8YDIvTHuBnik9uW7JdTy2+jECjVa/NMaY6AmlHPSvgUnAUcACYArwgaqeF/Ho6ghnKYia9n6wnK1XXUXGP/5O2uTw1/7fX7Wf+z68j/mb5tM5sTNesbLSxpjmeeikhxjbp2X1MltSDbTaecBIYKWqXiEivYAnWxRFG5V6/HF4fD5KFi+JSAJIjkvm/hPvZ3zf8azOX93q9jpKETpV7TB/izGRlp6UHvY2Q0kA+1U1ICJVIuID8oFWzwbWlkhCAmmTJ7F36VK08h4kPj78xxBh+mHTmX7Y9LC3bYwxLRHKNYAVItIFeAL4DMgGPolkUG5Iy8rCv2cPpRHoYjLGmLaoyTMAVa2eN/ExEVkI+FR1TWTDir7UCROQ5GRKFi8mdfx4t8MxxpiIC6Uc9EnVD2AA0CX4ukPxJCfTaeJEShYvQQN2p44xpuML5RrA7TVeJwHH43QFdZixANXSsrIoWbSI/atXkzJqlNvhGGNMRIXSBXR2zfci0h94KGIRuajTpJMhPp6SxUssARhjOryWFIPLAYaHO5C2wJuWRuoJ4ylZvJjmTJVpjDHtUZNnACLyVw7O0OwBjsGZLL5D8mVlkffLX1H+5ZckDR3qdjjGGBMxoVwDqHlfZBXwnKp22MI2nU45BTy/pmTRYksAxpgOrckuIFV9GqcExAJVfTYcX/4i8rCIbBCRNSIyNzjOoE2I69aNlDFjKFm8yO1QjDEmohqbD0BE5B4R2QlsAL4SkQIRuTsMx10MDFfVEcBXwF1haDNs0rKyKN/4NeWbvnU7FGOMiZjGzgB+AkwAjlPVdFXtCowFJojIT1tzUFVdpKpVwbcfARmtaS/c0k47FYCSJUtcjsQYYyKnsQRwGXCRqh74Gayqm4BLguvC5UrgzYZWisg1IrJCRFYUFBSE8bANi+/Th6QRI8I6R4AxxrQ1jSWAeFXdWXehqhYATVZLE5ElIvJ5PY9zamzzC5wLy8821I6qzlbVMao6pkePHk0dNmzSsk6jbO1aKrdti9oxjTEmmhpLABUtXAeAqp6mqsPrebwGICKXA9OAi7UN3nTvy8oCoGTJUpcjMcaYyGgsAYwUkeJ6HiXA0a05qIicCdwJTFfV0ta0FSkJmZkkHnGEdQMZYzqsxuYE9qqqr55Hmqq2tmD+34A0YLGIrBKRx1rZXkSkZWVR+tlnVO3a5XYoxhgTdi0pBdFqqnq4qvZX1WOCjx+7EUdT0k7PgkCAkrffdjsUY4wJO1cSQHuReMQRxA8YQMki6wYyxnQ8lgAaISKkZZ3Gvo8+wl9c7HY4xhgTVqHUAmrTKisrycnJoaysLCLt6+mnUzV6NBs2bsSTkhL29pOSksjIyCA+AvMQG2NMY9p9AsjJySEtLY3MzExEJOztqyrlX36JJyWFhAEDwt72rl27yMnJYdCgQWFt2xhjmtLuu4DKyspIT0+PyJc/ON1AXp8Pf8nesE8VKSKkp6dH7OzFGGMa0+4TABCxL/9qHp8PNEBg796wtx3p2I0xpiEdIgFEmic1FfF67UKwMaZDsQQQAhHB4/MRKC5pVjfQ7t27ycrKYsiQIWRlZVFYWBjBKI0xpnksAYTI6/OhAT+BfftC3ueBBx7g1FNPZePGjZx66qk88MADEYzQGGOap93fBVTTva9/wbpt4e2mOaqvj1+fPczpBvJ48BcX401Lq7XN5s2bmTZtGp9//jkAv//979m7dy+vvfYay5YtA+Dyyy9n0qRJPPjgg2GNzxhjWsrOAEIkHg+etDSnGyjE4qU7duygT58+APTp04f8/PxIhmiMMc3Soc4Afn32sIi27/X58O/ZQ6C0FG9qakSPZYwxkWZnAM3g6dQJRAjUuRsoLi6OQI2Lw9X39ffq1Yu8vDwA8vLy6NmzZ/SCNcaYJlgCaAbxevF26oS/uLhWN1CvXr3Iz89n165dlJeXM3/+fACmT5/O008/DcDTTz/NOeecU2+7xhjjhg7VBRQNHp8Pf0kJur8MSUkGID4+nrvvvpuxY8cyaNAghg4dCsCsWbO44IILeOqppxgwYAAvvfSSm6EbY0wtlgCayZuWRqUI/uJiPMEEAHDzzTdz8803H7L90qU2paQxpm2yLqBmkrg4PKmp+Iv3hHw3kDHGtEWuJgAR+ZmIqIh0dzOO5vL6fGhFBVpe7nYoxhjTYq4lABHpD2QBW9yKoaU8wYFgVhvIGNOeuXkG8EfgDqDd9aN44uPxpKQccjuoMca0J64kABGZDuSq6uoQtr1GRFaIyIqCgoIoRBcar89HoKyMQEWF26EYY0yLROwuIBFZAvSuZ9UvgJ8Dp4fSjqrOBmYDjBkzps2cLXh8Pti+nUBxMZ7u7eoShjHGABE8A1DV01R1eN0HsAkYBKwWkc1ABpAtIvUlizbLk5CAJymp0esAL730EsOGDcPj8bBixYooRmeMMU2LeheQqq5V1Z6qmqmqmUAOMFpVt0c7ltby+HwESksJVFbWu3748OHMmTOHk046KcqRGWNM0zrWQLA3Z8H2teFts/fRMKX+Ov5en4+q/Hw2ff4537/00kPKQd9zzz3hjcUYY8LI9QQQPAtolzxJSUhiIv6iIrdDMcaYZnM9AYRVA7/UI8nr86Gbvo36cY0xprWsFEQreX0+vF5PresA1eWgjTGmLbME0EqSlETv3r3JLyg4pBy0Mca0ZZYAWklESEpP565rr2Xs2LFMmzbtQDnouXPnkpGRwYcffsjUqVM544wzXI7WGGMO6ljXAFzi8fm4/uKL+cmsWXg7d6617txzz3UpKmOMaZydAYSBJyUFiYuz4nDGmHbFEkAYiAieNB+BkhK0xtzAxhjTllkCCBOvz4cGAgT27nU7FGOMCYklgDDxpKYgXi/+4hK3QzHGmJBYAggT8XjwpKURKCm2qSKNMe2CJYAw8vp8qN9PYN8+t0MxxpgmWQIII0+nTuDxECgu5umnn2bIkCEMGTKEp59+2u3QjDHmEDYOIIzE48HbqRMFW7Zw7733smLFCkSEY489lunTp9O1a1e3QzTGmAM6VAJ48JMH2bB7Q1jbHNptKHcef2eD6++8804GDhzI9ddfD8Bv/v53PKWlnDZ5Mt26dQMgKyuLhQsXctFFF4U1NmOMaQ3rAmqlmTNn8sILLxx4//K8efgDAfrVmCYyIyOD3NxcN8IzxpgGdagzgMZ+qUfKqFGjyM/PZ9u2bRQUFNC1a1dSfD7KS0tRVUQE4MCzMca0FR0qAbjlvPPO4+WXX2b79u3MnDmTrklJvLNoEVpWhiQnk5OTw6RJk9wOEwB/URGFL71EoGQv3q5d8XbpgrdLZ7xduhAXfO/x+RCPnRwa09FZAgiDmTNncvXVV7Nz507effddErxefnnvvezcsoX4nj1ZtGgRv/vd71yNsaqwkN3/+zSF//63c5uq1wt+f/0bezzOPAcHEkSNR9euBxJGzaTh7dIFiY+P7h9ljGkV1xKAiNwE3AhUAW+o6h1uxdJaw4YNo6SkhH79+tGnTx8A7rrpJsaffjoSH8/dd9994IJwtFXt3s3uf/2Lwmf/Q2D/ftLOOIPu111H4hFDCJSU4C8qOvgoLMRfVETVgffOc2VeHmXr1+MvLETLyxs8lic1tYGkUft9raSRlGRnG8a4xJUEICKTgXOAEapaLiI93YgjnNaurT0Z/Y+uuorLpk4lccgQPImJUY+natcudj31Twqfew4tK8M3ZQrdr/sxiUOGHNjG6/Ph9flgwICQ2w3s339I0qiq9f7g64rvvsNfWNh0faS4OCQhAU98PJKQ0MDDWedJSEDim1hf/YgPLo+vvZ2nnvY5cI1GDjwduG5T33Odazr1blt3GXLwbWNth6oZ2zb7CpRds2p7vN6w/1hy6wzgOuABVS0HUNV8l+KIGE9aGuTl4S8uxtOjR9SOW1VQ4HzxP/88WlGBb+pUuv/4WhIPOyws7XuSk/EkJxMfPNMJhVZW4t+z55CEEdizh0BZOVpRcfBR6TwHKirQisqDy8vKCRSXUBV8H6iss76iAqwSq+nA+j8xm04TJ4a1TbcSwBHARBH5LVAG/ExVP61vQxG5BrgGYEAzfqm6zZOQgCc5mUBxMUQhAVTm57P7qacofP4FtLKSzmdPI/3aH5M4eFDEj90UiY8nrnt34mrcGhsJWlV1IBnUSiCVFbWTzIH1wW0qK4INAAfqOAWfg+8P1HdSPbAKrb1NzX0Obl/ftg213Zw/thkbN7s2ldWyaosSBg4Me5sRSwAisgToXc+qXwSP2xUYBxwHvCgig7WeKmqqOhuYDTBmzJh29X+mx+ejascOAhUVeBISInKMyh072PXEkxS9+CLq99N5+nS6X3sNCZmZETleWyZxcUhcHKSk4HU7GGPagYglAFU9raF1InIdMCf4hf+JiASA7kBBpOJxg7c6ARSX4OmeHta2K/Py2PXEExS99DKqSufvn0P3a64hoR2dJRlj3OVWF9CrwCnAMhE5AkgAdroUS8R4EhPxJCbhLy4mLkwJoDI3l51PPEHRK3NAlS7nnkv6tdeQkJERlvaNMbHDrQTwT+CfIvI5UAFcXl/3T0fg8fmoKshHq6qc7okWqsjJZdfjj1P06qsAdPnBDLpffTXx/fqFKVJjTKxxJQGoagVwiRvHjpYzzzyTjz76iAknnMDLDz3knAW0YCxAxdat7Hz8cfa8+hoiQtfzzyP96qubdReOMcbUx0YCR8jtt99OaWkpjz/+OJKQ0OwEUPHdd+x87HH2zJuHeL10nTmT9Kt+RHzv+q6rG2NM83WoBLD9/vspXx/ectCJ3xtK75//vMH1dctB33PPPaSlpXHbbbexbNkyIHgxeNcu1O9HvI3fn1L+7bfseuwx9rw+H4mPp9slF9Ptyh8R36vdj5UzxrQxNga/leqWg37xxRc5//zza23j9flAFX9JwxPGl2/aRO7td7Bp6jSK31pEt8su4/Ali+l111325W+MiYgOdQbQ2C/1SKmvHHTdAWuSnIzExTmDwrp0qbUuUFZG1e5CNl11FZKURLcr/of0K66I+KApY4zpUAnALXXLQdclIk43UGERGgggHo/zxZ9fgL94D1peRvpVP6LbFVe06EKxMca0hCWAMKhbDro+Hp8Pdu+maucutGw//uJixOMhrkcP4kToedttUY7aGBPrLAGEQX3loCdOnMiGDRvYu3cvGRkZPPnkk0waOJCq/B0Hv/jT053yBbt3u/wXGGNikSWAMKlbDvr9998/ZJuqoiK0opK4bl1bNSjMGGPCwb6FoiiuzgVgY4xxk90GaowxMapDJID2XEaoPcdujGnf2n0CSEpKYteuXe3yi1RV2bVrF0lJSW6HYoyJQe3+GkBGRgY5OTkUFLTPqQSSkpLIsFLOxhgXtPsEEB8fz6BB7k97aIwx7U277wIyxhjTMpYAjDEmRlkCMMaYGCXt6e4ZESkAvmvh7t3pgPMOt4J9HgfZZ1GbfR61dYTPY6Cq9qi7sF0lgNYQkRWqOsbtONoK+zwOss+iNvs8auvIn4d1ARljTIyyBGCMMTEqlhLAbLcDaGPs8zjIPova7POorcN+HjFzDcAYY0xtsXQGYIwxpgZLAMYYE6NiIgGIyJki8qWIfC0is9yOxy0i0l9E3hGR9SLyhYjc4nZMbYGIeEVkpYjMdzsWt4lIFxF5WUQ2BP8/Ge92TG4RkZ8G/518LiLPiUiHK9vb4ROAiHiBR4EpwFHARSJylLtRuaYKuE1VvweMA26I4c+ipluA9W4H0Ub8GVioqkOBkcTo5yIi/YCbgTGqOhzwAjPdjSr8OnwCAI4HvlbVTapaATwPnONyTK5Q1TxVzQ6+LsH5x93P3ajcJSIZwFTgSbdjcZuI+ICTgKcAVLVCVYtcDcpdcUCyiMQBKcA2l+MJu1hIAP2ArTXe5xDjX3oAIpIJjAI+djkUt/0JuAMIuBxHWzAYKAD+FewSe1JEUt0Oyg2qmgv8HtgC5AF7VHWRu1GFXywkAKlnWUzf+yoinYBXgJ+oarHb8bhFRKYB+ar6mduxtBFxwGjgH6o6CtgHxOQ1MxHpitNTMAjoC6SKyCXuRhV+sZAAcoD+Nd5n0AFP5UIlIvE4X/7Pquoct+Nx2QRguohsxukaPEVE/u1uSK7KAXJUtfqs8GWchBCLTgO+VdUCVa0E5gAnuBxT2MVCAvgUGCIig0QkAedCzjyXY3KFiAhO/+56VX3E7Xjcpqp3qWqGqmbi/H/xtqp2uF95oVLV7cBWETkyuOhUYJ2LIblpCzBORFKC/25OpQNeEG/3U0I2RVWrRORG4C2cK/n/VNUvXA7LLROAS4G1IrIquOznqrrAvZBMG3MT8Gzwx9Im4AqX43GFqn4sIi8D2Th3z62kA5aEsFIQxhgTo2KhC8gYY0w9LAEYY0yMsgRgjDExyhKAMcbEKEsAxhgToywBmJgkInuDz5ki8sMwt/3zOu//G872jQkXSwAm1mUCzUoAwQqzjamVAFS1w40gNR2DJQAT6x4AJorIqmD9d6+IPCwin4rIGhG5FkBEJgXnUvgPsDa47FUR+SxYM/6a4LIHcCpIrhKRZ4PLqs82JNj25yKyVkQurNH2shp1+J8Njj41JqI6/EhgY5owC/iZqk4DCH6R71HV40QkEVguItVVII8Hhqvqt8H3V6rqbhFJBj4VkVdUdZaI3Kiqx9RzrBnAMTh19rsH93kvuG4UMAynTtVynFHbH4T7jzWmJjsDMKa204HLgqUyPgbSgSHBdZ/U+PIHuFlEVgMf4RQcHELjTgSeU1W/qu4A3gWOq9F2jqoGgFU4XVPGRJSdARhTmwA3qepbtRaKTMIpj1zz/WnAeFUtFZFlQFNTBjbWrVNe47Uf+7dposDOAEysKwHSarx/C7guWDYbETmigUlROgOFwS//oThTbFarrN6/jveAC4PXGXrgzL71SVj+CmNawH5lmFi3BqgKduX8L86cuJlAdvBCbAHw/Xr2Wwj8WETWAF/idANVmw2sEZFsVb24xvK5wHhgNc6kRHeo6vZgAjEm6qwaqDHGxCjrAjLGmBhlCcAYY2KUJQBjjIlRlgCMMSZGWQIwxpgYZQnAGGNilCUAY4yJUf8fOWTtNfuLx14AAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEGCAYAAAB7DNKzAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAAAl9ElEQVR4nO3dd3yV9d3/8dcni7BnmBlskCkzoN4urKLiqBOI9nbcVXs7umyrvdu7dlj91Vpvb7WtVi1VhrsOHKh1UJUwgiJLEMEMVsKeCST5/P7I4TZScgjhHK6Tc97PxyMPc13knPPOEfLONb7fr7k7IiIidUkKOoCIiMQ2FYWIiISlohARkbBUFCIiEpaKQkREwkoJOkA0dOjQwbt37x50DBGRRqWgoGCTu2ccvD8ui6J79+4sWLAg6BgiIo2KmRUear9OPYmISFgqChERCUtFISIiYakoREQkLBWFiIiEpaIQEZGwVBQiIhKWiqKWt5Zt5Ik5X7KzfH/QUUREYkZcDrhrqDeXbuDZghLufv0zLji+K3m5OQzq1jroWCIigbJ4XLho5MiR3tCR2Z+WbGNqfiEvL1pH+f5qjs9qQ15uNucN7Up6anKEk4qIxA4zK3D3kf+yX0VxaNv37ueFhSVMm1vEqtJdtEpP4ZIRWeSNyaZXRosIJRURiR0qigZyd+au2cLU/EJmLd3A/irnhF7tycvN4cyBnUhN1mUeEYkPdRWFrlEchpkxpmd7xvRsT9nOCp5ZUMz0uUXcOH0hGS2bcPnILCblZtOtTdOgo4qIRIWOKBqgqtqZvbKMqfmFvLOiFANO79+RvNwcTu6bQXKSRe21RUSiRUcUEZScZJzWvyOn9e9IydY9PDWvmKfmF/P28vlktm3KpNHZXD4qiw4tmgQdVUTkqOmIIkL2VVbz1rKNTM0vZM7qzaQmG+MHdSEvN5vcHu0w01GGiMQ2Xcw+hlaV7mL63CKeKyhmR3klvTu2IC83m4uGZ9K6aWpguUREwlFRBKB8fxWvLFrH1LlFLCreRtPUZM4f2pW8MdkMyWwTdDwRka9RUQRsydrtTJtbyIsfr2Pv/iqGZLYmLzeb84d2o2maBvKJSPBUFDFiR/l+Xvx4LVPzC1m5cRct01O4eHgmebnZ9OnUMuh4IpLAVBQxxt1ZULiVqfmFvL54A/uqqsnt0Y68MTmMH9iZtBQN5BORY0tFEcM276rg2YISps8tomjLHjq0SOPSkVlMHp1NVrtmQccTkQShomgEqqudf67axNT8Qv6xfCMOnNo3g7zcHE7r31ED+UQkqlQUjcz67XuZMa+Yp+YVUbqzgq6t02sG8o3OomPL9KDjiUgcUlE0UvurqvnH8o1MzS/ig1WbSEkyzhrYmbzcbMb2aq+BfCISMY12Cg8zaw78EdgHvOfu0wKOdEylJicxflAXxg/qwppNu5k+t5BnC0p4dfF6emY0Jy83h0uGZ9K6mQbyiUh0BHJEYWaPAxOAUncfVGv/eOB+IBl41N3vNrMrgW3u/oqZPe3ulx/u+ePpiOJQyvdX8dri9UzNL2Rh0TaapCRx3tCu5OVmc3xWGx1liEiDxNoRxRTgQeCJAzvMLBl4CPgGUALMN7OXgUxgcejLqo5tzNiUnprMRcMzuWh4JsvW7QgN5FvLcwUlDOzaiivG5HD+0K40bxLzB4wi0ggEdo3CzLoDMw8cUZjZWOAOdz8rtH176EtLgK3uPtPMnnL3iXU833XAdQDZ2dkjCgsLo/0txJRdFZX/N5Dvsw07adkkhW8O70Zebg79Omsgn4gcXsxdzD5EUVwCjHf3/whtXwnkAj+h5uijHPigPtco4v3UUzjuzsKibUzLL2Tm4vXsq6xmVPe25OXmcPbgzjRJ0XQhInJosXbq6VAOdWLd3X03cPWxDtNYmRkjctoyIqctP58wgOcKSpg2t5DvPf0Jv5qZxqUjM5k8Opuc9s2DjioijUQsFUUJkFVrOxNYF1CWuNC2eRrfPrkn157Ug4++2MzU/EIe/ecaHn5/NSf3zSAvN5tx/TuSonW/RSSMWCqK+UAfM+sBrAUmApODjRQfkpKMk/p04KQ+HdiwvZyn5xczY14R1z9ZQJfW6Uwclc3E0Vl0aqWBfCLyr4K6PXYGcCrQAdgI/MLdHzOzc4D/oeb22Mfd/c6GPH8iX6Oor8qqat75rJSpc4uYvbKM5CTjG8d1Im9MNif26kCSpgsRSTgxdzE7mlQUR6Zw826mzyvi2QUlbNm9j+7tm9UM5BuRSdvmaUHHE5FjREUhh1VRWcUbSzYwNb+Q+V9uJS0liQmDu5A3Jpvh2W01kE8kzqko5Iis2LCTaXMLeWHhWnZVVNK/c0uuGJPDhcO60UID+UTikopCGmR3RSUvL1rH1PxClq7bQfO0ZC4cVjOQb0DXVkHHE5EIUlHIUXF3FpVsZ2p+Ia8sWkdFZTXDs9twxZgczhnchfRUDeQTaexUFBIx2/bs4/mFa5k2t5DVZbtp0yyVS0dkMjk3hx4dNJBPpLFSUUjEuTtzVm9mWn4Rs5ZuoLLaOal3B/JyszljQCdSNZBPpFFpDFN4SCNjZpzQqwMn9OpA6Y5ynllQzIx5xXxn2kI6tmzCxNHZTByVRdc2TYOOKiJHQUcUElFV1c57K0qZml/IeyvLMGDccZ3Iy83m5D4ZGsgnEsN0RCHHRHKSMe64Tow7rhPFW/YwY14Rzywo5q1lG8lq15TJo3O4bGQm7Vs0CTqqiNSTjigk6vZVVjNrac1AvrlrtpCWnMTZgzuTl5vDqO4ayCcSK3QxW2LCqtKdTM0v4vmFJewsr6Rvpxbk5ebwzeHdaJWudb9FgqSikJiyd18Vryxax9S5hXxasp2mqclccHxXrhiTw6BurYOOJ5KQVBQSsz4t2ca0/CJeWrSW8v3VDM1qQ15uNucN6UrTNA3kEzlWVBQS87bv3c/fF5YwbW4Rn5fuolV6ChePyCQvN4feHVsEHU8k7qkopNFwd+at2cLUuUW8sWQ9+6ucMT3bccWYHM4c0Jm0FA3kE4kGFYU0Spt2VfDMgmKmzy2iZOteOrRowuWjMpk0OpvMts2CjicSV1QU0qhVVzvvf17GtPxC3vmsFAdO69eRK8Zkc0rfjiRrIJ/IUVNRSNxYu20vT80r4qn5xZTtrKBbm6ZMzs3mspFZZLTUQD6RhlJRSNzZX1XNW8s2MjW/kI++2ExqsnHmwM5ckZvDmJ7tNJBP5AhpCg+JO6nJSZwzuAvnDO7CF2W7mD63iOcKSnj10/X0ymhOXm4OF4/IpHVTDeQTORo6opC4Ur6/ipmfrmdqfiGfFG8jPTWJ84bUDOQbmtUm6HgiMU2nniThLFm7nWlzi3jpk7Xs2VfF4G6tycvN5vzju9IsTQfTIgdTUUjC2lm+nxc/XsvU/CJWbNxJyyYpXDS8G3ljcujbqWXQ8URihopCEp67U1C4lan5hby2eAP7qqoZ3aMdebnZjB/UmSYpmi5EEpuKQqSWzbsqeK6gZrqQoi17aN88jctGZTF5dDZZ7TSQTxKTikLkEKqrnQ9WbWJqfiFvL9+IA6f0zSAvN4fT+2sgnyQWFYXIYazfvpen5hXz1PwiNu6ooGvrdCaNzubyUVl0bJUedDyRqFNRiNTT/qpq/rG8lGlzC/nn55tISTLOHNiJK3JzGNurvQbySdzSgDuRekpNTmL8oM6MH9SZLzftZvq8Ip5dUMxrizcwqntbfnRWf0b3aBd0TJFjplEcUZjZhcC5QEfgIXd/M9zX64hCIq18fxXPFpTwwD8+p3RnBaf2y+DWM/tpNT6JK3UdUUR9Yn8ze9zMSs1syUH7x5vZCjNbZWa3hXsOd3/R3b8NXAVcHsW4IoeUnprMlWNyeP9Hp3H72f35pHgbEx74gBunL+SLsl1BxxOJqqgfUZjZycAu4Al3HxTalwysBL4BlADzgUlAMnDXQU9xjbuXhh53LzDN3ReGe00dUUi07Sjfz6OzV/PoB2uoqKzmkuGZ3HJGH7q1aRp0NJEGC/Ritpl1B2bWKoqxwB3uflZo+3YAdz+4JA483oC7gbfc/e3DvZ6KQo6VTbsq+OO7XzA1vxCAvDHZ3Hhabzq00HTn0vgEduqpDt2A4lrbJaF9dbkZOAO4xMxuONQXmNl1ZrbAzBaUlZVFLqlIGB1aNOG/zxvAuz86lYuGd+OJOYWc/Lt3uffNFewo3x90PJGICOqI4lLgLHf/j9D2lcBod785Eq+nIwoJyhdlu7jvrZXM/HQ9rZum8p1Te/HvY7vTNE3Tg0jsi7UjihIgq9Z2JrAuoCwiEdMrowUPTh7OzJtPYnh2G+5+/TNOvuddnpzzJfsqq4OOJ9IgQRXFfKCPmfUwszRgIvByQFlEIm5Qt9b89erRPHvDWHq0b87PX1rKuD+8xwsLS6iqjv1b0kVqO2xRhM7732hmbRvyAmY2A5gD9DOzEjO71t0rgZuAWcBy4Bl3X9qQ5xeJZaO6t+Pp68cw5epRtEpP5QfPLOLs+2cza+kGGsMYJhGoxzUKM+sNXE3N+IUFwF+BNz2G/5brGoXEoupq5/UlG7j3rRWsLtvN0Kw2/PisfpzYu0PQ0USACNwea2ZJwATgT0A18Dhwv7tviWTQSFBRSCyrrKrmhY/Xcv/bn7N2215O6NWeH53Vj2HZDTpoF4mYo7qYbWZDgHuBe4DngUuAHcA7kQwpkghSkpO4bGQW79x6Cr84bwArNuzkm3/8iG8/sYAVG3YGHU/kX9Tn1FMBsA14DHje3Stq/dkL7n5RVBM2gI4opDHZXVHJXz9cw8OzV7OropILj+/G987oQ0775kFHkwTT4FNPZtbT3VcftK+Hu6+JcMaIUVFIY7Rtzz7+/P5qpny0hsoq5/JRWdwyrg+dtBaGHCNHUxQL3X34IZ5sRIQzRoyKQhqz0h3lPPjuKmbMKyLJjKtO6M4Np/SibfO0oKNJnDvi9SjMrD8wEGhtZrVPL7UC9CuOSJR0bJXOry4YxLf/rSf3vb2SR/65mulzi/j2yT255qQetGiiZWTk2KrziMLMLgAuBM7n64PhdgJPuftHUU/XQDqikHiycuNO7n1zBbOWbqR98zRuGdeHb43N0Up7EnFHc+pprLvPiVqyKFBRSDxaVLyN3836jA9XbebMAZ2497KhtExPDTqWxJEjLgozewCos0Xc/ZbIxYssFYXEK3fn8Q+/5LevLSenfTMevmIEfTq1DDqWxImGrJmtn7QiMcbMuPakHgzs2oqbpi/kwoc+5J5Lh3LO4C5BR5M41ijWzD5SOqKQRLBheznfmVbAx0XbuP7knvzorH6kJAc1z6fEg4YcURx4YAbwE2AAte52cvfTI5pQRI5I59bpPH3dWH49cxkPz17N4rXbeWDSMNprdT2JsPr8+jGNmhleewC/BL6kZppwEQlYWkoSv75wEPdcMoQFhVs574EPWFS8LehYEmfqUxTt3f0xYL+7v+/u1wBjopxLRI7ApSOzeOE7J2BmXPrnOTw9vyjoSBJH6lMUBxb+XW9m55rZMGpWpBORGDKoW2tm3nwSuT3b8ZPnF3P7C4upqKwKOpbEgfoUxW/MrDXwQ+BW4FHg+1FNJSIN0rZ5GlOuHs2Np/VixrwiLns4n3Xb9gYdSxo53fUkEqdmLd3AD59ZRJOUJB6YPIwTemmBJAmvwetRmFmGmf3UzB4xs8cPfEQnpohEylkDO/PSTSfStnkaVzw6l0dmf6HlV6VB6nPq6SWgNfA28GqtDxGJcb0yWvDijScyflBnfvvaZ9w0/WN2V1QGHUsamfpMQ9nM3X8S9SQiEhUtmqTw0OThPDJ7Nf/vjc9YuXEnD185gp4ZLYKOJo1EfY4oZprZOVFPIiJRY2Zcf0ovnrw2l82793HBgx/y5tINQceSRqI+RfFdasqi3Mx2mNlOM9sR7WAiEnkn9u7AKzefRM+M5lz3ZAH3vrmCqmpdt5DwDlsU7t7S3ZPcPd3dW4W2Wx2LcCISed3aNOXp68cycVQWD7yziqunzGfbnn1Bx5IYVp+7nszMrjCzn4e2s8xsdPSjiUi0pKcmc/fFQ7jrosHkf7GZCQ98wJK124OOJTGqPqee/giMBSaHtncBD0UtkYgcM5NGZ/PMDWOpqnYu/tNHPF9QEnQkiUH1KYpcd78RKAdw962AVnkXiRPHZ7XhlZtPYnh2W3747CL++6Ul7KusDjqWxJB6zfVkZsmEVrsLTTuuv0UicaRDiyY8ee1orj+5J0/MKWTSX/LZuKM86FgSI+pTFP8L/B3oaGZ3Ah8Av41qKhE55lKSk7j9nON4aPJwlq/fwYQHPmDemi1Bx5IYUJ+7nqYBPwbuAtYDF7r7s9EOJiLBOHdIF1688URaNklh8l/ymfLhGk39keDqLAozyzWzRWa2C/gr8K67P+juy49dPBEJQt9OLXnxphM5rX9H7nhlGd9/+hP27tOU5Ykq3BHFQ9RMK94e+ANw3zFJdAhm1tzMCsxsQlAZRBJNq/RUHr5iBLee2ZeXFq3jm3/8kMLNu4OOJQEIVxRJ7v6Wu1eETjVlHOmTh2aaLTWzJQftH29mK8xslZndVo+n+gnwzJG+vogcnaQk46bT+zDl6tFs2FHOeQ98wLuflQYdS46xcEXRxswuOvBxiO36mAKMr70jdAfVQ8DZwABgkpkNMLPBZjbzoI+OZnYGsAzYeMTfnYhExCl9M3jlppPIbNuMa/42n/vf/pxqTf2RMOpcuMjM/hrmcR5aO/vwL2DWHZjp7oNC22OBO9z9rND27aEnvKuOx98JNKemVPYC33T3f7k918yuA64DyM7OHlFYWFifeCJyBMr3V/HTvy/mhYVrOXdIFx6YOIykJAs6lkRIXQsX1TnNuLtfHaUs3YDiWtslQG6YHP8FYGZXAZsOVRKhr3sEeARqVriLVFgR+Up6ajL3XjqUvp1acvfrn5HZpim3n3Nc0LEkyuqzHkWkHerXj8P+YHf3KZGPIiJHysy44ZRerNu2l4dnr6ZHh+ZMHJ0ddCyJoiCKogTIqrWdCawLIIeIHIX/njCALzfv4WcvLiG7XTNO6K01ueNV2AF3ZpZkZidE+DXnA33MrIeZpQETgZcj/BoiEmUpyUk8OHkYPTo054apBawu2xV0JImSsEURuh5wb0Of3MxmAHOAfmZWYmbXunslcBMwC1gOPOPuSxv6GiISnFbpqTx+1ShSk5O4Zsp8tu7WuhbxqD5zPb1pZheb2RHf2uDuk9y9i7ununumuz8W2v+au/d1917ufucRpxaRmJHVrhmPfGsk67aXc8PUAs08G4fqUxQ/AJ4F9mkpVBE5lBE5bbnnkiHMXbOFn/59seaGijOHvZjt7i2PRRARadwuOL4bazbt5n/e/pyeGc35z1N7Bx1JIkRLoYpIxHx3XB/OH9qV372xgjeWrA86jkSIlkIVkYgxM353yRCGZ7fhe09/wqcl24KOJBGgpVBFJKLSU5N55Fsj6dCiCf/xtwWs37436EhylLQUqohEXIcWTXj8qlHs2VfFtVMWsLuiMuhIchS0FKqIREXfTi15cPIwPtuwg+8+9TFVmm220dJSqCISNaf268gd5w/k7eWl3P26FsdsrOq8PdbMWrn7DjNrB5QCM2r9WTt316rrInJY3xrbndVlu/nLP9fQM6MFkzSBYKMTbhzFdGACUMDXZ3e10HbPKOYSkTjys3OP48vNu/l5aALBEzWBYKNS56knd58QmrbjFHfvWeujh7urJESk3lKSk3hg0jB6ZbTghqkFrCrVBIKNyeEmBXRqLmSLiByVlumpPHbVSJqk1EwguEUTCDYa9bnrKd/MRkU9iYjEvcy2NRMIbthRzg1PFlBRWRV0JKmH+hTFacAcM/vCzD41s8Vm9mm0g4lIfBqe3ZZ7Lx3KvC+3cPsLmkCwMQg7KWDoGsUNQOGxiSMiieC8oV1ZXbab+95eSa+MFtx4miYQjGVhi8Ld3czuc/cRxyqQiCSGW8b1Zs2mXdwzawXd2zfn3CFdgo4kddA1ChEJhJlx98VDGJHTlh888wmfFG8LOpLUQdcoRCQw6anJPHLlCDq2qplAcO02TSAYi+pTFGcDvYDTgfOoGYR3XjRDiUjiaN+iCY//+ygq9ldx7ZT57NIEgjGnPnM9Fbp7IbCXmhHZBz5ERCKiT6eWPJQ3nM9Ld3HLDE0gGGvqs8Ld+Wb2ObAGeB/4Eng9yrlEJMGc3DeDO84fyDuflXLnq5pAMJbU59TTr4ExwEp37wGMAz6MaioRSUhXjsnh6hO78/iHa5iar7vyY0W9Fi5y981Akpklufu7wPHRjSUiiepn5w7gtH4Z/OLlpcxeWRZ0HKF+RbHNzFoAs4FpZnY/oKtNIhIVyUnGA5OH06djC26ctpDPN+4MOlLCq09RXADsAb4PvAF8ge56EpEoatEkhceuGkWT1GSu+dt8Nu+qCDpSQqvPXU+73b3a3SuBV4EHQqeiRESiplubpjz67yMp3VHB9ZpAMFB1FoWZjTGz98zsBTMbZmZLgCXARjMbf+wiikiiOj6rDfdeNpQFhVu57XlNIBiUcHM9PQj8FGgNvAOc7e75ZtafmmVR3zgG+UQkwU0Y0pU1Zbu5962V9OjQnFvG9Qk6UsIJVxQp7v4mgJn9yt3zAdz9s5pJZUVEjo2bTu/Nmk27+UOoLM4b2jXoSAklXFFU1/r84AlYjtnxn5klUTOWoxWwwN3/dqxeW0Rig5lx18WDKd66h1ufXURm26YMy24bdKyEEe5i9lAz22FmO4Ehoc8PbA+uz5Ob2eNmVhq6vlF7/3gzW2Fmq8zstsM8zQVAN2A/UFKf1xWR+NMkJZmHrxxJp1bpfPuJBZRs3RN0pIRRZ1G4e7K7t3L3lu6eEvr8wHZqPZ9/CvC1C99mlgw8RM1kgwOASWY2wMwGm9nMgz46Av2AOe7+A+A7DfkmRSQ+tGuexuNXjaSispprpyxgZ/n+oCMlhPqMo2gwd58NbDlo92hglbuvdvd9wFPABe6+2N0nHPRRSs1RxNbQY3V/nEiC692xJX/KG8Gqsl3cPONjKquqD/8gOSpRLYo6dAOKa22XhPbV5QXgLDN7gJrR4YdkZteZ2QIzW1BWpmH/IvHspD4d+NUFA3lvRRn3vb0y6DhxL+xSqFFyqFum6rw47u57gGsP96Tu/gjwCMDIkSN1s7VInMvLzaGgcCuPzF7NJSOy6NGhedCR4lYQRxQlQFat7UxgXQA5RKSRu+3s/jRJSeY3M5cFHSWuBVEU84E+ZtbDzNKAicDLAeQQkUauY8t0bj69N//4rJT3VpQGHSduRbUozGwGMAfoZ2YlZnZtaM6om4BZwHLgGXdfGs0cIhK/rj6xBz06NOdXM5exr1IXtqMh2nc9TXL3Lu6e6u6Z7v5YaP9r7t7X3Xu5+53RzCAi8S0tJYmfTziO1WW7eWLOl0HHiUtBnHoSEYmo0/t34tR+Gdz/9ueU7dSU5JGmohCRuPDzCQPYu7+K389aEXSUuKOiEJG40CujBVef2J1nCopZXLI96DhxRUUhInHj5nF9aN88jTteWaq1KyJIRSEicaNVeio/Pqs/BYVbeekTDc+KFBWFiMSVS0ZkMiSzNXe9vpzdFZVBx4kLKgoRiStJScYvzhvIxh0V/PG9VUHHiQsqChGJOyNy2vLNYd34yz/XULRZ61YcLRWFiMSl287uT0qS8ZtXNQ/U0VJRiEhc6tQqnZtO782byzbyz8+19MDRUFGISNy69qQe5LRvxi9fWcZ+LXDUYCoKEYlbTVKS+dm5A1hVuosn5xQGHafRUlGISFw747iO/FufDtz39ko279I8UA2hohCRuGZm/OK8AezdV8Xv39SyqQ2hohCRuNe7Y0u+NbY7T80vYslazQN1pFQUIpIQvntGH9o1S+OXmgfqiKkoRCQhtG6ayq1n9WP+l1t55dP1QcdpVFQUIpIwLhuZxcCurbjrteXs2ad5oOpLRSEiCSM5ybjj/IGs317On9/7Iug4jYaKQkQSyqju7Th/aFcenr2a4i2aB6o+VBQiknBuP6c/SWb89rXlQUdpFFQUIpJwurRuyn+e2ovXl2zgoy82BR0n5qkoRCQhffvknmS2bcovX15GpeaBCktFISIJKT01mZ+dexwrNu5k+ryioOPENBWFiCSsswZ25oRe7bn3zZVs3b0v6DgxS0UhIgmrZh6ogeyqqOQPb2keqLqoKEQkofXr3JIrcrOZNreQ5et3BB0nJqkoRCThff8bfWndNFXzQNVBRSEiCa9NszR+cGY/8ldv4fUlG4KOE3NUFCIiwOTR2fTv3JI7X11O+f6qoOPElJgvCjPLNrOXzexxM7st6DwiEp8OzAO1dtteHn5/ddBxYkpUiyL0w73UzJYctH+8ma0ws1X1+OHfF3jV3a8BBkQtrIgkvDE923Pu4C786f1VrN22N+g4MSPaRxRTgPG1d5hZMvAQcDY1P/gnmdkAMxtsZjMP+ugIfAxMNLN3gHejnFdEEtzt5/THHe7SPFD/J6pF4e6zgS0H7R4NrHL31e6+D3gKuMDdF7v7hIM+SoGrgV+4++nAuXW9lpldZ2YLzGxBWVlZtL4lEYlzmW2bccMpvZj56Xrmrt4cdJyYEMQ1im5Aca3tktC+urwB3GJmfwa+rOuL3P0Rdx/p7iMzMjIiElREEtMNp/Sia+t07nhlGVXVul02iKKwQ+yr8/+Euy9x90vc/QZ3vzWKuUREAGialsxPzz2O5et38NR8zQMVRFGUAFm1tjOBdQHkEBGp07mDu5Dbox2/n7WC7Xv2Bx0nUEEUxXygj5n1MLM0YCLwcgA5RETqdGAeqO1793Pf24k9D1S0b4+dAcwB+plZiZld6+6VwE3ALGA58Iy7L41mDhGRhhjQtRWTRmfzZH4hKzfuDDpOYKJ919Mkd+/i7qnununuj4X2v+bufd29l7vfGc0MIiJH44dn9qN5WjK/emVZws4DFfMjs0VEgtSueRo/+EZfPli1iTeXbQw6TiBUFCIih3HFmBz6dmrBb15dlpDzQKkoREQOIyU5iTvOG0jxlr089sGaoOMccyoKEZF6OKF3B8YP7MxD765iw/byoOMcUyoKEZF6+q9zj6Oy2rn79cSaB0pFISJST1ntmnH9yT158ZN1FBQePI1d/FJRiIgcge+c2osurdO54+VlVCfIPFAqChGRI9AsLYXbzu7P4rXbebag+PAPiAMqChGRI3T+0K6M6t6We2atYEd5/M8DpaIQETlCB+aB2rx7H//79udBx4k6FYWISAMM6taaiaOymPLRl6wq3RV0nKhSUYiINNCtZ/ajaVoyv54Z3/NApQQdQESksWrfognfO6Mvv565jHF/eJ9kO9S6bMfWvZcNZUhmm4g+p4pCROQofGtsDqU7yineuifoKAA0TU2O+HOqKEREjkJqchK3n3Nc0DGiStcoREQkLBWFiIiEpaIQEZGwVBQiIhKWikJERMJSUYiISFgqChERCUtFISIiYVk8zk9iZmVAYQMf3gHYFME4jZ3ej6/ovfg6vR9fFw/vR467Zxy8My6L4miY2QJ3Hxl0jlih9+Mrei++Tu/H18Xz+6FTTyIiEpaKQkREwlJR/KtHgg4QY/R+fEXvxdfp/fi6uH0/dI1CRETC0hGFiIiEpaIQEZGwVBS1mNl4M1thZqvM7Lag8wTFzLLM7F0zW25mS83su0FnigVmlmxmH5vZzKCzBM3M2pjZc2b2WejvydigMwXFzL4f+neyxMxmmFl60JkiTUURYmbJwEPA2cAAYJKZDQg2VWAqgR+6+3HAGODGBH4vavsusDzoEDHifuANd+8PDCVB3xcz6wbcAox090FAMjAx2FSRp6L4ymhglbuvdvd9wFPABQFnCoS7r3f3haHPd1LzQ6BbsKmCZWaZwLnAo0FnCZqZtQJOBh4DcPd97r4t0FDBSgGamlkK0AxYF3CeiFNRfKUbUFxru4QE/+EIYGbdgWHA3ICjBO1/gB8D1QHniAU9gTLgr6FTcY+aWfOgQwXB3dcCvweKgPXAdnd/M9hUkaei+IodYl9C3ztsZi2A54HvufuOoPMExcwmAKXuXhB0lhiRAgwH/uTuw4DdQEJe0zOzttSceegBdAWam9kVwaaKPBXFV0qArFrbmcThIWR9mVkqNSUxzd1fCDpPwE4EzjezL6k5JXm6mU0NNlKgSoASdz9wlPkcNcWRiM4A1rh7mbvvB14ATgg4U8SpKL4yH+hjZj3MLI2aC1IvB5wpEGZm1Jx/Xu7ufwg6T9Dc/XZ3z3T37tT8vXjH3ePut8b6cvcNQLGZ9QvtGgcsCzBSkIqAMWbWLPTvZhxxeGE/JegAscLdK83sJmAWNXcuPO7uSwOOFZQTgSuBxWb2SWjfT939teAiSYy5GZgW+qVqNXB1wHkC4e5zzew5YCE1dwt+TBxO5aEpPEREJCydehIRkbBUFCIiEpaKQkREwlJRiIhIWCoKEREJS0UhEoaZ7Qr9t7uZTY7wc//0oO2PIvn8IpGiohCpn+7AERVFaEbicL5WFO4edyN6JT6oKETq527g38zsk9D6A8lmdo+ZzTezT83segAzOzW0lsd0YHFo34tmVhBas+C60L67qZlx9BMzmxbad+DoxULPvcTMFpvZ5bWe+71a60BMC40GFokqjcwWqZ/bgFvdfQJA6Af+dncfZWZNgA/N7MCsoaOBQe6+JrR9jbtvMbOmwHwze97dbzOzm9z9+EO81kXA8dSs89Ah9JjZoT8bBgykZh6yD6kZRf9BpL9Zkdp0RCHSMGcC3wpNcTIXaA/0Cf3ZvFolAXCLmS0C8qmZeLIP4Z0EzHD3KnffCLwPjKr13CXuXg18Qs0pMZGo0hGFSMMYcLO7z/raTrNTqZl2u/b2GcBYd99jZu8Bh1sqM9zppIpan1ehf8NyDOiIQqR+dgIta23PAr4Tmo4dM+tbx+I9rYGtoZLoT83SsgfsP/D4g8wGLg9dB8mgZjW5eRH5LkQaQL+NiNTPp0Bl6BTSFGrWjO4OLAxdUC4DLjzE494AbjCzT4EV1Jx+OuAR4FMzW+juebX2/x0YCyyiZvGsH7v7hlDRiBxzmj1WRETC0qknEREJS0UhIiJhqShERCQsFYWIiISlohARkbBUFCIiEpaKQkREwvr/nI2S7/BOuusAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEGCAYAAAB7DNKzAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAAAkiElEQVR4nO3de3iV5Z3u8e8vZ0ggBJJIyBEUUQSEEDmIINaqqFRp1Cowdqq21k7VVqcztTO7ndkz093Onk7tYZxp3ZXaWsCqYKUUlVoPCMoxnAUtCoEknM8J5Pzbf2RhYwwhYFbetZL7c13rIu+blbXucEHuPM/zHszdEREROZ2YoAOIiEhkU1GIiEibVBQiItImFYWIiLRJRSEiIm2KCzpAOKSnp3tBQUHQMUREosqaNWsOuHtGy/1dsigKCgpYvXp10DFERKKKmZW2tl9TTyIi0iYVhYiItElFISIibVJRiIhIm1QUIiLSJhWFiIi0SUUhIiJt6pLnUZyrlzbtYdu+4/RLSaRfcgL9UhLol5xIv5QEUhLjMLOgI4qIdDoVRTN/2rKXZ9eUtfq5hLiYj5VH03ZTqaSnJNI39Pn0lESS4mM7Ob2ISHhYV7xxUVFRkZ/rmdk19Q0cqqrlYGUtBypr/vJxVQ0HK2tD2zUcqKzlYFUN1XWNrb5OckIsfUOlkp6SECqR1kslrWcCCXGaBRSRYJnZGncvarlfI4oWEuNiyUrtQVZqj3Y9/0RtfZulcqCyhooj1WwsP8qhqlrqGlov5t5JcaSnNI1UTpVKeujPvskJZKf14JIBvUmM00hFRDqXiuIT6pkQR8++ceT27XnG57o7x6rrORgqlVOjkualcrCylu0HqlhTephDVbU0NuuVhNgYhuekMjo/jdH5aRTmpZHRKzGM352IiIqiU5kZqT3iSe0Rz6CPXZ/x4xoanSMnmkrk/f1VlOw8zJrSwzy5bAePL/kAgPx+PRmdl8bogqbyGJzZi9gYLbqLSMfRGkUUqqlvYFP5MdaUHmJNaVN5HKisBaBXYhyj8tOayiM/jZF5fUhJ1O8DInJmWqPoQhLjYj+cfoKmKa1dh06yullx/OhP7+EOMQYX9e/94fNH56eRk9ZDh/qKSLtpRNFFHa+uY92uI6zecZiSnYdZu/MIlTX1AGT2SvzLOkd+mhbJRQTQiKLb6ZUUz8TBGUwc3LQY0tDovLf3OKtLD1MSGnW8uGkP0HSOyKU5qRSGpqwK89NIT9EiuYg00YiiG9t3vPrD0lhTephN5ceobWg6L2RgejKFeX+ZrhqcmUKMFslFurTTjShUFPKh6roGNpUf/bA41pQe5mBVaJE8Ke4jxTEytw/JWiQX6VI09SRnlBQfS1FBX4oK+gJNi+SlB080lcbOpimrR1/5yyL5xVm9GTeoH9NGZjMsu7cWyEW6KI0o5Kwcq65j7c4jrAmtdazccYja+kYGZ6ZQXJjDtFED2n1Wu4hEFk09SVgcPVnHoo27mV9SxqodhzGDCeenU1yYzXWX9Nf0lEgUUVFI2JUerOL5teXMLyln56ET9EyIZcqw/txSmMO4Qf10xrhIhFNRSKdxd9aUHmZeSTkLN1RwvLqerNQkpo3KpnhUNoPP6xV0RBFpRdQWhZklA/8N1AKvu/vsM32NiiJyVNc18Kct+5hfUsbr7+2nodEZkZNK8ahsPnPpAPrpfA2RiBFRRWFms4CpwD53H9Zs/xTgx0As8At3/76Z3Qkccfffm9lv3f32M72+iiIyHaisYcG6CuaVlLG54hhxMcbkIZncUpjNpy7O1NnhIgGLtMNjnwT+C/j1qR1mFgs8BlwDlAGrzGwBkANsDD2toXNjSkdKT0nk7isGcvcVA9m65xjPl5Tz/NpyXtmyl9Qe8UwdkUVxYQ6FeX10qK1IBAls6snMCoCFp0YUZjYe+Gd3vy60/a3QU8uAw+6+0Myedvc7TvN69wL3AuTl5Y0uLS0N97cgHaCh0Vm27QDzS8p4afMequsaKejXk+LCHD47Krtd9/kQkY4RUVNP0GpR3ApMcfcvhrbvBMYC36Rp9FENLNUaRddVWVPPixt3M7+knLc/OAjAmIF9uaUwm+uHZ9E7KT7ghCJdW6RNPbWmtbkGd/cq4K7ODiOdLyUxjtuKcrmtKJeywyd4IbSe8c15G/nOC5u59pL+FBdmM/GCdOJidY9xkc4SSUVRBuQ2284BKgLKIgHLSevJV6+6gL+ZfD7ry44yv6SMBesr+P36CtJTEpk2cgDFhTkMHdA76KgiXV4kTT3FAe8BVwPlwCpghrtvPtvX1tRT11Rb38hr7zYdavvq1n3UNTgX9e/FLYU53DxyAJm9k4KOKBLVImqNwszmApOBdGAv8E/u/oSZ3QD8iKbDY2e5+3fP5fVVFF3f4apaFm6oYF5JOet2HSHGYOLgDIoLs7l2aH96JOhQW5GzFVFFEW4qiu7l/f2VHx5qW37kJCmJcdw4PIu/vrxAU1MiZ0FFIV1eY6OzYvsh5pWU8YcNuzlZ18C4QX25a8JAPn3xebrWlMgZqCikWzl6oo6nV+3kV2/toOJoNbl9e/CFywfyuaIceukwW5FWqSikW6pvaGTxO3uZtXQ7q0sPk5wQy21FuXzh8gIK0pODjicSUVQU0u1tKDvCL5ftYOGGCuobnasvyuSuCQO5/Px+umSICCoKkQ/tO1bNb5aXMnvFTg5W1TLkvF7cfUUBN4/MJileR0tJ96WiEGmhuq6BBesrmLV0O1v3HCetZzwzx+Zz5/h8ztM5GdINqShETsPdWf7BIWYt284rW/YSa8aNI7K4a8JARub2CTqeSKeJhms9iQTCzBh/fj/Gn9+PnQdP8ORbO3hm9S5eWFdBYV4f7powkCnD+hOv60tJN6URhUgrjlfX8dyaMp58awelB0+QlZrE58cXMH1MLn16JgQdTyQsNPUkcg4aGp3Xtu7jl29tZ9m2gyTFx1BcmMNdlxfo3t/S5agoRD6hrXuO8eSyHcxfW05tfSMTB6dz9xUDuXJwBjE661u6ABWFSAc5WFnD3JU7eWp5KXuP1TAoPZm7JhRQXJhDcqKW/SR6qShEOlhtfSMvbtrNrKXbWV92lF5JcUwfk8fnx+eTk6ZbuEr0UVGIhIm7U7LzCL9ctp0XN+3B3bnukv7cfcVAivLTdNa3RA0dHisSJmbG6Pw0RuenUXHkJE8tL2XOip28uGkPw7J7c/eEgdw4IovEOJ31LdFJIwqRMDhZ28D8tWX8ctkOtu2rJD0lkTvH5TNzXB7pKYlBxxNplaaeRALg7izddoBZS7fz2rv7iY81rhqSSXFhDlddlKFRhkQUTT2JBMDMmDg4g4mDM3h/fyVzV+zkhfUVLH5nL316xvOZEQMoLsxmZG4frWVIxNKIQqST1Tc0snTbAeaXlPPy5j3U1DcyKD2Z4sJspo3K1hFTEhhNPYlEoOPVdby4cQ/zSspYsf0QAOMG9aW4MIfrh/XX3fikU6koRCLcrkMn+N3acuavLWf7gSqS4mO47pL+FBfmMOH8fsTpooQSZioKkSjh7qzddYT5JWX8fv1ujp6sI7NXItNGZVNcmM1F/XsHHVG6KBWFSBSqqW/gta37mV9Sxqtb91Hf6AzN6k1xYTY3jRxAZi/dYEk6jopCJModqqpl4YYK5pWUs37XEWJjjEmD0ykuzOGaoefpNq7yiakoRLqQbfsqeX5tGc+XlFNxtJpeiXHcMDyLW0bnUJSfpqvZyjlRUYh0QY2NzvLtB5lfUs6LG3dTVdtATloPikdl89nCHAamJwcdUaKIikKkiztRW8/izXuZV1LGsm0HaHQozOtDcWEOU0dk6c58ckYqCpFuZM/Ral5YV868kjLe21tJQmwMV1/cdOmQKy/MICFOh9rKx6koRLohd2dzxTHml5TzwrpyDlbV0jc5gZsubbp0yPDsVF06RD6kohDp5uoaGnnzz/uZV1LOH9/ZS219IxdkplBcmM1nR2WTldoj6IgSsKguCjObBtwIZAKPufvitp6vohBp29GTdSzauJv5JWWs2nGY5IRYFj98Jdl9VBbd2emKIuwTlWY2y8z2mdmmFvunmNm7ZrbNzB5p6zXc/Xfu/iXgC8DtYYwr0i2k9ohn+pg8nr3vchY9OJETdQ38duXOoGNJhOqMFa0ngSnNd5hZLPAYcD0wFJhuZkPNbLiZLWzxyGz2pf8r9HUi0kGGDujN5AszeHrVLuoaGoOOIxEo7EXh7kuAQy12jwG2ufsH7l4LPA3c7O4b3X1qi8c+a/LvwIvuXhLuzCLdzYyx+ew7XsOftuwLOopEoKCOkcsGdjXbLgvtO50HgE8Dt5rZfa09wczuNbPVZrZ6//79HZdUpBu4akgGWalJzNH0k7QiqKJo7Xi8066qu/tP3H20u9/n7j87zXMed/cidy/KyMjosKAi3UFcbAy3X5bLm3/ez86DJ4KOIxEmqKIoA3KbbecAFQFlERHg9styMWDuKo0q5KOCKopVwGAzG2hmCcAdwIKAsogIkJXag6svPo9nV++itl6L2vIXnXF47FzgbWCImZWZ2T3uXg/cD7wMbAGecffN4c4iIm2bMTaPA5W1/PGdvUFHkQgSF+43cPfpp9m/CFgU7vcXkfabNDiD7D49mL2ilBtHZAUdRyKErgwmIh+KjTFmjM3jrfcPsv1AVdBxJEKoKETkI24ryiEuxpirQ2UlREUhIh+R2SuJa4Y2LWpX1zUEHUcigIpCRD5m5th8Dp+o4+XNe4KOIhFARSEiH3P5+f3I79eT2Ss0/SQqChFpRUyMMWNMHiu3H+LPe48HHUcCpqIQkVbdOjqHhNgYXf9JVBQi0rp+KYlcN6w/89aUaVG7m1NRiMhpzRybx7HqehZu2B10FAmQikJETmvswL6cn5HMnBWlQUeRAKkoROS0zIzpY/Io2XmELbuPBR1HAqKiEJE23To6h4S4GOboUNluS0UhIm3q0zOBqcOzeH5tOVU19UHHkQCoKETkjGaMzaOypp7fr9f9xbojFYWInNHo/DSGnNdL51R0UyoKETkjs6bLj28oO8rGsqNBx5FOpqIQkXaZNiqbpPgY5qzUobLdjYpCRNoltUc8N106gBfWVXC8ui7oONKJVBQi0m4zxuZzoraBF9ZpUbs7UVGISLtdmpPK0KzezF6xE3cPOo50EhWFiLSbmTFzXB5bdh9j3a4jQceRTqKiEJGzcvPIbJITYnWmdjeiohCRs5KSGMdNI7P5/YYKjp7UonZ3cMaiMLMYM7u8M8KISHSYOTaP6rpGni8pCzqKdIIzFoW7NwL/2QlZRCRKDMtO5dKcVOas1KJ2d9DeqafFZnaLmVlY04hI1Jg5Np/39layuvRw0FEkzNpbFA8DzwK1ZnbMzI6bmS5OL9KNTb00i16JcVrU7gbaVRTu3svdY9w93t17h7Z7hzuciESunglxfLYwmz9s3M3hqtqg40gYtfuoJzO7ycx+EHpMDWcoEYkOM8bmUVvfyDwtandp7SoKM/s+8DXgndDja6F9ItKNXdS/N6Pz07So3cW1d0RxA3CNu89y91nAlNA+EenmZozJ44P9VSz/4FDQUSRMzuaEuz7NPk7t4BxtMrNkM1ujKS+RyHPjiCxSe8Qze4UuP95Vtbco/g+w1syeNLNfAWtC+9pkZrPMbJ+ZbWqxf4qZvWtm28zskXa8/zeBZ9qZVUQ6UVJ8LLcU5vDy5j0cqKwJOo6EQbvOzAYagXHA/NBjvLs/3Y7Xf5KmaarmrxcLPAZcDwwFppvZUDMbbmYLWzwyzezTNK2L7D2bb0xEOs+MsbnUNTjPrdGidlcUd6YnuHujmd3v7s8AC87mxd19iZkVtNg9Btjm7h8AmNnTwM3u/j3gY1NLZnYVkExTqZw0s0Whs8VbPu9e4F6AvLy8s4kpIp/QBZm9GDuwL3NW7OTeiYOIidG5uV1Je6ee/mhm3zCzXDPre+pxju+ZDexqtl0W2tcqd/9Hd/86MAf4f62VROh5j7t7kbsXZWRknGM0ETlXM8bmsfPQCZa9fyDoKNLBzjiiCLk79OdXm+1zYNA5vGdrv2qc8bg6d3/yHN5LRDrJlGH96ZucwJwVO5k4WL+sdSXtXaN4xN0HtnicS0lA0wgit9l2DqD7KopEucS4WG4bncPid/ay71h10HGkA7X36rFfPdPzzsIqYLCZDTSzBOAOznLtQ0Qi0/QxeTQ0Os+s3nXmJ0vUCOsahZnNBd4GhphZmZnd4+71wP3Ay8AW4Bl333zO34GIRIyC9GQmXNCPuSt30dCoM7W7irCuUbj79NPsXwQsaud7i0gUmTk2n7+ZXcKS9/Zz1UWZQceRDtCuonD3geEOIiJdwzVDzyM9JZHZK3aqKLqINqeezOzvm318W4vPnfHMbBHpfuJjY/hcUQ6vbt1LxZGTQceRDnCmNYo7mn38rRafm4KISCumj8nDgd+u0qJ2V3CmorDTfNzatogIALl9ezJpcAa/XbWL+oZWz5GVKHKmovDTfNzatojIh2aOzWPPsWpe3bov6CjyCZ2pKC49dY9sYETo41Pbwzshn4hEqU9dlEn/3knMWal7ake7NovC3WOb3SM7LvTxqe34zgopItEnLjaGz12Wyxvv7WfXoRNBx5FP4GxuXCQiclbuuCwXA55epVFFNFNRiEjYDOjTg09dlMkzq8uo06J21FJRiEhYzRibx/7jNbzyju49Fq1UFCISVldemEl2nx7MXqHpp2ilohCRsIqNMe64LJel2w6w40BV0HHkHKgoRCTsPndZLrExxlwtakclFYWIhN15vZO45uLzeHZ1GTX1DUHHkbOkohCRTjFjbB6Hqmp5ebMWtaONikJEOsUVF6ST17cnc1aUBh1FzpKKQkQ6RUyMMX1MHss/OMS2fZVBx5GzoKIQkU5zW1EO8bHGXF3/KaqoKESk06SnJHLtJf2ZV1JGdZ0WtaOFikJEOtXMsXkcOVHHoo27g44i7aSiEJFONX5QPwalJzNHZ2pHDRWFiHQqs6ZF7dWlh3l3z/Gg40g7qChEpNPdMjqHhLgYHSobJVQUItLp+iYncMOw/sxfW86J2vqg48gZqChEJBAzxuZzvLqeheu1qB3pVBQiEojLCtIYnJnCbJ1TEfFUFCISCDNjxtg81u86wqbyo0HHkTaoKEQkMMWjckiKj2GORhURTUUhIoFJ7RnP1BEDeGFtOZU1WtSOVCoKEQnUjLF5VNU2sGBdRdBR5DQivijMLMbMvmtmPzWzvw46j4h0rFG5fbg4qzezV5Ti7kHHkVaEtSjMbJaZ7TOzTS32TzGzd81sm5k9coaXuRnIBuqAsnBlFZFgnFrU3lxxjA1lWtSOROEeUTwJTGm+w8xigceA64GhwHQzG2pmw81sYYtHJjAEeNvdHwa+Eua8IhKAaSMH0DMhVtd/ilBhLQp3XwIcarF7DLDN3T9w91rgaeBmd9/o7lNbPPbRNIo4HPra016X2MzuNbPVZrZ6//794fh2RCRMeiXFc/PIASxYX8Gx6rqg40gLQaxRZAO7mm2XhfadznzgOjP7KbDkdE9y98fdvcjdizIyMjomqYh0mhlj8jlZ18Dv1pYHHUVaiAvgPa2VfaddwXL3E8A94YsjIpFgeE4qw7NTmbNiJ3eOy8estR8VEoQgRhRlQG6z7RxAx8WJCDPH5rF1z3FKdh4+85Ol0wRRFKuAwWY20MwSgDuABQHkEJEI85lLB5CSGMdsLWpHlHAfHjsXeBsYYmZlZnaPu9cD9wMvA1uAZ9x9czhziEh0SE6MY9qoAfxhw26OnKgNOo6EhPuop+nunuXu8e6e4+5PhPYvcvcL3f18d/9uODOISHSZMSafmvpG5pVoUTtSRPyZ2SLSvQwd0JtReX2YozO1I4aKQkQizowxeby/v4qV21uehiVBUFGISMSZOmIAvZO0qB0pVBQiEnF6JMRSXJjDS5v28NrWfUHH6fZUFCISkb585SAK0nty15OrePiZdToKKkAqChGJSFmpPfj9A1fwwKcu4IV1FVzz6BJe3rwn6FjdkopCRCJWYlwsf3vtEF746gTSUxL58lNreGDuWg5W1gQdrVtRUYhIxBuWncqC+yfw8DUX8tKm3Vz76BIWbqjQ4bOdREUhIlEhPjaGB68ezMIHJpKd1oP756zlK78pYd/x6qCjdXkqChGJKkP692L+Vy7nm1Mu4tV393Hto0t4fm2ZRhdhpKIQkagTFxvDVyafz6IHJzIoPZmHfrueL/5qNXuOanQRDioKEYlaF2Sm8Ox9l/PtqUNZ9v4BrvnhG/x21U6NLjqYikJEolpsjHHPFQN56WuTGDqgN9+ct5HPz1pJ2eETQUfrMlQUItIlFKQnM/dL4/jXmy9hTelhrnt0CU8tL6WxUaOLT0pFISJdRkyMcef4Al7++iRG5aXx7d9tYsYvlrPzoEYXn4SKQkS6nNy+PXnqnjF8v3g4m8uPcd2PljBr6XaNLs6RikJEuiQz444xeSx+eBLjBvXlXxa+w+d+/jbv768MOlrUUVGISJeWldqDWV+4jP+87VLe23ucG378Jj9/433qGxqDjhY1VBQi0uWZGbeMzuGVh6/kygsz+N6LW7nlf97ivb3Hg44WFVQUItJtZPZO4ud3juan00ex6/BJpv5kKf/16p+p0+iiTSoKEelWzIzPXDqAPz40iWsuOY8fLH6PaY8tY3PF0aCjRSwVhYh0S/1SEnlsRiE/+6tC9h6r4eb/WsYPF79Lbb1GFy2pKESkW5syLIs/PjSJmy4dwE9e3cZnfrqUDWVHgo4VUVQUItLtpSUn8MPbR/LEXxdx5GQt0x5bxvdf3Ep1XUPQ0SKCikJEJOTqi89j8UNXctvoXH72xvvc8JM3WVN6KOhYgVNRiIg0k9ojnn+/dQS/vnsMNXWN3Pqzt/nXhe9wsrb7ji5UFCIirZh0YQYvPzSJmWPzeGLpdqb8eAnLPzgYdKxAqChERE4jJTGOf5s2nLlfGoc73PH4cr7zwiaqauqDjtapVBQiImcw/vx+vPT1idw1oYCnlpdy7aNLeGnTnm5zgyQVhYhIO/RMiOOfPnMJz355PMmJsdz3mzXM/MUKtu45FnS0sIv4ojCzPDNbYGazzOyRoPOISPdWVNCXRQ9O5F9uvoTNFce44cdv8u3fbeJwVW3Q0cImrEUR+uG+z8w2tdg/xczeNbNt7fjhfyHwB3e/GxgatrAiIu0UFxvD58cX8Po3JnPnuHzmrNzJ5B+8zi+Xbe+S142ycM6xmdkkoBL4tbsPC+2LBd4DrgHKgFXAdCAW+F6Ll7gbaACeAxx4yt1/eab3LSoq8tWrV3fUtyEi0qZ39xznXxe+w9JtB7ggM4XvTB3KpAszgo511sxsjbsXfWx/uBdjzKwAWNisKMYD/+zu14W2vwXg7i1L4tTXfwNY6e5LzOw5d7/1NM+7F7gXIC8vb3RpaWmHfy8iIqfj7ryyZR//9od3KD14gk9fnMk/3jiUgenJQUdrt9MVRRBrFNnArmbbZaF9p/MS8KCZ/QzYcbonufvj7l7k7kUZGdHX5CIS3cyMa4aex+KHJvHI9Rfx9vsHufbRN/jeoi0cr64LOt4nEhfAe1or+047rHH3TUCrowgRkUiTGBfLfVeeT3FhNv/x0rv8fMkHzCsp4++uG8Kto3OJjWntR2BkC2JEUQbkNtvOASoCyCEiEjaZvZL4j9suZcH9E8jvl8w3523k5seWsmpH9F07KoiiWAUMNrOBZpYA3AEsCCCHiEjYjcjpw3P3jefHd4zkYGUtt/3sbR6Yu5byIyeDjtZu4T48di7wNjDEzMrM7B53rwfuB14GtgDPuPvmcOYQEQmSmXHzyGz+9LdX8uDVg1m8eQ9X/+fr/OiV96LiYoNhP+opCDo8VkQiWdnhE3zvxa38YcNuBqQm8cgNF/OZEVmYBbt+EUlHPYmIdGs5aT15bEYhv713HGnJCTw4dy23/extNpZF5n27VRQiIgEZO6gfC+6/gu8XD2f7gSpuemwp33xuA/uP1wQd7SNUFCIiAYqNMe4Yk8drfzeZL14xkHklZVz1g9f5+RvvU1MfGesXKgoRkQjQOymef7xxKC8/NIkxA/vyvRe3ct2jS3jlnb2BX85cRSEiEkHOz0hh1hcu48m7LiM2xvjir1fz+Vkr+fPe44FlUlGIiESgyUMyeenrk/jO1KGs23WEKT9+k39esJmjJzr/ciAqChGRCBUfG8PdVwzk9W9M5o7Lcvn12zuY/IPXeOrtHdR34uXMVRQiIhGuX0oi3/3scBY+MJEh/Xvx7Rc2c+NPlvLWtgOd8v4qChGRKDF0QG/mfmkc/zOzkKraemb8YgVffmo1Ow+eCOv7qihERKKImXH98CxeefhK/u66Ibz55wN8+odv8H9f2kplTX1Y3lNFISIShZLiY/nqVRfw6t9OZuqILP779fe56gevs6a0469Oq6IQEYli/VOT+OHtI5n/N5dzUf9eFPTr+DvqBXHjIhER6WCFeWk8dc/YsLy2RhQiItImFYWIiLRJRSEiIm1SUYiISJtUFCIi0iYVhYiItElFISIibVJRiIhImyzoOyeFg5ntB0rP8cvTgc65JOPZUa6zo1xnR7nOTlfNle/uGS13dsmi+CTMbLW7FwWdoyXlOjvKdXaU6+x0t1yaehIRkTapKEREpE0qio97POgAp6FcZ0e5zo5ynZ1ulUtrFCIi0iaNKEREpE0qChERaZOKIsTMZpnZPjPbFHSW5sws18xeM7MtZrbZzL4WdCYAM0sys5Vmtj6U638Hnak5M4s1s7VmtjDoLKeY2Q4z22hm68xsddB5TjGzPmb2nJltDf07Gx8BmYaE/p5OPY6Z2deDzgVgZg+F/s1vMrO5ZpYUdCYAM/taKNPmjv670hpFiJlNAiqBX7v7sKDznGJmWUCWu5eYWS9gDTDN3d8JOJcBye5eaWbxwFLga+6+PMhcp5jZw0AR0NvdpwadB5qKAihy94g6UcvMfgW86e6/MLMEoKe7Hwk41ofMLBYoB8a6+7meSNtRWbJp+rc+1N1PmtkzwCJ3fzLgXMOAp4ExQC3wEvAVd/9zR7y+RhQh7r4E6Pi7kn9C7r7b3UtCHx8HtgDZwaYCb1IZ2owPPSLitw4zywFuBH4RdJZIZ2a9gUnAEwDuXhtJJRFyNfB+0CXRTBzQw8zigJ5ARcB5AC4Glrv7CXevB94APttRL66iiCJmVgCMAlYEHAX4cHpnHbAP+KO7R0Qu4EfA3wONAedoyYHFZrbGzO4NOkzIIGA/8MvQVN0vzCw56FAt3AHMDToEgLuXAz8AdgK7gaPuvjjYVABsAiaZWT8z6wncAOR21IurKKKEmaUA84Cvu/uxoPMAuHuDu48EcoAxoeFvoMxsKrDP3dcEnaUVE9y9ELge+GpoujNocUAh8D/uPgqoAh4JNtJfhKbCbgKeDToLgJmlATcDA4EBQLKZ/VWwqcDdtwD/DvyRpmmn9UB9R72+iiIKhNYA5gGz3X1+0HlaCk1VvA5MCTYJABOAm0LrAU8DnzKz3wQbqYm7V4T+3Ac8T9N8ctDKgLJmo8HnaCqOSHE9UOLue4MOEvJpYLu773f3OmA+cHnAmQBw9yfcvdDdJ9E0jd4h6xOgooh4oUXjJ4At7v7DoPOcYmYZZtYn9HEPmv4DbQ00FODu33L3HHcvoGnK4lV3D/w3PjNLDh2MQGhq51qapgsC5e57gF1mNiS062og0AMlWphOhEw7hewExplZz9D/zatpWjcMnJllhv7MA4rpwL+3uI56oWhnZnOByUC6mZUB/+TuTwSbCmj6DflOYGNoPQDgH9x9UXCRAMgCfhU6IiUGeMbdI+ZQ1Ah0HvB8088W4oA57v5SsJE+9AAwOzTN8wFwV8B5AAjNtV8DfDnoLKe4+wozew4ooWlqZy2RczmPeWbWD6gDvuruhzvqhXV4rIiItElTTyIi0iYVhYiItElFISIibVJRiIhIm1QUIiLSJhWFSBvMrDL0Z4GZzejg1/6HFttvdeTri3QUFYVI+xQAZ1UUoXNM2vKRonD3iDjDV6QlFYVI+3wfmBi6N8JDoQsi/oeZrTKzDWb2ZQAzmxy6f8gcYGNo3+9CFwLcfOpigGb2fZquQLrOzGaH9p0avVjotTeF7l9xe7PXfr3ZvSNmh84OFgkrnZkt0j6PAN84dW+L0A/8o+5+mZklAsvM7NRVRMcAw9x9e2j7bnc/FLrUySozm+fuj5jZ/aGLKrZUDIwELgXSQ1+zJPS5UcAlNF3aehlNZ+4v7ehvVqQ5jShEzs21wOdDl1VZAfQDBoc+t7JZSQA8aGbrgeU0Xfp5MG27ApgbujrvXpruLXBZs9cuc/dGYB1NU2IiYaURhci5MeABd3/5IzvNJtN0qe7m258Gxrv7CTN7HTjTrTPbmk6qafZxA/o/LJ1AIwqR9jkO9Gq2/TLwldAl4DGzC09zw59U4HCoJC4CxjX7XN2pr29hCXB7aB0kg6Y70K3skO9C5BzotxGR9tkA1IemkJ4EfkzTtE9JaEF5PzCtla97CbjPzDYA79I0/XTK48AGMytx95nN9j8PjKfp5jMO/L277wkVjUin09VjRUSkTZp6EhGRNqkoRESkTSoKERFpk4pCRETapKIQEZE2qShERKRNKgoREWnT/wcGWPqAO3Vu0QAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"import matplotlib.pyplot as plt\n",
"\n",
"# number of iterations\n",
"N = len(x)\n",
"\n",
"# iteration\n",
"iters = range(0,N)\n",
"\n",
"plt.figure\n",
"for i in range(0,len(x0)):\n",
" plt.plot(iters,[x[j][i] for j in range(0,N)],label=\"x\"+str(i))\n",
"plt.xlabel(\"Iteration\")\n",
"plt.ylabel(\"Primal Variables\")\n",
"plt.legend()\n",
"plt.show()\n",
"\n",
"plt.figure\n",
"for i in range(0,len(u[0])):\n",
" plt.plot(iters,[u[j][i] for j in range(0,N)],label=\"u\"+str(i))\n",
"for i in range(0,len(v[0])):\n",
" plt.plot(iters,[v[j][i] for j in range(0,N)],label=\"v\"+str(i))\n",
"plt.xlabel(\"Iteration\")\n",
"plt.ylabel(\"Dual Variables\")\n",
"plt.legend()\n",
"plt.show()\n",
"\n",
"plt.figure\n",
"plt.semilogy(iters,mu)\n",
"plt.xlabel(\"Iteration\")\n",
"plt.ylabel(\"Barrier Penalty\")\n",
"plt.show()\n",
"\n",
"plt.figure\n",
"plt.semilogy(range(1,N),E)\n",
"plt.xlabel(\"Iteration\")\n",
"plt.ylabel(\"Error\")\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"id": "a846e211",
"metadata": {},
"source": [
"\n",
"< [4.8 Inertia-Corrected Netwon Method for Equality Constrained NLPs](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [5.0 Special Topics](https://ndcbe.github.io/CBE60499/05.00-Special-Topics.html) >
"
]
},
{
"cell_type": "markdown",
"id": "f3e9a52a",
"metadata": {
"nbpages": {
"level": 1,
"link": "[4.9 Algorithms Homework 4: Interior Point Methods](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9-Algorithms-Homework-4:-Interior-Point-Methods)",
"section": "4.9 Algorithms Homework 4: Interior Point Methods"
}
},
"source": [
"# 4.9 Algorithms Homework 4: Interior Point Methods"
]
},
{
"cell_type": "markdown",
"id": "ba74c034",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.9.1 Tips and Tricks](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.1-Tips-and-Tricks)",
"section": "4.9.1 Tips and Tricks"
}
},
"source": [
"## 4.9.1 Tips and Tricks"
]
},
{
"cell_type": "markdown",
"id": "a8715f98",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.1.1 Background](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.1.1-Background)",
"section": "4.9.1.1 Background"
}
},
"source": [
"### 4.9.1.1 Background"
]
},
{
"cell_type": "markdown",
"id": "4844e9f9",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.1.1 Background](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.1.1-Background)",
"section": "4.9.1.1 Background"
}
},
"source": [
"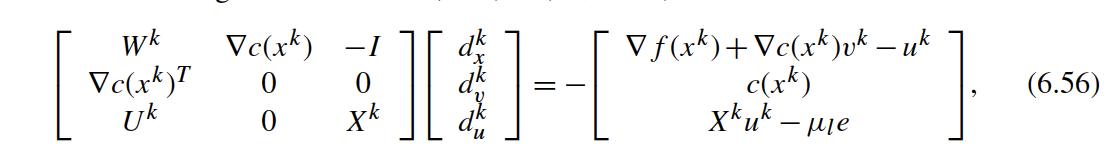\n",
"\n",
"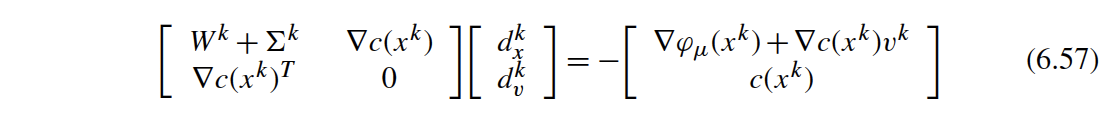\n",
"\n",
"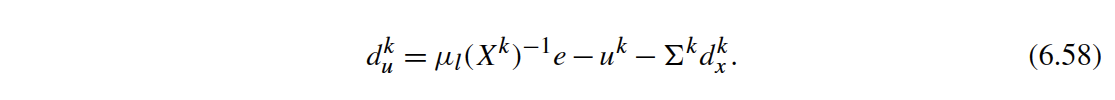\n",
"\n",
"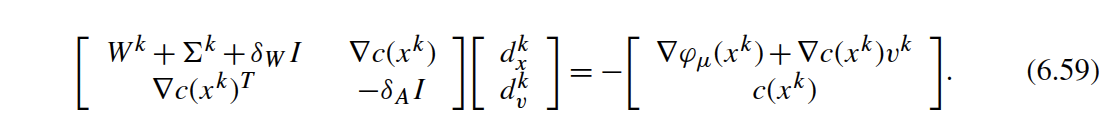"
]
},
{
"cell_type": "markdown",
"id": "11a91e88",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.1.2 Problem Formulation](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.1.2-Problem-Formulation)",
"section": "4.9.1.2 Problem Formulation"
}
},
"source": [
"### 4.9.1.2 Problem Formulation"
]
},
{
"cell_type": "markdown",
"id": "164bb509",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.1.2 Problem Formulation](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.1.2-Problem-Formulation)",
"section": "4.9.1.2 Problem Formulation"
}
},
"source": [
"Consider the following nonlinear program:\n",
"\n",
"$$\n",
"\\begin{align}\n",
"\t\\min_{x} \\quad & f(x) \\\\\n",
"\t\\mathrm{s.t.} \\quad & c(x) = 0 \\\\\n",
"\t& x_i \\geq 0, \\quad i \\in \\mathcal{I}\n",
"\\end{align}\n",
"$$\n",
"\n",
"where $x \\in \\mathbb{R}^{n}$, $f(x): \\mathbb{R}^{n} \\rightarrow \\mathbb{R}$, $c(x): \\mathbb{R}^{n} \\rightarrow \\mathbb{R}^{m}$ and $|\\mathcal{I} |$ = $r$ (i.e., there are $r$ variables with a lower bound and $r \\leq n$). This is an extension of (6.48) in Biegler (2010).\n",
"\n",
"This has the corresponding log-barrier approximation:\n",
"\n",
"$$\n",
"\\begin{align}\n",
"\t\\min_{x} \\quad & \\phi_{\\mu_l}(x) := f(x) - \\mu_l \\sum_{i \\in \\mathcal{I}} \\log(x_i) \\\\\n",
"\t\\mathrm{s.t.} \\quad & c(x) = 0\n",
"\\end{align}\n",
"$$\n",
"\n",
"which is an extension of (6.49) in Biegler (2010).\n",
"\n",
"Let the $n \\times r$ matrix $G$ encode which variables are bounded. If variable $i$ corresponds to the $j$th bound, then $G_{i,j} = 1$ and otherwise $G_{i,j} = 0$. $G$ is assembled as follows:\n",
"\n",
"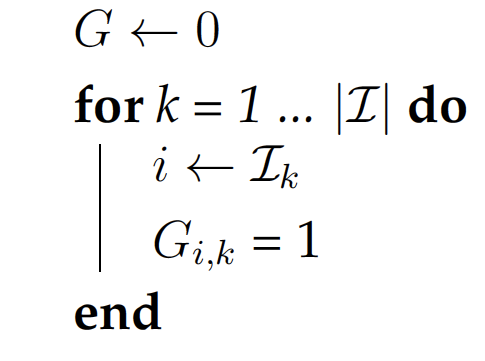\n",
"\n",
"Notice that $G$ is the gradient of $x \\geq 0$. $G^T G = I$ but the converse does not hold unless $r = n$."
]
},
{
"cell_type": "markdown",
"id": "c2fed8b8",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.1.3 Reformulation Example](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.1.3-Reformulation-Example)",
"section": "4.9.1.3 Reformulation Example"
}
},
"source": [
"### 4.9.1.3 Reformulation Example"
]
},
{
"cell_type": "markdown",
"id": "fae61884",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.1.3 Reformulation Example](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.1.3-Reformulation-Example)",
"section": "4.9.1.3 Reformulation Example"
}
},
"source": [
"Start with:\n",
"\n",
"$$\n",
"\t\\begin{align}\n",
"\t\t\\min_{x} \\quad & x_1^2 + x_2 \\\\\n",
"\t\t\\mathrm{s.t.} \\quad & x_1 + x_2 = 1 \\\\\n",
"\t\t& x_1 + 1 \\geq 0\n",
"\t\\end{align}\n",
"$$\n",
"\n",
"Add slack variable $x_3$ and convert the inequality constraint to an equality constraint and bound:\n",
"\n",
"$$\n",
"\t\\begin{align}\n",
"\t\t\\min_{x} \\quad & x_1^2 + x_2 \\\\\n",
"\t\t\\mathrm{s.t.} \\quad & x_1 + x_2 = 1 \\\\\n",
"\t\t& x_1 + 1 - x_3 = 0 \\\\\n",
"\t\t& x_3 \\geq 0\n",
"\t\\end{align}\n",
"$$\n",
"\n",
"Now assemble $G$:\n",
"\n",
"$$\n",
"\tG = \\begin{bmatrix}\n",
"\t\t0 \\\\\n",
"\t\t0 \\\\\n",
"\t\t1\n",
"\t\\end{bmatrix}\n",
"$$"
]
},
{
"cell_type": "markdown",
"id": "00e568fa",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.1.4 Primal Dual Optimality Conditions](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.1.4-Primal-Dual-Optimality-Conditions)",
"section": "4.9.1.4 Primal Dual Optimality Conditions"
}
},
"source": [
"### 4.9.1.4 Primal Dual Optimality Conditions"
]
},
{
"cell_type": "markdown",
"id": "b923aa13",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.1.4 Primal Dual Optimality Conditions](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.1.4-Primal-Dual-Optimality-Conditions)",
"section": "4.9.1.4 Primal Dual Optimality Conditions"
}
},
"source": [
"$$\n",
"\\newcommand{\\dims}[3]{\\underbrace{#1}_{#2 \\times #3}}\n",
"\\newcommand{\\I}[0]{\\mathcal{I}}\n",
"\\newcommand{\\dfx}[0]{\\dims{\\nabla f(x^k)}{n}{1}}\n",
"\\newcommand{\\cx}[0]{\\dims{c(x^k)}{m}{1}}\n",
"\\newcommand{\\dcx}[0]{\\dims{\\nabla c(x^k)}{n}{m}}\n",
"\\newcommand{\\dcxT}[0]{\\dims{\\nabla_x c(x^k)^T}{m}{n}}\n",
"\\newcommand{\\W}[0]{\\dims{W^k}{n}{n}}\n",
"\\newcommand{\\G}[0]{\\dims{G}{n}{r}}\n",
"\\newcommand{\\GT}[0]{\\dims{G^T}{r}{n}}\n",
"\\newcommand{\\vk}[0]{\\dims{v^k}{m}{1}}\n",
"\\newcommand{\\Xinv}[0]{\\dims{(\\hat{X}^k)^{-1}}{r}{r}}\n",
"\\newcommand{\\X}[0]{\\dims{\\hat{X}^k}{r}{r}}\n",
"\\newcommand{\\e}[0]{\\dims{e}{r}{1}}\n",
"\\newcommand{\\uk}[0]{\\dims{u^k}{r}{1}}\n",
"\\newcommand{\\dx}[0]{\\dims{d_x^k}{n}{1}}\n",
"\\newcommand{\\dv}[0]{\\dims{d_v^k}{m}{1}}\n",
"\\newcommand{\\du}[0]{\\dims{d_u^k}{r}{1}}\n",
"\\newcommand{\\Uk}[0]{\\dims{U^k}{r}{r}}\n",
"\\newcommand{\\Sk}[0]{\\dims{\\Sigma^k}{n}{n}}\n",
"\\newcommand{\\dphi}[0]{\\dims{\\nabla \\phi_{\\mu_l}}{n}{1}}\n",
"$$\n",
"\n",
"Next we extend (6.51) in Biegler (2010):\n",
" \n",
"$$\n",
"\\begin{gather}\n",
"\t\\dfx ~+~ \\dcx \\vk ~-~ \\G \\uk = \\dims{0}{n}{1} \\\\\n",
"\t\\X \\uk = \\mu \\e \\\\\n",
"\t\\cx = \\dims{0}{m}{1}\n",
"\\end{gather}\n",
"$$\n",
"\n",
"We now extend (6.56) in Biegler (2010):\n",
"\n",
"$$\n",
"\t\\begin{bmatrix}\n",
"\t\t\\W & \\dcx & \\G \\\\\n",
"\t\t\\dcxT & \\dims{0}{m}{m} & \\dims{0}{m}{r} \\\\\n",
"\t\t\\Uk \\GT & \\dims{0}{r}{m} & \\X\n",
"\t\\end{bmatrix} \n",
"\t\\begin{bmatrix}\n",
"\t\t\\dx \\\\\n",
"\t\t\\dv \\\\\n",
"\t\t\\du\n",
"\t\\end{bmatrix} = -\n",
"\t\\begin{bmatrix}\n",
"\t\\dfx ~+~ \\dcx \\vk ~-~ \\G \\uk \\\\\n",
"\t\\cx \\\\\n",
"\t\\X \\uk ~-~ \\mu_l \\e\n",
"\t\\end{bmatrix}\n",
"$$\n",
"\n",
"where $U^k = \\mathrm{diag}\\{u^k\\}$ and $W^k = \\nabla_{xx} L(x^k,v^k)$. Notice that $W^k$ does NOT include a contribution from the barrier term:\n",
"\n",
"$$\n",
"\\begin{equation}\n",
"\t\\W = \\dims{\\nabla^2 f(x^k)}{n}{n} + \\sum_{j=1}^{m} \\left( \\dims{\\nabla^2 c_{j}(x^k)}{n}{n} \\underbrace{v^k_{j}}_{\\mathrm{scalar}} \\right)\n",
"\\end{equation}\n",
"$$\n",
"\n",
"We can verify that $W^k$ does not include $\\hat{X}$ by showing that the KKT system above is a Newton step to solve the nonlinear system for the primal dual conditions.\n",
"\n",
"\n",
"The Newton step can be simplified, similar to (6.57) and (6.58) in Biegler (2010):\n",
"\n",
"$$\n",
"\\begin{equation}\n",
"\t\\begin{bmatrix}\n",
"\t\t\\W + \\Sk & \\dcx \\\\\n",
"\t\t\\dcxT & 0\n",
"\t\\end{bmatrix} \n",
"\t\\begin{bmatrix}\n",
"\t\t\\dx \\\\\n",
"\t\t\\dv\n",
"\t\\end{bmatrix} = -\n",
"\t\\begin{bmatrix}\n",
"\t\\dphi ~+~ \\dcx \\vk \\\\\n",
"\t\\cx\n",
"\t\\end{bmatrix}\n",
"\\end{equation}\n",
"$$\n",
"\n",
"and\n",
"\n",
"$$\n",
"\\begin{equation} \\label{eq:du}\n",
"\t\\du = \\mu_l \\Xinv \\e ~-~ \\uk ~-~ \\GT \\Sk \\dx\n",
"\\end{equation}\n",
"$$\n",
"\n",
"where\n",
"$$\n",
"\\begin{equation} \\label{eq:Sk}\n",
"\t\\Sk = \\G \\Xinv \\Uk \\GT\n",
"\\end{equation}\n",
"$$\n",
"\n",
"and \n",
"\n",
"$$\n",
"\\begin{equation}\n",
"\t\\dphi = \\dfx - \\mu_l \\G \\Xinv \\dims{e}{r}{1}\n",
"\\end{equation}\n",
"$$\n",
"\n",
"Notice that the equation for $\\du$ simplifies by substituting $G^T G = I$:\n",
"\n",
"$$\n",
"\t\\du = \\mu_l \\Xinv \\e ~-~ \\uk ~-~ \\Xinv \\Uk \\GT \\dx\n",
"$$\n",
"\n",
"Finally, inertia correction can be applied to simplified KKT step similar to (6.59) in Biegler (2010). "
]
},
{
"cell_type": "markdown",
"id": "1ca1ed21",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.9.2 Basic Interior Point Method for Inequality and Equality Constraint NLPs](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.2-Basic-Interior-Point-Method-for-Inequality-and-Equality-Constraint-NLPs)",
"section": "4.9.2 Basic Interior Point Method for Inequality and Equality Constraint NLPs"
}
},
"source": [
"## 4.9.2 Basic Interior Point Method for Inequality and Equality Constraint NLPs"
]
},
{
"cell_type": "markdown",
"id": "3fd841f9",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.9.2 Basic Interior Point Method for Inequality and Equality Constraint NLPs](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.2-Basic-Interior-Point-Method-for-Inequality-and-Equality-Constraint-NLPs)",
"section": "4.9.2 Basic Interior Point Method for Inequality and Equality Constraint NLPs"
}
},
"source": [
"Implement a basic interior point method for inequality and equality constrained nonlinear programs. See pg. 154 – 155 in Biegler (2010). You may skip the line search, i.e., always take a full step."
]
},
{
"cell_type": "markdown",
"id": "a7a244c5",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.2.1 Pseudocode](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.2.1-Pseudocode)",
"section": "4.9.2.1 Pseudocode"
}
},
"source": [
"### 4.9.2.1 Pseudocode"
]
},
{
"cell_type": "markdown",
"id": "23e86ba7",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.2.1 Pseudocode](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.2.1-Pseudocode)",
"section": "4.9.2.1 Pseudocode"
}
},
"source": [
"Write detailed pseudocode on paper or a whiteboard. Scan/take a photo and turn in."
]
},
{
"cell_type": "markdown",
"id": "d1ec363f",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.2.2 Python Implementation](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.2.2-Python-Implementation)",
"section": "4.9.2.2 Python Implementation"
}
},
"source": [
"### 4.9.2.2 Python Implementation"
]
},
{
"cell_type": "markdown",
"id": "2ad37a24",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.2.2 Python Implementation](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.2.2-Python-Implementation)",
"section": "4.9.2.2 Python Implementation"
}
},
"source": [
"Implement in Python. Hints: Reuse code from Algorithm 5.2 example."
]
},
{
"cell_type": "code",
"execution_count": 1,
"id": "ec182a38",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.2.2 Python Implementation](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.2.2-Python-Implementation)",
"section": "4.9.2.2 Python Implementation"
}
},
"outputs": [],
"source": [
"### Load Python libraries\n",
"import numpy as np\n",
"from scipy import linalg\n",
"\n",
"### Define helper functions\n",
"## Check is element of array is NaN\n",
"def check_nan(A):\n",
" return np.sum(np.isnan(A))\n",
"\n",
"## Calculate gradient with central finite difference\n",
"def my_grad_approx(x,f,eps1,verbose=False):\n",
" '''\n",
" Calculate gradient of function f using central difference formula\n",
" \n",
" Inputs:\n",
" x - point for which to evaluate gradient\n",
" f - function to consider\n",
" eps1 - perturbation size\n",
" \n",
" Outputs:\n",
" grad - gradient (vector)\n",
" '''\n",
" \n",
" n = len(x)\n",
" grad = np.zeros(n)\n",
" \n",
" if(verbose):\n",
" print(\"***** my_grad_approx at x = \",x,\"*****\")\n",
" \n",
" for i in range(0,n):\n",
" \n",
" # Create vector of zeros except eps in position i\n",
" e = np.zeros(n)\n",
" e[i] = eps1\n",
" \n",
" # Finite difference formula\n",
" my_f_plus = f(x + e)\n",
" my_f_minus = f(x - e)\n",
" \n",
" # Diagnostics\n",
" if(verbose):\n",
" print(\"e[\",i,\"] = \",e)\n",
" print(\"f(x + e[\",i,\"]) = \",my_f_plus)\n",
" print(\"f(x - e[\",i,\"]) = \",my_f_minus)\n",
" \n",
" \n",
" grad[i] = (my_f_plus - my_f_minus)/(2*eps1)\n",
" \n",
" if(verbose):\n",
" print(\"***** Done. ***** \\n\")\n",
" \n",
" return grad\n",
"\n",
"## Calculate gradient with central finite difference\n",
"def my_jac_approx(x,h,eps1,verbose=False):\n",
" '''\n",
" Calculate Jacobian of function h(x) using central difference formula\n",
" \n",
" Inputs:\n",
" x - point for which to evaluate gradient\n",
" h - vector-valued function to consider. h(x): R^n --> R^m\n",
" eps1 - perturbation size\n",
" \n",
" Outputs:\n",
" A - Jacobian (n x m matrix)\n",
" '''\n",
" \n",
" # Check h(x) at x\n",
" h_x0 = h(x)\n",
" \n",
" # Extract dimensions\n",
" n = len(x)\n",
" m = len(h_x0)\n",
" \n",
" # Initialize Jacobian matrix\n",
" A = np.zeros((n,m))\n",
" \n",
" # Calculate Jacobian by row\n",
" for i in range(0,n):\n",
" \n",
" # Create vector of zeros except eps in position i\n",
" e = np.zeros(n)\n",
" e[i] = eps1\n",
" \n",
" # Finite difference formula\n",
" my_h_plus = h(x + e)\n",
" my_h_minus = h(x - e)\n",
" \n",
" # Diagnostics\n",
" if(verbose):\n",
" print(\"e[\",i,\"] = \",e)\n",
" print(\"h(x + e[\",i,\"]) = \",my_h_plus)\n",
" print(\"h(x - e[\",i,\"]) = \",my_h_minus)\n",
" \n",
" \n",
" A[i,:] = (my_h_plus - my_h_minus)/(2*eps1)\n",
" \n",
" if(verbose):\n",
" print(\"***** Done. ***** \\n\")\n",
" \n",
" return A\n",
" \n",
"## Calculate Hessian using central finite difference\n",
"def my_hes_approx(x,grad,eps2):\n",
" '''\n",
" Calculate gradient of function my_f using central difference formula and my_grad\n",
" \n",
" Inputs:\n",
" x - point for which to evaluate gradient\n",
" grad - function to calculate the gradient\n",
" eps2 - perturbation size (for Hessian NOT gradient approximation)\n",
" \n",
" Outputs:\n",
" H - Hessian (matrix)\n",
" '''\n",
" \n",
" n = len(x)\n",
" H = np.zeros([n,n])\n",
" \n",
" for i in range(0,n):\n",
" # Create vector of zeros except eps in position i\n",
" e = np.zeros(n)\n",
" e[i] = eps2\n",
" \n",
" # Evaluate gradient twice\n",
" grad_plus = grad(x + e)\n",
" grad_minus = grad(x - e)\n",
" \n",
" # Notice we are building the Hessian by column (or row)\n",
" H[:,i] = (grad_plus - grad_minus)/(2*eps2)\n",
"\n",
" return H\n",
"\n",
"## Linear algebra calculation\n",
"def xxT(u):\n",
" '''\n",
" Calculates u*u.T to circumvent limitation with SciPy\n",
" \n",
" Arguments:\n",
" u - numpy 1D array\n",
" \n",
" Returns:\n",
" u*u.T\n",
" \n",
" Assume u is a nx1 vector.\n",
" Recall: NumPy does not distinguish between row or column vectors\n",
" \n",
" u.dot(u) returns a scalar. This functon returns an nxn matrix.\n",
" '''\n",
" \n",
" n = len(u)\n",
" A = np.zeros([n,n])\n",
" for i in range(0,n):\n",
" for j in range(0,n):\n",
" A[i,j] = u[i]*u[j]\n",
" \n",
" return A\n",
"\n",
"## Analyze Hessian\n",
"def analyze_hes(B):\n",
" print(B,\"\\n\")\n",
" \n",
" l = linalg.eigvals(B)\n",
" print(\"Eigenvalues: \",l,\"\\n\")\n"
]
},
{
"cell_type": "code",
"execution_count": 2,
"id": "f51b5c25",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.2.2 Python Implementation](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.2.2-Python-Implementation)",
"section": "4.9.2.2 Python Implementation"
}
},
"outputs": [],
"source": [
"## Assemble KKT matrix (equality constrained only)\n",
"def assemble_check_KKT(W,Sk,A,deltaA,deltaW,verbose):\n",
" \n",
" # YOUR SOLUTION HERE\n",
" \n",
" return KKT,inertia_correct,pos_ev,neg_ev,zero_ev"
]
},
{
"cell_type": "code",
"execution_count": 3,
"id": "ae9be074",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.2.2 Python Implementation](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.2.2-Python-Implementation)",
"section": "4.9.2.2 Python Implementation"
}
},
"outputs": [],
"source": [
"def barrier_subproblem(x0,v0,u0,calc_f,calc_c,var_bounds,mu,eps,max_iter=100,verbose=False):\n",
" '''\n",
" Basic Full Space Newton Method for Solving Barrier Subproblem Constrained NLP\n",
" \n",
" Input:\n",
" x0 - starting point (vector)\n",
" calc_f - function to calculate objective (returns scalar)\n",
" calc_c - function to calculate constraints (returns vector)\n",
" var_bounds - list of indicies for variables with lower bound\n",
" mu - barrier penalty\n",
" eps - tolerance for termination\n",
" \n",
" Histories (stored for debugging):\n",
" x - history of steps (primal variables)\n",
" v - history of steps (duals for constraints)\n",
" u - history of steps (duals for bounds)\n",
" f - history of objective evaluations\n",
" c - history of constraint evaluations\n",
" df - history of objective gradients\n",
" dL - history of Lagrange function gradients\n",
" A - history of constraint Jacobians\n",
" W - history of Lagrange Hessians\n",
" S - history of sigma matrix\n",
" \n",
" Outputs:\n",
" x - final value for primal variable\n",
" v - final value for constraint duals\n",
" u - final value for bound duals\n",
" \n",
" Notes:\n",
" 1. For simplicity, central finite difference is used \n",
" for all gradient calculations.\n",
" ''' \n",
" \n",
" ### Specifics for Algorithm 5.2\n",
" # Tuning parameters\n",
" delta_bar_W_min = 1E-20\n",
" delta_bar_W_0 = 1E-4\n",
" delta_bar_W_max = 1E40\n",
" delta_bar_A = 1E-8\n",
" kappa_u = 8\n",
" kappa_l = 1/3\n",
" \n",
" # Declare iteration histories as empty lists\n",
" x = []\n",
" v = []\n",
" u = []\n",
" f = []\n",
" L = []\n",
" c = []\n",
" df = []\n",
" dL = []\n",
" A = []\n",
" W = []\n",
"\n",
" # YOUR SOLUTION HERE"
]
},
{
"cell_type": "code",
"execution_count": 4,
"id": "6549fabb",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.2.2 Python Implementation](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.2.2-Python-Implementation)",
"section": "4.9.2.2 Python Implementation"
}
},
"outputs": [],
"source": [
"def interior_point(x0,calc_f,calc_c,var_bounds,max_iter=20):\n",
" \n",
" \n",
" # YOUR SOLUTION HERE\n",
" \n",
" return x, v, u, mu, E"
]
},
{
"cell_type": "markdown",
"id": "4fb21995",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.9.3 Test Problems](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.3-Test-Problems)",
"section": "4.9.3 Test Problems"
}
},
"source": [
"## 4.9.3 Test Problems"
]
},
{
"cell_type": "markdown",
"id": "2e7ab8ef",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.3.1 Problem 1: Convex](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.3.1-Problem-1:-Convex)",
"section": "4.9.3.1 Problem 1: Convex"
}
},
"source": [
"### 4.9.3.1 Problem 1: Convex"
]
},
{
"cell_type": "code",
"execution_count": 5,
"id": "4c290f53",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.3.1 Problem 1: Convex](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.3.1-Problem-1:-Convex)",
"section": "4.9.3.1 Problem 1: Convex"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 3.0000e+00 \t1.0000e+00 \t 2.00e+00 \t 9.06e-01 \t 2.00e+00 \t 3.56e-04 \t 0.00e+00 \t 0.00e+00\n",
"1 \t 1.0996e+00 \t1.3978e-10 \t 3.20e-04 \t 5.03e-04 \t 1.78e-04 \t 3.56e-04 \t 0.00e+00 \t 0.00e+00\n",
"2 \t 1.1000e+00 \t3.9524e-14 \t 1.26e-07 \t 1.70e-07 \t 3.94e-08 \t 5.91e-08 \t 0.00e+00 \t 0.00e+00\n",
"3 \t 1.1000e+00 \t0.0000e+00 \t 6.87e-11 \t 1.48e-11 \t 1.11e-10 \t 1.04e-10 \t 0.00e+00 \t 0.00e+00\n"
]
}
],
"source": [
"f = lambda x: x[0] + 2*x[1]\n",
"c = lambda x: (x[0] + x[1] - 1)*np.ones(1)\n",
"\n",
"# Indices of variables with lower bound of zero\n",
"vb = [1]\n",
"\n",
"x0 = np.ones(2)\n",
"u0 = np.ones(1)\n",
"v0 = np.ones(1)\n",
"\n",
"x_, v_, u_, E_ = barrier_subproblem(x0,v0,u0,f,c,vb,1E-1,1E-10,verbose=False)"
]
},
{
"cell_type": "markdown",
"id": "1f44a1a9",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.3.2 Problem 2: Convex](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.3.2-Problem-2:-Convex)",
"section": "4.9.3.2 Problem 2: Convex"
}
},
"source": [
"### 4.9.3.2 Problem 2: Convex"
]
},
{
"cell_type": "code",
"execution_count": 6,
"id": "08e17352",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.3.2 Problem 2: Convex](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.3.2-Problem-2:-Convex)",
"section": "4.9.3.2 Problem 2: Convex"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"\n",
"*** Barrier Subproblem 0 ***\n",
"mu = 10.0\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 3.0000e+00 \t1.0000e+00 \t 9.00e+00 \t 1.35e+01 \t 2.00e+00 \t 8.45e-03 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 1 ***\n",
"mu = 2.0\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 1.1008e+01 \t1.3978e-10 \t 7.92e+00 \t 1.14e+01 \t 4.22e-03 \t 8.45e-03 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 2 ***\n",
"mu = 0.4\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 2.9318e+00 \t0.0000e+00 \t 1.53e+00 \t 2.17e+00 \t 1.70e-04 \t 3.40e-04 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 3 ***\n",
"mu = 0.08000000000000002\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 1.3993e+00 \t2.5520e-10 \t 3.19e-01 \t 4.51e-01 \t 1.70e-04 \t 3.40e-04 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 4 ***\n",
"mu = 0.016000000000000004\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 1.0801e+00 \t5.3163e-11 \t 6.41e-02 \t 9.07e-02 \t 1.07e-05 \t 1.78e-05 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 5 ***\n",
"mu = 0.0020238577025077633\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 1.0160e+00 \t0.0000e+00 \t 1.40e-02 \t 1.98e-02 \t 1.15e-05 \t 1.86e-05 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 6 ***\n",
"mu = 9.104790579399288e-05\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 1.0020e+00 \t7.7571e-13 \t 1.93e-03 \t 2.73e-03 \t 7.76e-07 \t 8.83e-07 \t 0.00e+00 \t 0.00e+00\n",
"1 \t 1.0001e+00 \t0.0000e+00 \t 1.07e-07 \t 2.43e-09 \t 0.00e+00 \t 1.07e-07 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 7 ***\n",
"mu = 8.687702517211205e-07\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 1.0001e+00 \t0.0000e+00 \t 9.02e-05 \t 1.28e-04 \t 1.11e-10 \t 5.12e-09 \t 0.00e+00 \t 0.00e+00\n",
"1 \t 1.0000e+00 \t9.9920e-15 \t 4.95e-09 \t 6.52e-13 \t 3.88e-17 \t 4.95e-09 \t 0.00e+00 \t 0.00e+00\n"
]
}
],
"source": [
"f = lambda x: x[0] + 2*x[1]\n",
"c = lambda x: (x[0] + x[1] - 1)*np.ones(1)\n",
"\n",
"# Indices of variables with lower bound of zero\n",
"vb = [1]\n",
"\n",
"x0 = np.ones(2)\n",
"#u0 = np.ones(1)\n",
"#v0 = np.ones(1)\n",
"\n",
"# x_, v_, u_, E_ = barrier_subproblem(x0,v0,u0,f,c,vb,1E-1,1E-10,verbose=False)\n",
"\n",
"x, v, u, mu, E = interior_point(x0,f,c,vb)"
]
},
{
"cell_type": "code",
"execution_count": 7,
"id": "2efe01ca",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.3.2 Problem 2: Convex](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.3.2-Problem-2:-Convex)",
"section": "4.9.3.2 Problem 2: Convex"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEGCAYAAAB7DNKzAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAAAy70lEQVR4nO3deXxU9b3/8dcnO1nYsgBJWGXfEwMIiHVDQREktnXHrVLvFdvb3ntb79L2ent/9/bXX3t7b6tdEFGw1KUKFisq1qqgsoWwb4JAICFA2AmQ/fP740xkDJPJkMzMmSSf5+Mxj5kz58w5bxTmM+ec7yKqijHGGNOYKLcDGGOMiWxWKIwxxvhlhcIYY4xfViiMMcb4ZYXCGGOMXzFuBwiFtLQ07dOnj9sxjDGm1Vi/fv0xVU33ta5NFoo+ffpQUFDgdgxjjGk1RKSosXV26ckYY4xfViiMMcb4ZYXCGGOMX23yHoUxxoRSdXU1xcXFVFRUuB3lsiUkJJCdnU1sbGzAn7FCYYwxl6m4uJiUlBT69OmDiLgdJ2CqyvHjxykuLqZv374Bfy7kl55EZL6IHBWRrV7vdRWR90Rkt+e5SyOfnSIiu0Rkj4g8GeqsxhgTiIqKClJTU1tVkQAQEVJTUy/7TCgc9yheAKY0eO9J4H1VHQC871n+EhGJBp4BpgJDgbtFZGhooxpjTGBaW5Go15zcIS8UqroCONHg7RnAAs/rBcDtPj46FtijqntVtQp42fO59mfnMijb5XYKY0w75Varp26qWgrgec7wsU0WcNBrudjznk8iMltECkSkoKysLKhhXXWmFF65D974W7C5Q4wxfixYsIABAwYwYMAAFixY0PQHAhTJzWN9nR81+k2pqnNVNU9V89LTffZCb502/B60FkoK4OAat9MYYyLUiRMneOqpp1izZg1r167lqaee4uTJk0HZt1uF4oiI9ADwPB/1sU0x0NNrORs4FIZskaOuFta/AL3GQ4cu8Omv3E5kjIkA69atY+TIkVRUVHDu3DmGDRvGM888w+TJk+natStdunRh8uTJvPPOO0E5nlvNY5cCDwA/8Tz/ycc264ABItIXKAHuAu4JW8JIsPs9OFMMU/4TDm+BFT+DY3sgrb/byYwxHk+9uY3th84EdZ9DMzvyo9uGNbp+zJgxTJ8+nX/913/lwoUL3HfffcTGxtKz58Xf1tnZ2ZSUlAQlTziax74ErAIGiUixiDyCUyAmi8huYLJnGRHJFJFlAKpaA8wB3gV2AK+q6rZQ540oBfMhuRsMugXGzoboWFj9jNupjDER4Ic//CHvvfceBQUFfO9730N93MMMVsuskJ9RqOrdjay6wce2h4BbvJaXActCFC2ynToAu5fDNf/gFIjkDBh1F2z8A1z3L5CU5nZCYwz4/eUfSidOnKC8vJzq6moqKirIzs7mww8//GJ9cXEx1157bVCOFck3s9u39QtABHIfuPje+DlQUwHr5rmXyxgTEWbPns2Pf/xj7r33Xr7//e9z8803s3z5ck6ePMnJkydZvnw5N998c1COZUN4RKLaaihcCANuhs5e9/PTB8HAKbB2Lkz8NsR2cC+jMcY1CxcuJCYmhnvuuYfa2lomTJjAxo0b+cEPfsCYMWMA59JU165dg3I8KxSRaOdbcO4o5D186boJT8ALt8Kml3yvN8a0ebNmzWLWrFkAREdHs2bNxabzDz8c/O8Fu/QUiQrmQ6de0P+S2zjQeyJk5sCnT0NdXfizGWPaHSsUkebYHtj3EVz5AERFX7pexDmrOPE5fPZ2+PMZY9odKxSRZv3zEBUDOfc3vs2QGc4Zh3XAM8aEgRWKSFJdARsXweBpkNKt8e2iY2D838KBVXBwXfjyGWPaJSsUkWT7n+DCycBuUufcBwmdYJWdVRhjQssKRSQpmA+p/aHvNU1vG5/iFJQdb8KJvaHPZoxpt6xQRIoj2+DgarjyIeeGdSDGfhMkGlb/JrTZjDGtwpQpU+jcuTPTpk0L6n6tUESKguchOh5GX8a4hx17wMivO0ORn284N5Qxpr35x3/8R1588cWg79cKRSSoLIdNL8OwmZB4mT0px8+B6vNQ8FxoshljIo6vYca3bt3KDTfcQEpKStCPZz2zI8HW16HqbPN6WncbCv1vhDVzYfwTEJsQ/HzGmMa9/aQzDUAwdR8BU3/S6Gpfw4wPHz48uBm82BlFJCiYDxnDoOfY5n1+whPOkB9bXg1uLmNMxGo4zHgo2RmF20oKoXQj3PKzwG9iN9T3K84vkE+fhtH3QZTVf2PCxs8v/1BqOMx4UlJSyI5l3yhuK5gPsUkw8s7m70MEJnwLju2CPe8FL5sxJmI1HGY8lKxQuOnCKef+xIivQkLHlu1r2EzomGXDehjTDngPM/7kk0+ybt06/vrXvzJp0iS+9rWv8f7775Odnc27774blOO5dulJRAYBr3i91Q/4oar+j9c21+LMp73P89ZiVf33MEUMvc2vOi2W8h5q+b6iY+Gqv4Hl/+pczsrKbfk+jTERqbFhxq+//vqQHM+1MwpV3aWqo1V1NHAlcB5Y4mPTlfXbtakioepcdsrMdYYND4bcByC+I6x6Ojj7M8YYIufS0w3A56pa5HaQsDmwGsp2BHfyoYSOzvDk296Ak+3nP6UxJrQipVDcBbzUyLrxIrJJRN4WkUZnMReR2SJSICIFZWVloUkZTAXzIb4TDM8P7n7HPebc3F7z2+Du1xjzJarqdoRmaU5u1wuFiMQB04E/+lhdCPRW1VHAr4A3GtuPqs5V1TxVzUtPTw9J1qA5dxy2vwGj7oK4IDdp65QNw++A9QuckWiNMUGXkJDA8ePHW12xUFWOHz9OQsLldcyNhH4UU4FCVT3ScIWqnvF6vUxEfi0iaap6LKwJg23jIqitCs5NbF/Gz4HNr8D6F+Dq74TmGMa0Y9nZ2RQXF9Mqrl40kJCQQHZ29mV9JhIKxd00ctlJRLoDR1RVRWQszhnQ8XCGC7q6OmcWu14TIGNIaI7RYyT0uxZW/xauehxi4kJzHGPaqdjYWPr27et2jLBx9dKTiCQCk4HFXu89JiKPeRa/CmwVkU3AL4G7tLWd6zW07yNn/ohg3sT2ZcITUH4Ytr4W2uMYY9o8V88oVPU8kNrgvd96vX4aaFttPQvmQ2IqDJ0e2uNccQNkDHU64I26u/nDgxhj2j3Xb2a3K2dKYedbMPpeiIkP7bFEnLOKo9vh8/dDeyxjTJtmhSKcNvwetBaufDA8xxv+VUjpYcN6GGNaxApFuNTVOq2Q+l0HqVeE55gxcTDum7D3QyjdHJ5jGmPaHCsU4bL7PThTHPqb2A1d+RDEJdtZhTGm2axQhEvBfEjuDoOmhve4HTpD7ixnlNrTxeE9tjGmTbBCEQ6nDsDu5c4XdnRs+I8/ztPaePVvwn9sY0yrZ4UiHNYvcFoh5c5y5/hdesOw250cFafdyWCMabWsUIRabTUULoQBN0Pnnu7lGD8Hqs46xcIYYy6DFYpQ2/kWnDsa/pvYDWXlQp9JzuWnmip3sxhjWhUrFKFWMB869YL+N7idxOmAd/YQbPM1P5QxxvhmhSKUju1xxna68gGIinY7DfSfDGmDnKayrXzILGNM+FihCKX1z0NUDOTc73YSR1QUTJgDR7Y4nfCMMSYAVihCpbrCmXdi8DRI6eZ2motGfB2SMqwDnjEmYFYoQmX7n5wZ5ty+id1QbAKMm+0MFHh4q9tpjDGtgBWKUCmYD6n9oe81bie5VN4jEJsIq55xO4kxphWwQhEKR7bBwdXOOEuROA9EYlfIuQ+2/BHOHHI7jTEmwlmhCIWC5yE6Hkbf43aSxl31N86Q52t+53YSY0yEc3sq1P0iskVENopIgY/1IiK/FJE9IrJZRHLdyHlZKsth08swbKbzyz1Sde0HQ25zilrlWbfTGGMiWCScUVynqqNVNc/HuqnAAM9jNhD5o9ptfd0ZKiPSbmL7MuFbUHkaCl90O4kxJoJFQqHwZwawUB2rgc4i0sPtUH4VzIeMYdBzrNtJmpadB73Gw+pfQ22N22mMMRHK7UKhwHIRWS8is32szwIOei0Xe967hIjMFpECESkoKysLQdQAlBRC6UbIi9Cb2L5MeAJOH4Ttb7idxBgTodwuFBNVNRfnEtPjItKwLamvb1ufY0+o6lxVzVPVvPT09GDnDEzBfIhNgpF3unP85hg4FbpeAZ/+0ob1MMb45GqhUNVDnuejwBKg4fWaYsB7bO5sIDLbc1445dyfGPFVSOjodprA1Q/rUboJ9n/sdhpjTARyrVCISJKIpNS/Bm4CGnYVXgrM8rR+ugo4raqlYY4amM2vQvV557JTazPqbkhMtWE9jDE+uXlG0Q34WEQ2AWuBt1T1HRF5TEQ8c3eyDNgL7AGeBf7WnahNUHUuO2XmQmaO22kuX2wHGDsbdr8LR3e6ncYYE2Fi3Dqwqu4FRvl4/7derxV4PJy5muXAaijbAdOfdjtJ8435Bnz8C1j1NMxoxX8OY0zQuX0zu20omA/xnWB4vttJmi8pzelJvvkVOHvE7TTGmAhihaKlzh13mpaOugviktxO0zJXPe7M8b12rttJjDERxApFS21cBLVVrfMmdkNp/WHwrbBuHlSdczuNMSZCNFkoROSnItJRRGJF5H0ROSYi94UjXMSrq3Nmses1ATKGuJ0mOCY8ARWnYMMit5MYYyJEIGcUN6nqGWAaTr+GgcA/hjRVa7HvIzixt3WM6xSonuMge4xzU7uu1u00xpgIEEihiPU83wK8pKonQpindSmY7/Q/GDrd7STBI+KcVZwqgh1vup3GGBMBAikUb4rITiAPeF9E0oGK0MZqBc6Uws63YPS9EBPvdprgGjwNuvSxYT2MMUAAhUJVnwTGA3mqWg2cxxnVtX3b8Htn4p8rH3Q7SfBFRcP4OVCy3ukjYoxp1wK5mZ2I0+mtfi6ITJyzi/arrhbWvwD9roPUK9xOExqj74EOXWxYD2NMQJeengeqgAme5WLgP0KWqDXY/R6cKW5bN7EbiktyemvvWgbHdrudxhjjokAKxRWq+lOgGkBVL+B7+O/2o2A+JHeHQVPdThJaY2dDdCysesbtJMYYFwVSKKpEpAOeeSBE5AqgMqSpItmpA7B7OeTOcr5E27LkDKfH+aaXoNylyaCMMa4LpFD8CHgH6Ckii4D3ge+FNFUkW7/AaUKaO8vtJOExfg7UVDi9tY0x7VIgrZ7eA/KBB4GXcFo/fRjaWBGqthoKF8KAm6Fzz6a3bwvSB8HAKbDuWag673YaY4wLGi0UIpJb/wB6A6U4s8v18rzX/ux8C84dbds3sX2Z8AScP+5cgjLGtDv+5qP4uZ91Clwf5CyRr2A+dOoF/W9wO0l49Z7oTMi06hmn30hUtNuJjDFh1GihUNXrwhkk4h3b44ztdP0P2t8XZf2wHq89DLvehiHT3E5kjAmjQDrcJYjId0VksYi8LiJ/JyIJLT2wiPQUkQ9EZIeIbBORb/vY5loROS0iGz2PH7b0uM22/nmIioGc+12L4KohM6BzL+uAZ0w7FEirp4XAMOBXwNPAUODFIBy7Bvh7VR0CXAU8LiJDfWy3UlVHex7/HoTjXr7qCmfeicHTIKWbKxFcFx3jTGx0cDUcXOt2GmNMGAVSKAap6iOq+oHnMRtnqPEWUdVSVS30vD4L7ACyWrrfkNj+J7hwsv3dxG4o5z5I6GRnFca0M4EUig0iclX9goiMAz4JZggR6QPkAGt8rB4vIptE5G0RGeZnH7NFpEBECsrKgtw5rGA+pPaHvtcEd7+tTXwy5D3iDD9+Yq/baYwxYeKveewWEdkMjAM+FZH9IrIPWAUE7RtTRJKB14G/80yQ5K0Q6K2qo3Aufb3R2H5Uda6q5qlqXnp6erDiwZFtzuWWKx9ybuq2d+O+6dyrWfVrt5MYY8LEX/PYkDdtEZFYnCKxSFUXN1zvXThUdZmI/FpE0lT1WKizfaHgeYiOd0ZTNZDSHUbe6Qyzft0/Q2JXtxMZY0Ks0TMKVS3yfgAXcPpP1D9aREQEeA7Yoar/3cg23T3bISJjPXmPt/TYAassh00vw7CZ9oXobcIcqLkA655zO4kxJgwCaR47XUR2A/uAj4D9wNtBOPZE4H7geq/mr7eIyGMi8phnm68CW0VkE/BL4C7VME65tvV1qDprN7EbyhgC/SfD2t85LcKMMW2av0tP9X6M03z1L6qaIyLXAXe39MCq+jFNDFeuqk/jNMkNP1UoeA4yhkHPsa5EiGgTnoCF02Hlz2HS30Nsi7vWGGMiVCCtnqpV9TgQJSJRqvoBMDq0sSLAoUIo3QR5dhPbp77XODP8rfgp/GIo/OXfnCHYjTFtTiBnFKc8LZNWAItE5ChOZ7m2rWA+xCY5N27NpUTgvsWw70NYOw8++V/nMXAqjP2GU0SswBrTJgRSKGYAFcB3gHuBToA7PaTD5cIp2PI6jPw6JHR0O03kioqCK653HqcOOMW1cCHsegtSBzhTqY6+2+mkZ4xptSSc94bDJS8vTwsKCpq/gzW/g7e/B7M/dEZNNYGrroDtb8DaZ6GkwHNW9nUY+yh0a7S/pDHGZSKyXlXzfK1r9IxCRD5W1atF5Cxfbg4rgKpq2/yprer8Ms7MtSLRHLEJzvSpo+6CQxucy1KbXnIGVew1wSkYQ25r+9PIGtOG+OtHcbXnOUVVO3o9UtpskQA4sArKdlqT2GDIzIHbn4Hv7oDJ/w5nSuC1h+AXw+GD/4IzpW4nNMYEwG+rJxGJEpGt4QoTEQrmQ3wnGJ7vdpK2I7ErTPw2fGsD3PMqdB8BH/0E/mc4/PFB2P+JcyZnjIlIfm9mq2qdZ0C+Xqra9ts+njvmjBR75UMQl+R2mrYnKhoG3uw8jn/uFOUNL8K2JU5/lTGPOK3M4pPdTmqM8RJIP4oewDYReV9EltY/Qh3MFRsXQW2V03fChFbqFXDz/4Hv7oTpv3KKyFvfhf8eAm9/H47tdjuhMcYjkOaxT4U8RQQ4V1HF6fd/g3TKoUfGELfjtB9xiZA7y5k5sHid01pq3XOw5rfQ71oY8ygMnOJMnNTK1dYpFdW11NQqNXV11NSp86h1XtfWKdW1dZ5nZ7l+XU1dnedzX/5MTa1SW3fxdU3Dz3yxTcN911Fdp9R6PlOniqo6A7mpZ0A3z+VAZ1mdZ+/XAA2WG+6DLy1776OR/XvtA8XvoHJNtdj0/1n//6+05cPZuaJrYhx/mnN10Pfb5L8+Vf0o6EeNQElSxYdxeRTWjOAHbodpj0ScoVJ6jnXONAoXOCP3vnIvdOrpnOXlPgBJaW4n/ZILVbUcK6/kWHklx8urnOdzVZ73qjju9f6J81VhvRUTHSXE1D+iozzPQkxUlLMuun59FFFRIAginnF1RBDnyfPsvey8KYBEgRDlvC8X98Eln/nyMl7H8v7cJfv3fKYxTfXp9P9Z/x9ujd1FUxJC84OqyX4UnkmLfgUMAeKAaOBcJLd8am4/ioWr9vPDP21j2bcmMTQzYv947UdtDXz2tnOWse8jiI5zRvId8yhk54Wk53ddnXLyfFWjX/bHyqs4fu5iYThfVetzP8nxMaQlx5GaHE9qUhxpKfGkJcWRFB/T4Evb+aL2/gKPjRbPs/fypZ+5dJuLyzFR0uQXoTHemtWPwsvTwF3AH4E8YBYwIHjxIse0kZn8+M/bWbKhmKGZvqbvNmEVHeP0uRhyG5TtgnXzYONLsPkV6DHa6ZMx/A6I7eB3NxXVtZd86Zd5no+f+3IROHGukjofv52io4SuSXHOl35yPL17JTpFINlZTkuOIzUpnrQUpzAkxEaH5r+JMS4I5IyiQFXzRGSzqo70vPepqk4IS8JmaEnP7NkLC9hw8BSrnryemOhA7vWbsKo86xSKtfOgbAd06OLM5Z33CHTty/ZDZ1i0pogdpWecs4KzlZxr5Fd/Ulw0qfVf8p7nNM8ZQH0RSE+OJzU5ns4dYomKsl/opu1q6RnFeRGJAzaKyE+BUqDNth3Nz81i+fYjfPL5cb4yMIhTqprgiE9xxpDKewSKPoG1z6Krfg2fPk1h3Bh+VX4ta6JHk9MrlVHZnZ0v/uS4i0Wg/lJQcjwd4uxXvzGB8DeER56qFuBMLhQFzMEZGLAncEd44oXfdYMz6NQhlsWFxVYoIpkIh7vk8YfO6SyPupUplW9zv3zAC3Frqe3cl+jMGyApA5LTIcn70QHiO9jItsZcBn9nFM96hhd/CXhZVbfTDprKxsdEM21kD14vLKa8sobk+NbfLLMtUVVW7T3Oi6uKWL79CHWqXD+oL6PH/1+69OsEu/5MdMHzsOU1qDjleycxCZ6ikeZ5zrj4Ojnjy+8npraJprnGtESj/wI8s9kNwrmR/ZqIVHGxaBQF4+AiMgX4X5yWVPNU9ScN1otn/S3AeeBBVS0MxrH9yc/NZtGaA7y9pZSv5fUM9eFMAMora1hSWMzCVUXsPlpOl8RYvjGpL/eN603ProkXNxx+h/MAqKmC88fgXJnzKC+7+PqL947AkW1QfhTqqn0fvENX30XEV3GJS7azFdPmNDWExy6cs4inRGQUTtH4q4gcVtWJLTmwiEQDzwCTgWJgnYgs9Zy51JuK08JqADAO+I3nOaRye3WmT2oiSzaUWKFw2e4jZ3lxdRGLC0sor6xhZHYnfva1UUwb2aPplkUxcdAx03k0RRUqTjvDuJw72nhxObzFea443cgxO1w8W7mksKQ7w5NExTo90aNjISrGx7Ln4W/ZipEJo4DOqUUkCsgAuuHcyC4LwrHHAntUda/nGC/jTJLkXShmAAvVaZq1WkQ6i0gPVQ3psKMiwsycbP7n/c8oOXWBrM7+m1+a4KqpreO97UdYuKqIVXuPExcTxbSRPZg1vg+je3YOzUFFoENn55HWP4CQlZ6i0vAM5ejF98+UONPpniuDuiBPCinRXsUj2lNsfC3HeBUj7+UGBUqicHq5SSPPNLE+kGea//lG/zs0VTD9fbaJjza1QSQW69gkuOqxoO/Wb6EQkUnA3cDtwFbgZeA7qtrIz6nLkgUc9Fou5tKzBV/bZOG0vGqYdTYwG6BXr14tDjczJ4tf/OUz3thQwuPXBfDFYVqs7GwlL689wB/WHqD0dAVZnTvw/SmDuXNMT7omxbkd78ti4qFTlvNoiipcOOkUjKpzTtGoq4Ha6ouvv/RerXMZzOdy/bYNl+vfq/Xab8Nlz/6qzl963LpanDEzlItjZ3gvX+5zCz9vmicpI7yFQkQOAgdwisNTqnokyMf2VY4b/g0JZBvnTdW5wFxw+lG0LBr0Sk1kbJ+uLNlQwt9ee4X1cg0RVWV90UkWriri7a2lVNcqkwak8e8zhnP94Ayi20LfBRFnqPXErm4naV3qB4ZqfIOmPx+Szwbw+TbG3xnF1cG6ad2IYpymtvWygUPN2CZkZuZm8U+Lt7Cl5DQjszuH67DtwvmqGv608RALVzmd41ISYrj/qj7cd1Uv+qXbMOMGvhj8ybjOX6unUBYJgHXAABHpC5Tg3Ci/p8E2S4E5nvsX44DTob4/4e2WET340dJtLC4ssUIRJPuOneP3q4v4Y8FBzlTUMLh7Cv85cwS352SSGGfNUI2JRK79y1TVGhGZA7yL0zx2vqpuE5HHPOt/CyzDaRq7B6d5bFgniujUIZbJQ7qxdNMh/uXWIcTakB7NUlunfLDzKAtXF7HiszJiooSpI3owa3xv8np3sct6xkQ4V3/CqeoynGLg/d5vvV4r8Hi4c3nLz83irS2lfLSrjBuHdnMzSqtz4lwVrxYc5Periyg+eYFuHeP5zo0DuXtsTzI6JrgdzxgTIH83s3+Fnzs2qvqtkCSKMNcMTCc1KY4lG0qsUARo08FTLFxVxJubD1FVU8dV/bryz7cMYfLQbnZWZkwr5O+MonnDr7YxsdFR3DYqkz+sPcDp89V0Sox1O1JEqqiu5c+bS3lx1X42FZ8mKS6aO/N6cv/43gzsluJ2PGNMC/i7mb0gnEEi2R252bzw6X7e2lLKPeNa3kejLTl44jyL1hzglXUHOHm+mivSk3hq+jDyc7NISbCiakxb0OQ9ChFJB74PDAW+uLCsqteHMFdEGZ7Vkf4ZySzZUGyFwsuP/rSVhauLEGDy0G48ML4P469ItZvTxrQxgdzMXgS8AtwKPAY8QHCG8Gg1RIT83Cx++s4uio6fo3dqm52OI2BbS06zYFUR+TlZ/MPNg8i0YU6MabMCubOYqqrPAdWq+pGqPgxcFeJcEef20VmIwJINJW5HiQjzVu4lKS6aH00fZkXCmDYukEJRP/ZyqYjcKiI5OD2k25XMzh0Y3y+VJRtKaGr62Lbu0KkLvLm5lLvG9qJTB7sPYUxbF0ih+A8R6QT8PfAPwDycme7anfzcbIqOn6fwwEm3o7jq+U/2AfDQxD7uBjHGhEWThUJV/6yqp1V1q6pep6pXqurScISLNFOGd6dDbDSLC9vv5aczFdW8tPYgt47oQXaXxKY/YIxp9ZosFCLSV0T+W0QWi8jS+kc4wkWa5PgYbh7WjTc3HaKyptbtOK54ee0ByitreHRSP7ejGGPCJJBWT28AzwFvAnUhTdMK5Odm88bGQ/x1x1GmjujhdpywqqqpY/7H+xnfL5UR2Z3cjmOMCZNACkWFqv4y5ElaiYn908hIiWfxhpJ2Vyje2nKIw2cq+K/8EW5HMcaEUSA3s/9XRH4kIuNFJLf+EfJkESo6Srg9J4sPdh7lxLkqt+OEjaoyd8U+BmQk85WB6W7HMcaEUSCFYgTwKPAT4Oeex89CGSrS5edmUVOnvLkpbHMoue6TPcfZUXqGRyf1I6otzDpnjAlYIJeeZgL9VLX9/HxuwuDuHRnSoyOLN5TwwIQ+bscJi7kr95KWHM+MnEy3oxhjwiyQM4pNQOcQ52h17sjNYtPBU3xeVu52lJDbUXqGFZ+V8dDEPsTHRLsdxxgTZoEUim7AThF5t703j/U2fVQmUQJL2kGfinkr99EhNpp7bUBEY9qlQC49/SjYBxWR/wfcBlQBnwMPqeopH9vtB84CtUCNquYFO0tzZXRMYNKAdJZsKOG7kwe22ev2h09XsHRTCfeO603nxDi34xhjXBBIz+yPfD1aeNz3gOGqOhL4DPgnP9tep6qjI6lI1MvPzaLk1AXW7DvhdpSQeeHT/dTWKQ9P7Ot2FGOMSxotFCLysef5rIic8XqcFZEzLTmoqi5X1RrP4mpa6SCDNw3tTnJ8DEs2FLsdJSTKK2tYtKaIqcN70CvVhuswpr1qtFCo6tWe5xRV7ej1SFHVjkHM8DDwdmMxgOUisl5EZvvbiYjMFpECESkoKwvPdBkd4qKZOrw7y7Yc5kJV2xvS45V1BzlbUcM3JtnZhDHtmd9LTyISJSJbm7NjEfmLiGz18Zjhtc2/ADU4kyP5MlFVc4GpwOMick1jx1PVuaqap6p56enh6xCWn5tNeWUNy7cfDtsxw6Gmto75H+9jbJ+u5PTq4nYcY4yL/N7MVtU6EdkkIr1U9cDl7FhVb/S3XkQeAKYBN2gjEzyo6iHP81ERWQKMBVZcTo5QG9e3K1mdO7BkQwkzRme5HSdolm09TMmpC/zb9GFuRzHGuCyQ5rE9gG0i8n6wmseKyBScebinq+r5RrZJEpGU+tfATUCzzm5CKSpKuD0nkxWflXH0bIXbcYLCGa7jc/qlJXHD4Ay34xhjXBZI89inQnDcp4F44D0RAVitqo+JSCYwT1Vvwem/scSzPgb4g6q+E4IsLTYzJ5tnPvicpRsP8Y02MPz26r0n2Fpyhv+cOaLNNvs1xgSu0UIhIgnAY0B/YAvwnFdLpRZR1f6NvH8IuMXzei8wKhjHC7X+GcmMyu7E4sKSNlEonl25l9SkOPJz286lNGNM8/m79LQAyMMpElNxBgM0jcjPzWZ76Rl2Hm5Ry2HX7T5ylr/uPMqs8X1IiLXhOowx/gvFUFW9T1V/B3wVmBSmTK3SbaMyiYmSVj+kx7yV+4iPieL+8b3djmKMiRD+CkV1/YtgXXJqy7omxXHtoAyWbCihts5nI66Id/RsBUs2lPC1vGy6JtlwHcYYh79CMcq7NzYwMlg9s9uq/Nwsjp6t5JM9x9yO0iwLPy2iuq6OR65u/fdZjDHB469ndnSD3tgxIeqZ3WZcPziDjgkxLNnQ+i4/na+q4cXVRdw0tBt905LcjmOMiSCB9KMwAUqIjWbaqEze2XqY8srWdbXujwXFnL5Qzexr7GzCGPNlViiCLD8niwvVtbyztfUM6VFbp8z7eC+5vTpzZe+ubscxxkQYKxRBdmXvLvTqmtiqRpR9d9thDp64YGcTxhifrFAEmYgwMyeLTz8/TunpC27HaZKq8rsVe+mdmsjkod3djmOMiUBWKEIgPzcLVXhjwyG3ozSpoOgkmw6e4htX9yXahuswxvhghSIEeqcmkde7C4sLi2lkYNyIMXfFXrokxvLVK3u6HcUYE6GsUITIzNwsdh8tZ2tJ5HY5+bysnL/sOML9V/WmQ5wN12GM8c0KRYhMG5FJXHQUiyP4pvZzH+8jNjqK+8f3cTuKMSaCWaEIkU6Jsdw4NIOlGw9RXVvndpxLHCuv5PX1xdyRm0V6SrzbcYwxEcwKRQjNzMnm+LkqVnwWnjm8L8eLq4qorLHhOowxTbNCEUJfGZhO16Q4FkfYkB4Xqmp5cXURNw7JoH9GsttxjDERzgpFCMXFRHHbyB68t/0Ipy9UN/2BMHm9sJgT56p4tA1MsmSMCT1XCoWI/JuIlIjIRs/jlka2myIiu0Rkj4g8Ge6cwZCfm01VTR1vbyl1OwrgDNfx3Mf7GJXdibF9bbgOY0zT3Dyj+IWqjvY8ljVcKSLRwDM4s+sNBe4WkaHhDtlSI7M7cUV6EosjZEKjv+w4wr5j53j0mn545iM3xhi/IvnS01hgj6ruVdUq4GVghsuZLpuIkJ+bzdr9Jzh44rzbcXh2xV6yu3RgyjAbrsMYExg3C8UcEdksIvNFpIuP9VnAQa/lYs97PonIbBEpEJGCsrLIamV0e44T2+15KtYXnaSg6CSPXN2XmOhI/o1gjIkkIfu2EJG/iMhWH48ZwG+AK4DRQCnwc1+78PFeo+NhqOpcVc1T1bz09PRg/BGCJqtzB67q19X1IT3mrdxLx4QYvp5nw3UYYwIXE6odq+qNgWwnIs8Cf/axqhjw/kbLBiJ/lL1G5Odm873XNlN44BRX9vZ1AhVaRcfP8c62w/zNV64gKT5k/9uNMW2QW62eengtzgS2+thsHTBARPqKSBxwF7A0HPlCYerw7iTERrk2T8VzH+8jJkp4cEIfV45vjGm93LpQ/VMR2SIim4HrgO8AiEimiCwDUNUaYA7wLrADeFVVt7mUt8VSEmK5aWh33txUSmVNbViPffJcFa8WHOT20VlkdEwI67GNMa2fK9cgVPX+Rt4/BNzitbwMuKTpbGuVn5vF0k2H+GBnGVOGh6/V0e9XF1FRXcejNoOdMaYZrOlLGF3dP430lHgWF4bv8lNFdS0LVu3n2kHpDOyWErbjGmPaDisUYRQTHcWMUZl8sOsoJ89VheWYb2wo4Vh5FbNtuA5jTDNZoQiz/NxsqmuVP28OfQOuujrl2ZV7GZbZkfFXpIb8eMaYtskKRZgNzezI4O4pvB6GIT0+2HWUz8vOMduG6zDGtIAVChfk52ax8eApPi8rD+lx5q7YS2anBG4Z0aPpjY0xphFWKFwwY3QWUeLcPwiVTQdPsWbfCR6+ui+xNlyHMaYF7BvEBd06JjCxfxqLC0uoqwvNkB7PrtxLSnwMd46x4TqMMS1jhcIld+RmU3LqAuv2nwj6vg+eOM+yLaXcM64XKQmxQd+/MaZ9sULhkpuGdSMxLjok81TM/2QfUSI8OLFP0PdtjGl/rFC4JDEuhqnDe7BsSykV1cEb0uP0+WpeWXeQ6aMy6dGpQ9D2a4xpv6xQuOiO3CzOVtbw3vYjQdvnorVFnK+q5RvWwc4YEyRWKFx0Vb9UenRKCNqQHpU1tbzwyX4mDUhjaGbHoOzTGGOsULgoKkq4PSeLFbuPUXa2ssX7W7rxEEfPVvKonU0YY4LICoXL8nOyqK1Tlm5q2ZAeqs5wHYO7pzBpQFqQ0hljjBUK1w3olsKIrE4tvvz00WdlfHaknEcn2XAdxpjgskIRAfJzs9h26Ay7Dp9t9j6eXbmXbh3juW1UZhCTGWOMFYqIcNuoTKKjhMXNnCZ1a8lpPtlznIcm9iUuxv6XGmOCy605s18RkY2ex34R2djIdvs9U6ZuFJGCMMcMm7TkeK4dmM4bG0qobcaQHvNW7iUpLpq7x/YKQTpjTHvn1lSod9a/FpGfA6f9bH6dqh4LfSp35edm8/7Oo6z6/DhXX8bN6EOnLvDm5lIenNCHTh1suA5jTPC5ep1CnLuuXwdecjNHJLhhSAYpCTGXfVP7+U/2AfCQDddhjAkRty9oTwKOqOruRtYrsFxE1ovIbH87EpHZIlIgIgVlZWVBDxpqCbHRTBvZg7e3HuZcZU1AnzlTUc1Law9y64geZHdJDHFCY0x7FbJCISJ/EZGtPh4zvDa7G/9nExNVNReYCjwuItc0tqGqzlXVPFXNS09PD9KfIrxm5mRzobqWd7cdDmj7l9ceoLyyxjrYGWNCKmT3KFT1Rn/rRSQGyAeu9LOPQ57noyKyBBgLrAhmzkiS17sLPbt2YHFhCfm52X63raqpY/7H+xnfL5UR2Z3ClNAY0x65eenpRmCnqvq8KC8iSSKSUv8auAnYGsZ8YRcVJczMyeaTz49x+HSF323f2nKIw2cqmH2NnU0YY0LLzUJxFw0uO4lIpogs8yx2Az4WkU3AWuAtVX0nzBnDbmZOFqrwxsbG56lQVeau2MeAjGS+MrB1XmYzxrQerjSPBVDVB328dwi4xfN6LzAqzLFc1zctidxenVlcWMw3r/E9HMcne46zo/QMP71jJFFRNlyHMSa03G71ZHzIz83msyPlbDt0xuf6uSv3kpYcz4wcG67DGBN6Vigi0LSRPYiLjvI5TeqO0jOs+KyMhyb2IT4m2oV0xpj2xgpFBOqcGMf1gzNYuqmEmtq6L62bt3IfHWKjuXecDddhjAkPKxQRamZuFsfKq1i5++LoJYdPV7B0Uwl3julJ58Q4F9MZY9oTKxQR6rpBGXROjOV1ryE9Xvh0P7V1ysMT+7qYzBjT3lihiFBxMVFMH5XJe9uPcKaimvLKGhatKWLq8B70SrXhOowx4WOFIoLNzMmisqaOt7eU8sq6g5ytqOEbk+xswhgTXq71ozBNG92zM/3Skni1oJjDpysY26crOb26uB3LGNPO2BlFBBMRZuZksb7oJCWnLvCoDddhjHGBFYoId3tOFgD90pK4YXCGy2mMMe2RXXqKcD27JvIvtwxhWFZHG67DGOMKKxStgF1yMsa4yS49GWOM8csKhTHGGL+sUBhjjPHLCoUxxhi/rFAYY4zxywqFMcYYv6xQGGOM8csKhTHGGL9EVd3OEHQiUgYUNfPjacCxJrcKP8t1eSzX5bFcl6ct5uqtqum+VrTJQtESIlKgqnlu52jIcl0ey3V5LNflaW+57NKTMcYYv6xQGGOM8csKxaXmuh2gEZbr8liuy2O5Lk+7ymX3KIwxxvhlZxTGGGP8skJhjDHGLysUHiIyRUR2icgeEXnS7Tz1RGS+iBwVka1uZ6knIj1F5AMR2SEi20Tk225nAhCRBBFZKyKbPLmecjuTNxGJFpENIvJnt7N4E5H9IrJFRDaKSIHbeeqJSGcReU1Ednr+ro2PgEyDPP+d6h9nROTv3M4FICLf8fy93yoiL4lIQtD2bfconH/AwGfAZKAYWAfcrarbXQ0GiMg1QDmwUFWHu50HQER6AD1UtVBEUoD1wO1u//cSEQGSVLVcRGKBj4Fvq+pqN3PVE5HvAnlAR1Wd5naeeiKyH8hT1YjqQCYiC4CVqjpPROKARFU95XKsL3i+N0qAcara3A6+wcqShfP3faiqXhCRV4FlqvpCMPZvZxSOscAeVd2rqlXAy8AMlzMBoKorgBNu5/CmqqWqWuh5fRbYAWS5mwrUUe5ZjPU8IuKXkIhkA7cC89zO0hqISEfgGuA5AFWtiqQi4XED8LnbRcJLDNBBRGKAROBQsHZshcKRBRz0Wi4mAr74WgMR6QPkAGtcjgJ8cXlnI3AUeE9VIyIX8D/A94A6l3P4osByEVkvIrPdDuPRDygDnvdcrpsnIkluh2rgLuAlt0MAqGoJ8DPgAFAKnFbV5cHavxUKh/h4LyJ+iUYyEUkGXgf+TlXPuJ0HQFVrVXU0kA2MFRHXL9eJyDTgqKqudztLIyaqai4wFXjcc7nTbTFALvAbVc0BzgGRdO8wDpgO/NHtLAAi0gXnKkhfIBNIEpH7grV/KxSOYqCn13I2QTxta4s89wBeBxap6mK38zTkuUzxITDF3SQATASme+4FvAxcLyK/dzfSRap6yPN8FFiCcynWbcVAsdcZ4Ws4hSNSTAUKVfWI20E8bgT2qWqZqlYDi4EJwdq5FQrHOmCAiPT1/FK4C1jqcqaI5blp/BywQ1X/2+089UQkXUQ6e153wPnHs9PVUICq/pOqZqtqH5y/W39V1aD92msJEUnyNEjAc2nnJsD1Fnaqehg4KCKDPG/dALjeuMTL3UTIZSePA8BVIpLo+fd5A869w6CICdaOWjNVrRGROcC7QDQwX1W3uRwLABF5CbgWSBORYuBHqvqcu6mYCNwPbPHcDwD4Z1Vd5l4kAHoACzytUaKAV1U1opqiRqBuwBLnu4UY4A+q+o67kb7wBLDI8+NtL/CQy3kAEJFEnBaS33Q7Sz1VXSMirwGFQA2wgSAO52HNY40xxvhll56MMcb4ZYXCGGOMX1YojDHG+GWFwhhjjF9WKIwxxvhlhcIYP0Sk3PPcR0TuCfK+/7nB8qfB3L8xwWKFwpjA9AEuq1B4+nP486VCoapB60lrTDBZoTAmMD8BJnnmIPiOZ/DB/yci60Rks4h8E0BErvXM1fEHYIvnvTc8A+5tqx90T0R+gjPS50YRWeR5r/7sRTz73uqZJ+JOr31/6DVHwyJPL1xjQsp6ZhsTmCeBf6ifR8LzhX9aVceISDzwiYjUj9Y5Fhiuqvs8yw+r6gnPsCLrROR1VX1SROZ4BjBsKB8YDYwC0jyfWeFZlwMMwxmL7BOcXvIfB/sPa4w3O6MwpnluAmZ5hjBZA6QCAzzr1noVCYBvicgmYDXO4JMD8O9q4CXPSLhHgI+AMV77LlbVOmAjziUxY0LKziiMaR4BnlDVd7/0psi1OENiey/fCIxX1fMi8iHQ1BSV/i4nVXq9rsX+DZswsDMKYwJzFkjxWn4X+BvPcOuIyMBGJtbpBJz0FInBwFVe66rrP9/ACuBOz32QdJyZ3tYG5U9hTDPYrxFjArMZqPFcQnoB+F+cyz6FnhvKZcDtPj73DvCYiGwGduFcfqo3F9gsIoWqeq/X+0uA8cAmnAm0vqeqhz2Fxpiws9FjjTHG+GWXnowxxvhlhcIYY4xfViiMMcb4ZYXCGGOMX1YojDHG+GWFwhhjjF9WKIwxxvj1/wHGkZAa0gZrKgAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZAAAAEGCAYAAABLgMOSAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAAAkoElEQVR4nO3de5hddX3v8fdnLiEkBMh9NgkhUSOYwEzA4VbOsVCMB6gl6rE1VDGPtEYrFLE9aqRHhNPznPJY255ePNAo1HiqcJBrqpGLtEDVh0tASAgXSSPKkNsk4RJuSWbme/5Ya8edyVz27MusvWd/Xs+zn7XWb92+gWR/9/r9fuv3U0RgZmY2Uk1ZB2BmZvXJCcTMzEriBGJmZiVxAjEzs5I4gZiZWUlasg5gNE2bNi3mzp2bdRhmZnXl0Ucf3RER0/uXN1QCmTt3LmvXrs06DDOzuiLplwOVuwrLzMxK4gRiZmYlcQIxM7OSOIGYmVlJnEDMzKwkmSYQSddL2i7pyUH2S9LfSdooaZ2kkwr2nSPp2XTfitGL2szMIPsnkG8B5wyx/1xgfvpZDlwDIKkZ+Hq6fwFwgaQFVY3UzMwOkOl7IBHxgKS5QxyyBPh2JGPOPyjpSEk5YC6wMSI2AUi6MT32qWrEue7+23j1V+t5Zu7HaGkSrS1NtDY30dosWpubaGlqYlzLgestTckx+9dbmmhtSo5pbWmipUmMa26iqUnVCLloEcG+3qCnr499PcG+vj729R643tMb7O3tY19PHz19yXpPbyTH9faxL13v6e1jb7re2xcH3efA7X5xDBhb/2NGfo2DDhqIDvx/0P//iAb4X6R+R/U/pqhrDFRoViXvb89xzNSJFb1mrb9IOAt4oWC7Ky0bqPzUgS4gaTnJ0wtz5swpKYjd69fw7u7b+fiGE+mr8ENbk0gSTXMTLWlCOiA5NTcxrlm0FJTl97c0N9Ek0VPwJX7AF37hF30+QRR86ff0JcuxbqjvaU+HY41i4VGHN1wCGeiffgxRfnBhxEpgJUBnZ2dJXxen/6ffoun2m1h/yTz2TH7ngV/CvX3pl/Wv1wf+dZ7/5Z6U7R3ky72nr4+9Pfkv9wPX9/UGr+3pOeB6ESRPRc0HPuVMam1hXJpsWpo1bII6OFkdmLDy1xjoegdcu6mJ1hbR3KQSfqUf/L91uF/y1f4VP9CEa8M9+Rz0tDXgdftfw5nMqqu1qfItFrWeQLqAowu2ZwObgXGDlFdFU64DgIk7NzBx9vHVuo3VoAGT2rA5y1VT1hiybkQfzmrg42lvrNOAVyJiC/AIMF/SPEnjgKXpsdUx7Z3QMh62rqvaLczM6k2mTyCSbgDOBKZJ6gK+ArQCRMS1wBrgPGAj8AbwiXRfj6RLgLuAZuD6iNhQtUCbW2DGAtjyRNVuYWZWb7LuhXXBMPsDuHiQfWtIEszoyHXAhluTymv3njEzq/kqrNqRa4e3XoGXBxzV2Mys4TiBFKstaUhni9tBzMzACaR4MxeAmt2QbmaWcgIpVuuhMP1YN6SbmaWcQEaird1VWGZmKSeQkci1w2tbYfe2rCMxM8ucE8hIpG+kux3EzMwJZGTaTkiWbgcxM3MCGZHxR8DkuX4CMTPDCWTkch1uSDczwwlk5Nra4aVfJG+lm5k1MCeQkdrfkL4+2zjMzDLmBDJSbe3J0tVYZtbgnEBGatJMOKzNDelm1vCcQEqRa3dXXjNreE4gpWhrh+5nYd+bWUdiZpaZTBOIpHMkPStpo6QVA+z/vKTH08+TknolTUn3PS9pfbpv7agGnuuA6IXtT43qbc3MaklmCURSM/B14FxgAXCBpAWFx0TEX0bEoohYBHwJuD8idhUccla6v3O04gaSKixwNZaZNbQsn0BOATZGxKaI2AvcCCwZ4vgLgBtGJbLhHHlM8la6e2KZWQPLMoHMAl4o2O5Kyw4iaQJwDnBLQXEAd0t6VNLywW4iabmktZLWdnd3VyBskjnR29rdE8vMGlqWCUQDlMUgx/4O8JN+1VdnRMRJJFVgF0t6z0AnRsTKiOiMiM7p06eXF3GhXAds2wC9PZW7pplZHckygXQBRxdszwY2D3LsUvpVX0XE5nS5HbiNpEps9LS1Q89bsOPno3pbM7NakWUCeQSYL2mepHEkSWJ1/4MkHQH8JnBHQdlESZPy68D7gCdHJeq8fEO6q7HMrEFllkAioge4BLgLeBq4KSI2SPq0pE8XHPpB4O6IeL2gbCbwY0lPAA8DP4iIO0crdgCmzoeWQ92QbmYNqyXLm0fEGmBNv7Jr+21/C/hWv7JNQEeVwxtacwvMXOiuvGbWsPwmejly7cmovDFY27+Z2djlBFKOtnbY8wq89HzWkZiZjTonkHLsnxvE7SBm1nicQMoxYwGo2e0gZtaQnEDK0Toeph/nnlhm1pCcQMqV85AmZtaYnEDKleuA17bB7q1ZR2JmNqqcQMrlOdLNrEE5gZSr7YRkudUN6WbWWJxAyjX+cJjyNj+BmFnDcQKphLZ2d+U1s4bjBFIJuXZ4+Zfw5stZR2JmNmqcQCqhLf9G+vps4zAzG0VOIJWQnxvE1Vhm1kCcQCrhsBkwKecXCs2soWSaQCSdI+lZSRslrRhg/5mSXpH0ePq5othzR11bu3timVlDyWxCKUnNwNeBxSTzoz8iaXVEPNXv0H+PiPeXeO7oyXXAxntg7xswbkJmYZiZjZYsn0BOATZGxKaI2AvcCCwZhXOrI9cO0Qfbs8thZmajKcsEMgt4oWC7Ky3r73RJT0j6oaSFIzx39LS5Id3MGkuWc6JrgLL+c8M+BhwTEa9JOg+4HZhf5LnJTaTlwHKAOXPmlBzssI6cA+OPdEO6mTWMLJ9AuoCjC7ZnA5sLD4iIVyPitXR9DdAqaVox5xZcY2VEdEZE5/Tp0ysZ/4GkpBrLTyBm1iCyTCCPAPMlzZM0DlgKrC48QFKbJKXrp5DEu7OYczPR1g7bnoLefVlHYmZWdZlVYUVEj6RLgLuAZuD6iNgg6dPp/muBDwN/JKkHeBNYGhEBDHhuJn+QQrkO6N0DO34OMxcOf7yZWR3Lsg0kXy21pl/ZtQXr/wD8Q7HnZi6XDmmyZZ0TiJmNeX4TvZKmvgNaJ7gdxMwaghNIJTU1J08e7ollZg3ACaTS2tqTUXn7+rKOxMysqpxAKi3XAXtehZefzzoSM7OqcgKpNA/tbmYNwgmk0mYsgKYWj8xrZmOeE0iltRwC049zQ7qZjXlOINWQ60iqsGLA4bnMzMYEJ5BqaGuH17th99asIzEzqxonkGrIN6S7GsvMxrBhE4ikMyRNTNc/JumvJR1T/dDqWNsJydIN6WY2hhXzBHIN8IakDuALwC+Bb1c1qnp3yCSY8nbY8njWkZiZVU0xCaQnHQF3CfC3EfG3wKTqhjUG5NpdhWVmY1oxCWS3pC8BFwI/kNQMtFY3rDGgrR1e/hW8+VLWkZiZVUUxCeQjwB7goojYSjL3+F9WNaqxoHBodzOzMWjYBJImjVuAQ9KiHcBt1QxqTMgnEFdjmdkYVUwvrE8CNwP/mBbNAm6vxM0lnSPpWUkbJa0YYP9HJa1LPz9NG/Lz+56XtF7S45LWViKeipo4DSYd5ScQMxuzipmR8GLgFOAhgIh4TtKMcm+ctqV8HVgMdAGPSFodEU8VHPYL4Dcj4iVJ5wIrgVML9p8VETvKjaVqch1+AjGzMauYNpA9EbE3vyGpBajEGB2nABsjYlN6/RtJenrtFxE/jYh8K/SDwOwK3Hf05NqT+dH3vpF1JGZmFVdMArlf0uXAoZIWA98D/qUC954FvFCw3ZWWDeYPgB8WbAdwt6RHJS0f7CRJyyWtlbS2u7u7rIBHrK0dog+2bRjd+5qZjYJiEsgKoBtYD3wKWAP89wrcWwOUDfhkI+kskgTyxYLiMyLiJOBc4GJJ7xno3IhYGRGdEdE5ffr0cmMemf1DmnhuEDMbe4ZtA4mIPuAb6aeSuoCjC7ZnA5v7HySpHfgmcG5E7CyIa3O63C7pNpIqsQcqHGN5jjgaDp3syaXMbEwaNIFIWs8QbR0R0V7mvR8B5kuaB7wILAV+v18Mc4BbgQsj4ucF5ROBpojYna6/D/gfZcZTeVJSjeWeWGY2Bg31BPL+at44InokXQLcBTQD10fEBkmfTvdfC1wBTAX+jyRIhlXpBGYCt6VlLcB3I+LOasZbslw7PPSP0LsPmv0Cv5mNHYMmkIj4ZX5dUhtJFVEAj6QvF5YtItaQtKkUll1bsP6HwB8OcN4moKN/eU3KLYLevdD9LLQdn3U0ZmYVU8yLhH8IPAx8CPgw8KCki6od2JjRltb0uR3EzMaYYl4k/DxwYr4BW9JU4KfA9dUMbMyY+nZonZC+UPjRrKMxM6uYYrrxdgG7C7Z3c+D7GzaUpmaYebwb0s1szBmqF9afpKsvAg9JuoOkDWQJSZWWFSvXAU/cAH190ORZhM3Gqn379tHV1cVbb72VdSglGT9+PLNnz6a1tbgOP0NVYeUnjfqP9JN3R4mxNa5cOzzyDXjpF0mVlpmNSV1dXUyaNIm5c+eS9hKtGxHBzp076erqYt68eUWdM1QvrKsqFlmjK2xIdwIxG7PeeuutukweAJKYOnUqIxnyadhGdEnTSeZCXwiMz5dHxG+VEmRDmvEuaGpJGtKP/1DW0ZhZFdVj8sgbaezFVMh/B3gGmAdcBTxP8ha5FavlkCSJuCuvmWVk165dLF68mPnz57N48WJeeqn86baLSSBTI+I6YF9E3B8RFwGnlX3nRtPWkfTEikqMhG9mNjJXX301Z599Ns899xxnn302V199ddnXLCaB7EuXWyT9tqQTqbd5OWpBrh3e2AG7t2QdiZmNYc8//zzHH//rUS++9rWvceWVV3LHHXewbNkyAJYtW8btt99e9r2KeZHwf0o6AvhT4O+Bw4HPlX3nRpOfI33LOjj8qGxjMbOqu+pfNvDU5lcres0FRx3OV35nYUnnbtu2jVwuB0Aul2P79u1lx1PMcO7fT1dfAc4q+46NaubxgJJ2kGPPyToaM7OyDfUi4Rci4quS/p4BhnWPiEurGtlYc8hhSRdez5Fu1hBKfVIoV0tLC319ffu38y81zpw5ky1btpDL5diyZQszZswo+15DtYE8nS7XAo8O8LGR8twgZlZlM2fOZPv27ezcuZM9e/bw/e8nlUjnn38+q1atAmDVqlUsWbKk7HsN9SLhv0hqBo6PiM+XfSdL2kE23Apv7IIJU7KOxszGoNbWVq644gpOPfVU5s2bx3HHHQfAihUr+L3f+z2uu+465syZw/e+972y7zVkG0hE9Ep6d9l3scT+OdLXwdvOzDQUMxu7Lr30Ui699OBWhnvvvbei9ymmG+/PJK2WdKGkD+U/lbi5pHMkPStpo6QVA+yXpL9L96+TdFKx59aktoKeWGZmda6YbrxTgJ1A4dAlQTJXecnS6rGvA4tJhox/RNLqiHiq4LBzgfnp51TgGuDUIs+tPROnwuGz3ZBuZmNCMd14P1Gle58CbEynp0XSjSRDxRcmgSXAtyMiSGZCPFJSDphbxLm1KdfuIU3MbEwoZjDF8cAfcPBgiuVOazuLAyem6iJ5yhjumFlFnguApOXAcoA5c+aUF3EltLXDsz+Eva/DuIlZR2NmVrJi2kD+L9AG/BfgfpJhTHYPeUZxBhr2sf/7JoMdU8y5SWHEyojojIjO6dOnjzDEKsi1AwHbNmQdiZlZWYpJIO+IiC8Dr0fEKuC3gRMqcO8u4OiC7dnA5iKPKebc2rR/SBNXY5lZfRvJYIovSzoeOIKkDaJcjwDzJc2TNA5YCqzud8xq4ONpb6zTgFciYkuR59amw2fBoVOcQMxs1KxatYr58+czf/78/S8TVkIxvbBWSpoMfJnkS/qwdL0sEdEj6RLgLqAZuD4iNkj6dLr/WmANcB6wEXgD+MRQ55Yb06iQkmos98Qys1Gwa9currrqKtauXYsk3v3ud3P++eczefLksq891FhYT5FMJnVjRLxE0v7xtrLvWCAi1pAkicKyawvWA7i42HPrRq4DHrwGevZCy7isozGzMeKLX/wixxxzDJ/5zGcAuPLKK2ltbWXx4sVMmZKMfrF48WLuvPNOLrjggrLvN9QTyAUkVUN3S9oB3AD8v7QKycrR1g69e6H7mV+/nW5mY8sPV8DW9ZW9ZtsJcO7gE0EtXbqUyy67bH8Cuemmm1i6dClHH/3rJuPZs2fz4osvViScQdtAIuKJiPhSRLwd+CxwDPCQpH+V9MmK3L1R5RvSXY1lZhV04oknsn37djZv3swTTzzB5MmTOfTQQw86rlLzthfTBkJEPEjyIt8dwN8A/wB8oyIRNKIpb4fWicmQJidmHYyZVcUQTwrV9OEPf5ibb76ZrVu3snTpUqZNm8Z99923f39XVxdnnnlmRe5VzIuEJ5NUZ/1X4HlgJVD+MI6NrKkpeRR1Tywzq7ClS5fyyU9+kh07dnD//fdzyCGHcPnll/PSSy8BcPfdd/MXf/EXFbnXUI3o/wv4CPAScCNwRkR0VeSulrR9PP5d6OtLEoqZWQUsXLiQ3bt3M2vWrP1T2H75y1/m5JNPBuCKK67Y36BerqGeQPYA50bEzytyJztQWzvsXQm7NsG0d2QdjZmNIevXH9h4f9FFF3HRReWOPnWwoRrRr3LyqKL9c4O4GsvM6pPrTrIy/V3Q1Op2EDOrW04gWWkZBzPe5cmlzKxuDdWIftJg+wAi4rHKh9NgcunQ7hHJECdmVvciomLvWYy2ZPCP4g3ViP5XQ92HA2cotFLkFsHP/hlefRGOmJ11NGZWpvHjx7Nz506mTp1ad0kkIti5cyfjx48f/uDUoAkkIs6qSFQ2uLa0IX3LOicQszFg9uzZdHV10d3dnXUoJRk/fjyzZxf/XVTUm+jpMO4LOHBGwm+PODo70MyFgJIhTY47L+tozKxMra2tzJs3L+swRk0xb6J/BTiTJIGsAc4Ffgw4gZTrkMNg6jvckG5mdamYXlgfBs4GtkbEJ4AO4JCqRtVIch3uymtmdamYBPJmRPQBPZIOB7ZT5rwgkqZIukfSc+nyoJlNJB0t6d8kPS1pg6TPFuy7UtKLkh5PP/Vb/5Nrh1e74I1dWUdiZjYixSSQtZKOJBl991HgMeDhMu+7Arg3IuYD96bb/fUAfxoR7wJOAy6WtKBg/99ExKL0U58TS0FBQ7qfQsysvgybQCLiMxHxcjpT4GJgWVqVVY4lQH5i3lXABwa475b8uyYRsRt4GphV5n1rj+cGMbM6NWwCkfSe/AeYAxyZrpdjZn5mw3Q5Y5gY5pLMnPFQQfElktZJun6gKrC6MWEKHHG0n0DMrO4U04338wXr44FTSKqyhnyRUNKPgLYBdv1Z0dEl1zkMuAW4LCJeTYuvAf6c5IXGPyd56XHAoSYlLQeWA8yZM2cktx49be3uiWVmdWfYBBIRv1O4Lelo4KtFnPfewfZJ2iYpFxFbJOVIGuYHOq6VJHl8JyJuLbj2toJjvgF8f4g4VpJMgkVnZ+fI3tMfLbl2eHYN7Hkt6dprZlYHShlMsQs4vsz7rgaWpevLgDv6H6BkHIDrgKcj4q/77csVbH4QeLLMeLKV6wACttX3H8PMGksxLxL+PUlVESQJZxFQboX91cBNkv4A+BXwu+m9jgK+GRHnAWcAFwLrJT2ennd52uPqq5IWpXE9D3yqzHiyVTikyZzTso3FzKxIxbSBrC1Y7wFuiIiflHPTiNhJ8nJi//LNwHnp+o+BAUcji4gLy7l/zTn8KJgw1ZNLmVldKaYNZJWk6el6fY4QVuuk9I10N6SbWf0YtA1EiSsl7QCeAX4uqVvSFaMXXgNpa4ftT0PP3qwjMTMrylCN6JeRtEOcHBFTI2IycCpwhqTPjUZwDSXXDn37oPvprCMxMyvKUAnk48AFEfGLfEFEbAI+lu6zSmpL30h3NZaZ1YmhEkhrROzoX5i2g7RWL6QGNeVtMO4wv5FuZnVjqAQyVGW8K+orrakJ2k7wmFhmVjeG6oXVIenVAcpFwcyEVkFt7ckc6X290NScdTRmZkMa9AkkIpoj4vABPpMiwlVY1ZDrgH2vw65NWUdiZjasUoYysWrJeW4QM6sfTiC1ZPpx0DzOCcTM6oITSC1pboUZ73JDupnVBSeQWpPrSJ5AojZHnjczy3MCqTVt7fDmS/BKV9aRmJkNyQmk1niOdDOrE04gtWbmQkAe0sTMap4TSK0ZNxGmvdM9scys5mWSQCRNkXSPpOfS5eRBjnte0npJj0taO9Lz61au3VVYZlbzsnoCWQHcGxHzgXvT7cGcFRGLIqKzxPPrT1s7vPoivH7QWJZmZjUjqwSyBFiVrq8CPjDK59e2fEO6q7HMrIZllUBmRsQWgHQ5Y5DjArhb0qOSlpdwPpKWS1oraW13d53MyNt2QrJ0NZaZ1bBh50QvlaQfAW0D7PqzEVzmjIjYLGkGcI+kZyLigZHEERErgZUAnZ2d9fF23oQpcMQc98Qys5pWtQQSEe8dbJ+kbZJyEbFFUg7YPsg1NqfL7ZJuA04BHgCKOr+uuSHdzGpcVlVYq4Fl6foy4I7+B0iaKGlSfh14H/BksefXvVwH7NwIe3ZnHYmZ2YCySiBXA4slPQcsTreRdJSkNekxM4EfS3oCeBj4QUTcOdT5Y0pbOrT71ieHPs7MLCNVq8IaSkTsBM4eoHwzcF66vgnoGMn5Y0p+bpCt6+CY07ONxcxsAH4TvVZNysHE6e7Ka2Y1ywmkVklJNZZ7YplZjXICqWW5duh+Gnr2ZB2JmdlBnEBqWVs79PXA9qezjsTM7CBOILXMQ5qYWQ1zAqllk+fBuEl+odDMapITSC1rakrGxXJDupnVICeQWpfrgG1PQl9v1pGYmR3ACaTW5dph3xvJsCZmZjXECaTW5Yc0cTWWmdUYJ5BaN/1YaD4EtronlpnVFieQWtfcCjMXuCuvmdUcJ5B6kB/SJOpjPiwzawxOIPUg1w5vvQyvvJB1JGZm+zmB1IO2/Bvpbkg3s9rhBFIPZi4ENbkdxMxqSiYJRNIUSfdIei5dTh7gmGMlPV7weVXSZem+KyW9WLDvvFH/Q4ymcRNg2js9pImZ1ZSsnkBWAPdGxHzg3nT7ABHxbEQsiohFwLuBN4DbCg75m/z+iFjT//wxx3ODmFmNySqBLAFWpeurgA8Mc/zZwH9ExC+rGVRNy3XA7s3wWnfWkZiZAdklkJkRsQUgXc4Y5vilwA39yi6RtE7S9QNVgeVJWi5praS13d11/OW7f450t4OYWW2oWgKR9CNJTw7wWTLC64wDzge+V1B8DfB2YBGwBfirwc6PiJUR0RkRndOnTx/5H6RWtJ2QLF2NZWY1oqVaF46I9w62T9I2SbmI2CIpB2wf4lLnAo9FxLaCa+9fl/QN4PuViLmmHToZjpzjhnQzqxlZVWGtBpal68uAO4Y49gL6VV+lSSfvg8CTFY2uVuU63JXXzGpGVgnkamCxpOeAxek2ko6StL9HlaQJ6f5b+53/VUnrJa0DzgI+NzphZ6ytA3ZtgrdezToSM7PqVWENJSJ2kvSs6l++GTivYPsNYOoAx11Y1QBrVb4hfduTcMxvZBuLmTU8v4leT3L5IU1cjWVm2XMCqSeT2mDiDPfEMrOa4ARSb3Lt7ollZjXBCaTetLVD9zOw762sIzGzBucEUm9yHdDXA9ufyjoSM2twTiD1Zv+QJq7GMrNsOYHUmyPnwiGHuyHdzDLnBFJvmprSod3dldfMsuUEUo9y7bBtA/T1Zh2JmTUwJ5B61NYOPW/CjueyjsTMGpgTSD1yQ7qZ1QAnkHo07VhoGe92EDPLlBNIPWpugRkLnEDMLFNOIPUqP6RJRNaRmFmDcgKpV23t8NYr8PKvso7EzBpUJglE0u9K2iCpT1LnEMedI+lZSRslrSgonyLpHknPpcvJoxN5DcktSpauxjKzjGT1BPIk8CHggcEOkNQMfJ1kTvQFwAWSFqS7VwD3RsR84N50u7HMXABqdk8sM8tMVjMSPg0gaajDTgE2RsSm9NgbgSXAU+nyzPS4VcB9wBerE22Naj0Upr2zvCFNIpKXEaMXou/X632F230FZb3Q1zdAWW9yrcKy6Cvu/sUFWsFrFWnov5uFB47utcxKNXMhTJhS0UtmkkCKNAt4oWC7Czg1XZ8ZEVsAImKLpBmDXUTScmA5wJw5c6oUakZyHbDhVvi7kwqSQN/BX+QDlvVS1BezmY0NH70F5r+3opesWgKR9COgbYBdfxYRdxRziQHKRvyNFxErgZUAnZ2dY+sb85RPQu/e5BeumpIqrabmZL2pOdkuXG9qGqCscLvwGvnj+5flj+t/jfx1Cu5R1C/vIn91V/Jawyryr0lRTz2VvJZZGWYurPglq5ZAIqLcVNcFHF2wPRvYnK5vk5RLnz5ywPYy71WfZnfC7/5T1lGYWYOq5W68jwDzJc2TNA5YCqxO960GlqXry4BinmjMzKyCsurG+0FJXcDpwA8k3ZWWHyVpDUBE9ACXAHcBTwM3RcSG9BJXA4slPQcsTrfNzGwUKRqo7rWzszPWrl2bdRhmZnVF0qMRcdA7e7VchWVmZjXMCcTMzEriBGJmZiVxAjEzs5I4gZiZWUkaqheWpG7glyWePg3YUcFwKsVxjYzjGhnHNTK1GheUF9sxETG9f2FDJZBySFo7UDe2rDmukXFcI+O4RqZW44LqxOYqLDMzK4kTiJmZlcQJpHgrsw5gEI5rZBzXyDiukanVuKAKsbkNxMzMSuInEDMzK4kTiJmZlcQJpAiSzpH0rKSNklZkHQ+ApOslbZf0ZNaxFJJ0tKR/k/S0pA2SPpt1TACSxkt6WNITaVxXZR1TIUnNkn4m6ftZx5In6XlJ6yU9LqlmhrGWdKSkmyU9k/49O70GYjo2/e+U/7wq6bKs4wKQ9Ln07/yTkm6QNL5i13YbyNAkNQM/J5l3pItkoqsLIuKpjON6D/Aa8O2IOD7LWAqlM0TmIuIxSZOAR4EP1MB/LwETI+I1Sa3Aj4HPRsSDWcaVJ+lPgE7g8Ih4f9bxQJJAgM6IqKkX4yStAv49Ir6ZTjY3ISJezjis/dLvjBeBUyOi1BeXKxXLLJK/6wsi4k1JNwFrIuJblbi+n0CGdwqwMSI2RcRe4EZgScYxEREPALuyjqO/iNgSEY+l67tJJgOblW1UEInX0s3W9FMTv54kzQZ+G/hm1rHUOkmHA+8BrgOIiL21lDxSZwP/kXXyKNACHCqpBZjAr6cGL5sTyPBmAS8UbHdRA1+I9UDSXOBE4KGMQwH2VxM9DmwH7omImogL+N/AF4C+jOPoL4C7JT0qaXnWwaTeBnQD/5RW+X1T0sSsg+pnKXBD1kEARMSLwNeAXwFbgFci4u5KXd8JZHgaoKwmfrnWMkmHAbcAl0XEq1nHAxARvRGxCJgNnCIp86o/Se8HtkfEo1nHMoAzIuIk4Fzg4rTaNGstwEnANRFxIvA6UBPtkgBpldr5wPeyjgVA0mSSGpN5wFHAREkfq9T1nUCG1wUcXbA9mwo+Ao5FaRvDLcB3IuLWrOPpL63yuA84J9tIADgDOD9tb7gR+C1J/5xtSImI2JwutwO3kVTnZq0L6Cp4eryZJKHUinOBxyJiW9aBpN4L/CIiuiNiH3Ar8BuVurgTyPAeAeZLmpf+ulgKrM44ppqVNlZfBzwdEX+ddTx5kqZLOjJdP5TkH9YzmQYFRMSXImJ2RMwl+bv1rxFRsV+IpZI0Me0EQVpF9D4g8x5/EbEVeEHSsWnR2UCmHTT6uYAaqb5K/Qo4TdKE9N/m2STtkhXRUqkLjVUR0SPpEuAuoBm4PiI2ZBwWkm4AzgSmSeoCvhIR12UbFZD8or4QWJ+2NwBcHhFrsgsJgBywKu0h0wTcFBE102W2Bs0Ebku+c2gBvhsRd2Yb0n5/DHwn/UG3CfhExvEAIGkCSW/NT2UdS15EPCTpZuAxoAf4GRUc0sTdeM3MrCSuwjIzs5I4gZiZWUmcQMzMrCROIGZmVhInEDMzK4kTiFkJJL2WLudK+v0KX/vyfts/reT1zSrFCcSsPHOBESWQ9F2UoRyQQCKiYm8Om1WSE4hZea4G/nM6B8Tn0gEb/1LSI5LWSfoUgKQz03lSvgusT8tuTwcq3JAfrFDS1SQjpz4u6TtpWf5pR+m1n0zn6fhIwbXvK5gj4zvpW8dmVeU30c3KswL4b/k5PNJE8EpEnCzpEOAnkvKjn54CHB8Rv0i3L4qIXenQKo9IuiUiVki6JB30sb8PAYuADmBaes4D6b4TgYUk47T9hGREgB9X+g9rVshPIGaV9T7g4+kwLg8BU4H56b6HC5IHwKWSngAeJBmwcz5D+0/ADemowtuA+4GTC67dFRF9wOMkVWtmVeUnELPKEvDHEXHXAYXSmSRDjxduvxc4PSLekHQfMNxUo0NVS+0pWO/F/7ZtFPgJxKw8u4FJBdt3AX+UDmmPpHcOMuHREcBLafI4DjitYN++/Pn9PAB8JG1nmU4yM9/DFflTmJXAv1LMyrMO6Emror4F/C1J9dFjaUN2N/CBAc67E/i0pHXAsyTVWHkrgXWSHouIjxaU3wacDjxBMqnZFyJia5qAzEadR+M1M7OSuArLzMxK4gRiZmYlcQIxM7OSOIGYmVlJnEDMzKwkTiBmZlYSJxAzMyvJ/wfN8Cgk0bvA/gAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEGCAYAAAB7DNKzAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAAAmoElEQVR4nO3dd3yV9d3/8dcnC0jYGxIw7D2CDHFvsaIQauto1Tqq3j/tsHe11t53rd631rv2rva+XQ8HjluLdQQHoqhVXHUACXuJDEkChD0DWZ/fH+dE0xQOIZyT65zk/Xw88oBzSK7zxgfmnXN9ruv7NXdHRETkUJKCDiAiIvFNRSEiIhGpKEREJCIVhYiIRKSiEBGRiFKCDhALHTt29Ozs7KBjiIgklHnz5m1x9061n2+URZGdnc3cuXODjiEiklDMbN3BntepJxERiUhFISIiEakoREQkIhWFiIhEpKIQEZGIVBQiIhKRikJERCJSUdTw9pKNPPXJGrbuORB0FBGRuNEob7irr3eWbuLFeYX85xvLOKV/J3JHZXLmoC40T00OOpqISGCsMW5cNHr0aK/vndnLN+5ien4Rr8wvYtOuA7RqlsJ3hnUjd1QmY7Pbk5RkUU4rIhIfzGyeu4/+p+dVFAdXWeV8+tVW8goKeWvxRvaVVZLZtgWTc7qTm5NF384to5RWRCQ+qCiOwr6yCt5esom8giI+/nIzVQ7Ds9qQm5PJ+SO607Fls6i9lohIUFQUUVKyaz+vLSgmL7+IpRt2kZxkoXlGTiZnDdY8Q0QSl4oiBlZs3E1eQSGvFhSzcdd+WjVL4dxhXcnNyWJcL80zRCSxqChiqLLK+Wz1VvLyi3hr8Qb2hucZk0Z2Z8qoTPp2btVgWURE6ktF0UBKyyp5e+lG8vKL+Cg8zxiWGZpnXDBS8wwRiV8qigCU7N7Pa/OLmV5QxJLi0Dzj5H4dyR2VxdmaZ4hInFFRBGzlpt1MLyjilYIiNuzcT8tmKZw7tCu5ozI5rlcHzTNEJHAqijhRVeV8tiY0z3hzUWie0b1NcyblZDIlJ5N+XTTPEJFgqCjiUPU8Y3pBER99uYXKKmdoZmtyc7K4YER3OrXSPENEGo6KIs5t3n2A1xeE5hmLinaSnGSc1K8juTmZnD24Ky3SNM8QkdhSUSSQL2vMM4rD84wJQ7syJSeT43prniEisaGiSEBVVc7na7YxvaCQmYs2sudABd3aNGfSyEymjMqkv+YZIhJFKooEt7+8kneWbmJ6QREfrNxMZZUzuFtrpowK3Z/RuVXzoCOKSIJTUTQiW/Z8O89YWLiTJIMT+3ViSk4mZw/pQnqathkRkSOXsEVhZhnAQ0AZMNvdnzvc1zT2oqhpVckephcU8kpBMUU7SslIS+acoV2ZkpPF+D4dSNY8Q0TqKK6KwsymAhOBEncfWuP5CcCfgWTgcXe/x8wuA3a4++tm9ld3v+hwx29KRVGtqsr5Yu02pucXMXPRBnYfqKBr6+ZMGtmd3FGZDOzaOuiIIhLn4q0oTgb2AM9UF4WZJQMrgbOAQmAOcAkwCXjT3eeb2V/c/dLDHb8pFkVN+8sreXfZJqbnh+YZFVXOoG6tmZKTyaSR3encWvMMEflncVUUAGaWDcyoURTjgd+5+znhx78Of2ohsN3dZ5jZ8+5+8SGOdy1wLUDPnj2PXbduXaz/Cglha415xoLwPOOEvh2ZMiqTc4Z01TxDRL6RCEVxITDB3a8JP74MGAf8CngA2A98rBlF/a0q2cMrBUVMLyiiaEcp6WnJTBgSWm/q+D4dNc8QaeIOVRTx9OPkwb5LubvvBa5s6DCNUd/OLfnlOQP4xVn9mbN2G9MLinhj0QbyCoro0roZk0ZmkpuTyaBummeIyLfiqSgKgR41HmcBxQFladSSkoxxvTswrncHfnfBEP62rITpBYVM/XgNj364moFdWzFlVCaTRmbSRfMMkSYvnk49pRAaZp8BFBEaZl/q7kuO9Ng69VQ/W/ccCL3DyC9i/vod38wzcnNC84yMZvH0c4WIRFtczSjMbBpwKtAR2ATc7u5PmNl3gPsJXR471d3vqs/xVRRHb/Xm8DxjfhHrt5XSIjWZCUO7kpuTyQl9Nc8QaYziqihiTUURPe7O3HXbycsv4o2FxezaX0HnVs1C92fkZDG4u+YZIo2FikKO2v7ySt5fXkJeQRGzV5RQXukM7NqKyTmZTB6ZSdc2mmeIJDIVhUTV9r1lzFhYTF5BEQVf78AMju/TgdycLCYM7UpLzTNEEo6KQmJmzZa93+yf8fW2fbRITebsIV3IzcnkxL4dSUlOCjqiiNSBikJizt2Zt247eQVFvLFwAztLy+nUqhkXjOhObk4mQ7q3xkxDcJF4paKQBnWgIjzPyC/i/fA8o3+XluTmZDE5pzvd2rQIOqKI1KKikMBs31vGjEUbmJ5fSH54njG+dwdyczI5d1g3zTNE4oSKQuLCuq2hecb0giLWbd1H89Qkzh4cWm/qJM0zRAKlopC44u7kf72DvPxCZoTnGR1bhuYZU0ZpniESBBWFxK3QPGMz0wsKeW95aJ7Rr3NLckeF7s/o3lbzDJGGoKKQhLBjXxlvLNrA9Pwi5q7bjhkc16sDuaMyOXdoV1o1Tw06okijpaKQhPP11n3heUYha7fuo1lKEmcP6cqUnExO6qd5hki0qSgkYbk7Bet3MD2/iNcXFrNjXzkdW6Zx/ojuTMnJYmim5hki0aCikEahrKKK2StKmF5QxN+WlVBWWUXfzi3Jzclkck4mmZpniNSbikIanZ37ykPzjIJC5qzdDsC4Xu2ZMip0f0ZrzTNEjoiKQhq19dv2fXN/xpote2mWksSZg7swJSeTk/t3IlXzDJHDUlFIk+DuzF+/g+kFRby+oJjt+8rpkBGaZ+TmZDI8q43mGSKHoKKQJqesoooPVobuz3h3WQllFVX07pTBlPA8I6tdetARReKKikKatJ2l5cwM35/xxdptAIzt1Z4p4fWm2rTQPENERSEStn7bPl6dX0ReQRGrN+8lLSWJswaF9s84ZYDmGdJ0qShEanF3FhbuZHpBEa8tKGbb3jLaZ6Rx/vBu5I7KYoTmGdLEqChEIiivrOLDlZvJKyjinaWbQvOMjhnf3J/Ro73mGdL4qShE6mhnaTlvLd5AXn4Rn68JzzOy25M7KpPvaJ4hjZiKQqQeCrfv49X5xeTlF/JVeJ5x5qDO5OZkcUr/TqSlaJ4hjYeKQuQouDuLinaSlx+6P2Pr3jLapad+c3/GyB5tNc+QhKeiEImS8soqPvpyM3n5oXnGgYoqenXMYPLITHJzMunZQfMMSUwqCpEY2LW/nLcWbSSvoJDPVofmGaOPaUfuqEwmDutOm3TNMyRxqChEYqxoRymvhNebWlWyh7TkJE4f2JncUZmcNqCz5hkS91QUIg3E3VlctIu8gkJeX1DMlj1ltE1PZeLwbnx3VBY5PdsFHVHkoFQUIgGoqKzioy+3kFdQxNtLNnKgoorRx7TjX07tw2kDOpOUpAG4xI+ELgozmwycB3QGHnT3tyN9vopC4tHu/eW8PK+Qxz5aQ9GOUvp3acl1J/fhgpHdtWyIxIXAisLMpgITgRJ3H1rj+QnAn4Fk4HF3v6cOx2oH/NHdr470eSoKiWfllVXMWFjMI7NXs2LTbjLbtuCak3px0ZgepKelBB1PmrAgi+JkYA/wTHVRmFkysBI4CygE5gCXECqN39c6xFXuXhL+uv8GnnP3/EivqaKQRODuvL+ihEdmr+aLtdtol57K5eOzueL4bNpnpAUdT5qgQE89mVk2MKNGUYwHfufu54Qf/xrA3WuXRPXXG3AP8I67v3u411NRSKKZt24bD89ezbvLNtEiNZmLxvTgxyf31h7g0qAOVRRBvc/NBNbXeFwIjIvw+T8BzgTamFlfd3+k9ieY2bXAtQA9e/aMYlSR2Dv2mPY8fkV7vty0m0c+WM2zn63j2c/WccGI7lx3Sh8GdG0VdERpwoJ6R/E94Bx3vyb8+DJgrLv/JBqvp3cUkuiKdpTyxEdreH7O1+wrq+SMgZ25/tQ+jMluH3Q0acQO9Y4iqEstCoEeNR5nAcUBZRGJO5ltW/Db8wfzya9O56Yz+5P/9Xa+98inXPjw3/nbsk1UVcX/1YrSeARVFHOAfmbWy8zSgIuB1wLKIhK32mWk8bMz+/HJrafzu/MHs2Hnfq5+ei4T/vwhL88rpLyyKuiI0gQctijMbK6Z3RC+NPWImdk04FNggJkVmtnV7l4B3AjMApYBL7j7kvocX6QpSE9L4Ucn9GL2zady30UjMIx/fXEBp947m6kfr2FfWUXQEaURO+yMwsz6AlcCFwFzgSeBtz2O79TTjEIaO3dn9orNPDz7K75Yu4226alcoUtr5Sgd9eWxZpZE6Ma5h4EqYCrwZ3ffFs2g0aCikKbkYJfWXnNSL7LaablzOTJHVRRmNpzQu4rvEDpd9BxwInCZu4+MbtSjp6KQpqj60tpX5xfhwCRdWitHqN5FYWbzgB3AE8DL7n6gxp/lufuUKGc9aioKacqKd5TyuC6tlXo4mqLo7e6raz3Xy93XRDlj1KgoRGD73jKe+XQdT/19Ddv3lTP6mHZcf0ofTh+oVWvl4I6mKPLdfdRBDnZslDNGjYpC5FulZZW8MHc9j364WqvWSkRHXBRmNhAYAvwBuLnGH7UGbnb3IbEIGg0qCpF/Vl5ZxRsLN/Dw7K9YsWk33ds055qTenPxWK1aKyH1KYpJwGTgAv7xZrjdwPPu/vcY5IwKFYXIoR3s0torj+/Fdaf0pnlqctDxJEBHc+ppvLt/GrNkMaCiEKmbmpfW9u/SkvsvymFw99ZBx5KA1Ocdxf8Ch2wRd/9p9OJFl4pC5MjMXlHCzS8tZOe+cv717P5cc1JvkjXwbnLqs8y4vtOKNBGnDujMrJ+fzG15i/j9m8t5b3kJ//39EbppT4AE2TP7SOkdhUj9uDsvzivkjteWkGTGnZOHMHlkJqG9w6Sxq/cy42bWycz+aGYzzey96o/YxBSRIJkZ3x/dgzd/djIDurbipr8u4MZpBezYVxZ0NAlQXS6ifo7QCq+9gDuAtYSWCReRRqpnh3T+et14bj5nALMWb2TC/R/x8Zdbgo4lAalLUXRw9yeAcnf/wN2vAo6LcS4RCVhyknHDaX2Z/v9OIKNZMj984nPufH0p+8srg44mDawuRVEe/nWDmZ1nZjmEdqQTkSZgWFYbZvzkJC4ffwxTP1nDBQ98zNLiXUHHkgZUl6L4TzNrA/wr8EvgceCmmKYSkbjSIi2ZOycN5akrx7B9XzmTHvyYRz74ikptydok6KonETki2/aWcVveIt5aspGxvdrzJ11G22gczZ3ZnYAfA9nUuO8iPKuISyoKkdhyd16aV8jvwpfR3jFpCLk5uow20dXnhrtqrwIfAe8CmmKJCGbG90b3YFyvDvzihfn84oUF/G15CXdNHkrbdG3F2tjUpSjS3f1XMU8iIgmn+jLaRz74ivveWcm8tdv54/dGcGK/jkFHkyiqyzB7hpl9J+ZJRCQhHewy2jteX6LLaBuRuhTFzwiVxX4z22Vmu81M18aJyD+ovoz2ivHH8OQnazn/fz9mSfHOoGNJFBy2KNy9lbsnuXtzd28dfqx1iEXkn7RIS+aO8GW0O0rLmfzgJ7qMthGoy1pPZmY/NLN/Dz/uYWZjYx9NRBJV9Wq0Zwzswj1vLueSxz6jcPu+oGNJPdXl1NNDwHjg0vDjPcCDMUskIo1C+4w0Hv7hKO69cDhLi3dx7v0fkZdfSGO8d6uxq0tRjHP3G4D9AO6+HdD1byJyWNWX0b75s5MY0LUVv3hhATf+RavRJpo6rfVkZsmEd7sL34BXFdNUItKo9GhfYzXaJRs55/4PtRptAqlLUfwPMB3obGZ3AR8Dd8c0lYg0OtWX0b5ywwm0bJaiy2gTSJ3WejKzgcAZgAF/c/dlsQ52NLSEh0h8Ky2r5J43l/H0p+vo17kl9188kiHd2wQdq8k74h3uzGycmS0wsz3Ak8D77v5AvJeEiMS/6ston75qLDvDl9E+PFuX0carSKeeHiS0rHgH4E/AfQ2S6CDMLMPM5pnZxKAyiEj0ndK/E7N+fjJnDurCf72ly2jjVaSiSHL3d9z9gLu/CHQ60oOb2VQzKzGzxbWen2BmK8xslZndWodD/Qp44UhfX0TiX7uMNB76wSj++L0Ruow2TkVaFLCtmU051GN3z6vD8Z8CHgCeqX4ifAXVg8BZQCEwx8xeA5KB39f6+quA4cBSoHkdXk9EEpCZceGxWYzr1Z6b/hpejXZZCXflajXaeHDIYbaZPRnh67yu+1GYWTYww92Hhh+PB37n7ueEH/86fMDaJVH99XcBGcBgoBTIdfd/ujzXzK4FrgXo2bPnsevWratLPBGJM5VV/s1qtB1bNuPZa8bSt3OroGM1CfXeuCgKL5zNPxbFhcAEd78m/PgyQjf13XiY4/wI2OLuMw73mrrqSSTxLS7ayY+enENyErx43fH07KBd9GLtiK96imWWgzx32LZy96fqUhIi0jgMzWzDs9eM5UBFFZc+/hkbdpYGHanJCqIoCoEeNR5nAcUB5BCRODewa2ueuWosO/aV84PHP2fLngNBR2qSIhaFmSWZ2fFRfs05QD8z62VmacDFwGtRfg0RaSSGZ7XlySvHULyjlB8+/rnWiQpAxKIID43/u74HN7NpwKfAADMrNLOr3b0CuBGYBSwDXnD3JfV9DRFp/MZkt+exy0ezevNernhyDnsOVAQdqUmpy6mnt83su2Z2sNlCRO5+ibt3c/dUd89y9yfCz8909/7u3sfd7zri1CLS5JzUrxMPXJrD4qKdXPXUHErLtEZUQ6lLUfwCeBEo01aoIhKks4d05U/fH8Gctdu4/tl5HKhQWTSEI9kKNVVboYpI0CaNzOSeKcP4YOVmfjqtgIpK7XoQa9oKVUQSzkVjevLbiYOZtWQTv3xxAVVaTDCmIi3hUe0hQhsVnQ78B99uhTomhrlERCK66sRelJZXcu+sFaQ3S+GuyUOpxyhV6qAuRTHO3UeZWQGEtkINX9YqIhKoG07ry94DFTw0+yvSU5P5zXmDVBYxUJei0FaoIhK3bj5nAPvKKnn84zVkNEvhprP6Bx2p0alLUdTeCvVC4N9imkpEpI7MjN9OHMzeAxX8+W9fkp6WzHWn9Ak6VqNy2KJw9+fMbB7fboU6WbvciUg8SUoy7vnucErLK/n9m8tJT0vmsvHZQcdqNA5ZFGbW2t13mVl7oASYVuPP2rv7toYIKCJSF8lJxn0XjWR/eSX//uoSWqSlcOGxWUHHahQiXR77l/Cv84C5NT6qH4uIxJXU5CQeuHQUJ/TtwC0vLWDmog1BR2oUDlkU7j4xvGzHKe7eu8ZHL3fv3YAZRUTqrHlqMo9dPppRPdvx02kFvL+8JOhICe9wiwI6oUG2iEjCSE9LYeqVYxjYrRXXPzuPv3+1JehICa0uaz19Zma6uU5EEkrr5qk8c9U4jumQzjVPz2Xeuu1BR0pYdSmK04BPzewrM1toZovMbGGsg4mIHK32GWk8e/U4Ordqxo+e/ILFRTuDjpSQDrdxkQHXA30ILeFxPjAx/KuISNzr3Lo5z14zjlbNUrh86hesKtkddKSEU5cZxX3uvq72RwPlExE5alnt0nnux8eRZMalj33Ouq17g46UUDSjEJEmoVfHDJ67ZhxllVVc+tjnFO8oDTpSwtCMQkSajAFdW/F/V41jV2k5P3z8czbvPhB0pIRQl6I4F80oRKSRGJbVhqlXjmHDzv1c9sTn7NhXFnSkuFeXHe6qZxKlhFaQrf4QEUlIY7Lb89jlo1m9eS9XPDmH3fvLg44U1+qyw90FZvYlsAb4AFgLvBnjXCIiMXViv4489INRLCnaydVPz6W0TPtvH0pdTj39B3AcsNLdexFaRfaTmKYSEWkAZw7uwn0XjWTO2m1c9+w8DlSoLA6mLkVR7u5bgSQzS3L394GRsY0lItIwzh/Rnf+aMpwPV27mJ38poLxS+7LVVpei2GFmLYEPgefM7M9ARWxjiYg0nO+P6cHt5w/m7aWbuPnFBVRVaQxbU112uJtEaJB9E/ADoA1wZyxDiYg0tCtP6MW+skrunbWCFmkp3J07VPtvh9Vlh7vqWxirzOwNYGv4jm0RkUblhtP6sq+sggff/4r0tGT+7bxBKgsinHoys+PMbLaZ5ZlZjpktBhYDm8xsQsNFFBFpOL88ewA/Oj6bJz5ew33vfhl0nLgQ6R3FA8BthE41vQec6+6fmdlAQtuivtUA+UREGpSZ8duJgyktq+R//vYl6WnJXH9Kn6BjBSpSUaS4+9sAZnanu38G4O7L9VZMRBqzpCTj7inD2FdeyT1vLicjLZnLxmcHHSswkYqi5jVitVfParAZhZklEbqXozUw192fbqjXFpGmKznJ+NP3R1BaVsm/v7qEFmkpXHhsVtCxAhHp8tgRZrbLzHYDw8O/r348rC4HN7OpZlYSnm/UfH6Cma0ws1VmduthDjMJyATKgcK6vK6ISDSkJifxwKU5nNi3I7e8tIA3Fm4IOlIgDlkU7p7s7q3dvZW7p4R/X/04tY7Hfwr4h8G3mSUDDxJabHAwcImZDTazYWY2o9ZHZ2AA8Km7/wL4l/r8JUVE6qt5ajKPXn4so3q242fPF/De8k1BR2pwdbnhrt7c/UNgW62nxwKr3H21u5cBzwOT3H2Ru0+s9VFC6F1E9Wa3ur9eRBpceloKU68cw6Burbn+2Xz+vmpL0JEaVEyL4hAygfU1HheGnzuUPOAcM/tfQneHH5SZXWtmc81s7ubNm6OTVEQkrHXzVJ65aiy9OmRwzTNzm9SWqkEUxcEumTrkcNzd97n71e7+E3d/MMLnPeruo919dKdOnaISVESkpnYZaTxz9ViapSRx80sLqWwiS30EURSFQI8aj7OA4gByiIgcsS6tm3P7+UMo+HoHT36yJug4DSKIopgD9DOzXmaWBlwMvBZADhGRepk0sjtnDOzMH99ewdotew//BQkupkVhZtOAT4EBZlZoZle7ewVwIzALWAa84O5LYplDRCSazIy7coeRmpTErXkLG/1qs7G+6ukSd+/m7qnunuXuT4Sfn+nu/d29j7vfFcsMIiKx0LVNc35z3iA+W72Nv3zxddBxYiqIU08iIo3CRWN6cELfDvx+5jKKdtRewKLxUFGIiNSTmXHPlOE4cFveIhrrDgwqChGRo9CjfTq3nDOAD1Zu5uX8oqDjxISKQkTkKF0+PpvRx7TjzteXULJrf9Bxok5FISJylJKSjD9cOJwDFVX82yuLG90pKBWFiEgU9O7UkpvO6s/bSzfxxqLGtcqsikJEJEquObEXw7PacPurS9i2tyzoOFGjohARiZKU5CT+cOFwdu0v547XG899xCoKEZEoGti1NTec1pdX5xfzztLGsXeFikJEJMr+36l9Gdi1Fb+ZvoidpeVBxzlqKgoRkShLS0ni3gtHsHVvGXe/sSzoOEdNRSEiEgPDstrw45N689e56/noy8TeTE1FISISIz8/sx+9O2Vw68uL2HugIug49aaiEBGJkeapyfzhu8Mp3lnKH95aHnScelNRiIjE0Ojs9lwxPpunP13HF2u2BR2nXlQUIiIxdsuEAfRo34JfvbyQ/eWVQcc5YioKEZEYS09L4Z4pw1mzZS/3vbMy6DhHTEUhItIATujbkUvG9uCxj1azYP2OoOMcERWFiEgD+fV3BtG5VXNufmkBByoS5xSUikJEpIG0bp7K3VOGsnLTHh58/6ug49SZikJEpAGdPrALuTmZPPT+KpYW7wo6Tp2oKEREGthvJw6mbXoqt7y8gIrKqqDjHJaKQkSkgbXLSOM/Jg1lcdEuHv1oddBxDktFISISgHOHdePcoV25/90vWVWyJ+g4EakoREQCcsekIaSnJXPLSwuorIrffbZVFCIiAencqjm3nz+Y/K938PTf1wYd55BUFCIiAZo8MpPTBnTi3lkr+HrrvqDjHJSKQkQkQGbG3VOGkZJk/OrlhbjH3ykoFYWISMC6tWnBbecN4tPVW5n2xfqg4/wTFYWISBy4eEwPju/TgbtnLqN4R2nQcf5B3BeFmfU0s9fMbKqZ3Rp0HhGRWDAz7pkynMoq5zfTF8XVKaiYFkX4m3uJmS2u9fwEM1thZqvq8M2/P/CGu18FDI5ZWBGRgPXskM4tEwbw/orNTC8oCjrON2L9juIpYELNJ8wsGXgQOJfQN/5LzGywmQ0zsxm1PjoDBcDFZvYe8H6M84qIBOqK8dkce0w77nh9KSW79wcdB4hxUbj7h0Dtvf/GAqvcfbW7lwHPA5PcfZG7T6z1UQJcCdzu7qcD5x3qtczsWjOba2ZzN2/eHKu/kohITCUlGf/13eGUlldy+6tLgo4DBDOjyARqjvULw88dylvAT83sEWDtoT7J3R9199HuPrpTp05RCSoiEoS+nVty05n9eXPxRmYu2hB0HFICeE07yHOHnNq4+2LgwtjFERGJPz8+qRczF23gt68uZnzvDrTLSAssSxDvKAqBHjUeZwHFAeQQEYlbKclJ/OHC4ezYV86dM5YGmiWIopgD9DOzXmaWBlwMvBZADhGRuDaoW2tuOK0v0wuKeG/5psByxPry2GnAp8AAMys0s6vdvQK4EZgFLANecPf4mNiIiMSZG07ry4AurbgtbzG79pcHkiHWVz1d4u7d3D3V3bPc/Ynw8zPdvb+793H3u2KZQUQkkaWlhE5Blezez+9nLgskQ9zfmS0i0tSN6NGWH5/cm2lfrOeTVVsa/PVVFCIiCeCmM/vTq2MGt+YtZO+BigZ9bRWFiEgCaJ6azB8uHE7h9lLunbWiQV9bRSEikiDGZLfnivHZPP3pWuaurb3oReyoKEREEsjN5wwgs20LbnlpIfvLKxvkNVUUIiIJJKNZCvdMGc7qLXu5/90vG+Q1VRQiIgnmxH4duXhMDx798CsWFu6I+eupKEREEtBt5w2iU6tm3PLSQsoqqmL6WioKEZEE1Lp5KnfnDmP5xt08NHtVTF9LRSEikqDOGNSFySO788B7q1i+cVfMXkdFISKSwH57/hDatEjllpcWUlEZm1NQKgoRkQTWPiONOycNZWHhTh7/eE1MXkNFISKS4L4zrCsThnTlT++s5KvNe6J+/CB2uBMRkSgyM+6cPIS9L1Tgh9wvtP5UFCIijUDnVs35v6vHxeTYOvUkIiIRqShERCQiFYWIiESkohARkYhUFCIiEpGKQkREIlJRiIhIRCoKERGJyDwWt/EFzMw2A+vq+eUdgS1RjBMtynVklOvIKNeRaay5jnH3TrWfbJRFcTTMbK67jw46R23KdWSU68go15Fparl06klERCJSUYiISEQqin/2aNABDkG5joxyHRnlOjJNKpdmFCIiEpHeUYiISEQqChERiUhFUYOZTTCzFWa2ysxuDToPgJlNNbMSM1scdJaazKyHmb1vZsvMbImZ/SzoTABm1tzMvjCzBeFcdwSdqSYzSzazAjObEXSWama21swWmdl8M5sbdJ5qZtbWzF4ys+Xhf2fj4yDTgPB/p+qPXWb286BzAZjZTeF/84vNbJqZNY/asTWjCDGzZGAlcBZQCMwBLnH3pQHnOhnYAzzj7kODzFKTmXUDurl7vpm1AuYBk+Pgv5cBGe6+x8xSgY+Bn7n7Z0HmqmZmvwBGA63dfWLQeSBUFMBod4+rG8jM7GngI3d/3MzSgHR33xFwrG+Ev2cUAePcvb43+EYrSyahf+uD3b3UzF4AZrr7U9E4vt5RfGsssMrdV7t7GfA8MCngTLj7h8C2oHPU5u4b3D0//PvdwDIgM9hU4CHVu8unhj/i4qchM8sCzgMeDzpLvDOz1sDJwBMA7l4WTyURdgbwVdAlUUMK0MLMUoB0oDhaB1ZRfCsTWF/jcSFx8I0vEZhZNpADfB5wFOCb0zvzgRLgHXePi1zA/cAtQFXAOWpz4G0zm2dm1wYdJqw3sBl4Mnyq7nEzywg6VC0XA9OCDgHg7kXAH4GvgQ3ATnd/O1rHV1F8yw7yXFz8JBrPzKwl8DLwc3ffFXQeAHevdPeRQBYw1swCP2VnZhOBEnefF3SWgzjB3UcB5wI3hE93Bi0FGAU87O45wF4gLuaGAOFTYRcALwadBcDM2hE6A9IL6A5kmNkPo3V8FcW3CoEeNR5nEcW3bo1ReAbwMvCcu+cFnae28KmK2cCEYJMAcAJwQXge8Dxwupk9G2ykEHcvDv9aAkwndBo2aIVAYY13gy8RKo54cS6Q7+6bgg4Sdiawxt03u3s5kAccH62Dqyi+NQfoZ2a9wj8tXAy8FnCmuBUeGj8BLHP3PwWdp5qZdTKztuHftyD0P9DyQEMB7v5rd89y92xC/7bec/eo/cRXX2aWEb4YgfCpnbOBwK+wc/eNwHozGxB+6gwg0AslarmEODntFPY1cJyZpYf/3zyD0NwwKlKidaBE5+4VZnYjMAtIBqa6+5KAY2Fm04BTgY5mVgjc7u5PBJsKCP2EfBmwKDwPALjN3WcGFwmAbsDT4StSkoAX3D1uLkWNQ12A6aHvLaQAf3H3t4KN9I2fAM+Ff3BbDVwZcB4AzCyd0NWR1wWdpZq7f25mLwH5QAVQQBSX89DlsSIiEpFOPYmISEQqChERiUhFISIiEakoREQkIhWFiIhEpKIQicDM9oR/zTazS6N87NtqPf57NI8vEi0qCpG6yQaOqCjC93JE8g9F4e5Ru5NWJJpUFCJ1cw9wUngPgpvCCw/ea2ZzzGyhmV0HYGanhvfp+AuwKPzcK+EF95ZUL7pnZvcQWulzvpk9F36u+t2LhY+9OLxPxEU1jj27xh4Nz4XvwhWJKd2ZLVI3twK/rN5DIvwNf6e7jzGzZsAnZla9WudYYKi7rwk/vsrdt4WXFJljZi+7+61mdmN48cLapgAjgRFAx/DXfBj+sxxgCKF1yD4hdIf8x9H+y4rUpHcUIvVzNnB5ePmSz4EOQL/wn31RoyQAfmpmC4DPCC082Y/ITgSmhVfB3QR8AIypcexCd68C5hM6JSYSU3pHIVI/BvzE3Wf9w5NmpxJaErvm4zOB8e6+z8xmA4fbojLS6aQDNX5fif4flgagdxQidbMbaFXj8SzgX8JLrWNm/Q+xsU4bYHu4JAYCx9X4s/Lqr6/lQ+Ci8BykE6Gd3r6Iyt9CpB7004hI3SwEKsKnkJ4C/kzotE9+eKC8GZh8kK97C7jezBYCKwidfqr2KLDQzPLd/Qc1np8OjAcWENo86xZ33xguGpEGp9VjRUQkIp16EhGRiFQUIiISkYpCREQiUlGIiEhEKgoREYlIRSEiIhGpKEREJKL/D0v9ilie0TVJAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEGCAYAAAB7DNKzAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAAAiN0lEQVR4nO3deXjVhZ3v8fc3O1vYErJHUBQIYRFDcCu1KkJk62irxM7M09t2rHPrjFPv3F57Z+7TznMfp7135jptp860jlrrjMVadcoim3UD3NhkCQKKKBCSkLCHJfv3/nEONqbkJISc/E6Sz+t5zsM5v5Pzywce4JPf7/tbzN0RERFpT1zQAUREJLapKEREJCIVhYiIRKSiEBGRiFQUIiISUULQAaIhLS3NR48eHXQMEZFeZfPmzUfcPb3t8j5ZFKNHj2bTpk1BxxAR6VXMbP+FlmvXk4iIRKSiEBGRiFQUIiISkYpCREQiivmiMLPLzewJM3s+6CwiIv1RIEVhZk+aWbWZlbVZPsfM9pjZXjN7CMDd97n714PIKSIiwW1RPAXMab3AzOKBR4ESoAAoNbOCno8mIiKtBXIehbuvNbPRbRYXA3vdfR+AmT0LLATe78w6zexe4F6A/Pz8LuV6YXM5B46dJSkhjuSEOJIS4kiKD//a5nlyQhxJ8fG/f6/V+8nh53Fx1qUcIiKxJJZOuMsBDrZ6XQ7MMLORwMPA1Wb2XXf/wYU+7O6PAY8BFBUVdekmG8u2V/D6npqufPSCEuLsD0umneL5wxJq/d5nCyk5/N7ApHiuvWIkqSmJ3ZZZRKStWCqKC/347e5+FLivJwI89V+KaWlxGppbqG9qobG5hYam8CP8vL7N69Dz5k+f17d9r83r+lbPz6//dH1T+59vbqG5pf3eS0qI4+Zxo1gwNZubx48iJTG+J/6oRKQfiaWiKAfyWr3OBSp6OkRcnJESFx9T/+E2t3irovl9KR053cDKskqWbatk1c4qBicnMHtiJgumZnPDFSNJiI/5g9pEpBeIpaLYCFxpZmOAQ8Ai4J5gI8WG+DhjQFI8A5Ligd/vZro8HYrHjOBvbp/AO/uOsWTrIVbtrOKFLeWkDU5i7qQsFkzNYVr+MMw0LxGRrrEg7pltZouBm4A04DDwPXd/wsxuB34ExANPuvvDXVl/UVGR99eLAtY1NvP6nhqWbjvEK7uqqW9qIXf4ABZMyWbh1BzGZQ4JOqKIxCgz2+zuRX+wPIiiiLb+XBSt1dY1smbnYZZsq+DNvUdobnHGZw5h/pRsFkzJJm/EwKAjikgMUVH0c0dO17NiRyVLtlawef9xAK65bDgLpmQzd3IWaYOTA04oIkFTUcinDh47y7LtFSzdWsHuqlri44wbxqaxYEo2sydmMESH24r0SyoKuaA9VbUs3XaIJVsrKD9+juSEOG6ZMIoFU3K4aVx6TB39JSLRpaKQiNydLQdOsHTrIV7aUcmR0w0MSUlgzsRMFk7N4borRhKvM81F+jQVhXRaU3MLb310lCVbK1i9s4rT9U2kD0lm7qQsFk7NZmqeDrcV6YtUFNIldY3NvLa7miVbK3h1TzUNTS3kjxjIwqmhI6euzNDhtiJ9hYpCLtmpukZWl1WxNHy4bYvDhKxUFk7NZv6UbHKGDQg6oohcAhWFdKvq2jpWbK9kybYK3jtwAoDpo4ezYGoOcydlMWJQUrABReSiqSgkag4cDR1u+9v3DvFh9WkS4owbr0xj4dRsZhVkMjg5lq4UIyLtUVFI1Lk7u6tqWbK1gmXbKjh04hwpiXHcOiGDBVOy+fy4dJITdLitSKxSUUiPamlxthw4zpKtFby0o5JjZ0KH295WkMncyZncODadpARd3VYklqgoJDCNzS28ufcIy7dXsmZnFafqmkhNSWBWQSbzJmdxw9g0lYZIDFBRSExoaAqVxks7Klm9s4racGncNjGTuZNUGiJBUlFIzGloamH93hpe2l7Fmvd/XxqzJ2Zy++QsbrhCpSHSk1QUEtPqm5o/3T318vuHqa1rYuiARG4ryGBuePdUou7YJxJV7RWFjluUmJCcEM/N4zO4eXwG9U3NrP8wtHtqVVkVv9lcztABicyemMHtk1QaIj1NWxQS0+qbmln3wRFW7AhvadQ3MWxgIrMLQrunrr9ipEpDpJto15P0eudL46VwaZxuVRpzJ2dxnUpD5JKoKKRPqWtsZt2Hv9/SOF8acyZmcvsklYZIV6gopM+qa2xm7Qc1n5bGmYZmhg9MZE5huDQuH0mCSkOkQyoK6RfOl8ZLOyr5Xbg0RgxKYvbEDOZOyubay0eoNETaoaKQfqeusZk3wlsany2N0Ml9Kg2Rz1JRSL9W19jM63vCpbHrMGfDpTGnMFQaM8aoNERUFCJh50vjpR2VvBIujZGDkphdmMm8SVkUqzSkn1JRiFxAqDSqeWlH1WdKY05hJvMmZ1M8ZgTxcbo/uPQPKgqRDpxrOF8albyyq5pzjc2MGpLM7ZOymD8lm2n5wzBTaUjfpaIQuQhnG5p4dXc1y7ZV8NqeGhqaWsgZNoB5k0OlMTE7VaUhfY6KQqSLausaefn9wyzbVsG6D4/Q1OKMSRv0aWlclTEk6Igi3UJFIdINjp9pYPXOKpZtr+Dtj47S4nBVxmDmT85m3pRsxqQNCjqiSJepKES6WU1tPSvLKlm2rYKNnxwHoDAnlfmTs5k7OYvc4QMDTihycVQUIlFUceIcK3aESmNb+UkArrlsOPMmZzF3UhajUlMCTijSMRWFSA/Zf/QMy7eHSmN3VS1mMGPMCOZPyaakMIsRg5KCjihyQSoKkQDsra5l2bZKlm2vYF/NGeLjjBvGpjF/cha3Tcxk6IDEoCOKfKrXFoWZXQ78DTDU3b/Umc+oKCTWuDvvV576dEuj/Pg5kuLjmHlVOvOnZHHrhAwGJeuGkxKsQIrCzJ4E5gHV7l7Yavkc4MdAPPC4u/+wE+t6XkUhfYG7s638JMu2VbB8ewWHT9WTkhjHLeMzmD8li5vGjSIlMT7omNIPBVUUM4HTwNPni8LM4oEPgFlAObARKCVUGj9os4qvuXt1+HMqCulzWlqcjZ8cY/n2SlbsqOTomQYGJycwqyBUGjeOTScpQdedkp4R2K4nMxsNLG9VFNcB33f32eHX3wVw97Yl0XY9EYvCzO4F7gXIz8+/Zv/+/d3zGxDpIU3NLby97yjLt1WysqySU3VNDB0Qumvf/Cm6l4ZEXywVxZeAOe7+jfDrPwFmuPv97Xx+JPAwoS2QxzsqFNAWhfR+DU0trPuwhuXbK1mzs4ozDc2kDU6ipDB0NnjRZcOJ08UKpZu1VxRBTM8u9Le73bZy96PAfdGLIxJ7khLiuGVCBrdMyKCusZnXdlezfHslz206yL+/s5/M1BTmhi8hMiV3qK47JVEVRFGUA3mtXucCFQHkEOkVUhLjKZmURcmkLE7XN/HKrsMs21bJ029/whPrPyZvxADmTsqmpDCTySoNiYIgdj0lEBpm3wIcIjTMvsfdd3bX99SuJ+kPTp5tZPX7VSzbVsFbHx2lucXJGTaA2RMzKZmUyTX52j0lFyeoo54WAzcBacBh4Hvu/oSZ3Q78iNCRTk+6+8Pd+X1VFNLfnDjbwMvvH2ZVWRXrPjxCQ3ML6UOSmTMxk5LCTN21Tzql155w1xUqCunPausaeXV3NSt3VPH6B9XUNbYwYlASsyZkMGdSJjdckaZDbuWCVBQi/dDZhibe2FPDyrIqXt1dzen6JoakJHDrhAxKCjOZeVW6Tu6TT6koRPq5usZm1n94hJVlVfxu12FOnmtkYFI8Xxg/ipLCTL4wbpQuI9LPxdLhsSISgJTEeG4tyODWggwam1t4+6OjrCyrYs3OKl7aXklyQujaUyWFmdwyIUMXLJRPaYtCpJ9rDl9GZFVZFSvLKjl8qp7E+NBVbksKM5lVkKlLo/cT2vUkIh1qaXHeO3iCVWWVrCyrovz4OeLjjBljRlBSmMnsiZm6CVMfpqIQkYvi7uysOMXKskpW7qhi35EzmEHRZcOZU5jFnMJMcoYNCDqmdCMVhYh0mbvzweHTrCyrZFVZFburagGYkjuUOYVZlBRmMjptUMAp5VKpKESk2+yrOc2qnVWsKqtie/ge4ROyUikpDJ3gd2XGkIATSleoKEQkKg4eO8vqnVWsLKti8/7jAFyRPoiSwixKJmVSkJWq60/1EioKEYm6w6fqQqWxo4p3Pz5Ki0P+iIGUFGYypzCTqXnDVBoxTEUhIj3q6Ol61rx/mJVlVby19whNLU7W0BQWTs3hv912FYm69lTM0Ql3ItKjRg5OprQ4n9LifE6ebeR3uw6zfHsFP3vjI8ZlDuaPrs4NOqJ0kipdRKJu6MBE7rwmlye/Op3RIwey+N2DQUeSi6CiEJEeY2aUFuez4ZNj7K2uDTqOdJKKQkR61J3X5JIYbyzeoK2K3kJFISI9Km1wMrcVZPLilnLqGpuDjiOdoKIQkR5XWpzP8bONrN5ZFXQU6QQVhYj0uOuvGEn+iIEs3nAg6CjSCSoKEelxcXHGouI83tl3jH01p4OOIx1QUYhIIL50TS4JccazGzXUjnUqChEJxKghKcwqyOD5zeXUN2moHctUFCISmNLifI6daWDNzsNBR5EIVBQiEpgbx6aRO3yAhtoxTkUhIoGJiwudqf3WR0f5+MiZoONIO1QUIhKoL1+TS3yc8exGbVXEKhWFiARqVGoKt04YxfObymloagk6jlyAikJEAldanM/RMw28/L6G2rFIRSEigfvclenkDNNQO1apKEQkcPFxxqLpeazfe4T9RzXUjjUqChGJCV8uygsPtXWmdqxRUYhITMgcmsLN40fxm00HNdSOMSoKEYkZ9xTnc+R0A6/s0lA7lsR8UZjZBDP7mZk9b2Z/HnQeEYmemVelkz00hV9pqB1ToloUZvakmVWbWVmb5XPMbI+Z7TWzhyKtw913uft9wF1AUTTzikiw4uOMu6fns+7DIxw8djboOBIW7S2Kp4A5rReYWTzwKFACFAClZlZgZpPMbHmbx6jwZxYA64FXopxXRAJ21/Rc4gydqR1DoloU7r4WONZmcTGw1933uXsD8Cyw0N13uPu8No/q8HqWuvv1wFeimVdEgpc1dAA3jx/Fc5vKaWzWUDsWBDGjyAFaH/9WHl52QWZ2k5n9xMx+DqyI8HX3mtkmM9tUU1PTfWlFpMeVFudTU1vPK7uqg44iQEIA39MusMzb+2J3fx14vaOVuvtjwGMARUVF7a5PRGLf569KJ2toCos3HGBOYWbQcfq9ILYoyoG8Vq9zgYoAcohIjEqIj+OuojzWflijoXYMCKIoNgJXmtkYM0sCFgFLA8ghIjHsrumhnyd/s0lnagetw6Iwszgzu74rKzezxcDbwDgzKzezr7t7E3A/sBrYBTzn7ju7sn4R6btyhg3gpqvS+fWmgzRpqB2oDovC3VuA/9eVlbt7qbtnuXuiu+e6+xPh5Svc/Sp3v8LdH+7KukWk7ystzufwqXpe26MDVILU2V1Pa8zsTjO70CBaRCQqbh4/ilFDknX58YB1tigeBH4DNJjZKTOrNbNTUcwlIkJCfBx3T8/j9T3VHDpxLug4/VanisLdh7h7XHgXUmr4dWq0w4mI3FWUhwPP6fLjgen0UU9mtsDM/jH8mBfNUCIi5+WNGMjMK9N5TkPtwHSqKMzsh8ADwPvhxwPhZSIiUVdanE/lyTre+EBD7SB0dovidmCWuz/p7k8SutDf7dGLJSLye7dMGEW6htqBuZgT7oa1ej60m3OIiLQrMT6Ou4pyeXV3NZUnNdTuaZ0tir8H3jOzp8zsl8Dm8DIRkR6xaHo+LQ7PbSwPOkq/06kzs4EW4FrgxfDjOnd/NsrZREQ+lTdiIJ+7Mo1fbzxAc4uu+9mTOntm9v3uXhm+L8QSd6/qgWwiIp9xT3E+FSfrWKuhdo/q7K6nl83sr80sz8xGnH9ENZmISBu3FmSQNjhZ99TuYZ29H8XXwr9+q9UyBy7v3jgiIu1LjI/jy0W5PLZ2H1Un68gcmhJ0pH6hszOKh9x9TJuHSkJEetyi6Xk0t7guP96DOjuj+FZHXyci0hMuGzmIG8em8ezGgxpq9xDNKESk1yktzufQiXOs+1BD7Z6gGYWI9DqzCjIYOSiJxRsOcNO4UUHH6fM6VRTuPibaQUREOispIY4vFeXy+LqPqT5Vx6hUDbWjKeKuJzP7TqvnX27zns7MFpHALJqeHxpqb9aZ2tHW0YxiUavn323z3pxuziIi0mlj0gZx/RUjWbzhAC0aakdVR0Vh7Ty/0GsRkR5VWpxP+fFzrN97JOgofVpHReHtPL/QaxGRHnXbxAxGhIfaEj0dDbOnhO+NbcCAVvfJNkDTIxEJVHJCPHdOy+EXb35CTW096UOSg47UJ0XconD3+Fb3yE4IPz//OrGnQoqItGdRcT5NLc7zGmpHzcXcuEhEJOZckT6YGWNG8OxGDbWjRUUhIr3ePTPy2X/0LG/vOxp0lD5JRSEivd7siZkMG5ioy49HiYpCRHq9lMR47pyWy5qdVRw5XR90nD5HRSEifUJpcR6Nzc4LGmp3OxWFiPQJY0cNoXj0CBZvOIC7htrdSUUhIn1G6Yw8PtFQu9upKESkzygpzGLogEQWb9Dd77qTikJE+oyUxHjumJbD6rIqjmqo3W1UFCLSp5QW59PQ3MKLWw4FHaXPiPmiMLObzGydmf3MzG4KOo+IxLarMoZQdNlwDbW7UVSLwsyeNLNqMytrs3yOme0xs71m9lAHq3HgNKGLEOq4NxHpUGlxPvuOnOHdj48FHaVPiPYWxVO0ucGRmcUDjwIlQAFQamYFZjbJzJa3eYwC1rl7CfA/gL+Lcl4R6QPmTs4iNSVBlx/vJlEtCndfC7St9GJgr7vvc/cG4FlgobvvcPd5bR7V7t4S/txxoN1rCJvZvWa2ycw21dTUROX3IyK9Q2ioncvKHVUcP9MQdJxeL4gZRQ7Q+ti18vCyCzKzO8zs58C/Az9t7+vc/TF3L3L3ovT09G4LKyK906LiPBqaW3hhi/ZYX6ogiuJCt1Btd+Lk7i+6+zfd/W53fz16sUSkLxmfmcq0/GEaaneDIIqiHMhr9ToXqAggh4j0caXF+XxUc4aNnxwPOkqvFkRRbASuNLMxZpYELAKWBpBDRPq4eZOzGaKh9iWL9uGxi4G3gXFmVm5mX3f3JuB+YDWwC3jO3XdGM4eI9E8DkuL5o6tzeGlHJSfOaqjdVdE+6qnU3bPcPdHdc939ifDyFe5+lbtf4e4PRzODiPRvi6bn09CkM7UvRcyfmS0icikKslOZmqeh9qVQUYhIn3dPcT4fVp9mywENtbtCRSEifd68KVkMTk7gV+/q8uNdoaIQkT5vYFICC6dms3x7BSfPNgYdp9dRUYhIv1BanE99Uwu/3aqh9sVSUYhIv1CYM5TJuUM11O4CFYWI9BulxfnsrqrlvYMngo7Sq6goRKTfmD8lm0FJ8Sx+V2dqXwwVhYj0G4OTE1gwNYdl2ys4VaehdmepKESkX7mnOJ+6xhaWvKehdmepKESkX5mUO5TCnFSeeVdD7c5SUYhIv3N+qL2t/GTQUXoFFYWI9DsLpmQzUEPtTlNRiEi/MyQlkQVTslm6rYJaDbU7pKIQkX6ptDifc43NLNmqG2x2REUhIv3S5NyhFGSl8isNtTukohCRfsnMKJ2Rz/uVp9hxSEPtSFQUItJvLZyazYDEeN1TuwMqChHpt1JTEpk/JYslWys4Xd8UdJyYpaIQkX6ttDifsw3NLNVQu10qChHp16bmDWN85hDtfopARSEi/ZqZcc+MfHYcOskOnal9QSoKEen3Fk7NISUxjsUbtVVxISoKEen3hg5IZN7kbJa8d4gzGmr/ARWFiAihofaZhmaWbdNQuy0VhYgIMC1/GOMyhrB448Ggo8QcFYWICOEztYvz2HbwBDsrNNRuTUUhIhL2R1fnkpwQx7MbtFXRmopCRCRs6MBE5k7K4rfvHeJsg4ba56koRERaKZ2RT219E8u3VwYdJWaoKEREWim6bDhjRw3WmdqtqChERFoJDbXzee/ACXZVngo6TkxQUYiItHHH1TkkJcTxrLYqgF5QFGb2OTP7mZk9bmZvBZ1HRPq+4YOSuL0wkxffO8S5huag4wQuqkVhZk+aWbWZlbVZPsfM9pjZXjN7KNI63H2du98HLAd+Gc28IiLnlRbnU1vXpDO1if4WxVPAnNYLzCweeBQoAQqAUjMrMLNJZra8zWNUq4/eAyyOcl4REQCKx4xgfOYQ/va3ZTz62l4am1uCjhSYqBaFu68FjrVZXAzsdfd97t4APAssdPcd7j6vzaMawMzygZPu3u5kyczuNbNNZrappqYmWr8lEeknzIz/+MYMZhVk8A+r9/DFR9/st2dsBzGjyAFan/ZYHl4WydeBX0T6And/zN2L3L0oPT39EiOKiEDa4GQe/co0/vUr0zh8qp6FP32TR9bsob6pf80tgigKu8Ayj/QBd/+eu2uQLSKBKJmUxcvfnsmCKdn85NW9zP/n9Ww9eCLoWD0miKIoB/Javc4FNC0SkZg2fFASj9w9lSe/WsSpc03c8S9v8oMVu6hr7PtbF0EUxUbgSjMbY2ZJwCJgaQA5REQu2s3jM1jz4Ezunp7Hz9fuo+TH69j4SdtRbN8S7cNjFwNvA+PMrNzMvu7uTcD9wGpgF/Ccu++MZg4Rke6UmpLID+6YzDPfmEFjcwt3/fxtvr90Z5+9O565RxwP9EpFRUW+adOmoGOISD9wpr6Jf1i9h1++/Qk5wwbwf+6czA1j04KO1SVmttndi9ouj/kzs0VEYtmg5AS+v2Aiz33zOpLi4/jK4+/y3Re3c6quMeho3UZFISLSDaaPHsGKBz7HNz9/Ob/eeJDbHlnLq7sPBx2rW6goRES6SUpiPN8tmcB//tcbSB2QwNee2sSDv97KibMNQUe7JCoKEZFuNiVvGMv+4kb+8pYrWbqtglsfWcuqst57IyQVhYhIFCQnxPPgrKtYev+NZKQmc99/bOFbz2yhprY+6GgXTUUhIhJFBdmp/PZbN/DfZ4/j5fcPc9s/vcGSrYfoTUecqihERKIsMT6Ob31hLCseuJHRaYN44Nmt/NnTm6g6WRd0tE5RUYiI9JCxo4bw/H3X87dzJ7B+7xFm/dMbPLfxYMxvXagoRER6UHyc8Y3PXc6qB2ZSkJXKd17Yzp8+uYHy42eDjtYuFYWISABGpw1i8Z9dy//+YiFb9h9n9j+t5d/f/oSWltjbulBRiIgEJC7O+JNrL2P1t2cy7bLh/K8lO1n0b+/wyZEzQUf7DBWFiEjAcocP5OmvFfN/vzSZXZWnmPPjtfzb2n00x8jWhYpCRCQGmBl3FeXxuwc/z41j03h4xS7u/Ne3+PBwbdDRVBQiIrEkIzWFf/vTIn68aCr7j55h7k/W89NXP6SxuSWwTCoKEZEYY2YsnJrDyw9+nlkTM/jHNR+w8KdvsrPiZCB5VBQiIjEqbXAyj94zjZ/98TSqa+tZ+NM3eWTNHuqbevb2qyoKEZEYN6cwi989OJMFU7P5yat7mf/P69l68ESPfX8VhYhILzBsYBKP3DWVX3x1OrV1TdzxL2/ygxW7qGuM/taFikJEpBf5wvhRrP72TO6ens/P1+6j5Mfr2PDxsah+TxWFiEgvk5qSyA/umMQz35hBU0sLd/38bb63pIwz9U1R+X4qChGRXuqGsWmsemAmX71+NE+/s5/ZP1rLB1E470JFISLSiw1KTuD7Cyby3Dev4/L0weQMG9Dt3yOh29coIiI9bvroETz9teKorFtbFCIiEpGKQkREIlJRiIhIRCoKERGJSEUhIiIRqShERCQiFYWIiESkohARkYjMPTbuydqdzKwG2N/Fj6cBR7oxTrT1przKGj29KW9vygq9K++lZr3M3dPbLuyTRXEpzGyTuxcFnaOzelNeZY2e3pS3N2WF3pU3Wlm160lERCJSUYiISEQqij/0WNABLlJvyqus0dOb8vamrNC78kYlq2YUIiISkbYoREQkIhWFiIhEpKIIM7MnzazazMqCztIRM8szs9fMbJeZ7TSzB4LOFImZpZjZBjPbFs77d0Fn6oiZxZvZe2a2POgsHTGzT8xsh5ltNbNNQeeJxMyGmdnzZrY7/Pf3uqAztcfMxoX/TM8/TpnZXwWdqz1m9u3wv68yM1tsZindtm7NKELMbCZwGnja3QuDzhOJmWUBWe6+xcyGAJuBL7r7+wFHuyAzM2CQu582s0RgPfCAu78TcLR2mdmDQBGQ6u7zgs4TiZl9AhS5e8yfFGZmvwTWufvjZpYEDHT3EwHH6pCZxQOHgBnu3tWTeaPGzHII/bsqcPdzZvYcsMLdn+qO9WuLIszd1wLHgs7RGe5e6e5bws9rgV1ATrCp2uchp8MvE8OPmP0JxcxygbnA40Fn6UvMLBWYCTwB4O4NvaEkwm4BPorFkmglARhgZgnAQKCiu1asoujlzGw0cDXwbsBRIgrvytkKVAMvu3ss5/0R8B2gJeAcneXAGjPbbGb3Bh0mgsuBGuAX4d16j5vZoKBDddIiYHHQIdrj7oeAfwQOAJXASXdf013rV1H0YmY2GHgB+Ct3PxV0nkjcvdndpwK5QLGZxeTuPTObB1S7++ags1yEG9x9GlACfCu8GzUWJQDTgH9196uBM8BDwUbqWHgX2QLgN0FnaY+ZDQcWAmOAbGCQmf1xd61fRdFLhff1vwA84+4vBp2ns8K7Gl4H5gSbpF03AAvC+/2fBW42s/8INlJk7l4R/rUa+E+gONhE7SoHylttTT5PqDhiXQmwxd0PBx0kgluBj929xt0bgReB67tr5SqKXig8HH4C2OXujwSdpyNmlm5mw8LPBxD6S7070FDtcPfvunuuu48mtLvhVXfvtp/MupuZDQof0EB4N85tQEweuefuVcBBMxsXXnQLEJMHYLRRSgzvdgo7AFxrZgPD/z/cQmh22S1UFGFmthh4GxhnZuVm9vWgM0VwA/AnhH7aPX/o3u1Bh4ogC3jNzLYDGwnNKGL+sNNeIgNYb2bbgA3AS+6+KuBMkfwF8Ez478JU4O+DjROZmQ0EZhH6CT1mhbfSnge2ADsI/d/ebZfz0OGxIiISkbYoREQkIhWFiIhEpKIQEZGIVBQiIhKRikJERCJSUYhEYGanw7+ONrN7unnd/7PN67e6c/0i3UVFIdI5o4GLKorwFUcj+UxRuHu3nUkr0p1UFCKd80Pgc+GTG78dvsjhP5jZRjPbbmbfBDCzm8L3CvkVoROfMLPfhi/Yt/P8RfvM7IeErvS51cyeCS87v/Vi4XWXhe8zcXerdb/e6n4Oz4TPwhWJqoSgA4j0Eg8Bf33+3hTh//BPuvt0M0sG3jSz81frLAYK3f3j8Ouvufux8OVLNprZC+7+kJndH75QYlt3EDpreQqQFv7M2vB7VwMTCV1C+k1CZ+mv7+7frEhr2qIQ6ZrbgD8NXzr9XWAkcGX4vQ2tSgLgL8OX2HgHyGv1de25EVgcvuLuYeANYHqrdZe7ewuwldAuMZGo0haFSNcY8BfuvvozC81uInT57NavbwWuc/ezZvY60NEtKiPtTqpv9bwZ/RuWHqAtCpHOqQWGtHq9Gvjz8OXeMbOr2rkJz1DgeLgkxgPXtnqv8fzn21gL3B2eg6QTuivchm75XYh0gX4aEemc7UBTeBfSU8CPCe322RIeKNcAX7zA51YB94WvlrqH0O6n8x4DtpvZFnf/Sqvl/wlcB2wjdPe677h7VbhoRHqcrh4rIiIRadeTiIhEpKIQEZGIVBQiIhKRikJERCJSUYiISEQqChERiUhFISIiEf1/KX8ND8g2b18AAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"import matplotlib.pyplot as plt\n",
"\n",
"# number of iterations\n",
"N = len(x)\n",
"\n",
"# iteration\n",
"iters = range(0,N)\n",
"\n",
"plt.figure\n",
"for i in range(0,len(x0)):\n",
" plt.plot(iters,[x[j][i] for j in range(0,N)],label=\"x\"+str(i))\n",
"plt.xlabel(\"Iteration\")\n",
"plt.ylabel(\"Primal Variables\")\n",
"plt.legend()\n",
"plt.show()\n",
"\n",
"plt.figure\n",
"for i in range(0,len(u[0])):\n",
" plt.plot(iters,[u[j][i] for j in range(0,N)],label=\"u\"+str(i))\n",
"for i in range(0,len(v[0])):\n",
" plt.plot(iters,[v[j][i] for j in range(0,N)],label=\"v\"+str(i))\n",
"plt.xlabel(\"Iteration\")\n",
"plt.ylabel(\"Dual Variables\")\n",
"plt.legend()\n",
"plt.show()\n",
"\n",
"plt.figure\n",
"plt.semilogy(iters,mu)\n",
"plt.xlabel(\"Iteration\")\n",
"plt.ylabel(\"Barrier Penalty\")\n",
"plt.show()\n",
"\n",
"plt.figure\n",
"plt.semilogy(range(1,N),E)\n",
"plt.xlabel(\"Iteration\")\n",
"plt.ylabel(\"Error\")\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"id": "ce1653ce",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.3.3 Problem 3: Nonconvex](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.3.3-Problem-3:-Nonconvex)",
"section": "4.9.3.3 Problem 3: Nonconvex"
}
},
"source": [
"### 4.9.3.3 Problem 3: Nonconvex"
]
},
{
"cell_type": "code",
"execution_count": 8,
"id": "adaa8455",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.3.3 Problem 3: Nonconvex](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.3.3-Problem-3:-Nonconvex)",
"section": "4.9.3.3 Problem 3: Nonconvex"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"\n",
"*** Barrier Subproblem 0 ***\n",
"mu = 10.0\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 4.0000e+00 \t3.1623e+00 \t 9.00e+00 \t 6.17e+00 \t 8.25e+00 \t 8.06e+00 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 1 ***\n",
"mu = 2.0\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 4.0013e+01 \t4.4202e-10 \t 2.80e+01 \t 3.79e+00 \t 1.52e+00 \t 3.22e+00 \t 0.00e+00 \t 0.00e+00\n",
"1 \t 1.6354e+01 \t1.3323e-15 \t 6.22e+00 \t 9.26e-01 \t 2.49e-01 \t 1.35e+00 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 2 ***\n",
"mu = 0.4\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 1.2029e+01 \t5.9350e-11 \t 2.31e+00 \t 3.94e-01 \t 1.93e-01 \t 6.76e-01 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 3 ***\n",
"mu = 0.08000000000000002\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 1.0363e+01 \t5.0465e-11 \t 4.67e-01 \t 7.00e-02 \t 6.98e-02 \t 1.66e-01 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 4 ***\n",
"mu = 0.016000000000000004\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 1.0077e+01 \t8.9693e-12 \t 7.01e-02 \t 1.52e-02 \t 5.71e-03 \t 2.39e-02 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 5 ***\n",
"mu = 0.0020238577025077633\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 1.0016e+01 \t4.8606e-13 \t 1.42e-02 \t 3.45e-03 \t 7.38e-04 \t 4.77e-03 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 6 ***\n",
"mu = 9.104790579399288e-05\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 1.0002e+01 \t4.5590e-13 \t 1.94e-03 \t 4.78e-04 \t 9.46e-05 \t 6.54e-04 \t 0.00e+00 \t 0.00e+00\n",
"1 \t 1.0000e+01 \t6.1284e-14 \t 2.94e-07 \t 6.48e-09 \t 4.36e-07 \t 8.52e-07 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 7 ***\n",
"mu = 8.687702517211205e-07\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 1.0000e+01 \t4.4409e-16 \t 9.02e-05 \t 2.23e-05 \t 4.29e-06 \t 3.04e-05 \t 0.00e+00 \t 0.00e+00\n",
"1 \t 1.0000e+01 \t2.6645e-15 \t 1.67e-08 \t 1.36e-11 \t 1.69e-08 \t 2.21e-08 \t 0.00e+00 \t 0.00e+00\n",
"\n",
"*** Barrier Subproblem 8 ***\n",
"mu = 1e-09\n",
"Iter. \tf(x) \t\t||c(x)|| \tE \t\t||dx|| \t\t||dv|| \t\t||du|| \t\tdelta_A \tdelta_W\n",
"0 \t 1.0000e+01 \t1.1102e-16 \t 8.68e-07 \t 2.15e-07 \t 4.23e-08 \t 2.92e-07 \t 0.00e+00 \t 0.00e+00\n",
"1 \t 1.0000e+01 \t0.0000e+00 \t 1.36e-09 \t 1.33e-15 \t 3.33e-10 \t 1.60e-09 \t 0.00e+00 \t 0.00e+00\n"
]
}
],
"source": [
"f = lambda x: x[0] + 2*x[1] + x[2]**2\n",
"\n",
"def c(x):\n",
" rhs = np.zeros(2)\n",
" rhs[0] = x[0] + x[1] - 1\n",
" rhs[1] = x[2] - x[1] - 3\n",
" return rhs\n",
"\n",
"# Indices of variables with lower bound of zero\n",
"vb = [1,2]\n",
"\n",
"x0 = np.ones(3)\n",
"u0 = np.ones(2)\n",
"v0 = np.ones(2)\n",
"\n",
"## Test barrier subproblem\n",
"# xtest, vtest, utest, Etest = barrier_subproblem(x0,v0,u0,f,c,vb,1E-1,1E-10,max_iter=10,verbose=True)\n",
"\n",
"##\n",
"x, v, u, mu, E = interior_point(x0,f,c,vb)"
]
},
{
"cell_type": "code",
"execution_count": 9,
"id": "5b06a941",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.9.3.3 Problem 3: Nonconvex](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html#4.9.3.3-Problem-3:-Nonconvex)",
"section": "4.9.3.3 Problem 3: Nonconvex"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYAAAAEGCAYAAABsLkJ6AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAAAzFElEQVR4nO3dd3xU55Xw8d8ZFQRINCGqJCTRe7HAYAzG3Y4dt8SJ47ZeF7kktpM3iUuyu1m/ye6b3c1m0xzHuIG74xanOC7rhmFEkTGmGLCxECCLIpok1KU57x8zQhKojDR35o405/v5zGdm7tx57mGAe+7z3HvPI6qKMcaY2ONxOwBjjDHusARgjDExyhKAMcbEKEsAxhgToywBGGNMjIp3O4CuGDp0qGZlZbkdhjHG9CgfffTRQVVNO3F5j0oAWVlZFBQUuB2GMcb0KCKyq63lNgRkjDExyhKAMcbEKEsAxhgTo3rUOQBjjAm3+vp6iouLqampcTuULktKSiI9PZ2EhISg1rcEYIwxLRQXF5OSkkJWVhYi4nY4QVNVDh06RHFxMdnZ2UF9x9UhIBEZJCIvicg2EdkqIgvcjMcYY2pqakhNTe1RO38AESE1NbVLPRe3ewC/Bt5Q1a+LSCLQz+V4jDGmx+38m3Q1btcSgIgMABYDNwCoah1Q51Y8kbB+/3o84mHWsFluh2KMMa4OAeUApcATIvKxiDwqIv1PXElE8kSkQEQKSktLIx+lg3688sfc/d7dVNVXuR2KMaaHWb58OePHj2f8+PEsX77ckTbdTADxwBzgIVWdDVQC9524kqouVdVcVc1NSzvpTuYeY0/5HoqPFXO45jAvbH/B7XCMMT3I4cOHeeCBB1izZg1r167lgQce4MiRIyG362YCKAaKVXVN4P1L+BNCr+Qt8QIwbtA4ntj8hPUCjDFtWrduHTNmzKCmpobKykqmTp3Kgw8+yLnnnsuQIUMYPHgw5557Lm+88UbI23LtHICq7hORPSIyUVW3A2cDn7oVT7itKlnF6OTR/Otp/8q1r1/Lc9ue46bpN7kdljGmAw/8ZQuflpQ72uaUUQP4yVentvv53LlzueSSS/inf/onqqurufbaa0lISCAjI+P4Ounp6Xz55Zchx+L2ncB3As+IyEZgFvDv7oYTHvW+etbuW8uCUQuYmTaThaMXsmzLMusFGGPa9C//8i+8/fbbFBQUcM8999DW3O1OXKnk6mWgqroByHUzhkjYVLqJyvpKTht1GgDfnvltrn79ap7d9iw3T7/Z5eiMMe3p6Eg9nA4fPsyxY8eor6+npqaG9PR03n///eOfFxcXs2TJkpC343YPICZ4S7x4xMO8EfMAmJ42nUWjF7FsyzIq6ytdjs4YE23y8vL46U9/yjXXXMO9997L+eefz1tvvcWRI0c4cuQIb731Fueff37I23H7RrCYkF+Sz7Sh0xjYZ+DxZbfPvJ2rX7+a57Y9Z70AY8xxTz75JPHx8Vx99dU0NjZy2mmnsWHDBv75n/+ZuXPnAv4hoiFDhoS8LUsAYVZWW8bmQ5vJm5HXavn0tOksTl/Msi3LuGriVSQnJrsUoTEmmlx//fVcf/31AMTFxbFmzZrjn914442ObsuGgMJszd41+NR3fPy/pTtm3kFZbRnPbnvWhciMMbHOEkCYeUu8JCckM23otJM+mzp0KkvSl7B8y3Iq6ipciM4YE8ssAYSRqpJfks+8EfNI8LRdn/u2WbdRXlfOs1utF2CMiSxLAGG0q3wXJZUlLBy9sN11pqZOZUnGEpZ/ar0AY0xkWQIIo6byDwtGdTzNwR0z76CiroKntz4dibCMMQawBBBW+SX5ZKRkkJGS0eF6k1Mnc2bGmTy15SnK65y97dwYY9pjCSBM6hv95R/auvqnLXfMuoOK+gqe+fSZMEdmjOmJLrjgAgYNGsTFF1/sWJuWAMJkQ+kGqhqqOh3+aTJpyCTOzjybpz61XoAx5mQ//OEPeeqppxxt0xJAmOSX5BMnccfLPwTj9pm3U1FfwVOfOvuXbIzpOdoqB71582bOPvtsUlJSHN2W3QkcJt4SLzPSZpCSGPxf2MQhEzkn8xye/vRprp18bavSEcYYF/z9Pti3ydk2R0yHC3/e7sdtlYOeNu3k+4icYD2AMDhSc4RPD30a9PBPS7fNvI1j9cesF2BMDDuxHHS4WA8gDNbsXYOiQZ8AbmnikImcO+Zcnt76NNdNuc56Aca4qYMj9XA6sRx0//4nTZfuCOsBhIG3xEtKYgpTU7tXS/z2mbdTWV/J8i3OTPxsjOlZTiwHHS6uJgARKRKRTSKyQUQK3IzFKaqKt8TL/JHzifd0r4M1fvB4zhtzHs9sfYajNUedDdAYE9ValoO+7777WLduHe+++y6LFi3iyiuv5J133iE9PZ0333wz5G1FwxDQmap60O0gnLKzbCf7q/Z3a/y/pdtn3s7bu97myU+f5K45dzkUnTEm2rVXDvqss85yfFs2BOSwpvIP3Rn/b2nc4HGcn3U+z2x9hiM1R5wIzRhjWnE7ASjwloh8JCJ5ba0gInkiUiAiBaWlpREOr+u8JV6yBmQxOnl0yG3dNvM2qhuq7VyAMSYs3E4AC1V1DnAh8G0RWXziCqq6VFVzVTU3LS0t8hF2QV1jHQX7C0Ie/mkydtBYLsi6gGe3PcvhmsOOtGmMMU1cTQCqWhJ4PgC8CgR/22wU2nBgA9UN1SEP/7R028zbqGmosV6AMcZxriUAEekvIilNr4HzgM1uxeMEb4mXeIln7oi5jrWZMyiHC7Mv5Lltz1kvwBjjKDd7AMOBlSLyCbAW+JuqvuFiPCHzlniZOWwm/ROcvWnj1pm3UttYy7LNyxxt1xgT21xLAKpaqKozA4+pqvpvbsXihEPVh9h6eKujwz9Ncgb6ewHPb3+eQ9WHHG/fGBPdNmzYwIIFC5g6dSozZszghRdecKRdt08C9xqr964GQr/8sz23zbjN3wvYsiws7Rtjole/fv148skn2bJlC2+88Qbf/e53OXr0aMjtWgJwiLfEy8A+A5k8ZHJY2s8amMVF2Rfx/LbnOVjda+6bM8acoK1y0HV1dYwfPx6AUaNGMWzYMJy4LD4a7gTu8VSV/JJ85o+cT5wnLmzbyZuRx992/o0nNj/BD+f+MGzbMcb4/cfa/2Db4W2OtjlpyCTundd+fZ/OykGvXbuWuro6xo4dG3Is1gNwwI6jOyitLg3b8E+TrIFZXJxzMX/c/kfrBRjTi7VXDnrv3r1cd911PPHEE3g8oe++rQfggKbyDwtGOnMDWEdunXErfyv8G49vfpx75oavTrgxhg6P1MOprXLQ5eXlXHTRRfzsZz9j/vz5jmzHegAOyC/JJ3tgNiOTR4Z9W5kDMrko5yL+uP2PlFZFf2kMY0zXnVgOuq6ujssvv5zrr7+eK6+80rHtWAIIUW1jLQX7C8I+/NPSbTNuo8HXwOObH4/YNo0xkdFWOejnn3+eFStWsGzZMmbNmsWsWbPYsGFDyNuyIaAQrd+/ntrG2ogmgIwBGXx17Fd58bMXuXHajaT1i+4aScaY4LVXDrppmZOsBxCi/JJ84j3x5A7Pjeh282bk0eBr4LHNj0V0u8aY3sMSQIi8JV7mDJtDv4R+Ed1uRkoGl4y9hBe3v8j+yv0R3bYxpnewBBCCg9UH2X5ku2Pln7sqb0YePvVZL8AYh6mq2yF0S1fjtgQQgvySfCB85R86k56SzqXjLuWlz16yXoAxDklKSuLQoUM9LgmoKocOHSIpKSno79hJ4BB4S7wM7jOYSUMmuRbDLTNu4bUdr/Hopkf58fwfuxaHMb1Feno6xcXFjpRaiLSkpCTS09ODXt8SQDf51Ocv/zBqPh5xryM1Onk0l467lJc/f5mbpt/EiP4jXIvFmN4gISGB7Oxst8OICBsC6qbPj3zOoZpDrg3/tJQ3Iw9FeXTTo26HYozpQSwBdFMkyz90ZlTyKC4fdzkvf/4y+yr3uR2OMaaHcD0BiEiciHwsIn91O5au8JZ4GTdoHMP7D3c7FABumX4LAI9sfMTlSIwxPYXrCQC4G9jqdhBdUd1Qzfr96127/LMtI5NHcsW4K3hlxyuUHCtxOxxjTA/gagIQkXTgIqBHDV6v37+eOl9dVIz/t3TLjFsQhEc2WS/AGNM5t3sAvwLuAXztrSAieSJSICIF0XJZlrfES6InkVOGn+J2KK2M6D+CK8ZfwZ8+/5P1AowxnXItAYjIxcABVf2oo/VUdamq5qpqblpadBQ985Z4mTN8Dn3j+7odyklunn4zIsLSjUvdDsUYE+Xc7AEsBC4RkSLgeeAsEXnaxXiCcqDqADuO7oi64Z8mI/qP4Gvjv8ZrO16juKLY7XCMMVHMtQSgqverarqqZgFXAe+q6rVuxRMst8s/BKOpF2DnAowxHXH7HECP4y3xkpqUyvjB490OpV3D+w/n6xO+zp93/Jk9FXvcDscYE6WiIgGo6vuqerHbcXSmqfzDglELXC3/EIybp9+MRzx2X4Axpl3RvReLMtsOb+NI7ZGoHv5pMqzfMK6ceCV//uLP7Cm3XoAx5mSWALqgqfzD/JHzXY4kODdNu4l4TzxLN9kVQcaYk1kC6IL8knwmDJ7QY+bgTeuXxpUTruQvX/yF3eW73Q7HGBNlLAEEqaq+ivUH1veI4Z+Wbpx2I/GeeB7e+LDboRhjoowlgCAV7C+gwdcQVfV/gpHWL41vTPwGfy38K7vKd7kdjjEminSaAETkP0VkgIgkiMg7InJQRKL+en2n5Zfk0yeuD3OGzXE7lC67cdqNJHoS7e5gY0wrwfQAzlPVcuBioBiYAPwwrFFFIW+Jl1OGn0JSfPDzbUaLoX2HHu8FFJUVuR2OMSZKBJMAEgLPXwGeU9XDYYwnKu2r3EdhWWGPG/9v6R+n/SOJnkQ7F2CMOS6YBPAXEdkG5ALviEgaUBPesKJLTyj/0JmhfYdy1aSreH3n6+ws2+l2OMaYKNBpAlDV+4AFQK6q1gNVwKXhDiyaeEu8pPVNY9ygcW6HEpIbpt5An7g+1gswxgDBnQTuB3wbeCiwaBT+3kBMaPQ1kr/XX/5BRNwOJySpfVO5auJV/H3n3/lo/0c0+BrcDskY46L4INZ5AvgIaBr/KAZeBHrUHL7dtfXwVspqy3r08E9LN0y7gRc/e5Eb3riBBE8CWQOzGDtwLGMHNT8yUjJI8CR03pgxpkcLJgGMVdVvisi3AFS1Wnr6oXAX9LTyD50ZkjSEly95mYL9BXxx9Au+OPoFmw9u5s2iN1EUgHhPPFkDspqTwsCxjBs0jowBlhiM6U2CSQB1ItIX/HsHERkL1IY1qijiLfEyechkUvumuh2KY0Ylj+KS5EtaLatuqGZn2c7jSeGLo1/w6aFPeavorZMSQ87AHMYNGkfOIP9zZkomCXGWGIzpaYJJAD8B3gAyROQZ/DN53RDOoKJFZX0lnxz4hOunXu92KGHXN74vU1KnMCV1Sqvl1Q3VFJUVsePoDgrLCtlxdAfbDm/j7V1vNycGiWfMgDHHE0LOoBzGDRzHmAFjLDEYE8U6TQCq+raIrAfmAwLcraoHQ92wiCQBK4A+gTheUtWfhNquk9btW0eDNvSa8f/u6Bvfl8mpk5mcOrnV8pqGGorKA4nhqD8xbD+8nXd2v4NPfYA/MWQOyGw1lDR20FjGDBhDYlyiG38cY0wL7SYAETmx5sHewHOmiGSq6voQt10LnKWqx0QkAVgpIn9X1dUhtusYb4mXpLgkZg+b7XYoUScpPolJQyYxacikVsubEkPLoaTPjnzWKjHESRyZAzLJHpBNSmIKfeL6kBiXSGJcYvNrT/P7hLgE/3LPCesE1mu1TmBZDJ2mMqbbOuoB/HcHnylwVigbVlUFjgXeJgQeGkqbTssvySd3RK5zR6uHvgDxwJBsZ9qLQu0lhtrGWorK/ImhaTipqKyIyoZK6hrrmh++OkfiaEoWLRNLgifh5GTjSSQhLgGPePDgQUQQBI80vxaRkz5rmhHOI56T1j/pdVMbbbw+sZ22EpfQvKzp81bLAq/bS3rBfqfl59HAknhrC0YuYHj/4Y622W4CUNUzHd1SG0QkDv8lpuOAB1V1TRvr5AF5AJmZmeEO6bgvj31JUXkR35j4DWcaLN8Lj5wFfVLgzvUQH1tDIH3i+jBxyEQmDpnY4XqqSr2vntrGWmoba6lv9L+u8zUnidrG2rbXCSSQpnVart/y+3WNddQ21FJRV3H8vaL41Ieqtv0aRVXxEVje8nXTZ+rDhw8UfPiO93iMccJD5zwUuQTQJDBWfwdwOv4j9A+BP6hqyOUgVLURmCUig4BXRWSaqm4+YZ2lwFKA3NzciPUQHC3/oAp/vhNqK6DmKGx4GnJvDL3dXkhEjh+hp5Didjgha5Ug6DzBNH3n+Pc5+XV7n7fcphPfcVM0xBBtUpOcvxIxmKuAngQqgN8G3n8LeAq40qkgVPWoiLwPXABs7mT1iPCWeBnebzg5A3NCb2z9ctjxNlz4n7DpRVjx3zDrGojvE3rbJqo1DQUhEEec2+EY00owxeAmqupNqvpe4JGHvyR0SEQkLXDkT+A+g3OAbaG264RGXyOr967mtFGnhT4OeaQI3vwxZJ8Bc2+BJfdDeTF8/LQjsRpjTHcFkwA+FpHjt8GKyKnAKge2PRJ4T0Q2AuuAt1U1KspLbDm0hYq6itCHf3yN8Ort/hO/l/0ePB4YexZknAof/jc0xMz9dMaYKNTRZaCb8I/5JwDXi8juwPsxwKehblhVNwJReX2lt8SLIJw68tTQGlr9e9jthcsegoHp/mUisOQ+eOpyWP8kzLsl9ICNMaYbOjoHcHHEoogy3hIvU1KnMDhpcPcbObAV3vkpTLwIZn6r9Wc5Z0LGfPjwlzD7OkjoebOMGWN6vnaHgFR1V8sHUI2/B9D06JUq6irYWLoxtOGfxnp49Vbokwxf/bX/qL8lETjzfqgogY+fCi1gY4zppmDmA7hERD4HdgIfAEXA38Mcl2vW7ltLozayYNSC7jey4hew9xO4+FeQnNb2OtlnQOZp/nMB9TE1wZoxJkoEcxL4p/jrAH2mqtnA2ThzEjgq5Zfk0ze+L7PSZnWvgS/Xw4r/ghnfhCmXtL9e07mAir3+y0SNMSbCgkkA9ap6CPCIiEdV3wNmhTcs93hLvMwbMa97VSzrq+HV2yB5uP+a/85kL4YxC/3nAuqru749Y4wJQTAJ4KiIJOOv3PmMiPwa6JVzCe4p38Oeij3dH/5592dwcDtc9iD0HdT5+iL++wKO7YOPrBdgjImsYBLApfhPAH8P/7wAXwBfDWdQbsnfG0L5h6KVkP8gzL3Zf61/sLIXwZjTYaX1AowxkdVpAlDVSlVtVNUGVV2uqr8JDAn1Ot4SLyP7jyRrQFbXvlhbAX+63V/l89z/2/UNn3k/HNsPBU90/bvGGNNN7SYAEVkZeK4QkfIWjwoRKY9ciJHR4Gtgzd413Sv/8OaPoKwYLvsDJPbv+sazToesRbDyf6CuquvfN8aYbujoPoDTA88pqjqgxSNFVQdELsTI2HxwM8fqj3V9+OezN/139J52F2SGcOfwkvuh8gB8ZL0AY0xkdDgEJCIeEYmK6pzh5i3x4hFP18o/VB32l3keNhXO/FFoAWQt9F8VtPJX1gswxkREhwlAVX3AJyISuZlYXOIt8TItdRoD+wwM/kt/+74/CVz+B2dKOy/5kb8XUPBY6G0ZY0wngrkKaCSwRUTeEZE/Nz3CHVgkldeVs+ngpq5d/rnpJdjyiv9mrpEznAlkzALIWRLoBVQ606YxxrQjmAlhHgh7FC5bs3cNPvUFP/5fvtd/9J8+FxZ+19lgltwPj58P6x6DhXc527YxxrTQaQJQ1Q8iEYibvCVe+if0Z3ra9M5XbpresaHWf9VPXDA5tAsy5/urha76Ncy9qXtXFRljTBCCKQY3X0TWicgxEakTkcbedBmoquL9MlD+wRNE+Yem6R3PfQCGjgtPUGf+CKoOwtpHwtO+McYQ3DmA3+GfB/hzoC9wc2BZSEQkQ0TeE5GtIrJFRO4Otc3u2F2xm5LKkuCGf45P77jYP71juGTMg7Fng/c3UHssfNsxxsS0YBIAqroDiAvcEfwEsMSBbTcA31fVyfirjX5bRKY40G6XeEu8QBDlH3w++NMd/ukdLw1M7xhOS+6HqkOwznoBxpjwCGYvViUiicAGEflPEfkeEPLAtKruVdX1gdcVwFZgdKjtdpW3xMvo5NFkpGR0vOLq38OuVXDhf8CgTtZ1QsZcGHcOrPqNv9SEMcY4rKNSELmBl9cF1vsOUAlkAF9zMggRycI/P/CaNj7LE5ECESkoLS11crPU++pZu3dt5+UfDmyDd/5v29M7htOSH0H1YVi7NHLbNMbEjI56AI8EZgK7CchR1XJVfUBV/09gSMgRgVLTLwPfVdWTTi6r6lJVzVXV3LS0dmbX6qaNpRupaqjqePinsR5ezWt/esdwSj8Fxp8H3t9aL8AY47iOagHNxj8xfCPwkohsEJF7RWSMUxsXkQT8O/9nVPUVp9oNlrfES5zEMW/kvPZXCmZ6x3A64z6oPgJrHo78to0xvVpnpSC2B476pwD/AAwC3hWRkKeEFP+Yy2PAVlX9ZajtdUd+ST7Th05nQGI7te2Cnd4xnNJPgfHn+3sBNb3m6ltjTBQI6lIWEfEAw4Dh+E8AOzEYvxD/+YWzAr2LDSLyFQfaDUpZbRmbD25uf/inq9M7htOS+6DmqPUCjDGO6vA2VhFZhP8egMuAzcDzwPdUtSzUDavqSiCCA+qtrd67GkXbr//TNL3jta8EN71jOI2eAxMuhPzfwal5kNSFgnXGGNOOjq4C2gP8HP/lmbNV9TxVfdyJnX80yC/JJyUhhWlDp538YcvpHcedHfng2rLkXusFGGMc1VEP4HRV3RWxSCJIVVlVsopTR55KvOeEnyDU6R3DZdRsmPgVfy9gXp77vRJjTI/X0VVAvXLnD7CzfCf7Kve1PfwT6vSO4bTkPqgpgzV/cDsSY0wvEOZ6BtEpvyQfaKP8g1PTO4bLyJkw6WLI/z1UH3U7GmNMDxeTCcBb4iUzJZP0lPTmhU5O7xhOZ9wLtWWw+iG3IzHG9HDtngMQkd8C2t7nqtojZyupa6xj3b51XDL2hOv6m6Z3vOYlZ6Z3DJeRM/y9gNW/h/m3Qd/BbkdkjOmhOjoJXBCxKCLok9JPqG6obj38s/ll//SOZ/2Tc9M7htOS+2HbX/1DQWf92O1ojDE9VLsJQFWXRzKQSDle/mFEoPxDxT7/0f/oXFj4PXeDC9aIaTD5Ev/J4Pm3Q78hbkdkjOmBgpkRLE1EfiEir4vIu02PSAQXDt4SLzPTZpKcmNw8vWN9DVz+sPPTO4bTGfdCbbl/KMgYY7ohmJPAz+C/GSwb/wTxRcC6MMYUNodrDrP10Nbmyz/XPwmfvxXe6R3DZcQ0mHIprP6D/9yFMcZ0UTAJIFVVHwPqVfUDVb0R/wxePc6avWtQlIWjFgamd/xR+Kd3DKcz7oO6Cv/NYcYY00XBJID6wPNeEblIRGYD6R19IVp5S7wMSBzAlMGTIju9Y7gMnwJTLvOXh7BegDGmi4LZ8/1MRAYC3wd+ADwK9JCzpc1UFW+Jl/kj5xO39mH/9I4X/Dwy0zuG05L7oK7SXy7aGGO6oNOznqr618DLMuDM8IYTPoVlhRyoOsBpKTnw+gP+ujqzrnY7rNANmwxTL/dPG7ngO9A/1e2IjDE9RDBXAWWLyC9F5BUR+XPTIxLBOWnVl/45bBYUPOfO9I7hdMa9gV7Ab9yOxBjTgwRz3eOf8M/c9RfAF9Zowsi710tW/ABG7d0E33gKkoe5HZJzhk2CaVfA2kfgtDuh/1C3IzLG9ADBnAOoUdXfqOp7gauAPlDVD5zYuIg8LiIHRGSzE+21p7axlo/2ruO0wyXuTu8YTmfcC/VV1gswxgQtmATwaxH5iYgsEJE5TQ+Htr8MuMChttr1cclqanx1nKZ93Z/eMVzSJsL0r/t7AcecmLHTGNPbBTMENJ3A3L00DwFp4H1IVHWFiGSF2k5nXnzj34lPUOac94vePZHK4nv8dY28v4Hzfup2NI5RVRp8Sm2Dj7oGH7UNjYFnH7X1PuoaG6mt91Hb2PTeR219Y4v12/hei9f1jT58Cj5VfOrfngbeH38OxNH0+fH1aLle6+82f6/5O03rHm+Dprb8y6B1BcamZS2Xt1jU5ndavtET1mu3nRZf0laNuSMKQog6j16fy+IJaY62GUwCuBzIUdU6R7ccJBHJA/IAMjMzu9XGhJFncWD7e6xqmB3+7oab0ibAtK/Dukf9cxokO/uPJVQ19Y3sOHCMzw9U8Pn+YxSWVlJZ1xDYIbe1c2/078wbfI7slOI9Qp94D4nxHvrEx9EnwUNinIeEOA9xHsEjgPifPSII/mcE/zKPB2n67PjnIIHvSIvveDwgCNLi86Y2m9dvaqv5u03XJUiL6bJbXqsgx5edfAFD6/VO/r60sW7Ldlq1GAXXR0g0BBFFRg/u63ibop38zxKRF4A7VfWA41v3t58F/FVV25ict7Xc3FwtKOh6kdJGn3LmL95naHIir9yxsBtR9iAHd8CDc2H+HXD+v7kSQnVdI1+UHuOz/RV8fuAYnweedx+uOr4jj/cIY1L7MaBvQmCnHEefeE/rHXSr962XN71O7GCdPi3WSYz37+SNiUUi8pGq5p64PJgewHBgm4isA2qbFqpqjzmTGucRbl6Uzb+8toWCosPkZvXi6plDx8H0b8C6x/y9gJThYdtUdV3zEf1n+5t39HuONO/oE+KE7KH9mTZ6IJfPHs2E4SmMH5ZM1tD+JMT10DuwjeklgkkAPwl7FBFw5SkZ/M/bn/HwisLenQAAzrgHNv3Rfy7AgV5AVV2Df0e//xifHahgR+C5+Eh1qx19ztBkZqQP5Gtz0pkwPJnxw5MZk2o7emOiVTB3AjtyyWdbROQ5YAkwVESKgZ8ECs85rm9iHNfNH8Nv39vBF6XHGJuWHI7NRIfUsf7LXbvYC6isDezoWwzbfLbfv6NvkhjnISetP7MyBnPlKRlMGJ7MuGEpjEntZzt6Y3qYds8BiMhKVT1dRCpofVJeAFXVAZEIsKXungNocvBYLQt//i5XzBnN/7uiB8z8FYpDX8Dv5sKpt8IF/6/VRzX1jWzbV3F8J//5fv8QzpdHT97RNw3ZjB+e4j+iH9KPeNvRG9OjdPkcgKqeHnhOCWdgkTQ0uQ9fOyWdlz4q5v+cO5G0lCie+zdUqWNh5lVQ8DgsvBtSRgD+4Zzzf7WCPYf9O/vEeA9j05LJzRrMt4Zl+Hf0w5LJtB29Mb1eh0NAIuIBNgZzhU5PccuiHJ5bu5sn84v4/nkT3Q4nvBb/AD55Hlb+Ci78OQBP5e9iz+Fq/v3y6SwYm0rmkH52dYwxMarDQzxV9QGfiEj3LsCPQtlD+3PelOE8tXoXVXUNbocTXkNyYOa3/L2A8r1U1jbw8IpCFo0fytWnZpI9tL/t/I2JYcH08UcCW0TknZ5cDbSlvMU5HK2q54/r9rgdSvgt/gFoI6z8H57M38Xhyjq+e84Et6MyxkSBYC4DfSDsUUTYKWOGcMqYwTy6cifXzh/Tu8e6h2TDzG+hHy3jVd9sFk8YyyljBrsdlTEmCrS75xORJBH5LnAlMAlY5XQ1UDflLc6h+Eg1b2zZ53Yo4bf4B/h8DVxd/wrfO2e829EYY6JER4e+y4FcYBNwIfDfEYkoQs6dPJycof1ZuqKQzsph9HTH+qXzmi7hmvj3mD2wyu1wjDFRoqMEMEVVr1XVh4GvA4siFFNEeDzCzYty2FhcxurC3j2h+nJvEb+svYR4UVj5S7fDMcZEiY4SQH3TC1XtlZfLXDFnNKn9E1m64gu3Qwmbipp6HvmwkPETpiBzroX1T0JZsdthGWOiQEcJYKaIlAceFcCMptciUh6pAMMpKSGOfzgti/e2l/LZ/gq3wwmL5d4ijlbV+6/8WfR9f7H3D60XYIzpIAGoapyqDgg8UlQ1vsXriJeBCJfr5o+hb0Icj6wodDsUx5XX1PPIhzs5e9IwZmYMgkGZMDvQCzi80+3wjDEuC+Yy0F5tcP9EvpGbzrNrd/OD8ycyfECS2yE5ZtmqIsqq61tf97/o+7DhGfjNLBiYAWmT/NNJDpvc/LpPr6n+YYzpQMwnAICbTs/hqdW7eGJVEfddOMntcBxRXlPPox8Wcs7kYUxPH9j8waAMuOlt2PG/ULodSrdC0YfQUNO8zoB0GDYpkBAmNSeGpF7T8TPGYAkAgMzUflw4bSTPrNnFd84aR3Kfnv+zPLGyiPKahrbv+h01y/9o4muEI0XNCaF0OxzYCkUrT0gMo5sTwrCWiWEgxpiep+fv6RyStziHv23ay/Nrd3Pzohy3wwlJWXU9j64s5Nwpw5k2OoidsyfOXz00dSxM+krzcl8jHN3VnBCaEkTB49DQXDqalFFt9xj6DnL8z2aMcY6rCUBELgB+DcQBj6rqz92KZWbGIE7NHsLjK3fyD6dl9ejJTR5fuZOKmgbuPjvEu349cf6CckNyYOKFzct9vkBi2OZ/HAg8f7QM6lvcaJYysu0eQ18rRWFMNHAtAYhIHPAgcC5QDKwTkT+r6qduxXTrGTncuKyAv23cy2WzR7sVRkjKqut5fNVOzgv26L87PB5/jaEh2ScnhrLdzQmh6bF+eevEkDzCnwiaho/i+0BcH4hP8r9uesS1eB2fBHGJ7a/jiQvPn9WYXszNHsA8YIeqFgKIyPPApYBrCWDJhGGMG5bMwysKuXTWKER6XqnkxwJH/65U/PR4YHCW/zHxgublPh+U7Tm5x/DJ81B74oRz3d12fOdJor1EEpcI4gk8pPk10mKZnLDM08GyE5e31WaLdVuuR+DfXKt/ey1eH18e7LIWy9tcxsnLTlrXLdEQQxQZMQP6pzrapJsJYDTQsh5zMXDqiSuJSB6QB5CZGd5pCTweIW9RDve8vJGVOw6yaHxaWLfntLKqep5YuZMLpo5gyqgoumLH44HBY/yPCee3/kwVfA3+k80Ndf7nxlpoqD1hWeC5IfBZMOu0WlYHVYfbWCfQliqoz/8g8NqYaHLNyzD+HEebdDMBtJXeTzoUVNWlwFLwzwkc7qAunT2KX7y1naUrCntcAnhsZSEVtQ3c3ZMqfopAXIL/EW0zdKo2JwZaJIi2kkVn65607MTlLZOOto6h+U3XlrV62VabnWzHTb28QGO3DHP+EnU3E0AxkNHifTpQ4lIsx/WJj+OGhVn85xvb+bSkPLqOpDtwtKqOx1cVceG0EUwe2TNijnrHh2h67gUBxnTEzX/Z64DxIpItIonAVUBUzDR2zbwx9EuM45EPe055iEc/3Mmxnnb0b4xxlWsJIFBh9DvAm8BW4I+qusWteFoa2C+Bq+Zm8pdPSig5Wt35F1x2pLKOJ1bt5KLpI5k0wo7+jTHBcbVvq6qvq+oEVR2rqv/mZiwnuvH0LBT/NfXR7tGVhVTVN3JXqNf9G2Niig1utiN9cD8unjGS59bupqy6vvMvuORwZR3LVhXxlekjmTjCirgZY4JnCaADtyzKobKukefW7nY7lHY98qH/6P+7dvRvjOkiSwAdmDZ6IAvHpfLEqp3UNUTfdeGHjtWy3FvExTNGMX64Hf0bY7rGEkAn8haPZX95La9t+NLtUE7yyIc7qa5v5K6zxrkdijGmB7IE0InF44cyaUQKj3xYiEbRzSmHjtXyZH4RX7Wjf2NMN1kC6ISIkLc4h8/2H+P9z0rdDue4pSsKqbErf4wxIbAEEISLZ4xixIAkln4QHTeGHTxWy5P5u7hk5ijGDUt2OxxjTA9lCSAIifEebjw9i/zCQ2wqLnM7HJauKKS2oZE77ejfGBMCSwBB+ta8TFL6xPPwii9cjaO0wj/2f+ms0YxNs6N/Y0z3WQIIUkpSAlefmsnrm/ay53BV518Ik4c/+IK6Bh932pU/xpgQWQLogn9cmI1HhMdcKg9xoKKGp9fs4rLZo8mxo39jTIgsAXTBiIFJXDJrFC+s28PRqrqIb//hDwqpb1TuPMvG/o0xobME0EV5i3Oorm/k6dW7IrrdA+U1PL16F5fNGk320P4R3bYxpneyBNBFk0YM4IwJaSzz7qKmvjFi233ogy9o8Cl3nW1j/8YYZ1gC6IZbF+dw8Fgtf/o4MuUhDpTX8Oya3VwxezRjUu3o3xjjDEsA3bBgbCpTRw1g6YeF+HzhLw/x+/f9R//fsSt/jDEOciUBiMiVIrJFRHwikutGDKFoKg9RWFrJO9sOhHVb+8pqeHbtbr42x47+jTHOcqsHsBm4Aljh0vZDdtH0kYwe1JelYb4x7KH3d+Dz2ZU/xhjnuZIAVHWrqm53Y9tOiY/zcNPp2awrOsL63UfCso19ZTU8t3YPXz8lnYwh/cKyDWNM7Ir6cwAikiciBSJSUFoaPdU4Ab45N4MBSfE8siI8ReJ+//4OfKp8+0wb+zfGOC9sCUBE/ldENrfxuLQr7ajqUlXNVdXctLS0cIXbLf37xHPt/DG8sWUfRQcrHW275Gg1z6/dw5W5dvRvjAmPsCUAVT1HVae18XgtXNt0ww2nZZHg8fDoSmd7Ab9/fweKHf0bY8In6oeAot2wAUlcPns0LxYUc+hYrSNtlhyt5oV1e7gyN4P0wXb0b4wJD7cuA71cRIqBBcDfRORNN+Jwyi2Ls6lt8PGUQ+UhHnxvB4Ad/Rtjwsqtq4BeVdV0Ve2jqsNV9Xw34nDKuGEpnD1pGE/m76K6LrTyEMVHqvhjwR6+kZvB6EF9HYrQGGNOZkNADslbnMPhyjpeWl8cUjsPvue/r8CO/o0x4WYJwCHzsocwM2MQj35YSGM3y0MUH6nixYI9fHNuBqPs6N8YE2aWABwiIty6OIddh6p4a8u+brXx4Hs78IjY0b8xJiIsATjo/KkjyBzSj4dXFKLatV7AnsNVvFhQzFXzMhg50I7+jTHhZwnAQXEe4eZF2WzYc5SCXV0rD/G7d/1H/3cssaN/Y0xkWAJw2JWnZDC4XwIPfxD8jWG7D1Xx8vpivjUvgxEDk8IYnTHGNLME4LC+iXFctyCL/926nx0HjgX1nd+99zkej3CHjf0bYyLIEkAYXL9gDH3iPTwWRHmIXYcqeXn9l1w9L5PhA+zo3xgTOZYAwmBoch++dko6L6//ktKKjstD/O7dHcR7hDuWjI1QdMYY42cJIExuWZRDfaOP5d6idtcpOljJKx9/ydWnZjLMjv6NMRFmCSBMsof257wpw3lq9S4qaxvaXOe3gaP/28+wo39jTORZAgijvMVjKauu548Fe076bOfBSl79uJhr54+xo39jjCssAYTRKWMGkztmMI+t3ElDo6/VZ79993MS4z3cekaOS9EZY2KdJYAwu2VxDsVHqvn75ubyEIWlx/jTx19y7aljGJZiR//GGHdYAgizcycPJ2dof5a2KA/x23d3BI7+bezfGOMeSwBh5vEINy/KYdOXZeQXHuKL0mO8tuFLrl+QRVpKH7fDM8bEMLdmBPsvEdkmIhtF5FURGeRGHJFyxZzRDE1OZOmKQn77zuf0iY8jb7GN/Rtj3OVWD+BtYJqqzgA+A+53KY6ISEqI4/oFWby/vZTXPinh+gVjGJpsR//GGHe5NSXkW6radHH8aiDdjTgi6br5Y+ibEEffBDv6N8ZEh3i3AwBuBF5o70MRyQPyADIzMyMVk+MG90/k3y6fRpxHSLWjf2NMFJCuTlwSdMMi/wuMaOOjH6vqa4F1fgzkAldoEIHk5uZqQUGBs4EaY0wvJyIfqWruicvD1gNQ1XM6CegfgIuBs4PZ+RtjjHGWK0NAInIBcC9whqpWuRGDMcbEOreuAvodkAK8LSIbROQPLsVhjDExy5UegKra1FfGGOMyuxPYGGNilCUAY4yJUZYAjDEmRlkCMMaYGBW2G8HCQURKgV3d/PpQ4KCD4fR09ns0s9+iNfs9WusNv8cYVU07cWGPSgChEJGCtu6Ei1X2ezSz36I1+z1a682/hw0BGWNMjLIEYIwxMSqWEsBStwOIMvZ7NLPfojX7PVrrtb9HzJwDMMYY01os9QCMMca0YAnAGGNiVEwkABG5QES2i8gOEbnP7XjcIiIZIvKeiGwVkS0icrfbMUUDEYkTkY9F5K9ux+I2ERkkIi+JyLbAv5MFbsfkFhH5XuD/yWYReU5EktyOyWm9PgGISBzwIHAhMAX4lohMcTcq1zQA31fVycB84Nsx/Fu0dDew1e0gosSvgTdUdRIwkxj9XURkNHAXkKuq04A44Cp3o3Jer08AwDxgh6oWqmod8DxwqcsxuUJV96rq+sDrCvz/uUe7G5W7RCQduAh41O1Y3CYiA4DFwGMAqlqnqkddDcpd8UBfEYkH+gElLsfjuFhIAKOBPS3eFxPjOz0AEckCZgNrXA7Fbb8C7gF8LscRDXKAUuCJwJDYoyLS3+2g3KCqXwK/AHYDe4EyVX3L3aicFwsJQNpYFtPXvopIMvAy8F1VLXc7HreIyMXAAVX9yO1YokQ8MAd4SFVnA5VATJ4zE5HB+EcKsoFRQH8RudbdqJwXCwmgGMho8T6dXtiVC5aIJODf+T+jqq+4HY/LFgKXiEgR/qHBs0TkaXdDclUxUKyqTb3Cl/AnhFh0DrBTVUtVtR54BTjN5ZgcFwsJYB0wXkSyRSQR/4mcP7sckytERPCP725V1V+6HY/bVPV+VU1X1Sz8/y7eVdVed5QXLFXdB+wRkYmBRWcDn7oYkpt2A/NFpF/g/83Z9MIT4q7MCRxJqtogIt8B3sR/Jv9xVd3iclhuWQhcB2wSkQ2BZT9S1dfdC8lEmTuBZwIHS4XAP7ocjytUdY2IvASsx3/13Mf0wpIQVgrCGGNiVCwMARljjGmDJQBjjIlRlgCMMSZGWQIwxpgYZQnAGGNilCUAE5NE5FjgOUtErna47R+d8N7rZPvGOMUSgIl1WUCXEkCgwmxHWiUAVe11d5Ca3sESgIl1PwcWiciGQP33OBH5LxFZJyIbReRWABFZEphL4VlgU2DZn0Tko0DN+LzAsp/jryC5QUSeCSxr6m1IoO3NIrJJRL7Zou33W9ThfyZw96kxYdXr7wQ2phP3AT9Q1YsBAjvyMlWdKyJ9gFUi0lQFch4wTVV3Bt7fqKqHRaQvsE5EXlbV+0TkO6o6q41tXQHMwl9nf2jgOysCn80GpuKvU7UK/13bK53+wxrTkvUAjGntPOD6QKmMNUAqMD7w2doWO3+Au0TkE2A1/oKD4+nY6cBzqtqoqvuBD4C5LdouVlUfsAH/0JQxYWU9AGNaE+BOVX2z1UKRJfjLI7d8fw6wQFWrROR9oLMpAzsa1qlt8boR+79pIsB6ACbWVQApLd6/CdweKJuNiExoZ1KUgcCRwM5/Ev4pNpvUN33/BCuAbwbOM6Thn31rrSN/CmO6wY4yTKzbCDQEhnKW4Z8TNwtYHzgRWwpc1sb33gBuE5GNwHb8w0BNlgIbRWS9ql7TYvmrwALgE/yTEt2jqvsCCcSYiLNqoMYYE6NsCMgYY2KUJQBjjIlRlgCMMSZGWQIwxpgYZQnAGGNilCUAY4yJUZYAjDEmRv1/ZPmyyuwxTGMAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYAAAAEGCAYAAABsLkJ6AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAAAxf0lEQVR4nO3deXxU5fX48c+ZyR4yLGEnQEBRKgiCKCCioEZFECt1wbp9tS51b7UqdrHqr7UurV1tFbX96rfWHRQRkUVxoW4YNgUURYSEQAIkJBCyzZzfH3cCScgySWbmJpnzfr3mNTN3ee7JKHPmPvc+5xFVxRhjTOzxuB2AMcYYd1gCMMaYGGUJwBhjYpQlAGOMiVGWAIwxJkbFuR1Ac3Tv3l0zMzPdDsMYY9qVzz77bKeq9qi7vF0lgMzMTFasWOF2GMYY066IyHf1LbcuIGOMiVGWAIwxJkZZAjDGmBhlCcAYY2KUJQBjjIlRriYAEfmpiHwhIp+LyHMikuRmPMYYE0tcSwAi0g+4GRijqsMBLzDTrXiMMSbWuN0FFAcki0gckAJsczmeiPp0824Wfp6HP2AluI0x7nNtIJiq5orI74EtwH5gkaouqrudiFwDXAMwYMCA6AYZRlX+ANc/m01BSTmH9UjlplOGcPbIvng94nZoxpgY5WYXUFfgHGAQ0BdIFZFL6m6nqrNVdYyqjunR45CRzO3G8m92UVBSzv+ckEmcx8NPXlhF1iPvMic7hyp/wO3wjDExyM0uoNOAb1W1QFUrgTnACS7GE1FzsnPonBzPXWcN5c1bJvKPi0eTEOfh1hdXc9oj7/LSiq1UWiIwxkSRmwlgCzBORFJERIBTgfUuxhMxe8ureOuL7Uwb0YfEOC8ejzDl6D4suHkij196LKmJcdz+8hpO/cO7vPDpFksExpiocC0BqOrHwMtANrA2GMtst+KJpDfX5lFWGWDG6Ixayz0e4YxhvZl/04k8edkYuqTEc+cra5n08DL+8/EWKqosERhjIkfa06TwY8aM0fZYDfSi2R+Rt2c/7/xsEs7JTv1UlWVfFvCnpRtZvbWIvp2TuG7y4VwwJoPEOG8UIzbGdCQi8pmqjqm73O3bQDu8nMJSPty0ixmjMxr98gcQESYP7cmr15/A01ceT+/OSfzq1c+Z9PAynvlwM2WV/ihFbYyJBZYAIuy1Vc7QhnNH9Qt5HxHh5CN68Mp1J/DvH40lo2syd7/2BSc//A7/Wv6tJQJjTFhYAoggVeWV7ByOH9SN/t1Smr2/iHDikO68eO14/nP1WDLTU7n39XVMfOgdnnx/E/srLBEYY1rOEkAErc7Zw6aCfcxoxq//+ogIJxzWnReuHc/z14xjSM9O/OaN9Ux86G1mv/cNpRVVYYrYGBNL2tWUkO3NnOwcEuI8nDWiT9jaHDc4nXGD0/l0827+vGQj9y/YwOPvbuLqkwZz6biBpCbaf1JjTGjsDCBCKqoCvL56G6cf1QtfUnzY2z8usxv/vmosr1w3nmH9OvPAmxs48cG3efSdrykpqwz78YwxHY/9XIyQZV/mU1hayQ/q3PsfbscO7MYzVx7Pyi2F/GXpRh5+60tmv7eJq04cxOUTMiOSfNqTKn+ACn+AiirnUV5V+32FP+AMvFNQoPquaMV5cfB98Fn1wGsa2lZrb197/4PvDm079L+rRhRNb9t+7vQ2jRg7qBs9feGtmG8JIELmZOfSvVMCE4d0j8rxRg3oyr+uOJ41OUX8ZelG/rD4K554fxNXnjiIKyYMonOy+4mgvMpPUWklu/dVUFhawZ7SSsqq/A1/Odd5X97IuurX5VUBKqr8B95b4VXTUfzvFcdZAmgPikorWLphB5eNzyTOG91ethEZXXjy8uP4PHcPf1m6kT8t2chT73/LFRMyufLEQXRJSWj1MVSV0go/haUVFO6rdJ5LKyjcV0FhaSVFpRXsDj7X3Ka0GXctxXmEhDiP8/B6ar1ODL5OivfgS4oLrvMe2C6xxrbxNfeN85BYp62EOGeb6qKs1WM1RKB61MbB4Rv1rZMaaw5uKwh1h33Ut67mstrHalpz6sg2p13TNvXpnBz2Ni0BRMDra/Ko9CszRrfu7p/WGN6vM7MvG8MX2/bwt7e/5i9vf80/l2/m8hMGctWJg+ma6iSCQEApKatid/DLuqi0gt37anx5l1YGv9grDvx6LyqtpKKRekW+pDi6pibQNSWBHp0SOaJnWvB9PF1SnOVdU+PpkpxAcoK31pdxYvAL2cpkGxN5VgoiAs79+3L2V/h585aJTY7+jZYN24v569tfs2BtHinxXnp3Tjrwa72hbhKvR+iSHF/ry7tbSgJdUuOdL/GU4HPqwdedk+OjftZjjGlcQ6Ug7AwgzL7duY+VW4q4a8rQNvPlDzC0t49Hfziar3aU8NT737K3vIouwS/tLinxdAv+Yq9+3SUlgbTEODz2S9yYDssSQJjNzc7BI/D9Vg7+ipQjeqXx4Hkj3A7DGNMG2Ll6GAUCypyVuUw4vDu9wny13hhjws0SQBh9unk3OYX7I37vvzHGhIMlgDCak51LaoKX04f1cjsUY4xpkiWAMCmr9PPG2jymHN2HlAS7tGKMaftcTQAi0kVEXhaRDSKyXkTGuxlPayxat4O95VWu3vtvjDHN4fZP1T8DC1X1PBFJAJpfNL+NmJudQ9/OSYwblO52KMYYExLXzgBExAecBDwFoKoVqlrkVjytkV9Sxnsbd/L9Uf3svnljTLvhZhfQYKAA+JeIrBSRJ0Uk1cV4Wmzeqm34A+6WfjDGmOZyMwHEAaOBf6jqKGAfMKvuRiJyjYisEJEVBQUF0Y4xJHOycxmZ0ZnDe6a5HYoxxoTMzQSQA+So6sfB9y/jJIRaVHW2qo5R1TE9evSIaoChWJ9XzLq8YmbYvf/GmHbGtQSgqtuBrSJyZHDRqcA6t+Jpqbkrc4nzCGeP7Ot2KMYY0yxu3wV0E/Bs8A6gTcAVLsfTLP6A8urKXCYP7Um31NbX2TfGmGhyNQGo6irgkBKl7cXyr3eSX1LOjDZa+M0YYxpjI4FbYU52Dr6kOE75Xk+3QzHGmGazBNBCe8urWPjFds4e2ZfEOK/b4RhjTLNZAmihN9fmUVYZsLt/jDHtliWAFpqTnUtmegqjB3RxOxRjjGkRSwAtkFNYyoebdjFjdEabmvbRGGOawxJAC7y2ahsA59rdP8aYdswSQDOpKnOyczh+UDf6d2u3xUuNMcYSQHOtydnDNwX7mn/vvyq8cjW8dmNkAjPGmGZyeyRwuzMnO4eEOA9njejTvB1XPw9rX3ReHzkFhk4Nf3DGGNMMdgbQDBVVAeat3sbpR/XClxQf+o57C+Ctu6D/WOg5DBbcAeV7IxeoMcaEwBJAMyz7Mp/C0kp+0Nx7/xfeCRX7YPpfYdojUJwD7z4YmSCNMSZElgCaYU52Lt07JTBxSPfQd/pyIXz+Cpx0O/Q4EgaMg1GXwkd/hx1fRC5YY4xpgiWAEBWVVrB0ww7OOaYfcd4QP7ayYnjjVuh5FEz4ycHlWfdBog/m3wqBQETiNcaYplgCCNH8NXlU+ps57ePS+6B4m9P1E1ejXHRKNzj9/8HWj2DVs+EP1hhjQmAJIERzsnM4slcaR/XxhbbDlo/g0ydh7I8ho56K1yN/CANOgMW/gn27whusMcaEwBJACL7duY/sLUXMGN0vtNIPVeUw72bo3B9O+WX923g8zgXh8hJYcnd4AzbGmBBYAgjB3OwcPALfD3Xw1/t/gJ1fwrQ/QmKnhrfr+T0YfyOs/Dd892F4gjXGmBBZAmhCIKDMWZnLhMO708uX1PQOO9bB+4/AiAthyGlNb3/yHdB5AMz/KfgrWx+wMcaEyPUEICJeEVkpIvPdjqU+n27eTU7h/tDu/Q/4Yd5NkOSDM34X2gESUmHKg1CwHj58tHXBGmNMM7ieAIBbgPVuB9GQOdm5pCZ4OX1Yr6Y3/vRJyF0BZz4AqemhH2ToWXDkVGdwWNGWlgdrjDHN4GoCEJEMYCrwpJtxNKSs0s+CtXlMOboPKQlNlE0q2gJL7oXDs+Do85t/sCnBkcFv3tn8fY0xpgXcPgP4E3AH0OBoKBG5RkRWiMiKgoKCqAUGsHjdDkrKq5qu/KnqDOoC586elkwS06U/TJoFXy6ADQuav78xxjSTawlARKYB+ar6WWPbqepsVR2jqmN69OgRpegcc7Jz6Ns5iXGDm+jOWfsyfL0YTr0bugxo+QHHXe+MGn7zDqd2kDHGRJCbZwATgOkishl4HjhFRP7tYjy15JeU8d7GnXx/VD88nkZ+0e/b5RR76zcGjr+6dQf1xsPUR2DPVisWZ4yJONcSgKrepaoZqpoJzATeVtVL3IqnrnmrtuEPhFD64a27nJo/5/wNPN7WH3jgeBh1iXNH0I51rW/PGGMa4PY1gDZrTnYuIzM6c3jPtIY32rgE1rwAE291BnWFy2nBYnFvWLE4Y0zktIkEoKrLVHWa23FU27C9mHV5xcxo7N7/8r3O4K3uR8LE28IbQGq6UzF0y4ew+j/hbdsYY4LaRAJoa+Zm5xLnEc4e2bfhjd7+jdNXP/2vEJcY/iCOuRj6j4NFv4LS3eFv3xgT8ywB1OEPKHNX5jLpyJ50S02of6OcFfDxY3DcVTBgbGQCOVAsrhgWW7E4Y0z4WQKoY/nXO8kvKecHDV38rapwyj34+jq3fUZSr2HOraEr/88pL22MMWFkCaCOOdk5+JLiOOV7PevfYPmfIX+dc7tmUohzA7TGpFlOWWkrFmeMCTNLADXsLa9i4RfbOXtkXxLj6rmls+BLeO8hGP4DOPLM6ARVXSwuf50zj7AxxoSJJYAa3lybR1lloP67fwIBZ5KXhFQ4M8qDtIZOhSPPgmUPQNHW6B7bGNNhNZkARGSCiKQGX18iIo+IyMDIhxZ9c7JzyUxPYfSALoeu/Oyfzhy+Z9wPnaJbkgI4WCxu4azoH9sY0yGFcgbwD6BUREbiFG77DngmolG5ILdoPx99u4sZozMOnfZxTy4svgcGT4aRF7kSH10GOJPHbJgPX77pTgzGmA4llARQpaoKnAP8WVX/DDQyPLZ9enVlLqpwbt3Kn6rOiFz1w9l/almlz3AZfyP0+B4ssGJxxpjWCyUBlIjIXcClwBsi4gXiIxtWdKkqc7JzOD6zG/27pdRe+cVc+GohTP4FdM10Jb4DvPHO2IA9W+Ddh9yNxRjT7oWSAC4EyoErVXU70A94OKJRRdmanD18U7Dv0MJvpbud0sx9R8HYH7sTXF0DT4BjLoEP/wb5bXYiNWNMO9BkAgh+6b8CVNc72AnMjWRQ0TYnO4eEOA9njehTe8WiX8L+Qqfcg7eJGcGiKes+SExzJqFRdTsaY0w7FcpdQFcDLwOPBxf1A16NYExRVVEVYN7qbZx+VC98STV6tr55B1Y9CxNugd5HuxdgfQ4Ui/svrLJiccaYlgmlC+gGnMlbigFUdSPQwDDZ9mfZl/kUllbyg5r3/leUwuu3QPrhcNId7gXXmGMugf5jnbMUKxZnjGmBUBJAuapWVL8RkTigw/Q7zF2ZS/dOCUwc0v3gwmX3Q9F3cPZfID7JveAa4/HAtD9C2R5Y8mu3ozHGtEOhJIB3ReTnQLKIZAEvAa9HNqzoKCqtYOn6fM45ph9x3uBHkZvtzMZ17BWQOcHdAJvSaxiMvx6yn7FiccaYZgslAcwCCoC1wLXAAuCXkQwqWuavyaPCHzh477+/0in3kNoTsu51N7hQnTwLfBnOBWErFmeMaYZQ7gIKqOoTqnq+qp4XfN3qLiAR6S8i74jIehH5QkRuaW2bzTUnO4cje6UxrG+wqud//wo71sLUP0BS52iH0zKJnYLF4r5w5igwxpgQNXhvo4ispZG+flUd0cpjVwG3qWq2iKQBn4nIYlWNykzo3+7cR/aWIu6aMtQp/bDza6fY2vemw/fazOyUoRk6FY44E975HQw7Fzo3MpWlMcYENXZze0S/BVU1D8gLvi4RkfU4t5hGJQHMzc7BI/D9Uf2cSp+v3+Jc8D3r99E4fHiJwJSH4NGx8OadMPNZtyMyxrQDDXYBqep31Q+ckcAjgRE4dwV9F84gRCQTGAV8XM+6a0RkhYisKCgoCMvxAgFlzspcJhzenV6+JFj5DHz3AZz+G0jrFZZjRF3XgTWKxS10OxpjTDsQykCwq4BPgBnAecBHInJluAIQkU44I41/oqrFdder6mxVHaOqY3r0CE8Z5hXfFZJTuN+59784DxbdDZkTYdSlYWnfNeNvhB5DYcHtzlgGY4xpRCh3Ad0OjFLV/1HVy4FjgTvDcXARicf58n9WVeeEo81QzMnOITXBy+nDesGCn4G/HM7+s7uVPsMhLsGZqnLPFmfmMmOMaUQoCSAHKKnxvgRo9bRU4hTdfwpYr6qPtLa9UJVV+nljTR5nDu9DytcLnC6TSXdB+mHRCiGyMifAMRc7dzRZsThjTCMaTAAicquI3ArkAh+LyD0i8mvgI+DrMBx7Ak6J6VNEZFXwcVYY2m3U4nU7KCmv4oLhac6v/94jnK6TjiTrPkjoBG/cZsXijDENauwuoOpJX74JPqq9Fo4Dq+oHQNT7XOZk59C3cxLHf/0n2LcTfvhi26r0GQ6p3Z2BbK/fAqufg2N+6HZExpg2qMFvPlVtJ0NhQ1dQUs57G3fym5GFSPbTTqXPvse4HVZkjLoMVj7rFIs74kxI6eZ2RMaYNiaUu4B6iMjDIrJARN6ufkQjuHCbt3obcYFyfrDtIeg6yCmj0FFVF4vbXwRL7nE7GmNMGxTKReBngQ3AIOBeYDPwaQRjipg52Tn8tusbJOzZ7Nz1k5DS5D7tWu/hMO46yH4athwyxMIYE+NCSQDpqvoUUKmq76rqlcC4CMcVdhu2F0PeGmaUzYFRl8Dgk90OKTom3QW+fs7E9v4qt6MxxrQhoSSA6hKTeSIyVURGAe2u2Myrn33Hg/FPQHI3Z8RvrKguFrfjcysWZ4ypJZQE8BsR6QzcBvwMeBL4aUSjCjN/QEn+bDbDPd/imfp7SO7qdkjRNXQaDDkD3rkf9uS4HY0xpo0IpRz0fFXdo6qfq+pkVT1WVedFI7hwefutl5mQ/xo7+pwKR53jdjjRJwJnPQQagIUd+MK3MaZZGisHfYeqPiQif6WestCqenNEIwujoid/Q9evU1l4yUlchguDD9qCrplw8u2w9D746i044gy3IzLGuKyxM4DqOgIrgM/qebQbx132S1LLYfGCJ7jzvTsprYzRQmnjb4LuRzojoK1YnDExTxqb3EtEvMADqnp79EJq2JgxY3TFihXN3i9QXs7GEyawbdxgfjL2Swb5BvHHyX9kUOdBEYiyjdv8AfzvVOh2GBw2GTJPdCqhpnZ3OzJjTISIyGeqOqbu8kavAaiqH6f6Z7vmSUyk08kn029lLo+f8g92l+3mojcuYul3S90OLfoyT4RzH4dug2DVc/DS/8DDh8Gj45wy0uteg3273I7SGBMFjZ4BAIjIH4AhwEvAvurl0SzfXK2lZwAAxQsXkvuTnzLw/56h+Kj+3LrsVtbuXMsVw6/g5lE3E+fpYPWAQuGvhG2rYPP7zmPLR1DdPdZr+MGzg4EnWCkJY9qxhs4AQkkA/6pnsQYHhEVVaxJAYN8+vhp/Al1mXkjvn/+cCn8FD336EC98+QLH9z6eh056iPTk9DBH3M5UVcC2lbD5PaeraMvHULUfEGdUceZJTlIYeAIkd3E7WmNMiFqcANqS1iQAgK3X30DZ+vUc/vZSZyJ4YN4387jvw/vonNiZRyY9wsgeI8MVbvtXVQ65nznJ4Nv3YOsnzuQ5CPQZ4ZwdDDoJBoyDpM5uR2uMaUBrzgCSgB8Bw4Ck6uXt7QwAoOjVV8mbdReZL71E8tHDDyzfsHsDP33np2wv3c4dx93BzCNnHkgQpobKMshdEUwI70POJ+CvAPFAn2Ocs4PqhJCY1mRzxpjoaE0CeAmnGNwPgfuAi3Fm8bolEoE2prUJwF9UxFcnTiT9yivpeWvtwcx7yvfwiw9+wbs57zJt8DTuHn83yXHJrQ25Y6vcDzmfOslg8wfO60AliBf6joJBE52k0H+cU5LCGOOK1iSAlao6SkTWqOqI4Dy+b6nqKZEKtiGtTQAAW678EZXbtjH4zQWH/MoPaIAn1jzBo6se5fCuh/OnSX9igG9Aq44XUypKYevHTjLY/L7TfRSoAk8c9B1dOyF09EqsxrQhrUkAn6jq8SLyHnA9sB34RFUHhyGoM4E/A17gSVV9oLHtw5EACp9/nu333Mvg1+eROGRIvdssz13One/fSSAQ4Lcn/pbJAya36pgxq2Kfc2fRgYSQDeoHTzz0O9aZv9jXF5K6QKIPkny1nxM6OfMaGGNapTUJ4CrgFWAE8C+gE/ArVX28lQF5ga+ALJyJ5z8FLlLVdQ3tE44EUJmfz9cnT6L7TTfS4/rrG9wud28uty67lXW71nH10VdzwzE34PV4W3XsmFde4txZVH2X0baVTn2iBkn9iaHe5871L09IsyRiYl6zE4CIrMOZDOZ5Vf2m3o1aF9B44B5VPSP4/i4AVf1dQ/uEIwEAbP7hxQT272fw3MaHMpT7y/ndx7/jlY2vML7PeB486UG6JsVYJdFIqiyDsiIoK4byYijbE3wubuC57vo9ThdTo8S5IN1Q4kjqHDzTiHMuZosHPN6Dr2s+ai33OkX26l3ucZJO3WW1tpVDlyPO8uq4ocb7hpY1tU0o7TSyTSiadcNEpNqNAUmdIS6xRbs2lAAaG/10ETATWCQiO4HngBdUNa9FERyqH7C1xvscYGyY2m5UWlYW+Q8+SMXWrST079/gdoneRO454R5G9BjBbz/6LRfMv4BHTn6Eo3scHY0wO774JIjvDWm9W7a/qnMhutEkUU8S2bsDdm48uDxQ2fSxjHHbxa/AkNPC2mRjk8KvBlYDd4nIOOBC4GMR+Rp4TlWfaOWx60vvh5yOiMg1wDUAAwaE54JsWtZp5D/4ICWLl5B+5RVNbj9jyAyO7HYkty27jcsXXs6s42dx/hHn262ibhNxLiYnpLQuifgrIOB3uqO0+llrLKu5PBBcriGsq7l/oEZ7Ws8+gRrdYXowtrqxNri+7rIWvq/vuI1/gM3YNELtxooeR4a9yWYNBBORScAfgaNUtWXnIgfbcq0LCGDTjBl4EpPIfO4/Ie9TVFbErA9msTx3Oeccdg6/HPdLkuKSmt7RGGNc1KJicMEdjxORR0TkO5xJ4WfjdN+01qfAEBEZJCIJON1NUZtoxnf66exfuZLK/PyQ9+mS1IVHT3mU60Zex7xv5nHpm5eytWRr0zsaY0wb1GACEJH7ReQb4B/ANmCCqp6sqv9Q1Z2tPbCqVgE3Am/hzD3woqp+0dp2Q5WWlQXA3qXNqwjq9Xi5/pjr+dupfyN3by4Xzr+Q93Lei0SIxhgTUY2dAZQDU1R1jKr+XlXDPpmsqi5Q1SNU9TBV/W24229M4mGHkTB4MCWLF7do/5MyTuKFaS/Qr1M/blh6A4+uehR/wB/mKI0xJnIaTACqeq+qfhXNYKItLSuLfR9/QlVhYYv275/Wn/+b8n+cc9g5PLb6MW54+wb2lO8Jc5TGGBMZMT1CJi0rC/x+9r6zrMVtJMUl8f8m/D/uHn83n+R9woXzL2TdrgbHshljTJsR0wkgadhRxPXt0+JuoGoiwvlHnM8zU57Br34uXXApczfODVOUxhgTGY1dBB7d2COaQUaKiODLymLf8uX49+5reocmDO8+nBenvcjoXqO5+793c89/76HcXx6GSI0xJvwaGwn8h0bWKRD1aqCRkJaVxe6nn2Hf++/hmzKl1e11TerKY6c9xqOrHuWJtU+wfvd6/jjpj/Tt1DcM0RpjTPg0dhF4ciOPDvHlD5A8ahTe9PRWdwPV5PV4uXn0zfxl8l/YUryFC+ZfwPLc5WFr3xhjwiGkawAiMlxELhCRy6ofkQ4sWsTrJe2009i77F0C5eHtrpk8YDIvTHuBnik9uW7JdTy2+jECjVa/NMaY6AmlHPSvgUnAUcACYArwgaqeF/Ho6ghnKYia9n6wnK1XXUXGP/5O2uTw1/7fX7Wf+z68j/mb5tM5sTNesbLSxpjmeeikhxjbp2X1MltSDbTaecBIYKWqXiEivYAnWxRFG5V6/HF4fD5KFi+JSAJIjkvm/hPvZ3zf8azOX93q9jpKETpV7TB/izGRlp6UHvY2Q0kA+1U1ICJVIuID8oFWzwbWlkhCAmmTJ7F36VK08h4kPj78xxBh+mHTmX7Y9LC3bYwxLRHKNYAVItIFeAL4DMgGPolkUG5Iy8rCv2cPpRHoYjLGmLaoyTMAVa2eN/ExEVkI+FR1TWTDir7UCROQ5GRKFi8mdfx4t8MxxpiIC6Uc9EnVD2AA0CX4ukPxJCfTaeJEShYvQQN2p44xpuML5RrA7TVeJwHH43QFdZixANXSsrIoWbSI/atXkzJqlNvhGGNMRIXSBXR2zfci0h94KGIRuajTpJMhPp6SxUssARhjOryWFIPLAYaHO5C2wJuWRuoJ4ylZvJjmTJVpjDHtUZNnACLyVw7O0OwBjsGZLL5D8mVlkffLX1H+5ZckDR3qdjjGGBMxoVwDqHlfZBXwnKp22MI2nU45BTy/pmTRYksAxpgOrckuIFV9GqcExAJVfTYcX/4i8rCIbBCRNSIyNzjOoE2I69aNlDFjKFm8yO1QjDEmohqbD0BE5B4R2QlsAL4SkQIRuTsMx10MDFfVEcBXwF1haDNs0rKyKN/4NeWbvnU7FGOMiZjGzgB+AkwAjlPVdFXtCowFJojIT1tzUFVdpKpVwbcfARmtaS/c0k47FYCSJUtcjsQYYyKnsQRwGXCRqh74Gayqm4BLguvC5UrgzYZWisg1IrJCRFYUFBSE8bANi+/Th6QRI8I6R4AxxrQ1jSWAeFXdWXehqhYATVZLE5ElIvJ5PY9zamzzC5wLy8821I6qzlbVMao6pkePHk0dNmzSsk6jbO1aKrdti9oxjTEmmhpLABUtXAeAqp6mqsPrebwGICKXA9OAi7UN3nTvy8oCoGTJUpcjMcaYyGgsAYwUkeJ6HiXA0a05qIicCdwJTFfV0ta0FSkJmZkkHnGEdQMZYzqsxuYE9qqqr55Hmqq2tmD+34A0YLGIrBKRx1rZXkSkZWVR+tlnVO3a5XYoxhgTdi0pBdFqqnq4qvZX1WOCjx+7EUdT0k7PgkCAkrffdjsUY4wJO1cSQHuReMQRxA8YQMki6wYyxnQ8lgAaISKkZZ3Gvo8+wl9c7HY4xhgTVqHUAmrTKisrycnJoaysLCLt6+mnUzV6NBs2bsSTkhL29pOSksjIyCA+AvMQG2NMY9p9AsjJySEtLY3MzExEJOztqyrlX36JJyWFhAEDwt72rl27yMnJYdCgQWFt2xhjmtLuu4DKyspIT0+PyJc/ON1AXp8Pf8nesE8VKSKkp6dH7OzFGGMa0+4TABCxL/9qHp8PNEBg796wtx3p2I0xpiEdIgFEmic1FfF67UKwMaZDsQQQAhHB4/MRKC5pVjfQ7t27ycrKYsiQIWRlZVFYWBjBKI0xpnksAYTI6/OhAT+BfftC3ueBBx7g1FNPZePGjZx66qk88MADEYzQGGOap93fBVTTva9/wbpt4e2mOaqvj1+fPczpBvJ48BcX401Lq7XN5s2bmTZtGp9//jkAv//979m7dy+vvfYay5YtA+Dyyy9n0qRJPPjgg2GNzxhjWsrOAEIkHg+etDSnGyjE4qU7duygT58+APTp04f8/PxIhmiMMc3Soc4Afn32sIi27/X58O/ZQ6C0FG9qakSPZYwxkWZnAM3g6dQJRAjUuRsoLi6OQI2Lw9X39ffq1Yu8vDwA8vLy6NmzZ/SCNcaYJlgCaAbxevF26oS/uLhWN1CvXr3Iz89n165dlJeXM3/+fACmT5/O008/DcDTTz/NOeecU2+7xhjjhg7VBRQNHp8Pf0kJur8MSUkGID4+nrvvvpuxY8cyaNAghg4dCsCsWbO44IILeOqppxgwYAAvvfSSm6EbY0wtlgCayZuWRqUI/uJiPMEEAHDzzTdz8803H7L90qU2paQxpm2yLqBmkrg4PKmp+Iv3hHw3kDHGtEWuJgAR+ZmIqIh0dzOO5vL6fGhFBVpe7nYoxhjTYq4lABHpD2QBW9yKoaU8wYFgVhvIGNOeuXkG8EfgDqDd9aN44uPxpKQccjuoMca0J64kABGZDuSq6uoQtr1GRFaIyIqCgoIoRBcar89HoKyMQEWF26EYY0yLROwuIBFZAvSuZ9UvgJ8Dp4fSjqrOBmYDjBkzps2cLXh8Pti+nUBxMZ7u7eoShjHGABE8A1DV01R1eN0HsAkYBKwWkc1ABpAtIvUlizbLk5CAJymp0esAL730EsOGDcPj8bBixYooRmeMMU2LeheQqq5V1Z6qmqmqmUAOMFpVt0c7ltby+HwESksJVFbWu3748OHMmTOHk046KcqRGWNM0zrWQLA3Z8H2teFts/fRMKX+Ov5en4+q/Hw2ff4537/00kPKQd9zzz3hjcUYY8LI9QQQPAtolzxJSUhiIv6iIrdDMcaYZnM9AYRVA7/UI8nr86Gbvo36cY0xprWsFEQreX0+vF5PresA1eWgjTGmLbME0EqSlETv3r3JLyg4pBy0Mca0ZZYAWklESEpP565rr2Xs2LFMmzbtQDnouXPnkpGRwYcffsjUqVM544wzXI7WGGMO6ljXAFzi8fm4/uKL+cmsWXg7d6617txzz3UpKmOMaZydAYSBJyUFiYuz4nDGmHbFEkAYiAieNB+BkhK0xtzAxhjTllkCCBOvz4cGAgT27nU7FGOMCYklgDDxpKYgXi/+4hK3QzHGmJBYAggT8XjwpKURKCm2qSKNMe2CJYAw8vp8qN9PYN8+t0MxxpgmWQIII0+nTuDxECgu5umnn2bIkCEMGTKEp59+2u3QjDHmEDYOIIzE48HbqRMFW7Zw7733smLFCkSEY489lunTp9O1a1e3QzTGmAM6VAJ48JMH2bB7Q1jbHNptKHcef2eD6++8804GDhzI9ddfD8Bv/v53PKWlnDZ5Mt26dQMgKyuLhQsXctFFF4U1NmOMaQ3rAmqlmTNn8sILLxx4//K8efgDAfrVmCYyIyOD3NxcN8IzxpgGdagzgMZ+qUfKqFGjyM/PZ9u2bRQUFNC1a1dSfD7KS0tRVUQE4MCzMca0FR0qAbjlvPPO4+WXX2b79u3MnDmTrklJvLNoEVpWhiQnk5OTw6RJk9wOEwB/URGFL71EoGQv3q5d8XbpgrdLZ7xduhAXfO/x+RCPnRwa09FZAgiDmTNncvXVV7Nz507effddErxefnnvvezcsoX4nj1ZtGgRv/vd71yNsaqwkN3/+zSF//63c5uq1wt+f/0bezzOPAcHEkSNR9euBxJGzaTh7dIFiY+P7h9ljGkV1xKAiNwE3AhUAW+o6h1uxdJaw4YNo6SkhH79+tGnTx8A7rrpJsaffjoSH8/dd9994IJwtFXt3s3uf/2Lwmf/Q2D/ftLOOIPu111H4hFDCJSU4C8qOvgoLMRfVETVgffOc2VeHmXr1+MvLETLyxs8lic1tYGkUft9raSRlGRnG8a4xJUEICKTgXOAEapaLiI93YgjnNaurT0Z/Y+uuorLpk4lccgQPImJUY+natcudj31Twqfew4tK8M3ZQrdr/sxiUOGHNjG6/Ph9flgwICQ2w3s339I0qiq9f7g64rvvsNfWNh0faS4OCQhAU98PJKQ0MDDWedJSEDim1hf/YgPLo+vvZ2nnvY5cI1GDjwduG5T33Odazr1blt3GXLwbWNth6oZ2zb7CpRds2p7vN6w/1hy6wzgOuABVS0HUNV8l+KIGE9aGuTl4S8uxtOjR9SOW1VQ4HzxP/88WlGBb+pUuv/4WhIPOyws7XuSk/EkJxMfPNMJhVZW4t+z55CEEdizh0BZOVpRcfBR6TwHKirQisqDy8vKCRSXUBV8H6iss76iAqwSq+nA+j8xm04TJ4a1TbcSwBHARBH5LVAG/ExVP61vQxG5BrgGYEAzfqm6zZOQgCc5mUBxMUQhAVTm57P7qacofP4FtLKSzmdPI/3aH5M4eFDEj90UiY8nrnt34mrcGhsJWlV1IBnUSiCVFbWTzIH1wW0qK4INAAfqOAWfg+8P1HdSPbAKrb1NzX0Obl/ftg213Zw/thkbN7s2ldWyaosSBg4Me5sRSwAisgToXc+qXwSP2xUYBxwHvCgig7WeKmqqOhuYDTBmzJh29X+mx+ejascOAhUVeBISInKMyh072PXEkxS9+CLq99N5+nS6X3sNCZmZETleWyZxcUhcHKSk4HU7GGPagYglAFU9raF1InIdMCf4hf+JiASA7kBBpOJxg7c6ARSX4OmeHta2K/Py2PXEExS99DKqSufvn0P3a64hoR2dJRlj3OVWF9CrwCnAMhE5AkgAdroUS8R4EhPxJCbhLy4mLkwJoDI3l51PPEHRK3NAlS7nnkv6tdeQkJERlvaNMbHDrQTwT+CfIvI5UAFcXl/3T0fg8fmoKshHq6qc7okWqsjJZdfjj1P06qsAdPnBDLpffTXx/fqFKVJjTKxxJQGoagVwiRvHjpYzzzyTjz76iAknnMDLDz3knAW0YCxAxdat7Hz8cfa8+hoiQtfzzyP96qubdReOMcbUx0YCR8jtt99OaWkpjz/+OJKQ0OwEUPHdd+x87HH2zJuHeL10nTmT9Kt+RHzv+q6rG2NM83WoBLD9/vspXx/ectCJ3xtK75//vMH1dctB33PPPaSlpXHbbbexbNkyIHgxeNcu1O9HvI3fn1L+7bfseuwx9rw+H4mPp9slF9Ptyh8R36vdj5UzxrQxNga/leqWg37xxRc5//zza23j9flAFX9JwxPGl2/aRO7td7Bp6jSK31pEt8su4/Ali+l111325W+MiYgOdQbQ2C/1SKmvHHTdAWuSnIzExTmDwrp0qbUuUFZG1e5CNl11FZKURLcr/of0K66I+KApY4zpUAnALXXLQdclIk43UGERGgggHo/zxZ9fgL94D1peRvpVP6LbFVe06EKxMca0hCWAMKhbDro+Hp8Pdu+maucutGw//uJixOMhrkcP4kToedttUY7aGBPrLAGEQX3loCdOnMiGDRvYu3cvGRkZPPnkk0waOJCq/B0Hv/jT053yBbt3u/wXGGNikSWAMKlbDvr9998/ZJuqoiK0opK4bl1bNSjMGGPCwb6FoiiuzgVgY4xxk90GaowxMapDJID2XEaoPcdujGnf2n0CSEpKYteuXe3yi1RV2bVrF0lJSW6HYoyJQe3+GkBGRgY5OTkUFLTPqQSSkpLIsFLOxhgXtPsEEB8fz6BB7k97aIwx7U277wIyxhjTMpYAjDEmRlkCMMaYGCXt6e4ZESkAvmvh7t3pgPMOt4J9HgfZZ1GbfR61dYTPY6Cq9qi7sF0lgNYQkRWqOsbtONoK+zwOss+iNvs8auvIn4d1ARljTIyyBGCMMTEqlhLAbLcDaGPs8zjIPova7POorcN+HjFzDcAYY0xtsXQGYIwxpgZLAMYYE6NiIgGIyJki8qWIfC0is9yOxy0i0l9E3hGR9SLyhYjc4nZMbYGIeEVkpYjMdzsWt4lIFxF5WUQ2BP8/Ge92TG4RkZ8G/518LiLPiUiHK9vb4ROAiHiBR4EpwFHARSJylLtRuaYKuE1VvweMA26I4c+ipluA9W4H0Ub8GVioqkOBkcTo5yIi/YCbgTGqOhzwAjPdjSr8OnwCAI4HvlbVTapaATwPnONyTK5Q1TxVzQ6+LsH5x93P3ajcJSIZwFTgSbdjcZuI+ICTgKcAVLVCVYtcDcpdcUCyiMQBKcA2l+MJu1hIAP2ArTXe5xDjX3oAIpIJjAI+djkUt/0JuAMIuBxHWzAYKAD+FewSe1JEUt0Oyg2qmgv8HtgC5AF7VHWRu1GFXywkAKlnWUzf+yoinYBXgJ+oarHb8bhFRKYB+ar6mduxtBFxwGjgH6o6CtgHxOQ1MxHpitNTMAjoC6SKyCXuRhV+sZAAcoD+Nd5n0AFP5UIlIvE4X/7Pquoct+Nx2QRguohsxukaPEVE/u1uSK7KAXJUtfqs8GWchBCLTgO+VdUCVa0E5gAnuBxT2MVCAvgUGCIig0QkAedCzjyXY3KFiAhO/+56VX3E7Xjcpqp3qWqGqmbi/H/xtqp2uF95oVLV7cBWETkyuOhUYJ2LIblpCzBORFKC/25OpQNeEG/3U0I2RVWrRORG4C2cK/n/VNUvXA7LLROAS4G1IrIquOznqrrAvZBMG3MT8Gzwx9Im4AqX43GFqn4sIi8D2Th3z62kA5aEsFIQxhgTo2KhC8gYY0w9LAEYY0yMsgRgjDExyhKAMcbEKEsAxhgToywBmJgkInuDz5ki8sMwt/3zOu//G872jQkXSwAm1mUCzUoAwQqzjamVAFS1w40gNR2DJQAT6x4AJorIqmD9d6+IPCwin4rIGhG5FkBEJgXnUvgPsDa47FUR+SxYM/6a4LIHcCpIrhKRZ4PLqs82JNj25yKyVkQurNH2shp1+J8Njj41JqI6/EhgY5owC/iZqk4DCH6R71HV40QkEVguItVVII8Hhqvqt8H3V6rqbhFJBj4VkVdUdZaI3Kiqx9RzrBnAMTh19rsH93kvuG4UMAynTtVynFHbH4T7jzWmJjsDMKa204HLgqUyPgbSgSHBdZ/U+PIHuFlEVgMf4RQcHELjTgSeU1W/qu4A3gWOq9F2jqoGgFU4XVPGRJSdARhTmwA3qepbtRaKTMIpj1zz/WnAeFUtFZFlQFNTBjbWrVNe47Uf+7dposDOAEysKwHSarx/C7guWDYbETmigUlROgOFwS//oThTbFarrN6/jveAC4PXGXrgzL71SVj+CmNawH5lmFi3BqgKduX8L86cuJlAdvBCbAHw/Xr2Wwj8WETWAF/idANVmw2sEZFsVb24xvK5wHhgNc6kRHeo6vZgAjEm6qwaqDHGxCjrAjLGmBhlCcAYY2KUJQBjjIlRlgCMMSZGWQIwxpgYZQnAGGNilCUAY4yJUf8fOWTtNfuLx14AAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEGCAYAAAB7DNKzAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAAAl9ElEQVR4nO3dd3yV9d3/8dcni7BnmBlskCkzoN4urKLiqBOI9nbcVXs7umyrvdu7dlj91Vpvb7WtVi1VhrsOHKh1UJUwgiJLEMEMVsKeCST5/P7I4TZScgjhHK6Tc97PxyMPc13knPPOEfLONb7fr7k7IiIidUkKOoCIiMQ2FYWIiISlohARkbBUFCIiEpaKQkREwkoJOkA0dOjQwbt37x50DBGRRqWgoGCTu2ccvD8ui6J79+4sWLAg6BgiIo2KmRUear9OPYmISFgqChERCUtFISIiYakoREQkLBWFiIiEpaIQEZGwVBQiIhKWiqKWt5Zt5Ik5X7KzfH/QUUREYkZcDrhrqDeXbuDZghLufv0zLji+K3m5OQzq1jroWCIigbJ4XLho5MiR3tCR2Z+WbGNqfiEvL1pH+f5qjs9qQ15uNucN7Up6anKEk4qIxA4zK3D3kf+yX0VxaNv37ueFhSVMm1vEqtJdtEpP4ZIRWeSNyaZXRosIJRURiR0qigZyd+au2cLU/EJmLd3A/irnhF7tycvN4cyBnUhN1mUeEYkPdRWFrlEchpkxpmd7xvRsT9nOCp5ZUMz0uUXcOH0hGS2bcPnILCblZtOtTdOgo4qIRIWOKBqgqtqZvbKMqfmFvLOiFANO79+RvNwcTu6bQXKSRe21RUSiRUcUEZScZJzWvyOn9e9IydY9PDWvmKfmF/P28vlktm3KpNHZXD4qiw4tmgQdVUTkqOmIIkL2VVbz1rKNTM0vZM7qzaQmG+MHdSEvN5vcHu0w01GGiMQ2Xcw+hlaV7mL63CKeKyhmR3klvTu2IC83m4uGZ9K6aWpguUREwlFRBKB8fxWvLFrH1LlFLCreRtPUZM4f2pW8MdkMyWwTdDwRka9RUQRsydrtTJtbyIsfr2Pv/iqGZLYmLzeb84d2o2maBvKJSPBUFDFiR/l+Xvx4LVPzC1m5cRct01O4eHgmebnZ9OnUMuh4IpLAVBQxxt1ZULiVqfmFvL54A/uqqsnt0Y68MTmMH9iZtBQN5BORY0tFEcM276rg2YISps8tomjLHjq0SOPSkVlMHp1NVrtmQccTkQShomgEqqudf67axNT8Qv6xfCMOnNo3g7zcHE7r31ED+UQkqlQUjcz67XuZMa+Yp+YVUbqzgq6t02sG8o3OomPL9KDjiUgcUlE0UvurqvnH8o1MzS/ig1WbSEkyzhrYmbzcbMb2aq+BfCISMY12Cg8zaw78EdgHvOfu0wKOdEylJicxflAXxg/qwppNu5k+t5BnC0p4dfF6emY0Jy83h0uGZ9K6mQbyiUh0BHJEYWaPAxOAUncfVGv/eOB+IBl41N3vNrMrgW3u/oqZPe3ulx/u+ePpiOJQyvdX8dri9UzNL2Rh0TaapCRx3tCu5OVmc3xWGx1liEiDxNoRxRTgQeCJAzvMLBl4CPgGUALMN7OXgUxgcejLqo5tzNiUnprMRcMzuWh4JsvW7QgN5FvLcwUlDOzaiivG5HD+0K40bxLzB4wi0ggEdo3CzLoDMw8cUZjZWOAOdz8rtH176EtLgK3uPtPMnnL3iXU833XAdQDZ2dkjCgsLo/0txJRdFZX/N5Dvsw07adkkhW8O70Zebg79Omsgn4gcXsxdzD5EUVwCjHf3/whtXwnkAj+h5uijHPigPtco4v3UUzjuzsKibUzLL2Tm4vXsq6xmVPe25OXmcPbgzjRJ0XQhInJosXbq6VAOdWLd3X03cPWxDtNYmRkjctoyIqctP58wgOcKSpg2t5DvPf0Jv5qZxqUjM5k8Opuc9s2DjioijUQsFUUJkFVrOxNYF1CWuNC2eRrfPrkn157Ug4++2MzU/EIe/ecaHn5/NSf3zSAvN5tx/TuSonW/RSSMWCqK+UAfM+sBrAUmApODjRQfkpKMk/p04KQ+HdiwvZyn5xczY14R1z9ZQJfW6Uwclc3E0Vl0aqWBfCLyr4K6PXYGcCrQAdgI/MLdHzOzc4D/oeb22Mfd/c6GPH8iX6Oor8qqat75rJSpc4uYvbKM5CTjG8d1Im9MNif26kCSpgsRSTgxdzE7mlQUR6Zw826mzyvi2QUlbNm9j+7tm9UM5BuRSdvmaUHHE5FjREUhh1VRWcUbSzYwNb+Q+V9uJS0liQmDu5A3Jpvh2W01kE8kzqko5Iis2LCTaXMLeWHhWnZVVNK/c0uuGJPDhcO60UID+UTikopCGmR3RSUvL1rH1PxClq7bQfO0ZC4cVjOQb0DXVkHHE5EIUlHIUXF3FpVsZ2p+Ia8sWkdFZTXDs9twxZgczhnchfRUDeQTaexUFBIx2/bs4/mFa5k2t5DVZbtp0yyVS0dkMjk3hx4dNJBPpLFSUUjEuTtzVm9mWn4Rs5ZuoLLaOal3B/JyszljQCdSNZBPpFFpDFN4SCNjZpzQqwMn9OpA6Y5ynllQzIx5xXxn2kI6tmzCxNHZTByVRdc2TYOOKiJHQUcUElFV1c57K0qZml/IeyvLMGDccZ3Iy83m5D4ZGsgnEsN0RCHHRHKSMe64Tow7rhPFW/YwY14Rzywo5q1lG8lq15TJo3O4bGQm7Vs0CTqqiNSTjigk6vZVVjNrac1AvrlrtpCWnMTZgzuTl5vDqO4ayCcSK3QxW2LCqtKdTM0v4vmFJewsr6Rvpxbk5ebwzeHdaJWudb9FgqSikJiyd18Vryxax9S5hXxasp2mqclccHxXrhiTw6BurYOOJ5KQVBQSsz4t2ca0/CJeWrSW8v3VDM1qQ15uNucN6UrTNA3kEzlWVBQS87bv3c/fF5YwbW4Rn5fuolV6ChePyCQvN4feHVsEHU8k7qkopNFwd+at2cLUuUW8sWQ9+6ucMT3bccWYHM4c0Jm0FA3kE4kGFYU0Spt2VfDMgmKmzy2iZOteOrRowuWjMpk0OpvMts2CjicSV1QU0qhVVzvvf17GtPxC3vmsFAdO69eRK8Zkc0rfjiRrIJ/IUVNRSNxYu20vT80r4qn5xZTtrKBbm6ZMzs3mspFZZLTUQD6RhlJRSNzZX1XNW8s2MjW/kI++2ExqsnHmwM5ckZvDmJ7tNJBP5AhpCg+JO6nJSZwzuAvnDO7CF2W7mD63iOcKSnj10/X0ymhOXm4OF4/IpHVTDeQTORo6opC4Ur6/ipmfrmdqfiGfFG8jPTWJ84bUDOQbmtUm6HgiMU2nniThLFm7nWlzi3jpk7Xs2VfF4G6tycvN5vzju9IsTQfTIgdTUUjC2lm+nxc/XsvU/CJWbNxJyyYpXDS8G3ljcujbqWXQ8URihopCEp67U1C4lan5hby2eAP7qqoZ3aMdebnZjB/UmSYpmi5EEpuKQqSWzbsqeK6gZrqQoi17aN88jctGZTF5dDZZ7TSQTxKTikLkEKqrnQ9WbWJqfiFvL9+IA6f0zSAvN4fT+2sgnyQWFYXIYazfvpen5hXz1PwiNu6ooGvrdCaNzubyUVl0bJUedDyRqFNRiNTT/qpq/rG8lGlzC/nn55tISTLOHNiJK3JzGNurvQbySdzSgDuRekpNTmL8oM6MH9SZLzftZvq8Ip5dUMxrizcwqntbfnRWf0b3aBd0TJFjplEcUZjZhcC5QEfgIXd/M9zX64hCIq18fxXPFpTwwD8+p3RnBaf2y+DWM/tpNT6JK3UdUUR9Yn8ze9zMSs1syUH7x5vZCjNbZWa3hXsOd3/R3b8NXAVcHsW4IoeUnprMlWNyeP9Hp3H72f35pHgbEx74gBunL+SLsl1BxxOJqqgfUZjZycAu4Al3HxTalwysBL4BlADzgUlAMnDXQU9xjbuXhh53LzDN3ReGe00dUUi07Sjfz6OzV/PoB2uoqKzmkuGZ3HJGH7q1aRp0NJEGC/Ritpl1B2bWKoqxwB3uflZo+3YAdz+4JA483oC7gbfc/e3DvZ6KQo6VTbsq+OO7XzA1vxCAvDHZ3Hhabzq00HTn0vgEduqpDt2A4lrbJaF9dbkZOAO4xMxuONQXmNl1ZrbAzBaUlZVFLqlIGB1aNOG/zxvAuz86lYuGd+OJOYWc/Lt3uffNFewo3x90PJGICOqI4lLgLHf/j9D2lcBod785Eq+nIwoJyhdlu7jvrZXM/HQ9rZum8p1Te/HvY7vTNE3Tg0jsi7UjihIgq9Z2JrAuoCwiEdMrowUPTh7OzJtPYnh2G+5+/TNOvuddnpzzJfsqq4OOJ9IgQRXFfKCPmfUwszRgIvByQFlEIm5Qt9b89erRPHvDWHq0b87PX1rKuD+8xwsLS6iqjv1b0kVqO2xRhM7732hmbRvyAmY2A5gD9DOzEjO71t0rgZuAWcBy4Bl3X9qQ5xeJZaO6t+Pp68cw5epRtEpP5QfPLOLs+2cza+kGGsMYJhGoxzUKM+sNXE3N+IUFwF+BNz2G/5brGoXEoupq5/UlG7j3rRWsLtvN0Kw2/PisfpzYu0PQ0USACNwea2ZJwATgT0A18Dhwv7tviWTQSFBRSCyrrKrmhY/Xcv/bn7N2215O6NWeH53Vj2HZDTpoF4mYo7qYbWZDgHuBe4DngUuAHcA7kQwpkghSkpO4bGQW79x6Cr84bwArNuzkm3/8iG8/sYAVG3YGHU/kX9Tn1FMBsA14DHje3Stq/dkL7n5RVBM2gI4opDHZXVHJXz9cw8OzV7OropILj+/G987oQ0775kFHkwTT4FNPZtbT3VcftK+Hu6+JcMaIUVFIY7Rtzz7+/P5qpny0hsoq5/JRWdwyrg+dtBaGHCNHUxQL3X34IZ5sRIQzRoyKQhqz0h3lPPjuKmbMKyLJjKtO6M4Np/SibfO0oKNJnDvi9SjMrD8wEGhtZrVPL7UC9CuOSJR0bJXOry4YxLf/rSf3vb2SR/65mulzi/j2yT255qQetGiiZWTk2KrziMLMLgAuBM7n64PhdgJPuftHUU/XQDqikHiycuNO7n1zBbOWbqR98zRuGdeHb43N0Up7EnFHc+pprLvPiVqyKFBRSDxaVLyN3836jA9XbebMAZ2497KhtExPDTqWxJEjLgozewCos0Xc/ZbIxYssFYXEK3fn8Q+/5LevLSenfTMevmIEfTq1DDqWxImGrJmtn7QiMcbMuPakHgzs2oqbpi/kwoc+5J5Lh3LO4C5BR5M41ijWzD5SOqKQRLBheznfmVbAx0XbuP7knvzorH6kJAc1z6fEg4YcURx4YAbwE2AAte52cvfTI5pQRI5I59bpPH3dWH49cxkPz17N4rXbeWDSMNprdT2JsPr8+jGNmhleewC/BL6kZppwEQlYWkoSv75wEPdcMoQFhVs574EPWFS8LehYEmfqUxTt3f0xYL+7v+/u1wBjopxLRI7ApSOzeOE7J2BmXPrnOTw9vyjoSBJH6lMUBxb+XW9m55rZMGpWpBORGDKoW2tm3nwSuT3b8ZPnF3P7C4upqKwKOpbEgfoUxW/MrDXwQ+BW4FHg+1FNJSIN0rZ5GlOuHs2Np/VixrwiLns4n3Xb9gYdSxo53fUkEqdmLd3AD59ZRJOUJB6YPIwTemmBJAmvwetRmFmGmf3UzB4xs8cPfEQnpohEylkDO/PSTSfStnkaVzw6l0dmf6HlV6VB6nPq6SWgNfA28GqtDxGJcb0yWvDijScyflBnfvvaZ9w0/WN2V1QGHUsamfpMQ9nM3X8S9SQiEhUtmqTw0OThPDJ7Nf/vjc9YuXEnD185gp4ZLYKOJo1EfY4oZprZOVFPIiJRY2Zcf0ovnrw2l82793HBgx/y5tINQceSRqI+RfFdasqi3Mx2mNlOM9sR7WAiEnkn9u7AKzefRM+M5lz3ZAH3vrmCqmpdt5DwDlsU7t7S3ZPcPd3dW4W2Wx2LcCISed3aNOXp68cycVQWD7yziqunzGfbnn1Bx5IYVp+7nszMrjCzn4e2s8xsdPSjiUi0pKcmc/fFQ7jrosHkf7GZCQ98wJK124OOJTGqPqee/giMBSaHtncBD0UtkYgcM5NGZ/PMDWOpqnYu/tNHPF9QEnQkiUH1KYpcd78RKAdw962AVnkXiRPHZ7XhlZtPYnh2W3747CL++6Ul7KusDjqWxJB6zfVkZsmEVrsLTTuuv0UicaRDiyY8ee1orj+5J0/MKWTSX/LZuKM86FgSI+pTFP8L/B3oaGZ3Ah8Av41qKhE55lKSk7j9nON4aPJwlq/fwYQHPmDemi1Bx5IYUJ+7nqYBPwbuAtYDF7r7s9EOJiLBOHdIF1688URaNklh8l/ymfLhGk39keDqLAozyzWzRWa2C/gr8K67P+juy49dPBEJQt9OLXnxphM5rX9H7nhlGd9/+hP27tOU5Ykq3BHFQ9RMK94e+ANw3zFJdAhm1tzMCsxsQlAZRBJNq/RUHr5iBLee2ZeXFq3jm3/8kMLNu4OOJQEIVxRJ7v6Wu1eETjVlHOmTh2aaLTWzJQftH29mK8xslZndVo+n+gnwzJG+vogcnaQk46bT+zDl6tFs2FHOeQ98wLuflQYdS46xcEXRxswuOvBxiO36mAKMr70jdAfVQ8DZwABgkpkNMLPBZjbzoI+OZnYGsAzYeMTfnYhExCl9M3jlppPIbNuMa/42n/vf/pxqTf2RMOpcuMjM/hrmcR5aO/vwL2DWHZjp7oNC22OBO9z9rND27aEnvKuOx98JNKemVPYC33T3f7k918yuA64DyM7OHlFYWFifeCJyBMr3V/HTvy/mhYVrOXdIFx6YOIykJAs6lkRIXQsX1TnNuLtfHaUs3YDiWtslQG6YHP8FYGZXAZsOVRKhr3sEeARqVriLVFgR+Up6ajL3XjqUvp1acvfrn5HZpim3n3Nc0LEkyuqzHkWkHerXj8P+YHf3KZGPIiJHysy44ZRerNu2l4dnr6ZHh+ZMHJ0ddCyJoiCKogTIqrWdCawLIIeIHIX/njCALzfv4WcvLiG7XTNO6K01ueNV2AF3ZpZkZidE+DXnA33MrIeZpQETgZcj/BoiEmUpyUk8OHkYPTo054apBawu2xV0JImSsEURuh5wb0Of3MxmAHOAfmZWYmbXunslcBMwC1gOPOPuSxv6GiISnFbpqTx+1ShSk5O4Zsp8tu7WuhbxqD5zPb1pZheb2RHf2uDuk9y9i7ununumuz8W2v+au/d1917ufucRpxaRmJHVrhmPfGsk67aXc8PUAs08G4fqUxQ/AJ4F9mkpVBE5lBE5bbnnkiHMXbOFn/59seaGijOHvZjt7i2PRRARadwuOL4bazbt5n/e/pyeGc35z1N7Bx1JIkRLoYpIxHx3XB/OH9qV372xgjeWrA86jkSIlkIVkYgxM353yRCGZ7fhe09/wqcl24KOJBGgpVBFJKLSU5N55Fsj6dCiCf/xtwWs37436EhylLQUqohEXIcWTXj8qlHs2VfFtVMWsLuiMuhIchS0FKqIREXfTi15cPIwPtuwg+8+9TFVmm220dJSqCISNaf268gd5w/k7eWl3P26FsdsrOq8PdbMWrn7DjNrB5QCM2r9WTt316rrInJY3xrbndVlu/nLP9fQM6MFkzSBYKMTbhzFdGACUMDXZ3e10HbPKOYSkTjys3OP48vNu/l5aALBEzWBYKNS56knd58QmrbjFHfvWeujh7urJESk3lKSk3hg0jB6ZbTghqkFrCrVBIKNyeEmBXRqLmSLiByVlumpPHbVSJqk1EwguEUTCDYa9bnrKd/MRkU9iYjEvcy2NRMIbthRzg1PFlBRWRV0JKmH+hTFacAcM/vCzD41s8Vm9mm0g4lIfBqe3ZZ7Lx3KvC+3cPsLmkCwMQg7KWDoGsUNQOGxiSMiieC8oV1ZXbab+95eSa+MFtx4miYQjGVhi8Ld3czuc/cRxyqQiCSGW8b1Zs2mXdwzawXd2zfn3CFdgo4kddA1ChEJhJlx98VDGJHTlh888wmfFG8LOpLUQdcoRCQw6anJPHLlCDq2qplAcO02TSAYi+pTFGcDvYDTgfOoGYR3XjRDiUjiaN+iCY//+ygq9ldx7ZT57NIEgjGnPnM9Fbp7IbCXmhHZBz5ERCKiT6eWPJQ3nM9Ld3HLDE0gGGvqs8Ld+Wb2ObAGeB/4Eng9yrlEJMGc3DeDO84fyDuflXLnq5pAMJbU59TTr4ExwEp37wGMAz6MaioRSUhXjsnh6hO78/iHa5iar7vyY0W9Fi5y981Akpklufu7wPHRjSUiiepn5w7gtH4Z/OLlpcxeWRZ0HKF+RbHNzFoAs4FpZnY/oKtNIhIVyUnGA5OH06djC26ctpDPN+4MOlLCq09RXADsAb4PvAF8ge56EpEoatEkhceuGkWT1GSu+dt8Nu+qCDpSQqvPXU+73b3a3SuBV4EHQqeiRESiplubpjz67yMp3VHB9ZpAMFB1FoWZjTGz98zsBTMbZmZLgCXARjMbf+wiikiiOj6rDfdeNpQFhVu57XlNIBiUcHM9PQj8FGgNvAOc7e75ZtafmmVR3zgG+UQkwU0Y0pU1Zbu5962V9OjQnFvG9Qk6UsIJVxQp7v4mgJn9yt3zAdz9s5pJZUVEjo2bTu/Nmk27+UOoLM4b2jXoSAklXFFU1/r84AlYjtnxn5klUTOWoxWwwN3/dqxeW0Rig5lx18WDKd66h1ufXURm26YMy24bdKyEEe5i9lAz22FmO4Ehoc8PbA+uz5Ob2eNmVhq6vlF7/3gzW2Fmq8zstsM8zQVAN2A/UFKf1xWR+NMkJZmHrxxJp1bpfPuJBZRs3RN0pIRRZ1G4e7K7t3L3lu6eEvr8wHZqPZ9/CvC1C99mlgw8RM1kgwOASWY2wMwGm9nMgz46Av2AOe7+A+A7DfkmRSQ+tGuexuNXjaSispprpyxgZ/n+oCMlhPqMo2gwd58NbDlo92hglbuvdvd9wFPABe6+2N0nHPRRSs1RxNbQY3V/nEiC692xJX/KG8Gqsl3cPONjKquqD/8gOSpRLYo6dAOKa22XhPbV5QXgLDN7gJrR4YdkZteZ2QIzW1BWpmH/IvHspD4d+NUFA3lvRRn3vb0y6DhxL+xSqFFyqFum6rw47u57gGsP96Tu/gjwCMDIkSN1s7VInMvLzaGgcCuPzF7NJSOy6NGhedCR4lYQRxQlQFat7UxgXQA5RKSRu+3s/jRJSeY3M5cFHSWuBVEU84E+ZtbDzNKAicDLAeQQkUauY8t0bj69N//4rJT3VpQGHSduRbUozGwGMAfoZ2YlZnZtaM6om4BZwHLgGXdfGs0cIhK/rj6xBz06NOdXM5exr1IXtqMh2nc9TXL3Lu6e6u6Z7v5YaP9r7t7X3Xu5+53RzCAi8S0tJYmfTziO1WW7eWLOl0HHiUtBnHoSEYmo0/t34tR+Gdz/9ueU7dSU5JGmohCRuPDzCQPYu7+K389aEXSUuKOiEJG40CujBVef2J1nCopZXLI96DhxRUUhInHj5nF9aN88jTteWaq1KyJIRSEicaNVeio/Pqs/BYVbeekTDc+KFBWFiMSVS0ZkMiSzNXe9vpzdFZVBx4kLKgoRiStJScYvzhvIxh0V/PG9VUHHiQsqChGJOyNy2vLNYd34yz/XULRZ61YcLRWFiMSl287uT0qS8ZtXNQ/U0VJRiEhc6tQqnZtO782byzbyz8+19MDRUFGISNy69qQe5LRvxi9fWcZ+LXDUYCoKEYlbTVKS+dm5A1hVuosn5xQGHafRUlGISFw747iO/FufDtz39ko279I8UA2hohCRuGZm/OK8AezdV8Xv39SyqQ2hohCRuNe7Y0u+NbY7T80vYslazQN1pFQUIpIQvntGH9o1S+OXmgfqiKkoRCQhtG6ayq1n9WP+l1t55dP1QcdpVFQUIpIwLhuZxcCurbjrteXs2ad5oOpLRSEiCSM5ybjj/IGs317On9/7Iug4jYaKQkQSyqju7Th/aFcenr2a4i2aB6o+VBQiknBuP6c/SWb89rXlQUdpFFQUIpJwurRuyn+e2ovXl2zgoy82BR0n5qkoRCQhffvknmS2bcovX15GpeaBCktFISIJKT01mZ+dexwrNu5k+ryioOPENBWFiCSsswZ25oRe7bn3zZVs3b0v6DgxS0UhIgmrZh6ogeyqqOQPb2keqLqoKEQkofXr3JIrcrOZNreQ5et3BB0nJqkoRCThff8bfWndNFXzQNVBRSEiCa9NszR+cGY/8ldv4fUlG4KOE3NUFCIiwOTR2fTv3JI7X11O+f6qoOPElJgvCjPLNrOXzexxM7st6DwiEp8OzAO1dtteHn5/ddBxYkpUiyL0w73UzJYctH+8ma0ws1X1+OHfF3jV3a8BBkQtrIgkvDE923Pu4C786f1VrN22N+g4MSPaRxRTgPG1d5hZMvAQcDY1P/gnmdkAMxtsZjMP+ugIfAxMNLN3gHejnFdEEtzt5/THHe7SPFD/J6pF4e6zgS0H7R4NrHL31e6+D3gKuMDdF7v7hIM+SoGrgV+4++nAuXW9lpldZ2YLzGxBWVlZtL4lEYlzmW2bccMpvZj56Xrmrt4cdJyYEMQ1im5Aca3tktC+urwB3GJmfwa+rOuL3P0Rdx/p7iMzMjIiElREEtMNp/Sia+t07nhlGVXVul02iKKwQ+yr8/+Euy9x90vc/QZ3vzWKuUREAGialsxPzz2O5et38NR8zQMVRFGUAFm1tjOBdQHkEBGp07mDu5Dbox2/n7WC7Xv2Bx0nUEEUxXygj5n1MLM0YCLwcgA5RETqdGAeqO1793Pf24k9D1S0b4+dAcwB+plZiZld6+6VwE3ALGA58Iy7L41mDhGRhhjQtRWTRmfzZH4hKzfuDDpOYKJ919Mkd+/i7qnununuj4X2v+bufd29l7vfGc0MIiJH44dn9qN5WjK/emVZws4DFfMjs0VEgtSueRo/+EZfPli1iTeXbQw6TiBUFCIih3HFmBz6dmrBb15dlpDzQKkoREQOIyU5iTvOG0jxlr089sGaoOMccyoKEZF6OKF3B8YP7MxD765iw/byoOMcUyoKEZF6+q9zj6Oy2rn79cSaB0pFISJST1ntmnH9yT158ZN1FBQePI1d/FJRiIgcge+c2osurdO54+VlVCfIPFAqChGRI9AsLYXbzu7P4rXbebag+PAPiAMqChGRI3T+0K6M6t6We2atYEd5/M8DpaIQETlCB+aB2rx7H//79udBx4k6FYWISAMM6taaiaOymPLRl6wq3RV0nKhSUYiINNCtZ/ajaVoyv54Z3/NApQQdQESksWrfognfO6Mvv565jHF/eJ9kO9S6bMfWvZcNZUhmm4g+p4pCROQofGtsDqU7yineuifoKAA0TU2O+HOqKEREjkJqchK3n3Nc0DGiStcoREQkLBWFiIiEpaIQEZGwVBQiIhKWikJERMJSUYiISFgqChERCUtFISIiYVk8zk9iZmVAYQMf3gHYFME4jZ3ej6/ovfg6vR9fFw/vR467Zxy8My6L4miY2QJ3Hxl0jlih9+Mrei++Tu/H18Xz+6FTTyIiEpaKQkREwlJR/KtHgg4QY/R+fEXvxdfp/fi6uH0/dI1CRETC0hGFiIiEpaIQEZGwVBS1mNl4M1thZqvM7Lag8wTFzLLM7F0zW25mS83su0FnigVmlmxmH5vZzKCzBM3M2pjZc2b2WejvydigMwXFzL4f+neyxMxmmFl60JkiTUURYmbJwEPA2cAAYJKZDQg2VWAqgR+6+3HAGODGBH4vavsusDzoEDHifuANd+8PDCVB3xcz6wbcAox090FAMjAx2FSRp6L4ymhglbuvdvd9wFPABQFnCoS7r3f3haHPd1LzQ6BbsKmCZWaZwLnAo0FnCZqZtQJOBh4DcPd97r4t0FDBSgGamlkK0AxYF3CeiFNRfKUbUFxru4QE/+EIYGbdgWHA3ICjBO1/gB8D1QHniAU9gTLgr6FTcY+aWfOgQwXB3dcCvweKgPXAdnd/M9hUkaei+IodYl9C3ztsZi2A54HvufuOoPMExcwmAKXuXhB0lhiRAgwH/uTuw4DdQEJe0zOzttSceegBdAWam9kVwaaKPBXFV0qArFrbmcThIWR9mVkqNSUxzd1fCDpPwE4EzjezL6k5JXm6mU0NNlKgSoASdz9wlPkcNcWRiM4A1rh7mbvvB14ATgg4U8SpKL4yH+hjZj3MLI2aC1IvB5wpEGZm1Jx/Xu7ufwg6T9Dc/XZ3z3T37tT8vXjH3ePut8b6cvcNQLGZ9QvtGgcsCzBSkIqAMWbWLPTvZhxxeGE/JegAscLdK83sJmAWNXcuPO7uSwOOFZQTgSuBxWb2SWjfT939teAiSYy5GZgW+qVqNXB1wHkC4e5zzew5YCE1dwt+TBxO5aEpPEREJCydehIRkbBUFCIiEpaKQkREwlJRiIhIWCoKEREJS0UhEoaZ7Qr9t7uZTY7wc//0oO2PIvn8IpGiohCpn+7AERVFaEbicL5WFO4edyN6JT6oKETq527g38zsk9D6A8lmdo+ZzTezT83segAzOzW0lsd0YHFo34tmVhBas+C60L67qZlx9BMzmxbad+DoxULPvcTMFpvZ5bWe+71a60BMC40GFokqjcwWqZ/bgFvdfQJA6Af+dncfZWZNgA/N7MCsoaOBQe6+JrR9jbtvMbOmwHwze97dbzOzm9z9+EO81kXA8dSs89Ah9JjZoT8bBgykZh6yD6kZRf9BpL9Zkdp0RCHSMGcC3wpNcTIXaA/0Cf3ZvFolAXCLmS0C8qmZeLIP4Z0EzHD3KnffCLwPjKr13CXuXg18Qs0pMZGo0hGFSMMYcLO7z/raTrNTqZl2u/b2GcBYd99jZu8Bh1sqM9zppIpan1ehf8NyDOiIQqR+dgIta23PAr4Tmo4dM+tbx+I9rYGtoZLoT83SsgfsP/D4g8wGLg9dB8mgZjW5eRH5LkQaQL+NiNTPp0Bl6BTSFGrWjO4OLAxdUC4DLjzE494AbjCzT4EV1Jx+OuAR4FMzW+juebX2/x0YCyyiZvGsH7v7hlDRiBxzmj1WRETC0qknEREJS0UhIiJhqShERCQsFYWIiISlohARkbBUFCIiEpaKQkREwvr/nI2S7/BOuusAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEGCAYAAAB7DNKzAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAAAkiElEQVR4nO3de3iV5Z3u8e8vZ0ggBJJIyBEUUQSEEDmIINaqqFRp1Cowdqq21k7VVqcztTO7ndkz093Onk7tYZxp3ZXaWsCqYKUUlVoPCMoxnAUtCoEknM8J5Pzbf2RhYwwhYFbetZL7c13rIu+blbXucEHuPM/zHszdEREROZ2YoAOIiEhkU1GIiEibVBQiItImFYWIiLRJRSEiIm2KCzpAOKSnp3tBQUHQMUREosqaNWsOuHtGy/1dsigKCgpYvXp10DFERKKKmZW2tl9TTyIi0iYVhYiItElFISIibVJRiIhIm1QUIiLSJhWFiIi0SUUhIiJt6pLnUZyrlzbtYdu+4/RLSaRfcgL9UhLol5xIv5QEUhLjMLOgI4qIdDoVRTN/2rKXZ9eUtfq5hLiYj5VH03ZTqaSnJNI39Pn0lESS4mM7Ob2ISHhYV7xxUVFRkZ/rmdk19Q0cqqrlYGUtBypr/vJxVQ0HK2tD2zUcqKzlYFUN1XWNrb5OckIsfUOlkp6SECqR1kslrWcCCXGaBRSRYJnZGncvarlfI4oWEuNiyUrtQVZqj3Y9/0RtfZulcqCyhooj1WwsP8qhqlrqGlov5t5JcaSnNI1UTpVKeujPvskJZKf14JIBvUmM00hFRDqXiuIT6pkQR8++ceT27XnG57o7x6rrORgqlVOjkualcrCylu0HqlhTephDVbU0NuuVhNgYhuekMjo/jdH5aRTmpZHRKzGM352IiIqiU5kZqT3iSe0Rz6CPXZ/x4xoanSMnmkrk/f1VlOw8zJrSwzy5bAePL/kAgPx+PRmdl8bogqbyGJzZi9gYLbqLSMfRGkUUqqlvYFP5MdaUHmJNaVN5HKisBaBXYhyj8tOayiM/jZF5fUhJ1O8DInJmWqPoQhLjYj+cfoKmKa1dh06yullx/OhP7+EOMQYX9e/94fNH56eRk9ZDh/qKSLtpRNFFHa+uY92uI6zecZiSnYdZu/MIlTX1AGT2SvzLOkd+mhbJRQTQiKLb6ZUUz8TBGUwc3LQY0tDovLf3OKtLD1MSGnW8uGkP0HSOyKU5qRSGpqwK89NIT9EiuYg00YiiG9t3vPrD0lhTephN5ceobWg6L2RgejKFeX+ZrhqcmUKMFslFurTTjShUFPKh6roGNpUf/bA41pQe5mBVaJE8Ke4jxTEytw/JWiQX6VI09SRnlBQfS1FBX4oK+gJNi+SlB080lcbOpimrR1/5yyL5xVm9GTeoH9NGZjMsu7cWyEW6KI0o5Kwcq65j7c4jrAmtdazccYja+kYGZ6ZQXJjDtFED2n1Wu4hEFk09SVgcPVnHoo27mV9SxqodhzGDCeenU1yYzXWX9Nf0lEgUUVFI2JUerOL5teXMLyln56ET9EyIZcqw/txSmMO4Qf10xrhIhFNRSKdxd9aUHmZeSTkLN1RwvLqerNQkpo3KpnhUNoPP6xV0RBFpRdQWhZklA/8N1AKvu/vsM32NiiJyVNc18Kct+5hfUsbr7+2nodEZkZNK8ahsPnPpAPrpfA2RiBFRRWFms4CpwD53H9Zs/xTgx0As8At3/76Z3Qkccfffm9lv3f32M72+iiIyHaisYcG6CuaVlLG54hhxMcbkIZncUpjNpy7O1NnhIgGLtMNjnwT+C/j1qR1mFgs8BlwDlAGrzGwBkANsDD2toXNjSkdKT0nk7isGcvcVA9m65xjPl5Tz/NpyXtmyl9Qe8UwdkUVxYQ6FeX10qK1IBAls6snMCoCFp0YUZjYe+Gd3vy60/a3QU8uAw+6+0Myedvc7TvN69wL3AuTl5Y0uLS0N97cgHaCh0Vm27QDzS8p4afMequsaKejXk+LCHD47Krtd9/kQkY4RUVNP0GpR3ApMcfcvhrbvBMYC36Rp9FENLNUaRddVWVPPixt3M7+knLc/OAjAmIF9uaUwm+uHZ9E7KT7ghCJdW6RNPbWmtbkGd/cq4K7ODiOdLyUxjtuKcrmtKJeywyd4IbSe8c15G/nOC5u59pL+FBdmM/GCdOJidY9xkc4SSUVRBuQ2284BKgLKIgHLSevJV6+6gL+ZfD7ry44yv6SMBesr+P36CtJTEpk2cgDFhTkMHdA76KgiXV4kTT3FAe8BVwPlwCpghrtvPtvX1tRT11Rb38hr7zYdavvq1n3UNTgX9e/FLYU53DxyAJm9k4KOKBLVImqNwszmApOBdGAv8E/u/oSZ3QD8iKbDY2e5+3fP5fVVFF3f4apaFm6oYF5JOet2HSHGYOLgDIoLs7l2aH96JOhQW5GzFVFFEW4qiu7l/f2VHx5qW37kJCmJcdw4PIu/vrxAU1MiZ0FFIV1eY6OzYvsh5pWU8YcNuzlZ18C4QX25a8JAPn3xebrWlMgZqCikWzl6oo6nV+3kV2/toOJoNbl9e/CFywfyuaIceukwW5FWqSikW6pvaGTxO3uZtXQ7q0sPk5wQy21FuXzh8gIK0pODjicSUVQU0u1tKDvCL5ftYOGGCuobnasvyuSuCQO5/Px+umSICCoKkQ/tO1bNb5aXMnvFTg5W1TLkvF7cfUUBN4/MJileR0tJ96WiEGmhuq6BBesrmLV0O1v3HCetZzwzx+Zz5/h8ztM5GdINqShETsPdWf7BIWYt284rW/YSa8aNI7K4a8JARub2CTqeSKeJhms9iQTCzBh/fj/Gn9+PnQdP8ORbO3hm9S5eWFdBYV4f7powkCnD+hOv60tJN6URhUgrjlfX8dyaMp58awelB0+QlZrE58cXMH1MLn16JgQdTyQsNPUkcg4aGp3Xtu7jl29tZ9m2gyTFx1BcmMNdlxfo3t/S5agoRD6hrXuO8eSyHcxfW05tfSMTB6dz9xUDuXJwBjE661u6ABWFSAc5WFnD3JU7eWp5KXuP1TAoPZm7JhRQXJhDcqKW/SR6qShEOlhtfSMvbtrNrKXbWV92lF5JcUwfk8fnx+eTk6ZbuEr0UVGIhIm7U7LzCL9ctp0XN+3B3bnukv7cfcVAivLTdNa3RA0dHisSJmbG6Pw0RuenUXHkJE8tL2XOip28uGkPw7J7c/eEgdw4IovEOJ31LdFJIwqRMDhZ28D8tWX8ctkOtu2rJD0lkTvH5TNzXB7pKYlBxxNplaaeRALg7izddoBZS7fz2rv7iY81rhqSSXFhDlddlKFRhkQUTT2JBMDMmDg4g4mDM3h/fyVzV+zkhfUVLH5nL316xvOZEQMoLsxmZG4frWVIxNKIQqST1Tc0snTbAeaXlPPy5j3U1DcyKD2Z4sJspo3K1hFTEhhNPYlEoOPVdby4cQ/zSspYsf0QAOMG9aW4MIfrh/XX3fikU6koRCLcrkMn+N3acuavLWf7gSqS4mO47pL+FBfmMOH8fsTpooQSZioKkSjh7qzddYT5JWX8fv1ujp6sI7NXItNGZVNcmM1F/XsHHVG6KBWFSBSqqW/gta37mV9Sxqtb91Hf6AzN6k1xYTY3jRxAZi/dYEk6jopCJModqqpl4YYK5pWUs37XEWJjjEmD0ykuzOGaoefpNq7yiakoRLqQbfsqeX5tGc+XlFNxtJpeiXHcMDyLW0bnUJSfpqvZyjlRUYh0QY2NzvLtB5lfUs6LG3dTVdtATloPikdl89nCHAamJwcdUaKIikKkiztRW8/izXuZV1LGsm0HaHQozOtDcWEOU0dk6c58ckYqCpFuZM/Ral5YV868kjLe21tJQmwMV1/cdOmQKy/MICFOh9rKx6koRLohd2dzxTHml5TzwrpyDlbV0jc5gZsubbp0yPDsVF06RD6kohDp5uoaGnnzz/uZV1LOH9/ZS219IxdkplBcmM1nR2WTldoj6IgSsKguCjObBtwIZAKPufvitp6vohBp29GTdSzauJv5JWWs2nGY5IRYFj98Jdl9VBbd2emKIuwTlWY2y8z2mdmmFvunmNm7ZrbNzB5p6zXc/Xfu/iXgC8DtYYwr0i2k9ohn+pg8nr3vchY9OJETdQ38duXOoGNJhOqMFa0ngSnNd5hZLPAYcD0wFJhuZkPNbLiZLWzxyGz2pf8r9HUi0kGGDujN5AszeHrVLuoaGoOOIxEo7EXh7kuAQy12jwG2ufsH7l4LPA3c7O4b3X1qi8c+a/LvwIvuXhLuzCLdzYyx+ew7XsOftuwLOopEoKCOkcsGdjXbLgvtO50HgE8Dt5rZfa09wczuNbPVZrZ6//79HZdUpBu4akgGWalJzNH0k7QiqKJo7Xi8066qu/tP3H20u9/n7j87zXMed/cidy/KyMjosKAi3UFcbAy3X5bLm3/ez86DJ4KOIxEmqKIoA3KbbecAFQFlERHg9styMWDuKo0q5KOCKopVwGAzG2hmCcAdwIKAsogIkJXag6svPo9nV++itl6L2vIXnXF47FzgbWCImZWZ2T3uXg/cD7wMbAGecffN4c4iIm2bMTaPA5W1/PGdvUFHkQgSF+43cPfpp9m/CFgU7vcXkfabNDiD7D49mL2ilBtHZAUdRyKErgwmIh+KjTFmjM3jrfcPsv1AVdBxJEKoKETkI24ryiEuxpirQ2UlREUhIh+R2SuJa4Y2LWpX1zUEHUcigIpCRD5m5th8Dp+o4+XNe4KOIhFARSEiH3P5+f3I79eT2Ss0/SQqChFpRUyMMWNMHiu3H+LPe48HHUcCpqIQkVbdOjqHhNgYXf9JVBQi0rp+KYlcN6w/89aUaVG7m1NRiMhpzRybx7HqehZu2B10FAmQikJETmvswL6cn5HMnBWlQUeRAKkoROS0zIzpY/Io2XmELbuPBR1HAqKiEJE23To6h4S4GOboUNluS0UhIm3q0zOBqcOzeH5tOVU19UHHkQCoKETkjGaMzaOypp7fr9f9xbojFYWInNHo/DSGnNdL51R0UyoKETkjs6bLj28oO8rGsqNBx5FOpqIQkXaZNiqbpPgY5qzUobLdjYpCRNoltUc8N106gBfWVXC8ui7oONKJVBQi0m4zxuZzoraBF9ZpUbs7UVGISLtdmpPK0KzezF6xE3cPOo50EhWFiLSbmTFzXB5bdh9j3a4jQceRTqKiEJGzcvPIbJITYnWmdjeiohCRs5KSGMdNI7P5/YYKjp7UonZ3cMaiMLMYM7u8M8KISHSYOTaP6rpGni8pCzqKdIIzFoW7NwL/2QlZRCRKDMtO5dKcVOas1KJ2d9DeqafFZnaLmVlY04hI1Jg5Np/39layuvRw0FEkzNpbFA8DzwK1ZnbMzI6bmS5OL9KNTb00i16JcVrU7gbaVRTu3svdY9w93t17h7Z7hzuciESunglxfLYwmz9s3M3hqtqg40gYtfuoJzO7ycx+EHpMDWcoEYkOM8bmUVvfyDwtandp7SoKM/s+8DXgndDja6F9ItKNXdS/N6Pz07So3cW1d0RxA3CNu89y91nAlNA+EenmZozJ44P9VSz/4FDQUSRMzuaEuz7NPk7t4BxtMrNkM1ujKS+RyHPjiCxSe8Qze4UuP95Vtbco/g+w1syeNLNfAWtC+9pkZrPMbJ+ZbWqxf4qZvWtm28zskXa8/zeBZ9qZVUQ6UVJ8LLcU5vDy5j0cqKwJOo6EQbvOzAYagXHA/NBjvLs/3Y7Xf5KmaarmrxcLPAZcDwwFppvZUDMbbmYLWzwyzezTNK2L7D2bb0xEOs+MsbnUNTjPrdGidlcUd6YnuHujmd3v7s8AC87mxd19iZkVtNg9Btjm7h8AmNnTwM3u/j3gY1NLZnYVkExTqZw0s0Whs8VbPu9e4F6AvLy8s4kpIp/QBZm9GDuwL3NW7OTeiYOIidG5uV1Je6ee/mhm3zCzXDPre+pxju+ZDexqtl0W2tcqd/9Hd/86MAf4f62VROh5j7t7kbsXZWRknGM0ETlXM8bmsfPQCZa9fyDoKNLBzjiiCLk79OdXm+1zYNA5vGdrv2qc8bg6d3/yHN5LRDrJlGH96ZucwJwVO5k4WL+sdSXtXaN4xN0HtnicS0lA0wgit9l2DqD7KopEucS4WG4bncPid/ay71h10HGkA7X36rFfPdPzzsIqYLCZDTSzBOAOznLtQ0Qi0/QxeTQ0Os+s3nXmJ0vUCOsahZnNBd4GhphZmZnd4+71wP3Ay8AW4Bl333zO34GIRIyC9GQmXNCPuSt30dCoM7W7irCuUbj79NPsXwQsaud7i0gUmTk2n7+ZXcKS9/Zz1UWZQceRDtCuonD3geEOIiJdwzVDzyM9JZHZK3aqKLqINqeezOzvm318W4vPnfHMbBHpfuJjY/hcUQ6vbt1LxZGTQceRDnCmNYo7mn38rRafm4KISCumj8nDgd+u0qJ2V3CmorDTfNzatogIALl9ezJpcAa/XbWL+oZWz5GVKHKmovDTfNzatojIh2aOzWPPsWpe3bov6CjyCZ2pKC49dY9sYETo41Pbwzshn4hEqU9dlEn/3knMWal7ake7NovC3WOb3SM7LvTxqe34zgopItEnLjaGz12Wyxvv7WfXoRNBx5FP4GxuXCQiclbuuCwXA55epVFFNFNRiEjYDOjTg09dlMkzq8uo06J21FJRiEhYzRibx/7jNbzyju49Fq1UFCISVldemEl2nx7MXqHpp2ilohCRsIqNMe64LJel2w6w40BV0HHkHKgoRCTsPndZLrExxlwtakclFYWIhN15vZO45uLzeHZ1GTX1DUHHkbOkohCRTjFjbB6Hqmp5ebMWtaONikJEOsUVF6ST17cnc1aUBh1FzpKKQkQ6RUyMMX1MHss/OMS2fZVBx5GzoKIQkU5zW1EO8bHGXF3/KaqoKESk06SnJHLtJf2ZV1JGdZ0WtaOFikJEOtXMsXkcOVHHoo27g44i7aSiEJFONX5QPwalJzNHZ2pHDRWFiHQqs6ZF7dWlh3l3z/Gg40g7qChEpNPdMjqHhLgYHSobJVQUItLp+iYncMOw/sxfW86J2vqg48gZqChEJBAzxuZzvLqeheu1qB3pVBQiEojLCtIYnJnCbJ1TEfFUFCISCDNjxtg81u86wqbyo0HHkTaoKEQkMMWjckiKj2GORhURTUUhIoFJ7RnP1BEDeGFtOZU1WtSOVCoKEQnUjLF5VNU2sGBdRdBR5DQivijMLMbMvmtmPzWzvw46j4h0rFG5fbg4qzezV5Ti7kHHkVaEtSjMbJaZ7TOzTS32TzGzd81sm5k9coaXuRnIBuqAsnBlFZFgnFrU3lxxjA1lWtSOROEeUTwJTGm+w8xigceA64GhwHQzG2pmw81sYYtHJjAEeNvdHwa+Eua8IhKAaSMH0DMhVtd/ilBhLQp3XwIcarF7DLDN3T9w91rgaeBmd9/o7lNbPPbRNIo4HPra016X2MzuNbPVZrZ6//794fh2RCRMeiXFc/PIASxYX8Gx6rqg40gLQaxRZAO7mm2XhfadznzgOjP7KbDkdE9y98fdvcjdizIyMjomqYh0mhlj8jlZ18Dv1pYHHUVaiAvgPa2VfaddwXL3E8A94YsjIpFgeE4qw7NTmbNiJ3eOy8estR8VEoQgRhRlQG6z7RxAx8WJCDPH5rF1z3FKdh4+85Ol0wRRFKuAwWY20MwSgDuABQHkEJEI85lLB5CSGMdsLWpHlHAfHjsXeBsYYmZlZnaPu9cD9wMvA1uAZ9x9czhziEh0SE6MY9qoAfxhw26OnKgNOo6EhPuop+nunuXu8e6e4+5PhPYvcvcL3f18d/9uODOISHSZMSafmvpG5pVoUTtSRPyZ2SLSvQwd0JtReX2YozO1I4aKQkQizowxeby/v4qV21uehiVBUFGISMSZOmIAvZO0qB0pVBQiEnF6JMRSXJjDS5v28NrWfUHH6fZUFCISkb585SAK0nty15OrePiZdToKKkAqChGJSFmpPfj9A1fwwKcu4IV1FVzz6BJe3rwn6FjdkopCRCJWYlwsf3vtEF746gTSUxL58lNreGDuWg5W1gQdrVtRUYhIxBuWncqC+yfw8DUX8tKm3Vz76BIWbqjQ4bOdREUhIlEhPjaGB68ezMIHJpKd1oP756zlK78pYd/x6qCjdXkqChGJKkP692L+Vy7nm1Mu4tV393Hto0t4fm2ZRhdhpKIQkagTFxvDVyafz6IHJzIoPZmHfrueL/5qNXuOanQRDioKEYlaF2Sm8Ox9l/PtqUNZ9v4BrvnhG/x21U6NLjqYikJEolpsjHHPFQN56WuTGDqgN9+ct5HPz1pJ2eETQUfrMlQUItIlFKQnM/dL4/jXmy9hTelhrnt0CU8tL6WxUaOLT0pFISJdRkyMcef4Al7++iRG5aXx7d9tYsYvlrPzoEYXn4SKQkS6nNy+PXnqnjF8v3g4m8uPcd2PljBr6XaNLs6RikJEuiQz444xeSx+eBLjBvXlXxa+w+d+/jbv768MOlrUUVGISJeWldqDWV+4jP+87VLe23ucG378Jj9/433qGxqDjhY1VBQi0uWZGbeMzuGVh6/kygsz+N6LW7nlf97ivb3Hg44WFVQUItJtZPZO4ud3juan00ex6/BJpv5kKf/16p+p0+iiTSoKEelWzIzPXDqAPz40iWsuOY8fLH6PaY8tY3PF0aCjRSwVhYh0S/1SEnlsRiE/+6tC9h6r4eb/WsYPF79Lbb1GFy2pKESkW5syLIs/PjSJmy4dwE9e3cZnfrqUDWVHgo4VUVQUItLtpSUn8MPbR/LEXxdx5GQt0x5bxvdf3Ep1XUPQ0SKCikJEJOTqi89j8UNXctvoXH72xvvc8JM3WVN6KOhYgVNRiIg0k9ojnn+/dQS/vnsMNXWN3Pqzt/nXhe9wsrb7ji5UFCIirZh0YQYvPzSJmWPzeGLpdqb8eAnLPzgYdKxAqChERE4jJTGOf5s2nLlfGoc73PH4cr7zwiaqauqDjtapVBQiImcw/vx+vPT1idw1oYCnlpdy7aNLeGnTnm5zgyQVhYhIO/RMiOOfPnMJz355PMmJsdz3mzXM/MUKtu45FnS0sIv4ojCzPDNbYGazzOyRoPOISPdWVNCXRQ9O5F9uvoTNFce44cdv8u3fbeJwVW3Q0cImrEUR+uG+z8w2tdg/xczeNbNt7fjhfyHwB3e/GxgatrAiIu0UFxvD58cX8Po3JnPnuHzmrNzJ5B+8zi+Xbe+S142ycM6xmdkkoBL4tbsPC+2LBd4DrgHKgFXAdCAW+F6Ll7gbaACeAxx4yt1/eab3LSoq8tWrV3fUtyEi0qZ39xznXxe+w9JtB7ggM4XvTB3KpAszgo511sxsjbsXfWx/uBdjzKwAWNisKMYD/+zu14W2vwXg7i1L4tTXfwNY6e5LzOw5d7/1NM+7F7gXIC8vb3RpaWmHfy8iIqfj7ryyZR//9od3KD14gk9fnMk/3jiUgenJQUdrt9MVRRBrFNnArmbbZaF9p/MS8KCZ/QzYcbonufvj7l7k7kUZGdHX5CIS3cyMa4aex+KHJvHI9Rfx9vsHufbRN/jeoi0cr64LOt4nEhfAe1or+047rHH3TUCrowgRkUiTGBfLfVeeT3FhNv/x0rv8fMkHzCsp4++uG8Kto3OJjWntR2BkC2JEUQbkNtvOASoCyCEiEjaZvZL4j9suZcH9E8jvl8w3523k5seWsmpH9F07KoiiWAUMNrOBZpYA3AEsCCCHiEjYjcjpw3P3jefHd4zkYGUtt/3sbR6Yu5byIyeDjtZu4T48di7wNjDEzMrM7B53rwfuB14GtgDPuPvmcOYQEQmSmXHzyGz+9LdX8uDVg1m8eQ9X/+fr/OiV96LiYoNhP+opCDo8VkQiWdnhE3zvxa38YcNuBqQm8cgNF/OZEVmYBbt+EUlHPYmIdGs5aT15bEYhv713HGnJCTw4dy23/extNpZF5n27VRQiIgEZO6gfC+6/gu8XD2f7gSpuemwp33xuA/uP1wQd7SNUFCIiAYqNMe4Yk8drfzeZL14xkHklZVz1g9f5+RvvU1MfGesXKgoRkQjQOymef7xxKC8/NIkxA/vyvRe3ct2jS3jlnb2BX85cRSEiEkHOz0hh1hcu48m7LiM2xvjir1fz+Vkr+fPe44FlUlGIiESgyUMyeenrk/jO1KGs23WEKT9+k39esJmjJzr/ciAqChGRCBUfG8PdVwzk9W9M5o7Lcvn12zuY/IPXeOrtHdR34uXMVRQiIhGuX0oi3/3scBY+MJEh/Xvx7Rc2c+NPlvLWtgOd8v4qChGRKDF0QG/mfmkc/zOzkKraemb8YgVffmo1Ow+eCOv7qihERKKImXH98CxeefhK/u66Ibz55wN8+odv8H9f2kplTX1Y3lNFISIShZLiY/nqVRfw6t9OZuqILP779fe56gevs6a0469Oq6IQEYli/VOT+OHtI5n/N5dzUf9eFPTr+DvqBXHjIhER6WCFeWk8dc/YsLy2RhQiItImFYWIiLRJRSEiIm1SUYiISJtUFCIi0iYVhYiItElFISIibVJRiIhImyzoOyeFg5ntB0rP8cvTgc65JOPZUa6zo1xnR7nOTlfNle/uGS13dsmi+CTMbLW7FwWdoyXlOjvKdXaU6+x0t1yaehIRkTapKEREpE0qio97POgAp6FcZ0e5zo5ynZ1ulUtrFCIi0iaNKEREpE0qChERaZOKIsTMZpnZPjPbFHSW5sws18xeM7MtZrbZzL4WdCYAM0sys5Vmtj6U638Hnak5M4s1s7VmtjDoLKeY2Q4z22hm68xsddB5TjGzPmb2nJltDf07Gx8BmYaE/p5OPY6Z2deDzgVgZg+F/s1vMrO5ZpYUdCYAM/taKNPmjv670hpFiJlNAiqBX7v7sKDznGJmWUCWu5eYWS9gDTDN3d8JOJcBye5eaWbxwFLga+6+PMhcp5jZw0AR0NvdpwadB5qKAihy94g6UcvMfgW86e6/MLMEoKe7Hwk41ofMLBYoB8a6+7meSNtRWbJp+rc+1N1PmtkzwCJ3fzLgXMOAp4ExQC3wEvAVd/9zR7y+RhQh7r4E6Pi7kn9C7r7b3UtCHx8HtgDZwaYCb1IZ2owPPSLitw4zywFuBH4RdJZIZ2a9gUnAEwDuXhtJJRFyNfB+0CXRTBzQw8zigJ5ARcB5AC4Glrv7CXevB94APttRL66iiCJmVgCMAlYEHAX4cHpnHbAP+KO7R0Qu4EfA3wONAedoyYHFZrbGzO4NOkzIIGA/8MvQVN0vzCw56FAt3AHMDToEgLuXAz8AdgK7gaPuvjjYVABsAiaZWT8z6wncAOR21IurKKKEmaUA84Cvu/uxoPMAuHuDu48EcoAxoeFvoMxsKrDP3dcEnaUVE9y9ELge+GpoujNocUAh8D/uPgqoAh4JNtJfhKbCbgKeDToLgJmlATcDA4EBQLKZ/VWwqcDdtwD/DvyRpmmn9UB9R72+iiIKhNYA5gGz3X1+0HlaCk1VvA5MCTYJABOAm0LrAU8DnzKz3wQbqYm7V4T+3Ac8T9N8ctDKgLJmo8HnaCqOSHE9UOLue4MOEvJpYLu773f3OmA+cHnAmQBw9yfcvdDdJ9E0jd4h6xOgooh4oUXjJ4At7v7DoPOcYmYZZtYn9HEPmv4DbQ00FODu33L3HHcvoGnK4lV3D/w3PjNLDh2MQGhq51qapgsC5e57gF1mNiS062og0AMlWphOhEw7hewExplZz9D/zatpWjcMnJllhv7MA4rpwL+3uI56oWhnZnOByUC6mZUB/+TuTwSbCmj6DflOYGNoPQDgH9x9UXCRAMgCfhU6IiUGeMbdI+ZQ1Ah0HvB8088W4oA57v5SsJE+9AAwOzTN8wFwV8B5AAjNtV8DfDnoLKe4+wozew4ooWlqZy2RczmPeWbWD6gDvuruhzvqhXV4rIiItElTTyIi0iYVhYiItElFISIibVJRiIhIm1QUIiLSJhWFSBvMrDL0Z4GZzejg1/6HFttvdeTri3QUFYVI+xQAZ1UUoXNM2vKRonD3iDjDV6QlFYVI+3wfmBi6N8JDoQsi/oeZrTKzDWb2ZQAzmxy6f8gcYGNo3+9CFwLcfOpigGb2fZquQLrOzGaH9p0avVjotTeF7l9xe7PXfr3ZvSNmh84OFgkrnZkt0j6PAN84dW+L0A/8o+5+mZklAsvM7NRVRMcAw9x9e2j7bnc/FLrUySozm+fuj5jZ/aGLKrZUDIwELgXSQ1+zJPS5UcAlNF3aehlNZ+4v7ehvVqQ5jShEzs21wOdDl1VZAfQDBoc+t7JZSQA8aGbrgeU0Xfp5MG27ApgbujrvXpruLXBZs9cuc/dGYB1NU2IiYaURhci5MeABd3/5IzvNJtN0qe7m258Gxrv7CTN7HTjTrTPbmk6qafZxA/o/LJ1AIwqR9jkO9Gq2/TLwldAl4DGzC09zw59U4HCoJC4CxjX7XN2pr29hCXB7aB0kg6Y70K3skO9C5BzotxGR9tkA1IemkJ4EfkzTtE9JaEF5PzCtla97CbjPzDYA79I0/XTK48AGMytx95nN9j8PjKfp5jMO/L277wkVjUin09VjRUSkTZp6EhGRNqkoRESkTSoKERFpk4pCRETapKIQEZE2qShERKRNKgoREWnT/wcGWPqAO3Vu0QAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"import matplotlib.pyplot as plt\n",
"\n",
"# number of iterations\n",
"N = len(x)\n",
"\n",
"# iteration\n",
"iters = range(0,N)\n",
"\n",
"plt.figure\n",
"for i in range(0,len(x0)):\n",
" plt.plot(iters,[x[j][i] for j in range(0,N)],label=\"x\"+str(i))\n",
"plt.xlabel(\"Iteration\")\n",
"plt.ylabel(\"Primal Variables\")\n",
"plt.legend()\n",
"plt.show()\n",
"\n",
"plt.figure\n",
"for i in range(0,len(u[0])):\n",
" plt.plot(iters,[u[j][i] for j in range(0,N)],label=\"u\"+str(i))\n",
"for i in range(0,len(v[0])):\n",
" plt.plot(iters,[v[j][i] for j in range(0,N)],label=\"v\"+str(i))\n",
"plt.xlabel(\"Iteration\")\n",
"plt.ylabel(\"Dual Variables\")\n",
"plt.legend()\n",
"plt.show()\n",
"\n",
"plt.figure\n",
"plt.semilogy(iters,mu)\n",
"plt.xlabel(\"Iteration\")\n",
"plt.ylabel(\"Barrier Penalty\")\n",
"plt.show()\n",
"\n",
"plt.figure\n",
"plt.semilogy(range(1,N),E)\n",
"plt.xlabel(\"Iteration\")\n",
"plt.ylabel(\"Error\")\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"id": "a846e211",
"metadata": {},
"source": [
"\n",
"< [4.8 Inertia-Corrected Netwon Method for Equality Constrained NLPs](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [5.0 Special Topics](https://ndcbe.github.io/CBE60499/05.00-Special-Topics.html) > 
 "
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.6"
}
},
"nbformat": 4,
"nbformat_minor": 5
}
"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.6"
}
},
"nbformat": 4,
"nbformat_minor": 5
}

