# This code cell installs packages on Colab
import sys
if "google.colab" in sys.modules:
!wget "https://raw.githubusercontent.com/ndcbe/CBE60499/main/notebooks/helper.py"
import helper
helper.install_idaes()
helper.install_ipopt()
helper.download_figures(['cone1.png','cone2.png'])
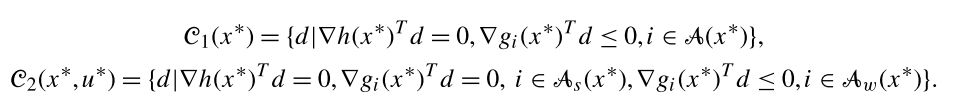

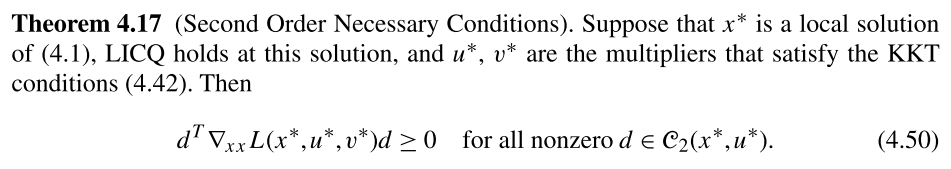





See errata here: http://numero.cheme.cmu.edu/content/errata2.pdf
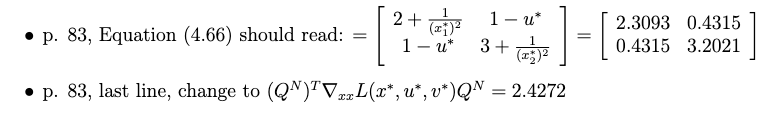
import numpy as np
# Define the Hessian of the Lagrange function
hessian_L = np.array([[2.3093, 0.4315], [0.4315, 3.2021]])
print(hessian_L)
[[2.3093 0.4315] [0.4315 3.2021]]
# Define the gradiant of the constraints
A = np.reshape(np.array([-2.2245, -1.7981]),(2,1))
print(A)
[[-2.2245] [-1.7981]]
Calculate the complete QR factorization.
$$ A = Q \times R $$# Calculate the COMPLETE QR factorization
Q, R = np.linalg.qr(A, mode='complete')
print(Q)
[[-0.77770385 -0.62863083] [-0.62863083 0.77770385]]
print(R)
[[2.86034331] [0. ]]
print(Q @ R)
[[-2.2245] [-1.7981]]
The second column of $Q$ is the null space of $A$. How do we know it is the null space? It corresponds to the second element of $R$ which is 0.
Finally, we can calculate the reduced Hessian:
# Calculate the reduced Hessian
print("Reduced Hessian w.r.t. null space of constraints:")
Q[:,1].T @ hessian_L @ Q[:,1]
Reduced Hessian w.r.t. null space of constraints:
2.4273753426093774
import pyomo.environ as pyo
m = pyo.ConcreteModel()
# Define variables
m.x1 = pyo.Var(initialize=1)
m.x2 = pyo.Var(initialize=1)
# Define constraints
# Note: changing this to an equality constraint
# changes the reduced_hessian
m.con1 = pyo.Constraint(expr=4 - m.x1*m.x2 <= 0 )
# Define objective
m.obj = pyo.Objective(expr=m.x1**2 - 4*m.x1 + 1.5*m.x2**2 - 7*m.x2 + m.x1*m.x2 + 9 - pyo.log(m.x1) - pyo.log(m.x2))
# Obtain dual solutions from first solve and send to warm start
m.dual = pyo.Suffix(direction=pyo.Suffix.IMPORT)
# Specify Ipopt as the solver and solve
opt = pyo.SolverFactory('ipopt')
opt.solve(m, tee=True)
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 0
Number of nonzeros in inequality constraint Jacobian.: 2
Number of nonzeros in Lagrangian Hessian.............: 3
Total number of variables............................: 2
variables with only lower bounds: 0
variables with lower and upper bounds: 0
variables with only upper bounds: 0
Total number of equality constraints.................: 0
Total number of inequality constraints...............: 1
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 1.5000000e+00 3.00e+00 2.67e+00 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 -3.3886674e-01 2.05e+00 5.62e+00 -1.0 1.78e+00 - 1.00e+00 2.75e-01f 1
2 -1.1897000e-01 0.00e+00 5.69e-01 -1.0 8.27e-01 - 1.00e+00 1.00e+00f 1
3 -4.7085742e-01 0.00e+00 6.15e-02 -1.7 1.54e-01 - 1.00e+00 1.00e+00h 1
4 -4.9093265e-01 0.00e+00 5.84e-04 -2.5 2.04e-02 - 1.00e+00 1.00e+00h 1
5 -4.9428887e-01 0.00e+00 4.51e-06 -3.8 5.92e-03 - 1.00e+00 1.00e+00h 1
6 -4.9445149e-01 0.00e+00 9.87e-09 -5.7 2.84e-04 - 1.00e+00 1.00e+00h 1
7 -4.9445337e-01 0.00e+00 1.29e-12 -8.6 3.29e-06 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 7
(scaled) (unscaled)
Objective...............: -4.9445336916038940e-01 -4.9445336916038940e-01
Dual infeasibility......: 1.2920775560587572e-12 1.2920775560587572e-12
Constraint violation....: 0.0000000000000000e+00 0.0000000000000000e+00
Complementarity.........: 2.5098574967664475e-09 2.5098574967664475e-09
Overall NLP error.......: 2.5098574967664475e-09 2.5098574967664475e-09
Number of objective function evaluations = 8
Number of objective gradient evaluations = 8
Number of equality constraint evaluations = 0
Number of inequality constraint evaluations = 8
Number of equality constraint Jacobian evaluations = 0
Number of inequality constraint Jacobian evaluations = 8
Number of Lagrangian Hessian evaluations = 7
Total CPU secs in IPOPT (w/o function evaluations) = 0.002
Total CPU secs in NLP function evaluations = 0.000
EXIT: Optimal Solution Found.
{'Problem': [{'Lower bound': -inf, 'Upper bound': inf, 'Number of objectives': 1, 'Number of constraints': 1, 'Number of variables': 2, 'Sense': 'unknown'}], 'Solver': [{'Status': 'ok', 'Message': 'Ipopt 3.13.2\\x3a Optimal Solution Found', 'Termination condition': 'optimal', 'Id': 0, 'Error rc': 0, 'Time': 0.04768204689025879}], 'Solution': [OrderedDict([('number of solutions', 0), ('number of solutions displayed', 0)])]}
m.dual[m.con1]
-0.5684977067847848
This is negative because of a sign convention in Pyomo. Notice it matches the book (expect the sign).
# Warning: this Pyomo feature is experimental
from pyomo.contrib.interior_point.inverse_reduced_hessian import inv_reduced_hessian_barrier
# https://github.com/Pyomo/pyomo/blob/main/pyomo/contrib/interior_point/inverse_reduced_hessian.py
Compute the reduced Hessian with respect to $x_1$
solve_result, inv_red_hes = inv_reduced_hessian_barrier(
m,
independent_variables= [m.x1], # Warning: these variables cannot be at their bounds
tee=True)
print("\nReduced Hessian w.r.t. x1:")
print(np.linalg.inv(inv_red_hes))
Ipopt 3.13.2: bound_relax_factor=0
honor_original_bounds=no
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 0
Number of nonzeros in inequality constraint Jacobian.: 2
Number of nonzeros in Lagrangian Hessian.............: 3
Total number of variables............................: 2
variables with only lower bounds: 0
variables with lower and upper bounds: 0
variables with only upper bounds: 0
Total number of equality constraints.................: 0
Total number of inequality constraints...............: 1
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 -4.9445337e-01 3.56e-08 3.85e-01 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 -4.7328569e-01 0.00e+00 3.92e-04 -1.7 1.17e-02 - 1.00e+00 1.00e+00h 1
2 -4.9381301e-01 0.00e+00 1.46e-04 -3.8 3.57e-02 - 1.00e+00 1.00e+00f 1
3 -4.9445098e-01 0.00e+00 1.74e-07 -5.7 1.06e-03 - 1.00e+00 1.00e+00h 1
4 -4.9445335e-01 0.00e+00 2.15e-12 -8.6 4.10e-06 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 4
(scaled) (unscaled)
Objective...............: -4.9445334641782601e-01 -4.9445334641782601e-01
Dual infeasibility......: 2.1520563109334034e-12 2.1520563109334034e-12
Constraint violation....: 0.0000000000000000e+00 0.0000000000000000e+00
Complementarity.........: 2.5123319576325299e-09 2.5123319576325299e-09
Overall NLP error.......: 2.5123319576325299e-09 2.5123319576325299e-09
Number of objective function evaluations = 5
Number of objective gradient evaluations = 5
Number of equality constraint evaluations = 0
Number of inequality constraint evaluations = 5
Number of equality constraint Jacobian evaluations = 0
Number of inequality constraint Jacobian evaluations = 5
Number of Lagrangian Hessian evaluations = 4
Total CPU secs in IPOPT (w/o function evaluations) = 0.001
Total CPU secs in NLP function evaluations = 0.000
EXIT: Optimal Solution Found.
Reduced Hessian w.r.t. x1:
[[1.99699045]]
Compute the reduced Hessian with respect to $x_2$
solve_result, inv_red_hes = inv_reduced_hessian_barrier(
m,
independent_variables= [m.x2], # Warning: these variables cannot be at their bounds
tee=True)
print("\nReduced Hessian w.r.t. x2:")
print(np.linalg.inv(inv_red_hes))
Ipopt 3.13.2: bound_relax_factor=0
honor_original_bounds=no
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 0
Number of nonzeros in inequality constraint Jacobian.: 2
Number of nonzeros in Lagrangian Hessian.............: 3
Total number of variables............................: 2
variables with only lower bounds: 0
variables with lower and upper bounds: 0
variables with only upper bounds: 0
Total number of equality constraints.................: 0
Total number of inequality constraints...............: 1
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 -4.9445335e-01 0.00e+00 3.85e-01 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 -4.7328569e-01 0.00e+00 3.92e-04 -1.7 1.17e-02 - 1.00e+00 1.00e+00h 1
2 -4.9381301e-01 0.00e+00 1.46e-04 -3.8 3.57e-02 - 1.00e+00 1.00e+00f 1
3 -4.9445098e-01 0.00e+00 1.74e-07 -5.7 1.06e-03 - 1.00e+00 1.00e+00h 1
4 -4.9445335e-01 0.00e+00 2.15e-12 -8.6 4.10e-06 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 4
(scaled) (unscaled)
Objective...............: -4.9445334641782779e-01 -4.9445334641782779e-01
Dual infeasibility......: 2.1527224447481785e-12 2.1527224447481785e-12
Constraint violation....: 0.0000000000000000e+00 0.0000000000000000e+00
Complementarity.........: 2.5123319576325299e-09 2.5123319576325299e-09
Overall NLP error.......: 2.5123319576325299e-09 2.5123319576325299e-09
Number of objective function evaluations = 5
Number of objective gradient evaluations = 5
Number of equality constraint evaluations = 0
Number of inequality constraint evaluations = 5
Number of equality constraint Jacobian evaluations = 0
Number of inequality constraint Jacobian evaluations = 5
Number of Lagrangian Hessian evaluations = 4
Total CPU secs in IPOPT (w/o function evaluations) = 0.001
Total CPU secs in NLP function evaluations = 0.000
EXIT: Optimal Solution Found.
Reduced Hessian w.r.t. x2:
[[2.76904325]]
Take away message: The reduced Hessian relative to all three bases (null space, $[1, 0]$, and $[0, 1]$) is positive definite.