
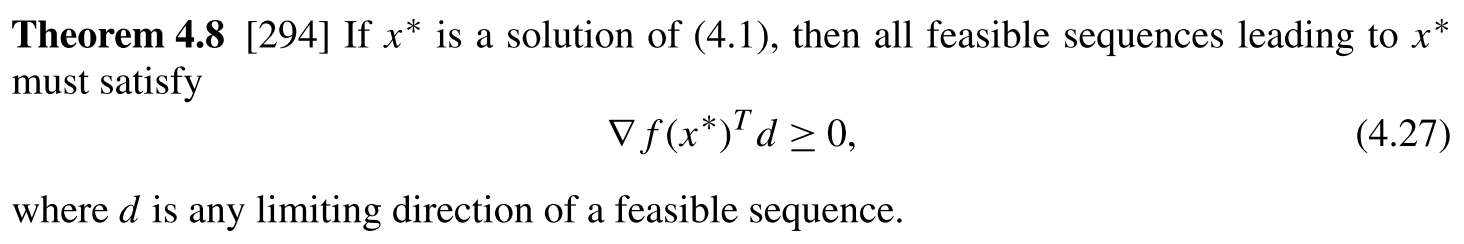

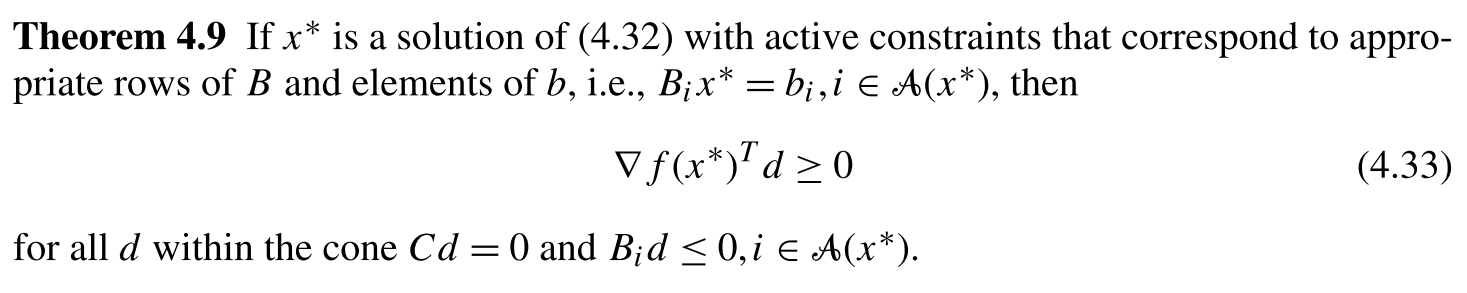

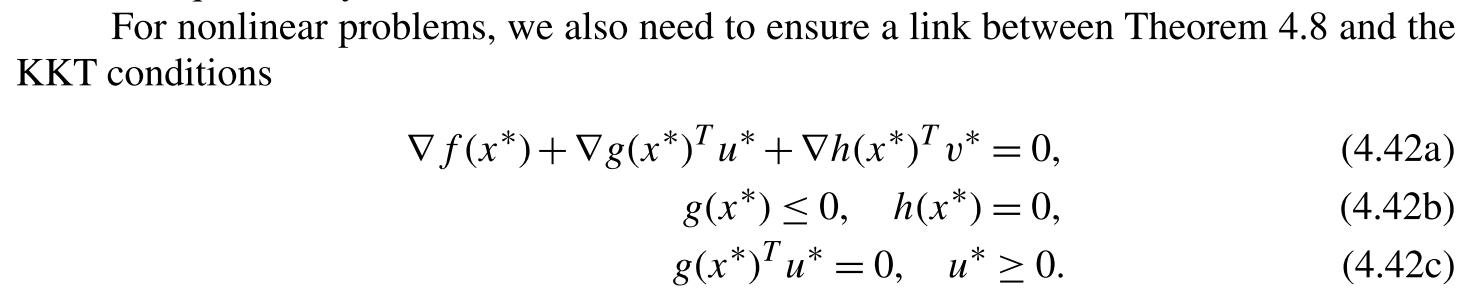
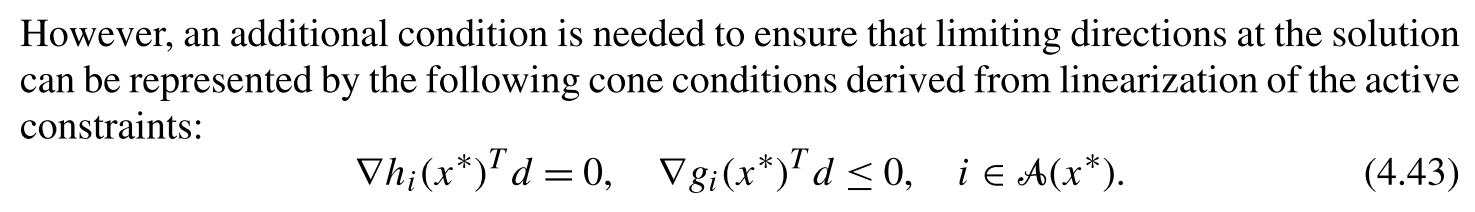
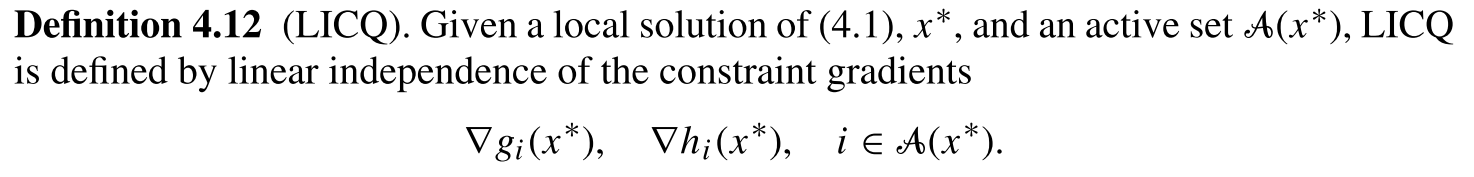

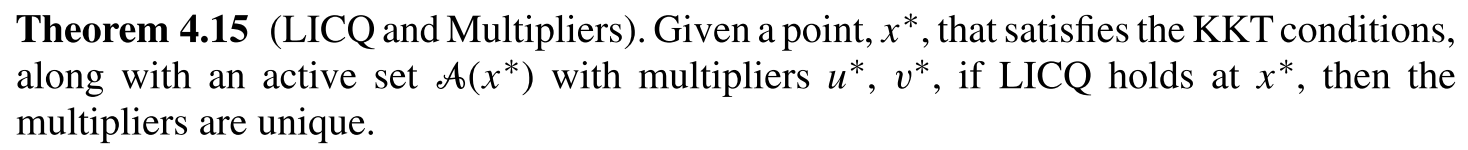

Consider the following two dimensional optimization problem:
$$ \begin{align} \min_{x_1,x_2} \quad & f(x) := x_1 \\ \mathrm{s.t.} \quad & g_1(x) := x_2 \leq x_1^3 \\ & g_2(x) := -x_1^3 \leq x_2 \end{align} $$This is an example from Section 4.3 in Nonlinear Programming by Biegler.
import numpy as np
import matplotlib.cm as cm
import matplotlib.pyplot as plt
from pyomo.environ import *
n = 101
x1 = np.linspace(-3,3,n)
plt.figure()
g1 = np.power(x1,3)
g2 = -g1
plt.plot(x1,g1,color="blue",linestyle="-",label="$x_2 \leq x_1^3$")
plt.fill_between(x1,g1,np.min(g1)*np.ones(n),color="blue",alpha=0.5)
plt.plot(x1,g2,color="red",linestyle="-",label="$-x_1^3 \leq x_2$")
plt.fill_between(x1,np.max(g2)*np.ones(n),g2,color="red",alpha=0.5)
plt.xlabel("$x_1$")
plt.ylabel("$x_2$")
plt.grid()
plt.legend(loc="center left")
plt.show()
Discussion
Where on the graph are both constraints satisfied? Choices:
## Create concrete Pyomo model
m = ConcreteModel()
## Set up to extract dual variables after model solve.
m.dual = Suffix(direction=Suffix.IMPORT)
## Declare variables with initial values
m.x1 = Var(initialize=1)
m.x2 = Var(initialize=1)
## Declare objective
m.OBJ = Objective(expr=m.x1, sense = minimize)
m.g1 = Constraint(expr=m.x2 <= m.x1**3)
m.g2 = Constraint(expr=-m.x1**3 <= m.x2)
## Specify IPOPT as solver
solver = SolverFactory('ipopt')
## Solve the model
results = solver.solve(m, tee = True)
## Return the solution
print("x1 = ",value(m.x1))
print("x2 = ",value(m.x2))
print("\n")
## Inspect dual variables
m.dual.display()
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 0
Number of nonzeros in inequality constraint Jacobian.: 4
Number of nonzeros in Lagrangian Hessian.............: 1
Total number of variables............................: 2
variables with only lower bounds: 0
variables with lower and upper bounds: 0
variables with only upper bounds: 0
Total number of equality constraints.................: 0
Total number of inequality constraints...............: 2
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 2
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 1.0000000e+00 0.00e+00 7.89e-01 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 9.7574511e-01 0.00e+00 1.04e-02 -1.0 2.54e-01 - 1.00e+00 1.00e+00f 1
2 6.6105230e-01 0.00e+00 2.39e-01 -1.7 4.64e+00 - 1.00e+00 3.73e-01f 1
3 4.6924687e-01 0.00e+00 2.74e-01 -1.7 1.92e-01 - 1.00e+00 1.00e+00h 1
4 3.2820073e-01 0.00e+00 3.14e-01 -1.7 1.62e-01 - 1.00e+00 8.72e-01h 1
5 2.6957767e-01 0.00e+00 1.60e-01 -1.7 5.86e-02 - 1.00e+00 1.00e+00f 1
6 1.8935274e-01 0.00e+00 2.24e+00 -2.5 2.21e-01 - 1.00e+00 3.63e-01f 1
7 1.3091124e-01 0.00e+00 3.19e-01 -2.5 5.84e-02 - 1.00e+00 1.00e+00h 1
8 9.6126564e-02 0.00e+00 2.03e+00 -2.5 4.69e-02 - 1.00e+00 7.41e-01h 1
9 7.1009142e-02 0.00e+00 2.58e-01 -2.5 2.51e-02 - 1.00e+00 1.00e+00f 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
10 5.1777995e-02 0.00e+00 1.21e+01 -2.5 3.18e-02 - 1.00e+00 6.04e-01h 1
11 4.0824512e-02 0.00e+00 1.97e-01 -2.5 1.10e-02 - 1.00e+00 1.00e+00f 1
12 3.4583313e-02 0.00e+00 5.91e+01 -2.5 1.80e-02 - 1.00e+00 3.47e-01h 2
13 2.6914569e-02 0.00e+00 1.79e-01 -2.5 7.67e-03 - 1.00e+00 1.00e+00h 1
14 2.0308733e-02 0.00e+00 2.01e-01 -2.5 6.61e-03 - 1.00e+00 1.00e+00h 1
15 1.9046691e-02 0.00e+00 3.31e-02 -2.5 1.26e-03 - 1.00e+00 1.00e+00h 1
16 1.2746908e-02 0.00e+00 5.71e+02 -3.8 1.83e-02 - 1.00e+00 3.44e-01f 1
17 8.7118644e-03 0.00e+00 3.19e-01 -3.8 4.04e-03 - 1.00e+00 1.00e+00f 1
18 7.5197334e-03 0.00e+00 1.09e+03 -3.8 3.10e-03 - 1.00e+00 3.85e-01f 2
19 5.1147446e-03 0.00e+00 3.19e-01 -3.8 2.40e-03 - 1.00e+00 1.00e+00f 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
20 3.3178215e-03 0.00e+00 3.78e-01 -3.8 1.80e-03 - 1.00e+00 1.00e+00f 1
21 2.2893616e-03 0.00e+00 3.40e-01 -3.8 1.03e-03 - 1.00e+00 1.00e+00f 1
22 1.8283227e-03 0.00e+00 8.34e+04 -3.8 4.48e-03 - 1.00e+00 1.03e-01f 2
23 4.5313818e-04 0.00e+00 8.82e-01 -3.8 1.38e-03 - 1.00e+00 1.00e+00f 1
24 3.0653152e-04 0.00e+00 3.16e+05 -5.7 1.47e-04 4.0 2.32e-01 1.00e+00h 1
25 -5.5285928e-04 0.00e+00 1.00e+00 -5.7 8.59e-04 - 1.00e+00 1.00e+00f 1
26 -1.1223885e-02 1.40e-06 1.36e+04 -5.7 7.96e-01 - 1.00e+00 1.34e-02f 1
27 -1.1107786e-02 1.36e-06 1.16e+03 -5.7 3.72e-03 - 1.00e+00 3.12e-02h 6
28 -7.4290268e-03 4.00e-07 4.64e-01 -5.7 3.68e-03 - 1.00e+00 1.00e+00h 1
29 -5.8687786e-03 1.92e-07 8.66e+02 -5.7 2.41e-03 - 1.00e+00 6.47e-01h 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
30 -5.8542172e-03 1.91e-07 3.64e+03 -5.7 1.86e-03 - 1.00e+00 7.81e-03f 8
31 -3.9974633e-03 5.39e-08 3.37e-01 -5.7 1.86e-03 - 1.00e+00 1.00e+00h 1
32 -2.9534118e-03 1.58e-08 5.23e+02 -5.7 1.12e-03 - 1.00e+00 9.29e-01h 1
33 -2.9344353e-03 1.53e-08 1.06e+04 -5.7 6.07e-04 - 1.00e+00 3.12e-02f 6
34 -2.3405157e-03 2.82e-09 1.76e-01 -5.7 5.94e-04 - 1.00e+00 1.00e+00h 1
35 -2.1660008e-03 1.62e-10 3.83e-02 -5.7 1.75e-04 - 1.00e+00 1.00e+00h 1
36 -2.1508378e-03 0.00e+00 6.75e-04 -5.7 1.52e-05 - 1.00e+00 1.00e+00h 1
37 -2.1544258e-03 0.00e+00 6.10e-06 -8.6 3.59e-06 - 1.00e+00 1.00e+00f 1
38 -2.1544329e-03 0.00e+00 7.78e-12 -9.0 7.05e-09 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 38
(scaled) (unscaled)
Objective...............: -2.1544328718688505e-03 -2.1544328718688505e-03
Dual infeasibility......: 7.7819972688075723e-12 7.7819972688075723e-12
Constraint violation....: 0.0000000000000000e+00 0.0000000000000000e+00
Complementarity.........: 9.0909382315597638e-10 9.0909382315597638e-10
Overall NLP error.......: 2.5317795697139416e-12 9.0909382315597638e-10
Number of objective function evaluations = 64
Number of objective gradient evaluations = 39
Number of equality constraint evaluations = 0
Number of inequality constraint evaluations = 64
Number of equality constraint Jacobian evaluations = 0
Number of inequality constraint Jacobian evaluations = 39
Number of Lagrangian Hessian evaluations = 38
Total CPU secs in IPOPT (w/o function evaluations) = 0.009
Total CPU secs in NLP function evaluations = 0.000
EXIT: Optimal Solution Found.
x1 = -0.0021544328718688505
x2 = 3.510966032529045e-27
dual : Direction=Suffix.IMPORT, Datatype=Suffix.FLOAT
Key : Value
g1 : -35907.30543965533
g2 : -35907.30543965533
Discussion