![\"Open](\"https://colab.research.google.com/assets/colab-badge.svg\" "\\"Open"){kind=icon}
![\"Download\"](\"https://img.shields.io/badge/Github-Download-blue.svg\" "\\"Download"){kind=icon}
"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "VIKbplFmN85I",
"nbpages": {
"level": 1,
"link": "[9.2 Uniform Random Variables: Legendre Polynomials](https://ndcbe.github.io/cbe67701-uncertainty-quantification/09.02-Uniform-Random-Variables-Legendre-Polynomials-Example.html#9.2-Uniform-Random-Variables:-Legendre-Polynomials)",
"section": "9.2 Uniform Random Variables: Legendre Polynomials"
}
},
"source": [
"# 9.2 Uniform Random Variables: Legendre Polynomials"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "X6nqgZlNN85J",
"nbpages": {
"level": 1,
"link": "[9.2 Uniform Random Variables: Legendre Polynomials](https://ndcbe.github.io/cbe67701-uncertainty-quantification/09.02-Uniform-Random-Variables-Legendre-Polynomials-Example.html#9.2-Uniform-Random-Variables:-Legendre-Polynomials)",
"section": "9.2 Uniform Random Variables: Legendre Polynomials"
}
},
"source": [
"Created by Kanishka Ghosh (kghosh@nd.edu)\n",
"\n",
"The following text, example, and code have been adapted from:\n",
"\n",
"McClarren, Ryan G (2018). *Uncertainty Quantification and Predictive Computational Science: A Foundation for Physical Scientists and Engineers, Chapter 9: Stochastic Collocation and Projection*, Springer, [https://link.springer.com/chapter/10.1007/978-3-319-99525-0_9](https://link.springer.com/chapter/10.1007/978-3-319-99525-0_9)"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 88
},
"colab_type": "code",
"executionInfo": {
"elapsed": 1112,
"status": "ok",
"timestamp": 1594690016961,
"user": {
"displayName": "Kanishka Ghosh",
"photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Ggs6_dpdWtDfmasHAbkJtmCveUsgqvE_5_E8TpIQQ=s64",
"userId": "16529478165777632155"
},
"user_tz": 240
},
"id": "rvuQ5gyk7BIc",
"nbpages": {
"level": 1,
"link": "[9.2 Uniform Random Variables: Legendre Polynomials](https://ndcbe.github.io/cbe67701-uncertainty-quantification/09.02-Uniform-Random-Variables-Legendre-Polynomials-Example.html#9.2-Uniform-Random-Variables:-Legendre-Polynomials)",
"section": "9.2 Uniform Random Variables: Legendre Polynomials"
},
"outputId": "c0966468-46a3-4d89-a73c-a25f559a029d"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Checking for figures/Fig-9.4_Table-9.7.png\n",
"\tCreating folder figures\n",
"\tDownloading https://ndcbe.github.io/cbe67701-uncertainty-quantification/figures/Fig-9.4_Table-9.7.png\n"
]
}
],
"source": [
"# Download figures (if needed)\n",
"import os, requests, urllib\n",
"\n",
"# GitHub pages url\n",
"url = \"https://ndcbe.github.io/cbe67701-uncertainty-quantification/\"\n",
"\n",
"# relative file paths to download\n",
"# this is the only line of code you need to change\n",
"file_paths = ['figures/Fig-9.4_Table-9.7.png']\n",
"\n",
"# loop over all files to download\n",
"for file_path in file_paths:\n",
" print(\"Checking for\",file_path)\n",
" # split each file_path into a folder and filename\n",
" stem, filename = os.path.split(file_path)\n",
" \n",
" # check if the folder name is not empty\n",
" if stem:\n",
" # check if the folder exists\n",
" if not os.path.exists(stem):\n",
" print(\"\\tCreating folder\",stem)\n",
" # if the folder does not exist, create it\n",
" os.mkdir(stem)\n",
" # if the file does not exist, create it by downloading from GitHub pages\n",
" if not os.path.isfile(file_path):\n",
" file_url = urllib.parse.urljoin(url,\n",
" urllib.request.pathname2url(file_path))\n",
" print(\"\\tDownloading\",file_url)\n",
" with open(file_path, 'wb') as f:\n",
" f.write(requests.get(file_url).content)\n",
" else:\n",
" print(\"\\tFile found!\")"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "PH3ltDE_-Qbu",
"nbpages": {
"level": 2,
"link": "[9.2.1 Generalized Polynomial Chaos](https://ndcbe.github.io/cbe67701-uncertainty-quantification/09.02-Uniform-Random-Variables-Legendre-Polynomials-Example.html#9.2.1-Generalized-Polynomial-Chaos)",
"section": "9.2.1 Generalized Polynomial Chaos"
}
},
"source": [
"## 9.2.1 Generalized Polynomial Chaos\n",
"Approach to approximate the mapping from input parameter to output random variable using different polynomial expansions when the input parameter is not normally distributed.\n",
"\n",
"## Uniform Random Variables: Legendre Polynomials\n",
"(adapted from McClarren 2018)\n",
"\n",
"If we consider a random variable $x$ is uniformly distributed in the range $[a,b]$, then $x$ can be written as $x \\sim \\mathcal{U}[a,b]$ and the PDF of $x$ is given as:\n",
"\n",
"
\n",
"\n",
"\\begin{align*}\n",
"f(x|a,b) = \\begin{cases}\n",
"\\frac{1}{b-a} \\quad x \\in [a,b]\\\\\n",
"0 \\quad \\quad \\mathrm{otherwise}\n",
"\\end{cases}\n",
"\\end{align*}\n",
"\n",
"
\n",
" \n",
"To correspond with the support with the standard definition of Legendre polynomials, the interval $[a,b]$ is mapped to $[-1,1]$ by defining random variable $z$ such that $z \\sim \\mathcal{U}[-1,1]$. $x$ and $z$ are related as:\n",
"\n",
"
\n",
"\n",
"\\begin{align*}\n",
"x = \\frac{b-a}{2}z + \\frac{a+b}{2} \\quad \\mathrm{and}, \\ z = \\frac{a+b-2x}{a-b}\n",
"\\end{align*}\n",
"\n",
"
\n",
"\n",
"Then, the expectation of a uniform random variable $g(x)$ transforms to:\n",
" \n",
"
\n",
"\n",
"\\begin{align*}\n",
"E[g(x)] = \\frac{1}{b-a} \\int\\limits_{a}^{b}g(x)dx = \\frac{1}{2} \\int\\limits_{-1}^{1}g \\left(\\frac{b-a}{2}z + \\frac{a+b}{2} \\right)dz\n",
"\\end{align*}\n",
"\n",
"
\n",
"\n",
"For a function in range $[-1,1]$, the Legendre polynomials form an orthogonal basis and are defined as:\n",
"\n",
"
\n",
"\n",
"\\begin{align*}\n",
"P_n(x) = \\frac{1}{2^n n!} \\frac{d^n}{dx^n} \\left[ (x^2 - 1)^n \\right]\n",
"\\end{align*}\n",
"\n",
"
\n",
"\n",
"where $n$ is the order of the polynomial.\n",
"\n",
"
\n",
"\n",
"The expansion of a square-integrable function $g(x)$ on the interval $[a,b]$ in terms of Legrende polynomials is then given as:\n",
"\n",
"
\n",
"\n",
"\\begin{align*}\n",
"g(x) = \\sum_{n=0}^{\\infty} c_n P_n \\left( \\frac{a+b-2x}{a-b}\\right), \\quad x \\in [a,b]\n",
"\\end{align*}\n",
"\n",
"
\n",
"\n",
"where $c_n$ is defined by\n",
"\n",
"\\begin{align*}\n",
"c_n = \\frac{2n+1}{2} \\int\\limits_{-1}^{1}g \\left( \\frac{b-a}{2}z + \\frac{a+b}{2} \\right)P_n(z)dz\n",
"\\end{align*}\n",
"\n",
"
\n",
"\n",
"As $P_0(x) = 1$ (from Table 9.6 of text), $c_0$ gives the mean of the expansion $G \\sim g(x)$\n",
"\n",
"
\n",
"\n",
"\\begin{align*}\n",
"c_0 = \\frac{1}{2}\\int\\limits_{-1}^{1}g \\left( \\frac{b-a}{2}z + \\frac{a+b}{2} \\right)dz = E[G]\n",
"\\end{align*}\n",
"\n",
"
\n",
"\n",
"The variance of the expansion G is equivalent to the sum of the squares of the Legendre polynomial coefficients with $n \\geq 1$:\n",
"\n",
"
\n",
"\n",
"\\begin{align*}\n",
"\\mathrm{Var}(G) = \\frac{1}{2}\\int\\limits_{-1}^{1} \\left( \\sum_{n=1}^{\\infty}c_n P_n (z) \\right)^2 dz - c_0^2 = \\sum_{n=1}^{\\infty}\\frac{c_n^2}{2n+1}\n",
"\\end{align*}"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "yvU3ngtBPGeZ",
"nbpages": {
"level": 2,
"link": "[9.2.2 Example: $G \\sim g(x) = cos(x)$ and $x \\sim \\mathcal{U}(0,2\\pi)$](https://ndcbe.github.io/cbe67701-uncertainty-quantification/09.02-Uniform-Random-Variables-Legendre-Polynomials-Example.html#9.2.2-Example:-$G-\\sim-g(x)-=-cos(x)$-and-$x-\\sim-\\mathcal{U}(0,2\\pi)$)",
"section": "9.2.2 Example: $G \\sim g(x) = cos(x)$ and $x \\sim \\mathcal{U}(0,2\\pi)$"
}
},
"source": [
"## 9.2.2 Example: $G \\sim g(x) = cos(x)$ and $x \\sim \\mathcal{U}(0,2\\pi)$\n",
"\n",
"The Legendre polynomial coefficients are given as:\n",
"\n",
"
\n",
"\n",
"\\begin{align*}\n",
"c_n = \\frac{2n+1}{2}\\int\\limits_{-1}^{1}\\cos(\\pi z+\\pi)P_n(z)dz\n",
"\\end{align*}\n",
"\n",
"
\n",
"\n",
"The variance of this function is given as:\n",
"\n",
"
\n",
"\n",
"\\begin{align*}\n",
"\\mathrm{Var}(G) = \\frac{1}{2\\pi}\\int\\limits_{0}^{2\\pi}\\cos^2(x)dx = \\frac{1}{2}\n",
"\\end{align*}\n",
"\n",
"The $n^{\\mathrm{th}}$-order approximations for $G$ using Legendre polynomials can be represented by $G_{approx,n}$ and are calculated as:\n",
"\n",
"
\n",
"\n",
"\\begin{align*}\n",
"G_{approx,n} = \\sum_{n=0}^{n} c_n P_n \\left( \\frac{a+b-2x}{a-b}\\right), \\quad x \\in [a,b]\n",
"\\end{align*}\n",
"\n",
"
\n",
"\n",
"and the corresponding variance is given by:\n",
"\n",
"
\n",
"\n",
"\\begin{align*}\n",
"\\mathrm{Var}(G_{approx,n}) = \\sum_{n=1}^{n}\\frac{c_n^2}{2n+1}\n",
"\\end{align*}\n",
"\n",
"
\n",
"\n",
"## Results from Textbook\n",
"\n",
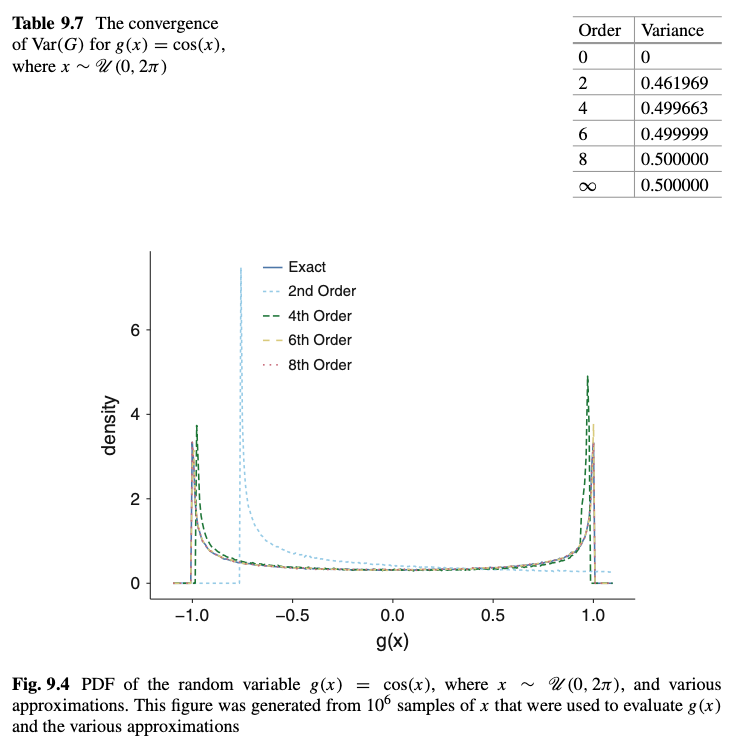
"Following is a screenshot of the results presented in the text (Pg. 201, Table 9.7 and Fig. 9.4):\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "KpN6w3UbW9fe",
"nbpages": {
"level": 2,
"link": "[9.2.2 Example: $G \\sim g(x) = cos(x)$ and $x \\sim \\mathcal{U}(0,2\\pi)$](https://ndcbe.github.io/cbe67701-uncertainty-quantification/09.02-Uniform-Random-Variables-Legendre-Polynomials-Example.html#9.2.2-Example:-$G-\\sim-g(x)-=-cos(x)$-and-$x-\\sim-\\mathcal{U}(0,2\\pi)$)",
"section": "9.2.2 Example: $G \\sim g(x) = cos(x)$ and $x \\sim \\mathcal{U}(0,2\\pi)$"
}
},
"source": [
"**Implementation Notes:**\n",
"* In this implementation, ```scipy.specials.eval_legendre()``` has been used evaluate the $n^{\\mathrm{th}}$-order Legendre polynomial\n",
"[https://docs.scipy.org/doc/scipy/reference/generated/scipy.special.eval_legendre.html](https://docs.scipy.org/doc/scipy/reference/generated/scipy.special.eval_legendre.html)\n",
"* To reduce runtime, 1000 samples of $x \\sim \\mathcal{U}(0,2\\pi)$ have been used for the following calculations"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "EyzmVqxso2ZW",
"nbpages": {
"level": 2,
"link": "[9.2.3 Importing libraries](https://ndcbe.github.io/cbe67701-uncertainty-quantification/09.02-Uniform-Random-Variables-Legendre-Polynomials-Example.html#9.2.3-Importing-libraries)",
"section": "9.2.3 Importing libraries"
}
},
"source": [
"## 9.2.3 Importing libraries"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 71
},
"colab_type": "code",
"executionInfo": {
"elapsed": 1371,
"status": "ok",
"timestamp": 1594690017228,
"user": {
"displayName": "Kanishka Ghosh",
"photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Ggs6_dpdWtDfmasHAbkJtmCveUsgqvE_5_E8TpIQQ=s64",
"userId": "16529478165777632155"
},
"user_tz": 240
},
"id": "RieCD1PGN85K",
"nbpages": {
"level": 2,
"link": "[9.2.3 Importing libraries](https://ndcbe.github.io/cbe67701-uncertainty-quantification/09.02-Uniform-Random-Variables-Legendre-Polynomials-Example.html#9.2.3-Importing-libraries)",
"section": "9.2.3 Importing libraries"
},
"outputId": "589f4057-53cc-4e2d-f5ac-1eb90ad43975"
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"/usr/local/lib/python3.6/dist-packages/statsmodels/tools/_testing.py:19: FutureWarning: pandas.util.testing is deprecated. Use the functions in the public API at pandas.testing instead.\n",
" import pandas.util.testing as tm\n"
]
}
],
"source": [
"## import all needed Python libraries here\n",
"import numpy as np\n",
"import pandas as pd\n",
"from scipy.stats import uniform\n",
"from scipy.special import legendre,eval_legendre\n",
"# from scipy.misc import derivative\n",
"from scipy import integrate\n",
"import matplotlib.pyplot as plt\n",
"import seaborn as sns"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "99rUgecEo6Ye",
"nbpages": {
"level": 2,
"link": "[9.2.4 Functions to calculate exact and $n^{\\mathrm{th}}$-order Legendre polynomial approximation of $g(x)$](https://ndcbe.github.io/cbe67701-uncertainty-quantification/09.02-Uniform-Random-Variables-Legendre-Polynomials-Example.html#9.2.4-Functions-to-calculate-exact-and-$n^{\\mathrm{th}}$-order-Legendre-polynomial-approximation-of-$g(x)$)",
"section": "9.2.4 Functions to calculate exact and $n^{\\mathrm{th}}$-order Legendre polynomial approximation of $g(x)$"
}
},
"source": [
"## 9.2.4 Functions to calculate exact and $n^{\\mathrm{th}}$-order Legendre polynomial approximation of $g(x)$"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"colab": {},
"colab_type": "code",
"executionInfo": {
"elapsed": 1368,
"status": "ok",
"timestamp": 1594690017229,
"user": {
"displayName": "Kanishka Ghosh",
"photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Ggs6_dpdWtDfmasHAbkJtmCveUsgqvE_5_E8TpIQQ=s64",
"userId": "16529478165777632155"
},
"user_tz": 240
},
"id": "Sx2HMWz5tFfJ",
"nbpages": {
"level": 2,
"link": "[9.2.4 Functions to calculate exact and $n^{\\mathrm{th}}$-order Legendre polynomial approximation of $g(x)$](https://ndcbe.github.io/cbe67701-uncertainty-quantification/09.02-Uniform-Random-Variables-Legendre-Polynomials-Example.html#9.2.4-Functions-to-calculate-exact-and-$n^{\\mathrm{th}}$-order-Legendre-polynomial-approximation-of-$g(x)$)",
"section": "9.2.4 Functions to calculate exact and $n^{\\mathrm{th}}$-order Legendre polynomial approximation of $g(x)$"
}
},
"outputs": [],
"source": [
"def g_x_exact(x):\n",
" '''\n",
" Function to create the exact form of the random variable, g(x), \n",
" being approximated\n",
" Argument:\n",
" x: Random variable from uniform distribution U[a,b]\n",
" Return:\n",
" Exact form of the random variable, g(x), being approximated (Here, cos(x))\n",
" '''\n",
" return np.cos(x)\n",
"\n",
"def transform_z_to_x(z,a,b):\n",
" '''\n",
" Helper function to return x in terms of z (Eq. 9.16 of text)\n",
" Arguments:\n",
" z: Random variable from uniform distribution U[-1,1]\n",
" a: Lower limit of uniform random variable x\n",
" b: Upper limit of uniform random variable x\n",
" Returns:\n",
" x: Random variable from uniform distribution U[a,b] in terms of z\n",
" '''\n",
" return ((b-a)/2)*z + (a+b)/2\n",
"\n",
"def transform_x_to_z(x,a,b):\n",
" '''\n",
" Helper function to return z in terms of x (Eq. 9.17 of text)\n",
" Arguments:\n",
" x: Random variable from uniform distribution U[a,b]\n",
" a: Lower limit of uniform random variable x\n",
" b: Upper limit of uniform random variable x\n",
" Returns:\n",
" z: Random variable from uniform distribution U[-1,1] in terms of x\n",
" '''\n",
" return (a+b - 2*x)/(a-b)\n",
"\n",
"def coef_n(a,b,n):\n",
" '''\n",
" Function to generate the Legendre polynomial coefficient of order n\n",
" Argument:\n",
" a: Lower limit of uniform random variable x\n",
" b: Upper limit of uniform random variable x\n",
" n: Order of Legendre polynomial\n",
" Return:\n",
" n-th order Legendre polynomial coefficient (Eq. 9.22 of text)\n",
" ''' \n",
" # Create a lambda function to return the integrand in terms of z as shown in\n",
" # Eq. 9.22 of text.\n",
" # Here, scipy.special.eval_legendre() has been used to evaluate the n-th \n",
" # order Legendre polynomial\n",
" # https://docs.scipy.org/doc/scipy/reference/generated/scipy.special.eval_legendre.html\n",
" integrand_func = lambda z: g_x_exact(transform_z_to_x(z,a,b))* \\\n",
" eval_legendre(n,z)\n",
" val,err = integrate.quad(integrand_func,-1,1)\n",
" return ((2*n + 1)/2)* val\n",
"\n",
"def g_x_approximation(x,a,b,n):\n",
" '''\n",
" Function to generate the n-th order Legendre polynomial expansion of the \n",
" random variable g(x), from Eq. 9.21 in text\n",
" Arguments:\n",
" x: Random variable from uniform distribution U[a,b]\n",
" a: Lower limit of uniform random variable x\n",
" b: Upper limit of uniform random variable x\n",
" n: Order of Legendre polynomial\n",
" Return:\n",
" n-th order Legendre polynomial expansion of g(x) (Eq. 9.21 of text)\n",
" '''\n",
" # calculating z in terms of x\n",
" z = transform_x_to_z(x,a,b)\n",
" # n-th order approximation of g(x)\n",
" expansion_sum = 0\n",
" # sum over 0 to n-th order Legendre polynomials following from Eq. 9.21 of text\n",
" for n_ in range(n+1):\n",
" expansion_sum += coef_n(a,b,n_) * eval_legendre(n_,z)\n",
" return expansion_sum"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "Ls776U73pO-5",
"nbpages": {
"level": 2,
"link": "[9.2.5 Function to calculate $\\mathrm{Var}(g(x))$, $E[G]$, and $\\mathrm{Var}(G)$](https://ndcbe.github.io/cbe67701-uncertainty-quantification/09.02-Uniform-Random-Variables-Legendre-Polynomials-Example.html#9.2.5-Function-to-calculate-$\\mathrm{Var}(g(x))$,-$E[G]$,-and-$\\mathrm{Var}(G)$)",
"section": "9.2.5 Function to calculate $\\mathrm{Var}(g(x))$, $E[G]$, and $\\mathrm{Var}(G)$"
}
},
"source": [
"## 9.2.5 Function to calculate $\\mathrm{Var}(g(x))$, $E[G]$, and $\\mathrm{Var}(G)$"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"colab": {},
"colab_type": "code",
"executionInfo": {
"elapsed": 1366,
"status": "ok",
"timestamp": 1594690017231,
"user": {
"displayName": "Kanishka Ghosh",
"photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Ggs6_dpdWtDfmasHAbkJtmCveUsgqvE_5_E8TpIQQ=s64",
"userId": "16529478165777632155"
},
"user_tz": 240
},
"id": "qG2eaRN6jUZW",
"nbpages": {
"level": 2,
"link": "[9.2.5 Function to calculate $\\mathrm{Var}(g(x))$, $E[G]$, and $\\mathrm{Var}(G)$](https://ndcbe.github.io/cbe67701-uncertainty-quantification/09.02-Uniform-Random-Variables-Legendre-Polynomials-Example.html#9.2.5-Function-to-calculate-$\\mathrm{Var}(g(x))$,-$E[G]$,-and-$\\mathrm{Var}(G)$)",
"section": "9.2.5 Function to calculate $\\mathrm{Var}(g(x))$, $E[G]$, and $\\mathrm{Var}(G)$"
}
},
"outputs": [],
"source": [
"def var_G_inf(a,b):\n",
" '''\n",
" Function to calculate the infinite-order approximation of variance of g(x) \n",
" following Eq. 9.27 of text\n",
" Arguments:\n",
" a: Lower limit of uniform random variable x\n",
" b: Upper limit of uniform random variable x\n",
" Return:\n",
" Variance of g(x)\n",
" '''\n",
" # Var(g(x))\n",
" # lambda function to define integrand g(x)^2\n",
" integrand_func = lambda x: g_x_exact(x)**2\n",
" val, err = integrate.quad(integrand_func,a,b)\n",
" return (1/(b-a)) * val\n",
"\n",
"def mean_G(a,b):\n",
" '''\n",
" Function to calculate the mean of the Legendre polynomial expansion G of g(x) \n",
" following Eq. 9.23 of text\n",
" Arguments:\n",
" a: Lower limit of uniform random variable x\n",
" b: Upper limit of uniform random variable x\n",
" Return:\n",
" Variance of G\n",
" '''\n",
" # lambda function to define integrand g(x)\n",
" integrand_func = lambda x: g_x_exact(x)\n",
" val, err = integrate.quad(integrand_func,a,b)\n",
" return (1/(b-a)) * val\n",
"\n",
"# function to calculate variance of G ~ g(x)\n",
"def var_G_approximation(a,b,n):\n",
" '''\n",
" Function to calculate the variance of the n-th order Legendre polynomial \n",
" expansion of g(x) following Eq. 9.24 of text\n",
" Arguments:\n",
" a: Lower limit of uniform random variable x\n",
" b: Upper limit of uniform random variable x\n",
" n: Highest order of Legendre polynomial used for the \n",
" Return:\n",
" Variance of n-th order Legendre polynomial expansion G of g(x)\n",
" '''\n",
" # Var(G(approx,n))\n",
" sum_sq_coef = 0\n",
" # sum of the squares coefficients with n >= 1\n",
" for n_ in range(n+1):\n",
" if n_ == 0:\n",
" pass\n",
" else:\n",
" sum_sq_coef += (1/(2*n_ + 1))*coef_n(a,b,n_)**2\n",
" return sum_sq_coef"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "4H3zDMcZlX33",
"nbpages": {
"level": 2,
"link": "[9.2.6 Generating samples from $\\mathcal{U}[0,2\\pi]$](https://ndcbe.github.io/cbe67701-uncertainty-quantification/09.02-Uniform-Random-Variables-Legendre-Polynomials-Example.html#9.2.6-Generating-samples-from-$\\mathcal{U}[0,2\\pi]$)",
"section": "9.2.6 Generating samples from $\\mathcal{U}[0,2\\pi]$"
}
},
"source": [
"## 9.2.6 Generating samples from $\\mathcal{U}[0,2\\pi]$"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"colab": {},
"colab_type": "code",
"executionInfo": {
"elapsed": 1364,
"status": "ok",
"timestamp": 1594690017232,
"user": {
"displayName": "Kanishka Ghosh",
"photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Ggs6_dpdWtDfmasHAbkJtmCveUsgqvE_5_E8TpIQQ=s64",
"userId": "16529478165777632155"
},
"user_tz": 240
},
"id": "PvzdhfhMOb0O",
"nbpages": {
"level": 2,
"link": "[9.2.6 Generating samples from $\\mathcal{U}[0,2\\pi]$](https://ndcbe.github.io/cbe67701-uncertainty-quantification/09.02-Uniform-Random-Variables-Legendre-Polynomials-Example.html#9.2.6-Generating-samples-from-$\\mathcal{U}[0,2\\pi]$)",
"section": "9.2.6 Generating samples from $\\mathcal{U}[0,2\\pi]$"
}
},
"outputs": [],
"source": [
"# Number of samples to dram from uniform distribution (1000 samples to reduce computation time)\n",
"n_samples = 1000\n",
"# Lower bound of interval for x~ U[0,2pi]\n",
"a = 0\n",
"# Upper bound of interval for x~ U[0,2pi]\n",
"b = 2*np.pi\n",
"# Orders of Legendre polynomials used for the approximation\n",
"n_vals = [0,2,4,6,8]\n",
"# n_samples number of samples drawn from U[0,1)\n",
"uniform_samples = np.random.random_sample(n_samples)\n",
"# Samples of x drawn from uniform distribution U[0,2pi)\n",
"x_vals = [(b - a) * u_samp + a for u_samp in uniform_samples]"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "j103-v9ZqBq_",
"nbpages": {
"level": 2,
"link": "[9.2.7 Convergence of variance for $g(x) = cos(x)$, where $ x \\sim \\mathcal{U} (0, 2\\pi )$](https://ndcbe.github.io/cbe67701-uncertainty-quantification/09.02-Uniform-Random-Variables-Legendre-Polynomials-Example.html#9.2.7-Convergence-of-variance-for-$g(x)-=-cos(x)$,-where-$-x-\\sim-\\mathcal{U}-(0,-2\\pi-)$)",
"section": "9.2.7 Convergence of variance for $g(x) = cos(x)$, where $ x \\sim \\mathcal{U} (0, 2\\pi )$"
}
},
"source": [
"## 9.2.7 Convergence of variance for $g(x) = cos(x)$, where $ x \\sim \\mathcal{U} (0, 2\\pi )$"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 235
},
"colab_type": "code",
"executionInfo": {
"elapsed": 1582,
"status": "ok",
"timestamp": 1594690017468,
"user": {
"displayName": "Kanishka Ghosh",
"photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Ggs6_dpdWtDfmasHAbkJtmCveUsgqvE_5_E8TpIQQ=s64",
"userId": "16529478165777632155"
},
"user_tz": 240
},
"id": "6LrSVEdIPPq1",
"nbpages": {
"level": 2,
"link": "[9.2.7 Convergence of variance for $g(x) = cos(x)$, where $ x \\sim \\mathcal{U} (0, 2\\pi )$](https://ndcbe.github.io/cbe67701-uncertainty-quantification/09.02-Uniform-Random-Variables-Legendre-Polynomials-Example.html#9.2.7-Convergence-of-variance-for-$g(x)-=-cos(x)$,-where-$-x-\\sim-\\mathcal{U}-(0,-2\\pi-)$)",
"section": "9.2.7 Convergence of variance for $g(x) = cos(x)$, where $ x \\sim \\mathcal{U} (0, 2\\pi )$"
},
"outputId": "10fb4cb3-3af6-4995-84bf-7f9fd1d9d7c3"
},
"outputs": [
{
"data": {
"text/html": [
"
| \n", " | Order | \n", "Variance | \n", "
|---|---|---|
| 0 | \n", "0 | \n", "0.000000 | \n", "
| 1 | \n", "2 | \n", "0.461969 | \n", "
| 2 | \n", "4 | \n", "0.499663 | \n", "
| 3 | \n", "6 | \n", "0.499999 | \n", "
| 4 | \n", "8 | \n", "0.500000 | \n", "
| 5 | \n", "Infinity | \n", "0.500000 | \n", "
"
]
}
],
"metadata": {
"colab": {
"collapsed_sections": [],
"name": "09.02-Uniform-Random-Variables-Legendre-Polynomials-Example.ipynb",
"provenance": []
},
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.3"
}
},
"nbformat": 4,
"nbformat_minor": 0
}