{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"*This notebook contains material from [cbe67701-uncertainty-quantification](https://ndcbe.github.io/cbe67701-uncertainty-quantification);\n",
"content is available [on Github](https://github.com/ndcbe/cbe67701-uncertainty-quantification.git).*"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"< [7.1 Latin Hypercube and Quasi-Monte Carlo Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html) | [Contents](toc.html) | [7.3 Meaningful Title Goes Here](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.03-Contributed-Example.html) 
 "
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "DnCs7XId4TeP",
"nbpages": {
"level": 1,
"link": "[7.2 Latin Hypercube Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2-Latin-Hypercube-Sampling)",
"section": "7.2 Latin Hypercube Sampling"
}
},
"source": [
"# 7.2 Latin Hypercube Sampling\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "5ZETasp64TeQ",
"nbpages": {
"level": 1,
"link": "[7.2 Latin Hypercube Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2-Latin-Hypercube-Sampling)",
"section": "7.2 Latin Hypercube Sampling"
}
},
"source": [
"Created by V.Vijay Kumar Naidu (vvelagal@nd.edu)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 1,
"link": "[7.2 Latin Hypercube Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2-Latin-Hypercube-Sampling)",
"section": "7.2 Latin Hypercube Sampling"
}
},
"source": [
"The text, examples, and codes in this notebook were adapted from the following references:\n",
"* https://en.wikipedia.org/wiki/Latin_hypercube_sampling\n",
"* McClarren, Ryan G (2018). *Uncertainty Quantification and Predictive Computational Science: A Foundation for Physical Scientists and Engineers, Chapter 7 : Sampling-Based Uncertainty Quantification Monte Carlo and Beyond*, Springer, https://link.springer.com/chapter/10.1007%2F978-3-319-99525-0_7"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "kQhVsePNSvu8",
"nbpages": {
"level": 1,
"link": "[7.2 Latin Hypercube Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2-Latin-Hypercube-Sampling)",
"section": "7.2 Latin Hypercube Sampling"
}
},
"outputs": [],
"source": [
"# Install Python libraries\n",
"!pip install -q sobol_seq\n",
"!pip install -q ghalton\n",
"!pip install -q pyDOE"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "KffZ1fJ_4TeQ",
"nbpages": {
"level": 1,
"link": "[7.2 Latin Hypercube Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2-Latin-Hypercube-Sampling)",
"section": "7.2 Latin Hypercube Sampling"
}
},
"outputs": [],
"source": [
"# Import\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"import scipy.sparse as sparse\n",
"import scipy.sparse.linalg as linalg\n",
"import scipy.integrate as integrate\n",
"import math\n",
"from scipy.stats.distributions import norm\n",
"from scipy.stats import gamma\n",
"import sobol_seq\n",
"import ghalton\n",
"from scipy import stats\n",
"from pyDOE import *\n",
"%matplotlib inline"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"nbpages": {
"level": 1,
"link": "[7.2 Latin Hypercube Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2-Latin-Hypercube-Sampling)",
"section": "7.2 Latin Hypercube Sampling"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Checking for figures/lhs_custom_distribution.png\n",
"\tFile found!\n",
"Checking for figures/chapter7-screenshot.PNG\n",
"\tFile found!\n"
]
}
],
"source": [
"# Download figures (if needed)\n",
"import os, requests, urllib\n",
"\n",
"# GitHub pages url\n",
"url = \"https://ndcbe.github.io/cbe67701-uncertainty-quantification/\"\n",
"\n",
"# relative file paths to download\n",
"# this is the only line of code you need to change\n",
"file_paths = ['figures/lhs_custom_distribution.png', 'figures/chapter7-screenshot.PNG']\n",
"\n",
"# loop over all files to download\n",
"for file_path in file_paths:\n",
" print(\"Checking for\",file_path)\n",
" # split each file_path into a folder and filename\n",
" stem, filename = os.path.split(file_path)\n",
" \n",
" # check if the folder name is not empty\n",
" if stem:\n",
" # check if the folder exists\n",
" if not os.path.exists(stem):\n",
" print(\"\\tCreating folder\",stem)\n",
" # if the folder does not exist, create it\n",
" os.mkdir(stem)\n",
" # if the file does not exist, create it by downloading from GitHub pages\n",
" if not os.path.isfile(file_path):\n",
" file_url = urllib.parse.urljoin(url,\n",
" urllib.request.pathname2url(file_path))\n",
" print(\"\\tDownloading\",file_url)\n",
" with open(file_path, 'wb') as f:\n",
" f.write(requests.get(file_url).content)\n",
" else:\n",
" print(\"\\tFile found!\")"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.2.1 Latin Hypercube Basics](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.1-Latin-Hypercube-Basics)",
"section": "7.2.1 Latin Hypercube Basics"
}
},
"source": [
"## 7.2.1 Latin Hypercube Basics\n",
"\n",
"Latin hypercube sampling (LHS) is a statistical method for generating a near random samples with equal intervals.\n",
"\n",
"To generalize the Latin square to a hypercube, we define a X = (X1, . . . , Xp) as a collection of p independent random variables. To generate N samples, we divide the domain of each Xj in N intervals. In total there are Np such intervals. The intervals are defined by the N + 1 edges:\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "7KFZKceKHWVX",
"nbpages": {
"level": 3,
"link": "[7.2.1.1 Latin Hypercube in 2D](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.1.1-Latin-Hypercube-in-2D)",
"section": "7.2.1.1 Latin Hypercube in 2D"
}
},
"source": [
"### 7.2.1.1 Latin Hypercube in 2D\n",
"\n",
"Makes a Latin Hyper Cube sample and returns a matrix X of size n by 2. For each column of X, the n values are randomly distributed with one from each interval (0,1/n), (1/n,2/n), ..., (1-1/n,1) and they are randomly permuted."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "30R2uAAp6aiR",
"nbpages": {
"level": 3,
"link": "[7.2.1.1 Latin Hypercube in 2D](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.1.1-Latin-Hypercube-in-2D)",
"section": "7.2.1.1 Latin Hypercube in 2D"
}
},
"outputs": [],
"source": [
"def latin_hypercube_2d_uniform(n):\n",
" lower_limits=np.arange(0,n)/n\n",
" upper_limits=np.arange(1,n+1)/n\n",
"\n",
" points=np.random.uniform(low=lower_limits,high=upper_limits,size=[2,n]).T\n",
" np.random.shuffle(points[:,1])\n",
" return points"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 341
},
"colab_type": "code",
"id": "lD6llSHp8nUH",
"nbpages": {
"level": 3,
"link": "[7.2.1.1 Latin Hypercube in 2D](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.1.1-Latin-Hypercube-in-2D)",
"section": "7.2.1.1 Latin Hypercube in 2D"
},
"outputId": "a245fe0e-5436-4fb4-f237-8651f745b45d"
},
"outputs": [
{
"data": {
"text/plain": [
""
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAUQAAAEzCAYAAABJzXq/AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAF1FJREFUeJzt3W2MXOd12PH/Wanimo1qR1EWdS1xSaIUQcZoIVfQSwzULuLWlAtIH6pEZMZuDchmlUQuWqcFJGygCgoIIy7cAEHVxttUcBKMbDH5kBABXQF1bDlITUY07CgWhQ1ovpmW0U0s10FKkLaypx/uXWm4mtmd2b0zd+7M/wcsuPeZe2bO5S4Pn5l7n3MjM5EkwUzdCUjSuLAgSlLJgihJJQuiJJUsiJJUsiBKUmnDghgRT0fEckR8o8fjERG/FhFnIuLFiHhX9WlK0vD1M0P8DHBgncfvBfaUX4eB/7b1tCRp9DYsiJn5ZeDVdXa5H/itLJwA3hYRb68qQUkalSo+Q3wH8K2O7UvlmCQ1yvUVPEd0Geu6HjAiDlO8reb6t9z4j/7h/tsGeqGzf/H/ANj943/bOOOGEteEHI1b31e/+tW/zMwfHziQagriJeDWju1bgFe67ZiZi8AiwE3z+/LUqVMDvdCDn/4KAM/+63uMM24ocU3I0bj1RcSFgYNKVbxlPgb8y/Js893A9zPzOxU8rySNVD+X3XwW+AqwNyIuRcRDEfFwRDxc7nIcOAucAf478PNDy1Zb127Dzp0wMwMnT8Dyct0ZSWNjw7fMmXlog8cT+IXKMtLwtNtw+DBcvlxsX7kKS0vFeKtVb27SGHClyjRZWHijGK5aWSnGJVkQp8rFi4ONS1PGgjhNduwYbFyaMhbEaXLkCGzffu3YzEwxLsmCOFVaLVhchPl5iIDZbbB3rydUpJIFcdq0WnD+fHEy5a67YW6u7oyksWFBlKSSBVGSSlHXfZnf8vduy/v+428OFHP6O38FwP63/x3jjBtKXBNyNG59Rx/+ya9m5h0DB+IMUZJeV9sM8ab5ffnqhZcHimlKxw3jmhvXhByNW19EOEOUpK2yIEpSyYKoydHZ2mznTlubaWBVdMyW6re2tdmFC0VrM2kAzhA1GXq1Njt3tp581EgWRE2GXi3MrlwdbR5qNAuiJkOvFmaz20abhxrNgqjJ0Ku12a7d9eSjRrIgajKsbW02P1+0NrObjwZgQdTk6Gxtdv68xVADs7mDccbV9FrGVR8HNneQpErY3ME442p6LeOqjwObO0hSJSyI61lehpMn3lgb227XnZGkIXItcy/tNix9uzhjmVmsjT18uHjMu9RJE8kZYi8LC0Ux7HT5cjEuaSJZEHvptTa217ikxrMg9tJrbWyvcUmNZ0Hs5ciR4mRKp+3bi3FJE8mC2EurVayFnd32xtrYxUVPqEgTzLPM65mbK76eXtl4X0mN5wxRkkoWREkq2e3GOONqei3jqo8Du91IUiXsdmOccTW9lnHVx4HdbiSpEhZESSpZECWpND4Fsd0ueg7ae1BSTcZjpUq7XfQavHy52Lb3oKQajMcMcWHhjWK4yt6DkkZsPAqivQcljYHxKIj2HpQ0BvoqiBFxICKWIuJMRDza5fEdEfHFiPhaRLwYER8YKIsjR4peg53sPShpxDYsiBFxHfAUcC+wHzgUEfvX7PZLwNHMvB04CPzXgbJotYpeg/Pz9h6UVJsNl+5FxD3AE5n5/nL7MYDM/ETHPp8Gzmbmr5T7fyozf3K957W5g3HjGNeEHI1b37CbO7wD+FbH9qVyrNMTwAcj4hJwHPhYtyeKiMMRcSoiTtW1hlqSeunnOsToMra2mh0CPpOZnypniL8dEe/MzGtaTWfmIrAIRXOHcV8obtz0xTUhR+PWd/ThgUNe188M8RJwa8f2LcAra/Z5CDgKkJlfAWaBmzefliSNXj8F8QVgT0TsiogbKE6aHFuzz0XgpwAiYh9FQfyLKhOVpGHbsCBm5mvAI8BzwMsUZ5NfiognI+K+crdfBD4aEX8KfBb4cPohoaSG6Wstc2YepzhZ0jn2eMf3p4F3V5uaJI3WeKxUkaQxYEGUpJIFEezFKAkYl36IdVqvFyO7a0tL0ug5Q7QXo6SSBbGJvRjXvsVfXq47I2ki+JZ5x47ibXK38XHU7S3+0lK9OUkTorYb1Y9Nt5vl5aKgrHQsu56Zgb17Of03s9W/3lbjTp6AK1evjZvbBTMz7N97y/jk2dC4JuRo3PqG3e1mss3Nwd69MLut2J7dVmzPzdWbVy9riuHrVla6j0vqW20zxJvm9+WrF14eKKYpHTeGGrdz55ve4j946BMwu41nn/5345NnQ+OakKNx64sIZ4hTo9vtFmZmYJeXCElbZUFsmm63Wxjnt/hSg1gQm6jVgvPni88Nz5+3GEoVsSBKUsmCKEklC6IklSyIklSyIEpSyYIoSSULoiSVLIiSVLLbjXHG1fRaxlUfB3a7kaRK2O3GOONqei3jqo8Du91IUiUsiJJUsiBKUsmCKEklC6Lqt/a2qu123RlpSnkbUtWr221VDx8uvm+16stLU8kZouq1sPBGMVx1+XIxLo2YBVH1unhxsHFpiCyIqteOHYONS0NkQVS9ut1Wdfv2YlwaMZs7GFd/3PIynDsLV67C7LbiHtMddxK0uYNxg9hKcwfPMqt+c3PeSlVjweYOxhlX02sZV30c2NxBkiphQZSkkgVRkkoWREkqWRAlqWRBlKSSBVGSShZESeOl3YaTJ+D550feH7OvghgRByJiKSLORMSjPfb5mYg4HREvRcQz1aYpaSqs9se8crXYXu2POaKiuGFBjIjrgKeAe4H9wKGI2L9mnz3AY8C7M/MngH87hFwlTbqa+2P2M0O8EziTmWcz8wfA54D71+zzUeCpzPweQGYuV5umpKlQc3/MDdcyR8QDwIHM/Ei5/SHgrsx8pGOf3wP+HHg3cB3wRGb+z/We1243xo1jXBNynOi4kyfgylVOz+0q4pbPFeOz2+Cuu/t6iq10u+lnhhhdxtZW0euBPcB7gUPAb0TE2970RBGHI+JURJyqq6mEpDG2a3dxs7FOMzPF+Aj00/7rEnBrx/YtwCtd9jmRmT8EzkXEEkWBfKFzp8xcBBah6HYz7p0zjJu+uCbkOPFx7TYPfuEVuHKVZ//3rxfNgltrP6Xr7ejDA6V4jX4K4gvAnojYBXwbOAj87Jp9fo9iZviZiLgZuA04u/m0JE2tVgv+uiikPNP1opah2fAtc2a+BjwCPAe8DBzNzJci4smIuK/c7TnguxFxGvgi8B8y87vDSlqShqGvjtmZeRw4vmbs8Y7vE/h4+SVJjeRKFUkqNbsgttvF0p6ZmZEv8ZE0eZp7k6nVJT6rV7WvLvGB4kNZSRpQc2eINS/xkTR5mlsQa17iI2nyNLcg7tgx2LgkbaC5BfHIEdi+/dqx7duLcUnahNpuVF9Jc4flZTh3tuidNrutWO84N7dx3GZfz7iJj2tCjsatbyvNHZp7lhmK4telAErSZtQ2Q7xpfl++euHlgWIasTB9o7h2uzgTfvFi8XnnkSOvXyY0VnlOaVwTcjRufRExpTPEpvHaSWmsNfekShN57aQ01iyIo+S1k9JYsyCOktdOSmPNgjhKXjspjTUL4ii1WrC4CPPzEFH8ubjoCRVpTHiWedRaLQugNKacIUpSyYIoSSULoiSVLIiSVGp2txvjjKs4rgk5Gre+rXS7cYYoSSW73RhnXE2vZVz1cbC1bjfOELU13gpWE8QLs7V5tjPThHGGqM2znZkmjAVRm2c7M00YC6I2z3ZmmjAWRG2e7cw0YSyI2jzbmWnCeJZZW2M7M00QZ4iSVLIgSlLJ5g7GGVfTaxlXfRxsrbmDnyFKg1pehnNn4cpVmN0Gu3YDs3VnpQrY3ME44waJWbtcEWD7dh589BmYmxvrY5uGOLC5gzQ6vZYrnjtbTz6qlAVRGkSvZYlXro42Dw2FBVEaRK9libPbRpuHhsKCKA2i13LFXbvryUeVsiBKg+i1XHFuru7MVAELojSoVgvOn4eVleJPly5ODAuiJJUsiJJU6qsgRsSBiFiKiDMR8eg6+z0QERkRm7ooUpLqtGFBjIjrgKeAe4H9wKGI2N9lvxuBfwOcrDpJSRqFfmaIdwJnMvNsZv4A+Bxwf5f9fhn4JHClwvyk6eJtXWu14VrmiHgAOJCZHym3PwTclZmPdOxzO/BLmfkvIuJLwL/PzFPrPa/dbowbx7hac1xehqWl4uz1qpkZ2Lv3TZf1NOHvso442Fq3m35miNFl7PUqGhEzwK8Cv7jhE0UcjohTEXGqrqYS0tg6d/baYgjFtuukR6afGeI9wBOZ+f5y+zGAzPxEuf1W4JvAX5chfxd4FbhvvVmi3W6MG8e4WnOcmYFu/x4j3lQom/B3WUccDL/bzQvAnojYFRE3AAeBY6sPZub3M/PmzNyZmTuBE2xQDCV14W1da7dhQczM14BHgOeAl4GjmflSRDwZEfcNO0Fpanhb19r11TE7M48Dx9eMPd5j3/duPS1pCq0uAVxYKNqM7dhRFEOXBo6MtxCQxom3da2VS/ckqWRBlKSSBVGSShZESSpZECWpZEGUpJIFUZJKG65lHha73Rg3jnFNyNG49Q27240kTYXaZoh2uzFuHOOakKNx6xt2txtJmgoWREkqWRAlqWRBlKSSBXFatdtw8gQ8/7x3d5NKFsRp1G7D4cNw5WqxfeFCsW1R1JSzIE6jhQW4fPnascuXi3FpilkQp9HFi4ONS1PCgjiNvLub1JUFcRp5dzepK5s7TGvc8jKnv/cDWFlh/1+9Art2w9zc+OU54rgm5Gjc+rbS3MG77k2ruTn4m+KXjn2+VZbA5g7GGVfbaxlXfRzY3EGSKmFBlKSSBVGSShZESSpZECWpZEGUpJIFUZJKFkRJKlkQpWmyvFw0Bp6ZsTFwFy7dk6ZFuw1L34aVFch8ozEwQKtVb25jwhmiNC0WFopi2MnGwNew241xxtX0WiOPe/55Ts/tKuKWz1372HveU/3r1RAHW+t24wxRmhaz2wYbn0K1fYb4lr913dh3zjBu+uKakOOm437kLA9+/gKsrPDsZx8rxrZvh8VFaK3/PI04vtLRhwcOeZ0zRE2vdrs40zotZ1xbLdi7t5gRRsD8fFkMPaGyyrPMmk6rt2Jdvfvg6hnXR5/pu3N4I83NFV9Pr2y87xRyhqjp1OtWrOfO1pOPxoIFUdOp1y1Xr1wdbR4aKxZETadet1z1jOtUsyBqOvW6Feuu3fXko7FgQdR0arWKM6zz89eecZ3kEyrakAVR06vVgvPni+Vs5897+Yn6K4gRcSAiliLiTEQ82uXxj0fE6Yh4MSK+EBHz1acqScO1YUGMiOuAp4B7gf3AoYjYv2a3rwF3ZOY/AH4X+GTViUrSsG3Y3CEi7gGeyMz3l9uPAWTmJ3rsfzvwXzLz3es9r80djBvHuCbkaNz6ht3c4R3Atzq2L5VjvTwEfL7bAxFxOCJORcSpurrsSFIv/Szdiy5jXatZRHwQuAPo2ksoMxeBRYCb5vfluC8UN2764pqQo3Hr20pzh34K4iXg1o7tW4BX1u4UEe8DFoD3ZKaX+0tqnH7eMr8A7ImIXRFxA3AQONa5Q/m54aeB+zJzufo0JWn4NiyImfka8AjwHPAycDQzX4qIJyPivnK3/wT8CPA7EfH1iDjW4+kkTbrOtmonTxQ3tmqIvtp/ZeZx4Piascc7vn9fxXlJaqK1bdWuXIWlpWK8ARe+u1JFUnW6tVVbWWnMjawsiJKq06utWq/xMWNBlFSdXm3Veo2PGQuipOp0a6s2M1OMN4AFUVJ11rZVm91W3NiqASdUwIIoTY5xuYtgZ1u1u+5uVI9J77onTYJedxGExszOxsGG3W6GxW43xo1jXBNy7Bp38kT3G2TNbitmaeOS55DjYPjdbiSNu153C/QuggOpbYZ40/y+fPXCywPFNKXjhnHNjWtCjl3jdu4s3iavNT9ffJ43LnkOOQ4gIpwhSlOt110EG3K5y7iwIEqToNddBD2hMhDPMkuTotWyAG6RM0RJKlkQJalkQZSkkgVRkkoWREkqWRAlqWRBlKSSBVGSSna7Mc64ml7LuOrjwG43klQJu90YZ1xNr2Vc9XFgtxtJqoQFUZJKFkRJKlkQJalkQZSkkgVRkkoWREnN0G4XN9OamSn+bLcrfwlvISBp/LXbcPgwXL5cbF+4UGxDpbdNcIYoafwtLLxRDFddvlyMV8iCKGn8Xbw42Pgm2dzBOONqei3jBog7eQKuXH3zjrPb4K67rxmyuYOkybZrd3EypdPMTDFeIZs7GGdcTa9l3IBx7XbxmeHFi7BjBxw50vWEylaaO3iWWVIztFqVnlHuxrfMklSyIEpVWF4uPvgf4kXDGj7fMktb1W7D0rdhZQUyh3bRsIbPGaK0VQsLRTHsNISLhjV8FkRpq0Z00bCGz4IobdWOHYONa2xZEKWtOnLkzRcNb99ejKtR+iqIEXEgIpYi4kxEPNrl8W0R8Wz5+MmI2Fl1otLYarVg795iGVkEzM/D4qInVBpow7PMEXEd8BTwT4FLwAsRcSwzT3fs9hDwvcz8+xFxEPgV4MFhJCyNpbm54uvplY331djqZ4Z4J3AmM89m5g+AzwH3r9nnfmC1U8PvAj8VEVFdmpI0fBuuZY6IB4ADmfmRcvtDwF2Z+UjHPt8o97lUbn+z3Ocvez2v3W6MG8e4JuRo3Pq20u2mn4L408D71xTEOzPzYx37vFTu01kQ78zM7655rsNAecUq7wS+sZmkG+JmoOd/CBNgko9vko8NJv/49mbmjZsJ7GelyiXg1o7tW4BXeuxzKSKuB94KvLr2iTJzEVgEiIhTm63iTeDxNdckHxtMx/FtNrafzxBfAPZExK6IuAE4CBxbs88x4F+V3z8A/GHW1VdMkjZpwxliZr4WEY8AzwHXAU9n5ksR8SRwKjOPAf8D+O2IOEMxMzw4zKQlaRj6au6QmceB42vGHu/4/grw0wO+9uKA+zeNx9dck3xs4PH1VFvHbEkaNy7dk6TS0AvipC/76+P4Ph4RpyPixYj4QkTM15HnZmx0bB37PRARGRGNOnPZz/FFxM+UP7+XIuKZUee4FX38bu6IiC9GxNfK388P1JHnZkTE0xGxXF4D3e3xiIhfK4/9xYh4V19PnJlD+6I4CfNNYDdwA/CnwP41+/w88Ovl9weBZ4eZUw3H90+A7eX3P9eU4+vn2Mr9bgS+DJwA7qg774p/dnuArwE/Wm7P1Z13xce3CPxc+f1+4HzdeQ9wfP8YeBfwjR6PfwD4PBDA3cDJfp532DPESV/2t+HxZeYXM/NyuXmC4jrOJujnZwfwy8AngSujTK4C/RzfR4GnMvN7AJm5POIct6Kf40tgdSnIW3nz9cVjKzO/TJdrnTvcD/xWFk4Ab4uIt2/0vMMuiO8AvtWxfakc67pPZr4GfB/4sSHnVZV+jq/TQxT/azXBhscWEbcDt2bmH4wysYr087O7DbgtIv44Ik5ExIGRZbd1/RzfE8AHI+ISxVUkH2NyDPpvExj+PVW6zfTWntbuZ59x1XfuEfFB4A7gPUPNqDrrHltEzAC/Cnx4VAlVrJ+f3fUUb5vfSzGz/6OIeGdm/t8h51aFfo7vEPCZzPxURNxDcS3xOzNzElr2bKquDHuGOMiyP9Zb9jem+jk+IuJ9wAJwX2ZeHVFuW7XRsd1IsR79SxFxnuJzmmMNOrHS7+/m72fmDzPzHLBEUSCboJ/jewg4CpCZXwFmKdY5T4K+/m2+yZA/+LweOAvs4o0Pdn9izT6/wLUnVY7W/YFtxcd3O8WH23vqzrfqY1uz/5do1kmVfn52B4DfLL+/meIt2I/VnXuFx/d54MPl9/vKghF15z7AMe6k90mVf861J1X+pK/nHEHSHwD+vCwKC+XYkxSzJSj+V/od4AzwJ8Duuv+iKz6+/wX8H+Dr5dexunOu6tjW7Nuogtjnzy6A/wycBv4MOFh3zhUf337gj8ti+XXgn9Wd8wDH9lngO8APKWaDDwEPAw93/OyeKo/9z/r93XSliiSVXKkiSSULoiSVLIiSVLIgSlLJgihJJQuiJJUsiJJUsiBKUun/A8Z74c1udeCIAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"n=20\n",
"p=latin_hypercube_2d_uniform(n)\n",
"plt.figure(figsize=[5,5])\n",
"plt.xlim([0,1])\n",
"plt.ylim([0,1])\n",
"plt.scatter(p[:,0],p[:,1],c='r')\n",
"\n",
"for i in np.arange(0,1,1/n):\n",
" plt.axvline(i)\n",
" plt.axhline(i)\n",
"plt.show"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "T3aFz5UHLhFf",
"nbpages": {
"level": 3,
"link": "[7.2.1.2 Latin-hypercube designs can be created using the following simple syntax](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.1.2-Latin-hypercube-designs-can-be-created-using-the-following-simple-syntax)",
"section": "7.2.1.2 Latin-hypercube designs can be created using the following simple syntax"
}
},
"source": [
"### 7.2.1.2 Latin-hypercube designs can be created using the following simple syntax\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[7.2.1.2 Latin-hypercube designs can be created using the following simple syntax](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.1.2-Latin-hypercube-designs-can-be-created-using-the-following-simple-syntax)",
"section": "7.2.1.2 Latin-hypercube designs can be created using the following simple syntax"
}
},
"source": [
"The following is adapted from:https://pythonhosted.org/pyDOE/randomized.html."
]
},
{
"cell_type": "markdown",
"metadata": {
"colab": {},
"colab_type": "code",
"id": "dCyvuRToLf7y",
"nbpages": {
"level": 3,
"link": "[7.2.1.2 Latin-hypercube designs can be created using the following simple syntax](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.1.2-Latin-hypercube-designs-can-be-created-using-the-following-simple-syntax)",
"section": "7.2.1.2 Latin-hypercube designs can be created using the following simple syntax"
}
},
"source": [
"```\n",
"lhs(n, [samples, criterion, iterations])\n",
"```"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "lvGXdBpOL8i5",
"nbpages": {
"level": 3,
"link": "[7.2.1.2 Latin-hypercube designs can be created using the following simple syntax](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.1.2-Latin-hypercube-designs-can-be-created-using-the-following-simple-syntax)",
"section": "7.2.1.2 Latin-hypercube designs can be created using the following simple syntax"
}
},
"source": [
"**n**: an integer that designates the number of factors (required).\n",
"\n",
"**samples**: an integer that designates the number of sample points to generate for each factor (default: n)\n",
"criterion: a string that tells lhs how to sample the points (default: None, which simply randomizes the points within the intervals):\n",
"\n",
"**“center” or “c”**: center the points within the sampling intervals\n",
"“maximin” or “m”: maximize the minimum distance between points, but place the point in a randomized location within its interval\n",
"\n",
"**“centermaximin” or “cm”**: same as “maximin”, but centered within the intervals\n",
"\n",
"**“correlation” or “corr”**: minimize the maximum correlation coefficient\n",
"\n",
"The output design scales all the variable ranges from zero to one which can then be transformed as the user wishes (like to a specific statistical distribution using the scipy.stats.distributions ppf (inverse cumulative distribution) function"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "W9KwhC8JL7wJ",
"nbpages": {
"level": 3,
"link": "[7.2.1.2 Latin-hypercube designs can be created using the following simple syntax](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.1.2-Latin-hypercube-designs-can-be-created-using-the-following-simple-syntax)",
"section": "7.2.1.2 Latin-hypercube designs can be created using the following simple syntax"
}
},
"outputs": [],
"source": [
"from scipy.stats.distributions import norm\n",
"from pyDOE import *\n",
"lhd = lhs(2, samples=5)\n",
"lhd = norm(loc=0, scale=1).ppf(lhd) # this applies to both factors here"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "QXvC3_JiM5_p",
"nbpages": {
"level": 3,
"link": "[7.2.1.2 Latin-hypercube designs can be created using the following simple syntax](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.1.2-Latin-hypercube-designs-can-be-created-using-the-following-simple-syntax)",
"section": "7.2.1.2 Latin-hypercube designs can be created using the following simple syntax"
}
},
"source": [
"Graphically, each transformation would look like the following, going from the blue sampled points (from using lhs) to the green sampled points that are normally distributed: (Adapted from https://pythonhosted.org/pyDOE/randomized.html)\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "B4vaJwj2NWd4",
"nbpages": {
"level": 3,
"link": "[7.2.1.2 Latin-hypercube designs can be created using the following simple syntax](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.1.2-Latin-hypercube-designs-can-be-created-using-the-following-simple-syntax)",
"section": "7.2.1.2 Latin-hypercube designs can be created using the following simple syntax"
}
},
"source": [
"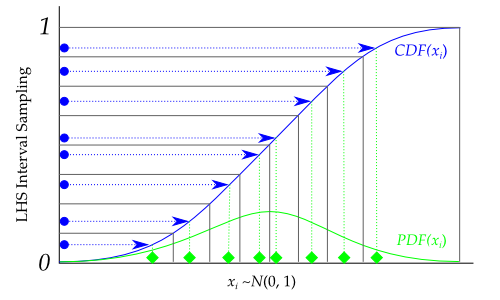"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "zrHRqUeibyNo",
"nbpages": {
"level": 3,
"link": "[7.2.1.2 Latin-hypercube designs can be created using the following simple syntax](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.1.2-Latin-hypercube-designs-can-be-created-using-the-following-simple-syntax)",
"section": "7.2.1.2 Latin-hypercube designs can be created using the following simple syntax"
}
},
"source": [
"An example for Latin-Hyper cube sampling"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 187
},
"colab_type": "code",
"id": "-Mb4AHDdRx_K",
"nbpages": {
"level": 3,
"link": "[7.2.1.2 Latin-hypercube designs can be created using the following simple syntax](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.1.2-Latin-hypercube-designs-can-be-created-using-the-following-simple-syntax)",
"section": "7.2.1.2 Latin-hypercube designs can be created using the following simple syntax"
},
"outputId": "7818b20e-d45c-46c6-e581-71073ef9deeb"
},
"outputs": [
{
"data": {
"text/plain": [
"array([[1.01038798, 2.96384621, 1.66664945, 4.08995188],\n",
" [0.98039537, 2.24799145, 3.68230066, 3.82708594],\n",
" [1.28011085, 2.28301199, 2.44501943, 4.6418306 ],\n",
" [0.91410412, 1.88397665, 2.71926383, 4.02262911],\n",
" [0.91979907, 1.73539308, 2.95722586, 4.15159108],\n",
" [0.96185965, 1.40469736, 3.04478481, 3.69932867],\n",
" [0.87127105, 1.74656817, 3.36550728, 3.65675587],\n",
" [1.04347425, 1.08778999, 2.13703733, 3.94872467],\n",
" [1.1143877 , 2.58203348, 4.47359066, 3.8801158 ],\n",
" [1.0641072 , 2.12054246, 4.13988503, 4.28057491]])"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"design = lhs(4, samples=10)\n",
"from scipy.stats.distributions import norm\n",
"means = [1, 2, 3, 4]\n",
"stdvs = [0.1, 0.5, 1, 0.25]\n",
"for i in range(4):\n",
" design[:, i] = norm(loc=means[i], scale=stdvs[i]).ppf(design[:, i])\n",
"\n",
"design"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.2.2 Advection-Diffusion-Reaction (ADR) Example](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2-Advection-Diffusion-Reaction-(ADR)-Example)",
"section": "7.2.2 Advection-Diffusion-Reaction (ADR) Example"
}
},
"source": [
"## 7.2.2 Advection-Diffusion-Reaction (ADR) Example"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "YoCFcxW3bAXw",
"nbpages": {
"level": 3,
"link": "[7.2.2.1 Set up diffusion reaction equation](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.1-Set-up-diffusion-reaction-equation)",
"section": "7.2.2.1 Set up diffusion reaction equation"
}
},
"source": [
"### 7.2.2.1 Set up diffusion reaction equation\n",
"\n",
"The steady advection-diffusion-reaction(ADR) equation in one-spatial dimension with a spatially constant, but uncertain, diffusion coefficient, a linear reaction term, and a prescribed uncertain source.\n",
"\n",
"$$\n",
"\\nu \\frac{du}{dx} - \\omega \\frac{d^2u}{dx^2} + \\kappa(x)u = S(x)\n",
"$$\n",
"The QoI is total reaction rate:$$\n",
"Q= \\int^{10}_{0} \\kappa(x_ u)u(x)dx\n",
"$$\n",
"where v and ω are spatially constant with means\n",
"$$\n",
"\\nu = 10, μ_{ω} = 20, \n",
"$$\n",
"and\n",
"$$\n",
"Var(v) = 0.0723493, Var(ω) = 0.3195214.\n",
"$$\n",
"\n",
"The reaction coefficient, κ(x), is given by \n",
"$$\n",
"κ(x) = κ_{l} \\space x ∈ (5, 7.5)\n",
"$$ \n",
" $$ \\space κ_{h} \\space otherwise$$ \n",
" \n",
" The value of the source is given by\n",
"$$S(x) = qx(10 − x),$$ "
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "eR3fNfymMbaE",
"nbpages": {
"level": 3,
"link": "[7.2.2.1 Set up diffusion reaction equation](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.1-Set-up-diffusion-reaction-equation)",
"section": "7.2.2.1 Set up diffusion reaction equation"
}
},
"outputs": [],
"source": [
"def ADRSource(Lx, Nx, Source, omega, v, kappa):\n",
" #Solves the diffusion equation with Generalized Source\n",
" A = sparse.dia_matrix((Nx,Nx),dtype=\"float\")\n",
" dx = Lx/Nx\n",
" i2dx2 = 1.0/(dx*dx)\n",
" #fill diagonal of A\n",
" A.setdiag(2*i2dx2*omega + np.sign(v)*v/dx + kappa)\n",
" #fill off diagonals of A\n",
" A.setdiag(-i2dx2*omega[1:Nx] + \n",
" 0.5*(1-np.sign(v[1:Nx]))*v[1:Nx]/dx,1)\n",
" A.setdiag(-i2dx2*omega[0:(Nx-1)] - \n",
" 0.5*(np.sign(v[0:(Nx-1)])+1)*v[0:(Nx-1)]/dx,-1)\n",
" #solve A x = Source\n",
" Solution = linalg.spsolve(A.tocsr(),Source)\n",
" Q = integrate.trapz(Solution*kappa,dx=dx)\n",
" return Solution, Q"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "YzNoqAe6bMTx",
"nbpages": {
"level": 3,
"link": "[7.2.2.1 Set up diffusion reaction equation](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.1-Set-up-diffusion-reaction-equation)",
"section": "7.2.2.1 Set up diffusion reaction equation"
}
},
"source": [
"Solve diffusion equation"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 332
},
"colab_type": "code",
"id": "ZGqMMZKvMbaG",
"nbpages": {
"level": 3,
"link": "[7.2.2.1 Set up diffusion reaction equation](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.1-Set-up-diffusion-reaction-equation)",
"section": "7.2.2.1 Set up diffusion reaction equation"
},
"outputId": "15a27e23-dd7b-4d74-cf85-d603bc3f69ad"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[10. 10. 10. ... 10. 10. 10.]\n",
"52.390252927703344\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAW4AAAD8CAYAAABXe05zAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAIABJREFUeJzt3Xd0lVW+xvHvTicNSIeEkAQIAUJJIxRFRURERyyINOlGr3XUKTp97lXvOKOOjp2OgjAM1hFHUUBFkJCEDqEEAiG0BEJ6P9n3D4LLq5QTyMk+5fdZi0USDjnPWUkeXva7i9JaI4QQwnG4mQ4ghBCiZaS4hRDCwUhxCyGEg5HiFkIIByPFLYQQDkaKWwghHIwUtxBCOBgpbiGEcDBS3EII4WA8bPFJQ0JCdExMjC0+tRBCOKWcnJxTWutQax5rk+KOiYkhOzvbFp9aCCGcklLqsLWPlaESIYRwMFLcQgjhYKS4hRDCwUhxCyGEg5HiFkIIByPFLYQQDkaKWwghHIxN5nELIS6f1prTVfUcKKqkuLKOkqp6ymsavv/zdl4eBPt5ERrgTbdQf8IDvVFKGUws2poUtxCG1TVa2FJQSubBEjLzT5N7vJwz1Q2X/ovNAnw8SOzcnsHdghnSLZik6I64u0mROzMpbiEMqG2w8NXeIj7dcYLVuSepqregFPSKCGRUYgQ9wgLoHuZPeKAPQX5eBLbzwE0ptIbq+kZOVdZTVFHLgaJK9p6sYOuRUv7+5T5e/AJC/L25pV8nbkuKpH9Ue7kad0LKFqe8p6amalnyLsRPHSiuZMnGAlbkHKG8tpEgPy9u7BPO8IRwBsYE0d7X87I/d2l1PevzTvPJ9mOs3lNEfWMT/bt0YNZVsdyUGIGHu9zSsmdKqRytdapVj5XiFsL2sg+V8MqaPL7eV4ynu+LGPhGMT4tmUFyQTQq1oraBD7YcZf63+Rw6XU1ciB+/uLEnNyVGyBW4nZLiFsJObMov4aUv97HhwGmC/byYNiSG8QOjCQ3wbpPnb2rSfJF7khdW7WXfyUr6d+nA02MS6RvVvk2eX1hPilsIwwpOV/Psp7l8tusEoQHe3Dcsjonp0fh6mbmtZGnSvL+5kL9+vpfTlXXMvCqWx26IN5ZH/FRLivuSXzWlVE/gnz/4UBzwB631S5eZTwinVVNv4eXV+5n/bT4e7opfjIxn1tVx+Hi6G83l7qa4K7ULI/tE8Jf/7GHOuny+zC3ilQlJJEbK1bejadEVt1LKHTgKpGutL7h3rFxxC1e04cApnnxvBwUl1dyRHMmvRyUQHuhjOtZ5bThwisf/uY2Sqnp+d0sv7hnUVca+DWvJFXdL74pcDxy4WGkL4Woqaht46v3tTJyTiZuCZRmDeHHcALstbYAh3UL49NGruapHCH/4aBePL99GXaPFdCxhpZYOcI0Hlp7vD5RSGUAGQHR09BXGEsIxbD1SysNLN3P0TA0Zw+J4bEQ87bzMDotYK8jPi3lTU3l1TR4vfLGPIyXVvHVPCsH+bXPjVFw+q4dKlFJewDGgj9b65MUeK0Mlwtk1NWlmrzvI85/vJTzQh39MGEBK1yDTsS7bJ9uP8cTybYQH+rBkVjpdgnxNR3I5thoquQnYfKnSFsLZlVbXM21hFn/5zx5G9gnn00evdujSBrilX2eWZgyirKaBu978jgPFlaYjiYtoSXFP4ALDJEK4ir0nKrj11fVsPHCaZ25P5LWJybRvd/mrHe1JcnRHlmUMorGpibvf+o7c4+WmI4kLsKq4lVK+wA3A+7aNI4T9+mzncW5/fT21DRaW3TeISenONxOjV6dA/nnfYDzc3LhnXiYH5crbLllV3Frraq11sNa6zNaBhLA3Wmv+sXo/9y/eTHx4AP9++CqSozuajmUz3UL9WXJvOlrD5LmZHC2tMR1J/IjsOiPERTRamnjq/R28+MU+7kiKZFnGILue5tdauoX6s2jGQCrqGpk8N5PiijrTkcQPSHELcQHV9Y1kvJPDsqwjPDy8Oy+M6298BWRbSoxsz4JpaRwvq2HWoixq6mWet72Q4hbiPE5X1jFh9ka+2lvEM7cn8sTInk43nm2N1Jgg/jE+ie1Hy3h02RYsTa2/t5FoOSluIX7kZHktd8/eyN6TFbx1TyqT0ruajmTUyD4R/PGW3qzafZJnVuaajiOQE3CE+H+OltYwac5GiivqWDR9IOlxwaYj2YVpQ2MpKKlh/vp8ugS1Y/rQWNORXJoUtxDNCk5XM2HORsprGnh7ZjopXZ135sjl+O3NvSg8U81/f7Kb2BA/ru0ZZjqSy5KhEiGAg8WVjHvrO6rqG3n33kFS2ufh7qZ4afwAeoYH8MjSLRw6VWU6ksuS4hYu70hJNRPnZNJgaWLpvYPkdJiL8PXyYM6UVNzcFBnvZFNV12g6kkuS4hYu7XhZDRPnbqSmwcLiWen06hRoOpLd6xLkyysTksgrquSXK7Zhi1O0xMVJcQuXVVxRx6S5mZypauDtGQOltFvg6h6h/HpUAp/uOMEbXx8wHcflSHELl1RaXc898zI5XlrLgulp9O/SwXQkh5MxLI5b+nXi+c/3sim/xHQclyLFLVxOdX0jUxdkcfBUFXOmpJIW49hbspqilOJ/7+hLdJAvjyzdQklVvelILkOKW7iURksTD7+7hR2FpbwyIYmreoSYjuTQAnw8eXViMiVV9fzyXzLe3VakuIXL0Frz+492sXpPEX8ek8iNfSJMR3IKiZHt+c3oBFbvKWLet/mm47gEKW7hMl5bm8fSTQX817XduGeQay9jb21Th8Qwsnc4z322h21HSk3HcXpS3MIlrMgp5PlV+7g9KZJf3djTdByno5Tir2P7EeLvzWPLt1LbIDsJ2pIUt3B66/YX8+R72xnaPZjn7uznkrv8tYUOvl78bWx/DhZX8dxne0zHcWpS3MKp7TpWxn8t3kz3MH/emJyCl4d8y9vSVT1CmDYkhgXrD7Eh75TpOE7L2jMnOyilViil9iilcpVSg20dTIgrVXimmukLsgjw8WDh9IEE+jjHob727tejEogL8eMX/9pGeW2D6ThOydrLj5eBz7TWCUB/QDblFXatrLqBaQuyqGmwsGjGQCLaO/9xY/ainZc7L4zrz4nyWv788W7TcZzSJYtbKRUIDAPmAWit67XWcttY2K3aBgv3vp1NwelqZt+TSnx4gOlILicpuiMPXted9zYXsnZvkek4TseaK+44oBhYoJTaopSaq5Ty+/GDlFIZSqlspVR2cXFxqwcVwhpNTZonlm9j06ESnh/Xn8Hd5CAEUx4a3p3uYf787oOdsotgK7OmuD2AZOANrXUSUAU8+eMHaa1na61TtdapoaGhrRxTCOs8+2kuK3cc5zejE7i1f2fTcVyat4c7z93Zl2NlNbywap/pOE7FmuIuBAq11pnN76/gbJELYVfmfZvP3G/zmTYkhnuvjjMdRwApXYOYnN6VBRvy2SoLc1rNJYtba30COKKUOrdq4XpA7jgIu7Jy+3GeXrmbUX0i+P0tvWWuth351aiehAf48OR722mwNJmO4xSsnVXyMLBEKbUdGAA8a7tIQrTMpvwSHlu+lZTojrw0fgDublLa9iTAx5P/uS2RPScqmP3NQdNxnIJVhwVrrbcCqTbOIkSL5RVVcO/b2UR1bMecKan4eLqbjiTO44be4dyUGMEra/YzZkBnojr6mo7k0GQZmXBYJ8trmTo/C093NxZNH0hHPy/TkcRF/O6W3igUz6yUZSBXSopbOKSK2gamL8jiTHU9C6al0SVIruDsXWSHdjw0vDv/2XmCdftlyvCVkOIWDqfB0sQDSzaz92QFr09KllPZHcisq2OJCfbljx/vor5RblReLilu4VC01jz53g7W7T/F/97Rl2t7hpmOJFrA28OdP/6sDweLq1iwXg5duFxS3MKhvPjFPt7bXMhjI+IZl9rFdBxxGa5LCGNErzBeXr2fE2W1puM4JClu4TCWbSrglTV53J3ahUeu7246jrgCf7ilD40WzfOr9pqO4pCkuIVD+HpfMb/9cCfD4kN5+vZEWWDj4KKDfZk+NIb3Nhey61iZ6TgOR4pb2L3dx8p5YHEO8eEBvD4pGU93+bZ1Bg9c15327Tx59tNcOR2+heQnQNi142U1zFiYRWA7TxZMS8Pf26o1Y8IBtG/nyaPX92B93mm+2ifTA1tCilvYrXNztSvrGpk/LU0OQ3BCk9K7EhPsy7Mrc2mUfUysJsUt7NK5udp5RZW8MTmZXp0CTUcSNuDl4caTNyWwv6iSf+UUmo7jMKS4hd3RWvO7D3aybv8pnr29L1f3kP3dndmNfSJI7dqRF1bto7peDlywhhS3sDuvrc3jn9lHeHh4d8alyVxtZ6eU4qnRCZyqrGPhhkOm4zgEKW5hVz7ccpTnV+3j9qRIHr8h3nQc0UZSugZxXc9Q3vr6oJwMbwUpbmE3Nh48zS9XbGNQXBDP3dlP5mq7mCdG9qSspoG562Qp/KVIcQu7kFdUQcbb2XQN9uOtyal4eci3pqtJjGzP6L4RzFt3kJKqetNx7Jr8dAjjiivqmLYgCy8PdxZMS6O9r6fpSMKQx0bEU91g4c2vD5iOYtekuIVR1fWNzFyUxenKeuZPS5V9tV1cj/AAbh8QyaINhygqlw2oLsSq4lZKHVJK7VBKbVVKZds6lHANlibNI0u3svNoGa9MSKJfVAfTkYQdeHREDyxNmtfW5pmOYrdacsV9ndZ6gNZazp4UV0xrzf98spsvc0/yx5/1YUTvcNORhJ3oGuzH2JQolmYdkavuC5ChEmHEvG/zWbjhELOuimXqkBjTcYSdeeDa7liatJwKfwHWFrcGVimlcpRSGed7gFIqQymVrZTKLi6WDWPEhX228zjPfJrLTYkR/GZ0L9NxhB2KDvZlTP/OLMks4HRlnek4dsfa4h6qtU4GbgIeVEoN+/EDtNaztdapWuvU0FBZoizOb3PBGR5dtpWkLh34+90DcHOTudri/B64rhu1jRbmyxFnP2FVcWutjzX/XgR8AAy0ZSjhnI6UVHPvomwi2vswZ0oqPp7upiMJO9Y9LIDRiZ1YtOEwZdWymvKHLlncSik/pVTAubeBkcBOWwcTzqW8toEZC7NobNIsmJZGsL+36UjCATx4XXcq6xpZ9N0h01HsijVX3OHAt0qpbcAmYKXW+jPbxhLOpNHSxMPvbiH/VBVvTEomLtTfdCThIHp3DmRErzDmr8+nsk52DjznksWttT6ote7f/KuP1vqZtggmnMfTK3P5el8xT9+WyJDuIabjCAfz0PAelFY3sDSzwHQUuyHTAYVNvf3dIRZuOMS9V8cyfmC06TjCAQ3o0oH02CDmr8+nQU7JAaS4hQ19tbeIP328ixG9wnnyJpn2Jy7ffdfEcbyslpXbj5uOYhekuIVN7DtZwcPvbqFnRCAvjx+Au0z7E1fg2vgwuof5M/ubg3IiPFLcwgZOV9YxY2EWPl7uzJuaip+czC6ukJubIuPqOHYfL2d93mnTcYyT4hatqrbBQsY7ORRX1DF3SiqdO7QzHUk4iTFJnQnx92b2OlkGL8UtWo3Wmqfe30HO4TO8OG4A/bvIbn+i9Xh7uDN9aAzf7Csm93i56ThGSXGLVvPa2jw+2HKUX4yM5+Z+nUzHEU5oUno0vl7uLn+8mRS3aBUrtx///pDfB6/rbjqOcFIdfL0Yl9qFj7cddektX6W4xRXbeqSUx5dvJbVrR/5yZ1855FfY1LQhMTQ2aZa48IIcKW5xRY6W1jBrUTZhgd68dU8K3h6ycZSwrZgQP66ND+XdTQXUN7rmghwpbnHZKusambkwi7oGC/OnysZRou1MHRJDcUUd/9npmgtypLjFZbE0aX6+bAv7iyp5dVIyPcIDTEcSLmRYj1BiQ/xYuOGQ6ShGSHGLy/KX/+TyZW4Rf/pZb66Jl4MzRNtyc1NMGdyVLQWlbC8sNR2nzUlxixZbuqmAOevymTYkhnsGx5iOI1zU2JQo/LzcXfKqW4pbtMiGvFP8/sOdXBMfyu9ulo2jhDkBPp6MTYnik23HOeVi51JKcQurHSyu5P7FOcSF+vHKxCQ83OXbR5g1ZUgM9ZYml9urW37yhFXOVNUzY2EWnu5uzJuaRqCPp+lIQtAt1J+ruoewdFMBlibX2TVQiltcUn1jE/cvzuFYWS2zp6TQJcjXdCQhvjcxPZpjZbV8s6/YdJQ2Y3VxK6XclVJblFKf2DKQsC9aa3734Q4y80v429h+pHQNMh1JiP/nht7hhPh78+4m1xkuackV96NArq2CCPs0+5uDLM8u5JHrezBmQKTpOEL8hKe7G3elRrFmTxEnylxj/xKrilspFQXcDMy1bRxhTz7fdYK/fLaHW/p14rERPUzHEeKCxqd1wdKkWZ59xHSUNmHtFfdLwK+AC24MoJTKUEplK6Wyi4tdZ6zJWe08WsbPl22lX1QHnr+rv2wcJexa12A/ru4RwjIXuUl5yeJWSt0CFGmtcy72OK31bK11qtY6NTRUVtI5spPltcxalE1HX0/mTEnBx1M2jhL2b8JA17lJac0V91DgVqXUIWAZMFwptdimqYQxNfUWZi3KpqK2gXnT0ggL8DEdSQirjOgVToi/l0vcpLxkcWutn9JaR2mtY4DxwBqt9WSbJxNtrqlJ89g/t7LzWBn/mJBEr06BpiMJYTUvDzfuSu3iEjcpZR63+N7zq/by2a4T/HZ0L67vFW46jhAtdu4m5XubC01HsakWFbfW+iut9S22CiPMWZFTyOtfHWBiejQzr4o1HUeIy9I12I+BsUG8l1OI1s57k1KuuAWb8kt46v3tDO0ezJ9v7SMzSIRDG5sSxcFTVWwucN7tXqW4Xdzh01Xc9042XYJ8eX1iCp6ycZRwcKP7dqKdpzsrcpx3uER+Sl1YWU0DMxZmoYH5U9No7ysbRwnH5+/twU19I/hk2zFqGyym49iEFLeLarA08dC7mykoqebNySnEhPiZjiREqxmbEkVFXSOf7zphOopNSHG7IK01f/p4F+v2n+KZ2/syKC7YdCQhWtWg2GCiOrZz2uESKW4XtGD9IZZkFnD/Nd0Yl9rFdBwhWp2bm+LO5Ci+zTvF8bIa03FanRS3i1mz5yRPr9zNyN7h/OrGnqbjCGEzdyZHoTW8v/mo6SitTorbhew5Uc7D726hd+dAXho/ADc3mfYnnFd0sC/pTjqnW4rbRRRX1DFzYTb+Ph7MnZKGr5eH6UhC2NydyWfndG8vLDMdpVVJcbuA2gYLGe9kU1JVz7ypaUS0l42jhGu4MTECL3c3Ptp6zHSUViXF7eS01vxyxXa2FJTy97sHkBjZ3nQkIdpM+3aeDE8I49/bjznVPt1S3E7u5dX7+fe2Y/x6VAKjEiNMxxGizY0Z0Jniijq+O3DadJRWI8XtxD7aepSXvtzP2JQo7r8mznQcIYy4LiGMAG8PPtrqPLNLpLidVM7hM/xyxXYGxgbx7O19ZeMo4bJ8PN0ZlRjBZztPOM0SeCluJ3SkpJr73smmU3sf3pycgpeHfJmFaxszIJKKukbW7ikyHaVVyE+0k6mobWDWomzqG5uYNzWNID8v05GEMG5wt2BCA7z50EmGS6S4nUijpYmHl24hr7iSNyan0D3M33QkIeyCu5viZ/06s3ZPMWU1DabjXDEpbifyzKe5fLW3mP8Zk8jQ7iGm4whhV8YM6Ey9pYnPdzr+joGXLG6llI9SapNSaptSapdS6s9tEUy0zDsbD7Ng/SFmXhXLxPRo03GEsDv9otoTE+zLx9scfzGONVfcdcBwrXV/YAAwSik1yLaxREus21/Mnz7exfCEMH4zupfpOELYJaUUo/t24ruDpympqjcd54pcsrj1WZXN73o2/3KeJUgOLq+oggeWbKZHmD//mJCEu2wcJcQFje7bCUuTdvgDFqwa41ZKuSultgJFwBda68zzPCZDKZWtlMouLi5u7ZziPE5X1jF9YRbeHu7MnZqKv7dsHCXExfTpHEjXYF8+3XHcdJQrYlVxa60tWusBQBQwUCmVeJ7HzNZap2qtU0NDQ1s7p/iRukYL9y/O4WR5HXOmpBDV0dd0JCHs3rnhkg0HHHu4pEWzSrTWpcBXwCibpBFW0Vrz1Ps7yDp0hhfu6k9SdEfTkYRwGDc3D5escuDhEmtmlYQqpTo0v90OGAHssXUwcWGvf3WA9zcf5fEb4vlZ/86m4wjhUPp0DiQ6yJeVDjxcYs0VdydgrVJqO5DF2THuT2wbS1zIf3Yc52+f72XMgM48PLy76ThCOJwfDpeccdDhEmtmlWzXWidprftprRO11v/dFsHET207UsrP/7mV5OgOPHdnP9k4SojL9P1wyW7HHC6RlZMO4mhpDbPeziY0wJvZU1Lx8XQ3HUkIh5UYGUhUx3as3CHFLWyksq6RmQuzqK23sGBaGiH+3qYjCeHQlFLc3LcTG/JOUVrteMMlUtx2ztKkeWTpFvYXVfLapGR6hAeYjiSEUxjdtxONTZovdp80HaXFpLjt3NMrd7NmTxF/vrUPw+JlfrwQraVfVHsiAn2kuEXreue7QyxYf4gZQ2OZPKir6ThCOBWlFCP7hPPN/mJq6h3rZBwpbjv19b5i/vTv3VyfEMZvb5aNo4SwhZG9I6htaOLbvFOmo7SIFLcd2neygoeWbCY+PEA2jhLChtLjggjw8XC4VZRS3HamuKKO6QuyaOflzrypqfjJxlFC2IynuxvXJ4TxZe5JGi1NpuNYTYrbjtQ2WMh4J5vTVXXMnZpK5w7tTEcSwumN7BPBmeoGcg6fMR3FalLcdkJrzS9XbGdLQSkv3T2AflEdTEcSwiUMiw/Fy8ONVQ40u0SK2078/cv9/HvbMX49KoFRiZ1MxxHCZfh7e3BV9xBW7T6B1o5xRowUtx34YEsh/1i9n3GpUdx/TZzpOEK4nJG9wzlSUsOeExWmo1hFituwrEMl/HrFDgbHBfP0bX1l4yghDLi+VzhK4TCLcaS4DTp8uoqMt7OJ6tiONyYn4+UhXw4hTAgN8CYluqPDnEUpTWFIaXU90xdkoYH509Lo4OtlOpIQLm1E73B2HSvnRFmt6SiXJMVtQG2DhYy3cygsrWHOlFRiQvxMRxLC5Q1PCANg7d4iw0kuTYq7jTU1nZ32t+lQCS/c1Z+0mCDTkYQQQI8wfyI7tGN1rhMUt1Kqi1JqrVIqVym1Syn1aFsEc1bPr9r7/bQ/OS9SCPuhlGJ4Qhjr805R22Dfm05Zc8XdCDyhte4FDAIeVEr1tm0s5/RuZgGvf3WAienRMu1PCDs0PCGMmgYLmfklpqNclDVnTh7XWm9ufrsCyAUibR3M2azdW8TvP9rJtT1D+e9b+8i0PyHs0OBuwfh4urEm176nBbZojFspFQMkAZm2COOsdh0r46Elm0mICODVicl4uMutBSHskY+nO0O7hbBmb5Fdr6K0ukGUUv7Ae8DPtdbl5/nzDKVUtlIqu7i4uDUzOrRjpTXMWJhFYDtP5k9Lw192+xPCrl2XEMaRkhoOFFeajnJBVhW3UsqTs6W9RGv9/vkeo7WerbVO1VqnhobKEVsA5bUNzFiYRXWdhQXT0wgP9DEdSQhxCdc1Twtcs8d+Z5dYM6tEAfOAXK31i7aP5BwaLE08uGQzeUWVvDE5hYSIQNORhBBWiOzQjoSIALueFmjNFfdQ4B5guFJqa/Ov0TbO5dC01vz2gx2s23+KZ+/oy1U9QkxHEkK0wHUJYWQfPkNZTYPpKOdlzaySb7XWSmvdT2s9oPnXp20RzlG9siaP5dmFPDK8O+NSu5iOI4RooesTwrA0adbtt8/7dTK9oZUt21TAi1/s447kSB67Id50HCHEZUiK7kgHX0+7HeeW4m5Fq3NP8tsPdzIsPpTn7uwnc7WFcFDuboqh3UP4dv8pu5wWKMXdSjYXnOHBdzfTp3Mgb0xKxlPmagvh0K7pEUpRRZ1dHq4g7dIK8ooqmbEwi/BAH+ZPS5OT2YVwAlfHn51U8M0++xvnluK+QifLa5k6fxMeboq3ZwwkxN/bdCQhRCvo1L4d8eH+fGOHNyiluK9AeW0D0xZkcaa6ngXTBtI1WPbVFsKZXN0jlKz8M9TU29dugVLcl6mu0cJ9b+ew/2QFb05OoW9Ue9ORhBCtbFh8KPWWJjbmnzYd5f+R4r4MTU2ax5dv47uDp/nbXf0YFi9L/IVwRumxQXh7uNndOLcUdwtprXl6ZS4rtx/nqZsSuD0pynQkIYSN+Hi6MzA2SIrb0b3+1QHmr89n+tAYMobJYQhCOLtr4kM5UFzF0dIa01G+J8XdAu9sPMzfPt/LbQM68/ube8sCGyFcwLmh0HV2dNUtxW2lj7Ye5Q8f7WRErzD+dld/3NyktIVwBT3C/IkI9LGraYFS3FZYu6eIJ5ZvY2BMEK9OlFWRQrgSpRRX9zi7/L3R0mQ6DiDFfUmb8ku4f3EOCZ0CmDs1FR9Pd9ORhBBtbFh8KOW1jWw/WmY6CiDFfVE7j5Yxc2EWkR3bsWj6QAJ8PE1HEkIYMKRbMAAb8k4ZTnKWFPcFHCyuZOr8TQT4eLB4ZjrBspRdCJcV7O9Nr06BrM+zj4U4UtzncbyshnvmbQLgnVnpdO7QznAiIYRpQ7sFk1NwhtoG88vfpbh/pKi8lolzMimvaWDRjIF0C/U3HUkIYQeGdA+mvrGJnMNnTEex6rDg+UqpIqXUzrYIZNLpyjomzc3kZHktC6ankRgp+48IIc4aGBuMh5tivR2Mc1tzxb0QGGXjHMaVVtczed4mCkqqmTc1jdSYINORhBB2xN/bg/5dOrDhgPlxbmsOC/4GKGmDLMaU1zYwZf4mDhRVMmdKKoOb7yALIcQPDekWzPbCUsprzZ7+7vJj3JV1jUybv4nc4+W8MTlZdvoTQlzQkG4hNGnIPGj2WrbVilsplaGUylZKZRcX28/S0Iupqbcwc2EW2wrLeGVCEtf3CjcdSQhhx5K7dsDH040NB8yOc7dacWutZ2utU7XWqaGh9n/VWttgIeOdbLIOlfD3uwcwKrGT6UhCCDvn7eFOWkwQGwzP53bJoZKzpZ3Duv2n+OvY/tzav7PpSEIIBzG4WzB7T1ZQXFFnLIM10wGXAt8BPZW7+gkyAAAHwklEQVRShUqpmbaPZTs19RZmLcpm3f5i/jq2H2NT5CAEIYT1hnY7e/r7dwfNXXV7XOoBWusJbRGkLVTXNzJzYTYb80/z/Nj+3CmlLYRoocTI9gT4eLAh75Sx/61fsridRVVdI9MXZpF9qIS/jxvAbUmRpiMJIRyQu5tiUFww6w3eoHSJMe7Kukamzt9EzuEzvDw+SUpbCHFFBscFc6SkhmOGjjNz+uIur21gyrxMth4p5ZUJSfxMbkQKIa7QwNizK6s35ZuZz+3UxV1SVc/kuZlsLyzj1YnJjO4rU/6EEFeuV6dAAnw8yMw3c4PSace4T5TVMnleJkdKqnnrnhRZXCOEaDXuboqBMUHGVlA65RX3oVNVjH1zAyfKalk0Y6CUthCi1aXHBXHwVBVF5bVt/txOV9x7TpQz9s3vqKpr5N170xkUJxtGCSFaX3rs2W7ZdKjtr7qdqrg3F5zh7rc24uGmWH7fYPpFdTAdSQjhpPp0DsTPy93IcInTjHF/s6+Y+xfnEBrgzeKZ6XQJ8jUdSQjhxDzc3UiJCTJyg9IprrhX5BQyY2EWXYP9+Nf9g6W0hRBtIj02iH0nKympqm/T53Xo4tZa88rq/fziX9sYFBfM8vsGERbgYzqWEMJFDIo7N5+7ba+6Hba4Gy1N/OaDHbzwxT7uSI5k/rQ0Anw8TccSQriQvpFn9+fObOOFOA45xl1d38hD725hzZ4iHh7encdviEcpZTqWEMLFeHm4kRzdsc1vUDrcFfeJslrGz97IV3uLePb2vjwxsqeUthDCmPTYYHJPlFNW3XbnUDpUcW87Usqtr37LgaJK5k5NZWJ6tOlIQggXlx4XhNaQ1YbzuR2muD/aepRxb32Hl4cb7z8wlOEJshpSCGHegC4d8HJ3a9OFOHY/xt3UpHnxi328ujaPgbFBvDEpmWB/b9OxhBACAB9Pd/p3aS9X3OdU1DZw/+IcXl2bx/i0LiyemS6lLYSwO6kxQew8WkZNvaVNns+q4lZKjVJK7VVK5SmlnrR1KIC9JyoY8+p6Vu8p4g+39OZ/7+iLl4dd/zsjhHBRaTEdabBoth4pbZPns+awYHfgNeAmoDcwQSnV25ahPtxylNteW09FXSPvzkpnxlWxMnNECGG3UqLPLsTJbqPhEmvGuAcCeVrrgwBKqWXAGGB3a4epa7Tw9Ce5vLPxMANjgnh1YhJhgbISUghh39r7etIzPICsw2fa5PmsKe5I4MgP3i8E0ls7SFl1A1MWbGLbkVIyhsXxyxt74ukuQyNCCMeQFtuRj7Yeo6lJ4+Zm2xECa4r7fAn0Tx6kVAaQARAd3fL51QE+HsQE+/Jf18QxKlGOGBNCOJaHh/fgFyN72ry0wbriLgS6/OD9KODYjx+ktZ4NzAZITU39SbFfipub4uXxSS39a0IIYRfC23BY15qxiCygh1IqVinlBYwHPrZtLCGEEBdyySturXWjUuoh4HPAHZivtd5l82RCCCHOy6qVk1rrT4FPbZxFCCGEFWTahhBCOBgpbiGEcDBS3EII4WCkuIUQwsFIcQshhINRWrd4rcylP6lSxcDhy/zrIcCpVozjCOQ1Oz9Xe70gr7mlumqtQ615oE2K+0oopbK11qmmc7Qlec3Oz9VeL8hrtiUZKhFCCAcjxS2EEA7GHot7tukABshrdn6u9npBXrPN2N0YtxBCiIuzxytuIYQQF2E3xW3iQGKTlFJdlFJrlVK5SqldSqlHTWdqK0opd6XUFqXUJ6aztAWlVAel1Aql1J7mr/dg05lsTSn1WPP39U6l1FKllNOdQaiUmq+UKlJK7fzBx4KUUl8opfY3/97RFs9tF8Vt4kBiO9AIPKG17gUMAh50gdd8zqNArukQbehl4DOtdQLQHyd/7UqpSOARIFVrncjZ7aDHm01lEwuBUT/62JPAaq11D2B18/utzi6Kmx8cSKy1rgfOHUjstLTWx7XWm5vfruDsD3Ok2VS2p5SKAm4G5prO0haUUoHAMGAegNa6XmtdajZVm/AA2imlPABfznNqlqPTWn8D/PhY9zHAoua3FwG32eK57aW4z3cgsdOX2DlKqRggCcg0m6RNvAT8CmgyHaSNxAHFwILm4aG5Sik/06FsSWt9FHgeKACOA2Va61VmU7WZcK31cTh7cQaE2eJJ7KW4rTqQ2BkppfyB94Cfa63LTeexJaXULUCR1jrHdJY25AEkA29orZOAKmz032d70TyuOwaIBToDfkqpyWZTORd7KW6rDiR2NkopT86W9hKt9fum87SBocCtSqlDnB0OG66UWmw2ks0VAoVa63P/m1rB2SJ3ZiOAfK11sda6AXgfGGI4U1s5qZTqBND8e5EtnsReitvlDiRWSinOjnvmaq1fNJ2nLWitn9JaR2mtYzj7NV6jtXbqKzGt9QngiFKqZ/OHrgd2G4zUFgqAQUop3+bv8+tx8huyP/AxMLX57anAR7Z4EqvOnLQ1Fz2QeChwD7BDKbW1+WO/aT7fUziXh4ElzRclB4HphvPYlNY6Uym1AtjM2dlTW3DCVZRKqaXAtUCIUqoQ+CPwF2C5UmomZ/8Bu8smzy0rJ4UQwrHYy1CJEEIIK0lxCyGEg5HiFkIIByPFLYQQDkaKWwghHIwUtxBCOBgpbiGEcDBS3EII4WD+D2zcViNvXo3OAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"Lx = 10\n",
"Nx = 2000\n",
"dx = Lx/Nx\n",
"Source_func = lambda x, q: q*x*(10-x)\n",
"kappa_func = lambda x, kappal, kappah: kappah + (kappal-kappah)*(x>5)*(x<7.5)\n",
"v_func = lambda x,v: v*np.ones(x.size)\n",
"omega_func = lambda x,omega: omega*np.ones(x.size)\n",
"\n",
"#nominal values\n",
"\n",
"import csv\n",
"\n",
"xs = np.linspace(dx/2,Lx-dx/2,Nx)\n",
"source = Source_func(xs, 1)\n",
"kappa = kappa_func(xs, 0.1, 2)\n",
"\n",
"omega_nom = 20\n",
"omega_var = 0.3195214\n",
"v_nom = 10\n",
"v_var = 0.0723493\n",
"kappal_nom = 0.1\n",
"kappal_var = 8.511570e-6\n",
"kappah_nom = 2\n",
"kappah_var = 0.002778142\n",
"q_nom = 1\n",
"q_var = 7.062353e-4\n",
"vs = v_func(xs, v_nom)\n",
"print(vs)\n",
"sol,Q = ADRSource(Lx, Nx, source, omega_func(xs, omega_nom), vs, kappa)\n",
"print(Q)\n",
"plt.plot(xs,sol)\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "8K4A3GjRMbaJ",
"nbpages": {
"level": 3,
"link": "[7.2.2.1 Set up diffusion reaction equation](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.1-Set-up-diffusion-reaction-equation)",
"section": "7.2.2.1 Set up diffusion reaction equation"
}
},
"source": [
"We are going to join gamma RVs with a normal copula. First we get the normal samples"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 648
},
"colab_type": "code",
"id": "5bv2qHTSMbaK",
"nbpages": {
"level": 3,
"link": "[7.2.2.1 Set up diffusion reaction equation](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.1-Set-up-diffusion-reaction-equation)",
"section": "7.2.2.1 Set up diffusion reaction equation"
},
"outputId": "adce1858-0e1a-46df-d404-499ef2d67e2b"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[[0. 0. 0. 0. 0.]\n",
" [0. 0. 0. 0. 0.]\n",
" [0. 0. 0. 0. 0.]\n",
" [0. 0. 0. 0. 0.]\n",
" [0. 0. 0. 0. 0.]]\n",
"[[ 1. 0.1 -0.05 0. 0. ]\n",
" [ 0.1 1. -0.4 0.3 0.5 ]\n",
" [-0.05 -0.4 1. 0.2 0. ]\n",
" [ 0. 0.3 0.2 1. -0.1 ]\n",
" [ 0. 0.5 0. -0.1 1. ]]\n",
"[[ 7.23493000e-02 1.52043249e-02 -3.92366580e-05 0.00000000e+00\n",
" 0.00000000e+00]\n",
" [ 1.52043249e-02 3.19521400e-01 -6.59651879e-04 8.93816670e-03\n",
" 7.51094687e-03]\n",
" [-3.92366580e-05 -6.59651879e-04 8.51157000e-06 3.07547395e-05\n",
" 0.00000000e+00]\n",
" [ 0.00000000e+00 8.93816670e-03 3.07547395e-05 2.77814200e-03\n",
" -1.40072194e-04]\n",
" [ 0.00000000e+00 7.51094687e-03 0.00000000e+00 -1.40072194e-04\n",
" 7.06235300e-04]]\n",
"[[0. 0. 0. 0. 0.]\n",
" [0. 0. 0. 0. 0.]\n",
" [0. 0. 0. 0. 0.]\n",
" [0. 0. 0. 0. 0.]\n",
" [0. 0. 0. 0. 0.]]\n",
"(array([3.20880078e-01, 7.14248146e-02, 2.58516363e-03, 4.68396801e-04,\n",
" 5.13602871e-06]), array([[-6.10221850e-02, -9.98104846e-01, -5.23689494e-03,\n",
" 5.95871096e-03, 2.80458596e-04],\n",
" [-9.97466874e-01, 6.06888498e-02, 2.39831973e-02,\n",
" -2.80393816e-02, -3.91132091e-03],\n",
" [ 2.05538173e-03, -8.80183607e-06, -1.78182587e-02,\n",
" 5.09130368e-02, -9.98542011e-01],\n",
" [-2.80167615e-02, 7.88889090e-03, -9.85095968e-01,\n",
" 1.67509882e-01, 2.60614743e-02],\n",
" [-2.33872832e-02, 6.43007420e-03, 1.69309850e-01,\n",
" 9.84137485e-01, 4.71091795e-02]]))\n",
"0.999986582967767\n"
]
}
],
"source": [
"means = [v_nom, omega_nom, kappal_nom, kappah_nom, q_nom]\n",
"varmat = np.zeros((5,5))\n",
"#fill in diagonal\n",
"corrmat = np.ones((5,5))\n",
"corrmat[0,:] = (1,.1,-0.05,0,0)\n",
"corrmat[1,:] = (.1,1,-.4,.3,.5)\n",
"corrmat[2,:] = (-0.05,-.4,1,.2,0)\n",
"corrmat[3,:] = (0,.3,0.2,1,-.1)\n",
"corrmat[4,:] = (0,.5,0,-.1,1)\n",
"print(corrmat-corrmat.transpose())\n",
"print(corrmat)\n",
"\n",
"\n",
"varmat[np.diag_indices(5)] = [v_var, omega_var, kappal_var, kappah_var, q_var]\n",
"for i in range(5):\n",
" for j in range(5):\n",
" varmat[i,j] = math.sqrt(varmat[i,i])*math.sqrt(varmat[j,j])*corrmat[i,j]\n",
"print(varmat)\n",
"print(varmat-varmat.transpose())\n",
"print(np.linalg.eig(varmat))\n",
"\n",
"# Warning: choosing a large number here will make the notebook take a long time\n",
"# to solve.\n",
"# samps = 10**6\n",
"samps = 10**4\n",
"# samps = 10**3\n",
"test = norm.cdf(np.random.multivariate_normal(np.zeros(5), corrmat, samps))\n",
"\n",
"print(np.max(test[:,0]))\n",
"import tabulate\n",
"#print(tabulate.tabulate(corrmat, tablefmt=\"latex\", floatfmt=\".2f\"))"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "pHqz2NbMbr05",
"nbpages": {
"level": 3,
"link": "[7.2.2.1 Set up diffusion reaction equation](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.1-Set-up-diffusion-reaction-equation)",
"section": "7.2.2.1 Set up diffusion reaction equation"
}
},
"source": [
"The distributions will be gammas"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 204
},
"colab_type": "code",
"id": "7RHUJw50bsj4",
"nbpages": {
"level": 3,
"link": "[7.2.2.1 Set up diffusion reaction equation](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.1-Set-up-diffusion-reaction-equation)",
"section": "7.2.2.1 Set up diffusion reaction equation"
},
"outputId": "9e2ea3e7-9c75-4f8b-8256-e293ae189de0"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"2.0011318620000007 0.04318279093895298 0.20780469421779907\n",
"[[ 1.00876724e+00 1.75153708e-01 -4.80376658e-04 -1.49687366e-03\n",
" 2.78620413e-04]\n",
" [ 1.75153708e-01 4.02281621e+00 -7.99696110e-03 -3.19230630e-02\n",
" 1.00074170e-01]\n",
" [-4.80376658e-04 -7.99696110e-03 9.97417876e-05 -8.24879554e-05\n",
" 1.85805384e-06]\n",
" [-1.49687366e-03 -3.19230630e-02 -8.24879554e-05 4.31871096e-02\n",
" 4.41484525e-04]\n",
" [ 2.78620413e-04 1.00074170e-01 1.85805384e-06 4.41484525e-04\n",
" 1.00649099e-02]] 40.66575412647241\n"
]
}
],
"source": [
"def gen_samps(samps,test):\n",
" #v will have v_nom = 10 v_var = 1 which makes alpha = 10 beta = 10 or theta = 1/10\n",
" vsamps = gamma.ppf(test[:,0], a = 100, scale = 1/10)\n",
" #print(np.mean(vsamps), np.var(vsamps), np.std(vsamps))\n",
" #plt.hist(vsamps)\n",
"\n",
" #omega will have omega_nom = 20, var = 4 which makes alpha = 100 beta = 5, theta = 1/5\n",
" omegasamps = gamma.ppf(test[:,1], a = 100, scale = 1/5)\n",
" #print(np.mean(omegasamps), np.var(omegasamps), np.std(omegasamps))\n",
" #plt.hist(omegasamps)\n",
"\n",
" #kappa_l will have kappa_l = 0.1 var = (0.01)^2 this makes alpha = 100 and theta = 1/1000\n",
" kappalsamps = gamma.ppf(test[:,2], a = 100, scale = 1/1000)\n",
" #print(np.mean(kappalsamps), np.var(kappalsamps), np.std(kappalsamps))\n",
" #plt.hist(kappalsamps)\n",
"\n",
" #kappa_h will have kappa_h = 2 var = .04 this makes alpha = 100 and theta = 1/50\n",
" kappahsamps = (test[:,3]>0.005)*(1.98582-4.82135) + (4.82135) # #gamma.ppf(test[:,3], a = 100, scale = 1/50)\n",
" print(np.mean(kappahsamps), np.var(kappahsamps), np.std(kappahsamps))\n",
" #plt.hist(kappahsamps)\n",
"\n",
" #q will have q = 1 var = 0.01 this makes alpha = 100 and theta = 1/100\n",
" qsamps = gamma.ppf(test[:,4], a = 100, scale = 1/100)\n",
" #print(np.mean(qsamps), np.var(qsamps),np.std(qsamps))\n",
" #plt.hist(qsamps)\n",
" \n",
" return vsamps,omegasamps,kappalsamps,kappahsamps,qsamps\n",
"vsamps,omegasamps,kappalsamps,kappahsamps,qsamps = gen_samps(samps,test)\n",
"\n",
"var_list = [vsamps,omegasamps,kappalsamps,kappahsamps,qsamps]\n",
"cormat_emp = np.zeros((5,5))\n",
"tmp = np.vstack((var_list[0],var_list[1],var_list[2],var_list[3],var_list[4]))\n",
"cormat_emp = np.cov(tmp)\n",
"sens = np.array([-1.74063875491,-0.970393472244,13.1587256647,17.7516305655,52.3902556893])\n",
"print(cormat_emp, np.dot(sens,np.dot(cormat_emp,sens)))"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 68
},
"colab_type": "code",
"id": "BJKHQE_PMbaP",
"nbpages": {
"level": 3,
"link": "[7.2.2.1 Set up diffusion reaction equation](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.1-Set-up-diffusion-reaction-equation)",
"section": "7.2.2.1 Set up diffusion reaction equation"
},
"outputId": "dbc1d1c6-ca5a-42f8-cd79-7357fedc1abf"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"9.996211170854629 19.991729539390022 0.10007439860826033 2.0011318620000007 1.0007749682671143\n"
]
}
],
"source": [
"Qs = np.zeros(samps)\n",
"print(np.mean(vsamps),np.mean(omegasamps),np.mean(kappalsamps), np.mean(kappahsamps),np.mean(qsamps))\n",
"for i in range(samps):\n",
" sol,Qs[i] = ADRSource(Lx, Nx, Source_func(xs, qsamps[i]), omega_func(xs, omegasamps[i]), v_func(xs, vsamps[i]),\n",
" kappa_func(xs, kappalsamps[i], kappahsamps[i]))\n"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 540
},
"colab_type": "code",
"id": "VGk7dr9mMbaR",
"nbpages": {
"level": 3,
"link": "[7.2.2.1 Set up diffusion reaction equation](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.1-Set-up-diffusion-reaction-equation)",
"section": "7.2.2.1 Set up diffusion reaction equation"
},
"outputId": "48a6c2d5-30af-45d1-9112-fcd9c536bd9c"
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYcAAAD8CAYAAACcjGjIAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAELRJREFUeJzt3X+s3XV9x/HnSwr+nAJSHWs7y2KzDc2c2ACOZDFg+GkoySCr2aQSliYGJy4mDvxjZCgJJIs4lsnSCVtxRiBoRqc40vEjm8lAyo+hUAkNMuhgcrWAOiau+t4f91M93s9p773n1HvuLc9HcnK/38/3/T3n/ck39HW/P84lVYUkSYNeNukGJEmLj+EgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkzrJJNzCqI444olavXj3pNiRpybj33nu/U1XL51K7ZMNh9erVbNu2bdJtSNKSkeQ/51rrZSVJUsdwkCR1DAdJUsdwkCR1Zg2HJNcmeSbJNwbGDk+yNcmj7edhbTxJrkqyI8mDSY4Z2GdDq380yYaB8Xck+Xrb56ok2d+TlCTNz1zOHP4eOHXG2EXAbVW1BritrQOcBqxpr43A1TAdJsAlwHHAscAlewKl1Wwc2G/mZ0mSFtis4VBV/wrsmjG8DtjcljcDZw2MX1fT7gIOTXIkcAqwtap2VdWzwFbg1LbttVX17zX9v6S7buC9JEkTMuo9hzdW1dMA7ecb2vgK4MmBup1tbF/jO4eMS5ImaH/fkB52v6BGGB/+5snGJNuSbJuamhqxRUnSbEb9hvS3kxxZVU+3S0PPtPGdwKqBupXAU238XTPG72zjK4fUD1VVm4BNAGvXrt1riMxm9UVfHnXXsTx++RkT+VxJmq9Rzxy2AHueONoA3Dwwfm57aul44Pl22elW4OQkh7Ub0ScDt7Zt309yfHtK6dyB95IkTcisZw5JPs/0b/1HJNnJ9FNHlwM3JjkfeAI4p5XfApwO7ABeAM4DqKpdST4O3NPqLq2qPTe5P8D0E1GvBL7SXpKkCZo1HKrqvXvZdNKQ2gIu2Mv7XAtcO2R8G/DW2fqQJC0cvyEtSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeqMFQ5J/iTJQ0m+keTzSV6R5Kgkdyd5NMkNSQ5ptS9v6zva9tUD73NxG38kySnjTUmSNK6RwyHJCuBDwNqqeitwELAeuAK4sqrWAM8C57ddzgeerao3A1e2OpIc3fZ7C3Aq8OkkB43alyRpfONeVloGvDLJMuBVwNPAicBNbftm4Ky2vK6t07aflCRt/PqqerGqvgXsAI4dsy9J0hhGDoeq+i/gL4AnmA6F54F7geeqancr2wmsaMsrgCfbvrtb/esHx4fs83OSbEyyLcm2qampUVuXJM1inMtKhzH9W/9RwK8ArwZOG1Jae3bZy7a9jfeDVZuqam1VrV2+fPn8m5Ykzck4l5XeDXyrqqaq6v+ALwK/AxzaLjMBrASeass7gVUAbfvrgF2D40P2kSRNwDjh8ARwfJJXtXsHJwEPA3cAZ7eaDcDNbXlLW6dtv72qqo2vb08zHQWsAb42Rl+SpDEtm71kuKq6O8lNwH3AbuB+YBPwZeD6JJ9oY9e0Xa4BPptkB9NnDOvb+zyU5Eamg2U3cEFV/XjUviRJ4xs5HACq6hLgkhnDjzHkaaOq+iFwzl7e5zLgsnF6kSTtP35DWpLUMRwkSR3DQZLUMRwkSR3DQZLUMRwkSR3DQZLUMRwkSR3DQZLUMRwkSR3DQZLUMRwkSR3DQZLUMRwkSR3DQZLUMRwkSR3DQZLUMRwkSR3DQZLUMRwkSR3DQZLUMRwkSR3DQZLUMRwkSR3DQZLUMRwkSR3DQZLUMRwkSR3DQZLUMRwkSR3DQZLUMRwkSZ2xwiHJoUluSvLNJNuTvDPJ4Um2Jnm0/Tys1SbJVUl2JHkwyTED77Oh1T+aZMO4k5IkjWfcM4e/BP65qn4DeBuwHbgIuK2q1gC3tXWA04A17bURuBogyeHAJcBxwLHAJXsCRZI0GSOHQ5LXAr8LXANQVT+qqueAdcDmVrYZOKstrwOuq2l3AYcmORI4BdhaVbuq6llgK3DqqH1JksY3zpnDrwFTwN8luT/JZ5K8GnhjVT0N0H6+odWvAJ4c2H9nG9vbuCRpQsYJh2XAMcDVVfV24H/42SWkYTJkrPYx3r9BsjHJtiTbpqam5tuvJGmOxgmHncDOqrq7rd/EdFh8u10uov18ZqB+1cD+K4Gn9jHeqapNVbW2qtYuX758jNYlSfsycjhU1X8DTyb59TZ0EvAwsAXY88TRBuDmtrwFOLc9tXQ88Hy77HQrcHKSw9qN6JPbmCRpQpaNuf8fA59LcgjwGHAe04FzY5LzgSeAc1rtLcDpwA7ghVZLVe1K8nHgnlZ3aVXtGrMvSdIYxgqHqnoAWDtk00lDagu4YC/vcy1w7Ti9SJL2H78hLUnqGA6SpI7hIEnqGA6SpI7hIEnqGA6SpI7hIEnqGA6SpI7hIEnqGA6SpI7hIEnqGA6SpI7hIEnqGA6SpI7hIEnqGA6SpI7hIEnqGA6SpI7hIEnqGA6SpI7hIEnqGA6SpI7hIEnqGA6SpI7hIEnqGA6SpI7hIEnqGA6SpI7hIEnqGA6SpI7hIEnqGA6SpI7hIEnqjB0OSQ5Kcn+SL7X1o5LcneTRJDckOaSNv7yt72jbVw+8x8Vt/JEkp4zbkyRpPPvjzOFCYPvA+hXAlVW1BngWOL+Nnw88W1VvBq5sdSQ5GlgPvAU4Ffh0koP2Q1+SpBGNFQ5JVgJnAJ9p6wFOBG5qJZuBs9ryurZO235Sq18HXF9VL1bVt4AdwLHj9CVJGs+4Zw6fAj4K/KStvx54rqp2t/WdwIq2vAJ4EqBtf77V/3R8yD6SpAkYORySvAd4pqruHRweUlqzbNvXPjM/c2OSbUm2TU1NzatfSdLcjXPmcAJwZpLHgeuZvpz0KeDQJMtazUrgqba8E1gF0La/Dtg1OD5kn59TVZuqam1VrV2+fPkYrUuS9mXkcKiqi6tqZVWtZvqG8u1V9QfAHcDZrWwDcHNb3tLWadtvr6pq4+vb00xHAWuAr43alyRpfMtmL5m3PwWuT/IJ4H7gmjZ+DfDZJDuYPmNYD1BVDyW5EXgY2A1cUFU//gX0JUmao/0SDlV1J3BnW36MIU8bVdUPgXP2sv9lwGX7oxdJ0vj8hrQkqWM4SJI6hoMkqWM4SJI6hoMkqWM4SJI6hoMkqWM4SJI6hoMkqWM4SJI6hoMkqWM4SJI6hoMkqWM4SJI6hoMkqWM4SJI6hoMkqWM4SJI6hoMkqWM4SJI6hoMkqWM4SJI6hoMkqWM4SJI6hoMkqWM4SJI6hoMkqWM4SJI6hoMkqWM4SJI6hoMkqWM4SJI6I4dDklVJ7kiyPclDSS5s44cn2Zrk0fbzsDaeJFcl2ZHkwSTHDLzXhlb/aJIN409LkjSOcc4cdgMfqarfBI4HLkhyNHARcFtVrQFua+sApwFr2msjcDVMhwlwCXAccCxwyZ5AkSRNxsjhUFVPV9V9bfn7wHZgBbAO2NzKNgNnteV1wHU17S7g0CRHAqcAW6tqV1U9C2wFTh21L0nS+PbLPYckq4G3A3cDb6yqp2E6QIA3tLIVwJMDu+1sY3sblyRNyNjhkOQ1wBeAD1fV9/ZVOmSs9jE+7LM2JtmWZNvU1NT8m5UkzclY4ZDkYKaD4XNV9cU2/O12uYj285k2vhNYNbD7SuCpfYx3qmpTVa2tqrXLly8fp3VJ0j6M87RSgGuA7VX1yYFNW4A9TxxtAG4eGD+3PbV0PPB8u+x0K3ByksPajeiT25gkaUKWjbHvCcD7gK8neaCNfQy4HLgxyfnAE8A5bdstwOnADuAF4DyAqtqV5OPAPa3u0qraNUZfkqQxjRwOVfVVht8vADhpSH0BF+zlva4Frh21F0nS/uU3pCVJHcNBktQxHCRJHcNBktQxHCRJHcNBktQxHCRJHcNBktQxHCRJHcNBktQxHCRJHcNBktQxHCRJHcNBktQxHCRJHcNBktQxHCRJHcNBktQxHCRJHcNBktQxHCRJHcNBktQxHCRJHcNBktQxHCRJHcNBktQxHCRJHcNBktQxHCRJHcNBktQxHCRJHcNBktQxHCRJnUUTDklOTfJIkh1JLpp0P5L0UrYowiHJQcBfA6cBRwPvTXL0ZLuSpJeuRREOwLHAjqp6rKp+BFwPrJtwT5L0krVs0g00K4AnB9Z3AsdNqBdJmtXqi748kc99/PIzFuRzFks4ZMhYdUXJRmBjW/1BkkfG+MwjgO+Msf+85YoF+ZgFn9cCORDndSDOCZzXL9SY/468aa6FiyUcdgKrBtZXAk/NLKqqTcCm/fGBSbZV1dr98V6LifNaOg7EOYHzOlAslnsO9wBrkhyV5BBgPbBlwj1J0kvWojhzqKrdST4I3AocBFxbVQ9NuC1JeslaFOEAUFW3ALcs4Eful8tTi5DzWjoOxDmB8zogpKq77ytJeolbLPccJEmLyAEdDklWJbkjyfYkDyW5cEhNklzV/mzHg0mOmUSv8zHHeb0ryfNJHmivP5tEr/OR5BVJvpbkP9q8/nxIzcuT3NCO191JVi98p3M3xzm9P8nUwLH6o0n0OookByW5P8mXhmxbUsdqj1nmtGSP1XwtmnsOvyC7gY9U1X1Jfgm4N8nWqnp4oOY0YE17HQdczeL/At5c5gXwb1X1ngn0N6oXgROr6gdJDga+muQrVXXXQM35wLNV9eYk64ErgN+fRLNzNJc5AdxQVR+cQH/juhDYDrx2yLaldqz22NecYOkeq3k5oM8cqurpqrqvLX+f6QO+YkbZOuC6mnYXcGiSIxe41XmZ47yWnHYMftBWD26vmTfF1gGb2/JNwElJhn2JclGY45yWpCQrgTOAz+ylZEkdK5jTnF4yDuhwGNROad8O3D1j07A/3bFk/qHdx7wA3tkuZ3wlyVsWtLERtVP6B4BngK1VtdfjVVW7geeB1y9sl/MzhzkB/F67rHlTklVDti9GnwI+CvxkL9uX3LFi9jnB0jxW8/aSCIckrwG+AHy4qr43c/OQXZbEb3azzOs+4E1V9Tbgr4B/XOj+RlFVP66q32b6W/LHJnnrjJIld7zmMKd/AlZX1W8B/8LPfttetJK8B3imqu7dV9mQsUV7rOY4pyV3rEZ1wIdDu877BeBzVfXFISVz+tMdi81s86qq7+25nNG+Q3JwkiMWuM2RVdVzwJ3AqTM2/fR4JVkGvA7YtaDNjWhvc6qq71bVi231b4F3LHBrozgBODPJ40z/FeUTk/zDjJqldqxmndMSPVYjOaDDoV3fvAbYXlWf3EvZFuDc9tTS8cDzVfX0gjU5grnMK8kv77m+m+RYpo/1dxeuy/lLsjzJoW35lcC7gW/OKNsCbGjLZwO31yL+ss5c5jTjHteZTN9DWtSq6uKqWllVq5n+cze3V9UfzihbUsdqLnNaisdqVAf600onAO8Dvt6u+QJ8DPhVgKr6G6a/lX06sAN4AThvAn3O11zmdTbwgSS7gf8F1i/m/zCbI4HNmf6fP70MuLGqvpTkUmBbVW1hOhQ/m2QH07+Frp9cu3Mylzl9KMmZTD+Ftgt4/8S6HdMSP1ZDHajHajZ+Q1qS1DmgLytJkkZjOEiSOoaDJKljOEiSOoaDJKljOEiSOoaDJKljOEiSOv8PiUgNr+39JlYAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYUAAAD8CAYAAACYebj1AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAEZxJREFUeJzt3H+s3XV9x/Hna1RxOrUFCmEtWzE2TjQT8QZwJMaBgQLG6iJJnZmNa9Z/2KbbEi0zi/NXgtsy1EzZiDDROJA5HQ0ysUGJ2zKRW0UEsWvVDroyel0R54hO9L0/zqcfD+Xe3p+cc7XPR3Jyvt/39/O93/f33HP76vfHOakqJEkC+LlxNyBJWj4MBUlSZyhIkjpDQZLUGQqSpM5QkCR1hoIkqTMUJEndnEIhyd4kX01yZ5LJVjsuyY4ku9vzqlZPkvcl2ZPkriRnDP2czW387iSbn5hdkiQtVObyieYke4GJqvr2UO3PgINVdXmSbcCqqnpzkouA3wMuAs4C3ltVZyU5DpgEJoACdgIvqqqHZtruCSecUOvWrVvwzknS0Wjnzp3frqrVC1l3xSK2uxF4aZu+FrgNeHOrf7gGafOFJCuTnNzG7qiqgwBJdgAbgOtm2sC6deuYnJxcRIuSdPRJ8h8LXXeu1xQK+EySnUm2ttpJVfUAQHs+sdXXAPcPrbuv1WaqP0aSrUkmk0xOTU3NfU8kSYs21yOFc6pqf5ITgR1Jvn6EsZmmVkeoP7ZQdRVwFcDExITf1idJIzSnI4Wq2t+eDwCfBM4EHmynhWjPB9rwfcApQ6uvBfYfoS5JWiZmDYUkT0vy9EPTwPnA3cB24NAdRJuBG9v0duB17S6ks4GH2+mlW4Dzk6xqdyqd32qSpGViLqePTgI+meTQ+L+rqk8nuQO4IckW4D7gkjb+ZgZ3Hu0BHgFeD1BVB5O8A7ijjXv7oYvOkqTlYU63pI7LxMREefeRJM1Pkp1VNbGQdf1EsySpMxQkSZ2hIEnqFvOJZs1g3bZPjWW7ey+/eCzblfSzwyMFSVJnKEiSOkNBktQZCpKkzlCQJHWGgiSpMxQkSZ2hIEnqDAVJUmcoSJI6Q0GS1BkKkqTOUJAkdYaCJKkzFCRJnaEgSeoMBUlSZyhIkjpDQZLUGQqSpM5QkCR1hoIkqTMUJEmdoSBJ6gwFSVJnKEiSOkNBktQZCpKkzlCQJHWGgiSpm3MoJDkmyZeT3NTmT01ye5LdST6W5Mmtfmyb39OWrxv6GZe1+q4kFyz1zkiSFmc+RwpvAO4dmn83cEVVrQceAra0+hbgoap6NnBFG0eS04BNwPOADcAHkhyzuPYlSUtpxVwGJVkLXAy8C/jDJAHOBX6zDbkW+FPgSmBjmwb4OPBXbfxG4Pqq+gHwrSR7gDOBf1uSPRHrtn1qbNvee/nFY9u2pKUz1yOF9wBvAn7c5o8HvlNVj7b5fcCaNr0GuB+gLX+4je/1adbpkmxNMplkcmpqah67IklarFlDIcnLgQNVtXO4PM3QmmXZkdb5SaHqqqqaqKqJ1atXz9aeJGkJzeX00TnAK5JcBDwFeAaDI4eVSVa0o4G1wP42fh9wCrAvyQrgmcDBofohw+tIkpaBWY8UquqyqlpbVesYXCj+bFW9Fvgc8Oo2bDNwY5ve3uZpyz9bVdXqm9rdSacC64EvLtmeSJIWbU4XmmfwZuD6JO8Evgxc3epXAx9pF5IPMggSquqeJDcAXwMeBS6tqh8tYvuSpCU2r1CoqtuA29r0NxncPXT4mO8Dl8yw/rsY3MEkSVqG/ESzJKkzFCRJnaEgSeoMBUlSZyhIkjpDQZLUGQqSpM5QkCR1hoIkqTMUJEmdoSBJ6gwFSVJnKEiSOkNBktQZCpKkzlCQJHWGgiSpMxQkSZ2hIEnqDAVJUmcoSJI6Q0GS1BkKkqTOUJAkdYaCJKkzFCRJnaEgSeoMBUlSZyhIkjpDQZLUGQqSpM5QkCR1hoIkqTMUJEndrKGQ5ClJvpjkK0nuSfK2Vj81ye1Jdif5WJInt/qxbX5PW75u6Gdd1uq7klzwRO2UJGlh5nKk8APg3Kp6AXA6sCHJ2cC7gSuqaj3wELCljd8CPFRVzwauaONIchqwCXgesAH4QJJjlnJnJEmLM2so1MD32uyT2qOAc4GPt/q1wCvb9MY2T1t+XpK0+vVV9YOq+hawBzhzSfZCkrQk5nRNIckxSe4EDgA7gG8A36mqR9uQfcCaNr0GuB+gLX8YOH64Ps06w9vammQyyeTU1NT890iStGBzCoWq+lFVnQ6sZfC/++dON6w9Z4ZlM9UP39ZVVTVRVROrV6+eS3uSpCUyr7uPquo7wG3A2cDKJCvaorXA/ja9DzgFoC1/JnBwuD7NOpKkZWAudx+tTrKyTf888DLgXuBzwKvbsM3AjW16e5unLf9sVVWrb2p3J50KrAe+uFQ7IklavBWzD+Fk4Np2p9DPATdU1U1JvgZcn+SdwJeBq9v4q4GPJNnD4AhhE0BV3ZPkBuBrwKPApVX1o6XdHUnSYswaClV1F/DCaerfZJq7h6rq+8AlM/ysdwHvmn+bkqRR8BPNkqTOUJAkdYaCJKkzFCRJnaEgSeoMBUlSZyhIkjpDQZLUGQqSpM5QkCR1hoIkqTMUJEmdoSBJ6gwFSVJnKEiSOkNBktQZCpKkzlCQJHWGgiSpMxQkSZ2hIEnqDAVJUmcoSJI6Q0GS1BkKkqTOUJAkdYaCJKkzFCRJnaEgSeoMBUlSZyhIkjpDQZLUGQqSpM5QkCR1s4ZCklOSfC7JvUnuSfKGVj8uyY4ku9vzqlZPkvcl2ZPkriRnDP2szW387iSbn7jdkiQtxFyOFB4F/qiqngucDVya5DRgG3BrVa0Hbm3zABcC69tjK3AlDEIEeCtwFnAm8NZDQSJJWh5mDYWqeqCqvtSm/we4F1gDbASubcOuBV7ZpjcCH66BLwArk5wMXADsqKqDVfUQsAPYsKR7I0lalHldU0iyDnghcDtwUlU9AIPgAE5sw9YA9w+ttq/VZqpLkpaJOYdCkl8A/gF4Y1V990hDp6nVEeqHb2drkskkk1NTU3NtT5K0BOYUCkmexCAQPlpVn2jlB9tpIdrzgVbfB5wytPpaYP8R6o9RVVdV1URVTaxevXo++yJJWqS53H0U4Grg3qr6y6FF24FDdxBtBm4cqr+u3YV0NvBwO710C3B+klXtAvP5rSZJWiZWzGHMOcBvAV9Ncmer/TFwOXBDki3AfcAlbdnNwEXAHuAR4PUAVXUwyTuAO9q4t1fVwSXZC0nSkpg1FKrqX5j+egDAedOML+DSGX7WNcA182lQkjQ6fqJZktQZCpKkzlCQJHWGgiSpMxQkSZ2hIEnqDAVJUmcoSJI6Q0GS1BkKkqTOUJAkdYaCJKkzFCRJnaEgSeoMBUlSZyhIkjpDQZLUGQqSpM5QkCR1hoIkqTMUJEmdoSBJ6gwFSVJnKEiSOkNBktQZCpKkzlCQJHWGgiSpMxQkSZ2hIEnqDAVJUmcoSJI6Q0GS1BkKkqRu1lBIck2SA0nuHqodl2RHkt3teVWrJ8n7kuxJcleSM4bW2dzG706y+YnZHUnSYszlSOFDwIbDatuAW6tqPXBrmwe4EFjfHluBK2EQIsBbgbOAM4G3HgoSSdLyMWsoVNXngYOHlTcC17bpa4FXDtU/XANfAFYmORm4ANhRVQer6iFgB48PGknSmC30msJJVfUAQHs+sdXXAPcPjdvXajPVJUnLyFJfaM40tTpC/fE/INmaZDLJ5NTU1JI2J0k6soWGwoPttBDt+UCr7wNOGRq3Fth/hPrjVNVVVTVRVROrV69eYHuSpIVYaChsBw7dQbQZuHGo/rp2F9LZwMPt9NItwPlJVrULzOe3miRpGVkx24Ak1wEvBU5Iso/BXUSXAzck2QLcB1zSht8MXATsAR4BXg9QVQeTvAO4o417e1UdfvFakjRms4ZCVb1mhkXnTTO2gEtn+DnXANfMqztJ0kj5iWZJUmcoSJI6Q0GS1BkKkqTOUJAkdYaCJKkzFCRJnaEgSeoMBUlSZyhIkjpDQZLUGQqSpM5QkCR1s35L6k+zdds+Ne4WJOmnikcKkqTOUJAkdT/Tp480OuM6Vbf38ovHsl3pZ5VHCpKkzlCQJHWGgiSpMxQkSZ2hIEnqDAVJUmcoSJI6Q0GS1BkKkqTOUJAkdYaCJKkzFCRJnaEgSeoMBUlSZyhIkjpDQZLUGQqSpG7koZBkQ5JdSfYk2Tbq7UuSZjbSUEhyDPB+4ELgNOA1SU4bZQ+SpJmN+kjhTGBPVX2zqv4PuB7YOOIeJEkzWDHi7a0B7h+a3wecNeIe9DNk3bZPjW3bey+/eCzbHec+H23G9Tsep1GHQqap1WMGJFuBrW32e0l2PeFdPdYJwLdHvM25sK/5ecL7yrsXtNpyfb1g+fY2tr5m+R0v59frlxe68qhDYR9wytD8WmD/8ICqugq4apRNDUsyWVUT49r+TOxrfuxr/pZrb/Y1P62vdQtdf9TXFO4A1ic5NcmTgU3A9hH3IEmawUiPFKrq0SS/C9wCHANcU1X3jLIHSdLMRn36iKq6Gbh51Nudh7GdupqFfc2Pfc3fcu3NvuZnUX2lqmYfJUk6Kvg1F5Kk7qgPhSTHJPlykpva/KlJbk+yO8nH2gXxUfe0N8lXk9yZZLLVjkuyo/W1I8mqUffV+liZ5ONJvp7k3iQvHndvSZ7TXqtDj+8meeO4+2q9/UGSe5LcneS6JE9ZJu+xN7Se7knyxlYby+uV5JokB5LcPVSbtpcMvK99Tc5dSc4YcV+XtNfsx0kmDht/WetrV5ILRtzXn7e/ybuSfDLJyoX2ddSHAvAG4N6h+XcDV1TVeuAhYMtYuoJfr6rTh2552wbc2vq6tc2Pw3uBT1fVrwAvYPDajbW3qtrVXqvTgRcBjwCfHHdfSdYAvw9MVNXzGdxcsYkxv8eSPB/4HQbfMPAC4OVJ1jO+1+tDwIbDajP1ciGwvj22AleOuK+7gd8APj9cbF/Xswl4XlvnA+1rfUbV1w7g+VX1q8C/A5ctuK+qOmofDD4ncStwLnATgw/XfRtY0Za/GLhlDH3tBU44rLYLOLlNnwzsGkNfzwC+RbsWtZx6G+rlfOBfl0Nf/OQT/McxuKnjJuCCcb/HgEuADw7N/wnwpnG+XsA64O7Z3lPA3wCvmW7cKPoaqt/GIOwPzV8GXDY0fwvw4lH31Za9CvjoQvs62o8U3sPgj+HHbf544DtV9Wib38fgD3vUCvhMkp3tE94AJ1XVAwDt+cQx9PUsYAr423bK7YNJnrZMejtkE3Bdmx5rX1X1n8BfAPcBDwAPAzsZ/3vsbuAlSY5P8lTgIgYfKl1Ov8eZepnuq3LG8Td6uOXU128D/9Sm593XURsKSV4OHKiqncPlaYaO4/asc6rqDAaHypcmeckYepjOCuAM4MqqeiHwv4zvNNbjtHPzrwD+fty9ALTz4BuBU4FfBJ7G4Hd6uJG+x6rqXgansHYAnwa+Ajx6xJWWj+XyN3q4ZdFXkrcw+F1+9FBpmmFH7OuoDQXgHOAVSfYy+LbWcxkcOaxMcujzG4/7Go5RqKr97fkAg3PjZwIPJjkZoD0fGHVfDP6Xsa+qbm/zH2cQEsuhNxj8g/ulqnqwzY+7r5cB36qqqar6IfAJ4NdYHu+xq6vqjKp6CXAQ2M34X69hM/Uy61fljMnY+0qyGXg58Npq54oW0tdRGwpVdVlVra3Bd4RsAj5bVa8FPge8ug3bDNw4yr6SPC3J0w9NMzhHfjeDrwPZPK6+AKrqv4D7kzynlc4DvrYcemtew09OHcH4+7oPODvJU5OEn7xeY32PASQ5sT3/EoMLp9cx/tdr2Ey9bAde1+5COht4+NBppjHbDmxKcmySUxlcCP/iqDaeZAPwZuAVVfXIovp6oi6E/DQ9gJcCN7XpZ7UXbQ+D0xDHjriXZzE4nP8KcA/wllY/nsFF8d3t+bgxvVanA5PAXcA/AquWQ2/AU4H/Bp45VFsOfb0N+DqDYP8IcOy432Otr39mEFBfAc4b5+vFIJAeAH7I4H+2W2bqhcHpkPcD3wC+ytDF3hH19ao2/QPgQYZuEgDe0vraBVw44r72MLh2cGd7/PVC+/ITzZKk7qg9fSRJejxDQZLUGQqSpM5QkCR1hoIkqTMUJEmdoSBJ6gwFSVL3/29WO/uOmIIrAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"52.38429950498757 60.93083101449816 44.256769035451256 5.846536644275092 15.192880831520508 2.154994384485121\n"
]
}
],
"source": [
"plt.hist(kappahsamps)\n",
"plt.show()\n",
"plt.hist(Qs)\n",
"plt.show()\n",
"print(np.mean(Qs),stats.scoreatpercentile(Qs,95) ,stats.scoreatpercentile(Qs,5),np.std(Qs), stats.kurtosis(Qs), stats.skew(Qs))\n",
"Qref = Qs.copy()\n",
"np.savetxt(fname=\"ref_\"+ str(samps) + \"_binomial.csv\", delimiter=\",\", X=Qref)"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "qpV0Y54GqvLa",
"nbpages": {
"level": 3,
"link": "[7.2.2.1 Set up diffusion reaction equation](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.1-Set-up-diffusion-reaction-equation)",
"section": "7.2.2.1 Set up diffusion reaction equation"
}
},
"source": [
"Now we will do 100 samples and compare"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 51
},
"colab_type": "code",
"id": "U3uCihlpMbaW",
"nbpages": {
"level": 3,
"link": "[7.2.2.1 Set up diffusion reaction equation](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.1-Set-up-diffusion-reaction-equation)",
"section": "7.2.2.1 Set up diffusion reaction equation"
},
"outputId": "1ae79b64-e021-4618-f22b-f6581a2e09e7"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"100\n",
"2.0141752999999993 0.07959828077091 0.2821316727538934\n"
]
}
],
"source": [
"samps = 100 #4*10**4\n",
"print (samps)\n",
"test = norm.cdf(np.random.multivariate_normal(np.zeros(5), corrmat, samps))\n",
"vsamps,omegasamps,kappalsamps,kappahsamps,qsamps = gen_samps(samps,test)"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 51
},
"colab_type": "code",
"id": "oG02l9jiMbaY",
"nbpages": {
"level": 3,
"link": "[7.2.2.1 Set up diffusion reaction equation](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.1-Set-up-diffusion-reaction-equation)",
"section": "7.2.2.1 Set up diffusion reaction equation"
},
"outputId": "6f8fd711-69ad-42d8-e29f-c4b5891620dd"
},
"outputs": [],
"source": [
"QSRS = np.zeros(samps)\n",
"for i in range(samps):\n",
" sol,QSRS[i] = ADRSource(Lx, Nx, Source_func(xs, qsamps[i]), omega_func(xs, omegasamps[i]), v_func(xs, vsamps[i]),\n",
" kappa_func(xs, kappalsamps[i], kappahsamps[i]))"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 281
},
"colab_type": "code",
"id": "_oWlAwu_eubW",
"nbpages": {
"level": 3,
"link": "[7.2.2.1 Set up diffusion reaction equation](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.1-Set-up-diffusion-reaction-equation)",
"section": "7.2.2.1 Set up diffusion reaction equation"
},
"outputId": "42a413c6-638b-467a-f7cc-44cc277ee392"
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAAD8CAYAAACMwORRAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAADe1JREFUeJzt3V2MXOV9x/Hvr3YSCk0KhgW5OHRBsmhQJAxdIVIklECSQkCAKqhAUesLq75JVWgrpU6rXkTqhZGqklaKolhAY1UtgdIQIxORWA6oL6pI1uHNjrFMiEtcu+ySQF5aqY2Tfy/mOKycXXZmd9bjefh+pNXMOXtm53k0nu+ePTNnnKpCktSWXxj1ACRJw2fcJalBxl2SGmTcJalBxl2SGmTcJalBxl2SGrS6n42SHAJ+CPwEOFZVU0nWAA8Ck8Ah4Ler6rWVGaYkaRCD7Ll/oKo2VNVUt7wF2F1V64Hd3bIk6RSQfs5Q7fbcp6rq1TnrDgDvr6qjSdYCT1bVxW/2c84555yanJxc3ogl6S1mz549r1bVxCC36euwDFDAV5IU8Nmq2gacV1VHAbrAn7vYD5mcnGR6enqQ8UnSW16S/xj0Nv3G/aqqOtIFfFeSFwYY1GZgM8AFF1ww6PgkSUvQ1zH3qjrSXc4AjwBXAK90h2PoLmcWuO22qpqqqqmJiYH+qpAkLdGicU9yRpJ3Hr8OfBjYCzwKbOw22wjsWKlBSpIG089hmfOAR5Ic3/4fqurxJF8HHkqyCXgZuG3lhilJGsSica+ql4BL51n/XeDalRiUJGl5PENVkhpk3CWpQcZdkhpk3CWpQf2exPSWNbnlsZHd96GtN4zsviWNN/fcJalBxl2SGmTcJalBxl2SGmTcJalBxl2SGmTcJalBxl2SGmTcJalBxl2SGmTcJalBxl2SGmTcJalBxl2SGmTcJalBxl2SGmTcJalBxl2SGmTcJalBxl2SGmTcJalBxl2SGmTcJalBxl2SGmTcJalBxl2SGmTcJalBxl2SGmTcJalBxl2SGtR33JOsSvJ0kp3d8oVJnkpyMMmDSd6+csOUJA1ikD33O4H9c5bvBu6pqvXAa8CmYQ5MkrR0fcU9yTrgBuDebjnANcDD3SbbgVtWYoCSpMH1u+f+KeDjwE+75bOB16vqWLd8GDh/vhsm2ZxkOsn07OzssgYrSerPonFPciMwU1V75q6eZ9Oa7/ZVta2qpqpqamJiYonDlCQNYnUf21wF3JTkI8BpwLvo7cmfmWR1t/e+DjiycsOUJA1i0T33qvpEVa2rqkngduCrVfVR4Ang1m6zjcCOFRulJGkgy3mf+58Af5TkRXrH4O8bzpAkScvVz2GZn6mqJ4Enu+svAVcMf0iSpOXyDFVJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGLRr3JKcl+VqSZ5PsS/LJbv2FSZ5KcjDJg0nevvLDlST1o5899/8FrqmqS4ENwHVJrgTuBu6pqvXAa8CmlRumJGkQi8a9en7ULb6t+yrgGuDhbv124JYVGaEkaWB9HXNPsirJM8AMsAv4FvB6VR3rNjkMnL/AbTcnmU4yPTs7O4wxS5IW0Vfcq+onVbUBWAdcAbxnvs0WuO22qpqqqqmJiYmlj1SS1LeB3i1TVa8DTwJXAmcmWd19ax1wZLhDkyQtVT/vlplIcmZ3/ReBDwL7gSeAW7vNNgI7VmqQkqTBrF58E9YC25OsovfL4KGq2pnkm8Dnk/wF8DRw3wqOU5I0gEXjXlXPAZfNs/4lesffJUmnGM9QlaQGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJatCi/0G2Rmdyy2Mjud9DW28Yyf1KGh733CWpQcZdkhpk3CWpQcZdkhpk3CWpQcZdkhpk3CWpQcZdkhpk3CWpQcZdkhpk3CWpQcZdkhpk3CWpQYvGPcm7kzyRZH+SfUnu7NavSbIrycHu8qyVH64kqR/97LkfA/64qt4DXAl8LMklwBZgd1WtB3Z3y5KkU8Cica+qo1X1je76D4H9wPnAzcD2brPtwC0rNUhJ0mAGOuaeZBK4DHgKOK+qjkLvFwBw7rAHJ0lamr7jnuSXgH8C7qqqHwxwu81JppNMz87OLmWMkqQB9RX3JG+jF/a/r6ovdKtfSbK2+/5aYGa+21bVtqqaqqqpiYmJYYxZkrSIft4tE+A+YH9V/dWcbz0KbOyubwR2DH94kqSl6Oc/yL4K+B3g+STPdOv+FNgKPJRkE/AycNvKDFGSNKhF415V/wpkgW9fO9zhLGxyy2Mn664kaex5hqokNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDFo17kvuTzCTZO2fdmiS7khzsLs9a2WFKkgbRz57754DrTli3BdhdVeuB3d2yJOkUsWjcq+qfge+dsPpmYHt3fTtwy5DHJUlahqUecz+vqo4CdJfnDm9IkqTlWvEXVJNsTjKdZHp2dnal706SxNLj/kqStQDd5cxCG1bVtqqaqqqpiYmJJd6dJGkQS437o8DG7vpGYMdwhiNJGoZ+3gr5APDvwMVJDifZBGwFPpTkIPChblmSdIpYvdgGVXXHAt+6dshjkSQNiWeoSlKDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNWjRk5j01jO55bGR3fehrTeM7L6llrjnLkkNMu6S1CDjLkkNMu6S1CDjLkkNMu6S1CDjLkkNMu6S1CDjLkkNMu6S1CDjLkkNMu6S1CDjLkkNMu6S1CDjLkkNMu6S1CDjLkkNMu6S1CDjLkkNMu6S1CDjLkkNMu6S1CDjLkkNMu6S1KDVox6ANNfklsdGcr+Htt4wkvvVyfVW+ve1rD33JNclOZDkxSRbhjUoSdLyLDnuSVYBnwauBy4B7khyybAGJklauuXsuV8BvFhVL1XV/wGfB24ezrAkScuxnLifD3xnzvLhbp0kacSW84Jq5llXP7dRshnY3C3+KMmBBX7eOcCryxjPqcp5jYHc/bOrTc1rDuc1QnP+ffXrxHn96qA/YDlxPwy8e87yOuDIiRtV1TZg22I/LMl0VU0tYzynJOc1XpzXeHFeC1vOYZmvA+uTXJjk7cDtwKPLGYwkaTiWvOdeVceS/D7wZWAVcH9V7RvayCRJS7ask5iq6kvAl4Y0lkUP3Ywp5zVenNd4cV4LSNXPvQYqSRpzfraMJDVoZHFPsirJ00l2dssXJnkqycEkD3Yv0o6VJIeSPJ/kmSTT3bo1SXZ189qV5KxRj3NQSc5M8nCSF5LsT/K+RuZ1cfdYHf/6QZK7GpnbHybZl2RvkgeSnNbIc+zObk77ktzVrRu7xyvJ/Ulmkuyds27eeaTnb7qPeXkuyeX93Mco99zvBPbPWb4buKeq1gOvAZtGMqrl+0BVbZjzNqYtwO5uXru75XHz18DjVfVrwKX0Hrexn1dVHegeqw3ArwP/AzzCmM8tyfnAHwBTVfVeem94uJ0xf44leS/we/TOjr8UuDHJesbz8foccN0J6xaax/XA+u5rM/CZvu6hqk76F733xO8GrgF20jsh6lVgdff99wFfHsXYljmvQ8A5J6w7AKztrq8FDox6nAPO6V3At+len2llXvPM88PAv7UwN944e3wNvTdN7AR+c9yfY8BtwL1zlv8c+Pi4Pl7AJLB3zvK88wA+C9wx33Zv9jWqPfdP0XtQftotnw28XlXHuuVx/SiDAr6SZE93Zi7AeVV1FKC7PHdko1uai4BZ4G+7w2j3JjmD8Z/XiW4HHuiuj/Xcquo/gb8EXgaOAt8H9jD+z7G9wNVJzk5yOvAReidSjvXjNcdC81jSR72c9LgnuRGYqao9c1fPs+k4vo3nqqq6nN6fUR9LcvWoBzQEq4HLgc9U1WXAfzMef/b2rTv2fBPwj6MeyzB0x2pvBi4EfgU4g96/yRON1XOsqvbTO7S0C3gceBY49qY3asOS+jiKPfergJuSHKL3SZLX0NuTPzPJ8ffdz/tRBqe6qjrSXc7QO3Z7BfBKkrUA3eXM6Ea4JIeBw1X1VLf8ML3Yj/u85roe+EZVvdItj/vcPgh8u6pmq+rHwBeA36CN59h9VXV5VV0NfA84yPg/XsctNI++PurlRCc97lX1iapaV1WT9P4U/mpVfRR4Ari122wjsONkj205kpyR5J3Hr9M7hruX3kcybOw2G7t5VdV/Ad9JcnG36lrgm4z5vE5wB28ckoHxn9vLwJVJTk8S3njMxvo5BpDk3O7yAuC36D1u4/54HbfQPB4Ffrd718yVwPePH755UyN+QeH9wM7u+kXA14AX6f15/I5Rv+Ax4Fwuovdn4rPAPuDPuvVn03vx+GB3uWbUY13C3DYA08BzwBeBs1qYVze304HvAr88Z93Yzw34JPACvR2MvwPeMe7PsW5e/0LvF9WzwLXj+njR+6V0FPgxvT3zTQvNg95hmU8D3wKep/cuqEXvwzNUJalBnqEqSQ0y7pLUIOMuSQ0y7pLUIOMuSQ0y7pLUIOMuSQ0y7pLUoP8HWGTWEnTNweIAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"51.754085783529696 59.55016400777867 44.19214310775517 6.711582319278186 19.857958480592576 3.271194643345333\n"
]
}
],
"source": [
"plt.hist(QSRS)\n",
"plt.show()\n",
"print(np.mean(QSRS),stats.scoreatpercentile(QSRS,95),stats.scoreatpercentile(QSRS,5),np.std(QSRS), \n",
" stats.kurtosis(QSRS), stats.skew(QSRS))"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "TqUABHh3i_vm",
"nbpages": {
"level": 3,
"link": "[7.2.2.2 Apply LHS](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.2-Apply-LHS)",
"section": "7.2.2.2 Apply LHS"
}
},
"source": [
"### 7.2.2.2 Apply LHS"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 264
},
"colab_type": "code",
"id": "78AGh7iQjANt",
"nbpages": {
"level": 3,
"link": "[7.2.2.2 Apply LHS](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.2-Apply-LHS)",
"section": "7.2.2.2 Apply LHS"
},
"outputId": "c3405446-3619-4454-e898-b85be5abb88c"
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXYAAAD8CAYAAABjAo9vAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAFENJREFUeJzt3XGIHOd5x/Hfc3dSmzYGC1ng1NJJETYmiTBxdDhX8kdrx22VYGISE5rEpIFUiIANCc0faRC4bUohYAiUWtAK26QFNSZgGwc7xpZBxQR6jm+FYqTICeLoJRcbrCjnOsGh0nmf/nGn+HTevZ2deWfed975fkDg06123xnv/t5nnndm1txdAIB8TMQeAAAgLIIdADJDsANAZgh2AMgMwQ4AmSHYASAzBDsAZIZgB4DMEOwAkJmpGC96zTXX+J49e2K8NAC0Vq/X+6W77xj1uCjBvmfPHs3Pz8d4aQBoLTNbLPI4WjEAkBmCHQAyQ7ADQGYqB7uZ/b6Z/dDMfmRmZ8zsH0IMDABQTojF0/+TdJu7/8bMtkj6gZk97e5zAZ4bADCmysHuq9/U8Zu1H7es/eHbOwAgkiA9djObNLNTkl6TdNzdXwjxvADq11tc1pET59RbXI49FAQS5Dx2d39L0gfN7GpJj5vZPnc/vf4xZnZI0iFJmp6eDvGyACrqLS7r7gfndHGlr61TEzp2cFb7d2+LPSxUFPSsGHd/XdJ/STow4HdH3X3G3Wd27Bh54RSABswtXNDFlb76Ll1a6Wtu4ULsISGAEGfF7Fir1GVm75J0u6SXqz4vgPrN7t2urVMTmjRpy9SEZvdujz0kBBCiFfMeSf9uZpNanSi+6+5PBnheADXbv3ubjh2c1dzCBc3u3U4bJhMhzop5SdLNAcYCIIL9u7cR6JnhylMAyAzBDgCZIdgBIDMEOwBkhmAHgMwQ7ACQGYIdADJDsANAZgh2AMgMwQ4AmSHYASAzBDsAZIZgB4DMEOwAkBmCHQAyQ7ADQGYIdgDIDMEOYCy9xWUdOXFOvcXl2EPBECG+8xRAR/QWl3X3g3O6uNLX1qkJHTs4y9fqJYiKHUBhcwsXdHGlr75Ll1b6mlu4EHtIGIBgB1DY7N7t2jo1oUmTtkxNaHbv9thDwgC0YgAUtn/3Nh07OKu5hQua3budNkyiCHYAY9m/exuBnrjKrRgz22VmJ8zsrJmdMbMvhxgYAKCcEBX7iqSvuvtJM7tKUs/Mjrv7jwM8NwBgTJUrdnd/1d1Prv33ryWdlXRd1ecFAJQT9KwYM9sj6WZJL4R8XgBAccGC3czeLelRSV9x9zcG/P6Qmc2b2fz58+dDvSwAYIMgwW5mW7Qa6sfc/bFBj3H3o+4+4+4zO3bsCPGyAIABQpwVY5IeknTW3b9VfUgAgCpCVOwfkfR5SbeZ2am1Px8P8LwAgBIqn+7o7j+QZAHGgsz0Fpe5QhGIgCtPUQvuAgjEw03AUAvuAgjEQ7CjFtwFEIiHVgxqwV0AgXgIdkiqZ6GTuwACcRDsYKETyAw9drDQCWSGYO+Izb5ZnoVOIC+0YjpgVKslt4VOLoxC1xHsHTCo1bIx8HJZ6GS9AKAV0wldarWwXgBQsXdC21otVVoplyexSyv97CcxYBhz98ZfdGZmxufn5xt/XaRvVCulSOjTY0euzKzn7jOjHkfFjqRsth5QtH+ey3oBUBbBjqQMaqVcrsBfef23IxeBARDsSMzG9QBJv6vSpyZMU5MTeust+ufAZgh2JGd9K+XIiXO/q9Lf6rv+8pZduu7qd9E/BzZBsCNpG1szd31oJ4EOjECwI2ltO1UTSAHBjuTVcZYLp0QiZwQ7OofbDuSHifpKBHuCyrxJeWMXV+TeOWgPJup3ItgTU+ZNmtMbu4kJitsO5IWJ+p0I9sSUeZPm8sZuaoIatCDLEU97MVG/U5BgN7OHJd0h6TV33xfiObuqzJs0lzd26Alqs7BevyCb0xFPF3Hm1DuFqti/LekBSf8R6Pk6q8ybNJc3dsgJapywzuWIp8u4P9CVggS7uz9vZntCPBfKvUlzeGOHnKDGCetcjngkFtGxih47khJqghonrHM54qGlhMsaC3YzOyTpkCRNT0839bJISJPV5LhhHfuIJ8S+oaWEyxoLdnc/KumotPpFG029LtIQ4gs0xhU7rIsKVWnn1FJCNbRi0IgQX6CRq1CVdi4tJVQX6nTH70j6U0nXmNmSpL9z94dCPDfysFk12cUWwvojlJCVdluOUlCvUGfFfDbE8yBfm1WTXWshDDpCodJGSLRi0Jhh1WTXWgiDjlDuufX67LcbzSHYkYS6Wwgpnd/dtSMUNI9gR6sVCezUFme7doSC5hHsaK2igZ3i4iyLnKjTROwBAGUNCuxBLrc+Jk3JtT56i8s6cuKceovLsYeCjFCxjymlXm3XFe1Vp9r6SK1FhHwQ7GPgg5iWcQK7ztZH2ck+xRYR8kCwj6HrH8SqRys53jZgnMl+4/ZzdgzqQrCPocsfxKpHK7ke7RSd7Idt//ojDkk6cuJcUu0itBPBPoYuf6Va1aOVsv8+9f1bdLIftv2X/+Q68SEOgn1MXf1KtapHK2X+fRv2b9E+/6jtz73Nl/oEnRuCvYLcP4zrVT2zpMy/j71/i4ZRkT7/qO3Puc3Xhgk6NwR7BTl/GAepulA57r+PuX83htF9d3xAy29erFRxbrb9OffbY0/QXUSwV5Dq+dFNq+swO+b+XR9GFy/1dd8Tp9V3r7XizLXf3rUCKAUEe0WxT7eLre4QCr1/i05C68PIzNR3D1ZxjhpDahVu1YmbAqh5BDsqSS2ENjPOJLQ+jLb9wVZ948kzQSrOImNIqcINNXF3vQBqGsGOSlIKoVHGnYTWh9GN114VpOIsMoaUKtw2Tdx4G8GOSlIKoVGqTEKhKs5x7m+Twr5s08SNt5m7N/6iMzMzPj8/3/jrIo6UzmGueyxF7w+fyv4o4j9f+JmePv2qPrbvPfrch6djD6fTzKzn7jOjHkfFjlqldoZH3TcDK7KtqVTjRfQWl/WNJ8/o4kpfL/7Pr3TjtVe1Zuxdxv3YMZZx7x9e9J7pOchxW3Pcpi6gYkdhZarvOnu0qbU0cuxH57hNXUCwo7AyZ0jUtbiaWotHSnMhmXPQu4lgR2Flq7c6espNn4ZX5r4xsY8oBk1+ksYeU5vWBLAqSLCb2QFJ/yxpUtKD7v7NEM+LtKRUvTXZIihz35gUjig2Tn6PnVzSoyeXkjrKKSr2JNk2lYPdzCYlHZH0Z5KWJL1oZt9z9x9XfW6kJ5XqrclJpsx9Y1K4sGfj5OdS9DGVkcIk2TYhKvZbJJ1z9wVJMrNHJN0piWBPVC7VT1OTTJn7xqSw6DjojpGPnVxq3UJoCpNk24QI9usk/Xzdz0uSPrzxQWZ2SNIhSZqe5iKHWKh+xlfmvjGptK02Tn4pjGlcKUySbRMi2G3A373jclZ3PyrpqLR65WmA1w0qlyp2FKqfcsrcNyaVttV6KY5plFQmyTYJEexLknat+3mnpFcCPG9julTFdrn6CTV5tzEc2459Pp4Qwf6ipBvM7L2SfiHpM5I+F+B5G9OlKrar1U+XJm+gcrC7+4qZ3SvpGa2e7viwu5+pPLIGda2K3az6ybUlVXbyznV/IG9BzmN39+9L+n6I54qhq1XsRjlXtWUm79j7g0kFZXHl6Zqmengpf1irtqRS2LZhYygzecds0cWeVNBuBHuDUv+wVmlJpbBto8Yw7uQds0XXpXUfhEewNyj1D+s4Ve3GyjiFbQs9hkH7o6mjkq6t+yAsgr1BbfiwFqlqB1XGKWxbHWPYeFOvpo5K2rbuk0IbDm8j2BvUtg/rMIMq43tuvT76ttW9f5s+KknpTpGbSaENhysR7A3L4UKLYZVxCttW5xhiHZWkHpwptOFwJYIdY2vbkUfIK05jbPew4By2XU1X9ym04XAlgh1DbRYQKVTnRYSudmNs96DgHLZdMar7tk30XUCwd0CZCi71w/+icmgTDArOIyfODdyucbY3ZGXflok+tqaOpgj2zJUN6BwCUcqnTbAxOIdt17DqfmOY5DJxt0mT+7xVwZ7ymQGpKhvQOQVijm2CYdu18e8lDQyT2FfV5vb/o4gm93lrgp0Ko5wqX0CdSyDm2iYYtl3r/35Yy4YzfJrX5D5vTbDn0hpoWpWAjh2IXa3sQtrs1NSUzvDpgib3eWuCPZfWQAyxA7qMLld2IW0WJqmc4dMlTe3z1gR7Tq0BjNblyq6IcY5mxg2TOo+U+Bw3ozXBLrWz8mxS21oXm42365XdZuo8mmniSInPcf1aFewYrm2tiyK32KWyG6zOoxmOlPIwEXsACGPQBzJlRca7f/c23XPr9QTLBpePZiZNwY9m6nxuNIeKPRNta120bbwpWN+6qutohiOlPJi7N/6iMzMzPj8/3/jr5i6nHnuXxlBE21ptqIeZ9dx9ZtTjqNgz0rZFqdjjrRqWTU4K9L4xDoIdnVUlLJuuoGldYRwEOzqrSljG+DYlet8oqlKwm9mnJf29pPdJusXdaZyjNaqEZYwKeljrqi3rBGhO1Yr9tKRPSfq3AGMBGle2z59KBc2iKgapFOzuflaSzCzMaICCUqhSYy/+SiyqYjB67GgdqtS3saiKQUYGu5k9J+naAb867O5PFH0hMzsk6ZAkTU9PFx4g6pNC1VsGVerbUmkJtV1bPwvDjAx2d789xAu5+1FJR6XVC5RCPCfKa3PV24YqtcmgSKEl1GZt/iwMQyumo9pc9aZepeYYFDlr82dhmKqnO35S0r9I2iHpKTM75e5/EWRkqFUbqt7NpFylbgyKx04uJTsJof2fhUG4V0yDUuvjpTaeXFyu2C+t9DU5OSG5a6XvVO8Ja8tnoei9Ygj2hnB43i2Xg+IXr/9Wj/zwZ+q7NGnS3/z5jbrn1utjDw8tVTTYuR97Q9p2v3RUc/le8nd9aCf3N0fjWDxtSKg+XlsOGdss5D5OfaEXeaIV06CqgUE7p35l9zET7pXYH/XgfuwJqnomR46nZaWmzD5mwr0S+yM+euwtwvdR1q/MPmb95Ersj/io2FuEfm39yuzjHM+DrqLq/qCNUx09diAAwuhKZfcHbZzN0WMHGpTylbAxlN0fIdaRmGQJdgAJCdHGoeIn2AEkpOo6EmeOrSLYASSlSluLhexVBDuAbHDm2CqCvSVYEAKKYSGbYG8FFoQAjIMrT1uAK/kAjINgbwFuJQBgHLRiWoAFoWawjoFcEOwtwYJQvVjHQE5oxQBiHQN5IdgBsY6BvNCKAcQ6BvJCsANrWMdALmjFAEBmKgW7md1vZi+b2Utm9riZXR1qYACAcqpW7Mcl7XP3myT9VNLXqw8JAFBFpWB392fdfWXtxzlJO6sPCQBQRcge+xclPT3sl2Z2yMzmzWz+/PnzAV8WbdZbXNaRE+fUW1yOPRQgGyPPijGz5yRdO+BXh939ibXHHJa0IunYsOdx96OSjkqrX2ZdarTICld7AvUYGezufvtmvzezL0i6Q9JH3Z3ARmF8jRlQj0rnsZvZAUlfk/Qn7v5mmCGhK/gaM6AeVS9QekDS70k6bmaSNOfuX6o8KnQCV3sC9agU7O5+faiBoJu42hMIjytPASAzBDsAZIZgB4DMEOwIhouNgDRw214EwcVGQDqo2BEEXy0HpINgRxB8tRyQDloxCIKLjYB0EOwIhouNgDTQigGAzBDsAJAZgh0AMkOwA0BmCHYAyAzBDgCZIdgBIDMEOwBkhmAHgMwQ7ACQGYIdADJDsANAZgh2AMgMwQ4AmakU7Gb2j2b2kpmdMrNnzeyPQg0MAFBO1Yr9fne/yd0/KOlJSfcFGBMAoIJKwe7ub6z78Q8lebXhAACqqvwNSmb2T5L+StL/Srq18ogAAJWMrNjN7DkzOz3gz52S5O6H3X2XpGOS7t3keQ6Z2byZzZ8/fz7cFgAArmDuYbonZrZb0lPuvm/UY2dmZnx+fj7I6wJAV5hZz91nRj2u6lkxN6z78ROSXq7yfEBZvcVlHTlxTr3F5dhDAaKr2mP/ppndKKkvaVHSl6oPCRhPb3FZdz84p4srfW2dmtCxg7Pav3tb7GEB0VQKdne/K9RAgLLmFi7o4kpffZcurfQ1t3CBYEenceUpWm9273ZtnZrQpElbpiY0u3d77CEBUVU+3RGIbf/ubTp2cFZzCxc0u3c71To6j2BHFvbv3kagA2toxQBAZgh2AMgMwQ4AmSHYASAzBDsAZIZgB4DMBLsJ2FgvanZeq7cgSN01kn4ZexAN6+I2S93cbra5fXa7+45RD4oS7G1hZvNF7qSWky5us9TN7Wab80UrBgAyQ7ADQGYI9s0djT2ACLq4zVI3t5ttzhQ9dgDIDBU7AGSGYB/BzO43s5fN7CUze9zMro49prqZ2afN7IyZ9c0s6zMIzOyAmf3EzM6Z2d/GHk8TzOxhM3vNzE7HHktTzGyXmZ0ws7Nr7+0vxx5TnQj20Y5L2ufuN0n6qaSvRx5PE05L+pSk52MPpE5mNinpiKSPSXq/pM+a2fvjjqoR35Z0IPYgGrYi6avu/j5Js5Luyfn/NcE+grs/6+4raz/OSdoZczxNcPez7v6T2ONowC2Szrn7grtflPSIpDsjj6l27v68pF/FHkeT3P1Vdz+59t+/lnRW0nVxR1Ufgn08X5T0dOxBIJjrJP183c9LyvjDjlVmtkfSzZJeiDuS+vANSpLM7DlJ1w741WF3f2LtMYe1ejh3rMmx1aXINneADfg7ThPLmJm9W9Kjkr7i7m/EHk9dCHZJ7n77Zr83sy9IukPSRz2T80NHbXNHLEnate7nnZJeiTQW1MzMtmg11I+5+2Oxx1MnWjEjmNkBSV+T9Al3fzP2eBDUi5JuMLP3mtlWSZ+R9L3IY0INzMwkPSTprLt/K/Z46kawj/aApKskHTezU2b2r7EHVDcz+6SZLUn6Y0lPmdkzscdUh7VF8XslPaPVxbTvuvuZuKOqn5l9R9J/S7rRzJbM7K9jj6kBH5H0eUm3rX2OT5nZx2MPqi5ceQoAmaFiB4DMEOwAkBmCHQAyQ7ADQGYIdgDIDMEOAJkh2AEgMwQ7AGTm/wH9Vvq+o4cjiAAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"#lhd will have the values in 0 to 1\n",
"lhd = lhs(5, samples=samps)\n",
"#now i need to turn these into samples from N(0,Corrmat)\n",
"#do cholesky fact\n",
"chol = np.linalg.cholesky(corrmat)\n",
"\n",
"lhs_unif = np.zeros((samps,5))\n",
"for i in range(samps):\n",
" lhs_unif[i,:] = np.dot(chol,norm.ppf(lhd[i,:]))\n",
"#print(lhs_unif)\n",
"#plt.plot(lhd[:,0],lhd[:,1],'.')\n",
"#plt.show()\n",
"plt.plot(lhs_unif[:,0],lhs_unif[:,1],'.')\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 34
},
"colab_type": "code",
"id": "veSJTwfsjEQ9",
"nbpages": {
"level": 3,
"link": "[7.2.2.2 Apply LHS](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.2-Apply-LHS)",
"section": "7.2.2.2 Apply LHS"
},
"outputId": "6f7f258d-b49c-42de-ace6-1aaa59d31a83"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"1.9858199999999997 4.930380657631324e-32 2.220446049250313e-16\n"
]
}
],
"source": [
"test_lhs = norm.cdf(lhs_unif)\n",
"\n",
"vsamps,omegasamps,kappalsamps,kappahsamps,qsamps = gen_samps(samps,test_lhs)"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 336
},
"colab_type": "code",
"id": "ATReERNLjI_E",
"nbpages": {
"level": 3,
"link": "[7.2.2.2 Apply LHS](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.2-Apply-LHS)",
"section": "7.2.2.2 Apply LHS"
},
"outputId": "21848535-183e-4072-d32b-9eee318588b7"
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXYAAAD8CAYAAABjAo9vAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAADPVJREFUeJzt3X+I5PV9x/Hnq5oUaizR3iqHer00iKn/5LRXaREkiRj8UaJCA0obpBXOghaF0Mbknwpt4QI1toUiPaNRWmOamojSiI1YIQSK5M4c/uhVTO0lUa93J2nQttCgvvvHfq/dnrvu7Mzszc77ng9YZua739nv58PneN6X787MpqqQJPXxU7MegCRpugy7JDVj2CWpGcMuSc0YdklqxrBLUjOGXZKaMeyS1Ixhl6RmTjyWB9u0aVNt3br1WB5Skubenj17XquqhVH3P6Zh37p1K7t37z6Wh5SkuZfk+2vZ30sxktSMYZekZgy7JDVj2CWpGcMuSc2sGvYkZyV5Msm+JM8nuXnYfluSV5LsHb4uX//hSpJWM8rLHd8EPl1VTyc5GdiT5PHhe3dU1Z+s3/AkSWu1atir6gBwYLj/RpJ9wBnrPTBJ0njWdI09yVbgPOCpYdNNSZ5Jck+SU6Y8NknSGEZ+52mS9wFfA26pqteT3An8IVDD7e3Aby/zvB3ADoAtW7ZMY8zS1G299RszO/b+nVfM7NjqaaQz9iTvYTHq91fV1wGq6mBVvVVVbwN3ARcs99yq2lVV26tq+8LCyB91IEka0yiviglwN7Cvqr6wZPvmJbtdDTw3/eFJktZqlEsxFwKfAp5NsnfY9jng2iTbWLwUsx+4YV1GKElak1FeFfNtIMt869HpD0eSNCnfeSpJzRh2SWrGsEtSM8f0LyhJq5nl68mlLjxjl6RmDLskNWPYJakZwy5JzRh2SWrGsEtSM4Zdkprxdex6B19LLs03z9glqRnDLknNGHZJasawS1Izhl2SmjHsktSMYZekZgy7JDVj2CWpGcMuSc0YdklqxrBLUjOGXZKaMeyS1Ixhl6RmDLskNWPYJakZwy5JzRh2SWrGsEtSM6uGPclZSZ5Msi/J80luHrafmuTxJC8Ot6es/3AlSasZ5Yz9TeDTVfWLwK8ANyY5F7gVeKKqzgaeGB5LkmZs1bBX1YGqenq4/wawDzgDuBK4b9jtPuCq9RqkJGl0a7rGnmQrcB7wFHB6VR2AxfgDp017cJKktRs57EneB3wNuKWqXl/D83Yk2Z1k9+HDh8cZoyRpDUYKe5L3sBj1+6vq68Pmg0k2D9/fDBxa7rlVtauqtlfV9oWFhWmMWZL0LkZ5VUyAu4F9VfWFJd96BLhuuH8d8PD0hydJWqsTR9jnQuBTwLNJ9g7bPgfsBL6a5HrgB8An12eIkqS1WDXsVfVtICt8++LpDkeSNCnfeSpJzRh2SWrGsEtSM4Zdkpox7JLUjGGXpGYMuyQ1Y9glqRnDLknNGHZJasawS1Izhl2SmjHsktSMYZekZgy7JDVj2CWpGcMuSc0YdklqxrBLUjOGXZKaMeyS1Ixhl6RmDLskNWPYJakZwy5JzRh2SWrGsEtSM4Zdkpox7JLUjGGXpGYMuyQ1Y9glqRnDLknNrBr2JPckOZTkuSXbbkvySpK9w9fl6ztMSdKoRjljvxe4dJntd1TVtuHr0ekOS5I0rlXDXlXfAn50DMYiSZqCSa6x35TkmeFSzSlTG5EkaSLjhv1O4IPANuAAcPtKOybZkWR3kt2HDx8e83CSpFGNFfaqOlhVb1XV28BdwAXvsu+uqtpeVdsXFhbGHackaURjhT3J5iUPrwaeW2lfSdKxdeJqOyR5APgIsCnJy8AfAB9Jsg0oYD9wwzqOUZK0BquGvaquXWbz3eswFknSFPjOU0lqxrBLUjOGXZKaMeyS1Ixhl6RmDLskNWPYJakZwy5JzRh2SWrGsEtSM4Zdkpox7JLUjGGXpGYMuyQ1Y9glqRnDLknNGHZJasawS1Izhl2SmjHsktSMYZekZgy7JDVj2CWpGcMuSc0YdklqxrBLUjOGXZKaMeyS1Ixhl6RmDLskNWPYJakZwy5Jzawa9iT3JDmU5Lkl205N8niSF4fbU9Z3mJKkUY1yxn4vcOlR224Fnqiqs4EnhseSpA1g1bBX1beAHx21+UrgvuH+fcBVUx6XJGlM415jP72qDgAMt6dNb0iSpEms+y9Pk+xIsjvJ7sOHD6/34STpuDdu2A8m2Qww3B5aaceq2lVV26tq+8LCwpiHkySNatywPwJcN9y/Dnh4OsORJE1qlJc7PgD8I3BOkpeTXA/sBC5J8iJwyfBYkrQBnLjaDlV17QrfunjKY5EkTYHvPJWkZgy7JDVj2CWpmVWvsUtaX1tv/cZMjrt/5xUzOa7Wn2fsktSMYZekZgy7JDVj2CWpGcMuSc0YdklqxrBLUjOGXZKaMeyS1Ixhl6RmDLskNWPYJakZwy5JzRh2SWrGsEtSM4ZdkprxD21sYLP6AwyS5ptn7JLUjGGXpGYMuyQ1Y9glqRnDLknNGHZJasawS1Izhl2SmjHsktSMYZekZgy7JDVj2CWpmYk+BCzJfuAN4C3gzaraPo1BSZLGN41Pd/xoVb02hZ8jSZoCL8VIUjOTnrEX8M0kBfxlVe06eockO4AdAFu2bJnwcJKmZZaf979/5xUzO/bxYNIz9gur6nzgMuDGJBcdvUNV7aqq7VW1fWFhYcLDSZJWM1HYq+rV4fYQ8BBwwTQGJUka39hhT3JSkpOP3Ac+Djw3rYFJksYzyTX204GHkhz5OV+uqsemMipJ0tjGDntVvQR8eIpjkSRNgS93lKRmDLskNWPYJakZwy5JzRh2SWrGsEtSM4Zdkpox7JLUjGGXpGYMuyQ1Y9glqZlp/Gm89mb5Bwkkaa08Y5ekZgy7JDVj2CWpGcMuSc0YdklqxrBLUjOGXZKa8XXsko65Wb03ZP/OK2Zy3GPNM3ZJasawS1Izhl2SmjHsktSMYZekZgy7JDVj2CWpGcMuSc3MzRuU/GMXkiY1y44cyzdHecYuSc0YdklqxrBLUjMThT3JpUleSPK9JLdOa1CSpPGNHfYkJwB/AVwGnAtcm+TcaQ1MkjSeSc7YLwC+V1UvVdVPgK8AV05nWJKkcU0S9jOAHy55/PKwTZI0Q5O8jj3LbKt37JTsAHYMD/8jyQsTHHM9bQJem/UgJuQcNoYOc4Ae89gwc8jnx37qJuDn1/KEScL+MnDWksdnAq8evVNV7QJ2TXCcYyLJ7qraPutxTMI5bAwd5gA95tFoDlvX8pxJLsV8Bzg7yQeSvBe4Bnhkgp8nSZqCsc/Yq+rNJDcBfw+cANxTVc9PbWSSpLFM9FkxVfUo8OiUxjJrG/5y0Qicw8bQYQ7QYx7H5RxS9Y7fd0qS5pgfKSBJzRy3YU9yQpLvJvm74fEHkjyV5MUkfzP8QnhDW2YO9yb51yR7h69tsx7japLsT/LsMN7dw7ZTkzw+rMXjSU6Z9TjfzQpzuC3JK0vW4vJZj/PdJHl/kgeT/HOSfUl+dQ7XYbk5zNs6nLNkrHuTvJ7klrWuxXEbduBmYN+Sx58H7qiqs4F/B66fyajW5ug5APxeVW0bvvbOYlBj+Ogw3iMvS7sVeGJYiyeGxxvd0XOAxX9PR9Zio/8u6s+Ax6rqQ8CHWfx3NW/rsNwcYI7WoapeODJW4JeA/wIeYo1rcVyGPcmZwBXAF4fHAT4GPDjsch9w1WxGN5qj59DMlSyuAczBWsy7JD8LXATcDVBVP6mqHzNH6/Auc5hnFwP/UlXfZ41rcVyGHfhT4PeBt4fHPwf8uKreHB7Pw8cjHD2HI/44yTNJ7kjy0zMY11oV8M0ke4Z3KQOcXlUHAIbb02Y2utEsNweAm4a1uGeDX8b4BeAw8KXh0t4Xk5zEfK3DSnOA+VmHo10DPDDcX9NaHHdhT/JrwKGq2rN08zK7btiXC60wB4DPAh8Cfhk4FfjMsR7bGC6sqvNZ/JTQG5NcNOsBjWG5OdwJfBDYBhwAbp/h+FZzInA+cGdVnQf8Jxv/ssvRVprDPK3D/xp+x/cJ4G/Hef5xF3bgQuATSfaz+ImUH2Px7Pf9SY68rn/Zj0fYQN4xhyR/XVUHatF/A19i8RM4N7SqenW4PcTitcQLgINJNgMMt4dmN8LVLTeHqjpYVW9V1dvAXWzstXgZeLmqnhoeP8hiJOdpHZadw5ytw1KXAU9X1cHh8ZrW4rgLe1V9tqrOHD574RrgH6rqN4AngV8fdrsOeHhGQ1zVCnP4zSULHxavwT03w2GuKslJSU4+ch/4OItjfoTFNYANvhYrzeHIWgyuZgOvRVX9G/DDJOcMmy4G/ok5WoeV5jBP63CUa/m/yzCwxrWY6J2nzXwG+EqSPwK+y/BLmDlzf5IFFi8t7QV+Z8bjWc3pwEOL/w9xIvDlqnosyXeArya5HvgB8MkZjnE1K83hr4aXmxawH7hhdkMcye+y+O/nvcBLwG+xeOI3L+sAy8/hz+dsHUjyM8Al/P+x7mQNa+E7TyWpmePuUowkdWfYJakZwy5JzRh2SWrGsEtSM4Zdkpox7JLUjGGXpGb+BzyVgQkvJkWgAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"52.091501134877944 60.53399286590944 44.78023096114341 4.899665382873159 1.1994249416182612 0.18626015216253644\n",
"52.38429950498757 60.93083101449816 44.256769035451256 5.846536644275092 15.192880831520508 2.154994384485121\n"
]
}
],
"source": [
"QLHS = np.zeros(samps)\n",
"for i in range(samps):\n",
" sol,QLHS[i] = ADRSource(Lx, Nx, Source_func(xs, qsamps[i]), omega_func(xs, omegasamps[i]), v_func(xs, vsamps[i]),\n",
" kappa_func(xs, kappalsamps[i], kappahsamps[i]))\n",
"plt.hist(QLHS)\n",
"plt.show()\n",
"print(np.mean(QLHS),stats.scoreatpercentile(QLHS,95),stats.scoreatpercentile(QLHS,5),np.std(QLHS), \n",
" stats.kurtosis(QLHS), stats.skew(QLHS))\n",
"print(np.mean(Qs),stats.scoreatpercentile(Qs,95) ,stats.scoreatpercentile(Qs,5),np.std(Qs), stats.kurtosis(Qs), stats.skew(Qs))"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[7.2.2.2 Apply LHS](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.2-Apply-LHS)",
"section": "7.2.2.2 Apply LHS"
}
},
"source": [
"Below is Figure 7.13 in McClarren (2018); it shows the convergence rates of different methods compared against a LHS with 10$^6$ samples."
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "01-H_CF8yAm3",
"nbpages": {
"level": 3,
"link": "[7.2.2.2 Apply LHS](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.2-Apply-LHS)",
"section": "7.2.2.2 Apply LHS"
}
},
"source": [
"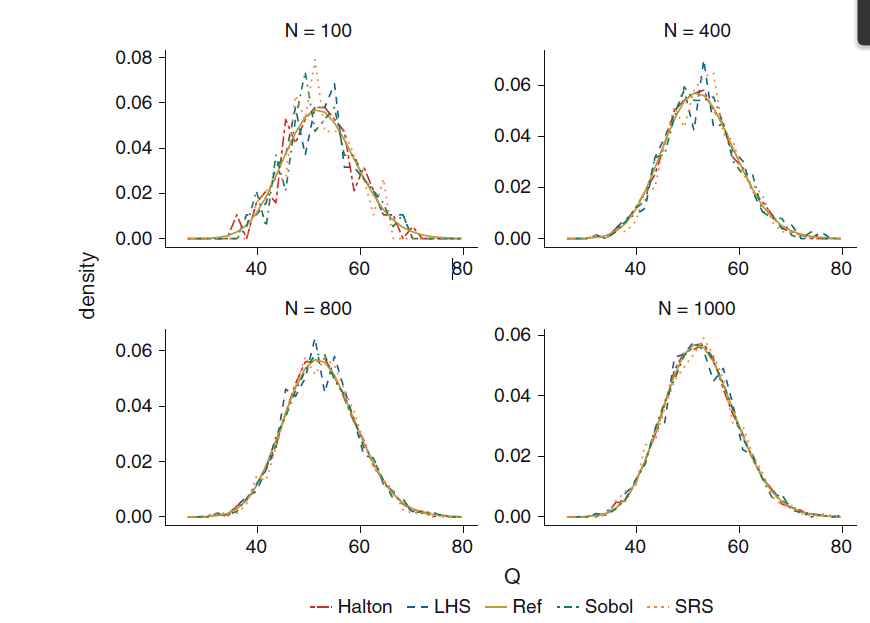\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"nbpages": {
"level": 3,
"link": "[7.2.2.2 Apply LHS](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.2-Apply-LHS)",
"section": "7.2.2.2 Apply LHS"
}
},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"< [7.1 Latin Hypercube and Quasi-Monte Carlo Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html) | [Contents](toc.html) | [7.3 Meaningful Title Goes Here](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.03-Contributed-Example.html)
"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "DnCs7XId4TeP",
"nbpages": {
"level": 1,
"link": "[7.2 Latin Hypercube Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2-Latin-Hypercube-Sampling)",
"section": "7.2 Latin Hypercube Sampling"
}
},
"source": [
"# 7.2 Latin Hypercube Sampling\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "5ZETasp64TeQ",
"nbpages": {
"level": 1,
"link": "[7.2 Latin Hypercube Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2-Latin-Hypercube-Sampling)",
"section": "7.2 Latin Hypercube Sampling"
}
},
"source": [
"Created by V.Vijay Kumar Naidu (vvelagal@nd.edu)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 1,
"link": "[7.2 Latin Hypercube Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2-Latin-Hypercube-Sampling)",
"section": "7.2 Latin Hypercube Sampling"
}
},
"source": [
"The text, examples, and codes in this notebook were adapted from the following references:\n",
"* https://en.wikipedia.org/wiki/Latin_hypercube_sampling\n",
"* McClarren, Ryan G (2018). *Uncertainty Quantification and Predictive Computational Science: A Foundation for Physical Scientists and Engineers, Chapter 7 : Sampling-Based Uncertainty Quantification Monte Carlo and Beyond*, Springer, https://link.springer.com/chapter/10.1007%2F978-3-319-99525-0_7"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "kQhVsePNSvu8",
"nbpages": {
"level": 1,
"link": "[7.2 Latin Hypercube Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2-Latin-Hypercube-Sampling)",
"section": "7.2 Latin Hypercube Sampling"
}
},
"outputs": [],
"source": [
"# Install Python libraries\n",
"!pip install -q sobol_seq\n",
"!pip install -q ghalton\n",
"!pip install -q pyDOE"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "KffZ1fJ_4TeQ",
"nbpages": {
"level": 1,
"link": "[7.2 Latin Hypercube Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2-Latin-Hypercube-Sampling)",
"section": "7.2 Latin Hypercube Sampling"
}
},
"outputs": [],
"source": [
"# Import\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"import scipy.sparse as sparse\n",
"import scipy.sparse.linalg as linalg\n",
"import scipy.integrate as integrate\n",
"import math\n",
"from scipy.stats.distributions import norm\n",
"from scipy.stats import gamma\n",
"import sobol_seq\n",
"import ghalton\n",
"from scipy import stats\n",
"from pyDOE import *\n",
"%matplotlib inline"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"nbpages": {
"level": 1,
"link": "[7.2 Latin Hypercube Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2-Latin-Hypercube-Sampling)",
"section": "7.2 Latin Hypercube Sampling"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Checking for figures/lhs_custom_distribution.png\n",
"\tFile found!\n",
"Checking for figures/chapter7-screenshot.PNG\n",
"\tFile found!\n"
]
}
],
"source": [
"# Download figures (if needed)\n",
"import os, requests, urllib\n",
"\n",
"# GitHub pages url\n",
"url = \"https://ndcbe.github.io/cbe67701-uncertainty-quantification/\"\n",
"\n",
"# relative file paths to download\n",
"# this is the only line of code you need to change\n",
"file_paths = ['figures/lhs_custom_distribution.png', 'figures/chapter7-screenshot.PNG']\n",
"\n",
"# loop over all files to download\n",
"for file_path in file_paths:\n",
" print(\"Checking for\",file_path)\n",
" # split each file_path into a folder and filename\n",
" stem, filename = os.path.split(file_path)\n",
" \n",
" # check if the folder name is not empty\n",
" if stem:\n",
" # check if the folder exists\n",
" if not os.path.exists(stem):\n",
" print(\"\\tCreating folder\",stem)\n",
" # if the folder does not exist, create it\n",
" os.mkdir(stem)\n",
" # if the file does not exist, create it by downloading from GitHub pages\n",
" if not os.path.isfile(file_path):\n",
" file_url = urllib.parse.urljoin(url,\n",
" urllib.request.pathname2url(file_path))\n",
" print(\"\\tDownloading\",file_url)\n",
" with open(file_path, 'wb') as f:\n",
" f.write(requests.get(file_url).content)\n",
" else:\n",
" print(\"\\tFile found!\")"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.2.1 Latin Hypercube Basics](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.1-Latin-Hypercube-Basics)",
"section": "7.2.1 Latin Hypercube Basics"
}
},
"source": [
"## 7.2.1 Latin Hypercube Basics\n",
"\n",
"Latin hypercube sampling (LHS) is a statistical method for generating a near random samples with equal intervals.\n",
"\n",
"To generalize the Latin square to a hypercube, we define a X = (X1, . . . , Xp) as a collection of p independent random variables. To generate N samples, we divide the domain of each Xj in N intervals. In total there are Np such intervals. The intervals are defined by the N + 1 edges:\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "7KFZKceKHWVX",
"nbpages": {
"level": 3,
"link": "[7.2.1.1 Latin Hypercube in 2D](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.1.1-Latin-Hypercube-in-2D)",
"section": "7.2.1.1 Latin Hypercube in 2D"
}
},
"source": [
"### 7.2.1.1 Latin Hypercube in 2D\n",
"\n",
"Makes a Latin Hyper Cube sample and returns a matrix X of size n by 2. For each column of X, the n values are randomly distributed with one from each interval (0,1/n), (1/n,2/n), ..., (1-1/n,1) and they are randomly permuted."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "30R2uAAp6aiR",
"nbpages": {
"level": 3,
"link": "[7.2.1.1 Latin Hypercube in 2D](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.1.1-Latin-Hypercube-in-2D)",
"section": "7.2.1.1 Latin Hypercube in 2D"
}
},
"outputs": [],
"source": [
"def latin_hypercube_2d_uniform(n):\n",
" lower_limits=np.arange(0,n)/n\n",
" upper_limits=np.arange(1,n+1)/n\n",
"\n",
" points=np.random.uniform(low=lower_limits,high=upper_limits,size=[2,n]).T\n",
" np.random.shuffle(points[:,1])\n",
" return points"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 341
},
"colab_type": "code",
"id": "lD6llSHp8nUH",
"nbpages": {
"level": 3,
"link": "[7.2.1.1 Latin Hypercube in 2D](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.1.1-Latin-Hypercube-in-2D)",
"section": "7.2.1.1 Latin Hypercube in 2D"
},
"outputId": "a245fe0e-5436-4fb4-f237-8651f745b45d"
},
"outputs": [
{
"data": {
"text/plain": [
""
]
},
"execution_count": 5,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAUQAAAEzCAYAAABJzXq/AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAF1FJREFUeJzt3W2MXOd12PH/Wanimo1qR1EWdS1xSaIUQcZoIVfQSwzULuLWlAtIH6pEZMZuDchmlUQuWqcFJGygCgoIIy7cAEHVxttUcBKMbDH5kBABXQF1bDlITUY07CgWhQ1ovpmW0U0s10FKkLaypx/uXWm4mtmd2b0zd+7M/wcsuPeZe2bO5S4Pn5l7n3MjM5EkwUzdCUjSuLAgSlLJgihJJQuiJJUsiJJUsiBKUmnDghgRT0fEckR8o8fjERG/FhFnIuLFiHhX9WlK0vD1M0P8DHBgncfvBfaUX4eB/7b1tCRp9DYsiJn5ZeDVdXa5H/itLJwA3hYRb68qQUkalSo+Q3wH8K2O7UvlmCQ1yvUVPEd0Geu6HjAiDlO8reb6t9z4j/7h/tsGeqGzf/H/ANj943/bOOOGEteEHI1b31e/+tW/zMwfHziQagriJeDWju1bgFe67ZiZi8AiwE3z+/LUqVMDvdCDn/4KAM/+63uMM24ocU3I0bj1RcSFgYNKVbxlPgb8y/Js893A9zPzOxU8rySNVD+X3XwW+AqwNyIuRcRDEfFwRDxc7nIcOAucAf478PNDy1Zb127Dzp0wMwMnT8Dyct0ZSWNjw7fMmXlog8cT+IXKMtLwtNtw+DBcvlxsX7kKS0vFeKtVb27SGHClyjRZWHijGK5aWSnGJVkQp8rFi4ONS1PGgjhNduwYbFyaMhbEaXLkCGzffu3YzEwxLsmCOFVaLVhchPl5iIDZbbB3rydUpJIFcdq0WnD+fHEy5a67YW6u7oyksWFBlKSSBVGSSlHXfZnf8vduy/v+428OFHP6O38FwP63/x3jjBtKXBNyNG59Rx/+ya9m5h0DB+IMUZJeV9sM8ab5ffnqhZcHimlKxw3jmhvXhByNW19EOEOUpK2yIEpSyYKoydHZ2mznTlubaWBVdMyW6re2tdmFC0VrM2kAzhA1GXq1Njt3tp581EgWRE2GXi3MrlwdbR5qNAuiJkOvFmaz20abhxrNgqjJ0Ku12a7d9eSjRrIgajKsbW02P1+0NrObjwZgQdTk6Gxtdv68xVADs7mDccbV9FrGVR8HNneQpErY3ME442p6LeOqjwObO0hSJSyI61lehpMn3lgb227XnZGkIXItcy/tNix9uzhjmVmsjT18uHjMu9RJE8kZYi8LC0Ux7HT5cjEuaSJZEHvptTa217ikxrMg9tJrbWyvcUmNZ0Hs5ciR4mRKp+3bi3FJE8mC2EurVayFnd32xtrYxUVPqEgTzLPM65mbK76eXtl4X0mN5wxRkkoWREkq2e3GOONqei3jqo8Du91IUiXsdmOccTW9lnHVx4HdbiSpEhZESSpZECWpND4Fsd0ueg7ae1BSTcZjpUq7XfQavHy52Lb3oKQajMcMcWHhjWK4yt6DkkZsPAqivQcljYHxKIj2HpQ0BvoqiBFxICKWIuJMRDza5fEdEfHFiPhaRLwYER8YKIsjR4peg53sPShpxDYsiBFxHfAUcC+wHzgUEfvX7PZLwNHMvB04CPzXgbJotYpeg/Pz9h6UVJsNl+5FxD3AE5n5/nL7MYDM/ETHPp8Gzmbmr5T7fyozf3K957W5g3HjGNeEHI1b37CbO7wD+FbH9qVyrNMTwAcj4hJwHPhYtyeKiMMRcSoiTtW1hlqSeunnOsToMra2mh0CPpOZnypniL8dEe/MzGtaTWfmIrAIRXOHcV8obtz0xTUhR+PWd/ThgUNe188M8RJwa8f2LcAra/Z5CDgKkJlfAWaBmzefliSNXj8F8QVgT0TsiogbKE6aHFuzz0XgpwAiYh9FQfyLKhOVpGHbsCBm5mvAI8BzwMsUZ5NfiognI+K+crdfBD4aEX8KfBb4cPohoaSG6Wstc2YepzhZ0jn2eMf3p4F3V5uaJI3WeKxUkaQxYEGUpJIFEezFKAkYl36IdVqvFyO7a0tL0ug5Q7QXo6SSBbGJvRjXvsVfXq47I2ki+JZ5x47ibXK38XHU7S3+0lK9OUkTorYb1Y9Nt5vl5aKgrHQsu56Zgb17Of03s9W/3lbjTp6AK1evjZvbBTMz7N97y/jk2dC4JuRo3PqG3e1mss3Nwd69MLut2J7dVmzPzdWbVy9riuHrVla6j0vqW20zxJvm9+WrF14eKKYpHTeGGrdz55ve4j946BMwu41nn/5345NnQ+OakKNx64sIZ4hTo9vtFmZmYJeXCElbZUFsmm63Wxjnt/hSg1gQm6jVgvPni88Nz5+3GEoVsSBKUsmCKEklC6IklSyIklSyIEpSyYIoSSULoiSVLIiSVLLbjXHG1fRaxlUfB3a7kaRK2O3GOONqei3jqo8Du91IUiUsiJJUsiBKUsmCKEklC6Lqt/a2qu123RlpSnkbUtWr221VDx8uvm+16stLU8kZouq1sPBGMVx1+XIxLo2YBVH1unhxsHFpiCyIqteOHYONS0NkQVS9ut1Wdfv2YlwaMZs7GFd/3PIynDsLV67C7LbiHtMddxK0uYNxg9hKcwfPMqt+c3PeSlVjweYOxhlX02sZV30c2NxBkiphQZSkkgVRkkoWREkqWRAlqWRBlKSSBVGSShZESeOl3YaTJ+D550feH7OvghgRByJiKSLORMSjPfb5mYg4HREvRcQz1aYpaSqs9se8crXYXu2POaKiuGFBjIjrgKeAe4H9wKGI2L9mnz3AY8C7M/MngH87hFwlTbqa+2P2M0O8EziTmWcz8wfA54D71+zzUeCpzPweQGYuV5umpKlQc3/MDdcyR8QDwIHM/Ei5/SHgrsx8pGOf3wP+HHg3cB3wRGb+z/We1243xo1jXBNynOi4kyfgylVOz+0q4pbPFeOz2+Cuu/t6iq10u+lnhhhdxtZW0euBPcB7gUPAb0TE2970RBGHI+JURJyqq6mEpDG2a3dxs7FOMzPF+Aj00/7rEnBrx/YtwCtd9jmRmT8EzkXEEkWBfKFzp8xcBBah6HYz7p0zjJu+uCbkOPFx7TYPfuEVuHKVZ//3rxfNgltrP6Xr7ejDA6V4jX4K4gvAnojYBXwbOAj87Jp9fo9iZviZiLgZuA04u/m0JE2tVgv+uiikPNP1opah2fAtc2a+BjwCPAe8DBzNzJci4smIuK/c7TnguxFxGvgi8B8y87vDSlqShqGvjtmZeRw4vmbs8Y7vE/h4+SVJjeRKFUkqNbsgttvF0p6ZmZEv8ZE0eZp7k6nVJT6rV7WvLvGB4kNZSRpQc2eINS/xkTR5mlsQa17iI2nyNLcg7tgx2LgkbaC5BfHIEdi+/dqx7duLcUnahNpuVF9Jc4flZTh3tuidNrutWO84N7dx3GZfz7iJj2tCjsatbyvNHZp7lhmK4telAErSZtQ2Q7xpfl++euHlgWIasTB9o7h2uzgTfvFi8XnnkSOvXyY0VnlOaVwTcjRufRExpTPEpvHaSWmsNfekShN57aQ01iyIo+S1k9JYsyCOktdOSmPNgjhKXjspjTUL4ii1WrC4CPPzEFH8ubjoCRVpTHiWedRaLQugNKacIUpSyYIoSSULoiSVLIiSVGp2txvjjKs4rgk5Gre+rXS7cYYoSSW73RhnXE2vZVz1cbC1bjfOELU13gpWE8QLs7V5tjPThHGGqM2znZkmjAVRm2c7M00YC6I2z3ZmmjAWRG2e7cw0YSyI2jzbmWnCeJZZW2M7M00QZ4iSVLIgSlLJ5g7GGVfTaxlXfRxsrbmDnyFKg1pehnNn4cpVmN0Gu3YDs3VnpQrY3ME44waJWbtcEWD7dh589BmYmxvrY5uGOLC5gzQ6vZYrnjtbTz6qlAVRGkSvZYlXro42Dw2FBVEaRK9libPbRpuHhsKCKA2i13LFXbvryUeVsiBKg+i1XHFuru7MVAELojSoVgvOn4eVleJPly5ODAuiJJUsiJJU6qsgRsSBiFiKiDMR8eg6+z0QERkRm7ooUpLqtGFBjIjrgKeAe4H9wKGI2N9lvxuBfwOcrDpJSRqFfmaIdwJnMvNsZv4A+Bxwf5f9fhn4JHClwvyk6eJtXWu14VrmiHgAOJCZHym3PwTclZmPdOxzO/BLmfkvIuJLwL/PzFPrPa/dbowbx7hac1xehqWl4uz1qpkZ2Lv3TZf1NOHvso442Fq3m35miNFl7PUqGhEzwK8Cv7jhE0UcjohTEXGqrqYS0tg6d/baYgjFtuukR6afGeI9wBOZ+f5y+zGAzPxEuf1W4JvAX5chfxd4FbhvvVmi3W6MG8e4WnOcmYFu/x4j3lQom/B3WUccDL/bzQvAnojYFRE3AAeBY6sPZub3M/PmzNyZmTuBE2xQDCV14W1da7dhQczM14BHgOeAl4GjmflSRDwZEfcNO0Fpanhb19r11TE7M48Dx9eMPd5j3/duPS1pCq0uAVxYKNqM7dhRFEOXBo6MtxCQxom3da2VS/ckqWRBlKSSBVGSShZESSpZECWpZEGUpJIFUZJKG65lHha73Rg3jnFNyNG49Q27240kTYXaZoh2uzFuHOOakKNx6xt2txtJmgoWREkqWRAlqWRBlKSSBXFatdtw8gQ8/7x3d5NKFsRp1G7D4cNw5WqxfeFCsW1R1JSzIE6jhQW4fPnascuXi3FpilkQp9HFi4ONS1PCgjiNvLub1JUFcRp5dzepK5s7TGvc8jKnv/cDWFlh/1+9Art2w9zc+OU54rgm5Gjc+rbS3MG77k2ruTn4m+KXjn2+VZbA5g7GGVfbaxlXfRzY3EGSKmFBlKSSBVGSShZESSpZECWpZEGUpJIFUZJKFkRJKlkQpWmyvFw0Bp6ZsTFwFy7dk6ZFuw1L34aVFch8ozEwQKtVb25jwhmiNC0WFopi2MnGwNew241xxtX0WiOPe/55Ts/tKuKWz1372HveU/3r1RAHW+t24wxRmhaz2wYbn0K1fYb4lr913dh3zjBu+uKakOOm437kLA9+/gKsrPDsZx8rxrZvh8VFaK3/PI04vtLRhwcOeZ0zRE2vdrs40zotZ1xbLdi7t5gRRsD8fFkMPaGyyrPMmk6rt2Jdvfvg6hnXR5/pu3N4I83NFV9Pr2y87xRyhqjp1OtWrOfO1pOPxoIFUdOp1y1Xr1wdbR4aKxZETadet1z1jOtUsyBqOvW6Feuu3fXko7FgQdR0arWKM6zz89eecZ3kEyrakAVR06vVgvPni+Vs5897+Yn6K4gRcSAiliLiTEQ82uXxj0fE6Yh4MSK+EBHz1acqScO1YUGMiOuAp4B7gf3AoYjYv2a3rwF3ZOY/AH4X+GTViUrSsG3Y3CEi7gGeyMz3l9uPAWTmJ3rsfzvwXzLz3es9r80djBvHuCbkaNz6ht3c4R3Atzq2L5VjvTwEfL7bAxFxOCJORcSpurrsSFIv/Szdiy5jXatZRHwQuAPo2ksoMxeBRYCb5vfluC8UN2764pqQo3Hr20pzh34K4iXg1o7tW4BX1u4UEe8DFoD3ZKaX+0tqnH7eMr8A7ImIXRFxA3AQONa5Q/m54aeB+zJzufo0JWn4NiyImfka8AjwHPAycDQzX4qIJyPivnK3/wT8CPA7EfH1iDjW4+kkTbrOtmonTxQ3tmqIvtp/ZeZx4Piascc7vn9fxXlJaqK1bdWuXIWlpWK8ARe+u1JFUnW6tVVbWWnMjawsiJKq06utWq/xMWNBlFSdXm3Veo2PGQuipOp0a6s2M1OMN4AFUVJ11rZVm91W3NiqASdUwIIoTY5xuYtgZ1u1u+5uVI9J77onTYJedxGExszOxsGG3W6GxW43xo1jXBNy7Bp38kT3G2TNbitmaeOS55DjYPjdbiSNu153C/QuggOpbYZ40/y+fPXCywPFNKXjhnHNjWtCjl3jdu4s3iavNT9ffJ43LnkOOQ4gIpwhSlOt110EG3K5y7iwIEqToNddBD2hMhDPMkuTotWyAG6RM0RJKlkQJalkQZSkkgVRkkoWREkqWRAlqWRBlKSSBVGSSna7Mc64ml7LuOrjwG43klQJu90YZ1xNr2Vc9XFgtxtJqoQFUZJKFkRJKlkQJalkQZSkkgVRkkoWREnN0G4XN9OamSn+bLcrfwlvISBp/LXbcPgwXL5cbF+4UGxDpbdNcIYoafwtLLxRDFddvlyMV8iCKGn8Xbw42Pgm2dzBOONqei3jBog7eQKuXH3zjrPb4K67rxmyuYOkybZrd3EypdPMTDFeIZs7GGdcTa9l3IBx7XbxmeHFi7BjBxw50vWEylaaO3iWWVIztFqVnlHuxrfMklSyIEpVWF4uPvgf4kXDGj7fMktb1W7D0rdhZQUyh3bRsIbPGaK0VQsLRTHsNISLhjV8FkRpq0Z00bCGz4IobdWOHYONa2xZEKWtOnLkzRcNb99ejKtR+iqIEXEgIpYi4kxEPNrl8W0R8Wz5+MmI2Fl1otLYarVg795iGVkEzM/D4qInVBpow7PMEXEd8BTwT4FLwAsRcSwzT3fs9hDwvcz8+xFxEPgV4MFhJCyNpbm54uvplY331djqZ4Z4J3AmM89m5g+AzwH3r9nnfmC1U8PvAj8VEVFdmpI0fBuuZY6IB4ADmfmRcvtDwF2Z+UjHPt8o97lUbn+z3Ocvez2v3W6MG8e4JuRo3Pq20u2mn4L408D71xTEOzPzYx37vFTu01kQ78zM7655rsNAecUq7wS+sZmkG+JmoOd/CBNgko9vko8NJv/49mbmjZsJ7GelyiXg1o7tW4BXeuxzKSKuB94KvLr2iTJzEVgEiIhTm63iTeDxNdckHxtMx/FtNrafzxBfAPZExK6IuAE4CBxbs88x4F+V3z8A/GHW1VdMkjZpwxliZr4WEY8AzwHXAU9n5ksR8SRwKjOPAf8D+O2IOEMxMzw4zKQlaRj6au6QmceB42vGHu/4/grw0wO+9uKA+zeNx9dck3xs4PH1VFvHbEkaNy7dk6TS0AvipC/76+P4Ph4RpyPixYj4QkTM15HnZmx0bB37PRARGRGNOnPZz/FFxM+UP7+XIuKZUee4FX38bu6IiC9GxNfK388P1JHnZkTE0xGxXF4D3e3xiIhfK4/9xYh4V19PnJlD+6I4CfNNYDdwA/CnwP41+/w88Ovl9weBZ4eZUw3H90+A7eX3P9eU4+vn2Mr9bgS+DJwA7qg774p/dnuArwE/Wm7P1Z13xce3CPxc+f1+4HzdeQ9wfP8YeBfwjR6PfwD4PBDA3cDJfp532DPESV/2t+HxZeYXM/NyuXmC4jrOJujnZwfwy8AngSujTK4C/RzfR4GnMvN7AJm5POIct6Kf40tgdSnIW3nz9cVjKzO/TJdrnTvcD/xWFk4Ab4uIt2/0vMMuiO8AvtWxfakc67pPZr4GfB/4sSHnVZV+jq/TQxT/azXBhscWEbcDt2bmH4wysYr087O7DbgtIv44Ik5ExIGRZbd1/RzfE8AHI+ISxVUkH2NyDPpvExj+PVW6zfTWntbuZ59x1XfuEfFB4A7gPUPNqDrrHltEzAC/Cnx4VAlVrJ+f3fUUb5vfSzGz/6OIeGdm/t8h51aFfo7vEPCZzPxURNxDcS3xOzNzElr2bKquDHuGOMiyP9Zb9jem+jk+IuJ9wAJwX2ZeHVFuW7XRsd1IsR79SxFxnuJzmmMNOrHS7+/m72fmDzPzHLBEUSCboJ/jewg4CpCZXwFmKdY5T4K+/m2+yZA/+LweOAvs4o0Pdn9izT6/wLUnVY7W/YFtxcd3O8WH23vqzrfqY1uz/5do1kmVfn52B4DfLL+/meIt2I/VnXuFx/d54MPl9/vKghF15z7AMe6k90mVf861J1X+pK/nHEHSHwD+vCwKC+XYkxSzJSj+V/od4AzwJ8Duuv+iKz6+/wX8H+Dr5dexunOu6tjW7Nuogtjnzy6A/wycBv4MOFh3zhUf337gj8ti+XXgn9Wd8wDH9lngO8APKWaDDwEPAw93/OyeKo/9z/r93XSliiSVXKkiSSULoiSVLIiSVLIgSlLJgihJJQuiJJUsiJJUsiBKUun/A8Z74c1udeCIAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"n=20\n",
"p=latin_hypercube_2d_uniform(n)\n",
"plt.figure(figsize=[5,5])\n",
"plt.xlim([0,1])\n",
"plt.ylim([0,1])\n",
"plt.scatter(p[:,0],p[:,1],c='r')\n",
"\n",
"for i in np.arange(0,1,1/n):\n",
" plt.axvline(i)\n",
" plt.axhline(i)\n",
"plt.show"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "T3aFz5UHLhFf",
"nbpages": {
"level": 3,
"link": "[7.2.1.2 Latin-hypercube designs can be created using the following simple syntax](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.1.2-Latin-hypercube-designs-can-be-created-using-the-following-simple-syntax)",
"section": "7.2.1.2 Latin-hypercube designs can be created using the following simple syntax"
}
},
"source": [
"### 7.2.1.2 Latin-hypercube designs can be created using the following simple syntax\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[7.2.1.2 Latin-hypercube designs can be created using the following simple syntax](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.1.2-Latin-hypercube-designs-can-be-created-using-the-following-simple-syntax)",
"section": "7.2.1.2 Latin-hypercube designs can be created using the following simple syntax"
}
},
"source": [
"The following is adapted from:https://pythonhosted.org/pyDOE/randomized.html."
]
},
{
"cell_type": "markdown",
"metadata": {
"colab": {},
"colab_type": "code",
"id": "dCyvuRToLf7y",
"nbpages": {
"level": 3,
"link": "[7.2.1.2 Latin-hypercube designs can be created using the following simple syntax](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.1.2-Latin-hypercube-designs-can-be-created-using-the-following-simple-syntax)",
"section": "7.2.1.2 Latin-hypercube designs can be created using the following simple syntax"
}
},
"source": [
"```\n",
"lhs(n, [samples, criterion, iterations])\n",
"```"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "lvGXdBpOL8i5",
"nbpages": {
"level": 3,
"link": "[7.2.1.2 Latin-hypercube designs can be created using the following simple syntax](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.1.2-Latin-hypercube-designs-can-be-created-using-the-following-simple-syntax)",
"section": "7.2.1.2 Latin-hypercube designs can be created using the following simple syntax"
}
},
"source": [
"**n**: an integer that designates the number of factors (required).\n",
"\n",
"**samples**: an integer that designates the number of sample points to generate for each factor (default: n)\n",
"criterion: a string that tells lhs how to sample the points (default: None, which simply randomizes the points within the intervals):\n",
"\n",
"**“center” or “c”**: center the points within the sampling intervals\n",
"“maximin” or “m”: maximize the minimum distance between points, but place the point in a randomized location within its interval\n",
"\n",
"**“centermaximin” or “cm”**: same as “maximin”, but centered within the intervals\n",
"\n",
"**“correlation” or “corr”**: minimize the maximum correlation coefficient\n",
"\n",
"The output design scales all the variable ranges from zero to one which can then be transformed as the user wishes (like to a specific statistical distribution using the scipy.stats.distributions ppf (inverse cumulative distribution) function"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "W9KwhC8JL7wJ",
"nbpages": {
"level": 3,
"link": "[7.2.1.2 Latin-hypercube designs can be created using the following simple syntax](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.1.2-Latin-hypercube-designs-can-be-created-using-the-following-simple-syntax)",
"section": "7.2.1.2 Latin-hypercube designs can be created using the following simple syntax"
}
},
"outputs": [],
"source": [
"from scipy.stats.distributions import norm\n",
"from pyDOE import *\n",
"lhd = lhs(2, samples=5)\n",
"lhd = norm(loc=0, scale=1).ppf(lhd) # this applies to both factors here"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "QXvC3_JiM5_p",
"nbpages": {
"level": 3,
"link": "[7.2.1.2 Latin-hypercube designs can be created using the following simple syntax](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.1.2-Latin-hypercube-designs-can-be-created-using-the-following-simple-syntax)",
"section": "7.2.1.2 Latin-hypercube designs can be created using the following simple syntax"
}
},
"source": [
"Graphically, each transformation would look like the following, going from the blue sampled points (from using lhs) to the green sampled points that are normally distributed: (Adapted from https://pythonhosted.org/pyDOE/randomized.html)\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "B4vaJwj2NWd4",
"nbpages": {
"level": 3,
"link": "[7.2.1.2 Latin-hypercube designs can be created using the following simple syntax](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.1.2-Latin-hypercube-designs-can-be-created-using-the-following-simple-syntax)",
"section": "7.2.1.2 Latin-hypercube designs can be created using the following simple syntax"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "zrHRqUeibyNo",
"nbpages": {
"level": 3,
"link": "[7.2.1.2 Latin-hypercube designs can be created using the following simple syntax](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.1.2-Latin-hypercube-designs-can-be-created-using-the-following-simple-syntax)",
"section": "7.2.1.2 Latin-hypercube designs can be created using the following simple syntax"
}
},
"source": [
"An example for Latin-Hyper cube sampling"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 187
},
"colab_type": "code",
"id": "-Mb4AHDdRx_K",
"nbpages": {
"level": 3,
"link": "[7.2.1.2 Latin-hypercube designs can be created using the following simple syntax](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.1.2-Latin-hypercube-designs-can-be-created-using-the-following-simple-syntax)",
"section": "7.2.1.2 Latin-hypercube designs can be created using the following simple syntax"
},
"outputId": "7818b20e-d45c-46c6-e581-71073ef9deeb"
},
"outputs": [
{
"data": {
"text/plain": [
"array([[1.01038798, 2.96384621, 1.66664945, 4.08995188],\n",
" [0.98039537, 2.24799145, 3.68230066, 3.82708594],\n",
" [1.28011085, 2.28301199, 2.44501943, 4.6418306 ],\n",
" [0.91410412, 1.88397665, 2.71926383, 4.02262911],\n",
" [0.91979907, 1.73539308, 2.95722586, 4.15159108],\n",
" [0.96185965, 1.40469736, 3.04478481, 3.69932867],\n",
" [0.87127105, 1.74656817, 3.36550728, 3.65675587],\n",
" [1.04347425, 1.08778999, 2.13703733, 3.94872467],\n",
" [1.1143877 , 2.58203348, 4.47359066, 3.8801158 ],\n",
" [1.0641072 , 2.12054246, 4.13988503, 4.28057491]])"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"design = lhs(4, samples=10)\n",
"from scipy.stats.distributions import norm\n",
"means = [1, 2, 3, 4]\n",
"stdvs = [0.1, 0.5, 1, 0.25]\n",
"for i in range(4):\n",
" design[:, i] = norm(loc=means[i], scale=stdvs[i]).ppf(design[:, i])\n",
"\n",
"design"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.2.2 Advection-Diffusion-Reaction (ADR) Example](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2-Advection-Diffusion-Reaction-(ADR)-Example)",
"section": "7.2.2 Advection-Diffusion-Reaction (ADR) Example"
}
},
"source": [
"## 7.2.2 Advection-Diffusion-Reaction (ADR) Example"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "YoCFcxW3bAXw",
"nbpages": {
"level": 3,
"link": "[7.2.2.1 Set up diffusion reaction equation](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.1-Set-up-diffusion-reaction-equation)",
"section": "7.2.2.1 Set up diffusion reaction equation"
}
},
"source": [
"### 7.2.2.1 Set up diffusion reaction equation\n",
"\n",
"The steady advection-diffusion-reaction(ADR) equation in one-spatial dimension with a spatially constant, but uncertain, diffusion coefficient, a linear reaction term, and a prescribed uncertain source.\n",
"\n",
"$$\n",
"\\nu \\frac{du}{dx} - \\omega \\frac{d^2u}{dx^2} + \\kappa(x)u = S(x)\n",
"$$\n",
"The QoI is total reaction rate:$$\n",
"Q= \\int^{10}_{0} \\kappa(x_ u)u(x)dx\n",
"$$\n",
"where v and ω are spatially constant with means\n",
"$$\n",
"\\nu = 10, μ_{ω} = 20, \n",
"$$\n",
"and\n",
"$$\n",
"Var(v) = 0.0723493, Var(ω) = 0.3195214.\n",
"$$\n",
"\n",
"The reaction coefficient, κ(x), is given by \n",
"$$\n",
"κ(x) = κ_{l} \\space x ∈ (5, 7.5)\n",
"$$ \n",
" $$ \\space κ_{h} \\space otherwise$$ \n",
" \n",
" The value of the source is given by\n",
"$$S(x) = qx(10 − x),$$ "
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "eR3fNfymMbaE",
"nbpages": {
"level": 3,
"link": "[7.2.2.1 Set up diffusion reaction equation](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.1-Set-up-diffusion-reaction-equation)",
"section": "7.2.2.1 Set up diffusion reaction equation"
}
},
"outputs": [],
"source": [
"def ADRSource(Lx, Nx, Source, omega, v, kappa):\n",
" #Solves the diffusion equation with Generalized Source\n",
" A = sparse.dia_matrix((Nx,Nx),dtype=\"float\")\n",
" dx = Lx/Nx\n",
" i2dx2 = 1.0/(dx*dx)\n",
" #fill diagonal of A\n",
" A.setdiag(2*i2dx2*omega + np.sign(v)*v/dx + kappa)\n",
" #fill off diagonals of A\n",
" A.setdiag(-i2dx2*omega[1:Nx] + \n",
" 0.5*(1-np.sign(v[1:Nx]))*v[1:Nx]/dx,1)\n",
" A.setdiag(-i2dx2*omega[0:(Nx-1)] - \n",
" 0.5*(np.sign(v[0:(Nx-1)])+1)*v[0:(Nx-1)]/dx,-1)\n",
" #solve A x = Source\n",
" Solution = linalg.spsolve(A.tocsr(),Source)\n",
" Q = integrate.trapz(Solution*kappa,dx=dx)\n",
" return Solution, Q"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "YzNoqAe6bMTx",
"nbpages": {
"level": 3,
"link": "[7.2.2.1 Set up diffusion reaction equation](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.1-Set-up-diffusion-reaction-equation)",
"section": "7.2.2.1 Set up diffusion reaction equation"
}
},
"source": [
"Solve diffusion equation"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 332
},
"colab_type": "code",
"id": "ZGqMMZKvMbaG",
"nbpages": {
"level": 3,
"link": "[7.2.2.1 Set up diffusion reaction equation](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.1-Set-up-diffusion-reaction-equation)",
"section": "7.2.2.1 Set up diffusion reaction equation"
},
"outputId": "15a27e23-dd7b-4d74-cf85-d603bc3f69ad"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[10. 10. 10. ... 10. 10. 10.]\n",
"52.390252927703344\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAW4AAAD8CAYAAABXe05zAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAIABJREFUeJzt3Xd0lVW+xvHvTicNSIeEkAQIAUJJIxRFRURERyyINOlGr3XUKTp97lXvOKOOjp2OgjAM1hFHUUBFkJCEDqEEAiG0BEJ6P9n3D4LLq5QTyMk+5fdZi0USDjnPWUkeXva7i9JaI4QQwnG4mQ4ghBCiZaS4hRDCwUhxCyGEg5HiFkIIByPFLYQQDkaKWwghHIwUtxBCOBgpbiGEcDBS3EII4WA8bPFJQ0JCdExMjC0+tRBCOKWcnJxTWutQax5rk+KOiYkhOzvbFp9aCCGcklLqsLWPlaESIYRwMFLcQgjhYKS4hRDCwUhxCyGEg5HiFkIIByPFLYQQDkaKWwghHIxN5nELIS6f1prTVfUcKKqkuLKOkqp6ymsavv/zdl4eBPt5ERrgTbdQf8IDvVFKGUws2poUtxCG1TVa2FJQSubBEjLzT5N7vJwz1Q2X/ovNAnw8SOzcnsHdghnSLZik6I64u0mROzMpbiEMqG2w8NXeIj7dcYLVuSepqregFPSKCGRUYgQ9wgLoHuZPeKAPQX5eBLbzwE0ptIbq+kZOVdZTVFHLgaJK9p6sYOuRUv7+5T5e/AJC/L25pV8nbkuKpH9Ue7kad0LKFqe8p6amalnyLsRPHSiuZMnGAlbkHKG8tpEgPy9u7BPO8IRwBsYE0d7X87I/d2l1PevzTvPJ9mOs3lNEfWMT/bt0YNZVsdyUGIGHu9zSsmdKqRytdapVj5XiFsL2sg+V8MqaPL7eV4ynu+LGPhGMT4tmUFyQTQq1oraBD7YcZf63+Rw6XU1ciB+/uLEnNyVGyBW4nZLiFsJObMov4aUv97HhwGmC/byYNiSG8QOjCQ3wbpPnb2rSfJF7khdW7WXfyUr6d+nA02MS6RvVvk2eX1hPilsIwwpOV/Psp7l8tusEoQHe3Dcsjonp0fh6mbmtZGnSvL+5kL9+vpfTlXXMvCqWx26IN5ZH/FRLivuSXzWlVE/gnz/4UBzwB631S5eZTwinVVNv4eXV+5n/bT4e7opfjIxn1tVx+Hi6G83l7qa4K7ULI/tE8Jf/7GHOuny+zC3ilQlJJEbK1bejadEVt1LKHTgKpGutL7h3rFxxC1e04cApnnxvBwUl1dyRHMmvRyUQHuhjOtZ5bThwisf/uY2Sqnp+d0sv7hnUVca+DWvJFXdL74pcDxy4WGkL4Woqaht46v3tTJyTiZuCZRmDeHHcALstbYAh3UL49NGruapHCH/4aBePL99GXaPFdCxhpZYOcI0Hlp7vD5RSGUAGQHR09BXGEsIxbD1SysNLN3P0TA0Zw+J4bEQ87bzMDotYK8jPi3lTU3l1TR4vfLGPIyXVvHVPCsH+bXPjVFw+q4dKlFJewDGgj9b65MUeK0Mlwtk1NWlmrzvI85/vJTzQh39MGEBK1yDTsS7bJ9uP8cTybYQH+rBkVjpdgnxNR3I5thoquQnYfKnSFsLZlVbXM21hFn/5zx5G9gnn00evdujSBrilX2eWZgyirKaBu978jgPFlaYjiYtoSXFP4ALDJEK4ir0nKrj11fVsPHCaZ25P5LWJybRvd/mrHe1JcnRHlmUMorGpibvf+o7c4+WmI4kLsKq4lVK+wA3A+7aNI4T9+mzncW5/fT21DRaW3TeISenONxOjV6dA/nnfYDzc3LhnXiYH5crbLllV3Frraq11sNa6zNaBhLA3Wmv+sXo/9y/eTHx4AP9++CqSozuajmUz3UL9WXJvOlrD5LmZHC2tMR1J/IjsOiPERTRamnjq/R28+MU+7kiKZFnGILue5tdauoX6s2jGQCrqGpk8N5PiijrTkcQPSHELcQHV9Y1kvJPDsqwjPDy8Oy+M6298BWRbSoxsz4JpaRwvq2HWoixq6mWet72Q4hbiPE5X1jFh9ka+2lvEM7cn8sTInk43nm2N1Jgg/jE+ie1Hy3h02RYsTa2/t5FoOSluIX7kZHktd8/eyN6TFbx1TyqT0ruajmTUyD4R/PGW3qzafZJnVuaajiOQE3CE+H+OltYwac5GiivqWDR9IOlxwaYj2YVpQ2MpKKlh/vp8ugS1Y/rQWNORXJoUtxDNCk5XM2HORsprGnh7ZjopXZ135sjl+O3NvSg8U81/f7Kb2BA/ru0ZZjqSy5KhEiGAg8WVjHvrO6rqG3n33kFS2ufh7qZ4afwAeoYH8MjSLRw6VWU6ksuS4hYu70hJNRPnZNJgaWLpvYPkdJiL8PXyYM6UVNzcFBnvZFNV12g6kkuS4hYu7XhZDRPnbqSmwcLiWen06hRoOpLd6xLkyysTksgrquSXK7Zhi1O0xMVJcQuXVVxRx6S5mZypauDtGQOltFvg6h6h/HpUAp/uOMEbXx8wHcflSHELl1RaXc898zI5XlrLgulp9O/SwXQkh5MxLI5b+nXi+c/3sim/xHQclyLFLVxOdX0jUxdkcfBUFXOmpJIW49hbspqilOJ/7+hLdJAvjyzdQklVvelILkOKW7iURksTD7+7hR2FpbwyIYmreoSYjuTQAnw8eXViMiVV9fzyXzLe3VakuIXL0Frz+492sXpPEX8ek8iNfSJMR3IKiZHt+c3oBFbvKWLet/mm47gEKW7hMl5bm8fSTQX817XduGeQay9jb21Th8Qwsnc4z322h21HSk3HcXpS3MIlrMgp5PlV+7g9KZJf3djTdByno5Tir2P7EeLvzWPLt1LbIDsJ2pIUt3B66/YX8+R72xnaPZjn7uznkrv8tYUOvl78bWx/DhZX8dxne0zHcWpS3MKp7TpWxn8t3kz3MH/emJyCl4d8y9vSVT1CmDYkhgXrD7Eh75TpOE7L2jMnOyilViil9iilcpVSg20dTIgrVXimmukLsgjw8WDh9IEE+jjHob727tejEogL8eMX/9pGeW2D6ThOydrLj5eBz7TWCUB/QDblFXatrLqBaQuyqGmwsGjGQCLaO/9xY/ainZc7L4zrz4nyWv788W7TcZzSJYtbKRUIDAPmAWit67XWcttY2K3aBgv3vp1NwelqZt+TSnx4gOlILicpuiMPXted9zYXsnZvkek4TseaK+44oBhYoJTaopSaq5Ty+/GDlFIZSqlspVR2cXFxqwcVwhpNTZonlm9j06ESnh/Xn8Hd5CAEUx4a3p3uYf787oOdsotgK7OmuD2AZOANrXUSUAU8+eMHaa1na61TtdapoaGhrRxTCOs8+2kuK3cc5zejE7i1f2fTcVyat4c7z93Zl2NlNbywap/pOE7FmuIuBAq11pnN76/gbJELYVfmfZvP3G/zmTYkhnuvjjMdRwApXYOYnN6VBRvy2SoLc1rNJYtba30COKKUOrdq4XpA7jgIu7Jy+3GeXrmbUX0i+P0tvWWuth351aiehAf48OR722mwNJmO4xSsnVXyMLBEKbUdGAA8a7tIQrTMpvwSHlu+lZTojrw0fgDublLa9iTAx5P/uS2RPScqmP3NQdNxnIJVhwVrrbcCqTbOIkSL5RVVcO/b2UR1bMecKan4eLqbjiTO44be4dyUGMEra/YzZkBnojr6mo7k0GQZmXBYJ8trmTo/C093NxZNH0hHPy/TkcRF/O6W3igUz6yUZSBXSopbOKSK2gamL8jiTHU9C6al0SVIruDsXWSHdjw0vDv/2XmCdftlyvCVkOIWDqfB0sQDSzaz92QFr09KllPZHcisq2OJCfbljx/vor5RblReLilu4VC01jz53g7W7T/F/97Rl2t7hpmOJFrA28OdP/6sDweLq1iwXg5duFxS3MKhvPjFPt7bXMhjI+IZl9rFdBxxGa5LCGNErzBeXr2fE2W1puM4JClu4TCWbSrglTV53J3ahUeu7246jrgCf7ilD40WzfOr9pqO4pCkuIVD+HpfMb/9cCfD4kN5+vZEWWDj4KKDfZk+NIb3Nhey61iZ6TgOR4pb2L3dx8p5YHEO8eEBvD4pGU93+bZ1Bg9c15327Tx59tNcOR2+heQnQNi142U1zFiYRWA7TxZMS8Pf26o1Y8IBtG/nyaPX92B93mm+2ifTA1tCilvYrXNztSvrGpk/LU0OQ3BCk9K7EhPsy7Mrc2mUfUysJsUt7NK5udp5RZW8MTmZXp0CTUcSNuDl4caTNyWwv6iSf+UUmo7jMKS4hd3RWvO7D3aybv8pnr29L1f3kP3dndmNfSJI7dqRF1bto7peDlywhhS3sDuvrc3jn9lHeHh4d8alyVxtZ6eU4qnRCZyqrGPhhkOm4zgEKW5hVz7ccpTnV+3j9qRIHr8h3nQc0UZSugZxXc9Q3vr6oJwMbwUpbmE3Nh48zS9XbGNQXBDP3dlP5mq7mCdG9qSspoG562Qp/KVIcQu7kFdUQcbb2XQN9uOtyal4eci3pqtJjGzP6L4RzFt3kJKqetNx7Jr8dAjjiivqmLYgCy8PdxZMS6O9r6fpSMKQx0bEU91g4c2vD5iOYtekuIVR1fWNzFyUxenKeuZPS5V9tV1cj/AAbh8QyaINhygqlw2oLsSq4lZKHVJK7VBKbVVKZds6lHANlibNI0u3svNoGa9MSKJfVAfTkYQdeHREDyxNmtfW5pmOYrdacsV9ndZ6gNZazp4UV0xrzf98spsvc0/yx5/1YUTvcNORhJ3oGuzH2JQolmYdkavuC5ChEmHEvG/zWbjhELOuimXqkBjTcYSdeeDa7liatJwKfwHWFrcGVimlcpRSGed7gFIqQymVrZTKLi6WDWPEhX228zjPfJrLTYkR/GZ0L9NxhB2KDvZlTP/OLMks4HRlnek4dsfa4h6qtU4GbgIeVEoN+/EDtNaztdapWuvU0FBZoizOb3PBGR5dtpWkLh34+90DcHOTudri/B64rhu1jRbmyxFnP2FVcWutjzX/XgR8AAy0ZSjhnI6UVHPvomwi2vswZ0oqPp7upiMJO9Y9LIDRiZ1YtOEwZdWymvKHLlncSik/pVTAubeBkcBOWwcTzqW8toEZC7NobNIsmJZGsL+36UjCATx4XXcq6xpZ9N0h01HsijVX3OHAt0qpbcAmYKXW+jPbxhLOpNHSxMPvbiH/VBVvTEomLtTfdCThIHp3DmRErzDmr8+nsk52DjznksWttT6ote7f/KuP1vqZtggmnMfTK3P5el8xT9+WyJDuIabjCAfz0PAelFY3sDSzwHQUuyHTAYVNvf3dIRZuOMS9V8cyfmC06TjCAQ3o0oH02CDmr8+nQU7JAaS4hQ19tbeIP328ixG9wnnyJpn2Jy7ffdfEcbyslpXbj5uOYhekuIVN7DtZwcPvbqFnRCAvjx+Au0z7E1fg2vgwuof5M/ubg3IiPFLcwgZOV9YxY2EWPl7uzJuaip+czC6ukJubIuPqOHYfL2d93mnTcYyT4hatqrbBQsY7ORRX1DF3SiqdO7QzHUk4iTFJnQnx92b2OlkGL8UtWo3Wmqfe30HO4TO8OG4A/bvIbn+i9Xh7uDN9aAzf7Csm93i56ThGSXGLVvPa2jw+2HKUX4yM5+Z+nUzHEU5oUno0vl7uLn+8mRS3aBUrtx///pDfB6/rbjqOcFIdfL0Yl9qFj7cddektX6W4xRXbeqSUx5dvJbVrR/5yZ1855FfY1LQhMTQ2aZa48IIcKW5xRY6W1jBrUTZhgd68dU8K3h6ycZSwrZgQP66ND+XdTQXUN7rmghwpbnHZKusambkwi7oGC/OnysZRou1MHRJDcUUd/9npmgtypLjFZbE0aX6+bAv7iyp5dVIyPcIDTEcSLmRYj1BiQ/xYuOGQ6ShGSHGLy/KX/+TyZW4Rf/pZb66Jl4MzRNtyc1NMGdyVLQWlbC8sNR2nzUlxixZbuqmAOevymTYkhnsGx5iOI1zU2JQo/LzcXfKqW4pbtMiGvFP8/sOdXBMfyu9ulo2jhDkBPp6MTYnik23HOeVi51JKcQurHSyu5P7FOcSF+vHKxCQ83OXbR5g1ZUgM9ZYml9urW37yhFXOVNUzY2EWnu5uzJuaRqCPp+lIQtAt1J+ruoewdFMBlibX2TVQiltcUn1jE/cvzuFYWS2zp6TQJcjXdCQhvjcxPZpjZbV8s6/YdJQ2Y3VxK6XclVJblFKf2DKQsC9aa3734Q4y80v429h+pHQNMh1JiP/nht7hhPh78+4m1xkuackV96NArq2CCPs0+5uDLM8u5JHrezBmQKTpOEL8hKe7G3elRrFmTxEnylxj/xKrilspFQXcDMy1bRxhTz7fdYK/fLaHW/p14rERPUzHEeKCxqd1wdKkWZ59xHSUNmHtFfdLwK+AC24MoJTKUEplK6Wyi4tdZ6zJWe08WsbPl22lX1QHnr+rv2wcJexa12A/ru4RwjIXuUl5yeJWSt0CFGmtcy72OK31bK11qtY6NTRUVtI5spPltcxalE1HX0/mTEnBx1M2jhL2b8JA17lJac0V91DgVqXUIWAZMFwptdimqYQxNfUWZi3KpqK2gXnT0ggL8DEdSQirjOgVToi/l0vcpLxkcWutn9JaR2mtY4DxwBqt9WSbJxNtrqlJ89g/t7LzWBn/mJBEr06BpiMJYTUvDzfuSu3iEjcpZR63+N7zq/by2a4T/HZ0L67vFW46jhAtdu4m5XubC01HsakWFbfW+iut9S22CiPMWZFTyOtfHWBiejQzr4o1HUeIy9I12I+BsUG8l1OI1s57k1KuuAWb8kt46v3tDO0ezJ9v7SMzSIRDG5sSxcFTVWwucN7tXqW4Xdzh01Xc9042XYJ8eX1iCp6ycZRwcKP7dqKdpzsrcpx3uER+Sl1YWU0DMxZmoYH5U9No7ysbRwnH5+/twU19I/hk2zFqGyym49iEFLeLarA08dC7mykoqebNySnEhPiZjiREqxmbEkVFXSOf7zphOopNSHG7IK01f/p4F+v2n+KZ2/syKC7YdCQhWtWg2GCiOrZz2uESKW4XtGD9IZZkFnD/Nd0Yl9rFdBwhWp2bm+LO5Ci+zTvF8bIa03FanRS3i1mz5yRPr9zNyN7h/OrGnqbjCGEzdyZHoTW8v/mo6SitTorbhew5Uc7D726hd+dAXho/ADc3mfYnnFd0sC/pTjqnW4rbRRRX1DFzYTb+Ph7MnZKGr5eH6UhC2NydyWfndG8vLDMdpVVJcbuA2gYLGe9kU1JVz7ypaUS0l42jhGu4MTECL3c3Ptp6zHSUViXF7eS01vxyxXa2FJTy97sHkBjZ3nQkIdpM+3aeDE8I49/bjznVPt1S3E7u5dX7+fe2Y/x6VAKjEiNMxxGizY0Z0Jniijq+O3DadJRWI8XtxD7aepSXvtzP2JQo7r8mznQcIYy4LiGMAG8PPtrqPLNLpLidVM7hM/xyxXYGxgbx7O19ZeMo4bJ8PN0ZlRjBZztPOM0SeCluJ3SkpJr73smmU3sf3pycgpeHfJmFaxszIJKKukbW7ikyHaVVyE+0k6mobWDWomzqG5uYNzWNID8v05GEMG5wt2BCA7z50EmGS6S4nUijpYmHl24hr7iSNyan0D3M33QkIeyCu5viZ/06s3ZPMWU1DabjXDEpbifyzKe5fLW3mP8Zk8jQ7iGm4whhV8YM6Ey9pYnPdzr+joGXLG6llI9SapNSaptSapdS6s9tEUy0zDsbD7Ng/SFmXhXLxPRo03GEsDv9otoTE+zLx9scfzGONVfcdcBwrXV/YAAwSik1yLaxREus21/Mnz7exfCEMH4zupfpOELYJaUUo/t24ruDpympqjcd54pcsrj1WZXN73o2/3KeJUgOLq+oggeWbKZHmD//mJCEu2wcJcQFje7bCUuTdvgDFqwa41ZKuSultgJFwBda68zzPCZDKZWtlMouLi5u7ZziPE5X1jF9YRbeHu7MnZqKv7dsHCXExfTpHEjXYF8+3XHcdJQrYlVxa60tWusBQBQwUCmVeJ7HzNZap2qtU0NDQ1s7p/iRukYL9y/O4WR5HXOmpBDV0dd0JCHs3rnhkg0HHHu4pEWzSrTWpcBXwCibpBFW0Vrz1Ps7yDp0hhfu6k9SdEfTkYRwGDc3D5escuDhEmtmlYQqpTo0v90OGAHssXUwcWGvf3WA9zcf5fEb4vlZ/86m4wjhUPp0DiQ6yJeVDjxcYs0VdydgrVJqO5DF2THuT2wbS1zIf3Yc52+f72XMgM48PLy76ThCOJwfDpeccdDhEmtmlWzXWidprftprRO11v/dFsHET207UsrP/7mV5OgOPHdnP9k4SojL9P1wyW7HHC6RlZMO4mhpDbPeziY0wJvZU1Lx8XQ3HUkIh5UYGUhUx3as3CHFLWyksq6RmQuzqK23sGBaGiH+3qYjCeHQlFLc3LcTG/JOUVrteMMlUtx2ztKkeWTpFvYXVfLapGR6hAeYjiSEUxjdtxONTZovdp80HaXFpLjt3NMrd7NmTxF/vrUPw+JlfrwQraVfVHsiAn2kuEXreue7QyxYf4gZQ2OZPKir6ThCOBWlFCP7hPPN/mJq6h3rZBwpbjv19b5i/vTv3VyfEMZvb5aNo4SwhZG9I6htaOLbvFOmo7SIFLcd2neygoeWbCY+PEA2jhLChtLjggjw8XC4VZRS3HamuKKO6QuyaOflzrypqfjJxlFC2IynuxvXJ4TxZe5JGi1NpuNYTYrbjtQ2WMh4J5vTVXXMnZpK5w7tTEcSwumN7BPBmeoGcg6fMR3FalLcdkJrzS9XbGdLQSkv3T2AflEdTEcSwiUMiw/Fy8ONVQ40u0SK2078/cv9/HvbMX49KoFRiZ1MxxHCZfh7e3BV9xBW7T6B1o5xRowUtx34YEsh/1i9n3GpUdx/TZzpOEK4nJG9wzlSUsOeExWmo1hFituwrEMl/HrFDgbHBfP0bX1l4yghDLi+VzhK4TCLcaS4DTp8uoqMt7OJ6tiONyYn4+UhXw4hTAgN8CYluqPDnEUpTWFIaXU90xdkoYH509Lo4OtlOpIQLm1E73B2HSvnRFmt6SiXJMVtQG2DhYy3cygsrWHOlFRiQvxMRxLC5Q1PCANg7d4iw0kuTYq7jTU1nZ32t+lQCS/c1Z+0mCDTkYQQQI8wfyI7tGN1rhMUt1Kqi1JqrVIqVym1Syn1aFsEc1bPr9r7/bQ/OS9SCPuhlGJ4Qhjr805R22Dfm05Zc8XdCDyhte4FDAIeVEr1tm0s5/RuZgGvf3WAienRMu1PCDs0PCGMmgYLmfklpqNclDVnTh7XWm9ufrsCyAUibR3M2azdW8TvP9rJtT1D+e9b+8i0PyHs0OBuwfh4urEm176nBbZojFspFQMkAZm2COOsdh0r46Elm0mICODVicl4uMutBSHskY+nO0O7hbBmb5Fdr6K0ukGUUv7Ae8DPtdbl5/nzDKVUtlIqu7i4uDUzOrRjpTXMWJhFYDtP5k9Lw192+xPCrl2XEMaRkhoOFFeajnJBVhW3UsqTs6W9RGv9/vkeo7WerbVO1VqnhobKEVsA5bUNzFiYRXWdhQXT0wgP9DEdSQhxCdc1Twtcs8d+Z5dYM6tEAfOAXK31i7aP5BwaLE08uGQzeUWVvDE5hYSIQNORhBBWiOzQjoSIALueFmjNFfdQ4B5guFJqa/Ov0TbO5dC01vz2gx2s23+KZ+/oy1U9QkxHEkK0wHUJYWQfPkNZTYPpKOdlzaySb7XWSmvdT2s9oPnXp20RzlG9siaP5dmFPDK8O+NSu5iOI4RooesTwrA0adbtt8/7dTK9oZUt21TAi1/s447kSB67Id50HCHEZUiK7kgHX0+7HeeW4m5Fq3NP8tsPdzIsPpTn7uwnc7WFcFDuboqh3UP4dv8pu5wWKMXdSjYXnOHBdzfTp3Mgb0xKxlPmagvh0K7pEUpRRZ1dHq4g7dIK8ooqmbEwi/BAH+ZPS5OT2YVwAlfHn51U8M0++xvnluK+QifLa5k6fxMeboq3ZwwkxN/bdCQhRCvo1L4d8eH+fGOHNyiluK9AeW0D0xZkcaa6ngXTBtI1WPbVFsKZXN0jlKz8M9TU29dugVLcl6mu0cJ9b+ew/2QFb05OoW9Ue9ORhBCtbFh8KPWWJjbmnzYd5f+R4r4MTU2ax5dv47uDp/nbXf0YFi9L/IVwRumxQXh7uNndOLcUdwtprXl6ZS4rtx/nqZsSuD0pynQkIYSN+Hi6MzA2SIrb0b3+1QHmr89n+tAYMobJYQhCOLtr4kM5UFzF0dIa01G+J8XdAu9sPMzfPt/LbQM68/ube8sCGyFcwLmh0HV2dNUtxW2lj7Ye5Q8f7WRErzD+dld/3NyktIVwBT3C/IkI9LGraYFS3FZYu6eIJ5ZvY2BMEK9OlFWRQrgSpRRX9zi7/L3R0mQ6DiDFfUmb8ku4f3EOCZ0CmDs1FR9Pd9ORhBBtbFh8KOW1jWw/WmY6CiDFfVE7j5Yxc2EWkR3bsWj6QAJ8PE1HEkIYMKRbMAAb8k4ZTnKWFPcFHCyuZOr8TQT4eLB4ZjrBspRdCJcV7O9Nr06BrM+zj4U4UtzncbyshnvmbQLgnVnpdO7QznAiIYRpQ7sFk1NwhtoG88vfpbh/pKi8lolzMimvaWDRjIF0C/U3HUkIYQeGdA+mvrGJnMNnTEex6rDg+UqpIqXUzrYIZNLpyjomzc3kZHktC6ankRgp+48IIc4aGBuMh5tivR2Mc1tzxb0QGGXjHMaVVtczed4mCkqqmTc1jdSYINORhBB2xN/bg/5dOrDhgPlxbmsOC/4GKGmDLMaU1zYwZf4mDhRVMmdKKoOb7yALIcQPDekWzPbCUsprzZ7+7vJj3JV1jUybv4nc4+W8MTlZdvoTQlzQkG4hNGnIPGj2WrbVilsplaGUylZKZRcX28/S0Iupqbcwc2EW2wrLeGVCEtf3CjcdSQhhx5K7dsDH040NB8yOc7dacWutZ2utU7XWqaGh9n/VWttgIeOdbLIOlfD3uwcwKrGT6UhCCDvn7eFOWkwQGwzP53bJoZKzpZ3Duv2n+OvY/tzav7PpSEIIBzG4WzB7T1ZQXFFnLIM10wGXAt8BPZW7+gkyAAAHwklEQVRShUqpmbaPZTs19RZmLcpm3f5i/jq2H2NT5CAEIYT1hnY7e/r7dwfNXXV7XOoBWusJbRGkLVTXNzJzYTYb80/z/Nj+3CmlLYRoocTI9gT4eLAh75Sx/61fsridRVVdI9MXZpF9qIS/jxvAbUmRpiMJIRyQu5tiUFww6w3eoHSJMe7Kukamzt9EzuEzvDw+SUpbCHFFBscFc6SkhmOGjjNz+uIur21gyrxMth4p5ZUJSfxMbkQKIa7QwNizK6s35ZuZz+3UxV1SVc/kuZlsLyzj1YnJjO4rU/6EEFeuV6dAAnw8yMw3c4PSace4T5TVMnleJkdKqnnrnhRZXCOEaDXuboqBMUHGVlA65RX3oVNVjH1zAyfKalk0Y6CUthCi1aXHBXHwVBVF5bVt/txOV9x7TpQz9s3vqKpr5N170xkUJxtGCSFaX3rs2W7ZdKjtr7qdqrg3F5zh7rc24uGmWH7fYPpFdTAdSQjhpPp0DsTPy93IcInTjHF/s6+Y+xfnEBrgzeKZ6XQJ8jUdSQjhxDzc3UiJCTJyg9IprrhX5BQyY2EWXYP9+Nf9g6W0hRBtIj02iH0nKympqm/T53Xo4tZa88rq/fziX9sYFBfM8vsGERbgYzqWEMJFDIo7N5+7ba+6Hba4Gy1N/OaDHbzwxT7uSI5k/rQ0Anw8TccSQriQvpFn9+fObOOFOA45xl1d38hD725hzZ4iHh7encdviEcpZTqWEMLFeHm4kRzdsc1vUDrcFfeJslrGz97IV3uLePb2vjwxsqeUthDCmPTYYHJPlFNW3XbnUDpUcW87Usqtr37LgaJK5k5NZWJ6tOlIQggXlx4XhNaQ1YbzuR2muD/aepRxb32Hl4cb7z8wlOEJshpSCGHegC4d8HJ3a9OFOHY/xt3UpHnxi328ujaPgbFBvDEpmWB/b9OxhBACAB9Pd/p3aS9X3OdU1DZw/+IcXl2bx/i0LiyemS6lLYSwO6kxQew8WkZNvaVNns+q4lZKjVJK7VVK5SmlnrR1KIC9JyoY8+p6Vu8p4g+39OZ/7+iLl4dd/zsjhHBRaTEdabBoth4pbZPns+awYHfgNeAmoDcwQSnV25ahPtxylNteW09FXSPvzkpnxlWxMnNECGG3UqLPLsTJbqPhEmvGuAcCeVrrgwBKqWXAGGB3a4epa7Tw9Ce5vLPxMANjgnh1YhJhgbISUghh39r7etIzPICsw2fa5PmsKe5I4MgP3i8E0ls7SFl1A1MWbGLbkVIyhsXxyxt74ukuQyNCCMeQFtuRj7Yeo6lJ4+Zm2xECa4r7fAn0Tx6kVAaQARAd3fL51QE+HsQE+/Jf18QxKlGOGBNCOJaHh/fgFyN72ry0wbriLgS6/OD9KODYjx+ktZ4NzAZITU39SbFfipub4uXxSS39a0IIYRfC23BY15qxiCygh1IqVinlBYwHPrZtLCGEEBdyySturXWjUuoh4HPAHZivtd5l82RCCCHOy6qVk1rrT4FPbZxFCCGEFWTahhBCOBgpbiGEcDBS3EII4WCkuIUQwsFIcQshhINRWrd4rcylP6lSxcDhy/zrIcCpVozjCOQ1Oz9Xe70gr7mlumqtQ615oE2K+0oopbK11qmmc7Qlec3Oz9VeL8hrtiUZKhFCCAcjxS2EEA7GHot7tukABshrdn6u9npBXrPN2N0YtxBCiIuzxytuIYQQF2E3xW3iQGKTlFJdlFJrlVK5SqldSqlHTWdqK0opd6XUFqXUJ6aztAWlVAel1Aql1J7mr/dg05lsTSn1WPP39U6l1FKllNOdQaiUmq+UKlJK7fzBx4KUUl8opfY3/97RFs9tF8Vt4kBiO9AIPKG17gUMAh50gdd8zqNArukQbehl4DOtdQLQHyd/7UqpSOARIFVrncjZ7aDHm01lEwuBUT/62JPAaq11D2B18/utzi6Kmx8cSKy1rgfOHUjstLTWx7XWm5vfruDsD3Ok2VS2p5SKAm4G5prO0haUUoHAMGAegNa6XmtdajZVm/AA2imlPABfznNqlqPTWn8D/PhY9zHAoua3FwG32eK57aW4z3cgsdOX2DlKqRggCcg0m6RNvAT8CmgyHaSNxAHFwILm4aG5Sik/06FsSWt9FHgeKACOA2Va61VmU7WZcK31cTh7cQaE2eJJ7KW4rTqQ2BkppfyB94Cfa63LTeexJaXULUCR1jrHdJY25AEkA29orZOAKmz032d70TyuOwaIBToDfkqpyWZTORd7KW6rDiR2NkopT86W9hKt9fum87SBocCtSqlDnB0OG66UWmw2ks0VAoVa63P/m1rB2SJ3ZiOAfK11sda6AXgfGGI4U1s5qZTqBND8e5EtnsReitvlDiRWSinOjnvmaq1fNJ2nLWitn9JaR2mtYzj7NV6jtXbqKzGt9QngiFKqZ/OHrgd2G4zUFgqAQUop3+bv8+tx8huyP/AxMLX57anAR7Z4EqvOnLQ1Fz2QeChwD7BDKbW1+WO/aT7fUziXh4ElzRclB4HphvPYlNY6Uym1AtjM2dlTW3DCVZRKqaXAtUCIUqoQ+CPwF2C5UmomZ/8Bu8smzy0rJ4UQwrHYy1CJEEIIK0lxCyGEg5HiFkIIByPFLYQQDkaKWwghHIwUtxBCOBgpbiGEcDBS3EII4WD+D2zcViNvXo3OAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"Lx = 10\n",
"Nx = 2000\n",
"dx = Lx/Nx\n",
"Source_func = lambda x, q: q*x*(10-x)\n",
"kappa_func = lambda x, kappal, kappah: kappah + (kappal-kappah)*(x>5)*(x<7.5)\n",
"v_func = lambda x,v: v*np.ones(x.size)\n",
"omega_func = lambda x,omega: omega*np.ones(x.size)\n",
"\n",
"#nominal values\n",
"\n",
"import csv\n",
"\n",
"xs = np.linspace(dx/2,Lx-dx/2,Nx)\n",
"source = Source_func(xs, 1)\n",
"kappa = kappa_func(xs, 0.1, 2)\n",
"\n",
"omega_nom = 20\n",
"omega_var = 0.3195214\n",
"v_nom = 10\n",
"v_var = 0.0723493\n",
"kappal_nom = 0.1\n",
"kappal_var = 8.511570e-6\n",
"kappah_nom = 2\n",
"kappah_var = 0.002778142\n",
"q_nom = 1\n",
"q_var = 7.062353e-4\n",
"vs = v_func(xs, v_nom)\n",
"print(vs)\n",
"sol,Q = ADRSource(Lx, Nx, source, omega_func(xs, omega_nom), vs, kappa)\n",
"print(Q)\n",
"plt.plot(xs,sol)\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "8K4A3GjRMbaJ",
"nbpages": {
"level": 3,
"link": "[7.2.2.1 Set up diffusion reaction equation](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.1-Set-up-diffusion-reaction-equation)",
"section": "7.2.2.1 Set up diffusion reaction equation"
}
},
"source": [
"We are going to join gamma RVs with a normal copula. First we get the normal samples"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 648
},
"colab_type": "code",
"id": "5bv2qHTSMbaK",
"nbpages": {
"level": 3,
"link": "[7.2.2.1 Set up diffusion reaction equation](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.1-Set-up-diffusion-reaction-equation)",
"section": "7.2.2.1 Set up diffusion reaction equation"
},
"outputId": "adce1858-0e1a-46df-d404-499ef2d67e2b"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[[0. 0. 0. 0. 0.]\n",
" [0. 0. 0. 0. 0.]\n",
" [0. 0. 0. 0. 0.]\n",
" [0. 0. 0. 0. 0.]\n",
" [0. 0. 0. 0. 0.]]\n",
"[[ 1. 0.1 -0.05 0. 0. ]\n",
" [ 0.1 1. -0.4 0.3 0.5 ]\n",
" [-0.05 -0.4 1. 0.2 0. ]\n",
" [ 0. 0.3 0.2 1. -0.1 ]\n",
" [ 0. 0.5 0. -0.1 1. ]]\n",
"[[ 7.23493000e-02 1.52043249e-02 -3.92366580e-05 0.00000000e+00\n",
" 0.00000000e+00]\n",
" [ 1.52043249e-02 3.19521400e-01 -6.59651879e-04 8.93816670e-03\n",
" 7.51094687e-03]\n",
" [-3.92366580e-05 -6.59651879e-04 8.51157000e-06 3.07547395e-05\n",
" 0.00000000e+00]\n",
" [ 0.00000000e+00 8.93816670e-03 3.07547395e-05 2.77814200e-03\n",
" -1.40072194e-04]\n",
" [ 0.00000000e+00 7.51094687e-03 0.00000000e+00 -1.40072194e-04\n",
" 7.06235300e-04]]\n",
"[[0. 0. 0. 0. 0.]\n",
" [0. 0. 0. 0. 0.]\n",
" [0. 0. 0. 0. 0.]\n",
" [0. 0. 0. 0. 0.]\n",
" [0. 0. 0. 0. 0.]]\n",
"(array([3.20880078e-01, 7.14248146e-02, 2.58516363e-03, 4.68396801e-04,\n",
" 5.13602871e-06]), array([[-6.10221850e-02, -9.98104846e-01, -5.23689494e-03,\n",
" 5.95871096e-03, 2.80458596e-04],\n",
" [-9.97466874e-01, 6.06888498e-02, 2.39831973e-02,\n",
" -2.80393816e-02, -3.91132091e-03],\n",
" [ 2.05538173e-03, -8.80183607e-06, -1.78182587e-02,\n",
" 5.09130368e-02, -9.98542011e-01],\n",
" [-2.80167615e-02, 7.88889090e-03, -9.85095968e-01,\n",
" 1.67509882e-01, 2.60614743e-02],\n",
" [-2.33872832e-02, 6.43007420e-03, 1.69309850e-01,\n",
" 9.84137485e-01, 4.71091795e-02]]))\n",
"0.999986582967767\n"
]
}
],
"source": [
"means = [v_nom, omega_nom, kappal_nom, kappah_nom, q_nom]\n",
"varmat = np.zeros((5,5))\n",
"#fill in diagonal\n",
"corrmat = np.ones((5,5))\n",
"corrmat[0,:] = (1,.1,-0.05,0,0)\n",
"corrmat[1,:] = (.1,1,-.4,.3,.5)\n",
"corrmat[2,:] = (-0.05,-.4,1,.2,0)\n",
"corrmat[3,:] = (0,.3,0.2,1,-.1)\n",
"corrmat[4,:] = (0,.5,0,-.1,1)\n",
"print(corrmat-corrmat.transpose())\n",
"print(corrmat)\n",
"\n",
"\n",
"varmat[np.diag_indices(5)] = [v_var, omega_var, kappal_var, kappah_var, q_var]\n",
"for i in range(5):\n",
" for j in range(5):\n",
" varmat[i,j] = math.sqrt(varmat[i,i])*math.sqrt(varmat[j,j])*corrmat[i,j]\n",
"print(varmat)\n",
"print(varmat-varmat.transpose())\n",
"print(np.linalg.eig(varmat))\n",
"\n",
"# Warning: choosing a large number here will make the notebook take a long time\n",
"# to solve.\n",
"# samps = 10**6\n",
"samps = 10**4\n",
"# samps = 10**3\n",
"test = norm.cdf(np.random.multivariate_normal(np.zeros(5), corrmat, samps))\n",
"\n",
"print(np.max(test[:,0]))\n",
"import tabulate\n",
"#print(tabulate.tabulate(corrmat, tablefmt=\"latex\", floatfmt=\".2f\"))"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "pHqz2NbMbr05",
"nbpages": {
"level": 3,
"link": "[7.2.2.1 Set up diffusion reaction equation](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.1-Set-up-diffusion-reaction-equation)",
"section": "7.2.2.1 Set up diffusion reaction equation"
}
},
"source": [
"The distributions will be gammas"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 204
},
"colab_type": "code",
"id": "7RHUJw50bsj4",
"nbpages": {
"level": 3,
"link": "[7.2.2.1 Set up diffusion reaction equation](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.1-Set-up-diffusion-reaction-equation)",
"section": "7.2.2.1 Set up diffusion reaction equation"
},
"outputId": "9e2ea3e7-9c75-4f8b-8256-e293ae189de0"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"2.0011318620000007 0.04318279093895298 0.20780469421779907\n",
"[[ 1.00876724e+00 1.75153708e-01 -4.80376658e-04 -1.49687366e-03\n",
" 2.78620413e-04]\n",
" [ 1.75153708e-01 4.02281621e+00 -7.99696110e-03 -3.19230630e-02\n",
" 1.00074170e-01]\n",
" [-4.80376658e-04 -7.99696110e-03 9.97417876e-05 -8.24879554e-05\n",
" 1.85805384e-06]\n",
" [-1.49687366e-03 -3.19230630e-02 -8.24879554e-05 4.31871096e-02\n",
" 4.41484525e-04]\n",
" [ 2.78620413e-04 1.00074170e-01 1.85805384e-06 4.41484525e-04\n",
" 1.00649099e-02]] 40.66575412647241\n"
]
}
],
"source": [
"def gen_samps(samps,test):\n",
" #v will have v_nom = 10 v_var = 1 which makes alpha = 10 beta = 10 or theta = 1/10\n",
" vsamps = gamma.ppf(test[:,0], a = 100, scale = 1/10)\n",
" #print(np.mean(vsamps), np.var(vsamps), np.std(vsamps))\n",
" #plt.hist(vsamps)\n",
"\n",
" #omega will have omega_nom = 20, var = 4 which makes alpha = 100 beta = 5, theta = 1/5\n",
" omegasamps = gamma.ppf(test[:,1], a = 100, scale = 1/5)\n",
" #print(np.mean(omegasamps), np.var(omegasamps), np.std(omegasamps))\n",
" #plt.hist(omegasamps)\n",
"\n",
" #kappa_l will have kappa_l = 0.1 var = (0.01)^2 this makes alpha = 100 and theta = 1/1000\n",
" kappalsamps = gamma.ppf(test[:,2], a = 100, scale = 1/1000)\n",
" #print(np.mean(kappalsamps), np.var(kappalsamps), np.std(kappalsamps))\n",
" #plt.hist(kappalsamps)\n",
"\n",
" #kappa_h will have kappa_h = 2 var = .04 this makes alpha = 100 and theta = 1/50\n",
" kappahsamps = (test[:,3]>0.005)*(1.98582-4.82135) + (4.82135) # #gamma.ppf(test[:,3], a = 100, scale = 1/50)\n",
" print(np.mean(kappahsamps), np.var(kappahsamps), np.std(kappahsamps))\n",
" #plt.hist(kappahsamps)\n",
"\n",
" #q will have q = 1 var = 0.01 this makes alpha = 100 and theta = 1/100\n",
" qsamps = gamma.ppf(test[:,4], a = 100, scale = 1/100)\n",
" #print(np.mean(qsamps), np.var(qsamps),np.std(qsamps))\n",
" #plt.hist(qsamps)\n",
" \n",
" return vsamps,omegasamps,kappalsamps,kappahsamps,qsamps\n",
"vsamps,omegasamps,kappalsamps,kappahsamps,qsamps = gen_samps(samps,test)\n",
"\n",
"var_list = [vsamps,omegasamps,kappalsamps,kappahsamps,qsamps]\n",
"cormat_emp = np.zeros((5,5))\n",
"tmp = np.vstack((var_list[0],var_list[1],var_list[2],var_list[3],var_list[4]))\n",
"cormat_emp = np.cov(tmp)\n",
"sens = np.array([-1.74063875491,-0.970393472244,13.1587256647,17.7516305655,52.3902556893])\n",
"print(cormat_emp, np.dot(sens,np.dot(cormat_emp,sens)))"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 68
},
"colab_type": "code",
"id": "BJKHQE_PMbaP",
"nbpages": {
"level": 3,
"link": "[7.2.2.1 Set up diffusion reaction equation](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.1-Set-up-diffusion-reaction-equation)",
"section": "7.2.2.1 Set up diffusion reaction equation"
},
"outputId": "dbc1d1c6-ca5a-42f8-cd79-7357fedc1abf"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"9.996211170854629 19.991729539390022 0.10007439860826033 2.0011318620000007 1.0007749682671143\n"
]
}
],
"source": [
"Qs = np.zeros(samps)\n",
"print(np.mean(vsamps),np.mean(omegasamps),np.mean(kappalsamps), np.mean(kappahsamps),np.mean(qsamps))\n",
"for i in range(samps):\n",
" sol,Qs[i] = ADRSource(Lx, Nx, Source_func(xs, qsamps[i]), omega_func(xs, omegasamps[i]), v_func(xs, vsamps[i]),\n",
" kappa_func(xs, kappalsamps[i], kappahsamps[i]))\n"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 540
},
"colab_type": "code",
"id": "VGk7dr9mMbaR",
"nbpages": {
"level": 3,
"link": "[7.2.2.1 Set up diffusion reaction equation](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.1-Set-up-diffusion-reaction-equation)",
"section": "7.2.2.1 Set up diffusion reaction equation"
},
"outputId": "48a6c2d5-30af-45d1-9112-fcd9c536bd9c"
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYcAAAD8CAYAAACcjGjIAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAELRJREFUeJzt3X+s3XV9x/HnSwr+nAJSHWs7y2KzDc2c2ACOZDFg+GkoySCr2aQSliYGJy4mDvxjZCgJJIs4lsnSCVtxRiBoRqc40vEjm8lAyo+hUAkNMuhgcrWAOiau+t4f91M93s9p773n1HvuLc9HcnK/38/3/T3n/ck39HW/P84lVYUkSYNeNukGJEmLj+EgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkzrJJNzCqI444olavXj3pNiRpybj33nu/U1XL51K7ZMNh9erVbNu2bdJtSNKSkeQ/51rrZSVJUsdwkCR1DAdJUsdwkCR1Zg2HJNcmeSbJNwbGDk+yNcmj7edhbTxJrkqyI8mDSY4Z2GdDq380yYaB8Xck+Xrb56ok2d+TlCTNz1zOHP4eOHXG2EXAbVW1BritrQOcBqxpr43A1TAdJsAlwHHAscAlewKl1Wwc2G/mZ0mSFtis4VBV/wrsmjG8DtjcljcDZw2MX1fT7gIOTXIkcAqwtap2VdWzwFbg1LbttVX17zX9v6S7buC9JEkTMuo9hzdW1dMA7ecb2vgK4MmBup1tbF/jO4eMS5ImaH/fkB52v6BGGB/+5snGJNuSbJuamhqxRUnSbEb9hvS3kxxZVU+3S0PPtPGdwKqBupXAU238XTPG72zjK4fUD1VVm4BNAGvXrt1riMxm9UVfHnXXsTx++RkT+VxJmq9Rzxy2AHueONoA3Dwwfm57aul44Pl22elW4OQkh7Ub0ScDt7Zt309yfHtK6dyB95IkTcisZw5JPs/0b/1HJNnJ9FNHlwM3JjkfeAI4p5XfApwO7ABeAM4DqKpdST4O3NPqLq2qPTe5P8D0E1GvBL7SXpKkCZo1HKrqvXvZdNKQ2gIu2Mv7XAtcO2R8G/DW2fqQJC0cvyEtSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeoYDpKkjuEgSeqMFQ5J/iTJQ0m+keTzSV6R5Kgkdyd5NMkNSQ5ptS9v6zva9tUD73NxG38kySnjTUmSNK6RwyHJCuBDwNqqeitwELAeuAK4sqrWAM8C57ddzgeerao3A1e2OpIc3fZ7C3Aq8OkkB43alyRpfONeVloGvDLJMuBVwNPAicBNbftm4Ky2vK6t07aflCRt/PqqerGqvgXsAI4dsy9J0hhGDoeq+i/gL4AnmA6F54F7geeqancr2wmsaMsrgCfbvrtb/esHx4fs83OSbEyyLcm2qampUVuXJM1inMtKhzH9W/9RwK8ArwZOG1Jae3bZy7a9jfeDVZuqam1VrV2+fPn8m5Ykzck4l5XeDXyrqqaq6v+ALwK/AxzaLjMBrASeass7gVUAbfvrgF2D40P2kSRNwDjh8ARwfJJXtXsHJwEPA3cAZ7eaDcDNbXlLW6dtv72qqo2vb08zHQWsAb42Rl+SpDEtm71kuKq6O8lNwH3AbuB+YBPwZeD6JJ9oY9e0Xa4BPptkB9NnDOvb+zyU5Eamg2U3cEFV/XjUviRJ4xs5HACq6hLgkhnDjzHkaaOq+iFwzl7e5zLgsnF6kSTtP35DWpLUMRwkSR3DQZLUMRwkSR3DQZLUMRwkSR3DQZLUMRwkSR3DQZLUMRwkSR3DQZLUMRwkSR3DQZLUMRwkSR3DQZLUMRwkSR3DQZLUMRwkSR3DQZLUMRwkSR3DQZLUMRwkSR3DQZLUMRwkSR3DQZLUMRwkSR3DQZLUMRwkSR3DQZLUMRwkSR3DQZLUMRwkSZ2xwiHJoUluSvLNJNuTvDPJ4Um2Jnm0/Tys1SbJVUl2JHkwyTED77Oh1T+aZMO4k5IkjWfcM4e/BP65qn4DeBuwHbgIuK2q1gC3tXWA04A17bURuBogyeHAJcBxwLHAJXsCRZI0GSOHQ5LXAr8LXANQVT+qqueAdcDmVrYZOKstrwOuq2l3AYcmORI4BdhaVbuq6llgK3DqqH1JksY3zpnDrwFTwN8luT/JZ5K8GnhjVT0N0H6+odWvAJ4c2H9nG9vbuCRpQsYJh2XAMcDVVfV24H/42SWkYTJkrPYx3r9BsjHJtiTbpqam5tuvJGmOxgmHncDOqrq7rd/EdFh8u10uov18ZqB+1cD+K4Gn9jHeqapNVbW2qtYuX758jNYlSfsycjhU1X8DTyb59TZ0EvAwsAXY88TRBuDmtrwFOLc9tXQ88Hy77HQrcHKSw9qN6JPbmCRpQpaNuf8fA59LcgjwGHAe04FzY5LzgSeAc1rtLcDpwA7ghVZLVe1K8nHgnlZ3aVXtGrMvSdIYxgqHqnoAWDtk00lDagu4YC/vcy1w7Ti9SJL2H78hLUnqGA6SpI7hIEnqGA6SpI7hIEnqGA6SpI7hIEnqGA6SpI7hIEnqGA6SpI7hIEnqGA6SpI7hIEnqGA6SpI7hIEnqGA6SpI7hIEnqGA6SpI7hIEnqGA6SpI7hIEnqGA6SpI7hIEnqGA6SpI7hIEnqGA6SpI7hIEnqGA6SpI7hIEnqGA6SpI7hIEnqGA6SpI7hIEnqjB0OSQ5Kcn+SL7X1o5LcneTRJDckOaSNv7yt72jbVw+8x8Vt/JEkp4zbkyRpPPvjzOFCYPvA+hXAlVW1BngWOL+Nnw88W1VvBq5sdSQ5GlgPvAU4Ffh0koP2Q1+SpBGNFQ5JVgJnAJ9p6wFOBG5qJZuBs9ryurZO235Sq18HXF9VL1bVt4AdwLHj9CVJGs+4Zw6fAj4K/KStvx54rqp2t/WdwIq2vAJ4EqBtf77V/3R8yD6SpAkYORySvAd4pqruHRweUlqzbNvXPjM/c2OSbUm2TU1NzatfSdLcjXPmcAJwZpLHgeuZvpz0KeDQJMtazUrgqba8E1gF0La/Dtg1OD5kn59TVZuqam1VrV2+fPkYrUuS9mXkcKiqi6tqZVWtZvqG8u1V9QfAHcDZrWwDcHNb3tLWadtvr6pq4+vb00xHAWuAr43alyRpfMtmL5m3PwWuT/IJ4H7gmjZ+DfDZJDuYPmNYD1BVDyW5EXgY2A1cUFU//gX0JUmao/0SDlV1J3BnW36MIU8bVdUPgXP2sv9lwGX7oxdJ0vj8hrQkqWM4SJI6hoMkqWM4SJI6hoMkqWM4SJI6hoMkqWM4SJI6hoMkqWM4SJI6hoMkqWM4SJI6hoMkqWM4SJI6hoMkqWM4SJI6hoMkqWM4SJI6hoMkqWM4SJI6hoMkqWM4SJI6hoMkqWM4SJI6hoMkqWM4SJI6hoMkqWM4SJI6hoMkqWM4SJI6hoMkqWM4SJI6I4dDklVJ7kiyPclDSS5s44cn2Zrk0fbzsDaeJFcl2ZHkwSTHDLzXhlb/aJIN409LkjSOcc4cdgMfqarfBI4HLkhyNHARcFtVrQFua+sApwFr2msjcDVMhwlwCXAccCxwyZ5AkSRNxsjhUFVPV9V9bfn7wHZgBbAO2NzKNgNnteV1wHU17S7g0CRHAqcAW6tqV1U9C2wFTh21L0nS+PbLPYckq4G3A3cDb6yqp2E6QIA3tLIVwJMDu+1sY3sblyRNyNjhkOQ1wBeAD1fV9/ZVOmSs9jE+7LM2JtmWZNvU1NT8m5UkzclY4ZDkYKaD4XNV9cU2/O12uYj285k2vhNYNbD7SuCpfYx3qmpTVa2tqrXLly8fp3VJ0j6M87RSgGuA7VX1yYFNW4A9TxxtAG4eGD+3PbV0PPB8u+x0K3ByksPajeiT25gkaUKWjbHvCcD7gK8neaCNfQy4HLgxyfnAE8A5bdstwOnADuAF4DyAqtqV5OPAPa3u0qraNUZfkqQxjRwOVfVVht8vADhpSH0BF+zlva4Frh21F0nS/uU3pCVJHcNBktQxHCRJHcNBktQxHCRJHcNBktQxHCRJHcNBktQxHCRJHcNBktQxHCRJHcNBktQxHCRJHcNBktQxHCRJHcNBktQxHCRJHcNBktQxHCRJHcNBktQxHCRJHcNBktQxHCRJHcNBktQxHCRJHcNBktQxHCRJHcNBktQxHCRJHcNBktQxHCRJHcNBktQxHCRJnUUTDklOTfJIkh1JLpp0P5L0UrYowiHJQcBfA6cBRwPvTXL0ZLuSpJeuRREOwLHAjqp6rKp+BFwPrJtwT5L0krVs0g00K4AnB9Z3AsdNqBdJmtXqi748kc99/PIzFuRzFks4ZMhYdUXJRmBjW/1BkkfG+MwjgO+Msf+85YoF+ZgFn9cCORDndSDOCZzXL9SY/468aa6FiyUcdgKrBtZXAk/NLKqqTcCm/fGBSbZV1dr98V6LifNaOg7EOYHzOlAslnsO9wBrkhyV5BBgPbBlwj1J0kvWojhzqKrdST4I3AocBFxbVQ9NuC1JeslaFOEAUFW3ALcs4Eful8tTi5DzWjoOxDmB8zogpKq77ytJeolbLPccJEmLyAEdDklWJbkjyfYkDyW5cEhNklzV/mzHg0mOmUSv8zHHeb0ryfNJHmivP5tEr/OR5BVJvpbkP9q8/nxIzcuT3NCO191JVi98p3M3xzm9P8nUwLH6o0n0OookByW5P8mXhmxbUsdqj1nmtGSP1XwtmnsOvyC7gY9U1X1Jfgm4N8nWqnp4oOY0YE17HQdczeL/At5c5gXwb1X1ngn0N6oXgROr6gdJDga+muQrVXXXQM35wLNV9eYk64ErgN+fRLNzNJc5AdxQVR+cQH/juhDYDrx2yLaldqz22NecYOkeq3k5oM8cqurpqrqvLX+f6QO+YkbZOuC6mnYXcGiSIxe41XmZ47yWnHYMftBWD26vmTfF1gGb2/JNwElJhn2JclGY45yWpCQrgTOAz+ylZEkdK5jTnF4yDuhwGNROad8O3D1j07A/3bFk/qHdx7wA3tkuZ3wlyVsWtLERtVP6B4BngK1VtdfjVVW7geeB1y9sl/MzhzkB/F67rHlTklVDti9GnwI+CvxkL9uX3LFi9jnB0jxW8/aSCIckrwG+AHy4qr43c/OQXZbEb3azzOs+4E1V9Tbgr4B/XOj+RlFVP66q32b6W/LHJnnrjJIld7zmMKd/AlZX1W8B/8LPfttetJK8B3imqu7dV9mQsUV7rOY4pyV3rEZ1wIdDu877BeBzVfXFISVz+tMdi81s86qq7+25nNG+Q3JwkiMWuM2RVdVzwJ3AqTM2/fR4JVkGvA7YtaDNjWhvc6qq71bVi231b4F3LHBrozgBODPJ40z/FeUTk/zDjJqldqxmndMSPVYjOaDDoV3fvAbYXlWf3EvZFuDc9tTS8cDzVfX0gjU5grnMK8kv77m+m+RYpo/1dxeuy/lLsjzJoW35lcC7gW/OKNsCbGjLZwO31yL+ss5c5jTjHteZTN9DWtSq6uKqWllVq5n+cze3V9UfzihbUsdqLnNaisdqVAf600onAO8Dvt6u+QJ8DPhVgKr6G6a/lX06sAN4AThvAn3O11zmdTbwgSS7gf8F1i/m/zCbI4HNmf6fP70MuLGqvpTkUmBbVW1hOhQ/m2QH07+Frp9cu3Mylzl9KMmZTD+Ftgt4/8S6HdMSP1ZDHajHajZ+Q1qS1DmgLytJkkZjOEiSOoaDJKljOEiSOoaDJKljOEiSOoaDJKljOEiSOv8PiUgNr+39JlYAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYUAAAD8CAYAAACYebj1AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAEZxJREFUeJzt3H+s3XV9x/Hna1RxOrUFCmEtWzE2TjQT8QZwJMaBgQLG6iJJnZmNa9Z/2KbbEi0zi/NXgtsy1EzZiDDROJA5HQ0ysUGJ2zKRW0UEsWvVDroyel0R54hO9L0/zqcfD+Xe3p+cc7XPR3Jyvt/39/O93/f33HP76vfHOakqJEkC+LlxNyBJWj4MBUlSZyhIkjpDQZLUGQqSpM5QkCR1hoIkqTMUJEndnEIhyd4kX01yZ5LJVjsuyY4ku9vzqlZPkvcl2ZPkriRnDP2czW387iSbn5hdkiQtVObyieYke4GJqvr2UO3PgINVdXmSbcCqqnpzkouA3wMuAs4C3ltVZyU5DpgEJoACdgIvqqqHZtruCSecUOvWrVvwzknS0Wjnzp3frqrVC1l3xSK2uxF4aZu+FrgNeHOrf7gGafOFJCuTnNzG7qiqgwBJdgAbgOtm2sC6deuYnJxcRIuSdPRJ8h8LXXeu1xQK+EySnUm2ttpJVfUAQHs+sdXXAPcPrbuv1WaqP0aSrUkmk0xOTU3NfU8kSYs21yOFc6pqf5ITgR1Jvn6EsZmmVkeoP7ZQdRVwFcDExITf1idJIzSnI4Wq2t+eDwCfBM4EHmynhWjPB9rwfcApQ6uvBfYfoS5JWiZmDYUkT0vy9EPTwPnA3cB24NAdRJuBG9v0duB17S6ks4GH2+mlW4Dzk6xqdyqd32qSpGViLqePTgI+meTQ+L+rqk8nuQO4IckW4D7gkjb+ZgZ3Hu0BHgFeD1BVB5O8A7ijjXv7oYvOkqTlYU63pI7LxMREefeRJM1Pkp1VNbGQdf1EsySpMxQkSZ2hIEnqFvOJZs1g3bZPjWW7ey+/eCzblfSzwyMFSVJnKEiSOkNBktQZCpKkzlCQJHWGgiSpMxQkSZ2hIEnqDAVJUmcoSJI6Q0GS1BkKkqTOUJAkdYaCJKkzFCRJnaEgSeoMBUlSZyhIkjpDQZLUGQqSpM5QkCR1hoIkqTMUJEmdoSBJ6gwFSVJnKEiSOkNBktQZCpKkzlCQJHWGgiSpm3MoJDkmyZeT3NTmT01ye5LdST6W5Mmtfmyb39OWrxv6GZe1+q4kFyz1zkiSFmc+RwpvAO4dmn83cEVVrQceAra0+hbgoap6NnBFG0eS04BNwPOADcAHkhyzuPYlSUtpxVwGJVkLXAy8C/jDJAHOBX6zDbkW+FPgSmBjmwb4OPBXbfxG4Pqq+gHwrSR7gDOBf1uSPRHrtn1qbNvee/nFY9u2pKUz1yOF9wBvAn7c5o8HvlNVj7b5fcCaNr0GuB+gLX+4je/1adbpkmxNMplkcmpqah67IklarFlDIcnLgQNVtXO4PM3QmmXZkdb5SaHqqqqaqKqJ1atXz9aeJGkJzeX00TnAK5JcBDwFeAaDI4eVSVa0o4G1wP42fh9wCrAvyQrgmcDBofohw+tIkpaBWY8UquqyqlpbVesYXCj+bFW9Fvgc8Oo2bDNwY5ve3uZpyz9bVdXqm9rdSacC64EvLtmeSJIWbU4XmmfwZuD6JO8Evgxc3epXAx9pF5IPMggSquqeJDcAXwMeBS6tqh8tYvuSpCU2r1CoqtuA29r0NxncPXT4mO8Dl8yw/rsY3MEkSVqG/ESzJKkzFCRJnaEgSeoMBUlSZyhIkjpDQZLUGQqSpM5QkCR1hoIkqTMUJEmdoSBJ6gwFSVJnKEiSOkNBktQZCpKkzlCQJHWGgiSpMxQkSZ2hIEnqDAVJUmcoSJI6Q0GS1BkKkqTOUJAkdYaCJKkzFCRJnaEgSeoMBUlSZyhIkjpDQZLUGQqSpM5QkCR1hoIkqTMUJEndrKGQ5ClJvpjkK0nuSfK2Vj81ye1Jdif5WJInt/qxbX5PW75u6Gdd1uq7klzwRO2UJGlh5nKk8APg3Kp6AXA6sCHJ2cC7gSuqaj3wELCljd8CPFRVzwauaONIchqwCXgesAH4QJJjlnJnJEmLM2so1MD32uyT2qOAc4GPt/q1wCvb9MY2T1t+XpK0+vVV9YOq+hawBzhzSfZCkrQk5nRNIckxSe4EDgA7gG8A36mqR9uQfcCaNr0GuB+gLX8YOH64Ps06w9vammQyyeTU1NT890iStGBzCoWq+lFVnQ6sZfC/++dON6w9Z4ZlM9UP39ZVVTVRVROrV6+eS3uSpCUyr7uPquo7wG3A2cDKJCvaorXA/ja9DzgFoC1/JnBwuD7NOpKkZWAudx+tTrKyTf888DLgXuBzwKvbsM3AjW16e5unLf9sVVWrb2p3J50KrAe+uFQ7IklavBWzD+Fk4Np2p9DPATdU1U1JvgZcn+SdwJeBq9v4q4GPJNnD4AhhE0BV3ZPkBuBrwKPApVX1o6XdHUnSYswaClV1F/DCaerfZJq7h6rq+8AlM/ysdwHvmn+bkqRR8BPNkqTOUJAkdYaCJKkzFCRJnaEgSeoMBUlSZyhIkjpDQZLUGQqSpM5QkCR1hoIkqTMUJEmdoSBJ6gwFSVJnKEiSOkNBktQZCpKkzlCQJHWGgiSpMxQkSZ2hIEnqDAVJUmcoSJI6Q0GS1BkKkqTOUJAkdYaCJKkzFCRJnaEgSeoMBUlSZyhIkjpDQZLUGQqSpM5QkCR1s4ZCklOSfC7JvUnuSfKGVj8uyY4ku9vzqlZPkvcl2ZPkriRnDP2szW387iSbn7jdkiQtxFyOFB4F/qiqngucDVya5DRgG3BrVa0Hbm3zABcC69tjK3AlDEIEeCtwFnAm8NZDQSJJWh5mDYWqeqCqvtSm/we4F1gDbASubcOuBV7ZpjcCH66BLwArk5wMXADsqKqDVfUQsAPYsKR7I0lalHldU0iyDnghcDtwUlU9AIPgAE5sw9YA9w+ttq/VZqpLkpaJOYdCkl8A/gF4Y1V990hDp6nVEeqHb2drkskkk1NTU3NtT5K0BOYUCkmexCAQPlpVn2jlB9tpIdrzgVbfB5wytPpaYP8R6o9RVVdV1URVTaxevXo++yJJWqS53H0U4Grg3qr6y6FF24FDdxBtBm4cqr+u3YV0NvBwO710C3B+klXtAvP5rSZJWiZWzGHMOcBvAV9Ncmer/TFwOXBDki3AfcAlbdnNwEXAHuAR4PUAVXUwyTuAO9q4t1fVwSXZC0nSkpg1FKrqX5j+egDAedOML+DSGX7WNcA182lQkjQ6fqJZktQZCpKkzlCQJHWGgiSpMxQkSZ2hIEnqDAVJUmcoSJI6Q0GS1BkKkqTOUJAkdYaCJKkzFCRJnaEgSeoMBUlSZyhIkjpDQZLUGQqSpM5QkCR1hoIkqTMUJEmdoSBJ6gwFSVJnKEiSOkNBktQZCpKkzlCQJHWGgiSpMxQkSZ2hIEnqDAVJUmcoSJI6Q0GS1BkKkqRu1lBIck2SA0nuHqodl2RHkt3teVWrJ8n7kuxJcleSM4bW2dzG706y+YnZHUnSYszlSOFDwIbDatuAW6tqPXBrmwe4EFjfHluBK2EQIsBbgbOAM4G3HgoSSdLyMWsoVNXngYOHlTcC17bpa4FXDtU/XANfAFYmORm4ANhRVQer6iFgB48PGknSmC30msJJVfUAQHs+sdXXAPcPjdvXajPVJUnLyFJfaM40tTpC/fE/INmaZDLJ5NTU1JI2J0k6soWGwoPttBDt+UCr7wNOGRq3Fth/hPrjVNVVVTVRVROrV69eYHuSpIVYaChsBw7dQbQZuHGo/rp2F9LZwMPt9NItwPlJVrULzOe3miRpGVkx24Ak1wEvBU5Iso/BXUSXAzck2QLcB1zSht8MXATsAR4BXg9QVQeTvAO4o417e1UdfvFakjRms4ZCVb1mhkXnTTO2gEtn+DnXANfMqztJ0kj5iWZJUmcoSJI6Q0GS1BkKkqTOUJAkdYaCJKkzFCRJnaEgSeoMBUlSZyhIkjpDQZLUGQqSpM5QkCR1s35L6k+zdds+Ne4WJOmnikcKkqTOUJAkdT/Tp480OuM6Vbf38ovHsl3pZ5VHCpKkzlCQJHWGgiSpMxQkSZ2hIEnqDAVJUmcoSJI6Q0GS1BkKkqTOUJAkdYaCJKkzFCRJnaEgSeoMBUlSZyhIkjpDQZLUGQqSpG7koZBkQ5JdSfYk2Tbq7UuSZjbSUEhyDPB+4ELgNOA1SU4bZQ+SpJmN+kjhTGBPVX2zqv4PuB7YOOIeJEkzWDHi7a0B7h+a3wecNeIe9DNk3bZPjW3bey+/eCzbHec+H23G9Tsep1GHQqap1WMGJFuBrW32e0l2PeFdPdYJwLdHvM25sK/5ecL7yrsXtNpyfb1g+fY2tr5m+R0v59frlxe68qhDYR9wytD8WmD/8ICqugq4apRNDUsyWVUT49r+TOxrfuxr/pZrb/Y1P62vdQtdf9TXFO4A1ic5NcmTgU3A9hH3IEmawUiPFKrq0SS/C9wCHANcU1X3jLIHSdLMRn36iKq6Gbh51Nudh7GdupqFfc2Pfc3fcu3NvuZnUX2lqmYfJUk6Kvg1F5Kk7qgPhSTHJPlykpva/KlJbk+yO8nH2gXxUfe0N8lXk9yZZLLVjkuyo/W1I8mqUffV+liZ5ONJvp7k3iQvHndvSZ7TXqtDj+8meeO4+2q9/UGSe5LcneS6JE9ZJu+xN7Se7knyxlYby+uV5JokB5LcPVSbtpcMvK99Tc5dSc4YcV+XtNfsx0kmDht/WetrV5ILRtzXn7e/ybuSfDLJyoX2ddSHAvAG4N6h+XcDV1TVeuAhYMtYuoJfr6rTh2552wbc2vq6tc2Pw3uBT1fVrwAvYPDajbW3qtrVXqvTgRcBjwCfHHdfSdYAvw9MVNXzGdxcsYkxv8eSPB/4HQbfMPAC4OVJ1jO+1+tDwIbDajP1ciGwvj22AleOuK+7gd8APj9cbF/Xswl4XlvnA+1rfUbV1w7g+VX1q8C/A5ctuK+qOmofDD4ncStwLnATgw/XfRtY0Za/GLhlDH3tBU44rLYLOLlNnwzsGkNfzwC+RbsWtZx6G+rlfOBfl0Nf/OQT/McxuKnjJuCCcb/HgEuADw7N/wnwpnG+XsA64O7Z3lPA3wCvmW7cKPoaqt/GIOwPzV8GXDY0fwvw4lH31Za9CvjoQvs62o8U3sPgj+HHbf544DtV9Wib38fgD3vUCvhMkp3tE94AJ1XVAwDt+cQx9PUsYAr423bK7YNJnrZMejtkE3Bdmx5rX1X1n8BfAPcBDwAPAzsZ/3vsbuAlSY5P8lTgIgYfKl1Ov8eZepnuq3LG8Td6uOXU128D/9Sm593XURsKSV4OHKiqncPlaYaO4/asc6rqDAaHypcmeckYepjOCuAM4MqqeiHwv4zvNNbjtHPzrwD+fty9ALTz4BuBU4FfBJ7G4Hd6uJG+x6rqXgansHYAnwa+Ajx6xJWWj+XyN3q4ZdFXkrcw+F1+9FBpmmFH7OuoDQXgHOAVSfYy+LbWcxkcOaxMcujzG4/7Go5RqKr97fkAg3PjZwIPJjkZoD0fGHVfDP6Xsa+qbm/zH2cQEsuhNxj8g/ulqnqwzY+7r5cB36qqqar6IfAJ4NdYHu+xq6vqjKp6CXAQ2M34X69hM/Uy61fljMnY+0qyGXg58Npq54oW0tdRGwpVdVlVra3Bd4RsAj5bVa8FPge8ug3bDNw4yr6SPC3J0w9NMzhHfjeDrwPZPK6+AKrqv4D7kzynlc4DvrYcemtew09OHcH4+7oPODvJU5OEn7xeY32PASQ5sT3/EoMLp9cx/tdr2Ey9bAde1+5COht4+NBppjHbDmxKcmySUxlcCP/iqDaeZAPwZuAVVfXIovp6oi6E/DQ9gJcCN7XpZ7UXbQ+D0xDHjriXZzE4nP8KcA/wllY/nsFF8d3t+bgxvVanA5PAXcA/AquWQ2/AU4H/Bp45VFsOfb0N+DqDYP8IcOy432Otr39mEFBfAc4b5+vFIJAeAH7I4H+2W2bqhcHpkPcD3wC+ytDF3hH19ao2/QPgQYZuEgDe0vraBVw44r72MLh2cGd7/PVC+/ITzZKk7qg9fSRJejxDQZLUGQqSpM5QkCR1hoIkqTMUJEmdoSBJ6gwFSVL3/29WO/uOmIIrAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"52.38429950498757 60.93083101449816 44.256769035451256 5.846536644275092 15.192880831520508 2.154994384485121\n"
]
}
],
"source": [
"plt.hist(kappahsamps)\n",
"plt.show()\n",
"plt.hist(Qs)\n",
"plt.show()\n",
"print(np.mean(Qs),stats.scoreatpercentile(Qs,95) ,stats.scoreatpercentile(Qs,5),np.std(Qs), stats.kurtosis(Qs), stats.skew(Qs))\n",
"Qref = Qs.copy()\n",
"np.savetxt(fname=\"ref_\"+ str(samps) + \"_binomial.csv\", delimiter=\",\", X=Qref)"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "qpV0Y54GqvLa",
"nbpages": {
"level": 3,
"link": "[7.2.2.1 Set up diffusion reaction equation](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.1-Set-up-diffusion-reaction-equation)",
"section": "7.2.2.1 Set up diffusion reaction equation"
}
},
"source": [
"Now we will do 100 samples and compare"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 51
},
"colab_type": "code",
"id": "U3uCihlpMbaW",
"nbpages": {
"level": 3,
"link": "[7.2.2.1 Set up diffusion reaction equation](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.1-Set-up-diffusion-reaction-equation)",
"section": "7.2.2.1 Set up diffusion reaction equation"
},
"outputId": "1ae79b64-e021-4618-f22b-f6581a2e09e7"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"100\n",
"2.0141752999999993 0.07959828077091 0.2821316727538934\n"
]
}
],
"source": [
"samps = 100 #4*10**4\n",
"print (samps)\n",
"test = norm.cdf(np.random.multivariate_normal(np.zeros(5), corrmat, samps))\n",
"vsamps,omegasamps,kappalsamps,kappahsamps,qsamps = gen_samps(samps,test)"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 51
},
"colab_type": "code",
"id": "oG02l9jiMbaY",
"nbpages": {
"level": 3,
"link": "[7.2.2.1 Set up diffusion reaction equation](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.1-Set-up-diffusion-reaction-equation)",
"section": "7.2.2.1 Set up diffusion reaction equation"
},
"outputId": "6f8fd711-69ad-42d8-e29f-c4b5891620dd"
},
"outputs": [],
"source": [
"QSRS = np.zeros(samps)\n",
"for i in range(samps):\n",
" sol,QSRS[i] = ADRSource(Lx, Nx, Source_func(xs, qsamps[i]), omega_func(xs, omegasamps[i]), v_func(xs, vsamps[i]),\n",
" kappa_func(xs, kappalsamps[i], kappahsamps[i]))"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 281
},
"colab_type": "code",
"id": "_oWlAwu_eubW",
"nbpages": {
"level": 3,
"link": "[7.2.2.1 Set up diffusion reaction equation](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.1-Set-up-diffusion-reaction-equation)",
"section": "7.2.2.1 Set up diffusion reaction equation"
},
"outputId": "42a413c6-638b-467a-f7cc-44cc277ee392"
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAAD8CAYAAACMwORRAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAADe1JREFUeJzt3V2MXOV9x/Hvr3YSCk0KhgW5OHRBsmhQJAxdIVIklECSQkCAKqhAUesLq75JVWgrpU6rXkTqhZGqklaKolhAY1UtgdIQIxORWA6oL6pI1uHNjrFMiEtcu+ySQF5aqY2Tfy/mOKycXXZmd9bjefh+pNXMOXtm53k0nu+ePTNnnKpCktSWXxj1ACRJw2fcJalBxl2SGmTcJalBxl2SGmTcJalBxl2SGrS6n42SHAJ+CPwEOFZVU0nWAA8Ck8Ah4Ler6rWVGaYkaRCD7Ll/oKo2VNVUt7wF2F1V64Hd3bIk6RSQfs5Q7fbcp6rq1TnrDgDvr6qjSdYCT1bVxW/2c84555yanJxc3ogl6S1mz549r1bVxCC36euwDFDAV5IU8Nmq2gacV1VHAbrAn7vYD5mcnGR6enqQ8UnSW16S/xj0Nv3G/aqqOtIFfFeSFwYY1GZgM8AFF1ww6PgkSUvQ1zH3qjrSXc4AjwBXAK90h2PoLmcWuO22qpqqqqmJiYH+qpAkLdGicU9yRpJ3Hr8OfBjYCzwKbOw22wjsWKlBSpIG089hmfOAR5Ic3/4fqurxJF8HHkqyCXgZuG3lhilJGsSica+ql4BL51n/XeDalRiUJGl5PENVkhpk3CWpQcZdkhpk3CWpQf2exPSWNbnlsZHd96GtN4zsviWNN/fcJalBxl2SGmTcJalBxl2SGmTcJalBxl2SGmTcJalBxl2SGmTcJalBxl2SGmTcJalBxl2SGmTcJalBxl2SGmTcJalBxl2SGmTcJalBxl2SGmTcJalBxl2SGmTcJalBxl2SGmTcJalBxl2SGmTcJalBxl2SGmTcJalBxl2SGmTcJalBxl2SGtR33JOsSvJ0kp3d8oVJnkpyMMmDSd6+csOUJA1ikD33O4H9c5bvBu6pqvXAa8CmYQ5MkrR0fcU9yTrgBuDebjnANcDD3SbbgVtWYoCSpMH1u+f+KeDjwE+75bOB16vqWLd8GDh/vhsm2ZxkOsn07OzssgYrSerPonFPciMwU1V75q6eZ9Oa7/ZVta2qpqpqamJiYonDlCQNYnUf21wF3JTkI8BpwLvo7cmfmWR1t/e+DjiycsOUJA1i0T33qvpEVa2rqkngduCrVfVR4Ang1m6zjcCOFRulJGkgy3mf+58Af5TkRXrH4O8bzpAkScvVz2GZn6mqJ4Enu+svAVcMf0iSpOXyDFVJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGLRr3JKcl+VqSZ5PsS/LJbv2FSZ5KcjDJg0nevvLDlST1o5899/8FrqmqS4ENwHVJrgTuBu6pqvXAa8CmlRumJGkQi8a9en7ULb6t+yrgGuDhbv124JYVGaEkaWB9HXNPsirJM8AMsAv4FvB6VR3rNjkMnL/AbTcnmU4yPTs7O4wxS5IW0Vfcq+onVbUBWAdcAbxnvs0WuO22qpqqqqmJiYmlj1SS1LeB3i1TVa8DTwJXAmcmWd19ax1wZLhDkyQtVT/vlplIcmZ3/ReBDwL7gSeAW7vNNgI7VmqQkqTBrF58E9YC25OsovfL4KGq2pnkm8Dnk/wF8DRw3wqOU5I0gEXjXlXPAZfNs/4lesffJUmnGM9QlaQGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJapBxl6QGGXdJatCi/0G2Rmdyy2Mjud9DW28Yyf1KGh733CWpQcZdkhpk3CWpQcZdkhpk3CWpQcZdkhpk3CWpQcZdkhpk3CWpQcZdkhpk3CWpQcZdkhpk3CWpQYvGPcm7kzyRZH+SfUnu7NavSbIrycHu8qyVH64kqR/97LkfA/64qt4DXAl8LMklwBZgd1WtB3Z3y5KkU8Cica+qo1X1je76D4H9wPnAzcD2brPtwC0rNUhJ0mAGOuaeZBK4DHgKOK+qjkLvFwBw7rAHJ0lamr7jnuSXgH8C7qqqHwxwu81JppNMz87OLmWMkqQB9RX3JG+jF/a/r6ovdKtfSbK2+/5aYGa+21bVtqqaqqqpiYmJYYxZkrSIft4tE+A+YH9V/dWcbz0KbOyubwR2DH94kqSl6Oc/yL4K+B3g+STPdOv+FNgKPJRkE/AycNvKDFGSNKhF415V/wpkgW9fO9zhLGxyy2Mn664kaex5hqokNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDFo17kvuTzCTZO2fdmiS7khzsLs9a2WFKkgbRz57754DrTli3BdhdVeuB3d2yJOkUsWjcq+qfge+dsPpmYHt3fTtwy5DHJUlahqUecz+vqo4CdJfnDm9IkqTlWvEXVJNsTjKdZHp2dnal706SxNLj/kqStQDd5cxCG1bVtqqaqqqpiYmJJd6dJGkQS437o8DG7vpGYMdwhiNJGoZ+3gr5APDvwMVJDifZBGwFPpTkIPChblmSdIpYvdgGVXXHAt+6dshjkSQNiWeoSlKDjLskNci4S1KDjLskNci4S1KDjLskNci4S1KDjLskNWjRk5j01jO55bGR3fehrTeM7L6llrjnLkkNMu6S1CDjLkkNMu6S1CDjLkkNMu6S1CDjLkkNMu6S1CDjLkkNMu6S1CDjLkkNMu6S1CDjLkkNMu6S1CDjLkkNMu6S1CDjLkkNMu6S1CDjLkkNMu6S1CDjLkkNMu6S1CDjLkkNMu6S1KDVox6ANNfklsdGcr+Htt4wkvvVyfVW+ve1rD33JNclOZDkxSRbhjUoSdLyLDnuSVYBnwauBy4B7khyybAGJklauuXsuV8BvFhVL1XV/wGfB24ezrAkScuxnLifD3xnzvLhbp0kacSW84Jq5llXP7dRshnY3C3+KMmBBX7eOcCryxjPqcp5jYHc/bOrTc1rDuc1QnP+ffXrxHn96qA/YDlxPwy8e87yOuDIiRtV1TZg22I/LMl0VU0tYzynJOc1XpzXeHFeC1vOYZmvA+uTXJjk7cDtwKPLGYwkaTiWvOdeVceS/D7wZWAVcH9V7RvayCRJS7ask5iq6kvAl4Y0lkUP3Ywp5zVenNd4cV4LSNXPvQYqSRpzfraMJDVoZHFPsirJ00l2dssXJnkqycEkD3Yv0o6VJIeSPJ/kmSTT3bo1SXZ189qV5KxRj3NQSc5M8nCSF5LsT/K+RuZ1cfdYHf/6QZK7GpnbHybZl2RvkgeSnNbIc+zObk77ktzVrRu7xyvJ/Ulmkuyds27eeaTnb7qPeXkuyeX93Mco99zvBPbPWb4buKeq1gOvAZtGMqrl+0BVbZjzNqYtwO5uXru75XHz18DjVfVrwKX0Hrexn1dVHegeqw3ArwP/AzzCmM8tyfnAHwBTVfVeem94uJ0xf44leS/we/TOjr8UuDHJesbz8foccN0J6xaax/XA+u5rM/CZvu6hqk76F733xO8GrgF20jsh6lVgdff99wFfHsXYljmvQ8A5J6w7AKztrq8FDox6nAPO6V3At+len2llXvPM88PAv7UwN944e3wNvTdN7AR+c9yfY8BtwL1zlv8c+Pi4Pl7AJLB3zvK88wA+C9wx33Zv9jWqPfdP0XtQftotnw28XlXHuuVx/SiDAr6SZE93Zi7AeVV1FKC7PHdko1uai4BZ4G+7w2j3JjmD8Z/XiW4HHuiuj/Xcquo/gb8EXgaOAt8H9jD+z7G9wNVJzk5yOvAReidSjvXjNcdC81jSR72c9LgnuRGYqao9c1fPs+k4vo3nqqq6nN6fUR9LcvWoBzQEq4HLgc9U1WXAfzMef/b2rTv2fBPwj6MeyzB0x2pvBi4EfgU4g96/yRON1XOsqvbTO7S0C3gceBY49qY3asOS+jiKPfergJuSHKL3SZLX0NuTPzPJ8ffdz/tRBqe6qjrSXc7QO3Z7BfBKkrUA3eXM6Ea4JIeBw1X1VLf8ML3Yj/u85roe+EZVvdItj/vcPgh8u6pmq+rHwBeA36CN59h9VXV5VV0NfA84yPg/XsctNI++PurlRCc97lX1iapaV1WT9P4U/mpVfRR4Ari122wjsONkj205kpyR5J3Hr9M7hruX3kcybOw2G7t5VdV/Ad9JcnG36lrgm4z5vE5wB28ckoHxn9vLwJVJTk8S3njMxvo5BpDk3O7yAuC36D1u4/54HbfQPB4Ffrd718yVwPePH755UyN+QeH9wM7u+kXA14AX6f15/I5Rv+Ax4Fwuovdn4rPAPuDPuvVn03vx+GB3uWbUY13C3DYA08BzwBeBs1qYVze304HvAr88Z93Yzw34JPACvR2MvwPeMe7PsW5e/0LvF9WzwLXj+njR+6V0FPgxvT3zTQvNg95hmU8D3wKep/cuqEXvwzNUJalBnqEqSQ0y7pLUIOMuSQ0y7pLUIOMuSQ0y7pLUIOMuSQ0y7pLUoP8HWGTWEnTNweIAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"51.754085783529696 59.55016400777867 44.19214310775517 6.711582319278186 19.857958480592576 3.271194643345333\n"
]
}
],
"source": [
"plt.hist(QSRS)\n",
"plt.show()\n",
"print(np.mean(QSRS),stats.scoreatpercentile(QSRS,95),stats.scoreatpercentile(QSRS,5),np.std(QSRS), \n",
" stats.kurtosis(QSRS), stats.skew(QSRS))"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "TqUABHh3i_vm",
"nbpages": {
"level": 3,
"link": "[7.2.2.2 Apply LHS](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.2-Apply-LHS)",
"section": "7.2.2.2 Apply LHS"
}
},
"source": [
"### 7.2.2.2 Apply LHS"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 264
},
"colab_type": "code",
"id": "78AGh7iQjANt",
"nbpages": {
"level": 3,
"link": "[7.2.2.2 Apply LHS](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.2-Apply-LHS)",
"section": "7.2.2.2 Apply LHS"
},
"outputId": "c3405446-3619-4454-e898-b85be5abb88c"
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXYAAAD8CAYAAABjAo9vAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAFENJREFUeJzt3XGIHOd5x/Hfc3dSmzYGC1ng1NJJETYmiTBxdDhX8kdrx22VYGISE5rEpIFUiIANCc0faRC4bUohYAiUWtAK26QFNSZgGwc7xpZBxQR6jm+FYqTICeLoJRcbrCjnOsGh0nmf/nGn+HTevZ2deWfed975fkDg06123xnv/t5nnndm1txdAIB8TMQeAAAgLIIdADJDsANAZgh2AMgMwQ4AmSHYASAzBDsAZIZgB4DMEOwAkJmpGC96zTXX+J49e2K8NAC0Vq/X+6W77xj1uCjBvmfPHs3Pz8d4aQBoLTNbLPI4WjEAkBmCHQAyQ7ADQGYqB7uZ/b6Z/dDMfmRmZ8zsH0IMDABQTojF0/+TdJu7/8bMtkj6gZk97e5zAZ4bADCmysHuq9/U8Zu1H7es/eHbOwAgkiA9djObNLNTkl6TdNzdXwjxvADq11tc1pET59RbXI49FAQS5Dx2d39L0gfN7GpJj5vZPnc/vf4xZnZI0iFJmp6eDvGyACrqLS7r7gfndHGlr61TEzp2cFb7d2+LPSxUFPSsGHd/XdJ/STow4HdH3X3G3Wd27Bh54RSABswtXNDFlb76Ll1a6Wtu4ULsISGAEGfF7Fir1GVm75J0u6SXqz4vgPrN7t2urVMTmjRpy9SEZvdujz0kBBCiFfMeSf9uZpNanSi+6+5PBnheADXbv3ubjh2c1dzCBc3u3U4bJhMhzop5SdLNAcYCIIL9u7cR6JnhylMAyAzBDgCZIdgBIDMEOwBkhmAHgMwQ7ACQGYIdADJDsANAZgh2AMgMwQ4AmSHYASAzBDsAZIZgB4DMEOwAkBmCHQAyQ7ADQGYIdgDIDMEOYCy9xWUdOXFOvcXl2EPBECG+8xRAR/QWl3X3g3O6uNLX1qkJHTs4y9fqJYiKHUBhcwsXdHGlr75Ll1b6mlu4EHtIGIBgB1DY7N7t2jo1oUmTtkxNaHbv9thDwgC0YgAUtn/3Nh07OKu5hQua3budNkyiCHYAY9m/exuBnrjKrRgz22VmJ8zsrJmdMbMvhxgYAKCcEBX7iqSvuvtJM7tKUs/Mjrv7jwM8NwBgTJUrdnd/1d1Prv33ryWdlXRd1ecFAJQT9KwYM9sj6WZJL4R8XgBAccGC3czeLelRSV9x9zcG/P6Qmc2b2fz58+dDvSwAYIMgwW5mW7Qa6sfc/bFBj3H3o+4+4+4zO3bsCPGyAIABQpwVY5IeknTW3b9VfUgAgCpCVOwfkfR5SbeZ2am1Px8P8LwAgBIqn+7o7j+QZAHGgsz0Fpe5QhGIgCtPUQvuAgjEw03AUAvuAgjEQ7CjFtwFEIiHVgxqwV0AgXgIdkiqZ6GTuwACcRDsYKETyAw9drDQCWSGYO+Izb5ZnoVOIC+0YjpgVKslt4VOLoxC1xHsHTCo1bIx8HJZ6GS9AKAV0wldarWwXgBQsXdC21otVVoplyexSyv97CcxYBhz98ZfdGZmxufn5xt/XaRvVCulSOjTY0euzKzn7jOjHkfFjqRsth5QtH+ey3oBUBbBjqQMaqVcrsBfef23IxeBARDsSMzG9QBJv6vSpyZMU5MTeust+ufAZgh2JGd9K+XIiXO/q9Lf6rv+8pZduu7qd9E/BzZBsCNpG1szd31oJ4EOjECwI2ltO1UTSAHBjuTVcZYLp0QiZwQ7OofbDuSHifpKBHuCyrxJeWMXV+TeOWgPJup3ItgTU+ZNmtMbu4kJitsO5IWJ+p0I9sSUeZPm8sZuaoIatCDLEU97MVG/U5BgN7OHJd0h6TV33xfiObuqzJs0lzd26Alqs7BevyCb0xFPF3Hm1DuFqti/LekBSf8R6Pk6q8ybNJc3dsgJapywzuWIp8u4P9CVggS7uz9vZntCPBfKvUlzeGOHnKDGCetcjngkFtGxih47khJqghonrHM54qGlhMsaC3YzOyTpkCRNT0839bJISJPV5LhhHfuIJ8S+oaWEyxoLdnc/KumotPpFG029LtIQ4gs0xhU7rIsKVWnn1FJCNbRi0IgQX6CRq1CVdi4tJVQX6nTH70j6U0nXmNmSpL9z94dCPDfysFk12cUWwvojlJCVdluOUlCvUGfFfDbE8yBfm1WTXWshDDpCodJGSLRi0Jhh1WTXWgiDjlDuufX67LcbzSHYkYS6Wwgpnd/dtSMUNI9gR6sVCezUFme7doSC5hHsaK2igZ3i4iyLnKjTROwBAGUNCuxBLrc+Jk3JtT56i8s6cuKceovLsYeCjFCxjymlXm3XFe1Vp9r6SK1FhHwQ7GPgg5iWcQK7ztZH2ck+xRYR8kCwj6HrH8SqRys53jZgnMl+4/ZzdgzqQrCPocsfxKpHK7ke7RSd7Idt//ojDkk6cuJcUu0itBPBPoYuf6Va1aOVsv8+9f1bdLIftv2X/+Q68SEOgn1MXf1KtapHK2X+fRv2b9E+/6jtz73Nl/oEnRuCvYLcP4zrVT2zpMy/j71/i4ZRkT7/qO3Puc3Xhgk6NwR7BTl/GAepulA57r+PuX83htF9d3xAy29erFRxbrb9OffbY0/QXUSwV5Dq+dFNq+swO+b+XR9GFy/1dd8Tp9V3r7XizLXf3rUCKAUEe0WxT7eLre4QCr1/i05C68PIzNR3D1ZxjhpDahVu1YmbAqh5BDsqSS2ENjPOJLQ+jLb9wVZ948kzQSrOImNIqcINNXF3vQBqGsGOSlIKoVHGnYTWh9GN114VpOIsMoaUKtw2Tdx4G8GOSlIKoVGqTEKhKs5x7m+Twr5s08SNt5m7N/6iMzMzPj8/3/jrIo6UzmGueyxF7w+fyv4o4j9f+JmePv2qPrbvPfrch6djD6fTzKzn7jOjHkfFjlqldoZH3TcDK7KtqVTjRfQWl/WNJ8/o4kpfL/7Pr3TjtVe1Zuxdxv3YMZZx7x9e9J7pOchxW3Pcpi6gYkdhZarvOnu0qbU0cuxH57hNXUCwo7AyZ0jUtbiaWotHSnMhmXPQu4lgR2Flq7c6espNn4ZX5r4xsY8oBk1+ksYeU5vWBLAqSLCb2QFJ/yxpUtKD7v7NEM+LtKRUvTXZIihz35gUjig2Tn6PnVzSoyeXkjrKKSr2JNk2lYPdzCYlHZH0Z5KWJL1oZt9z9x9XfW6kJ5XqrclJpsx9Y1K4sGfj5OdS9DGVkcIk2TYhKvZbJJ1z9wVJMrNHJN0piWBPVC7VT1OTTJn7xqSw6DjojpGPnVxq3UJoCpNk24QI9usk/Xzdz0uSPrzxQWZ2SNIhSZqe5iKHWKh+xlfmvjGptK02Tn4pjGlcKUySbRMi2G3A373jclZ3PyrpqLR65WmA1w0qlyp2FKqfcsrcNyaVttV6KY5plFQmyTYJEexLknat+3mnpFcCPG9julTFdrn6CTV5tzEc2459Pp4Qwf6ipBvM7L2SfiHpM5I+F+B5G9OlKrar1U+XJm+gcrC7+4qZ3SvpGa2e7viwu5+pPLIGda2K3az6ybUlVXbyznV/IG9BzmN39+9L+n6I54qhq1XsRjlXtWUm79j7g0kFZXHl6Zqmengpf1irtqRS2LZhYygzecds0cWeVNBuBHuDUv+wVmlJpbBto8Yw7uQds0XXpXUfhEewNyj1D+s4Ve3GyjiFbQs9hkH7o6mjkq6t+yAsgr1BbfiwFqlqB1XGKWxbHWPYeFOvpo5K2rbuk0IbDm8j2BvUtg/rMIMq43tuvT76ttW9f5s+KknpTpGbSaENhysR7A3L4UKLYZVxCttW5xhiHZWkHpwptOFwJYIdY2vbkUfIK05jbPew4By2XU1X9ym04XAlgh1DbRYQKVTnRYSudmNs96DgHLZdMar7tk30XUCwd0CZCi71w/+icmgTDArOIyfODdyucbY3ZGXflok+tqaOpgj2zJUN6BwCUcqnTbAxOIdt17DqfmOY5DJxt0mT+7xVwZ7ymQGpKhvQOQVijm2CYdu18e8lDQyT2FfV5vb/o4gm93lrgp0Ko5wqX0CdSyDm2iYYtl3r/35Yy4YzfJrX5D5vTbDn0hpoWpWAjh2IXa3sQtrs1NSUzvDpgib3eWuCPZfWQAyxA7qMLld2IW0WJqmc4dMlTe3z1gR7Tq0BjNblyq6IcY5mxg2TOo+U+Bw3ozXBLrWz8mxS21oXm42365XdZuo8mmniSInPcf1aFewYrm2tiyK32KWyG6zOoxmOlPIwEXsACGPQBzJlRca7f/c23XPr9QTLBpePZiZNwY9m6nxuNIeKPRNta120bbwpWN+6qutohiOlPJi7N/6iMzMzPj8/3/jr5i6nHnuXxlBE21ptqIeZ9dx9ZtTjqNgz0rZFqdjjrRqWTU4K9L4xDoIdnVUlLJuuoGldYRwEOzqrSljG+DYlet8oqlKwm9mnJf29pPdJusXdaZyjNaqEZYwKeljrqi3rBGhO1Yr9tKRPSfq3AGMBGle2z59KBc2iKgapFOzuflaSzCzMaICCUqhSYy/+SiyqYjB67GgdqtS3saiKQUYGu5k9J+naAb867O5PFH0hMzsk6ZAkTU9PFx4g6pNC1VsGVerbUmkJtV1bPwvDjAx2d789xAu5+1FJR6XVC5RCPCfKa3PV24YqtcmgSKEl1GZt/iwMQyumo9pc9aZepeYYFDlr82dhmKqnO35S0r9I2iHpKTM75e5/EWRkqFUbqt7NpFylbgyKx04uJTsJof2fhUG4V0yDUuvjpTaeXFyu2C+t9DU5OSG5a6XvVO8Ja8tnoei9Ygj2hnB43i2Xg+IXr/9Wj/zwZ+q7NGnS3/z5jbrn1utjDw8tVTTYuR97Q9p2v3RUc/le8nd9aCf3N0fjWDxtSKg+XlsOGdss5D5OfaEXeaIV06CqgUE7p35l9zET7pXYH/XgfuwJqnomR46nZaWmzD5mwr0S+yM+euwtwvdR1q/MPmb95Ersj/io2FuEfm39yuzjHM+DrqLq/qCNUx09diAAwuhKZfcHbZzN0WMHGpTylbAxlN0fIdaRmGQJdgAJCdHGoeIn2AEkpOo6EmeOrSLYASSlSluLhexVBDuAbHDm2CqCvSVYEAKKYSGbYG8FFoQAjIMrT1uAK/kAjINgbwFuJQBgHLRiWoAFoWawjoFcEOwtwYJQvVjHQE5oxQBiHQN5IdgBsY6BvNCKAcQ6BvJCsANrWMdALmjFAEBmKgW7md1vZi+b2Utm9riZXR1qYACAcqpW7Mcl7XP3myT9VNLXqw8JAFBFpWB392fdfWXtxzlJO6sPCQBQRcge+xclPT3sl2Z2yMzmzWz+/PnzAV8WbdZbXNaRE+fUW1yOPRQgGyPPijGz5yRdO+BXh939ibXHHJa0IunYsOdx96OSjkqrX2ZdarTICld7AvUYGezufvtmvzezL0i6Q9JH3Z3ARmF8jRlQj0rnsZvZAUlfk/Qn7v5mmCGhK/gaM6AeVS9QekDS70k6bmaSNOfuX6o8KnQCV3sC9agU7O5+faiBoJu42hMIjytPASAzBDsAZIZgB4DMEOwIhouNgDRw214EwcVGQDqo2BEEXy0HpINgRxB8tRyQDloxCIKLjYB0EOwIhouNgDTQigGAzBDsAJAZgh0AMkOwA0BmCHYAyAzBDgCZIdgBIDMEOwBkhmAHgMwQ7ACQGYIdADJDsANAZgh2AMgMwQ4AmakU7Gb2j2b2kpmdMrNnzeyPQg0MAFBO1Yr9fne/yd0/KOlJSfcFGBMAoIJKwe7ub6z78Q8lebXhAACqqvwNSmb2T5L+StL/Srq18ogAAJWMrNjN7DkzOz3gz52S5O6H3X2XpGOS7t3keQ6Z2byZzZ8/fz7cFgAArmDuYbonZrZb0lPuvm/UY2dmZnx+fj7I6wJAV5hZz91nRj2u6lkxN6z78ROSXq7yfEBZvcVlHTlxTr3F5dhDAaKr2mP/ppndKKkvaVHSl6oPCRhPb3FZdz84p4srfW2dmtCxg7Pav3tb7GEB0VQKdne/K9RAgLLmFi7o4kpffZcurfQ1t3CBYEenceUpWm9273ZtnZrQpElbpiY0u3d77CEBUVU+3RGIbf/ubTp2cFZzCxc0u3c71To6j2BHFvbv3kagA2toxQBAZgh2AMgMwQ4AmSHYASAzBDsAZIZgB4DMBLsJ2FgvanZeq7cgSN01kn4ZexAN6+I2S93cbra5fXa7+45RD4oS7G1hZvNF7qSWky5us9TN7Wab80UrBgAyQ7ADQGYI9s0djT2ACLq4zVI3t5ttzhQ9dgDIDBU7AGSGYB/BzO43s5fN7CUze9zMro49prqZ2afN7IyZ9c0s6zMIzOyAmf3EzM6Z2d/GHk8TzOxhM3vNzE7HHktTzGyXmZ0ws7Nr7+0vxx5TnQj20Y5L2ufuN0n6qaSvRx5PE05L+pSk52MPpE5mNinpiKSPSXq/pM+a2fvjjqoR35Z0IPYgGrYi6avu/j5Js5Luyfn/NcE+grs/6+4raz/OSdoZczxNcPez7v6T2ONowC2Szrn7grtflPSIpDsjj6l27v68pF/FHkeT3P1Vdz+59t+/lnRW0nVxR1Ufgn08X5T0dOxBIJjrJP183c9LyvjDjlVmtkfSzZJeiDuS+vANSpLM7DlJ1w741WF3f2LtMYe1ejh3rMmx1aXINneADfg7ThPLmJm9W9Kjkr7i7m/EHk9dCHZJ7n77Zr83sy9IukPSRz2T80NHbXNHLEnate7nnZJeiTQW1MzMtmg11I+5+2Oxx1MnWjEjmNkBSV+T9Al3fzP2eBDUi5JuMLP3mtlWSZ+R9L3IY0INzMwkPSTprLt/K/Z46kawj/aApKskHTezU2b2r7EHVDcz+6SZLUn6Y0lPmdkzscdUh7VF8XslPaPVxbTvuvuZuKOqn5l9R9J/S7rRzJbM7K9jj6kBH5H0eUm3rX2OT5nZx2MPqi5ceQoAmaFiB4DMEOwAkBmCHQAyQ7ADQGYIdgDIDMEOAJkh2AEgMwQ7AGTm/wH9Vvq+o4cjiAAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"#lhd will have the values in 0 to 1\n",
"lhd = lhs(5, samples=samps)\n",
"#now i need to turn these into samples from N(0,Corrmat)\n",
"#do cholesky fact\n",
"chol = np.linalg.cholesky(corrmat)\n",
"\n",
"lhs_unif = np.zeros((samps,5))\n",
"for i in range(samps):\n",
" lhs_unif[i,:] = np.dot(chol,norm.ppf(lhd[i,:]))\n",
"#print(lhs_unif)\n",
"#plt.plot(lhd[:,0],lhd[:,1],'.')\n",
"#plt.show()\n",
"plt.plot(lhs_unif[:,0],lhs_unif[:,1],'.')\n",
"plt.show()"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 34
},
"colab_type": "code",
"id": "veSJTwfsjEQ9",
"nbpages": {
"level": 3,
"link": "[7.2.2.2 Apply LHS](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.2-Apply-LHS)",
"section": "7.2.2.2 Apply LHS"
},
"outputId": "6f7f258d-b49c-42de-ace6-1aaa59d31a83"
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"1.9858199999999997 4.930380657631324e-32 2.220446049250313e-16\n"
]
}
],
"source": [
"test_lhs = norm.cdf(lhs_unif)\n",
"\n",
"vsamps,omegasamps,kappalsamps,kappahsamps,qsamps = gen_samps(samps,test_lhs)"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 336
},
"colab_type": "code",
"id": "ATReERNLjI_E",
"nbpages": {
"level": 3,
"link": "[7.2.2.2 Apply LHS](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.2-Apply-LHS)",
"section": "7.2.2.2 Apply LHS"
},
"outputId": "21848535-183e-4072-d32b-9eee318588b7"
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXYAAAD8CAYAAABjAo9vAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAADPVJREFUeJzt3X+I5PV9x/Hnq5oUaizR3iqHer00iKn/5LRXaREkiRj8UaJCA0obpBXOghaF0Mbknwpt4QI1toUiPaNRWmOamojSiI1YIQSK5M4c/uhVTO0lUa93J2nQttCgvvvHfq/dnrvu7Mzszc77ng9YZua739nv58PneN6X787MpqqQJPXxU7MegCRpugy7JDVj2CWpGcMuSc0YdklqxrBLUjOGXZKaMeyS1Ixhl6RmTjyWB9u0aVNt3br1WB5Skubenj17XquqhVH3P6Zh37p1K7t37z6Wh5SkuZfk+2vZ30sxktSMYZekZgy7JDVj2CWpGcMuSc2sGvYkZyV5Msm+JM8nuXnYfluSV5LsHb4uX//hSpJWM8rLHd8EPl1VTyc5GdiT5PHhe3dU1Z+s3/AkSWu1atir6gBwYLj/RpJ9wBnrPTBJ0njWdI09yVbgPOCpYdNNSZ5Jck+SU6Y8NknSGEZ+52mS9wFfA26pqteT3An8IVDD7e3Aby/zvB3ADoAtW7ZMY8zS1G299RszO/b+nVfM7NjqaaQz9iTvYTHq91fV1wGq6mBVvVVVbwN3ARcs99yq2lVV26tq+8LCyB91IEka0yiviglwN7Cvqr6wZPvmJbtdDTw3/eFJktZqlEsxFwKfAp5NsnfY9jng2iTbWLwUsx+4YV1GKElak1FeFfNtIMt869HpD0eSNCnfeSpJzRh2SWrGsEtSM8f0LyhJq5nl68mlLjxjl6RmDLskNWPYJakZwy5JzRh2SWrGsEtSM4Zdkprxdex6B19LLs03z9glqRnDLknNGHZJasawS1Izhl2SmjHsktSMYZekZgy7JDVj2CWpGcMuSc0YdklqxrBLUjOGXZKaMeyS1Ixhl6RmDLskNWPYJakZwy5JzRh2SWrGsEtSM6uGPclZSZ5Msi/J80luHrafmuTxJC8Ot6es/3AlSasZ5Yz9TeDTVfWLwK8ANyY5F7gVeKKqzgaeGB5LkmZs1bBX1YGqenq4/wawDzgDuBK4b9jtPuCq9RqkJGl0a7rGnmQrcB7wFHB6VR2AxfgDp017cJKktRs57EneB3wNuKWqXl/D83Yk2Z1k9+HDh8cZoyRpDUYKe5L3sBj1+6vq68Pmg0k2D9/fDBxa7rlVtauqtlfV9oWFhWmMWZL0LkZ5VUyAu4F9VfWFJd96BLhuuH8d8PD0hydJWqsTR9jnQuBTwLNJ9g7bPgfsBL6a5HrgB8An12eIkqS1WDXsVfVtICt8++LpDkeSNCnfeSpJzRh2SWrGsEtSM4Zdkpox7JLUjGGXpGYMuyQ1Y9glqRnDLknNGHZJasawS1Izhl2SmjHsktSMYZekZgy7JDVj2CWpGcMuSc0YdklqxrBLUjOGXZKaMeyS1Ixhl6RmDLskNWPYJakZwy5JzRh2SWrGsEtSM4Zdkpox7JLUjGGXpGYMuyQ1Y9glqRnDLknNrBr2JPckOZTkuSXbbkvySpK9w9fl6ztMSdKoRjljvxe4dJntd1TVtuHr0ekOS5I0rlXDXlXfAn50DMYiSZqCSa6x35TkmeFSzSlTG5EkaSLjhv1O4IPANuAAcPtKOybZkWR3kt2HDx8e83CSpFGNFfaqOlhVb1XV28BdwAXvsu+uqtpeVdsXFhbGHackaURjhT3J5iUPrwaeW2lfSdKxdeJqOyR5APgIsCnJy8AfAB9Jsg0oYD9wwzqOUZK0BquGvaquXWbz3eswFknSFPjOU0lqxrBLUjOGXZKaMeyS1Ixhl6RmDLskNWPYJakZwy5JzRh2SWrGsEtSM4Zdkpox7JLUjGGXpGYMuyQ1Y9glqRnDLknNGHZJasawS1Izhl2SmjHsktSMYZekZgy7JDVj2CWpGcMuSc0YdklqxrBLUjOGXZKaMeyS1Ixhl6RmDLskNWPYJakZwy5Jzawa9iT3JDmU5Lkl205N8niSF4fbU9Z3mJKkUY1yxn4vcOlR224Fnqiqs4EnhseSpA1g1bBX1beAHx21+UrgvuH+fcBVUx6XJGlM415jP72qDgAMt6dNb0iSpEms+y9Pk+xIsjvJ7sOHD6/34STpuDdu2A8m2Qww3B5aaceq2lVV26tq+8LCwpiHkySNatywPwJcN9y/Dnh4OsORJE1qlJc7PgD8I3BOkpeTXA/sBC5J8iJwyfBYkrQBnLjaDlV17QrfunjKY5EkTYHvPJWkZgy7JDVj2CWpmVWvsUtaX1tv/cZMjrt/5xUzOa7Wn2fsktSMYZekZgy7JDVj2CWpGcMuSc0YdklqxrBLUjOGXZKaMeyS1Ixhl6RmDLskNWPYJakZwy5JzRh2SWrGsEtSM4ZdkprxD21sYLP6AwyS5ptn7JLUjGGXpGYMuyQ1Y9glqRnDLknNGHZJasawS1Izhl2SmjHsktSMYZekZgy7JDVj2CWpmYk+BCzJfuAN4C3gzaraPo1BSZLGN41Pd/xoVb02hZ8jSZoCL8VIUjOTnrEX8M0kBfxlVe06eockO4AdAFu2bJnwcJKmZZaf979/5xUzO/bxYNIz9gur6nzgMuDGJBcdvUNV7aqq7VW1fWFhYcLDSZJWM1HYq+rV4fYQ8BBwwTQGJUka39hhT3JSkpOP3Ac+Djw3rYFJksYzyTX204GHkhz5OV+uqsemMipJ0tjGDntVvQR8eIpjkSRNgS93lKRmDLskNWPYJakZwy5JzRh2SWrGsEtSM4Zdkpox7JLUjGGXpGYMuyQ1Y9glqZlp/Gm89mb5Bwkkaa08Y5ekZgy7JDVj2CWpGcMuSc0YdklqxrBLUjOGXZKa8XXsko65Wb03ZP/OK2Zy3GPNM3ZJasawS1Izhl2SmjHsktSMYZekZgy7JDVj2CWpGcMuSc3MzRuU/GMXkiY1y44cyzdHecYuSc0YdklqxrBLUjMThT3JpUleSPK9JLdOa1CSpPGNHfYkJwB/AVwGnAtcm+TcaQ1MkjSeSc7YLwC+V1UvVdVPgK8AV05nWJKkcU0S9jOAHy55/PKwTZI0Q5O8jj3LbKt37JTsAHYMD/8jyQsTHHM9bQJem/UgJuQcNoYOc4Ae89gwc8jnx37qJuDn1/KEScL+MnDWksdnAq8evVNV7QJ2TXCcYyLJ7qraPutxTMI5bAwd5gA95tFoDlvX8pxJLsV8Bzg7yQeSvBe4Bnhkgp8nSZqCsc/Yq+rNJDcBfw+cANxTVc9PbWSSpLFM9FkxVfUo8OiUxjJrG/5y0Qicw8bQYQ7QYx7H5RxS9Y7fd0qS5pgfKSBJzRy3YU9yQpLvJvm74fEHkjyV5MUkfzP8QnhDW2YO9yb51yR7h69tsx7japLsT/LsMN7dw7ZTkzw+rMXjSU6Z9TjfzQpzuC3JK0vW4vJZj/PdJHl/kgeT/HOSfUl+dQ7XYbk5zNs6nLNkrHuTvJ7klrWuxXEbduBmYN+Sx58H7qiqs4F/B66fyajW5ug5APxeVW0bvvbOYlBj+Ogw3iMvS7sVeGJYiyeGxxvd0XOAxX9PR9Zio/8u6s+Ax6rqQ8CHWfx3NW/rsNwcYI7WoapeODJW4JeA/wIeYo1rcVyGPcmZwBXAF4fHAT4GPDjsch9w1WxGN5qj59DMlSyuAczBWsy7JD8LXATcDVBVP6mqHzNH6/Auc5hnFwP/UlXfZ41rcVyGHfhT4PeBt4fHPwf8uKreHB7Pw8cjHD2HI/44yTNJ7kjy0zMY11oV8M0ke4Z3KQOcXlUHAIbb02Y2utEsNweAm4a1uGeDX8b4BeAw8KXh0t4Xk5zEfK3DSnOA+VmHo10DPDDcX9NaHHdhT/JrwKGq2rN08zK7btiXC60wB4DPAh8Cfhk4FfjMsR7bGC6sqvNZ/JTQG5NcNOsBjWG5OdwJfBDYBhwAbp/h+FZzInA+cGdVnQf8Jxv/ssvRVprDPK3D/xp+x/cJ4G/Hef5xF3bgQuATSfaz+ImUH2Px7Pf9SY68rn/Zj0fYQN4xhyR/XVUHatF/A19i8RM4N7SqenW4PcTitcQLgINJNgMMt4dmN8LVLTeHqjpYVW9V1dvAXWzstXgZeLmqnhoeP8hiJOdpHZadw5ytw1KXAU9X1cHh8ZrW4rgLe1V9tqrOHD574RrgH6rqN4AngV8fdrsOeHhGQ1zVCnP4zSULHxavwT03w2GuKslJSU4+ch/4OItjfoTFNYANvhYrzeHIWgyuZgOvRVX9G/DDJOcMmy4G/ok5WoeV5jBP63CUa/m/yzCwxrWY6J2nzXwG+EqSPwK+y/BLmDlzf5IFFi8t7QV+Z8bjWc3pwEOL/w9xIvDlqnosyXeArya5HvgB8MkZjnE1K83hr4aXmxawH7hhdkMcye+y+O/nvcBLwG+xeOI3L+sAy8/hz+dsHUjyM8Al/P+x7mQNa+E7TyWpmePuUowkdWfYJakZwy5JzRh2SWrGsEtSM4Zdkpox7JLUjGGXpGb+BzyVgQkvJkWgAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"name": "stdout",
"output_type": "stream",
"text": [
"52.091501134877944 60.53399286590944 44.78023096114341 4.899665382873159 1.1994249416182612 0.18626015216253644\n",
"52.38429950498757 60.93083101449816 44.256769035451256 5.846536644275092 15.192880831520508 2.154994384485121\n"
]
}
],
"source": [
"QLHS = np.zeros(samps)\n",
"for i in range(samps):\n",
" sol,QLHS[i] = ADRSource(Lx, Nx, Source_func(xs, qsamps[i]), omega_func(xs, omegasamps[i]), v_func(xs, vsamps[i]),\n",
" kappa_func(xs, kappalsamps[i], kappahsamps[i]))\n",
"plt.hist(QLHS)\n",
"plt.show()\n",
"print(np.mean(QLHS),stats.scoreatpercentile(QLHS,95),stats.scoreatpercentile(QLHS,5),np.std(QLHS), \n",
" stats.kurtosis(QLHS), stats.skew(QLHS))\n",
"print(np.mean(Qs),stats.scoreatpercentile(Qs,95) ,stats.scoreatpercentile(Qs,5),np.std(Qs), stats.kurtosis(Qs), stats.skew(Qs))"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[7.2.2.2 Apply LHS](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.2-Apply-LHS)",
"section": "7.2.2.2 Apply LHS"
}
},
"source": [
"Below is Figure 7.13 in McClarren (2018); it shows the convergence rates of different methods compared against a LHS with 10$^6$ samples."
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "01-H_CF8yAm3",
"nbpages": {
"level": 3,
"link": "[7.2.2.2 Apply LHS](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.2-Apply-LHS)",
"section": "7.2.2.2 Apply LHS"
}
},
"source": [
"\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"nbpages": {
"level": 3,
"link": "[7.2.2.2 Apply LHS](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html#7.2.2.2-Apply-LHS)",
"section": "7.2.2.2 Apply LHS"
}
},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"< [7.1 Latin Hypercube and Quasi-Monte Carlo Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html) | [Contents](toc.html) | [7.3 Meaningful Title Goes Here](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.03-Contributed-Example.html) 
 "
]
}
],
"metadata": {
"colab": {
"name": "07.02-Latin-Hypercube-sampling.ipynb",
"provenance": []
},
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.3"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
"
]
}
],
"metadata": {
"colab": {
"name": "07.02-Latin-Hypercube-sampling.ipynb",
"provenance": []
},
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.3"
}
},
"nbformat": 4,
"nbformat_minor": 1
}

