{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"*This notebook contains material from [cbe67701-uncertainty-quantification](https://ndcbe.github.io/cbe67701-uncertainty-quantification);\n",
"content is available [on Github](https://github.com/ndcbe/cbe67701-uncertainty-quantification.git).*"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"< [7.0 Sampling-Based Uncertainty Quantification: Monte Carlo and Beyond](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.00-Sampling-Based-Uncertainty-Quantification.html) | [Contents](toc.html) | [7.2 Latin Hypercube Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html) 
 "
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 1,
"link": "[7.1 Latin Hypercube and Quasi-Monte Carlo Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1-Latin-Hypercube-and-Quasi-Monte-Carlo-Sampling)",
"section": "7.1 Latin Hypercube and Quasi-Monte Carlo Sampling"
}
},
"source": [
"# 7.1 Latin Hypercube and Quasi-Monte Carlo Sampling\n",
"\n",
"Created by Dezhao Huang (dhuang2@nd.edu)\n",
"\n",
"These examples and codes were adapted from:\n",
"* https://risk-engineering.org/notebook/monte-carlo-LHS.html\n",
"* McClarren, Ryan G (2018). *Uncertainty Quantification and Predictive Computational Science: A Foundation for Physical Scientists and Engineers*, *Chapter 7 : Sampling-Based Uncertainty Quantification Monte Carlo and Beyond*, Springer, https://link.springer.com/chapter/10.1007%2F978-3-319-99525-0_7\n",
"\n",
"## Chapter 7 Overview\n",
"\n",
"1. Basic Monte Carlo methods: maximum likelihood estimation and methods of moments\n",
"2. Design based sampling: Latin Hypercube Sampling\n",
"3. Quasi-Monte Carlo: Halton sequences and Sobol sequence"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"autoscroll": false,
"ein.hycell": false,
"ein.tags": "worksheet-0",
"nbpages": {
"level": 1,
"link": "[7.1 Latin Hypercube and Quasi-Monte Carlo Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1-Latin-Hypercube-and-Quasi-Monte-Carlo-Sampling)",
"section": "7.1 Latin Hypercube and Quasi-Monte Carlo Sampling"
},
"slideshow": {
"slide_type": "-"
}
},
"outputs": [],
"source": [
"# Load libraries\n",
"import math\n",
"import numpy\n",
"import scipy.stats\n",
"import matplotlib.pyplot as plt\n",
"plt.style.use(\"bmh\")\n",
"import sympy\n",
"from IPython.display import Image\n",
"from IPython.core.display import HTML "
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"nbpages": {
"level": 1,
"link": "[7.1 Latin Hypercube and Quasi-Monte Carlo Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1-Latin-Hypercube-and-Quasi-Monte-Carlo-Sampling)",
"section": "7.1 Latin Hypercube and Quasi-Monte Carlo Sampling"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Requirement already satisfied: sobol_seq in /anaconda3/lib/python3.7/site-packages (0.2.0)\n",
"Requirement already satisfied: numpy in /anaconda3/lib/python3.7/site-packages (from sobol_seq) (1.16.2)\n",
"Requirement already satisfied: scipy in /anaconda3/lib/python3.7/site-packages (from sobol_seq) (1.2.1)\n",
"Requirement already satisfied: pyDOE in /anaconda3/lib/python3.7/site-packages (0.3.8)\n",
"Requirement already satisfied: scipy in /anaconda3/lib/python3.7/site-packages (from pyDOE) (1.2.1)\n",
"Requirement already satisfied: numpy in /anaconda3/lib/python3.7/site-packages (from pyDOE) (1.16.2)\n"
]
}
],
"source": [
"## Install missing packages\n",
"!pip install sobol_seq\n",
"\n",
"import sobol_seq\n",
"\n",
"!pip install pyDOE\n",
"from pyDOE import lhs"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"nbpages": {
"level": 1,
"link": "[7.1 Latin Hypercube and Quasi-Monte Carlo Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1-Latin-Hypercube-and-Quasi-Monte-Carlo-Sampling)",
"section": "7.1 Latin Hypercube and Quasi-Monte Carlo Sampling"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Checking for figures/LHS.png\n",
"\tFile found!\n"
]
}
],
"source": [
"# Download figures (if needed)\n",
"import os, requests, urllib\n",
"\n",
"# GitHub pages url\n",
"url = \"https://ndcbe.github.io/cbe67701-uncertainty-quantification/\"\n",
"\n",
"# relative file paths to download\n",
"# this is the only line of code you need to change\n",
"file_paths = ['figures/LHS.png']\n",
"\n",
"# loop over all files to download\n",
"for file_path in file_paths:\n",
" print(\"Checking for\",file_path)\n",
" # split each file_path into a folder and filename\n",
" stem, filename = os.path.split(file_path)\n",
" \n",
" # check if the folder name is not empty\n",
" if stem:\n",
" # check if the folder exists\n",
" if not os.path.exists(stem):\n",
" print(\"\\tCreating folder\",stem)\n",
" # if the folder does not exist, create it\n",
" os.mkdir(stem)\n",
" # if the file does not exist, create it by downloading from GitHub pages\n",
" if not os.path.isfile(file_path):\n",
" file_url = urllib.parse.urljoin(url,\n",
" urllib.request.pathname2url(file_path))\n",
" print(\"\\tDownloading\",file_url)\n",
" with open(file_path, 'wb') as f:\n",
" f.write(requests.get(file_url).content)\n",
" else:\n",
" print(\"\\tFile found!\")"
]
},
{
"cell_type": "markdown",
"metadata": {
"ein.tags": "worksheet-0",
"nbpages": {
"level": 1,
"link": "[7.1 Latin Hypercube and Quasi-Monte Carlo Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1-Latin-Hypercube-and-Quasi-Monte-Carlo-Sampling)",
"section": "7.1 Latin Hypercube and Quasi-Monte Carlo Sampling"
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
"The simplest 1D integration problem, \n",
"\n",
"$\\int_1^5 x^2$\n",
"\n",
"We can estimate this integral using a standard Monte Carlo method, where we use the fact that the expectation of a random variable is related to its integral\n",
"\n",
"$\\mathbb{E}(f(x)) = \\int_I f(x) dx$\n",
"\n",
"We will sample a large number $N$ of points in $I$ and calculate their average, and multiply by the range over which we are integrating.\n"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"autoscroll": false,
"ein.hycell": false,
"ein.tags": "worksheet-0",
"nbpages": {
"level": 1,
"link": "[7.1 Latin Hypercube and Quasi-Monte Carlo Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1-Latin-Hypercube-and-Quasi-Monte-Carlo-Sampling)",
"section": "7.1 Latin Hypercube and Quasi-Monte Carlo Sampling"
},
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Analytical result: 41.333333333333336\n"
]
}
],
"source": [
"# First, let's take a look at the analytical result:\n",
"result = {} \n",
"x = sympy.Symbol(\"x\")\n",
"i = sympy.integrate(x**2)\n",
"result[\"analytical\"] = float(i.subs(x, 5) - i.subs(x, 1))\n",
"print(\"Analytical result: {}\".format(result[\"analytical\"]))"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 1,
"link": "[7.1 Latin Hypercube and Quasi-Monte Carlo Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1-Latin-Hypercube-and-Quasi-Monte-Carlo-Sampling)",
"section": "7.1 Latin Hypercube and Quasi-Monte Carlo Sampling"
}
},
"source": [
"Monte Carlo Simulator : $ = (b-a)\\frac{1}{N}\\sum_{i = 0}^{N-1} f(x_i)$"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"autoscroll": false,
"ein.hycell": false,
"ein.tags": "worksheet-0",
"nbpages": {
"level": 1,
"link": "[7.1 Latin Hypercube and Quasi-Monte Carlo Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1-Latin-Hypercube-and-Quasi-Monte-Carlo-Sampling)",
"section": "7.1 Latin Hypercube and Quasi-Monte Carlo Sampling"
},
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Simple Monte Carlo result: 40.6994232474979\n"
]
}
],
"source": [
"# Second, use the simple monte carlo method to calculate the integral\n",
"N = 1000\n",
"accum = 0\n",
"for i in range(N):\n",
" x = numpy.random.uniform(1, 5)\n",
" accum += x**2\n",
"interval_length = 5 - 1\n",
"result[\"MC\"] = interval_length * accum / float(N)\n",
"print(\"Simple Monte Carlo result: {}\".format(result[\"MC\"]))\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"ein.tags": "worksheet-0",
"nbpages": {
"level": 2,
"link": "[7.1.1 Latin hypercube sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1.1-Latin-hypercube-sampling)",
"section": "7.1.1 Latin hypercube sampling"
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
"## 7.1.1 Latin hypercube sampling\n",
"\n",
"Try to pick a design that fills the design space given a fixed number of samples.\n",
"\n",
"The LHS figure below is from McClarren (2018).\n",
"\n",
"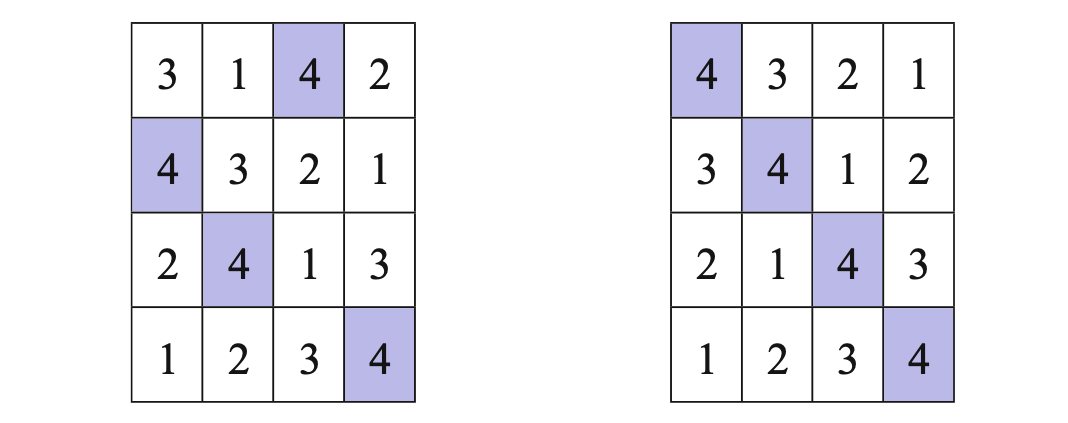\n"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"autoscroll": false,
"ein.hycell": false,
"ein.tags": "worksheet-0",
"nbpages": {
"level": 2,
"link": "[7.1.1 Latin hypercube sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1.1-Latin-hypercube-sampling)",
"section": "7.1.1 Latin hypercube sampling"
},
"scrolled": false,
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Latin hypercube result: 41.33359084466315\n"
]
}
],
"source": [
"N = 1000\n",
"\n",
"seq = lhs(2, N)\n",
"accum = 0\n",
"for i in range(N):\n",
" x = 1 + seq[i][0]*(5 - 1)\n",
" y = 1 + seq[i][1]*(5**2 - 1**2)\n",
" accum += x**2\n",
"volume = 5 - 1\n",
"result[\"LHS\"] = volume * accum / float(N)\n",
"print(\"Latin hypercube result: {}\".format(result[\"LHS\"]))"
]
},
{
"cell_type": "markdown",
"metadata": {
"ein.tags": "worksheet-0",
"nbpages": {
"level": 2,
"link": "[7.1.2 Quasi MC: Halton’s low discrepency sequences](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1.2-Quasi-MC:-Halton’s-low-discrepency-sequences)",
"section": "7.1.2 Quasi MC: Halton’s low discrepency sequences"
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
"## 7.1.2 Quasi MC: Halton’s low discrepency sequences"
]
},
{
"cell_type": "markdown",
"metadata": {
"ein.tags": "worksheet-0",
"nbpages": {
"level": 2,
"link": "[7.1.2 Quasi MC: Halton’s low discrepency sequences](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1.2-Quasi-MC:-Halton’s-low-discrepency-sequences)",
"section": "7.1.2 Quasi MC: Halton’s low discrepency sequences"
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
"Quasi-Monte Carlo(QMC) simulation is the traditional MCS but using deterministic sequences.\n",
"\n",
"A [low discrepancy (or quasi-random) sequence](https://en.wikipedia.org/wiki/Low-discrepancy_sequence) is a deterministic mathematical sequence of numbers that has the property of low discrepancy. This means that there are no clusters of points and that the sequence fills space roughly uniformly. The [Halton sequence](https://en.wikipedia.org/wiki/Halton_sequence) is a low discrepancy sequence that has useful properties for pseudo-stochastic sampling methods (also called “quasi-Monte Carlo” methods)."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"autoscroll": false,
"ein.hycell": false,
"ein.tags": "worksheet-0",
"nbpages": {
"level": 2,
"link": "[7.1.2 Quasi MC: Halton’s low discrepency sequences](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1.2-Quasi-MC:-Halton’s-low-discrepency-sequences)",
"section": "7.1.2 Quasi MC: Halton’s low discrepency sequences"
},
"slideshow": {
"slide_type": "-"
}
},
"outputs": [],
"source": [
"def halton(dim: int, nbpts: int):\n",
" h = numpy.full(nbpts * dim, numpy.nan)\n",
" p = numpy.full(nbpts, numpy.nan)\n",
" P = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31]\n",
" lognbpts = math.log(nbpts + 1)\n",
" for i in range(dim):\n",
" b = P[i]\n",
" n = int(math.ceil(lognbpts / math.log(b)))\n",
" for t in range(n):\n",
" p[t] = pow(b, -(t + 1))\n",
" for j in range(nbpts):\n",
" d = j + 1\n",
" sum_ = math.fmod(d, b) * p[0]\n",
" for t in range(1, n):\n",
" d = math.floor(d / b)\n",
" sum_ += math.fmod(d, b) * p[t]\n",
"\n",
" h[j*dim + i] = sum_\n",
" return h.reshape(nbpts, dim)"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"autoscroll": false,
"ein.hycell": false,
"ein.tags": "worksheet-0",
"nbpages": {
"level": 2,
"link": "[7.1.2 Quasi MC: Halton’s low discrepency sequences](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1.2-Quasi-MC:-Halton’s-low-discrepency-sequences)",
"section": "7.1.2 Quasi MC: Halton’s low discrepency sequences"
},
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXAAAAEGCAYAAAB8Ys7jAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAIABJREFUeJzsvX2UZEd1J/iLyu+vyvrsqv5StxANbSHckhAILFjAggF7jy1GZoRgZtZey+sPmmGNF++x53g8LD4zMLA+DMyxB++wLJ7ZOW7E7A7IXmG8Y5kvb+MRNN22JYPobnV1V1VnVlZlVlbld+bL2D8yX+lVVMR78fWqlVT+zukjVebLePfGjXsj4t4bNwilFGOMMcYYY4weJm41AWOMMcYYY+hhbMDHGGOMMUYUYwM+xhhjjDGiGBvwMcYYY4wRxdiAjzHGGGOMKMYGfIwxxhhjRDE24GO8KEEIeRMhhBJCjt1qWsYY48WKsQE/ICCE/Doh5DwhpEII2SSEfJMQ8nbmmQ8NjSYlhDjD575DCPkYIeS4xDu+Sgj5DOfzk8M2X29A/+uHbZzUbWOMMX7YMDbgBwc/DuCzAN4M4H4A3wLwJ4SQB5jnrgE4DODY8LmPA3gjgGcIIT+2b9SOMcYYgRgb8AMCSulPUEr/HaX0IqX0+5TSDwL4OwAPM486lNICpfTm8LlzAF4P4BkAf0gIsTJmCCH/ghDyd4SQBiHkBiHk04SQvODZkwC+Mfzz+eFK/KvD7wgh5IOEkKuEkA4h5Aoh5FeZ318jhHyYEPJJQkiZEFIkhPyvhJBIAI3/dNhumxBSIoR8hRCS8nz/VkLIXxJCmoSQFULI/0EImfV8Twghv0MIWSOE1Agh5wghHyCE9DzPfIgQcpl5757dBiHkVYSQPxu2UyKE/N+EkBNsO4SQhwgh3yOE1Akhf0EIuYNp+1WEkD8lhGwN2/qvhJD7ZXka48WFsQE/oBga4hyA9aBnKaVdAL8L4KUA7rVEQhPALwK4E8DPAXgTgE8Jnr0B4KHh/78Ggx2CO/G8F8DvAPgogFdgsGP4KCHkMaaNfwLgJga7ivcD+FUA/52IOELIwwB+A8D/COAUgLcC+LLn+x8H8CUA5wD8KIB3ADgJ4D8TQsjwsfcD+DUAv45Bv10A8M9F7/Sh5U4AXwNwHsB9GOymHAD/LyEk6Xn0MIBfAfAPAfwYgCkMdl1uO68A8HUAlWEb9wD4BIZ2QJKnMV5MoJSO/x3AfwB+C8AmgGOezz4E4LLg+dMAKIBHfNr8KoAugBrzrz787et9fvv3AbQBTAz/ftPwN8eGf79++PdJ5nc3AHyM+ewTAK56/r4G4AnmmT8F8Ec+9HwAwHMAYj68fpT57LYhjXcP/14G8C+YZ/4TgJ5fn7O8AvgcgHPMMwkADQDv8LTTAzDveeZRAH0AyeHf/wHAJbePdXga/3tx/RuvwA8gCCHvBfBPAbyTUros+7Phf4Oqn/1nAHcz/36SQ8PDhJCvE0JWCSE1AP8RQBzAoiQ9IIRMYuCr/zrz1dcAnCSEpD2fXWSeWQGw4NP84wBiAJYIIZ8jhPxjQkjO8/2rAfzq0A1RG/Lw7PC7U0PajgL4/5h2vxnI2F68GsDfZ961ASCJwe7AxSqltOT5ewUDuR0a/v0qAH9OKe37vEfIkwbdY4SM6K0mYIz9BSHkgwD+FwA/TSn9Lwo/vWv43ysBz21RSlmfbo/5+34AXwDwEQzcCxUArwXwhxgYcVWwkwpvu9/h/Ea4gKGUrhBCTmMQ9P1xAP8MwL8ihNxPKb0x/O2/wmBVy6IAwPWvB014fQ69MebvieF7Psr5/Ybn/3k8ur9nP+MhiKcxXmQYG/ADBELIhzFwDfwkpfRrCr+LYeDLfQ57V7I6eD2AdUrpb3ne8c6A37jGaSfwSCndIoQsY5Al8/94nv1vADxPKW2YEEkpbWPgavlTQsg/A1DEwC/8bwB8G8Ar2MnKC0LICoAHADzp+ZjN+lkDcIgQEqGUOsPP2DjDtzHwSV+hQ7+GJr4D4C2EkAnBKjyQpzFeXBgb8AMCQsi/BvBLAN4N4PuEENdV0aSUVj2PRjzf5TEIdH0AAx/423y23yr4PoD5YaDxLzAw6O8N+M0SBqvVnySEfB5Ae0j3RwD8LiHkBxj4cH8cg0DeWRMCh7RNAPivGMQKHsQg6Ou6FH4bwJ8RQj6Bwc5hGwM3wz8A8D5KaRODwO/vEEK+h0Ha5k8DeAvzqr8AkB4+979jYLxZ2v/lkI7/kxDySQAlDIKL7wDwSUrpVUm2PgbgrwD8R0LI72Kw87kXwDKl9LwkT2O8mHCrnfDjf/vzD4OtM+/f5zzPfMjzeR9AFYPMiY/BE+z0ecdXAXyG8/lJMEFMDDJHihgEOJ/EYGLxBu7eBE8Qc/jZ/4yBX9cB8NXhZwQDN8zzGARQrwL4Veb91wD8FvPZZ9w2BLw8jIH/uoJBsPBvATzGPPMGAP8FA0NXxyAt818DiA6/n8DA+K4Pv/9PGEyGPaadnx/S3cQg0+VRMAFbAK/EIEOkMnzuMoD/DcCMR3a+wdDhZ68Z0lwf0v1XAF4jy9P434vrHxkKbYwxxtgHEEJ+DoNJbrz7HcMY4yyUMcYYY4wRxdiAjzHGGGOMKMYulDHGGGOMEcV4BT7GGGOMMaIYG/AxxhhjjBHFvkbCv/rVr9JEIrGfrxxjjDHGGGk0Go31Bx98cJ733b4a8EQigdOnT2v/fmlpCSdOnAh+8IcEB41f4ODxfND4BQ4ez6b8XrhwYUn03Ui5UGIxtkTEDzcOGr/AweP5oPELHDyew+R3pAx4Ps+t9/9Di4PGL3DweD5o/AIHj+cw+R0pA76+Hnj3wA8VDhq/wMHj+aDxCxw8nsPkd6QM+Hjm/uHHQeP5oPELHDyexyvwITodttzxDzcOGr/AweP5oPELHDyew+Q30IATQj47vJT1bwXfE0LIp4YXqv41IcTWnYl70GwerGqWB41f4ODxfND4BQ4ez2HyK7MC/xyAt/t8/xMY1Aw+hcEltf/WnCw+Fhelb9v6ocBB4xc4eDwfNH6Bg8dzmPwGGnBK6dcBlH0eeQjAv6cDfAvAFCHksC0CvSgUbt2tTu1eH9c3W2j3bNxnIIdbye+twkHj2ZTfWzEuTTGWsT3YOMhzFIObwV0sDz+7aaHtXYjHda5LNEe718cnvnEd6/UO5jJxfOANtyERVQ8ftHt9FGsdLGTjUr+/Vfy6UKXXRlu3mmcvbPIvggm/tsblfsOPZ9M+3w+ZqSLMMW3DgPMukOWWOFxbW8Njjz2GaDQKx3Hw8MMP4+zZsygUCshkMohEItja2sL8/DzK5TIopZifn0exWEQ2m0W/38fS0hIWFhZQKpVACMHMzAxKpRImJyfhOA7q9ToWFxexsnoTzT7BkfkZbFXKyOfz6HQ6aDabWFxcRKFQQDweRy6Xw8bGBqanp9FsNtFqtXa+TyaTSKVSuHazhG6rhVMpBxGnhtXKDCYaFaRSKcTjcVSrVczNzaFaraLb7e783stTfmYOf3zhKpqdHurRHB46GUV+cnDJea1W4/IUi8Wwvr6+w1OhUEAsFkM+n8f6+roRT5VKBbOzs9je3kan09n53uWpXNnEn1zrItqtYypB8FOvfjnKpaKUnFie+hT44pUWMs42etE0HvqRWXRaDS5P8Xgca2tre3hKpDJYLpZw5NAsnE5biycZObk8dZ0+vni1g5yzhX40hYdeMY9Woy419nhyarTaWK/WcPvxoyiXijtyqtVq2Nra0pLTZgeYc8og8TRyvU08d8XBy04ek9Ynv7Enw1On00Gt3gCyM0CtjFQyITX2arUaarXaHp5iiSS+9L0KYr0GGpEc3nEqDer0fOXk5SmZzuBLz5Qw0WtiOzKJd7wkjlhkQpkn2/oEDE5jyo49npyExlemnCwh5CSAP6GU3sX57g8wuJrqj4Z/fx/Amyile1bg58+fp/txlJ63MgGgPTO77W00OphN6610rm+28KlvXkcqFkGr5+D9D9yG41NJ3994+d3vlYUfvaq0qPDOk/GtWGnqyEsEP/pNjlnbGJcq72JlrisXEc+mfa7z+/3QKwtH6b/z4IMP3sf7zsYK/AkA7yOEnANwP4Aqz3jbwPT0tNRzxVoH6/UOUrEINhodLFdb+MJfr/kOND9BJqIT+MAbbsNarYNDmoJeyMYxl4nvKNuhbPC2yuX3VhgwEb06tHjbmk7F0Hb6aPf63N/xZMzKc63W0TamstCRlwh+9PP4lTUqNsalDEQy15WLSI/9xpxMf6jKzKZe+dEoa7d0EGjACSF/hMEFs3OEkGUA/xxADAAopZ/G4ELan8TgktUGgP8+LGKbzSYmJycDn2MFSSl8B5qMIBPRCSOjoaNsLr8yiiI7yE2Ng47Sum0tV1s4d7GIT59fFvYzT8amiq0Dm8bRz7Cw/KoaFXdcusHMhWHbNvtFJHPdSU6kx7w+V+kPVZnpjGWdnYis3dJBoAGnlL474HsK4Kw1inzQarWknmMFCcB3oNla4QUZFNVJwOU3SFFkB7mucfBCV2kT0QnEIhOoNLu+/cyTsalie/lXMWwieem0IzIsLL+6RsXti5l0DJQClWbX2m5NJHPdSc5Pj7193u71cXF1G6VaB+m4XH+o6JitFXuQzGTtlg5G5mbsdq8PJz0t3HqzYAXpN9BsbJfDcHO4+aNBiiKr9DYmKhEtMkZNpp9n5hd2VpLedlh5qvJiM5NIpx2RYWFzhHXGorcvbm53QCnFdCq2q19Mdit+409nZ+ry7EeT289rtTZK9S4OkTjmM2auLBayE5BLZ8fpa+1EwswDHwkD7gpzziljPTKjpXx+A83GdjkMP22hUNgJfvitBju9PqZTMWy2ukKll31OBiwtskYtqJ/bvT7++Onv48J2KtA4qho6nnwOZePKRs1UzqzR8soY0BuL3r44nBu4DL0ytjF5mboQvSgUClg8enzXruGRMws4nk/ucdVl4lEQAjx6ZgE/ejgXiqtMduKfSce4+hMkM1bGNjESBtwVZt7iqoIFT5Aq7dsMerlIJtW2zr/82mM45lEC1ed0ITJqvP7zU5hirYP1NqSMo6qhY+WTT0a1jJqfnIPGC8+Q8mSsaix5LkNvv1zfbEnLZz+QTCZ3xkwiGsHF1W2sbrVxLJ/ckYO3n+czCSXjbZMv79iuNLv45dceQzwyobQTCdJjE4yEAXeFWWnbXVX4QcdfrLpyChpobg6pCOzgikcmuO3IPqcLnlHTzVaJxJNo1R2pSZD1lwbFH7zy8VtJ62QkyfDLe2c+QMayYA2I9/9tyccWUqkUptIDmla22gCAfCK6Sw66u2LbKcRs3+ksfIL02AQjYcBdYT535Xm87I7bfFcVflCZmXWzLWRXTjIKVKlUfKPXsqv+sLM4eMqmI59EdAI/cSKB2PTirmBlEI0qLhyXBpM0SZ6cZcYL752FlWJoGQpeek3lYzPLqVKp4MTk5K7MJJ5bT8dto5NC7Acb7tUgPTbBSBhwYNCRtx9d2OnAsHM+w3CJeCGj8Ln8NDeg50J2cNnK4vADq2w68inWOpiansGMZyUsQ6NJaqONNElZfnmujm486xuYtznJ6srHdpbT7OzsDk13zKbxwTeesJbLrppCLAO/iURGPi6/YWBkDDgAbG9v7xwtVZ0ZVYNYNmZePwT5Um9stvD1v7mOZ+tx6VWlH1h3g2p6lipU+s+r+HflOnj3A3ciEZU/KGKS2mgzTVJ2MnX9z5/4xnVku1XUYtvCw2Uqk6yKsVeRj80sp3avj6W1Cl6aTEvFRfwgirGopBCbQFY+XrtlGyNlwNnC6CqC1wliybSvu0IK8qWuVNs4GW0gEUlaNbBhpGeJ+kBWPl7F73XVD4rYnGz92rKZ5+/yvJimWBLIV2U3oLOjkh3fstlLsucV5pwy/njJMT75KOKX5ct2bMqFrHzCvNBhpAy4Xz6lzSCWLEzdEH6+1MlkFH9biSOb7uHoZNLaysF2epZJH+y4TZLRHcXfiue1DororuJk27LtcnKN3ZWmI4xLqOwGVDKBZKGavRQ0+V1c3cZarY1eIotq22xRoqK/tmNTLmTlc+DzwF2I8iltBrHc9kxmYBOl8dL1liMEr73rNu2UPx4dJulZPOhOhKzM3vu6Y6i2euhWClqr+LBhW9a8wDxvHMtOYGFkmuhkL/lNfqVaB6V6Fz+S6iCanjFalIQVo/LyXKp3cOnmNs4IdER2gXHg88BdiNJxbAaxZAY9b+VoS2m8dEVaVRyZTUv/lqWRR4dt376uIrEyq7Z6OD6VxFpHj98geGW22eopG9wwDGQiOoGF6ReMg2gcy8Y4bGQCBfGsA5evdDyCQySOVx7L4Z6XHjfy55uMY7+2XZ5L9UF/nbtYwFOXK0YxqAOfRuhCVBjdZhAraDIQrRxtpme5dG1u6tdQ8OPDtruBl+Gie6w+jOL33hXgWr2D+UwMh7IJJYMbhoEEdvNruiuUzTTZ72qHu3d9cdwxPykd1LYRwHfbdCfw3z+/LGzb5fnSzW2cu1hAJh7Vlq2LF/uFDvuGarWKqampPZ/zIs9+6Xd+CJoMRCtH2d97ETRQRfwGweaxeRmwGS4mx+qr1SpS2clQqumRCYJa28FCNq6llDIGUtWl4pWxya5QRK9p+qiNQD5LR2HlBjArLrFquyyFl+dULIJGx/HNvkpEJ3DmcA5PXa5YcdHo6rEMRsqAz83NCb9zB5pNF4ZO4SuVVUvQacBuIiddvMtF2Mfmve/hKa1pcGlyesb6CUHvtjibiICCYi6dMJ7UeAsHVdrZMa2zKwyiUbUImMqhnRubLXz+UjGw+qGXDj89Buz7t708N7o9ZBJRNLv+p311dx+8vgvi1wQjZcCr1SoymYzvM7Yq7pnU4DBNz3KN8GR3E1uxLSUjZuPYvE5ND16QVEf5Vktla6svLx+uzPLJ6C6Xl05boiCrjktlo7KJjW7EuIqjLGyXJl6ptlGstXFqNi3Nc5AeqxrPoPHKBu5Zt6cfHaqFynh9J2O3dDFSBrzb7QY+IzPYWYGrbntNfchBq+QXcoSB5xWNmKyyi3jWrenh9a+b+E1TE9SKseLx4dI4mVQb9rJGTef06TevrOPCdt2oiiPbpknwT/XQzmQyimKtja2OfLqrjB7L6phs6QOWZ9UxwHsv28+ivpPhVxcjZcBl8imDBigvCOkX1JCB6gQQtEoW5QjLQEbZ/Qa9bk0PlgbdCe7okcP4wPGYceBMJR3MVluqk1ex1sGztbi1XGYbwT+d+jp3H8nhXWcWAl11rp7MzC/48qEC2QlHZULQrb0j6rtxHvgQbj6lyYk4VuDfW6sbbdl1q+7J+NG9OcIqCBqsfoNep6aHyYqQfcaVsWmWjGo6mK22VCavhWwcd2Y7+G4tYt3Xq+vflpWtjpvD1ZN7c038zAOvtBKXsXGeg0ejTu0dUZ+M88CHyGQyxkFKVuCnD2WMtuy6Pvd3/ughEEC4aklEJ3B4Nm9sHHnwG/QqCmxjRcg+87N3+vsKVVPgbKSD2WqLpT0RncCbTx/BGxK5fcnJF8mDR5dqfZ0gePWk0CLWSkOIxquOnbBRe4fXJ2H5v4ERM+CRSMQ4SMkTuG7tC8BOVUQ/flXakTUApjzLQkZW7DPbnRQOC9rTSYGzlQ5m2paI9mQ8immDSYClUdW/fSgb1xpHquPEqyfpjNlKmQXPaOrYibBq7/jpsSlGyoBvbW1h8WjeOMjFCpw3AEzzmUVQGVhbW1uYnp5WCpjo9IHsIQdVyCgE+0y01xS2p3Oc3TSoaqstEe2ujAGz7B8vjSr+bZ1xpFs4y+07b7kE2zVm/HgNgop83X5u9/qBZ068MraNkTLg8/PzVhWSB1eJOj3+BaY8qPo9ZQfW/Py8csBEh9+dQw7xCOrt3h4Xge2Ki37POB3x6VPd4+wq8rFZcTCIdmAgY/e9Jtk/MuDJQ2cH6Ral8nMl+Z0wbsQPafMU9ilS1bEiM/m4Mg4DI2XAy+Uy0um0UZaD3wDwCmQ6FcNMOoZK0+5JRtmB1e71cXV1DcnpQ0oBE1XsOuTQcZCJR9HqOUoGMohfmbo07jPLhYGMRc+FcZzdRVirQRHtwAtj+ka1heVqa8/VYl7YmLR5u0+VgLS3KBUhwHxm74GooH50eVblycYp0v1yEXrf4+XXNkbKgFNKjX7PSyH0FjbyCmSzJb7A1BRBRs2lc6ZXwfp1KjwSbzKRuWDrVJjWdjFF1/HfkrI8m9b78ML2Ee4g2oHBmG73+nj8UhFrtcE7zxzOKWf/mBgm2XHEFqUSlSIO6kevHqtMIKYVIW1P0H5jz/ued73ErpfAi5Ey4KZbETaf9+NfW0Kz6+wIkxWIyhH0MGZ2J57Gps9N2DbAUyDvIQcb9T5k0e718cWrHazUr2v5VnXrfbjQXeGa9Mf8/DyKtQ7KjS5OzWWw1e7h0bsXhO2YxGtMeWEne1Ep4qB+ZPVYdgIxrQgZVklgdvJh34OUvbx3FiNlwIvForAeuIwAdkXCBf5e3foHYdyEPeeUEUnPhFLLxAs/BWIHKaBe70MWxVoHOWcLqVheaQXM0q+bD63jljI1nsViEYtHj++My6OTCRzLq636be0cgniR7Z+g53T12NSFFlZJ4CBXF61XAOSl21TBSBlw3r1yKgLwDoD8MOOCXSXouCVYBbJ1E/a11SROHjnE9dWrHI4xNbDePtFxqahMsP1oCq22+glUth3deh+q8jc1ntls1jieYcM37gYng+5Jle0f73Os/E30WNaFJqJJdgIwdUl531OrVpR+r4KRMuA86Ky23O9tZbPsmXEt3YQ9l4n5BlplD8fYXCXbyHv3m2AfesU8OrEs8smoNQWync3hhYwP3n2nHy8m8QzTCcCVkek9qTyjJ3vuQVcmqrzLTAA29Mf7nprSL9UwUga8VqthdnZ212f7udpy2wvaegPqN2Hz2uXxq3M4xuYqWVVhVGlpNepYPGpeUtZPtjar+wX54GfSMVAKYblVnox5CCu9EbBzT6pIz3jy72vosR9sT342LmXxQlbGOhgpA76wsDcYsJ+rLZXJQLdOxK5cbw6/OodjbK6SebyK2nQPB6nQsrCwYKWmhx9ERtdWFoeX/pvbHVA6yCTi8cKTMYswd1SA+T2pfrnhvLFIk+p6bAMiGZu4ZWRkIyNjXUgZcELI2wF8EkAEwGcopR9lvr8NwB8CmBo+8xuU0ict04pSqYTjx4/v+VxkUNo9uzfTqEwGKqsCUbs8fmUGuo1VsntKT8eg8dI1ZWtwl0olLBw+6lugSPYSAT+wPtqw0ssO5wYuNdH4E41pL/YjvVFUT0S2Mp8oN5zX9o2banpsA7qxMt3URvedxVoHTnUNt58Ql8wwQaABJ4REAPwegLcCWAbwNCHkCUrps57HfgvA45TSf0sIuRPAkwBO2iaWECL9LLuNtXEzjck2TzY9azoVQ9vpo93rC/mVGegqysDylU9Grd1mvtHYe+2cHwghvgYl6BIBW/nfJhMYz6UmMgYyY9pmrrsfzV4ZqVbm88sNZ9tW0WMRVHlXnQRl9UcmF/xMro0jR9Vu1pKFzAr8NQAuU0qvAgAh5ByAhwB4DTgFMDn8/zyAVZtEupiZmZF+1isw2ZtpdNKYZCCbnrVcbeHcxSI+fX4Zc5k4fvk+O0dwVfkyXfGZTHSujHkK5NIlukTAVv636QTGo1/UfzJjOsjP7hfM1jXwOpX5/HLDVXnmwaRmT1jnGUQ2wdt/VxuR0A7AyRjwowBueP5eBnA/88yHAPwZIeSfAMgAeIsV6hiUSiXpurph+YFVVrYqdVUS0QnEIhOoNLs7z91YLWDq5XdIvcsmX6Y1lv0muqDf+8nYSxfvEgFbmQxhBoFV+GVpVMl1N3ULhVWZD1DTYxcyNXv8wNsV2XKb8WyCt//uyXatleJgIWPAefsd9kz7uwF8jlL6u4SQ1wH4D4SQuyilfe9Da2treOyxxxCNRuE4Dh5++GGcPXsWhUIBmUwGkUgEW1tbmJ+fR7lcBqV0cFKtWEQ2mwUhBEtLS1hYWECpVEKfAr1EDqSxiempPBzHQb1ex+LiIgqFAt5zKoZudBKkuYVmbQvVTgfNZnPn+3g8jlwuh42NDXRiGaS7VdyVprjSdPDcledxaCqLVCqFSqWC2dlZbG9vo9Pp7Pw+lUohHo+jWq1ibm4O1WoV3W4Xi4uLWFm9iT9faqDScnAk2cfRdAopZxvZ7ATy0T6WlpZ28mFrtRoWFhbgVNdwJtfG1UYE92S7yCamsL6+vounWCyGfD6P9fV15PN5dHx4mp6exvLGFuacMnrxLOacMq7eiOLo7GQgT4+cBGhqDrFeE4WVG3t4Opbq4yfvfSlq1couOSXTGVSaPcSdFo4cXsTazRUQQjAzM4NCcQ1/ttRCo93BYpLip179cpRLxV08RSIRrK2tCXn6hbunUNqsIYEejmYjKKzcQDKZRCqVQq9SxokMQHo1zGSBqTiwtLTkKyfv2OtvbcGJz4NubeDuXAvP1WO4J9tBvFvDxkZ9R06lUmmHp1KphFQmiy/9bRGk18JWJI93nIwgmYhLyanVamFrawvNZhOtVmvn+2gsgQaiiLRrODQ/t0dOsUQSd2T7iPVqaMRzoLUNLFV7O983EcdEext3pR0stXq4fO060rEJ0FQeqFeQn8ztGnssT5OTk/jZOzNY33Rw8vgiCis3fMdev1pEubl77G3XGtjYruP240dRLhV35NRqtVCr1ZT06fvXlhHv1HEsGUUGNawnMpgm/vrE4ynlOCis1OGkpzHnlDGbiuJmq4fnrjyP4wuzgfrEysnliadPj5wEOiSDJEmisHLDd+z52T1f4xxUX2RokD9EKX3b8O/fBABK6Uc8zzwD4O2U0hvDv68CeC2ldM3b1vnz5+np06d93+eH9fV15KZmQil96s7w7orDtL3rmy186pvXkYpF0Oo50sfh273+ziphe7MsdaO1TIEuG3yxPL3/gduUVn1BvwcGMnZ51lnVevvPdDzItiPiS4Z+L7/ed8teLCyikZW7jasDVeDHA49n2fa8/MgExkUy0NEL3V2WDr9eXLhw4TsPPvjgfbzvZFbgTwM4RQi5HcAKgEe7bygMAAAgAElEQVQBvId55jqABwF8jhDyIwCSAEraFAuwtV3DZ/6mpr2N8oPqVjBImLp1VbzbsUK9Hih4W8efdXhit4VB23qZbXl9yLOuCyDIxaWS726SKilLf50jY7cfE9EIVrbaWK62cMfs3mp2fjTajmuowu99PJ794PYza7SDLiYOSvu1keorA1V+VRBowCmlPULI+wB8BYMUwc9SSp8hhHwYwLcppU8A+J8A/DtCyAcwcK/8HDUtHchDdgbr9YKw9KkpZP3bMsK0kdfKXobKMz4yiilrjEx5CjLQMn3i8hyGwQniUWWFFZQqKXsYhHfh7UI2jpl0DBdXtwEA5y4W8cE3DnzGKitA2bhGGPB7n8olvyaGM2gMqcSzTM4m3PJLjYc53U8yn/225/+fBfCAXdI4qJV9S5/yEEblPFnjojIh8Gj0XoYqPOxjSTFt8CRjoIP6xOVZli8V+Qbl7KoYiqBUSVn6eRfeJqITeOTMAla32sgnothsda3V19FZUOjokN/7VC75ld2N8GBz0jI58T2+1HiIZCKOD7xhUVj6lEVYJ9hMszRkaYzFYjvPiYyPjZV+EE8i3kRlBUxWyi7PMnypytePR9UV/1QyilR8sBPk1Q2RlYtXxl4czydxLJ+0Xl9Hp3SErD9ediyIeOZBtBuR3YHYch8GteU3flT4VcVIGfBUNhdq8r4sRMLUmTD8aMznXyhB6Wd8TI2mH08ueC4D20Gxdq+PxsQg+JeIBt+OrnM4Q8Sj6vHp3z+/vBODee/rjmntNoCBjMOqr2MDsq4DlXEv4pkH3m5ERY9tuQ+D2vIbP149to2RMeDtXh9f/u5VXNhOGSXve9szca3whKkzYfjRuL6+jkwms/M+VqGDLlNlYVIQieXte2t1q5Ojq0RzThnrkRlj+Yog4lFlteYt/tTqOai2eoEBNWFbayU8fg1G9XXCcBO6kOlj1XHvxzMP7G7E9uRlo/aO3/jx6rFtjIwBL9Y6uN6MKBkMWytlWQXRNSgiwbMzt6vQOit92wc7Th/KWF0RukoUTySllciW+8iF7E5G17fKG0e9WBrr9U3t+jphF7qS6WPV/uDx7Fe6wLacVehXqb0jGj/jFTgGnTyfnMBGXZx1IuuHU1kx2CiCo7vy7XQ63PforPRN3Uk83lSVSqYezES3hdl0WjpIpOvXNd196fDOoz8bpUaTgcwpX5X2RAZU1zXFA8uzTOkCWVeIjlyDFnp+tXdkINJjGxgZA56ITuDNJ9L4e9OLUj5aP0OrsmIwLYJjskJqNptK9MsWzLJ5o7lKWQGZfPXnrjyPl92xN71PVK5UFbZWrLK87xhah29ou+2W0WQwnYphJh1DpalfbdNGn3j7I8iQsjzbiFWZ8uC30BPV3pGFSI9tYGQMOAAcPXIYiUSC+51qqVdZpTGtBGcyOEX5ozz6dQ/0hOk/9UI2X/1lJ4/tMd5+5UrDoMMW2IqYvLLGi4uLgZMBKyMvD5st80uv96tmvguWZxuxKhEPJuM7qPaOLG55HviLBX75lKorTNkVlI6xlKFLZmD58cvSr3Ogx7b/1MYOgOVZplypLA1BdNiezNiKmDxDG5QjzJOR7ilfEWzmS8uMQ5Znk1iVjdOwItjyvY/zwIeIx9UuLJVRSNnqeqrGMogumYHlxy8LHSW0tXWVqU0jqwwszyrlSk1Ok4p+a2sFJzK0QTIWych28FZHd3iQGYc8nnViVbZOw3rbs32uQcSvLYyUAc/lcr7fs364sC7/NV3ty273gvhl36Gq1KYrL2//ueUNVG80D+JZhS+T06S83x7KxkNbwbl8Z1P+6WUiGdkwLCytuqdS2XaC5CU7rlVr7+iehjXl2Q/tXh91xHfONtjGSBnwjY2NPeUVRSsFGWW2VT/adGUm2u7x+A2iSyV/1ZQPb/81uj1kElE0u8G1afxW7TyeZY2VyYTE+62NHYpIJq6s78018TMPvNJ39xdmCp1ufR0/BAU0Zcd1EO82au+4CLP2zuBsw3YoFSBHyoBPT0/v+ttv1pRRZhOFN1kB8QYWb7vH8uuFrHvIRnqWCLvdGwnp2jR+hfn9eA6CjrHz9iP7W9XxoRNwu9aMKmc2ycBkfNjyiYvaV5GxH+8y8pYNEIsu3zZxoblyjiVSoQXMR8qAN5tNTE4Obm4LSi2TFW6YqxuXTt4AYAcWT2k2N6o7/LJtqtxXuJ+X4QadSNy1audUlBTxrEKTSWojmyapUktDJ7B9ewbWTxbKug9F+mNLL0Tjb7vWwGY/joUh37ZPRMsiyIdu6/BbrFvFbDofSvmDkTLgrVYLgHxqmYxwbfsSvTA9BOTyyyKoqp6rEKYpkDJQdduwQUlWaUQ8hwFbpXjZtkr1Di7d3MYZQcDVK+tupWB94SAb/PPTHxt6IXIVfu0HRVzY3sJMOgZKEXjCMSwE+dBNUxNdOfPONtjCSBlwtla0bGqZLagaPtNDQKL8UT/DzE4YJimQOtDJR/eu2m3nzNo83CTTVqk+kPO5iwU8dbkSeOy6nTpslScZvvZLf0SuwmdrcaRiEdzc7oBSiulUzFrutgqC+kk2VhVkxNmzDTYxUgacVyta9iZsXcimyfEgGgCyg1OUPyra4oomDNUUSBt+P91Vrc2cWd3DTbx2blRbePxSEeUGf7XotnXp5jbOXSxInxhV5dckVdLFfuoPz1V4Z7aD79YiOJwblMn1Hm4Ke4HB0ubXT7KxqiD9GeeBD5FMBvu3bc7eQQE31WJagNpN2C6/orbZ99sI3NoueqXq9/Pj2Uujn4xV6oTIBLk+8Y3rWK62sFbr4NRcxretM4dzeOpyRZp/GX69MEmV9H5n4uM20bFEdAJvPLWAN6SndvpG1UDapDFI/jKxKva9rP6oylgFI2XAU6nUzv+LfK82Z++ggJsfvAPIpVN1cHr5lYGNwK0tv5+ucQjiOUjGtuuEuP2RTwyyRbbaPRydFB/lV+VfVca2MkRUYxfu97KV+fyQy6YxOfnCu3Vzt0VQOcFpq/CVC57+5BVlrIKRMuCVSsU3Q8F2TYeO098xALJXuLm/tZGeValUkEhnlQaaaeDWlt9Pt3KcqYxt1wnx9seZwzk8endwPQyVAKCXX9lTwWFkTslOjDqV+Vi+/GRsgz/VE5w2Cl+54OlPYaVolFnlh5Ey4LOzs77fh5G/Op2K4Zdfe2xHaWUK97MDaLnaQiwywc019kMuP6010Ey3uDp+PxX4KZCJjNu9Pjq9/q6iUaZ1QsIymC5cflUzllT6X2Y8yE6MqpX5eHwFyVjGrWUjiDvIGGrj0uo2zhyxEwfgjZcgfk0wUgZ8e3vb9wSXLWVjV3HxyIS2H3gqGcPnmeCXrPLdLFeVDacNN1KQ3y+fjCrfBuTFjWoLy9UW8om98QRdGbOV/7yTrilkDabOxOnyG5ZRkR0PKhkZKpX5eLKONv1lbMqPbBC3VG9jrdbF5y8V8dQVccaQKtjxEjSmTTBSBpxXGJ1VGtXVCa8d05W8dwC1e318+lvLWqvXFHGMC1R5V/+6g9PLT14jG8eLdq+Pxy8VsVYb9MWZw7ldfMkUv+fJmK38pzrpmkJ34nT5tWlUvGNZJeipmpEhQwdP1oWq/gUHNoO4l1a38flLRd/6PTaSIsYXOgzB5gjbClrK5E+rwh1A7V5fezI4euQwPnA8Jn0SkD0SzFv9mxjx41NJY3dKsdZBudHFqbkMtto9PHr3wi6aeDKWUSCbJVF1oBv8dflVMSp+4J0ulO0X1YyMIIhkLZvrz+s7m0HcM0dyeOqKOGOIZxdcvlQM+rge+BCiWtGmvlmZ/GkW+5GV4fKr6jZxg60mq38RTE93en9/dDKBY3lxrWjTk6wswjwgohv89fLLMyqq7ire6cKwy0WIIJK1TF60qO9U9cmkmBtvN/uFv15TXjCO88CHYFOubM3GOifydLIy2r3+jjICwTO5bIqZ6EiwyerfjxeT051BSuPlWfckq7efeT5yWeVTMfi6wV9WxqbuKt5Y9uuXMCGStcy49pO9SkzCpJgb25eUQmvBqJoqqoKRMuBsYXQ/Y2CqfH7QWfmzQTaZGhCyheD9akaHsfpiDYLqxbp+SuPlWWeCFimtqsx0DH5Q8JdHv9/lBjruKpkgrww/svoT9BxP1jLjWqbvgt5toywuexBPZ0E0vtBhiGq1iqmpqV2f8QaIDeXzg45h8Q4m2RoQPH5FtIsMtW5Q14VISWwfmHHh5VllAto5fSm4PFhVZrZqgYuMqdunfjLWNWJBQd4gfmT1RzcGJTOug2Qv824bO3S2L3UCudeLG0hlJ0PZ9YyUAZ+bm5N6zlT5ZFYVqoL0DibZGhCy/Lo02a6q6Kcktg/MuGB5luGL3d3wLg9WldlUMrpzUYXJJcos/Wyf/tKrxDnCNoyYCxVjJhuQ1dUz2XEtkn27519K2vt72ztQFT1z5dNpthFfvR5KXZeRMuDVahWZjP8VVIBZoE1WKVQNJm87FuQvjTSqiCZS+1KZjQe/EqlsH9vKuZaVsYhO0eXBgJrv9PfPLw/KJySieO/r7FWTY43eaqmM6cnczntlVtOitvwMqIoxkw3I6q5wdWTswqUjqJS0l+8wUgNl2nLl8/JUD89ZSiJgMVIGvNvt7vy/anRZ1jCHeQkCO5iC/KUrlc6+VWbjIahEqs2CSO7fvbZ6zqztycRbbrXZdVBt9aRO4OrQmpqgAPTcEaoGVDaYqRKQ1XEprG83MdvTuyPStBSuzXpJQW258iFOLbTUVqlRSQh5O4BPAogA+Ayl9KOcZx4B8CEAFMAlSul7LNIJ4IV8Sp3osqxhvlX5xFyDmJ3Ber1gdKu2yXMuTaISqbpuG17ao5ttcSQTwdnjaspte6tsmiqpQiucwaJEZ+EgWqgEFaTS2WH6BcpVXQq1RgdZTZeCaSlcGws02WqXrnxWKzM4Mp29NT5wQkgEwO8BeCuAZQBPE0KeoJQ+63nmFIDfBPAApbRCCDlknVK8kE+pIwRZw8xzdQSlXtnaku1RhlpZejIJK/CUiKqXSA0CK7/vrdV3/p50qtoBQ5G/VFU2Jjs4VVqXVvbWuFfpY29bMjTqGjAbk6T77rvSbTzTiGidfDSlw3SBphq8T0QnMNGoIDF/64pZvQbAZUrpVQAghJwD8BCAZz3P/A8Afo9SWgEASumabUIB7PjNdISgInjvVlOmLGUY6VkAMJnL4gNvmJGiWVYxdS50CHuFe/pQZudvmggukCQLE6Oru4NThTumdTJu2DEkQ6OJATMNlLvvLnda3EJksqVqg+gwObwTBJ3gva6/XwYyBvwogBuev5cB3M888zIAIIT8JQZulg9RSv/UCoUeRCIRAHLpWTYCjzIKEUZ6lpdf2cEqulWbhe6FDjrKK5IHT37u34leXdqXalphT4UH2f5VaXMhG98Z04B6xg07hmSMs43JWHfH6b576WYJJw7P79Jb3VK1PNpMDu8EQSfe4pWxbcgYcML5jHLaOQXgTQCOAfgGIeQuSumm96G1tTU89thjiEajcBwHDz/8MM6ePYtCoYBMJoNIJIKtrS3Mz8+jXC6DUor5+XkUi0Vks1mUSiVsbW1hYWEBpVIJhBA48RksrZSQymTxpb8tgvRa2Irk8Y6TESQTceTzeayvryOfz6PT6aDZbGJxcRGFQgHxeBy5XA4bGxuYnp5Gs9lEq9Xa+T4aS+D2LEWiV0UzngXqZSxVu5iZX8DzN1Ywl88iFYvj3lwTlxsxvDTbR7dSQDt1mMvT1dU1zPQqcOJpzDllXFtNYi4TQ3VrG8hMgzSriEUmMDMzg1KphGazCcdxUK/Xd2iKxWI7PKWzk3jib26CDnl++LYJ9EgKizN5FFZucHlKJpP4hbuncHNtA0cXZlAuFdHpdLC4uIiV1Zsotgj6rW3clXZwvdXD5aUbyEax83sZOQFAdWsbX7rWQ6a3jVQ8ip+69yWoltcxOTm5m6eVGzs89avrqLRaQN/xldN2rYGv/aCIZ2uD67neeGoBuWwalUoFs7Oz2N7eRqfTwcz8Au7NNbHWJkhk4uhWCqjH5lGtVtHtdgN5yk/P4k++8wOsNgdlhB++LYlYbgFoVlEqrO7IaQ9PjJy8Y29mfgF//PT3UW4DNJbCG2aaiEQiXDmlUqldPDVbbazRLGZ7ZUwm49hqd/DclefxkmOLOzydvX8R126sYG4qg8Z2FQUfOdWqdRRqtV36FMRTKpvDl797FdebEcwnJ/DmE2kcPXJYSp9cnlqVIrrTGZSHcnLS05hzyshm44j2ejgeqaKTnAStbWCp2lMae6V6F3NOGU48gxmngsvXgNuPHFKWk5+NeOQkQLKLoLUyNjdKSKVSWN8oo5/MIdFvo997YWy5Mtza2sLc3Jz02GP1SWicKWVtMfMAIa/DYEX9tuHfvwkAlNKPeJ75NIBvUUo/N/z7zwH8BqX0aW9b58+fp6dPn/Z9nx8ajQbS6TT3u+ubLXzqm9eRikXQ6jl4/wPyZVv90O71A32hAKS3vp/4xvWd2dv9rWjF4MevbZ696Vlr9Q4OZWOYzyS0fb26tAXx7G07EY1gq93Dr77+OO6Y5f+GlZ8f2JVlGGOKbfNX7juElywEH9ayLR9diPpEZVXOytirF9OpmHSpWh54Oia7Q9dF0KpfZkz74cKFC9958MEH7+N9J7MCfxrAKULI7QBWADwKgM0w+SKAdwP4HCFkDgOXylVtigUol8vCjggq9G9ywYGML1Q3EOR3XNqP3yCeVaGTnuXXr7q0uTwHtT2TjuHi6jYA4NzFIj74xhNGbjObec5+YNuMtLcBBBtw0/Q5XbBy0C3a5QU7rm3GWPzcq2FdsxbkqgvSYxMEGnBKaY8Q8j4AX8HAv/1ZSukzhJAPA/g2pfSJ4Xd/jxDyLAAHwK9TSjdsE+u3WzARnApMJwrZ9Kx2r49Ko4t5n3xZmwNfNT0rqF91aHN5nmz1fIs4JaITeOTMAla32sgnothsdY2DiiIlDOMkn7fN1ZVlqQJTpulzKvD6/Xly0Cna5UXX2ZuHbhog9YLXVpjXrAVN9EFeDhNI5YFTSp8E8CTz2W97/p8C+LXhv9AwPz/v+72s4A5l41avHAP0B4Bfylqj2UJ6xT9fVmWFaTM9SyZAqKKUXp7p80todBzfmtjH80kcyyetrY5t5DnLwpvl9MWrHazUrxtVcbR9stAdx6l4BPV2LzD/X2WnosKzKt22rllTtRNBuhNkt0wwUicxi8Wicl1dVnD5ZNT6lWOAWcaDyE1jki/rfc5WepYXtt0LXp7/pjGBTCKKZtcJJZtCdGQ9zLrZvHcWax3knC2kYnntKo62d5jecdzoOMjEo2j1xHJw6ZLtO1WeZSCbeeJHo6md8NMdHbsli5Ey4Dr3yrGC0y0FG2QsbRo0t631Tlsp1Y9Ht630LBaqBk92hbTeaWM+k9i5lMKvbd3URlHf2UyVlHnnQjaOfjSFVtvfQPrBZn56u9dHx+nvHE6Zz8Sl5ADIp0B2en30Ikkuz2H5oGVotGEnRAjrPkxgxAy4H4KS993OD+vyBhWDJuvOuLa6hpNHDu15RvXQjupN4rIwCRCKVkhenk3qj5gcdpFtz7S+TiI6gYdeMY9OLKu96re1cGBPGHovhbZRB8bb/ksz2HPptA0fdGkY5M0P6VWdEEzsxK3CSBnwWq2G2dm95Td5tTU2Wz0rJ7FUK76ZHMRg20rStpY/j/ecyk3itqGyQhLx7IVJvY9bcUmE3ztbjTpOnJAvG8zCluvH5SURjaBQ6+y0LYKqcfT2VdSp7bl02tQF+d7XHcPHv7aEensQAPfW19FxLdl0qYnslg2MlAFfWFjgfs6WPf3415bQ7DpWTmKF5euVOco+PcsPfsgOLt1MENu5sip9KJKxlz6Teh86fSJqT7e+jvedLL+yLhm21IGpS0wlNdO0cuJ2fHJPX5nq2Warh2bX2Qm4euvrmFzIYcOlFjSmTTBSBrxUKuH48eN7PvcKPy2InMtiv+uA+Pm378618A8euAvA3vszZQeXTiaI7fK1oj7kDXaRjF3YqPehqph+GSqq9XVYePm9lbV3ElH51Ezd1fI7f/QQCICJ2rrxzpiFX32d/XKBiGQTNKZNMFIGnBDeqf7dwncvgtURnK06ICbFdLzKUev0tW/CDqKDB5Fi2iqjKpN3K5Kxi/2q9yHTno1+8fJ7q2vvyKZmmsaR3n0HvzaIrAtStb6ObZmJIJJN0Jg2wUgZ8JmZGeF3XuHrKq9OpT4WpsV0vMrRTme0b8I23ebqnrKThaiv/WQMqLmPvGVWbU5AKqmZQfDyK2MYVYyn6ko5LNccS4eTCK42rRM0ZvVKdtFgCyLZBI1pE4yUAS+VSjhx4oT1qoMudCv1eWGafuRVjm6lgKNTSa2gm8ydgX7v1j1l575fN+3SlXEQnbfKLWQ7NdPLr4xhVDGeOhdThOGaY+lAYxN+5QNMg8aiNi+ubqNU6/geEDOBSDYyY1oXI2XAJycnQ51F/ZRD1ijaCHq6ylGheeXVjrfoUdCdgaIDLbqn7Lzv1027dGVsa5tru463TGqmCv2Tk7sL/csYRhUjKzrlG9YqVIaOxnZV+KyfnunqlsvzWq2NUr2LQySO+Yy9ksB+uwBgr4xtYqQMuOM4oRXWd8ETgIpRtOl7cxxHSJMIskWPwshv975f5kgyj69Wp4c/sGhgdFahsu3xUjNVDaQrYx3o1N4JM87hBy8d2wKeg/RMZiyKTryu1zvIxKMgBMaFwPZTxkEYKQNer9exeHRm36PLqpXgbPne6vU65ub25gjLVgH0K3pkO7+d936dI8mlzS2s1x1rBsb2KlQlCC1TU0Mk4yDo8mAzzqErExHPMnrmNxb9Try+oBMJ40JgqotIXRnLYKQM+OLionaGgckKw7QSnO6uwb3EmeXDRhVAk+2oSlEsVd5vP34Uc6sFq4FU2VWobnteqE5gPBnLQJcH3TgHK3eRTGT0TMRzWHqmazNEEE2CIr51ZSyDkTLg7qXGqkFKGwbAZo6qrLF0+XV5KNaCb8J26VUNWAJylzer3miuynu5VJQ2MDbcILZ3caoTmFfGLsKuvaMa5+DJXbTTkBkfPJ55fcfGoEz6RDexgQee7vjxLeLXBkbKgMdiMa3fBfn9ppJR4dF7FyYDQHcCcPll61QE3YTtB1YR3H4wqelhk/dYLCZlYGy7QWz6gFUmMHZM68YmgOAJ2I9eVbcQjy/Z8eGnx34xKNvxGhN46QzawejaLRmMlAHP5/Nav/MzAO4VVfOZGA5l9a+oCiO10eXXqxiyN2GLaAyrpocfVHjnyVh328/yLjp+rjMZqJxw9DMqLL86sQkbmSUqbiHRQRnZ8aGqx2HFa7zQKWHgIohvXbslg5Ex4O1eH1eWC3j5HbdbWWG4BoBMENTaDhayce2slrBSs9bX15HJZPYMENWCVDvuF4fvfrFR08MWimslRKcjgRkrKpNJkHxUdxaq8vYzKq6MvbtB1UnSxgE0P4jkzvIlOz5YnoNoCrsyoGkJgyC+XX7DwEgYcLfz0G7iyVX/G2pEEBmAUr2DbCICCoq5ND81MAhhpTa6M7eJb9A78GbSMUynYths7Xa/qBhmm75EHq1fWWrhyjNmN9SwkHGhqRgI1UwTP+TzeW41TZka3C6CUiVFV6OpQFbuMs/xeLYlax3I6O+NagvL1RbyCf4ZED++D/wK3O3glySB5y3lrnoHRT4ZVVIYFn4rBBMaO53OLnp1fIPewVlpit0vYRpmWRRrHbTbHaRiGemj3zI0y/jQVYymaaqkF51OB1uMAam2etqnd3mpkqKr0cLO/Ra1z/Jcqndw6eY2ziik5tqETBD38UtFrNUGfXfmcE5poefVY9sYCQPudnDcqWE2nbVWo8M7KEyK1otWCLJbM5ESNZtN3/fqVOYLux64lx+XRlkDsZCN41CSYqWmf0MNDzI+dK/RDDtV0otms4nFmTlrp3ddeGniXY0W9olMv/a9PJfqg/46d7GApy5XQjkZqipP3iKo3Oji1FwGW+0eHr17QYnGID02wUgYcLeDVyszODKdtRLECoNG1cpxQUoUlD96Kyrz+YF111AKpWJPiegEfurVL8cbOjDOrOC1LeNDt5kqKZsT7bcAsHV2gd1h6NS4kYFMuquX50s3t3HuYkG7/LMMParyZOHty6OTCRzLq9E3zgPHoIMnGhUk5gd1BWwGsXQRpGBBNAb5UoPyR2WNs9/gDKvuyM3tDiilmE7FlBSzXCruFCwLc4Uo6jtbqZKyu6/vX1veCczbrJzHo8m7ywwjMCib7uo9z3HmcA5PXa6EFqC0EZ8ynWDHeeBDxOO7E/NNg1iAvgGTUbAgGoN8qf/wZcGD2cQ3aNtIevk5nIuDUuwJmIrocGXgylhX8VTkyes7W6mSsruvbLfGDczbMjx+6Xa2d2ay6a66euzFfmew6EywLo0T0XEeOAAgl8vt+lvGeLV7g5uwedkXJgbMHayJaAQrW20sV1u4Yza95zkVJWKVtj2R4/7OFmxlz3iViT1cEqSYrAx+8Z5B7WQdxbMVF7Fh2GR3X5FEgtv3uvyrLEaC9Ee1Pdl4i44es3SFlcEiy7OKe/REBvjFhX4o7suRMuBrpXWUe1HpAcX6ZNmbsE0M2EKWf4eg266OErEKMNHaBhDOZai89+msTnjK5O3DoP5kZbBSLGFmalLLkNrKh5ZdGJgExty+n3bKcNIze/pex/CEUfdcpT1Zmjc2NpDNZqXpEFUXVLmoQnb3Jsuzins05VSt+/ZdjIwBb/f6+PJSG89L5Ai7YFPo2JuwTetJsHcImlx/5rbpVYB2oyb1O5uV+lTh7WOZdDAWrAwOH3qh0L/qykynpocOzzYCY27fX1/L4rZDM8q/ZyFr1GytMEWQoXl6elr65GNQdUGbfnOZVbWXZln3aDuRse7bdzEyBrxY68DptJCKZaUHVJCgTQ0Ye4eg7g2RvfAAACAASURBVPVnLE3ubzabzcBi8CpGiac0Jj50YPeBKJ10MFYGmxsl4bM20sFsuIx0V/q84/yTEcfK1lrGqNlcYQbx6oftWgO//52ydu2dMPz3QPB5Dl7fybhHJxqbobhPgBEy4AvZOOYSwA3FHGH3JmyRP85ku8wOJABWVwatVivwGZWVVxj1Ptw+MEkH88pAxLPtdDAT+eis9AF+xToZGfPAmwyCjJpqTREZI6kzrja26+DVfGexX9UFvW2KeNYpt7CTTVZtW6XTi5Ex4Ino7hxhHZ+gDoIGKDuQbObzyuSPyhqlMOt9JKL20sFEPNvwb6us3Pza0lnpU/B3Zzo5wiLZBBk11QlMxkjq7Gp4Nd9F71epuGgjJVbEs0na8tn7x3ngAF7IEZaBzsAKI2Bi4neVyR+VNUqqyqta78PWtlbEs616H7I7LpkUUdWVPu8znRxh3cksDNeDzq6GV/NdBLefg2Ryq84N8MDK59qNFbzy5XdYo8ULKQNOCHk7gE8CiAD4DKX0o4Ln3gngCwBeTSn9tjUqh0gm7QW0WIQRMGn3zG7CZvn1c+XYrsutU+/DRvaGSMY8+mXqfejA1Fcu6mveZyJ+/frJJFir43ow2Y3wkEwmlekIkomtBZsfgmgWFUebyYVXYyjQgBNCIgB+D8BbASwDeJoQ8gSl9FnmuRyA9wP4qzAIBYBUKiX9rOp2WXQTtu6qxVUik5uwvfzarv2yn/U+VHjwkzGrQEH1PnRhw1fOU3beZzx+Zdx2fmMyqHKeCnR3I37jS0WPXcjswGws2HThVxxNNptMBzIr8NcAuEwpvQoAhJBzAB4C8Czz3O8A+BiAD1ql0INKpRKYleGFynbZ78Z52ZmX53oxuQnby6/NkrX7Xe/DhYxbRkXGQfU+dOFnIG3X1OHxKyNr0Zg0rZzHQndl6ze+VPUYkCtXoCJ/myWBee15i6MVNPiVhYwBPwrghufvZQD3ex8ghNwD4Dil9E8IIaEZ8NnZWesK5Ha87I3zLGRcL7o3Yc/OvnCIx2bu637W+/BCxi3j5TkIPJpMqkqybeuU75WFO45z+ek935nIWrVynmk9HxENfqUruvEs2j31k4l+OzDVMrw2SwLz2vP2k8qYVoXMaCecz+jOl4RMAPgEgJ8LamhtbQ2PPfYYotEoHMfBww8/jLNnz6JQKCCTySASiWBrawvz8/Mol8uglGJ+fh7FYhHZbBbr5TK+s9rA9+pxvCzTxRtun8b83CwKxTV0oylMxifQaTWwuLiIQqGAWCyGfD6P9fV15PN5dDqdQSnL4ffxeBzZVAb35pq41ozi9iww26sAThJLKwUkk0mkUilUKhXMzs5ie3sbnU5n5/epVAqbHWDOKYPE08j1NvHcFQcvO3kMhUIBP3tnBtudFKK9JpxOC8uFvTwBQK1Ww8LCAkqlEgghmJmZQalUQq/XQ6vVQr1ex+LiIh45CTT7CRyZn0Fh5QbS2UmsbzeQoF0cPXJ4h6dcLoeNjQ1MT0+j2Wyi1Wrt0JxMJpGOJ3BvromrjSjuyFJ0KwW0U4d3eIrH46hWq5ibm0O1WkW32935fSaTQWM7gsLWFnrJPKZ6mziUJrjWdPDcledxZG5qF083i2uod/s4tjCPankdP//KHMr1DuL9Nta3G5hzyphNRXGz1cNzV55HJkbQaDT2yCmIp/ZECgUfOQXxFDT2AGBlfRONZgd3pjvo9BpY2ZhCpFXF5OQkHMfZkZPf2JuZX8Dl68u4WGhhuUlwJtPAj73yFJxOexdP//jlSTSQRaRdQ7fVQFmSp5n5Bdyba6LQIjiej4NsraGROsTlqden+PNnV/boU6lU2sXT2fsXce3GCvKZGHrtJgorYn3K5XLoVdZxe5bC6dQwlwWm4sDS0hKisQS++FwVC7SKL39vCu94WRb9XldbTnRrA3fnWniuHsM92Q7i3Ro2Nuqo1WqYnp3H0moRk8kolydWn64tLQHtJl6SBOJODauVGUw0KlJjz7URv3jPDArlKpLEAZwullYGPNVqNWxsbBiNPaFxppT6P0DI6wB8iFL6tuHfvwkAlNKPDP/OA7gCwHX0LAIoA/hpNpB5/vx5evr06SA7L8Rff/8K/v0PBvmjrZ6D9z9wGw5l5W7C9kO719feLrurMnfmtRn9XlpaEmYomK4GRTyrIIh32cwB7+8LKzd8szJs78BU2jOVtfv75WoLa7UOTs1lcHu0irfdd6f0ylF2TMrI9vpmC5/65vVd+mQrt5pHg/u+u9INPNNM7+iviTx579E98yCSremY89NjGVy4cOE7Dz744H2872RW4E8DOEUIuR3ACoBHAbzH/ZJSWgUw5/5NCPkqgA+GkYXCyx8Nq2qbip84rHrbi4uLwsFjI1PCTc/az9vMvTTyfu+XF70f9T5cusNIlXT7I5+IYq3WwVa7h61EXirgZjtVEgj3rkkeDe77rjQdK24L0XtsuQgBtaqDIh26pfXAKaU9Qsj7AHwFgzTCz1JKnyGEfBjAtymlT4RGHQNe/qhOuqDtWhA6qVkytKys3sTj18AdPGEVorKhQC5kL5zw/p6XF+32k+hSZt0VEitjmVo2urIGdvfHmcM5PHr3AsjWWqCPOoxUSWB/L/vwvu+5K8/jZXfcZnS6USXWolsSGDC/lAV4EdQDp5Q+CeBJ5rPfFjz7JnOy+EilUns6WTVdMIxaEDqQoaVOo1iu1rjpYDaUz1b1PhF0aGRTzNiKkmxZYJNJiJWx6LSkLfD6Y83ZW4LYi7BSJb00qZZylXHh+O1iFqZzyosv1ZPBtiYmlaqDomwWnbRJWYzUSUxvIXgvZAehSuW8sFcnMjP715dqvulgJqtBILh4z43NFj5/qah0LRoLVRpZGbMVJdlLAkRXg6nUcQmqZWPT7872Rzwelz60YzNVUgey7oSgZ1wZq+hYUGaL7SJtLoJolMlmEdktGxgpA16tVjE1NeX7jIwyyFbOMxkEpulZxVoHCaeBU3N5rYtUZRDk91uptlGstXFqNi2lNDbAyjjokgBeP6qu1vxq2YR9RLtc2cTj391UOrRjK1WSBz+5yuzYZJ7xytjUX29DPjKH2nQvZVmrddCXsFu6GCkDPjc35/u97Am2F8NFqjIzeyOSQ6ftaF2kKgs/v99kMopirY2tTg9HJ5NWlUYEVsZB/cT7XubCXtmyBGG7mfqpSazX17UO7dhGkFxlXB6iCdXbP0F6zINoHOgG81UDw0G0+R1468XU+ZXFSBnwarWKTCbD/U627kgiKlc5z0QpZQdV0Mz+jlNpkOys1nbZhH7vILz7SA7vOrNg7SajIBp5Mg4yYOz3Ni92CPuSiHivGWqsRQY7QeKe+CZ5QM7lwXNLsf3jp8d+8MtsUek/mcCwrv7w+mhjTY9fGYyUAe92u9zPVeuOBA1EU6W0FQClTg+3Ka72bPiuVf1+NjNgvDK2qURe2KyLLWpLlnbq9ELPBPGjxSsHv5vkXfhNpt73uM/wdkN9gR7rQCdWFRQYNtV/to9EdssGRsqAB9WKVqk74jcQTZXSVgCU5Vf2YIyf75oH1SCQDf5EfezybFuJvLBZF9vUB7+4uCjlItGdzIJo8crB7yZ53fdw+zrlnxdtu0ogi6DAsIwLTgW3NA/8xQSZWtG6dUdE7enOyiqDSjRgWX5lS2qKfNeid+sYyiD+dIO4Ls+7M4bauLS6jTNHzOTqpV3logCVtlQNgEyOsMlkFrQYYav4iW6u0n0Pr3+WVsQ8hxlf8Y5Jv8Cw7RTiW54H/mKByI+ksiLUSS8LY1b20iMasCy/QQMryHfNQ7HWwVqtjQlCUKq3rfBlEsR1eX4hY6iNtVoXn79UxFNX5O/aDII7AYVxmMkrh6lkDO1eX1i8Kcg36sZ2eKWOZSCzGLGRmshLp/NOil56/Xi2WXXTC56cw9xhehGW/xsYMQMeiUSE38luQ3XTy4IGqCqCThfy+NXJyAjCVDKKUr2LWttBNhFB3kKKmkkQ1+V5J2NodRufv1T0DUzbDDgvV1uIRSaM0iNd2perg1jEp7+1LBxvfmPaHa9+pY5lafFbjKhU8ZN5Tz4gs8OPZ9urXxk9E/Gjks3iN178+DXFSBnwra0tTE/vLb8pCxPftsoADULQ6UI/flUzMoKw2erhUCaOxRxBn1JUWz3jPGMTJfTynIhO4MyRHJ66Is4YUq1n4kfrVDKGz18qotzQP7jkIhGdQCwygXKj62s0/Ma0TqljmXhGWKeM3fcE7Vb9eLa5m5bVM13ILghN7ZYfRsqAz8/PG/3e1qEPdoCqrtqCThfa4lcGC9k45rMvBHRUB7bIYOhuQVmeVbNAZOqZiNpv9/r49LeWrW3fg066Fmsd5GfEOcJssE3GeNsswKa7swmaIILGta3dtKyese2aXFDCoztMPR4pA14ul5FO764dodLhtnzb3gE6nYrh3EW1lD3R6UK2MiCPX9swMbZ+SqQbxOXxrJIFQql6PROvP9zmylTUt95+O5Nr45EHXmFkaF3oFGATVaM0iQ348V2sdUC3NnDiNrNxLcNr0CleFqo8y+5kwtTjkTLgbO1ynUFmYzu5a9Xm9PHp82qrNt4A5/ESVKtddvIyOSrsBxunFFm+3/USsywQgF/PRKctm8FSgH9gptntWat0qVOZU6Q/tssVe0883p1rYfHIUaP+la10aToB+tUrl20/SI9NMFIGnN2K2KoF7rdaCDJ6Mqs2Gb8kjxe/rZfs5BVmWpaNU4os30gtKNPB9qWqEWblE0b9G9GBmXrc7M5KL2yu2G0f1vKeeHyuHgvlxKPoOd0JUKZeuUz7YxfKEMVicSefst3ro9PrWwlMsEKwWbpSti2ewvjdTiO7WggrLSuId9n0tz0ukHoFQN6YLhX3jY0JTvfATLdSsDahAmrZE376Y2M3IjrxeE+2E8qJxyDILMqCClNp7VQ9dss2RsqAu/fDsdHlX37tMe0DCDzYLF2pklLHKozffXiyq4Ww65rzeFdJf2P5rlUrO22EUe2QhTUlDUhHFPljN5xcCFz5Q1Z/THYjgPjEY7xb840/hSF7lQBv0C5Elb6gey1NMFIG3AUbXY5HJqwquc3SlSoGlPWXlupdZPP8AyCyqwWdlZSpAqmmv3n5rsG+28ePH1sTnExg2yRYzNJvK/c9DP1xweN5MhnFxkYdgJ0Tz7LQmahlY1W8Xfd+LD6AETPgtVoNs7Oz+7KqtFW6khdkCzoA5A6SOaeML15pGa0W2OeCYEOBVNPfvKjVaqhHMsarYtlyoTKGVfWcgCiwzZODO6b9+ODlub8Yiq3JwI9nXt+rZoXJGktdnmViVUHu1yAZm2CkDPjCwiDAFeR7tTH78Qae6SCQNY7uIHHiGWy2zS5lVYWNzBITWhYWFkCiZgZmV/Bs6H8NKjHsV2FP9ZyASjqiO6ZF4MnD9Oo3G/pjomdentm+V9Exk1gVoFf/Jog+nryCZGyCkTLgpVIJx48fB+Dvew0j48J9p8kpMdkVvDtIZpwKIulp7dWCDoL8frZuRhcZAFfGJpPRruBZt4dMIopmV+8eSZkVl8lBJu+Y5kEkD9MVtIn+qOoZ20d+PKv0neqOWHUhpUMfT15rN1d8ZWyCkTLghBDu57z8WpOAlN/qQsZIKpXW5MAdJJevAS89qZ8VYSs9S5QOZuLeECmQK2OTyYitTmlSrCnoNKXpQSbvmFaZDFQmONmxIGsQVQwnr49EeuxCVsd0s9Bs5biLvmNlE8SvCUbKgM/MzOz5TJRfa/uiAZXfi9LnVFYXiegEbj9ySNt420zPCiqArwo/BeLJWBWi4Jno1KFqWy5uVFtYrraQT+hPZi6/qpOB7AShMhZkFxgqbg6erGcNZWyahSazy9xs9bTdsKxsbIxpEUbKgJdKJSwePb5rNWGrIL0Lk9lZJn1OZWVZKpW08kdNL6RgEVQAXxV+CnT5xk28/I7bjV1fbD+bbpt57obHLxWxVhv075nDegdyXBmHla+/u656B5dubuOMIKgsu8BQWYiIzjeweqzLk04Wjd8us1TrYK3ewXwmhkPZhBU3rK4ey2CkDHgqk92jhKr1DoJgEqHXqR7nh8nJSannWMNsOz1LtKLVhZ8CTbQbeHL1uvX0LNsGsljroNzo4tRcBlvtHh69e0Er6OfK2GTcyaRJluoDns9dLOCpy+K66rILDJXnWFnz9NhmIFEGol0mmSCotR0sZONSZ0BkIKvHOhgpA16u85XQZv0KkXFRTVVSTZ/jwXEc4XdBQUUbRbu8sBEg9WvPVaCTSYIlyfSs/VZ6UXtHJxM4lvcP2Ipod2Wsk7nT7vVxo9rC4z4lcN12L93cxrmLBaPYhYgGmRRL77tEeiyrZzp9FQTvRJdNREBBMZdO7Nod6o4/Pz02xUgZ8Hi/zVXCMI2LrWP1OrN3vV7H3NzecqMyQUW2T3QKHdk8jBDUnktf0qlhNp2VSs+ylTqnQ6+tbAmvjFXGsTsGlqstrNU6ODWX8U2TPHM4h6cui+uq60DXqPH0WLUtkVtLd8x65ZlPRve4CE3Gn0iPbWCkDPjRI4fxgeMxqzOvFyapfy5EA0tnoAdd4qwSVFQxOGGchJS9Ym21MoMj01mhK8DkWHOQgbSdKhlEO6B/4a07BvKJKNZqHWy1ezg6Kb6tR3fV6te/ukaNp8cyO0TZYmG6Y9YrT9ZFaLKDG19qPIR7OajuqTyZ049h1BLRHejsZaheA6MTVJQ1YKLrp3RXOCr1YCYaFSTm9/oM/fzmNiYa26mSQbS7EF14K7tj2WgMAqiP3h18/6nqTjWof3V1g6fHppUtVXVMdSybuG3GlxoPEYvFfL8X1YxQOf1oo5YIC92B7uWX5YM12qbXoLGpWWx+rYmx9PoX0/Hd926yMvOTschvbiMwaTtVMoh2Fzx+VXYsYe1GgeD+Vd3VuXLm8RzUVhAtYZ3gZGnUmRSC7JYJRsqA5/PiMqMioaiefjStJcKDrrJ5+WXTwb5XqgvTwVyorDLY1Cw2HdMkCJqITuC9rzuGj39tCfV2D79/fllY08NPxixsBiZtp0rKgsevyo5F5sCL7tF4mf6VpcEr5196Fb8uiF9bQbTYikmwdMvqj9+koDKmVSFlwAkhbwfwSQARAJ+hlH6U+f7XAPwCgB6AEoCfp5QuWaYV6+vryGQy3O9EQlE9/Rg0AGTdMSolZ2X4VU0HU11lBKVjmhrLzVYPza6zyy3Bq+nRr4plzMKmX5fXlsyuxjTYyxvTtiYm06Pxtlb5e0rt3lzD9OTuMro2gsY2YhJeelT0x29S8LNbpggcoYSQCIDfA/BWAMsAniaEPEEpfdbz2HcB3EcpbRBCfgXAxwC8yzaxfjOZSCgqg1BmiyRTStKWX9bLr8uHbDqYjnvhnT96CAQQ1oY2UWbZmh5NxcscbPp1bfuIZcAb06K+Vp0sbByNN919Antlvzi3m2dRxUUbiyDvO7ztBY1lVf3xmxRu9Qr8NQAuU0qvAgAh5ByAhwDsGHBK6V94nv8WgH9kk0gXnU5H+J2fUGwMQkBOqDqGU6SYLL+JqHw6mKlPkAfZfjSp6VHtdKynMHph85SqjbZEY5rta53JIoyj8SIE1Q/yyrlaXt/1/Z4VerWFL/z1WuhZULoGmQc/++Nnt0whY8CPArjh+XsZwP0+zz8G4MsmRInQbDZ9v3eF4q15AeydyXUhI1SdfGuRYvL4lV0Jh+ET5NGuEjTmKQ37Wa3ewGefCa+ipM1TqjbaChrTLnRkpDtWALVSq7JBV5delme2Hyk1K5fLQqdEss6OUzQpyMpYBzIGnFdKi3vNMiHkHwG4D8Abed+vra3hscceQzQaheM4ePjhh3H27FkUCgVkMhlEIhFsbW1hfn4e5XIZlFLMz8+jWCwim80imUxiaWkJCwsLKJVKIIRgZmYGpVIJk5OTcBwHW9s1fPGag0mnimg0hs1+Atl+Dd1oGg+dnka33cLi4iIKhQLi8ThyuRw2NjYwPT2NZrOJVuuF75PJJFKpFCqVCmZnZ7G9vY1HTgIkuwhaK6NaXkc8Hke1WsXc3Byq1Sq63S7O3r+IazdWMDeVQWO7ioIPT6V6F3NOGU48gxmngsvXgKML87i+WsBsPov19XXU6/UdmmKxGPL5PPrVdTSRR7XTQbPZFPIUbzdRqPrz1Gu1cSQTwaRTBUkkkXSaWFoq7uLJ/b0rp8pmFX98rYtEr45sfAI//aqXorJRQpMkEG1v4660g6tNBz+4uoSpdGyPnFieUtkcbtxcA4klkOyUcVe6jytNB89deR5zk2llOXU6nZ3vU6nULjm951QM1bqDk8cXUVi5gSbimBjSvNTq4fK165hMRHbJCRhcRMCOvUdOAr1oHrn4BAorN+CkpzHnlDGbiuJmq4fnrjyP4wuz6Ajk1On28IPVdaTRQ6/bFvJE6lu4N9fE39XjuCfbQaRVxeZma8/YY+Xk6lOpsLpn7PF4akam8eSFy1huTmA6GcGDJ9I4euTwrrG3vr6OfD6/w5PL83QqilKri+euPI8Th+eFcnIcB7VabZecHjkJdEgGs7k0trfWcFuGINrbxlSWYCoOLC0t+dqI1ZsFdCJJTKeiaDXqu3iazE/j3lwTy60J3JaJoFspoJ06vGvsffm7V3G9GcF8cgJv9vAcj8fRjeZQUBh7zVYbyM4AtTKymTTS6TSWlpak5MSzEb7GOejKe0LI6wB8iFL6tuHfvwkAlNKPMM+9BcC/AfBGSukar63z58/T06dP+77PD0tLS4H5lNc3W/jUN68Pi1v1QCnFdCqGVs/B+x+4zSifOQy4qxd39fHe1x3bOURyb66Jn3nglftCY7vXV0oH63hunWH71suPzGrWu4K7O9vE9f7kTkVJ09xu2QyMIJpttuV99v/6y7/Bhe2UdF1tU794ELz645WrH1RlLqPHsuPR+/6g2JSoPR2eVWjxu5xcBhcuXPjOgw8+eB/vO5kV+NMAThFCbgewAuBRAO/xPkAIuQfAHwB4u8h420A8Huyb827HDucG2zFb+cw6UI2ue7d75Q6s1awIgmo6GC9XnMePKOtBWFGyC7zr3gWjipIsrSYlEGy35UWx1kG5DWkfug2/eBB0Tryquhtk9FglbiXjIhG11+7p1xWXpUWGX10EGnBKaY8Q8j4AX8EgjfCzlNJnCCEfBvBtSukTAD4OIAvgC8Pi5dcppT9tm9hcLvgGb54/T+bIbhirclkF8w4urwLRdGrXYNKh0SZfQbniPH549PhVlKTplHFFSZZW3RIIYbTlxUI2DhpLodVwtBYYfnTpyp1njFV93C5ENMjoMQuZiouqQVh2QaJaV5wHHi3dqDq/spDKA6eUPgngSeaz3/b8/1ss08XFxsZGoE8I2DuYgk5shbUqNw08dSsFqeCgC3aQy6ZnycJG6V5Rn/B4NgFLaz4Z1boDkdeWrVKviegE/tuTccSmF7UOTPmtlsO60EMls0pEg6wey7Tl0quT4qpTV1wnX72gyK8KRuok5vT0tHEbvA5+sd6EvTXxwk0eQUrEG+S207N0FcULv3x9lmcTeGnNSxankmlLpcSwjCGdm53B5KTekXCRPHhjxXXP7dcE5jdeZfV4J97SC74qUcXlosuXzo4asGO3RBgpA75da2CzHzd2B7AdHFYdBdP0rGazKV3wn6cwYaRn+fkSbdRy9vJsCpdWkzIAXr5USwzLrFz///bONUaS66rjv7vdO9PzfvbO2Ou1Fztr2VaIjeNg88EJaHlYkYgly8QmigLSCsmx4UP4BIqErPCBhwQIhCWDIIJEAgyRZVYoKAiT4Chah/jt2JKTXcezD7vnsTPTMz0z3T09c/nQXeOa2qq6j7rVM6Wuv7RSz3Z11fnXuffce88995wgX9NBMkwfYauPpDNy04E7rr3q6Nj/jm1LJbo43emHbbityzYdRGYMeKO1y//+eJ5X1te0d+xN0oymFTPtdTCbZW29XteWMazDhA0grnKH+GHKLW625OccfEaaOT1MeLnIrxPH12Y2Gfx91Ma47eEyEx93mAz+76N07Me+jW3DUomN1i6XVus88/o8K1vhhS78cuq+a9t2pMPXFpkx4PO1Jm/X+qwrYdvMZMLum2Yl7GCHCOYRjpMxqsMEf2M6k9IxnC6zAoblTu52Tg9/qGTa+XWS5orWiVhJw1Vgu7EJepxt91s8ua5UG8zXGpyaGnRyGAjsi4JMlmcSPTcOmTHgM8N93DHc5NVawaoSdtJIk6Q71qrwrLAiAqZ5hHUGIZMZh67hdJkVMIyz7uD32vvrLNQaoXlidHm7CpX0oHpuklzRJj5Z166CJIO2Duc4meP6sSfXaKnIfK3BWrPF8dGSs9WmTTtK8zxHZgx4f/EInzo1w/2D48pGmEakic2OdVD+uPCssCICpdLBHjoKprCNqmjuYnPTQ6lk7orw3uNircnixjZCQHkoujpNHFyESpogjK+NrCoj6sJV4G+LcTpRtVldzlFuG90iE3ddP8Ijd6oLXdhCZyAZOFpgqZHeeY7MGHCAkeFBRkf35zrRnXEkLerrYpYZbJCqIgLrsj/1Q0c68bU6KWyTGjRPjsG+/mu+Uw0Q3nsc7CtwTPTx6J0z1gWlXYRKmqDQ18/F1TrjpSKr9ZbRQO1y5eOHarLhtcWojImqNutxtpmUqAYtl5OJOJgMJIUhdyuAIDJlwFdWVugfHLYK5bE5YRa8n+uG4ZcprIjAOwtXWdrYcZbUx0Oc2yY4yzRJYZtEnv3LzVGjASL4Hm2Nt/ecbhgAaPP+rzfmeHltgIWNJuWhoxwb7tceqMM2qW0NY9i9dWLBTV0rHmfd9AFB6AxarlZHUfDcdYu19qRBNZC4OtsQhkwZ8KmpKWvfm+6swtSfmcTFESaTv4jADTNlpt9fdjrD2ue26cz8oxqhJ2MaFc398Ov03c2i8QBh6y+Nu1/SCi06mK81ubBZRBwR1Bo7zAz3GQ+QatvZvQAAEZ1JREFUnqxpp4hwlZrW42wbo96NATZOz957Xqg1WNzY5pjoozwUP5DUiulUpIeMGfD19XVmyjPWy0bdWYUfOspM0mniZguNrQ3njXWf22a7xVB/ka1tdxXt98lvceDplmHpxD3lPd/09GoclzTyjpwYlKyuS4b7C0gk04Nq332YzC4jgcKg2wZU13mc36rtWMeo68ywbQdblZ699zzUV0QItNx16+vr+UlMaCdGdzkC626OqZSZViVsj6/Le+53N/Q7q2gfJpfNgSed5aYuZ5vTq1H3c2kg/fJ/8sZhTk/MMlYqaukhSmYbf7hp2/HP9lV7UHGbqR5n2xh1HV62g60qgm28VNzXf3TcdQdd0OHQwIsfNQnlSXISS9W40jrBGeTr8p4qt40NXMwI94zDwHXKZ+lytjm9app3xBRB+Z+4d5aRwfYzdfQQJbPpxMZ2deIiv87x66+jv7+9WZ3GRmySQUEngs204HXSWP84ZMqAm8TM2uYt8EPVuEw6jW6j8ncaFd8k+wEuBkDvGlczQlDr2CQDn85yPmneEVMEQzPfvHCRj9/+ESeRJyarJNvViYv8On4dpx0cYONmVUWwVestIxdOklh/FTJlwAcGBrSvTerfBr3GpdtpdBpVsNN84fZ4vqYrAJNZUtJ8H7YdU6Vj0wx8quV8nIw6x8lNEQzNfPHKDi8sXbSOPFG5W2xTsEbp1UV+naCObd6r7TF+HQTlSXqSVdWPkyBTBtwkMbqtf9tlpw3eS9Wogp1mozUYe3/dhmrjanGR78Pm3al0HMXZRb6P4Hcm78w0HNULzaRwxDryRMUtSQrWuKyRSfPrJC1wkOQYf/A+upOahz92DAFa5wJM+3ESZMqAV6tVxsfH9/5OMgpHpdx0FWkQ1cjiGlWw0xS2N5XP0WmoNsbNZb4PP1SdJqjjqGeqMvAlzfdh8s5swlG90MzRnWWag5OphmbGyR9VUDFOr8H3bxrCqaNjF9zikCS/jgo2/dgWmTLg09MfxlMmHYXDOrzLHXEbF06w07QabqpZ2/gETQyzbnSCjs78OjaB6UDicoPaJveOJ+/lpVFumB534vv1wyb3js0sNuq6OF3b6ljFLQpJNtltbEJa/TgMmTLg1WqVoaEhIPkoHNbhXTQMD7YuHH9nuLrwIV8V0vAJmrhAdIyzjs78OlbxspE3LBws6Qa1be6d/uIRBnbrTlwzQYTJr8q94/KUb1wRhqCOTWG6D5Bkk912Q9S2H5siUwZ8e3t773MauUlcNAyde6ky54XxjYPtasTlyUKd6BCV0YT9nF0fnjENB9NdWehELkQZyDgdJ+Uf1Lkq905S+OWNK8Kg2669e6rS5cb9LiolsG5fT7ohCmZ8TZEpA+6Pp4x6sUmNku6sU2c2Gbe01Mmcpxs/aruB59I46kaHqIymn3PUPoWtfoP30w0HSzP3TpyOXR9yUeXeMUWQi1/euCIMuu3ato36fxeVEhiSuYhMkMeBdxCMpwy+2DRmbLYukiiYZM7z+KoGJRtZbPy2cdCNDlEZTb+Og7ySlgZz+Z5UULkwPPnjYoSjXDNp5d4xQRgX3UyOunHRtu/e/7u4lMBpIEw/eRx4Byo/kqvdaZNMfaZLK5PMeUNDQ9ruEVNZbP22cTCNDglr7H4dB3mlse+hQtJDIarcO8E2HRd6CqSae8cEUbrQeb+6/mDbAUx3IHEFlc1Iy/8NGTPghUIh9vukfnGbTH2mncHEiBQKBW2jZSqLid/W9awPoldLQR37eSVNCRy8XxL5bRAm/+b6h3xVoaemOe1d7nEE7xm1n6HzflX92IPtAKbSmcv3orMxrMvXBpky4Gtra0xMTER+n7Sz2WTq8+Bv2KrE/LpGZG1tjdnjY85zRUTJkcasPOw5ED2Di9OxrlvCdYf1y+96MKv4+B507h0VkuYE8aDqx96zvPdsM4BF9THX70VnY1iHry0yZcDL5TKgDpmzXSLaZurzb0zaJOaPQrlcdjoDVCFJNIUHXQMXZYw8HcfJaJIS2GWHTWMw8/PtVu4d20HIZhM4iEZrl1ZpjEZrN/LZrvPrxHGw3RgOz04YPqip2nQSZMqALy8vU+grpZa43naTx2sUSRLzh2F5eZnBwUGjQUm3c+qGZ6U164syRh5nXdjm9LAxYi7y6wTh56tjoHXaQqO1S7O1Gxp9kWQQcuWiHG+tslocj1wtRYXYupjMuBgEVCuRoM0wbdMmyJQBl1I6j54IIm7ppYpIWdxoGiXmV0HKqIPO4UhyPNjU0IbBdNYX9q5NOavkc+kWcnG6MYgg36SbjMEQusfuu2HfJl6S0ExXLspjgyJ2tRQXYpv0/bgYBExXIqZt2gSZMuDlchlRTMdPGweTQzu6ifl1ELb0ihtI0joerNtpTDMFuuCsks+FWyjuXjqbWHHyu15eB0Po+gpH9j0zaWimCxfle1vh+0omIbZR0JnI6a5iXIUQ5y6UDubn57npppusOmSSGbrpoZ2kBRL2ntvh60FlCJMcD3axgoma3ZgMGH7OjdYul1brPPP6PCtb2878zmmFBoZtYimTZgV0nBSmfnSXbiGdgfZL99/Ijy78hFtvuVaPJiG2Uc93MZFLcso6DK517EemDLhXV860QyZVrAu/mQ38dfQ836BuJWyT48GQPL7Yf+8kmQI9zp7OrlQbzNcanJoadLYZF8bftpq76nSjanKhWytRl6upH91V3zE5sXp9RPIuVy6apIORzSnruPumVQ8TNA24EOIB4C+BAvB3Uso/DnzfD3wN+DhwFXhESvmeW1GjoVJ80iPZ3YgEiWsAXucwqYStgv86W5eCLmzen6ez0VKR+VqDtWaL46MlJ5txnkyeeyPpfeI2vtPYNNMJldTVn03fcZW1L0oeU6Orm2tHV9euUxOnCaUBF0IUgKeAXwIuAz8QQpyVUr7tu+wMsCKl/IgQ4lHgT4BHXAtbq9WYmpoK/S6u0bo4kp3Ub6b6XZg8Hl+vc5hUwjaRz8bImHLVNSoeZ79Md10/wiN3zig342wMhm0eGT93Ux98GN8kMqZxgtZDGln7dDh7UHEziU3XDYAwdpEo9GPC1xQ6M/CfBc5LKd8FEEL8C/Ag4DfgDwJPdj5/A/hrIYSQjrdfZ2ZmrH5n4/czRZJOFCXPxFSZi6t1q0rYJvKZNtg0Zxwe55nhPuPoEht0Y7YVayBnZhLnukmjPftld521T4ezBxU3k4gQk4gkk1WMSj+2dksHOgb8OHDJ9/dl4N6oa6SULSFEFZgCllwI6WFxcZETJ05Y/dbE72eDJJ0oqmGdffk8r62XEp1605XPpMGmZTCCnL90/43WM1tduJ5tmeKD+QWeeXc3Ua6btPdobNxycdDh7EFpHA24h71HF+5DlX6S2C0VdAy4CPm/4Mxa5xoWFhY4c+YMxWKRnZ0dHnroIZ544gkqlQpDQ0MUCgXW1tYol8ssLy8jpaRcLjM/P8/w8DBbW1vMzc0xMzPD4uIiQggmJydZXFxkdHSUnZ0dNjY2mJ2dpVKpcPToUcbGxlhaWmJsbIxms8nW1hazs7N89iTU5QCzk2NUrlxiYmKCra0t6vX63u9LpRIDAwOsrKwwNTXF+vo6zWZz7/uBgQH6+vqoVquMTkzy0yNNtrebrPWNsb1SYak1rOQE7SXW4584xsX35xkpFdhp1jl/6QNoNTlZOkJpp8bV9UmObK5wdTOaU6VSoa+vj5GREa5evbqP02R5hrtHtlhqQGGoxPZKhVpxOpbT9PQ01WqV7e3tve+HhoYoIbh7ZIsfbx7lY8M7tKoL1EvHruFkqqcLlyvIVpObS0fo26nx/kqbcxSn2dlZdqvzrDb09RTFabhQoHJlXqmniakyd43UqTV3aQwOsb1SYUWOGbU9v56WllfYrRe5ZWCXoz7OYW1vt9mEgVnmrlzL6XOnjlLd2OHkiVkqVy5p9SdbPZm2vWB/WlpeYbte5NTADgUf5yg9PXHvLO9dusL0+BCb61UqAU6Pf+IYc1c+4NjkMLXqChUFp92Njb33KApFbhwSDO5U2e4fpFCvMjc3b8zJ09Py4so1ba9erzM3NxfZ9nT0FGmcVV4OIcTPAU9KKX+l8/fvA0gp/8h3zbc615wTQhSBClAOulDOnTsnb7vtttjnxWFzczO1E00u0GjtOtvobLR2efq7F7i8KZkadJfLwqV8rjd10+CcBlxyX13f4OmXFvdmkIeVs0scNs5ptGU/ktqtV1555eXTp0/fE/adzgz8B8ApIcRPAVeAR4HPBa45C/wGcA54GPgf1/5vaC9F0oqndAETN4TOvX715FGOTsw6a1iu5XMZqeLd0zXnNOCSe3V5qWu5bg4LDhvnNNqyH2naLaUB7/i0fxv4Fu0wwq9KKd8SQnwFeElKeRb4e+DrQojzwDJtI+8co6Ojadz20GJifIyJFBvWYUSvcR4dHU3dgBw29BrnNO2WVhy4lPKbwDcD//cHvs914NfcinYtdnZ20n7EoUKv8YXe49xrfKH3OKfJN1PrtY2NjYMWoavoNb7Qe5x7jS/0Huc0+WbKgKdZHPQwotf4Qu9x7jW+0Huc0+SbKQNeqVQOWoSuotf4Qu9x7jW+0Huc0+SbKQP+3HPPHbQIXUWv8YXe49xrfKH3OKfJN1MG/Nlnnz1oEbqKXuMLvce51/hC73FOk2+mDHir1TpoEbqKXuMLvce51/hC73FOk6/yJKZLPP/884vAnO3vl5eXpycnJ53mVznM6DW+0Huce40v9B5nB3xvOn36dGhZn64a8Bw5cuTI4Q6ZcqHkyJEjR44PkRvwHDly5MgoDqUBF0I8IIR4RwhxXgjxeyHf9wshnul8/30hxMnuS+kOGnx/VwjxthDiDSHE80KIw5vRSxMqzr7rHhZCSCFEaDa2rECHrxDisx09vyWE+Kduy+gaGu36RiHEt4UQr3ba9qcPQk5XEEJ8VQixIIT4YcT3QgjxV5338YYQ4u7ED5VSHqp/tBNmXQBuBvqA14E7Atc8Djzd+fwo8MxBy50y318ABjufv5hlvrqcO9eNAC8ALwL3HLTcKev4FPAqMNH5+9hBy90Fzn8LfLHz+Q7gvYOWOyHnTwJ3Az+M+P7TwH/Srp9wH/D9pM88jDPwvRJuUsom4JVw8+NB4B87n78BnBZChBWVyAKUfKWU35ZSbnb+fBG4ocsyuoaOjgH+EPhToN5N4VKADt/fAp6SUq4ASCkXuiyja+hwloCXqm8MeL+L8jmHlPIF2tlYo/Ag8DXZxovAuBDiuiTPPIwGPKyE2/Goa6SULcAr4ZZF6PD14wztUTzLUHIWQvwMcEJK+R/dFCwl6Oj4VuBWIcT3hBAvCiEe6Jp06UCH85PA54UQl2lnO/2d7oh2YDDt60popZPtMpyVcMsItLkIIT4P3AN8KlWJ0kcsZyHEEeAvgN/slkApQ0fHRdpulJ+nvcL6rhDio1LK1ZRlSws6nH8d+Acp5Z91Kn99vcN5N33xDgTO7dZhnIFfBvwVQG/g2qXV3jWdEm5jxC9dDjN0+CKE+EXgy8BnpJSNLsmWFlScR4CPAt8RQrxH2194NsMbmbpt+t+llNtSyp8A79A26FmFDuczwL8CSCnPASVguivSHQy0+roJDqMB3yvhJoToo71JeTZwjVfCDVIs4dYlKPl23Al/Q9t4Z903CgrOUsqqlHJaSnlSSnmStt//M1LKlw5G3MTQadPP0d6sRggxTdul8m5XpXQLHc4XgdMAQojbaRvwxa5K2V2cBb7QiUa5D6hKKT9IdMeD3rmN2a39Ee1d7C93/u8rtDsxtBX9b8B54P+Amw9a5pT5/jcwD7zW+Xf2oGVOm3Pg2u+Q4SgUTR0L4M+Bt4E3gUcPWuYucL4D+B7tCJXXgF8+aJkT8v1n4ANgm/Zs+wzwGPCYT8dPdd7Hmy7adH6UPkeOHDkyisPoQsmRI0eOHBrIDXiOHDlyZBS5Ac+RI0eOjCI34Dly5MiRUeQGPEeOHDkyityA58iRI0dGkRvwHDly5MgocgOeI0eOHBnF/wP9cIf2ITw8nQAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"N = 1000\n",
"seq = halton(2, N)\n",
"plt.title(\"2D Halton sequence\")\n",
"plt.scatter(seq[:,0], seq[:,1], marker=\".\", alpha=0.7);"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"autoscroll": false,
"ein.hycell": false,
"ein.tags": "worksheet-0",
"nbpages": {
"level": 2,
"link": "[7.1.2 Quasi MC: Halton’s low discrepency sequences](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1.2-Quasi-MC:-Halton’s-low-discrepency-sequences)",
"section": "7.1.2 Quasi MC: Halton’s low discrepency sequences"
},
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXAAAAEGCAYAAAB8Ys7jAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAIABJREFUeJzsvXmcZEd15/uNXG5mVta+91JqIallCYR2IcCAJUtisT2WJfNkZGNbHnlm3jwxXsczMONna+zH4JmHn818HrZnzNjYAx8wAw+sseVFAgsbIzCoQUgIa2mJ6kW1ZFZlLZmVmTeXeH/cvNk3b90l7pJZXXT9Pp/+VGfmvRFx4pw4EXHixDlCSskBDnCAAxxg/yGx1w04wAEOcIADhMOBAj/AAQ5wgH2KAwV+gAMc4AD7FAcK/AAHOMAB9ikOFPgBDnCAA+xTHCjwAxzgAAfYpzhQ4BYIIR4UQrywF3UJIe4TQjQHUff5gAuN3qCw948Q4hYhhBRCHN3Ldh3g/MIFo8CFEDkhxK8LIZ4XQlSFEGtCiK8IIX7G8tj7gdfuURP/BDgyiIo6ykFa/hWEEI8IIfaK9oFDCPEGIcRfd2ivCSEWhRCfFEIc2+u2ueCLwCHg5UFUJoT4QSHEF4QQ60KIihDiBSHER4UQo4Oo/wBquGAUOPC7wE8AvwS8Evhe4IPAuPmAlLIspSzuReOklFUp5coAq2xhKIRDwG3ABvAXQojZAbZhTyCEuBJ4BHgeuB24ErgP+DZwXiooKaUupVyWUrb7XZcQ4nuB/w+jj94AXA08AGwBmX7Xf4AAkFJeEP8wFNS7fJ55EHjB/hm4B2Ow7wCfwRjkdwPPAtvAJ4Exy3sfBh4FfgE423nvU8C0R133AU37Z+C7gROdMr4C3GBr8+3AU0AN+AbwPYAE3ulBZ09dne9e3Xnvn1i+ewXGQH65U/9TwI/b3nsM+BDwfwLLwHqH/rzlGQH8OrAKlIGPAz/v0IafBJ4B6sAZ4P8CUra6/nvn+9UOT9+LsRD5FWAFKADv9eHzzwEFBZl5L/CtDu2ngd+z8dnk0a2dvqkCnwcOA28CvgZUOrJwxEGufhR4scO7R4FXeMjDLR3+HLV9vgP4204bnwHeYqPhOuBLnTqeA96OMVH9sgfdvw18VaF/LsOQ6w2gBPw18GrbM/d0aK1h7CJ+sNPuNzjRZXmvCdxn+TzXkasCxpj7e+BNDv3j1x+zwB92ZKWGMYb/aRCazqd/F9IKfAl4qxBiMuB7hzAUyw8Db8NQqJ8EfhpDOL8PeCPw72zvvQZDqN7aeeZq4A8C1p0A3gf8LHA9hkB9QgiRAhBCHAEeAr7c+f3ngf8nYB0IIfLAP+181C0/DQOf7dDwauC/AX8ohLjVVsTbgUkMen8U+CHg31h+/xmMyeyXOu08AfyqrQ3fj9E//6NT1y9irPp6nuvUlcZYGf4CRr//WaetbwT+NfDvhBBv8yB5CZjweQYMhfzPMXZs93Xo+y+2ZxKdNv40hmwcxjCH/RrwLzvtPMpuvhwC/g/gRzrtHgE+I4QQPm2y4/3AfwSuAb4K/IkQYhxACDEEPIyh9F6DsQP9BQwl5oUl4DIhxGvcHhBCzAFfwJhI34hhenwWeEwIMdN55jqMyfp/dtr3fuADAelDCJED/gajj96GMSk9DDzS2U1Z4dUfOYwJ9hrgxzD4+q8wlL0STecd9noGGdQ/jMG1iGE6+AaGMroTEJZnHmT3CrxJ78r5g50yZizffQDLigVjpVCmd7X2ZowVwnGXuu5j9wpcAtdbvntt57vv6nx+L8ZqKml55q2orcBlp43lzv8lxkot5fZe590/BX7f8vkx4Bu2Z34PeNzy+Qy2VTHGJGil9++AT9ie+VkMJapZ6vq67ZlvAk/ZvnsSeL8HDQmMXUMbWAP+Evi3wIIP7Xdh7A4Stn681vLML3W+u8Hy3c8DRZtcSeAyy3eXd7673UUebsF5BX635Zn5zndv6Xz+Zw5yeEXnGa8V+BDGwkBiKPPPdHgxZaPhS7b3BHAS+LnO548AX7Q98y4CrsA7fXHGLpvA54DfDtAf92Osuo+60O1L0/n274JZgUsp/x64FGNm/SOMLdmngId8Vj1nZa9dfBlYllIWbN/ZVzXPSCk3LZ//vvPXvmLwbDaGMuq2pfN3rvP3lcBXpJQtyzOPK5bdAq4FbgB+HHgJ+AkppdXzYUgI8RtCiG92DrPKGLsJ+0Hf122fz5pt7Bx6HcHYPlvxBdvnV2Fsfa34PJDF4JuJJ23PLGNMyPbvXFeZUsq2lPKnMVbL78LYav8L4FtCiFvM54QQdwsh/lYI8XKH9o8CGoZi6BaHYT6x1o2tTcvAlBAiafmuIKXseiFJKZ8Dihg8DYJu30splzH4apWPb1nlUEr5jxjmAVdIKXeklD+IYUJ7D4YJ7T3As5YV703ADUKIsvkPw7RxMXDcUv/f0ws731VwE0afb9jqe6OlLhNe/XEDxrg841GPH03nFVJ73YBBoqOcvtj595tCiHdibNnfhKEsnNCwF+PyXT8mw7ZNOZuhIxMO37l9doVFgTwrhBgG/lQIca2Ust75/v/G2KX8IvCPGPbc3wTGbEXpts/W/hCW73ybZPvs9G5s/OgM8I8BHxNCvBvDZv2rGFvmmzG2/u/DWFWXMHZAf4ShxE048khK2bB/Z6HHDUHNJ7C778FbPpQhpfw2xm7yw0KIf49hQ/83wE916vgsxgRohzlhCIX6zUPZLu2dic5KQwLjLOIuh/d3bJ+j9IcKTecVLpgVuAu+1fnbD8+LK20uV6+31RkHngFusq3sXheyrA9hbJ2twvsm4KNSyj+RUj6JceB2eZBCO6u/sxgmLCvsn7+JcQBrxZswTCgvBqkzDKSUeqceUxbegGH2+GUp5Zc7K+Q4fbBnhBDdnYUQ4nJgivjl40ohRHfCFUJ8FxbPK1VIKUv07my+irFrOiulfMH2z9ydfhN/vq92/h62fHctvZPZV4FLgC2HuoK4VT4BvMrDl16FpvMKF4wCF0J8XgjxvwshbhRCHBNC3Ab8DsZ28m/6UKUE/lgIcZUQ4k0YtvM/l1I+H2Mdv4OxPfxdIcSVncPF91rqV2+ssTv5beA9lonnWeBOIcRrhBCvxDg3OOxWhgd+E/hZIcSPCyGOCyF+EcN7xor3AT8shHi3EOJyIcQ9GDbJ3+wo19gghPgXQoj/KoR4ixDisk7f/VuMA7JPdx57FkPJ3i+EuEQI8RMYh45xYQfjQPgGIcSNGCv7pzC8UeLCRzFs4H8shLi6s6v47xiToqt8COOS2fuFELcKIV4hhHi1EOL9wFWc65//F0hiHLy+UQhxcce3/r1CCHOx8lvA6zrfXS6EuAtjN2fFCxhnUw8KIa4QQryh8561fR/FMPH9uRDizZ26bhZCvEcI8UMB+uNjnboeEkLc3qHtNiHEjwSg6bzCBaPAgb/AOHl+GGNw/iGGa+B3y/74fv8Dhr3vEeCvMFYjPxVnBVLKsxhuWa/HsP19APjlzs+1EEX+PoZM/FLn889jCPzfYGwtz2IcPgbFBzC8N36r087XYXhpdCGlfBjDE+Yngac7z/4O8B9C1OeHf8DwZ/4ghq36ixgeRT+H4Y6IlPLPMCbD/4ihWN/BuX6JA0sYE+KnMOzEVeAu2Tk5iwNSyh2MM4s5DBfUj2BM0mW85ePzwALGGPkWBv9fh3Ew/qFO2Sud74oYrqbPYijaYx3akFI+geGV9A6MPnw3hkxZ29jE8MSZxTBhfRD495wzrSClrGHszr7aadNznTpfgyGfQfrjezDk6+Md2j4I5FRpOt8gYpSXA3QghPgwxkm3fZU5iLpNe/7VUsqn/J4/wOAhhHgQQxletgd1H8PwXPpBKeX/2oP6L8ZYTb9RShnmQPMAFlxQh5jfiRBC/EsMz4yXMU79fwv48oHyPgBA56D+LIbSPAb8Z4xV61/vZbsOEA8OFPj+xzEMF685jEOmRzB8mg9wADAORv8DhivnOoa55n+zeBodYB/jwIRygAMc4AD7FBfSIeYBDnCAA3xH4UCBH+AABzjAPsVAbeCPPfaYzGQOolEe4AAHOIAqdnZ2irfddptjMK2BKvBMJsMVV1wR+v3FxUWOHbOH4fjOxYVGL1x4NF9o9MKFR3NUek+cOOHq676vTCjpdHqvmzBQXGj0woVH84VGL1x4NPeT3n2lwMfG7DGUvrNxodELFx7NFxq9cOHR3E9695UCLxb3JNvZnuFCoxcuPJovNHrhwqO5n/TuKwV+MHN/5+NCo/lCoxcuPJoPVuAd6HqsQenOe1xo9MKFR/OFRi9ceDT3k15fBS6E+AMhxKoQ4mmX34UQ4r8IIV4QQnxDCHF9/M00UK1W+1X0eYkLjV648Gi+0OiFC4/mftKrsgL/MEaeRTe8DSPd0HGMBLC/G71Zzpifn/d/6DsIFxq9cOHRfKHRCxcezf2kVyXt1N9iBMFxw53AH0sDXwLGhRCH4mqgFcvLy/4PfQfhQqMXLgya9Vab1bKO3mrvC3qt7Y0DZ5eWYi3vfEc/eRzHRZ4jwGnL5zOd72IPgK5pmv9DFuitNhvVJuO5FFoyPnN/v8q1I5lOs1rW+17P+YSgPN5v0FttPvHkCtv1FiOZJLfMn18+0XbZtrf3nmvmIsmi3mrzjZUaS0ursZS3H9BPmY5DgTslYnUMcbi6usr9999PKpWi1Wpx991388ADD7C8vEw+nyeZTLK1tcXMzAzr6+tIKZmZmWFlZYXh4WHa7TaLi4vMzc1RKBQQQjA5OUmhUGB0dJRWq0WlUmF+fp6zS0s8tVJjraUxm6jy2ssP0242qFarzM/Ps7y8jKZpjIyMsLa2xsTEBNVqlVqt1v09m82Sy+UolUpMTU2xvb1NtV7ny8UkWn2DRDrDGy+bobK9xfT0NJubmzQaje77Jk2lzU204Qla1S0S0EMTQLlc3kXT8uoqT63UKLe2GUs0ueWaS1lbXSGdTjM2NkaxWGRsbAxd1x1pWi0WSeZGSLUbNPW6I02j4xMUSlukaHLk0CGWl5fJ5XJomsbm5qYnTV58cqPJiU/Ly8s9NGmaxurqamQ+6bre/X2vabLyKT06Ra5aJJ9Ks1FLU9psMjq8dV7Q1AYeX2mTrm8htSHecGyU9c1tqrUERxMVqlXBailHq7LpKXtefKqRQjRqTGSyiOo2J1+qcsnCkUA0BRlPbSCZG0Uvl5gYG1PmU1TZm5qd49SZlxkfySMwbmNG4ZOr8lUJJ9vJovFnUsqrHH77r8BjUsqPdT4/C9wipdy1An/88cdlv67S21cOq2WdTz21Sl5LUtFbvP3qWWby7jOh6qo6TLlhVjCrZZ2/e/JZKtlppXqC1hn3ykoVfv38nX7N2t7vr5+sc8nFF4cuK86doCnb2VSC9WqDe6+dYzqvKcuJSnv0Vpu//sq3OC3HQsldELndSxmPi8cAJ06ceOK222670em3OFbgDwHvEkJ8HLgZ2HRS3nFgYmLC8XsnRo3nUoxkkt3vxrLupAZhdJByATaqTbbrLfKa8c5mramkiMdzKdraMBVdrR7r4FGpM2y7osCtn61td+PxfoVdqWnJBPdcM8dmrclYNkWtUg5VbkVv8pETyzRakvFcKhblNJ5LMZRO8MTZbQTwyPPr3HvtfE97oypLLZngpuOHuaylsTCeCdzmIHK7FzLuVG8qN9K3unwVuBDiY8AtwLQQ4gzwq0AaQEr5exhJgr8PI7v0DjEn7rWiWq0yOjq663s3RqkIntf7TrAPQD8BDKrwrfW8/mgObXTStx774LnrqhnfOsO2Kwqc+nksm+pp+62HhCOP9wpBV7nW5wFHpaYlE135KrnItF8dHzmxzNdf3iavJbmYnKvMBmm/lkxw+/FJijsNJofS7Ojtbrl+ik91DOmtNo+fXGWplffcHbq1OYjc7oWMO9WbbDf6VpcvRVLKe31+l8ADsbXIA7WacyJtN0ZZB4oXgjJatVzz2SAK34qmXueIQj32wbPTaPvWGaVdYeHUz/a2b1V0jvS9JWoIugW3P3/rpRO+Ss1Npr2wUW3SaEnyWoqK3kRLCUeZDWNCmBnWmBvWAis91TG0UW3Saujks6OOfeLX5iByuxcy7lTv0pnT/i+FxL7KienmTxmFUeZsf9dVM+w02n1hdBCFb4Wq/6jb4PE73gjbrrBw4pO97QtHDg+sPX4wJ5dsOsFKWadY0Tk8mvV93lTYQuCr1ML4CI/nUoznUlxMlnRS8GPXzTvKbBgTQtixpPreeC6Fnhl3NQ267dLsZqggC6hByjjs3kH00w98Xynw5eVl1wOuMIzaq0MOVXjRa4V98IDz1r3fUNmu2/nktFoZPk8OMcdzKYa0BCfObCOBR55b514XZWk+b1XY0wpmPC8eu/VnEGUZ1nynMpac7PsqE8TN0y1GZg47tt3e5qF0IvAuaBAuvl7129urOo7DYF8p8GzWffUTBnt1yKGKoPSaK+6wdEUR/iiToZZMdFdZKS2ejE1xDGQtmeD2yyZZqzSYyKXZabRDnY949b0bj1VMCf1aTVvb4NaHUfidz+WU+zCILJ8PCzKn9satt6zYVwo8l8vFWp65wipUdKbz6YEdcqhCld4wh5h+ZQQV/iiTobXu6VSDO2fbkS+LxDWQZ4Y1Zm02YS/FZp2MVCYPNx7HtbgIujM1actrCT79dMG1D73a5zd5+sm1tc2quwi91eZkscpGtcloNrVnCzKn9tZa8eotK84vjeWDUqkUv4eC7NxE6qxeB70Fc6rP/K68vq5Er8ohph9dURVGlBN/a92JWinywItzZxXUPBV08nCTaWt/DqUT6M02eivaxOYHa9sTAhot6aoM3RY/KvQHGccquwizzo1qk8WNGsfGs4znUn1ZkPmNI6f2LvVDb3WwrxT41NRUrOVtVJvsNNpM5zUqeotiRedzL5QGtgVzEnY4pyCm0nB0wXnQWgXJSXlaVzEqgyqqy1WU7bq17mxmJPLAM8vbqDZJJwVD6Wg8tPblaln3nByCTh5uMm32Z7Gi88jz6zz0TLHvMmlt+1bN8G7xvIdgW/zYy3CjP+g49ttFmHWOZlMcG89y++WTXDKZi72fgvi6W9sbt96yYl8p8O3tbd+rpUFgV1pSGsKQTAg2qs2+b8GchF1Kut/J2rZjG5wEyUt5qgyqOFyuwp74W+uubxYjDzwtmeCuq2b46NeW0ZuSTz9diE3x+U10QSdCL5nWkglSiQQ7ensg5zTWto/nUq6eWaa5Yrve6i5+zHap0O83joPugu3tvmTSMFnEHUco7M4ubr1lxb5S4GECo/vZK61Kq9Fqs7hRo1xvMpxJRV65+cFN2M3vJpNtxwHgJkhuwqSqVPbC5cpe92IxnksPFb1Nq03s9lC/iS7oROgn04O8jGJOfKc36iyMZ8hrKexd5meuUDJ5eNAc5vxiUF5YYXnRz4QO+0qBB/WnVBEGq9LaqDY5Np4llRQ0W5KdRnuXAMcJN2E3v8slph0FL4wg3XrpBELAdF47r1wl7YjLZ7afis9vogsyEfrRO8jLKHqr7XlwCe7mCuhd8XrR70Wz2+LE66zIXqefmStIf3iFQbDvStwWigd+4B0E9acM6oLUaLUZySTZabT7dghih5Owd1eji4uOPtFBBrWbnf18RRi/aCcMUvEFgZ2Gs0tLDE8fDuQ73y+ojBczXkqhojM9lO4qb3NVnk4K3nn9PHnNfex48dhp4vU7K7JPNnFM3m6LPyde+C0UD/zAOwjqRhjEBclkwJCW4M5XTfd9paqijLzoVR3Ue+XrHtabx43msFvr88mv38nd88lVneXzJDa2suITvX83qk02qk2+XapS0VsA/NRNh0PLtX3idVpRW8+K7HIdx+QdZ9CsuN2frdhXCjxoYHRVRloZUNFbpDszbb+gfJodQyD4vJYgIWCr1hzYriLSpR4LzUEjLJ7vsNNweqPOdlOQz/SPJqcEDV6mCL/xslFtsqO3mbEcXua1BI2WZKveJJtKUvO78OQj1/aJ1++saEjb7WYZdfKOM2jW+Z7QYWDY3NxkfHw80DsqjIzLXqq66lS9BBGGXnt7Pv10gUZLkk4K7rpqZiArvCjK1qQ5jstJ5xt2xX0Zz/BCQue0zVUvrrsITn1ot3HDblOEF6+crrp/+ukCbdlms9qETJszWwlPB4Cgcu11VlSs6DzyXPxulkFW8X7PRh3HXthXo2B6erov5cax5Yojpri9jB+4bDISXdYDp4re6vuhrIkoE6LJ4zARFsPC78p4XBe7nOTsDa+8iEYy03PhKi4PCnsfntqodz9vVJucXKsy2uGT6mRrp8E0n5zaqNNqQyqZ5NCwxumNOpdMOe9kw4xjt7OiVCLRkev4dzFBVvFez/ZLb8E+U+Cbm5uksznf0+gwiLrliiOmuL2M1fUS46Phg8H30xMjiHtmEJ5sbm6Sz+d9LyfFSYebwuxHbA07DTvlbQ4fPsdjPzkKIuv2PrxoPNO94LS4UeOzz68bq2gtoZw4xE7DeC5FOimoN9vkNEGrbbjiPvr8OuNnnBNNmDx2QxQa45Jxa0iBit6OpFv86I2CfaXAa7oe6DR6kIgjpri9jBTNSG3qhyeG3mpTKOs8+sI6O3qbIc0I+DQz3Hvoa6VPxQ5rotFo9K3tTvBSmIOwu5v0mvCSo6ATilMf3nPNHCfXqnz2+fXuzuz7rphkq2aUGQQmH3/kmlkAao02EkkiITz97+0028uMSmNUuPm6h9UtXvRGxb5S4NmxabaXNroDqljR2ay29jyADcR3k9FahmxGZ3ycq1ZTsFfKOqdKNa4+NMyJM9usVRrMDmtKuTed7LDWd6w+s1HbrrKS81KYg7hEY/cR9pKjsPG97eF7L53K8cQZY7wMpRM88tw6T5zdJpUQ3Hh01DNkrgk7X995/Tw7jTbpBPzJk6ueh+Zh/MCD0OjXbj+ZMNuQTAjKdeNmdhTdcuAH3kFts8hIJsN2vUUmJfjM0wWaUnJ6o97XADZW+JkOoipLaxmLZ/rnPxoGpmBP5tIslmqslHUkMJFLuwq4lx3WnIRTiUS3P4P6zLrxI0jcCjeFOYhdgBO9bnIU14RipWtHb/Ibf7PI+k6DRMJw2VOJLOh0RmGmx2u0JFrK/dA8qB+4iaim0h534bSRPs6+c7S2YaNq3MhutWUk3XLgB97B6PAw9yxMUqzofObpAk8tl8lrSS6a6F8AGyvcLhT0K3phv+xmYWEdXDccGeGWSyd47GSJnUa765Fgjz/hZoftrv6eN0wxZn8GodlLSQc9kwjzWxwIQq+peIsV3TfbkkpZM3mNs802qYQgkRC028ZhoEpkQa/0eH6H5l40u02acZxHdDMspYzEzcWdBnMOO0drG4bSiV3xYIJOJP0cx/tKgbeFEWRKSmhLujkBs6nELuXdj7CwdqXQ7+iFyWQwm2Q/YO9H++C697pMV9CdTCNudtjNWhO92eahZ4o9SjalQLPZpkar7aqkBxlDJArC8DhOmZsZ1rjx6CirZZ3hTJKfuOGQ0iToxFe/Pjf5hhC72mGF06TpNPasOzcVmO1bKesIYHLIfedobYP1pzATST/H8fkp1Q7QW23+4fllTssqQ1qCkUySiyeccwL2KzOHU/RCq1vWi2tVLply3gWEmVC2traYmJhw/C3uCcrtgodTP9ptqjN5zTP+hNs7eid0gXXALxXP0ezXpiHN8Dd28qBwUjCDivUepB4vHjuVe7JYZa3SQEslYomYaUzC845mIr+wvE589YoVYvJtQWzy5vGJQDywx0e379xUyrLuYKzvh41dr2oXD8LjoNg3Cnyj2mSlPUQ+Y9yWvPNV06STidDhU60IMuCsQaGAHrcsN9epsBPKzMyMa3vjnKDcyutuORWS+oZZ8ToNeJNmvzaZt2a95MDuCTMIb6Wg9bjx2K3ctUqDr57dIp9OMpINFjHTTc7dzERa0ohO+JETyzRavWF5g5Zl5dtKfSjwxOO3c3Mqy6mNWjLB4dEs917rPGn5IYycq/I4DPaNAh/PpZhJ1jirpxnJJD1jlQTpZNUB5/bcPdfM8eJalUc7bllOAhXWHW19fZ2hoaFd38c9QbmVZ2ZdUUnqG/bAzz7gTZq92mTlrWrMGqfygqQ+U0VQ3rjx2K1cLZUgn05y+ewQWvcSi3+7wk5gFb1NW/aG5TUPK1XGjFPSkSPJWiiTltfOLQy9Yc4Rwsi5Ko/DYN8ocC2Z4Or5PK+bno18tdUK1QHn9pyWTHDJVI7xjluWk0CFtcdKFwmLe4JyK09LBk/qG/XAz6TZq01hJgqnK+BWU4yTL3sQWC9+qNiBzUnDjcdu7V+rNMikEqQSIpBnRJAwrU71Oh1Weo0Zr6QjlWK01HBeB50qsXOi7saCyrkqj8Ng3yhwgPm5WbJZ746zMlGlk1WVoddzfkolrNJx23rFPUF5leeU1Lcf6PJtcsq3TWEmCtMccGqjzkXjGSp6u2se8vNlV2m73dfdLZPNrrgjFpORlyLVkgl+4MopPvzVJY6NZ8l06Ak7gbmFaVWRXZUx45V0ZCQ5G6R7HWGXgSCxc1Rvu8ZxCxMOTChdrKysePpTxpHNw+15FSUdV5B/E170qpYXNRtP2MnHhMr5wq4Drpuu7HqwxGXmsCcrMAe4ii+7H5x8olV3cTvFFQ4dXfCVW73V5k+eXOXZwg55LcXFqWyg2DZWPg6lE10vno2qfwrBIIeVJrzkzm8ch0GQ2Dkqt13juoUJ/aHXxL5S4H555cLamlWVYRwmAiv8lJsTvUE9Kfw8A1TKCku36oRq5dtGPd2zve9XYCdzgJvR7Exf9jARAaPs4hLDw0pyayhc2Tm8NbxCgu6GzAnR7NNMUvBSqcqO3gqcQtBNJlRC0/YjP2SQ2DleY8J+CzOVDHYL00lu+pUPE/aZAvfDfvH9hXC7hbAKzUmQB+GVoTqhWvk2m0p0+RZnLBK3AX54NLvLja5f8TjcnlORW/Mg8GJyaKndrrMqMN0QzdAThYrO/LDWvW0YNVqlo4loQGEtgu4U3cZEo9VmKJ1gu25Mas1W7y1Mv8iVg47LdP5qOAeUy2WmpqZ6vvO7aNJPRPErVlFOdnrjVGiDCNQUxHxj8m278HJVefNNAAAgAElEQVQgxaaKIDb1sH2jclZlr8vksZ/cxmHKspsGpofSIGBHD59CMEzSDadxHAei7JDt9wvufvUMY9lUz1mGn4J2o79f9MI+U+Bzc735HFUumgRBEIUcdbZVUU52eoN6nwT1LogbQZWOlDAzc+6AK+4JWUU2rKsw1RCrUWTB5LGKvd/a/qCLB+s1d3sy4qiTgsrBoRPNKuUP4uIVOGflymupnh2J3wTlNqZU6Q0DpVErhHgr8AEgCXxISvkbtt8vAv4IGO88824p5cMxt5VCocDCwkL3c5RVpFOI0yCDMEjdbhcK/JSTlV6zDDcPB3t9YbwL+gFVpWm292hii7fceEVPPwWZkKMMevsqTDU3ahQ5NHkcRP7CTBhW5TKeS7EwlgnkrWWt223FrZp0wz6Og9DYL6WuasbyesZtTKnQGxa+ClwIkQQ+CNwBnAG+IoR4SEr5jOWxXwY+IaX8XSHEK4GHgYvjbqywxVBQ6XQnRW2NZ20KR9BBqLqC9RpsfsrJpLdfk0vch7JhYW1vrSZDm3Oi7oqcVmEq70fZzZg8DiJ/YSYMuxeKV0hfN6isuFVkyj6OVWm0HsCq+u4HOaiPw4zlRL8KvWGhImmvAV6QUr7YaczHgTsBqwKXwGjn/2PAy3E20sTkZG+KMS3Z69vrd6hgxqI241lfe2SkKxxhEjKorDZ6PCxs8VKcJhfrZ5Pefk0u1n4a1FbVCdb2apnh0OacqLctwyrioLsZa3+bPDZvvRYqOtP5tGfdbu10ix1j92kOu2MIu+K2wz6OVWm0hnZQ8d0PcxgdZ+xxEyr0hoWKhB4BTls+nwFutj3zIPDXQoh/BeSB22NpnQ2FQqHHn1JvtfnkU6sUKw2m82nuvbb3ZN4ucKc7sajNeNbrnXCS9ih5qsKowkxrQCBrvBR7YgOnRAcmvf2aXMw+3OuMRm6HmEHhddsyTm8St3dV3cysbXr9ZJ1LLr7Y+FGC6Pz1q8spUJdbtqqNapOXSlXmO5ey3n71rPLu0TohBHHV84J9HKvSaI0mqOK7r3php58LF73V5ttnl7nskov7UoeKAnda/9tF7F7gw1LK3xRCvA74H0KIq6SUbetDq6ur3H///aRSKVqtFnfffTcPPPAAy8vL5PN5kskkW1tbzMzMsL6+jpSSmZkZVlZWGB4eRgjB4uIic3OGctuut3ju5QoXZeqcLaf59suCTFtnfn6e5eVlRDLFZLpJqlZiSMuTb26zIDZZauS5fbbB5fNDzE3mWTpzmomJCarVKpVqlcbYNLXNIvlcjlwuR6lUYmpqiu3tbXT9XPm5XA5N09jc3GR6epq10gblap2Ljh5mbXWlS9PrJ+vspEb4ptwik9Q5Xc7yzPMvQU0yk0ogqlW+XciQra4xkkxSrGU5+dK3Gc6kKRaLVCoVfujKOU6ffZl8NkOjVmWpWGRsbAxd16lWq902aZrGyMgIa2trTExMUCpWqdVq3d+z2WwPTS8XN8hVS4jMONlqkdMvS6ZGhro0bW5u0mg0uu+r8AkMTwOTT0IIJicnWV5dRWhD5FKCnZ0K2U4/ZzWNsbExdopFtFSK1dVVT5qqVXeavv/SCYobWyRlnc1KjVy1SC6VoVITnHypykWH5nxpqpfWWVGkqVAoMDo6SqvVolKpdMtMp9MMDY/w8kqB2akJ2s0G1WqV9OgUuWqRfCrN+k6KYrLO2MYG65sVhuvrpIbGydbXOHVWMjs+4it7S0WDT2dW18hVN7t8PLMsECJBrlqkKvNMtzfJVBM8s5XlpdEqdyyMsdNIIPUq7YbO6Zd7acoND/OFk+vIRg09M87N0y2ymsYPXDbC0mqBmckJNtaKofhUq9Uol8u+48nk0+j8PItnDD69+ZjG6toO38hmSOslJpNQ2Rlhu/AyYyMjPXzaWVvlSKJCoZ5lIbGDrOUoViWVSoWp2Tkee/IkOy2BzAxx0zRMjo/7jicv2bPz6ezSEk+u6jQbDV5c+xZveOVF7JS3Q40nV+Xsd0+/o5AflFK+pfP5PQBSyvdZnvkm8FYp5enO5xeB10opV61lPf744/KKK67wrM8LxWKxJ8Pz2c0a/+mxxe7nd996bFe0PL3V3rVScVthRVmN+r2rt9p87OvL3cBQ1x4aJpkUXTu80wp8q7TumdE6jhXEXkTpG9ISIOlenrHWaedxXHUOenfhdQhndee7eqyFGBrzTTUXpj4wVuBnt2p8cXGTTNLI4v6+t13KsYmcZ3mrZZ1PPbVKXkuyVWty2/FJLnUJlRwUcfBYb7V3hYV1u8HqNN6t9FX0Fm+/ejb2S3oni1U++8I6h9I1Vlu50HWcOHHiidtuu+1Gp99UVuBfAY4LIV4BnAXeAfyo7ZlTwG3Ah4UQVwJZoBC4pT6oVCpdxustY3F/7WHjJtvUULob4tX83emU3WvLF8WbwO9dLdkbGKqit/iehXGm8umup4N9y2il1464lJOq2SDqZGHtn0LFCKg/ndfYqDY5uVbtKgcvmoNiUJ42TvAKfnbPNecSC48ntzjTsSd7nef4wY3We66Z49nVCqdLdVpSkkoI0kn/QzW76e+zz6/zhEuW+aCIg8daZzLa0du+cX76mZ7OCfZJen6sxshQ+LMdL/iWKKVsCiHeBfwVhovgH0gpvymE+DXgq1LKh4BfBH5fCPHzGOaV+2QfQnCZyUF7VnPpBO+4dq7H3SuscrMHjdebbfSWWuQ0FYEwA0OZjP38ixvdK8ewW9iiJn+N66p8HJOFtX+m82mQsFXbrRziTgC7V542fsHPzMTCy7U8I9lkaM8QO+yjTksm+K7ZPDctjLK209i10HGDfaKJM2l4XDyOooTjmtydxpjd5/7KS2Y4Pju6ZzZwOj7dD9u++xXL/58Bvjvepu2GmRzUz90rSkwUa8aOh54pKg+mIG5IqoMibPJXCK90vQQyyq1Na99KabT/1EZ9Vz/sFONPABt29xBl1+EnD11ZeOnbXPqK4G6sTm31cld1y7rjR/tF4xnGc+6hksPAlGsvrxmVPo+qhKNO7m59bve5z9U30JLjoevxwr66iZlOpwF/5eXkjWBPtusG1a2Z27sqbkgXjWdIJwVbHfdFt0Fh0utWjpfwhlEIKgIZdRA/8tw6xZ0G00Np3n717C7l0PCg2a3NXgM+ykQWddfhJw9aMsHYUDaWPlYx4QW55OYUHteMYhjVayOdTnva7IP0eRw7rKA3sP1CB9jHZnFlOVL7vLCvFPjY2BgQLP52mK1pHArLTSjMsKaNlkRLCc+Yzia9bvAS3jC+4NZAR14CGXbwFso6T5zdBmCxVOOOyyd3letFc5jbs2FvzA4iVgyoy7QfgviR+8F+d+H0Rp2F8UwsJh4waHbqX73ZZqWseyYbjhtRbsB6hQ6wjk2/cRwF+0qBF4tF8vk8oB5/2yvZrte7cQQOchIKq32sorc8I8BZ6Q2KML7g9hjIbgIZBQLjkMQ8RrOX60azU5+qKNmwN2ZV43pERRCZ9oWiH7kfnO4upJOCRkvGYgsvFoscOrqwa5f88LeKLJZqnCrVuP7oiFKfx3m4vl33znYf9iJTlHHsh32lwMPMZFFu14WNq+KlWIK0J+rMrUqDW6CjuA9dZoY1rj860r145XSY5kazU5+q9KXqRBbXLcOgiGt1tlFtstNoM5FLU9xpeCag9oPZZ9Zcr1u1JlpKKAf48sLY2NiuMxGz/dcdHqFUbXDH8cldO1cne3mch+t+2e7DXmQ6WIF3oOt64Hf67UrmtHLzimYXaGWsQG8cvuD2Q5d+KG/oHKb5ZAN3o9lNWd966QRC4Bl0SmWQxXXLMCjs9Ibl53jOSMjwxNltBPDI8+u7biYHgZbszfU6nks5BlIL2l691aa4vcPQiBF543MvlLp3A4bSRpLm2WFtl0uwk6IOsnr2otMcjzt6k08+VXA14YTVJWH0lir2lQKvVquh3uvnQLQK0VqlwX/70lnSyQQj2aRrNDtreyp6k1OlOhdNZMhrvezwo3fQvuBxwI8XbjRrSSPujWmPhd0HXqCewi1MdMh+wEqvKj/d2n/78UmKOw0mh9Ls6N4JqFXg1CfW4oLKn/l8rrrGlwqCWy+d6PEmu/NV06STCdcsOfYdbc/qWUv0ZFZyu9TjJBtap05VE05QB+mweksF+0qBx+0jHAes9sIX16vUm22GMykunsj6RrOr6E0efOQlyvUmw5kUD97xih4l7kdvnAdtg1htqsCNZvPw11QW1sFv0m6NVuc1iMNGh+wHrPSqrCi92j8zrDEXIQG128QQ18U383mRGTf+Cnp2PW67KC9TmbkDkxIeeqboGffELxmDlwlHpQw39FNv7SsF7uUXvVcwVynPFipU9BarZV05Z+GpUp1yvcmQlqRcb3J6s84VM+fe8aN3EEkZoHdgA7EHALKW70azXVnYB781Wp1fbskwk16/Ah9Z6fWyx9511QwV3Ug24db+KLsIN7c+L5qDyp/5fLZaROaM3alKe53oCnroHCQZg92Eo1qGG/qpt/aVAte0vV8huuHEmW3ObtWRSK4+NMw7r/e3P140kWE4k+quwBfGMj2/J9NpT//1QWz77bdezRRcccUWsQ/EW+Z3+4F3s+Ro584VnAZ/HEH5VdoYF90b1SZJi9+7mz12o9rkIyeWaUsYSid6+sEpqUCYXYRdOS1t1fjLZ9dpdHJCxpEUxHx+8UyLY0ctO4cQdyyCHjqHTcYQpAzXtvdRb+0rBT7SiTZ2vsG+/brzVTO77NlOyGuG2eT0Zp2FsV4buN5q88WXddYWVz2Vht+AjTuGCRgDLi4/XftAlOledyv7BGI/Vwh6yBRm0ovbJ9xK01S6yQ/NnQvX4GSP/a7Zoa4Ln5etOArsq/8//8c1nloqk9eSXEwutqQgWjLBoalxZdu+SntVDp1VZcPPNdnqOdNQbG8/9da+UuBra2u+4RXjQlhhctt+uSGvpbhiJoXeavestjeqTZL1bfLZ6R6lEfTWWKwxTDpJcONwJXMqfySTpFHZhJmJ7u9Bs+SoKBT7M359GtVU5eVmmqyVdilH+4Lg+6+Y4u9e2vS1FUeBVcHpTeO8Ia+lqOiG+2Cc5jmncRwm+UI/4verjK/PvVDadWfCq7391Fv7SoFPTEz4PxQDBiFMfvWN51K0teEeZdmv1GpesNMG4ZPgusHqClirlHt+67edX6VPTQ+YMJEC3Xhr0pTTdkepsy8IDo1mueea7MDyl+otI3PPxWRJJwU/dl14d0QnmONYbxnpDU1s11tkUwlWyrqSH3vUQ2enm70f+/qya4IYMG4Tr5R1sqkE5XqTZEL4jq1+6q19pcCr1Sqjo6P+D/rAb5YNo/i8hClsfa8/mkMbnewO2qC3SuO6Xm2nLS5PDSflZuex0wSiGtfGWo9b/6tGdQx7jdyt/O5qd2td2bY8SA8ZFf/6sKhWq2Tzw3zsa8tdv/VrDg+TSQq+9nI8fux+cJK9Qlnvxus/Vapxx/HJnklEb7V59Pl1Fks1JJIhLUmrLT3jGZn0xqG3nLCvFHitVotchsqKK85VX5T6mnqdIy4n5crtCnG9ehCppsDZbW5jq8LEdG8IX+vKMKhJyO8dtz6NKy6KW/kmTYvFuuN7cbk0BuVlRTcOTK2Hl3GjVquxUW1S3GkAhmiWqk3efHySUq0Zmx+7F+zxXk6uVcmlRHeYOA0Xu2nrh189w5CW8t0VxaG33LCvFPjU7Fzg1ZcdKoMxLu8OrwBRKvXZ/UeDtssUuOm8RkWPFpGwH3Bym9PrCU5sr0QOTKX6Thwual7w41k/fYTDXLT5yIllvnZ2Gy2V4NJJ98NL8/kwE/38/DwilWJ6yMhNayT3SHPJVI65pXN+7E5RRONaXDglrBjJJF0TxFjfsZq2DvzAFaG32jz25ElOy7FIisV+e8staUMc9jW/AFF+9Tn5j1pXo36TmcrqMg4laafbLQqjae+cGTa25faDs4eeKXI0UeFMPRUpMFXQd7xc1DaqTU5t1B2vkavCibdmP5WLS+eSGvvA69auE8JctKm32lQaLYqVBs1Wm7QLqVEmelOu771unjsuNzK227NSOUURheDhZt1g1mWNze/n4RN2YXfgB05HGFsJ8tlorlxWV6BHnguWtCFwe+vRAkRls86HOKqDR2V1qWpSUEGPy59mpJCbGTZ4ZLV3Xn90pGvftE5II5kk5WqCkVy0wFT2d4IeQDqtzvw8DYLA2k+HknWOLrhnfTIVvZaE935u0fXWrhcdQS7aZJIJcukEzbak1W7ziW+sct+Nh10n+mxa/dDRhCnXWjKx6x1THpzOe6QkVndOLXkuM9JG9dzlO69+DbOwcxvHcWDfKPDxXIqUlmXD5pURZjulJTtJGxrBkzYEaW/UAFG5nHPi2SArK6/VpapJQRXWQX3izDZrlQazwxq3XjrRY+8sVhqu9S4XNeanJ1zrDTqAwhxAOq3O4pQRKw8260nXcq2KvtZosV1rks8439r1oiPIRZt3Xj/PTqPFs6sVhjMp9KZ03Q0NaYnuod8jz61zr6K3iptc28t3mnzi9kgyJ3jT7v/ppwuxL+ZU6A2LfaPAtWSCG2YEIzOzXcZF2U712z0tDjt6qVRyPL2O0vYwJoWgZa+UdSQwkTOiugnBLnun0wSsJRPIWhktORW4bjeENQlZV2dxy4iVBwuJumu51rbrzTaZVIIdveV4a9eLjiC8zGsp/vnNR/jo15bRm+4eFlqyN0n3dr3Fi2tVFsYzVPS256LKTa7t5TuNnyBjSnWBV9HbtCWxT9QmVOgNi32jwAFmp6cZ7nRsmEQNVgRVsGFW+1Ht6FNTzoosyuQQ1wGtV9mmecqMDDed13rsnWPZFIWyzqMv7I697EazFVFv7AWlJ+6+spabaronu7W2fSqf5idvnGe53Nh1azdu5LUU99142Jdue5Luv3p2jTNb9e55jxm/xc4nFR6D8/hRHVPWM6h0UvDO6+dd+6zfizlVesNgXynw7e3t7o0me6cHyXtpIqgwDMIzwworvXZEmRxU3o1injo8mnVMont4NNvty5WyzqlSjWuPjPRMwF40m+0a5CWruNz53MpdWlqDsd7VmbXvd8d7GYwvuArdZt+aiR+SCUG53iSVFD3xW+x88uOxCaeDb1VsVJtsVJt8u1SlorcA+KmbdtvyrXQEkZEg40OV3jDYVwrcGhjd78Q6TrejuGNhqCJMIPg46O1nQl+zLydzhkllfafB3LB2zkPGh+a4L1n5od8+8U4JHex9309Zi0qfljyX+GGjahywNlvSMwWbaqKSj319uWtjv+HIiLKNHYwFXjppZBDKaykaLWdbvpWOsEmf7eNj1w3Pg4QOBpz8or3yXjpdSojqehj3FstrAAX1H41rp9DPCcvalzccGeGOyyd7bvv50TyoELowmJ2Xnd5BLhb6kRDEzKpjX1RZ+aQi1xvVJsVKo3uhZm1n98G3X5veeb1Rjzn+45IVLx459emBH3gHbv6UToPavJTw9Ze3fSOq+aFftlC3W29+sbHdENfgj0tJhsl8s7y8zKGjC66TWj9t+HYMQpnaeTzICapfCUHMItz4pCLX47kU0/k0p0o1JDA1pB4Kwip3P3WTvy0/KLx45NSnO8UDP3DA3R3HaVCvlnUaLRlbRLW4baFOE0yxondzBI5kknzv4WD+o3EN/jiUZNjMN+lMVim41CBMWINQpnaZHuQENQhPLCc+qbjVaUkjf+odx3sv+vghrAlK1ZRkPud2scupT+WBG6EBr8DodmEZz6X6GlEtKjaqzV0TjP2iQoPdyQ28EGTw+wlsVCUZOvONTLJdb7huTwcRo8XEIJSpk0wPaoLqF32+sqWY4MA8EA+CMHIXJBepynP2QGAHCR062NzcZHx8XOnZQa5k/OAk0E4TTDqZ6Jm9W7UyMB2oLlUPk37bdsOu7tr1MiOZjOP1/73wBOq3Mg0i0ybinMj6sbP041MYmlURRu5Ulb7fc25p6fpJ775S4NPT/VFmbrE74hgkbgKtclGhUetPNutB2HbDTqBzMzPcs5Db9d5eeQL1G0Flut8TWZwZnNz4FJTmIAgjd6pK3+85N9r7Se++UuCbm5vk83n/BxXhNhjiHCReAu13UaEYM70mBnVQFmZ1t7m5yeF8PpZAVvsBQWW6nxOZitwHzV7kdD8j7nFsR1C5U1X6fs+5yWg/6d1Xo6DRaMRanttgiHOQBFU81gESN70mVAR20PZmE240B11ZBU09txe0QnCZ7udEFsZE4OUl5HY/o19yHQWqSt/rOTcZ7Se9StwXQrwV+ACQBD4kpfwNh2fuAR7EiFf0pJTyR2NsJxB/XF23weA3SIIM+CCKx3QrrLfaZJIJfuSqmehEerTLK87zXtibwZvHqoMsSPv3klYILtP9PNsJayJwaqPX/Yy4x/FeTsBOkLZsEHvqBy6ESAIfBO4AzgBfEUI8JKV8xvLMceA9wHdLKUtCiNl+NDbuuLpug8FrkDgF+/cL3uOmeKyCB3SD6VcaLfLpJDOtEj/w2ld1y41ytVgVqkkovN6PMpji4HGQHdRe29bD0Nuvg9WwJgI3uD0f5zje6wlYpS17HQ/8NcALUsoXAYQQHwfuBJ6xPPPPgA9KKUsAUsrVuBsK9MWO5DYY3L63B/t3i/fgBzuz33DxGFs1I/BObafNZC5NRaa7CkVvtV1jaseFoEko/GgKM5ji4HEQRbPXtvV+2oL94HbRymtyCJIr025OMevyoznIImDQN1fD5LbtJ49VpPUIcNry+Qxws+2ZywGEEH+PYWZ5UEr5l7G00IJkMhl3ka5wY5Z1wHvFe/CDfSL4i2fXOLNZpy0lh0Y1LpnMkcs0ugrFnkPQKaZ2VDqjJqGIYzDFweMgZgbVZ/u1TY9LpoO2L0y6NScXOT9oSSO7jfXdNx9zl4mg7erXBOyUsT5sbtt+6i0VaoXDd/acnyngOHALcBT4OyHEVVLKDetDq6ur3H///aRSKVqtFnfffTcPPPAAy8vL5PN5kskkW1tbzMzMsL6+jpSSmZkZVlZWGB4eplAosLW1xdzcHIVCASEEk5OTFAoFcsPDbFcbiGaNI4cOsby8TDqdZmxsjGKxyNjYGLquU61WmZ+fZ3l5GU3TGBkZYW1tjYmJCarVKrVajanZOR578iTbrQQpLcsNM4LZ6Wm2t7ep1uu88aJJttcLjA3n+fLZHURtg0xmhGqpwGKx2S3fi6ZycZnZZJNqvc1h6hRbw9w616Sit7n58qM0yiVks8H62hrrm9scPjTP8fQ26WyTQiPNcW0bUR9ltbKhRJP5ezabJZfLGTGKxyf4/D++TKvZQM+Mc9Nkk/lkg+264OKkznxmnOLKMo1GIzBNC4kGWSY5fXqlh0+jo6O0Wi0qlUq3TCufarUajUajS9PZpSWapJiZGGVro+RL09TUFNvb2+i6zvz8PEtnTpPL5dA0jc3NTaanp9nc3NxFUyqZZKnoLHvZoTxfeGkDGlUamTFeOwOpZEKZJi/ZO336NMlkMhBNy8vLPTSNTUzy+W+dpdnh483TLUaHh2kLQXF9kyOH5tjeKPXQ1EplobbN0USDpZ0hnnruJaaHNWamplheXUVoQ+RSgnp1h/n5eU6eOotWrTGuDaFVSywV0uQSbVfZGx4bY32zQlI2yI5Nk6sWGUppbNeSnD61wlAm40jTTitBrlokqY2QrG5x8qUqlywc8ZS9O79rijNLy0yOjbK9UaJcLjvqCFU+lXd2+HIxiVbfIJlK8z1XHGZptUir1mYu2UJWdda2R9A313bx6ZZ5yfaOzsKRw13ZK5VKbG1tucqen97zVM7SbnG3PyDE6zBW1G/pfH4PgJTyfZZnfg/4kpTyw53PnwXeLaX8irWsxx9/XF5xxRWe9XlhZ2eHoaGhXd+b5oXiToPpoXSgqGVOWC3rfOqpVfJakore4u1Xz7pmRQdCe0borbbnaf1mucL/em6rx96+WWsC6leLg9I5lk1FvkIfZDUL9PSJlceDtm+6rWLd5CGOst1kOgjc+OgXMc/JXHbXVTOOsugm+253KOznRNYy/8nlo4wNO5sVzgebdpj+9EJUHp84ceKJ22677Uan31RW4F8BjgshXgGcBd4B2D1MPgPcC3xYCDGNYVJ5MXSLXbC+vu7YEYWyzhNntwFYLNW44/LJwFdwrXDbCrmZCKJ4RpjvOm3jl1aLbNeT3fp2Gu1IdKnQGfWAzO/9nryZ6QQIepI6WHl8vkTmi7pN9yrbTaaDwKl9qqnz7GnjTm3UHd+zm5rAPSOWU91W2/nq0stdBe6UlWlQN6hVzKTWcWEmK3Fb87qVFweP3eAriVLKphDiXcBfYdi3/0BK+U0hxK8BX5VSPtT57c1CiGeAFvBLUsq1uBvrtVsQGHYdiWSt0oi0QnUToigDWWVA2ZVTNin6fsAW5FAqDlj7oVDpeNTktW6fWHk8qANGP8+bqErFi/d+O2AVOLXPq++sisaeNu6i8Yzre1YZ9cqIZa17KJ3gked7My+ZNHvdUjZ3vEGTtKjCL9iaG7+tweas73iFro6Dx25QGhFSyoeBh23f/Yrl/xL4hc6/vmFmxtkvemZY4/qjIxTKOkvbOp9/cYMnl8qRtl9utyTDDuQwymh+bpZ7jmp9WY2EPZSKCms/TA+lQUDFkqh6xMLjQazGVD1vouxMvHjvJtNB2m8qY5Xk1PYd0O3HJ3dF1lPpcy+arGXozTYPPVPsVfQdmrtJsFO7M9ubCR2KlQbT+XTsHldhFlT2d4oVnVQiQV5LWCKLGvGNrOVF5bEX9tVNzJWVFVd/ytsvm2R9p8HnX9zoW3JSCD+QnQaGn+eASW8/zAZxmSf8aPDbIkPvGcLimV4e98vn2URUzxsVeClFL5n2g5+92EsJZVMJnji7TbGTEUk13K8KTdYy9FZ7l6JfOnOaY8eOMZ5LkUkK/uH0JqmE4JHn17uKulDWu9l4TpVq3GG+OrEAACAASURBVHE8mlnUjjALKredRUJAvdXu2MwNV2BreVF47Id9pcCdTmR7VhSaEc3PuqJzen6vbm1ZB4bKYU2/8uhBPOYJldRSKgdfVmXRT5qdYO2H8VwqduVtwk0pRqE3zCRs0rtS1hHA5FA69AQeVtFbaa612jTakiEtyXbNZl7qPONngAibcDzo7s5tZ7FVa5JNJbh4IoeW2h26up8yva8UuBOsQlzRW9z5qmnSHd9TO1PCnnD3Q+nv9Q3AOPyf/Whw2nK62RBV6u4HHwZ5aBY3wkzC1sM4q226nxeY3BT9RrVJuw3j2RQVvdWzcp0Z1rjhyAhrOw2mhtJMBwz7oCIrYXZ3TjsL03vHKcFDv7GvFHi5XGZqaqrnO7sQex3G9TPYuypMwcprCd/B50RvnAjkMaIluP2yyZ4r/H4KxP67PWGFU/+bNPu5osXpXtZvM42XMonC47CTj5Y0EiXce+38nkxcJs3nYuLvXrlqyQT3XuffvkJZZ6WsM5k7t5OI4vKnCi2Z4K6rZji1Ueei8Qx5LYWbCPVzHO8rBT43t/ugLYgQmwplo2rYqYbS/kyNc6XspJS8Zm0negeJrr00neDEmW3WKg1mLfZSa99br0q7neYDvpOWSXN3YHa2+G7ubUER1GYf9Hen572USVQeR5l8+j1xucGkWdWO7ga91ebRF9Y5VaqxWKpxw5ERRxdK87Axzp2b3morLyj6OY73z34RKBQKjt+bjDa3TqtlHb3VdnzurqtmulfgP/10wfE5K0yl72VXV4VdsHYa7W67neBG76Bg0r6+Y2QHn7CsckxoHXPVp58u8KmnVvnEkys9fWrljTlg3371rKvAFwoGTx59fp3FUo2vn91mSEt03dui8MFUpk7tjON3JzgtAOz0urXVTY73GlHbZqXZKh9BsVFtsqO3ufbICMcmstxx+WSPC2VFP3fYGIRn4E+jH1+t6Oc43lcrcCGcbvWfg4q5o6K3aUuUPVXitJEGtVn60RsHvFaUPfbS59bZaTjbS712KU5eKF79LYQwBmajzXWHRyhVG9xxfJK8lvK9SOGHoDb7oL87wY/nTjzu123EOM4QnNwQg0bGjEuurX07N6x17eS+bowxmE2DjOV+juN9pcAnJyc9f1cZYGEPfuLaaga5OONEr+ogVHlOJTRu117qYY9069MwimhycpJU5lx5s5aBCe4XKVQQ1Gbv9PtQOkGhojM9lA50aOjWd048VkmsEFQRxzUpqLgh+sFrHDvR5kavV996uTGq0uilR4Is7Pz0VhTsKwVeKBQ8/SlV0jntlddBmIszdnpVB6Hqc/aIiB/92jKttnNoXK9JzH6gY75ntaE7XdRwGpSFQoFDRxccJ7qo5xEqNldf2RC2v4r1urXTSab9blGGUcRxneXE4YboNo7dxkhQX3cwbkaeKtW5aCLTtxyZqgs7P70VBftKgY+Ojnr+bj9Ucztk6MfhTdhYwV6w06tahupz9tC4ejNcaFy3A53xXIohLdG9kPHIc+vce52RncRtUOaGh10nOtXr4V6D1I/3Xr+bNteZvEZFj8f1Mzc8HGiREVYRxxWWIKgbohNf7HJtPtNotXfRpuK5ZEdFb/LgIy9RrjcZzqR48I5X9CVHpir89FYU7CsF3mq1fJ8xB6BXrIa4EbfNzISdXtUygqwg3Ca8IEkc3OKIaEnD9XCt0mAil2an0fYdlNvVhuNv5iB38twJsjNxi56novzjjs2it9p84eQ6K62q8iIjbBviVEqqbohufDHlWm8ZGaYefd44XxlKJxjSEt3DR73ZDkXvqVKdcr3JkJakXG9yerPOFTPBeBXnIk9Fb4XFvlLglUqF6elppWedGO8VxjQK4raZmbDTq1pGkLqsghq0fSpxRGaGNWaHtV0D0G1QimaNkUxmF9+8FLRK/3td+FA1ScS9MtuoNpGNGvnssPIiI0ob4t55+pXnxpdKpcLoxCSfeHKFlbLOYqnGdYdH2Gm0ufNVhrw/8vw6Dz1TVHK3teOiiQzDmVR3Bb4wlomN5jAIoreCYl8p8CDJQe2CDue27UNaAiRdr4qop/xx28xMONGrWkaYwRr0HZU4Ik4KR2+1XQ9zjxw6xD0L6Z7n/XZTKv3vpkyCmiTiVILjuRR6ZlzZNdItcNX5Cje+zM/Pd/t9cijNqVKNUrXRPbA2TVV2d1tV5DXDbHJ6s87CmHHJZhBw28ntaVLj8wlBk4NaB5tVCRQqxgHMtCWMadQY2P04GO1nMtQ4oBpHxMoHv8Nck+agCtrPu8etjLyWICFgq9Z0jELYL5iD/abJJmNzR3zlJg4vkkHHAXIbF8vLyxw6utDlx/VHR7jj+GSXdyrOCH7Ia6nAZpMo8OLPXic1Pm+QTqdDv9sTxjSfBknkSyFB/JvDIAq9Jvo5aMNMXH4rXieaveqxmnHSScE7r5/vrvL9EgWYh6+NliSdFNx11cxAFJt1sB9O1HnbMf9YL1G9SIJMAHG6qton741qE5H0Dlur6oywl4Hp7PDiTxzj2A37SoGPjY2FftfJpOKmEIL6T/cr7VMUemEw7Qw6cfmtrtxodqtno9pko9rk26UaFb2JEPBj183zyW+s7kqxZy/DagKq6MZWfRCWCetgX6ufi/fuxauoOwXVc4JCWefRF3oTMAQ5oHSD9fnJdJP5Q21P2fFzRogq23Erf69dYtRx7IV9pcCLxSL5vHMuPRXYBUb1oMsO1dVQVCEJQq9TXXsd8dCtfV6rq6A8Hs+lSCcFFb1JXkuiNyUvrlWVUuwNKuOPV70LiSpD6YRnRqA4dgp+tJqyv1LWOVWqce2RkVhcVZ2eT9VKkd0f7bFygrq9xh2V1GtHEVVveWFfKfB+zmSgfgNOJZJgHKtfVXrd6orDlhgHnG58Sunc30F5rCUTvPP6eYQAvWmksxrNJrsp9rzu2/Tr7EKlzWa9rWqOTz9d8PTkiWOn4Edr91Axl2axVGO9c8PSeqvWqryCTn49yRC0fCT3R2usnFOlGtcfHQk0+YYJduVkqrMfjrrtKA5W4B3out7X8oPcgPNzbQoburYn/rUivW51qdoS+w23G59Wv1+zvzcqwXmc11Lcd+PhHvPY9UdHuum43GJJw95F5DPrfWG9zna97enJ4+cSq8pHL1qtddxwZIQ7Lj93qOi2QHC6fetVtymLje1SJPdHp1g5Qcpzy6xjPVR32s3aTXX33XhYbeXeR721rxR4tVrta/leqxS3SIJuCGqzdBokqvR6TTx+tsRBwO3Gp1MCjrA8tg/yuGJd9/ugLNHSu37vbp48Xi6xcU3GQWTffCbogsDk0WKxFqmtVnmyx8rxgpMZzx7syi3piJOpTtV02k+9ta8UuKo/ZZRB57ZKCbJltNssf+DKKd/2OA0SVXpVTAFhAjHFFb3OeoPSvhOwu/3F5TMbx8p6EIfATn7vTnBziY1zMg4i+267PhWZicrjMKYvJ146BbtyuyXsZKpTNZ0e+IF3YPqPel2Hzmv9MRUEERqrzXKr1uQT31h1DRJlwmmQmMlfVdvnO4gDBGIKo7x2mYBcyvDqx6g+s3GumAdxCOzk9+6HQZ9tOPHMzazjJzN6q83JU2e57JKLI7XVLu9hYxE57W7cFjpOpjp7v1ujNZoB3Bqlg6TGACTTad/r0AkBjVa4oEx+UF3VWc0nbkGiVPyUNS0+ZRE0EFNQ5eU0eL0Gjav7WASa414xD8JLJQy9VvvzoZH0QM427Dxzkle/nYHJn3S1zontlVjjnEeJRWSlTW+1PRc65rNejgNDaSPUrsAICXDboQM/cADaqRzb9YrndWhTacaRQScM7OaTH7lmlj/71prSSsU+SEZGRmJrV1ivAfPU3S/9nJOyDqMAo9Acx4rZPrH220slDL3W6I/9XLD4wS6vfvw2+TOh5WJta5yxiFQXOl6Lk9uPT1LcaTA5lGZHbyPT/XEhhH2mwJs7m7sCHcHuK917lSEadrt8Ndq7g0Sp2jDX1tYYHh6OpV1BlZG5yvvo15bRm0b6Oa8Vk9PgDaMAvWj22yarTBheZbhNrE73BeIy04ThsX3BoqX2bsFihR+/Tf6kqyVGctOxtVXVYUBlBx1HxM+ZYY05SwC3RmUTZibCE+iBfaXApycnuWdheJeAOAnOXsX6cVNkQWN7AExMxMv0oAd7Fb1Nq62Wfs5t8Aat041mlW2ynwLpZ1TDsAjD4/NpwWKHp3msw5/losb89ERs5hNzx6uloodDMNvol7rPS9bsv9Uq5dDt8cO+UuDVapXR0VFHAdkrf16ndvitOlWFZLuyQy2RHdjFm6iXNeLggcljO1TNI15t8LvAESWqYdz0eiHqgmUvY4hoyQQZmrHV269wCCqp+/wmK/O3Uggeq2JfKfBaLbz/6CCFVlWReQmJ3mrztcU1Tstm9+KQPV9lnAjjMdIPuPE4jgNFvwscqu6YcR5shpXpsJPlIFwjnbyRrJ+jjGM7+nHQrHojW3UsxkmvHftKgbv5U/p16KCCTwWBn5BsVJsstfPkM/75KvvZnn7vbOy8c+NxHJOJtQy3bOV+9Ib1QXaTzzA+wlEWI/12jXS6sWz3konTLzqqXDj15XjOSAVYqOhM53tdCcPokn76ge+tFguIs0tLrJZ1w9WnA7NDP/XUKp94cqXnNxNOQrtX0FttVst6N56K2+HTeC7FoUSFin7u9mI/22+uZFQOw0wa7Hywf+cHJ94tLy+7Pm8q1zj8h2eGNWV6o7TDTz696A1Tnh+sB379OPS0h034xlK5cz/jnOyGodlLtsLKhWdfyo4Xoc3EGUaXBKU3CJS4J4R4K/ABIAl8SEr5Gy7PvR34n8BNUsqvxtZKjM7+xmqdpaXVnplPZUWxV1HnnGhQjaeiJRNcd2yKm0cnQ+ertNfttWpTXcm4JWSIK1N6Nrs7amBYmrwQZeUWpF4/+fSi13o5zTSfuV1rV43fHeeBnxOs7qeLGzVabcmZrXpPkK52QB73a/fsxhsz1sq0gythGF0SRKaDwrd2IUQS+CBwB3AG+IoQ4iEp5TO250aAnwG+3I+GblSbbDaT5DO9na0S6GcvbLluNFgFxi+eykh+iNF8uHyVVvgNAmt/+W2nnYQ+TOZwcB4MtVYuFppUEMY8FLRevwGfyznTa41+Z41SeNdVMz12/B29ycPfKiqlBxxE/HNzrL24VuXR59cZzaZIJgS3XDrORC7tSbNXm+M0+fhFFfW79GMNEKcycQahNyhUlnKvAV6QUr4IIIT4OHAn8IztuV8H/jPwr2NtYQfjuRRTiTqn9WxPp9qVMzivBs8HL5Wgs3epVOqeXkdpvxlJLZkQxkRoizUdVCE52QfD7HCcBkN5fV3pxD5KPOgoCKpQ/BYPVh471ZNMCMp1g3fmpG96MD3y/DqffKrQTQrs1x5V+Yt64K8lE1wylWP8jOF+OpJN8sSZ7e4k8/rJurJXRty7Z7ddsF0Ze/FMSyZ8E3BY4cbjOKDSG0eA05bPZ4CbrQ8IIa4DFqSUfyaE6IsC15IJvvvKBZqprKPfZdyBfvrhtaLqPmhiamoqlnrzWoLFjVo3S7f1VmWoFY7NPhhlh2MfDFNpOLrQ9iyjojf5028W+PZ6NVQ86CgIo1C8Jl83HltNEcOZFK32uQBKWjJBKpFgR2/vSgrs1R4VPsVlsvA6ME7n1eNjx717dtoFuynjuEJNxDWOnaAi9U6hj7rqRwiRAH4LuM+voNXVVe6//35SqRStVou7776bBx54gOXlZfL5PMlkkq2tLWZmZlhfX0dKyczMDCsrKwwPD1MqlUin04zMzXH65QJCCCYnJykUCoyOjtJqtSiXy4ynk2i1ImOpNOnWGIuLS4yNjaHrOtVqlfn5eZaXl9E0jZGREdbW1piYmKBarVKr1ZianeNzX3+BUiNBJpvlNbMJZqen2d7eRtf17vu5XA5N01jf2CCdH0fWK8hWs/u7E03NVpsvFSBd34R0jje8YpzaToW5uTkKhV6ams0mtVqNSqXSLTOdTjM2NkaxWHSlKTuUZ2m1yNzMJM16nbWtCpeOpZgVNWoS1kqbFGtlpqam0Le2WBCbLNXzLCQqNLbTbDQybG5uMj09zebmJo1Go1t+M5khoVc4rums6kO8tHiaoXSCmZkZdoorJDq3CsvlsiNNJp+sNNXaAr3W5GiiSrPW4vTLy6TaDUc+DY+N8egzS7C9w0gqx6tHG1w/ladWKbNUKjE1NcX29jbVep3s2DS1zSLDQ0NomuZKk4rsWWl6w1SDeksyPzvB0pnTjjSp8GlkZITFxUUWFha6smf+ns1medslOVaL60y/coaNrTJJWUc2GyyeWSadyTKT0hH1Cq89PMK1U5BJnPvdiyYvPpEdIVctkkkPodeanHypyiULRwLR5DSeFsQm27UE01qWjZWzTOTSruPJiU87xWVEQD45yV670eyR92pJUMvkyVWLaOk8zareQ7MqTduFl8lJZx1RLpdZW1uLJHuuyln6LAWFEK8DHpRSvqXz+T0AUsr3dT6PAScB87rRPLAO/KD9IPPxxx+XV1xxhZ+ed8Xi4qJSVC+91Y40Y5/drPGfHlvsfn73rcccU3KZdQVZsayWdT711Cp5zfCAePvVs64ztyq9fu0B70PGIP3Vj0Mla5kLYpM333Sla5mrZZ1PPLnSDax/3ZGRXYH1z0e3UTeE4bGJqHLuVmY/+s7a1iBRNqPU57aDrujNbiKKvKYWRdGtDpX+j8JjgBMnTjxx22233ej0m8oK/CvAcSHEK4CzwDuAHzV/lFJuAtPmZyHEY8C/jtsLBdT9KeOwd6uk5AJL+Mj0ufCRbsoegiV6COM/6nbb0M/jRbW/+nEgbC0zl5j2tcGP51JcTJZ0UvBjnYTFVnhtb4OYxgZx+SuKj3AQvqnSEpa/Kl5OZlutNEftY6f3vRSyNRBY1Atrqv2/p/HApZRNIcS7gL/CcCP8AynlN4UQvwZ8VUr5UN9aZ0PUWNEm/IRmZlhTTsllHuqdOLONBB55br2bBd2p3iBuXGHo7c09mOCR59aVPBSCoB8HwmaZi4uLDHvQrDLY3OzUQVZaeqvNx76+3JWBe6915mlUxCXTXgi6wgzKXz+FaR9rZlz/Qlnn0Rd234aNWq/XBL4XF9b6yWOlkx8p5cPAw7bvfsXl2VuiN8sZcbjjqAZFUk3JpSUT3H7ZJGuVBhO5NDuNtuvV20ar7ejG5TahhKHX6/DI66Cl36tN1fJVaPYbbG5KPsjBU6GsdyflU6Uadxx3zmwfFf10MTPRT1c8N990r5jZ6UyWTzy5wkpZ51SpxrVH/D1ogtDlddDc7zshTnK+126E5w2iJjjQW21OFqtsVJu+EfaCzMgzwxqzlvCRVl90a4YgpyS+XhNKWHrNttvTRXm5jfXTZqxavt5qs9MyYmdoyd0xNILAiX9BB6+0/e0HnHgc92Q6CFc8p/JdFbtMsl1vMJlLs1iqsb7TYM7HgyYIXV67tDhNgE4xXxxdmGNMzGLHvlLgm5ubjI+Ph3rX7WJEHDOwly+6NeC+UxJfJ7dH82ZdeWPDk964blf2Oz5GkDCtuWqRLyw1HGNoRFVmqv1hXqm+9vAwG9UmU0PeZrQosMt0PybTQbjiOZXvpmDb9TJmXP8bjoxwx+WTu3KjRqXLawEWh7nEycT2/7f3rUGOXNd530U3Gq/BawaYmX3MLrUUGUpiRO6SsmQnerCWa7H8QwxZCkXarMTOJlVW6PzRr7hc5WIpP+w4laScRFVxylElthXJsl7ZUiRKIq2XFcqRuCQlijK1XHJnZ3bnAWDwGAANNNC4+QE0ttG43X37hQcHXxWLuzs9t8+599zT5557HmZy7kVv2WGuFHgul7N/yAT6LLTTmSgevHOZ2QFcg1MryCwW3dghyCioRp91o93F1/6u2I/xtYiJ5t3oPMLq1kLjnSMnZVoFqX+c3qq0A/mo2M2Hfl7j4RAev3fNUrl4tZaNMh3Ux1SLt/fjwpCVwciaVzMFu5bP47GNmG8FqKaRoMdyseUSElPOvegtO8yVAq9Wq0gk3LUnMhbBN1PeitrrX65ccX/556TgvibkxYaCb/3iAF98pTD0C5J203FLJzdwY6E5cYtU5K5t0wFtzgS5hmQsi41MZCr1a/Tz2i8kFrJU3l6tZaNMe3F3WH1MvNLqpI6PHiwFW61WcTyRsP2QsniZpRBRo4vNbB950Vt2mCsF3ul0XP8ua3LNfFh7dYWZnuwlFMtKt0rCILOu0xvxC+Yl6qqlk9v58eMCSQ8nm02bs6tvyrj9bZOtRa5fVyfz6sdH1CjTXsL4vHYbsgJPHR/e/WG3j6144eUj6Ev5/JKE+04kUWp2RlxsrH3kRW/ZYa4UuNd4Sv3ksoREEw5WenLQoVh6xaH5BVNhe4U3rQJdQXSvkYQQzmycuHWJ6/F4zLOJWevKO69+fERXVtewX1dGaHTDt91cW4VW+uEGc7I/tH1s9m4rXnj7ngZtpUtCCE+c5YtUm2oc+CzBz3hKlpDohePcyeTQr2V22ejEKrcDSyHzxERPq0AXzwfEjYLzM9afZxObKQueefX6EVXUHr7z8lVs0bRnRWM112ZuLDcnJDNenXystThws3fzVgM0m3O3pw0v915WmHoc+KzAzI/kRomaNR82Ew6zsrV+fumNAhGU38wv2AmwGwXnF8+8dbO9WqZePqIVuYtqTxwrkewGZnPthztC/w6eSofxcAhKtzcMBzUikUhYvttObuzm3I3hEKTVHuQ+nisFLgjC2L+5nXgzITETDtbzTisfOv3QsPi1g1lqcdAp4WZwquDc8MyCcRPHwyHTMsOsu5FJXJRlYiIiYREFQ16An7HvVorSSVkHnnfry9xeerVoOneCICBlo2S9fBitPmZmc2uVjOR17/gl0yzMlQKv1WrIZrMj/+blcsapkBifd/Kld6MUWPxawaqQVUXuhzM+eW4dCWl2l90Nz6wNZtzEdhafsR+pHxE+rI46RhrP5QUk86uWtey9wOqEoZV1CAv+dOcZXsYrPcu509Y4yDsc45ra7b8gT9hOZdoJZncnM5DP58f+bZrt0py4CNwoBRa/VjDrllORu7hWltFQVADAb73n+MQtcV444dlug+k3sRM58UOmzBLHjDSur64iHve3lr0eZjIaVHcenrnT1niSdzh2+8+PE7YZnO5jJ5grBX5wcIB4PD7yb9OOxuAVQjdKgcWvm3doiUQJSURHpRPrXuMGdjzz1OBgwYmc+CFTrI46FbmLN0oyzqzcykHQ+FXUHjpqvzOM00bLTioBagjK8OGZO6dy7Qd4+PVywrZCkPzOlQI3q10uCd6zzKzghx/MjVKwq9XO+44nz/XDmDoq9ezrDBqU0mEyFdCPtzW7kDOrwWEGJxafV+vQ2FFH6fawXWvj2SsHyGzfssQ1fofZn1IID78rx51a7vcdkBfo94nV3DmVaz/ghl+/5ihIfmd3JzNgdhQJ8tLJaQlSp5aQFXiPXnapxQlJxG+957gnQZzURWhmeQWffXEXL9w4BAFw7mRyWMpVb3FX5H5Rft6MwElDv/nj4RC2Ku1hk9+RcMV83lH2pwZjhctJ3AHZ0cO7T4J0KVjBDb9+zNHChTLA3t4eM54yyGJMTjK//P6ImPHr5r1eBHGS6ctbN3dRbPZv7SmAYqMz7CHa7fVdDLVW36/83JUDpl95VqCf8zMroWGTX32Y3d7eHo6d3HB0kjDWazFWuPQbPB9vViMRzfDML92qxZ2JiVxy/VZCkPzOlQI36w/nNu7Tr0JMQDAfEbt+eEG91+wdUdG665AfVvpKJoVctV/KgADIxkQ883clvLRTBwFwz/ElfPBMBt99o4LUwG1m9CsHDTd8moXZXdhIOD6qGy12Y4VLP2EW2WQVTx8Ph/DMayW8fLMOin5VR4GQYW2hCxuJkfGnFeI6KfDsY7eYKwVuBqcbwM8MNA1BRsNYCfkkonAysX4ne82t8a0rB2Mdavyy0sUQwRNn1/Gh2zOotVUkJQFffKUAoG+Rl+UuVhLh4SXmZqU15lcOEl74ZIXZNTvO0+eNa+6mFCsvWJb1X79etoynV7o9fO7lvWGRp52aglg4hFxCGuF5lgpTzSvmSoHX6/1O6iw42QB+ZqDpn/H7UqheryOZydqGygUdhSMJITx4xzKKzQ6W42E0lfGuQ36dBDSev/9mdXipl42K2ES/P6nW4u6xe9bwRklm+pWDhFc+jcqXKrJjGiYZeTVGL4VlPH06KqJQV5CNibhe7n90j6UkCORWSWWN50mcHmcBVnrLK+ZKga+trfkyTpAhVHYC6OTIuLa2hkJdwV5dwXI8PLSAxFDIU/EjN8fW/JKENUPXIT38mtO1tTWmi+Chu/obQG9tnlmJDf3Kk8oB8MqnUfn2OoorOiYVQ22kF4BlzRV9NM0nPrABAEN51S6bNZ6nkcMxDZeNX3qLhblS4IVCARsbG57HmVbsuNMj4+7ePr5bELFZbuFaWcbfy8XxzGsltLvU9ZEzqLAzv+a0UChg7fiJW/5UKQRKR8MJ/X6nE/jxTr3y3brpj0wHCePHwox/VjQNy92i8Tzp9ZuWy8YvvcXCXDmcCCG+jaUJ5SR9bix/4n5dGbbwMqKlUjQ7Pbz72BJUlaIsd/DyzTqi4dDwyOmVBidj2M2ZH3NKCBlu7IfflQMocOnVIj7/8h5znqaxjn6+00+ZnhTM+Ncsas1VonR72KsriIqj8qrnmWcuFbVnuU944UX2vSDINZ4rC3x5eXnaJHiC8ab+W1cO0FTMu/4cW80hWalhr65AFEI4loyi0Ki7bgJrpIE3ZM2sMwor2cbsd4HxyAUWtDUeXvh1esO476slGbdPMNpkEph3mdbDGPv+hZ/u43q5hc1yC/edSA5lzQnPflrN0yq7EeQaz5UCLxQKcx0/arypv/Rq0fICp1Iq4rF7Nobt1pqdnqcmsBoeuD0LQmA7o+uOpgAAIABJREFUhtnmUdSeabIN63fj4RBAgKbSQ1wK4cG3L5sqff0a67MZtbjvFyYUbTIpzLtMG6FZ1Pt1BU2lh3tPJHHQ7ODCncvDNdPzbOeTnnbrQD8Q5BrPlQJPpVLTJsEzNAFX1J6tNZBKpSAJIRxPRce6f2jHSieXMWYxvWbPXi3KqMjdsSiPitxFsdlvE6Ul21hFpRQafUt9OR7G5e1DlBr9TkcsRaxfY23DXS3JeG7C0SaTwltBpvVgNT5eW5KGLceAWzzzWNeZmIi4FEKhoSCXCLs+MWrwO/uU51QZ5BrPlQJXVdXR87wttaaRSMBjDej51QseqyYIq1ypEU6zSo2V9LTNk4mJyMXDw2Qb1sbSH1dz8TBA+oqeAsjGwqbv13jWr8vtKzG84DLaZNYTRZzK9CyDt/GxqqqWBsIYaD+EFDYlRSZ5SWn1LqPMBbnGc6XAG40Gcrkc17M8izntRAI7a8CMX2NNkM+8uAu1B1senGaVpqIiTmeiePDOZZxZvuV7loR+P8ALd/Z9eyxXDCv8TO8KMnt/o9FAKruMz764i2Kzg1w8jCfOrgfS6DdI8H44nMj0rMOu8bE2J7XaIZ653jE1EIxjNjs95BISGor16WuSceVWDSCMMhfkGs+VAnfSHNRuMR1ZAFOCGb96RRwWCJQu5eLBTVZpJiaOKG/9WKx0euMzelpYriAWz4W6ghduHAIANsstXLhzGcdTUd8b/QYFNw1+3wqw68upzYkEArnXNTUQeMf08qxXmL2LJXOLpsYDOGkOyiNMPBaAF3g9vpvxa7zt//IrBW6hnVZWKe/7d3d3IWbWQClFt0chhm6FYDmdz2lFHTht8Dtrl5jGeXbSH5QnRjwul6GGs2go5gYCz5henvUKs3fpL97DAkE8HMLuzo3FJSYAhMNh7md5hInHAnALP47vVvzqFaHTOjBBN+t18h4jwuEw0jERkhiC3OoiLrlvb+V2Q7sJf9TDyYfDiUyz6PNbSbH82HoDwayYlQYzudHPSTocxm+cXecuA2wli8a58POSkjW+HV2SEMIjd+fxmRd3oXQpvvxKAR9YDU7NzpUCT6fTzH+36otoJ0x2FoAV3DRJdQIzfo3gFdpJ+YS9vCedTqOh9PC2bAyiQNAdJDNRxV3da6cb2pgODoqhzz6IZgm8a8yij4cmp8reKLfXK22uYlZ20M9JWE0jIYnDFm5uP0hByLPx4+1m/IbSg9rD0K0Zik65GiEh5CEAfwxAAPCnlNI/NPz8EwD+OYAugAKAf0Yp3fSZVhSLRSQSiZF/M244qxhjDX4ctdw0SXUKFr9eMCmfsJf3FItFHDu5gUxMHH5g7WpwBEV7oaEMomwkx3zwfjicrrGTuXWj4IxyeyoT4S5mZQdtTjY3d5BJJV3T6GYueGCk5YHbs67GN86hUq8AuYxruqxguwsIIQKATwG4AGAbwI8IIZcopa/qHnsRwP2U0iYh5OMA/gjAx/wmlmWtDGtVh0O2McZ6eD1quWmS6hROrTM7TMon7OU96XR6eAzdqrSxkYkM5y5o/+awL+WgQUIuEQYoRpol+O2+cLrGTubWjYJjyS1vMSte6Hn2ooT9lmcjLYS449U4Z83Dmie6rMBD0S8BeJ1S+gYAEEI+B+BhAEMFTin9tu75HwJ40k8iNSjKeOU2bRH36optjLGfcNMk1SlY/HrBpC55vLyn2WqjUW3h2dfHywzok6CcJjHZwZg5qvWlBDCivIzhjZ6P7A7WWPt48LaRs5NRXtej8e+eT686nr0oYb/lmVVn3e34+jmr+LyP9eCZrRMAtnR/3wbwXovnLwL4uheizCDL47WTtUXkiTF2CrsLjKCVIYtfHtqs4Pclj5/vUdQeLl8r4jWlhevlFu49kRz7GAflx7fqS6m9+0a1xQxv9AKrNdbD70tcr40pvMiQnmev+8hIi5cTkhktXvcL7xq7AY+WY5XSYuZEEUKeBHA/gA+yfr6/v4+LFy9CFEWoqopHH30UTz31FHZ3d5FIJCAIAmq1GvL5PA4ODkApRT6fx97eHpaWlhCNRrG5udmvk10ogBCC5eVlFAoFpFIpfPhUGOXaITZOHMfO9lY/oiGdRrFYRDqdhqIokGUZ6+vr2N3dhSRJSCaTKJVKyGazkGUZrVYL6+vruLGzg5/st1HtClgJtfEP3rGBVrMBRVGwsrqG69s3kUzEoRIRh4U61vJ5VKtVdDqd4fg8PAH9gu8snmKxGIrFIhqNxnDMcDiM+FISf/PqdRz0JCRFintWJZw4dsyWp93dXUSjUcRiMZTLZaysrODw8BCKogx/HovFIEkSqtUqcrmc7zylUimoqjrGUzqdxubNPVRVAaelNpZiDRw2wzgjyWhXQ6jTFEqlErrhBNR6GcfDPey3lnD1zWtYTiY88wRCsEGq2GvHcUJooVHsISmsjvBULlWQCKk4FWmhRwmUVgub5T1LnuxkT1VV1Go1yLKMhiwjms6hVS0iEYuN8HSzWEFMLoNEMojKRWzdpFhJxrnXaX9nf2SdVDEKtA5xMtTBXiuON65dx1JE5FonN/tJL3uqqqJer4+sU7O4C2qxTjd2dkDFKJKxMOR6nSl70XgCf/NmBejI6ETSeF8eEIWQK55S6+vY3PZnP8XjcWxubnraT6bK2a7lPSHklwE8TSn98ODvvwsAlNI/MDz3IID/DOCDlNJ91ljPP/88veuuuyzfZ4XNzc2Jxczu1xV88af7Q4vso+9eHcm0MsaQBxHRofGrry/RUPp+Wq0Qlp42XkwjvZy3rME3f/RzbNE04uHQWNEuniJaXmm0sgQVtYfPvrSLYqODXCLsy7u1NW4oXfzF5V10VMqUJ79PHpPOUtWv/872lqN9zEur2Z4NAk72kFe9dfny5RfOnz9/P+tnPBb4jwDcQQh5G4AbAB4H8Ov6BwghZwH8CYCHzJS3H5CkyWVJ2mVaCSGCersLIUQC87lLEvuDkYwIrjuRTyO9nPedkhDCvaeyeG86x1SiWlr12eNJlOUOLtyx7Cvtdq4BSQjhiXutM0ntMBa3PFjjv7i8i5duHiIhibgN0UAuxY28+DGelSLTGx76WPIPrfPFvmu/31H5QkgndUnvdA8FqbdsOaSUdgkhvwPgG+iHEX6aUvozQsgnAfyYUnoJwL8DsATgrwbFy69TSj/iN7HJZNLvIU3Bk2m1FBGh9qhpFqdXSzeZTA5bqkWEEOrtLkSh393bbSfyaaSXO3lnJpWCNOg2r504tPnTb9BVQ4W7oOA2UYS19qyNn0wmB0qKDizHfgZfEJfiduM5lVe7gk7az0IE6Ki3yj3QsH3YpDE8OB62N1gmdUnvdA8Fqbe4PlGU0q8B+Jrh335f9+cHfaaLiVKpZOsT8hNmmVb6NHazaAA/LN39YhHfL0m4Xm5BpRRxSUB3cMR2Ww88SCvFTAEkpBBCBKi1urYlC3b3C3huP4xWp4ftWnvMRTUPLbjM3CGsjd8slYZx77chBkkk+A0folucwg2vVopM/7NaqwtJvNXUuNOoAvms5dj6XrBNxdxgCToTkwWzPWQm/0HqrbnKxFxKp8fCx6bhz9ULiZms+GHpCrEkmoo8LIr/0b+fR1wSPSmvoI7OVs0fvvxKAR2VIiwQPHJ33tIH/n/3VLy00xoW6RKFURfVpKJoAHdrOOoOEXAbYsPfY238SDY78Q8TC254tTIGjDVBHnv3Kjo9IB0V0WrUbV0vz145wGa5H4107mSSabBMq9qk0YhjuYn0tGSz1h8rL5gbBa6oPXz/F3vYURMjNRmmWQ7WCn5YumKvM1IU/1gqaqn8eD9kVkqQ97LROO9mCkBfd6ahqIMWaWy6KnIXotpBQhJRb3cQDd86cUyqEJXGn7EpAe8a3nKHiGgofctT+z2Woi7L8rBxxzQrYWZiIiICwfWKjOPJCBevVh8eSRitCfLVn5eG+7PQaOLS6w3Tfct71xG0O9AujDgdFU3dRHpa5MEaB4G5UeAVuQu1oyARTQ0nyEtab9Dww6rqKm08ds+G7Rh+WSK8NdRZZXjNPlhOy4EuCSrWlmK4fTmKJ86uDa22SUbL8DQlMEMmJg7cIVGEhXF3iFFRt1otX2j2egrtqD38bL+BaquL8uDikGcsqw+PsSaItj+r9SYO25LpvuW96wjaHWi3F4xuorBAmH56P9bYDHOjwDMxEUokMzZBfi+gny4Zr1bV+vo61xh+WSI8NdTNyvBqFtf1ShundOnvTj9ktXAKoQ5FPCIgLk3enWDXlMAOLH6tZEqrFe21oJPmqnjy3DoSkrN9oKg9vHyzjkZ7kPqtqNiqtnFX3tt+MlOwp04eR/KwbLpveWXGDyPJbN559pSxKJ7Zx35RDxz9xXpvTkUyf3xkgvz0HU67Q48RvLWijRslHg65SjVn1TLWw6oMr+brZs0d74esIncRa1eRT+Rsu68EBT+sOj2/djK1u7uLYyc3PBV0qshdXCu30FC6IAT4zfuPc/++Rt+B3EGj0wPQRTIaxkY64phvI1i+4kxMRGl/z/ZkySszXowkq7h+u71g5E/jg0VKkDXf50aBA0AiFmNGhfi1yafZwYVlBUSjUS7LzLhRzBSpHTQrWoug+PIrhZHftyrD68fcZWIihLDkKr7dL/h9oWg3L9FodCTiwk1Bp/7RvYuEJEBWenijJOPMCl+JZI2+TDSM92yk8J6NFN69vuTYijeD0VecjAh44FjE8b7182SsjSV3uri8fQgK4Hq5hQ+dySIWFobvsNoLev7s+IhGvZVbsMJcKfBYLBbo+NPo4GJloYmRCLdlpgnSfl1xpEiNG6Oh9NCjo37L9CAuWwuJYyk3vyzX99+5hl447tuJatr1YuxOR2IkgmcMERdOCzp97J5VyB0VvR6wXWvj2SsHyGzzZQfr6VuOhXHfiZRlmJ4bGD9iasjZPvbzZKwfi1KKHqUghKBHKf7Pz4sghAzfwdoLbuQiSL01Vwq8XC4HdpsLTLYlkwa9cFfkLq6WZNw+sJ72CgeWlz0sOFGkrI3BUjjGZ1g0+DV39WoVp097r508rYxTo7KzOx3tFQ7Q7Eius0sVtYev/rwEMRRCFz1sZCKOFI7Vuvk1h0aZ6sqHAFaYvLj1R1tBP67x4vGdawnInR6iYqivrCO33uHUKDGjP0i9NVcKfGVlfNH9xqTDufS+ts1KC89dOcALA+vp2GoOycOGI6vWiSI12xj633eyefyYO7/WmIdu3pBJHgvUStlZnY70a+wmu1R/L2FMmHFSv5q1bmZz6NQqN8qkIjfHnrGaPy+nO1ZUEevikdVbVqO72FBgLBnFmwcBBKu35kqBHx4eTjQTcxLQhORqScY3XyuBEGCn1kaxoYA0G44iGvRjuukcoo9X1n7fqUVvVxfDbtPbrTHvODy1sHlCJnme4a3XwaKptD++xk7AGwnhBix63VrlepkqMdbY6oPr5XTHiirSn4j0pRrM3mFsIQeM559Y0R+k3porBe62wcE0sjV5oKfrVCaC69UWtitthELASjyMD+QUCIOEErtsLzfg2Ri8m8euLgZvIwRFUUzXy4nysKObx0IfXi6aNAkxNoGwKjBm1oxBURRPJxfeSAi/xnZ6x8KCVWMWK0PBpnAqU25Y47IuVh+5Oz+izDWw5ISVf2JFv9+NWfSYKwXuJp5ymmUznRy5H7g9i/UlCU2lX+nwoNnB9/YJmjt7w5jrsEBMs73cgkd58DxjpRALdYW7EcLK6prpejn1hVrRzWOhP/v6Aa6XW9gst3DfifHLRWMTCKt6HWY86WV6Fi5d7cb247KatY/d+uLNKh7quzixxjXePX3mxV2oPXC7b1gfBTP6F3HgA7iJp5xkaKCTj4WRLkKA1aSE7WobFEBcEpDqVtAWssOytR2VuvJxTgJ2G5ug3wWE1R1Ej+vbN00vbjMxEfFwCIWGglw87Il/Hgu9qfSGdWgu3Dl+uchqwcVabysZ1GR61nIQzODHZbXZPnbji+dJZdePyyqToNXdMftdox/cbA7M6F/EgQ/gJhwnIYVAQbF32MZKIoxGuwul27PtXO8GjsqmMjb/E/eu48IdywD66ePffEmG2qEjZWvHjuAz4h6y2tj5JQnnTiaHCRNWF3WZZALJw565hUdu/b/jkXdeC33N5HKRV5lZfdw0mZ5WDoIbuLX4NVkNR5zFRdvV5rdLZde/n1UmgXWBaYTRD+5kDhZhhAM4LYyuqD184Sf7eHWvga5KcaPWwos3DkEIwX0nkr40pdXDyfHSbPPrXQvvf3seNJIYK1uryc2sWW1mQi0J/I0Q4tEIHrsnNZa9JwmhoVWcT0iotfolW3t0/NjLgtfICS8XxlZjaTI9jRyESUIvq3lRwUfyfLVWAPva/LwXuFZlErzel1jSP82GDrOEarWKTIY/Rrgid1FsdhAiBIRQVFsqomIIYYGg1Oz4buU4PV7abf7GYQ2nl/ulKPVKmxXT+lax2rQ1Nl4yGWPUndwH+BE54RVmY2n8+uGa8Bte6rMYf08vq6TVcK4EGfNndG+EhRDyFhmkVh9JL/cldnCqt5xgbhS4ovYQiqehcFZJA/oTn4uHsVluQQwRZGMiOmrfkbXi0odqJ9QsQbCKqrAaK5fLjY1jFtNqVwPFzWachntG49kuRp3n2Kthmh86J2sc5GWkU7j96Jn9nl4JRiLOsk3twHJvsOD2I+n142rcx35iLhS4JhSSXIYSkx1ZUE+cXceFO2/5lautLgC46mjjRqjNQuh4xqpWq/2O6QMYb863Km1TP55ZeysndLvdwE6UvvF5jWezYkJ6Jce7qYJ2T7CSOnjDPo1rPCtw+9Ez+z29EpTLBd8MAj8jk6zg5eMa5BrPhQLXFul4qIetuoJiQzENQzNCEkIjz/IU6fEzpdcshI5nrE6nM/J3Y9bms1cOhvVJrMZzQ7eb33Gq9FnPazxLwmhDAFYxId5NFaR7gnUq0pS2VWSEBuMazwrcfvR43BSbxe7U6QT8O2HajRPkGs+FAtfCx35wM4Q2beFbVw5GSj/6iSBSelkhdDxjsWpFP3bPGt4oyXj2ygFXQwX9u6xKYxrhhlenSp/1vD5m1qwhgBsE5Z4w8nC90h6JjLAL+wwyRtgLgnQ38PLspBInK93dbuxJNUE58nHgkhDCg3csIyIXIccyaCo915tZUXso1PuZUaxQQr9Tes1C6HjG0mpFG10wZ1ZiyGyL3IkEPNasEXb08Wa9WYH1/M721jBm1q9iQl7QULq4Xm7jVDbCPL0ZaTyViTiKjOCNEZ7GfURQ7gYrnp24n/Tg9YNr8OteRKvHLoQIKnKXOc4iDhwDZRuJodzpufZjav7oF24cggA4dzI5ZsnbKQ2nQm0VQmc3ViKRMHXBOEkkAPisWaOSMBvPzOpwE4Uzlgau8xVqHx5jlx8WggipbChdPP2tN1Fvd7EUEfH0hbeNKXEWD05S23l8o5MKF/Wjlg0PzHjmTcwxwo0y9uteJCGFsFlpDWWEdboN8o5jbhS4JITwD29fBokmXfsxtbBCoO/SKDbGQwmD8Je6tWQEQQDAdsE4HdOP4k4a7E4pXsLDNJ41mqyssKBDKq+X26i3u4hLAurtrmmbMSMPTuZAz68ZJhFFY5eu7vYDwlL8ZjzbJebox9Kez8REV8rYr33eUHo4mYpApRIEQkaadmv0gtjlH7vH3ChwAJDrdZz2UJpRH1ZIAOQS7FDCWQnnqtVqOHYyzZ3FaAU7gXWiJBJSCCEC1Aa+dz+jOmq1GrLZrC1NdiGVftB0KhvBUkQcWlc8bcachozWajUkUmlL69artchjPftxCc5bYlW/xmZ8Gt1PwK0KgHEpBFCgOTiNP3bPmis/uB/7PCGFsF1rj1nget43SBW/mskGcmqaKwWez+c9/b4xrNBNKOEkkc/nLV0wTmElsHadYzRoVrFWl+WRu/OmNLk5duvX2EpxaUolKoawV1dQbXVdW1RmdCakvttkq9rGRprtAzeOw1JYlhfjKzlb69aLtchrPfNcglt9QFjvMVP8ZvvYyv2kr4JYaCgDA0wajpuOio794H6gofRwOhOFKBB0VTq0wPW877XjgeUezJUCPzg4QDweB+CtchtvCOK0USiVEOv1j4hBFuDSR7iYdY7R5ljfQKChqCNHRuO4bo7d+jW2UlxaZJJ2n6FFJjlpH8dDZ0ISubuzmyksKwt2Z7+Iw7Zga926tRZ5rWe7S3C7DwjrPWaKX7/GvHzqx8olwgDFiHtlWslamZiIZFQYnpA1HvX0nhBagZVGmCsFTgfno1mrARIEFLWHn9w8xPY2CYxH1jza9dXkPc673VDUcAY229BaZFKx2cFyPGwbmWQmM35tfEXtoaP2mDXBreYsKpBAk4yc1udx223JrO42S/Eb15gHxrEAjIzrd7KWIwORDu6ndGzp6W0U+bPHnWKuFLh29JqnGiBuUZG72OnEAAEj4Ul+RAPYdZGxihvnPc67Lf2aWV4xLQdgRH5JwtqSxLVpzWTGj41vbOzw8LtyI+45qzlbX1vFYyelwGqgBHEp7+Q9LMXv1hVqHCuo4AOnF/rNTg+5hISGwr7QTwqrrmmxw1wp8L29PZw+ffotX7kNGFwUtip4sRYdXo74cfLg6SKjhe+ZxY1zH+cdln5V1B6++9M3sUXTXPw52bRmMuPHxjc2dggPQiqNtLLmTJPpIA2QIC7lWYYE73s0nt2+DwBTlnjer48zZ3Xg0cbmNRB5dJEbfnkxV5pP6ys3KatimmgoPUjRON6dSEDt9S9HqMK2mJ1Y5bxdZHizIM02lpvSrxW5i0ovjESE/2TFqzTsfLxeFJwXg2Iee7x6NSR4eDbKlVUEinZRzGMgfP7lvWEpitOZ6PDuZ/Tegz/KikcXBbnGXJJGCHkIwB8DEAD8KaX0Dw0/jwD4MwD3ASgB+Bil9Jq/pPahXygrf+csNDkwwgldmZjYV7IqRoTIqCicbibeLjJOIw+MG0sf1sdb+jUTExETQ9gPqONQUOGhbzWDws5KDdqFyWo3aBeBwrMHNLqFEEG93YUoEGZ4Km+UlYZphh3b7hBCiADgUwAuANgG8CNCyCVK6au6xy4CKFNK304IeRzAvwXwMb+JrR4e4uubiuVCzeoFp1O6JCGEs6sikvnVEaVgVBROm8zyKhunkQfGjWXs/s1T+tWMZy+Y1MfcahNb0VCv17HiIbfBb/BYqV5dmHY8Gz8QhNwyXLxEoOjvdpYiIroqHbOw9WMdyP1EP54CeF749QIeyn4JwOuU0jcAgBDyOQAPA9Ar8IcBPD348xcA/BdCCKFurpstEEmu4HCnarlQs3rB6Yau4+vriEbHi9jrf48nw9Ktr9JJ5AFrY+l//5G789iqtLFhkxLP4pkHbkIEJwE7GtbW1iZKjx2MVqoQGrdSvZ447HhmnRL9iEDR023scqV/Nys81Y3caDK5nPOWv2IFHgV+AsCW7u/bAN5r9gyltEsIqQJYAVD0g0gNnXoZyUjYcqFm9YLTDV2FQgEbGxuWz1htpqAVmF1ol54O3sJEPDwbEXSIoBfY0eCG3yBhtFK1XqxeawLpYcezmUz7EYGip5tFvtPwVDPoZfJkqIYP339XIMYDj3ZjJfIbLWueZ7C/v4+LFy9CFEWoqopHH30UTz31FHZ3d5FIJCAIAmq1GvL5PA4ODkApRT6fx97eHpaWlqC0W/iV5R6iqRUoh2Xs79zE8vIyCoUCUqkUVFVFo9HAP3rHGrZu3EQiGkGnJWOnWEQ6nYaiKJBlGevr69jd3YUkSUgmkyiVSshms5BlGa1Wa/jzaDSKWCyGcrmMlZUVHB4eQlGU4c9jsRgkSUK1WkUul0O1WkWn0xn+3MjT+/NdyIqKE+vL2NneGl5u1Ot1rK2toVAogBAy5ElRFBSLRTQajeGY4XAY6XQaRQZPO9tbIzwhugRBruCk0MNuK4Grb17DcjLhK0/aOiV163TYGuWp0emh3erhZKiJSkvC9i6B0G0zeVIUBfv7+47WSYEItSXjZKiNYiuKze2bkKBiZXUNG6SKWktAXpJwWLiJOPLcPOllz2qd9LJn5KleLCAv9qC0FGwIKmKhHDY3N4c8VSoVpNPpwGXPCU+/stxGKBJHmEio1RvYOJHHzvaWpew52U+VSgXZbNaWp061ip2iM56Msse7Tnqe2s0mjscFSO0SsmIYYjeFzc0dRzoinFpBTC4iJkbQ6yi4+uY1nDq25nqdTJWznZeDEPLLAJ6mlH548PffBQBK6R/onvnG4JnnCSEigF0AeaML5fnnn6d33XWX5fus0Gw2TTO43orwyu8suBCc0uGGZ7tCTNO+XLSi4ajJNDAfPHuVG71MZsMqHj274Vr+Ll++/ML58+fvZ/2MxwL/EYA7CCFvA3ADwOMAft3wzCUA/xTA8wA+CuCv/fZ/A/2jV1DxlLMIr/zOSnSEEzrc8BxkiKAfsKLhqMk0MB88e5UbvUweFm5OLxNz4NP+HQDfQD+M8NOU0p8RQj4J4MeU0ksA/juAPyeEvA7gAH0l7ztSqVQQw84s/OB3FhSYEzrc8jwrfDrFUZNp4OjwrMmkqKQDewfXDR+l9GsAvmb4t9/X/bkF4B/7S9o4VFUN+hUzhaPGL3D0eD5q/AJHj+cg+Z1+gLQDNBqNaZMwURw1foGjx/NR4xc4ejwHye9cKfBZbQAbFI4av8DR4/mo8QscPZ6D5HeuFPju7u60SZgojhq/wNHj+ajxCxw9noPkd64U+Fe+8pVpkzBRHDV+gaPH81HjFzh6PAfJ71wp8C996UvTJmGiOGr8AkeP56PGL3D0eA6S37lS4N1ud9okTBRHjV/g6PF81PgFjh7PQfJrm4npJ5577rkCgE23v39wcJBbXl72tb7KLOOo8QscPZ6PGr/A0ePZB35Pnz9/nlkRa6IKfIEFFlhgAf8wVy6UBRZYYIEFbmGhwBdYYIEF5hQzqcAJIQ8RQl4flVsKAAADtklEQVQjhLxOCPnXjJ9HCCF/Ofj53xJCbps8lf6Bg99PEEJeJYT8hBDyHCFktisBccCOZ91zHyWEUEIIsxrbvICHX0LIY4N1/hkh5H9Nmka/wSHXpwgh3yaEvDiQ7V+bBp1+gRDyaULIPiHkFZOfE0LIfxrMx08IIec8v5RSOlP/oV8w6yqAMwAkAC8DeKfhmX8J4L8O/vw4gL+cNt0B8/sAgPjgzx+fZ355eR48lwTwPQA/BHD/tOkOeI3vAPAigOzg76vTpnsCPP83AB8f/PmdAK5Nm26PPH8AwDkAr5j8/NcAfB39/gnvA/C3Xt85ixb4sIUbpVQBoLVw0+NhAP9z8OcvADhPCGE1lZgH2PJLKf02pbQ5+OsPAZycMI1+g2eNAeDfAPgjAK1JEhcAePj9FwA+RSktAwCldH/CNPoNHp4pAK00YRrAzQnS5zsopd9DvxqrGR4G8Ge0jx8CyBBCjnl55ywqcFYLtxNmz1BKuwC0Fm7zCB5+9biI/ld8nmHLMyHkLIANSulXJ0lYQOBZ4zsB3EkI+QEh5IeEkIcmRl0w4OH5aQBPEkK20a92+q8mQ9rU4HSv22I2GkaOwrcWbnMCbl4IIU8CuB/ABwOlKHhY8kwICQH4jwB+c1IEBQyeNRbRd6N8CP0T1vcJIXdTSisB0xYUeHh+AsD/oJT++0Hnrz8f8NwLnrypwHe9NYsW+DYAfcfTkxg/Wg2fGbRwS8P66DLL4OEXhJAHAfwegI9QStsToi0o2PGcBHA3gO8QQq6h7y+8NMcXmbwy/b8ppR1K6ZsAXkNfoc8reHi+CODzAEApfR5AFEBuItRNB1x73QlmUYEPW7gRQiT0LykvGZ7RWrgBAbZwmxBs+R24E/4EfeU9775RwIZnSmmVUpqjlN5GKb0Nfb//RyilP54OuZ7BI9NfQf+yGoSQHPoulTcmSqW/4OH5OoDzAEAIeQf6CrwwUSoni0sA/skgGuV9AKqU0h1PI0775tbitvYX6N9i/97g3z6J/iYG+gv9VwBeB/D/AJyZNs0B8/ssgD0ALw3+uzRtmoPm2fDsdzDHUSica0wA/AcArwL4KYDHp03zBHh+J4AfoB+h8hKAX502zR75/SyAHQAd9K3tiwB+G8Bv69b4U4P5+KkfMr1IpV9ggQUWmFPMogtlgQUWWGABDiwU+AILLLDAnGKhwBdYYIEF5hQLBb7AAgssMKdYKPAFFlhggTnFQoEvsMACC8wpFgp8gQUWWGBOsVDgCyywwAJziv8PF3u6DFnasXUAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"N = 1000\n",
"plt.title(\"Simpling Random Sampling Sequence\")\n",
"plt.scatter(numpy.random.uniform(size=N), numpy.random.uniform(size=N), marker=\".\", alpha=0.5);"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"autoscroll": false,
"ein.hycell": false,
"ein.tags": "worksheet-0",
"nbpages": {
"level": 2,
"link": "[7.1.2 Quasi MC: Halton’s low discrepency sequences](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1.2-Quasi-MC:-Halton’s-low-discrepency-sequences)",
"section": "7.1.2 Quasi MC: Halton’s low discrepency sequences"
},
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Quasi-Monte Carlo result (Halton): 41.21870562744141\n"
]
}
],
"source": [
"seq = halton(2, N)\n",
"accum = 0\n",
"for i in range(N):\n",
" x = 1 + seq[i][0]*(5 - 1)\n",
" y = 1 + seq[i][1]*(5**2 - 1**2)\n",
" accum += x**2\n",
"volume = 5 - 1\n",
"result[\"QMCH\"] = volume * accum / float(N)\n",
"print(\"Quasi-Monte Carlo result (Halton): {}\".format(result[\"QMCH\"]))"
]
},
{
"cell_type": "markdown",
"metadata": {
"ein.tags": "worksheet-0",
"nbpages": {
"level": 2,
"link": "[7.1.2 Quasi MC: Halton’s low discrepency sequences](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1.2-Quasi-MC:-Halton’s-low-discrepency-sequences)",
"section": "7.1.2 Quasi MC: Halton’s low discrepency sequences"
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
"Another quasi-random sequence commonly used for this purpose is the **Sobol’ sequence**. This equence was designed to make integral estiamtes on the p-dimensional hypercube converge as quickly as possible."
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.1.2 Quasi MC: Halton’s low discrepency sequences](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1.2-Quasi-MC:-Halton’s-low-discrepency-sequences)",
"section": "7.1.2 Quasi MC: Halton’s low discrepency sequences"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXAAAAEGCAYAAAB8Ys7jAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAIABJREFUeJzsvXuQZNdZJ/g7eTNvviors/LRVf0otdSyhGQL25IlGQQDAknYMA4bKYwWsQ5WDu3s7CIeMyzMwi7LaJgIDMwQOxALw8QQxrsYzHjWqwkFeDGSvfLCWAZbbWksydjqlrq6q7semZWPysy6mTfz3rN/ZN3SrVv3cV43u9Odv4iK7qr7OOf7ne/7zus73yWUUswxxxxzzDF7SFztCswxxxxzzCGGuQOfY4455phRzB34HHPMMceMYu7A55hjjjlmFHMHPsccc8wxo5g78DnmmGOOGcXcgc9xzYMQQgkhH5F8x4377/leVfWaY46rjbkDv05BCPlFQsgLhJAWIaRNCPkbQsj7Pfc8te/0KCHE2r/vRULIbxFCVhnKqBBCfpcQ8iYhZEgIqRNC/poQ8lh8ks0xx/WDuQO/fvGDAD4O4AcAvBfAlwH8OSHkezz3XQBwHMCp/fv+FYDvB/AqIeS+iDI+A+D7APxjALcCeD+ATwGoqBFhjjmuc1BK5z/zH1BKAeDrAH7b9ftTAM753JcC8AKA1wEkAt5VAkABfCCizBSA3wBwGYAJ4DUAP+G5hwL4OUw6hD6AKwB+3nPPcQB/BqANwADwPIC7Xddv3H/P94bU5dR+GY39d7wB4Bdd15P7nLwJYADgVQD/2POO0wD+cv/5iwB+Zr8uf+i65wKAX/E894cAnvf87WcA/P1+Wa8D+F8AJD3v+TUAvwOgCWALwL8GoHne8+Q+r0MA2wD+Lx6Z5j/X7s98BD4HAIAQkgBQwMR5hYJSOgLw2wDeBuCugNt6ALoAPkQIyYe87tcB/CMA/wTAHQA+CeCThJAHPPf9c0wc4Z0AfhPAbxFCHtmvOwHwnwDcBuADAO7FxJk9SwipRsnjwu8DKAJ4EMDtAJ4AsO66/ocAHsFkRnE7Js7zNwkhT7jq8TQmM4z7AXxw/yeIo0AQQp4C8AsAfnm/rJ/bL/efe279GQAbmMyOfhYTHn/S9Z5/gQlfvw/gOzGZBb3EKtMc1ziudg8y/7k2fgD8Ciaj11Ouvz0FnxH4/rXbMBnRPhryzocx6RBMAF/FZKT4g67rOUxGhT/lee5pAF9w/U4B/LHnnj8F8Df7/39g/563u66nMXFsv7r/+42IHoG/DOCpgGs3AbAB3Ob5+68CeGn//w/ul3Gr63oNk9E48wh8n5c9AO/33POTANqe9zzjuecvAXxq///5/bJ/QVSm+c+1/ZNk8PFzfJuDEPJTAP5nAB+klK5H3e88tv9vYDY0SunThJDPAvgeTEaIPwjgZwkhv08pfRKTEbwO4P/zPPpFTEaebrzg+f0/YzKaBIB3ANihlL7mKntICPnb/Wus+DcA/h0h5IcxGe3/BaXUqdvdmMj81clA+wBJANb+/98OoEEp/ZarHnVCyDc56uDIkwXwGUKIm18NQIYQUqOU1vf/9pLn2cuYOGbnPRkAfxVQDotMc1zDmDvw6xyEkF8A8C8wcd7PcTx6x/6/58NuopQOAXxh/+djhJBfAfAvCSH/yn2bt1o+f/OCeH73u5/lPe66/hEh5C8x6Rh+AMD/Qwh5mlL6Eby14X8fJqNjv7JZy7NxtP4p1/+dsn4MwLdwFE3X/02funiXRoPqxCLTHNcw5mvg1zEIIb+GyZrqj/A4b0JICsDPY+JcvCPAKHxj/98agHOYLKF8v+ee78NkM82N7/L8/t2ud70KoEoIeburjmlM1sK97wkFpXSDUvpHlNKfxGQN/L8mhCwCeHH/lhsopec8P04n9iqAGiHkFlc9qphE4LixDeCE5293uv7/KiYbimd8yjpHKWUdHb+2/573BVxnkWmOaxjzEfh1CkLIv8Fk4+oxAN8khKzsXzIopR3XrZrrWhETR/NPMVkDfx+l1A54fwWTiI4/wmRtuY3JqP1jmEQ8vEQpHRFCfheTEXkdk87gxwB8CMBDnld+gBDy0wA+h8kI+b8C8OP7174A4O8A/Ckh5EkAHQD/KybLB/+Wg5P/HcBnAXxz/9lHAFwC0KWU7hJCPg7g3xNC/hkmSzp5AO8BUKOU/iaAz+/L+klCyM9gMjr+TQBjT1HPAfgpQsjTANYA/PeYRK80AYBS2iOE/DqAX99f2ngWE1v9TgB3Ukr/JxZ59t/z2wCeIoQY++/JYtJhf4xSeo5BpjmuZVztRfj5z9X5wWSK7PfzCdc9T7n+bmPiGM8C+C24NjsD3p/GJMLk7zBxTE5Y3h8AWHXdxxpG+E8wiTTZw2Rz8hc993jDCL8I/jDC38NkVmEA2AHwFwDe4bquAfhnmIT2mZhs0H4RwI95yvkrTEa+65hEjzyPw5uYBQB/DKCFyWj8KfiHET6BSac22L/3bwH8D67rFxARjojJUs3PYdIpmZhE5/xHHpnmP9fuD9lvxDnmmCMmEEKexySa57+92nWZ49sL8zXwOeaYY44ZxdyBzzHHHHPMKOZLKHPMMcccM4r5CHyOOeaYY0Yxd+BzzDHHHDOKqcaBP//88zSdTk+zyDnmmGOOmcbe3l7jgQceqPldm6oDT6fTuO2224SfX1tbw+nTpxXW6NrG9SYvcP3JfL3JC1x/MsvKe/bs2bWgazO1hJJKpaJv+jbC9SYvcP3JfL3JC1x/Mscp70w58GKxeLWrMFVcb/IC15/M15u8wPUnc5zyzpQDbzQivzXwbYXrTV7g+pP5epMXuP5kjlPemXLg85772x/Xm8zXm7zA9SfzfAS+D9P0pj7+9sb1Ji9w/cl8vckLXH8yxylvpAMnhHycELJNCHkl4DohhPwuIeQcIeS/EEK4v//HCsMw4nr1NYnrTV7g+pP5epMXuP5kjlNelhH4J/DWp6v88MMAbtn/+e/AkX+ZFysrK9E3fRvhepMXuP5kvt7kBa4/meOUN9KB08k3AZsht3wIwP9JJ/gygBIh5LiqCrqxubkZx2uvWcjKa1o2tnsmTMv3mwvXJK5mG18NvmZZp0X5mmWZRRCnvCoO8pzE5KslDtb3/7ah4N2HoKVS2O6ZKGWT0LWZWr4Xgq7r3M+Ylo22MUZeT+DpV+roDi0U0hoefdfyTHAmIrMoHK5K2YkZfPrlranzNU15ZeDmStcSMC1bmK9ZkVkGh/iKUV4VDtz7cVYg4IOo29vbeOKJJ5BMJmFZFh555BE8+eST2NzcRD6fh6Zp2N3dRa1WQ7PZBKUUtVoNW1tbyOTyePFSB+PxDkbpIr6rBiS1BMrlMur1OhYXF2FZFvr9PlZWVrC5uYlUKoVisYhGo4FisQjTNGEYxsF1XddRKBSw3WhAyxaQtEcYm8OD65lMBtlsFq1WC5VKBd1uF6ZpHlzPZrPQdR2dTgfVahWdTgej0ejgepBMpXIFl65solJaRDJB0Ov1sLy8jHq9DkLIgUypVAqNRoNZpssbG/gvWwO0rBSKdA8mzWA5ZYMaJna6BZidndhkctppYWEBAAJlimonXdexvb19qJ20VAp2MovxXgfVchmGYWAwGEi108A08bcNDfqwDZLK4DtPLCJrNKDpi0gaHbxxYYgbT64okSlM93q9HnZ3d5XINBqNUDm2jIvrV1AuFpBOJZW0U+XYMp5/+Tz2LAKazuGeKpBILyBhdHBKs7A5yOP8mxdQymdRKBSws7ODpaWlQJl6vR56vd41oXtES4Kk8xj12yiXSoHtFCWTu52M4fBAtxKpNO45uYC1tTUpmQKdL0s6WULIjQD+nFJ6h8+1f4fJJ5w+tf/7NwHcTyk9MgJ/4YUXqOhR+u2eib9++ZvoZ6romxY+/M5jqOXlezaZkUTc5fEewd3umfjM17eR1zXsDsbQkwSWDW65vKMt3usy8MocV/u4ueqbFj70jiq+cK7FXQ4LF2H3qDxWPi2uPvzOYyhmksJlRckcp355y5kGX/fXTNz+tjPC7zt79uyLDzzwwN1+11SMwJ8B8NOEkD8D8F4AHT/nLYtSNglbX0DfnJBdzPBVPUgp2sYY3aGFvK6hO7TQGYyVdAxBYCnPqesCZ/xoKZtEIT15bymbxMN31LA3slHMsBtClFLH3eEtLS0d+p2HLx6Dd3NVSGuo5nU8+q5ldAZjZr5YuIi6xyuvDFh1mZcvL1cOP7x8OWUjswDTsgMHB9MaUE1Lt45Vy3FUHwCDAyeEfArA/QCqhJB1AP8ckw/RglL6B5h8xftHAJzD5IOzH42jorqWwH2nstAXy1wKA4QrhZ9yqoRXAaLKc9f1uNbHj7xnkX1t0ceoePuiKKWOs8MzLRtbrS4y+QXm9hE1+CAHxCMLCxdR9xiGgcXFReYyvXDrF4sui/AVxJWuJbj4csrWjDasy6Zv2XHrl6gtyuhWq1FXUn8/RHorSuljEdcpgCeV1SgEY3OIkwyN6W2oMKUIG0nITuWCFCBs5OKuqzUwuRWY16i8iFLqoOuquMoaTfztTuKAKx6+eA0+bq6C7nFzNRgMhMv306+oUbEoXyJcBdnhKc3GekDZcQ2oZG1RRrdk2jgKU00nKwuWeEq/hopSCj/lVDGVC1KAMGNw1zWVLilzkGHwvjtMqf2uq+SKpEu+nSwLX3HMoNzw8sSyjOC9Bzgc7fKjty8L1ydIv8KcTFwdsBdhdrg5yKOQ8W8r0aWZKMjaogxXccaBz5QD39zcjNzwCWooXqUQ6X15p2h+cCtwt35FmYMMq7Pfu8Nk9V4XHan4Tf8zRgM0W2V2xEEdiurOLognlpGp+57tnnmIq0uXr+D2t50R2gyV1S+VHbAXYXZ4/s0LuPmm4DJkZ0YOeJeX/OqhgisWvyWKmXLgmUzmyN9YlZpXKXh7X5EpWhCcutq9LIB41wVVvFtkpBI0/b942cYNJ/kciLtt4+rsVLWBl6vFfE5qM1RGv1TLxuIwdS2BciEv3SYskVK8y0t+UMGVn99ShZly4Nls9tDvKpXaC97eV2SKxiqvqqmc3/0qliBERipBfB0rFaSMO8zAREbm7oNRKpZqvFwN+j2pzVAVo1UVOsDjML12rKIs1vXrOLiK0itZecMwUw681Wod2rGPU6kBvt5X1gj8lMCRV8VULmwJQFWHxzNSCeLL28asXEW9V2Rk7n1GJCzTD26uNlotHD+1KrQZyoooB+O3Ts974pnHYbK0sUhZbojyJcJVlF7JyhuGmXLglUrl0O8ijSSzPhpWnowjDHIubnllp3JRkTiqY99ZNo79+PK2sRd+TrVv2pEbiyJTX+8zeyObex8kCpVKRWgzlGcG4fCV0xN48G1l1BZ0383pWl4XXoLisUV3G6uIs1a1Gcoqe9iehp9eRem0DGbKgXe73UNHS3kbSXZ9lCVCQ8QRuh1F2xjjjR0DZyrZI/K6wdt58d4vuxHI6pS8fIXJDBzl6pNnN2HTw6dN/d4r0tnzPGNaNuo9E8+da2LPtJn1y5GXdzOUFQ5fmVQCZ9e72OmPcGxBD6ybTJghqy12u13o2dyEr9eb2Bux88VTFi9fQXYYVicWHYnSaRnMlAP3S4zO2kimZeN8w0DbGGMxk+TerHE7tLhGq21jjLX2AM+93kRpPYn7ysPAZ3g7L577ZTs6Ga6ikt8fCrPUCEYWZWpPkREZ6zMOX1s9ExdbA7z7ZIE9cmlf3rjCRB2+tnomKIClbCq0bjJLNay2aAyHB3yttQa48wQ7X0D8XHntMEz/WXQkzg86zJQDF42ndAzMaZjTpQxK2STXuhjvejOPgjlK8MaOgedebx44pGypGvlcHId8ZKISRNeaHb6i2thtMLnU4YyLUe3pjVZhaSMWzhy+ytkU1loDNPdGWF7QmfRrZWWFmTMRx+Xw1eibePZbb412g+qmak8kDJliFd2NNsq5FC62BmgZk1kB6xIoq36pssMo/Y/SkXkc+D6ceErehnEMbDGTxOlSBg/eWsaZcvjUyO95Focmc/z2TCWL0nry4Fmj3QBKbFOvsPDGONYYg8Dr/L183Vce4syNN4aW4TYY2XVhdxuJjuzcfL3nZAEP3VpGNX90ndkPm5ubyFaOR3Imlb5VS+DEYgaP3bnCxJWfQ1I56h10Giik0+gOLdx1qoCHbmHniyffiyo7lA1ImMeB7yObzQo1jDfJU5TzljkwIXv81u2Q2jtsX7MOc0gq84SElS96YMLLF9X4llxk1oXdbSSTXY93ecqtW9lslokzFbHaons0qju8hVwOj65Whfhi1S+VdigbkDAPI9yHrutCDaNi/Zf1eZE4UW9dD6JDAhLBs+Z6mUaeENkDE16+8lk99o92+LWRrINk4ctXt3SdSb/CHFecaRaAGDo8nS3UV8YWZc9OqAhIcLi61j/oMDV0Oh0cP7Uo5CBl139Zn/cqGCD+pZdOp4NSqXTobzy5XqaRJ0T2wIR3Tfv/PftNXKKG0OZpEFhymFwtrvb22zhKv4IcVxwnT1lGvUHtzmKLfnrtBxlb9OPranG10WCTVwQz5cCr1apSB+lANmeCF24FY4kTDUK1enQTkyfXS5jRi47YVOTj8MLha7tnYtvOIp9WlzKANYdJHFx5n/fjKufTxkHwc1yq0yywjnqDZpostuin136Q1S0vX1eLK1Z5RTBTDrzT6SCfzytzkIC6nAlBkJnKOfKyvC9oVOL9u8woJM7UBY5sFc3EFVMXmvb6gcdoVXIV9LyXq4ZPG/NAdsnOC9ZRr1+7s9qin14DYtkeeSC7rMK6dOnlKkheFZgpBz4ajY78TbZR4sqZ4EBmKufI65VFRqllRiHTSF3wncsZ3Fc7JjXtVTWjkh2xseiWn07zQGZGKpsbx9vurLboJ7NMtkdWyNgiz9KlF7JtHIaZcuB+8ZSya13TWPsUncqFxQiLKrXMiC3OfBwOTh4/jnRafNqrckYlu3HIwldQjLDoxjfrKDiO3Distugns2xnKbo5yVouz9KlF/M48H0ExVPKrHWJKqw7S507FwcLWB0ha4wwD2RGbDJcseTjcGR2t7FsWKLMjEp245CFLz+dllm6URFmJzNAYLHFvcZRmWUHB596aRON/gjVfAqPvXtFOV+8S5duzOPA98G6jsSrDLwK2zcnOTgGIxvru0OsltJIawl85K4V5HWxRPF+yOfzWIxhhiCzhyBi3N58HNtdE4uZpC9f3jbm7TRUz6hkNw6j+PLTaW9OjvM7Bm6OyMnhLk8mzE41/MohPjLLjPw3dgf48loHWoLgQtPAXScL+I4aW85x1nJl6hfX+jcwYw5c0zSm+1RvfrhhWjY+eXYTL13pIqUlMBxZOG/ZMMc2AOCj95xgVpwoR6hpWqyyAIfzP6Q0glxKfRxxXk8gQYBGz4RNKTa6Jt5oGiAEePzuw3z5tTFPpxE3X8CEs5yeQL1voppPSTk/P3kdvlp7I6zvDvH515t4MSInhxssfE2DJ3c5jb4JSid/C7JjkcGBadn4i2/soLk3AiEEBMDnvrmDl6/0lPIlWj+A3W+JIJ5Wiwm7u7vM9+pa4iBe1bRsZXVoG2OMLIq8rsEc29ASBMORjbyexMii6AzGysra3d09WKqJy8h0LYGH76hBT04SQz39Sl0pX6Zl4+lX6hhZFAu6hltrORgja5+/o3zxtLFfWdu9SeIgZ3M1NlCA7P8rA6+8br5sAKcW04dycqgGlaw/K75wroVnXmvg0y9vodXpKHtv2xjDpsDJYhrZVAKlTBKVvK6cL0e3RGxDRqejMFMj8FqtxnxvHEH7AA4iG25EFnqS4OF3VPF/v9LAyKJcCbKcOoZtvJQq1di+helG37Rh2RDK0hgFdx6avmnhg7dXkE4mYI79+Qpq4yiu4mrvIJn2RjaqeR19U44vr7xuvnYHk1lR31STk8N7bZp8uZec0oUlrrqGwbHHM+UctASQTiYwiEjY5Yc4ueLxW7yYKQfebDaRy+UCr7sbgWWdUia7m3vq+dF7TihLqOTGxnYD3aEWy7cwRULtVCTGOr6YweN3B/Pl18YsXKk+pOEtn/fwEitXXnm9eXtEvwIUxVmcfHnh5Wu8twtUisx1DYPfprxqW5TlKspvyWCmHDgNme95G+HhO2qhRiarNN5DDSoSKnnfkdGI0kMaDkRC7VQnxgriy6+NWbiKa1NO5PASD1deef3eLeJXoziTPT8RhqgDOVtXLnPVNQpe+1Nti7LhpGF+SxYz5cDDpiLeRtgb2aFGNs0RCCA2iltZPoZHT+lK0wYAYqF200iMBbzVxrwzhLg25UQOL/HkCfHTadHNPB79Yo3Z5uWR5UCOV+ZpRcR468mqX7LhpPMllH1sbW0dxFOyKGyYIcQ5AvFC9Ai6I6+qtAEORAxmWnxtbW3h+KlVocM4MvHLQVDFVZAOuHVaFKL6xRKzzZIxkOV4uRtemYM6k7gyLIrMQGXCSVW0cRBmyoE735VTkZMjrhGIH0SPoHu/oyfjRGWP40+Lr4WFhVjTG7Bshsrm4/B7JqjzVfGtRFUpDnj1S/R4uZ/M7rrGvcGqSr9YTzXH9T1MYMYcuANVCqtiBBIE1RkOnfqKOFFVx/FZ+HJCN3lHTg5f1KZYmvJ6dtR1FVypXCaIIyOkU2ce/ZI5Xh6GuOzQqUtcfAFqljh5MFMOvNfroVKpxJaTQ1VmN1X5OBx53RDpdOJa7/fylUslhBTYzdcq6eCHyuWprmezXpdB0Ei+0+3CSheY9SvujJA8+iV6vNzR6yDbkt00dN+rOt+LF25Zg2ZZfnasCjPlwJeXlwGoycnh52BU9aiiUzSvcjryhoGlMxPt8KKMxcuXqAN0P7c5zAnzFYUoHmRHZix8edPV/l0jgdbGNrN+xZ0R0oswTkTtcHl5OdQWZTcNHcSV7yUIQVyx2LEomDSUEPJ+AL8DQAPwh5TS3/BcvwHA/wGgtH/PL1FKP6u4rqjX61hdXQUgH7oXlGOCpUeNgogj8FNOt7xBYN2s4jW0QwmoUgk8eIt/Aio3X6IO0P3cKc0Q5ktk34PnOk99Hr6jFpnkrG2MkRzuIp+pMOtXXJ1xEFg447XDer2O9NJyqC3KbBo64OVKduM0iCsWOxZFZOsTQjQAvwfgIQDrAL5CCHmGUvqa67ZfAfBpSum/JYS8HcBnAdyourKEEKnn3Xk/1tqDyBwTosbC6whMy8b5hoG2MT50GpJVXhYj4jW0gwRUyQRevNxFY2+E5QU9lmyF7uf2mjT0OcfIRpYtvNwRFpYrOjLzDg7+5GubsGyEdi6lbBJ6UkOd46QlD8fujJlPv1IXWtpyHJrK0SohhNsWAbEkdTxcqVi/9tMfWb8VBhaPdC+Ac5TSN/Yr82cAPgTA7cApgMX9/xcBXFFZSQflclnqeadBz+8Y+Pzrzcij4zIjMlZH4CiOo8inS5mDI+ZjBnlZRw2iyw1bPRMEQDmXYnKUog7QeW6PBK8VetPS5lIJrmPmPEYqszyT0gjMMWXSr+9/xw0wSYq7w2NZXnJkTRBgZEXXJ+h5FofGw1e5XOa2RUdukYgg3mU8kf2PMPll/VYYWBz4SQCXXL+vA3iv556nAPwVIeRnAOQBPKikdh7U6/XAOHBW6FoCN1eyeHE9ydST+61bqoxPdee+OF3K4MFbyzhTnkwlN1zy+oHVyGSWGxp9E8++3sSeyZ9fwimbh696iMxuI+ubFj70jipSWoLZmFmNVHZ5Jpc6POIN46y905DW6ShZRXKq8Dg0Xr6cNua1ReBouKEqvmQDI8LkD9NpWbDU0m/8752EPgbgE5TS3yaEfDeAPyaE3EEpPZS6a3t7G0888QSSySQsy8IjjzyCJ598Epubm8jn89A0Dbu7u6jVamg2m6CUolarYWtrCwsLCyCEYG1tDeVqDc+/cgGDMYWVXsC9VYqlYhGWZaHf72NlZQWbm5tIpVIoFotoNBooFoswTROGYWBlZQX3lYewSBLVUh4b65ewtLQEwzAwGAwOns9kMshms2i1WqhUKmjv7uKliy1s2HkcT/Rx141V5DJpdDodFJfK2NppIUVsnDx+nFkmalOskg42hzmcThrIDoDxsIKNeh2JRAKNRiNQJqrnkTA6OKVZ2Bzkcf7NCyjlsygUCtjZ2TmQaWe3D2OQwKlEHz0jgc2GDjqY7Ix3u12Ypnnw/mw2C13X0el0Jh9j7XXwDyomsqUqjHYDu61mpEzAJNIgqJ2GozGanS5uOHUCO9tbh2TSNA3b29sH7bS5uQld11EoFNBrNFBNUowHXaxqNhZTVexsb8D2tFO324UxHCJTrGLQaWAhl4Ou6+i12yinADLYRVmjyCaqWFtbO9JOFzfryBhdJPRFpI0WLm8lsJhOotfrYXl5sjdBCEG5XEa9Xsfi4uJh3du4jO87lkQiswCz18Zedxdtl+65ZRoMBtjd3UW3v4evre0c6Nadpyso5HOHdG+3PzjgzNtOnU4Ho9Ho4P3pbA615BBksAc9vYh7awTm2MbJlTI21i8daqfl5WVsbm1jYFEcP1ZFe6eB7MICljUDdDBAKl1Ct34Fo47ua0+pxQqyRgP5ZArtQQrn37yAk8eqgfY0GAzQ6/UOdO9Hb1/GpctXUFzIY6+7i40AmdztVKpU8cVXL8IcWxinF3Fv1UaxUAAwiexJFyoY9VpIaongdvLY0/tvXESnb4BYQ9DxCGvrb7WT2568Mg2QRNZoIKkXQIwuzr9p4MzqyQN70jQNa2trkTKF2VOgc446p7/vkJ+ilL5v//dfBgBK6cdc97wK4P2U0kv7v78B4Lsopdvud73wwgv0tttuCy0vDI1GA9VqFds9E5/5+vbBSOzD7zwWS6/sRVC5sutnpmX7Tgsded33uWWTHYHHyRXgz1cxkwyts1dmP1miptBhvMg8HwdfrDotGp4ps/4r+3yUzDKIyxZZ4dYFIDxaTVbes2fPvvjAAw/c7XeNZQT+FQC3EEJuAnAZwI8D+AnPPRcBPADgE4SQ2wFkANSFaxyAfr+ParUaemJMdeOxHMhRnYzHK2+YbKxHzKdxipLlgEkUV26ZebhyQzZ8bJp8bbd2sbhUDp3Ci+qX7PokAtb8AAAgAElEQVQv6/NBfAV1dlFt7AfWw0vTyHHEe85DRF5WRDpwSumYEPLTAD6HSYjgxymlrxJCfg3AVymlzwD4HwH8e0LIP8VkeeVxGkMKLufjoEGOS3XjsTaUqgNA3rJTi5PDDroWnGOCx8jiPLTC2sFEHdeuHJOPmVVx0m5afBmDBM52t0KdQBz65YZqvqI6O96P/PIMXqaRs4f3nMdV/6jxfkz3Zz1/+1XX/18D8D1qq3YU7o+D+jku1YrO2lBeZQLkjtQ6Cps1GjCyVeYcEzxQreisHUzU6HaVdPBD99zOzZds/pIoqObf4etUoo/1YTLUCajWL0A+Nw6LbEHZGHuNDZy58Ubp9/n5gDhmT7KpC+YfNd5HKpUKvS6j6LI5E9zKJJs10FHYheTh0D2VRiar6DJKHTa63RsQLr5U5i8JA+8ygV89/fgyDIJCli/6Qla/VOXGCUJUNsYTiQFOrdrMYYki8d+qZk8qUhdE+S0ZzJQDLxaLkfeIKLrqnAmyuRyc55sDHYUMe44JXogquup8HG6+0ukc12xgGmueDniWCdwI42u7lcWxpUVhvkRmT3Fz5qcLblvcGercYYkygxeZmbnM0qVTRm6hwFVfHsyUA280Gsjn88z3s/bcqnMmBDkzVqN3nj//5gXcfJP89JgVsnyJdjBuvrr1K1yzARVLGyJ88TjBML6sfgd6tcRVX9nZk+xx/LyeiEwT4NUFd5mrifB0CarTCcvMzGW4klkWZMVMOfBischlbKyjQtXrm07ZMrkcdC2B49WykPP+1EubaPRHWMom8b5bK745TILKvNp8pUYTZ8bKlez6rWNoO/0RbErx0XuOo5RVm+8m7F6WWaUfZJYJRDgLOjHMup7sLpMM86HPxG2PPEtQovrlbo9mxIxDBjPlwPcGQ/z5G/wn5ETCxuKAO/9DSiPIpSLWTU2T6/2mZePvt/v46qVdUAAv7o2x0x/h+GKay9CuJl+OzDJr6sxl7eeg2e6a+NrGLgYjigutAX79h29GXleXZyPsXt42DoLsOnEU2sYYbWOMoWWjOxiDEGCrZ6LRN3FiMcP0DqfM7X478r447TFurpwycnoC9b6JG9NUSSfkh5ly4O1uH92hHtvaXYzfHgUwUYSH76jhT762CXNM8fQr9VDHahgG87udEdLG7hCNvRGK6SQs20YuxnXOOEYUjsyOETf6Zizt4h5RnmvuwTBtZFIahmMblzpD3FZjSyzFykHQvTxtHPV+91F+1QeO8noCa+0BuoMReiML39juI0EInv1WE4/ducJVTpjMcSXQciNurg5AJ8fYU7aaTtoPM+XAbzh1AoVuS+nUCoj/E05u9E0blg2m5D088aPOlK26oKOaS2F5QUc+rYFSHNoIZQHLMlVcpzi9Mn/hXCuWdnHnoLm1mgMoYFOgkElitZjmelcYF1E8qYwR1rVE5ElXUfRNG6dLGSS1LDrGCJYNHF9MY29kcw8OKseWsd0zj3AyTTuMkytgol97IxvVvI6t4cJ8CQUAdra38Oi7VoU+5BBmRNOMZGCdvpmWjfMXL+NtZ25kktP93rtXF/HQLWUUM0nsjWxurkQ/0aYC7phZnqgY3s7EzVc1r+Pxu49jszfCajEduXziLTvs2H4UT6pjhKM4k9ngLmUng46VxTRAgb0Rf4Iz07Lx/MvncYkWj3AyTTtkLU9FQMBqoj9fQgEAXeePdGAxojg2Tdzl8x4yceqcMoYHp/REN2x59Z9FqeM0NC2VOhidsbSLaGfixxfL5qUXYVyw8KTrcqc5ec4uyHS8fpEcImvUbWOMvpVAPsP+iTZVsz3eswuq+Bp2ErHNJGbKgRcK0fGU3kZiMqKYNk1ED5k4dV7Ss1wOUsW6NIvTjOtot2nZ+NIVEztrb31iLKpdZDoTEb54nADLeYBMjj0s1lsP3rMLqnP2sOa79/JF0lnf1Lay4ZFR9eA9u6CKrx5djL5ZEDPlwHd2dkLTK/o1EuvoOo5NOVEFcOqcMlooZKvKc1+4ITJDkImrDUPbGEMbdpHPVJnjf6eR+8IBrxMIuqYiRljk7MI0uXLe68fX3VWgUDvmq18y4ZFhEDm7oIqvKL8lg5ly4EtLS6HXgxppGiGCDmSOADtwDH+zoWOlOpE5jjVnmWPoLHG1UYruNzqz9QWuDw/EOWrzQsQJ+F1zv2dnmGZySrL5OJy6TIsrr5xuvqrlMhYZnbDsoaNrga8ovyWDmXLghmFgcfHwdITFYaoaXbM4JFVHgHUtgTTG0LWEdO6LIBlUjW6icl/4KXrQ9ftOZaEvlrn4imvUxiKn7HuOJ63IkZ3K1AVxcsXqNP3sOKy+QbOYsMifa4kvHnl5MVMOfDAYHPpddc6EMLD0vKqPADvyqlpz9srw8B01JQ7JzziiOp0grsbmECdjWMcX5SuOLIfu97CkDlCdusANVcsEPE7Ta8dR8MoZZYvXGl+88vJgphy4N2ZWtcMMA0vPq2q65yAo/zkgtqTilWFvZCvr8LzGEcVF0HWWuOgo56KCr7izHDrvWUweBxCuX7Ij/zC+VC0T8DhN2dj3KFu81vi66vnArxV4Y2ZVO8wwsJQlMkILa/yg/OeiSyp+MrA4JBG+orgIuh4VF+3mK6cn8ODbyr65XmT5mlZMsiNvmH7JjPxZ+FKxTMBji47McSVdU8VXUOfFy9c8H/g+MpnDORd4G8q0bNR7Jp57vXlwCEEmbjjoPt4cE07jt40x3tgxcKYy+Sq9V14HspujLHy5M8+5v7DOGwsbxoXf9SCZHTh8ZVIJnF3vYqc/wrEFXXlGOd5nRJ2RIy9LhycTfRE3Xzy6ldTTuNwZCNkha1myfPnZYxCi+IrSaRnMlAPPZrNH/sbaUE7PutUzsdYa4M4TBa6RFauB8hqyO8HVWnui1KX1SZY3P3kBuREG64jbGYUkCDCyKNPRf+87RBxakMwOHL62eiYogKVsKrJeInzxdnaikRzZbDbW/B/T4st5jkW3vrRu4KIxFLJD5x1x5S8Js8ewQVsYX1E6LYOZcuCtVkt4N9fpWcu5FC62BmgZk5EIy+iC1UBFDNlp/Dd2DDz3evOQo9wLkVfVWqwf3KOQ3cEYepJwhfbxfuzAbYxRbezw1eibePZbTebj3H4bYVFOgJVjmeWWRrOJL53rM+sMr/NSwZdKh9k2xkiYPZRzFW47dOrCY2OifPnZI+9s0oGM34rCTDnwSqUi/Kx7mnPXqQIeuqWMap4tTzargYoasq4lcKaSRWk9eWgaluWU109ZZdf7S9kkHr6jxpVThSeHidcYWdpY1xI4sZjBY3euKF/njGt/JAjJXBHdjT6TzsikDRDliyUclHfGaaULGIxsbjsE+GxMhi8/e2SFlxMZvxWFmXLg3W4XejYnNBoQWf/lPQQgY8h+9dvpdplPcPkpKyAWreJXl6B+iDcfhxt+xjjmkFnFOqfbCajMqxIGN2eJscGsM6qPwrMgrEzRGed9J3Ski1VurnhsMajuxUySyX+ILiP5cdLl0GlezJQDN4ZDqVNjvOu/vIcAgu5jHaUcmeaHJPtnyflCKYQNXoYrVr78jHGjYca6xhlULjCdvCpezu4rm3j0XTcwOYq4ctCEIcxhivJljUZCXPEeyPHWPZdKcPkPVhuIskNVH+3ww0w58Eyxiu5Gm/vINg9kDwH4rbWKdjpB8aM8OV9UHNQJgkg+Djf8jLFybFn50W7WAznTyBXi5SxbqnLpVhw5aNzgObwk2qGwxkWrsEV33VWHhrLa4eI8DnyCQaeBQjp9RGFklFhFzoQwyChNUPwoT84Xv0MHMs5IRa4XN7zGeHH9ClR+dYnnQI6fs4pbv4x2AyixT6/d9VaZYsGpK8/hJdEOJSwuOk79mpZte3VobX0eBw4AWMjl8OhqlevIdhhU5kwIgsyozhtiFjVSDHJKMmuWbkwjdUGpkEehaysbBfN2oF4OZTpgFv1q7zSYZfFC9YxBRFaRDiUorC5u/QrqoHlTBvDmXpqHEe7D74MOMkocZ86EgzpLjOoSyZTUGjOrvIAcXyrDGXOZNB5916LwKFj1jErmeRb9kvmgg4oZg8oRL6stBsk8Df2SGdCIdjAybRyFmXLgnU4HpVLp0N9klDjOnAneOoqM6rZ3WoHLCSKdTJiBxc0XK1dOG4vwFceMSmbUxsKXn047ssSpW04ZKke8rLYYJPM0U2MA/DMO0Q4mSF4VmCkHXq1Wff8uqsQyxm1aNj710iYa/RGWskm879aKb04OP7Aq6onlGgrdnrI1uyB54+aLZ6Tj18YyYYkqZlSiozYWvvzkdcpoG2OkNIKP3LXC/J1O2TA72REviy2G2bFMLqFcKoEHb/HPjeMH3g5DtIMJklcFZsqBdzod5PPRn6DiIVrUuDd2B/jyWgeETJS0uTfCSiHNdfoySlH3el08+i6xwyphZctkURThq22M0TbG0BIEO/0Rzu8YuDkgv4RfG7PypXqTKkgWmTV1L/zkdfi60DLQNy3YNsUH31Fjckw8TnAafPmV0dhqBNoxr37Veya2eiaK6SRevNxFvW+ikE4ydXq8HYboAIbVb4lgphz4aDRius8hutE3Qan6epiWjb/4xg6aeyNQEBBQZFP8py+j7huNRkrX48PqEidfeT2BtfYA3cEY/ZEFAKjkU76dXVAbs/CgegPaD+5cGSmNIJeSK8Mrr2nZGFk2Egmgb1rIpTS8ut3H3tjGckQSKgeiYXZx8KVrCTx8Rw0X20PcUEpD1xLMdhwF07Lx3LkmLrYGGNk2CICNronzOwYA4KP3nFDGlej9ALvfEgFTixFC3k8I+SYh5Bwh5JcC7nmUEPIaIeRVQsifqq3mBLx5db9wroVnXmvg0y9vwbRsZfVoG2PYFDhZTGMxncByQQelUD6KqRxbxnbPVFr3MMTFV9+0cbqUwa21HPIpDXoycdDZeSGTO9lZC43LGQFvOSQ9STCyKJ5+pS7FlVteZzngmdcayGgJvPP4AlYKOjRCUM6lAjkTxTT4Mi0bT79Sx/PnWwdcqcqP3TbG2DNtvPtkAWfKWZypZLFnWsjrSYwsysWVadmRtsZyjx+uaj5wQogG4PcAPARgHcBXCCHPUEpfc91zC4BfBvA9lNIWIeRYHJXlyavLMtWVyUdcyiZxppyDniR49J3HMLIhtI4eVL5p2Xj+5fO4RIvKDmmEIc781w5fbWOMQiYJy6YoZZO+nR1rjLAfX3F929GLvmnDssGdodEPbnndbdA3LXzoHTUAwLOvN7FnsiWhchCl29Piy0+v9hpH21g2B81KIY0P3F7Bf3h5GyMrWL/8wMKFDF9XOx/4vQDOUUrfAABCyJ8B+BCA11z3/CMAv0cpbQEApXRbdUUBcK0jRa3vyTSIiqlnVPltY4yOnUQ+Hc8HBXjD7WQOALn5yqUSoYmxgtqYha+4OiCnfN5wOxbO3PJ63+skeXrs3Xz7ICy6PS2+8nriCFfE08Yqc9B89J4TSsNree4JQlzr3wCbAz8J4JLr93UA7/XccysAEEL+MwANwFOU0r9UUkMXNE0LvMZzBBi4OomBeMovZZNIp5Ko+6RxVXGakifcTsVozc1XGG1BbczCV1zH4EXC7Vg5c8sb1AYsuuaWk0W349zA9MruzWbpbWOVOWhUhtdG3cOqW2F+SxYsrUZ8/ubd6koCuAXA/QBOAfhrQsgdlNK2+6bt7W088cQTSCaTsCwLjzzyCJ588klsbm4in89D0zTs7u6iVquh2WyCUoparYatrS0sLCygXq9jd3cXy8vLqNfrIISgXC5jc3sbZ+sWhqMxiokx7n/XzdjZ3kIqlUKxWMTG+gaKxSJM04RhGFhZWUGvsYHjiQFawxRWEwMkRgvY2mphMBhgZWUFm5ubyGQyyGazaLVaqFQq6Ha7ME3z4Ho2m4Wu6+h0OqhWq+h0OhiNRgfXvTLVd3awZ1o4tXIMvcY2jmljGEMbq4kRMijj0qWtA5nq9TreXhghU8gDowHoeIS19U0QLYkXNkdIDrugeh73reYxGr5VZ13XUSgUsLOzg6WlJRiGcUSmAZLIGg0k9QKI0cX5Nw2cWT15INPeSMeGS6Z2fwBjkMCpRB+7gySubGsgpoFSpYqN7QYyGsHK8rGDdgKAXq93pJ3q9ToWFxdhWRb6/f5BnZx2ajQaGAwGGI1G6O3tIVOsYtBpIJtOI5PLY5V0sDNM43jSQrd+BYvJ44fa6b7yEKl8EWRkYGP9EirHlvH8y+exa2nQdR131RJYrtUi28mre1YyAwy6OJUYYWuQwxsXLmIhnUS5XMbG+oavTAObwByMcSphoDXQcekKBbHMQzIVCgVcunQJmqYdaqe9xiZsDt0rLpXxxW9cxng8gpku4Z7yGMvaGP0hsJowodMlrK9vH7Gnh1ZTaHYMnDq+gq0rl7nayWtPbt27uLENa2BjWbNADRO7ewWYnZ0DmS5duoRUKnUgU+XYMlZJB7sDDTVdR7d+BTnwtxOr7u32egftkNF1FItF3FceQsssIAULG+uXfO3ph88U0drtI2EPYZomnn/5PLpWAkk9g/fUCI5Vq77t1Gq1sLu7y+QjgmQKdM40IuyAEPLdmIyo37f/+y8DAKX0Y657/gDAlymln9j//fMAfolS+hX3u1544QV62223hZYXhr29PeRyuSM933bPxGe+vn2wdvjhdx5jznYmmjmQF0HpXsNGcY68bojKGlWXMFlVpqqNwt7eHpLpjO+7/dorDDJ64dYBkRmI3yjU79N0fm3MCz85i5lkrNElbvDy5SfztGxR1do/j27JtvHZs2dffOCBB+72u8YyAv8KgFsIITcBuAzgxwH8hOee/wTgMQCfIIRUMVlSeUO4xgFoNpu+xi06HfROt+Lc2BE5NNFsNo80vMhUjnd5yQu/+1UnUnLLrJeOKTmQI7Ksouo0p/eZoPb3a2Ne+MmpKvxUdDM0jC8/madli6rW/nl0S0UbByHS01FKx4SQnwbwOUzWtz9OKX2VEPJrAL5KKX1m/9oPEUJeA2AB+EVK6Y7qylJKuTLx8UJV4/IkoAqD3+zIaxxA+EiYN8NcELz3h8kjkyCIUqpsfdbPkYhuhoo4RPczQTKN90PTeEaZsh0yK2Q2Q8P4ipr1h71XVA6VGQ4BPt1ikVcUTLWnlH4WwGc9f/tV1/8pgJ/f/4kNtVoNiRR7Jj4/hDkXFRthYQ6T18hqtZrv392yRo2EZQ0hSPYgeWSXZz70HRWlDsmrF6KbobIIMvgv14HWlW3hpRnRDpkFcW2G1mq1SJtS9fGKODMcsupWkB2rwEydxNza2sLp06el8peEOReREZsXsh858JM3DFEGJJuAKoov2XAr7/3rG5u4/W1nIrmSieEP40Om84iqk5/Bp4Yd5DNV5s5VtEOWjbMO0h0Rvq5sbuJLzXSoTfHONIMgmu9FJV8sdiyKmXLgzo6s6GjD3ZhtY+ybk4N3xOYFr8MMUxSW7+hFGZCMQ/Ly9caOgTMBOUwcyCYIKhejv94ddwy/iH6JJFUqZZNAKou+T6ho2DO8HbLKOOug+7j4SmXRHY4ObKrRN5FMJHxnebIfr7gW+Irre5jAjDlwWbjzWKy1B/j86028uJ4MbSBeBeBxmKo2aqIMSLTD8/L13OtNlCL4kt0g7bZbofeblo3zDQNtY8x9EtLdWca13JBJJvDi5S4ae6PI3CW6lsD33lRCIrcovDnKsuSigi9V6+oAkNc1FNKTj3bk9ASe/VYTeyM71AZkAhV47LFtjDGy7KnNcmQxUw681+uhUqkc/M5LmNOY53cMfP71JpNCi0YgsDR41OjeK68XMpuFPHy9sWPgOUa+nOdEN0jDZHanWV1rD3C6lGE+Mi2yNs/DleNgtnomCHAod0kYF4O9Pk7X+NKN8uz3TIMvXq4Ge308+q5VdAZjmGMbz7zWiDX1Mwtf3hlUTk9wzYzC+IqyYxnMlANfXl4++L/MNOfmShYvrie5RtU8X65hRdSowi2vFypiuVn5OlPJosTBl7tMXq7CZHY6vMVMEqdLGTx4axlnyuFLOt5nRT90wDqTaPRNrtwlXnlV6tc0+BLhanl5+cCmTMtmHll7HXEQVyIcHs1DU0VKSzB3FmF8hem0LGbKgdfrdayurgKQP36r+sMEIkoTVQ+3vF6o+pqIinr6Icqwg/gKk9nd4U2SiYU7I9HwMVGudC2BE4sZrtwlbnmDOFOxYRvFF29uHAciXLllVm2LogOVoDw0rAjjK0ynZTFTDpyQt071y4YZiawLBymr7KZaUD3c8gJy8azT5ivMsMP48srsrYPM/oLshw5Y+eLhyi2vH2fFTDL2pGsyh5dEzgN421ilLcp0vrxr5W65wp4P02lZzJQDL5fLB//3EgaoP9rNOiqJK7ObW17ZeNZp8xVm2GF8uWUOkkNmf0HUmOM4GWhaNpApwLTsQP0KGzSo6kxkDi8FOa4wvqLaOAgs+iUTNsu7Vu6VK+h5UXlZMFMOvF6vH4qnVBFmFASeUUkcmfBMy8aFy5t425kboWsJKYfkYNp8BXUwYXy5ZZaB7IEcrzGq7qQdvrJGA0a2GqhfQTMnlZ2Jaq6AcL68dswCVv0K6nxls3fyZHr0QkReVsyUA19cDI4RVu1EeUYlqkdszrN0YOFsd0sq30sQVL+Pp4MJ48stM097xX28PC79SqdyofrlJ4ds5zuNo/hhS3ZZgbhoXv1iWa5jgV9SMl67CfNbspgpB25ZVuA1FU5UZo1Z5YjNefZYEth2PavSyFSMVOLgyy2zs4QQVZ9pHC+X1a+g5ThzMEYhk+OKvojjdK1Krpw6By3ZLWsGPlBaYuYKEJdZdubkfX5vZHPbYZjfksVMOfB+v49qNThmVsaJqs6ZILNp6DwLY4BCdoEr34voxqSKsEQVfDky51IJ5vrEtQfhhah+hS3HnX/TwM038Y0Kw9ado9p+Wlw59fRbsqODATdXorME2aRrfs/zdHamZWO7tYvFpbKSmY0XM+PATctGarFysOHDAhWhY6LKLbNp6Dy70y2gUshxL710h5MTbg++Lfo4twNVYYmyfDky89RHdkQquj4qG2qnawmcWT0pZNheJ8LaAcsunakIaUylS0JhiSKzBJFNVpbnWeCUYQwSQsuCLJgJB+4QkdlrYCe5hI/ctYK8Hl11HvLjyEIns2moawmYnR3oJfb1woPj3KkEzq53sd01sZhJMvGlIixRFm6Zed4vamTuk4oJAvzD2ys4vphhfp613DBZVH3wlrXDU+GQukP2fC9+5XbrV4S4EgXvJivL8yxwyjiV6GN9mIxltjMTDrxtjCdGtmfh670uAOCj95xgVhzVcaAiEFHMVCrFVUZeTyBBgEbPhE0pNrom3mgaIAR4/O5wvnjlj4svR2bn/Y2+CZZ0yrxG5uQIaRojXGgauNwZ4uubPXzX6SIee/cKlxMXDbUD+Ns4CO68NSmNIJdSE6fuRr1nYqtnophJMud78St31AkfuMRphw7iShvswLRsjCwbuVQCxpCgkFVfBjAjDryUTSKlEVwwNOT1JEYWVd6bxZ2IhtchAUCxWGR+v2nZePqVOkYWxUJaw63VHF7b7iOvazDHbHyxGnacSaG8Mn/hXEtp7DVweOR9vmGgb1pIJBLQEgSN/miqusXTxmHQtQQevqOGT57dxMiiePqVutIpu2nZeO71JtZaA4wtG5pGmPO9eBEls+oN1aAyeO2RFd6lzHvftoIT1dL1uwauawl85K4VfO4rLVwBe0IeB1HOOY5DGkHgcUiNRgP5fJ7pve68F33TwgffUUU6lYA5pkr5ipsrt8xxbbi5uTpTzmJk21hrDZAgBNV8Sum6cBRfPG0chb5pw6bgzjrIgrYxxt7Ixp0nCtjpm8inNQxGbPle3DAtG2tXtgJj/aed0S+OAYI3r4rRbUNfjucwz0w4cADI60l83+2nQNN5ZflLHExrZ54naqFtjJEvsMePeqeExxfTePzuE0rzvfDIIAr36Ix1miuaObA7tFDJp/DwHTV0BmMA4M6BIcuXzAhcJH+Jik3IlcU0Hr6jhr2RLaRbdkCs/zQHUgCbLovw5W2HWnkpjuoDmCEHDgD2eIRjZTU5E9yYxnpY2xgjryeYDMxR4hVtD//wPUXuTSK3UanKMeEgbq72BkOYrm9ERq2HymQOdL+XZVPcD6J8OToxHgxREihXJH+JbM6eo5zx1fkg1l+jh843eK8H5c+RHZnzdngyGTzdXLV3GkL1ZcFMOXDDMCLvERmV+Cmnqqmc30musJGLW4ntwZA7ayCvw+blK85NJtOycfZCA5fo6JDBxJFlUXSdVQVfbp1YJR1UazVuHkXyl8jOnmT1661Y/yEK2cIRrsI6O9mRuUiHJ5vB07mXxW+JYqYc+MrKSuh1maxqbsJVTuX8TnKFKUFQvGwca4OifMW1ydQ2xtiw88in2Q0mjjw0QVDFl1snNoZ5oWUokZnQNLly3ut32CvofEMQlyKO1CuTSIcnm8HTQZTfksFMOfComFmZrGos72FpPJEZgBt+8bJxrQ2q4ksUflwdT/RxyUwyO6WoEe61yJdbJ1YTfSY5VeQvmSZXQIgdhZxv8OOS15H6ySTS4Xn5AsQyeKqK9ffDTDlwXQ/e8BPJxxEE0QxwMjOAQ3LuK/F4Nw1A7cZhHHxFlcOzdv3uG5bw3mKVa3kmbIQrw5dsZxxWX0cnhp3EgZxBnKnMXxIXV34I4svPjqPqzONIg2QSWfpz8yWaRIxXXh7MlAMvFAqHfledj8OBn9NlaTzREVqQ4TryqprKxcUXSzms64ulxUUsSDoQFXyp6oyD4OhEjy6GlgdcHScrk9jMuT+IL68ds4DHkQZ2HJIzS9G8KiLysmKmHPjOzg4WXKkoRfNxsCint7FZRl8iI7Qww3XkVTWVU52/hLccN4K48raxH6LaTwVf01pecuQN4yzO/CUqllXC7vfji6WNwxD3RqWypesAACAASURBVHsQX0HvjeJLVt4wzJQDX1o6HE+p2mGGgXWzildxvIbb6JtIJibTdbe8KqZyoo5AJs6aJ/IHONrGfnVhTUIkw9e0uHLkDStPxiH5RUH1TfvISFlmWYX3/qg2jkKcG+1RCeH83hslv6y8YZgpB24YxqHk6LyK7eS/aBtjodNqLEohs6GV0xN49ltN7O2fcPuB48Q3GbyocxHhq94z8dzrb9VJNM466D4vV9429sJtLG1jjDd2DJyphH/cWMUGVtQI1Inzf/qVOtfgwJE3qjxRh+Tl60++tgnLRmj94k5s1u3vYZDISEW9xLXR7k0It9Mf4VhEvpco+aN0WgYz5cAHg8GRv7E2pDv/xVp7gNMlviP5cYVauQ3XHNt45rXGQU++2zdxMuIZ3hEZL19bPRNrrQHuPFHg7vBYckx4efVrYzfcSZvW2gM893oTpfUkU3pemQ2ssPo7I7YEAUYW5RocDAYDrtwyMrOhlEZgjqPrx8sXb2f3tbUdXKJjoaiXuI/aO3xt9UxQAEvZ6HwvUfJH6bQMZsqBy8RTuvNfnC5l8OCtZZwph4/cHPAsu4gomOMoTMs+1JOvnjwR+YxMuWFw+CrnUrjYGqBlTEYiKpep/O6LamPHWN7YMfDc601mZxkXX+4R7u5gkgmwb7KP9CvHlrl0S+bUaS51eIYQlaI3jkM+IrH+DkTk521nh69G3zw0G2YJ/w06NTqPA9/H5uYmjp9alc7lUMommZ03IP/lFVZ4e/KN9UtYYIgfDStXRe6Lu04V8NAtZeY8Iax8+d2314iOmdW1BM5UsiitJ4U29lTy5dUr3hwhF9evoDvUmdaPVZw6FZmJhIU3iuQJ4Y31d8Arv8x+14nFDB67c0VJLqGrHgdOCHk/gN8BoAH4Q0rpbwTc92EA/xHAPZTSryqr5T6SelppLocgiMb/qgj3chtbJpNheibs4NG1zJfffTajzDLLSCr58qtHVJO7+Sou5FDoUqaOSEV4JO/IOogTGed45+kK3rtYZm43nlxCblyN1AF+ZbLasQgiHTghRAPwewAeArAO4CuEkGcopa957isA+FkAfxtHRQFgnEihOzRibRCZ+F/RONEgZLPZ0HpGHciZhgLLpi/w3pfNZpm54lnPZ+lgppFXxcvXD5/J4tF3LTJ1RF6+ALFw0qj6sRxBl9GtQj6HRUG+eGY4qs5P8MCvzIEVbMeyYBmB3wvgHKX0DQAghPwZgA8BeM1z378E8FsAfkFpDV2wjC4K6fQRw1PZKDLxv0GOS3S00mq1fHevWQ/kTCP3hWy8tPe+RrOJL53rK3NKPB3M1eBru9FEpVQSioQSDScNAs8RdBmugvTaD7y5hNy4Gh2en25tcMjLCxYHfhLAJdfv6wDe676BEHIngFVK6Z8TQmJz4MeqVTy6mlOay0H1cWk/xyU6WqlUKr5/Zz2Q46dM1xpfXiRzRXQ3+sqcEk8HczX4WqlVhWVTzT3PEXQZroL0GojXHoM6PNEOmjXFQZi8smBhg/j87SBAjBCSAPC/AXg86kXb29t44oknkEwmYVkWHnnkETz55JPY3NxEPp+HpmnY3d1FrVZDs9kEpRS1Wg1bW1tYWFhAq9VCKpXC8vIytq5cBiEEyBSQNRpIp3IwB2Ocf9PAmdWT2NzcRCqVQrFYRKPRQLFYhGmaMAwDKysr2NzchJZK4UtXTGjDLmx9AfedymJsDvGjty/j0uUrWMznMOj3sNFqoVKpoNvtwjTNg+ez2Sx0XUen00G1WkWn08FoNDq47sjU63SwlCLQBh0sJQkyKOONC1eAVBZ5XcNgr4/l5WXU63UQQlAul1Gv1zEejzEYDNDv9w/emUqlkFsoYJV00BzqWElSdOtXsJg8js3NTei6jkKhgJ2dHSwtLcEwDAwGAyyurGBtfRMmkrAGBk4lhmgMMlhbvwIdFpNMlzc28NL2CP0xsJQw8Q/uuBHddgvfW7GhF5Yw2N1Bt90CAPR6PV+ZFhcXYVnWEZmcdjLHY6xoFuzBEKl0Cd36FYx308jk8tjYbmC5VsZ4OMRgMDh4PpPJIJvNTkZ2pSXUW7tIYoyTx4+j19jAimaiOyRYTZhIWUVcudLwbSdH94atJrb2de+NS1eAwRi1ZALEMNDoLMDqt5lkyi0U8DevXUTT1lFIUrzrmI6Tx4/jvvIQFkmiWsrjyvolaGT1oJ38ZArTvfvKQ+gLJdiDPjbWLx20E01mUMimYPR6gfYEAJ1uF+lCBaNeCyRBsJSykRq0kNNzsPodrDX2sLKygr3GJkYB9uTo1pBqGA2GOJUYoDlI4+LlDaTo+IhMly5dwunTp4/IlEpn8KVLfRCzj3G6gO9eSYFa4wN7XFosoL/bwUaIjwjTvezCApY1A3QwONAto5XCC5sjJIddUD2P+1bzGA3faocge1pZWcH5i5ehGUOUUxkkjRa2mhkkx4Mj7dTr9bCzsxPqI8L8XqhzphHBuoSQ7wbwFKX0ffu//zIAUEo/tv97EcB5AL39R1YANAF80LuR+cILL9Dbbrstys8HYm1t7chubtgmS1Svut0z8Zmvbx98+ujD7zwWWxY+07K5p3Jra2uBUTfu96kYNVwrfDkyi4zswmSTOVbtfScAphEbC19+Oi0D3pBXP9ni5ipI5mnol1cXeMt02wnAbscybXz27NkXH3jggbv9rrGMwL8C4BZCyE0ALgP4cQA/4VyklHYAHMwDCSHPA/iFOKJQ/OIpZaZyceaY8Ksn79plWIywyA6589y1zNfKysoR2WTCEmXzl8iso7Lw5afTMmvuPMt1qnPjsHIVFBc9jfQFXl3gKVM0GdxVjQOnlI4JIT8N4HOYhBF+nFL6KiHk1wB8lVL6TGy18yAonlLU4GVC0WTWRlmVhidGmAdXi69PvbSJ7e7kg7j/zXuO+37GzK+NZcISVUB045CFL6+8Xr36wO0VbOyOcMNSmumzbzwcxMEXC1dhdsyrX1G5S1jqy1qmaId31ePAKaWfBfBZz99+NeDe++Wr5Y+wsDo3eBRTdHRW75nY6pkoZ1NoG2Oc3zFwc0RODneZTGGJhTwKXVu5QzpSTsx8mZaNv9/u4+8udtA0xrDtycbKE/eePCK7XxvLhCWqBq/Ti+LLK2/bGKNtjKElCLa7Jp569k0MxzYW0kk89dBNkU6ch4O4+QriKsyOefXLm7tku2tiMZPER+5aYf7OKWuZoh0eq98SwUydxGRNjO4oZqNvMuXj4IVp2XjuXBMXWwNcaBrQkwl8/vUmXozIyeGtY2RYoq7jB27OghD+r6XzIE6+nBHSxu4Q9f4IAKAlJsfN/UavQW0sGpaoGqq58sqb1xNYaw/QG45BCGBZFAuZJHrDMS51hritxpaIS2WCNlG4O4hcKvHWMofCDxzk9QQSBGj0TNiUYqNr4o2mAUKAx+8+odRmRDu8+Qcd9tHpdFAqsX/D+wvnWkpjPh20jTH2TBvvPlnAld0h9AQRym4YBtOy8eVvXcElWjy0IRQn4uDLGSFVF3TU8imMLIp0MoFaQF6VsDaOWuuM+5CGG6q48srbN22cLmWQ1AgGIwtvtgbYMy0spJNYLaaZ38vCxTT40rUEipnkoWWh+8pDLjsOgmnZePqVOkYWxYKu4dZaDq9tTUJQzTFV+uELpzwRvnj9Fg9myoFXq+wxs9P6ismpYhqg4Epg5EaQUrSNMbbtrFDSHxGw8CWa+8Lh6t4birj/TAkpLRE4owhq46g9B9l4bR7w5MaJ4ssrr3Oytju0UM3rePzu49jsjbBaZFsDd8oV/fxfHPDypS+IddBB713MJNE3LXzw9grSyQTMMeXKNMpStgxfPH6LFzPlwDudDvL5vO81kQMAoj2q32676o3QUjaJimbiiqkrX//2kzuKrzg/hOFGUBtHOc04O2yALXWB934Wvrzy+vFVysrn41B1uIwFUbZoD/oASkee4dUv73uPL2bw+N0nlCSg8j4rw1eY35LFTDnw0Wjk+3eRfBwqMge6G1AkJ0eYUuhaAt+5nMF9tWNHjuXLTHvDTo+F8SWjwDzrrEFtHOU04zwGLxI+xsqXn7yy69IsHUxceUJYbHFj/dKR50T0K0hneXOqs5QtE7ETpNMqMFMOPCieUiT+NywjXRzrgjx5JhycPH4c6bQe+g6VccJhfMUVoueFu429bRHmNGXi26MgEj7G2qGoiBFmycfhhUx8exhYbNFPZtEOhbezE7FDpxzRiJ15PvB9OPGUKvIlBClMXOuCPHkmvPJGvSMKvNN/PwQ5SNWdnbuN/dqC56MNKvgS1S/WDkU2Rpg1H0dQHVUkxuLVLz+Z4+pQvBCxQ3cdRWZGVz0O/FpBPp+XSl/qht8zKrO7sTqBMKXwrpuJLBOInh7zg7uucXV2jswq1mhV8SUcPsbQociujapayxZdghLRryCZVXUoInKqCKcM4iqu9W9gxhy4pmlKj0t7n1G1jqrKCWiadqS+vMsEqo9LR73XkZ+XL+d+R2YVSzYq+VJh4H4y9U0t+kEPVMyovBBdghLRL69e+0HlGj3PUpwowrhikVcUM+XAd3d3cfxUUUphw5RA1TqqKiewu7uLpaWlI3XkWSaIK39JWGfHw5f3/vvKQywtLSkztGnyFeVg/GRa73QwSuWlBgeqHJLIEpQIX7u7u8gvFrm4AsSWVESW4kQQxpWfHavCTDnwWq0mZdgszkXFOqqIUvsZf61Wi3wuqqy4+Ap6Ly9f3vvThbcUPQ5Di4sv1pwc3mWov2sQtDa2pQcHvJEXLIhrc69UqTI5YxVLKqr2QSJlCuGKxY5FMVMOvNlsIpfLCRu2tzEbfRPJRCK0kVRtYIUhyFE68sqWpYIvv3wvfu/l5ct7/3hvF6gUA++X3TiNiy9vTo6d/gjHFvRQp9w2xtCGPeQz5dgGB6Zlo94z8dy5JvZMO5YYfl6+NrYb6A612O1Q9DmRWXcYVyx2LIqZcuBRucuj4G7MXCqBZ1+PVmpVG1hBMC0b5xsG2sb4yHF8FnnjPA7t8NU2xlhrD5jyvfDy5b1/68rlwHtlN07dXMU1st/qmaAAlrKpSKdcyiaRSRI0OE7x8vDr8LXVM3GxNcC7TxZiHYWyIqORqdoh72AqyB5Z4Geysn4rDDPlwL1TEV4FczemObbxzGsN5rSgcRxjdwzMcZCnS5lDR4Cjpl4i680ifJ3fMfD515vMCu1dJuCJ5Q2TWSbiYlpcNfomnv1WE3sjO9Ip61oC999xIwZIxjI4cPgqZ1NYaw3Q3BthOSAHjRe8H4bg4Wpl+RgePaVPzQ55BlNh9sjyrB9f8yWUfWxtbR3EU8oc7XYO7IhMyVSOSty5HE6XMnjw1jLOlN9aonDLG/Y8i/LL8HVzJYsX15NCXAWVGcRjmMwyG4zT4urEYgaP3bnCPOJrNupH8oF7eRHVOTdf7zlZwEO3lpmzWvLke+HlymljGTt0lz8te2R51o+vKDuWwUw5cPf34WTjX0WmZCwJlUQ3PkrZ5BFl8X4PT+aAiexReJHpa9hp1yAew74BKDIdFgm3U6FbrPe75fXjBRA/0CKzgc3KlwhXbpnj2GRX0eH52aO3bFZbjPqupQxmyoG7oSJOlHdKFhX7rHLjwwvZ2HJZvkSmr0FKPY28KjLhdnHmVQmDHy+UYiqdichxfCDc0bPypSoowalr3B2eysNespgpB97r9VCpVABM5+gtTy8bpEwyuRzc8srGll8NvoKUOoxHt8wykDnA5FfvOE6empaNrWYHhdJSqH6pOKgTVQ+Z4/h+bRzGl2gbs9ijbI4jFpl5bVGVTvthphz48vLhjxq4CVN99Ja3l/UqUy6VkDb4crWG7Z6p7MTd1eDLT6nDjD65UIZp2dxcqchf4q2jirwqYfX99MtbGAwIzna3QvUriCvR2YBINr4w+LVx2Du9dsxaZxZ7nEaOI17dEpGXFTPlwOv1OlZXV32vqZ728vayXmWSNQrTsvH8Kxewbi8qP3EHTI+vIHh5dIwsY+xgkK1wGdk0prRx8XUyYeDyMBWqX0FciTgk0Wx8vAjj683Lm7j5xhtisUe/dpcdrIguLzkI81uymCkHTggJvKZi2iubY8KtTLJrzm1jjMGYIp9Rm8PEXderzZcbjoEWNA11TiOLM3+JA1m+gmYIQ4OikI0voob1WdXrt2F8pY0+XuxsCfHFol/edpdNjyC6vOQgzG/JYqYceLlcDr0uM+1VnWNCds25lE3CSi8If6qNtY7XCl+OkTUGGRQyfB1enPlL3BDlK2yGUG/nUCsVlESIsMgim41PBV+aviDMl4h+hS3ZRcmiYiaNTEFoWZAFM+PATcvGhcubeNuZG5mJUBE6JjOCk1lz1rUE7q1SFDxf5ImCo5R5PYG+aSvPfeFANV+OkZ1/8wJuvokvfE7UuGXXRmVD7XQtgXGvDT0kdYAfZGYDMo7QtGx86qVNNPojVPMpPPbuFSG+dKOFQrYqxJeMfoksQ6kYvWeNBoxsVcnGtxcz4cAdIqy9Mf565wo+ctcK0wdeeZQ1jnVA2fcvFYtY4uztnZNkb7YMrCzoOFbQmQ3tavOlawmsVJaE1i1FjFskN463TNlQu8XFRa46u8sWnT2JOsJ6z8TZ9S4ogAtNA3edKOA7juWZnZLD15VtDSeOVYX4UgVWvmQGB86R/HQqp2Tj2w8z4cDbxhhtYwyzP8TrfQuEAI/ffYLZyERDx1RC5P2WZXGVUe+Z2OqZSBGC9fYQe6aF9c4QD91SxonFDHM9ryZfjszevDXm2FY+Dc3rCSQIsDsYo5DRDh2B5z3ZG3VPEFe8bRwEd96alEaQS6nVX9Oy0eyPYFMKCmBnb4S//OYOXt7occdaL6QSoffHbYsAXyfB2+F5j+QXixYKuVwsHdF0os0lUcomkdIIMjCR1zWYY4rOYKzs/aZlY7tnAsDBVC0OeJdUTMsOvb/f7zO/27RsPHeuiYutAb5R7yFBAC1BEEcanTj5cmR2jPhD76gCBHjmtQY+/fJWJGesMC0bT79Sx8iiSGkE339TCXsj+9CITBWcZS0/Z8TTxmHQtQQevqMGPUkwsiiefqWulKtPv7yFL77Zhp5MYHlBRzWXQnVBF+IqSuYwvlTB4ev+m5cmvCksx3sk/+2V8ARwMpiJEbiuJfCRu1bwH86OcaOlMSeYcSNowyKOAxpR9Ygqz6lr5Rh7/GjbGGPPtPHukwXs9E1kkgmYFkUll0KVc9oWtrkTN1/uD8DqWgLJRAJ7pq0s/tqB28j6pgU9mRCatkdthEXxpfKDt33ThmVDKIteGNxc3bSUxfffXMLZy92DDIK868KpxUrgbGpa9uh04HGU4z2S/x03qu0g3JgJBw4AeT2J+1eAQm1ZWc4EQP0BjShEleeu6yrp4IfuuZ1JVrfSrBTSePiOGvZGtlKuWOovi8sbG1j4/9s799jIrvu+f868OMPh8DEkl9Rq11JWD0uOUFuKLCtGEDtYOTHS1ooFP+RCaZWuC8SV/U/+KmAgCFwUSFO0RYoaaIrUaNKmTZrUcBeFg8CSHSSIJcfWyo1iAcnqRS13OeQMORwOh3d453H6x8ylLu/euXPOvecOOeF8gQU4e+/MPb/H+Z1zfud3vnfpvHL5mAnei8JUkqUQpXQqwWaYvky81Fi3lDMqZ897l/O8dzkfetM4aFNvVP1Rp4JI17+8KaCN9RvMTMisIJsJV+UQZCwTXA5B0K1ndbf1oCmUHdgvbxjG74c5dpw8IXany6ubTW553lAzKLBGma0N+l1T3DgOhtk7nU4rP8+LMKWcJjl7wm4az6QGc6XHuYGpO9hF9S9Htig2HoaxCuBzc2rlVjpBM6hGNOpSLkw9q7utU1N6Gx9hqgt0B5goJWzDsGu12e5kyE+plY+NgvfCC90gMMzeqj7thzClnGFnuCZ9a6eZOar193uOn3+ZmBzoDnamVgNRbDwMYxXAK5UK+Xw+8J4wQdPPOcMYT5VjIqgzuNtaL98y5sCD2hvmwESUErYgzOdSnEtY3LAzSrOvUfBeuBH28FKQvVV8ehDCzFZNsHiqIMi3nFp/FX2FtadqXwzyU1OrzSg2HgalAC6E+Djwm0AS+G0p5a97rv8K8HmgDZSBfyqlXDPcVqWRzNQhAF1HN8kx4bQ13ZqPNSDFqStQ2+Dzckw8fv95PjSVV8qt+g02pkm63IjjsJfO7CwqJweMhpUSgn3rjqWi8jPCrLJM9UVTq80TnYELIZLAV4GPAevA94UQV6WUr7luewV4VEp5IIT4AvAbwGdNN9a27eOffYxoKoem6+hxcEzYto1tcFPHNGOfgzCOPuh6t93iXDE8E57JHGpc+jr2jL5Ph61mCZPacH/H5ICnml7y9uMghFllmeyLJlabOvLqQsUDHwNel1K+CSCE+H3gSeAogEspv+O6/yXgGZONdGBZ1tHfQQ5t6hCAjqPHwTFhWRZ3LC4Z2WSNm7FP19EHXXfbOGw7TNCvjoLhEHo2NlHNEham0gQ66SUdG4dZZUXpi8PkDpOCiurTQVAJ4HcCN1yf14EPBdx/BfhjvwtbW1tcuXKFVCpFp9Phqaee4rnnnqNUKpHP50kmk+zt7bG8vMzOzg5SSpaXl9nc3GRmZoZsNsva2horKyu8dbPElNUgmZkhY1W5tZVkJp2g0WiwurrKQaVEK51mbm6OSqXC3Nwctm1jWRarq6uUSiUymQyFQoHt7W0WFhawLItms3l0PZvNksvlqFarzM4vcEdin06zRXpqnnr5FrIxTSaToVarsbS0xE+f69Jo2ly88zwb6zeUZAKo1ev8ZSVB6nCPTCrJR378PexuV8jlcuxVd/hw8ZDc/BLWboXKZom5uTk2y2WulbvYts1sssNH338P21ubA2VKzy6SsypMpzLUm0neeOttLq6eo16v935jdZW19RK5XO6YTLVajVardaQTVZn263UW0glSzV3mU0kycoG1tQ1mZ2fpdDrs7+8zn06SaVaYS6VJd+ZYW9tgenqara2toXZqWBbZuSWatQr5XO7ITouLi7fJlJ7K8t0bDYTdoD1V4CdX08hOO1Cm+mGbZlNyIXFArZnm5maCRKvJysoKzZ0yh0JQLBYpl8tHMjm+d3Njg5ZMsLK4QK26E+h7nU6HjUqVpLXLhWSXUjPPG2+9TbGQPyaTvbfHRVFj4zDPxUSDVj3NbmtqqJ2qtRqZmQU61h4JuN1O+/s8+d5lbpa2yGUk7cMm61tbXCt3OGy1mUu0j3wrHdCf3njnJmnrkIVMjrRVpVTJMEWbZrN5ZAenPzn2r9frWIeHR3acmZ4e6HsHlRKiL9N+rcZCWpBs1lhICbIUWVvbCJRpw8dOpVLpmEz5wix//nqZbusQe2qeDy11yE1N3eZ77v5Y3triu+sWCXufzlSBD5/P0HHZIZfLMT09zdraWqT+NAhi2CvvhRCfBn5OSvn5/udfBB6TUn7J595ngC8CH5FSHnqvv/jii/KBBx4IfF4Q1tbWIr/UOArsTjeW471b+zb/+9Ut8pkke802l+8rcs9ijo31GwNrhN3fadgdPvX3zgXOLkxtBulgmL78rrttrCLLdDrBE/cVWZ4ZfCJUV1feZ+jqS+d7a2tr3HHhotJ3dP3P25ZPPrSsRHAWt74cG0fpw3H0Ra/cT/740lBuHBVdqfh0EK5du/by5cuXH/W7pjIDXwfcbOQXgFvem4QQTwBfZkDwNoFMJpi4PQgmdtrD5BtV4OaxWNtt8sL1HV5eT/HR1cH1o7r52DD6Ku/bPH9dnx/ErWtdAiq3jQfBSSdkUwlevlmnctBiZSZjlFEurH+1Ol2tVEcmk1F+lq7/udMuu1ab33ulRKfLUFvGra9MJnOM7CnMydE4+uIx/p1MQokbR6mUVMGnw0IlgH8fuE8I8WPATeBp4B+5bxBCPAz8FvBxKeWW8Vb2USgUjn3WyS9Hma2HyQfq3H9UXrVt8cL1nSOHlunBpUdhKxB09LW5b7NWbfLw+YJWKWXYl0JkkonbbOwHp9Ns7tsIoDg9+GCII7eJDawgGY5WBJkE0+mEMo97oVDQ3stQvdcdXNJJgd2WSsEybn1lp/PHyJ7ums9q0WPEVVbrlttud7n6WsUIW6GKT4fFUI1JKdtCiC8Cf0KvjPBrUsofCSG+AvxASnkV+DfADPCH/bdPvCOl/ITpxm5vbw/NCfkhygZQmIAUZrDIJBPcs5jj5fXU0XdbjRosLwR+x10va8qpHX0Vp9O8U21StVqcm8kodbCoL4VQsbHTaSoNm29d31Hi5IhLV3BcZmfpnU4mlILfVqXCd3emlPxF17fcwWU6nTjG/aGyYvNSPJjS2cZWhfph5ojs6Yn7i1wq5oynqMIeg3fKFFVXIcN0FTZuqUBpyJNSfhP4puf/ftX19xOG2+WLhYVeMIvC5aBb/qUb/KMMFt7RvNnYV/pekFOHcWK3vh65UOBj9xVZUmQdjPpSCMfGw5BJJjg/m+VzH1g1xl9ikldFNagkcwXqh5aSv4TxLXdwifIiBz+dhdXXynKRQt2iftjjVlEN3hD9LUiqCLsK8Xuuqk+HwVidxLQsi2x+xhiXQxAc58xn9FjqotYKuztc1bKUCP+DDjuEXQ1E2V9Q/a6frqqVno1VA0OUvLAJXTltUJHZ7xmpbkvZX6KW/IXNG/vpbC6bCq2v9uGhso+ErcU3UXYZRl9+z+0q9uMwGKsA3mw2R8Ll4Ld7r8rs59eZw85Ums3mwPapOHXU1UCU/YWwBFwNy+JbhquLVA6YRO3wKjL7PaNtH/KZ919U2/wb4Fumq7FU/CuKvprNppK+otTix01S521nkH9tVPz7sQmMVQBfXV1FpOJjw3Pgdc6DVjd0Z47Swfy4onWcOk7mQAemA192bon6xq6xAyuqB0xGoSu/Z8yurmpNLrz3mj7go+pfUfQ1iAPdBJeQg0F9wvSAp+JfJjnfvRirAO5wJ5uehcR5ZDoKrUoDrAAAFGJJREFUY54fV7SOU8c1Y9Nl5NNBs1ahMDVl7PdU+Uvi0JUKd8naejQ+cNP6V/WvKPry82uTXELuNqqQ1DkrijCDtIp/ReV8D8JYBfBstvdeR5OzkLiPTEdhzHPkjRIwTc/YwjLyqSKfy/GZ9y+HTkFFGYxH4Ve3rTiyau8qDWpzFOqAk9CXn8xxcAn5wSvfdDoRaZBW0VdUGwdhrAJ4Lpfz/X8/o2zt20od3hQj3yD4dTBVAqFcLmc8YEalE42Dkc+NXC4XOgVlejCOkiZQDWaDfFoHXl9V1dlJ6ctP5qhcQqrwyqdb9uq1u4q+TNh4EMYqgFerVd/dXLcSvfWuw0bUsMs0d5XKsOPJXidUfWa1WiWXyBoNmF6HAz060aj6GjZIeG2s08FMD8ZR0gQ6Nvbz6Si5d1WdnZS+/GSOuurV0ZdbPlU7Bdl9mL4G2dgExiqALy4uDrzmKFGXHjOM4zjGdE6SXZidIpvuvXg5nzF37HhxcZFMDBSmbocbpb7qhz3uko/eM08qkfDlL/HaWGfAiIPuNWyaQMfGXrj9KyHg7z+4yB2zWeWgpqqHk9LXoH4cduAYRQlolHRaUNyKirEK4PV6feiJprA8DjqOU9632dzvvfm93mzzRrtLq9NFCHj20fNKzqPyzHq9zh0zM8bzgG6MUl9zUyl+sL7H927USCUS/MSdBT738Ooxmbw21hkwTO5dDEKUHLEf/Hy6vG+zsXfIrf6/V0v7PH7XHJ/7wKqyb6lyq5yEvra3zJ5MPPKvbIrNfZtKw+b8rHreWcVOUQY7lbgVFmMVwFWI0b3pFNOcCXany/PXd1irNpFSkkkJ7HaHmakUdlsa42mGd+U1nQd0w9FXpWEzhJgyFOxOl+df3+GdapNWt0u3K0n1bbF90LpNX3421pE/Tl05v2/Sv/xeUvL89R3eqlqU91ukEoJkQlBp3K6rYe00fT4iDPz8y+QLDhz/ertqsd1oUZxO862/3bltYmACP3PPAkKgfCr5qI0n/EKHUwPVespMMhHppFgQdq02B60uD58vULVafOJ9i3z7jV3sttQi5FHB6upqbMQ9Xnz79apxXUFfX3aXD9xZYLvRW7Vcr1hIYHE6fZu+gmysootR6Mukf3nldfzrkTtneflGDRAkhWApf7uuhiFIF6PyKwdu//qFB1eM/a7jXw8s5/lhq86Dy3kOWt1QE6lBOvFL0ehgUgfeh049pQ5nQlhelXMzGd6zMM2zj06H5pgIevbNjQ1loqMoiEtXcFxfq4UpPvlQr0QQ/Gcyg2yskueM41TiIAzTmaquvPK69fX43fN89NI86WRCf9Y3hPNllFz6Xl3duHmLB++9dFt7o/DQ9L6bRkKofH6QTqKW3k7qwPsIKscJU88axpEH5Q3DjPbDnt1NZoweOvA+X6e23CSvStBG7yAbq3Qi06cSHfgFl2FHtVV15ZXXVF46SBdx6cnB0L44k7/tfhObkNPphDLlhRdBOom62TspI+xjEDF62HrWUfCquNuockzYjfl8jsJU09ihA3dbdGvLR8GrAoNtrNKJopwHGISgAzmDdKajKz95TeSlg/QVJ0+ISl88qO8d+45JOgbVr+lM+AbZWplE7IRf6HBqUKvVmJ+fv+3/w9azRj3Uooqwx4Qb9b1jREemZk5hDuOMgisE3rWxyjF0L7yzMZ3zAIMQpPNB/qWjq0E+rQsdfQUFpKgTBJW+uOGReVS+5SDMhM9rax1dmbKxH8YqgC8tLR39bYKPw2s00DvUooqwx4SXlpaOOY6pQzRhSwdHwYS3tLSkfAx9UDuDzgPoboTGrSu3T4dFGH35XQszQQjjW16ZR+Vbw+TUWfno6MqEjQdhrAJ4rVYjn88bPV7uNpruoZYgqASBYQ7jyOtuqy5Vrcnj0t72xpFLrdVqpGQ68u+G5aAx5VuquvLaOAxM2UF3RRrWt/xkjsu3dPcvVKG7yopq40EYqwDearWA+Pg4TC3lTAUBR1433I6uEpDi5HoxeZLP0XHTtrlg4Hf9AonKAD1q32ratnaePi72TN0VaVjf8vNrL0z0xTD7F6rQWTWoyBsWYxXAnXrKuPg4TC3lTAWBYfWjShuhETp3WH3p5i3dOp5PJ7lwMfzrv7zt0+WgiUtfg3T1vUqS3Y0tZd+Kmz1TZ0UaVleOX4fRl05fDLN/oQPVVcOkDrwPp54yjMOqGt/EUs7UADOsflTlOWE7t1dfn3xo2Ze0S3dF4Ae3jjPNCrXmitKApztY6G6EmtaXn29lDnfJZ5eUfStu9kw3hvlXWF2VSiXuuHBxqK9E7YtxE6+pPm9SB96HNx+s47Be41caNqlEYqiRTG1iBcHudCnv2zx/fYeDVvfIoYflzVSfE6Zzu/W1a7X579dKdCWBgTls3tKt45l0NlDHbhbIMFUmOhuhOgijr/lcCpHO0rDVfUvHH6NWcagOeLq6yufzt+nrzW2LS4vBLzfW7YtxTvR0nhdX/hvGLIAnk8nQ33Ubfzqd4FvXdziwu0ONZGrDbxAch9nct1mrNnn4fOEo+KUU5Y2Dw8Str3RS0OpIZrOpwMBsohpINuuB1SFO50oIlNrk9xtxlKaF0VcmmeCn7ikisgVl31L1RxNVHHHpKplMMus6Qbm22+T56zvMr6eM90WdAcbudHmjYrFrtSP5lff+KHFrGMYqgO/t7bGwsHD0WZcD2DG+3e5y9bWKFoVqXIQ/zkykOJ3mnWqTqtXi3EyGuWyKjcpxeb3QfdlB2HSDt6Z6UGCOkhN3dLxW2YcB9JvuWdtes00mJbRmr6dNXwDW/j539eXV1VUQolZx6A4AOvpy+vFn3r/Cm9sWz1/fUQ6YcfVFL0X0XfNZZW6jYbryxi2TGKsAvry8fPR32GPwTi1wlF17kzMT98ztkQsFPnZf8Yj3wi2vH3Q4TMIeg3d+T4fSVSUnPkiHQTK7dTWfS/HJh5a1jk6fRn058g57ZhTOnjA+rjMA6OrLkTmTTHBpMcf8esr4prGuvhx5Z7Mp7prP8sT9RS4Vg1M63u8O0tWwfhwFYxXAd3Z2mJ6eBqIf7Q67az/IWcMG9aC2uOV1nh2mfMxETW3UvLD7uUEd3iuztw2386r4PztK/e8o9eXIG/RMk5w9QQh7gElXX24bm9o0jkrW5Z0cDAveOroK8umoGKsALl3J3qh1omGXYn7OGpVadFBb3PJGKR+Lk/siCIOeG9Th5ZCEvordotb/jopiAd6VN8hGo+DsiXJ2QVdfXhur2lSVSyiMvnQGEl1dDfPpKBirAO5eigzKt5o+fqsy6w2aaUbp9G55o5SPDXLOUejL77lBwcrEcjNq/a+33WCeYuFIT8VF32e6f38UXCFRzi7o6kvXxrpcQmEHYNUBT1dXkxRKH5ubm8fqKb0KN320W3XWG/bY9rBnv3njFvdeulsrXTIIfs45Kn15fzNos3O/UuLS3XeHenZUbhxvG+OgWHDa6ujpoqjxsx988GiFMKhaxfRkxfRpTh19efvxMOhyCcUxAEfxL115dTBWATzs+zBVZyqqyzRvR/PrYFE6vdM5aba5Vt80ftrOgelUgc6AMGiz81yyzYWL3cj7EiZ1ZXoGfKwG+jCtvMQ3NVmJ+zTnMH1lp/XqosNwCZkcgKP6V1zvw4QxC+DDEGWmortM83u2yjFjlU7vdM7lVIKyZrpEB1FmKiZJgtzByDrUfx1WXPwlDkzNgN2HkBw9nUsljJIpqSDu05zD9HUu2eQfFotak6kog0vUiUrc/hUFSlYXQnwc+E0gCfy2lPLXPdengN8FfgLYBj4rpXzbbFNhf3+fxQE1wg7CzlR0l2nDEKXTOw4nLItCLh9rmWOYmYppkiB3B7uYaGlvssbJ9+Ig6gzY76j9QatLvXwr1GzXb/BVJcU6aX3RtEKVJYYNmFFTKlGP5O/X60PjVlgMbYkQIgl8FfgYsA58XwhxVUr5muu2K0BVSnmvEOJp4F8DnzXd2JUV/Zehqio/zDJtGMJ2esfhKrUZlubykdMJYQJp2DK7MPpyd7As787MdPhropSi7Vpt0knBM4+sBr7uzQ3dTu3V2UGry3I+QyEZnujI0bWuzU9aX5mpOaNliSqIklIJoy+3TRbSCe20oCpUtP8Y8LqU8k0AIcTvA08C7gD+JPBr/b//CPiPQgghDdfPlMtlLl68qPUdVeXHkWP2Qjcl02nskikWtJ4xivp4U/Sl3mcv5zPcuLFJIa9f6x9m4Ni12uxabd6uNmnYbYSAZx89r2R7XX8ZpLMwPu0nR5iyufD6smjYHQB+6YP6+mpUSrHMeFURlt8obFov1dw1Mgj5QUUzdwI3XJ/XgQ8NukdK2RZC1IBFoOK+aWtriytXrpBKpeh0Ojz11FM899xzlEol8vk8yWSSvb09lpeX2dnZQUrJ8vIym5ubzMzMYFkWa2trrKysUC6XEUJQLBYpl8vMzs7S6XRoNBqsrq5SKpVIp9PMzc1RqVSYm5tjt2FjWdbR9UwmQ6FQYHt7m4WFBSzLotlsMru6ytp6iWw2Sy6Xo1qtsri4SL1ex7bto+/ncjkymR4p/9LSErVajVardXTdT6afWuySKSzQ3NumvlsFeqkhP5ls26ZSqQTKZNvHZUqm0yym2ySbVXKZGey9HdYqh0fXVWXaqATL9OHiIVOFBdoHe2zeunnMTkEyDbOTbdtsbW1hWRaL51a4KGo0mgmyUznq5VtMdYpHdtKVyWunxXMrnGeXPdHh3HSSYqtKebeAtOq3+d4gmQ4qZVKzs+wN8T3btvlw8ZDc/BLWboXtrU0KhQK7u7vMzc1Fkmluocj5xD7tZov01Dz18i2ENTO0P+naSSRTzCRaXErX2Utlybf3eeOtt7l08c7A/uSVqbRXY39/P1Cmf3Bvka2dKinayHaLtXW1GKEq0y88uMKNm7fIZ6doNS02BvQnVZm8dnJ8d6+ZZDrRS5VNs6wUI/xkGgQxbJIshPg08HNSys/3P/8i8JiU8kuue37Uv2e9//mN/j3b7t968cUX5QMPPBD4vCAcHBzEdqLpNCKsvHanG+tKIk54ZY5blobd5vdeKWG3JfO5YDKlOGDKp0dl84bdY1psdcLr66z0Y8cmGdlibiY8I+G1a9devnz58qN+11Q0vw6413gXgFuD7hFCpIA5YEe/qcEol8umf/JUI6y8znJv3II33C5z3LLkMymeffQ8n/3AysiDN5jz6VHZPJ9J8UsfjKavs9KPHZvsbleG3xwSKtr/PnCfEOLHhBAZ4Gngqueeq8A/6f/9KeDbpvPfALOzs6Z/8lTjrMkLJyPzSQ5442jjqPoaR5mjIE55h+bA+zntLwJ/Qq+M8GtSyh8JIb4C/EBKeRX4L8B/E0K8Tm/m/XQcje10OnH87KnFWZMXzp7MZ01eOHsyxymv0hAqpfymlPJ+KeU9Usp/1f+/X+0Hb6SUTSnlp6WU90opH3MqVkyj0WjE8bOnFmdNXjh7Mp81eeHsyRynvGOVJI3z5aCnEWdNXjh7Mp81eeHsyRynvGMVwEul0kk3YaQ4a/LC2ZP5rMkLZ0/mOOUdqwD+jW9846SbMFKcNXnh7Ml81uSFsydznPKOVQD/+te/ftJNGCnOmrxw9mQ+a/LC2ZM5TnnHKoC32+2TbsJIcdbkhbMn81mTF86ezHHKO/Qkpkm88MILZWAt7Pd3dnaWisVifFXxpwxnTV44ezKfNXnh7MlsQN67Ll++7Ptan5EG8AkmmGCCCcxhrFIoE0wwwQQTvItJAJ9gggkmGFOcugAuhPi4EOJvhBCvCyH+hc/1KSHEH/Svf08IcffoW2kWCjL/ihDiNSHEXwkhXhBCxPOG1BFhmLyu+z4lhJBCCF8mtnGCisxCiM/07fwjIcT/GHUbTULBp98jhPiOEOKVvl///Em00xSEEF8TQmwJIf56wHUhhPgPfX38lRDiESMPllKemn/0uFbeAC4BGeD/Ae/z3PPPgf/U//tp4A9Out0jkPlngOn+318YZ5lV5O3fVwD+DHgJePSk2z0CG98HvAIs9D+fO+l2xyzvfwa+0P/7fcDbJ93uiDL/NPAI8NcDrv888MeAAB4HvmfiuadtBn709h8ppQ04b/9x40ngd/p//xFwWQghRthG0xgqs5TyO1LKg/7Hl+hR+o4rVGwM8C+B3wCao2xcTFCR+Z8BX5VSVgGklFsjbqNJqMgrAYemb47bKarHClLKPyOYQvtJ4HdlDy8B80KIO6I+97QFcL+3/9w56B4pZRtw3v4zrlCR2Y0r9EbyccVQeYUQDwMXpZT/d5QNixEqNr4fuF8I8RdCiJf6LxIfV6jI+2vAM0KIdeCbwJf4uw3dfq4Esy+biw6/mbS3zlHlnnGCsjxCiGeAR4GPxNqieBEorxAiAfx74NlRNWgEULFxil4a5aP0Vlh/LoR4SEq5G3Pb4oCKvJ8D/quU8t8KIX6SHh31Q1LKbvzNOxHEErdO2wz81Lz9Z4RQkRkhxBPAl4FPSCkPR9S2ODBM3gLwEPCnQoi36eULr475RqaqX/8fKWVLSvkW8Df0Avo4QkXeK8D/ApBSvghkgaWRtO5koNTPdXHaAvipefvPCDFU5n5K4bfoBe9xzo3CEHmllDUp5ZKU8m4p5d30cv6fkFL+4GSaawQqfv0NepvVCCGW6KVUYuHVHwFU5H0HuAwghHiQXgD/u/yutavAP+5XozwO1KSUG5F/9aR3bwfs1v4tvV3sL/f/7yv0OjH0DP2HwOvAXwKXTrrNI5D5eWAT+GH/39WTbnOc8nru/VPGvApF0cYC+HfAa8CrwNMn3eaY5X0f8Bf0KlR+CPzsSbc5orz/E9gAWvRm21eAXwZ+2WXfr/b18aopn54cpZ9gggkmGFOcthTKBBNMMMEEipgE8AkmmGCCMcUkgE8wwQQTjCkmAXyCCSaYYEwxCeATTDDBBGOKSQCfYIIJJhhTTAL4BBNMMMGYYhLAJ5hgggnGFP8f59E3CBw4PbgAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"seq = sobol_seq.i4_sobol_generate(2, N)\n",
"plt.title(\"2D Sobol sequence\")\n",
"plt.scatter(seq[:,0], seq[:,1], marker=\".\", alpha=0.5);"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.1.2 Quasi MC: Halton’s low discrepency sequences](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1.2-Quasi-MC:-Halton’s-low-discrepency-sequences)",
"section": "7.1.2 Quasi MC: Halton’s low discrepency sequences"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Quasi-Monte Carlo result (Sobol): 41.31674468994141\n"
]
}
],
"source": [
"seq = sobol_seq.i4_sobol_generate(2, N)\n",
"\n",
"accum = 0\n",
"for i in range(N):\n",
" x = 1 + seq[i][0]*(5 - 1)\n",
" y = 1 + seq[i][1]*(5**2 - 1**2)\n",
" accum += x**2\n",
"volume = 5 - 1\n",
"result[\"QMCS\"] = volume * accum / float(N)\n",
"print(\"Quasi-Monte Carlo result (Sobol): {}\".format(result[\"QMCS\"]))"
]
},
{
"cell_type": "markdown",
"metadata": {
"ein.tags": "worksheet-0",
"nbpages": {
"level": 2,
"link": "[7.1.3 Comparison (1 dimensional)](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1.3-Comparison-(1-dimensional))",
"section": "7.1.3 Comparison (1 dimensional)"
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
"## 7.1.3 Comparison (1 dimensional)\n",
"\n",
"We can compare the error of our different estimates (each used the same number of runs):"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"autoscroll": false,
"ein.hycell": false,
"ein.tags": "worksheet-0",
"nbpages": {
"level": 2,
"link": "[7.1.3 Comparison (1 dimensional)](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1.3-Comparison-(1-dimensional))",
"section": "7.1.3 Comparison (1 dimensional)"
},
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"MC result: 40.699423 Error: 6.339101E-01\n",
"LHS result: 41.333591 Error: 2.575113E-04\n",
"QMCH result: 41.218706 Error: 1.146277E-01\n",
"QMCS result: 41.316745 Error: 1.658864E-02\n"
]
}
],
"source": [
"for m in [\"MC\", \"LHS\", \"QMCH\", \"QMCS\"]:\n",
" print(\"{:4} result: {:.8} Error: {:E}\".format(m, result[m], abs(result[m]-result[\"analytical\"])))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"< [7.0 Sampling-Based Uncertainty Quantification: Monte Carlo and Beyond](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.00-Sampling-Based-Uncertainty-Quantification.html) | [Contents](toc.html) | [7.2 Latin Hypercube Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html)
"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 1,
"link": "[7.1 Latin Hypercube and Quasi-Monte Carlo Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1-Latin-Hypercube-and-Quasi-Monte-Carlo-Sampling)",
"section": "7.1 Latin Hypercube and Quasi-Monte Carlo Sampling"
}
},
"source": [
"# 7.1 Latin Hypercube and Quasi-Monte Carlo Sampling\n",
"\n",
"Created by Dezhao Huang (dhuang2@nd.edu)\n",
"\n",
"These examples and codes were adapted from:\n",
"* https://risk-engineering.org/notebook/monte-carlo-LHS.html\n",
"* McClarren, Ryan G (2018). *Uncertainty Quantification and Predictive Computational Science: A Foundation for Physical Scientists and Engineers*, *Chapter 7 : Sampling-Based Uncertainty Quantification Monte Carlo and Beyond*, Springer, https://link.springer.com/chapter/10.1007%2F978-3-319-99525-0_7\n",
"\n",
"## Chapter 7 Overview\n",
"\n",
"1. Basic Monte Carlo methods: maximum likelihood estimation and methods of moments\n",
"2. Design based sampling: Latin Hypercube Sampling\n",
"3. Quasi-Monte Carlo: Halton sequences and Sobol sequence"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"autoscroll": false,
"ein.hycell": false,
"ein.tags": "worksheet-0",
"nbpages": {
"level": 1,
"link": "[7.1 Latin Hypercube and Quasi-Monte Carlo Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1-Latin-Hypercube-and-Quasi-Monte-Carlo-Sampling)",
"section": "7.1 Latin Hypercube and Quasi-Monte Carlo Sampling"
},
"slideshow": {
"slide_type": "-"
}
},
"outputs": [],
"source": [
"# Load libraries\n",
"import math\n",
"import numpy\n",
"import scipy.stats\n",
"import matplotlib.pyplot as plt\n",
"plt.style.use(\"bmh\")\n",
"import sympy\n",
"from IPython.display import Image\n",
"from IPython.core.display import HTML "
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"nbpages": {
"level": 1,
"link": "[7.1 Latin Hypercube and Quasi-Monte Carlo Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1-Latin-Hypercube-and-Quasi-Monte-Carlo-Sampling)",
"section": "7.1 Latin Hypercube and Quasi-Monte Carlo Sampling"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Requirement already satisfied: sobol_seq in /anaconda3/lib/python3.7/site-packages (0.2.0)\n",
"Requirement already satisfied: numpy in /anaconda3/lib/python3.7/site-packages (from sobol_seq) (1.16.2)\n",
"Requirement already satisfied: scipy in /anaconda3/lib/python3.7/site-packages (from sobol_seq) (1.2.1)\n",
"Requirement already satisfied: pyDOE in /anaconda3/lib/python3.7/site-packages (0.3.8)\n",
"Requirement already satisfied: scipy in /anaconda3/lib/python3.7/site-packages (from pyDOE) (1.2.1)\n",
"Requirement already satisfied: numpy in /anaconda3/lib/python3.7/site-packages (from pyDOE) (1.16.2)\n"
]
}
],
"source": [
"## Install missing packages\n",
"!pip install sobol_seq\n",
"\n",
"import sobol_seq\n",
"\n",
"!pip install pyDOE\n",
"from pyDOE import lhs"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"nbpages": {
"level": 1,
"link": "[7.1 Latin Hypercube and Quasi-Monte Carlo Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1-Latin-Hypercube-and-Quasi-Monte-Carlo-Sampling)",
"section": "7.1 Latin Hypercube and Quasi-Monte Carlo Sampling"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Checking for figures/LHS.png\n",
"\tFile found!\n"
]
}
],
"source": [
"# Download figures (if needed)\n",
"import os, requests, urllib\n",
"\n",
"# GitHub pages url\n",
"url = \"https://ndcbe.github.io/cbe67701-uncertainty-quantification/\"\n",
"\n",
"# relative file paths to download\n",
"# this is the only line of code you need to change\n",
"file_paths = ['figures/LHS.png']\n",
"\n",
"# loop over all files to download\n",
"for file_path in file_paths:\n",
" print(\"Checking for\",file_path)\n",
" # split each file_path into a folder and filename\n",
" stem, filename = os.path.split(file_path)\n",
" \n",
" # check if the folder name is not empty\n",
" if stem:\n",
" # check if the folder exists\n",
" if not os.path.exists(stem):\n",
" print(\"\\tCreating folder\",stem)\n",
" # if the folder does not exist, create it\n",
" os.mkdir(stem)\n",
" # if the file does not exist, create it by downloading from GitHub pages\n",
" if not os.path.isfile(file_path):\n",
" file_url = urllib.parse.urljoin(url,\n",
" urllib.request.pathname2url(file_path))\n",
" print(\"\\tDownloading\",file_url)\n",
" with open(file_path, 'wb') as f:\n",
" f.write(requests.get(file_url).content)\n",
" else:\n",
" print(\"\\tFile found!\")"
]
},
{
"cell_type": "markdown",
"metadata": {
"ein.tags": "worksheet-0",
"nbpages": {
"level": 1,
"link": "[7.1 Latin Hypercube and Quasi-Monte Carlo Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1-Latin-Hypercube-and-Quasi-Monte-Carlo-Sampling)",
"section": "7.1 Latin Hypercube and Quasi-Monte Carlo Sampling"
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
"The simplest 1D integration problem, \n",
"\n",
"$\\int_1^5 x^2$\n",
"\n",
"We can estimate this integral using a standard Monte Carlo method, where we use the fact that the expectation of a random variable is related to its integral\n",
"\n",
"$\\mathbb{E}(f(x)) = \\int_I f(x) dx$\n",
"\n",
"We will sample a large number $N$ of points in $I$ and calculate their average, and multiply by the range over which we are integrating.\n"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"autoscroll": false,
"ein.hycell": false,
"ein.tags": "worksheet-0",
"nbpages": {
"level": 1,
"link": "[7.1 Latin Hypercube and Quasi-Monte Carlo Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1-Latin-Hypercube-and-Quasi-Monte-Carlo-Sampling)",
"section": "7.1 Latin Hypercube and Quasi-Monte Carlo Sampling"
},
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Analytical result: 41.333333333333336\n"
]
}
],
"source": [
"# First, let's take a look at the analytical result:\n",
"result = {} \n",
"x = sympy.Symbol(\"x\")\n",
"i = sympy.integrate(x**2)\n",
"result[\"analytical\"] = float(i.subs(x, 5) - i.subs(x, 1))\n",
"print(\"Analytical result: {}\".format(result[\"analytical\"]))"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 1,
"link": "[7.1 Latin Hypercube and Quasi-Monte Carlo Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1-Latin-Hypercube-and-Quasi-Monte-Carlo-Sampling)",
"section": "7.1 Latin Hypercube and Quasi-Monte Carlo Sampling"
}
},
"source": [
"Monte Carlo Simulator : $ = (b-a)\\frac{1}{N}\\sum_{i = 0}^{N-1} f(x_i)$"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"autoscroll": false,
"ein.hycell": false,
"ein.tags": "worksheet-0",
"nbpages": {
"level": 1,
"link": "[7.1 Latin Hypercube and Quasi-Monte Carlo Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1-Latin-Hypercube-and-Quasi-Monte-Carlo-Sampling)",
"section": "7.1 Latin Hypercube and Quasi-Monte Carlo Sampling"
},
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Simple Monte Carlo result: 40.6994232474979\n"
]
}
],
"source": [
"# Second, use the simple monte carlo method to calculate the integral\n",
"N = 1000\n",
"accum = 0\n",
"for i in range(N):\n",
" x = numpy.random.uniform(1, 5)\n",
" accum += x**2\n",
"interval_length = 5 - 1\n",
"result[\"MC\"] = interval_length * accum / float(N)\n",
"print(\"Simple Monte Carlo result: {}\".format(result[\"MC\"]))\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"ein.tags": "worksheet-0",
"nbpages": {
"level": 2,
"link": "[7.1.1 Latin hypercube sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1.1-Latin-hypercube-sampling)",
"section": "7.1.1 Latin hypercube sampling"
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
"## 7.1.1 Latin hypercube sampling\n",
"\n",
"Try to pick a design that fills the design space given a fixed number of samples.\n",
"\n",
"The LHS figure below is from McClarren (2018).\n",
"\n",
"\n"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"autoscroll": false,
"ein.hycell": false,
"ein.tags": "worksheet-0",
"nbpages": {
"level": 2,
"link": "[7.1.1 Latin hypercube sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1.1-Latin-hypercube-sampling)",
"section": "7.1.1 Latin hypercube sampling"
},
"scrolled": false,
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Latin hypercube result: 41.33359084466315\n"
]
}
],
"source": [
"N = 1000\n",
"\n",
"seq = lhs(2, N)\n",
"accum = 0\n",
"for i in range(N):\n",
" x = 1 + seq[i][0]*(5 - 1)\n",
" y = 1 + seq[i][1]*(5**2 - 1**2)\n",
" accum += x**2\n",
"volume = 5 - 1\n",
"result[\"LHS\"] = volume * accum / float(N)\n",
"print(\"Latin hypercube result: {}\".format(result[\"LHS\"]))"
]
},
{
"cell_type": "markdown",
"metadata": {
"ein.tags": "worksheet-0",
"nbpages": {
"level": 2,
"link": "[7.1.2 Quasi MC: Halton’s low discrepency sequences](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1.2-Quasi-MC:-Halton’s-low-discrepency-sequences)",
"section": "7.1.2 Quasi MC: Halton’s low discrepency sequences"
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
"## 7.1.2 Quasi MC: Halton’s low discrepency sequences"
]
},
{
"cell_type": "markdown",
"metadata": {
"ein.tags": "worksheet-0",
"nbpages": {
"level": 2,
"link": "[7.1.2 Quasi MC: Halton’s low discrepency sequences](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1.2-Quasi-MC:-Halton’s-low-discrepency-sequences)",
"section": "7.1.2 Quasi MC: Halton’s low discrepency sequences"
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
"Quasi-Monte Carlo(QMC) simulation is the traditional MCS but using deterministic sequences.\n",
"\n",
"A [low discrepancy (or quasi-random) sequence](https://en.wikipedia.org/wiki/Low-discrepancy_sequence) is a deterministic mathematical sequence of numbers that has the property of low discrepancy. This means that there are no clusters of points and that the sequence fills space roughly uniformly. The [Halton sequence](https://en.wikipedia.org/wiki/Halton_sequence) is a low discrepancy sequence that has useful properties for pseudo-stochastic sampling methods (also called “quasi-Monte Carlo” methods)."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"autoscroll": false,
"ein.hycell": false,
"ein.tags": "worksheet-0",
"nbpages": {
"level": 2,
"link": "[7.1.2 Quasi MC: Halton’s low discrepency sequences](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1.2-Quasi-MC:-Halton’s-low-discrepency-sequences)",
"section": "7.1.2 Quasi MC: Halton’s low discrepency sequences"
},
"slideshow": {
"slide_type": "-"
}
},
"outputs": [],
"source": [
"def halton(dim: int, nbpts: int):\n",
" h = numpy.full(nbpts * dim, numpy.nan)\n",
" p = numpy.full(nbpts, numpy.nan)\n",
" P = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31]\n",
" lognbpts = math.log(nbpts + 1)\n",
" for i in range(dim):\n",
" b = P[i]\n",
" n = int(math.ceil(lognbpts / math.log(b)))\n",
" for t in range(n):\n",
" p[t] = pow(b, -(t + 1))\n",
" for j in range(nbpts):\n",
" d = j + 1\n",
" sum_ = math.fmod(d, b) * p[0]\n",
" for t in range(1, n):\n",
" d = math.floor(d / b)\n",
" sum_ += math.fmod(d, b) * p[t]\n",
"\n",
" h[j*dim + i] = sum_\n",
" return h.reshape(nbpts, dim)"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"autoscroll": false,
"ein.hycell": false,
"ein.tags": "worksheet-0",
"nbpages": {
"level": 2,
"link": "[7.1.2 Quasi MC: Halton’s low discrepency sequences](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1.2-Quasi-MC:-Halton’s-low-discrepency-sequences)",
"section": "7.1.2 Quasi MC: Halton’s low discrepency sequences"
},
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXAAAAEGCAYAAAB8Ys7jAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAIABJREFUeJzsvX2UZEd1J/iLyu+vyvrsqv5StxANbSHckhAILFjAggF7jy1GZoRgZtZey+sPmmGNF++x53g8LD4zMLA+DMyxB++wLJ7ZOW7E7A7IXmG8Y5kvb+MRNN22JYPobnV1V1VnVlZlVlbld+bL2D8yX+lVVMR78fWqlVT+zukjVebLePfGjXsj4t4bNwilFGOMMcYYY4weJm41AWOMMcYYY+hhbMDHGGOMMUYUYwM+xhhjjDGiGBvwMcYYY4wRxdiAjzHGGGOMKMYGfIwxxhhjRDE24GO8KEEIeRMhhBJCjt1qWsYY48WKsQE/ICCE/Doh5DwhpEII2SSEfJMQ8nbmmQ8NjSYlhDjD575DCPkYIeS4xDu+Sgj5DOfzk8M2X29A/+uHbZzUbWOMMX7YMDbgBwc/DuCzAN4M4H4A3wLwJ4SQB5jnrgE4DODY8LmPA3gjgGcIIT+2b9SOMcYYgRgb8AMCSulPUEr/HaX0IqX0+5TSDwL4OwAPM486lNICpfTm8LlzAF4P4BkAf0gIsTJmCCH/ghDyd4SQBiHkBiHk04SQvODZkwC+Mfzz+eFK/KvD7wgh5IOEkKuEkA4h5Aoh5FeZ318jhHyYEPJJQkiZEFIkhPyvhJBIAI3/dNhumxBSIoR8hRCS8nz/VkLIXxJCmoSQFULI/0EImfV8Twghv0MIWSOE1Agh5wghHyCE9DzPfIgQcpl5757dBiHkVYSQPxu2UyKE/N+EkBNsO4SQhwgh3yOE1Akhf0EIuYNp+1WEkD8lhGwN2/qvhJD7ZXka48WFsQE/oBga4hyA9aBnKaVdAL8L4KUA7rVEQhPALwK4E8DPAXgTgE8Jnr0B4KHh/78Ggx2CO/G8F8DvAPgogFdgsGP4KCHkMaaNfwLgJga7ivcD+FUA/52IOELIwwB+A8D/COAUgLcC+LLn+x8H8CUA5wD8KIB3ADgJ4D8TQsjwsfcD+DUAv45Bv10A8M9F7/Sh5U4AXwNwHsB9GOymHAD/LyEk6Xn0MIBfAfAPAfwYgCkMdl1uO68A8HUAlWEb9wD4BIZ2QJKnMV5MoJSO/x3AfwB+C8AmgGOezz4E4LLg+dMAKIBHfNr8KoAugBrzrz787et9fvv3AbQBTAz/ftPwN8eGf79++PdJ5nc3AHyM+ewTAK56/r4G4AnmmT8F8Ec+9HwAwHMAYj68fpT57LYhjXcP/14G8C+YZ/4TgJ5fn7O8AvgcgHPMMwkADQDv8LTTAzDveeZRAH0AyeHf/wHAJbePdXga/3tx/RuvwA8gCCHvBfBPAbyTUros+7Phf4Oqn/1nAHcz/36SQ8PDhJCvE0JWCSE1AP8RQBzAoiQ9IIRMYuCr/zrz1dcAnCSEpD2fXWSeWQGw4NP84wBiAJYIIZ8jhPxjQkjO8/2rAfzq0A1RG/Lw7PC7U0PajgL4/5h2vxnI2F68GsDfZ961ASCJwe7AxSqltOT5ewUDuR0a/v0qAH9OKe37vEfIkwbdY4SM6K0mYIz9BSHkgwD+FwA/TSn9Lwo/vWv43ysBz21RSlmfbo/5+34AXwDwEQzcCxUArwXwhxgYcVWwkwpvu9/h/Ea4gKGUrhBCTmMQ9P1xAP8MwL8ihNxPKb0x/O2/wmBVy6IAwPWvB014fQ69MebvieF7Psr5/Ybn/3k8ur9nP+MhiKcxXmQYG/ADBELIhzFwDfwkpfRrCr+LYeDLfQ57V7I6eD2AdUrpb3ne8c6A37jGaSfwSCndIoQsY5Al8/94nv1vADxPKW2YEEkpbWPgavlTQsg/A1DEwC/8bwB8G8Ar2MnKC0LICoAHADzp+ZjN+lkDcIgQEqGUOsPP2DjDtzHwSV+hQ7+GJr4D4C2EkAnBKjyQpzFeXBgb8AMCQsi/BvBLAN4N4PuEENdV0aSUVj2PRjzf5TEIdH0AAx/423y23yr4PoD5YaDxLzAw6O8N+M0SBqvVnySEfB5Ae0j3RwD8LiHkBxj4cH8cg0DeWRMCh7RNAPivGMQKHsQg6Ou6FH4bwJ8RQj6Bwc5hGwM3wz8A8D5KaRODwO/vEEK+h0Ha5k8DeAvzqr8AkB4+979jYLxZ2v/lkI7/kxDySQAlDIKL7wDwSUrpVUm2PgbgrwD8R0LI72Kw87kXwDKl9LwkT2O8mHCrnfDjf/vzD4OtM+/f5zzPfMjzeR9AFYPMiY/BE+z0ecdXAXyG8/lJMEFMDDJHihgEOJ/EYGLxBu7eBE8Qc/jZ/4yBX9cB8NXhZwQDN8zzGARQrwL4Veb91wD8FvPZZ9w2BLw8jIH/uoJBsPBvATzGPPMGAP8FA0NXxyAt818DiA6/n8DA+K4Pv/9PGEyGPaadnx/S3cQg0+VRMAFbAK/EIEOkMnzuMoD/DcCMR3a+wdDhZ68Z0lwf0v1XAF4jy9P434vrHxkKbYwxxtgHEEJ+DoNJbrz7HcMY4yyUMcYYY4wRxdiAjzHGGGOMKMYulDHGGGOMEcV4BT7GGGOMMaIYG/AxxhhjjBHFvkbCv/rVr9JEIrGfrxxjjDHGGGk0Go31Bx98cJ733b4a8EQigdOnT2v/fmlpCSdOnAh+8IcEB41f4ODxfND4BQ4ez6b8XrhwYUn03Ui5UGIxtkTEDzcOGr/AweP5oPELHDyew+R3pAx4Ps+t9/9Di4PGL3DweD5o/AIHj+cw+R0pA76+Hnj3wA8VDhq/wMHj+aDxCxw8nsPkd6QM+Hjm/uHHQeP5oPELHDyexyvwITodttzxDzcOGr/AweP5oPELHDyew+Q30IATQj47vJT1bwXfE0LIp4YXqv41IcTWnYl70GwerGqWB41f4ODxfND4BQ4ez2HyK7MC/xyAt/t8/xMY1Aw+hcEltf/WnCw+Fhelb9v6ocBB4xc4eDwfNH6Bg8dzmPwGGnBK6dcBlH0eeQjAv6cDfAvAFCHksC0CvSgUbt2tTu1eH9c3W2j3bNxnIIdbye+twkHj2ZTfWzEuTTGWsT3YOMhzFIObwV0sDz+7aaHtXYjHda5LNEe718cnvnEd6/UO5jJxfOANtyERVQ8ftHt9FGsdLGTjUr+/Vfy6UKXXRlu3mmcvbPIvggm/tsblfsOPZ9M+3w+ZqSLMMW3DgPMukOWWOFxbW8Njjz2GaDQKx3Hw8MMP4+zZsygUCshkMohEItja2sL8/DzK5TIopZifn0exWEQ2m0W/38fS0hIWFhZQKpVACMHMzAxKpRImJyfhOA7q9ToWFxexsnoTzT7BkfkZbFXKyOfz6HQ6aDabWFxcRKFQQDweRy6Xw8bGBqanp9FsNtFqtXa+TyaTSKVSuHazhG6rhVMpBxGnhtXKDCYaFaRSKcTjcVSrVczNzaFaraLb7e783stTfmYOf3zhKpqdHurRHB46GUV+cnDJea1W4/IUi8Wwvr6+w1OhUEAsFkM+n8f6+roRT5VKBbOzs9je3kan09n53uWpXNnEn1zrItqtYypB8FOvfjnKpaKUnFie+hT44pUWMs42etE0HvqRWXRaDS5P8Xgca2tre3hKpDJYLpZw5NAsnE5biycZObk8dZ0+vni1g5yzhX40hYdeMY9Woy419nhyarTaWK/WcPvxoyiXijtyqtVq2Nra0pLTZgeYc8og8TRyvU08d8XBy04ek9Ynv7Enw1On00Gt3gCyM0CtjFQyITX2arUaarXaHp5iiSS+9L0KYr0GGpEc3nEqDer0fOXk5SmZzuBLz5Qw0WtiOzKJd7wkjlhkQpkn2/oEDE5jyo49npyExlemnCwh5CSAP6GU3sX57g8wuJrqj4Z/fx/Amyile1bg58+fp/txlJ63MgGgPTO77W00OphN6610rm+28KlvXkcqFkGr5+D9D9yG41NJ3994+d3vlYUfvaq0qPDOk/GtWGnqyEsEP/pNjlnbGJcq72JlrisXEc+mfa7z+/3QKwtH6b/z4IMP3sf7zsYK/AkA7yOEnANwP4Aqz3jbwPT0tNRzxVoH6/UOUrEINhodLFdb+MJfr/kOND9BJqIT+MAbbsNarYNDmoJeyMYxl4nvKNuhbPC2yuX3VhgwEb06tHjbmk7F0Hb6aPf63N/xZMzKc63W0TamstCRlwh+9PP4lTUqNsalDEQy15WLSI/9xpxMf6jKzKZe+dEoa7d0EGjACSF/hMEFs3OEkGUA/xxADAAopZ/G4ELan8TgktUGgP8+LGKbzSYmJycDn2MFSSl8B5qMIBPRCSOjoaNsLr8yiiI7yE2Ng47Sum0tV1s4d7GIT59fFvYzT8amiq0Dm8bRz7Cw/KoaFXdcusHMhWHbNvtFJHPdSU6kx7w+V+kPVZnpjGWdnYis3dJBoAGnlL474HsK4Kw1inzQarWknmMFCcB3oNla4QUZFNVJwOU3SFFkB7mucfBCV2kT0QnEIhOoNLu+/cyTsalie/lXMWwieem0IzIsLL+6RsXti5l0DJQClWbX2m5NJHPdSc5Pj7193u71cXF1G6VaB+m4XH+o6JitFXuQzGTtlg5G5mbsdq8PJz0t3HqzYAXpN9BsbJfDcHO4+aNBiiKr9DYmKhEtMkZNpp9n5hd2VpLedlh5qvJiM5NIpx2RYWFzhHXGorcvbm53QCnFdCq2q19Mdit+409nZ+ry7EeT289rtTZK9S4OkTjmM2auLBayE5BLZ8fpa+1EwswDHwkD7gpzziljPTKjpXx+A83GdjkMP22hUNgJfvitBju9PqZTMWy2ukKll31OBiwtskYtqJ/bvT7++Onv48J2KtA4qho6nnwOZePKRs1UzqzR8soY0BuL3r44nBu4DL0ytjF5mboQvSgUClg8enzXruGRMws4nk/ucdVl4lEQAjx6ZgE/ejgXiqtMduKfSce4+hMkM1bGNjESBtwVZt7iqoIFT5Aq7dsMerlIJtW2zr/82mM45lEC1ed0ITJqvP7zU5hirYP1NqSMo6qhY+WTT0a1jJqfnIPGC8+Q8mSsaix5LkNvv1zfbEnLZz+QTCZ3xkwiGsHF1W2sbrVxLJ/ckYO3n+czCSXjbZMv79iuNLv45dceQzwyobQTCdJjE4yEAXeFWWnbXVX4QcdfrLpyChpobg6pCOzgikcmuO3IPqcLnlHTzVaJxJNo1R2pSZD1lwbFH7zy8VtJ62QkyfDLe2c+QMayYA2I9/9tyccWUqkUptIDmla22gCAfCK6Sw66u2LbKcRs3+ksfIL02AQjYcBdYT535Xm87I7bfFcVflCZmXWzLWRXTjIKVKlUfKPXsqv+sLM4eMqmI59EdAI/cSKB2PTirmBlEI0qLhyXBpM0SZ6cZcYL752FlWJoGQpeek3lYzPLqVKp4MTk5K7MJJ5bT8dto5NC7Acb7tUgPTbBSBhwYNCRtx9d2OnAsHM+w3CJeCGj8Ln8NDeg50J2cNnK4vADq2w68inWOpiansGMZyUsQ6NJaqONNElZfnmujm486xuYtznJ6srHdpbT7OzsDk13zKbxwTeesJbLrppCLAO/iURGPi6/YWBkDDgAbG9v7xwtVZ0ZVYNYNmZePwT5Um9stvD1v7mOZ+tx6VWlH1h3g2p6lipU+s+r+HflOnj3A3ciEZU/KGKS2mgzTVJ2MnX9z5/4xnVku1XUYtvCw2Uqk6yKsVeRj80sp3avj6W1Cl6aTEvFRfwgirGopBCbQFY+XrtlGyNlwNnC6CqC1wliybSvu0IK8qWuVNs4GW0gEUlaNbBhpGeJ+kBWPl7F73XVD4rYnGz92rKZ5+/yvJimWBLIV2U3oLOjkh3fstlLsucV5pwy/njJMT75KOKX5ct2bMqFrHzCvNBhpAy4Xz6lzSCWLEzdEH6+1MlkFH9biSOb7uHoZNLaysF2epZJH+y4TZLRHcXfiue1DororuJk27LtcnKN3ZWmI4xLqOwGVDKBZKGavRQ0+V1c3cZarY1eIotq22xRoqK/tmNTLmTlc+DzwF2I8iltBrHc9kxmYBOl8dL1liMEr73rNu2UPx4dJulZPOhOhKzM3vu6Y6i2euhWClqr+LBhW9a8wDxvHMtOYGFkmuhkL/lNfqVaB6V6Fz+S6iCanjFalIQVo/LyXKp3cOnmNs4IdER2gXHg88BdiNJxbAaxZAY9b+VoS2m8dEVaVRyZTUv/lqWRR4dt376uIrEyq7Z6OD6VxFpHj98geGW22eopG9wwDGQiOoGF6ReMg2gcy8Y4bGQCBfGsA5evdDyCQySOVx7L4Z6XHjfy55uMY7+2XZ5L9UF/nbtYwFOXK0YxqAOfRuhCVBjdZhAraDIQrRxtpme5dG1u6tdQ8OPDtruBl+Gie6w+jOL33hXgWr2D+UwMh7IJJYMbhoEEdvNruiuUzTTZ72qHu3d9cdwxPykd1LYRwHfbdCfw3z+/LGzb5fnSzW2cu1hAJh7Vlq2LF/uFDvuGarWKqampPZ/zIs9+6Xd+CJoMRCtH2d97ETRQRfwGweaxeRmwGS4mx+qr1SpS2clQqumRCYJa28FCNq6llDIGUtWl4pWxya5QRK9p+qiNQD5LR2HlBjArLrFquyyFl+dULIJGx/HNvkpEJ3DmcA5PXa5YcdHo6rEMRsqAz83NCb9zB5pNF4ZO4SuVVUvQacBuIiddvMtF2Mfmve/hKa1pcGlyesb6CUHvtjibiICCYi6dMJ7UeAsHVdrZMa2zKwyiUbUImMqhnRubLXz+UjGw+qGXDj89Buz7t708N7o9ZBJRNLv+p311dx+8vgvi1wQjZcCr1SoymYzvM7Yq7pnU4DBNz3KN8GR3E1uxLSUjZuPYvE5ND16QVEf5Vktla6svLx+uzPLJ6C6Xl05boiCrjktlo7KJjW7EuIqjLGyXJl6ptlGstXFqNi3Nc5AeqxrPoPHKBu5Zt6cfHaqFynh9J2O3dDFSBrzb7QY+IzPYWYGrbntNfchBq+QXcoSB5xWNmKyyi3jWrenh9a+b+E1TE9SKseLx4dI4mVQb9rJGTef06TevrOPCdt2oiiPbpknwT/XQzmQyimKtja2OfLqrjB7L6phs6QOWZ9UxwHsv28+ivpPhVxcjZcBl8imDBigvCOkX1JCB6gQQtEoW5QjLQEbZ/Qa9bk0PlgbdCe7okcP4wPGYceBMJR3MVluqk1ex1sGztbi1XGYbwT+d+jp3H8nhXWcWAl11rp7MzC/48qEC2QlHZULQrb0j6rtxHvgQbj6lyYk4VuDfW6sbbdl1q+7J+NG9OcIqCBqsfoNep6aHyYqQfcaVsWmWjGo6mK22VCavhWwcd2Y7+G4tYt3Xq+vflpWtjpvD1ZN7c038zAOvtBKXsXGeg0ejTu0dUZ+M88CHyGQyxkFKVuCnD2WMtuy6Pvd3/ughEEC4aklEJ3B4Nm9sHHnwG/QqCmxjRcg+87N3+vsKVVPgbKSD2WqLpT0RncCbTx/BGxK5fcnJF8mDR5dqfZ0gePWk0CLWSkOIxquOnbBRe4fXJ2H5v4ERM+CRSMQ4SMkTuG7tC8BOVUQ/flXakTUApjzLQkZW7DPbnRQOC9rTSYGzlQ5m2paI9mQ8immDSYClUdW/fSgb1xpHquPEqyfpjNlKmQXPaOrYibBq7/jpsSlGyoBvbW1h8WjeOMjFCpw3AEzzmUVQGVhbW1uYnp5WCpjo9IHsIQdVyCgE+0y01xS2p3Oc3TSoaqstEe2ujAGz7B8vjSr+bZ1xpFs4y+07b7kE2zVm/HgNgop83X5u9/qBZ068MraNkTLg8/PzVhWSB1eJOj3+BaY8qPo9ZQfW/Py8csBEh9+dQw7xCOrt3h4Xge2Ki37POB3x6VPd4+wq8rFZcTCIdmAgY/e9Jtk/MuDJQ2cH6Ral8nMl+Z0wbsQPafMU9ilS1bEiM/m4Mg4DI2XAy+Uy0um0UZaD3wDwCmQ6FcNMOoZK0+5JRtmB1e71cXV1DcnpQ0oBE1XsOuTQcZCJR9HqOUoGMohfmbo07jPLhYGMRc+FcZzdRVirQRHtwAtj+ka1heVqa8/VYl7YmLR5u0+VgLS3KBUhwHxm74GooH50eVblycYp0v1yEXrf4+XXNkbKgFNKjX7PSyH0FjbyCmSzJb7A1BRBRs2lc6ZXwfp1KjwSbzKRuWDrVJjWdjFF1/HfkrI8m9b78ML2Ee4g2oHBmG73+nj8UhFrtcE7zxzOKWf/mBgm2XHEFqUSlSIO6kevHqtMIKYVIW1P0H5jz/ued73ErpfAi5Ey4KZbETaf9+NfW0Kz6+wIkxWIyhH0MGZ2J57Gps9N2DbAUyDvIQcb9T5k0e718cWrHazUr2v5VnXrfbjQXeGa9Mf8/DyKtQ7KjS5OzWWw1e7h0bsXhO2YxGtMeWEne1Ep4qB+ZPVYdgIxrQgZVklgdvJh34OUvbx3FiNlwIvForAeuIwAdkXCBf5e3foHYdyEPeeUEUnPhFLLxAs/BWIHKaBe70MWxVoHOWcLqVheaQXM0q+bD63jljI1nsViEYtHj++My6OTCRzLq636be0cgniR7Z+g53T12NSFFlZJ4CBXF61XAOSl21TBSBlw3r1yKgLwDoD8MOOCXSXouCVYBbJ1E/a11SROHjnE9dWrHI4xNbDePtFxqahMsP1oCq22+glUth3deh+q8jc1ntls1jieYcM37gYng+5Jle0f73Os/E30WNaFJqJJdgIwdUl531OrVpR+r4KRMuA86Ky23O9tZbPsmXEt3YQ9l4n5BlplD8fYXCXbyHv3m2AfesU8OrEs8smoNQWync3hhYwP3n2nHy8m8QzTCcCVkek9qTyjJ3vuQVcmqrzLTAA29Mf7nprSL9UwUga8VqthdnZ212f7udpy2wvaegPqN2Hz2uXxq3M4xuYqWVVhVGlpNepYPGpeUtZPtjar+wX54GfSMVAKYblVnox5CCu9EbBzT6pIz3jy72vosR9sT342LmXxQlbGOhgpA76wsDcYsJ+rLZXJQLdOxK5cbw6/OodjbK6SebyK2nQPB6nQsrCwYKWmhx9ERtdWFoeX/pvbHVA6yCTi8cKTMYswd1SA+T2pfrnhvLFIk+p6bAMiGZu4ZWRkIyNjXUgZcELI2wF8EkAEwGcopR9lvr8NwB8CmBo+8xuU0ict04pSqYTjx4/v+VxkUNo9uzfTqEwGKqsCUbs8fmUGuo1VsntKT8eg8dI1ZWtwl0olLBw+6lugSPYSAT+wPtqw0ssO5wYuNdH4E41pL/YjvVFUT0S2Mp8oN5zX9o2banpsA7qxMt3URvedxVoHTnUNt58Ql8wwQaABJ4REAPwegLcCWAbwNCHkCUrps57HfgvA45TSf0sIuRPAkwBO2iaWECL9LLuNtXEzjck2TzY9azoVQ9vpo93rC/mVGegqysDylU9Grd1mvtHYe+2cHwghvgYl6BIBW/nfJhMYz6UmMgYyY9pmrrsfzV4ZqVbm88sNZ9tW0WMRVHlXnQRl9UcmF/xMro0jR9Vu1pKFzAr8NQAuU0qvAgAh5ByAhwB4DTgFMDn8/zyAVZtEupiZmZF+1isw2ZtpdNKYZCCbnrVcbeHcxSI+fX4Zc5k4fvk+O0dwVfkyXfGZTHSujHkK5NIlukTAVv636QTGo1/UfzJjOsjP7hfM1jXwOpX5/HLDVXnmwaRmT1jnGUQ2wdt/VxuR0A7AyRjwowBueP5eBnA/88yHAPwZIeSfAMgAeIsV6hiUSiXpurph+YFVVrYqdVUS0QnEIhOoNLs7z91YLWDq5XdIvcsmX6Y1lv0muqDf+8nYSxfvEgFbmQxhBoFV+GVpVMl1N3ULhVWZD1DTYxcyNXv8wNsV2XKb8WyCt//uyXatleJgIWPAefsd9kz7uwF8jlL6u4SQ1wH4D4SQuyilfe9Da2treOyxxxCNRuE4Dh5++GGcPXsWhUIBmUwGkUgEW1tbmJ+fR7lcBqV0cFKtWEQ2mwUhBEtLS1hYWECpVEKfAr1EDqSxiempPBzHQb1ex+LiIgqFAt5zKoZudBKkuYVmbQvVTgfNZnPn+3g8jlwuh42NDXRiGaS7VdyVprjSdPDcledxaCqLVCqFSqWC2dlZbG9vo9Pp7Pw+lUohHo+jWq1ibm4O1WoV3W4Xi4uLWFm9iT9faqDScnAk2cfRdAopZxvZ7ATy0T6WlpZ28mFrtRoWFhbgVNdwJtfG1UYE92S7yCamsL6+vounWCyGfD6P9fV15PN5dHx4mp6exvLGFuacMnrxLOacMq7eiOLo7GQgT4+cBGhqDrFeE4WVG3t4Opbq4yfvfSlq1couOSXTGVSaPcSdFo4cXsTazRUQQjAzM4NCcQ1/ttRCo93BYpLip179cpRLxV08RSIRrK2tCXn6hbunUNqsIYEejmYjKKzcQDKZRCqVQq9SxokMQHo1zGSBqTiwtLTkKyfv2OtvbcGJz4NubeDuXAvP1WO4J9tBvFvDxkZ9R06lUmmHp1KphFQmiy/9bRGk18JWJI93nIwgmYhLyanVamFrawvNZhOtVmvn+2gsgQaiiLRrODQ/t0dOsUQSd2T7iPVqaMRzoLUNLFV7O983EcdEext3pR0stXq4fO060rEJ0FQeqFeQn8ztGnssT5OTk/jZOzNY33Rw8vgiCis3fMdev1pEubl77G3XGtjYruP240dRLhV35NRqtVCr1ZT06fvXlhHv1HEsGUUGNawnMpgm/vrE4ynlOCis1OGkpzHnlDGbiuJmq4fnrjyP4wuzgfrEysnliadPj5wEOiSDJEmisHLDd+z52T1f4xxUX2RokD9EKX3b8O/fBABK6Uc8zzwD4O2U0hvDv68CeC2ldM3b1vnz5+np06d93+eH9fV15KZmQil96s7w7orDtL3rmy186pvXkYpF0Oo50sfh273+ziphe7MsdaO1TIEuG3yxPL3/gduUVn1BvwcGMnZ51lnVevvPdDzItiPiS4Z+L7/ed8teLCyikZW7jasDVeDHA49n2fa8/MgExkUy0NEL3V2WDr9eXLhw4TsPPvjgfbzvZFbgTwM4RQi5HcAKgEe7bygMAAAgAElEQVQBvId55jqABwF8jhDyIwCSAEraFAuwtV3DZ/6mpr2N8oPqVjBImLp1VbzbsUK9Hih4W8efdXhit4VB23qZbXl9yLOuCyDIxaWS726SKilLf50jY7cfE9EIVrbaWK62cMfs3mp2fjTajmuowu99PJ794PYza7SDLiYOSvu1keorA1V+VRBowCmlPULI+wB8BYMUwc9SSp8hhHwYwLcppU8A+J8A/DtCyAcwcK/8HDUtHchDdgbr9YKw9KkpZP3bMsK0kdfKXobKMz4yiilrjEx5CjLQMn3i8hyGwQniUWWFFZQqKXsYhHfh7UI2jpl0DBdXtwEA5y4W8cE3DnzGKitA2bhGGPB7n8olvyaGM2gMqcSzTM4m3PJLjYc53U8yn/225/+fBfCAXdI4qJV9S5/yEEblPFnjojIh8Gj0XoYqPOxjSTFt8CRjoIP6xOVZli8V+Qbl7KoYiqBUSVn6eRfeJqITeOTMAla32sgnothsda3V19FZUOjokN/7VC75ld2N8GBz0jI58T2+1HiIZCKOD7xhUVj6lEVYJ9hMszRkaYzFYjvPiYyPjZV+EE8i3kRlBUxWyi7PMnypytePR9UV/1QyilR8sBPk1Q2RlYtXxl4czydxLJ+0Xl9Hp3SErD9ediyIeOZBtBuR3YHYch8GteU3flT4VcVIGfBUNhdq8r4sRMLUmTD8aMznXyhB6Wd8TI2mH08ueC4D20Gxdq+PxsQg+JeIBt+OrnM4Q8Sj6vHp3z+/vBODee/rjmntNoCBjMOqr2MDsq4DlXEv4pkH3m5ERY9tuQ+D2vIbP149to2RMeDtXh9f/u5VXNhOGSXve9szca3whKkzYfjRuL6+jkwms/M+VqGDLlNlYVIQieXte2t1q5Ojq0RzThnrkRlj+Yog4lFlteYt/tTqOai2eoEBNWFbayU8fg1G9XXCcBO6kOlj1XHvxzMP7G7E9uRlo/aO3/jx6rFtjIwBL9Y6uN6MKBkMWytlWQXRNSgiwbMzt6vQOit92wc7Th/KWF0RukoUTySllciW+8iF7E5G17fKG0e9WBrr9U3t+jphF7qS6WPV/uDx7Fe6wLacVehXqb0jGj/jFTgGnTyfnMBGXZx1IuuHU1kx2CiCo7vy7XQ63PforPRN3Uk83lSVSqYezES3hdl0WjpIpOvXNd196fDOoz8bpUaTgcwpX5X2RAZU1zXFA8uzTOkCWVeIjlyDFnp+tXdkINJjGxgZA56ITuDNJ9L4e9OLUj5aP0OrsmIwLYJjskJqNptK9MsWzLJ5o7lKWQGZfPXnrjyPl92xN71PVK5UFbZWrLK87xhah29ou+2W0WQwnYphJh1DpalfbdNGn3j7I8iQsjzbiFWZ8uC30BPV3pGFSI9tYGQMOAAcPXIYiUSC+51qqVdZpTGtBGcyOEX5ozz6dQ/0hOk/9UI2X/1lJ4/tMd5+5UrDoMMW2IqYvLLGi4uLgZMBKyMvD5st80uv96tmvguWZxuxKhEPJuM7qPaOLG55HviLBX75lKorTNkVlI6xlKFLZmD58cvSr3Ogx7b/1MYOgOVZplypLA1BdNiezNiKmDxDG5QjzJOR7ilfEWzmS8uMQ5Znk1iVjdOwItjyvY/zwIeIx9UuLJVRSNnqeqrGMogumYHlxy8LHSW0tXWVqU0jqwwszyrlSk1Ok4p+a2sFJzK0QTIWych28FZHd3iQGYc8nnViVbZOw3rbs32uQcSvLYyUAc/lcr7fs364sC7/NV3ty273gvhl36Gq1KYrL2//ueUNVG80D+JZhS+T06S83x7KxkNbwbl8Z1P+6WUiGdkwLCytuqdS2XaC5CU7rlVr7+iehjXl2Q/tXh91xHfONtjGSBnwjY2NPeUVRSsFGWW2VT/adGUm2u7x+A2iSyV/1ZQPb/81uj1kElE0u8G1afxW7TyeZY2VyYTE+62NHYpIJq6s78018TMPvNJ39xdmCp1ufR0/BAU0Zcd1EO82au+4CLP2zuBsw3YoFSBHyoBPT0/v+ttv1pRRZhOFN1kB8QYWb7vH8uuFrHvIRnqWCLvdGwnp2jR+hfn9eA6CjrHz9iP7W9XxoRNwu9aMKmc2ycBkfNjyiYvaV5GxH+8y8pYNEIsu3zZxoblyjiVSoQXMR8qAN5tNTE4Obm4LSi2TFW6YqxuXTt4AYAcWT2k2N6o7/LJtqtxXuJ+X4QadSNy1audUlBTxrEKTSWojmyapUktDJ7B9ewbWTxbKug9F+mNLL0Tjb7vWwGY/joUh37ZPRMsiyIdu6/BbrFvFbDofSvmDkTLgrVYLgHxqmYxwbfsSvTA9BOTyyyKoqp6rEKYpkDJQdduwQUlWaUQ8hwFbpXjZtkr1Di7d3MYZQcDVK+tupWB94SAb/PPTHxt6IXIVfu0HRVzY3sJMOgZKEXjCMSwE+dBNUxNdOfPONtjCSBlwtla0bGqZLagaPtNDQKL8UT/DzE4YJimQOtDJR/eu2m3nzNo83CTTVqk+kPO5iwU8dbkSeOy6nTpslScZvvZLf0SuwmdrcaRiEdzc7oBSiulUzFrutgqC+kk2VhVkxNmzDTYxUgacVyta9iZsXcimyfEgGgCyg1OUPyra4oomDNUUSBt+P91Vrc2cWd3DTbx2blRbePxSEeUGf7XotnXp5jbOXSxInxhV5dckVdLFfuoPz1V4Z7aD79YiOJwblMn1Hm4Ke4HB0ubXT7KxqiD9GeeBD5FMBvu3bc7eQQE31WJagNpN2C6/orbZ99sI3NoueqXq9/Pj2Uujn4xV6oTIBLk+8Y3rWK62sFbr4NRcxretM4dzeOpyRZp/GX69MEmV9H5n4uM20bFEdAJvPLWAN6SndvpG1UDapDFI/jKxKva9rP6oylgFI2XAU6nUzv+LfK82Z++ggJsfvAPIpVN1cHr5lYGNwK0tv5+ucQjiOUjGtuuEuP2RTwyyRbbaPRydFB/lV+VfVca2MkRUYxfu97KV+fyQy6YxOfnCu3Vzt0VQOcFpq/CVC57+5BVlrIKRMuCVSsU3Q8F2TYeO098xALJXuLm/tZGeValUkEhnlQaaaeDWlt9Pt3KcqYxt1wnx9seZwzk8endwPQyVAKCXX9lTwWFkTslOjDqV+Vi+/GRsgz/VE5w2Cl+54OlPYaVolFnlh5Ey4LOzs77fh5G/Op2K4Zdfe2xHaWUK97MDaLnaQiwywc019kMuP6010Ey3uDp+PxX4KZCJjNu9Pjq9/q6iUaZ1QsIymC5cflUzllT6X2Y8yE6MqpX5eHwFyVjGrWUjiDvIGGrj0uo2zhyxEwfgjZcgfk0wUgZ8e3vb9wSXLWVjV3HxyIS2H3gqGcPnmeCXrPLdLFeVDacNN1KQ3y+fjCrfBuTFjWoLy9UW8om98QRdGbOV/7yTrilkDabOxOnyG5ZRkR0PKhkZKpX5eLKONv1lbMqPbBC3VG9jrdbF5y8V8dQVccaQKtjxEjSmTTBSBpxXGJ1VGtXVCa8d05W8dwC1e318+lvLWqvXFHGMC1R5V/+6g9PLT14jG8eLdq+Pxy8VsVYb9MWZw7ldfMkUv+fJmK38pzrpmkJ34nT5tWlUvGNZJeipmpEhQwdP1oWq/gUHNoO4l1a38flLRd/6PTaSIsYXOgzB5gjbClrK5E+rwh1A7V5fezI4euQwPnA8Jn0SkD0SzFv9mxjx41NJY3dKsdZBudHFqbkMtto9PHr3wi6aeDKWUSCbJVF1oBv8dflVMSp+4J0ulO0X1YyMIIhkLZvrz+s7m0HcM0dyeOqKOGOIZxdcvlQM+rge+BCiWtGmvlmZ/GkW+5GV4fKr6jZxg60mq38RTE93en9/dDKBY3lxrWjTk6wswjwgohv89fLLMyqq7ire6cKwy0WIIJK1TF60qO9U9cmkmBtvN/uFv15TXjCO88CHYFOubM3GOifydLIy2r3+jjICwTO5bIqZ6EiwyerfjxeT051BSuPlWfckq7efeT5yWeVTMfi6wV9WxqbuKt5Y9uuXMCGStcy49pO9SkzCpJgb25eUQmvBqJoqqoKRMuBsYXQ/Y2CqfH7QWfmzQTaZGhCyheD9akaHsfpiDYLqxbp+SuPlWWeCFimtqsx0DH5Q8JdHv9/lBjruKpkgrww/svoT9BxP1jLjWqbvgt5toywuexBPZ0E0vtBhiGq1iqmpqV2f8QaIDeXzg45h8Q4m2RoQPH5FtIsMtW5Q14VISWwfmHHh5VllAto5fSm4PFhVZrZqgYuMqdunfjLWNWJBQd4gfmT1RzcGJTOug2Qv824bO3S2L3UCudeLG0hlJ0PZ9YyUAZ+bm5N6zlT5ZFYVqoL0DibZGhCy/Lo02a6q6Kcktg/MuGB5luGL3d3wLg9WldlUMrpzUYXJJcos/Wyf/tKrxDnCNoyYCxVjJhuQ1dUz2XEtkn27519K2vt72ztQFT1z5dNpthFfvR5KXZeRMuDVahWZjP8VVIBZoE1WKVQNJm87FuQvjTSqiCZS+1KZjQe/EqlsH9vKuZaVsYhO0eXBgJrv9PfPLw/KJySieO/r7FWTY43eaqmM6cnczntlVtOitvwMqIoxkw3I6q5wdWTswqUjqJS0l+8wUgNl2nLl8/JUD89ZSiJgMVIGvNvt7vy/anRZ1jCHeQkCO5iC/KUrlc6+VWbjIahEqs2CSO7fvbZ6zqztycRbbrXZdVBt9aRO4OrQmpqgAPTcEaoGVDaYqRKQ1XEprG83MdvTuyPStBSuzXpJQW258iFOLbTUVqlRSQh5O4BPAogA+Ayl9KOcZx4B8CEAFMAlSul7LNIJ4IV8Sp3osqxhvlX5xFyDmJ3Ber1gdKu2yXMuTaISqbpuG17ao5ttcSQTwdnjaspte6tsmiqpQiucwaJEZ+EgWqgEFaTS2WH6BcpVXQq1RgdZTZeCaSlcGws02WqXrnxWKzM4Mp29NT5wQkgEwO8BeCuAZQBPE0KeoJQ+63nmFIDfBPAApbRCCDlknVK8kE+pIwRZw8xzdQSlXtnaku1RhlpZejIJK/CUiKqXSA0CK7/vrdV3/p50qtoBQ5G/VFU2Jjs4VVqXVvbWuFfpY29bMjTqGjAbk6T77rvSbTzTiGidfDSlw3SBphq8T0QnMNGoIDF/64pZvQbAZUrpVQAghJwD8BCAZz3P/A8Afo9SWgEASumabUIB7PjNdISgInjvVlOmLGUY6VkAMJnL4gNvmJGiWVYxdS50CHuFe/pQZudvmggukCQLE6Oru4NThTumdTJu2DEkQ6OJATMNlLvvLnda3EJksqVqg+gwObwTBJ3gva6/XwYyBvwogBuev5cB3M888zIAIIT8JQZulg9RSv/UCoUeRCIRAHLpWTYCjzIKEUZ6lpdf2cEqulWbhe6FDjrKK5IHT37u34leXdqXalphT4UH2f5VaXMhG98Z04B6xg07hmSMs43JWHfH6b576WYJJw7P79Jb3VK1PNpMDu8EQSfe4pWxbcgYcML5jHLaOQXgTQCOAfgGIeQuSumm96G1tTU89thjiEajcBwHDz/8MM6ePYtCoYBMJoNIJIKtrS3Mz8+jXC6DUor5+XkUi0Vks1mUSiVsbW1hYWEBpVIJhBA48RksrZSQymTxpb8tgvRa2Irk8Y6TESQTceTzeayvryOfz6PT6aDZbGJxcRGFQgHxeBy5XA4bGxuYnp5Gs9lEq9Xa+T4aS+D2LEWiV0UzngXqZSxVu5iZX8DzN1Ywl88iFYvj3lwTlxsxvDTbR7dSQDt1mMvT1dU1zPQqcOJpzDllXFtNYi4TQ3VrG8hMgzSriEUmMDMzg1KphGazCcdxUK/Xd2iKxWI7PKWzk3jib26CDnl++LYJ9EgKizN5FFZucHlKJpP4hbuncHNtA0cXZlAuFdHpdLC4uIiV1Zsotgj6rW3clXZwvdXD5aUbyEax83sZOQFAdWsbX7rWQ6a3jVQ8ip+69yWoltcxOTm5m6eVGzs89avrqLRaQN/xldN2rYGv/aCIZ2uD67neeGoBuWwalUoFs7Oz2N7eRqfTwcz8Au7NNbHWJkhk4uhWCqjH5lGtVtHtdgN5yk/P4k++8wOsNgdlhB++LYlYbgFoVlEqrO7IaQ9PjJy8Y29mfgF//PT3UW4DNJbCG2aaiEQiXDmlUqldPDVbbazRLGZ7ZUwm49hqd/DclefxkmOLOzydvX8R126sYG4qg8Z2FQUfOdWqdRRqtV36FMRTKpvDl797FdebEcwnJ/DmE2kcPXJYSp9cnlqVIrrTGZSHcnLS05hzyshm44j2ejgeqaKTnAStbWCp2lMae6V6F3NOGU48gxmngsvXgNuPHFKWk5+NeOQkQLKLoLUyNjdKSKVSWN8oo5/MIdFvo997YWy5Mtza2sLc3Jz02GP1SWicKWVtMfMAIa/DYEX9tuHfvwkAlNKPeJ75NIBvUUo/N/z7zwH8BqX0aW9b58+fp6dPn/Z9nx8ajQbS6TT3u+ubLXzqm9eRikXQ6jl4/wPyZVv90O71A32hAKS3vp/4xvWd2dv9rWjF4MevbZ696Vlr9Q4OZWOYzyS0fb26tAXx7G07EY1gq93Dr77+OO6Y5f+GlZ8f2JVlGGOKbfNX7juElywEH9ayLR9diPpEZVXOytirF9OpmHSpWh54Oia7Q9dF0KpfZkz74cKFC9958MEH7+N9J7MCfxrAKULI7QBWADwKgM0w+SKAdwP4HCFkDgOXylVtigUol8vCjggq9G9ywYGML1Q3EOR3XNqP3yCeVaGTnuXXr7q0uTwHtT2TjuHi6jYA4NzFIj74xhNGbjObec5+YNuMtLcBBBtw0/Q5XbBy0C3a5QU7rm3GWPzcq2FdsxbkqgvSYxMEGnBKaY8Q8j4AX8HAv/1ZSukzhJAPA/g2pfSJ4Xd/jxDyLAAHwK9TSjdsE+u3WzARnApMJwrZ9Kx2r49Ko4t5n3xZmwNfNT0rqF91aHN5nmz1fIs4JaITeOTMAla32sgnothsdY2DiiIlDOMkn7fN1ZVlqQJTpulzKvD6/Xly0Cna5UXX2ZuHbhog9YLXVpjXrAVN9EFeDhNI5YFTSp8E8CTz2W97/p8C+LXhv9AwPz/v+72s4A5l41avHAP0B4Bfylqj2UJ6xT9fVmWFaTM9SyZAqKKUXp7p80todBzfmtjH80kcyyetrY5t5DnLwpvl9MWrHazUrxtVcbR9stAdx6l4BPV2LzD/X2WnosKzKt22rllTtRNBuhNkt0wwUicxi8Wicl1dVnD5ZNT6lWOAWcaDyE1jki/rfc5WepYXtt0LXp7/pjGBTCKKZtcJJZtCdGQ9zLrZvHcWax3knC2kYnntKo62d5jecdzoOMjEo2j1xHJw6ZLtO1WeZSCbeeJHo6md8NMdHbsli5Ey4Dr3yrGC0y0FG2QsbRo0t631Tlsp1Y9Ht630LBaqBk92hbTeaWM+k9i5lMKvbd3URlHf2UyVlHnnQjaOfjSFVtvfQPrBZn56u9dHx+nvHE6Zz8Sl5ADIp0B2en30Ikkuz2H5oGVotGEnRAjrPkxgxAy4H4KS993OD+vyBhWDJuvOuLa6hpNHDu15RvXQjupN4rIwCRCKVkhenk3qj5gcdpFtz7S+TiI6gYdeMY9OLKu96re1cGBPGHovhbZRB8bb/ksz2HPptA0fdGkY5M0P6VWdEEzsxK3CSBnwWq2G2dm95Td5tTU2Wz0rJ7FUK76ZHMRg20rStpY/j/ecyk3itqGyQhLx7IVJvY9bcUmE3ztbjTpOnJAvG8zCluvH5SURjaBQ6+y0LYKqcfT2VdSp7bl02tQF+d7XHcPHv7aEensQAPfW19FxLdl0qYnslg2MlAFfWFjgfs6WPf3415bQ7DpWTmKF5euVOco+PcsPfsgOLt1MENu5sip9KJKxlz6Teh86fSJqT7e+jvedLL+yLhm21IGpS0wlNdO0cuJ2fHJPX5nq2Warh2bX2Qm4euvrmFzIYcOlFjSmTTBSBrxUKuH48eN7PvcKPy2InMtiv+uA+Pm378618A8euAvA3vszZQeXTiaI7fK1oj7kDXaRjF3YqPehqph+GSqq9XVYePm9lbV3ElH51Ezd1fI7f/QQCICJ2rrxzpiFX32d/XKBiGQTNKZNMFIGnBDeqf7dwncvgtURnK06ICbFdLzKUev0tW/CDqKDB5Fi2iqjKpN3K5Kxi/2q9yHTno1+8fJ7q2vvyKZmmsaR3n0HvzaIrAtStb6ObZmJIJJN0Jg2wUgZ8JmZGeF3XuHrKq9OpT4WpsV0vMrRTme0b8I23ebqnrKThaiv/WQMqLmPvGVWbU5AKqmZQfDyK2MYVYyn6ko5LNccS4eTCK42rRM0ZvVKdtFgCyLZBI1pE4yUAS+VSjhx4oT1qoMudCv1eWGafuRVjm6lgKNTSa2gm8ydgX7v1j1l575fN+3SlXEQnbfKLWQ7NdPLr4xhVDGeOhdThOGaY+lAYxN+5QNMg8aiNi+ubqNU6/geEDOBSDYyY1oXI2XAJycnQ51F/ZRD1ijaCHq6ylGheeXVjrfoUdCdgaIDLbqn7Lzv1027dGVsa5tru463TGqmCv2Tk7sL/csYRhUjKzrlG9YqVIaOxnZV+KyfnunqlsvzWq2NUr2LQySO+Yy9ksB+uwBgr4xtYqQMuOM4oRXWd8ETgIpRtOl7cxxHSJMIskWPwshv975f5kgyj69Wp4c/sGhgdFahsu3xUjNVDaQrYx3o1N4JM87hBy8d2wKeg/RMZiyKTryu1zvIxKMgBMaFwPZTxkEYKQNer9exeHRm36PLqpXgbPne6vU65ub25gjLVgH0K3pkO7+d936dI8mlzS2s1x1rBsb2KlQlCC1TU0Mk4yDo8mAzzqErExHPMnrmNxb9Try+oBMJ40JgqotIXRnLYKQM+OLionaGgckKw7QSnO6uwb3EmeXDRhVAk+2oSlEsVd5vP34Uc6sFq4FU2VWobnteqE5gPBnLQJcH3TgHK3eRTGT0TMRzWHqmazNEEE2CIr51ZSyDkTLg7qXGqkFKGwbAZo6qrLF0+XV5KNaCb8J26VUNWAJylzer3miuynu5VJQ2MDbcILZ3caoTmFfGLsKuvaMa5+DJXbTTkBkfPJ55fcfGoEz6RDexgQee7vjxLeLXBkbKgMdiMa3fBfn9ppJR4dF7FyYDQHcCcPll61QE3YTtB1YR3H4wqelhk/dYLCZlYGy7QWz6gFUmMHZM68YmgOAJ2I9eVbcQjy/Z8eGnx34xKNvxGhN46QzawejaLRmMlAHP5/Nav/MzAO4VVfOZGA5l9a+oCiO10eXXqxiyN2GLaAyrpocfVHjnyVh328/yLjp+rjMZqJxw9DMqLL86sQkbmSUqbiHRQRnZ8aGqx2HFa7zQKWHgIohvXbslg5Ex4O1eH1eWC3j5HbdbWWG4BoBMENTaDhayce2slrBSs9bX15HJZPYMENWCVDvuF4fvfrFR08MWimslRKcjgRkrKpNJkHxUdxaq8vYzKq6MvbtB1UnSxgE0P4jkzvIlOz5YnoNoCrsyoGkJgyC+XX7DwEgYcLfz0G7iyVX/G2pEEBmAUr2DbCICCoq5ND81MAhhpTa6M7eJb9A78GbSMUynYths7Xa/qBhmm75EHq1fWWrhyjNmN9SwkHGhqRgI1UwTP+TzeW41TZka3C6CUiVFV6OpQFbuMs/xeLYlax3I6O+NagvL1RbyCf4ZED++D/wK3O3glySB5y3lrnoHRT4ZVVIYFn4rBBMaO53OLnp1fIPewVlpit0vYRpmWRRrHbTbHaRiGemj3zI0y/jQVYymaaqkF51OB1uMAam2etqnd3mpkqKr0cLO/Ra1z/Jcqndw6eY2ziik5tqETBD38UtFrNUGfXfmcE5poefVY9sYCQPudnDcqWE2nbVWo8M7KEyK1otWCLJbM5ESNZtN3/fqVOYLux64lx+XRlkDsZCN41CSYqWmf0MNDzI+dK/RDDtV0otms4nFmTlrp3ddeGniXY0W9olMv/a9PJfqg/46d7GApy5XQjkZqipP3iKo3Oji1FwGW+0eHr17QYnGID02wUgYcLeDVyszODKdtRLECoNG1cpxQUoUlD96Kyrz+YF111AKpWJPiegEfurVL8cbOjDOrOC1LeNDt5kqKZsT7bcAsHV2gd1h6NS4kYFMuquX50s3t3HuYkG7/LMMParyZOHty6OTCRzLq9E3zgPHoIMnGhUk5gd1BWwGsXQRpGBBNAb5UoPyR2WNs9/gDKvuyM3tDiilmE7FlBSzXCruFCwLc4Uo6jtbqZKyu6/vX1veCczbrJzHo8m7ywwjMCib7uo9z3HmcA5PXa6EFqC0EZ8ynWDHeeBDxOO7E/NNg1iAvgGTUbAgGoN8qf/wZcGD2cQ3aNtIevk5nIuDUuwJmIrocGXgylhX8VTkyes7W6mSsruvbLfGDczbMjx+6Xa2d2ay6a66euzFfmew6EywLo0T0XEeOAAgl8vt+lvGeLV7g5uwedkXJgbMHayJaAQrW20sV1u4Yza95zkVJWKVtj2R4/7OFmxlz3iViT1cEqSYrAx+8Z5B7WQdxbMVF7Fh2GR3X5FEgtv3uvyrLEaC9Ee1Pdl4i44es3SFlcEiy7OKe/REBvjFhX4o7suRMuBrpXWUe1HpAcX6ZNmbsE0M2EKWf4eg266OErEKMNHaBhDOZai89+msTnjK5O3DoP5kZbBSLGFmalLLkNrKh5ZdGJgExty+n3bKcNIze/pex/CEUfdcpT1Zmjc2NpDNZqXpEFUXVLmoQnb3Jsuzins05VSt+/ZdjIwBb/f6+PJSG89L5Ai7YFPo2JuwTetJsHcImlx/5rbpVYB2oyb1O5uV+lTh7WOZdDAWrAwOH3qh0L/qykynpocOzzYCY27fX1/L4rZDM8q/ZyFr1GytMEWQoXl6elr65GNQdUGbfnOZVbWXZln3aDuRse7bdzEyBrxY68DptJCKZaUHVJCgTQ0Ye4eg7g2RvfAAACAASURBVPVnLE3ubzabzcBi8CpGiac0Jj50YPeBKJ10MFYGmxsl4bM20sFsuIx0V/q84/yTEcfK1lrGqNlcYQbx6oftWgO//52ydu2dMPz3QPB5Dl7fybhHJxqbobhPgBEy4AvZOOYSwA3FHGH3JmyRP85ku8wOJABWVwatVivwGZWVVxj1Ptw+MEkH88pAxLPtdDAT+eis9AF+xToZGfPAmwyCjJpqTREZI6kzrja26+DVfGexX9UFvW2KeNYpt7CTTVZtW6XTi5Ex4Ino7hxhHZ+gDoIGKDuQbObzyuSPyhqlMOt9JKL20sFEPNvwb6us3Pza0lnpU/B3Zzo5wiLZBBk11QlMxkjq7Gp4Nd9F71epuGgjJVbEs0na8tn7x3ngAF7IEZaBzsAKI2Bi4neVyR+VNUqqyqta78PWtlbEs616H7I7LpkUUdWVPu8znRxh3cksDNeDzq6GV/NdBLefg2Ryq84N8MDK59qNFbzy5XdYo8ULKQNOCHk7gE8CiAD4DKX0o4Ln3gngCwBeTSn9tjUqh0gm7QW0WIQRMGn3zG7CZvn1c+XYrsutU+/DRvaGSMY8+mXqfejA1Fcu6mveZyJ+/frJJFir43ow2Y3wkEwmlekIkomtBZsfgmgWFUebyYVXYyjQgBNCIgB+D8BbASwDeJoQ8gSl9FnmuRyA9wP4qzAIBYBUKiX9rOp2WXQTtu6qxVUik5uwvfzarv2yn/U+VHjwkzGrQEH1PnRhw1fOU3beZzx+Zdx2fmMyqHKeCnR3I37jS0WPXcjswGws2HThVxxNNptMBzIr8NcAuEwpvQoAhJBzAB4C8Czz3O8A+BiAD1ql0INKpRKYleGFynbZ78Z52ZmX53oxuQnby6/NkrX7Xe/DhYxbRkXGQfU+dOFnIG3X1OHxKyNr0Zg0rZzHQndl6ze+VPUYkCtXoCJ/myWBee15i6MVNPiVhYwBPwrghufvZQD3ex8ghNwD4Dil9E8IIaEZ8NnZWesK5Ha87I3zLGRcL7o3Yc/OvnCIx2bu637W+/BCxi3j5TkIPJpMqkqybeuU75WFO45z+ek935nIWrVynmk9HxENfqUruvEs2j31k4l+OzDVMrw2SwLz2vP2k8qYVoXMaCecz+jOl4RMAPgEgJ8LamhtbQ2PPfYYotEoHMfBww8/jLNnz6JQKCCTySASiWBrawvz8/Mol8uglGJ+fh7FYhHZbBbr5TK+s9rA9+pxvCzTxRtun8b83CwKxTV0oylMxifQaTWwuLiIQqGAWCyGfD6P9fV15PN5dDqdQSnL4ffxeBzZVAb35pq41ozi9iww26sAThJLKwUkk0mkUilUKhXMzs5ie3sbnU5n5/epVAqbHWDOKYPE08j1NvHcFQcvO3kMhUIBP3tnBtudFKK9JpxOC8uFvTwBQK1Ww8LCAkqlEgghmJmZQalUQq/XQ6vVQr1ex+LiIh45CTT7CRyZn0Fh5QbS2UmsbzeQoF0cPXJ4h6dcLoeNjQ1MT0+j2Wyi1Wrt0JxMJpGOJ3BvromrjSjuyFJ0KwW0U4d3eIrH46hWq5ibm0O1WkW32935fSaTQWM7gsLWFnrJPKZ6mziUJrjWdPDcledxZG5qF083i2uod/s4tjCPankdP//KHMr1DuL9Nta3G5hzyphNRXGz1cNzV55HJkbQaDT2yCmIp/ZECgUfOQXxFDT2AGBlfRONZgd3pjvo9BpY2ZhCpFXF5OQkHMfZkZPf2JuZX8Dl68u4WGhhuUlwJtPAj73yFJxOexdP//jlSTSQRaRdQ7fVQFmSp5n5Bdyba6LQIjiej4NsraGROsTlqden+PNnV/boU6lU2sXT2fsXce3GCvKZGHrtJgorYn3K5XLoVdZxe5bC6dQwlwWm4sDS0hKisQS++FwVC7SKL39vCu94WRb9XldbTnRrA3fnWniuHsM92Q7i3Ro2Nuqo1WqYnp3H0moRk8kolydWn64tLQHtJl6SBOJODauVGUw0KlJjz7URv3jPDArlKpLEAZwullYGPNVqNWxsbBiNPaFxppT6P0DI6wB8iFL6tuHfvwkAlNKPDP/OA7gCwHX0LAIoA/hpNpB5/vx5evr06SA7L8Rff/8K/v0PBvmjrZ6D9z9wGw5l5W7C9kO719feLrurMnfmtRn9XlpaEmYomK4GRTyrIIh32cwB7+8LKzd8szJs78BU2jOVtfv75WoLa7UOTs1lcHu0irfdd6f0ylF2TMrI9vpmC5/65vVd+mQrt5pHg/u+u9INPNNM7+iviTx579E98yCSremY89NjGVy4cOE7Dz744H2872RW4E8DOEUIuR3ACoBHAbzH/ZJSWgUw5/5NCPkqgA+GkYXCyx8Nq2qbip84rHrbi4uLwsFjI1PCTc/az9vMvTTyfu+XF70f9T5cusNIlXT7I5+IYq3WwVa7h61EXirgZjtVEgj3rkkeDe77rjQdK24L0XtsuQgBtaqDIh26pfXAKaU9Qsj7AHwFgzTCz1JKnyGEfBjAtymlT4RGHQNe/qhOuqDtWhA6qVkytKys3sTj18AdPGEVorKhQC5kL5zw/p6XF+32k+hSZt0VEitjmVo2urIGdvfHmcM5PHr3AsjWWqCPOoxUSWB/L/vwvu+5K8/jZXfcZnS6USXWolsSGDC/lAV4EdQDp5Q+CeBJ5rPfFjz7JnOy+EilUns6WTVdMIxaEDqQoaVOo1iu1rjpYDaUz1b1PhF0aGRTzNiKkmxZYJNJiJWx6LSkLfD6Y83ZW4LYi7BSJb00qZZylXHh+O1iFqZzyosv1ZPBtiYmlaqDomwWnbRJWYzUSUxvIXgvZAehSuW8sFcnMjP715dqvulgJqtBILh4z43NFj5/qah0LRoLVRpZGbMVJdlLAkRXg6nUcQmqZWPT7872Rzwelz60YzNVUgey7oSgZ1wZq+hYUGaL7SJtLoJolMlmEdktGxgpA16tVjE1NeX7jIwyyFbOMxkEpulZxVoHCaeBU3N5rYtUZRDk91uptlGstXFqNi2lNDbAyjjokgBeP6qu1vxq2YR9RLtc2cTj391UOrRjK1WSBz+5yuzYZJ7xytjUX29DPjKH2nQvZVmrddCXsFu6GCkDPjc35/u97Am2F8NFqjIzeyOSQ6ftaF2kKgs/v99kMopirY2tTg9HJ5NWlUYEVsZB/cT7XubCXtmyBGG7mfqpSazX17UO7dhGkFxlXB6iCdXbP0F6zINoHOgG81UDw0G0+R1468XU+ZXFSBnwarWKTCbD/U627kgiKlc5z0QpZQdV0Mz+jlNpkOys1nbZhH7vILz7SA7vOrNg7SajIBp5Mg4yYOz3Ni92CPuSiHivGWqsRQY7QeKe+CZ5QM7lwXNLsf3jp8d+8MtsUek/mcCwrv7w+mhjTY9fGYyUAe92u9zPVeuOBA1EU6W0FQClTg+3Ka72bPiuVf1+NjNgvDK2qURe2KyLLWpLlnbq9ELPBPGjxSsHv5vkXfhNpt73uM/wdkN9gR7rQCdWFRQYNtV/to9EdssGRsqAB9WKVqk74jcQTZXSVgCU5Vf2YIyf75oH1SCQDf5EfezybFuJvLBZF9vUB7+4uCjlItGdzIJo8crB7yZ53fdw+zrlnxdtu0ogi6DAsIwLTgW3NA/8xQSZWtG6dUdE7enOyiqDSjRgWX5lS2qKfNeid+sYyiD+dIO4Ls+7M4bauLS6jTNHzOTqpV3logCVtlQNgEyOsMlkFrQYYav4iW6u0n0Pr3+WVsQ8hxlf8Y5Jv8Cw7RTiW54H/mKByI+ksiLUSS8LY1b20iMasCy/QQMryHfNQ7HWwVqtjQlCUKq3rfBlEsR1eX4hY6iNtVoXn79UxFNX5O/aDII7AYVxmMkrh6lkDO1eX1i8Kcg36sZ2eKWOZSCzGLGRmshLp/NOil56/Xi2WXXTC56cw9xhehGW/xsYMQMeiUSE38luQ3XTy4IGqCqCThfy+NXJyAjCVDKKUr2LWttBNhFB3kKKmkkQ1+V5J2NodRufv1T0DUzbDDgvV1uIRSaM0iNd2perg1jEp7+1LBxvfmPaHa9+pY5lafFbjKhU8ZN5Tz4gs8OPZ9urXxk9E/Gjks3iN178+DXFSBnwra0tTE/vLb8pCxPftsoADULQ6UI/flUzMoKw2erhUCaOxRxBn1JUWz3jPGMTJfTynIhO4MyRHJ66Is4YUq1n4kfrVDKGz18qotzQP7jkIhGdQCwygXKj62s0/Ma0TqljmXhGWKeM3fcE7Vb9eLa5m5bVM13ILghN7ZYfRsqAz8/PG/3e1qEPdoCqrtqCThfa4lcGC9k45rMvBHRUB7bIYOhuQVmeVbNAZOqZiNpv9/r49LeWrW3fg066Fmsd5GfEOcJssE3GeNsswKa7swmaIILGta3dtKyese2aXFDCoztMPR4pA14ul5FO764dodLhtnzb3gE6nYrh3EW1lD3R6UK2MiCPX9swMbZ+SqQbxOXxrJIFQql6PROvP9zmylTUt95+O5Nr45EHXmFkaF3oFGATVaM0iQ348V2sdUC3NnDiNrNxLcNr0CleFqo8y+5kwtTjkTLgbO1ynUFmYzu5a9Xm9PHp82qrNt4A5/ESVKtddvIyOSrsBxunFFm+3/USsywQgF/PRKctm8FSgH9gptntWat0qVOZU6Q/tssVe0883p1rYfHIUaP+la10aToB+tUrl20/SI9NMFIGnN2K2KoF7rdaCDJ6Mqs2Gb8kjxe/rZfs5BVmWpaNU4os30gtKNPB9qWqEWblE0b9G9GBmXrc7M5KL2yu2G0f1vKeeHyuHgvlxKPoOd0JUKZeuUz7YxfKEMVicSefst3ro9PrWwlMsEKwWbpSti2ewvjdTiO7WggrLSuId9n0tz0ukHoFQN6YLhX3jY0JTvfATLdSsDahAmrZE376Y2M3IjrxeE+2E8qJxyDILMqCClNp7VQ9dss2RsqAu/fDsdHlX37tMe0DCDzYLF2pklLHKozffXiyq4Ww65rzeFdJf2P5rlUrO22EUe2QhTUlDUhHFPljN5xcCFz5Q1Z/THYjgPjEY7xb840/hSF7lQBv0C5Elb6gey1NMFIG3AUbXY5HJqwquc3SlSoGlPWXlupdZPP8AyCyqwWdlZSpAqmmv3n5rsG+28ePH1sTnExg2yRYzNJvK/c9DP1xweN5MhnFxkYdgJ0Tz7LQmahlY1W8Xfd+LD6AETPgtVoNs7Oz+7KqtFW6khdkCzoA5A6SOaeML15pGa0W2OeCYEOBVNPfvKjVaqhHMsarYtlyoTKGVfWcgCiwzZODO6b9+ODlub8Yiq3JwI9nXt+rZoXJGktdnmViVUHu1yAZm2CkDPjCwiDAFeR7tTH78Qae6SCQNY7uIHHiGWy2zS5lVYWNzBITWhYWFkCiZgZmV/Bs6H8NKjHsV2FP9ZyASjqiO6ZF4MnD9Oo3G/pjomdentm+V9Exk1gVoFf/Jog+nryCZGyCkTLgpVIJx48fB+Dvew0j48J9p8kpMdkVvDtIZpwKIulp7dWCDoL8frZuRhcZAFfGJpPRruBZt4dMIopmV+8eSZkVl8lBJu+Y5kEkD9MVtIn+qOoZ20d+PKv0neqOWHUhpUMfT15rN1d8ZWyCkTLghBDu57z8WpOAlN/qQsZIKpXW5MAdJJevAS89qZ8VYSs9S5QOZuLeECmQK2OTyYitTmlSrCnoNKXpQSbvmFaZDFQmONmxIGsQVQwnr49EeuxCVsd0s9Bs5biLvmNlE8SvCUbKgM/MzOz5TJRfa/uiAZXfi9LnVFYXiegEbj9ySNt420zPCiqArwo/BeLJWBWi4Jno1KFqWy5uVFtYrraQT+hPZi6/qpOB7AShMhZkFxgqbg6erGcNZWyahSazy9xs9bTdsKxsbIxpEUbKgJdKJSwePb5rNWGrIL0Lk9lZJn1OZWVZKpW08kdNL6RgEVQAXxV+CnT5xk28/I7bjV1fbD+bbpt57obHLxWxVhv075nDegdyXBmHla+/u656B5dubuOMIKgsu8BQWYiIzjeweqzLk04Wjd8us1TrYK3ewXwmhkPZhBU3rK4ey2CkDHgqk92jhKr1DoJgEqHXqR7nh8nJSannWMNsOz1LtKLVhZ8CTbQbeHL1uvX0LNsGsljroNzo4tRcBlvtHh69e0Er6OfK2GTcyaRJluoDns9dLOCpy+K66rILDJXnWFnz9NhmIFEGol0mmSCotR0sZONSZ0BkIKvHOhgpA16u85XQZv0KkXFRTVVSTZ/jwXEc4XdBQUUbRbu8sBEg9WvPVaCTSYIlyfSs/VZ6UXtHJxM4lvcP2Ipod2Wsk7nT7vVxo9rC4z4lcN12L93cxrmLBaPYhYgGmRRL77tEeiyrZzp9FQTvRJdNREBBMZdO7Nod6o4/Pz02xUgZ8Hi/zVXCMI2LrWP1OrN3vV7H3NzecqMyQUW2T3QKHdk8jBDUnktf0qlhNp2VSs+ylTqnQ6+tbAmvjFXGsTsGlqstrNU6ODWX8U2TPHM4h6cui+uq60DXqPH0WLUtkVtLd8x65ZlPRve4CE3Gn0iPbWCkDPjRI4fxgeMxqzOvFyapfy5EA0tnoAdd4qwSVFQxOGGchJS9Ym21MoMj01mhK8DkWHOQgbSdKhlEO6B/4a07BvKJKNZqHWy1ezg6Kb6tR3fV6te/ukaNp8cyO0TZYmG6Y9YrT9ZFaLKDG19qPIR7OajuqTyZ049h1BLRHejsZaheA6MTVJQ1YKLrp3RXOCr1YCYaFSTm9/oM/fzmNiYa26mSQbS7EF14K7tj2WgMAqiP3h18/6nqTjWof3V1g6fHppUtVXVMdSybuG3GlxoPEYvFfL8X1YxQOf1oo5YIC92B7uWX5YM12qbXoLGpWWx+rYmx9PoX0/Hd926yMvOTschvbiMwaTtVMoh2Fzx+VXYsYe1GgeD+Vd3VuXLm8RzUVhAtYZ3gZGnUmRSC7JYJRsqA5/PiMqMioaiefjStJcKDrrJ5+WXTwb5XqgvTwVyorDLY1Cw2HdMkCJqITuC9rzuGj39tCfV2D79/fllY08NPxixsBiZtp0rKgsevyo5F5sCL7tF4mf6VpcEr5196Fb8uiF9bQbTYikmwdMvqj9+koDKmVSFlwAkhbwfwSQARAJ+hlH6U+f7XAPwCgB6AEoCfp5QuWaYV6+vryGQy3O9EQlE9/Rg0AGTdMSolZ2X4VU0HU11lBKVjmhrLzVYPza6zyy3Bq+nRr4plzMKmX5fXlsyuxjTYyxvTtiYm06Pxtlb5e0rt3lzD9OTuMro2gsY2YhJeelT0x29S8LNbpggcoYSQCIDfA/BWAMsAniaEPEEpfdbz2HcB3EcpbRBCfgXAxwC8yzaxfjOZSCgqg1BmiyRTStKWX9bLr8uHbDqYjnvhnT96CAQQ1oY2UWbZmh5NxcscbPp1bfuIZcAb06K+Vp0sbByNN919Antlvzi3m2dRxUUbiyDvO7ztBY1lVf3xmxRu9Qr8NQAuU0qvAgAh5ByAhwDsGHBK6V94nv8WgH9kk0gXnU5H+J2fUGwMQkBOqDqGU6SYLL+JqHw6mKlPkAfZfjSp6VHtdKynMHph85SqjbZEY5rta53JIoyj8SIE1Q/yyrlaXt/1/Z4VerWFL/z1WuhZULoGmQc/++Nnt0whY8CPArjh+XsZwP0+zz8G4MsmRInQbDZ9v3eF4q15AeydyXUhI1SdfGuRYvL4lV0Jh+ET5NGuEjTmKQ37Wa3ewGefCa+ipM1TqjbaChrTLnRkpDtWALVSq7JBV5delme2Hyk1K5fLQqdEss6OUzQpyMpYBzIGnFdKi3vNMiHkHwG4D8Abed+vra3hscceQzQaheM4ePjhh3H27FkUCgVkMhlEIhFsbW1hfn4e5XIZlFLMz8+jWCwim80imUxiaWkJCwsLKJVKIIRgZmYGpVIJk5OTcBwHW9s1fPGag0mnimg0hs1+Atl+Dd1oGg+dnka33cLi4iIKhQLi8ThyuRw2NjYwPT2NZrOJVuuF75PJJFKpFCqVCmZnZ7G9vY1HTgIkuwhaK6NaXkc8Hke1WsXc3Byq1Sq63S7O3r+IazdWMDeVQWO7ioIPT6V6F3NOGU48gxmngsvXgKML87i+WsBsPov19XXU6/UdmmKxGPL5PPrVdTSRR7XTQbPZFPIUbzdRqPrz1Gu1cSQTwaRTBUkkkXSaWFoq7uLJ/b0rp8pmFX98rYtEr45sfAI//aqXorJRQpMkEG1v4660g6tNBz+4uoSpdGyPnFieUtkcbtxcA4klkOyUcVe6jytNB89deR5zk2llOXU6nZ3vU6nULjm951QM1bqDk8cXUVi5gSbimBjSvNTq4fK165hMRHbJCRhcRMCOvUdOAr1oHrn4BAorN+CkpzHnlDGbiuJmq4fnrjyP4wuz6Ajk1On28IPVdaTRQ6/bFvJE6lu4N9fE39XjuCfbQaRVxeZma8/YY+Xk6lOpsLpn7PF4akam8eSFy1huTmA6GcGDJ9I4euTwrrG3vr6OfD6/w5PL83QqilKri+euPI8Th+eFcnIcB7VabZecHjkJdEgGs7k0trfWcFuGINrbxlSWYCoOLC0t+dqI1ZsFdCJJTKeiaDXqu3iazE/j3lwTy60J3JaJoFspoJ06vGvsffm7V3G9GcF8cgJv9vAcj8fRjeZQUBh7zVYbyM4AtTKymTTS6TSWlpak5MSzEb7GOejKe0LI6wB8iFL6tuHfvwkAlNKPMM+9BcC/AfBGSukar63z58/T06dP+77PD0tLS4H5lNc3W/jUN68Pi1v1QCnFdCqGVs/B+x+4zSifOQy4qxd39fHe1x3bOURyb66Jn3nglftCY7vXV0oH63hunWH71suPzGrWu4K7O9vE9f7kTkVJ09xu2QyMIJpttuV99v/6y7/Bhe2UdF1tU794ELz645WrH1RlLqPHsuPR+/6g2JSoPR2eVWjxu5xcBhcuXPjOgw8+eB/vO5kV+NMAThFCbgewAuBRAO/xPkAIuQfAHwB4u8h420A8Huyb827HDucG2zFb+cw6UI2ue7d75Q6s1awIgmo6GC9XnMePKOtBWFGyC7zr3gWjipIsrSYlEGy35UWx1kG5DWkfug2/eBB0Tryquhtk9FglbiXjIhG11+7p1xWXpUWGX10EGnBKaY8Q8j4AX8EgjfCzlNJnCCEfBvBtSukTAD4OIAvgC8Pi5dcppT9tm9hcLvgGb54/T+bIbhirclkF8w4urwLRdGrXYNKh0SZfQbniPH549PhVlKTplHFFSZZW3RIIYbTlxUI2DhpLodVwtBYYfnTpyp1njFV93C5ENMjoMQuZiouqQVh2QaJaV5wHHi3dqDq/spDKA6eUPgngSeaz3/b8/1ss08XFxsZGoE8I2DuYgk5shbUqNw08dSsFqeCgC3aQy6ZnycJG6V5Rn/B4NgFLaz4Z1boDkdeWrVKviegE/tuTccSmF7UOTPmtlsO60EMls0pEg6wey7Tl0quT4qpTV1wnX72gyK8KRuok5vT0tHEbvA5+sd6EvTXxwk0eQUrEG+S207N0FcULv3x9lmcTeGnNSxankmlLpcSwjCGdm53B5KTekXCRPHhjxXXP7dcE5jdeZfV4J97SC74qUcXlosuXzo4asGO3RBgpA75da2CzHzd2B7AdHFYdBdP0rGazKV3wn6cwYaRn+fkSbdRy9vJsCpdWkzIAXr5USwzLrFz///bONUaS66rjv7vdO9PzfvbO2Ou1Fztr2VaIjeNg88EJaHlYkYgly8QmigLSCsmx4UP4BIqErPCBhwQIhCWDIIJEAgyRZVYoKAiT4Chah/jt2JKTXcezD7vnsTPTMz0z3T09c/nQXeOa2qq6j7rVM6Wuv7RSz3Z11fnXuffce88995wgX9NBMkwfYauPpDNy04E7rr3q6Nj/jm1LJbo43emHbbityzYdRGYMeKO1y//+eJ5X1te0d+xN0oymFTPtdTCbZW29XteWMazDhA0grnKH+GHKLW625OccfEaaOT1MeLnIrxPH12Y2Gfx91Ma47eEyEx93mAz+76N07Me+jW3DUomN1i6XVus88/o8K1vhhS78cuq+a9t2pMPXFpkx4PO1Jm/X+qwrYdvMZMLum2Yl7GCHCOYRjpMxqsMEf2M6k9IxnC6zAoblTu52Tg9/qGTa+XWS5orWiVhJw1Vgu7EJepxt91s8ua5UG8zXGpyaGnRyGAjsi4JMlmcSPTcOmTHgM8N93DHc5NVawaoSdtJIk6Q71qrwrLAiAqZ5hHUGIZMZh67hdJkVMIyz7uD32vvrLNQaoXlidHm7CpX0oHpuklzRJj5Z166CJIO2Duc4meP6sSfXaKnIfK3BWrPF8dGSs9WmTTtK8zxHZgx4f/EInzo1w/2D48pGmEakic2OdVD+uPCssCICpdLBHjoKprCNqmjuYnPTQ6lk7orw3uNircnixjZCQHkoujpNHFyESpogjK+NrCoj6sJV4G+LcTpRtVldzlFuG90iE3ddP8Ijd6oLXdhCZyAZOFpgqZHeeY7MGHCAkeFBRkf35zrRnXEkLerrYpYZbJCqIgLrsj/1Q0c68bU6KWyTGjRPjsG+/mu+Uw0Q3nsc7CtwTPTx6J0z1gWlXYRKmqDQ18/F1TrjpSKr9ZbRQO1y5eOHarLhtcWojImqNutxtpmUqAYtl5OJOJgMJIUhdyuAIDJlwFdWVugfHLYK5bE5YRa8n+uG4ZcprIjAOwtXWdrYcZbUx0Oc2yY4yzRJYZtEnv3LzVGjASL4Hm2Nt/ecbhgAaPP+rzfmeHltgIWNJuWhoxwb7tceqMM2qW0NY9i9dWLBTV0rHmfd9AFB6AxarlZHUfDcdYu19qRBNZC4OtsQhkwZ8KmpKWvfm+6swtSfmcTFESaTv4jADTNlpt9fdjrD2ue26cz8oxqhJ2MaFc398Ov03c2i8QBh6y+Nu1/SCi06mK81ubBZRBwR1Bo7zAz3GQ+QatvZvQAAEZ1JREFUnqxpp4hwlZrW42wbo96NATZOz957Xqg1WNzY5pjoozwUP5DUiulUpIeMGfD19XVmyjPWy0bdWYUfOspM0mniZguNrQ3njXWf22a7xVB/ka1tdxXt98lvceDplmHpxD3lPd/09GoclzTyjpwYlKyuS4b7C0gk04Nq332YzC4jgcKg2wZU13mc36rtWMeo68ywbQdblZ699zzUV0QItNx16+vr+UlMaCdGdzkC626OqZSZViVsj6/Le+53N/Q7q2gfJpfNgSed5aYuZ5vTq1H3c2kg/fJ/8sZhTk/MMlYqaukhSmYbf7hp2/HP9lV7UHGbqR5n2xh1HV62g60qgm28VNzXf3TcdQdd0OHQwIsfNQnlSXISS9W40jrBGeTr8p4qt40NXMwI94zDwHXKZ+lytjm9app3xBRB+Z+4d5aRwfYzdfQQJbPpxMZ2deIiv87x66+jv7+9WZ3GRmySQUEngs204HXSWP84ZMqAm8TM2uYt8EPVuEw6jW6j8ncaFd8k+wEuBkDvGlczQlDr2CQDn85yPmneEVMEQzPfvHCRj9/+ESeRJyarJNvViYv8On4dpx0cYONmVUWwVestIxdOklh/FTJlwAcGBrSvTerfBr3GpdtpdBpVsNN84fZ4vqYrAJNZUtJ8H7YdU6Vj0wx8quV8nIw6x8lNEQzNfPHKDi8sXbSOPFG5W2xTsEbp1UV+naCObd6r7TF+HQTlSXqSVdWPkyBTBtwkMbqtf9tlpw3eS9Wogp1mozUYe3/dhmrjanGR78Pm3al0HMXZRb6P4Hcm78w0HNULzaRwxDryRMUtSQrWuKyRSfPrJC1wkOQYf/A+upOahz92DAFa5wJM+3ESZMqAV6tVxsfH9/5OMgpHpdx0FWkQ1cjiGlWw0xS2N5XP0WmoNsbNZb4PP1SdJqjjqGeqMvAlzfdh8s5swlG90MzRnWWag5OphmbGyR9VUDFOr8H3bxrCqaNjF9zikCS/jgo2/dgWmTLg09MfxlMmHYXDOrzLHXEbF06w07QabqpZ2/gETQyzbnSCjs78OjaB6UDicoPaJveOJ+/lpVFumB534vv1wyb3js0sNuq6OF3b6ljFLQpJNtltbEJa/TgMmTLg1WqVoaEhIPkoHNbhXTQMD7YuHH9nuLrwIV8V0vAJmrhAdIyzjs78OlbxspE3LBws6Qa1be6d/uIRBnbrTlwzQYTJr8q94/KUb1wRhqCOTWG6D5Bkk912Q9S2H5siUwZ8e3t773MauUlcNAyde6ky54XxjYPtasTlyUKd6BCV0YT9nF0fnjENB9NdWehELkQZyDgdJ+Uf1Lkq905S+OWNK8Kg2669e6rS5cb9LiolsG5fT7ohCmZ8TZEpA+6Pp4x6sUmNku6sU2c2Gbe01Mmcpxs/aruB59I46kaHqIymn3PUPoWtfoP30w0HSzP3TpyOXR9yUeXeMUWQi1/euCIMuu3ato36fxeVEhiSuYhMkMeBdxCMpwy+2DRmbLYukiiYZM7z+KoGJRtZbPy2cdCNDlEZTb+Og7ySlgZz+Z5UULkwPPnjYoSjXDNp5d4xQRgX3UyOunHRtu/e/7u4lMBpIEw/eRx4Byo/kqvdaZNMfaZLK5PMeUNDQ9ruEVNZbP22cTCNDglr7H4dB3mlse+hQtJDIarcO8E2HRd6CqSae8cEUbrQeb+6/mDbAUx3IHEFlc1Iy/8NGTPghUIh9vukfnGbTH2mncHEiBQKBW2jZSqLid/W9awPoldLQR37eSVNCRy8XxL5bRAm/+b6h3xVoaemOe1d7nEE7xm1n6HzflX92IPtAKbSmcv3orMxrMvXBpky4Gtra0xMTER+n7Sz2WTq8+Bv2KrE/LpGZG1tjdnjY85zRUTJkcasPOw5ED2Di9OxrlvCdYf1y+96MKv4+B507h0VkuYE8aDqx96zvPdsM4BF9THX70VnY1iHry0yZcDL5TKgDpmzXSLaZurzb0zaJOaPQrlcdjoDVCFJNIUHXQMXZYw8HcfJaJIS2GWHTWMw8/PtVu4d20HIZhM4iEZrl1ZpjEZrN/LZrvPrxHGw3RgOz04YPqip2nQSZMqALy8vU+grpZa43naTx2sUSRLzh2F5eZnBwUGjQUm3c+qGZ6U164syRh5nXdjm9LAxYi7y6wTh56tjoHXaQqO1S7O1Gxp9kWQQcuWiHG+tslocj1wtRYXYupjMuBgEVCuRoM0wbdMmyJQBl1I6j54IIm7ppYpIWdxoGiXmV0HKqIPO4UhyPNjU0IbBdNYX9q5NOavkc+kWcnG6MYgg36SbjMEQusfuu2HfJl6S0ExXLspjgyJ2tRQXYpv0/bgYBExXIqZt2gSZMuDlchlRTMdPGweTQzu6ifl1ELb0ihtI0joerNtpTDMFuuCsks+FWyjuXjqbWHHyu15eB0Po+gpH9j0zaWimCxfle1vh+0omIbZR0JnI6a5iXIUQ5y6UDubn57npppusOmSSGbrpoZ2kBRL2ntvh60FlCJMcD3axgoma3ZgMGH7OjdYul1brPPP6PCtb2878zmmFBoZtYimTZgV0nBSmfnSXbiGdgfZL99/Ijy78hFtvuVaPJiG2Uc93MZFLcso6DK517EemDLhXV860QyZVrAu/mQ38dfQ836BuJWyT48GQPL7Yf+8kmQI9zp7OrlQbzNcanJoadLYZF8bftpq76nSjanKhWytRl6upH91V3zE5sXp9RPIuVy6apIORzSnruPumVQ8TNA24EOIB4C+BAvB3Uso/DnzfD3wN+DhwFXhESvmeW1GjoVJ80iPZ3YgEiWsAXucwqYStgv86W5eCLmzen6ez0VKR+VqDtWaL46MlJ5txnkyeeyPpfeI2vtPYNNMJldTVn03fcZW1L0oeU6Orm2tHV9euUxOnCaUBF0IUgKeAXwIuAz8QQpyVUr7tu+wMsCKl/IgQ4lHgT4BHXAtbq9WYmpoK/S6u0bo4kp3Ub6b6XZg8Hl+vc5hUwjaRz8bImHLVNSoeZ79Md10/wiN3zig342wMhm0eGT93Ux98GN8kMqZxgtZDGln7dDh7UHEziU3XDYAwdpEo9GPC1xQ6M/CfBc5LKd8FEEL8C/Ag4DfgDwJPdj5/A/hrIYSQjrdfZ2ZmrH5n4/czRZJOFCXPxFSZi6t1q0rYJvKZNtg0Zxwe55nhPuPoEht0Y7YVayBnZhLnukmjPftld521T4ezBxU3k4gQk4gkk1WMSj+2dksHOgb8OHDJ9/dl4N6oa6SULSFEFZgCllwI6WFxcZETJ05Y/dbE72eDJJ0oqmGdffk8r62XEp1605XPpMGmZTCCnL90/43WM1tduJ5tmeKD+QWeeXc3Ua6btPdobNxycdDh7EFpHA24h71HF+5DlX6S2C0VdAy4CPm/4Mxa5xoWFhY4c+YMxWKRnZ0dHnroIZ544gkqlQpDQ0MUCgXW1tYol8ssLy8jpaRcLjM/P8/w8DBbW1vMzc0xMzPD4uIiQggmJydZXFxkdHSUnZ0dNjY2mJ2dpVKpcPToUcbGxlhaWmJsbIxms8nW1hazs7N89iTU5QCzk2NUrlxiYmKCra0t6vX63u9LpRIDAwOsrKwwNTXF+vo6zWZz7/uBgQH6+vqoVquMTkzy0yNNtrebrPWNsb1SYak1rOQE7SXW4584xsX35xkpFdhp1jl/6QNoNTlZOkJpp8bV9UmObK5wdTOaU6VSoa+vj5GREa5evbqP02R5hrtHtlhqQGGoxPZKhVpxOpbT9PQ01WqV7e3tve+HhoYoIbh7ZIsfbx7lY8M7tKoL1EvHruFkqqcLlyvIVpObS0fo26nx/kqbcxSn2dlZdqvzrDb09RTFabhQoHJlXqmniakyd43UqTV3aQwOsb1SYUWOGbU9v56WllfYrRe5ZWCXoz7OYW1vt9mEgVnmrlzL6XOnjlLd2OHkiVkqVy5p9SdbPZm2vWB/WlpeYbte5NTADgUf5yg9PXHvLO9dusL0+BCb61UqAU6Pf+IYc1c+4NjkMLXqChUFp92Njb33KApFbhwSDO5U2e4fpFCvMjc3b8zJ09Py4so1ba9erzM3NxfZ9nT0FGmcVV4OIcTPAU9KKX+l8/fvA0gp/8h3zbc615wTQhSBClAOulDOnTsnb7vtttjnxWFzczO1E00u0GjtOtvobLR2efq7F7i8KZkadJfLwqV8rjd10+CcBlxyX13f4OmXFvdmkIeVs0scNs5ptGU/ktqtV1555eXTp0/fE/adzgz8B8ApIcRPAVeAR4HPBa45C/wGcA54GPgf1/5vaC9F0oqndAETN4TOvX715FGOTsw6a1iu5XMZqeLd0zXnNOCSe3V5qWu5bg4LDhvnNNqyH2naLaUB7/i0fxv4Fu0wwq9KKd8SQnwFeElKeRb4e+DrQojzwDJtI+8co6Ojadz20GJifIyJFBvWYUSvcR4dHU3dgBw29BrnNO2WVhy4lPKbwDcD//cHvs914NfcinYtdnZ20n7EoUKv8YXe49xrfKH3OKfJN1PrtY2NjYMWoavoNb7Qe5x7jS/0Huc0+WbKgKdZHPQwotf4Qu9x7jW+0Huc0+SbKQNeqVQOWoSuotf4Qu9x7jW+0Huc0+SbKQP+3HPPHbQIXUWv8YXe49xrfKH3OKfJN1MG/Nlnnz1oEbqKXuMLvce51/hC73FOk2+mDHir1TpoEbqKXuMLvce51/hC73FOk6/yJKZLPP/884vAnO3vl5eXpycnJ53mVznM6DW+0Huce40v9B5nB3xvOn36dGhZn64a8Bw5cuTI4Q6ZcqHkyJEjR44PkRvwHDly5MgoDqUBF0I8IIR4RwhxXgjxeyHf9wshnul8/30hxMnuS+kOGnx/VwjxthDiDSHE80KIw5vRSxMqzr7rHhZCSCFEaDa2rECHrxDisx09vyWE+Kduy+gaGu36RiHEt4UQr3ba9qcPQk5XEEJ8VQixIIT4YcT3QgjxV5338YYQ4u7ED5VSHqp/tBNmXQBuBvqA14E7Atc8Djzd+fwo8MxBy50y318ABjufv5hlvrqcO9eNAC8ALwL3HLTcKev4FPAqMNH5+9hBy90Fzn8LfLHz+Q7gvYOWOyHnTwJ3Az+M+P7TwH/Srp9wH/D9pM88jDPwvRJuUsom4JVw8+NB4B87n78BnBZChBWVyAKUfKWU35ZSbnb+fBG4ocsyuoaOjgH+EPhToN5N4VKADt/fAp6SUq4ASCkXuiyja+hwloCXqm8MeL+L8jmHlPIF2tlYo/Ag8DXZxovAuBDiuiTPPIwGPKyE2/Goa6SULcAr4ZZF6PD14wztUTzLUHIWQvwMcEJK+R/dFCwl6Oj4VuBWIcT3hBAvCiEe6Jp06UCH85PA54UQl2lnO/2d7oh2YDDt60popZPtMpyVcMsItLkIIT4P3AN8KlWJ0kcsZyHEEeAvgN/slkApQ0fHRdpulJ+nvcL6rhDio1LK1ZRlSws6nH8d+Acp5Z91Kn99vcN5N33xDgTO7dZhnIFfBvwVQG/g2qXV3jWdEm5jxC9dDjN0+CKE+EXgy8BnpJSNLsmWFlScR4CPAt8RQrxH2194NsMbmbpt+t+llNtSyp8A79A26FmFDuczwL8CSCnPASVguivSHQy0+roJDqMB3yvhJoToo71JeTZwjVfCDVIs4dYlKPl23Al/Q9t4Z903CgrOUsqqlHJaSnlSSnmStt//M1LKlw5G3MTQadPP0d6sRggxTdul8m5XpXQLHc4XgdMAQojbaRvwxa5K2V2cBb7QiUa5D6hKKT9IdMeD3rmN2a39Ee1d7C93/u8rtDsxtBX9b8B54P+Amw9a5pT5/jcwD7zW+Xf2oGVOm3Pg2u+Q4SgUTR0L4M+Bt4E3gUcPWuYucL4D+B7tCJXXgF8+aJkT8v1n4ANgm/Zs+wzwGPCYT8dPdd7Hmy7adH6UPkeOHDkyisPoQsmRI0eOHBrIDXiOHDlyZBS5Ac+RI0eOjCI34Dly5MiRUeQGPEeOHDkyityA58iRI0dGkRvwHDly5MgocgOeI0eOHBnF/wP9cIf2ITw8nQAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"N = 1000\n",
"seq = halton(2, N)\n",
"plt.title(\"2D Halton sequence\")\n",
"plt.scatter(seq[:,0], seq[:,1], marker=\".\", alpha=0.7);"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"autoscroll": false,
"ein.hycell": false,
"ein.tags": "worksheet-0",
"nbpages": {
"level": 2,
"link": "[7.1.2 Quasi MC: Halton’s low discrepency sequences](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1.2-Quasi-MC:-Halton’s-low-discrepency-sequences)",
"section": "7.1.2 Quasi MC: Halton’s low discrepency sequences"
},
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXAAAAEGCAYAAAB8Ys7jAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAIABJREFUeJzsvXmcZEd15/uNXG5mVta+91JqIallCYR2IcCAJUtisT2WJfNkZGNbHnlm3jwxXsczMONna+zH4JmHn818HrZnzNjYAx8wAw+sseVFAgsbIzCoQUgIa2mJ6kW1ZFZlLZmVmTeXeH/cvNk3b90l7pJZXXT9Pp/+VGfmvRFx4pw4EXHixDlCSskBDnCAAxxg/yGx1w04wAEOcIADhMOBAj/AAQ5wgH2KAwV+gAMc4AD7FAcK/AAHOMAB9ikOFPgBDnCAA+xTHCjwAxzgAAfYpzhQ4BYIIR4UQrywF3UJIe4TQjQHUff5gAuN3qCw948Q4hYhhBRCHN3Ldh3g/MIFo8CFEDkhxK8LIZ4XQlSFEGtCiK8IIX7G8tj7gdfuURP/BDgyiIo6ykFa/hWEEI8IIfaK9oFDCPEGIcRfd2ivCSEWhRCfFEIc2+u2ueCLwCHg5UFUJoT4QSHEF4QQ60KIihDiBSHER4UQo4Oo/wBquGAUOPC7wE8AvwS8Evhe4IPAuPmAlLIspSzuReOklFUp5coAq2xhKIRDwG3ABvAXQojZAbZhTyCEuBJ4BHgeuB24ErgP+DZwXiooKaUupVyWUrb7XZcQ4nuB/w+jj94AXA08AGwBmX7Xf4AAkFJeEP8wFNS7fJ55EHjB/hm4B2Ow7wCfwRjkdwPPAtvAJ4Exy3sfBh4FfgE423nvU8C0R133AU37Z+C7gROdMr4C3GBr8+3AU0AN+AbwPYAE3ulBZ09dne9e3Xnvn1i+ewXGQH65U/9TwI/b3nsM+BDwfwLLwHqH/rzlGQH8OrAKlIGPAz/v0IafBJ4B6sAZ4P8CUra6/nvn+9UOT9+LsRD5FWAFKADv9eHzzwEFBZl5L/CtDu2ngd+z8dnk0a2dvqkCnwcOA28CvgZUOrJwxEGufhR4scO7R4FXeMjDLR3+HLV9vgP4204bnwHeYqPhOuBLnTqeA96OMVH9sgfdvw18VaF/LsOQ6w2gBPw18GrbM/d0aK1h7CJ+sNPuNzjRZXmvCdxn+TzXkasCxpj7e+BNDv3j1x+zwB92ZKWGMYb/aRCazqd/F9IKfAl4qxBiMuB7hzAUyw8Db8NQqJ8EfhpDOL8PeCPw72zvvQZDqN7aeeZq4A8C1p0A3gf8LHA9hkB9QgiRAhBCHAEeAr7c+f3ngf8nYB0IIfLAP+181C0/DQOf7dDwauC/AX8ohLjVVsTbgUkMen8U+CHg31h+/xmMyeyXOu08AfyqrQ3fj9E//6NT1y9irPp6nuvUlcZYGf4CRr//WaetbwT+NfDvhBBv8yB5CZjweQYMhfzPMXZs93Xo+y+2ZxKdNv40hmwcxjCH/RrwLzvtPMpuvhwC/g/gRzrtHgE+I4QQPm2y4/3AfwSuAb4K/IkQYhxACDEEPIyh9F6DsQP9BQwl5oUl4DIhxGvcHhBCzAFfwJhI34hhenwWeEwIMdN55jqMyfp/dtr3fuADAelDCJED/gajj96GMSk9DDzS2U1Z4dUfOYwJ9hrgxzD4+q8wlL0STecd9noGGdQ/jMG1iGE6+AaGMroTEJZnHmT3CrxJ78r5g50yZizffQDLigVjpVCmd7X2ZowVwnGXuu5j9wpcAtdbvntt57vv6nx+L8ZqKml55q2orcBlp43lzv8lxkot5fZe590/BX7f8vkx4Bu2Z34PeNzy+Qy2VTHGJGil9++AT9ie+VkMJapZ6vq67ZlvAk/ZvnsSeL8HDQmMXUMbWAP+Evi3wIIP7Xdh7A4Stn681vLML3W+u8Hy3c8DRZtcSeAyy3eXd7673UUebsF5BX635Zn5zndv6Xz+Zw5yeEXnGa8V+BDGwkBiKPPPdHgxZaPhS7b3BHAS+LnO548AX7Q98y4CrsA7fXHGLpvA54DfDtAf92Osuo+60O1L0/n274JZgUsp/x64FGNm/SOMLdmngId8Vj1nZa9dfBlYllIWbN/ZVzXPSCk3LZ//vvPXvmLwbDaGMuq2pfN3rvP3lcBXpJQtyzOPK5bdAq4FbgB+HHgJ+AkppdXzYUgI8RtCiG92DrPKGLsJ+0Hf122fz5pt7Bx6HcHYPlvxBdvnV2Fsfa34PJDF4JuJJ23PLGNMyPbvXFeZUsq2lPKnMVbL78LYav8L4FtCiFvM54QQdwsh/lYI8XKH9o8CGoZi6BaHYT6x1o2tTcvAlBAiafmuIKXseiFJKZ8Dihg8DYJu30splzH4apWPb1nlUEr5jxjmAVdIKXeklD+IYUJ7D4YJ7T3As5YV703ADUKIsvkPw7RxMXDcUv/f0ws731VwE0afb9jqe6OlLhNe/XEDxrg841GPH03nFVJ73YBBoqOcvtj595tCiHdibNnfhKEsnNCwF+PyXT8mw7ZNOZuhIxMO37l9doVFgTwrhBgG/lQIca2Ust75/v/G2KX8IvCPGPbc3wTGbEXpts/W/hCW73ybZPvs9G5s/OgM8I8BHxNCvBvDZv2rGFvmmzG2/u/DWFWXMHZAf4ShxE048khK2bB/Z6HHDUHNJ7C778FbPpQhpfw2xm7yw0KIf49hQ/83wE916vgsxgRohzlhCIX6zUPZLu2dic5KQwLjLOIuh/d3bJ+j9IcKTecVLpgVuAu+1fnbD8+LK20uV6+31RkHngFusq3sXheyrA9hbJ2twvsm4KNSyj+RUj6JceB2eZBCO6u/sxgmLCvsn7+JcQBrxZswTCgvBqkzDKSUeqceUxbegGH2+GUp5Zc7K+Q4fbBnhBDdnYUQ4nJgivjl40ohRHfCFUJ8FxbPK1VIKUv07my+irFrOiulfMH2z9ydfhN/vq92/h62fHctvZPZV4FLgC2HuoK4VT4BvMrDl16FpvMKF4wCF0J8XgjxvwshbhRCHBNC3Ab8DsZ28m/6UKUE/lgIcZUQ4k0YtvM/l1I+H2Mdv4OxPfxdIcSVncPF91rqV2+ssTv5beA9lonnWeBOIcRrhBCvxDg3OOxWhgd+E/hZIcSPCyGOCyF+EcN7xor3AT8shHi3EOJyIcQ9GDbJ3+wo19gghPgXQoj/KoR4ixDisk7f/VuMA7JPdx57FkPJ3i+EuEQI8RMYh45xYQfjQPgGIcSNGCv7pzC8UeLCRzFs4H8shLi6s6v47xiToqt8COOS2fuFELcKIV4hhHi1EOL9wFWc65//F0hiHLy+UQhxcce3/r1CCHOx8lvA6zrfXS6EuAtjN2fFCxhnUw8KIa4QQryh8561fR/FMPH9uRDizZ26bhZCvEcI8UMB+uNjnboeEkLc3qHtNiHEjwSg6bzCBaPAgb/AOHl+GGNw/iGGa+B3y/74fv8Dhr3vEeCvMFYjPxVnBVLKsxhuWa/HsP19APjlzs+1EEX+PoZM/FLn889jCPzfYGwtz2IcPgbFBzC8N36r087XYXhpdCGlfBjDE+Yngac7z/4O8B9C1OeHf8DwZ/4ghq36ixgeRT+H4Y6IlPLPMCbD/4ihWN/BuX6JA0sYE+KnMOzEVeAu2Tk5iwNSyh2MM4s5DBfUj2BM0mW85ePzwALGGPkWBv9fh3Ew/qFO2Sud74oYrqbPYijaYx3akFI+geGV9A6MPnw3hkxZ29jE8MSZxTBhfRD495wzrSClrGHszr7aadNznTpfgyGfQfrjezDk6+Md2j4I5FRpOt8gYpSXA3QghPgwxkm3fZU5iLpNe/7VUsqn/J4/wOAhhHgQQxletgd1H8PwXPpBKeX/2oP6L8ZYTb9RShnmQPMAFlxQh5jfiRBC/EsMz4yXMU79fwv48oHyPgBA56D+LIbSPAb8Z4xV61/vZbsOEA8OFPj+xzEMF685jEOmRzB8mg9wADAORv8DhivnOoa55n+zeBodYB/jwIRygAMc4AD7FBfSIeYBDnCAA3xH4UCBH+AABzjAPsVAbeCPPfaYzGQOolEe4AAHOIAqdnZ2irfddptjMK2BKvBMJsMVV1wR+v3FxUWOHbOH4fjOxYVGL1x4NF9o9MKFR3NUek+cOOHq676vTCjpdHqvmzBQXGj0woVH84VGL1x4NPeT3n2lwMfG7DGUvrNxodELFx7NFxq9cOHR3E9695UCLxb3JNvZnuFCoxcuPJovNHrhwqO5n/TuKwV+MHN/5+NCo/lCoxcuPJoPVuAd6HqsQenOe1xo9MKFR/OFRi9ceDT3k15fBS6E+AMhxKoQ4mmX34UQ4r8IIV4QQnxDCHF9/M00UK1W+1X0eYkLjV648Gi+0OiFC4/mftKrsgL/MEaeRTe8DSPd0HGMBLC/G71Zzpifn/d/6DsIFxq9cOHRfKHRCxcezf2kVyXt1N9iBMFxw53AH0sDXwLGhRCH4mqgFcvLy/4PfQfhQqMXLgya9Vab1bKO3mrvC3qt7Y0DZ5eWYi3vfEc/eRzHRZ4jwGnL5zOd72IPgK5pmv9DFuitNhvVJuO5FFoyPnN/v8q1I5lOs1rW+17P+YSgPN5v0FttPvHkCtv1FiOZJLfMn18+0XbZtrf3nmvmIsmi3mrzjZUaS0ursZS3H9BPmY5DgTslYnUMcbi6usr9999PKpWi1Wpx991388ADD7C8vEw+nyeZTLK1tcXMzAzr6+tIKZmZmWFlZYXh4WHa7TaLi4vMzc1RKBQQQjA5OUmhUGB0dJRWq0WlUmF+fp6zS0s8tVJjraUxm6jy2ssP0242qFarzM/Ps7y8jKZpjIyMsLa2xsTEBNVqlVqt1v09m82Sy+UolUpMTU2xvb1NtV7ny8UkWn2DRDrDGy+bobK9xfT0NJubmzQaje77Jk2lzU204Qla1S0S0EMTQLlc3kXT8uoqT63UKLe2GUs0ueWaS1lbXSGdTjM2NkaxWGRsbAxd1x1pWi0WSeZGSLUbNPW6I02j4xMUSlukaHLk0CGWl5fJ5XJomsbm5qYnTV58cqPJiU/Ly8s9NGmaxurqamQ+6bre/X2vabLyKT06Ra5aJJ9Ks1FLU9psMjq8dV7Q1AYeX2mTrm8htSHecGyU9c1tqrUERxMVqlXBailHq7LpKXtefKqRQjRqTGSyiOo2J1+qcsnCkUA0BRlPbSCZG0Uvl5gYG1PmU1TZm5qd49SZlxkfySMwbmNG4ZOr8lUJJ9vJovFnUsqrHH77r8BjUsqPdT4/C9wipdy1An/88cdlv67S21cOq2WdTz21Sl5LUtFbvP3qWWby7jOh6qo6TLlhVjCrZZ2/e/JZKtlppXqC1hn3ykoVfv38nX7N2t7vr5+sc8nFF4cuK86doCnb2VSC9WqDe6+dYzqvKcuJSnv0Vpu//sq3OC3HQsldELndSxmPi8cAJ06ceOK222670em3OFbgDwHvEkJ8HLgZ2HRS3nFgYmLC8XsnRo3nUoxkkt3vxrLupAZhdJByATaqTbbrLfKa8c5mramkiMdzKdraMBVdrR7r4FGpM2y7osCtn61td+PxfoVdqWnJBPdcM8dmrclYNkWtUg5VbkVv8pETyzRakvFcKhblNJ5LMZRO8MTZbQTwyPPr3HvtfE97oypLLZngpuOHuaylsTCeCdzmIHK7FzLuVG8qN9K3unwVuBDiY8AtwLQQ4gzwq0AaQEr5exhJgr8PI7v0DjEn7rWiWq0yOjq663s3RqkIntf7TrAPQD8BDKrwrfW8/mgObXTStx774LnrqhnfOsO2Kwqc+nksm+pp+62HhCOP9wpBV7nW5wFHpaYlE135KrnItF8dHzmxzNdf3iavJbmYnKvMBmm/lkxw+/FJijsNJofS7Ojtbrl+ik91DOmtNo+fXGWplffcHbq1OYjc7oWMO9WbbDf6VpcvRVLKe31+l8ADsbXIA7WacyJtN0ZZB4oXgjJatVzz2SAK34qmXueIQj32wbPTaPvWGaVdYeHUz/a2b1V0jvS9JWoIugW3P3/rpRO+Ss1Npr2wUW3SaEnyWoqK3kRLCUeZDWNCmBnWmBvWAis91TG0UW3Saujks6OOfeLX5iByuxcy7lTv0pnT/i+FxL7KienmTxmFUeZsf9dVM+w02n1hdBCFb4Wq/6jb4PE73gjbrrBw4pO97QtHDg+sPX4wJ5dsOsFKWadY0Tk8mvV93lTYQuCr1ML4CI/nUoznUlxMlnRS8GPXzTvKbBgTQtixpPreeC6Fnhl3NQ267dLsZqggC6hByjjs3kH00w98Xynw5eVl1wOuMIzaq0MOVXjRa4V98IDz1r3fUNmu2/nktFoZPk8OMcdzKYa0BCfObCOBR55b514XZWk+b1XY0wpmPC8eu/VnEGUZ1nynMpac7PsqE8TN0y1GZg47tt3e5qF0IvAuaBAuvl7129urOo7DYF8p8GzWffUTBnt1yKGKoPSaK+6wdEUR/iiToZZMdFdZKS2ejE1xDGQtmeD2yyZZqzSYyKXZabRDnY949b0bj1VMCf1aTVvb4NaHUfidz+WU+zCILJ8PCzKn9satt6zYVwo8l8vFWp65wipUdKbz6YEdcqhCld4wh5h+ZQQV/iiTobXu6VSDO2fbkS+LxDWQZ4Y1Zm02YS/FZp2MVCYPNx7HtbgIujM1actrCT79dMG1D73a5zd5+sm1tc2quwi91eZkscpGtcloNrVnCzKn9tZa8eotK84vjeWDUqkUv4eC7NxE6qxeB70Fc6rP/K68vq5Er8ohph9dURVGlBN/a92JWinywItzZxXUPBV08nCTaWt/DqUT6M02eivaxOYHa9sTAhot6aoM3RY/KvQHGccquwizzo1qk8WNGsfGs4znUn1ZkPmNI6f2LvVDb3WwrxT41NRUrOVtVJvsNNpM5zUqeotiRedzL5QGtgVzEnY4pyCm0nB0wXnQWgXJSXlaVzEqgyqqy1WU7bq17mxmJPLAM8vbqDZJJwVD6Wg8tPblaln3nByCTh5uMm32Z7Gi88jz6zz0TLHvMmlt+1bN8G7xvIdgW/zYy3CjP+g49ttFmHWOZlMcG89y++WTXDKZi72fgvi6W9sbt96yYl8p8O3tbd+rpUFgV1pSGsKQTAg2qs2+b8GchF1Kut/J2rZjG5wEyUt5qgyqOFyuwp74W+uubxYjDzwtmeCuq2b46NeW0ZuSTz9diE3x+U10QSdCL5nWkglSiQQ7ensg5zTWto/nUq6eWaa5Yrve6i5+zHap0O83joPugu3tvmTSMFnEHUco7M4ubr1lxb5S4GECo/vZK61Kq9Fqs7hRo1xvMpxJRV65+cFN2M3vJpNtxwHgJkhuwqSqVPbC5cpe92IxnksPFb1Nq03s9lC/iS7oROgn04O8jGJOfKc36iyMZ8hrKexd5meuUDJ5eNAc5vxiUF5YYXnRz4QO+0qBB/WnVBEGq9LaqDY5Np4llRQ0W5KdRnuXAMcJN2E3v8slph0FL4wg3XrpBELAdF47r1wl7YjLZ7afis9vogsyEfrRO8jLKHqr7XlwCe7mCuhd8XrR70Wz2+LE66zIXqefmStIf3iFQbDvStwWigd+4B0E9acM6oLUaLUZySTZabT7dghih5Owd1eji4uOPtFBBrWbnf18RRi/aCcMUvEFgZ2Gs0tLDE8fDuQ73y+ojBczXkqhojM9lO4qb3NVnk4K3nn9PHnNfex48dhp4vU7K7JPNnFM3m6LPyde+C0UD/zAOwjqRhjEBclkwJCW4M5XTfd9paqijLzoVR3Ue+XrHtabx43msFvr88mv38nd88lVneXzJDa2suITvX83qk02qk2+XapS0VsA/NRNh0PLtX3idVpRW8+K7HIdx+QdZ9CsuN2frdhXCjxoYHRVRloZUNFbpDszbb+gfJodQyD4vJYgIWCr1hzYriLSpR4LzUEjLJ7vsNNweqPOdlOQz/SPJqcEDV6mCL/xslFtsqO3mbEcXua1BI2WZKveJJtKUvO78OQj1/aJ1++saEjb7WYZdfKOM2jW+Z7QYWDY3NxkfHw80DsqjIzLXqq66lS9BBGGXnt7Pv10gUZLkk4K7rpqZiArvCjK1qQ5jstJ5xt2xX0Zz/BCQue0zVUvrrsITn1ot3HDblOEF6+crrp/+ukCbdlms9qETJszWwlPB4Cgcu11VlSs6DzyXPxulkFW8X7PRh3HXthXo2B6erov5cax5Yojpri9jB+4bDISXdYDp4re6vuhrIkoE6LJ4zARFsPC78p4XBe7nOTsDa+8iEYy03PhKi4PCnsfntqodz9vVJucXKsy2uGT6mRrp8E0n5zaqNNqQyqZ5NCwxumNOpdMOe9kw4xjt7OiVCLRkev4dzFBVvFez/ZLb8E+U+Cbm5uksznf0+gwiLrliiOmuL2M1fUS46Phg8H30xMjiHtmEJ5sbm6Sz+d9LyfFSYebwuxHbA07DTvlbQ4fPsdjPzkKIuv2PrxoPNO94LS4UeOzz68bq2gtoZw4xE7DeC5FOimoN9vkNEGrbbjiPvr8OuNnnBNNmDx2QxQa45Jxa0iBit6OpFv86I2CfaXAa7oe6DR6kIgjpri9jBTNSG3qhyeG3mpTKOs8+sI6O3qbIc0I+DQz3Hvoa6VPxQ5rotFo9K3tTvBSmIOwu5v0mvCSo6ATilMf3nPNHCfXqnz2+fXuzuz7rphkq2aUGQQmH3/kmlkAao02EkkiITz97+0028uMSmNUuPm6h9UtXvRGxb5S4NmxabaXNroDqljR2ay29jyADcR3k9FahmxGZ3ycq1ZTsFfKOqdKNa4+NMyJM9usVRrMDmtKuTed7LDWd6w+s1HbrrKS81KYg7hEY/cR9pKjsPG97eF7L53K8cQZY7wMpRM88tw6T5zdJpUQ3Hh01DNkrgk7X995/Tw7jTbpBPzJk6ueh+Zh/MCD0OjXbj+ZMNuQTAjKdeNmdhTdcuAH3kFts8hIJsN2vUUmJfjM0wWaUnJ6o97XADZW+JkOoipLaxmLZ/rnPxoGpmBP5tIslmqslHUkMJFLuwq4lx3WnIRTiUS3P4P6zLrxI0jcCjeFOYhdgBO9bnIU14RipWtHb/Ibf7PI+k6DRMJw2VOJLOh0RmGmx2u0JFrK/dA8qB+4iaim0h534bSRPs6+c7S2YaNq3MhutWUk3XLgB97B6PAw9yxMUqzofObpAk8tl8lrSS6a6F8AGyvcLhT0K3phv+xmYWEdXDccGeGWSyd47GSJnUa765Fgjz/hZoftrv6eN0wxZn8GodlLSQc9kwjzWxwIQq+peIsV3TfbkkpZM3mNs802qYQgkRC028ZhoEpkQa/0eH6H5l40u02acZxHdDMspYzEzcWdBnMOO0drG4bSiV3xYIJOJP0cx/tKgbeFEWRKSmhLujkBs6nELuXdj7CwdqXQ7+iFyWQwm2Q/YO9H++C697pMV9CdTCNudtjNWhO92eahZ4o9SjalQLPZpkar7aqkBxlDJArC8DhOmZsZ1rjx6CirZZ3hTJKfuOGQ0iToxFe/Pjf5hhC72mGF06TpNPasOzcVmO1bKesIYHLIfedobYP1pzATST/H8fkp1Q7QW23+4fllTssqQ1qCkUySiyeccwL2KzOHU/RCq1vWi2tVLply3gWEmVC2traYmJhw/C3uCcrtgodTP9ptqjN5zTP+hNs7eid0gXXALxXP0ezXpiHN8Dd28qBwUjCDivUepB4vHjuVe7JYZa3SQEslYomYaUzC845mIr+wvE589YoVYvJtQWzy5vGJQDywx0e379xUyrLuYKzvh41dr2oXD8LjoNg3Cnyj2mSlPUQ+Y9yWvPNV06STidDhU60IMuCsQaGAHrcsN9epsBPKzMyMa3vjnKDcyutuORWS+oZZ8ToNeJNmvzaZt2a95MDuCTMIb6Wg9bjx2K3ctUqDr57dIp9OMpINFjHTTc7dzERa0ohO+JETyzRavWF5g5Zl5dtKfSjwxOO3c3Mqy6mNWjLB4dEs917rPGn5IYycq/I4DPaNAh/PpZhJ1jirpxnJJD1jlQTpZNUB5/bcPdfM8eJalUc7bllOAhXWHW19fZ2hoaFd38c9QbmVZ2ZdUUnqG/bAzz7gTZq92mTlrWrMGqfygqQ+U0VQ3rjx2K1cLZUgn05y+ewQWvcSi3+7wk5gFb1NW/aG5TUPK1XGjFPSkSPJWiiTltfOLQy9Yc4Rwsi5Ko/DYN8ocC2Z4Or5PK+bno18tdUK1QHn9pyWTHDJVI7xjluWk0CFtcdKFwmLe4JyK09LBk/qG/XAz6TZq01hJgqnK+BWU4yTL3sQWC9+qNiBzUnDjcdu7V+rNMikEqQSIpBnRJAwrU71Oh1Weo0Zr6QjlWK01HBeB50qsXOi7saCyrkqj8Ng3yhwgPm5WbJZ746zMlGlk1WVoddzfkolrNJx23rFPUF5leeU1Lcf6PJtcsq3TWEmCtMccGqjzkXjGSp6u2se8vNlV2m73dfdLZPNrrgjFpORlyLVkgl+4MopPvzVJY6NZ8l06Ak7gbmFaVWRXZUx45V0ZCQ5G6R7HWGXgSCxc1Rvu8ZxCxMOTChdrKysePpTxpHNw+15FSUdV5B/E170qpYXNRtP2MnHhMr5wq4Drpuu7HqwxGXmsCcrMAe4ii+7H5x8olV3cTvFFQ4dXfCVW73V5k+eXOXZwg55LcXFqWyg2DZWPg6lE10vno2qfwrBIIeVJrzkzm8ch0GQ2Dkqt13juoUJ/aHXxL5S4H555cLamlWVYRwmAiv8lJsTvUE9Kfw8A1TKCku36oRq5dtGPd2zve9XYCdzgJvR7Exf9jARAaPs4hLDw0pyayhc2Tm8NbxCgu6GzAnR7NNMUvBSqcqO3gqcQtBNJlRC0/YjP2SQ2DleY8J+CzOVDHYL00lu+pUPE/aZAvfDfvH9hXC7hbAKzUmQB+GVoTqhWvk2m0p0+RZnLBK3AX54NLvLja5f8TjcnlORW/Mg8GJyaKndrrMqMN0QzdAThYrO/LDWvW0YNVqlo4loQGEtgu4U3cZEo9VmKJ1gu25Mas1W7y1Mv8iVg47LdP5qOAeUy2WmpqZ6vvO7aNJPRPErVlFOdnrjVGiDCNQUxHxj8m278HJVefNNAAAgAElEQVQgxaaKIDb1sH2jclZlr8vksZ/cxmHKspsGpofSIGBHD59CMEzSDadxHAei7JDt9wvufvUMY9lUz1mGn4J2o79f9MI+U+Bzc735HFUumgRBEIUcdbZVUU52eoN6nwT1LogbQZWOlDAzc+6AK+4JWUU2rKsw1RCrUWTB5LGKvd/a/qCLB+s1d3sy4qiTgsrBoRPNKuUP4uIVOGflymupnh2J3wTlNqZU6Q0DpVErhHgr8AEgCXxISvkbtt8vAv4IGO88824p5cMxt5VCocDCwkL3c5RVpFOI0yCDMEjdbhcK/JSTlV6zDDcPB3t9YbwL+gFVpWm292hii7fceEVPPwWZkKMMevsqTDU3ahQ5NHkcRP7CTBhW5TKeS7EwlgnkrWWt223FrZp0wz6Og9DYL6WuasbyesZtTKnQGxa+ClwIkQQ+CNwBnAG+IoR4SEr5jOWxXwY+IaX8XSHEK4GHgYvjbqywxVBQ6XQnRW2NZ20KR9BBqLqC9RpsfsrJpLdfk0vch7JhYW1vrSZDm3Oi7oqcVmEq70fZzZg8DiJ/YSYMuxeKV0hfN6isuFVkyj6OVWm0HsCq+u4HOaiPw4zlRL8KvWGhImmvAV6QUr7YaczHgTsBqwKXwGjn/2PAy3E20sTkZG+KMS3Z69vrd6hgxqI241lfe2SkKxxhEjKorDZ6PCxs8VKcJhfrZ5Pefk0u1n4a1FbVCdb2apnh0OacqLctwyrioLsZa3+bPDZvvRYqOtP5tGfdbu10ix1j92kOu2MIu+K2wz6OVWm0hnZQ8d0PcxgdZ+xxEyr0hoWKhB4BTls+nwFutj3zIPDXQoh/BeSB22NpnQ2FQqHHn1JvtfnkU6sUKw2m82nuvbb3ZN4ucKc7sajNeNbrnXCS9ih5qsKowkxrQCBrvBR7YgOnRAcmvf2aXMw+3OuMRm6HmEHhddsyTm8St3dV3cysbXr9ZJ1LLr7Y+FGC6Pz1q8spUJdbtqqNapOXSlXmO5ey3n71rPLu0TohBHHV84J9HKvSaI0mqOK7r3php58LF73V5ttnl7nskov7UoeKAnda/9tF7F7gw1LK3xRCvA74H0KIq6SUbetDq6ur3H///aRSKVqtFnfffTcPPPAAy8vL5PN5kskkW1tbzMzMsL6+jpSSmZkZVlZWGB4eRgjB4uIic3OGctuut3ju5QoXZeqcLaf59suCTFtnfn6e5eVlRDLFZLpJqlZiSMuTb26zIDZZauS5fbbB5fNDzE3mWTpzmomJCarVKpVqlcbYNLXNIvlcjlwuR6lUYmpqiu3tbXT9XPm5XA5N09jc3GR6epq10gblap2Ljh5mbXWlS9PrJ+vspEb4ptwik9Q5Xc7yzPMvQU0yk0ogqlW+XciQra4xkkxSrGU5+dK3Gc6kKRaLVCoVfujKOU6ffZl8NkOjVmWpWGRsbAxd16lWq902aZrGyMgIa2trTExMUCpWqdVq3d+z2WwPTS8XN8hVS4jMONlqkdMvS6ZGhro0bW5u0mg0uu+r8AkMTwOTT0IIJicnWV5dRWhD5FKCnZ0K2U4/ZzWNsbExdopFtFSK1dVVT5qqVXeavv/SCYobWyRlnc1KjVy1SC6VoVITnHypykWH5nxpqpfWWVGkqVAoMDo6SqvVolKpdMtMp9MMDY/w8kqB2akJ2s0G1WqV9OgUuWqRfCrN+k6KYrLO2MYG65sVhuvrpIbGydbXOHVWMjs+4it7S0WDT2dW18hVN7t8PLMsECJBrlqkKvNMtzfJVBM8s5XlpdEqdyyMsdNIIPUq7YbO6Zd7acoND/OFk+vIRg09M87N0y2ymsYPXDbC0mqBmckJNtaKofhUq9Uol8u+48nk0+j8PItnDD69+ZjG6toO38hmSOslJpNQ2Rlhu/AyYyMjPXzaWVvlSKJCoZ5lIbGDrOUoViWVSoWp2Tkee/IkOy2BzAxx0zRMjo/7jicv2bPz6ezSEk+u6jQbDV5c+xZveOVF7JS3Q40nV+Xsd0+/o5AflFK+pfP5PQBSyvdZnvkm8FYp5enO5xeB10opV61lPf744/KKK67wrM8LxWKxJ8Pz2c0a/+mxxe7nd996bFe0PL3V3rVScVthRVmN+r2rt9p87OvL3cBQ1x4aJpkUXTu80wp8q7TumdE6jhXEXkTpG9ISIOlenrHWaedxXHUOenfhdQhndee7eqyFGBrzTTUXpj4wVuBnt2p8cXGTTNLI4v6+t13KsYmcZ3mrZZ1PPbVKXkuyVWty2/FJLnUJlRwUcfBYb7V3hYV1u8HqNN6t9FX0Fm+/ejb2S3oni1U++8I6h9I1Vlu50HWcOHHiidtuu+1Gp99UVuBfAY4LIV4BnAXeAfyo7ZlTwG3Ah4UQVwJZoBC4pT6oVCpdxustY3F/7WHjJtvUULob4tX83emU3WvLF8WbwO9dLdkbGKqit/iehXGm8umup4N9y2il1464lJOq2SDqZGHtn0LFCKg/ndfYqDY5uVbtKgcvmoNiUJ42TvAKfnbPNecSC48ntzjTsSd7nef4wY3We66Z49nVCqdLdVpSkkoI0kn/QzW76e+zz6/zhEuW+aCIg8daZzLa0du+cX76mZ7OCfZJen6sxshQ+LMdL/iWKKVsCiHeBfwVhovgH0gpvymE+DXgq1LKh4BfBH5fCPHzGOaV+2QfQnCZyUF7VnPpBO+4dq7H3SuscrMHjdebbfSWWuQ0FYEwA0OZjP38ixvdK8ewW9iiJn+N66p8HJOFtX+m82mQsFXbrRziTgC7V542fsHPzMTCy7U8I9lkaM8QO+yjTksm+K7ZPDctjLK209i10HGDfaKJM2l4XDyOooTjmtydxpjd5/7KS2Y4Pju6ZzZwOj7dD9u++xXL/58Bvjvepu2GmRzUz90rSkwUa8aOh54pKg+mIG5IqoMibPJXCK90vQQyyq1Na99KabT/1EZ9Vz/sFONPABt29xBl1+EnD11ZeOnbXPqK4G6sTm31cld1y7rjR/tF4xnGc+6hksPAlGsvrxmVPo+qhKNO7m59bve5z9U30JLjoevxwr66iZlOpwF/5eXkjWBPtusG1a2Z27sqbkgXjWdIJwVbHfdFt0Fh0utWjpfwhlEIKgIZdRA/8tw6xZ0G00Np3n717C7l0PCg2a3NXgM+ykQWddfhJw9aMsHYUDaWPlYx4QW55OYUHteMYhjVayOdTnva7IP0eRw7rKA3sP1CB9jHZnFlOVL7vLCvFPjY2BgQLP52mK1pHArLTSjMsKaNlkRLCc+Yzia9bvAS3jC+4NZAR14CGXbwFso6T5zdBmCxVOOOyyd3letFc5jbs2FvzA4iVgyoy7QfgviR+8F+d+H0Rp2F8UwsJh4waHbqX73ZZqWseyYbjhtRbsB6hQ6wjk2/cRwF+0qBF4tF8vk8oB5/2yvZrte7cQQOchIKq32sorc8I8BZ6Q2KML7g9hjIbgIZBQLjkMQ8RrOX60azU5+qKNmwN2ZV43pERRCZ9oWiH7kfnO4upJOCRkvGYgsvFoscOrqwa5f88LeKLJZqnCrVuP7oiFKfx3m4vl33znYf9iJTlHHsh32lwMPMZFFu14WNq+KlWIK0J+rMrUqDW6CjuA9dZoY1rj860r145XSY5kazU5+q9KXqRBbXLcOgiGt1tlFtstNoM5FLU9xpeCag9oPZZ9Zcr1u1JlpKKAf48sLY2NiuMxGz/dcdHqFUbXDH8cldO1cne3mch+t+2e7DXmQ6WIF3oOt64Hf67UrmtHLzimYXaGWsQG8cvuD2Q5d+KG/oHKb5ZAN3o9lNWd966QRC4Bl0SmWQxXXLMCjs9Ibl53jOSMjwxNltBPDI8+u7biYHgZbszfU6nks5BlIL2l691aa4vcPQiBF543MvlLp3A4bSRpLm2WFtl0uwk6IOsnr2otMcjzt6k08+VXA14YTVJWH0lir2lQKvVquh3uvnQLQK0VqlwX/70lnSyQQj2aRrNDtreyp6k1OlOhdNZMhrvezwo3fQvuBxwI8XbjRrSSPujWmPhd0HXqCewi1MdMh+wEqvKj/d2n/78UmKOw0mh9Ls6N4JqFXg1CfW4oLKn/l8rrrGlwqCWy+d6PEmu/NV06STCdcsOfYdbc/qWUv0ZFZyu9TjJBtap05VE05QB+mweksF+0qBx+0jHAes9sIX16vUm22GMykunsj6RrOr6E0efOQlyvUmw5kUD97xih4l7kdvnAdtg1htqsCNZvPw11QW1sFv0m6NVuc1iMNGh+wHrPSqrCi92j8zrDEXIQG128QQ18U383mRGTf+Cnp2PW67KC9TmbkDkxIeeqboGffELxmDlwlHpQw39FNv7SsF7uUXvVcwVynPFipU9BarZV05Z+GpUp1yvcmQlqRcb3J6s84VM+fe8aN3EEkZoHdgA7EHALKW70azXVnYB781Wp1fbskwk16/Ah9Z6fWyx9511QwV3Ug24db+KLsIN7c+L5qDyp/5fLZaROaM3alKe53oCnroHCQZg92Eo1qGG/qpt/aVAte0vV8huuHEmW3ObtWRSK4+NMw7r/e3P140kWE4k+quwBfGMj2/J9NpT//1QWz77bdezRRcccUWsQ/EW+Z3+4F3s+Ro584VnAZ/HEH5VdoYF90b1SZJi9+7mz12o9rkIyeWaUsYSid6+sEpqUCYXYRdOS1t1fjLZ9dpdHJCxpEUxHx+8UyLY0ctO4cQdyyCHjqHTcYQpAzXtvdRb+0rBT7SiTZ2vsG+/brzVTO77NlOyGuG2eT0Zp2FsV4buN5q88WXddYWVz2Vht+AjTuGCRgDLi4/XftAlOledyv7BGI/Vwh6yBRm0ovbJ9xK01S6yQ/NnQvX4GSP/a7Zoa4Ln5etOArsq/8//8c1nloqk9eSXEwutqQgWjLBoalxZdu+SntVDp1VZcPPNdnqOdNQbG8/9da+UuBra2u+4RXjQlhhctt+uSGvpbhiJoXeavestjeqTZL1bfLZ6R6lEfTWWKwxTDpJcONwJXMqfySTpFHZhJmJ7u9Bs+SoKBT7M359GtVU5eVmmqyVdilH+4Lg+6+Y4u9e2vS1FUeBVcHpTeO8Ia+lqOiG+2Cc5jmncRwm+UI/4verjK/PvVDadWfCq7391Fv7SoFPTEz4PxQDBiFMfvWN51K0teEeZdmv1GpesNMG4ZPgusHqClirlHt+67edX6VPTQ+YMJEC3Xhr0pTTdkepsy8IDo1mueea7MDyl+otI3PPxWRJJwU/dl14d0QnmONYbxnpDU1s11tkUwlWyrqSH3vUQ2enm70f+/qya4IYMG4Tr5R1sqkE5XqTZEL4jq1+6q19pcCr1Sqjo6P+D/rAb5YNo/i8hClsfa8/mkMbnewO2qC3SuO6Xm2nLS5PDSflZuex0wSiGtfGWo9b/6tGdQx7jdyt/O5qd2td2bY8SA8ZFf/6sKhWq2Tzw3zsa8tdv/VrDg+TSQq+9nI8fux+cJK9Qlnvxus/Vapxx/HJnklEb7V59Pl1Fks1JJIhLUmrLT3jGZn0xqG3nLCvFHitVotchsqKK85VX5T6mnqdIy4n5crtCnG9ehCppsDZbW5jq8LEdG8IX+vKMKhJyO8dtz6NKy6KW/kmTYvFuuN7cbk0BuVlRTcOTK2Hl3GjVquxUW1S3GkAhmiWqk3efHySUq0Zmx+7F+zxXk6uVcmlRHeYOA0Xu2nrh189w5CW8t0VxaG33LCvFPjU7Fzg1ZcdKoMxLu8OrwBRKvXZ/UeDtssUuOm8RkWPFpGwH3Bym9PrCU5sr0QOTKX6Thwual7w41k/fYTDXLT5yIllvnZ2Gy2V4NJJ98NL8/kwE/38/DwilWJ6yMhNayT3SHPJVI65pXN+7E5RRONaXDglrBjJJF0TxFjfsZq2DvzAFaG32jz25ElOy7FIisV+e8staUMc9jW/AFF+9Tn5j1pXo36TmcrqMg4laafbLQqjae+cGTa25faDs4eeKXI0UeFMPRUpMFXQd7xc1DaqTU5t1B2vkavCibdmP5WLS+eSGvvA69auE8JctKm32lQaLYqVBs1Wm7QLqVEmelOu771unjsuNzK227NSOUURheDhZt1g1mWNze/n4RN2YXfgB05HGFsJ8tlorlxWV6BHnguWtCFwe+vRAkRls86HOKqDR2V1qWpSUEGPy59mpJCbGTZ4ZLV3Xn90pGvftE5II5kk5WqCkVy0wFT2d4IeQDqtzvw8DYLA2k+HknWOLrhnfTIVvZaE935u0fXWrhcdQS7aZJIJcukEzbak1W7ziW+sct+Nh10n+mxa/dDRhCnXWjKx6x1THpzOe6QkVndOLXkuM9JG9dzlO69+DbOwcxvHcWDfKPDxXIqUlmXD5pURZjulJTtJGxrBkzYEaW/UAFG5nHPi2SArK6/VpapJQRXWQX3izDZrlQazwxq3XjrRY+8sVhqu9S4XNeanJ1zrDTqAwhxAOq3O4pQRKw8260nXcq2KvtZosV1rks8439r1oiPIRZt3Xj/PTqPFs6sVhjMp9KZ03Q0NaYnuod8jz61zr6K3iptc28t3mnzi9kgyJ3jT7v/ppwuxL+ZU6A2LfaPAtWSCG2YEIzOzXcZF2U712z0tDjt6qVRyPL2O0vYwJoWgZa+UdSQwkTOiugnBLnun0wSsJRPIWhktORW4bjeENQlZV2dxy4iVBwuJumu51rbrzTaZVIIdveV4a9eLjiC8zGsp/vnNR/jo15bRm+4eFlqyN0n3dr3Fi2tVFsYzVPS256LKTa7t5TuNnyBjSnWBV9HbtCWxT9QmVOgNi32jwAFmp6cZ7nRsmEQNVgRVsGFW+1Ht6FNTzoosyuQQ1wGtV9mmecqMDDed13rsnWPZFIWyzqMv7I697EazFVFv7AWlJ+6+spabaronu7W2fSqf5idvnGe53Nh1azdu5LUU99142Jdue5Luv3p2jTNb9e55jxm/xc4nFR6D8/hRHVPWM6h0UvDO6+dd+6zfizlVesNgXynw7e3t7o0me6cHyXtpIqgwDMIzwworvXZEmRxU3o1injo8mnVMont4NNvty5WyzqlSjWuPjPRMwF40m+0a5CWruNz53MpdWlqDsd7VmbXvd8d7GYwvuArdZt+aiR+SCUG53iSVFD3xW+x88uOxCaeDb1VsVJtsVJt8u1SlorcA+KmbdtvyrXQEkZEg40OV3jDYVwrcGhjd78Q6TrejuGNhqCJMIPg46O1nQl+zLydzhkllfafB3LB2zkPGh+a4L1n5od8+8U4JHex9309Zi0qfljyX+GGjahywNlvSMwWbaqKSj319uWtjv+HIiLKNHYwFXjppZBDKaykaLWdbvpWOsEmf7eNj1w3Pg4QOBpz8or3yXjpdSojqehj3FstrAAX1H41rp9DPCcvalzccGeGOyyd7bvv50TyoELowmJ2Xnd5BLhb6kRDEzKpjX1RZ+aQi1xvVJsVKo3uhZm1n98G3X5veeb1Rjzn+45IVLx459emBH3gHbv6UToPavJTw9Ze3fSOq+aFftlC3W29+sbHdENfgj0tJhsl8s7y8zKGjC66TWj9t+HYMQpnaeTzICapfCUHMItz4pCLX47kU0/k0p0o1JDA1pB4Kwip3P3WTvy0/KLx45NSnO8UDP3DA3R3HaVCvlnUaLRlbRLW4baFOE0yxondzBI5kknzv4WD+o3EN/jiUZNjMN+lMVim41CBMWINQpnaZHuQENQhPLCc+qbjVaUkjf+odx3sv+vghrAlK1ZRkPud2scupT+WBG6EBr8DodmEZz6X6GlEtKjaqzV0TjP2iQoPdyQ28EGTw+wlsVCUZOvONTLJdb7huTwcRo8XEIJSpk0wPaoLqF32+sqWY4MA8EA+CMHIXJBepynP2QGAHCR062NzcZHx8XOnZQa5k/OAk0E4TTDqZ6Jm9W7UyMB2oLlUPk37bdsOu7tr1MiOZjOP1/73wBOq3Mg0i0ybinMj6sbP041MYmlURRu5Ulb7fc25p6fpJ775S4NPT/VFmbrE74hgkbgKtclGhUetPNutB2HbDTqBzMzPcs5Db9d5eeQL1G0Flut8TWZwZnNz4FJTmIAgjd6pK3+85N9r7Se++UuCbm5vk83n/BxXhNhjiHCReAu13UaEYM70mBnVQFmZ1t7m5yeF8PpZAVvsBQWW6nxOZitwHzV7kdD8j7nFsR1C5U1X6fs+5yWg/6d1Xo6DRaMRanttgiHOQBFU81gESN70mVAR20PZmE240B11ZBU09txe0QnCZ7udEFsZE4OUl5HY/o19yHQWqSt/rOTcZ7Se9StwXQrwV+ACQBD4kpfwNh2fuAR7EiFf0pJTyR2NsJxB/XF23weA3SIIM+CCKx3QrrLfaZJIJfuSqmehEerTLK87zXtibwZvHqoMsSPv3klYILtP9PNsJayJwaqPX/Yy4x/FeTsBOkLZsEHvqBy6ESAIfBO4AzgBfEUI8JKV8xvLMceA9wHdLKUtCiNl+NDbuuLpug8FrkDgF+/cL3uOmeKyCB3SD6VcaLfLpJDOtEj/w2ld1y41ytVgVqkkovN6PMpji4HGQHdRe29bD0Nuvg9WwJgI3uD0f5zje6wlYpS17HQ/8NcALUsoXAYQQHwfuBJ6xPPPPgA9KKUsAUsrVuBsK9MWO5DYY3L63B/t3i/fgBzuz33DxGFs1I/BObafNZC5NRaa7CkVvtV1jaseFoEko/GgKM5ji4HEQRbPXtvV+2oL94HbRymtyCJIr025OMevyoznIImDQN1fD5LbtJ49VpPUIcNry+Qxws+2ZywGEEH+PYWZ5UEr5l7G00IJkMhl3ka5wY5Z1wHvFe/CDfSL4i2fXOLNZpy0lh0Y1LpnMkcs0ugrFnkPQKaZ2VDqjJqGIYzDFweMgZgbVZ/u1TY9LpoO2L0y6NScXOT9oSSO7jfXdNx9zl4mg7erXBOyUsT5sbtt+6i0VaoXDd/acnyngOHALcBT4OyHEVVLKDetDq6ur3H///aRSKVqtFnfffTcPPPAAy8vL5PN5kskkW1tbzMzMsL6+jpSSmZkZVlZWGB4eplAosLW1xdzcHIVCASEEk5OTFAoFcsPDbFcbiGaNI4cOsby8TDqdZmxsjGKxyNjYGLquU61WmZ+fZ3l5GU3TGBkZYW1tjYmJCarVKrVajanZOR578iTbrQQpLcsNM4LZ6Wm2t7ep1uu88aJJttcLjA3n+fLZHURtg0xmhGqpwGKx2S3fi6ZycZnZZJNqvc1h6hRbw9w616Sit7n58qM0yiVks8H62hrrm9scPjTP8fQ26WyTQiPNcW0bUR9ltbKhRJP5ezabJZfLGTGKxyf4/D++TKvZQM+Mc9Nkk/lkg+264OKkznxmnOLKMo1GIzBNC4kGWSY5fXqlh0+jo6O0Wi0qlUq3TCufarUajUajS9PZpSWapJiZGGVro+RL09TUFNvb2+i6zvz8PEtnTpPL5dA0jc3NTaanp9nc3NxFUyqZZKnoLHvZoTxfeGkDGlUamTFeOwOpZEKZJi/ZO336NMlkMhBNy8vLPTSNTUzy+W+dpdnh483TLUaHh2kLQXF9kyOH5tjeKPXQ1EplobbN0USDpZ0hnnruJaaHNWamplheXUVoQ+RSgnp1h/n5eU6eOotWrTGuDaFVSywV0uQSbVfZGx4bY32zQlI2yI5Nk6sWGUppbNeSnD61wlAm40jTTitBrlokqY2QrG5x8qUqlywc8ZS9O79rijNLy0yOjbK9UaJcLjvqCFU+lXd2+HIxiVbfIJlK8z1XHGZptUir1mYu2UJWdda2R9A313bx6ZZ5yfaOzsKRw13ZK5VKbG1tucqen97zVM7SbnG3PyDE6zBW1G/pfH4PgJTyfZZnfg/4kpTyw53PnwXeLaX8irWsxx9/XF5xxRWe9XlhZ2eHoaGhXd+b5oXiToPpoXSgqGVOWC3rfOqpVfJakore4u1Xz7pmRQdCe0borbbnaf1mucL/em6rx96+WWsC6leLg9I5lk1FvkIfZDUL9PSJlceDtm+6rWLd5CGOst1kOgjc+OgXMc/JXHbXVTOOsugm+253KOznRNYy/8nlo4wNO5sVzgebdpj+9EJUHp84ceKJ22677Uan31RW4F8BjgshXgGcBd4B2D1MPgPcC3xYCDGNYVJ5MXSLXbC+vu7YEYWyzhNntwFYLNW44/LJwFdwrXDbCrmZCKJ4RpjvOm3jl1aLbNeT3fp2Gu1IdKnQGfWAzO/9nryZ6QQIepI6WHl8vkTmi7pN9yrbTaaDwKl9qqnz7GnjTm3UHd+zm5rAPSOWU91W2/nq0stdBe6UlWlQN6hVzKTWcWEmK3Fb87qVFweP3eAriVLKphDiXcBfYdi3/0BK+U0hxK8BX5VSPtT57c1CiGeAFvBLUsq1uBvrtVsQGHYdiWSt0oi0QnUToigDWWVA2ZVTNin6fsAW5FAqDlj7oVDpeNTktW6fWHk8qANGP8+bqErFi/d+O2AVOLXPq++sisaeNu6i8Yzre1YZ9cqIZa17KJ3gked7My+ZNHvdUjZ3vEGTtKjCL9iaG7+tweas73iFro6Dx25QGhFSyoeBh23f/Yrl/xL4hc6/vmFmxtkvemZY4/qjIxTKOkvbOp9/cYMnl8qRtl9utyTDDuQwymh+bpZ7jmp9WY2EPZSKCms/TA+lQUDFkqh6xMLjQazGVD1vouxMvHjvJtNB2m8qY5Xk1PYd0O3HJ3dF1lPpcy+arGXozTYPPVPsVfQdmrtJsFO7M9ubCR2KlQbT+XTsHldhFlT2d4oVnVQiQV5LWCKLGvGNrOVF5bEX9tVNzJWVFVd/ytsvm2R9p8HnX9zoW3JSCD+QnQaGn+eASW8/zAZxmSf8aPDbIkPvGcLimV4e98vn2URUzxsVeClFL5n2g5+92EsJZVMJnji7TbGTEUk13K8KTdYy9FZ7l6JfOnOaY8eOMZ5LkUkK/uH0JqmE4JHn17uKulDWu9l4TpVq3GG+OrEAACAASURBVHE8mlnUjjALKredRUJAvdXu2MwNV2BreVF47Id9pcCdTmR7VhSaEc3PuqJzen6vbm1ZB4bKYU2/8uhBPOYJldRSKgdfVmXRT5qdYO2H8VwqduVtwk0pRqE3zCRs0rtS1hHA5FA69AQeVtFbaa612jTakiEtyXbNZl7qPONngAibcDzo7s5tZ7FVa5JNJbh4IoeW2h26up8yva8UuBOsQlzRW9z5qmnSHd9TO1PCnnD3Q+nv9Q3AOPyf/Whw2nK62RBV6u4HHwZ5aBY3wkzC1sM4q226nxeY3BT9RrVJuw3j2RQVvdWzcp0Z1rjhyAhrOw2mhtJMBwz7oCIrYXZ3TjsL03vHKcFDv7GvFHi5XGZqaqrnO7sQex3G9TPYuypMwcprCd/B50RvnAjkMaIluP2yyZ4r/H4KxP67PWGFU/+bNPu5osXpXtZvM42XMonC47CTj5Y0EiXce+38nkxcJs3nYuLvXrlqyQT3XuffvkJZZ6WsM5k7t5OI4vKnCi2Z4K6rZji1Ueei8Qx5LYWbCPVzHO8rBT43t/ugLYgQmwplo2rYqYbS/kyNc6XspJS8Zm0negeJrr00neDEmW3WKg1mLfZSa99br0q7neYDvpOWSXN3YHa2+G7ubUER1GYf9Hen572USVQeR5l8+j1xucGkWdWO7ga91ebRF9Y5VaqxWKpxw5ERRxdK87Axzp2b3morLyj6OY73z34RKBQKjt+bjDa3TqtlHb3VdnzurqtmulfgP/10wfE5K0yl72VXV4VdsHYa7W67neBG76Bg0r6+Y2QHn7CsckxoHXPVp58u8KmnVvnEkys9fWrljTlg3371rKvAFwoGTx59fp3FUo2vn91mSEt03dui8MFUpk7tjON3JzgtAOz0urXVTY73GlHbZqXZKh9BsVFtsqO3ufbICMcmstxx+WSPC2VFP3fYGIRn4E+jH1+t6Oc43lcrcCGcbvWfg4q5o6K3aUuUPVXitJEGtVn60RsHvFaUPfbS59bZaTjbS712KU5eKF79LYQwBmajzXWHRyhVG9xxfJK8lvK9SOGHoDb7oL87wY/nTjzu123EOM4QnNwQg0bGjEuurX07N6x17eS+bowxmE2DjOV+juN9pcAnJyc9f1cZYGEPfuLaaga5OONEr+ogVHlOJTRu117qYY9069MwimhycpJU5lx5s5aBCe4XKVQQ1Gbv9PtQOkGhojM9lA50aOjWd048VkmsEFQRxzUpqLgh+sFrHDvR5kavV996uTGq0uilR4Is7Pz0VhTsKwVeKBQ8/SlV0jntlddBmIszdnpVB6Hqc/aIiB/92jKttnNoXK9JzH6gY75ntaE7XdRwGpSFQoFDRxccJ7qo5xEqNldf2RC2v4r1urXTSab9blGGUcRxneXE4YboNo7dxkhQX3cwbkaeKtW5aCLTtxyZqgs7P70VBftKgY+Ojnr+bj9Ucztk6MfhTdhYwV6w06tahupz9tC4ejNcaFy3A53xXIohLdG9kPHIc+vce52RncRtUOaGh10nOtXr4V6D1I/3Xr+bNteZvEZFj8f1Mzc8HGiREVYRxxWWIKgbohNf7HJtPtNotXfRpuK5ZEdFb/LgIy9RrjcZzqR48I5X9CVHpir89FYU7CsF3mq1fJ8xB6BXrIa4EbfNzISdXtUygqwg3Ca8IEkc3OKIaEnD9XCt0mAil2an0fYdlNvVhuNv5iB38twJsjNxi56novzjjs2it9p84eQ6K62q8iIjbBviVEqqbohufDHlWm8ZGaYefd44XxlKJxjSEt3DR73ZDkXvqVKdcr3JkJakXG9yerPOFTPBeBXnIk9Fb4XFvlLglUqF6elppWedGO8VxjQK4raZmbDTq1pGkLqsghq0fSpxRGaGNWaHtV0D0G1QimaNkUxmF9+8FLRK/3td+FA1ScS9MtuoNpGNGvnssPIiI0ob4t55+pXnxpdKpcLoxCSfeHKFlbLOYqnGdYdH2Gm0ufNVhrw/8vw6Dz1TVHK3teOiiQzDmVR3Bb4wlomN5jAIoreCYl8p8CDJQe2CDue27UNaAiRdr4qop/xx28xMONGrWkaYwRr0HZU4Ik4KR2+1XQ9zjxw6xD0L6Z7n/XZTKv3vpkyCmiTiVILjuRR6ZlzZNdItcNX5Cje+zM/Pd/t9cijNqVKNUrXRPbA2TVV2d1tV5DXDbHJ6s87CmHHJZhBw28ntaVLj8wlBk4NaB5tVCRQqxgHMtCWMadQY2P04GO1nMtQ4oBpHxMoHv8Nck+agCtrPu8etjLyWICFgq9Z0jELYL5iD/abJJmNzR3zlJg4vkkHHAXIbF8vLyxw6utDlx/VHR7jj+GSXdyrOCH7Ia6nAZpMo8OLPXic1Pm+QTqdDv9sTxjSfBknkSyFB/JvDIAq9Jvo5aMNMXH4rXieaveqxmnHSScE7r5/vrvL9EgWYh6+NliSdFNx11cxAFJt1sB9O1HnbMf9YL1G9SIJMAHG6qton741qE5H0Dlur6oywl4Hp7PDiTxzj2A37SoGPjY2FftfJpOKmEIL6T/cr7VMUemEw7Qw6cfmtrtxodqtno9pko9rk26UaFb2JEPBj183zyW+s7kqxZy/DagKq6MZWfRCWCetgX6ufi/fuxauoOwXVc4JCWefRF3oTMAQ5oHSD9fnJdJP5Q21P2fFzRogq23Erf69dYtRx7IV9pcCLxSL5vHMuPRXYBUb1oMsO1dVQVCEJQq9TXXsd8dCtfV6rq6A8Hs+lSCcFFb1JXkuiNyUvrlWVUuwNKuOPV70LiSpD6YRnRqA4dgp+tJqyv1LWOVWqce2RkVhcVZ2eT9VKkd0f7bFygrq9xh2V1GtHEVVveWFfKfB+zmSgfgNOJZJgHKtfVXrd6orDlhgHnG58Sunc30F5rCUTvPP6eYQAvWmksxrNJrsp9rzu2/Tr7EKlzWa9rWqOTz9d8PTkiWOn4Edr91Axl2axVGO9c8PSeqvWqryCTn49yRC0fCT3R2usnFOlGtcfHQk0+YYJduVkqrMfjrrtKA5W4B3out7X8oPcgPNzbQoburYn/rUivW51qdoS+w23G59Wv1+zvzcqwXmc11Lcd+PhHvPY9UdHuum43GJJw95F5DPrfWG9zna97enJ4+cSq8pHL1qtddxwZIQ7Lj93qOi2QHC6fetVtymLje1SJPdHp1g5Qcpzy6xjPVR32s3aTXX33XhYbeXeR721rxR4tVrta/leqxS3SIJuCGqzdBokqvR6TTx+tsRBwO3Gp1MCjrA8tg/yuGJd9/ugLNHSu37vbp48Xi6xcU3GQWTffCbogsDk0WKxFqmtVnmyx8rxgpMZzx7syi3piJOpTtV02k+9ta8UuKo/ZZRB57ZKCbJltNssf+DKKd/2OA0SVXpVTAFhAjHFFb3OeoPSvhOwu/3F5TMbx8p6EIfATn7vTnBziY1zMg4i+267PhWZicrjMKYvJ146BbtyuyXsZKpTNZ0e+IF3YPqPel2Hzmv9MRUEERqrzXKr1uQT31h1DRJlwmmQmMlfVdvnO4gDBGIKo7x2mYBcyvDqx6g+s3GumAdxCOzk9+6HQZ9tOPHMzazjJzN6q83JU2e57JKLI7XVLu9hYxE57W7cFjpOpjp7v1ujNZoB3Bqlg6TGACTTad/r0AkBjVa4oEx+UF3VWc0nbkGiVPyUNS0+ZRE0EFNQ5eU0eL0Gjav7WASa414xD8JLJQy9VvvzoZH0QM427Dxzkle/nYHJn3S1zontlVjjnEeJRWSlTW+1PRc65rNejgNDaSPUrsAICXDboQM/cADaqRzb9YrndWhTacaRQScM7OaTH7lmlj/71prSSsU+SEZGRmJrV1ivAfPU3S/9nJOyDqMAo9Acx4rZPrH220slDL3W6I/9XLD4wS6vfvw2+TOh5WJta5yxiFQXOl6Lk9uPT1LcaTA5lGZHbyPT/XEhhH2mwJs7m7sCHcHuK917lSEadrt8Ndq7g0Sp2jDX1tYYHh6OpV1BlZG5yvvo15bRm0b6Oa8Vk9PgDaMAvWj22yarTBheZbhNrE73BeIy04ThsX3BoqX2bsFihR+/Tf6kqyVGctOxtVXVYUBlBx1HxM+ZYY05SwC3RmUTZibCE+iBfaXApycnuWdheJeAOAnOXsX6cVNkQWN7AExMxMv0oAd7Fb1Nq62Wfs5t8Aat041mlW2ynwLpZ1TDsAjD4/NpwWKHp3msw5/losb89ERs5hNzx6uloodDMNvol7rPS9bsv9Uq5dDt8cO+UuDVapXR0VFHAdkrf16ndvitOlWFZLuyQy2RHdjFm6iXNeLggcljO1TNI15t8LvAESWqYdz0eiHqgmUvY4hoyQQZmrHV269wCCqp+/wmK/O3Uggeq2JfKfBaLbz/6CCFVlWReQmJ3mrztcU1Tstm9+KQPV9lnAjjMdIPuPE4jgNFvwscqu6YcR5shpXpsJPlIFwjnbyRrJ+jjGM7+nHQrHojW3UsxkmvHftKgbv5U/p16KCCTwWBn5BsVJsstfPkM/75KvvZnn7vbOy8c+NxHJOJtQy3bOV+9Ib1QXaTzzA+wlEWI/12jXS6sWz3konTLzqqXDj15XjOSAVYqOhM53tdCcPokn76ge+tFguIs0tLrJZ1w9WnA7NDP/XUKp94cqXnNxNOQrtX0FttVst6N56K2+HTeC7FoUSFin7u9mI/22+uZFQOw0wa7Hywf+cHJ94tLy+7Pm8q1zj8h2eGNWV6o7TDTz696A1Tnh+sB379OPS0h034xlK5cz/jnOyGodlLtsLKhWdfyo4Xoc3EGUaXBKU3CJS4J4R4K/ABIAl8SEr5Gy7PvR34n8BNUsqvxtZKjM7+xmqdpaXVnplPZUWxV1HnnGhQjaeiJRNcd2yKm0cnQ+ertNfttWpTXcm4JWSIK1N6Nrs7amBYmrwQZeUWpF4/+fSi13o5zTSfuV1rV43fHeeBnxOs7qeLGzVabcmZrXpPkK52QB73a/fsxhsz1sq0gythGF0SRKaDwrd2IUQS+CBwB3AG+IoQ4iEp5TO250aAnwG+3I+GblSbbDaT5DO9na0S6GcvbLluNFgFxi+eykh+iNF8uHyVVvgNAmt/+W2nnYQ+TOZwcB4MtVYuFppUEMY8FLRevwGfyznTa41+Z41SeNdVMz12/B29ycPfKiqlBxxE/HNzrL24VuXR59cZzaZIJgS3XDrORC7tSbNXm+M0+fhFFfW79GMNEKcycQahNyhUlnKvAV6QUr4IIIT4OHAn8IztuV8H/jPwr2NtYQfjuRRTiTqn9WxPp9qVMzivBs8HL5Wgs3epVOqeXkdpvxlJLZkQxkRoizUdVCE52QfD7HCcBkN5fV3pxD5KPOgoCKpQ/BYPVh471ZNMCMp1g3fmpG96MD3y/DqffKrQTQrs1x5V+Yt64K8lE1wylWP8jOF+OpJN8sSZ7e4k8/rJurJXRty7Z7ddsF0Ze/FMSyZ8E3BY4cbjOKDSG0eA05bPZ4CbrQ8IIa4DFqSUfyaE6IsC15IJvvvKBZqprKPfZdyBfvrhtaLqPmhiamoqlnrzWoLFjVo3S7f1VmWoFY7NPhhlh2MfDFNpOLrQ9iyjojf5028W+PZ6NVQ86CgIo1C8Jl83HltNEcOZFK32uQBKWjJBKpFgR2/vSgrs1R4VPsVlsvA6ME7n1eNjx717dtoFuynjuEJNxDWOnaAi9U6hj7rqRwiRAH4LuM+voNXVVe6//35SqRStVou7776bBx54gOXlZfL5PMlkkq2tLWZmZlhfX0dKyczMDCsrKwwPD1MqlUin04zMzXH65QJCCCYnJykUCoyOjtJqtSiXy4ynk2i1ImOpNOnWGIuLS4yNjaHrOtVqlfn5eZaXl9E0jZGREdbW1piYmKBarVKr1ZianeNzX3+BUiNBJpvlNbMJZqen2d7eRtf17vu5XA5N01jf2CCdH0fWK8hWs/u7E03NVpsvFSBd34R0jje8YpzaToW5uTkKhV6ams0mtVqNSqXSLTOdTjM2NkaxWHSlKTuUZ2m1yNzMJM16nbWtCpeOpZgVNWoS1kqbFGtlpqam0Le2WBCbLNXzLCQqNLbTbDQybG5uMj09zebmJo1Go1t+M5khoVc4rums6kO8tHiaoXSCmZkZdoorJDq3CsvlsiNNJp+sNNXaAr3W5GiiSrPW4vTLy6TaDUc+DY+N8egzS7C9w0gqx6tHG1w/ladWKbNUKjE1NcX29jbVep3s2DS1zSLDQ0NomuZKk4rsWWl6w1SDeksyPzvB0pnTjjSp8GlkZITFxUUWFha6smf+ns1medslOVaL60y/coaNrTJJWUc2GyyeWSadyTKT0hH1Cq89PMK1U5BJnPvdiyYvPpEdIVctkkkPodeanHypyiULRwLR5DSeFsQm27UE01qWjZWzTOTSruPJiU87xWVEQD45yV670eyR92pJUMvkyVWLaOk8zareQ7MqTduFl8lJZx1RLpdZW1uLJHuuyln6LAWFEK8DHpRSvqXz+T0AUsr3dT6PAScB87rRPLAO/KD9IPPxxx+XV1xxhZ+ed8Xi4qJSVC+91Y40Y5/drPGfHlvsfn73rcccU3KZdQVZsayWdT711Cp5zfCAePvVs64ztyq9fu0B70PGIP3Vj0Mla5kLYpM333Sla5mrZZ1PPLnSDax/3ZGRXYH1z0e3UTeE4bGJqHLuVmY/+s7a1iBRNqPU57aDrujNbiKKvKYWRdGtDpX+j8JjgBMnTjxx22233ej0m8oK/CvAcSHEK4CzwDuAHzV/lFJuAtPmZyHEY8C/jtsLBdT9KeOwd6uk5AJL+Mj0ufCRbsoegiV6COM/6nbb0M/jRbW/+nEgbC0zl5j2tcGP51JcTJZ0UvBjnYTFVnhtb4OYxgZx+SuKj3AQvqnSEpa/Kl5OZlutNEftY6f3vRSyNRBY1Atrqv2/p/HApZRNIcS7gL/CcCP8AynlN4UQvwZ8VUr5UN9aZ0PUWNEm/IRmZlhTTsllHuqdOLONBB55br2bBd2p3iBuXGHo7c09mOCR59aVPBSCoB8HwmaZi4uLDHvQrDLY3OzUQVZaeqvNx76+3JWBe6915mlUxCXTXgi6wgzKXz+FaR9rZlz/Qlnn0Rd234aNWq/XBL4XF9b6yWOlkx8p5cPAw7bvfsXl2VuiN8sZcbjjqAZFUk3JpSUT3H7ZJGuVBhO5NDuNtuvV20ar7ejG5TahhKHX6/DI66Cl36tN1fJVaPYbbG5KPsjBU6GsdyflU6Uadxx3zmwfFf10MTPRT1c8N990r5jZ6UyWTzy5wkpZ51SpxrVH/D1ogtDlddDc7zshTnK+126E5w2iJjjQW21OFqtsVJu+EfaCzMgzwxqzlvCRVl90a4YgpyS+XhNKWHrNttvTRXm5jfXTZqxavt5qs9MyYmdoyd0xNILAiX9BB6+0/e0HnHgc92Q6CFc8p/JdFbtMsl1vMJlLs1iqsb7TYM7HgyYIXV67tDhNgE4xXxxdmGNMzGLHvlLgm5ubjI+Ph3rX7WJEHDOwly+6NeC+UxJfJ7dH82ZdeWPDk964blf2Oz5GkDCtuWqRLyw1HGNoRFVmqv1hXqm+9vAwG9UmU0PeZrQosMt0PybTQbjiOZXvpmDb9TJmXP8bjoxwx+WTu3KjRqXLawEWh7nEycT2/7f3rUGOXNd530U3Gq/BawaYmX3MLrUUGUpiRO6SsmQnerCWa7H8QwxZCkXarMTOJlVW6PzRr7hc5WIpP+w4laScRFVxylElthXJsl7ZUiRKIq2XFcqRuCQlijK1XHJnZ3bnAWDwGAANNNC4+QE0ttG43X37hQcHXxWLuzs9t8+599zT5557HmZy7kVv2WGuFHgul7N/yAT6LLTTmSgevHOZ2QFcg1MryCwW3dghyCioRp91o93F1/6u2I/xtYiJ5t3oPMLq1kLjnSMnZVoFqX+c3qq0A/mo2M2Hfl7j4RAev3fNUrl4tZaNMh3Ux1SLt/fjwpCVwciaVzMFu5bP47GNmG8FqKaRoMdyseUSElPOvegtO8yVAq9Wq0gk3LUnMhbBN1PeitrrX65ccX/556TgvibkxYaCb/3iAF98pTD0C5J203FLJzdwY6E5cYtU5K5t0wFtzgS5hmQsi41MZCr1a/Tz2i8kFrJU3l6tZaNMe3F3WH1MvNLqpI6PHiwFW61WcTyRsP2QsniZpRBRo4vNbB950Vt2mCsF3ul0XP8ua3LNfFh7dYWZnuwlFMtKt0rCILOu0xvxC+Yl6qqlk9v58eMCSQ8nm02bs6tvyrj9bZOtRa5fVyfz6sdH1CjTXsL4vHYbsgJPHR/e/WG3j6144eUj6Ev5/JKE+04kUWp2RlxsrH3kRW/ZYa4UuNd4Sv3ksoREEw5WenLQoVh6xaH5BVNhe4U3rQJdQXSvkYQQzmycuHWJ6/F4zLOJWevKO69+fERXVtewX1dGaHTDt91cW4VW+uEGc7I/tH1s9m4rXnj7ngZtpUtCCE+c5YtUm2oc+CzBz3hKlpDohePcyeTQr2V22ejEKrcDSyHzxERPq0AXzwfEjYLzM9afZxObKQueefX6EVXUHr7z8lVs0bRnRWM112ZuLDcnJDNenXystThws3fzVgM0m3O3pw0v915WmHoc+KzAzI/kRomaNR82Ew6zsrV+fumNAhGU38wv2AmwGwXnF8+8dbO9WqZePqIVuYtqTxwrkewGZnPthztC/w6eSofxcAhKtzcMBzUikUhYvttObuzm3I3hEKTVHuQ+nisFLgjC2L+5nXgzITETDtbzTisfOv3QsPi1g1lqcdAp4WZwquDc8MyCcRPHwyHTMsOsu5FJXJRlYiIiYREFQ16An7HvVorSSVkHnnfry9xeerVoOneCICBlo2S9fBitPmZmc2uVjOR17/gl0yzMlQKv1WrIZrMj/+blcsapkBifd/Kld6MUWPxawaqQVUXuhzM+eW4dCWl2l90Nz6wNZtzEdhafsR+pHxE+rI46RhrP5QUk86uWtey9wOqEoZV1CAv+dOcZXsYrPcu509Y4yDsc45ra7b8gT9hOZdoJZncnM5DP58f+bZrt0py4CNwoBRa/VjDrllORu7hWltFQVADAb73n+MQtcV444dlug+k3sRM58UOmzBLHjDSur64iHve3lr0eZjIaVHcenrnT1niSdzh2+8+PE7YZnO5jJ5grBX5wcIB4PD7yb9OOxuAVQjdKgcWvm3doiUQJSURHpRPrXuMGdjzz1OBgwYmc+CFTrI46FbmLN0oyzqzcykHQ+FXUHjpqvzOM00bLTioBagjK8OGZO6dy7Qd4+PVywrZCkPzOlQI3q10uCd6zzKzghx/MjVKwq9XO+44nz/XDmDoq9ezrDBqU0mEyFdCPtzW7kDOrwWEGJxafV+vQ2FFH6fawXWvj2SsHyGzfssQ1fofZn1IID78rx51a7vcdkBfo94nV3DmVaz/ghl+/5ihIfmd3JzNgdhQJ8tLJaQlSp5aQFXiPXnapxQlJxG+957gnQZzURWhmeQWffXEXL9w4BAFw7mRyWMpVb3FX5H5Rft6MwElDv/nj4RC2Ku1hk9+RcMV83lH2pwZjhctJ3AHZ0cO7T4J0KVjBDb9+zNHChTLA3t4eM54yyGJMTjK//P6ImPHr5r1eBHGS6ctbN3dRbPZv7SmAYqMz7CHa7fVdDLVW36/83JUDpl95VqCf8zMroWGTX32Y3d7eHo6d3HB0kjDWazFWuPQbPB9vViMRzfDML92qxZ2JiVxy/VZCkPzOlQI36w/nNu7Tr0JMQDAfEbt+eEG91+wdUdG665AfVvpKJoVctV/KgADIxkQ883clvLRTBwFwz/ElfPBMBt99o4LUwG1m9CsHDTd8moXZXdhIOD6qGy12Y4VLP2EW2WQVTx8Ph/DMayW8fLMOin5VR4GQYW2hCxuJkfGnFeI6KfDsY7eYKwVuBqcbwM8MNA1BRsNYCfkkonAysX4ne82t8a0rB2Mdavyy0sUQwRNn1/Gh2zOotVUkJQFffKUAoG+Rl+UuVhLh4SXmZqU15lcOEl74ZIXZNTvO0+eNa+6mFCsvWJb1X79etoynV7o9fO7lvWGRp52aglg4hFxCGuF5lgpTzSvmSoHX6/1O6iw42QB+ZqDpn/H7UqheryOZydqGygUdhSMJITx4xzKKzQ6W42E0lfGuQ36dBDSev/9mdXipl42K2ES/P6nW4u6xe9bwRklm+pWDhFc+jcqXKrJjGiYZeTVGL4VlPH06KqJQV5CNibhe7n90j6UkCORWSWWN50mcHmcBVnrLK+ZKga+trfkyTpAhVHYC6OTIuLa2hkJdwV5dwXI8PLSAxFDIU/EjN8fW/JKENUPXIT38mtO1tTWmi+Chu/obQG9tnlmJDf3Kk8oB8MqnUfn2OoorOiYVQ22kF4BlzRV9NM0nPrABAEN51S6bNZ6nkcMxDZeNX3qLhblS4IVCARsbG57HmVbsuNMj4+7ePr5bELFZbuFaWcbfy8XxzGsltLvU9ZEzqLAzv+a0UChg7fiJW/5UKQRKR8MJ/X6nE/jxTr3y3brpj0wHCePHwox/VjQNy92i8Tzp9ZuWy8YvvcXCXDmcCCG+jaUJ5SR9bix/4n5dGbbwMqKlUjQ7Pbz72BJUlaIsd/DyzTqi4dDwyOmVBidj2M2ZH3NKCBlu7IfflQMocOnVIj7/8h5znqaxjn6+00+ZnhTM+Ncsas1VonR72KsriIqj8qrnmWcuFbVnuU944UX2vSDINZ4rC3x5eXnaJHiC8ab+W1cO0FTMu/4cW80hWalhr65AFEI4loyi0Ki7bgJrpIE3ZM2sMwor2cbsd4HxyAUWtDUeXvh1esO476slGbdPMNpkEph3mdbDGPv+hZ/u43q5hc1yC/edSA5lzQnPflrN0yq7EeQaz5UCLxQKcx0/arypv/Rq0fICp1Iq4rF7Nobt1pqdnqcmsBoeuD0LQmA7o+uOpgAAIABJREFUhtnmUdSeabIN63fj4RBAgKbSQ1wK4cG3L5sqff0a67MZtbjvFyYUbTIpzLtMG6FZ1Pt1BU2lh3tPJHHQ7ODCncvDNdPzbOeTnnbrQD8Q5BrPlQJPpVLTJsEzNAFX1J6tNZBKpSAJIRxPRce6f2jHSieXMWYxvWbPXi3KqMjdsSiPitxFsdlvE6Ul21hFpRQafUt9OR7G5e1DlBr9TkcsRaxfY23DXS3JeG7C0SaTwltBpvVgNT5eW5KGLceAWzzzWNeZmIi4FEKhoSCXCLs+MWrwO/uU51QZ5BrPlQJXVdXR87wttaaRSMBjDej51QseqyYIq1ypEU6zSo2V9LTNk4mJyMXDw2Qb1sbSH1dz8TBA+oqeAsjGwqbv13jWr8vtKzG84DLaZNYTRZzK9CyDt/GxqqqWBsIYaD+EFDYlRSZ5SWn1LqPMBbnGc6XAG40Gcrkc17M8izntRAI7a8CMX2NNkM+8uAu1B1senGaVpqIiTmeiePDOZZxZvuV7loR+P8ALd/Z9eyxXDCv8TO8KMnt/o9FAKruMz764i2Kzg1w8jCfOrgfS6DdI8H44nMj0rMOu8bE2J7XaIZ653jE1EIxjNjs95BISGor16WuSceVWDSCMMhfkGs+VAnfSHNRuMR1ZAFOCGb96RRwWCJQu5eLBTVZpJiaOKG/9WKx0euMzelpYriAWz4W6ghduHAIANsstXLhzGcdTUd8b/QYFNw1+3wqw68upzYkEArnXNTUQeMf08qxXmL2LJXOLpsYDOGkOyiNMPBaAF3g9vpvxa7zt//IrBW6hnVZWKe/7d3d3IWbWQClFt0chhm6FYDmdz2lFHTht8Dtrl5jGeXbSH5QnRjwul6GGs2go5gYCz5henvUKs3fpL97DAkE8HMLuzo3FJSYAhMNh7md5hInHAnALP47vVvzqFaHTOjBBN+t18h4jwuEw0jERkhiC3OoiLrlvb+V2Q7sJf9TDyYfDiUyz6PNbSbH82HoDwayYlQYzudHPSTocxm+cXecuA2wli8a58POSkjW+HV2SEMIjd+fxmRd3oXQpvvxKAR9YDU7NzpUCT6fTzH+36otoJ0x2FoAV3DRJdQIzfo3gFdpJ+YS9vCedTqOh9PC2bAyiQNAdJDNRxV3da6cb2pgODoqhzz6IZgm8a8yij4cmp8reKLfXK22uYlZ20M9JWE0jIYnDFm5uP0hByLPx4+1m/IbSg9rD0K0Zik65GiEh5CEAfwxAAPCnlNI/NPz8EwD+OYAugAKAf0Yp3fSZVhSLRSQSiZF/M244qxhjDX4ctdw0SXUKFr9eMCmfsJf3FItFHDu5gUxMHH5g7WpwBEV7oaEMomwkx3zwfjicrrGTuXWj4IxyeyoT4S5mZQdtTjY3d5BJJV3T6GYueGCk5YHbs67GN86hUq8AuYxruqxguwsIIQKATwG4AGAbwI8IIZcopa/qHnsRwP2U0iYh5OMA/gjAx/wmlmWtDGtVh0O2McZ6eD1quWmS6hROrTM7TMon7OU96XR6eAzdqrSxkYkM5y5o/+awL+WgQUIuEQYoRpol+O2+cLrGTubWjYJjyS1vMSte6Hn2ooT9lmcjLYS449U4Z83Dmie6rMBD0S8BeJ1S+gYAEEI+B+BhAEMFTin9tu75HwJ40k8iNSjKeOU2bRH36optjLGfcNMk1SlY/HrBpC55vLyn2WqjUW3h2dfHywzok6CcJjHZwZg5qvWlBDCivIzhjZ6P7A7WWPt48LaRs5NRXtej8e+eT686nr0oYb/lmVVn3e34+jmr+LyP9eCZrRMAtnR/3wbwXovnLwL4uheizCDL47WTtUXkiTF2CrsLjKCVIYtfHtqs4Pclj5/vUdQeLl8r4jWlhevlFu49kRz7GAflx7fqS6m9+0a1xQxv9AKrNdbD70tcr40pvMiQnmev+8hIi5cTkhktXvcL7xq7AY+WY5XSYuZEEUKeBHA/gA+yfr6/v4+LFy9CFEWoqopHH30UTz31FHZ3d5FIJCAIAmq1GvL5PA4ODkApRT6fx97eHpaWlhCNRrG5udmvk10ogBCC5eVlFAoFpFIpfPhUGOXaITZOHMfO9lY/oiGdRrFYRDqdhqIokGUZ6+vr2N3dhSRJSCaTKJVKyGazkGUZrVYL6+vruLGzg5/st1HtClgJtfEP3rGBVrMBRVGwsrqG69s3kUzEoRIRh4U61vJ5VKtVdDqd4fg8PAH9gu8snmKxGIrFIhqNxnDMcDiM+FISf/PqdRz0JCRFintWJZw4dsyWp93dXUSjUcRiMZTLZaysrODw8BCKogx/HovFIEkSqtUqcrmc7zylUimoqjrGUzqdxubNPVRVAaelNpZiDRw2wzgjyWhXQ6jTFEqlErrhBNR6GcfDPey3lnD1zWtYTiY88wRCsEGq2GvHcUJooVHsISmsjvBULlWQCKk4FWmhRwmUVgub5T1LnuxkT1VV1Go1yLKMhiwjms6hVS0iEYuN8HSzWEFMLoNEMojKRWzdpFhJxrnXaX9nf2SdVDEKtA5xMtTBXiuON65dx1JE5FonN/tJL3uqqqJer4+sU7O4C2qxTjd2dkDFKJKxMOR6nSl70XgCf/NmBejI6ETSeF8eEIWQK55S6+vY3PZnP8XjcWxubnraT6bK2a7lPSHklwE8TSn98ODvvwsAlNI/MDz3IID/DOCDlNJ91ljPP/88veuuuyzfZ4XNzc2Jxczu1xV88af7Q4vso+9eHcm0MsaQBxHRofGrry/RUPp+Wq0Qlp42XkwjvZy3rME3f/RzbNE04uHQWNEuniJaXmm0sgQVtYfPvrSLYqODXCLsy7u1NW4oXfzF5V10VMqUJ79PHpPOUtWv/872lqN9zEur2Z4NAk72kFe9dfny5RfOnz9/P+tnPBb4jwDcQQh5G4AbAB4H8Ov6BwghZwH8CYCHzJS3H5CkyWVJ2mVaCSGCersLIUQC87lLEvuDkYwIrjuRTyO9nPedkhDCvaeyeG86x1SiWlr12eNJlOUOLtyx7Cvtdq4BSQjhiXutM0ntMBa3PFjjv7i8i5duHiIhibgN0UAuxY28+DGelSLTGx76WPIPrfPFvmu/31H5QkgndUnvdA8FqbdsOaSUdgkhvwPgG+iHEX6aUvozQsgnAfyYUnoJwL8DsATgrwbFy69TSj/iN7HJZNLvIU3Bk2m1FBGh9qhpFqdXSzeZTA5bqkWEEOrtLkSh393bbSfyaaSXO3lnJpWCNOg2r504tPnTb9BVQ4W7oOA2UYS19qyNn0wmB0qKDizHfgZfEJfiduM5lVe7gk7az0IE6Ki3yj3QsH3YpDE8OB62N1gmdUnvdA8Fqbe4PlGU0q8B+Jrh335f9+cHfaaLiVKpZOsT8hNmmVb6NHazaAA/LN39YhHfL0m4Xm5BpRRxSUB3cMR2Ww88SCvFTAEkpBBCBKi1urYlC3b3C3huP4xWp4ftWnvMRTUPLbjM3CGsjd8slYZx77chBkkk+A0folucwg2vVopM/7NaqwtJvNXUuNOoAvms5dj6XrBNxdxgCToTkwWzPWQm/0HqrbnKxFxKp8fCx6bhz9ULiZms+GHpCrEkmoo8LIr/0b+fR1wSPSmvoI7OVs0fvvxKAR2VIiwQPHJ33tIH/n/3VLy00xoW6RKFURfVpKJoAHdrOOoOEXAbYsPfY238SDY78Q8TC254tTIGjDVBHnv3Kjo9IB0V0WrUbV0vz145wGa5H4107mSSabBMq9qk0YhjuYn0tGSz1h8rL5gbBa6oPXz/F3vYURMjNRmmWQ7WCn5YumKvM1IU/1gqaqn8eD9kVkqQ97LROO9mCkBfd6ahqIMWaWy6KnIXotpBQhJRb3cQDd86cUyqEJXGn7EpAe8a3nKHiGgofctT+z2Woi7L8rBxxzQrYWZiIiICwfWKjOPJCBevVh8eSRitCfLVn5eG+7PQaOLS6w3Tfct71xG0O9AujDgdFU3dRHpa5MEaB4G5UeAVuQu1oyARTQ0nyEtab9Dww6rqKm08ds+G7Rh+WSK8NdRZZXjNPlhOy4EuCSrWlmK4fTmKJ86uDa22SUbL8DQlMEMmJg7cIVGEhXF3iFFRt1otX2j2egrtqD38bL+BaquL8uDikGcsqw+PsSaItj+r9SYO25LpvuW96wjaHWi3F4xuorBAmH56P9bYDHOjwDMxEUokMzZBfi+gny4Zr1bV+vo61xh+WSI8NdTNyvBqFtf1ShundOnvTj9ktXAKoQ5FPCIgLk3enWDXlMAOLH6tZEqrFe21oJPmqnjy3DoSkrN9oKg9vHyzjkZ7kPqtqNiqtnFX3tt+MlOwp04eR/KwbLpveWXGDyPJbN559pSxKJ7Zx35RDxz9xXpvTkUyf3xkgvz0HU67Q48RvLWijRslHg65SjVn1TLWw6oMr+brZs0d74esIncRa1eRT+Rsu68EBT+sOj2/djK1u7uLYyc3PBV0qshdXCu30FC6IAT4zfuPc/++Rt+B3EGj0wPQRTIaxkY64phvI1i+4kxMRGl/z/ZkySszXowkq7h+u71g5E/jg0VKkDXf50aBA0AiFmNGhfi1yafZwYVlBUSjUS7LzLhRzBSpHTQrWoug+PIrhZHftyrD68fcZWIihLDkKr7dL/h9oWg3L9FodCTiwk1Bp/7RvYuEJEBWenijJOPMCl+JZI2+TDSM92yk8J6NFN69vuTYijeD0VecjAh44FjE8b7182SsjSV3uri8fQgK4Hq5hQ+dySIWFobvsNoLev7s+IhGvZVbsMJcKfBYLBbo+NPo4GJloYmRCLdlpgnSfl1xpEiNG6Oh9NCjo37L9CAuWwuJYyk3vyzX99+5hl447tuJatr1YuxOR2IkgmcMERdOCzp97J5VyB0VvR6wXWvj2SsHyGzzZQfr6VuOhXHfiZRlmJ4bGD9iasjZPvbzZKwfi1KKHqUghKBHKf7Pz4sghAzfwdoLbuQiSL01Vwq8XC4HdpsLTLYlkwa9cFfkLq6WZNw+sJ72CgeWlz0sOFGkrI3BUjjGZ1g0+DV39WoVp097r508rYxTo7KzOx3tFQ7Q7Eius0sVtYev/rwEMRRCFz1sZCKOFI7Vuvk1h0aZ6sqHAFaYvLj1R1tBP67x4vGdawnInR6iYqivrCO33uHUKDGjP0i9NVcKfGVlfNH9xqTDufS+ts1KC89dOcALA+vp2GoOycOGI6vWiSI12xj633eyefyYO7/WmIdu3pBJHgvUStlZnY70a+wmu1R/L2FMmHFSv5q1bmZz6NQqN8qkIjfHnrGaPy+nO1ZUEevikdVbVqO72FBgLBnFmwcBBKu35kqBHx4eTjQTcxLQhORqScY3XyuBEGCn1kaxoYA0G44iGvRjuukcoo9X1n7fqUVvVxfDbtPbrTHvODy1sHlCJnme4a3XwaKptD++xk7AGwnhBix63VrlepkqMdbY6oPr5XTHiirSn4j0pRrM3mFsIQeM559Y0R+k3porBe62wcE0sjV5oKfrVCaC69UWtitthELASjyMD+QUCIOEErtsLzfg2Ri8m8euLgZvIwRFUUzXy4nysKObx0IfXi6aNAkxNoGwKjBm1oxBURRPJxfeSAi/xnZ6x8KCVWMWK0PBpnAqU25Y47IuVh+5Oz+izDWw5ISVf2JFv9+NWfSYKwXuJp5ymmUznRy5H7g9i/UlCU2lX+nwoNnB9/YJmjt7w5jrsEBMs73cgkd58DxjpRALdYW7EcLK6prpejn1hVrRzWOhP/v6Aa6XW9gst3DfifHLRWMTCKt6HWY86WV6Fi5d7cb247KatY/d+uLNKh7quzixxjXePX3mxV2oPXC7b1gfBTP6F3HgA7iJp5xkaKCTj4WRLkKA1aSE7WobFEBcEpDqVtAWssOytR2VuvJxTgJ2G5ug3wWE1R1Ej+vbN00vbjMxEfFwCIWGglw87Il/Hgu9qfSGdWgu3Dl+uchqwcVabysZ1GR61nIQzODHZbXZPnbji+dJZdePyyqToNXdMftdox/cbA7M6F/EgQ/gJhwnIYVAQbF32MZKIoxGuwul27PtXO8GjsqmMjb/E/eu48IdywD66ePffEmG2qEjZWvHjuAz4h6y2tj5JQnnTiaHCRNWF3WZZALJw565hUdu/b/jkXdeC33N5HKRV5lZfdw0mZ5WDoIbuLX4NVkNR5zFRdvV5rdLZde/n1UmgXWBaYTRD+5kDhZhhAM4LYyuqD184Sf7eHWvga5KcaPWwos3DkEIwX0nkr40pdXDyfHSbPPrXQvvf3seNJIYK1uryc2sWW1mQi0J/I0Q4tEIHrsnNZa9JwmhoVWcT0iotfolW3t0/NjLgtfICS8XxlZjaTI9jRyESUIvq3lRwUfyfLVWAPva/LwXuFZlErzel1jSP82GDrOEarWKTIY/Rrgid1FsdhAiBIRQVFsqomIIYYGg1Oz4buU4PV7abf7GYQ2nl/ulKPVKmxXT+lax2rQ1Nl4yGWPUndwH+BE54RVmY2n8+uGa8Bte6rMYf08vq6TVcK4EGfNndG+EhRDyFhmkVh9JL/cldnCqt5xgbhS4ovYQiqehcFZJA/oTn4uHsVluQQwRZGMiOmrfkbXi0odqJ9QsQbCKqrAaK5fLjY1jFtNqVwPFzWachntG49kuRp3n2Kthmh86J2sc5GWkU7j96Jn9nl4JRiLOsk3twHJvsOD2I+n142rcx35iLhS4JhSSXIYSkx1ZUE+cXceFO2/5lautLgC46mjjRqjNQuh4xqpWq/2O6QMYb863Km1TP55ZeysndLvdwE6UvvF5jWezYkJ6Jce7qYJ2T7CSOnjDPo1rPCtw+9Ez+z29EpTLBd8MAj8jk6zg5eMa5BrPhQLXFul4qIetuoJiQzENQzNCEkIjz/IU6fEzpdcshI5nrE6nM/J3Y9bms1cOhvVJrMZzQ7eb33Gq9FnPazxLwmhDAFYxId5NFaR7gnUq0pS2VWSEBuMazwrcfvR43BSbxe7U6QT8O2HajRPkGs+FAtfCx35wM4Q2beFbVw5GSj/6iSBSelkhdDxjsWpFP3bPGt4oyXj2ygFXQwX9u6xKYxrhhlenSp/1vD5m1qwhgBsE5Z4w8nC90h6JjLAL+wwyRtgLgnQ38PLspBInK93dbuxJNUE58nHgkhDCg3csIyIXIccyaCo915tZUXso1PuZUaxQQr9Tes1C6HjG0mpFG10wZ1ZiyGyL3IkEPNasEXb08Wa9WYH1/M721jBm1q9iQl7QULq4Xm7jVDbCPL0ZaTyViTiKjOCNEZ7GfURQ7gYrnp24n/Tg9YNr8OteRKvHLoQIKnKXOc4iDhwDZRuJodzpufZjav7oF24cggA4dzI5ZsnbKQ2nQm0VQmc3ViKRMHXBOEkkAPisWaOSMBvPzOpwE4Uzlgau8xVqHx5jlx8WggipbChdPP2tN1Fvd7EUEfH0hbeNKXEWD05S23l8o5MKF/Wjlg0PzHjmTcwxwo0y9uteJCGFsFlpDWWEdboN8o5jbhS4JITwD29fBokmXfsxtbBCoO/SKDbGQwmD8Je6tWQEQQDAdsE4HdOP4k4a7E4pXsLDNJ41mqyssKBDKq+X26i3u4hLAurtrmmbMSMPTuZAz68ZJhFFY5eu7vYDwlL8ZjzbJebox9Kez8REV8rYr33eUHo4mYpApRIEQkaadmv0gtjlH7vH3ChwAJDrdZz2UJpRH1ZIAOQS7FDCWQnnqtVqOHYyzZ3FaAU7gXWiJBJSCCEC1Aa+dz+jOmq1GrLZrC1NdiGVftB0KhvBUkQcWlc8bcachozWajUkUmlL69artchjPftxCc5bYlW/xmZ8Gt1PwK0KgHEpBFCgOTiNP3bPmis/uB/7PCGFsF1rj1nget43SBW/mskGcmqaKwWez+c9/b4xrNBNKOEkkc/nLV0wTmElsHadYzRoVrFWl+WRu/OmNLk5duvX2EpxaUolKoawV1dQbXVdW1RmdCakvttkq9rGRprtAzeOw1JYlhfjKzlb69aLtchrPfNcglt9QFjvMVP8ZvvYyv2kr4JYaCgDA0wajpuOio794H6gofRwOhOFKBB0VTq0wPW877XjgeUezJUCPzg4QDweB+CtchtvCOK0USiVEOv1j4hBFuDSR7iYdY7R5ljfQKChqCNHRuO4bo7d+jW2UlxaZJJ2n6FFJjlpH8dDZ0ISubuzmyksKwt2Z7+Iw7Zga926tRZ5rWe7S3C7DwjrPWaKX7/GvHzqx8olwgDFiHtlWslamZiIZFQYnpA1HvX0nhBagZVGmCsFTgfno1mrARIEFLWHn9w8xPY2CYxH1jza9dXkPc673VDUcAY229BaZFKx2cFyPGwbmWQmM35tfEXtoaP2mDXBreYsKpBAk4yc1udx223JrO42S/Eb15gHxrEAjIzrd7KWIwORDu6ndGzp6W0U+bPHnWKuFLh29JqnGiBuUZG72OnEAAEj4Ul+RAPYdZGxihvnPc67Lf2aWV4xLQdgRH5JwtqSxLVpzWTGj41vbOzw8LtyI+45qzlbX1vFYyelwGqgBHEp7+Q9LMXv1hVqHCuo4AOnF/rNTg+5hISGwr7QTwqrrmmxw1wp8L29PZw+ffotX7kNGFwUtip4sRYdXo74cfLg6SKjhe+ZxY1zH+cdln5V1B6++9M3sUXTXPw52bRmMuPHxjc2dggPQiqNtLLmTJPpIA2QIC7lWYYE73s0nt2+DwBTlnjer48zZ3Xg0cbmNRB5dJEbfnkxV5pP6ys3KatimmgoPUjRON6dSEDt9S9HqMK2mJ1Y5bxdZHizIM02lpvSrxW5i0ovjESE/2TFqzTsfLxeFJwXg2Iee7x6NSR4eDbKlVUEinZRzGMgfP7lvWEpitOZ6PDuZ/Tegz/KikcXBbnGXJJGCHkIwB8DEAD8KaX0Dw0/jwD4MwD3ASgB+Bil9Jq/pPahXygrf+csNDkwwgldmZjYV7IqRoTIqCicbibeLjJOIw+MG0sf1sdb+jUTExETQ9gPqONQUOGhbzWDws5KDdqFyWo3aBeBwrMHNLqFEEG93YUoEGZ4Km+UlYZphh3b7hBCiADgUwAuANgG8CNCyCVK6au6xy4CKFNK304IeRzAvwXwMb+JrR4e4uubiuVCzeoFp1O6JCGEs6sikvnVEaVgVBROm8zyKhunkQfGjWXs/s1T+tWMZy+Y1MfcahNb0VCv17HiIbfBb/BYqV5dmHY8Gz8QhNwyXLxEoOjvdpYiIroqHbOw9WMdyP1EP54CeF749QIeyn4JwOuU0jcAgBDyOQAPA9Ar8IcBPD348xcA/BdCCKFurpstEEmu4HCnarlQs3rB6Yau4+vriEbHi9jrf48nw9Ktr9JJ5AFrY+l//5G789iqtLFhkxLP4pkHbkIEJwE7GtbW1iZKjx2MVqoQGrdSvZ447HhmnRL9iEDR023scqV/Nys81Y3caDK5nPOWv2IFHgV+AsCW7u/bAN5r9gyltEsIqQJYAVD0g0gNnXoZyUjYcqFm9YLTDV2FQgEbGxuWz1htpqAVmF1ol54O3sJEPDwbEXSIoBfY0eCG3yBhtFK1XqxeawLpYcezmUz7EYGip5tFvtPwVDPoZfJkqIYP339XIMYDj3ZjJfIbLWueZ7C/v4+LFy9CFEWoqopHH30UTz31FHZ3d5FIJCAIAmq1GvL5PA4ODkApRT6fx97eHpaWlqC0W/iV5R6iqRUoh2Xs79zE8vIyCoUCUqkUVFVFo9HAP3rHGrZu3EQiGkGnJWOnWEQ6nYaiKJBlGevr69jd3YUkSUgmkyiVSshms5BlGa1Wa/jzaDSKWCyGcrmMlZUVHB4eQlGU4c9jsRgkSUK1WkUul0O1WkWn0xn+3MjT+/NdyIqKE+vL2NneGl5u1Ot1rK2toVAogBAy5ElRFBSLRTQajeGY4XAY6XQaRQZPO9tbIzwhugRBruCk0MNuK4Grb17DcjLhK0/aOiV163TYGuWp0emh3erhZKiJSkvC9i6B0G0zeVIUBfv7+47WSYEItSXjZKiNYiuKze2bkKBiZXUNG6SKWktAXpJwWLiJOPLcPOllz2qd9LJn5KleLCAv9qC0FGwIKmKhHDY3N4c8VSoVpNPpwGXPCU+/stxGKBJHmEio1RvYOJHHzvaWpew52U+VSgXZbNaWp061ip2iM56Msse7Tnqe2s0mjscFSO0SsmIYYjeFzc0dRzoinFpBTC4iJkbQ6yi4+uY1nDq25nqdTJWznZeDEPLLAJ6mlH548PffBQBK6R/onvnG4JnnCSEigF0AeaML5fnnn6d33XWX5fus0Gw2TTO43orwyu8suBCc0uGGZ7tCTNO+XLSi4ajJNDAfPHuVG71MZsMqHj274Vr+Ll++/ML58+fvZ/2MxwL/EYA7CCFvA3ADwOMAft3wzCUA/xTA8wA+CuCv/fZ/A/2jV1DxlLMIr/zOSnSEEzrc8BxkiKAfsKLhqMk0MB88e5UbvUweFm5OLxNz4NP+HQDfQD+M8NOU0p8RQj4J4MeU0ksA/juAPyeEvA7gAH0l7ztSqVQQw84s/OB3FhSYEzrc8jwrfDrFUZNp4OjwrMmkqKQDewfXDR+l9GsAvmb4t9/X/bkF4B/7S9o4VFUN+hUzhaPGL3D0eD5q/AJHj+cg+Z1+gLQDNBqNaZMwURw1foGjx/NR4xc4ejwHye9cKfBZbQAbFI4av8DR4/mo8QscPZ6D5HeuFPju7u60SZgojhq/wNHj+ajxCxw9noPkd64U+Fe+8pVpkzBRHDV+gaPH81HjFzh6PAfJ71wp8C996UvTJmGiOGr8AkeP56PGL3D0eA6S37lS4N1ud9okTBRHjV/g6PF81PgFjh7PQfJrm4npJ5577rkCgE23v39wcJBbXl72tb7KLOOo8QscPZ6PGr/A0ePZB35Pnz9/nlkRa6IKfIEFFlhgAf8wVy6UBRZYYIEFbmGhwBdYYIEF5hQzqcAJIQ8RQl4flVsKAAADtklEQVQjhLxOCPnXjJ9HCCF/Ofj53xJCbps8lf6Bg99PEEJeJYT8hBDyHCFktisBccCOZ91zHyWEUEIIsxrbvICHX0LIY4N1/hkh5H9Nmka/wSHXpwgh3yaEvDiQ7V+bBp1+gRDyaULIPiHkFZOfE0LIfxrMx08IIec8v5RSOlP/oV8w6yqAMwAkAC8DeKfhmX8J4L8O/vw4gL+cNt0B8/sAgPjgzx+fZ355eR48lwTwPQA/BHD/tOkOeI3vAPAigOzg76vTpnsCPP83AB8f/PmdAK5Nm26PPH8AwDkAr5j8/NcAfB39/gnvA/C3Xt85ixb4sIUbpVQBoLVw0+NhAP9z8OcvADhPCGE1lZgH2PJLKf02pbQ5+OsPAZycMI1+g2eNAeDfAPgjAK1JEhcAePj9FwA+RSktAwCldH/CNPoNHp4pAK00YRrAzQnS5zsopd9DvxqrGR4G8Ge0jx8CyBBCjnl55ywqcFYLtxNmz1BKuwC0Fm7zCB5+9biI/ld8nmHLMyHkLIANSulXJ0lYQOBZ4zsB3EkI+QEh5IeEkIcmRl0w4OH5aQBPEkK20a92+q8mQ9rU4HSv22I2GkaOwrcWbnMCbl4IIU8CuB/ABwOlKHhY8kwICQH4jwB+c1IEBQyeNRbRd6N8CP0T1vcJIXdTSisB0xYUeHh+AsD/oJT++0Hnrz8f8NwLnrypwHe9NYsW+DYAfcfTkxg/Wg2fGbRwS8P66DLL4OEXhJAHAfwegI9QStsToi0o2PGcBHA3gO8QQq6h7y+8NMcXmbwy/b8ppR1K6ZsAXkNfoc8reHi+CODzAEApfR5AFEBuItRNB1x73QlmUYEPW7gRQiT0LykvGZ7RWrgBAbZwmxBs+R24E/4EfeU9775RwIZnSmmVUpqjlN5GKb0Nfb//RyilP54OuZ7BI9NfQf+yGoSQHPoulTcmSqW/4OH5OoDzAEAIeQf6CrwwUSoni0sA/skgGuV9AKqU0h1PI0775tbitvYX6N9i/97g3z6J/iYG+gv9VwBeB/D/AJyZNs0B8/ssgD0ALw3+uzRtmoPm2fDsdzDHUSica0wA/AcArwL4KYDHp03zBHh+J4AfoB+h8hKAX502zR75/SyAHQAd9K3tiwB+G8Bv69b4U4P5+KkfMr1IpV9ggQUWmFPMogtlgQUWWGABDiwU+AILLLDAnGKhwBdYYIEF5hQLBb7AAgssMKdYKPAFFlhggTnFQoEvsMACC8wpFgp8gQUWWGBOsVDgCyywwAJziv8PF3u6DFnasXUAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"N = 1000\n",
"plt.title(\"Simpling Random Sampling Sequence\")\n",
"plt.scatter(numpy.random.uniform(size=N), numpy.random.uniform(size=N), marker=\".\", alpha=0.5);"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"autoscroll": false,
"ein.hycell": false,
"ein.tags": "worksheet-0",
"nbpages": {
"level": 2,
"link": "[7.1.2 Quasi MC: Halton’s low discrepency sequences](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1.2-Quasi-MC:-Halton’s-low-discrepency-sequences)",
"section": "7.1.2 Quasi MC: Halton’s low discrepency sequences"
},
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Quasi-Monte Carlo result (Halton): 41.21870562744141\n"
]
}
],
"source": [
"seq = halton(2, N)\n",
"accum = 0\n",
"for i in range(N):\n",
" x = 1 + seq[i][0]*(5 - 1)\n",
" y = 1 + seq[i][1]*(5**2 - 1**2)\n",
" accum += x**2\n",
"volume = 5 - 1\n",
"result[\"QMCH\"] = volume * accum / float(N)\n",
"print(\"Quasi-Monte Carlo result (Halton): {}\".format(result[\"QMCH\"]))"
]
},
{
"cell_type": "markdown",
"metadata": {
"ein.tags": "worksheet-0",
"nbpages": {
"level": 2,
"link": "[7.1.2 Quasi MC: Halton’s low discrepency sequences](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1.2-Quasi-MC:-Halton’s-low-discrepency-sequences)",
"section": "7.1.2 Quasi MC: Halton’s low discrepency sequences"
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
"Another quasi-random sequence commonly used for this purpose is the **Sobol’ sequence**. This equence was designed to make integral estiamtes on the p-dimensional hypercube converge as quickly as possible."
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.1.2 Quasi MC: Halton’s low discrepency sequences](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1.2-Quasi-MC:-Halton’s-low-discrepency-sequences)",
"section": "7.1.2 Quasi MC: Halton’s low discrepency sequences"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXAAAAEGCAYAAAB8Ys7jAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAIABJREFUeJzsvXuQZNdZJ/g7eTNvviors/LRVf0otdSyhGQL25IlGQQDAknYMA4bKYwWsQ5WDu3s7CIeMyzMwi7LaJgIDMwQOxALw8QQxrsYzHjWqwkFeDGSvfLCWAZbbWksydjqlrq6q7semZWPysy6mTfz3rN/ZN3SrVv3cV43u9Odv4iK7qr7OOf7ne/7zus73yWUUswxxxxzzDF7SFztCswxxxxzzCGGuQOfY4455phRzB34HHPMMceMYu7A55hjjjlmFHMHPsccc8wxo5g78DnmmGOOGcXcgc9xzYMQQgkhH5F8x4377/leVfWaY46rjbkDv05BCPlFQsgLhJAWIaRNCPkbQsj7Pfc8te/0KCHE2r/vRULIbxFCVhnKqBBCfpcQ8iYhZEgIqRNC/poQ8lh8ks0xx/WDuQO/fvGDAD4O4AcAvBfAlwH8OSHkezz3XQBwHMCp/fv+FYDvB/AqIeS+iDI+A+D7APxjALcCeD+ATwGoqBFhjjmuc1BK5z/zH1BKAeDrAH7b9ftTAM753JcC8AKA1wEkAt5VAkABfCCizBSA3wBwGYAJ4DUAP+G5hwL4OUw6hD6AKwB+3nPPcQB/BqANwADwPIC7Xddv3H/P94bU5dR+GY39d7wB4Bdd15P7nLwJYADgVQD/2POO0wD+cv/5iwB+Zr8uf+i65wKAX/E894cAnvf87WcA/P1+Wa8D+F8AJD3v+TUAvwOgCWALwL8GoHne8+Q+r0MA2wD+Lx6Z5j/X7s98BD4HAIAQkgBQwMR5hYJSOgLw2wDeBuCugNt6ALoAPkQIyYe87tcB/CMA/wTAHQA+CeCThJAHPPf9c0wc4Z0AfhPAbxFCHtmvOwHwnwDcBuADAO7FxJk9SwipRsnjwu8DKAJ4EMDtAJ4AsO66/ocAHsFkRnE7Js7zNwkhT7jq8TQmM4z7AXxw/yeIo0AQQp4C8AsAfnm/rJ/bL/efe279GQAbmMyOfhYTHn/S9Z5/gQlfvw/gOzGZBb3EKtMc1ziudg8y/7k2fgD8Ciaj11Ouvz0FnxH4/rXbMBnRPhryzocx6RBMAF/FZKT4g67rOUxGhT/lee5pAF9w/U4B/LHnnj8F8Df7/39g/563u66nMXFsv7r/+42IHoG/DOCpgGs3AbAB3Ob5+68CeGn//w/ul3Gr63oNk9E48wh8n5c9AO/33POTANqe9zzjuecvAXxq///5/bJ/QVSm+c+1/ZNk8PFzfJuDEPJTAP5nAB+klK5H3e88tv9vYDY0SunThJDPAvgeTEaIPwjgZwkhv08pfRKTEbwO4P/zPPpFTEaebrzg+f0/YzKaBIB3ANihlL7mKntICPnb/Wus+DcA/h0h5IcxGe3/BaXUqdvdmMj81clA+wBJANb+/98OoEEp/ZarHnVCyDc56uDIkwXwGUKIm18NQIYQUqOU1vf/9pLn2cuYOGbnPRkAfxVQDotMc1zDmDvw6xyEkF8A8C8wcd7PcTx6x/6/58NuopQOAXxh/+djhJBfAfAvCSH/yn2bt1o+f/OCeH73u5/lPe66/hEh5C8x6Rh+AMD/Qwh5mlL6Eby14X8fJqNjv7JZy7NxtP4p1/+dsn4MwLdwFE3X/02funiXRoPqxCLTHNcw5mvg1zEIIb+GyZrqj/A4b0JICsDPY+JcvCPAKHxj/98agHOYLKF8v+ee78NkM82N7/L8/t2ud70KoEoIeburjmlM1sK97wkFpXSDUvpHlNKfxGQN/L8mhCwCeHH/lhsopec8P04n9iqAGiHkFlc9qphE4LixDeCE5293uv7/KiYbimd8yjpHKWUdHb+2/573BVxnkWmOaxjzEfh1CkLIv8Fk4+oxAN8khKzsXzIopR3XrZrrWhETR/NPMVkDfx+l1A54fwWTiI4/wmRtuY3JqP1jmEQ8vEQpHRFCfheTEXkdk87gxwB8CMBDnld+gBDy0wA+h8kI+b8C8OP7174A4O8A/Ckh5EkAHQD/KybLB/+Wg5P/HcBnAXxz/9lHAFwC0KWU7hJCPg7g3xNC/hkmSzp5AO8BUKOU/iaAz+/L+klCyM9gMjr+TQBjT1HPAfgpQsjTANYA/PeYRK80AYBS2iOE/DqAX99f2ngWE1v9TgB3Ukr/JxZ59t/z2wCeIoQY++/JYtJhf4xSeo5BpjmuZVztRfj5z9X5wWSK7PfzCdc9T7n+bmPiGM8C+C24NjsD3p/GJMLk7zBxTE5Y3h8AWHXdxxpG+E8wiTTZw2Rz8hc993jDCL8I/jDC38NkVmEA2AHwFwDe4bquAfhnmIT2mZhs0H4RwI95yvkrTEa+65hEjzyPw5uYBQB/DKCFyWj8KfiHET6BSac22L/3bwH8D67rFxARjojJUs3PYdIpmZhE5/xHHpnmP9fuD9lvxDnmmCMmEEKexySa57+92nWZ49sL8zXwOeaYY44ZxdyBzzHHHHPMKOZLKHPMMcccM4r5CHyOOeaYY0Yxd+BzzDHHHDOKqcaBP//88zSdTk+zyDnmmGOOmcbe3l7jgQceqPldm6oDT6fTuO2224SfX1tbw+nTpxXW6NrG9SYvcP3JfL3JC1x/MsvKe/bs2bWgazO1hJJKpaJv+jbC9SYvcP3JfL3JC1x/Mscp70w58GKxeLWrMFVcb/IC15/M15u8wPUnc5zyzpQDbzQivzXwbYXrTV7g+pP5epMXuP5kjlPemXLg85772x/Xm8zXm7zA9SfzfAS+D9P0pj7+9sb1Ji9w/cl8vckLXH8yxylvpAMnhHycELJNCHkl4DohhPwuIeQcIeS/EEK4v//HCsMw4nr1NYnrTV7g+pP5epMXuP5kjlNelhH4J/DWp6v88MMAbtn/+e/AkX+ZFysrK9E3fRvhepMXuP5kvt7kBa4/meOUN9KB08k3AZsht3wIwP9JJ/gygBIh5LiqCrqxubkZx2uvWcjKa1o2tnsmTMv3mwvXJK5mG18NvmZZp0X5mmWZRRCnvCoO8pzE5KslDtb3/7ah4N2HoKVS2O6ZKGWT0LWZWr4Xgq7r3M+Ylo22MUZeT+DpV+roDi0U0hoefdfyTHAmIrMoHK5K2YkZfPrlranzNU15ZeDmStcSMC1bmK9ZkVkGh/iKUV4VDtz7cVYg4IOo29vbeOKJJ5BMJmFZFh555BE8+eST2NzcRD6fh6Zp2N3dRa1WQ7PZBKUUtVoNW1tbyOTyePFSB+PxDkbpIr6rBiS1BMrlMur1OhYXF2FZFvr9PlZWVrC5uYlUKoVisYhGo4FisQjTNGEYxsF1XddRKBSw3WhAyxaQtEcYm8OD65lMBtlsFq1WC5VKBd1uF6ZpHlzPZrPQdR2dTgfVahWdTgej0ejgepBMpXIFl65solJaRDJB0Ov1sLy8jHq9DkLIgUypVAqNRoNZpssbG/gvWwO0rBSKdA8mzWA5ZYMaJna6BZidndhkctppYWEBAAJlimonXdexvb19qJ20VAp2MovxXgfVchmGYWAwGEi108A08bcNDfqwDZLK4DtPLCJrNKDpi0gaHbxxYYgbT64okSlM93q9HnZ3d5XINBqNUDm2jIvrV1AuFpBOJZW0U+XYMp5/+Tz2LAKazuGeKpBILyBhdHBKs7A5yOP8mxdQymdRKBSws7ODpaWlQJl6vR56vd41oXtES4Kk8xj12yiXSoHtFCWTu52M4fBAtxKpNO45uYC1tTUpmQKdL0s6WULIjQD+nFJ6h8+1f4fJJ5w+tf/7NwHcTyk9MgJ/4YUXqOhR+u2eib9++ZvoZ6romxY+/M5jqOXlezaZkUTc5fEewd3umfjM17eR1zXsDsbQkwSWDW65vKMt3usy8MocV/u4ueqbFj70jiq+cK7FXQ4LF2H3qDxWPi2uPvzOYyhmksJlRckcp355y5kGX/fXTNz+tjPC7zt79uyLDzzwwN1+11SMwJ8B8NOEkD8D8F4AHT/nLYtSNglbX0DfnJBdzPBVPUgp2sYY3aGFvK6hO7TQGYyVdAxBYCnPqesCZ/xoKZtEIT15bymbxMN31LA3slHMsBtClFLH3eEtLS0d+p2HLx6Dd3NVSGuo5nU8+q5ldAZjZr5YuIi6xyuvDFh1mZcvL1cOP7x8OWUjswDTsgMHB9MaUE1Lt45Vy3FUHwCDAyeEfArA/QCqhJB1AP8ckw/RglL6B5h8xftHAJzD5IOzH42jorqWwH2nstAXy1wKA4QrhZ9yqoRXAaLKc9f1uNbHj7xnkX1t0ceoePuiKKWOs8MzLRtbrS4y+QXm9hE1+CAHxCMLCxdR9xiGgcXFReYyvXDrF4sui/AVxJWuJbj4csrWjDasy6Zv2XHrl6gtyuhWq1FXUn8/RHorSuljEdcpgCeV1SgEY3OIkwyN6W2oMKUIG0nITuWCFCBs5OKuqzUwuRWY16i8iFLqoOuquMoaTfztTuKAKx6+eA0+bq6C7nFzNRgMhMv306+oUbEoXyJcBdnhKc3GekDZcQ2oZG1RRrdk2jgKU00nKwuWeEq/hopSCj/lVDGVC1KAMGNw1zWVLilzkGHwvjtMqf2uq+SKpEu+nSwLX3HMoNzw8sSyjOC9Bzgc7fKjty8L1ydIv8KcTFwdsBdhdrg5yKOQ8W8r0aWZKMjaogxXccaBz5QD39zcjNzwCWooXqUQ6X15p2h+cCtwt35FmYMMq7Pfu8Nk9V4XHan4Tf8zRgM0W2V2xEEdiurOLognlpGp+57tnnmIq0uXr+D2t50R2gyV1S+VHbAXYXZ4/s0LuPmm4DJkZ0YOeJeX/OqhgisWvyWKmXLgmUzmyN9YlZpXKXh7X5EpWhCcutq9LIB41wVVvFtkpBI0/b942cYNJ/kciLtt4+rsVLWBl6vFfE5qM1RGv1TLxuIwdS2BciEv3SYskVK8y0t+UMGVn99ShZly4Nls9tDvKpXaC97eV2SKxiqvqqmc3/0qliBERipBfB0rFaSMO8zAREbm7oNRKpZqvFwN+j2pzVAVo1UVOsDjML12rKIs1vXrOLiK0itZecMwUw681Wod2rGPU6kBvt5X1gj8lMCRV8VULmwJQFWHxzNSCeLL28asXEW9V2Rk7n1GJCzTD26uNlotHD+1KrQZyoooB+O3Ts974pnHYbK0sUhZbojyJcJVlF7JyhuGmXLglUrl0O8ijSSzPhpWnowjDHIubnllp3JRkTiqY99ZNo79+PK2sRd+TrVv2pEbiyJTX+8zeyObex8kCpVKRWgzlGcG4fCV0xN48G1l1BZ0383pWl4XXoLisUV3G6uIs1a1Gcoqe9iehp9eRem0DGbKgXe73UNHS3kbSXZ9lCVCQ8QRuh1F2xjjjR0DZyrZI/K6wdt58d4vuxHI6pS8fIXJDBzl6pNnN2HTw6dN/d4r0tnzPGNaNuo9E8+da2LPtJn1y5GXdzOUFQ5fmVQCZ9e72OmPcGxBD6ybTJghqy12u13o2dyEr9eb2Bux88VTFi9fQXYYVicWHYnSaRnMlAP3S4zO2kimZeN8w0DbGGMxk+TerHE7tLhGq21jjLX2AM+93kRpPYn7ysPAZ3g7L577ZTs6Ga6ikt8fCrPUCEYWZWpPkREZ6zMOX1s9ExdbA7z7ZIE9cmlf3rjCRB2+tnomKIClbCq0bjJLNay2aAyHB3yttQa48wQ7X0D8XHntMEz/WXQkzg86zJQDF42ndAzMaZjTpQxK2STXuhjvejOPgjlK8MaOgedebx44pGypGvlcHId8ZKISRNeaHb6i2thtMLnU4YyLUe3pjVZhaSMWzhy+ytkU1loDNPdGWF7QmfRrZWWFmTMRx+Xw1eibePZbb412g+qmak8kDJliFd2NNsq5FC62BmgZk1kB6xIoq36pssMo/Y/SkXkc+D6ceErehnEMbDGTxOlSBg/eWsaZcvjUyO95Focmc/z2TCWL0nry4Fmj3QBKbFOvsPDGONYYg8Dr/L183Vce4syNN4aW4TYY2XVhdxuJjuzcfL3nZAEP3VpGNX90ndkPm5ubyFaOR3Imlb5VS+DEYgaP3bnCxJWfQ1I56h10Giik0+gOLdx1qoCHbmHniyffiyo7lA1ImMeB7yObzQo1jDfJU5TzljkwIXv81u2Q2jtsX7MOc0gq84SElS96YMLLF9X4llxk1oXdbSSTXY93ecqtW9lslokzFbHaons0qju8hVwOj65Whfhi1S+VdigbkDAPI9yHrutCDaNi/Zf1eZE4UW9dD6JDAhLBs+Z6mUaeENkDE16+8lk99o92+LWRrINk4ctXt3SdSb/CHFecaRaAGDo8nS3UV8YWZc9OqAhIcLi61j/oMDV0Oh0cP7Uo5CBl139Zn/cqGCD+pZdOp4NSqXTobzy5XqaRJ0T2wIR3Tfv/PftNXKKG0OZpEFhymFwtrvb22zhKv4IcVxwnT1lGvUHtzmKLfnrtBxlb9OPranG10WCTVwQz5cCr1apSB+lANmeCF24FY4kTDUK1enQTkyfXS5jRi47YVOTj8MLha7tnYtvOIp9WlzKANYdJHFx5n/fjKufTxkHwc1yq0yywjnqDZpostuin136Q1S0vX1eLK1Z5RTBTDrzT6SCfzytzkIC6nAlBkJnKOfKyvC9oVOL9u8woJM7UBY5sFc3EFVMXmvb6gcdoVXIV9LyXq4ZPG/NAdsnOC9ZRr1+7s9qin14DYtkeeSC7rMK6dOnlKkheFZgpBz4ajY78TbZR4sqZ4EBmKufI65VFRqllRiHTSF3wncsZ3Fc7JjXtVTWjkh2xseiWn07zQGZGKpsbx9vurLboJ7NMtkdWyNgiz9KlF7JtHIaZcuB+8ZSya13TWPsUncqFxQiLKrXMiC3OfBwOTh4/jnRafNqrckYlu3HIwldQjLDoxjfrKDiO3Distugns2xnKbo5yVouz9KlF/M48H0ExVPKrHWJKqw7S507FwcLWB0ha4wwD2RGbDJcseTjcGR2t7FsWKLMjEp245CFLz+dllm6URFmJzNAYLHFvcZRmWUHB596aRON/gjVfAqPvXtFOV+8S5duzOPA98G6jsSrDLwK2zcnOTgGIxvru0OsltJIawl85K4V5HWxRPF+yOfzWIxhhiCzhyBi3N58HNtdE4uZpC9f3jbm7TRUz6hkNw6j+PLTaW9OjvM7Bm6OyMnhLk8mzE41/MohPjLLjPw3dgf48loHWoLgQtPAXScL+I4aW85x1nJl6hfX+jcwYw5c0zSm+1RvfrhhWjY+eXYTL13pIqUlMBxZOG/ZMMc2AOCj95xgVpwoR6hpWqyyAIfzP6Q0glxKfRxxXk8gQYBGz4RNKTa6Jt5oGiAEePzuw3z5tTFPpxE3X8CEs5yeQL1voppPSTk/P3kdvlp7I6zvDvH515t4MSInhxssfE2DJ3c5jb4JSid/C7JjkcGBadn4i2/soLk3AiEEBMDnvrmDl6/0lPIlWj+A3W+JIJ5Wiwm7u7vM9+pa4iBe1bRsZXVoG2OMLIq8rsEc29ASBMORjbyexMii6AzGysra3d09WKqJy8h0LYGH76hBT04SQz39Sl0pX6Zl4+lX6hhZFAu6hltrORgja5+/o3zxtLFfWdu9SeIgZ3M1NlCA7P8rA6+8br5sAKcW04dycqgGlaw/K75wroVnXmvg0y9vodXpKHtv2xjDpsDJYhrZVAKlTBKVvK6cL0e3RGxDRqejMFMj8FqtxnxvHEH7AA4iG25EFnqS4OF3VPF/v9LAyKJcCbKcOoZtvJQq1di+helG37Rh2RDK0hgFdx6avmnhg7dXkE4mYI79+Qpq4yiu4mrvIJn2RjaqeR19U44vr7xuvnYHk1lR31STk8N7bZp8uZec0oUlrrqGwbHHM+UctASQTiYwiEjY5Yc4ueLxW7yYKQfebDaRy+UCr7sbgWWdUia7m3vq+dF7TihLqOTGxnYD3aEWy7cwRULtVCTGOr6YweN3B/Pl18YsXKk+pOEtn/fwEitXXnm9eXtEvwIUxVmcfHnh5Wu8twtUisx1DYPfprxqW5TlKspvyWCmHDgNme95G+HhO2qhRiarNN5DDSoSKnnfkdGI0kMaDkRC7VQnxgriy6+NWbiKa1NO5PASD1deef3eLeJXoziTPT8RhqgDOVtXLnPVNQpe+1Nti7LhpGF+SxYz5cDDpiLeRtgb2aFGNs0RCCA2iltZPoZHT+lK0wYAYqF200iMBbzVxrwzhLg25UQOL/HkCfHTadHNPB79Yo3Z5uWR5UCOV+ZpRcR468mqX7LhpPMllH1sbW0dxFOyKGyYIcQ5AvFC9Ai6I6+qtAEORAxmWnxtbW3h+KlVocM4MvHLQVDFVZAOuHVaFKL6xRKzzZIxkOV4uRtemYM6k7gyLIrMQGXCSVW0cRBmyoE735VTkZMjrhGIH0SPoHu/oyfjRGWP40+Lr4WFhVjTG7Bshsrm4/B7JqjzVfGtRFUpDnj1S/R4uZ/M7rrGvcGqSr9YTzXH9T1MYMYcuANVCqtiBBIE1RkOnfqKOFFVx/FZ+HJCN3lHTg5f1KZYmvJ6dtR1FVypXCaIIyOkU2ce/ZI5Xh6GuOzQqUtcfAFqljh5MFMOvNfroVKpxJaTQ1VmN1X5OBx53RDpdOJa7/fylUslhBTYzdcq6eCHyuWprmezXpdB0Ei+0+3CSheY9SvujJA8+iV6vNzR6yDbkt00dN+rOt+LF25Zg2ZZfnasCjPlwJeXlwGoycnh52BU9aiiUzSvcjryhoGlMxPt8KKMxcuXqAN0P7c5zAnzFYUoHmRHZix8edPV/l0jgdbGNrN+xZ0R0oswTkTtcHl5OdQWZTcNHcSV7yUIQVyx2LEomDSUEPJ+AL8DQAPwh5TS3/BcvwHA/wGgtH/PL1FKP6u4rqjX61hdXQUgH7oXlGOCpUeNgogj8FNOt7xBYN2s4jW0QwmoUgk8eIt/Aio3X6IO0P3cKc0Q5ktk34PnOk99Hr6jFpnkrG2MkRzuIp+pMOtXXJ1xEFg447XDer2O9NJyqC3KbBo64OVKduM0iCsWOxZFZOsTQjQAvwfgIQDrAL5CCHmGUvqa67ZfAfBpSum/JYS8HcBnAdyourKEEKnn3Xk/1tqDyBwTosbC6whMy8b5hoG2MT50GpJVXhYj4jW0gwRUyQRevNxFY2+E5QU9lmyF7uf2mjT0OcfIRpYtvNwRFpYrOjLzDg7+5GubsGyEdi6lbBJ6UkOd46QlD8fujJlPv1IXWtpyHJrK0SohhNsWAbEkdTxcqVi/9tMfWb8VBhaPdC+Ac5TSN/Yr82cAPgTA7cApgMX9/xcBXFFZSQflclnqeadBz+8Y+Pzrzcij4zIjMlZH4CiOo8inS5mDI+ZjBnlZRw2iyw1bPRMEQDmXYnKUog7QeW6PBK8VetPS5lIJrmPmPEYqszyT0gjMMWXSr+9/xw0wSYq7w2NZXnJkTRBgZEXXJ+h5FofGw1e5XOa2RUdukYgg3mU8kf2PMPll/VYYWBz4SQCXXL+vA3iv556nAPwVIeRnAOQBPKikdh7U6/XAOHBW6FoCN1eyeHE9ydST+61bqoxPdee+OF3K4MFbyzhTnkwlN1zy+oHVyGSWGxp9E8++3sSeyZ9fwimbh696iMxuI+ubFj70jipSWoLZmFmNVHZ5Jpc6POIN46y905DW6ShZRXKq8Dg0Xr6cNua1ReBouKEqvmQDI8LkD9NpWbDU0m/8752EPgbgE5TS3yaEfDeAPyaE3EEpPZS6a3t7G0888QSSySQsy8IjjzyCJ598Epubm8jn89A0Dbu7u6jVamg2m6CUolarYWtrCwsLCyCEYG1tDeVqDc+/cgGDMYWVXsC9VYqlYhGWZaHf72NlZQWbm5tIpVIoFotoNBooFoswTROGYWBlZQX3lYewSBLVUh4b65ewtLQEwzAwGAwOns9kMshms2i1WqhUKmjv7uKliy1s2HkcT/Rx141V5DJpdDodFJfK2NppIUVsnDx+nFkmalOskg42hzmcThrIDoDxsIKNeh2JRAKNRiNQJqrnkTA6OKVZ2Bzkcf7NCyjlsygUCtjZ2TmQaWe3D2OQwKlEHz0jgc2GDjqY7Ix3u12Ypnnw/mw2C13X0el0Jh9j7XXwDyomsqUqjHYDu61mpEzAJNIgqJ2GozGanS5uOHUCO9tbh2TSNA3b29sH7bS5uQld11EoFNBrNFBNUowHXaxqNhZTVexsb8D2tFO324UxHCJTrGLQaWAhl4Ou6+i12yinADLYRVmjyCaqWFtbO9JOFzfryBhdJPRFpI0WLm8lsJhOotfrYXl5sjdBCEG5XEa9Xsfi4uJh3du4jO87lkQiswCz18Zedxdtl+65ZRoMBtjd3UW3v4evre0c6Nadpyso5HOHdG+3PzjgzNtOnU4Ho9Ho4P3pbA615BBksAc9vYh7awTm2MbJlTI21i8daqfl5WVsbm1jYFEcP1ZFe6eB7MICljUDdDBAKl1Ct34Fo47ua0+pxQqyRgP5ZArtQQrn37yAk8eqgfY0GAzQ6/UOdO9Hb1/GpctXUFzIY6+7i40AmdztVKpU8cVXL8IcWxinF3Fv1UaxUAAwiexJFyoY9VpIaongdvLY0/tvXESnb4BYQ9DxCGvrb7WT2568Mg2QRNZoIKkXQIwuzr9p4MzqyQN70jQNa2trkTKF2VOgc446p7/vkJ+ilL5v//dfBgBK6cdc97wK4P2U0kv7v78B4Lsopdvud73wwgv0tttuCy0vDI1GA9VqFds9E5/5+vbBSOzD7zwWS6/sRVC5sutnpmX7Tgsded33uWWTHYHHyRXgz1cxkwyts1dmP1miptBhvMg8HwdfrDotGp4ps/4r+3yUzDKIyxZZ4dYFIDxaTVbes2fPvvjAAw/c7XeNZQT+FQC3EEJuAnAZwI8D+AnPPRcBPADgE4SQ2wFkANSFaxyAfr+ParUaemJMdeOxHMhRnYzHK2+YbKxHzKdxipLlgEkUV26ZebhyQzZ8bJp8bbd2sbhUDp3Ci+qX7PokAtb8AAAgAElEQVQv6/NBfAV1dlFt7AfWw0vTyHHEe85DRF5WRDpwSumYEPLTAD6HSYjgxymlrxJCfg3AVymlzwD4HwH8e0LIP8VkeeVxGkMKLufjoEGOS3XjsTaUqgNA3rJTi5PDDroWnGOCx8jiPLTC2sFEHdeuHJOPmVVx0m5afBmDBM52t0KdQBz65YZqvqI6O96P/PIMXqaRs4f3nMdV/6jxfkz3Zz1/+1XX/18D8D1qq3YU7o+D+jku1YrO2lBeZQLkjtQ6Cps1GjCyVeYcEzxQreisHUzU6HaVdPBD99zOzZds/pIoqObf4etUoo/1YTLUCajWL0A+Nw6LbEHZGHuNDZy58Ubp9/n5gDhmT7KpC+YfNd5HKpUKvS6j6LI5E9zKJJs10FHYheTh0D2VRiar6DJKHTa63RsQLr5U5i8JA+8ygV89/fgyDIJCli/6Qla/VOXGCUJUNsYTiQFOrdrMYYki8d+qZk8qUhdE+S0ZzJQDLxaLkfeIKLrqnAmyuRyc55sDHYUMe44JXogquup8HG6+0ukc12xgGmueDniWCdwI42u7lcWxpUVhvkRmT3Fz5qcLblvcGercYYkygxeZmbnM0qVTRm6hwFVfHsyUA280Gsjn88z3s/bcqnMmBDkzVqN3nj//5gXcfJP89JgVsnyJdjBuvrr1K1yzARVLGyJ88TjBML6sfgd6tcRVX9nZk+xx/LyeiEwT4NUFd5mrifB0CarTCcvMzGW4klkWZMVMOfBischlbKyjQtXrm07ZMrkcdC2B49WykPP+1EubaPRHWMom8b5bK745TILKvNp8pUYTZ8bKlez6rWNoO/0RbErx0XuOo5RVm+8m7F6WWaUfZJYJRDgLOjHMup7sLpMM86HPxG2PPEtQovrlbo9mxIxDBjPlwPcGQ/z5G/wn5ETCxuKAO/9DSiPIpSLWTU2T6/2mZePvt/v46qVdUAAv7o2x0x/h+GKay9CuJl+OzDJr6sxl7eeg2e6a+NrGLgYjigutAX79h29GXleXZyPsXt42DoLsOnEU2sYYbWOMoWWjOxiDEGCrZ6LRN3FiMcP0DqfM7X478r447TFurpwycnoC9b6JG9NUSSfkh5ly4O1uH92hHtvaXYzfHgUwUYSH76jhT762CXNM8fQr9VDHahgG87udEdLG7hCNvRGK6SQs20YuxnXOOEYUjsyOETf6Zizt4h5RnmvuwTBtZFIahmMblzpD3FZjSyzFykHQvTxtHPV+91F+1QeO8noCa+0BuoMReiML39juI0EInv1WE4/ducJVTpjMcSXQciNurg5AJ8fYU7aaTtoPM+XAbzh1AoVuS+nUCoj/E05u9E0blg2m5D088aPOlK26oKOaS2F5QUc+rYFSHNoIZQHLMlVcpzi9Mn/hXCuWdnHnoLm1mgMoYFOgkElitZjmelcYF1E8qYwR1rVE5ElXUfRNG6dLGSS1LDrGCJYNHF9MY29kcw8OKseWsd0zj3AyTTuMkytgol97IxvVvI6t4cJ8CQUAdra38Oi7VoU+5BBmRNOMZGCdvpmWjfMXL+NtZ25kktP93rtXF/HQLWUUM0nsjWxurkQ/0aYC7phZnqgY3s7EzVc1r+Pxu49jszfCajEduXziLTvs2H4UT6pjhKM4k9ngLmUng46VxTRAgb0Rf4Iz07Lx/MvncYkWj3AyTTtkLU9FQMBqoj9fQgEAXeePdGAxojg2Tdzl8x4yceqcMoYHp/REN2x59Z9FqeM0NC2VOhidsbSLaGfixxfL5qUXYVyw8KTrcqc5ec4uyHS8fpEcImvUbWOMvpVAPsP+iTZVsz3eswuq+Bp2ErHNJGbKgRcK0fGU3kZiMqKYNk1ED5k4dV7Ss1wOUsW6NIvTjOtot2nZ+NIVEztrb31iLKpdZDoTEb54nADLeYBMjj0s1lsP3rMLqnP2sOa79/JF0lnf1Lay4ZFR9eA9u6CKrx5djL5ZEDPlwHd2dkLTK/o1EuvoOo5NOVEFcOqcMlooZKvKc1+4ITJDkImrDUPbGEMbdpHPVJnjf6eR+8IBrxMIuqYiRljk7MI0uXLe68fX3VWgUDvmq18y4ZFhEDm7oIqvKL8lg5ly4EtLS6HXgxppGiGCDmSOADtwDH+zoWOlOpE5jjVnmWPoLHG1UYruNzqz9QWuDw/EOWrzQsQJ+F1zv2dnmGZySrL5OJy6TIsrr5xuvqrlMhYZnbDsoaNrga8ovyWDmXLghmFgcfHwdITFYaoaXbM4JFVHgHUtgTTG0LWEdO6LIBlUjW6icl/4KXrQ9ftOZaEvlrn4imvUxiKn7HuOJ63IkZ3K1AVxcsXqNP3sOKy+QbOYsMifa4kvHnl5MVMOfDAYHPpddc6EMLD0vKqPADvyqlpz9srw8B01JQ7JzziiOp0grsbmECdjWMcX5SuOLIfu97CkDlCdusANVcsEPE7Ta8dR8MoZZYvXGl+88vJgphy4N2ZWtcMMA0vPq2q65yAo/zkgtqTilWFvZCvr8LzGEcVF0HWWuOgo56KCr7izHDrvWUweBxCuX7Ij/zC+VC0T8DhN2dj3KFu81vi66vnArxV4Y2ZVO8wwsJQlMkILa/yg/OeiSyp+MrA4JBG+orgIuh4VF+3mK6cn8ODbyr65XmT5mlZMsiNvmH7JjPxZ+FKxTMBji47McSVdU8VXUOfFy9c8H/g+MpnDORd4G8q0bNR7Jp57vXlwCEEmbjjoPt4cE07jt40x3tgxcKYy+Sq9V14HspujLHy5M8+5v7DOGwsbxoXf9SCZHTh8ZVIJnF3vYqc/wrEFXXlGOd5nRJ2RIy9LhycTfRE3Xzy6ldTTuNwZCNkha1myfPnZYxCi+IrSaRnMlAPPZrNH/sbaUE7PutUzsdYa4M4TBa6RFauB8hqyO8HVWnui1KX1SZY3P3kBuREG64jbGYUkCDCyKNPRf+87RBxakMwOHL62eiYogKVsKrJeInzxdnaikRzZbDbW/B/T4st5jkW3vrRu4KIxFLJD5x1x5S8Js8ewQVsYX1E6LYOZcuCtVkt4N9fpWcu5FC62BmgZk5EIy+iC1UBFDNlp/Dd2DDz3evOQo9wLkVfVWqwf3KOQ3cEYepJwhfbxfuzAbYxRbezw1eibePZbTebj3H4bYVFOgJVjmeWWRrOJL53rM+sMr/NSwZdKh9k2xkiYPZRzFW47dOrCY2OifPnZI+9s0oGM34rCTDnwSqUi/Kx7mnPXqQIeuqWMap4tTzargYoasq4lcKaSRWk9eWgaluWU109ZZdf7S9kkHr6jxpVThSeHidcYWdpY1xI4sZjBY3euKF/njGt/JAjJXBHdjT6TzsikDRDliyUclHfGaaULGIxsbjsE+GxMhi8/e2SFlxMZvxWFmXLg3W4XejYnNBoQWf/lPQQgY8h+9dvpdplPcPkpKyAWreJXl6B+iDcfhxt+xjjmkFnFOqfbCajMqxIGN2eJscGsM6qPwrMgrEzRGed9J3Ski1VurnhsMajuxUySyX+ILiP5cdLl0GlezJQDN4ZDqVNjvOu/vIcAgu5jHaUcmeaHJPtnyflCKYQNXoYrVr78jHGjYca6xhlULjCdvCpezu4rm3j0XTcwOYq4ctCEIcxhivJljUZCXPEeyPHWPZdKcPkPVhuIskNVH+3ww0w58Eyxiu5Gm/vINg9kDwH4rbWKdjpB8aM8OV9UHNQJgkg+Djf8jLFybFn50W7WAznTyBXi5SxbqnLpVhw5aNzgObwk2qGwxkWrsEV33VWHhrLa4eI8DnyCQaeBQjp9RGFklFhFzoQwyChNUPwoT84Xv0MHMs5IRa4XN7zGeHH9ClR+dYnnQI6fs4pbv4x2AyixT6/d9VaZYsGpK8/hJdEOJSwuOk79mpZte3VobX0eBw4AWMjl8OhqlevIdhhU5kwIgsyozhtiFjVSDHJKMmuWbkwjdUGpkEehaysbBfN2oF4OZTpgFv1q7zSYZfFC9YxBRFaRDiUorC5u/QrqoHlTBvDmXpqHEe7D74MOMkocZ86EgzpLjOoSyZTUGjOrvIAcXyrDGXOZNB5916LwKFj1jErmeRb9kvmgg4oZg8oRL6stBsk8Df2SGdCIdjAybRyFmXLgnU4HpVLp0N9klDjOnAneOoqM6rZ3WoHLCSKdTJiBxc0XK1dOG4vwFceMSmbUxsKXn047ssSpW04ZKke8rLYYJPM0U2MA/DMO0Q4mSF4VmCkHXq1Wff8uqsQyxm1aNj710iYa/RGWskm879aKb04OP7Aq6onlGgrdnrI1uyB54+aLZ6Tj18YyYYkqZlSiozYWvvzkdcpoG2OkNIKP3LXC/J1O2TA72REviy2G2bFMLqFcKoEHb/HPjeMH3g5DtIMJklcFZsqBdzod5PPRn6DiIVrUuDd2B/jyWgeETJS0uTfCSiHNdfoySlH3el08+i6xwyphZctkURThq22M0TbG0BIEO/0Rzu8YuDkgv4RfG7PypXqTKkgWmTV1L/zkdfi60DLQNy3YNsUH31Fjckw8TnAafPmV0dhqBNoxr37Veya2eiaK6SRevNxFvW+ikE4ydXq8HYboAIbVb4lgphz4aDRius8hutE3Qan6epiWjb/4xg6aeyNQEBBQZFP8py+j7huNRkrX48PqEidfeT2BtfYA3cEY/ZEFAKjkU76dXVAbs/CgegPaD+5cGSmNIJeSK8Mrr2nZGFk2Egmgb1rIpTS8ut3H3tjGckQSKgeiYXZx8KVrCTx8Rw0X20PcUEpD1xLMdhwF07Lx3LkmLrYGGNk2CICNronzOwYA4KP3nFDGlej9ALvfEgFTixFC3k8I+SYh5Bwh5JcC7nmUEPIaIeRVQsifqq3mBLx5db9wroVnXmvg0y9vwbRsZfVoG2PYFDhZTGMxncByQQelUD6KqRxbxnbPVFr3MMTFV9+0cbqUwa21HPIpDXoycdDZeSGTO9lZC43LGQFvOSQ9STCyKJ5+pS7FlVteZzngmdcayGgJvPP4AlYKOjRCUM6lAjkTxTT4Mi0bT79Sx/PnWwdcqcqP3TbG2DNtvPtkAWfKWZypZLFnWsjrSYwsysWVadmRtsZyjx+uaj5wQogG4PcAPARgHcBXCCHPUEpfc91zC4BfBvA9lNIWIeRYHJXlyavLMtWVyUdcyiZxppyDniR49J3HMLIhtI4eVL5p2Xj+5fO4RIvKDmmEIc781w5fbWOMQiYJy6YoZZO+nR1rjLAfX3F929GLvmnDssGdodEPbnndbdA3LXzoHTUAwLOvN7FnsiWhchCl29Piy0+v9hpH21g2B81KIY0P3F7Bf3h5GyMrWL/8wMKFDF9XOx/4vQDOUUrfAABCyJ8B+BCA11z3/CMAv0cpbQEApXRbdUUBcK0jRa3vyTSIiqlnVPltY4yOnUQ+Hc8HBXjD7WQOALn5yqUSoYmxgtqYha+4OiCnfN5wOxbO3PJ63+skeXrs3Xz7ICy6PS2+8nriCFfE08Yqc9B89J4TSsNree4JQlzr3wCbAz8J4JLr93UA7/XccysAEEL+MwANwFOU0r9UUkMXNE0LvMZzBBi4OomBeMovZZNIp5Ko+6RxVXGakifcTsVozc1XGG1BbczCV1zH4EXC7Vg5c8sb1AYsuuaWk0W349zA9MruzWbpbWOVOWhUhtdG3cOqW2F+SxYsrUZ8/ubd6koCuAXA/QBOAfhrQsgdlNK2+6bt7W088cQTSCaTsCwLjzzyCJ588klsbm4in89D0zTs7u6iVquh2WyCUoparYatrS0sLCygXq9jd3cXy8vLqNfrIISgXC5jc3sbZ+sWhqMxiokx7n/XzdjZ3kIqlUKxWMTG+gaKxSJM04RhGFhZWUGvsYHjiQFawxRWEwMkRgvY2mphMBhgZWUFm5ubyGQyyGazaLVaqFQq6Ha7ME3z4Ho2m4Wu6+h0OqhWq+h0OhiNRgfXvTLVd3awZ1o4tXIMvcY2jmljGEMbq4kRMijj0qWtA5nq9TreXhghU8gDowHoeIS19U0QLYkXNkdIDrugeh73reYxGr5VZ13XUSgUsLOzg6WlJRiGcUSmAZLIGg0k9QKI0cX5Nw2cWT15INPeSMeGS6Z2fwBjkMCpRB+7gySubGsgpoFSpYqN7QYyGsHK8rGDdgKAXq93pJ3q9ToWFxdhWRb6/f5BnZx2ajQaGAwGGI1G6O3tIVOsYtBpIJtOI5PLY5V0sDNM43jSQrd+BYvJ44fa6b7yEKl8EWRkYGP9EirHlvH8y+exa2nQdR131RJYrtUi28mre1YyAwy6OJUYYWuQwxsXLmIhnUS5XMbG+oavTAObwByMcSphoDXQcekKBbHMQzIVCgVcunQJmqYdaqe9xiZsDt0rLpXxxW9cxng8gpku4Z7yGMvaGP0hsJowodMlrK9vH7Gnh1ZTaHYMnDq+gq0rl7nayWtPbt27uLENa2BjWbNADRO7ewWYnZ0DmS5duoRUKnUgU+XYMlZJB7sDDTVdR7d+BTnwtxOr7u32egftkNF1FItF3FceQsssIAULG+uXfO3ph88U0drtI2EPYZomnn/5PLpWAkk9g/fUCI5Vq77t1Gq1sLu7y+QjgmQKdM40IuyAEPLdmIyo37f/+y8DAKX0Y657/gDAlymln9j//fMAfolS+hX3u1544QV62223hZYXhr29PeRyuSM933bPxGe+vn2wdvjhdx5jznYmmjmQF0HpXsNGcY68bojKGlWXMFlVpqqNwt7eHpLpjO+7/dorDDJ64dYBkRmI3yjU79N0fm3MCz85i5lkrNElbvDy5SfztGxR1do/j27JtvHZs2dffOCBB+72u8YyAv8KgFsIITcBuAzgxwH8hOee/wTgMQCfIIRUMVlSeUO4xgFoNpu+xi06HfROt+Lc2BE5NNFsNo80vMhUjnd5yQu/+1UnUnLLrJeOKTmQI7Ksouo0p/eZoPb3a2Ne+MmpKvxUdDM0jC8/madli6rW/nl0S0UbByHS01FKx4SQnwbwOUzWtz9OKX2VEPJrAL5KKX1m/9oPEUJeA2AB+EVK6Y7qylJKuTLx8UJV4/IkoAqD3+zIaxxA+EiYN8NcELz3h8kjkyCIUqpsfdbPkYhuhoo4RPczQTKN90PTeEaZsh0yK2Q2Q8P4ipr1h71XVA6VGQ4BPt1ikVcUTLWnlH4WwGc9f/tV1/8pgJ/f/4kNtVoNiRR7Jj4/hDkXFRthYQ6T18hqtZrv392yRo2EZQ0hSPYgeWSXZz70HRWlDsmrF6KbobIIMvgv14HWlW3hpRnRDpkFcW2G1mq1SJtS9fGKODMcsupWkB2rwEydxNza2sLp06el8peEOReREZsXsh858JM3DFEGJJuAKoov2XAr7/3rG5u4/W1nIrmSieEP40Om84iqk5/Bp4Yd5DNV5s5VtEOWjbMO0h0Rvq5sbuJLzXSoTfHONIMgmu9FJV8sdiyKmXLgzo6s6GjD3ZhtY+ybk4N3xOYFr8MMUxSW7+hFGZCMQ/Ly9caOgTMBOUwcyCYIKhejv94ddwy/iH6JJFUqZZNAKou+T6ho2DO8HbLKOOug+7j4SmXRHY4ObKrRN5FMJHxnebIfr7gW+Irre5jAjDlwWbjzWKy1B/j86028uJ4MbSBeBeBxmKo2aqIMSLTD8/L13OtNlCL4kt0g7bZbofeblo3zDQNtY8x9EtLdWca13JBJJvDi5S4ae6PI3CW6lsD33lRCIrcovDnKsuSigi9V6+oAkNc1FNKTj3bk9ASe/VYTeyM71AZkAhV47LFtjDGy7KnNcmQxUw681+uhUqkc/M5LmNOY53cMfP71JpNCi0YgsDR41OjeK68XMpuFPHy9sWPgOUa+nOdEN0jDZHanWV1rD3C6lGE+Mi2yNs/DleNgtnomCHAod0kYF4O9Pk7X+NKN8uz3TIMvXq4Ge308+q5VdAZjmGMbz7zWiDX1Mwtf3hlUTk9wzYzC+IqyYxnMlANfXl4++L/MNOfmShYvrie5RtU8X65hRdSowi2vFypiuVn5OlPJosTBl7tMXq7CZHY6vMVMEqdLGTx4axlnyuFLOt5nRT90wDqTaPRNrtwlXnlV6tc0+BLhanl5+cCmTMtmHll7HXEQVyIcHs1DU0VKSzB3FmF8hem0LGbKgdfrdayurgKQP36r+sMEIkoTVQ+3vF6o+pqIinr6Icqwg/gKk9nd4U2SiYU7I9HwMVGudC2BE4sZrtwlbnmDOFOxYRvFF29uHAciXLllVm2LogOVoDw0rAjjK0ynZTFTDpyQt071y4YZiawLBymr7KZaUD3c8gJy8azT5ivMsMP48srsrYPM/oLshw5Y+eLhyi2vH2fFTDL2pGsyh5dEzgN421ilLcp0vrxr5W65wp4P02lZzJQDL5fLB//3EgaoP9rNOiqJK7ObW17ZeNZp8xVm2GF8uWUOkkNmf0HUmOM4GWhaNpApwLTsQP0KGzSo6kxkDi8FOa4wvqLaOAgs+iUTNsu7Vu6VK+h5UXlZMFMOvF6vH4qnVBFmFASeUUkcmfBMy8aFy5t425kboWsJKYfkYNp8BXUwYXy5ZZaB7IEcrzGq7qQdvrJGA0a2GqhfQTMnlZ2Jaq6AcL68dswCVv0K6nxls3fyZHr0QkReVsyUA19cDI4RVu1EeUYlqkdszrN0YOFsd0sq30sQVL+Pp4MJ48stM097xX28PC79SqdyofrlJ4ds5zuNo/hhS3ZZgbhoXv1iWa5jgV9SMl67CfNbspgpB25ZVuA1FU5UZo1Z5YjNefZYEth2PavSyFSMVOLgyy2zs4QQVZ9pHC+X1a+g5ThzMEYhk+OKvojjdK1Krpw6By3ZLWsGPlBaYuYKEJdZdubkfX5vZHPbYZjfksVMOfB+v49qNThmVsaJqs6ZILNp6DwLY4BCdoEr34voxqSKsEQVfDky51IJ5vrEtQfhhah+hS3HnX/TwM038Y0Kw9ado9p+Wlw59fRbsqODATdXorME2aRrfs/zdHamZWO7tYvFpbKSmY0XM+PATctGarFysOHDAhWhY6LKLbNp6Dy70y2gUshxL710h5MTbg++Lfo4twNVYYmyfDky89RHdkQquj4qG2qnawmcWT0pZNheJ8LaAcsunakIaUylS0JhiSKzBJFNVpbnWeCUYQwSQsuCLJgJB+4QkdlrYCe5hI/ctYK8Hl11HvLjyEIns2moawmYnR3oJfb1woPj3KkEzq53sd01sZhJMvGlIixRFm6Zed4vamTuk4oJAvzD2ys4vphhfp613DBZVH3wlrXDU+GQukP2fC9+5XbrV4S4EgXvJivL8yxwyjiV6GN9mIxltjMTDrxtjCdGtmfh670uAOCj95xgVhzVcaAiEFHMVCrFVUZeTyBBgEbPhE0pNrom3mgaIAR4/O5wvnjlj4svR2bn/Y2+CZZ0yrxG5uQIaRojXGgauNwZ4uubPXzX6SIee/cKlxMXDbUD+Ns4CO68NSmNIJdSE6fuRr1nYqtnophJMud78St31AkfuMRphw7iShvswLRsjCwbuVQCxpCgkFVfBjAjDryUTSKlEVwwNOT1JEYWVd6bxZ2IhtchAUCxWGR+v2nZePqVOkYWxUJaw63VHF7b7iOvazDHbHyxGnacSaG8Mn/hXEtp7DVweOR9vmGgb1pIJBLQEgSN/miqusXTxmHQtQQevqOGT57dxMiiePqVutIpu2nZeO71JtZaA4wtG5pGmPO9eBEls+oN1aAyeO2RFd6lzHvftoIT1dL1uwauawl85K4VfO4rLVwBe0IeB1HOOY5DGkHgcUiNRgP5fJ7pve68F33TwgffUUU6lYA5pkr5ipsrt8xxbbi5uTpTzmJk21hrDZAgBNV8Sum6cBRfPG0chb5pw6bgzjrIgrYxxt7Ixp0nCtjpm8inNQxGbPle3DAtG2tXtgJj/aed0S+OAYI3r4rRbUNfjucwz0w4cADI60l83+2nQNN5ZflLHExrZ54naqFtjJEvsMePeqeExxfTePzuE0rzvfDIIAr36Ix1miuaObA7tFDJp/DwHTV0BmMA4M6BIcuXzAhcJH+Jik3IlcU0Hr6jhr2RLaRbdkCs/zQHUgCbLovw5W2HWnkpjuoDmCEHDgD2eIRjZTU5E9yYxnpY2xgjryeYDMxR4hVtD//wPUXuTSK3UanKMeEgbq72BkOYrm9ERq2HymQOdL+XZVPcD6J8OToxHgxREihXJH+JbM6eo5zx1fkg1l+jh843eK8H5c+RHZnzdngyGTzdXLV3GkL1ZcFMOXDDMCLvERmV+Cmnqqmc30musJGLW4ntwZA7ayCvw+blK85NJtOycfZCA5fo6JDBxJFlUXSdVQVfbp1YJR1UazVuHkXyl8jOnmT1661Y/yEK2cIRrsI6O9mRuUiHJ5vB07mXxW+JYqYc+MrKSuh1maxqbsJVTuX8TnKFKUFQvGwca4OifMW1ydQ2xtiw88in2Q0mjjw0QVDFl1snNoZ5oWUokZnQNLly3ut32CvofEMQlyKO1CuTSIcnm8HTQZTfksFMOfComFmZrGos72FpPJEZgBt+8bJxrQ2q4ksUflwdT/RxyUwyO6WoEe61yJdbJ1YTfSY5VeQvmSZXQIgdhZxv8OOS15H6ySTS4Xn5AsQyeKqK9ffDTDlwXQ/e8BPJxxEE0QxwMjOAQ3LuK/F4Nw1A7cZhHHxFlcOzdv3uG5bw3mKVa3kmbIQrw5dsZxxWX0cnhp3EgZxBnKnMXxIXV34I4svPjqPqzONIg2QSWfpz8yWaRIxXXh7MlAMvFAqHfledj8OBn9NlaTzREVqQ4TryqprKxcUXSzms64ulxUUsSDoQFXyp6oyD4OhEjy6GlgdcHScrk9jMuT+IL68ds4DHkQZ2HJIzS9G8KiLysmKmHPjOzg4WXKkoRfNxsCint7FZRl8iI7Qww3XkVTWVU52/hLccN4K48raxH6LaTwVf01pecuQN4yzO/CUqllXC7vfji6WNwxD3RqWypesAACAASURBVHsQX0HvjeJLVt4wzJQDX1o6HE+p2mGGgXWzildxvIbb6JtIJibTdbe8KqZyoo5AJs6aJ/IHONrGfnVhTUIkw9e0uHLkDStPxiH5RUH1TfvISFlmWYX3/qg2jkKcG+1RCeH83hslv6y8YZgpB24YxqHk6LyK7eS/aBtjodNqLEohs6GV0xN49ltN7O2fcPuB48Q3GbyocxHhq94z8dzrb9VJNM466D4vV9429sJtLG1jjDd2DJyphH/cWMUGVtQI1Inzf/qVOtfgwJE3qjxRh+Tl60++tgnLRmj94k5s1u3vYZDISEW9xLXR7k0It9Mf4VhEvpco+aN0WgYz5cAHg8GRv7E2pDv/xVp7gNMlviP5cYVauQ3XHNt45rXGQU++2zdxMuIZ3hEZL19bPRNrrQHuPFHg7vBYckx4efVrYzfcSZvW2gM893oTpfUkU3pemQ2ssPo7I7YEAUYW5RocDAYDrtwyMrOhlEZgjqPrx8sXb2f3tbUdXKJjoaiXuI/aO3xt9UxQAEvZ6HwvUfJH6bQMZsqBy8RTuvNfnC5l8OCtZZwph4/cHPAsu4gomOMoTMs+1JOvnjwR+YxMuWFw+CrnUrjYGqBlTEYiKpep/O6LamPHWN7YMfDc601mZxkXX+4R7u5gkgmwb7KP9CvHlrl0S+bUaS51eIYQlaI3jkM+IrH+DkTk521nh69G3zw0G2YJ/w06NTqPA9/H5uYmjp9alc7lUMommZ03IP/lFVZ4e/KN9UtYYIgfDStXRe6Lu04V8NAtZeY8Iax8+d2314iOmdW1BM5UsiitJ4U29lTy5dUr3hwhF9evoDvUmdaPVZw6FZmJhIU3iuQJ4Y31d8Arv8x+14nFDB67c0VJLqGrHgdOCHk/gN8BoAH4Q0rpbwTc92EA/xHAPZTSryqr5T6SelppLocgiMb/qgj3chtbJpNheibs4NG1zJfffTajzDLLSCr58qtHVJO7+Sou5FDoUqaOSEV4JO/IOogTGed45+kK3rtYZm43nlxCblyN1AF+ZbLasQgiHTghRAPwewAeArAO4CuEkGcopa957isA+FkAfxtHRQFgnEihOzRibRCZ+F/RONEgZLPZ0HpGHciZhgLLpi/w3pfNZpm54lnPZ+lgppFXxcvXD5/J4tF3LTJ1RF6+ALFw0qj6sRxBl9GtQj6HRUG+eGY4qs5P8MCvzIEVbMeyYBmB3wvgHKX0DQAghPwZgA8BeM1z378E8FsAfkFpDV2wjC4K6fQRw1PZKDLxv0GOS3S00mq1fHevWQ/kTCP3hWy8tPe+RrOJL53rK3NKPB3M1eBru9FEpVQSioQSDScNAs8RdBmugvTaD7y5hNy4Gh2en25tcMjLCxYHfhLAJdfv6wDe676BEHIngFVK6Z8TQmJz4MeqVTy6mlOay0H1cWk/xyU6WqlUKr5/Zz2Q46dM1xpfXiRzRXQ3+sqcEk8HczX4WqlVhWVTzT3PEXQZroL0GojXHoM6PNEOmjXFQZi8smBhg/j87SBAjBCSAPC/AXg86kXb29t44oknkEwmYVkWHnnkETz55JPY3NxEPp+HpmnY3d1FrVZDs9kEpRS1Wg1bW1tYWFhAq9VCKpXC8vIytq5cBiEEyBSQNRpIp3IwB2Ocf9PAmdWT2NzcRCqVQrFYRKPRQLFYhGmaMAwDKysr2NzchJZK4UtXTGjDLmx9AfedymJsDvGjty/j0uUrWMznMOj3sNFqoVKpoNvtwjTNg+ez2Sx0XUen00G1WkWn08FoNDq47sjU63SwlCLQBh0sJQkyKOONC1eAVBZ5XcNgr4/l5WXU63UQQlAul1Gv1zEejzEYDNDv9w/emUqlkFsoYJV00BzqWElSdOtXsJg8js3NTei6jkKhgJ2dHSwtLcEwDAwGAyyurGBtfRMmkrAGBk4lhmgMMlhbvwIdFpNMlzc28NL2CP0xsJQw8Q/uuBHddgvfW7GhF5Yw2N1Bt90CAPR6PV+ZFhcXYVnWEZmcdjLHY6xoFuzBEKl0Cd36FYx308jk8tjYbmC5VsZ4OMRgMDh4PpPJIJvNTkZ2pSXUW7tIYoyTx4+j19jAimaiOyRYTZhIWUVcudLwbSdH94atJrb2de+NS1eAwRi1ZALEMNDoLMDqt5lkyi0U8DevXUTT1lFIUrzrmI6Tx4/jvvIQFkmiWsrjyvolaGT1oJ38ZArTvfvKQ+gLJdiDPjbWLx20E01mUMimYPR6gfYEAJ1uF+lCBaNeCyRBsJSykRq0kNNzsPodrDX2sLKygr3GJkYB9uTo1pBqGA2GOJUYoDlI4+LlDaTo+IhMly5dwunTp4/IlEpn8KVLfRCzj3G6gO9eSYFa4wN7XFosoL/bwUaIjwjTvezCApY1A3QwONAto5XCC5sjJIddUD2P+1bzGA3faocge1pZWcH5i5ehGUOUUxkkjRa2mhkkx4Mj7dTr9bCzsxPqI8L8XqhzphHBuoSQ7wbwFKX0ffu//zIAUEo/tv97EcB5AL39R1YANAF80LuR+cILL9Dbbrstys8HYm1t7chubtgmS1Svut0z8Zmvbx98+ujD7zwWWxY+07K5p3Jra2uBUTfu96kYNVwrfDkyi4zswmSTOVbtfScAphEbC19+Oi0D3pBXP9ni5ipI5mnol1cXeMt02wnAbscybXz27NkXH3jggbv9rrGMwL8C4BZCyE0ALgP4cQA/4VyklHYAHMwDCSHPA/iFOKJQ/OIpZaZyceaY8Ksn79plWIywyA6589y1zNfKysoR2WTCEmXzl8iso7Lw5afTMmvuPMt1qnPjsHIVFBc9jfQFXl3gKVM0GdxVjQOnlI4JIT8N4HOYhBF+nFL6KiHk1wB8lVL6TGy18yAonlLU4GVC0WTWRlmVhidGmAdXi69PvbSJ7e7kg7j/zXuO+37GzK+NZcISVUB045CFL6+8Xr36wO0VbOyOcMNSmumzbzwcxMEXC1dhdsyrX1G5S1jqy1qmaId31ePAKaWfBfBZz99+NeDe++Wr5Y+wsDo3eBRTdHRW75nY6pkoZ1NoG2Oc3zFwc0RODneZTGGJhTwKXVu5QzpSTsx8mZaNv9/u4+8udtA0xrDtycbKE/eePCK7XxvLhCWqBq/Ti+LLK2/bGKNtjKElCLa7Jp569k0MxzYW0kk89dBNkU6ch4O4+QriKsyOefXLm7tku2tiMZPER+5aYf7OKWuZoh0eq98SwUydxGRNjO4oZqNvMuXj4IVp2XjuXBMXWwNcaBrQkwl8/vUmXozIyeGtY2RYoq7jB27OghD+r6XzIE6+nBHSxu4Q9f4IAKAlJsfN/UavQW0sGpaoGqq58sqb1xNYaw/QG45BCGBZFAuZJHrDMS51hritxpaIS2WCNlG4O4hcKvHWMofCDxzk9QQSBGj0TNiUYqNr4o2mAUKAx+8+odRmRDu8+Qcd9tHpdFAqsX/D+wvnWkpjPh20jTH2TBvvPlnAld0h9AQRym4YBtOy8eVvXcElWjy0IRQn4uDLGSFVF3TU8imMLIp0MoFaQF6VsDaOWuuM+5CGG6q48srbN22cLmWQ1AgGIwtvtgbYMy0spJNYLaaZ38vCxTT40rUEipnkoWWh+8pDLjsOgmnZePqVOkYWxYKu4dZaDq9tTUJQzTFV+uELpzwRvnj9Fg9myoFXq+wxs9P6ismpYhqg4Epg5EaQUrSNMbbtrFDSHxGw8CWa+8Lh6t4birj/TAkpLRE4owhq46g9B9l4bR7w5MaJ4ssrr3Oytju0UM3rePzu49jsjbBaZFsDd8oV/fxfHPDypS+IddBB713MJNE3LXzw9grSyQTMMeXKNMpStgxfPH6LFzPlwDudDvL5vO81kQMAoj2q32676o3QUjaJimbiiqkrX//2kzuKrzg/hOFGUBtHOc04O2yALXWB934Wvrzy+vFVysrn41B1uIwFUbZoD/oASkee4dUv73uPL2bw+N0nlCSg8j4rw1eY35LFTDnw0Wjk+3eRfBwqMge6G1AkJ0eYUuhaAt+5nMF9tWNHjuXLTHvDTo+F8SWjwDzrrEFtHOU04zwGLxI+xsqXn7yy69IsHUxceUJYbHFj/dKR50T0K0hneXOqs5QtE7ETpNMqMFMOPCieUiT+NywjXRzrgjx5JhycPH4c6bQe+g6VccJhfMUVoueFu429bRHmNGXi26MgEj7G2qGoiBFmycfhhUx8exhYbNFPZtEOhbezE7FDpxzRiJ15PvB9OPGUKvIlBClMXOuCPHkmvPJGvSMKvNN/PwQ5SNWdnbuN/dqC56MNKvgS1S/WDkU2Rpg1H0dQHVUkxuLVLz+Z4+pQvBCxQ3cdRWZGVz0O/FpBPp+XSl/qht8zKrO7sTqBMKXwrpuJLBOInh7zg7uucXV2jswq1mhV8SUcPsbQociujapayxZdghLRryCZVXUoInKqCKcM4iqu9W9gxhy4pmlKj0t7n1G1jqrKCWiadqS+vMsEqo9LR73XkZ+XL+d+R2YVSzYq+VJh4H4y9U0t+kEPVMyovBBdghLRL69e+0HlGj3PUpwowrhikVcUM+XAd3d3cfxUUUphw5RA1TqqKiewu7uLpaWlI3XkWSaIK39JWGfHw5f3/vvKQywtLSkztGnyFeVg/GRa73QwSuWlBgeqHJLIEpQIX7u7u8gvFrm4AsSWVESW4kQQxpWfHavCTDnwWq0mZdgszkXFOqqIUvsZf61Wi3wuqqy4+Ap6Ly9f3vvThbcUPQ5Di4sv1pwc3mWov2sQtDa2pQcHvJEXLIhrc69UqTI5YxVLKqr2QSJlCuGKxY5FMVMOvNlsIpfLCRu2tzEbfRPJRCK0kVRtYIUhyFE68sqWpYIvv3wvfu/l5ct7/3hvF6gUA++X3TiNiy9vTo6d/gjHFvRQp9w2xtCGPeQz5dgGB6Zlo94z8dy5JvZMO5YYfl6+NrYb6A612O1Q9DmRWXcYVyx2LIqZcuBRucuj4G7MXCqBZ1+PVmpVG1hBMC0b5xsG2sb4yHF8FnnjPA7t8NU2xlhrD5jyvfDy5b1/68rlwHtlN07dXMU1st/qmaAAlrKpSKdcyiaRSRI0OE7x8vDr8LXVM3GxNcC7TxZiHYWyIqORqdoh72AqyB5Z4Geysn4rDDPlwL1TEV4FczemObbxzGsN5rSgcRxjdwzMcZCnS5lDR4Cjpl4i680ifJ3fMfD515vMCu1dJuCJ5Q2TWSbiYlpcNfomnv1WE3sjO9Ip61oC999xIwZIxjI4cPgqZ1NYaw3Q3BthOSAHjRe8H4bg4Wpl+RgePaVPzQ55BlNh9sjyrB9f8yWUfWxtbR3EU8oc7XYO7IhMyVSOSty5HE6XMnjw1jLOlN9aonDLG/Y8i/LL8HVzJYsX15NCXAWVGcRjmMwyG4zT4urEYgaP3bnCPOJrNupH8oF7eRHVOTdf7zlZwEO3lpmzWvLke+HlymljGTt0lz8te2R51o+vKDuWwUw5cPf34WTjX0WmZCwJlUQ3PkrZ5BFl8X4PT+aAiexReJHpa9hp1yAew74BKDIdFgm3U6FbrPe75fXjBRA/0CKzgc3KlwhXbpnj2GRX0eH52aO3bFZbjPqupQxmyoG7oSJOlHdKFhX7rHLjwwvZ2HJZvkSmr0FKPY28KjLhdnHmVQmDHy+UYiqdichxfCDc0bPypSoowalr3B2eysNespgpB97r9VCpVABM5+gtTy8bpEwyuRzc8srGll8NvoKUOoxHt8wykDnA5FfvOE6empaNrWYHhdJSqH6pOKgTVQ+Z4/h+bRzGl2gbs9ijbI4jFpl5bVGVTvthphz48vLhjxq4CVN99Ja3l/UqUy6VkDb4crWG7Z6p7MTd1eDLT6nDjD65UIZp2dxcqchf4q2jirwqYfX99MtbGAwIzna3QvUriCvR2YBINr4w+LVx2Du9dsxaZxZ7nEaOI17dEpGXFTPlwOv1OlZXV32vqZ728vayXmWSNQrTsvH8Kxewbi8qP3EHTI+vIHh5dIwsY+xgkK1wGdk0prRx8XUyYeDyMBWqX0FciTgk0Wx8vAjj683Lm7j5xhtisUe/dpcdrIguLzkI81uymCkHTggJvKZi2iubY8KtTLJrzm1jjMGYIp9Rm8PEXderzZcbjoEWNA11TiOLM3+JA1m+gmYIQ4OikI0voob1WdXrt2F8pY0+XuxsCfHFol/edpdNjyC6vOQgzG/JYqYceLlcDr0uM+1VnWNCds25lE3CSi8If6qNtY7XCl+OkTUGGRQyfB1enPlL3BDlK2yGUG/nUCsVlESIsMgim41PBV+aviDMl4h+hS3ZRcmiYiaNTEFoWZAFM+PATcvGhcubeNuZG5mJUBE6JjOCk1lz1rUE7q1SFDxf5ImCo5R5PYG+aSvPfeFANV+OkZ1/8wJuvokvfE7UuGXXRmVD7XQtgXGvDT0kdYAfZGYDMo7QtGx86qVNNPojVPMpPPbuFSG+dKOFQrYqxJeMfoksQ6kYvWeNBoxsVcnGtxcz4cAdIqy9Mf565wo+ctcK0wdeeZQ1jnVA2fcvFYtY4uztnZNkb7YMrCzoOFbQmQ3tavOlawmsVJaE1i1FjFskN463TNlQu8XFRa46u8sWnT2JOsJ6z8TZ9S4ogAtNA3edKOA7juWZnZLD15VtDSeOVYX4UgVWvmQGB86R/HQqp2Tj2w8z4cDbxhhtYwyzP8TrfQuEAI/ffYLZyERDx1RC5P2WZXGVUe+Z2OqZSBGC9fYQe6aF9c4QD91SxonFDHM9ryZfjszevDXm2FY+Dc3rCSQIsDsYo5DRDh2B5z3ZG3VPEFe8bRwEd96alEaQS6nVX9Oy0eyPYFMKCmBnb4S//OYOXt7occdaL6QSoffHbYsAXyfB2+F5j+QXixYKuVwsHdF0os0lUcomkdIIMjCR1zWYY4rOYKzs/aZlY7tnAsDBVC0OeJdUTMsOvb/f7zO/27RsPHeuiYutAb5R7yFBAC1BEEcanTj5cmR2jPhD76gCBHjmtQY+/fJWJGesMC0bT79Sx8iiSGkE339TCXsj+9CITBWcZS0/Z8TTxmHQtQQevqMGPUkwsiiefqWulKtPv7yFL77Zhp5MYHlBRzWXQnVBF+IqSuYwvlTB4ev+m5cmvCksx3sk/+2V8ARwMpiJEbiuJfCRu1bwH86OcaOlMSeYcSNowyKOAxpR9Ygqz6lr5Rh7/GjbGGPPtPHukwXs9E1kkgmYFkUll0KVc9oWtrkTN1/uD8DqWgLJRAJ7pq0s/tqB28j6pgU9mRCatkdthEXxpfKDt33ThmVDKIteGNxc3bSUxfffXMLZy92DDIK868KpxUrgbGpa9uh04HGU4z2S/x03qu0g3JgJBw4AeT2J+1eAQm1ZWc4EQP0BjShEleeu6yrp4IfuuZ1JVrfSrBTSePiOGvZGtlKuWOovi8sbG1j4/9s799jIrvu+f868OMPh8DEkl9Rq11JWD0uOUFuKLCtGEDtYOTHS1ooFP+RCaZWuC8SV/U/+KmAgCFwUSFO0RYoaaIrUaNKmTZrUcBeFg8CSHSSIJcfWyo1iAcnqRS13OeQMORwOh3d453H6x8ylLu/euXPOvecOOeF8gQU4e+/MPb/H+Z1zfud3vnfpvHL5mAnei8JUkqUQpXQqwWaYvky81Fi3lDMqZ897l/O8dzkfetM4aFNvVP1Rp4JI17+8KaCN9RvMTMisIJsJV+UQZCwTXA5B0K1ndbf1oCmUHdgvbxjG74c5dpw8IXany6ubTW553lAzKLBGma0N+l1T3DgOhtk7nU4rP8+LMKWcJjl7wm4az6QGc6XHuYGpO9hF9S9Htig2HoaxCuBzc2rlVjpBM6hGNOpSLkw9q7utU1N6Gx9hqgt0B5goJWzDsGu12e5kyE+plY+NgvfCC90gMMzeqj7thzClnGFnuCZ9a6eZOar193uOn3+ZmBzoDnamVgNRbDwMYxXAK5UK+Xw+8J4wQdPPOcMYT5VjIqgzuNtaL98y5sCD2hvmwESUErYgzOdSnEtY3LAzSrOvUfBeuBH28FKQvVV8ehDCzFZNsHiqIMi3nFp/FX2FtadqXwzyU1OrzSg2HgalAC6E+Djwm0AS+G0p5a97rv8K8HmgDZSBfyqlXDPcVqWRzNQhAF1HN8kx4bQ13ZqPNSDFqStQ2+Dzckw8fv95PjSVV8qt+g02pkm63IjjsJfO7CwqJweMhpUSgn3rjqWi8jPCrLJM9UVTq80TnYELIZLAV4GPAevA94UQV6WUr7luewV4VEp5IIT4AvAbwGdNN9a27eOffYxoKoem6+hxcEzYto1tcFPHNGOfgzCOPuh6t93iXDE8E57JHGpc+jr2jL5Ph61mCZPacH/H5ICnml7y9uMghFllmeyLJlabOvLqQsUDHwNel1K+CSCE+H3gSeAogEspv+O6/yXgGZONdGBZ1tHfQQ5t6hCAjqPHwTFhWRZ3LC4Z2WSNm7FP19EHXXfbOGw7TNCvjoLhEHo2NlHNEham0gQ66SUdG4dZZUXpi8PkDpOCiurTQVAJ4HcCN1yf14EPBdx/BfhjvwtbW1tcuXKFVCpFp9Phqaee4rnnnqNUKpHP50kmk+zt7bG8vMzOzg5SSpaXl9nc3GRmZoZsNsva2horKyu8dbPElNUgmZkhY1W5tZVkJp2g0WiwurrKQaVEK51mbm6OSqXC3Nwctm1jWRarq6uUSiUymQyFQoHt7W0WFhawLItms3l0PZvNksvlqFarzM4vcEdin06zRXpqnnr5FrIxTSaToVarsbS0xE+f69Jo2ly88zwb6zeUZAKo1ev8ZSVB6nCPTCrJR378PexuV8jlcuxVd/hw8ZDc/BLWboXKZom5uTk2y2WulbvYts1sssNH338P21ubA2VKzy6SsypMpzLUm0neeOttLq6eo16v935jdZW19RK5XO6YTLVajVardaQTVZn263UW0glSzV3mU0kycoG1tQ1mZ2fpdDrs7+8zn06SaVaYS6VJd+ZYW9tgenqara2toXZqWBbZuSWatQr5XO7ITouLi7fJlJ7K8t0bDYTdoD1V4CdX08hOO1Cm+mGbZlNyIXFArZnm5maCRKvJysoKzZ0yh0JQLBYpl8tHMjm+d3Njg5ZMsLK4QK26E+h7nU6HjUqVpLXLhWSXUjPPG2+9TbGQPyaTvbfHRVFj4zDPxUSDVj3NbmtqqJ2qtRqZmQU61h4JuN1O+/s8+d5lbpa2yGUk7cMm61tbXCt3OGy1mUu0j3wrHdCf3njnJmnrkIVMjrRVpVTJMEWbZrN5ZAenPzn2r9frWIeHR3acmZ4e6HsHlRKiL9N+rcZCWpBs1lhICbIUWVvbCJRpw8dOpVLpmEz5wix//nqZbusQe2qeDy11yE1N3eZ77v5Y3triu+sWCXufzlSBD5/P0HHZIZfLMT09zdraWqT+NAhi2CvvhRCfBn5OSvn5/udfBB6TUn7J595ngC8CH5FSHnqvv/jii/KBBx4IfF4Q1tbWIr/UOArsTjeW471b+zb/+9Ut8pkke802l+8rcs9ijo31GwNrhN3fadgdPvX3zgXOLkxtBulgmL78rrttrCLLdDrBE/cVWZ4ZfCJUV1feZ+jqS+d7a2tr3HHhotJ3dP3P25ZPPrSsRHAWt74cG0fpw3H0Ra/cT/740lBuHBVdqfh0EK5du/by5cuXH/W7pjIDXwfcbOQXgFvem4QQTwBfZkDwNoFMJpi4PQgmdtrD5BtV4OaxWNtt8sL1HV5eT/HR1cH1o7r52DD6Ku/bPH9dnx/ErWtdAiq3jQfBSSdkUwlevlmnctBiZSZjlFEurH+1Ol2tVEcmk1F+lq7/udMuu1ab33ulRKfLUFvGra9MJnOM7CnMydE4+uIx/p1MQokbR6mUVMGnw0IlgH8fuE8I8WPATeBp4B+5bxBCPAz8FvBxKeWW8Vb2USgUjn3WyS9Hma2HyQfq3H9UXrVt8cL1nSOHlunBpUdhKxB09LW5b7NWbfLw+YJWKWXYl0JkkonbbOwHp9Ns7tsIoDg9+GCII7eJDawgGY5WBJkE0+mEMo97oVDQ3stQvdcdXNJJgd2WSsEybn1lp/PHyJ7ums9q0WPEVVbrlttud7n6WsUIW6GKT4fFUI1JKdtCiC8Cf0KvjPBrUsofCSG+AvxASnkV+DfADPCH/bdPvCOl/ITpxm5vbw/NCfkhygZQmIAUZrDIJBPcs5jj5fXU0XdbjRosLwR+x10va8qpHX0Vp9O8U21StVqcm8kodbCoL4VQsbHTaSoNm29d31Hi5IhLV3BcZmfpnU4mlILfVqXCd3emlPxF17fcwWU6nTjG/aGyYvNSPJjS2cZWhfph5ojs6Yn7i1wq5oynqMIeg3fKFFVXIcN0FTZuqUBpyJNSfhP4puf/ftX19xOG2+WLhYVeMIvC5aBb/qUb/KMMFt7RvNnYV/pekFOHcWK3vh65UOBj9xVZUmQdjPpSCMfGw5BJJjg/m+VzH1g1xl9ikldFNagkcwXqh5aSv4TxLXdwifIiBz+dhdXXynKRQt2iftjjVlEN3hD9LUiqCLsK8Xuuqk+HwVidxLQsi2x+xhiXQxAc58xn9FjqotYKuztc1bKUCP+DDjuEXQ1E2V9Q/a6frqqVno1VA0OUvLAJXTltUJHZ7xmpbkvZX6KW/IXNG/vpbC6bCq2v9uGhso+ErcU3UXYZRl9+z+0q9uMwGKsA3mw2R8Ll4Ld7r8rs59eZw85Ums3mwPapOHXU1UCU/YWwBFwNy+JbhquLVA6YRO3wKjL7PaNtH/KZ919U2/wb4Fumq7FU/CuKvprNppK+otTix01S521nkH9tVPz7sQmMVQBfXV1FpOJjw3Pgdc6DVjd0Z47Swfy4onWcOk7mQAemA192bon6xq6xAyuqB0xGoSu/Z8yurmpNLrz3mj7go+pfUfQ1iAPdBJeQg0F9wvSAp+JfJjnfvRirAO5wJ5uehcR5ZDoKrUoDrAAAFGJJREFUY54fV7SOU8c1Y9Nl5NNBs1ahMDVl7PdU+Uvi0JUKd8naejQ+cNP6V/WvKPry82uTXELuNqqQ1DkrijCDtIp/ReV8D8JYBfBstvdeR5OzkLiPTEdhzHPkjRIwTc/YwjLyqSKfy/GZ9y+HTkFFGYxH4Ve3rTiyau8qDWpzFOqAk9CXn8xxcAn5wSvfdDoRaZBW0VdUGwdhrAJ4Lpfz/X8/o2zt20od3hQj3yD4dTBVAqFcLmc8YEalE42Dkc+NXC4XOgVlejCOkiZQDWaDfFoHXl9V1dlJ6ctP5qhcQqrwyqdb9uq1u4q+TNh4EMYqgFerVd/dXLcSvfWuw0bUsMs0d5XKsOPJXidUfWa1WiWXyBoNmF6HAz060aj6GjZIeG2s08FMD8ZR0gQ6Nvbz6Si5d1WdnZS+/GSOuurV0ZdbPlU7Bdl9mL4G2dgExiqALy4uDrzmKFGXHjOM4zjGdE6SXZidIpvuvXg5nzF37HhxcZFMDBSmbocbpb7qhz3uko/eM08qkfDlL/HaWGfAiIPuNWyaQMfGXrj9KyHg7z+4yB2zWeWgpqqHk9LXoH4cduAYRQlolHRaUNyKirEK4PV6feiJprA8DjqOU9632dzvvfm93mzzRrtLq9NFCHj20fNKzqPyzHq9zh0zM8bzgG6MUl9zUyl+sL7H927USCUS/MSdBT738Ooxmbw21hkwTO5dDEKUHLEf/Hy6vG+zsXfIrf6/V0v7PH7XHJ/7wKqyb6lyq5yEvra3zJ5MPPKvbIrNfZtKw+b8rHreWcVOUQY7lbgVFmMVwFWI0b3pFNOcCXany/PXd1irNpFSkkkJ7HaHmakUdlsa42mGd+U1nQd0w9FXpWEzhJgyFOxOl+df3+GdapNWt0u3K0n1bbF90LpNX3421pE/Tl05v2/Sv/xeUvL89R3eqlqU91ukEoJkQlBp3K6rYe00fT4iDPz8y+QLDhz/ertqsd1oUZxO862/3bltYmACP3PPAkKgfCr5qI0n/EKHUwPVespMMhHppFgQdq02B60uD58vULVafOJ9i3z7jV3sttQi5FHB6upqbMQ9Xnz79apxXUFfX3aXD9xZYLvRW7Vcr1hIYHE6fZu+gmysootR6Mukf3nldfzrkTtneflGDRAkhWApf7uuhiFIF6PyKwdu//qFB1eM/a7jXw8s5/lhq86Dy3kOWt1QE6lBOvFL0ehgUgfeh049pQ5nQlhelXMzGd6zMM2zj06H5pgIevbNjQ1loqMoiEtXcFxfq4UpPvlQr0QQ/Gcyg2yskueM41TiIAzTmaquvPK69fX43fN89NI86WRCf9Y3hPNllFz6Xl3duHmLB++9dFt7o/DQ9L6bRkKofH6QTqKW3k7qwPsIKscJU88axpEH5Q3DjPbDnt1NZoweOvA+X6e23CSvStBG7yAbq3Qi06cSHfgFl2FHtVV15ZXXVF46SBdx6cnB0L44k7/tfhObkNPphDLlhRdBOom62TspI+xjEDF62HrWUfCquNuockzYjfl8jsJU09ihA3dbdGvLR8GrAoNtrNKJopwHGISgAzmDdKajKz95TeSlg/QVJ0+ISl88qO8d+45JOgbVr+lM+AbZWplE7IRf6HBqUKvVmJ+fv+3/w9azRj3Uooqwx4Qb9b1jREemZk5hDuOMgisE3rWxyjF0L7yzMZ3zAIMQpPNB/qWjq0E+rQsdfQUFpKgTBJW+uOGReVS+5SDMhM9rax1dmbKxH8YqgC8tLR39bYKPw2s00DvUooqwx4SXlpaOOY6pQzRhSwdHwYS3tLSkfAx9UDuDzgPoboTGrSu3T4dFGH35XQszQQjjW16ZR+Vbw+TUWfno6MqEjQdhrAJ4rVYjn88bPV7uNpruoZYgqASBYQ7jyOtuqy5Vrcnj0t72xpFLrdVqpGQ68u+G5aAx5VuquvLaOAxM2UF3RRrWt/xkjsu3dPcvVKG7yopq40EYqwDearWA+Pg4TC3lTAUBR1433I6uEpDi5HoxeZLP0XHTtrlg4Hf9AonKAD1q32ratnaePi72TN0VaVjf8vNrL0z0xTD7F6rQWTWoyBsWYxXAnXrKuPg4TC3lTAWBYfWjShuhETp3WH3p5i3dOp5PJ7lwMfzrv7zt0+WgiUtfg3T1vUqS3Y0tZd+Kmz1TZ0UaVleOX4fRl05fDLN/oQPVVcOkDrwPp54yjMOqGt/EUs7UADOsflTlOWE7t1dfn3xo2Ze0S3dF4Ae3jjPNCrXmitKApztY6G6EmtaXn29lDnfJZ5eUfStu9kw3hvlXWF2VSiXuuHBxqK9E7YtxE6+pPm9SB96HNx+s47Be41caNqlEYqiRTG1iBcHudCnv2zx/fYeDVvfIoYflzVSfE6Zzu/W1a7X579dKdCWBgTls3tKt45l0NlDHbhbIMFUmOhuhOgijr/lcCpHO0rDVfUvHH6NWcagOeLq6yufzt+nrzW2LS4vBLzfW7YtxTvR0nhdX/hvGLIAnk8nQ33Ubfzqd4FvXdziwu0ONZGrDbxAch9nct1mrNnn4fOEo+KUU5Y2Dw8Str3RS0OpIZrOpwMBsohpINuuB1SFO50oIlNrk9xtxlKaF0VcmmeCn7ikisgVl31L1RxNVHHHpKplMMus6Qbm22+T56zvMr6eM90WdAcbudHmjYrFrtSP5lff+KHFrGMYqgO/t7bGwsHD0WZcD2DG+3e5y9bWKFoVqXIQ/zkykOJ3mnWqTqtXi3EyGuWyKjcpxeb3QfdlB2HSDt6Z6UGCOkhN3dLxW2YcB9JvuWdtes00mJbRmr6dNXwDW/j539eXV1VUQolZx6A4AOvpy+vFn3r/Cm9sWz1/fUQ6YcfVFL0X0XfNZZW6jYbryxi2TGKsAvry8fPR32GPwTi1wlF17kzMT98ztkQsFPnZf8Yj3wi2vH3Q4TMIeg3d+T4fSVSUnPkiHQTK7dTWfS/HJh5a1jk6fRn058g57ZhTOnjA+rjMA6OrLkTmTTHBpMcf8esr4prGuvhx5Z7Mp7prP8sT9RS4Vg1M63u8O0tWwfhwFYxXAd3Z2mJ6eBqIf7Q67az/IWcMG9aC2uOV1nh2mfMxETW3UvLD7uUEd3iuztw2386r4PztK/e8o9eXIG/RMk5w9QQh7gElXX24bm9o0jkrW5Z0cDAveOroK8umoGKsALl3J3qh1omGXYn7OGpVadFBb3PJGKR+Lk/siCIOeG9Th5ZCEvordotb/jopiAd6VN8hGo+DsiXJ2QVdfXhur2lSVSyiMvnQGEl1dDfPpKBirAO5eigzKt5o+fqsy6w2aaUbp9G55o5SPDXLOUejL77lBwcrEcjNq/a+33WCeYuFIT8VF32e6f38UXCFRzi7o6kvXxrpcQmEHYNUBT1dXkxRKH5ubm8fqKb0KN320W3XWG/bY9rBnv3njFvdeulsrXTIIfs45Kn15fzNos3O/UuLS3XeHenZUbhxvG+OgWHDa6ujpoqjxsx988GiFMKhaxfRkxfRpTh19efvxMOhyCcUxAEfxL115dTBWATzs+zBVZyqqyzRvR/PrYFE6vdM5aba5Vt80ftrOgelUgc6AMGiz81yyzYWL3cj7EiZ1ZXoGfKwG+jCtvMQ3NVmJ+zTnMH1lp/XqosNwCZkcgKP6V1zvw4QxC+DDEGWmortM83u2yjFjlU7vdM7lVIKyZrpEB1FmKiZJgtzByDrUfx1WXPwlDkzNgN2HkBw9nUsljJIpqSDu05zD9HUu2eQfFotak6kog0vUiUrc/hUFSlYXQnwc+E0gCfy2lPLXPdengN8FfgLYBj4rpXzbbFNhf3+fxQE1wg7CzlR0l2nDEKXTOw4nLItCLh9rmWOYmYppkiB3B7uYaGlvssbJ9+Ig6gzY76j9QatLvXwr1GzXb/BVJcU6aX3RtEKVJYYNmFFTKlGP5O/X60PjVlgMbYkQIgl8FfgYsA58XwhxVUr5muu2K0BVSnmvEOJp4F8DnzXd2JUV/Zehqio/zDJtGMJ2esfhKrUZlubykdMJYQJp2DK7MPpyd7As787MdPhropSi7Vpt0knBM4+sBr7uzQ3dTu3V2UGry3I+QyEZnujI0bWuzU9aX5mpOaNliSqIklIJoy+3TRbSCe20oCpUtP8Y8LqU8k0AIcTvA08C7gD+JPBr/b//CPiPQgghDdfPlMtlLl68qPUdVeXHkWP2Qjcl02nskikWtJ4xivp4U/Sl3mcv5zPcuLFJIa9f6x9m4Ni12uxabd6uNmnYbYSAZx89r2R7XX8ZpLMwPu0nR5iyufD6smjYHQB+6YP6+mpUSrHMeFURlt8obFov1dw1Mgj5QUUzdwI3XJ/XgQ8NukdK2RZC1IBFoOK+aWtriytXrpBKpeh0Ojz11FM899xzlEol8vk8yWSSvb09lpeX2dnZQUrJ8vIym5ubzMzMYFkWa2trrKysUC6XEUJQLBYpl8vMzs7S6XRoNBqsrq5SKpVIp9PMzc1RqVSYm5tjt2FjWdbR9UwmQ6FQYHt7m4WFBSzLotlsMru6ytp6iWw2Sy6Xo1qtsri4SL1ex7bto+/ncjkymR4p/9LSErVajVardXTdT6afWuySKSzQ3NumvlsFeqkhP5ls26ZSqQTKZNvHZUqm0yym2ySbVXKZGey9HdYqh0fXVWXaqATL9OHiIVOFBdoHe2zeunnMTkEyDbOTbdtsbW1hWRaL51a4KGo0mgmyUznq5VtMdYpHdtKVyWunxXMrnGeXPdHh3HSSYqtKebeAtOq3+d4gmQ4qZVKzs+wN8T3btvlw8ZDc/BLWboXtrU0KhQK7u7vMzc1Fkmluocj5xD7tZov01Dz18i2ENTO0P+naSSRTzCRaXErX2Utlybf3eeOtt7l08c7A/uSVqbRXY39/P1Cmf3Bvka2dKinayHaLtXW1GKEq0y88uMKNm7fIZ6doNS02BvQnVZm8dnJ8d6+ZZDrRS5VNs6wUI/xkGgQxbJIshPg08HNSys/3P/8i8JiU8kuue37Uv2e9//mN/j3b7t968cUX5QMPPBD4vCAcHBzEdqLpNCKsvHanG+tKIk54ZY5blobd5vdeKWG3JfO5YDKlOGDKp0dl84bdY1psdcLr66z0Y8cmGdlibiY8I+G1a9devnz58qN+11Q0vw6413gXgFuD7hFCpIA5YEe/qcEol8umf/JUI6y8znJv3II33C5z3LLkMymeffQ8n/3AysiDN5jz6VHZPJ9J8UsfjKavs9KPHZvsbleG3xwSKtr/PnCfEOLHhBAZ4Gngqueeq8A/6f/9KeDbpvPfALOzs6Z/8lTjrMkLJyPzSQ5442jjqPoaR5mjIE55h+bA+zntLwJ/Qq+M8GtSyh8JIb4C/EBKeRX4L8B/E0K8Tm/m/XQcje10OnH87KnFWZMXzp7MZ01eOHsyxymv0hAqpfymlPJ+KeU9Usp/1f+/X+0Hb6SUTSnlp6WU90opH3MqVkyj0WjE8bOnFmdNXjh7Mp81eeHsyRynvGOVJI3z5aCnEWdNXjh7Mp81eeHsyRynvGMVwEul0kk3YaQ4a/LC2ZP5rMkLZ0/mOOUdqwD+jW9846SbMFKcNXnh7Ml81uSFsydznPKOVQD/+te/ftJNGCnOmrxw9mQ+a/LC2ZM5TnnHKoC32+2TbsJIcdbkhbMn81mTF86ezHHKO/Qkpkm88MILZWAt7Pd3dnaWisVifFXxpwxnTV44ezKfNXnh7MlsQN67Ll++7Ptan5EG8AkmmGCCCcxhrFIoE0wwwQQTvItJAJ9gggkmGFOcugAuhPi4EOJvhBCvCyH+hc/1KSHEH/Svf08IcffoW2kWCjL/ihDiNSHEXwkhXhBCxPOG1BFhmLyu+z4lhJBCCF8mtnGCisxCiM/07fwjIcT/GHUbTULBp98jhPiOEOKVvl///Em00xSEEF8TQmwJIf56wHUhhPgPfX38lRDiESMPllKemn/0uFbeAC4BGeD/Ae/z3PPPgf/U//tp4A9Out0jkPlngOn+318YZ5lV5O3fVwD+DHgJePSk2z0CG98HvAIs9D+fO+l2xyzvfwa+0P/7fcDbJ93uiDL/NPAI8NcDrv888MeAAB4HvmfiuadtBn709h8ppQ04b/9x40ngd/p//xFwWQghRthG0xgqs5TyO1LKg/7Hl+hR+o4rVGwM8C+B3wCao2xcTFCR+Z8BX5VSVgGklFsjbqNJqMgrAYemb47bKarHClLKPyOYQvtJ4HdlDy8B80KIO6I+97QFcL+3/9w56B4pZRtw3v4zrlCR2Y0r9EbyccVQeYUQDwMXpZT/d5QNixEqNr4fuF8I8RdCiJf6LxIfV6jI+2vAM0KIdeCbwJf4uw3dfq4Esy+biw6/mbS3zlHlnnGCsjxCiGeAR4GPxNqieBEorxAiAfx74NlRNWgEULFxil4a5aP0Vlh/LoR4SEq5G3Pb4oCKvJ8D/quU8t8KIX6SHh31Q1LKbvzNOxHEErdO2wz81Lz9Z4RQkRkhxBPAl4FPSCkPR9S2ODBM3gLwEPCnQoi36eULr475RqaqX/8fKWVLSvkW8Df0Avo4QkXeK8D/ApBSvghkgaWRtO5koNTPdXHaAvipefvPCDFU5n5K4bfoBe9xzo3CEHmllDUp5ZKU8m4p5d30cv6fkFL+4GSaawQqfv0NepvVCCGW6KVUYuHVHwFU5H0HuAwghHiQXgD/u/yutavAP+5XozwO1KSUG5F/9aR3bwfs1v4tvV3sL/f/7yv0OjH0DP2HwOvAXwKXTrrNI5D5eWAT+GH/39WTbnOc8nru/VPGvApF0cYC+HfAa8CrwNMn3eaY5X0f8Bf0KlR+CPzsSbc5orz/E9gAWvRm21eAXwZ+2WXfr/b18aopn54cpZ9gggkmGFOcthTKBBNMMMEEipgE8AkmmGCCMcUkgE8wwQQTjCkmAXyCCSaYYEwxCeATTDDBBGOKSQCfYIIJJhhTTAL4BBNMMMGYYhLAJ5hgggnGFP8f59E3CBw4PbgAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"seq = sobol_seq.i4_sobol_generate(2, N)\n",
"plt.title(\"2D Sobol sequence\")\n",
"plt.scatter(seq[:,0], seq[:,1], marker=\".\", alpha=0.5);"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.1.2 Quasi MC: Halton’s low discrepency sequences](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1.2-Quasi-MC:-Halton’s-low-discrepency-sequences)",
"section": "7.1.2 Quasi MC: Halton’s low discrepency sequences"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Quasi-Monte Carlo result (Sobol): 41.31674468994141\n"
]
}
],
"source": [
"seq = sobol_seq.i4_sobol_generate(2, N)\n",
"\n",
"accum = 0\n",
"for i in range(N):\n",
" x = 1 + seq[i][0]*(5 - 1)\n",
" y = 1 + seq[i][1]*(5**2 - 1**2)\n",
" accum += x**2\n",
"volume = 5 - 1\n",
"result[\"QMCS\"] = volume * accum / float(N)\n",
"print(\"Quasi-Monte Carlo result (Sobol): {}\".format(result[\"QMCS\"]))"
]
},
{
"cell_type": "markdown",
"metadata": {
"ein.tags": "worksheet-0",
"nbpages": {
"level": 2,
"link": "[7.1.3 Comparison (1 dimensional)](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1.3-Comparison-(1-dimensional))",
"section": "7.1.3 Comparison (1 dimensional)"
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
"## 7.1.3 Comparison (1 dimensional)\n",
"\n",
"We can compare the error of our different estimates (each used the same number of runs):"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"autoscroll": false,
"ein.hycell": false,
"ein.tags": "worksheet-0",
"nbpages": {
"level": 2,
"link": "[7.1.3 Comparison (1 dimensional)](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.01-Sampling-Based-Uncertainty-Quantification.html#7.1.3-Comparison-(1-dimensional))",
"section": "7.1.3 Comparison (1 dimensional)"
},
"slideshow": {
"slide_type": "-"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"MC result: 40.699423 Error: 6.339101E-01\n",
"LHS result: 41.333591 Error: 2.575113E-04\n",
"QMCH result: 41.218706 Error: 1.146277E-01\n",
"QMCS result: 41.316745 Error: 1.658864E-02\n"
]
}
],
"source": [
"for m in [\"MC\", \"LHS\", \"QMCH\", \"QMCS\"]:\n",
" print(\"{:4} result: {:.8} Error: {:E}\".format(m, result[m], abs(result[m]-result[\"analytical\"])))"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"< [7.0 Sampling-Based Uncertainty Quantification: Monte Carlo and Beyond](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.00-Sampling-Based-Uncertainty-Quantification.html) | [Contents](toc.html) | [7.2 Latin Hypercube Sampling](https://ndcbe.github.io/cbe67701-uncertainty-quantification/07.02-Latin-Hypercube-sampling.html) 
 "
]
}
],
"metadata": {
"anaconda-cloud": null,
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.3"
},
"name": "monte-carlo-LHS.ipynb"
},
"nbformat": 4,
"nbformat_minor": 1
}
"
]
}
],
"metadata": {
"anaconda-cloud": null,
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.3"
},
"name": "monte-carlo-LHS.ipynb"
},
"nbformat": 4,
"nbformat_minor": 1
}

