{
"cells": [
{
"cell_type": "markdown",
"id": "3e406844",
"metadata": {},
"source": [
"\n",
"*This notebook contains material from [CBE60499](https://ndcbe.github.io/CBE60499);\n",
"content is available [on Github](git@github.com:ndcbe/CBE60499.git).*\n"
]
},
{
"cell_type": "markdown",
"id": "567be855",
"metadata": {},
"source": [
"\n",
"< [4.7 Simple Netwon Method for Equality Constrained NLPs](https://ndcbe.github.io/CBE60499/04.07-Interior-Point1.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [4.9 Algorithms Homework 4: Interior Point Methods](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html) > 
 "
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 1,
"link": "[4.8 Inertia-Corrected Netwon Method for Equality Constrained NLPs](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8-Inertia-Corrected-Netwon-Method-for-Equality-Constrained-NLPs)",
"section": "4.8 Inertia-Corrected Netwon Method for Equality Constrained NLPs"
}
},
"source": [
"# 4.8 Inertia-Corrected Netwon Method for Equality Constrained NLPs\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 1,
"link": "[4.8 Inertia-Corrected Netwon Method for Equality Constrained NLPs](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8-Inertia-Corrected-Netwon-Method-for-Equality-Constrained-NLPs)",
"section": "4.8 Inertia-Corrected Netwon Method for Equality Constrained NLPs"
}
},
"source": [
"Background:\n",
"\n",
"\n",
"\n",
"The Algorithm:\n",
"\n",
"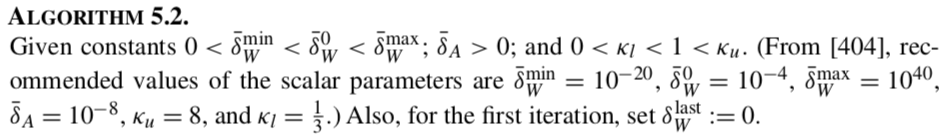\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.8.1 Helper Functions](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.1-Helper-Functions)",
"section": "4.8.1 Helper Functions"
}
},
"source": [
"## 4.8.1 Helper Functions"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.8.1 Helper Functions](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.1-Helper-Functions)",
"section": "4.8.1 Helper Functions"
}
},
"outputs": [],
"source": [
"# Load required Python libraries.\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"from scipy import linalg\n",
"\n",
"## Check is element of array is NaN\n",
"def check_nan(A):\n",
" return np.sum(np.isnan(A))\n",
"\n",
"## Calculate gradient with central finite difference\n",
"## Calculate gradient with central finite difference\n",
"def my_grad_approx(x,f,eps1,verbose=False):\n",
" '''\n",
" Calculate gradient of function f using central difference formula\n",
" \n",
" Inputs:\n",
" x - point for which to evaluate gradient\n",
" f - function to consider\n",
" eps1 - perturbation size\n",
" \n",
" Outputs:\n",
" grad - gradient (vector)\n",
" '''\n",
" \n",
" n = len(x)\n",
" grad = np.zeros(n)\n",
" \n",
" if(verbose):\n",
" print(\"***** my_grad_approx at x = \",x,\"*****\")\n",
" \n",
" for i in range(0,n):\n",
" \n",
" # Create vector of zeros except eps in position i\n",
" e = np.zeros(n)\n",
" e[i] = eps1\n",
" \n",
" # Finite difference formula\n",
" my_f_plus = f(x + e)\n",
" my_f_minus = f(x - e)\n",
" \n",
" # Diagnostics\n",
" if(verbose):\n",
" print(\"e[\",i,\"] = \",e)\n",
" print(\"f(x + e[\",i,\"]) = \",my_f_plus)\n",
" print(\"f(x - e[\",i,\"]) = \",my_f_minus)\n",
" \n",
" \n",
" grad[i] = (my_f_plus - my_f_minus)/(2*eps1)\n",
" \n",
" if(verbose):\n",
" print(\"***** Done. ***** \\n\")\n",
" \n",
" return grad\n",
"\n",
"def my_jac_approx(x,h,eps1,verbose=False):\n",
" '''\n",
" Calculate Jacobian of function h(x) using central difference formula\n",
" \n",
" Inputs:\n",
" x - point for which to evaluate gradient\n",
" h - vector-valued function to consider. h(x): R^n --> R^m\n",
" eps1 - perturbation size\n",
" \n",
" Outputs:\n",
" A - Jacobian (n x m matrix)\n",
" '''\n",
" \n",
" # Check h(x) at x\n",
" h_x0 = h(x)\n",
" \n",
" # Extract dimensions\n",
" n = len(x)\n",
" m = len(h_x0)\n",
" \n",
" # Initialize Jacobian matrix\n",
" A = np.zeros((n,m))\n",
" \n",
" # Calculate Jacobian by row\n",
" for i in range(0,n):\n",
" \n",
" # Create vector of zeros except eps in position i\n",
" e = np.zeros(n)\n",
" e[i] = eps1\n",
" \n",
" # Finite difference formula\n",
" my_h_plus = h(x + e)\n",
" my_h_minus = h(x - e)\n",
" \n",
" # Diagnostics\n",
" if(verbose):\n",
" print(\"e[\",i,\"] = \",e)\n",
" print(\"h(x + e[\",i,\"]) = \",my_h_plus)\n",
" print(\"h(x - e[\",i,\"]) = \",my_h_minus)\n",
" \n",
" \n",
" A[i,:] = (my_h_plus - my_h_minus)/(2*eps1)\n",
" \n",
" if(verbose):\n",
" print(\"***** Done. ***** \\n\")\n",
" \n",
" return A\n",
" \n",
"## Calculate gradient using central finite difference and my_hes_approx\n",
"def my_hes_approx(x,grad,eps2):\n",
" '''\n",
" Calculate gradient of function my_f using central difference formula and my_grad\n",
" \n",
" Inputs:\n",
" x - point for which to evaluate gradient\n",
" grad - function to calculate the gradient\n",
" eps2 - perturbation size (for Hessian NOT gradient approximation)\n",
" \n",
" Outputs:\n",
" H - Hessian (matrix)\n",
" '''\n",
" \n",
" n = len(x)\n",
" H = np.zeros([n,n])\n",
" \n",
" for i in range(0,n):\n",
" # Create vector of zeros except eps in position i\n",
" e = np.zeros(n)\n",
" e[i] = eps2\n",
" \n",
" # Evaluate gradient twice\n",
" grad_plus = grad(x + e)\n",
" grad_minus = grad(x - e)\n",
" \n",
" # Notice we are building the Hessian by column (or row)\n",
" H[:,i] = (grad_plus - grad_minus)/(2*eps2)\n",
"\n",
" return H\n",
"\n",
"## Linear algebra calculation\n",
"def xxT(u):\n",
" '''\n",
" Calculates u*u.T to circumvent limitation with SciPy\n",
" \n",
" Arguments:\n",
" u - numpy 1D array\n",
" \n",
" Returns:\n",
" u*u.T\n",
" \n",
" Assume u is a nx1 vector.\n",
" Recall: NumPy does not distinguish between row or column vectors\n",
" \n",
" u.dot(u) returns a scalar. This functon returns an nxn matrix.\n",
" '''\n",
" \n",
" n = len(u)\n",
" A = np.zeros([n,n])\n",
" for i in range(0,n):\n",
" for j in range(0,n):\n",
" A[i,j] = u[i]*u[j]\n",
" \n",
" return A\n",
"\n",
"## Analyze Hessian\n",
"def analyze_hes(B):\n",
" print(B,\"\\n\")\n",
" \n",
" l = linalg.eigvals(B)\n",
" print(\"Eigenvalues: \",l,\"\\n\")"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.8.2 Algorithm 5.2](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.2-Algorithm-5.2)",
"section": "4.8.2 Algorithm 5.2"
}
},
"source": [
"## 4.8.2 Algorithm 5.2"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.8.2 Algorithm 5.2](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.2-Algorithm-5.2)",
"section": "4.8.2 Algorithm 5.2"
}
},
"outputs": [],
"source": [
"def assemble_check_KKT(W,A,deltaA,deltaW,verbose):\n",
" \n",
" n = np.size(W,0)\n",
" \n",
" if(np.size(W,1) != n):\n",
" print(\"WARNING: W is not square. Somthing is broken.\")\n",
" \n",
" rA = np.size(A,0)\n",
" m = np.size(A,1)\n",
" \n",
" if(rA != n):\n",
" print(\"WARNING: A does not have the corrent number of rows.\")\n",
" \n",
" # Assemble KKT matrix\n",
" KKT_top = np.concatenate((W + deltaW*np.eye(n),A),axis=1)\n",
" KKT_bot = np.concatenate((A.T,-deltaA*np.eye(m)),axis=1)\n",
" KKT = np.concatenate((KKT_top,KKT_bot),axis=0)\n",
" \n",
" # Check inertia of KKT matrix.\n",
" # Out of simplicity, we will just calculate the eigenvalues.\n",
" # Biegler, 2010 explains a more sophisticates (and computationally efficient)\n",
" # strategy\n",
" l, eigvec = linalg.eig(KKT)\n",
"\n",
" zero_tol = 1E-12\n",
"\n",
" # Count number of positive eigenvalues\n",
" pos_ev = sum(l >= zero_tol)\n",
"\n",
" # Count number of eigenvalues close to zero\n",
" zero_ev = sum(np.abs(l) < zero_tol)\n",
"\n",
" # Count number of negative eigenvalues\n",
" neg_ev = sum(l <= -zero_tol)\n",
"\n",
" inertia_correct = (n == pos_ev and m == neg_ev)\n",
" \n",
" if(verbose):\n",
" print(\"deltaA = \",deltaA,\" deltaW = \",deltaW,\"intertia =(\",pos_ev,\",\",neg_ev,\",\",zero_ev,\")\\n\")\n",
" \n",
" return KKT,inertia_correct,pos_ev,neg_ev,zero_ev\n",
" \n",
"def alg52(x0,calc_f,calc_h,eps1=1E-6,eps2=1E-6,max_iter=10,verbose=False):\n",
" '''\n",
" Basic Full Space Newton Method for Equality Constrained NLP\n",
" \n",
" Input:\n",
" x0 - starting point (vector)\n",
" calc_f - function to calculate objective (returns scalar)\n",
" calc_h - function to calculate constraints (returns vector)\n",
" eps1 - tolerance for primal and dual steps\n",
" eps2 - tolerance for gradient of L1\n",
" \n",
" Outputs:\n",
" x - history of steps (primal variables)\n",
" v - history of steps (dual variables)\n",
" f - history of objective evaluations\n",
" h - history of constraint evaluations\n",
" df - history of objective gradients\n",
" dL - history of Lagrange function gradients\n",
" A - history of constraint Jacobians\n",
" W - history of Lagrange Hessians\n",
" \n",
" Notes:\n",
" 1. For simplicity, central finite difference is used \n",
" for all gradient calculations.\n",
" '''\n",
"\n",
" ### Specifics for Algorithm 5.2\n",
" # Tuning parameters\n",
" delta_bar_W_min = 1E-20\n",
" delta_bar_W_0 = 1E-4\n",
" delta_bar_W_max = 1E40\n",
" delta_bar_A = 1E-8\n",
" kappa_u = 8\n",
" kappa_l = 1/3\n",
" \n",
" # Declare iteration histories as empty lists\n",
" x = []\n",
" v = []\n",
" f = []\n",
" L = []\n",
" h = []\n",
" df = []\n",
" dL = []\n",
" A = []\n",
" W = []\n",
"\n",
" # Set for first iteration\n",
" delta_A = 0.0\n",
" delta_W = 0.0\n",
" delta_W_last = 0.0\n",
" \n",
" # Flag for iterations\n",
" flag = True\n",
" \n",
" # Iteration counter\n",
" k = 0\n",
" \n",
" # Copy initial point to primal variable history\n",
" n = len(x0)\n",
" x.append(x0)\n",
" \n",
" # Evaluate objective and constraints at initial point\n",
" f.append(calc_f(x0))\n",
" h.append(calc_h(x0))\n",
" \n",
" # Determine number of equality constraints\n",
" m = len(h[0])\n",
" \n",
" # Initial dual variables with vector of ones\n",
" v.append(np.ones(m))\n",
" \n",
" # Print header for iteration information\n",
" print(\"Iter. \\tf(x) \\t\\t||h(x)|| \\t||grad_L(x)|| \\t||dx|| \\t\\t||dv|| \\t\\tdelta_A \\tdelta_W\")\n",
" \n",
" while(flag and k < max_iter):\n",
" \n",
" # STEP 1. Construct KKT matrix\n",
" \n",
" if(k > 0):\n",
" # Evaluate objective function\n",
" f.append(calc_f(x[k]))\n",
" \n",
" # Evaluate constraint function\n",
" h.append(calc_h(x[k]))\n",
" \n",
" # Evaluate objective gradient\n",
" df.append(my_grad_approx(x[k],calc_f,1E-6))\n",
" \n",
" # Evaluate constraint Jacobian\n",
" A.append(my_jac_approx(x[k],calc_h,1E-6))\n",
" \n",
" # Evaluate gradient of Lagrange function\n",
" L_func = lambda x_ : calc_f(x_) + (calc_h(x_)).dot(v[k])\n",
" L_grad = lambda x_ : my_grad_approx(x_,L_func,1E-6)\n",
" dL.append(L_grad(x[k]))\n",
" norm_dL = linalg.norm(dL[k])\n",
" \n",
" # Evaluate Hessian of Lagrange function\n",
" W.append(my_hes_approx(x[k],L_grad,1E-6))\n",
" \n",
" if(verbose):\n",
" print(\"*** k =\",k,\" ***\")\n",
" print(\"x_k =\",x[k])\n",
" print(\"v_k =\",v[k])\n",
" print(\"f_k =\",f[k])\n",
" print(\"df_k =\",df[k])\n",
" print(\"h_k =\",h[k])\n",
" print(\"A_k =\\n\",A[k])\n",
" print(\"W_k =\\n\",W[k])\n",
" print(\"\\n\")\n",
" \n",
" ######\n",
" # Algorithm 5.2: Add intertia correction to Algorithm 5.1\n",
" \n",
" ### ALG. 5.2, STEP 1\n",
" delta_A = 0\n",
" delta_W = 0\n",
" \n",
" KKT,inertia_correct,pos_ev,neg_ev,zero_ev = assemble_check_KKT(W[k],A[k],delta_A,delta_W,verbose)\n",
" \n",
" if not inertia_correct:\n",
" ### ALG. 5.2, STEP 2\n",
" # Assume zero eigenvalue is from rank-deficient Jacobian.\n",
" # Set delta_A to non-zero value\n",
" if zero_ev != 0:\n",
" delta_A = delta_bar_A\n",
" \n",
" ### ALG. 5.2, STEP 3\n",
" if delta_W_last == 0:\n",
" delta_W = delta_bar_W_0\n",
" else:\n",
" delta_W = max(delta_bar_W_min,kappa_l*delta_W_last)\n",
"\n",
" while (not inertia_correct) and flag:\n",
" ### ALG. 5.2, STEP 4\n",
" KKT,inertia_correct,pos_ev,neg_ev,zero_ev = assemble_check_KKT(W[k],A[k],delta_A,delta_W,verbose)\n",
" \n",
" ### ALG. 5.2, STEP 5\n",
" if not inertia_correct:\n",
" delta_W = kappa_u*delta_W\n",
" \n",
" ### ALG. 5.2, STEP 6\n",
" if delta_W > delta_bar_W_max:\n",
" flag = False\n",
" print(\"Abort step computation. KKT matrix is severely ill-conditioned.\")\n",
" \n",
" delta_W_last = delta_W\n",
" \n",
" ## STEP 2. Solve linear system.\n",
" \n",
" if flag:\n",
" b = -np.concatenate((dL[k],h[k]),axis=0)\n",
" z = linalg.solve(KKT,b)\n",
" else:\n",
" z = []\n",
" \n",
" ## STEP 3. Take step\n",
" if flag:\n",
" dx = z[0:n]\n",
" dv = z[n:(n+m+1)]\n",
" \n",
" x.append(x[k] + dx)\n",
" v.append(v[k] + dv)\n",
" \n",
" norm_dx = linalg.norm(dx)\n",
" norm_dv = linalg.norm(dv)\n",
" \n",
" ## Print iteration information\n",
" print(k,' \\t{0: 1.4e} \\t{1:1.4e} \\t{2:1.4e}'.format(f[k],linalg.norm(h[k]),norm_dL),end='')\n",
" \n",
" if flag:\n",
" print(' \\t{0: 1.4e} \\t{1: 1.4e}'.format(norm_dx,norm_dv),end='')\n",
" else:\n",
" print(' \\t ------- \\t -------',end='')\n",
" \n",
" print(' \\t{0: 1.4e} \\t{1: 1.4e}'.format(delta_A,delta_W),end='\\n')\n",
" \n",
" # Increment counter\n",
" k = k + 1\n",
" \n",
" ## Check convergence criteria\n",
" if(flag):\n",
" flag = norm_dx > eps1 and norm_dv > eps1 and norm_dL > eps2\n",
" \n",
" if(not flag and k > max_iter):\n",
" print(\"Reached maximum number of iterations.\")\n",
" \n",
" return x,v,f,h,df,dL,A,W"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.8.3 Example Problem 2](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.3-Example-Problem-2)",
"section": "4.8.3 Example Problem 2"
}
},
"source": [
"## 4.8.3 Example Problem 2\n",
"\n",
"(Where is Example Problem 1? We are using the same number scheme as the previous notebook.)\n",
"\n",
"Consider:\n",
"$$\\begin{align}\\min_x \\quad & x_1^2 + 2 x_2^2 \\\\\n",
"\\mathrm{s.t.} \\quad & x_1 + x_2 = 1 \\\\\n",
" & x_1 + x_2 = 1 \\end{align}$$\n",
"\n",
"### Test Algorithm 5.2 with redundant constraints."
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.8.3 Example Problem 2](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.3-Example-Problem-2)",
"section": "4.8.3 Example Problem 2"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Iter. \tf(x) \t\t||h(x)|| \t||grad_L(x)|| \t||dx|| \t\t||dv|| \t\tdelta_A \tdelta_W\n",
"0 \t 3.0000e+00 \t1.4142e+00 \t7.2111e+00 \t 7.4537e-01 \t 2.3571e+00 \t 1.0000e-08 \t 1.0000e-04\n",
"1 \t 6.6667e-01 \t2.3373e-08 \t2.9368e-04 \t 5.4908e-05 \t 9.4088e-05 \t 1.0000e-08 \t 3.3333e-05\n",
"2 \t 6.6667e-01 \t9.4991e-13 \t3.7259e-09 \t 1.1908e-09 \t 6.4780e-11 \t 1.0000e-08 \t 1.1111e-05\n",
"\n",
"x* = [0.66666667 0.33333333]\n",
"\n",
"v* = [-0.66666666 -0.66666667]\n"
]
}
],
"source": [
"## Define functions\n",
"def my_f2(x):\n",
" return x[0]**2 + 2*x[1]**2\n",
"\n",
"def my_h2(x):\n",
" h = np.zeros(2)\n",
" h[0] = x[0] + x[1] - 1\n",
" h[1] = h[0]\n",
" return h\n",
"\n",
"## Declare initial point\n",
"x0 = np.array((1,1))\n",
"\n",
"## Run Algorithm 5.2 on test problem\n",
"results = alg52(x0,my_f2,my_h2,verbose=False)\n",
"\n",
"## Display results\n",
"xstar = results[0][-1]\n",
"print(\"\\nx* =\",xstar)\n",
"\n",
"## Display results\n",
"vstar = results[1][-1]\n",
"print(\"\\nv* =\",vstar)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.8.3.1 Test Algorithm 5.2 without redundant constraints.](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.3.1-Test-Algorithm-5.2-without-redundant-constraints.)",
"section": "4.8.3.1 Test Algorithm 5.2 without redundant constraints."
}
},
"source": [
"### 4.8.3.1 Test Algorithm 5.2 without redundant constraints."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.8.3.1 Test Algorithm 5.2 without redundant constraints.](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.3.1-Test-Algorithm-5.2-without-redundant-constraints.)",
"section": "4.8.3.1 Test Algorithm 5.2 without redundant constraints."
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Iter. \tf(x) \t\t||h(x)|| \t||grad_L(x)|| \t||dx|| \t\t||dv|| \t\tdelta_A \tdelta_W\n",
"0 \t 3.0000e+00 \t1.0000e+00 \t5.8310e+00 \t 7.4537e-01 \t 2.3335e+00 \t 0.0000e+00 \t 0.0000e+00\n",
"1 \t 6.6667e-01 \t1.3978e-10 \t2.9473e-04 \t 4.5326e-05 \t 1.5285e-04 \t 0.0000e+00 \t 0.0000e+00\n",
"2 \t 6.6667e-01 \t0.0000e+00 \t4.5431e-09 \t 1.4393e-09 \t 2.0170e-09 \t 0.0000e+00 \t 0.0000e+00\n",
"\n",
"x* = [0.66666667 0.33333333]\n",
"\n",
"v* = [-1.33333333]\n"
]
}
],
"source": [
"## Define functions\n",
"def my_h2b(x):\n",
" return (x[0] + x[1] - 1)*np.ones(1)\n",
"\n",
"## Run Algorithm 5.2 on test problem\n",
"results = alg52(x0,my_f2,my_h2b,verbose=False)\n",
"\n",
"## Display results\n",
"xstar = results[0][-1]\n",
"print(\"\\nx* =\",xstar)\n",
"\n",
"## Display results\n",
"vstar = results[1][-1]\n",
"print(\"\\nv* =\",vstar)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.8.3.2 Discussion](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.3.2-Discussion)",
"section": "4.8.3.2 Discussion"
}
},
"source": [
"### 4.8.3.2 Discussion\n",
"\n",
"* Compare the multipliers with and without the redundant constraint."
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.8.4 Example Problem 3](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.4-Example-Problem-3)",
"section": "4.8.4 Example Problem 3"
}
},
"source": [
"## 4.8.4 Example Problem 3\n",
"\n",
"Let us try a model where $\\nabla h(x^k)^T$ is full rank but there are multiple local optima.\n",
"\n",
"Consider:\n",
"$$\\begin{align}\\min_x \\quad & x_1^3 - x_2 -x_1 x_2 - x_2^2 \\\\\n",
"\\mathrm{s.t.} \\quad & x_1^2 + x_2^2 = 1\n",
"\\end{align}$$"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.8.4 Example Problem 3](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.4-Example-Problem-3)",
"section": "4.8.4 Example Problem 3"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYQAAAD8CAYAAAB3u9PLAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAABgfUlEQVR4nO2dd3xUVfr/32cmvfdCQhop9F4E6R1EQJq9oK5ldXV/flfXLa5bbKura9fVtaIroiAgIlUCIr23QAiBdNJ7m8zM+f1xAyIkEJLJ3DvJfb9e9zUzmTv3fHIzuZ97znnO8wgpJTo6Ojo6Oga1Bejo6OjoaAPdEHR0dHR0AN0QdHR0dHQa0Q1BR0dHRwfQDUFHR0dHpxHdEHR0dHR0ABsYghCiqxBikxAiRQhxVAjxaBP7CCHE60KINCHEISHEwLa2q6Ojo6NjW5xscAwz8H9Syn1CCG9grxBivZTy2AX7TAMSGrdhwDuNjzo6Ojo6GqHNPQQpZZ6Ucl/j80ogBYi4aLdZwKdSYQfgJ4QIb2vbOjo6Ojq2wxY9hPMIIWKAAcDOi96KALIueJ3d+LO8Jo5xH3AfgJub26CoqKg2abJYJUUV9QR4ueDsZPspE6vVisGg/akYXadt0XXals6qs8JkptzUQJiHK842Om5qamqRlDK4VR+WUtpkA7yAvcCcJt77Dhh5weuNwKArHTMxMVG2ldp6k3xnyVZ5tqiizcdqik2bNrXLcW2NrtO26DptS2fTmVlcKm/5YLFMevoV+ZvFK2Vpda1NjiullMAe2crruE16CEIIZ2Ap8LmUclkTu2QDXS94HQnk2qLtK+Hm4swD86+1R1M6Ojo6l0VKydL9R3luTTJGYeDFG6Zyfd/uCCHUlgbYYMhIKL/JB0CKlPKVZnZbCTwshFiMMplcLqW8ZLhIR0dHp6OSV17JUyvXs/VUBkNjInlh9hS6+PmoLesX2KKHcC1wO3BYCHGg8Wd/BKIApJTvAquB6UAaUAMstEG7Ojo6OppHSsmy/Ud5fu1mrFbJU9PHcfPgfhgM2ugVXEibDUFKuRW47G/WOK71UFvb0tHR0XEkskvL+cu3G9iWnsmQ6EiemzWJrgF+astqFptGGamNlFIzY3E6OjqdF4vVyqKdB3jth58wCAN/mT6emwb31WSv4EI6hCHUm8y4ujjpZqCjo6M6R3Lz+euqjRzJzWdsYix/vW4CYb7eastqEQ5tCPkllazffoLMs6UE+nkwb0J/Av08z79vtUrNO7KOjk7HoKquntc2bePzXQcJ9HTn5bnTmd470aFuVB3aEF78aCPCIAjx9+JkZhFbD6Qza2wfDqfl0ie+i24GOjo67Y6UklWHT/DS+i0UVlZz85B+/Hb8CHzc3dSWdtU4rCGcyS3hyKk81r79IABb9p1i0Xe72Xc8m+z8MgD+cPdE4ru2bsGejo6OzpU4kV/EP1b/wJ6MHHqFh/DGjdfTL9Jxs/I4rCGcyi4iOjyA8qpafL3cCQ/y4fjpfO6fOwIfT3fe/XorB07k6Iago6Njc0qra3kjeTtf7jmEt5srf79+InMH9MLoAOk3LofDGsLA7pF88f1eFq3ajZ+3Bys3H+aWaYMY3DOq8f2u7DycwbyJ/dUVqnHqG8zklFWQU15BblkF+RVVlNbUUlJTS2lNLdX1JmobzNSaGmiwWLBKiUVKkBInoxFnowEngwF3F2c8XVzwdHXBx80VP3c3/Dzc8fdwJ8Tbs3HzIsTbCxcno9q/to5OqzBbrXy8fR9vJe+gxmTixsF9eWTcCPw8HG94qCkc1hD8fTy4fcYQ1u84QUiANwO6RxJ0wYTyln2nGD80QUWF2qOgsorDOfkczjnLyYJi0gqLySotx6rklwKUBSXnLuR+7m4Eenrg7uKMu7MzLk5GjEIgGjezxYLZasVktlDb0ECNqYGqunpyyiooq6mlvLYOeZEGAYR4exHh50Okvw/RAf5EBfgRE+hHbFCAPU+Hjk6LkVLy/dFUnt+VQmGdiZHdonlyyhjiQwLVlmZTHNYQAMYMimfMoHgA1vyUwt/fW0NxWQ2VNXVUVNdx05TOXYcnp6yCHemZbEvPZNvJdEqT9wPgZDAQE+hH97BgruuTREyAP138vOni60OItxdORtt0ey1WK+W1dRRWVlNQVU1BRRW55ZXklleQU1bBnowcvj10/Bem4e/qTI/MYhJCAkkMCSIxNIiEkCDcnB36q6rjwOw4ncXL63/kcG4+EZ5uvHfrbEYnxKotq11w6P8ys9mCk5MRq1UyaXgSVilZuvEgowbE8bcHpqktz+5IKUk5W8i6YydZn5LGqaISAII8Pejm48mkgf3oGxlGj7AQu1xgjQYDAZ4eBHh6kETTczl1DWaySss4U1zGqcISth89RnltHV/uOUyd2QyAQQjigvzpGR5Cj7AQencJpUd4CF6uLu3+O+h0Xg5m5/Hqxp/YfjqLMB8vnps1Gb+ygg5rBuDghkBjfO/rX2zG1GDhibsmMH1kT5VF2Z/s0nKWHzzGioMpZJWWYxCCIdGRLBjUhxHdoogPDmTz5s2MHa69HpObsxMJIUovYFIP6G6tYezYsVisVrJKy0nNL+J4fiEpeYXsPJ3NykPHAWXoqVtwAL27hNEvMow+EWEkhQbhbNTnJ3TaxpHcfN7evIMfTqQT4OHOk1PGcNPgvrg5O5GcXKi2vGaRUvK33RvadAyHNQQpJU5GA1JKlqw/wCd/vxVQhikcfaa/JVitkuST6Xy+6yDbTmUAMDwuivtHDWVCUjf8Pd1VVtg2jAYDMYH+xAT6M7nnz3NBRVXVHM0t4EhuPodzz7Ll5GmWH1Sqtbo5OdE7IpQBXbswoGs4A7p2wd/Dsc+Djv04nHOWN5N3sPnkaXzcXPnt+BHcPmwAng7QE5VS8vc9G/n4+N42HcdhDcFilTgZBf/5ehu94sJIiArGapUd3gxMZjMrDx3no217OVVUQpiPFw+NvYYb+vciQmOpdNuDIC9PxiTGMiZR6bZLKckpq+Bg9lkOZudxIDuPj7bt5X2rFYBuQQEMjOrCoKgIBkdHEOHn41ArR3XaFyklO09n8f5Pe/jpVAa+7m78dvwIbh3aH283V7XltQgpJS/u38xHKXu4u8dgnm7DsRzWEM5NfH6xZi9v/H4eABLJFRKvOixmi5VlB47yVvIO8iur6BEWzEtzpjG1V0KnHiYRQhDp70ukvy/X9UkCoNbUwJHcfPZl5bIvM5c1R0/y1b4jAIR6ezEoOoKh0REMiYkkLihAN4hOiNliZcPxNP770x6O5OYT5OnBYxOu5Zah/R1uburNw9t458gObknsz1ODJ3Q+QzBbrDgZDXy6ahddw/zpm9gFKTtm70BKyaYT6by8YSunikroFxHGc7MnMyIuSr+QNYO7izNDYiIZEhMJKMNrJwuK2JOZw96MHHafyWb1kRMABHp6MDg6giHRyv4JwYF6ypMOTGVdPV/vO8KinQfILa8gOsCPv82YwOx+PXF1wEi2tw9v5+UDPzInrhfPDJvS5muC450Bfu4dfLxyF889PAMAq5QYO9gFMru0nL999wM/pp0hJtCf1xfMYFKPeN0IrhKDQZAUFkxSWDC3Du2PlJLMknJ2Z2Sz+0w2uzOyWXvsJAC+7m4MiY5gaEwkQ2O6khgSpBtEB+DE2UK+2HOIlYdSqDE1MCQ6kj9OHcO4pDiHvZF8/+hOXty/mVmxPXlpxHUYbHBdcEhDADiSlkdSTAjX9I3pcL0Ds8XKJzv28cam7RgNBv44dQw3D+nXqYeGbIkQguhAP6ID/Zg3sDegmK9iEDnsOpPFhuOnAPB1c2VITCQv3DDV4YYSOju1pgbWp6SxeM8h9mXl4upkZFqvJG4f1p9eXULVltcmPjm+l2f3buK66O68fO0Mm13/HNYQeseH8/oTc4GO1TvIKinjd8vWcDA7j3GJcTx93XiHyaXuyJybh7ihfy8Acssq2NXYe0gvKsHTxbnZz5otVoSg2X/Kc4WbLFYrKw6m8MzqTfx5+jjmDOjVLr9LZ0ZKyaGcsyzdf5TVR05QVW8iOsCP308ezQ39e3WIFBOfHt/L07vWM7lrAq+Ouh4nG94M28QQhBAfAjOAAill7ybeHwusAE43/miZlPLvbW3XuTEnTkfpHaw5msqfV65HIPjX3Glc1ztJHx5SiS5+Pszu35PZ/a+8ruXCld1SSixWiRDKgrpzaT4Aluw9zJd7DhMT5I+pcdGdXrPDNmSWlPHtoeOsPJRCRkkZbk5OTOmVwNwBvRkcFdFhzvGi4/v4y671TIyM543Rs3A22HbUwFY9hI+BN4FPL7PPj1LKGW1tqCP+AzVYLDy/ZjP/232QfhFhvDxvOpH+vmrL0mkBf1y+jhqTidEJsYyMj25M/fHz9/Nc7+CVDVtpsFgZnxRHTlkFccFKDhzd71tPRnEZa4+lsvbYSY7mFSCAITGR/GrkEKb0THCYsNGW8nnqfp7atY6JkfG8PeYGXNphCNkmhiCl3CKEiLHFsa7Ecx+so6rWxAuPXG+P5tqdito6Hlmyih2ns1g4fBCPTbxWnytwIG4c3Ic1R0/y6Y79PL1qI85GAz3DQhgZH8O0XolEB/qxeM8h9mbm8MaN1/P90VROFhYTF+QPoPcArwKrVXI49yybTqSzKTWdE/lFAPSLCOPxSaOY3juJ8A46vLr45EH+tGMt4yO68daY2e1iBmDfOYThQoiDQC7wOynl0as9gNlsYfPeNK7tH2d7dSqQXVrO/Z8vJ7OkjOdnTz4/fq3jOPSLDP9FQZT0whI2paaz83QWRVXVTOwRz4aUND5buAAhBDllFfi6uRHk5XmZo+qco6Cyim2nMtmWnsG2U5kUVddgFIKBURE8OWUMk3vE06WDL8hcdGIfT+1cx5gucbw99gZcje132RZSXpyguJUHUnoIq5qZQ/ABrFLKKiHEdOA1KWWTuamFEPcB9wEEBwcPWrJkyfn3UnMq+GBNGndMjKNXtJ9NdLeVqqoqvLy8rvpz2VW1vHYwDYuU3N8rliT/9r2zaa1Oe+NoOq1SIiXn5wwupKy+gUUnMjhZVs2NCZG4GARHSiqI9fFkbEQwVikv+YyUkkPFFUR4uhHo5tLmHoSjnc+y+gbSyqtILVO2szV1AHg7O9Hd35vegT70DvDBU6U1A/Y+nxsrz7Ko9Az93Px4ODgRZ3Hl+dJx48btlVIObk17djmrUsqKC56vFkK8LYQIklIWNbHve8B7AElJSXLs2LHn39v18UbcXJy45+brcLtM1Ic9SU5O5kKNLeFYXgG//3Qpnu5ufHj7XOKC278OQGt0qoGj65RSnjcJJ6OB/oNL+elUBvuz8tiXmUtpTQ1ZdWZmjx5J/66XllrMKinjwdc/AsDb1ZWk0CASQgKJDwkkPljZAjzdW2wUWj6f5bV1pJwtJCWvgPUZp8mrP0teRSUAHi7ODIqK4NaYSK7tFk330GBNzB3a83wuOr6PRZk72nXO4GLsYghCiDAgX0ophRBDAQNQfDXHkFKyZd8prukboxkzaA3Hzxay8JOv8XBx4ZO75hEV4Ke2JB0bIoT4RQj0uQR9tw7tz+I9h1ifksa4xLhmx7pDfbxYfM9NHM8v5MTZQo7nF7Lq8Akq6+vP7+Pj5kpsoD8xQf5EB/jR1d+PqABfIv18r8os7EVZTR2ZJWWcLi4hraCYtMISUguKyCk7f59IgKsL18THsLDrQPpHdqFneIjN6nI4Iv89totn9vxgVzMA24WdfgGMBYKEENnA04AzgJTyXWAe8KAQwgzUAjfJqxyrSs0opLC0ilEDutlCsiqkFRSz8NOleLi4sGjhfD2SqBNhsVqpazDj6+bKbcP6N7ufi5MT/buG/6L3IKWkoLKakwXFpBcVk15UyumiUnakZ7HiYMovPu/qZCTc14dwH6VcaW1pMRmu+wjwdD9fCc/XzRUvN1e8XV1bfdE1W6xU1Zuoqq9XSq5W11JSU0NRVQ1nK6rIr6gkr7ySrNJyKup+NjNng4GYIH/6RoRx46A+9AgPoWdYCIf37NJsT8bevHNkB//cl8y0qCReGzXTbmYAtosyuvkK77+JEpbaarYeSEcIGNHPMYtT5FdUce9ny3AyCD66c65uBp0Mo8HAXcMHnl9/cDUIIQj18SLUx4uR8dG/eO9cgaGskvLGutiV5JVXkFdRxe6MHAoqKlmXVdDssd2cnHB1dsLNyQk3ZyeMBgNGg8DYOFZtkVaklJitkvoGM3VmM/UNZmoaGpo9po+bK6E+XoT5eNMvMpyu/r7ny6RGBfjpUXSX4c1D2/jXgS3MjOnJKyNn2HTRWUtwmJXK2w+epkdsKAG+HmpLuWpqTA08+MUKKurq+XzhAmIC/dWWpKMSLk62/Ze7sMBQU2zatIkBw4ZTWlN7fiuvraOqvp7KOhPVJhN1DWbqzWbqGsxYrFYsUmKxWhEIDEJgMCjDYOeMw9XZCS9XF3zcXPFydcXP3Y0ATw8CPd0J8PRwiPoBWkNKycsHfuTNw9u4Ia4X/xpxnSoLbh3CEMqrajl66iwLZw1TW8pVY7VKfr9sDcfPFvL2zTPpER6itiSdToQQAj8PN/w83IhFvxHRIlJK/rFnIx+m7OGm+H48e80U1bIvOIQh7DmWhVVKrukTo7aUq+btLTtYfzyNJ6eMYWxix1g/oaOjYxusUvLUznV8nrqfhT0G85fBE1QNCnAIQ9h9NBNPdxd6dgtTW8pVsTUtg7eSdzC7X0/uvGaA2nJ0dHQ0hNlq5ffbV7P01BEe7H0NTwwYo3qEmMMYwsDukQ4VhlZcVcOT36whPjiQp68br/ofWkdHRzvUW8w88uNK1mam8lj/UfymzwhNXCM0f4UtKqsiO7+MAd0j1ZbSYqSU/Hnlesrr6vnX3Gm4O/C6CR0dHdtS02Di3h+WsjYzlaeHTOSRvtdqwgzAAXoIB07kANA/KUJlJS1n6f6jbEpN58kpY0gKC1Zbjo6OjkaoMNVx7w9fs6cwhxeHT2NBQj+1Jf0CzRvCoZO5uLo4kRTtGNE5eeWVPL9mM0NjIrljmD5voKOjo1BQW8WdG5aQVl7E66NmMiOmh9qSLkHzhnD4ZC49Y0NxcnKMxSzPfZ+MVVp5btZkTeRe0dHRUZ+sqjJuW7+YgtpqPhg/n9FdtLnAVtNzCFIqKSv6JHRRW0qL+DHtDOuPp/HA6GH6SmQdHR0ATpYVsWDN55TW1/L5pJs0awag8R5Cg8WK2WKllwOEmzZYLDz3fTLRAX4sHD5QbTk6OjoaYG9BNnf/8DUuRiOLJ99Cz4BQtSVdFk33EExmKwA94rRvCIv3HOJ0cSm/nzLa5ukJdHR0HI9N2ae4df1iAlzdWTb1ds2bAWi9h2C24u/jQYi/tgt8VNbV81byDq6J7co4fTWyjk6n55v0Izz+02q6+wfz8YQFBLk7RoU8TRuCyWyle0yIZmJ0m+ODn/ZQVlvHE5NHa16rjo5O+yGl5N2jO/nnvmSGh0Xx3ti5eLu4qi2rxWjaEMwWK4kaDzetbjCzaPdRpvZMoKeeuE5Hp9NisVr5x56NfHx8L9fH9OBf117XrvWP2wNNq5US4rs2ndZXKyTnFFFtMvHgaMfLxKqjo2Mb6ixm/m/rKr7LOM69PYfwx0HjL6mX7Qho2hBA24ZQa2pgU04hYxJi9RXJOjqdlNK6Wu5LXsrugmz+MHAc9/d23JtDTRuCEBAVpt0c7isOpVDVYObeawerLUVHR0cFsirLuHPjErKrynlz9CxNrj6+GjRtCE4Gg2ZXKFutkk937CfKy53B0Y6TZ0lHR8c2HCrK455NX2OyWPh80k0MCe2qtqQ2Y5N1CEKID4UQBUKII828L4QQrwsh0oQQh4QQLVq55eyk3TG47aczSS8qYXyk9qOgdHR0bMvazFQWrP0cF4ORr6fe1iHMAGy3MO1jYOpl3p8GJDRu9wHvtOSgWq5/8MXugwR4uDMoxE9tKTo6OnZCSskHx3bzQPIykvyDWT79ThL8tDvPebXYZMhISrlFCBFzmV1mAZ9KKSWwQwjhJ4QIl1LmXe64zk7aNITCymo2nUhn4YhBOBssasvRaSVSQmkpZGRAcbHyvKzs0seyMqirA4vl5+2uu+BPfwKjUdnc3MDPD/z9f3688HlgIMTEKK91HBOz1cpnpWfYmJXP1KhE/j3yetydtFXr5MfC/W36vFCu0W2n0RBWSSl7N/HeKuAFKeXWxtcbgd9LKfc0se99KL0IgoODBy1ZssQm+mzJhqwCvj6Vw9NDeuAtzXh5aXslNUBVVVWn1Vlff+lmMimPAC4u4OSkbOcu8Bc/F0LZQHk0m6swGhWdUoLV+rNZmM2XPjeblfaEAFdXZXNx+fn5uc3WdOa/uy2ptpp5p+gkR+rKmeodzgK/KM2FlZZSxSdiIyvGvrpXStmqSBd7TSo3deaadCIp5XvAewBJSUly7Nix7Sirdbz+n8/pFR7CzddNJTk5GS1qvJjOoNNshpQU2LcP9u5VHg8ehOBgSEyE2NhfbnFxyt17a/6vW6NTSqUncvo0pKcrj+e21FQoKYH+/WHQIBg4UHlMSlJMqbV0hr97e5NVWcbCH77iTH0lCwPieHrGArUlXYLZauHxg6/iWtu2uwp7GUI2cOGsSySQa6e2bUpGcRnH8gp4YvJotaV0eioqIDkZNmyAXbvg8GGIjPz5gnrDDTBggHaGaYSAoCBlGzLk0vdLSn42s1Wr4G9/g7NnoV8/GDoUJk6EMWNAwzfSHY6d+Zk8mPwNFilZNOlG6o+fVltSkyzJWkdqZQZP9ljIEv7Z6uPYyxBWAg8LIRYDw4DyK80faJU1x1IBmNYrUWUlnY+GBuXCv369sh08CNdco1woX3xRubv28VFbZesJCFB+l4kTf/5ZWRns3w/btsFLL8GNNyqGN2mSsg0e3LYehE7z/C/1AH/ZuY4obz/eHzeXbr6BJGvQEE5WZvJFxlrGhgxmVHDbqjTaxBCEEF8AY4EgIUQ28DTgDCClfBdYDUwH0oAaYKEt2lWD9Slp9IsII9zXW20pnYKyMli+HL75BjZvVoZ6Jk2Cp5+GkSPBw0Nthe2Lnx+MG6dsf/oTVFXBjz8qhnjvvZCTo7x3ww0waxZ461/LNmO2Wnl27w98lLKHMV3ieH30THxd3NSW1SR1FhMvn1iEv4s3D8bPa/PxbBVldPMV3pfAQ7ZoS03yyis5kpvP/00cqbaUDk1NjTJk8sUX8MMPMH48LFgA778PIZ08f6CXF0ybpmwAeXmwbh18+SU89BBMngw33wzTpyuRTzpXR2ldLQ9vWc5PZzO4u8dg/jhoPE4GbUY7Anx0egVZNfk80+chvJzafnek6ZXKWmNzajoA45P0mge2xmRSLmyFhTB7NgwbplzYPv4YfPVqpM0SHg533qlsJSWwdCm8+abSe5g5E+bMUSbb9ZpNV+Z4aQG/2rSU/JoqXhwxnQXxfdWWdFn2lqSwKvdHZkWMZYB/kk2OqV3r0yCbT54h0s+HuKAAtaV0GPLzlcnT6Gh44QXlDjg1FdauVWL9dTNoOQEB8KtfKb2qo0eVCfXcXGWY7YUXlAgnnaZZnXGcOd8vot5iYcnUWzVvBgClpgrivbpyV+z1NjumbggtxGS2sPN0FqMTYvVUFTZg3z7lrrZ7d2UcfP162LpVCRHt7MNCtiA8HB59VDm/K1fCiRMQH68YxpEmE8x0TsxWK8/v3cSvNy8nyS+Yb6+7k/5BXdSW1SImhg3jlQH/h4vBdovjdENoIQez86hpaGBEXJTaUhwWsxm+/hpGjVKGhXr2hLQ0eO896H3JckYdWzFgAHz0kWIKUVHKPMOECYpRWK1qq1OPkroa7tzwJf85upPbkwby5ZRbCfVwrFl5o7DtJVw3hBay60w2AhgSE6m2FIdDSli2DPr0gZdfhkceURZm/f73SkoHHfsQEgJPPQVnzsDdd8Pf/66YxerVyt+oM3GwKI/rv/uY3QXZvDRiOv8YNhkXPX5XN4SWsi8rl4SQIHzd9dCNq2HTJmWtwN//Dq+8osTTz5+vT3KqiYsL3Hor7N6tzN/87nfKgrdt29RW1v5IKVl0fB/z13wGwNdTb2O+BucLzFYLZ2t/nvSxVYqhK6EbQguwWiUHs/MY0DVcbSkOw759MGWKEu3y6KPK62nTWpcmQqd9EEIZujt8WOkx3Hyzspaho84x1DSYeOynVTy1ax3Xhsew6rqF9A3S5v/0i8c/4fmUD9mYvwsp5fl5y/Y2Bt0QWsDp4hKq6k30i9Tml0dLnD0Lt90GM2YoF5eUFLjlFtBwKHenx2hUIrpOnICxY5X5hXvu6VhRSallhcxa/SnL04/yWP9RfDB+Hv5u7mrLahZnYcTd6MrBslT+c2opp6tyANo9oEX/N20Bh3PyAegTEaqyEu1itSqTw337QteucPIk/PrXyvCEjmPg5gb/7/8pYb/e3tCrFyxa5PjzC0vSDjHzu08ora9l0cSbeKTvtZrLVHoxQwJ7UWupJ8ErioqGar7IXMPWwv08d+wDzlTntltPQR/JbQEpZwtwd3bS1x80Q1qaMuTQ0AAbNyqTxzqOi68vvPqq0tP71a8UU/jvf5UIJUeiusHE07vW8/Wpw4wIi+bVUdcT4u4YmQHHhgwmvSqH/v5J9PNPZGfxYf6XsYbyhqpfDCHZGr2H0AJSzhaSGBqMUR/3+AVWK7zxhjJpPGeOso5AN4OOw+DBysTzuHFKQr0PPnCc3sKR4rPMWPURS08d5jd9RrBo4o0OYwZWqcQCezl58EH6cqI8wujhHUuRqYx47658eHrF+SEkW6P3EK6AlJIT+UVM6ZmgthRNUVSkzA1UVyvRKYl68tcOiZMT/OEPcP31yjzDypXw6afaXUEupeST43t5bu8mAt08+GLyLVwT5lhdG0Pj2oIbIseSmZpHXm0RX2at4/ouoxkW2JvjFWeI9Ypon7bb5agdiOLqGspr64gP1gPmz7Fvn5LPf+BA2LJFN4POQO/eivFHRSm1GY4dU1vRpRTUVrHwh6/46+4NjAyPYfWMux3ODC7E2eBMN69I7t/zDJUNNdwWPZ1E72iu6zKq3drUewhX4FRhCQDdgvX5A1DuDv/v/+Cdd2Be27Pt6jgQLi7KEOEnnyjrFrT0HdiUfYrfbfuOqgYTfx86iduTBnaIFDNTwkZQaqpkQuhQhBBIKW2+OvlCdEO4AmeKSwGICfRXWYm6NDTAY48pSeeSk5UIFJ3OyZ13KnNFc+bAnj3w7LPqFempbjDx/N5NfJa6n+7+wSyefAsJfkHqiGkHPJzcuDN2BkahnOD2NjndEK5ARkkZLkYj4T6OlePEllRUKKmUvb2VimVaKUmpox4DBypmcNNNypqTpUvtX6xoX2EOj21dRUZlKff0GMLjA8fgZnT8S1qD1Yyz4eff45wZ2AN9DuEKZJeWE+Hng8Hg+N3P1lBaqlQo69kTVqzQzUDnZ4KCYM0aJUPtddcp1dzsQb3FzMv7tzB/zWc0WC18MfkWnhoyoUOYQX5dMffs+ht7StSZpNEN4QrklFUQ4efAhXrbQHGxUt93+HB46y19tbHOpTg5KZlU4+Jg6lSlN9meHCk+y6zvPuGNw9uYFduL76937InjC5FS8ubJL6mx1BHlEaaKBpv8iwshpgohTggh0oQQTzbx/lghRLkQ4kDj9hdbtGsP8iuqOmX95IICpXTlxInw73/rOYh0msdoVMqb9u2rpNYuK7N9GyaLhdcObmX26k8pqa/lw/HzeGXkDHw0Wuu4NWzI38m+0uPcFXs9IW7qBLG0uY8lhDACbwGTgGxgtxBipZTy4j7Pj1LKGW1tz56YzBaKqmsI9XGMBS22Ij9fMYM5c5QspboZ6FwJg0HpRf6//6fkQlq/XqngZgsOFOXyxLbVpJYVMSu2J38bOgk/V+3mIWoNRfVlvH/qG/r4xjM9XL2a7bboIQwF0qSU6VJKE7AYmGWD46pOSXUNAMFeniorsR91dUpSuhtugH/8QzcDnZYjhNKbHDlSSXHe0NC249WaG3huzw/M+X4RlaZ6Phg/j9dGzexwZiCl5O20JZilmUcSbz6/ME0NRFuTJAkh5gFTpZT3Nr6+HRgmpXz4gn3GAktRehC5wO+klEebOd59wH0AwcHBg5YsWdImfW0ho7KG5/ee4IHesfQP8mtyn6qqKry8tN+DaKnOM2eUlBRxce2vqSk62vlUG7V0pqWBq6uS6LAlXKzzUG0pn5acochSz1ivEBb4ReFhUH/SuD3O5wmyWWnYxRhrb4bS9lWe48aN2yulHNyqD0sp27QB84H/XvD6duCNi/bxAbwan08HTrbk2ImJiVJNtpw8LZOefkXuzchudp9NmzbZT1AbaInOl16ScsAAKaur219Pc3Sk86kF1NJZViZl9+5S/uc/Ldv/nM6Cmir58OblMvqT5+WE5e/J7XkZ7SeyFdj6fFY2VMtbt/9J/mbvP6XZarbJMYE9spXXc1tYbjZw4X1AJEov4ELTqbjg+WohxNtCiCApZZEN2m83ymvrAPBz71hd1KZYvVqpaLZzp/3jyXU6Hr6+St6jkSOhe3cYPfry+1uk5KOUPbxy4EfqLWb+X7+RPND7Glw7QCjp5fgwfSXlpkqe7nWfXdcbNIctzvZuIEEIEQvkADcBt1y4gxAiDMiXUkohxFCUuQvNl9+oqK0HwNvNVWUl7UtampK4bPnylnfxdXSuREICfPYZ3HijkjU1sply5PsLc/n72cNkZNUwKjyWp4dOJN634+cOO1R2krVntzE3cgIJ3toInW2zIUgpzUKIh4G1gBH4UEp5VAjxQOP77wLzgAeFEGagFripsWujaapNJgC8XDtulRcp4b77lIL3I0aorUanozFpEtx/Pzz0kHLDcWGQQn5NJf/ct5ll6UfwN7rw9pjZTItK6hA5iK5EvcXEGycXE+YWyC3R09SWcx6b9MeklKuB1Rf97N0Lnr8JvGmLtuxJjakBgxC4OXfcbutHH0FlpVL3WEenPfjDH2DAACW9xbx5ypqCj1L28Pqhn2iwWniw9zX0LbMwLbq72lLtxpKs9eTWFvJMn4dwM2rnhrPjXulsQG1DA25OTh32juXsWXjySSVm3En/Jui0E66uysK1BQsk5u7HeTt1M5lVZUyMjOepIROI9vYnOTlZbZl2I6smn6+zNjAuZDAD/JPUlvML9MvAZTCZLbg4qT/R0148+qhS+rJfP7WV6HR0PBJzCf7jRp7cl0N3/2A+nrCAsREqxTariJSSd9K+wtXowj1xs9WWcwm6IVyGBosFZ7Xy+rYza9fC3r3w8cdqK9HpyKSWFfKv/VtYl3WSoCBPrF9M48+P92FkROdMjLWpYDcHy1J5KH4B/i7ay5GmG8JlsFglxg6a5fQf/4BnnoFOEFGrowI5VeW8fugnvjp1GE8nFx7rP4q7ewzmiwpXnntWCXPubFQ2VPN++jd094lharg2Izh0Q7gMEomhA84fbN0KeXnaqXal03E4W1PJW4e3s/jkAQSChd0H83CfEfi7KXced9wBTz8NBw92vqHKT86soqqhlof73KhqeorLoRtCJ+Sf/4THH9cnknVsR05VOf85upPFJw8ikSyI78dDfYbTxfOXwyKurkoCvBdfhM8/V0msCqRWZrAmbxuzIsYQ6xWhtpxm0S8Jl8EgBFbtL5e4Ko4cUSpdffWV2kp0OgIZlaW8c3gHS9MPAzA3rg8P9R1OVy+/Zj9z//1Krqz0dPVyZtkTq7TybtrX+Ll4c6uG1hw0hW4Il8HJYMBitaotw6b8619KdJFbx0kjr6MCB4pyeffIDtZmpuJsMHJzQn/u7zWMCC/fK37Wx0dZDPnvf8Mbb9hBrMqsP7uDE5UZPJZ0Gx5O2p600w3hMjgbjZjMFrVl2Iz6emW16IkTaivRcUQsVisbs9P4MGUPO/Iz8XVx48Hew7mr+yBCPK4uA+g998C118Jrr3XsSnyVDdV8fPpbevnEMT5kiNpyrohuCJfB1clIndmstgybkZys1EYODVVbiY4jUW6q48uTB/n0xD6yq8oJ9/Dmz4PHc1NCP7ycW5fnq1s3pSbzzp1KidaOyqIz31FlruHB+PkOscBVN4TL4ObsTL3ZgsVqxdgBbmNWrFCK3+joXAkpJQeL8/j8xH6+PZNCncXM0NCu/GnQOCZ1TcTJBv8Ps2Yp38mOaghnqnP5Pu8npncZpemJ5AvRDeEyeLg4A1BrasCrA2Q8XblSSVOho9McRbXVLD99lKWnjpBSWoCHkzM3xPXm1sT+9A60beH3mTNh4UJ44QWbHlYTSCl579QyPJ3cuU3jE8kXohvCZTiX5bSq3uTwhlBTo9Q56N558ofptJA6i5nk7FN8c/ooG7PSMEsr/QLD+cewycyO7YW3S/t894cMgbIyOHmyXQ6vKrtKjnCwLJUHus3D29lxSvDqhnAZfBpNoKKunjBfb5XVtI3qahg7Vq+RrKNQZzGzLe8M32UcZ13mSSob6gly82Bhj8EsiO9Lgl9Qu2swGGDMGNi+HaK0UQ7AJjRYzfw3fTmR7iFMC79WbTlXhW4Il8HXXYnNPFc5zZGpq9N7B52dSlM9W/NOsyYzlY3ZaVQ1mPB2dmVKVCIzY3syIizaJnMDV0NSkhL11pEMYVXuFnJrC/lb7wdwMjhWLjTdEC6Dv4cSM1xaU6uykrajG0Lnw2K1kmGq5r2jO9mUc4rd+dmYpRV/V3dmRPdganQSw8OiVC1T2b07fP21UkinI1DRUM0XmWsZ5N+DwQE91ZZz1eiGcBkCPJXiwiXVNSoraTt1dcrdmE7HxSolJ8uK2F2QzfazGfyUd4YyUx2che5+wfyq11DGRXRjYHCE3XsCzXGuh9BRWJy5hlpznSZTW7cE3RAuQ4CnOwIorHJsQ6ipgYYGiIlRW4mOrZBSkl9bxeHisxwuPsuh4jz2FeZQYVLqgIe6ezGhazyBZbXcPW4qYR7anANLTFRqencEztYW813uViaFXUO0Z7jaclqFTQxBCDEVeA2lpvJ/pZQvXPS+aHx/OlAD3CWl3GeLttsTZ6MRfw93Cquq1ZbSJjIzwcUFOmhphw6NlJKC2ipOVZRwuqKEk2VFpJQWcKK0ULn7R8m5Fe8byPSo7gwOjWRISCRRXn4IIUhOTtasGQB4eoKvr3LD4uh8lvEdBmHQVI3kq6XNhiCEMAJvAZOAbGC3EGKllPLYBbtNAxIat2HAO42PmifUx4v8iiq1ZbSJurqOnR7AETFbrVSY6igz1VFWX0txXQ2FtdUU1laRX1tFTlUFOdXl5FRXUGv++Wrp4eRMd/8QpkV3J8kviN6BYfT0D8HDWTt1ea8Wd3dw9ByS6VU5JBfsZW7XCQS5+qktp9XYoocwFEiTUqYDCCEWA7OACw1hFvCplFICO4QQfkKIcCllng3ab1fCfLzJLa9QW0abqK/XDeEcDVYLZ6srKaqroaiumpK6Giob6qluMFHdYKLeYsZktdJgtWC2WrFIK1YpkchfXLQKCwv5MrkUUOpmWKU8v59FSixWK2ZpxWSxUG8xU2+xUGdpoMbcQFVjO80R4OpOhJcv8b6BjOkSR4y3P7E+AcT6+BPu6dPhanS4uoKj55D86PQKPJ3cmRc5UVUdDda2jWbYwhAigKwLXmdz6d1/U/tEAJcYghDiPuA+AP+gMNWLb1urKsgsKm1WR1VVleoar0R1NQQGal8n2O58SikpMNeTbqoi3VRFXkMt+eY6is31NHftcRYCF2HECYGTEBiEwIDAAAjEL9ZwWK1W8vJ+jj4TCAQgAKMQGFE+b0TgIgz4CgNBwhk3J1fcnI24GYx4GpzwMDjhZTDiZXDGz+iMj9EZpwuLp1QD1RWYz1ZwkjNc7RouR/h+/uY3YDJpXyc0fT6zKGSf4ThjrL3Z+9MudYQ1Uuy3vE2ft4UhNHW7cnEHsCX7KD+U8j3gPYDwrnFy7NixbRLXVtJd9rI5dwsDhl1zfl3ChSQnJ6O2xiuxfz9s357M/Plj1ZZyRdpyPustZjblnGJNRipbctMpqVcu2O5OzsT7BnKNdxdivP2J9PIl2N2TIDdPAtw88HZxxdPJ5aoibxzh7w6OofPuu+Gdd7SvEy49n1JKnjj4GoF1vjw65C5cjeoN3ZmtdSw5/WybjmELQ8gGul7wOhLIbcU+l2C2qN+P7Oqv5HfPKi1v0hAcAVdXxx+jvRyFtUqs/ZdpB6kw1RPg6s7YiDiGhHSlX1A4iX7Bmgmz1LkURx7S3F96nGMV6fw6fr6qZgCQUZWsiSGj3UCCECIWyAFuAm65aJ+VwMON8wvDgPKWzB+YLepfxaIC/ADIKC6jdxfHzBsdGQkmkzJO66j/eE1RVFvNO0d28HnqfkxWC9dFd2d+fF9VVtzqtI76eigqcsxyrlJKPs/8nmBXfyaHXaO2HE5VfI+XU5c2HaPNfwYppVkI8TCwFiXs9EMp5VEhxAON778LrEYJOU1DCTtd2JJjmy1WpJSq5hGPauwhnCkuVU1DW/HxUUJOc3Kga9cr7+8I7MrP4sHN31BWX8sNcb15qM9wYn0C1Jalc5WkpSnrYxxxnvxA2QmOV5zh1/HzcTY4q6qluqGAvNo99AtYCCxt9XFs4stSytUoF/0Lf/buBc8l8NDVHtcqoaC0itAA9eKo3V2c6eLrw2kHNgRQSmaeONExDOF/qQf4y851RHn78cXkm0n0C1Zbkk4rOXHCMVfQSyn5LGO1ZnoHpyvXAZI476ltOo7m+9UZuSVqSyAuyJ9ThcVqy2gT5wzB0Xnv6E7+uGMN14bH8M30O3QzcHAc1RDO9Q4WdJ2keu8AIL1yLcFuvfBxiWzTcTRvCGc0YAgJIUGcKizB4sDB0q6ujm8IG7PTeG7vJq6L7s6H4+fh6+KYk/w6P+OohvBl5joCXXyZFKb++trS+nRKTaeI9Z7S5mNp2hAMQpCeo/6deUJIICaLhYySMrWltBpPT/jpJ7VVtJ5KUz1PbFtND/8QXh45o0OUNO3sSKl8JwcNUlvJ1XGsPJ3D5WnMiRyvid7BmaoNCAzEeI1v87E0/V/l7CRIz1bfEJJClWIhqflFKitpPV5ekJEBWVlX3leLfHpiH8V1NbwwfBpuKqZr1rEdKSlKlFH//moruTqWZm/E28mDqeEj1JaClJLTlRsIcx+Iu1Pbgyq0bQhGA6eyi5AqB9HHBwfiZDBwLK9AVR1tZfp0pa6yo1FnMfPBsV2MjYijX5BjZpHUuZQVK5S6yo4UYVRCJTuLj3Bdl1G4GdUvq1tcn0JlQzax3rYpKKFtQ3AyUFVTT0GJusnlXJ2d6BYcQMrZQlV1tJVZsxzTEHblZ1FSX8sdSQPVlqJjQ1auVL6TjsQekYaTMHJ9l9FqSwHgTOUPGHAiymuMTY6neUMAOJmp/oW4V3goR3LzVe+ttIXJk5X6teXlaiu5OrbkpuNiMDI8LFptKTo24uxZOH5cqansKJSZKjlKBuNDh+Lnon5KcSklZ6p+oIvHUFyNPjY5prYNwWhACEjNUH+opk9EKKU1teSUOW7mU29vGD8evvxSbSVXR0pJAT0CQnB3Un8CT8c2fPYZzJih1OlwFFbnbcUsrNwQOU5tKYAyXFRtPku0d9snk8+haUMQAiJD/TihAUPoH6mMXe/P0nzG7svy2GPw0ktgsaitpOUU1FZrusiLztVRXw+vvqp8Fx2FBmsDq/N+IlaG0tVDGylsMqqSERjp6jnSZsfUtCEAJEWHcOKM+oaQEBKEh4sz+7OumJNP04waBcHBsGyZ2kpaTmVDPd7O6k/g6diGzz+HXr1gwAC1lbScn4oOUmqqYJCMV1sKoAwXZVZtJsx9oM2Gi8ABDKF7TCh5RRWUV9Zeeed2xMlooH9kOHszc1TV0VaEgCefhBdecJwMqJ7OLtSYTWrL0LEBFgu8+KLyHXQkvsvdShf3YGIIUVsKAOUNGVQ0ZBHlZdvJbe0bQqzSPUs5k6+yEhgSHUlqfhFlNXVqS2kTM2YoZTU3blRbScvwc3GjqK5GbRk6NmDFCqWGsgOUPjjPmepcjlWkMz382sYySOqTVfUjAF09R9n0uNo3hBjFkVPS1TeEoTGRSGBPRrbaUtqEwaDcof3xj44xl5DoF8zx0gKHjvDSUVKwP/208r1zpLUHa/O24ySMjA8dqraU82RXbyPANRFPZ9v2WDRvCN6ebkSH+3M0/azaUugTEYabkxM7Tjvoct8LuPVWJeHdW2+preTK9A4MpcJUT0ZlmdpSdNrASy9BVJSyGM1RMFkb+KFgNyOC+uHr7KW2HADqLOUU1h0m0tP2K6U1bwgAveO7cORkrup3iC5ORgZFR7A9PVNVHbbAYID334e//x0yNf7rjAyPAeCHnDR1hei0mhMn4N//hnfecazewbaiQ1SZa5gSNlxtKefJrd6BxEqkDaOLzuEQhtA3IZzSylqy8svUlsKIuChOFZWQX6Hu6mlbkJQEv/0tPPigtieYo739SfANYm1mqtpSdFqB1Qr33Qd/+YvSQ3Ak1p3dTqhbIH39EtSWcp7s6m24Gf0Jcu1u82M7hiEkRgBwMFX9CJ+R3ZTVsltPZaisxDY88YTSQ9D6YrWZsT3YmZ/F6Qr106HrXB0ffKCsPXjoqktkqUtBXQmHyk4yMXQoBqGNS6VVWsit2UmEx3BEO2jSxm95BWLCA/DxcuPACfUNITE0iGAvT7amnVFbik1wcYH//hcefVQpZ6hVbkzoh5Mw8NmJ/WpL0bkKDh9WJpHff18p4+pIJBfsQSIZFzJEbSnnKa5Lod5aQYRn+1Rpa5MhCCEChBDrhRAnGx/9m9nvjBDisBDigBBiz1WLNAj6JUZowhCEEIyKj+GnUxmYLY5bMOdChg2Dv/1NmezTap6jEHcvZsT04H8nD1BUW622HJ0WUFSkJK979VXo00dtNVdPcsFeevrEEe4epLaU8+TU7AQE4R7tY1Jt7SE8CWyUUiYAGxtfN8c4KWV/KeXg1jQ0ICmC7PwyCkvVH7sfkxhLRV09+xx81fKFPPCAEht+663aDUV9pN+1mCxm3jjkwJV+OgkNDTBvHixYoHynHI0z1blk1OQxJkRbGXbzanYT6JqEm9G3XY7fVkOYBXzS+PwTYHYbj9csA3so1eH3HVd/DcC1cVE4G438cOKU2lJsymuvQXW10sXXInE+Adyc0J9Fqfs5Uqx+GLJO8zzyiJJM8dln1VbSOrYWHkAguDaov9pSztNgraaw7ijhHq26p24Roi2hnEKIMiml3wWvS6WUlwwbCSFOA6WABP4jpXzvMse8D7gPIDg4eNCSJUsAsFolf/v8EH1j/Zg7Uv00yG8eOkVeTR1P9orC21v7ideqqqrw8rpyHLXZrKQlDg+HwEA7CLuIK+mstpr5Y+5B/Iwu/CWsN0aVYhhbej7VRg2dhYVQUAA9eijhzS1Ba+fzI7EBN1y4Wf4yNYSaOmtdT1AQ9AkhRQtxr28+6mncuHF7WzsSg5TyshuwATjSxDYLKLto39JmjtGl8TEEOAiMvlK7UkoSExPlhfzfy9/IOY/9V2qBr/celklPvyI/XvGd2lJaxKZNm1q879GjUoaHS/npp+2npzlaovO7Myky+pPn5esHt7a/oGa4mvOpJvbW+fbbUnbtKuWpU1f3OS2dz5yaAjl982/k8uxNl7ynps7dhW/KT1NHyQZL7WX3A/bIFlxfm9qu6N9SyolSyt5NbCuAfCFEOEDjY5NpSaWUuY2PBcA3QKvWgA/uFUV2QTl5RerXJBjfvRtOBgN7C0vVlmJzevaEDRvgD3+ADz9UW82lTI/uzuzYXrx6cCv7CtUPNNBReO01JXFdcjLExamtpvVsLzoEwDWB2poJz689QJBbT5wMbu3WRlvnEFYCdzY+vxNYcfEOQghPIYT3uefAZJQexlUzpKeyqmX3UfWX1vp7uDM8Loo9BWWqr6BuD3r2hB9+gL/+VVldqjX+PmwS4Z4+PLR5OQW16gcadHZefBFef93xzQBgR/Fh4jwjCHVTYcy0GRqstRTXHSfUvX+7ttNWQ3gBmCSEOAlManyNEKKLEGJ14z6hwFYhxEFgF/CdlHJNaxqLiwwk0NeTXUe0sShseu9ESupNHMh27KI5zZGYCJs2wT//qdz9aQkfFzfeHXMDZaY6frVpKXXmBrUldVqeeUZZfLZ5M0SrP73XJioaqjlecZqhgb3VlvILiuqOIbEQ4t6vXdtpkyFIKYullBOklAmNjyWNP8+VUk5vfJ4upezXuPWSUrY67kAIwdDeUew+monVqv5d+aTu8TgJwarDJ9SW0m5066b8o7/5Jvzud8qks1boHRjGqyOv51BRHr/d+i0Wa8dYF+IomExK2pMvvlB6BpGRaitqO3tLjmFFMiSgl9pSfkFB7UFAEOLWvkblECuVL2R43xjKKms5roH6CF5urvQN8uX7Iydo0Grwvg2IjoadO5VVp5MnK1EkWmFKVCJ/HjyBNZmpPLVrXYccvtMiubkwZgycPQvbtytRaR2B/aUn8HHyJMFbW0mXCuoO4e8Sh4uxfSMaHc4QrukTQ2SoH6UV2iiYMiw0gJKaWn7qILmNmiMgAFavhmuugcGDYc9VrzdvP+7pOYQHe1/D/1IP8NzeTboptDNbt8KQIUqhpaVLwcd2FRxVRUrJ/rLj9PdPwqiR3EWg5C8qrDtKsHvfdm/Lqd1bsDG+3u4s/dfdass4T68Ab/w93PnmwDHGJjr4bNoVMBrhuecUQ5g+XZlbWLhQbVUKTwwYQ02DifeP7cIsrfxl8ASEI+VZdgCkVOpn/OMf8MknMHWq2opsS1ZtPiWmCvr5Jaot5ReUm87QYK1u9+EicEBD0BpOBgMz+3bnf7sOUlJdQ4Cnh9qS2p05c5RFRzfcoMwvvPoq+Pmpq0kIwV+HTsLJYOSDlN3UW8z8Y+hkjC1dGaVzWYqKlGylx48rQ0SOHknUFIfLTgJoKtU1KBPKAEFuPdu9Lf2/xQbMG9ibBquVbw4cU1uK3ejRQxk28vRUEpetaVXcmG0RQvDnweP5de/h/C/1AL/eslyPPrIB33wDfftC166wY0fHNAOAo+XpBLr4Eu6mnWR2AEV1KTgbvPBx7trubemGYAMSQoIYFNWFJXsPayL6yV54eSlDCB9/rCTHu/NO5U5STYQQPDFwDH8ZMoF1mancsn4xxXXamG9yNPLylOR0TzwBX30F//oXuLurrar9OFaRTg+fWM0NNRbXHyfItXu71D+4GN0QbMRNg/uSUVLGtg5QXvNqmTABjhxRch/16qUYhNrzunf3GMLbY2ZztCSfWas/4USphkKjNI7VCu++q/QKEhLg0CG49lq1VbUvJfXlFNaX0sMnVm0pv8AiGyg1nSLQLcku7emGYCOm9EwgwMOd/+0+oLYUVfDygldeUSKR3nxTiUb64Qd1NU2L7s6XU27BZLEw5/tFegnOKyAlfP89DBwIixYpixKffbZj9wrOcaJSiRJM8olRV8hFlJtOY5UNBLjqhtAiLFYr+08oKbHVDDd0cXJi/qA+bDqRTnapRqvM2IFBg2DXLqVW869+paxb2LtXPT39g7qw8ro7ifcN5P7kZby4bzNmfQHbJWzfrtTDeOwxePppJbS0t7YW67YraVVZGDAQ5xmhtpRfUFKvTHQHuNpnotvhDcFoMPDEv1eQmVeKEEJVU7h5cF8MQvD5roOqadACBgPcfDOkpCiRSNdfDzfeCKkq3aCHeXjz5dRbuTmhP28f2c4dG77Uq641cvQozJ6t/H3uvFNZfHjDDaCxYfR2J60yi64eobgaXdSW8gtK609hFK54O9tnGbhDG8K5EpYDe3Rl8dp9AFhUnNQN8/VmSs8Evt53hOp6k2o6tIKLi5La4ORJ6NcPRoyAu+9WxqTtjZvRieeHT+XFEdPZW5jD9FUf8VPeGfsL0Qh798Jtt8G4cTB6tGLWd98NTp00ED2tKot47/aP4rlaSutP4ecSi0HYpyC1QxuCofE25pZpg1i/4zgATkZ1f6U7hw+ksr6er/e1KqFrh8TTU6nClpqqhCxOm6ZciFassH+5zgXxfVk+/Q58XFy5bf1iXty3mQZrx007ciFmsxItNHKkspakb1/FrB97DNzaL6Oy5ikzVVLWUEmsxoaLAMpMp/FzsV+cr2MbgkExhH6JEUgJB1OV3Phqhn72iwxncHQEH23fi8ncOS40LSUgAP78Zzh9WplfeO45JYrllVeg3I7TLj38Q1g5/U5uSujH20e2M2/NZ6RXlNhPgJ0pKVFWlcfFKSmqf/tbOHVKCSf1bZ/SvA7FmWqlNnqMZxeVlfySeksFtZYi/Fxi7NamQxsC/DxsNHl4dxavUYaNrI3zCGrNJ9w/cihnK6r49lCKKu1rHRcXuOUWJWHe//4Hu3dDbCzcey9UVtqn1+Dh7MLzw6fx1ujZnKko5bpVH7HidMdZWGg2w9q1cOaMkrH22DFYvhx+/BHmzeu8Q0NNkVWjJMqM9ghTWckvqTApIey+uiG0HGNjL2HB5AH8uD8d+HnYSK0FJiPjo+kZHsJ7W3frKZmvwDXXKOmTDx+G7t0hO1tJo/zoo8qq2Pb29OtiurNu5j1cExpFhGfLsrTVWTSUA/wCrFblgv/QQxARoUQLeXgo6SY++UQJJ9W5lOzaAjyMbvi7aCtLX3mDEgrr42K/zKsObwhCCCxWKzFdAugTH05qxs8LkNKzi1RJky2E4IFRQ8koKWP1ET32vSVERCj1Fnr0UPIjBQTAXXcpwxx/+APs26dc8NqDUA9vPpown8Ehl4/kWHrqMM/s2cht6xbzfUVu+4i5SiwWJcz38cchJuZnM9i+XTHUkBAIDVVbpbbJrS2gi3uw5lYoV5iyEBjxdrbfUJbDGwJwPoHZ23+cT1xEAACfr97DYy8v5+VPN/GvT+2/Qmpi93gSQgJ5d8tOvZdwlSQmKne3KSlKHh0plTDWsDDl8YMPINPOC8KXnjrMUzvX4SSMLOwxmOSqAt48tM2+Iho5fRreew/mz1cu+AsXgqursqjs0CFlAr+j5htqD87WFhPurq38RQAVDdl4OYdjEPYb3+swI4lfrT/Ap6t2ISXcft1gjqTl8fQDU0HCix9vZOPOVCYMs19aW4NB8ODoYTz29WrWHD3JdX3ss9KwIyEE9O+vbC+8oJjAhg2wfj08+aTSi5g0SdmGD1cuju3B4eKzPL83maeHTOTGBKWE4fFjx9iRn8l9lmG4GNs3JDAvD7ZtU37v9euhulr5nWfMUDLNRmgvOMZhsEorBfUljAhu39KUraGyIQdvZ/v+cdtkCEKI+cBfgR7AUCllk2VThBBTgdcAI/BfKeULbWn3YnIKyvh28xEWzhxGl2BfPli+g9iIAAYkKUMAcyf2Y+32FLsaAsDUnom8E7KTN5K3M6VnguohsY5OVJQSK3/33crw0cGDikG8/bYyvOTpqayUHjRIGS8fNKjtlbyklLx68EeGhkaeNwOA7IYaPD08bGoGUkJOjjI8tnevsu3bB/X1MGwYTJyoDAn17t35Fo61F2WmSszSQrCrv9pSfoGUksqGHILd7FvKs609hCPAHOA/ze0ghDACbwGTgGxgtxBipZTSZiEdOw9nEODrwZwJyj+s2WLl+Q/XA5B5tpT9x3MIDfBGSmnXcUKDQfDb8dfy0OKVLDtwlAWD+tit7Y6OwQADBijb448rF9PTp3++mL7+uvLo4qKYQ0KCEsl04ebldeV2duRnsiX3NDvnPXz+Z1lVZZRaTCR6dcEq5fn1MC2lokLReuF28qSiXcqfTe3uu5VsslFRugG0F4X1ZQAEufqpquNiTNZKGqxVdp0/gDYagpQyBa4YzTMUSJNSpjfuuxiYBdjMEPokdOHDFTvOvw7y98TP253b/rSI6HB/KmvquW/ucFUmjcYnxTGgazhvbNrO9X264+7ibHcNnQEhlHHzuDglrBKUi2tmJhw4oMTdnzwJ69b9fBH29laMISYGgoLA318p9HPh41c1JxgT2IO6Eg/yjWDBzKb8LHJMtdzk3Y3CAoHFAnV1UFoKZWVNPxYV/dxube0vjSkuThkCGjBAGf7RL/72o7ShAoBAF20tyKhqyAPAy86GIGwRqy+ESAZ+19SQkRBiHjBVSnlv4+vbgWFSyocv3rfx/fuA+wCCg4MHLVmypEUaXvsmhdgwL5K6+rI/rZjoUC+6hXuTVViNv5cLsWFe547fit+weaqqqvC6wq1mWlkV/zpwkpmx4UyPVifWuSU6tYA9dTY0gMmkDMlYLErsvsXyy+f7RQHpopzrahKQEtKcSzjmUkiUu5H+RfGAcgEXQontNxqVrannrq7KZs81APrf/fIc5DTrDPt5wDoVb65c7dBeOmvcjlEY+BlhBQ/h2nB18wjjxo3bK6Uc3Jp2r/jVFEJsAJq6iv1JSrmiBW00dQVu1oWklO8B7wEkJSXJsWPHtqAJ8A7txoYdJ9hyLJcAH29unDmOuIjAFn22LSQnJ3MljWOBA3Ur2Ziexe/nziTQy/5lNluiUwtoTefO/Ex+vXk51QOUr2x6XjnjwuIZVAHTbh2rrrgWoLXz2Rxq6czPNMGZ/UwZPQkXw5V77/bSmVJWRGEhjB42DXengHZv7xxXNAQp5cQ2tpENXJg1KhKweRD3oB5dGZAUSV5ROREhfr94z95zB03x2MSRXP/Wp7yRvJ2/zpigqhadljMsNIqvp97GS/s3E+bhzWP9RzEiLJqdW3/6xX5rM1MZGxGHq7HDBO51CiobqnE1uLTIDOxJjbkAg3DGzWjfyW57fHt3AwlCiFggB7gJuKU9GhKC82ZwoQmobQYAcUEB3DSkH1/sPshNg/vSPSxYbUk6LSTWJ4C3x9zQ7I3FidJC7k9eRqJfEC+OmE7/IG3lxNFpnipzLV5O2qsAVGMuwsMYZPdrV5viIIUQNwghsoHhwHdCiLWNP+8ihFgNIKU0Aw8Da4EUYImU8mjbZDerp8nnWuE3Y4fj4+bKM6s3qVq3Qad1NPedSvIP5qPx86k01TPn+0U8v3eTZtNb6PySGkstHk7aS/Vaay7C3an9h7wvpk2GIKX8RkoZKaV0lVKGSimnNP48V0o5/YL9VkspE6WU3aSUz7ZVtKPi5+HG/00cyZ7MHL49dFxtOTo2ZFxkN9bOvIcb4/vyn6M7uW7VR+wv1EZ6C53mqbOYcDe6qi3jEmotJbgbHcwQtExtXQMbdp7Q3J343AG96RsRxovrtlBRW6e2HB0b4uPixvPDp/HpxBupbWhg7hq9t6B16q0mXA3aqpIGUGcpsfv8AXRgQ1izLYU/vfkdBxprJGgFg0Hw9HXjKamp5dUf1MmFo9O+jO4Sy5qZd7Ogm9JbmPndxxwpPqu2LJ0mMFnNOBu0FQggpZV6SwWuRvuvjeiwhjDt2h74eLnxxfcqVnhvhl5dQrmlcYL5ULZ+oeiI+Li48cKIaXw0YT5l9XXMXv0prx3c2mmqszkKFmnByY7J41qCyVqFxIqb0c/ubXdYQ3BzdWbu+H5s2XeKrPxSteVcwm/HjyDE24s/rViHyawPKXRUxkV0Y93Me5ge3Z1/H9zK/DWfc7oDV2dzNCzSilFo6zJYb1FWT7sa7V+fQVtnwsbMn9QfJ6ORL77fp7aUS/Byc+Vv10/gZGEx727ZpbYcnXbEz9Wd10fP5M3RszhdUcL0VR/xv9QDmpvf6oxo8W9gslYC4GLwtnvbHdoQAv08mTqiO6u2HKG0okZtOZcwNjGOWX178N7W3RzNtX8hHx37MiOmB2tn3sPAoC78cccafrVpKSV12vte6qiLyVoFgIvR/qk8OrQhANw6fTD1DRa+Wn9AbSlN8oepY/H3cOMPy9dhMuvjyx2dMA9vFk26iacGT2BL7mmmffsh285mqC2r02IUBixSWwWsGqzKTYKzwf4pbjq8IcRGBDJqYDe+2nCA2roGteVcgp+HG3+7fiKpBUW8mbxdbTk6dsAgBPf0HMKyabfj6ezCreu+4IW9yfqEswo4GYxYpLbOu7nREJyEbgjtwp0zhlBRVcfyTYfUltIk45O6MXdAL97fuptdZ7LVlqNjJ3oHhrHquru4KaE/7x7dwc1rvyC3ukJtWZ0KZ+FMg1VbQR16D6Gd6ZPQhUE9uvLZ6j3UmbTXSwD449SxRAX48cSy7ymr0ResdRY8nF14fvhUXh81k5TSAqZ/+yHrs06qLavT4GJwwmTV1jXBLOsBcDLYfwV1pzAEgHtuuIaismpWJh9RW0qTeLq68K+50yiuquGpb9drMvpBp/2YGduTb2fcRYSXL7/atJTn927CbNXW2HZHxM3oSp3VpLaMX2BpNASj0A2h3VDSY0fw6apd1Ju01UU8R5+IMH474VrWp6Tx5d7DasvRsTNxPgEsm3Y7tyUO4D9Hd3L7hsUU1FapLatD4250pdasrR65xWoCBALb1etuKZ3GEADunTOcwtJqViRr92K7cPggRnaL5rnvkzmWV6C2HB0742p04plrpvDytdexvzCX61Z9xM78TLVldVg8nNypstSqLeMXSMwYhLMqGZs7lSGc6yV88u0uzc4lGAyCF+dMJcDTnUeXrKJcT4DXKZnbrQ8rpt+Jt7Mrt65bzKIT+/RhxHbAy8mdGnMdVg2FnlqlGYNdStVcSqcyBCEE980dQVFZNcs2ajPiCCDA04NX58/gbHklTyxbg9WqXwg6I0n+wSyffgeju8Ty1M51PLFttZ451cb4OHsikVSbtdNLkFgRKqXT6FSGADCwR1eG9orik293UV2rrcmkC+nfNZw/TB3L5pOneXvLDrXl6KiEj4sb/x0/j0f6XstXpw5z45rPya+pVFtWh8HXWVkNXNagnbkaKSUGlS7Nnc4QAB5cMJKyylo+X71HbSmX5eYhfZnVrwdvJu9g4/FTasvRUQmDEDzWfxTvjZ3DyfIiZn73CYeK8tSW1SHwc1byBZWZtLP+QyIBdSo+dkpD6BkXxoShifzv+70Ul1WrLadZhBD8bcZE+nQJ5fGl33P8bKHaknRUZHJUIkun3Y6TwcD8tZ+z8vQxtSU5PAEuSkbREg0Zgpq0tabyfCHEUSGEVQgx+DL7nRFCHBZCHBBCaOK2/MEF12IyW/jvN9pOF+Hm7MSbN83E282VX3+xgsJK7RqYTvvTwz+EldfdRb/AMB75cSWvHPhRn2xuAwGuShGaYlO5ykp+RiCQqDPJ3dYewhFgDrClBfuOk1L2l1I2axz2pGuoP3PG92VF8mHO5Go7P32ojxdv3zyT0ppaHl68kroGfWKxMxPo5sFnk25mfrc+vH7oJ3679Vt9srmVeBrdcTe6UlSvnZopQhgc0xCklClSyhO2EmNv7pl9Da4uzry5uCV+pi69uoTy0pxpHMo5yxPLvseir2Lt1LgYjbw4YjqPDxjNitPHuG3dYopq9d7j1SKEINjVn4I6DRkCRqRKCffsNYcggXVCiL1CiPvs1OYV8ffx4K6ZQ/lxfzq7j2p/8c/EHvH8fsoY1qWk8ez3yfpQQSdHCMFDfUbw1ujZHCk5y9w1i8io1M6FzVEIcQsgv65YbRnnMQpnrFKdHp+40kVFCLEBCGvirT9JKVc07pMM/E5K2eT8gBCii5QyVwgRAqwHfiOlbPK2vNEw7gMIDg4etGTJkpb+Lq2iwWzllWXHcDYaePSGHhgNVze7X1VVhZeXfQtZfJ2Ww4bsAmbFhjMtuqk/zaWoobM16DpbR1p9Ja8WnkAA/y+4O3Guijat6WwONXVuEAc4SiaPyOsRV4jusYfOMu+NlPtsJCrnGUQr7tnHjRu3t9VD81LKNm9AMjC4hfv+FcU8rrhvYmKitAfJu0/Kobe9LL9cu++qP7tp0ybbC7oCFotV/u7r1TLp6Vfkkj2HWvQZNXS2Bl1n60krK5Ijl74tkz57Sa7LTJVSalNnU6ipc3n2Jjl9829kWX3FFfe1h85DxZ/Kj1OHywZLXas+D+yRrbyWt/uQkRDCUwjhfe45MBllMvqKWCz2GRIZPagbQ3tH897SbZSUa7+kocEgeHbWZEbFx/D0qo18f8Rhp3F0bEg330CWTbuDJP9g7k9expI07a7G1xIR7iEA5NRqI6z7XNprs7R/2pq2hp3eIITIBoYD3wkh1jb+vIsQYnXjbqHAViHEQWAX8J2Uck1Ljl9ZZp8TIoTgsdvGUlPfwNtLfrRLm23FxcnIawtmMLBrFx5ftoYf9IVrOkCwuyf/m3Qz14ZF88S21ayuyFVbkuY5ZwhZNdqoa24UbgBYrA5mCFLKb6SUkVJKVyllqJRySuPPc6WU0xufp0sp+zVuvaSUz7b0+HW1ZjJP28e1YyMCuWnKAL7dcpTDaY7xT+Th4sy7t8yiZ3gIj371HT+mnVFbko4G8HR24YPx85kR04MlZZk8s2cjVj0AoVlC3AJwMTiTVXNWbSkAOBkUQ2iQ9s+vpO2VygKWfLzVbs3dM3s4wf5evPjxRswWxwjr9HJz5f3bbiA+OICHF6/kp1N6wXYdJSz19VEzmegVxn+P7ebxbd/pBXeawSgMdPUIJaNGG+lAnIUn8HMpTXuiaUPw8HRh4/eHyMu2z8IxT3cXfnfHOFIzClm8Zp9d2rQFvu5ufHj7XGIC/XnwfyvYcvK02pJ0NIBBCG71j+ax/qNYeuoIj/y4gnp9AVuTRHuEc6ZaGyMDzkallnKD1f7rSjRtCF7eLhiNBr60Yy9hzKB4Rg3sxnvLtpFTUGa3dtuKv6c7H985j/jgQB5a/K2eDE8HUObHHul7LX8ePJ7VGSe494el1DRoN8uvWsR4dqHEVEFFg/qL+1wMSliryWL/rLaaNgSDUTB19kDWf3uA/Lwyu7QphODxO8ZjNAhe+GijQy3+8vdw56M759IzLJhHl6zSo490znNvz6G8OHwaP509w50bl1DVUK+2JE0R69kFgNPVOSorAReDkoHVZLV/Sm5NGwLAgjtHArD4I/tF/4QGevPrBSPZdSSD739KsVu7tsDX3Y0Pbp9D/8hwHvt6NYt3H1Rbko5GWJDQj9dHzWRfYQ53bFhChUmvxneOWK8IANKr1DcEV+M5Q9B7CJcQEubL1NkDWbdiP2dz7Lcsf+6E/vRN6MK/P9uk6RTZTXFuonl0Qix//e4H3t68w6F6Ojrtx4yYHrw1ejaHi/O4bf1iyuq1UylMTfxdfAh08eVUVZbaUnASHhiEM/UW+2dg1bwhANx8z2gMRsFn7yXbrU2DQfDnX02m3mTm+Y82ONwF1d3FmTdvup5Z/Xrw+qbtLD6ZrSfE0wFganQS/xk7h+Olhdy07n+U1Gl/MaY96ObVlTQNGIIQAleDr24IzREU4sOMeUPYuPqg3dYlAESHB/Dg/JH8uO+Uww0dATgbjTw/awr3jBjE5twiHl78LTWmBrVl6WiA8ZHxfDh+PqcrSrll/Re6KQCJ3lFk1xRQo4H6ym5Gf2ot9k9U6BCGAHDjwlG4ujnz6Ts/2LfdKQPpnxTBy4s2kV/seLVsDQbB45NHc1NCJJtPnub2j5ZQUKmd+rE66jGySwwfjJunm0Ijid7RSCQnK9XvJfT0v5F472l2b9dhDMHP35M5tw7nx43HSD1mv4kfg0Hwl/umYLFY+cf7a7FaHWvo6BxjI4J5++aZnC4q5cb3F+vlOHUAxRT+O26uYgrrvqC4E5tConc0ACmV6q/jifeZTrT3OLu36zCGADD3thH4+Hrw4Zsb7NpuRIgfj94yht1HM/ly3X67tm1LxibG8dndC7BKyc0fLGbtsZNqS9LRAKO6xPLh+Hmcrizl9vWLKa/vnNFH3s4edPUIJaVCfUNQC4cyBE8vN26+ZxT7d6azd3uaXduePa4PowZ2460vfyQ1o8CubduSnuEhfHXfzSSGKmsVXv9hm8P2enRsx7XhMfxn7BzSyou5Y8OXnTYktadPHMcrzmCVnTMAw6EMAWDG/KGERfjz/mvrsNgx35AQgj/fOxlfLzeeens1tXWOOzkb4u3ForvmMad/L97espOHFq+kvLZzXgB0fmZsRBxvj5nN0ZJ87tr4VadcvNbTJ44qcw2ZGkl0Z28czhBcXJy4++GJnD6Zz4ZVB+zatp+3O399YBoZeSX8+/NNdm3b1rg4OfHsrEn8edo4fkw7w9z/fM6xPMft+ejYholdE3hz9CwOFuVy98avqDU77o1Pa+jjFw/AkXL7jkBoBYczBIDRk3rRo29XPn5rI7U19r2LGdIrijtmDGVF8hHW73Ds1BBCCG4b1p9FC+djtlq56b+L+WrvYYdbc6FjW6ZGJ/HqyJnsLsjm15uXY7KoU/BdDULdAglxDeBQWeecX3NIQxBCcP9jUygprrJreuxz3DdnOH3iw3nug3UU2qmIT3syoGsXlt1/K4OjI3jq2w08vmwNVXWdb7hA52euj+3Bc9dMZVPOKX67dWWnSp3dxy+ew2Vpmp1HsFjb73/TIQ0BoEefroyd0puvP9tGgZ0S353DycnIsw/PwMXZiUUb0x16PuEcAZ4evH/bDTw6bgTfHznBDf/5nEPZnXMcVUfh5sT+57OkPrFtdacpstPfL5EKc7XqeY3yaw+wu/A1dhS8TK25hLM1+/ku61d8n/1rcqp3YJW277k5rCEA3P2bSQC89+o6u7cdGujN3x+cTkFZHS987HipLZrCaDDw4JhhLFo4H4vVyi0ffsm7W3bpKS86Mff2HMpj/UexLP0Iz+xxrOy/raWvXyIAB8tSVdNQWn+K3YWvU27KoNx0mj1Fb3Ks7Au6+84l2msMe4veorje9kPWDm0IoeF+3HjXKH7ccJQDu9Lt3v6wPtFMHBjOmp9SWLax4xQ0HxgVwTcP3MakHvG8+sNP3PbREjJLytSWpaMSv+kzgru6D+LDlD28fWS72nLanSBXPyLdQ1U1hJSyrwhx78PEiFeYEvkmVQ25+LvG081nKn0C7sDbuSsFtba/5rTJEIQQLwkhjgshDgkhvhFC+DWz31QhxAkhRJoQ4sm2tHkx8++4lrAIf956aTXmBvtPfo3vH8aIfrG88tkmDpxQP3WurfB1d+OVedN5ac400gpKmP3OZyzec6hT3CHq/BIhBH8ZMpHZsb14af8WFp1wnGqCraW/fxJHyk/RYFVnOFhiwc3of/61j0sUdeafcxs5G9wxt0OJzbb2ENYDvaWUfYFU4A8X7yCEMAJvAdOAnsDNQoiebWz3PK5uzjz4u2lkpheyfPEOWx22xRiE4G8PTiM82IcnX//WIfMdNYcQguv7dmflr2+nX2QYf121kbs/XUp2qf2zMOqoi0EIXrp2OhMj4/nLznV8e9rxkj1eDQP8k6i3mjhWrs6q5QDXJM7W7KOqIY9yUwYN1mpKTWlsyv0DW88+Q7kpg3CPITZvt02GIKVcJ6U8V6R1BxDZxG5DgTQpZbqU0gQsBma1pd2LuWZ0EsNGJXL8iDp36D6ebrz021k0mC3sOtrxityH+3rz4R1z+euMCRzKyeeNTR1/2EDnUpwNRt4cPYshIZF8mXawQ/cW+/omEOoWSIVZnVookZ7DcXcKZGv+P9hd+Dpezl0YHfZ3At2642RwZVDwQ4S497H530DY6oBCiG+BL6WUn13083nAVCnlvY2vbweGSSkfbuY49wH3Nb7sDRyxicD2IwgoUltEC9B12hZdp23RddqOJCmld2s+6HSlHYQQG4CwJt76k5RyReM+fwLMwOdNHaKJnzXrQlLK94D3Go+7R0o5+Eoa1cQRNIKu09boOm2LrtN2CCH2tPazVzQEKeXEKzR+JzADmCCb7m5kA10veB0J5F6NSB0dHR2d9qetUUZTgd8DM6WUzU157wYShBCxQggX4CZgZVva1dHR0dGxPW2NMnoT8AbWCyEOCCHeBRBCdBFCrAZonHR+GFgLpABLpJRHW3j899qozx44gkbQddoaXadt0XXajlZrtNmkso6Ojo6OY+PQK5V1dHR0dGyHbgg6Ojo6OoCGDEELaTBaghBivhDiqBDCKoRoNvxMCHFGCHG4cW6l1WFgreUqdKp9PgOEEOuFECcbH/2b2U+V83ml8yMUXm98/5AQYqC9tF2FxrFCiPLGc3dACPEXe2ts1PGhEKJACNHk2iItnMtGHVfSqfr5FEJ0FUJsEkKkNP6fP9rEPld/PqWUmtiAyYBT4/N/Av9sYh8jcAqIA1yAg0BPO+vsASQBycDgy+x3BghS8XxeUadGzueLwJONz59s6u+u1vlsyfkBpgPfo6y3uQbYqUGNY4FVan0XL9AxGhgIHGnmfVXP5VXoVP18AuHAwMbn3iipg9r83dRMD0FqJA3GlZBSpkgpNV8qrYU6VT+fje190vj8E2C2ndu/HC05P7OAT6XCDsBPCBGuMY2aQEq5BSi5zC5qn0ugRTpVR0qZJ6Xc1/i8EiWCM+Ki3a76fGrGEC7ibhRnu5gIIOuC19lcehK0ggTWCSH2Nqbj0CJaOJ+hUso8UL7kQEgz+6lxPltyftQ+hy1tf7gQ4qAQ4nshRC/7SLtq1D6XV4NmzqcQIgYYAOy86K2rPp9XXKlsS+ydBqO1tERnC7hWSpkrhAhBWadxvPHOw2bYQKfq5/MqDtPu57MJWnJ+7HIOL0NL2t8HREspq4QQ04HlQEJ7C2sFap/LlqKZ8ymE8AKWAr+VUlZc/HYTH7ns+bSrIUgHSYNxJZ0tPEZu42OBEOIblK69TS9gNtCp+vkUQuQLIcKllHmN3dmCZo7R7uezCVpyftROzXLF9i+8UEgpVwsh3hZCBEkptZakTe1z2SK0cj6FEM4oZvC5lHJZE7tc9fnUzJCR6EBpMIQQnkII73PPUSbMtZi1VQvncyVwZ+PzO4FLejYqns+WnJ+VwB2NER3XAOXnhsDsxBU1CiHChBCi8flQlP/7YjtqbClqn8sWoYXz2dj+B0CKlPKVZna7+vOp5kz5RTPiaSjjXQcat3cbf94FWH3RzHkqSmTFn1TQeQOK89YD+cDai3WiRHwcbNyOalWnRs5nILARONn4GKCl89nU+QEeAB5ofC5QCkCdAg5zmcgzFTU+3HjeDqIEbIywt8ZGHV8AeUBD43fzHq2dyxbqVP18AiNRhn8OXXDNnN7W86mnrtDR0dHRATQ0ZKSjo6Ojoy66Iejo6OjoALoh6Ojo6Og0ohuCjo6Ojg6gG4KOjo6OTiO6Iejo6OjoALoh6Ojo6Og08v8BV1Ayn9vJfp4AAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAELCAYAAADHksFtAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAAAy4UlEQVR4nO3deXxU5dn/8c+VjSSEEEggELZACLtsYQtbwQ13HtyqVnEttWqfPm2ttbVV299jtXa1ta2igkur2LoUqrgiiArIKhD2EEDCFkIgZF9mrt8fM/RJaZbJMjlzkuv9es0rs5w553uyzJVz3+fct6gqxhhjTF3CnA5gjDEmtFmhMMYYUy8rFMYYY+plhcIYY0y9rFAYY4yplxUKY4wx9XK0UIjIAhHJE5GsOl6fISKFIvKF//Zga2c0xpj2LsLh7T8PPAm8WM8yn6jqZY1ZaVJSkqampjYpUElJCR07dmzSe0OB2/OD+/fB7fnB/ftg+Rtvw4YN+ararbbXHC0UqrpSRFJber2pqamsX7++Se9dsWIFM2bMaNlArcjt+cH9++D2/OD+fbD8jSciB+p6zQ19FJkisllE3hGR4U6HMcaY9kacHsLDf0TxlqqOqOW1eMCrqsUicgnwhKqm17GeecA8gOTk5IxFixY1KU9xcTFxcXFNem8ocHt+cP8+uD0/uH8fLH/jzZw5c4Oqjqv1RVV19AakAlkBLrsfSGpouYyMDG2q5cuXN/m9ocDt+VXdvw9uz6/q/n2w/I0HrNc6PlNDuulJRHqIiPjvT8DXVHbC2VTGGNO+ONqZLSKvADOAJBHJBR4CIgFU9SngauCbIlINlAHX+SufMcaYVuL0WU/XN/D6k/hOnzXGGOMQp6+jMMaYdqmovIrdx4o5VVpJTFQ4fbrE0rtLDP7W9pBihcIYY1pJeZWHJZsP8+q6g2z68iTesxrS+3aN5b9Gp5BOaLWwW6EwxpggU1Xe3nqER5fu5NCpMgZ2j+PumQMZ3SeBxLgOlFZWk51XzLIdefz+o2w6hENB3H5umtSPsDDnjzCsUBhjTBAVllXxoze38vaWIwzrGc8vrhrJlIGJ/9HENDktibmZqew5VsR3XvyMh5ZsY/muPJ68YSxxHZz9qLZCYYwxQbIvv4Tbnl/HwYJS7rtoMN+YnkZ4A0cI6cmd+N64DuRG9+fhf27n6j+v4qXbJ9KtU4dWSv2fQvo6CmOMcautuYVc+afPOFVaySvzJnHXjIENFokzRISbMlNZeMt4DpwoZe6CtRSWVgU5cd2sUBhjTAvbfPAUNzy7htioCN68awrjU7s2aT3TB3Vj/twM9uYV8/UX11Pl8bZw0sBYoTDGmBZ04EQJtz6/joTYSF79xiRSk5o3XPi09G788pqRrN1fwCNv72ihlI1jhcIYY1rIyZJKbl24DlXlxdsm0rtLbIusd/boXtwxtT/Pr9rP21uOtMg6G8MKhTHGtICKag/feGkDuSfLmD93HP2beSRxtvsvHsKoPgk88I+t5J0ub9F1N8QKhTHGtIAfvZHF2v0F/OraUU3uk6hPRHgYv7l2FGWVHn70Zq2zRweNFQpjjGmm1zbk8vrGXP77vHSuGJUStO2kdYvj3gsH8+GOY3yw/VjQtnM2KxTGGNMM2XnF/OQfWUwa0JVvn1frvGot6pYpqQxKjuPhJdsoq/QEfXtghcIYY5qsvMrDPS9vJCYqnCeuGxPwdRLNERkexv+bPYJDp8p49pOcoG8PrFAYY0yT/XzpDnYeLeLX144iOT661bY7cUAis4Yn8/TKHE4UVwR9e1YojDGmCVZl5/Pi6gPcNqU/Mwd3b/Xtf3/WEEorq/nDR9lB35YVCmOMaaSSimp+8MYWUhNj+f6swY5kGNg9jmsy+vDy519ytDC4p8taoTDGmEb65Xu7yD1ZxuNXjyImKtyxHPecOxCPKk+v3BvU7VihMMaYRli7r4DnV+3n5sxUJvRv+eslGqNP11jmjOnFy59/yfGi4PVVOFooRGSBiOSJSK1Xj4jP70UkW0S2iMjY1s5ojDFnlFd5uP/1LfTpGsN9FznT5HS2u2cOpNLj5flV+4K2DaePKJ4HLqrn9YuBdP9tHvDnVshkjDG1evrjHHLyS3jkv84hNio0pvPpn9SRWcN68Jc1X1JaWR2UbThaKFR1JVBQzyKzgRfVZw2QICI9g5WnotpDWXVozVVrjAkNB06U8McV2Vw6sifTB3VzOs6/uWNafwrLqnhtQ25Q1u/0EUVDegEHazzO9T/X4oorqpny2Ee8u8+5yUGMMaFJVXlw8TaiwsN48LJhTsf5Dxn9ujC6TwLPfboPj7fl/9kNjWOnutV2mWOt3wURmYeveYrk5GRWrFjR6I31jPbw8cFqln20vFWusAyG4uLiJu17KHH7Prg9P7h/H1o6/7qj1Xy8u4IbhkSxY+Magj0rRFPyn9u9mrxSZfmKFUS09OeXqjp6A1KBrDpeexq4vsbjXUDPhtaZkZGhTfHO1iPa7wdv6Yfbjzbp/aFg+fLlTkdoNrfvg9vzq7p/H1oyf0lFlU585EO9+Hcrtara02LrrY8T339gvdbxmRrqTU9LgLn+s58mAYWqGrRZO84b2p3OHYRX1n4ZrE0YY1zmqY9zOHq6nJ/OHk5EeKh/ZAaHo01PIvIKMANIEpFc4CEgEkBVnwKWApcA2UApcGsw80SGhzGtVwRLd+Zx+FQZKQkxwdycMSbEHTpVxtMf7+WykT2DMseEWzhaKFT1+gZeV+DuVooDwFd6R/BWThV/W3+Q/zl/UGtu2hgTYn7xzk7AN7tce9Y+j6Pq0S02jGnpSby67mBQzh4wxrjDhgMFLNl8mHnTB7TY3NduZYWiFjdM6MuRwnI+3p3ndBRjjAO8XuVn/9xOcnwH7vxKmtNxHGeFohbnD0smKS6KV9cdbHhhY0yb8+amQ2zOLeS+WUPo2CHUryIIPisUtYgMD+PyUSks33WcwjK7AM+Y9qSkoppfvLuTUX0SmDMmKNf3uo4VijrMHt2Lymov72076nQUY0wreurjveQVVfDgZcMIc+mFty3NCkUdRvXuTL/EWJZ8cdjpKMaYVpJ7spT5K3O4YlQKGf26OB0nZFihqIOIMHtUCqv25pN3OrizRxljQsNj7+xExE6HPZsVinpcMToFr8JbW4J2MbgxJkSs21/AW1uO8I3paXax7VmsUNRjYPdODE+JZ/Fma34ypi07czpsj/hovvGVAU7HCTlWKBowe3QKmw+eYn9+idNRjDFB8vrGXLYeKuT+i4eEzIREocQKRQMuH5WCCCy2Tm1j2qTiimoef28XY/omMHt0itNxQpIVigb07BzD+NSuvJNl/RTGtEV/XpHNcf/psCJ2OmxtrFAEYNbwHuw8WmTNT8a0MQcLSnnmk33MGdOLMX3tdNi6WKEIwKzhyQB28Z0xbczPl+4gXIT7LhrsdJSQZoUiAL27xDKiV7wVCmPakFV783kn6yh3z0yjZ2c7HbY+VigCdNHwHmz88hTH7OI7Y1yv2uPlZ//cTu8uMdwxzU6HbYgVigDNGt4DgPe3H3M4iTGmuRatO8jOo0U8cMlQoiPDnY4T8qxQBGhg9zgGJHXkvSxrfjLGzQpLq/j1+7uYNKArF43o4XQcV7BCESARYdaIHqzJOUFhqQ09boxb/fbD3RSWVfHgZcPtdNgAWaFohFnDe1DtVZbttOYnY9xoz7EiXlpzgOsn9GVYSrzTcVzD0UIhIheJyC4RyRaR+2t5fYaIFIrIF/7bg07kPGNkr8707BzNu9b8ZIzrqCo/e2s7HaPC+e4Fg5yO4yqODWoiIuHAH4ELgFxgnYgsUdXtZy36iape1uoBaxEWJpw7pDtvbjpERbWHDhHWCWaMWyzbkccne/J58LJhJMZ1cDqOqzh5RDEByFbVHFWtBBYBsx3ME5DzhnantNLD2n0FTkcxxgSootrD/769nYHd47gps5/TcVxHVNWZDYtcDVykqnf4H98ETFTVe2osMwN4Hd8Rx2HgXlXdVsf65gHzAJKTkzMWLVrUpFzFxcXExcXV+XqFR7lnWSkz+kTwtaGh919JQ/ndwO374Pb84P59ODv/kr2VvLGninvHdWBEUuiPDuvE93/mzJkbVHVcrS+qqiM34Brg2RqPbwL+cNYy8UCc//4lwJ5A1p2RkaFNtXz58gaXuWXB5zr98Y/U6/U2eTvBEkj+UOf2fXB7flX370PN/AfyS3TQA0v1m39Z71ygRnLi+w+s1zo+U51sesoF+tR43BvfUcO/qOppVS32318KRIpIUutFrN25Q7pz4EQpOTZIoDEhTVV5cEkWEWHCg5cNdzqOazlZKNYB6SLSX0SigOuAJTUXEJEe4j/RWUQm4Mt7otWTnmXmkO4ALN+Z53ASY0x93s06yopdx/nuhYPp0Tna6Tiu5VihUNVq4B7gPWAH8DdV3SYid4rInf7FrgayRGQz8HvgOv8hkqN6d4llUHIcH1mhMCZkFVdU89N/bmdYz3hutg7sZnG0V8ffnLT0rOeeqnH/SeDJ1s4ViJlDuvPcJ/soKq+iU3Sk03GMMWf53Qe7OVZUzp9uHEtEuF1b3Bz23Wui84YkU+1VPt2T73QUY8xZDhZ5WbhqP9eN78tYm5Co2axQNNHYvgl0jom05idjQozHqyzMqiAhJpIf2IRELSL0TygOURHhYUxLT+Lj3cdRVRtczJgQseDTfeQUenniumEkxEY5HadNsCOKZpie3o28ogp2Hyt2OooxBsg5Xsyv3t/FmO7hXDEqxek4bYYVimaYmu67pOOTPccdTmKM8XiV+17bQnRkODcPi7Kj/BZkhaIZUhJiGNg9jpXWoW2M415YtZ/1B07y0OXDSIi2j7aWZN/NZpqWnsTnOScor/I4HcWYdmt/fgmPv7eT84Z0Z86YXk7HaXOsUDTT9PRuVFR7Wb//pNNRjGmXvF7lvte3EBkexiNzzrEmpyCwQtFMEwd0JTJcrJ/CGIcsXLWftfsKePCyYTZMR5BYoWim2KgIxvXrav0Uxjhg++HT/OKdnZw/NJmrM3o7HafNskLRAqamJ7HjyGnyisqdjmJMu1Fe5eHbizbROTaSX1xlTU7BZIWiBUxP7wbAZ9l2VGFMa/n50h3sySvmN9eOsqlNg8wKRQsYnhJPl9hIPtlthcKY1vDh9mO8uPoAd0ztzzT/P2omeKxQtICwMGFqejdW7sknBEZBN6ZNO1hQyvf+vpnhKfF838ZyahVWKFrItPQk8osr2Hm0yOkoxrRZFdUe7n55I15V/vy1DDpEhDsdqV2wQtFCptlwHsYE3SNv72BLbiG/umYUfRNjnY7TblihaCE9O8eQ3j2OT+w0WWOCYvEXh/7VLzFreA+n47QrViha0LT0bny+r8CG8zCmhWUdKuQHr29hfGoXfnDxEKfjtDtWKFrQtPQkKqu9rN1X4HQUY9qM/OIK5r24nq6xUfzpaxlE2rSmrc7R77iIXCQiu0QkW0Tur+V1EZHf+1/fIiJjncgZqDPDeXy215qfjGkJldVe7vrLRk6UVDJ/7ji6dbLrJZzgWKEQkXDgj8DFwDDgehEZdtZiFwPp/ts84M+tGrKRYqMiGN0ngdV7TzgdxRjXU1V+8o8s1u4v4PGrRzKiV2enI7VbTh5RTACyVTVHVSuBRcDss5aZDbyoPmuABBHp2dpBGyMzLYmsQ4UUllY5HcUYV/v9smxeXX+Q/z53ILNH29DhTgpozmwRiQW+B/RV1a+LSDowWFXfasa2ewEHazzOBSYGsEwv4EgtGefhO+ogOTmZFStWNClUcXFxk98L0LHIg1fhuX9+zNjk1p+SvLn5Q4Hb98Ht+cH5ffgkt4rnsiqZkhLBmMjDrFjxH3/y9XI6f3OFWv5AP8kWAhuATP/jXODvQHMKRW0jeJ19WXMgy/ieVJ0PzAcYN26czpgxo0mhVqxYQVPfC5BZ7eG3m97ndExPZswY3uT1NFVz84cCt++D2/ODs/uwcvdxXnh/HVMHJrHglvFERTS+4cPtP4NQyx/oTyBNVR8HqgBUtYzaP8QbIxfoU+Nxb+BwE5YJKR0iwhmf2pVV1qFtTKNtO1zIN/+ygYHd4/jzjWObVCRMywv0p1ApIjH4/5sXkTSgopnbXgeki0h/EYkCrgOWnLXMEmCu/+ynSUChqjbuGNQBmWmJ7D5WzPGi5n6LjGk/DhaUcuvCdcTHRPL8rRPoFB3pdCTjF2iheBh4F+gjIn8FlgH3NWfDqloN3AO8B+wA/qaq20TkThG507/YUiAHyAaeAe5qzjZby+Q033Aeq3Ps7CdjAnGksIzrn1lDRbWX52+dYDPVhZiA+ihU9X0R2QBMwtfk9G1VbXbbiqouxVcMaj73VI37Ctzd3O20thEp8XSKjmD13nyuGJXidBxjQtrxogq+9sznnCqt4q93TGRwj05ORzJnCfSspyXAK8ASVS0JbiT3iwgPY2L/RFbZ9RTG1OtkSSU3Pfc5RwrLefH2CYzqk+B0JFOLQJuefg1MA7aLyN9F5GoRsWPDekxOS+TAiVJyT5Y6HcWYkHS6vIqbF64lJ7+EZ28ex/jUrk5HMnUIqFCo6seqehcwAN8pqNcCecEM5naTByYC2FGFMbU4XV7FLQvWsv3waZ66cSxTBiY5HcnUI+Bzz/xnPV0F3AmMB14IVqi2YFD3TiR2jLLhPIw5S2FpFTc9+zlbcgt58oYxnDsk2elIpgGB9lG8iu+q6Xfxjc+0QlW9wQzmdmFhQmZaIqv2+qZHFWnuZSfGuN/JkkpufO5z9hwr5qkbMzh/mBUJNwj0iGIhvovu7lTVj6xIBGZyWhLHTleQk2/9/8bkF1dw/TNr2JNXzNNzrUi4Sb1HFCJyrqp+BMQCs8/+r1hV3whiNtebnPZ//RRp3eIcTmOMc/JOl/O1Zz/n4MlSFtw8nqnp1ifhJg01PX0F+Ai4vJbXFLBCUY9+ibGkdI5m9d58bprUz+k4xjjiwIkSbnpuLfnFFSy8ZQKZ/n+gjHvUWyhU9SH/3Z+p6r6ar4lI/6ClaiNEhMy0JD7aeQyvVwkLs34K075sP3yauQvW4vF6efnrkxht10m4UqB9FK/X8txrLRmkrZqclsjJ0ip2HD3tdBRjWtXafQV8df5qIsOFv9+ZaUXCxRrqoxgCDAc6i8iVNV6KB+yCuwCcuZ5i9d4TDE+xGbpM+/Dh9mPc/fJGenWJ4aXbJ9IrIcbpSKYZGuqjGAxcBiTw7/0URcDXg5SpTenZOYYBSR1ZtfcEd0wb4HQcY4Lu9Q253Pf6FoanxLPwlvEkxtk8127XUB/FYmCxiGSq6upWytTmZKYl8o9Nh6jyeIkMt/H1Tdv17Cc5/O/bO5gyMJGnbxpHXIfWn+XRtLxAP7XuFJGEMw9EpIuILAhOpLZncloSJZUeth4qdDqKMUGhqjz+7k7+9+0dXDyiBwtuGW9Fog0JtFCMVNVTZx6o6klgTFAStUGTBvgGO1uVbbPembbH41V+9OZW/rRiL9dP6MuTN4ylQ0S407FMCwq0UISJSJczD0SkK4HPt93uJcZ1YGjPeBsg0LQ5FdUe7nl5I6+sPcg9Mwfy8zkjCLfTwNucQD/sfw2sEpHX8F1ody3wSNBStUGT0xJ5ac0Byqs8REfaf1vG/Yorqpn34npW7T3Bjy8daidrtGGBDjP+Ir6RY48Bx4ErVfWlYAZrayanJVJZ7WXjgZNORzGm2U4UV3DDM2v4fF8Bv75mlBWJNq4xp+B0BUpU9Q/Acbsyu3Em9O9KeJhY85NxvUOnyrjm6dXsOlrE0zdmcFVGb6cjmSALdJjxh4Bx+K6rWAhEAn8BpjRlo/4+jleBVGA/cK2/g/zs5fbju2bDA1Sr6rimbC8UdIqOZGTvzqzam4/v22iM+2TnFXHTc2sprqjmpdsnMqG/zUrXHgR6RDEHuAIoAVDVw0BzZkC/H1imqunAMv/jusxU1dFuLhJnTE5LZHNuIUXlVU5HMabRvjh4iqufWk2VR3l1XqYViXYk0EJRqaqKryMbEenYzO3O5v9myHsB+K9mrs8VpqQl4fEq6/YXOB3FmEZZsSuP6+evIT46kte/mcmwlHinI5lWJL7P/wYWErkXSAcuAB4FbgNe9vdXNH6jIqdUNaHG45Oq2qWW5fYBJ/EVqKdVdX4965wHzANITk7OWLRoUVOiUVxcTFxccOaOqPQody0r5by+EVw/JDjDGgQzf2tx+z64PT/8+z58dqiKBVmV9IoL47vjOpDQIfRHF3D7z8CJ/DNnztxQZ8uNqgZ0w1ckfgn8CrgggOU/BLJquc0GTp217Mk61pHi/9od2AxMDyRrRkaGNtXy5cub/N5AXPf0ar34dyuDtv5g528Nbt8Ht+dX/b99mP/xXu33g7f0uqdX6+mySmdDNYLbfwZO5AfWax2fqQFfNKeqHwAfNGL58+t6TUSOiUhPVT0iIj2BvDrWcdj/NU9E3gQmACsDzRCKpgxM5Ffv76agpJKuHaOcjmNMrbyq/HzpDuavzOGSc3rw26+Otqut27F6jyFF5FP/1yIROV3LbZ+I3NWE7S4BbvbfvxlYXMu2O4pIpzP3gQvxHZG4WmaabwrINTl2mqwJTVUeL89srWD+yhzmZvbjD9fbkBztXb2FQlWn+r92UtX4s2/4Tpn9dhO2+xhwgYjswdek9RiAiKSIyFL/MsnApyKyGVgLvK2q7zZhWyFlZO/OdIwK958ma0xoKa2s5o4X1rP6sIfvXTCIn14x3IbkMIE3PYnIWGAqvo7lT1V1k6qeEJEZjd2oqp4Azqvl+cPAJf77OcCoxq471EWGhzFxQCKrsu2IwoSWgpJKbn1+HVtzT3HL8Ci+dV6605FMiAjo9AUReRDfaayJQBLwvIj8GEBVjwQvXts0OS2RnPwSjhSWOR3FGAByT5Zy9VOr2HnkNH++MYMZfSKdjmRCSKDnuV0PjFfVh1T1IWAS8LXgxWrbMtP+b3pUY5y28+hprvrzKo4XVfDS7ROZNbyH05FMiAm0UOzn3+fI7gDsbfE07cTQHvF0iY3kM2t+Mg5bk3OCa5/yTV759zvtamtTu3r7KETkD/j6JCqAbSJy5vTY84FPg5ytzQoLEzLTElm9Nx9VRcQ6C03re3NTLve9toW+XWN54bYJ9O4S63QkE6Ia6sxe7/+6Hd+YTF58A/QtD2ao9iAzLYmlW49y4EQpqUnNHRHFmMCpKk8s28PvPtxD5oBEnroxg86x1idh6tZQoXgZ3wRFtwEH8DVV9cE3guyPghutbZvs76f4bG++FQrTaiqrvdz/xhbe2HiIK8f24rErRxIVEfpDchhnNfQb8jjQBeivqhmqOgYYAHTGN5yHaaIBSR3pER9t81OYVlNYWsXcBZ/zxsZDfOf8Qfz6mlFWJExAGjqiuAwY5B8HBABVPS0i3wR2Av8TxGxtmogwOS2Rj3cfx+tVwuyiJhNEB06UcNvz6/iyoJTffnUUc8bYZEMmcA39O6E1i0SNJz34hxw3TZeZlsiJkkp2HStyOoppw1bsyuPyP3xKfnElL90+0YqEabSGCsV2EZl79pMiciO+IwrTDJMH+sZ9suYnEwyqyh+XZ3Pr8+tISYjhn/dMZdKARKdjGRdqqOnpbuANEbkN2IDvKGI8EINv1jvTDL0SYkhNjGX13nxun2pTkJuWU1xRzb1/28y7245yxagUHrvqHGKjAh6xx5h/U+9vjqoeAiaKyLnAcECAd1R1WWuEaw8y05J4a/Nhqj1eIsKtY9E0386jp7nn5U3syy/hx5cO5fap/e1aHdMsAf2LoaofAR8FOUu7NGVgIq+s/ZKthwoZ0/c/JvkzJmCqyourD/DI0h3ER0fy0m0T/tW8aUxz2LGow860Ga/ae8IKhWmyvNPl/PCNrSzbmce5Q7rz+NUjSYoLznS7pv2xtg6HJcV1YEiPTjY/hWkSVeVv6w9y/m8+5tPsfB66fBjP3TzOioRpUXZEEQImpyXx188PUF7lITrSZhIzgcnOK+an/9zGJ3vymZDalceuOocB3eKcjmXaICsUIWDKwEQWfLaPDQdOMsXalE0DTpVW8sSyPby0+gDRkeH8bPZwbpzYzy7aNEFjhSIETBqQSGS4sHL3cSsUpk6FZVW8uGo/z322j9NlVXx1fF++d+Ega2YyQWeFIgR07BBBRr8ufLz7OD+8ZKjTcUyIOXyqjL9+foAXVx2gqKKac4d0594LBzMsJd7paKadcKRQiMg1wMPAUGCCqq6vY7mLgCeAcOBZVX2s1UK2sumDuvH4u7vIO11O9/joht9gWszxogp2HyvieFEFhWVVnC6rAiAyIoyo8DDiYyLp1qkD3eI6kJIQTUJsVNAzlVZWs2LXcV5dd5CVe44DcPGIHtw1YyAjenUO+vaNqcmpI4os4Erg6boWEJFw4I/ABUAusE5Elqjq9taJ2Lqmp/sKxco9+VydYWPxBNOx0+W8v+0oy3bmkXWokPziyka9v3NMJKmJsfRL7Eg//9fUxFj6JsbSrYnNQOVVHnYeLWLjgZOs2H2cNTknqKz20rNzNN+aOZBrxvWhT1ebWMg4w5FCoao7gIauFp0AZKtqjn/ZRcBsfJMotTnDesaTFBfFyt3HrVAEgcervJN1hIWf7WfDgZMA9E/qyMzB3RnSM56hPTqR3DmazjGRxEdHEiZQ6fFSWe3lVGkV+cUV5BVVcOhkGQcKSjhwopRNB0/y1pbDeGsMjxkVHkbnKGXArtWkJMSQFBdFxw4RxHWIoENEGFUepdrrpaTCQ15RBXmnyzl4spS9x0vw+FeU1q0jcyf1Y+aQ7kwakEi4dVIbh0ktg8O23sZFVgD31tb0JCJXAxep6h3+xzcBE1X1njrWNQ+YB5CcnJyxaNGiJmUqLi4mLs6ZUwyf3lJO1nEPT5wbS1gTh1xwMn9Lacl98HiVTw5V886+Ko6VKsmxwpReEWQkR5DSUZo9tEW1V8kvU/JKveSVKifKlbziSoqqwzlRphRVKpXe2t/bKQoSOoTRNVroGx9Gv05hpHYOIynG+cub3P57ZPkbb+bMmRtUdVxtrwXtiEJEPgR61PLSA6q6OJBV1PJcnVVNVecD8wHGjRunM2bMCCTmf1ixYgVNfW9zneycy+pXN5OUPoaRvROatA4n87eUltqHrEOF3P/GFrIOlXJOr848PCeNC4f3CPp/6Gfnr/Z4Kan0UFntJTJciAgPo0NEGJEhPLaX23+PLH/LClqhUNXzm7mKXHzTrp7RGzjczHWGtGnp3QBYuft4kwuF8bX3/+aD3Tz36T66xEbx5A1juPScno4NjBcRHkbnEDhKMKapQvm3dx2QLiL9RSQKuA5Y4nCmoEqK68DwlHhW7rbhPJrqaGE5X52/hvkrc7h2XG+WffcrXDYyxUZPNaYZHCkUIjJHRHKBTOBtEXnP/3yKiCwFUNVq4B7gPWAH8DdV3eZE3tY0fVA3Nn55kqLyKqejuM76/QVc9odPyT5WxFM3ZvDolSPpHBvpdCxjXM+RQqGqb6pqb1XtoKrJqjrL//xhVb2kxnJLVXWQqqap6iNOZG1t09O7Ue1Vm/Wukd7acpjrn1lDXIdw3rx7CheNqK17zBjTFKHc9NQuZfTrQseocFbuPu50FNf4x6ZD/PcrmxjdJ4HFd09lUHInpyMZ06bYEB4hJioijMy0RFbuOY6qWtt6A17bkMv3X9vMpP6JPHfLOJvu05ggsCOKEDR9UDcOFpSx/0Sp01FC2uIvDvH91zYzdWASC24Zb0XCmCCxQhGCptc4TdbUbtXefO79+2Ym9u/KM3PHERNl83gYEyxWKEJQalJH+naN5WMrFLXafayIb7y0gdTEjjx94zib7MmYILNCEaLOHdKdz7LzKav0OB0lpOSdLufWheuIjgxn4a3j7fRXY1qBFYoQdd7Q7lRUe/ks2y6+O6PK4+XulzdSUFLJwlvG07uLjaZqTGuwQhGiJvZPpGNUOMt2HnM6Ssh4/N2drNt/kseuOsfmZDCmFVmhCFFREWFMH9SNZTvy8HqdG+E3VLybdYRnPtnH3Mx+zB7dy+k4xrQrVihC2HlDk8krqmDb4dNOR3HUvvwSvv/3LYzqk8ADl9pUsca0NisUIWzm4G6IwIc72m/zU5XHy/8s2kR4uPCnr42lQ4Sd4WRMa7NCEcIS4zowtm+Xdt1P8YePstmcW8ijc86hV0KM03GMaZesUIS484Z2J+vQaY4WljsdpdVt/PIkf1yezZVje3HxOT2djmNMu2WFIsSdPzQZoN0dVZRUVPPdV7+gR3w0D18x3Ok4xrRrVihCXHr3OHp3ieHD7e2rUDz2zk4OFJTym2tHER9tF9UZ4yQrFCFORJg1vAefZZ9oN5MZ7Srw8NKaA9w6uT8TByQ6HceYds8KhQtcPKIHlR4vH+3MczpK0JVXeViQVUGfrjHcO2uQ03GMMVihcIWxfbvQvVMHlm494nSUoHti2R6OlSqPzhlpw4YbEyKsULhAWJhw8YgerNh1nJKKaqfjBE3WoULmr8xhWq8IpqYnOR3HGOPnSKEQkWtEZJuIeEVkXD3L7ReRrSLyhYisb82Moebic3pSUe1l+a622fzk8So/fGMrXTtGcd2QKKfjGGNqcOqIIgu4ElgZwLIzVXW0qtZZUNqD8aldSYqL4p2so05HCYqX137J1kOF/OSyYXSMtOlfjQkljhQKVd2hqruc2LZbhYf5zn5avjOvzc1RkV9cwS/f3cnktEQuH2kX1hkTakK9j0KB90Vkg4jMczqM0y45pyellZ42N/Pdo0t3Ulbl4WezRyBiRxPGhBpRDc4Q1iLyIdCjlpceUNXF/mVWAPeqaq39DyKSoqqHRaQ78AHwLVWttbnKX0jmASQnJ2csWrSoSbmLi4uJi4tr0nuDzeNVvr28lBFJ4dw5KrrWZUI5f212FXh4dG05lw2I5OpBvr4Jt+3D2dyeH9y/D5a/8WbOnLmhziZ+VXXsBqwAxgW47MP4ikqDy2ZkZGhTLV++vMnvbQ33v75Zh/7kHS2pqKr19VDPX1NltUcv/M3HOvnRZVpaUf2v5920D7Vxe35V9++D5W88YL3W8Zkask1PItJRRDqduQ9ciK8TvF2bM6Y3pZUe3tvm/k7t5z/bz65jRTx0+TBiomz4cGNClVOnx84RkVwgE3hbRN7zP58iIkv9iyUDn4rIZmAt8LaqvutE3lAyrl8XeneJ4Y2Nh5yO0ixHCsv43Ye7OW9Idy4Ylux0HGNMPRy59FVV3wTerOX5w8Al/vs5wKhWjhbywsKEK8f04snl2RwtLKdH59r7KkLd/761g2qv8vAVw60D25gQF7JNT6Zuc8b2xquw+At3HlWs3H2ct7ce4Z6ZA+nTNdbpOMaYBlihcKH+SR0Z2zeB1zfmnunod42Kag8PLdlG/6SOzPvKAKfjGGMCYIXCpeaM7c3uY8VsO3za6SiNMv/jHPbll/Cz2cNt/mtjXMIKhUtdPrInkeHiqk7tgwWlPLk8m0tH9mRaejen4xhjAmSFwqUSYqM4b0gyi784REV16A/poao8uDiLiDDhJ5cOczqOMaYRrFC42A0T+3KipJJ3tob+NRXvbTvK8l3H+c4Fg1x7ppYx7ZUVChebOjCJAUkdeWH1fqej1Ku4opqf/nM7Q3vGc8vkVKfjGGMayQqFi4WFCTdl9mPTl6fYmlvodJw6/e6D3Rw9Xc4jc0YQEW6/csa4jf3VutxVGb2JjQrnxRA9qthx5DQLV+3nuvF9Gdu3i9NxjDFNYIXC5eKjI5kzpheLNx/mZEml03H+jderPPDmVhJiIvnBRYOdjmOMaSIrFG3A3MxUKqu9vLr+oNNR/s2r6w+y8ctT/PCSoSTE2vSmxriVFYo2YHCPTkwa0JWXVh/A4w2NK7XzTpfz6NIdTOjflavG9nI6jjGmGaxQtBG3Tx3AoVNlfH7U+WsqVJUH/pFFRbWXx648xwb9M8blrFC0EecN6c7g5E68lVOJ1+Gjire2HOGD7cf43oWDGNDNvbOMGWN8rFC0EWFhwl0z0zhcrLy/3bkL8E4UV/DQkm2M6pPA7VNt0D9j2gIrFG3Ipef0pEes8JsPdjvSV6GqPLhkG8Xl1fzy6pGEh1mTkzFtgRWKNiQiPIw56VHsPlbsyFwVr288xNtbjvDt89MZlNyp1bdvjAkOKxRtzPge4QzrGc9vPthNeVXrdWznHC/mwcVZTBrQlTu/ktZq2zXGBJ8VijYmTIQfXTKU3JNlPPfpvlbZZkW1h2+9somoiDB++9XR1uRkTBvjSKEQkV+KyE4R2SIib4pIQh3LXSQiu0QkW0Tub+WYrjU1PYlZw5N58qNsDp8qC/r2fvnuLrYdPs3jV42kZ+eYoG/PGNO6nDqi+AAYoaojgd3AD89eQETCgT8CFwPDgOtFxCYyCNCPLx2GV5UHF28L6nSp/9h0iGc/3cfczH5cOLxH0LZjjHGOI4VCVd9X1Wr/wzVA71oWmwBkq2qOqlYCi4DZrZXR7fp0jeXeCwfz4Y5j/CNIHdsbDhRw32tbmNi/Kz+2yYiMabNCoY/iNuCdWp7vBdQcvCjX/5wJ0G1T+5PRrwsPLd7GwYLSFl33wYJS5r24gZSEaJ66MYOoiFD4VTLGBIMEq1lCRD4EamuLeEBVF/uXeQAYB1ypZwURkWuAWap6h//xTcAEVf1WHdubB8wDSE5Ozli0aFGTchcXFxMX596ric/Of6zEy8Ory0iODeNHE6OJCm9+R3NxpfLo2jJOlis/mRRDz7iWLRJt7WfgRm7fB8vfeDNnztygquNqfVFVHbkBNwOrgdg6Xs8E3qvx+IfADwNZd0ZGhjbV8uXLm/zeUFBb/veyjmi/H7yl31m0ST0eb7PWf7KkQi/+3UpNf2CpfrbneLPWVZe2+DNwG7fvg+VvPGC91vGZ6tRZTxcBPwCuUNW62kTWAeki0l9EooDrgCWtlbEtuXB4D753wSDe2HSIR5buaHLn9uFTZVz79Gqy84qZf1MGkwcmtXBSY0woinBou08CHYAP/COLrlHVO0UkBXhWVS9R1WoRuQd4DwgHFqjqNofyut495w7kREklz326j9JKD/9v9vBGTUu6bn8B97y8kdIKD8/fOt6KhDHtiCOFQlUH1vH8YeCSGo+XAktbK1dbJiI8dPkwOnYI54/L97Ivv5hfXj2KPl1j631fWaWHP63I5k8r9tK7Swwv3DaBIT3iWym1MSYUOHVEYRwgInx/1hD6J8Xx8JJtzPrdSuZmpjI3sx8pCf9+odzJkkpe35jLws/2c+hUGVeO6cVPZw+nU3SkQ+mNMU6xQtEOXZ3Rm0kDuvLYOzt5euVenvp4LwO7x9G3ayxhAodOlbPz6GlUYXxqF3597SgmDUh0OrYxxiFWKNqp3l1iefKGsXz/RAnvZh3l830FHC0sx6tK9/hoLho+iPOGdmdEr85ORzXGOMwKRTvXL7Ej3/hKGt+wEV+NMXWwy2mNMcbUywqFMcaYelmhMMYYUy8rFMYYY+plhcIYY0y9rFAYY4yplxUKY4wx9bJCYYwxpl5Bm7jISSJyHDjQxLcnAfktGKe1uT0/uH8f3J4f3L8Plr/x+qlqt9peaJOFojlEZL3WNcuTC7g9P7h/H9yeH9y/D5a/ZVnTkzHGmHpZoTDGGFMvKxT/ab7TAZrJ7fnB/fvg9vzg/n2w/C3I+iiMMcbUy44ojDHG1MsKhTHGmHpZofATkYtEZJeIZIvI/U7naSwRWSAieSKS5XSWphCRPiKyXER2iMg2Efm205kaS0SiRWStiGz278NPnc7UFCISLiKbROQtp7M0hYjsF5GtIvKFiKx3Ok9jiUiCiLwmIjv9fw+ZjmeyPgrfHwawG7gAyAXWAder6nZHgzWCiEwHioEXVXWE03kaS0R6Aj1VdaOIdAI2AP/lsp+BAB1VtVhEIoFPgW+r6hqHozWKiHwXGAfEq+plTudpLBHZD4xTVVdecCciLwCfqOqzIhIFxKrqKScz2RGFzwQgW1VzVLUSWATMdjhTo6jqSqDA6RxNpapHVHWj/34RsAPo5WyqxlGfYv/DSP/NVf+JiUhv4FLgWaeztEciEg9MB54DUNVKp4sEWKE4oxdwsMbjXFz2IdWWiEgqMAb43OEojeZvtvkCyAM+UFW37cPvgPsAr8M5mkOB90Vkg4jMczpMIw0AjgML/c1/z4pIR6dDWaHwkVqec9V/gm2FiMQBrwP/o6qnnc7TWKrqUdXRQG9ggoi4phlQRC4D8lR1g9NZmmmKqo4FLgbu9jfLukUEMBb4s6qOAUoAx/tMrVD45AJ9ajzuDRx2KEu75W/Xfx34q6q+4XSe5vA3F6wALnI2SaNMAa7wt/EvAs4Vkb84G6nxVPWw/2se8Ca+pmW3yAVyaxyJvoavcDjKCoXPOiBdRPr7O4+uA5Y4nKld8XcEPwfsUNXfOJ2nKUSkm4gk+O/HAOcDOx0N1Qiq+kNV7a2qqfj+Bj5S1RsdjtUoItLRfzIE/iabCwHXnAmoqkeBgyIy2P/UeYDjJ3REOB0gFKhqtYjcA7wHhAMLVHWbw7EaRUReAWYASSKSCzykqs85m6pRpgA3AVv9bfwAP1LVpc5FarSewAv+s+jCgL+pqitPMXWxZOBN3/8dRAAvq+q7zkZqtG8Bf/X/05oD3OpwHjs91hhjTP2s6ckYY0y9rFAYY4yplxUKY4wx9bJCYYwxpl5WKIwxxtTLCoUxxph6WaEwhn+N0fSEf3jwrSIy4KzXU0WkrMY1Hk3dzsMicq///qrmrKuWdcf4h9auFJGklly3ad+sUBjj80MgR1WHA78H7qplmb3+cZz+jfg0+m9JVSc3OmX96yvz57PhZ0yLskJh2j3/UA9zVPUJ/1P7gIENvCfVP6nMn4CNQB8R+Yd/xNJtNUctFZEH/JNifQgMrvF8cY37//HeGtt4xv/8+/6hQc4MVfG2f5KkLBH5akt9P4w5mw3hYYxvTKY+NZqVugIfBvC+wcCtqnoXgIjcpqoF/g/zdSLyOpCKb9ykMfj+3jbim5TpbLW9FyAd3yRaXxeRvwFXAX/BN9jgYVW91L/tzo3daWMCZUcUxsBo4EFVHe1vunkf+CKA9x04a/a6/xaRzcAafKMRpwPTgDdVtdQ/bHpdg03W9l6Afap6JssGfIUHYCtwvoj8QkSmqWphAHmNaRIrFMZAF6AUQEQi8I04+s8A3ldy5o6IzMB3ZJKpqqOATUC0/+V6B1Rr4L0VNRb14G8FUNXdQAa+gvGoiDwYQF5jmsQKhTG++dIn+e9/B3hbVfc1ch2dgZOqWioiQ2qsbyUwx39GUifg8ka8t04ikgKUqupfgF8RAnMWmLbL+iiMgVeAd0QkG1gNNGX6zHeBO0VkC7ALXxMSqrpRRF7F15R1APgk0Pc24BzglyLiBaqAbzYhszEBsWHGjQmAfx7vt1Q15Kc29c9QN05V853OYtoGa3oyJjAeoHNzL7gLpjMX3AGRgNfhOKYNsSMKY4wx9bIjCmOMMfWyQmGMMaZeViiMMcbUywqFMcaYelmhMMYYUy8rFMYYY+plhcIYY0y9rFAYY4yp1/8HvDmK8ScbidcAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"## Copied from notebook with Algorithm 5.1\n",
"def my_f3(x):\n",
" return x[0]**3 - x[1] - x[0]*x[1] - x[1]**2\n",
"\n",
"def my_h3(x):\n",
" return (x[0]**2 + x[1]**2 - 1)*np.ones(1)\n",
"\n",
"def visualize(xk=[]):\n",
" n1 = 101\n",
" n2 = 101\n",
" x1eval = np.linspace(-2,2,n1)\n",
" x2eval = np.linspace(-2,2,n2)\n",
" \n",
" X, Y = np.meshgrid(x1eval, x2eval)\n",
" \n",
" Z = np.zeros([n2,n1])\n",
" \n",
" for i in range(0,n1):\n",
" for j in range(0,n2):\n",
" Z[j,i] = my_f3((X[j,i], Y[j,i]))\n",
" \n",
" fig, ax = plt.subplots(1,1)\n",
" CS = ax.contour(X, Y, Z)\n",
" ax.clabel(CS, inline=1, fontsize=12)\n",
"\n",
" # Add grid\n",
" plt.grid()\n",
" \n",
" # Add unit circle\n",
" circ = plt.Circle((0, 0), radius=1, edgecolor='b', facecolor='None')\n",
" ax.add_patch(circ)\n",
" \n",
" # Plot iteration history\n",
" if len(xk) > 0:\n",
" for i in range(0,len(xk)):\n",
" if i == len(xk) - 1:\n",
" c = \"red\"\n",
" else:\n",
" c = \"black\"\n",
" plt.scatter((xk[i][0]),(xk[i][1]),marker='o',color=c)\n",
" \n",
" plt.xlim([-2,2])\n",
" plt.ylim([-2,2])\n",
" \n",
"visualize()\n",
"\n",
"nt = 200\n",
"theta = np.linspace(0,2*np.pi,nt)\n",
"obj = np.zeros(nt)\n",
"\n",
"\n",
"for i in range(0,nt):\n",
" x_ = np.cos(theta[i])\n",
" y_ = np.sin(theta[i])\n",
" \n",
" obj[i] = my_f3((x_,y_))\n",
"\n",
"\n",
"plt.figure()\n",
"plt.plot(theta,obj)\n",
"plt.xlabel('$\\\\theta$ [radians]')\n",
"plt.ylabel('Objective')\n",
"plt.grid()"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.8.4.1 Starting Point Near Global Min ($\\theta_0 = 1.0$)](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.4.1-Starting-Point-Near-Global-Min-($\\theta_0-=-1.0$))",
"section": "4.8.4.1 Starting Point Near Global Min ($\\theta_0 = 1.0$)"
}
},
"source": [
"### 4.8.4.1 Starting Point Near Global Min ($\\theta_0 = 1.0$)"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.8.4.1 Starting Point Near Global Min ($\\theta_0 = 1.0$)](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.4.1-Starting-Point-Near-Global-Min-($\\theta_0-=-1.0$))",
"section": "4.8.4.1 Starting Point Near Global Min ($\\theta_0 = 1.0$)"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Iter. \tf(x) \t\t||h(x)|| \t||grad_L(x)|| \t||dx|| \t\t||dv|| \t\tdelta_A \tdelta_W\n",
"0 \t-6.9105e-01 \t0.0000e+00 \t3.7501e+00 \t 1.1171e+00 \t 1.1455e+00 \t 0.0000e+00 \t 0.0000e+00\n",
"1 \t-4.0104e+00 \t1.2480e+00 \t2.1729e+00 \t 4.2318e-01 \t 3.9672e-01 \t 0.0000e+00 \t 0.0000e+00\n",
"2 \t-2.4216e+00 \t1.7908e-01 \t3.3575e-01 \t 8.3649e-02 \t 1.0205e-01 \t 0.0000e+00 \t 0.0000e+00\n",
"3 \t-2.1438e+00 \t6.9971e-03 \t1.7074e-02 \t 3.5294e-03 \t 6.5710e-03 \t 0.0000e+00 \t 0.0000e+00\n",
"4 \t-2.1324e+00 \t1.2457e-05 \t4.6327e-05 \t 6.3597e-06 \t 1.9707e-05 \t 0.0000e+00 \t 0.0000e+00\n",
"5 \t-2.1323e+00 \t4.0446e-11 \t1.4043e-09 \t 2.8044e-10 \t 3.3891e-11 \t 0.0000e+00 \t 0.0000e+00\n",
"\n",
"x* = [0.24215301 0.97023807]\n",
"\n",
"v* = [1.64012795]\n",
"\n",
"theta* = 1.326212035697004 = 1.3262120356970035\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYQAAAD8CAYAAAB3u9PLAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAABhxklEQVR4nO2dd3xUVfr/32cmvfdCQhop9F4E6R1EUIoNG+qyurq6P7+r6+q6brGtrq5dV9eKKKKgICJVAiK9t5AQAgkppPc2mZnz++MGpAQIyWTuneS+X6/7ykzmzj2f3Mzczz3nPOd5hJQSHR0dHR0dg9oCdHR0dHS0gW4IOjo6OjqAbgg6Ojo6Oo3ohqCjo6OjA+iGoKOjo6PTiG4IOjo6OjqADQxBCNFZCLFBCJEihDgshHikiX2EEOINIUS6EOKAEKJ/a9vV0dHR0bEtTjY4hhn4PynlHiGEN7BbCLFWSnnknH2mAAmN2xDg3cafOjo6OjoaodU9BCllnpRyT+PjSiAFiLhgtxnAZ1JhG+AnhAhvbds6Ojo6OrbDFj2EswghYoB+wPYLXooATp3zPLvxd3lNHGM+MB/Azc1tQFRUVKs0WaySoop6ArxccHay/ZSJ1WrFYND+VIyu07boOm1LR9VZYTJTbmogzMMVZxsdNy0trUhKGdyiN0spbbIBXsBuYGYTr/0ADD/n+XpgwJWOmZiYKFtLbb1Jvrt4szxdVNHqYzXFhg0b2uS4tkbXaVt0nbalo+nMKi6Vt324SCY986r8/aLlsrS61ibHlVJKYJds4XXcJj0EIYQzsARYKKVc2sQu2UDnc55HArm2aPtKuLk4c/+ca+3RlI6Ojs5lkVKyZO9hnl+VjFEYeOnGyVzfuytCCLWlATYYMhLKX/IhkCKlfPUSuy0HHhJCLEKZTC6XUl40XKSjo6PTXskrr+Tp5WvZfDyTwTGRvHjDJDr5+agt6zxs0UO4FrgDOCiE2Nf4uyeBKAAp5XvASmAqkA7UAPNs0K6Ojo6O5pFSsnTvYV5YvRGrVfL01DHcOrAPBoM2egXn0mpDkFJuBi77lzWOaz3Y2rZ0dHR0HIns0nL++v06tmRkMSg6kudnTKBzgJ/asi6JTaOM1EZKqZmxOB0dnY6LxWplwfZ9vP7TLxiEgb9OHcstA3trsldwLu3CEOpNZlxdnHQz0NHRUZ1Dufn8bcV6DuXmMzoxlr9dN44wX2+1ZTULhzaE/JJK1m5NJet0KYF+Hswe15dAP8+zr1utUvOOrKOj0z6oqqvn9Q1bWLhjP4Ge7rwyaypTeyY61I2qQxvCSx+vRxgEIf5eHMsqYvO+DGaM7sXB9Fx6xXfSzUBHR6fNkVKy4mAqL6/dRGFlNbcO6sMfxg7Dx91NbWlXjcMawsncEg4dz2P1Ow8AsGnPcRb8sJM9R7PJzi8D4M/3jCe+c8sW7Ono6OhcidT8Iv658id2ZebQIzyEN2++nj6RjpuVx2EN4Xh2EdHhAZRX1eLr5U54kA9HT+Tz21nD8PF0571vNrMvNUc3BB0dHZtTWl3Lm8lb+WrXAbzdXPnH9eOZ1a8HRgdIv3E5HNYQ+neN5Msfd7NgxU78vD1YvvEgt00ZwMDuUY2vd2b7wUxmj++rrlCNU99gJqesgpzyCnLLKsivqKK0ppaSmlpKa2qprjdR22Cm1tRAg8WCVUosUoKUOBmNOBsNOBkMuLs44+nigqerCz5urvi5u+Hn4Y6/hzsh3p6Nmxch3l64OBnV/rN1dFqE2Wrlk617eDt5GzUmEzcP7M3DY4bh5+F4w0NN4bCG4O/jwR3TBrF2WyohAd706xpJ0DkTypv2HGfs4AQVFWqPgsoqDubkczDnNMcKikkvLOZUaTlWJb8UoCwoOXMh93N3I9DTA3cXZ9ydnXFxMmIUAtG4mS0WzFYrJrOF2oYGakwNVNXVk1NWQVlNLeW1dcgLNAggxNuLCD8fIv19iA7wJyrAj5hAP2KDAux5OnR0mo2Ukh8Pp/HCjhQK60wM7xLNE5NGER8SqLY0m+KwhgAwakA8owbEA7DqlxT+8f4qistqqKypo6K6jlsmdew6PDllFWzLyGJLRhZbjmVQmrwXACeDgZhAP7qGBXNdryRiAvzp5OdNJ18fQry9cDLapttrsVopr62jsLKagqpqCiqqyC2vJLe8gpyyCnZl5vD9gaPnmYa/qzPdsopJCAkkMSSIxNAgEkKCcHN26I+qjgOz7cQpXln7Mwdz84nwdOP9uTcwMiFWbVltgkN/y8xmC05ORqxWyYShSVilZMn6/YzoF8ff75+itjy7I6Uk5XQha44cY21KOseLSgAI8vSgi48nE/r3oXdkGN3CQuxygTUaDAR4ehDg6UESTc/l1DWYOVVaxsniMo4XlrD18BHKa+v4atdB6sxmAAxCEBfkT/fwELqFhdCzUyjdwkPwcnVp879Bp+OyPzuP19b/wtYTpwjz8eL5GRPxKytot2YADm4INMb3vvHlRkwNFh6/exxTh3dXWZT9yS4t57v9R1i2P4VTpeUYhGBQdCQ3DejFsC5RxAcHsnHjRkYP1V6Pyc3ZiYQQpRcwoRt0tdYwevRoLFYrp0rLScsv4mh+ISl5hWw/kc3yA0cBZeipS3AAPTuF0ScyjF4RYSSFBuFs1OcndFrHodx83tm4jZ9SMwjwcOeJSaO4ZWBv3JydSE4uVFveJZFS8ved61p1DIc1BCklTkYDUkoWr93Hp/+YCyjDFI4+098crFZJ8rEMFu7Yz5bjmQAMjYvityMGMy6pC/6e7iorbB1Gg4GYQH9iAv2Z2P3XuaCiqmoO5xZwKDefg7mn2XTsBN/tV6q1ujk50TMilH6dO9Gvczj9OnfC38Oxz4OO/TiYc5q3krex8dgJfNxc+cPYYdwxpB+eDtATlVLyj13r+eTo7lYdx2ENwWKVOBkF//1mCz3iwkiICsZqle3eDExmM8sPHOXjLbs5XlRCmI8XD46+hhv79iBCY6l024IgL09GJcYyKlHptkspySmrYH/2afZn57EvO4+Pt+zmA6sVgC5BAfSP6sSAqAgGRkcQ4efjUCtHddoWKSXbT5zig1928cvxTHzd3fjD2GHMHdwXbzdXteU1CyklL+3dyMcpu7in20CeacWxHNYQzkx8frlqN2/+aTYAEskVEq86LGaLlaX7DvN28jbyK6voFhbMyzOnMLlHQoceJhFCEOnvS6S/L9f1SgKg1tTAodx89pzKZU9WLqsOH+PrPYcACPX2YkB0BIOjIxgUE0lcUIBuEB0Qs8XKuqPp/O+XXRzKzSfI04NHx13LbYP7Otzc1FsHt/DuoW3cltiXpweO63iGYLZYcTIa+GzFDjqH+dM7sRNSts/egZSSDakZvLJuM8eLSugTEcbzN0xkWFyUfiG7BO4uzgyKiWRQTCSgDK8dKyhiV1YOuzNz2Hkym5WHUgEI9PRgYHQEg6KV/ROCA/WUJ+2Yyrp6vtlziAXb95FbXkF0gB9/nzaOG/p0x9UBI9neObiVV/b9zMy4Hjw7ZFKrrwmOdwb4tXfwyfIdPP/QNACsUmJsZxfI7NJy/v7DT/ycfpKYQH/euGkaE7rF60ZwlRgMgqSwYJLCgpk7uC9SSrJKytmZmc3Ok9nszMxm9ZFjAPi6uzEoOoLBMZEMjulMYkiQbhDtgNTThXy56wDLD6RQY2pgUHQkT04exZikOIe9kfzg8HZe2ruRGbHdeXnYdRhscF1wSEMAOJSeR1JMCNf0jml3vQOzxcqn2/bw5oatGA0Gnpw8ilsH9enQQ0O2RAhBdKAf0YF+zO7fE1DMVzGIHHacPMW6o8cB8HVzZVBMJC/eONnhhhI6OrWmBtampLNo1wH2nMrF1cnIlB5J3DGkLz06haotr1V8enQ3z+3ewHXRXXnl2mk2u/45rCH0jA/njcdnAe2rd3CqpIw/Ll3F/uw8xiTG8cx1Yx0ml7ojc2Ye4sa+PQDILatgR2PvIaOoBE8X50u+12yxIgSX/FKeKdxksVpZtj+FZ1du4C9TxzCzX482+Vs6MlJKDuScZsnew6w8lEpVvYnoAD/+NHEkN/bt0S5STHx2dDfP7FjLxM4JvDbiepxseDNsE0MQQnwETAMKpJQ9m3h9NLAMONH4q6VSyn+0tl3nxpw47aV3sOpwGn9ZvhaB4N+zpnBdzyR9eEglOvn5cEPf7tzQ98rrWs5d2S2lxGKVCKEsqDuT5gNg8e6DfLXrIDFB/pgaF93pNTtsQ1ZJGd8fOMryAylklpTh5uTEpB4JzOrXk4FREe3mHC84uoe/7ljL+Mh43hw5A2eDbUcNbNVD+AR4C/jsMvv8LKWc1tqG2uMXqMFi4YVVG/li5376RITxyuypRPr7qi1Lpxk8+d0aakwmRibEMjw+ujH1x6+fzzO9g1fXbabBYmVsUhw5ZRXEBSs5cHS/bzmZxWWsPpLG6iPHOJxXgAAGxUTym+GDmNQ9wWHCRpvLwrS9PL1jDeMj43ln1I24tMEQsk0MQUq5SQgRY4tjXYnnP1xDVa2JFx++3h7NtTkVtXU8vHgF206cYt7QATw6/lp9rsCBuHlgL1YdPsZn2/byzIr1OBsNdA8LYXh8DFN6JBId6MeiXQfYnZXDmzdfz4+H0zhWWExckD8AX3zxBU899RRZWVlERUXx3HPPMXfuXJX/Km1itUoO5p5mQ2oGG9IySM0vAqBPRBiPTRjB1J5JhLfT4dVFx/bz1LbVjI3owtujbmgTMwD7ziEMFULsB3KBP0opD1/tAcxmCxt3p3Nt3zjbq1OB7NJyfrvwO7JKynjhholnx691HIc+keHnFUTJKCxhQ1oG20+coqiqmvHd4lmXks7n825CCEFOWQW+bm4EeXmycOFC5s+fT01NDQCZmZnMnz8fQDeFRgoqq9hyPIstGZlsOZ5FUXUNRiHoHxXBE5NGMbFbPJ3a+YLMBal7eHr7GkZ1iuOd0Tfiamy7y7aQ8sIExS08kNJDWHGJOQQfwCqlrBJCTAVel1I2mZtaCDEfmA8QHBw8YPHixWdfS8up4MNV6dw5Po4e0X420d1aqqqq8PLyuur3ZVfV8vr+dCxS8tsesST5t+2dTUt12htH02mVEik5O2dwLmX1DSxIzeRYWTU3J0TiYhAcKqkg1seT0RHB7D9wAHNDw3nvkRJyhRPDuncl0M2l1XNIjnY+y+obSC+vIq1M2U7X1AHg7exEV39vegb60DPAB0+V1gzY+3yurzzNgtKT9HHz46HgRJzFledLx4wZs1tKObAl7dnFEJrY9yQwUEpZdLn9kpKSZGpq6tnnL32ynh9+Pszqdx/A7TJRH/YkOTmZ0aNHX9V7juQVMO+zJbg7O/HRHbOIC277OgAt0akGjq5TSnnWJJyMBk4Wl/LL8Uz2nspjT1YupTU1+Hu48+rs6+gfHcGF3z9nvwDiHvkLAN6uriSFBpEQEkh8SCDxwcoW4OnebKPQ8vksr60j5XQhKXkFrN17gLx6C3kVlQB4uDgzIEpZD3Jtl2i6hgZrYu7QnudzwdE9LZozEEK02BDsYrNCiDAgX0ophRCDAQNQfDXHkFKyac9xrukdoxkzaAlHTxcy79Nv8HBx4dO7ZxMV4Ke2JB0bIoQ4LwT6TIK+uYP7smjXAdampDMmMY5wX2+ioqLIzMw87/3mynLqf/iKF959n9TThRzNL2TFwVQq6+vP7uPj5kpsoD8xQf5EB/jR2d+PqABfIv18r8os7EVZTR1ZJWWcKC4hvaCY9MIS0gqKyCmrOLtPgKsL18THMK9zf/pGdqJ7eIjN6nI4Iv87soNnd/3UphPITWGrsNMvgdFAkBAiG3gGcAaQUr4HzAYeEEKYgVrgFnmVXZO0zEIKS6sY0a+LLSSrQnpBMfM+W4KHiwsL5s3RI4k6EBarlboGM75urtw+pC8Azz333HlzCADurq48+4ffc8vA3md/J6WkoLKaYwXFZBQVk1FUyomiUrZlnGLZ/pTz2nF1MhLu60O4j1KutLa0mEzXPQR4up+thOfr5oqXmyverq4tvuiaLVaq6k1U1dcrJVeraympqaGoqobTFVXkV1SSV17JqdJyKup+NTNng4GYIH96R4Rx84BedAsPoXtYCAd37dBsT8bevHtoG//ak8yUqCReHzHdbmYAtosyuvUKr7+FEpbaYjbvy0AIGNbHMYtT5FdUcd/nS3EyCD6+a5ZuBh0Mo8HA3UP7n11/AL9OHF8pykgIQaiPF6E+XgyPjz7vtTMFhk6VlDfWxa4kr7yCvIoqdmbmUFBRyZpTBZfU5ebkhKuzE25OTrg5O2E0GDAaBMbGsWqLtCKlxGyV1DeYqTObqW8wU3PB3Me5+Li5EurjRZiPN30iw+ns73u2TGpUgJ8eRXcZ3jqwhX/v28T0mO68OnyaTRedNQeHWam8df8JusWGEuDrobaUq6bG1MADXy6joq6ehfNuIibQX21JOirh4nT+V27u3Lmtiig6t8BQU2zYsIF+Q4ZSWlN7diuvraOqvp7KOhPVJhN1DWbqzWbqGsxYrFYsUmKxWhEIDEJgMCjDYGeMw9XZCS9XF3zcXPFydcXP3Y0ATw8CPd0J8PRwiPoBWkNKySv7fuatg1u4Ma4H/x52nSoLbh3CEMqrajl8/DTzZgxRW8pVY7VK/rR0FUdPF/LOrdPpFh6itiSdDoQQAj8PN/w83IhFvxHRIlJK/rlrPR+l7OKW+D48d80k1bIvOIQh7DpyCquUXNMrRm0pV807m7ax9mg6T0waxejE9rF+QkdHxzZYpeTp7WtYmLaXed0G8teB41QNCnAIQ9h5OAtPdxe6dwlTW8pVsTk9k7eTt3FDn+7cdU0/teXo6OhoCLPVyp+2rmTJ8UM80PMaHu83SvUIMYcxhP5dIx0qDK24qoYnvl1FfHAgz1w3VvV/tI6Ojnaot5h5+OflrM5K49G+I/h9r2GauEZo/gpbVFZFdn4Z/bpGqi2l2Ugp+cvytZTX1fPvWVNwd+B1Ezo6OralpsHEfT8tYXVWGs8MGs/Dva/VhBmAA/QQ9qXmANA3KUJlJc1nyd7DbEjL4IlJo0gKC1Zbjo6OjkaoMNVx30/fsKswh5eGTuGmhD5qSzoPzRvCgWO5uLo4kRTtGNE5eeWVvLBqI4NjIrlziD5voKOjo1BQW8Vd6xaTXl7EGyOmMy2mm9qSLkLzhnDwWC7dY0NxcnKMxSzP/5iMVVp5fsZETeRe0dHRUZ9TVWXcvnYRBbXVfDh2DiM7aXOBrabnEKRUUlb0SuiktpRm8XP6SdYeTef+kUP0lcg6OjoAHCsr4qZVCymtr2XhhFs0awag8R5Cg8WK2WKlhwOEmzZYLDz/YzLRAX7MG9pfbTk6OjoaYHdBNvf89A0uRiOLJt5G94BQtSVdFk33EExmKwDd4rRvCIt2HeBEcSl/mjTyovQEOjo6HY8N2ceZu3YRAa7uLJ18h+bNALTeQzBb8ffxIMRf2wU+KuvqeTt5G9fEdmaMvhpZR6fD823GIR77ZSVd/YP5ZNxNBLl7qi2pWWjaEExmK11jQjQTo3spPvxlF2W1dTw+caTmtero6LQdUkreO7ydf+1JZmhYFO+PnoW3i6vaspqNpg3BbLGSqPFw0+oGMwt2HmZy9wS664nrdHQ6LBarlX/uWs8nR3dzfUw3/n3tdW1a/7gt0LRaKSG+c9NpfbVCck4R1SYTD4x0vEysOjo6tqHOYub/Nq/gh8yj3Nd9EE8OGHtRjW1HQNOTyqBtQ6g1NbAhp5BRCbH6imSdFrNw4UJiYmIwGAzExMSwcOFCtSXpXAWldbXcsXYRP2Qe5c/9x/CXgeMc0gxA4z0EISAqTLs53JcdSKGqwcx917aonrWODgsXLjyvjGZmZibz588HaFXhHB37cKqyjLvWLya7qpy3Rs7Q5Orjq0HTPQQng0GzK5StVsln2/YS5eXOwGjHybOkoy2eeuqp82oqA9TU1PDUU0+ppEinuRwoymPmqgUU19WwcMItDm8GYCNDEEJ8JIQoEEIcusTrQgjxhhAiXQhxQAjRrJVbzk7a7XZtPZFFRlEJYyO1HwWlo12ysrKu6vc62mB1Vho3rV6Ii8HIN5NvZ1BoZ7Ul2QRb9RA+ASZf5vUpQELjNh94tzkH1XL9gy937ifAw50BIX5qS9FxYG43GDgBWIATwK2Nv4+KilJPlM4lkVLy4ZGd3J+8lCT/YL6behcJftqd57xabDKHIKXcJISIucwuM4DPpJQS2CaE8BNChEsp8y53XGcnbRpCYWU1G1IzmDdsAM4Gi9pydFqIlFBaCpmZUFysPC4ru/hnWRnU1YHF8ut2993w1FNgNCqbmxv4+YG//68/z30cGAgxMcrzMzzfowfvWiycWbIUA3zQ+Pi6556zxynQuQrMViufl55k/al8Jkcl8p/h1+PupK1aJz8X7m3V+4VyjW49jYawQkrZs4nXVgAvSik3Nz5fD/xJSrmriX3no/QiCA4OHrB48WKb6LMl604V8M3xHJ4Z1A1vacbLS9srqQGqqqo6rM76+os3k0n5CeDiAk5OynbmAn/hYyGUDZSfZnMVRqOiU0qwWn81C7P54sdms9KeEODqqmzG0nw8qMf1nA3ABLgMGGCTv70j/99tSbXVzLtFxzhUV85k73Bu8ovSXCRRKVV8KtazbPRru6WULYp0sVeUUVNnrkknklK+D7wPkJSUJEePHt2GslrGG/9dSI/wEG69bjLJycloUeOFdASdZjOkpMCePbB7t/Jz/34IDobERIiNPX+Li1Pu3lvyvW6JTimVnsiJE5CRARn3PsFJYjlBLGkkUkIAfdlHf3Yz4LPRDBgASUmKKbWUjvB/b2tOVZYx76evOVlfybyAOJ6ZdpPaki7CbLXw2P7XcK1t3apoexlCNnDurEskkGuntm1KZnEZR/IKeHziSLWldHgqKiA5Gdatgx074OBBiIyEAQOgf3+48Ubo1+/8YRo1EQKCgpRt0CA4ecu/iDnn9RL82UN/1jGAFSvg73+H06ehTx8YPBjGj4dRo0DDN9Ltju35WTyQ/C0WKVkw4Wbqj55QW1KTLD61hrTKTJ7oNo/F/KvFx7GXISwHHhJCLAKGAOVXmj/QKquOpAEwpUeiyko6Hg0NyoV/7Vpl278frrlGuVC+9BL07Qs+PmqrbD5fdO/OI0eOnJ1DCKCUoaxnR/c8vvpK+VKXlcHevbBlC7z8Mtx8s2J4EyYo28CBretB6FyaL9L28dfta4jy9uODMbPo4htIsgYN4VhlFl9mrmZ0yEBGBLeuSqNNDEEI8SUwGggSQmQDzwDOAFLK94CVwFQgHagB5tmiXTVYm5JOn4gwwn291ZbSISgrg+++g2+/hY0blaGeCRPgmWdg+HDw8FBbYct58vBhnu/Rg9uOHCEKyEIxiScPHz67j58fjBmjbE89BVVV8PPPiiHedx/k5Civ3XgjzJgB3vrHstWYrVae2/0TH6fsYlSnON4YOR1fFze1ZTVJncXEK6kL8Hfx5oH42a0+nq2ijG69wusSeNAWbalJXnklh3Lz+b/xw9WW0q6pqYEVK+DLL+Gnn2DsWLjpJvjgAwhpZ/kDz734xwBPXmF/Ly+YMkXZAPLyYM0a+OorePBBmDgRbr0Vpk5VIp90ro7Suloe2vQdv5zO5J5uA3lywFicDNqMdgT4+MQyTtXk82yvB/Fyav3dkaZTV2iNjWkZAIxN0mse2BqTSbmwFRbCDTfAkCHKhe2TT8BXr0Z6ScLD4a67lK2kBJYsgbfeUnoP06fDzJnKZLtes+nKHC0t4DcblpBfU8VLw6ZyU3xvtSVdlt0lKazI/ZkZEaPp559kk2Nq1/o0yMZjJ4n08yEuKEBtKe2G/Hxl8jQ6Gl58UbkDTkuD1auVWH/dDJpPQAD85jdKr+rwYWVCPTdXGWZ78UUlwkmnaVZmHmXmjwuot1hYPHmu5s0AoNRUQbxXZ+6Ovd5mx9QNoZmYzBa2nzjFyIRYPVWFDdizR7mr7dpVGQdfuxY2b1ZCRNvbsJAahIfDI48o53f5ckhNhfh4xTAONZlgpmNitlp5YfcGfrfxO5L8gvn+urvoG9RJbVnNYnzYEF7t93+4GGy3OE43hGayPzuPmoYGhsXpKQVaitkM33wDI0Yow0Ldu0N6Orz/PvS8aDmjjq3o1w8+/lgxhagoZZ5h3DjFKKxWtdWpR0ldDXet+4r/Ht7OHUn9+WrSXEI9HGtW3ihsewnXDaGZ7DiZjQAGxUSqLcXhkBKWLoVeveCVV+Dhh5WFWX/6k5LSQcc+hITA00/DyZNwzz3wj38oZrFypfI/6kjsL8rj+h8+YWdBNi8Pm8o/h0zERY/f1Q2huew5lUtCSBC+7nroxtWwYYOyVuAf/4BXX1Xi6efM0Sc51cTFBebOhZ07lfmbP/5RWfC2ZYvaytoeKSULju5hzqrPAfhm8u3M0eB8gdlq4XTtr5M+tkoxdCV0Q2gGVqtkf3Ye/TqHqy3FYdizByZNUqJdHnlEeT5lSsvSROi0DUIoQ3cHDyo9hltvVdYytNc5hpoGE4/+soKnd6zh2vAYVlw3j95B2vxOv3T0U15I+Yj1+TuQUp6dt2xrY9ANoRmcKC6hqt5En0htfni0xOnTcPvtMG2acnFJSYHbbgMNh3J3eIxGJaIrNRVGj1bmF+69t31FJaWVFTJj5Wd8l3GYR/uO4MOxs/F3c1db1iVxFkbcja7sL0vjv8eXcKIqB6DNA1r0r2kzOJiTD0CviFCVlWgXq1WZHO7dGzp3hmPH4He/U4YndBwDNzf4f/9PCfv19oYePWDBAsefX1icfoDpP3xKaX0tC8bfwsO9r9VcptILGRTYg1pLPQleUVQ0VPNl1io2F+7l+SMfcrI6t816CvpIbjNIOV2Au7OTvv7gEqSnK0MODQ2wfr0yeazjuPj6wmuvKT293/xGMYX//U+JUHIkqhtMPLNjLd8cP8iwsGheG3E9Ie6OkRlwdMhAMqpy6OufRB//RLYXH+SLzFWUN1SdN4Rka/QeQjNIOV1IYmgwRn3c4zysVnjzTWXSeOZMZR2Bbgbth4EDlYnnMWOUhHoffug4vYVDxaeZtuJjlhw/yO97DWPB+JsdxgysUokF9nLy4MOM74jyCKObdyxFpjLivTvz0YllZ4eQbI3eQ7gCUkpS84uY1D1BbSmaoqhImRuorlaiUxL15K/tEicn+POf4frrlXmG5cvhs8+0u4JcSsmnR3fz/O4NBLp58OXE27gmzLG6NobGtQU3Ro4mKy2PvNoivjq1hus7jWRIYE+OVpwk1iuibdpuk6O2I4qrayivrSM+WA+YP8OePUo+//79YdMm3Qw6Aj17KsYfFaXUZjhyRG1FF1NQW8W8n77mbzvXMTw8hpXT7nE4MzgXZ4MzXbwi+e2uZ6lsqOH26KkkekdzXacRbdam3kO4AscLSwDoEqzPH4Byd/h//wfvvguzW59tV8eBcHFRhgg//VRZt6Clz8CG7OP8ccsPVDWY+MfgCdyR1L9dpJiZFDaMUlMl40IHI4RASmnz1cnnohvCFThZXApATKC/ykrUpaEBHn1USTqXnKxEoOh0TO66S5krmjkTdu2C555Tr0hPdYOJF3Zv4PO0vXT1D2bRxNtI8AtSR0wb4OHkxl2x0zAK5QS3tcnphnAFMkvKcDEaCfdxrBwntqSiQkml7O2tVCzTSklKHfXo318xg1tuUdacLFli/2JFewpzeHTzCjIrS7m32yAe6z8KN6PjX9IarGacDb/+HWfMwB7ocwhXILu0nAg/HwwGx+9+toTSUqVCWffusGyZbgY6vxIUBKtWKRlqBw48TVRUdwwGAzExMSxcuLDN2q23mHll7ybmrPqcBquFLyfextODxrULM8ivK+beHX9nV4k6kzSOfwbbmJyyCiL8HKhQrw0pLlYyY44YAf/5j552QudinJxgwoQv+OKLBiyW94GpZGZmMn/+fADmzp1r0/YOFZ/mj7/8wNGyQmbG9eRvg8fjo9HylleLlJK3jn1FjaWOKI8wVTTYpIcghJgshEgVQqQLIZ5o4vXRQohyIcS+xu2vtmjXHuRXVHXI+skFBUrpyvHjdTPQuTxPP/0kFss84ACwBvClpqaGp556ymZtmCwWXt+/mRtWfkZJfS0fjZ3Nq8OntRszAFiXv509pUe5O/Z6QtzUCWJpdQ9BCGEE3gYmANnATiHEcinlhX2en6WU01rbnj0xmS0UVdcQ6uMYC1psRX6+YgYzZypZSnUz0LkcWVlZwJmy6f8B1gMTGn/fevYV5fL4lpWklRUxI7Y7fx88AT9X7eYhaglF9WV8cPxbevnGMzVcvZrttughDAbSpZQZUkoTsAiYYYPjqk5JdQ0AwV6eKiuxH3V1SlK6G2+Ef/5TNwOdKxN1Xk6L/wdsBr6mc+fW1R6vNTfw/K6fmPnjAipN9Xw4djavj5je7sxASsk76YsxSzMPJ956dmGaGojWJkkSQswGJksp72t8fgcwREr50Dn7jAaWoPQgcoE/SikPX+J484H5AMHBwQMWL17cKn2tIbOyhhd2p3J/z1j6Bvk1uU9VVRVeXtrvQTRX58mTSkqKuNZ9l1tMezufamMPnSUlJWRmZmI9r/xaAj4+riQkuDbrGBfqPFBbymclJymy1DPaK4Sb/KLwMKg/5dkW5zOVbJYbdjDK2pPBtH6V55gxY3ZLKQe26M1SylZtwBzgf+c8vwN484J9fACvxsdTgWPNOXZiYqJUk03HTsikZ16VuzOzL7nPhg0b7CeoFTRH58svS9mvn5TV1W2v51K0p/OpBeyl8/PPP5fR0dFSCCGjo6Pl++9/Jbt2lfK//23e+8/oLKipkg9t/E5Gf/qCHPfd+3JrXmbbiW4Btj6flQ3Vcu7Wp+Tvd/9Lmq1mmxwT2CVbeD23heVmA53PeR6J0gs413Qqznm8UgjxjhAiSEpZZIP224zy2joA/NzbVxe1KVauVCqabd9u/3hyHcdn7ty5F0UUjR4Nw4dD164wcuTl32+Rko9TdvHqvp+pt5j5f32Gc3/Pa3BtB6Gkl+OjjOWUmyp5psd8u643uBS2ONs7gQQhRCyQA9wC3HbuDkKIMCBfSimFEINR5i40X36jorYeAG+35nV7HZX0dCVx2XffKbUMdHRsQUICfP453HyzkjU18hLlyPcW5vKP0wfJPFXDiPBYnhk8nnjf9p877EDZMVaf3sKsyHEkeGsj51KrDUFKaRZCPASsBozAR1LKw0KI+xtffw+YDTwghDADtcAtjV0bTVNtMgHg5dp+q7xICfPnKwXvhw1TW41Oe2PCBPjtb+HBB5UbjnODFPJrKvnXno0szTiEv9GFd0bdwJSopHaRg+hK1FtMvHlsEWFugdwWPUVtOWexSX9MSrkSWHnB79475/FbwFu2aMue1JgaMAiBm3P77bZ+/DFUVip1j3V02oI//xn69VPSW8yerawp+DhlF28c+IUGq4UHel5D7zILU6K7qi3Vbiw+tZbc2kKe7fUgbkbt3HC23yudDahtaMDNyand3rGcPg1PPAFr1yorTnV02gJXV/jgA7jpJom561HeSdtIVlUZ4yPjeXrQOKK9/UlOTlZbpt04VZPPN6fWMSZkIP38k9SWcx76ZeAymMwWXJzUn+hpKx55RCl92aeP2kp02jseibkEP7meJ/bk0NU/mE/G3cToCJVim1VESsm76V/janTh3rgb1JZzEbohXIYGiwVntfL6tjGrV8Pu3fDJJ2or0WnPpJUV8u+9m1hz6hhBQZ5Yv5zCXx7rxfCIjplXc0PBTvaXpfFg/E34u2gvR5puCJfBYpUY22mW03/+E559FjpARK2OCuRUlfPGgV/4+vhBPJ1ceLTvCO7pNpAvK1x5/jklzLmjUdlQzQcZ39LVJ4bJ4dqM4NAN4TJIJIZ2OH+weTPk5Wmn2pVO++F0TSVvH9zKomP7EAjmdR3IQ72G4e+m3HnceSc88wzs39/xhio/PbmCqoZaHup1s6rpKS6HbggdkH/9Cx57TJ9I1rEdOVXl/PfwdhYd249EclN8Hx7sNZROnucPi7i6wv/7f/DSS9CGJRM0R1plJqvytjAjYhSxXhFqy7kk+iXhMhiEwKr95RJXxaFDSqWrr79WW4lOeyCzspR3D25jScZBAGbF9eLB3kPp7OV3yff89rdKrqyMDPVyZtkTq7TyXvo3+Ll4M1dDaw6aQjeEy+BkMGA5L2GX4/PvfyvRRW7tJ428jgrsK8rlvUPbWJ2VhrPByK0JffltjyFEePle8b0+PspiyP/8B9580w5iVWbt6W2kVmbyaNLteDhpe9JON4TL4Gw0YjJb1JZhM+rrldWiqalqK9FxRCxWK+uz0/koZRfb8rPwdXHjgZ5DubvrAEI8ri4D6L33wrXXwuuvg0Gbw+k2obKhmk9OfE8PnzjGhgxSW84V0Q3hMrg6Gakzm9WWYTOSk5XayKGhaivRcSTKTXV8dWw/n6XuIbuqnHAPb/4ycCy3JPTBy7lleb66dFFqMm/fDkOH2liwhlhw8geqzDU8ED/HIRa46oZwGdycnak3W7BYrRjbwW3MsmVK8RsdnSshpWR/cR4LU/fy/ckU6ixmBod25qkBY5jQOREnG3wfZsxQPpPt1RBOVufyY94vTO00QtMTyeeiG8Jl8HBxBqDW1IBXO8h4uny5kqZCR+dSFNVW892Jwyw5foiU0gI8nJy5Ma4ncxP70jPQtoXfp0+HefPgxRdtelhNIKXk/eNL8XRy53aNTySfi24Il+FMltOqepPDG0JNjVLnoGvHyR+m00zqLGaSs4/z7YnDrD+Vjlla6RMYzj+HTOSG2B54u7TNZ3/QICgrg2PH2uTwqrKj5BD7y9K4v8tsvJ0dpwSvbgiXwafRBCrq6gnz9VZZTeuorlYKljjAMKaOHaizmNmSd5IfMo+yJusYlQ31BLl5MK/bQG6K702CX1CbazAYYNQo2LoVorRRDsAmNFjN/C/jOyLdQ5gSfq3acq4K3RAug6+7Ept5pnKaI1NXp/cOOjqVpno2551gVVYa67PTqWow4e3syqSoRKbHdmdYWLRN5gauhqQkJeqtPRnCitxN5NYW8vee9+NkcKxcaLohXAZ/DyVmuLSmVmUlrUc3hI6HxWol01TN+4e3syHnODvzszFLK/6u7kyL7sbk6CSGhkWpWqaya1f45hulkE57oKKhmi+zVjPAvxsDA7qrLeeq0Q3hMgR4KsWFS6prVFbSeurqlLsxnfaLVUqOlRWxsyCbracz+SXvJGWmOjgNXf2C+U2PwYyJ6EL/4Ai79wQuxZkeQnthUdYqas11mkxt3Rx0Q7gMAZ7uCKCwyrENoaYGGhogJkZtJTq2QkpJfm0VB4tPc7D4NAeK89hTmEOFSakDHuruxbjO8QSW1XLPmMmEeWhzDiwxUanp3R44XVvMD7mbmRB2DdGe4WrLaRE2MQQhxGTgdZSayv+TUr54weui8fWpQA1wt5Ryjy3abkucjUb8PdwprKpWW0qryMoCFxdop6Ud2jVSSgpqqzheUcKJihKOlRWRUlpAammhcvePknMr3jeQqVFdGRgayaCQSKK8/BBCkJycrFkzAPD0BF9f5YbF0fk88wcMwqCpGslXS6sNQQhhBN4GJgDZwE4hxHIp5ZFzdpsCJDRuQ4B3G39qnlAfL/IrqtSW0Srq6tp3egBHxGy1UmGqo8xUR1l9LcV1NRTWVlNYW0V+bRU5VRXkVJeTU11BrfnXq6WHkzNd/UOYEt2VJL8gegaG0d0/BA9n7dTlvVrc3cHRc0hmVOWQXLCbWZ3HEeTqp7acFmOLHsJgIF1KmQEghFgEzADONYQZwGdSSglsE0L4CSHCpZR5Nmi/TQnz8Sa3vEJtGa2ivl43hDM0WC2crq6kqK6GorpqSupqqGyop7rBRHWDiXqLGZPVSoPVgtlqxSKtWKVEIs+7aBUWFvJVcimg1M2wSnl2P4uUWKxWzNKKyWKh3mKm3mKhztJAjbmBqsZ2LkWAqzsRXr7E+wYyqlMcMd7+xPoEEOvjT7inT7ur0eHqCo6eQ/LjE8vwdHJnduR4VXU0WFs3mmELQ4gATp3zPJuL7/6b2icCuMgQhBDzgfkA/kFhqhfftlZVkFVUekkdVVVVqmu8EtXVEBiofZ1gu/MppaTAXE+GqYoMUxV5DbXkm+soNtdzqWuPsxC4CCNOCJyEwCAEBgQGQCDOW8NhtVrJy/s1+kwgEIAAjEJgRHm/EYGLMOArDAQJZ9ycXHFzNuJmMOJpcMLD4ISXwYiXwRk/ozM+Rmeczi2eUg1UV2A+XcExTnK1a7gc4fP5+9+DyaR9ndD0+TxFIXsMRxll7cnuX3aoI6yRYr/vWvV+WxhCU7crF3YAm7OP8ksp3wfeBwjvHCdHjx7dKnGtJcNlNxtzN9FvyDVn1yWcS3JyMmprvBJ798LWrcnMmTNabSlXpDXns95iZkPOcVZlprEpN4OSeuWC7e7kTLxvINd4dyLG259IL1+C3T0JcvMkwM0DbxdXPJ1criryxhH+7+AYOu+5B959V/s64eLzKaXk8f2vE1jnyyOD7sbVqN7Qndlax+ITz7XqGLYwhGyg8znPI4HcFuxzEWaL+v3Izv5KfvdTpeVNGoIj4Orq+GO0l6OwVom1/yp9PxWmegJc3RkdEcegkM70CQon0S9YM2GWOhfjyEOae0uPcqQig9/Fz1HVDAAyq5I1MWS0E0gQQsQCOcAtwG0X7LMceKhxfmEIUN6c+QOzRf2rWFSAHwCZxWX07OSYeaMjI8FkUsZpHfWL1xRFtdW8e2gbC9P2YrJauC66K3Pie6uy4lanZdTXQ1GRY5ZzlVKyMOtHgl39mRh2jdpyOF7xI15OnVp1jFb/G6SUZiHEQ8BqlLDTj6SUh4UQ9ze+/h6wEiXkNB0l7HRec45ttliRUqqaRzyqsYdwsrhUNQ2txcdHCTnNyYHOna+8vyOwI/8UD2z8lrL6Wm6M68mDvYYS6xOgtiydqyQ9XVkf44jz5PvKUjlacZLfxc/B2eCsqpbqhgLyanfRJ2AesKTFx7GJL0spV6Jc9M/93XvnPJbAg1d7XKuEgtIqQgPUi6N2d3Gmk68PJxzYEEApmZma2j4M4Yu0ffx1+xqivP34cuKtJPoFqy1Jp4WkpjrmCnopJZ9nrtRM7+BE5RpAEuc9uVXH0Xy/OjO3RG0JxAX5c7ywWG0ZreKMITg67x/ezpPbVnFteAzfTr1TNwMHx1EN4Uzv4KbOE1TvHQBkVK4m2K0HPi6RrTqO5g3hpAYMISEkiOOFJVgcOFja1dXxDWF9djrP797AddFd+WjsbHxdHHOSX+dXHNUQvspaQ6CLLxPC1F9fW1qfQanpOLHek1p9LE0bgkEIMnLUvzNPCAnEZLGQWVKmtpQW4+kJv/yitoqWU2mq5/EtK+nmH8Irw6e1i5KmHR0plc/kgAFqK7k6jpRncLA8nZmRYzXROzhZtQ6BgRivsa0+lqa/Vc5Ogoxs9Q0hKVQpFpKWX6Sykpbj5QWZmXDq1JX31SKfpe6huK6GF4dOwU3FdM06tiMlRYky6ttXbSVXx5Ls9Xg7eTA5fJjaUpBScqJyHWHu/XF3an1QhbYNwWjgeHYRUuUg+vjgQJwMBo7kFaiqo7VMnarUVXY06ixmPjyyg9ERcfQJcswskjoXs2yZUlfZkSKMSqhke/Ehrus0Ajej+mV1i+tTqGzIJtbbNgUltG0ITgaqauopKFE3uZyrsxNdggNIOV2oqo7WMmOGYxrCjvxTlNTXcmdSf7Wl6NiQ5cuVz6QjsUuk4ySMXN9ppNpSADhZ+RMGnIjyGmWT42neEACOZal/Ie4RHsqh3HzVeyutYeJEpX5tebnaSq6OTbkZuBiMDA2LVluKjo04fRqOHlVqKjsKZaZKDpPJ2NDB+Lmon1JcSsnJqp/o5DEYV6OPTY6pbUMwGhAC0jLVH6rpFRFKaU0tOWWOm/nU2xvGjoWvvlJbydWRUlJAt4AQ3J3Un8DTsQ2ffw7Tpil1OhyFlXmbMQsrN0aOUVsKoAwXVZtPE+3d+snkM2jaEISAyFA/UjVgCH0jlbHrvac0n7H7sjz6KLz8MlgsaitpPgW11Zou8qJzddTXw2uvKZ9FR6HB2sDKvF+IlaF09tBGCpvMqmQERjp7DrfZMTVtCABJ0SGknlTfEBJCgvBwcWbvqSvm5NM0I0ZAcDAsXaq2kuZT2VCPt7P6E3g6tmHhQujRA/r1U1tJ8/mlaD+lpgoGyHi1pQDKcFFW1UbC3PvbbLgIHMAQusaEkldUQXll7ZV3bkOcjAb6RoazOytHVR2tRQh44gl48UXHyYDq6exCjdmktgwdG2CxwEsvKZ9BR+KH3M10cg8mhhC1pQBQ3pBJRcMporxsO7mtfUOIVbpnKSfzVVYCg6IjScsvoqymTm0prWLaNKWs5vr1aitpHn4ubhTV1agtQ8cGLFum1FB2gNIHZzlZncuRigymhl/bWAZJfU5V/QxAZ88RNj2u9g0hRnHklAz1DWFwTCQS2JWZrbaUVmEwKHdoTz7pGHMJiX7BHC0tcOgILx0lBfszzyifO0dae7A6bytOwsjY0MFqSzlLdvUWAlwT8XS2bY9F84bg7elGdLg/hzNOqy2FXhFhuDk5se2Egy73PYe5c5WEd2+/rbaSK9MzMJQKUz2ZlWVqS9FpBS+/DFFRymI0R8FkbeCngp0MC+qDr7OX2nIAqLOUU1h3kEhP26+U1rwhAPSM78ShY7mq3yG6OBkZEB3B1owsVXXYAoMBPvgA/vEPyNL4nzM8PAaAn3LS1RWi02JSU+E//4F333Ws3sGWogNUmWuYFDZUbSlnya3ehsRKpA2ji87gEIbQOyGc0spaTuWXqS2FYXFRHC8qIb9C3dXTtiApCf7wB3jgAW1PMEd7+5PgG8TqrDS1pei0AKsV5s+Hv/5V6SE4EmtObyXULZDefglqSzlLdvUW3Iz+BLl2tfmxHcMQEiMA2J+mfoTP8C7KatnNxzNVVmIbHn9c6SFofbHa9NhubM8/xYkK9dOh61wdH36orD148KpLZKlLQV0JB8qOMT50MAahjUulVVrIrdlOhMdQRBto0sZfeQViwgPw8XJjX6r6hpAYGkSwlyeb00+qLcUmuLjA//4HjzyilDPUKjcn9MFJGPg8da/aUnSugoMHlUnkDz5Qyrg6EskFu5BIxoQMUlvKWYrrUqi3VhDh2TZV2lplCEKIACHEWiHEscaf/pfY76QQ4qAQYp8QYtdVizQI+iRGaMIQhBCMiI/hl+OZmC2OWzDnXIYMgb//XZns02qeoxB3L6bFdOOLY/soqq1WW45OMygqUpLXvfYa9OqltpqrJ7lgN9194gh3D1JbyllyarYDgnCPtjGp1vYQngDWSykTgPWNzy/FGCllXynlwJY01C8pguz8MgpL1R+7H5UYS0VdPXscfNXyudx/vxIbPneudkNRH+5zLSaLmTcPOHClnw5CQwPMng033aR8phyNk9W5ZNbkMSpEWxl282p2EuiahJvRt02O31pDmAF82vj4U+CGVh7vkvTvplSH33NU/TUA18ZF4Ww08lPqcbWl2JTXX4fqaqWLr0XifAK4NaEvC9L2cqhY/TBknUvz8MNKMsXnnlNbScvYXLgPgeDaoL5qSzlLg7WawrrDhHu06J66WYjWhHIKIcqklH7nPC+VUl40bCSEOAGUAhL4r5Ty/csccz4wHyA4OHjA4sWLAbBaJX9feIDesX7MGq5+GuS3Dhwnr6aOJ3pE4e2t/cRrVVVVeHldOY7abFbSEoeHQ2CgHYRdwJV0VlvNPJm7Hz+jC38N64lRpRjG5p5PtVFDZ2EhFBRAt25KeHNz0Nr5/Fisww0XbpXnp4ZQU2etayoFQZ8SUjQP9/pLRz2NGTNmd0tHYpBSXnYD1gGHmthmAGUX7Ft6iWN0avwZAuwHRl6pXSkliYmJ8lz+75Vv5cxH/ye1wDe7D8qkZ16Vnyz7QW0pzWLDhg3N3vfwYSnDw6X87LO203MpmqPzh5MpMvrTF+Qb+ze3vaBLcDXnU03srfOdd6Ts3FnK48ev7n1aOp85NQVy6sbfy++yN1z0mpo6dxa+JT9LGyEbLLWX3Q/YJZtxfW1qu6J/SynHSyl7NrEtA/KFEOEAjT+bTEsqpcxt/FkAfAu0aA34wB5RZBeUk1ekfk2CsV274GQwsLuwVG0pNqd7d1i3Dv78Z/joI7XVXMzU6K7cENuD1/ZvZk+h+oEGOgqvv64krktOhrg4tdW0nK1FBwC4JlBbM+H5tfsIcuuOk8Gtzdpo7RzCcuCuxsd3Acsu3EEI4SmE8D7zGJiI0sO4agZ1V1a17Dys/tJafw93hsZFsaugTPUV1G1B9+7w00/wt78pq0u1xj+GTCDc04cHN35HQa36gQYdnZdegjfecHwzANhWfJA4zwhC3VQYM70EDdZaiuuOEuret03baa0hvAhMEEIcAyY0PkcI0UkIsbJxn1BgsxBiP7AD+EFKuaoljcVFBhLo68mOQ9pYFDa1ZyIl9Sb2ZTt20ZxLkZgIGzbAv/6l3P1pCR8XN94bdSNlpjp+s2EJdeYGtSV1WJ59Vll8tnEjRKs/vdcqKhqqOVpxgsGBPdWWch5FdUeQWAhx79Om7bTKEKSUxVLKcVLKhMafJY2/z5VSTm18nCGl7NO49ZBStjjuQAjB4J5R7DychdWq/l35hK7xOAnBioOpaktpM7p0Ub7ob70Ff/yjMumsFXoGhvHa8Os5UJTHHzZ/j8XaPtaFOAomk5L25MsvlZ5BZKTailrP7pIjWJEMCuihtpTzKKjdDwhC3NrWqBxipfK5DO0dQ1llLUc1UB/By82V3kG+/HgolQatBu/bgOho2L5dWXU6caISRaIVJkUl8peB41iVlcbTO9a0y+E7LZKbC6NGwenTsHWrEpXWHthbmoqPkycJ3tpKulRQdwB/lzhcjG0b0ehwhnBNrxgiQ/0ordBGwZQhoQGU1NTySzvJbXQpAgJg5Uq45hoYOBB2XfV687bj3u6DeKDnNXyRto/nd2/QTaGN2bwZBg1SCi0tWQI+tqvgqCpSSvaWHaWvfxJGjeQuAiV/UWHdYYLde7d5W05t3oKN8fV2Z8m/71Fbxll6BHjj7+HOt/uOMDrRwWfTroDRCM8/rxjC1KnK3MK8eWqrUni83yhqGkx8cGQHZmnlrwPHIRwpz7IDIKVSP+Of/4RPP4XJk9VWZFtO1eZTYqqgj1+i2lLOo9x0kgZrdZsPF4EDGoLWcDIYmN67K1/s2E9JdQ0Bnh5qS2pzZs5UFh3deKMyv/Daa+Dnp64mIQR/GzwBJ4ORD1N2Um8x88/BEzE2d2WUzmUpKlKylR49qgwROXokUVMcLDsGoKlU16BMKAMEuXVv87b0b4sNmN2/Jw1WK9/uO6K2FLvRrZsybOTpqSQuW9WiuDHbIoTgLwPH8rueQ/kibR+/2/SdHn1kA779Fnr3hs6dYdu29mkGAIfLMwh08SXcTTvJ7ACK6lJwNnjh49y5zdvSDcEGJIQEMSCqE4t3H9RE9JO98PJShhA++URJjnfXXcqdpJoIIXi8/yj+Omgca7LSuG3tIorrtDHf5Gjk5SnJ6R5/HL7+Gv79b3B3V1tV23GkIoNuPrGaG2osrj9KkGvXNql/cCG6IdiIWwb2JrOkjC3toLzm1TJuHBw6pOQ+6tFDMQi153Xv6TaId0bdwOGSfGas/JTUUg2FRmkcqxXee0/pFSQkwIEDcO21aqtqW0rqyymsL6WbT6zaUs7DIhsoNR0n0C3JLu3phmAjJnVPIMDDnS927lNbiip4ecGrryqRSG+9pUQj/fSTupqmRHflq0m3YbJYmPnjAr0E5xWQEn78Efr3hwULlEWJzz3XvnsFZ0itVKIEk3xi1BVyAeWmE1hlAwGuuiE0C4vVyt5UJSW2muGGLk5OzBnQiw2pGWSXarTKjB0YMAB27FBqNf/mN8q6hd271dPTN6gTy6+7i3jfQH6bvJSX9mzErC9gu4itW5V6GI8+Cs88o4SW9tTWYt02Jb3qFAYMxHlGqC3lPErqlYnuAFf7THQ7vCEYDQYe/88ysvJKEUKoagq3DuyNQQgW7tivmgYtYDDArbdCSooSiXT99XDzzZCm0g16mIc3X02ey60JfXnn0FbuXPeVXnWtkcOH4YYblP/PXXcpiw9vvBE0Noze5qRXnqKzRyiuRhe1pZxHaf1xjMIVb2f7LAN3aEM4U8Kyf7fOLFq9BwCLipO6Yb7eTOqewDd7DlFdb1JNh1ZwcVFSGxw7Bn36wLBhcM89ypi0vXEzOvHC0Mm8NGwquwtzmLriY37JO2l/IRph9264/XYYMwZGjlTM+p57wKmDBqKnV50i3rvto3iultL64/i5xGIQ9ilI7dCGYGi8jbltygDWbjsKgJNR3T/prqH9qayv55s9LUro2i7x9FSqsKWlKSGLU6YoF6Jly+xfrvOm+N58N/VOfFxcuX3tIl7as5EGa/tNO3IuZrMSLTR8uLKWpHdvxawffRTc2i6jsuYpM1VS1lBJrMaGiwDKTCfwc7FfnK9jG4JBMYQ+iRFICfvTlNz4aoZ+9okMZ2B0BB9v3Y3J3DEuNM0lIAD+8hc4cUKZX3j+eSWK5dVXodyO0y7d/ENYPvUubknowzuHtjJ71edkVJTYT4CdKSlRVpXHxSkpqv/wBzh+XAkn9W2b0rwOxclqpTZ6jGcnlZWcT72lglpLEX4uMXZr06ENAX4dNpo4tCuLVinDRtbGeQS15hN+O3wwpyuq+P5Aiirtax0XF7jtNiVh3hdfwM6dEBsL990HlZX26TV4OLvwwtApvD3yBk5WlHLdio9ZdqL9LCw0m2H1ajh5UslYe+QIfPcd/PwzzJ7dcYeGmuJUjZIoM9ojTGUl51NhUkLYfXVDaD7Gxl7CTRP78fPeDODXYSO1FpgMj4+me3gI72/eqadkvgLXXKOkTz54ELp2hexsJY3yI48oq2Lb2tOvi+nKmun3ck1oFBGezcvSVmfRUA7wc7BalQv+gw9CRIQSLeThoaSb+PRTJZxU52KyawvwMLrh76KtLH3lDUoorI+L/TKvOrwhCCGwWK3EdAqgV3w4aZm/LkDKyC5SJU22EIL7Rwwms6SMlYf02PfmEBGh1Fvo1k3JjxQQAHffrQxz/PnPsGePcsFrC0I9vPl43BwGhlw+kmPJ8YM8u2s9t69ZxI8VuW0j5iqxWJQw38ceg5iYX81g61bFUENCIDRUbZXaJre2gE7uwZpboVxhOoXAiLez/YayHN4QgLMJzN55cg5xEQEALFy5i0df+Y5XPtvAvz+z/wqp8V3jSQgJ5L1N2/VewlWSmKjc3aakKHl0pFTCWMPClJ8ffghZdl4QvuT4QZ7evgYnYWRet4EkVxXw1oEt9hXRyIkT8P77MGeOcsGfNw9cXZVFZQcOKBP47TXfUFtwuraYcHdt5S8CqGjIxss5HIOw3/heuxlJ/HrtPj5bsQMp4Y7rBnIoPY9n7p8MEl76ZD3rt6cxboj90toaDIIHRg7h0W9WsurwMa7rZZ+Vhu0JIaBvX2V78UXFBNatg7Vr4YknlF7EhAnKNnSocnFsCw4Wn+aF3ck8M2g8NycoJQyPHjnCtvws5luG4GJs25DAvDzYskX5u9euhepq5W+eNk3JNBuhveAYh8EqrRTUlzAsuG1LU7aEyoYcvJ3t+89tlSEIIeYAfwO6AYOllE2WTRFCTAZeB4zA/6SUL7am3QvJKSjj+42HmDd9CJ2Cffnwu23ERgTQL0kZApg1vg+rt6bY1RAAJndP5N2Q7byZvJVJ3RNUD4l1dKKilFj5e+5Rho/271cM4p13lOElT09lpfSAAcp4+YABra/kJaXktf0/Mzg08qwZAGQ31ODp4WFTM5AScnKU4bHdu5Vtzx6or4chQ2D8eGVIqGfPjrdwrK0oM1VilhaCXf3VlnIeUkoqG3IIdrNvKc/W9hAOATOB/15qByGEEXgbmABkAzuFEMullDYL6dh+MJMAXw9mjlO+sGaLlRc+WgtA1ulS9h7NITTAGymlXccJDQbBH8Zey4OLlrN032FuGtDLbm23dwwG6NdP2R57TLmYnjjx68X0jTeUny4uijkkJCiRTOduXl5Xbmdbfhabck+wffZDZ393qqqMUouJRK9OWKU8ux6muVRUKFrP3Y4dU7RL+aup3XOPkk02Kko3gLaisL4MgCBXP1V1XIjJWkmDtcqu8wfQSkOQUqbAFaN5BgPpUsqMxn0XATMAmxlCr4ROfLRs29nnQf6e+Hm7c/tTC4gO96eypp75s4aqMmk0NimOfp3DeXPDVq7v1RV3F2e7a+gICKGMm8fFKWGVoFxcs7Jg3z4l7v7YMViz5teLsLe3YgwxMRAUBP7+SqGfc39+XZPKqMBu1JV4kG8EC2Y25J8ix1TLLd5dKCwQWCxQVwelpVBW1vTPoqJf262tPd+Y4uKUIaB+/ZThH/3ibz9KGyoACHTR1oKMqoY8ALzsbAjCFrH6Qohk4I9NDRkJIWYDk6WU9zU+vwMYIqV86MJ9G1+fD8wHCA4OHrB48eJmaXj92xRiw7xI6uzL3vRiokO96BLuzanCavy9XIgN8zpz/Bb8hZemqqoKryvcaqaXVfHvfceYHhvO1Gh1Yp2bo1ML2FNnQwOYTMqQjMWixO5bLOc/3isKyBDlXFeTgJSQ7lzCEZdCotyN9C2KB5QLuBBKbL/RqGxNPXZ1VTZ7rgHQ/++XZz8nWGPYy/3WyXhz5WqH9tJZ43aEwsDPCSt4ENeGq5tHGDNmzG4p5cCWtHvFj6YQYh3Q1FXsKSnlsma00dQV+JIuJKV8H3gfICkpSY4ePboZTYB3aBfWbUtl05FcAny8uXn6GOIiApv13taQnJzMlTSOBvbVLWd9xin+NGs6gV72L7PZHJ1aQGs6t+dn8buN31HdT/nIZuSVMyYsngEVMGXuaHXFNQOtnc9LoZbO/CwTnNzLpJETcDFcufduL50pZUUUFsLIIVNwdwpo8/bOcEVDkFKOb2Ub2cC5WaMiAZsHcQ/o1pl+SZHkFZUTEeJ33mv2njtoikfHD+f6tz/jzeSt/G3aOFW16DSfIaFRfDP5dl7eu5EwD28e7TuCYWHRbN/8y3n7rc5KY3REHK7GdhO41yGobKjG1eDSLDOwJzXmAgzCGTejfSe77fHp3QkkCCFigRzgFuC2tmhICM6awbkmoLYZAMQFBXDLoD58uXM/twzsTdewYLUl6TSTWJ8A3hl14yVvLFJLC/lt8lIS/YJ4adhU+gZpKyeOzqWpMtfi5aS9CkA15iI8jEF2v3a1Kg5SCHGjECIbGAr8IIRY3fj7TkKIlQBSSjPwELAaSAEWSykPt072JfU0+Vgr/H70UHzcXHl25QZV6zbotIxLfaaS/IP5eOwcKk31zPxxAS/s3qDZ9BY651NjqcXDSXupXmvNRbg7tf2Q94W0yhCklN9KKSOllK5SylAp5aTG3+dKKaees99KKWWilLKLlPK51op2VPw83Pi/8cPZlZXD9weOqi1Hx4aMiezC6un3cnN8b/57eDvXrfiYvYXaSG+hc2nqLCbcja5qy7iIWksJ7kYHMwQtU1vXwLrtqZq7E5/Vrye9I8J4ac0mKmrr1JajY0N8XNx4YegUPht/M7UNDcxapfcWtE691YSrQVtV0gDqLCV2nz+AdmwIq7ak8NRbP7CvsUaCVjAYBM9cN5aSmlpe+0mdXDg6bcvITrGsmn4PN3VRegvTf/iEQ8Wn1Zal0wQmqxlng7YCAaS0Um+pwNVo/7UR7dYQplzbDR8vN778UcUK75egR6dQbmucYD6QrV8o2iM+Lm68OGwKH4+bQ1l9HTes/IzX92/uMNXZHAWLtOBkx+RxzcFkrUJixc3oZ/e2260huLk6M2tsHzbtOc6p/FK15VzEH8YOI8Tbi6eWrcFk1ocU2itjIrqwZvq9TI3uyn/2b2bOqoWcaMfV2RwNi7RiFNq6DNZblNXTrkb712fQ1pmwMXMm9MXJaOTLH/eoLeUivNxc+fv14zhWWMx7m3aoLUenDfFzdeeNkdN5a+QMTlSUMHXFx3yRtk9z81sdES3+D0zWSgBcDN52b7tdG0KgnyeTh3VlxaZDlFbUqC3nIkYnxjGjdzfe37yTw7n2L+SjY1+mxXRj9fR76R/UiSe3reI3G5ZQUqe9z6WOupisVQC4GO2fyqNdGwLA3KkDqW+w8PXafWpLaZI/Tx6Nv4cbf/5uDSazPr7c3gnz8GbBhFt4euA4NuWeYMr3H7HldKbasjosRmHAIrVVwKrBqtwkOBvsn+Km3RtCbEQgI/p34et1+6ita1BbzkX4ebjx9+vHk1ZQxFvJW9WWo2MHDEJwb/dBLJ1yB57OLsxd8yUv7k7WJ5xVwMlgxCK1dd7NjYbgJHRDaBPumjaIiqo6vttwQG0pTTI2qQuz+vXgg8072XEyW205OnaiZ2AYK667m1sS+vLe4W3cuvpLcqsr1JbVoXAWzjRYtRXUofcQ2pheCZ0Y0K0zn6/cRZ1Je70EgCcnjyYqwI/Hl/5IWY2+YK2j4OHswgtDJ/PGiOmklBYw9fuPWHvqmNqyOgwuBidMVm1dE8yyHgAng/1XUHcIQwC498ZrKCqrZnnyIbWlNImnqwv/njWF4qoanv5+rSajH3Tajumx3fl+2t1EePnymw1LeGH3BsxWbY1tt0fcjK7UWU1qyzgPS6MhGIVuCG2Gkh47gs9W7KDepK0u4hl6RYTxh3HXsjYlna92H1Rbjo6difMJYOmUO7g9sR//PbydO9YtoqC2Sm1Z7Rp3oyu1Zm31yC1WEyAQ2K5ed3PpMIYAcN/MoRSWVrMsWbsX23lDBzC8SzTP/5jMkbwCteXo2BlXoxPPXjOJV669jr2FuVy34mO252epLavd4uHkTpWlVm0Z5yExYxDOqmRs7lCGcKaX8On3OzQ7l2AwCF6aOZkAT3ceWbyCcj0BXodkVpdeLJt6F97Orsxds4gFqXv0YcQ2wMvJnRpzHVYNhZ5apRmDXUrVXEyHMgQhBPNnDaOorJql67UZcQQQ4OnBa3Omcbq8kseXrsJq1S8EHZEk/2C+m3onIzvF8vT2NTy+ZaWeOdXG+Dh7IpFUm7XTS5BYESql0+hQhgDQv1tnBveI4tPvd1Bdq63JpHPp2zmcP08ezcZjJ3hn0za15eiohI+LG/8bO5uHe1/L18cPcvOqheTXVKotq93g66ysBi5r0M5cjZQSg0qX5g5nCAAP3DScsspaFq7cpbaUy3LroN7M6NONt5K3sf7ocbXl6KiEQQge7TuC90fP5Fh5EdN/+JQDRXlqy2oX+Dkr+YLKTNpZ/yGRgDoVHzukIXSPC2Pc4ES++HE3xWXVasu5JEII/j5tPL06hfLYkh85erpQbUk6KjIxKpElU+7AyWBgzuqFLD9xRG1JDk+Ai5JRtERDhqAmra2pPEcIcVgIYRVCDLzMfieFEAeFEPuEEJq4LX/gpmsxmS3871ttp4twc3birVum4+3myu++XEZhpXYNTKft6eYfwvLr7qZPYBgP/7ycV/f9rE82t4IAV6UITbGpXGUlvyIQSNSZ5G5tD+EQMBPY1Ix9x0gp+0opL2kc9qRzqD8zx/ZmWfJBTuZqOz99qI8X79w6ndKaWh5atJy6Bn1isSMT6ObB5xNuZU6XXrxx4Bf+sPl7fbK5hXga3XE3ulJUr52aKUIYHNMQpJQpUspUW4mxN/fecA2uLs68tag5fqYuPTqF8vLMKRzIOc3jS3/Eoq9i7dC4GI28NGwqj/UbybITR7h9zSKKavXe49UihCDY1Z+COg0ZAkakSgn37DWHIIE1QojdQoj5dmrzivj7eHD39MH8vDeDnYe1v/hnfLd4/jRpFGtS0nnux2R9qKCDI4TgwV7DeHvkDRwqOc2sVQvIrNTOhc1RCHELIL+uWG0ZZzEKZ6xSnR6fuNJFRQixDghr4qWnpJTLGvdJBv4opWxyfkAI0UlKmSuECAHWAr+XUjZ5W95oGPMBgoODByxevLi5f0uLaDBbeXXpEZyNBh65sRtGw9XN7ldVVeHlZd9CFt+k57Auu4AZseFMiW7qX3MxauhsCbrOlpFeX8lrhakI4P8FdyXOVdGmNZ2XQk2d68Q+DpPFw/J6xBWie+yhs8x7PeU+64nKeRbRgnv2MWPG7G7x0LyUstUbkAwMbOa+f0Mxjyvum5iYKO1B8s5jcvDtr8ivVu+56vdu2LDB9oKugMVilX/8ZqVMeuZVuXjXgWa9Rw2dLUHX2XLSy4rk8CXvyKTPX5ZrstKklNrU2RRq6vwue4OcuvH3sqy+4or72kPngeLP5CdpQ2WDpa5F7wd2yRZey9t8yEgI4SmE8D7zGJiIMhl9RSwW+wyJjBzQhcE9o3l/yRZKyrVf0tBgEDw3YyIj4mN4ZsV6fjzksNM4Ojaki28gS6fcSZJ/ML9NXsridO2uxtcSEe4hAOTUaiOs+0zaa7O0f9qa1oad3iiEyAaGAj8IIVY3/r6TEGJl426hwGYhxH5gB/CDlHJVc45fWWafEyKE4NHbR1NT38A7i3+2S5utxcXJyOs3TaN/5048tnQVP+kL13SAYHdPvphwK9eGRfP4lpWsrMhVW5LmOWMIp2q0UdfcKNwAsFgdzBCklN9KKSOllK5SylAp5aTG3+dKKac2Ps6QUvZp3HpIKZ9r7vHras1knbCPa8dGBHLLpH58v+kwB9Md40vk4eLMe7fNoHt4CI98/QM/p59UW5KOBvB0duHDsXOYFtONxWVZPLtrPVY9AOGShLgF4GJw5lTNabWlAOBkUAyhQdo/v5K2VyoLWPzJZrs1d+8NQwn29+KlT9ZjtjhGWKeXmysf3H4j8cEBPLRoOb8c1wu26yhhqW+MmM54rzD+d2Qnj235QS+4cwmMwkBnj1Aya7SRDsRZeAK/ltK0J5o2BA9PF9b/eIC8bPssHPN0d+GPd44hLbOQRav22KVNW+Dr7sZHd8wiJtCfB75YxqZjJ9SWpKMBDEIw1z+aR/uOYMnxQzz88zLq9QVsTRLtEc7Jam2MDDgblVrKDVb7ryvRtCF4ebtgNBr4yo69hFED4hnRvwvvL91CTkGZ3dptLf6e7nxy12zigwN5cNH3ejI8HUCZH3u497X8ZeBYVmamct9PS6hp0G6WX7WI8exEiamCigb1F/e5GJSwVpPF/lltNW0IBqNg8g39Wfv9PvLzyuzSphCCx+4ci9EgePHj9Q61+Mvfw52P75pF97BgHlm8Qo8+0jnLfd0H89LQKfxy+iR3rV9MVUO92pI0RaxnJwBOVOeorARcDEoGVpPV/im5NW0IADfdNRyARR/bL/onNNCb3900nB2HMvnxlxS7tWsLfN3d+PCOmfSNDOfRb1ayaOd+tSXpaISbEvrwxojp7CnM4c51i6kw6dX4zhDrFQFARpX6huBqPGMIeg/hIkLCfJl8Q3/WLNvL6Rz7LcufNa4vvRM68Z/PN2g6RXZTnJloHpkQy99++Il3Nm5zqJ6OTtsxLaYbb4+8gYPFedy+dhFl9dqpFKYm/i4+BLr4crzqlNpScBIeGIQz9Rb7Z2DVvCEA3HrvSAxGwefvJ9utTYNB8JffTKTeZOaFj9c53AXV3cWZt265nhl9uvHGhq0sOpatJ8TTAWBydBL/HT2To6WF3LLmC0rqtL8Y0x508epMugYMQQiBq8FXN4RLERTiw7TZg1i/cr/d1iUARIcH8MCc4fy857jDDR0BOBuNvDBjEvcOG8DG3CIeWvQ9NaYGtWXpaICxkfF8NHYOJypKuW3tl7opAIneUWTXFFCjgfrKbkZ/ai32T1ToEIYAcPO8Ebi6OfPZuz/Zt91J/embFMErCzaQX+x4tWwNBsFjE0dyS0IkG4+d4I6PF1NQqZ36sTrqMbxTDB+Oma2bQiOJ3tFIJMcq1e8ldPe/mXjvKXZv12EMwc/fk5lzh/Lz+iOkHbHfxI/BIPjr/ElYLFb++cFqrFbHGjo6w+iIYN65dTonikq5+YNFejlOHUAxhf+NmaWYwpovKe7AppDoHQ1ASqX663jifaYS7T3G7u06jCEAzLp9GD6+Hnz01jq7thsR4scjt41i5+Esvlqz165t25LRiXF8fs9NWKXk1g8XsfrIMbUl6WiAEZ1i+WjsbE5UlnLH2kWU13fM6CNvZw86e4SSUqG+IaiFQxmCp5cbt947gr3bM9i9Nd2ubd8wphcj+nfh7a9+Ji2zwK5t25Lu4SF8Pf9WEkOVtQpv/LTFYXs9Orbj2vAY/jt6Junlxdy57qsOG5La3SeOoxUnscqOGYDhUIYAMG3OYMIi/Png9TVY7JhvSAjBX+6biK+XG0+/s5LaOsednA3x9mLB3bOZ2bcH72zazoOLllNe2zEvADq/MjoijndG3cDhknzuXv91h1y81t0njipzDVkaSXRnbxzOEFxcnLjnofGcOJbPuhX77Nq2n7c7f7t/Cpl5Jfxn4Qa7tm1rXJyceG7GBP4yZQw/p59k1n8XciTPcXs+OrZhfOcE3ho5g/1Fudyz/mtqzY5749MSevnFA3Co3L4jEFrB4QwBYOSEHnTr3ZlP3l5PbY1972IG9YjizmmDWZZ8iLXbHDs1hBCC24f0ZcG8OZitVm753yK+3n3Q4dZc6NiWydFJvDZ8OjsLsvndxu8wWdQp+K4GoW6BhLgGcKCsY86vOaQhCCH47aOTKCmusmt67DPMnzmUXvHhPP/hGgrtVMSnLenXuRNLfzuXgdERPP39Oh5buoqquo43XKDzK9fHduP5ayazIec4f9i8vEOlzu7lF8/BsnTNziNYrG333XRIQwDo1qszoyf15JvPt1Bgp8R3Z3ByMvLcQ9NwcXZiwfoMh55POEOApwcf3H4jj4wZxo+HUrnxvws5kN0xx1F1FG5N7Hs2S+rjW1Z2mCI7ff0SqTBXq57XKL92HzsLX2dbwSvUmks4XbOXH079hh+zf0dO9Tas0vY9N4c1BIB7fj8BgPdfW2P3tkMDvfnHA1MpKKvjxU8cL7VFUxgNBh4YNYQF8+ZgsVq57aOveG/TDj3lRQfmvu6DebTvCJZmHOLZXY6V/bel9PZLBGB/WZpqGkrrj7Oz8A3KTZmUm06wq+gtjpR9SVffWUR7jWJ30dsU19t+yNqhDSE03I+b7x7Bz+sOs29Hht3bH9IrmvH9w1n1SwpL17efgub9oyL49v7bmdAtntd++oXbP15MVkmZ2rJ0VOL3vYZxd9cBfJSyi3cObVVbTpsT5OpHpHuoqoaQUvY1Ie69GB/xKpMi36KqIRd/13i6+EymV8CdeDt3pqDW9tecVhmCEOJlIcRRIcQBIcS3Qgi/S+w3WQiRKoRIF0I80Zo2L2TOndcSFuHP2y+vxNxg/8mvsX3DGNYnllc/38C+VPVT59oKX3c3Xp09lZdnTiG9oIQb3v2cRbsOdIg7RJ3zEULw10HjuSG2By/v3cSCVMepJthS+voncaj8OA1WdYaDJRbcjP5nn/u4RFFn/jW3kbPBHXMblNhsbQ9hLdBTStkbSAP+fOEOQggj8DYwBegO3CqE6N7Kds/i6ubMA3+cQlZGId8t2marwzYbgxD8/YEphAf78MQb3ztkvqNLIYTg+t5dWf67O+gTGcbfVqznns+WkF1q/yyMOupiEIKXr53K+Mh4/rp9Dd+fcLxkj1dDP/8k6q0mjpSrs2o5wDWJ0zV7qGrIo9yUSYO1mlJTOhty/8zm089Sbsok3GOQzdttlSFIKddIKc8Uad0GRDax22AgXUqZIaU0AYuAGa1p90KuGZnEkBGJHD2kzh26j6cbL/9hBg1mCzsOt78i9+G+3nx05yz+Nm0cB3LyeXND+x820LkYZ4ORt0bOYFBIJF+l72/XvcXevgmEugVSYVanFkqk51DcnQLZnP9Pdha+gZdzJ0aG/YNAt644GVwZEPwgIe69bP4/ELY6oBDie+ArKeXnF/x+NjBZSnlf4/M7gCFSyocucZz5wPzGpz2BQzYR2HYEAUVqi2gGuk7bouu0LbpO25EkpfRuyRudrrSDEGIdENbES09JKZc17vMUYAYWNnWIJn53SReSUr4PvN943F1SyoFX0qgmjqARdJ22RtdpW3SdtkMIsaul772iIUgpx1+h8buAacA42XR3IxvofM7zSCD3akTq6Ojo6LQ9rY0ymgz8CZgupbzUlPdOIEEIESuEcAFuAZa3pl0dHR0dHdvT2iijtwBvYK0QYp8Q4j0AIUQnIcRKgMZJ54eA1UAKsFhKebiZx3+/lfrsgSNoBF2nrdF12hZdp+1osUabTSrr6Ojo6Dg2Dr1SWUdHR0fHduiGoKOjo6MDaMgQtJAGozkIIeYIIQ4LIaxCiEuGnwkhTgohDjbOrbQ4DKylXIVOtc9ngBBirRDiWONP/0vsp8r5vNL5EQpvNL5+QAjR317arkLjaCFEeeO52yeE+Ku9NTbq+EgIUSCEaHJtkRbOZaOOK+lU/XwKIToLITYIIVIav+ePNLHP1Z9PKaUmNmAi4NT4+F/Av5rYxwgcB+IAF2A/0N3OOrsBSUAyMPAy+50EglQ8n1fUqZHz+RLwROPjJ5r6v6t1PptzfoCpwI8o622uAbZrUONoYIVan8VzdIwE+gOHLvG6qufyKnSqfj6BcKB/42NvlNRBrf5saqaHIDWSBuNKSClTpJSaL5XWTJ2qn8/G9j5tfPwpcIOd278czTk/M4DPpMI2wE8IEa4xjZpASrkJKLnMLmqfS6BZOlVHSpknpdzT+LgSJYIz4oLdrvp8asYQLuAeFGe7kAjg1DnPs7n4JGgFCawRQuxuTMehRbRwPkOllHmgfMiBkEvsp8b5bM75UfscNrf9oUKI/UKIH4UQPewj7apR+1xeDZo5n0KIGKAfsP2Cl676fF5xpbItsXcajJbSHJ3N4FopZa4QIgRlncbRxjsPm2EDnaqfz6s4TJufzyZozvmxyzm8DM1pfw8QLaWsEkJMBb4DEtpaWAtQ+1w2F82cTyGEF7AE+IOUsuLCl5t4y2XPp10NQTpIGowr6WzmMXIbfxYIIb5F6drb9AJmA52qn08hRL4QIlxKmdfYnS24xDHa/Hw2QXPOj9qpWa7Y/rkXCinlSiHEO0KIICml1pK0qX0um4VWzqcQwhnFDBZKKZc2sctVn0/NDBmJdpQGQwjhKYTwPvMYZcJci1lbtXA+lwN3NT6+C7ioZ6Pi+WzO+VkO3NkY0XENUH5mCMxOXFGjECJMCCEaHw9G+d4X21Fjc1H7XDYLLZzPxvY/BFKklK9eYrerP59qzpRfMCOejjLeta9xe6/x952AlRfMnKehRFY8pYLOG1Gctx7IB1ZfqBMl4mN/43ZYqzo1cj4DgfXAscafAVo6n02dH+B+4P7GxwKlANRx4CCXiTxTUeNDjedtP0rAxjB7a2zU8SWQBzQ0fjbv1dq5bKZO1c8nMBxl+OfAOdfMqa09n3rqCh0dHR0dQENDRjo6Ojo66qIbgo6Ojo4OoBuCjo6Ojk4juiHo6Ojo6AC6Iejo6OjoNKIbgo6Ojo4OoBuCjo6Ojk4j/x+yp66Cbe8KuQAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"theta0 = 1.0\n",
"x0 = np.array((np.sin(theta0),np.cos(theta0)))\n",
"\n",
"## Run Algorithm 5.1 on test problem\n",
"results = alg52(x0,my_f3,my_h3)\n",
"\n",
"## Display results\n",
"xstar = results[0][-1]\n",
"print(\"\\nx* =\",xstar)\n",
"\n",
"## Display results\n",
"vstar = results[1][-1]\n",
"print(\"\\nv* =\",vstar)\n",
"\n",
"## Convert into theta\n",
"print(\"\\ntheta* =\",np.arccos(xstar[0]),\"=\",np.arcsin(xstar[1]))\n",
"\n",
"## Visualize\n",
"visualize(results[0])"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.8.4.2 Starting Point Near Local Min ($\\theta_0 = \\pi$)](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.4.2-Starting-Point-Near-Local-Min-($\\theta_0-=-\\pi$))",
"section": "4.8.4.2 Starting Point Near Local Min ($\\theta_0 = \\pi$)"
}
},
"source": [
"### 4.8.4.2 Starting Point Near Local Min ($\\theta_0 = \\pi$)"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.8.4.2 Starting Point Near Local Min ($\\theta_0 = \\pi$)](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.4.2-Starting-Point-Near-Local-Min-($\\theta_0-=-\\pi$))",
"section": "4.8.4.2 Starting Point Near Local Min ($\\theta_0 = \\pi$)"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Iter. \tf(x) \t\t||h(x)|| \t||grad_L(x)|| \t||dx|| \t\t||dv|| \t\tdelta_A \tdelta_W\n",
"0 \t 2.2204e-16 \t0.0000e+00 \t1.4142e+00 \t 5.0002e-01 \t 2.4998e-01 \t 0.0000e+00 \t 0.0000e+00\n",
"1 \t-6.2504e-01 \t2.5002e-01 \t1.0000e+00 \t 3.0322e-01 \t 4.1490e-01 \t 0.0000e+00 \t 3.2768e+00\n",
"2 \t-7.1455e-01 \t9.1941e-02 \t8.2867e-01 \t 6.9738e+00 \t 3.9656e+00 \t 0.0000e+00 \t 0.0000e+00\n",
"3 \t-1.9540e+02 \t4.8634e+01 \t5.3609e+01 \t 7.3453e+00 \t 8.9486e+00 \t 0.0000e+00 \t 3.2768e+00\n",
"4 \t-6.6453e+01 \t5.3954e+01 \t7.3649e+01 \t 3.6845e+00 \t 4.7204e+00 \t 0.0000e+00 \t 8.7381e+00\n",
"5 \t-2.0079e+01 \t1.3575e+01 \t2.6604e+00 \t 1.7791e+00 \t 2.6030e-01 \t 0.0000e+00 \t 0.0000e+00\n",
"6 \t-6.7442e+00 \t3.1651e+00 \t9.2895e-01 \t 7.7547e-01 \t 2.3764e-01 \t 0.0000e+00 \t 0.0000e+00\n",
"7 \t-3.0811e+00 \t6.0135e-01 \t3.5585e-01 \t 2.3833e-01 \t 1.8564e-01 \t 0.0000e+00 \t 0.0000e+00\n",
"8 \t-2.2251e+00 \t5.6802e-02 \t8.3998e-02 \t 2.7726e-02 \t 5.2689e-02 \t 0.0000e+00 \t 0.0000e+00\n",
"9 \t-2.1336e+00 \t7.6871e-04 \t2.8474e-03 \t 3.8422e-04 \t 1.6169e-03 \t 0.0000e+00 \t 0.0000e+00\n",
"\n",
"x* = [0.24215303 0.97023814]\n",
"\n",
"v* = [1.64012726]\n",
"\n",
"theta* = 1.3262120118414 (using arccos)\n",
"\n",
"theta* = 1.3262123260037786 (using arcsin)\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYQAAAD8CAYAAAB3u9PLAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAABi3UlEQVR4nO2dd3xUVfr/32cmvfdCQhop9F4E6R1EUAQbNtRFXV3dn1913XVdd91FXdta0cUusiIKAiJSJSDSQ4dACIGEkJBCep3MzPn9cQNSAoRkMvdOct+v131lyp17PrmZ3M895zzneYSUEh0dHR0dHYPaAnR0dHR0tIFuCDo6Ojo6gG4IOjo6Ojr16Iago6OjowPohqCjo6OjU49uCDo6Ojo6gA0MQQjRXgixXgiRKoQ4KIR4ooF9hBDiHSFEuhBinxCid3Pb1dHR0dGxLU42OIYZ+D8p5S4hhDeQIoRYI6U8dN4+E4CE+m0A8EH9Tx0dHR0djdDsHoKUMldKuav+cTmQCkRctNsU4EupsBXwE0KEN7dtHR0dHR3bYYsewjmEEDFAL2DbRW9FACfPe55d/1puA8eYBcwCcHNz6xMVFdUsTRarpLCslgAvF5ydbD9lYrVaMRi0PxWj67QtjqRTSkltbe0l77m6umI0GlVQdSmOdD5tqbPMZKbUVEeYhyvONjpuWlpaoZQyuEkfllLaZAO8gBRgagPv/QgMPu/5OqDP1Y6ZmJgom0t1rUl+sHCTPF1Y1uxjNcT69etb5Li2RtdpWxxJZ3R0tAQu2aKjo9WWdw5HOp+2IOtMsbzzkwUy6YU35R8WLJPFldU2Oa6UUgI7ZROv4zbpIQghnIFFwHwp5eIGdskG2p/3PBLIsUXbV8PNxZmHp19vj6Z0dDRJVlbWNb2u03JIKVm0+yAvrUzGKAy8evN4buzeESGE2tIAGwwZCeU3+QRIlVK+eZndlgGPCSEWoEwml0opLxku0tHRsT1RUVFkZmY2+LqO/cgtLef5ZWvYdCyT/jGRvHLTONr5+agt6wJs0UO4Hrgb2C+E2FP/2l+AKAAp5YfACmAikA5UATNt0K6Ojk4jmD17NrNmzaKqqurcax4eHsyePVtFVW0HKSWLdx/k5VUbsFolz08cwR19e2AwaKNXcD7NNgQp5Sbgir9Z/bjWo81tS0dH59qZMWMGAM899xxZWVlERUUxe/bsc6/rtBzZxaX87Ye1bM7Iol90JC9NGUP7AD+1ZV0Wm0YZqY2UUjNjcTo6WmLGjBm6AdgRi9XKvG17ePvnXzEIA3+bOJLb+3bXZK/gfFqFIdSazLi6OOlmoKOjozoHcvL4+/J1HMjJY3hiLH+/YRRhvt5qy2oUDm0IeUXlrNlyhKzTxQT6eTBtVE8C/TzPvW+1Ss07so6OTuugoqaWt9dvZv72vQR6uvPGLROZ2DXRoW5UHdoQXv1sHcIgCPH34mhWIZv2ZDBleDf2p+fQLb6dbgY6OjotjpSS5fuP8NqajRSUV3JHvx78ceQgfNzd1JZ2zTisIZzIKeLAsVxWzXkEgI27jjHvxx3sOpxNdl4JAH++fzTx7Zu2YE9HR0fnahzJK+SfK35mZ+YpuoSH8O5tN9Ij0nGz8jisIRzLLiQ6PIDSimp8vdwJD/Lh8PE8HrplED6e7nz43Sb2HDmlG4KOjo7NKa6s5t3kLXyzcx/ebq68eONobunVBaMDpN+4Eg5rCL07RvL1TynMW74DP28Plm3Yz50T+tC3c1T9++3Ztj+TaaN7qitU49TWmTlVUsap0jJySsrIK6uguKqaoqpqiquqqaw1UV1nptpUR53FglVKLFKClDgZjTgbDTgZDLi7OOPp4oKnqws+bq74ubvh5+GOv4c7Id6e9ZsXId5euDhpI3+Ojs61YrZa+XzLLt5P3kqVycRtfbvz+IhB+Hk43vBQQzisIfj7eHD3pH6s2XqEkABvenWMJOi8CeWNu44xsn+Cigq1R355BftP5bH/1GmO5p8hveAMJ4tLsSr5pQBlQcnZC7mfuxuBnh64uzjj7uyMi5MRoxCI+s1ssWC2WjGZLVTX1VFlqqOippZTJWWUVFVTWl2DvEiDAEK8vYjw8yHS34foAH+iAvyICfQjNijAnqdDR6fRSCn56WAaL29PpaDGxOAO0Tw7bhjxIYFqS7MpDmsIAMP6xDOsTzwAK39N5cW5KzlTUkV5VQ1llTXcPq5t1+E5VVLG1owsNmdksfloBsXJuwFwMhiICfSjY1gwN3RLIibAn3Z+3rTz9SHE2wsno226vRarldLqGgrKK8mvqCS/rIKc0nJySss4VVLGzsxT/LDv8AWm4e/qTKesMySEBJIYEkRiaBAJIUG4OTv0V1XHgdl6/CRvrPmF/Tl5RHi6MXfGTQxNiFVbVovg0P9lZrMFJycjVqtkzMAkrFKyaN1ehvSK4x8PT1Bbnt2RUpJ6uoDVh46yJjWdY4VFAAR5etDBx5MxvXvQPTKMTmEhdrnAGg0GAjw9CPD0IImG53Jq6sycLC7hxJkSjhUUseXgIUqra/hm535qzGYADEIQF+RP5/AQOoWF0LVdKJ3CQ/BydWnx30Gn7bI3O5e31v3KluMnCfPx4qUpY/EryW+1ZgAObgjUx/e+8/UGTHUWnrlvFBMHd1ZZlP3JLi5lyd5DLN2bysniUgxC0C86klv7dGNQhyjigwPZsGEDwwdqr8fk5uxEQojSCxjTCTpaqxg+fDgWq5WTxaWk5RVyOK+A1NwCth3PZtm+w4Ay9NQhOICu7cLoERlGt4gwkkKDcNZIfn8dx+VATh5zNmzl5yMZBHi48+y4Ydzetztuzk4kJxeoLe+ySCn5x461zTqGwxqClBInowEpJQvX7OGLF5Vl+Rar1eFn+huD1SpJPprB/O172XxMyWQ5MC6Kh4b0Z1RSB/w93VVW2DyMBgMxgf7EBPoztvNvc0GFFZUczMnnQE4e+3NOs/HocZbsVaq1ujk50TUilF7t29GrfTi92rfD38Oxz4OO/dh/6jTvJW9lw9Hj+Li58seRg7h7QC88HaAnKqXkxZ3r+PxwSrOO47CGYLFKnIyC/363mS5xYSREBWO1ylZvBiazmWX7DvPZ5hSOFRYR5uPFo8Ov4+aeXYjQWCrdliDIy5NhibEMS1S67VJKTpWUsTf7NHuzc9mTnctnm1P4yGoFoENQAL2j2tEnKoK+0RFE+Pk41MpRnZZFSsm24yf56Ned/HosE193N/44chAz+vfE281VbXmNQkrJq7s38FnqTu7v1JcXmnEshzWEsxOfX69M4d0/TQNAIrlK4lWHxWyxsnjPQd5P3kpeeQWdwoJ5beoExndJaNPDJEIIIv19ifT35YZuSQBUm+o4kJPHrpM57MrKYeXBo3y76wAAod5e9ImOoH90BP1iIokLCtANog1itlhZezidj3/dyYGcPII8PXhy1PXc2b+nw81Nvbd/Mx8c2MqdiT15vu+otmcIZosVJ6OBL5dvp32YP90T2yFl6+wdSClZfySDN9Zu4lhhET0iwnjpprEMiovSL2SXwd3FmX4xkfSLiQSU4bWj+YXszDpFSuYpdpzIZsWBIwAEenrQNzqCftHK/gnBgXrKk1ZMeU0t3+06wLxte8gpLSM6wI9/TBrFTT064+qAkWxz9m/hjT2/MDWuC/8aMK7Z1wTHOwP81jv4fNl2XnpsEgBWKTG2sgtkdnEp//jxZ35JP0FMoD/v3DqJMZ3idSO4RgwGQVJYMElhwczo3xMpJVlFpezIzGbHiWx2ZGaz6tBRAHzd3egXHUH/mEj6x7QnMSRIN4hWwJHTBXy9cx/L9qVSZaqjX3Qkfxk/jBFJcQ57I/nRwW28unsDU2I789qgGzDY4LrgkIYAcCA9l6SYEK7rHtPqegdmi5Uvtu7i3fVbMBoM/GX8MO7o16NNDw3ZEiEE0YF+RAf6Ma13V0AxX8UgTrH9xEnWHj4GgK+bK/1iInnl5vEON5TQ1qk21bEmNZ0FO/ex62QOrk5GJnRJ4u4BPenSLlRtec3ii8MpzE5Zzw3RHXnj+kk2u/45rCF0jQ/nnWduAVpX7+BkUQlPLV7J3uxcRiTG8cINIx0ml7ojc3Ye4uaeXQDIKSlje33vIaOwCE8X58t+1myxIgSX/ac8W7jJYrWydG8q/1qxnr9OHMHUXl1a5Hdpy0gp2XfqNIt2H2TFgSNU1JqIDvDjT2OHcnPPLq0ixcSXh1N4YfsaxrZP4K0hN+Jkw5thmxiCEOJTYBKQL6Xs2sD7w4GlwPH6lxZLKV9sbrvO9TlxWkvvYOXBNP66bA0Cweu3TOCGrkn68JBKtPPz4aaenbmp59XXtZy/sltKicUqEUJZUHc2zQfAwpT9fLNzPzFB/pjqF93pNTtsQ1ZRCT/sO8yyfalkFpXg5uTEuC4J3NKrK32jIlrNOZ53eBd/276G0ZHxvDt0Cs4G244a2KqH8DnwHvDlFfb5RUo5qbkNtcZ/oDqLhZdXbuB/O/bSIyKMN6ZNJNLfV21ZOo3gL0tWU2UyMTQhlsHx0fWpP377fp7tHby5dhN1Fisjk+I4VVJGXLCSA0f3+6aTeaaEVYfSWHXoKAdz8xFAv5hIfje4H+M6JzhM2GhjmZ+2m+e3r2Z0ZDxzht2MSwsMIdvEEKSUG4UQMbY41tV46ZPVVFSbeOXxG+3RXItTVl3D4wuXs/X4SWYO7MOTo6/X5wociNv6dmPlwaN8uXU3Lyxfh7PRQOewEAbHxzChSyLRgX4s2LmPlKxTvHvbjfx0MI2jBWeIC/IH0HuA14DVKtmfc5r1RzJYn5bBkbxCAHpEhPH0mCFM7JpEeCsdXl1wdC/PbV3FyIgOvD/sphYxA7DvHMJAIcReIAd4Skp58FoPYDZb2JCSzvU942yvTgWyi0t5aP4SsopKePmmsefGr3Uchx6R4RcURMkoKGJ9Wgbbjp+ksKKS0Z3iWZuazlczb0UIwamSMnzd3Ajy8rzCUXXOkl9eweZjWWzOyGTzsSwKK6swCkHvqAieHTeMsZ3iadfKF2TOO7KL57etZli7OOYMvxlXY8tdtoWUFycobuKBlB7C8svMIfgAVillhRBiIvC2lLLB3NRCiFnALIDg4OA+CxcuPPde2qkyPlmZzj2j4+gS7WcT3c2loqICLy+va/5cdkU1b+9NxyIlD3WJJcm/Ze9smqrT3jiaTquUSMm5OYPzKamtY96RTI6WVHJbQiQuBsGBojJifTwZHhGMVcpLPiOlZN+ZMiI83Qh0c2l2D8LRzmdJbR3ppRWklSjb6aoaALydnejo703XQB+6BvjgqdKaAXufz3Xlp5lXfIIebn48FpyIs7j6fOmIESNSpJR9m9KeXc6qlLLsvMcrhBBzhBBBUsrCBvadC8wFSEpKksOHDz/33vbP1+Hm4sQDd9yA2xWiPuxJcnIy52tsDIdy8/nTl4vwdHfj07tvIS645esANEWnGji6TinlOZNwMhro2beYX49lsvtkLruyciiuquJkjZmbhg6mZ/tLSy2eLCrhkXc+A8Db1ZWk0CASQgKJDwkkPljZAjzdG20UWj6fpdU1pJ4uIDU3nzWZx8mtPU1uWTkAHi7O9ImKYEZMJNd3iKZjaLAm5g7teT7nHd7FvKytLTpncDF2MQQhRBiQJ6WUQoj+gAE4cy3HkFKycdcxruseoxkzaAqHTxcw84vv8HBx4Yv7phEV4Ke2JB0bIoS4IAT6bIK+Gf17smDnPtakpjMiMe6yY92hPl4seOB2DucVcOR0AYfzCli+/wjltbXn9vFxcyU20J+YIH+iA/xo7+9HVIAvkX6+12QW9qKkqoasohKOnykiPf8M6QVFpOUXcqrk3H0iAa4uXBcfw8z2vekZ2Y7O4SE2q8vhiHx8aDv/2vmzXc0AbBd2+jUwHAgSQmQDLwDOAFLKD4FpwCNCCDNQDdwur3GsKi2zgILiCob06mALyaqQnn+GmV8uwsPFhXkzp+uRRG0Ii9VKTZ0ZXzdX7hrQ87L7uTg50bN9+AW9Bykl+eWVHM0/Q0bhGTIKizleWMzWjJMs3Zt6weddnYyE+/oQ7qOUK60uPkOm6y4CPN3PVcLzdXPFy80Vb1fXJl90zRYrFbUmKmprlZKrldUUVVVRWFHF6bIK8srKyS0t52RxKWU1v5mZs8FATJA/3SPCuK1PNzqFh9A5LIT9O7drtidjbz44sJV/70pmQlQSbw+ZbDczANtFGd1xlfffQwlLbTKb9mQgBAzq4ZjFKfLKKnjwq8U4GQSf3XuLbgZtDKPBwH0De59bf3AtCCEI9fEi1MeLwfHRF7x3tsDQyaLS+rrY5eSWlpFbVsGOzFPkl5Wz+mT+ZY/t5uSEq7MTbk5OuDk7YTQYMBoExvqxaou0IqXEbJXU1pmpMZuprTNTVVd32WP6uLkS6uNFmI83PSLDae/ve65MalSAnx5FdwXe27eZ1/dsZHJMZ94cPMmmi84ag8OsVN6y9zidYkMJ8PVQW8o1U2Wq45Gvl1JWU8v8mbcSE+ivtiQdlXBxsu2/3PkFhhpi/fr19BowkOKq6nNbaXUNFbW1lNeYqDSZqKkzU2s2U1NnxmK1YpESi9WKQGAQAoNBGQY7axyuzk54ubrg4+aKl6srfu5uBHh6EOjpToCnh0PUD9AaUkre2PML7+3fzM1xXXh90A2qLLh1CEMorajm4LHTzJwyQG0p14zVKvnT4pUcPl3AnDsm0yk8RG1JOm0IIQR+Hm74ebgRi34jokWklPxz5zo+Td3J7fE9mH3dONWyLziEIew8dBKrlFzXLUZtKdfMnI1bWXM4nWfHDWN4YutYP6Gjo2MbrFLy/LbVzE/bzcxOfflb31GqBgU4hCHsOJiFp7sLnTuEqS3lmtiUnsn7yVu5qUdn7r2ul9pydHR0NITZauVPW1aw6NgBHul6Hc/0GqZ6hJjDGELvjpEOFYZ2pqKKZ79fSXxwIC/cMFL1P7SOjo52qLWYefyXZazKSuPJnkP4Q7dBmrhGaP4KW1hSQXZeCb06RqotpdFIKfnrsjWU1tTy+i0TcHfgdRM6Ojq2parOxIM/L2JVVhov9BvN492v14QZgAP0EPYcOQVAz6QIlZU0nkW7D7I+LYNnxw0jKSxYbTk6OjoaocxUw4M/f8fOglO8OnACtyb0UFvSBWi+h7DvaA6uLk4kRTtGdE5uaTkvr9xA/5hI7hmgzxvoNI/58+cTExODwWAgJiaG+fPnqy1Jp4nkV1dw26r/sbswh3eGTNacGYAD9BD2H82hc2woTk6OsZjlpZ+SsUorL00Zq4ncKzqOy/z585k1axZVVVUAZGZmMmvWLABmzJihpjSda+RkRQl3rVlAfnUln4ycztB22lxgq+kegpRKyopuCe3UltIofkk/wZrD6Tw8dIC+Elmn2Tz33HPnzOAsVVVVPPfccyop0mkKR0sKuXXlfIprq5k/5nbNmgFovIdQZ7Fitljp4gDhpnUWCy/9lEx0gB8zB/ZWW45OKyArK+uaXtfRHin52dz/83e4GI0sGHsnnQNC1ZZ0RTTdQzCZrQB0itO+ISzYuY/jZ4r507ihNk9PoNM2iYqKuqbXdbTF+uxjzFizgABXdxaPv1vzZgAaN4Q6sxV/Hw9C/LVd4KO8ppb3k7dyXWx7RuirkXVsxOzZs/HwuDB3l4eHB7Nnz1ZJkU5j+T7jAL9bv4h430C+HX8X7b391JbUKDRtCCazlY4xIZqJ0b0cn/y6k5LqGp4ZO1TzWnUchxkzZjB37lyio6MRQhAdHc3cuXP1CWUNI6XkgwNb+X+bltMvNJKvx95JkLvjlEvV9NiG2WIlUePhppV1ZubtOMj4zgl01hPX6diYGTNm6AbgIFisVv65cx2fH07hxphOvH79DS1a/7gl0LRaKSG+fcNpfbVC8qlCKk0mHhnqeJlYdXR0bEONxcz/bVrOj5mHebBzP/7SZ+Ql9bIdAU0bAmjbEKpNdaw/VcCwhFh9RbKOThuluKaaWcmL2JGfzZ97j+Chro57c6hpQxACosK0m8N96b5UKurMPHh9X7Wl6OjoqMDJ8hLuXbeQ7IpS3hs6hUkxndSW1Cw0bQhOBoNmVyhbrZIvt+4mysudvtGOk2dJR0fHNuwrzOWB9d9hsliYP+Z2+oW2V1tSs7FJlJEQ4lMhRL4Q4sBl3hdCiHeEEOlCiH1CiEat3HJ20u4Y3JbjWWQUFjEyUvtRUDraRs9X5Hisykrj1lXzcTEY+W78Xa3CDMB2YaefA+Ov8P4EIKF+mwV80JiDarn+wdc79hLg4U6fED+1peg4MJ+OHs31d91FRmYmGVIyqD5fkW4K2kRKySeHdvBw8mKS/INZMvFeEvy0O895rdhkyEhKuVEIEXOFXaYAX0opJbBVCOEnhAiXUuZe6bjOTto0hILyStYfyWDmoD44Gyxqy9FpIlJCcTFkZsKZM8rjkpJLf5aUQE0NWCy/bffdB889B0ajsrm5gZ8f+Pv/9vP8x4GBEBOjPD/Lpt//ntvWreNslHoM8BFAfb4iPdxUW5itVr4qPsG6k3mMj0rkP4NvxN1JW7VOfinY3azPC+Ua3XzqDWG5lLJrA+8tB16RUm6qf74O+JOUcmcD+85C6UUQHBzcZ+HChTbRZ0vWnsznu2OneKFfJ7ylGS8vba+kBqioqGizOmtrL91MJuUngIsLODkp29kL/MWPhVA2UH6azRUYjYpOKcFq/c0szOZLH5vNSntCgKursjkV5+FOLa7nbQAmYD/Qp0+fZv/ubfnvbksqrWY+KDzKgZpSxnuHc6tflObCSoup4AuxjqXD30qRUjYp0sVek8oNnbkGnUhKOReYC5CUlCSHDx/egrKaxjv/nU+X8BDuuGE8ycnJaFHjxbQFnWYzpKbCrl2QkqL83LsXgoMhMRFiYy/c4uKUu/em/F83RaeUSk/k+HHIyICMB57lBLEcJ5Y0EikigJ7soTcpfBWYxcaN/0dSkmJKTaUt/N1bmpPlJcz8+VtO1JYzMyCOFybdqrakSzBbLTy99y1cq12bdRx7GUI2cP6sSySQY6e2bUrmmRIO5ebzzNihaktp85SVQXIyrF0L27fD/v0QGQl9+kDv3nDzzdCr14XDNGoiBAQFKVu/fpA943UiLb8NORbhzy56s5Y+xMf/kcmT4fRp6NED+veH0aNh2DDQ8I10q2NbXhaPJH+PRUrmjbmN2sPH1ZbUIAtPriatPJNnO81kIf9u8nHsZQjLgMeEEAuAAUDp1eYPtMrKQ2kATOiSqLKStkddnXLhX7NG2fbuheuuUy6Ur74KPXuCj4/aKhvPiVmz8P/gg3NzCAEUM5B1ZI2CV9ZGA8r8xe7dsHkzvPYa3HabYnhjxihb377N60HoXJ7/pe3hb9tWE+Xtx0cjbqGDbyDJGjSEo+VZfJ25iuEhfRkS3LwqjTYxBCHE18BwIEgIkQ28ADgDSCk/BFYAE4F0oAqYaYt21WBNajo9IsII9/VWW0qboKQEliyB77+HDRuUoZ4xY+CFF2DwYLgoGahDMXjOHDYBMXPn0s5iIcdo5MSsWdw/Z865ffz8YMQIZXvuOaiogF9+UQzxwQfh1CnlvZtvhilTwFv/WjYbs9XK7JSf+Sx1J8PaxfHO0Mn4uripLatBaiwm3jgyD38Xbx6Jn9bs49kqyuiOq7wvgUdt0Zaa5JaWcyAnj/8bPVhtKa2aqipYvhy+/hp+/hlGjoRbb4WPPoKQVpY/cPCcOVBvAJH125Xw8oIJE5QNIDcXVq+Gb76BRx+FsWPhjjtg4kQl8knn2iiuqeaxjUv49XQm93fqy1/6jMTJoM1oR4DPji/lZFUe/+r2KF5Ozb870vRKZa2xIS0DgJFJes0DW2MyKRe2ggK46SYYMEC5sH3+Ofjq1UgvS3g43HuvshUVwaJF8N57Su9h8mSYOlWZbNdrNl2dw8X5/G79IvKqKnh10ERuje+utqQrklKUyvKcX5gSMZxe/kk2OaZ2rU+DbDh6gkg/H+KCAtSW0mrIy4N//AOio+GVV5Q74LQ0WLVKifXXzaDxBATA736n9KoOHlQm1HNylGG2V15RIpx0GmZF5mGm/jSPWouFheNnaN4MAIpNZcR7tee+2BttdkzdEBqJyWxh2/GTDE2I1VNV2IBdu5S72o4dlXHwNWtg0yYlRLS1DQupQXg4PPGEcn6XLYMjRyA+XjGMAw0mmGmbmK1WXk5Zz+83LCHJL5gfbriXnkHt1JbVKEaHDeDNXv+Hi8F2i+N0Q2gke7NzqaqrY1CcXs+2qZjN8N13MGSIMizUuTOkp8PcudD1kuWMOraiVy/47DPFFKKilHmGUaMUo7Ba1VanHkU1Vdy79hv+e3Abdyf15ptxMwj1cKxZeaOw7SVcN4RGsv1ENgLoF3O1aT+di5ESFi+Gbt3gjTfg8ceVhVl/+pOS0kHHPoSEwPPPw4kTcP/98OKLilmsWKH8jdoSewtzufHHz9mRn81rgybyzwFjcdHjd3VDaCy7TuaQEBKEr7seunEtrF+vrBV48UV4800lnn76dH2SU01cXGDGDNixQ5m/eeopZcHb5s1qK2t5pJTMO7yL6Su/AuC78XcxXYPzBWarhdPVv0362CrF0NXQDaERWK2Svdm59GofrrYUh2HXLhg3Tol2eeIJ5fmECU1LE6HTMgihDN3t36/0GO64Q1nL0FrnGKrqTDz563Ke376a68NjWH7DTLoHafN/+tXDX/By6qesy9uOlPLcvGVLG4NuCI3g+JkiKmpN9IjU5pdHS5w+DXfdBZMmKReX1FS4807QcCh3m8doVCK6jhyB4cOV+YUHHmhdUUlpJQVMWfElSzIO8mTPIXwychr+bu5qy7oszsKIu9GVvSVp/PfYIo5XnAJo8YAW/d+0Eew/lQdAt4hQlZVoF6tVmRzu3h3at4ejR+H3v1eGJ3QcAzc3+H//Twn79faGLl1g3jzHn19YmL6PyT9+QXFtNfNG387j3a/XXKbSi+kX2IVqSy0JXlGU1VXyddZKNhXs5qVDn3CiMqfFegr6SG4jSD2dj7uzk77+4DKkpytDDnV1sG6dMnms47j4+sJbbyk9vd/9TjGFjz9WIpQcico6Ey9sX8N3x/YzKCyat4bcSIi7Y2QGHB7Sl4yKU/T0T6KHfyLbzuznf5krKa2ruGAIydboPYRGkHq6gMTQYIz6uMcFWK3w7rvKpPHUqco6At0MWg99+yoTzyNGKAn1PvnEcXoLB86cZtLyz1h0bD9/6DaIeaNvcxgzsEolFtjLyYNPMpYQ5RFGJ+9YCk0lxHu359PjS88NIdkavYdwFaSUHMkrZFznBLWlaIrCQmVuoLJSiU5J1JO/tkqcnODPf4Ybb1TmGZYtgy+/1O4KciklXxxO4aWU9QS6efD12Du5LsyxujaG+rUFN0cOJystl9zqQr45uZob2w1lQGBXDpedINYromXabpGjtiLOVFZRWl1DfLAeMH+WXbuUfP69e8PGjboZtAW6dlWMPypKqc1w6JDaii4lv7qCmT9/y993rGVweAwrJt3vcGZwPs4GZzp4RfLQzn9RXlfFXdETSfSO5oZ2Q1qsTb2HcBWOFRQB0CFYnz8A5e7w//4PPvgApjU/266OA+HiogwRfvGFsm5BS9+B9dnHeGrzj1TUmXix/xjuTurdKlLMjAsbRLGpnFGh/RFCIKW0+erk89EN4SqcOFMMQEygv8pK1KWuDp58Ukk6l5ysRKDotE3uvVeZK5o6FXbuhNmz1SvSU1ln4uWU9XyVtpuO/sEsGHsnCX5B6ohpATyc3Lg3dhJGoZzgljY53RCuQmZRCS5GI+E+jpXjxJaUlSmplL29lYplWilJqaMevXsrZnD77cqak0WL7F+saFfBKZ7ctJzM8mIe6NSPp3sPw83o+Je0OqsZZ8Nvv8dZM7AH+hzCVcguLiXCzweDwfG7n02huFipUNa5MyxdqpuBzm8EBcHKlUqG2htuUKq52YNai5k3dm9k+sqvqLNa+HrsnTzfb1SrMIO8mjM8sP0f7CxSZ5JGN4SrcKqkjAg/ByrUa0POnFHqFQ8cCO+/r6821rkUJyclk2pcHIwfr/QmW5IDZ04z5ccveHf/ZqbEduGnGx174vh8pJS8d/Qbqiw1RHmEqaLBJv/iQojxQogjQoh0IcSzDbw/XAhRKoTYU7/9zRbt2oO8soo2WT85P18pXTl6NPznP3oOIp3LYzQq5U27d1dSa5eU2L4Nk8XC23s3cdOKLymqrebTkdN4c/AkfDRa67gprM3bxq7iw9wXeyMhbuoEsTS7jyWEMALvA2OAbGCHEGKZlPLiPs8vUspJzW3PnpjMFgorqwj1cYwFLbYiL08xg6lTlSyluhnoXA2DQelF/r//p+RCWrNGqeBmC/YU5vDM5hWklRQyJbYz/+g/Bj9X7eYhagqFtSV8dOx7uvnGMzFcvZrttugh9AfSpZQZUkoTsACYYoPjqk5RZRUAwV6eKiuxHzU1SlK6m2+Gf/5TNwOdxiOE0pscPFhJcV5X17zjVZvreGnnz0z9aR7lplo+GTmNt4dMbnVmIKVkTvpCzNLM44l3nFuYpgaiuUmShBDTgPFSygfrn98NDJBSPnbePsOBRSg9iBzgKSnlwcscbxYwCyA4OLjPwoULm6WvOWSWV/FyyhEe7hpLzyC/BvepqKjAy0v7PYjG6jxxQklJERfX8poaorWdT7VRS2d6Ori6KokOG8PFOvdVF/Nl0QkKLbUM9wrhVr8oPAzqTxq3xPk8QjbLDNsZZu1Kf5q/ynPEiBEpUsq+TfqwlLJZGzAd+Pi853cD7160jw/gVf94InC0McdOTEyUarLx6HGZ9MKbMiUz+7L7rF+/3n6CmkFjdL72mpS9eklZWdnyei5HazqfWkAtnSUlUnbsKOV//9u4/c/qzK+qkI9tWCKjv3hZjloyV27JzWw5kU3A1uezvK5SztjynPxDyr+l2Wq2yTGBnbKJ13NbWG42cP59QCRKL+B80yk77/EKIcQcIUSQlLLQBu23GKXVNQD4ubeuLmpDrFihVDTbts3+8eQ6rQ9fXyXv0eDB0LEjDB165f0tUvJZ6k7e3PMLtRYz/6/HYB7ueh2urSCU9Ep8mrGMUlM5L3SZZdf1BpfDFmd7B5AghIgFTgG3A3eev4MQIgzIk1JKIUR/lLkLzZffKKuuBcDbzVVlJS1LerqSuGzJksZ38XV0rkZCAnz1Fdx2m5I1NfIy5ch3F+Tw4un9ZJ6sYkh4LC/0H028b+vPHbav5CirTm/mlshRJHhrI3S22YYgpTQLIR4DVgFG4FMp5UEhxMP1738ITAMeEUKYgWrg9vqujaapNJkA8HJtvVVepIRZs5SC94MGqa1Gp7UxZgw89BA8+qhyw3F+kEJeVTn/3rWBxRkH8De6MGfYTUyISmoVOYiuRq3FxLtHFxDmFsid0RPUlnMOm/THpJQrgBUXvfbheY/fA96zRVv2pMpUh0EI3Jxbb7f1s8+gvFype6yj0xL8+c/Qq5eS3mLaNGVNwWepO3ln36/UWS080vU6updYmBDdUW2pdmPhyTXkVBfwr26P4mbUzg1n673S2YDqujrcnJxa7R3L6dPw7LNKzLiT/k3QaSFcXZWFa7feKjF3PMyctA1kVZQwOjKe5/uNItrbn+TkZLVl2o2TVXl8d3ItI0L60ss/SW05F6BfBq6AyWzBxUn9iZ6W4oknlNKXPXqorUSnteORmEPwX9bx7K5TdPQP5vNRtzI8QqXYZhWRUvJB+re4Gl14IO4mteVcgm4IV6DOYsFZrby+LcyqVZCSAp9/rrYSndZMWkkBr+/eyOqTRwkK8sT69QT++nQ3Bke0zcRY6/N3sLckjUfjb8XfRXs50nRDuAIWq8TYSrOc/vOf8K9/QRuIqNVRgVMVpbyz71e+PbYfTycXnuw5hPs79eXrMldemq2EObc1yusq+Sjjezr6xDA+XJsRHLohXAGJxNAK5w82bYLcXO1Uu9JpPZyuKuf9/VtYcHQPAsHMjn15rNsg/N2UO4977oEXXoC9e9veUOUXJ5ZTUVfNY91uUzU9xZXQDaEN8u9/w9NP6xPJOrbjVEUp/z24jQVH9yKR3Brfg0e7DaSd54XDIq6uSgK8V1+F+fNVEqsCaeWZrMzdzJSIYcR6Ragt57Lol4QrYBACq/aXS1wTBw4ola6+/VZtJTqtgczyYj7Yv5VFGfsBuCWuG492H0h7L7/Lfuahh5RcWRkZ6uXMsidWaeXD9O/wc/FmhobWHDSEbghXwMlgwGK1qi3Dprz+uhJd5NZ60sjrqMCewhw+PLCVVVlpOBuM3JHQk4e6DCDCy/eqn/XxURZD/uc/8O67dhCrMmtOb+VIeSZPJt2Fh5O2J+10Q7gCzkYjJrNFbRk2o7ZWWS165IjaSnQcEYvVyrrsdD5N3cnWvCx8Xdx4pOtA7uvYhxCPa8sA+sADcP318PbbrbsSX3ldJZ8f/4EuPnGMDOmntpyrohvCFXB1MlJjNqstw2YkJyu1kUND1Vai40iUmmr45uhevjyyi+yKUsI9vPlr35HcntADL+em5fnq0EGpybxtm1KitbUy78SPVJireCR+ukMscNUN4Qq4OTtTa7ZgsVoxtoLbmKVLleI3OjpXQ0rJ3jO5zD+ymx9OpFJjMdM/tD3P9RnBmPaJONng/2HKFOU72VoN4URlDj/l/srEdkM0PZF8ProhXAEPF2cAqk11eLWCjKfLlilpKnR0LkdhdSVLjh9k0bEDpBbn4+HkzM1xXZmR2JOugbYt/D55MsycCa+8YtPDagIpJXOPLcbTyZ27ND6RfD66IVyBs1lOK2pNDm8IVVVKnYOObSd/mE4jqbGYSc4+xvfHD7LuZDpmaaVHYDj/HDCWm2K74O3SMt/9fv2gpASOHm2Rw6vK9qID7C1J4+EO0/B2dpwSvLohXAGfehMoq6klzNdbZTXNo7IShg/XayTrKNRYzGzOPcGPmYdZnXWU8rpagtw8mNmpL7fGdyfBL6jFNRgMMGwYbNkCUdooB2AT6qxmPs5YQqR7CBPCr1dbzjWhG8IV8HVXYjPPVk5zZGpq9N5BW6fcVMum3OOszEpjXXY6FXUmvJ1dGReVyOTYzgwKi7bJ3MC1kJSkRL21JkNYnrORnOoC/tH1YZwMjpULTTeEK+DvocQMF1dVq6yk+eiG0PawWK1kmiqZe3Ab608dY0deNmZpxd/VnUnRnRgfncTAsChVy1R27AjffacU0mkNlNVV8nXWKvr4d6JvQGe15VwzuiFcgQBPpbhwUWWVykqaT02Ncjem03qxSsnRkkJ25Gez5XQmv+aeoMRUA6eho18wv+vSnxERHegdHGH3nsDlONtDaC0syFpJtblGk6mtG4NuCFcgwNMdARRUOLYhVFVBXR3ExKitRMdWSCnJq65g/5nT7D9zmn1nctlVcIoyk1IHPNTdi1Ht4wksqeb+EeMJ89DmHFhiolLTuzVwuvoMP+ZsYkzYdUR7hqstp0nYxBCEEOOBt1FqKn8spXzlovdF/fsTgSrgPinlLlu03ZI4G434e7hTUFGptpRmkZUFLi7QSks7tGqklORXV3CsrIjjZUUcLSkktTifI8UFyt0/Ss6teN9AJkZ1pG9oJP1CIony8kMIQXJysmbNAMDTE3x9lRsWR+erzB8xCIOmaiRfK802BCGEEXgfGANkAzuEEMuklIfO220CkFC/DQA+qP+peUJ9vMgrq1BbRrOoqWnd6QEcEbPVSpmphhJTDSW11ZypqaKgupKC6gryqis4VVHGqcpSTlWWUW3+7Wrp4eRMR/8QJkR3JMkviK6BYXT2D8HDWTt1ea8Vd3dw9BySGRWnSM5P4Zb2owhy9VNbTpOxRQ+hP5AupcwAEEIsAKYA5xvCFOBLKaUEtgoh/IQQ4VLKXBu036KE+XiTU1qmtoxmUVurG8JZ6qwWTleWU1hTRWFNJUU1VZTX1VJZZ6KyzkStxYzJaqXOasFstWKRVqxSIpEXXLQKCgr4JrkYUOpmWKU8t59FSixWK2ZpxWSxUGsxU2uxUGOpo8pcR0V9O5cjwNWdCC9f4n0DGdYujhhvf2J9Aoj18Sfc06fV1ehwdQVHzyH52fGleDq5My1ytKo66qzNG82whSFEACfPe57NpXf/De0TAVxiCEKIWcAsAP+gMNWLb1srysgqLL6sjoqKCtU1Xo3KSggM1L5OsN35lFKSb64lw1RBhqmC3Lpq8sw1nDHXcrlrj7MQuAgjTgichMAgBAYEBkAgLljDYbVayc39LfpMIBCAAIxCYET5vBGBizDgKwwECWfcnFxxczbiZjDiaXDCw+CEl8GIl8EZP6MzPkZnnM4vnlIJVJZhPl3GUU5wrWu4HOH7+Yc/gMmkfZ3Q8Pk8SQG7DIcZZu1Kyq/b1RFWzxm/Jc36vC0MoaHblYs7gI3ZR3lRyrnAXIDw9nFy+PDhzRLXXDJcUtiQs5FeA647ty7hfJKTk1Fb49XYvRu2bElm+vThaku5Ks05n7UWM+tPHWNlZhobczIoqlUu2O5OzsT7BnKddztivP2J9PIl2N2TIDdPAtw88HZxxdPJ5Zoibxzh7w6OofP+++GDD7SvEy49n1JKntn7NoE1vjzR7z5cjeoN3ZmtNSw8PrtZx7CFIWQD7c97HgnkNGGfSzBb1O9HtvdX8rufLC5t0BAcAVdXxx+jvRIF1Uqs/Tfpeykz1RLg6s7wiDj6hbSnR1A4iX7Bmgmz1LkURx7S3F18mENlGfw+frqqZgCQWZGsiSGjHUCCECIWOAXcDtx50T7LgMfq5xcGAKWNmT8wW9S/ikUF+AGQeaaEru0cM290ZCSYTMo4raP+4zVEYXUlHxzYyvy03ZisFm6I7sj0+O6qrLjVaRq1tVBY6JjlXKWUzM/6iWBXf8aGXae2HI6V/YSXU7tmHaPZfwYppVkI8RiwCiXs9FMp5UEhxMP1738IrEAJOU1HCTud2Zhjmy1WpJSq5hGPqu8hnDhTrJqG5uLjo4ScnjoF7dtffX9HYHveSR7Z8D0ltdXcHNeVR7sNJNYnQG1ZOtdIerqyPsYR58n3lBzhcNkJfh8/HWeDs6paKuvyya3eSY+AmcCiJh/HJr4spVyBctE//7UPz3ssgUev9bhWCfnFFYQGqBdH7e7iTDtfH447sCGAUjLzyJHWYQj/S9vD37atJsrbj6/H3kGiX7DaknSayJEjjrmCXkrJV5krNNM7OF6+GpDEeY9v1nE036/OzClSWwJxQf4cKzijtoxmcdYQHJ25B7fxl60ruT48hu8n3qObgYPjqIZwtndwa/sxqvcOADLKVxHs1gUfl8hmHUfzhnBCA4aQEBLEsYIiLA4cLO3q6viGsC47nZdS1nNDdEc+HTkNXxfHnOTX+Q1HNYRvslYT6OLLmDD119cW12ZQbDpGrPe4Zh9L04ZgEIKMU+rfmSeEBGKyWMgsKlFbSpPx9IRff1VbRdMpN9XyzOYVdPIP4Y3Bk1pFSdO2jpTKd7JPH7WVXBuHSjPYX5rO1MiRmugdnKhYi8BAjNfIZh9L0/9Vzk6CjGz1DSEpVCkWkpZXqLKSpuPlBZmZcPLk1ffVIl8e2cWZmipeGTgBNxXTNevYjtRUJcqoZ0+1lVwbi7LX4e3kwfjwQWpLQUrJ8fK1hLn3xt2p+UEV2jYEo4Fj2YVIlYPo44MDcTIYOJSbr6qO5jJxolJX2dGosZj55NB2hkfE0SPIMbNI6lzK0qVKXWVHijAqopxtZw5wQ7shuBnVL6t7pjaV8rpsYr1tU1BC24bgZKCiqpb8InWTy7k6O9EhOIDU0wWq6mguU6Y4piFszztJUW019yT1VluKjg1Ztkz5TjoSO0U6TsLIje2Gqi0FgBPlP2PAiSivYTY5nuYNAeBolvoX4i7hoRzIyVO9t9Icxo5V6teWlqqt5NrYmJOBi8HIwLBotaXo2IjTp+HwYaWmsqNQYirnIJmMDO2Pn4v6KcWllJyo+Jl2Hv1xNfrY5JjaNgSjASEgLVP9oZpuEaEUV1VzqsRxM596e8PIkfDNN2oruTZSi/LpFBCCu5P6E3g6tuGrr2DSJKVOh6OwIncTZmHl5sgRaksBlOGiSvNpor2bP5l8Fk0bghAQGerHEQ0YQs9IZex690nNZ+y+Ik8+Ca+9BhaL2koaT351paaLvOhcG7W18NZbynfRUaiz1rEi91diZSjtPbSRwiazIhmBkfaeg212TE0bAkBSdAhHTqhvCAkhQXi4OLP75FVz8mmaIUMgOBgWL1ZbSeMpr6vF21n9CTwd2zB/PnTpAr16qa2k8fxauJdiUxl9ZLzaUgBluCirYgNh7r1tNlwEDmAIHWNCyS0so7S8+uo7tyBORgM9I8NJyTqlqo7mIgQ8+yy88orjZED1dHahymxSW4aODbBY4NVXle+gI/FjzibauQcTQ4jaUgAorcukrO4kUV62ndzWviHEKt2z1BN5KiuBftGRpOUVUlJVo7aUZjFpklJWc906tZU0Dj8XNwprqtSWoWMDli5Vaig7QOmDc5yozOFQWQYTw6+vL4OkPicrfgGgvecQmx5X+4YQozhyaob6htA/JhIJ7MzMVltKszAYlDu0v/zFMeYSEv2COVyc79ARXjpKCvYXXlC+d4609mBV7hachJGRof3VlnKO7MrNBLgm4uls2x6L5g3B29ON6HB/DmacVlsK3SLCcHNyYutxB13uex4zZigJ795/X20lV6drYChlployy0vUlqLTDF57DaKilMVojoLJWsfP+TsYFNQDX2cvteUAUGMppaBmP5Getl8prXlDAOga344DR3NUv0N0cTLSJzqCLRlZquqwBQYDfPQRvPgiZGn81xkcHgPAz6fS1RWi02SOHIH//Ac++MCxegebC/dRYa5iXNhAtaWcI6dyKxIrkTaMLjqLQxhC94RwisurOZlXorYUBsVFcaywiLwydVdP24KkJPjjH+GRR7Q9wRzt7U+CbxCrstLUlqLTBKxWmDUL/vY3pYfgSKw+vYVQt0C6+yWoLeUc2ZWbcTP6E+Ta0ebHdgxDSIwAYG+a+hE+gzsoq2U3HctUWYlteOYZpYeg9cVqk2M7sS3vJMfL1E+HrnNtfPKJsvbg0WsukaUu+TVF7Cs5yujQ/hiENi6VVmkhp2obER4DES2gSRu/5VWICQ/Ax8uNPUfUN4TE0CCCvTzZlH5CbSk2wcUFPv4YnnhCKWeoVW5L6IGTMPDVkd1qS9G5BvbvVyaRP/pIKePqSCTn70QiGRHST20p5zhTk0qttYwIz5ap0tYsQxBCBAgh1gghjtb/9L/MfieEEPuFEHuEEDuvWaRB0CMxQhOGIIRgSHwMvx7LxGxx3II55zNgAPzjH8pkn1bzHIW4ezEpphP/O7qHwupKteXoNILCQiV53VtvQbduaqu5dpLzU+jsE0e4e5DaUs5xqmobIAj3aBmTam4P4VlgnZQyAVhX//xyjJBS9pRS9m1KQ72SIsjOK6GgWP2x+2GJsZTV1LLLwVctn8/DDyux4TNmaDcU9fEe12OymHl3nwNX+mkj1NXBtGlw663Kd8rROFGZQ2ZVLsNCtJVhN7dqB4GuSbgZfVvk+M01hCnAF/WPvwBuaubxLkvvTkp1+F2H1V8DcH1cFM5GIz8fOaa2FJvy9ttQWal08bVInE8AdyT0ZF7abg6cUT8MWefyPP64kkxx9my1lTSNTQV7EAiuD+qptpRz1FkrKag5SLhHk+6pG4VoTiinEKJESul33vNiKeUlw0ZCiONAMSCB/0op517hmLOAWQDBwcF9Fi5cCIDVKvnH/H10j/XjlsHqp0F+b98xcqtqeLZLFN7e2k+8VlFRgZfX1eOozWYlLXF4OAQG2kHYRVxNZ6XVzF9y9uJndOFvYV0xqhTD2NjzqTZq6CwogPx86NRJCW9uDFo7n5+Jtbjhwh3ywtQQauqsdj1CftAXhBTOxL328lFPI0aMSGnqSAxSyituwFrgQAPbFKDkon2LL3OMdvU/Q4C9wNCrtSulJDExUZ7P/73xvZz65MdSC3yXsl8mvfCm/Hzpj2pLaRTr169v9L4HD0oZHi7ll1+2nJ7L0RidP55IldFfvCzf2bup5QVdhms5n2pib51z5kjZvr2Ux45d2+e0dD5PVeXLiRv+IJdkr7/kPTV17ih4T36ZNkTWWaqvuB+wUzbi+trQdlX/llKOllJ2bWBbCuQJIcIB6n82mJZUSplT/zMf+B5o0hrwvl2iyM4vJbdQ/ZoEIzt2wMlgIKWgWG0pNqdzZ1i7Fv78Z/j0U7XVXMrE6I7cFNuFt/ZuYleB+oEGOgpvv60krktOhrg4tdU0nS2F+wC4LlBbM+F51XsIcuuMk8Gtxdpo7hzCMuDe+sf3Aksv3kEI4SmE8D77GBiL0sO4Zvp1Vla17Dio/tJafw93BsZFsTO/RPUV1C1B587w88/w978rq0u1xosDxhDu6cOjG5aQX61+oEFb59VX4Z13HN8MALae2U+cZwShbiqMmV6GOms1Z2oOE+res0Xbaa4hvAKMEUIcBcbUP0cI0U4IsaJ+n1BgkxBiL7Ad+FFKubIpjcVFBhLo68n2A9pYFDaxayJFtSb2ZDt20ZzLkZgI69fDv/+t3P1pCR8XNz4cdjMlphp+t34RNeY6tSW1Wf71L2Xx2YYNEK3+9F6zKKur5HDZcfoHdlVbygUU1hxCYiHEvUeLttMsQ5BSnpFSjpJSJtT/LKp/PUdKObH+cYaUskf91kVK2eS4AyEE/btGseNgFlar+nflYzrG4yQEy/cfUVtKi9Ghg/KP/t578NRTyqSzVugaGMZbg29kX2Euf9z0AxZr61gX4iiYTErak6+/VnoGkZFqK2o+KUWHsCLpF9BFbSkXkF+9FxCEuLWsUTnESuXzGdg9hpLyag5roD6Cl5sr3YN8+enAEeq0GrxvA6KjYds2ZdXp2LFKFIlWGBeVyF/7jmJlVhrPb1/dKofvtEhODgwbBqdPw5YtSlRaa2B38RF8nDxJ8NZW0qX8mn34u8ThYmzZiEaHM4TrusUQGepHcZk2CqYMCA2gqKqaX1tJbqPLERAAK1bAdddB376w85rXm7ccD3TuxyNdr+N/aXt4KWW9bgotzKZN0K+fUmhp0SLwsV0FR1WRUrK75DA9/ZMwaiR3ESj5iwpqDhLs3r3F23Jq8RZsjK+3O4tev19tGefoEuCNv4c73+85xPBEB59NuwpGI7z0kmIIEycqcwszZ6qtSuGZXsOoqjPx0aHtmKWVv/UdhXCkPMsOgJRK/Yx//hO++ALGj1dbkW05WZ1HkamMHn6Jaku5gFLTCeqslS0+XAQOaAhaw8lgYHL3jvxv+16KKqsI8PRQW1KLM3Wqsujo5puV+YW33gI/P3U1CSH4e/8xOBmMfJK6g1qLmX/2H4uxsSujdK5IYaGSrfTwYWWIyNEjiRpif8lRAE2lugZlQhkgyK1zi7el/7fYgGm9u1JntfL9nkNqS7EbnTopw0aenkrispVNihuzLUII/tp3JL/vOpD/pe3h9xuX6NFHNuD776F7d2jfHrZubZ1mAHCwNINAF1/C3bSTzA6gsCYVZ4MXPs7tW7wt3RBsQEJIEH2i2rEwZb8mop/shZeXMoTw+edKcrx771XuJNVECMEzvYfxt36jWJ2Vxp1rFnCmRhvzTY5Gbq6SnO6ZZ+Dbb+H118HdXW1VLcehsgw6+cRqbqjxTO1hglw7tkj9g4vRDcFG3N63O5lFJWxuBeU1r5XTp+djtXbmyy//Q2hoAQ89tEX1Cmz3d+rHnGE3cbAojykrvuBIsYZCozSO1Qoffqj0ChISYN8+uP56tVW1LEW1pRTUFtPJJ1ZtKRdgkXUUm44R6JZkl/Z0Q7AR4zonEODhzv927FFbil2ZP38+s2bN4uTJVOBJrNbxfPyxKwkJhfz8s7raJkR35Jtxd2KyWJj60zy9BOdVkBJ++gl694Z585RFibNnt+5ewVmOlCtRgkk+MeoKuYhS03Gsso4AV90QGoXFamX3ESUltprhhi5OTkzv0431RzLILtZolZkW4LnnnqOq6vwhmV1YrX0pLX2R3/1OWbeQkqKaPHoGtWPZDfcS7xvIQ8mLeXXXBsz6ArZL2LJFqYfx5JPwwgtKaGlXbS3WbVHSK05iwECcZ4TaUi6gqFaZ6A5wtc9Et8MbgtFg4Jn/LCUrtxghhKqmcEff7hiEYP72vappsDdZWQ0NkUnOnHmP1FQlEunGG+G22yBNpRv0MA9vvhk/gzsSejLnwBbuWfuNXnWtnoMH4aablL/Pvfcqiw9vvhk0Noze4qSXn6S9RyiuRhe1pVxAce0xjMIVb2f7LAN3aEM4W8Kyd6f2LFi1CwCLipO6Yb7ejOucwHe7DlBZa1JNhz2Jimp4RWdUVBQuLkpqg6NHoUcPGDQI7r9fGZO2N25GJ14eOJ5XB00kpeAUE5d/xq+5J+wvRCOkpMBdd8GIETB0qGLW998PTm00ED294iTx3i0fxXOtFNcew88lFoOwT0FqhzYEQ/1tzJ0T+rBm62EAnIzq/kr3DuxNeW0t3+1qUkJXh2P27Nl4eFy49sLDw4PZ55XK8vRUqrClpSkhixMmKBeipUvtX67z1vjuLJl4Dz4urty1ZgGv7tpAnbX1ph05H7NZiRYaPFhZS9K9u2LWTz4Jbi2XUVnzlJjKKakrJ1Zjw0UAJabj+LnYL87XsQ3BoBhCj8QIpIS9aUpufDVDP3tEhtM3OoLPtqRgMrf+C82MGTOYO3cu0dHRCCGIjo5m7ty5zGigkG5AAPz1r3D8OPzud8qq54QEePNNKLXjtEsn/xCWTbyX2xN6MOfAFqat/IqMsiL7CbAzRUXKqvK4OCVF9R//CMeOKeGkvi1TmtehOFGp1EaP8WynspILqbWUUW0pxM8lxm5tOrQhwG/DRmMHdmTBSmXYyFo/j6DWfMJDg/tzuqyCH/alqtK+vZkxYwYnTpzAarVy4sSJBs3gfFxc4M47lYR5//sf7NgBsbHw4INQXm6fXoOHswsvD5zA+0Nv4kRZMTcs/4ylx1vPwkKzGVatghMnlIy1hw7BkiXwyy8wbVrbHRpqiJNVSqLMaI8wlZVcSJlJmZ/z1Q2h8Rjrewm3ju3FL7szgN+GjdRaYDI4PprO4SHM3bRDT8l8Fa67TkmfvH8/dOwI2dlKGuUnnlBWxba0p98Q05HVkx/gutAoIjwbl6WtxqKhHODnYbUqF/xHH4WICCVayMNDSTfxxRdKOKnOpWRX5+NhdMPfRVtZ+krrlFBYHxf7ZV51eEMQQmCxWolpF0C3+HDSMn9bgJSRXahKmmwhBA8P6U9mUQkrDuix740hIkKpt9Cpk5IfKSAA7rtPGeb4859h1y7lgtcShHp489mo6fQNuXIkx6Jj+/nXznXctXoBP5XltIyYa8Rige3b4emnISbmNzPYskUx1JAQCA1VW6W2yanOp517sOZWKJeZTiIw4u1sv6EshzcE4FwCszl/mU5cRAAA81fs5Mk3lvDGl+t5/Uv7r5Aa3TGehJBAPty4Te8lXCOJicrdbWqqkkdHSrjjDggLU35+8gk0GO3agiw6tp/nt63GSRiZ2akvyRX5vLdvs31F1HP8OMydC9OnKxf8mTPB1VVZVLZvnzKB31rzDbUEp6vPEO6urfxFAGV12Xg5h2MQ9hvfazUjid+u2cOXy7cjJdx9Q18OpOfywsPjQcKrn69j3bY0Rg2wX1pbg0HwyNABPPndClYePMoN3eyz0rA1IQT07Klsr7yimMDatbBmDTz7rNKLGDNG2QYOVC6OLcH+M6d5OSWZF/qN5rYEpYTh4UOH2JqXxSzLAFyMLRsSmJsLmzcrv/eaNVBZqfzOkyYpmWYjtBcc4zBYpZX82iIGBbdsacqmUF53Cm9n+/5xm9VDEEJMF0IcFEJYhRB9r7DfeCHEESFEuhDi2ea02RCn8kv4YcMBZk4ewF8fHMvabWl4e7rSKymSXh0juWV0D1Ztsf8E7/jOiSSEBPJu8pZzk986DTN//nxiYmJISUkhJiaG+fPnX7JPVJQSK//115CXBwsWKNXc5syBpCRl7mHKFHjxRVi+XLmQNhcpJW/t/YX+oZHcltDjnM7tmelsWvcz3y5Y0PxGzrWlzKEsW6b0kCZNgnbtlBXDn3yi9JyWLFF+r3nzlIVkuhk0jxJTOWZpIdjVX20pFyClVMUQmttDOABMBf57uR2EEEbgfWAMkA3sEEIsk1LaLKRj2/5MAnw9mDpKcXmzxcrLn64BIOt0MbsPnyI0wBsppV3HCQ0GwR9HXs+jC5axeM9Bbu3TzW5tOxJn8yGdTYGRmZnJrFmzAC4bsWQwQK9eyvb008rF9PhxZa4hJUUJr0xJUSKaevdWwltjYy/cvLyurm1rXhYbc46zbdpj53TWerjQ1QClJ7KZ9d6VdTZEWZmi9fzt6FFFu5TQp4+y3X+/kk02KqrtrRy2FwW1JQAEufqpquNiTNZy6qwVdp0/gGYagpQyFa4azdMfSJdSZtTvuwCYAtjMELoltOPTpVvPPQ/y98TP2527nptHdLg/5VW1zLploCqTRiOT4ujVPpx312/hxm4dcXdxtrsGrXNpPiSoqqriueeea/SFVghl3DwuTgmrBOXimpUFe/YocfdHj8Lq1b9dhL29FWOIiYGgIPD3Vwr9nP/z26ojDAvsRE2RB88++x+qTF549kqgyCip3ptLbaUXf/rT2wwcOIPiYigpocGfhYW/tVtdfaExxcUpQ0C9eil3/PrF334U15UBEOiirQUZFXVK99bLzoYgbBGrL4RIBp6SUl5SaVcIMQ0YL6V8sP753cAAKeVjlznWLGAWQHBwcJ+FCxc2SsPb36cSG+ZFUntfdqefITrUiw7h3pwsqMTfy4XYMK+zx2/Cb3h5Kioq8LrKrWZ6SQWv7znK5NhwJkarE+vcGJ1qkXJe9rvIyEiys7PPPe/Tp0+LtVtXByYT1NYq0Tpms/Lz/Me7RT4ZopQbqhKoqzNzzKWEw26FRHk40e10LCABiYuLM05OSplRo5EGH7u6Kps91wBo+e9+Pmrp3MtxVht287B1PN5cvdqhvXRWuR2iIPArwvIfxbXu2oaNRowYkSKlvOwQ/pW46ldTCLEWaOgq9pyUcmkj2mjoCnxZF5JSzgXmAiQlJcnhw4c3ognwDu3A2q1H2HgohwAfb26bPIK4iMBGfbY5JCcnczWNw4E9NctYl3GSP90ymUAv+5fZbIxOtbjvvvvIzFRirl9//XWeeuopAKKjozlx4oSKymBbXha/37CEyl6S//73Y2ojg6lNzWBMvxE89dRozei8HFr+u5+PWjrzskxwYjfjho7BxXD13ru9dKaWFFJQAEMHTMDdKaDF2zvLVSeVpZSjpZRdG9gaYwagzBucnzUqErB5EHefTu15+t5RvPrHybz77LQLzEDNDKhneXL0YGrq6ng3eYvaUjRHY/IhqcWA0Ci+G38XJytKGDRkMDU//kLJ4jW4SOU+56zOVVlp1Gp0wZrO5Smvq8TV4NIoM7AnVeZ8DMIZN6N9J7vtsQ5hB5AghIgVQrgAtwPLWqIhISAixA+40AS0sOAkLiiA2/v1YGHKfg6f1qt3nc/5+ZCAK+ZDUoNYnwDmDLuZ+Xc9ynuPP01UuDKue1Zn34ljeSh5MTf++Dl7CrWxYE2ncVSYq/Fy0l4FoCpzIR7GILtfu5obdnqzECIbGAj8KIRYVf96OyHECgAppRl4DFgFpAILpZQHmyf7snoafKwV/jB8ID5urvxrxXpN9Fq0xNl8SH369GlUPiQ1EEI0qDPJP5jPRk6n3FTL1J/m8XLKes2mt9C5kCpLNR5O2kv1Wm0uxN2p5Ye8L6ZZhiCl/F5KGSmldJVShkopx9W/niOlnHjefiuklIlSyg5SSvXHAVTCz8ON/xs9mJ1Zp/hh32G15ejYkBGRHVg1+QFui+/Ofw9u44bln7G7QO8taJ0aiwl3o6vaMi6h2lKEu9HBDEHLVNfUsXbbEc3did/SqyvdI8J4dfVGyqpr1JajY0N8XNx4eeAEvhx9G9V1ddyyUu8taJ1aqwlXg7aqpAHUWIrsPn8ArdgQVm5O5bn3fmRPfY0ErWAwCF64YSRFVdW89bM6uXB0Wpah7WJZOfl+bu2g9BYm//g5B86cVluWTgOYrGacDdrK4COllVpLGa5G+6+NaLWGMOH6Tvh4ufH1TypWeL8MXdqFcme/Hny9Yy/7svULRWvEx8WNVwZN4LNR0ympreGmFV/y9t5NbaY6m6NgkRac7Jg8rjGYrBVIrLgZ/ezedqs1BDdXZ24Z2YONu45xMq9YbTmX8MeRgwjx9uK5pasxmfUhhdbKiIgOrJ78ABOjO/KfvZuYvnI+x1txdTZHwyKtGIW2LoO1FmX1tKvR/vUZtHUmbMz0MT1xMhr5+qddaku5BC83V/5x4yiOFpzhw43b1Zaj04L4ubrzztDJvDd0CsfLipi4/DP+l7ZHc/NbbREt/g1M1nIAXAzedm+7VRtCoJ8n4wd1ZPnGAxSXVV39A3ZmeGIcU7p3Yu6mHRzMsX8hHx37MimmE6smP0DvoHb8ZetKfrd+EUU12vte6qiLyVoBgIvR/qk8WrUhAMyY2JfaOgvfrtmjtpQG+fP44fh7uPHnJasxmfXx5dZOmIc388bczvN9R7Ex5zgTfviUzacz1ZbVZjEKAxaprdT0dVblJsHZYP8UN63eEGIjAhnSuwPfrt1DdU2d2nIuwc/DjX/cOJq0/ELe09NatAkMQvBA534snnA3ns4uzFj9Na+kJOsTzirgZDBikdo67+Z6Q3ASuiG0CPdO6kdZRQ1L1u9TW0qDjEzqwC29uvDRph1sP5F99Q/otAq6Boax/Ib7uD2hJx8e3Modq74mp7JMbVltCmfhTJ1VW0Edeg+hhemW0I4+ndrz1Yqd1Ji010sA+Mv44UQF+PHM4p8oqdIXrLUVPJxdeHngeN4ZMpnU4nwm/vApa04eVVtWm8HF4ITJqq1rglnWAuBksP8K6jZhCAAP3HwdhSWVLEs+oLaUBvF0deH1WyZwpqKK539Yo8noB52WY3JsZ36YdB8RXr78bv0iXk5Zj9mqrbHt1oib0ZUaq0ltGRdgqTcEo9ANocXo06k9vZIi+HL5dmpN2uoinqVbRBh/HHU9a1LT+SZlv9pydOxMnE8AiyfczV2JvfjvwW3cvXYB+dUVastq1bgbXak2a6tHbrGaAIHAaPe224whADw4dSAFxZUsTdbuxXbmwD4M7hDNSz8lcyg3X205OnbG1ejEv64bxxvX38DughxuWP4Z2/Ky1JbVavFwcqfCUq22jAuQmDEIZ1UyNrcpQzjbS/jih+2anUswGASvTh1PgKc7TyxcTqmeAK9NckuHbiydeC/ezq7MWL2AeUd26cOILYCXkztV5hqsGgo9tUozhuaVu28ybcoQhBDMumUQhSWVLF6nzYgjgABPD96aPonTpeU8s3glVqt+IWiLJPkHs2TiPQxtF8vz21bzzOYVeuZUG+Pj7IlEUmnWTi9BYkWolE6jTRkCQO9O7enfJYovfthOZbW2JpPOp2f7cP48fjgbjh5nzsatasvRUQkfFzc+HjmNx7tfz7fH9nPbyvnkVZWrLavV4OusrAYuqdPOXI2UEoNKl+Y2ZwgAj9w6mJLyauav2Km2lCtyR7/uTOnRifeSt7Lu8DG15eiohEEInuw5hLnDp3K0tJDJP37BvsJctWW1CvyclXxBJSbtrP+QSECdio9t0hA6x4Uxqn8i//sphTMllWrLuSxCCP4xaTTd2oXy9KKf9FrMbZyxUYksmnA3TgYD01fNZ9nxQ2pLcngCXJSMokUaMgQ1aW5N5elCiINCCKsQou8V9jshhNgvhNgjhNDEbfkjt16PyWzh4++1nS7CzdmJ926fjLebK7//eikF5do1MJ2Wp5N/CMtuuI8egWE8/ssy3tzziz7Z3AwCXJUiNGdMpSor+Q2BQKLOJHdzewgHgKnAxkbsO0JK2VNKeVnjsCftQ/2ZOrI7S5P3cyJH2/npQ328mHPHZIqrqnlswTJq6vSJxbZMoJsHX425g+kduvHOvl/546Yf9MnmJuJpdMfd6EphrXZqpghhcExDkFKmSimP2EqMvXngputwdXHmvQWN8TN16dIulNemTmDfqdM8s/gnLPoq1jaNi9HIq4Mm8nSvoSw9foi7Vi+gsFrvPV4rQgiCXf3Jr9GQIWBEqpRwz15zCBJYLYRIEULMslObV8Xfx4P7Jvfnl90Z7Dio/cU/ozvF86dxw1idms7sn5L1oYI2jhCCR7sN4v2hN3Gg6DS3rJxHZrl2LmyOQohbAHk1Z9SWcQ6jcMYq1enxiatdVIQQa4GwBt56Tkq5tH6fZOApKWWD8wNCiHZSyhwhRAiwBviDlLLB2/J6w5gFEBwc3GfhwoWN/V2aRJ3ZypuLD+FsNPDEzZ0wGq5tdr+iogIvL/sWsvgu/RRrs/OZEhvOhOiG/jSXoobOpqDrbBrpteW8VXAEAfy/4I7EuSratKbzcqipc63Yw0GyeFzeiLhKdI89dJZ4r6PUZx1Rp/6FaMI9+4gRI1KaPDQvpWz2BiQDfRu5799RzOOq+yYmJkp7kLzjqOx/1xvym1W7rvmz69evt72gq2CxWOVT362QSS+8KRfu3Neoz6ihsynoOptOekmhHLxojkz66jW5OitNSqlNnQ2hps4l2evlxA1/kCW1ZVfd1x469535Un6eNlDWWWqa9Hlgp2zitbzFh4yEEJ5CCO+zj4GxKJPRV8Visc+QyNA+HejfNZq5izZTVKr9koYGg2D2lLEMiY/hheXr+OmAw07j6NiQDr6BLJ5wD0n+wTyUvJiF6dpdja8lItxDADhVrY2w7rNpr83S/mlrmht2erMQIhsYCPwohFhV/3o7IcSK+t1CgU1CiL3AduBHKeXKxhy/vMQ+J0QIwZN3Daeqto45C3+xS5vNxcXJyNu3TqJ3+3Y8vXglP+sL13SAYHdP/jfmDq4Pi+aZzStYUZajtiTNc9YQTlZpo665UbgBYLE6mCFIKb+XUkZKKV2llKFSynH1r+dIKSfWP86QUvao37pIKWc39vg11WayjtvHtWMjArl9XC9+2HiQ/emO8U/k4eLMh3dOoXN4CE98+yO/pJ9QW5KOBvB0duGTkdOZFNOJhSVZ/GvnOqx6AMJlCXELwMXgzMmq02pLAcDJoBhCnbR/fiVtr1QWsPDzTXZr7oGbBhLs78Wrn6/DbHGMsE4vN1c+uutm4oMDeGzBMn49phds11HCUt8ZMpnRXmF8fGgHT2/+US+4cxmMwkB7j1Ayq7SRDsRZeAK/ldK0J5o2BA9PF9b9tI/cbPssHPN0d+Gpe0aQllnAgpW77NKmLfB1d+PTu28hJtCfR/63lI1Hj6stSUcDGIRghn80T/YcwqJjB3j8l6XU6gvYGiTaI5wTldoYGXA2KrWU66z2X1eiaUPw8nbBaDTwjR17CcP6xDOkdwfmLt7MqfwSu7XbXPw93fn83mnEBwfy6IIf9GR4OoAyP/Z49+v5a9+RrMg8woM/L6KqTrtZftUixrMdRaYyyurUX9znYlDCWk0W+2e11bQhGIyC8Tf1Zs0Pe8jLLbFLm0IInr5nJEaD4JXP1jnU4i9/D3c+u/cWOocF88TC5Xr0kc45Huzcn1cHTuDX0ye4d91CKupq1ZakKWI92wFwvPKUykrAxaBkYDVZ7Z+SW9OGAHDrvYMBWPCZ/aJ/QgO9+f2tg9l+IJOffk21W7u2wNfdjU/unkrPyHCe/G4FC3bsVVuSjka4NaEH7wyZzK6CU9yzdiFlJr0a31livSIAyKhQ3xBcjWcNQe8hXEJImC/jb+rN6qW7OX3KfsvybxnVk+4J7fjPV+s1nSK7Ic5ONA9NiOXvP/7MnA1bHaqno9NyTIrpxPtDb2L/mVzuWrOAklrtVApTE38XHwJdfDlWcVJtKTgJDwzCmVqL/TOwat4QAO54YCgGo+Crucl2a9NgEPz1d2OpNZl5+bO1DndBdXdx5r3bb2RKj068s34LC45m6wnxdAAYH53Ef4dP5XBxAbev/h9FNdpfjGkPOni1J10DhiCEwNXgqxvC5QgK8WHStH6sW7HXbusSAKLDA3hk+mB+2XXM4YaOAJyNRl6eMo4HBvVhQ04hjy34gSpTndqydDTAyMh4Ph05neNlxdy55mvdFIBE7yiyq/Kp0kB9ZTejP9UW+ycqdAhDALht5hBc3Zz58oOf7dvuuN70TIrgjXnryTvjeLVsDQbB02OHcntCJBuOHufuzxaSX66d+rE66jG4XQyfjJimm0I9id7RSCRHy9XvJXT2v4147wl2b9dhDMHP35OpMwbyy7pDpB2y38SPwSD426xxWCxW/vnRKqxWxxo6OsvwiGDm3DGZ44XF3PbRAr0cpw6gmMLHI25RTGH115xpw6aQ6B0NQGq5+ut44n0mEu09wu7tOowhANxy1yB8fD349L21dm03IsSPJ+4cxo6DWXyzerdd27YlwxPj+Or+W7FKyR2fLGDVoaNqS9LRAEPaxfLpyGkcLy/m7jULKK1tm9FH3s4etPcIJbVMfUNQC4cyBE8vN+54YAi7t2WQsiXdrm3fNKIbQ3p34P1vfiEtM9+ubduSzuEhfDvrDhJDlbUK7/y82WF7PTq24/rwGP47fCrppWe4Z+03bTYktbNPHIfLTmCVbTMAw6EMAWDS9P6ERfjz0dursdgx35AQgr8+OBZfLzeen7OC6hrHnZwN8fZi3n3TmNqzC3M2buPRBcsorW6bFwCd3xgeEcecYTdxsCiP+9Z92yYXr3X2iaPCXEWWRhLd2RuHMwQXFyfuf2w0x4/msXb5Hru27eftzt8fnkBmbhH/mb/erm3bGhcnJ2ZPGcNfJ4zgl/QT3PLf+RzKddyej45tGN0+gfeGTmFvYQ73r/uWarPj3vg0hW5+8QAcKLXvCIRWcDhDABg6pgudurfn8/fXUV1l37uYfl2iuGdSf5YmH2DNVsdODSGE4K4BPZk3czpmq5XbP17Atyn7HW7NhY5tGR+dxFuDJ7MjP5vfb1iCyaJOwXc1CHULJMQ1gH0lbXN+zSENQQjBQ0+Oo+hMhV3TY59l1tSBdIsP56VPVlNgpyI+LUmv9u1Y/NAM+kZH8PwPa3l68UoqatrecIHOb9wY24mXrhvP+lPH+OOmZW0qdXY3v3j2l6Rrdh7BYm25/02HNASATt3aM3xcV777ajP5dkp8dxYnJyOzH5uEi7MT89ZlOPR8wlkCPD346K6beWLEIH46cISb/zuffdltcxxVR+GOxJ7nsqQ+s3lFmymy09MvkTJzpep5jfKq97Cj4G225r9BtbmI01W7+fHk7/gp+/ecqtyKVdq+5+awhgBw/x/GADD3rdV2bzs00JsXH5lIfkkNr3zueKktGsJoMPDIsAHMmzkdi9XKnZ9+w4cbt+spL9owD3buz5M9h7A44wD/2ulY2X+bSne/RAD2lqSppqG49hg7Ct6h1JRJqek4Owvf41DJ13T0vYVor2GkFL7PmVrbD1k7tCGEhvtx231D+GXtQfZsz7B7+wO6RTO6dzgrf01l8brWU9C8d1QE3z98F2M6xfPWz79y12cLySoqUVuWjkr8odsg7uvYh09TdzLnwBa15bQ4Qa5+RLqHqmoIqSXfEuLejdERbzIu8j0q6nLwd42ng894ugXcg7dze/KrbX/NaZYhCCFeE0IcFkLsE0J8L4Twu8x+44UQR4QQ6UKIZ5vT5sVMv+d6wiL8ef+1FZjr7D/5NbJnGIN6xPLmV+vZc0T91Lm2wtfdjTenTeS1qRNIzy/ipg++YsHOfW3iDlHnQoQQ/K3faG6K7cJruzcy74jjVBNsKj39kzhQeow6qzrDwRILbkb/c899XKKoMf+W28jZ4I65BUpsNreHsAboKqXsDqQBf754ByGEEXgfmAB0Bu4QQnRuZrvncHVz5pGnJpCVUcCSBVttddhGYxCCfzwygfBgH5595weHzHd0OYQQ3Ni9I8t+fzc9IsP4+/J13P/lIrKL7Z+FUUddDELw2vUTGR0Zz9+2reaH446X7PFa6OWfRK3VxKFSdVYtB7gmcbpqFxV1uZSaMqmzVlJsSmd9zp/ZdPpflJoyCffoZ/N2m2UIUsrVUsqzRVq3ApEN7NYfSJdSZkgpTcACYEpz2r2Y64YmMWBIIocPqHOH7uPpxmt/nEKd2cL2g62vyH24rzef3nMLf580in2n8nh3fesfNtC5FGeDkfeGTqFfSCTfpO9t1b3F7r4JhLoFUmZWpxZKpOdA3J0C2ZT3T3YUvIOXczuGhr1IoFtHnAyu9Al+lBD3bjb/GwhbHVAI8QPwjZTyq4tenwaMl1I+WP/8bmCAlPKxyxxnFjCr/mlX4IBNBLYcQUCh2iIaga7Ttug6bYuu03YkSSm9m/JBp6vtIIRYC4Q18NZzUsql9fs8B5iB+Q0dooHXLutCUsq5wNz64+6UUva9mkY1cQSNoOu0NbpO26LrtB1CiJ1N/exVDUFKOfoqjd8LTAJGyYa7G9lA+/OeRwI51yJSR0dHR6flaW6U0XjgT8BkKeXlprx3AAlCiFghhAtwO7CsOe3q6Ojo6Nie5kYZvQd4A2uEEHuEEB8CCCHaCSFWANRPOj8GrAJSgYVSyoONPP7cZuqzB46gEXSdtkbXaVt0nbajyRptNqmso6Ojo+PYOPRKZR0dHR0d26Ebgo6Ojo4OoCFD0EIajMYghJguhDgohLAKIS4bfiaEOCGE2F8/t9LkMLCmcg061T6fAUKINUKIo/U//S+znyrn82rnRyi8U//+PiFEb3tpuwaNw4UQpfXnbo8Q4m/21liv41MhRL4QosG1RVo4l/U6rqZT9fMphGgvhFgvhEit/z9/ooF9rv18Sik1sQFjAaf6x/8G/t3APkbgGBAHuAB7gc521tkJSAKSgb5X2O8EEKTi+byqTo2cz1eBZ+sfP9vQ312t89mY8wNMBH5CWW9zHbBNgxqHA8vV+i6ep2Mo0Bs4cJn3VT2X16BT9fMJhAO96x97o6QOavZ3UzM9BKmRNBhXQ0qZKqXUfKm0RupU/XzWt/dF/eMvgJvs3P6VaMz5mQJ8KRW2An5CiHCNadQEUsqNQNEVdlH7XAKN0qk6UspcKeWu+sflKBGcERftds3nUzOGcBH3ozjbxUQAJ897ns2lJ0ErSGC1ECKlPh2HFtHC+QyVUuaC8iUHQi6znxrnszHnR+1z2Nj2Bwoh9gohfhJCdLGPtGtG7XN5LWjmfAohYoBewLaL3rrm83nVlcq2xN5pMJpKY3Q2guullDlCiBCUdRqH6+88bIYNdKp+Pq/hMC1+PhugMefHLufwCjSm/V1AtJSyQggxEVgCJLS0sCag9rlsLJo5n0IIL2AR8EcpZdnFbzfwkSueT7sagnSQNBhX09nIY+TU/8wXQnyP0rW36QXMBjpVP59CiDwhRLiUMre+O5t/mWO0+PlsgMacH7VTs1y1/fMvFFLKFUKIOUKIICml1pK0qX0uG4VWzqcQwhnFDOZLKRc3sMs1n0/NDBmJVpQGQwjhKYTwPvsYZcJci1lbtXA+lwH31j++F7ikZ6Pi+WzM+VkG3FMf0XEdUHp2CMxOXFWjECJMCCHqH/dH+b8/Y0eNjUXtc9kotHA+69v/BEiVUr55md2u/XyqOVN+0Yx4Osp415767cP619sBKy6aOU9Diax4TgWdN6M4by2QB6y6WCdKxMfe+u2gVnVq5HwGAuuAo/U/A7R0Phs6P8DDwMP1jwVKAahjwH6uEHmmosbH6s/bXpSAjUH21liv42sgF6ir/24+oLVz2Uidqp9PYDDK8M++866ZE5t7PvXUFTo6Ojo6gIaGjHR0dHR01EU3BB0dHR0dQDcEHR0dHZ16dEPQ0dHR0QF0Q9DR0dHRqUc3BB0dHR0dQDcEHR0dHZ16/j8AjTaPQGWE0wAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"theta0 = np.pi\n",
"x0 = np.array((np.sin(theta0),np.cos(theta0)))\n",
"\n",
"## Run Algorithm 5.1 on test problem\n",
"results = alg52(x0,my_f3,my_h3)\n",
"\n",
"## Display results\n",
"xstar = results[0][-1]\n",
"print(\"\\nx* =\",xstar)\n",
"\n",
"## Display results\n",
"vstar = results[1][-1]\n",
"print(\"\\nv* =\",vstar)\n",
"\n",
"## Convert into theta\n",
"print(\"\\ntheta* =\",np.arccos(xstar[0]),\"(using arccos)\")\n",
"print(\"\\ntheta* =\",np.arcsin(xstar[1]),\"(using arcsin)\")\n",
"\n",
"## Visualize\n",
"visualize(results[0])"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.8.4.3 Starting Point Near Global Max ($\\theta_0 = 5.5$)](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.4.3-Starting-Point-Near-Global-Max-($\\theta_0-=-5.5$))",
"section": "4.8.4.3 Starting Point Near Global Max ($\\theta_0 = 5.5$)"
}
},
"source": [
"### 4.8.4.3 Starting Point Near Global Max ($\\theta_0 = 5.5$)"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.8.4.3 Starting Point Near Global Max ($\\theta_0 = 5.5$)](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.4.3-Starting-Point-Near-Global-Max-($\\theta_0-=-5.5$))",
"section": "4.8.4.3 Starting Point Near Global Max ($\\theta_0 = 5.5$)"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Iter. \tf(x) \t\t||h(x)|| \t||grad_L(x)|| \t||dx|| \t\t||dv|| \t\tdelta_A \tdelta_W\n",
"0 \t-1.0621e+00 \t0.0000e+00 \t6.9215e-01 \t 5.6411e-01 \t 4.3032e-01 \t 0.0000e+00 \t 3.2768e+00\n",
"1 \t-2.0216e+00 \t3.1822e-01 \t2.0226e+00 \t 2.3706e-01 \t 1.1375e+00 \t 0.0000e+00 \t 8.7381e+00\n",
"2 \t-1.9886e+00 \t5.6197e-02 \t1.3940e+00 \t 4.4244e-01 \t 4.9825e-02 \t 0.0000e+00 \t 0.0000e+00\n",
"3 \t-2.4244e+00 \t1.9575e-01 \t5.4298e-01 \t 1.2207e-01 \t 1.5280e-02 \t 0.0000e+00 \t 0.0000e+00\n",
"4 \t-2.1566e+00 \t1.4900e-02 \t3.8186e-02 \t 1.0366e-02 \t 1.9242e-03 \t 0.0000e+00 \t 0.0000e+00\n",
"5 \t-2.1325e+00 \t1.0745e-04 \t2.7129e-04 \t 7.4929e-05 \t 1.7543e-05 \t 0.0000e+00 \t 0.0000e+00\n",
"6 \t-2.1323e+00 \t5.6144e-09 \t3.7221e-09 \t 2.8396e-09 \t 2.9955e-09 \t 0.0000e+00 \t 0.0000e+00\n",
"\n",
"x* = [0.24215301 0.97023807]\n",
"\n",
"v* = [1.64012795]\n",
"\n",
"theta* = 1.3262120357119471 (using arccos)\n",
"\n",
"theta* = 1.3262120357119473 (using arcsin)\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYQAAAD8CAYAAAB3u9PLAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAABiVElEQVR4nO2dd3xUVfr/32cmvfdCQgqk0HuR3qsIioAFG+qiru66P7+r667ruq51dXXturhWZEUUBESkSlCk9xYIIZCQQnpvk5k5vz9uQEogIZnMvZPc9+s1r8xkbu755GRyP/ec85znEVJKdHR0dHR0DGoL0NHR0dHRBroh6Ojo6OgAuiHo6Ojo6NSjG4KOjo6ODqAbgo6Ojo5OPboh6Ojo6OgANjAEIURHIcQmIUSyEOKIEOLRBo4RQoi3hBCpQoiDQoh+LW1XR0dHR8e2ONngHGbg/6SUe4UQ3sAeIcR6KeXRC46ZAsTXPwYD79d/1dHR0dHRCC0eIUgpc6SUe+uflwPJQMQlh80APpcK2wE/IUR4S9vW0dHR0bEdthghnEcIEQP0BXZc8lYEcOaC15n138tp4BzzgfkAbm5u/aOiolqkyWKVFJTVEuDlgrOT7ZdMrFYrBoP2l2J0nbZF12lb2qvOMpOZUlMdYR6uONvovCkpKQVSyuBm/bCU0iYPwAvYA8xs4L3vgeEXvN4I9G/snAkJCbKlVNea5PtLtsizBWUtPldDbNq0qVXOa2t0nbZF12lb2pvOjMJieftHi2XiM6/L3y1eKYsrq21yXimlBHbLZl7HbTJCEEI4A0uBRVLKZQ0ckgl0vOB1JJBti7Ybw83FmQdnD7NHUzo6OjpXRUrJ0n1HeHFNEkZh4JWbJnNDry4IIdSWBthgykgov8lHQLKU8vUrHLYSeEQIsRhlMblUSnnZdJGOjo5OWyWntJynV65ny8l0BsVE8vKNk+jg56O2rIuwxQhhGHAncEgIsb/+e38BogCklB8Aq4GpQCpQBcyzQbs6Ojo6mkdKybJ9R3hp7WasVsnTU8dw24DeGAzaGBVcSIsNQUq5Bbjqb1Y/r/VwS9vS0dHRcSQyi0v523cb2JqWwcDoSF6cMYGOAX5qy7oiNo0yUhsppWbm4nR0dNovFquVhTv28+aPv2AQBv42dSy3DuilyVHBhbQJQ6g1mXF1cdLNQEdHR3UOZ+fy91UbOZydy+iEWP5+/TjCfL3VltUkHNoQcovKWb/tOBlniwn082DWuD4E+nmef99qlZp3ZB0dnbZBRU0tb27ayqKdBwj0dOe1m6cytUeCQ92oOrQhvPLJRoRBEOLvxYmMArbsT2PG6J4cSs2mZ1wH3Qx0dHRaHSklqw4d59X1P5FfXsltA3vzh7FD8XF3U1vaNeOwhnA6u4jDJ3NY+95DAPy09yQLv9/F3mOZZOaWAPDne8cT17F5G/Z0dHR0GuN4bgHPrf6R3elZdA8P4e1bbqB3pONm5XFYQziZWUB0eAClFdX4erkTHuTDsVO5PHDzUHw83fngmy3sP56lG4KOjo7NKa6s5u2kbXy1+yDebq7844bx3Ny3O0YHSL9xNRzWEPp1ieTLH/awcNUu/Lw9WLn5ELdP6c+AblH173dkx6F0Zo3vo65QjVNbZyarpIys0jKyS8rILauguKqaoqpqiquqqaw1UV1nptpUR53FglVKLFKClDgZjTgbDTgZDLi7OOPp4oKnqws+bq74ubvh5+GOv4c7Id6e9Q8vQry9cHEyqv1r6+g0C7PVyqfb9vJu0naqTCZuGdCL348Zip+H400PNYTDGoK/jwd3ThvI+u3HCQnwpm+XSIIuWFD+ae9Jxg6KV1Gh9sgrr+BQVi6Hss5yIq+Q1PxCzhSXYlXySwHKhpJzF3I/dzcCPT1wd3HG3dkZFycjRiEQ9Q+zxYLZasVktlBdV0eVqY6KmlqySsooqaqmtLoGeYkGAYR4exHh50Okvw/RAf5EBfgRE+hHbFCAPbtDR6fJSCn54UgKL+1MJr/GxPDO0Tw5aRRxIYFqS7MpDmsIAKP6xzGqfxwAa35J5h8L1lBYUkV5VQ1llTXcOql91+HJKilje1oGW9My2HoijeKkfQA4GQzEBPrRJSyY63smEhPgTwc/bzr4+hDi7YWT0TbDXovVSml1DfnlleRVVJJXVkF2aTnZpWVklZSxOz2L7w4eu8g0/F2d6ZpRSHxIIAkhQSSEBhEfEoSbs0N/VHUcmO2nzvDa+p85lJ1LhKcbC+beyMj4WLVltQoO/V9mNltwcjJitUomDEnEKiVLNx5gRN9OPPvgFLXl2R0pJcln81l39ATrk1M5WVAEQJCnB519PJnQrze9IsPoGhZilwus0WAgwNODAE8PEml4LaemzsyZ4hJOF5ZwMr+IbUeOUlpdw1e7D1FjNgNgEIJOQf50Cw+ha1gIPTqE0jU8BC9Xl1b/HXTaLwcyc3hj4y9sO3WGMB8vXpwxEb+SvDZrBuDghkB9fO9bX27GVGfhiXvGMXV4N5VF2Z/M4lKWHzjKigPJnCkuxSAEA6MjmdO/J0M7RxEXHMjmzZsZPUR7IyY3ZyfiQ5RRwISu0MVaxejRo7FYrZwpLiUlt4Bjufkk5+Sz41QmKw8eA5Spp87BAfToEEbvyDB6RoSRGBqEs1Ffn9BpGYezc3lv83Z+PJ5GgIc7T04axa0DeuHm7ERSUr7a8q6IlJJnd21o0Tkc1hCklDgZDUgpWbJ+P5/9Yy6gTFM4+kp/U7BaJUkn0li08wBbT6YDMKRTFA+MGMS4xM74e7qrrLBlGA0GYgL9iQn0Z2K3X9eCCioqOZKdx+HsXA5ln+WnE6dYfkCp1urm5ESPiFD6duxA347h9O3YAX8Px+4HHftxKOss7yRtZ/OJU/i4ufKHsUO5c3BfPB1gJCql5B+7N/LpsT0tOo/DGoLFKnEyCv7zzVa6dwojPioYq1W2eTMwmc2sPHiMT7bu4WRBEWE+Xjw8+jpu6tOdCI2l0m0Ngrw8GZUQy6gEZdgupSSrpIwDmWc5kJnD/swcPtm6hw+tVgA6BwXQL6oD/aMiGBAdQYSfj0PtHNVpXaSU7Dh1hg9/2c0vJ9PxdXfjD2OHMndQH7zdXNWW1ySklLyybzOfJO/m3q4DeKYF53JYQzi38Pnlmj28/adZAEgkjSRedVjMFivL9h/h3aTt5JZX0DUsmFdnTmFy9/h2PU0ihCDS35dIf1+u75kIQLWpjsPZuew9k83ejGzWHDnB13sPAxDq7UX/6AgGRUcwMCaSTkEBukG0Q8wWKxuOpfLfX3ZzODuXIE8PHhs3jNsH9XG4tal3Dm3l/cPbuT2hD08PGNf+DMFsseJkNPD5qp10DPOnV0IHpGybowMpJZuOp/Hahi2cLCiid0QYL944kaGdovQL2RVwd3FmYEwkA2MiAWV67UReAbszstiTnsWu05msPnwcgEBPDwZERzAwWjk+PjhQT3nShimvqeWbvYdZuGM/2aVlRAf48ey0cdzYuxuuDhjJ9t6hbby2/2dmdurO84Mntfia4Hg9wK+jg09X7uTFR6YBYJUSYxu7QGYWl/Ls9z/yc+ppYgL9eWvONCZ0jdON4BoxGASJYcEkhgUzd1AfpJRkFJWyKz2TXacz2ZWeydqjJwDwdXdjYHQEg2IiGRTTkYSQIN0g2gDHz+bz5e6DrDyYTJWpjoHRkfxl8ijGJHZy2BvJD4/s4JV9m5kR241Xh16PwQbXBYc0BIDDqTkkxoRwXa+YNjc6MFusfLZ9L29v2obRYOAvk0dx28De7XpqyJYIIYgO9CM60I9Z/XoAivkqBpHFztNn2HDsJAC+bq4MjInk5ZsmO9xUQnun2lTH+uRUFu8+yN4z2bg6GZnSPZE7B/ehe4dQteW1iM+O7eGFPZu4ProLrw2bZrPrn8MaQo+4cN564magbY0OzhSV8MdlaziQmcOYhE48c/1Yh8ml7sicW4e4qU93ALJLythZP3pIKyjC08X5ij9rtlgRgiv+U54r3GSxWllxIJnnV2/ir1PHMLNv91b5XdozUkoOZp1l6b4jrD58nIpaE9EBfvxp4khu6tO9TaSY+PzYHp7ZuZ6JHeN5Y8QNONnwZtgmhiCE+BiYBuRJKXs08P5oYAVwqv5by6SU/2hpu871OXHayuhgzZEU/rpyPQLBv26ewvU9EvXpIZXo4OfDjX26cWOfxve1XLizW0qJxSoRQtlQdy7NB8CSPYf4avchYoL8MdVvutNrdtiGjKISvjt4jJUHk0kvKsHNyYlJ3eO5uW8PBkRFtJk+XnhsL3/buZ7xkXG8PXIGzgbbzhrYaoTwKfAO8PlVjvlZSjmtpQ21xX+gOouFl9Zs5n+7DtA7IozXZk0l0t9XbVk6TeAvy9dRZTIxMj6W4XHR9ak/fv18nhsdvL5hC3UWK2MTO5FVUkanYCUHju73zSe9sIS1R1NYe/QER3LyEMDAmEh+M3wgk7rFO0zYaFNZlLKPp3euY3xkHO+NugmXVphCtokhSCl/EkLE2OJcjfHiR+uoqDbx8u9vsEdzrU5ZdQ2/X7KK7afOMG9Ifx4bP0xfK3AgbhnQkzVHTvD59n08s2ojzkYD3cJCGB4Xw5TuCUQH+rF490H2ZGTx9i038MORFE7kF9IpyB9AHwFeA1ar5FD2WTYdT2NTShrHcwsA6B0RxuMTRjC1RyLhbXR6dfGJAzy1fS1jIzrz7qgbW8UMwL5rCEOEEAeAbOCPUsoj13oCs9nC5j2pDOvTyfbqVCCzuJQHFi0no6iEl26ceH7+Wsdx6B0ZflFBlLT8IjalpLHj1BkKKioZ3zWODcmpfDFvDkIIskrK8HVzI8jL8ypn1TlHXnkFW09msDUtna0nMyiorMIoBP2iInhy0igmdo2jQxvfkLnw+F6e3rGOUR068d7om3A1tt5lW0h5aYLiZp5IGSGsusIagg9glVJWCCGmAm9KKRvMTS2EmA/MBwgODu6/ZMmS8++lZJXx0ZpU7hrfie7RfjbR3VIqKirw8vK65p/LrKjmzQOpWKTkge6xJPq37p1Nc3XaG0fTaZUSKTm/ZnAhJbV1LDyezomSSm6Jj8TFIDhcVEasjyejI4KxSnnZz0gpOVhYRoSnG4FuLi0eQThaf5bU1pFaWkFKifI4W1UDgLezE138vekR6EOPAB88VdozYO/+3Fh+loXFp+nt5scjwQk4i8bXS8eMGbNHSjmgOe3ZpVellGUXPF8thHhPCBEkpSxo4NgFwAKAxMREOXr06PPv7fx0I24uTtx32/W4XSXqw54kJSVxocamcDQnjz99vhRPdzc+vvNmOgW3fh2A5uhUA0fXKaU8bxJORgN9BhTzy8l09p3JYW9GNsVVVZypMXPjyOH06Xh5qcUzRSU89NYnAHi7upIYGkR8SCBxIYHEBSuPAE/3JhuFlvuztLqG5LP5JOfksT79FDm1Z8kpKwfAw8WZ/lERzI2JZFjnaLqEBmti7dCe/bnw2F4WZmxv1TWDS7GLIQghwoBcKaUUQgwCDEDhtZxDSslPe09yXa8YzZhBczh2Np95n32Dh4sLn90zi6gAP7Ul6dgQIcRFIdDnEvTNHdSHxbsPsj45lTEJna441x3q48Xi+27lWG4+x8/mcyw3n1WHjlNeW3v+GB83V2ID/YkJ8ic6wI+O/n5EBfgS6ed7TWZhL0qqasgoKuFUYRGpeYWk5heRkldAVsn5+0QCXF24Li6GeR370SeyA93CQ2xWl8MR+e/RnTy/+0e7mgHYLuz0S2A0ECSEyASeAZwBpJQfALOAh4QQZqAauFVe41xVSno++cUVjOjb2RaSVSE1r5B5ny/Fw8WFhfNm65FE7QiL1UpNnRlfN1fuGNznise5ODnRp2P4RaMHKSV55ZWcyCskraCQtIJiThUUsz3tDCsOJF/0865ORsJ9fQj3UcqVVhcXku66lwBP9/OV8HzdXPFyc8Xb1bXZF12zxUpFrYmK2lql5GplNUVVVRRUVHG2rILcsnJySss5U1xKWc2vZuZsMBAT5E+viDBu6d+TruEhdAsL4dDunZodydib9w9v5597k5gSlcibI6bbzQzAdlFGtzXy/jsoYanNZsv+NISAob0dszhFblkF93+xDCeD4JO7b9bNoJ1hNBi4Z0i/8/sPrgUhBKE+XoT6eDE8Lvqi984VGDpTVFpfF7ucnNIycsoq2JWeRV5ZOevO5F3x3G5OTrg6O+Hm5ISbsxNGgwGjQWCsn6u2SCtSSsxWSW2dmRqzmdo6M1V1dVc8p4+bK6E+XoT5eNM7MpyO/r7ny6RGBfjpUXRX4Z2DW/nX/p+YHtON14dPs+mms6bgMDuVtx04RdfYUAJ8PdSWcs1Umep46MsVlNXUsmjeHGIC/dWWpKMSLk62/Ze7sMBQQ2zatIm+g4dQXFV9/lFaXUNFbS3lNSYqTSZq6szUms3U1JmxWK1YpMRitSIQGITAYFCmwc4Zh6uzE16uLvi4ueLl6oqfuxsBnh4EeroT4OnhEPUDtIaUktf2/8w7h7ZyU6fu/Gvo9apsuHUIQyitqObIybPMmzFYbSnXjNUq+dOyNRw7m897t02na3iI2pJ02hFCCPw83PDzcCMW/UZEi0gpeW73Rj5O3s2tcb154bpJqmVfcAhD2H30DFYpua5njNpSrpn3ftrO+mOpPDlpFKMT2sb+CR0dHdtglZKnd6xjUco+5nUdwN8GjFM1KMAhDGHXkQw83V3o1jlMbSnXxJbUdN5N2s6Nvbtx93V91Zajo6OjIcxWK3/atpqlJw/zUI/reKLvKNUjxBzGEPp1iXSoMLTCiiqe/HYNccGBPHP9WNX/0Do6Otqh1mLm9z+vZG1GCo/1GcHveg7VxDVC81fYgpIKMnNL6NslUm0pTUZKyV9Xrqe0ppZ/3TwFdwfeN6Gjo2NbqupM3P/jUtZmpPDMwPH8vtcwTZgBOMAIYf/xLAD6JEaorKTpLN13hE0paTw5aRSJYcFqy9HR0dEIZaYa7v/xG3bnZ/HKkCnMie+ttqSL0LwhHDyRjauLE4nRjhGdk1NazktrNjMoJpK7BuvrBjo6Ogp51RXcvWEJqaUFvDViOtNiuqot6TI0bwiHTmTTLTYUJyfH2Mzy4g9JWKWVF2dM1ETuFR0dHfU5U1HCHesXk1ddyUdjZzOygzY32Gp6DUFKJWVFz/gOaktpEj+nnmb9sVQeHDlY34mso6MDwImSAuasWURxbTWLJtyqWTMAjY8Q6ixWzBYr3R0g3LTOYuHFH5KIDvBj3pB+asvR0dHRAHvyMrn3x29wMRpZPPF2ugWEqi3pqmh6hGAyWwHo2kn7hrB490FOFRbzp0kjbZ6eQEdHx/HYlHmSuesXE+DqzrLJd2reDEDrIwSzFX8fD0L8tV3go7ymlneTtnNdbEfG6LuRdXTaPd+mHebxX1bTxT+YT8fNIcjdMSrkaX6E0CUmRDMxulfio192U1JdwxMTR2pea1tl0aJFxMTEYDAYiImJYdGiRWpL0mmHSCl5//B2/t+WVQwMjeTLibc7jBmAxkcIZouVBI2Hm1bWmVm46wiTu8XTTU9cpwqLFi1i/vz5VFVVAZCens78+fMBmDt3rprSdNoRFquV53Zv5NNje7ghpiv/GnZ9q9Y/bg00PUKQEuI6NpzWVyskZRVQaTLx0EjHy8TaVnjqqafOm8E5qqqqeOqpp1RSpNPeqKlPRfHpsT3c320gb46Y7nBmABofIYC2DaHaVMemrHxGxcfqO5JVJCMj45q+r6NjS4prqpmftJRdeZn8ud8YHujhuDeHmh4hCAFRYdrN4b7iYDIVdWbuHzZAbSntmqioqGv6fmNocT1Ci5p04Ex5CTevWciBghzeGTnDoc0ANG4ITgaDZncoW62Sz7fvI8rLnQHRjpNnqS3ywgsv4OFxcSU9Dw8PXnjhhWs+17n1iPT0dKSU59cj1LwAa1GTDhwsyGHmmoUU1lSxaMKtmkxFca3YxBCEEB8LIfKEEIev8L4QQrwlhEgVQhwUQjRp55azk3YjdradyiCtoIixkdqPgmrrzJ07lwULFhAdHY0QgujoaBYsWNCsBWUtrkdoUVN7Z21GCnPWLsLFYOSbyXcwMLSj2pJsgq1GCJ8Ck6/y/hQgvv4xH3i/KSfVcv2DL3cdIMDDnf4hfmpL0UExhdOnT2O1Wjl9+nSzo4vsvR7x8fjxpAuBVQhOC8E8V9fL7vz1NRLtIKXko6O7eDBpGYn+wSyfejfxftpd57xWbLKoLKX8SQgRc5VDZgCfSyklsF0I4SeECJdS5lztvM5O2jSE/PJKNh1PY97Q/jgbLGrL0WkmUkJxMaSnQ2Gh8tzf/wmKiqyAH+Bf/9UPFxc/Ro4Ei0V53HMPPPUUGI3Kw80N/PzA3//Xrxc+DwyEmBjl9Tk+Hj+eWzZu5FyUegzwjsnE/DvuAH4NmY2KiiI9Pf0y/c1dI9FpHmarlS+KT7PxTC6ToxL49/AbcHfSVq2Tn/P3tejnhXKNbjn1hrBKStmjgfdWAS9LKbfUv94I/ElKubuBY+ejjCIIDg7uv2TJEpvosyUbzuTxzcksnhnYFW9pxstL2zupASoqKtqtztrayx8mk/IVwMUFnJyUh9lcS0VFKVKaATNgQQgroaEh+Pp6A0qwg9lcgdGo6JQSrNZfzcJsvvy52ay0JwS4uioPp+Jc3KnF9YIHgAk47uJCz549ASgqKiI9PR2r1Xr+dzIYDERHRxMQEGD3/mwNtK6z0mrm/YITHK4pZbJ3OHP8ojBobKq4mAo+ExtZMfqNPVLK5kW6SClt8kC5wTl8hfe+B4Zf8Hoj0L+xcyYkJEgtctMHX8iZH3whpZRy06ZN6oppIu1BZ12dlAcPSvnpp1L+7ndSDhsmpZeXlLGxUk6aJOWDD0r5z39KuWSJlLt2SVlYKKXVevl5vvjiCxkdHS2FEDI6Olp+8cUXNtFptUqZny/lzp1SLl4s5Yv8Sc7nAzmBtTKaU9KbUjmCzfJRXpdwpzxyREqzuemaGqI9/N1bm4yyYjlu+QLZ+fN/yr9/95XachqkzmKWf9j7Lznnlz9JYLds5nXcXvsQMoELV10igWw7tW1T0gtLOJqTxxMTR6otpd1TVgZJSbBhA+zcCYcOQWQk9O8P/frBTTdB374XT9M0hblz57bKDmchIChIeQwcCOm3/pPoC94vwp+99GMD/fHwmMP06XD2LPTuDYMGzeXdd+cyahRo+Ea6zbEjN4OHkr7FIiULJ9xC7bFTaktqkCVn1pFSns6TXeexhH82+zz2MoSVwCNCiMXAYKBUNrJ+oFXWHE0BYEr3BJWVtD/q6pQL//r1yuPAAbjuOhg/Hl55Bfr0AR8ftVU2nY3jxl20hhBAMUPYyCdsZMGCXsydCyUlsG8fbN0Kr74Kt9yiGN6ECcpjwABlDUPH9vwvZT9/27GOKG8/PhxzM519A0nSoCGcKM/gy/S1jA4ZwIjgllVptIkhCCG+BEYDQUKITOAZwBlASvkBsBqYCqQCVcA8W7SrBuuTU+kdEUZ4/XyyTutSUgLLl8O338LmzRAbq1wIn3kGhg+HS7YfOBT3btjAx+PHM27jRjoCGcCzLi5M/fjj8yMUPz8YM0Z5PPUUVFTAzz8rhnj//ZCVpbx3000wYwZ46x/LFmO2Wnlhz498krybUR068dbI6fi6uKktq0FqLCZeO74QfxdvHoqb1eLz2SrK6LZG3pfAw7ZoS01ySss5nJ3L/40frraUNk1VFaxaBV9+CT/+CGPHwpw58OGHENLG8gfeu2HD+ecxwCeNHO/lBVOmKA+AnBxYtw6++goefhgmToTbboOpU5XIJ51ro7immkd+Ws4vZ9O5t+sA/tJ/LE4GbUY7AnxyagVnqnJ5vufDeDm1/O5I87mMtMTmlDQAxibqNQ9sjcmkXNjy8+HGG2HwYOXC9umn4KtXI70i4eFw993Ko6gIli6Fd95RRg/Tp8PMmUqEk16zqXGOFefxm01Lya2q4JWhU5kT10ttSVdlT1Eyq7J/ZkbEaPr6J9rknNq1Pg2y+cRpIv186BR09VA/naaTmwvPPgvR0fDyy8odcEoKrF2rxPrrZtB0AgLgN79RRlVHjigL6tnZyjTbyy8rey10GmZ1+jFm/rCQWouFJZPnat4MAIpNZcR5deSe2Btsdk7dEJqIyWxhx6kzjIyP1VNV2IC9e5W72i5dlHnw9ethyxYIDm5700JqEB4Ojz6q9O/KlXD8OMTFKYZxuMEEM+0Ts9XKS3s28dvNy0n0C+a76++mT1AHtWU1ifFhg3m97//hYrDd5jjdEJrIgcwcqurqGNpJ3x3aXMxm+OYbGDFCmRbq1g1SU2HBAuhx2XZGHVvRty988oliClFRyjrDuHGKUVyw163dUVRTxd0bvuI/R3ZwZ2I/vpo0l1APx1qVNwrbXsJ1Q2giO09nIoCBMZFqS3E4pIRly6BnT3jtNfj97yEtDf70JyWlg459CAmBp5+G06fh3nvhH/9QzGL1auVv1J44UJDDDd9/yq68TF4dOpXnBk/ERY/f1Q2hqew9k018SBC+7nroxrWwaZOyV+Af/4DXX1fi6WfP1hc51cTFBebOhV27lPWbP/4RRo1S/jZtHSklC4/tZfaaLwD4ZvIdzNbgeoHZauFs9a+LPtJOjq0bQhOwWiUHMnPo2zFcbSkOw969MGmSEu3y6KPK6ylTlN26OtpACGXq7tAhZcRw223KXoa2usZQVWfisV9W8fTOdQwLj2HV9fPoFaTN/+lXjn3GS8kfszF3J1LK8+uWrW0MuiE0gVOFRVTUmugdqc0Pj9pcWM2rY8eBDBt2imnTlItLcjLcfjtoOJS73WM0KhFdx4/D6NHK+sJ997WtqKSUknxmrP6c5WlHeKzPCD4aOwt/N3e1ZV0RZ2HE3ejKgZIU/nNyKacqsgBaPaBF/zdtAoeycgHoGRGqshLt8Ws1rwykvJ/MzO/ZuXMpzz23mN/+Vpme0HEM3Nzg//0/JezX2xu6d4eFCx1/fWFJ6kGmf/8ZxbXVLBx/K7/vNUxzmUovZWBgd6ottcR7RVFWV8mXGWvYkr+PF49+xOnK7FYbKeiG0ASSz+bh7uyk7z9oAKWaVziQhJKRZBxm8+M899yT6grTaTa+vvDGG8pu8ddfV6b+HLEWT2WdiT/+8j1PbF1Nv+AIVt8wj+EdYtSW1SRGhwygt18CffwTuTV6EvHeUfwvfQ1HStMumkKyNbohNIHks/kkhAZj1Oc9LsJqhfT06cB2YBkwHFAmoPVqXo7PgAHKwvOYMUpCvY8+cpzRwuHCs0xb9QlLTx7idz2HsnD8LYS4O0aaWKtUYoG9nDz4KG05UR5hdPWOpcBUQpx3Rz4+teL8FJKt0a9wjSCl5HhuAYmhbadMni0oKIDJk8HV9S5gKPAm8GtQu17Nq23g5AR//rMSLfb++8oidGmp2qqujJSST5N3M/OHhdRYzHw58Xb+r+9Ih7qZM9TvLbgpcjReTu7kVBfw1Zl13NBhJHOjpzAwoDuxXhGt03arnLUNUVhZRWl1DXHBesD8OfbuVfL59+sHH36YgofHxXcrHh4evPDCCyqp02kNevRQwlKjomDQIDh6VG1Fl5NXXcG8H7/m77s2MDw8htXT7uW6MMe9MXE2ONPZK5IHdj9PeV0Vd0RPJcE7mus7jGi1NvVo8EY4mV8EQOdgff0A4PPP4f/+T7lbnDUL4HYMBslTTz1FRkYGUVFRvPDCC61SYEZHXVxc4O234bPPlH0Lv34G1GdT5kn+uPV7KupM/GPQBO5M7NcmUsxMChtKsamccaGDEEIgpbT57uQL0Q2hEU4XFgMQE+ivshJ1qauDxx5Tks4lJSkRKOdorQpjOtrk7ruVXeczZ8Lu3fDCC+oV6amsM/HSnk18kbKPLv7BLJ54O/F+bWd618PJjbtjp2EUSge3tsnphtAI6UUluBiNhPs4Vo4TW1JWpqRS9vZWKpZda0lKnbZHv36KGdx6K0ybpqTdtnexor35WTy2ZRXp5cXc13Ugj/cbhZvR8S9pdVYzzoZff49zZmAP9DWERsgsLiXCzweDwfGHn82huFipUNatG6xYoZuBzq8EBcGaNUqG2uuvV6q52YNai5nX9v3E7DVfUGe18OXE23l64Lg2YQa5NYXct/NZdheps0ijG0IjZJWUEeHnQIV6bUhhoVKveMgQePddfbexzuU4OSmZVDt1UqLOyspat73DhWeZ8f1nvH1oKzNiu/PDDY69cHwhUkreOfEVVZYaojzCVNFgk39xIcRkIcRxIUSqEOKyHUlCiNFCiFIhxP76x99s0a49yC2raJf1k/PylNKV48fDv/+t5yDSuTJGo1LetFcvJbV2SYnt2zBZLLx5YAs3rv6cotpqPh47i9eHT8NHo7WOm8OG3B3sLT7GPbE3EOKmThBLi8dYQggj8C4wAcgEdgkhVkopLx3z/CylnNbS9uyJyWyhoLKKUB/H2NBiK3JzFTOYOVPJUqqbgU5jGAzKKPL//T8lF9L69UoFN1uwvyCbJ7auJqWkgBmx3Xh20AT8XLWbh6g5FNSW8OHJb+npG8fUcPVqtttihDAISJVSpkkpTcBiYIYNzqs6RZVVAAR7eaqsxH7U1ChJ6W66CZ57TjcDnaYjhDKaHD5cSXFeV9ey81Wb63hx94/M/GEh5aZaPho7izdHTG9zZiCl5L3UJZilmd8n3HZ+Y5oaiJYmSRJCzAImSynvr399JzBYSvnIBceMBpaijCCygT9KKY9c4XzzgfkAwcHB/ZcsWdIifS0hvbyKl/Yc58EesfQJ8mvwmIqKCry8tD+CaKrO06eVlBSdOrW+poZoa/2pNmrpTE0FV1fo2LFpx1+q82B1MZ8XnabAUstorxDm+EXhYVB/0bg1+vM4maw07GSUtQeDSGjx+caMGbNHSjmgWT8spWzRA5gN/PeC13cCb19yjA/gVf98KnCiKedOSEiQavLTiVMy8ZnX5Z70zCses2nTJvsJagFN0fnqq1L27StlZWXr67kSbak/tYBaOktKpOzSRcr//Kdpx5/TmVdVIR/ZvFxGf/aSHLd8gdyWk956IpuBrfuzvK5Szt32lPzdnn9Ks9Vsk3MCu2Uzr+e2sNxM4ML7gEiUUcCFplN2wfPVQoj3hBBBUsoCG7TfapRW1wDg5962hqgNsXq1ktlyxw77x5PrtD18fZWazcOHQ5cuMHLk1Y+3SMknybt5ff/P1FrM/L/ew3mwx3W4toFQ0qvxcdpKSk3lPNN9vl33G1wJW/T2LiBeCBELZAG3ArdfeIAQIgzIlVJKIcQglLULzZffKKuuBcDbzVVlJa1LaqpSIGX58qYP8XV0GiM+Hr74Am65RcmaGnmFcuT78rP5x9lDpJ+pYkR4LM8MGk+cb9vPHXaw5ARrz27l5shxxHtrI3S2xYYgpTQLIR4B1gJG4GMp5REhxIP1738AzAIeEkKYgWrg1vqhjaapNJkA8HJtu1VepIT585WC90OHqq1Gp60xYQI88AA8/LByw3FhkEJuVTn/3LuZZWmH8Te68N6oG5kSldgmchA1Rq3FxNsnFhPmFsjt0VPUlnMem4zHpJSrgdWXfO+DC56/A7xji7bsSZWpDoMQuDm33WHrJ59AeblS91hHpzX485+hb18lvcWsWcqegk+Sd/PWwV+os1p4qMd19CqxMCW6i9pS7caSM+vJrs7n+Z4P42bUzg1n273S2YDqujrcnJza7B3L2bPw5JNKzLiT/knQaSVcXZWNa3PmSMxdjvFeymYyKkoYHxnH0wPHEe3tT1JSktoy7caZqly+ObOBMSED6OufqLaci9AvA1fBZLbg4qT+Qk9r8eijcO+90Lu32kp02joeCdkE/2UjT+7Noot/MJ+Om8PoCJVim1VESsn7qV/janThvk43qi3nMnRDuAp1FgvOauX1bWXWroU9e+DTT9VWotOWSSnJ51/7fmLdmRMEBXli/XIKf328J8Mj2mdirE15uzhQksLDcXPwd9FejjTdEK6CxSoxttEsp889B88/D+0golZHBbIqSnnr4C98ffIQnk4uPNZnBPd2HcCXZa68+IIS5tzeKK+r5MO0b+niE8PkcG1GcOiGcBUkEkMbXD/YsgVycrRT7Uqn7XC2qpx3D21j8Yn9CATzugzgkZ5D8XdT7jzuugueeQYOHGh/U5WfnV5FRV01j/S8RdX0FFdDN4R2yD//CY8/ri8k69iOrIpS/nNkB4tPHEAimRPXm4d7DqGD58XTIq6uSgK8V16BRYtUEqsCKeXprMnZyoyIUcR6Ragt54rol4SrYBACq/a3S1wThw8rla6+/lptJTptgfTyYt4/tJ2laYcAuLlTTx7uNYSOXn5X/JkHHlByZaWlqZczy55YpZUPUr/Bz8WbuRrac9AQuiFcBSeDAYvVqrYMm/KvfynRRW5tJ428jgrsL8jmg8PbWZuRgrPByG3xfXig+2AivHwb/VkfH2Uz5L//DW+/bQexKrP+7HaOl6fzWOIdeDhpe9FON4Sr4Gw0YjJb1JZhM2prld2ix4+rrUTHEbFYrWzMTOXj5N1sz83A18WNh3oM4Z4u/QnxuLYMoPfdB8OGwZtvtu1KfOV1lXx66ju6+3RibMhAteU0im4IV8HVyUiN2ay2DJuRlKTURg4NVVuJjiNRaqrhqxMH+Pz4XjIrSgn38OavA8Zya3xvvJybl+erc2elJvOOHUqJ1rbKwtPfU2Gu4qG42Q6xwVU3hKvg5uxMrdmCxWrF2AZuY1asUIrf6Og0hpSSA4U5LDq+j+9OJ1NjMTMotCNP9R/DhI4JONng/2HGDOUz2VYN4XRlNj/k/MLUDiM0vZB8IbohXAUPF2cAqk11eLWBjKcrVyppKnR0rkRBdSXLTx1h6cnDJBfn4eHkzE2dejA3oQ89Am1b+H36dJg3D15+2aan1QRSShacXIankzt3aHwh+UJ0Q7gK57KcVtSaHN4QqqqUOgdd2k/+MJ0mUmMxk5R5km9PHWHjmVTM0krvwHCeGzyRG2O74+3SOp/9gQOhpAROnGiV06vKzqLDHChJ4cHOs/B2dpwSvLohXAWfehMoq6klzNdbZTUto7ISRo/WayTrKNRYzGzNOc336cdYl3GC8rpagtw8mNd1AHPiehHvF9TqGgwGGDUKtm2DKG2UA7AJdVYz/01bTqR7CFPCh6kt55rQDeEq+LorsZnnKqc5MjU1+uigvVNuqmVLzinWZKSwMTOVijoT3s6uTIpKYHpsN4aGRdtkbeBaSExUot7akiGsyv6J7Op8nu3xIE4Gx8qFphvCVfD3UGKGi6uqVVbScnRDaH9YrFbSTZUsOLKDTVkn2ZWbiVla8Xd1Z1p0VyZHJzIkLErVMpVdusA33yiFdNoCZXWVfJmxlv7+XRkQ0E1tOdeMbghXIcBTKS5cVFmlspKWU1Oj3I3ptF2sUnKipIBdeZlsO5vOLzmnKTHVwFno4hfMb7oPYkxEZ/oFR9h9JHAlzo0Q2gqLM9ZQba7RZGrrpqAbwlUI8HRHAPkVjm0IVVVQVwcxMWor0bEVUkpyqys4VHiWQ4VnOViYw978LMpMSh3wUHcvxnWMI7CkmnvHTCbMQ5trYAkJSk3vtsDZ6kK+z97ChLDriPYMV1tOs7CJIQghJgNvotRU/q+U8uVL3hf1708FqoB7pJR7bdF2a+JsNOLv4U5+RaXaUlpERga4uEAbLe3QppFSklddwcmyIk6VFXGipIDk4jyOF+crd/8oObfifAOZGtWFAaGRDAyJJMrLDyEESUlJmjUDAE9P8PVVblgcnS/Sv8cgDJqqkXyttNgQhBBG4F1gApAJ7BJCrJRSHr3gsClAfP1jMPB+/VfNE+rjRW5ZhdoyWkRNTdtOD+CImK1Wykw1lJhqKKmtprCmivzqSvKrK8itriCrooysylKyKsuoNv96tfRwcqaLfwhToruQ6BdEj8AwuvmH4OGsnbq814q7Ozh6Dsm0iiyS8vZwc8dxBLn6qS2n2dhihDAISJVSpgEIIRYDM4ALDWEG8LmUUgLbhRB+QohwKWWODdpvVcJ8vMkuLVNbRouordUN4Rx1VgtnK8spqKmioKaSopoqyutqqawzUVlnotZixmS1Ume1YLZasUgrVimRyIsuWvn5+XyVVAwodTOsUp4/ziIlFqsVs7RisliotZiptViosdRRZa6jor6dKxHg6k6Ely9xvoGM6tCJGG9/Yn0CiPXxJ9zTp83V6HB1BUfPIfnJqRV4OrkzK3K8qjrqrC2bzbCFIUQAZy54ncnld/8NHRMBXGYIQoj5wHwA/6Aw1YtvWyvKyCgovqKOiooK1TU2RmUlBAZqXyfYrj+llOSZa0kzVZBmqiCnrppccw2F5lqudO1xFgIXYcQJgZMQGITAgMAACMRFezisVis5Ob9GnwkEAhCAUQiMKD9vROAiDPgKA0HCGTcnV9ycjbgZjHganPAwOOFlMOJlcMbP6IyP0RmnC4unVAKVZZjPlnGC01zrHi5H+Hz+7ndgMmlfJzTcn2fIZ6/hGKOsPdjzy051hNVT6Le8RT9vC0No6Hbl0gFgU45RvinlAmABQHjHTnL06NEtEtdS0lz2sDn7J/oOvu78voQLSUpKQm2NjbFvH2zblsTs2aPVltIoLenPWouZTVknWZOewk/ZaRTVKhdsdydn4nwDuc67AzHe/kR6+RLs7kmQmycBbh54u7ji6eRyTZE3jvB3B8fQee+98P772tcJl/enlJInDrxJYI0vjw68B1ejelN3ZmsNS0690KJz2MIQMoGOF7yOBLKbccxlmC3qjyM7+iv53c8UlzZoCI6Aq6vjz9FejfxqJdb+q9QDlJlqCXB1Z3REJwaGdKR3UDgJfsGaCbPUuRxHntLcV3yMo2Vp/DZutqpmAJBekaSJKaNdQLwQIhbIAm4Fbr/kmJXAI/XrC4OB0qasH5gt6l/FogL8AEgvLKFHB8fMGx0ZCSaTMk/rqP94DVFQXcn7h7ezKGUfJquF66O7MDuulyo7bnWaR20tFBQ4ZjlXKSWLMn4g2NWfiWHXqS2Hk2U/4OXUoUXnaPGfQUppFkI8AqxFCTv9WEp5RAjxYP37HwCrUUJOU1HCTuc15dxmixUppap5xKPqRwinC4tV09BSfHyUkNOsLOjYsfHjHYGduWd4aPO3lNRWc1OnHjzccwixPgFqy9K5RlJTlf0xjrhOvr/kOMfKTvPbuNk4G5xV1VJZl0dO9W56B8wDljb7PDbxZSnlapSL/oXf++CC5xJ4+FrPa5WQV1xBaIB6cdTuLs508PXhlAMbAiglM48fbxuG8L+U/fxtxzqivP34cuJtJPgFqy1Jp5kcP+6YO+illHyRvlozo4NT5esASSfvyS06j+bH1enZRWpLoFOQPyfzC9WW0SLOGYKjs+DIDv6yfQ3DwmP4dupduhk4OI5qCOdGB3M6TlB9dACQVr6WYLfu+LhEtug8mjeE0xowhPiQIE7mF2Fx4GBpV1fHN4SNmam8uGcT10d34eOxs/B1ccxFfp1fcVRD+CpjHYEuvkwIU39/bXFtGsWmk8R6T2rxuTRtCAYhSMtS/848PiQQk8VCelGJ2lKajacn/PKL2iqaT7mplie2rqarfwivDZ/WJkqatnekVD6T/furreTaOFqaxqHSVGZGjtXE6OB0xQYEBmK8xrb4XJr+r3J2EqRlqm8IiaFKsZCU3AKVlTQfLy9IT4czZxo/Vot8fnwvhTVVvDxkCm4qpmvWsR3JyUqUUZ8+aiu5NpZmbsTbyYPJ4UPVloKUklPlGwhz74e7U8uDKrRtCEYDJzMLkCoH0ccFB+JkMHA0J09VHS1l6lSlrrKjUWMx89HRnYyO6ETvIMfMIqlzOStWKHWVHSnCqIhydhQe5voOI3Azql9Wt7A2mfK6TGK9bVNQQtuG4GSgoqqWvCJ1k8u5OjvROTiA5LP5qupoKTNmOKYh7Mw9Q1FtNXcl9lNbio4NWblS+Uw6ErtFKk7CyA0dRqotBYDT5T9iwIkor1E2OZ/mDQHgRIb6F+Lu4aEczs5VfbTSEiZOVOrXlpaqreTa+Ck7DReDkSFh0WpL0bERZ8/CsWNKTWVHocRUzhHSGRs6CD8X9VOKSyk5XfEjHTwG4Wr0sck5tW0IRgNCQEq6+lM1PSNCKa6qJqvEcTOfenvD2LHw1VdqK7k2kovy6BoQgruT+gt4Orbhiy9g2jSlToejsDpnC2Zh5abIMWpLAZTpokrzWaK9W76YfA5NG4IQEBnqx3ENGEKfSGXuet8ZzWfsviqPPQavvgoWi9pKmk5edaWmi7zoXBu1tfDGG8pn0VGos9axOucXYmUoHT20kcImvSIJgZGOnsNtdk5NGwJAYnQIx0+rbwjxIUF4uDiz70yjOfk0zYgREBwMy5apraTplNfV4u2s/gKejm1YtAi6d4e+fdVW0nR+KThAsamM/jJObSmAMl2UUbGZMPd+NpsuAgcwhC4xoeQUlFFaXt34wa2Ik9FAn8hw9mRkqaqjpQgBTz4JL7/sOBlQPZ1dqDKb1JahYwMsFnjlFeUz6Eh8n72FDu7BxBCithQASuvSKas7Q5SXbRe3tW8IscrwLPl0rspKYGB0JCm5BZRU1agtpUVMm6aU1dy4UW0lTcPPxY2Cmiq1ZejYgBUrlBrKDlD64DynK7M5WpbG1PBh9WWQ1OdMxc8AdPQcYdPzat8QYhRHTk5T3xAGxUQigd3pmWpLaREGg3KH9pe/OMZaQoJfMMeK8xw6wktHScH+zDPK586R9h6szdmGkzAyNnSQ2lLOk1m5lQDXBDydbTti0bwheHu6ER3uz5G0s2pLoWdEGG5OTmw/5aDbfS9g7lwl4d2776qtpHF6BIZSZqolvbxEbSk6LeDVVyEqStmM5iiYrHX8mLeLoUG98XX2UlsOADWWUvJrDhHpafud0po3BIAecR04fCJb9TtEFycj/aMj2JaWoaoOW2AwwIcfwj/+ARka/3WGh8cA8GNWqrpCdJrN8ePw73/D++871uhga8FBKsxVTAoboraU82RXbkdiJdKG0UXncAhD6BUfTnF5NWdyS9SWwtBOUZwsKCK3TN3d07YgMRH+8Ad46CFtLzBHe/sT7xvE2owUtaXoNAOrFebPh7/9TRkhOBLrzm4j1C2QXn7xaks5T2blVtyM/gS5drH5uR3DEBIiADiQon6Ez/DOym7ZLSfTVVZiG554QhkhaH2z2vTYruzIPcOpMvXToetcGx99pOw9ePiaS2SpS15NEQdLTjA+dBAGoY1LpVVayK7aQYTHEEQraNLGb9kIMeEB+Hi5sf+4+oaQEBpEsJcnW1JPqy3FJri4wH//C48+qpQz1Cq3xPfGSRj44vg+taXoXAOHDimLyB9+qJRxdSSS8nYjkYwJGai2lPMU1iRTay0jwrN1qrS1yBCEEAFCiPVCiBP1X/2vcNxpIcQhIcR+IcTuaxZpEPROiNCEIQghGBEXwy8n0zFbHLdgzoUMHgzPPqss9mk1z1GIuxfTYrryvxP7KaiuVFuOThMoKFCS173xBvTsqbaaaycpbw/dfDoR7h6ktpTzZFXtAAThHq1jUi0dITwJbJRSxgMb619fiTFSyj5SygHNaahvYgSZuSXkF6s/dz8qIZaymlr2Oviu5Qt58EElNnzuXO2Gov6+9zBMFjNvH3TgSj/thLo6mDUL5sxRPlOOxunKbNKrchgVoq0MuzlVuwh0TcTN6Nsq52+pIcwAPqt//hlwYwvPd0X6dVWqw+89pv4egGGdonA2Gvnx+Em1pdiUN9+EykpliK9FOvkEcFt8Hxam7ONwofphyDpX5ve/V5IpvvCC2kqax5b8/QgEw4L6qC3lPHXWSvJrjhDu0ax76iYhWhLKKYQokVL6XfC6WEp52bSREOIUUAxI4D9SygVXOed8YD5AcHBw/yVLlgBgtUqeXXSQXrF+3Dxc/TTI7xw8SU5VDU92j8LbW/uJ1yoqKvDyajyO2mxW0hKHh0NgoB2EXUJjOiutZv6SfQA/owt/C+uBUaUYxqb2p9qooTM/H/LyoGtXJby5KWitPz8RG3DDhdvkxakh1NRZ7XqcvKDPCCmYh3vtlaOexowZs6e5MzFIKa/6ADYAhxt4zABKLjm2+Arn6FD/NQQ4AIxsrF0pJQkJCfJC/u+1b+XMx/4rtcA3ew7JxGdel5+u+F5tKU1i06ZNTT72yBEpw8Ol/Pzz1tNzJZqi8/vTyTL6s5fkWwe2tL6gK3At/akm9tb53ntSduwo5cmT1/ZzWurPrKo8OXXz7+TyzE2Xvaemzl3578jPU0bIOkv1VY8DdssmXF8bejTq31LK8VLKHg08VgC5QohwgPqvDaYllVJm13/NA74FmrUHfED3KDLzSskpUL8mwdgunXEyGNiTX6y2FJvTrRts2AB//jN8/LHaai5nanQXboztzhsHtrA3X/1AAx2FN99UEtclJUGnTmqraT7bCg4CcF2gtlbCc6v3E+TWDSeDW6u10dI1hJXA3fXP7wZWXHqAEMJTCOF97jkwEWWEcc0M7Kbsatl1RP2ttf4e7gzpFMXuvBLVd1C3Bt26wY8/wt//ruwu1Rr/GDyBcE8fHt68nLxq9QMN2juvvAJvveX4ZgCwvfAQnTwjCHVTYc70CtRZqymsOUaoe59WbaelhvAyMEEIcQKYUP8aIUQHIcTq+mNCgS1CiAPATuB7KeWa5jTWKTKQQF9Pdh7WxqawqT0SKKo1sT/TsYvmXImEBNi0Cf75T+XuT0v4uLjxwaibKDHV8JtNS6kx16ktqd3y/PPK5rPNmyFa/eW9FlFWV8mxslMMCuyhtpSLKKg5isRCiHvvVm2nRYYgpSyUUo6TUsbXfy2q/362lHJq/fM0KWXv+kd3KWWz4w6EEAzqEcWuIxlYrerflU/oEoeTEKw6dFxtKa1G587KP/o778Af/6gsOmuFHoFhvDH8Bg4W5PCHLd9hsbaNfSGOgsmkpD358ktlZBAZqbailrOn6ChWJAMDuqst5SLyqg8AghC31jUqh9ipfCFDesVQUl7NMQ3UR/Byc6VXkC8/HD5OnVaD921AdDTs2KHsOp04UYki0QqTohL464BxrMlI4emd69rk9J0Wyc6GUaPg7FnYtk2JSmsL7Cs+jo+TJ/He2kq6lFdzEH+XTrgYWzei0eEM4bqeMUSG+lFcpo2CKYNDAyiqquaXNpLb6EoEBMDq1XDddTBgAOy+5v3mrcd93QbyUI/r+F/Kfl7cs0k3hVZmyxYYOFAptLR0KfjYroKjqkgp2VdyjD7+iRg1krsIlPxF+TVHCHbv1eptObV6CzbG19udpf+6V20Z5+ke4I2/hzvf7j/K6AQHX01rBKMRXnxRMYSpU5W1hXnz1Fal8ETfUVTVmfjw6E7M0srfBoxDOFKeZQdASqV+xnPPwWefweTJaiuyLWeqcykyldHbL0FtKRdRajpNnbWy1aeLwAENQWs4GQxM79WF/+08QFFlFQGeHmpLanVmzlQ2Hd10k7K+8MYb4OenriYhBH8fNAEng5GPkndRazHz3KCJGJu6M0rnqhQUKNlKjx1TpogcPZKoIQ6VnADQVKprUBaUAYLcurV6W/p/iw2Y1a8HdVYr3+4/qrYUu9G1qzJt5OmpJC5b06y4MdsihOCvA8by2x5D+F/Kfn7703I9+sgGfPst9OoFHTvC9u1t0wwAjpSmEejiS7ibdpLZARTUJONs8MLHuWOrt6Ubgg2IDwmif1QHluw5pInoJ3vh5aVMIXz6qZIc7+67lTtJNRFC8ES/Ufxt4DjWZaRw+/rFFNZoY73J0cjJUZLTPfEEfP01/Otf4O6utqrW42hZGl19YjU31VhYe4wg1y6tUv/gUnRDsBG3DuhFelEJW9tAec1rZdw4OHxYyX3UvbtiEGqv697bdSDvjbqRI0W5zFj9GceLNRQapXGsVvjgA2VUEB8PBw/CsGFqq2pdimpLya8tpqtPrNpSLsIi6yg2nSTQLdEu7emGYCMmdYsnwMOd/+3ar7YUVfDygtdfVyKR3nlHiUb68Ud1NU2J7sJXk27HZLEw84eFegnORpASfvgB+vWDhQuVTYkvvNC2RwXnOF6uRAkm+sSoK+QSSk2nsMo6Alx1Q2gSFquVfceVlNhqhhu6ODkxu39PNh1PI7NYo1Vm7ED//rBzp1Kr+Te/UfYt7Nmjnp4+QR1Yef3dxPkG8kDSMl7ZuxmzvoHtMrZtU+phPPYYPPOMElraQ1ubdVuV1IozGDDQyTNCbSkXUVSrLHQHuNpnodvhDcFoMPDEv1eQkVOMEEJVU7htQC8MQrBo5wHVNGgBgwFuuw2Sk5VIpBtugFtugRSVbtDDPLz5avJcbovvw3uHt3HXhq/0qmv1HDkCN96o/H3uvlvZfHjTTaCxafRWJ7X8DB09QnE1uqgt5SKKa09iFK54O9tnG7hDG8K5Epb9unZk8dq9AFhUXNQN8/VmUrd4vtl7mMpak2o6tIKLi5La4MQJ6N0bhg6Fe+9V5qTtjZvRiZeGTOaVoVPZk5/F1FWf8EvOafsL0Qh79sAdd8CYMTBypGLW994LTu00ED214gxx3q0fxXOtFNeexM8lFoOwT0FqhzYEQ/1tzO1T+rN++zEAnIzq/kp3D+lHeW0t3+xtVkLXNomnp1KFLSVFCVmcMkW5EK1YYf9ynXPierF86l34uLhyx/rFvLJ3M3XWtpt25ELMZiVaaPhwZS9Jr16KWT/2GLi1XkZlzVNiKqekrpxYjU0XAZSYTuHnYr84X8c2BINiCL0TIpASDqQoufHVDP3sHRnOgOgIPtm2B5O5fVxomkpAAPz1r3DqlLK+8OKLShTL669DqR2XXbr6h7By6t3cGt+b9w5vY9aaL0grK7KfADtTVKTsKu/USUlR/Yc/wMmTSjipb+uU5nUoTlcqtdFjPDuorORiai1lVFsK8HOJsVubDm0I8Ou00cQhXVi8Rpk2stavI6i1nvDA8EGcLavgu4PJqrSvdVxc4PbblYR5//sf7NoFsbFw//1QXm6fUYOHswsvDZnCuyNv5HRZMdev+oQVp9rOxkKzGdauhdOnlYy1R4/C8uXw888wa1b7nRpqiDNVSqLMaI8wlZVcTJlJCWH31Q2h6RjrRwlzJvbl531pwK/TRmptMBkeF0238BAWbNmlp2RuhOuuU9InHzoEXbpAZqaSRvnRR5Vdsa3t6dfHdGHd9Pu4LjSKCM+mZWmrsWgoB/gFWK3KBf/hhyEiQokW8vBQ0k189pkSTqpzOZnVeXgY3fB30VaWvtI6JRTWx8V+mVcd3hCEEFisVmI6BNAzLpyU9F83IKVlFqiSJlsIwYMjBpFeVMLqw3rse1OIiFDqLXTtquRHCgiAe+5Rpjn+/GfYu1e54LUGoR7efDJuNgNCrh7JsfTkIZ7fvZE71i3mh7Ls1hFzjVgsSpjv449DTMyvZrBtm2KoISEQGqq2Sm2TXZ1HB/dgze1QLjOdQWDE29l+U1kObwjA+QRm7/1lNp0iAgBYtHo3j722nNc+38S/Prf/DqnxXeKIDwnkg5926KOEayQhQbm7TU5W8uhIqYSxhoUpXz/6CDLsvCF86clDPL1jHU7CyLyuA0iqyOOdg1vtK6KeU6dgwQKYPVu54M+bB66uyqaygweVBfy2mm+oNThbXUi4u7byFwGU1WXi5RyOQdhvfq/NzCR+vX4/n6/aiZRw5/UDOJyawzMPTgYJr3y6kY07Uhg32H5pbQ0GwUMjB/PYN6tZc+QE1/e0z07DtoQQ0KeP8nj5ZcUENmyA9evhySeVUcSECcpjyBDl4tgaHCo8y0t7knhm4HhuiVdKGB47epTtuRnMtwzGxdi6IYE5ObB1q/J7r18PlZXK7zxtmpJpNkJ7wTEOg1VayastYmhw65ambA7ldVl4O9v3j9siQxBCzAb+DnQFBkkpGyybIoSYDLwJGIH/Silfbkm7l5KVV8J3mw8zb/pgOgT78tHy7cRGBNA3UZkCuHl8b9ZuS7arIQBM7pbA+yE7eDtpG5O6xaseEuvoREUpsfL33qtMHx04oBjEe+8p00uenspO6f79lfny/v1bXslLSskbB35mUGjkeTMAyKyrwtPDw6ZmICVkZSnTY3v2KI+9e6G2FgYPhvHjlSmhHj3a38ax1qLEVI5ZWgh29VdbykVIKSmvyyLYzb6lPFs6QjgMzAT+c6UDhBBG4F1gApAJ7BJCrJRS2iykY8ehdAJ8PZg5TvmHNVusvPTxegAyzhaz71gWoQHeSCntOk9oMAj+MHYYDy9eybL9R5jTv6fd2m7rGAzQt6/yePxx5WJ66tSvF9O33lK+urgo5hAfr0QyXfjw8mq8ne25GfyUfYodsx45/70zFSUUW0wkeHXAKuX5/TBNpaxM0Xrh48QJRbuUv5ravfcq2WSjonQDaC3ya0sACHL1U1XHpZis5dRZK+y6fgAtNAQpZTI0Gs0zCEiVUqbVH7sYmAHYzBB6xnfg4xXbz78O8vfEz9udO55aSHS4P+VVtcy/eYgqi0ZjEzvRt2M4b2/axg09u+Du4mx3De0BIZR5806dlLBKUC6uGRmwf78Sd3/iBKxb9+tF2NtbMYaYGAgKAn9/pdDPhV+/rjrOqMCu1BR5kGsEC2Y25Z4hy1TNrd6dyc8TWCxQUwPFxVBS0vDXgoJf262uvtiYOnVSpoD69lWmf/SLv/0orisDINBFWxsyKupyAPCysyEIW8TqCyGSgD82NGUkhJgFTJZS3l//+k5gsJTykUuPrX9/PjAfIDg4uP+SJUuapOHNb5OJDfMisaMv+1ILiQ71onO4N2fyK/H3ciE2zOvc+ZvxG16ZiooKvBq51UwtqeBf+08wPTacqdHqxDo3RacWsKfOujowmZQpGYtFid23WC5+vk/kkSZKub4qHikh1bmIoy75RLkb6VMQBygXcCGU2H6jUXk09NzVVXnYcw+A/ne/Ogc4xTrDPh60Tsabxqsd2ktnldtR8gO/ICzvYVzrrm0dYcyYMXuklAOa026jH00hxAagoavYU1LKFU1oo6Er8BVdSEq5AFgAkJiYKEePHt2EJsA7tDMbth/np6PZBPh4c8v0MXSKCGzSz7aEpKQkGtM4Gthfs5KNaWf4083TCfSyf5nNpujUAlrTuSM3g99uXk5lX+Ujm5ZTypiwOPqXwZS5o9UV1wS01p9XQi2duRkmOL2PSSMn4GJofPRuL53JJQXk58PIwVNwdwpo9fbO0aghSCnHt7CNTODCrFGRgM2DuPt37UjfxEhyCkqJCPG76D17rx00xGPjh3PDu5/zdtI2/j5tnKpadJrO4NAovpl8B6/u20yYhzeP9RnB0LBodmz55aLj1makMDqiE67GNhO41y4or6vE1eDSJDOwJ1XmPAzCGTejfRe77fHp3QXECyFigSzgVuD21mhICM6bwYUmoLYZAHQKCuDWgb35ctcBbh3Qiy5hwWpL0mkisT4BvDfqpiveWBwvzueBpGUk+AXxytCp9AnSVk4cnStTYa7Gy0l7FYCqzAV4GIPsfu1qURykEOImIUQmMAT4Xgixtv77HYQQqwGklGbgEWAtkAwskVIeaZnsK+pp8LlW+N3oIfi4ufL86k2q1m3QaR5X+kwl+gfzydjZlJtqmfnDQl7as0mz6S10LqbKUo2Hk/ZSvVabC3B3av0p70tpkSFIKb+VUkZKKV2llKFSykn138+WUk694LjVUsoEKWVnKeULLRXtqPh5uPF/44ezOyOL7w4eU1uOjg0ZE9mZtdPv45a4XvznyA6uX/UJ+/K1kd5C58rUWEy4G13VlnEZ1ZYi3I0OZghaprqmjg07jmvuTvzmvj3oFRHGK+t+oqy6Rm05OjbEx8WNl4ZM4fPxt1BdV8fNa/TRgtaptZpwNWirShpAjaXI7usH0IYNYc3WZJ5653v219dI0AoGg+CZ68dSVFXNGz+qkwtHp3UZ2SGWNdPvZU5nZbQw/ftPOVx4Vm1ZOg1gsppxNmgrEEBKK7WWMlyN9t8b0WYNYcqwrvh4ufHlDypWeL8C3TuEcnv9AvPBTP1C0RbxcXHj5aFT+GTcbEpqa7hx9ee8eWBLu6nO5ihYpAUnOyaPawomawUSK25GP7u33WYNwc3VmZvH9uanvSc5k1ustpzL+MPYoYR4e/HUinWYzPqUQltlTERn1k2/j6nRXfj3gS3MXrOIU224OpujYZFWjEJbl8Fai7J72tVo//oM2uoJGzN7Qh+cjEa+/GGv2lIuw8vNlWdvGMeJ/EI++Gmn2nJ0WhE/V3feGjmdd0bO4FRZEVNXfcL/UvZrbn2rPaLFv4HJWg6Ai8Hb7m23aUMI9PNk8tAurPrpMMVlVWrLuYzRCZ2Y0asrC7bs4ki2/Qv56NiXaTFdWTv9PvoFdeAv29fwm01LKarR3udSR11M1goAXIz2T+XRpg0BYO7UAdTWWfh6/X61pTTInyePxt/DjT8vX4fJrM8vt3XCPLxZOOFWnh4wjp+yTzHlu4/ZejZdbVntFqMwYJHaKmBVZ1VuEpwN9k9x0+YNITYikBH9OvP1hv1U19SpLecy/DzcePaG8aTkFfBO0ja15ejYAYMQ3NdtIMum3Imnswtz133Jy3uS9AVnFXAyGLFIbfW7ud4QnIRuCK3C3dMGUlZRw/JNB9WW0iBjEztzc9/ufLhlFztPZ6otR8dO9AgMY9X193BrfB8+OLKd29Z+SXZlmdqy2hXOwpk6q7aCOvQRQivTM74D/bt25IvVu6kxaW+UAPCXyaOJCvDjiWU/UFKlb1hrL3g4u/DSkMm8NWI6ycV5TP3uY9afOaG2rHaDi8EJk1Vb1wSzrAXAyWD/HdTtwhAA7rvpOgpKKlmZdFhtKQ3i6erCv26eQmFFFU9/t16T0Q86rcf02G58N+0eIrx8+c2mpby0ZxNmq7bmttsibkZXaqwmtWVchKXeEIxCN4RWQ0mPHcHnq3ZSa9LWEPEcPSPC+MO4YaxPTuWrPYfUlqNjZzr5BLBsyp3ckdCX/xzZwZ0bFpNXXaG2rDaNu9GVarO2RuQWqwkQCGxXr7uptBtDALh/5hDyiytZkaTdi+28If0Z3jmaF39I4mhOntpydOyMq9GJ56+bxGvDrmdffjbXr/qEHbkZastqs3g4uVNhqVZbxkVIzBiEsyoZm9uVIZwbJXz23U7NriUYDIJXZk4mwNOdR5esolRPgNcuublzT1ZMvRtvZ1fmrlvMwuN79WnEVsDLyZ0qcw1WDYWeWqUZg11K1VxOuzIEIQTzbx5KQUklyzZqM+IIIMDTgzdmT+NsaTlPLFuD1apfCNojif7BLJ96FyM7xPL0jnU8sXW1njnVxvg4eyKRVJq1M0qQWBEqpdNoV4YA0K9rRwZ1j+Kz73ZSWa2txaQL6dMxnD9PHs3mE6d476ftasvRUQkfFzf+O3YWv+81jK9PHuKWNYvIrSpXW1abwddZ2Q1cUqedtRopJQaVLs3tzhAAHpoznJLyahat3q22lKty28BezOjdlXeStrPx2Em15eiohEEIHuszggWjZ3KitIDp33/GwYIctWW1CfyclXxBJSbt7P+QSECdio/t0hC6dQpj3KAE/vfDHgpLKtWWc0WEEDw7bTw9O4Ty+NIfOHY2X21JOioyMSqBpVPuxMlgYPbaRaw8dVRtSQ5PgIuSUbRIQ4agJi2tqTxbCHFECGEVQgy4ynGnhRCHhBD7hRCauC1/aM4wTGYL//1W2+ki3JydeOfW6Xi7ufLbL1eQX65dA9Npfbr6h7Dy+nvoHRjG739eyev7f9YXm1tAgKtShKbQVKqykl8RCCTqLHK3dIRwGJgJ/NSEY8dIKftIKa9oHPakY6g/M8f2YkXSIU5nazs/faiPF+/dNp3iqmoeWbySmjp9YbE9E+jmwRcTbmN25568dfAX/rDlO32xuZl4Gt1xN7pSUKudmilCGBzTEKSUyVLK47YSY2/uu/E6XF2ceWdxU/xMXbp3COXVmVM4mHWWJ5b9gEXfxdqucTEaeWXoVB7vO5IVp45yx7rFFFTro8drRQhBsKs/eTUaMgSMSJUS7tlrDUEC64QQe4QQ8+3UZqP4+3hwz/RB/LwvjV1HtL/5Z3zXOP40aRTrklN54YckfaqgnSOE4OGeQ3l35I0cLjrLzWsWkl6unQuboxDiFkBuTaHaMs5jFM5YpTojPtHYRUUIsQEIa+Ctp6SUK+qPSQL+KKVscH1ACNFBSpkthAgB1gO/k1I2eFtebxjzAYKDg/svWbKkqb9Ls6gzW3l92VGcjQYevakrRsO1re5XVFTg5WXfQhbfpGaxITOPGbHhTIlu6E9zOWrobA66zuaRWlvOG/nHEcD/C+5CJ1dFm9Z0Xgk1dW4Q+zlCBr+XNyAaie6xh84S742U+mwkKut5RDPu2ceMGbOn2VPzUsoWP4AkYEATj/07ink0emxCQoK0B0m7TshBd7wmv1q795p/dtOmTbYX1AgWi1X+8ZvVMvGZ1+WS3Qeb9DNq6GwOus7mk1pSIIcvfU8mfvGqXJeRIqXUps6GUFPn8sxNcurm38mS2rJGj7WHzoOFn8tPU4bIOktNs34e2C2beS1v9SkjIYSnEML73HNgIspidKNYLPaZEhnZvzODekSzYOlWikq1X9LQYBC8MGMiI+JieGbVRn447LDLODo2pLNvIMum3EWifzAPJC1jSap2d+NriQj3EACyqrUR1n0u7bVZ2j9tTUvDTm8SQmQCQ4DvhRBr67/fQQixuv6wUGCLEOIAsBP4Xkq5pinnLy+xT4cIIXjsjtFU1dbx3pKf7dJmS3FxMvLmnGn069iBx5et4Ud945oOEOzuyf8m3MawsGie2Lqa1WXZakvSPOcM4UyVNuqaG4UbABargxmClPJbKWWklNJVShkqpZxU//1sKeXU+udpUsre9Y/uUsoXmnr+mmozGafs49qxEYHcOqkv3/10hEOpjvFP5OHizAe3z6BbeAiPfv09P6eeVluSjgbwdHbho7GzmRbTlSUlGTy/eyNWPQDhioS4BeBicOZM1Vm1pQDgZFAMoU7aP7+StncqC1jy6Ra7NXffjUMI9vfilU83YrY4Rlinl5srH95xE3HBATyyeCW/nNQLtusoYalvjZjOeK8w/nt0F49v/V4vuHMFjMJAR49Q0qu0kQ7EWXgCv5bStCeaNgQPTxc2/nCQnEz7bBzzdHfhj3eNISU9n8Vr9tqlTVvg6+7Gx3feTEygPw/9bwU/nTiltiQdDWAQgrn+0TzWZwRLTx7m9z+voFbfwNYg0R7hnK7UxsyAs1GppVxntf++Ek0bgpe3C0ajga/sOEoY1T+OEf06s2DZVrLySuzWbkvx93Tn07tnERccyMOLv9OT4ekAyvrY73sN468DxrI6/Tj3/7iUqjrtZvlVixjPDhSZyiirU39zn4tBCWs1Weyf1VbThmAwCibf2I/13+0nN6fELm0KIXj8rrEYDYKXP9noUJu//D3c+eTum+kWFsyjS1bp0Uc657m/2yBeGTKFX86e5u6NS6ioq1VbkqaI9ewAwKnKLJWVgItBycBqsto/JbemDQFgzt3DAVj8if2if0IDvfntnOHsPJzOD78k261dW+Dr7sZHd86kT2Q4j32zmsW7DqgtSUcjzInvzVsjprM3P4u7NiyhzKRX4ztHrFcEAGkV6huCq/GcIegjhMsICfNl8o39WLdiH2ez7Lct/+ZxfegV34F/f7FJ0ymyG+LcQvPI+Fj+/v2PvLd5u0ONdHRaj2kxXXl35I0cKszhjvWLKanVTqUwNfF38SHQxZeTFWfUloKT8MAgnKm12D8Dq+YNAeC2+0ZiMAq+WJBktzYNBsFffzORWpOZlz7Z4HAXVHcXZ9659QZm9O7KW5u2sfhEpp4QTweAydGJ/Gf0TI4V53Pruv9RVKP9zZj2oLNXR1I1YAhCCFwNvrohXImgEB+mzRrIxtUH7LYvASA6PICHZg/n570nHW7qCMDZaOSlGZO4b2h/NmcX8Mji76gy1aktS0cDjI2M4+OxszlVVszt67/UTQFI8I4isyqPKg3UV3Yz+lNtsX+iQocwBIBb5o3A1c2Zz9//0b7tTupHn8QIXlu4idxCx6tlazAIHp84klvjI9l84hR3frKEvHLt1I/VUY/hHWL4aMws3RTqSfCORiI5Ua7+KKGb/y3EeU+xe7sOYwh+/p7MnDuEnzceJeWo/RZ+DAbB3+ZPwmKx8tyHa7FaHWvq6ByjI4J577bpnCoo5pYPF+vlOHUAxRT+O+ZmxRTWfUlhOzaFBO9oAJLL1d/HE+czlWjvMXZv12EMAeDmO4bi4+vBx+9ssGu7ESF+PHr7KHYdyeCrdfvs2rYtGZ3QiS/unYNVSm77aDFrj55QW5KOBhjRIZaPx87iVHkxd65fTGlt+4w+8nb2oKNHKMll6huCWjiUIXh6uXHbfSPYtyONPdtS7dr2jWN6MqJfZ9796mdS0vPs2rYt6RYewtfzbyMhVNmr8NaPWx121KNjO4aFx/Cf0TNJLS3krg1ftduQ1G4+nThWdhqrbJ8BGA5lCADTZg8iLMKfD99ch8WO+YaEEPz1/on4ernx9Hurqa5x3MXZEG8vFt4zi5l9uvPeTzt4ePFKSqvb5wVA51dGR3TivVE3cqQol3s2ft0uN6918+lEhbmKDI0kurM3DmcILi5O3PvIeE6dyGXDqv12bdvP252/PziF9Jwi/r1ok13btjUuTk68MGMCf50yhp9TT3PzfxZxNMdxRz46tmF8x3jeGTmDAwXZ3Lvxa6rNjnvj0xx6+sUBcLjUvjMQWsHhDAFg5ITudO3VkU/f3Uh1lX3vYgZ2j+KuaYNYkXSY9dsdOzWEEII7Bvdh4bzZmK1Wbv3vYr7ec8jh9lzo2JbJ0Ym8MXw6u/Iy+e3m5Zgs6hR8V4NQt0BCXAM4WNI+19cc0hCEEDzw2CSKCivsmh77HPNnDqFnXDgvfrSOfDsV8WlN+nbswLIH5jIgOoKnv9vA48vWUFHT/qYLdH7lhtiuvHjdZDZlneQPW1a2q9TZPf3iOFSSqtl1BIu19f43HdIQALr27MjoST345out5Nkp8d05nJyMvPDINFycnVi4Mc2h1xPOEeDpwYd33MSjY4byw+Hj3PSfRRzMbJ/zqDoKtyX0OZ8l9Ymtq9tNkZ0+fgmUmStVz2uUW72fXflvsj3vNarNRZyt2sf3Z37DD5m/JatyO1Zp+5GbwxoCwL2/mwDAgjfW2b3t0EBv/vHQVPJKanj5U8dLbdEQRoOBh0YNZuG82VisVm7/+Cs++GmnnvKiHXN/t0E81mcEy9IO8/xux8r+21x6+SUAcKAkRTUNxbUn2ZX/FqWmdEpNp9hd8A5HS76ki+/NRHuNYk/BuxTW2n7K2qENITTcj1vuGcHPG46wf2ea3dsf3DOa8f3CWfNLMss2tp2C5v2iIvj2wTuY0DWON378hTs+WUJGUYnasnRU4nc9h3JPl/58nLyb9w5vU1tOqxPk6keke6iqhpBc8jUh7j0ZH/E6kyLfoaIuG3/XODr7TKZnwF14O3ckr9r215wWGYIQ4lUhxDEhxEEhxLdCCL8rHDdZCHFcCJEqhHiyJW1eyuy7hhEW4c+7r67GXGf/xa+xfcIY2juW17/YxP7j6qfOtRW+7m68Pmsqr86cQmpeETe+/wWLdx9sF3eIOhcjhOBvA8dzY2x3Xt33EwuPO041webSxz+Rw6UnqbOqMx0sseBm9D//2sclihrzr7mNnA3umFuhxGZLRwjrgR5Syl5ACvDnSw8QQhiBd4EpQDfgNiFEtxa2ex5XN2ce+uMUMtLyWb54u61O22QMQvDsQ1MID/bhybe+c8h8R1dCCMENvbqw8rd30jsyjL+v2si9ny8ls9j+WRh11MUgBK8Om8r4yDj+tmMd351yvGSP10Jf/0RqrSaOlqqzaznANZGzVXupqMuh1JROnbWSYlMqm7L/zJazz1NqSifcY6DN222RIUgp10kpzxVp3Q5ENnDYICBVSpkmpTQBi4EZLWn3Uq4bmcjgEQkcO6zOHbqPpxuv/mEGdWYLO4+0vSL34b7efHzXzfx92jgOZuXy9qa2P22gcznOBiPvjJzBwJBIvko90KZHi7184wl1C6TMrE4tlEjPIbg7BbIl9zl25b+Fl3MHRob9g0C3LjgZXOkf/DAh7j1t/jcQtjqhEOI74Csp5ReXfH8WMFlKeX/96zuBwVLKR65wnvnA/PqXPYDDNhHYegQBBWqLaAK6Ttui67Qtuk7bkSil9G7ODzo1doAQYgMQ1sBbT0kpV9Qf8xRgBhY1dIoGvndFF5JSLgAW1J93t5RyQGMa1cQRNIKu09boOm2LrtN2CCF2N/dnGzUEKeX4Rhq/G5gGjJMNDzcygY4XvI4Esq9FpI6Ojo5O69PSKKPJwJ+A6VLKKy157wLihRCxQggX4FZgZUva1dHR0dGxPS2NMnoH8AbWCyH2CyE+ABBCdBBCrAaoX3R+BFgLJANLpJRHmnj+BS3UZw8cQSPoOm2NrtO26DptR7M12mxRWUdHR0fHsXHonco6Ojo6OrZDNwQdHR0dHUBDhqCFNBhNQQgxWwhxRAhhFUJcMfxMCHFaCHGofm2l2WFgzeUadKrdnwFCiPVCiBP1X/2vcJwq/dlY/wiFt+rfPyiE6GcvbdegcbQQorS+7/YLIf5mb431Oj4WQuQJIRrcW6SFvqzX0ZhO1ftTCNFRCLFJCJFc/3/+aAPHXHt/Sik18QAmAk71z/8J/LOBY4zASaAT4AIcALrZWWdXIBFIAgZc5bjTQJCK/dmoTo305yvAk/XPn2zo765Wfzalf4CpwA8o+22uA3ZoUONoYJVan8ULdIwE+gGHr/C+qn15DTpV708gHOhX/9wbJXVQiz+bmhkhSI2kwWgMKWWylFLzpdKaqFP1/qxv77P6558BN9q5/avRlP6ZAXwuFbYDfkKIcI1p1ARSyp+AoqsconZfAk3SqTpSyhwp5d765+UoEZwRlxx2zf2pGUO4hHtRnO1SIoAzF7zO5PJO0AoSWCeE2FOfjkOLaKE/Q6WUOaB8yIGQKxynRn82pX/U7sOmtj9ECHFACPGDEKK7faRdM2r35bWgmf4UQsQAfYEdl7x1zf3Z6E5lW2LvNBjNpSk6m8AwKWW2ECIEZZ/Gsfo7D5thA52q9+c1nKbV+7MBmtI/dunDq9CU9vcC0VLKCiHEVGA5EN/awpqB2n3ZVDTTn0IIL2Ap8AcpZdmlbzfwI1ftT7sagnSQNBiN6WziObLrv+YJIb5FGdrb9AJmA52q96cQIlcIES6lzKkfzuZd4Ryt3p8N0JT+UTs1S6PtX3ihkFKuFkK8J4QIklJqLUmb2n3ZJLTSn0IIZxQzWCSlXNbAIdfcn5qZMhJtKA2GEMJTCOF97jnKgrkWs7ZqoT9XAnfXP78buGxko2J/NqV/VgJ31Ud0XAeUnpsCsxONahRChAkhRP3zQSj/94V21NhU1O7LJqGF/qxv/yMgWUr5+hUOu/b+VHOl/JIV8VSU+a799Y8P6r/fAVh9ycp5CkpkxVMq6LwJxXlrgVxg7aU6USI+DtQ/jmhVp0b6MxDYCJyo/xqgpf5sqH+AB4EH658LlAJQJ4FDXCXyTEWNj9T32wGUgI2h9tZYr+NLIAeoq/9s3qe1vmyiTtX7ExiOMv1z8IJr5tSW9qeeukJHR0dHB9DQlJGOjo6OjrrohqCjo6OjA+iGoKOjo6NTj24IOjo6OjqAbgg6Ojo6OvXohqCjo6OjA+iGoKOjo6NTz/8HW+8swHyjABcAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"theta0 = 5.5\n",
"x0 = np.array((np.sin(theta0),np.cos(theta0)))\n",
"\n",
"## Run Algorithm 5.1 on test problem\n",
"results = alg52(x0,my_f3,my_h3)\n",
"\n",
"## Display results\n",
"xstar = results[0][-1]\n",
"print(\"\\nx* =\",xstar)\n",
"\n",
"## Display results\n",
"vstar = results[1][-1]\n",
"print(\"\\nv* =\",vstar)\n",
"\n",
"## Convert into theta\n",
"print(\"\\ntheta* =\",np.arccos(xstar[0]),\"(using arccos)\")\n",
"print(\"\\ntheta* =\",np.arcsin(xstar[1]),\"(using arcsin)\")\n",
"\n",
"## Visualize\n",
"visualize(results[0])"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.8.4.3 Starting Point Near Global Max ($\\theta_0 = 5.5$)](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.4.3-Starting-Point-Near-Global-Max-($\\theta_0-=-5.5$))",
"section": "4.8.4.3 Starting Point Near Global Max ($\\theta_0 = 5.5$)"
}
},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"id": "f3f70c86",
"metadata": {},
"source": [
"\n",
"< [4.7 Simple Netwon Method for Equality Constrained NLPs](https://ndcbe.github.io/CBE60499/04.07-Interior-Point1.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [4.9 Algorithms Homework 4: Interior Point Methods](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html) >
"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 1,
"link": "[4.8 Inertia-Corrected Netwon Method for Equality Constrained NLPs](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8-Inertia-Corrected-Netwon-Method-for-Equality-Constrained-NLPs)",
"section": "4.8 Inertia-Corrected Netwon Method for Equality Constrained NLPs"
}
},
"source": [
"# 4.8 Inertia-Corrected Netwon Method for Equality Constrained NLPs\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 1,
"link": "[4.8 Inertia-Corrected Netwon Method for Equality Constrained NLPs](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8-Inertia-Corrected-Netwon-Method-for-Equality-Constrained-NLPs)",
"section": "4.8 Inertia-Corrected Netwon Method for Equality Constrained NLPs"
}
},
"source": [
"Background:\n",
"\n",
"\n",
"\n",
"The Algorithm:\n",
"\n",
"\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.8.1 Helper Functions](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.1-Helper-Functions)",
"section": "4.8.1 Helper Functions"
}
},
"source": [
"## 4.8.1 Helper Functions"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.8.1 Helper Functions](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.1-Helper-Functions)",
"section": "4.8.1 Helper Functions"
}
},
"outputs": [],
"source": [
"# Load required Python libraries.\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"from scipy import linalg\n",
"\n",
"## Check is element of array is NaN\n",
"def check_nan(A):\n",
" return np.sum(np.isnan(A))\n",
"\n",
"## Calculate gradient with central finite difference\n",
"## Calculate gradient with central finite difference\n",
"def my_grad_approx(x,f,eps1,verbose=False):\n",
" '''\n",
" Calculate gradient of function f using central difference formula\n",
" \n",
" Inputs:\n",
" x - point for which to evaluate gradient\n",
" f - function to consider\n",
" eps1 - perturbation size\n",
" \n",
" Outputs:\n",
" grad - gradient (vector)\n",
" '''\n",
" \n",
" n = len(x)\n",
" grad = np.zeros(n)\n",
" \n",
" if(verbose):\n",
" print(\"***** my_grad_approx at x = \",x,\"*****\")\n",
" \n",
" for i in range(0,n):\n",
" \n",
" # Create vector of zeros except eps in position i\n",
" e = np.zeros(n)\n",
" e[i] = eps1\n",
" \n",
" # Finite difference formula\n",
" my_f_plus = f(x + e)\n",
" my_f_minus = f(x - e)\n",
" \n",
" # Diagnostics\n",
" if(verbose):\n",
" print(\"e[\",i,\"] = \",e)\n",
" print(\"f(x + e[\",i,\"]) = \",my_f_plus)\n",
" print(\"f(x - e[\",i,\"]) = \",my_f_minus)\n",
" \n",
" \n",
" grad[i] = (my_f_plus - my_f_minus)/(2*eps1)\n",
" \n",
" if(verbose):\n",
" print(\"***** Done. ***** \\n\")\n",
" \n",
" return grad\n",
"\n",
"def my_jac_approx(x,h,eps1,verbose=False):\n",
" '''\n",
" Calculate Jacobian of function h(x) using central difference formula\n",
" \n",
" Inputs:\n",
" x - point for which to evaluate gradient\n",
" h - vector-valued function to consider. h(x): R^n --> R^m\n",
" eps1 - perturbation size\n",
" \n",
" Outputs:\n",
" A - Jacobian (n x m matrix)\n",
" '''\n",
" \n",
" # Check h(x) at x\n",
" h_x0 = h(x)\n",
" \n",
" # Extract dimensions\n",
" n = len(x)\n",
" m = len(h_x0)\n",
" \n",
" # Initialize Jacobian matrix\n",
" A = np.zeros((n,m))\n",
" \n",
" # Calculate Jacobian by row\n",
" for i in range(0,n):\n",
" \n",
" # Create vector of zeros except eps in position i\n",
" e = np.zeros(n)\n",
" e[i] = eps1\n",
" \n",
" # Finite difference formula\n",
" my_h_plus = h(x + e)\n",
" my_h_minus = h(x - e)\n",
" \n",
" # Diagnostics\n",
" if(verbose):\n",
" print(\"e[\",i,\"] = \",e)\n",
" print(\"h(x + e[\",i,\"]) = \",my_h_plus)\n",
" print(\"h(x - e[\",i,\"]) = \",my_h_minus)\n",
" \n",
" \n",
" A[i,:] = (my_h_plus - my_h_minus)/(2*eps1)\n",
" \n",
" if(verbose):\n",
" print(\"***** Done. ***** \\n\")\n",
" \n",
" return A\n",
" \n",
"## Calculate gradient using central finite difference and my_hes_approx\n",
"def my_hes_approx(x,grad,eps2):\n",
" '''\n",
" Calculate gradient of function my_f using central difference formula and my_grad\n",
" \n",
" Inputs:\n",
" x - point for which to evaluate gradient\n",
" grad - function to calculate the gradient\n",
" eps2 - perturbation size (for Hessian NOT gradient approximation)\n",
" \n",
" Outputs:\n",
" H - Hessian (matrix)\n",
" '''\n",
" \n",
" n = len(x)\n",
" H = np.zeros([n,n])\n",
" \n",
" for i in range(0,n):\n",
" # Create vector of zeros except eps in position i\n",
" e = np.zeros(n)\n",
" e[i] = eps2\n",
" \n",
" # Evaluate gradient twice\n",
" grad_plus = grad(x + e)\n",
" grad_minus = grad(x - e)\n",
" \n",
" # Notice we are building the Hessian by column (or row)\n",
" H[:,i] = (grad_plus - grad_minus)/(2*eps2)\n",
"\n",
" return H\n",
"\n",
"## Linear algebra calculation\n",
"def xxT(u):\n",
" '''\n",
" Calculates u*u.T to circumvent limitation with SciPy\n",
" \n",
" Arguments:\n",
" u - numpy 1D array\n",
" \n",
" Returns:\n",
" u*u.T\n",
" \n",
" Assume u is a nx1 vector.\n",
" Recall: NumPy does not distinguish between row or column vectors\n",
" \n",
" u.dot(u) returns a scalar. This functon returns an nxn matrix.\n",
" '''\n",
" \n",
" n = len(u)\n",
" A = np.zeros([n,n])\n",
" for i in range(0,n):\n",
" for j in range(0,n):\n",
" A[i,j] = u[i]*u[j]\n",
" \n",
" return A\n",
"\n",
"## Analyze Hessian\n",
"def analyze_hes(B):\n",
" print(B,\"\\n\")\n",
" \n",
" l = linalg.eigvals(B)\n",
" print(\"Eigenvalues: \",l,\"\\n\")"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.8.2 Algorithm 5.2](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.2-Algorithm-5.2)",
"section": "4.8.2 Algorithm 5.2"
}
},
"source": [
"## 4.8.2 Algorithm 5.2"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.8.2 Algorithm 5.2](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.2-Algorithm-5.2)",
"section": "4.8.2 Algorithm 5.2"
}
},
"outputs": [],
"source": [
"def assemble_check_KKT(W,A,deltaA,deltaW,verbose):\n",
" \n",
" n = np.size(W,0)\n",
" \n",
" if(np.size(W,1) != n):\n",
" print(\"WARNING: W is not square. Somthing is broken.\")\n",
" \n",
" rA = np.size(A,0)\n",
" m = np.size(A,1)\n",
" \n",
" if(rA != n):\n",
" print(\"WARNING: A does not have the corrent number of rows.\")\n",
" \n",
" # Assemble KKT matrix\n",
" KKT_top = np.concatenate((W + deltaW*np.eye(n),A),axis=1)\n",
" KKT_bot = np.concatenate((A.T,-deltaA*np.eye(m)),axis=1)\n",
" KKT = np.concatenate((KKT_top,KKT_bot),axis=0)\n",
" \n",
" # Check inertia of KKT matrix.\n",
" # Out of simplicity, we will just calculate the eigenvalues.\n",
" # Biegler, 2010 explains a more sophisticates (and computationally efficient)\n",
" # strategy\n",
" l, eigvec = linalg.eig(KKT)\n",
"\n",
" zero_tol = 1E-12\n",
"\n",
" # Count number of positive eigenvalues\n",
" pos_ev = sum(l >= zero_tol)\n",
"\n",
" # Count number of eigenvalues close to zero\n",
" zero_ev = sum(np.abs(l) < zero_tol)\n",
"\n",
" # Count number of negative eigenvalues\n",
" neg_ev = sum(l <= -zero_tol)\n",
"\n",
" inertia_correct = (n == pos_ev and m == neg_ev)\n",
" \n",
" if(verbose):\n",
" print(\"deltaA = \",deltaA,\" deltaW = \",deltaW,\"intertia =(\",pos_ev,\",\",neg_ev,\",\",zero_ev,\")\\n\")\n",
" \n",
" return KKT,inertia_correct,pos_ev,neg_ev,zero_ev\n",
" \n",
"def alg52(x0,calc_f,calc_h,eps1=1E-6,eps2=1E-6,max_iter=10,verbose=False):\n",
" '''\n",
" Basic Full Space Newton Method for Equality Constrained NLP\n",
" \n",
" Input:\n",
" x0 - starting point (vector)\n",
" calc_f - function to calculate objective (returns scalar)\n",
" calc_h - function to calculate constraints (returns vector)\n",
" eps1 - tolerance for primal and dual steps\n",
" eps2 - tolerance for gradient of L1\n",
" \n",
" Outputs:\n",
" x - history of steps (primal variables)\n",
" v - history of steps (dual variables)\n",
" f - history of objective evaluations\n",
" h - history of constraint evaluations\n",
" df - history of objective gradients\n",
" dL - history of Lagrange function gradients\n",
" A - history of constraint Jacobians\n",
" W - history of Lagrange Hessians\n",
" \n",
" Notes:\n",
" 1. For simplicity, central finite difference is used \n",
" for all gradient calculations.\n",
" '''\n",
"\n",
" ### Specifics for Algorithm 5.2\n",
" # Tuning parameters\n",
" delta_bar_W_min = 1E-20\n",
" delta_bar_W_0 = 1E-4\n",
" delta_bar_W_max = 1E40\n",
" delta_bar_A = 1E-8\n",
" kappa_u = 8\n",
" kappa_l = 1/3\n",
" \n",
" # Declare iteration histories as empty lists\n",
" x = []\n",
" v = []\n",
" f = []\n",
" L = []\n",
" h = []\n",
" df = []\n",
" dL = []\n",
" A = []\n",
" W = []\n",
"\n",
" # Set for first iteration\n",
" delta_A = 0.0\n",
" delta_W = 0.0\n",
" delta_W_last = 0.0\n",
" \n",
" # Flag for iterations\n",
" flag = True\n",
" \n",
" # Iteration counter\n",
" k = 0\n",
" \n",
" # Copy initial point to primal variable history\n",
" n = len(x0)\n",
" x.append(x0)\n",
" \n",
" # Evaluate objective and constraints at initial point\n",
" f.append(calc_f(x0))\n",
" h.append(calc_h(x0))\n",
" \n",
" # Determine number of equality constraints\n",
" m = len(h[0])\n",
" \n",
" # Initial dual variables with vector of ones\n",
" v.append(np.ones(m))\n",
" \n",
" # Print header for iteration information\n",
" print(\"Iter. \\tf(x) \\t\\t||h(x)|| \\t||grad_L(x)|| \\t||dx|| \\t\\t||dv|| \\t\\tdelta_A \\tdelta_W\")\n",
" \n",
" while(flag and k < max_iter):\n",
" \n",
" # STEP 1. Construct KKT matrix\n",
" \n",
" if(k > 0):\n",
" # Evaluate objective function\n",
" f.append(calc_f(x[k]))\n",
" \n",
" # Evaluate constraint function\n",
" h.append(calc_h(x[k]))\n",
" \n",
" # Evaluate objective gradient\n",
" df.append(my_grad_approx(x[k],calc_f,1E-6))\n",
" \n",
" # Evaluate constraint Jacobian\n",
" A.append(my_jac_approx(x[k],calc_h,1E-6))\n",
" \n",
" # Evaluate gradient of Lagrange function\n",
" L_func = lambda x_ : calc_f(x_) + (calc_h(x_)).dot(v[k])\n",
" L_grad = lambda x_ : my_grad_approx(x_,L_func,1E-6)\n",
" dL.append(L_grad(x[k]))\n",
" norm_dL = linalg.norm(dL[k])\n",
" \n",
" # Evaluate Hessian of Lagrange function\n",
" W.append(my_hes_approx(x[k],L_grad,1E-6))\n",
" \n",
" if(verbose):\n",
" print(\"*** k =\",k,\" ***\")\n",
" print(\"x_k =\",x[k])\n",
" print(\"v_k =\",v[k])\n",
" print(\"f_k =\",f[k])\n",
" print(\"df_k =\",df[k])\n",
" print(\"h_k =\",h[k])\n",
" print(\"A_k =\\n\",A[k])\n",
" print(\"W_k =\\n\",W[k])\n",
" print(\"\\n\")\n",
" \n",
" ######\n",
" # Algorithm 5.2: Add intertia correction to Algorithm 5.1\n",
" \n",
" ### ALG. 5.2, STEP 1\n",
" delta_A = 0\n",
" delta_W = 0\n",
" \n",
" KKT,inertia_correct,pos_ev,neg_ev,zero_ev = assemble_check_KKT(W[k],A[k],delta_A,delta_W,verbose)\n",
" \n",
" if not inertia_correct:\n",
" ### ALG. 5.2, STEP 2\n",
" # Assume zero eigenvalue is from rank-deficient Jacobian.\n",
" # Set delta_A to non-zero value\n",
" if zero_ev != 0:\n",
" delta_A = delta_bar_A\n",
" \n",
" ### ALG. 5.2, STEP 3\n",
" if delta_W_last == 0:\n",
" delta_W = delta_bar_W_0\n",
" else:\n",
" delta_W = max(delta_bar_W_min,kappa_l*delta_W_last)\n",
"\n",
" while (not inertia_correct) and flag:\n",
" ### ALG. 5.2, STEP 4\n",
" KKT,inertia_correct,pos_ev,neg_ev,zero_ev = assemble_check_KKT(W[k],A[k],delta_A,delta_W,verbose)\n",
" \n",
" ### ALG. 5.2, STEP 5\n",
" if not inertia_correct:\n",
" delta_W = kappa_u*delta_W\n",
" \n",
" ### ALG. 5.2, STEP 6\n",
" if delta_W > delta_bar_W_max:\n",
" flag = False\n",
" print(\"Abort step computation. KKT matrix is severely ill-conditioned.\")\n",
" \n",
" delta_W_last = delta_W\n",
" \n",
" ## STEP 2. Solve linear system.\n",
" \n",
" if flag:\n",
" b = -np.concatenate((dL[k],h[k]),axis=0)\n",
" z = linalg.solve(KKT,b)\n",
" else:\n",
" z = []\n",
" \n",
" ## STEP 3. Take step\n",
" if flag:\n",
" dx = z[0:n]\n",
" dv = z[n:(n+m+1)]\n",
" \n",
" x.append(x[k] + dx)\n",
" v.append(v[k] + dv)\n",
" \n",
" norm_dx = linalg.norm(dx)\n",
" norm_dv = linalg.norm(dv)\n",
" \n",
" ## Print iteration information\n",
" print(k,' \\t{0: 1.4e} \\t{1:1.4e} \\t{2:1.4e}'.format(f[k],linalg.norm(h[k]),norm_dL),end='')\n",
" \n",
" if flag:\n",
" print(' \\t{0: 1.4e} \\t{1: 1.4e}'.format(norm_dx,norm_dv),end='')\n",
" else:\n",
" print(' \\t ------- \\t -------',end='')\n",
" \n",
" print(' \\t{0: 1.4e} \\t{1: 1.4e}'.format(delta_A,delta_W),end='\\n')\n",
" \n",
" # Increment counter\n",
" k = k + 1\n",
" \n",
" ## Check convergence criteria\n",
" if(flag):\n",
" flag = norm_dx > eps1 and norm_dv > eps1 and norm_dL > eps2\n",
" \n",
" if(not flag and k > max_iter):\n",
" print(\"Reached maximum number of iterations.\")\n",
" \n",
" return x,v,f,h,df,dL,A,W"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.8.3 Example Problem 2](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.3-Example-Problem-2)",
"section": "4.8.3 Example Problem 2"
}
},
"source": [
"## 4.8.3 Example Problem 2\n",
"\n",
"(Where is Example Problem 1? We are using the same number scheme as the previous notebook.)\n",
"\n",
"Consider:\n",
"$$\\begin{align}\\min_x \\quad & x_1^2 + 2 x_2^2 \\\\\n",
"\\mathrm{s.t.} \\quad & x_1 + x_2 = 1 \\\\\n",
" & x_1 + x_2 = 1 \\end{align}$$\n",
"\n",
"### Test Algorithm 5.2 with redundant constraints."
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.8.3 Example Problem 2](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.3-Example-Problem-2)",
"section": "4.8.3 Example Problem 2"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Iter. \tf(x) \t\t||h(x)|| \t||grad_L(x)|| \t||dx|| \t\t||dv|| \t\tdelta_A \tdelta_W\n",
"0 \t 3.0000e+00 \t1.4142e+00 \t7.2111e+00 \t 7.4537e-01 \t 2.3571e+00 \t 1.0000e-08 \t 1.0000e-04\n",
"1 \t 6.6667e-01 \t2.3373e-08 \t2.9368e-04 \t 5.4908e-05 \t 9.4088e-05 \t 1.0000e-08 \t 3.3333e-05\n",
"2 \t 6.6667e-01 \t9.4991e-13 \t3.7259e-09 \t 1.1908e-09 \t 6.4780e-11 \t 1.0000e-08 \t 1.1111e-05\n",
"\n",
"x* = [0.66666667 0.33333333]\n",
"\n",
"v* = [-0.66666666 -0.66666667]\n"
]
}
],
"source": [
"## Define functions\n",
"def my_f2(x):\n",
" return x[0]**2 + 2*x[1]**2\n",
"\n",
"def my_h2(x):\n",
" h = np.zeros(2)\n",
" h[0] = x[0] + x[1] - 1\n",
" h[1] = h[0]\n",
" return h\n",
"\n",
"## Declare initial point\n",
"x0 = np.array((1,1))\n",
"\n",
"## Run Algorithm 5.2 on test problem\n",
"results = alg52(x0,my_f2,my_h2,verbose=False)\n",
"\n",
"## Display results\n",
"xstar = results[0][-1]\n",
"print(\"\\nx* =\",xstar)\n",
"\n",
"## Display results\n",
"vstar = results[1][-1]\n",
"print(\"\\nv* =\",vstar)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.8.3.1 Test Algorithm 5.2 without redundant constraints.](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.3.1-Test-Algorithm-5.2-without-redundant-constraints.)",
"section": "4.8.3.1 Test Algorithm 5.2 without redundant constraints."
}
},
"source": [
"### 4.8.3.1 Test Algorithm 5.2 without redundant constraints."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.8.3.1 Test Algorithm 5.2 without redundant constraints.](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.3.1-Test-Algorithm-5.2-without-redundant-constraints.)",
"section": "4.8.3.1 Test Algorithm 5.2 without redundant constraints."
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Iter. \tf(x) \t\t||h(x)|| \t||grad_L(x)|| \t||dx|| \t\t||dv|| \t\tdelta_A \tdelta_W\n",
"0 \t 3.0000e+00 \t1.0000e+00 \t5.8310e+00 \t 7.4537e-01 \t 2.3335e+00 \t 0.0000e+00 \t 0.0000e+00\n",
"1 \t 6.6667e-01 \t1.3978e-10 \t2.9473e-04 \t 4.5326e-05 \t 1.5285e-04 \t 0.0000e+00 \t 0.0000e+00\n",
"2 \t 6.6667e-01 \t0.0000e+00 \t4.5431e-09 \t 1.4393e-09 \t 2.0170e-09 \t 0.0000e+00 \t 0.0000e+00\n",
"\n",
"x* = [0.66666667 0.33333333]\n",
"\n",
"v* = [-1.33333333]\n"
]
}
],
"source": [
"## Define functions\n",
"def my_h2b(x):\n",
" return (x[0] + x[1] - 1)*np.ones(1)\n",
"\n",
"## Run Algorithm 5.2 on test problem\n",
"results = alg52(x0,my_f2,my_h2b,verbose=False)\n",
"\n",
"## Display results\n",
"xstar = results[0][-1]\n",
"print(\"\\nx* =\",xstar)\n",
"\n",
"## Display results\n",
"vstar = results[1][-1]\n",
"print(\"\\nv* =\",vstar)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.8.3.2 Discussion](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.3.2-Discussion)",
"section": "4.8.3.2 Discussion"
}
},
"source": [
"### 4.8.3.2 Discussion\n",
"\n",
"* Compare the multipliers with and without the redundant constraint."
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.8.4 Example Problem 3](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.4-Example-Problem-3)",
"section": "4.8.4 Example Problem 3"
}
},
"source": [
"## 4.8.4 Example Problem 3\n",
"\n",
"Let us try a model where $\\nabla h(x^k)^T$ is full rank but there are multiple local optima.\n",
"\n",
"Consider:\n",
"$$\\begin{align}\\min_x \\quad & x_1^3 - x_2 -x_1 x_2 - x_2^2 \\\\\n",
"\\mathrm{s.t.} \\quad & x_1^2 + x_2^2 = 1\n",
"\\end{align}$$"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.8.4 Example Problem 3](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.4-Example-Problem-3)",
"section": "4.8.4 Example Problem 3"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYQAAAD8CAYAAAB3u9PLAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAABgfUlEQVR4nO2dd3xUVfr/32cmvfdCQhop9F4E6R1EQJq9oK5ldXV/flfXLa5bbKura9fVtaIroiAgIlUCIr23QAiBdNJ7m8zM+f1xAyIkEJLJ3DvJfb9e9zUzmTv3fHIzuZ97znnO8wgpJTo6Ojo6Oga1Bejo6OjoaAPdEHR0dHR0AN0QdHR0dHQa0Q1BR0dHRwfQDUFHR0dHpxHdEHR0dHR0ABsYghCiqxBikxAiRQhxVAjxaBP7CCHE60KINCHEISHEwLa2q6Ojo6NjW5xscAwz8H9Syn1CCG9grxBivZTy2AX7TAMSGrdhwDuNjzo6Ojo6GqHNPQQpZZ6Ucl/j80ogBYi4aLdZwKdSYQfgJ4QIb2vbOjo6Ojq2wxY9hPMIIWKAAcDOi96KALIueJ3d+LO8Jo5xH3AfgJub26CoqKg2abJYJUUV9QR4ueDsZPspE6vVisGg/akYXadt0XXals6qs8JkptzUQJiHK842Om5qamqRlDK4VR+WUtpkA7yAvcCcJt77Dhh5weuNwKArHTMxMVG2ldp6k3xnyVZ5tqiizcdqik2bNrXLcW2NrtO26DptS2fTmVlcKm/5YLFMevoV+ZvFK2Vpda1NjiullMAe2crruE16CEIIZ2Ap8LmUclkTu2QDXS94HQnk2qLtK+Hm4swD86+1R1M6Ojo6l0VKydL9R3luTTJGYeDFG6Zyfd/uCCHUlgbYYMhIKL/JB0CKlPKVZnZbCTwshFiMMplcLqW8ZLhIR0dHp6OSV17JUyvXs/VUBkNjInlh9hS6+PmoLesX2KKHcC1wO3BYCHGg8Wd/BKIApJTvAquB6UAaUAMstEG7Ojo6OppHSsmy/Ud5fu1mrFbJU9PHcfPgfhgM2ugVXEibDUFKuRW47G/WOK71UFvb0tHR0XEkskvL+cu3G9iWnsmQ6EiemzWJrgF+astqFptGGamNlFIzY3E6OjqdF4vVyqKdB3jth58wCAN/mT6emwb31WSv4EI6hCHUm8y4ujjpZqCjo6M6R3Lz+euqjRzJzWdsYix/vW4CYb7eastqEQ5tCPkllazffoLMs6UE+nkwb0J/Av08z79vtUrNO7KOjk7HoKquntc2bePzXQcJ9HTn5bnTmd470aFuVB3aEF78aCPCIAjx9+JkZhFbD6Qza2wfDqfl0ie+i24GOjo67Y6UklWHT/DS+i0UVlZz85B+/Hb8CHzc3dSWdtU4rCGcyS3hyKk81r79IABb9p1i0Xe72Xc8m+z8MgD+cPdE4ru2bsGejo6OzpU4kV/EP1b/wJ6MHHqFh/DGjdfTL9Jxs/I4rCGcyi4iOjyA8qpafL3cCQ/y4fjpfO6fOwIfT3fe/XorB07k6Iago6Njc0qra3kjeTtf7jmEt5srf79+InMH9MLoAOk3LofDGsLA7pF88f1eFq3ajZ+3Bys3H+aWaYMY3DOq8f2u7DycwbyJ/dUVqnHqG8zklFWQU15BblkF+RVVlNbUUlJTS2lNLdX1JmobzNSaGmiwWLBKiUVKkBInoxFnowEngwF3F2c8XVzwdHXBx80VP3c3/Dzc8fdwJ8Tbs3HzIsTbCxcno9q/to5OqzBbrXy8fR9vJe+gxmTixsF9eWTcCPw8HG94qCkc1hD8fTy4fcYQ1u84QUiANwO6RxJ0wYTyln2nGD80QUWF2qOgsorDOfkczjnLyYJi0gqLySotx6rklwKUBSXnLuR+7m4Eenrg7uKMu7MzLk5GjEIgGjezxYLZasVktlDb0ECNqYGqunpyyiooq6mlvLYOeZEGAYR4exHh50Okvw/RAf5EBfgRE+hHbFCAPU+Hjk6LkVLy/dFUnt+VQmGdiZHdonlyyhjiQwLVlmZTHNYQAMYMimfMoHgA1vyUwt/fW0NxWQ2VNXVUVNdx05TOXYcnp6yCHemZbEvPZNvJdEqT9wPgZDAQE+hH97BgruuTREyAP138vOni60OItxdORtt0ey1WK+W1dRRWVlNQVU1BRRW55ZXklleQU1bBnowcvj10/Bem4e/qTI/MYhJCAkkMCSIxNIiEkCDcnB36q6rjwOw4ncXL63/kcG4+EZ5uvHfrbEYnxKotq11w6P8ys9mCk5MRq1UyaXgSVilZuvEgowbE8bcHpqktz+5IKUk5W8i6YydZn5LGqaISAII8Pejm48mkgf3oGxlGj7AQu1xgjQYDAZ4eBHh6kETTczl1DWaySss4U1zGqcISth89RnltHV/uOUyd2QyAQQjigvzpGR5Cj7AQencJpUd4CF6uLu3+O+h0Xg5m5/Hqxp/YfjqLMB8vnps1Gb+ygg5rBuDghkBjfO/rX2zG1GDhibsmMH1kT5VF2Z/s0nKWHzzGioMpZJWWYxCCIdGRLBjUhxHdoogPDmTz5s2MHa69HpObsxMJIUovYFIP6G6tYezYsVisVrJKy0nNL+J4fiEpeYXsPJ3NykPHAWXoqVtwAL27hNEvMow+EWEkhQbhbNTnJ3TaxpHcfN7evIMfTqQT4OHOk1PGcNPgvrg5O5GcXKi2vGaRUvK33RvadAyHNQQpJU5GA1JKlqw/wCd/vxVQhikcfaa/JVitkuST6Xy+6yDbTmUAMDwuivtHDWVCUjf8Pd1VVtg2jAYDMYH+xAT6M7nnz3NBRVXVHM0t4EhuPodzz7Ll5GmWH1Sqtbo5OdE7IpQBXbswoGs4A7p2wd/Dsc+Djv04nHOWN5N3sPnkaXzcXPnt+BHcPmwAng7QE5VS8vc9G/n4+N42HcdhDcFilTgZBf/5ehu94sJIiArGapUd3gxMZjMrDx3no217OVVUQpiPFw+NvYYb+vciQmOpdNuDIC9PxiTGMiZR6bZLKckpq+Bg9lkOZudxIDuPj7bt5X2rFYBuQQEMjOrCoKgIBkdHEOHn41ArR3XaFyklO09n8f5Pe/jpVAa+7m78dvwIbh3aH283V7XltQgpJS/u38xHKXu4u8dgnm7DsRzWEM5NfH6xZi9v/H4eABLJFRKvOixmi5VlB47yVvIO8iur6BEWzEtzpjG1V0KnHiYRQhDp70ukvy/X9UkCoNbUwJHcfPZl5bIvM5c1R0/y1b4jAIR6ezEoOoKh0REMiYkkLihAN4hOiNliZcPxNP770x6O5OYT5OnBYxOu5Zah/R1uburNw9t458gObknsz1ODJ3Q+QzBbrDgZDXy6ahddw/zpm9gFKTtm70BKyaYT6by8YSunikroFxHGc7MnMyIuSr+QNYO7izNDYiIZEhMJKMNrJwuK2JOZw96MHHafyWb1kRMABHp6MDg6giHRyv4JwYF6ypMOTGVdPV/vO8KinQfILa8gOsCPv82YwOx+PXF1wEi2tw9v5+UDPzInrhfPDJvS5muC450Bfu4dfLxyF889PAMAq5QYO9gFMru0nL999wM/pp0hJtCf1xfMYFKPeN0IrhKDQZAUFkxSWDC3Du2PlJLMknJ2Z2Sz+0w2uzOyWXvsJAC+7m4MiY5gaEwkQ2O6khgSpBtEB+DE2UK+2HOIlYdSqDE1MCQ6kj9OHcO4pDiHvZF8/+hOXty/mVmxPXlpxHUYbHBdcEhDADiSlkdSTAjX9I3pcL0Ds8XKJzv28cam7RgNBv44dQw3D+nXqYeGbIkQguhAP6ID/Zg3sDegmK9iEDnsOpPFhuOnAPB1c2VITCQv3DDV4YYSOju1pgbWp6SxeM8h9mXl4upkZFqvJG4f1p9eXULVltcmPjm+l2f3buK66O68fO0Mm13/HNYQeseH8/oTc4GO1TvIKinjd8vWcDA7j3GJcTx93XiHyaXuyJybh7ihfy8Acssq2NXYe0gvKsHTxbnZz5otVoSg2X/Kc4WbLFYrKw6m8MzqTfx5+jjmDOjVLr9LZ0ZKyaGcsyzdf5TVR05QVW8iOsCP308ezQ39e3WIFBOfHt/L07vWM7lrAq+Ouh4nG94M28QQhBAfAjOAAill7ybeHwusAE43/miZlPLvbW3XuTEnTkfpHaw5msqfV65HIPjX3Glc1ztJHx5SiS5+Pszu35PZ/a+8ruXCld1SSixWiRDKgrpzaT4Aluw9zJd7DhMT5I+pcdGdXrPDNmSWlPHtoeOsPJRCRkkZbk5OTOmVwNwBvRkcFdFhzvGi4/v4y671TIyM543Rs3A22HbUwFY9hI+BN4FPL7PPj1LKGW1tqCP+AzVYLDy/ZjP/232QfhFhvDxvOpH+vmrL0mkBf1y+jhqTidEJsYyMj25M/fHz9/Nc7+CVDVtpsFgZnxRHTlkFccFKDhzd71tPRnEZa4+lsvbYSY7mFSCAITGR/GrkEKb0THCYsNGW8nnqfp7atY6JkfG8PeYGXNphCNkmhiCl3CKEiLHFsa7Ecx+so6rWxAuPXG+P5tqdito6Hlmyih2ns1g4fBCPTbxWnytwIG4c3Ic1R0/y6Y79PL1qI85GAz3DQhgZH8O0XolEB/qxeM8h9mbm8MaN1/P90VROFhYTF+QPoPcArwKrVXI49yybTqSzKTWdE/lFAPSLCOPxSaOY3juJ8A46vLr45EH+tGMt4yO68daY2e1iBmDfOYThQoiDQC7wOynl0as9gNlsYfPeNK7tH2d7dSqQXVrO/Z8vJ7OkjOdnTz4/fq3jOPSLDP9FQZT0whI2paaz83QWRVXVTOwRz4aUND5buAAhBDllFfi6uRHk5XmZo+qco6Cyim2nMtmWnsG2U5kUVddgFIKBURE8OWUMk3vE06WDL8hcdGIfT+1cx5gucbw99gZcje132RZSXpyguJUHUnoIq5qZQ/ABrFLKKiHEdOA1KWWTuamFEPcB9wEEBwcPWrJkyfn3UnMq+GBNGndMjKNXtJ9NdLeVqqoqvLy8rvpz2VW1vHYwDYuU3N8rliT/9r2zaa1Oe+NoOq1SIiXn5wwupKy+gUUnMjhZVs2NCZG4GARHSiqI9fFkbEQwVikv+YyUkkPFFUR4uhHo5tLmHoSjnc+y+gbSyqtILVO2szV1AHg7O9Hd35vegT70DvDBU6U1A/Y+nxsrz7Ko9Az93Px4ODgRZ3Hl+dJx48btlVIObk17djmrUsqKC56vFkK8LYQIklIWNbHve8B7AElJSXLs2LHn39v18UbcXJy45+brcLtM1Ic9SU5O5kKNLeFYXgG//3Qpnu5ufHj7XOKC278OQGt0qoGj65RSnjcJJ6OB/oNL+elUBvuz8tiXmUtpTQ1ZdWZmjx5J/66XllrMKinjwdc/AsDb1ZWk0CASQgKJDwkkPljZAjzdW2wUWj6f5bV1pJwtJCWvgPUZp8mrP0teRSUAHi7ODIqK4NaYSK7tFk330GBNzB3a83wuOr6PRZk72nXO4GLsYghCiDAgX0ophRBDAQNQfDXHkFKyZd8prukboxkzaA3Hzxay8JOv8XBx4ZO75hEV4Ke2JB0bIoT4RQj0uQR9tw7tz+I9h1ifksa4xLhmx7pDfbxYfM9NHM8v5MTZQo7nF7Lq8Akq6+vP7+Pj5kpsoD8xQf5EB/jR1d+PqABfIv18r8os7EVZTR2ZJWWcLi4hraCYtMISUguKyCk7f59IgKsL18THsLDrQPpHdqFneIjN6nI4Iv89totn9vxgVzMA24WdfgGMBYKEENnA04AzgJTyXWAe8KAQwgzUAjfJqxyrSs0opLC0ilEDutlCsiqkFRSz8NOleLi4sGjhfD2SqBNhsVqpazDj6+bKbcP6N7ufi5MT/buG/6L3IKWkoLKakwXFpBcVk15UyumiUnakZ7HiYMovPu/qZCTc14dwH6VcaW1pMRmu+wjwdD9fCc/XzRUvN1e8XV1bfdE1W6xU1Zuoqq9XSq5W11JSU0NRVQ1nK6rIr6gkr7ySrNJyKup+NjNng4GYIH/6RoRx46A+9AgPoWdYCIf37NJsT8bevHNkB//cl8y0qCReGzXTbmYAtosyuvkK77+JEpbaarYeSEcIGNHPMYtT5FdUce9ny3AyCD66c65uBp0Mo8HAXcMHnl9/cDUIIQj18SLUx4uR8dG/eO9cgaGskvLGutiV5JVXkFdRxe6MHAoqKlmXVdDssd2cnHB1dsLNyQk3ZyeMBgNGg8DYOFZtkVaklJitkvoGM3VmM/UNZmoaGpo9po+bK6E+XoT5eNMvMpyu/r7ny6RGBfjpUXSX4c1D2/jXgS3MjOnJKyNn2HTRWUtwmJXK2w+epkdsKAG+HmpLuWpqTA08+MUKKurq+XzhAmIC/dWWpKMSLk62/Ze7sMBQU2zatIkBw4ZTWlN7fiuvraOqvp7KOhPVJhN1DWbqzWbqGsxYrFYsUmKxWhEIDEJgMCjDYOeMw9XZCS9XF3zcXPFydcXP3Y0ATw8CPd0J8PRwiPoBWkNKycsHfuTNw9u4Ia4X/xpxnSoLbh3CEMqrajl66iwLZw1TW8pVY7VKfr9sDcfPFvL2zTPpER6itiSdToQQAj8PN/w83IhFvxHRIlJK/rFnIx+m7OGm+H48e80U1bIvOIQh7DmWhVVKrukTo7aUq+btLTtYfzyNJ6eMYWxix1g/oaOjYxusUvLUznV8nrqfhT0G85fBE1QNCnAIQ9h9NBNPdxd6dgtTW8pVsTUtg7eSdzC7X0/uvGaA2nJ0dHQ0hNlq5ffbV7P01BEe7H0NTwwYo3qEmMMYwsDukQ4VhlZcVcOT36whPjiQp68br/ofWkdHRzvUW8w88uNK1mam8lj/UfymzwhNXCM0f4UtKqsiO7+MAd0j1ZbSYqSU/Hnlesrr6vnX3Gm4O/C6CR0dHdtS02Di3h+WsjYzlaeHTOSRvtdqwgzAAXoIB07kANA/KUJlJS1n6f6jbEpN58kpY0gKC1Zbjo6OjkaoMNVx7w9fs6cwhxeHT2NBQj+1Jf0CzRvCoZO5uLo4kRTtGNE5eeWVPL9mM0NjIrljmD5voKOjo1BQW8WdG5aQVl7E66NmMiOmh9qSLkHzhnD4ZC49Y0NxcnKMxSzPfZ+MVVp5btZkTeRe0dHRUZ+sqjJuW7+YgtpqPhg/n9FdtLnAVtNzCFIqKSv6JHRRW0qL+DHtDOuPp/HA6GH6SmQdHR0ATpYVsWDN55TW1/L5pJs0awag8R5Cg8WK2WKllwOEmzZYLDz3fTLRAX4sHD5QbTk6OjoaYG9BNnf/8DUuRiOLJ99Cz4BQtSVdFk33EExmKwA94rRvCIv3HOJ0cSm/nzLa5ukJdHR0HI9N2ae4df1iAlzdWTb1ds2bAWi9h2C24u/jQYi/tgt8VNbV81byDq6J7co4fTWyjk6n55v0Izz+02q6+wfz8YQFBLk7RoU8TRuCyWyle0yIZmJ0m+ODn/ZQVlvHE5NHa16rjo5O+yGl5N2jO/nnvmSGh0Xx3ti5eLu4qi2rxWjaEMwWK4kaDzetbjCzaPdRpvZMoKeeuE5Hp9NisVr5x56NfHx8L9fH9OBf117XrvWP2wNNq5US4rs2ndZXKyTnFFFtMvHgaMfLxKqjo2Mb6ixm/m/rKr7LOM69PYfwx0HjL6mX7Qho2hBA24ZQa2pgU04hYxJi9RXJOjqdlNK6Wu5LXsrugmz+MHAc9/d23JtDTRuCEBAVpt0c7isOpVDVYObeawerLUVHR0cFsirLuHPjErKrynlz9CxNrj6+GjRtCE4Gg2ZXKFutkk937CfKy53B0Y6TZ0lHR8c2HCrK455NX2OyWPh80k0MCe2qtqQ2Y5N1CEKID4UQBUKII828L4QQrwsh0oQQh4QQLVq55eyk3TG47aczSS8qYXyk9qOgdHR0bMvazFQWrP0cF4ORr6fe1iHMAGy3MO1jYOpl3p8GJDRu9wHvtOSgWq5/8MXugwR4uDMoxE9tKTo6OnZCSskHx3bzQPIykvyDWT79ThL8tDvPebXYZMhISrlFCBFzmV1mAZ9KKSWwQwjhJ4QIl1LmXe64zk7aNITCymo2nUhn4YhBOBssasvRaSVSQmkpZGRAcbHyvKzs0seyMqirA4vl5+2uu+BPfwKjUdnc3MDPD/z9f3688HlgIMTEKK91HBOz1cpnpWfYmJXP1KhE/j3yetydtFXr5MfC/W36vFCu0W2n0RBWSSl7N/HeKuAFKeXWxtcbgd9LKfc0se99KL0IgoODBy1ZssQm+mzJhqwCvj6Vw9NDeuAtzXh5aXslNUBVVVWn1Vlff+lmMimPAC4u4OSkbOcu8Bc/F0LZQHk0m6swGhWdUoLV+rNZmM2XPjeblfaEAFdXZXNx+fn5uc3WdOa/uy2ptpp5p+gkR+rKmeodzgK/KM2FlZZSxSdiIyvGvrpXStmqSBd7TSo3deaadCIp5XvAewBJSUly7Nix7Sirdbz+n8/pFR7CzddNJTk5GS1qvJjOoNNshpQU2LcP9u5VHg8ehOBgSEyE2NhfbnFxyt17a/6vW6NTSqUncvo0pKcrj+e21FQoKYH+/WHQIBg4UHlMSlJMqbV0hr97e5NVWcbCH77iTH0lCwPieHrGArUlXYLZauHxg6/iWtu2uwp7GUI2cOGsSySQa6e2bUpGcRnH8gp4YvJotaV0eioqIDkZNmyAXbvg8GGIjPz5gnrDDTBggHaGaYSAoCBlGzLk0vdLSn42s1Wr4G9/g7NnoV8/GDoUJk6EMWNAwzfSHY6d+Zk8mPwNFilZNOlG6o+fVltSkyzJWkdqZQZP9ljIEv7Z6uPYyxBWAg8LIRYDw4DyK80faJU1x1IBmNYrUWUlnY+GBuXCv369sh08CNdco1woX3xRubv28VFbZesJCFB+l4kTf/5ZWRns3w/btsFLL8GNNyqGN2mSsg0e3LYehE7z/C/1AH/ZuY4obz/eHzeXbr6BJGvQEE5WZvJFxlrGhgxmVHDbqjTaxBCEEF8AY4EgIUQ28DTgDCClfBdYDUwH0oAaYKEt2lWD9Slp9IsII9zXW20pnYKyMli+HL75BjZvVoZ6Jk2Cp5+GkSPBw0Nthe2Lnx+MG6dsf/oTVFXBjz8qhnjvvZCTo7x3ww0waxZ461/LNmO2Wnl27w98lLKHMV3ieH30THxd3NSW1SR1FhMvn1iEv4s3D8bPa/PxbBVldPMV3pfAQ7ZoS03yyis5kpvP/00cqbaUDk1NjTJk8sUX8MMPMH48LFgA778PIZ08f6CXF0ybpmwAeXmwbh18+SU89BBMngw33wzTpyuRTzpXR2ldLQ9vWc5PZzO4u8dg/jhoPE4GbUY7Anx0egVZNfk80+chvJzafnek6ZXKWmNzajoA45P0mge2xmRSLmyFhTB7NgwbplzYPv4YfPVqpM0SHg533qlsJSWwdCm8+abSe5g5E+bMUSbb9ZpNV+Z4aQG/2rSU/JoqXhwxnQXxfdWWdFn2lqSwKvdHZkWMZYB/kk2OqV3r0yCbT54h0s+HuKAAtaV0GPLzlcnT6Gh44QXlDjg1FdauVWL9dTNoOQEB8KtfKb2qo0eVCfXcXGWY7YUXlAgnnaZZnXGcOd8vot5iYcnUWzVvBgClpgrivbpyV+z1NjumbggtxGS2sPN0FqMTYvVUFTZg3z7lrrZ7d2UcfP162LpVCRHt7MNCtiA8HB59VDm/K1fCiRMQH68YxpEmE8x0TsxWK8/v3cSvNy8nyS+Yb6+7k/5BXdSW1SImhg3jlQH/h4vBdovjdENoIQez86hpaGBEXJTaUhwWsxm+/hpGjVKGhXr2hLQ0eO896H3JckYdWzFgAHz0kWIKUVHKPMOECYpRWK1qq1OPkroa7tzwJf85upPbkwby5ZRbCfVwrFl5o7DtJVw3hBay60w2AhgSE6m2FIdDSli2DPr0gZdfhkceURZm/f73SkoHHfsQEgJPPQVnzsDdd8Pf/66YxerVyt+oM3GwKI/rv/uY3QXZvDRiOv8YNhkXPX5XN4SWsi8rl4SQIHzd9dCNq2HTJmWtwN//Dq+8osTTz5+vT3KqiYsL3Hor7N6tzN/87nfKgrdt29RW1v5IKVl0fB/z13wGwNdTb2O+BucLzFYLZ2t/nvSxVYqhK6EbQguwWiUHs/MY0DVcbSkOw759MGWKEu3y6KPK62nTWpcmQqd9EEIZujt8WOkx3Hyzspaho84x1DSYeOynVTy1ax3Xhsew6rqF9A3S5v/0i8c/4fmUD9mYvwsp5fl5y/Y2Bt0QWsDp4hKq6k30i9Tml0dLnD0Lt90GM2YoF5eUFLjlFtBwKHenx2hUIrpOnICxY5X5hXvu6VhRSallhcxa/SnL04/yWP9RfDB+Hv5u7mrLahZnYcTd6MrBslT+c2opp6tyANo9oEX/N20Bh3PyAegTEaqyEu1itSqTw337QteucPIk/PrXyvCEjmPg5gb/7/8pYb/e3tCrFyxa5PjzC0vSDjHzu08ora9l0cSbeKTvtZrLVHoxQwJ7UWupJ8ErioqGar7IXMPWwv08d+wDzlTntltPQR/JbQEpZwtwd3bS1x80Q1qaMuTQ0AAbNyqTxzqOi68vvPqq0tP71a8UU/jvf5UIJUeiusHE07vW8/Wpw4wIi+bVUdcT4u4YmQHHhgwmvSqH/v5J9PNPZGfxYf6XsYbyhqpfDCHZGr2H0AJSzhaSGBqMUR/3+AVWK7zxhjJpPGeOso5AN4OOw+DBysTzuHFKQr0PPnCc3sKR4rPMWPURS08d5jd9RrBo4o0OYwZWqcQCezl58EH6cqI8wujhHUuRqYx47658eHrF+SEkW6P3EK6AlJIT+UVM6ZmgthRNUVSkzA1UVyvRKYl68tcOiZMT/OEPcP31yjzDypXw6afaXUEupeST43t5bu8mAt08+GLyLVwT5lhdG0Pj2oIbIseSmZpHXm0RX2at4/ouoxkW2JvjFWeI9Ypon7bb5agdiOLqGspr64gP1gPmz7Fvn5LPf+BA2LJFN4POQO/eivFHRSm1GY4dU1vRpRTUVrHwh6/46+4NjAyPYfWMux3ODC7E2eBMN69I7t/zDJUNNdwWPZ1E72iu6zKq3drUewhX4FRhCQDdgvX5A1DuDv/v/+Cdd2Be27Pt6jgQLi7KEOEnnyjrFrT0HdiUfYrfbfuOqgYTfx86iduTBnaIFDNTwkZQaqpkQuhQhBBIKW2+OvlCdEO4AmeKSwGICfRXWYm6NDTAY48pSeeSk5UIFJ3OyZ13KnNFc+bAnj3w7LPqFempbjDx/N5NfJa6n+7+wSyefAsJfkHqiGkHPJzcuDN2BkahnOD2NjndEK5ARkkZLkYj4T6OlePEllRUKKmUvb2VimVaKUmpox4DBypmcNNNypqTpUvtX6xoX2EOj21dRUZlKff0GMLjA8fgZnT8S1qD1Yyz4eff45wZ2AN9DuEKZJeWE+Hng8Hg+N3P1lBaqlQo69kTVqzQzUDnZ4KCYM0aJUPtddcp1dzsQb3FzMv7tzB/zWc0WC18MfkWnhoyoUOYQX5dMffs+ht7StSZpNEN4QrklFUQ4efAhXrbQHGxUt93+HB46y19tbHOpTg5KZlU4+Jg6lSlN9meHCk+y6zvPuGNw9uYFduL76937InjC5FS8ubJL6mx1BHlEaaKBpv8iwshpgohTggh0oQQTzbx/lghRLkQ4kDj9hdbtGsP8iuqOmX95IICpXTlxInw73/rOYh0msdoVMqb9u2rpNYuK7N9GyaLhdcObmX26k8pqa/lw/HzeGXkDHw0Wuu4NWzI38m+0uPcFXs9IW7qBLG0uY8lhDACbwGTgGxgtxBipZTy4j7Pj1LKGW1tz56YzBaKqmsI9XGMBS22Ij9fMYM5c5QspboZ6FwJg0HpRf6//6fkQlq/XqngZgsOFOXyxLbVpJYVMSu2J38bOgk/V+3mIWoNRfVlvH/qG/r4xjM9XL2a7bboIQwF0qSU6VJKE7AYmGWD46pOSXUNAMFeniorsR91dUpSuhtugH/8QzcDnZYjhNKbHDlSSXHe0NC249WaG3huzw/M+X4RlaZ6Phg/j9dGzexwZiCl5O20JZilmUcSbz6/ME0NRFuTJAkh5gFTpZT3Nr6+HRgmpXz4gn3GAktRehC5wO+klEebOd59wH0AwcHBg5YsWdImfW0ho7KG5/ee4IHesfQP8mtyn6qqKry8tN+DaKnOM2eUlBRxce2vqSk62vlUG7V0pqWBq6uS6LAlXKzzUG0pn5acochSz1ivEBb4ReFhUH/SuD3O5wmyWWnYxRhrb4bS9lWe48aN2yulHNyqD0sp27QB84H/XvD6duCNi/bxAbwan08HTrbk2ImJiVJNtpw8LZOefkXuzchudp9NmzbZT1AbaInOl16ScsAAKaur219Pc3Sk86kF1NJZViZl9+5S/uc/Ldv/nM6Cmir58OblMvqT5+WE5e/J7XkZ7SeyFdj6fFY2VMtbt/9J/mbvP6XZarbJMYE9spXXc1tYbjZw4X1AJEov4ELTqbjg+WohxNtCiCApZZEN2m83ymvrAPBz71hd1KZYvVqpaLZzp/3jyXU6Hr6+St6jkSOhe3cYPfry+1uk5KOUPbxy4EfqLWb+X7+RPND7Glw7QCjp5fgwfSXlpkqe7nWfXdcbNIctzvZuIEEIEQvkADcBt1y4gxAiDMiXUkohxFCUuQvNl9+oqK0HwNvNVWUl7UtampK4bPnylnfxdXSuREICfPYZ3HijkjU1sply5PsLc/n72cNkZNUwKjyWp4dOJN634+cOO1R2krVntzE3cgIJ3toInW2zIUgpzUKIh4G1gBH4UEp5VAjxQOP77wLzgAeFEGagFripsWujaapNJgC8XDtulRcp4b77lIL3I0aorUanozFpEtx/Pzz0kHLDcWGQQn5NJf/ct5ll6UfwN7rw9pjZTItK6hA5iK5EvcXEGycXE+YWyC3R09SWcx6b9MeklKuB1Rf97N0Lnr8JvGmLtuxJjakBgxC4OXfcbutHH0FlpVL3WEenPfjDH2DAACW9xbx5ypqCj1L28Pqhn2iwWniw9zX0LbMwLbq72lLtxpKs9eTWFvJMn4dwM2rnhrPjXulsQG1DA25OTh32juXsWXjySSVm3En/Jui0E66uysK1BQsk5u7HeTt1M5lVZUyMjOepIROI9vYnOTlZbZl2I6smn6+zNjAuZDAD/JPUlvML9MvAZTCZLbg4qT/R0148+qhS+rJfP7WV6HR0PBJzCf7jRp7cl0N3/2A+nrCAsREqxTariJSSd9K+wtXowj1xs9WWcwm6IVyGBosFZ7Xy+rYza9fC3r3w8cdqK9HpyKSWFfKv/VtYl3WSoCBPrF9M48+P92FkROdMjLWpYDcHy1J5KH4B/i7ay5GmG8JlsFglxg6a5fQf/4BnnoFOEFGrowI5VeW8fugnvjp1GE8nFx7rP4q7ewzmiwpXnntWCXPubFQ2VPN++jd094lharg2Izh0Q7gMEomhA84fbN0KeXnaqXal03E4W1PJW4e3s/jkAQSChd0H83CfEfi7KXced9wBTz8NBw92vqHKT86soqqhlof73KhqeorLoRtCJ+Sf/4THH9cnknVsR05VOf85upPFJw8ikSyI78dDfYbTxfOXwyKurkoCvBdfhM8/V0msCqRWZrAmbxuzIsYQ6xWhtpxm0S8Jl8EgBFbtL5e4Ko4cUSpdffWV2kp0OgIZlaW8c3gHS9MPAzA3rg8P9R1OVy+/Zj9z//1Krqz0dPVyZtkTq7TybtrX+Ll4c6uG1hw0hW4Il8HJYMBitaotw6b8619KdJFbx0kjr6MCB4pyeffIDtZmpuJsMHJzQn/u7zWMCC/fK37Wx0dZDPnvf8Mbb9hBrMqsP7uDE5UZPJZ0Gx5O2p600w3hMjgbjZjMFrVl2Iz6emW16IkTaivRcUQsVisbs9P4MGUPO/Iz8XVx48Hew7mr+yBCPK4uA+g998C118Jrr3XsSnyVDdV8fPpbevnEMT5kiNpyrohuCJfB1clIndmstgybkZys1EYODVVbiY4jUW6q48uTB/n0xD6yq8oJ9/Dmz4PHc1NCP7ycW5fnq1s3pSbzzp1KidaOyqIz31FlruHB+PkOscBVN4TL4ObsTL3ZgsVqxdgBbmNWrFCK3+joXAkpJQeL8/j8xH6+PZNCncXM0NCu/GnQOCZ1TcTJBv8Ps2Yp38mOaghnqnP5Pu8npncZpemJ5AvRDeEyeLg4A1BrasCrA2Q8XblSSVOho9McRbXVLD99lKWnjpBSWoCHkzM3xPXm1sT+9A60beH3mTNh4UJ44QWbHlYTSCl579QyPJ3cuU3jE8kXohvCZTiX5bSq3uTwhlBTo9Q56N558ofptJA6i5nk7FN8c/ooG7PSMEsr/QLD+cewycyO7YW3S/t894cMgbIyOHmyXQ6vKrtKjnCwLJUHus3D29lxSvDqhnAZfBpNoKKunjBfb5XVtI3qahg7Vq+RrKNQZzGzLe8M32UcZ13mSSob6gly82Bhj8EsiO9Lgl9Qu2swGGDMGNi+HaK0UQ7AJjRYzfw3fTmR7iFMC79WbTlXhW4Il8HXXYnNPFc5zZGpq9N7B52dSlM9W/NOsyYzlY3ZaVQ1mPB2dmVKVCIzY3syIizaJnMDV0NSkhL11pEMYVXuFnJrC/lb7wdwMjhWLjTdEC6Dv4cSM1xaU6uykrajG0Lnw2K1kmGq5r2jO9mUc4rd+dmYpRV/V3dmRPdganQSw8OiVC1T2b07fP21UkinI1DRUM0XmWsZ5N+DwQE91ZZz1eiGcBkCPJXiwiXVNSoraTt1dcrdmE7HxSolJ8uK2F2QzfazGfyUd4YyUx2che5+wfyq11DGRXRjYHCE3XsCzXGuh9BRWJy5hlpznSZTW7cE3RAuQ4CnOwIorHJsQ6ipgYYGiIlRW4mOrZBSkl9bxeHisxwuPsuh4jz2FeZQYVLqgIe6ezGhazyBZbXcPW4qYR7anANLTFRqencEztYW813uViaFXUO0Z7jaclqFTQxBCDEVeA2lpvJ/pZQvXPS+aHx/OlAD3CWl3GeLttsTZ6MRfw93Cquq1ZbSJjIzwcUFOmhphw6NlJKC2ipOVZRwuqKEk2VFpJQWcKK0ULn7R8m5Fe8byPSo7gwOjWRISCRRXn4IIUhOTtasGQB4eoKvr3LD4uh8lvEdBmHQVI3kq6XNhiCEMAJvAZOAbGC3EGKllPLYBbtNAxIat2HAO42PmifUx4v8iiq1ZbSJurqOnR7AETFbrVSY6igz1VFWX0txXQ2FtdUU1laRX1tFTlUFOdXl5FRXUGv++Wrp4eRMd/8QpkV3J8kviN6BYfT0D8HDWTt1ea8Wd3dw9ByS6VU5JBfsZW7XCQS5+qktp9XYoocwFEiTUqYDCCEWA7OACw1hFvCplFICO4QQfkKIcCllng3ab1fCfLzJLa9QW0abqK/XDeEcDVYLZ6srKaqroaiumpK6Giob6qluMFHdYKLeYsZktdJgtWC2WrFIK1YpkchfXLQKCwv5MrkUUOpmWKU8v59FSixWK2ZpxWSxUG8xU2+xUGdpoMbcQFVjO80R4OpOhJcv8b6BjOkSR4y3P7E+AcT6+BPu6dPhanS4uoKj55D86PQKPJ3cmRc5UVUdDda2jWbYwhAigKwLXmdz6d1/U/tEAJcYghDiPuA+AP+gMNWLb1urKsgsKm1WR1VVleoar0R1NQQGal8n2O58SikpMNeTbqoi3VRFXkMt+eY6is31NHftcRYCF2HECYGTEBiEwIDAAAjEL9ZwWK1W8vJ+jj4TCAQgAKMQGFE+b0TgIgz4CgNBwhk3J1fcnI24GYx4GpzwMDjhZTDiZXDGz+iMj9EZpwuLp1QD1RWYz1ZwkjNc7RouR/h+/uY3YDJpXyc0fT6zKGSf4ThjrL3Z+9MudYQ1Uuy3vE2ft4UhNHW7cnEHsCX7KD+U8j3gPYDwrnFy7NixbRLXVtJd9rI5dwsDhl1zfl3ChSQnJ6O2xiuxfz9s357M/Plj1ZZyRdpyPustZjblnGJNRipbctMpqVcu2O5OzsT7BnKNdxdivP2J9PIl2N2TIDdPAtw88HZxxdPJ5aoibxzh7w6OofPuu+Gdd7SvEy49n1JKnjj4GoF1vjw65C5cjeoN3ZmtdSw5/WybjmELQ8gGul7wOhLIbcU+l2C2qN+P7Oqv5HfPKi1v0hAcAVdXxx+jvRyFtUqs/ZdpB6kw1RPg6s7YiDiGhHSlX1A4iX7Bmgmz1LkURx7S3F96nGMV6fw6fr6qZgCQUZWsiSGj3UCCECIWyAFuAm65aJ+VwMON8wvDgPKWzB+YLepfxaIC/ADIKC6jdxfHzBsdGQkmkzJO66j/eE1RVFvNO0d28HnqfkxWC9dFd2d+fF9VVtzqtI76eigqcsxyrlJKPs/8nmBXfyaHXaO2HE5VfI+XU5c2HaPNfwYppVkI8TCwFiXs9EMp5VEhxAON778LrEYJOU1DCTtd2JJjmy1WpJSq5hGPauwhnCkuVU1DW/HxUUJOc3Kga9cr7+8I7MrP4sHN31BWX8sNcb15qM9wYn0C1Jalc5WkpSnrYxxxnvxA2QmOV5zh1/HzcTY4q6qluqGAvNo99AtYCCxt9XFs4stSytUoF/0Lf/buBc8l8NDVHtcqoaC0itAA9eKo3V2c6eLrw2kHNgRQSmaeONExDOF/qQf4y851RHn78cXkm0n0C1Zbkk4rOXHCMVfQSyn5LGO1ZnoHpyvXAZI476ltOo7m+9UZuSVqSyAuyJ9ThcVqy2gT5wzB0Xnv6E7+uGMN14bH8M30O3QzcHAc1RDO9Q4WdJ2keu8AIL1yLcFuvfBxiWzTcTRvCGc0YAgJIUGcKizB4sDB0q6ujm8IG7PTeG7vJq6L7s6H4+fh6+KYk/w6P+OohvBl5joCXXyZFKb++trS+nRKTaeI9Z7S5mNp2hAMQpCeo/6deUJIICaLhYySMrWltBpPT/jpJ7VVtJ5KUz1PbFtND/8QXh45o0OUNO3sSKl8JwcNUlvJ1XGsPJ3D5WnMiRyvid7BmaoNCAzEeI1v87E0/V/l7CRIz1bfEJJClWIhqflFKitpPV5ekJEBWVlX3leLfHpiH8V1NbwwfBpuKqZr1rEdKSlKlFH//moruTqWZm/E28mDqeEj1JaClJLTlRsIcx+Iu1Pbgyq0bQhGA6eyi5AqB9HHBwfiZDBwLK9AVR1tZfp0pa6yo1FnMfPBsV2MjYijX5BjZpHUuZQVK5S6yo4UYVRCJTuLj3Bdl1G4GdUvq1tcn0JlQzax3rYpKKFtQ3AyUFVTT0GJusnlXJ2d6BYcQMrZQlV1tJVZsxzTEHblZ1FSX8sdSQPVlqJjQ1auVL6TjsQekYaTMHJ9l9FqSwHgTOUPGHAiymuMTY6neUMAOJmp/oW4V3goR3LzVe+ttIXJk5X6teXlaiu5OrbkpuNiMDI8LFptKTo24uxZOH5cqansKJSZKjlKBuNDh+Lnon5KcSklZ6p+oIvHUFyNPjY5prYNwWhACEjNUH+opk9EKKU1teSUOW7mU29vGD8evvxSbSVXR0pJAT0CQnB3Un8CT8c2fPYZzJih1OlwFFbnbcUsrNwQOU5tKYAyXFRtPku0d9snk8+haUMQAiJD/TihAUPoH6mMXe/P0nzG7svy2GPw0ktgsaitpOUU1FZrusiLztVRXw+vvqp8Fx2FBmsDq/N+IlaG0tVDGylsMqqSERjp6jnSZsfUtCEAJEWHcOKM+oaQEBKEh4sz+7OumJNP04waBcHBsGyZ2kpaTmVDPd7O6k/g6diGzz+HXr1gwAC1lbScn4oOUmqqYJCMV1sKoAwXZVZtJsx9oM2Gi8ABDKF7TCh5RRWUV9Zeeed2xMlooH9kOHszc1TV0VaEgCefhBdecJwMqJ7OLtSYTWrL0LEBFgu8+KLyHXQkvsvdShf3YGIIUVsKAOUNGVQ0ZBHlZdvJbe0bQqzSPUs5k6+yEhgSHUlqfhFlNXVqS2kTM2YoZTU3blRbScvwc3GjqK5GbRk6NmDFCqWGsgOUPjjPmepcjlWkMz382sYySOqTVfUjAF09R9n0uNo3hBjFkVPS1TeEoTGRSGBPRrbaUtqEwaDcof3xj44xl5DoF8zx0gKHjvDSUVKwP/208r1zpLUHa/O24ySMjA8dqraU82RXbyPANRFPZ9v2WDRvCN6ebkSH+3M0/azaUugTEYabkxM7Tjvoct8LuPVWJeHdW2+preTK9A4MpcJUT0ZlmdpSdNrASy9BVJSyGM1RMFkb+KFgNyOC+uHr7KW2HADqLOUU1h0m0tP2K6U1bwgAveO7cORkrup3iC5ORgZFR7A9PVNVHbbAYID334e//x0yNf7rjAyPAeCHnDR1hei0mhMn4N//hnfecazewbaiQ1SZa5gSNlxtKefJrd6BxEqkDaOLzuEQhtA3IZzSylqy8svUlsKIuChOFZWQX6Hu6mlbkJQEv/0tPPigtieYo739SfANYm1mqtpSdFqB1Qr33Qd/+YvSQ3Ak1p3dTqhbIH39EtSWcp7s6m24Gf0Jcu1u82M7hiEkRgBwMFX9CJ+R3ZTVsltPZaisxDY88YTSQ9D6YrWZsT3YmZ/F6Qr106HrXB0ffKCsPXjoqktkqUtBXQmHyk4yMXQoBqGNS6VVWsit2UmEx3BEO2jSxm95BWLCA/DxcuPACfUNITE0iGAvT7amnVFbik1wcYH//hcefVQpZ6hVbkzoh5Mw8NmJ/WpL0bkKDh9WJpHff18p4+pIJBfsQSIZFzJEbSnnKa5Lod5aQYRn+1Rpa5MhCCEChBDrhRAnGx/9m9nvjBDisBDigBBiz1WLNAj6JUZowhCEEIyKj+GnUxmYLY5bMOdChg2Dv/1NmezTap6jEHcvZsT04H8nD1BUW622HJ0WUFSkJK979VXo00dtNVdPcsFeevrEEe4epLaU8+TU7AQE4R7tY1Jt7SE8CWyUUiYAGxtfN8c4KWV/KeXg1jQ0ICmC7PwyCkvVH7sfkxhLRV09+xx81fKFPPCAEht+663aDUV9pN+1mCxm3jjkwJV+OgkNDTBvHixYoHynHI0z1blk1OQxJkRbGXbzanYT6JqEm9G3XY7fVkOYBXzS+PwTYHYbj9csA3so1eH3HVd/DcC1cVE4G438cOKU2lJsymuvQXW10sXXInE+Adyc0J9Fqfs5Uqx+GLJO8zzyiJJM8dln1VbSOrYWHkAguDaov9pSztNgraaw7ijhHq26p24Roi2hnEKIMiml3wWvS6WUlwwbCSFOA6WABP4jpXzvMse8D7gPIDg4eNCSJUsAsFolf/v8EH1j/Zg7Uv00yG8eOkVeTR1P9orC21v7ideqqqrw8rpyHLXZrKQlDg+HwEA7CLuIK+mstpr5Y+5B/Iwu/CWsN0aVYhhbej7VRg2dhYVQUAA9eijhzS1Ba+fzI7EBN1y4Wf4yNYSaOmtdT1AQ9AkhRQtxr28+6mncuHF7WzsSg5TyshuwATjSxDYLKLto39JmjtGl8TEEOAiMvlK7UkoSExPlhfzfy9/IOY/9V2qBr/celklPvyI/XvGd2lJaxKZNm1q879GjUoaHS/npp+2npzlaovO7Myky+pPn5esHt7a/oGa4mvOpJvbW+fbbUnbtKuWpU1f3OS2dz5yaAjl982/k8uxNl7ynps7dhW/KT1NHyQZL7WX3A/bIFlxfm9qu6N9SyolSyt5NbCuAfCFEOEDjY5NpSaWUuY2PBcA3QKvWgA/uFUV2QTl5RerXJBjfvRtOBgN7C0vVlmJzevaEDRvgD3+ADz9UW82lTI/uzuzYXrx6cCv7CtUPNNBReO01JXFdcjLExamtpvVsLzoEwDWB2poJz689QJBbT5wMbu3WRlvnEFYCdzY+vxNYcfEOQghPIYT3uefAZJQexlUzpKeyqmX3UfWX1vp7uDM8Loo9BWWqr6BuD3r2hB9+gL/+VVldqjX+PmwS4Z4+PLR5OQW16gcadHZefBFef93xzQBgR/Fh4jwjCHVTYcy0GRqstRTXHSfUvX+7ttNWQ3gBmCSEOAlManyNEKKLEGJ14z6hwFYhxEFgF/CdlHJNaxqLiwwk0NeTXUe0sShseu9ESupNHMh27KI5zZGYCJs2wT//qdz9aQkfFzfeHXMDZaY6frVpKXXmBrUldVqeeUZZfLZ5M0SrP73XJioaqjlecZqhgb3VlvILiuqOIbEQ4t6vXdtpkyFIKYullBOklAmNjyWNP8+VUk5vfJ4upezXuPWSUrY67kAIwdDeUew+monVqv5d+aTu8TgJwarDJ9SW0m5066b8o7/5Jvzud8qks1boHRjGqyOv51BRHr/d+i0Wa8dYF+IomExK2pMvvlB6BpGRaitqO3tLjmFFMiSgl9pSfkFB7UFAEOLWvkblECuVL2R43xjKKms5roH6CF5urvQN8uX7Iydo0Grwvg2IjoadO5VVp5MnK1EkWmFKVCJ/HjyBNZmpPLVrXYccvtMiubkwZgycPQvbtytRaR2B/aUn8HHyJMFbW0mXCuoO4e8Sh4uxfSMaHc4QrukTQ2SoH6UV2iiYMiw0gJKaWn7qILmNmiMgAFavhmuugcGDYc9VrzdvP+7pOYQHe1/D/1IP8NzeTboptDNbt8KQIUqhpaVLwcd2FRxVRUrJ/rLj9PdPwqiR3EWg5C8qrDtKsHvfdm/Lqd1bsDG+3u4s/dfdass4T68Ab/w93PnmwDHGJjr4bNoVMBrhuecUQ5g+XZlbWLhQbVUKTwwYQ02DifeP7cIsrfxl8ASEI+VZdgCkVOpn/OMf8MknMHWq2opsS1ZtPiWmCvr5Jaot5ReUm87QYK1u9+EicEBD0BpOBgMz+3bnf7sOUlJdQ4Cnh9qS2p05c5RFRzfcoMwvvPoq+Pmpq0kIwV+HTsLJYOSDlN3UW8z8Y+hkjC1dGaVzWYqKlGylx48rQ0SOHknUFIfLTgJoKtU1KBPKAEFuPdu9Lf2/xQbMG9ibBquVbw4cU1uK3ejRQxk28vRUEpetaVXcmG0RQvDnweP5de/h/C/1AL/eslyPPrIB33wDfftC166wY0fHNAOAo+XpBLr4Eu6mnWR2AEV1KTgbvPBx7trubemGYAMSQoIYFNWFJXsPayL6yV54eSlDCB9/rCTHu/NO5U5STYQQPDFwDH8ZMoF1mancsn4xxXXamG9yNPLylOR0TzwBX30F//oXuLurrar9OFaRTg+fWM0NNRbXHyfItXu71D+4GN0QbMRNg/uSUVLGtg5QXvNqmTABjhxRch/16qUYhNrzunf3GMLbY2ZztCSfWas/4USphkKjNI7VCu++q/QKEhLg0CG49lq1VbUvJfXlFNaX0sMnVm0pv8AiGyg1nSLQLcku7emGYCOm9EwgwMOd/+0+oLYUVfDygldeUSKR3nxTiUb64Qd1NU2L7s6XU27BZLEw5/tFegnOKyAlfP89DBwIixYpixKffbZj9wrOcaJSiRJM8olRV8hFlJtOY5UNBLjqhtAiLFYr+08oKbHVDDd0cXJi/qA+bDqRTnapRqvM2IFBg2DXLqVW869+paxb2LtXPT39g7qw8ro7ifcN5P7kZby4bzNmfQHbJWzfrtTDeOwxePppJbS0t7YW67YraVVZGDAQ5xmhtpRfUFKvTHQHuNpnotvhDcFoMPDEv1eQmVeKEEJVU7h5cF8MQvD5roOqadACBgPcfDOkpCiRSNdfDzfeCKkq3aCHeXjz5dRbuTmhP28f2c4dG77Uq641cvQozJ6t/H3uvFNZfHjDDaCxYfR2J60yi64eobgaXdSW8gtK609hFK54O9tnGbhDG8K5EpYDe3Rl8dp9AFhUnNQN8/VmSs8Evt53hOp6k2o6tIKLi5La4ORJ6NcPRoyAu+9WxqTtjZvRieeHT+XFEdPZW5jD9FUf8VPeGfsL0Qh798Jtt8G4cTB6tGLWd98NTp00ED2tKot47/aP4rlaSutP4ecSi0HYpyC1QxuCofE25pZpg1i/4zgATkZ1f6U7hw+ksr6er/e1KqFrh8TTU6nClpqqhCxOm6ZciFassH+5zgXxfVk+/Q58XFy5bf1iXty3mQZrx007ciFmsxItNHKkspakb1/FrB97DNzaL6Oy5ikzVVLWUEmsxoaLAMpMp/FzsV+cr2MbgkExhH6JEUgJB1OV3Phqhn72iwxncHQEH23fi8ncOS40LSUgAP78Zzh9WplfeO45JYrllVeg3I7TLj38Q1g5/U5uSujH20e2M2/NZ6RXlNhPgJ0pKVFWlcfFKSmqf/tbOHVKCSf1bZ/SvA7FmWqlNnqMZxeVlfySeksFtZYi/Fxi7NamQxsC/DxsNHl4dxavUYaNrI3zCGrNJ9w/cihnK6r49lCKKu1rHRcXuOUWJWHe//4Hu3dDbCzcey9UVtqn1+Dh7MLzw6fx1ujZnKko5bpVH7HidMdZWGg2w9q1cOaMkrH22DFYvhx+/BHmzeu8Q0NNkVWjJMqM9ghTWckvqTApIey+uiG0HGNjL2HB5AH8uD8d+HnYSK0FJiPjo+kZHsJ7W3frKZmvwDXXKOmTDx+G7t0hO1tJo/zoo8qq2Pb29OtiurNu5j1cExpFhGfLsrTVWTSUA/wCrFblgv/QQxARoUQLeXgo6SY++UQJJ9W5lOzaAjyMbvi7aCtLX3mDEgrr42K/zKsObwhCCCxWKzFdAugTH05qxs8LkNKzi1RJky2E4IFRQ8koKWP1ET32vSVERCj1Fnr0UPIjBQTAXXcpwxx/+APs26dc8NqDUA9vPpown8Ehl4/kWHrqMM/s2cht6xbzfUVu+4i5SiwWJcz38cchJuZnM9i+XTHUkBAIDVVbpbbJrS2gi3uw5lYoV5iyEBjxdrbfUJbDGwJwPoHZ23+cT1xEAACfr97DYy8v5+VPN/GvT+2/Qmpi93gSQgJ5d8tOvZdwlSQmKne3KSlKHh0plTDWsDDl8YMPINPOC8KXnjrMUzvX4SSMLOwxmOSqAt48tM2+Iho5fRreew/mz1cu+AsXgqursqjs0CFlAr+j5htqD87WFhPurq38RQAVDdl4OYdjEPYb3+swI4lfrT/Ap6t2ISXcft1gjqTl8fQDU0HCix9vZOPOVCYMs19aW4NB8ODoYTz29WrWHD3JdX3ss9KwIyEE9O+vbC+8oJjAhg2wfj08+aTSi5g0SdmGD1cuju3B4eKzPL83maeHTOTGBKWE4fFjx9iRn8l9lmG4GNs3JDAvD7ZtU37v9euhulr5nWfMUDLNRmgvOMZhsEorBfUljAhu39KUraGyIQdvZ/v+cdtkCEKI+cBfgR7AUCllk2VThBBTgdcAI/BfKeULbWn3YnIKyvh28xEWzhxGl2BfPli+g9iIAAYkKUMAcyf2Y+32FLsaAsDUnom8E7KTN5K3M6VnguohsY5OVJQSK3/33crw0cGDikG8/bYyvOTpqayUHjRIGS8fNKjtlbyklLx68EeGhkaeNwOA7IYaPD08bGoGUkJOjjI8tnevsu3bB/X1MGwYTJyoDAn17t35Fo61F2WmSszSQrCrv9pSfoGUksqGHILd7FvKs609hCPAHOA/ze0ghDACbwGTgGxgtxBipZTSZiEdOw9nEODrwZwJyj+s2WLl+Q/XA5B5tpT9x3MIDfBGSmnXcUKDQfDb8dfy0OKVLDtwlAWD+tit7Y6OwQADBijb448rF9PTp3++mL7+uvLo4qKYQ0KCEsl04ebldeV2duRnsiX3NDvnPXz+Z1lVZZRaTCR6dcEq5fn1MC2lokLReuF28qSiXcqfTe3uu5VsslFRugG0F4X1ZQAEufqpquNiTNZKGqxVdp0/gDYagpQyBa4YzTMUSJNSpjfuuxiYBdjMEPokdOHDFTvOvw7y98TP253b/rSI6HB/KmvquW/ucFUmjcYnxTGgazhvbNrO9X264+7ibHcNnQEhlHHzuDglrBKUi2tmJhw4oMTdnzwJ69b9fBH29laMISYGgoLA318p9HPh41c1JxgT2IO6Eg/yjWDBzKb8LHJMtdzk3Y3CAoHFAnV1UFoKZWVNPxYV/dxube0vjSkuThkCGjBAGf7RL/72o7ShAoBAF20tyKhqyAPAy86GIGwRqy+ESAZ+19SQkRBiHjBVSnlv4+vbgWFSyocv3rfx/fuA+wCCg4MHLVmypEUaXvsmhdgwL5K6+rI/rZjoUC+6hXuTVViNv5cLsWFe547fit+weaqqqvC6wq1mWlkV/zpwkpmx4UyPVifWuSU6tYA9dTY0gMmkDMlYLErsvsXyy+f7RQHpopzrahKQEtKcSzjmUkiUu5H+RfGAcgEXQontNxqVrannrq7KZs81APrf/fIc5DTrDPt5wDoVb65c7dBeOmvcjlEY+BlhBQ/h2nB18wjjxo3bK6Uc3Jp2r/jVFEJsAJq6iv1JSrmiBW00dQVu1oWklO8B7wEkJSXJsWPHtqAJ8A7txoYdJ9hyLJcAH29unDmOuIjAFn22LSQnJ3MljWOBA3Ur2Ziexe/nziTQy/5lNluiUwtoTefO/Ex+vXk51QOUr2x6XjnjwuIZVAHTbh2rrrgWoLXz2Rxq6czPNMGZ/UwZPQkXw5V77/bSmVJWRGEhjB42DXengHZv7xxXNAQp5cQ2tpENXJg1KhKweRD3oB5dGZAUSV5ROREhfr94z95zB03x2MSRXP/Wp7yRvJ2/zpigqhadljMsNIqvp97GS/s3E+bhzWP9RzEiLJqdW3/6xX5rM1MZGxGHq7HDBO51CiobqnE1uLTIDOxJjbkAg3DGzWjfyW57fHt3AwlCiFggB7gJuKU9GhKC82ZwoQmobQYAcUEB3DSkH1/sPshNg/vSPSxYbUk6LSTWJ4C3x9zQ7I3FidJC7k9eRqJfEC+OmE7/IG3lxNFpnipzLV5O2qsAVGMuwsMYZPdrV5viIIUQNwghsoHhwHdCiLWNP+8ihFgNIKU0Aw8Da4EUYImU8mjbZDerp8nnWuE3Y4fj4+bKM6s3qVq3Qad1NPedSvIP5qPx86k01TPn+0U8v3eTZtNb6PySGkstHk7aS/Vaay7C3an9h7wvpk2GIKX8RkoZKaV0lVKGSimnNP48V0o5/YL9VkspE6WU3aSUz7ZVtKPi5+HG/00cyZ7MHL49dFxtOTo2ZFxkN9bOvIcb4/vyn6M7uW7VR+wv1EZ6C53mqbOYcDe6qi3jEmotJbgbHcwQtExtXQMbdp7Q3J343AG96RsRxovrtlBRW6e2HB0b4uPixvPDp/HpxBupbWhg7hq9t6B16q0mXA3aqpIGUGcpsfv8AXRgQ1izLYU/vfkdBxprJGgFg0Hw9HXjKamp5dUf1MmFo9O+jO4Sy5qZd7Ogm9JbmPndxxwpPqu2LJ0mMFnNOBu0FQggpZV6SwWuRvuvjeiwhjDt2h74eLnxxfcqVnhvhl5dQrmlcYL5ULZ+oeiI+Li48cKIaXw0YT5l9XXMXv0prx3c2mmqszkKFmnByY7J41qCyVqFxIqb0c/ubXdYQ3BzdWbu+H5s2XeKrPxSteVcwm/HjyDE24s/rViHyawPKXRUxkV0Y93Me5ge3Z1/H9zK/DWfc7oDV2dzNCzSilFo6zJYb1FWT7sa7V+fQVtnwsbMn9QfJ6ORL77fp7aUS/Byc+Vv10/gZGEx727ZpbYcnXbEz9Wd10fP5M3RszhdUcL0VR/xv9QDmpvf6oxo8W9gslYC4GLwtnvbHdoQAv08mTqiO6u2HKG0okZtOZcwNjGOWX178N7W3RzNtX8hHx37MiOmB2tn3sPAoC78cccafrVpKSV12vte6qiLyVoFgIvR/qk8OrQhANw6fTD1DRa+Wn9AbSlN8oepY/H3cOMPy9dhMuvjyx2dMA9vFk26iacGT2BL7mmmffsh285mqC2r02IUBixSWwWsGqzKTYKzwf4pbjq8IcRGBDJqYDe+2nCA2roGteVcgp+HG3+7fiKpBUW8mbxdbTk6dsAgBPf0HMKyabfj6ezCreu+4IW9yfqEswo4GYxYpLbOu7nREJyEbgjtwp0zhlBRVcfyTYfUltIk45O6MXdAL97fuptdZ7LVlqNjJ3oHhrHquru4KaE/7x7dwc1rvyC3ukJtWZ0KZ+FMg1VbQR16D6Gd6ZPQhUE9uvLZ6j3UmbTXSwD449SxRAX48cSy7ymr0ResdRY8nF14fvhUXh81k5TSAqZ/+yHrs06qLavT4GJwwmTV1jXBLOsBcDLYfwV1pzAEgHtuuIaismpWJh9RW0qTeLq68K+50yiuquGpb9drMvpBp/2YGduTb2fcRYSXL7/atJTn927CbNXW2HZHxM3oSp3VpLaMX2BpNASj0A2h3VDSY0fw6apd1Ju01UU8R5+IMH474VrWp6Tx5d7DasvRsTNxPgEsm3Y7tyUO4D9Hd3L7hsUU1FapLatD4250pdasrR65xWoCBALb1etuKZ3GEADunTOcwtJqViRr92K7cPggRnaL5rnvkzmWV6C2HB0742p04plrpvDytdexvzCX61Z9xM78TLVldVg8nNypstSqLeMXSMwYhLMqGZs7lSGc6yV88u0uzc4lGAyCF+dMJcDTnUeXrKJcT4DXKZnbrQ8rpt+Jt7Mrt65bzKIT+/RhxHbAy8mdGnMdVg2FnlqlGYNdStVcSqcyBCEE980dQVFZNcs2ajPiCCDA04NX58/gbHklTyxbg9WqXwg6I0n+wSyffgeju8Ty1M51PLFttZ451cb4OHsikVSbtdNLkFgRKqXT6FSGADCwR1eG9orik293UV2rrcmkC+nfNZw/TB3L5pOneXvLDrXl6KiEj4sb/x0/j0f6XstXpw5z45rPya+pVFtWh8HXWVkNXNagnbkaKSUGlS7Nnc4QAB5cMJKyylo+X71HbSmX5eYhfZnVrwdvJu9g4/FTasvRUQmDEDzWfxTvjZ3DyfIiZn73CYeK8tSW1SHwc1byBZWZtLP+QyIBdSo+dkpD6BkXxoShifzv+70Ul1WrLadZhBD8bcZE+nQJ5fGl33P8bKHaknRUZHJUIkun3Y6TwcD8tZ+z8vQxtSU5PAEuSkbREg0Zgpq0tabyfCHEUSGEVQgx+DL7nRFCHBZCHBBCaOK2/MEF12IyW/jvN9pOF+Hm7MSbN83E282VX3+xgsJK7RqYTvvTwz+EldfdRb/AMB75cSWvHPhRn2xuAwGuShGaYlO5ykp+RiCQqDPJ3dYewhFgDrClBfuOk1L2l1I2axz2pGuoP3PG92VF8mHO5Go7P32ojxdv3zyT0ppaHl68kroGfWKxMxPo5sFnk25mfrc+vH7oJ3679Vt9srmVeBrdcTe6UlSvnZopQhgc0xCklClSyhO2EmNv7pl9Da4uzry5uCV+pi69uoTy0pxpHMo5yxPLvseir2Lt1LgYjbw4YjqPDxjNitPHuG3dYopq9d7j1SKEINjVn4I6DRkCRqRKCffsNYcggXVCiL1CiPvs1OYV8ffx4K6ZQ/lxfzq7j2p/8c/EHvH8fsoY1qWk8ez3yfpQQSdHCMFDfUbw1ujZHCk5y9w1i8io1M6FzVEIcQsgv65YbRnnMQpnrFKdHp+40kVFCLEBCGvirT9JKVc07pMM/E5K2eT8gBCii5QyVwgRAqwHfiOlbPK2vNEw7gMIDg4etGTJkpb+Lq2iwWzllWXHcDYaePSGHhgNVze7X1VVhZeXfQtZfJ2Ww4bsAmbFhjMtuqk/zaWoobM16DpbR1p9Ja8WnkAA/y+4O3Guijat6WwONXVuEAc4SiaPyOsRV4jusYfOMu+NlPtsJCrnGUQr7tnHjRu3t9VD81LKNm9AMjC4hfv+FcU8rrhvYmKitAfJu0/Kobe9LL9cu++qP7tp0ybbC7oCFotV/u7r1TLp6Vfkkj2HWvQZNXS2Bl1n60krK5Ijl74tkz57Sa7LTJVSalNnU6ipc3n2Jjl9829kWX3FFfe1h85DxZ/Kj1OHywZLXas+D+yRrbyWt/uQkRDCUwjhfe45MBllMvqKWCz2GRIZPagbQ3tH897SbZSUa7+kocEgeHbWZEbFx/D0qo18f8Rhp3F0bEg330CWTbuDJP9g7k9expI07a7G1xIR7iEA5NRqI6z7XNprs7R/2pq2hp3eIITIBoYD3wkh1jb+vIsQYnXjbqHAViHEQWAX8J2Uck1Ljl9ZZp8TIoTgsdvGUlPfwNtLfrRLm23FxcnIawtmMLBrFx5ftoYf9IVrOkCwuyf/m3Qz14ZF88S21ayuyFVbkuY5ZwhZNdqoa24UbgBYrA5mCFLKb6SUkVJKVyllqJRySuPPc6WU0xufp0sp+zVuvaSUz7b0+HW1ZjJP28e1YyMCuWnKAL7dcpTDaY7xT+Th4sy7t8yiZ3gIj371HT+mnVFbko4G8HR24YPx85kR04MlZZk8s2cjVj0AoVlC3AJwMTiTVXNWbSkAOBkUQ2iQ9s+vpO2VygKWfLzVbs3dM3s4wf5evPjxRswWxwjr9HJz5f3bbiA+OICHF6/kp1N6wXYdJSz19VEzmegVxn+P7ebxbd/pBXeawSgMdPUIJaNGG+lAnIUn8HMpTXuiaUPw8HRh4/eHyMu2z8IxT3cXfnfHOFIzClm8Zp9d2rQFvu5ufHj7XGIC/XnwfyvYcvK02pJ0NIBBCG71j+ax/qNYeuoIj/y4gnp9AVuTRHuEc6ZaGyMDzkallnKD1f7rSjRtCF7eLhiNBr60Yy9hzKB4Rg3sxnvLtpFTUGa3dtuKv6c7H985j/jgQB5a/K2eDE8HUObHHul7LX8ePJ7VGSe494el1DRoN8uvWsR4dqHEVEFFg/qL+1wMSliryWL/rLaaNgSDUTB19kDWf3uA/Lwyu7QphODxO8ZjNAhe+GijQy3+8vdw56M759IzLJhHl6zSo490znNvz6G8OHwaP509w50bl1DVUK+2JE0R69kFgNPVOSorAReDkoHVZLV/Sm5NGwLAgjtHArD4I/tF/4QGevPrBSPZdSSD739KsVu7tsDX3Y0Pbp9D/8hwHvt6NYt3H1Rbko5GWJDQj9dHzWRfYQ53bFhChUmvxneOWK8IANKr1DcEV+M5Q9B7CJcQEubL1NkDWbdiP2dz7Lcsf+6E/vRN6MK/P9uk6RTZTXFuonl0Qix//e4H3t68w6F6Ojrtx4yYHrw1ejaHi/O4bf1iyuq1UylMTfxdfAh08eVUVZbaUnASHhiEM/UW+2dg1bwhANx8z2gMRsFn7yXbrU2DQfDnX02m3mTm+Y82ONwF1d3FmTdvup5Z/Xrw+qbtLD6ZrSfE0wFganQS/xk7h+Olhdy07n+U1Gl/MaY96ObVlTQNGIIQAleDr24IzREU4sOMeUPYuPqg3dYlAESHB/Dg/JH8uO+Uww0dATgbjTw/awr3jBjE5twiHl78LTWmBrVl6WiA8ZHxfDh+PqcrSrll/Re6KQCJ3lFk1xRQo4H6ym5Gf2ot9k9U6BCGAHDjwlG4ujnz6Ts/2LfdKQPpnxTBy4s2kV/seLVsDQbB45NHc1NCJJtPnub2j5ZQUKmd+rE66jGySwwfjJunm0Ijid7RSCQnK9XvJfT0v5F472l2b9dhDMHP35M5tw7nx43HSD1mv4kfg0Hwl/umYLFY+cf7a7FaHWvo6BxjI4J5++aZnC4q5cb3F+vlOHUAxRT+O26uYgrrvqC4E5tConc0ACmV6q/jifeZTrT3OLu36zCGADD3thH4+Hrw4Zsb7NpuRIgfj94yht1HM/ly3X67tm1LxibG8dndC7BKyc0fLGbtsZNqS9LRAKO6xPLh+Hmcrizl9vWLKa/vnNFH3s4edPUIJaVCfUNQC4cyBE8vN26+ZxT7d6azd3uaXduePa4PowZ2460vfyQ1o8CubduSnuEhfHXfzSSGKmsVXv9hm8P2enRsx7XhMfxn7BzSyou5Y8OXnTYktadPHMcrzmCVnTMAw6EMAWDG/KGERfjz/mvrsNgx35AQgj/fOxlfLzeeens1tXWOOzkb4u3ForvmMad/L97espOHFq+kvLZzXgB0fmZsRBxvj5nN0ZJ87tr4VadcvNbTJ44qcw2ZGkl0Z28czhBcXJy4++GJnD6Zz4ZVB+zatp+3O399YBoZeSX8+/NNdm3b1rg4OfHsrEn8edo4fkw7w9z/fM6xPMft+ejYholdE3hz9CwOFuVy98avqDU77o1Pa+jjFw/AkXL7jkBoBYczBIDRk3rRo29XPn5rI7U19r2LGdIrijtmDGVF8hHW73Ds1BBCCG4b1p9FC+djtlq56b+L+WrvYYdbc6FjW6ZGJ/HqyJnsLsjm15uXY7KoU/BdDULdAglxDeBQWeecX3NIQxBCcP9jUygprrJreuxz3DdnOH3iw3nug3UU2qmIT3syoGsXlt1/K4OjI3jq2w08vmwNVXWdb7hA52euj+3Bc9dMZVPOKX67dWWnSp3dxy+ew2Vpmp1HsFjb73/TIQ0BoEefroyd0puvP9tGgZ0S353DycnIsw/PwMXZiUUb0x16PuEcAZ4evH/bDTw6bgTfHznBDf/5nEPZnXMcVUfh5sT+57OkPrFtdacpstPfL5EKc7XqeY3yaw+wu/A1dhS8TK25hLM1+/ku61d8n/1rcqp3YJW277k5rCEA3P2bSQC89+o6u7cdGujN3x+cTkFZHS987HipLZrCaDDw4JhhLFo4H4vVyi0ffsm7W3bpKS86Mff2HMpj/UexLP0Iz+xxrOy/raWvXyIAB8tSVdNQWn+K3YWvU27KoNx0mj1Fb3Ks7Au6+84l2msMe4veorje9kPWDm0IoeF+3HjXKH7ccJQDu9Lt3v6wPtFMHBjOmp9SWLax4xQ0HxgVwTcP3MakHvG8+sNP3PbREjJLytSWpaMSv+kzgru6D+LDlD28fWS72nLanSBXPyLdQ1U1hJSyrwhx78PEiFeYEvkmVQ25+LvG081nKn0C7sDbuSsFtba/5rTJEIQQLwkhjgshDgkhvhFC+DWz31QhxAkhRJoQ4sm2tHkx8++4lrAIf956aTXmBvtPfo3vH8aIfrG88tkmDpxQP3WurfB1d+OVedN5ac400gpKmP3OZyzec6hT3CHq/BIhBH8ZMpHZsb14af8WFp1wnGqCraW/fxJHyk/RYFVnOFhiwc3of/61j0sUdeafcxs5G9wxt0OJzbb2ENYDvaWUfYFU4A8X7yCEMAJvAdOAnsDNQoiebWz3PK5uzjz4u2lkpheyfPEOWx22xRiE4G8PTiM82IcnX//WIfMdNYcQguv7dmflr2+nX2QYf121kbs/XUp2qf2zMOqoi0EIXrp2OhMj4/nLznV8e9rxkj1eDQP8k6i3mjhWrs6q5QDXJM7W7KOqIY9yUwYN1mpKTWlsyv0DW88+Q7kpg3CPITZvt02GIKVcJ6U8V6R1BxDZxG5DgTQpZbqU0gQsBma1pd2LuWZ0EsNGJXL8iDp36D6ebrz021k0mC3sOtrxityH+3rz4R1z+euMCRzKyeeNTR1/2EDnUpwNRt4cPYshIZF8mXawQ/cW+/omEOoWSIVZnVookZ7DcXcKZGv+P9hd+Dpezl0YHfZ3At2642RwZVDwQ4S497H530DY6oBCiG+BL6WUn13083nAVCnlvY2vbweGSSkfbuY49wH3Nb7sDRyxicD2IwgoUltEC9B12hZdp23RddqOJCmld2s+6HSlHYQQG4CwJt76k5RyReM+fwLMwOdNHaKJnzXrQlLK94D3Go+7R0o5+Eoa1cQRNIKu09boOm2LrtN2CCH2tPazVzQEKeXEKzR+JzADmCCb7m5kA10veB0J5F6NSB0dHR2d9qetUUZTgd8DM6WUzU157wYShBCxQggX4CZgZVva1dHR0dGxPW2NMnoT8AbWCyEOCCHeBRBCdBFCrAZonHR+GFgLpABLpJRHW3j899qozx44gkbQddoaXadt0XXajlZrtNmkso6Ojo6OY+PQK5V1dHR0dGyHbgg6Ojo6OoCGDEELaTBaghBivhDiqBDCKoRoNvxMCHFGCHG4cW6l1WFgreUqdKp9PgOEEOuFECcbH/2b2U+V83ml8yMUXm98/5AQYqC9tF2FxrFCiPLGc3dACPEXe2ts1PGhEKJACNHk2iItnMtGHVfSqfr5FEJ0FUJsEkKkNP6fP9rEPld/PqWUmtiAyYBT4/N/Av9sYh8jcAqIA1yAg0BPO+vsASQBycDgy+x3BghS8XxeUadGzueLwJONz59s6u+u1vlsyfkBpgPfo6y3uQbYqUGNY4FVan0XL9AxGhgIHGnmfVXP5VXoVP18AuHAwMbn3iipg9r83dRMD0FqJA3GlZBSpkgpNV8qrYU6VT+fje190vj8E2C2ndu/HC05P7OAT6XCDsBPCBGuMY2aQEq5BSi5zC5qn0ugRTpVR0qZJ6Xc1/i8EiWCM+Ki3a76fGrGEC7ibhRnu5gIIOuC19lcehK0ggTWCSH2Nqbj0CJaOJ+hUso8UL7kQEgz+6lxPltyftQ+hy1tf7gQ4qAQ4nshRC/7SLtq1D6XV4NmzqcQIgYYAOy86K2rPp9XXKlsS+ydBqO1tERnC7hWSpkrhAhBWadxvPHOw2bYQKfq5/MqDtPu57MJWnJ+7HIOL0NL2t8HREspq4QQ04HlQEJ7C2sFap/LlqKZ8ymE8AKWAr+VUlZc/HYTH7ns+bSrIUgHSYNxJZ0tPEZu42OBEOIblK69TS9gNtCp+vkUQuQLIcKllHmN3dmCZo7R7uezCVpyftROzXLF9i+8UEgpVwsh3hZCBEkptZakTe1z2SK0cj6FEM4oZvC5lHJZE7tc9fnUzJCR6EBpMIQQnkII73PPUSbMtZi1VQvncyVwZ+PzO4FLejYqns+WnJ+VwB2NER3XAOXnhsDsxBU1CiHChBCi8flQlP/7YjtqbClqn8sWoYXz2dj+B0CKlPKVZna7+vOp5kz5RTPiaSjjXQcat3cbf94FWH3RzHkqSmTFn1TQeQOK89YD+cDai3WiRHwcbNyOalWnRs5nILARONn4GKCl89nU+QEeAB5ofC5QCkCdAg5zmcgzFTU+3HjeDqIEbIywt8ZGHV8AeUBD43fzHq2dyxbqVP18AiNRhn8OXXDNnN7W86mnrtDR0dHRATQ0ZKSjo6Ojoy66Iejo6OjoALoh6Ojo6Og0ohuCjo6Ojg6gG4KOjo6OTiO6Iejo6OjoALoh6Ojo6Og08v8BV1Ayn9vJfp4AAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAELCAYAAADHksFtAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAAAy4UlEQVR4nO3deXxU5dn/8c+VjSSEEEggELZACLtsYQtbwQ13HtyqVnEttWqfPm2ttbVV299jtXa1ta2igkur2LoUqrgiiArIKhD2EEDCFkIgZF9mrt8fM/RJaZbJMjlzkuv9es0rs5w553uyzJVz3+fct6gqxhhjTF3CnA5gjDEmtFmhMMYYUy8rFMYYY+plhcIYY0y9rFAYY4yplxUKY4wx9XK0UIjIAhHJE5GsOl6fISKFIvKF//Zga2c0xpj2LsLh7T8PPAm8WM8yn6jqZY1ZaVJSkqampjYpUElJCR07dmzSe0OB2/OD+/fB7fnB/ftg+Rtvw4YN+ararbbXHC0UqrpSRFJber2pqamsX7++Se9dsWIFM2bMaNlArcjt+cH9++D2/OD+fbD8jSciB+p6zQ19FJkisllE3hGR4U6HMcaY9kacHsLDf0TxlqqOqOW1eMCrqsUicgnwhKqm17GeecA8gOTk5IxFixY1KU9xcTFxcXFNem8ocHt+cP8+uD0/uH8fLH/jzZw5c4Oqjqv1RVV19AakAlkBLrsfSGpouYyMDG2q5cuXN/m9ocDt+VXdvw9uz6/q/n2w/I0HrNc6PlNDuulJRHqIiPjvT8DXVHbC2VTGGNO+ONqZLSKvADOAJBHJBR4CIgFU9SngauCbIlINlAHX+SufMcaYVuL0WU/XN/D6k/hOnzXGGOMQp6+jMMaYdqmovIrdx4o5VVpJTFQ4fbrE0rtLDP7W9pBihcIYY1pJeZWHJZsP8+q6g2z68iTesxrS+3aN5b9Gp5BOaLWwW6EwxpggU1Xe3nqER5fu5NCpMgZ2j+PumQMZ3SeBxLgOlFZWk51XzLIdefz+o2w6hENB3H5umtSPsDDnjzCsUBhjTBAVllXxoze38vaWIwzrGc8vrhrJlIGJ/9HENDktibmZqew5VsR3XvyMh5ZsY/muPJ68YSxxHZz9qLZCYYwxQbIvv4Tbnl/HwYJS7rtoMN+YnkZ4A0cI6cmd+N64DuRG9+fhf27n6j+v4qXbJ9KtU4dWSv2fQvo6CmOMcautuYVc+afPOFVaySvzJnHXjIENFokzRISbMlNZeMt4DpwoZe6CtRSWVgU5cd2sUBhjTAvbfPAUNzy7htioCN68awrjU7s2aT3TB3Vj/twM9uYV8/UX11Pl8bZw0sBYoTDGmBZ04EQJtz6/joTYSF79xiRSk5o3XPi09G788pqRrN1fwCNv72ihlI1jhcIYY1rIyZJKbl24DlXlxdsm0rtLbIusd/boXtwxtT/Pr9rP21uOtMg6G8MKhTHGtICKag/feGkDuSfLmD93HP2beSRxtvsvHsKoPgk88I+t5J0ub9F1N8QKhTHGtIAfvZHF2v0F/OraUU3uk6hPRHgYv7l2FGWVHn70Zq2zRweNFQpjjGmm1zbk8vrGXP77vHSuGJUStO2kdYvj3gsH8+GOY3yw/VjQtnM2KxTGGNMM2XnF/OQfWUwa0JVvn1frvGot6pYpqQxKjuPhJdsoq/QEfXtghcIYY5qsvMrDPS9vJCYqnCeuGxPwdRLNERkexv+bPYJDp8p49pOcoG8PrFAYY0yT/XzpDnYeLeLX144iOT661bY7cUAis4Yn8/TKHE4UVwR9e1YojDGmCVZl5/Pi6gPcNqU/Mwd3b/Xtf3/WEEorq/nDR9lB35YVCmOMaaSSimp+8MYWUhNj+f6swY5kGNg9jmsy+vDy519ytDC4p8taoTDGmEb65Xu7yD1ZxuNXjyImKtyxHPecOxCPKk+v3BvU7VihMMaYRli7r4DnV+3n5sxUJvRv+eslGqNP11jmjOnFy59/yfGi4PVVOFooRGSBiOSJSK1Xj4jP70UkW0S2iMjY1s5ojDFnlFd5uP/1LfTpGsN9FznT5HS2u2cOpNLj5flV+4K2DaePKJ4HLqrn9YuBdP9tHvDnVshkjDG1evrjHHLyS3jkv84hNio0pvPpn9SRWcN68Jc1X1JaWR2UbThaKFR1JVBQzyKzgRfVZw2QICI9g5WnotpDWXVozVVrjAkNB06U8McV2Vw6sifTB3VzOs6/uWNafwrLqnhtQ25Q1u/0EUVDegEHazzO9T/X4oorqpny2Ee8u8+5yUGMMaFJVXlw8TaiwsN48LJhTsf5Dxn9ujC6TwLPfboPj7fl/9kNjWOnutV2mWOt3wURmYeveYrk5GRWrFjR6I31jPbw8cFqln20vFWusAyG4uLiJu17KHH7Prg9P7h/H1o6/7qj1Xy8u4IbhkSxY+Magj0rRFPyn9u9mrxSZfmKFUS09OeXqjp6A1KBrDpeexq4vsbjXUDPhtaZkZGhTfHO1iPa7wdv6Yfbjzbp/aFg+fLlTkdoNrfvg9vzq7p/H1oyf0lFlU585EO9+Hcrtara02LrrY8T339gvdbxmRrqTU9LgLn+s58mAYWqGrRZO84b2p3OHYRX1n4ZrE0YY1zmqY9zOHq6nJ/OHk5EeKh/ZAaHo01PIvIKMANIEpFc4CEgEkBVnwKWApcA2UApcGsw80SGhzGtVwRLd+Zx+FQZKQkxwdycMSbEHTpVxtMf7+WykT2DMseEWzhaKFT1+gZeV+DuVooDwFd6R/BWThV/W3+Q/zl/UGtu2hgTYn7xzk7AN7tce9Y+j6Pq0S02jGnpSby67mBQzh4wxrjDhgMFLNl8mHnTB7TY3NduZYWiFjdM6MuRwnI+3p3ndBRjjAO8XuVn/9xOcnwH7vxKmtNxHGeFohbnD0smKS6KV9cdbHhhY0yb8+amQ2zOLeS+WUPo2CHUryIIPisUtYgMD+PyUSks33WcwjK7AM+Y9qSkoppfvLuTUX0SmDMmKNf3uo4VijrMHt2Lymov72076nQUY0wreurjveQVVfDgZcMIc+mFty3NCkUdRvXuTL/EWJZ8cdjpKMaYVpJ7spT5K3O4YlQKGf26OB0nZFihqIOIMHtUCqv25pN3OrizRxljQsNj7+xExE6HPZsVinpcMToFr8JbW4J2MbgxJkSs21/AW1uO8I3paXax7VmsUNRjYPdODE+JZ/Fma34ypi07czpsj/hovvGVAU7HCTlWKBowe3QKmw+eYn9+idNRjDFB8vrGXLYeKuT+i4eEzIREocQKRQMuH5WCCCy2Tm1j2qTiimoef28XY/omMHt0itNxQpIVigb07BzD+NSuvJNl/RTGtEV/XpHNcf/psCJ2OmxtrFAEYNbwHuw8WmTNT8a0MQcLSnnmk33MGdOLMX3tdNi6WKEIwKzhyQB28Z0xbczPl+4gXIT7LhrsdJSQZoUiAL27xDKiV7wVCmPakFV783kn6yh3z0yjZ2c7HbY+VigCdNHwHmz88hTH7OI7Y1yv2uPlZ//cTu8uMdwxzU6HbYgVigDNGt4DgPe3H3M4iTGmuRatO8jOo0U8cMlQoiPDnY4T8qxQBGhg9zgGJHXkvSxrfjLGzQpLq/j1+7uYNKArF43o4XQcV7BCESARYdaIHqzJOUFhqQ09boxb/fbD3RSWVfHgZcPtdNgAWaFohFnDe1DtVZbttOYnY9xoz7EiXlpzgOsn9GVYSrzTcVzD0UIhIheJyC4RyRaR+2t5fYaIFIrIF/7bg07kPGNkr8707BzNu9b8ZIzrqCo/e2s7HaPC+e4Fg5yO4yqODWoiIuHAH4ELgFxgnYgsUdXtZy36iape1uoBaxEWJpw7pDtvbjpERbWHDhHWCWaMWyzbkccne/J58LJhJMZ1cDqOqzh5RDEByFbVHFWtBBYBsx3ME5DzhnantNLD2n0FTkcxxgSootrD/769nYHd47gps5/TcVxHVNWZDYtcDVykqnf4H98ETFTVe2osMwN4Hd8Rx2HgXlXdVsf65gHzAJKTkzMWLVrUpFzFxcXExcXV+XqFR7lnWSkz+kTwtaGh919JQ/ndwO374Pb84P59ODv/kr2VvLGninvHdWBEUuiPDuvE93/mzJkbVHVcrS+qqiM34Brg2RqPbwL+cNYy8UCc//4lwJ5A1p2RkaFNtXz58gaXuWXB5zr98Y/U6/U2eTvBEkj+UOf2fXB7flX370PN/AfyS3TQA0v1m39Z71ygRnLi+w+s1zo+U51sesoF+tR43BvfUcO/qOppVS32318KRIpIUutFrN25Q7pz4EQpOTZIoDEhTVV5cEkWEWHCg5cNdzqOazlZKNYB6SLSX0SigOuAJTUXEJEe4j/RWUQm4Mt7otWTnmXmkO4ALN+Z53ASY0x93s06yopdx/nuhYPp0Tna6Tiu5VihUNVq4B7gPWAH8DdV3SYid4rInf7FrgayRGQz8HvgOv8hkqN6d4llUHIcH1mhMCZkFVdU89N/bmdYz3hutg7sZnG0V8ffnLT0rOeeqnH/SeDJ1s4ViJlDuvPcJ/soKq+iU3Sk03GMMWf53Qe7OVZUzp9uHEtEuF1b3Bz23Wui84YkU+1VPt2T73QUY8xZDhZ5WbhqP9eN78tYm5Co2axQNNHYvgl0jom05idjQozHqyzMqiAhJpIf2IRELSL0TygOURHhYUxLT+Lj3cdRVRtczJgQseDTfeQUenniumEkxEY5HadNsCOKZpie3o28ogp2Hyt2OooxBsg5Xsyv3t/FmO7hXDEqxek4bYYVimaYmu67pOOTPccdTmKM8XiV+17bQnRkODcPi7Kj/BZkhaIZUhJiGNg9jpXWoW2M415YtZ/1B07y0OXDSIi2j7aWZN/NZpqWnsTnOScor/I4HcWYdmt/fgmPv7eT84Z0Z86YXk7HaXOsUDTT9PRuVFR7Wb//pNNRjGmXvF7lvte3EBkexiNzzrEmpyCwQtFMEwd0JTJcrJ/CGIcsXLWftfsKePCyYTZMR5BYoWim2KgIxvXrav0Uxjhg++HT/OKdnZw/NJmrM3o7HafNskLRAqamJ7HjyGnyisqdjmJMu1Fe5eHbizbROTaSX1xlTU7BZIWiBUxP7wbAZ9l2VGFMa/n50h3sySvmN9eOsqlNg8wKRQsYnhJPl9hIPtlthcKY1vDh9mO8uPoAd0ztzzT/P2omeKxQtICwMGFqejdW7sknBEZBN6ZNO1hQyvf+vpnhKfF838ZyahVWKFrItPQk8osr2Hm0yOkoxrRZFdUe7n55I15V/vy1DDpEhDsdqV2wQtFCptlwHsYE3SNv72BLbiG/umYUfRNjnY7TblihaCE9O8eQ3j2OT+w0WWOCYvEXh/7VLzFreA+n47QrViha0LT0bny+r8CG8zCmhWUdKuQHr29hfGoXfnDxEKfjtDtWKFrQtPQkKqu9rN1X4HQUY9qM/OIK5r24nq6xUfzpaxlE2rSmrc7R77iIXCQiu0QkW0Tur+V1EZHf+1/fIiJjncgZqDPDeXy215qfjGkJldVe7vrLRk6UVDJ/7ji6dbLrJZzgWKEQkXDgj8DFwDDgehEZdtZiFwPp/ts84M+tGrKRYqMiGN0ngdV7TzgdxRjXU1V+8o8s1u4v4PGrRzKiV2enI7VbTh5RTACyVTVHVSuBRcDss5aZDbyoPmuABBHp2dpBGyMzLYmsQ4UUllY5HcUYV/v9smxeXX+Q/z53ILNH29DhTgpozmwRiQW+B/RV1a+LSDowWFXfasa2ewEHazzOBSYGsEwv4EgtGefhO+ogOTmZFStWNClUcXFxk98L0LHIg1fhuX9+zNjk1p+SvLn5Q4Hb98Ht+cH5ffgkt4rnsiqZkhLBmMjDrFjxH3/y9XI6f3OFWv5AP8kWAhuATP/jXODvQHMKRW0jeJ19WXMgy/ieVJ0PzAcYN26czpgxo0mhVqxYQVPfC5BZ7eG3m97ndExPZswY3uT1NFVz84cCt++D2/ODs/uwcvdxXnh/HVMHJrHglvFERTS+4cPtP4NQyx/oTyBNVR8HqgBUtYzaP8QbIxfoU+Nxb+BwE5YJKR0iwhmf2pVV1qFtTKNtO1zIN/+ygYHd4/jzjWObVCRMywv0p1ApIjH4/5sXkTSgopnbXgeki0h/EYkCrgOWnLXMEmCu/+ynSUChqjbuGNQBmWmJ7D5WzPGi5n6LjGk/DhaUcuvCdcTHRPL8rRPoFB3pdCTjF2iheBh4F+gjIn8FlgH3NWfDqloN3AO8B+wA/qaq20TkThG507/YUiAHyAaeAe5qzjZby+Q033Aeq3Ps7CdjAnGksIzrn1lDRbWX52+dYDPVhZiA+ihU9X0R2QBMwtfk9G1VbXbbiqouxVcMaj73VI37Ctzd3O20thEp8XSKjmD13nyuGJXidBxjQtrxogq+9sznnCqt4q93TGRwj05ORzJnCfSspyXAK8ASVS0JbiT3iwgPY2L/RFbZ9RTG1OtkSSU3Pfc5RwrLefH2CYzqk+B0JFOLQJuefg1MA7aLyN9F5GoRsWPDekxOS+TAiVJyT5Y6HcWYkHS6vIqbF64lJ7+EZ28ex/jUrk5HMnUIqFCo6seqehcwAN8pqNcCecEM5naTByYC2FGFMbU4XV7FLQvWsv3waZ66cSxTBiY5HcnUI+Bzz/xnPV0F3AmMB14IVqi2YFD3TiR2jLLhPIw5S2FpFTc9+zlbcgt58oYxnDsk2elIpgGB9lG8iu+q6Xfxjc+0QlW9wQzmdmFhQmZaIqv2+qZHFWnuZSfGuN/JkkpufO5z9hwr5qkbMzh/mBUJNwj0iGIhvovu7lTVj6xIBGZyWhLHTleQk2/9/8bkF1dw/TNr2JNXzNNzrUi4Sb1HFCJyrqp+BMQCs8/+r1hV3whiNtebnPZ//RRp3eIcTmOMc/JOl/O1Zz/n4MlSFtw8nqnp1ifhJg01PX0F+Ai4vJbXFLBCUY9+ibGkdI5m9d58bprUz+k4xjjiwIkSbnpuLfnFFSy8ZQKZ/n+gjHvUWyhU9SH/3Z+p6r6ar4lI/6ClaiNEhMy0JD7aeQyvVwkLs34K075sP3yauQvW4vF6efnrkxht10m4UqB9FK/X8txrLRmkrZqclsjJ0ip2HD3tdBRjWtXafQV8df5qIsOFv9+ZaUXCxRrqoxgCDAc6i8iVNV6KB+yCuwCcuZ5i9d4TDE+xGbpM+/Dh9mPc/fJGenWJ4aXbJ9IrIcbpSKYZGuqjGAxcBiTw7/0URcDXg5SpTenZOYYBSR1ZtfcEd0wb4HQcY4Lu9Q253Pf6FoanxLPwlvEkxtk8127XUB/FYmCxiGSq6upWytTmZKYl8o9Nh6jyeIkMt/H1Tdv17Cc5/O/bO5gyMJGnbxpHXIfWn+XRtLxAP7XuFJGEMw9EpIuILAhOpLZncloSJZUeth4qdDqKMUGhqjz+7k7+9+0dXDyiBwtuGW9Fog0JtFCMVNVTZx6o6klgTFAStUGTBvgGO1uVbbPembbH41V+9OZW/rRiL9dP6MuTN4ylQ0S407FMCwq0UISJSJczD0SkK4HPt93uJcZ1YGjPeBsg0LQ5FdUe7nl5I6+sPcg9Mwfy8zkjCLfTwNucQD/sfw2sEpHX8F1ody3wSNBStUGT0xJ5ac0Byqs8REfaf1vG/Yorqpn34npW7T3Bjy8daidrtGGBDjP+Ir6RY48Bx4ErVfWlYAZrayanJVJZ7WXjgZNORzGm2U4UV3DDM2v4fF8Bv75mlBWJNq4xp+B0BUpU9Q/Acbsyu3Em9O9KeJhY85NxvUOnyrjm6dXsOlrE0zdmcFVGb6cjmSALdJjxh4Bx+K6rWAhEAn8BpjRlo/4+jleBVGA/cK2/g/zs5fbju2bDA1Sr6rimbC8UdIqOZGTvzqzam4/v22iM+2TnFXHTc2sprqjmpdsnMqG/zUrXHgR6RDEHuAIoAVDVw0BzZkC/H1imqunAMv/jusxU1dFuLhJnTE5LZHNuIUXlVU5HMabRvjh4iqufWk2VR3l1XqYViXYk0EJRqaqKryMbEenYzO3O5v9myHsB+K9mrs8VpqQl4fEq6/YXOB3FmEZZsSuP6+evIT46kte/mcmwlHinI5lWJL7P/wYWErkXSAcuAB4FbgNe9vdXNH6jIqdUNaHG45Oq2qWW5fYBJ/EVqKdVdX4965wHzANITk7OWLRoUVOiUVxcTFxccOaOqPQody0r5by+EVw/JDjDGgQzf2tx+z64PT/8+z58dqiKBVmV9IoL47vjOpDQIfRHF3D7z8CJ/DNnztxQZ8uNqgZ0w1ckfgn8CrgggOU/BLJquc0GTp217Mk61pHi/9od2AxMDyRrRkaGNtXy5cub/N5AXPf0ar34dyuDtv5g528Nbt8Ht+dX/b99mP/xXu33g7f0uqdX6+mySmdDNYLbfwZO5AfWax2fqQFfNKeqHwAfNGL58+t6TUSOiUhPVT0iIj2BvDrWcdj/NU9E3gQmACsDzRCKpgxM5Ffv76agpJKuHaOcjmNMrbyq/HzpDuavzOGSc3rw26+Otqut27F6jyFF5FP/1yIROV3LbZ+I3NWE7S4BbvbfvxlYXMu2O4pIpzP3gQvxHZG4WmaabwrINTl2mqwJTVUeL89srWD+yhzmZvbjD9fbkBztXb2FQlWn+r92UtX4s2/4Tpn9dhO2+xhwgYjswdek9RiAiKSIyFL/MsnApyKyGVgLvK2q7zZhWyFlZO/OdIwK958ma0xoKa2s5o4X1rP6sIfvXTCIn14x3IbkMIE3PYnIWGAqvo7lT1V1k6qeEJEZjd2oqp4Azqvl+cPAJf77OcCoxq471EWGhzFxQCKrsu2IwoSWgpJKbn1+HVtzT3HL8Ci+dV6605FMiAjo9AUReRDfaayJQBLwvIj8GEBVjwQvXts0OS2RnPwSjhSWOR3FGAByT5Zy9VOr2HnkNH++MYMZfSKdjmRCSKDnuV0PjFfVh1T1IWAS8LXgxWrbMtP+b3pUY5y28+hprvrzKo4XVfDS7ROZNbyH05FMiAm0UOzn3+fI7gDsbfE07cTQHvF0iY3kM2t+Mg5bk3OCa5/yTV759zvtamtTu3r7KETkD/j6JCqAbSJy5vTY84FPg5ytzQoLEzLTElm9Nx9VRcQ6C03re3NTLve9toW+XWN54bYJ9O4S63QkE6Ia6sxe7/+6Hd+YTF58A/QtD2ao9iAzLYmlW49y4EQpqUnNHRHFmMCpKk8s28PvPtxD5oBEnroxg86x1idh6tZQoXgZ3wRFtwEH8DVV9cE3guyPghutbZvs76f4bG++FQrTaiqrvdz/xhbe2HiIK8f24rErRxIVEfpDchhnNfQb8jjQBeivqhmqOgYYAHTGN5yHaaIBSR3pER9t81OYVlNYWsXcBZ/zxsZDfOf8Qfz6mlFWJExAGjqiuAwY5B8HBABVPS0i3wR2Av8TxGxtmogwOS2Rj3cfx+tVwuyiJhNEB06UcNvz6/iyoJTffnUUc8bYZEMmcA39O6E1i0SNJz34hxw3TZeZlsiJkkp2HStyOoppw1bsyuPyP3xKfnElL90+0YqEabSGCsV2EZl79pMiciO+IwrTDJMH+sZ9suYnEwyqyh+XZ3Pr8+tISYjhn/dMZdKARKdjGRdqqOnpbuANEbkN2IDvKGI8EINv1jvTDL0SYkhNjGX13nxun2pTkJuWU1xRzb1/28y7245yxagUHrvqHGKjAh6xx5h/U+9vjqoeAiaKyLnAcECAd1R1WWuEaw8y05J4a/Nhqj1eIsKtY9E0386jp7nn5U3syy/hx5cO5fap/e1aHdMsAf2LoaofAR8FOUu7NGVgIq+s/ZKthwoZ0/c/JvkzJmCqyourD/DI0h3ER0fy0m0T/tW8aUxz2LGow860Ga/ae8IKhWmyvNPl/PCNrSzbmce5Q7rz+NUjSYoLznS7pv2xtg6HJcV1YEiPTjY/hWkSVeVv6w9y/m8+5tPsfB66fBjP3TzOioRpUXZEEQImpyXx188PUF7lITrSZhIzgcnOK+an/9zGJ3vymZDalceuOocB3eKcjmXaICsUIWDKwEQWfLaPDQdOMsXalE0DTpVW8sSyPby0+gDRkeH8bPZwbpzYzy7aNEFjhSIETBqQSGS4sHL3cSsUpk6FZVW8uGo/z322j9NlVXx1fF++d+Ega2YyQWeFIgR07BBBRr8ufLz7OD+8ZKjTcUyIOXyqjL9+foAXVx2gqKKac4d0594LBzMsJd7paKadcKRQiMg1wMPAUGCCqq6vY7mLgCeAcOBZVX2s1UK2sumDuvH4u7vIO11O9/joht9gWszxogp2HyvieFEFhWVVnC6rAiAyIoyo8DDiYyLp1qkD3eI6kJIQTUJsVNAzlVZWs2LXcV5dd5CVe44DcPGIHtw1YyAjenUO+vaNqcmpI4os4Erg6boWEJFw4I/ABUAusE5Elqjq9taJ2Lqmp/sKxco9+VydYWPxBNOx0+W8v+0oy3bmkXWokPziyka9v3NMJKmJsfRL7Eg//9fUxFj6JsbSrYnNQOVVHnYeLWLjgZOs2H2cNTknqKz20rNzNN+aOZBrxvWhT1ebWMg4w5FCoao7gIauFp0AZKtqjn/ZRcBsfJMotTnDesaTFBfFyt3HrVAEgcervJN1hIWf7WfDgZMA9E/qyMzB3RnSM56hPTqR3DmazjGRxEdHEiZQ6fFSWe3lVGkV+cUV5BVVcOhkGQcKSjhwopRNB0/y1pbDeGsMjxkVHkbnKGXArtWkJMSQFBdFxw4RxHWIoENEGFUepdrrpaTCQ15RBXmnyzl4spS9x0vw+FeU1q0jcyf1Y+aQ7kwakEi4dVIbh0ktg8O23sZFVgD31tb0JCJXAxep6h3+xzcBE1X1njrWNQ+YB5CcnJyxaNGiJmUqLi4mLs6ZUwyf3lJO1nEPT5wbS1gTh1xwMn9Lacl98HiVTw5V886+Ko6VKsmxwpReEWQkR5DSUZo9tEW1V8kvU/JKveSVKifKlbziSoqqwzlRphRVKpXe2t/bKQoSOoTRNVroGx9Gv05hpHYOIynG+cub3P57ZPkbb+bMmRtUdVxtrwXtiEJEPgR61PLSA6q6OJBV1PJcnVVNVecD8wHGjRunM2bMCCTmf1ixYgVNfW9zneycy+pXN5OUPoaRvROatA4n87eUltqHrEOF3P/GFrIOlXJOr848PCeNC4f3CPp/6Gfnr/Z4Kan0UFntJTJciAgPo0NEGJEhPLaX23+PLH/LClqhUNXzm7mKXHzTrp7RGzjczHWGtGnp3QBYuft4kwuF8bX3/+aD3Tz36T66xEbx5A1juPScno4NjBcRHkbnEDhKMKapQvm3dx2QLiL9RSQKuA5Y4nCmoEqK68DwlHhW7rbhPJrqaGE5X52/hvkrc7h2XG+WffcrXDYyxUZPNaYZHCkUIjJHRHKBTOBtEXnP/3yKiCwFUNVq4B7gPWAH8DdV3eZE3tY0fVA3Nn55kqLyKqejuM76/QVc9odPyT5WxFM3ZvDolSPpHBvpdCxjXM+RQqGqb6pqb1XtoKrJqjrL//xhVb2kxnJLVXWQqqap6iNOZG1t09O7Ue1Vm/Wukd7acpjrn1lDXIdw3rx7CheNqK17zBjTFKHc9NQuZfTrQseocFbuPu50FNf4x6ZD/PcrmxjdJ4HFd09lUHInpyMZ06bYEB4hJioijMy0RFbuOY6qWtt6A17bkMv3X9vMpP6JPHfLOJvu05ggsCOKEDR9UDcOFpSx/0Sp01FC2uIvDvH91zYzdWASC24Zb0XCmCCxQhGCptc4TdbUbtXefO79+2Ym9u/KM3PHERNl83gYEyxWKEJQalJH+naN5WMrFLXafayIb7y0gdTEjjx94zib7MmYILNCEaLOHdKdz7LzKav0OB0lpOSdLufWheuIjgxn4a3j7fRXY1qBFYoQdd7Q7lRUe/ks2y6+O6PK4+XulzdSUFLJwlvG07uLjaZqTGuwQhGiJvZPpGNUOMt2HnM6Ssh4/N2drNt/kseuOsfmZDCmFVmhCFFREWFMH9SNZTvy8HqdG+E3VLybdYRnPtnH3Mx+zB7dy+k4xrQrVihC2HlDk8krqmDb4dNOR3HUvvwSvv/3LYzqk8ADl9pUsca0NisUIWzm4G6IwIc72m/zU5XHy/8s2kR4uPCnr42lQ4Sd4WRMa7NCEcIS4zowtm+Xdt1P8YePstmcW8ijc86hV0KM03GMaZesUIS484Z2J+vQaY4WljsdpdVt/PIkf1yezZVje3HxOT2djmNMu2WFIsSdPzQZoN0dVZRUVPPdV7+gR3w0D18x3Ok4xrRrVihCXHr3OHp3ieHD7e2rUDz2zk4OFJTym2tHER9tF9UZ4yQrFCFORJg1vAefZZ9oN5MZ7Srw8NKaA9w6uT8TByQ6HceYds8KhQtcPKIHlR4vH+3MczpK0JVXeViQVUGfrjHcO2uQ03GMMVihcIWxfbvQvVMHlm494nSUoHti2R6OlSqPzhlpw4YbEyKsULhAWJhw8YgerNh1nJKKaqfjBE3WoULmr8xhWq8IpqYnOR3HGOPnSKEQkWtEZJuIeEVkXD3L7ReRrSLyhYisb82Moebic3pSUe1l+a622fzk8So/fGMrXTtGcd2QKKfjGGNqcOqIIgu4ElgZwLIzVXW0qtZZUNqD8aldSYqL4p2so05HCYqX137J1kOF/OSyYXSMtOlfjQkljhQKVd2hqruc2LZbhYf5zn5avjOvzc1RkV9cwS/f3cnktEQuH2kX1hkTakK9j0KB90Vkg4jMczqM0y45pyellZ42N/Pdo0t3Ulbl4WezRyBiRxPGhBpRDc4Q1iLyIdCjlpceUNXF/mVWAPeqaq39DyKSoqqHRaQ78AHwLVWttbnKX0jmASQnJ2csWrSoSbmLi4uJi4tr0nuDzeNVvr28lBFJ4dw5KrrWZUI5f212FXh4dG05lw2I5OpBvr4Jt+3D2dyeH9y/D5a/8WbOnLmhziZ+VXXsBqwAxgW47MP4ikqDy2ZkZGhTLV++vMnvbQ33v75Zh/7kHS2pqKr19VDPX1NltUcv/M3HOvnRZVpaUf2v5920D7Vxe35V9++D5W88YL3W8Zkask1PItJRRDqduQ9ciK8TvF2bM6Y3pZUe3tvm/k7t5z/bz65jRTx0+TBiomz4cGNClVOnx84RkVwgE3hbRN7zP58iIkv9iyUDn4rIZmAt8LaqvutE3lAyrl8XeneJ4Y2Nh5yO0ixHCsv43Ye7OW9Idy4Ylux0HGNMPRy59FVV3wTerOX5w8Al/vs5wKhWjhbywsKEK8f04snl2RwtLKdH59r7KkLd/761g2qv8vAVw60D25gQF7JNT6Zuc8b2xquw+At3HlWs3H2ct7ce4Z6ZA+nTNdbpOMaYBlihcKH+SR0Z2zeB1zfmnunod42Kag8PLdlG/6SOzPvKAKfjGGMCYIXCpeaM7c3uY8VsO3za6SiNMv/jHPbll/Cz2cNt/mtjXMIKhUtdPrInkeHiqk7tgwWlPLk8m0tH9mRaejen4xhjAmSFwqUSYqM4b0gyi784REV16A/poao8uDiLiDDhJ5cOczqOMaYRrFC42A0T+3KipJJ3tob+NRXvbTvK8l3H+c4Fg1x7ppYx7ZUVChebOjCJAUkdeWH1fqej1Ku4opqf/nM7Q3vGc8vkVKfjGGMayQqFi4WFCTdl9mPTl6fYmlvodJw6/e6D3Rw9Xc4jc0YQEW6/csa4jf3VutxVGb2JjQrnxRA9qthx5DQLV+3nuvF9Gdu3i9NxjDFNYIXC5eKjI5kzpheLNx/mZEml03H+jderPPDmVhJiIvnBRYOdjmOMaSIrFG3A3MxUKqu9vLr+oNNR/s2r6w+y8ctT/PCSoSTE2vSmxriVFYo2YHCPTkwa0JWXVh/A4w2NK7XzTpfz6NIdTOjflavG9nI6jjGmGaxQtBG3Tx3AoVNlfH7U+WsqVJUH/pFFRbWXx648xwb9M8blrFC0EecN6c7g5E68lVOJ1+Gjire2HOGD7cf43oWDGNDNvbOMGWN8rFC0EWFhwl0z0zhcrLy/3bkL8E4UV/DQkm2M6pPA7VNt0D9j2gIrFG3Ipef0pEes8JsPdjvSV6GqPLhkG8Xl1fzy6pGEh1mTkzFtgRWKNiQiPIw56VHsPlbsyFwVr288xNtbjvDt89MZlNyp1bdvjAkOKxRtzPge4QzrGc9vPthNeVXrdWznHC/mwcVZTBrQlTu/ktZq2zXGBJ8VijYmTIQfXTKU3JNlPPfpvlbZZkW1h2+9somoiDB++9XR1uRkTBvjSKEQkV+KyE4R2SIib4pIQh3LXSQiu0QkW0Tub+WYrjU1PYlZw5N58qNsDp8qC/r2fvnuLrYdPs3jV42kZ+eYoG/PGNO6nDqi+AAYoaojgd3AD89eQETCgT8CFwPDgOtFxCYyCNCPLx2GV5UHF28L6nSp/9h0iGc/3cfczH5cOLxH0LZjjHGOI4VCVd9X1Wr/wzVA71oWmwBkq2qOqlYCi4DZrZXR7fp0jeXeCwfz4Y5j/CNIHdsbDhRw32tbmNi/Kz+2yYiMabNCoY/iNuCdWp7vBdQcvCjX/5wJ0G1T+5PRrwsPLd7GwYLSFl33wYJS5r24gZSEaJ66MYOoiFD4VTLGBIMEq1lCRD4EamuLeEBVF/uXeQAYB1ypZwURkWuAWap6h//xTcAEVf1WHdubB8wDSE5Ozli0aFGTchcXFxMX596ric/Of6zEy8Ory0iODeNHE6OJCm9+R3NxpfLo2jJOlis/mRRDz7iWLRJt7WfgRm7fB8vfeDNnztygquNqfVFVHbkBNwOrgdg6Xs8E3qvx+IfADwNZd0ZGhjbV8uXLm/zeUFBb/veyjmi/H7yl31m0ST0eb7PWf7KkQi/+3UpNf2CpfrbneLPWVZe2+DNwG7fvg+VvPGC91vGZ6tRZTxcBPwCuUNW62kTWAeki0l9EooDrgCWtlbEtuXB4D753wSDe2HSIR5buaHLn9uFTZVz79Gqy84qZf1MGkwcmtXBSY0woinBou08CHYAP/COLrlHVO0UkBXhWVS9R1WoRuQd4DwgHFqjqNofyut495w7kREklz326j9JKD/9v9vBGTUu6bn8B97y8kdIKD8/fOt6KhDHtiCOFQlUH1vH8YeCSGo+XAktbK1dbJiI8dPkwOnYI54/L97Ivv5hfXj2KPl1j631fWaWHP63I5k8r9tK7Swwv3DaBIT3iWym1MSYUOHVEYRwgInx/1hD6J8Xx8JJtzPrdSuZmpjI3sx8pCf9+odzJkkpe35jLws/2c+hUGVeO6cVPZw+nU3SkQ+mNMU6xQtEOXZ3Rm0kDuvLYOzt5euVenvp4LwO7x9G3ayxhAodOlbPz6GlUYXxqF3597SgmDUh0OrYxxiFWKNqp3l1iefKGsXz/RAnvZh3l830FHC0sx6tK9/hoLho+iPOGdmdEr85ORzXGOMwKRTvXL7Ej3/hKGt+wEV+NMXWwy2mNMcbUywqFMcaYelmhMMYYUy8rFMYYY+plhcIYY0y9rFAYY4yplxUKY4wx9bJCYYwxpl5Bm7jISSJyHDjQxLcnAfktGKe1uT0/uH8f3J4f3L8Plr/x+qlqt9peaJOFojlEZL3WNcuTC7g9P7h/H9yeH9y/D5a/ZVnTkzHGmHpZoTDGGFMvKxT/ab7TAZrJ7fnB/fvg9vzg/n2w/C3I+iiMMcbUy44ojDHG1MsKhTHGmHpZofATkYtEZJeIZIvI/U7naSwRWSAieSKS5XSWphCRPiKyXER2iMg2Efm205kaS0SiRWStiGz278NPnc7UFCISLiKbROQtp7M0hYjsF5GtIvKFiKx3Ok9jiUiCiLwmIjv9fw+ZjmeyPgrfHwawG7gAyAXWAder6nZHgzWCiEwHioEXVXWE03kaS0R6Aj1VdaOIdAI2AP/lsp+BAB1VtVhEIoFPgW+r6hqHozWKiHwXGAfEq+plTudpLBHZD4xTVVdecCciLwCfqOqzIhIFxKrqKScz2RGFzwQgW1VzVLUSWATMdjhTo6jqSqDA6RxNpapHVHWj/34RsAPo5WyqxlGfYv/DSP/NVf+JiUhv4FLgWaeztEciEg9MB54DUNVKp4sEWKE4oxdwsMbjXFz2IdWWiEgqMAb43OEojeZvtvkCyAM+UFW37cPvgPsAr8M5mkOB90Vkg4jMczpMIw0AjgML/c1/z4pIR6dDWaHwkVqec9V/gm2FiMQBrwP/o6qnnc7TWKrqUdXRQG9ggoi4phlQRC4D8lR1g9NZmmmKqo4FLgbu9jfLukUEMBb4s6qOAUoAx/tMrVD45AJ9ajzuDRx2KEu75W/Xfx34q6q+4XSe5vA3F6wALnI2SaNMAa7wt/EvAs4Vkb84G6nxVPWw/2se8Ca+pmW3yAVyaxyJvoavcDjKCoXPOiBdRPr7O4+uA5Y4nKld8XcEPwfsUNXfOJ2nKUSkm4gk+O/HAOcDOx0N1Qiq+kNV7a2qqfj+Bj5S1RsdjtUoItLRfzIE/iabCwHXnAmoqkeBgyIy2P/UeYDjJ3REOB0gFKhqtYjcA7wHhAMLVHWbw7EaRUReAWYASSKSCzykqs85m6pRpgA3AVv9bfwAP1LVpc5FarSewAv+s+jCgL+pqitPMXWxZOBN3/8dRAAvq+q7zkZqtG8Bf/X/05oD3OpwHjs91hhjTP2s6ckYY0y9rFAYY4yplxUKY4wx9bJCYYwxpl5WKIwxxtTLCoUxxph6WaEwhn+N0fSEf3jwrSIy4KzXU0WkrMY1Hk3dzsMicq///qrmrKuWdcf4h9auFJGklly3ad+sUBjj80MgR1WHA78H7qplmb3+cZz+jfg0+m9JVSc3OmX96yvz57PhZ0yLskJh2j3/UA9zVPUJ/1P7gIENvCfVP6nMn4CNQB8R+Yd/xNJtNUctFZEH/JNifQgMrvF8cY37//HeGtt4xv/8+/6hQc4MVfG2f5KkLBH5akt9P4w5mw3hYYxvTKY+NZqVugIfBvC+wcCtqnoXgIjcpqoF/g/zdSLyOpCKb9ykMfj+3jbim5TpbLW9FyAd3yRaXxeRvwFXAX/BN9jgYVW91L/tzo3daWMCZUcUxsBo4EFVHe1vunkf+CKA9x04a/a6/xaRzcAafKMRpwPTgDdVtdQ/bHpdg03W9l6Afap6JssGfIUHYCtwvoj8QkSmqWphAHmNaRIrFMZAF6AUQEQi8I04+s8A3ldy5o6IzMB3ZJKpqqOATUC0/+V6B1Rr4L0VNRb14G8FUNXdQAa+gvGoiDwYQF5jmsQKhTG++dIn+e9/B3hbVfc1ch2dgZOqWioiQ2qsbyUwx39GUifg8ka8t04ikgKUqupfgF8RAnMWmLbL+iiMgVeAd0QkG1gNNGX6zHeBO0VkC7ALXxMSqrpRRF7F15R1APgk0Pc24BzglyLiBaqAbzYhszEBsWHGjQmAfx7vt1Q15Kc29c9QN05V853OYtoGa3oyJjAeoHNzL7gLpjMX3AGRgNfhOKYNsSMKY4wx9bIjCmOMMfWyQmGMMaZeViiMMcbUywqFMcaYelmhMMYYUy8rFMYYY+plhcIYY0y9rFAYY4yp1/8HvDmK8ScbidcAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"## Copied from notebook with Algorithm 5.1\n",
"def my_f3(x):\n",
" return x[0]**3 - x[1] - x[0]*x[1] - x[1]**2\n",
"\n",
"def my_h3(x):\n",
" return (x[0]**2 + x[1]**2 - 1)*np.ones(1)\n",
"\n",
"def visualize(xk=[]):\n",
" n1 = 101\n",
" n2 = 101\n",
" x1eval = np.linspace(-2,2,n1)\n",
" x2eval = np.linspace(-2,2,n2)\n",
" \n",
" X, Y = np.meshgrid(x1eval, x2eval)\n",
" \n",
" Z = np.zeros([n2,n1])\n",
" \n",
" for i in range(0,n1):\n",
" for j in range(0,n2):\n",
" Z[j,i] = my_f3((X[j,i], Y[j,i]))\n",
" \n",
" fig, ax = plt.subplots(1,1)\n",
" CS = ax.contour(X, Y, Z)\n",
" ax.clabel(CS, inline=1, fontsize=12)\n",
"\n",
" # Add grid\n",
" plt.grid()\n",
" \n",
" # Add unit circle\n",
" circ = plt.Circle((0, 0), radius=1, edgecolor='b', facecolor='None')\n",
" ax.add_patch(circ)\n",
" \n",
" # Plot iteration history\n",
" if len(xk) > 0:\n",
" for i in range(0,len(xk)):\n",
" if i == len(xk) - 1:\n",
" c = \"red\"\n",
" else:\n",
" c = \"black\"\n",
" plt.scatter((xk[i][0]),(xk[i][1]),marker='o',color=c)\n",
" \n",
" plt.xlim([-2,2])\n",
" plt.ylim([-2,2])\n",
" \n",
"visualize()\n",
"\n",
"nt = 200\n",
"theta = np.linspace(0,2*np.pi,nt)\n",
"obj = np.zeros(nt)\n",
"\n",
"\n",
"for i in range(0,nt):\n",
" x_ = np.cos(theta[i])\n",
" y_ = np.sin(theta[i])\n",
" \n",
" obj[i] = my_f3((x_,y_))\n",
"\n",
"\n",
"plt.figure()\n",
"plt.plot(theta,obj)\n",
"plt.xlabel('$\\\\theta$ [radians]')\n",
"plt.ylabel('Objective')\n",
"plt.grid()"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.8.4.1 Starting Point Near Global Min ($\\theta_0 = 1.0$)](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.4.1-Starting-Point-Near-Global-Min-($\\theta_0-=-1.0$))",
"section": "4.8.4.1 Starting Point Near Global Min ($\\theta_0 = 1.0$)"
}
},
"source": [
"### 4.8.4.1 Starting Point Near Global Min ($\\theta_0 = 1.0$)"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.8.4.1 Starting Point Near Global Min ($\\theta_0 = 1.0$)](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.4.1-Starting-Point-Near-Global-Min-($\\theta_0-=-1.0$))",
"section": "4.8.4.1 Starting Point Near Global Min ($\\theta_0 = 1.0$)"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Iter. \tf(x) \t\t||h(x)|| \t||grad_L(x)|| \t||dx|| \t\t||dv|| \t\tdelta_A \tdelta_W\n",
"0 \t-6.9105e-01 \t0.0000e+00 \t3.7501e+00 \t 1.1171e+00 \t 1.1455e+00 \t 0.0000e+00 \t 0.0000e+00\n",
"1 \t-4.0104e+00 \t1.2480e+00 \t2.1729e+00 \t 4.2318e-01 \t 3.9672e-01 \t 0.0000e+00 \t 0.0000e+00\n",
"2 \t-2.4216e+00 \t1.7908e-01 \t3.3575e-01 \t 8.3649e-02 \t 1.0205e-01 \t 0.0000e+00 \t 0.0000e+00\n",
"3 \t-2.1438e+00 \t6.9971e-03 \t1.7074e-02 \t 3.5294e-03 \t 6.5710e-03 \t 0.0000e+00 \t 0.0000e+00\n",
"4 \t-2.1324e+00 \t1.2457e-05 \t4.6327e-05 \t 6.3597e-06 \t 1.9707e-05 \t 0.0000e+00 \t 0.0000e+00\n",
"5 \t-2.1323e+00 \t4.0446e-11 \t1.4043e-09 \t 2.8044e-10 \t 3.3891e-11 \t 0.0000e+00 \t 0.0000e+00\n",
"\n",
"x* = [0.24215301 0.97023807]\n",
"\n",
"v* = [1.64012795]\n",
"\n",
"theta* = 1.326212035697004 = 1.3262120356970035\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYQAAAD8CAYAAAB3u9PLAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAABhxklEQVR4nO2dd3xUVfr/32cmvfdCQhop9F4E6R1EUIoNG+qyurq6P7+r6+q6brGtrq5dV9eKKKKgICJVAiK9t5AQAgkppPc2mZnz++MGpAQIyWTuneS+X6/7ykzmzj2f3Mzczz3nPOd5hJQSHR0dHR0dg9oCdHR0dHS0gW4IOjo6OjqAbgg6Ojo6Oo3ohqCjo6OjA+iGoKOjo6PTiG4IOjo6OjqADQxBCNFZCLFBCJEihDgshHikiX2EEOINIUS6EOKAEKJ/a9vV0dHR0bEtTjY4hhn4PynlHiGEN7BbCLFWSnnknH2mAAmN2xDg3cafOjo6OjoaodU9BCllnpRyT+PjSiAFiLhgtxnAZ1JhG+AnhAhvbds6Ojo6OrbDFj2EswghYoB+wPYLXooATp3zPLvxd3lNHGM+MB/Azc1tQFRUVKs0WaySoop6ArxccHay/ZSJ1WrFYND+VIyu07boOm1LR9VZYTJTbmogzMMVZxsdNy0trUhKGdyiN0spbbIBXsBuYGYTr/0ADD/n+XpgwJWOmZiYKFtLbb1Jvrt4szxdVNHqYzXFhg0b2uS4tkbXaVt0nbalo+nMKi6Vt324SCY986r8/aLlsrS61ibHlVJKYJds4XXcJj0EIYQzsARYKKVc2sQu2UDnc55HArm2aPtKuLk4c/+ca+3RlI6Ojs5lkVKyZO9hnl+VjFEYeOnGyVzfuytCCLWlATYYMhLKX/IhkCKlfPUSuy0HHhJCLEKZTC6XUl40XKSjo6PTXskrr+Tp5WvZfDyTwTGRvHjDJDr5+agt6zxs0UO4FrgDOCiE2Nf4uyeBKAAp5XvASmAqkA7UAPNs0K6Ojo6O5pFSsnTvYV5YvRGrVfL01DHcOrAPBoM2egXn0mpDkFJuBi77lzWOaz3Y2rZ0dHR0HIns0nL++v06tmRkMSg6kudnTKBzgJ/asi6JTaOM1EZKqZmxOB0dnY6LxWplwfZ9vP7TLxiEgb9OHcstA3trsldwLu3CEOpNZlxdnHQz0NHRUZ1Dufn8bcV6DuXmMzoxlr9dN44wX2+1ZTULhzaE/JJK1m5NJet0KYF+Hswe15dAP8+zr1utUvOOrKOj0z6oqqvn9Q1bWLhjP4Ge7rwyaypTeyY61I2qQxvCSx+vRxgEIf5eHMsqYvO+DGaM7sXB9Fx6xXfSzUBHR6fNkVKy4mAqL6/dRGFlNbcO6sMfxg7Dx91NbWlXjcMawsncEg4dz2P1Ow8AsGnPcRb8sJM9R7PJzi8D4M/3jCe+c8sW7Ono6OhcidT8Iv658id2ZebQIzyEN2++nj6RjpuVx2EN4Xh2EdHhAZRX1eLr5U54kA9HT+Tz21nD8PF0571vNrMvNUc3BB0dHZtTWl3Lm8lb+WrXAbzdXPnH9eOZ1a8HRgdIv3E5HNYQ+neN5Msfd7NgxU78vD1YvvEgt00ZwMDuUY2vd2b7wUxmj++rrlCNU99gJqesgpzyCnLLKsivqKK0ppaSmlpKa2qprjdR22Cm1tRAg8WCVUosUoKUOBmNOBsNOBkMuLs44+nigqerCz5urvi5u+Hn4Y6/hzsh3p6Nmxch3l64OBnV/rN1dFqE2Wrlk617eDt5GzUmEzcP7M3DY4bh5+F4w0NN4bCG4O/jwR3TBrF2WyohAd706xpJ0DkTypv2HGfs4AQVFWqPgsoqDubkczDnNMcKikkvLOZUaTlWJb8UoCwoOXMh93N3I9DTA3cXZ9ydnXFxMmIUAtG4mS0WzFYrJrOF2oYGakwNVNXVk1NWQVlNLeW1dcgLNAggxNuLCD8fIv19iA7wJyrAj5hAP2KDAux5OnR0mo2Ukh8Pp/HCjhQK60wM7xLNE5NGER8SqLY0m+KwhgAwakA8owbEA7DqlxT+8f4qistqqKypo6K6jlsmdew6PDllFWzLyGJLRhZbjmVQmrwXACeDgZhAP7qGBXNdryRiAvzp5OdNJ18fQry9cDLapttrsVopr62jsLKagqpqCiqqyC2vJLe8gpyyCnZl5vD9gaPnmYa/qzPdsopJCAkkMSSIxNAgEkKCcHN26I+qjgOz7cQpXln7Mwdz84nwdOP9uTcwMiFWbVltgkN/y8xmC05ORqxWyYShSVilZMn6/YzoF8ff75+itjy7I6Uk5XQha44cY21KOseLSgAI8vSgi48nE/r3oXdkGN3CQuxygTUaDAR4ehDg6UESTc/l1DWYOVVaxsniMo4XlrD18BHKa+v4atdB6sxmAAxCEBfkT/fwELqFhdCzUyjdwkPwcnVp879Bp+OyPzuP19b/wtYTpwjz8eL5GRPxKytot2YADm4INMb3vvHlRkwNFh6/exxTh3dXWZT9yS4t57v9R1i2P4VTpeUYhGBQdCQ3DejFsC5RxAcHsnHjRkYP1V6Pyc3ZiYQQpRcwoRt0tdYwevRoLFYrp0rLScsv4mh+ISl5hWw/kc3yA0cBZeipS3AAPTuF0ScyjF4RYSSFBuFs1OcndFrHodx83tm4jZ9SMwjwcOeJSaO4ZWBv3JydSE4uVFveJZFS8ved61p1DIc1BCklTkYDUkoWr93Hp/+YCyjDFI4+098crFZJ8rEMFu7Yz5bjmQAMjYvityMGMy6pC/6e7iorbB1Gg4GYQH9iAv2Z2P3XuaCiqmoO5xZwKDefg7mn2XTsBN/tV6q1ujk50TMilH6dO9Gvczj9OnfC38Oxz4OO/TiYc5q3krex8dgJfNxc+cPYYdwxpB+eDtATlVLyj13r+eTo7lYdx2ENwWKVOBkF//1mCz3iwkiICsZqle3eDExmM8sPHOXjLbs5XlRCmI8XD46+hhv79iBCY6l024IgL09GJcYyKlHptkspySmrYH/2afZn57EvO4+Pt+zmA6sVgC5BAfSP6sSAqAgGRkcQ4efjUCtHddoWKSXbT5zig1928cvxTHzd3fjD2GHMHdwXbzdXteU1CyklL+3dyMcpu7in20CeacWxHNYQzkx8frlqN2/+aTYAEskVEq86LGaLlaX7DvN28jbyK6voFhbMyzOnMLlHQoceJhFCEOnvS6S/L9f1SgKg1tTAodx89pzKZU9WLqsOH+PrPYcACPX2YkB0BIOjIxgUE0lcUIBuEB0Qs8XKuqPp/O+XXRzKzSfI04NHx13LbYP7Otzc1FsHt/DuoW3cltiXpweO63iGYLZYcTIa+GzFDjqH+dM7sRNSts/egZSSDakZvLJuM8eLSugTEcbzN0xkWFyUfiG7BO4uzgyKiWRQTCSgDK8dKyhiV1YOuzNz2Hkym5WHUgEI9PRgYHQEg6KV/ROCA/WUJ+2Yyrp6vtlziAXb95FbXkF0gB9/nzaOG/p0x9UBI9neObiVV/b9zMy4Hjw7ZFKrrwmOdwb4tXfwyfIdPP/QNACsUmJsZxfI7NJy/v7DT/ycfpKYQH/euGkaE7rF60ZwlRgMgqSwYJLCgpk7uC9SSrJKytmZmc3Ok9nszMxm9ZFjAPi6uzEoOoLBMZEMjulMYkiQbhDtgNTThXy56wDLD6RQY2pgUHQkT04exZikOIe9kfzg8HZe2ruRGbHdeXnYdRhscF1wSEMAOJSeR1JMCNf0jml3vQOzxcqn2/bw5oatGA0Gnpw8ilsH9enQQ0O2RAhBdKAf0YF+zO7fE1DMVzGIHHacPMW6o8cB8HVzZVBMJC/eONnhhhI6OrWmBtampLNo1wH2nMrF1cnIlB5J3DGkLz06haotr1V8enQ3z+3ewHXRXXnl2mk2u/45rCH0jA/njcdnAe2rd3CqpIw/Ll3F/uw8xiTG8cx1Yx0ml7ojc2Ye4sa+PQDILatgR2PvIaOoBE8X50u+12yxIgSX/FKeKdxksVpZtj+FZ1du4C9TxzCzX482+Vs6MlJKDuScZsnew6w8lEpVvYnoAD/+NHEkN/bt0S5STHx2dDfP7FjLxM4JvDbiepxseDNsE0MQQnwETAMKpJQ9m3h9NLAMONH4q6VSyn+0tl3nxpw47aV3sOpwGn9ZvhaB4N+zpnBdzyR9eEglOvn5cEPf7tzQ98rrWs5d2S2lxGKVCKEsqDuT5gNg8e6DfLXrIDFB/pgaF93pNTtsQ1ZJGd8fOMryAylklpTh5uTEpB4JzOrXk4FREe3mHC84uoe/7ljL+Mh43hw5A2eDbUcNbNVD+AR4C/jsMvv8LKWc1tqG2uMXqMFi4YVVG/li5376RITxyuypRPr7qi1Lpxk8+d0aakwmRibEMjw+ujH1x6+fzzO9g1fXbabBYmVsUhw5ZRXEBSs5cHS/bzmZxWWsPpLG6iPHOJxXgAAGxUTym+GDmNQ9wWHCRpvLwrS9PL1jDeMj43ln1I24tMEQsk0MQUq5SQgRY4tjXYnnP1xDVa2JFx++3h7NtTkVtXU8vHgF206cYt7QATw6/lp9rsCBuHlgL1YdPsZn2/byzIr1OBsNdA8LYXh8DFN6JBId6MeiXQfYnZXDmzdfz4+H0zhWWExckD8AX3zxBU899RRZWVlERUXx3HPPMXfuXJX/Km1itUoO5p5mQ2oGG9IySM0vAqBPRBiPTRjB1J5JhLfT4dVFx/bz1LbVjI3owtujbmgTMwD7ziEMFULsB3KBP0opD1/tAcxmCxt3p3Nt3zjbq1OB7NJyfrvwO7JKynjhholnx691HIc+keHnFUTJKCxhQ1oG20+coqiqmvHd4lmXks7n825CCEFOWQW+bm4EeXmycOFC5s+fT01NDQCZmZnMnz8fQDeFRgoqq9hyPIstGZlsOZ5FUXUNRiHoHxXBE5NGMbFbPJ3a+YLMBal7eHr7GkZ1iuOd0Tfiamy7y7aQ8sIExS08kNJDWHGJOQQfwCqlrBJCTAVel1I2mZtaCDEfmA8QHBw8YPHixWdfS8up4MNV6dw5Po4e0X420d1aqqqq8PLyuur3ZVfV8vr+dCxS8tsesST5t+2dTUt12htH02mVEik5O2dwLmX1DSxIzeRYWTU3J0TiYhAcKqkg1seT0RHB7D9wAHNDw3nvkRJyhRPDuncl0M2l1XNIjnY+y+obSC+vIq1M2U7X1AHg7exEV39vegb60DPAB0+V1gzY+3yurzzNgtKT9HHz46HgRJzFledLx4wZs1tKObAl7dnFEJrY9yQwUEpZdLn9kpKSZGpq6tnnL32ynh9+Pszqdx/A7TJRH/YkOTmZ0aNHX9V7juQVMO+zJbg7O/HRHbOIC277OgAt0akGjq5TSnnWJJyMBk4Wl/LL8Uz2nspjT1YupTU1+Hu48+rs6+gfHcGF3z9nvwDiHvkLAN6uriSFBpEQEkh8SCDxwcoW4OnebKPQ8vksr60j5XQhKXkFrN17gLx6C3kVlQB4uDgzIEpZD3Jtl2i6hgZrYu7QnudzwdE9LZozEEK02BDsYrNCiDAgX0ophRCDAQNQfDXHkFKyac9xrukdoxkzaAlHTxcy79Nv8HBx4dO7ZxMV4Ke2JB0bIoQ4LwT6TIK+uYP7smjXAdampDMmMY5wX2+ioqLIzMw87/3mynLqf/iKF959n9TThRzNL2TFwVQq6+vP7uPj5kpsoD8xQf5EB/jR2d+PqABfIv18r8os7EVZTR1ZJWWcKC4hvaCY9MIS0gqKyCmrOLtPgKsL18THMK9zf/pGdqJ7eIjN6nI4Iv87soNnd/3UphPITWGrsNMvgdFAkBAiG3gGcAaQUr4HzAYeEEKYgVrgFnmVXZO0zEIKS6sY0a+LLSSrQnpBMfM+W4KHiwsL5s3RI4k6EBarlboGM75urtw+pC8Azz333HlzCADurq48+4ffc8vA3md/J6WkoLKaYwXFZBQVk1FUyomiUrZlnGLZ/pTz2nF1MhLu60O4j1KutLa0mEzXPQR4up+thOfr5oqXmyverq4tvuiaLVaq6k1U1dcrJVeraympqaGoqobTFVXkV1SSV17JqdJyKup+NTNng4GYIH96R4Rx84BedAsPoXtYCAd37dBsT8bevHtoG//ak8yUqCReHzHdbmYAtosyuvUKr7+FEpbaYjbvy0AIGNbHMYtT5FdUcd/nS3EyCD6+a5ZuBh0Mo8HA3UP7n11/AL9OHF8pykgIQaiPF6E+XgyPjz7vtTMFhk6VlDfWxa4kr7yCvIoqdmbmUFBRyZpTBZfU5ebkhKuzE25OTrg5O2E0GDAaBMbGsWqLtCKlxGyV1DeYqTObqW8wU3PB3Me5+Li5EurjRZiPN30iw+ns73u2TGpUgJ8eRXcZ3jqwhX/v28T0mO68OnyaTRedNQeHWam8df8JusWGEuDrobaUq6bG1MADXy6joq6ehfNuIibQX21JOirh4nT+V27u3Lmtiig6t8BQU2zYsIF+Q4ZSWlN7diuvraOqvp7KOhPVJhN1DWbqzWbqGsxYrFYsUmKxWhEIDEJgMCjDYGeMw9XZCS9XF3zcXPFydcXP3Y0ATw8CPd0J8PRwiPoBWkNKySv7fuatg1u4Ma4H/x52nSoLbh3CEMqrajl8/DTzZgxRW8pVY7VK/rR0FUdPF/LOrdPpFh6itiSdDoQQAj8PN/w83IhFvxHRIlJK/rlrPR+l7OKW+D48d80k1bIvOIQh7DpyCquUXNMrRm0pV807m7ax9mg6T0waxejE9rF+QkdHxzZYpeTp7WtYmLaXed0G8teB41QNCnAIQ9h5OAtPdxe6dwlTW8pVsTk9k7eTt3FDn+7cdU0/teXo6OhoCLPVyp+2rmTJ8UM80PMaHu83SvUIMYcxhP5dIx0qDK24qoYnvl1FfHAgz1w3VvV/tI6Ojnaot5h5+OflrM5K49G+I/h9r2GauEZo/gpbVFZFdn4Z/bpGqi2l2Ugp+cvytZTX1fPvWVNwd+B1Ezo6OralpsHEfT8tYXVWGs8MGs/Dva/VhBmAA/QQ9qXmANA3KUJlJc1nyd7DbEjL4IlJo0gKC1Zbjo6OjkaoMNVx30/fsKswh5eGTuGmhD5qSzoPzRvCgWO5uLo4kRTtGNE5eeWVvLBqI4NjIrlziD5voKOjo1BQW8Vd6xaTXl7EGyOmMy2mm9qSLkLzhnDwWC7dY0NxcnKMxSzP/5iMVVp5fsZETeRe0dHRUZ9TVWXcvnYRBbXVfDh2DiM7aXOBrabnEKRUUlb0SuiktpRm8XP6SdYeTef+kUP0lcg6OjoAHCsr4qZVCymtr2XhhFs0awag8R5Cg8WK2WKlhwOEmzZYLDz/YzLRAX7MG9pfbTk6OjoaYHdBNvf89A0uRiOLJt5G94BQtSVdFk33EExmKwDd4rRvCIt2HeBEcSl/mjTyovQEOjo6HY8N2ceZu3YRAa7uLJ18h+bNALTeQzBb8ffxIMRf2wU+KuvqeTt5G9fEdmaMvhpZR6fD823GIR77ZSVd/YP5ZNxNBLl7qi2pWWjaEExmK11jQjQTo3spPvxlF2W1dTw+caTmtero6LQdUkreO7ydf+1JZmhYFO+PnoW3i6vaspqNpg3BbLGSqPFw0+oGMwt2HmZy9wS664nrdHQ6LBarlX/uWs8nR3dzfUw3/n3tdW1a/7gt0LRaKSG+c9NpfbVCck4R1SYTD4x0vEysOjo6tqHOYub/Nq/gh8yj3Nd9EE8OGHtRjW1HQNOTyqBtQ6g1NbAhp5BRCbH6imSdFrNw4UJiYmIwGAzExMSwcOFCtSXpXAWldbXcsXYRP2Qe5c/9x/CXgeMc0gxA4z0EISAqTLs53JcdSKGqwcx917aonrWODgsXLjyvjGZmZibz588HaFXhHB37cKqyjLvWLya7qpy3Rs7Q5Orjq0HTPQQng0GzK5StVsln2/YS5eXOwGjHybOkoy2eeuqp82oqA9TU1PDUU0+ppEinuRwoymPmqgUU19WwcMItDm8GYCNDEEJ8JIQoEEIcusTrQgjxhhAiXQhxQAjRrJVbzk7a7XZtPZFFRlEJYyO1HwWlo12ysrKu6vc62mB1Vho3rV6Ii8HIN5NvZ1BoZ7Ul2QRb9RA+ASZf5vUpQELjNh94tzkH1XL9gy937ifAw50BIX5qS9FxYG43GDgBWIATwK2Nv4+KilJPlM4lkVLy4ZGd3J+8lCT/YL6behcJftqd57xabDKHIKXcJISIucwuM4DPpJQS2CaE8BNChEsp8y53XGcnbRpCYWU1G1IzmDdsAM4Gi9pydFqIlFBaCpmZUFysPC4ru/hnWRnU1YHF8ut2993w1FNgNCqbmxv4+YG//68/z30cGAgxMcrzMzzfowfvWiycWbIUA3zQ+Pi6556zxynQuQrMViufl55k/al8Jkcl8p/h1+PupK1aJz8X7m3V+4VyjW49jYawQkrZs4nXVgAvSik3Nz5fD/xJSrmriX3no/QiCA4OHrB48WKb6LMl604V8M3xHJ4Z1A1vacbLS9srqQGqqqo6rM76+os3k0n5CeDiAk5OynbmAn/hYyGUDZSfZnMVRqOiU0qwWn81C7P54sdms9KeEODqqmzG0nw8qMf1nA3ABLgMGGCTv70j/99tSbXVzLtFxzhUV85k73Bu8ovSXCRRKVV8KtazbPRru6WULYp0sVeUUVNnrkknklK+D7wPkJSUJEePHt2GslrGG/9dSI/wEG69bjLJycloUeOFdASdZjOkpMCePbB7t/Jz/34IDobERIiNPX+Li1Pu3lvyvW6JTimVnsiJE5CRARn3PsFJYjlBLGkkUkIAfdlHf3Yz4LPRDBgASUmKKbWUjvB/b2tOVZYx76evOVlfybyAOJ6ZdpPaki7CbLXw2P7XcK1t3apoexlCNnDurEskkGuntm1KZnEZR/IKeHziSLWldHgqKiA5Gdatgx074OBBiIyEAQOgf3+48Ubo1+/8YRo1EQKCgpRt0CA4ecu/iDnn9RL82UN/1jGAFSvg73+H06ehTx8YPBjGj4dRo0DDN9Ltju35WTyQ/C0WKVkw4Wbqj55QW1KTLD61hrTKTJ7oNo/F/KvFx7GXISwHHhJCLAKGAOVXmj/QKquOpAEwpUeiyko6Hg0NyoV/7Vpl278frrlGuVC+9BL07Qs+PmqrbD5fdO/OI0eOnJ1DCKCUoaxnR/c8vvpK+VKXlcHevbBlC7z8Mtx8s2J4EyYo28CBretB6FyaL9L28dfta4jy9uODMbPo4htIsgYN4VhlFl9mrmZ0yEBGBLeuSqNNDEEI8SUwGggSQmQDzwDOAFLK94CVwFQgHagB5tmiXTVYm5JOn4gwwn291ZbSISgrg+++g2+/hY0blaGeCRPgmWdg+HDw8FBbYct58vBhnu/Rg9uOHCEKyEIxiScPHz67j58fjBmjbE89BVVV8PPPiiHedx/k5Civ3XgjzJgB3vrHstWYrVae2/0TH6fsYlSnON4YOR1fFze1ZTVJncXEK6kL8Hfx5oH42a0+nq2ijG69wusSeNAWbalJXnklh3Lz+b/xw9WW0q6pqYEVK+DLL+Gnn2DsWLjpJvjgAwhpZ/kDz734xwBPXmF/Ly+YMkXZAPLyYM0a+OorePBBmDgRbr0Vpk5VIp90ro7Suloe2vQdv5zO5J5uA3lywFicDNqMdgT4+MQyTtXk82yvB/Fyav3dkaZTV2iNjWkZAIxN0mse2BqTSbmwFRbCDTfAkCHKhe2TT8BXr0Z6ScLD4a67lK2kBJYsgbfeUnoP06fDzJnKZLtes+nKHC0t4DcblpBfU8VLw6ZyU3xvtSVdlt0lKazI/ZkZEaPp559kk2Nq1/o0yMZjJ4n08yEuKEBtKe2G/Hxl8jQ6Gl58UbkDTkuD1auVWH/dDJpPQAD85jdKr+rwYWVCPTdXGWZ78UUlwkmnaVZmHmXmjwuot1hYPHmu5s0AoNRUQbxXZ+6Ovd5mx9QNoZmYzBa2nzjFyIRYPVWFDdizR7mr7dpVGQdfuxY2b1ZCRNvbsJAahIfDI48o53f5ckhNhfh4xTAONZlgpmNitlp5YfcGfrfxO5L8gvn+urvoG9RJbVnNYnzYEF7t93+4GGy3OE43hGayPzuPmoYGhsXpKQVaitkM33wDI0Yow0Ldu0N6Orz/PvS8aDmjjq3o1w8+/lgxhagoZZ5h3DjFKKxWtdWpR0ldDXet+4r/Ht7OHUn9+WrSXEI9HGtW3ihsewnXDaGZ7DiZjQAGxUSqLcXhkBKWLoVeveCVV+Dhh5WFWX/6k5LSQcc+hITA00/DyZNwzz3wj38oZrFypfI/6kjsL8rj+h8+YWdBNi8Pm8o/h0zERY/f1Q2huew5lUtCSBC+7nroxtWwYYOyVuAf/4BXX1Xi6efM0Sc51cTFBebOhZ07lfmbP/5RWfC2ZYvaytoeKSULju5hzqrPAfhm8u3M0eB8gdlq4XTtr5M+tkoxdCV0Q2gGVqtkf3Ye/TqHqy3FYdizByZNUqJdHnlEeT5lSsvSROi0DUIoQ3cHDyo9hltvVdYytNc5hpoGE4/+soKnd6zh2vAYVlw3j95B2vxOv3T0U15I+Yj1+TuQUp6dt2xrY9ANoRmcKC6hqt5En0htfni0xOnTcPvtMG2acnFJSYHbbgMNh3J3eIxGJaIrNRVGj1bmF+69t31FJaWVFTJj5Wd8l3GYR/uO4MOxs/F3c1db1iVxFkbcja7sL0vjv8eXcKIqB6DNA1r0r2kzOJiTD0CviFCVlWgXq1WZHO7dGzp3hmPH4He/U4YndBwDNzf4f/9PCfv19oYePWDBAsefX1icfoDpP3xKaX0tC8bfwsO9r9VcptILGRTYg1pLPQleUVQ0VPNl1io2F+7l+SMfcrI6t816CvpIbjNIOV2Au7OTvv7gEqSnK0MODQ2wfr0yeazjuPj6wmuvKT293/xGMYX//U+JUHIkqhtMPLNjLd8cP8iwsGheG3E9Ie6OkRlwdMhAMqpy6OufRB//RLYXH+SLzFWUN1SdN4Rka/QeQjNIOV1IYmgwRn3c4zysVnjzTWXSeOZMZR2Bbgbth4EDlYnnMWOUhHoffug4vYVDxaeZtuJjlhw/yO97DWPB+JsdxgysUokF9nLy4MOM74jyCKObdyxFpjLivTvz0YllZ4eQbI3eQ7gCUkpS84uY1D1BbSmaoqhImRuorlaiUxL15K/tEicn+POf4frrlXmG5cvhs8+0u4JcSsmnR3fz/O4NBLp58OXE27gmzLG6NobGtQU3Ro4mKy2PvNoivjq1hus7jWRIYE+OVpwk1iuibdpuk6O2I4qrayivrSM+WA+YP8OePUo+//79YdMm3Qw6Aj17KsYfFaXUZjhyRG1FF1NQW8W8n77mbzvXMTw8hpXT7nE4MzgXZ4MzXbwi+e2uZ6lsqOH26KkkekdzXacRbdam3kO4AscLSwDoEqzPH4Byd/h//wfvvguzW59tV8eBcHFRhgg//VRZt6Clz8CG7OP8ccsPVDWY+MfgCdyR1L9dpJiZFDaMUlMl40IHI4RASmnz1cnnohvCFThZXApATKC/ykrUpaEBHn1USTqXnKxEoOh0TO66S5krmjkTdu2C555Tr0hPdYOJF3Zv4PO0vXT1D2bRxNtI8AtSR0wb4OHkxl2x0zAK5QS3tcnphnAFMkvKcDEaCfdxrBwntqSiQkml7O2tVCzTSklKHfXo318xg1tuUdacLFli/2JFewpzeHTzCjIrS7m32yAe6z8KN6PjX9IarGacDb/+HWfMwB7ocwhXILu0nAg/HwwGx+9+toTSUqVCWffusGyZbgY6vxIUBKtWKRlqBw48TVRUdwwGAzExMSxcuLDN2q23mHll7ybmrPqcBquFLyfextODxrULM8ivK+beHX9nV4k6kzSOfwbbmJyyCiL8HKhQrw0pLlYyY44YAf/5j552QudinJxgwoQv+OKLBiyW94GpZGZmMn/+fADmzp1r0/YOFZ/mj7/8wNGyQmbG9eRvg8fjo9HylleLlJK3jn1FjaWOKI8wVTTYpIcghJgshEgVQqQLIZ5o4vXRQohyIcS+xu2vtmjXHuRXVHXI+skFBUrpyvHjdTPQuTxPP/0kFss84ACwBvClpqaGp556ymZtmCwWXt+/mRtWfkZJfS0fjZ3Nq8OntRszAFiXv509pUe5O/Z6QtzUCWJpdQ9BCGEE3gYmANnATiHEcinlhX2en6WU01rbnj0xmS0UVdcQ6uMYC1psRX6+YgYzZypZSnUz0LkcWVlZwJmy6f8B1gMTGn/fevYV5fL4lpWklRUxI7Y7fx88AT9X7eYhaglF9WV8cPxbevnGMzVcvZrttughDAbSpZQZUkoTsAiYYYPjqk5JdQ0AwV6eKiuxH3V1SlK6G2+Ef/5TNwOdKxN1Xk6L/wdsBr6mc+fW1R6vNTfw/K6fmPnjAipN9Xw4djavj5je7sxASsk76YsxSzMPJ956dmGaGojWJkkSQswGJksp72t8fgcwREr50Dn7jAaWoPQgcoE/SikPX+J484H5AMHBwQMWL17cKn2tIbOyhhd2p3J/z1j6Bvk1uU9VVRVeXtrvQTRX58mTSkqKuNZ9l1tMezufamMPnSUlJWRmZmI9r/xaAj4+riQkuDbrGBfqPFBbymclJymy1DPaK4Sb/KLwMKg/5dkW5zOVbJYbdjDK2pPBtH6V55gxY3ZLKQe26M1SylZtwBzgf+c8vwN484J9fACvxsdTgWPNOXZiYqJUk03HTsikZ16VuzOzL7nPhg0b7CeoFTRH58svS9mvn5TV1W2v51K0p/OpBeyl8/PPP5fR0dFSCCGjo6Pl++9/Jbt2lfK//23e+8/oLKipkg9t/E5Gf/qCHPfd+3JrXmbbiW4Btj6flQ3Vcu7Wp+Tvd/9Lmq1mmxwT2CVbeD23heVmA53PeR6J0gs413Qqznm8UgjxjhAiSEpZZIP224zy2joA/NzbVxe1KVauVCqabd9u/3hyHcdn7ty5F0UUjR4Nw4dD164wcuTl32+Rko9TdvHqvp+pt5j5f32Gc3/Pa3BtB6Gkl+OjjOWUmyp5psd8u643uBS2ONs7gQQhRCyQA9wC3HbuDkKIMCBfSimFEINR5i40X36jorYeAG+35nV7HZX0dCVx2XffKbUMdHRsQUICfP453HyzkjU18hLlyPcW5vKP0wfJPFXDiPBYnhk8nnjf9p877EDZMVaf3sKsyHEkeGsj51KrDUFKaRZCPASsBozAR1LKw0KI+xtffw+YDTwghDADtcAtjV0bTVNtMgHg5dp+q7xICfPnKwXvhw1TW41Oe2PCBPjtb+HBB5UbjnODFPJrKvnXno0szTiEv9GFd0bdwJSopHaRg+hK1FtMvHlsEWFugdwWPUVtOWexSX9MSrkSWHnB79475/FbwFu2aMue1JgaMAiBm3P77bZ+/DFUVip1j3V02oI//xn69VPSW8yerawp+DhlF28c+IUGq4UHel5D7zILU6K7qi3Vbiw+tZbc2kKe7fUgbkbt3HC23yudDahtaMDNyand3rGcPg1PPAFr1yorTnV02gJXV/jgA7jpJom561HeSdtIVlUZ4yPjeXrQOKK9/UlOTlZbpt04VZPPN6fWMSZkIP38k9SWcx76ZeAymMwWXJzUn+hpKx55RCl92aeP2kp02jseibkEP7meJ/bk0NU/mE/G3cToCJVim1VESsm76V/janTh3rgb1JZzEbohXIYGiwVntfL6tjGrV8Pu3fDJJ2or0WnPpJUV8u+9m1hz6hhBQZ5Yv5zCXx7rxfCIjplXc0PBTvaXpfFg/E34u2gvR5puCJfBYpUY22mW03/+E559FjpARK2OCuRUlfPGgV/4+vhBPJ1ceLTvCO7pNpAvK1x5/jklzLmjUdlQzQcZ39LVJ4bJ4dqM4NAN4TJIJIZ2OH+weTPk5Wmn2pVO++F0TSVvH9zKomP7EAjmdR3IQ72G4e+m3HnceSc88wzs39/xhio/PbmCqoZaHup1s6rpKS6HbggdkH/9Cx57TJ9I1rEdOVXl/PfwdhYd249EclN8Hx7sNZROnucPi7i6wv/7f/DSS9CGJRM0R1plJqvytjAjYhSxXhFqy7kk+iXhMhiEwKr95RJXxaFDSqWrr79WW4lOeyCzspR3D25jScZBAGbF9eLB3kPp7OV3yff89rdKrqyMDPVyZtkTq7TyXvo3+Ll4M1dDaw6aQjeEy+BkMGA5L2GX4/PvfyvRRW7tJ428jgrsK8rlvUPbWJ2VhrPByK0JffltjyFEePle8b0+PspiyP/8B9580w5iVWbt6W2kVmbyaNLteDhpe9JON4TL4Gw0YjJb1JZhM+rrldWiqalqK9FxRCxWK+uz0/koZRfb8rPwdXHjgZ5DubvrAEI8ri4D6L33wrXXwuuvg0Gbw+k2obKhmk9OfE8PnzjGhgxSW84V0Q3hMrg6Gakzm9WWYTOSk5XayKGhaivRcSTKTXV8dWw/n6XuIbuqnHAPb/4ycCy3JPTBy7lleb66dFFqMm/fDkOH2liwhlhw8geqzDU8ED/HIRa46oZwGdycnak3W7BYrRjbwW3MsmVK8RsdnSshpWR/cR4LU/fy/ckU6ixmBod25qkBY5jQOREnG3wfZsxQPpPt1RBOVufyY94vTO00QtMTyeeiG8Jl8HBxBqDW1IBXO8h4uny5kqZCR+dSFNVW892Jwyw5foiU0gI8nJy5Ma4ncxP70jPQtoXfp0+HefPgxRdtelhNIKXk/eNL8XRy53aNTySfi24Il+FMltOqepPDG0JNjVLnoGvHyR+m00zqLGaSs4/z7YnDrD+Vjlla6RMYzj+HTOSG2B54u7TNZ3/QICgrg2PH2uTwqrKj5BD7y9K4v8tsvJ0dpwSvbgiXwafRBCrq6gnz9VZZTeuorlYKljjAMKaOHaizmNmSd5IfMo+yJusYlQ31BLl5MK/bQG6K702CX1CbazAYYNQo2LoVorRRDsAmNFjN/C/jOyLdQ5gSfq3acq4K3RAug6+7Ept5pnKaI1NXp/cOOjqVpno2551gVVYa67PTqWow4e3syqSoRKbHdmdYWLRN5gauhqQkJeqtPRnCitxN5NYW8vee9+NkcKxcaLohXAZ/DyVmuLSmVmUlrUc3hI6HxWol01TN+4e3syHnODvzszFLK/6u7kyL7sbk6CSGhkWpWqaya1f45hulkE57oKKhmi+zVjPAvxsDA7qrLeeq0Q3hMgR4KsWFS6prVFbSeurqlLsxnfaLVUqOlRWxsyCbracz+SXvJGWmOjgNXf2C+U2PwYyJ6EL/4Ai79wQuxZkeQnthUdYqas11mkxt3Rx0Q7gMAZ7uCKCwyrENoaYGGhogJkZtJTq2QkpJfm0VB4tPc7D4NAeK89hTmEOFSakDHuruxbjO8QSW1XLPmMmEeWhzDiwxUanp3R44XVvMD7mbmRB2DdGe4WrLaRE2MQQhxGTgdZSayv+TUr54weui8fWpQA1wt5Ryjy3abkucjUb8PdwprKpWW0qryMoCFxdop6Ud2jVSSgpqqzheUcKJihKOlRWRUlpAammhcvePknMr3jeQqVFdGRgayaCQSKK8/BBCkJycrFkzAPD0BF9f5YbF0fk88wcMwqCpGslXS6sNQQhhBN4GJgDZwE4hxHIp5ZFzdpsCJDRuQ4B3G39qnlAfL/IrqtSW0Srq6tp3egBHxGy1UmGqo8xUR1l9LcV1NRTWVlNYW0V+bRU5VRXkVJeTU11BrfnXq6WHkzNd/UOYEt2VJL8gegaG0d0/BA9n7dTlvVrc3cHRc0hmVOWQXLCbWZ3HEeTqp7acFmOLHsJgIF1KmQEghFgEzADONYQZwGdSSglsE0L4CSHCpZR5Nmi/TQnz8Sa3vEJtGa2ivl43hDM0WC2crq6kqK6GorpqSupqqGyop7rBRHWDiXqLGZPVSoPVgtlqxSKtWKVEIs+7aBUWFvJVcimg1M2wSnl2P4uUWKxWzNKKyWKh3mKm3mKhztJAjbmBqsZ2LkWAqzsRXr7E+wYyqlMcMd7+xPoEEOvjT7inT7ur0eHqCo6eQ/LjE8vwdHJnduR4VXU0WFs3mmELQ4gATp3zPJuL7/6b2icCuMgQhBDzgfkA/kFhqhfftlZVkFVUekkdVVVVqmu8EtXVEBiofZ1gu/MppaTAXE+GqYoMUxV5DbXkm+soNtdzqWuPsxC4CCNOCJyEwCAEBgQGQCDOW8NhtVrJy/s1+kwgEIAAjEJgRHm/EYGLMOArDAQJZ9ycXHFzNuJmMOJpcMLD4ISXwYiXwRk/ozM+Rmeczi2eUg1UV2A+XcExTnK1a7gc4fP5+9+DyaR9ndD0+TxFIXsMRxll7cnuX3aoI6yRYr/vWvV+WxhCU7crF3YAm7OP8ksp3wfeBwjvHCdHjx7dKnGtJcNlNxtzN9FvyDVn1yWcS3JyMmprvBJ798LWrcnMmTNabSlXpDXns95iZkPOcVZlprEpN4OSeuWC7e7kTLxvINd4dyLG259IL1+C3T0JcvMkwM0DbxdXPJ1criryxhH+7+AYOu+5B959V/s64eLzKaXk8f2vE1jnyyOD7sbVqN7Qndlax+ITz7XqGLYwhGyg8znPI4HcFuxzEWaL+v3Izv5KfvdTpeVNGoIj4Orq+GO0l6OwVom1/yp9PxWmegJc3RkdEcegkM70CQon0S9YM2GWOhfjyEOae0uPcqQig9/Fz1HVDAAyq5I1MWS0E0gQQsQCOcAtwG0X7LMceKhxfmEIUN6c+QOzRf2rWFSAHwCZxWX07OSYeaMjI8FkUsZpHfWL1xRFtdW8e2gbC9P2YrJauC66K3Pie6uy4lanZdTXQ1GRY5ZzlVKyMOtHgl39mRh2jdpyOF7xI15OnVp1jFb/G6SUZiHEQ8BqlLDTj6SUh4UQ9ze+/h6wEiXkNB0l7HRec45ttliRUqqaRzyqsYdwsrhUNQ2txcdHCTnNyYHOna+8vyOwI/8UD2z8lrL6Wm6M68mDvYYS6xOgtiydqyQ9XVkf44jz5PvKUjlacZLfxc/B2eCsqpbqhgLyanfRJ2AesKTFx7GJL0spV6Jc9M/93XvnPJbAg1d7XKuEgtIqQgPUi6N2d3Gmk68PJxzYEEApmZma2j4M4Yu0ffx1+xqivP34cuKtJPoFqy1Jp4WkpjrmCnopJZ9nrtRM7+BE5RpAEuc9uVXH0Xy/OjO3RG0JxAX5c7ywWG0ZreKMITg67x/ezpPbVnFteAzfTr1TNwMHx1EN4Uzv4KbOE1TvHQBkVK4m2K0HPi6RrTqO5g3hpAYMISEkiOOFJVgcOFja1dXxDWF9djrP797AddFd+WjsbHxdHHOSX+dXHNUQvspaQ6CLLxPC1F9fW1qfQanpOLHek1p9LE0bgkEIMnLUvzNPCAnEZLGQWVKmtpQW4+kJv/yitoqWU2mq5/EtK+nmH8Irw6e1i5KmHR0plc/kgAFqK7k6jpRncLA8nZmRYzXROzhZtQ6BgRivsa0+lqa/Vc5Ogoxs9Q0hKVQpFpKWX6Sykpbj5QWZmXDq1JX31SKfpe6huK6GF4dOwU3FdM06tiMlRYky6ttXbSVXx5Ls9Xg7eTA5fJjaUpBScqJyHWHu/XF3an1QhbYNwWjgeHYRUuUg+vjgQJwMBo7kFaiqo7VMnarUVXY06ixmPjyyg9ERcfQJcswskjoXs2yZUlfZkSKMSqhke/Ehrus0Ajej+mV1i+tTqGzIJtbbNgUltG0ITgaqauopKFE3uZyrsxNdggNIOV2oqo7WMmOGYxrCjvxTlNTXcmdSf7Wl6NiQ5cuVz6QjsUuk4ySMXN9ppNpSADhZ+RMGnIjyGmWT42neEACOZal/Ie4RHsqh3HzVeyutYeJEpX5tebnaSq6OTbkZuBiMDA2LVluKjo04fRqOHlVqKjsKZaZKDpPJ2NDB+Lmon1JcSsnJqp/o5DEYV6OPTY6pbUMwGhAC0jLVH6rpFRFKaU0tOWWOm/nU2xvGjoWvvlJbydWRUlJAt4AQ3J3Un8DTsQ2ffw7Tpil1OhyFlXmbMQsrN0aOUVsKoAwXVZtPE+3d+snkM2jaEISAyFA/UjVgCH0jlbHrvac0n7H7sjz6KLz8MlgsaitpPgW11Zou8qJzddTXw2uvKZ9FR6HB2sDKvF+IlaF09tBGCpvMqmQERjp7DrfZMTVtCABJ0SGknlTfEBJCgvBwcWbvqSvm5NM0I0ZAcDAsXaq2kuZT2VCPt7P6E3g6tmHhQujRA/r1U1tJ8/mlaD+lpgoGyHi1pQDKcFFW1UbC3PvbbLgIHMAQusaEkldUQXll7ZV3bkOcjAb6RoazOytHVR2tRQh44gl48UXHyYDq6exCjdmktgwdG2CxwEsvKZ9BR+KH3M10cg8mhhC1pQBQ3pBJRcMporxsO7mtfUOIVbpnKSfzVVYCg6IjScsvoqymTm0prWLaNKWs5vr1aitpHn4ubhTV1agtQ8cGLFum1FB2gNIHZzlZncuRigymhl/bWAZJfU5V/QxAZ88RNj2u9g0hRnHklAz1DWFwTCQS2JWZrbaUVmEwKHdoTz7pGHMJiX7BHC0tcOgILx0lBfszzyifO0dae7A6bytOwsjY0MFqSzlLdvUWAlwT8XS2bY9F84bg7elGdLg/hzNOqy2FXhFhuDk5se2Egy73PYe5c5WEd2+/rbaSK9MzMJQKUz2ZlWVqS9FpBS+/DFFRymI0R8FkbeCngp0MC+qDr7OX2nIAqLOUU1h3kEhP26+U1rwhAPSM78ShY7mq3yG6OBkZEB3B1owsVXXYAoMBPvgA/vEPyNL4nzM8PAaAn3LS1RWi02JSU+E//4F333Ws3sGWogNUmWuYFDZUbSlnya3ehsRKpA2ji87gEIbQOyGc0spaTuWXqS2FYXFRHC8qIb9C3dXTtiApCf7wB3jgAW1PMEd7+5PgG8TqrDS1pei0AKsV5s+Hv/5V6SE4EmtObyXULZDefglqSzlLdvUW3Iz+BLl2tfmxHcMQEiMA2J+mfoTP8C7KatnNxzNVVmIbHn9c6SFofbHa9NhubM8/xYkK9dOh61wdH36orD148KpLZKlLQV0JB8qOMT50MAahjUulVVrIrdlOhMdQRBto0sZfeQViwgPw8XJjX6r6hpAYGkSwlyeb00+qLcUmuLjA//4HjzyilDPUKjcn9MFJGPg8da/aUnSugoMHlUnkDz5Qyrg6EskFu5BIxoQMUlvKWYrrUqi3VhDh2TZV2lplCEKIACHEWiHEscaf/pfY76QQ4qAQYp8QYtdVizQI+iRGaMIQhBCMiI/hl+OZmC2OWzDnXIYMgb//XZns02qeoxB3L6bFdOOLY/soqq1WW45OMygqUpLXvfYa9OqltpqrJ7lgN9194gh3D1JbyllyarYDgnCPtjGp1vYQngDWSykTgPWNzy/FGCllXynlwJY01C8pguz8MgpL1R+7H5UYS0VdPXscfNXyudx/vxIbPneudkNRH+5zLSaLmTcPOHClnw5CQwPMng033aR8phyNk9W5ZNbkMSpEWxl282p2EuiahJvRt02O31pDmAF82vj4U+CGVh7vkvTvplSH33NU/TUA18ZF4Ww08lPqcbWl2JTXX4fqaqWLr0XifAK4NaEvC9L2cqhY/TBknUvz8MNKMsXnnlNbScvYXLgPgeDaoL5qSzlLg7WawrrDhHu06J66WYjWhHIKIcqklH7nPC+VUl40bCSEOAGUAhL4r5Ty/csccz4wHyA4OHjA4sWLAbBaJX9feIDesX7MGq5+GuS3Dhwnr6aOJ3pE4e2t/cRrVVVVeHldOY7abFbSEoeHQ2CgHYRdwJV0VlvNPJm7Hz+jC38N64lRpRjG5p5PtVFDZ2EhFBRAt25KeHNz0Nr5/Fisww0XbpXnp4ZQU2etayoFQZ8SUjQP9/pLRz2NGTNmd0tHYpBSXnYD1gGHmthmAGUX7Ft6iWN0avwZAuwHRl6pXSkliYmJ8lz+75Vv5cxH/ye1wDe7D8qkZ16Vnyz7QW0pzWLDhg3N3vfwYSnDw6X87LO203MpmqPzh5MpMvrTF+Qb+ze3vaBLcDXnU03srfOdd6Ts3FnK48ev7n1aOp85NQVy6sbfy++yN1z0mpo6dxa+JT9LGyEbLLWX3Q/YJZtxfW1qu6J/SynHSyl7NrEtA/KFEOEAjT+bTEsqpcxt/FkAfAu0aA34wB5RZBeUk1ekfk2CsV274GQwsLuwVG0pNqd7d1i3Dv78Z/joI7XVXMzU6K7cENuD1/ZvZk+h+oEGOgqvv64krktOhrg4tdW0nK1FBwC4JlBbM+H5tfsIcuuOk8Gtzdpo7RzCcuCuxsd3Acsu3EEI4SmE8D7zGJiI0sO4agZ1V1a17Dys/tJafw93hsZFsaugTPUV1G1B9+7w00/wt78pq0u1xj+GTCDc04cHN35HQa36gQYdnZdegjfecHwzANhWfJA4zwhC3VQYM70EDdZaiuuOEuret03baa0hvAhMEEIcAyY0PkcI0UkIsbJxn1BgsxBiP7AD+EFKuaoljcVFBhLo68mOQ9pYFDa1ZyIl9Sb2ZTt20ZxLkZgIGzbAv/6l3P1pCR8XN94bdSNlpjp+s2EJdeYGtSV1WJ59Vll8tnEjRKs/vdcqKhqqOVpxgsGBPdWWch5FdUeQWAhx79Om7bTKEKSUxVLKcVLKhMafJY2/z5VSTm18nCGl7NO49ZBStjjuQAjB4J5R7DychdWq/l35hK7xOAnBioOpaktpM7p0Ub7ob70Ff/yjMumsFXoGhvHa8Os5UJTHHzZ/j8XaPtaFOAomk5L25MsvlZ5BZKTailrP7pIjWJEMCuihtpTzKKjdDwhC3NrWqBxipfK5DO0dQ1llLUc1UB/By82V3kG+/HgolQatBu/bgOho2L5dWXU6caISRaIVJkUl8peB41iVlcbTO9a0y+E7LZKbC6NGwenTsHWrEpXWHthbmoqPkycJ3tpKulRQdwB/lzhcjG0b0ehwhnBNrxgiQ/0ordBGwZQhoQGU1NTySzvJbXQpAgJg5Uq45hoYOBB2XfV687bj3u6DeKDnNXyRto/nd2/QTaGN2bwZBg1SCi0tWQI+tqvgqCpSSvaWHaWvfxJGjeQuAiV/UWHdYYLde7d5W05t3oKN8fV2Z8m/71Fbxll6BHjj7+HOt/uOMDrRwWfTroDRCM8/rxjC1KnK3MK8eWqrUni83yhqGkx8cGQHZmnlrwPHIRwpz7IDIKVSP+Of/4RPP4XJk9VWZFtO1eZTYqqgj1+i2lLOo9x0kgZrdZsPF4EDGoLWcDIYmN67K1/s2E9JdQ0Bnh5qS2pzZs5UFh3deKMyv/Daa+Dnp64mIQR/GzwBJ4ORD1N2Um8x88/BEzE2d2WUzmUpKlKylR49qgwROXokUVMcLDsGoKlU16BMKAMEuXVv87b0b4sNmN2/Jw1WK9/uO6K2FLvRrZsybOTpqSQuW9WiuDHbIoTgLwPH8rueQ/kibR+/2/SdHn1kA779Fnr3hs6dYdu29mkGAIfLMwh08SXcTTvJ7ACK6lJwNnjh49y5zdvSDcEGJIQEMSCqE4t3H9RE9JO98PJShhA++URJjnfXXcqdpJoIIXi8/yj+Omgca7LSuG3tIorrtDHf5Gjk5SnJ6R5/HL7+Gv79b3B3V1tV23GkIoNuPrGaG2osrj9KkGvXNql/cCG6IdiIWwb2JrOkjC3toLzm1TJuHBw6pOQ+6tFDMQi153Xv6TaId0bdwOGSfGas/JTUUg2FRmkcqxXee0/pFSQkwIEDcO21aqtqW0rqyymsL6WbT6zaUs7DIhsoNR0n0C3JLu3phmAjJnVPIMDDnS927lNbiip4ecGrryqRSG+9pUQj/fSTupqmRHflq0m3YbJYmPnjAr0E5xWQEn78Efr3hwULlEWJzz3XvnsFZ0itVKIEk3xi1BVyAeWmE1hlAwGuuiE0C4vVyt5UJSW2muGGLk5OzBnQiw2pGWSXarTKjB0YMAB27FBqNf/mN8q6hd271dPTN6gTy6+7i3jfQH6bvJSX9mzErC9gu4itW5V6GI8+Cs88o4SW9tTWYt02Jb3qFAYMxHlGqC3lPErqlYnuAFf7THQ7vCEYDQYe/88ysvJKEUKoagq3DuyNQQgW7tivmgYtYDDArbdCSooSiXT99XDzzZCm0g16mIc3X02ey60JfXnn0FbuXPeVXnWtkcOH4YYblP/PXXcpiw9vvBE0Noze5qRXnqKzRyiuRhe1pZxHaf1xjMIVb2f7LAN3aEM4U8Kyf7fOLFq9BwCLipO6Yb7eTOqewDd7DlFdb1JNh1ZwcVFSGxw7Bn36wLBhcM89ypi0vXEzOvHC0Mm8NGwquwtzmLriY37JO2l/IRph9264/XYYMwZGjlTM+p57wKmDBqKnV50i3rvto3iultL64/i5xGIQ9ilI7dCGYGi8jbltygDWbjsKgJNR3T/prqH9qayv55s9LUro2i7x9FSqsKWlKSGLU6YoF6Jly+xfrvOm+N58N/VOfFxcuX3tIl7as5EGa/tNO3IuZrMSLTR8uLKWpHdvxawffRTc2i6jsuYpM1VS1lBJrMaGiwDKTCfwc7FfnK9jG4JBMYQ+iRFICfvTlNz4aoZ+9okMZ2B0BB9v3Y3J3DEuNM0lIAD+8hc4cUKZX3j+eSWK5dVXodyO0y7d/ENYPvUubknowzuHtjJ71edkVJTYT4CdKSlRVpXHxSkpqv/wBzh+XAkn9W2b0rwOxclqpTZ6jGcnlZWcT72lglpLEX4uMXZr06ENAX4dNpo4tCuLVinDRtbGeQS15hN+O3wwpyuq+P5Aiirtax0XF7jtNiVh3hdfwM6dEBsL990HlZX26TV4OLvwwtApvD3yBk5WlHLdio9ZdqL9LCw0m2H1ajh5UslYe+QIfPcd/PwzzJ7dcYeGmuJUjZIoM9ojTGUl51NhUkLYfXVDaD7Gxl7CTRP78fPeDODXYSO1FpgMj4+me3gI72/eqadkvgLXXKOkTz54ELp2hexsJY3yI48oq2Lb2tOvi+nKmun3ck1oFBGezcvSVmfRUA7wc7BalQv+gw9CRIQSLeThoaSb+PRTJZxU52KyawvwMLrh76KtLH3lDUoorI+L/TKvOrwhCCGwWK3EdAqgV3w4aZm/LkDKyC5SJU22EIL7Rwwms6SMlYf02PfmEBGh1Fvo1k3JjxQQAHffrQxz/PnPsGePcsFrC0I9vPl43BwGhlw+kmPJ8YM8u2s9t69ZxI8VuW0j5iqxWJQw38ceg5iYX81g61bFUENCIDRUbZXaJre2gE7uwZpboVxhOoXAiLez/YayHN4QgLMJzN55cg5xEQEALFy5i0df+Y5XPtvAvz+z/wqp8V3jSQgJ5L1N2/VewlWSmKjc3aakKHl0pFTCWMPClJ8ffghZdl4QvuT4QZ7evgYnYWRet4EkVxXw1oEt9hXRyIkT8P77MGeOcsGfNw9cXZVFZQcOKBP47TXfUFtwuraYcHdt5S8CqGjIxss5HIOw3/heuxlJ/HrtPj5bsQMp4Y7rBnIoPY9n7p8MEl76ZD3rt6cxboj90toaDIIHRg7h0W9WsurwMa7rZZ+Vhu0JIaBvX2V78UXFBNatg7Vr4YknlF7EhAnKNnSocnFsCw4Wn+aF3ck8M2g8NycoJQyPHjnCtvws5luG4GJs25DAvDzYskX5u9euhepq5W+eNk3JNBuhveAYh8EqrRTUlzAsuG1LU7aEyoYcvJ3t+89tlSEIIeYAfwO6AYOllE2WTRFCTAZeB4zA/6SUL7am3QvJKSjj+42HmDd9CJ2Cffnwu23ERgTQL0kZApg1vg+rt6bY1RAAJndP5N2Q7byZvJVJ3RNUD4l1dKKilFj5e+5Rho/271cM4p13lOElT09lpfSAAcp4+YABra/kJaXktf0/Mzg08qwZAGQ31ODp4WFTM5AScnKU4bHdu5Vtzx6or4chQ2D8eGVIqGfPjrdwrK0oM1VilhaCXf3VlnIeUkoqG3IIdrNvKc/W9hAOATOB/15qByGEEXgbmABkAzuFEMullDYL6dh+MJMAXw9mjlO+sGaLlRc+WgtA1ulS9h7NITTAGymlXccJDQbBH8Zey4OLlrN032FuGtDLbm23dwwG6NdP2R57TLmYnjjx68X0jTeUny4uijkkJCiRTOduXl5Xbmdbfhabck+wffZDZ393qqqMUouJRK9OWKU8ux6muVRUKFrP3Y4dU7RL+aup3XOPkk02Kko3gLaisL4MgCBXP1V1XIjJWkmDtcqu8wfQSkOQUqbAFaN5BgPpUsqMxn0XATMAmxlCr4ROfLRs29nnQf6e+Hm7c/tTC4gO96eypp75s4aqMmk0NimOfp3DeXPDVq7v1RV3F2e7a+gICKGMm8fFKWGVoFxcs7Jg3z4l7v7YMViz5teLsLe3YgwxMRAUBP7+SqGfc39+XZPKqMBu1JV4kG8EC2Y25J8ix1TLLd5dKCwQWCxQVwelpVBW1vTPoqJf262tPd+Y4uKUIaB+/ZThH/3ibz9KGyoACHTR1oKMqoY8ALzsbAjCFrH6Qohk4I9NDRkJIWYDk6WU9zU+vwMYIqV86MJ9G1+fD8wHCA4OHrB48eJmaXj92xRiw7xI6uzL3vRiokO96BLuzanCavy9XIgN8zpz/Bb8hZemqqoKryvcaqaXVfHvfceYHhvO1Gh1Yp2bo1ML2FNnQwOYTMqQjMWixO5bLOc/3isKyBDlXFeTgJSQ7lzCEZdCotyN9C2KB5QLuBBKbL/RqGxNPXZ1VTZ7rgHQ/++XZz8nWGPYy/3WyXhz5WqH9tJZ43aEwsDPCSt4ENeGq5tHGDNmzG4p5cCWtHvFj6YQYh3Q1FXsKSnlsma00dQV+JIuJKV8H3gfICkpSY4ePboZTYB3aBfWbUtl05FcAny8uXn6GOIiApv13taQnJzMlTSOBvbVLWd9xin+NGs6gV72L7PZHJ1aQGs6t+dn8buN31HdT/nIZuSVMyYsngEVMGXuaHXFNQOtnc9LoZbO/CwTnNzLpJETcDFcufduL50pZUUUFsLIIVNwdwpo8/bOcEVDkFKOb2Ub2cC5WaMiAZsHcQ/o1pl+SZHkFZUTEeJ33mv2njtoikfHD+f6tz/jzeSt/G3aOFW16DSfIaFRfDP5dl7eu5EwD28e7TuCYWHRbN/8y3n7rc5KY3REHK7GdhO41yGobKjG1eDSLDOwJzXmAgzCGTejfSe77fHp3QkkCCFigRzgFuC2tmhICM6awbkmoLYZAMQFBXDLoD58uXM/twzsTdewYLUl6TSTWJ8A3hl14yVvLFJLC/lt8lIS/YJ4adhU+gZpKyeOzqWpMtfi5aS9CkA15iI8jEF2v3a1Kg5SCHGjECIbGAr8IIRY3fj7TkKIlQBSSjPwELAaSAEWSykPt072JfU0+Vgr/H70UHzcXHl25QZV6zbotIxLfaaS/IP5eOwcKk31zPxxAS/s3qDZ9BY651NjqcXDSXupXmvNRbg7tf2Q94W0yhCklN9KKSOllK5SylAp5aTG3+dKKaees99KKWWilLKLlPK51op2VPw83Pi/8cPZlZXD9weOqi1Hx4aMiezC6un3cnN8b/57eDvXrfiYvYXaSG+hc2nqLCbcja5qy7iIWksJ7kYHMwQtU1vXwLrtqZq7E5/Vrye9I8J4ac0mKmrr1JajY0N8XNx4YegUPht/M7UNDcxapfcWtE691YSrQVtV0gDqLCV2nz+AdmwIq7ak8NRbP7CvsUaCVjAYBM9cN5aSmlpe+0mdXDg6bcvITrGsmn4PN3VRegvTf/iEQ8Wn1Zal0wQmqxlng7YCAaS0Um+pwNVo/7UR7dYQplzbDR8vN778UcUK75egR6dQbmucYD6QrV8o2iM+Lm68OGwKH4+bQ1l9HTes/IzX92/uMNXZHAWLtOBkx+RxzcFkrUJixc3oZ/e2260huLk6M2tsHzbtOc6p/FK15VzEH8YOI8Tbi6eWrcFk1ocU2itjIrqwZvq9TI3uyn/2b2bOqoWcaMfV2RwNi7RiFNq6DNZblNXTrkb712fQ1pmwMXMm9MXJaOTLH/eoLeUivNxc+fv14zhWWMx7m3aoLUenDfFzdeeNkdN5a+QMTlSUMHXFx3yRtk9z81sdES3+D0zWSgBcDN52b7tdG0KgnyeTh3VlxaZDlFbUqC3nIkYnxjGjdzfe37yTw7n2L+SjY1+mxXRj9fR76R/UiSe3reI3G5ZQUqe9z6WOupisVQC4GO2fyqNdGwLA3KkDqW+w8PXafWpLaZI/Tx6Nv4cbf/5uDSazPr7c3gnz8GbBhFt4euA4NuWeYMr3H7HldKbasjosRmHAIrVVwKrBqtwkOBvsn+Km3RtCbEQgI/p34et1+6ita1BbzkX4ebjx9+vHk1ZQxFvJW9WWo2MHDEJwb/dBLJ1yB57OLsxd8yUv7k7WJ5xVwMlgxCK1dd7NjYbgJHRDaBPumjaIiqo6vttwQG0pTTI2qQuz+vXgg8072XEyW205OnaiZ2AYK667m1sS+vLe4W3cuvpLcqsr1JbVoXAWzjRYtRXUofcQ2pheCZ0Y0K0zn6/cRZ1Je70EgCcnjyYqwI/Hl/5IWY2+YK2j4OHswgtDJ/PGiOmklBYw9fuPWHvqmNqyOgwuBidMVm1dE8yyHgAng/1XUHcIQwC498ZrKCqrZnnyIbWlNImnqwv/njWF4qoanv5+rSajH3Tajumx3fl+2t1EePnymw1LeGH3BsxWbY1tt0fcjK7UWU1qyzgPS6MhGIVuCG2Gkh47gs9W7KDepK0u4hl6RYTxh3HXsjYlna92H1Rbjo6difMJYOmUO7g9sR//PbydO9YtoqC2Sm1Z7Rp3oyu1Zm31yC1WEyAQ2K5ed3PpMIYAcN/MoRSWVrMsWbsX23lDBzC8SzTP/5jMkbwCteXo2BlXoxPPXjOJV669jr2FuVy34mO252epLavd4uHkTpWlVm0Z5yExYxDOqmRs7lCGcKaX8On3OzQ7l2AwCF6aOZkAT3ceWbyCcj0BXodkVpdeLJt6F97Orsxds4gFqXv0YcQ2wMvJnRpzHVYNhZ5apRmDXUrVXEyHMgQhBPNnDaOorJql67UZcQQQ4OnBa3Omcbq8kseXrsJq1S8EHZEk/2C+m3onIzvF8vT2NTy+ZaWeOdXG+Dh7IpFUm7XTS5BYESql0+hQhgDQv1tnBveI4tPvd1Bdq63JpHPp2zmcP08ezcZjJ3hn0za15eiohI+LG/8bO5uHe1/L18cPcvOqheTXVKotq93g66ysBi5r0M5cjZQSg0qX5g5nCAAP3DScsspaFq7cpbaUy3LroN7M6NONt5K3sf7ocbXl6KiEQQge7TuC90fP5Fh5EdN/+JQDRXlqy2oX+Dkr+YLKTNpZ/yGRgDoVHzukIXSPC2Pc4ES++HE3xWXVasu5JEII/j5tPL06hfLYkh85erpQbUk6KjIxKpElU+7AyWBgzuqFLD9xRG1JDk+Ai5JRtERDhqAmra2pPEcIcVgIYRVCDLzMfieFEAeFEPuEEJq4LX/gpmsxmS3871ttp4twc3birVum4+3myu++XEZhpXYNTKft6eYfwvLr7qZPYBgP/7ycV/f9rE82t4IAV6UITbGpXGUlvyIQSNSZ5G5tD+EQMBPY1Ix9x0gp+0opL2kc9qRzqD8zx/ZmWfJBTuZqOz99qI8X79w6ndKaWh5atJy6Bn1isSMT6ObB5xNuZU6XXrxx4Bf+sPl7fbK5hXga3XE3ulJUr52aKUIYHNMQpJQpUspUW4mxN/fecA2uLs68tag5fqYuPTqF8vLMKRzIOc3jS3/Eoq9i7dC4GI28NGwqj/UbybITR7h9zSKKavXe49UihCDY1Z+COg0ZAkakSgn37DWHIIE1QojdQoj5dmrzivj7eHD39MH8vDeDnYe1v/hnfLd4/jRpFGtS0nnux2R9qKCDI4TgwV7DeHvkDRwqOc2sVQvIrNTOhc1RCHELIL+uWG0ZZzEKZ6xSnR6fuNJFRQixDghr4qWnpJTLGvdJBv4opWxyfkAI0UlKmSuECAHWAr+XUjZ5W95oGPMBgoODByxevLi5f0uLaDBbeXXpEZyNBh65sRtGw9XN7ldVVeHlZd9CFt+k57Auu4AZseFMiW7qX3MxauhsCbrOlpFeX8lrhakI4P8FdyXOVdGmNZ2XQk2d68Q+DpPFw/J6xBWie+yhs8x7PeU+64nKeRbRgnv2MWPG7G7x0LyUstUbkAwMbOa+f0Mxjyvum5iYKO1B8s5jcvDtr8ivVu+56vdu2LDB9oKugMVilX/8ZqVMeuZVuXjXgWa9Rw2dLUHX2XLSy4rk8CXvyKTPX5ZrstKklNrU2RRq6vwue4OcuvH3sqy+4or72kPngeLP5CdpQ2WDpa5F7wd2yRZey9t8yEgI4SmE8D7zGJiIMhl9RSwW+wyJjBzQhcE9o3l/yRZKyrVf0tBgEDw3YyIj4mN4ZsV6fjzksNM4Ojaki28gS6fcSZJ/ML9NXsridO2uxtcSEe4hAOTUaiOs+0zaa7O0f9qa1oad3iiEyAaGAj8IIVY3/r6TEGJl426hwGYhxH5gB/CDlHJVc45fWWafEyKE4NHbR1NT38A7i3+2S5utxcXJyOs3TaN/5048tnQVP+kL13SAYHdPvphwK9eGRfP4lpWsrMhVW5LmOWMIp2q0UdfcKNwAsFgdzBCklN9KKSOllK5SylAp5aTG3+dKKac2Ps6QUvZp3HpIKZ9r7vHras1knbCPa8dGBHLLpH58v+kwB9Md40vk4eLMe7fNoHt4CI98/QM/p59UW5KOBvB0duHDsXOYFtONxWVZPLtrPVY9AOGShLgF4GJw5lTNabWlAOBkUAyhQdo/v5K2VyoLWPzJZrs1d+8NQwn29+KlT9ZjtjhGWKeXmysf3H4j8cEBPLRoOb8c1wu26yhhqW+MmM54rzD+d2Qnj235QS+4cwmMwkBnj1Aya7SRDsRZeAK/ltK0J5o2BA9PF9b/eIC8bPssHPN0d+GPd44hLbOQRav22KVNW+Dr7sZHd8wiJtCfB75YxqZjJ9SWpKMBDEIw1z+aR/uOYMnxQzz88zLq9QVsTRLtEc7Jam2MDDgblVrKDVb7ryvRtCF4ebtgNBr4yo69hFED4hnRvwvvL91CTkGZ3dptLf6e7nxy12zigwN5cNH3ejI8HUCZH3u497X8ZeBYVmamct9PS6hp0G6WX7WI8exEiamCigb1F/e5GJSwVpPF/lltNW0IBqNg8g39Wfv9PvLzyuzSphCCx+4ci9EgePHj9Q61+Mvfw52P75pF97BgHlm8Qo8+0jnLfd0H89LQKfxy+iR3rV9MVUO92pI0RaxnJwBOVOeorARcDEoGVpPV/im5NW0IADfdNRyARR/bL/onNNCb3900nB2HMvnxlxS7tWsLfN3d+PCOmfSNDOfRb1ayaOd+tSXpaISbEvrwxojp7CnM4c51i6kw6dX4zhDrFQFARpX6huBqPGMIeg/hIkLCfJl8Q3/WLNvL6Rz7LcufNa4vvRM68Z/PN2g6RXZTnJloHpkQy99++Il3Nm5zqJ6OTtsxLaYbb4+8gYPFedy+dhFl9dqpFKYm/i4+BLr4crzqlNpScBIeGIQz9Rb7Z2DVvCEA3HrvSAxGwefvJ9utTYNB8JffTKTeZOaFj9c53AXV3cWZt265nhl9uvHGhq0sOpatJ8TTAWBydBL/HT2To6WF3LLmC0rqtL8Y0x508epMugYMQQiBq8FXN4RLERTiw7TZg1i/cr/d1iUARIcH8MCc4fy857jDDR0BOBuNvDBjEvcOG8DG3CIeWvQ9NaYGtWXpaICxkfF8NHYOJypKuW3tl7opAIneUWTXFFCjgfrKbkZ/ai32T1ToEIYAcPO8Ebi6OfPZuz/Zt91J/embFMErCzaQX+x4tWwNBsFjE0dyS0IkG4+d4I6PF1NQqZ36sTrqMbxTDB+Oma2bQiOJ3tFIJMcq1e8ldPe/mXjvKXZv12EMwc/fk5lzh/Lz+iOkHbHfxI/BIPjr/ElYLFb++cFqrFbHGjo6w+iIYN65dTonikq5+YNFejlOHUAxhf+NmaWYwpovKe7AppDoHQ1ASqX663jifaYS7T3G7u06jCEAzLp9GD6+Hnz01jq7thsR4scjt41i5+Esvlqz165t25LRiXF8fs9NWKXk1g8XsfrIMbUl6WiAEZ1i+WjsbE5UlnLH2kWU13fM6CNvZw86e4SSUqG+IaiFQxmCp5cbt947gr3bM9i9Nd2ubd8wphcj+nfh7a9+Ji2zwK5t25Lu4SF8Pf9WEkOVtQpv/LTFYXs9Orbj2vAY/jt6Junlxdy57qsOG5La3SeOoxUnscqOGYDhUIYAMG3OYMIi/Png9TVY7JhvSAjBX+6biK+XG0+/s5LaOsednA3x9mLB3bOZ2bcH72zazoOLllNe2zEvADq/MjoijndG3cDhknzuXv91h1y81t0njipzDVkaSXRnbxzOEFxcnLjnofGcOJbPuhX77Nq2n7c7f7t/Cpl5Jfxn4Qa7tm1rXJyceG7GBP4yZQw/p59k1n8XciTPcXs+OrZhfOcE3ho5g/1Fudyz/mtqzY5749MSevnFA3Co3L4jEFrB4QwBYOSEHnTr3ZlP3l5PbY1972IG9YjizmmDWZZ8iLXbHDs1hBCC24f0ZcG8OZitVm753yK+3n3Q4dZc6NiWydFJvDZ8OjsLsvndxu8wWdQp+K4GoW6BhLgGcKCsY86vOaQhCCH47aOTKCmusmt67DPMnzmUXvHhPP/hGgrtVMSnLenXuRNLfzuXgdERPP39Oh5buoqquo43XKDzK9fHduP5ayazIec4f9i8vEOlzu7lF8/BsnTNziNYrG333XRIQwDo1qszoyf15JvPt1Bgp8R3Z3ByMvLcQ9NwcXZiwfoMh55POEOApwcf3H4jj4wZxo+HUrnxvws5kN0xx1F1FG5N7Hs2S+rjW1Z2mCI7ff0SqTBXq57XKL92HzsLX2dbwSvUmks4XbOXH079hh+zf0dO9Tas0vY9N4c1BIB7fj8BgPdfW2P3tkMDvfnHA1MpKKvjxU8cL7VFUxgNBh4YNYQF8+ZgsVq57aOveG/TDj3lRQfmvu6DebTvCJZmHOLZXY6V/bel9PZLBGB/WZpqGkrrj7Oz8A3KTZmUm06wq+gtjpR9SVffWUR7jWJ30dsU19t+yNqhDSE03I+b7x7Bz+sOs29Hht3bH9IrmvH9w1n1SwpL17efgub9oyL49v7bmdAtntd++oXbP15MVkmZ2rJ0VOL3vYZxd9cBfJSyi3cObVVbTpsT5OpHpHuoqoaQUvY1Ie69GB/xKpMi36KqIRd/13i6+EymV8CdeDt3pqDW9tecVhmCEOJlIcRRIcQBIcS3Qgi/S+w3WQiRKoRIF0I80Zo2L2TOndcSFuHP2y+vxNxg/8mvsX3DGNYnllc/38C+VPVT59oKX3c3Xp09lZdnTiG9oIQb3v2cRbsOdIg7RJ3zEULw10HjuSG2By/v3cSCVMepJthS+voncaj8OA1WdYaDJRbcjP5nn/u4RFFn/jW3kbPBHXMblNhsbQ9hLdBTStkbSAP+fOEOQggj8DYwBegO3CqE6N7Kds/i6ubMA3+cQlZGId8t2marwzYbgxD8/YEphAf78MQb3ztkvqNLIYTg+t5dWf67O+gTGcbfVqznns+WkF1q/yyMOupiEIKXr53K+Mh4/rp9Dd+fcLxkj1dDP/8k6q0mjpSrs2o5wDWJ0zV7qGrIo9yUSYO1mlJTOhty/8zm089Sbsok3GOQzdttlSFIKddIKc8Uad0GRDax22AgXUqZIaU0AYuAGa1p90KuGZnEkBGJHD2kzh26j6cbL/9hBg1mCzsOt78i9+G+3nx05yz+Nm0cB3LyeXND+x820LkYZ4ORt0bOYFBIJF+l72/XvcXevgmEugVSYVanFkqk51DcnQLZnP9Pdha+gZdzJ0aG/YNAt644GVwZEPwgIe69bP4/ELY6oBDie+ArKeXnF/x+NjBZSnlf4/M7gCFSyocucZz5wPzGpz2BQzYR2HYEAUVqi2gGuk7bouu0LbpO25EkpfRuyRudrrSDEGIdENbES09JKZc17vMUYAYWNnWIJn53SReSUr4PvN943F1SyoFX0qgmjqARdJ22RtdpW3SdtkMIsaul772iIUgpx1+h8buAacA42XR3IxvofM7zSCD3akTq6Ojo6LQ9rY0ymgz8CZgupbzUlPdOIEEIESuEcAFuAZa3pl0dHR0dHdvT2iijtwBvYK0QYp8Q4j0AIUQnIcRKgMZJ54eA1UAKsFhKebiZx3+/lfrsgSNoBF2nrdF12hZdp+1osUabTSrr6Ojo6Dg2Dr1SWUdHR0fHduiGoKOjo6MDaMgQtJAGozkIIeYIIQ4LIaxCiEuGnwkhTgohDjbOrbQ4DKylXIVOtc9ngBBirRDiWONP/0vsp8r5vNL5EQpvNL5+QAjR317arkLjaCFEeeO52yeE+Ku9NTbq+EgIUSCEaHJtkRbOZaOOK+lU/XwKIToLITYIIVIav+ePNLHP1Z9PKaUmNmAi4NT4+F/Av5rYxwgcB+IAF2A/0N3OOrsBSUAyMPAy+50EglQ8n1fUqZHz+RLwROPjJ5r6v6t1PptzfoCpwI8o622uAbZrUONoYIVan8VzdIwE+gOHLvG6qufyKnSqfj6BcKB/42NvlNRBrf5saqaHIDWSBuNKSClTpJSaL5XWTJ2qn8/G9j5tfPwpcIOd278czTk/M4DPpMI2wE8IEa4xjZpASrkJKLnMLmqfS6BZOlVHSpknpdzT+LgSJYIz4oLdrvp8asYQLuAeFGe7kAjg1DnPs7n4JGgFCawRQuxuTMehRbRwPkOllHmgfMiBkEvsp8b5bM75UfscNrf9oUKI/UKIH4UQPewj7apR+1xeDZo5n0KIGKAfsP2Cl676fF5xpbItsXcajJbSHJ3N4FopZa4QIgRlncbRxjsPm2EDnaqfz6s4TJufzyZozvmxyzm8DM1pfw8QLaWsEkJMBb4DEtpaWAtQ+1w2F82cTyGEF7AE+IOUsuLCl5t4y2XPp10NQTpIGowr6WzmMXIbfxYIIb5F6drb9AJmA52qn08hRL4QIlxKmdfYnS24xDHa/Hw2QXPOj9qpWa7Y/rkXCinlSiHEO0KIICml1pK0qX0um4VWzqcQwhnFDBZKKZc2sctVn0/NDBmJdpQGQwjhKYTwPvMYZcJci1lbtXA+lwN3NT6+C7ioZ6Pi+WzO+VkO3NkY0XENUH5mCMxOXFGjECJMCCEaHw9G+d4X21Fjc1H7XDYLLZzPxvY/BFKklK9eYrerP59qzpRfMCOejjLeta9xe6/x952AlRfMnKehRFY8pYLOG1Gctx7IB1ZfqBMl4mN/43ZYqzo1cj4DgfXAscafAVo6n02dH+B+4P7GxwKlANRx4CCXiTxTUeNDjedtP0rAxjB7a2zU8SWQBzQ0fjbv1dq5bKZO1c8nMBxl+OfAOdfMqa09n3rqCh0dHR0dQENDRjo6Ojo66qIbgo6Ojo4OoBuCjo6Ojk4juiHo6Ojo6AC6Iejo6OjoNKIbgo6Ojo4OoBuCjo6Ojk4j/x+yp66Cbe8KuQAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"theta0 = 1.0\n",
"x0 = np.array((np.sin(theta0),np.cos(theta0)))\n",
"\n",
"## Run Algorithm 5.1 on test problem\n",
"results = alg52(x0,my_f3,my_h3)\n",
"\n",
"## Display results\n",
"xstar = results[0][-1]\n",
"print(\"\\nx* =\",xstar)\n",
"\n",
"## Display results\n",
"vstar = results[1][-1]\n",
"print(\"\\nv* =\",vstar)\n",
"\n",
"## Convert into theta\n",
"print(\"\\ntheta* =\",np.arccos(xstar[0]),\"=\",np.arcsin(xstar[1]))\n",
"\n",
"## Visualize\n",
"visualize(results[0])"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.8.4.2 Starting Point Near Local Min ($\\theta_0 = \\pi$)](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.4.2-Starting-Point-Near-Local-Min-($\\theta_0-=-\\pi$))",
"section": "4.8.4.2 Starting Point Near Local Min ($\\theta_0 = \\pi$)"
}
},
"source": [
"### 4.8.4.2 Starting Point Near Local Min ($\\theta_0 = \\pi$)"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.8.4.2 Starting Point Near Local Min ($\\theta_0 = \\pi$)](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.4.2-Starting-Point-Near-Local-Min-($\\theta_0-=-\\pi$))",
"section": "4.8.4.2 Starting Point Near Local Min ($\\theta_0 = \\pi$)"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Iter. \tf(x) \t\t||h(x)|| \t||grad_L(x)|| \t||dx|| \t\t||dv|| \t\tdelta_A \tdelta_W\n",
"0 \t 2.2204e-16 \t0.0000e+00 \t1.4142e+00 \t 5.0002e-01 \t 2.4998e-01 \t 0.0000e+00 \t 0.0000e+00\n",
"1 \t-6.2504e-01 \t2.5002e-01 \t1.0000e+00 \t 3.0322e-01 \t 4.1490e-01 \t 0.0000e+00 \t 3.2768e+00\n",
"2 \t-7.1455e-01 \t9.1941e-02 \t8.2867e-01 \t 6.9738e+00 \t 3.9656e+00 \t 0.0000e+00 \t 0.0000e+00\n",
"3 \t-1.9540e+02 \t4.8634e+01 \t5.3609e+01 \t 7.3453e+00 \t 8.9486e+00 \t 0.0000e+00 \t 3.2768e+00\n",
"4 \t-6.6453e+01 \t5.3954e+01 \t7.3649e+01 \t 3.6845e+00 \t 4.7204e+00 \t 0.0000e+00 \t 8.7381e+00\n",
"5 \t-2.0079e+01 \t1.3575e+01 \t2.6604e+00 \t 1.7791e+00 \t 2.6030e-01 \t 0.0000e+00 \t 0.0000e+00\n",
"6 \t-6.7442e+00 \t3.1651e+00 \t9.2895e-01 \t 7.7547e-01 \t 2.3764e-01 \t 0.0000e+00 \t 0.0000e+00\n",
"7 \t-3.0811e+00 \t6.0135e-01 \t3.5585e-01 \t 2.3833e-01 \t 1.8564e-01 \t 0.0000e+00 \t 0.0000e+00\n",
"8 \t-2.2251e+00 \t5.6802e-02 \t8.3998e-02 \t 2.7726e-02 \t 5.2689e-02 \t 0.0000e+00 \t 0.0000e+00\n",
"9 \t-2.1336e+00 \t7.6871e-04 \t2.8474e-03 \t 3.8422e-04 \t 1.6169e-03 \t 0.0000e+00 \t 0.0000e+00\n",
"\n",
"x* = [0.24215303 0.97023814]\n",
"\n",
"v* = [1.64012726]\n",
"\n",
"theta* = 1.3262120118414 (using arccos)\n",
"\n",
"theta* = 1.3262123260037786 (using arcsin)\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYQAAAD8CAYAAAB3u9PLAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAABi3UlEQVR4nO2dd3xUVfr/32cmvfdCQhop9F4E6R1EUAQbNtRFXV3dn1913XVdd91FXdta0cUusiIKAiJSJSDSQ4dACIGEkJBCep3MzPn9cQNSAoRkMvdOct+v131lyp17PrmZ3M895zzneYSUEh0dHR0dHYPaAnR0dHR0tIFuCDo6Ojo6gG4IOjo6Ojr16Iago6OjowPohqCjo6OjU49uCDo6Ojo6gA0MQQjRXgixXgiRKoQ4KIR4ooF9hBDiHSFEuhBinxCid3Pb1dHR0dGxLU42OIYZ+D8p5S4hhDeQIoRYI6U8dN4+E4CE+m0A8EH9Tx0dHR0djdDsHoKUMldKuav+cTmQCkRctNsU4EupsBXwE0KEN7dtHR0dHR3bYYsewjmEEDFAL2DbRW9FACfPe55d/1puA8eYBcwCcHNz6xMVFdUsTRarpLCslgAvF5ydbD9lYrVaMRi0PxWj67QtjqRTSkltbe0l77m6umI0GlVQdSmOdD5tqbPMZKbUVEeYhyvONjpuWlpaoZQyuEkfllLaZAO8gBRgagPv/QgMPu/5OqDP1Y6ZmJgom0t1rUl+sHCTPF1Y1uxjNcT69etb5Li2RtdpWxxJZ3R0tAQu2aKjo9WWdw5HOp+2IOtMsbzzkwUy6YU35R8WLJPFldU2Oa6UUgI7ZROv4zbpIQghnIFFwHwp5eIGdskG2p/3PBLIsUXbV8PNxZmHp19vj6Z0dDRJVlbWNb2u03JIKVm0+yAvrUzGKAy8evN4buzeESGE2tIAGwwZCeU3+QRIlVK+eZndlgGPCSEWoEwml0opLxku0tHRsT1RUVFkZmY2+LqO/cgtLef5ZWvYdCyT/jGRvHLTONr5+agt6wJs0UO4Hrgb2C+E2FP/2l+AKAAp5YfACmAikA5UATNt0K6Ojk4jmD17NrNmzaKqqurcax4eHsyePVtFVW0HKSWLdx/k5VUbsFolz08cwR19e2AwaKNXcD7NNgQp5Sbgir9Z/bjWo81tS0dH59qZMWMGAM899xxZWVlERUUxe/bsc6/rtBzZxaX87Ye1bM7Iol90JC9NGUP7AD+1ZV0Wm0YZqY2UUjNjcTo6WmLGjBm6AdgRi9XKvG17ePvnXzEIA3+bOJLb+3bXZK/gfFqFIdSazLi6OOlmoKOjozoHcvL4+/J1HMjJY3hiLH+/YRRhvt5qy2oUDm0IeUXlrNlyhKzTxQT6eTBtVE8C/TzPvW+1Ss07so6OTuugoqaWt9dvZv72vQR6uvPGLROZ2DXRoW5UHdoQXv1sHcIgCPH34mhWIZv2ZDBleDf2p+fQLb6dbgY6OjotjpSS5fuP8NqajRSUV3JHvx78ceQgfNzd1JZ2zTisIZzIKeLAsVxWzXkEgI27jjHvxx3sOpxNdl4JAH++fzTx7Zu2YE9HR0fnahzJK+SfK35mZ+YpuoSH8O5tN9Ij0nGz8jisIRzLLiQ6PIDSimp8vdwJD/Lh8PE8HrplED6e7nz43Sb2HDmlG4KOjo7NKa6s5t3kLXyzcx/ebq68eONobunVBaMDpN+4Eg5rCL07RvL1TynMW74DP28Plm3Yz50T+tC3c1T9++3Ztj+TaaN7qitU49TWmTlVUsap0jJySsrIK6uguKqaoqpqiquqqaw1UV1nptpUR53FglVKLFKClDgZjTgbDTgZDLi7OOPp4oKnqws+bq74ubvh5+GOv4c7Id6e9ZsXId5euDhpI3+Ojs61YrZa+XzLLt5P3kqVycRtfbvz+IhB+Hk43vBQQzisIfj7eHD3pH6s2XqEkABvenWMJOi8CeWNu44xsn+Cigq1R355BftP5bH/1GmO5p8hveAMJ4tLsSr5pQBlQcnZC7mfuxuBnh64uzjj7uyMi5MRoxCI+s1ssWC2WjGZLVTX1VFlqqOippZTJWWUVFVTWl2DvEiDAEK8vYjw8yHS34foAH+iAvyICfQjNijAnqdDR6fRSCn56WAaL29PpaDGxOAO0Tw7bhjxIYFqS7MpDmsIAMP6xDOsTzwAK39N5cW5KzlTUkV5VQ1llTXcPq5t1+E5VVLG1owsNmdksfloBsXJuwFwMhiICfSjY1gwN3RLIibAn3Z+3rTz9SHE2wsno226vRarldLqGgrKK8mvqCS/rIKc0nJySss4VVLGzsxT/LDv8AWm4e/qTKesMySEBJIYEkRiaBAJIUG4OTv0V1XHgdl6/CRvrPmF/Tl5RHi6MXfGTQxNiFVbVovg0P9lZrMFJycjVqtkzMAkrFKyaN1ehvSK4x8PT1Bbnt2RUpJ6uoDVh46yJjWdY4VFAAR5etDBx5MxvXvQPTKMTmEhdrnAGg0GAjw9CPD0IImG53Jq6sycLC7hxJkSjhUUseXgIUqra/hm535qzGYADEIQF+RP5/AQOoWF0LVdKJ3CQ/BydWnx30Gn7bI3O5e31v3KluMnCfPx4qUpY/EryW+1ZgAObgjUx/e+8/UGTHUWnrlvFBMHd1ZZlP3JLi5lyd5DLN2bysniUgxC0C86klv7dGNQhyjigwPZsGEDwwdqr8fk5uxEQojSCxjTCTpaqxg+fDgWq5WTxaWk5RVyOK+A1NwCth3PZtm+w4Ay9NQhOICu7cLoERlGt4gwkkKDcNZIfn8dx+VATh5zNmzl5yMZBHi48+y4Ydzetztuzk4kJxeoLe+ySCn5x461zTqGwxqClBInowEpJQvX7OGLF5Vl+Rar1eFn+huD1SpJPprB/O172XxMyWQ5MC6Kh4b0Z1RSB/w93VVW2DyMBgMxgf7EBPoztvNvc0GFFZUczMnnQE4e+3NOs/HocZbsVaq1ujk50TUilF7t29GrfTi92rfD38Oxz4OO/dh/6jTvJW9lw9Hj+Li58seRg7h7QC88HaAnKqXkxZ3r+PxwSrOO47CGYLFKnIyC/363mS5xYSREBWO1ylZvBiazmWX7DvPZ5hSOFRYR5uPFo8Ov4+aeXYjQWCrdliDIy5NhibEMS1S67VJKTpWUsTf7NHuzc9mTnctnm1P4yGoFoENQAL2j2tEnKoK+0RFE+Pk41MpRnZZFSsm24yf56Ned/HosE193N/44chAz+vfE281VbXmNQkrJq7s38FnqTu7v1JcXmnEshzWEsxOfX69M4d0/TQNAIrlK4lWHxWyxsnjPQd5P3kpeeQWdwoJ5beoExndJaNPDJEIIIv19ifT35YZuSQBUm+o4kJPHrpM57MrKYeXBo3y76wAAod5e9ImOoH90BP1iIokLCtANog1itlhZezidj3/dyYGcPII8PXhy1PXc2b+nw81Nvbd/Mx8c2MqdiT15vu+otmcIZosVJ6OBL5dvp32YP90T2yFl6+wdSClZfySDN9Zu4lhhET0iwnjpprEMiovSL2SXwd3FmX4xkfSLiQSU4bWj+YXszDpFSuYpdpzIZsWBIwAEenrQNzqCftHK/gnBgXrKk1ZMeU0t3+06wLxte8gpLSM6wI9/TBrFTT064+qAkWxz9m/hjT2/MDWuC/8aMK7Z1wTHOwP81jv4fNl2XnpsEgBWKTG2sgtkdnEp//jxZ35JP0FMoD/v3DqJMZ3idSO4RgwGQVJYMElhwczo3xMpJVlFpezIzGbHiWx2ZGaz6tBRAHzd3egXHUH/mEj6x7QnMSRIN4hWwJHTBXy9cx/L9qVSZaqjX3Qkfxk/jBFJcQ57I/nRwW28unsDU2I789qgGzDY4LrgkIYAcCA9l6SYEK7rHtPqegdmi5Uvtu7i3fVbMBoM/GX8MO7o16NNDw3ZEiEE0YF+RAf6Ma13V0AxX8UgTrH9xEnWHj4GgK+bK/1iInnl5vEON5TQ1qk21bEmNZ0FO/ex62QOrk5GJnRJ4u4BPenSLlRtec3ii8MpzE5Zzw3RHXnj+kk2u/45rCF0jQ/nnWduAVpX7+BkUQlPLV7J3uxcRiTG8cINIx0ml7ojc3Ye4uaeXQDIKSlje33vIaOwCE8X58t+1myxIgSX/ac8W7jJYrWydG8q/1qxnr9OHMHUXl1a5Hdpy0gp2XfqNIt2H2TFgSNU1JqIDvDjT2OHcnPPLq0ixcSXh1N4YfsaxrZP4K0hN+Jkw5thmxiCEOJTYBKQL6Xs2sD7w4GlwPH6lxZLKV9sbrvO9TlxWkvvYOXBNP66bA0Cweu3TOCGrkn68JBKtPPz4aaenbmp59XXtZy/sltKicUqEUJZUHc2zQfAwpT9fLNzPzFB/pjqF93pNTtsQ1ZRCT/sO8yyfalkFpXg5uTEuC4J3NKrK32jIlrNOZ53eBd/276G0ZHxvDt0Cs4G244a2KqH8DnwHvDlFfb5RUo5qbkNtcZ/oDqLhZdXbuB/O/bSIyKMN6ZNJNLfV21ZOo3gL0tWU2UyMTQhlsHx0fWpP377fp7tHby5dhN1Fisjk+I4VVJGXLCSA0f3+6aTeaaEVYfSWHXoKAdz8xFAv5hIfje4H+M6JzhM2GhjmZ+2m+e3r2Z0ZDxzht2MSwsMIdvEEKSUG4UQMbY41tV46ZPVVFSbeOXxG+3RXItTVl3D4wuXs/X4SWYO7MOTo6/X5wociNv6dmPlwaN8uXU3Lyxfh7PRQOewEAbHxzChSyLRgX4s2LmPlKxTvHvbjfx0MI2jBWeIC/IH0HuA14DVKtmfc5r1RzJYn5bBkbxCAHpEhPH0mCFM7JpEeCsdXl1wdC/PbV3FyIgOvD/sphYxA7DvHMJAIcReIAd4Skp58FoPYDZb2JCSzvU942yvTgWyi0t5aP4SsopKePmmsefGr3Uchx6R4RcURMkoKGJ9Wgbbjp+ksKKS0Z3iWZuazlczb0UIwamSMnzd3Ajy8rzCUXXOkl9eweZjWWzOyGTzsSwKK6swCkHvqAieHTeMsZ3iadfKF2TOO7KL57etZli7OOYMvxlXY8tdtoWUFycobuKBlB7C8svMIfgAVillhRBiIvC2lLLB3NRCiFnALIDg4OA+CxcuPPde2qkyPlmZzj2j4+gS7WcT3c2loqICLy+va/5cdkU1b+9NxyIlD3WJJcm/Ze9smqrT3jiaTquUSMm5OYPzKamtY96RTI6WVHJbQiQuBsGBojJifTwZHhGMVcpLPiOlZN+ZMiI83Qh0c2l2D8LRzmdJbR3ppRWklSjb6aoaALydnejo703XQB+6BvjgqdKaAXufz3Xlp5lXfIIebn48FpyIs7j6fOmIESNSpJR9m9KeXc6qlLLsvMcrhBBzhBBBUsrCBvadC8wFSEpKksOHDz/33vbP1+Hm4sQDd9yA2xWiPuxJcnIy52tsDIdy8/nTl4vwdHfj07tvIS645esANEWnGji6TinlOZNwMhro2beYX49lsvtkLruyciiuquJkjZmbhg6mZ/tLSy2eLCrhkXc+A8Db1ZWk0CASQgKJDwkkPljZAjzdG20UWj6fpdU1pJ4uIDU3nzWZx8mtPU1uWTkAHi7O9ImKYEZMJNd3iKZjaLAm5g7teT7nHd7FvKytLTpncDF2MQQhRBiQJ6WUQoj+gAE4cy3HkFKycdcxruseoxkzaAqHTxcw84vv8HBx4Yv7phEV4Ke2JB0bIoS4IAT6bIK+Gf17smDnPtakpjMiMe6yY92hPl4seOB2DucVcOR0AYfzCli+/wjltbXn9vFxcyU20J+YIH+iA/xo7+9HVIAvkX6+12QW9qKkqoasohKOnykiPf8M6QVFpOUXcqrk3H0iAa4uXBcfw8z2vekZ2Y7O4SE2q8vhiHx8aDv/2vmzXc0AbBd2+jUwHAgSQmQDLwDOAFLKD4FpwCNCCDNQDdwur3GsKi2zgILiCob06mALyaqQnn+GmV8uwsPFhXkzp+uRRG0Ii9VKTZ0ZXzdX7hrQ87L7uTg50bN9+AW9Bykl+eWVHM0/Q0bhGTIKizleWMzWjJMs3Zt6weddnYyE+/oQ7qOUK60uPkOm6y4CPN3PVcLzdXPFy80Vb1fXJl90zRYrFbUmKmprlZKrldUUVVVRWFHF6bIK8srKyS0t52RxKWU1v5mZs8FATJA/3SPCuK1PNzqFh9A5LIT9O7drtidjbz44sJV/70pmQlQSbw+ZbDczANtFGd1xlfffQwlLbTKb9mQgBAzq4ZjFKfLKKnjwq8U4GQSf3XuLbgZtDKPBwH0De59bf3AtCCEI9fEi1MeLwfHRF7x3tsDQyaLS+rrY5eSWlpFbVsGOzFPkl5Wz+mT+ZY/t5uSEq7MTbk5OuDk7YTQYMBoExvqxaou0IqXEbJXU1pmpMZuprTNTVVd32WP6uLkS6uNFmI83PSLDae/ve65MalSAnx5FdwXe27eZ1/dsZHJMZ94cPMmmi84ag8OsVN6y9zidYkMJ8PVQW8o1U2Wq45Gvl1JWU8v8mbcSE+ivtiQdlXBxsu2/3PkFhhpi/fr19BowkOKq6nNbaXUNFbW1lNeYqDSZqKkzU2s2U1NnxmK1YpESi9WKQGAQAoNBGQY7axyuzk54ubrg4+aKl6srfu5uBHh6EOjpToCnh0PUD9AaUkre2PML7+3fzM1xXXh90A2qLLh1CEMorajm4LHTzJwyQG0p14zVKvnT4pUcPl3AnDsm0yk8RG1JOm0IIQR+Hm74ebgRi34jokWklPxz5zo+Td3J7fE9mH3dONWyLziEIew8dBKrlFzXLUZtKdfMnI1bWXM4nWfHDWN4YutYP6Gjo2MbrFLy/LbVzE/bzcxOfflb31GqBgU4hCHsOJiFp7sLnTuEqS3lmtiUnsn7yVu5qUdn7r2ul9pydHR0NITZauVPW1aw6NgBHul6Hc/0GqZ6hJjDGELvjpEOFYZ2pqKKZ79fSXxwIC/cMFL1P7SOjo52qLWYefyXZazKSuPJnkP4Q7dBmrhGaP4KW1hSQXZeCb06RqotpdFIKfnrsjWU1tTy+i0TcHfgdRM6Ojq2parOxIM/L2JVVhov9BvN492v14QZgAP0EPYcOQVAz6QIlZU0nkW7D7I+LYNnxw0jKSxYbTk6OjoaocxUw4M/f8fOglO8OnACtyb0UFvSBWi+h7DvaA6uLk4kRTtGdE5uaTkvr9xA/5hI7hmgzxvoNI/58+cTExODwWAgJiaG+fPnqy1Jp4nkV1dw26r/sbswh3eGTNacGYAD9BD2H82hc2woTk6OsZjlpZ+SsUorL00Zq4ncKzqOy/z585k1axZVVVUAZGZmMmvWLABmzJihpjSda+RkRQl3rVlAfnUln4ycztB22lxgq+kegpRKyopuCe3UltIofkk/wZrD6Tw8dIC+Elmn2Tz33HPnzOAsVVVVPPfccyop0mkKR0sKuXXlfIprq5k/5nbNmgFovIdQZ7Fitljp4gDhpnUWCy/9lEx0gB8zB/ZWW45OKyArK+uaXtfRHin52dz/83e4GI0sGHsnnQNC1ZZ0RTTdQzCZrQB0itO+ISzYuY/jZ4r507ihNk9PoNM2iYqKuqbXdbTF+uxjzFizgABXdxaPv1vzZgAaN4Q6sxV/Hw9C/LVd4KO8ppb3k7dyXWx7RuirkXVsxOzZs/HwuDB3l4eHB7Nnz1ZJkU5j+T7jAL9bv4h430C+HX8X7b391JbUKDRtCCazlY4xIZqJ0b0cn/y6k5LqGp4ZO1TzWnUchxkzZjB37lyio6MRQhAdHc3cuXP1CWUNI6XkgwNb+X+bltMvNJKvx95JkLvjlEvV9NiG2WIlUePhppV1ZubtOMj4zgl01hPX6diYGTNm6AbgIFisVv65cx2fH07hxphOvH79DS1a/7gl0LRaKSG+fcNpfbVC8qlCKk0mHhnqeJlYdXR0bEONxcz/bVrOj5mHebBzP/7SZ+Ql9bIdAU0bAmjbEKpNdaw/VcCwhFh9RbKOThuluKaaWcmL2JGfzZ97j+Chro57c6hpQxACosK0m8N96b5UKurMPHh9X7Wl6OjoqMDJ8hLuXbeQ7IpS3hs6hUkxndSW1Cw0bQhOBoNmVyhbrZIvt+4mysudvtGOk2dJR0fHNuwrzOWB9d9hsliYP+Z2+oW2V1tSs7FJlJEQ4lMhRL4Q4sBl3hdCiHeEEOlCiH1CiEat3HJ20u4Y3JbjWWQUFjEyUvtRUDraRs9X5Hisykrj1lXzcTEY+W78Xa3CDMB2YaefA+Ov8P4EIKF+mwV80JiDarn+wdc79hLg4U6fED+1peg4MJ+OHs31d91FRmYmGVIyqD5fkW4K2kRKySeHdvBw8mKS/INZMvFeEvy0O895rdhkyEhKuVEIEXOFXaYAX0opJbBVCOEnhAiXUuZe6bjOTto0hILyStYfyWDmoD44Gyxqy9FpIlJCcTFkZsKZM8rjkpJLf5aUQE0NWCy/bffdB889B0ajsrm5gZ8f+Pv/9vP8x4GBEBOjPD/Lpt//ntvWreNslHoM8BFAfb4iPdxUW5itVr4qPsG6k3mMj0rkP4NvxN1JW7VOfinY3azPC+Ua3XzqDWG5lLJrA+8tB16RUm6qf74O+JOUcmcD+85C6UUQHBzcZ+HChTbRZ0vWnsznu2OneKFfJ7ylGS8vba+kBqioqGizOmtrL91MJuUngIsLODkp29kL/MWPhVA2UH6azRUYjYpOKcFq/c0szOZLH5vNSntCgKursjkV5+FOLa7nbQAmYD/Qp0+fZv/ubfnvbksqrWY+KDzKgZpSxnuHc6tflObCSoup4AuxjqXD30qRUjYp0sVek8oNnbkGnUhKOReYC5CUlCSHDx/egrKaxjv/nU+X8BDuuGE8ycnJaFHjxbQFnWYzpKbCrl2QkqL83LsXgoMhMRFiYy/c4uKUu/em/F83RaeUSk/k+HHIyICMB57lBLEcJ5Y0EikigJ7soTcpfBWYxcaN/0dSkmJKTaUt/N1bmpPlJcz8+VtO1JYzMyCOFybdqrakSzBbLTy99y1cq12bdRx7GUI2cP6sSySQY6e2bUrmmRIO5ebzzNihaktp85SVQXIyrF0L27fD/v0QGQl9+kDv3nDzzdCr14XDNGoiBAQFKVu/fpA943UiLb8NORbhzy56s5Y+xMf/kcmT4fRp6NED+veH0aNh2DDQ8I10q2NbXhaPJH+PRUrmjbmN2sPH1ZbUIAtPriatPJNnO81kIf9u8nHsZQjLgMeEEAuAAUDp1eYPtMrKQ2kATOiSqLKStkddnXLhX7NG2fbuheuuUy6Ur74KPXuCj4/aKhvPiVmz8P/gg3NzCAEUM5B1ZI2CV9ZGA8r8xe7dsHkzvPYa3HabYnhjxihb377N60HoXJ7/pe3hb9tWE+Xtx0cjbqGDbyDJGjSEo+VZfJ25iuEhfRkS3LwqjTYxBCHE18BwIEgIkQ28ADgDSCk/BFYAE4F0oAqYaYt21WBNajo9IsII9/VWW0qboKQEliyB77+HDRuUoZ4xY+CFF2DwYLgoGahDMXjOHDYBMXPn0s5iIcdo5MSsWdw/Z865ffz8YMQIZXvuOaiogF9+UQzxwQfh1CnlvZtvhilTwFv/WjYbs9XK7JSf+Sx1J8PaxfHO0Mn4uripLatBaiwm3jgyD38Xbx6Jn9bs49kqyuiOq7wvgUdt0Zaa5JaWcyAnj/8bPVhtKa2aqipYvhy+/hp+/hlGjoRbb4WPPoKQVpY/cPCcOVBvAJH125Xw8oIJE5QNIDcXVq+Gb76BRx+FsWPhjjtg4kQl8knn2iiuqeaxjUv49XQm93fqy1/6jMTJoM1oR4DPji/lZFUe/+r2KF5Ozb870vRKZa2xIS0DgJFJes0DW2MyKRe2ggK46SYYMEC5sH3+Ofjq1UgvS3g43HuvshUVwaJF8N57Su9h8mSYOlWZbNdrNl2dw8X5/G79IvKqKnh10ERuje+utqQrklKUyvKcX5gSMZxe/kk2OaZ2rU+DbDh6gkg/H+KCAtSW0mrIy4N//AOio+GVV5Q74LQ0WLVKifXXzaDxBATA736n9KoOHlQm1HNylGG2V15RIpx0GmZF5mGm/jSPWouFheNnaN4MAIpNZcR7tee+2BttdkzdEBqJyWxh2/GTDE2I1VNV2IBdu5S72o4dlXHwNWtg0yYlRLS1DQupQXg4PPGEcn6XLYMjRyA+XjGMAw0mmGmbmK1WXk5Zz+83LCHJL5gfbriXnkHt1JbVKEaHDeDNXv+Hi8F2i+N0Q2gke7NzqaqrY1CcXs+2qZjN8N13MGSIMizUuTOkp8PcudD1kuWMOraiVy/47DPFFKKilHmGUaMUo7Ba1VanHkU1Vdy79hv+e3Abdyf15ptxMwj1cKxZeaOw7SVcN4RGsv1ENgLoF3O1aT+di5ESFi+Gbt3gjTfg8ceVhVl/+pOS0kHHPoSEwPPPw4kTcP/98OKLilmsWKH8jdoSewtzufHHz9mRn81rgybyzwFjcdHjd3VDaCy7TuaQEBKEr7seunEtrF+vrBV48UV4800lnn76dH2SU01cXGDGDNixQ5m/eeopZcHb5s1qK2t5pJTMO7yL6Su/AuC78XcxXYPzBWarhdPVv0362CrF0NXQDaERWK2Svdm59GofrrYUh2HXLhg3Tol2eeIJ5fmECU1LE6HTMgihDN3t36/0GO64Q1nL0FrnGKrqTDz563Ke376a68NjWH7DTLoHafN/+tXDX/By6qesy9uOlPLcvGVLG4NuCI3g+JkiKmpN9IjU5pdHS5w+DXfdBZMmKReX1FS4807QcCh3m8doVCK6jhyB4cOV+YUHHmhdUUlpJQVMWfElSzIO8mTPIXwychr+bu5qy7oszsKIu9GVvSVp/PfYIo5XnAJo8YAW/d+0Eew/lQdAt4hQlZVoF6tVmRzu3h3at4ejR+H3v1eGJ3QcAzc3+H//Twn79faGLl1g3jzHn19YmL6PyT9+QXFtNfNG387j3a/XXKbSi+kX2IVqSy0JXlGU1VXyddZKNhXs5qVDn3CiMqfFegr6SG4jSD2dj7uzk77+4DKkpytDDnV1sG6dMnms47j4+sJbbyk9vd/9TjGFjz9WIpQcico6Ey9sX8N3x/YzKCyat4bcSIi7Y2QGHB7Sl4yKU/T0T6KHfyLbzuznf5krKa2ruGAIydboPYRGkHq6gMTQYIz6uMcFWK3w7rvKpPHUqco6At0MWg99+yoTzyNGKAn1PvnEcXoLB86cZtLyz1h0bD9/6DaIeaNvcxgzsEolFtjLyYNPMpYQ5RFGJ+9YCk0lxHu359PjS88NIdkavYdwFaSUHMkrZFznBLWlaIrCQmVuoLJSiU5J1JO/tkqcnODPf4Ybb1TmGZYtgy+/1O4KciklXxxO4aWU9QS6efD12Du5LsyxujaG+rUFN0cOJystl9zqQr45uZob2w1lQGBXDpedINYromXabpGjtiLOVFZRWl1DfLAeMH+WXbuUfP69e8PGjboZtAW6dlWMPypKqc1w6JDaii4lv7qCmT9/y993rGVweAwrJt3vcGZwPs4GZzp4RfLQzn9RXlfFXdETSfSO5oZ2Q1qsTb2HcBWOFRQB0CFYnz8A5e7w//4PPvgApjU/266OA+HiogwRfvGFsm5BS9+B9dnHeGrzj1TUmXix/xjuTurdKlLMjAsbRLGpnFGh/RFCIKW0+erk89EN4SqcOFMMQEygv8pK1KWuDp58Ukk6l5ysRKDotE3uvVeZK5o6FXbuhNmz1SvSU1ln4uWU9XyVtpuO/sEsGHsnCX5B6ohpATyc3Lg3dhJGoZzgljY53RCuQmZRCS5GI+E+jpXjxJaUlSmplL29lYplWilJqaMevXsrZnD77cqak0WL7F+saFfBKZ7ctJzM8mIe6NSPp3sPw83o+Je0OqsZZ8Nvv8dZM7AH+hzCVcguLiXCzweDwfG7n02huFipUNa5MyxdqpuBzm8EBcHKlUqG2htuUKq52YNai5k3dm9k+sqvqLNa+HrsnTzfb1SrMIO8mjM8sP0f7CxSZ5JGN4SrcKqkjAg/ByrUa0POnFHqFQ8cCO+/r6821rkUJyclk2pcHIwfr/QmW5IDZ04z5ccveHf/ZqbEduGnGx174vh8pJS8d/Qbqiw1RHmEqaLBJv/iQojxQogjQoh0IcSzDbw/XAhRKoTYU7/9zRbt2oO8soo2WT85P18pXTl6NPznP3oOIp3LYzQq5U27d1dSa5eU2L4Nk8XC23s3cdOKLymqrebTkdN4c/AkfDRa67gprM3bxq7iw9wXeyMhbuoEsTS7jyWEMALvA2OAbGCHEGKZlPLiPs8vUspJzW3PnpjMFgorqwj1cYwFLbYiL08xg6lTlSyluhnoXA2DQelF/r//p+RCWrNGqeBmC/YU5vDM5hWklRQyJbYz/+g/Bj9X7eYhagqFtSV8dOx7uvnGMzFcvZrttugh9AfSpZQZUkoTsACYYoPjqk5RZRUAwV6eKiuxHzU1SlK6m2+Gf/5TNwOdxiOE0pscPFhJcV5X17zjVZvreGnnz0z9aR7lplo+GTmNt4dMbnVmIKVkTvpCzNLM44l3nFuYpgaiuUmShBDTgPFSygfrn98NDJBSPnbePsOBRSg9iBzgKSnlwcscbxYwCyA4OLjPwoULm6WvOWSWV/FyyhEe7hpLzyC/BvepqKjAy0v7PYjG6jxxQklJERfX8poaorWdT7VRS2d6Ori6KokOG8PFOvdVF/Nl0QkKLbUM9wrhVr8oPAzqTxq3xPk8QjbLDNsZZu1Kf5q/ynPEiBEpUsq+TfqwlLJZGzAd+Pi853cD7160jw/gVf94InC0McdOTEyUarLx6HGZ9MKbMiUz+7L7rF+/3n6CmkFjdL72mpS9eklZWdnyei5HazqfWkAtnSUlUnbsKOV//9u4/c/qzK+qkI9tWCKjv3hZjloyV27JzWw5kU3A1uezvK5SztjynPxDyr+l2Wq2yTGBnbKJ13NbWG42cP59QCRKL+B80yk77/EKIcQcIUSQlLLQBu23GKXVNQD4ubeuLmpDrFihVDTbts3+8eQ6rQ9fXyXv0eDB0LEjDB165f0tUvJZ6k7e3PMLtRYz/6/HYB7ueh2urSCU9Ep8mrGMUlM5L3SZZdf1BpfDFmd7B5AghIgFTgG3A3eev4MQIgzIk1JKIUR/lLkLzZffKKuuBcDbzVVlJS1LerqSuGzJksZ38XV0rkZCAnz1Fdx2m5I1NfIy5ch3F+Tw4un9ZJ6sYkh4LC/0H028b+vPHbav5CirTm/mlshRJHhrI3S22YYgpTQLIR4DVgFG4FMp5UEhxMP1738ITAMeEUKYgWrg9vqujaapNJkA8HJtvVVepIRZs5SC94MGqa1Gp7UxZgw89BA8+qhyw3F+kEJeVTn/3rWBxRkH8De6MGfYTUyISmoVOYiuRq3FxLtHFxDmFsid0RPUlnMOm/THpJQrgBUXvfbheY/fA96zRVv2pMpUh0EI3Jxbb7f1s8+gvFype6yj0xL8+c/Qq5eS3mLaNGVNwWepO3ln36/UWS080vU6updYmBDdUW2pdmPhyTXkVBfwr26P4mbUzg1n673S2YDqujrcnJxa7R3L6dPw7LNKzLiT/k3QaSFcXZWFa7feKjF3PMyctA1kVZQwOjKe5/uNItrbn+TkZLVl2o2TVXl8d3ItI0L60ss/SW05F6BfBq6AyWzBxUn9iZ6W4oknlNKXPXqorUSnteORmEPwX9bx7K5TdPQP5vNRtzI8QqXYZhWRUvJB+re4Gl14IO4mteVcgm4IV6DOYsFZrby+LcyqVZCSAp9/rrYSndZMWkkBr+/eyOqTRwkK8sT69QT++nQ3Bke0zcRY6/N3sLckjUfjb8XfRXs50nRDuAIWq8TYSrOc/vOf8K9/QRuIqNVRgVMVpbyz71e+PbYfTycXnuw5hPs79eXrMldemq2EObc1yusq+Sjjezr6xDA+XJsRHLohXAGJxNAK5w82bYLcXO1Uu9JpPZyuKuf9/VtYcHQPAsHMjn15rNsg/N2UO4977oEXXoC9e9veUOUXJ5ZTUVfNY91uUzU9xZXQDaEN8u9/w9NP6xPJOrbjVEUp/z24jQVH9yKR3Brfg0e7DaSd54XDIq6uSgK8V1+F+fNVEqsCaeWZrMzdzJSIYcR6Ragt57Lol4QrYBACq/aXS1wTBw4ola6+/VZtJTqtgczyYj7Yv5VFGfsBuCWuG492H0h7L7/Lfuahh5RcWRkZ6uXMsidWaeXD9O/wc/FmhobWHDSEbghXwMlgwGK1qi3Dprz+uhJd5NZ60sjrqMCewhw+PLCVVVlpOBuM3JHQk4e6DCDCy/eqn/XxURZD/uc/8O67dhCrMmtOb+VIeSZPJt2Fh5O2J+10Q7gCzkYjJrNFbRk2o7ZWWS165IjaSnQcEYvVyrrsdD5N3cnWvCx8Xdx4pOtA7uvYhxCPa8sA+sADcP318PbbrbsSX3ldJZ8f/4EuPnGMDOmntpyrohvCFXB1MlJjNqstw2YkJyu1kUND1Vai40iUmmr45uhevjyyi+yKUsI9vPlr35HcntADL+em5fnq0EGpybxtm1KitbUy78SPVJireCR+ukMscNUN4Qq4OTtTa7ZgsVoxtoLbmKVLleI3OjpXQ0rJ3jO5zD+ymx9OpFJjMdM/tD3P9RnBmPaJONng/2HKFOU72VoN4URlDj/l/srEdkM0PZF8ProhXAEPF2cAqk11eLWCjKfLlilpKnR0LkdhdSVLjh9k0bEDpBbn4+HkzM1xXZmR2JOugbYt/D55MsycCa+8YtPDagIpJXOPLcbTyZ27ND6RfD66IVyBs1lOK2pNDm8IVVVKnYOObSd/mE4jqbGYSc4+xvfHD7LuZDpmaaVHYDj/HDCWm2K74O3SMt/9fv2gpASOHm2Rw6vK9qID7C1J4+EO0/B2dpwSvLohXAGfehMoq6klzNdbZTXNo7IShg/XayTrKNRYzGzOPcGPmYdZnXWU8rpagtw8mNmpL7fGdyfBL6jFNRgMMGwYbNkCUdooB2AT6qxmPs5YQqR7CBPCr1dbzjWhG8IV8HVXYjPPVk5zZGpq9N5BW6fcVMum3OOszEpjXXY6FXUmvJ1dGReVyOTYzgwKi7bJ3MC1kJSkRL21JkNYnrORnOoC/tH1YZwMjpULTTeEK+DvocQMF1dVq6yk+eiG0PawWK1kmiqZe3Ab608dY0deNmZpxd/VnUnRnRgfncTAsChVy1R27AjffacU0mkNlNVV8nXWKvr4d6JvQGe15VwzuiFcgQBPpbhwUWWVykqaT02Ncjem03qxSsnRkkJ25Gez5XQmv+aeoMRUA6eho18wv+vSnxERHegdHGH3nsDlONtDaC0syFpJtblGk6mtG4NuCFcgwNMdARRUOLYhVFVBXR3ExKitRMdWSCnJq65g/5nT7D9zmn1nctlVcIoyk1IHPNTdi1Ht4wksqeb+EeMJ89DmHFhiolLTuzVwuvoMP+ZsYkzYdUR7hqstp0nYxBCEEOOBt1FqKn8spXzlovdF/fsTgSrgPinlLlu03ZI4G434e7hTUFGptpRmkZUFLi7QSks7tGqklORXV3CsrIjjZUUcLSkktTifI8UFyt0/Ss6teN9AJkZ1pG9oJP1CIony8kMIQXJysmbNAMDTE3x9lRsWR+erzB8xCIOmaiRfK802BCGEEXgfGANkAzuEEMuklIfO220CkFC/DQA+qP+peUJ9vMgrq1BbRrOoqWnd6QEcEbPVSpmphhJTDSW11ZypqaKgupKC6gryqis4VVHGqcpSTlWWUW3+7Wrp4eRMR/8QJkR3JMkviK6BYXT2D8HDWTt1ea8Vd3dw9BySGRWnSM5P4Zb2owhy9VNbTpOxRQ+hP5AupcwAEEIsAKYA5xvCFOBLKaUEtgoh/IQQ4VLKXBu036KE+XiTU1qmtoxmUVurG8JZ6qwWTleWU1hTRWFNJUU1VZTX1VJZZ6KyzkStxYzJaqXOasFstWKRVqxSIpEXXLQKCgr4JrkYUOpmWKU8t59FSixWK2ZpxWSxUGsxU2uxUGOpo8pcR0V9O5cjwNWdCC9f4n0DGdYujhhvf2J9Aoj18Sfc06fV1ehwdQVHzyH52fGleDq5My1ytKo66qzNG82whSFEACfPe57NpXf/De0TAVxiCEKIWcAsAP+gMNWLb1srysgqLL6sjoqKCtU1Xo3KSggM1L5OsN35lFKSb64lw1RBhqmC3Lpq8sw1nDHXcrlrj7MQuAgjTgichMAgBAYEBkAgLljDYbVayc39LfpMIBCAAIxCYET5vBGBizDgKwwECWfcnFxxczbiZjDiaXDCw+CEl8GIl8EZP6MzPkZnnM4vnlIJVJZhPl3GUU5wrWu4HOH7+Yc/gMmkfZ3Q8Pk8SQG7DIcZZu1Kyq/b1RFWzxm/Jc36vC0MoaHblYs7gI3ZR3lRyrnAXIDw9nFy+PDhzRLXXDJcUtiQs5FeA647ty7hfJKTk1Fb49XYvRu2bElm+vThaku5Ks05n7UWM+tPHWNlZhobczIoqlUu2O5OzsT7BnKddztivP2J9PIl2N2TIDdPAtw88HZxxdPJ5Zoibxzh7w6OofP+++GDD7SvEy49n1JKntn7NoE1vjzR7z5cjeoN3ZmtNSw8PrtZx7CFIWQD7c97HgnkNGGfSzBb1O9HtvdX8rufLC5t0BAcAVdXxx+jvRIF1Uqs/Tfpeykz1RLg6s7wiDj6hbSnR1A4iX7Bmgmz1LkURx7S3F18mENlGfw+frqqZgCQWZGsiSGjHUCCECIWOAXcDtx50T7LgMfq5xcGAKWNmT8wW9S/ikUF+AGQeaaEru0cM290ZCSYTMo4raP+4zVEYXUlHxzYyvy03ZisFm6I7sj0+O6qrLjVaRq1tVBY6JjlXKWUzM/6iWBXf8aGXae2HI6V/YSXU7tmHaPZfwYppVkI8RiwCiXs9FMp5UEhxMP1738IrEAJOU1HCTud2Zhjmy1WpJSq5hGPqu8hnDhTrJqG5uLjo4ScnjoF7dtffX9HYHveSR7Z8D0ltdXcHNeVR7sNJNYnQG1ZOtdIerqyPsYR58n3lBzhcNkJfh8/HWeDs6paKuvyya3eSY+AmcCiJh/HJr4spVyBctE//7UPz3ssgUev9bhWCfnFFYQGqBdH7e7iTDtfH447sCGAUjLzyJHWYQj/S9vD37atJsrbj6/H3kGiX7DaknSayJEjjrmCXkrJV5krNNM7OF6+GpDEeY9v1nE036/OzClSWwJxQf4cKzijtoxmcdYQHJ25B7fxl60ruT48hu8n3qObgYPjqIZwtndwa/sxqvcOADLKVxHs1gUfl8hmHUfzhnBCA4aQEBLEsYIiLA4cLO3q6viGsC47nZdS1nNDdEc+HTkNXxfHnOTX+Q1HNYRvslYT6OLLmDD119cW12ZQbDpGrPe4Zh9L04ZgEIKMU+rfmSeEBGKyWMgsKlFbSpPx9IRff1VbRdMpN9XyzOYVdPIP4Y3Bk1pFSdO2jpTKd7JPH7WVXBuHSjPYX5rO1MiRmugdnKhYi8BAjNfIZh9L0/9Vzk6CjGz1DSEpVCkWkpZXqLKSpuPlBZmZcPLk1ffVIl8e2cWZmipeGTgBNxXTNevYjtRUJcqoZ0+1lVwbi7LX4e3kwfjwQWpLQUrJ8fK1hLn3xt2p+UEV2jYEo4Fj2YVIlYPo44MDcTIYOJSbr6qO5jJxolJX2dGosZj55NB2hkfE0SPIMbNI6lzK0qVKXWVHijAqopxtZw5wQ7shuBnVL6t7pjaV8rpsYr1tU1BC24bgZKCiqpb8InWTy7k6O9EhOIDU0wWq6mguU6Y4piFszztJUW019yT1VluKjg1Ztkz5TjoSO0U6TsLIje2Gqi0FgBPlP2PAiSivYTY5nuYNAeBolvoX4i7hoRzIyVO9t9Icxo5V6teWlqqt5NrYmJOBi8HIwLBotaXo2IjTp+HwYaWmsqNQYirnIJmMDO2Pn4v6KcWllJyo+Jl2Hv1xNfrY5JjaNgSjASEgLVP9oZpuEaEUV1VzqsRxM596e8PIkfDNN2oruTZSi/LpFBCCu5P6E3g6tuGrr2DSJKVOh6OwIncTZmHl5sgRaksBlOGiSvNpor2bP5l8Fk0bghAQGerHEQ0YQs9IZex690nNZ+y+Ik8+Ca+9BhaL2koaT351paaLvOhcG7W18NZbynfRUaiz1rEi91diZSjtPbSRwiazIhmBkfaeg212TE0bAkBSdAhHTqhvCAkhQXi4OLP75FVz8mmaIUMgOBgWL1ZbSeMpr6vF21n9CTwd2zB/PnTpAr16qa2k8fxauJdiUxl9ZLzaUgBluCirYgNh7r1tNlwEDmAIHWNCyS0so7S8+uo7tyBORgM9I8NJyTqlqo7mIgQ8+yy88orjZED1dHahymxSW4aODbBY4NVXle+gI/FjzibauQcTQ4jaUgAorcukrO4kUV62ndzWviHEKt2z1BN5KiuBftGRpOUVUlJVo7aUZjFpklJWc906tZU0Dj8XNwprqtSWoWMDli5Vaig7QOmDc5yozOFQWQYTw6+vL4OkPicrfgGgvecQmx5X+4YQozhyaob6htA/JhIJ7MzMVltKszAYlDu0v/zFMeYSEv2COVyc79ARXjpKCvYXXlC+d4609mBV7hachJGRof3VlnKO7MrNBLgm4uls2x6L5g3B29ON6HB/DmacVlsK3SLCcHNyYutxB13uex4zZigJ795/X20lV6drYChlployy0vUlqLTDF57DaKilMVojoLJWsfP+TsYFNQDX2cvteUAUGMppaBmP5Getl8prXlDAOga344DR3NUv0N0cTLSJzqCLRlZquqwBQYDfPQRvPgiZGn81xkcHgPAz6fS1RWi02SOHIH//Ac++MCxegebC/dRYa5iXNhAtaWcI6dyKxIrkTaMLjqLQxhC94RwisurOZlXorYUBsVFcaywiLwydVdP24KkJPjjH+GRR7Q9wRzt7U+CbxCrstLUlqLTBKxWmDUL/vY3pYfgSKw+vYVQt0C6+yWoLeUc2ZWbcTP6E+Ta0ebHdgxDSIwAYG+a+hE+gzsoq2U3HctUWYlteOYZpYeg9cVqk2M7sS3vJMfL1E+HrnNtfPKJsvbg0WsukaUu+TVF7Cs5yujQ/hiENi6VVmkhp2obER4DES2gSRu/5VWICQ/Ax8uNPUfUN4TE0CCCvTzZlH5CbSk2wcUFPv4YnnhCKWeoVW5L6IGTMPDVkd1qS9G5BvbvVyaRP/pIKePqSCTn70QiGRHST20p5zhTk0qttYwIz5ap0tYsQxBCBAgh1gghjtb/9L/MfieEEPuFEHuEEDuvWaRB0CMxQhOGIIRgSHwMvx7LxGxx3II55zNgAPzjH8pkn1bzHIW4ezEpphP/O7qHwupKteXoNILCQiV53VtvQbduaqu5dpLzU+jsE0e4e5DaUs5xqmobIAj3aBmTam4P4VlgnZQyAVhX//xyjJBS9pRS9m1KQ72SIsjOK6GgWP2x+2GJsZTV1LLLwVctn8/DDyux4TNmaDcU9fEe12OymHl3nwNX+mkj1NXBtGlw663Kd8rROFGZQ2ZVLsNCtJVhN7dqB4GuSbgZfVvk+M01hCnAF/WPvwBuaubxLkvvTkp1+F2H1V8DcH1cFM5GIz8fOaa2FJvy9ttQWal08bVInE8AdyT0ZF7abg6cUT8MWefyPP64kkxx9my1lTSNTQV7EAiuD+qptpRz1FkrKag5SLhHk+6pG4VoTiinEKJESul33vNiKeUlw0ZCiONAMSCB/0op517hmLOAWQDBwcF9Fi5cCIDVKvnH/H10j/XjlsHqp0F+b98xcqtqeLZLFN7e2k+8VlFRgZfX1eOozWYlLXF4OAQG2kHYRVxNZ6XVzF9y9uJndOFvYV0xqhTD2NjzqTZq6CwogPx86NRJCW9uDFo7n5+Jtbjhwh3ywtQQauqsdj1CftAXhBTOxL328lFPI0aMSGnqSAxSyituwFrgQAPbFKDkon2LL3OMdvU/Q4C9wNCrtSulJDExUZ7P/73xvZz65MdSC3yXsl8mvfCm/Hzpj2pLaRTr169v9L4HD0oZHi7ll1+2nJ7L0RidP55IldFfvCzf2bup5QVdhms5n2pib51z5kjZvr2Ux45d2+e0dD5PVeXLiRv+IJdkr7/kPTV17ih4T36ZNkTWWaqvuB+wUzbi+trQdlX/llKOllJ2bWBbCuQJIcIB6n82mJZUSplT/zMf+B5o0hrwvl2iyM4vJbdQ/ZoEIzt2wMlgIKWgWG0pNqdzZ1i7Fv78Z/j0U7XVXMrE6I7cFNuFt/ZuYleB+oEGOgpvv60krktOhrg4tdU0nS2F+wC4LlBbM+F51XsIcuuMk8Gtxdpo7hzCMuDe+sf3Aksv3kEI4SmE8D77GBiL0sO4Zvp1Vla17Dio/tJafw93BsZFsTO/RPUV1C1B587w88/w978rq0u1xosDxhDu6cOjG5aQX61+oEFb59VX4Z13HN8MALae2U+cZwShbiqMmV6GOms1Z2oOE+res0Xbaa4hvAKMEUIcBcbUP0cI0U4IsaJ+n1BgkxBiL7Ad+FFKubIpjcVFBhLo68n2A9pYFDaxayJFtSb2ZDt20ZzLkZgI69fDv/+t3P1pCR8XNz4cdjMlphp+t34RNeY6tSW1Wf71L2Xx2YYNEK3+9F6zKKur5HDZcfoHdlVbygUU1hxCYiHEvUeLttMsQ5BSnpFSjpJSJtT/LKp/PUdKObH+cYaUskf91kVK2eS4AyEE/btGseNgFlar+nflYzrG4yQEy/cfUVtKi9Ghg/KP/t578NRTyqSzVugaGMZbg29kX2Euf9z0AxZr61gX4iiYTErak6+/VnoGkZFqK2o+KUWHsCLpF9BFbSkXkF+9FxCEuLWsUTnESuXzGdg9hpLyag5roD6Cl5sr3YN8+enAEeq0GrxvA6KjYds2ZdXp2LFKFIlWGBeVyF/7jmJlVhrPb1/dKofvtEhODgwbBqdPw5YtSlRaa2B38RF8nDxJ8NZW0qX8mn34u8ThYmzZiEaHM4TrusUQGepHcZk2CqYMCA2gqKqaX1tJbqPLERAAK1bAdddB376w85rXm7ccD3TuxyNdr+N/aXt4KWW9bgotzKZN0K+fUmhp0SLwsV0FR1WRUrK75DA9/ZMwaiR3ESj5iwpqDhLs3r3F23Jq8RZsjK+3O4tev19tGefoEuCNv4c73+85xPBEB59NuwpGI7z0kmIIEycqcwszZ6qtSuGZXsOoqjPx0aHtmKWVv/UdhXCkPMsOgJRK/Yx//hO++ALGj1dbkW05WZ1HkamMHn6Jaku5gFLTCeqslS0+XAQOaAhaw8lgYHL3jvxv+16KKqsI8PRQW1KLM3Wqsujo5puV+YW33gI/P3U1CSH4e/8xOBmMfJK6g1qLmX/2H4uxsSujdK5IYaGSrfTwYWWIyNEjiRpif8lRAE2lugZlQhkgyK1zi7el/7fYgGm9u1JntfL9nkNqS7EbnTopw0aenkrispVNihuzLUII/tp3JL/vOpD/pe3h9xuX6NFHNuD776F7d2jfHrZubZ1mAHCwNINAF1/C3bSTzA6gsCYVZ4MXPs7tW7wt3RBsQEJIEH2i2rEwZb8mop/shZeXMoTw+edKcrx771XuJNVECMEzvYfxt36jWJ2Vxp1rFnCmRhvzTY5Gbq6SnO6ZZ+Dbb+H118HdXW1VLcehsgw6+cRqbqjxTO1hglw7tkj9g4vRDcFG3N63O5lFJWxuBeU1r5XTp+djtXbmyy//Q2hoAQ89tEX1Cmz3d+rHnGE3cbAojykrvuBIsYZCozSO1Qoffqj0ChISYN8+uP56tVW1LEW1pRTUFtPJJ1ZtKRdgkXUUm44R6JZkl/Z0Q7AR4zonEODhzv927FFbil2ZP38+s2bN4uTJVOBJrNbxfPyxKwkJhfz8s7raJkR35Jtxd2KyWJj60zy9BOdVkBJ++gl694Z585RFibNnt+5ewVmOlCtRgkk+MeoKuYhS03Gsso4AV90QGoXFamX3ESUltprhhi5OTkzv0431RzLILtZolZkW4LnnnqOq6vwhmV1YrX0pLX2R3/1OWbeQkqKaPHoGtWPZDfcS7xvIQ8mLeXXXBsz6ArZL2LJFqYfx5JPwwgtKaGlXbS3WbVHSK05iwECcZ4TaUi6gqFaZ6A5wtc9Et8MbgtFg4Jn/LCUrtxghhKqmcEff7hiEYP72vappsDdZWQ0NkUnOnHmP1FQlEunGG+G22yBNpRv0MA9vvhk/gzsSejLnwBbuWfuNXnWtnoMH4aablL/Pvfcqiw9vvhk0Noze4qSXn6S9RyiuRhe1pVxAce0xjMIVb2f7LAN3aEM4W8Kyd6f2LFi1CwCLipO6Yb7ejOucwHe7DlBZa1JNhz2Jimp4RWdUVBQuLkpqg6NHoUcPGDQI7r9fGZO2N25GJ14eOJ5XB00kpeAUE5d/xq+5J+wvRCOkpMBdd8GIETB0qGLW998PTm00ED294iTx3i0fxXOtFNcew88lFoOwT0FqhzYEQ/1tzJ0T+rBm62EAnIzq/kr3DuxNeW0t3+1qUkJXh2P27Nl4eFy49sLDw4PZ55XK8vRUqrClpSkhixMmKBeipUvtX67z1vjuLJl4Dz4urty1ZgGv7tpAnbX1ph05H7NZiRYaPFhZS9K9u2LWTz4Jbi2XUVnzlJjKKakrJ1Zjw0UAJabj+LnYL87XsQ3BoBhCj8QIpIS9aUpufDVDP3tEhtM3OoLPtqRgMrf+C82MGTOYO3cu0dHRCCGIjo5m7ty5zGigkG5AAPz1r3D8OPzud8qq54QEePNNKLXjtEsn/xCWTbyX2xN6MOfAFqat/IqMsiL7CbAzRUXKqvK4OCVF9R//CMeOKeGkvi1TmtehOFGp1EaP8WynspILqbWUUW0pxM8lxm5tOrQhwG/DRmMHdmTBSmXYyFo/j6DWfMJDg/tzuqyCH/alqtK+vZkxYwYnTpzAarVy4sSJBs3gfFxc4M47lYR5//sf7NgBsbHw4INQXm6fXoOHswsvD5zA+0Nv4kRZMTcs/4ylx1vPwkKzGVatghMnlIy1hw7BkiXwyy8wbVrbHRpqiJNVSqLMaI8wlZVcSJlJmZ/z1Q2h8Rjrewm3ju3FL7szgN+GjdRaYDI4PprO4SHM3bRDT8l8Fa67TkmfvH8/dOwI2dlKGuUnnlBWxba0p98Q05HVkx/gutAoIjwbl6WtxqKhHODnYbUqF/xHH4WICCVayMNDSTfxxRdKOKnOpWRX5+NhdMPfRVtZ+krrlFBYHxf7ZV51eEMQQmCxWolpF0C3+HDSMn9bgJSRXahKmmwhBA8P6U9mUQkrDuix740hIkKpt9Cpk5IfKSAA7rtPGeb4859h1y7lgtcShHp489mo6fQNuXIkx6Jj+/nXznXctXoBP5XltIyYa8Rige3b4emnISbmNzPYskUx1JAQCA1VW6W2yanOp517sOZWKJeZTiIw4u1sv6EshzcE4FwCszl/mU5cRAAA81fs5Mk3lvDGl+t5/Uv7r5Aa3TGehJBAPty4Te8lXCOJicrdbWqqkkdHSrjjDggLU35+8gk0GO3agiw6tp/nt63GSRiZ2akvyRX5vLdvs31F1HP8OMydC9OnKxf8mTPB1VVZVLZvnzKB31rzDbUEp6vPEO6urfxFAGV12Xg5h2MQ9hvfazUjid+u2cOXy7cjJdx9Q18OpOfywsPjQcKrn69j3bY0Rg2wX1pbg0HwyNABPPndClYePMoN3eyz0rA1IQT07Klsr7yimMDatbBmDTz7rNKLGDNG2QYOVC6OLcH+M6d5OSWZF/qN5rYEpYTh4UOH2JqXxSzLAFyMLRsSmJsLmzcrv/eaNVBZqfzOkyYpmWYjtBcc4zBYpZX82iIGBbdsacqmUF53Cm9n+/5xm9VDEEJMF0IcFEJYhRB9r7DfeCHEESFEuhDi2ea02RCn8kv4YcMBZk4ewF8fHMvabWl4e7rSKymSXh0juWV0D1Ztsf8E7/jOiSSEBPJu8pZzk986DTN//nxiYmJISUkhJiaG+fPnX7JPVJQSK//115CXBwsWKNXc5syBpCRl7mHKFHjxRVi+XLmQNhcpJW/t/YX+oZHcltDjnM7tmelsWvcz3y5Y0PxGzrWlzKEsW6b0kCZNgnbtlBXDn3yi9JyWLFF+r3nzlIVkuhk0jxJTOWZpIdjVX20pFyClVMUQmttDOABMBf57uR2EEEbgfWAMkA3sEEIsk1LaLKRj2/5MAnw9mDpKcXmzxcrLn64BIOt0MbsPnyI0wBsppV3HCQ0GwR9HXs+jC5axeM9Bbu3TzW5tOxJn8yGdTYGRmZnJrFmzAC4bsWQwQK9eyvb008rF9PhxZa4hJUUJr0xJUSKaevdWwltjYy/cvLyurm1rXhYbc46zbdpj53TWerjQ1QClJ7KZ9d6VdTZEWZmi9fzt6FFFu5TQp4+y3X+/kk02KqrtrRy2FwW1JQAEufqpquNiTNZy6qwVdp0/gGYagpQyFa4azdMfSJdSZtTvuwCYAtjMELoltOPTpVvPPQ/y98TP2527nptHdLg/5VW1zLploCqTRiOT4ujVPpx312/hxm4dcXdxtrsGrXNpPiSoqqriueeea/SFVghl3DwuTgmrBOXimpUFe/YocfdHj8Lq1b9dhL29FWOIiYGgIPD3Vwr9nP/z26ojDAvsRE2RB88++x+qTF549kqgyCip3ptLbaUXf/rT2wwcOIPiYigpocGfhYW/tVtdfaExxcUpQ0C9eil3/PrF334U15UBEOiirQUZFXVK99bLzoYgbBGrL4RIBp6SUl5SaVcIMQ0YL6V8sP753cAAKeVjlznWLGAWQHBwcJ+FCxc2SsPb36cSG+ZFUntfdqefITrUiw7h3pwsqMTfy4XYMK+zx2/Cb3h5Kioq8LrKrWZ6SQWv7znK5NhwJkarE+vcGJ1qkXJe9rvIyEiys7PPPe/Tp0+LtVtXByYT1NYq0Tpms/Lz/Me7RT4ZopQbqhKoqzNzzKWEw26FRHk40e10LCABiYuLM05OSplRo5EGH7u6Kps91wBo+e9+Pmrp3MtxVht287B1PN5cvdqhvXRWuR2iIPArwvIfxbXu2oaNRowYkSKlvOwQ/pW46ldTCLEWaOgq9pyUcmkj2mjoCnxZF5JSzgXmAiQlJcnhw4c3ognwDu3A2q1H2HgohwAfb26bPIK4iMBGfbY5JCcnczWNw4E9NctYl3GSP90ymUAv+5fZbIxOtbjvvvvIzFRirl9//XWeeuopAKKjozlx4oSKymBbXha/37CEyl6S//73Y2ojg6lNzWBMvxE89dRozei8HFr+u5+PWjrzskxwYjfjho7BxXD13ru9dKaWFFJQAEMHTMDdKaDF2zvLVSeVpZSjpZRdG9gaYwagzBucnzUqErB5EHefTu15+t5RvPrHybz77LQLzEDNDKhneXL0YGrq6ng3eYvaUjRHY/IhqcWA0Ci+G38XJytKGDRkMDU//kLJ4jW4SOU+56zOVVlp1Gp0wZrO5Smvq8TV4NIoM7AnVeZ8DMIZN6N9J7vtsQ5hB5AghIgVQrgAtwPLWqIhISAixA+40AS0sOAkLiiA2/v1YGHKfg6f1qt3nc/5+ZCAK+ZDUoNYnwDmDLuZ+Xc9ynuPP01UuDKue1Zn34ljeSh5MTf++Dl7CrWxYE2ncVSYq/Fy0l4FoCpzIR7GILtfu5obdnqzECIbGAj8KIRYVf96OyHECgAppRl4DFgFpAILpZQHmyf7snoafKwV/jB8ID5urvxrxXpN9Fq0xNl8SH369GlUPiQ1EEI0qDPJP5jPRk6n3FTL1J/m8XLKes2mt9C5kCpLNR5O2kv1Wm0uxN2p5Ye8L6ZZhiCl/F5KGSmldJVShkopx9W/niOlnHjefiuklIlSyg5SSvXHAVTCz8ON/xs9mJ1Zp/hh32G15ejYkBGRHVg1+QFui+/Ofw9u44bln7G7QO8taJ0aiwl3o6vaMi6h2lKEu9HBDEHLVNfUsXbbEc3did/SqyvdI8J4dfVGyqpr1JajY0N8XNx4eeAEvhx9G9V1ddyyUu8taJ1aqwlXg7aqpAHUWIrsPn8ArdgQVm5O5bn3fmRPfY0ErWAwCF64YSRFVdW89bM6uXB0Wpah7WJZOfl+bu2g9BYm//g5B86cVluWTgOYrGacDdrK4COllVpLGa5G+6+NaLWGMOH6Tvh4ufH1TypWeL8MXdqFcme/Hny9Yy/7svULRWvEx8WNVwZN4LNR0ympreGmFV/y9t5NbaY6m6NgkRac7Jg8rjGYrBVIrLgZ/ezedqs1BDdXZ24Z2YONu45xMq9YbTmX8MeRgwjx9uK5pasxmfUhhdbKiIgOrJ78ABOjO/KfvZuYvnI+x1txdTZHwyKtGIW2LoO1FmX1tKvR/vUZtHUmbMz0MT1xMhr5+qddaku5BC83V/5x4yiOFpzhw43b1Zaj04L4ubrzztDJvDd0CsfLipi4/DP+l7ZHc/NbbREt/g1M1nIAXAzedm+7VRtCoJ8n4wd1ZPnGAxSXVV39A3ZmeGIcU7p3Yu6mHRzMsX8hHx37MimmE6smP0DvoHb8ZetKfrd+EUU12vte6qiLyVoBgIvR/qk8WrUhAMyY2JfaOgvfrtmjtpQG+fP44fh7uPHnJasxmfXx5dZOmIc388bczvN9R7Ex5zgTfviUzacz1ZbVZjEKAxaprdT0dVblJsHZYP8UN63eEGIjAhnSuwPfrt1DdU2d2nIuwc/DjX/cOJq0/ELe09NatAkMQvBA534snnA3ns4uzFj9Na+kJOsTzirgZDBikdo67+Z6Q3ASuiG0CPdO6kdZRQ1L1u9TW0qDjEzqwC29uvDRph1sP5F99Q/otAq6Boax/Ib7uD2hJx8e3Modq74mp7JMbVltCmfhTJ1VW0Edeg+hhemW0I4+ndrz1Yqd1Ji010sA+Mv44UQF+PHM4p8oqdIXrLUVPJxdeHngeN4ZMpnU4nwm/vApa04eVVtWm8HF4ITJqq1rglnWAuBksP8K6jZhCAAP3HwdhSWVLEs+oLaUBvF0deH1WyZwpqKK539Yo8noB52WY3JsZ36YdB8RXr78bv0iXk5Zj9mqrbHt1oib0ZUaq0ltGRdgqTcEo9ANocXo06k9vZIi+HL5dmpN2uoinqVbRBh/HHU9a1LT+SZlv9pydOxMnE8AiyfczV2JvfjvwW3cvXYB+dUVastq1bgbXak2a6tHbrGaAIHAaPe224whADw4dSAFxZUsTdbuxXbmwD4M7hDNSz8lcyg3X205OnbG1ejEv64bxxvX38DughxuWP4Z2/Ky1JbVavFwcqfCUq22jAuQmDEIZ1UyNrcpQzjbS/jih+2anUswGASvTh1PgKc7TyxcTqmeAK9NckuHbiydeC/ezq7MWL2AeUd26cOILYCXkztV5hqsGgo9tUozhuaVu28ybcoQhBDMumUQhSWVLF6nzYgjgABPD96aPonTpeU8s3glVqt+IWiLJPkHs2TiPQxtF8vz21bzzOYVeuZUG+Pj7IlEUmnWTi9BYkWolE6jTRkCQO9O7enfJYovfthOZbW2JpPOp2f7cP48fjgbjh5nzsatasvRUQkfFzc+HjmNx7tfz7fH9nPbyvnkVZWrLavV4OusrAYuqdPOXI2UEoNKl+Y2ZwgAj9w6mJLyauav2Km2lCtyR7/uTOnRifeSt7Lu8DG15eiohEEInuw5hLnDp3K0tJDJP37BvsJctWW1CvyclXxBJSbtrP+QSECdio9t0hA6x4Uxqn8i//sphTMllWrLuSxCCP4xaTTd2oXy9KKf9FrMbZyxUYksmnA3TgYD01fNZ9nxQ2pLcngCXJSMokUaMgQ1aW5N5elCiINCCKsQou8V9jshhNgvhNgjhNDEbfkjt16PyWzh4++1nS7CzdmJ926fjLebK7//eikF5do1MJ2Wp5N/CMtuuI8egWE8/ssy3tzziz7Z3AwCXJUiNGdMpSor+Q2BQKLOJHdzewgHgKnAxkbsO0JK2VNKeVnjsCftQ/2ZOrI7S5P3cyJH2/npQ328mHPHZIqrqnlswTJq6vSJxbZMoJsHX425g+kduvHOvl/546Yf9MnmJuJpdMfd6EphrXZqpghhcExDkFKmSimP2EqMvXngputwdXHmvQWN8TN16dIulNemTmDfqdM8s/gnLPoq1jaNi9HIq4Mm8nSvoSw9foi7Vi+gsFrvPV4rQgiCXf3Jr9GQIWBEqpRwz15zCBJYLYRIEULMslObV8Xfx4P7Jvfnl90Z7Dio/cU/ozvF86dxw1idms7sn5L1oYI2jhCCR7sN4v2hN3Gg6DS3rJxHZrl2LmyOQohbAHk1Z9SWcQ6jcMYq1enxiatdVIQQa4GwBt56Tkq5tH6fZOApKWWD8wNCiHZSyhwhRAiwBviDlLLB2/J6w5gFEBwc3GfhwoWN/V2aRJ3ZypuLD+FsNPDEzZ0wGq5tdr+iogIvL/sWsvgu/RRrs/OZEhvOhOiG/jSXoobOpqDrbBrpteW8VXAEAfy/4I7EuSratKbzcqipc63Yw0GyeFzeiLhKdI89dJZ4r6PUZx1Rp/6FaMI9+4gRI1KaPDQvpWz2BiQDfRu5799RzOOq+yYmJkp7kLzjqOx/1xvym1W7rvmz69evt72gq2CxWOVT362QSS+8KRfu3Neoz6ihsynoOptOekmhHLxojkz66jW5OitNSqlNnQ2hps4l2evlxA1/kCW1ZVfd1x469535Un6eNlDWWWqa9Hlgp2zitbzFh4yEEJ5CCO+zj4GxKJPRV8Visc+QyNA+HejfNZq5izZTVKr9koYGg2D2lLEMiY/hheXr+OmAw07j6NiQDr6BLJ5wD0n+wTyUvJiF6dpdja8lItxDADhVrY2w7rNpr83S/mlrmht2erMQIhsYCPwohFhV/3o7IcSK+t1CgU1CiL3AduBHKeXKxhy/vMQ+J0QIwZN3Daeqto45C3+xS5vNxcXJyNu3TqJ3+3Y8vXglP+sL13SAYHdP/jfmDq4Pi+aZzStYUZajtiTNc9YQTlZpo665UbgBYLE6mCFIKb+XUkZKKV2llKFSynH1r+dIKSfWP86QUvao37pIKWc39vg11WayjtvHtWMjArl9XC9+2HiQ/emO8U/k4eLMh3dOoXN4CE98+yO/pJ9QW5KOBvB0duGTkdOZFNOJhSVZ/GvnOqx6AMJlCXELwMXgzMmq02pLAcDJoBhCnbR/fiVtr1QWsPDzTXZr7oGbBhLs78Wrn6/DbHGMsE4vN1c+uutm4oMDeGzBMn49phds11HCUt8ZMpnRXmF8fGgHT2/+US+4cxmMwkB7j1Ayq7SRDsRZeAK/ldK0J5o2BA9PF9b9tI/cbPssHPN0d+Gpe0aQllnAgpW77NKmLfB1d+PTu28hJtCfR/63lI1Hj6stSUcDGIRghn80T/YcwqJjB3j8l6XU6gvYGiTaI5wTldoYGXA2KrWU66z2X1eiaUPw8nbBaDTwjR17CcP6xDOkdwfmLt7MqfwSu7XbXPw93fn83mnEBwfy6IIf9GR4OoAyP/Z49+v5a9+RrMg8woM/L6KqTrtZftUixrMdRaYyyurUX9znYlDCWk0W+2e11bQhGIyC8Tf1Zs0Pe8jLLbFLm0IInr5nJEaD4JXP1jnU4i9/D3c+u/cWOocF88TC5Xr0kc45Huzcn1cHTuDX0ye4d91CKupq1ZakKWI92wFwvPKUykrAxaBkYDVZ7Z+SW9OGAHDrvYMBWPCZ/aJ/QgO9+f2tg9l+IJOffk21W7u2wNfdjU/unkrPyHCe/G4FC3bsVVuSjka4NaEH7wyZzK6CU9yzdiFlJr0a31livSIAyKhQ3xBcjWcNQe8hXEJImC/jb+rN6qW7OX3KfsvybxnVk+4J7fjPV+s1nSK7Ic5ONA9NiOXvP/7MnA1bHaqno9NyTIrpxPtDb2L/mVzuWrOAklrtVApTE38XHwJdfDlWcVJtKTgJDwzCmVqL/TOwat4QAO54YCgGo+Crucl2a9NgEPz1d2OpNZl5+bO1DndBdXdx5r3bb2RKj068s34LC45m6wnxdAAYH53Ef4dP5XBxAbev/h9FNdpfjGkPOni1J10DhiCEwNXgqxvC5QgK8WHStH6sW7HXbusSAKLDA3hk+mB+2XXM4YaOAJyNRl6eMo4HBvVhQ04hjy34gSpTndqydDTAyMh4Ph05neNlxdy55mvdFIBE7yiyq/Kp0kB9ZTejP9UW+ycqdAhDALht5hBc3Zz58oOf7dvuuN70TIrgjXnryTvjeLVsDQbB02OHcntCJBuOHufuzxaSX66d+rE66jG4XQyfjJimm0I9id7RSCRHy9XvJXT2v4147wl2b9dhDMHP35OpMwbyy7pDpB2y38SPwSD426xxWCxW/vnRKqxWxxo6OsvwiGDm3DGZ44XF3PbRAr0cpw6gmMLHI25RTGH115xpw6aQ6B0NQGq5+ut44n0mEu09wu7tOowhANxy1yB8fD349L21dm03IsSPJ+4cxo6DWXyzerdd27YlwxPj+Or+W7FKyR2fLGDVoaNqS9LRAEPaxfLpyGkcLy/m7jULKK1tm9FH3s4etPcIJbVMfUNQC4cyBE8vN+54YAi7t2WQsiXdrm3fNKIbQ3p34P1vfiEtM9+ubduSzuEhfDvrDhJDlbUK7/y82WF7PTq24/rwGP47fCrppWe4Z+03bTYktbNPHIfLTmCVbTMAw6EMAWDS9P6ERfjz0dursdgx35AQgr8+OBZfLzeen7OC6hrHnZwN8fZi3n3TmNqzC3M2buPRBcsorW6bFwCd3xgeEcecYTdxsCiP+9Z92yYXr3X2iaPCXEWWRhLd2RuHMwQXFyfuf2w0x4/msXb5Hru27eftzt8fnkBmbhH/mb/erm3bGhcnJ2ZPGcNfJ4zgl/QT3PLf+RzKddyej45tGN0+gfeGTmFvYQ73r/uWarPj3vg0hW5+8QAcKLXvCIRWcDhDABg6pgudurfn8/fXUV1l37uYfl2iuGdSf5YmH2DNVsdODSGE4K4BPZk3czpmq5XbP17Atyn7HW7NhY5tGR+dxFuDJ7MjP5vfb1iCyaJOwXc1CHULJMQ1gH0lbXN+zSENQQjBQ0+Oo+hMhV3TY59l1tSBdIsP56VPVlNgpyI+LUmv9u1Y/NAM+kZH8PwPa3l68UoqatrecIHOb9wY24mXrhvP+lPH+OOmZW0qdXY3v3j2l6Rrdh7BYm25/02HNASATt3aM3xcV777ajP5dkp8dxYnJyOzH5uEi7MT89ZlOPR8wlkCPD346K6beWLEIH46cISb/zuffdltcxxVR+GOxJ7nsqQ+s3lFmymy09MvkTJzpep5jfKq97Cj4G225r9BtbmI01W7+fHk7/gp+/ecqtyKVdq+5+awhgBw/x/GADD3rdV2bzs00JsXH5lIfkkNr3zueKktGsJoMPDIsAHMmzkdi9XKnZ9+w4cbt+spL9owD3buz5M9h7A44wD/2ulY2X+bSne/RAD2lqSppqG49hg7Ct6h1JRJqek4Owvf41DJ13T0vYVor2GkFL7PmVrbD1k7tCGEhvtx231D+GXtQfZsz7B7+wO6RTO6dzgrf01l8brWU9C8d1QE3z98F2M6xfPWz79y12cLySoqUVuWjkr8odsg7uvYh09TdzLnwBa15bQ4Qa5+RLqHqmoIqSXfEuLejdERbzIu8j0q6nLwd42ng894ugXcg7dze/KrbX/NaZYhCCFeE0IcFkLsE0J8L4Twu8x+44UQR4QQ6UKIZ5vT5sVMv+d6wiL8ef+1FZjr7D/5NbJnGIN6xPLmV+vZc0T91Lm2wtfdjTenTeS1qRNIzy/ipg++YsHOfW3iDlHnQoQQ/K3faG6K7cJruzcy74jjVBNsKj39kzhQeow6qzrDwRILbkb/c899XKKoMf+W28jZ4I65BUpsNreHsAboKqXsDqQBf754ByGEEXgfmAB0Bu4QQnRuZrvncHVz5pGnJpCVUcCSBVttddhGYxCCfzwygfBgH5595weHzHd0OYQQ3Ni9I8t+fzc9IsP4+/J13P/lIrKL7Z+FUUddDELw2vUTGR0Zz9+2reaH446X7PFa6OWfRK3VxKFSdVYtB7gmcbpqFxV1uZSaMqmzVlJsSmd9zp/ZdPpflJoyCffoZ/N2m2UIUsrVUsqzRVq3ApEN7NYfSJdSZkgpTcACYEpz2r2Y64YmMWBIIocPqHOH7uPpxmt/nEKd2cL2g62vyH24rzef3nMLf580in2n8nh3fesfNtC5FGeDkfeGTqFfSCTfpO9t1b3F7r4JhLoFUmZWpxZKpOdA3J0C2ZT3T3YUvIOXczuGhr1IoFtHnAyu9Al+lBD3bjb/GwhbHVAI8QPwjZTyq4tenwaMl1I+WP/8bmCAlPKxyxxnFjCr/mlX4IBNBLYcQUCh2iIaga7Ttug6bYuu03YkSSm9m/JBp6vtIIRYC4Q18NZzUsql9fs8B5iB+Q0dooHXLutCUsq5wNz64+6UUva9mkY1cQSNoOu0NbpO26LrtB1CiJ1N/exVDUFKOfoqjd8LTAJGyYa7G9lA+/OeRwI51yJSR0dHR6flaW6U0XjgT8BkKeXlprx3AAlCiFghhAtwO7CsOe3q6Ojo6Nie5kYZvQd4A2uEEHuEEB8CCCHaCSFWANRPOj8GrAJSgYVSyoONPP7cZuqzB46gEXSdtkbXaVt0nbajyRptNqmso6Ojo+PYOPRKZR0dHR0d26Ebgo6Ojo4OoCFD0EIajMYghJguhDgohLAKIS4bfiaEOCGE2F8/t9LkMLCmcg061T6fAUKINUKIo/U//S+znyrn82rnRyi8U//+PiFEb3tpuwaNw4UQpfXnbo8Q4m/21liv41MhRL4QosG1RVo4l/U6rqZT9fMphGgvhFgvhEit/z9/ooF9rv18Sik1sQFjAaf6x/8G/t3APkbgGBAHuAB7gc521tkJSAKSgb5X2O8EEKTi+byqTo2cz1eBZ+sfP9vQ312t89mY8wNMBH5CWW9zHbBNgxqHA8vV+i6ep2Mo0Bs4cJn3VT2X16BT9fMJhAO96x97o6QOavZ3UzM9BKmRNBhXQ0qZKqXUfKm0RupU/XzWt/dF/eMvgJvs3P6VaMz5mQJ8KRW2An5CiHCNadQEUsqNQNEVdlH7XAKN0qk6UspcKeWu+sflKBGcERftds3nUzOGcBH3ozjbxUQAJ897ns2lJ0ErSGC1ECKlPh2HFtHC+QyVUuaC8iUHQi6znxrnszHnR+1z2Nj2Bwoh9gohfhJCdLGPtGtG7XN5LWjmfAohYoBewLaL3rrm83nVlcq2xN5pMJpKY3Q2guullDlCiBCUdRqH6+88bIYNdKp+Pq/hMC1+PhugMefHLufwCjSm/V1AtJSyQggxEVgCJLS0sCag9rlsLJo5n0IIL2AR8EcpZdnFbzfwkSueT7sagnSQNBhX09nIY+TU/8wXQnyP0rW36QXMBjpVP59CiDwhRLiUMre+O5t/mWO0+PlsgMacH7VTs1y1/fMvFFLKFUKIOUKIICml1pK0qX0uG4VWzqcQwhnFDOZLKRc3sMs1n0/NDBmJVpQGQwjhKYTwPvsYZcJci1lbtXA+lwH31j++F7ikZ6Pi+WzM+VkG3FMf0XEdUHp2CMxOXFWjECJMCCHqH/dH+b8/Y0eNjUXtc9kotHA+69v/BEiVUr55md2u/XyqOVN+0Yx4Osp415767cP619sBKy6aOU9Diax4TgWdN6M4by2QB6y6WCdKxMfe+u2gVnVq5HwGAuuAo/U/A7R0Phs6P8DDwMP1jwVKAahjwH6uEHmmosbH6s/bXpSAjUH21liv42sgF6ir/24+oLVz2Uidqp9PYDDK8M++866ZE5t7PvXUFTo6Ojo6gIaGjHR0dHR01EU3BB0dHR0dQDcEHR0dHZ16dEPQ0dHR0QF0Q9DR0dHRqUc3BB0dHR0dQDcEHR0dHZ16/j8AjTaPQGWE0wAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"theta0 = np.pi\n",
"x0 = np.array((np.sin(theta0),np.cos(theta0)))\n",
"\n",
"## Run Algorithm 5.1 on test problem\n",
"results = alg52(x0,my_f3,my_h3)\n",
"\n",
"## Display results\n",
"xstar = results[0][-1]\n",
"print(\"\\nx* =\",xstar)\n",
"\n",
"## Display results\n",
"vstar = results[1][-1]\n",
"print(\"\\nv* =\",vstar)\n",
"\n",
"## Convert into theta\n",
"print(\"\\ntheta* =\",np.arccos(xstar[0]),\"(using arccos)\")\n",
"print(\"\\ntheta* =\",np.arcsin(xstar[1]),\"(using arcsin)\")\n",
"\n",
"## Visualize\n",
"visualize(results[0])"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.8.4.3 Starting Point Near Global Max ($\\theta_0 = 5.5$)](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.4.3-Starting-Point-Near-Global-Max-($\\theta_0-=-5.5$))",
"section": "4.8.4.3 Starting Point Near Global Max ($\\theta_0 = 5.5$)"
}
},
"source": [
"### 4.8.4.3 Starting Point Near Global Max ($\\theta_0 = 5.5$)"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.8.4.3 Starting Point Near Global Max ($\\theta_0 = 5.5$)](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.4.3-Starting-Point-Near-Global-Max-($\\theta_0-=-5.5$))",
"section": "4.8.4.3 Starting Point Near Global Max ($\\theta_0 = 5.5$)"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Iter. \tf(x) \t\t||h(x)|| \t||grad_L(x)|| \t||dx|| \t\t||dv|| \t\tdelta_A \tdelta_W\n",
"0 \t-1.0621e+00 \t0.0000e+00 \t6.9215e-01 \t 5.6411e-01 \t 4.3032e-01 \t 0.0000e+00 \t 3.2768e+00\n",
"1 \t-2.0216e+00 \t3.1822e-01 \t2.0226e+00 \t 2.3706e-01 \t 1.1375e+00 \t 0.0000e+00 \t 8.7381e+00\n",
"2 \t-1.9886e+00 \t5.6197e-02 \t1.3940e+00 \t 4.4244e-01 \t 4.9825e-02 \t 0.0000e+00 \t 0.0000e+00\n",
"3 \t-2.4244e+00 \t1.9575e-01 \t5.4298e-01 \t 1.2207e-01 \t 1.5280e-02 \t 0.0000e+00 \t 0.0000e+00\n",
"4 \t-2.1566e+00 \t1.4900e-02 \t3.8186e-02 \t 1.0366e-02 \t 1.9242e-03 \t 0.0000e+00 \t 0.0000e+00\n",
"5 \t-2.1325e+00 \t1.0745e-04 \t2.7129e-04 \t 7.4929e-05 \t 1.7543e-05 \t 0.0000e+00 \t 0.0000e+00\n",
"6 \t-2.1323e+00 \t5.6144e-09 \t3.7221e-09 \t 2.8396e-09 \t 2.9955e-09 \t 0.0000e+00 \t 0.0000e+00\n",
"\n",
"x* = [0.24215301 0.97023807]\n",
"\n",
"v* = [1.64012795]\n",
"\n",
"theta* = 1.3262120357119471 (using arccos)\n",
"\n",
"theta* = 1.3262120357119473 (using arcsin)\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYQAAAD8CAYAAAB3u9PLAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/Z1A+gAAAACXBIWXMAAAsTAAALEwEAmpwYAABiVElEQVR4nO2dd3xUVfr/32cmvfdCQgqk0HuR3qsIioAFG+qiru66P7+r667ruq51dXXturhWZEUUBESkSlCk9xYIIZCQQnpvk5k5vz9uQEogIZnMvZPc9+s1r8xkbu755GRyP/ec85znEVJKdHR0dHR0DGoL0NHR0dHRBroh6Ojo6OgAuiHo6Ojo6NSjG4KOjo6ODqAbgo6Ojo5OPboh6Ojo6OgANjAEIURHIcQmIUSyEOKIEOLRBo4RQoi3hBCpQoiDQoh+LW1XR0dHR8e2ONngHGbg/6SUe4UQ3sAeIcR6KeXRC46ZAsTXPwYD79d/1dHR0dHRCC0eIUgpc6SUe+uflwPJQMQlh80APpcK2wE/IUR4S9vW0dHR0bEdthghnEcIEQP0BXZc8lYEcOaC15n138tp4BzzgfkAbm5u/aOiolqkyWKVFJTVEuDlgrOT7ZdMrFYrBoP2l2J0nbZF12lb2qvOMpOZUlMdYR6uONvovCkpKQVSyuBm/bCU0iYPwAvYA8xs4L3vgeEXvN4I9G/snAkJCbKlVNea5PtLtsizBWUtPldDbNq0qVXOa2t0nbZF12lb2pvOjMJieftHi2XiM6/L3y1eKYsrq21yXimlBHbLZl7HbTJCEEI4A0uBRVLKZQ0ckgl0vOB1JJBti7Ybw83FmQdnD7NHUzo6OjpXRUrJ0n1HeHFNEkZh4JWbJnNDry4IIdSWBthgykgov8lHQLKU8vUrHLYSeEQIsRhlMblUSnnZdJGOjo5OWyWntJynV65ny8l0BsVE8vKNk+jg56O2rIuwxQhhGHAncEgIsb/+e38BogCklB8Aq4GpQCpQBcyzQbs6Ojo6mkdKybJ9R3hp7WasVsnTU8dw24DeGAzaGBVcSIsNQUq5Bbjqb1Y/r/VwS9vS0dHRcSQyi0v523cb2JqWwcDoSF6cMYGOAX5qy7oiNo0yUhsppWbm4nR0dNovFquVhTv28+aPv2AQBv42dSy3DuilyVHBhbQJQ6g1mXF1cdLNQEdHR3UOZ+fy91UbOZydy+iEWP5+/TjCfL3VltUkHNoQcovKWb/tOBlniwn082DWuD4E+nmef99qlZp3ZB0dnbZBRU0tb27ayqKdBwj0dOe1m6cytUeCQ92oOrQhvPLJRoRBEOLvxYmMArbsT2PG6J4cSs2mZ1wH3Qx0dHRaHSklqw4d59X1P5FfXsltA3vzh7FD8XF3U1vaNeOwhnA6u4jDJ3NY+95DAPy09yQLv9/F3mOZZOaWAPDne8cT17F5G/Z0dHR0GuN4bgHPrf6R3elZdA8P4e1bbqB3pONm5XFYQziZWUB0eAClFdX4erkTHuTDsVO5PHDzUHw83fngmy3sP56lG4KOjo7NKa6s5u2kbXy1+yDebq7844bx3Ny3O0YHSL9xNRzWEPp1ieTLH/awcNUu/Lw9WLn5ELdP6c+AblH173dkx6F0Zo3vo65QjVNbZyarpIys0jKyS8rILauguKqaoqpqiquqqaw1UV1nptpUR53FglVKLFKClDgZjTgbDTgZDLi7OOPp4oKnqws+bq74ubvh5+GOv4c7Id6e9Q8vQry9cHEyqv1r6+g0C7PVyqfb9vJu0naqTCZuGdCL348Zip+H400PNYTDGoK/jwd3ThvI+u3HCQnwpm+XSIIuWFD+ae9Jxg6KV1Gh9sgrr+BQVi6Hss5yIq+Q1PxCzhSXYlXySwHKhpJzF3I/dzcCPT1wd3HG3dkZFycjRiEQ9Q+zxYLZasVktlBdV0eVqY6KmlqySsooqaqmtLoGeYkGAYR4exHh50Okvw/RAf5EBfgRE+hHbFCAPbtDR6fJSCn54UgKL+1MJr/GxPDO0Tw5aRRxIYFqS7MpDmsIAKP6xzGqfxwAa35J5h8L1lBYUkV5VQ1llTXcOql91+HJKilje1oGW9My2HoijeKkfQA4GQzEBPrRJSyY63smEhPgTwc/bzr4+hDi7YWT0TbDXovVSml1DfnlleRVVJJXVkF2aTnZpWVklZSxOz2L7w4eu8g0/F2d6ZpRSHxIIAkhQSSEBhEfEoSbs0N/VHUcmO2nzvDa+p85lJ1LhKcbC+beyMj4WLVltQoO/V9mNltwcjJitUomDEnEKiVLNx5gRN9OPPvgFLXl2R0pJcln81l39ATrk1M5WVAEQJCnB519PJnQrze9IsPoGhZilwus0WAgwNODAE8PEml4LaemzsyZ4hJOF5ZwMr+IbUeOUlpdw1e7D1FjNgNgEIJOQf50Cw+ha1gIPTqE0jU8BC9Xl1b/HXTaLwcyc3hj4y9sO3WGMB8vXpwxEb+SvDZrBuDghkB9fO9bX27GVGfhiXvGMXV4N5VF2Z/M4lKWHzjKigPJnCkuxSAEA6MjmdO/J0M7RxEXHMjmzZsZPUR7IyY3ZyfiQ5RRwISu0MVaxejRo7FYrZwpLiUlt4Bjufkk5+Sz41QmKw8eA5Spp87BAfToEEbvyDB6RoSRGBqEs1Ffn9BpGYezc3lv83Z+PJ5GgIc7T04axa0DeuHm7ERSUr7a8q6IlJJnd21o0Tkc1hCklDgZDUgpWbJ+P5/9Yy6gTFM4+kp/U7BaJUkn0li08wBbT6YDMKRTFA+MGMS4xM74e7qrrLBlGA0GYgL9iQn0Z2K3X9eCCioqOZKdx+HsXA5ln+WnE6dYfkCp1urm5ESPiFD6duxA347h9O3YAX8Px+4HHftxKOss7yRtZ/OJU/i4ufKHsUO5c3BfPB1gJCql5B+7N/LpsT0tOo/DGoLFKnEyCv7zzVa6dwojPioYq1W2eTMwmc2sPHiMT7bu4WRBEWE+Xjw8+jpu6tOdCI2l0m0Ngrw8GZUQy6gEZdgupSSrpIwDmWc5kJnD/swcPtm6hw+tVgA6BwXQL6oD/aMiGBAdQYSfj0PtHNVpXaSU7Dh1hg9/2c0vJ9PxdXfjD2OHMndQH7zdXNWW1ySklLyybzOfJO/m3q4DeKYF53JYQzi38Pnlmj28/adZAEgkjSRedVjMFivL9h/h3aTt5JZX0DUsmFdnTmFy9/h2PU0ihCDS35dIf1+u75kIQLWpjsPZuew9k83ejGzWHDnB13sPAxDq7UX/6AgGRUcwMCaSTkEBukG0Q8wWKxuOpfLfX3ZzODuXIE8PHhs3jNsH9XG4tal3Dm3l/cPbuT2hD08PGNf+DMFsseJkNPD5qp10DPOnV0IHpGybowMpJZuOp/Hahi2cLCiid0QYL944kaGdovQL2RVwd3FmYEwkA2MiAWV67UReAbszstiTnsWu05msPnwcgEBPDwZERzAwWjk+PjhQT3nShimvqeWbvYdZuGM/2aVlRAf48ey0cdzYuxuuDhjJ9t6hbby2/2dmdurO84Mntfia4Hg9wK+jg09X7uTFR6YBYJUSYxu7QGYWl/Ls9z/yc+ppYgL9eWvONCZ0jdON4BoxGASJYcEkhgUzd1AfpJRkFJWyKz2TXacz2ZWeydqjJwDwdXdjYHQEg2IiGRTTkYSQIN0g2gDHz+bz5e6DrDyYTJWpjoHRkfxl8ijGJHZy2BvJD4/s4JV9m5kR241Xh16PwQbXBYc0BIDDqTkkxoRwXa+YNjc6MFusfLZ9L29v2obRYOAvk0dx28De7XpqyJYIIYgO9CM60I9Z/XoAivkqBpHFztNn2HDsJAC+bq4MjInk5ZsmO9xUQnun2lTH+uRUFu8+yN4z2bg6GZnSPZE7B/ehe4dQteW1iM+O7eGFPZu4ProLrw2bZrPrn8MaQo+4cN564magbY0OzhSV8MdlaziQmcOYhE48c/1Yh8ml7sicW4e4qU93ALJLythZP3pIKyjC08X5ij9rtlgRgiv+U54r3GSxWllxIJnnV2/ir1PHMLNv91b5XdozUkoOZp1l6b4jrD58nIpaE9EBfvxp4khu6tO9TaSY+PzYHp7ZuZ6JHeN5Y8QNONnwZtgmhiCE+BiYBuRJKXs08P5oYAVwqv5by6SU/2hpu871OXHayuhgzZEU/rpyPQLBv26ewvU9EvXpIZXo4OfDjX26cWOfxve1XLizW0qJxSoRQtlQdy7NB8CSPYf4avchYoL8MdVvutNrdtiGjKISvjt4jJUHk0kvKsHNyYlJ3eO5uW8PBkRFtJk+XnhsL3/buZ7xkXG8PXIGzgbbzhrYaoTwKfAO8PlVjvlZSjmtpQ21xX+gOouFl9Zs5n+7DtA7IozXZk0l0t9XbVk6TeAvy9dRZTIxMj6W4XHR9ak/fv18nhsdvL5hC3UWK2MTO5FVUkanYCUHju73zSe9sIS1R1NYe/QER3LyEMDAmEh+M3wgk7rFO0zYaFNZlLKPp3euY3xkHO+NugmXVphCtokhSCl/EkLE2OJcjfHiR+uoqDbx8u9vsEdzrU5ZdQ2/X7KK7afOMG9Ifx4bP0xfK3AgbhnQkzVHTvD59n08s2ojzkYD3cJCGB4Xw5TuCUQH+rF490H2ZGTx9i038MORFE7kF9IpyB9AHwFeA1ar5FD2WTYdT2NTShrHcwsA6B0RxuMTRjC1RyLhbXR6dfGJAzy1fS1jIzrz7qgbW8UMwL5rCEOEEAeAbOCPUsoj13oCs9nC5j2pDOvTyfbqVCCzuJQHFi0no6iEl26ceH7+Wsdx6B0ZflFBlLT8IjalpLHj1BkKKioZ3zWODcmpfDFvDkIIskrK8HVzI8jL8ypn1TlHXnkFW09msDUtna0nMyiorMIoBP2iInhy0igmdo2jQxvfkLnw+F6e3rGOUR068d7om3A1tt5lW0h5aYLiZp5IGSGsusIagg9glVJWCCGmAm9KKRvMTS2EmA/MBwgODu6/ZMmS8++lZJXx0ZpU7hrfie7RfjbR3VIqKirw8vK65p/LrKjmzQOpWKTkge6xJPq37p1Nc3XaG0fTaZUSKTm/ZnAhJbV1LDyezomSSm6Jj8TFIDhcVEasjyejI4KxSnnZz0gpOVhYRoSnG4FuLi0eQThaf5bU1pFaWkFKifI4W1UDgLezE138vekR6EOPAB88VdozYO/+3Fh+loXFp+nt5scjwQk4i8bXS8eMGbNHSjmgOe3ZpVellGUXPF8thHhPCBEkpSxo4NgFwAKAxMREOXr06PPv7fx0I24uTtx32/W4XSXqw54kJSVxocamcDQnjz99vhRPdzc+vvNmOgW3fh2A5uhUA0fXKaU8bxJORgN9BhTzy8l09p3JYW9GNsVVVZypMXPjyOH06Xh5qcUzRSU89NYnAHi7upIYGkR8SCBxIYHEBSuPAE/3JhuFlvuztLqG5LP5JOfksT79FDm1Z8kpKwfAw8WZ/lERzI2JZFjnaLqEBmti7dCe/bnw2F4WZmxv1TWDS7GLIQghwoBcKaUUQgwCDEDhtZxDSslPe09yXa8YzZhBczh2Np95n32Dh4sLn90zi6gAP7Ul6dgQIcRFIdDnEvTNHdSHxbsPsj45lTEJna441x3q48Xi+27lWG4+x8/mcyw3n1WHjlNeW3v+GB83V2ID/YkJ8ic6wI+O/n5EBfgS6ed7TWZhL0qqasgoKuFUYRGpeYWk5heRkldAVsn5+0QCXF24Li6GeR370SeyA93CQ2xWl8MR+e/RnTy/+0e7mgHYLuz0S2A0ECSEyASeAZwBpJQfALOAh4QQZqAauFVe41xVSno++cUVjOjb2RaSVSE1r5B5ny/Fw8WFhfNm65FE7QiL1UpNnRlfN1fuGNznise5ODnRp2P4RaMHKSV55ZWcyCskraCQtIJiThUUsz3tDCsOJF/0865ORsJ9fQj3UcqVVhcXku66lwBP9/OV8HzdXPFyc8Xb1bXZF12zxUpFrYmK2lql5GplNUVVVRRUVHG2rILcsnJySss5U1xKWc2vZuZsMBAT5E+viDBu6d+TruEhdAsL4dDunZodydib9w9v5597k5gSlcibI6bbzQzAdlFGtzXy/jsoYanNZsv+NISAob0dszhFblkF93+xDCeD4JO7b9bNoJ1hNBi4Z0i/8/sPrgUhBKE+XoT6eDE8Lvqi984VGDpTVFpfF7ucnNIycsoq2JWeRV5ZOevO5F3x3G5OTrg6O+Hm5ISbsxNGgwGjQWCsn6u2SCtSSsxWSW2dmRqzmdo6M1V1dVc8p4+bK6E+XoT5eNM7MpyO/r7ny6RGBfjpUXRX4Z2DW/nX/p+YHtON14dPs+mms6bgMDuVtx04RdfYUAJ8PdSWcs1Umep46MsVlNXUsmjeHGIC/dWWpKMSLk62/Ze7sMBQQ2zatIm+g4dQXFV9/lFaXUNFbS3lNSYqTSZq6szUms3U1JmxWK1YpMRitSIQGITAYFCmwc4Zh6uzE16uLvi4ueLl6oqfuxsBnh4EeroT4OnhEPUDtIaUktf2/8w7h7ZyU6fu/Gvo9apsuHUIQyitqObIybPMmzFYbSnXjNUq+dOyNRw7m897t02na3iI2pJ02hFCCPw83PDzcCMW/UZEi0gpeW73Rj5O3s2tcb154bpJqmVfcAhD2H30DFYpua5njNpSrpn3ftrO+mOpPDlpFKMT2sb+CR0dHdtglZKnd6xjUco+5nUdwN8GjFM1KMAhDGHXkQw83V3o1jlMbSnXxJbUdN5N2s6Nvbtx93V91Zajo6OjIcxWK3/atpqlJw/zUI/reKLvKNUjxBzGEPp1iXSoMLTCiiqe/HYNccGBPHP9WNX/0Do6Otqh1mLm9z+vZG1GCo/1GcHveg7VxDVC81fYgpIKMnNL6NslUm0pTUZKyV9Xrqe0ppZ/3TwFdwfeN6Gjo2NbqupM3P/jUtZmpPDMwPH8vtcwTZgBOMAIYf/xLAD6JEaorKTpLN13hE0paTw5aRSJYcFqy9HR0dEIZaYa7v/xG3bnZ/HKkCnMie+ttqSL0LwhHDyRjauLE4nRjhGdk1NazktrNjMoJpK7BuvrBjo6Ogp51RXcvWEJqaUFvDViOtNiuqot6TI0bwiHTmTTLTYUJyfH2Mzy4g9JWKWVF2dM1ETuFR0dHfU5U1HCHesXk1ddyUdjZzOygzY32Gp6DUFKJWVFz/gOaktpEj+nnmb9sVQeHDlY34mso6MDwImSAuasWURxbTWLJtyqWTMAjY8Q6ixWzBYr3R0g3LTOYuHFH5KIDvBj3pB+asvR0dHRAHvyMrn3x29wMRpZPPF2ugWEqi3pqmh6hGAyWwHo2kn7hrB490FOFRbzp0kjbZ6eQEdHx/HYlHmSuesXE+DqzrLJd2reDEDrIwSzFX8fD0L8tV3go7ymlneTtnNdbEfG6LuRdXTaPd+mHebxX1bTxT+YT8fNIcjdMSrkaX6E0CUmRDMxulfio192U1JdwxMTR2pea1tl0aJFxMTEYDAYiImJYdGiRWpL0mmHSCl5//B2/t+WVQwMjeTLibc7jBmAxkcIZouVBI2Hm1bWmVm46wiTu8XTTU9cpwqLFi1i/vz5VFVVAZCens78+fMBmDt3rprSdNoRFquV53Zv5NNje7ghpiv/GnZ9q9Y/bg00PUKQEuI6NpzWVyskZRVQaTLx0EjHy8TaVnjqqafOm8E5qqqqeOqpp1RSpNPeqKlPRfHpsT3c320gb46Y7nBmABofIYC2DaHaVMemrHxGxcfqO5JVJCMj45q+r6NjS4prqpmftJRdeZn8ud8YHujhuDeHmh4hCAFRYdrN4b7iYDIVdWbuHzZAbSntmqioqGv6fmNocT1Ci5p04Ex5CTevWciBghzeGTnDoc0ANG4ITgaDZncoW62Sz7fvI8rLnQHRjpNnqS3ywgsv4OFxcSU9Dw8PXnjhhWs+17n1iPT0dKSU59cj1LwAa1GTDhwsyGHmmoUU1lSxaMKtmkxFca3YxBCEEB8LIfKEEIev8L4QQrwlhEgVQhwUQjRp55azk3YjdradyiCtoIixkdqPgmrrzJ07lwULFhAdHY0QgujoaBYsWNCsBWUtrkdoUVN7Z21GCnPWLsLFYOSbyXcwMLSj2pJsgq1GCJ8Ck6/y/hQgvv4xH3i/KSfVcv2DL3cdIMDDnf4hfmpL0UExhdOnT2O1Wjl9+nSzo4vsvR7x8fjxpAuBVQhOC8E8V9fL7vz1NRLtIKXko6O7eDBpGYn+wSyfejfxftpd57xWbLKoLKX8SQgRc5VDZgCfSyklsF0I4SeECJdS5lztvM5O2jSE/PJKNh1PY97Q/jgbLGrL0WkmUkJxMaSnQ2Gh8tzf/wmKiqyAH+Bf/9UPFxc/Ro4Ei0V53HMPPPUUGI3Kw80N/PzA3//Xrxc+DwyEmBjl9Tk+Hj+eWzZu5FyUegzwjsnE/DvuAH4NmY2KiiI9Pf0y/c1dI9FpHmarlS+KT7PxTC6ToxL49/AbcHfSVq2Tn/P3tejnhXKNbjn1hrBKStmjgfdWAS9LKbfUv94I/ElKubuBY+ejjCIIDg7uv2TJEpvosyUbzuTxzcksnhnYFW9pxstL2zupASoqKtqtztrayx8mk/IVwMUFnJyUh9lcS0VFKVKaATNgQQgroaEh+Pp6A0qwg9lcgdGo6JQSrNZfzcJsvvy52ay0JwS4uioPp+Jc3KnF9YIHgAk47uJCz549ASgqKiI9PR2r1Xr+dzIYDERHRxMQEGD3/mwNtK6z0mrm/YITHK4pZbJ3OHP8ojBobKq4mAo+ExtZMfqNPVLK5kW6SClt8kC5wTl8hfe+B4Zf8Hoj0L+xcyYkJEgtctMHX8iZH3whpZRy06ZN6oppIu1BZ12dlAcPSvnpp1L+7ndSDhsmpZeXlLGxUk6aJOWDD0r5z39KuWSJlLt2SVlYKKXVevl5vvjiCxkdHS2FEDI6Olp+8cUXNtFptUqZny/lzp1SLl4s5Yv8Sc7nAzmBtTKaU9KbUjmCzfJRXpdwpzxyREqzuemaGqI9/N1bm4yyYjlu+QLZ+fN/yr9/95XachqkzmKWf9j7Lznnlz9JYLds5nXcXvsQMoELV10igWw7tW1T0gtLOJqTxxMTR6otpd1TVgZJSbBhA+zcCYcOQWQk9O8P/frBTTdB374XT9M0hblz57bKDmchIChIeQwcCOm3/pPoC94vwp+99GMD/fHwmMP06XD2LPTuDYMGzeXdd+cyahRo+Ea6zbEjN4OHkr7FIiULJ9xC7bFTaktqkCVn1pFSns6TXeexhH82+zz2MoSVwCNCiMXAYKBUNrJ+oFXWHE0BYEr3BJWVtD/q6pQL//r1yuPAAbjuOhg/Hl55Bfr0AR8ftVU2nY3jxl20hhBAMUPYyCdsZMGCXsydCyUlsG8fbN0Kr74Kt9yiGN6ECcpjwABlDUPH9vwvZT9/27GOKG8/PhxzM519A0nSoCGcKM/gy/S1jA4ZwIjgllVptIkhCCG+BEYDQUKITOAZwBlASvkBsBqYCqQCVcA8W7SrBuuTU+kdEUZ4/XyyTutSUgLLl8O338LmzRAbq1wIn3kGhg+HS7YfOBT3btjAx+PHM27jRjoCGcCzLi5M/fjj8yMUPz8YM0Z5PPUUVFTAzz8rhnj//ZCVpbx3000wYwZ46x/LFmO2Wnlhz498krybUR068dbI6fi6uKktq0FqLCZeO74QfxdvHoqb1eLz2SrK6LZG3pfAw7ZoS01ySss5nJ3L/40frraUNk1VFaxaBV9+CT/+CGPHwpw58OGHENLG8gfeu2HD+ecxwCeNHO/lBVOmKA+AnBxYtw6++goefhgmToTbboOpU5XIJ51ro7immkd+Ws4vZ9O5t+sA/tJ/LE4GbUY7AnxyagVnqnJ5vufDeDm1/O5I87mMtMTmlDQAxibqNQ9sjcmkXNjy8+HGG2HwYOXC9umn4KtXI70i4eFw993Ko6gIli6Fd95RRg/Tp8PMmUqEk16zqXGOFefxm01Lya2q4JWhU5kT10ttSVdlT1Eyq7J/ZkbEaPr6J9rknNq1Pg2y+cRpIv186BR09VA/naaTmwvPPgvR0fDyy8odcEoKrF2rxPrrZtB0AgLgN79RRlVHjigL6tnZyjTbyy8rey10GmZ1+jFm/rCQWouFJZPnat4MAIpNZcR5deSe2Btsdk7dEJqIyWxhx6kzjIyP1VNV2IC9e5W72i5dlHnw9ethyxYIDm5700JqEB4Ojz6q9O/KlXD8OMTFKYZxuMEEM+0Ts9XKS3s28dvNy0n0C+a76++mT1AHtWU1ifFhg3m97//hYrDd5jjdEJrIgcwcqurqGNpJ3x3aXMxm+OYbGDFCmRbq1g1SU2HBAuhx2XZGHVvRty988oliClFRyjrDuHGKUVyw163dUVRTxd0bvuI/R3ZwZ2I/vpo0l1APx1qVNwrbXsJ1Q2giO09nIoCBMZFqS3E4pIRly6BnT3jtNfj97yEtDf70JyWlg459CAmBp5+G06fh3nvhH/9QzGL1auVv1J44UJDDDd9/yq68TF4dOpXnBk/ERY/f1Q2hqew9k018SBC+7nroxrWwaZOyV+Af/4DXX1fi6WfP1hc51cTFBebOhV27lPWbP/4RRo1S/jZtHSklC4/tZfaaLwD4ZvIdzNbgeoHZauFs9a+LPtJOjq0bQhOwWiUHMnPo2zFcbSkOw969MGmSEu3y6KPK6ylTlN26OtpACGXq7tAhZcRw223KXoa2usZQVWfisV9W8fTOdQwLj2HV9fPoFaTN/+lXjn3GS8kfszF3J1LK8+uWrW0MuiE0gVOFRVTUmugdqc0Pj9pcWM2rY8eBDBt2imnTlItLcjLcfjtoOJS73WM0KhFdx4/D6NHK+sJ997WtqKSUknxmrP6c5WlHeKzPCD4aOwt/N3e1ZV0RZ2HE3ejKgZIU/nNyKacqsgBaPaBF/zdtAoeycgHoGRGqshLt8Ws1rwykvJ/MzO/ZuXMpzz23mN/+Vpme0HEM3Nzg//0/JezX2xu6d4eFCx1/fWFJ6kGmf/8ZxbXVLBx/K7/vNUxzmUovZWBgd6ottcR7RVFWV8mXGWvYkr+PF49+xOnK7FYbKeiG0ASSz+bh7uyk7z9oAKWaVziQhJKRZBxm8+M899yT6grTaTa+vvDGG8pu8ddfV6b+HLEWT2WdiT/+8j1PbF1Nv+AIVt8wj+EdYtSW1SRGhwygt18CffwTuTV6EvHeUfwvfQ1HStMumkKyNbohNIHks/kkhAZj1Oc9LsJqhfT06cB2YBkwHFAmoPVqXo7PgAHKwvOYMUpCvY8+cpzRwuHCs0xb9QlLTx7idz2HsnD8LYS4O0aaWKtUYoG9nDz4KG05UR5hdPWOpcBUQpx3Rz4+teL8FJKt0a9wjSCl5HhuAYmhbadMni0oKIDJk8HV9S5gKPAm8GtQu17Nq23g5AR//rMSLfb++8oidGmp2qqujJSST5N3M/OHhdRYzHw58Xb+r+9Ih7qZM9TvLbgpcjReTu7kVBfw1Zl13NBhJHOjpzAwoDuxXhGt03arnLUNUVhZRWl1DXHBesD8OfbuVfL59+sHH36YgofHxXcrHh4evPDCCyqp02kNevRQwlKjomDQIDh6VG1Fl5NXXcG8H7/m77s2MDw8htXT7uW6MMe9MXE2ONPZK5IHdj9PeV0Vd0RPJcE7mus7jGi1NvVo8EY4mV8EQOdgff0A4PPP4f/+T7lbnDUL4HYMBslTTz1FRkYGUVFRvPDCC61SYEZHXVxc4O234bPPlH0Lv34G1GdT5kn+uPV7KupM/GPQBO5M7NcmUsxMChtKsamccaGDEEIgpbT57uQL0Q2hEU4XFgMQE+ivshJ1qauDxx5Tks4lJSkRKOdorQpjOtrk7ruVXeczZ8Lu3fDCC+oV6amsM/HSnk18kbKPLv7BLJ54O/F+bWd618PJjbtjp2EUSge3tsnphtAI6UUluBiNhPs4Vo4TW1JWpqRS9vZWKpZda0lKnbZHv36KGdx6K0ybpqTdtnexor35WTy2ZRXp5cXc13Ugj/cbhZvR8S9pdVYzzoZff49zZmAP9DWERsgsLiXCzweDwfGHn82huFipUNatG6xYoZuBzq8EBcGaNUqG2uuvV6q52YNai5nX9v3E7DVfUGe18OXE23l64Lg2YQa5NYXct/NZdheps0ijG0IjZJWUEeHnQIV6bUhhoVKveMgQePddfbexzuU4OSmZVDt1UqLOyspat73DhWeZ8f1nvH1oKzNiu/PDDY69cHwhUkreOfEVVZYaojzCVNFgk39xIcRkIcRxIUSqEOKyHUlCiNFCiFIhxP76x99s0a49yC2raJf1k/PylNKV48fDv/+t5yDSuTJGo1LetFcvJbV2SYnt2zBZLLx5YAs3rv6cotpqPh47i9eHT8NHo7WOm8OG3B3sLT7GPbE3EOKmThBLi8dYQggj8C4wAcgEdgkhVkopLx3z/CylnNbS9uyJyWyhoLKKUB/H2NBiK3JzFTOYOVPJUqqbgU5jGAzKKPL//T8lF9L69UoFN1uwvyCbJ7auJqWkgBmx3Xh20AT8XLWbh6g5FNSW8OHJb+npG8fUcPVqtttihDAISJVSpkkpTcBiYIYNzqs6RZVVAAR7eaqsxH7U1ChJ6W66CZ57TjcDnaYjhDKaHD5cSXFeV9ey81Wb63hx94/M/GEh5aZaPho7izdHTG9zZiCl5L3UJZilmd8n3HZ+Y5oaiJYmSRJCzAImSynvr399JzBYSvnIBceMBpaijCCygT9KKY9c4XzzgfkAwcHB/ZcsWdIifS0hvbyKl/Yc58EesfQJ8mvwmIqKCry8tD+CaKrO06eVlBSdOrW+poZoa/2pNmrpTE0FV1fo2LFpx1+q82B1MZ8XnabAUstorxDm+EXhYVB/0bg1+vM4maw07GSUtQeDSGjx+caMGbNHSjmgWT8spWzRA5gN/PeC13cCb19yjA/gVf98KnCiKedOSEiQavLTiVMy8ZnX5Z70zCses2nTJvsJagFN0fnqq1L27StlZWXr67kSbak/tYBaOktKpOzSRcr//Kdpx5/TmVdVIR/ZvFxGf/aSHLd8gdyWk956IpuBrfuzvK5Szt32lPzdnn9Ks9Vsk3MCu2Uzr+e2sNxM4ML7gEiUUcCFplN2wfPVQoj3hBBBUsoCG7TfapRW1wDg5962hqgNsXq1ktlyxw77x5PrtD18fZWazcOHQ5cuMHLk1Y+3SMknybt5ff/P1FrM/L/ew3mwx3W4toFQ0qvxcdpKSk3lPNN9vl33G1wJW/T2LiBeCBELZAG3ArdfeIAQIgzIlVJKIcQglLULzZffKKuuBcDbzVVlJa1LaqpSIGX58qYP8XV0GiM+Hr74Am65RcmaGnmFcuT78rP5x9lDpJ+pYkR4LM8MGk+cb9vPHXaw5ARrz27l5shxxHtrI3S2xYYgpTQLIR4B1gJG4GMp5REhxIP1738AzAIeEkKYgWrg1vqhjaapNJkA8HJtu1VepIT585WC90OHqq1Gp60xYQI88AA8/LByw3FhkEJuVTn/3LuZZWmH8Te68N6oG5kSldgmchA1Rq3FxNsnFhPmFsjt0VPUlnMem4zHpJSrgdWXfO+DC56/A7xji7bsSZWpDoMQuDm33WHrJ59AeblS91hHpzX485+hb18lvcWsWcqegk+Sd/PWwV+os1p4qMd19CqxMCW6i9pS7caSM+vJrs7n+Z4P42bUzg1n273S2YDqujrcnJza7B3L2bPw5JNKzLiT/knQaSVcXZWNa3PmSMxdjvFeymYyKkoYHxnH0wPHEe3tT1JSktoy7caZqly+ObOBMSED6OufqLaci9AvA1fBZLbg4qT+Qk9r8eijcO+90Lu32kp02joeCdkE/2UjT+7Noot/MJ+Om8PoCJVim1VESsn7qV/janThvk43qi3nMnRDuAp1FgvOauX1bWXWroU9e+DTT9VWotOWSSnJ51/7fmLdmRMEBXli/XIKf328J8Mj2mdirE15uzhQksLDcXPwd9FejjTdEK6CxSoxttEsp889B88/D+0golZHBbIqSnnr4C98ffIQnk4uPNZnBPd2HcCXZa68+IIS5tzeKK+r5MO0b+niE8PkcG1GcOiGcBUkEkMbXD/YsgVycrRT7Uqn7XC2qpx3D21j8Yn9CATzugzgkZ5D8XdT7jzuugueeQYOHGh/U5WfnV5FRV01j/S8RdX0FFdDN4R2yD//CY8/ri8k69iOrIpS/nNkB4tPHEAimRPXm4d7DqGD58XTIq6uSgK8V16BRYtUEqsCKeXprMnZyoyIUcR6Ragt54rol4SrYBACq/a3S1wThw8rla6+/lptJTptgfTyYt4/tJ2laYcAuLlTTx7uNYSOXn5X/JkHHlByZaWlqZczy55YpZUPUr/Bz8WbuRrac9AQuiFcBSeDAYvVqrYMm/KvfynRRW5tJ428jgrsL8jmg8PbWZuRgrPByG3xfXig+2AivHwb/VkfH2Uz5L//DW+/bQexKrP+7HaOl6fzWOIdeDhpe9FON4Sr4Gw0YjJb1JZhM2prld2ix4+rrUTHEbFYrWzMTOXj5N1sz83A18WNh3oM4Z4u/QnxuLYMoPfdB8OGwZtvtu1KfOV1lXx66ju6+3RibMhAteU0im4IV8HVyUiN2ay2DJuRlKTURg4NVVuJjiNRaqrhqxMH+Pz4XjIrSgn38OavA8Zya3xvvJybl+erc2elJvOOHUqJ1rbKwtPfU2Gu4qG42Q6xwVU3hKvg5uxMrdmCxWrF2AZuY1asUIrf6Og0hpSSA4U5LDq+j+9OJ1NjMTMotCNP9R/DhI4JONng/2HGDOUz2VYN4XRlNj/k/MLUDiM0vZB8IbohXAUPF2cAqk11eLWBjKcrVyppKnR0rkRBdSXLTx1h6cnDJBfn4eHkzE2dejA3oQ89Am1b+H36dJg3D15+2aan1QRSShacXIankzt3aHwh+UJ0Q7gK57KcVtSaHN4QqqqUOgdd2k/+MJ0mUmMxk5R5km9PHWHjmVTM0krvwHCeGzyRG2O74+3SOp/9gQOhpAROnGiV06vKzqLDHChJ4cHOs/B2dpwSvLohXAWfehMoq6klzNdbZTUto7ISRo/WayTrKNRYzGzNOc336cdYl3GC8rpagtw8mNd1AHPiehHvF9TqGgwGGDUKtm2DKG2UA7AJdVYz/01bTqR7CFPCh6kt55rQDeEq+LorsZnnKqc5MjU1+uigvVNuqmVLzinWZKSwMTOVijoT3s6uTIpKYHpsN4aGRdtkbeBaSExUot7akiGsyv6J7Op8nu3xIE4Gx8qFphvCVfD3UGKGi6uqVVbScnRDaH9YrFbSTZUsOLKDTVkn2ZWbiVla8Xd1Z1p0VyZHJzIkLErVMpVdusA33yiFdNoCZXWVfJmxlv7+XRkQ0E1tOdeMbghXIcBTKS5cVFmlspKWU1Oj3I3ptF2sUnKipIBdeZlsO5vOLzmnKTHVwFno4hfMb7oPYkxEZ/oFR9h9JHAlzo0Q2gqLM9ZQba7RZGrrpqAbwlUI8HRHAPkVjm0IVVVQVwcxMWor0bEVUkpyqys4VHiWQ4VnOViYw978LMpMSh3wUHcvxnWMI7CkmnvHTCbMQ5trYAkJSk3vtsDZ6kK+z97ChLDriPYMV1tOs7CJIQghJgNvotRU/q+U8uVL3hf1708FqoB7pJR7bdF2a+JsNOLv4U5+RaXaUlpERga4uEAbLe3QppFSklddwcmyIk6VFXGipIDk4jyOF+crd/8oObfifAOZGtWFAaGRDAyJJMrLDyEESUlJmjUDAE9P8PVVblgcnS/Sv8cgDJqqkXyttNgQhBBG4F1gApAJ7BJCrJRSHr3gsClAfP1jMPB+/VfNE+rjRW5ZhdoyWkRNTdtOD+CImK1Wykw1lJhqKKmtprCmivzqSvKrK8itriCrooysylKyKsuoNv96tfRwcqaLfwhToruQ6BdEj8AwuvmH4OGsnbq814q7Ozh6Dsm0iiyS8vZwc8dxBLn6qS2n2dhihDAISJVSpgEIIRYDM4ALDWEG8LmUUgLbhRB+QohwKWWODdpvVcJ8vMkuLVNbRouordUN4Rx1VgtnK8spqKmioKaSopoqyutqqawzUVlnotZixmS1Ume1YLZasUgrVimRyIsuWvn5+XyVVAwodTOsUp4/ziIlFqsVs7RisliotZiptViosdRRZa6jor6dKxHg6k6Ely9xvoGM6tCJGG9/Yn0CiPXxJ9zTp83V6HB1BUfPIfnJqRV4OrkzK3K8qjrqrC2bzbCFIUQAZy54ncnld/8NHRMBXGYIQoj5wHwA/6Aw1YtvWyvKyCgovqKOiooK1TU2RmUlBAZqXyfYrj+llOSZa0kzVZBmqiCnrppccw2F5lqudO1xFgIXYcQJgZMQGITAgMAACMRFezisVis5Ob9GnwkEAhCAUQiMKD9vROAiDPgKA0HCGTcnV9ycjbgZjHganPAwOOFlMOJlcMbP6IyP0RmnC4unVAKVZZjPlnGC01zrHi5H+Hz+7ndgMmlfJzTcn2fIZ6/hGKOsPdjzy051hNVT6Le8RT9vC0No6Hbl0gFgU45RvinlAmABQHjHTnL06NEtEtdS0lz2sDn7J/oOvu78voQLSUpKQm2NjbFvH2zblsTs2aPVltIoLenPWouZTVknWZOewk/ZaRTVKhdsdydn4nwDuc67AzHe/kR6+RLs7kmQmycBbh54u7ji6eRyTZE3jvB3B8fQee+98P772tcJl/enlJInDrxJYI0vjw68B1ejelN3ZmsNS0690KJz2MIQMoGOF7yOBLKbccxlmC3qjyM7+iv53c8UlzZoCI6Aq6vjz9FejfxqJdb+q9QDlJlqCXB1Z3REJwaGdKR3UDgJfsGaCbPUuRxHntLcV3yMo2Vp/DZutqpmAJBekaSJKaNdQLwQIhbIAm4Fbr/kmJXAI/XrC4OB0qasH5gt6l/FogL8AEgvLKFHB8fMGx0ZCSaTMk/rqP94DVFQXcn7h7ezKGUfJquF66O7MDuulyo7bnWaR20tFBQ4ZjlXKSWLMn4g2NWfiWHXqS2Hk2U/4OXUoUXnaPGfQUppFkI8AqxFCTv9WEp5RAjxYP37HwCrUUJOU1HCTuc15dxmixUppap5xKPqRwinC4tV09BSfHyUkNOsLOjYsfHjHYGduWd4aPO3lNRWc1OnHjzccwixPgFqy9K5RlJTlf0xjrhOvr/kOMfKTvPbuNk4G5xV1VJZl0dO9W56B8wDljb7PDbxZSnlapSL/oXf++CC5xJ4+FrPa5WQV1xBaIB6cdTuLs508PXhlAMbAiglM48fbxuG8L+U/fxtxzqivP34cuJtJPgFqy1Jp5kcP+6YO+illHyRvlozo4NT5esASSfvyS06j+bH1enZRWpLoFOQPyfzC9WW0SLOGYKjs+DIDv6yfQ3DwmP4dupduhk4OI5qCOdGB3M6TlB9dACQVr6WYLfu+LhEtug8mjeE0xowhPiQIE7mF2Fx4GBpV1fHN4SNmam8uGcT10d34eOxs/B1ccxFfp1fcVRD+CpjHYEuvkwIU39/bXFtGsWmk8R6T2rxuTRtCAYhSMtS/848PiQQk8VCelGJ2lKajacn/PKL2iqaT7mplie2rqarfwivDZ/WJkqatnekVD6T/furreTaOFqaxqHSVGZGjtXE6OB0xQYEBmK8xrb4XJr+r3J2EqRlqm8IiaFKsZCU3AKVlTQfLy9IT4czZxo/Vot8fnwvhTVVvDxkCm4qpmvWsR3JyUqUUZ8+aiu5NpZmbsTbyYPJ4UPVloKUklPlGwhz74e7U8uDKrRtCEYDJzMLkCoH0ccFB+JkMHA0J09VHS1l6lSlrrKjUWMx89HRnYyO6ETvIMfMIqlzOStWKHWVHSnCqIhydhQe5voOI3Azql9Wt7A2mfK6TGK9bVNQQtuG4GSgoqqWvCJ1k8u5OjvROTiA5LP5qupoKTNmOKYh7Mw9Q1FtNXcl9lNbio4NWblS+Uw6ErtFKk7CyA0dRqotBYDT5T9iwIkor1E2OZ/mDQHgRIb6F+Lu4aEczs5VfbTSEiZOVOrXlpaqreTa+Ck7DReDkSFh0WpL0bERZ8/CsWNKTWVHocRUzhHSGRs6CD8X9VOKSyk5XfEjHTwG4Wr0sck5tW0IRgNCQEq6+lM1PSNCKa6qJqvEcTOfenvD2LHw1VdqK7k2kovy6BoQgruT+gt4Orbhiy9g2jSlToejsDpnC2Zh5abIMWpLAZTpokrzWaK9W76YfA5NG4IQEBnqx3ENGEKfSGXuet8ZzWfsviqPPQavvgoWi9pKmk5edaWmi7zoXBu1tfDGG8pn0VGos9axOucXYmUoHT20kcImvSIJgZGOnsNtdk5NGwJAYnQIx0+rbwjxIUF4uDiz70yjOfk0zYgREBwMy5apraTplNfV4u2s/gKejm1YtAi6d4e+fdVW0nR+KThAsamM/jJObSmAMl2UUbGZMPd+NpsuAgcwhC4xoeQUlFFaXt34wa2Ik9FAn8hw9mRkqaqjpQgBTz4JL7/sOBlQPZ1dqDKb1JahYwMsFnjlFeUz6Eh8n72FDu7BxBCithQASuvSKas7Q5SXbRe3tW8IscrwLPl0rspKYGB0JCm5BZRU1agtpUVMm6aU1dy4UW0lTcPPxY2Cmiq1ZejYgBUrlBrKDlD64DynK7M5WpbG1PBh9WWQ1OdMxc8AdPQcYdPzat8QYhRHTk5T3xAGxUQigd3pmWpLaREGg3KH9pe/OMZaQoJfMMeK8xw6wktHScH+zDPK586R9h6szdmGkzAyNnSQ2lLOk1m5lQDXBDydbTti0bwheHu6ER3uz5G0s2pLoWdEGG5OTmw/5aDbfS9g7lwl4d2776qtpHF6BIZSZqolvbxEbSk6LeDVVyEqStmM5iiYrHX8mLeLoUG98XX2UlsOADWWUvJrDhHpafud0po3BIAecR04fCJb9TtEFycj/aMj2JaWoaoOW2AwwIcfwj/+ARka/3WGh8cA8GNWqrpCdJrN8ePw73/D++871uhga8FBKsxVTAoboraU82RXbkdiJdKG0UXncAhD6BUfTnF5NWdyS9SWwtBOUZwsKCK3TN3d07YgMRH+8Ad46CFtLzBHe/sT7xvE2owUtaXoNAOrFebPh7/9TRkhOBLrzm4j1C2QXn7xaks5T2blVtyM/gS5drH5uR3DEBIiADiQon6Ez/DOym7ZLSfTVVZiG554QhkhaH2z2vTYruzIPcOpMvXToetcGx99pOw9ePiaS2SpS15NEQdLTjA+dBAGoY1LpVVayK7aQYTHEEQraNLGb9kIMeEB+Hi5sf+4+oaQEBpEsJcnW1JPqy3FJri4wH//C48+qpQz1Cq3xPfGSRj44vg+taXoXAOHDimLyB9+qJRxdSSS8nYjkYwJGai2lPMU1iRTay0jwrN1qrS1yBCEEAFCiPVCiBP1X/2vcNxpIcQhIcR+IcTuaxZpEPROiNCEIQghGBEXwy8n0zFbHLdgzoUMHgzPPqss9mk1z1GIuxfTYrryvxP7KaiuVFuOThMoKFCS173xBvTsqbaaaycpbw/dfDoR7h6ktpTzZFXtAAThHq1jUi0dITwJbJRSxgMb619fiTFSyj5SygHNaahvYgSZuSXkF6s/dz8qIZaymlr2Oviu5Qt58EElNnzuXO2Gov6+9zBMFjNvH3TgSj/thLo6mDUL5sxRPlOOxunKbNKrchgVoq0MuzlVuwh0TcTN6Nsq52+pIcwAPqt//hlwYwvPd0X6dVWqw+89pv4egGGdonA2Gvnx+Em1pdiUN9+EykpliK9FOvkEcFt8Hxam7ONwofphyDpX5ve/V5IpvvCC2kqax5b8/QgEw4L6qC3lPHXWSvJrjhDu0ax76iYhWhLKKYQokVL6XfC6WEp52bSREOIUUAxI4D9SygVXOed8YD5AcHBw/yVLlgBgtUqeXXSQXrF+3Dxc/TTI7xw8SU5VDU92j8LbW/uJ1yoqKvDyajyO2mxW0hKHh0NgoB2EXUJjOiutZv6SfQA/owt/C+uBUaUYxqb2p9qooTM/H/LyoGtXJby5KWitPz8RG3DDhdvkxakh1NRZ7XqcvKDPCCmYh3vtlaOexowZs6e5MzFIKa/6ADYAhxt4zABKLjm2+Arn6FD/NQQ4AIxsrF0pJQkJCfJC/u+1b+XMx/4rtcA3ew7JxGdel5+u+F5tKU1i06ZNTT72yBEpw8Ol/Pzz1tNzJZqi8/vTyTL6s5fkWwe2tL6gK3At/akm9tb53ntSduwo5cmT1/ZzWurPrKo8OXXz7+TyzE2Xvaemzl3578jPU0bIOkv1VY8DdssmXF8bejTq31LK8VLKHg08VgC5QohwgPqvDaYllVJm13/NA74FmrUHfED3KDLzSskpUL8mwdgunXEyGNiTX6y2FJvTrRts2AB//jN8/LHaai5nanQXboztzhsHtrA3X/1AAx2FN99UEtclJUGnTmqraT7bCg4CcF2gtlbCc6v3E+TWDSeDW6u10dI1hJXA3fXP7wZWXHqAEMJTCOF97jkwEWWEcc0M7Kbsatl1RP2ttf4e7gzpFMXuvBLVd1C3Bt26wY8/wt//ruwu1Rr/GDyBcE8fHt68nLxq9QMN2juvvAJvveX4ZgCwvfAQnTwjCHVTYc70CtRZqymsOUaoe59WbaelhvAyMEEIcQKYUP8aIUQHIcTq+mNCgS1CiAPATuB7KeWa5jTWKTKQQF9Pdh7WxqawqT0SKKo1sT/TsYvmXImEBNi0Cf75T+XuT0v4uLjxwaibKDHV8JtNS6kx16ktqd3y/PPK5rPNmyFa/eW9FlFWV8mxslMMCuyhtpSLKKg5isRCiHvvVm2nRYYgpSyUUo6TUsbXfy2q/362lHJq/fM0KWXv+kd3KWWz4w6EEAzqEcWuIxlYrerflU/oEoeTEKw6dFxtKa1G587KP/o778Af/6gsOmuFHoFhvDH8Bg4W5PCHLd9hsbaNfSGOgsmkpD358ktlZBAZqbailrOn6ChWJAMDuqst5SLyqg8AghC31jUqh9ipfCFDesVQUl7NMQ3UR/Byc6VXkC8/HD5OnVaD921AdDTs2KHsOp04UYki0QqTohL464BxrMlI4emd69rk9J0Wyc6GUaPg7FnYtk2JSmsL7Cs+jo+TJ/He2kq6lFdzEH+XTrgYWzei0eEM4bqeMUSG+lFcpo2CKYNDAyiqquaXNpLb6EoEBMDq1XDddTBgAOy+5v3mrcd93QbyUI/r+F/Kfl7cs0k3hVZmyxYYOFAptLR0KfjYroKjqkgp2VdyjD7+iRg1krsIlPxF+TVHCHbv1eptObV6CzbG19udpf+6V20Z5+ke4I2/hzvf7j/K6AQHX01rBKMRXnxRMYSpU5W1hXnz1Fal8ETfUVTVmfjw6E7M0srfBoxDOFKeZQdASqV+xnPPwWefweTJaiuyLWeqcykyldHbL0FtKRdRajpNnbWy1aeLwAENQWs4GQxM79WF/+08QFFlFQGeHmpLanVmzlQ2Hd10k7K+8MYb4OenriYhBH8fNAEng5GPkndRazHz3KCJGJu6M0rnqhQUKNlKjx1TpogcPZKoIQ6VnADQVKprUBaUAYLcurV6W/p/iw2Y1a8HdVYr3+4/qrYUu9G1qzJt5OmpJC5b06y4MdsihOCvA8by2x5D+F/Kfn7703I9+sgGfPst9OoFHTvC9u1t0wwAjpSmEejiS7ibdpLZARTUJONs8MLHuWOrt6Ubgg2IDwmif1QHluw5pInoJ3vh5aVMIXz6qZIc7+67lTtJNRFC8ES/Ufxt4DjWZaRw+/rFFNZoY73J0cjJUZLTPfEEfP01/Otf4O6utqrW42hZGl19YjU31VhYe4wg1y6tUv/gUnRDsBG3DuhFelEJW9tAec1rZdw4OHxYyX3UvbtiEGqv697bdSDvjbqRI0W5zFj9GceLNRQapXGsVvjgA2VUEB8PBw/CsGFqq2pdimpLya8tpqtPrNpSLsIi6yg2nSTQLdEu7emGYCMmdYsnwMOd/+3ar7YUVfDygtdfVyKR3nlHiUb68Ud1NU2J7sJXk27HZLEw84eFegnORpASfvgB+vWDhQuVTYkvvNC2RwXnOF6uRAkm+sSoK+QSSk2nsMo6Alx1Q2gSFquVfceVlNhqhhu6ODkxu39PNh1PI7NYo1Vm7ED//rBzp1Kr+Te/UfYt7Nmjnp4+QR1Yef3dxPkG8kDSMl7ZuxmzvoHtMrZtU+phPPYYPPOMElraQ1ubdVuV1IozGDDQyTNCbSkXUVSrLHQHuNpnodvhDcFoMPDEv1eQkVOMEEJVU7htQC8MQrBo5wHVNGgBgwFuuw2Sk5VIpBtugFtugRSVbtDDPLz5avJcbovvw3uHt3HXhq/0qmv1HDkCN96o/H3uvlvZfHjTTaCxafRWJ7X8DB09QnE1uqgt5SKKa09iFK54O9tnG7hDG8K5Epb9unZk8dq9AFhUXNQN8/VmUrd4vtl7mMpak2o6tIKLi5La4MQJ6N0bhg6Fe+9V5qTtjZvRiZeGTOaVoVPZk5/F1FWf8EvOafsL0Qh79sAdd8CYMTBypGLW994LTu00ED214gxx3q0fxXOtFNeexM8lFoOwT0FqhzYEQ/1tzO1T+rN++zEAnIzq/kp3D+lHeW0t3+xtVkLXNomnp1KFLSVFCVmcMkW5EK1YYf9ynXPierF86l34uLhyx/rFvLJ3M3XWtpt25ELMZiVaaPhwZS9Jr16KWT/2GLi1XkZlzVNiKqekrpxYjU0XAZSYTuHnYr84X8c2BINiCL0TIpASDqQoufHVDP3sHRnOgOgIPtm2B5O5fVxomkpAAPz1r3DqlLK+8OKLShTL669DqR2XXbr6h7By6t3cGt+b9w5vY9aaL0grK7KfADtTVKTsKu/USUlR/Yc/wMmTSjipb+uU5nUoTlcqtdFjPDuorORiai1lVFsK8HOJsVubDm0I8Ou00cQhXVi8Rpk2stavI6i1nvDA8EGcLavgu4PJqrSvdVxc4PbblYR5//sf7NoFsbFw//1QXm6fUYOHswsvDZnCuyNv5HRZMdev+oQVp9rOxkKzGdauhdOnlYy1R4/C8uXw888wa1b7nRpqiDNVSqLMaI8wlZVcTJlJCWH31Q2h6RjrRwlzJvbl531pwK/TRmptMBkeF0238BAWbNmlp2RuhOuuU9InHzoEXbpAZqaSRvnRR5Vdsa3t6dfHdGHd9Pu4LjSKCM+mZWmrsWgoB/gFWK3KBf/hhyEiQokW8vBQ0k189pkSTqpzOZnVeXgY3fB30VaWvtI6JRTWx8V+mVcd3hCEEFisVmI6BNAzLpyU9F83IKVlFqiSJlsIwYMjBpFeVMLqw3rse1OIiFDqLXTtquRHCgiAe+5Rpjn+/GfYu1e54LUGoR7efDJuNgNCrh7JsfTkIZ7fvZE71i3mh7Ls1hFzjVgsSpjv449DTMyvZrBtm2KoISEQGqq2Sm2TXZ1HB/dgze1QLjOdQWDE29l+U1kObwjA+QRm7/1lNp0iAgBYtHo3j722nNc+38S/Prf/DqnxXeKIDwnkg5926KOEayQhQbm7TU5W8uhIqYSxhoUpXz/6CDLsvCF86clDPL1jHU7CyLyuA0iqyOOdg1vtK6KeU6dgwQKYPVu54M+bB66uyqaygweVBfy2mm+oNThbXUi4u7byFwGU1WXi5RyOQdhvfq/NzCR+vX4/n6/aiZRw5/UDOJyawzMPTgYJr3y6kY07Uhg32H5pbQ0GwUMjB/PYN6tZc+QE1/e0z07DtoQQ0KeP8nj5ZcUENmyA9evhySeVUcSECcpjyBDl4tgaHCo8y0t7knhm4HhuiVdKGB47epTtuRnMtwzGxdi6IYE5ObB1q/J7r18PlZXK7zxtmpJpNkJ7wTEOg1VayastYmhw65ambA7ldVl4O9v3j9siQxBCzAb+DnQFBkkpGyybIoSYDLwJGIH/Silfbkm7l5KVV8J3mw8zb/pgOgT78tHy7cRGBNA3UZkCuHl8b9ZuS7arIQBM7pbA+yE7eDtpG5O6xaseEuvoREUpsfL33qtMHx04oBjEe+8p00uenspO6f79lfny/v1bXslLSskbB35mUGjkeTMAyKyrwtPDw6ZmICVkZSnTY3v2KI+9e6G2FgYPhvHjlSmhHj3a38ax1qLEVI5ZWgh29VdbykVIKSmvyyLYzb6lPFs6QjgMzAT+c6UDhBBG4F1gApAJ7BJCrJRS2iykY8ehdAJ8PZg5TvmHNVusvPTxegAyzhaz71gWoQHeSCntOk9oMAj+MHYYDy9eybL9R5jTv6fd2m7rGAzQt6/yePxx5WJ66tSvF9O33lK+urgo5hAfr0QyXfjw8mq8ne25GfyUfYodsx45/70zFSUUW0wkeHXAKuX5/TBNpaxM0Xrh48QJRbuUv5ravfcq2WSjonQDaC3ya0sACHL1U1XHpZis5dRZK+y6fgAtNAQpZTI0Gs0zCEiVUqbVH7sYmAHYzBB6xnfg4xXbz78O8vfEz9udO55aSHS4P+VVtcy/eYgqi0ZjEzvRt2M4b2/axg09u+Du4mx3De0BIZR5806dlLBKUC6uGRmwf78Sd3/iBKxb9+tF2NtbMYaYGAgKAn9/pdDPhV+/rjrOqMCu1BR5kGsEC2Y25Z4hy1TNrd6dyc8TWCxQUwPFxVBS0vDXgoJf262uvtiYOnVSpoD69lWmf/SLv/0orisDINBFWxsyKupyAPCysyEIW8TqCyGSgD82NGUkhJgFTJZS3l//+k5gsJTykUuPrX9/PjAfIDg4uP+SJUuapOHNb5OJDfMisaMv+1ILiQ71onO4N2fyK/H3ciE2zOvc+ZvxG16ZiooKvBq51UwtqeBf+08wPTacqdHqxDo3RacWsKfOujowmZQpGYtFid23WC5+vk/kkSZKub4qHikh1bmIoy75RLkb6VMQBygXcCGU2H6jUXk09NzVVXnYcw+A/ne/Ogc4xTrDPh60Tsabxqsd2ktnldtR8gO/ICzvYVzrrm0dYcyYMXuklAOa026jH00hxAagoavYU1LKFU1oo6Er8BVdSEq5AFgAkJiYKEePHt2EJsA7tDMbth/np6PZBPh4c8v0MXSKCGzSz7aEpKQkGtM4Gthfs5KNaWf4083TCfSyf5nNpujUAlrTuSM3g99uXk5lX+Ujm5ZTypiwOPqXwZS5o9UV1wS01p9XQi2duRkmOL2PSSMn4GJofPRuL53JJQXk58PIwVNwdwpo9fbO0aghSCnHt7CNTODCrFGRgM2DuPt37UjfxEhyCkqJCPG76D17rx00xGPjh3PDu5/zdtI2/j5tnKpadJrO4NAovpl8B6/u20yYhzeP9RnB0LBodmz55aLj1makMDqiE67GNhO41y4or6vE1eDSJDOwJ1XmPAzCGTejfRe77fHp3QXECyFigSzgVuD21mhICM6bwYUmoLYZAHQKCuDWgb35ctcBbh3Qiy5hwWpL0mkisT4BvDfqpiveWBwvzueBpGUk+AXxytCp9AnSVk4cnStTYa7Gy0l7FYCqzAV4GIPsfu1qURykEOImIUQmMAT4Xgixtv77HYQQqwGklGbgEWAtkAwskVIeaZnsK+pp8LlW+N3oIfi4ufL86k2q1m3QaR5X+kwl+gfzydjZlJtqmfnDQl7as0mz6S10LqbKUo2Hk/ZSvVabC3B3av0p70tpkSFIKb+VUkZKKV2llKFSykn138+WUk694LjVUsoEKWVnKeULLRXtqPh5uPF/44ezOyOL7w4eU1uOjg0ZE9mZtdPv45a4XvznyA6uX/UJ+/K1kd5C58rUWEy4G13VlnEZ1ZYi3I0OZghaprqmjg07jmvuTvzmvj3oFRHGK+t+oqy6Rm05OjbEx8WNl4ZM4fPxt1BdV8fNa/TRgtaptZpwNWirShpAjaXI7usH0IYNYc3WZJ5653v219dI0AoGg+CZ68dSVFXNGz+qkwtHp3UZ2SGWNdPvZU5nZbQw/ftPOVx4Vm1ZOg1gsppxNmgrEEBKK7WWMlyN9t8b0WYNYcqwrvh4ufHlDypWeL8C3TuEcnv9AvPBTP1C0RbxcXHj5aFT+GTcbEpqa7hx9ee8eWBLu6nO5ihYpAUnOyaPawomawUSK25GP7u33WYNwc3VmZvH9uanvSc5k1ustpzL+MPYoYR4e/HUinWYzPqUQltlTERn1k2/j6nRXfj3gS3MXrOIU224OpujYZFWjEJbl8Fai7J72tVo//oM2uoJGzN7Qh+cjEa+/GGv2lIuw8vNlWdvGMeJ/EI++Gmn2nJ0WhE/V3feGjmdd0bO4FRZEVNXfcL/UvZrbn2rPaLFv4HJWg6Ai8Hb7m23aUMI9PNk8tAurPrpMMVlVWrLuYzRCZ2Y0asrC7bs4ki2/Qv56NiXaTFdWTv9PvoFdeAv29fwm01LKarR3udSR11M1goAXIz2T+XRpg0BYO7UAdTWWfh6/X61pTTInyePxt/DjT8vX4fJrM8vt3XCPLxZOOFWnh4wjp+yTzHlu4/ZejZdbVntFqMwYJHaKmBVZ1VuEpwN9k9x0+YNITYikBH9OvP1hv1U19SpLecy/DzcePaG8aTkFfBO0ja15ejYAYMQ3NdtIMum3Imnswtz133Jy3uS9AVnFXAyGLFIbfW7ud4QnIRuCK3C3dMGUlZRw/JNB9WW0iBjEztzc9/ufLhlFztPZ6otR8dO9AgMY9X193BrfB8+OLKd29Z+SXZlmdqy2hXOwpk6q7aCOvQRQivTM74D/bt25IvVu6kxaW+UAPCXyaOJCvDjiWU/UFKlb1hrL3g4u/DSkMm8NWI6ycV5TP3uY9afOaG2rHaDi8EJk1Vb1wSzrAXAyWD/HdTtwhAA7rvpOgpKKlmZdFhtKQ3i6erCv26eQmFFFU9/t16T0Q86rcf02G58N+0eIrx8+c2mpby0ZxNmq7bmttsibkZXaqwmtWVchKXeEIxCN4RWQ0mPHcHnq3ZSa9LWEPEcPSPC+MO4YaxPTuWrPYfUlqNjZzr5BLBsyp3ckdCX/xzZwZ0bFpNXXaG2rDaNu9GVarO2RuQWqwkQCGxXr7uptBtDALh/5hDyiytZkaTdi+28If0Z3jmaF39I4mhOntpydOyMq9GJ56+bxGvDrmdffjbXr/qEHbkZastqs3g4uVNhqVZbxkVIzBiEsyoZm9uVIZwbJXz23U7NriUYDIJXZk4mwNOdR5esolRPgNcuublzT1ZMvRtvZ1fmrlvMwuN79WnEVsDLyZ0qcw1WDYWeWqUZg11K1VxOuzIEIQTzbx5KQUklyzZqM+IIIMDTgzdmT+NsaTlPLFuD1apfCNojif7BLJ96FyM7xPL0jnU8sXW1njnVxvg4eyKRVJq1M0qQWBEqpdNoV4YA0K9rRwZ1j+Kz73ZSWa2txaQL6dMxnD9PHs3mE6d476ftasvRUQkfFzf+O3YWv+81jK9PHuKWNYvIrSpXW1abwddZ2Q1cUqedtRopJQaVLs3tzhAAHpoznJLyahat3q22lKty28BezOjdlXeStrPx2Em15eiohEEIHuszggWjZ3KitIDp33/GwYIctWW1CfyclXxBJSbt7P+QSECdio/t0hC6dQpj3KAE/vfDHgpLKtWWc0WEEDw7bTw9O4Ty+NIfOHY2X21JOioyMSqBpVPuxMlgYPbaRaw8dVRtSQ5PgIuSUbRIQ4agJi2tqTxbCHFECGEVQgy4ynGnhRCHhBD7hRCauC1/aM4wTGYL//1W2+ki3JydeOfW6Xi7ufLbL1eQX65dA9Npfbr6h7Dy+nvoHRjG739eyev7f9YXm1tAgKtShKbQVKqykl8RCCTqLHK3dIRwGJgJ/NSEY8dIKftIKa9oHPakY6g/M8f2YkXSIU5nazs/faiPF+/dNp3iqmoeWbySmjp9YbE9E+jmwRcTbmN25568dfAX/rDlO32xuZl4Gt1xN7pSUKudmilCGBzTEKSUyVLK47YSY2/uu/E6XF2ceWdxU/xMXbp3COXVmVM4mHWWJ5b9gEXfxdqucTEaeWXoVB7vO5IVp45yx7rFFFTro8drRQhBsKs/eTUaMgSMSJUS7tlrDUEC64QQe4QQ8+3UZqP4+3hwz/RB/LwvjV1HtL/5Z3zXOP40aRTrklN54YckfaqgnSOE4OGeQ3l35I0cLjrLzWsWkl6unQuboxDiFkBuTaHaMs5jFM5YpTojPtHYRUUIsQEIa+Ctp6SUK+qPSQL+KKVscH1ACNFBSpkthAgB1gO/k1I2eFtebxjzAYKDg/svWbKkqb9Ls6gzW3l92VGcjQYevakrRsO1re5XVFTg5WXfQhbfpGaxITOPGbHhTIlu6E9zOWrobA66zuaRWlvOG/nHEcD/C+5CJ1dFm9Z0Xgk1dW4Q+zlCBr+XNyAaie6xh84S742U+mwkKut5RDPu2ceMGbOn2VPzUsoWP4AkYEATj/07ink0emxCQoK0B0m7TshBd7wmv1q795p/dtOmTbYX1AgWi1X+8ZvVMvGZ1+WS3Qeb9DNq6GwOus7mk1pSIIcvfU8mfvGqXJeRIqXUps6GUFPn8sxNcurm38mS2rJGj7WHzoOFn8tPU4bIOktNs34e2C2beS1v9SkjIYSnEML73HNgIspidKNYLPaZEhnZvzODekSzYOlWikq1X9LQYBC8MGMiI+JieGbVRn447LDLODo2pLNvIMum3EWifzAPJC1jSap2d+NriQj3EACyqrUR1n0u7bVZ2j9tTUvDTm8SQmQCQ4DvhRBr67/fQQixuv6wUGCLEOIAsBP4Xkq5pinnLy+xT4cIIXjsjtFU1dbx3pKf7dJmS3FxMvLmnGn069iBx5et4Ud945oOEOzuyf8m3MawsGie2Lqa1WXZakvSPOcM4UyVNuqaG4UbABargxmClPJbKWWklNJVShkqpZxU//1sKeXU+udpUsre9Y/uUsoXmnr+mmozGafs49qxEYHcOqkv3/10hEOpjvFP5OHizAe3z6BbeAiPfv09P6eeVluSjgbwdHbho7GzmRbTlSUlGTy/eyNWPQDhioS4BeBicOZM1Vm1pQDgZFAMoU7aP7+StncqC1jy6Ra7NXffjUMI9vfilU83YrY4Rlinl5srH95xE3HBATyyeCW/nNQLtusoYalvjZjOeK8w/nt0F49v/V4vuHMFjMJAR49Q0qu0kQ7EWXgCv5bStCeaNgQPTxc2/nCQnEz7bBzzdHfhj3eNISU9n8Vr9tqlTVvg6+7Gx3feTEygPw/9bwU/nTiltiQdDWAQgrn+0TzWZwRLTx7m9z+voFbfwNYg0R7hnK7UxsyAs1GppVxntf++Ek0bgpe3C0ajga/sOEoY1T+OEf06s2DZVrLySuzWbkvx93Tn07tnERccyMOLv9OT4ekAyvrY73sN468DxrI6/Tj3/7iUqjrtZvlVixjPDhSZyiirU39zn4tBCWs1Weyf1VbThmAwCibf2I/13+0nN6fELm0KIXj8rrEYDYKXP9noUJu//D3c+eTum+kWFsyjS1bp0Uc657m/2yBeGTKFX86e5u6NS6ioq1VbkqaI9ewAwKnKLJWVgItBycBqsto/JbemDQFgzt3DAVj8if2if0IDvfntnOHsPJzOD78k261dW+Dr7sZHd86kT2Q4j32zmsW7DqgtSUcjzInvzVsjprM3P4u7NiyhzKRX4ztHrFcEAGkV6huCq/GcIegjhMsICfNl8o39WLdiH2ez7Lct/+ZxfegV34F/f7FJ0ymyG+LcQvPI+Fj+/v2PvLd5u0ONdHRaj2kxXXl35I0cKszhjvWLKanVTqUwNfF38SHQxZeTFWfUloKT8MAgnKm12D8Dq+YNAeC2+0ZiMAq+WJBktzYNBsFffzORWpOZlz7Z4HAXVHcXZ9659QZm9O7KW5u2sfhEpp4QTweAydGJ/Gf0TI4V53Pruv9RVKP9zZj2oLNXR1I1YAhCCFwNvrohXImgEB+mzRrIxtUH7LYvASA6PICHZg/n570nHW7qCMDZaOSlGZO4b2h/NmcX8Mji76gy1aktS0cDjI2M4+OxszlVVszt67/UTQFI8I4isyqPKg3UV3Yz+lNtsX+iQocwBIBb5o3A1c2Zz9//0b7tTupHn8QIXlu4idxCx6tlazAIHp84klvjI9l84hR3frKEvHLt1I/VUY/hHWL4aMws3RTqSfCORiI5Ua7+KKGb/y3EeU+xe7sOYwh+/p7MnDuEnzceJeWo/RZ+DAbB3+ZPwmKx8tyHa7FaHWvq6ByjI4J577bpnCoo5pYPF+vlOHUAxRT+O+ZmxRTWfUlhOzaFBO9oAJLL1d/HE+czlWjvMXZv12EMAeDmO4bi4+vBx+9ssGu7ESF+PHr7KHYdyeCrdfvs2rYtGZ3QiS/unYNVSm77aDFrj55QW5KOBhjRIZaPx87iVHkxd65fTGlt+4w+8nb2oKNHKMll6huCWjiUIXh6uXHbfSPYtyONPdtS7dr2jWN6MqJfZ9796mdS0vPs2rYt6RYewtfzbyMhVNmr8NaPWx121KNjO4aFx/Cf0TNJLS3krg1ftduQ1G4+nThWdhqrbJ8BGA5lCADTZg8iLMKfD99ch8WO+YaEEPz1/on4ernx9Hurqa5x3MXZEG8vFt4zi5l9uvPeTzt4ePFKSqvb5wVA51dGR3TivVE3cqQol3s2ft0uN6918+lEhbmKDI0kurM3DmcILi5O3PvIeE6dyGXDqv12bdvP252/PziF9Jwi/r1ok13btjUuTk68MGMCf50yhp9TT3PzfxZxNMdxRz46tmF8x3jeGTmDAwXZ3Lvxa6rNjnvj0xx6+sUBcLjUvjMQWsHhDAFg5ITudO3VkU/f3Uh1lX3vYgZ2j+KuaYNYkXSY9dsdOzWEEII7Bvdh4bzZmK1Wbv3vYr7ec8jh9lzo2JbJ0Ym8MXw6u/Iy+e3m5Zgs6hR8V4NQt0BCXAM4WNI+19cc0hCEEDzw2CSKCivsmh77HPNnDqFnXDgvfrSOfDsV8WlN+nbswLIH5jIgOoKnv9vA48vWUFHT/qYLdH7lhtiuvHjdZDZlneQPW1a2q9TZPf3iOFSSqtl1BIu19f43HdIQALr27MjoST345out5Nkp8d05nJyMvPDINFycnVi4Mc2h1xPOEeDpwYd33MSjY4byw+Hj3PSfRRzMbJ/zqDoKtyX0OZ8l9Ymtq9tNkZ0+fgmUmStVz2uUW72fXflvsj3vNarNRZyt2sf3Z37DD5m/JatyO1Zp+5GbwxoCwL2/mwDAgjfW2b3t0EBv/vHQVPJKanj5U8dLbdEQRoOBh0YNZuG82VisVm7/+Cs++GmnnvKiHXN/t0E81mcEy9IO8/xux8r+21x6+SUAcKAkRTUNxbUn2ZX/FqWmdEpNp9hd8A5HS76ki+/NRHuNYk/BuxTW2n7K2qENITTcj1vuGcHPG46wf2ea3dsf3DOa8f3CWfNLMss2tp2C5v2iIvj2wTuY0DWON378hTs+WUJGUYnasnRU4nc9h3JPl/58nLyb9w5vU1tOqxPk6keke6iqhpBc8jUh7j0ZH/E6kyLfoaIuG3/XODr7TKZnwF14O3ckr9r215wWGYIQ4lUhxDEhxEEhxLdCCL8rHDdZCHFcCJEqhHiyJW1eyuy7hhEW4c+7r67GXGf/xa+xfcIY2juW17/YxP7j6qfOtRW+7m68Pmsqr86cQmpeETe+/wWLdx9sF3eIOhcjhOBvA8dzY2x3Xt33EwuPO041webSxz+Rw6UnqbOqMx0sseBm9D//2sclihrzr7mNnA3umFuhxGZLRwjrgR5Syl5ACvDnSw8QQhiBd4EpQDfgNiFEtxa2ex5XN2ce+uMUMtLyWb54u61O22QMQvDsQ1MID/bhybe+c8h8R1dCCMENvbqw8rd30jsyjL+v2si9ny8ls9j+WRh11MUgBK8Om8r4yDj+tmMd351yvGSP10Jf/0RqrSaOlqqzaznANZGzVXupqMuh1JROnbWSYlMqm7L/zJazz1NqSifcY6DN222RIUgp10kpzxVp3Q5ENnDYICBVSpkmpTQBi4EZLWn3Uq4bmcjgEQkcO6zOHbqPpxuv/mEGdWYLO4+0vSL34b7efHzXzfx92jgOZuXy9qa2P22gcznOBiPvjJzBwJBIvko90KZHi7184wl1C6TMrE4tlEjPIbg7BbIl9zl25b+Fl3MHRob9g0C3LjgZXOkf/DAh7j1t/jcQtjqhEOI74Csp5ReXfH8WMFlKeX/96zuBwVLKR65wnvnA/PqXPYDDNhHYegQBBWqLaAK6Ttui67Qtuk7bkSil9G7ODzo1doAQYgMQ1sBbT0kpV9Qf8xRgBhY1dIoGvndFF5JSLgAW1J93t5RyQGMa1cQRNIKu09boOm2LrtN2CCF2N/dnGzUEKeX4Rhq/G5gGjJMNDzcygY4XvI4Esq9FpI6Ojo5O69PSKKPJwJ+A6VLKKy157wLihRCxQggX4FZgZUva1dHR0dGxPS2NMnoH8AbWCyH2CyE+ABBCdBBCrAaoX3R+BFgLJANLpJRHmnj+BS3UZw8cQSPoOm2NrtO26DptR7M12mxRWUdHR0fHsXHonco6Ojo6OrZDNwQdHR0dHUBDhqCFNBhNQQgxWwhxRAhhFUJcMfxMCHFaCHGofm2l2WFgzeUadKrdnwFCiPVCiBP1X/2vcJwq/dlY/wiFt+rfPyiE6GcvbdegcbQQorS+7/YLIf5mb431Oj4WQuQJIRrcW6SFvqzX0ZhO1ftTCNFRCLFJCJFc/3/+aAPHXHt/Sik18QAmAk71z/8J/LOBY4zASaAT4AIcALrZWWdXIBFIAgZc5bjTQJCK/dmoTo305yvAk/XPn2zo765Wfzalf4CpwA8o+22uA3ZoUONoYJVan8ULdIwE+gGHr/C+qn15DTpV708gHOhX/9wbJXVQiz+bmhkhSI2kwWgMKWWylFLzpdKaqFP1/qxv77P6558BN9q5/avRlP6ZAXwuFbYDfkKIcI1p1ARSyp+AoqsconZfAk3SqTpSyhwp5d765+UoEZwRlxx2zf2pGUO4hHtRnO1SIoAzF7zO5PJO0AoSWCeE2FOfjkOLaKE/Q6WUOaB8yIGQKxynRn82pX/U7sOmtj9ECHFACPGDEKK7faRdM2r35bWgmf4UQsQAfYEdl7x1zf3Z6E5lW2LvNBjNpSk6m8AwKWW2ECIEZZ/Gsfo7D5thA52q9+c1nKbV+7MBmtI/dunDq9CU9vcC0VLKCiHEVGA5EN/awpqB2n3ZVDTTn0IIL2Ap8AcpZdmlbzfwI1ftT7sagnSQNBiN6WziObLrv+YJIb5FGdrb9AJmA52q96cQIlcIES6lzKkfzuZd4Ryt3p8N0JT+UTs1S6PtX3ihkFKuFkK8J4QIklJqLUmb2n3ZJLTSn0IIZxQzWCSlXNbAIdfcn5qZMhJtKA2GEMJTCOF97jnKgrkWs7ZqoT9XAnfXP78buGxko2J/NqV/VgJ31Ud0XAeUnpsCsxONahRChAkhRP3zQSj/94V21NhU1O7LJqGF/qxv/yMgWUr5+hUOu/b+VHOl/JIV8VSU+a799Y8P6r/fAVh9ycp5CkpkxVMq6LwJxXlrgVxg7aU6USI+DtQ/jmhVp0b6MxDYCJyo/xqgpf5sqH+AB4EH658LlAJQJ4FDXCXyTEWNj9T32wGUgI2h9tZYr+NLIAeoq/9s3qe1vmyiTtX7ExiOMv1z8IJr5tSW9qeeukJHR0dHB9DQlJGOjo6OjrrohqCjo6OjA+iGoKOjo6NTj24IOjo6OjqAbgg6Ojo6OvXohqCjo6OjA+iGoKOjo6NTz/8HW+8swHyjABcAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"theta0 = 5.5\n",
"x0 = np.array((np.sin(theta0),np.cos(theta0)))\n",
"\n",
"## Run Algorithm 5.1 on test problem\n",
"results = alg52(x0,my_f3,my_h3)\n",
"\n",
"## Display results\n",
"xstar = results[0][-1]\n",
"print(\"\\nx* =\",xstar)\n",
"\n",
"## Display results\n",
"vstar = results[1][-1]\n",
"print(\"\\nv* =\",vstar)\n",
"\n",
"## Convert into theta\n",
"print(\"\\ntheta* =\",np.arccos(xstar[0]),\"(using arccos)\")\n",
"print(\"\\ntheta* =\",np.arcsin(xstar[1]),\"(using arcsin)\")\n",
"\n",
"## Visualize\n",
"visualize(results[0])"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.8.4.3 Starting Point Near Global Max ($\\theta_0 = 5.5$)](https://ndcbe.github.io/CBE60499/04.08-Interior-Point2.html#4.8.4.3-Starting-Point-Near-Global-Max-($\\theta_0-=-5.5$))",
"section": "4.8.4.3 Starting Point Near Global Max ($\\theta_0 = 5.5$)"
}
},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"id": "f3f70c86",
"metadata": {},
"source": [
"\n",
"< [4.7 Simple Netwon Method for Equality Constrained NLPs](https://ndcbe.github.io/CBE60499/04.07-Interior-Point1.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [4.9 Algorithms Homework 4: Interior Point Methods](https://ndcbe.github.io/CBE60499/04.09-Algorithms4.html) > 
 "
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.6"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.6"
}
},
"nbformat": 4,
"nbformat_minor": 2
}

