{
"cells": [
{
"cell_type": "markdown",
"id": "0bbc6dd5",
"metadata": {},
"source": [
"\n",
"*This notebook contains material from [CBE60499](https://ndcbe.github.io/CBE60499);\n",
"content is available [on Github](git@github.com:ndcbe/CBE60499.git).*\n"
]
},
{
"cell_type": "markdown",
"id": "e0d652d6",
"metadata": {},
"source": [
"\n",
"< [4.1 Convexity Revisited](https://ndcbe.github.io/CBE60499/04.01-Convexity.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [4.3 Analysis of KKT Conditions](https://ndcbe.github.io/CBE60499/04.03-KKT-Multipliers.html) > 
 "
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 1,
"link": "[4.2 Local Optimality Conditions](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2-Local-Optimality-Conditions)",
"section": "4.2 Local Optimality Conditions"
}
},
"source": [
"# 4.2 Local Optimality Conditions"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 1,
"link": "[4.2 Local Optimality Conditions](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2-Local-Optimality-Conditions)",
"section": "4.2 Local Optimality Conditions"
}
},
"source": [
"**Reference** Section 4.2 in Biegler (2010)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.2.1 Unconstrained Optimality Conditions](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.1-Unconstrained-Optimality-Conditions)",
"section": "4.2.1 Unconstrained Optimality Conditions"
}
},
"source": [
"## 4.2.1 Unconstrained Optimality Conditions"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.2.1 Unconstrained Optimality Conditions](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.1-Unconstrained-Optimality-Conditions)",
"section": "4.2.1 Unconstrained Optimality Conditions"
}
},
"source": [
"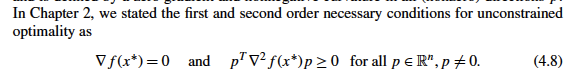"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.2.2 Karush-Kuhn-Tucker (KKT) Necessary Conditions](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.2-Karush-Kuhn-Tucker-(KKT)-Necessary-Conditions)",
"section": "4.2.2 Karush-Kuhn-Tucker (KKT) Necessary Conditions"
}
},
"source": [
"## 4.2.2 Karush-Kuhn-Tucker (KKT) Necessary Conditions"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.2.2 Karush-Kuhn-Tucker (KKT) Necessary Conditions](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.2-Karush-Kuhn-Tucker-(KKT)-Necessary-Conditions)",
"section": "4.2.2 Karush-Kuhn-Tucker (KKT) Necessary Conditions"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.2.2 Karush-Kuhn-Tucker (KKT) Necessary Conditions](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.2-Karush-Kuhn-Tucker-(KKT)-Necessary-Conditions)",
"section": "4.2.2 Karush-Kuhn-Tucker (KKT) Necessary Conditions"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.2.3 Kinematic Interpretation via Example](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3-Kinematic-Interpretation-via-Example)",
"section": "4.2.3 Kinematic Interpretation via Example"
}
},
"source": [
"## 4.2.3 Kinematic Interpretation via Example\n",
"\n",
"Consider the following two dimensional optimization problem:\n",
"\n",
"$$\n",
"\\begin{align} \\min_{x_1,x_2} \\quad & f(x) := x_1^2 - 4 x_1 + \\frac{3}{2} x_2^2 -7x_2 + x_1 x_2 + 9 - \\mathrm{ln}(x_1) - \\mathrm{ln}(x_2) \\\\\n",
"\\mathrm{s.t.} \\quad & g(x) := 4 - x_1 x_2 \\leq 0 \\\\\n",
" & h(x) := 2 x_1 - x_2 = 0\n",
"\\end{align}\n",
"$$"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.2.3 Kinematic Interpretation via Example](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3-Kinematic-Interpretation-via-Example)",
"section": "4.2.3 Kinematic Interpretation via Example"
}
},
"outputs": [],
"source": [
"import numpy as np\n",
"import matplotlib.cm as cm\n",
"import matplotlib.pyplot as plt\n",
"from pyomo.environ import *"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.1 Define Function for Visualization](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.1-Define-Function-for-Visualization)",
"section": "4.2.3.1 Define Function for Visualization"
}
},
"source": [
"### 4.2.3.1 Define Function for Visualization"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.1 Define Function for Visualization](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.1-Define-Function-for-Visualization)",
"section": "4.2.3.1 Define Function for Visualization"
}
},
"outputs": [],
"source": [
"## Objective function\n",
"def f(x):\n",
" return x[0]**2 - 4*x[0] + 1.5*x[1]**2 - 7*x[1] + x[0]*x[1] + 9 - np.log(x[0]) - np.log(x[1])\n",
"\n",
"## Gradient of objective f(x)\n",
"def df(x):\n",
" return np.array((2*x[0] - 4 + x[1] - 1/x[0], 3*x[1] - 7 + x[0] - 1/x[1]))\n",
"\n",
"## Gradient of inequality constraint g(x)\n",
"def dg(x):\n",
" return np.array((-x[1], -x[0]))\n",
"\n",
"## Gradient of equality constraint h(x)\n",
"def dh(x):\n",
" return np.array([2, -1])\n",
"\n",
"## Function that plots contour of objective, solution, and optionally g(x) <= 0 and h(x) = 0\n",
"def visualize(xsln,plot_g,plot_h):\n",
" ## Create contour plot\n",
" \n",
" n1 = 101\n",
" n2 = 101\n",
" x1eval = np.linspace(0.05,10,n1)\n",
" x2eval = np.linspace(0.05,10,n2)\n",
" \n",
" X, Y = np.meshgrid(x1eval, x2eval)\n",
" \n",
" Z = np.zeros([n2,n1])\n",
" \n",
" for i in range(0,n1):\n",
" for j in range(0,n2):\n",
" Z[j,i] = f((X[j,i], Y[j,i]))\n",
" \n",
" fig, ax = plt.subplots()\n",
" CS = ax.contour(X, Y, Z)\n",
" ax.clabel(CS, inline=1, fontsize=10)\n",
" \n",
" ## Plot g(x) <= 0\n",
" if(plot_g):\n",
" g_x2 = np.zeros(n1)\n",
" for i in range(0,n1):\n",
" # Inverted g(x) = 0 to calculate x2 explicitly from x1\n",
" g_x2[i] = 4 / x1eval[i]\n",
" \n",
" plt.plot(x1eval,g_x2,color=\"blue\",linestyle=\"-.\",label=\"$g(x) \\leq 0$\")\n",
" \n",
" ## Plot h(x) = 0\n",
" if(plot_h):\n",
" h_x2 = 2*x1eval\n",
" plt.plot(x1eval,h_x2,color=\"red\",linestyle=\"--\",label=\"$h(x) = 0$\")\n",
" \n",
" ## Plot solution\n",
" plt.scatter(xsln[0],xsln[1],marker=\"*\",color=\"black\",label=\"$x^{*}$\")\n",
" \n",
" ## Adjust x and y limits\n",
" plt.xlim([-1,10])\n",
" plt.ylim([-1,10])\n",
" \n",
" ## Add legend\n",
" plt.legend()\n",
" \n",
"## Function that draws gradient of f(x) and optionally g(x) and h(x)\n",
"def draw_gradients(x,with_g,with_h):\n",
" dh_x = dh(x)\n",
" \n",
" ## Draw gradient of f(x) [objective]\n",
" df_x = df(x)\n",
" plt.arrow(x[0],x[1],df_x[0],df_x[1],color=\"black\",width=0.1)\n",
" \n",
" ## Draw gradient of g(x) [inequality]\n",
" if(with_g):\n",
" dg_x = dg(x)\n",
" plt.arrow(x[0],x[1],dg_x[0],dg_x[1],color=\"blue\",width=0.1)\n",
" \n",
" ## Draw gradient of h(x) [equality]\n",
" if(with_h):\n",
" dh_x = dh(x)\n",
" plt.arrow(x[0],x[1],dh_x[0],dh_x[1],color=\"red\",width=0.1)\n",
" \n",
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.2 Define function to solve optimization problem with Pyomo](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.2-Define-function-to-solve-optimization-problem-with-Pyomo)",
"section": "4.2.3.2 Define function to solve optimization problem with Pyomo"
}
},
"source": [
"### 4.2.3.2 Define function to solve optimization problem with Pyomo"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.2 Define function to solve optimization problem with Pyomo](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.2-Define-function-to-solve-optimization-problem-with-Pyomo)",
"section": "4.2.3.2 Define function to solve optimization problem with Pyomo"
}
},
"outputs": [],
"source": [
"def solve_opt(consider_g,consider_h):\n",
" \n",
" ## Create concrete Pyomo model\n",
" m = ConcreteModel()\n",
" \n",
" ## Declare variables with initial values\n",
" m.x1 = Var(bounds=(0,100),initialize=10)\n",
" m.x2 = Var(bounds=(0,100),initialize=10)\n",
" \n",
" ## Declare objective\n",
" m.OBJ = Objective(expr=m.x1**2 - 4*m.x1 + 1.5*m.x2**2 - 7*m.x2 + m.x1 * m.x2 + 9 - log(m.x1) - log(m.x2), sense = minimize)\n",
" \n",
" if(consider_g):\n",
" ## Add inequality constraint\n",
" m.con1 = Constraint(expr=4 - m.x1*m.x2 <= 0)\n",
" \n",
" if(consider_h):\n",
" ## Add equality constraint\n",
" m.con2 = Constraint(expr=2*m.x1 - m.x2 == 0)\n",
" \n",
" ## Specify IPOPT as solver\n",
" solver = SolverFactory('ipopt')\n",
"\n",
" ## Solve the model\n",
" results = solver.solve(m, tee = True)\n",
" \n",
" ## Return the solution\n",
" return [value(m.x1),value(m.x2)]\n",
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.3 Take 1: Unconstrained](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.3-Take-1:-Unconstrained)",
"section": "4.2.3.3 Take 1: Unconstrained"
}
},
"source": [
"### 4.2.3.3 Take 1: Unconstrained"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.3 Take 1: Unconstrained](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.3-Take-1:-Unconstrained)",
"section": "4.2.3.3 Take 1: Unconstrained"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Ipopt 3.12.10: \n",
"\n",
"******************************************************************************\n",
"This program contains Ipopt, a library for large-scale nonlinear optimization.\n",
" Ipopt is released as open source code under the Eclipse Public License (EPL).\n",
" For more information visit http://projects.coin-or.org/Ipopt\n",
"******************************************************************************\n",
"\n",
"This is Ipopt version 3.12.10, running with linear solver mumps.\n",
"NOTE: Other linear solvers might be more efficient (see Ipopt documentation).\n",
"\n",
"Number of nonzeros in equality constraint Jacobian...: 0\n",
"Number of nonzeros in inequality constraint Jacobian.: 0\n",
"Number of nonzeros in Lagrangian Hessian.............: 3\n",
"\n",
"Total number of variables............................: 2\n",
" variables with only lower bounds: 0\n",
" variables with lower and upper bounds: 2\n",
" variables with only upper bounds: 0\n",
"Total number of equality constraints.................: 0\n",
"Total number of inequality constraints...............: 0\n",
" inequality constraints with only lower bounds: 0\n",
" inequality constraints with lower and upper bounds: 0\n",
" inequality constraints with only upper bounds: 0\n",
"\n",
"iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls\n",
" 0 2.4439483e+02 0.00e+00 3.29e+01 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0\n",
" 1 -8.0094510e-01 0.00e+00 4.03e-01 -1.0 8.53e+00 - 9.05e-01 1.00e+00f 1\n",
" 2 -8.7120418e-01 0.00e+00 2.51e-03 -1.0 1.31e-01 - 1.00e+00 1.00e+00f 1\n",
" 3 -8.7421973e-01 0.00e+00 5.46e-04 -2.5 3.76e-02 - 1.00e+00 1.00e+00f 1\n",
" 4 -8.7422408e-01 0.00e+00 1.29e-06 -3.8 1.78e-03 - 1.00e+00 1.00e+00f 1\n",
" 5 -8.7422408e-01 0.00e+00 6.93e-10 -5.7 4.12e-05 - 1.00e+00 1.00e+00f 1\n",
" 6 -8.7422408e-01 0.00e+00 9.45e-14 -8.6 4.81e-07 - 1.00e+00 1.00e+00f 1\n",
"\n",
"Number of Iterations....: 6\n",
"\n",
" (scaled) (unscaled)\n",
"Objective...............: -8.7422408318635370e-01 -8.7422408318635370e-01\n",
"Dual infeasibility......: 9.4500693109869893e-14 9.4500693109869893e-14\n",
"Constraint violation....: 0.0000000000000000e+00 0.0000000000000000e+00\n",
"Complementarity.........: 2.5065634500861016e-09 2.5065634500861016e-09\n",
"Overall NLP error.......: 2.5065634500861016e-09 2.5065634500861016e-09\n",
"\n",
"\n",
"Number of objective function evaluations = 7\n",
"Number of objective gradient evaluations = 7\n",
"Number of equality constraint evaluations = 0\n",
"Number of inequality constraint evaluations = 0\n",
"Number of equality constraint Jacobian evaluations = 0\n",
"Number of inequality constraint Jacobian evaluations = 0\n",
"Number of Lagrangian Hessian evaluations = 6\n",
"Total CPU secs in IPOPT (w/o function evaluations) = 0.010\n",
"Total CPU secs in NLP function evaluations = 0.000\n",
"\n",
"EXIT: Optimal Solution Found.\n",
"\b"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAAD8CAYAAACMwORRAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzs3Xd4leX5wPHve1b23jshOyQhQNhhb0UcICgKuGuHWqu11dYuW2vV1vpztHVPEMEBorL3DIQRIHvvvcfZz++PYKp1AiEn4/lcl5cmec8590mO93nP/d7P/ShCCCRJkqShRWXrACRJkqS+J5O7JEnSECSTuyRJ0hAkk7skSdIQJJO7JEnSECSTuyRJ0hD0vcldUZTXFEWpUxTl7Je+56koynZFUfLP/9vj8oYpSZIkXYgfcub+BrDgf773a2CnECIa2Hn+a0mSJGmAUH7IIiZFUcKBzUKIxPNf5wIzhBDViqIEAHuEELGXM1BJkiTph9Nc5O38hBDVAOcTvO+3Hagoyl3AXQBOTk5j4+LiLvIhpeHEYDaT19SIRqXC1c4ONzt7nHQ6FFsHNsAJBPntNahQ8NA54aZzQqMM7UtrbaZqDJYuHDXuOKjdUSlqW4d08SzlIDpB5QMqTzj/is/IyGgQQvhcyF1dbHL/wYQQLwEvAaSmporjx49f7oeUhoAuk4mdxYVsLchnT2kxXSYT9nZ2zImIZEFUNFNDw7HTXPaX76BjtlrYW5fFB2VHOd5UhEZRM9MvgSWhExntEY6iDL23x+ruLI43rqWo4zAaxZ5E94WM9lyKq9bP1qFdMGE8hmh/FkzpoHJCcf4xOCxBpbIrvdD76teyjEzu0sXQm03sLy1la2E+O4oLaTMYcNbqmDViBAujYpgeFo69RmvrMAec0o56PihP59PKDNrNeiKd/VgSOoGFgaNx0tjZOrw+12goJaPpfXJbdwAQ6zqbVK/leNqFfettWoxVdJjqCHZK6a8wv5cQAoxHEB3PgukE6Cai9no7QwiReiH3c7HJ/SmgUQjxhKIovwY8hRAPfd/9yOQuXSqjxcLh8jK2FOazrTCfZr0eJ62WmREjuCIqlhnhMtH/L73FyLbqTDaUHSGnrQontR1XBI1maehEIpy/taI6aLWb6jjRtIGzLZ9iFkbmBTxEvNvcrx1nthop6TzK8cZ1qBQ1U3xuJ8gx2QYRf7OeJL8PhBWVw6y+T+6KoqwFZgDeQC3we+Bj4H0gFCgDrhdCNH3fg8nkLvUls9XKkYpyPi/IY2tBPk36bpy0WmaPiOTKqFimhcnSzZcJITjXWsH6siPsqM7EJCyM84pkWegk0nzjUA+x2nyXuYXTzR+T7HE1Tppv7ta2CgsqRU1R+2Fy2rYz0+8+HDRu/Rzp91MU5fKcufcVmdyly+WLRP9Zfi5bCvNp0etx1umYHxnNouhYJoeEolUP4gttfazZ2MHH5cf5sPwotfpWAuzdWRI6kauDU3HTOdo6vEtiMpmoqKhAr9d/77ECgYKCVZjptrTiqPZAACZrN2pFi0alu/wBf4m9vT3BwcFotV/99CmTuyQBJouFQ+VlbM7PZVthAe1GAx729iyMjuWq6FjGBQWjGoIXFi+G2Wphf10275cdJqOpGDuVlgWBo1geNpkoF39bh3dRiouLcXFxwcvL6wdfQG41VqNVOSCwYrEaQVEwWfXoVI64aC+oSeWiCSFobGykvb2diIiIr/xMJndJ+h8Gs5l9pSV8kp/DzqJCus1m/J2cuSo2jsUxcST4+A7JDpKLUdBew/ulh/m86hQGq4mxniO4IWzyoCvZZGdnExcX971/V6O1G5OlC4O1C7WiwVnrQ5OhFDdtIDq1AyarHr2lDWeNT7+9RoQQ5OTkEB8f/5Xvy+T+HYqqG3l1SzolNU2U1jZjNFvQatToNGqc7XV4uDji7uyAj5sT/p4u+Hm4EOjlSpC3G77uzqhVg+fFLX2zTqORncWFfJKXw97SEsxWK1EenlwdF8/imHhC3AZerdUWWoxdbKo4zvqyw9TqWwly8GRZ2CSuCh6Ls8be1uF9r+zs7K8lxy8zWrrosrSgoKBR2aFVHNCpHegw1WMWRtx1QQCYrQbaTfW46QJRgG5LG2ZhwF7tik7l0K/xy+T+HfIrG7jvxY8J9/Mkwt8De50Ws8WK0WyhrUtPc3s3ze1d1Ld20tTe9ZXbatQqgrzcCPVzJ8zXgzA/DyL8PYkI8MLD+fL9kaXLp7m7m88K8tiUm82xqkoAxgYEcnVsPItiYnG3l39Xs9XCnros1pUc4nRLKU5qO64KTmV52CSCHD1tHd63+q7kLoSg09xIp7kJR407LtqebiGrsNJoKMFDF9xbZ28z1aKg4KTxotPchEWY0Kkc6LK04KYNQKu6PG90MrlfRgaTmbqWDqoa26hsaKWivoWKhlZKa5spq2vGYLL0Huvp4khkoBeRAV5EBXkTHeRNZIAXjvb9eyFGungVba1sys1hY242+U2NaFUqZoaP4Nr4BGaERciOGyCrtYK1JQfZUXMGIQQz/BJYEZ5GknvogCtrfd+ZO/S0QXaZmzAJPS4aXwQCvaUNN10AAFZhpsFQgrddBJ3mJlSosFO7oFHp6DQ3oqDC8Vs6cC5H/DK59wOrVVDT3EZxdRPFNU0UVjdSWNVIUXUjXQZT73EhPu7EhvgQE+xDXIgvcSG+eLs52TBy6fsIIciqr+OjnGw25WXT0NWFm509i2JiuS4ugRT/gAGXyPpbnb6V9aVH+KginTZTN4luIdwYPoWZfiPRqAZGN9IPSe5fMFuNCAQqRU27qQ43rT8CQYepHkVR46h2p81ci7PGB62qZ+FXk6EMR4079mpXhBB9/pqQyX2AsVoF1U1t5Fc2kFdRT35lPbnl9VQ0tPYe4+3mRHyoLwmhfsSH+ZEQ6icT/gBltlo5WFbKhzlZbC8qQG82M8LDg+viRnJtXAIBLi62DtGmus1GPq06wdqSg5R3NRJg784N4VNYHJxq89WvF5Lcv2AVVtpNtZiFAbWiQ61ocNJ4o7e0IhA4qN1QKWoMlk66LM24aQN6Z9h8keCtwozJqket6L61hTIrK4v09HRmz56Nu7s7Lt/wOpLJfZDo6DaQW1FPTlkd2WW15JTXUVzTxBe/dn8PFxLC/EgM9ycxwp+EUD9Z0hlg2g0GPivI48PscxyrqkQB0kLDWBI/knmRUcN6RaxFWNlfl8O7Jfs53VyKs8ae60LGszxsMj72rjaJ6WKS+xdMVj0CgVaxR1EUOs1NIAROWi8AWo1VaFUOOKjdUL7UQWS2Gmkz1aBRdBitXThqPHBQu3/trP706dPcdtttrF69mnvuuecbz/plch/EuvRGcsrryCqrI6ukhrOlNVTU95zhqxSFyEAvkkcEkBwRQPKIQEJ9v/4ikWyjtKWFD3PO8WF2FpXtbbjo7FgcG8fShESSff2G9d/pbEs575bsZ3fNOVSKioWBKdwUkcYI5/4d4HUpyf1/dZqbsAoTLlo/uswt6C1tuOuCvjJ50iostJvqetspTdZuOs3NuOsCv3Z/mzdvpqSkhBEjRpCWloar69ffAGVyH2JaOro5V1JDZnE1Z4prOFtcTYfeCIC7kz3JIwJJiQwkJSqQhFA/dFp5kc+WrEJwpKKc9Vln2VKQj8FiJsbLm2UJiVwTF4+nw+Be5XkpKruaWFNygE0VGRisJtJ84lgZMZWUfppK2ZfJ3Ww10m6qw4oZjWKHg9oNnbrnb/tFOUZvae+5GKsNQFFUGCydGKwdXD3vBn798K+YOXsav/3tb+nuMPLcc89TU1ODv/+3LxCTyX2Is1oFxTWNnC6qJrOomsyiKkpqmwHQadQkhPkxOiqIMdHBjBoRgLPD0JvyN1i0GfRszstlfdZZTtfWoFOpmRsZybKEJKaEhg3b1bAtxk42lB1hXelhWk1dJLmHsipiGlN941BdxkVRF5PcW1tbmTx5MocOHcLtG9Y7mK1G1IoGRVF97SLqF6tbHTXuCGFFb+nAZO3i1JE8fvPor1l9282sf+9D3trwbzzsA3vfHC4kfpnch7jm9i5OFVZxqrCKkwWVZJfVYrEKVIpCbIgPY6ODGRsdzOioIFydBv5ik6Eop6Ge9Vln+Sgnixa9niAXV65PSOT6hMRhexFWbzHySUUG75QcoLq7mQgnH1ZGTGNBYMpl6bC5mOS+Zs0abrrpJtasWcONN974ncd2mZuxCDMuWh/MViMtxgq87MJRFBVmq5FOcyMOajcswsycmfPQd5nYs2cPir0BjcoOe3XP6+DbOm1kcpfoNpjILK7mRH4FJ/IrOVNcjdFsQVEgNtiX1JhgxsWGMDoqSJ7Z9zOD2cz2ogLWnTvDwfIyVIrCjLAIbkxMZnp4BJphuOLZbLWws+YsbxbvpaC9Bj97N24On8ri4FQcNH3XRHAhyX3FihVs2rQJg8GA2WxGo9FgZ2fH4sWLWbNmzbfeTgjr+WRuoNPchJsuAKuwoLe0YbIacNP5s/f459yx4l58vH04dOjQ+fZKFU4aL8xWI92Wlt5++S/X8GVyl77GYDJztqSGjLwKjueVk1nUk+zVKoX4UD/Gx4UyPjaEUZGB2Mmafb8pa23h/XNnWZ91lvquTvydnLl+ZCLLRyYR6GKbjhJbEkJwqCGPN4r2cLq5FHetI8vDJ7MsdBIu2ktfGXwhyb2goIDFixdTUlJCd3c3Dg4OREREsGnTJiIjI7/39kJYaTVVYRVWVIoataLFUe1BWVUxixZezYb3P+Tee+/lwQcfZMz0KDx0IZiFEYOlHbWiwypMWLHgpg3sPYuXyV36XgaTmcyiao7llpOeW8a5khosVoGdVs3oqCDGx4UyMT6MmCAfVKrhWRfuTyaLhV0lRaw9k8n+shIURWFmeAQrkkYxLTR8WM4vOtVcwptFezlYn4uT2o4loRNYEZ6Gp53zRd/nhZZlNmzYwI033oidnR0Gg4G1a9eydOnSC3pMg6UDgRU7lQvd3d3MmDWN3/3htyxacA379u3jwYceYNu+jbhq/Wgz1eCgdsdO3bPGpcVYibPGp7c3XiZ36YJ1dBs4UVDJ0ewy0nPKKKxuBMDD2YGJ8WFMSghjYnyYXFjVDyraWnnv7BnWnTtDY3cXwa6u3DAymWUjk/B2HH6dNnltVbxRtJedNWfRqdRcEzKOmyOm4Wd/4cPcLjS5L1u2jG3btvHoo4/y2GOPMX/+fNatW3fBj/tl3eZWzMKIy/nWyFZjDR66YPTWdoSw4KjxRKWoMVn1tJpq8LYL/874ZXKXLkh9SwdHc8o4nF3K0eyy3oFpMcE+TEoIY8rIcEZFBspNLi4jo8XC9sIC1pw9zeGKcrQqFQuiYrg5eRSpAUHDrm++tKOeN4v38nnVKRQUrgoaw6oR0y9oUNmFJvdjx44RGhqKn58ftbW1lJeXk5p6QXn0a0zWbtpMdSiARmXf20b5xVm7VtWzSKrNVIsaDU5ar94LrDK5S33KahXkVdZzOKuEw1mlnCqowmy14mSvY3xcKGkjw5mSGIGv+8V/XJa+W2FTI++eOc0H2Vm0Gw3EenmzMjmFa+IScNQOr1Ww1d3NvFW0j00Vx7EiWBCQwq2RMwh18v7e2/Zln/ulMlg6exI5KgQ9Iw4cNZ5oVfaYrHo6TA04a72/MmFSJnfpsurUG0nPKePguRIOnSuhprkd6DmrT0uMYGpSBInh/sOyTny5dZlMfJKbzduZp8hqqMdFZ8eShJGsTE4hwv3yTCIcqOr0rbxTvJ+PytMxWS3MDxzFrSNmEP4dG3sPpOT+ZUJYaTFV4aT2RKd2pMlQjp3aCSdNz6cSizCjQi0365D6jxCCwqpGDpwr5sDZYk4XVmGxCtydHUgbGc605BFMjA+T7ZZ9TAjBiZoq3jp9ii0FeZisVqaHhbN61BimhYUPq8VRDYZ21hQfYEP5EQwWM3P9k7gtauY3jjb4oTsx9af/rmZto8PUgEZljwoVrjr/8z/vmSevoKa6qJXEhOSv3F4md6lftHXqOZxVyr6zRRw6V0Jrpx6NWkVqTAjTk0cwPTkSf8/huWDncqnr7GDt2UzWnMmkvquTcHcPViWnsCR+JC52w+dNtdnYwbvFB1hfdgS9xfSNSf5i9lDtbxarCbWqp9T2RQ7uMrdQW19JcWMmBs8CJvvc0TufRiZ3qd+ZLVYyi6rYm1nEvswiSut6RiTEhfgyMyWSGaOiiAocuP+TDTZGi4UtBXm8efokJ2uqcdbqWDoykdXJowlzd7d1eP2mxdjJu8UHeL/scE+SD0jijshZhDv7YjKZqKioQK/X2zrMC6az01LneIQTre9hFWaSPRYzwftmHDRuMrlLtlVS08SezEL2nC7kTHE1QkCwjxszR0UxMyWS5IjAH9RTX93UxufpOdQ2t3PNlETiQ/t3suBgcLqmmjdOn+Sz/FzMViuzIyK5NWUME4NDhs2baYuxk3eK97O+7AgGi4n5gaO4PXLWD7rwOpB1mhs5Uv8m51q34Gcfyw0Rz8vkLg0c9a0d7MssYvepQtJzyzBbrHi7OjIzJYpZo6MZGx2MRv3NF2Tve/Fjgr3dCfRy5fNjOSyfPoqrJo3EYrXKi7j/o7ajg3fPnGbNmdM06buJ9/bhttFjWRQdO2y2CGw2dvB28X7Wlx7BLCwsDEzh9shZA3qv1x+iwVCM0dJFkFOiTO7SwNTebeDg2WJ2nszn4LkS9EYzMcE+vPebm792rN5o5ran1/HCvdfh4ezAcx8fwNvVidHRQWzPyONkQSVLpiazcFwcisKwOUv9PnqziY052bx+6gR5TY34ODqxalQKKxJH4eEwPDb8bjS081bRPj4sP4pZWFkcnMptI2bg5zC4S1ay5i4NCt1GE4fOldBtNLFoQsLXfl7V2Mqb2zI4kl3KVRMTyCqrZd7YGN7ansGyGaPwcnHk9a3HeOTG2UQFDe6P35eDEIIDZaW8diqDvaUl2Gs0LIkfyW2jxw6bVsp6fRtvFO3ho/JjqBSF60LGs3rEdLzsBueFfpncpUGvtrmd5zceZFRkIH7uzry+9Rir56XS1qln4+FzvPKLZQA8+9F+ooO8uWL8wOtnHkjyGht47WQGH+dkY7JamBsZxZ1jUhkbEGTr0PpFdXczrxTs4tPKE+jUGm4Im8zNEdNw7YMBZf3pYpL78CjISYPGF2OLr540Eq1Gzemialo79WzPyOO6tCSg58xUrVJRe35hldUqei/SdhtMbD2eS31rB4smJhDgOfymLn5ZjJc3T8yZzwOT0ngr8yTvZJ5mW2EBY/wDuGvsOOaMiBrS/fIBDh48mrSEVSOm83L+Dt4o2ssHZUdZGTGN5WGT+3TU8EAjr0xJA063wYRWo8ZktuDr7kxGXgUFVQ29Z+lGs4X0nDLGRocAPVveATS0dvLvzYc5lFVCfUsnf3xrG80d3TZ7HgOJj5MTD0xK4+Btd/GH6bOo6+rk7k83Me+d11l3NhOD2WzrEC+rMCdv/pxyA+9MvodRHuG8mL+Na/c9zYayI5isQ/O5y+QuDSgJYf6oFIWVT6zh169+RmVDK4qiMDY6GACT2UJGfgVqlULyiACA3o6bT46cQ6tR8/PrpvHIitk42es4eK4YgPYuPXszC9l1qsA2T2yAcNRqWTVqNLtW3c6zC67EQaPl4V3bmf7mK/wnI512g+Fbb2uxWvnL/j3sKBq8v8MY1wD+MXYVr0z4EWFO3jyZtYnr9z/DlqpTWIXV1uH1KZncpQEl0MuVf/7kan5z0xzSRoZz24Lx3LZgPFqNmvYuPedKa9iRkc+VE86fxZt6zrqqGlupqG8lKdyfQK+eUozBZCHEp6dL4sGXNnPgbDFvbD3G79/cSnvX4Fvg0pc0KhVXxcSx6YabefOaJUR5evG3g/tJe/1lnj50AJPF8rXbNHV3E+Dsws8+38zLJ47ZIOq+k+wRxr/H38k/x67GSWPP7zLfZ9WhFzhcn0d/Xoe8nC6p5q4oyv3AHYAAzgC3CiGG9/81Up+IC/ElLqRnOJSjnRaNWsXKv63Fx82ZZdNHkZYYAYDu/I5S2aV1ODvYEeLbk8zPFFfj5+GMEIJtGbmoVSp+s2IOADf99V1aOvW4OPZM4jt4roTIAK9hOTJBURSmhoYzNTSczNoa/pNxjGNVFd+4DaCPkxNLExL5ODebCUE9JbFTNdXo1GoSfL59kNdApSgKk31imegdzbbqTP6dv537Mt5grOcI7oldQIJbsK1DvCQXndwVRQkC7gUShBDdiqK8D9wAvNFHsUkSAFqNmt+smIPBZKayoZURAV4YTGZO5Ffg7+lKoJcrzg469EYzHi49G10cyy0nyNsNg8lCbnk981JjAKiobyEuxBeT2UJLRzcvf3aUsrpmKhvbSBsZzv1Lpg3bvvlkP39euOIqjBbLt/4OXso4RqSHJ8l+/hjMZjKqq/gkLwcfR0cenDyVWK/B15qqUlQsCExhtn8iH5an81rhbm45/CJz/JP4cfQ8Qpy8bB3iRbnUsowGcFAURQM4AlWXHpIkfTM7rYYRAT2bGmjUKkxmCznldT0/02korG7Aw9mBLr2RQ1klJIT5gRA0tHUyPjYUgKb2bjRqFWqVig37Mqlv7eC5n13L8z+7lrqWDroMJls+xQFB9y2bs5S3trKrpIgfp44Heko7NyeN4uPlNzE2IIgX0o/0Z5h9TqvSsDxsMh9Me4DbI2dyoD6HZQee4emsT2gxdn7nbUs7G8hpreynSH+Yi07uQohK4GmgDKgGWoUQ2/73OEVR7lIU5biiKMfr6+svPlJJOk9RFNQqFRPiw5iVEgVAoJcbbo72rHxiDX9Zu5MAT1cmxofR2qVHbzQT6OWKyWyhvL4FIcDVyZ49mYWsntvTOqzTqLHXacmvlK/Rb/N25kkSfX2J8fLGer4d9Ys2yrTQMDQqFeWtrUDPgLM2w+Cs0Dpr7PlR9Fw+nPoAi4PGsqHsCNfue5o3i/ait3z9zd8qrOyry+LBE2/zZNZGLAPkwuyllGU8gKuBCKAFWK8oys1CiHe+fJwQ4iXgJehZxHQJsUrSt/J1d+bvdy9m7+lCXJ3siQvtqQGX17Xidb5Uk1tRT3ZZLWOjg6lqaMVqFYwM/2KetiC/sp5Qn+GxgvOHMpjNbMg+x/jAYI5VVfL8wquA82NqFQWtWk1lext7Snq6kvydnek0Gnni4D4Km5pw0mn525z5eDoMvn1hve1deTjxWm4In8LzuVt4IW8rkc5+pPnGfeU4laJiZcQ0WoxdlHc1oFYGRp/KpUQxBygWQtQLIUzAh8DkvglLki7O9FGRjI4KwkHXMyt7fmoMp4uqeHzNTp77+AC+7s7MHxfL5qPZjIsN6b3dgbPFeLs54enqOGS6JfqC0WLheFUli997h6buboJc/7sorKi5iWePHuKX27bQYTLyi0lTqOno4P/SD9NlMvHmNUsIcXNne+HgbZ0EiHD25e9jV/HmpJ8yxSf2G4/JbavicEMeP4me1/u9NlM3VV3N/RXm11xKt0wZMFFRFEegG5gNyNkC0oAS7OPO0z+6im3H8xgfF8KcMT0XVrVqVW83Tnl9C0eyS7liXE975fmTUglwsbPjmflX8LNxjTy2bw9vnDqBVq3mWFUF9moN9hoNv06bRrJfzyegvx8+gKudPTcmJqNVq4lw92B3STHLE5O/55EGvni3bx7ZYBVW3inezyTvGMKdfWkydJDRVMSWqlO0mrrwtHPm4ZHX4KHr3/2HLzq5CyGOKoqyATgBmIGTnC+/SNJAEuDpyup5Xx3LMX1UJE+/v4eWjm6yy2oJ8/Nk1pie+r1KpWCxWtlyLJdZKVE42A2vzam/SaSnF29cs4T6rk5+v3sn+8tK+OXkqawaNbr3mIzqSpq6u1kYFUL4+QFlZ+pqmB8ZDTBkxzXvqj1HaWcDv09aCsCL+dvw1Dlxa+RMEt1DeCl/B+8UH+BH0XPQqfpv4ssl/aaFEL8XQsQJIRKFECuFEN++vE2SBpCx0cHcfdUk8isbGBMdzF1XTkSrVveWZI7nlvPoG1uY//DLPLluN0XVjTaOeGDwcXTixSsX896S5RwoK2X5hvc4XtXTJdJlMuFiZ0f4+R2h9peVoFZURHj0JHq1StX7+81uqOdfx4/y9KEDg3L0gUVY2V6dicFiYmP5cZaFTUKjUnO4Po+TTcW4ah2p7u4pydwVPYebI9LQqTR0mQ2937/c5OAwadianhzJ9OTI3q+/2MQYYHxcKK/84no+2H+GDw6c4b09pxgTHcTSqcnMHh2NVvPN7YLDxUhfP1666hpO1VT3/s7aDQYKGhsJdnUD4LP8PGK9vHuT/Rdn7mfqavntru1cE5dAcUszd23+mOcWLsLVzt5mz+dC6S0mtlaf5vFzH+Fr58qioDEAbCg7QqSLH/4O7mwoPUJpZz13RM3GQ+dMaWcD/8rbSqupC4sQPJ5yI96XcQSxTO6SdN6XF+4oisKY6GDGRAfzYPt0Nh3O4oP9mTzy2ud4ue7l2ilJLJmahJ/H8FvV+mUp/gG9/+3t6ES70cD+0hIOV5RT19nJz8ZNxN2+Z7zuFyWZvx3cxxXRMdyaMoZOo5GHd27DZBkY7YM/lJPGjqfHrGRvbRZ/z97MupJDpHpF4u/gzrKwyYQ5eTPKPYynsjcBsL8uh+ONhYQ4evNE7Hyez93CgbocrgkZd9lilMldkr6Hh4sjq+elsnLOWA5nl/L+3lO8uuUor29NZ3pyJMtnpJAaEzxsV7Z+YXxQMKtHjebfGelMDgnjTzNm93bXmCwWtGo1O4sLaTcY+NHYnoVQXSYTViHoMBoBOFBeyqbcHNJCw7g1ZYzNnssPNd0vgel+CRS21xLm5E2X2Yi9uucazZbqU3SbTQghOFifQ7RLADP8ejancVDrONlcLJO7JA0EKpXClJHhTBkZTmVDKxv2Z/LxwbPsOlVAZIAXy2emcOX4+GF9AfaK6FiuiP5vu2BDVxdV7W293TT/OnaUZSOTen+eXllBm8FAmLs7v9qxFXuNhuUjE3n5xHHs1GpWJI3q9+dwMSJd/DBbLbhoHXjoxDvM9k/ineJ9PJt6K3vrstGptCS5h+Bl50KHSU9BRw2Lg3ou8luFFdVl6I0fdsndYrFe+GtnAAAgAElEQVSSm11FfW0bnZ0Gujp7rgFrtGp0WjWOTna4uDrg4uqAu4cjnl7OaIZ5fVX6uiBvN+67dio/unISW4/nsm7PqZ5e+o8OcM2URJbPGEWgl5utw7S58tYW0qsqSPbzp6KtFbVKxdL4kQB0GI28e+Y0Px0/gfVZZ+k0Gnlo8lS8HB1x0Go5WFbae8bfaTTipBvYG2toVGp+EX8lh+vzqDO08fSYlcS7BZHdWoGTRkeoU8/cnS3Vp/CxcyPQoedC85cTu95iIqu1nJFuIdipL+0kYdgk94qyRja8d5RD+3JpbvruORH/y93dEW9fV/wC3PDzd8M/wJ3AIA8Czv+j1crkP1zZ6zRcPXkkiyclcLqoirW7T7Fm1wne3XmCmSmRrJg1hpTIwGFbshkdEMjogEAAgl3dCHN3J6O6imhPL9aezcTHyYnJwaEsWvs2f5o5Gy/HnpWsO4sKsQiBVq3mRHUV72Seoqy1hVtSxrAoJu67HtLmJvnEfOXr0s4GAhzcsVfryGqt4FRTCbP9Ewly9ATAbLWgUak51ljIxvJjtJv1VHY1cW/cQqb5Xvw2ksMmuXd3G9m59QzjJ0UxZVosI6L8cHTS4ehoh6KA0WjBZDLT3WWkrbWb9rZumps6aWrsoKG+nfr6NirKGslIL0Lf/d/5EiqVgn+AO8GhXoSEeREW4U1YuA9hI3xwcrKz4TOW+pOiKKREBpESGURNUzvr953mg/2Z7DxZQHyoLytmjWHe2Jhh32UzNiCIP+zZibuDA7PCR/DrKdPYVVxEvLcPo/x6Ls62GfTsLS3h7WuXsq0wn835uUwICuHGpGRePJbOhOAQfBydbPxMfrhE9xBeKtiBgsLGiuNcFTyWcV5RaFQ9rbcalRqj1cwT5z7mlhEzuCp4LJsrT3CoPveSkvuw2SBbCIHRaMbuEuuhQghamruormymsqKJyoomKsqaKC9rpKK0EaPxvz27fv5uRET6MiLKlxHRfkRG+xMY5NG736c0tHUbTXx6NJs1u05SUtOEj5sTN8xMYUlaMq5Og6ft73LIqq/rnQH/WX4umbU1/DptOgB/3LsLgFWjRvNSxjHSQsK4IjoGRVG4au3bPDptJuODBtes9fTGAk41lRDrGsj08xdV4b9n7f/O305RRy1Pjr4Zi7BytCGfIw0F3BM7H61KIzfI/i6KolxyYv/ifjw8nfDwdCIh6asvMIvFSm11C6UlDZQU1VNcWEdRQS3pRwqwWnreRB0cdURF+xEVG0B0rD+x8YEEh3rJhD8EOei0LJ2azHVTkjiUVcK7O0/w3McHeeXzdK6eNJKbZo8hyHt41uW/vLmHq509Z+rqqO3oIL+pkc8L8vhsxSo+ycvB18mJZD9/FEXhZHUV/s7OxHv72DDyizPeK4rxXlG9X++ry2aCVxR2ai1Nhg42VhznpfF3AaBWVGS3VaJRqVBQ+Lj84na9GjbJvT+o1SoCgz0JDPZkUtp/625Gg5nSknoK8moozK8lP7eGzzed5CN9T3nH0cmOmLgA4kYGEp8QRHxiEB6e/TuHQrp8VCqFtMQI0hIjyKuo592dJ9iwP5P3955m9phoVs0Z2zudcjiaEBRMemUF129Yy4LIaH4zdQaeDo7UdXYS7elNiFvPG+Ce0mJS/AMGzEjdS5HfVk2woycjnP34qCKdyd4xhDh5YRVWyrua2FadyYvjbue1wt00GTsu6jGGTVlmoLFYrJSVNJCbXdXzT1YVRQV1WM4v5vAPdCchMYiEpBASk0MIH+GDWj305nIMV/UtHazdfZIN+zLp0BtJjQlh9bxUJieEDduLr51GI/YaTe9ip1s3fsAto8YwPTyCIxXlbMg6y9Vx8UwNDbdtoH1sX102Wa0V3B09l9KOet4q3ke4sw9TfeJ45PR7PDN2Nf4O7hdclpHJfQAxGEzk59aQfbaCrLOVZJ2toKmh513b0cmOkUnBJKWEkpQSSkxcADqd/OA12HV0G/jo4FnW7DpBbXMH0UHe3DJvHHPHxqAZxm/mJouFvx7Yi06jYXXyaO785CNuTBrF4pg4XOyGVqNCTmslvzn9HpEufugUDYGOHvw4eh4Pn1pDqlckS0MnXlTNXSb3AUwIQW1NK2dPl3M2s5wzp8ooK2kAQKfTkJAYRPKYMEaNDiNuZJBM9oOYyWxhy7Ec3th2nOKaJoK8XFk5N5XFk0ZiP0z/rg1dXTy6ewcqRWGkjy8/GTfhKz8vam7iZE0118Yl9O4INViZrRY2VhwnyT2UEc6+1BvaeCF3Kz+NnY+/vTsqlUom96GutaWLs6fLOX2ylMyTpRQV1CIE2NlpSBwVyujUcEanRhAZ7SfLOIOQ1SrYf6aI17Ye40xxNZ4ujtw8ewxLpyXj7DC0zlh/KIPZjJ2m5w3OKkRvIv/rgb28fOI4ib5+PDptBuMCB1cHzXdpN3Xz57Mf8rukpThp7OSZ+3DU3tbNmVNlnMwo4dTxEkqKe/YAdXF1IGVMGGPHjyB1wgj8AtxtHKl0IYQQnMiv5NUt6RzJLsXFwY4bZqZw48zRuDs72Dq8AcEqBJtys3ny4H5qOju4IiqGX6dN651KOZi1Grv4feb72Kt1JHuEclPEVJnch7umxg5OZZRw4lgxJ44VUV/XDkBIqBepEyMZNzGS5NGhfdIWKvWPrNIaXv08nd2nC3Gw03L9tGRWzhmLl+vgWchzOXWZTLx84hj/yTiGVQjuHJPK3WPHD/hxBT/EywU7cdc6six8skzu0n8JISgrbSTjaCHHjhSSebIMo9GMVqcmZUw44ydFMX5SJIHBnrYOVfoBCiobeH3rMbYez0WnUXNtWhK3zEvFx122zQJUtbfx5KH9bMrNwc/JmV9NmcbVsXFDovtIlmWk72QwmMg8WcaxI4UcO1JARVkTAKHh3kycEs3EKdEkJAaj1sha/UBWWtvMa1vS+Sw9G7VKxXVpSdwyfxy+MskDPdv9PbZvD5m1NYwNCOR302eR5Otn67AuiUzu0gWprGji6MECjh7KJ/NkKWazFRdXB8ZPimTS1BjGTYjEUc7HGbAq6lt4bcsxNh/JQqVSuDYtiVtlkgd66vEfZJ/jyYP7aeruYvnIJB6cnIang6OtQ7soMrlLF62z00DG0SKOHMzjyMEC2tu60erUjEmNYPK0WCZPjcHdQ9Z4B6LKhlZe25LOJ4d7kvySqcncOn8c3m7y79VmMPBc+mHePH0SR62WX0ycwk1JowbdRt0yuUt9wmK2cvZMOYf35XFwXw411a2oVAqJo0JImx5H2ow4fHxdbR2m9D8qG1p59fN0PjlyDo1axbLpKdwyLxUPl8F5ttqX8hsb+eO+XRwqLyPB24c/zpzN2IAgW4f1g8nkLvU5IQSF+bUc3JfLgd05va2WCYnBTJsVz9SZcfj6Df7Ws6GkrK6FVz47wmfpOdjpNKyYOZqVc8YO+0mUQgg+L8jnL/t3U93RwZL4kfxqyjS8HQf+m59M7tJlV17ayL7d2ezbnU1Rfi3Qk+inz45n2qwEvH2G94bRA0lxTRP/2XyYbRl5uDjYsWpuKjfOTMHRfvC3CF6KLpOJ59IP89rJDBy0Wh6clMaNickDulQjk7vUryrKm9i3K4u9u3oSvaJA8ugwZsxJYNrMeFzdfvgZkRBiSLSsDUR5FfW8uOkQ+84U4eniyB0Lx3NdWhI67fAca/CFgqZGfr9nJ4crykn28+exmXMGbFeNTO6SzZSVNLB3Zxa7t5+jvKwRtVrFuImRzJw7ksnTYrG3//ZFUxaLFbVahdlskfvVXkaZRdU8v/EAx/MqCPB05cdXTWLh+LgBfcZ6uQkh2Jibw+MH9tDU3c3K5BTunzgF1wE2nEwmd8nmhBAU5tWye8c5dm8/S31dOw6OOlbfMZ0lN0z4xtuYzRbKSxt56s+bmDoznmU3TZJzcS4TIQRHsst47uMD5JTXERXoxT3XpJGWGDGsPzm1GfT8/fBB3sk8hY+TE7+bNpOFUTED5ncik7s0oFitgjOnStmx9SzjJ0YydebX94O0mK18+P5RqitbKMirYcz4CG65cwbVlc3k59YwbdbF7yEpfTurVbDjZB4vbDxEeX0LY6KDuO/aqSRFBNg6NJs6XVPNb3ZtJ6uhnhnhEfxpxuwBMatGJndpUKmtbuE/z+8kJtaf+KRgNm44zk9+Po9D+3LJz62morwJg97Ez36x4GtbGkp9w2Sx8NGBs7z06RGa2ruYOyaan12TRojP8B00Z7ZaefP0SZ45chAhBPdPnMItKWPQ2LB8dTHJXX72lWyiqqKJ11/aw+SpMdywago1VS3Y22uws9Pw9qv7WHbTZJ7512pGjQmnuqoZ6CkpSH1Lq1azbPooNv7pVu66ciL7zxaz5I9v8tT7e2jp6LZ1eDahUam4ffRYtt58C5NDQnn8wF6uW/cuZ+tqbR3aBZHJXbIJg8FMW1s3776xnzde2sPRQwXMX5TC3l1ZjBkfQUiYFyaThbAIb0qLezYo+aL+KZN833Oy13H3okls/NOtXDUpgXV7TnH1717n7R0ZGE1mW4dnE0Eurry06BqeX3gVNZ0dXLvuXZ44uI9uk8nWof0gl1SWURTFHXgFSAQEcJsQ4vC3HS/LMtL/yj5XyWv/2kVOdhXX3ziRPTuzeOjRxcQl9Kwe/L+nPsfb14UVq9N6u2qgZ479pxtPUl3ZzBVXjyY2PtCWT2PIKahs4J8f7udQVgnB3m7cd+1UZo2OGjAXGPtbq17PEwf3se7cGcLc3Hl81lwmhYT22+PboizzLLBFCBEHjAKyL/H+pGHCYu7ZCDwmNoCY+EBuuXMGOjstLi4OxCUEYbFYqa9r48zpMubMT+q50fnzkJKiel7/zx4qyhoJCvHk5Rd20tjQbqNnMjRFBXnz/D3X8sI912Gv0/DLlzdz5zPryS4bXKWJvuJmb89fZ8/j3WuvB+Cmj9bzm13baTMYbBzZt7vo5K4oiiswDXgVQAhhFEK09FVg0tD2xVjh9vZujEYzk6fGMG5iJJHRPYtIuruM7NhyhuhYf3z93bBaRe9tdm49g6+/G7f/eCbLbpqEg6OOk8dLANDrTeRmV1FbLV+KfWFSQhhrHrmZR1bMpqi6iZufWMMf3tpGQ2unrUOziUkhoXy2YhV3jkll3bkzLHjnDXYVF9k6rG900WUZRVFSgJeALHrO2jOA+4QQnf9z3F3AXQChoaFjS0tLLylgaejq7NDz6/vXEhLqCYqCi4s9CxalEBHpi9FgRmenIetsBVs3n2bm3JGkjA1Hrzfxx4fXc8dPZhMZ7cejD63D3k7L6ZOlXHXtWJavnCw3Du8j7d0GXvnsKGt3n8ROq+GOhRO4cWbKsF3perqmml/t2EpeUyPXxiXw6LQZuNtfni0Q+7UVUlGUVOAIMEUIcVRRlGeBNiHEo992G1lzl75PZ6eBrZtPYbUKrrl+3NdWrH768QmamjqYf+UofP3cOHwgj4z0IuYsSKKspIEdW87w5P/djMlk4aF73+H3jy/tHVUsV8D2jbK6Zv6+YS/7zxQT4uPOg9dPZ2rSCFuHZRMGs5kXjx/lX8fT8bB34C+z5jBnRFSfP05/19wrgAohxNHzX28AxlzC/UkSTk52XLd8AktvnIhGo6axoZ0P3jtK5smeT3yOTnY0NXb0TqI8cayYsHAfOtr15OfUsHhJz+u/vLQBN3dHdDoNHe169uw4xy9+/BZP/XkT1ZXNNnt+Q0GorwfP/uQanvvZtahVCve9uJH7XvyY8vrhVwqz02i4f+IUPlq2Am9HR+7avJEHtn1Oq15v69AuPrkLIWqAckVRYs9/azY9JRpJ6jNe3i7MXZhEUEjPPq9mswV9d08r2tGD+VSUNRKbEEhnpwGj0cy4iZEAtDR34uHphADWvXOIIwfyufeXC3FxdeDD99Nt9XSGlCkjw1n325Xcd+1UMvIqWPqnt3hx0yG6jYOjVbAvjfT146PlN3HP+Il8kpfDgnffZHeJbWvxl9otcw/wrqIomUAK8PilhyRJX+Xq5oiXd88o4eSUUJqbOlm97AU+23SSGXNGEhMXQF52NV7eztjZaWlv66astBF7ex0Wi5Xd28+x+s7pRMX4kzYjDovFSlvb8Fyg09e0GjWr56Xy0R9uYc6YaF75/ChL//gWe04XDrv1CDq1mvsnTuHDZStws7fn9k0f8fDObXQYjTaJ55KuhAghTgEXVAeSpEvhF+DOE/9cQXFhHe4eTnh49tTTiwpqeweTZZ4so7KsibSZcRzen0dktB8BQR4IIbCz0/SshrX79imV0oXzcXfmL7cu5Lq0JJ5Yu4tf/HsTaYkRPLRsBsHDbJRBoq8fG5ffxD+PHuLlE8c5WF7KU3MWMCE4pF/jkCtUpUEpItK3N7EDzL9yFK/9ezebPjjOW6/tY2RyMKNGh7FxwzEWLh4N9Kxw3b87B19/N3R2GqzW4XVm2R/GRgez5jc38Ysl0ziRX8H1j73FK58dHXarXO00Gn41ZRrrli5HrahY8eH7PL5/DwZz//0eZHKXhoQZc0ayfOVkqqtauOXO6cyYM5K6mla0Og1jx/d0cjTUt3PyeDGLru657j9MF1tedlq1mpvnjOXDP9zC1KQRvPjJIW74yzsczyu3dWj9bmxAEJ+uWMWKpFG8cjKDq9e9S3Z9Xb88tpwKKQ1ZQgheeGYrsfGBxCcGs/mjDIwGM/f+cuFXjjl6qIBxEyPlDPnL5OC5Ev723i4qGlq5alICP79uGh7Ol6cffCDbU1LMr3ZspVWv54HJU7h9dCqqH3iGIUf+StL/OHwgj3dfP4CiwMLFoxk/KRJvH9febf0y0ov49c/XEBTiyQ0rJzNnQZLshb8Muo0mXvnsKG9vz8DZQcf9S6axaGLCsJtV09TdxSO7trOtsICJQSH8fd5CAly+f99hmdwl6VvU17Xh4+v6te9brYKDe3NY8+ZBCvJq8A9wY/nKycy7YpRc2XoZFFQ28Oc1O8gsqmZCXCiPrJg97GbHCyFYn3WWP+3bjVal5i+z5nJFdMx33kYmd0n6Dt+1CbcQgvRDBbzz+n5ysqrw8XXhxlVpzF8kk3xfs1oFG/Zn8tzHB7BYrNx91SRWzBqDZpiVxUpamrl/62ecrq3h+oREfj99Fo7ab+7iksldki6REIKM9CLefnU/WWcr8PFz5cZVU1iwKAWtVpZr+lJdSwd/XbuTvZlFJIT58bub5xIT7GPrsPqVyWLh2aOH+dfxo4S7e/DsgitJ9PX72nEyuUtSHxFCcOJYMW+9so+ssxX4+btx821TmbsguXc6pXTphBBsP5HH397bTXuXgVsXjOOOhRPQDrPrHofLy3hg2+c0dnfxqynTuDVlzFc+ZcrkLkl9TAjB8aNFvPnyXnKzqwgM9mD1HT2tlirV8LoYeDm1dHTz1Po9fJ6eQ1SQN39YOY+EsK+fwQ5lzd3d/GrHVnYUFzIrfARPzp2Pp4MjIJO7JF02QggO78/jjZf3UlxYR0SkL7f+aAYTp0QPu46Py2lvZiGPr9lJU3sXt8wbx51XTBhWI4WFELydeYrH9+/Fw8GBZxdcyfigYJncJelys1oFe3dm8cbLe6iqaGZkcjB3/HgWiaP6b8u1oa69S8/T6/fyyZEsooK8+dPq+cSF+No6rH51rq6We7Z8SllrC/dPnMzPxk+SyV2S+oPZbGHr5tO89do+mho6mDglmtt/PIvwEcPrguDltO9MEX9+dwct7d3cvnA8ty0cj1Y9fGrxHUYjv9m1HYvVygtXLpbJXZL6k15v4uP301n79iH03UbmXTmK1XdMw9vn6z310oVr7dTz5Pu7+Tw9h4QwPx67ZQER/p62DqvfCCEwWizYa7UyuUuSLbS2dLHmzQNs+uA4Go2a61dM5PqbJuHgoLN1aEPCjhN5PL5mJ91GE/dck8YNM0YPqwvasuYuSTZWXdnMq//ezd6dWXh6O3PrXTOYuzBZzq3pAw2tnTz27nb2nylmYnwof1g1H193Z1uH1S9kcpekAeLcmXL+8387yD5XSVSMPz++by7Jo8NsHdagJ4TgwwNn+PuGveg0an570xzmjPnupftDgUzukjSACCHYvf0cr7y4k/q6dqbNiueun87GL2B4zVK5HMrqmvnt61s4W1LD4kkj+eWyGTjZD90SmEzukjQA6fUm1r97mHXvHEIIuGHlZJbdPAk7uRvUJTFZLLy0+QivbU0nyNuNv952BSPD/W0d1mUhk7skDWB1Na289MJO9u7Mwj/AjbvvncfkaTFyEdQlysiv4NHXt9DQ2slPrp7MqjmpQ+5iq0zukjQInMoo4YV/bKWkuJ7xk6L46f3zCAwePu19l0Nbp57H3t3OzpMFTIwP47Fb5uPl6vT9NxwkZHKXpEHCbLawccNx3nplLyazhRtunswNK6egsxs+S+37mhCCDw6c4e/r9+DsYMefb1nAhPihcRFbJndJGmQa6tv5z3Pb2bMji8BgD+775ULGjBth67AGtfzKBn79yqeU1DZxx8IJ3HXlRNSqwd2KKpO7JA1SJ44V8exTn1NV0czs+Yn86J65eHgOnbJCf+s2mHhi3S4+OZxFakwwf7ltIT5ug7cnXiZ3SRrEjAYza946wLq3D+HgaMeP7pnDvCuS5QXXS7Dp8DmeWLsLJwcdj992BeNiQ2wd0kWRyV2ShoDS4nqe+dunnMusYHRqOPf/6koCgjxsHdagVVjVwC9f/pSy2mZ+fNVkbp0/btB108jkLklDhNUq+HTjCV55YSdWq+DWH83g6qXj5BiDi9SlN/LYuzvYejyXaUkjeOyW+bg42ts6rB9MJndJGmLq69p49snPOHqogITEYB54ZBGh4d62DmtQEkKwbs8p/rFhH/5eLjx911WDZs9WmdwlaQgSQrBz61lefGYreoOJW++awXXLJ8iz+It0urCKh17eTHuXgd+tnMuCcXG2Dul7XUxyl68OSRrgFEVhzoIkXllzN6njI3np+Z088NO3qChvsnVog9KoyEDWPHIT8WF+PPLa5zzzwT7MFqutw+pz8sxdkgYRIQQ7tpzhxX9uw2yycNfP5rDo2jGyo+YimMwW/vHBPtbtOcX42BCeuONK3J0dbB3WN5JlGUkaJhrq23j6L5vJSC9i3MRIHnhkEV7eLrYOa1DaeOgcj6/diZ+7M/+4ezFRQQPvmoZNyjKKoqgVRTmpKMrmS70vSZJ+GG8fV/76zI387IEFZJ4s5a6VL3Fwb66twxqUrp48kpfvvx690cQtT73H3tOFtg6pT/RFzf0+ILsP7keSpAugKApXL0nlxdfvwM/fjT88vJ5nnviU7m6jrUMbdJJHBPDOwzcR7u/JL/6zide3ptOfVY3L4ZKSu6IowcCVwCt9E44kSRcqNNybZ1+6leU3T+bzT07y01tfpSCvxtZhDTq+7s688otlzBsby3MfH+T3b27FaDLbOqyLdqln7v8EHgK+9VKzoih3KYpyXFGU4/X19Zf4cJIkfROtVs0dP5nFE8/eRGeXgXvvfJ2P1x8b9Gef/c1ep+Hx2xZy96JJbD6azd3PfkBzR7etw7ooF53cFUVZBNQJITK+6zghxEtCiFQhRKqPz+BYMCBJg9WY1Aj+8+adjBkXwQvPbOWPj2ygvW1wJidbURSFu66cyF9vv4LsslpWP7mW0tpmW4d1wS7lzH0KsFhRlBLgPWCWoijv9ElUkiRdNHcPJx57ajk/umcORw7k85NbXyEnq9LWYQ0681Nj+ffPl9LZbWT1k2vJyK+wdUgX5KKTuxDiYSFEsBAiHLgB2CWEuLnPIpMk6aIpisLSGyfyj3+twmoV3H/3m2z64Lgs01ygUSMCefOhG/B0deIn//chW48Nno4kuUJVkoawhMRg/vXGHYwZN4Ln/r6FJ/74seymuUDBPu68/uBykiL8efi1z3hz2+B4k+yT5C6E2COEWNQX9yVJUt9ydXPksaeWc8tdM9i9/Rz33vk6lRVydMGFcHOy54V7rmPu2Bie/Wg/T6/fi9U6sBO8PHOXpGFApVK46ZY0Hv/HjTQ2dPDT217l6KECW4c1qNhpNfz1tiu4afYY1u4+ycOvfTagWyVlcpekYSR1QiQvvHYb/gHuPPrL91j71sFBUWIYKFQqhQeWTufn101le0Ye977wMZ36gVnmksldkoaZgEAP/vmfW5g+O4HX/r2bx3/3EXq9ydZhDSqr5qbyx1XzyMiv4K5n1tPc3mXrkL5GJndJGobs7bU88sdr/7+9e4/Puf7/OP547drRhs1swxza8HWMaMnh25JT+UYkcviGX+kgh5SlpINQfb+SckiIFCpyLMX320ESqRA5jS1iNsbWGGHsuub9+2P7+upbsdN1fa7r2ut+u7nZrl2fz+f5sXnuc30+n+v9ZtDD7Vj/ZSIjhyzgl8zTVsfyKF1bNWLy4Dv4OT2LQa8u5fjJX62O9Bta7kqVUSJCn/6tGf9yb9IOZzF00DyS96VbHcujxF8by+vDe5CZfYb7XlnC4YxsqyNdouWuVBnXsk1dps7+P/x8bSQMWcCmrz3nXm53cH3d6sx+tCc5uXbun/wBB47+YnUkQMtdKQXE1I5k+tx7uSY2guefWsqKD763OpJHaVgrirkje4EID7y6lH2pGVZH0nJXSuULqxTCpNf70+bm+syc+jkzp37m9vdyu5PYquHMHXk3gQF+PPTaMvYcsnZkTi13pdQlgYF+PDOhB9173cCKDzbz4nMryL3gvvdyu5uakaHMHXk3FcoF8PDU5ez4+ahlWbTclVK/YbP5MOTRTjw4rANff7mXMQmLOHv2gtWxPEa18ArMTbibsPLlGDZ9pWUFr+WulPodEaFXv5aMHtuN3TtSeXzoQk6eOGt1LI8RFVaeOSN7UcnCgtdyV0r9qfa3Xsv4l+8mNeUXRg6ZT8axU1ZH8hiRoSGXCn749JUuPwev5a6UuqIWrerwz6l/5+SJszz68HzSUnXQsc/rIpQAABRhSURBVMKKDA1h9qM9qRgcyJBpK1x6F42Wu1Lqqho3qcErr/cn94KDhCELSDmoU2YWVpVK5Zn9WC+Cg/wZMm0FP6dnuWS7Wu5KqUKp85cqTJ7RH4CEoQs58NNxixN5jmrhFZg1oie+PsLgKctIzXT+O1m13JVShVYrJoLJbwzA39/GE4+8qwVfBDUjQ5k54i4ceRcZMnU5mdlnnLo9ceVwn3FxcWbr1q0u254r5eXlkX7gOAd3HebgrsNkpv7C2dPnOJN9jjxHHv6BfgQE+RMcGkxEdDiVq4dTJSaSaxrXILxqGCJi9S4oVWhH007w+LCFXLjgYNL0e4itE2V1JI+RmHKMB19bRtVK+bdMVgwOvOoyIvKDMSauKNvRci8Be66dH9ftYePy79j00RayC0bV8/ERwqqEEhIaTHDFctj8bNjP27mQk8uvJ85wIv3kb975V75SCLWb1qJhq3o0bF2Phq3+QvmwEKt2S6lCOZp2goShC3HY83hlRn9qxURYHcljbElKZfjrK6lXI5JZI+4iKMDvis/XcncRYwzrFm3kzScWknX0JEEhgdzY5Xqu79CE2Ka1qNWwOgFBAX+6fJ4jjxPHsjnyUzqH9qRyaHcqyT8c4MCPh7iYdxEfH6H+jXVp1TWONne2oEa9aBfunVKFl3Y4i4ShCwF4deYAoqtXsjiR51i7/SeenLOa1o2uYfLgrvjZbH/6XC13Fzh2KINpQ+aw5d8/Ur9FHfqO6UFcp6b4B/qXeN05Z8+TtHk/P67bzeY12/hp20EA6jSLoV3fv9K2TxsiqoeXeDtKlaaUg5mMHLKAoCB/Xps1kIjIClZH8hjLN+zkxffX0q11I567p+Ofnp7VcneylMRUHot/DvsFO/e92I87ht6K7Qq/bUsqMy2LDcu/Y92ijezbvB8fH6HF7c3pMeJ2rrulsZ6nV24jeV86o4a/S3jlEF6bOZCKoeWsjuQxZn68iTlrvufB21syuEurP3yOlrsTnck+y7Abn+Lc6XO8tmEC0XWqunT7R/an89k7X7FmzhdkZ54mtmkt+jx5J/G9Wjr1F4xShbXrx8OMfvR9YutG8fK0vxMUVPJXs2WBMYbnF37Gx98mMm5AJ7q2avS75xSn3PVWyEKaMng2xw5m8NzSBJcXO0B0narc+0Jf3kuZycg5g3HkOnip3xQGNXyM9Us26STHynLXXleTp8ffSfLeo7zwzAryHBetjuQRRIRn+nWgRb0aTHj3C7Ymp5bKerXcC2H/jwdZv+Rb+o3pQeO/NrA0i3+gP50HtWfOrld5bmkCfgG+vNDnNR6Lf5bkHw5Ymk2p1vH1eOTxzmz+dj/TXvmXHnQUkp+vjUkPdqFmVCiPz/6YlOMnS7xOLfdCWDb5Y8pVCKLHo7dbHeUSHx8fbrqrJbO2T+KxNwdzJDmdYS2eYtqQOeScybE6nirDbu/enL4D2rBm1XYWL9xkdRyPUb5cIFMe7oaPjw8j3viQ02fPl2h9Wu6FsHN9Iq26xhESGmx1lN+x2Wz87f72vJM8je7DO/PJ7M8Z3PwJEr9LtjqaKsPufagt7To1Yt6sdWxYt9fqOB6jekQokx/qytGs04x+aw2OvOKf2tJyv4pzv+aQmZbFNY1qWB3lioIrBjNkyr1M+nIsjlwHj930LEsmfaQvi5UlRISEp7rSoFE0E8d/xE9J6VZH8hjN6kQzpm97vtubwrSVG4q9Hi33q7iQkwtAUPkgi5MUTtObG/Hmjlf4a48bmfPku7wy6A3suXarY6kyyD/Al3ETe1EhtBxjRy/VyT6KoHubxvRuex3vrt3GvzbvK9Y6tNyvws/fFwD7Bc8pyOCKwTyz+DHuebYnn73zFc/eMZELOTpNmnK9sEohjPtnL06dPMeEp5fhcORZHcljjOwZT/O60by8ZF2xltdyv4rgiuUYMPZumrb9/b2n7kxEGDiuNyPnDGbb5zt5vsckcj3oF5TyHnXrVSVhTBd27Uhl7htfWh3HY/jZbEy8/3ZmjbirWMsXu9xFpIaIrBORvSKyR0RGFHdd7kxE6D+2F3WbxzptG6dOnaJRo0acOlX6U5h1HtSekXMGs/XTHbx6/0w9B68s0a5TY7r1jGP54u/1AmsRhFcIpl6NyGItW5IjdweQYIxpALQEhopIwxKsr8xavXo1iYmJrFmzxinrv+2+dgwc15u1723g3/P0yElZ46HhHanfsBqvvPQJ6UdKfh+3urJil7sxJt0Ys63g41+BvYAOX1gE/fr1IyQkhIEDBwIwYMAAQkJC6NevX6lvq++YO2ne4VpmPDKPY4dcN4+jUv/h52fj6Qk98PERXnh2BXa7nn93plI55y4i1wDNgO//4GsPishWEdmamen58y6ePX2OdYu/YfbjC8hKL9nRx/jx46lZsyZ+fvljOfv5+VGrVi0mTJhQGlF/w2az8fi8oQDMe/r9Ul+/UoVRpWooI5/qQvK+dBbMXW91HK9W4nIXkRBgOfCoMeb0/37dGPOmMSbOGBMXEeHZg/mfPJ7NxAHT2fbFTnx8hLHdJ5KWfLTY66tTpw7jx4/HbrcTHByM3W5n3Lhx1K5duxRT/1dE9XB6juzKukXfkLI3zSnbUOpqbmpbn85dr+ODdzexc3uK1XG8VonKXUT8yC/294wxK0onknu6kHOBLxZ+TcXKFUiY+zAPvNyfCuHlOZ5SslcjS5YsITg4mHHjxhEcHMzSpUtLKfEf6zK4IwDffrTFqdtR6koeHtGJqtXCmPTCKs6d1dt0naEkd8sI8Baw1xjzaulFck/7Nu/n8L4jdB7UDoC05KOERlUkvNp/Z54pzp0oo0aNIikpiYSEBJKSkhg1alSpZf4jlaPDqdMshh8+3+HU7Sh1JUHl/Bn1TFeOHzvFnDfWWh3HK5XkyL0N0B9oJyI/Fvz5Wynlcjs7v0okNLIiDVvVAyA16SiB5QK5eNnYD8YYzp46y/olmwr9pqEbbriBqKj8yYWjoqKIiyvSkM3FUiUmkpPHS/+2S6WKonHTmvTofSOfrNzGDj09U+pKcrfMRmOMGGOaGGOuK/jjnHv5LGaMYe37G7j57vxZUg7uSiFp834qR1citkmtS89bPftzZiUs4NP5X3F/45F898kPVkW+Iv9AP87rS2HlBgY+cDNVqoUyZeJqcnMdVsfxKvoO1ULIc+TRJL4hWUdOkHMmh49mfIr9gp1b+rS59JzvV//A18u/o8M98by0egx9n+pRooutznRodyo16lezOoZSBAX5M2JUZ9IOn2DJe99aHceraLkXgq+fL/G9WjFz5Hye7zGJCuEh3P1EN6rGRl16zvsvraDTwLaXhinwC/Alacv+S19PSUzlZIb1p0KOHcrg0O7DNGxZz+ooSgEQd2Nt2rZvyPvzN+qbm0qRlnshxXVqyjtJ0xg552Hue7EfSVsOkJeX/yaMz+Z/RaWqYb85kl/y8ke063cTDruDheOWMmPE2wy94UkWjnfu3TBXYoxh+rC5+Af6c1vBhWGl3MFDj3TAZvNh9utfWB3Fa2i5F1FUrQjyHHlkZ5xi/7aDAJzO+pXGbepz8WL+3TIrpq6mWp0qXHtTA95+ehFnT59j1NtDeWvPa6QkpnI661eX57548SKzE+azec127n2hLxHVw12eQak/UzmiAn0HtOGb9Ul6cbWUaLkXg83XRqeBbanTPAaAwOBAfjlyAv8APzLTslj0j5UMHNebbz7cTJ4jj1v6/pWI6uHYLzhI/DYZe8GFo9zzuS45VZN7PpeJA6azfMpqug/vTPdHOjt9m0oV1V19biQisjxzZ6zVAe5KgZZ7CdhsNgBirq3Jti928uStE3j7mUV0eagjsU1qkbz1APVa1CW2SU0g//RNfM9WhFcNY8+mJF7sO4UnO45n4sDp5J7PLfV8uedz+XD6vxhYdzhfvr+RQS/1Y8iUe/Hx0W+7cj8BAX4MuP9m9iUeZeP6JKvjeDz9X14KGrWux8xtL9Ox/83c92Jf7nmuJzlnz3PiWDZVYyPx8/fj8L4jHN57hEat67F7416WTl5F8w5NeHPHZPIceXy7amupZDHG8PPOFN55djH9aw9jxoh5VI2NYtLasfQZfSf57z1Tyj117NyEGjXDWTB3/aXTnKp4fK0O4C18fHzocE/8pc+zjhzn5PFs6reoC8DKqaupVjuK8pVC2LVhHzX+Uo1uQ28D4GLexUsTaRhjEBFyzuSQdfQkYVEVCQwJvPQq4T8cdgfZGafISs8mIyWTAzsOcXDXYfZt3s+J9JP4+AjNOzZhzHsjPG6iEVV22Ww+9B8Uz0tjV7Lhq73c3E5HES8uLXcnCY2sSFhUKI+3e56YxjXZv/0g/Z6+i9R9R0hNPkLvUd2A/GEMqtWuQoXw8gCXjqx3fr2XZ7r849L6AoL88Q/0w2HPw2HP+920fz4+QvV61WjatiHN2zfhhs7NCK8a5qK9Var0xLdrwIK31rN4wSbib2mgrzaLScvdSUJCgxm77HE+nvUZlaMr0fvJblSODmfxP1cSWrkCtRrWwGF3cGBHCqcyT//mnnmA2k1r8cT8YWRnnOb8mfPknMnBfsGBzc+Gr5+NgHIBVKoSSliVUCKqh1OzQTQBQQEW7a1Spcdm8+Huv7fi1X+sZvsPh2geF2N1JI+k5e5kXQd3uvSxw+7gZMYp+o6+E4Cd6xNJ3rKf2tfFULP+b+c5qRwdTsf+N7s0q1Luon2na3lr5jo+XLJFy72Y9IKqC/n6+dK4TX1e/r/X+Xjmp7z97GKqxERyS982V19YqTLEP8CXv93RjO++SeZ4erbVcTySlruL9RhxO72f6E7G4V8YOK43XR++lfJhIVbHUsrt/K1bMwA+Xa3DUxeHnpaxwOV31Sil/liVqqE0vyGWz9bspP+geL2wWkR65K6Uclvtb23M8WOnSNyt00IWlZa7UspttYmvh5+/jfVr91odxeNouSul3Fa54ACaXR/DdxuTdbyZItJyV0q5tZZt6pJ+NJsjaTrWe1FouSul3Np1118DwM5thyzN4Wm03JVSbq16zUqEhgWze2eq1VE8ipa7UsqtiQh/qV+V/cnHrY7iUbTclVJuL7ZuJCmHMslzXLQ6isfQcldKub1q0WFczDNkuMEk855Cy10p5fYiIisAkJXp+vmHPZWWu1LK7QWHBAJw9mzpT0fprbTclVJuz9c3v6ryHHkWJ/EcWu5KKbd3Pid/5rHAID+Lk3gOLXellNvLzDgNQFglHR67sLTclVJuL3lfOv7+vtSsVdnqKB5Dy10p5dbs9jy+/jKRxk1rYPPVyios/ZdSSrm1Vcu3kpnxKz37trQ6ikcpUbmLyG0ikiQi+0VkdGmFUkopuz2PGa99yqxpn9P8hhjiboy1OpJHKfY0eyJiA2YAHYE0YIuIrDLGJJZWOKVU2fXm61/w4dIt9OjdggeGttdp9oqoJHOotgD2G2N+BhCRxUA3QMtdKVViffq3psl1NbnplgZWR/FIJTktEw1cPgZnWsFjvyEiD4rIVhHZmpmZWYLNKaXKkvDK5bXYS6Ak5f5Hr5F+Nw+WMeZNY0ycMSYuIiKiBJtTSilVWCUp9zSgxmWfVweOliyOUkqp0lCSct8C1BWRGBHxB/oAq0onllJKqZIo9gVVY4xDRIYBnwI2YJ4xZk+pJVNKKVVsJblbBmPMGmBNKWVRSilVSvQdqkop5YW03JVSygtpuSullBfScldKKS+k5a6UUl5Iy10ppbyQlrtSSnkhLXellPJCWu5KKeWFtNyVUsoLabkrpZQX0nJXSikvpOWulFJeSMtdKaW8kBjzu5nxnLcxkUwgxWUb/K/KwC8WbNdKus9lg+5z2VDPGFO+KAuUaDz3ojLGWDKJqohsNcbEWbFtq+g+lw26z2WDiGwt6jJ6WkYppbyQlrtSSnmhslLub1odwAK6z2WD7nPZUOR9dukFVaWUUq5RVo7clVKqTNFyV0opL+T15S4it4lIkojsF5HRVudxNhGpISLrRGSviOwRkRFWZ3IFEbGJyHYR+cTqLK4gIqEiskxE9hV8r1tZncnZROSxgp/p3SKySEQCrc5U2kRknohkiMjuyx6rJCKfi8hPBX+HFWZdXl3uImIDZgCdgYZAXxFpaG0qp3MACcaYBkBLYGgZ2GeAEcBeq0O40FTg38aY+kBTvHzfRSQaeASIM8Y0BmxAH2tTOcU7wG3/89hoYK0xpi6wtuDzq/LqcgdaAPuNMT8bY3KBxUA3izM5lTEm3RizreDjX8n/Tx9tbSrnEpHqwO3AXKuzuIKIVADigbcAjDG5xphsa1O5hC8QJCK+QDngqMV5Sp0x5mvgxP883A2YX/DxfKB7Ydbl7eUeDaRe9nkaXl50lxORa4BmwPfWJnG6KcATwEWrg7hILJAJvF1wKmquiARbHcqZjDFHgFeAw0A6cMoY85m1qVwmyhiTDvkHb0BkYRby9nKXP3isTNz7KSIhwHLgUWPMaavzOIuIdAEyjDE/WJ3FhXyB5sBMY0wz4CyFfKnuqQrOM3cDYoBqQLCI3GNtKvfm7eWeBtS47PPqeOFLuf8lIn7kF/t7xpgVVudxsjbAHSJyiPzTbu1E5F1rIzldGpBmjPnPK7Jl5Je9N+sAHDTGZBpj7MAKoLXFmVzluIhUBSj4O6MwC3l7uW8B6opIjIj4k38BZpXFmZxKRIT8c7F7jTGvWp3H2YwxTxljqhtjriH/+/ulMcarj+iMMceAVBGpV/BQeyDRwkiucBhoKSLlCn7G2+PlF5EvswoYWPDxQOCjwizk0lEhXc0Y4xCRYcCn5F9dn2eM2WNxLGdrA/QHdonIjwWPjTHGrLEwkyp9w4H3Cg5afgbutTiPUxljvheRZcA28u8I244XDkMgIouAtkBlEUkDxgL/BJaIyCDyf8n1KtS6dPgBpZTyPt5+WkYppcokLXellPJCWu5KKeWFtNyVUsoLabkrpZQX0nJXSikvpOWulFJe6P8By5cDQH2a63AAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Solve optimization problem\n",
"xsln = solve_opt(False,False)\n",
"\n",
"# Create contour plot\n",
"visualize(xsln,False,False)\n",
"\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.4 Take 2. With $g(x) \\leq 0$](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.4-Take-2.-With-$g(x)-\\leq-0$)",
"section": "4.2.3.4 Take 2. With $g(x) \\leq 0$"
}
},
"source": [
"### 4.2.3.4 Take 2. With $g(x) \\leq 0$"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.4 Take 2. With $g(x) \\leq 0$](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.4-Take-2.-With-$g(x)-\\leq-0$)",
"section": "4.2.3.4 Take 2. With $g(x) \\leq 0$"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Ipopt 3.12.10: \n",
"\n",
"******************************************************************************\n",
"This program contains Ipopt, a library for large-scale nonlinear optimization.\n",
" Ipopt is released as open source code under the Eclipse Public License (EPL).\n",
" For more information visit http://projects.coin-or.org/Ipopt\n",
"******************************************************************************\n",
"\n",
"This is Ipopt version 3.12.10, running with linear solver mumps.\n",
"NOTE: Other linear solvers might be more efficient (see Ipopt documentation).\n",
"\n",
"Number of nonzeros in equality constraint Jacobian...: 0\n",
"Number of nonzeros in inequality constraint Jacobian.: 2\n",
"Number of nonzeros in Lagrangian Hessian.............: 3\n",
"\n",
"Total number of variables............................: 2\n",
" variables with only lower bounds: 0\n",
" variables with lower and upper bounds: 2\n",
" variables with only upper bounds: 0\n",
"Total number of equality constraints.................: 0\n",
"Total number of inequality constraints...............: 1\n",
" inequality constraints with only lower bounds: 0\n",
" inequality constraints with lower and upper bounds: 0\n",
" inequality constraints with only upper bounds: 1\n",
"\n",
"iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls\n",
" 0 2.4439483e+02 0.00e+00 3.60e+00 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0\n",
" 1 4.4804168e+01 0.00e+00 3.92e+00 -1.0 2.13e+02 - 8.82e-01 4.46e-01f 1\n",
" 2 5.4337665e+00 0.00e+00 1.68e+00 -1.0 2.39e+00 - 1.00e+00 1.00e+00f 1\n",
" 3 5.2037708e-02 0.00e+00 8.16e-01 -1.0 9.15e-01 - 1.00e+00 1.00e+00f 1\n",
" 4 -4.4584904e-01 0.00e+00 1.06e-01 -1.7 2.32e-01 - 1.00e+00 1.00e+00h 1\n",
" 5 -4.8930521e-01 0.00e+00 1.81e-03 -2.5 5.28e-02 - 1.00e+00 1.00e+00h 1\n",
" 6 -4.9427819e-01 0.00e+00 8.51e-06 -3.8 8.98e-03 - 1.00e+00 1.00e+00h 1\n",
" 7 -4.9445150e-01 0.00e+00 7.69e-09 -5.7 3.02e-04 - 1.00e+00 1.00e+00h 1\n",
" 8 -4.9445337e-01 0.00e+00 8.06e-13 -8.6 3.28e-06 - 1.00e+00 1.00e+00h 1\n",
"\n",
"Number of Iterations....: 8\n",
"\n",
" (scaled) (unscaled)\n",
"Objective...............: -4.9445336916190996e-01 -4.9445336916190996e-01\n",
"Dual infeasibility......: 8.0590836175421712e-13 8.0590836175421712e-13\n",
"Constraint violation....: 0.0000000000000000e+00 0.0000000000000000e+00\n",
"Complementarity.........: 2.5083384199831901e-09 2.5083384199831901e-09\n",
"Overall NLP error.......: 2.5083384199831901e-09 2.5083384199831901e-09\n",
"\n",
"\n",
"Number of objective function evaluations = 9\n",
"Number of objective gradient evaluations = 9\n",
"Number of equality constraint evaluations = 0\n",
"Number of inequality constraint evaluations = 9\n",
"Number of equality constraint Jacobian evaluations = 0\n",
"Number of inequality constraint Jacobian evaluations = 9\n",
"Number of Lagrangian Hessian evaluations = 8\n",
"Total CPU secs in IPOPT (w/o function evaluations) = 0.012\n",
"Total CPU secs in NLP function evaluations = 0.000\n",
"\n",
"EXIT: Optimal Solution Found.\n",
"\b"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAAD8CAYAAACMwORRAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzsnXd4VGXa/z9napJJ772QXkihQ0LviiKgolRdy677urruuquur66oq67u6rs/ddfeAREVQUWQ3msIJCG9997L9PP7YyDKgkpJMinnc125IDOnfM/M5DvPuZ/7uW9BFEUkJCQkJIYWMmsLkJCQkJDofSRzl5CQkBiCSOYuISEhMQSRzF1CQkJiCCKZu4SEhMQQRDJ3CQkJiSHIL5q7IAjvCYJQJwhC5o8ecxUEYYcgCPnn/nXpW5kSEhISElfC5YzcPwDm/ddjjwK7RFEMB3ad+11CQkJCYoAgXM4iJkEQgoFvRFGMO/d7LjBNFMVqQRB8gL2iKEb2pVAJCQkJictHcZX7eYmiWA1wzuA9f2pDQRDuBe4F0Gg0o6Oioq7ylP3H+e87QbCujuGMzmgkr6kRhUyGo1qNk9oGjUqF9Jb8PCIi+e01yBBwUWlwUmlQCEN7aq3NUI3O1IWdwhlbuTMyQW5tSVePqRzETpB5gMwVzn3iU1NTG0RR9LiSQ12tuV82oii+BbwFMGbMGPHkyZN9fcprorUVnJ3hn/+EP/zB2mqGL10GA7uKC9lekM/e0mK6DAZs1GpmhYQyLyycyYHBqBV9/vEddBjNJvbVZfFF2TFONhWhEORM94phSeAEklyCEYbgiKW6O4uTjesp6jiCQrAhznk+Sa4346j0sra0K0bUn0Bs/xcYjoNMg2B/H9guQSZTl17psfo1LDMYzN1shr/9DWbPhgkTrK1GAkBrNHCgtJTthfnsLC6kTafDXqlixogRzA+LYGpQMDYKpbVlDjhKO+r5ovw431am0m7UEmrvxZLA8cz3TUKjUFtbXq/TqCsltekzclt3AhDpOJMxbktxVQf95D4t+io6DHX4axL7S+YvIooi6I8idvwLDKdANQG528epoiiOuZLjXK25vwQ0iqL4giAIjwKuoij++ZeOMxjMXWJgozeZOFJexrbCfL4vzKdZq0WjVDI9ZATXhUUyLVgy+v9Ga9LzfXU6n5cdJaetCo1czXV+SdwcOIEQ+5+MqA5a2g11nGr6nMyWbzGKeub4/Jlop9kXbWc06ynpPMbJxg3IBDnJHnfhZxdvBcWXxmLy+0E0I7Od0fvmLgjCemAa4A7UAn8FvgI+AwKBMuAWURSbfulkg8Xca2osI3hfX2srkfg5jGYzRyvK+a4gj+0F+TRpu9EolcwcEcr1YZFMCZJCNz9GFEXOtlawsewoO6vTMYgmxrqFcmvgRFI8o5APsdh8l7GFM81fEe+yEI3i0tnaZtGETJBT1H6EnLYdTPd6EFuFUz8r/WUEQeibkXtvMVjMPT4eQkNh0yZrK5G4XM4b/db8XLYV5tOi1WKvUjE3NJwF4ZFMCghEKR/EE229TLO+g6/KT/Jl+TFqta342DizJHACC/3H4KSy69VzGQwGKioq0Gq1vXrc3kBEREDALBrpNrViJ3dBBAzmbuSCEoVM1a96bGxs8Pf3R6m88O5TMvdeYvJkUCph925rK5G4GgwmE4fLy/gmP5fvCwto1+twsbFhfngkN4RHMtbPH9kQnFi8GoxmEwfqsvms7AipTcWoZUrm+SawNGgSYQ7evXKO4uJiHBwccHNzG7ATuq36apQyW0TMmMx6EAQMZi0qmR0OyitKUrlqRFGksbGR9vZ2QkJCLnhOMvde4oYboLISTp2ythKJa0VnNLK/tISv83PYVVRIt9GIt8aeGyKjuDEiihgPzwFrOP1NQXsNn5Ue4buq0+jMBka7juC2oEnXHLLJzs4mKipqwL3OenM3BlMXOnMXckGBvdKDJl0pTkpfVHJbDGYtWlMb9gqPftMuiiI5OTlER0df8Lhk7j9DUXUj7247TklNE6W1zeiNJpQKOSqFHHsbFS4Odjjb2+LhpOHbdxMpzXPi6z21+Lk74elsj1w2tOKRw5FOvZ5dxYV8nZfDvtISjGYzYS6uLIyK5saIaAKcBl6s1Rq06LvYUnGSjWVHqNW24mfryq1BE7nBfzT2CpsrPl52dvZFZmVN9KYuukwtCAgoZGqUgi0quS0dhnqMoh5nlR8ARrOOdkM9TipfBKDb1IZR1GEjd0Qls+0zfZd6vSRz/xnyKxt48N9fEezlSoi3CzYqJUaTGb3RRFuXlub2bprbu6hv7eTM1vE0F0QSf+cbACjkMvzcnAj0cibI04UgLxdCvF0J8XHDxb7v3mSJvqO5u5utBXlsyc3mRFUlAKN9fFkYGc2CiEicbaT31Wg2sbcuiw0lhznTUopGruYG/zEsDZqIn53rZR9nIJm7KIp0GhvpNDZhp3DGQWnJFjKLZhp1Jbio/Hvi7G2GWgQENAo3Oo1NmEQDKpktXaYWnJQ+KGVX/kV3OUjm3oc88qiZf/5D4GBGOVWNrVTUt1DR0EppbTNldc3oDKaebV0d7Aj1dSPUx40wP3fC/dwJ9XHDzqZ/J2Ikrp6Ktla25OawOTeb/KZGlDIZ04NHsCg6hmlBIVLGDZDVWsH6kkPsrMlAFEWmecWwLDiFkc6BvxiyGEjmfh6jWU+XsQmDqMVB4YmIiNbUhpPKBwCzaKRBV4K7OoROYxMyZKjlDihkKjqNjQjIsPuJDJxrRTL3PuTFF+GRR6CjAzSaC58zm0Vqmtsorm6iuKaJwupGCqsaKapupEtn6NkuwMOZyAAPIvw9iArwJCrAE3en/zqYxIBCFEWy6uvYlJPNlrxsGrq6cFLbsCAiksVRMSR6+wy4uHF/U6dtZWPpUTZVHKfN0E2cUwC3Bycz3SsWhezS2UgD0dzPYzTrERGRCXLaDXU4Kb0REekw1CMIcuzkzrQZa7FXeKCUWRZ+NenKsFM4YyN3RBTFXv9MSObeh7z5JvzmN1BRAX5+l7eP2SxS3dRGfmUDeRX15FfWk1teT0VDa8827k4aogM9iQn0IjrIi5hAL8nwByhGs5lDZaV8mZPFjqICtEYjI1xcWBwVy6KoGHwcHKwt0ap0G/V8W3WK9SWHKO9qxMfGmduCk7nRf8xFq18HsrkDdHd3M2/ePDZtW4soMyIXVMgFBRqFO1pTKyIicpMtc2bP5bsdX6MX2nFS+vTUsDlv8GbRiMGsRS6oLplCuW3bNh588EFMJhN33303jz566WK6krn3IRs2wG23wdmzEBNzbcfq6NaRW1FPTlkd2WW15JTXUVzT1FOczNvFgZggL+KCvYkL8SYm0EsK6Qww2nU6thbk8WX2WU5UVSIAKYFBLImOZU5o2LBeEWsSzRyoy2FtyQHONJdir7BhccA4lgZNwsPGERj45v76669jNBp58MEHMZi1iIgoBRsEQaDT2ASiiEbpxpo1a/ANdmP58uXYyp0QfpRBZDTraTPUoBBU6M1d2ClcsJU794zqTSYTERER7NixA39/f8aOHcv69euJuYTBSObeh+Tnw+bNsGoVePbB6uwurZ6c8jqyyurIKqkhs7SGinrLCF8mCIT6uhE/wof4EB/iR/gS6Ok87MMBA4XSlha+zDnLl9lZVLa34aBSc2NkFDfHxBHv6TWs36fMlnLWlhxgT81ZZIKM+b6JLA9JQVfeNCDMPTs7m1//+te0tLSwcuVK3nzzTQoKCpg0aRLr1q0jODgYgOnTp/OXv/yF2bNn8+e//JG2tlbeeO0djqYe4InHn2T7dzsvqDxpFk20G+qQCwrkRnt27NrGN1u/5qYFN3PdddcBcOTIEZ566im2b98OwPPPPw/AY489dkmdvWHu0kzRJQgPh4cf7rvj29moGBXuz6hw/57HWjq6OVtSQ3pxNRnFNWw/kcsXBzIAcNbYED/Cl8RQXxLDfIkJ9EKllN46axDk7MxDE5J5cPwkjlaUszErk8+zzrI24wwRbu7cGhPHTVHRuNr27irPwUCccwDPJy6jsquJdSUH2VKRyteVqbzis4guow5buQpBEJg27ZePtWDBD3+D06bBHXdYfhoa4OabL9x2795fPp7RaGT58uW8++67JCUlcd999xEXF4der6eoqKjH2AHWrFnDk08+SV1dHZmns/jo8zdo1JUQERPC6dTMi8Ix2XkZfLv1a/Z8f4jy8gomT01m7vxZTJ8+HbNowmjWUViajb//DzFef39/jh079svCrwHJIS6B0QhFReDuDq6Xn/F1TTjb25IcF0JynGVlmtksUlzTyJmiatKLqkkvqmJ/RhEAKoWcmCAvksL8GBXuT8IIH+xth16Vv4GMTBCYFBDIpIBA1kzT8k1eLhuzMnn2wF5ePHSA2aGh3BozkuTAoGG3GtbPzpU/xdzIPWEz+bzsKIZ2E6Wd9djKVbipHQAb6OfK/F9++SUJCQkkJSUBEBMTg6enJw0NDTg7O1+w7ZQpUxBFkZdffpm9e/fiYOeA0axHLihQqVS0tbXh6OjYc5e29JblFOQV8vvf/5733nsPZw97DOYubFW2tOlrQBAwiSZ05k70pi5UcssXf1/f5Unmfgnq6iAyEv7zH8vEqjWQyQRCfd0J9XVnccpIAJrbuzhdWMXpwirSCir5aMdJ3t9+ApkgEBngwehwf0aH+5MU5oejpm9ycCUuxlFtw7KRCSwbmUBOQz0bszLZlJPFt/l5+Dk4cktMHLfExA27SVhnlYa7w2aSlZWFl40zTfoOKroaefdrJW5qe5yUdpdlcD8embu7X95I/b9JT08nMfGHsr6ZmZnMmzcPW1vbi2reZGRkUF1djbu7Ow7n3rPzE6Q6nQ5RqaXdoMNB6YHRrGfPsS2UZTXz3XfbuPmWW9Dpu5kzew533LUSdz9HnJV+RATH8XHlOsxY0qgrKirw8fG58gu5AqSY+yXQ62HjRhg/HsLCrK3mp+nWGUgvruZUfgWn8ivJKK5GbzQhCBDp78mYCH/GRgaQFOYnjez7GZ3RyI6iAjaczeBQeRkyQWBaUAi3x8UzNTgExTBa8Xw+hiyKIm2Gbhr17ehMBhQyOW4qB5xVdsj6uCLlK6+8QkFBAa+//jqnT58mOTmZjIwMRowYQUBAAPn5+djY2FBdXc3cuXPZsGEDDzzwAA8//DBz584FoLGxkZSUFLKzsxFFM4Igw2jW0Wlswknlg1k0oTW1UddQw9G9Z3APtGXK+Nmo5HYYjUbCI0L5ZvsmwoPiGDN2DO98+BoxsTHYKVwuiOFLMfc+RKWC5cutreKXsVUrGR8VyPioQAB0BiOZJTWk5lVwMq+cz/ad4ZNdp5DLBKIDvRgXFci4yAASQn1RSzH7PkWtULAgIooFEVGUtbbw2dlMNmZlsvubr/DW2HNLbBxLY0fi6+Boban9hiAIOKnscFTa0mnU0aBrp1bbQoOuDReVPa6qvivzsXLlSq6//nrGjh3LxIkTCQ4OZsSIEQDMmTOHgwcPMmnSJBYvXsw///lPoqOjeeKJJ3jkkUd6zH3Pnj09E6TnM2XkgpKF826ltrYOEBAAmSBHROSxp/7YE4JRKBQ89/KTLLp+KUaTieWrbyUmNhazaKDNUIOT0rfXwzTSyP0nOHbMsoApLs7aSq4encFIelE1J3LLOZ5bxtmSGkxmEbVSTlKYH+OiApkQHUSEnwcy2fCKC1sDg8nE7pIi1mekc6CsBEEQmB4cwrKRCUwJDB6y9Yt+LhWyy6ijUddOh1GLTJDhotLgqrL/yQVRV0tHRwf29vYAvPTSS7S2tvLss88CkJaWxssvv8zHH3/8s8dYvHgxzz//PJGRFzed05k6EDGjljkgCALthjoUgrqnNnyHoQGjqMdR6UWboQZbuTNquWWNS4u+EnuFR0/oRxq59zErVsCYMbB+vbWVXD1qpYKxkQGMjQzgt0yio1vHqYJKjmWXcTynjP+36SD/b9NBXOxtmRAdxMSYICZEB0kLq/oIpVzO3NBw5oaGU9HWyqeZGWw4m8Gu4iL8HR25LTaeW2NH4m43fDJt7BRq7BRqtCY9Dbp2GnUdNOk6cFZpcFPbo5T1jkW98sorfPrppyiVSpKTk3n55Zd7nktKSmL69OmYTCbkP1HzX6/Xc9NNN13S2AHUcvsLflcIaoyiHrDUhtea2nFR+dNtakUhqHrq0hjMWoyioU/qxksj958gORlsbGDXLmsr6TvqWzo4llPGkexSjmWX0dTeBUCEvwcTY4JIjg0mIdRXanLRh+hNJnYUFrAu8wxHKspRymTMC4tgRXwCY3z8hkTe/JUsYtKZDDTq2mk1dAPgrLLDTeWASj64xqEGczdthjoEQCGzsYzi5U49o3alzLJIqs1QixwFGqXbD6mV0iKmvmXJEsjOhqwsayvpH8xmkbzKeo5klXAkq5TTBVUYzWY0NirGRQWSEhtMclwIns72v3wwiauisKmRtRln+CI7i3a9jkg3d1bGJ3JTVAx2ysG7CvZqVqjqzUYadR206jsRASelLW5qB9TywfU66EydFiNHhoiZdkMtdgpXlDIbDGYtHYYG7JXuF1SYlMy9j7n/fli3Dpp+sTPs0KRTq+d4ThmHzpZw+GwJNc3tgGVUnxIXwuSRIcQFew/ZOLE16TIY+Do3m4/TT5PVUI+DSs2SmFhWxicS4tw3lQj7kmspP2A4Z/It50zeUWmL+yA0eQBRNNNiqEIjd0Ult6NJV45arkGjsCymMYlGZMilZh19zbPPwhNPgFYL6mGeRSiKIoVVjRw8W8zBzGLOFFZhMos429uSEhvMlPgRTIgOktItexlRFDlVU8VHZ06zrSAPg9nM1KBgVieMYkpQ8KBZHNUbtWUMZhNNug6aDR2I4uAz+fMhF62pjQ5DAwqZDTJkOKq8zz1vqScvExRUFbYQFxN/wf6Sufci77wD99wDpaUQGGhtNQOLtk4tR7JK2Z9ZxOGzJbR2alHIZYyJCGBq/Aimxofi7Tq8Fuz0NXWdHazPTGddRjr1XZ0EO7uwKj6RJdGxOAzw0UdvFg4zmk006Tto0nciiuKgM/nzmMwG5DKL5vMe3G1qpdPYSFFeOY1u+5nkcTfOKl9AMvde5ZtvLL1Ujx2DceOsrWbgYjSZSS+qYl96EfvTiyitawYgKsCT6YmhTEsII8x34DZGHmzoTSa2FeTx4Zk00mqqsVequDk2jtXxSQT91zL6gUJfVIUcKib/35hFE+lnT3FIuQazaCTe5UbGu6/AVuEkmXtvcfIkjB0LX30FCxdaW83goaSmib3phew9U0hGcTWiCP4eTkxPCGN6YijxIb6XlVNf3dTGd8dzqG1u56bkOKIDvfpB/eDiTE01H5xJY2t+LkazmZkhodyZOIoJ/gED6su0L0v+DkWTz87OJjDck6P1H3K2dRteNpHcFvKaZO69RUUFBATAG2/Ar39tbTWDk/rWDvanF7HndCHHc8swmsy4O9oxPTGMGUnhjA73RyG/9ITsg//+Cn93Z3zdHPnuRA5LpyZww8RYTGazNIn7X9R2dLA24wzrMs7QpO0m2t2DXyWNZkF45IBoEdgf9dyNZhON+g6adR092TXuasdBl0IJF75eDbpi9KYu/DRxkrn3FkYjbNliWcgkxdyvnfZuHYcyi9mVls+hsyVo9UYi/D349PEVF22r1Rv51T828PoDi3Gxt+XVrw7i7qghKdyPHal5pBVUsmRyPPPHRiEIfV9db7CgNRrYnJPN+6dPkdfUiIedhlUJiSyLS8DF1noNv/uzWYfRbKJR107zuewaZ5Ud7mqHXlsM1R9IqZASg5ZuvYHDZ0vo1htYMP7iTjRVja18+H0qR7NLuWFCDFlltcwZHcFHO1K5dVoCbg52vL/9BH+5fSZhfu5WuIKBjSiKHCwr5b3TqewrLcFGoWBJdCy/ShptlVRKa3RiMvzI5AUsFSrd1Q4XlTXIysri+PHjzJw5E2dn554qkNZEKj/QDxw9akmFvJzmAhKXj61Kycyk8Es+V9vczn++PkJCqC8pccG8v/0Eq+eMoa1Ti52NkpsmWYr9nCqoJK+yXjL3SyAIApODgpkcFExeYwPvpaWy8Wwm6zLOMDs0jHtGjWG0z2U2Bx6kKGVyvG2dcVXb06C1mHyLoRNXlT1uKoee0J7BYODVV1+lra2N3/3ud1ZW3btI5v4zPPEEdHTAkSPWVjJ8OF+2eOHEWJQKOWeKqmnt1LIjNa+nrr0oishlMmrPLawym8WeSdpunYHtJ3Opb+1gwYQYfFyHT9XFSxHh5s4Ls+byx4kpfJSexifpZ/i+sIBR3j7cO3oss0aEDZp8+atBJVPga+eCm8n+XO0ai9G7qRxwVWsoLy/nzjvvZMSIEbS3t+PoOHQ+L9LM1M/w2muWVaoS/Uu3zoBSIcdgNOHpbE9qXgUFVQ1cN85yq6o3mjieU8bo8AAAzOdCiw2tnbzxzREOZ5VQ39LJmo++p7mj22rXMZDw0Gj448QUDv3qXp6aOoO6rk5+8+0W5nzyPhsy09EZjdaW2Keo5UpWXL+EoiPp2MlV/O8Tj3PHffcwafY0Fi9ZwnXXXTekjB0kc/9ZIiMhJMTaKoYXMUHeyASBlS+s49F3t1LZ0IogCIw+12/WYDSRml+BXCYQP8LSyeZ8xs3XR8+iVMj5/eIp/GXZTDQ2Kg6dLQagvUvLvvRCdp8usM6FDRDslEpWJSSxe9Vd/Gve9dgqlDy2ewdTP3yHN1OP067T/eS+JrOZvx3Yy86ivn8NW1tbiY2NpbW1tdeOuWbNGl564UX2f7WdkrP5PPX3v1GrbaHLXqBV30V/zj/2B5K5/wzZ2fDyy9DZaW0lwwdfN0f+77cLeXz5LFJig/nVvHH8at44lAo57V1azpbWsDM1n+vHnxvFGywjzqrGVirqWxkZ7I2vm2UEpjOYCPCwLOx5+K1vOJhZzAfbT/DXD7fT3qW9tIBhgkIm44aIKLbctoIPb1pCmKsbfz90gJT33+Yfhw9iMJku2qepuxsfewfu/+4b3j51ok/1ffvtt2RlZbF169ZeO+aPe6Nu3PAZIY5eBNi5IxMEqrqbKO6so8OgHTImf03mLgjCQ4IgnBUEIVMQhPWCIAypxp1pafDHP0J5ubWVDD+iAjxZlDISJ40NPq4OKOQyVv59Pa9vPszEmCCuP5dlozrXUSq7tA57WzUBnhYzzyiuxsvFHlEU+T41F7lMxuPLZvHRI7dTUNVAS+cP5n7obAk1Te39f5EDAEEQmBwYzCeLbuGrpctJCQziRFXFJdsAemg03BwTR4SbO+P9LCGx0zXVZNXX9ZqeZcuWYW9vz+rVqwFYtWoV9vb2LFu27JqPfb43qlqtxsHB0lTDXmlDiMYTX1tXzKJIeVcDZV0NdBv113w+a3PVE6qCIPgBDwAxoih2C4LwGXAb8EEvabM63paaPtTUQFSUdbUMZ5QKOY8vm4XOYKSyoZURPm7oDEZO5Vfg7eqIr5sj9rYqtHojLg6WRhcncsvxc3dCZzCRW17PnDERAFTUtxAV4InBaKKlo5u3tx6jrK6ZysY2UmKDeWjJlGGbNx/v5c3r192A3mT6ydfgrdQThLq4Eu/ljc5oJLW6iq/zcvCws+PhSZOJdLu27KWnn36a06dPU1JSgtFoRKlUEhQUxDPPPHNNx62urmb58uVs3ryZBx54gO3bt/e0zzvf/s9BaUuLvpMGXTslnXU4KG3xVDsNyoVQcO1hGQVgKwiCArADqq5d0sDhx+YuYX3USgUjfCxNDRRyGQajiZxyy6hRrVJQWN2Ai70tXVo9h7NKiAnyAlGkoa2TcZGWlWhN7d0o5DLkMhmf70+nvrWDV+9fxGv3L6KupYMuncGalzggUP1Ec5by1lZ2lxRx3xhLsSWFTMaKkQl8tXQ5o338eP340Ws+d1hYGE8//TQGgwGNRoPBYGDNmjWEhoZe9TG7urou6o361FNPXbSdTBBwVdsT6uCFu9qRDqOWwo5aarpbMJovDlP9GJ3JMOBG+1dt7qIoVgL/AMqAaqBVFMXv/3s7QRDuFQThpCAIJ+vr669eqRXwsczXSeY+wBAEAblMxvjoIGYkhgHg6+aEk50NK19Yx9/W78LH1ZEJ0UG0dmnR6o34ujliMJoor2+xlIzV2LA3vZDVsy3rQlQKOTYqJfmVg+sz2p98nJ5GnKcnEW7umM+lo55Po0wJDEIhk1F+bgJUbzLRpru6eY3PPvsMjUbDmjVr0Gg0bNy48Zp029nZceTIEWbPng1YYu9Hfia/WS7I8LBxJNTeG2eVHc36Tgo7amnQtWMWzRdtL4oiHUYtFV2N1HS3DJiY/bWEZVyAhUAI0AJsFARhhSiKn/x4O1EU3wLeAssK1WvQ2u84O4NKJZn7YMDT2Z5//uZG9p0pxFFjQ1SgJwDlda24nQvV5FbUk11Wy+hwf6oaWjGbRWKDz9fTFsmvrCfQY/A1w+hLdEYjn2efZZyvPyeqKnlt/g3AuTK1goBSLqeyvY29JZasJG97ezr1el44tJ/CpiY0KiW/D424onP+6U9/4tVXX8XLy4sVK1ZQbqVJL6VMjo+tC64qe+q0rdRrW1HLFDgoLyzlIAgCbmoHjKIZg9k4YMJ61xJMmgUUi6JYDyAIwpfAJOCTn91rECEIltCMZO6Dh6kJF96+zx0TwSPvfMtz63ZRWtdMcmwwc8dG8vcNexgbGdCz3cHMYtydNLg62vU0VpCwjMBPVlXy7P69eGo0+P0oF7youYmv83I4VlFBvLc3f5iYTE1HB59knKbLYODDm5bw/KH9dBuuLId+7NixPf/38vLCy8u6FUHVciUBGne6jXpsfqLapNakp9Ooxc/Wtecxk9mMSTRbLWZ/LWctAyYIgmAHdAMzgSFXOMbbG6qrra1C4mrx93DmH7++ge9P5jEuKoBZoyyjSKVcRlTAudF9fQtHs0u5bqwlvfLcoFQCcFCreWXuddw/tpFn9u/lg9OnUMrlnKiqwEauwEah4NGUKcR7We6A/nnkII5qG26Pi0cplxPi7IJ2iCyQslWoLvm4KIo06jrQKGxQy5UYzSa6jDpaDV2YRDMKmRxvG+eL6tr0NVdt7qIoHhOWcOk3AAAgAElEQVQE4XPgFGAE0jgXfhlKeHtDSYm1VUhcCz6ujqyec2HNpakJofzjs720dHSTXVZLkJcrM0ZZ4vcymYDJbGbbiVxmJIZhqx68tcF7i1BXNz64aQn1XZ38dc8uDpSV8KdJk1mVkNSzTWp1JU3d3cwPCyD4XIGyjLoaYjx9e+LQQ/GOqN3Yjd5sxNfWcs11ujYUggx3tSO2ChX12jYa9R14qB1/sdRDb8brrylbRhTFv4qiGCWKYpwoiitFUfzp5W2DFCksMzQZHe7Pb26YSH5lA6PC/bn3+gko5fKeP66TueU88cE25j72Ni9u2ENRdaOVFQ8MPOw0/Pv6G/l0yVIOlpWy9PNPOVlVCVgaezuo1QSf6wh1oKwEuSBDoVLS2Gh5/XpayhkM1HV2UNPR3lM+YjAhiiJt+i7MopkWfRcuKg2CINBh0NJl1CEXZBjMljsWDxtH3FT2yAQBk2hGb770nYwoijQ2NmJj0zvLhaSSv79AdTWYzeA3tIvoScAFsXZRFEkrqOSLAxnsTMvHYDQxKtyPmyfHMzMpHKWif2+xByqna6oRBIEEL2+25ufyZXYW79y4CIDHdn1PpJs7C8LCaa9vQKu1ZM/oTSZatN3YKVUYzCZMZhFXW9tBVcDMLIq0GjrRm43IsGTXADTrOwCwlavoNOpQyZQ4KC1mbTSbaDdqezJunFUa5MKF42sbGxv8/f1RKi+8W5RK/vYB59MhJYY+Pw4ZCILAqHB/RoX783D7VLYcyeKLA+n85b3vcHPcx6LkkSyZPBIvF+vX/7Ymid4//IG422lo1+s4UFrCkYpy6jo7uX/sBNztHXC3/+F1WrFpI5MDg/h1QgKdej2P7fqev06dgZudnTUu4ZrYV5vFP7K/YblLCmPcQjlUns+tQZMI0rhTr23jpewtvBi/ggN1OZxsLEVlo+B/IufyWu42/O0EbgoY+8snuUokc/8FSkvho49g1SoICrK2Gglr4OJgx+o5Y1g5azRHskv5bN9p3t12jPe3H2dqfChLpyUyJsJ/SMaTr4Rxfv6sTkjijdTjTAoI4ulpM3uyawwmE0q5nF3FhbTrdPx6tGUhVJfBgFkU6dBbFgAdLC9lS24OKYFB3Jk4ymrXcrlM9YphqlcMhe21BGnc6fpRRs226tN0Gw2Iosih+hzCHXyY5mUpm2ErV5HWXCyZuzWproYnn4Rx4yRzH+7IZALJscEkxwZT2dDK5wfS+epQJrtPFxDq48bS6YlcPy56WE/AXhceyXXhkT2/N3R1UdXe1pNN858Tx7g1dmTP88crK2jT6QhyduaRnduxUShYGhvH26dOopbLWTYyod+v4WoIdfDCaDbhoLTlz6c+Yab3SD4p3s+/xtzJvrpsVDIlI50DcFM70GHQUtBRw41+liiLWTQjE3q/huOwM3eTyUxudhX1tW10duro6rTMASuUclRKOXYaNQ6Otjg42uLsYkdioj1arRy12srCJQYUfu5OPLhoMr++fiLbT+ayYe9pnlu3i1c3HeSm5DiWTkvA183J2jKtTnlrC8erKoj38qairRW5TMbN0bEAdOj1rM04w/+MG8/GrEw69Xr+PGkybnZ22CqVHCor7Rnxd+r1aFSXTkUcKChkcv4QfT1H6vOo07Xxj1EriXbyI7u1Ao1CRaDGUndnW/VpPNROPdk1PzZ2rclAVms5sU4BqH8ip/6y9VzT3oOIirJGPv/0GIf359LcdGU1fJ2d7XD3dMTLxwkvbye8fZzx9XPB59yPUilNrg1XbFQKFk6K5caJMZwpqmL9ntOs232KtbtOMT0xlGUzRpEY6jtsQzZJPr4k+fgC4O/oRJCzM6nVVYS7urE+Mx0PjYZJ/oEsWP8xT0+f2RN331VUiEkUUcrlnKqu4pP005S1tnBH4igWRAzsKn4TPS5ckVva2YCPrTM2chVZrRWcbiphpnccfnaWBU9GswmFTM6JxkI2l5+g3ailsquJB6LmM8Xz6nvPDhtz7+7Ws2t7BuMmhpE8JZIRYV7YaVTY2akRBNDrTRgMRrq79LS1dtPe1k1zUydNjR188LEvXdWNGAxppB4vQtv9Q3EpmUzA28cZ/0A3AoLcCApxJyjYg6ARHmg00nB/uCAIAomhfiSG+lHT1M7G/Wf44kA6u9IKiA70ZNmMUcwZHTHss2xG+/jx1N5dONvaMiN4BI8mT2F3cRHR7h4keFkmZ9t0WvaVlvDxopv5vjCfb/JzGe8XwO0j4/n3ieOM9w/Aw05j5Su5fOKcA3irYCcCApsrTnKD/2jGuoWhkFlSbxUyOXqzkRfOfsUdI6Zxg/9ovqk8xeH63Gsy92GTCimKInq9EfVVxEOjoyEmBr74wnKcluYuqiubqaxoorKiiYqyJsrLGqkobUSv/yGH1cvbiZBQT0aEeTIi3IvQcG98/Vx6+n1KDG269Qa+PZbNut1plNQ04eGk4bbpiSxJicdRM6RaH1wxWfV1xHhYVghvzc8lvbaGR1OmArBm324AViUk8VbqCVICgrguPAJBELhh/cc8MWU64/z8rab9ajjeWMDpphIiHX2Zem5SFX4Ytb+Rv4OijlpeTFqBSTRzrCGfow0F/C5yLkqZQkqF/DkEQbgqYwcIDobi4h+O4+KqwcVVQ8zICz9gJpOZ2uoWSksaKCmqp7iwjqKCWo4fLcBssnyJ2tqpCAv3IizSh/BIbyKjffEPdJMMfwhiq1Jy8+R4FieP5HBWCWt3neLVrw7xznfHWTgxluUzR+HnPjzj8ueNHcBRbUNGXR21HR3kNzXyXUEeW5et4uu8HDw1GuK9vBEEgbTqKrzt7Yl297Ci8qtjnFsY49zCen7fX5fNeLcw1HIlTboONlec5K1x9wKWqpTZbZUoZDIEBL4qv7quV8PG3K+F0FA4fPiXa47I5TJ8/V3x9XdlYsoPcTe9zkhpST0FeTUU5teSn1vDd1vS2KS1hHfsNGoionyIivUlOsaP6Dg/XFzt+/qyJPoJmUwgJS6ElLgQ8irqWbvrFJ8fSOezfWeYOSqcVbNG91SnHI6M9/PneGUFt3y+nnmh4Tw+eRqutnbUdXYS7upOgJPlC3BvaTGJ3j6YLlF2d7CR31aNv50rI+y92FRxnEnuEQRo3DCLZsq7mvi+Op1/j72L9wr30HRuYdSVIpn7ZRAaCm1t0NgI7lfRaEalVhAe6UN45A8LPkwmM2UlDeRmV1l+sqrYuPYoJpPlg+vt60xMnB8xIwOIiw8geIQHcrnU8nawE+HvwZrVc7l/YTLr96Tx+f50dqTmMSYigNVzxjApJmjYTb4q5XL+MDGZX48ei41Cgfxci7+s+jrG+Vrujo9WlFPZ1sbCqGicbWx/7nCDgrvCZvT8P9zBB8O5ZiDlnY18VLyfBX6jaDd0s7cui1dGr+axqzjHsIm5XwtbtsDChXDsmCXfva/Q6Qzk59aQnVlBVmYlWZkVNDVYvrXtNGpiR/ozMjGQkYmBRET5oFJJ382DnY5uHZsOZbJu9ylqmzsI93PnjjljmT06AsUw/jI3mEw8f3AfKoWC1fFJ3PP1Jm4fmcCNEVE4DLG85JzWSh4/8ymhDl6oBAW+di7cFz6Hx06vY4xbKDcHTriqmLtk7pfB2bMQFwfr1sHtt/ffeUVRpLamlcwz5WSml5NxuoyykgYAVCoFMXF+xI8KIiEpiKhYP8nsBzEGo4ltJ3L44PuTFNc04efmyMrZY7hxYiw2w/R9bejq4ok9O5EJArEenvx27PgLni9qbiKtpppFUTGDqi7NpTCaTWyuOMlI50BG2HtSr2vj9dzt/E/kXLxtnJHJZJK59wXd3WBnB888A//7v9bV0trSReaZcs6klZKeVkpRQS2iCGq1griEQJLGBJM0JoTQcC8pjDMIMZtFDmQU8d72E2QUV+PqYMeKmaO4eUo89rZDa8R6ueiMRtQKyxecWRR7jPz5g/t4+9RJ4jy9eGLKNMb6Dq4Mmp+j3dDNs5lf8uTIm9Eo1NLIvS/x84M5c+D9962t5ELa27rJOF1GWmoJp0+WUFJs6QHq4GhL4qggRo8bwZjxI/DycbayUokrQRRFTuVX8u624xzNLsXBVs1t0xO5fXoSzvaDP+bcG5hFkS252bx46AA1nR1cFxbBoylT8Hcc/BlIrfou/pr+GTZyFfEugSwPmSyZe18xcyZ4eMCnn1pbyc/T1NjB6dQSTp0o5tSJIurr2gEICHRjzIRQxk4IJT4p8KrTQiX6n6zSGt797jh7zhRiq1Zyy5R4Vs4ajZvj4FnI05d0GQy8feoEb6aewCyK3DNqDL8ZPW7Alyu4HN4u2IWz0o5bgydJ5t5XDMbWa6IoUlbaSOqxQk4cLSQ9rQy93ohSJSdxVDDjJoYxbmIovv6uv3wwCatTUNnA+9tPsP1kLiqFnEUpI7ljzhg8nKW0WYCq9jZePHyALbk5eGnseSR5Cgsjo4ZE9pEUlpH4WXQ6A+lpZZw4WsiJowVUlDUBEBjszoTkcCYkhxMT549cIcXqBzKltc28t+04W49nI5fJWJwykjvmjsVTMnnA0u7vmf17Sa+tYbSPL09OncFIT+s22b5WJHPvQ06etEymvvoqhIdbW03vUFnRxLFDBRw7nE96WilGoxkHR1vGTQxl4uQIxo4PxU6qjzNgqahv4b1tJ/jmaBYymcCilJHcKZk8YInHf5F9lhcPHaCpu4ulsSN5eFIKrraDryEISObep5w6BffeC2+8AWOu6CUeHHR26kg9VsTRQ3kcPVRAe1s3SpWcUWNCmDQlkkmTI3B2kWK8A5HKhlbe23acr49YTH7J5HjunDsWdyfp/WrT6Xj1+BE+PJOGnVLJHyYks3xkQs9CqcGCZO4SvYLJaCYzo5wj+/M4tD+HmupWZDKBuIQAUqZGkTItCg9PR2vLlPgvKhtaefe743x99CwKuYxbpyZyx5wxuDgMztFqb5Lf2Mia/bs5XF5GjLsHa6bPZLTP4GmMLJm7RK8jiiKF+bUc2p/LwT05PamWMXH+TJkRzeTpUXh6Df7Us6FEWV0L72w9ytbjOahVCpZNT2LlrNHDvhKlKIp8V5DP3w7sobqjgyXRsTySPAX3QdC7VTL3PuaOO8BggLVrra3EepSXNrJ/Tzb792RTlF8LWIx+6sxopsyIwd1jeDeMHkgU1zTx5jdH+D41DwdbNatmj+H26YnY2Qz+FMFroctg4NXjR3gvLRVbpZKHJ6Zwe1z8gA7VSObex9xyC6SnQ26utZUMDCrKm9i/O4t9uy1GLwgQnxTEtFkxTJkejaPT5Y+IRFEcEilrA5G8inr+veUw+zOKcHWw4+7541icMhKVcniWNThPQVMjf927iyMV5cR7efPM9FkDNqtGMvc+5tFH4eWXLeUI5MO7oc5FlJU0sG9XFnt2nKW8rBG5XMbYCaFMnx3LpCmR2Nj89KIpk8mMXC7DaDShGOadivqS9KJqXtt8kJN5Ffi4OnLfDROZPy5qQI9Y+xpRFNmcm8NzB/fS1N3NyvhEHpqQjOMAK04mmXsf8/bbloyZkhIICrK2moGJKIoU5tWyZ+dZ9uzIpL6uHVs7FavvnsqS28Zfch+j0UR5aSMvPbuFydOjuXX5RKkuTh8hiiJHs8t49auD5JTXEebrxu9uSiElLmRY3zm16bT888ghPkk/jYdGw5NTpjM/LGLAvCaSufcxu3dbyhDs2gUzZvzy9sMds1kk43QpO7dnMm5CKJOnX9wP0mQ08+Vnx6iubKEgr4ZR40K4455pVFc2k59bw5QZV99DUuKnMZtFdqbl8frmw5TXtzAq3I8HF01mZIjPL+88hDlTU83ju3eQ1VDPtOAQnp42c0DUqpHMvY8pLbW03HvrLbjnHmurGfzUVrfw5mu7iIj0JnqkP5s/P8lvfz+Hw/tzyc+tpqK8CZ3WwP1/mHdRS0OJ3sFgMrHpYCZvfXuUpvYuZo8K5/6bUgjwGL6F5oxmMx+eSeOVo4cQRZGHJiRzR+IoFFYMX12NuUv3vleAvz8olVBYaG0lg5+qiibef2svkyZHcNuqZGqqWrCxUaBWK/j43f3cunwSr/xnNQmjgqmuagYsIQWJ3kUpl3Pr1AQ2P30n914/gQOZxSxZ8yEvfbaXlo5ua8uzCgqZjLuSRrN9xR1MCgjkuYP7WLxhLZl1tdaWdkVI5n4FyOUQEgIFBdZWMvjR6Yy0tXWz9oMDfPDWXo4dLmDugkT27c5i1LgQAoLcMBhMBIW4U1psaVByPv4pmXzvo7FR8ZsFE9n89J3cMDGGDXtPs/DJ9/l4Zyp6g9Ha8qyCn4Mjby24idfm30BNZweLNqzlhUP76TYYrC3tsrimsIwgCM7AO0AcIAK/EkXxyE9tP9jDMgCLFkF2NuTkWFvJ0CD7bCXv/Wc3OdlV3HL7BPbuyuLPT9xIVIxl9eD/e+k73D0dWLY6pSerBix17L/dnEZ1ZTPXLUwiMtrXmpcx5CiobOD/vjzA4awS/N2deHDRZGYkhQ2YCcb+plWr5YVD+9lwNoMgJ2eemzGbiQGB/XZ+a4Rl/gVsE0UxCkgAsq/xeAOe666DlBRLCWCJq8dktDQCj4j0ISLalzvumYZKrcTBwZaoGD9MJjP1dW1knClj1tyRlp3OveYlRfW8/+ZeKsoa8Qtw5e3Xd9HY0G6lKxmahPm589rvFvH67xZjo1Lwp7e/4Z5XNpJdNrhCE72Fk40Nz8+cw9pFtwCwfNNGHt+9gzadzsrKfpqrNndBEByBKcC7AKIo6kVRbOktYQOVe+6Bd94ZfLXdBxrnywq3t3ej1xuZNDmCsRNCCQ23LCLp7tKzc1sG4ZHeeHo7YTaLPfvs2p6Bp7cTd903nVuXT8TWTkXayRIAtFoDudlV1FYP+Y9ivzAxJoh1f1nBX5bNpKi6iRUvrOOpj76nobXT2tKswsSAQLYuW8U9o8aw4WwG8z75gN3FRdaWdUmuOiwjCEIi8BaQhWXUngo8KIpi539tdy9wL0BgYODo0tLSaxI8EBDFH/qqSvQenR1aHn1oPQGBriAIODjYMG9BIiGhnuh1RlRqBVmZFWz/5gzTZ8eSODoYrdbAmsc2cvdvZxIa7sUTf96AjVrJmbRSblg0mqUrJ0mNw3uJ9m4d72w9xvo9aaiVCu6eP57bpycO25WuZ2qqeWTndvKaGlkUFcMTU6bhbNM3LRD7OyyjAEYB/xFFMQnoBB79741EUXxLFMUxoiiO8fDwuIbTDQxE0TKp+vDD1lYy9NDY2/DC/y0jLMKbEaGe3PM/MwkJ9QRApbYYSHFBHe6eDvj6uwCQdrIYvwBXDAYj3289g05r4PFnFrN20wOcOllMV+cPt81Go6n/L2oI4WCr5qElU/j8yVWMCvfjX5sOcMszH3MgY2COXPuaBG8fNt+2gt+Nm8DXeTnM/eRDdhYNnGyLazH3CqBCFMVj537/HIvZD2kEAe6/H+bOtbaSoYlGo2bx0vHcfPsEFAo5jQ3tfPHpMdLTLHd8dho1TY0dPZUoT50oJijYg452Lfk5Ndy4xDK4KS9twMnZDpVKQUe7lr07z/KH+z7ipWe3UF3ZbLXrGwoEerrwr9/exKv3L0IuE3jw35t58N9fUV4//EJhaoWChyYks+nWZbjb2XHvN5v54/ff0arVWlva1Zu7KIo1QLkgCJHnHpqJJUQz5Hn4YVi40Noqhgdu7g7Mnj8SvwBLn1ej0YS225KKduxQPhVljUTG+NLZqUOvNzJ2QigALc2duLhqEIENnxzm6MF8HvjTfBwcbfnys+PWupwhRXJsMBv+dyUPLppMal4FNz/9Ef/ecphu/eBIFexNYj292LR0ec8oft7aD9lTYt07mmvNlvkdsFYQhHQgEXju2iUNfEwmSypka6u1lQwPHJ3scHO3lBKOTwykuamT1be+ztYtaUybFUtElA952dW4udujVitpb+umrLQRGxsVJpOZPTvOsvqeqYRFeJMyLQqTyUxb2/BcoNPbKBVyVs8Zw6an7mDWqHDe+e4YN6/5iL1nCofdegSVXM5DE5L58tZlONnYcNeWTTy263s69Hqr6LmmmRBRFE8DQ7Dp3M9z+rSl1d7GjXDzzdZWM7zw8nHmhf9bRnFhHc4uGlxcLa3kigpqewqTpaeVUVnWRMr0KI4cyCM03AsfPxdEUUStVlhWw6p/ukqlxJXj4WzP3+6cz+KUkbywfjd/eGMLKXEh/PnWafgPs1IGcZ5ebF66nP87dpi3T53kUHkpL82ax3j/gH7VIa1QvQpiYy2rVc+csbaS4UtIqGePsQPMvT6B997Yw5YvTvLRe/uJjfcnISmIzZ+fYP6NSYBlheuBPTl4ejuhUiswm4fXyLI/GB3uz7rHl/OHJVM4lV/BLc98xDtbjw27Va5qhYJHkqew4ealyAUZy778jOcO7EVn7L/XQTL3q8DGBqKjLSN4iYHBtFmxLF05ieqqFu64ZyrTZsVSV9OKUqVg9LgRADTUt5N2spgFCy3z/tJahb5BKZezYtZovnzqDiaPHMG/vz7MbX/7hJN55daW1u+M9vHj22WrWDYygXfSUlm4YS3Z9XX9cm6pKuRVsmIF7NsH5cPv8zpoEEWR11/ZTmS0L9Fx/nyzKRW9zsgDf5p/wTbHDhcwdkKoVEO+jzh0toS/f7qbioZWbpgYw+8XT8HFvm/ywQcye0uKeWTndlq1Wv44KZm7ksYgu8wRhlTytx/5xz/gT3+ChgZwc7O2Gomf4sjBPNa+fxBBgPk3JjFuYijuHo49bf1Sjxfx6O/X4Rfgym0rJzFr3kipG1Qf0K038M7WY3y8IxV7WxUPLZnCggkxw65WTVN3F3/ZvYPvCwuY4BfAP+fMx8fhl/sOS+bej+zYAXPmSI07Bgv1dW14eDpe9LjZLHJoXw7rPjxEQV4N3j5OLF05iTnXJUgrW/uAgsoGnl23k/SiasZHBfKXZTOHXe14URTZmJXJ0/v3oJTJ+duM2VwXHvGz+0jm3o/U1YGXl6Wn6kMPWVuNxOXwc024RVHk+OECPnn/ADlZVXh4OnD7qhTmLpBMvrcxm0U+P5DOq18dxGQy85sbJrJsxigUwywsVtLSzEPbt3KmtoZbYuL469QZ2CkvncUlmXs/4+dnabv30UfWViLRW4iiSOrxIj5+9wBZmRV4eDly+6pk5i1IRKmUwjW9SV1LB8+v38W+9CJigrx4csVsIvwHf4mSK8FgMvGvY0f4z8ljBDu78K951xPn6XXRdpK59zM33gi5uZYfiaGFKIqcOlHMR+/sJyuzAi9vJ1b8ajKz58X3VKeUuHZEUWTHqTz+/uke2rt03DlvLHfPH49ymM17HCkv44/ff0djdxePJE/hzsRRF9xlSubezxw7BmYzTJxobSUSfYUoipw8VsSHb+8jN7sKX38XVt9tSbWUyYbXZGBf0tLRzUsb9/Ld8RzC/Nx5auUcYoIuHsEOZZq7u3lk53Z2FhcyI3gEL86ei6utpfSsZO4SEn2EKIocOZDHB2/vo7iwjpBQT+789TQmJIcPu4yPvmRfeiHPrdtFU3sXd8wZyz3XjR9WJYVFUeTj9NM8d2AfLra2/Gve9Yzz85fM3Rps2wZdXbB4sbWVSPQHZrPIvl1ZfPD2XqoqmomN9+fu+2YQl9B/LdeGOu1dWv6xcR9fH80izM+dp1fPJSrA09qy+pWzdbX8btu3lLW28NCESdw/bqJk7v3NnDnQ3AwnTlhbiUR/YjSa2P7NGT56bz9NDR1MSA7nrvtmEDxieE0I9iX7M4p4du1OWtq7uWv+OH41fxxK+fCJxXfo9Ty+ewcms5nXr79RMvf+prIS3N1Brba2EglroNUa+Oqz46z/+DDabj1zrk9g9d1TcPe4OKde4spp7dTy4md7+O54DjFBXjxzxzxCvF2tLavfEEURvcmEjVIpmbuEhDVobeli3YcH2fLFSRQKObcsm8Atyydia6uytrQhwc5TeTy3bhfdegO/uymF26YlDasJbSnmbiWefBI8PS0dmiSGN9WVzbz7xh727crC1d2eO++dxuz58VLdml6gobWTZ9bu4EBGMROiA3lq1Vw8ne2tLatfkMzdSkydaplUleLuEuc5m1HOm/9vJ9lnKwmL8Oa+B2cTnxRkbVmDHlEU+fJgBv/8fB8qhZz/XT6LWaN+fun+UEAydyvxxBPw3HPQ0gKXUQNIYpggiiJ7dpzlnX/vor6unSkzorn3f2by/9u77/Coiq+B49/JpieEhBAIEEqC9CqELkWqBUSRrqAUEelNAfmpIIr0KoL0KihFqQqK0pEmUqSEEFoooaVAepn3j0kIIL6kbHKzm/k8z322ZPfu2UDOvXfmzEzBQrlrLpWscOVWKP9b/AunLt3ktToV+LB9I1wcrbcJLCPJXV8rmkGDBmow0/79Rkei5SRCCBo3r8ii1X3o2qMBB/edp3unuSxfuJvY2Ny3zqg5FSvgwcJh7enxUk02/fkPncat4J9LN40OK0fRyd0M6tRRKzPt3m10JFpO5OhoR5ceDVi06gPq1C/NsoW76dl5Lvt2nct164yak53JRN/W9Zg3uB0JCUl0m/Q9S7Yf1itsJdPNMmZSu7Za2efAAaMj0XK6v49eYvbUbVy6eJuadZ6j7+DmFPbJPeV9WSEiMoaxK39lx7FAapcrzth3W+Dp5vLsN1oI3SxjoFdeUXPNhIQYHYmW01WtXoI5S3vSe0AzTh2/Qs+3v2XZgl3ExeaudUbNyc3FkYnvteTjzk04FhhMxy9XcPDMZaPDMpRO7mbSujVICZs2GR2JZglsbU282bEWC1d9QL0GZVi+aA/vdfmWvw4HGR2axRJC0LZ+ZZYN74ybsyN9Zq1nzqb9JCYlGR2aIXSzjJlICb6+UKmSTvBa+v11OIgZk37menAoTVpU5P3+zfDIZz3NCtktOjae8d//zqYDp/Ev7cOX3V/GK6/l1sTrZhkDCQE9e0KpUkZHoskx/OsAACAASURBVFmiajX8mL/8fd7q9gK7dpymR+e5bNtyXHe4ZpCTgx1jurZgdNfmnLp4k87jVnL4XO5azV6fuWtaDnP54m2mTdjCPyeCed6/BIOHv0qhIh5Gh2WxLly/w4fzt3AlJJQPWtWlW4saFjd1gR7ElAMkJcGVK1CihNGRaJYsKUmyZcNfLJi9g6QkSbf3G9G6bQ09jUEGRcXEMXblb2w7co4GlfwY+24L8jg7Gh1WmulmmRygb1+oWRMSE42ORLNkNjaCVm9UZ8F3valSrThzZvzKkA+WceXSHaNDs0jOjvaM6/4yH7VvxP5/LvHW+O8ICL5tdFhZSp+5m9m+fRAUBB06gL31jobWspGUkh3bTvHNtG3ExMbTrVcj2nSopc/iM+j4het8NH8z96Ni+bRLM16qUdbokJ5JN8tomhW7d/cB0yds5cDeACpU9mHYqNfwKaoHP2XE3YhIPpq/hWOB1+jStDr9X38B2xx8sNTNMjnEzZswa5Zqf9c0c8nn6cqYCe346JPXuHzxDh+8M59N64/qipoM8HRzYe7AN+nQqCrLfztKv1nrCXsQbXRYZqWTexb4/XcYMAB27jQ6Es3aCCFo9nJl5q/oRYXKRZk5+WdGDV3N3Tv3jQ7N4tjZmhje4UU+69KcYxeu03XCKgKvWU+fRqaTuxDCJIQ4JoTYbI6ArMEbb0DevLB4sdGRaNYqv5cbX03rRL+hL3Hi2GV6dZnHvl3njA7LIrWuW4H5g9sRExfPu5NWs+v4BaNDMgtznLkPBM6YYT9Ww8kJOnWCdesgPNzoaDRrJYSg9Zv+fLO4JwW98zJ65Bqmjd9CdHSc0aFZnMp+hVgx8i1KeOdjyLcbWbztkMU3d2UquQshfIBXgQXmCcd6dOsG0dHw/fdGR6JZu2Il8jNjXjc6vF2Xnzcdo2+3hQQG6LnN06uAuysLhrSnefUyzPppH58t3UZcvOVO5papahkhxFrgKyAPMExK2fIpr+kF9AIoVqxY9cuXc8dMbVKqeWby5NHTAGvZ568jF5nw+Qbuh0fTq19TWrf1RwjLGo1pNCkl87ceZO7mA1QtWZgpvV/Dw9XJ0JiytVpGCNESuCWlPPr/vU5KOU9K6S+l9Pfy8srox1kcIdTZ+59/whndaKVlk2r+vny79D2q1fBl9rRtjPl4LfcjrKsKJKsJIej1am2+6vEKZ66E8M7EVVwOCTU6rHTLTLNMPeA1IcQlYDXQWAixwixRWYm331YrNOmOVS07uXu4MHZSB97v35Q/956nT7cFnD19zeiwLE4L/zLMHdSWyOg43pm4iqPng40OKV0ynNyllCOllD5SyhJAR+B3KeXbZovMChQsCK1aqeQeFWV0NFpuIoSgbafaTJ3TlaQkyeDeS9m47ojFdxJmtyp+hVn6UUfyubnQZ+Z6th22nIokXeeexYYMUQtoh4UZHYmWG5Wv6MOcJT2pVsOPWVN+YfyYn3Q1TTr5eLmzeFgHKvl6M3LRVpZut4yDpJ5+QNNygaQkyapl+1g6fyfFfb0YPb4dRfS6rekSG5/Ap0u38evRADq9+DxD2zbMtqmD9fQDOdi5c3D4sNFRaLmVjY3grXdfYNzUTty984C+3RdycH+g0WFZFAc7W77q/gpvNanGqj+OMXLR1hxdKqmTezaQUq2xOmSI0ZFouZ1/rZLMXtQd70LufPLhalYt22cRTQw5hY2NYGjbhgxqU59fjwYwYPZPRMbkzGYundyzgRCwfLkasao97tq1a8THxxsdRq5SqLAH0799l4ZNyrNo7h+M+/RHYmL0v0F6dG3mz5iuzTl6Pphe09YQej/nVUzo5J5NatSAAgXUWXxuJaUkKCiIJUuW0LFjR7y9vfHx8WHzZj0tUXZzdLTj4zFv0OODxuz6/TRD+izjzu0Io8OyKK3qVGBK79cIunGXHlPXEBKasyZv0x2q2ejyZWjfHr76Cho3NjqarCel5OzZs+zatYuff/6ZvXv3Eh0djclk4sGDB9ja2tKhQweWLVuGjY0+zzDKn/vOM+6zH3FytmfsxA6ULlvI6JAsytHzwQz6ZgNuzo7MGfgmxQq4m/0z9GIdOVxMDJQpA15ecOgQWFs+S0xM5OTJk+zatYutW7dy4MABkpKSkFIS9UShv7OzM61ateK7777TiT0HuHjhFp98+D3hYVGMHP06dRuUMToki3L6cgj9vv4RWxvBnIFvUrJwfrPuX1fL5HCOjvDFF3D0KKxebXQ05tetWzf8/f0ZMWIE27dv5/79+0RGRj41sb/yyiusXLlSJ/YcwrdkAWYt6EYJPy9Gj1zD+u8PGh2SRSlfvCALhrQDIXhv6hrOXr1ldEj6zD27JSVB9eoQGqrKIx0cjI7IfM6cOUOzZs24c+cOsbGxT32Nk5MTLVq0YO3atZhMpmyOUHuWmJh4Jny+gb07z9KmQ03e798s22q5rcGVW2H0nrGWyOg4vhnQhgolvM2yX33mbgFsbGDSJNX+Pnu20dGYT1xcHNu3b3/Ylv40Tk5ONGnShDVr1ujEnkM5Otrxv7FteL1dDdZ/f4gvP11PXGzOreXOaYoVcGfBkPa4OTvwwYx1HA+6blgsOrkboGlTaNECPv8cbtwwOprMSUxMZPHixfj4+DBq1CjCw8OJjIzExsYGV1fXh69zcnKiUaNGrF+//j+Tv5YzmEw29BnUnF79mrL79zN8PHQVkZFPvxLT/q2wpxsLhrbHI48z/Wb9aFiC18ndILNmQWws9OtndCQZI6Vk3bp1+Pr60r9/f27fvk1kZCSg2tSbNWvGxIkTcXZ2xsHBgfr167Nhwwbs7OwMjlxLCyEE7TrXZsRnrTl1/CrD+i4n9F6k0WFZjIIeeZg/pB35jEzwUsps26pXry61VOPHSwlSrltndCRpl5SUJLdv3y7Lli0rXVxcJPBwc3FxkXXr1pWHDh16+PpTp07J0aNHy9jYWAOj1jLj4P7z8tVGX8l3O8yWITfCjA7HooSE3pevfbJI1h/0tTx18UaG9wMckenMt7pD1UAJCfDyy/Dee6r+Pac7cOAAAwYM4MyZMw/P0gFcXFzw8/Nj5syZNGrUyLgAtSxz6sRV/jdsNc4uDkyc+TY+RfWkY2l189593pv6AxFRsXw7uC1lixZI9z50nbsFklJNT5CTnThxgkGDBnHw4MHHyhpdXFwoUKAAM2bMoGXLlno5NysXGHCTEYO+w2SyYeLMtyjum3tWVsus63cj6Dn1B2LiElgwpB1+hTzT9X5dLWOBhFAJ/uuvc97cM4GBgbzxxhvUrl2bnTt3PkzsLi4ueHt7M2/ePAIDA2nVqpVO7LnAc6W9mTK7CwBD+y7nwvkQgyOyHIU93Zg7sC22NoLe09dy9XbWL/Cgk3sOkJAAK1bA+vVGR6Jcu3aNrl27UqlSJTZt2kR0dDRSSpydnfHw8GDy5MlcuXKFzp0760FIuUxxXy+mfNMVe3sTHw1YoRN8OhQr4M6cgW+SkJhEnxnruB32IEs/TzfLmEliYiI3LoRw8eQVLp68wu2rd4iMiOJBWBSJCYnYO9rh4GSPi7sLXkU8ye/jibdvAUpULIpnIQ/CwgR58xo7JcGdO3cYM2YMCxYsIDEx8eFsjU5OTtja2jJq1CgGDBiAk5OxK8FrxrsefI9h/ZYTG5vApFlv4/dcQaNDshinL9+k17S1FMqnSibzujg+8z26zT2bxcfF8/cf/7B33Z/s33CYsORZ9WxsBB7e7ri6u+CS1xmTnYn4mHhio+O4f+8B926EkpSU+nvPk8+VklWKU75OGfI9V5GAkNJ8ODz7hq5GREQwceJEpk2bRmJi4sPRpQ4ODphMJgYNGsTw4cNxc3PLtpi0nO968D2G9l1OQnwik2d30W3w6XD43FX6f/0jZYoWYO7AN3Fy+P9LhHVyzyZSSv5YtZd5Hy3n7vVQnFwdqdWyOtWbVsavSnGKl/fBwem/k3NiQiL3boZx7fwNLv1zlUunrhJw9AIX/r5EQEIHLtGGxiV/5L2eUO+NmhQtUyRLvkd0dDSzZs3iiy++ICEhgejoaADs7OywtbWle/fujB49mvz5zTsJkmY9gq/cZWjf5QBMndNVL92XDjuOnWf4/C3UrVCCKb1bYff/jNrWyT0b3Lx0i5l95nP4l78pW/M5On3cBv/mVbB3tM/0vqMjY/jnQCDde+fj1IWCVGUcnuIEzz3vS+NOL9CoYz28fNLXy/408fHxLFy4kFGjRhETE/Owo9RkMmFvb0/btm0ZN24cPj4+mf4szfpdvnibIX2W4eRkz7S57+BVQF/hpdW6PSf48rsdtK5bgU/fbvafhQk6uWexy6evMrjBp8THxtP9y8681rdFlsyREhEBL7wAly4l8XmfPVzY+QtnDwViYyOo+Wo12gx8laovVkx3hUpSUhKrV69m2LBhREREPKxVF0Lg6OhIs2bNmDx5MqVKlTL7d9KsW8DZG3zYfwWe+V2ZNucd8ro7Gx2SxZizaT/ztx6k16u16d2yzlNfo5N7FnoQFkm/WiOJiohi2p6xFHkuaxc0uHoVatUCOzvYvRts42+wfclOts7/jbDbEfhVKU7H4W/QoF3tZx5gpJRs2bKFgQMHEhIS8tgAJGdnZ2rWrMn06dOpUqVKln4nzbqd/PsKIwZ9h1+pgkyc+RZOTpm/ms0NpJSMXr6dTQdOM6Zrc1rVqfCv12QkuevpB9JobIcpsoVdB3lyz+ls+8y//pLS3V1KPz8pg4PVc7HRsXLrgt9k9/IDZVPRVr5Tur/c+f0+mZSU9NR97Ny5U1aqVOmpUwVUr15d7tu3L9u+j2b99u06K5vX+0J+PGSVTIhPNDocixEXnyDfn7ZG1ugzXR4+d+VfPycD0w/o5J4G548FyaairVz62ffZ/tkHD0qZJ4+UpUtLef166vOJiYly99oDsmelwbKpaCsHvjBKnjsS+PDnR44ckXXr1pXOzs7/SuplypSR27Zt+88DgqZlxuYfj8qmdcbKqV9t1v/H0iEiMlq+OWaJbDhktrx0895jP8tIctcjUNJg7ZRNOLs50WbQq9n+2TVrws8/w7VrsHhx6vM2NjbUf7M2c49NYvC83lwLuEG/miMZ02kiLzV7mfr167N///7HRpUWLVqUJUuWcObMGZo3b65HlWpZ4tXXq9Gpaz22bjzG6uX7jQ7HYuRxdmT6B62xsbFh4Dc/EREZk6n96eSeBid2naZOK39c3V0M+fx69eDYMRg5Uj1OSkr9mclk4pWeTRjz6zDsn5Ps+f4Q93eAXbQaaOTi4oKXlxczZ84kKCiItm3b6qSuZblu7zeicfMKLJr7B3v+OGN0OBbDx8udKe+34vrdCEYs3EpCYtKz3/QfdHJ/hqj70dwOvkuJCkUNjaNUKTUPzcWLULmyWmA7PDycMmXK8O6771K9VjW2Bf3EUbkLIQU1RCPKOFZm7NixXL16le7du+tFMrRsI4Rg6MhWlKtQhAmfb+D8OQtflSYbPf9cET7u1IQ/z1xm5o97MrwfndyfITY6DgCnPDljyL2U4OwM0dFRtG/fnYCAAFasWEFMTAwJCQnEOD7gpPN+vCp4UDS2NAkn7bER+p9Zy372DraMmdAON3dnPhuxRi/2kQ6v16tIh0ZVWbHjL34+dDZD+9B/9c9gZ6/OduNj4w2ORClYEKKj19CoURLbt38LjCAxUZWzmkwm+vbty6Xgi3x3Yj5vf9KW7Ut28slrE4iN1sukadnPI58rY8a3Izw0irGj1pKQkGh0SBZjSNsGVCtVhIk//JGxHaS3BzYzmyVWyyQlJcllo3+QAUcvGBpHTIyU06dLmTevlI6OiVKdw6dsu6Sbm588cODAv963dcFvsplNOznipbEyNibOgMg1Tcod207KpnXGyjkzthsdikW5E/5Anr0SkqFqmQw3wgohigLLAG8gCZgnpZyR0f3lVEIIunzWzrDPT0yEpUthxAiIjARV/GKDEElIGYsQZ5CyFibTKaKj/9109HKPJgghmNJzDlN7zmH4sv66Q1XLdo2bV+T0qWDWrT5IhUo+1H+xnNEhWQRPNxc83TJWyJGZZpkEYKiUshxQG+grhCifif1pj5AS1q4FX18YMABu305J7ODkBAUKnMDVtRGTJv2Bq2szEhJCadIERo2CuLjH9/VS98a8M6YDO1bu4ZdFv2f/l9E04P3+zShbvjCTx23mxrVQo8OxehlO7lLKG1LKv5Lv3wfOAFkzfWEuIiVs3w7lysG776ppCFJmC3B2hrp1Ydcu2LQpnsDAjQwdOpTAwDVs3nyTbt1g3Djw94ejRx/fb6eP36Ba00rMHrCIm5duZfv30jQ7OxOjxrbBxkbwxSfriY/X7e9ZySwdqkKIEsDzwMGn/KyXEOKIEOLI7du3zfFxhoqMiOKP1fv4dtgy7t4w79nH/v1Qowa0aQPnzqUmdRcXqFQJtmyBffvUa2rUqEHBgmqBhIIFC9KgQTUWLoSNG+HuXTUvzYgRkDw1OyaTiWGL+gKwaNR3Zo1b09LKu5A7Q0a2JODsDZYt2GV0OFYt08ldCOEKrAMGSSkjnvy5lHKelNJfSunv5WXZk/mHhoQxoess/vrtBDY2gs9en0BwwPVM7/fECXjxRWjWTJ1xP5rUfX1h1So4fhwaNXr2vlq1gn/+gXfeUVcAj5a2e/l40nZIK/5YtY/LZ4IzHbemZUT9RmV5uVVVvl+xnxPHLhsdjtXKVHIXQtihEvtKKWUOWQE0a8RGx/Lb8t3kze/G0AUf8N7ELrh55iHkcsavRs6fh9atoXZt1dSS0qbu4gLe3jBvHgQGqoSdnj5Qd3dYuBD27gWTCe7dg/bt1dVAy97NADiw4XCG49a0zPpgYHMKFfZg0hcbiYrUZbpZIcPJXaiSi4XAGSnlVPOFlDOdPRTIlbPXeLlHYwCCA67jXjAvnoVTV56RaZw+OTgYunZVI023bIHo6NTBSR4eMHkyXLkCnTtnbk1V5+QptU+ehN9/V000+Yt4UrKqL0d/PZ7xHWtaJjk52/Ph/1oRcjOc+d/sMDocq5SZM/d6QBegsRDi7+TtFTPFleOc2Hka9wJ5KV+nDABXz13H0dmRpEfmfpBSEhkeya4f9j910NCdO9Cvn5pKYPVqiIlRpY5OTpAnD3z6qZogrHdvNY+7uTRsqA4olSurxwfvdWHLsaZcvWq+z9C09KpYpRhtOtRi849/cVw3z5hdZqpl9kophZSyspSyavK21ZzB5RRSSnZ8t4eG7dUqKRdPXubcoUDyF8mHX+XiD1+35dtfmTt0GduW7qRnxSH8uVmVrEREqBLF4sVhwQKV1OPjwcFBnV0PHqyS7/DhKtFnBcfkBdYTE8HeDs6G1uG55+CDDyAoKGs+U9Oe5Z33GuJd2J3pE7YQF5dgdDhWRU8/kAaJCYlUblCeu9fuEf0gmg2ztxEfG8+LHes9fM3BLUfZve5Pmr7dgHFbPqbTyDZc/Oc6EyaAjw9Mm6ba1GNj1Vm5oyP07AmXL8OXX4JbNi07aTJBVZel9G74Dd26qbb5UqVUm/yhQ9kTg6alcHKyZ+CHLxN85R4/rDxgdDhWRSf3NLC1s6VBuzrMGbKU0W0m4ebpSvuPWlPIr+DD13w3bj3N32lElUYViI+HPftsmfxpIJ9/Dvfvg030VRxtwnF0hI4dVWfq119D/vzZ+11uXrrFpVNXqPOiN3PnwqVL8OGHqrKmVi3Vubt8eWoJpaZlNf9aJWnUpDzfLd2rBzeZkU7uaeTfvApLzs1kyPwP6P5lZ84dvkBiohqEsX3pTvIV8qBh+3qsXAnFisHuZRu4Elef6KgE/MQaypkWU99hOON7rWHZMnU2n92klMzqtwB7R3teSu4YLlwYxo9Xg6VmzIDQUHVFER6u3pNSwaNpWen9AU0xmWz49uvfjA7Faujknk4Fi3uRmJBI2K1wAv+6CED43fsI97KUKyd5/32wu7mFB0nehFGOsnarKOETxeStfdlwaxr3Q64Scfd+tsedlJTEt0OXcmjrMbp90QkvH8/Hfp4nj5rm4MwZVWtfoIB6/qWXoFu3bA9Xy2Xye7nRqWs99u06pztXzUQn9www2Zpo/k4jnqvmy86dMHmqI98vu0fQRTsSIu9Sgh+54dSBGiUO0fbNRL5Z/wINm3sSH5vA6QMBxCd3HMXFxBF6KzzL442LiWNC11msm76F1/u/zOsDXv7P19rYQMWK6r6U8Npr0KCBehwVBZ06wQ8/pA600jRzebNjLbwK5GHB7B1pLivW/ptemieDjhyBAQNMHD8OdlHFKMs2nmcsibYexORtxorvinNu469UfKEcfpWLAar5pkHbOngW8uCf/ef4YdIGbgSFULJqCQZ/+z72jvZmjTEuJo6t83fw/cSfuHPtHj3GdabD8NfTPCukEDBsWOrjgADYuVOVcTo5wauvqqkSXnkF8uY1a+haLuTgYEfXng2ZMm4ze3edo36jskaHZNH0mXs6nT6tmioaNIADB9TZbDhlOOU8kbh8DRkyuxP7b7alfr0Y7t0Mo5BfAezs7bhy9hpXzlyjQt0ynNp7hjVTNlKtaWXmHZ9CYkIiBzYeMUt8UkqCTlxmySer6VKyH7MHLqKQX0Em7fiMjiPeyNR0v1WrqpLNnTtVU82ePWqglZcXNG8Os2bBhQtm+RpaLtXs5coULebJsgW7SErSZ++Zoc/c0+jSJfjoI9i0SU2pm7JItYuLqlUfP96Grl0bPJzL5WZQCKEhYZStWQqAH2dsoXDJguTJ58rJPWcpWrowrfu+BEBSYhJxySs9SSkRQhD9IJq710PxKJgXR1dHTCbTY/EkxCcQdiucuzfCuHX5NheOX+LiySucPRTIvRuh2NgIqjWrzMcrB1KlUQWz/R5MJjUoqmFDmDkTDh6En36CDRtUm/2AAeoAUKSI6qTNl0/9jjQtLUwmG7r0aMC4z35kz84zNGysZxHPKJ3cn+HmTfjkE1ixAhIS1AaqWcLeHkaPVgOBHBwef597gbx4FHRnWOPR+FYsRuCxi3Qe9SZXz17jasA1OnzYGlDTGBQu6Y2bZx6Ah2fWJ3af4X8tv3q4Pwcne+wd7UiITyQhPvFfy/7Z2Ah8yhSmSqPyVGtSmRovP49nIY+s+aUkM5nUFMR168LEiWoenH37VGIHGDRITX0QEKAenz0LJUqkDqjStKdp0LgcyxbuYvWy/TR4sZxeXCaDdHL/D6GhanDRN9+oUZ0pC2A4OqqkNnw4DBny32elru4ufLZ2GJvmbid/kXx0GN6a/EU8WT3+R9zzu1G8fFES4hO4cPwy4bcjHquZByhZpTgfLe1H2K0IYh7EEP0gmvjYBEx2JmztTDg4O5DP2x0Pb3e8fDwpVq4IDk4OTw8mmzz3nNpSDBwIISHqvpRqVsuwMFVPX78+vPCCqqt3dzckXC2HMplsaP9WHaZ+tYVjRy9Rzd/X6JAskk7uT3jwAKZOVWeiiYlqqgBQZ+kmE/Tpo6YS8EjjSXGr3s0f3k+ITyD0VjidRrwBwIldpwk4HEjJqr4UK/v4Oif5i3jSrEtDs3wno6RU2YBqxvr2W9i9W7XVjx+vfr9CQIUKKuHXqgWNG0PJksbFrOUMTZpXYuGcP/jph8M6uWeQ7lBNFhsL06erwUXjx6tSv5gYNR+6o6OaxTEoSM3YmNbE/iRbO1sq1ivLxHe/ZtOcbSz+ZDXevgV4sVO9Z7/ZwplManrjKVPUNAdhYbBjB3z+ufqd//gj9Oql5q4HNU3xwIFw6pSxcWvGsHew5ZXXnufPfQGE3AgzOhyLJLKzntTf318eOWKeqhBzSUiAZcvUqkVRUan12zY2qh29ZUt1Fl+ihPk+87cVu7n8z1WqvFgR/+ZVzLdjCyalqrRxdlajZg8dUguYbNwITZrAtm3w8cdqZssqVdRtxYqpg60063PzRhhd237N293q07WnZV/FZpYQ4qiU0j8978m1zTIpC1APHarOEh8dlOPkpJoUpk6F8lnQWd/07QbPflEuI8Tj7fU1a6rZNFPOPUwm8PSErVthyZLU13l5qWad8uXV1rlzxq+stJzFu5A71Wr4sX3rCbr0aKA7VtMp1zXLSKnOAsuVU7Xa/7UA9S+/ZE1i19LOZEpdJrBpUzW5WUgI3LgBv/6qZtps1Uo1qa1cqebKT+kjmTFDHSDik4uK/v4bDh9WHeWa5WjSoiIhN8M5fUovC5leuerMff9+VYd99uzjZ+ouLuDnp+q207JOqWYsb2+1NW2a+pyUcP26eh5UfX3JkqmLnowZo+rxU37m56d+7uen1qn19VWPfXXfXY5Sr0EZ7OxN7NpxhgqVihodjkXJFW3ux4+rzrnDhx+f5dDFRbXZzpih2tb1VZ/1CgxUC4efP6/a9oOC1O3ly6ljF3x9UxcuGTZMNc+NHase79mj5twvWlQ1++j/K9ln1NDVXL18h6Vr+ubaphnd5v6E8+fVH+mvv6rL9ZTjmIuLmgVxyhQ1t3pm1inVLMOTNfgpEhLU0oZBQalNOgB376auQQvQrl1qzb6Tk6rw8fFRnb9FiqitShU1chfUuAh7804VlGvVrleKQwcCuRYcik/RfM9+gwZYaXIPDoaRI1WHaXy8qqcG9cfq4ADjxkGPHuZdp1SzTLa2avnD4sUff37x4scfb9yoFi2/ckUdDIKD1bZvn2oOiotTnbkpyT1/fjVyecIEddDo3h0KFlSbt7e6LVAgdXtyhLOWqmr1EgCc+OuSTu7pYFXJ/fZt1ba6cKFK6CmdaU5O6o941CjV5p5V65Rq1qtmTbU9jZRq8fOU5p2kJDWCuUYN9TgsTJV23rz531Mlu7mpBdKHDlWvHzpUHRDq1VOdwHv3qmqh/PnVrbu76nDODXyK5cPdw4VTJ67ySutqRodjMawiuUdEqIFHM2aopJ6yRJyDg/oDGDRI/bFl1zqlWu4ihCrJTGFjo04kUnh7qzZ/UMk9JERtDm2/2wAACX5JREFUt2/DrVup9yskz+8WGqoqul5S88px4oSaV//Jz3R3V53Dnp7qdsQIdeVw9SqsW6eakooUUU1M16+r13t4qGZJS2q6FkJQumwhAgNCjA7Folh0co+OVgn9yy9VUo+OVs/b2amk3qOHmtgru9cp1bT/klKZ5ef336/x9VVNPimqV1dn/nfvqu3OHTU249499TjlNuVK9dQpGDxYzdtTpIiayfTR1bRMJpXo3d3VPPwpt+PHQ+nSqgDht9/gvffUCdGlS6r81M0tdXN1zd4rB79SBThy6AKJCUmYbHUnWVpYRHIPD398MYj4eFiwQJ0dxcamVsCYTCqxt2un2tWNWKdU08zN1TW1iSctWrRQCd/VVT1u3BjWrFHNPaGh6jY8XN0PD1fb+fOpzUr79qlChLffVol80aLUqqFHOTurwgQ3N3W7bZs6kVq/Xt2fO1ddIfz6q6pMcnV9fHNxefz20Q7sJxUu4kFSouTWrXAKFdaj1NIixyf3//1PJerRo1UyX71a/ce7fz+1/VIINf9L8+YwaRKUKmVoyJpmKBubx0fpFiumtrTq3RveekslbFBn/XXrqoPA/ftqe/R+RIS6TZnKOSBADThLafpZtkxNmf3/sbdPbU4dOBCOHVOTzIFqbtq/rzQBAfb06WOHT1F1IHh0K1BAndSBGrBmMkGlSupxSIh67OSkttxSHZej69xHj1bJOipK/QPa2qrml0c7pZydVUfX9OmqFE3TtJwlKkpdLURGqllXU07MIiNT7yckqL4xULOHBgWpSiNQM7Hu3BnH5Yv3cXVzIz7ejqio1IMBQJkyanAiqH4HGxv44w/1uHRpdWWSwsEhNdGnbPXqqc9N+bwyZdRBBtTBRQj1OgcHdRB7citRIjX/nDiRWhmVlKS+u4OD2mwzeDptVXXuY8emJnZ4fPARqEu5smXVqNK6dbM/Pk3T0ibl7Dqt3n//8cfffAPnz92lT7eFjBnfjroNygDqRC8qSvW1pTQpgTrRS1kpDVQF3Z07qa99couJeXwCuosXH28GXrhQXZ2krOnwNF27wtKl6n7NmupANX68usLx9Ex9ncmUmuhTDhQODuo7Dx6sDnavvw79+6vb4GDYvDntv7tH5cjk/tVX6hfzZEJPIQT07ateY0m9/pqmZUxMtOotdnRKHZxiMqmmo5TmoxTPP//4406d0vdZP//8+OPbt9VtUpK6Wkg5KMTGqgNDTMzjB4PVq1PXJHBwUAeb2NjU16fcf/RxweS1ehIS1OOUg9X9++pgkxE5rllm8mT47LP/TuwphFADS1q2NGOAmqblSL9vP8VXo39i3vJe+JbMffM8W3yzzLRp/53YhVBH6JgYVTfcrJmetVHTcouAszewt7elWHFd15xWOSa5z5qlqmFSatVtbFR5VHS06qxo0ULNAvjCC4+3YWmaZt3i4xPZ/ftpKlYpqmvc0yFHJPcFC9S0AA4Oqk69TBk1Oq9JE9VZqkeWalrutXHdEW7fus/gEboNNj0yldyFEC8BMwATsEBKOT4j+/HwgE8+Ucuq1aqVvp51TdOsU3x8IvO+/o2f1hymWg1f/Gv9P8N6tX/JcHIXQpiA2UAzIBg4LITYKKU8nd59vfmm2jRN01KkJPY2HWryXt8muXYu94zKzJl7TSBQShkEIIRYDbQG0p3cNU3TntSxS10qVy1G/RfLGR2KRcpM70QR4Oojj4OTn3uMEKKXEOKIEOLI7ZSCUU3TtGfwzJ9HJ/ZMyExyf9o10r+K5qWU86SU/lJKf69H50XVNE3Tskxmknsw8OiKtT7A9cyFo2mapplDZpL7YaCUEMJXCGEPdAQ2micsTdM0LTMy3KEqpUwQQvQDtqFKIRdJKf8xW2SapmlahmWqzl1KuRXYaqZYNE3TNDPRY3k1TdOskE7umqZpVkgnd03TNCukk7umaZoV0sld0zTNCunkrmmaZoV0ctc0TbNCOrlrmqZZIZ3cNU3TrJBO7pqmaVZIJ3dN0zQrpJO7pmmaFdLJXdM0zQrp5K5pmmaFhJT/Whkv6z5MiNvA5Wz7wFT5gTsGfK6R9HfOHfR3zh3KSCnzpOcNmZrPPb2klIYsoiqEOCKl9Dfis42iv3PuoL9z7iCEOJLe9+hmGU3TNCukk7umaZoVyi3JfZ7RARhAf+fcQX/n3CHd3zlbO1Q1TdO07JFbztw1TdNyFZ3cNU3TrJDVJ3chxEtCiHNCiEAhxAij48lqQoiiQog/hBBnhBD/CCEGGh1TdhBCmIQQx4QQm42OJTsIIdyFEGuFEGeT/63rGB1TVhNCDE7+P31KCLFKCOFodEzmJoRYJIS4JYQ49chz+YQQvwohziffeqRlX1ad3IUQJmA28DJQHugkhChvbFRZLgEYKqUsB9QG+uaC7wwwEDhjdBDZaAbwi5SyLFAFK//uQogiwADAX0pZETABHY2NKkssAV564rkRwA4pZSlgR/LjZ7Lq5A7UBAKllEFSyjhgNdDa4JiylJTyhpTyr+T791F/9EWMjSprCSF8gFeBBUbHkh2EEG5AA2AhgJQyTkoZZmxU2cIWcBJC2ALOwHWD4zE7KeVu4N4TT7cGlibfXwq8npZ9WXtyLwJcfeRxMFae6B4lhCgBPA8cNDaSLDcd+AhIMjqQbOIH3AYWJzdFLRBCuBgdVFaSUl4DJgNXgBtAuJRyu7FRZZuCUsoboE7egAJpeZO1J3fxlOdyRe2nEMIVWAcMklJGGB1PVhFCtARuSSmPGh1LNrIFqgFzpJTPA5Gk8VLdUiW3M7cGfIHCgIsQ4m1jo8rZrD25BwNFH3nsgxVeyj1JCGGHSuwrpZTrjY4ni9UDXhNCXEI1uzUWQqwwNqQsFwwESylTrsjWopK9NWsKXJRS3pZSxgPrgboGx5RdQoQQhQCSb2+l5U3WntwPA6WEEL5CCHtUB8xGg2PKUkIIgWqLPSOlnGp0PFlNSjlSSukjpSyB+vf9XUpp1Wd0UsqbwFUhRJnkp5oApw0MKTtcAWoLIZyT/483wco7kR+xEXgn+f47wIa0vClbZ4XMblLKBCFEP2Abqnd9kZTyH4PDymr1gC7ASSHE38nPfSyl3GpgTJr59QdWJp+0BAHdDI4nS0kpDwoh1gJ/oSrCjmGF0xAIIVYBjYD8Qohg4DNgPPCDEKIH6iDXLk370tMPaJqmWR9rb5bRNE3LlXRy1zRNs0I6uWuaplkhndw1TdOskE7umqZpVkgnd03TNCukk7umaZoV+j8kfwJoKeEYtgAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Solve optimization problem\n",
"xsln = solve_opt(True,False)\n",
"\n",
"# Create contour plot\n",
"visualize(xsln,True,False)\n",
"\n",
"# Draw gradient\n",
"draw_gradients(xsln,True,False)\n",
"\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.5 Take 3. With $g(x) \\leq 0$ and $h(x) = 0$](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.5-Take-3.-With-$g(x)-\\leq-0$-and-$h(x)-=-0$)",
"section": "4.2.3.5 Take 3. With $g(x) \\leq 0$ and $h(x) = 0$"
}
},
"source": [
"### 4.2.3.5 Take 3. With $g(x) \\leq 0$ and $h(x) = 0$"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.5 Take 3. With $g(x) \\leq 0$ and $h(x) = 0$](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.5-Take-3.-With-$g(x)-\\leq-0$-and-$h(x)-=-0$)",
"section": "4.2.3.5 Take 3. With $g(x) \\leq 0$ and $h(x) = 0$"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Ipopt 3.12.10: \n",
"\n",
"******************************************************************************\n",
"This program contains Ipopt, a library for large-scale nonlinear optimization.\n",
" Ipopt is released as open source code under the Eclipse Public License (EPL).\n",
" For more information visit http://projects.coin-or.org/Ipopt\n",
"******************************************************************************\n",
"\n",
"This is Ipopt version 3.12.10, running with linear solver mumps.\n",
"NOTE: Other linear solvers might be more efficient (see Ipopt documentation).\n",
"\n",
"Number of nonzeros in equality constraint Jacobian...: 2\n",
"Number of nonzeros in inequality constraint Jacobian.: 2\n",
"Number of nonzeros in Lagrangian Hessian.............: 3\n",
"\n",
"Total number of variables............................: 2\n",
" variables with only lower bounds: 0\n",
" variables with lower and upper bounds: 2\n",
" variables with only upper bounds: 0\n",
"Total number of equality constraints.................: 1\n",
"Total number of inequality constraints...............: 1\n",
" inequality constraints with only lower bounds: 0\n",
" inequality constraints with lower and upper bounds: 0\n",
" inequality constraints with only upper bounds: 1\n",
"\n",
"iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls\n",
" 0 2.4439483e+02 1.00e+01 2.05e+00 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0\n",
" 1 4.4148045e+01 5.54e+00 2.30e+00 -1.0 2.13e+02 - 8.84e-01 4.46e-01f 1\n",
" 2 8.2513369e+00 4.16e-01 1.12e+00 -1.0 3.36e+00 - 1.00e+00 9.25e-01f 1\n",
" 3 1.0558961e+00 0.00e+00 8.05e-01 -1.0 9.84e-01 - 1.00e+00 1.00e+00f 1\n",
" 4 2.1482166e-01 0.00e+00 1.14e-01 -1.7 2.30e-01 - 1.00e+00 1.00e+00f 1\n",
" 5 1.6203098e-01 0.00e+00 9.32e-04 -2.5 2.25e-02 - 1.00e+00 1.00e+00h 1\n",
" 6 1.5801768e-01 0.00e+00 1.94e-06 -3.8 3.61e-03 - 1.00e+00 1.00e+00h 1\n",
" 7 1.5786332e-01 0.00e+00 1.79e-09 -5.7 1.44e-04 - 1.00e+00 1.00e+00h 1\n",
" 8 1.5786148e-01 0.00e+00 2.44e-13 -8.6 1.73e-06 - 1.00e+00 1.00e+00h 1\n",
"\n",
"Number of Iterations....: 8\n",
"\n",
" (scaled) (unscaled)\n",
"Objective...............: 1.5786147595031963e-01 1.5786147595031963e-01\n",
"Dual infeasibility......: 2.4449104235876087e-13 2.4449104235876087e-13\n",
"Constraint violation....: 0.0000000000000000e+00 0.0000000000000000e+00\n",
"Complementarity.........: 2.5065016939133549e-09 2.5065016939133549e-09\n",
"Overall NLP error.......: 2.5065016939133549e-09 2.5065016939133549e-09\n",
"\n",
"\n",
"Number of objective function evaluations = 9\n",
"Number of objective gradient evaluations = 9\n",
"Number of equality constraint evaluations = 9\n",
"Number of inequality constraint evaluations = 9\n",
"Number of equality constraint Jacobian evaluations = 9\n",
"Number of inequality constraint Jacobian evaluations = 9\n",
"Number of Lagrangian Hessian evaluations = 8\n",
"Total CPU secs in IPOPT (w/o function evaluations) = 0.011\n",
"Total CPU secs in NLP function evaluations = 0.000\n",
"\n",
"EXIT: Optimal Solution Found.\n",
"\b"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAAD8CAYAAACMwORRAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzsnXd4VHX2h987PTPpvRdSCSGFJr1IEyyINAVR3N+q6y6ra1t1Xd11113dddVd26prV1AUFVCpUqRDgEAC6aSH9JBkkkyf+/vjQhTpIckkZN7n4YFk5t45d2b43O8995zPEURRxIkTJ06cXF3IHB2AEydOnDjpepzi7sSJEydXIU5xd+LEiZOrEKe4O3HixMlViFPcnThx4uQqxCnuTpw4cXIVclFxFwThPUEQagVBOPqT33kLgrBJEISCU397dW+YTpw4ceLkcriUlfsHwHU/+93jwGZRFGOBzad+duLEiRMnvQThUpqYBEGIBL4VRTHp1M95wERRFKsEQQgCtomiGN+dgTpx4sSJk0tH0cntAkRRrAI4JfD+53uiIAj3APcA6HS6oQkJCZ18yZ7j9PlOEBwbR3/GZLWS39iAQibDXa3GQ61Bp1LR6z6S9nbIz4eoKPDwcHQ0iIgU6KuRIeCl0uGh0qEQru5bay2WKky2drQKT1zknsgEuaND6jy2chDbQOYHMm849Y0/ePBgvSiKfpezq86K+yUjiuLbwNsAw4YNEw8cONDdL3lFNDeDpye8+CI89JCjo+m/tFssbC4+zobCAraVFtNusaBRq5kSFc11MbGMC49Erej2r++l0dzcK4QdwGq38UNtNl+W7eNAYxEKQc6kgETmhI8kzSsS4SpcsVQZsjnQ8ClFrXtQCBqSPGeQ5j0Xd2WAo0O7bERzOqL+P2DZDzIdgut94DIHmUxdern76tG0TF8Qd7sd/vY3mDoVRo50dDROAIxWCztKS9lwvIDvi4/TYjLhqlRx7YABzIiJY0JEJBqFsmeDOnwYtmyBBx/stZd4pa11fFm+n+8qD6K3Gol2DWBO+DXMCE5Dp1A7Orwup8FUysHGz8lr/h6AePfJDPNZgLc64rzbNJlP0GqpJVSX2lNhXhRRFMG8F7H1P2A5BKqRyH0+PiiK4rDL2U9nxf0FoEEUxecFQXgc8BZF8fcX209fEHcnvRuzzcae8jLWHy9g4/ECThqN6JRKJkUNYGZMPBMje0Dom5pg6FAwmSArC7x6d7GY0WZmY1UmK8v2kttyAp1czcyQNOaGjyTK9bwZ1T6L3lLLocaVHG36DqtoZlrQ7xnoMfWs51ntZkra9nGgYQUyQc4Yv/8jRJvsgIjPjSTy20G0I3O5tuvFXRCET4GJgC9QA/wJWAV8DoQDZcA8URQbL/ZifUXcq6ulFXxwsKMjcXIhrHY7eyvKWVeYz4bCAhqNBnRKJZMHRHN9TDzjI7ohdWO3w+zZsHYt/PADjB7dtfvvRkRR5FhzBV+U7eX7qkwsoo3hPtHMDx/FWP8E5FdZbr7d2sSRk6tI9pqFTnHuE7BdtCET5BTp95DbsolJAQ/gougdKbafIghC96zcu4q+Iu7JyRAdDV9/7ehInFwqp4V+bUEe648X0GQ04qpSMT06lhti4xkdFo5S3gU32v7xD3j8cfjPf+D++698fw7ipLmVVeUH+Kp8HzXGZoI0nswJH8ms0GF4qLRd+loWi4WKigqMRmOX7rcrEBERELCLVgy2ZrRyL0TAYjcgF5QoZKoejUej0RAaGopSeebVp1Pcu4hx40CplFKqTvoeFpuN3eVlfFuQx8bjhejNJrw0GmbExnNjbDzDQ0KRdSZPXlEBAwZIK/fPPuu1ufbLwWq3saM2h8/L9nCwsRi1TMl1wSksiBhNjFtgl7xGcXExbm5u+Pj49Nobus3mKpQyF0Ts2OxmEAQsdiMqmRY35WUVqXQaURRpaGhAr9cTFRV1xmNOce8ibrwRKivh0CFHR+LkSjFZrWwvLeGbglw2Fx3HYLUSqHPlxvgEbopLINHP//IE54cfYMgQcHPrvqAdRKG+ms9L97DuxGFMdgtDvQdwa8ToK07Z5OTkkJCQ0OuE3Ww3YLG1Y7K3IxcUuCr9aDSV4qEMRiV3wWI3YrS14Krw67HYRVEkNzeXgQMHnvF7p7hfgKKqBt5dv5+S6kZKa05ittpQKuSoFHJcNSq83LR4urrg56Hju3dTKc334JutNYT4euDv6YpcdnXlI/sjbWYzm4uP801+Lj+UlmC124nx8mZWwkBuihtI2PnKGS0WSE/vU/n1K6HJ3M6aigN8UbaHGmMzIS7ezI8YxY2hQ3FVaC57fzk5OWeJlSMx29pptzUhIKCQqVEKLqjkLrRa6rCKZjxVIQBY7Sb0ljo8VMEIgMHWglU0oZG7o5K5dFt853q/nOJ+AQoq63ngjVVEBngTFeiFRqXEarNjttpoaTdyUm/gpL6duuY2jqy9hpOF8STf9SYACrmMEB8PwgM8ifD3IiLAi6hAb6KCfPBy7b4P2Un3cdJgYG1hPmvyckg/UQnA0KBgZsUP5Ia4eDw1P/lcH31UanzIzISkJAdF3PNY7Ta21WazomQ3R5pK0cnV3Bg6jAURowjRel/yfnqTuIuiSJu1gTZrI1qFJ25KqVrILtppMJXgpQrtyLO3WGoQENApfGizNmITLahkLrTbmvBQBqGUXf6J7lJwins38tjjdl78l8DOrHJONDRTUddERX0zpTUnKas9icli63iut5uW6GAfooN8iAnxJTbEl+ggH7Sanr0R46TzVLQ0syYvl9V5ORQ0NqCUyZgUOYDZAxO5NuMIynnz4Ne/htdfd3SoDiO7uYJPS3bxfXUWoigyMSCRhZFjGewZftGURW8S99NY7WbarY1YRCNuCn9ERIy2FjxUQQDYRSv1phJ81VG0WRuRIUMtd0MhU9FmbUBAhvY8FThXilPcu5F//hMeewxaW0GnO/Mxu12k+mQLxVWNFFc3cryqgeMnGiiqaqDdZOl4XpifJ/FhfsSF+pEQ5k9CmD++Hj/bmZNehSiKZNfV8nVuDmvyc3AtKWX1i/+hOSKC+vXrSIm4Ojs8L4daYzNflO7l64r9tFgMJHmEcVvkGCYFDEIhO3c1Um8U99NY7WZERGSCHL2lFg9lICIirZY6BEGOVu5Ji7UGV4UfSpnU+NVoKkOr8EQjd0cUxS7/TjjFvRt56y341a+k4oiQkEvbxm4XqWpsoaCynvyKOgoq68grr6OivrnjOb4eOgaG+5MYHsDAiAASwwOcgt9Lsba3Yxw6FKGyklmPPkiRhzsDvLy4JWEQsxMSCboKb6heDgarme9OHOLTkl2UtzcQpPHk1sgx3BQ67Kzu194s7gAGg4HrrruOr9cvQ5RZkQsq5IICncIXo60ZERG5zYVpU6ezbtM3mAU9HsqgDg+b0wJvF61Y7EbkguqcJZTr16/ngQcewGaz8ctf/pLHHz+3ma5T3LuRFSvg1lvh2DFITLyyfbUaTORV1JFbVktOWQ255bUUVzd2mJMFermRGBFAUmQgSVGBJIYHOFM6vQFRhFdfhbg49JMmsbYwn69yjpF+ohIBGBsewZyBg5gWHdPz1ge9CJtoZ0dtLstKdnDkZCmuCg23hI1gQcRo/DTuQO8X99dffx2r1coDDzyAxW5EREQpaBAEgTZrI4giOqUPzzzzDMGRPixatAgXuQfCTyqIrHYzLZZqFIIKs70drcILF7lnx6reZrMRFxfHpk2bCA0NZfjw4Xz66acknkNgnOLejRQUwOrVcMcd4N8N3dntRjO55bVkl9WSXVLN0dJqKuqkFb5MEIgO9iF5QBDJUUEkDwgm3N+z36cDehSDAVzOfaO8tKmJr3KP8VVONpX6FtxUam6KT2BuYhLJ/gH9+nM62lTOspIdbK0+hkyQMSM4lUVRYzGVN/YKcc/JyeHee++lqamJxYsX89Zbb1FYWMjo0aNZvnw5kZGRAEyaNIk//OEPTJ06ld//4WFaWpp587V32HtwB089+TQb1n1/hvOkXbSht9QiFxTIra5s2ryeb9d+w803zGXmzJkA7Nmzhz//+c9s2LABgOeeew6AJ5544pxxdoW49xJbvd5FbCw88kj37V+rUTEkNpQhsaEdv2tqNXCspJrM4iqyiqvZkJ7HlzuyAPDUaUgeEExqdDCpMcEkhgegUjo/um7h0CGYMQO++ALGjz/r4QhPTx4cOYYHrhnN3opyvsg+ysrsYyzLOkKcjy/zE5O4OWEg3i5d2+XZF0jyDOO51IVUtjeyvGQnayoO8k3lQV4Omk271YSLXIUgCEycePF93XDDj/8HJ06EJUukP/X1MHfumc/dtu3i+7NarSxatIh3332XtLQ07rvvPpKSkjCbzRQVFXUIO8AzzzzD008/TW1tLUcPZ/PRyjdpMJUQlxjF4YNHz0rH5ORn8d3ab9i6cRfl5RWMmzCG6TOmMGnSJOyiDavdxPHSHEJDf8zxhoaGsm/fvosHfgU4FeIcWK1QVAS+vuB96RVfV4SnqwtjkqIYkyR1ptntIsXVDRwpqiKzqIrMohNszyoCQKWQkxgRQFpMCENiQ0kZEISry9Xn8tfjnDwJc+aASnXRfJxMEBgdFs7osHCemWjk2/w8vsg+yrM7tvHPXTuYGh3N/MTBjAmP6Fw3bB8mROvNo4k3cXfMZFaW7cWit1HaVoeLXIWP2g3QQA8783/11VekpKSQlpYGQGJiIv7+/tTX1+Pp6XnGc8ePH48oirz00kts27YNN60bVrsZuaBApVLR0tKCu7t7x1XagnmLKMw/zu9+9zvee+89PP1csdjbcVG50GKuBkHAJtow2dsw29pRyaUTf3df5TnF/RzU1kJ8PPz3v9KNVUcgkwlEB/sSHezLLWMHA3BS387h4yc4fPwEGYWVfLTpAO9vSEcmCMSH+TE0NpShsaGkxYTgruueGtyrFrtdysNVVsL27dKZ/RJxV2tYODiFhYNTyK2v44vso3ydm813BfmEuLkzLzGJeYlJ/e4mrKdKxy9jJpOdnU2AxpNGcysV7Q28+40SH7UrHkrtJQncT1fmvr6XtlL/OZmZmaSm/mjre/ToUa677jpcXFzO8rzJysqiqqoKX19f3E59ZqdvkJpMJkSlEb3FhJvSD6vdzNZ9ayjLPsm6deuZO28eJrOBaVOnseT/FuMb4o6nMoS4yCQ+rlyOHamMuqKigqCgoMs/kMvAmXM/B2azdFV+zTUQE+PoaM6PwWQhs7iKQwUVHCqoJKu4CrPVhiBAfKg/w+JCGR4fRlpMiHNlfzGeew7+8Ad45RX47W+veHcmq5VNRYWsOJbFrvIyZILAxIgobktKZkJkFIp+1PF8OocsiiItFgMNZj0mmwWFTI6Pyg1PlRZZNztSvvzyyxQWFvL6669z+PBhxowZQ1ZWFgMGDCAsLIyCggI0Gg1VVVVMnz6dFStWcP/99/PII48wffp0ABoaGhg7diw5OTmIoh1BkGG1m2izNuKhCsIu2jDaWqitr2bvtiP4hrsw/pqpqORarFYrsXHRfLvha2Ijkhg2fBjvfPgaiYMS0Sq8zsjhO3Pu3YhKBYsWOTqKi+OiVnJNQjjXJIQDYLJYOVpSzcH8Cg7kl/P5D0f4ZPMh5DKBgeEBjEgIZ0R8GCnRwaidOfsfEUUoLoYFC2Dp0i7ZpVqh4Ia4BG6IS6CsuYnPjx3li+yjbPl2FYE6V+YNSmLBoMEEu7l3yev1BQRBwEOlxV3pQpvVRL1JT42xiXpTC14qV7xV3WfzsXjxYq6//nqGDx/OqFGjiIyMZMCAAQBMmzaNnTt3Mnr0aG655RZefPFFBg4cyFNPPcVjjz3WIe5bt27tuEF6ulJGLiiZdd18ampqAQEBkAlyRESe+PPDHSkYhULB3196mtnXL8Bqs7HozvkkDhqEXbTQYqnGQxnc5Wka58r9POzbJzUw9eVuc5PFSmZRFel55ezPK+NYSTU2u4haKSctJoQRCeGMHBhBXIgfMln/ygufE4tFsgPtrt3bbGwpKeLTrEx2lJUgCAKTIqNYODiF8eGRV61/0YVKIdutJhpMelqtRmSCDC+VDm+V63kbojpLa2srrq6uALzwwgs0Nzfz7LPPApCRkcFLL73Exx9/fMF93HLLLTz33HPEx589dM5ka0XEjlrmhiAI6C21KAR1hzd8q6Ueq2jGXRlAi6UaF7knarnU49JkrsRV4deR+nGu3LuZ22+HYcPg008dHUnnUSsVDI8PY3h8GL9mNK0GE4cKK9mXU8b+3DJe+Xonr3y9Ey9XF0YOjGBUYgQjB0b0n8YqiwXuuQceflg6i3ejsAMo5XKmR8cyPTqWipZmPjuaxYpjWWwuLiLU3Z1bByUzf9BgfLX9p9JGq1CjVagx2szUm/Q0mFppNLXiqdLho3ZFKesaiXr55Zf57LPPUCqVjBkzhpdeeqnjsbS0NCZNmoTNZkN+Hs9/s9nMzTfffE5hB1DLXc/4WSGosYpmQPKGN9r0eKlCMdiaUQiqDl8ai92IVbR0i2+8c+V+HsaMAY0GNm92dCTdR11TK/tyy9iTU8q+nDIa9e0AxIX6MSoxgjGDIkmJDu6aIRe9kYcfhpdeguXL4bbbHBKC2WZj0/FClh89wp6KcpQyGdfFxHF7cgrDgkKuirr5y2liMtksNJj0NFsMAHiqtPio3FDJ+9Y61GI30GKpRQAUMo20ipd7dKzalTKpSarFUoMcBTqlz4+llc4mpu5lzhzIyYHsbEdH0jPY7SL5lXXsyS5hT3YphwtPYLXb0WlUjEgIZ+ygSMYkReHv6XrxnfUFvvxSKpheulTqRO0FHG9sYFnWEb7MyUZvNhHv48vi5FRuTkhE281XFd1JZzpUzXYrDaZWms1tiICH0gUftRtqed96H0y2NknIkSFiR2+pQavwRinTYLEbabXU46r0PcNh0inu3czSpdKCrvGik2GvTtqMZvbnlrHrWAm7j5VQfVIPSKv6sUlRjBscRVJkYN/ME+fnSzm3xESp7FHVu+we2i0WvsnL4ePMw2TX1+GmUjMncRCLk1OJ8uzdw7jPxZXYD1hOiXzTKZF3V7rg2wdFHkAU7TRZTqCTe6OSa2k0laOW69AppGYam2hFhrzLhnX0rWudHiQwUOppMZlA3Q+rCHUaFZNSY5iUGoMoihw/0cDOY8XsPFrMhxvTeW/9fjxdXRg7KJLxyQMYOTCi75Rb/uMfkqB//nmvE3YArVLJgiQp/36o+gQfHTnMsszDfHD4EBMiIrkzZQjjIyL7RXOUUqYg0MUTH7UbjaZWTlpaabEY+pzISykXGS5yd8mDxqZBISg7hF0U7Zw0lSETFNhEy0X2dmk4V+7n4Z134O67obQUwsMdHU3voqXNyJ7sUrYfLWL3sRKa24wo5DKGxYUxIXkAE5KjCfTuxQ07ZrO0eu9DpVC1ba18ejST5VmZ1LW3EenpxR3JqcwZOAi3Xr766ErjMKvdRqO5lUZzG6Io9jmRP43NbkEuk2I+rcEGWzNt1gaK8stp8NnOaL9f4qkKBpxpmS7l22+lWar79sGIEY6OpvditdnJLDrBD5lFbM8sorT2JAAJYf5MSo1mYkoMMcG9ZDDyunXSh+nj4+hIOo3ZZmN9YT4fHskgo7oKV6WKuYOSuDM5jYiftdH3FrrDFfJqEfmfYxdtZB47xC7lM9hFK8leN3GN7+24KDyc4t5VHDgAw4fDqlUwa5ajo+k7lFQ3si3zONuOHCeruApRhFA/DyalxDApNZrkqOBLqqmvamxh3f5cak7quXlMEgPDA64ssAMHpBKo22+Hd9+9sn31Eo5UV/HBkQzWFuRhtduZHBXNXalDGBka1jtOpqfoTsvfq1Hkc3JyCI/1Z2/dhxxrXk+AJp5bo15zintXUVEBYWHw5ptw772OjqZvUtfcyvbMIrYePs7+vDKsNju+7lompcZwbVosQ2NDUcjPfUP2gTdWEerrSbCPO+vSc1kwIYUbRw3CZrdf/k3cxkYYMkTyjzl06LJ8Y/oCNa2tLMs6wvKsIzQaDQz09eMXaUO5ITYetcLxt9V6ws/darfRYG7lpKm1o7rGV+3e50oo4cz3q95UjNnWToguySnuXYXVCmvWSEUVzpz7laM3mNh1tJjNGQXsOlaC0WwlLtSPz568/aznGs1WfvGvFbx+/y14ubrw6qqd+LrrSIsNYdPBfDIKK5kzLpkZwxMQhIu469ntcNNNsHEj7Nx5VefYjFYLq3NzeP/wIfIbG/DT6rgjJZWFSSl4ncefvifoyWEdVruNBpOek6eqazxVWnzVbl3WDNUTdFUpZB+sY+sZFAq45RansHcVbi5qrhuewAv33MjmF37FC/fcwO1ThpzzuY36NgZHBbHkn5/xztp9FFc34uXmwl8+3kSYvyd3TR/OlzsyKapquHj64d//hu++g5dfvqqFHUCjkKps1i26kw9nzSHRz48X9+xizPtv89TW7yluOunoELsdhUxOgIsn0W6BeKl0NJnbOa6vodrQxIaNG1i8ePFZ2xgMBiZMmIDNZjvHHiXMZjPjx4/HarV2Orb169cTHx9PTEwMzz//fKf3c6n0ndOZA9i7F4xGLmm4gJNLx0WlZHJa7Dkfqzmp57/f7CElOpixSZG8vyGdO6cNo6XNiFaj5ObRUoXLocJK8ivriAm5SIpl0SLJZuDXv+7qw+i1CILAuIhIxkVEkt9Qz3sZB/ni2FGWZx1hanQMdw8ZxtCgSxwO3EdRyuQEunjirXal3iit5Lek7yI2KeGs1N57773HLbfccl7rAQCVSsXkyZNZsWIFizrhKmiz2fjNb35zxpi9m2666Zxj9roKp7hfgKeegtZW2LPH0ZH0H07bFs8aNQilQs6Roiqa24xsOpjf4WsviiJymYyaU41VdrvYcZPWYLKw4UAedVV13DA+laCAAHjsMYcdj6OJ8/Hl+SnTeXjUWD7KzOCTzCNsPF7IkMAg7hk6nCkDYnq+Xv5cq6X586UTcHs7nHJePINOjmJSyRQEa73wsbly/FgeHn7eXDN2FGVFJXzy8cdMmzqNZcuWsXz58o5tfjpm749//CMtLS288sor3HzzzTzxxBOdEvf9+/cTExPT4UR56623snr1aqe4O4rXXuuVPS5XPQaTBaVCjsVqw9/TlYP5FRSeqGfmCCkPabba2J9bxiPzJgJgF0VkCNQ3t/Hx9wepqm/Cc/NGnvluC8+98gRebv3HiOt8+Ol0PDxqLPcNu4aV2Ud5J+MAv/puDQO8vLg7bRg3JyT2ipuv3YVarqTgWC7zb1vAnzf9la+/+pq3PnyX5JHDLjhmLyMjgzVr1gCQlJREenr6WfseN24cer3+rN//61//YsqUKQBUVlYSFhbW8ZhzzJ6DOY8BnJNuJDEikG/35rD4+eX4e7kR6uuBIAgMPTVv1mK1cbCgArlMIHmANMnmdMXNN3uPoVTI+V3OdoK/eJ2H//gGu7JLuOGaRPTtRg4VVmKzi1yb2osnsHQzWqWSO1LSWDg4hXWF+bx9MJ0ntmzi5X27uSt1CAuTUs7bFGWz23l+13auCQllyoAreA8vNEpJq73w450cxWSxWGhsbOSJ3z+OTCbDS6HF09OLvMoidO6uNJvbcVe6IAjCWWP2Tqdr5HI5KpUKvV7fMaEJYMeOHRd9/XMVrjjH7DmQnByp7+XeeyVvdyfdT7CPO//+9Sxyy2vJKa3h2rRYmtuMvL9hP/p2I8erGvj+YAHXX3NqFW+xolIqONHQTEVdM+Nbqgj+z4tw//2Y/AMJ85Maex55+1vC/T3JK6/jhyPHeWTeBNy0/XcUoUIm48a4BG6IjWdneSlvHUznH7t28Eb6fhYnp/LANaPOcgNtNBgIcnVj6bpveXjUGO4eMtxB0V8+2dnZpKSkIDuVa887lsOo1GEM8A7BZDJxwtBIg1mJv9qDopz8s8bsncZkMqHRnPm9uZSVe2hoKOXl5R2PVVRUEBwc3NWHeQZXJO6CIDwI/BIQgSzgLlEUjRfequ+QkSG5ws6cCQkJjo6mf5EQ5k9CmD8AWrUShVzG4n98ip+HK/MnpDD21CBx1amJUjmltbga2gj7+59h1CiyfvMwAfvzEEWRjQfzkMtkPLlQ+o+26LllNLUZO8R917ESooN8erdlQjchCALjwiMZFx5JZk01bx1MJ/1ExTnHAPrpdMxNTGJVXg7XhEgphsPVVajkchL9/Hs69MviyJEjpKSkdPycmZnJrFmzCPMPQrCDt6BFL5o5VHSMexcuZsWXX/D7hx5hw4YNZ4zZ8/PzQ/kzh85LWbkPHz6cgoICiouLCQkJ4bPPPjsjz98ddFrcBUEIAe4HEkVRNAiC8DlwK/BBF8XmcAIDpb+rq53i7kiUCjlPLpyCyWKlsr6ZAUE+mCxWDhVUEOjtTrCPO64uKowmM17hIfD5p6QfPUGIrwcmi4288jqmDYsDoKKuiYQwfyxWG02tBv63dh9ltSepbGhh7KBIHpwzvld1d/YkyQGBvD7zRsw223nfg7cPphPt5U1yQCAmq5WDVSf4Jj8XP62WR0aPI96ndzaIHTlyhBE/KYU9evQoSae8haZNm0bW/kOMHDWK2+68j98/+zSacB/uffR+/vT0n845Zu9yUSgUvPbaa0yfPh2bzcYvfvELBg0adOUHdgGutM5dAbgIgqAAtMCJKw+p9/BTcXfieNRKBQOCpKEGCrkMi9VGbnmt9JhKwXEzeO3aTruvP7uzS0iMCABRpL6ljRHxUsNCo96AQi5DLpOxcnsmdc2tvLp0Nq8tnU1tUyvtpq5x5OvLqM5TElje3MyWkiLuGyaJpEIm4/bBKaxasIihQSG8vn9vT4Z5Wbz44ossWLCg4+eioiJcTjV2LV26lA8//BBXnY70vfu5Y9Z8fNXuJI0cwvsbvqTa0ITVbmP58uXcc88959y/yWbBYDVfMIaZM2eSn5/P8ePHefLJJ7vu4M5Dp8VdFMVK4F9AGVAFNIuiuPHnzxME4R5BEA4IgnCgrq6u85E6gCDpfp1T3HsZgiAgl8m4ZmCEdHP0zTcJfumfeLioWfyPT/nbp5sJ8nZn5MAImtuNGM1Wgn3csVhtlNc1IYrgrtNZu+PIAAAgAElEQVSwLfM4d06Vmv5UCjkalZKCyr71He1JPs7MIMnfnzgfX+ynylFPl1GODY9AIZNR3twMSAZnLaa+kaH96Zg9ALkgw0/jTrRrIJ4qLSfNbeQ0ljP5+unExp3dnyGKIq1WIxXtDVQbms5589QRXElaxguYBUQBTcAXgiDcLoriJz99niiKbwNvg2Q/cAWx9jienlIppFPcezHp6fDAA/hPnsyLr77MD1nFuOs0JIRLOeDy2mZ8TpVC5lXUkVNWw9DYUE7UN2O3iwyKlC7PRFGkoLKOcL++NwyjOzFZrazMOcaI4FDST1Ty2owbgVPVH4KAUi6nUt/CtpJiAAJdXWkzm3l+13aONzaiUyn5XXScIw/hkvjFL35x1u+UMjlBLl54q1ypNTZz7dzrabOacFOeaeUgCAI+ajesoh2L3dpr0npXkpaZAhSLolgniqIF+AoY3TVh9Q4EQUrNOMW9l9LQIDW0BAbCxx+DTMaElGjSYkJwUUk3vaYPi+NI0Qn+vnwzr67aib+nK9OHx/PtvhyGx/9Yd7zzaDG+Hjq83bW9ZuXVGzDbbBw4UclNn31Co8FAiLt7x2NFJxv5z77dPLpxPa0WMw+NGkN1ayuv7N9Du8XChzfPIczDE4Ol8y37vQG1XEmYzpdInT+uinNXWBltZtqsRvzUP74/Nrsds81xx34l1TJlwEhBELSAAZgM9A1XsMsgMBCqqhwdhZOzsNth8WLpzLtz53k92kP9PPnXvTey8UA+IxLCmDJEWkUq5bKOapzyuib25pQyc7hUXnlqUeoEcFOreXn6TJYOb+Cv27fxweFDKOVy0k9UoJEr0CgUPD52PMkB0hXQi3t24q7WcFtSMkq5nChPL4xX4MfSm3BRnLujURRFGkyt6BQa1HIlVruNdquJZks7NtGOQiYnUOOJQtazg+Y7Le6iKO4TBGElcAiwAhmcSr9cTQQGQkmJo6NwchbHjsEPP0jGYMMvXG8d5O3OndPONNSbkBLNvz7fRlOrgZyyGiICvLl2iNSYI5MJ2Ox21qfncW1qDC7qvusN3lVEe/vwwc1zqGtv409bN7OjrIRHR4/jjpS0juccrKqk0WBgRkwYkadmvWbVVpPoL9VzS6Pmrr6zpt5qwGy3EuwiHXOtqQWFIMNX7Y6LQkWdsYUGcyt+avcetXq4ojp3URT/BPypi2LplQQGSgZiTnoZgwdDbi6EhnZq86GxofzqxlH8cKSIIbGh3DAyEYVc1iFAB/LKeeqD9fzDRc0N1wxk7vhkBgT13QlOXYWfVscb19/Esdoa/rNvD98V5PHo6HEMCw6h3WLBTa0m8tREqB1lJcgFWUfNvCAIHe+vwWJBbzZhF0X8da59bh6sKIroLQZclRqazO14qXQIgkCrxUi71YSXSofFbsUFFX4ad6x2GzJBwCbasYl2VD1gQez0c78IVVVSBiDk6jbR6zuUl8P330smUl0sCD9dWYqiSEZhJV/uyOL7jAIsVhtDYkOYOy6ZyWmxKBU9e4ndWzlcXYUgCKQEBLK2II+vcrJ556bZADyxeSPxPr4MV2kYlJjY8f62Wyyc0LfgqdFgtFqx2GyEe3he/hAWB2IT7ZxoP0m7zYRCkBPtJk0KK2+rRxAE3JUunDS1oVWo8dNIeXiTzUKdqQWbaEcUIUTrjfIcqZqu8nN32g9chNPlkE56AWYzzJsnpWSmT4cubt/+acpAEASGxIYyJDaUR/QTWLMnmy93ZPKH99bh4/4Ds8cMZs64wQR49b+u1p+SGvjjfxBfrQ692cSO0hL2VJRT29bG0uEjaamsBH58f6tb9XioNfhqddjsdir1LX3uJrZckBGm80FvMVBtbKbR1IpWoUYpU+Cl0qGWK3GRq6kxNgGgtxhot5pQyRT4azyoNTbTajXipeo+X5O+c6p0EKWl8Ne/Sn87cTCPPCJNLH/vvS4X9gvh5ablzmnDWPXMXby6dDaJEQG8u34fN/zxXR556xvS88r7nDh1ByNCQrkzJY03D+5Hp1Lxl4mTO6pr7KfenxaTEbso4nfKrOn0722iiNVmo8looKTpJPXtbY45iMvETelCrFsgWoUatUyBXbR3pJhaLO3YRbGjDl4lU+CtcgVAQKDdaurW2Jwr94tQVQVPPy0N8YmIcHQ0/ZjPPoNXX4Xf/U5avTsAmUxgzKBIxgyKpLK+mZU7Mlm16yhbDhcSHeTDgkmpXD9iYL++ATszNp6ZsT/aqda3t2O22ToEr66tDS/Nj3XibRYLNrsdtUJBRUszgiDgpXGhvr0NAQEfbffaNWdnZ7N//34mT56Mp6fnWUZhl4pGrkQURWSCjIr2RtyULjSa9IRpfWm1GhEQcFGoUMjk2Ox2THYLnkrpBNddN5r7nbjbbHbyck5QV9NCW5uJ9jbp7KlQylEp5Wh1atzcXXBzd8HTS0tqqitGo5zzuKA66QkaGuCee2D0aPjnPx0dDQAhvh48MHsc914/ig0H8lix7bBUS//1Tm4ek8SCiSkE+3g4OkyHU97chOVUrbdU8y10zHO12e00Gtrx1+loNBiwiyLBOlcUcjkyQaDVbJa8+gWhc4PRLwGLxcKrr75KS0sLv/3tb69oX4IgEOjiSavFiFW0Ear1wUWh4qSpFbkg67iJ2mxpRyHIO/LtPxV2u2jHbLdisllQy69skdBvxL2irIGVn+1j9/Y8TjZe3iWfp6cWX393AoI8CAj0IDDIk+AQL4JO/VEqnTfXuhUfH1i2DNLSQNm7VsUalYJZowdx06hEjhSd4NOth1m+5RDLNh9iUmo0C68dQmp08FVZAngppAUFk9MkWRKo5ArUCjntFjNquYJGgwGFTIZOqaJK30CwmzuKU742erMJUQSZINBmNtNoMGC2WfHRavHUdN2w7/Lycu666y4GDBiAXq/H/SdNWp3FVXlmo5PZbkUpUyATZBisZgw2M25Klw6xP71yb7MaaTK302oxsmjXq9yfMIPx/p0fLN5vxN1gMLN5QxYjRsUwZnw8A2IC0OpUaLVqBAHMZhsWixVDu5mWZgP6FgMnG9tobGjlg4+Daa9qwGLJ4OD+IoyGH82lZDKBwCBPQsN9CIvwISLKl4hIPyIG+KHTOZf7V4QoQl6eZMl5442OjuaCCIJAanQIqdEhVDfq+WL7Eb7ckcnmjEIGhvuz8NohTBsa1++rbLRKJSf0euSCDDe1mkBXN/RmExqFEu2pE7fNbkdvMhHl5UWz0UizyYhOqcLbxYXa9jZ0StVZXvOXwvnG51VXVxN42iWwG3CRq6gztQDQZG7DQ6VDJ1efURpqF0WqDE34qt3wVruyJHoiu+vyrkjc+00ppCiKmM1W1J3Ihw4cCImJ8OWX0n6aTrZTVXmSyopGKisaqShrpLysgYrSBszmH7vxAgI9iIr2Z0CMPwNiA4iODSQ4xKtj3qeTi/D661KOfdcu6aZHH8NgtvDdvhyWb8mgpLoRPw8dt05KZc7YZNx1/WdQyLlK+wwWCy6nxLzZaKTdYiHoVL77hL6FluZmZk+bzpcb1hPs54+HWhLDgoYGgt3c0HVi/uX27dt5+umnufvuu1m+fDlr1qy54FDsrqTNaqTdakYjV57hTXNa3GuNLZjtFkK1PmTnZNPkK2dvfSG/jZ+OUqZwlkJeCEEQOiXsAJGRUFz84368vHV4eetIHHxmA43NZqemqonSknpKiuooPl5LUWEN+/cWYrdJJ1EXrYqY2ABi4oOIjQ8kfmAwoeE+TsH/Ofv2wYMPwrRpMOyyvtO9BheVkrnjkrllzGB2Z5ewbPMhXl21i3fW7WfWqEEsmjyEEN/+mZd3+Ul6TSYIGKwWLDYbRquVZqORA9t+IDcnh+3fb+YXixdL9fFmM0q5DE0nZ72eb3xeT6BTaND9xJdGbzGgU6iRCTKsdhtN5jYidX6AVEmT01KJQiZDQGBV+dlzWy+FfrNyvxKWLpV8qZqaOtc3YzZZKS2pozC/muMFNRTkVVNUUIPRKKV3tDo1cQlBJAwKZmBiCAOTQvDydu3io+hD1NfDkCEgl8PBg+Dt7eiIuoz8ijqWbT7EuvRc7HaRyUNiuWPK0A53yquRc63cf4pdFKlta6PJaOCJ+37NxrVrMZvNWK1WFAoFarWam266iZfffhtBAG8X7TknRV2MrKws5syZg6+vL7t3776SQ7pi6owtuCtdUMuV1BlbsNhtBGu9EEWRo9nHePbk97wx/P/4smwfjeZWnkia7Vy5dwfR0dDSIhVt+HZi0IxKrSA2PojY+B8bPmw2O2Ul9eTlnJD+ZJ/gi2V7sdnsAAQGe5KYFELi4DCSksOIHOCHXN4P2hJsNrj9dqipgd27ryphB4gL9eOZO6ezdNYYPt2awcrtmWw6mM+wuDDunDaM0YkR/e7mq0wQCHR1xU+r5Z9//zt5x45RUlKC1WpFqVQSERHB4089hdlmw1Oj6ZSwV1VVsWjRIlavXs39999/xvg8R3C6axVOlVGe+rfZbqXVauKGkCHoLQa21Wbz8tA7eaITr+FcuV8Ca9bArFlSpqA7U78mk4WCvGpyjlaQfbSS7KMVNNa3AtLqftDgUAanhjM4NZy4hCBUqqvw3Gy3w9/+Jpn63H23o6PpdloNJr7edZTlWw5Rc7KV2BBflkwbztShcSiukpP5xVbuP2flypXcdtttqNRqzCYTHy9bxtDJ1+LtosVTo7nsksj29nYmT57MX/7yF6ZOncr27dt57LHH2LNnz+UeSrdgsJqpNDSikSsREKgsLGH44DSeOLycYT7RzA0f2amcu1PcL4FjxyApCZYvh9tu67nXFUWRmupmjh4p52hmOVmHyygrqQdApVKQmBRC8pAIUtIiSBgU0vfF3m6HPuQv0pVYrDbWp+fywcYDFFc3EuLjzuKpw7hp1CA0ffxzvVxxnz9/Phs3buQPTz7Js88+y/hrr+W9Tz7GX3dmqtJktdJuseCp0fT5qx1RFGkyt+GiUFGUV4hXVBCv523gN/HTCdR4IpPJnOLeHRgMoNVKNgR//KNjY2luaufokXKOZJSSmVFKUWENoghqtYKklHDShkWSNiyK6NiAvpXGKSuD666Dt96CceMcHY3DsNtFdmQV8d6GdLKKq/B203L75CHMHZ+Mq0vfLK29XHFPT08nPDycgIAAampqKC0rY8QpW+efdnNW6fXUt7ehUSoJdu1cBU1vJCcnh9CYSJ49+hVPD56LTqF2rty7k5AQqXDj/fcdHcmZ6FsMZB0uI+NgCYcPlFBSLM0AdXN3IXVIBENHDGDYNQMICPJ0cKQXwGSC8eMhJwcOHIC43j+WrbsRRZFDBZW8u34/e3NKcXNRc+ukVG6blIana9c18fQElyvul4ooijQZjVS3tmK12/DQaAh0dUUl7/tXOsHREfwp83M0chXJXuEsihrnvKHaXSQkSCv43oabuwujx8czerzk59HY0MrhgyUcSi/mUHoRO7blAhAW7sOwkdEMHxlNclp4p8tCu4WHH4b9+6VGAqewA1LJ7dC4UIbGhZJdWs276/bzv7X7+GTzIeaNT2bxlKH4uHefo2BfQBAkKwN3tZr69nbq2ttoMZnw1Wrx0+r6lIXwz/FQafn3sCX8r3AzSqFzJZvOlfsl0hdHr4miSFlpAwf3HSd973EyM8owm60oVXJSh0QyYlQMI0ZFExzqwIqU5cth0SJ46CF48UXHxdEHKKys5/0N6Ww4kIdKIWf22MEsmTYMP8/eXTabk5NDQkJCt+fFzTYb1a16mo1GabSdq2ufy8eLokhubm6X+Lk7xb0fYTJZyMwoI33vcdL3FlJR1ghAeKQvI8fEMnJMLIlJocgVPbjiWbIEjh+HLVt6nW9Mb6W05iTvrd/P2v05yGUybhk7mCXTh+PfS0W+uLgYNzc3fHx8ekRo28xmqlr1GCwWtEolQW7uHdYGvRlRFGloaECv1xMVFXXGY05x70YOHJBupr76KsTGOjqarqGyopF9uwrZt7uAzIxSrFY7bu4ujBgVzahxcQy/Jhptd/vjiCK0tkInrVb7MxV1Tby3Pp1v92YjkwnMHjuYu3qhyFssFioqKjAajT32miLQbjHTYpRG+WlVSjzUUkdob0aj0RAaGoryZycjp7h3I4cOSa6zb77ZZ7vhL0hbm4mD+4rYuyufvbsK0bcYUKrkDBkWJeX0x8Xh6dVFOV5RlEzylyyROsScXBGV9c28t34/3+yRRH7OuGTumj4cX4/+nZMHaDGZeHX/Hj48koFWqeShkWNYNDilz+XjneLupEuwWe0czSpnz/Z8dm3PpbqqGZlMICkljLETEhg7MQE//yuwRn3lFXjgAcmb/dFHuy7wfk5lfTPvrtvPN3uPoZDLmD8hlSXThuHl1r0DL/oCBQ0NPLN9C7vLy0j09eOZSZMZGtR3BiM7xd1JlyOKIscLati1PY+dW3M7Si0Tk0IZf+1Axk1KwD/gMsyv9uyRyh5nzIBVq/pt01J3UlbbxDtr97J2fy5qlYKFk9JYPGVov3KiPBeiKLKusIC/7dhKVWsrcwYO4rEx4/Ht5mlPXYFT3LuZJUvAYpHmRvRXyksb2L41h+1bcygqqAEkoZ8weSDjr03E1+8CufO6OskQTKmUDMG8vHoo6v5JcXUjb327h40H83FzUXPH1GHcNikVrebqaPbpLO0WC6/u38N7GQdxUSp5ZNRYbktK7tWpGqe4dzPz5kFmpjQ/wglUlDeyfUs2P2yRhF4QIDktgolTEhk/aSDuHj9bES1dCu+8I63e09LOeKi75kg6kZwo31izm+1ZRXi7afnljBHcMnYwKmX/bnMpbGzgT9s2s6einOSAQP46aQqD/QMcHdY5cYp7N/P44/DSS1IzUw9aQfcJykrq+WFzNls3HaO8rAG5XMbwkdFMmjqI0ePj0WiU0N4uNStNnHjGtjabHblchtVqQ9HPJxV1J5lFVby2eicH8isI8nbnvhtHMWNEQq9esXY3oiiyOi+Xv+/cRqPBwOLkVB4cOQb3XjY02Snu3cz//idVzJSUQESEo6PpnYiiyPH8GrZ+f4ytm45SV6tnsLWWCffdzKy7rj3nNlarjfLSBl54dg3jJg1k/qJRfcsXpw8hiiJ7c8p4ddVOcstriQn24bc3j2VsUlS/vnJqMRl5cc8uPsk8jJ9Ox9PjJzEjJq7XvCdOce9mtmyByZNh82a49tw65eQn2O0iuet2ETVvJq0jRuO3bf1Zz7FZ7Xz1+T6qKpsozK9myIgoltw9karKkxTkVTP+2q73JHEifTbfZ+Tz+urdlNc1MSQ2hAdmj2NwVNDFN76KOVJdxZNbNpFdX8fEyCj+MnEyoe6On5blFPduprRUGrn39tv9wmr8yjGZJIfHvDzpBmpMzBkP11Q18dZrm4mLD2Tg4FBWrzzAr383jd3b8yjIq6KivBGT0cLSh647a6Shk67BYrPx9c6jvP3dXhr17UwdEsvSm8cS5teLjea6GavdzodHMnh57y5EUeTBkWNYkjqkU0NCuorOiLvz2vcyCA2VCj2OH3d0JH2EBx+E9HT44IOzhP1ERSPvv72N0ePiuPWOMVSfaEKjUaBWK/j43e3MXzSal/97JylDIqk6cRKQUgpOuhalXM78CSms/std3HP9SHYcLWbOMx/ywufbaGrthU55PYBCJuP/0oay4fYljA4L5+87f+CWFcs4Wlvj6NAuC6e4XwZyOURFQWGhoyPpA3z6Kfz3v/DIIzB79lkPm0xWWloMLPtgBx+8vY19uwuZfkMqP2zJZsiIKMIifLBYbERE+VJaLA0oOZ3/dIp816PTqPjVDaNY/Ze7uHFUIiu2HWbW0+/z8fcHMVusjg7PIYS4ufP2DTfz2owbqW5rZfaKZTy/azsGi8XRoV0SV5SWEQTBE3gHSEKyc/iFKIrnnV3V19MyIOlUTg7k5jo6kl5OWRm88IJUXnQB06acY5W8998t5OacYN5tI9m2OZvfP3UTCYlS9+ArL6zD19+NhXeO7aiqAcnH/rvVGVRVnmTmrDTiBwb3yGH1Fwor6/n3VzvYnV1CqK8HD8wex7VpMb3mBmNP02w08vyu7aw4lkWEhyd/v3Yqo8LCe+z1HZGW+Q+wXhTFBCAFyLnC/fV6Zs6EsWMlexQn58BgkMblhYdLLmvnEXabVRoEHhcfRNzAYJbcPRGVWombmwsJiSHYbHbqalvIOlLGlOmDpY1OveclRXW8/9Y2KsoaCAnz5n+vb6ahXt8TR9dviAnx5bXfzub1396CRqXg0f99y90vf0FOWd9KTXQVHhoNz02exrLZ8wBY9PUXPLllEy0mk4MjOz+dFndBENyB8cC7AKIomkVRbOqqwHord98t9eH00wXMhRFFqY13zpyLnv1O2wrr9QbMZiujx8UxfGQ00bFSE4mh3cz367OIjQ/EP9ADu13s2Gbzhiz8Az34v/smMX/RKFy0KjIOlABgNFrIyzlBTdVV/1XsEUYlRrD8D7fzh4WTKapq5Pbnl/PnjzZS39zm6NAcwqiwcNYuvIO7hwxjxbEsrvvkA7YUFzk6rHNyJS1qA4A64H1BEFKAg8ADoiie8akLgnAPcA9AeHjPXcZ0J6L441xVJz/hlVfg88/h+ecv+ezn6aXjNw9OB6Ct1UhBfjX//OtqEATc3DTMWzgKAKvFhkqtIPtoBS3NBoaOGICXtytGowWrxUZUtD8Af3v6KzRqJUcySrlx9lAWLB7d9weHOxiFXMbccclMHxbPO2v38enWDDZnFPDLGddw26TUftfp6qJU8sTYCcyMieOx7zfwy2++ZnZCIk+Nn4inpveMQOx0zl0QhGHAXmCMKIr7BEH4D9AiiuJT59vmasi5i6J0U3XmTHjjDUdH04vYvRsmTJDemFWrOn1p09ZmYsO3h7HbRW6eN/ysjtXvVh2isbGV6den4B/gwZ6d+RzcX8SU6wZTVlLP9+uz+Ocrt2Ox2Pj9/Z/wp7/P7bAqdnbAdg1ltSd5ceUP7MgqJszPk0fmTWDc4AGODsshmKxW3jiwj/8e2I+XxoW/XTuFKQNiLr7hZdLTOfcKoEIUxX2nfl4JDLmC/fUJBEGySJk+3dGR9CJqa2H+fCnP/uGHV5Sz0unU3LLgGubeNhKFQk5DvZ4vP9tHZkYpAFqdmsaG1g4nykPpxURE+tGqN1KQW81Nc6Tvf3lpPR6eWlQqBa16I9u+P8ZD933EC8+uoary5JUfcz8m3N+L//z6Zl5dOhu5TOCBN1bzwBurKK/rf6kwtULBgyPH8PX8hfhqtdzz7Woe3riO5h4cTHI+Oi3uoihWA+WCIMSf+tVkILtLourlPPIIzJrl6Ch6ERUVoFLBypXg2bXNLz6+bkydMZiQMGnOq9Vqw2iQStH27SqgoqyB+MRg2tpMmM1Who+Uhn80nWzDy1uHCKz4ZDd7dxZw/6MzcHN34avP93dpjP2VMYMiWfHHxTwwexwH8yuY+5ePeGPNbgzmvlEq2JUM8g/g6wWL+O2IkXyTn8t1yz5ka4ljc/FXWi3zW2CZIAiZQCrw9ysPqfdjs0mlkM3Njo6k66mpqWHs2LGsWrXq0jcaMkTqQv2Z02NX4e6hxcdXshJOTg3nZGMbd85/nbVrMpg4ZRBxCUHk51Th4+uKWq1E32KgrLQBjUaFzWZn66Zj3Hn3BGLiAhk7MQGbzU5LS/9s0OlqlAo5d04bxtd/XsKUIbG8s24fc5/5iG1Hjve7fgSVXM6DI8fw1fyFeGg0/N+ar3li80ZazWaHxHNF4i6K4mFRFIeJopgsiuLNoij2i+vdw4dh4EDYtMnRkXQt6enpDBo0iD179lBcXHzxDdauhSeflM52PTSAOCDIk+f/vZA/PzeP3z12PdOvTwGgqLCmw6IgM6OMyrJGRo6NZc+OfKJjAwgK8UIURdRqhdQNq+79A5P7En6ervztrhn876F5aNVKHnpzDQ+8sZqKfpiqSfIPYPWCRdw7dDhfZB9l5vIP2VdR3uNxODtUO8GgQVK36pEjjo6k6/jggw+YOHEiDQ0NaDQa3N0vMkavpARuv10SeAesTKKi/fHy/nFG6PTrU3jvza2s+fIAH723nUHJoaSkRbB6ZTozbpKuKARBYMfWXPwDPVCpFdjt/Wtl2RMMjQ1l+ZOLeGjOeA4VVDDvrx/xztp9/a7LVa1Q8NiY8ayYuwC5IGPhV5/z9x3bMFl77n1winsn0Giklfvhw46O5MqxWCz86le/4je/+Q3t7e0AyOXyC4u70Qhz50rNSitXgovjy78mThnEgsWjqTrRxJK7JzBxyiBqq5tRqhQMHSFVctTX6ck4UMwNs6T7/s5ehe5BKZdz+5ShfPXnJYwbPIA3vtnNrX/7hAP5Pb96dTRDg0L4buEdLBycwjsZB5m1Yhk5dbU98tpOce8kKSl9X9zr6+sZO3YsH330UYewA8hksguL++9+J7k8fvghREf3QKSXxoT/b++8w6Mqvj/8TjY9AQKE0CEEEAUEpBfpCU0EvgpSpBhARIpIURT9qYgUQUBAilQpUqQpUqR3kI6U0EtIKEmAJLT0nd8fQxJCDSl7k828z3Of3buZu/fsJvncueecOadBaT7q602NN18BIE/e7JQslY9tm04SGHCbZYv+pWSp/JQolQ9QM3kpJf/uPkdcnNlI060SDzdXRn/YnEl9/kdsnJke45fx7bz1hGaxgmTOdnYMq+/N7BbvEBoRwf+WLGTG4QOY0zkmocU9hVSooJJEbt0y2pKUcfToUcqUKcORI0eIiHjyn+2Z4n7+PMyZA59/nuFThoQQVKrqxV/LDvLj0D8p4ulOhw9qAYnFxw4fuMT/fbaEbh2m8c/qo8TGxhlpslVSq4wnS/6vE76Nq7Bu32ne/e43/t57MssFXOt5FmPd+52pV6wYI3ftoOOKpVy/m35lM3Q99xSycSM0apQ5G3csXLiQDz/8MMls/VGyZ8/Onj17KFOmzNPf4D6AI+0AACAASURBVMQJePVVsM08KxNDgu+Qx+PJC5bZLNm9/TQL5+7m/Nkb5Mufg7adatKoWXm9sjUdOH/1Jj8s3MSxi9ep9moRhnRomOVqx0spWep3gu93bMXOxsTwBj40K/nKc4/RzTosSHAw5M2rih7272+0Nclny5YtNGzY8LljXFxcOHXqFIULF0588c4d2Lo1w8/Wn8fzmnBLKdm/5zwL5uzktN818nhko33nN2ncXIt8WmM2S5btPMakP3cRF2em59s16NCgIrZZrLXi5bBQ+q9fy39BN2hTuizf1m2A8zOyzrS4W5iCBVXbvXnzjLYk+YSHh/P777+zevVq1q1b99Qx9vb2BAUF4Ra/IElKaNNGlRU4exa8rHepuZSSQ/svMn/WTvxOBJInb3bad65Fk+YVsLPTpQvSkuCwe4xctJntxy5SumhevunowyuF8hhtlkWJiYtjwr69TD24D0+3nExo8hZlPfI+MU6Lu4Vp0UKt3TlzxmhLXp5p06YxaNAg7t9Xdd6cnJzIli0bd+7cITo6mujoaEymh2I2fjwMGKDqsw8aZKDVlkNKyeEDl5g3cwd+JwLJmy8HHbvWxqdJuYTqlJrUI6Vk4+Gz/Lh4K3cfROHbpArdm1bDLovVANobcIWBG9ZxK+IBg2vVwbdCxSR3mVrcLcy+fSobsEYNoy15OcLDwylSpAh37twBlBvm+++/Z8CAAQQGBhIWFkbZsmXV4F27oF49ePttWLEiy+UPSik5uO8ic2ds58ypaxQolJMu3VWqpY1N1vou0pOwexGMWbqNdftPU6KgO991akTpok/OYK2Z0IgIBm9az6ZLF2jg6cVon8bkclKlZ7W4a5JF3759mTlzJpEPixsVLlyYCxcuYPe4v+/uXRU4dXKCgwfTvG5MZkJKyd6dZ/ltxnYuXQimWHEPfD+qR/VaJbNsd6L0YPuxC4xYuJnbdx/wQaMqfNisWpYqKSylZP6xo4zYuZ2cTk5MaPIWVQsW0uJuBP/8Aw8ewDvvGG1J8jh37hzlypVLEHZnZ2eWL19OkyZNnn7A/PlQrpxK7NdgNku2b/bjtxnbuBYYSplyhej+cQPKlreOXgUZgbsPIvlp6Xb+/tePEgXd+b5LY14t7GG0WRblZHAQff9Zw5XwMPpXr0mfqjW0uFuaRo0gNBQOHDDakuTRsGFDtm3bhtlsxsbGhtq1a7Nt27YnBwYFqXQgzVOJjY1j/er/mDd7B7dv3qN6rZJ0+7gBnl5ZKyCYnuw4fpEfft9E2N0IujWtStemVbEzZR1f/L3oaL7aspE4s5nJb7XQ4m5prl4Fd3dwcDDakhezceNGWrVqlZDf7uTkxJEjRyhVqlTSgatXq/rs69dD7doGWJp5iIyM4c8/9rNo/h4iI6Jp9FZ5unSvg3ueF9Tm0SSL8PuRjP5jK+v2n6Z00bwM+6AJxfLlMtosiyGlJDouDkc7Oy3umqcTGxtLiRIl8PdXTS8cHBzw9fVl6tSpSQdevAiVKql2U7t3Z4i6MZmB8LAHLJy7i1XLD2Jra6JNh+q0eb8GTk72RptmFWw6fJYRCzcTER1D31Zv0q7eG1kqoK197gbxzTfg4aE6NGVUJk6cyJAhQxJSH7Nly4a/vz85c+ZMHBQZCbVqKYE/dMiq89nTi+tXQ5k1bSvbN/uRy90V3x718GlaDlMWW6CTHtwMv8+w3zey8/glqr9WhO86N8bDzdVosyyCFneDqFtXBVUzqt/99u3beHp6cvdhHQsXFxdGjRpFn8evRj16wIwZsGqVSn3UpJiTxwP4deImTp28SolX8vFxPx/KvVHUaLMyPVJKVuw6zthl27G3NfH1+954V3z+0n1rwNI9VDUPqVMHDh9WmYMZkS+//JLoR2qu58mTh549eyYdZDZDjhzw5Zda2NOAMq8XZsL0D/jyu1aEh91nYO/5DPt6OUHXs17zirRECMG7tcux+KuOFPHIyecz1vDdvA3cjzSm21FGRs/c04D4ImL//JPxGmefOnWKihUrJkl9XLVq1bPry0iZ5RYqpTeRkTEs/X0vSxbsQUpo16km73WsgYPuBpUqYuLimL76X2av309B9xyM7NqMMp75jDYrXdAzd4OoUUN1Ztqxw2hLnqRHjx5ERUUBqk57zZo1kwp7eLgqa/nvv2pfC3ua4+hoR6dudZi96GNq1H6FebN20L3DNHZvP5Plyt6mJXYmE71b1mJ6/zbExprxHbOE3zYc0B22HqLFPQ1wdYXKlWHLFqMtScratWs5fPhwgoA4ODgkzY6RErp2VVelmKzXsd7SeOTLwdfD3mHMpI44Otrz3ZdL+XrQEq4F3jbatExNpZKFWPxVR+qW92Liyl30+WUlt+7cN9osw9HinkY0a6ZqzQQFGW2JIiYmho8++ighp93R0ZEPP/yQEiVKJA4aN07Vixk9WuezW5AKlTyZOrc7PT/x4cR/V+je8VfmzdxOdFTW6jOalmR3cWT0h80Z0qEhR84H0m74Avad8jfaLEPR4p5GtGypJsJ//220JYqJEydy+3bijNDBwYFhw4YlDti5EwYPVnUTMlNBeivB1tbEu+2qMWvRx9SqU4r5s3fyYadfOXzgotGmZVqEELSuXY55gzuQ3dmRXpNWMPXvPcSZs2YLRR1QTSOkVOt+Xn/deIG/efMmnp6eCTntLi4ujBs3jh49eiQO+uAD2LNHFQR7Xr9UjUU4fOAiE8as41pgKA0bl+Wjvj7kzOVitFmZloioGEYt2cLfe/2o/EohhndtSp4cmTcnXue5G8wPP8Dt28rbYSRdu3bl999/T0h/LFGiBKdPn06szw4QF6d8SAUKGGSl5nGio2JZOG8XS+bvwcnZgY/6etOoWTlddTIVrNp7klGLtuDiZM+Irs2oUqrwiw/KgGhx13D8+HGqVq2aJPVx3bp11KlTRw2YMUMFCAoWNNBKzfPwvxTC+B/XcPJYIG9U9qT/4LfIXzDniw/UPJUL127y2Yw1XAkK5eO3a+LbuEqmK12gUyEzAGYzXL5szLmllHTv3j0h9dFkMlG3bt1EYV+1Sq1C/flnYwzUJIuixfIwbkoXPvmsKWf8rtGj03RWLNlHXFzW9B2nluIF3FkwuD0+lV5h8qrdDJi2irsPIo02K93RM/c05uOPYflyuH5d5b5bkpUrV9KpU6ckrfP8/Pzw9PSECxdUQbASJVR3JUdHyxqnSREhwXeYMHot+/acp3TZQgwc0pwinu5Gm5UpkVKyZNtRxi3bQb7c2fipx9uZpmerdstkAHbvVnW32rYFewsWBIyKisLT05MbN24ASth79+7NmDFjICICatYEf39VJ8HT03KGaVKNlJLN608wZfx6IqNi8O1Rj3faVtPFyFLIfxeu8fmM1dx9EMU3nXxoUuVVo016IdotkwGoVQs6dbKssAOMHTs2oScqqNTHb7/9Vu388AMcPaq6Kmlhz3QIIfBu8jozF/akctXiTP9lMwN7zyMwQC9+Sgnlixdg4ZD3ea1oXobMXsf45TuItUKXl565pwM3bsDSpdC7N9hY4PIZFBSEl5dXwoIlFxcXJk2ahK+vrxoQHg7r1kG7dulvjCZdkVKy6Z/jTPl5A7ExcfTo403z/1XUGTUpICY2jnHLd7Bk21GqlirMqO5v4eaaMfsX6Jl7BmHLFvjkE3ha97r0YMCAAcQ8Uj6gSJEidOnSBS5dUjXac+TQwm4lCCHwaVqOGQt6UKZcYSb+tI6vBi7m1s0MWpI0A2Nna2Jw2/p826kRRy5co/OPizh/9abRZqUZqRZ3IYRJCHFECLE6LQyyBv73P6Wnc+ak/7mOHDnCypUrE8Td2dmZmTNnYnP3Lvj4qHZ5GqvDPU92Ro5vT5+BTTh2xJ8enaaze/sZo83KlLSsWYYZ/dsQGR3DB2MWs/2/C0ablCakxcy9H3AqDd7HanBygvbtVdZMeHj6nUdKSbdu3YiIiADA1tYWHx8fataooVag+vvDF1+knwEaQxFC0PLdykyZ0528+XLw3ZdLGT9qDRERurb5y1LOKz8Lvnwfz3y5GPDrKuas35/pK3amStyFEIWAt4CZaWOO9eDrq5JUlixJv3MsXbqUs2fPJuzb2dkxadIk+Okn+PNPGDNGZclorJoinu5MmO5L2441Wff3EXr7zuL82RtGm5Xp8HBzZeaA92hUqRST/tzNt3PXEx2TeYu5pSqgKoRYBowEsgGDpJTNnzKmB9ADoEiRIpXiGzRbO1KqOjPZssHevWn//hERERQtWpSQkBBApT7279+f4Y0aqfrs776rriw60JalOHzwEj9+/xd3wyPo0ceblq0r62DrSyKlZMbafUxbvZcKxQswtmcLchocaLVoQFUI0RwIllIeet44KeV0KWVlKWXlPHkyx4KBtEAINXv/9184lQ5Oqx9//DFhsRIoX/tXX30F+fNDq1Ywc6YW9ixIxcrF+HXuh1SsUozJ49czdMgy7t6JMNqsTIUQgh5vVWdkt2acuhJEl9GL8A8KNdqslyY1bplaQAshxGVgMdBACLEgTayyEjp2VKtU0zqweu3aNcaMGZMk9XHi+PE4OznBK68oZ7+u9JhlccvpwrAxbfmorzf/7jpHL9+ZnPa7arRZmY7GlUsx7dPW3I+IpsvoRRw6F2i0SS9FisVdSvmllLKQlNITaAdskVJ2TDPLrIC8eVWv6Tlz4KEOpwn9+vVLkvro5eVF+2PH4P33ITbz+gg1aYcQgtbtqzNuamfMZkn/nnNZtfxgpg8SWpryXgWY+3k7cmV3odfEFaw/kHkyknSeezozYADUqQNhadT0fv/+/axZsyZB3J2cnFjeqRPip5/AzQ1sbdPmRBqroHTZQkz9rTsVq3gxaew/jBr6p86meUkK5XFjzqC2vF4sH1/OXsvcDZnjIqlXqGYipJSUL1+e48ePAyo75qOGDZm0Z49yx+zaBQ4OBlupyYiYzZJF83Yzd8Y2ihbLw3ej2lCwUC6jzcpURMXE8s3c9Ww8dJb29d9gYOu6FisdrFeoZmDOnIEDB1L3HgsXLuTixcQ2bK4mE+OuXFGz9aVLtbBrnomNjeD9D95kxLj23Lp5j95dZ7Fvz3mjzcpUONjZMrJrM95vWJFFW4/w5ey1GTpVUou7BZBS9VgdMCDl73H//n369euXkCHj7OzMyC5dsAsOhgULdEEwTbKoXK04k2d3JV9+N/7vs8Usmrc7U7gYMgo2NoKBrevy6Tu12XjoLJ9M/pP7kRnTzaXF3QIIoQoyLl+e8vcYPnx4QnYMqAyZzuPHq/rCTZumgZWarEL+Ajn5+dcPqNuwNLOnbWXENyuJjIx58YGaBDr7VGZo50YcOhdIj/FLCb2bhhkTaYQWdwtRpQp4eKhZ/MsSEBDAzz//nFBmoIajIxt9fHBycFCrpDSal8TR0Y4hQ/9Ht48bsH2LHwN6zeNmyJ0XH6hJ4O0aZRjbswUXr9+i27ilBIVmrOJtWtwtiL8/VK+uqka+DH379k3IjskBLDGbKbdjR/oWrtFYPUII2nWqyfej2xJ45Ra9u83m7OnrRpuVqajzuhe/9H2HkLB7dP3pD64Ep1FaXBqgxd2C5M2rar1//rnqtZoc9uzZw8aNG4mNjUUAC2xsKGQ2I/74A3Lqpsma1FO9Vkkm/PoBdrYmBvaax54dmSeXOyNQqWQhfv20NRHRMXQfu4QL1zJG2WAt7hbE0VE1RTp0CBYvfvF4s9lMt27dEnztX9jY0NxsRowdCzVqpLO1mqxEseIeTJrpi6dXHr77cikrluwz2qRMRemieZk5oA0IwYfjlnI6INhok7S4W5r334cKFWDIEIiKev7Y3377jYCAAADyA9+azUS2aAF9+6a/oZosR85croz5pRO16r7K1AkbmTphA2azzqRJLl75czNzwHs4Otjx0fhlnLxsbGVOLe4WxsZGVeL194fJk5897u7duwwcODAh9THc2ZklH32E44IFuiCYJt1wdLTj62Hv0KpNFVYs2c/wb1YQHZVxc7kzGkU83Jg54D2yOzvw8YTl/HfxmmG2aHE3AG9vaNwYvv8erj8jfjV06FCioqKwBd4EcuTIQdsJE3R2jCbdMZls6PVpI3r08WbHllMMGbiI+/dfcJupSaBA7uzMHPgeObM502fSSsMEXou7QUyapNwyffo8+bNLly4xZcoUIiIiGAlsBxYMHoyDXoGqsRBCCNp0qM4X37bkxH8BDOo9n9Db9198oAaAvDmzMWNAG3IZKPBa3A2iZEn47jtYsUJtj9KrVy+io6P5HzAIWOHhQf1PPjHASk1Wp2Hj1/l+9HsE+N9kQK+5BN/Q6bfJxcPNNUHg+05aaXEfvBZ3Axk4ULloHq3Su337dnbs2EGxuDjmAAeE4NW1a3U3HY1hVK1RglET3if09n0+/XgugQG3jTYp0+Dh5sqvn7Ymh4sjvSausGgWjRZ3A7G1hQ0b4L331H5cXBzdunUj7sEDlgMxwJLWrSlbqZKRZmo0lC1XmJ9+6UR0VCwDe83D/1KI0SZlGvLlysav/dvg4mRPr4kruHj9lkXOq8XdYIRQJQl++QW6d1/HxYsXiQKmAd0cHPhiyhSjTdRoACjxSj7GTu4EwMDe87lwLshgizIPBXJnZ1q/1tjaCHr+vIyAkPRfyarFPQMQGwu//RbLvHk25JWSIsA8FxfqDB+Ou7u70eZpNAkULZaHsVM6Y29v4vNPFmiBfwmKeLgxtd+7xMaZ6TVhOSFh99L1fLpZRxoRFxfH9QtBXDp+hUvHrxAScJP7dx5wL+wBcbFx2Dva4eBkj4ubC3kK5sa9UG7cC3lwNbwwA788gf+VN6jBIXbSgDgk/sDhsmVpu2wZlCpl9MfTaJJwLfA2g/rMJyoqljGTOuJVIq/RJmUa/Pxv0GP8MvLnUimTOVwcX3hMSpp1aHFPBTHRMRzdepJdy/9lz18HCHtYVc/GRpAznxuubi645HDGZGciJjKGqIho7ty6x+0bochHVv7F4IqQHixjMk7EMJsP6MN0zPb22JhMqpxkx47Qti2ULasXMWkyBNcCbzOw93xiY+L4aXInihbLY7RJmYYDZwLo+8tKShX2YFq/d3FysHvueC3uFkJKydZFu5j++XxuXQvFydWRas0rUcm7HF7li1K0dCEcnBJz0u/fh3XrYO5c2LQJ7GzjiL4XhjPXcSGAbPgznTFU4xLvMYI/+YL6jKUHM6jFVQpzD+zs1JYjB3ToAO3aQaVKWug1hhJ45RYDe88HYNzUzrp130uw+cg5Bs9YQ80ynozt+TZ2JtMzx2pxtwA3LgczsdcMDvxzlFerlqD9kHeo3Kg89o72ScaFh8Pq1UrQd+wAe3u4+1i552zZIDoaphUdwQdnv+IzBzdMXfrx6wwfwmV1KjCC3OIYJUQ4Dcz+1COAPESoNBsHB3ByUiLfvr2qJWyjQygay+N/KYQBvebh5GTP+GldyOOR3WiTMg3Ldx5j+MLNtKxZhm86+jwz5VmLezrj7xdA/zrfEBMVQ9fhHWjRuzGmR662t27Bn38qQd+3Twn6vcdiJtmzqwBq48bQuTM0biRxGtSbWxcuEDt3Lnnz5eP8+WCaNnUlKMiR7zuu4cKa5ZwOuI8Nkqo2wbwTd5oKhCBACbqLC5hM8O67qjJZ7drqAqDRWIizp6/zWd8F5HZ3ZfzULuRwczbapEzD1L/3MGPtPnq8VZ2ezZ9e7VWLezpyL+w+fap9yYM7Dxi/cxgFS+QHVH32lSvht9/g6FHlObn/yCptIcDVVaU7vv02dOoEDRsq4U9CbGwSQQ4IgGrV1Pvt2AG2MdfZ8Mtq1s7eSti9GLwIp539JepEnSfh8hIv9AAtWqiT1a//lJNpNGnP8aNX+OLThXiVzMvoie/j5KT/7pKDlJLv5m/g771+DO3ciLdrlHliTErEHSmlxbZKlSrJzMqwtmNlY7u28vhOP3nlipTjx0tZvryUDg5SOjtLqeRbbTY2UmbLJmWOHFL6+kq5aZOUMTGPvWF0tJSdOkl59KiUZvNTz3n4sJRublJ6eUkZGKhei4qIkmtnbpJdS/WR3qK17OLUSm6z9ZRmF9ekRgihjHB2lrJ1ayn/+kvKiIj0/ZI0WZ7d20/LRrV+kEMGLJKxMXFGm5NpiI6JlR+NXyqr9PpZHjhz5YmfAwflS+qtFvdkcO7IRektWssPvZfI115Tgu7klFRLTSYpXV2lzJ1byo8/lnLnTiljY5/zpv37qwMXLXruufftUxr9yitSXruW+HpcXJzcsWyv7P56f+ktWst+r/SQZ6r4KOOyZUtqHKjXHB2lbN5cyqVLpbx3L22+HI3mMVavPCS9awyT40auluZnTFw0T3LnfoR8d+hvsu6AyfLyjdtJfqbFPY3x85Pyu++krOY6QdYTnaSLw70kemlrK6WLi5R580r56adKiJP1t7x0qXqDvn2TZceuXeo8w4c/+bPY2Fi5ZsYm2dqjq/SxaSMndJ8sH8z9XcpmzZSYP0voHRyk9PaWcsECKcPCXu6L0WhewKypW6R3jWFy4dxdRpuSqQgIDpX1B02VLb+ZLcPvJd5pa3FPJWaz8pIMHixloUJqdm5vL+WbfCTLMEGC2nd2lrJwYSm/+OK5XpWnc+aMEtfq1aWMikr2YWfPJp4n7il3u/fC7snJ/WZLH5s2snPJPvLk3jNSPngg5cqVUv7vf8ropwm9q6v6ULVrSzlzppQ3b77Eh9Fono7ZbJYjvl0hvWsMkzu2+BltTqbi8LlAWaX3z/LjCctlTKz6Z9fingLMZjXj/vRTNQN3cVEz8gR3Cw+kt2gtS9iukF5eUg4dKuWpU6k4YbduUrq7S3nlSb9acrh4UcoyZZTNT+PothOyQ9GespHte3LJ6D8Tb4ujoqRcu1bK9u2VoGfLpvzyjwq9i4sS+qpVpZwyRcrr11P4ITUaKaMiY2Tf7rPlW/VGyrOnr734AE0CK3cdl2/0HCfHLt0mpdTinmxiY6XcsUPKnj2Vj9zVVfnMH9U5JyfluShTMkx6i9Zy5nfr0ubk0dFSnjyZ4sMvXJCySpXnv8W9sHvy+/fGSm/RWo72/UVGR0UnHRATo6K8vr4q6pstm4oCP/oFODsroS9fXkWPU3gx0mRtbt+6K9u3miDbt5ogb9/ScZ6XYdTiLfKNnuPk2n2ntLg/j+TqmYODlBUqSPnzz0rP7obek96itVw6dlXqDFi9WsqQkDT5LPGTcbNZyiVLnh64NZvN8rdvFktv0VoObjxMRj6IfPqbxcaq6O/HH7/4Svfaa1KOGqWuMBpNMjl7+ppsVnek7N/zNxkT87wsA82jRMfGym5jl8h6A6docX+cqCgp16yRsl2753siHBye7Ykwm81y3nd/yLOHUiFoBw6oWbCvb+o+0GNs2KA+Q9Omz75urJ25SfrYtJFfNBkmoyKjnz4oHrNZyv37VSZPvI/Kzi7pF+boqDYvLxVt9tP+VM2L2bz+uPSuMUxOnbDBaFMyFTfD78nTV4IsK+5AYWArcAo4CfR70TGWEPdHY4hOTlJmz55Umx6PIc6alc4xxJs3pSxaVMoiRdLlRFOnqs9SoICUW7Y8fcy6WZult2gtR3ackPzUtPjo8hdfqOhxfHT50S8yPrpcqJCKQr90dFmTlZg0dp0OsKYQS4t7fqDiw+fZgLNA6ecdk17ifueOlIsXqxnsi7L/fHyk/P13C2X/xcWplER7ezUjTicOH1Z58EJIOWTI05Nw5n+/VHqL1nLtzE0pO8mpUyqa7OWlvmQHh6RfsJ1dCvNCNVmF6OhY2afbLNnCe7S8Fnj7xQdoEjDULQP8Bfg8b0xaintoqJRz50pZv34GXrczbpwyZPLkdD/V3btSdu2qTvf661IePJj057GxsfJzn6HyLecO8vqloNSd7MIF5Xt/0YquXLlU1Hrnzqfnb2qyHNevhcpWjcbIXr4zZXS09r8nF8PEHfAErgDZn/KzHsBB4GCRIkVS9QGDg6WcPl3KmjXVZNj1BSvuV61K+xX398Lvyy2LdslpA+fKm9deMPsIDpZyzBiLzmBXrVIuGpNJeUoiH4mjBgfclG85d5DDO4xPuxNeuaKizxUqpKIWg1RZRNd0ulxWYMfWU9K7xjA5c8pmo03JNBgi7oArcAh450VjUzJzv3ZNyl9+kbJSJSXoLi5P145s2aTs2FHKf/55qbVBL8XtG6Hy/1qOkj91myKnfzZP9q46WAacufrkwJAQJVYGERqqZvFvvPFkJs2crxdJb9FaXvYLSPsTX7+uotJVqz79lxV/9XV1VVHuNWsSf1nt2qlfZv/+KnCisWrGjvhb+tQcJv87fNloUzIFFhd3wA5YDwxIzvjkivvly1L+9JNyLzxvMujmJmX37lJu3fr0yWBaEvkgUv4x5i/5U7cpCa992fQHeXDD0aQDo6KkrFFD+doN9jnfv68eb92Ssk0bKU+fljIk8Kb0Fq3lopEr0vfkN2+qaHWdOk+/zYr3mzk5qch2/C/ZyUnKggXVQgSN1fLgfpTs3PoX2fGdifL+vWek6WoSSIm4p7i7g1BV5WcBp6SU41L6PvGcOwfDh6t2oa++Cl9/DcePQ1QUPHigquG6uIC7O/TqBevXq/rpM2ZAvXrpX7789P7zXDl9labdGgAQePYabnlzkLtAYucZKSV8/jns3QsffGB4lyTnhyW1jx+HLVvUd+leMDfFKxTj0Mb/0vfkuXND166wfTsEB8Ovv4KPj2oyki2bGnP3LkREwM6d6pcMav/qVVXwvlu3JzucaKwCJ2d7Pvv6bYJuhDNjymajzbFKUiOJtYBOwHEhxNGHrw2RUq5NzsFSgp8fLFkC8+dDUBCYzUqA4rGzU6XIH+0sV7GiMZp5bJsfbh45KF1DNasOOHMNR2dHzHHmhDFyyR88mDCZg00/pHrzFjg8680sTN26EBgIjg/78O673Ymoy+F8EgCFC1vAgPhfYIcOT/YcUmTAcQAAFG5JREFUtLV9sqMJKJFfuBBWrVJjmzWzgKEaS1K2fBHeaVuN5Yv3Uc+7DOXfKGq0SVZFimfuUspdUkohpSwnpazwcHuhsB8+rCa3hQpB1arw449w+bL6X46KSuweV7SoGvfvv0qYxowxrmWolJLNC3dS9z3VJeXScX/O7D+Pe8FceJV7+Ad5+jRrPhjKNA8f1ssidC87gH9XH7K8sc8gXtjj4sDeDk6H1qBECfj4Y7h40YKGuLhA69bw119Qq5bqM/gsIiPh5k1o00Ydc+uW5ezUWIQuH9YlXwE3fv5xDdHRsUabY1VYtOnmf/9BnTowfjxcu6buxKOjlfA4OkLJksodc/SoEvwffoCyZQ33bhAXG0e5OqW5dfU2Efci+GvyemKiYqjfrlbCmH2bT7LDsTjev3zOiHVf0/7Ldwg8e81Aq5+OyQQVXObSs+4UfH1h1iz1vb/3Huzfb0FDAgJg8+bEWzNXV3Wr9jQePIC//4bixeGPP9Rtn8YqcHKyp99nTQm8cps/ft9rtDlWhUUbbcbGqg3U7NxsVsLSpYuamHl6WtKa5GNrZ0udNjX4pe8s8hZ1p1SVErzbvzk53BMbAS9ceJjmEwdRvk1dAOwcbDlz4HzCz/39Asjunp2cHjksbv+j3LgczOUTV+j4f9Xo9C188w1MnAjTpsHSpaq1X+/eSuwd0tOvVLSompXfuJF0CwxUV/arV5Wv/vZt5coxmZT7pm1bNUsYPjwdjdNYksrVilOvYWkWzt1Fw0ZlyV8wp9EmWQUW7aFqMlWWdnYHKVNGxRvfeQcKFrTY6dOEIP8Q8hbNw/51R6jUqBymX39lw7L97HUrzVdLBmBrp66XH74+gK4jOlClSQUWjVjJ8V2nCDx7jabdGtLpmzaG2C6l5Ou3R3Jsmx+zT08gT6HcCT+7exfmzIHJk5W2BgSAh4eaNDsb3es4NhZCQhIvAMWKqai7xmq4GXIH33ZTqVTVi+9GGvP/kZFJSQ9Vi7plChWCK1fg0CHo2zfzCTtA3qJ5iIuNIyw4nPPzV8Onn3LnRihl33wNs1ldKFdMWEOBEvl4vfZrzPlqEffvPOCzOb2ZdXI8/n4B3Lll+QwQs9nMrwPnsn/tEXx/aJ9E2EElsHzyCZw6pX4/Hh7q9SZNwNfX4uYmxdYW8ueHN96Apk21sFsh7nmy075zLXZvP8N/R/yNNscqsKi458mTKBqZGZOtiUbNX6fEN59AgQI4dvfl5rVQ7B3sCAm8xaKRK+kytC27/9xPXGwc9du/SZ5CuYmJisVv71liHgaOoiOjCQ0OT3d7oyOj+bHzJJb/vIZWfZvS6pOmzxxrY6PiHKBc2y1aqDgJqFl8+/bK7X3/frqbrclivNuuGnk8sjFz8mYs6VGwVizqc7cazGbo2BFT0A3YvZti0dn4u9cMBjceRu78OWn+kQ9e5YqyZvpGyr75Gl7ligCwYe426rSuQe78OTm55wx/jPmL6xeDKF7Bk/6/foS9o32amhkdGc3aGZtZMvpPbl69TbcRHWg7uBUimRFqIWDQoMT9s2dh2zZYvFjFTN56S7nWmjVTMVGNJjU4ONjRuXtdxo5Yza7tZ6hdT9+hpQYt7inBzw927YIJE6ByZcoAUw+PZsvCXVSoX4ac+dyIuB/J7Rth5PfywM7ejiunr3Ll1FWqNKnAiV2nWDZ+NRW9y9GydxNGvP8ze1cdpO57NVNtmpSSS8evsGPpXtbN3sLt66G8Xvs1Bs/rS4X6ZVP13hUqqHjnrl1q9r58OSxbppJc6tWDt99WQl+8eKo/hiaL4tO0HH8s2Mu8mdupVacUNjYGp8plYrS4p4SyZeH0aShQIOElGxsbvDvWSdi/dTWI0KAwXq1aEoCVE9ZQoHhesuVy5fjO0xR+pQAtezcBwBxnJjoqBlDiLIQg4l4Et66FkjNvDhxdHTGZTElMiI2JJSw4nFvXwwj2D+HCf5e5dPwKp/ef5/b1UGxsBBV9yjHk936Ur1cmzT66yaQWRdWtq7Js9u2DP/9UaeuffKK2wEAVTwkIgFy5VGq7RpMcTCYbOnWrw4hvV7Jz2ynqNihttEmZFi3uL0NAAPzzD3Tv/sJosJtHDnLmdWNQg+8oVrYI549cosNX7xJw+ioBZ6/S9rOWgCpjUKB4PrLnVkvy410mx3ac4uvmIxPez8HJHntHO2Jj4oiNiSPm4cUgHhsbQaFSBShfrzQVG5ajStM3yJ0/fVPKTCaoWVNto0fD+fOwe3fiV/Ppp6r0wdmzav/0aZXuGr+gSqN5GnUavMa8WdtZPG8Pdeq/lmw3oiYpWtyTS3S0Winp56eczY/M2p+Gq5sL3y4bxN/TNuBeMBdtB7fEvWBuFo9aiZt7doqWLkxsTCwX/vMnPOQO+b3yJjm+ePmifD63D2HBd4i8F0nEvQhiomIx2ZmwtTPh4OxArnxu5MznRp5CuSnyWkEcnIwteFCihNri6ddPlZUAFZytVw/CwlQufe3a8OabUL06uLkZYq4mg2Iy2fDe+zUYN3INRw5dpmLlYkablCnR4p5cBg1SPoilS18o7I/yds9GCc9jY2IJDQ6n/Rf/A+DYdj/OHjhP8QrFKPJq0jsB94K58elUN21sN4g6iV4qzGZVO2zHDlUnbNQoVQpBCChTRgl+tWrQoIH22WugYaPXmTV1K3/+cUCLewqxaCpkpmXxYpg0Cfr3V0tpU4itnS1la73K6A9+4e+p65nzf4vJV8yD+u1rvfjgTI7JBC1bwtixqsxBWJiqPvD992r9w8qV0KMHLFqkxt++rWb+J04Ya7fGGOwdbGnW4g3+3X2WoOthRpuTKbHoCtXKlSvLgwcPWux8acKtW2pFZLlysHXrs+ufvASbFuzA/2QA5euXpXKj8mlgZOZHSrhwQa2GLVBAXQDq11dFIRs2VCWehwxRv4by5dVj2bLWsW5C83RuXA+jc+tf6Ohbm87dM/ddbGpJyQpV7ZZ5Eblzq+lkhQppIuxAkqwajUKIpP76qlXhzp3EGmEmk/pVrF0Lv/2WOC5PHuXWKV1abR06QE5dmsQqyJffjYpVvNiw9hidutXRgdWXRLtlnkV8wXlQAdTMWCshk2MyJTZh8faGDRtUgPb6ddi4UVUXffttVSr699+hTx9VJRjUEoSqVSHmYVLR0aNw4ACEhhrzWTQpo2HjsgTdCMfvRKDRpmQ69Mz9WUyerHL5du1SKR2aDEO+fGrz9k58TUpVRjpfPrWfK5cKzMbfbA0dqvLx43/m5aV+7uWlvG7Fiqn9Yjp2l6GoVacUdvYmtm8+RZnXLdFZxnrQPven8e+/KtWjcWO1OsdG3+Bkds6fh5MnVTvHCxdUg5ILF8DfP7EMdbFiiY1LBg1SJRaGDVP7O3dC9uyqc1XOnMb3GMhKfDVwMQH+N5m7tHeWdc1on3tacPOmKmZesCDMm6eF3Up4PAc/nthYVTr+4sVElw6oOPqjpY7btEnM2XdyUhk+hQqp4G/BgmorX16t3AW1LMI+bUsFZVmq1yrJ/r3nuRoYSqHCuV58gAbQ4p6UuDh4/331X7xnj47MZQFsbVXfkKKPte+cMyfp/qpVqlz1lSvqYhAYqLbdu5U7KDpaBXPjxd3dXbUw/PFHddHo2hXy5lVbvnzq0cMjcUvXxiiZnAqVPAE4dviyFveXQIv7owih8u/atFENWzWah1StqranIaW64Yt375jNMHgwVKmi9sPCVGrnjRvPLpWcPbvqijVwoBo/cKC6INSqpYLAu3apbCF3d/Xo5qYCzlmBQkVy4ZbThRPHAmjWsqLR5mQatLjHExen/lu++MJoSzSZDCFUSmY8Njbw1VeJ+/nyKZ8/KHEPClJbSIjqJBj/vMzD+m6hoSqvv4mqK8exY6qu/uPndHNTweHcudXjF1+oO4eAAFWxs00b5S66dUvdXbi5qZtRF5fMFTMQQvDKq/k5fzbIaFMyFVrcQd1r+/jA9OmJ99UaTTrg4qIydLy8nj2mWDHl8omnUiU18791S203b6oVvLdvq/34x/i0zxMn1GLq6tWVuP/9d9JuWiaTEno3N1WHP/5x1Ch45RXVonbTJvjwQ3VHcfmySj/Nnj1xc3W17J2DV0kPDu6/QFysGZOtjoMlBy3uUVFqinPjxkvVjNFoLIWra6KLJzk0bqwE39VV7TdooEoihYWpu4KwMAgPV8/Dw9V27lyiW2n3bpUt1LGjEvLZsxOzhh7F2Vm1Z8yeXT2uX6/cRitWqOfTpqk7hI0bVWaSq2vSzcUl6ePzevUWKJgTc5wkODic/AV0LCw5aHEfOFBNi5Yvh5IljbZGo0k1NjZJcwGKFFFbcunZU+UVZFNVqPH1VWWdw8NVI/W7d5M+v3NHPcaXcj57Vi04i3f9zJsHCxY8/5z29mqeBaqm0JEjqsgcKHfTnt2vcPasPb162VGosLoQPLp5eKg5GqgFayYTvP662g8KUvtOTmrLKglwWTvPfeFC9Vc8cCD89JPR1mg0VsmDB+pu4f59uHdPXQju31db/PPYWLVmEFT10IsXVaYRQK9esG1bNP6X7uKaPTsxMXY8eJB4MQAoVUr1CwDlWbWxUaWgQLmazp1LHOvgkCj08VutWuq88ecrVUpdZEBdXIRQ4xwc1EXs8c3TU6XCgoqRxGdGmc3qszs4qM02hdNpnef+smzerIqKjxz54rEajSZFxM+uk8tHHyXdnzIFzp25RS/fWQwd1YaadUoBKgfiwQOIiEh0KQH8/LMS1XiGDlVxivixj2+RkUkL0F26lLQn8KxZ6u4kOvrZNnfuDHPnqudVq6oL1ahR6g4nd+7EcSZTotDHXygcHNRn7t9fXexatYK+fdVjYCCsXp387+5Rsra4z5yppg1pVBBMo9GkD5ERKlrs6JT4v2oyKddRvPsonjfeSLrfvv3LnWvduqT7ISHq0WxWdwvxF4WoKHVhiIxMejFYvDixJ4GDg7rYREUljo9//uh+3oe9emJj1X78xeruXXWxSQlZT9ylhK+/hg8+UD72+KiTRqPJsIQE3wEgZy7j/l9tbBLdOM+jVavE587Oie6d5JAzp1rTEM9rryn31OjRL2crZMWqkJMmwYgRqmaMRqPJFJw9fR17e1uKFHU32pRMQ9YS9717VfC0RQv1qNFoMjwxMXHs2OJH2fKFdY77S5B1vqmQEJUrVaSIinxkpiV6Gk0WZtXyg4QE36V1e116+2VIlbgLIZoIIc4IIc4LITL2uv3vv1ch82XL1JI8jUaToYmJiWPy+PVMm7iRilWKUbnac5b1ap4gxeIuhDABk4GmQGmgvRCidFoZluaMHq1WVjweStdoNBmS6b9s4s+lB3inbVWGj22XZWu5p5TUZMtUBc5LKS8CCCEWAy0Bv7QwLM1xclINODQaTaagXaealKtQhNr1XzPalExJatwyBYGAR/YDH76WBCFEDyHEQSHEwZD4hFGNRqN5Abnds2lhTwWpEfen3SM9UctASjldSllZSlk5z6N1UTUajUaTbqRG3AOBRzvWFgKupc4cjUaj0aQFqRH3A0BJIUQxIYQ90A5YlTZmaTQajSY1pDigKqWMFUL0AdYDJmC2lPJkmlmm0Wg0mhSTqtoyUsq1wNo0skWj0Wg0aUTWWaGq0Wg0WQgt7hqNRmOFaHHXaDQaK0SLu0aj0VghWtw1Go3GCtHirtFoNFaIFneNRqOxQrS4azQajRWixV2j0WisEC3uGo1GY4VocddoNBorRIu7RqPRWCFa3DUajcYK0eKu0Wg0VoiQ8onOeOl3MiFCAH+LnTARd+CmAec1Ev2Zswb6M2cNSkkps73MAamq5/6ySCkNaaIqhDgopaxsxLmNQn/mrIH+zFkDIcTBlz1Gu2U0Go3GCtHirtFoNFZIVhH36UYbYAD6M2cN9GfOGrz0Z7ZoQFWj0Wg0liGrzNw1Go0mS6HFXaPRaKwQqxd3IUQTIcQZIcR5IcQXRtuT3gghCgshtgohTgkhTgoh+hltkyUQQpiEEEeEEKuNtsUSCCHchBDLhBCnH/6uaxhtU3ojhOj/8G/6hBBikRDC0Wib0hohxGwhRLAQ4sQjr+USQmwUQpx7+JgzOe9l1eIuhDABk4GmQGmgvRCitLFWpTuxwEAp5WtAdaB3FvjMAP2AU0YbYUEmAP9IKV8FymPln10IURD4BKgspSwLmIB2xlqVLvwGNHnstS+AzVLKksDmh/svxKrFHagKnJdSXpRSRgOLgZYG25SuSCmvSykPP3x+F/VPX9BYq9IXIUQh4C1gptG2WAIhRHagDjALQEoZLaUMM9Yqi2ALOAkhbAFn4JrB9qQ5UsodwO3HXm4JzH34fC7QKjnvZe3iXhAIeGQ/ECsXukcRQngCbwD7jLUk3fkZ+BwwG22IhfACQoA5D11RM4UQLkYblZ5IKa8CPwFXgOtAuJRyg7FWWYy8UsrroCZvgEdyDrJ2cRdPeS1L5H4KIVyB5cCnUso7RtuTXgghmgPBUspDRttiQWyBisBUKeUbwH2SeaueWXnoZ24JFAMKAC5CiI7GWpWxsXZxDwQKP7JfCCu8lXscIYQdSth/l1KuMNqedKYW0EIIcRnldmsghFhgrEnpTiAQKKWMvyNbhhJ7a8YbuCSlDJFSxgArgJoG22QpgoQQ+QEePgYn5yBrF/cDQEkhRDEhhD0qALPKYJvSFSGEQPliT0kpxxltT3ojpfxSSllISumJ+v1ukVJa9YxOSnkDCBBClHr4UkPAz0CTLMEVoLoQwvnh33hDrDyI/AirgC4Pn3cB/krOQRatCmlppJSxQog+wHpUdH22lPKkwWalN7WATsBxIcTRh68NkVKuNdAmTdrTF/j94aTlIuBrsD3pipRynxBiGXAYlRF2BCssQyCEWATUA9yFEIHAt8Ao4A8hRDfURa5Nst5Llx/QaDQa68Pa3TIajUaTJdHirtFoNFaIFneNRqOxQrS4azQajRWixV2j0WisEC3uGo1GY4VocddoNBor5P8BGHBSk4B6kL4AAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Solve optimization problem\n",
"xsln = solve_opt(True,True)\n",
"\n",
"# Create contour plot\n",
"visualize(xsln,True,True)\n",
"\n",
"# Draw gradient\n",
"draw_gradients(xsln,True,True)\n",
"\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.6 Discussion](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.6-Discussion)",
"section": "4.2.3.6 Discussion"
}
},
"source": [
"### 4.2.3.6 Discussion\n",
"\n",
"Why are the gradient vectors not the same length? I thought the forces were balanced..."
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.7 Analysis without Constraints](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.7-Analysis-without-Constraints)",
"section": "4.2.3.7 Analysis without Constraints"
}
},
"source": [
"### 4.2.3.7 Analysis without Constraints"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.7 Analysis without Constraints](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.7-Analysis-without-Constraints)",
"section": "4.2.3.7 Analysis without Constraints"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.8 Analysis with Constraints](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.8-Analysis-with-Constraints)",
"section": "4.2.3.8 Analysis with Constraints"
}
},
"source": [
"### 4.2.3.8 Analysis with Constraints"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.8 Analysis with Constraints](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.8-Analysis-with-Constraints)",
"section": "4.2.3.8 Analysis with Constraints"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"id": "469d15ba",
"metadata": {},
"source": [
"\n",
"< [4.1 Convexity Revisited](https://ndcbe.github.io/CBE60499/04.01-Convexity.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [4.3 Analysis of KKT Conditions](https://ndcbe.github.io/CBE60499/04.03-KKT-Multipliers.html) >
"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 1,
"link": "[4.2 Local Optimality Conditions](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2-Local-Optimality-Conditions)",
"section": "4.2 Local Optimality Conditions"
}
},
"source": [
"# 4.2 Local Optimality Conditions"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 1,
"link": "[4.2 Local Optimality Conditions](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2-Local-Optimality-Conditions)",
"section": "4.2 Local Optimality Conditions"
}
},
"source": [
"**Reference** Section 4.2 in Biegler (2010)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.2.1 Unconstrained Optimality Conditions](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.1-Unconstrained-Optimality-Conditions)",
"section": "4.2.1 Unconstrained Optimality Conditions"
}
},
"source": [
"## 4.2.1 Unconstrained Optimality Conditions"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.2.1 Unconstrained Optimality Conditions](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.1-Unconstrained-Optimality-Conditions)",
"section": "4.2.1 Unconstrained Optimality Conditions"
}
},
"source": [
"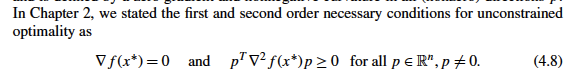"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.2.2 Karush-Kuhn-Tucker (KKT) Necessary Conditions](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.2-Karush-Kuhn-Tucker-(KKT)-Necessary-Conditions)",
"section": "4.2.2 Karush-Kuhn-Tucker (KKT) Necessary Conditions"
}
},
"source": [
"## 4.2.2 Karush-Kuhn-Tucker (KKT) Necessary Conditions"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.2.2 Karush-Kuhn-Tucker (KKT) Necessary Conditions](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.2-Karush-Kuhn-Tucker-(KKT)-Necessary-Conditions)",
"section": "4.2.2 Karush-Kuhn-Tucker (KKT) Necessary Conditions"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.2.2 Karush-Kuhn-Tucker (KKT) Necessary Conditions](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.2-Karush-Kuhn-Tucker-(KKT)-Necessary-Conditions)",
"section": "4.2.2 Karush-Kuhn-Tucker (KKT) Necessary Conditions"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.2.3 Kinematic Interpretation via Example](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3-Kinematic-Interpretation-via-Example)",
"section": "4.2.3 Kinematic Interpretation via Example"
}
},
"source": [
"## 4.2.3 Kinematic Interpretation via Example\n",
"\n",
"Consider the following two dimensional optimization problem:\n",
"\n",
"$$\n",
"\\begin{align} \\min_{x_1,x_2} \\quad & f(x) := x_1^2 - 4 x_1 + \\frac{3}{2} x_2^2 -7x_2 + x_1 x_2 + 9 - \\mathrm{ln}(x_1) - \\mathrm{ln}(x_2) \\\\\n",
"\\mathrm{s.t.} \\quad & g(x) := 4 - x_1 x_2 \\leq 0 \\\\\n",
" & h(x) := 2 x_1 - x_2 = 0\n",
"\\end{align}\n",
"$$"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"nbpages": {
"level": 2,
"link": "[4.2.3 Kinematic Interpretation via Example](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3-Kinematic-Interpretation-via-Example)",
"section": "4.2.3 Kinematic Interpretation via Example"
}
},
"outputs": [],
"source": [
"import numpy as np\n",
"import matplotlib.cm as cm\n",
"import matplotlib.pyplot as plt\n",
"from pyomo.environ import *"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.1 Define Function for Visualization](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.1-Define-Function-for-Visualization)",
"section": "4.2.3.1 Define Function for Visualization"
}
},
"source": [
"### 4.2.3.1 Define Function for Visualization"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.1 Define Function for Visualization](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.1-Define-Function-for-Visualization)",
"section": "4.2.3.1 Define Function for Visualization"
}
},
"outputs": [],
"source": [
"## Objective function\n",
"def f(x):\n",
" return x[0]**2 - 4*x[0] + 1.5*x[1]**2 - 7*x[1] + x[0]*x[1] + 9 - np.log(x[0]) - np.log(x[1])\n",
"\n",
"## Gradient of objective f(x)\n",
"def df(x):\n",
" return np.array((2*x[0] - 4 + x[1] - 1/x[0], 3*x[1] - 7 + x[0] - 1/x[1]))\n",
"\n",
"## Gradient of inequality constraint g(x)\n",
"def dg(x):\n",
" return np.array((-x[1], -x[0]))\n",
"\n",
"## Gradient of equality constraint h(x)\n",
"def dh(x):\n",
" return np.array([2, -1])\n",
"\n",
"## Function that plots contour of objective, solution, and optionally g(x) <= 0 and h(x) = 0\n",
"def visualize(xsln,plot_g,plot_h):\n",
" ## Create contour plot\n",
" \n",
" n1 = 101\n",
" n2 = 101\n",
" x1eval = np.linspace(0.05,10,n1)\n",
" x2eval = np.linspace(0.05,10,n2)\n",
" \n",
" X, Y = np.meshgrid(x1eval, x2eval)\n",
" \n",
" Z = np.zeros([n2,n1])\n",
" \n",
" for i in range(0,n1):\n",
" for j in range(0,n2):\n",
" Z[j,i] = f((X[j,i], Y[j,i]))\n",
" \n",
" fig, ax = plt.subplots()\n",
" CS = ax.contour(X, Y, Z)\n",
" ax.clabel(CS, inline=1, fontsize=10)\n",
" \n",
" ## Plot g(x) <= 0\n",
" if(plot_g):\n",
" g_x2 = np.zeros(n1)\n",
" for i in range(0,n1):\n",
" # Inverted g(x) = 0 to calculate x2 explicitly from x1\n",
" g_x2[i] = 4 / x1eval[i]\n",
" \n",
" plt.plot(x1eval,g_x2,color=\"blue\",linestyle=\"-.\",label=\"$g(x) \\leq 0$\")\n",
" \n",
" ## Plot h(x) = 0\n",
" if(plot_h):\n",
" h_x2 = 2*x1eval\n",
" plt.plot(x1eval,h_x2,color=\"red\",linestyle=\"--\",label=\"$h(x) = 0$\")\n",
" \n",
" ## Plot solution\n",
" plt.scatter(xsln[0],xsln[1],marker=\"*\",color=\"black\",label=\"$x^{*}$\")\n",
" \n",
" ## Adjust x and y limits\n",
" plt.xlim([-1,10])\n",
" plt.ylim([-1,10])\n",
" \n",
" ## Add legend\n",
" plt.legend()\n",
" \n",
"## Function that draws gradient of f(x) and optionally g(x) and h(x)\n",
"def draw_gradients(x,with_g,with_h):\n",
" dh_x = dh(x)\n",
" \n",
" ## Draw gradient of f(x) [objective]\n",
" df_x = df(x)\n",
" plt.arrow(x[0],x[1],df_x[0],df_x[1],color=\"black\",width=0.1)\n",
" \n",
" ## Draw gradient of g(x) [inequality]\n",
" if(with_g):\n",
" dg_x = dg(x)\n",
" plt.arrow(x[0],x[1],dg_x[0],dg_x[1],color=\"blue\",width=0.1)\n",
" \n",
" ## Draw gradient of h(x) [equality]\n",
" if(with_h):\n",
" dh_x = dh(x)\n",
" plt.arrow(x[0],x[1],dh_x[0],dh_x[1],color=\"red\",width=0.1)\n",
" \n",
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.2 Define function to solve optimization problem with Pyomo](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.2-Define-function-to-solve-optimization-problem-with-Pyomo)",
"section": "4.2.3.2 Define function to solve optimization problem with Pyomo"
}
},
"source": [
"### 4.2.3.2 Define function to solve optimization problem with Pyomo"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.2 Define function to solve optimization problem with Pyomo](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.2-Define-function-to-solve-optimization-problem-with-Pyomo)",
"section": "4.2.3.2 Define function to solve optimization problem with Pyomo"
}
},
"outputs": [],
"source": [
"def solve_opt(consider_g,consider_h):\n",
" \n",
" ## Create concrete Pyomo model\n",
" m = ConcreteModel()\n",
" \n",
" ## Declare variables with initial values\n",
" m.x1 = Var(bounds=(0,100),initialize=10)\n",
" m.x2 = Var(bounds=(0,100),initialize=10)\n",
" \n",
" ## Declare objective\n",
" m.OBJ = Objective(expr=m.x1**2 - 4*m.x1 + 1.5*m.x2**2 - 7*m.x2 + m.x1 * m.x2 + 9 - log(m.x1) - log(m.x2), sense = minimize)\n",
" \n",
" if(consider_g):\n",
" ## Add inequality constraint\n",
" m.con1 = Constraint(expr=4 - m.x1*m.x2 <= 0)\n",
" \n",
" if(consider_h):\n",
" ## Add equality constraint\n",
" m.con2 = Constraint(expr=2*m.x1 - m.x2 == 0)\n",
" \n",
" ## Specify IPOPT as solver\n",
" solver = SolverFactory('ipopt')\n",
"\n",
" ## Solve the model\n",
" results = solver.solve(m, tee = True)\n",
" \n",
" ## Return the solution\n",
" return [value(m.x1),value(m.x2)]\n",
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.3 Take 1: Unconstrained](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.3-Take-1:-Unconstrained)",
"section": "4.2.3.3 Take 1: Unconstrained"
}
},
"source": [
"### 4.2.3.3 Take 1: Unconstrained"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.3 Take 1: Unconstrained](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.3-Take-1:-Unconstrained)",
"section": "4.2.3.3 Take 1: Unconstrained"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Ipopt 3.12.10: \n",
"\n",
"******************************************************************************\n",
"This program contains Ipopt, a library for large-scale nonlinear optimization.\n",
" Ipopt is released as open source code under the Eclipse Public License (EPL).\n",
" For more information visit http://projects.coin-or.org/Ipopt\n",
"******************************************************************************\n",
"\n",
"This is Ipopt version 3.12.10, running with linear solver mumps.\n",
"NOTE: Other linear solvers might be more efficient (see Ipopt documentation).\n",
"\n",
"Number of nonzeros in equality constraint Jacobian...: 0\n",
"Number of nonzeros in inequality constraint Jacobian.: 0\n",
"Number of nonzeros in Lagrangian Hessian.............: 3\n",
"\n",
"Total number of variables............................: 2\n",
" variables with only lower bounds: 0\n",
" variables with lower and upper bounds: 2\n",
" variables with only upper bounds: 0\n",
"Total number of equality constraints.................: 0\n",
"Total number of inequality constraints...............: 0\n",
" inequality constraints with only lower bounds: 0\n",
" inequality constraints with lower and upper bounds: 0\n",
" inequality constraints with only upper bounds: 0\n",
"\n",
"iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls\n",
" 0 2.4439483e+02 0.00e+00 3.29e+01 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0\n",
" 1 -8.0094510e-01 0.00e+00 4.03e-01 -1.0 8.53e+00 - 9.05e-01 1.00e+00f 1\n",
" 2 -8.7120418e-01 0.00e+00 2.51e-03 -1.0 1.31e-01 - 1.00e+00 1.00e+00f 1\n",
" 3 -8.7421973e-01 0.00e+00 5.46e-04 -2.5 3.76e-02 - 1.00e+00 1.00e+00f 1\n",
" 4 -8.7422408e-01 0.00e+00 1.29e-06 -3.8 1.78e-03 - 1.00e+00 1.00e+00f 1\n",
" 5 -8.7422408e-01 0.00e+00 6.93e-10 -5.7 4.12e-05 - 1.00e+00 1.00e+00f 1\n",
" 6 -8.7422408e-01 0.00e+00 9.45e-14 -8.6 4.81e-07 - 1.00e+00 1.00e+00f 1\n",
"\n",
"Number of Iterations....: 6\n",
"\n",
" (scaled) (unscaled)\n",
"Objective...............: -8.7422408318635370e-01 -8.7422408318635370e-01\n",
"Dual infeasibility......: 9.4500693109869893e-14 9.4500693109869893e-14\n",
"Constraint violation....: 0.0000000000000000e+00 0.0000000000000000e+00\n",
"Complementarity.........: 2.5065634500861016e-09 2.5065634500861016e-09\n",
"Overall NLP error.......: 2.5065634500861016e-09 2.5065634500861016e-09\n",
"\n",
"\n",
"Number of objective function evaluations = 7\n",
"Number of objective gradient evaluations = 7\n",
"Number of equality constraint evaluations = 0\n",
"Number of inequality constraint evaluations = 0\n",
"Number of equality constraint Jacobian evaluations = 0\n",
"Number of inequality constraint Jacobian evaluations = 0\n",
"Number of Lagrangian Hessian evaluations = 6\n",
"Total CPU secs in IPOPT (w/o function evaluations) = 0.010\n",
"Total CPU secs in NLP function evaluations = 0.000\n",
"\n",
"EXIT: Optimal Solution Found.\n",
"\b"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAAD8CAYAAACMwORRAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzs3Xd4leX5wPHve1b23jshOyQhQNhhb0UcICgKuGuHWqu11dYuW2vV1vpztHVPEMEBorL3DIQRIHvvvcfZz++PYKp1AiEn4/lcl5cmec8590mO93nP/d7P/ShCCCRJkqShRWXrACRJkqS+J5O7JEnSECSTuyRJ0hAkk7skSdIQJJO7JEnSECSTuyRJ0hD0vcldUZTXFEWpUxTl7Je+56koynZFUfLP/9vj8oYpSZIkXYgfcub+BrDgf773a2CnECIa2Hn+a0mSJGmAUH7IIiZFUcKBzUKIxPNf5wIzhBDViqIEAHuEELGXM1BJkiTph9Nc5O38hBDVAOcTvO+3Hagoyl3AXQBOTk5j4+LiLvIhpeHEYDaT19SIRqXC1c4ONzt7nHQ6FFsHNsAJBPntNahQ8NA54aZzQqMM7UtrbaZqDJYuHDXuOKjdUSlqW4d08SzlIDpB5QMqTzj/is/IyGgQQvhcyF1dbHL/wYQQLwEvAaSmporjx49f7oeUhoAuk4mdxYVsLchnT2kxXSYT9nZ2zImIZEFUNFNDw7HTXPaX76BjtlrYW5fFB2VHOd5UhEZRM9MvgSWhExntEY6iDL23x+ruLI43rqWo4zAaxZ5E94WM9lyKq9bP1qFdMGE8hmh/FkzpoHJCcf4xOCxBpbIrvdD76teyjEzu0sXQm03sLy1la2E+O4oLaTMYcNbqmDViBAujYpgeFo69RmvrMAec0o56PihP59PKDNrNeiKd/VgSOoGFgaNx0tjZOrw+12goJaPpfXJbdwAQ6zqbVK/leNqFfettWoxVdJjqCHZK6a8wv5cQAoxHEB3PgukE6Cai9no7QwiReiH3c7HJ/SmgUQjxhKIovwY8hRAPfd/9yOQuXSqjxcLh8jK2FOazrTCfZr0eJ62WmREjuCIqlhnhMtH/L73FyLbqTDaUHSGnrQontR1XBI1maehEIpy/taI6aLWb6jjRtIGzLZ9iFkbmBTxEvNvcrx1nthop6TzK8cZ1qBQ1U3xuJ8gx2QYRf7OeJL8PhBWVw6y+T+6KoqwFZgDeQC3we+Bj4H0gFCgDrhdCNH3fg8nkLvUls9XKkYpyPi/IY2tBPk36bpy0WmaPiOTKqFimhcnSzZcJITjXWsH6siPsqM7EJCyM84pkWegk0nzjUA+x2nyXuYXTzR+T7HE1Tppv7ta2CgsqRU1R+2Fy2rYz0+8+HDRu/Rzp91MU5fKcufcVmdyly+WLRP9Zfi5bCvNp0etx1umYHxnNouhYJoeEolUP4gttfazZ2MHH5cf5sPwotfpWAuzdWRI6kauDU3HTOdo6vEtiMpmoqKhAr9d/77ECgYKCVZjptrTiqPZAACZrN2pFi0alu/wBf4m9vT3BwcFotV/99CmTuyQBJouFQ+VlbM7PZVthAe1GAx729iyMjuWq6FjGBQWjGoIXFi+G2Wphf10275cdJqOpGDuVlgWBo1geNpkoF39bh3dRiouLcXFxwcvL6wdfQG41VqNVOSCwYrEaQVEwWfXoVI64aC+oSeWiCSFobGykvb2diIiIr/xMJndJ+h8Gs5l9pSV8kp/DzqJCus1m/J2cuSo2jsUxcST4+A7JDpKLUdBew/ulh/m86hQGq4mxniO4IWzyoCvZZGdnExcX971/V6O1G5OlC4O1C7WiwVnrQ5OhFDdtIDq1AyarHr2lDWeNT7+9RoQQ5OTkEB8f/5Xvy+T+HYqqG3l1SzolNU2U1jZjNFvQatToNGqc7XV4uDji7uyAj5sT/p4u+Hm4EOjlSpC3G77uzqhVg+fFLX2zTqORncWFfJKXw97SEsxWK1EenlwdF8/imHhC3AZerdUWWoxdbKo4zvqyw9TqWwly8GRZ2CSuCh6Ls8be1uF9r+zs7K8lxy8zWrrosrSgoKBR2aFVHNCpHegw1WMWRtx1QQCYrQbaTfW46QJRgG5LG2ZhwF7tik7l0K/xy+T+HfIrG7jvxY8J9/Mkwt8De50Ws8WK0WyhrUtPc3s3ze1d1Ld20tTe9ZXbatQqgrzcCPVzJ8zXgzA/DyL8PYkI8MLD+fL9kaXLp7m7m88K8tiUm82xqkoAxgYEcnVsPItiYnG3l39Xs9XCnros1pUc4nRLKU5qO64KTmV52CSCHD1tHd63+q7kLoSg09xIp7kJR407LtqebiGrsNJoKMFDF9xbZ28z1aKg4KTxotPchEWY0Kkc6LK04KYNQKu6PG90MrlfRgaTmbqWDqoa26hsaKWivoWKhlZKa5spq2vGYLL0Huvp4khkoBeRAV5EBXkTHeRNZIAXjvb9eyFGungVba1sys1hY242+U2NaFUqZoaP4Nr4BGaERciOGyCrtYK1JQfZUXMGIQQz/BJYEZ5GknvogCtrfd+ZO/S0QXaZmzAJPS4aXwQCvaUNN10AAFZhpsFQgrddBJ3mJlSosFO7oFHp6DQ3oqDC8Vs6cC5H/DK59wOrVVDT3EZxdRPFNU0UVjdSWNVIUXUjXQZT73EhPu7EhvgQE+xDXIgvcSG+eLs52TBy6fsIIciqr+OjnGw25WXT0NWFm509i2JiuS4ugRT/gAGXyPpbnb6V9aVH+KginTZTN4luIdwYPoWZfiPRqAZGN9IPSe5fMFuNCAQqRU27qQ43rT8CQYepHkVR46h2p81ci7PGB62qZ+FXk6EMR4079mpXhBB9/pqQyX2AsVoF1U1t5Fc2kFdRT35lPbnl9VQ0tPYe4+3mRHyoLwmhfsSH+ZEQ6icT/gBltlo5WFbKhzlZbC8qQG82M8LDg+viRnJtXAIBLi62DtGmus1GPq06wdqSg5R3NRJg784N4VNYHJxq89WvF5Lcv2AVVtpNtZiFAbWiQ61ocNJ4o7e0IhA4qN1QKWoMlk66LM24aQN6Z9h8keCtwozJqket6L61hTIrK4v09HRmz56Nu7s7Lt/wOpLJfZDo6DaQW1FPTlkd2WW15JTXUVzTxBe/dn8PFxLC/EgM9ycxwp+EUD9Z0hlg2g0GPivI48PscxyrqkQB0kLDWBI/knmRUcN6RaxFWNlfl8O7Jfs53VyKs8ae60LGszxsMj72rjaJ6WKS+xdMVj0CgVaxR1EUOs1NIAROWi8AWo1VaFUOOKjdUL7UQWS2Gmkz1aBRdBitXThqPHBQu3/trP706dPcdtttrF69mnvuuecbz/plch/EuvRGcsrryCqrI6ukhrOlNVTU95zhqxSFyEAvkkcEkBwRQPKIQEJ9v/4ikWyjtKWFD3PO8WF2FpXtbbjo7FgcG8fShESSff2G9d/pbEs575bsZ3fNOVSKioWBKdwUkcYI5/4d4HUpyf1/dZqbsAoTLlo/uswt6C1tuOuCvjJ50iostJvqetspTdZuOs3NuOsCv3Z/mzdvpqSkhBEjRpCWloar69ffAGVyH2JaOro5V1JDZnE1Z4prOFtcTYfeCIC7kz3JIwJJiQwkJSqQhFA/dFp5kc+WrEJwpKKc9Vln2VKQj8FiJsbLm2UJiVwTF4+nw+Be5XkpKruaWFNygE0VGRisJtJ84lgZMZWUfppK2ZfJ3Ww10m6qw4oZjWKHg9oNnbrnb/tFOUZvae+5GKsNQFFUGCydGKwdXD3vBn798K+YOXsav/3tb+nuMPLcc89TU1ODv/+3LxCTyX2Is1oFxTWNnC6qJrOomsyiKkpqmwHQadQkhPkxOiqIMdHBjBoRgLPD0JvyN1i0GfRszstlfdZZTtfWoFOpmRsZybKEJKaEhg3b1bAtxk42lB1hXelhWk1dJLmHsipiGlN941BdxkVRF5PcW1tbmTx5MocOHcLtG9Y7mK1G1IoGRVF97SLqF6tbHTXuCGFFb+nAZO3i1JE8fvPor1l9282sf+9D3trwbzzsA3vfHC4kfpnch7jm9i5OFVZxqrCKkwWVZJfVYrEKVIpCbIgPY6ODGRsdzOioIFydBv5ik6Eop6Ge9Vln+Sgnixa9niAXV65PSOT6hMRhexFWbzHySUUG75QcoLq7mQgnH1ZGTGNBYMpl6bC5mOS+Zs0abrrpJtasWcONN974ncd2mZuxCDMuWh/MViMtxgq87MJRFBVmq5FOcyMOajcswsycmfPQd5nYs2cPir0BjcoOe3XP6+DbOm1kcpfoNpjILK7mRH4FJ/IrOVNcjdFsQVEgNtiX1JhgxsWGMDoqSJ7Z9zOD2cz2ogLWnTvDwfIyVIrCjLAIbkxMZnp4BJphuOLZbLWws+YsbxbvpaC9Bj97N24On8ri4FQcNH3XRHAhyX3FihVs2rQJg8GA2WxGo9FgZ2fH4sWLWbNmzbfeTgjr+WRuoNPchJsuAKuwoLe0YbIacNP5s/f459yx4l58vH04dOjQ+fZKFU4aL8xWI92Wlt5++S/X8GVyl77GYDJztqSGjLwKjueVk1nUk+zVKoX4UD/Gx4UyPjaEUZGB2Mmafb8pa23h/XNnWZ91lvquTvydnLl+ZCLLRyYR6GKbjhJbEkJwqCGPN4r2cLq5FHetI8vDJ7MsdBIu2ktfGXwhyb2goIDFixdTUlJCd3c3Dg4OREREsGnTJiIjI7/39kJYaTVVYRVWVIoataLFUe1BWVUxixZezYb3P+Tee+/lwQcfZMz0KDx0IZiFEYOlHbWiwypMWLHgpg3sPYuXyV36XgaTmcyiao7llpOeW8a5khosVoGdVs3oqCDGx4UyMT6MmCAfVKrhWRfuTyaLhV0lRaw9k8n+shIURWFmeAQrkkYxLTR8WM4vOtVcwptFezlYn4uT2o4loRNYEZ6Gp53zRd/nhZZlNmzYwI033oidnR0Gg4G1a9eydOnSC3pMg6UDgRU7lQvd3d3MmDWN3/3htyxacA379u3jwYceYNu+jbhq/Wgz1eCgdsdO3bPGpcVYibPGp7c3XiZ36YJ1dBs4UVDJ0ewy0nPKKKxuBMDD2YGJ8WFMSghjYnyYXFjVDyraWnnv7BnWnTtDY3cXwa6u3DAymWUjk/B2HH6dNnltVbxRtJedNWfRqdRcEzKOmyOm4Wd/4cPcLjS5L1u2jG3btvHoo4/y2GOPMX/+fNatW3fBj/tl3eZWzMKIy/nWyFZjDR66YPTWdoSw4KjxRKWoMVn1tJpq8LYL/874ZXKXLkh9SwdHc8o4nF3K0eyy3oFpMcE+TEoIY8rIcEZFBspNLi4jo8XC9sIC1pw9zeGKcrQqFQuiYrg5eRSpAUHDrm++tKOeN4v38nnVKRQUrgoaw6oR0y9oUNmFJvdjx44RGhqKn58ftbW1lJeXk5p6QXn0a0zWbtpMdSiARmXf20b5xVm7VtWzSKrNVIsaDU5ar94LrDK5S33KahXkVdZzOKuEw1mlnCqowmy14mSvY3xcKGkjw5mSGIGv+8V/XJa+W2FTI++eOc0H2Vm0Gw3EenmzMjmFa+IScNQOr1Ww1d3NvFW0j00Vx7EiWBCQwq2RMwh18v7e2/Zln/ulMlg6exI5KgQ9Iw4cNZ5oVfaYrHo6TA04a72/MmFSJnfpsurUG0nPKePguRIOnSuhprkd6DmrT0uMYGpSBInh/sOyTny5dZlMfJKbzduZp8hqqMdFZ8eShJGsTE4hwv3yTCIcqOr0rbxTvJ+PytMxWS3MDxzFrSNmEP4dG3sPpOT+ZUJYaTFV4aT2RKd2pMlQjp3aCSdNz6cSizCjQi0365D6jxCCwqpGDpwr5sDZYk4XVmGxCtydHUgbGc605BFMjA+T7ZZ9TAjBiZoq3jp9ii0FeZisVqaHhbN61BimhYUPq8VRDYZ21hQfYEP5EQwWM3P9k7gtauY3jjb4oTsx9af/rmZto8PUgEZljwoVrjr/8z/vmSevoKa6qJXEhOSv3F4md6lftHXqOZxVyr6zRRw6V0Jrpx6NWkVqTAjTk0cwPTkSf8/huWDncqnr7GDt2UzWnMmkvquTcHcPViWnsCR+JC52w+dNtdnYwbvFB1hfdgS9xfSNSf5i9lDtbxarCbWqp9T2RQ7uMrdQW19JcWMmBs8CJvvc0TufRiZ3qd+ZLVYyi6rYm1nEvswiSut6RiTEhfgyMyWSGaOiiAocuP+TDTZGi4UtBXm8efokJ2uqcdbqWDoykdXJowlzd7d1eP2mxdjJu8UHeL/scE+SD0jijshZhDv7YjKZqKioQK/X2zrMC6az01LneIQTre9hFWaSPRYzwftmHDRuMrlLtlVS08SezEL2nC7kTHE1QkCwjxszR0UxMyWS5IjAH9RTX93UxufpOdQ2t3PNlETiQ/t3suBgcLqmmjdOn+Sz/FzMViuzIyK5NWUME4NDhs2baYuxk3eK97O+7AgGi4n5gaO4PXLWD7rwOpB1mhs5Uv8m51q34Gcfyw0Rz8vkLg0c9a0d7MssYvepQtJzyzBbrHi7OjIzJYpZo6MZGx2MRv3NF2Tve/Fjgr3dCfRy5fNjOSyfPoqrJo3EYrXKi7j/o7ajg3fPnGbNmdM06buJ9/bhttFjWRQdO2y2CGw2dvB28X7Wlx7BLCwsDEzh9shZA3qv1x+iwVCM0dJFkFOiTO7SwNTebeDg2WJ2nszn4LkS9EYzMcE+vPebm792rN5o5ran1/HCvdfh4ezAcx8fwNvVidHRQWzPyONkQSVLpiazcFwcisKwOUv9PnqziY052bx+6gR5TY34ODqxalQKKxJH4eEwPDb8bjS081bRPj4sP4pZWFkcnMptI2bg5zC4S1ay5i4NCt1GE4fOldBtNLFoQsLXfl7V2Mqb2zI4kl3KVRMTyCqrZd7YGN7ansGyGaPwcnHk9a3HeOTG2UQFDe6P35eDEIIDZaW8diqDvaUl2Gs0LIkfyW2jxw6bVsp6fRtvFO3ho/JjqBSF60LGs3rEdLzsBueFfpncpUGvtrmd5zceZFRkIH7uzry+9Rir56XS1qln4+FzvPKLZQA8+9F+ooO8uWL8wOtnHkjyGht47WQGH+dkY7JamBsZxZ1jUhkbEGTr0PpFdXczrxTs4tPKE+jUGm4Im8zNEdNw7YMBZf3pYpL78CjISYPGF2OLr540Eq1Gzemialo79WzPyOO6tCSg58xUrVJRe35hldUqei/SdhtMbD2eS31rB4smJhDgOfymLn5ZjJc3T8yZzwOT0ngr8yTvZJ5mW2EBY/wDuGvsOOaMiBrS/fIBDh48mrSEVSOm83L+Dt4o2ssHZUdZGTGN5WGT+3TU8EAjr0xJA063wYRWo8ZktuDr7kxGXgUFVQ29Z+lGs4X0nDLGRocAPVveATS0dvLvzYc5lFVCfUsnf3xrG80d3TZ7HgOJj5MTD0xK4+Btd/GH6bOo6+rk7k83Me+d11l3NhOD2WzrEC+rMCdv/pxyA+9MvodRHuG8mL+Na/c9zYayI5isQ/O5y+QuDSgJYf6oFIWVT6zh169+RmVDK4qiMDY6GACT2UJGfgVqlULyiACA3o6bT46cQ6tR8/PrpvHIitk42es4eK4YgPYuPXszC9l1qsA2T2yAcNRqWTVqNLtW3c6zC67EQaPl4V3bmf7mK/wnI512g+Fbb2uxWvnL/j3sKBq8v8MY1wD+MXYVr0z4EWFO3jyZtYnr9z/DlqpTWIXV1uH1KZncpQEl0MuVf/7kan5z0xzSRoZz24Lx3LZgPFqNmvYuPedKa9iRkc+VE86fxZt6zrqqGlupqG8lKdyfQK+eUozBZCHEp6dL4sGXNnPgbDFvbD3G79/cSnvX4Fvg0pc0KhVXxcSx6YabefOaJUR5evG3g/tJe/1lnj50AJPF8rXbNHV3E+Dsws8+38zLJ47ZIOq+k+wRxr/H38k/x67GSWPP7zLfZ9WhFzhcn0d/Xoe8nC6p5q4oyv3AHYAAzgC3CiGG9/81Up+IC/ElLqRnOJSjnRaNWsXKv63Fx82ZZdNHkZYYAYDu/I5S2aV1ODvYEeLbk8zPFFfj5+GMEIJtGbmoVSp+s2IOADf99V1aOvW4OPZM4jt4roTIAK9hOTJBURSmhoYzNTSczNoa/pNxjGNVFd+4DaCPkxNLExL5ODebCUE9JbFTNdXo1GoSfL59kNdApSgKk31imegdzbbqTP6dv537Mt5grOcI7oldQIJbsK1DvCQXndwVRQkC7gUShBDdiqK8D9wAvNFHsUkSAFqNmt+smIPBZKayoZURAV4YTGZO5Ffg7+lKoJcrzg469EYzHi49G10cyy0nyNsNg8lCbnk981JjAKiobyEuxBeT2UJLRzcvf3aUsrpmKhvbSBsZzv1Lpg3bvvlkP39euOIqjBbLt/4OXso4RqSHJ8l+/hjMZjKqq/gkLwcfR0cenDyVWK/B15qqUlQsCExhtn8iH5an81rhbm45/CJz/JP4cfQ8Qpy8bB3iRbnUsowGcFAURQM4AlWXHpIkfTM7rYYRAT2bGmjUKkxmCznldT0/02korG7Aw9mBLr2RQ1klJIT5gRA0tHUyPjYUgKb2bjRqFWqVig37Mqlv7eC5n13L8z+7lrqWDroMJls+xQFB9y2bs5S3trKrpIgfp44Heko7NyeN4uPlNzE2IIgX0o/0Z5h9TqvSsDxsMh9Me4DbI2dyoD6HZQee4emsT2gxdn7nbUs7G8hpreynSH+Yi07uQohK4GmgDKgGWoUQ2/73OEVR7lIU5biiKMfr6+svPlJJOk9RFNQqFRPiw5iVEgVAoJcbbo72rHxiDX9Zu5MAT1cmxofR2qVHbzQT6OWKyWyhvL4FIcDVyZ49mYWsntvTOqzTqLHXacmvlK/Rb/N25kkSfX2J8fLGer4d9Ys2yrTQMDQqFeWtrUDPgLM2w+Cs0Dpr7PlR9Fw+nPoAi4PGsqHsCNfue5o3i/ait3z9zd8qrOyry+LBE2/zZNZGLAPkwuyllGU8gKuBCKAFWK8oys1CiHe+fJwQ4iXgJehZxHQJsUrSt/J1d+bvdy9m7+lCXJ3siQvtqQGX17Xidb5Uk1tRT3ZZLWOjg6lqaMVqFYwM/2KetiC/sp5Qn+GxgvOHMpjNbMg+x/jAYI5VVfL8wquA82NqFQWtWk1lext7Snq6kvydnek0Gnni4D4Km5pw0mn525z5eDoMvn1hve1deTjxWm4In8LzuVt4IW8rkc5+pPnGfeU4laJiZcQ0WoxdlHc1oFYGRp/KpUQxBygWQtQLIUzAh8DkvglLki7O9FGRjI4KwkHXMyt7fmoMp4uqeHzNTp77+AC+7s7MHxfL5qPZjIsN6b3dgbPFeLs54enqOGS6JfqC0WLheFUli997h6buboJc/7sorKi5iWePHuKX27bQYTLyi0lTqOno4P/SD9NlMvHmNUsIcXNne+HgbZ0EiHD25e9jV/HmpJ8yxSf2G4/JbavicEMeP4me1/u9NlM3VV3N/RXm11xKt0wZMFFRFEegG5gNyNkC0oAS7OPO0z+6im3H8xgfF8KcMT0XVrVqVW83Tnl9C0eyS7liXE975fmTUglwsbPjmflX8LNxjTy2bw9vnDqBVq3mWFUF9moN9hoNv06bRrJfzyegvx8+gKudPTcmJqNVq4lw92B3STHLE5O/55EGvni3bx7ZYBVW3inezyTvGMKdfWkydJDRVMSWqlO0mrrwtHPm4ZHX4KHr3/2HLzq5CyGOKoqyATgBmIGTnC+/SNJAEuDpyup5Xx3LMX1UJE+/v4eWjm6yy2oJ8/Nk1pie+r1KpWCxWtlyLJdZKVE42A2vzam/SaSnF29cs4T6rk5+v3sn+8tK+OXkqawaNbr3mIzqSpq6u1kYFUL4+QFlZ+pqmB8ZDTBkxzXvqj1HaWcDv09aCsCL+dvw1Dlxa+RMEt1DeCl/B+8UH+BH0XPQqfpv4ssl/aaFEL8XQsQJIRKFECuFEN++vE2SBpCx0cHcfdUk8isbGBMdzF1XTkSrVveWZI7nlvPoG1uY//DLPLluN0XVjTaOeGDwcXTixSsX896S5RwoK2X5hvc4XtXTJdJlMuFiZ0f4+R2h9peVoFZURHj0JHq1StX7+81uqOdfx4/y9KEDg3L0gUVY2V6dicFiYmP5cZaFTUKjUnO4Po+TTcW4ah2p7u4pydwVPYebI9LQqTR0mQ2937/c5OAwadianhzJ9OTI3q+/2MQYYHxcKK/84no+2H+GDw6c4b09pxgTHcTSqcnMHh2NVvPN7YLDxUhfP1666hpO1VT3/s7aDQYKGhsJdnUD4LP8PGK9vHuT/Rdn7mfqavntru1cE5dAcUszd23+mOcWLsLVzt5mz+dC6S0mtlaf5vFzH+Fr58qioDEAbCg7QqSLH/4O7mwoPUJpZz13RM3GQ+dMaWcD/8rbSqupC4sQPJ5yI96XcQSxTO6SdN6XF+4oisKY6GDGRAfzYPt0Nh3O4oP9mTzy2ud4ue7l2ilJLJmahJ/H8FvV+mUp/gG9/+3t6ES70cD+0hIOV5RT19nJz8ZNxN2+Z7zuFyWZvx3cxxXRMdyaMoZOo5GHd27DZBkY7YM/lJPGjqfHrGRvbRZ/z97MupJDpHpF4u/gzrKwyYQ5eTPKPYynsjcBsL8uh+ONhYQ4evNE7Hyez93CgbocrgkZd9lilMldkr6Hh4sjq+elsnLOWA5nl/L+3lO8uuUor29NZ3pyJMtnpJAaEzxsV7Z+YXxQMKtHjebfGelMDgnjTzNm93bXmCwWtGo1O4sLaTcY+NHYnoVQXSYTViHoMBoBOFBeyqbcHNJCw7g1ZYzNnssPNd0vgel+CRS21xLm5E2X2Yi9uucazZbqU3SbTQghOFifQ7RLADP8ejancVDrONlcLJO7JA0EKpXClJHhTBkZTmVDKxv2Z/LxwbPsOlVAZIAXy2emcOX4+GF9AfaK6FiuiP5vu2BDVxdV7W293TT/OnaUZSOTen+eXllBm8FAmLs7v9qxFXuNhuUjE3n5xHHs1GpWJI3q9+dwMSJd/DBbLbhoHXjoxDvM9k/ineJ9PJt6K3vrstGptCS5h+Bl50KHSU9BRw2Lg3ou8luFFdVl6I0fdsndYrFe+GtnAAAgAElEQVSSm11FfW0bnZ0Gujp7rgFrtGp0WjWOTna4uDrg4uqAu4cjnl7OaIZ5fVX6uiBvN+67dio/unISW4/nsm7PqZ5e+o8OcM2URJbPGEWgl5utw7S58tYW0qsqSPbzp6KtFbVKxdL4kQB0GI28e+Y0Px0/gfVZZ+k0Gnlo8lS8HB1x0Go5WFbae8bfaTTipBvYG2toVGp+EX8lh+vzqDO08fSYlcS7BZHdWoGTRkeoU8/cnS3Vp/CxcyPQoedC85cTu95iIqu1nJFuIdipL+0kYdgk94qyRja8d5RD+3JpbvruORH/y93dEW9fV/wC3PDzd8M/wJ3AIA8Czv+j1crkP1zZ6zRcPXkkiyclcLqoirW7T7Fm1wne3XmCmSmRrJg1hpTIwGFbshkdEMjogEAAgl3dCHN3J6O6imhPL9aezcTHyYnJwaEsWvs2f5o5Gy/HnpWsO4sKsQiBVq3mRHUV72Seoqy1hVtSxrAoJu67HtLmJvnEfOXr0s4GAhzcsVfryGqt4FRTCbP9Ewly9ATAbLWgUak51ljIxvJjtJv1VHY1cW/cQqb5Xvw2ksMmuXd3G9m59QzjJ0UxZVosI6L8cHTS4ehoh6KA0WjBZDLT3WWkrbWb9rZumps6aWrsoKG+nfr6NirKGslIL0Lf/d/5EiqVgn+AO8GhXoSEeREW4U1YuA9hI3xwcrKz4TOW+pOiKKREBpESGURNUzvr953mg/2Z7DxZQHyoLytmjWHe2Jhh32UzNiCIP+zZibuDA7PCR/DrKdPYVVxEvLcPo/x6Ls62GfTsLS3h7WuXsq0wn835uUwICuHGpGRePJbOhOAQfBydbPxMfrhE9xBeKtiBgsLGiuNcFTyWcV5RaFQ9rbcalRqj1cwT5z7mlhEzuCp4LJsrT3CoPveSkvuw2SBbCIHRaMbuEuuhQghamruormymsqKJyoomKsqaKC9rpKK0EaPxvz27fv5uRET6MiLKlxHRfkRG+xMY5NG736c0tHUbTXx6NJs1u05SUtOEj5sTN8xMYUlaMq5Og6ft73LIqq/rnQH/WX4umbU1/DptOgB/3LsLgFWjRvNSxjHSQsK4IjoGRVG4au3bPDptJuODBtes9fTGAk41lRDrGsj08xdV4b9n7f/O305RRy1Pjr4Zi7BytCGfIw0F3BM7H61KIzfI/i6KolxyYv/ifjw8nfDwdCIh6asvMIvFSm11C6UlDZQU1VNcWEdRQS3pRwqwWnreRB0cdURF+xEVG0B0rD+x8YEEh3rJhD8EOei0LJ2azHVTkjiUVcK7O0/w3McHeeXzdK6eNJKbZo8hyHt41uW/vLmHq509Z+rqqO3oIL+pkc8L8vhsxSo+ycvB18mJZD9/FEXhZHUV/s7OxHv72DDyizPeK4rxXlG9X++ry2aCVxR2ai1Nhg42VhznpfF3AaBWVGS3VaJRqVBQ+Lj84na9GjbJvT+o1SoCgz0JDPZkUtp/625Gg5nSknoK8moozK8lP7eGzzed5CN9T3nH0cmOmLgA4kYGEp8QRHxiEB6e/TuHQrp8VCqFtMQI0hIjyKuo592dJ9iwP5P3955m9phoVs0Z2zudcjiaEBRMemUF129Yy4LIaH4zdQaeDo7UdXYS7elNiFvPG+Ce0mJS/AMGzEjdS5HfVk2woycjnP34qCKdyd4xhDh5YRVWyrua2FadyYvjbue1wt00GTsu6jGGTVlmoLFYrJSVNJCbXdXzT1YVRQV1WM4v5vAPdCchMYiEpBASk0MIH+GDWj305nIMV/UtHazdfZIN+zLp0BtJjQlh9bxUJieEDduLr51GI/YaTe9ip1s3fsAto8YwPTyCIxXlbMg6y9Vx8UwNDbdtoH1sX102Wa0V3B09l9KOet4q3ke4sw9TfeJ45PR7PDN2Nf4O7hdclpHJfQAxGEzk59aQfbaCrLOVZJ2toKmh513b0cmOkUnBJKWEkpQSSkxcADqd/OA12HV0G/jo4FnW7DpBbXMH0UHe3DJvHHPHxqAZxm/mJouFvx7Yi06jYXXyaO785CNuTBrF4pg4XOyGVqNCTmslvzn9HpEufugUDYGOHvw4eh4Pn1pDqlckS0MnXlTNXSb3AUwIQW1NK2dPl3M2s5wzp8ooK2kAQKfTkJAYRPKYMEaNDiNuZJBM9oOYyWxhy7Ec3th2nOKaJoK8XFk5N5XFk0ZiP0z/rg1dXTy6ewcqRWGkjy8/GTfhKz8vam7iZE0118Yl9O4INViZrRY2VhwnyT2UEc6+1BvaeCF3Kz+NnY+/vTsqlUom96GutaWLs6fLOX2ylMyTpRQV1CIE2NlpSBwVyujUcEanRhAZ7SfLOIOQ1SrYf6aI17Ye40xxNZ4ujtw8ewxLpyXj7DC0zlh/KIPZjJ2m5w3OKkRvIv/rgb28fOI4ib5+PDptBuMCB1cHzXdpN3Xz57Mf8rukpThp7OSZ+3DU3tbNmVNlnMwo4dTxEkqKe/YAdXF1IGVMGGPHjyB1wgj8AtxtHKl0IYQQnMiv5NUt6RzJLsXFwY4bZqZw48zRuDs72Dq8AcEqBJtys3ny4H5qOju4IiqGX6dN651KOZi1Grv4feb72Kt1JHuEclPEVJnch7umxg5OZZRw4lgxJ44VUV/XDkBIqBepEyMZNzGS5NGhfdIWKvWPrNIaXv08nd2nC3Gw03L9tGRWzhmLl+vgWchzOXWZTLx84hj/yTiGVQjuHJPK3WPHD/hxBT/EywU7cdc6six8skzu0n8JISgrbSTjaCHHjhSSebIMo9GMVqcmZUw44ydFMX5SJIHBnrYOVfoBCiobeH3rMbYez0WnUXNtWhK3zEvFx122zQJUtbfx5KH9bMrNwc/JmV9NmcbVsXFDovtIlmWk72QwmMg8WcaxI4UcO1JARVkTAKHh3kycEs3EKdEkJAaj1sha/UBWWtvMa1vS+Sw9G7VKxXVpSdwyfxy+MskDPdv9PbZvD5m1NYwNCOR302eR5Otn67AuiUzu0gWprGji6MECjh7KJ/NkKWazFRdXB8ZPimTS1BjGTYjEUc7HGbAq6lt4bcsxNh/JQqVSuDYtiVtlkgd66vEfZJ/jyYP7aeruYvnIJB6cnIang6OtQ7soMrlLF62z00DG0SKOHMzjyMEC2tu60erUjEmNYPK0WCZPjcHdQ9Z4B6LKhlZe25LOJ4d7kvySqcncOn8c3m7y79VmMPBc+mHePH0SR62WX0ycwk1JowbdRt0yuUt9wmK2cvZMOYf35XFwXw411a2oVAqJo0JImx5H2ow4fHxdbR2m9D8qG1p59fN0PjlyDo1axbLpKdwyLxUPl8F5ttqX8hsb+eO+XRwqLyPB24c/zpzN2IAgW4f1g8nkLvU5IQSF+bUc3JfLgd05va2WCYnBTJsVz9SZcfj6Df7Ws6GkrK6FVz47wmfpOdjpNKyYOZqVc8YO+0mUQgg+L8jnL/t3U93RwZL4kfxqyjS8HQf+m59M7tJlV17ayL7d2ezbnU1Rfi3Qk+inz45n2qwEvH2G94bRA0lxTRP/2XyYbRl5uDjYsWpuKjfOTMHRfvC3CF6KLpOJ59IP89rJDBy0Wh6clMaNickDulQjk7vUryrKm9i3K4u9u3oSvaJA8ugwZsxJYNrMeFzdfvgZkRBiSLSsDUR5FfW8uOkQ+84U4eniyB0Lx3NdWhI67fAca/CFgqZGfr9nJ4crykn28+exmXMGbFeNTO6SzZSVNLB3Zxa7t5+jvKwRtVrFuImRzJw7ksnTYrG3//ZFUxaLFbVahdlskfvVXkaZRdU8v/EAx/MqCPB05cdXTWLh+LgBfcZ6uQkh2Jibw+MH9tDU3c3K5BTunzgF1wE2nEwmd8nmhBAU5tWye8c5dm8/S31dOw6OOlbfMZ0lN0z4xtuYzRbKSxt56s+bmDoznmU3TZJzcS4TIQRHsst47uMD5JTXERXoxT3XpJGWGDGsPzm1GfT8/fBB3sk8hY+TE7+bNpOFUTED5ncik7s0oFitgjOnStmx9SzjJ0YydebX94O0mK18+P5RqitbKMirYcz4CG65cwbVlc3k59YwbdbF7yEpfTurVbDjZB4vbDxEeX0LY6KDuO/aqSRFBNg6NJs6XVPNb3ZtJ6uhnhnhEfxpxuwBMatGJndpUKmtbuE/z+8kJtaf+KRgNm44zk9+Po9D+3LJz62morwJg97Ez36x4GtbGkp9w2Sx8NGBs7z06RGa2ruYOyaan12TRojP8B00Z7ZaefP0SZ45chAhBPdPnMItKWPQ2LB8dTHJXX72lWyiqqKJ11/aw+SpMdywago1VS3Y22uws9Pw9qv7WHbTZJ7512pGjQmnuqoZ6CkpSH1Lq1azbPooNv7pVu66ciL7zxaz5I9v8tT7e2jp6LZ1eDahUam4ffRYtt58C5NDQnn8wF6uW/cuZ+tqbR3aBZHJXbIJg8FMW1s3776xnzde2sPRQwXMX5TC3l1ZjBkfQUiYFyaThbAIb0qLezYo+aL+KZN833Oy13H3okls/NOtXDUpgXV7TnH1717n7R0ZGE1mW4dnE0Eurry06BqeX3gVNZ0dXLvuXZ44uI9uk8nWof0gl1SWURTFHXgFSAQEcJsQ4vC3HS/LMtL/yj5XyWv/2kVOdhXX3ziRPTuzeOjRxcQl9Kwe/L+nPsfb14UVq9N6u2qgZ479pxtPUl3ZzBVXjyY2PtCWT2PIKahs4J8f7udQVgnB3m7cd+1UZo2OGjAXGPtbq17PEwf3se7cGcLc3Hl81lwmhYT22+PboizzLLBFCBEHjAKyL/H+pGHCYu7ZCDwmNoCY+EBuuXMGOjstLi4OxCUEYbFYqa9r48zpMubMT+q50fnzkJKiel7/zx4qyhoJCvHk5Rd20tjQbqNnMjRFBXnz/D3X8sI912Gv0/DLlzdz5zPryS4bXKWJvuJmb89fZ8/j3WuvB+Cmj9bzm13baTMYbBzZt7vo5K4oiiswDXgVQAhhFEK09FVg0tD2xVjh9vZujEYzk6fGMG5iJJHRPYtIuruM7NhyhuhYf3z93bBaRe9tdm49g6+/G7f/eCbLbpqEg6OOk8dLANDrTeRmV1FbLV+KfWFSQhhrHrmZR1bMpqi6iZufWMMf3tpGQ2unrUOziUkhoXy2YhV3jkll3bkzLHjnDXYVF9k6rG900WUZRVFSgJeALHrO2jOA+4QQnf9z3F3AXQChoaFjS0tLLylgaejq7NDz6/vXEhLqCYqCi4s9CxalEBHpi9FgRmenIetsBVs3n2bm3JGkjA1Hrzfxx4fXc8dPZhMZ7cejD63D3k7L6ZOlXHXtWJavnCw3Du8j7d0GXvnsKGt3n8ROq+GOhRO4cWbKsF3perqmml/t2EpeUyPXxiXw6LQZuNtfni0Q+7UVUlGUVOAIMEUIcVRRlGeBNiHEo992G1lzl75PZ6eBrZtPYbUKrrl+3NdWrH768QmamjqYf+UofP3cOHwgj4z0IuYsSKKspIEdW87w5P/djMlk4aF73+H3jy/tHVUsV8D2jbK6Zv6+YS/7zxQT4uPOg9dPZ2rSCFuHZRMGs5kXjx/lX8fT8bB34C+z5jBnRFSfP05/19wrgAohxNHzX28AxlzC/UkSTk52XLd8AktvnIhGo6axoZ0P3jtK5smeT3yOTnY0NXb0TqI8cayYsHAfOtr15OfUsHhJz+u/vLQBN3dHdDoNHe169uw4xy9+/BZP/XkT1ZXNNnt+Q0GorwfP/uQanvvZtahVCve9uJH7XvyY8vrhVwqz02i4f+IUPlq2Am9HR+7avJEHtn1Oq15v69AuPrkLIWqAckVRYs9/azY9JRpJ6jNe3i7MXZhEUEjPPq9mswV9d08r2tGD+VSUNRKbEEhnpwGj0cy4iZEAtDR34uHphADWvXOIIwfyufeXC3FxdeDD99Nt9XSGlCkjw1n325Xcd+1UMvIqWPqnt3hx0yG6jYOjVbAvjfT146PlN3HP+Il8kpfDgnffZHeJbWvxl9otcw/wrqIomUAK8PilhyRJX+Xq5oiXd88o4eSUUJqbOlm97AU+23SSGXNGEhMXQF52NV7eztjZaWlv66astBF7ex0Wi5Xd28+x+s7pRMX4kzYjDovFSlvb8Fyg09e0GjWr56Xy0R9uYc6YaF75/ChL//gWe04XDrv1CDq1mvsnTuHDZStws7fn9k0f8fDObXQYjTaJ55KuhAghTgEXVAeSpEvhF+DOE/9cQXFhHe4eTnh49tTTiwpqeweTZZ4so7KsibSZcRzen0dktB8BQR4IIbCz0/SshrX79imV0oXzcXfmL7cu5Lq0JJ5Yu4tf/HsTaYkRPLRsBsHDbJRBoq8fG5ffxD+PHuLlE8c5WF7KU3MWMCE4pF/jkCtUpUEpItK3N7EDzL9yFK/9ezebPjjOW6/tY2RyMKNGh7FxwzEWLh4N9Kxw3b87B19/N3R2GqzW4XVm2R/GRgez5jc38Ysl0ziRX8H1j73FK58dHXarXO00Gn41ZRrrli5HrahY8eH7PL5/DwZz//0eZHKXhoQZc0ayfOVkqqtauOXO6cyYM5K6mla0Og1jx/d0cjTUt3PyeDGLru657j9MF1tedlq1mpvnjOXDP9zC1KQRvPjJIW74yzsczyu3dWj9bmxAEJ+uWMWKpFG8cjKDq9e9S3Z9Xb88tpwKKQ1ZQgheeGYrsfGBxCcGs/mjDIwGM/f+cuFXjjl6qIBxEyPlDPnL5OC5Ev723i4qGlq5alICP79uGh7Ol6cffCDbU1LMr3ZspVWv54HJU7h9dCqqH3iGIUf+StL/OHwgj3dfP4CiwMLFoxk/KRJvH9febf0y0ov49c/XEBTiyQ0rJzNnQZLshb8Muo0mXvnsKG9vz8DZQcf9S6axaGLCsJtV09TdxSO7trOtsICJQSH8fd5CAly+f99hmdwl6VvU17Xh4+v6te9brYKDe3NY8+ZBCvJq8A9wY/nKycy7YpRc2XoZFFQ28Oc1O8gsqmZCXCiPrJg97GbHCyFYn3WWP+3bjVal5i+z5nJFdMx33kYmd0n6Dt+1CbcQgvRDBbzz+n5ysqrw8XXhxlVpzF8kk3xfs1oFG/Zn8tzHB7BYrNx91SRWzBqDZpiVxUpamrl/62ecrq3h+oREfj99Fo7ab+7iksldki6REIKM9CLefnU/WWcr8PFz5cZVU1iwKAWtVpZr+lJdSwd/XbuTvZlFJIT58bub5xIT7GPrsPqVyWLh2aOH+dfxo4S7e/DsgitJ9PX72nEyuUtSHxFCcOJYMW+9so+ssxX4+btx821TmbsguXc6pXTphBBsP5HH397bTXuXgVsXjOOOhRPQDrPrHofLy3hg2+c0dnfxqynTuDVlzFc+ZcrkLkl9TAjB8aNFvPnyXnKzqwgM9mD1HT2tlirV8LoYeDm1dHTz1Po9fJ6eQ1SQN39YOY+EsK+fwQ5lzd3d/GrHVnYUFzIrfARPzp2Pp4MjIJO7JF02QggO78/jjZf3UlxYR0SkL7f+aAYTp0QPu46Py2lvZiGPr9lJU3sXt8wbx51XTBhWI4WFELydeYrH9+/Fw8GBZxdcyfigYJncJelys1oFe3dm8cbLe6iqaGZkcjB3/HgWiaP6b8u1oa69S8/T6/fyyZEsooK8+dPq+cSF+No6rH51rq6We7Z8SllrC/dPnMzPxk+SyV2S+oPZbGHr5tO89do+mho6mDglmtt/PIvwEcPrguDltO9MEX9+dwct7d3cvnA8ty0cj1Y9fGrxHUYjv9m1HYvVygtXLpbJXZL6k15v4uP301n79iH03UbmXTmK1XdMw9vn6z310oVr7dTz5Pu7+Tw9h4QwPx67ZQER/p62DqvfCCEwWizYa7UyuUuSLbS2dLHmzQNs+uA4Go2a61dM5PqbJuHgoLN1aEPCjhN5PL5mJ91GE/dck8YNM0YPqwvasuYuSTZWXdnMq//ezd6dWXh6O3PrXTOYuzBZzq3pAw2tnTz27nb2nylmYnwof1g1H193Z1uH1S9kcpekAeLcmXL+8387yD5XSVSMPz++by7Jo8NsHdagJ4TgwwNn+PuGveg0an570xzmjPnupftDgUzukjSACCHYvf0cr7y4k/q6dqbNiueun87GL2B4zVK5HMrqmvnt61s4W1LD4kkj+eWyGTjZD90SmEzukjQA6fUm1r97mHXvHEIIuGHlZJbdPAk7uRvUJTFZLLy0+QivbU0nyNuNv952BSPD/W0d1mUhk7skDWB1Na289MJO9u7Mwj/AjbvvncfkaTFyEdQlysiv4NHXt9DQ2slPrp7MqjmpQ+5iq0zukjQInMoo4YV/bKWkuJ7xk6L46f3zCAwePu19l0Nbp57H3t3OzpMFTIwP47Fb5uPl6vT9NxwkZHKXpEHCbLawccNx3nplLyazhRtunswNK6egsxs+S+37mhCCDw6c4e/r9+DsYMefb1nAhPihcRFbJndJGmQa6tv5z3Pb2bMji8BgD+775ULGjBth67AGtfzKBn79yqeU1DZxx8IJ3HXlRNSqwd2KKpO7JA1SJ44V8exTn1NV0czs+Yn86J65eHgOnbJCf+s2mHhi3S4+OZxFakwwf7ltIT5ug7cnXiZ3SRrEjAYza946wLq3D+HgaMeP7pnDvCuS5QXXS7Dp8DmeWLsLJwcdj992BeNiQ2wd0kWRyV2ShoDS4nqe+dunnMusYHRqOPf/6koCgjxsHdagVVjVwC9f/pSy2mZ+fNVkbp0/btB108jkLklDhNUq+HTjCV55YSdWq+DWH83g6qXj5BiDi9SlN/LYuzvYejyXaUkjeOyW+bg42ts6rB9MJndJGmLq69p49snPOHqogITEYB54ZBGh4d62DmtQEkKwbs8p/rFhH/5eLjx911WDZs9WmdwlaQgSQrBz61lefGYreoOJW++awXXLJ8iz+It0urCKh17eTHuXgd+tnMuCcXG2Dul7XUxyl68OSRrgFEVhzoIkXllzN6njI3np+Z088NO3qChvsnVog9KoyEDWPHIT8WF+PPLa5zzzwT7MFqutw+pz8sxdkgYRIQQ7tpzhxX9uw2yycNfP5rDo2jGyo+YimMwW/vHBPtbtOcX42BCeuONK3J0dbB3WN5JlGUkaJhrq23j6L5vJSC9i3MRIHnhkEV7eLrYOa1DaeOgcj6/diZ+7M/+4ezFRQQPvmoZNyjKKoqgVRTmpKMrmS70vSZJ+GG8fV/76zI387IEFZJ4s5a6VL3Fwb66twxqUrp48kpfvvx690cQtT73H3tOFtg6pT/RFzf0+ILsP7keSpAugKApXL0nlxdfvwM/fjT88vJ5nnviU7m6jrUMbdJJHBPDOwzcR7u/JL/6zide3ptOfVY3L4ZKSu6IowcCVwCt9E44kSRcqNNybZ1+6leU3T+bzT07y01tfpSCvxtZhDTq+7s688otlzBsby3MfH+T3b27FaDLbOqyLdqln7v8EHgK+9VKzoih3KYpyXFGU4/X19Zf4cJIkfROtVs0dP5nFE8/eRGeXgXvvfJ2P1x8b9Gef/c1ep+Hx2xZy96JJbD6azd3PfkBzR7etw7ooF53cFUVZBNQJITK+6zghxEtCiFQhRKqPz+BYMCBJg9WY1Aj+8+adjBkXwQvPbOWPj2ygvW1wJidbURSFu66cyF9vv4LsslpWP7mW0tpmW4d1wS7lzH0KsFhRlBLgPWCWoijv9ElUkiRdNHcPJx57ajk/umcORw7k85NbXyEnq9LWYQ0681Nj+ffPl9LZbWT1k2vJyK+wdUgX5KKTuxDiYSFEsBAiHLgB2CWEuLnPIpMk6aIpisLSGyfyj3+twmoV3H/3m2z64Lgs01ygUSMCefOhG/B0deIn//chW48Nno4kuUJVkoawhMRg/vXGHYwZN4Ln/r6FJ/74seymuUDBPu68/uBykiL8efi1z3hz2+B4k+yT5C6E2COEWNQX9yVJUt9ydXPksaeWc8tdM9i9/Rz33vk6lRVydMGFcHOy54V7rmPu2Bie/Wg/T6/fi9U6sBO8PHOXpGFApVK46ZY0Hv/HjTQ2dPDT217l6KECW4c1qNhpNfz1tiu4afYY1u4+ycOvfTagWyVlcpekYSR1QiQvvHYb/gHuPPrL91j71sFBUWIYKFQqhQeWTufn101le0Ye977wMZ36gVnmksldkoaZgEAP/vmfW5g+O4HX/r2bx3/3EXq9ydZhDSqr5qbyx1XzyMiv4K5n1tPc3mXrkL5GJndJGobs7bU88sdr/7+9e4/Puf7/OP547drRhs1swxza8HWMaMnh25JT+UYkcviGX+kgh5SlpINQfb+SckiIFCpyLMX320ESqRA5jS1iNsbWGGHsuub9+2P7+upbsdN1fa7r2ut+u7nZrl2fz+f5sXnuc30+n+v9ZtDD7Vj/ZSIjhyzgl8zTVsfyKF1bNWLy4Dv4OT2LQa8u5fjJX62O9Bta7kqVUSJCn/6tGf9yb9IOZzF00DyS96VbHcujxF8by+vDe5CZfYb7XlnC4YxsqyNdouWuVBnXsk1dps7+P/x8bSQMWcCmrz3nXm53cH3d6sx+tCc5uXbun/wBB47+YnUkQMtdKQXE1I5k+tx7uSY2guefWsqKD763OpJHaVgrirkje4EID7y6lH2pGVZH0nJXSuULqxTCpNf70+bm+syc+jkzp37m9vdyu5PYquHMHXk3gQF+PPTaMvYcsnZkTi13pdQlgYF+PDOhB9173cCKDzbz4nMryL3gvvdyu5uakaHMHXk3FcoF8PDU5ez4+ahlWbTclVK/YbP5MOTRTjw4rANff7mXMQmLOHv2gtWxPEa18ArMTbibsPLlGDZ9pWUFr+WulPodEaFXv5aMHtuN3TtSeXzoQk6eOGt1LI8RFVaeOSN7UcnCgtdyV0r9qfa3Xsv4l+8mNeUXRg6ZT8axU1ZH8hiRoSGXCn749JUuPwev5a6UuqIWrerwz6l/5+SJszz68HzSUnXQsc/rIpQAABRhSURBVMKKDA1h9qM9qRgcyJBpK1x6F42Wu1Lqqho3qcErr/cn94KDhCELSDmoU2YWVpVK5Zn9WC+Cg/wZMm0FP6dnuWS7Wu5KqUKp85cqTJ7RH4CEoQs58NNxixN5jmrhFZg1oie+PsLgKctIzXT+O1m13JVShVYrJoLJbwzA39/GE4+8qwVfBDUjQ5k54i4ceRcZMnU5mdlnnLo9ceVwn3FxcWbr1q0u254r5eXlkX7gOAd3HebgrsNkpv7C2dPnOJN9jjxHHv6BfgQE+RMcGkxEdDiVq4dTJSaSaxrXILxqGCJi9S4oVWhH007w+LCFXLjgYNL0e4itE2V1JI+RmHKMB19bRtVK+bdMVgwOvOoyIvKDMSauKNvRci8Be66dH9ftYePy79j00RayC0bV8/ERwqqEEhIaTHDFctj8bNjP27mQk8uvJ85wIv3kb975V75SCLWb1qJhq3o0bF2Phq3+QvmwEKt2S6lCOZp2goShC3HY83hlRn9qxURYHcljbElKZfjrK6lXI5JZI+4iKMDvis/XcncRYwzrFm3kzScWknX0JEEhgdzY5Xqu79CE2Ka1qNWwOgFBAX+6fJ4jjxPHsjnyUzqH9qRyaHcqyT8c4MCPh7iYdxEfH6H+jXVp1TWONne2oEa9aBfunVKFl3Y4i4ShCwF4deYAoqtXsjiR51i7/SeenLOa1o2uYfLgrvjZbH/6XC13Fzh2KINpQ+aw5d8/Ur9FHfqO6UFcp6b4B/qXeN05Z8+TtHk/P67bzeY12/hp20EA6jSLoV3fv9K2TxsiqoeXeDtKlaaUg5mMHLKAoCB/Xps1kIjIClZH8hjLN+zkxffX0q11I567p+Ofnp7VcneylMRUHot/DvsFO/e92I87ht6K7Qq/bUsqMy2LDcu/Y92ijezbvB8fH6HF7c3pMeJ2rrulsZ6nV24jeV86o4a/S3jlEF6bOZCKoeWsjuQxZn68iTlrvufB21syuEurP3yOlrsTnck+y7Abn+Lc6XO8tmEC0XWqunT7R/an89k7X7FmzhdkZ54mtmkt+jx5J/G9Wjr1F4xShbXrx8OMfvR9YutG8fK0vxMUVPJXs2WBMYbnF37Gx98mMm5AJ7q2avS75xSn3PVWyEKaMng2xw5m8NzSBJcXO0B0narc+0Jf3kuZycg5g3HkOnip3xQGNXyM9Us26STHynLXXleTp8ffSfLeo7zwzAryHBetjuQRRIRn+nWgRb0aTHj3C7Ymp5bKerXcC2H/jwdZv+Rb+o3pQeO/NrA0i3+gP50HtWfOrld5bmkCfgG+vNDnNR6Lf5bkHw5Ymk2p1vH1eOTxzmz+dj/TXvmXHnQUkp+vjUkPdqFmVCiPz/6YlOMnS7xOLfdCWDb5Y8pVCKLHo7dbHeUSHx8fbrqrJbO2T+KxNwdzJDmdYS2eYtqQOeScybE6nirDbu/enL4D2rBm1XYWL9xkdRyPUb5cIFMe7oaPjw8j3viQ02fPl2h9Wu6FsHN9Iq26xhESGmx1lN+x2Wz87f72vJM8je7DO/PJ7M8Z3PwJEr9LtjqaKsPufagt7To1Yt6sdWxYt9fqOB6jekQokx/qytGs04x+aw2OvOKf2tJyv4pzv+aQmZbFNY1qWB3lioIrBjNkyr1M+nIsjlwHj930LEsmfaQvi5UlRISEp7rSoFE0E8d/xE9J6VZH8hjN6kQzpm97vtubwrSVG4q9Hi33q7iQkwtAUPkgi5MUTtObG/Hmjlf4a48bmfPku7wy6A3suXarY6kyyD/Al3ETe1EhtBxjRy/VyT6KoHubxvRuex3vrt3GvzbvK9Y6tNyvws/fFwD7Bc8pyOCKwTyz+DHuebYnn73zFc/eMZELOTpNmnK9sEohjPtnL06dPMeEp5fhcORZHcljjOwZT/O60by8ZF2xltdyv4rgiuUYMPZumrb9/b2n7kxEGDiuNyPnDGbb5zt5vsckcj3oF5TyHnXrVSVhTBd27Uhl7htfWh3HY/jZbEy8/3ZmjbirWMsXu9xFpIaIrBORvSKyR0RGFHdd7kxE6D+2F3WbxzptG6dOnaJRo0acOlX6U5h1HtSekXMGs/XTHbx6/0w9B68s0a5TY7r1jGP54u/1AmsRhFcIpl6NyGItW5IjdweQYIxpALQEhopIwxKsr8xavXo1iYmJrFmzxinrv+2+dgwc15u1723g3/P0yElZ46HhHanfsBqvvPQJ6UdKfh+3urJil7sxJt0Ys63g41+BvYAOX1gE/fr1IyQkhIEDBwIwYMAAQkJC6NevX6lvq++YO2ne4VpmPDKPY4dcN4+jUv/h52fj6Qk98PERXnh2BXa7nn93plI55y4i1wDNgO//4GsPishWEdmamen58y6ePX2OdYu/YfbjC8hKL9nRx/jx46lZsyZ+fvljOfv5+VGrVi0mTJhQGlF/w2az8fi8oQDMe/r9Ul+/UoVRpWooI5/qQvK+dBbMXW91HK9W4nIXkRBgOfCoMeb0/37dGPOmMSbOGBMXEeHZg/mfPJ7NxAHT2fbFTnx8hLHdJ5KWfLTY66tTpw7jx4/HbrcTHByM3W5n3Lhx1K5duxRT/1dE9XB6juzKukXfkLI3zSnbUOpqbmpbn85dr+ODdzexc3uK1XG8VonKXUT8yC/294wxK0onknu6kHOBLxZ+TcXKFUiY+zAPvNyfCuHlOZ5SslcjS5YsITg4mHHjxhEcHMzSpUtLKfEf6zK4IwDffrTFqdtR6koeHtGJqtXCmPTCKs6d1dt0naEkd8sI8Baw1xjzaulFck/7Nu/n8L4jdB7UDoC05KOERlUkvNp/Z54pzp0oo0aNIikpiYSEBJKSkhg1alSpZf4jlaPDqdMshh8+3+HU7Sh1JUHl/Bn1TFeOHzvFnDfWWh3HK5XkyL0N0B9oJyI/Fvz5Wynlcjs7v0okNLIiDVvVAyA16SiB5QK5eNnYD8YYzp46y/olmwr9pqEbbriBqKj8yYWjoqKIiyvSkM3FUiUmkpPHS/+2S6WKonHTmvTofSOfrNzGDj09U+pKcrfMRmOMGGOaGGOuK/jjnHv5LGaMYe37G7j57vxZUg7uSiFp834qR1citkmtS89bPftzZiUs4NP5X3F/45F898kPVkW+Iv9AP87rS2HlBgY+cDNVqoUyZeJqcnMdVsfxKvoO1ULIc+TRJL4hWUdOkHMmh49mfIr9gp1b+rS59JzvV//A18u/o8M98by0egx9n+pRooutznRodyo16lezOoZSBAX5M2JUZ9IOn2DJe99aHceraLkXgq+fL/G9WjFz5Hye7zGJCuEh3P1EN6rGRl16zvsvraDTwLaXhinwC/Alacv+S19PSUzlZIb1p0KOHcrg0O7DNGxZz+ooSgEQd2Nt2rZvyPvzN+qbm0qRlnshxXVqyjtJ0xg552Hue7EfSVsOkJeX/yaMz+Z/RaWqYb85kl/y8ke063cTDruDheOWMmPE2wy94UkWjnfu3TBXYoxh+rC5+Af6c1vBhWGl3MFDj3TAZvNh9utfWB3Fa2i5F1FUrQjyHHlkZ5xi/7aDAJzO+pXGbepz8WL+3TIrpq6mWp0qXHtTA95+ehFnT59j1NtDeWvPa6QkpnI661eX57548SKzE+azec127n2hLxHVw12eQak/UzmiAn0HtOGb9Ul6cbWUaLkXg83XRqeBbanTPAaAwOBAfjlyAv8APzLTslj0j5UMHNebbz7cTJ4jj1v6/pWI6uHYLzhI/DYZe8GFo9zzuS45VZN7PpeJA6azfMpqug/vTPdHOjt9m0oV1V19biQisjxzZ6zVAe5KgZZ7CdhsNgBirq3Jti928uStE3j7mUV0eagjsU1qkbz1APVa1CW2SU0g//RNfM9WhFcNY8+mJF7sO4UnO45n4sDp5J7PLfV8uedz+XD6vxhYdzhfvr+RQS/1Y8iUe/Hx0W+7cj8BAX4MuP9m9iUeZeP6JKvjeDz9X14KGrWux8xtL9Ox/83c92Jf7nmuJzlnz3PiWDZVYyPx8/fj8L4jHN57hEat67F7416WTl5F8w5NeHPHZPIceXy7amupZDHG8PPOFN55djH9aw9jxoh5VI2NYtLasfQZfSf57z1Tyj117NyEGjXDWTB3/aXTnKp4fK0O4C18fHzocE/8pc+zjhzn5PFs6reoC8DKqaupVjuK8pVC2LVhHzX+Uo1uQ28D4GLexUsTaRhjEBFyzuSQdfQkYVEVCQwJvPQq4T8cdgfZGafISs8mIyWTAzsOcXDXYfZt3s+J9JP4+AjNOzZhzHsjPG6iEVV22Ww+9B8Uz0tjV7Lhq73c3E5HES8uLXcnCY2sSFhUKI+3e56YxjXZv/0g/Z6+i9R9R0hNPkLvUd2A/GEMqtWuQoXw8gCXjqx3fr2XZ7r849L6AoL88Q/0w2HPw2HP+920fz4+QvV61WjatiHN2zfhhs7NCK8a5qK9Var0xLdrwIK31rN4wSbib2mgrzaLScvdSUJCgxm77HE+nvUZlaMr0fvJblSODmfxP1cSWrkCtRrWwGF3cGBHCqcyT//mnnmA2k1r8cT8YWRnnOb8mfPknMnBfsGBzc+Gr5+NgHIBVKoSSliVUCKqh1OzQTQBQQEW7a1Spcdm8+Huv7fi1X+sZvsPh2geF2N1JI+k5e5kXQd3uvSxw+7gZMYp+o6+E4Cd6xNJ3rKf2tfFULP+b+c5qRwdTsf+N7s0q1Luon2na3lr5jo+XLJFy72Y9IKqC/n6+dK4TX1e/r/X+Xjmp7z97GKqxERyS982V19YqTLEP8CXv93RjO++SeZ4erbVcTySlruL9RhxO72f6E7G4V8YOK43XR++lfJhIVbHUsrt/K1bMwA+Xa3DUxeHnpaxwOV31Sil/liVqqE0vyGWz9bspP+geL2wWkR65K6Uclvtb23M8WOnSNyt00IWlZa7UspttYmvh5+/jfVr91odxeNouSul3Fa54ACaXR/DdxuTdbyZItJyV0q5tZZt6pJ+NJsjaTrWe1FouSul3Np1118DwM5thyzN4Wm03JVSbq16zUqEhgWze2eq1VE8ipa7UsqtiQh/qV+V/cnHrY7iUbTclVJuL7ZuJCmHMslzXLQ6isfQcldKub1q0WFczDNkuMEk855Cy10p5fYiIisAkJXp+vmHPZWWu1LK7QWHBAJw9mzpT0fprbTclVJuz9c3v6ryHHkWJ/EcWu5KKbd3Pid/5rHAID+Lk3gOLXellNvLzDgNQFglHR67sLTclVJuL3lfOv7+vtSsVdnqKB5Dy10p5dbs9jy+/jKRxk1rYPPVyios/ZdSSrm1Vcu3kpnxKz37trQ6ikcpUbmLyG0ikiQi+0VkdGmFUkopuz2PGa99yqxpn9P8hhjiboy1OpJHKfY0eyJiA2YAHYE0YIuIrDLGJJZWOKVU2fXm61/w4dIt9OjdggeGttdp9oqoJHOotgD2G2N+BhCRxUA3QMtdKVViffq3psl1NbnplgZWR/FIJTktEw1cPgZnWsFjvyEiD4rIVhHZmpmZWYLNKaXKkvDK5bXYS6Ak5f5Hr5F+Nw+WMeZNY0ycMSYuIiKiBJtTSilVWCUp9zSgxmWfVweOliyOUkqp0lCSct8C1BWRGBHxB/oAq0onllJKqZIo9gVVY4xDRIYBnwI2YJ4xZk+pJVNKKVVsJblbBmPMGmBNKWVRSilVSvQdqkop5YW03JVSygtpuSullBfScldKKS+k5a6UUl5Iy10ppbyQlrtSSnkhLXellPJCWu5KKeWFtNyVUsoLabkrpZQX0nJXSikvpOWulFJeSMtdKaW8kBjzu5nxnLcxkUwgxWUb/K/KwC8WbNdKus9lg+5z2VDPGFO+KAuUaDz3ojLGWDKJqohsNcbEWbFtq+g+lw26z2WDiGwt6jJ6WkYppbyQlrtSSnmhslLub1odwAK6z2WD7nPZUOR9dukFVaWUUq5RVo7clVKqTNFyV0opL+T15S4it4lIkojsF5HRVudxNhGpISLrRGSviOwRkRFWZ3IFEbGJyHYR+cTqLK4gIqEiskxE9hV8r1tZncnZROSxgp/p3SKySEQCrc5U2kRknohkiMjuyx6rJCKfi8hPBX+HFWZdXl3uImIDZgCdgYZAXxFpaG0qp3MACcaYBkBLYGgZ2GeAEcBeq0O40FTg38aY+kBTvHzfRSQaeASIM8Y0BmxAH2tTOcU7wG3/89hoYK0xpi6wtuDzq/LqcgdaAPuNMT8bY3KBxUA3izM5lTEm3RizreDjX8n/Tx9tbSrnEpHqwO3AXKuzuIKIVADigbcAjDG5xphsa1O5hC8QJCK+QDngqMV5Sp0x5mvgxP883A2YX/DxfKB7Ydbl7eUeDaRe9nkaXl50lxORa4BmwPfWJnG6KcATwEWrg7hILJAJvF1wKmquiARbHcqZjDFHgFeAw0A6cMoY85m1qVwmyhiTDvkHb0BkYRby9nKXP3isTNz7KSIhwHLgUWPMaavzOIuIdAEyjDE/WJ3FhXyB5sBMY0wz4CyFfKnuqQrOM3cDYoBqQLCI3GNtKvfm7eWeBtS47PPqeOFLuf8lIn7kF/t7xpgVVudxsjbAHSJyiPzTbu1E5F1rIzldGpBmjPnPK7Jl5Je9N+sAHDTGZBpj7MAKoLXFmVzluIhUBSj4O6MwC3l7uW8B6opIjIj4k38BZpXFmZxKRIT8c7F7jTGvWp3H2YwxTxljqhtjriH/+/ulMcarj+iMMceAVBGpV/BQeyDRwkiucBhoKSLlCn7G2+PlF5EvswoYWPDxQOCjwizk0lEhXc0Y4xCRYcCn5F9dn2eM2WNxLGdrA/QHdonIjwWPjTHGrLEwkyp9w4H3Cg5afgbutTiPUxljvheRZcA28u8I244XDkMgIouAtkBlEUkDxgL/BJaIyCDyf8n1KtS6dPgBpZTyPt5+WkYppcokLXellPJCWu5KKeWFtNyVUsoLabkrpZQX0nJXSikvpOWulFJe6P8By5cDQH2a63AAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Solve optimization problem\n",
"xsln = solve_opt(False,False)\n",
"\n",
"# Create contour plot\n",
"visualize(xsln,False,False)\n",
"\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.4 Take 2. With $g(x) \\leq 0$](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.4-Take-2.-With-$g(x)-\\leq-0$)",
"section": "4.2.3.4 Take 2. With $g(x) \\leq 0$"
}
},
"source": [
"### 4.2.3.4 Take 2. With $g(x) \\leq 0$"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.4 Take 2. With $g(x) \\leq 0$](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.4-Take-2.-With-$g(x)-\\leq-0$)",
"section": "4.2.3.4 Take 2. With $g(x) \\leq 0$"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Ipopt 3.12.10: \n",
"\n",
"******************************************************************************\n",
"This program contains Ipopt, a library for large-scale nonlinear optimization.\n",
" Ipopt is released as open source code under the Eclipse Public License (EPL).\n",
" For more information visit http://projects.coin-or.org/Ipopt\n",
"******************************************************************************\n",
"\n",
"This is Ipopt version 3.12.10, running with linear solver mumps.\n",
"NOTE: Other linear solvers might be more efficient (see Ipopt documentation).\n",
"\n",
"Number of nonzeros in equality constraint Jacobian...: 0\n",
"Number of nonzeros in inequality constraint Jacobian.: 2\n",
"Number of nonzeros in Lagrangian Hessian.............: 3\n",
"\n",
"Total number of variables............................: 2\n",
" variables with only lower bounds: 0\n",
" variables with lower and upper bounds: 2\n",
" variables with only upper bounds: 0\n",
"Total number of equality constraints.................: 0\n",
"Total number of inequality constraints...............: 1\n",
" inequality constraints with only lower bounds: 0\n",
" inequality constraints with lower and upper bounds: 0\n",
" inequality constraints with only upper bounds: 1\n",
"\n",
"iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls\n",
" 0 2.4439483e+02 0.00e+00 3.60e+00 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0\n",
" 1 4.4804168e+01 0.00e+00 3.92e+00 -1.0 2.13e+02 - 8.82e-01 4.46e-01f 1\n",
" 2 5.4337665e+00 0.00e+00 1.68e+00 -1.0 2.39e+00 - 1.00e+00 1.00e+00f 1\n",
" 3 5.2037708e-02 0.00e+00 8.16e-01 -1.0 9.15e-01 - 1.00e+00 1.00e+00f 1\n",
" 4 -4.4584904e-01 0.00e+00 1.06e-01 -1.7 2.32e-01 - 1.00e+00 1.00e+00h 1\n",
" 5 -4.8930521e-01 0.00e+00 1.81e-03 -2.5 5.28e-02 - 1.00e+00 1.00e+00h 1\n",
" 6 -4.9427819e-01 0.00e+00 8.51e-06 -3.8 8.98e-03 - 1.00e+00 1.00e+00h 1\n",
" 7 -4.9445150e-01 0.00e+00 7.69e-09 -5.7 3.02e-04 - 1.00e+00 1.00e+00h 1\n",
" 8 -4.9445337e-01 0.00e+00 8.06e-13 -8.6 3.28e-06 - 1.00e+00 1.00e+00h 1\n",
"\n",
"Number of Iterations....: 8\n",
"\n",
" (scaled) (unscaled)\n",
"Objective...............: -4.9445336916190996e-01 -4.9445336916190996e-01\n",
"Dual infeasibility......: 8.0590836175421712e-13 8.0590836175421712e-13\n",
"Constraint violation....: 0.0000000000000000e+00 0.0000000000000000e+00\n",
"Complementarity.........: 2.5083384199831901e-09 2.5083384199831901e-09\n",
"Overall NLP error.......: 2.5083384199831901e-09 2.5083384199831901e-09\n",
"\n",
"\n",
"Number of objective function evaluations = 9\n",
"Number of objective gradient evaluations = 9\n",
"Number of equality constraint evaluations = 0\n",
"Number of inequality constraint evaluations = 9\n",
"Number of equality constraint Jacobian evaluations = 0\n",
"Number of inequality constraint Jacobian evaluations = 9\n",
"Number of Lagrangian Hessian evaluations = 8\n",
"Total CPU secs in IPOPT (w/o function evaluations) = 0.012\n",
"Total CPU secs in NLP function evaluations = 0.000\n",
"\n",
"EXIT: Optimal Solution Found.\n",
"\b"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAAD8CAYAAACMwORRAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzsnXd4VGXa/z9napJJ772QXkihQ0LviiKgolRdy677urruuquur66oq67u6rs/ddfeAREVQUWQ3msIJCG9997L9PP7YyDKgkpJMinnc125IDOnfM/M5DvPuZ/7uW9BFEUkJCQkJIYWMmsLkJCQkJDofSRzl5CQkBiCSOYuISEhMQSRzF1CQkJiCCKZu4SEhMQQRDJ3CQkJiSHIL5q7IAjvCYJQJwhC5o8ecxUEYYcgCPnn/nXpW5kSEhISElfC5YzcPwDm/ddjjwK7RFEMB3ad+11CQkJCYoAgXM4iJkEQgoFvRFGMO/d7LjBNFMVqQRB8gL2iKEb2pVAJCQkJictHcZX7eYmiWA1wzuA9f2pDQRDuBe4F0Gg0o6Oioq7ylP3H+e87QbCujuGMzmgkr6kRhUyGo1qNk9oGjUqF9Jb8PCIi+e01yBBwUWlwUmlQCEN7aq3NUI3O1IWdwhlbuTMyQW5tSVePqRzETpB5gMwVzn3iU1NTG0RR9LiSQ12tuV82oii+BbwFMGbMGPHkyZN9fcprorUVnJ3hn/+EP/zB2mqGL10GA7uKC9lekM/e0mK6DAZs1GpmhYQyLyycyYHBqBV9/vEddBjNJvbVZfFF2TFONhWhEORM94phSeAEklyCEYbgiKW6O4uTjesp6jiCQrAhznk+Sa4346j0sra0K0bUn0Bs/xcYjoNMg2B/H9guQSZTl17psfo1LDMYzN1shr/9DWbPhgkTrK1GAkBrNHCgtJTthfnsLC6kTafDXqlixogRzA+LYGpQMDYKpbVlDjhKO+r5ovw431am0m7UEmrvxZLA8cz3TUKjUFtbXq/TqCsltekzclt3AhDpOJMxbktxVQf95D4t+io6DHX4axL7S+YvIooi6I8idvwLDKdANQG528epoiiOuZLjXK25vwQ0iqL4giAIjwKuoij++ZeOMxjMXWJgozeZOFJexrbCfL4vzKdZq0WjVDI9ZATXhUUyLVgy+v9Ga9LzfXU6n5cdJaetCo1czXV+SdwcOIEQ+5+MqA5a2g11nGr6nMyWbzGKeub4/Jlop9kXbWc06ynpPMbJxg3IBDnJHnfhZxdvBcWXxmLy+0E0I7Od0fvmLgjCemAa4A7UAn8FvgI+AwKBMuAWURSbfulkg8Xca2osI3hfX2srkfg5jGYzRyvK+a4gj+0F+TRpu9EolcwcEcr1YZFMCZJCNz9GFEXOtlawsewoO6vTMYgmxrqFcmvgRFI8o5APsdh8l7GFM81fEe+yEI3i0tnaZtGETJBT1H6EnLYdTPd6EFuFUz8r/WUEQeibkXtvMVjMPT4eQkNh0yZrK5G4XM4b/db8XLYV5tOi1WKvUjE3NJwF4ZFMCghEKR/EE229TLO+g6/KT/Jl+TFqta342DizJHACC/3H4KSy69VzGQwGKioq0Gq1vXrc3kBEREDALBrpNrViJ3dBBAzmbuSCEoVM1a96bGxs8Pf3R6m88O5TMvdeYvJkUCph925rK5G4GgwmE4fLy/gmP5fvCwto1+twsbFhfngkN4RHMtbPH9kQnFi8GoxmEwfqsvms7AipTcWoZUrm+SawNGgSYQ7evXKO4uJiHBwccHNzG7ATuq36apQyW0TMmMx6EAQMZi0qmR0OyitKUrlqRFGksbGR9vZ2QkJCLnhOMvde4oYboLISTp2ythKJa0VnNLK/tISv83PYVVRIt9GIt8aeGyKjuDEiihgPzwFrOP1NQXsNn5Ue4buq0+jMBka7juC2oEnXHLLJzs4mKipqwL3OenM3BlMXOnMXckGBvdKDJl0pTkpfVHJbDGYtWlMb9gqPftMuiiI5OTlER0df8Lhk7j9DUXUj7247TklNE6W1zeiNJpQKOSqFHHsbFS4Odjjb2+LhpOHbdxMpzXPi6z21+Lk74elsj1w2tOKRw5FOvZ5dxYV8nZfDvtISjGYzYS6uLIyK5saIaAKcBl6s1Rq06LvYUnGSjWVHqNW24mfryq1BE7nBfzT2CpsrPl52dvZFZmVN9KYuukwtCAgoZGqUgi0quS0dhnqMoh5nlR8ARrOOdkM9TipfBKDb1IZR1GEjd0Qls+0zfZd6vSRz/xnyKxt48N9fEezlSoi3CzYqJUaTGb3RRFuXlub2bprbu6hv7eTM1vE0F0QSf+cbACjkMvzcnAj0cibI04UgLxdCvF0J8XHDxb7v3mSJvqO5u5utBXlsyc3mRFUlAKN9fFkYGc2CiEicbaT31Wg2sbcuiw0lhznTUopGruYG/zEsDZqIn53rZR9nIJm7KIp0GhvpNDZhp3DGQWnJFjKLZhp1Jbio/Hvi7G2GWgQENAo3Oo1NmEQDKpktXaYWnJQ+KGVX/kV3OUjm3oc88qiZf/5D4GBGOVWNrVTUt1DR0EppbTNldc3oDKaebV0d7Aj1dSPUx40wP3fC/dwJ9XHDzqZ/J2Ikrp6Ktla25OawOTeb/KZGlDIZ04NHsCg6hmlBIVLGDZDVWsH6kkPsrMlAFEWmecWwLDiFkc6BvxiyGEjmfh6jWU+XsQmDqMVB4YmIiNbUhpPKBwCzaKRBV4K7OoROYxMyZKjlDihkKjqNjQjIsPuJDJxrRTL3PuTFF+GRR6CjAzSaC58zm0Vqmtsorm6iuKaJwupGCqsaKapupEtn6NkuwMOZyAAPIvw9iArwJCrAE3en/zqYxIBCFEWy6uvYlJPNlrxsGrq6cFLbsCAiksVRMSR6+wy4uHF/U6dtZWPpUTZVHKfN0E2cUwC3Bycz3SsWhezS2UgD0dzPYzTrERGRCXLaDXU4Kb0REekw1CMIcuzkzrQZa7FXeKCUWRZ+NenKsFM4YyN3RBTFXv9MSObeh7z5JvzmN1BRAX5+l7eP2SxS3dRGfmUDeRX15FfWk1teT0VDa8827k4aogM9iQn0IjrIi5hAL8nwByhGs5lDZaV8mZPFjqICtEYjI1xcWBwVy6KoGHwcHKwt0ap0G/V8W3WK9SWHKO9qxMfGmduCk7nRf8xFq18HsrkDdHd3M2/ePDZtW4soMyIXVMgFBRqFO1pTKyIicpMtc2bP5bsdX6MX2nFS+vTUsDlv8GbRiMGsRS6oLplCuW3bNh588EFMJhN33303jz566WK6krn3IRs2wG23wdmzEBNzbcfq6NaRW1FPTlkd2WW15JTXUVzT1FOczNvFgZggL+KCvYkL8SYm0EsK6Qww2nU6thbk8WX2WU5UVSIAKYFBLImOZU5o2LBeEWsSzRyoy2FtyQHONJdir7BhccA4lgZNwsPGERj45v76669jNBp58MEHMZi1iIgoBRsEQaDT2ASiiEbpxpo1a/ANdmP58uXYyp0QfpRBZDTraTPUoBBU6M1d2ClcsJU794zqTSYTERER7NixA39/f8aOHcv69euJuYTBSObeh+Tnw+bNsGoVePbB6uwurZ6c8jqyyurIKqkhs7SGinrLCF8mCIT6uhE/wof4EB/iR/gS6Ok87MMBA4XSlha+zDnLl9lZVLa34aBSc2NkFDfHxBHv6TWs36fMlnLWlhxgT81ZZIKM+b6JLA9JQVfeNCDMPTs7m1//+te0tLSwcuVK3nzzTQoKCpg0aRLr1q0jODgYgOnTp/OXv/yF2bNn8+e//JG2tlbeeO0djqYe4InHn2T7dzsvqDxpFk20G+qQCwrkRnt27NrGN1u/5qYFN3PdddcBcOTIEZ566im2b98OwPPPPw/AY489dkmdvWHu0kzRJQgPh4cf7rvj29moGBXuz6hw/57HWjq6OVtSQ3pxNRnFNWw/kcsXBzIAcNbYED/Cl8RQXxLDfIkJ9EKllN46axDk7MxDE5J5cPwkjlaUszErk8+zzrI24wwRbu7cGhPHTVHRuNr27irPwUCccwDPJy6jsquJdSUH2VKRyteVqbzis4guow5buQpBEJg27ZePtWDBD3+D06bBHXdYfhoa4OabL9x2795fPp7RaGT58uW8++67JCUlcd999xEXF4der6eoqKjH2AHWrFnDk08+SV1dHZmns/jo8zdo1JUQERPC6dTMi8Ix2XkZfLv1a/Z8f4jy8gomT01m7vxZTJ8+HbNowmjWUViajb//DzFef39/jh079svCrwHJIS6B0QhFReDuDq6Xn/F1TTjb25IcF0JynGVlmtksUlzTyJmiatKLqkkvqmJ/RhEAKoWcmCAvksL8GBXuT8IIH+xth16Vv4GMTBCYFBDIpIBA1kzT8k1eLhuzMnn2wF5ePHSA2aGh3BozkuTAoGG3GtbPzpU/xdzIPWEz+bzsKIZ2E6Wd9djKVbipHQAb6OfK/F9++SUJCQkkJSUBEBMTg6enJw0NDTg7O1+w7ZQpUxBFkZdffpm9e/fiYOeA0axHLihQqVS0tbXh6OjYc5e29JblFOQV8vvf/5733nsPZw97DOYubFW2tOlrQBAwiSZ05k70pi5UcssXf1/f5Unmfgnq6iAyEv7zH8vEqjWQyQRCfd0J9XVnccpIAJrbuzhdWMXpwirSCir5aMdJ3t9+ApkgEBngwehwf0aH+5MU5oejpm9ycCUuxlFtw7KRCSwbmUBOQz0bszLZlJPFt/l5+Dk4cktMHLfExA27SVhnlYa7w2aSlZWFl40zTfoOKroaefdrJW5qe5yUdpdlcD8embu7X95I/b9JT08nMfGHsr6ZmZnMmzcPW1vbi2reZGRkUF1djbu7Ow7n3rPzE6Q6nQ5RqaXdoMNB6YHRrGfPsS2UZTXz3XfbuPmWW9Dpu5kzew533LUSdz9HnJV+RATH8XHlOsxY0qgrKirw8fG58gu5AqSY+yXQ62HjRhg/HsLCrK3mp+nWGUgvruZUfgWn8ivJKK5GbzQhCBDp78mYCH/GRgaQFOYnjez7GZ3RyI6iAjaczeBQeRkyQWBaUAi3x8UzNTgExTBa8Xw+hiyKIm2Gbhr17ehMBhQyOW4qB5xVdsj6uCLlK6+8QkFBAa+//jqnT58mOTmZjIwMRowYQUBAAPn5+djY2FBdXc3cuXPZsGEDDzzwAA8//DBz584FoLGxkZSUFLKzsxFFM4Igw2jW0Wlswknlg1k0oTW1UddQw9G9Z3APtGXK+Nmo5HYYjUbCI0L5ZvsmwoPiGDN2DO98+BoxsTHYKVwuiOFLMfc+RKWC5cutreKXsVUrGR8VyPioQAB0BiOZJTWk5lVwMq+cz/ad4ZNdp5DLBKIDvRgXFci4yAASQn1RSzH7PkWtULAgIooFEVGUtbbw2dlMNmZlsvubr/DW2HNLbBxLY0fi6+Boban9hiAIOKnscFTa0mnU0aBrp1bbQoOuDReVPa6qvivzsXLlSq6//nrGjh3LxIkTCQ4OZsSIEQDMmTOHgwcPMmnSJBYvXsw///lPoqOjeeKJJ3jkkUd6zH3Pnj09E6TnM2XkgpKF826ltrYOEBAAmSBHROSxp/7YE4JRKBQ89/KTLLp+KUaTieWrbyUmNhazaKDNUIOT0rfXwzTSyP0nOHbMsoApLs7aSq4encFIelE1J3LLOZ5bxtmSGkxmEbVSTlKYH+OiApkQHUSEnwcy2fCKC1sDg8nE7pIi1mekc6CsBEEQmB4cwrKRCUwJDB6y9Yt+LhWyy6ijUddOh1GLTJDhotLgqrL/yQVRV0tHRwf29vYAvPTSS7S2tvLss88CkJaWxssvv8zHH3/8s8dYvHgxzz//PJGRFzed05k6EDGjljkgCALthjoUgrqnNnyHoQGjqMdR6UWboQZbuTNquWWNS4u+EnuFR0/oRxq59zErVsCYMbB+vbWVXD1qpYKxkQGMjQzgt0yio1vHqYJKjmWXcTynjP+36SD/b9NBXOxtmRAdxMSYICZEB0kLq/oIpVzO3NBw5oaGU9HWyqeZGWw4m8Gu4iL8HR25LTaeW2NH4m43fDJt7BRq7BRqtCY9Dbp2GnUdNOk6cFZpcFPbo5T1jkW98sorfPrppyiVSpKTk3n55Zd7nktKSmL69OmYTCbkP1HzX6/Xc9NNN13S2AHUcvsLflcIaoyiHrDUhtea2nFR+dNtakUhqHrq0hjMWoyioU/qxksj958gORlsbGDXLmsr6TvqWzo4llPGkexSjmWX0dTeBUCEvwcTY4JIjg0mIdRXanLRh+hNJnYUFrAu8wxHKspRymTMC4tgRXwCY3z8hkTe/JUsYtKZDDTq2mk1dAPgrLLDTeWASj64xqEGczdthjoEQCGzsYzi5U49o3alzLJIqs1QixwFGqXbD6mV0iKmvmXJEsjOhqwsayvpH8xmkbzKeo5klXAkq5TTBVUYzWY0NirGRQWSEhtMclwIns72v3wwiauisKmRtRln+CI7i3a9jkg3d1bGJ3JTVAx2ysG7CvZqVqjqzUYadR206jsRASelLW5qB9TywfU66EydFiNHhoiZdkMtdgpXlDIbDGYtHYYG7JXuF1SYlMy9j7n/fli3Dpp+sTPs0KRTq+d4ThmHzpZw+GwJNc3tgGVUnxIXwuSRIcQFew/ZOLE16TIY+Do3m4/TT5PVUI+DSs2SmFhWxicS4tw3lQj7kmspP2A4Z/It50zeUWmL+yA0eQBRNNNiqEIjd0Ult6NJV45arkGjsCymMYlGZMilZh19zbPPwhNPgFYL6mGeRSiKIoVVjRw8W8zBzGLOFFZhMos429uSEhvMlPgRTIgOktItexlRFDlVU8VHZ06zrSAPg9nM1KBgVieMYkpQ8KBZHNUbtWUMZhNNug6aDR2I4uAz+fMhF62pjQ5DAwqZDTJkOKq8zz1vqScvExRUFbYQFxN/wf6Sufci77wD99wDpaUQGGhtNQOLtk4tR7JK2Z9ZxOGzJbR2alHIZYyJCGBq/Aimxofi7Tq8Fuz0NXWdHazPTGddRjr1XZ0EO7uwKj6RJdGxOAzw0UdvFg4zmk006Tto0nciiuKgM/nzmMwG5DKL5vMe3G1qpdPYSFFeOY1u+5nkcTfOKl9AMvde5ZtvLL1Ujx2DceOsrWbgYjSZSS+qYl96EfvTiyitawYgKsCT6YmhTEsII8x34DZGHmzoTSa2FeTx4Zk00mqqsVequDk2jtXxSQT91zL6gUJfVIUcKib/35hFE+lnT3FIuQazaCTe5UbGu6/AVuEkmXtvcfIkjB0LX30FCxdaW83goaSmib3phew9U0hGcTWiCP4eTkxPCGN6YijxIb6XlVNf3dTGd8dzqG1u56bkOKIDvfpB/eDiTE01H5xJY2t+LkazmZkhodyZOIoJ/gED6su0L0v+DkWTz87OJjDck6P1H3K2dRteNpHcFvKaZO69RUUFBATAG2/Ar39tbTWDk/rWDvanF7HndCHHc8swmsy4O9oxPTGMGUnhjA73RyG/9ITsg//+Cn93Z3zdHPnuRA5LpyZww8RYTGazNIn7X9R2dLA24wzrMs7QpO0m2t2DXyWNZkF45IBoEdgf9dyNZhON+g6adR092TXuasdBl0IJF75eDbpi9KYu/DRxkrn3FkYjbNliWcgkxdyvnfZuHYcyi9mVls+hsyVo9UYi/D349PEVF22r1Rv51T828PoDi3Gxt+XVrw7i7qghKdyPHal5pBVUsmRyPPPHRiEIfV9db7CgNRrYnJPN+6dPkdfUiIedhlUJiSyLS8DF1noNv/uzWYfRbKJR107zuewaZ5Ud7mqHXlsM1R9IqZASg5ZuvYHDZ0vo1htYMP7iTjRVja18+H0qR7NLuWFCDFlltcwZHcFHO1K5dVoCbg52vL/9BH+5fSZhfu5WuIKBjSiKHCwr5b3TqewrLcFGoWBJdCy/ShptlVRKa3RiMvzI5AUsFSrd1Q4XlTXIysri+PHjzJw5E2dn554qkNZEKj/QDxw9akmFvJzmAhKXj61Kycyk8Es+V9vczn++PkJCqC8pccG8v/0Eq+eMoa1Ti52NkpsmWYr9nCqoJK+yXjL3SyAIApODgpkcFExeYwPvpaWy8Wwm6zLOMDs0jHtGjWG0z2U2Bx6kKGVyvG2dcVXb06C1mHyLoRNXlT1uKoee0J7BYODVV1+lra2N3/3ud1ZW3btI5v4zPPEEdHTAkSPWVjJ8OF+2eOHEWJQKOWeKqmnt1LIjNa+nrr0oishlMmrPLawym8WeSdpunYHtJ3Opb+1gwYQYfFyHT9XFSxHh5s4Ls+byx4kpfJSexifpZ/i+sIBR3j7cO3oss0aEDZp8+atBJVPga+eCm8n+XO0ai9G7qRxwVWsoLy/nzjvvZMSIEbS3t+PoOHQ+L9LM1M/w2muWVaoS/Uu3zoBSIcdgNOHpbE9qXgUFVQ1cN85yq6o3mjieU8bo8AAAzOdCiw2tnbzxzREOZ5VQ39LJmo++p7mj22rXMZDw0Gj448QUDv3qXp6aOoO6rk5+8+0W5nzyPhsy09EZjdaW2Keo5UpWXL+EoiPp2MlV/O8Tj3PHffcwafY0Fi9ZwnXXXTekjB0kc/9ZIiMhJMTaKoYXMUHeyASBlS+s49F3t1LZ0IogCIw+12/WYDSRml+BXCYQP8LSyeZ8xs3XR8+iVMj5/eIp/GXZTDQ2Kg6dLQagvUvLvvRCdp8usM6FDRDslEpWJSSxe9Vd/Gve9dgqlDy2ewdTP3yHN1OP067T/eS+JrOZvx3Yy86ivn8NW1tbiY2NpbW1tdeOuWbNGl564UX2f7WdkrP5PPX3v1GrbaHLXqBV30V/zj/2B5K5/wzZ2fDyy9DZaW0lwwdfN0f+77cLeXz5LFJig/nVvHH8at44lAo57V1azpbWsDM1n+vHnxvFGywjzqrGVirqWxkZ7I2vm2UEpjOYCPCwLOx5+K1vOJhZzAfbT/DXD7fT3qW9tIBhgkIm44aIKLbctoIPb1pCmKsbfz90gJT33+Yfhw9iMJku2qepuxsfewfu/+4b3j51ok/1ffvtt2RlZbF169ZeO+aPe6Nu3PAZIY5eBNi5IxMEqrqbKO6so8OgHTImf03mLgjCQ4IgnBUEIVMQhPWCIAypxp1pafDHP0J5ubWVDD+iAjxZlDISJ40NPq4OKOQyVv59Pa9vPszEmCCuP5dlozrXUSq7tA57WzUBnhYzzyiuxsvFHlEU+T41F7lMxuPLZvHRI7dTUNVAS+cP5n7obAk1Te39f5EDAEEQmBwYzCeLbuGrpctJCQziRFXFJdsAemg03BwTR4SbO+P9LCGx0zXVZNXX9ZqeZcuWYW9vz+rVqwFYtWoV9vb2LFu27JqPfb43qlqtxsHB0lTDXmlDiMYTX1tXzKJIeVcDZV0NdBv113w+a3PVE6qCIPgBDwAxoih2C4LwGXAb8EEvabM63paaPtTUQFSUdbUMZ5QKOY8vm4XOYKSyoZURPm7oDEZO5Vfg7eqIr5sj9rYqtHojLg6WRhcncsvxc3dCZzCRW17PnDERAFTUtxAV4InBaKKlo5u3tx6jrK6ZysY2UmKDeWjJlGGbNx/v5c3r192A3mT6ydfgrdQThLq4Eu/ljc5oJLW6iq/zcvCws+PhSZOJdLu27KWnn36a06dPU1JSgtFoRKlUEhQUxDPPPHNNx62urmb58uVs3ryZBx54gO3bt/e0zzvf/s9BaUuLvpMGXTslnXU4KG3xVDsNyoVQcO1hGQVgKwiCArADqq5d0sDhx+YuYX3USgUjfCxNDRRyGQajiZxyy6hRrVJQWN2Ai70tXVo9h7NKiAnyAlGkoa2TcZGWlWhN7d0o5DLkMhmf70+nvrWDV+9fxGv3L6KupYMuncGalzggUP1Ec5by1lZ2lxRx3xhLsSWFTMaKkQl8tXQ5o338eP340Ws+d1hYGE8//TQGgwGNRoPBYGDNmjWEhoZe9TG7urou6o361FNPXbSdTBBwVdsT6uCFu9qRDqOWwo5aarpbMJovDlP9GJ3JMOBG+1dt7qIoVgL/AMqAaqBVFMXv/3s7QRDuFQThpCAIJ+vr669eqRXwsczXSeY+wBAEAblMxvjoIGYkhgHg6+aEk50NK19Yx9/W78LH1ZEJ0UG0dmnR6o34ujliMJoor2+xlIzV2LA3vZDVsy3rQlQKOTYqJfmVg+sz2p98nJ5GnKcnEW7umM+lo55Po0wJDEIhk1F+bgJUbzLRpru6eY3PPvsMjUbDmjVr0Gg0bNy48Zp029nZceTIEWbPng1YYu9Hfia/WS7I8LBxJNTeG2eVHc36Tgo7amnQtWMWzRdtL4oiHUYtFV2N1HS3DJiY/bWEZVyAhUAI0AJsFARhhSiKn/x4O1EU3wLeAssK1WvQ2u84O4NKJZn7YMDT2Z5//uZG9p0pxFFjQ1SgJwDlda24nQvV5FbUk11Wy+hwf6oaWjGbRWKDz9fTFsmvrCfQY/A1w+hLdEYjn2efZZyvPyeqKnlt/g3AuTK1goBSLqeyvY29JZasJG97ezr1el44tJ/CpiY0KiW/D424onP+6U9/4tVXX8XLy4sVK1ZQbqVJL6VMjo+tC64qe+q0rdRrW1HLFDgoLyzlIAgCbmoHjKIZg9k4YMJ61xJMmgUUi6JYDyAIwpfAJOCTn91rECEIltCMZO6Dh6kJF96+zx0TwSPvfMtz63ZRWtdMcmwwc8dG8vcNexgbGdCz3cHMYtydNLg62vU0VpCwjMBPVlXy7P69eGo0+P0oF7youYmv83I4VlFBvLc3f5iYTE1HB59knKbLYODDm5bw/KH9dBuuLId+7NixPf/38vLCy8u6FUHVciUBGne6jXpsfqLapNakp9Ooxc/Wtecxk9mMSTRbLWZ/LWctAyYIgmAHdAMzgSFXOMbbG6qrra1C4mrx93DmH7++ge9P5jEuKoBZoyyjSKVcRlTAudF9fQtHs0u5bqwlvfLcoFQCcFCreWXuddw/tpFn9u/lg9OnUMrlnKiqwEauwEah4NGUKcR7We6A/nnkII5qG26Pi0cplxPi7IJ2iCyQslWoLvm4KIo06jrQKGxQy5UYzSa6jDpaDV2YRDMKmRxvG+eL6tr0NVdt7qIoHhOWcOk3AAAgAElEQVQE4XPgFGAE0jgXfhlKeHtDSYm1VUhcCz6ujqyec2HNpakJofzjs720dHSTXVZLkJcrM0ZZ4vcymYDJbGbbiVxmJIZhqx68tcF7i1BXNz64aQn1XZ38dc8uDpSV8KdJk1mVkNSzTWp1JU3d3cwPCyD4XIGyjLoaYjx9e+LQQ/GOqN3Yjd5sxNfWcs11ujYUggx3tSO2ChX12jYa9R14qB1/sdRDb8brrylbRhTFv4qiGCWKYpwoiitFUfzp5W2DFCksMzQZHe7Pb26YSH5lA6PC/bn3+gko5fKeP66TueU88cE25j72Ni9u2ENRdaOVFQ8MPOw0/Pv6G/l0yVIOlpWy9PNPOVlVCVgaezuo1QSf6wh1oKwEuSBDoVLS2Gh5/XpayhkM1HV2UNPR3lM+YjAhiiJt+i7MopkWfRcuKg2CINBh0NJl1CEXZBjMljsWDxtH3FT2yAQBk2hGb770nYwoijQ2NmJj0zvLhaSSv79AdTWYzeA3tIvoScAFsXZRFEkrqOSLAxnsTMvHYDQxKtyPmyfHMzMpHKWif2+xByqna6oRBIEEL2+25ufyZXYW79y4CIDHdn1PpJs7C8LCaa9vQKu1ZM/oTSZatN3YKVUYzCZMZhFXW9tBVcDMLIq0GjrRm43IsGTXADTrOwCwlavoNOpQyZQ4KC1mbTSbaDdqezJunFUa5MKF42sbGxv8/f1RKi+8W5RK/vYB59MhJYY+Pw4ZCILAqHB/RoX783D7VLYcyeKLA+n85b3vcHPcx6LkkSyZPBIvF+vX/7Ymid4//IG422lo1+s4UFrCkYpy6jo7uX/sBNztHXC3/+F1WrFpI5MDg/h1QgKdej2P7fqev06dgZudnTUu4ZrYV5vFP7K/YblLCmPcQjlUns+tQZMI0rhTr23jpewtvBi/ggN1OZxsLEVlo+B/IufyWu42/O0EbgoY+8snuUokc/8FSkvho49g1SoICrK2Gglr4OJgx+o5Y1g5azRHskv5bN9p3t12jPe3H2dqfChLpyUyJsJ/SMaTr4Rxfv6sTkjijdTjTAoI4ulpM3uyawwmE0q5nF3FhbTrdPx6tGUhVJfBgFkU6dBbFgAdLC9lS24OKYFB3Jk4ymrXcrlM9YphqlcMhe21BGnc6fpRRs226tN0Gw2Iosih+hzCHXyY5mUpm2ErV5HWXCyZuzWproYnn4Rx4yRzH+7IZALJscEkxwZT2dDK5wfS+epQJrtPFxDq48bS6YlcPy56WE/AXhceyXXhkT2/N3R1UdXe1pNN858Tx7g1dmTP88crK2jT6QhyduaRnduxUShYGhvH26dOopbLWTYyod+v4WoIdfDCaDbhoLTlz6c+Yab3SD4p3s+/xtzJvrpsVDIlI50DcFM70GHQUtBRw41+liiLWTQjE3q/huOwM3eTyUxudhX1tW10duro6rTMASuUclRKOXYaNQ6Otjg42uLsYkdioj1arRy12srCJQYUfu5OPLhoMr++fiLbT+ayYe9pnlu3i1c3HeSm5DiWTkvA183J2jKtTnlrC8erKoj38qairRW5TMbN0bEAdOj1rM04w/+MG8/GrEw69Xr+PGkybnZ22CqVHCor7Rnxd+r1aFSXTkUcKChkcv4QfT1H6vOo07Xxj1EriXbyI7u1Ao1CRaDGUndnW/VpPNROPdk1PzZ2rclAVms5sU4BqH8ip/6y9VzT3oOIirJGPv/0GIf359LcdGU1fJ2d7XD3dMTLxwkvbye8fZzx9XPB59yPUilNrg1XbFQKFk6K5caJMZwpqmL9ntOs232KtbtOMT0xlGUzRpEY6jtsQzZJPr4k+fgC4O/oRJCzM6nVVYS7urE+Mx0PjYZJ/oEsWP8xT0+f2RN331VUiEkUUcrlnKqu4pP005S1tnBH4igWRAzsKn4TPS5ckVva2YCPrTM2chVZrRWcbiphpnccfnaWBU9GswmFTM6JxkI2l5+g3ailsquJB6LmM8Xz6nvPDhtz7+7Ws2t7BuMmhpE8JZIRYV7YaVTY2akRBNDrTRgMRrq79LS1dtPe1k1zUydNjR188LEvXdWNGAxppB4vQtv9Q3EpmUzA28cZ/0A3AoLcCApxJyjYg6ARHmg00nB/uCAIAomhfiSG+lHT1M7G/Wf44kA6u9IKiA70ZNmMUcwZHTHss2xG+/jx1N5dONvaMiN4BI8mT2F3cRHR7h4keFkmZ9t0WvaVlvDxopv5vjCfb/JzGe8XwO0j4/n3ieOM9w/Aw05j5Su5fOKcA3irYCcCApsrTnKD/2jGuoWhkFlSbxUyOXqzkRfOfsUdI6Zxg/9ovqk8xeH63Gsy92GTCimKInq9EfVVxEOjoyEmBr74wnKcluYuqiubqaxoorKiiYqyJsrLGqkobUSv/yGH1cvbiZBQT0aEeTIi3IvQcG98/Vx6+n1KDG269Qa+PZbNut1plNQ04eGk4bbpiSxJicdRM6RaH1wxWfV1xHhYVghvzc8lvbaGR1OmArBm324AViUk8VbqCVICgrguPAJBELhh/cc8MWU64/z8rab9ajjeWMDpphIiHX2Zem5SFX4Ytb+Rv4OijlpeTFqBSTRzrCGfow0F/C5yLkqZQkqF/DkEQbgqYwcIDobi4h+O4+KqwcVVQ8zICz9gJpOZ2uoWSksaKCmqp7iwjqKCWo4fLcBssnyJ2tqpCAv3IizSh/BIbyKjffEPdJMMfwhiq1Jy8+R4FieP5HBWCWt3neLVrw7xznfHWTgxluUzR+HnPjzj8ueNHcBRbUNGXR21HR3kNzXyXUEeW5et4uu8HDw1GuK9vBEEgbTqKrzt7Yl297Ci8qtjnFsY49zCen7fX5fNeLcw1HIlTboONlec5K1x9wKWqpTZbZUoZDIEBL4qv7quV8PG3K+F0FA4fPiXa47I5TJ8/V3x9XdlYsoPcTe9zkhpST0FeTUU5teSn1vDd1vS2KS1hHfsNGoionyIivUlOsaP6Dg/XFzt+/qyJPoJmUwgJS6ElLgQ8irqWbvrFJ8fSOezfWeYOSqcVbNG91SnHI6M9/PneGUFt3y+nnmh4Tw+eRqutnbUdXYS7upOgJPlC3BvaTGJ3j6YLlF2d7CR31aNv50rI+y92FRxnEnuEQRo3DCLZsq7mvi+Op1/j72L9wr30HRuYdSVIpn7ZRAaCm1t0NgI7lfRaEalVhAe6UN45A8LPkwmM2UlDeRmV1l+sqrYuPYoJpPlg+vt60xMnB8xIwOIiw8geIQHcrnU8nawE+HvwZrVc7l/YTLr96Tx+f50dqTmMSYigNVzxjApJmjYTb4q5XL+MDGZX48ei41Cgfxci7+s+jrG+Vrujo9WlFPZ1sbCqGicbWx/7nCDgrvCZvT8P9zBB8O5ZiDlnY18VLyfBX6jaDd0s7cui1dGr+axqzjHsIm5XwtbtsDChXDsmCXfva/Q6Qzk59aQnVlBVmYlWZkVNDVYvrXtNGpiR/ozMjGQkYmBRET5oFJJ382DnY5uHZsOZbJu9ylqmzsI93PnjjljmT06AsUw/jI3mEw8f3AfKoWC1fFJ3PP1Jm4fmcCNEVE4DLG85JzWSh4/8ymhDl6oBAW+di7cFz6Hx06vY4xbKDcHTriqmLtk7pfB2bMQFwfr1sHtt/ffeUVRpLamlcwz5WSml5NxuoyykgYAVCoFMXF+xI8KIiEpiKhYP8nsBzEGo4ltJ3L44PuTFNc04efmyMrZY7hxYiw2w/R9bejq4ok9O5EJArEenvx27PgLni9qbiKtpppFUTGDqi7NpTCaTWyuOMlI50BG2HtSr2vj9dzt/E/kXLxtnJHJZJK59wXd3WBnB888A//7v9bV0trSReaZcs6klZKeVkpRQS2iCGq1griEQJLGBJM0JoTQcC8pjDMIMZtFDmQU8d72E2QUV+PqYMeKmaO4eUo89rZDa8R6ueiMRtQKyxecWRR7jPz5g/t4+9RJ4jy9eGLKNMb6Dq4Mmp+j3dDNs5lf8uTIm9Eo1NLIvS/x84M5c+D9962t5ELa27rJOF1GWmoJp0+WUFJs6QHq4GhL4qggRo8bwZjxI/DycbayUokrQRRFTuVX8u624xzNLsXBVs1t0xO5fXoSzvaDP+bcG5hFkS252bx46AA1nR1cFxbBoylT8Hcc/BlIrfou/pr+GTZyFfEugSwPmSyZe18xcyZ4eMCnn1pbyc/T1NjB6dQSTp0o5tSJIurr2gEICHRjzIRQxk4IJT4p8KrTQiX6n6zSGt797jh7zhRiq1Zyy5R4Vs4ajZvj4FnI05d0GQy8feoEb6aewCyK3DNqDL8ZPW7Alyu4HN4u2IWz0o5bgydJ5t5XDMbWa6IoUlbaSOqxQk4cLSQ9rQy93ohSJSdxVDDjJoYxbmIovv6uv3wwCatTUNnA+9tPsP1kLiqFnEUpI7ljzhg8nKW0WYCq9jZePHyALbk5eGnseSR5Cgsjo4ZE9pEUlpH4WXQ6A+lpZZw4WsiJowVUlDUBEBjszoTkcCYkhxMT549cIcXqBzKltc28t+04W49nI5fJWJwykjvmjsVTMnnA0u7vmf17Sa+tYbSPL09OncFIT+s22b5WJHPvQ06etEymvvoqhIdbW03vUFnRxLFDBRw7nE96WilGoxkHR1vGTQxl4uQIxo4PxU6qjzNgqahv4b1tJ/jmaBYymcCilJHcKZk8YInHf5F9lhcPHaCpu4ulsSN5eFIKrraDryEISObep5w6BffeC2+8AWOu6CUeHHR26kg9VsTRQ3kcPVRAe1s3SpWcUWNCmDQlkkmTI3B2kWK8A5HKhlbe23acr49YTH7J5HjunDsWdyfp/WrT6Xj1+BE+PJOGnVLJHyYks3xkQs9CqcGCZO4SvYLJaCYzo5wj+/M4tD+HmupWZDKBuIQAUqZGkTItCg9PR2vLlPgvKhtaefe743x99CwKuYxbpyZyx5wxuDgMztFqb5Lf2Mia/bs5XF5GjLsHa6bPZLTP4GmMLJm7RK8jiiKF+bUc2p/LwT05PamWMXH+TJkRzeTpUXh6Df7Us6FEWV0L72w9ytbjOahVCpZNT2LlrNHDvhKlKIp8V5DP3w7sobqjgyXRsTySPAX3QdC7VTL3PuaOO8BggLVrra3EepSXNrJ/Tzb792RTlF8LWIx+6sxopsyIwd1jeDeMHkgU1zTx5jdH+D41DwdbNatmj+H26YnY2Qz+FMFroctg4NXjR3gvLRVbpZKHJ6Zwe1z8gA7VSObex9xyC6SnQ26utZUMDCrKm9i/O4t9uy1GLwgQnxTEtFkxTJkejaPT5Y+IRFEcEilrA5G8inr+veUw+zOKcHWw4+7541icMhKVcniWNThPQVMjf927iyMV5cR7efPM9FkDNqtGMvc+5tFH4eWXLeUI5MO7oc5FlJU0sG9XFnt2nKW8rBG5XMbYCaFMnx3LpCmR2Nj89KIpk8mMXC7DaDShGOadivqS9KJqXtt8kJN5Ffi4OnLfDROZPy5qQI9Y+xpRFNmcm8NzB/fS1N3NyvhEHpqQjOMAK04mmXsf8/bbloyZkhIICrK2moGJKIoU5tWyZ+dZ9uzIpL6uHVs7FavvnsqS28Zfch+j0UR5aSMvPbuFydOjuXX5RKkuTh8hiiJHs8t49auD5JTXEebrxu9uSiElLmRY3zm16bT888ghPkk/jYdGw5NTpjM/LGLAvCaSufcxu3dbyhDs2gUzZvzy9sMds1kk43QpO7dnMm5CKJOnX9wP0mQ08+Vnx6iubKEgr4ZR40K4455pVFc2k59bw5QZV99DUuKnMZtFdqbl8frmw5TXtzAq3I8HF01mZIjPL+88hDlTU83ju3eQ1VDPtOAQnp42c0DUqpHMvY8pLbW03HvrLbjnHmurGfzUVrfw5mu7iIj0JnqkP5s/P8lvfz+Hw/tzyc+tpqK8CZ3WwP1/mHdRS0OJ3sFgMrHpYCZvfXuUpvYuZo8K5/6bUgjwGL6F5oxmMx+eSeOVo4cQRZGHJiRzR+IoFFYMX12NuUv3vleAvz8olVBYaG0lg5+qiibef2svkyZHcNuqZGqqWrCxUaBWK/j43f3cunwSr/xnNQmjgqmuagYsIQWJ3kUpl3Pr1AQ2P30n914/gQOZxSxZ8yEvfbaXlo5ua8uzCgqZjLuSRrN9xR1MCgjkuYP7WLxhLZl1tdaWdkVI5n4FyOUQEgIFBdZWMvjR6Yy0tXWz9oMDfPDWXo4dLmDugkT27c5i1LgQAoLcMBhMBIW4U1psaVByPv4pmXzvo7FR8ZsFE9n89J3cMDGGDXtPs/DJ9/l4Zyp6g9Ha8qyCn4Mjby24idfm30BNZweLNqzlhUP76TYYrC3tsrimsIwgCM7AO0AcIAK/EkXxyE9tP9jDMgCLFkF2NuTkWFvJ0CD7bCXv/Wc3OdlV3HL7BPbuyuLPT9xIVIxl9eD/e+k73D0dWLY6pSerBix17L/dnEZ1ZTPXLUwiMtrXmpcx5CiobOD/vjzA4awS/N2deHDRZGYkhQ2YCcb+plWr5YVD+9lwNoMgJ2eemzGbiQGB/XZ+a4Rl/gVsE0UxCkgAsq/xeAOe666DlBRLCWCJq8dktDQCj4j0ISLalzvumYZKrcTBwZaoGD9MJjP1dW1knClj1tyRlp3OveYlRfW8/+ZeKsoa8Qtw5e3Xd9HY0G6lKxmahPm589rvFvH67xZjo1Lwp7e/4Z5XNpJdNrhCE72Fk40Nz8+cw9pFtwCwfNNGHt+9gzadzsrKfpqrNndBEByBKcC7AKIo6kVRbOktYQOVe+6Bd94ZfLXdBxrnywq3t3ej1xuZNDmCsRNCCQ23LCLp7tKzc1sG4ZHeeHo7YTaLPfvs2p6Bp7cTd903nVuXT8TWTkXayRIAtFoDudlV1FYP+Y9ivzAxJoh1f1nBX5bNpKi6iRUvrOOpj76nobXT2tKswsSAQLYuW8U9o8aw4WwG8z75gN3FRdaWdUmuOiwjCEIi8BaQhWXUngo8KIpi539tdy9wL0BgYODo0tLSaxI8EBDFH/qqSvQenR1aHn1oPQGBriAIODjYMG9BIiGhnuh1RlRqBVmZFWz/5gzTZ8eSODoYrdbAmsc2cvdvZxIa7sUTf96AjVrJmbRSblg0mqUrJ0mNw3uJ9m4d72w9xvo9aaiVCu6eP57bpycO25WuZ2qqeWTndvKaGlkUFcMTU6bhbNM3LRD7OyyjAEYB/xFFMQnoBB79741EUXxLFMUxoiiO8fDwuIbTDQxE0TKp+vDD1lYy9NDY2/DC/y0jLMKbEaGe3PM/MwkJ9QRApbYYSHFBHe6eDvj6uwCQdrIYvwBXDAYj3289g05r4PFnFrN20wOcOllMV+cPt81Go6n/L2oI4WCr5qElU/j8yVWMCvfjX5sOcMszH3MgY2COXPuaBG8fNt+2gt+Nm8DXeTnM/eRDdhYNnGyLazH3CqBCFMVj537/HIvZD2kEAe6/H+bOtbaSoYlGo2bx0vHcfPsEFAo5jQ3tfPHpMdLTLHd8dho1TY0dPZUoT50oJijYg452Lfk5Ndy4xDK4KS9twMnZDpVKQUe7lr07z/KH+z7ipWe3UF3ZbLXrGwoEerrwr9/exKv3L0IuE3jw35t58N9fUV4//EJhaoWChyYks+nWZbjb2XHvN5v54/ff0arVWlva1Zu7KIo1QLkgCJHnHpqJJUQz5Hn4YVi40Noqhgdu7g7Mnj8SvwBLn1ej0YS225KKduxQPhVljUTG+NLZqUOvNzJ2QigALc2duLhqEIENnxzm6MF8HvjTfBwcbfnys+PWupwhRXJsMBv+dyUPLppMal4FNz/9Ef/ecphu/eBIFexNYj292LR0ec8oft7aD9lTYt07mmvNlvkdsFYQhHQgEXju2iUNfEwmSypka6u1lQwPHJ3scHO3lBKOTwykuamT1be+ztYtaUybFUtElA952dW4udujVitpb+umrLQRGxsVJpOZPTvOsvqeqYRFeJMyLQqTyUxb2/BcoNPbKBVyVs8Zw6an7mDWqHDe+e4YN6/5iL1nCofdegSVXM5DE5L58tZlONnYcNeWTTy263s69Hqr6LmmmRBRFE8DQ7Dp3M9z+rSl1d7GjXDzzdZWM7zw8nHmhf9bRnFhHc4uGlxcLa3kigpqewqTpaeVUVnWRMr0KI4cyCM03AsfPxdEUUStVlhWw6p/ukqlxJXj4WzP3+6cz+KUkbywfjd/eGMLKXEh/PnWafgPs1IGcZ5ebF66nP87dpi3T53kUHkpL82ax3j/gH7VIa1QvQpiYy2rVc+csbaS4UtIqGePsQPMvT6B997Yw5YvTvLRe/uJjfcnISmIzZ+fYP6NSYBlheuBPTl4ejuhUiswm4fXyLI/GB3uz7rHl/OHJVM4lV/BLc98xDtbjw27Va5qhYJHkqew4ealyAUZy778jOcO7EVn7L/XQTL3q8DGBqKjLSN4iYHBtFmxLF05ieqqFu64ZyrTZsVSV9OKUqVg9LgRADTUt5N2spgFCy3z/tJahb5BKZezYtZovnzqDiaPHMG/vz7MbX/7hJN55daW1u+M9vHj22WrWDYygXfSUlm4YS3Z9XX9cm6pKuRVsmIF7NsH5cPv8zpoEEWR11/ZTmS0L9Fx/nyzKRW9zsgDf5p/wTbHDhcwdkKoVEO+jzh0toS/f7qbioZWbpgYw+8XT8HFvm/ywQcye0uKeWTndlq1Wv44KZm7ksYgu8wRhlTytx/5xz/gT3+ChgZwc7O2Gomf4sjBPNa+fxBBgPk3JjFuYijuHo49bf1Sjxfx6O/X4Rfgym0rJzFr3kipG1Qf0K038M7WY3y8IxV7WxUPLZnCggkxw65WTVN3F3/ZvYPvCwuY4BfAP+fMx8fhl/sOS+bej+zYAXPmSI07Bgv1dW14eDpe9LjZLHJoXw7rPjxEQV4N3j5OLF05iTnXJUgrW/uAgsoGnl23k/SiasZHBfKXZTOHXe14URTZmJXJ0/v3oJTJ+duM2VwXHvGz+0jm3o/U1YGXl6Wn6kMPWVuNxOXwc024RVHk+OECPnn/ADlZVXh4OnD7qhTmLpBMvrcxm0U+P5DOq18dxGQy85sbJrJsxigUwywsVtLSzEPbt3KmtoZbYuL469QZ2CkvncUlmXs/4+dnabv30UfWViLRW4iiSOrxIj5+9wBZmRV4eDly+6pk5i1IRKmUwjW9SV1LB8+v38W+9CJigrx4csVsIvwHf4mSK8FgMvGvY0f4z8ljBDu78K951xPn6XXRdpK59zM33gi5uZYfiaGFKIqcOlHMR+/sJyuzAi9vJ1b8ajKz58X3VKeUuHZEUWTHqTz+/uke2rt03DlvLHfPH49ymM17HCkv44/ff0djdxePJE/hzsRRF9xlSubezxw7BmYzTJxobSUSfYUoipw8VsSHb+8jN7sKX38XVt9tSbWUyYbXZGBf0tLRzUsb9/Ld8RzC/Nx5auUcYoIuHsEOZZq7u3lk53Z2FhcyI3gEL86ei6utpfSsZO4SEn2EKIocOZDHB2/vo7iwjpBQT+789TQmJIcPu4yPvmRfeiHPrdtFU3sXd8wZyz3XjR9WJYVFUeTj9NM8d2AfLra2/Gve9Yzz85fM3Rps2wZdXbB4sbWVSPQHZrPIvl1ZfPD2XqoqmomN9+fu+2YQl9B/LdeGOu1dWv6xcR9fH80izM+dp1fPJSrA09qy+pWzdbX8btu3lLW28NCESdw/bqJk7v3NnDnQ3AwnTlhbiUR/YjSa2P7NGT56bz9NDR1MSA7nrvtmEDxieE0I9iX7M4p4du1OWtq7uWv+OH41fxxK+fCJxXfo9Ty+ewcms5nXr79RMvf+prIS3N1Brba2EglroNUa+Oqz46z/+DDabj1zrk9g9d1TcPe4OKde4spp7dTy4md7+O54DjFBXjxzxzxCvF2tLavfEEURvcmEjVIpmbuEhDVobeli3YcH2fLFSRQKObcsm8Atyydia6uytrQhwc5TeTy3bhfdegO/uymF26YlDasJbSnmbiWefBI8PS0dmiSGN9WVzbz7xh727crC1d2eO++dxuz58VLdml6gobWTZ9bu4EBGMROiA3lq1Vw8ne2tLatfkMzdSkydaplUleLuEuc5m1HOm/9vJ9lnKwmL8Oa+B2cTnxRkbVmDHlEU+fJgBv/8fB8qhZz/XT6LWaN+fun+UEAydyvxxBPw3HPQ0gKXUQNIYpggiiJ7dpzlnX/vor6unSkzorn3f2by/9u77/Coiq+B49/JpieEhBAIEEqC9CqELkWqBUSRrqAUEelNAfmpIIr0KoL0KihFqQqK0pEmUqSEEFoooaVAepn3j0kIIL6kbHKzm/k8z322ZPfu2UDOvXfmzEzBQrlrLpWscOVWKP9b/AunLt3ktToV+LB9I1wcrbcJLCPJXV8rmkGDBmow0/79Rkei5SRCCBo3r8ii1X3o2qMBB/edp3unuSxfuJvY2Ny3zqg5FSvgwcJh7enxUk02/fkPncat4J9LN40OK0fRyd0M6tRRKzPt3m10JFpO5OhoR5ceDVi06gPq1C/NsoW76dl5Lvt2nct164yak53JRN/W9Zg3uB0JCUl0m/Q9S7Yf1itsJdPNMmZSu7Za2efAAaMj0XK6v49eYvbUbVy6eJuadZ6j7+DmFPbJPeV9WSEiMoaxK39lx7FAapcrzth3W+Dp5vLsN1oI3SxjoFdeUXPNhIQYHYmW01WtXoI5S3vSe0AzTh2/Qs+3v2XZgl3ExeaudUbNyc3FkYnvteTjzk04FhhMxy9XcPDMZaPDMpRO7mbSujVICZs2GR2JZglsbU282bEWC1d9QL0GZVi+aA/vdfmWvw4HGR2axRJC0LZ+ZZYN74ybsyN9Zq1nzqb9JCYlGR2aIXSzjJlICb6+UKmSTvBa+v11OIgZk37menAoTVpU5P3+zfDIZz3NCtktOjae8d//zqYDp/Ev7cOX3V/GK6/l1sTrZhkDCQE9e0KpUkZHoskx/OsAACAASURBVFmiajX8mL/8fd7q9gK7dpymR+e5bNtyXHe4ZpCTgx1jurZgdNfmnLp4k87jVnL4XO5azV6fuWtaDnP54m2mTdjCPyeCed6/BIOHv0qhIh5Gh2WxLly/w4fzt3AlJJQPWtWlW4saFjd1gR7ElAMkJcGVK1CihNGRaJYsKUmyZcNfLJi9g6QkSbf3G9G6bQ09jUEGRcXEMXblb2w7co4GlfwY+24L8jg7Gh1WmulmmRygb1+oWRMSE42ORLNkNjaCVm9UZ8F3valSrThzZvzKkA+WceXSHaNDs0jOjvaM6/4yH7VvxP5/LvHW+O8ICL5tdFhZSp+5m9m+fRAUBB06gL31jobWspGUkh3bTvHNtG3ExMbTrVcj2nSopc/iM+j4het8NH8z96Ni+bRLM16qUdbokJ5JN8tomhW7d/cB0yds5cDeACpU9mHYqNfwKaoHP2XE3YhIPpq/hWOB1+jStDr9X38B2xx8sNTNMjnEzZswa5Zqf9c0c8nn6cqYCe346JPXuHzxDh+8M59N64/qipoM8HRzYe7AN+nQqCrLfztKv1nrCXsQbXRYZqWTexb4/XcYMAB27jQ6Es3aCCFo9nJl5q/oRYXKRZk5+WdGDV3N3Tv3jQ7N4tjZmhje4UU+69KcYxeu03XCKgKvWU+fRqaTuxDCJIQ4JoTYbI6ArMEbb0DevLB4sdGRaNYqv5cbX03rRL+hL3Hi2GV6dZnHvl3njA7LIrWuW4H5g9sRExfPu5NWs+v4BaNDMgtznLkPBM6YYT9Ww8kJOnWCdesgPNzoaDRrJYSg9Zv+fLO4JwW98zJ65Bqmjd9CdHSc0aFZnMp+hVgx8i1KeOdjyLcbWbztkMU3d2UquQshfIBXgQXmCcd6dOsG0dHw/fdGR6JZu2Il8jNjXjc6vF2Xnzcdo2+3hQQG6LnN06uAuysLhrSnefUyzPppH58t3UZcvOVO5papahkhxFrgKyAPMExK2fIpr+kF9AIoVqxY9cuXc8dMbVKqeWby5NHTAGvZ568jF5nw+Qbuh0fTq19TWrf1RwjLGo1pNCkl87ceZO7mA1QtWZgpvV/Dw9XJ0JiytVpGCNESuCWlPPr/vU5KOU9K6S+l9Pfy8srox1kcIdTZ+59/whndaKVlk2r+vny79D2q1fBl9rRtjPl4LfcjrKsKJKsJIej1am2+6vEKZ66E8M7EVVwOCTU6rHTLTLNMPeA1IcQlYDXQWAixwixRWYm331YrNOmOVS07uXu4MHZSB97v35Q/956nT7cFnD19zeiwLE4L/zLMHdSWyOg43pm4iqPng40OKV0ynNyllCOllD5SyhJAR+B3KeXbZovMChQsCK1aqeQeFWV0NFpuIoSgbafaTJ3TlaQkyeDeS9m47ojFdxJmtyp+hVn6UUfyubnQZ+Z6th22nIokXeeexYYMUQtoh4UZHYmWG5Wv6MOcJT2pVsOPWVN+YfyYn3Q1TTr5eLmzeFgHKvl6M3LRVpZut4yDpJ5+QNNygaQkyapl+1g6fyfFfb0YPb4dRfS6rekSG5/Ap0u38evRADq9+DxD2zbMtqmD9fQDOdi5c3D4sNFRaLmVjY3grXdfYNzUTty984C+3RdycH+g0WFZFAc7W77q/gpvNanGqj+OMXLR1hxdKqmTezaQUq2xOmSI0ZFouZ1/rZLMXtQd70LufPLhalYt22cRTQw5hY2NYGjbhgxqU59fjwYwYPZPRMbkzGYundyzgRCwfLkasao97tq1a8THxxsdRq5SqLAH0799l4ZNyrNo7h+M+/RHYmL0v0F6dG3mz5iuzTl6Pphe09YQej/nVUzo5J5NatSAAgXUWXxuJaUkKCiIJUuW0LFjR7y9vfHx8WHzZj0tUXZzdLTj4zFv0OODxuz6/TRD+izjzu0Io8OyKK3qVGBK79cIunGXHlPXEBKasyZv0x2q2ejyZWjfHr76Cho3NjqarCel5OzZs+zatYuff/6ZvXv3Eh0djclk4sGDB9ja2tKhQweWLVuGjY0+zzDKn/vOM+6zH3FytmfsxA6ULlvI6JAsytHzwQz6ZgNuzo7MGfgmxQq4m/0z9GIdOVxMDJQpA15ecOgQWFs+S0xM5OTJk+zatYutW7dy4MABkpKSkFIS9UShv7OzM61ateK7777TiT0HuHjhFp98+D3hYVGMHP06dRuUMToki3L6cgj9vv4RWxvBnIFvUrJwfrPuX1fL5HCOjvDFF3D0KKxebXQ05tetWzf8/f0ZMWIE27dv5/79+0RGRj41sb/yyiusXLlSJ/YcwrdkAWYt6EYJPy9Gj1zD+u8PGh2SRSlfvCALhrQDIXhv6hrOXr1ldEj6zD27JSVB9eoQGqrKIx0cjI7IfM6cOUOzZs24c+cOsbGxT32Nk5MTLVq0YO3atZhMpmyOUHuWmJh4Jny+gb07z9KmQ03e798s22q5rcGVW2H0nrGWyOg4vhnQhgolvM2yX33mbgFsbGDSJNX+Pnu20dGYT1xcHNu3b3/Ylv40Tk5ONGnShDVr1ujEnkM5Otrxv7FteL1dDdZ/f4gvP11PXGzOreXOaYoVcGfBkPa4OTvwwYx1HA+6blgsOrkboGlTaNECPv8cbtwwOprMSUxMZPHixfj4+DBq1CjCw8OJjIzExsYGV1fXh69zcnKiUaNGrF+//j+Tv5YzmEw29BnUnF79mrL79zN8PHQVkZFPvxLT/q2wpxsLhrbHI48z/Wb9aFiC18ndILNmQWws9OtndCQZI6Vk3bp1+Pr60r9/f27fvk1kZCSg2tSbNWvGxIkTcXZ2xsHBgfr167Nhwwbs7OwMjlxLCyEE7TrXZsRnrTl1/CrD+i4n9F6k0WFZjIIeeZg/pB35jEzwUsps26pXry61VOPHSwlSrltndCRpl5SUJLdv3y7Lli0rXVxcJPBwc3FxkXXr1pWHDh16+PpTp07J0aNHy9jYWAOj1jLj4P7z8tVGX8l3O8yWITfCjA7HooSE3pevfbJI1h/0tTx18UaG9wMckenMt7pD1UAJCfDyy/Dee6r+Pac7cOAAAwYM4MyZMw/P0gFcXFzw8/Nj5syZNGrUyLgAtSxz6sRV/jdsNc4uDkyc+TY+RfWkY2l189593pv6AxFRsXw7uC1lixZI9z50nbsFklJNT5CTnThxgkGDBnHw4MHHyhpdXFwoUKAAM2bMoGXLlno5NysXGHCTEYO+w2SyYeLMtyjum3tWVsus63cj6Dn1B2LiElgwpB1+hTzT9X5dLWOBhFAJ/uuvc97cM4GBgbzxxhvUrl2bnTt3PkzsLi4ueHt7M2/ePAIDA2nVqpVO7LnAc6W9mTK7CwBD+y7nwvkQgyOyHIU93Zg7sC22NoLe09dy9XbWL/Cgk3sOkJAAK1bA+vVGR6Jcu3aNrl27UqlSJTZt2kR0dDRSSpydnfHw8GDy5MlcuXKFzp0760FIuUxxXy+mfNMVe3sTHw1YoRN8OhQr4M6cgW+SkJhEnxnruB32IEs/TzfLmEliYiI3LoRw8eQVLp68wu2rd4iMiOJBWBSJCYnYO9rh4GSPi7sLXkU8ye/jibdvAUpULIpnIQ/CwgR58xo7JcGdO3cYM2YMCxYsIDEx8eFsjU5OTtja2jJq1CgGDBiAk5OxK8FrxrsefI9h/ZYTG5vApFlv4/dcQaNDshinL9+k17S1FMqnSibzujg+8z26zT2bxcfF8/cf/7B33Z/s33CYsORZ9WxsBB7e7ri6u+CS1xmTnYn4mHhio+O4f+8B926EkpSU+nvPk8+VklWKU75OGfI9V5GAkNJ8ODz7hq5GREQwceJEpk2bRmJi4sPRpQ4ODphMJgYNGsTw4cNxc3PLtpi0nO968D2G9l1OQnwik2d30W3w6XD43FX6f/0jZYoWYO7AN3Fy+P9LhHVyzyZSSv5YtZd5Hy3n7vVQnFwdqdWyOtWbVsavSnGKl/fBwem/k3NiQiL3boZx7fwNLv1zlUunrhJw9AIX/r5EQEIHLtGGxiV/5L2eUO+NmhQtUyRLvkd0dDSzZs3iiy++ICEhgejoaADs7OywtbWle/fujB49mvz5zTsJkmY9gq/cZWjf5QBMndNVL92XDjuOnWf4/C3UrVCCKb1bYff/jNrWyT0b3Lx0i5l95nP4l78pW/M5On3cBv/mVbB3tM/0vqMjY/jnQCDde+fj1IWCVGUcnuIEzz3vS+NOL9CoYz28fNLXy/408fHxLFy4kFGjRhETE/Owo9RkMmFvb0/btm0ZN24cPj4+mf4szfpdvnibIX2W4eRkz7S57+BVQF/hpdW6PSf48rsdtK5bgU/fbvafhQk6uWexy6evMrjBp8THxtP9y8681rdFlsyREhEBL7wAly4l8XmfPVzY+QtnDwViYyOo+Wo12gx8laovVkx3hUpSUhKrV69m2LBhREREPKxVF0Lg6OhIs2bNmDx5MqVKlTL7d9KsW8DZG3zYfwWe+V2ZNucd8ro7Gx2SxZizaT/ztx6k16u16d2yzlNfo5N7FnoQFkm/WiOJiohi2p6xFHkuaxc0uHoVatUCOzvYvRts42+wfclOts7/jbDbEfhVKU7H4W/QoF3tZx5gpJRs2bKFgQMHEhIS8tgAJGdnZ2rWrMn06dOpUqVKln4nzbqd/PsKIwZ9h1+pgkyc+RZOTpm/ms0NpJSMXr6dTQdOM6Zrc1rVqfCv12QkuevpB9JobIcpsoVdB3lyz+ls+8y//pLS3V1KPz8pg4PVc7HRsXLrgt9k9/IDZVPRVr5Tur/c+f0+mZSU9NR97Ny5U1aqVOmpUwVUr15d7tu3L9u+j2b99u06K5vX+0J+PGSVTIhPNDocixEXnyDfn7ZG1ugzXR4+d+VfPycD0w/o5J4G548FyaairVz62ffZ/tkHD0qZJ4+UpUtLef166vOJiYly99oDsmelwbKpaCsHvjBKnjsS+PDnR44ckXXr1pXOzs7/SuplypSR27Zt+88DgqZlxuYfj8qmdcbKqV9t1v/H0iEiMlq+OWaJbDhktrx0895jP8tIctcjUNJg7ZRNOLs50WbQq9n+2TVrws8/w7VrsHhx6vM2NjbUf7M2c49NYvC83lwLuEG/miMZ02kiLzV7mfr167N///7HRpUWLVqUJUuWcObMGZo3b65HlWpZ4tXXq9Gpaz22bjzG6uX7jQ7HYuRxdmT6B62xsbFh4Dc/EREZk6n96eSeBid2naZOK39c3V0M+fx69eDYMRg5Uj1OSkr9mclk4pWeTRjz6zDsn5Ps+f4Q93eAXbQaaOTi4oKXlxczZ84kKCiItm3b6qSuZblu7zeicfMKLJr7B3v+OGN0OBbDx8udKe+34vrdCEYs3EpCYtKz3/QfdHJ/hqj70dwOvkuJCkUNjaNUKTUPzcWLULmyWmA7PDycMmXK8O6771K9VjW2Bf3EUbkLIQU1RCPKOFZm7NixXL16le7du+tFMrRsI4Rg6MhWlKtQhAmfb+D8OQtflSYbPf9cET7u1IQ/z1xm5o97MrwfndyfITY6DgCnPDljyL2U4OwM0dFRtG/fnYCAAFasWEFMTAwJCQnEOD7gpPN+vCp4UDS2NAkn7bER+p9Zy372DraMmdAON3dnPhuxRi/2kQ6v16tIh0ZVWbHjL34+dDZD+9B/9c9gZ6/OduNj4w2ORClYEKKj19CoURLbt38LjCAxUZWzmkwm+vbty6Xgi3x3Yj5vf9KW7Ut28slrE4iN1sukadnPI58rY8a3Izw0irGj1pKQkGh0SBZjSNsGVCtVhIk//JGxHaS3BzYzmyVWyyQlJcllo3+QAUcvGBpHTIyU06dLmTevlI6OiVKdw6dsu6Sbm588cODAv963dcFvsplNOznipbEyNibOgMg1Tcod207KpnXGyjkzthsdikW5E/5Anr0SkqFqmQw3wgohigLLAG8gCZgnpZyR0f3lVEIIunzWzrDPT0yEpUthxAiIjARV/GKDEElIGYsQZ5CyFibTKaKj/9109HKPJgghmNJzDlN7zmH4sv66Q1XLdo2bV+T0qWDWrT5IhUo+1H+xnNEhWQRPNxc83TJWyJGZZpkEYKiUshxQG+grhCifif1pj5AS1q4FX18YMABu305J7ODkBAUKnMDVtRGTJv2Bq2szEhJCadIERo2CuLjH9/VS98a8M6YDO1bu4ZdFv2f/l9E04P3+zShbvjCTx23mxrVQo8OxehlO7lLKG1LKv5Lv3wfOAFkzfWEuIiVs3w7lysG776ppCFJmC3B2hrp1Ydcu2LQpnsDAjQwdOpTAwDVs3nyTbt1g3Djw94ejRx/fb6eP36Ba00rMHrCIm5duZfv30jQ7OxOjxrbBxkbwxSfriY/X7e9ZySwdqkKIEsDzwMGn/KyXEOKIEOLI7du3zfFxhoqMiOKP1fv4dtgy7t4w79nH/v1Qowa0aQPnzqUmdRcXqFQJtmyBffvUa2rUqEHBgmqBhIIFC9KgQTUWLoSNG+HuXTUvzYgRkDw1OyaTiWGL+gKwaNR3Zo1b09LKu5A7Q0a2JODsDZYt2GV0OFYt08ldCOEKrAMGSSkjnvy5lHKelNJfSunv5WXZk/mHhoQxoess/vrtBDY2gs9en0BwwPVM7/fECXjxRWjWTJ1xP5rUfX1h1So4fhwaNXr2vlq1gn/+gXfeUVcAj5a2e/l40nZIK/5YtY/LZ4IzHbemZUT9RmV5uVVVvl+xnxPHLhsdjtXKVHIXQtihEvtKKWUOWQE0a8RGx/Lb8t3kze/G0AUf8N7ELrh55iHkcsavRs6fh9atoXZt1dSS0qbu4gLe3jBvHgQGqoSdnj5Qd3dYuBD27gWTCe7dg/bt1dVAy97NADiw4XCG49a0zPpgYHMKFfZg0hcbiYrUZbpZIcPJXaiSi4XAGSnlVPOFlDOdPRTIlbPXeLlHYwCCA67jXjAvnoVTV56RaZw+OTgYunZVI023bIHo6NTBSR4eMHkyXLkCnTtnbk1V5+QptU+ehN9/V000+Yt4UrKqL0d/PZ7xHWtaJjk52/Ph/1oRcjOc+d/sMDocq5SZM/d6QBegsRDi7+TtFTPFleOc2Hka9wJ5KV+nDABXz13H0dmRpEfmfpBSEhkeya4f9j910NCdO9Cvn5pKYPVqiIlRpY5OTpAnD3z6qZogrHdvNY+7uTRsqA4olSurxwfvdWHLsaZcvWq+z9C09KpYpRhtOtRi849/cVw3z5hdZqpl9kophZSyspSyavK21ZzB5RRSSnZ8t4eG7dUqKRdPXubcoUDyF8mHX+XiD1+35dtfmTt0GduW7qRnxSH8uVmVrEREqBLF4sVhwQKV1OPjwcFBnV0PHqyS7/DhKtFnBcfkBdYTE8HeDs6G1uG55+CDDyAoKGs+U9Oe5Z33GuJd2J3pE7YQF5dgdDhWRU8/kAaJCYlUblCeu9fuEf0gmg2ztxEfG8+LHes9fM3BLUfZve5Pmr7dgHFbPqbTyDZc/Oc6EyaAjw9Mm6ba1GNj1Vm5oyP07AmXL8OXX4JbNi07aTJBVZel9G74Dd26qbb5UqVUm/yhQ9kTg6alcHKyZ+CHLxN85R4/rDxgdDhWRSf3NLC1s6VBuzrMGbKU0W0m4ebpSvuPWlPIr+DD13w3bj3N32lElUYViI+HPftsmfxpIJ9/Dvfvg030VRxtwnF0hI4dVWfq119D/vzZ+11uXrrFpVNXqPOiN3PnwqVL8OGHqrKmVi3Vubt8eWoJpaZlNf9aJWnUpDzfLd2rBzeZkU7uaeTfvApLzs1kyPwP6P5lZ84dvkBiohqEsX3pTvIV8qBh+3qsXAnFisHuZRu4Elef6KgE/MQaypkWU99hOON7rWHZMnU2n92klMzqtwB7R3teSu4YLlwYxo9Xg6VmzIDQUHVFER6u3pNSwaNpWen9AU0xmWz49uvfjA7Faujknk4Fi3uRmJBI2K1wAv+6CED43fsI97KUKyd5/32wu7mFB0nehFGOsnarKOETxeStfdlwaxr3Q64Scfd+tsedlJTEt0OXcmjrMbp90QkvH8/Hfp4nj5rm4MwZVWtfoIB6/qWXoFu3bA9Xy2Xye7nRqWs99u06pztXzUQn9www2Zpo/k4jnqvmy86dMHmqI98vu0fQRTsSIu9Sgh+54dSBGiUO0fbNRL5Z/wINm3sSH5vA6QMBxCd3HMXFxBF6KzzL442LiWNC11msm76F1/u/zOsDXv7P19rYQMWK6r6U8Npr0KCBehwVBZ06wQ8/pA600jRzebNjLbwK5GHB7B1pLivW/ptemieDjhyBAQNMHD8OdlHFKMs2nmcsibYexORtxorvinNu469UfKEcfpWLAar5pkHbOngW8uCf/ef4YdIGbgSFULJqCQZ/+z72jvZmjTEuJo6t83fw/cSfuHPtHj3GdabD8NfTPCukEDBsWOrjgADYuVOVcTo5wauvqqkSXnkF8uY1a+haLuTgYEfXng2ZMm4ze3edo36jskaHZNH0mXs6nT6tmioaNIADB9TZbDhlOOU8kbh8DRkyuxP7b7alfr0Y7t0Mo5BfAezs7bhy9hpXzlyjQt0ynNp7hjVTNlKtaWXmHZ9CYkIiBzYeMUt8UkqCTlxmySer6VKyH7MHLqKQX0Em7fiMjiPeyNR0v1WrqpLNnTtVU82ePWqglZcXNG8Os2bBhQtm+RpaLtXs5coULebJsgW7SErSZ++Zoc/c0+jSJfjoI9i0SU2pm7JItYuLqlUfP96Grl0bPJzL5WZQCKEhYZStWQqAH2dsoXDJguTJ58rJPWcpWrowrfu+BEBSYhJxySs9SSkRQhD9IJq710PxKJgXR1dHTCbTY/EkxCcQdiucuzfCuHX5NheOX+LiySucPRTIvRuh2NgIqjWrzMcrB1KlUQWz/R5MJjUoqmFDmDkTDh6En36CDRtUm/2AAeoAUKSI6qTNl0/9jjQtLUwmG7r0aMC4z35kz84zNGysZxHPKJ3cn+HmTfjkE1ixAhIS1AaqWcLeHkaPVgOBHBwef597gbx4FHRnWOPR+FYsRuCxi3Qe9SZXz17jasA1OnzYGlDTGBQu6Y2bZx6Ah2fWJ3af4X8tv3q4Pwcne+wd7UiITyQhPvFfy/7Z2Ah8yhSmSqPyVGtSmRovP49nIY+s+aUkM5nUFMR168LEiWoenH37VGIHGDRITX0QEKAenz0LJUqkDqjStKdp0LgcyxbuYvWy/TR4sZxeXCaDdHL/D6GhanDRN9+oUZ0pC2A4OqqkNnw4DBny32elru4ufLZ2GJvmbid/kXx0GN6a/EU8WT3+R9zzu1G8fFES4hO4cPwy4bcjHquZByhZpTgfLe1H2K0IYh7EEP0gmvjYBEx2JmztTDg4O5DP2x0Pb3e8fDwpVq4IDk4OTw8mmzz3nNpSDBwIISHqvpRqVsuwMFVPX78+vPCCqqt3dzckXC2HMplsaP9WHaZ+tYVjRy9Rzd/X6JAskk7uT3jwAKZOVWeiiYlqqgBQZ+kmE/Tpo6YS8EjjSXGr3s0f3k+ITyD0VjidRrwBwIldpwk4HEjJqr4UK/v4Oif5i3jSrEtDs3wno6RU2YBqxvr2W9i9W7XVjx+vfr9CQIUKKuHXqgWNG0PJksbFrOUMTZpXYuGcP/jph8M6uWeQ7lBNFhsL06erwUXjx6tSv5gYNR+6o6OaxTEoSM3YmNbE/iRbO1sq1ivLxHe/ZtOcbSz+ZDXevgV4sVO9Z7/ZwplManrjKVPUNAdhYbBjB3z+ufqd//gj9Oql5q4HNU3xwIFw6pSxcWvGsHew5ZXXnufPfQGE3AgzOhyLJLKzntTf318eOWKeqhBzSUiAZcvUqkVRUan12zY2qh29ZUt1Fl+ihPk+87cVu7n8z1WqvFgR/+ZVzLdjCyalqrRxdlajZg8dUguYbNwITZrAtm3w8cdqZssqVdRtxYqpg60063PzRhhd237N293q07WnZV/FZpYQ4qiU0j8978m1zTIpC1APHarOEh8dlOPkpJoUpk6F8lnQWd/07QbPflEuI8Tj7fU1a6rZNFPOPUwm8PSErVthyZLU13l5qWad8uXV1rlzxq+stJzFu5A71Wr4sX3rCbr0aKA7VtMp1zXLSKnOAsuVU7Xa/7UA9S+/ZE1i19LOZEpdJrBpUzW5WUgI3LgBv/6qZtps1Uo1qa1cqebKT+kjmTFDHSDik4uK/v4bDh9WHeWa5WjSoiIhN8M5fUovC5leuerMff9+VYd99uzjZ+ouLuDnp+q207JOqWYsb2+1NW2a+pyUcP26eh5UfX3JkqmLnowZo+rxU37m56d+7uen1qn19VWPfXXfXY5Sr0EZ7OxN7NpxhgqVihodjkXJFW3ux4+rzrnDhx+f5dDFRbXZzpih2tb1VZ/1CgxUC4efP6/a9oOC1O3ly6ljF3x9UxcuGTZMNc+NHase79mj5twvWlQ1++j/K9ln1NDVXL18h6Vr+ubaphnd5v6E8+fVH+mvv6rL9ZTjmIuLmgVxyhQ1t3pm1inVLMOTNfgpEhLU0oZBQalNOgB376auQQvQrl1qzb6Tk6rw8fFRnb9FiqitShU1chfUuAh7804VlGvVrleKQwcCuRYcik/RfM9+gwZYaXIPDoaRI1WHaXy8qqcG9cfq4ADjxkGPHuZdp1SzTLa2avnD4sUff37x4scfb9yoFi2/ckUdDIKD1bZvn2oOiotTnbkpyT1/fjVyecIEddDo3h0KFlSbt7e6LVAgdXtyhLOWqmr1EgCc+OuSTu7pYFXJ/fZt1ba6cKFK6CmdaU5O6o941CjV5p5V65Rq1qtmTbU9jZRq8fOU5p2kJDWCuUYN9TgsTJV23rz531Mlu7mpBdKHDlWvHzpUHRDq1VOdwHv3qmqh/PnVrbu76nDODXyK5cPdw4VTJ67ySutqRodjMawiuUdEqIFHM2aopJ6yRJyDg/oDGDRI/bFl1zqlWu4ihCrJTGFjo04kUnh7qzZ/UMk9JERtDm2/2wAACX5JREFUt2/DrVup9yskz+8WGqoqul5S88px4oSaV//Jz3R3V53Dnp7qdsQIdeVw9SqsW6eakooUUU1M16+r13t4qGZJS2q6FkJQumwhAgNCjA7Folh0co+OVgn9yy9VUo+OVs/b2amk3qOHmtgru9cp1bT/klKZ5ef336/x9VVNPimqV1dn/nfvqu3OHTU249499TjlNuVK9dQpGDxYzdtTpIiayfTR1bRMJpXo3d3VPPwpt+PHQ+nSqgDht9/gvffUCdGlS6r81M0tdXN1zd4rB79SBThy6AKJCUmYbHUnWVpYRHIPD398MYj4eFiwQJ0dxcamVsCYTCqxt2un2tWNWKdU08zN1TW1iSctWrRQCd/VVT1u3BjWrFHNPaGh6jY8XN0PD1fb+fOpzUr79qlChLffVol80aLUqqFHOTurwgQ3N3W7bZs6kVq/Xt2fO1ddIfz6q6pMcnV9fHNxefz20Q7sJxUu4kFSouTWrXAKFdaj1NIixyf3//1PJerRo1UyX71a/ce7fz+1/VIINf9L8+YwaRKUKmVoyJpmKBubx0fpFiumtrTq3RveekslbFBn/XXrqoPA/ftqe/R+RIS6TZnKOSBADThLafpZtkxNmf3/sbdPbU4dOBCOHVOTzIFqbtq/rzQBAfb06WOHT1F1IHh0K1BAndSBGrBmMkGlSupxSIh67OSkttxSHZej69xHj1bJOipK/QPa2qrml0c7pZydVUfX9OmqFE3TtJwlKkpdLURGqllXU07MIiNT7yckqL4xULOHBgWpSiNQM7Hu3BnH5Yv3cXVzIz7ejqio1IMBQJkyanAiqH4HGxv44w/1uHRpdWWSwsEhNdGnbPXqqc9N+bwyZdRBBtTBRQj1OgcHdRB7citRIjX/nDiRWhmVlKS+u4OD2mwzeDptVXXuY8emJnZ4fPARqEu5smXVqNK6dbM/Pk3T0ibl7Dqt3n//8cfffAPnz92lT7eFjBnfjroNygDqRC8qSvW1pTQpgTrRS1kpDVQF3Z07qa99couJeXwCuosXH28GXrhQXZ2krOnwNF27wtKl6n7NmupANX68usLx9Ex9ncmUmuhTDhQODuo7Dx6sDnavvw79+6vb4GDYvDntv7tH5cjk/tVX6hfzZEJPIQT07ateY0m9/pqmZUxMtOotdnRKHZxiMqmmo5TmoxTPP//4406d0vdZP//8+OPbt9VtUpK6Wkg5KMTGqgNDTMzjB4PVq1PXJHBwUAeb2NjU16fcf/RxweS1ehIS1OOUg9X9++pgkxE5rllm8mT47LP/TuwphFADS1q2NGOAmqblSL9vP8VXo39i3vJe+JbMffM8W3yzzLRp/53YhVBH6JgYVTfcrJmetVHTcouAszewt7elWHFd15xWOSa5z5qlqmFSatVtbFR5VHS06qxo0ULNAvjCC4+3YWmaZt3i4xPZ/ftpKlYpqmvc0yFHJPcFC9S0AA4Oqk69TBk1Oq9JE9VZqkeWalrutXHdEW7fus/gEboNNj0yldyFEC8BMwATsEBKOT4j+/HwgE8+Ucuq1aqVvp51TdOsU3x8IvO+/o2f1hymWg1f/Gv9P8N6tX/JcHIXQpiA2UAzIBg4LITYKKU8nd59vfmm2jRN01KkJPY2HWryXt8muXYu94zKzJl7TSBQShkEIIRYDbQG0p3cNU3TntSxS10qVy1G/RfLGR2KRcpM70QR4Oojj4OTn3uMEKKXEOKIEOLI7ZSCUU3TtGfwzJ9HJ/ZMyExyf9o10r+K5qWU86SU/lJKf69H50XVNE3Tskxmknsw8OiKtT7A9cyFo2mapplDZpL7YaCUEMJXCGEPdAQ2micsTdM0LTMy3KEqpUwQQvQDtqFKIRdJKf8xW2SapmlahmWqzl1KuRXYaqZYNE3TNDPRY3k1TdOskE7umqZpVkgnd03TNCukk7umaZoV0sld0zTNCunkrmmaZoV0ctc0TbNCOrlrmqZZIZ3cNU3TrJBO7pqmaVZIJ3dN0zQrpJO7pmmaFdLJXdM0zQrp5K5pmmaFhJT/Whkv6z5MiNvA5Wz7wFT5gTsGfK6R9HfOHfR3zh3KSCnzpOcNmZrPPb2klIYsoiqEOCKl9Dfis42iv3PuoL9z7iCEOJLe9+hmGU3TNCukk7umaZoVyi3JfZ7RARhAf+fcQX/n3CHd3zlbO1Q1TdO07JFbztw1TdNyFZ3cNU3TrJDVJ3chxEtCiHNCiEAhxAij48lqQoiiQog/hBBnhBD/CCEGGh1TdhBCmIQQx4QQm42OJTsIIdyFEGuFEGeT/63rGB1TVhNCDE7+P31KCLFKCOFodEzmJoRYJIS4JYQ49chz+YQQvwohziffeqRlX1ad3IUQJmA28DJQHugkhChvbFRZLgEYKqUsB9QG+uaC7wwwEDhjdBDZaAbwi5SyLFAFK//uQogiwADAX0pZETABHY2NKkssAV564rkRwA4pZSlgR/LjZ7Lq5A7UBAKllEFSyjhgNdDa4JiylJTyhpTyr+T791F/9EWMjSprCSF8gFeBBUbHkh2EEG5AA2AhgJQyTkoZZmxU2cIWcBJC2ALOwHWD4zE7KeVu4N4TT7cGlibfXwq8npZ9WXtyLwJcfeRxMFae6B4lhCgBPA8cNDaSLDcd+AhIMjqQbOIH3AYWJzdFLRBCuBgdVFaSUl4DJgNXgBtAuJRyu7FRZZuCUsoboE7egAJpeZO1J3fxlOdyRe2nEMIVWAcMklJGGB1PVhFCtARuSSmPGh1LNrIFqgFzpJTPA5Gk8VLdUiW3M7cGfIHCgIsQ4m1jo8rZrD25BwNFH3nsgxVeyj1JCGGHSuwrpZTrjY4ni9UDXhNCXEI1uzUWQqwwNqQsFwwESylTrsjWopK9NWsKXJRS3pZSxgPrgboGx5RdQoQQhQCSb2+l5U3WntwPA6WEEL5CCHtUB8xGg2PKUkIIgWqLPSOlnGp0PFlNSjlSSukjpSyB+vf9XUpp1Wd0UsqbwFUhRJnkp5oApw0MKTtcAWoLIZyT/483wco7kR+xEXgn+f47wIa0vClbZ4XMblLKBCFEP2Abqnd9kZTyH4PDymr1gC7ASSHE38nPfSyl3GpgTJr59QdWJp+0BAHdDI4nS0kpDwoh1gJ/oSrCjmGF0xAIIVYBjYD8Qohg4DNgPPCDEKIH6iDXLk370tMPaJqmWR9rb5bRNE3LlXRy1zRNs0I6uWuaplkhndw1TdOskE7umqZpVkgnd03TNCukk7umaZoV+j8kfwJoKeEYtgAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Solve optimization problem\n",
"xsln = solve_opt(True,False)\n",
"\n",
"# Create contour plot\n",
"visualize(xsln,True,False)\n",
"\n",
"# Draw gradient\n",
"draw_gradients(xsln,True,False)\n",
"\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.5 Take 3. With $g(x) \\leq 0$ and $h(x) = 0$](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.5-Take-3.-With-$g(x)-\\leq-0$-and-$h(x)-=-0$)",
"section": "4.2.3.5 Take 3. With $g(x) \\leq 0$ and $h(x) = 0$"
}
},
"source": [
"### 4.2.3.5 Take 3. With $g(x) \\leq 0$ and $h(x) = 0$"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.5 Take 3. With $g(x) \\leq 0$ and $h(x) = 0$](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.5-Take-3.-With-$g(x)-\\leq-0$-and-$h(x)-=-0$)",
"section": "4.2.3.5 Take 3. With $g(x) \\leq 0$ and $h(x) = 0$"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Ipopt 3.12.10: \n",
"\n",
"******************************************************************************\n",
"This program contains Ipopt, a library for large-scale nonlinear optimization.\n",
" Ipopt is released as open source code under the Eclipse Public License (EPL).\n",
" For more information visit http://projects.coin-or.org/Ipopt\n",
"******************************************************************************\n",
"\n",
"This is Ipopt version 3.12.10, running with linear solver mumps.\n",
"NOTE: Other linear solvers might be more efficient (see Ipopt documentation).\n",
"\n",
"Number of nonzeros in equality constraint Jacobian...: 2\n",
"Number of nonzeros in inequality constraint Jacobian.: 2\n",
"Number of nonzeros in Lagrangian Hessian.............: 3\n",
"\n",
"Total number of variables............................: 2\n",
" variables with only lower bounds: 0\n",
" variables with lower and upper bounds: 2\n",
" variables with only upper bounds: 0\n",
"Total number of equality constraints.................: 1\n",
"Total number of inequality constraints...............: 1\n",
" inequality constraints with only lower bounds: 0\n",
" inequality constraints with lower and upper bounds: 0\n",
" inequality constraints with only upper bounds: 1\n",
"\n",
"iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls\n",
" 0 2.4439483e+02 1.00e+01 2.05e+00 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0\n",
" 1 4.4148045e+01 5.54e+00 2.30e+00 -1.0 2.13e+02 - 8.84e-01 4.46e-01f 1\n",
" 2 8.2513369e+00 4.16e-01 1.12e+00 -1.0 3.36e+00 - 1.00e+00 9.25e-01f 1\n",
" 3 1.0558961e+00 0.00e+00 8.05e-01 -1.0 9.84e-01 - 1.00e+00 1.00e+00f 1\n",
" 4 2.1482166e-01 0.00e+00 1.14e-01 -1.7 2.30e-01 - 1.00e+00 1.00e+00f 1\n",
" 5 1.6203098e-01 0.00e+00 9.32e-04 -2.5 2.25e-02 - 1.00e+00 1.00e+00h 1\n",
" 6 1.5801768e-01 0.00e+00 1.94e-06 -3.8 3.61e-03 - 1.00e+00 1.00e+00h 1\n",
" 7 1.5786332e-01 0.00e+00 1.79e-09 -5.7 1.44e-04 - 1.00e+00 1.00e+00h 1\n",
" 8 1.5786148e-01 0.00e+00 2.44e-13 -8.6 1.73e-06 - 1.00e+00 1.00e+00h 1\n",
"\n",
"Number of Iterations....: 8\n",
"\n",
" (scaled) (unscaled)\n",
"Objective...............: 1.5786147595031963e-01 1.5786147595031963e-01\n",
"Dual infeasibility......: 2.4449104235876087e-13 2.4449104235876087e-13\n",
"Constraint violation....: 0.0000000000000000e+00 0.0000000000000000e+00\n",
"Complementarity.........: 2.5065016939133549e-09 2.5065016939133549e-09\n",
"Overall NLP error.......: 2.5065016939133549e-09 2.5065016939133549e-09\n",
"\n",
"\n",
"Number of objective function evaluations = 9\n",
"Number of objective gradient evaluations = 9\n",
"Number of equality constraint evaluations = 9\n",
"Number of inequality constraint evaluations = 9\n",
"Number of equality constraint Jacobian evaluations = 9\n",
"Number of inequality constraint Jacobian evaluations = 9\n",
"Number of Lagrangian Hessian evaluations = 8\n",
"Total CPU secs in IPOPT (w/o function evaluations) = 0.011\n",
"Total CPU secs in NLP function evaluations = 0.000\n",
"\n",
"EXIT: Optimal Solution Found.\n",
"\b"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAAD8CAYAAACMwORRAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzsnXd4VHX2h987PTPpvRdSCSGFJr1IEyyINAVR3N+q6y6ra1t1Xd11113dddVd26prV1AUFVCpUqRDgEAC6aSH9JBkkkyf+/vjQhTpIckkZN7n4YFk5t45d2b43O8995zPEURRxIkTJ06cXF3IHB2AEydOnDjpepzi7sSJEydXIU5xd+LEiZOrEKe4O3HixMlViFPcnThx4uQqxCnuTpw4cXIVclFxFwThPUEQagVBOPqT33kLgrBJEISCU397dW+YTpw4ceLkcriUlfsHwHU/+93jwGZRFGOBzad+duLEiRMnvQThUpqYBEGIBL4VRTHp1M95wERRFKsEQQgCtomiGN+dgTpx4sSJk0tH0cntAkRRrAI4JfD+53uiIAj3APcA6HS6oQkJCZ18yZ7j9PlOEBwbR3/GZLWS39iAQibDXa3GQ61Bp1LR6z6S9nbIz4eoKPDwcHQ0iIgU6KuRIeCl0uGh0qEQru5bay2WKky2drQKT1zknsgEuaND6jy2chDbQOYHMm849Y0/ePBgvSiKfpezq86K+yUjiuLbwNsAw4YNEw8cONDdL3lFNDeDpye8+CI89JCjo+m/tFssbC4+zobCAraVFtNusaBRq5kSFc11MbGMC49Erej2r++l0dzcK4QdwGq38UNtNl+W7eNAYxEKQc6kgETmhI8kzSsS4SpcsVQZsjnQ8ClFrXtQCBqSPGeQ5j0Xd2WAo0O7bERzOqL+P2DZDzIdgut94DIHmUxdern76tG0TF8Qd7sd/vY3mDoVRo50dDROAIxWCztKS9lwvIDvi4/TYjLhqlRx7YABzIiJY0JEJBqFsmeDOnwYtmyBBx/stZd4pa11fFm+n+8qD6K3Gol2DWBO+DXMCE5Dp1A7Orwup8FUysHGz8lr/h6AePfJDPNZgLc64rzbNJlP0GqpJVSX2lNhXhRRFMG8F7H1P2A5BKqRyH0+PiiK4rDL2U9nxf0FoEEUxecFQXgc8BZF8fcX209fEHcnvRuzzcae8jLWHy9g4/ECThqN6JRKJkUNYGZMPBMje0Dom5pg6FAwmSArC7x6d7GY0WZmY1UmK8v2kttyAp1czcyQNOaGjyTK9bwZ1T6L3lLLocaVHG36DqtoZlrQ7xnoMfWs51ntZkra9nGgYQUyQc4Yv/8jRJvsgIjPjSTy20G0I3O5tuvFXRCET4GJgC9QA/wJWAV8DoQDZcA8URQbL/ZifUXcq6ulFXxwsKMjcXIhrHY7eyvKWVeYz4bCAhqNBnRKJZMHRHN9TDzjI7ohdWO3w+zZsHYt/PADjB7dtfvvRkRR5FhzBV+U7eX7qkwsoo3hPtHMDx/FWP8E5FdZbr7d2sSRk6tI9pqFTnHuE7BdtCET5BTp95DbsolJAQ/gougdKbafIghC96zcu4q+Iu7JyRAdDV9/7ehInFwqp4V+bUEe648X0GQ04qpSMT06lhti4xkdFo5S3gU32v7xD3j8cfjPf+D++698fw7ipLmVVeUH+Kp8HzXGZoI0nswJH8ms0GF4qLRd+loWi4WKigqMRmOX7rcrEBERELCLVgy2ZrRyL0TAYjcgF5QoZKoejUej0RAaGopSeebVp1Pcu4hx40CplFKqTvoeFpuN3eVlfFuQx8bjhejNJrw0GmbExnNjbDzDQ0KRdSZPXlEBAwZIK/fPPuu1ufbLwWq3saM2h8/L9nCwsRi1TMl1wSksiBhNjFtgl7xGcXExbm5u+Pj49Nobus3mKpQyF0Ts2OxmEAQsdiMqmRY35WUVqXQaURRpaGhAr9cTFRV1xmNOce8ibrwRKivh0CFHR+LkSjFZrWwvLeGbglw2Fx3HYLUSqHPlxvgEbopLINHP//IE54cfYMgQcHPrvqAdRKG+ms9L97DuxGFMdgtDvQdwa8ToK07Z5OTkkJCQ0OuE3Ww3YLG1Y7K3IxcUuCr9aDSV4qEMRiV3wWI3YrS14Krw67HYRVEkNzeXgQMHnvF7p7hfgKKqBt5dv5+S6kZKa05ittpQKuSoFHJcNSq83LR4urrg56Hju3dTKc334JutNYT4euDv6YpcdnXlI/sjbWYzm4uP801+Lj+UlmC124nx8mZWwkBuihtI2PnKGS0WSE/vU/n1K6HJ3M6aigN8UbaHGmMzIS7ezI8YxY2hQ3FVaC57fzk5OWeJlSMx29pptzUhIKCQqVEKLqjkLrRa6rCKZjxVIQBY7Sb0ljo8VMEIgMHWglU0oZG7o5K5dFt853q/nOJ+AQoq63ngjVVEBngTFeiFRqXEarNjttpoaTdyUm/gpL6duuY2jqy9hpOF8STf9SYACrmMEB8PwgM8ifD3IiLAi6hAb6KCfPBy7b4P2Un3cdJgYG1hPmvyckg/UQnA0KBgZsUP5Ia4eDw1P/lcH31UanzIzISkJAdF3PNY7Ta21WazomQ3R5pK0cnV3Bg6jAURowjRel/yfnqTuIuiSJu1gTZrI1qFJ25KqVrILtppMJXgpQrtyLO3WGoQENApfGizNmITLahkLrTbmvBQBqGUXf6J7lJwins38tjjdl78l8DOrHJONDRTUddERX0zpTUnKas9icli63iut5uW6GAfooN8iAnxJTbEl+ggH7Sanr0R46TzVLQ0syYvl9V5ORQ0NqCUyZgUOYDZAxO5NuMIynnz4Ne/htdfd3SoDiO7uYJPS3bxfXUWoigyMSCRhZFjGewZftGURW8S99NY7WbarY1YRCNuCn9ERIy2FjxUQQDYRSv1phJ81VG0WRuRIUMtd0MhU9FmbUBAhvY8FThXilPcu5F//hMeewxaW0GnO/Mxu12k+mQLxVWNFFc3cryqgeMnGiiqaqDdZOl4XpifJ/FhfsSF+pEQ5k9CmD++Hj/bmZNehSiKZNfV8nVuDmvyc3AtKWX1i/+hOSKC+vXrSIm4Ojs8L4daYzNflO7l64r9tFgMJHmEcVvkGCYFDEIhO3c1Um8U99NY7WZERGSCHL2lFg9lICIirZY6BEGOVu5Ji7UGV4UfSpnU+NVoKkOr8EQjd0cUxS7/TjjFvRt56y341a+k4oiQkEvbxm4XqWpsoaCynvyKOgoq68grr6OivrnjOb4eOgaG+5MYHsDAiAASwwOcgt9Lsba3Yxw6FKGyklmPPkiRhzsDvLy4JWEQsxMSCboKb6heDgarme9OHOLTkl2UtzcQpPHk1sgx3BQ67Kzu194s7gAGg4HrrruOr9cvQ5RZkQsq5IICncIXo60ZERG5zYVpU6ezbtM3mAU9HsqgDg+b0wJvF61Y7EbkguqcJZTr16/ngQcewGaz8ctf/pLHHz+3ma5T3LuRFSvg1lvh2DFITLyyfbUaTORV1JFbVktOWQ255bUUVzd2mJMFermRGBFAUmQgSVGBJIYHOFM6vQFRhFdfhbg49JMmsbYwn69yjpF+ohIBGBsewZyBg5gWHdPz1ge9CJtoZ0dtLstKdnDkZCmuCg23hI1gQcRo/DTuQO8X99dffx2r1coDDzyAxW5EREQpaBAEgTZrI4giOqUPzzzzDMGRPixatAgXuQfCTyqIrHYzLZZqFIIKs70drcILF7lnx6reZrMRFxfHpk2bCA0NZfjw4Xz66acknkNgnOLejRQUwOrVcMcd4N8N3dntRjO55bVkl9WSXVLN0dJqKuqkFb5MEIgO9iF5QBDJUUEkDwgm3N+z36cDehSDAVzOfaO8tKmJr3KP8VVONpX6FtxUam6KT2BuYhLJ/gH9+nM62lTOspIdbK0+hkyQMSM4lUVRYzGVN/YKcc/JyeHee++lqamJxYsX89Zbb1FYWMjo0aNZvnw5kZGRAEyaNIk//OEPTJ06ld//4WFaWpp587V32HtwB089+TQb1n1/hvOkXbSht9QiFxTIra5s2ryeb9d+w803zGXmzJkA7Nmzhz//+c9s2LABgOeeew6AJ5544pxxdoW49xJbvd5FbCw88kj37V+rUTEkNpQhsaEdv2tqNXCspJrM4iqyiqvZkJ7HlzuyAPDUaUgeEExqdDCpMcEkhgegUjo/um7h0CGYMQO++ALGjz/r4QhPTx4cOYYHrhnN3opyvsg+ysrsYyzLOkKcjy/zE5O4OWEg3i5d2+XZF0jyDOO51IVUtjeyvGQnayoO8k3lQV4Omk271YSLXIUgCEycePF93XDDj/8HJ06EJUukP/X1MHfumc/dtu3i+7NarSxatIh3332XtLQ07rvvPpKSkjCbzRQVFXUIO8AzzzzD008/TW1tLUcPZ/PRyjdpMJUQlxjF4YNHz0rH5ORn8d3ab9i6cRfl5RWMmzCG6TOmMGnSJOyiDavdxPHSHEJDf8zxhoaGsm/fvosHfgU4FeIcWK1QVAS+vuB96RVfV4SnqwtjkqIYkyR1ptntIsXVDRwpqiKzqIrMohNszyoCQKWQkxgRQFpMCENiQ0kZEISry9Xn8tfjnDwJc+aASnXRfJxMEBgdFs7osHCemWjk2/w8vsg+yrM7tvHPXTuYGh3N/MTBjAmP6Fw3bB8mROvNo4k3cXfMZFaW7cWit1HaVoeLXIWP2g3QQA8783/11VekpKSQlpYGQGJiIv7+/tTX1+Pp6XnGc8ePH48oirz00kts27YNN60bVrsZuaBApVLR0tKCu7t7x1XagnmLKMw/zu9+9zvee+89PP1csdjbcVG50GKuBkHAJtow2dsw29pRyaUTf3df5TnF/RzU1kJ8PPz3v9KNVUcgkwlEB/sSHezLLWMHA3BS387h4yc4fPwEGYWVfLTpAO9vSEcmCMSH+TE0NpShsaGkxYTgruueGtyrFrtdysNVVsL27dKZ/RJxV2tYODiFhYNTyK2v44vso3ydm813BfmEuLkzLzGJeYlJ/e4mrKdKxy9jJpOdnU2AxpNGcysV7Q28+40SH7UrHkrtJQncT1fmvr6XtlL/OZmZmaSm/mjre/ToUa677jpcXFzO8rzJysqiqqoKX19f3E59ZqdvkJpMJkSlEb3FhJvSD6vdzNZ9ayjLPsm6deuZO28eJrOBaVOnseT/FuMb4o6nMoS4yCQ+rlyOHamMuqKigqCgoMs/kMvAmXM/B2azdFV+zTUQE+PoaM6PwWQhs7iKQwUVHCqoJKu4CrPVhiBAfKg/w+JCGR4fRlpMiHNlfzGeew7+8Ad45RX47W+veHcmq5VNRYWsOJbFrvIyZILAxIgobktKZkJkFIp+1PF8OocsiiItFgMNZj0mmwWFTI6Pyg1PlRZZNztSvvzyyxQWFvL6669z+PBhxowZQ1ZWFgMGDCAsLIyCggI0Gg1VVVVMnz6dFStWcP/99/PII48wffp0ABoaGhg7diw5OTmIoh1BkGG1m2izNuKhCsIu2jDaWqitr2bvtiP4hrsw/pqpqORarFYrsXHRfLvha2Ijkhg2fBjvfPgaiYMS0Sq8zsjhO3Pu3YhKBYsWOTqKi+OiVnJNQjjXJIQDYLJYOVpSzcH8Cg7kl/P5D0f4ZPMh5DKBgeEBjEgIZ0R8GCnRwaidOfsfEUUoLoYFC2Dp0i7ZpVqh4Ia4BG6IS6CsuYnPjx3li+yjbPl2FYE6V+YNSmLBoMEEu7l3yev1BQRBwEOlxV3pQpvVRL1JT42xiXpTC14qV7xV3WfzsXjxYq6//nqGDx/OqFGjiIyMZMCAAQBMmzaNnTt3Mnr0aG655RZefPFFBg4cyFNPPcVjjz3WIe5bt27tuEF6ulJGLiiZdd18ampqAQEBkAlyRESe+PPDHSkYhULB3196mtnXL8Bqs7HozvkkDhqEXbTQYqnGQxnc5Wka58r9POzbJzUw9eVuc5PFSmZRFel55ezPK+NYSTU2u4haKSctJoQRCeGMHBhBXIgfMln/ygufE4tFsgPtrt3bbGwpKeLTrEx2lJUgCAKTIqNYODiF8eGRV61/0YVKIdutJhpMelqtRmSCDC+VDm+V63kbojpLa2srrq6uALzwwgs0Nzfz7LPPApCRkcFLL73Exx9/fMF93HLLLTz33HPEx589dM5ka0XEjlrmhiAI6C21KAR1hzd8q6Ueq2jGXRlAi6UaF7knarnU49JkrsRV4deR+nGu3LuZ22+HYcPg008dHUnnUSsVDI8PY3h8GL9mNK0GE4cKK9mXU8b+3DJe+Xonr3y9Ey9XF0YOjGBUYgQjB0b0n8YqiwXuuQceflg6i3ejsAMo5XKmR8cyPTqWipZmPjuaxYpjWWwuLiLU3Z1bByUzf9BgfLX9p9JGq1CjVagx2szUm/Q0mFppNLXiqdLho3ZFKesaiXr55Zf57LPPUCqVjBkzhpdeeqnjsbS0NCZNmoTNZkN+Hs9/s9nMzTfffE5hB1DLXc/4WSGosYpmQPKGN9r0eKlCMdiaUQiqDl8ai92IVbR0i2+8c+V+HsaMAY0GNm92dCTdR11TK/tyy9iTU8q+nDIa9e0AxIX6MSoxgjGDIkmJDu6aIRe9kYcfhpdeguXL4bbbHBKC2WZj0/FClh89wp6KcpQyGdfFxHF7cgrDgkKuirr5y2liMtksNJj0NFsMAHiqtPio3FDJ+9Y61GI30GKpRQAUMo20ipd7dKzalTKpSarFUoMcBTqlz4+llc4mpu5lzhzIyYHsbEdH0jPY7SL5lXXsyS5hT3YphwtPYLXb0WlUjEgIZ+ygSMYkReHv6XrxnfUFvvxSKpheulTqRO0FHG9sYFnWEb7MyUZvNhHv48vi5FRuTkhE281XFd1JZzpUzXYrDaZWms1tiICH0gUftRtqed96H0y2NknIkSFiR2+pQavwRinTYLEbabXU46r0PcNh0inu3czSpdKCrvGik2GvTtqMZvbnlrHrWAm7j5VQfVIPSKv6sUlRjBscRVJkYN/ME+fnSzm3xESp7FHVu+we2i0WvsnL4ePMw2TX1+GmUjMncRCLk1OJ8uzdw7jPxZXYD1hOiXzTKZF3V7rg2wdFHkAU7TRZTqCTe6OSa2k0laOW69AppGYam2hFhrzLhnX0rWudHiQwUOppMZlA3Q+rCHUaFZNSY5iUGoMoihw/0cDOY8XsPFrMhxvTeW/9fjxdXRg7KJLxyQMYOTCi75Rb/uMfkqB//nmvE3YArVLJgiQp/36o+gQfHTnMsszDfHD4EBMiIrkzZQjjIyL7RXOUUqYg0MUTH7UbjaZWTlpaabEY+pzISykXGS5yd8mDxqZBISg7hF0U7Zw0lSETFNhEy0X2dmk4V+7n4Z134O67obQUwsMdHU3voqXNyJ7sUrYfLWL3sRKa24wo5DKGxYUxIXkAE5KjCfTuxQ07ZrO0eu9DpVC1ba18ejST5VmZ1LW3EenpxR3JqcwZOAi3Xr766ErjMKvdRqO5lUZzG6Io9jmRP43NbkEuk2I+rcEGWzNt1gaK8stp8NnOaL9f4qkKBpxpmS7l22+lWar79sGIEY6OpvditdnJLDrBD5lFbM8sorT2JAAJYf5MSo1mYkoMMcG9ZDDyunXSh+nj4+hIOo3ZZmN9YT4fHskgo7oKV6WKuYOSuDM5jYiftdH3FrrDFfJqEfmfYxdtZB47xC7lM9hFK8leN3GN7+24KDyc4t5VHDgAw4fDqlUwa5ajo+k7lFQ3si3zONuOHCeruApRhFA/DyalxDApNZrkqOBLqqmvamxh3f5cak7quXlMEgPDA64ssAMHpBKo22+Hd9+9sn31Eo5UV/HBkQzWFuRhtduZHBXNXalDGBka1jtOpqfoTsvfq1Hkc3JyCI/1Z2/dhxxrXk+AJp5bo15zintXUVEBYWHw5ptw772OjqZvUtfcyvbMIrYePs7+vDKsNju+7lompcZwbVosQ2NDUcjPfUP2gTdWEerrSbCPO+vSc1kwIYUbRw3CZrdf/k3cxkYYMkTyjzl06LJ8Y/oCNa2tLMs6wvKsIzQaDQz09eMXaUO5ITYetcLxt9V6ws/darfRYG7lpKm1o7rGV+3e50oo4cz3q95UjNnWToguySnuXYXVCmvWSEUVzpz7laM3mNh1tJjNGQXsOlaC0WwlLtSPz568/aznGs1WfvGvFbx+/y14ubrw6qqd+LrrSIsNYdPBfDIKK5kzLpkZwxMQhIu469ntcNNNsHEj7Nx5VefYjFYLq3NzeP/wIfIbG/DT6rgjJZWFSSl4ncefvifoyWEdVruNBpOek6eqazxVWnzVbl3WDNUTdFUpZB+sY+sZFAq45RansHcVbi5qrhuewAv33MjmF37FC/fcwO1ThpzzuY36NgZHBbHkn5/xztp9FFc34uXmwl8+3kSYvyd3TR/OlzsyKapquHj64d//hu++g5dfvqqFHUCjkKps1i26kw9nzSHRz48X9+xizPtv89TW7yluOunoELsdhUxOgIsn0W6BeKl0NJnbOa6vodrQxIaNG1i8ePFZ2xgMBiZMmIDNZjvHHiXMZjPjx4/HarV2Orb169cTHx9PTEwMzz//fKf3c6n0ndOZA9i7F4xGLmm4gJNLx0WlZHJa7Dkfqzmp57/f7CElOpixSZG8vyGdO6cNo6XNiFaj5ObRUoXLocJK8ivriAm5SIpl0SLJZuDXv+7qw+i1CILAuIhIxkVEkt9Qz3sZB/ni2FGWZx1hanQMdw8ZxtCgSxwO3EdRyuQEunjirXal3iit5Lek7yI2KeGs1N57773HLbfccl7rAQCVSsXkyZNZsWIFizrhKmiz2fjNb35zxpi9m2666Zxj9roKp7hfgKeegtZW2LPH0ZH0H07bFs8aNQilQs6Roiqa24xsOpjf4WsviiJymYyaU41VdrvYcZPWYLKw4UAedVV13DA+laCAAHjsMYcdj6OJ8/Hl+SnTeXjUWD7KzOCTzCNsPF7IkMAg7hk6nCkDYnq+Xv5cq6X586UTcHs7nHJePINOjmJSyRQEa73wsbly/FgeHn7eXDN2FGVFJXzy8cdMmzqNZcuWsXz58o5tfjpm749//CMtLS288sor3HzzzTzxxBOdEvf9+/cTExPT4UR56623snr1aqe4O4rXXuuVPS5XPQaTBaVCjsVqw9/TlYP5FRSeqGfmCCkPabba2J9bxiPzJgJgF0VkCNQ3t/Hx9wepqm/Cc/NGnvluC8+98gRebv3HiOt8+Ol0PDxqLPcNu4aV2Ud5J+MAv/puDQO8vLg7bRg3JyT2ipuv3YVarqTgWC7zb1vAnzf9la+/+pq3PnyX5JHDLjhmLyMjgzVr1gCQlJREenr6WfseN24cer3+rN//61//YsqUKQBUVlYSFhbW8ZhzzJ6DOY8BnJNuJDEikG/35rD4+eX4e7kR6uuBIAgMPTVv1mK1cbCgArlMIHmANMnmdMXNN3uPoVTI+V3OdoK/eJ2H//gGu7JLuOGaRPTtRg4VVmKzi1yb2osnsHQzWqWSO1LSWDg4hXWF+bx9MJ0ntmzi5X27uSt1CAuTUs7bFGWz23l+13auCQllyoAreA8vNEpJq73w450cxWSxWGhsbOSJ3z+OTCbDS6HF09OLvMoidO6uNJvbcVe6IAjCWWP2Tqdr5HI5KpUKvV7fMaEJYMeOHRd9/XMVrjjH7DmQnByp7+XeeyVvdyfdT7CPO//+9Sxyy2vJKa3h2rRYmtuMvL9hP/p2I8erGvj+YAHXX3NqFW+xolIqONHQTEVdM+Nbqgj+z4tw//2Y/AMJ85Maex55+1vC/T3JK6/jhyPHeWTeBNy0/XcUoUIm48a4BG6IjWdneSlvHUznH7t28Eb6fhYnp/LANaPOcgNtNBgIcnVj6bpveXjUGO4eMtxB0V8+2dnZpKSkIDuVa887lsOo1GEM8A7BZDJxwtBIg1mJv9qDopz8s8bsncZkMqHRnPm9uZSVe2hoKOXl5R2PVVRUEBwc3NWHeQZXJO6CIDwI/BIQgSzgLlEUjRfequ+QkSG5ws6cCQkJjo6mf5EQ5k9CmD8AWrUShVzG4n98ip+HK/MnpDD21CBx1amJUjmltbga2gj7+59h1CiyfvMwAfvzEEWRjQfzkMtkPLlQ+o+26LllNLUZO8R917ESooN8erdlQjchCALjwiMZFx5JZk01bx1MJ/1ExTnHAPrpdMxNTGJVXg7XhEgphsPVVajkchL9/Hs69MviyJEjpKSkdPycmZnJrFmzCPMPQrCDt6BFL5o5VHSMexcuZsWXX/D7hx5hw4YNZ4zZ8/PzQ/kzh85LWbkPHz6cgoICiouLCQkJ4bPPPjsjz98ddFrcBUEIAe4HEkVRNAiC8DlwK/BBF8XmcAIDpb+rq53i7kiUCjlPLpyCyWKlsr6ZAUE+mCxWDhVUEOjtTrCPO64uKowmM17hIfD5p6QfPUGIrwcmi4288jqmDYsDoKKuiYQwfyxWG02tBv63dh9ltSepbGhh7KBIHpwzvld1d/YkyQGBvD7zRsw223nfg7cPphPt5U1yQCAmq5WDVSf4Jj8XP62WR0aPI96ndzaIHTlyhBE/KYU9evQoSae8haZNm0bW/kOMHDWK2+68j98/+zSacB/uffR+/vT0n845Zu9yUSgUvPbaa0yfPh2bzcYvfvELBg0adOUHdgGutM5dAbgIgqAAtMCJKw+p9/BTcXfieNRKBQOCpKEGCrkMi9VGbnmt9JhKwXEzeO3aTruvP7uzS0iMCABRpL6ljRHxUsNCo96AQi5DLpOxcnsmdc2tvLp0Nq8tnU1tUyvtpq5x5OvLqM5TElje3MyWkiLuGyaJpEIm4/bBKaxasIihQSG8vn9vT4Z5Wbz44ossWLCg4+eioiJcTjV2LV26lA8//BBXnY70vfu5Y9Z8fNXuJI0cwvsbvqTa0ITVbmP58uXcc88959y/yWbBYDVfMIaZM2eSn5/P8ePHefLJJ7vu4M5Dp8VdFMVK4F9AGVAFNIuiuPHnzxME4R5BEA4IgnCgrq6u85E6gCDpfp1T3HsZgiAgl8m4ZmCEdHP0zTcJfumfeLioWfyPT/nbp5sJ8nZn5MAImtuNGM1Wgn3csVhtlNc1IYrgrtNZu+PIAAAgAElEQVSwLfM4d06Vmv5UCjkalZKCyr71He1JPs7MIMnfnzgfX+ynylFPl1GODY9AIZNR3twMSAZnLaa+kaH96Zg9ALkgw0/jTrRrIJ4qLSfNbeQ0ljP5+unExp3dnyGKIq1WIxXtDVQbms5589QRXElaxguYBUQBTcAXgiDcLoriJz99niiKbwNvg2Q/cAWx9jienlIppFPcezHp6fDAA/hPnsyLr77MD1nFuOs0JIRLOeDy2mZ8TpVC5lXUkVNWw9DYUE7UN2O3iwyKlC7PRFGkoLKOcL++NwyjOzFZrazMOcaI4FDST1Ty2owbgVPVH4KAUi6nUt/CtpJiAAJdXWkzm3l+13aONzaiUyn5XXScIw/hkvjFL35x1u+UMjlBLl54q1ypNTZz7dzrabOacFOeaeUgCAI+ajesoh2L3dpr0npXkpaZAhSLolgniqIF+AoY3TVh9Q4EQUrNOMW9l9LQIDW0BAbCxx+DTMaElGjSYkJwUUk3vaYPi+NI0Qn+vnwzr67aib+nK9OHx/PtvhyGx/9Yd7zzaDG+Hjq83bW9ZuXVGzDbbBw4UclNn31Co8FAiLt7x2NFJxv5z77dPLpxPa0WMw+NGkN1ayuv7N9Du8XChzfPIczDE4Ol8y37vQG1XEmYzpdInT+uinNXWBltZtqsRvzUP74/Nrsds81xx34l1TJlwEhBELSAAZgM9A1XsMsgMBCqqhwdhZOzsNth8WLpzLtz53k92kP9PPnXvTey8UA+IxLCmDJEWkUq5bKOapzyuib25pQyc7hUXnlqUeoEcFOreXn6TJYOb+Cv27fxweFDKOVy0k9UoJEr0CgUPD52PMkB0hXQi3t24q7WcFtSMkq5nChPL4xX4MfSm3BRnLujURRFGkyt6BQa1HIlVruNdquJZks7NtGOQiYnUOOJQtazg+Y7Le6iKO4TBGElcAiwAhmcSr9cTQQGQkmJo6NwchbHjsEPP0jGYMMvXG8d5O3OndPONNSbkBLNvz7fRlOrgZyyGiICvLl2iNSYI5MJ2Ox21qfncW1qDC7qvusN3lVEe/vwwc1zqGtv409bN7OjrIRHR4/jjpS0juccrKqk0WBgRkwYkadmvWbVVpPoL9VzS6Pmrr6zpt5qwGy3EuwiHXOtqQWFIMNX7Y6LQkWdsYUGcyt+avcetXq4ojp3URT/BPypi2LplQQGSgZiTnoZgwdDbi6EhnZq86GxofzqxlH8cKSIIbGh3DAyEYVc1iFAB/LKeeqD9fzDRc0N1wxk7vhkBgT13QlOXYWfVscb19/Esdoa/rNvD98V5PHo6HEMCw6h3WLBTa0m8tREqB1lJcgFWUfNvCAIHe+vwWJBbzZhF0X8da59bh6sKIroLQZclRqazO14qXQIgkCrxUi71YSXSofFbsUFFX4ad6x2GzJBwCbasYl2VD1gQez0c78IVVVSBiDk6jbR6zuUl8P330smUl0sCD9dWYqiSEZhJV/uyOL7jAIsVhtDYkOYOy6ZyWmxKBU9e4ndWzlcXYUgCKQEBLK2II+vcrJ556bZADyxeSPxPr4MV2kYlJjY8f62Wyyc0LfgqdFgtFqx2GyEe3he/hAWB2IT7ZxoP0m7zYRCkBPtJk0KK2+rRxAE3JUunDS1oVWo8dNIeXiTzUKdqQWbaEcUIUTrjfIcqZqu8nN32g9chNPlkE56AWYzzJsnpWSmT4cubt/+acpAEASGxIYyJDaUR/QTWLMnmy93ZPKH99bh4/4Ds8cMZs64wQR49b+u1p+SGvjjfxBfrQ692cSO0hL2VJRT29bG0uEjaamsBH58f6tb9XioNfhqddjsdir1LX3uJrZckBGm80FvMVBtbKbR1IpWoUYpU+Cl0qGWK3GRq6kxNgGgtxhot5pQyRT4azyoNTbTajXipeo+X5O+c6p0EKWl8Ne/Sn87cTCPPCJNLH/vvS4X9gvh5ablzmnDWPXMXby6dDaJEQG8u34fN/zxXR556xvS88r7nDh1ByNCQrkzJY03D+5Hp1Lxl4mTO6pr7KfenxaTEbso4nfKrOn0722iiNVmo8looKTpJPXtbY45iMvETelCrFsgWoUatUyBXbR3pJhaLO3YRbGjDl4lU+CtcgVAQKDdaurW2Jwr94tQVQVPPy0N8YmIcHQ0/ZjPPoNXX4Xf/U5avTsAmUxgzKBIxgyKpLK+mZU7Mlm16yhbDhcSHeTDgkmpXD9iYL++ATszNp6ZsT/aqda3t2O22ToEr66tDS/Nj3XibRYLNrsdtUJBRUszgiDgpXGhvr0NAQEfbffaNWdnZ7N//34mT56Mp6fnWUZhl4pGrkQURWSCjIr2RtyULjSa9IRpfWm1GhEQcFGoUMjk2Ox2THYLnkrpBNddN5r7nbjbbHbyck5QV9NCW5uJ9jbp7KlQylEp5Wh1atzcXXBzd8HTS0tqqitGo5zzuKA66QkaGuCee2D0aPjnPx0dDQAhvh48MHsc914/ig0H8lix7bBUS//1Tm4ek8SCiSkE+3g4OkyHU97chOVUrbdU8y10zHO12e00Gtrx1+loNBiwiyLBOlcUcjkyQaDVbJa8+gWhc4PRLwGLxcKrr75KS0sLv/3tb69oX4IgEOjiSavFiFW0Ear1wUWh4qSpFbkg67iJ2mxpRyHIO/LtPxV2u2jHbLdisllQy69skdBvxL2irIGVn+1j9/Y8TjZe3iWfp6cWX393AoI8CAj0IDDIk+AQL4JO/VEqnTfXuhUfH1i2DNLSQNm7VsUalYJZowdx06hEjhSd4NOth1m+5RDLNh9iUmo0C68dQmp08FVZAngppAUFk9MkWRKo5ArUCjntFjNquYJGgwGFTIZOqaJK30CwmzuKU742erMJUQSZINBmNtNoMGC2WfHRavHUdN2w7/Lycu666y4GDBiAXq/H/SdNWp3FVXlmo5PZbkUpUyATZBisZgw2M25Klw6xP71yb7MaaTK302oxsmjXq9yfMIPx/p0fLN5vxN1gMLN5QxYjRsUwZnw8A2IC0OpUaLVqBAHMZhsWixVDu5mWZgP6FgMnG9tobGjlg4+Daa9qwGLJ4OD+IoyGH82lZDKBwCBPQsN9CIvwISLKl4hIPyIG+KHTOZf7V4QoQl6eZMl5442OjuaCCIJAanQIqdEhVDfq+WL7Eb7ckcnmjEIGhvuz8NohTBsa1++rbLRKJSf0euSCDDe1mkBXN/RmExqFEu2pE7fNbkdvMhHl5UWz0UizyYhOqcLbxYXa9jZ0StVZXvOXwvnG51VXVxN42iWwG3CRq6gztQDQZG7DQ6VDJ1efURpqF0WqDE34qt3wVruyJHoiu+vyrkjc+00ppCiKmM1W1J3Ihw4cCImJ8OWX0n6aTrZTVXmSyopGKisaqShrpLysgYrSBszmH7vxAgI9iIr2Z0CMPwNiA4iODSQ4xKtj3qeTi/D661KOfdcu6aZHH8NgtvDdvhyWb8mgpLoRPw8dt05KZc7YZNx1/WdQyLlK+wwWCy6nxLzZaKTdYiHoVL77hL6FluZmZk+bzpcb1hPs54+HWhLDgoYGgt3c0HVi/uX27dt5+umnufvuu1m+fDlr1qy54FDsrqTNaqTdakYjV57hTXNa3GuNLZjtFkK1PmTnZNPkK2dvfSG/jZ+OUqZwlkJeCEEQOiXsAJGRUFz84368vHV4eetIHHxmA43NZqemqonSknpKiuooPl5LUWEN+/cWYrdJJ1EXrYqY2ABi4oOIjQ8kfmAwoeE+TsH/Ofv2wYMPwrRpMOyyvtO9BheVkrnjkrllzGB2Z5ewbPMhXl21i3fW7WfWqEEsmjyEEN/+mZd3+Ul6TSYIGKwWLDYbRquVZqORA9t+IDcnh+3fb+YXixdL9fFmM0q5DE0nZ72eb3xeT6BTaND9xJdGbzGgU6iRCTKsdhtN5jYidX6AVEmT01KJQiZDQGBV+dlzWy+FfrNyvxKWLpV8qZqaOtc3YzZZKS2pozC/muMFNRTkVVNUUIPRKKV3tDo1cQlBJAwKZmBiCAOTQvDydu3io+hD1NfDkCEgl8PBg+Dt7eiIuoz8ijqWbT7EuvRc7HaRyUNiuWPK0A53yquRc63cf4pdFKlta6PJaOCJ+37NxrVrMZvNWK1WFAoFarWam266iZfffhtBAG8X7TknRV2MrKws5syZg6+vL7t3776SQ7pi6owtuCtdUMuV1BlbsNhtBGu9EEWRo9nHePbk97wx/P/4smwfjeZWnkia7Vy5dwfR0dDSIhVt+HZi0IxKrSA2PojY+B8bPmw2O2Ul9eTlnJD+ZJ/gi2V7sdnsAAQGe5KYFELi4DCSksOIHOCHXN4P2hJsNrj9dqipgd27ryphB4gL9eOZO6ezdNYYPt2awcrtmWw6mM+wuDDunDaM0YkR/e7mq0wQCHR1xU+r5Z9//zt5x45RUlKC1WpFqVQSERHB4089hdlmw1Oj6ZSwV1VVsWjRIlavXs39999/xvg8R3C6axVOlVGe+rfZbqXVauKGkCHoLQa21Wbz8tA7eaITr+FcuV8Ca9bArFlSpqA7U78mk4WCvGpyjlaQfbSS7KMVNNa3AtLqftDgUAanhjM4NZy4hCBUqqvw3Gy3w9/+Jpn63H23o6PpdloNJr7edZTlWw5Rc7KV2BBflkwbztShcSiukpP5xVbuP2flypXcdtttqNRqzCYTHy9bxtDJ1+LtosVTo7nsksj29nYmT57MX/7yF6ZOncr27dt57LHH2LNnz+UeSrdgsJqpNDSikSsREKgsLGH44DSeOLycYT7RzA0f2amcu1PcL4FjxyApCZYvh9tu67nXFUWRmupmjh4p52hmOVmHyygrqQdApVKQmBRC8pAIUtIiSBgU0vfF3m6HPuQv0pVYrDbWp+fywcYDFFc3EuLjzuKpw7hp1CA0ffxzvVxxnz9/Phs3buQPTz7Js88+y/hrr+W9Tz7GX3dmqtJktdJuseCp0fT5qx1RFGkyt+GiUFGUV4hXVBCv523gN/HTCdR4IpPJnOLeHRgMoNVKNgR//KNjY2luaufokXKOZJSSmVFKUWENoghqtYKklHDShkWSNiyK6NiAvpXGKSuD666Dt96CceMcHY3DsNtFdmQV8d6GdLKKq/B203L75CHMHZ+Mq0vfLK29XHFPT08nPDycgIAAampqKC0rY8QpW+efdnNW6fXUt7ehUSoJdu1cBU1vJCcnh9CYSJ49+hVPD56LTqF2rty7k5AQqXDj/fcdHcmZ6FsMZB0uI+NgCYcPlFBSLM0AdXN3IXVIBENHDGDYNQMICPJ0cKQXwGSC8eMhJwcOHIC43j+WrbsRRZFDBZW8u34/e3NKcXNRc+ukVG6blIana9c18fQElyvul4ooijQZjVS3tmK12/DQaAh0dUUl7/tXOsHREfwp83M0chXJXuEsihrnvKHaXSQkSCv43oabuwujx8czerzk59HY0MrhgyUcSi/mUHoRO7blAhAW7sOwkdEMHxlNclp4p8tCu4WHH4b9+6VGAqewA1LJ7dC4UIbGhZJdWs276/bzv7X7+GTzIeaNT2bxlKH4uHefo2BfQBAkKwN3tZr69nbq2ttoMZnw1Wrx0+r6lIXwz/FQafn3sCX8r3AzSqFzJZvOlfsl0hdHr4miSFlpAwf3HSd973EyM8owm60oVXJSh0QyYlQMI0ZFExzqwIqU5cth0SJ46CF48UXHxdEHKKys5/0N6Ww4kIdKIWf22MEsmTYMP8/eXTabk5NDQkJCt+fFzTYb1a16mo1GabSdq2ufy8eLokhubm6X+Lk7xb0fYTJZyMwoI33vcdL3FlJR1ghAeKQvI8fEMnJMLIlJocgVPbjiWbIEjh+HLVt6nW9Mb6W05iTvrd/P2v05yGUybhk7mCXTh+PfS0W+uLgYNzc3fHx8ekRo28xmqlr1GCwWtEolQW7uHdYGvRlRFGloaECv1xMVFXXGY05x70YOHJBupr76KsTGOjqarqGyopF9uwrZt7uAzIxSrFY7bu4ujBgVzahxcQy/Jhptd/vjiCK0tkInrVb7MxV1Tby3Pp1v92YjkwnMHjuYu3qhyFssFioqKjAajT32miLQbjHTYpRG+WlVSjzUUkdob0aj0RAaGoryZycjp7h3I4cOSa6zb77ZZ7vhL0hbm4mD+4rYuyufvbsK0bcYUKrkDBkWJeX0x8Xh6dVFOV5RlEzylyyROsScXBGV9c28t34/3+yRRH7OuGTumj4cX4/+nZMHaDGZeHX/Hj48koFWqeShkWNYNDilz+XjneLupEuwWe0czSpnz/Z8dm3PpbqqGZlMICkljLETEhg7MQE//yuwRn3lFXjgAcmb/dFHuy7wfk5lfTPvrtvPN3uPoZDLmD8hlSXThuHl1r0DL/oCBQ0NPLN9C7vLy0j09eOZSZMZGtR3BiM7xd1JlyOKIscLati1PY+dW3M7Si0Tk0IZf+1Axk1KwD/gMsyv9uyRyh5nzIBVq/pt01J3UlbbxDtr97J2fy5qlYKFk9JYPGVov3KiPBeiKLKusIC/7dhKVWsrcwYO4rEx4/Ht5mlPXYFT3LuZJUvAYpHmRvRXyksb2L41h+1bcygqqAEkoZ8weSDjr03E1+8CufO6OskQTKmUDMG8vHoo6v5JcXUjb327h40H83FzUXPH1GHcNikVrebqaPbpLO0WC6/u38N7GQdxUSp5ZNRYbktK7tWpGqe4dzPz5kFmpjQ/wglUlDeyfUs2P2yRhF4QIDktgolTEhk/aSDuHj9bES1dCu+8I63e09LOeKi75kg6kZwo31izm+1ZRXi7afnljBHcMnYwKmX/bnMpbGzgT9s2s6einOSAQP46aQqD/QMcHdY5cYp7N/P44/DSS1IzUw9aQfcJykrq+WFzNls3HaO8rAG5XMbwkdFMmjqI0ePj0WiU0N4uNStNnHjGtjabHblchtVqQ9HPJxV1J5lFVby2eicH8isI8nbnvhtHMWNEQq9esXY3oiiyOi+Xv+/cRqPBwOLkVB4cOQb3XjY02Snu3cz//idVzJSUQESEo6PpnYiiyPH8GrZ+f4ytm45SV6tnsLWWCffdzKy7rj3nNlarjfLSBl54dg3jJg1k/qJRfcsXpw8hiiJ7c8p4ddVOcstriQn24bc3j2VsUlS/vnJqMRl5cc8uPsk8jJ9Ox9PjJzEjJq7XvCdOce9mtmyByZNh82a49tw65eQn2O0iuet2ETVvJq0jRuO3bf1Zz7FZ7Xz1+T6qKpsozK9myIgoltw9karKkxTkVTP+2q73JHEifTbfZ+Tz+urdlNc1MSQ2hAdmj2NwVNDFN76KOVJdxZNbNpFdX8fEyCj+MnEyoe6On5blFPduprRUGrn39tv9wmr8yjGZJIfHvDzpBmpMzBkP11Q18dZrm4mLD2Tg4FBWrzzAr383jd3b8yjIq6KivBGT0cLSh647a6Shk67BYrPx9c6jvP3dXhr17UwdEsvSm8cS5teLjea6GavdzodHMnh57y5EUeTBkWNYkjqkU0NCuorOiLvz2vcyCA2VCj2OH3d0JH2EBx+E9HT44IOzhP1ERSPvv72N0ePiuPWOMVSfaEKjUaBWK/j43e3MXzSal/97JylDIqk6cRKQUgpOuhalXM78CSms/std3HP9SHYcLWbOMx/ywufbaGrthU55PYBCJuP/0oay4fYljA4L5+87f+CWFcs4Wlvj6NAuC6e4XwZyOURFQWGhoyPpA3z6Kfz3v/DIIzB79lkPm0xWWloMLPtgBx+8vY19uwuZfkMqP2zJZsiIKMIifLBYbERE+VJaLA0oOZ3/dIp816PTqPjVDaNY/Ze7uHFUIiu2HWbW0+/z8fcHMVusjg7PIYS4ufP2DTfz2owbqW5rZfaKZTy/azsGi8XRoV0SV5SWEQTBE3gHSEKyc/iFKIrnnV3V19MyIOlUTg7k5jo6kl5OWRm88IJUXnQB06acY5W8998t5OacYN5tI9m2OZvfP3UTCYlS9+ArL6zD19+NhXeO7aiqAcnH/rvVGVRVnmTmrDTiBwb3yGH1Fwor6/n3VzvYnV1CqK8HD8wex7VpMb3mBmNP02w08vyu7aw4lkWEhyd/v3Yqo8LCe+z1HZGW+Q+wXhTFBCAFyLnC/fV6Zs6EsWMlexQn58BgkMblhYdLLmvnEXabVRoEHhcfRNzAYJbcPRGVWombmwsJiSHYbHbqalvIOlLGlOmDpY1OveclRXW8/9Y2KsoaCAnz5n+vb6ahXt8TR9dviAnx5bXfzub1396CRqXg0f99y90vf0FOWd9KTXQVHhoNz02exrLZ8wBY9PUXPLllEy0mk4MjOz+dFndBENyB8cC7AKIomkVRbOqqwHord98t9eH00wXMhRFFqY13zpyLnv1O2wrr9QbMZiujx8UxfGQ00bFSE4mh3cz367OIjQ/EP9ADu13s2Gbzhiz8Az34v/smMX/RKFy0KjIOlABgNFrIyzlBTdVV/1XsEUYlRrD8D7fzh4WTKapq5Pbnl/PnjzZS39zm6NAcwqiwcNYuvIO7hwxjxbEsrvvkA7YUFzk6rHNyJS1qA4A64H1BEFKAg8ADoiie8akLgnAPcA9AeHjPXcZ0J6L441xVJz/hlVfg88/h+ecv+ezn6aXjNw9OB6Ct1UhBfjX//OtqEATc3DTMWzgKAKvFhkqtIPtoBS3NBoaOGICXtytGowWrxUZUtD8Af3v6KzRqJUcySrlx9lAWLB7d9weHOxiFXMbccclMHxbPO2v38enWDDZnFPDLGddw26TUftfp6qJU8sTYCcyMieOx7zfwy2++ZnZCIk+Nn4inpveMQOx0zl0QhGHAXmCMKIr7BEH4D9AiiuJT59vmasi5i6J0U3XmTHjjDUdH04vYvRsmTJDemFWrOn1p09ZmYsO3h7HbRW6eN/ysjtXvVh2isbGV6den4B/gwZ6d+RzcX8SU6wZTVlLP9+uz+Ocrt2Ox2Pj9/Z/wp7/P7bAqdnbAdg1ltSd5ceUP7MgqJszPk0fmTWDc4AGODsshmKxW3jiwj/8e2I+XxoW/XTuFKQNiLr7hZdLTOfcKoEIUxX2nfl4JDLmC/fUJBEGySJk+3dGR9CJqa2H+fCnP/uGHV5Sz0unU3LLgGubeNhKFQk5DvZ4vP9tHZkYpAFqdmsaG1g4nykPpxURE+tGqN1KQW81Nc6Tvf3lpPR6eWlQqBa16I9u+P8ZD933EC8+uoary5JUfcz8m3N+L//z6Zl5dOhu5TOCBN1bzwBurKK/rf6kwtULBgyPH8PX8hfhqtdzz7Woe3riO5h4cTHI+Oi3uoihWA+WCIMSf+tVkILtLourlPPIIzJrl6Ch6ERUVoFLBypXg2bXNLz6+bkydMZiQMGnOq9Vqw2iQStH27SqgoqyB+MRg2tpMmM1Who+Uhn80nWzDy1uHCKz4ZDd7dxZw/6MzcHN34avP93dpjP2VMYMiWfHHxTwwexwH8yuY+5ePeGPNbgzmvlEq2JUM8g/g6wWL+O2IkXyTn8t1yz5ka4ljc/FXWi3zW2CZIAiZQCrw9ysPqfdjs0mlkM3Njo6k66mpqWHs2LGsWrXq0jcaMkTqQv2Z02NX4e6hxcdXshJOTg3nZGMbd85/nbVrMpg4ZRBxCUHk51Th4+uKWq1E32KgrLQBjUaFzWZn66Zj3Hn3BGLiAhk7MQGbzU5LS/9s0OlqlAo5d04bxtd/XsKUIbG8s24fc5/5iG1Hjve7fgSVXM6DI8fw1fyFeGg0/N+ar3li80ZazWaHxHNF4i6K4mFRFIeJopgsiuLNoij2i+vdw4dh4EDYtMnRkXQt6enpDBo0iD179lBcXHzxDdauhSeflM52PTSAOCDIk+f/vZA/PzeP3z12PdOvTwGgqLCmw6IgM6OMyrJGRo6NZc+OfKJjAwgK8UIURdRqhdQNq+79A5P7En6ervztrhn876F5aNVKHnpzDQ+8sZqKfpiqSfIPYPWCRdw7dDhfZB9l5vIP2VdR3uNxODtUO8GgQVK36pEjjo6k6/jggw+YOHEiDQ0NaDQa3N0vMkavpARuv10SeAesTKKi/fHy/nFG6PTrU3jvza2s+fIAH723nUHJoaSkRbB6ZTozbpKuKARBYMfWXPwDPVCpFdjt/Wtl2RMMjQ1l+ZOLeGjOeA4VVDDvrx/xztp9/a7LVa1Q8NiY8ayYuwC5IGPhV5/z9x3bMFl77n1winsn0Giklfvhw46O5MqxWCz86le/4je/+Q3t7e0AyOXyC4u70Qhz50rNSitXgovjy78mThnEgsWjqTrRxJK7JzBxyiBqq5tRqhQMHSFVctTX6ck4UMwNs6T7/s5ehe5BKZdz+5ShfPXnJYwbPIA3vtnNrX/7hAP5Pb96dTRDg0L4buEdLBycwjsZB5m1Yhk5dbU98tpOce8kKSl9X9zr6+sZO3YsH330UYewA8hksguL++9+J7k8fvghREf3QKSXxoT/b++8w6Mqvj/8TjY9AQKE0CEEEAUEpBfpCU0EvgpSpBhARIpIURT9qYgUQUBAilQpUqQpUqR3kI6U0EtIKEmAJLT0nd8fQxJCDSl7k828z3Of3buZu/fsJvncueecOadBaT7q602NN18BIE/e7JQslY9tm04SGHCbZYv+pWSp/JQolQ9QM3kpJf/uPkdcnNlI060SDzdXRn/YnEl9/kdsnJke45fx7bz1hGaxgmTOdnYMq+/N7BbvEBoRwf+WLGTG4QOY0zkmocU9hVSooJJEbt0y2pKUcfToUcqUKcORI0eIiHjyn+2Z4n7+PMyZA59/nuFThoQQVKrqxV/LDvLj0D8p4ulOhw9qAYnFxw4fuMT/fbaEbh2m8c/qo8TGxhlpslVSq4wnS/6vE76Nq7Bu32ne/e43/t57MssFXOt5FmPd+52pV6wYI3ftoOOKpVy/m35lM3Q99xSycSM0apQ5G3csXLiQDz/8MMls/VGyZ8/Onj17KFOmzNPf4D6AI+0AACAASURBVMQJePVVsM08KxNDgu+Qx+PJC5bZLNm9/TQL5+7m/Nkb5Mufg7adatKoWXm9sjUdOH/1Jj8s3MSxi9ep9moRhnRomOVqx0spWep3gu93bMXOxsTwBj40K/nKc4/RzTosSHAw5M2rih7272+0Nclny5YtNGzY8LljXFxcOHXqFIULF0588c4d2Lo1w8/Wn8fzmnBLKdm/5zwL5uzktN818nhko33nN2ncXIt8WmM2S5btPMakP3cRF2em59s16NCgIrZZrLXi5bBQ+q9fy39BN2hTuizf1m2A8zOyzrS4W5iCBVXbvXnzjLYk+YSHh/P777+zevVq1q1b99Qx9vb2BAUF4Ra/IElKaNNGlRU4exa8rHepuZSSQ/svMn/WTvxOBJInb3bad65Fk+YVsLPTpQvSkuCwe4xctJntxy5SumhevunowyuF8hhtlkWJiYtjwr69TD24D0+3nExo8hZlPfI+MU6Lu4Vp0UKt3TlzxmhLXp5p06YxaNAg7t9Xdd6cnJzIli0bd+7cITo6mujoaEymh2I2fjwMGKDqsw8aZKDVlkNKyeEDl5g3cwd+JwLJmy8HHbvWxqdJuYTqlJrUI6Vk4+Gz/Lh4K3cfROHbpArdm1bDLovVANobcIWBG9ZxK+IBg2vVwbdCxSR3mVrcLcy+fSobsEYNoy15OcLDwylSpAh37twBlBvm+++/Z8CAAQQGBhIWFkbZsmXV4F27oF49ePttWLEiy+UPSik5uO8ic2ds58ypaxQolJMu3VWqpY1N1vou0pOwexGMWbqNdftPU6KgO991akTpok/OYK2Z0IgIBm9az6ZLF2jg6cVon8bkclKlZ7W4a5JF3759mTlzJpEPixsVLlyYCxcuYPe4v+/uXRU4dXKCgwfTvG5MZkJKyd6dZ/ltxnYuXQimWHEPfD+qR/VaJbNsd6L0YPuxC4xYuJnbdx/wQaMqfNisWpYqKSylZP6xo4zYuZ2cTk5MaPIWVQsW0uJuBP/8Aw8ewDvvGG1J8jh37hzlypVLEHZnZ2eWL19OkyZNnn7A/PlQrpxK7NdgNku2b/bjtxnbuBYYSplyhej+cQPKlreOXgUZgbsPIvlp6Xb+/tePEgXd+b5LY14t7GG0WRblZHAQff9Zw5XwMPpXr0mfqjW0uFuaRo0gNBQOHDDakuTRsGFDtm3bhtlsxsbGhtq1a7Nt27YnBwYFqXQgzVOJjY1j/er/mDd7B7dv3qN6rZJ0+7gBnl5ZKyCYnuw4fpEfft9E2N0IujWtStemVbEzZR1f/L3oaL7aspE4s5nJb7XQ4m5prl4Fd3dwcDDakhezceNGWrVqlZDf7uTkxJEjRyhVqlTSgatXq/rs69dD7doGWJp5iIyM4c8/9rNo/h4iI6Jp9FZ5unSvg3ueF9Tm0SSL8PuRjP5jK+v2n6Z00bwM+6AJxfLlMtosiyGlJDouDkc7Oy3umqcTGxtLiRIl8PdXTS8cHBzw9fVl6tSpSQdevAiVKql2U7t3Z4i6MZmB8LAHLJy7i1XLD2Jra6JNh+q0eb8GTk72RptmFWw6fJYRCzcTER1D31Zv0q7eG1kqoK197gbxzTfg4aE6NGVUJk6cyJAhQxJSH7Nly4a/vz85c+ZMHBQZCbVqKYE/dMiq89nTi+tXQ5k1bSvbN/uRy90V3x718GlaDlMWW6CTHtwMv8+w3zey8/glqr9WhO86N8bDzdVosyyCFneDqFtXBVUzqt/99u3beHp6cvdhHQsXFxdGjRpFn8evRj16wIwZsGqVSn3UpJiTxwP4deImTp28SolX8vFxPx/KvVHUaLMyPVJKVuw6zthl27G3NfH1+954V3z+0n1rwNI9VDUPqVMHDh9WmYMZkS+//JLoR2qu58mTh549eyYdZDZDjhzw5Zda2NOAMq8XZsL0D/jyu1aEh91nYO/5DPt6OUHXs17zirRECMG7tcux+KuOFPHIyecz1vDdvA3cjzSm21FGRs/c04D4ImL//JPxGmefOnWKihUrJkl9XLVq1bPry0iZ5RYqpTeRkTEs/X0vSxbsQUpo16km73WsgYPuBpUqYuLimL76X2av309B9xyM7NqMMp75jDYrXdAzd4OoUUN1Ztqxw2hLnqRHjx5ERUUBqk57zZo1kwp7eLgqa/nvv2pfC3ua4+hoR6dudZi96GNq1H6FebN20L3DNHZvP5Plyt6mJXYmE71b1mJ6/zbExprxHbOE3zYc0B22HqLFPQ1wdYXKlWHLFqMtScratWs5fPhwgoA4ODgkzY6RErp2VVelmKzXsd7SeOTLwdfD3mHMpI44Otrz3ZdL+XrQEq4F3jbatExNpZKFWPxVR+qW92Liyl30+WUlt+7cN9osw9HinkY0a6ZqzQQFGW2JIiYmho8++ighp93R0ZEPP/yQEiVKJA4aN07Vixk9WuezW5AKlTyZOrc7PT/x4cR/V+je8VfmzdxOdFTW6jOalmR3cWT0h80Z0qEhR84H0m74Avad8jfaLEPR4p5GtGypJsJ//220JYqJEydy+3bijNDBwYFhw4YlDti5EwYPVnUTMlNBeivB1tbEu+2qMWvRx9SqU4r5s3fyYadfOXzgotGmZVqEELSuXY55gzuQ3dmRXpNWMPXvPcSZs2YLRR1QTSOkVOt+Xn/deIG/efMmnp6eCTntLi4ujBs3jh49eiQO+uAD2LNHFQR7Xr9UjUU4fOAiE8as41pgKA0bl+Wjvj7kzOVitFmZloioGEYt2cLfe/2o/EohhndtSp4cmTcnXue5G8wPP8Dt28rbYSRdu3bl999/T0h/LFGiBKdPn06szw4QF6d8SAUKGGSl5nGio2JZOG8XS+bvwcnZgY/6etOoWTlddTIVrNp7klGLtuDiZM+Irs2oUqrwiw/KgGhx13D8+HGqVq2aJPVx3bp11KlTRw2YMUMFCAoWNNBKzfPwvxTC+B/XcPJYIG9U9qT/4LfIXzDniw/UPJUL127y2Yw1XAkK5eO3a+LbuEqmK12gUyEzAGYzXL5szLmllHTv3j0h9dFkMlG3bt1EYV+1Sq1C/flnYwzUJIuixfIwbkoXPvmsKWf8rtGj03RWLNlHXFzW9B2nluIF3FkwuD0+lV5h8qrdDJi2irsPIo02K93RM/c05uOPYflyuH5d5b5bkpUrV9KpU6ckrfP8/Pzw9PSECxdUQbASJVR3JUdHyxqnSREhwXeYMHot+/acp3TZQgwc0pwinu5Gm5UpkVKyZNtRxi3bQb7c2fipx9uZpmerdstkAHbvVnW32rYFewsWBIyKisLT05MbN24ASth79+7NmDFjICICatYEf39VJ8HT03KGaVKNlJLN608wZfx6IqNi8O1Rj3faVtPFyFLIfxeu8fmM1dx9EMU3nXxoUuVVo016IdotkwGoVQs6dbKssAOMHTs2oScqqNTHb7/9Vu388AMcPaq6Kmlhz3QIIfBu8jozF/akctXiTP9lMwN7zyMwQC9+Sgnlixdg4ZD3ea1oXobMXsf45TuItUKXl565pwM3bsDSpdC7N9hY4PIZFBSEl5dXwoIlFxcXJk2ahK+vrxoQHg7r1kG7dulvjCZdkVKy6Z/jTPl5A7ExcfTo403z/1XUGTUpICY2jnHLd7Bk21GqlirMqO5v4eaaMfsX6Jl7BmHLFvjkE3ha97r0YMCAAcQ8Uj6gSJEidOnSBS5dUjXac+TQwm4lCCHwaVqOGQt6UKZcYSb+tI6vBi7m1s0MWpI0A2Nna2Jw2/p826kRRy5co/OPizh/9abRZqUZqRZ3IYRJCHFECLE6LQyyBv73P6Wnc+ak/7mOHDnCypUrE8Td2dmZmTNnYnP3Lvj4qHZ5GqvDPU92Ro5vT5+BTTh2xJ8enaaze/sZo83KlLSsWYYZ/dsQGR3DB2MWs/2/C0ablCakxcy9H3AqDd7HanBygvbtVdZMeHj6nUdKSbdu3YiIiADA1tYWHx8fataooVag+vvDF1+knwEaQxFC0PLdykyZ0528+XLw3ZdLGT9qDRERurb5y1LOKz8Lvnwfz3y5GPDrKuas35/pK3amStyFEIWAt4CZaWOO9eDrq5JUlixJv3MsXbqUs2fPJuzb2dkxadIk+Okn+PNPGDNGZclorJoinu5MmO5L2441Wff3EXr7zuL82RtGm5Xp8HBzZeaA92hUqRST/tzNt3PXEx2TeYu5pSqgKoRYBowEsgGDpJTNnzKmB9ADoEiRIpXiGzRbO1KqOjPZssHevWn//hERERQtWpSQkBBApT7279+f4Y0aqfrs776rriw60JalOHzwEj9+/xd3wyPo0ceblq0r62DrSyKlZMbafUxbvZcKxQswtmcLchocaLVoQFUI0RwIllIeet44KeV0KWVlKWXlPHkyx4KBtEAINXv/9184lQ5Oqx9//DFhsRIoX/tXX30F+fNDq1Ywc6YW9ixIxcrF+HXuh1SsUozJ49czdMgy7t6JMNqsTIUQgh5vVWdkt2acuhJEl9GL8A8KNdqslyY1bplaQAshxGVgMdBACLEgTayyEjp2VKtU0zqweu3aNcaMGZMk9XHi+PE4OznBK68oZ7+u9JhlccvpwrAxbfmorzf/7jpHL9+ZnPa7arRZmY7GlUsx7dPW3I+IpsvoRRw6F2i0SS9FisVdSvmllLKQlNITaAdskVJ2TDPLrIC8eVWv6Tlz4KEOpwn9+vVLkvro5eVF+2PH4P33ITbz+gg1aYcQgtbtqzNuamfMZkn/nnNZtfxgpg8SWpryXgWY+3k7cmV3odfEFaw/kHkyknSeezozYADUqQNhadT0fv/+/axZsyZB3J2cnFjeqRPip5/AzQ1sbdPmRBqroHTZQkz9rTsVq3gxaew/jBr6p86meUkK5XFjzqC2vF4sH1/OXsvcDZnjIqlXqGYipJSUL1+e48ePAyo75qOGDZm0Z49yx+zaBQ4OBlupyYiYzZJF83Yzd8Y2ihbLw3ej2lCwUC6jzcpURMXE8s3c9Ww8dJb29d9gYOu6FisdrFeoZmDOnIEDB1L3HgsXLuTixcQ2bK4mE+OuXFGz9aVLtbBrnomNjeD9D95kxLj23Lp5j95dZ7Fvz3mjzcpUONjZMrJrM95vWJFFW4/w5ey1GTpVUou7BZBS9VgdMCDl73H//n369euXkCHj7OzMyC5dsAsOhgULdEEwTbKoXK04k2d3JV9+N/7vs8Usmrc7U7gYMgo2NoKBrevy6Tu12XjoLJ9M/pP7kRnTzaXF3QIIoQoyLl+e8vcYPnx4QnYMqAyZzuPHq/rCTZumgZWarEL+Ajn5+dcPqNuwNLOnbWXENyuJjIx58YGaBDr7VGZo50YcOhdIj/FLCb2bhhkTaYQWdwtRpQp4eKhZ/MsSEBDAzz//nFBmoIajIxt9fHBycFCrpDSal8TR0Y4hQ/9Ht48bsH2LHwN6zeNmyJ0XH6hJ4O0aZRjbswUXr9+i27ilBIVmrOJtWtwtiL8/VK+uqka+DH379k3IjskBLDGbKbdjR/oWrtFYPUII2nWqyfej2xJ45Ra9u83m7OnrRpuVqajzuhe/9H2HkLB7dP3pD64Ep1FaXBqgxd2C5M2rar1//rnqtZoc9uzZw8aNG4mNjUUAC2xsKGQ2I/74A3Lqpsma1FO9Vkkm/PoBdrYmBvaax54dmSeXOyNQqWQhfv20NRHRMXQfu4QL1zJG2WAt7hbE0VE1RTp0CBYvfvF4s9lMt27dEnztX9jY0NxsRowdCzVqpLO1mqxEseIeTJrpi6dXHr77cikrluwz2qRMRemieZk5oA0IwYfjlnI6INhok7S4W5r334cKFWDIEIiKev7Y3377jYCAAADyA9+azUS2aAF9+6a/oZosR85croz5pRO16r7K1AkbmTphA2azzqRJLl75czNzwHs4Otjx0fhlnLxsbGVOLe4WxsZGVeL194fJk5897u7duwwcODAh9THc2ZklH32E44IFuiCYJt1wdLTj62Hv0KpNFVYs2c/wb1YQHZVxc7kzGkU83Jg54D2yOzvw8YTl/HfxmmG2aHE3AG9vaNwYvv8erj8jfjV06FCioqKwBd4EcuTIQdsJE3R2jCbdMZls6PVpI3r08WbHllMMGbiI+/dfcJupSaBA7uzMHPgeObM502fSSsMEXou7QUyapNwyffo8+bNLly4xZcoUIiIiGAlsBxYMHoyDXoGqsRBCCNp0qM4X37bkxH8BDOo9n9Db9198oAaAvDmzMWNAG3IZKPBa3A2iZEn47jtYsUJtj9KrVy+io6P5HzAIWOHhQf1PPjHASk1Wp2Hj1/l+9HsE+N9kQK+5BN/Q6bfJxcPNNUHg+05aaXEfvBZ3Axk4ULloHq3Su337dnbs2EGxuDjmAAeE4NW1a3U3HY1hVK1RglET3if09n0+/XgugQG3jTYp0+Dh5sqvn7Ymh4sjvSausGgWjRZ3A7G1hQ0b4L331H5cXBzdunUj7sEDlgMxwJLWrSlbqZKRZmo0lC1XmJ9+6UR0VCwDe83D/1KI0SZlGvLlysav/dvg4mRPr4kruHj9lkXOq8XdYIRQJQl++QW6d1/HxYsXiQKmAd0cHPhiyhSjTdRoACjxSj7GTu4EwMDe87lwLshgizIPBXJnZ1q/1tjaCHr+vIyAkPRfyarFPQMQGwu//RbLvHk25JWSIsA8FxfqDB+Ou7u70eZpNAkULZaHsVM6Y29v4vNPFmiBfwmKeLgxtd+7xMaZ6TVhOSFh99L1fLpZRxoRFxfH9QtBXDp+hUvHrxAScJP7dx5wL+wBcbFx2Dva4eBkj4ubC3kK5sa9UG7cC3lwNbwwA788gf+VN6jBIXbSgDgk/sDhsmVpu2wZlCpl9MfTaJJwLfA2g/rMJyoqljGTOuJVIq/RJmUa/Pxv0GP8MvLnUimTOVwcX3hMSpp1aHFPBTHRMRzdepJdy/9lz18HCHtYVc/GRpAznxuubi645HDGZGciJjKGqIho7ty6x+0bochHVv7F4IqQHixjMk7EMJsP6MN0zPb22JhMqpxkx47Qti2ULasXMWkyBNcCbzOw93xiY+L4aXInihbLY7RJmYYDZwLo+8tKShX2YFq/d3FysHvueC3uFkJKydZFu5j++XxuXQvFydWRas0rUcm7HF7li1K0dCEcnBJz0u/fh3XrYO5c2LQJ7GzjiL4XhjPXcSGAbPgznTFU4xLvMYI/+YL6jKUHM6jFVQpzD+zs1JYjB3ToAO3aQaVKWug1hhJ45RYDe88HYNzUzrp130uw+cg5Bs9YQ80ynozt+TZ2JtMzx2pxtwA3LgczsdcMDvxzlFerlqD9kHeo3Kg89o72ScaFh8Pq1UrQd+wAe3u4+1i552zZIDoaphUdwQdnv+IzBzdMXfrx6wwfwmV1KjCC3OIYJUQ4Dcz+1COAPESoNBsHB3ByUiLfvr2qJWyjQygay+N/KYQBvebh5GTP+GldyOOR3WiTMg3Ldx5j+MLNtKxZhm86+jwz5VmLezrj7xdA/zrfEBMVQ9fhHWjRuzGmR662t27Bn38qQd+3Twn6vcdiJtmzqwBq48bQuTM0biRxGtSbWxcuEDt3Lnnz5eP8+WCaNnUlKMiR7zuu4cKa5ZwOuI8Nkqo2wbwTd5oKhCBACbqLC5hM8O67qjJZ7drqAqDRWIizp6/zWd8F5HZ3ZfzULuRwczbapEzD1L/3MGPtPnq8VZ2ezZ9e7VWLezpyL+w+fap9yYM7Dxi/cxgFS+QHVH32lSvht9/g6FHlObn/yCptIcDVVaU7vv02dOoEDRsq4U9CbGwSQQ4IgGrV1Pvt2AG2MdfZ8Mtq1s7eSti9GLwIp539JepEnSfh8hIv9AAtWqiT1a//lJNpNGnP8aNX+OLThXiVzMvoie/j5KT/7pKDlJLv5m/g771+DO3ciLdrlHliTErEHSmlxbZKlSrJzMqwtmNlY7u28vhOP3nlipTjx0tZvryUDg5SOjtLqeRbbTY2UmbLJmWOHFL6+kq5aZOUMTGPvWF0tJSdOkl59KiUZvNTz3n4sJRublJ6eUkZGKhei4qIkmtnbpJdS/WR3qK17OLUSm6z9ZRmF9ekRgihjHB2lrJ1ayn/+kvKiIj0/ZI0WZ7d20/LRrV+kEMGLJKxMXFGm5NpiI6JlR+NXyqr9PpZHjhz5YmfAwflS+qtFvdkcO7IRektWssPvZfI115Tgu7klFRLTSYpXV2lzJ1byo8/lnLnTiljY5/zpv37qwMXLXruufftUxr9yitSXruW+HpcXJzcsWyv7P56f+ktWst+r/SQZ6r4KOOyZUtqHKjXHB2lbN5cyqVLpbx3L22+HI3mMVavPCS9awyT40auluZnTFw0T3LnfoR8d+hvsu6AyfLyjdtJfqbFPY3x85Pyu++krOY6QdYTnaSLw70kemlrK6WLi5R580r56adKiJP1t7x0qXqDvn2TZceuXeo8w4c/+bPY2Fi5ZsYm2dqjq/SxaSMndJ8sH8z9XcpmzZSYP0voHRyk9PaWcsECKcPCXu6L0WhewKypW6R3jWFy4dxdRpuSqQgIDpX1B02VLb+ZLcPvJd5pa3FPJWaz8pIMHixloUJqdm5vL+WbfCTLMEGC2nd2lrJwYSm/+OK5XpWnc+aMEtfq1aWMikr2YWfPJp4n7il3u/fC7snJ/WZLH5s2snPJPvLk3jNSPngg5cqVUv7vf8ropwm9q6v6ULVrSzlzppQ3b77Eh9Fono7ZbJYjvl0hvWsMkzu2+BltTqbi8LlAWaX3z/LjCctlTKz6Z9fingLMZjXj/vRTNQN3cVEz8gR3Cw+kt2gtS9iukF5eUg4dKuWpU6k4YbduUrq7S3nlSb9acrh4UcoyZZTNT+PothOyQ9GespHte3LJ6D8Tb4ujoqRcu1bK9u2VoGfLpvzyjwq9i4sS+qpVpZwyRcrr11P4ITUaKaMiY2Tf7rPlW/VGyrOnr734AE0CK3cdl2/0HCfHLt0mpdTinmxiY6XcsUPKnj2Vj9zVVfnMH9U5JyfluShTMkx6i9Zy5nfr0ubk0dFSnjyZ4sMvXJCySpXnv8W9sHvy+/fGSm/RWo72/UVGR0UnHRATo6K8vr4q6pstm4oCP/oFODsroS9fXkWPU3gx0mRtbt+6K9u3miDbt5ogb9/ScZ6XYdTiLfKNnuPk2n2ntLg/j+TqmYODlBUqSPnzz0rP7obek96itVw6dlXqDFi9WsqQkDT5LPGTcbNZyiVLnh64NZvN8rdvFktv0VoObjxMRj6IfPqbxcaq6O/HH7/4Svfaa1KOGqWuMBpNMjl7+ppsVnek7N/zNxkT87wsA82jRMfGym5jl8h6A6docX+cqCgp16yRsl2753siHBye7Ykwm81y3nd/yLOHUiFoBw6oWbCvb+o+0GNs2KA+Q9Omz75urJ25SfrYtJFfNBkmoyKjnz4oHrNZyv37VSZPvI/Kzi7pF+boqDYvLxVt9tP+VM2L2bz+uPSuMUxOnbDBaFMyFTfD78nTV4IsK+5AYWArcAo4CfR70TGWEPdHY4hOTlJmz55Umx6PIc6alc4xxJs3pSxaVMoiRdLlRFOnqs9SoICUW7Y8fcy6WZult2gtR3ackPzUtPjo8hdfqOhxfHT50S8yPrpcqJCKQr90dFmTlZg0dp0OsKYQS4t7fqDiw+fZgLNA6ecdk17ifueOlIsXqxnsi7L/fHyk/P13C2X/xcWplER7ezUjTicOH1Z58EJIOWTI05Nw5n+/VHqL1nLtzE0pO8mpUyqa7OWlvmQHh6RfsJ1dCvNCNVmF6OhY2afbLNnCe7S8Fnj7xQdoEjDULQP8Bfg8b0xaintoqJRz50pZv34GXrczbpwyZPLkdD/V3btSdu2qTvf661IePJj057GxsfJzn6HyLecO8vqloNSd7MIF5Xt/0YquXLlU1Hrnzqfnb2qyHNevhcpWjcbIXr4zZXS09r8nF8PEHfAErgDZn/KzHsBB4GCRIkVS9QGDg6WcPl3KmjXVZNj1BSvuV61K+xX398Lvyy2LdslpA+fKm9deMPsIDpZyzBiLzmBXrVIuGpNJeUoiH4mjBgfclG85d5DDO4xPuxNeuaKizxUqpKIWg1RZRNd0ulxWYMfWU9K7xjA5c8pmo03JNBgi7oArcAh450VjUzJzv3ZNyl9+kbJSJSXoLi5P145s2aTs2FHKf/55qbVBL8XtG6Hy/1qOkj91myKnfzZP9q46WAacufrkwJAQJVYGERqqZvFvvPFkJs2crxdJb9FaXvYLSPsTX7+uotJVqz79lxV/9XV1VVHuNWsSf1nt2qlfZv/+KnCisWrGjvhb+tQcJv87fNloUzIFFhd3wA5YDwxIzvjkivvly1L+9JNyLzxvMujmJmX37lJu3fr0yWBaEvkgUv4x5i/5U7cpCa992fQHeXDD0aQDo6KkrFFD+doN9jnfv68eb92Ssk0bKU+fljIk8Kb0Fq3lopEr0vfkN2+qaHWdOk+/zYr3mzk5qch2/C/ZyUnKggXVQgSN1fLgfpTs3PoX2fGdifL+vWek6WoSSIm4p7i7g1BV5WcBp6SU41L6PvGcOwfDh6t2oa++Cl9/DcePQ1QUPHigquG6uIC7O/TqBevXq/rpM2ZAvXrpX7789P7zXDl9labdGgAQePYabnlzkLtAYucZKSV8/jns3QsffGB4lyTnhyW1jx+HLVvUd+leMDfFKxTj0Mb/0vfkuXND166wfTsEB8Ovv4KPj2oyki2bGnP3LkREwM6d6pcMav/qVVXwvlu3JzucaKwCJ2d7Pvv6bYJuhDNjymajzbFKUiOJtYBOwHEhxNGHrw2RUq5NzsFSgp8fLFkC8+dDUBCYzUqA4rGzU6XIH+0sV7GiMZp5bJsfbh45KF1DNasOOHMNR2dHzHHmhDFyyR88mDCZg00/pHrzFjg8680sTN26EBgIjg/78O673Ymoy+F8EgCFC1vAgPhfYIcOT/YcUmTAcQAAFG5JREFUtLV9sqMJKJFfuBBWrVJjmzWzgKEaS1K2fBHeaVuN5Yv3Uc+7DOXfKGq0SVZFimfuUspdUkohpSwnpazwcHuhsB8+rCa3hQpB1arw449w+bL6X46KSuweV7SoGvfvv0qYxowxrmWolJLNC3dS9z3VJeXScX/O7D+Pe8FceJV7+Ad5+jRrPhjKNA8f1ssidC87gH9XH7K8sc8gXtjj4sDeDk6H1qBECfj4Y7h40YKGuLhA69bw119Qq5bqM/gsIiPh5k1o00Ydc+uW5ezUWIQuH9YlXwE3fv5xDdHRsUabY1VYtOnmf/9BnTowfjxcu6buxKOjlfA4OkLJksodc/SoEvwffoCyZQ33bhAXG0e5OqW5dfU2Efci+GvyemKiYqjfrlbCmH2bT7LDsTjev3zOiHVf0/7Ldwg8e81Aq5+OyQQVXObSs+4UfH1h1iz1vb/3Huzfb0FDAgJg8+bEWzNXV3Wr9jQePIC//4bixeGPP9Rtn8YqcHKyp99nTQm8cps/ft9rtDlWhUUbbcbGqg3U7NxsVsLSpYuamHl6WtKa5GNrZ0udNjX4pe8s8hZ1p1SVErzbvzk53BMbAS9ceJjmEwdRvk1dAOwcbDlz4HzCz/39Asjunp2cHjksbv+j3LgczOUTV+j4f9Xo9C188w1MnAjTpsHSpaq1X+/eSuwd0tOvVLSompXfuJF0CwxUV/arV5Wv/vZt5coxmZT7pm1bNUsYPjwdjdNYksrVilOvYWkWzt1Fw0ZlyV8wp9EmWQUW7aFqMlWWdnYHKVNGxRvfeQcKFrTY6dOEIP8Q8hbNw/51R6jUqBymX39lw7L97HUrzVdLBmBrp66XH74+gK4jOlClSQUWjVjJ8V2nCDx7jabdGtLpmzaG2C6l5Ou3R3Jsmx+zT08gT6HcCT+7exfmzIHJk5W2BgSAh4eaNDsb3es4NhZCQhIvAMWKqai7xmq4GXIH33ZTqVTVi+9GGvP/kZFJSQ9Vi7plChWCK1fg0CHo2zfzCTtA3qJ5iIuNIyw4nPPzV8Onn3LnRihl33wNs1ldKFdMWEOBEvl4vfZrzPlqEffvPOCzOb2ZdXI8/n4B3Lll+QwQs9nMrwPnsn/tEXx/aJ9E2EElsHzyCZw6pX4/Hh7q9SZNwNfX4uYmxdYW8ueHN96Apk21sFsh7nmy075zLXZvP8N/R/yNNscqsKi458mTKBqZGZOtiUbNX6fEN59AgQI4dvfl5rVQ7B3sCAm8xaKRK+kytC27/9xPXGwc9du/SZ5CuYmJisVv71liHgaOoiOjCQ0OT3d7oyOj+bHzJJb/vIZWfZvS6pOmzxxrY6PiHKBc2y1aqDgJqFl8+/bK7X3/frqbrclivNuuGnk8sjFz8mYs6VGwVizqc7cazGbo2BFT0A3YvZti0dn4u9cMBjceRu78OWn+kQ9e5YqyZvpGyr75Gl7ligCwYe426rSuQe78OTm55wx/jPmL6xeDKF7Bk/6/foS9o32amhkdGc3aGZtZMvpPbl69TbcRHWg7uBUimRFqIWDQoMT9s2dh2zZYvFjFTN56S7nWmjVTMVGNJjU4ONjRuXtdxo5Yza7tZ6hdT9+hpQYt7inBzw927YIJE6ByZcoAUw+PZsvCXVSoX4ac+dyIuB/J7Rth5PfywM7ejiunr3Ll1FWqNKnAiV2nWDZ+NRW9y9GydxNGvP8ze1cdpO57NVNtmpSSS8evsGPpXtbN3sLt66G8Xvs1Bs/rS4X6ZVP13hUqqHjnrl1q9r58OSxbppJc6tWDt99WQl+8eKo/hiaL4tO0HH8s2Mu8mdupVacUNjYGp8plYrS4p4SyZeH0aShQIOElGxsbvDvWSdi/dTWI0KAwXq1aEoCVE9ZQoHhesuVy5fjO0xR+pQAtezcBwBxnJjoqBlDiLIQg4l4Et66FkjNvDhxdHTGZTElMiI2JJSw4nFvXwwj2D+HCf5e5dPwKp/ef5/b1UGxsBBV9yjHk936Ur1cmzT66yaQWRdWtq7Js9u2DP/9UaeuffKK2wEAVTwkIgFy5VGq7RpMcTCYbOnWrw4hvV7Jz2ynqNihttEmZFi3uL0NAAPzzD3Tv/sJosJtHDnLmdWNQg+8oVrYI549cosNX7xJw+ioBZ6/S9rOWgCpjUKB4PrLnVkvy410mx3ac4uvmIxPez8HJHntHO2Jj4oiNiSPm4cUgHhsbQaFSBShfrzQVG5ajStM3yJ0/fVPKTCaoWVNto0fD+fOwe3fiV/Ppp6r0wdmzav/0aZXuGr+gSqN5GnUavMa8WdtZPG8Pdeq/lmw3oiYpWtyTS3S0Winp56eczY/M2p+Gq5sL3y4bxN/TNuBeMBdtB7fEvWBuFo9aiZt7doqWLkxsTCwX/vMnPOQO+b3yJjm+ePmifD63D2HBd4i8F0nEvQhiomIx2ZmwtTPh4OxArnxu5MznRp5CuSnyWkEcnIwteFCihNri6ddPlZUAFZytVw/CwlQufe3a8OabUL06uLkZYq4mg2Iy2fDe+zUYN3INRw5dpmLlYkablCnR4p5cBg1SPoilS18o7I/yds9GCc9jY2IJDQ6n/Rf/A+DYdj/OHjhP8QrFKPJq0jsB94K58elUN21sN4g6iV4qzGZVO2zHDlUnbNQoVQpBCChTRgl+tWrQoIH22WugYaPXmTV1K3/+cUCLewqxaCpkpmXxYpg0Cfr3V0tpU4itnS1la73K6A9+4e+p65nzf4vJV8yD+u1rvfjgTI7JBC1bwtixqsxBWJiqPvD992r9w8qV0KMHLFqkxt++rWb+J04Ya7fGGOwdbGnW4g3+3X2WoOthRpuTKbHoCtXKlSvLgwcPWux8acKtW2pFZLlysHXrs+ufvASbFuzA/2QA5euXpXKj8mlgZOZHSrhwQa2GLVBAXQDq11dFIRs2VCWehwxRv4by5dVj2bLWsW5C83RuXA+jc+tf6Ohbm87dM/ddbGpJyQpV7ZZ5Eblzq+lkhQppIuxAkqwajUKIpP76qlXhzp3EGmEmk/pVrF0Lv/2WOC5PHuXWKV1abR06QE5dmsQqyJffjYpVvNiw9hidutXRgdWXRLtlnkV8wXlQAdTMWCshk2MyJTZh8faGDRtUgPb6ddi4UVUXffttVSr699+hTx9VJRjUEoSqVSHmYVLR0aNw4ACEhhrzWTQpo2HjsgTdCMfvRKDRpmQ69Mz9WUyerHL5du1SKR2aDEO+fGrz9k58TUpVRjpfPrWfK5cKzMbfbA0dqvLx43/m5aV+7uWlvG7Fiqn9Yjp2l6GoVacUdvYmtm8+RZnXLdFZxnrQPven8e+/KtWjcWO1OsdG3+Bkds6fh5MnVTvHCxdUg5ILF8DfP7EMdbFiiY1LBg1SJRaGDVP7O3dC9uyqc1XOnMb3GMhKfDVwMQH+N5m7tHeWdc1on3tacPOmKmZesCDMm6eF3Up4PAc/nthYVTr+4sVElw6oOPqjpY7btEnM2XdyUhk+hQqp4G/BgmorX16t3AW1LMI+bUsFZVmq1yrJ/r3nuRoYSqHCuV58gAbQ4p6UuDh4/331X7xnj47MZQFsbVXfkKKPte+cMyfp/qpVqlz1lSvqYhAYqLbdu5U7KDpaBXPjxd3dXbUw/PFHddHo2hXy5lVbvnzq0cMjcUvXxiiZnAqVPAE4dviyFveXQIv7owih8u/atFENWzWah1StqranIaW64Yt375jNMHgwVKmi9sPCVGrnjRvPLpWcPbvqijVwoBo/cKC6INSqpYLAu3apbCF3d/Xo5qYCzlmBQkVy4ZbThRPHAmjWsqLR5mQatLjHExen/lu++MJoSzSZDCFUSmY8Njbw1VeJ+/nyKZ8/KHEPClJbSIjqJBj/vMzD+m6hoSqvv4mqK8exY6qu/uPndHNTweHcudXjF1+oO4eAAFWxs00b5S66dUvdXbi5qZtRF5fMFTMQQvDKq/k5fzbIaFMyFVrcQd1r+/jA9OmJ99UaTTrg4qIydLy8nj2mWDHl8omnUiU18791S203b6oVvLdvq/34x/i0zxMn1GLq6tWVuP/9d9JuWiaTEno3N1WHP/5x1Ch45RXVonbTJvjwQ3VHcfmySj/Nnj1xc3W17J2DV0kPDu6/QFysGZOtjoMlBy3uUVFqinPjxkvVjNFoLIWra6KLJzk0bqwE39VV7TdooEoihYWpu4KwMAgPV8/Dw9V27lyiW2n3bpUt1LGjEvLZsxOzhh7F2Vm1Z8yeXT2uX6/cRitWqOfTpqk7hI0bVWaSq2vSzcUl6ePzevUWKJgTc5wkODic/AV0LCw5aHEfOFBNi5Yvh5IljbZGo0k1NjZJcwGKFFFbcunZU+UVZFNVqPH1VWWdw8NVI/W7d5M+v3NHPcaXcj57Vi04i3f9zJsHCxY8/5z29mqeBaqm0JEjqsgcKHfTnt2vcPasPb162VGosLoQPLp5eKg5GqgFayYTvP662g8KUvtOTmrLKglwWTvPfeFC9Vc8cCD89JPR1mg0VsmDB+pu4f59uHdPXQju31db/PPYWLVmEFT10IsXVaYRQK9esG1bNP6X7uKaPTsxMXY8eJB4MQAoVUr1CwDlWbWxUaWgQLmazp1LHOvgkCj08VutWuq88ecrVUpdZEBdXIRQ4xwc1EXs8c3TU6XCgoqRxGdGmc3qszs4qM02hdNpnef+smzerIqKjxz54rEajSZFxM+uk8tHHyXdnzIFzp25RS/fWQwd1YaadUoBKgfiwQOIiEh0KQH8/LMS1XiGDlVxivixj2+RkUkL0F26lLQn8KxZ6u4kOvrZNnfuDHPnqudVq6oL1ahR6g4nd+7EcSZTotDHXygcHNRn7t9fXexatYK+fdVjYCCsXp387+5Rsra4z5yppg1pVBBMo9GkD5ERKlrs6JT4v2oyKddRvPsonjfeSLrfvv3LnWvduqT7ISHq0WxWdwvxF4WoKHVhiIxMejFYvDixJ4GDg7rYREUljo9//uh+3oe9emJj1X78xeruXXWxSQlZT9ylhK+/hg8+UD72+KiTRqPJsIQE3wEgZy7j/l9tbBLdOM+jVavE587Oie6d5JAzp1rTEM9rryn31OjRL2crZMWqkJMmwYgRqmaMRqPJFJw9fR17e1uKFHU32pRMQ9YS9717VfC0RQv1qNFoMjwxMXHs2OJH2fKFdY77S5B1vqmQEJUrVaSIinxkpiV6Gk0WZtXyg4QE36V1e116+2VIlbgLIZoIIc4IIc4LITL2uv3vv1ch82XL1JI8jUaToYmJiWPy+PVMm7iRilWKUbnac5b1ap4gxeIuhDABk4GmQGmgvRCidFoZluaMHq1WVjweStdoNBmS6b9s4s+lB3inbVWGj22XZWu5p5TUZMtUBc5LKS8CCCEWAy0Bv7QwLM1xclINODQaTaagXaealKtQhNr1XzPalExJatwyBYGAR/YDH76WBCFEDyHEQSHEwZD4hFGNRqN5Abnds2lhTwWpEfen3SM9UctASjldSllZSlk5z6N1UTUajUaTbqRG3AOBRzvWFgKupc4cjUaj0aQFqRH3A0BJIUQxIYQ90A5YlTZmaTQajSY1pDigKqWMFUL0AdYDJmC2lPJkmlmm0Wg0mhSTqtoyUsq1wNo0skWj0Wg0aUTWWaGq0Wg0WQgt7hqNRmOFaHHXaDQaK0SLu0aj0VghWtw1Go3GCtHirtFoNFaIFneNRqOxQrS4azQajRWixV2j0WisEC3uGo1GY4VocddoNBorRIu7RqPRWCFa3DUajcYK0eKu0Wg0VoiQ8onOeOl3MiFCAH+LnTARd+CmAec1Ev2Zswb6M2cNSkkps73MAamq5/6ySCkNaaIqhDgopaxsxLmNQn/mrIH+zFkDIcTBlz1Gu2U0Go3GCtHirtFoNFZIVhH36UYbYAD6M2cN9GfOGrz0Z7ZoQFWj0Wg0liGrzNw1Go0mS6HFXaPRaKwQqxd3IUQTIcQZIcR5IcQXRtuT3gghCgshtgohTgkhTgoh+hltkyUQQpiEEEeEEKuNtsUSCCHchBDLhBCnH/6uaxhtU3ojhOj/8G/6hBBikRDC0Wib0hohxGwhRLAQ4sQjr+USQmwUQpx7+JgzOe9l1eIuhDABk4GmQGmgvRCitLFWpTuxwEAp5WtAdaB3FvjMAP2AU0YbYUEmAP9IKV8FymPln10IURD4BKgspSwLmIB2xlqVLvwGNHnstS+AzVLKksDmh/svxKrFHagKnJdSXpRSRgOLgZYG25SuSCmvSykPP3x+F/VPX9BYq9IXIUQh4C1gptG2WAIhRHagDjALQEoZLaUMM9Yqi2ALOAkhbAFn4JrB9qQ5UsodwO3HXm4JzH34fC7QKjnvZe3iXhAIeGQ/ECsXukcRQngCbwD7jLUk3fkZ+BwwG22IhfACQoA5D11RM4UQLkYblZ5IKa8CPwFXgOtAuJRyg7FWWYy8UsrroCZvgEdyDrJ2cRdPeS1L5H4KIVyB5cCnUso7RtuTXgghmgPBUspDRttiQWyBisBUKeUbwH2SeaueWXnoZ24JFAMKAC5CiI7GWpWxsXZxDwQKP7JfCCu8lXscIYQdSth/l1KuMNqedKYW0EIIcRnldmsghFhgrEnpTiAQKKWMvyNbhhJ7a8YbuCSlDJFSxgArgJoG22QpgoQQ+QEePgYn5yBrF/cDQEkhRDEhhD0qALPKYJvSFSGEQPliT0kpxxltT3ojpfxSSllISumJ+v1ukVJa9YxOSnkDCBBClHr4UkPAz0CTLMEVoLoQwvnh33hDrDyI/AirgC4Pn3cB/krOQRatCmlppJSxQog+wHpUdH22lPKkwWalN7WATsBxIcTRh68NkVKuNdAmTdrTF/j94aTlIuBrsD3pipRynxBiGXAYlRF2BCssQyCEWATUA9yFEIHAt8Ao4A8hRDfURa5Nst5Llx/QaDQa68Pa3TIajUaTJdHirtFoNFaIFneNRqOxQrS4azQajRWixV2j0WisEC3uGo1GY4VocddoNBor5P8BGHBSk4B6kL4AAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"# Solve optimization problem\n",
"xsln = solve_opt(True,True)\n",
"\n",
"# Create contour plot\n",
"visualize(xsln,True,True)\n",
"\n",
"# Draw gradient\n",
"draw_gradients(xsln,True,True)\n",
"\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.6 Discussion](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.6-Discussion)",
"section": "4.2.3.6 Discussion"
}
},
"source": [
"### 4.2.3.6 Discussion\n",
"\n",
"Why are the gradient vectors not the same length? I thought the forces were balanced..."
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.7 Analysis without Constraints](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.7-Analysis-without-Constraints)",
"section": "4.2.3.7 Analysis without Constraints"
}
},
"source": [
"### 4.2.3.7 Analysis without Constraints"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.7 Analysis without Constraints](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.7-Analysis-without-Constraints)",
"section": "4.2.3.7 Analysis without Constraints"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.8 Analysis with Constraints](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.8-Analysis-with-Constraints)",
"section": "4.2.3.8 Analysis with Constraints"
}
},
"source": [
"### 4.2.3.8 Analysis with Constraints"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[4.2.3.8 Analysis with Constraints](https://ndcbe.github.io/CBE60499/04.02-Local-Optimality.html#4.2.3.8-Analysis-with-Constraints)",
"section": "4.2.3.8 Analysis with Constraints"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"id": "469d15ba",
"metadata": {},
"source": [
"\n",
"< [4.1 Convexity Revisited](https://ndcbe.github.io/CBE60499/04.01-Convexity.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [4.3 Analysis of KKT Conditions](https://ndcbe.github.io/CBE60499/04.03-KKT-Multipliers.html) > 
 "
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.6"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.6"
}
},
"nbformat": 4,
"nbformat_minor": 2
}

