{
"cells": [
{
"cell_type": "markdown",
"id": "d5f6ea4f",
"metadata": {},
"source": [
"\n",
"*This notebook contains material from [CBE60499](https://ndcbe.github.io/CBE60499);\n",
"content is available [on Github](git@github.com:ndcbe/CBE60499.git).*\n"
]
},
{
"cell_type": "markdown",
"id": "3fffdc48",
"metadata": {},
"source": [
"\n",
"< [3.5 Quasi-Newton Methods for Unconstrained Optimization](https://ndcbe.github.io/CBE60499/03.05-Quasi-Newton-Method.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [3.7 Algorithms Homework 1](https://ndcbe.github.io/CBE60499/03.07-Algorithms1.html) > 
 "
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 1,
"link": "[3.6 Descent and Globalization](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6-Descent-and-Globalization)",
"section": "3.6 Descent and Globalization"
}
},
"source": [
"# 3.6 Descent and Globalization"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"nbpages": {
"level": 1,
"link": "[3.6 Descent and Globalization](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6-Descent-and-Globalization)",
"section": "3.6 Descent and Globalization"
}
},
"outputs": [],
"source": [
"import matplotlib.pyplot as plt\n",
"import numpy as np"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.6.1 Define Test Function and Derivatives](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.1-Define-Test-Function-and-Derivatives)",
"section": "3.6.1 Define Test Function and Derivatives"
}
},
"source": [
"## 3.6.1 Define Test Function and Derivatives\n",
"\n",
"Let's get started by defining a test function we will use throughout the notebook.\n",
"\n",
"Consider a scalar function $f(x): \\mathbb{R} \\rightarrow \\mathbb{R}$ to allow for easier visualization. Let\n",
"\n",
"$$f(x) = 0.5 (x-1)^4 + (x+1)^3 - 10 x^2 + 5 x$$\n",
"\n",
"$$f'(x) = 6 - 8 x - 3 x^2 + 2 x^3$$\n",
"\n",
"$$f''(x) = -8 - 6 x + 6 x^2 $$"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.6.1 Define Test Function and Derivatives](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.1-Define-Test-Function-and-Derivatives)",
"section": "3.6.1 Define Test Function and Derivatives"
}
},
"outputs": [],
"source": [
"## Define f(x)\n",
"f = lambda x : 0.5*(x-1)**4 + (x+1)**3 - 10*x**2 + 5*x\n",
"\n",
"## Define f'(x)\n",
"df = lambda x : 6 - 8*x - 3*x**2 + 2*x**3\n",
"\n",
"## Define f''(x)\n",
"ddf = lambda x : -8 - 6*x + 6*x**2"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.6.1 Define Test Function and Derivatives](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.1-Define-Test-Function-and-Derivatives)",
"section": "3.6.1 Define Test Function and Derivatives"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXkAAAEGCAYAAACAd+UpAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAABBkUlEQVR4nO3deZzN1f/A8deZzQxj3/elkC1rJBGiJEvf0CaFSouU9mjToq9UtEqWflSWdkrFV5ZIIbJm34mxjMEMZn///jgzY2jGLPd+5nPnzvv5eHwe5m6f856L9z33fM55HyMiKKWU8k8BbgeglFLKOZrklVLKj2mSV0opP6ZJXiml/JgmeaWU8mNBbgeQXpkyZaRGjRq5fv3p06cpUqSI9wJymMbrLI3XWRqvs3IS7+rVq4+JSNkMHxQRnzmaN28unli0aJFHr89rGq+zNF5nabzOykm8wCrJJK/qcI1SSvkxTfJKKeXHNMkrpZQf0ySvlFJ+TJO8Ukr5MU3ySinlxzTJK6WUH/ObJC8ixCfHux2GUkr5FJ9a8ZpbSclJdJvRjZAzIVzX8Tq3w1FKKZ/hF0k+MCCQFhVbEBMR43YoSinlU/xmuObVjq/Ss1JPt8NQSimf4jdJPtWcbXOYsnaK22EopZRP8EqSN8aUMMZ8bYzZYozZbIxpbYwpZYyZb4zZnvJnSW+0lZXxq8bz0aqPSJbkvGhOKaV8mrd68u8Cc0XkMqAxsBl4FlggIrWBBSm3HTflpiksHbCUAON3X1KUUirHPM6ExphiQDtgMoCIxIvICaAnMDXlaVOBmzxtKzvKFC5DSGAI8UnxbD22NS+aVEopn2VsKWIPTmBME2ACsAnbi18NPAr8IyIl0j0vSkT+NWRjjBkEDAIoX75885kzZ+Y6lpiYGMLDwwEY8fcINkVv4vOWnxMSEJLrczopfbz5gcbrLI3XWb4ab0RsBMsjl9OjUo/zRiByEm+HDh1Wi0iLDB/MrNB8dg+gBZAItEq5/S7wKnDigudFZXUub24asvLASpmzdY5H53OaP29i4As0XmdpvN7xwsIXpMjIInLg5IHz7vfWpiHemCd/ADggIitSbn+NHX8/bIypKCKHjDEVgSNeaCvbrqh8RdrPIoIxJi+bV0qpbHm5/cv0bdSXysUqO3J+j8fkRSQC2G+MqZty17XYoZvvgbtT7rsbmO1pW7kxbf002nzShvgkLXmglPIdUWejOH72OMYY6papm/ULcslbU1CGANOMMeuBJsDrwCigszFmO9A55XaeKx5anPCQcE7GnnSjeaWUytDj/3ucxuMbcybhjKPteKWsgYisxY7NX+hab5zfE93qdOPG2jfqcI1SyqcMbTWUNlXbUDi4sKPtFIjJ5MYYjp89zqjfRukiKaWUqyRlRmPjCo25t9m9jrdXIJI82HIHzy98nj//+dPtUJRSBdjT85/mmfnPpCV7p/lFFcrs6Hd5P1pVbuXoBQ6llLoYESE6PppAE5hnQ8gFJsmnv4K9+ehmLitzmY7TK6XylDGG8d3G5+mwcYEZrkm14sAKGn3UiE/Xfep2KEqpAuSTNZ+w8/hOgDytrVXgkvwVla/g9Wtfp+dlWnteKZU3Tsae5Kn5T/HW72/ledsFZrgmVYAJ4Ok2TwPnrnLrsI1SyknFQ4uz7oF1FA0pmudtF7iefKqos1F0+qwTn6//3O1QlFJ+LLUabpViVSgeWjzP2y+wSb5YoWKEBPpmdUqllH9Yf3g9DcY1YMLqCa7FUOCGa1IFBgTy0x0/6VCNUsox9crU47/X/pdbGtziWgwFNsnDubH4H7b+wKm4U/S9vK/LESml/EVSchLBgcE81eYpV+MosMM1qUSEd1e8y7hV4/JsBZpSyr8t27eMxuMbsy1ym9uhFOyePNje/IxeMyhWqJgO3SilvCJJkihduDQVwyu6HYr25AHKFilLoaBCxCXGsWzfMrfDUUrlc+2qt+PX/r9StFDeT5m8kCb5dJ6e/zSdP+vM4ZjDboeilMqH5u+cz3sr3st52YLjx50JCE3y5xnWdhhf3/I15cPLux2KUiof+uLvLxi/anzOdqLbuxcqVYLPPnMkpgI/Jp9ehfAKdK3dFbDLkN1YuKCUyr8mdp/IsTPHCA0Kzf6L3n8fEhOhfXtHYtKefAaW7l1KtXeqsWTvErdDUUrlA4t2L+LYmWMYYyhbpGzOXtylC4wcCVWrOhKbJvkMNK3YlF71elGzRE23Q1FK+bgzCWe45etbePDHB3N3gk6d4JlnvBtUOjpck4HwkHA+6fmJ22EopfKBwsGF+aXfL5QILZGzFyYlwahR0L8/VK7sRGiA9uQvKiY+hju/vZMvNn7hdihKKR/0z6l/ALtfa/US1XP24lmz4PnnYcUK7weWjib5iygUWIg9J/Zw4NQBt0NRSvmYlf+spNZ7tfh609e5O8HYsVCzJvR0dm8LHa65iODAYBb3X0xQgL5NSqnz1S9bn0dbPUrnWp1z/uKVK2HZMnj3XQgM9H5w6WhPPgupCX7VwVV8sPIDl6NRSrlNREhKTiI8JJzRnUfnbqr12LFQrBgMGOD9AC+gST6bxq8az9t/vM3p+NNuh6KUctGUtVO4Zso1HD+by1WqyckQFAQPPQRFnS974LVxCGNMILAK+EdEuhljSgFfADWAPcAtIhLlrfby2jtd3iEhKYEiIUXcDkUp5aLCwYUpXbg0xQvlcrFkQIBd3ZpHVW+92ZN/FNic7vazwAIRqQ0sSLmdb4WHhFMyrCTJksw3m77RssRKFVC3NryV2bfNJjAgF2Ppx47Bhg325zyqeuuVJG+MqQLcCExKd3dPYGrKz1OBm7zRlttmbZlF769688O2H9wORSmVh4YvGM53m7/z7CRjx0KTJvDPP16JKTuMN3qkxpivgf8CRYEnU4ZrTohIiXTPiRKRkhm8dhAwCKB8+fLNZ86cmes4YmJiCA8Pz/Xrs0NE+CPyD1qXbu1x/fm8iNebNF5nabzO8iTeuKQ4hq4bSqPijXjokodydY7AmBha33Ybx1u0YNOIEVk+PyfxdujQYbWItMjwQRHx6AC6AeNSfm4PzEn5+cQFz4vK6lzNmzcXTyxatMij1+dURHSEHD9zPNevz+t4PaXxOkvjdZan8cYmxEp8YnzuT/D66yIgsnp1tp6ek3iBVZJJXvXGcE0boIcxZg8wE+hojPkcOGyMqQiQ8ucRL7TlM2ITY2k5qWXu61UopXxebGIsry99nbMJZykUVIjgwODcnejMGTtU06ULNGvm3SCz4HGSF5FhIlJFRGoAtwELReRO4Hvg7pSn3Q3M9rQtXxIaFMprHV7jubbPuR2KUsoh83bM4/mFz/Pbvt88O9Fff8Hp0zB8uHcCywEnl3KOAr40xtwD7AP6ONiWK/o17pf2c3RctE9s9aWU8p6el/Vk0+BNXFbmMs9OdPXV9mJriRJeiSsnvLoYSkQWi0i3lJ8jReRaEamd8qdz+1u57L0V79FgXAOOnParESmlCqzNRzez8chGAM8T/OHDdk68CwkedMWrV7St1pYba99I0RDtySvlDx766SF6zuxJYnKiZydKSIA2bWDgQO8ElgtaecsLmlZsykfdPgIgWZIJMPrZqVR+Nv3m6ew/td/z4oSffgo7d9qLri7RbORFh2MOc9Xkq5i1ZZbboSilcmFtxFpEhIpFK9KyckvPThYXB6+8Ai1bQrdu3gkwFzTJe1Hx0OKEh4RjyJvlykop71kXsY4WE1rw4Z8feueEkyfDvn3w6qt5VsIgIzpc40WhQaHM7zff45WwSqm816h8I97t8u55s+ZyTcQO1Vx9NXTORb15L9KevJelJvivN33NXd/dRbIkuxyRUupiziac5diZYwSYAAa3HEyxQsU8P6kxsHgxTJvmai8eNMk7Zv/J/Ww/vp3ouGi3Q1FKXcSQn4fQcmJL7+0VERsL8fEQGgrVqnnnnB7QJO+QoVcOZUn/JbnbNUYplWfub34/j135mPf2inj3XahTB477xtIgTfIOMcYQHBjM2YSzPDDnATYf3Zz1i5RSeeZU3CkArqh8BUNaDfHOSU+ehNGjoX59KFXKO+f0kCZ5hx0/e5zZW2fz695f3Q5FKZVid9RuLn3vUqaunZr1k3Ni1Cjbg3/tNe+e1wM6u8ZhlYtVZsvgLTpso5QPKVekHN3rdKdNtTbeO+m+fXbRU79+eV5p8mK0J58HUhP8uoh1vLjoRd06UCmXJCYnEp8UT5GQIkzuOZlLS13qvZN/8omdSeNDvXjQJJ+nvt38LZ+s+YSjZ466HYpSBdLj8x7nus+uIy4xzvsnf+klWLnSJ2bUpKfDNXnopfYvMaTVEMoULuN2KEoVSK0qtyI8JJxCQYW8d1IRiIqyF1obNfLeeb1Ee/J5KMAEUKZwGUSEt39/m92nd7sdklIFQmrPve/lfXn92te9e/I5c6BGDVi92rvn9RJN8i6IPBvJW3+8xc8RP7sdilJ+b8PhDVz6/qWsP7He+ydPTISnn4aKFeHyy71/fi/Q4RoXlClchpX3rmT7X9vdDkUpv1citAQNyzWkYlhF7598wgTYsgVmzYLgXO7/6jDtybukavGqBJgAjp4+yrO/POv55gRKqfPEJcYhIlQtXpWf+/5M2UJlvdvA0aPw/PPQoQP06OHdc3uRJnmXzds5j3dXvMu6iHVuh6KU30hISqDHzB4MnTvUuUZ++AFiYuCDD1wvQnYxOlzjsjsvv5Nrql9D1eJV3Q5FKb8RGBBIk/JNqFO6jnONDBwInTr53JTJC2mS9wGpCX7OtjlEnonk7iZ3uxyRUvnX6fjTFAkpwhud33CmgaQkOw7foIHPJ3jQ4RqfISJ8tOojxq8eT1JyktvhKJUvfbjyQ5p83ISImAjnGpkwwc6k+esv59rwIu3J+whjDF/0/gIRITAg0O1wlMqXmlVsRttqbZ1bcHj0KAwfDu3bQ9OmzrThZdqT9yHhIeEULVSUhKQEHv7pYTYe2eh2SErlC8fP2trtrau25pOenxAU4FD/9Zln8sXF1vQ0yfugI6eP8N2W71i4e6HboSjl89YfXk+td2vx9aavnW1o4UL4v/+Dxx+HevWcbcuLdLjGB1UuVpm/H/qbEqEl3A5FKZ93SclL6F2/N22qerFscEZ27ICGDWHECGfb8TKPe/LGmKrGmEXGmM3GmL+NMY+m3F/KGDPfGLM95c+SnodbcKQm+C3HtnDdZ9dx9LRWrlQqvb0n9qaVDZ7UYxIVizqwojW9QYPsxdawMGfb8TJvDNckAk+ISD3gSmCwMaY+8CywQERqAwtSbqscOnL6CNuPb+fI6SNuh6KUz4iJj6Ht/7Xl3u/vdb6xFStg9mz7s0OlC155BaZPd+TUnid5ETkkIn+l/BwNbAYqAz2B1L21pgI3edpWQdSueju2PryVBuUaAOj0SqWwkxRe6fAKT7R+wtmGYmOhf3945BH7swP+/tsm+d9/d+T0GG/uUmSMqQEsARoC+0SkRLrHokTkX0M2xphBwCCA8uXLN585c2au24+JiSE8PDzXr89rOY33mwPfsCxyGa83fJ3QwFAHI8uYv7+/btN4s3Y8/jgn4k9QK7xWjl+bm3hrTpxI9enTWTd6NFFXXJHjNrMiAk8/fTlbthTl889XUrx4QtpjOYm3Q4cOq0WkRSaNiFcOIBxYDdyccvvEBY9HZXWO5s2biycWLVrk0evzWk7j/Xzd59Lnyz4SnxjvTEBZ8Pf3120ab9a6fN5Fqo2tJrEJsTl+bY7j/fNPkcBAkQEDctxWds2ZIwIi77zz78dyEi+wSjLJq16ZXWOMCQa+AaaJyLcpdx82xlQUkUPGmIqADip7qO/lfbmj0R0YY4iJjyHQBBIWnL8uAinliQ+7fsiBUwe8u7NTRmJj4Y47bJ34t992pIn4eDsbs25deOghR5oAvDO7xgCTgc0iMibdQ98DqUVY7gZme9qWsitjkyWZbtO7cfOXN+um4MrvHT19lI9XfQxArZK1aFe9nfONFipkywh/9hmUdGZi4LhxsG0bjBnjbCl6b/Tk2wD9gA3GmLUp9w0HRgFfGmPuAfYBfbzQlsJuIzigyQBCg0Ix+WTVnVK59cHKD3jz9ze5/tLrqVGihvMNxsXZJH/XXY41cewYvPwyXH893HCDY80AXkjyIvIbkFmmudbT86uMpa9UuergKuqWrkvRQkVdjEgpZ7x4zYv0rt87bxL8/v3QujW8/z785z+ONfPSSxAdbXvxTvfTtKxBPncy9iTXfXYdD//8sNuhKOU1e07sodeXvYg6G0VgQCCNyjdyvtGkJNt7P3ECGjnX3vr1MH48PPgg1K/vWDNp/KKsQVISfPMNlCxZ8IYuiocW5/ObP6dJhSZuh6KU1+w4voNl+5ax9+ReSobl0WL50aNh8WL45BO49FJHmkhMtHuNlCmTd9UR/KInv3gx3Hor/Pijw8uafVTX2l2pVLQSIsKo30ZxMPqg2yEplStnE84C0KlWJ3Y9uivvOi8LF9oLrbfeahc/OWTMGFi92haxLF3asWbO4xdJvmNHaNsWPv20BjExbkfjnl1Ruxi5dCSfrfvM7VCUyrE1h9ZQ671aLNq9CIDCwYXzrvHff4fLLoNJkxwbJN+6FV580Q719+7tSBMZ8oskbwy88QZERYXwzjtuR+OeS0pdwtr71/J0m6cBSJZklyNSKvtqlKhB6yqt8+YC64Wefx5WrgSHVvAmJ8O999raZh9+mLel6P0iyYO9IN6mzTFGj7bTkwqqS0pdgjGGwzGHaTGhhdakVz5v0e5FJCUnUTKsJN/e+i01S9bMu8afew6WL7c/FyniWDPjxsFvv8HYsXZ9VV7ymyQPcO+9uzh9Gl5/3e1I3JeYnEhwYDBhQboiVvmu1QdX0/HTjnz454d53/ikSTZZzJnjaDN79sCzz9o58XffneXTvc6vknyNGmfo399+Hdq71+1o3FW5WGWW37Oc1lVbA7A2Yq2ujlU+p3ml5ky/eTr3N78/bxtetgwGD4bOne2qJIckJtrruMbAxx+7s2OgXyV5sNOSjLEXOAq61NWwK/9ZSfMJzZn01ySXI1IKTsefZsDsAeyK2gXA7Y1ud74WTXrbt0OPHlC9OsyYAYGBjjX18svw6692bVX16o41c1F+l+SrVrWlnz/7DDZscDsa39CiUgvGXj+WOxrd4XYoSnEo5hA/bvuRP/b/4U4A770HAQHw88+OzmP83/9g5Ejbk3dwVmaW/C7Jgx3/Kl4cnnrK1msu6AJMAI+0eoQiIUWIT4pnyE9DOHDqgNthqQImIiYCgEtLXcqOR3bQ9/K+7gTyzjvwxx9wySWONXHwINx5p13R+qELlxvS84sVrxcqVcoO2wwdCt9+C716uR2R79h0dBNT103l6mpXc2vDW3Nxgk326+7evRARASdPQuXKMHy4fXzAAHulyRh7hIXBlVfaKWpgVxOGhUGVKvZrV+XKzpbgUz5hzaE1tP2/tnzc7WP6Xt6XYoWK5W0AycnUnDgRate2/+YcWtEKdhz+9tvh9Gn46isonIfT/TPil0ke7DWVKVPg0UfhuuugqNbuAqBJhSbseGQH5YqUA+BQ9KF/b4CcnAxbtthNi9esgTNn4KOP7GP332/nggEEBdmvTFddde61IrbOhIg9z4kTtuhTqueesx8OqYyx67wnpVwvmDYNataExo0dndKm8laj8o0Y1HwQHWp2yPvGReCxx6g+fTpcfbUtGuOgl16CJUvg00+hXj1Hm8oWv03yQUE2L111le3VO1T3P19KTfC7o3bT9OOmjGg/gqFXDrUPjh4Nb755brFBaCi0bHlu3Ovtt+14ZvXqtgDHhdMFpky5eONbt8KBAzbxpx6XXWYfi4mx33HBtlGvHrRoAf36wbVa0DS/OR1/mpd/fZkX2r1A0UJFGXP9mKxf5G0idvz2vffY37s3VR94wNHmvvjCzsq85x77z9YX+G2SBztKcN998O67dn7q5Ze7HZFvqXr4LIPjLuc/Qz6En/pC2bI2cd9wg60V0aKFTcBB6f6ZtGzpWaPFitmByozK7xUuDLt32zJ9q1fbY+5c2+a119phoPvvtzUs2reHVq10qMeH/XXoL95d8S5tqrah52U93Qni5Zdtx+XBB9nZpw9VHZzDuHSpLWJ59dW2No2v8OskD/Df/8J338EDD9hRhgC/vNScA1FRMHkyTJ9O0Jo1jDQG2rWDEyd4YcN7dO3cldYDB7oTW0AA1Khhjx497H2pwz4Ahw/bK1ovvGBvFy0KHTrY/8R167oRscrAvpP7qFa8Gm2rt2XHkB1ULV7VnUBOn7blaQcOtFl3yRLHmtqyBXr2tCONs2fbL8C+wu9TXqlSdvThjz/sNb8CKy7O/nnsGDz9tO2djxljh0sWLyaqShmmb5zOnG3Orv7LMWPOzWNu1crOi42MtP95+/aFjRvttwOAL7+Exx6zFQUTEjI/p3LM1LVTqfN+HdZGrAVwL8EnJdlrOkuXwoQJjvbuIiLsl9/gYDsrs1Qpx5rKFb/vyYP9CjV5MjzzDHTrBhUquB1RHhGBn36yn3IlS9qvNLVr25kxVc//z1cyrCSrB60mPMQWaNpx3F6czfNZENlRqhTcfLM90tu0yV6IeecdKFaMei1a2A+1Xr3cWWpYAHWv253tx7dTr4xLVxxF4LXX7FDf119DiRKONnf6tM0pR47YRU8187DsTnb5fU8ezi0pPnPGXhApEHPnFyywV527dbNj2ddcc+6xqhn3rkqEliAoIIik5CT+88V/6Da9W/4qhTBihO3lz5oFvXtTcvVqO5STmuAXL4ZTp1wM0D/9uO1H7p51NyJCqbBSvNbxtbxdwZoqOdnOm37xRceTO9h5At262QloX3xhL2H5ogKR5MFO1HjzTduxHTfO7WgcNn48dOpkZ7FMmGDntQ8dmu2XBwYEMv7G8bzW8TWMMYhI/ilbXKSIHRydPJk/vvnGLpQAu6Fmly5Qrpzt2X/5pf3UVx7bc2IP6w+vJ/JspHtBJCTYr+zvvQePP27HZoOcG6g4edIWHFu61K6u79bNsaY8VmCSPNi58zfcAE8+ab/Z+5WjR8/9Un362ClF27fb6UW5mIHSplob2lVvB8CHf35I5886czbprDcjdpwEBtpFV2CT/4IFMGiQ3SDi1lttwv/yS3eDzKc2Hd3EhpO2bshDVzzE8nuWU6ZwGfcCuuceu8biv/+Ft95ydAw+KsrWNVu5EmbOhDt8vFpIgRiTT2WM/YBv1Mhes1u+HAq58K3Sq5KTYeJEGDbMDgiuWmXrcTzyiNeaCA8Jp1RYKUIDfGjKQE4FBECbNvYYO9bOtJg589y82gUL7DWLvn3t3NuUIZ6EBDh+3A7tpx6nTtkvAalHbKz9axA5NxQYHGwX9oaG2qNIEXspoWRJe5QqBeXL588ZoCJCv+/6cfLUSR6WhzHGuDM8k97gwXaW2L33OtrM0aN2ceWmTfZLYvfujjbnHSLiM0fz5s3FE4sWLcrW877/3v53fOopj5rzWHbjzdSGDSKtWtlf5pprRDZt8kZYGUpOTpZFixbJsdPH5N7Z98rhmMOOteUt2Xl/ExNFdu4U2fTAu5IQHCoCcrDIpTK+0svSssxOMSY1dWd+BAeLFCokEhoqEhZmj6CgrF9njEi5ciJNmoh07SrSvfs/8sYbIl99JbJqlUhUlONvUY7sOr5L4hLjRERk05FN8s28b9wN6NdfRV5/PdtP9/T/2/btIvXq2b/nuXM9OlW25CReYJVkklcLVE8+Vffudk3NW2/ZcbV8uZhy+XK7IKhYMbt++s47HZ1Bklq2+Pf9vzPz75kMbjk4beVsfhERAevWnTvWr4dt2yA+HuARitKfOwp9S3/5jPsOjqBX+Cd88MJuypU3lC2ZSKlyQZQuba/pFS5sj7CwzCvVJibaXn5srL0kEBV17oiMtPEcPHju2LmzDD/8cP45ype315NSj0aNbMWHkiUdfrMusO/kPhp+1JBn2jzDi9e8SL2y9Tgccjhvg0hv/HgYMsQWGRsyxLFt+1LNnWvr0QQG2p/Tz2PwdQUyyYNdnb9kiR2a/fNP35z6lCERm8ybN7dDMk88YTNBHuletzv7hu6jZJjNMp+u+5SONTtSpViVPIshO86ehQ0birF6tf08XL7cXodOVbWqTZY33GDXUdWtC3XqFKNs2f4Y0x/276fMrl2MuMbYbH3ppXYY5667oOF12bqoFxRkc094uF1InNW/scWLf6dZs/bs3g27dsGOHbB5sz2mT7cX+1JVr27jb9oUrrjCHuUc+MyNjoumaKGiVCtejZEdR9K7fh7uQJ2RM2fsJIKJE6FrVzsO72CCF7ETNoYNg4YN7cStfJMrUmXWxffWAXQBtgI7gGcv9ty8Gq5JtW2bSMmSIg0bipw65VHTuZLjr48//mi/2x875kg8Wbkw3mOnj0n46+Ey5KchrsST3unTIr/8IvL88yJt24qEhJwbFqlZU+S220TGjBFZtEgkMjKHJz9xQmTwYJFSpewJy5cXefxxO87jRRf795CcLHLwoB0mGDVK5Pbb7dBBQMC537NaNZHevUXeflvkjz9EYmM9i+fzdZ9LqTdKyb4T+3IcryOSkkSaNbPjXMOG2bG2HMhpvNHR9n0GkVtuEYmJydHLPZYvhmuMMYHAh0Bn4ADwpzHmexHxibkttWvbyRVdutjRju++89GyB6kLPF580XbfTpxwdLOD7CpduDTrHlhHqTC7xG/n8Z2cjDtJs4rNHG9bxA65zJtnj2XL7LBLQID9kvPoo1Cs2Abuu6+R5190ihe3y+LHjIEff4SpU+1UvW7doFYtOHTINuzgNypj7AbQFSvaIcZUMTG2WOiff9pj5Uq7BgjspILmze215rZtbU2V7AzzJCQlEBwYzFVVr+KmujcRFuzyPsHJyfYNCAiw0yMrVrS1lRy0YIG9hrt3r52w88wz+Xg9XWbZ3xsH0BqYl+72MGBYZs/P6558qvfft5/Ww4Z51HyOZSve6GjbPQORO+8UOXPG8bgyk1W8fb7sI6XeKCWn40870n50tMg334j0728706k92EaNRJ54wn7ROXky+/F65OhR27MUERk6VCQwUOSGG0RmzMj135G34j10SOTbb0WefFKkdetz32qMse/V4MEiX34pcviCa+fJycly61e3Sv9Z/fM03ovasUOkQweRTz/1+FTZiffkSZH777fvV+3aIr/95nGzueatnryxjzvDGNMb6CIi96bc7ge0EpGH0z1nEDAIoHz58s1nzpyZ6/ZiYmIIz8X4nAiMGVOHOXMq8dxzm+jU6UiuY8iJ7MRb+913qfT99+y8/34O9Onjanciq3hjEmPYGbOTxiUaA7D02FKuKn0VgSb3e2hGRobw229l+P330qxZU5KEhADCwxO44oooWrY8TosWxylTJj5X8XpL4X37KD9vHuV/+YXQI0dILFyYiC5d2DFkSI7O41S8cXEBbN5clA0bSrB+fXE2bixObKz9O6le/TSNGh+jWZMYGjc+wQ+nJhESEMJtVW9Lu9ie1/ECBMTHU3XGDKpPm0ZycDDbhw7lcOfOHp3zYvGKwPLlpXnnndocO1aIPn32M2DAHgoVcm8RYE7e3w4dOqwWkYzX3GaW/b1xAH2ASelu9wPez+z5bvXkRUTi4uwsxJAQkZ9/9iiMbLtovMnJ9s9jx+xgsw/Iyfu7bN8yYQQyafWkHLezd6/I2LEibdpI2hTGSy4ReewxO6YeH+/9eL0iKUlk4UKRAQNEhqRcp0hOttP8Vq0693eaibyKNz5eZPlyO7bfutefYh6vKlRcJSBSv77IQw/ZaZxHjlz8PI7Fu3ix7UaDyK23ivzzj1dOm1m8S5eKXH21be6yy0R+/90rzXksX4zJY8fh0xdKqQIcdLjNXAkJsWPyHTvCTTfBnDm2MoArfv7Zbu/+zTd27D0fzvFsXaU1c26fQ6da9k1cuncpgqStor3QwYN2q7SZM+1MGLDTBV96yVYhaNAgH4yJBgTY0scd0u1+tHev/SWGD7czdG691R4NG7r2CwUFCXUuP0GrViV5ILY2t3/diFuvN0SsseV9pk49V/qjQQM7XbB9e7vWyNGJXJIyc+zkSfvzvHl25ZFD1q2zG5X9+KMtWjhunF04GxLiWJPuyCz7e+PATtHcBdQEQoB1QIPMnu9mTz7VsWN23DIszHYonJRhvNOn25U0TZpk3ZXKY568v9d9dp3Ufq+2JCadmxERGSkyfrxI+/bneuyNG9uO77Zt7sbrVcePi0yaJNK587npMLNm2cfi49N6+HkVb68vekm7/2snyZl8s4iPt7NzRo0S6dJFpEiRc9c/6tQRufdekalTRaZP/yOrLyfZs327SN++Ii+8cO6+uDgvnPh8ixYtkrg4kS++sMP8IFKihP09TztzGckj3urJO5rkbdt0BbYBO4HnLvZcX0jyIvaCVP369h+3kxde/hXv++/bbHfNNXbano/x5P09HX9aNh3ZJGfOiEybGS/VHh4oQVXWpH1FHjFCZPNm78Uq4kNJPr3Dh0XGjbNXkUVshrnkEpGnnpLV77+f42mB2ZGcnCwLdy1MS+pT1kyRiasnSlJyUrZen5r0R48W6d7dJsbUpF++vMh//mMfW7o0h8ly40aRgQPtReuwMJGXX87Fb5e15GTb1B137JFy5WzcNWrYzsTx44406RX5Jsnn5PCVJC9iZyjUqSNStKhdPe2E8+IdM8b+dfTsKXL2rDMNeii3729Skh1LHzDAvp+U2yABz5aWnk/PljVrROITEzLtVXrCJ5P8hWbPFrn++nN1EMqWFbnvvizH73Piu83fCSOQH7f96JXzJSWJrFsnMnToVunXz35GpSb9gAC77qR/f5EPPrCdpAzLM7z+un1BaKjIww/bRQBeFBsrMm+evTRSs2ZqbMnSo4fITz858lnqdfllTD7fqlDBbjDUqZM9Jk2yix0d06WL3aVp9GhHS6TmpS1bbBnWzz+HffvswsTevaFfv4Y0b72HYqFFMAbeWf4BU9dNZfHdiykeWtztsPNWjx72iIpi05gx1N+1y66DSB2vHzwYKlWyY9PNmmVeQyGdxOREPvrzIyoVrUSv+r3oVqcbn/3ns7TrI54KCLB13Xr2PEj79nUAu2nG8uV2r45Vq+w4d/o93a8uv537is7k0FW9KNqqPk3Cr6P2E4Zij91LocqeVa+MjrYrhFO3BV61yo63x8XZ4nCdOtl57qVK/UGfPld51FZ+5B/ZxCGVK9ttA3v3thuBb9sGr7zi5QVTy5bZzT3q1bOLbfK5yEi7gcLUqXZhTkCAzU+jRtky74ULpz7z3NSwKsWq0LRC07QEv2DXAuqXrU/FohXz/hdwS8mSHLn2Wuq/+uq5+xIT7Zu4ahU8/7wtXdmunb06mEEB81NxpyhWqBiBJpDJaybTtGJTetXvRVBAEHdefqej4Zcrd+7zCmy//tAfezg5+WtKzptBhX/+Ivmw4bk9YTz7aX2gOdAcM8bOLShXzh5ly9oFW6GhdjFXoUL2QmhcnC1VcfasrWxw9KjtE+3fbz8TUxUtaj8LBw+21787djz3b27x4oyn2vo7TfJZKFHCTnZ56CEYOdIm+qlTbWEqT1X84Qeb2D/5BAYM8PyELomPt+/Rp5/CDz/Y8ryNGtkCcHfcYRcoXkzv+r3TaqLEJsbS56s+XH/p9czoNQOwQ4pZzdn2S0FBdhnrkSN2Ceb8+XaPuR077OOHDkG/ftCiBS9V3cmE07+y9/H9hAQVYnH/xZQILZG38R4/brNu48aY5CQq3diUSidO2MI6T4whoE8fRlaqwiOHbc879YiIsL/ikSO2aFxUlE3qsbHntiY25vyicKVL2xoy7drZOkQ1akCTJnYVu0+uWneRJvlsCA62GyzVrWv3wN6+3dZFql/fg5NOnUqdsWNtkaW+fb0Wa14Rsfnn00/ttMfISNsTe/hhO6zVpEnuzhsaFMrye5enXrTnUPQh2v5fWyZ0n0DHms4uZfdZ5crZEoi3325vJyez58Qe3vllOM+fPkqZMWNoXzmB4GqQ8FYFQr74lhIdOtiE+/ffdupmlSq2e+xFxf7+247RrFljayvs2AGXXWYrqgUG2rG6yy6z7acI4Fx5hjZtsm5DxH6hCQrKB1NofZQm+Wwyxu4oVbcuDBxovxKOGmULQea45/DDDzBwIFHNmlHqm2/y1cTcnTvtB9y0afZbTWioXVfQr58dlvHG5YQ6peuk/RwVG0WtkrWoXLQyAH8d+ov5O+fzQIsHCtT4vYiw6egmwkPCqV6iOtFx0Yzf+y3XTvmK7jWuo8PGjXRYtcom22rV7It++gkeeODcScqWtd3er7+23eBff7XfEIoXt+Mixthj4ED7F/u//8GiRXbe+smTtoznkSN2xwxjqPT99/Y5NWrYcph3333+GgEv7IlnTP7cWMWnZHZF1o3Dl2bXXExEhJ1KBiIdO9oVmtl2/LhIsWIiLVrIrz/95FiM3hQRYWd31q9/Iq0GSvv2dup3Xs/0fOO3NyTstTA5FWvLhq44sEJWHFiR4eycfDG7Jp0L441PjJeI6AgREYmOi5aQV0Nk6M9D0x4/GXtSLurECZElS0SmTBF59VVblKVr13NVTP/7X8lwV5TUx4cPtzuilCkjUquWXRaarn7Ssi+/9O05iBfI7/8eLgadQul9yck2yYWH25w9alQO6lLNnSty6JBP/6M7dkxkwgSRa689t36nVq1oeeMNkX0ZV57NM0dPH037+cZpN8ol716SluSX7Vsmu6N2i0j++0+9cOHC83bcajGhhXSf3j3t9g9bf5CDp7w71VCSkuyHwZEjdg5/RMS5wmuJiRedypnf3l9/jvdiSV4vUeSSMXaSw7p19uLPs89CnTp22lhSUgYvOHHCfrUFWyu2QoU8jDZ7Dh2yG+5cd50Nb9AgO/Xxuedg40aYPHkVTz9tv/G7Kf2G0VNvmsoXvb9IuzDbf1Z/hvx8rjDYFxu/YNNRn6hs/S8x8TH8deivtNuvb3mdtv/XNu32Iy0fYVDzQWm3u9Xp5v0ZRwEBdrimbFk79l++/Lnxx8BAHQj3A5rkPVSrlh1iX7zYXkwaMMAOT375pZ1lAtjpJzffbOcQRkS4Ge55ROx1udGj7UWwypXhwQdhzx674dRff8HWrXbaaIMGbkebsdKFS9O8UvO029/d+h2vdrDTEBOSE7hr1l1MWTsFgGRJ5p7Z9/DLrl8A+y02PinvptWtP7ye15a8RlKy7QW8+uurXDnpSuIS7RSSTuU68fRVT6dddO7XuB/d6ng+rq0KNk3yXnLNNbBihU3uZ8/aGlTVqtl9PmL6P2wvYE2c6HoP/sQJmD3bXo+rUcPWyXrmGTv3+OWXbY9961Z7Ublp0/zXkWtQrgFNKjQBIMgEsWPIDh5t9SgAkWci+d+u/7ErahcAh2IOEfpaaNqHQOSZSB6b+xjrItYBdt753B1zOXr6KGB73usPrycmPgaAqLNRLNq9iBOxJwDYFrmNlxe/TESM/SCftWUWFd6qwN4TewFYdXAVLyx6gf2n9gNwV+O7+O7W79K+hbQq3Yp7mt1TMKeLKsdokvciY6BPH7vS88cf7a48h16dRPiMiXxxyXAmnLnzvH1G80JkpK2o+eST0KKFnV980012dkyzZnZq6P79dhbcCy/kk2qP2WSMoWrxqlQuZmfmlC1Slv2P7ee+ZvcBEBwQzAvtXkj7UNh/aj8T/5rI3pM2KW8+upkbpt3Anwf/BGDNoTU0Ht+YFQdWAHamT8dPO7Lh8AYAdkXtYsSvI9hzYg8AVYtVpUfdHgQY+9/s1ga3EjMshholagD2A+nGOjcSEph/Zlep/EenUDogMNBOf+9aZwcyfzDbKl/Hs/GvsOd++/jll9vHixQpTfXqtkftaWJNTrbJeutWm7BXrbLHnj328ZAQaN3aJvL27e0i23w0c9OrUnvKZYuU5eUOL6fd36RCE2KGx6QNlzQo14BlA5dxWZnLAKhXth5f9/maBuXs2FWzis1YfPdiGpVvBECnWp1IeCGBoAD736p5peZMqDQh7fxFQoo4/8spdQFN8k665BLMBx9Q5+ab2VUqkM2bbQ//p5/satDExEa88IJdin355Xa1XurS7nLl7Cr2gIDz57dFR8OxY+eOgwft4qydO8+tDgQ7DfqKK+wYe8uW0KqVd1bpFgSpHwLhIeFcVfVcrZMyhcvQq36vtNslw0pyTY1r0m6nJnelfIn+q3RCYqLtVtesCffZoQGDXSFbvz489RScPg1Tp64mKKg569fbWTrz59uaHPHZuBZojB16KV/efjh07Wr/rF3bfmD4wD7fSikfoEneCc89Bx99ZKeuZDLfsEgRqF8/mvbtz78/tbd+5IgtBSJybiGiMbaSY5kytohTNgoSKqUKOE3y3jZ3rp2TeP/9uZpQbgwUK2YPpZTylM6u8aYjR6B/fzsvcexYt6NRSintyXuNiF0Ce+KEHVzXq5xKKR+gPXlvSUiwS15Hj7bF1JVSygdoT95bQkLsyqKUOdZKKeULtCfvqdhYu8x1zRp721+Wiyql/IImeU+NGGE3YTh0yO1IlFLqXzTJe2LVKnjzTXvBtWtXt6NRSql/0SSfW/Hxdpu0ChVsjQKllPJBeuE1tyZOhA0b4PvvoUQJt6NRSqkMedSTN8a8aYzZYoxZb4z5zhhTIt1jw4wxO4wxW40x13scqa8ZNAi++Qa6d3c7EqWUypSnwzXzgYYicjmwDRgGYIypD9wGNAC6AOOMMf5RaSUx0S54Cg62uz0ppZQP8yjJi8j/RCQx5eZyoErKzz2BmSISJyK7gR1AS0/a8hnvvGNLSR486HYkSimVJW9eeB0I/Jzyc2Vgf7rHDqTcl7/t2wcvvWQLtVf08obKSinlACNZrNA0xvwCZLQx6XMiMjvlOc8BLYCbRUSMMR8Cf4jI5ymPTwZ+EpFvMjj/IGAQQPny5ZvPnDkz179MTEwM4eHhuX59VuqPGEHp5ctZOWUKcV7Yq9XpeL1N43WWxussf463Q4cOq0WkRYYPiohHB3A38AdQON19w4Bh6W7PA1pnda7mzZuLJxYtWuTR6y9q3jy7OdNrr3ntlI7G6wCN11kar7P8OV5glWSSVz2dXdMFeAboISJn0j30PXCbMaaQMaYmUBtY6Ulbrps1Cy691O6IrZRS+YSn8+Q/AAoB81P2xVwuIg+IyN/GmC+BTUAiMFhEkjxsy10ffmg3VS1UyO1IlFIq2zxK8iJy6UUeGwmM9OT8PuGff2wZ4Ro17A7bSimVj2hZg6w88gi0aAFnzmT9XKWU8jGa5C9m4UL49lt47DEoXNjtaJRSKsc0yWcmOdleZK1WDZ54wu1olFIqV7RAWWamTbMbgUybBqGhbkejlFK5oj35zGzbBq1awW23uR2JUkrlmvbkM/Pqq/DCCxCgn4NK+bqEhAQOHDhAbGxsps8pXrw4mzdvzsOoPJNRvKGhoVSpUoXg4OBsn0eT/IWOHIHdu20vPiTE7WiUUtlw4MABihYtSo0aNTCZ7LMcHR1N0aJF8ziy3LswXhEhMjKSAwcOULNmzWyfR7upF3r5Zbj6at2zVal8JDY2ltKlS2ea4P2BMYbSpUtf9NtKRjTJp7dlC3z8Mdx/v1aZVCqf8ecEnyo3v6Mm+fSef97Oh3/pJbcjUUopr9Akn2rNGrud3+OPa/kCpVSOvffee9SrV4++ffsya9YsXnnllYs+/8knn2ThwoWOx6UXXlNt3w41a9rVrUoplUPjxo3j559/pmbNmlx11VV8//33F33+kCFDuO++++jYsaOjcWmST3XLLdCrFwT6x1a0ShVUQ4fC2rX/vj8pKSzX/72bNLE7f2bmgQceYNeuXfTo0YM777yTQoUKUaZMGQB69uxJr169uOuuu/j4449ZsmQJ06ZNo3r16kRGRhIREUEFL2xClBkdrgH49VdbxkATvFIqF8aPH0+lSpVYtGgR5cqVo1mzZmmPTZgwgVdeeYWlS5fy9ttv8/7776c91qxZM5YtW+ZobNqTX7oU2reHyZNh4EC3o1FKeSizHnd09Nk8mSd/6NAhyqa7rle+fHleeeUVOnTowHfffUepUqXSHitXrhwHDx50NJ6C3ZMXsTNqKlTQ8gVKKa8ICwv711z2DRs2ULp06X8l9NjYWMLCwhyNp2An+QULYMkSGD5cSwkrpbyiXr167NixI+32ypUr+fnnn1mzZg1vvfUWu3fvTnts27ZtNGzY0NF4Cm6SF4EXX4SqVWHQILejUUr5iXbt2rFmzRpEhLi4OO677z4++eQTKlWqxNtvv83AgQMRERISEtixYwctWrRwNJ6COyZ/+LAtXTB8uO7bqpTy2J49e9J+7tSpEwsWLKBTp06sW7cu7f4ePXrQo0cPAObMmUPv3r0JCnI2DRfcJF+hgi0nrJRSXjZ8+HBWrFhx0eckJibyRB5sSFQwk/yhQ1CypG4GopRyRPny5dN67Jnp06dPnsRSMMfkH3gAmje34/JKKeXHCl6S37gRvv/ernAtAFXrlFIFW8FL8qNGQZEiMGSI25EopZTjClaS37ULZsyABx+EdKvOlFLKXxWsJD9jBgQF2XLCSinlRamlhitXrsyIESPS7n/nnXf49NNPL/ra2267je3btzsSl1eSvDHmSWOMGGPKpLtvmDFmhzFmqzHmem+047Hhw2H9et31SSnldePGjeOnn35i5MiRafclJibyySefcMcdd1z0tQ8++CCjR492JC6Pp1AaY6oCnYF96e6rD9wGNAAqAb8YY+qISJKn7eVaYqLtxdet61oISqk80r79v+4K7tHDfos/cwa6dv33a/r3t8exY9C79/mPLV580eYuLDUcHh4OwMKFC2nWrBlBQUEkJibSunVr3nzzTdq3b8+wYcMICAhg5MiRtG3blv79+5OYmOj1xVHeONtY4Glgdrr7egIzRSQO2G2M2QG0BP7wQns5FxMD9erBK6/AgAGuhKCU8l/jx49n7ty5LFq0KK2OPMCyZcto3rw5AEFBQUyZMoXevXvz3nvvMXfu3LQFUwEBAVx66aWsW7cu7fne4lGSN8b0AP4RkXUXbDBbGVie7vaBlPsyOscgYBDYBQSLs/jEvJiYmJgMX1/pu++oc+AAf505wykPzu9tmcXrqzReZ2m8uVe8eHGio6PP3fHDD/96TlJSEgmpz8ngcQCio22ZkwsfT3/uTIgIMTExFEpXJmXfvn3UqFEjLbZq1apxyy230L17d3755Rfi4uKIi4sDoGTJkuzcuZM6deqkxRudQbuxsbE5et+zTPLGmF+AjLYteQ4YDlyX0csyuC/DlUciMgGYANCiRQtpn8HXrOxavHgx/3p9UhLcdx9ceSXNBg/O9bmdkGG8PkzjdZbGm3ubN2/OslZ8dHS0o/XkjTGEh4ef10axYsUwxpx337Zt2yhRogQxMTHn3Z+UlESpUqXS7sss3tDQUJo2bZrtuLJM8iLSKZNfqBFQE0jtxVcB/jLGtMT23Kume3oVwNnK+JmZMwd27IB0F0OUUiovXFh2+NtvvyUyMpIlS5bQrVs3Vq5cSYkSJQCb/Bs0aOD1GHI9u0ZENohIORGpISI1sIm9mYhEAN8DtxljChljagK1gZVeiTinxoyBatXg5ptdaV4pVXDdcMMNLFmyBIBjx47x7LPPMnnyZOrUqcPDDz/Mo48+CsDhw4cJCwujogMz/xwpUCYifxtjvgQ2AYnAYNdm1nz4IRw8aGfWKKWUQ9KXGk5VvXp1Spcuzfbt26lduzbb0lW+feSRR9J+nj59Ovfff78jcXkt86X05tPfHgm4P0bSsKE9lFLKBaNGjeLQoUPUrl070+eUKFGCfv36OdK+/654/ecf6NsXdu50OxKlVAFWt25d2rVrd9HnDBgwwLHNQ/w3yX/wAcycCQH++ysqpVRW/DMDnj0LEyZAz55Qs6bb0SillGv8M8l/9RUcPw4PP+x2JEop5Sr/TPLjxtkaNR06uB2JUkq5yv+SfEICXHMNPPOM7vyklMozGZUaHjFiBFOmTEl7ztChQ9PmzWemU6dOREVFeS0u/0vywcHwxhtaiEwplacyKjWc3vHjx1m+fHmWM2369evHuHHjvBaXXyX5oOhomDsXkpPdDkUp5aL2U9ozZe0UABKSEmg/pT0zN80E4EzCGdpPac8XG78A4GTsSdpPac+3m78F4NiZY7Sf0p4fttoiZRExEVm2l77U8OHDh9NKDYeHhxMWFgbA119/TZcuXWybJ09St25dtm7dCsDtt9/OxIkTAejRowczZszwxtsAOLTi1S0V5s2zK1zXr4dGjdwORylVQGRWavjJJ59M+3nZsmX0TqlTX7x4cT744AP69+/Po48+SlRUFPfddx9gq1HGxcURGRnplYJq/pPkk5OpNHs2XHWVJnilCrjF/Ren/RwcGMzi/ovTyvYWDi583uPFQ4ufd7tM4TLn3a4QnlER3pw7dOgQZcuWTbvduXNnvvrqKwYPHsy6devOe265cuWIiIigRo0aHrfrP8M1CxZQ+MABeOghtyNRSql/CQsLIzY2Nu12cnIymzdvJiwsjOPHj5/33NjYWEJDQ73Srv8k+XHjiC9R4t/bdimllA+4sOzw2LFjqVevHjNmzGDgwIEkJCQAdvORiIgIqlev7pV2/SPJnz0La9dyqGtXu6uLUkr5mBtvvDFtR6dt27YxadIk3n77bdq2bUu7du147bXXAFi9ejVXXnml12rZ+MeYfFgYbN/Ovvnz8c5nn1JK5UxGpYbTa9u2LcOGDePEiRPUqVOHzZs3pz02ZsyYtJ8/++wzHvLisLN/9OQBgoJISpmqpJRSvujtt99m3759F31Ow4YNufbaa73Wpn/05JVSKh9o1apVls9JnUrpLf7Tk1dKFWgi4nYIjsvN76hJXimV74WGhhIZGenXiV5EiIyMzPHUSh2uUUrle1WqVOHAgQMcPXo00+d4c+55Xsgo3tDQUKpUqZKj82iSV0rle8HBwdTMYoOgxYsX07Rp0zyKyHPeileHa5RSyo9pkldKKT+mSV4ppfyY8aWr0caYo8BeD05RBjjmpXDygsbrLI3XWRqvs3ISb3URKZvRAz6V5D1ljFklIi3cjiO7NF5nabzO0nid5a14dbhGKaX8mCZ5pZTyY/6W5Ce4HUAOabzO0nidpfE6yyvx+tWYvFJKqfP5W09eKaVUOprklVLKj/lVkjfGvGqMWW+MWWuM+Z8xppLbMV2MMeZNY8yWlJi/M8aUcDumizHG9DHG/G2MSTbG+OxUNGNMF2PMVmPMDmPMs27HkxVjzCfGmCPGmI1ux5IdxpiqxphFxpjNKf8eHnU7posxxoQaY1YaY9alxPuy2zFlhzEm0Bizxhgzx5Pz+FWSB94UkctFpAkwB3jR5XiyMh9oKCKXA9uAYS7Hk5WNwM3AErcDyYwxJhD4ELgBqA/cboyp725UWZoCdHE7iBxIBJ4QkXrAlcBgH3+P44COItIYaAJ0McZc6W5I2fIosDnLZ2XBr5K8iJxKd7MI4NNXlUXkfyKSmHJzOZCzGqJ5TEQ2i8hWt+PIQktgh4jsEpF4YCbQ0+WYLkpElgDH3Y4ju0TkkIj8lfJzNDYRVXY3qsyJFZNyMzjl8OncYIypAtwITPL0XH6V5AGMMSONMfuBvvh+Tz69gcDPbgfhByoD+9PdPoAPJ6D8zhhTA2gKrHA5lItKGfpYCxwB5ouIT8cLvAM8DSR7eqJ8l+SNMb8YYzZmcPQEEJHnRKQqMA142N1os4435TnPYb8CT3Mv0rRYsozXx5kM7vPpXlt+ZYwJB74Bhl7wLdrniEhSyjBuFaClMaahyyFlyhjTDTgiIqu9cb58t2mIiHTK5lOnAz8CLzkYTpayitcYczfQDbhWfGDRQg7eX191AKia7nYV4KBLsfgtY0wwNsFPE5Fv3Y4nu0TkhDFmMfYaiK9e6G4D9DDGdAVCgWLGmM9F5M7cnCzf9eQvxhhTO93NHsAWt2LJDmNMF+AZoIeInHE7Hj/xJ1DbGFPTGBMC3AZ873JMfsUYY4DJwGYRGeN2PFkxxpRNnblmjAkDOuHDuUFEholIFRGpgf33uzC3CR78LMkDo1KGFtYD12GvTvuyD4CiwPyUaZ/j3Q7oYowx/zHGHABaAz8aY+a5HdOFUi5kPwzMw14Q/FJE/nY3qoszxswA/gDqGmMOGGPucTumLLQB+gEdU/7drk3pdfqqisCilLzwJ3ZM3qNpifmJljVQSik/5m89eaWUUulokldKKT+mSV4ppfyYJnmllPJjmuSVUsqPaZJXSik/pkleKaX8mCZ5pS7CGHNFSr3/UGNMkZR65D5b90SpC+liKKWyYIx5DVtDJAw4ICL/dTkkpbJNk7xSWUipgfMnEAtcJSJJLoekVLbpcI1SWSsFhGPrDIW6HItSOaI9eaWyYIz5HrvDVE2gooi4vk+BUtmV7+rJK5WXjDF3AYkiMj1l/9jfjTEdRWSh27EplR3ak1dKKT+mY/JKKeXHNMkrpZQf0ySvlFJ+TJO8Ukr5MU3ySinlxzTJK6WUH9Mkr5RSfuz/AQ/kisdVNAryAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"plt.figure()\n",
"xplt = np.arange(-3,4,0.1)\n",
"\n",
"fplt = f(xplt)\n",
"dfplt = df(xplt)\n",
"ddfplt = ddf(xplt)\n",
"\n",
"plt.plot(xplt, fplt, label=\"f(x)\", color=\"b\", linestyle=\"-\")\n",
"plt.plot(xplt, dfplt, label=\"f'(x)\", color=\"r\", linestyle=\"--\")\n",
"plt.plot(xplt, ddfplt, label=\"f''(x)\", color=\"g\", linestyle=\":\")\n",
"plt.xlabel(\"x\")\n",
"plt.legend()\n",
"plt.grid()\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.6.2 Geometric Insights into Newton Steps](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.2-Geometric-Insights-into-Newton-Steps)",
"section": "3.6.2 Geometric Insights into Newton Steps"
}
},
"source": [
"## 3.6.2 Geometric Insights into Newton Steps"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.2.1 Motivation](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.2.1-Motivation)",
"section": "3.6.2.1 Motivation"
}
},
"source": [
"### 3.6.2.1 Motivation\n",
"\n",
"We can interpret Newton-type methods for unconstrained optimization as root finding of $\\nabla f(x) = 0$.\n",
"\n",
"At iteration $k$, we assemble an approximation to $f(x)$ using a Taylor series expansion:\n",
"\n",
"$$f(x^k + p^k) \\approx f(x^k) + \\nabla f(x^k)^T p^k + \\frac{1}{2} (p^k)^T (B^k) p^k$$\n",
"\n",
"and solve for $p^k$ such that $f(x^k + p^k)=0$. This gives:\n",
"\n",
"$$p^k = -(B^k)^{-1} \\nabla f(x^k)$$\n",
"\n",
"The choice of $B^k$ determines the algorithm classification:\n",
"* Pure **Newton Method**, $B^k = \\nabla^2 f(x^k)$\n",
"* **Steepest Descent**, $B^k = \\frac{1}{\\alpha} I$, where scalar $\\alpha$ is sometimes known as the dampening factor\n",
"* **Levenberg-Marquart**, $B^k = \\nabla^2 f(x^k) + \\delta I$, where scalar $\\delta$ is chosen to ensure $B^k$ is positive definite.\n",
"* **Broyden Methods**, $B^{k}$ is approximated using history of gradient evaluations, i.e., $\\nabla f(x^0), ... \\nabla f(x^k)$. We will study the SR1 and BFGS formulas in this family of methods.\n",
"\n",
"This section **explores how choosing $B^k$ impacts the shape of the approximation and calculated step.**"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.2.2 Compute and Plot Steps](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.2.2-Compute-and-Plot-Steps)",
"section": "3.6.2.2 Compute and Plot Steps"
}
},
"source": [
"### 3.6.2.2 Compute and Plot Steps\n",
"\n",
"Define a function that:\n",
"* Computes the i. Newton, ii. Levenberg-Marquardt and iii. Steepest Descent Step for a given starting point $x_0$\n",
"* Plots the step in terms of $f(x)$ and $f'(x)$"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.2.2 Compute and Plot Steps](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.2.2-Compute-and-Plot-Steps)",
"section": "3.6.2.2 Compute and Plot Steps"
}
},
"outputs": [],
"source": [
"def calc_step(x0, epsLM):\n",
" \n",
" # Evaluate f(x0), f'(x0) and f''(x0)\n",
" f0 = f(x0)\n",
" df0 = df(x0)\n",
" ddf0 = ddf(x0)\n",
" print(\"x0 = \",x0)\n",
" print(\"f(x0) =\",f0)\n",
" print(\"f'(x0) =\",df0)\n",
" print(\"f''(x0) =\",ddf0)\n",
" \n",
" \n",
" ### Calculate steps\n",
" \n",
" # Newtwon Step\n",
" xN = x0 - df0 / ddf0\n",
" \n",
" print(\"\\n### Newton Step ###\")\n",
" print(\"xN = \",xN)\n",
" print(\"pN = xN - x0 = \",xN - x0)\n",
" f_xN = f(xN)\n",
" print(\"f(xN) = \",f_xN)\n",
" print(\"f(xN) - f(x0) = \",f_xN - f0)\n",
" \n",
" # Levenberg-Marquardt Step\n",
" # Recall the eigenvalue of a 1x1 matrix is just that value\n",
" dffLM = np.amax([ddf0, epsLM])\n",
" xLM = x0 - df0 / dffLM\n",
" \n",
" print(\"\\n### Levenberg-Marquardt Step ###\")\n",
" print(\"xLM = \",xLM)\n",
" print(\"pLM = xLM - x0 = \",xN - x0)\n",
" f_xLM = f(xLM)\n",
" print(\"f(xLM) = \",f_xLM)\n",
" print(\"f(xLM) - f(x0) = \",f_xLM - f0)\n",
" \n",
" \n",
" # Steepest Descent Step\n",
" xSD = x0 - df0 / 1\n",
" \n",
" print(\"\\n### Steepest Descent Step ###\")\n",
" print(\"xSD = \",xSD)\n",
" print(\"pSD = xSD - x0 = \",xSD - x0)\n",
" f_xSD = f(xSD)\n",
" print(\"f(xSD) = \",f_xSD)\n",
" print(\"f(xSD) - f(x0) = \",f_xSD - f0)\n",
" \n",
" ### Plot Surrogates on x vs f(x)\n",
" \n",
" ### Plot f(x)\n",
" plt.figure()\n",
" plt.scatter(x0,f0,label=\"$x_0$\",color=\"black\")\n",
" plt.plot(xplt, fplt, label=\"f(x)\",color=\"purple\")\n",
" \n",
" ### Plot approximation for Newton's method\n",
" fN = lambda x : f0 + df0*(x - x0) + 0.5*ddf0*(x-x0)**2\n",
" plt.plot(xplt, fN(xplt),label=\"Newton\",linestyle=\"--\",color=\"red\")\n",
" plt.scatter(xN, f(xN),color=\"red\",marker=\"x\")\n",
" \n",
" \n",
" ### Plot approximation for LM\n",
" fLM = lambda x : f0 + df0*(x-x0) + 0.5*dffLM*(x-x0)**2\n",
" plt.plot(xplt, fLM(xplt),label=\"LM\",linestyle=\"--\",color=\"blue\")\n",
" plt.scatter(xLM, f(xLM),color=\"blue\",marker=\"x\")\n",
"\n",
" ### Plot approximation for SD\n",
" fSD = lambda x : f0 + df0*(x-x0) + 0.5*(x-x0)**2\n",
" plt.plot(xplt, fSD(xplt),label=\"Steepest\",linestyle=\"--\",color=\"green\")\n",
" plt.scatter(xSD, f(xSD),color=\"green\",marker=\"x\")\n",
" \n",
" #plt.plot([x0, xLM],[f0, f(xLM)],label=\"LM\",color=\"green\",marker=\"o\")\n",
" #plt.plot([x0,xSD],[f0,f(xSD)],label=\"Steepest\",color=\"blue\",marker=\"s\")\n",
" \n",
" plt.xlim((-3.5,4.5))\n",
" plt.ylim((-12.5,22.5))\n",
" plt.xlabel(\"$x$\")\n",
" plt.ylabel(\"$f(x)$\")\n",
" plt.legend()\n",
" plt.title(\"Function and Surrogates\")\n",
" plt.grid()\n",
" plt.show()\n",
" \n",
" ### Plot Surrogates on x vs f(x)\n",
" plt.figure()\n",
" plt.scatter(x0,df0,label=\"$x_0$\",color=\"black\")\n",
" plt.plot(xplt, dfplt, label=\"f'(x)\",color=\"purple\")\n",
" \n",
" \n",
" ### Plot approximation for Newton's method\n",
" dfN = lambda x : df0 + ddf0*(x-x0)\n",
" plt.plot(xplt, dfN(xplt),label=\"Newton\",linestyle=\"--\",color=\"red\")\n",
" plt.scatter(xN, df(xN),color=\"red\",marker=\"x\")\n",
" \n",
" \n",
" ### Plot approximation for LM\n",
" dfLM = lambda x : df0 + dffLM*(x-x0)\n",
" plt.plot(xplt, dfLM(xplt),label=\"LM\",linestyle=\"--\",color=\"blue\")\n",
" plt.scatter(xLM, df(xLM),color=\"blue\",marker=\"x\")\n",
"\n",
" ### Plot approximation for SD\n",
" dfSD = lambda x : df0 + (x-x0)\n",
" plt.plot(xplt, dfSD(xplt),label=\"Steepest\",linestyle=\"--\",color=\"green\")\n",
" plt.scatter(xSD, df(xSD),color=\"green\",marker=\"x\")\n",
" \n",
" \n",
" plt.xlim((-3.5,4.5))\n",
" plt.ylim((-50,50))\n",
" plt.xlabel(\"$x$\")\n",
" plt.ylabel(\"$f'(x)$\")\n",
" plt.legend()\n",
" plt.title(\"First Derivative and Surrogates\")\n",
" plt.grid()\n",
" plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.2.3 Consider $x_0 = -3$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.2.3-Consider-$x_0-=--3$)",
"section": "3.6.2.3 Consider $x_0 = -3$"
}
},
"source": [
"### 3.6.2.3 Consider $x_0 = -3$"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.2.3 Consider $x_0 = -3$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.2.3-Consider-$x_0-=--3$)",
"section": "3.6.2.3 Consider $x_0 = -3$"
},
"scrolled": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"x0 = -3\n",
"f(x0) = 15.0\n",
"f'(x0) = -51\n",
"f''(x0) = 64\n",
"\n",
"### Newton Step ###\n",
"xN = -2.203125\n",
"pN = xN - x0 = 0.796875\n",
"f(xN) = -8.660857647657394\n",
"f(xN) - f(x0) = -23.660857647657394\n",
"\n",
"### Levenberg-Marquardt Step ###\n",
"xLM = -2.203125\n",
"pLM = xLM - x0 = 0.796875\n",
"f(xLM) = -8.660857647657394\n",
"f(xLM) - f(x0) = -23.660857647657394\n",
"\n",
"### Steepest Descent Step ###\n",
"xSD = 48.0\n",
"pSD = xSD - x0 = 51.0\n",
"f(xSD) = 2534689.5\n",
"f(xSD) - f(x0) = 2534674.5\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEWCAYAAAB42tAoAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAABOnUlEQVR4nO3dd1wUd/7H8deHIggi3YIgxYoVezdgSUyzxDRjSeIlppe7XO7SY3LnXe6X3hPTi0Zz9mhM1Kixxk4UQRSxIShNpIm07++PRQ4NIODuzu7yfT4ePGRnZmfeOy772ZnvzPcrSik0TdM0rSZORgfQNE3TbJsuFJqmaVqtdKHQNE3TaqULhaZpmlYrXSg0TdO0WulCoWmaptVKFwrNYYjIMBFJNDrH5YjIehG5x+gcmlZXulBoZiMiR0XknIjkV/kJsuD2lIi0v/BYKbVRKdXJUtuzBhHxEZHPReSUiOSJyEER+bvRuepCRGaKyLdG59DMz8XoAJrDuVEptcboEHbsTcATiATOAh2Bbg1ZkYi4KKVKL5nmrJQqu+KUWqOijyg0i6s40hhV5XHlN08RCas4MrhTRI6LSKaIPFtlWWcReUZEDld8w94lIiEisqFikd8rjlxuE5FoEUmp8tzIitM8OSKyX0TGVpn3pYi8LyIrKta7TUTa1fIa/lvxLf+siGwQka51XZeIjBaRAxXPfQ+QWnZXP2CuUuqMUqpcKXVAKbXgkn1V+QWv6mksEblLRDaLyJsikg3MrMj2oYj8KCIFQMxl9ou/iPwgIrkiskNE/ikim6rMf1tETlTM3yUiwyqmjwGeAW6r+P/4vWK6t4h8JiJpInKyYn3OFfPai8ivFfslU0Tm17JfNAPpQqHZiqFAJ2Ak8IKIRFZM/wswCbgOaA5MBwqVUsMr5vdUSjVTSl30ISMirsAPwCqgBfAIMEdEqp6amgS8BPgCScCsWvKtBDpUrGs3MOeS+dWuS0QCgIXAc0AAcBgYUst2fgNmicjdItKhluVqMgBIrsh54fXcUfG7F7CN2vfL+0AB0Aq4s+Knqh1AFOAHzAX+KyLuSqmfgH8B8yv+P3pWLP8VUAq0B3oBVwMX2mf+UZHDFwgG3m3A69WsQBcKzdyWVHxTzRGRJfV43ktKqXNKqd+B34ELHzT3AM8ppRKVye9Kqaw6rG8g0Ax4RSlVrJRaCyzH9IF+wSKl1PaK0zNzMH0AVksp9blSKk8pdR6YCfQUEe86rOs6IF4ptUApVQK8BZyqJfcjFc9/GIgXkSQRubYOr/eCVKXUu0qpUqXUuYppS5VSm5VS5RW5qt0vFd/0JwIvKqUKlVLxmD7oq+6Hb5VSWRXrfx1ww1Tg/0BEWgLXAo8rpQqUUumYTq3dXrFICRAKBCmlipRSm6pbj2Y8XSg0cxuvlPKp+Blfj+dV/fAsxPRhBhCC6Vt4fQUBJyo+HC84BrSpwzYvUnH665WK01+5wNGKWQF1WFcQcOLCDGXqhfMENagolv9SSvUB/IHvMX1r96vpOZeobt1Vp9W2XwIxtVueqOG5iMgTIpJQcbooB/Dm4v1QVSjgCqRd+PIAfIzpSAbgb5hOw22vOAU2vQ6vTzOALhSaNRQAHlUet6rHc08ANbYd1CIVCBGRqu/xtsDJBqzrDmAcMArTB2NYxfTa2houSMNU7ExPEJGqj2ujlMrFdDrHEwjHtB+h9n1ZXXfQVafVtl8yMJ0mCq4yr2r2YcDfgVsBX6WUD6YG9wv74dJtnwDOAwFVvjw0V0p1rXh9p5RS9yqlgoD7gA+kylVsmu3QhUKzhljgdhFxFZG+wM31eO6nwD9EpIOY9BAR/4p5p4GIGp63DdMH698qthsN3AjMa0B+L0wfeFmYPqT/VY/nrgC6ishNFY3Qj1JLoRSR50Wkn4g0ERF34DEgB0hUSmVg+kCfUnGUM536F9Ea90vF1VCLMDWCe4hIZ2Baled6YSokGYCLiLyAqd3ogtNA2IUipJRKw9QG8bqINBcRJxFpJyJXVbzWW0TkQlE6g6nQ6CuybJAuFJo1PI/pA+0MpgbfufV47huYTr+sAnKBz4CmFfNmAl9VnNa4teqTlFLFwFhM58gzgQ+AaUqpAw3I/zWm0zMngXhMDc51opTKBG4BXsFUaDoAm2t7CvBFReZUYDRwvVIqv2L+vcCTFevqCmypzwupw355GNNR0yngG+A7TEUS4GdMjfoHMe2PIi4+NfXfin+zRGR3xe/TgCaY9tsZYAHQumJeP2CbiOQDy4DHlFJH6vN6NOsQPXCRpmk1EZH/AK2UUpde/aQ1IvqIQtO0SiLSueL0nohIf+BPwGKjc2nG0ndma5pWlRem001BQDrwOrDU0ESa4fSpJ03TNK1W+tSTpmmaViuHO/UUEBCgwsLCzLrOgoICPD09zbpOSzAiZ2F2EQlH3GnXsgCf4LptW+9P89I5zcceMoJlcu7atStTKRVY7UyllEP99OnTR5nbunXrzL5OSzAi55Knf1Og1I6v9tf5OXp/mpfOaT72kFEpy+QEdqoaPlf1qSftiqQkFQEQHFVTLw6aptk7XSi0K9JlYHPu77KBFl10odA0R+VwbRSadcX8pRcxfzE6haZplqQLhXZFsg5l4xPqjXMTZ6OjAFBSUkJKSgpFRUVXvC5vb28SEhLMkMqyzJXT3d2d4OBgXF1dzZBKcyS6UGhXpH+XPAa0SWDu0drG4rGelJQUvLy8CAsLw9RRa8Pl5eXh5eVlpmSWY46cSimysrJISUkhPDzcTMk0R6HbKLQGU+WKlNJWBLcoMTpKpaKiIvz9/a+4SDQ2IoK/v79ZjsQ0x6MLhdZgmYlZFONGcIhtfSjrItEwer9pNdGFQmuwlNhMAILbuRmcRNM0S9KFQmuwE3FnAQjp2vwyS2qaZs90odAarNPQQP45aj3thra+/MKNyDvvvENkZCSTJ09myZIlvPzyy7Uu/9e//pW1a9daKZ2m1Z++6klrsE7XRvDstTWNRNp4ffDBB6xcuZLw8HAGDx7MsmXLal3+kUce4d5772XEiBFWSqjZk4RFCSAQOSHSsAw2UShEJATTcJOtgHJgtlLqbRHxA+ZjGsz+KHCrUuqMUTm1ix38+QjebZrRslv1/YgZ7afHf+JU7KkGP7+srAxn54vvD2kV1Yoxb42p8Tn3338/ycnJjB07lilTpuDm5kZAgOmu9XHjxjFx4kSmTZvGxx9/zIYNG5gzZw6hoaFkZWVx6tQpWrWqcThtrZHa8toWXNxcDC0UtnLqqRR4QikVCQwEHhKRLsBTwC9KqQ7ALxWPNRsxZWIh06KPGR3Dpnz00UcEBQWxbt06WrRoQe/evSvnzZ49m5dffpmNGzfy+uuv8+6771bO6927N5s31zaUttZYZSVm4d/J39AMNnFEoZRKA9Iqfs8TkQSgDTAOiK5Y7CtgPfB3AyJq1Tha2IJeIbZ753Jt3/zr4kpvZEtLSyMw8H9HWy1btuTll18mJiaGxYsX4+fnVzmvRYsWpKamXlFezfEUZhVyLvsc/h11obiIiIQBvYBtQMuKIoJSKk1EWtTwnBnADDD9Ma5fv96smfLz882+TkuwZs7inGIy1NV4eW6s9zYtmdPb25u8vDyzrKusrKxB61JKkZ+fj4hw9uzZi9axa9cu/Pz8SE5Ovmh6bm4urVu3btD2GpqzOkVFRRb7v7GHvyNby3h2v+nKwtTzqRflsnrOmvofN+IHaAbsAm6qeJxzyfwzl1uHHo/COuJ/SFKg1JwHN9X7uZbMGR8fb7Z15ebmNuh5oaGhKiMjQ61cuVJNnjy5cvq2bdtUz5491cmTJ1X79u1VcnJy5bwbbrhBbd261ao5q2PO/Xcpe/g7srWMe77Yo2YyU2UezLxoeqMdj0JEXIGFwByl1KKKyadFpHXF/NaYBnvXbMDR3dkAhHaz/b6QjDJ8+HD27NmDUorz589z77338vnnnxMUFMTrr7/O9OnTUUpRUlJCUlISffv2NTqyZmOyDmbh5OKET5iPoTlsolCIqe+Az4AEpdQbVWYtA+6s+P1OYKm1s2nV63FdMF/du4mu14UaHcXmHD16lICAADw8PBg1ahS//PILbm5u/P7775WN22PHjmXdunWICMuXL+fmm2/GxcXmzgRrBstKzMK3nS/Orsb2zmwr78whwFRgn4jEVkx7BngF+F5E/gQcB24xJp52qTZ9WzOtr77R7nKeeeYZtm3bVusypaWlPPHEE1ZKpNmTrINZhjdkg40UCqXUJqCmHslGWjOLVje/fRpH0+au9Ly1k9FRbFrLli0ZO3Zsrcvccov+/qP9kSpXZB3Kot2YdkZHsY1CodmfP/9Z4elawJpbjU6iaY7p7PGzlJ0vs4kjCptoo9Dsz7HCQEIDCoyOoWkOK+tgFoAuFJp9KsopIq28FWEhZUZH0TSHlZlo6sY/oFOAwUl0odAa4Pi2NABC2+kzl9URkYsap1977TVmzpx5ReuMjY3lxx9/vMJkmj3JOphFE68meLb0NDqKLhRa/R3bY7qHIqy7voeiOm5ubixatIjMzEyzrVMXisYn+2A2AZ0CbGLkQV0otHrrf0d71r6+h6gJ4UZHsUkuLi7MmDGDN9988w/zMjIymDhxIv369aNfv36VHQF2796dnJwclFL4+/vz9ddfAzB16lRWrVrFCy+8wPz584mKimL+/PlkZ2czfvx4evTowYgRI9i7dy8AM2fOZPr06URHRxMREcE777xjvReumVVmYqZNtE+AvupJawDvtt7E/KWX0THqJjr6j9NuvRUefBAKC+G66/44/6674K67kKwsuPHGi+fVsX+dhx56iB49evC3v/3toumPPfYYf/7znxk6dCjHjx/nmmuuISEhgSFDhrB582ZCQ0OJiIhg48aNTJs2jd9++40PP/yQl19+mZ07d/Lee+8BpjEsevXqxZIlS1i+fDnTpk0jNjYWgAMHDrBu3Try8vLo1KkTDzzwAK6urnXKrdmGknMlnD1+Fr+7/S6/sBXoQqHV248v7cDJWRjznO5yoibNmzdn2rRpvPPOOzRt2rRy+po1a4iPj698nJubS15eHsOGDWPDhg2EhobywAMPMHv2bE6ePImfnx/NmjX7w/o3bdrEwoULAbjqqqvIysri7FlTB3LXX389bm5uuLm50aJFC06fPk1wcLCFX7FmTtlJ2aBsoyEbdKHQGuDfbzTBWRRjnjM6SR3UdgTg4VHrfOXvX+cjiOo8/vjj9O7dm7vvvrtyWnl5OVu3br2oeICpX6j333+f48ePM2vWLBYvXsyCBQsYNmxY9dlMnWRe5MK5bDc3t8ppzs7OlJaWNvg1aMawpUtjQbdRaA1wtCCQsIB8o2PYPD8/P2699VY+++yzymlXX3115ekjoPJ0UUhICJmZmRw6dIiIiAiGDh3Ka6+9VlkovLy8LupKfPjw4cyZMweAjRs3EhAQQPPmza3wqjRr0IVCs2vF+cWklrUktI3+lloXTzzxxEVXP73zzjvs3LmTHj160KVLFz766KPKeQMGDKBjx44ADBs2jJMnTzJ06FAAYmJiiI+Pr2zMnjlzZuV6XnzxRb766ivrvjDNorISs/AK8qJJsyZGRwH0qSetnlJ2nqKctoS1M7Y3S1uWn/+/o62WLVtSWFhY+TggIID58+dX+7xvvvmm8vfBgwdTXl5e+djPz48dO3ZctPzSpabOlKuOxHfp/RpxcXENexGaobIOGj/8aVX6iEKrl6O7TIfEoV3/2MCqaZp5ZCXaRq+xF+gjCq1eht7XlYM9jhLUs6PRUTTNIdnKONlV6UKh1UuTZk3oMDrM6Bia5rAqG7L1qSfNXs19aDOf373R6Bia5rCyEm3riifQhUKrp9lzPPl8obfRMTTNYV0YJ9s33NfoKJV0odDq5ViBP2H+eZdfUNO0BrkwTraTi+18PNtOEs3mlRaVcqK0NWFtSoyOYtOq63Jj5syZiAhJSUmV0958801EhJ07d1oznmbjbGWc7Kp0odDqLHXPacpwITRCv20aonv37sybN6/y8YIFC+jSpYuBiTRbU15aTtahLAI620YfTxfov3itzlL2VoxD0cX4gVTs0fjx4ytvkktOTsbb25vAwECDU2m2JPtwNmXny2jRrYXRUS6iL4/V6mzwfd0pvOUczk26Gx2lzq6gl3GysqShvYxXq3nz5oSEhBAXF8fSpUu57bbb+OKLLxq+Qs3hpMelA9hcobCZIwoR+VxE0kUkrsq0mSJyUkRiK36q+bO2nDlz5hAWFsauXbsICwur7IStMWvq19Rm+p+xR7fffjvz5s1jyZIlTJgwweg4mo1Jj0sHgYBI2zr1ZEtHFF8C7wFfXzL9TaXUa9YOM2fOHGbMmFHZT8+xY8eYMWMGAJMnT7Z2HJvwzsRfyctVPLs62ugodXYFvYzj76+u6AiiOjfeeCNPPvkkffv21b29an+QEZeBX3s/XJva1kBTNnNEoZTaAGQbneOCZ599lsLCQnrRi9PvZABQWFjIs88+a3Ay43y/2pfVO3yMjmHXmjZtyn/+859G/T7SapYel06LrrZ12gls64iiJg+LyDRgJ/CEUurMpQuIyAxgBph661xvhq+BjzzyCABLftrBq0P/w3OZL+ATZvoGaI71W0J+fr5Fsx3O70x0m9+veBuWzOnt7X3RuA1XoqysrEHrKiwspE2bNpWPH374Yc6fP4+rqyt5eXlcf/31gKnX17KyMgoKCq4oc0NzVqeoqMhi/zeWfn+ag5EZy4vLyTyYiUc/j8tmsHpOpZTN/ABhQFyVxy0BZ0xHPrOAzy+3jj59+ihzCA0NVYDq1SlaMRPVM2iQAlRoaKhZ1m8J69ats9i689LyFCj1r6uvfBuWzBkfH2+2deXm5pptXZZkzpzm3H+XsuT/u7kYmTEtNk3NZKbaN2/fZZe1RE5gp6rhc9VmTj1VRyl1WilVppQqBz4B+ltr27NmzcLDw4OCM6bTTs6+Pnh4eDBr1ixrRbAphzecBKB9V7fLLKlpWkPY6hVPYENtFNURkdZVHk4ArDYKy+TJk5k9ezZlHucBOO/vwuzZsxttQ3bWiUICJJN2fXyMjqJpDik9Lh0nVyf8O9jWXdlgQ4VCRL4DtgKdRCRFRP4E/J+I7BORvUAM8GdrZpo8eTJJRw7hlB9Avn9poy0SACOe6EVGeQC9JnU2OoqmOaSMuAwCOgXg3MT2Ro+0mcZspdSkaiZ/Vs00q4vZMZrW5/yMjmETxEmMjqBpDil9fzrBA4KNjlEtmzmisGW3ekfTPamt0TEM9UDXDbwwfL3RMTTNIRXnF5NzJIfAbrbZpYsuFHVQ5l9GottR0g+mGx3FMCsS23H0pM0cgGqaQ8mIN100Y4v3UIAuFHWytnAnn9/3ISu+XW90FEMU5RSRUtaa9qGlRkexC7NmzaJr16706NGDqKgotm3bxltvvVV5l79RcnJy+OCDDwzNoFXPlq94Al0o6qR9kOnmqZ0JBwxOYowjm06icKJdZ9vqVsAWbd26leXLl7N792727t3LmjVrCAkJ0YVCq1V6XDouTV3wCfcxOkq1dKGog679OgKQmJtmcBJjJG0zjeHbvo8eAvVy0tLSCAgIwM3NdL9JQEAACxYsIDU1lZiYGGJiYgBYtWoVgwYNonfv3txyyy3k5+cDsGvXLq666ir69OnDNddcQ1qa6T0XHR3N448/zuDBg+nWrRvbt28HoKCggAcffJB+/frRq1evym7M9+/fT//+/YmKiqJHjx4cOnSIp556isOHDxMVFcWTTz5p7V2j1SI9Lp3ALoE4OdvmR7I+6VwHrVu1hvgmnHC2ma6orEoEejVNoP3wIKOj1Fv0l9F/mHZr11t5sN+DFJYUct2cP3ZIfFfUXdwVdRdZ57K4ceHF/Yyvv2t9rdu7+uqrefnll+nYsSOjRo3itttu49FHH+WNN95g3bp1BAQEkJmZyT//+U/WrFmDp6cn//nPf3jjjTd4+umneeSRR1i6dCmBgYHMnz+fZ599ls8//xwwFYUtW7awYcMGpk+fTlxcHLNmzWL48OF888035OTk0L9/f0aNGsVHH33EY489xuTJkykuLqasrIxXXnmFuLg4YmNjG7o7NQtJj0un3dXtjI5RI10o6sBZnHE/24qMZo2zUNzwcn9ueNnoFPahWbNm7Nq1i40bN7Ju3Tpuu+02XnnllYuW+e2334iPj2fIkCEAFBcXM2jQIBITE4mLi2P06NGAqQ+n1q3/d8/ppEmmK8iHDx9Obm4uOTk5rFq1isLCQt5//33A1FfT8ePHGTRoELNmzSIlJYWbbrqJDh06WOPlaw1QmFVIflq+zbZPgC4UdTbtyERKE8uMjqHVU21HAB6uHrXO92/qf9kjiOo4OzsTHR1NdHQ03bt356uvvrpovlKK0aNH89133100fd++fXTt2pWtW7dWu14R+cNjpRTffvstvXv3vmheZGQkAwYMYMWKFVxzzTV8+umnRERE1Pu1aJaXsb/iiicbLhS2eULMBk0dehNtD/lxPve80VGsbmCzOJ4ftt7oGHYhMTGRQ4cOVT6OjY0lNDQULy+vyh5eBw4cyObNm0lKSgJMvc0ePHiQTp06kZGRUVkoSkpK2L9/f+W65s+fD8CmTZvw9vbG29uba665ho8++uhCJ5rs2bMHMA21GhERwaOPPsrYsWPZu3fvRRk025G+37aveAJdKOqswKuQPZ2OEPvDXqOjWFVJYQk7CzpT8TmkXUZ+fj533nknXbp0oUePHsTHxzNz5kxmzJjBtddeS0xMDIGBgXz55ZdMmjSJHj16MHDgQA4cOECTJk1YsGABf//73+nZsydRUVFs2bKlct2+vr4MHjyY+++/n88+M3Va8Pzzz1NaWkqPHj3o1q0bzz//PGAqKt26dSMqKooDBw4wbdo0/P39GTJkCN26ddON2TYkPS4dt+ZueLXxMjpKjfSppzrakbeHpZO+InJJFAMm9zM6jtUc25pKGaG076zfKnXRp0+fiz7cL3jkkUcqxzgBGDFiBDt27PjDclFRUWzYsKHadU+cOJF///vfF01r2rQpb7/9Nl5eF3/IPP300zz99NN/WMfcuXPr9Do068mIy6BFtxZ/OLVoS/QRRR0NGzkQgPisVIOTWFfSVtP50/a99bCdmmZuSinTpbE22nXHBfprYh1FdYuCFXBUGteVT4f3FgDQbnBLg5M0brY+MpzWMPlp+ZzLPmfT7ROgjyjqzNvdG5fC5pzy+MNIrA6tTTt3bgr6jVY9bPuNrGn2KG236YbK1r1aX2ZJY+lCUQ9euS3J8ckyOoZVjf/3ABaeHKi7F9c0C0jbnQYCraJaGR2lVvrUUz08rR7gyI/HKC4opolnE6PjWEVxfjFNmjWO16pp1pa2K42ATgE2/zemjyjq4dqY0bTM9uVMcuM4/VRWXIa3Vxn/GLne6Cia5pBSd6XSurdtn3YCXSjqJcs9izX997Pmq81GR7GKk7tOUURTWrXRbxNNM7f80/nkncyjdR9dKBxKhlcmm677Lyu27b/8wg4gaYvpjtF2PW33RiBNs1eVDdn6iMKx9O7VC4DD5Y3jEtmkPabuHtoPdtwrnubMmUNYWBhOTk6EhYUxZ84cs6w3JiaG1atXA/Dcc8/x6KOPmmW9muO4UCha9bLthmzQjdn1EtI8BMqdSfXIMTqKVSQdLMeNIoL72f43noaYM2cOM2bMqBxQ6NixY8yYMQOAyZMnX9G6X3rpJV544QXS09PZs2cPy5Ytu+K8mmNJ25WGXwc/3L3djY5yWfqIoh5cnV3xyA0ky7txNGYPH+PBMzG/4eTimG+TZ5999g+jzhUWFvLss89e8bqHDx+OUoo33niDefPm4ezsTEFBAXfeeSf33nuv2Y5cNPuVtjvNLk47gQ0VChH5XETSRSSuyjQ/EVktIocq/vU1MiOAf2ELzvmeIvdkrtFRLO6Gl/vzwtpoo2NYzPHjx+s1vT727dtHWloabm5ulf0wLVq0iJtvvplPPvlEH2E0coVZhZw9dtYuGrLBhgoF8CUw5pJpTwG/KKU6AL9UPDbUe5H/5O9fx1CUU2R0FIsqLSrl0OqjlBU77hgcbdu2rdf0ukpLS2Py5MksXboUT09Pfv75ZwBSUlIICQkBTGNWaI1X2i77acgGGyoUSqkNwKWtxOOAC6O+fAWMt2am6vQd1oemxe5kHsg0OopFJa09Tserw5jzcPWD6DiCWbNm4eHhcdE0Dw8PZs2a1eB1FhYWctNNN/H6668TGRnJ888/z8yZMwEIDg4mJSUFgPLy8gZvQ7N/9nTFE4AoGxpoQETCgOVKqW4Vj3OUUj5V5p9RSv3h9JOIzABmALRs2bLPvHnzzJorPz+fZs2aAXA86zj/99H3jMwZxoRXB5h1O1eqas4r9fvH6Tw+71a++vtC2o7xN8s6LzBnzkt5e3vTvn37Oi///fff89JLL5GSkkJwcDAvvvgit956K2AaitSc3/wLCgr461//iru7OwMHDuS2224zy3rNmTMpKYmzZ8+aZV2XsuT/u7lYK+P+mfvJP5jPgLkN+wyxRM6YmJhdSqm+1c5UStnMDxAGxFV5nHPJ/DOXW0efPn2Uua1bt67y9+0p2xUzUf16vGT27Vypqjmv1KzR6xQolXsy12zrvMCcOS8VHx9vtnXl5pr/tVuCOXOac/9dypL/7+ZirYxvR7ytvr/5+wY/3xI5gZ2qhs9Vmzn1VIPTItIaoOLfdIPzEOFrGnf4uGfhZZa0b/GHXAlxPolXkL7ZTtPM6dyZc5xJPkOr3rZ//8QFtl4olgF3Vvx+J7DUwCwA+DX1w/W8Bxk+ZykpLDE6jsUknPYj0ifN6Bia5nBO7TkFQFCfIIOT1J3NFAoR+Q7YCnQSkRQR+RPwCjBaRA4BoyseG0pECDzfknLf4+xbcMDoOBbz0l/zeOIJ3bW4pplb6i7TKJn20pANNnRntlJqUg2zRlo1SB2EeYZw2vMUyVtO0Xtad6PjWMQNL/c3OkKDKaVsevxhW6Vs6MIWR3Zq9ym823rjEeBx+YVthM0cUdiTHx5czHOf3EhQB0+jo1jEsc0prHtjD+dzzxsdpd7c3d3JysrSH3r1pJQiKysLd3fb707C3qXuSrWbG+0usJkjCnvi18oPz0BPMhMc816Khf+XxBPLosm8MRu35m5Gx6mXC/cqZGRkXPG6ioqK7OKD01w53d3dCQ4ONkMirSZFZ4vIPpRNz2k9jY5SL7pQNEBSdhKfjlxM0Ko7GGt0GAtISHQiUDLw7xBodJR6c3V1JTw83CzrWr9+Pb0qegy2ZfaSU/tfQ7Y9tU+APvXUIEopDnbeyha/JpSVOF4XF/GpPkQ2P2l0DE1zOCe2ngCgTf82BiepH10oGiDUJxRRQrFvKgdXJhsdx6xUuSIhP4TIIMfv9FDTrO3E5hP4d/K3q4Zs0IWiQZo4N8G/PBB8k9m9+IjRccwqPT6TM8qXyM66MVjTzEmVK05sOUHIkBCjo9SbbqNooPb+EWT6JnNgh2Pdoe0b5s22z/fTpntHo6NomkPJPJBJ0Zki2g65st6JjaCPKBqoT4c+NC89jxQ5VnfjTZo1of/dXWnT174a2zTN1p3YYmqfsMcjCl0oGui9697j9QP30T6k2OgoZrX8he0seMJxuxbXNKOc2HwCjwAP/Duatzdma9CF4goERAaQkXDl1+vbkrfec+H/Pm5udAxNczjHNx8nZHCIXfYaoAtFAx3OPswTvk/zT/dQkjccMzqO2cSfDSKyZeMYE1zTrKUgvYDsQ9l2edoJdKFoMC83L5J9DpDTIpU93zvGJbJnj58lrbwVkR1KjY6iaQ7FntsnQBeKBgv0CKSpkwf4JhO/zTIjgllbwirTmzmyd1ODk2iaYzm++TjOTZztqmvxqnShaCARob1/O1x8Ezl0pInRccwicVsOAF1iWhobRNMczInNJwjqG4SLu33ekaALxRWI8IvAxfcgSWcDjI5iFtM+HsLJXaeIuMo+D481zRaVFpWStiuN4MH22+GiLhRXYHDIYNrmB9DVJdHoKGYhTkJQ71Y4N3E2OoqmOYzUnamUFZfZ5Y12F+hCcQX+NuRvfBzxH4LPJ1Nyzv6HRX2i73qWPrPN6Bia5lCObz4OQMhg+z1S14XiCgVGBlKuFCe2pRgd5Yrkpebxxq5o9m0/Z3QUTXMoKVtS8Ovgh2cL+x3orN6FQkQ8RUSfmwBOnD3B1UnX8I9uHZn/zD6j41yR35eYOjfsNdR+38yaZmuUMnUEaM+nnaAOhUJEnETkDhFZISLpwAEgTUT2i8irItLB8jFtU6BnIKklJ3HziyMu0b6vfNqz1nSTXa+x9nt4rGm2JutgFoWZhXZ7/8QFdTmiWAe0A54GWimlQpRSLYBhwG/AKyIyxYIZbZa7iztBXkE09/ud+Bz7vD76gj17TaPatY7Sl8Zqmrmc2GzfN9pdUJeLekcppf7QUquUygYWAgtFxNXsyexEhG8ESYFHiS/vRElhCa4e9rkrCoqc6R94BHGyv+FPNc1WHVl7BI9ADwI62fcl9Jc9orhQJETkLamhN6vqCok5ichREdknIrEistOS26qvCN8Izvmfphg3ds9NMDpOg80/Ppgf0voZHUPTHIYqVySvSabd6HaIk/11BFhVfRqz84FlIuIJICJXi8hmy8SqVoxSKkop1deK27ys0RGjGekTzT18BMXnjY5zRez9zaxptuT0vtMUnC4gYnSE0VGuWJ0LhVLqOeA7YL2IbAKeAJ6yVDB7MaXHFL699xuCOU1pgX2OTTH/sS2M8N1DZmKW0VE0zWEkrzZ1FuoIhUKUqtvYyCIyEngOEKA1MFYpZZVbkkXkCHAGUMDHSqnZl8yfAcwAaNmyZZ958+aZdfv5+fk0a9asxvllqoyNt26hib8vgz/qZtZt18flctbkm3sKmHc4mmU//2aVu7IbmtPadE7zsoec5sy498m9nM84T78vzX9K1xL7MiYmZleNZ2yUUnX6AdYCQyt+7w7EAiPq+vwr+QGCKv5tAfwODK9p2T59+ihzW7duXY3zTuefVq4vu6q+Q2coL86qspIys2+/rmrLWZthzWPVoGZ7zRumFg3NaW06p3nZQ05zZSwuLFb/dP+nWvn4SrOs71KW2JfATlXD52p9Tj2NUEptqvh9H3At8M+G1a76UUqlVvybDiwG+ltju3UR4BGAs5MzTdqmkkdzDq4+YnSkeikvLSc2N5xeYdlGR9E0h3F803FKi0ppN7qd0VHMoi433NV0pVMaMLK2Zcyh4k5wrwu/A1cDcZbaXn05iRMRvhGUh5luWNv6rX0NYnRkwwnyaE6v3ro3F00zl+TVyTi5OhF6VajRUcyiLp8Oa0XkERG56B50EWkCDBKRr4A7LZLOpCWwSUR+B7YDK5RSP1lwe/UW4RtBbsAZXChh92/21aB97mwxV/vvpN/1LYyOomkOI3l1Mm2HtKWJp3332HBBXW64OwSUAYtFpDWQA7gDzsAq4E2lVKylAiqlkoGellq/OUT4RPDr0V/pSCL7U32NjlMv3SZ04OcJRqfQNMeRfzqfU7GnGDFrhNFRzKYuhWKwUmqGiNwDtAUCgXNKqRyLJrMjN3S8gRaeLXBu/yvNmroAg42OVGf2fDe5ptmiI7+Y2inbXe0Y7RNQt1NPP4vIVkyngKYBQUCRRVPZmdHtRvPs8GfpPjqM/ONnLlypZRcimmfw9wHrjY6haQ7j8KrDNPVrSqterYyOYjaXPaJQSj0hIhHAeiAcGAt0FZFiIE4pdZtlI9o+pRSn8k9BGJw468XWD/cw+MHeRse6rNNxGaSUBdGq9UGjozQq53PPk3Uwi6yDWZw7cw5VpigvK0eVKVw9XPEJ88EnzAfvUG+HOcfdWCilSF6dTMSoCJycHecCkTqN9K2UShaRUUqpyk8UEWkGGHd3mQ05V3qOoDeCeDzoz3zIazT/eCWDHzQ61eXtWXIMCKRXtI/RURyWUoqsg1kcWnGIwz8f5vTe0+Sfyq/z872CvAiLDiNsRBjhI8LxDbevNrDGJjMhk7zUPIe4G7uqOhUKgKpFouJxPqZuxhs9D1cPWjVrxVn/HMI5wt5kL6Mj1UnsJtMHVtSEcIOTOJ70/ens/nQ3B384yJnDpkunA7sG0n5Me/w7+ePfyZ+ATgF4BHggzoKTsxPiLBTnFZNzLIeco6af9H3pHFl7hH1zTQNj+YT70H1yd3rd3QvfCF00bM3hVYcBx+i2o6o6FwqtdhG+ERzNO0pnlyT2F3Q2Ok6d7IlvQrjLcXxC7Xv0LVuhyhWHfjzEtre3kbwmGWc3ZyJGRjDoL4PocF0HfMJ8LrsONy83vIK8CBn0v/ELlFJkHsjkyNojHFp+iE3/2sTGf24kLCaMXtN7Ud6i3IKvSquPpJVJ+HfyxyfUx+goZqULhZlE+Eaw8dhGJgSc4cdToWQfPoNfO9v+xnfj9YqhGUcwXcymNZQqV+ybu49fX/qV7KRsvNp4MeJfI+hzbx88AjyueP0iQmBkIIGRgfR/qD+5KbnEfhVL7OexLJ66GLcWbjR/qTm9pveySl9dWvXOZZ/jyNojDHpikNFRzM5xWlsMFuETwYncE7TvabriKXbxYYMTXd6UD4fwyIKrjI5h105sPcFngz4zfWA3d2PivIk8duQxhj09zCxFojrNg5sz/NnhPHLoESb/NBm3QDdWPLCCdzu8y86Pd1JWXGaR7Wq1S1yWSHlpOZETI42OYnb6iMJMJkROoJ1fO7pFduaFn1+i3YC7jI5Uq7TY05zPLyF0cBs9DkUD5J7MZfWTq4n7Lo5mrZsx7stx9Jza06r7UpyE9te0J6pJFCHFIax/cT0r7l/Btre2cd0H1xEeo9uerClhYQLebb0J6mvfwyJXRx9RmElUqyim9ZxGhyHtcQJO/37a6Ei1mv3nBCKGBZGbkmt0FLsTNz+OD7t9yIHFBxj23DAeOfgIUXdGGVZwRUwF409b/8SkHyZRVlzG1yO+ZtGUReSfrvsVVlrDnc89z+FVh4mcGIkFu74zjC4UZlKuytl+cjun3E5R5OHDv546iyq33RvvNu/1oof7IbzbehsdxW4UnS1i8dTFLLx9If6d/Ll/7/2M+McImjSzjXsdRISON3TkgbgHGP78cOL/G897nd5j1+xddnUTqD06uOIgZcVlDnnaCXShMKthXwzjk92foHx8WVowmuT1x42OVK3SolK2ZndkSPtTRkexG8c3HeejHh+x77t9XDXzKqZvmo5/B3+jY1XLtakrMS/HcP/e+wnqE8Ty+5Yzb9w8CtILjI7msBIWJtCsdbOLrlZzJLpQmImTOBHuE07ymWSiopsDsP4L2xybYu/CQ+TjxdBo3cdTXeyavYuvYr7CydWJ6ZumE/1iNE4utv+nE9ApgKmrpzLm7TEcXnWYD3t8yKGVh4yO5XCKC4pJWplE5wmdHba9z/bf7XYkwjeC5DPJ9J3WDV+y+XW9bV59snlxOgBD7nCMvvItRZUpVj66kuX3LSdiVAQzds0geGCw0bHqRZyEAY8O4N4d9+LZwpO5181l5aMr9ZVRZpT0UxIlhSV0mdjF6CgWo696MqMI3wg2n9hM8O3B9GQL29Js84P4lhciCQrfSttBjne9t7mcO3OOfU/t48zOMwz880BGvzrarvvuadm9Jfduv5c1T61h29vbSNuVxi0LbsGrtX30ImDLEhYm4BHgQehw2/x7Nwf7fefboAjfCHLP51LYpJAeXsfwkzOczz1vdKw/aNWjBRNf1UWiJmdPnOXzwZ+TE5vDjZ/eyDVvXGPXReICF3cXxrw1hpvn38yp2FPM7jObE1tOGB3LrpWeL+Xg8oN0Gt/JLk5HNpTjvjID3BR5E2unrcXT1ZMRt/gxwXsdTbxs44qYC9JiT/Puzb9yOi7D6Cg2KftwNl8M+4K81Dx6vNqD3n+y/V6A66vrrV25Z9s9uHq48mX0l+z4cIfRkexW8upkivOKHfq0E+hCYVZhPmHEhMfg5uJG8IBgzmWdI+tgltGxLrJ2dhKPLryKtP3ZRkexORnxGXwx7AuK84uZtnYaPlE+RkeymBbdWnDvjntpN7odPz74Iz8+8iPlpbrPqPpKWJiAm7cb4SMc++ZGXSjMSCnFwviFbEvZRvDAYOLowthetnVov3lDGV7k0n1Ce6Oj2JS03Wl8MfwLUHDXr3cR1Mfx7q69VFPfpty+7HYGPTGIHe/tYN74eRTn29eY70YqKSwhYVECncd3dvg+tnShMCMR4YEVD/DZns8I7BpIU6cidpzrZlPXr2863IpB/gcd/o1dH6m7Uvkq5iuaNGvC3RvvpkXXFkZHshonZyeufu1qrvvgOpJWJvHF8C/IPanv1q+L/d/v53zueXr9qZfRUSxOFwozu3CJrJOzE53bFlGKK9u/tY0R5HKOnSWuqD1DeuhuHS5I35/Ot9d8S1O/pty98W782vsZHckQ/R7ox6Tlk8g+lM2nAz7l9D7b7oLGFuz+ZDcBnQNoO9Txe1/WhcLMLhQKgB5jghDK+XVZjrGhKuz74SgAQ6/X3XaAqeH6m9Hf4NzEmalrpuId0rj3S4drO3D3prtBwZfDv+T4ZtvsWcAWpO9P58SWE/S+t7dD9u10KbsoFCIyRkQSRSRJRJ4yOk9tInwjOH72OCVlJbS/ph2RJLBpTzOjYwEw7OGe5JzIZ+h9XY2OYrjclFy+GfUNZcVlTF09Fb92jfNI4lKterZi+pbpeLbw5JtR33BwuW0cDdua3Z/sxrmJMz2n9TQ6ilXYfKEQEWfgfeBaoAswSURs9lq0CN8IylQZJ3JP0GZAG6JZx7AI22nQbh7c3GY6sTNKQUYB34z+hnPZ55jy85RG1SZRFz6hPty96W5adGvBvPHz+P3r342OZFNKzpXw+9e/E3lTpMXGHLE1Nl8ogP5AklIqWSlVDMwDxhmcqUbjO4/n0COHaOvdFq/WXnRoW0q3zsb33FlSWML1LXbw0z93Gh3FUCXnSpg3dh45R3O4Y8UdjeLqpobwDPRk2tpphMeEs+TOJWx9c6vRkWxGwsIEis4U0ftex7vHpiZi690Pi8jNwBil1D0Vj6cCA5RSD1dZZgYwA6Bly5Z95s2bZ9YM+fn5NGvWsNNH8TPjyYnLpeMzkQT0tuw58NpyHluRyV2v3cwbt3xPrweN/QZ9JfvzSqhyRfxL8WRuzKTLzC4EDg+sdXmjctaXJXOWF5eT8K8EMn/NJPSuUEKnhTb4nLw97M+6ZIx9LJbirGL6fd3PsE4ALbEvY2Jidiml+lY7Uyll0z/ALcCnVR5PBd6tafk+ffooc1u3bl29ln9v23tq6YGlSimltry+RbXlqJrQarPZc12qtpwzo9cpoUylx2dYPMfl1Hd/msuqJ1epmcxUW17fUqfljcpZX5bOWVZSppbctUTNZKb6+YmfVXl5eYPWYw/783IZMxIy1Exmqo2vbLROoBpYYl8CO1UNn6v2cOopBajayXswkGpQljp5e9vbzNk3B4A2A9rQi938cqqroTczLd/egkFecQRGBhiWwUg7PtzBlle30O+hfgz880Cj49gVJxcnxn42lv6P9Gfr61tZft9yyssa513cuz/djZOLE1F3RRkdxarsoVDsADqISLiINAFuB5YZnKlWVS+Rbd27NR0kmVy82fhhnCF5UnefYmdhF24Y1Di77Ti08hArH15Jxxs6MuatMY3ickZzEydhzNtjGPrMUHZ/spsl05ZQVtK4uiovOVdC7JexdBrXiWYtbfsUmrnZfKFQSpUCDwM/AwnA90qp/camql2EbwSHsw8DptHGwnt44s45ls3JMyRP9rE8Ynz2cOP9bQzZvpGyDmaxcNJCWvZoycTvJjp0D5+WJiKMnDWSkf8eyb65+1hw2wJKz5caHctqdn28i3NZ5xjw6ACjo1idXfzVKKV+VEp1VEq1U0rNMjrP5UT4RnCm6Axnzp0BoN3IcAaxlWVxEYaMo91tQgfWnulFtwkdrL5tI53PPc+8cfNwdnXmtiW3NfrLgs1l6FNDGfP2GA4sPsD88fMpOVdidCSLKzlXwub/bCYsOsyhx52oiV0UCnsT4RsBwPGzpjtbw0eEM5jNfPNqqtWvkijOLyb78BmrbtMWqHLFoimLyDqUxS3/vQWfUB+jIzmUAY8O4MZPbiTp5yTmXj/X4TsT3P3JbvJP5XPVi1cZHcUQulBYwHUdrqPwmUJ6tjLdtRk6LJQmzoqSM4VWz/LLG7/Tor0Xv31qTPuIUdbPXM/BHw4y5q0xhEWHGR3HIfW+pzcTvpnAsQ3H+ObqbyjKKTI6kkWUFpWy+T+bCb0qtNG+l3ShsAB3F3eaujatfOzW3I2gvkFs+eogzwxeb9UsP3x/DneKiLq58XQrnrAogQ3/2EDU9Cj6PdTP6DgOrcfkHtzy/S2k7jT1wFuQYTs9JZvL7k93k5ea12iPJkAXCot5af1LfLTzo8rHYTFhHD7hyitbh3Nqb7pVMqhyxfID7RjdOg53H3erbNNoWQezWHLXEtoMaMP1H1yvr3CygsibIpm0bBKZBzL58qovHaqb8tKiUja9som2w9o22qMJ0IXCYlYcWsGihEWVj8NHhNNapaJwYsUbiVbJsG/RIU6UteGGqx2/sRFM3ZR8f/P3ODdx5pb/3oKLm4vRkRqN9mPaM+XnKeSm5PLFsC84c8Qx2sV2f7abvJOmo4nG/KVDFwoLaefXrvJeCoC2Q9ri5lxOiJxg2c/Wufpm+WzTfYnXPd7RKtszklKKFQ+uID0unZvm3NTouww3QujwUKb9Mo2inCK+GPoF6futc+RsKaXnS9n8ymZChoQ4/FCnl6MLhYVE+ERw7OwxSstN15m7ergSMjiEYe47WX2qO+eyz1k8wx0vtOfr+zbROqqlxbdltD2f7+H3r35n+PPDaX9N42mPsTVt+rXhrl/vQinFF8O+IOW3FKMjNdimVzaRm5JL9EvRjfpoAnShsJgI3whKy0tJyf3fH0r4iHCCzx0ivEkqx7elWTxD2NBgpn401OLbMdqp2FP8+NCPRIyK4KoXGm+Do61o2b0l0zdPx8Pfg69Hfk3ST0lGR6q39P3pbJy1ke53dCdiZITRcQynC4WFRPhGEOARQEZBRuW0sJgwmlLIov+W0elay7751r8Vy9yHNlNa5Nh3zp7PPc/3N3+PR4AHN829CSdn/Za2Bb7hvty96W78O/nz3Y3fsW/uPqMj1Vl5WTk/3PMDbs3duOata4yOYxP0X5WFRIdFk/FkBv3a/O/yzOCBwbi6u3Jk7RHyT+VTUmi5RubnXnDixU/a4NzE2WLbMJpSiuX3LyfnSA4Tv5uIZ6Cn0ZG0Kpq1bMad6+6k7dC2LJq8iBPzTlzoAdqm7Xh/Bym/pTDm7TH6PVVBFwoLqe6cpoubCyFDQti/NIk2rctY+NQOi2z79+8T2ZzXgwevO2pYf/nWEPtFLHHfxRH9UjShwxpftwr2wN3bnckrJ9P1tq4kf5zM8vuW23RngkWnivjlmV9of217ut/R3eg4NkMXCgt6/KfHefaXZy+aFj4inNyjmbRwOcO7X1qmB8oPXjxNUwq5680oi6zfFmQkZPDjwz8SPiKcoU87fjuMPXNxd2Hi3Im0ndyW3Z/sZu71cyk6a3t3cSulOPjGQUSEGz66odE3YFelC4UFJWQmsDp59UXTwmLCcEKY2msfW/J6sHtOglm3efb4Wb490Ic7Ou7CN9zHrOu2FSXnSlhw6wKaNGvChG8m6HYJOyBOQvg94Yz9fCxH1x3l88GfcybZtu612PHBDs7sOMPIf4/Eu62+vLoq/RdmQRE+ERw+c/iiaUF9g2jSrAndOpXiST7vzsw06zaPbT9NaJNTPPiC4w5Q9PNffiY9Lp0JX0/AK8jL6DhaPfS6uxdTVk0hLzWP2X1mc3D5QaMjAZD4QyI/PfoTfgP96Peg7vblUrpQWFCEbwTZ57LJKcqpnObs6kzo8FBSt59kWtfdfJfUjzNHcmpcR331uLkj+89F0HtypNnWaUsSFiWw66NdDPrrINqP0fdL2KPwmHBm7JqBb4Qv3934Hb888wvlpcaNmHdy+0kW3r6Q1r1b0+WFLg7drtdQulBY0IXuxo+cOXLx9KsjyDqYxf3PBbD5myNmO0V09kA+BekFDvtGz03JZdk9y2jdpzUjZ400Oo52BXwjfJm+eTq97+3Npn9v4purvyH/dL7Vc2QfzmbuDXPxbOnJpOWTcG7quFcJXgldKCyoo39HerXqRVHpxQ13ncd1BiD/ZA59ppjvm//s55oTFZxhyOBIllZeVs7iaYspKy5j4tyJDn3Zb2Ph4u7CjbNvZNyX40j5LYUPun7A3jl7rXYJbWFmIXOunYMqV0z5aUqjG960PnShsKDuLbuz+77dDAoZdNF0nzAfWvZoSeLSRHKOneWu9ptY+sy2K9pWyo40fsoawsTejnlJ7JZXt3B03VGuffda/Dv6Gx1HM6OoO6OYsWsG/h38WTxlMd/d+B25KZbtgfbU76f4bNBn5J7IZdKySfo9dRm6UBik07hOnNh8AmdXJ349FsobH7hd0frefzQRhXDf/7UzU0LbcXL7SdY9v46ut3Yl6q4oo+NoFhAYGcjdm+7mmjev4cjaI3zQ9QO2v7fdImNy7/l8D58N/IzigmKmrJpCyOAQs2/D0ehCYWF/WvonJi2c9IfpncZ1QpUrDq86zMNjDrPhbBTLX9jeoG3Ezk/k9d8GM6HlOsKHO9ab/nzeeRbesRCvIC+u/0iPL+HInJydGPj4QB7Y9wBBfYNY+chK3uv4Hrtm76Ks+Mpv0ispLGHp3UtZ9qdlhAwO4b499+kbNetIFwoLyy/JZ2fqzj9Mb927Nc2Dm5O4NJGH5wyip3sid/8zokGDGi18Lw1/pzNMf/W8OSLblJ8e/YmcIzlM+HYCTX2bXv4Jmt3za+fH1DVTmfLzFLyCvFh+33Le6/QeOz/aSWFW/YcTPnfmHFte28L7ke8T+1Usw58fzpRVuk2iPnShsLAInwiO5hylrPzib0QiQsexHTm86jBOrk7Mne9MvvLkyfH1v678Hxujif3dCc8QD3PFtgn7v99P7JexDHt2mP7m18iICO2ubsf0LdO548c78Aj0YMUDK3it5Wt8Peprdny4g7zUvBobvksKS0jdmcqKB1fwZvCbrH5yNT7hPkxbM42Yl2P0TZr1ZNNDgInITOBe4EIXrM8opX40LlH9Ve1uPNTn4g+7zuM6s/ODnSSvSabL2E4semkHfW/pXOd17/gqHk/fJnQZ256W3QJJWG/m8AY6e+Isy+9bTpsBbRj+/HCj42gGERE6XNuB9mPak7Y7jYSFCSQsTODHB3/kxwd/xNXDlebBzWke3BzPFp7kpeWRnZRN3sk8AJzdnOl+R3cGPDqAVlGtDH419sumC0WFN5VSrxkdoqEu3EuRfCb5D4Ui9KpQmng1IXFpIp1u7MS1L5juCC0tKuXUvgyC+7Wucb15qXncdk8zmjoXsy+/HCcXx/mGVF5WzuKpiykvLeemOTfh7KovhW3sRISgPkEE9QlixKwRZMRnkLw6mbMnzpKXkkduSi4nt5+kWetmRIyKwK+DH37t/QgfEa57gDUDeygUdq1TQCfGdhpLU9c/nl93cXOhw7UdOPjDQcrLyisPh29vv4P4jBb8su10taPTnY7L4KExSRwtHcCGt+McqkgAbHltC8d+Pca4L8bh187P6DiajRERWnRtQYuuLYyO0miILfcPX3Hq6S4gF9gJPKGU+kNPYiIyA5gB0LJlyz7z5s0za478/HyaNbNMw9fpNac5MOsAUe9G4d3N1BFZ4ncZPDx7PE6UM77Nr4y7J5+gaNMH5qJHc/h039Wcx42/9F3K9a/+74PUkjnNqbaceYl57HloDwHDAoh8IdLQq5wcYX/aEnvIaQ8ZwTI5Y2Jidiml+lY7Uyll6A+wBoir5mcc0BJwxtToPgv4/HLr69OnjzK3devWXfE6SstKq51+7sw59bLLy2rV31ZdNP3QmqPq4e7rlQf5CpSa9+hmpZRSf+u/Tk2N2KgOrjpikZzWUFPO83nn1Tsd3lFvBL+hCrMLrRuqGva+P22NPeS0h4xKWSYnsFPV8Llq+KknpdSouiwnIp8Ayy0cxyImLZzEkTNH+O2e3/4wz93HndCrQklcmsjo/4yunN5+ZCjv7g3lpcNn+PSRHVz7ZG8AXtl6lUPeeQ2w8rGVZCdlc+e6O/WlsJpmQ2z65LaIVG3NnYDpSMPueLt5k5Rd8wDzncd3Jisxi/S4P95D4dfOl7/9GE3z4OYADlsk9v93P7GfxzL06aGEXRVmdBxN06qw6UIB/J+I7BORvUAM8GejAzVEhG8EWeeyOFt0ttr5XW/ripOLE3u+2GPlZLbh7PGzLJ+xnDb92xA9M9roOJqmXcKmC4VSaqpSqrtSqodSaqxSKs3oTA1R2d14zpFq53sGetLxxo7s+3afTY8nbAkXXQo7V18Kq2m2yKYLhaOoei9FTaLujqIgvYBDPx6yViybsOnfmzi24RjXvX+dvhRW02yULhRW0N6vPQ/1e4i23m1rXKbDtR3wbOlJ7Bex1gtmsOObjrN+5nq6TepGj6k9jI6jaVoNDL/qqTFo7tac9657r9ZlnFyc6DmtJ7+9+Rv5p/MdvsOyc9nnWHjHQnxCfbjhoxt0r7CaZsP0EYWVlJSVcCr/VK3LRN0dRXlpOXu/3WulVMZQSrHsT8vIP5XPzfNvxq35lY3FoWmaZelCYSVTFk9h+Be1d24XGBlImwFtiP0i1mrDQRohdUkqB5YcYNQrowjqG2R0HE3TLkMXCiupqbvxS0XdHUXG/gxSd6ZaKZl1nYo9xeEPD9Phug4MfHyg0XE0TasDXSisJMI3gpLyEk7mnax1uW63d8PF3cUhG7XP555nwW0LcG3uyrgvxznszYOa5mh0obCSulwiC+Du7U7kxEj2zd1HybkSa0SzCqUUy+5ZRvbhbCKfi9RdP2uaHdGFwkrqWigAek3vxfmz54n7zi57LKnWtne2Ef/feEb+ayQ+UT5Gx9E0rR50obCSEO8Q/j3y3/QL6nfZZcNiwmjVqxWbXtlEeVm5FdJZ1omtJ1j919V0GteJwU8ONjqOpmn1pAuFlbg4ufDU0Kfo3rL7ZZcVEYY9M4zsQ9nEL4i3QjrLKcgoYMGtC/Bu6834L8fr+yU0zQ7pQmFFp/JPsSt1V52WjbwpkoDIADbO2ogqt89LZctLy1l0xyIKMgq4ZcEtuPu4Gx1J07QG0IXCimaun8mYOWPqtKw4CUOfHkr6vnQOLj9o4WSWsfpvq0lek8z1H1xP6141j/+taZpt04XCiiJ8I8gszCT3fG6dlu8+qTs+4T5smLXhohvw7OEIY8/ne/jtzd/o/2h/ek3vZXQcTdOugC4UVlTZ3fiZ6rsbv5STixNnXAJJ3Z7K4VWHAVOR+HOfDcyMXm+pmFfs+ObjLL9/ORGjI7jm9WuMjqNp2hXShcKK6nOJLJiKQk7T1uTixZcTl1cWibdjryLnrNjkkcXZ42f5/qbv8Qn14eb5N+Pkot9immbv9F+xFdW3UIiT8OaeaFyCWuBacJYw5xO8HXsVj0X9ypu7htvcnc3F+cXMGzeP0qJSJv0wSY97rWkOQhcKK/Jx92HexHmM7zy+zs8RJ+EfibeSRzOuZSVOlNtkkSgrLmP+TfM5ve80E+dNJKBzgNGRNE0zE10orOy2brfRzq9dnZdX5Yq/DdvKj1xLa04xkK38uc8GmzrtpMoVS+5aQvLqZG785EY6XNvB6EiappmRLhRWdiDzAEsOLKnTslXbJK7umU6nsZ0YLWv5Ora7zRQLpRQ//fkn4r6LY+QrI+l1t77CSdMcjS4UVvZV7Ffc+t9bL9vdOJhOO/l4K1ObxO6ruO6D63Br5sKDzb7Bp3m5TZx+2vTvTWx/ZzsD/zKQIX8bYnQcTdMsQBcKK6trd+MXzFwfXdkm0bxNc0b9ZxSu+TmMn+5r4aSXt+2dbax9di09pvTg6lev1t1zaJqDMrxQiMgtIrJfRMpFpO8l854WkSQRSRQRh7ggv75XPgEXHTn0va8vIUNCWPWXVRSkF5g9X11t/NdGfnrsJyJvimTs52Nt4uhG0zTLMLxQAHHATcCGqhNFpAtwO9AVGAN8ICLO1o9nXg0pFFWJk3Dj7Bs5n3eepdOXUl5q3d5llVKseXqN6Uhiag9unn8zzq52/9+iaVotDC8USqkEpVRiNbPGAfOUUueVUkeAJKC/ddOZX4h3CM7i3OBCARDYJZAxb43h0IpDLH9gudXG11blipWPrGTzK5vpc38fxn85Xt9Qp2mNgFjrQ+ZyRGQ98Fel1M6Kx+8Bvymlvq14/BmwUim1oJrnzgBmALRs2bLPvHnzzJotPz+fZs2amW198bnxBLkH4dPE54rWc+SzIxz/9jhtp7YlfHq42XNWVVpQSuKriWT+mknwbcFE3BfR4DYJS+Y0J53TvOwhpz1kBMvkjImJ2aWU6lvdPBezbqkGIrIGaFXNrGeVUktrelo106qtakqp2cBsgL59+6ro6OiGxKzR+vXrMec6ozHPuq666ip+cPuBPZ/todvAbtAFs+a8ID0une/v+57sw9mMfm00g/4y6Ioars29Py1F5zQve8hpDxnB+jmtUiiUUqMa8LQUIKTK42Ag1TyJjLXj5A42Ht/IXwb95YrWIyLc8NENFGYU8uPDPxL5XCRmqkGV9n67l+X3LcetuRt3rr2T0OGh5t2Apmk2z5ZPMC8DbhcRNxEJBzoA2w3OZBZrj6zliVVP1Lm78do4uTgx8buJhAwOIeEfCax8dCUlhSVXvN681DyW3LmExVMXE9Q3iBm7Z+gioWmNlOGFQkQmiEgKMAhYISI/Ayil9gPfA/HAT8BDSqnL36VmB+rb3fjluHq4MnX1VNpMbMP2d7fzce+PObmjbvdpXKo4v5h1L67j3Q7vEjcvjqHPDGXaL9Pwau1llqyaptkfq5x6qo1SajGwuIZ5s4BZ1k1keRf6eko+k0zPVj3Nsk7Xpq60f7g9Ix4YwdK7lvLZoM8Y/ORgev+pN37t/S77/NyUXOIXxrPp35soOF1A19u6MvJfI/GNMP7GPk3TjGV4oWiMrvReilrXPTKCB/Y9wE+P/cTmVzaz+ZXNtOjegs4TOtPhug408WxCeVk5qkxRnF/MkbVHSFyWyKk9pwAIGRLC7UtuJ3hgsNmzaZpmn3ShMICPuw++7r4WKRQA7j7ujP9qPNEvR3Ng8QEOLD7Ahn9sYMPLG/64sEDIoBBGvjKSTjd2IiAyQHfFoWnaRXShMEjcg3G08Gxh0W34hPow8PGBDHx8IAXpBRzfdJzysnKcnJ0QZ8HZ1ZmgfkF4BnpaNIemafZNFwqDBHkFWXV7ni08ibwp0qrb1DTNMRh+1VNjteHYBh5c8WCduhvXNE0zki4UBknMTOTDnR+SkptidBRN07Ra6UJhEEte+aRpmmZOulAYRBcKTdPshS4UBjFHd+OapmnWoAuFQVycXIjwjeBM0Rmjo2iaptXKZsajMBcRyQCOmXm1AUCmmddpCTqneemc5mUPOe0hI1gmZ6hSKrC6GQ5XKCxBRHbWNKCHLdE5zUvnNC97yGkPGcH6OfWpJ03TNK1WulBomqZptdKFom5mGx2gjnRO89I5zcsectpDRrByTt1GoWmaptVKH1FomqZptdKFQtM0TauVLhR1JCL/EJG9IhIrIqtExLr9hNeRiLwqIgcqsi4WER+jM1VHRG4Rkf0iUi4iNnU5ooiMEZFEEUkSkaeMzlMTEflcRNJFJM7oLDURkRARWSciCRX/348Znak6IuIuIttF5PeKnC8ZnakmIuIsIntEZLm1tqkLRd29qpTqoZSKApYDLxicpyargW5KqR7AQeBpg/PUJA64Cahm2D3jiIgz8D5wLdAFmCQiXYxNVaMvgTFGh7iMUuAJpVQkMBB4yEb353lghFKqJxAFjBGRgcZGqtFjQII1N6gLRR0ppXKrPPQEbPIqAKXUKqVUacXD3wCbHPxaKZWglEo0Okc1+gNJSqlkpVQxMA8YZ3CmaimlNgDZRueojVIqTSm1u+L3PEwfcG2MTfVHyiS/4qFrxY/N/Y2LSDBwPfCpNberC0U9iMgsETkBTMZ2jyiqmg6sNDqEnWkDnKjyOAUb/GCzRyISBvQCthkcpVoVp3RigXRgtVLKFnO+BfwNKLfmRnWhqEJE1ohIXDU/4wCUUs8qpUKAOcDDtpqzYplnMR32z7HlnDZIqplmc98s7Y2INAMWAo9fcnRuM5RSZRWnloOB/iLSzeBIFxGRG4B0pdQua29bj5ldhVJqVB0XnQusAF60YJwaXS6niNwJ3ACMVAbeKFOP/WlLUoCQKo+DgVSDsjgEEXHFVCTmKKUWGZ3ncpRSOSKyHlP7jy1dKDAEGCsi1wHuQHMR+VYpNcXSG9ZHFHUkIh2qPBwLHDAqS21EZAzwd2CsUqrQ6Dx2aAfQQUTCRaQJcDuwzOBMdktEBPgMSFBKvWF0npqISOCFKwRFpCkwChv7G1dKPa2UClZKhWF6X661RpEAXSjq45WK0yZ7gasxXXlgi94DvIDVFZfyfmR0oOqIyAQRSQEGAStE5GejMwFUXAjwMPAzpobX75VS+41NVT0R+Q7YCnQSkRQR+ZPRmaoxBJgKjKh4P8ZWfCO2Na2BdRV/3zswtVFY7fJTW6e78NA0TdNqpY8oNE3TtFrpQqFpmqbVShcKTdM0rVa6UGiapmm10oVC0zRNq5UuFJqmaVqtdKHQNE3TaqULhaZZQcWYDKMrfv+niLxjdCZNqyvd15OmWceLwMsi0gJTD6pjDc6jaXWm78zWNCsRkV+BZkB0xdgMmmYX9KknTbMCEemOqT+h87pIaPZGFwpNszARaY1pXJBxQIGIXGNwJE2rF10oNM2CRMQDWIRp3OgE4B/ATENDaVo96TYKTdM0rVb6iELTNE2rlS4UmqZpWq10odA0TdNqpQuFpmmaVitdKDRN07Ra6UKhaZqm1UoXCk3TNK1W/w8H5U0wrcDPmwAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEWCAYAAAB42tAoAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAABK2ElEQVR4nO3dd3gVZdrH8e+dSjqQ0EPvLQRCr0FBQA0iiqKoiG3VVbHsurqoL7sra0dlRd1dsYKCYsGAgqKhSgsdAiR0A6EFQnp/3j/OIZtAEgKckzlJ7s915eKcmTkzvzMhc888M/OMGGNQSimlyuJmdQCllFKuTQuFUkqpcmmhUEopVS4tFEoppcqlhUIppVS5tFAopZQqlxYKdQERSReRVlbnuBTOyiwig0Rkj6Pn60gi0kJEjIh4WJ1FVU9aKGowETkoIln2jey5n8bGGH9jzP7LmF+kiCReZJqPRSRXRNLsPztE5CURCbr8bwKXm7mUfEZE2hSb70pjTPsrna+VRGSgiPwmImdF5LSIrBaRXlbnqgj7/9FhVueo6bRQqCj7Rvbcz9HyJhYRdwcs81VjTABQD5gE9AVWi4jfpc5I96LLJyKBwELgX0BdoAnwNyDnMuYlIuJ23jBd/zWAFgp1geJ71fYjgPdE5AcRyQCGisi1IhJnPyI4IiJ/sm/kfwQaFz86KW85xphsY8wGYDQQjK1onMtwj4jsEpEzIrJERJqfl++PIpIAJBTPLCJ9ReRY8YImIjeKyDb7694iskZEUkQkSUTeEREv+7gV9o9stee/tfhRkog8IyLzz1tXb4vIDPvrIBGZZZ/vERF5sazCWl6OYt/nQRFJsK+DmSIi9nHuIvK6iJwSkf3AdeWs5nb2df2FMabAGJNljPnJGHNufUwVkdnFlluiGUtElonINBFZDWQCrcpY//eLyF77Ecv3xX/3InKNiOyxH9G8KyLLReQ++7jWIvKriCTbv88cEaltH/cZ0AyItv8+nrYP72s/QkoRka0iEllsWXeLyH77/80DIjKhnHWjKsoYoz819Ac4CAwrZbgB2thffwycBQZg27GoBSQBg+zj6wA97K8jgcSLLPNj4MVShn8KzLO/HgPsBToCHsBzwG/n5fsZ2x6yTymZ9wHDi03/FfCM/XUEtiMYD6AFsAt4vLTvfv53Appj21gG2t+729dFX/v774B/A35AfWA98Icy1kNFciwEamPbWJ4ERtrHPQjsBpra10GMfXqPUpYTCCQDnwCjgDrnjZ8KzC72vkXxeQHLgMNAZ3tWz/PXP3AVcAroAXhjO3pZYf98CJAKjLV/fjKQB9xnH98GGG7/XD1gBfBWWf9HsR0RJQPXYvv/ONz+vp59vacC7e3TNgI6W/13Vh1+9IhCfWffM0sRke/KmGaBMWa1MabQGJON7Q+9k4gEGmPOGGM2OSDHUWwbHoA/AC8ZY3YZY/KBfwLhxY8q7ONPG2OySpnXF8BtACISgG2j8gWAMWajMWatMSbfGHMQ24Z9SEUCGmMOAZuwFTKwbSAzjTFrRaQBtg3x48aYDGPMCeBNYHwZ86pIjpeNMSnGmMPYikG4ffgt2DamvxtjTgMvlZM5FRiIbeP+X+CkfY+/QUW+s93Hxpid9qx59mHF1/8E4ENjzCZjTA7wLNBPRFpgW/c7jTHf2H+XM4BjxfLtNcb8bIzJMcacBKaXsh6KuwP4wRjzg/3/489ArH05AIVAFxHxMcYkGWN2XsL3VGXQQqHGGGNq23/GlDHN7+e9vwnbH+YhezNCPwfkaAKctr9uDrx9roDZh4t9mrIyFfc5MFZEvLHtyW6yb+QRkXYistDePJWKrQiFXELOz7EXIeB2+/tzmT2BpGK5/43tyOICFcxxrNjrTMDf/roxJb//ofIC2wvu3caYUKCL/fNvlfeZ85S2rosPa1w8gzEmHdtefpPzsxpjDFB0wYOI1BeRufamulRgNuX/PpoD44rt3KRgK4SNjDEZwK3YjriSRGSRiHS4hO+pyqCFQlVEiS6GjTEbjDE3YNsIfgd8Wdp0FSUi/sAwYKV90O/YmmxqF/vxMcb8Vlam8/LFYdtwjaLkxhzgPWzNNm2NMYHAX7EVoYr6CogUkVDgxmLz/h3bCeKQYpkDjTGdy5jPleRIwtbsdE6zioY3xuzG1vzXxT4oA/AtNknD0j52kWFHsW3AARDb+apg4Ig9a2ixcVL8PbajIQOE2dfDHZRcD+cv+3fgs/P+b/gZY162f78lxpjh2JqddmM7ilJXSAuFuiQi4iUiE0QkyN4MkQoU2EcfB4Klgpe6ioi3iERgKzZngI/so94HnhWRzvbpgkRk3CVG/Rx4DBiMbeN+ToA9c7p9b/Oh8z53HCjzfgx788gye9YDxphd9uFJwE/AGyISKCJu9hO1ZTWjXCxHeb4EHhORUBGpAzxT1oQi0kFEnrIXNkSkKbYjorX2SbYAg0Wkmf339uwl5Djnc2CSiITbj+L+CayzN6ktArqKyBj7CfI/UrIYBQDpQIqINAH+fN68z/99zAaiRGSE/aR+LbFdcBAqIg1EZLS9UOXY51uAumJaKNTluBM4aG8qeBDbXuC5vdUvgP32ZoGyrnp6WkTSsDUpfQpsBPrbmw4wxnwLvALMtS9jB7ajg0vxBbYT0b8aY04VG/4nbEcZadj2Nued97mpwCf2/LeUMe/PsR0BfX7e8LsALyAOW+Gbj23PtjQXy1Ge/wJLgK3Yzpl8U860aUAfYJ3Yrlpbi219PgVgb+OfB2zD9ntYeAk5sM/jF+B54GtsRxCtsZ+bsa/7ccCr2JqjOmE7p3Du8ty/YTsJfhZbUTn/u7wEPGf/ffzJGPM7cAO2I7CT2I4w/oxtW+Zm/15Hsf3fGgI8fKnfR11IbE2GSinlfGK7DyMRmGCMibE6j6oYPaJQSjmVvZmotr1Z6ty5mLUX+ZhyIVoolFLO1g/bvS2ngChsV9qVdlmzclHa9KSUUqpcekShlFKqXNWuQ6+QkBDTokULh84zIyMDP79L7q+u0mlOx9KcjlUVclaFjOCcnBs3bjxljKlX6kgr+g1x5k9ERIRxtJiYGIfP0xmcmfPJiBjz6xubHDIvXZ+OpTkdpypkNMY5OYFYo309qcu179dDTN8YybZVqVZHUUpZQAuFuqjofx0EIOqxltYGUUpZQguFuqjo5QF08t5Lq8gKdymklHKQ1a+tZuVLKy8+oRNVu5PZyrHOHj7LijNdearPamyPDnBteXl5JCYmkp2dfcXzCgoKYteuXQ5I5VyOylmrVi1CQ0Px9PR0QCrlCKbQsPbNtYT2Cb34xE6khUKV6+DaY7Ty9CJqYt2LT+wCEhMTCQgIoEWLFtg6Kr18aWlpBAQEOCiZ8zgipzGG5ORkEhMTadlSmxhdxeHVh0lPSqfTLZ0szaGFQpWr2y3t2XOLbc+mKsjOznZIkahpRITg4GBOnjxpdRRVTNxXcbh7u9Pu+naW5tBzFKpMhfmF5GXaHmgmblVnw6tF4vLoenMtptCw6+tdtB3VFu8Ab0uzaKFQZVr13nbq+2ewbtYOq6MoVeP8/tvvpB1No9M4a5udQAuFKsfCz86QYXzpOEKvdlKqsu38aqet2SnK2mYn0EKhyhG9tSmRdbcTGBpodZQqZcaMGXTs2JEmTZowderUouFvvfUWn376abmfHT9+PAkJCU5OqFydKTTsmu8azU6ghUKVIeHng+zObU3U0HSro1Q57777Lj/88APTpk0rGpafn8+HH37I7bffXu5nH3roIV599VVnR1QuzpWanUCvelJliH7nINCCqMdbWx3lsi1+fDHHthy77M8XFBTg7u5eYljD8IaMfGtkmZ958MEH2b9/P6NHj+aOO+7A398fgF9//ZUePXrg4eFBfn4+/fr147XXXiMyMpJnn30WNzc3pk2bxqBBg7j77rvJz8/Hw0P/PGsqV2p2Ai0UqgxDxzfk5dxltBgYaXWUKuX9999n8eLFxMTEEBISUjR89erVREREAODh4cHHH3/MzTffzIwZM1i8eDHr1q0DwM3NjTZt2rB169ai6VXNcq7Zqc3INi7R7ARaKFQZut/Wge63dbA6xhUpb8+/Ihx5w11SUhIdO3Yset+5c2fuvPNOoqKiWLNmDV5eXkXj6tevz9GjR7VQ1FC/r3GtZifQcxSqFJvm7GLZW1sozC+0Okq14ePjc0G3Itu3b6d27docP368xPDs7Gx8fHwqM55yIedusmsf1d7qKEW0UKgLvD7lNLc82aTK3I1dFXTs2JG9e/cWvf/mm29ITk5mxYoVPPbYY6SkpBSNi4+Pp3PnzhakVFYzhYa4+XG2ZqdA12h2Ai0U6jx5mXn8eLgz17XejbuX+8U/oCpk1KhRrFixAoBTp07xzDPPMGvWLNq1a8cjjzzC5MmTATh+/Dg+Pj40atTIyrjKIgeXHyTtSBpdbutidZQSXOochYi4A7HAEWPM9SJSF5gHtAAOArcYY85Yl7D6W/2fnaSYcKJu1B5EL9fBgwcvGNa8eXOCg4NJSEigbdu2xMfHF4177LHHil5//vnn/OEPf6iMmMoFbZu9DS9/L5dqdgLXO6KYDBTvL/kZ4BdjTFvgF/t75UTRs1PwIodrnnStPZrq4OWXXyYpKancaWrXrs3EiRMrKZFyJfnZ+eyav4uON3XE09e1dtRcplCISChwHfBBscE3AJ/YX38CjKnkWDXOyt31GBq8Hf+G/lZHqXbat2/P4MGDy51m0qRJev9EDRW/MJ6c1By6TuhqdZQLiO2Z2tYTkfnAS0AA8Cd701OKMaZ2sWnOGGPqlPLZB4AHABo0aBAxd+5ch2ZLT08vunHKlTkiZ0F2ARmJ2QS28XNQqgs5c30GBQXRpo1jHrBU2g13rsiROffu3cvZs2cdMq/zVYW/Iysz7nh+B2lxafT9si/iXn5Pvs7IOXTo0I3GmJ6ljjTGWP4DXA+8a38dCSy0v045b7ozF5tXRESEcbSYmBiHz9MZNKcxcXFxDptXamqqw+blTI7M6cj1d76q8P/TqoyZyZnmH17/MIufWFyh6Z2RE4g1ZWxXXaXpaQAwWkQOAnOBq0RkNnBcRBoB2P89YV3E6m9S25W8PXa51TGUqnHi5sdRkFvgks1O4CLnKIwxzxpjQo0xLYDxwK/GmDuA74FzZ/YmAgssiljtnd53hs/29uPkCddoiqzKRISnnnqq6P3rr79eohfZy7FlyxZ++OGHK0ymXNX2OdsJ6RBCox6ueVm0SxSKcrwMDBeRBGC4/b1ygh/fiKMAD6ImhVx8YlUub29vvvnmG06dOuWweWqhqL5SDqVwaMUhuk7o6rJPGXS5QmGMWWaMud7+OtkYc7Uxpq3939NW56uuohcK9eUkvSa6Tv8yVZWHhwcPPPAAb7755gXjTp48yU033USvXr3o1asXq1evBqBr166kpKRgjCE4OLjouRV33nknP/30Ey+88ALz5s0jPDycefPmcfr0acaMGUNYWBhXXXUV27ZtA2Dq1Kncc889REZG0qpVK2bMmFF5X1xdlh1f2J4g2fV212x2Ahe74U5ZIy8zj8W/d2Zs2224eQyyOo5jRUZeOOyWW+DhhyEzE6699sLxd98Nd9+NJCdDVFTJccuWVWixf/zjHwkLC+Ppp58uMXzy5Mk88cQTDBw4kMOHDzNixAh27drFgAEDWL16Nc2bN6dVq1asXLmSu+66i7Vr1/Lee+/x97//ndjYWN555x0AHn30Ubp37853333HwoULueuuu9iyZQsAu3fvJiYmhrS0NNq3b89DDz2Ep6drXZevbIwxbJu9jab9m1Kn1QUXdLoMLRSKlENnubb5HsbdUcvqKNVGYGAgd911FzNmzCjRwd/SpUuJi4srep+amkpaWhqDBg1ixYoVNG/enIceeoj//Oc/HDlyhLp165Z6GeSqVav4+uuvARgyZAjJyclFl7Ved911eHt74+3tTf369Tl+/DihoaFO/sbqchzbfIyTO09y7bul7LC4EC0UinodQ/j8YDU9N1HeEYCvb7njTXBwhY8gSvP444/To0cPJk2aVDSssLCQNWvWXNA77ODBg5k5cyaHDx9m2rRpfPvtt8yfP59Bg0o/wjOl3P90rn3b2/t/ncm5u7uTn59/2d9BOdfmDzfj7u1Ol/Gu3ROCy52jUJXLFBr2/XrI6hjVUt26dbnllluYNWtW0bBrrrmmqPkIKGouatq0KadOnSIhIYFWrVoxcOBAXn/99aJCERAQQFpaWtHnBg8ezJw5cwBYuXIlISEhBAbqs82rkrysPLbP2U7HsR3xqePa3cproajh9iw+QJurm/PpA6usjlItPfXUUyWufpoxYwaxsbGEhYXRqVMn3n///aJxffr0oV0726MvBw0axJEjRxg4cCAAQ4cOJS4uruhk9tSpU4vm83//93988sknqKpl93e7yU7Jpvu93a2OclHa9FTDRc88DLQiclJLq6NUG+np6UWvGzRoQGZmZtH7kJAQ5s2bV+rnPvvss6LX/fv3p7Dwfw+Oqlu3Lhs2bCgx/YIFttuKij+J7/z7NXbs2HF5X0I53eZZm6ndojYth7r+354eUdRw0avq0K3WHpr1a2J1FKVqjJSDKRz45QDhk8IRN9e8d6I4LRQ1WHLCaVandiGqZ/ldXyulHGvzR5tBIPzucKujVIgWihrsx+m7KMSdqHvqWR1FqRqjsKCQLR9tofXw1gQ1C7I6ToXoOYoa7PpnujCv1m/0vLOv1VGUqjEO/HKA1N9TGf7acKujVJgWihqsdvMgbnmzv9UxlKpRNn+4GZ+6PnQY08HqKBWmTU811MbZu3gjahmpialWR1GqxshMzmT3t7vpOqErHt5VZz9dC0UN9dkbJ5iysC/uXq7/BLeqprQuN6ZOnYqIsHfv3qJhb775JiJCbGxsZcZTFtr66VYKcguqxL0TxWmhqIFMoSF6Rwuurrcdv/rOe+SpKqlr164Uf0zv/Pnz6dRJe+utKUyhIfa9WEL7hdKwW0Or41wSLRQ10K6F+9if35yoYVlWR6lRxowZU3ST3P79+wkKCqJePb3irKbY/8t+Tiecptcfe1kd5ZJVnUYy5TDR7yUCbbj+ibZWR3G6K+hlnORkudxexksVGBhI06ZN2bFjBwsWLODWW2/lo48+uvwZqiplw8wN+Ib40unmqncUqUcUNdDRJKG33w5Ce7nmYxers/HjxzN37ly+++47brzxRqvjqEpy9vBZ4qPj6X5f9yp1EvucqpdYXbG3twwhP7tmdD19Bb2MExxsrugIojRRUVH8+c9/pmfPntrbaw2y8T8bMcbQ88GeVke5LFooapjC/ELcPNzwqKW/eiv4+PjwyiuvFPUSq6q//Jx8Nv13E+2ub0ft5rWtjnNZdGtRw9zRZg3GCF8c0hvtnCUzM7PEE+WefPLJEuPHjx9f2ZGUhXZ9s4uMExn0erjqncQ+RwtFDZKbnsvCQ10Z32GL1VGqteLdg1/MMke3bSmXE/tuLHVa16H1Na2tjnLZ9GR2DbL8ne2kEUjUzfpsbKUqw/Ftxzm86jA9H+pZJboTL4sWihok+ot0apHF1ZNd+/m8SlUX62asw6OWR5XpTrwsWihqCFNoiI5rxfAG2/AN8bU6jlLVXvqxdLZ9to1ud3fDN7hq/83pOYoaIj87n0dG7qNDhHbZoVRlWD9zPQV5BfR7op/VUa6YFooawtPXk6eiI62OoVSNkJeZR+x7sbQf3Z7gdsFWx7li2vRUQyyZFsuZAylWx1CqRtjyyRaykrPo91TVP5oALRQ1womdJxn1XA9m3LPF6ig1wrRp0+jcuTNhYWGEh4ezbt063nrrLTIzMy3NlZKSwrvvvmtphpqgsKCQtdPX0rhXY5oNbGZ1HIfQQlED/PDmHgxuRN3XwOoo1d6aNWtYuHAhmzZtYtu2bSxdupSmTZtqoahB4qPjOb33NP3/1B+RqntJbHFaKGqA6B89aOKWRPfbqs6jF6uqpKQkQkJC8Pb2BiAkJIT58+dz9OhRhg4dytChQwH46aef6NevHz169GDcuHGkp6cDsHHjRoYMGUJERAQjRowgKSkJgMjISB5//HH69+9Ply5dWL9+PQAZGRk8/PDD9OrVi+7duxd1Y75z50569+5NeHg4YWFhJCQk8Mwzz7Bv3z7Cw8P585//XNmrpsb47fXfCGoeRMexHa2O4jB6Mruay0nN4aejnZnQcTPiVvN6i438OPKCYbd0voWHez1MZl4m1865sJ/xu8Pv5u7wu0nOSibq65L9jC+7e1m5y7vmmmv4+9//Trt27Rg2bBi33norjz32GNOnTycmJoaQkBBOnTrFiy++yNKlS/Hz8+OVV15h+vTpPPvsszz66KMsWLCAevXqMW/ePKZMmcKHH34I2IrCb7/9xooVK7jnnnvYsWMH06ZNY/DgwXz22WekpKTQu3dvhg0bxvvvv8/kyZOZMGECubm5FBQU8PLLL7Njxw62bNlyuatTXUTiukR+X/07I94cgZtH9dkP10JRza35cBfphBN1i4/VUWoEf39/Nm7cyMqVK4mJieHWW2/l5ZdfLjHN2rVriYuLY8CAAQDk5ubSr18/9uzZw44dOxg+fDgABQUFNGr0v+J+2223ATB48GBSU1NJSUnhp59+IjMzk5kzZwKQnZ3N4cOH6devH9OmTSMxMZGxY8fStm31f/aIK/jttd/wDvKuco86vRgtFNVc5OPh7Ol4gGZ9ulodxRLlHQH4evqWOz7YJ/iiRxClcXd3JzIyksjISLp27conn3xSYrwxhuHDh/PFF1+UGL59+3Y6d+7MmjVrSp3v+e3dIoIxhtmzZ9OjR48S4zp27EifPn1YtGgRI0aM4IMPPqBVq1aX/F1UxZ3YcYJdX+9i0JRBeAd4Wx3HoarPsZEqU7sRLalVW/t3qgx79uwhISGh6P2WLVto3rw5AQEBpKWlAdC3b19Wr17N3r17AVtvs/Hx8bRv356TJ08WFYq8vDx27txZNK958+YBsGrVKoKCgggKCmLEiBG8//77GGMA2Lx5M2B71GqrVq147LHHGD16NNu2bSuRQTneymkr8fTzpO8Tfa2O4nAuUShEpKmIxIjILhHZKSKT7cPrisjPIpJg/7eO1Vmrkp0L9nJ7i9Xs+/WQ1VFqjPT0dCZOnEinTp0ICwsjLi6OqVOn8sADDzBq1CiGDh1KvXr1+Pjjj7ntttsICwujb9++7N69Gy8vL+bPn89f/vIXunXrRnh4OL/99lvRvOvUqUP//v158MEHmTVrFgDPP/88+fn5hIWF0aVLF55//nnAVlS6dOlCeHg4u3fv5q677iI4OJgBAwbQpUsXPZntYKd2n2LHvB30fqR3le+uo1TGGMt/gEZAD/vrACAe6AS8CjxjH/4M8MrF5hUREWEcLSYmxuHzdIbzc744LMaAMUc3H7MmUBmcuT7j4uIcNq/U1FSHzetKDRkyxGzYsKHUcY7M6cj1d76q8Hd0uRm/ufMb86LPiyb9eLpjA5XBGesSiDVlbFdd4ojCGJNkjNlkf50G7AKaADcA5xp4PwHGWBKwiopeE0Ivv500Ctf7J5RyltN7T7P98+30fKgnfvWrZ19qLncyW0RaAN2BdUADY0wS2IqJiNS3MltVcnzHSdZndOJvV62wOopyAH3Aketa+dJK3Dzc6P+n6vvUSDH2k2CuQET8geXANGPMNyKSYoypXWz8GWPMBecpROQB4AGABg0aRMydO9ehudLT0/H393foPJ2heM7Vr5zgucW3MPv5b2hyVV2Lk5XkzPUZFBREmzZtHDKvgoIC3N3dHTIvZ3Jkzr1793L27FmHzOt8VeHv6FIzZh/LZv0d62k8ujFtHnPM/7uKcMa6HDp06EZjTM9SR5bVJlXZP4AnsAR4stiwPUAj87/zGHsuNh89R2Hz8X0rTWTtTaawoNC6QGXQcxSOpecoHOdSM0b/Idr8w+sf5uzvZ50TqAw18hyF2C4QnwXsMsZMLzbqe2Ci/fVEYEFlZ6uqJv53IDFnulfpxy8q5cpO7zvN5lmbCb8nnMDQQKvjOJVLFApgAHAncJWIbLH/XAu8DAwXkQRguP29uogzB1LIz863OoZS1VrM8zG4e7kz5IUhVkdxOpc4mW2MWQWUtet7dWVmqQ6mRG0jencbDmY2wN3L9dvYlapqkjYlseOLHQz860ACGgVYHcfpXOWIQjmIKTQs3N2anvUPa5FQykl+efYXfOr6MODpAVZHqRRaKKqZrV/F83tBE6JG5FkdpUqYM2cOLVq0wM3NjRYtWjBnzhyHzHfo0KH8/PPPADz33HM89thjDpmvst7+X/az76d9DJoyiFpBNaNrHJdoelKOE/2fJIS2XPeUPnviYubMmcMDDzxQ9EChQ4cO8cADDwAwYcKEK5r33/72N1544QVOnDjB5s2b+f777684r7KeMYZfnvmFwKaB9Hq4l9VxKo0eUVQz0evq0dsvjgZd6lkdxeVNmTLlgqfOZWZmMmXKlCue9+DBgzHGMH36dObOnYu7uzsZGRlMnDiR+++/32FHLqpyxc2P42jsUYb+fSgetWrOfrYWimrmtWl5vPhCrtUxqoTDhw9f0vBLsX37dpKSkvD29iYgwHay85tvvuHmm2/mv//9rx5hVEEFuQX8OuVX6nWuR9idYVbHqVRaKKqZIZPDGfZ0j4tPqGjWrPQH35c1vKKSkpKYMGECCxYswM/PjyVLlgCQmJhI06ZNAarEHd+qpHUz1nE64TTDXx2Om3vN2nTWrG9bza1+5QTrZu2wOkaVMW3aNHx9S3YJ7evry7Rp0y57npmZmYwdO5Y33niDjh078vzzzzN16lQAQkNDSUxMBKCwsPCyl6EqX1pSGsv/tpy217Wl7bU172mBNaeRrZrLOp3FtMXXk3RkA33utTpN1XDuhPWUKVM4fPgwzZo1Y9q0aVd0ItvX17fEE+oGDx5c9H7s2LE88sgjLFq0iKioqLJmoVzQ0r8spSC3gJFvjbQ6iiW0UFQTv87YQRa9iLq1enZz7CwTJky44iucKsrPz4+PPvqoUpalHOf3335n22fbGPjsQOq2ca0ONiuLNj1VEwu/ysKfNCIfrZnPxlbKGQoLCvnhkR8IaBLAoL8OsjqOZbRQVAOm0BC9uy1DgjfhHVi9HuqulJU2fbCJY5uPcc3r1+Dl72V1HMtooagGDq85QobxYUCfE1ZHUarayDqdxa9TfqX5kOZ0vrWz1XEspecoqoHmA0I5kZ7Hsl9rWx3FJRhjsPVcry6FcaGHmLmCJU8sIedsDqNmjKrx/5/0iKKa8PT1xNPf0+oYlqtVqxbJycm60btExhiSk5OpVatm9F10MQk/JrD1060MeGYADcL0mfN6RFHFHd10jKv6ZfLuP8/iFmF1Guudu1fh5MmTVzyv7OzsKrHhdFTOWrVqERoa6oBEVVtOag4L/7CQep3qMfi5wVbHcQlaKKq4hdPj2ZM7mPqtEjiFc551XJV4enrSsmVLh8xr2bJldO/e3SHzcqaqkrOqWPrMUlITU7n3t3vx8NZNJGihqPKif65FC4/f6XxDG5avOGJ1nMuWn5NPVnIWmcmZ5KbZ+qoSN7H9uAs+dX3wq+eHp59njW8vVs6TsiWFre9tpc/jfQjtq0dX52ihqMIyT2Wy9ERX7g9bj7g1tTrORRljOJ1wmhO/niAmJoZTcac4ueskKQdTyMuo2PMzPGp54FvPlzot61C3XV1C2ocQ3C6YBmENCGoepEVEXba8zDziX4+nTqs6XPXiVVbHcSlaKKqwX97eQTa9ibrN3+ooZTp7+Cz7l+7nwK8HOBhzkLSjaQDsdttNnVZ1COkYQqthrfCt54tvsC8+wT54B3ojIphCgzGGwrxCsk5nkXEyg8yTmWQcz+DM/jPsWbCHzSc3Fy3Lt54vTXo3oUmfJjTt35RmA5rVqK6g1ZX5+S8/k3Uki3G/jMPLr+beM1Ea/Suqwuq38OWuVqsY8khvq6OUkHkqk51f7mT7nO38/tvvAPjV96PlVS1pMbQFSW5JjLxjpEM24llnskjek0zS5iSOrj/KkfVHSPghAYzt6KPZoGa0Gt6K1te0pkFYAz3iUKXaE72HDe9soMnNTWh5lWPOcVUnWiiqsD73dnGZDgCNMRz49QDr3lrH3sV7KcwvpH6X+lz90tW0H92ekI4hRRvpZcuWOWxP36eOD6F9Q23tyQ/ZhmWfzebwqsPsX7qf/T/vZ+nTS1n69FJqt6hNh7Ed6HhjR0L7hda4rqJV6VKPpLJg0gIahjek1f2trI7jkrRQVFFHNx0j/WQW7UZYu/dTmF9I3Ndx/PbqbyRtSsK/oT99n+xL2IQwy64/rxVUi3bXtaPdde0AWxfRCT8ksPvb3Wx4ZwNrp6/Fr4EfXcZ3IezOMBr1aKRHGjVUYUEh3975LflZ+dw09yZ2JGk3/aXRQlFF/fuJ3fxjxWBOxp8muG3l92hpCg3bv9hOzPMxpBxIIbh9MFEfRBF2R5jLXVIY0CiAHvf2oMe9PchJzSHhhwTivooj9r1Y1r29jpAOIYTdGUa3id0IbBJodVxViVa/upqDMQcZ/eFoQtqHQJLViVyTa/1FqwqL3tCAfgE7CG5b+Y9kTFyXyOLJizmy7giNejRixPQRtB/dHnFz/b1y70BvuozvQpfxXcg6k0XcV3Fs+2wbv075lZjnY2h3fTt6PNCDNiPbWB1VOVni2kRino+hy/guhN8dbnUcl6aFogpK3JDE5qyOvDRiWaUuNy0pjaVPL2Xb7G34N/Tnho9uoNtd3apEgSiNTx0fIh6IIOKBCE7vO83mWZvZ/OFm9ny/h8CmgdQdXpeMThn41ddnfFQ3aUlpfHnTlwQ1C+K696/TpseL0EJRBS18MwFoRNRDlXdD0M6vdrLowUXkZuQy8NmBDHx2IN4B1adL87qt63L1P68m8m+RxEfHE/t+LPs/3M+bc96k621d6f1Ybxp1b2R1TOUA+Tn5fHnTl2SnZHPvmnupFeT63bRYTQtFFbTol1q09DhMp6jWTl9Wdko2PzzyA9vnbKdJ7yaM+XSMrS23mnL3dKfj2I50HNuRRZ8sgvWw9ZOtbPl4C80GNaP/n/vT7rp2VfYoqqYzxrDooUUkrklk3Pxx2uFfBWmhqII++a0tB9Ycc/rG6kDMAb676zvSktKI/Fskg/46CDePmnNJqV9zPyInRnL1tKvZ/OFm1r29jrmj5xLSIYR+T/WznbjXG/qqlPX/Ws+Wj7Yw+PnBdLqpk9Vxqoya81dfjdRtXYeIOzo6bf7GGNa+vZbPhn+Gp58n9665lyEvDKlRRaK4WrVr0e/Jfjy27zHGfj4WDx8Pou+P5q0Wb7H61dXkpOZYHVFVwP5f9rPkySW0v6E9kVMjrY5TpejuUBUz/YZl+Pq58eDnzun+OD8nn0UPLWLLR1voMKYDYz4dU63ORVwJNw83ut7WlS7ju3Aw5iCrX1nN0r8sZdVLq+j1x170mdwHv3p64tsVHdt6jC9v+pKQDiHc+NmN2nR4iS65UIiIH5BtjClwQh5VjsL8Ql5b2JFBjffzoBPmn34snXlj55G4JpHBzw8mcmqk/kGVQkRoeVVLWl7VkqMbj7LqpVWs/OdK1kxfQ8QfIhjw5wEENA6wOqayO73vNLNHzMY7wJsJP0zQHZ/LcNFCISJuwHhgAtALyAG8ReQk8APwH2NMglNTKgA2ztnNscJORF3n+NWdHJ/Mp8M+JSs5i5u/vJnO42r2M4IrqnFEY26Zfwundp9i1UurWP+v9cS+G0v3e7sz4C8DqN28ttURa7S0pDQ+G/4ZhfmFTIyZSFCzIKsjVUkVaXSOAVoDzwINjTFNjTH1gUHAWuBlEbnDiRmVXfSsE7hRwLVPOfYk3PFtx/lo8EfkZ+czaeUkLRKXIaRDCGM+GcOj8Y/S7e5ubPpgE/9q8y++v+97zuw/Y3W8GinrTBazR8wm40QGE36cQL2O9ayOVGVVpOlpmDHmgocFGGNOA18DX4uIPqy5EkTHNqR/4A6C23Zz2DyPrD/C7JGz8fT15K6ldxHSofpe+loZ6rSqQ9S/oxj83GBWv7qaTf/dxJaPt9Dtzm4M/OtAgtsGWx2xRsg+m83n131O8p5kbl90O016NbE6UpV20SOKc0VCRN6SMm5fLK2QKMfKTsmmtncWN0Y6bu/04PKDfHr1p/jU8WHSyklaJBwoqGkQ1/7rWiYfmEzvR3uzY+4OZnaYybd3fsup3aesjletZZ7K5NOrP+XohqPc9MVNtBqmPcJeqUu53jEd+N5+MhsRuUZEVjsnVkkiMlJE9ojIXhF5pjKW6Wpq1a5FzJnuPLkg0iHzO7TiEHNGziGoWRCTVk6iTss6DpmvKimgUQAj3xzJ5AOT6ftEX3Z9s4uZnWby9W1fc2LnCavjVTtpSWl8PORjTu48yfgF4+k41nmXkdckFb7qyRjznIjcDiwTkRwgA3D6RltE3IGZwHAgEdggIt8bY+KcvWxXknkqE98QX4fM69iWY3wR9QW1W9Rm4rKJeklnJfBv6M81r1/DgL8MYM30NWx4ZwM75u2g002dGDRlEA3DG1odscpLOZjCp8M+JeO47ZxEi8gWVkeqNip8RCEiVwP3YysQ9YDHjDErnRWsmN7AXmPMfmNMLjAXuKESlusyMk5kUL9eIf+6efkVzys5Idl2qWCQN3f8dIcWiUrmV8+PYS8NY/LByQz66yD2/bSPf3f/N1+M/oIj649YHa/KOrblGB8N+ois5CzuXHqnFgkHE2NMxSYU+RV4wRizSkS6Ap8BTxpjfnVqQJGbgZHGmPvs7+8E+hhjHik2zQPAAwANGjSImDt3rkMzpKen4+9v3XOpt/7nBI9/cQv/fvAr2t1a9pUbF8uZcyqHLY9uoSCrgPAZ4fg2c8wRyqWyen1WVGXkzE/P58g3R0j8OpH81Hzq9KxDswnNCOoWVOEeTWv6+jy57CS7X9mNh78HXV/qin+by19GTV6XQ4cO3WiM6VnqSGPMZf0AjYDfLvfzl7CcccAHxd7fCfyrrOkjIiKMo8XExDh8npfinrYrTBApJjcjt9zpysuZdSbLvNvlXfNP/3+aIxuOODjhpbF6fVZUZebMTs02q15ZZV5r8JqZylTzQd8PzO4Fu01hQeFFP1tT12dhQaH55blfbOur3wcmLSntiudZU9elMcYAsaaM7epFm57KudIpCbi6vGkcJBFoWux9KHDUictzKYX5hSza155RzXbi6Xt5VyEXFhQyf/x8Tu05xfgF42ncs7GDU6or5R3gzYCnBzD5wGSuffda0o+lM/eGubwX9h5bPt5CQa52hFBc9tls5o2dx8oXVxJ+TzgTYybi39D1jwSqqgrdcCcij4pIs+IDRcQL6CcinwATnZLOZgPQVkRa2pc5HvjeictzKRs+ieN4YX2irq9YE2Fplj6zlH1L9nHtzGtpeZW1z9hW5fP08aTXQ714NOHRoj6JFkxawNst32b1q6vJTsm2OqLlDi47yPth7xO/MJ6Rb49k9AejXe7xu9VNRdbuSOAe4AsRaQmkALUAd+An4E1jzBZnBTTG5IvII8AS+zI/NMbsdNbyXE3zXvV5/fpljPpT+GV9ftvsbax5fQ29/tiLiPsjHBtOOY2bhxthd4TRdUJX9v20jzWvr2HpX5ay4h8rCJ8UTu9HehPcrmbdvJefnc8vU35h7fS11G1bl3tW30Non8p7eFdNdtFCYYzJBt4F3rXfgR0CZBljUpycrXiGH7D1K1XjNAyrz1PR9S/rs0c2HOH7+76nRWQLRrw5wsHJVGUQEdqMaEObEW1I2pzE2ulriX0/lvX/Wk+bUW3o81gfjNflH21WFYnrEvn+3u85ufMkPR/uyfBXh+Pl52V1rBqj3KYnERkjIv8SkXZguwPbGJNUmUWiJkvacpwvHv2NtKNpl/zZ9GPpzLtxHv4N/Rn31TjcPd2dkFBVpkbdG3HjZzfyxOEniPxbJMc2H2POqDmsv3M9q15eRfqxdKsjOlzqkVS+vetbZvWdRfaZbCb8OIHrZl6nRaKSlVsojDHfAc2Bq0Xk0UpJpIp888/d3P5Of45uPXlJnyssKOTr278m+0w24xeMd9iNeso1+Df0Z8gLQ3j80OOMnTMW73re/PLsL7zZ9E2+vPlLEn5IoDC/0OqYVyQvK48VL67gnXbvsPPLnQx8diB/3P1H2oxsY3W0Gqki5yhaGWPeE5GNwL+cHUj9T/SvfrT1PED7UZfWV83qV1dzMOYgo2eNpmE3veO3unL3cqfr7V1JbpxMl0Zd2PTfTWz9ZCu7vt6FX30/utzWhbA7w2jUo1GF78mwWtaZLGLfj2Xd2+vIOJ5Bx5s6Mvy14drFjMUqUigWi8gaoKGI3ANsBXbaz10oJ0k7mkZMclceiVgDVPxKpcS1icQ8H0PnWzsTPincafmUawlpH8I1r1/D1f+8moQfE9j22TZi37NtcIPbBdPhxg50uLEDTXo1ccmHUZ09fJa1b69l0382kZueS+sRrRn010E0H9zc6miKip3M/pOItAKWYdtijQY6i0gusMMYc6tzI9ZMP7+1k1z6MvrO2hX+TH56Pl9P+pqgpkFc//71VWYvUjmOu5c7HW7oQIcbOpB1Jou4+XHEfRXHmjfWsPqV1QQ0CaD96Pa0vqY1LSJbUKt2LcuyZqdkE/d1HNvnbOfgsoOIm9BlfBf6/7m/Hgm7mApdfGyM2S8iw4wx8eeGiYg/0MVpyWq4dcuzqSNnGPCHiq1iYwzxb8Zz9vezTFo5ydINgHINPnV8iLg/goj7I8g6k0XCogR2fbOLrZ9uJfa9WMRNaNyrMS2vbknTfk1p0rsJfvWd1/eXMYaTcSc5EHOA/T/vZ++PeynILaBu27oM+b8hhN8drk8EdFGX0nts/Hnv07E94U45wSvrInlyx0k8alXsV7T1k62c/PUkQ18cStN+TS/+AVWj+NTxIeyOMMLuCKMgt4DEdYns/3k/+3/ez+qXV2MKbZfY1m5Rm8a9GlOvcz2C2wUT0j6Eum3rXvJzpgvzCzm97zSndp3iZNxJjm87TvxP8aw4swKAoGZB9HyoJ10ndKVxz8Z69Ovi9HZGF9agS8Ue3ZiamMriyYsJCgti4DMDnZxKVXXuXu40H9Sc5oOaM/TvQ8nNyCVpUxJH1h/hyLojHI09Stz8OCh2e4Z3oDe+9XzxDfHFr54fnn6eiIjtfIdAQU4BmcmZZCVnkZmcScaJDArz/nflVWDTQOr0qEOf8X1oeVVLaresrcWhCtFC4YJeGbWMuHgPPk4YcNETj8YYFj20iIK8Ato/3R4390t5FpVS4OXnVVQ4zsnLyuPMvjOc2nOK5Phk0o+lk3Uqi4yTGaQmppKXlQcGTKHBFBrcvdzxCfahdovaNIpohF8DP0I6hFCvYz1COoTgHejNsmXL6BHZw8Jvqi6XFgoXNDumCfV80it0dcqOuTuIXxjP8NeHk9sktxLSqZrA08eT+l3qU7/L5fUKoKoX3f10MQdXJbIjpy1RQ85edNqMkxksfmwxTXo3oe/jfSshnVKqJtJC4WKi39oHQNSjF793YvFji8k+m83oD0drk5NSyml06+JiomP86eC1jzZXl3+j0Z7v97Bj7g4GPzeY+p21eUAp5Tx6jsLF9OqQxqh6aUDrMqfJTc9l0cOLqN+1vl7lpJRyOi0ULmba6siLTrPynytJO5LGuC/H4e6lvcIqpZxLm55cyJ4f95OfnV/uNKf3nmbNG2sIuzOMpv31xjqllPNpoXARBbkFDLwukAe7rSl3usWPL8bd251hrwyrpGRKqZpOC4WLWDtrJ6dMCNdce2FT0rnuFeIXxZOwKIHBzw8moFFAZUdUStVQWihcRPQnp/EgjxFPdC4xfGrkMp6IWEFeVh5LHl9CcPtgvpqdy9TIZdYEVUrVOFooXET0llAG19lOULOgomGm0JByVnh7yxCea/0Fp/ee5mBeE97eNpSUs1J0pKGUUs6kVz25gH2/HiIupw33j1peYri4CW9uHIyE/YTHzkR20YF5+29kcvhy23AXfACNUqr60ULhApr3b0LMm1toH9nhgnHiJgwbnMe6nQX8zHAALRJKqUqlTU8uwKOWB5GPh9MovMEF45Ljk9nw3kY20oPT1AXgiYgV2uyklKo0WigsdvbwWf7UcxkJPx+8YJwpNEzvM488PGjX2ZPCAsPk8OW8vWWIFgulVKXRQmGxJW/u5I2NkRxPSL1gXNLmJLxSTlLQoDHTtw0vOmcxOXw5tYOMNj8ppSqFnqOwWPSCQoIlmX73db5g3C/P/IJPsA9/2T2+qCgUneDWIqGUqiR6RGGh/Ox8fjjYiWtb7rqgz6b9S/ezf+l+Bj83mFq1a5UYp0VCKVWZtFBYaM0HOzlt6hJ1Q8kiYQoNS59ZSlBz2wPolVLKStr0ZKHfd6VTX04y4smSzU67v9tN0sYkxnwyBg9v/RUppaylRxQWun3mAJJygwkMDSwaZoxhxT9WENwumK4TulqYTimlbLRQWKQgtwAAN4+Sv4L4hfEc23KMgX8dqI83VUq5BN0SWWTGLStp73WA1MT/XRZrjGHF31dQp1Udut6uRxNKKdeghcIi0cuD8HTLL9HstG/JPo7GHmXgswNx99Qn1ymlXIMWCgukHDrLypQuRHU/UjTMGMPyvy0nqFkQ3e7qZmE6pZQqyfJCISKvichuEdkmIt+KSO1i454Vkb0iskdERlgY06EWv7GTfDyJuju4aNiBXw6QuDaRAc8M0OdgK6VciuWFAvgZ6GKMCQPigWcBRKQTMB7oDIwE3hWRarEFjf7eECKn6DOpU9GwFf9YQUCTALrf093CZEopdSHLC4Ux5idjTL797Vog1P76BmCuMSbHGHMA2Av0tiKjo427zYMXb4srOnI4tOIQh1YcYsDTA/S+CaWUy3G1rdI9wDz76ybYCsc5ifZhVd6Yl/qUeL/61dX41vOlx/09LEqklFJlE2Oc31W1iCwFGpYyaooxZoF9milAT2CsMcaIyExgjTFmtn38LOAHY8zXpcz/AeABgAYNGkTMnTvXofnT09Px9/d3yLz2zj9JUDNP6vWuDUDGoQxi746l+d3NaTGxxRXN25E5nUlzOpbmdJyqkBGck3Po0KEbjTGl9xlkjLH8B5gIrAF8iw17Fni22PslQL+LzSsiIsI4WkxMjMPm1c5zv7kmeEPR+wX3LTAv1nrRpJ9Iv+J5OzKnM2lOx9KcjlMVMhrjnJxArClju2r5OQoRGQn8BRhtjMksNup7YLyIeItIS6AtsN6KjI4Sv+QA8XktiRqaAUD68XS2fbaNbhO74VfPz+J0SilVOlc4R/EO4A38LCIAa40xDxpjdorIl0AckA/80RhTYGHOKxb9ziGgJVGPtwZgw7sbKMgpoO8Tfa0NppRS5bC8UBhj2pQzbhowrRLjOFX0ytp0rRVP8wHtyMvKI/bdWNpFtSOkfYjV0ZRSqkyWNz3VFBknMlh7tgNRPY4CsPXTrWSeyqT/n/pbnEwppcpn+RFFTeFX34+k/SnkZ3fBFBrWTl9L456NaTaomdXRlFKqXFooKlGdlrUB2PP9HpLjk7lp7k3Yz8sopZTL0qanSpCXmcf1DdazZFosAOtmrCOwaSCdbup0kU8qpZT1tFBUgtX/2cmiE73JTM3n1O5THPjlAD0f6nnBQ4uUUsoV6ZaqEkTPTsGLHIY/0YUN723A3cudHvdqdx1KqapBC0UliN7WnKtCtuHl78XWj7fSaVwn/OrrDXZKqapBC4WT7flxPwl5LYm6OpPtn28nJzWHXg/3sjqWUkpVmBYKJ0s7mc2QoC1c91hrNszcQINuDQjtF3rxDyqllIvQQuFkPe/qxLKUcMQUcnzbcXr9sZdeEquUqlK0UDhR5qlMzhxIASD23Vi8A73pentXa0MppdQl0kLhRN88v5l6rfyJ/XQHO7/aSbe7u+Hl52V1LKWUuiRaKJwoepEQ4naajIPJFOYV6klspVSVpIXCSXLTc1n8e2eubb2HzR9upuVVLbWXWKVUlaSFwklW/XsnqQQxqEcGZw+dpft93a2OpJRSl0ULhZNEz0nFm2x8clOoVbsWHW/saHUkpZS6LNp7rJM88noLen+9gb2z9tLjvh541NJVrZSqmvSIwklaX9Wc1p28KcgpoPu92uyklKq6dDfXCRa+sJ60M/mkrtpOw/CGNOreyOpISil12bRQOMErb3uTlhPAjTnHGPWvUVbHUUqpK6JNTw52ak8yv6V2YWDwLty93fVObKVUlaeFwsF+fHMXhbgTkrKXjjd2xKeuj9WRlFLqimihcLDoRe40kmOYzEzC7wm3Oo5SSl0xPUfhQKbQcPBMIIN8YqkTUptWV7eyOpJSSl0xPaJwIHETlu5pSofMWLrd3Q1x0+7ElVJVnxYKBzKFhh1f7MANIeyOMKvjKKWUQ2jTk4OYQkOvgF3080igW+8mBLcNtjqSUko5hB5ROEhc9D42ZnaiMDWNrhP0klilVPWhhcJBot9LBCBETtP51s4Wp1FKKcfRQuEg0b/VJUy20W5Ea/wb+FsdRymlHEYLhQOc3HWKNWld6GE20vUObXZSSlUvWigcID+ngHtCvqe513E63NDB6jhKKeVQetWTA9TrGEzbgj20HdcOL38vq+MopZRD6RHFFcpJzeHrh38h80yWXu2klKqWtFBcoeUzdzD+wxHk+tSm9fDWVsdRSimHc5lCISJ/EhEjIiHFhj0rIntFZI+IjLAyX1kWzE7Fh0z63dEKNw+XWZ1KKeUwLnGOQkSaAsOBw8WGdQLGA52BxsBSEWlnjCmwJuWFTKFh4e629GUt3Sfp406VUtWTq+wCvwk8DZhiw24A5hpjcowxB4C9QG8rwpVl+zcJHC4MpZtvAqF9Qq2Oo5RSTmH5EYWIjAaOGGO2ipTobbUJsLbY+0T7sNLm8QDwAECDBg1YtmyZQzOmp6eXOs+F/0wG2tG6XyHLVyx36DIvR1k5XY3mdCzN6ThVISNYkNMY4/QfYCmwo5SfG4B1QJB9uoNAiP31TOCOYvOYBdx0sWVFREQYR4uJiSl1eOx/Y81fedEc/u2ww5d5OcrK6Wo0p2NpTsepChmNcU5OINaUsV2tlCMKY8yw0oaLSFegJXDuaCIU2CQivbEdQTQtNnkocNTJUS9J/PfxhIT6arOTUqpas/QchTFmuzGmvjGmhTGmBbbi0MMYcwz4HhgvIt4i0hJoC6y3MG4J859cTXQ0tLm+jT6gSClVrVl+jqIsxpidIvIlEAfkA380LnTF0ycfFbKZQbw8odDqKEop5VSuctUTAPYji1PF3k8zxrQ2xrQ3xvxoZbbislOyiUnpTn+PDTTt3/TiH1BKqSrMpQpFVfHzG1vIwJ8BPbO02UkpVe1pobgM3358Fl8yuHaqS93WoZRSTuGy5yhcmUnLYLh7DG2GX2d1FKVUFZGTn0NuQS4B3gEArE1cy+ms06TlpJGWm0ZqTiqt6rRiTIcxANz93d2cyjxFem46MRNjOO8+s0qlheIS5aTm0Do7jp6P9NRmJ6WqMWMMmXmZRRvxtJw0ACIaRwDwza5v2Hd6X4nxTQKb8PehfwdgzNwxbD2+lbQc2/i8wjxGtB7B4jsWA3Dr/Fs5fPZwiWXe2OHGokKx69Qu8gvzCfQOJLcgF28P70r65hfSQnGJtny6lYKcAjqN62R1FKXUeQpNIW5ia1E/mnaUxNTEog11Wm4aOfk53B9xPwCzNs1ixeEVRXv0aTlp5GbksilyEwBRX0SxKGFRifm3rduW+EfjAZixbgbLDy1HEAK8AwjwCqBXk15F07YLbkegdyABXgG2f70DaB/cvmj83Jvm4iZuBHgHFE3n7/W/xyivu2+dc1bSZdBCcYkeftyb+m59eaGfXu2klCPkFeQVbajTctNoF9wOL3cv4k7GsS5xXYk99rTcNF4d/ir+Xv78O/bf/HfTf4s+m5qTSkZeBrnP5eLp7sk/V/6TmRtmlliWh5sH9/W4DxFh6/GtLDu4rGgjHVQryHYhvt2dYXcyqNmgoo18gFcAIb5FnVvz7a3f4unuiZ+nX6nNQq8Of7Xc792vab8rW3GVSAvFJUjccJRNBd14rHG8NjupGi87P5ujaUdLtLGn5aQxpMUQGvo3ZOuxrXy27bOi8QeOHsDzgCf/ifoPHUI68NHmj3j4h4fJzs8uMd89j+yhXXA7fkz4kT/9/Kei4d7u3gR4B/D84Ofx9/Knlkct6vvVp03dNgR4BRTtmRca271N9/e4n1FtRhVt5M/9e86MUTOYMWpGiWUX7z/p1i63lvv96/jUudxVV+VoobgEX/11M9CYkXfWszqKUpekeHu7r6cvgd6BpOWksezgsqJmmXMb9NHtR9OzcU92ndzFE0ueKDEuLSeNWaNncUOHG1h+cDkj54y8YFk/TviRkW1Gsv/Mft6Lfa9oIy25QmNpTH6hbbe9U71OPNLrkRJ77IHegTTwawDApO6TuKnTTUWf93Iv+ZjhieETmRg+sczv3K1hN7o17ObAtVhzaaG4BEtW+xPK7wx7YYDVUVQNYIwp0axy7nWjgEZ0qteJ3IJcpq+Zzvb92/k68+uivfqxHcdyR9gdHE8/Ts//9izayJ/b0359+Os81f8pktKTGD13dIllCkLTwKb0bNwTEeF01mkCvAOo71fftsH2CiA00Na3WViDMD6+4eMSG/kA7wCaBzUH4MaON5LRMaNo3suWLSMyMrLofZ/QPvQJ7VPm96/rU5e6PnUdtTrVFdBCUUFZp7NYmdWTGwN/wdN39MU/oGqk/MJ8cvJz8PPyA2Dj0Y0kZyUXNcuk5qTSNKgpYzuOBeDBhQ+SlJ5Uohhc1/Y6po+YDkDwq8FFe+DnPNzzYWZeNxNBePaXZ3HDjcCTgUVt7SnZKQD4e/kzvNXwEs0uAd4BDGhq29FpHtScDfdvKNFs4+vpW3QyuENIB9bfX3b3ao0CGpW7R6+qDy0UFXRk41Ee4HuG3KFXO1U3Ofk5JfbYC0wBPRr1ACB6TzQJpxNKtMPX96vPi1e9CMBtX9/GhiMbij6blZ/FkOZDWHb3MgBu/+Z24pPjSyxvVJtRRYVi+4ntpOemE+Bl22tvXbc1beu2BUBEeHPEm3i5e5XYY28W1AwAT3dPMv6awbpV6xg6dOgF38vPy48Pb/iwzO/t7eFNz8Y9r2zlqRpBC0UFHYo5SB33NEa8ONjqKDWeret824b0ePpxjqQdKXFVTEZuRtElkLO3zSbmQIxtQ27fmLu7ubP8btuDpm756ha+ivuqxPybBjbl8BO269tnbpjJkn1LAPDx8CHQO5DwhuFF07YIamG7xNHrf80vreu2Lhr/0Q0fYYy5oHnmnNX3rC73uz7S+5Fyx/t6+lp6I5aqGbRQVIApNES/c5AO3RvjU8fH6jhVUqEpJD03nbScNA5lHCI7P5taHrWIT45nXeK6Env0qTmp/OOqf1C7Vm0+2fIJ78W+d8EJ15S/pBDgHcBrv73GG2veuGB5k7pPwsPNg81Jm1myb0mJppdgn+Ci6cZ1Gkd4w/ASG/Hi7eJzxs7B3c0dfy9/PNwu/HN5adhL5X7v/k37X8FaU8o1aKGogAPzj/F22r287P6N1VEqXW5BLsfSj5XYY0/NSaV/0/40DmhM3Mk4PtnySYk99tScVN4e+TZdG3Rl3o553Bd9H+m56SXmGx4RTreG3fh538888uP/9prdxZ0A7wCe7PcktWvVxtPdk0DvQEIDQ/+3sfcKKGpHv6vbXQxqNuiCPXZ3cQfgjRFv8MaICwvJOeM6jyv3+wf7Bpc7XqmaQAtFBWxYIAiF3Pxid6ujXFROfg5puWl4uXsR6B1IZl4myw4uK3F5Y2pOKiPbjKRPaB/2n9nP5MWTSc1JLVEM3hn1DuM6j2PN72uI/CTyguV8e+u3jOkwhoMpB3lr3VtFJ1LPnRTNK8wDoE3dNtzf4/4SJ1QT9yfSNMh2w+JtXW9jRJsRRRv5Wh61SjSl3N71dm7venuZ3zesQRhhDcIcug6VUiVpoSjHnDlzmDJlCrWTviOcTaw9vofWtHT4cjLzMktc9ZKak0o933p0rt+ZgsICpq+ZfsHdqde1vY6J4RNJyU6h+7+7k5aTxtnss+Qvt10h8+LQF5kyeAqnMk9x3ecXdl5Yu1Zt+oT2wRjD0bSjRZc9ntvgn9uQdwjpwAdRH5Rougn0DqRlbdt6GNVmFDnP5ZT53SIaRxT1jXPOsvRlRc07egmkUq5Pzp0YrC5E5CRwyAGzqgs0p2RX7IX2eZ92wPydIQQ4ddGprKc5HUtzOk5VyAjOydncGFPq3cTVrlA4g4jEGmNc/jpCzelYmtOxqkLOqpARKj+nPrhIKaVUubRQKKWUKpcWior5j9UBKkhzOpbmdKyqkLMqZIRKzqnnKJRSSpVLjyiUUkqVSwuFUkqpcmmhqCAR+YeIbBORLSLyk4g0tjpTaUTkNRHZbc/6rYjUtjpTaURknIjsFJFCEXGpyxFFZKSI7BGRvSLyjNV5yiIiH4rICRHZYXWWsohIUxGJEZFd9t/3ZKszlUZEaonIehHZas/5N6szlUVE3EVks4gsrKxlaqGouNeMMWHGmHBgIfCCxXnK8jPQxRgTBsQDz1qcpyw7gLHACquDFCci7sBMYBTQCbhNRFy1b/mPgQsfMeda8oGnjDEdgb7AH110feYAVxljugHhwEgR6WttpDJNBnZV5gK1UFSQMSa12Fs/wCWvAjDG/GSMOfekm7VAqJV5ymKM2WWM2WN1jlL0BvYaY/YbY3KBucANFmcqlTFmBa7bSwAAxpgkY8wm++s0bBu4JtamupCxOddzpaf9x+X+xkUkFLgO+KAyl6uF4hKIyDQR+R2YgOseURR3D/Cj1SGqmCbA78XeJ+KCG7aqSERaAN2BdRZHKZW9SWcLcAL42RjjijnfAp7G1p1QpdFCUYyILBWRHaX83ABgjJlijGkKzAHKf6KMhTnt00zBdtg/x5VzuqDSngLkcnuWVY2I+ANfA4+fd3TuMowxBfam5VCgt4h0sThSCSJyPXDCGLOxspetvccWY4wZVsFJPwcWAf/nxDhlulhOEZkIXA9cbSy8UeYS1qcrSQSaFnsfChy1KEu1ICKe2IrEHGOMyz/UxRiTIiLLsJ3/caULBQYAo0XkWqAWECgis40xdzh7wXpEUUEi0rbY29HAbquylEdERgJ/AUYbYzKtzlMFbQDaikhLEfECxgPfW5ypyhLbw0VmAbuMMdOtzlMWEal37gpBEfEBhuFif+PGmGeNMaHGmBbY/l/+WhlFArRQXIqX7c0m24BrsF154IreAQKAn+2X8r5vdaDSiMiNIpII9AMWicgSqzMB2C8EeARYgu3E65fGmJ3WpiqdiHwBrAHai0iiiNxrdaZSDADuBK6y/3/cYt8jdjWNgBj73/cGbOcoKu3yU1enXXgopZQqlx5RKKWUKpcWCqWUUuXSQqGUUqpcWiiUUkqVSwuFUkqpcmmhUEopVS4tFEoppcqlhUKpSmB/JsNw++sXRWSG1ZmUqijt60mpyvF/wN9FpD62HlRHW5xHqQrTO7OVqiQishzwByLtz2ZQqkrQpielKoGIdMXWn1COFglV1WihUMrJRKQRtueC3ABkiMgIiyMpdUm0UCjlRCLiC3yD7bnRu4B/AFMtDaXUJdJzFEoppcqlRxRKKaXKpYVCKaVUubRQKKWUKpcWCqWUUuXSQqGUUqpcWiiUUkqVSwuFUkqpcv0/WmM9jql8sK4AAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"calc_step(-3,1E-2)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.2.3 Consider $x_0 = -3$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.2.3-Consider-$x_0-=--3$)",
"section": "3.6.2.3 Consider $x_0 = -3$"
}
},
"source": [
"**Discussion**\n",
"* In this case, do we expect the Newton and LM steps to be the same? Explain.\n",
"* Why does $f(x)$ increase with a steepest descent ($B^k = I$) step? I thought the main idea was that because $B^k$ is **positive definite** the step is in a **descent direction**!"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.2.4 Consider $x_0 = 0$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.2.4-Consider-$x_0-=-0$)",
"section": "3.6.2.4 Consider $x_0 = 0$"
}
},
"source": [
"### 3.6.2.4 Consider $x_0 = 0$"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.2.4 Consider $x_0 = 0$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.2.4-Consider-$x_0-=-0$)",
"section": "3.6.2.4 Consider $x_0 = 0$"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"x0 = 0\n",
"f(x0) = 1.5\n",
"f'(x0) = 6\n",
"f''(x0) = -8\n",
"\n",
"### Newton Step ###\n",
"xN = 0.75\n",
"pN = xN - x0 = 0.75\n",
"f(xN) = 3.486328125\n",
"f(xN) - f(x0) = 1.986328125\n",
"\n",
"### Levenberg-Marquardt Step ###\n",
"xLM = -600.0\n",
"pLM = xLM - x0 = 0.75\n",
"f(xLM) = 65014556401.5\n",
"f(xLM) - f(x0) = 65014556400.0\n",
"\n",
"### Steepest Descent Step ###\n",
"xSD = -6.0\n",
"pSD = xSD - x0 = -6.0\n",
"f(xSD) = 685.5\n",
"f(xSD) - f(x0) = 684.0\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEWCAYAAAB42tAoAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAABeFklEQVR4nO3dd3iN5xvA8e+TTSKCRIiR2GLG3mpTaqtRq6X016rRpUMHWi1dWkpLS1G7du1dxB6xiU2IkQTZ8zy/P97QIImMc857TvJ8riuXnHfe58W5z7OFlBJFURRFSYuN3gEoiqIolk0lCkVRFCVdKlEoiqIo6VKJQlEURUmXShSKoihKulSiUBRFUdKlEoWSYwghmgghzusdx/MIIXYKIV7XOw5FySiVKBSjEUJcFULECCEiU/x4mfB+UghR9tFrKeVuKWUFU93PHIQQbkKI2UKI20KICCFEoBDiQ73jygghxFghxHy941CMz07vAJQcp6OUcqveQVixyYAz4As8BMoDVbJyISGEnZQy8alttlLKpGxHqeQqqkShmFxySaNVitePv3kKIXySSwYDhRDXhRAhQogxKY61FUJ8IoS4lPwN+4gQooQQYlfyIceTSy69hBDNhBBBKc71Ta7meSCEOC2E6JRi3xwhxDQhxLrk6x4QQpRJ5z38nfwt/6EQYpcQonJGryWEaC2EOJd87i+ASOdx1QEWSinvSykNUspzUsplTz2rx1/wUlZjCSFeFUL4CyEmCyHCgLHJsf0qhFgvhIgCmj/nuRQSQvwjhAgXQhwSQnwlhNiTYv/PQogbyfuPCCGaJG9vB3wC9Er++zievD2/EGKWECJYCHEz+Xq2yfvKCiH+TX4uIUKIJek8F0VHKlEolqIxUAFoCXwuhPBN3v4u0AdoD7gCg4BoKWXT5P3VpZQuUsonPmSEEPbAP8BmoDAwHFgghEhZNdUHGAcUAC4CE9KJbwNQLvlaR4EFT+1P9VpCCHdgOfAp4A5cAhqlc5/9wAQhxGtCiHLpHJeWesDl5DgfvZ9Xkn/PBxwg/ecyDYgCigADk39SOgT4AQWBhcDfQggnKeVG4GtgSfLfR/Xk4+cCiUBZoAbQBnjUPvNlchwFgOLA1Cy8X8UMVKJQjG1V8jfVB0KIVZk4b5yUMkZKeRw4Djz6oHkd+FRKeV5qjkspQzNwvfqACzBRShkvpdwOrEX7QH9khZTyYHL1zAK0D8BUSSlnSykjpJRxwFiguhAifwau1R44I6VcJqVMAH4CbqcT9/Dk898GzgghLgohXszA+33klpRyqpQyUUoZk7xttZTSX0ppSI4r1eeS/E2/O/CFlDJaSnkG7YM+5XOYL6UMTb7+D4AjWoJ/hhDCE3gRGCWljJJS3kWrWuudfEgC4A14SSljpZR7UruOoj+VKBRj6yKldEv+6ZKJ81J+eEajfZgBlED7Fp5ZXsCN5A/HR64BxTJwzyckV39NTK7+CgeuJu9yz8C1vIAbj3ZIbRbOG6QhOVl+LaWsBRQClqJ9ay+Y1jlPSe3aKbel91w80Notb6RxLkKI94QQZ5Orix4A+XnyOaTkDdgDwY++PAAz0EoyAKPRquEOJleBDcrA+1N0oBKFYg5RQN4Ur4tk4twbQJptB+m4BZQQQqT8N14SuJmFa70CdAZaoX0w+iRvT6+t4ZFgtGSnnSCESPk6PVLKcLTqHGegFNpzhPSfZWrTQafclt5zuYdWTVQ8xb6UsTcBPgR6AgWklG5oDe6PnsPT974BxAHuKb48uEopKye/v9tSyiFSSi/gDWC6SNGLTbEcKlEo5hAA9BZC2AshagM9MnHuH8CXQohyQlNNCFEoed8doHQa5x1A+2AdnXzfZkBHYHEW4s+H9oEXivYh/XUmzl0HVBZCdEtuhB5BOolSCPGZEKKOEMJBCOEEjAQeAOellPfQPtD7JZdyBpH5JJrmc0nuDbUCrRE8rxCiIjAgxbn50BLJPcBOCPE5WrvRI3cAn0dJSEoZjNYG8YMQwlUIYSOEKCOEeCH5vb4shHiUlO6jJRrVI8sCqUShmMNnaB9o99EafBdm4twf0apfNgPhwCwgT/K+scDc5GqNnilPklLGA53Q6shDgOnAACnluSzEPw+teuYmcAatwTlDpJQhwMvARLREUw7wT+8U4M/kmG8BrYEOUsrI5P1DgA+Sr1UZ2JuZN5KB5/I2WqnpNvAXsAgtSQJsQmvUD0R7HrE8WTX1d/KfoUKIo8m/DwAc0J7bfWAZUDR5Xx3ggBAiElgDjJRSXsnM+1HMQ6iFixRFSYsQYhJQREr5dO8nJRdRJQpFUR4TQlRMrt4TQoi6wGBgpd5xKfpSI7MVRUkpH1p1kxdwF/gBWK1rRIruVNWToiiKki5V9aQoiqKkK8dVPbm7u0sfHx+jXjMqKgpnZ2ejXtMUVJzGpeI0LkuIMzA0kMj4SHzdfcljn+eZ/caM8c4dcHCAAgWMcrknmOJZHjlyJERK6ZHqTilljvqpVauWNLYdO3YY/ZqmoOI0LhWncekd5/zj8yVjkbOPzk7zGGPEmJQk5bvvSglSvvJKti+XKlM8S+CwTONzNceVKBRFUVLzStVXKJinIC+Wy8zUWZkTHw+vvgqLFsHbb8NPP5nsVmalEoWiKDnatQfXMEgDpQqUMnmS6NABtm6Fb76BDz8EkZFJXqyAShSKouRYcYlx9Pi7ByHRIQS+HYi9rb3J7uXgAHXqQL9+MDCHDU/MFYkiISGBoKAgYmNjs3R+/vz5OXv2rJGjMj5TxOnk5ETx4sWxtzfdfzBFMZV3Nr3D4VuHWdlrpcmSRGAgREeDnx98nZlZwKxIrkgUQUFB5MuXDx8fH0QWyoIRERHky5fPBJEZl7HjlFISGhpKUFAQpUqVMtp1FcUcFpxYwK+Hf+WDhh/QpWIXk9zjwAF46SUoWhQCAsAmhw44yKFv60mxsbEUKlQoS0kiNxNCUKhQoSyXxBRFL2funWHo2qE09W7K1y1N8zV/3Tpo0QJcXWHFipybJCCXJApAJYksUs9NsUbe+b0Z5DeIJT2WYGdj/IqT2bOhc2eoWBH27oWyOXwVjVxR9aQoSu4gpSQmMQZnB2emtjfNEtxSwrJl0LKl9qcV1EpnW64pUSiKkvN96/8tdX6vQ2h0RpZVz5ykJLh/X+vy+vff8M8/uSNJgEoUZjVlyhR8fX3p27cvq1atYvz48eke//7777N9+3YzRaco1m3b5W18sv0TqhauSsE8GV1iPGNiYqBHD2jTRhsv4eysdYfNLVTVkxlNnz6dDRs2UKpUKRo2bMiaNWvSPX748OEMGTKEFi1amClCRbFONx7eoPfy3lR0r8gfnf4wattaWBh06qS1Rfz8s/kTxNkVZ0GAb1df8944BYtIFEKIEmjLTRYBDMBMKeXPQoiCwBK0xeyvAj2llPezc6+NozZyO+B2ps5JSkrC1tY2zf1F/IrQ7qd26V7jf//7H5cvX6ZTp07069cPR0dH3N3dAejcuTPdu3dnwIABzJgxg127drFgwQK8vb0JDQ3l9u3bFCmS5jLLipKrxSbG0n1pd+IS41jeczkuDi5Gu/b169CuHVy6BEuWwMsvG+3SGbb3+73YOdrpmigspeopEXhPSukL1AeGCSEqAR8B26SU5YBtya+t0m+//YaXlxc7duygcOHC1KxZ8/G+mTNnMn78eHbv3s0PP/zA1Kn/NcLVrFkTf//0llhWlNztYexDJJK5XeZS0b2iUa/96qtw6xZs2qRPkgAIPR9KoQqF9Ll5MosoUUgpg4Hg5N8jhBBngWJAZ6BZ8mFzgZ3Ah9m51/O++afG2APZgoOD8fD4bzZfT09Pxo8fT/PmzVm5ciUFC/5Xv1q4cGFu3bpltHsrSk7j6eLJ/sH7sbVJu9SfVbNmQWQkVK1q9EtnSHRoNDFhMRQqrxLFE4QQPkAN4ADgmZxEkFIGCyEKp3HOUGAoaB+6O3fufGJ//vz5iYiIyHJMSUlJ2Tr/ESklkZGRCCF4+PDhE9c8cuQIBQsW5PLly09sDw8Pp2jRohm6v7HifFpsbOwzzzQ7IiMjjXo9U1FxGpex4zwXfo7FQYt5v/z7uNgZp7opMjKSsWNPc/BgQd5///zjQXR6Pd6Hpx8CcCvu1hPPzux/52nNP67HD+ACHAG6Jb9+8NT++8+7RmrrUZw5cybzk7OnEB4enq3zH/H29pb37t2TGzZskH379n28/cCBA7J69ery5s2bsmzZsvLy5cuP97300kty3759Zo3zadl9fk/Te12CjFJxGpcx47wTeUcW/7G49J7sLUOiQox23eHDA6UQUjZqJGVEhNEum2XH/jwmxzJWhgQ++R7NvR6FpbRRIISwB5YDC6SUK5I33xFCFE3eXxRtsXer17RpU44dO4aUkri4OIYMGcLs2bPx8vLihx9+YNCgQUgpSUhI4OLFi9SuXVvvkBXFYiQaEum1rBch0SGs6LWCQnmzXy0jJXz8MUydWo7OnWHLFnAxXpt4loUGhmJjZ4Obj5uucVhEohBaX7ZZwFkp5Y8pdq0BHk3YOxBYbe7YjOnq1au4u7uTN29eWrVqxbZt23B0dOT48eOPG7c7derEjh07EEKwdu1aevTogZ2dxdUQKopuRm8Zzc6rO5n50kxqFq35/BMyYPhwmDgROnW6ybJlkOfZVVJ1EXo+lAJlCmBrb/z2l8ywlE+gRkB/4KQQIiB52yfARGCpEGIwcB3Qqd+B8X3yySccOHAg3WMSExN57733zBSRoli+kOgQFp5cyMh6I+lfvb/Rrtu9O3h5QYMGF7C1LWa062ZXaGCo7g3ZYCGJQkq5B0hrhExLc8ZiLp6ennTq1CndY17Wqz+eolgo97zuHHvjGO553bN9rTt3tCqmfv2geXPtx5L6BEiDJPRCKGXaldE7FMuoelIURUlPSHQI3/p/S5IhiaL5imZ7EaKLF6FhQ/jf/+B25sbfms3D6w9JikuyiBKFShSKoli0R43Xn+/4nPOh57N9vUOHtCQRHg7btoGlTnoQGqhNbKgShaIoynOM3jKa7Ve289tLv1HJo1K2rrVhAzRrpvVo8veHevWME6MphJwPAcC9Qvar2bJLJQozEUI80TD9/fffM3bs2GxdMyAggPXr12czMkWxXPOOz2Py/smMqDuCV/1ezfb1Ll+GChW0Cf7Kl89+fKYUGhiKQz4HnD2d9Q5FJQpzcXR0ZMWKFYSEhBjtmipRKDnZg9gHDN8wnOY+zfm+zfdZvo6U2qR+AMOGwf79llvdlFJYYBjuFdwtYpVJlSjMxM7OjqFDhzJ58uRn9t27d4/u3btTp04d6tSp83gSwKpVq/LgwQOklBQqVIh58+YB0L9/fzZv3sznn3/OkiVL8PPzY8mSJYSFhdGlSxeqVatG/fr1OXHiBABjx45l0KBBNGvWjNKlSzNlyhTzvXFFySI3Jzc299vMkh5Lstx4nZQEb78N1atrDdhgPetIhJwPsYj2CbCQ7rFm16zZs9t69oS33oLoaGjf/oldeZKSYPBgbSrJkBBtBZOUMtinbtiwYVSrVo3Ro0c/sX3kyJG88847NG7cmOvXr9O2bVvOnj1Lo0aN8Pf3x9vbm9KlS7N7924GDBjA/v37+fXXXxk/fjyHDx/ml19+AeCNN96gRo0arFq1iu3btzNgwAACAgIAOHfuHDt27CAiIoIKFSrw5ptvYm+fvZ4jimIK8UnxbL+ynXZl21GveNYbEWJitK6vK1bABx9A6dJGDNLEEmISeHj9IQVfM+4CTFmVOxOFTlxdXRkwYABTpkwhT4qhn1u3buXMmTOPX4eHhxMREUGTJk3YtWsX3t7evPnmm8ycOZObN29SsGBBXFKZX2D//v2sXLkSgBYtWhAaGsrDh9qkYh06dMDR0RFHR0cKFy7MnTt3KF68uInfsaJkjpSSYeuG8cexPzjxvxNU9czatK1hYdC5s9Zg/dNPMHKkceM0tbCLYSAtoyEbcmuiSK8EkDfvM/tjUk4z7u6erVE5o0aNombNmrz22muPtxkMBvbt2/dE8gBtTqhp06Zx/fp1JkyYwMqVK1m2bBlNmjRJ9dravF5PelS/6ejo+Hibra0tiYmJWX4PimIq0w5N449jf/BJ40+ynCQApkyBgwdh0SLo1cuIAZqJJXWNBdVGYXYFCxakZ8+ezJo16/G2Nm3aPK4+Ah5XF5UoUYKQkBAuXLhA6dKlady4Md9///3jRJEvX74nphVv2LAhCxYsAGDnzp24u7vj6upqhnelKNm3/cp2Rm0cRcfyHfmyxZdZusaj70qffgr79llnkgCVKBTgvffee6L305QpUzh8+DDVqlWjUqVK/Pbbb4/31atXj/LJ/fiaNGnCzZs3ady4MQDNmzfnzJkzjxuzP/7448fX+eijj5g7d65535iiZFFYTBgv//0yFdwrML/bfGxE5j+a/v0XatfWRlrb2UFN48wXqIvQ86Hk88qHg4tltLznzqonHURGRj7+3dPTk+jo6Mev3d3dWbJkSarn/fXXX49/b9iwIQaD4fHrggULcujQocevIyIiWL362Ql2nx6vcerUqUzHryimVDBPQSa3nUzDEg1xdcx8KXjZMq3hunRpiI83QYBmFhqo//KnKakShaIoujFIA+dDtGk5BlQfQNmCZTN9jalTtU6LtWrBnj1QsqSxozS/0POWMWvsIypRKIqim0+3f4rfDD8uhF7I0vkzZsCIEVoPp61boaBl9CbNFktZJzslVfWkKIouFpxYwDd7vmFozaFZKkmANqTp7l345BOw1XdtH6N53JCtqp4URcnNDt48yOA1g3nB+wWmtp+aqWkqIiK0Xk1xcVCoEHz2Wc5JEqBVO4Hl9HgClSgURTGz25G36bK4C175vFjWcxkOthnv2XPnjjaxwsSJ2mC6nOjROtkFShXQO5THVNWToihm5Z7Xnf7V+tO/ev9MrVR34QK0a6d1f12zBlq0MGGQOnq0TraNneV8j7ecSHK41KbcGDt2LEIILj6arQyYPHkyQggOHz5szvAUxeQM0kBIdAh2NnZMaj2JKoWrZPjclIsN7djxzHRsOYqlrJOdkkoUOqtatSqLFy9+/HrZsmVUqpS9xVkUxRL9efVPasyowZ3IO5k+N08erdvr3r1Qt64JgrMQhkQDoRdCca9oGXM8PaIShc66dOnyeJDc5cuXyZ8/Px4eHjpHpSjGNf/EfOZfn0+7Mu0o7Fw4w+ft369Ny1GlChw+DOXKmTBICxB2KYykuCQKV8n4MzKHXNlGkclZxklKymOMWcZT5erqSokSJTh16hSrV6+mV69e/Pnnn1m/oKJYmH039jF4zWCq56/OtA7TMtTDSUqYMEHr0bRoEfTuDRawfo/J3T11F8DiEoXFlCiEELOFEHeFEKdSbBsrhLgphAhI/smRNZO9e/dm8eLFrFq1iq5du+odjqIYzdUHV+m8uDMlXEswrvK4DPVwSkrSVqL77DNtWo5u3cwQqIW4e+ouCHD3tayqJ0sqUcwBfgHmPbV9spQy6+sgpiKTs4wTERHzeJrxbM4ynqqOHTvywQcfULt2bTXbq5KjuDm50cynGV82/5LgU8HPPT4mBl55BVatgtGjtW6wuaEk8ci9U/coWLYg9nksa1Exi0kUUspdQggfveN4WtS9KKLuROFS2cVka9fmyZOHSZMmPZ4lVlGsXaIhkURDIm5Obix9eSkAwTw/UezbB2vXautJDB9u6igtz91Tdylc2bKqncCCEkU63hZCDAAOA+9JKe8/fYAQYigwFLSZWXc+9ZU/f/78T6zbkBnxMfEYYg2EPwjPVr/m6OhoihUr9vj122+/TVxcHPb29kRERNChQwdAmwE2KSmJqKioTMeclJSU5feZntjY2GeeaXZERkYa9XqmouLMup8v/MyFyAv8WP1HHGy06qb04oyPFzg4SGxsYN48J4oWjTV6yT0j9HyWhngDIYEh5K2T97kxmD1OKaXF/AA+wKkUrz0BW7S2lAnA7Oddo1atWvJpZ86ceWZbRsXcj5E3D92UcRFxWb6GuYSHh5vkutl5fqnZsWOHUa9nKirOrPl5/8+Sscj3N73/xPa04jx+XEpvbynXrzd9bM+j57MMDgiWYxkrTy4++dxjTREncFim8blqMY3ZqZFS3pFSJkkpDcDvgNl7UNs6aZPIJMappUMV5Xn+Of8P72x6hy4VuzCx1cTnHr9zJzRpAomJkNuXcLfUHk9gQb2eUiOEKJriZVfA7Cvu2DlotXOJsSpRKEp6jgYfpffy3tQsWpP5Xedja5P+TH1Ll0LbtlqC2LcPqmZ9iewc4e6pu9jY21ConGWNygYLaqMQQiwCmgHuQogg4AugmRDCD5DAVeANs8dlIxD2gqS4JHPfWlGsiouDC/WL12d+1/k4Ozine+yBA9rYiMaNYfVqKGA589/p5t6pe7hXcMfWwfKmwrWYRCGl7JPK5llmDyQVNvY2qupJUdIQmxiLo60j5QuVZ9uAbRk6p25dbdGh/v3BycnEAVqJu6fvUryeZda/WXTVk6WwcbBRJQpFSUWiIZFuS7rxxtrnF/YTEgRvvQXnz2tjI4YMUUnikfjIeB5ceYBHFcucvkcligywsbfBkGjAkGjQOxRFsRhSSoatG8aGixuo7VU73WPDw+Gjj6rx66+wfbuZArQi987cA7DIMRSgEkWGCHttoF12q58mTJhA5cqVqVatGn5+fhw4cICffvqJ6OhoY4SZZQ8ePGD69Om6xqBYn2/9v2Xm0Zl81OgjhtYamuZxwcHwwgtw/Hh+5syBN980X4zWwpJ7PIFKFBli46A9puz0fNq3bx9r167l6NGjnDhxgq1bt1KiRAmVKBSrtOTUEj7a9hG9q/RmQssJaR539aq2jsSFC/D116cYONB8MVqTu6fuYpfHDrdSbnqHkiqVKDLAxl57TNlppwgODsbd3R1HR0cA3N3dWbZsGbdu3aJ58+Y0b94cgM2bN9OgQQNq1qzJyy+/TGRkJABHjhzhhRdeoFatWrRt25bgYG06hGbNmjFq1CgaNmxIvXr1OHjwIABRUVEMGjSIOnXqUKNGjcdTmZ8+fZq6devi5+dHtWrVuHDhAh999BGXLl3Cz8+PDz74IMvvUck9CuQpQPty7fmz85/YiLQ/Rjw9oWZNbbxE3bph5gvQytw9dRePSh7Y2FrmR7LF9Hoyp2Zzmj2zrWflnrxV5y2iE6Jpv+DJSWqTkpLoUbgHAwoNICQ6hB5Ln5xnfOerO597zzZt2jB+/HjKly9Pq1at6NWrFyNGjODHH39kx44duLu7ExISwldffcXWrVtxdnZm0qRJ/Pjjj3z88ccMHz6c1atX4+HhwZIlSxgzZgyzZ88GtKSwd+9eNm7cyKBBgzh16hQTJkygRYsWzJ49mwcPHlC3bl1atWrFb7/9xsiRI+nbty/x8fEkJSUxceJETp06RUBAQFYfqZJLxCTEkMc+D23KtKFNmTZpHrdlC9SpA25usHy5ts3CZhmxKHdP3aVMmzJ6h5GmXJkossLGLns9n1xcXDhy5Ai7d+9mx44d9OrVi4kTnxy5un//fs6cOUOjRo0AiI+Pp0GDBpw/f55Tp07RunVrQEtcRYv+NxaxTx+tZ3GjRo0IDw/nwYMHbN68mTVr1vD999rEu7GxsVy/fp0GDRowYcIEgoKC6NatG+Vy+kowitHcibxDo9mN+KjxR7xe8/U0j/v9d/jf/7T1XaZONWOAVio6NJrI4EiLbZ+AXJoo0isB5LXP+8z+iIgIkkKTiH0QS5G8RTJUgkiNra0tzZo1o1mzZlStWpW5c+c+sV9KSevWrVm0aNET20+ePEnlypXZt29fqtd9elZbIQRSSpYvX06FChWe2Ofr60u9evVYt24dbdu25Y8//qB06dJZej9K7hEZH0mHhR0Ijgymumf1VI+REsaN037atYNvvjFzkFbq3unkHk8WnCgss0LMAtk62mpdZJOy1kX2/PnzXLhw4fHrgIAAvL29yZcv3+MZX+vXr4+/vz8XL14EtBlnAwMDqVChAvfu3XucKBISEjh9+vTjay1ZsgTQGszz589P/vz5adu2LVOnTn00uSLHjh0DtOVWS5cuzYgRI+jUqRMnTpx4IgZFeVqiIZFey3px7PYxlvRYQp1idZ49JlEbFzFuHLz2GqxZAy4uOgRrhe6etuweT6ASRYbZOSXP+ZTFLrKRkZEMHDiQSpUqUa1aNc6cOcPYsWMZOnQoL774Is2bN8fDw4M5c+bQp08fqlWrRv369Tl37hwODg4sW7aMDz/8kOrVq+Pn58fevXsfX7tAgQI0bNiQUaNGMWuWNpj9s88+IyEhgWrVqlGlShU+++wzQEsqVapUwc/Pj3PnzjFgwAAKFSpEo0aNqFKlimrMVp7waKzE+gvrmd5+Oi+VfynV40JDYfNm+PRTmDUL7C1r3R2LdvfUXRxdHclXLJ/eoaQpV1Y9ZYWdo/aokmKTIG/mz69Vq9YTH+6PDB8+nOEpVmhp0aIFhw4deuY4Pz8/du3aleq1u3fvzjfffENERMTjlfjy5MnDjBkznjn2448/5uOPP35m+8KFCzP8XpTcQwhBBfcKfNL4E96o/ezo6/v3wdVV69104oTWeK1kzr1T9yhcpbDJFkYzBpUoMsjWUU03ruQu4XHhuDq68m6Dd1Pdf+WKNvtrhw4webJKElkhpeTuqbv49vDVO5R0qaqnDLKxtcHG3vLmfNq5cye1a6c/fYKiZNa6wHWU+rkUh24+W7oFOHYMGjSAkBDo0SPVQ5QMiAyOJCYsxqLbJ0Alikyxc7RT61IoOd7BmwfpuawnpdxKUdG94jP7t26Fpk3B0RH8/SG5N7eSBcFHtYGzRWsUfc6R+lKJIhPsHO1U1ZOSo10IvUCHhR3wdPZk3SvryOf4ZAPrgwdaCaJUKdi7F3wtu8bE4gUfDQYBRfyK6B1KulQbRSbYOtliCNW6yFrqUHtFyaq7UXdpO78tABv7bcTTxfOZY9zctK6v1atD/vxmDjAHCj4SjHsFdxxcHPQOJV3q0y4THvd8srB2CkUxBjcnN1qXbs36V9ZTvlD5x9uTkmDkSK3bK2jVTipJGMetI7coWtOyq51AJYpMUT2flJwoNjGWkOgQHGwdmNFxxhMD6mJjoU8fmDIFzp3TMcgcKPJOJBE3IyhaSyWKHEWVKJScJsmQRP+V/Wk0uxExCTFP7HvwQJuK4++/4fvv4bvv9Ikxp3rckK1KFNZpwYIF+Pj4YGNjg4+PD0uXLgW0iQFt7LK+fnbz5s3ZsmULAJ9++ikjRowwWsyKkllSSkZsGMGyM8t4o9Yb5LHP83hfbKxWxbR3LyxcCO+9p2OgOdSjRFGkhmU3ZINqzH7GggULGDp06OPFhK5du8bw4cNxcnKib9++2DraZrmL7Lhx4/j888+5e/cux44dY82aNcYMXVEyZdy/45h+eDofNPzgmUF1Tk4wYADUqAEtW+oUYA4XfCSYguUK4pTf8hcOVyWKp4wZM+aZFediYmIYM2YMoFU/ZbXqqWnTpkgp+fHHH1m8eDG2trZERUUxcOBAhgwZwoIFC7Idv6JkxLzj8xj37zhe83uNSa0mPd6+e7c2NgLg/fdVkjCl4KPBVlHtBBaUKIQQs4UQd4UQp1JsKyiE2CKEuJD8ZwFTx3H9+vV0t9s52ZEUn4TBkPlZZE+ePElwcDCOjo6P52RasWIFPXr04Pfff1clDMVs2pVtx4eNPmRmx5mP5xhatgxat4bRo7UpwxXTiQ6N5uG1h1bRkA0WlCiAOUC7p7Z9BGyTUpYDtiW/NqmSJUumu/1Rz6fMliqCg4Pp27cvq1evxtnZmU2bNgEQFBREiRIltGvb2mY1bEXJkGPBx0hISqCwc2EmtpqInY1W+/zLL9CzJ9SqBf/8AxY8P12OEHzEehqywYIShZRyF/D0orqdgUer+8wFupg6jgkTJpA375PTw+bJk4cJE7QF5B9PN56Jdoro6Gi6devGDz/8gK+vL5999hljx44FoHjx4gQFBQFkqZSiKBm178Y+Gv/ZmNFbRj/eJiV8/DEMHw6dO2vTcxQsqGOQuYQ19XgCENKCyphCCB9grZSySvLrB1JKtxT770spn6l+EkIMBYYCeHp61lq8ePET+/Pnz0/ZsmUzHMfSpUsZN24cQUFBFC9enM8++4zevXsDIA2SyAuROLg74FjIMdPv8WlRUVG8//77ODk5Ub9+fXr16pXlayUlJZmkVHLx4kUePnxotOtFRkbiYgWr2uSkOC9FXmLU8VHkt8/PFL8pFHTQsoHBAOPHVyJ//gRGjLiAKQu11vA8zRXj6bGniQyMpN7Celk63xRxNm/e/IiUMvUZRqWUFvMD+ACnUrx+8NT++8+7Rq1ateTTzpw588y2zAgPD3/i9e3jt2XYpbBsXdMUno7TWLL7/J62Y8cOo17PVHJKnBdDL8oi3xeRxX4oJq/cvyKllDI8XMqbN7X98fFSGgymjVFK63ie5orx59I/y6U9lmb5fFPECRyWaXyuWkzVUxruCCGKAiT/eVfneACt+knNIqtYAyklPf7uQUJSApv7b8bHzYfbt+GFF6B9e216Dnt71SZhTjH3Y7h/+T5Falr++IlHLH0cxRpgIDAx+c/V+oajsctjR/S9aKSUFr0qlaIIIZjdaTaJhkQqeVQiMFAbbX3njtbLSfWfML/bx24D4FXLS+dIMs5iShRCiEXAPqCCECJICDEYLUG0FkJcAFonv9adnZMd0iBJildTeSiWKTwunHnH5wFQo2gN6hSrw/790LAhREbCzp3w4ov6xphb3TpyC7CehmywoBKFlLJPGruMMuTHmN/+U/Z8ejT/U04lLaizg5IxMQkxdFzUkb039lK3WF0quldESnj3XW2a8I0bIRN9OxQju330NvlL5ieve97nH2whcvanXDInJydCQ0MpVKiQUZKFXZ7kRBGTCDl4umUpJaGhoTg5Wf4UA4omPimeHn/3YPe13SzotoCK7hVJStKqmJYtAzs7KGzZq27meLeO3LKagXaP5IpE8Wiswr1797J0fmxs7DMflg/DHmIfa0/e+5bzrSC1OLPLycmJ4sWLG/Waimk8mgl2/YX1zHhpBr2r9GHcOG1962XLwMt6qsRzrNiHsYRdCKP6gOp6h5IpuSJR2NvbU6pUqSyfv3PnTmrUqPHEtjlvzsGQYGCQ/6Dshmc0qcWp5B67ru3i79N/813r7xhUfShDh8Iff8DAgWpKDkvxqCHbmtonIJckClNw93Xn9OLTqueTYjGal2pOwP8CKONSja5dYe1aGDMGvvxSdX+1FDf23QCgWN1iOkeSORbT68naePh6EPsglqg7UXqHouRiUkpmX5nN5kubAajmWY3evWHdOpg2Db76SiUJS3LD/waFKhSyqoZsUIkiy9x93QG4dzZr7R6KYgxf7vqSv67/xbrAdY+3ffopLF8Ob72lY2DKM6RBcmPvDUo0KqF3KJmmEkUWeVTyACDkbIjOkSi51Xf+3/HFzi9o69mW/oUn8/332vZ69aBrV31jU54Vci6E2PuxlGyU+gzVlkwliizK55UPh3wOqkSh6GLqgamM3jqaXpV70Sx8As2b2TB1Khhx7kbFyG7s1donrLFEoRqzs0gIgYevByFnVIlCMS8pJSfunKBrxa60jf6LIZ/YUrkybNgA+XPwuB5rd8P/Bnnd81KofCG9Q8k0VaLIBndfd1WiUMwqLjEOIQQzOs6g7rUlDBpoT7VqD9m1S42TsHTX/a9TomEJq+wlqRJFNrj7uhMZHEnsw1i9Q1FygUUnF1FpeiWuP7yOjbDBq4g9ffrAxIknVEnCwkXdjSLsQphVVjuBShTZohq0FXNZenop/Vb2o5hLCS4c13rcDRgACxaAg4MaTWfprLl9AlSiyBYPXy1RqOonxZSWn1nOK8tfoW7RhiT9tZaO7fISrK2kqcZIWInr/texdbC1qqnFU1KN2dngVsoNW0dbVaJQTGbr5a30Xt6b6u51uf/Lei6fdWHePChqXTNA5Ho3/G/gVdvr8czT1kaVKLLBxtaGQuULce+MKlEoplGraC26eg8m+LuNBF/Nx6ZNkLx8u2IlEmMTCT4STPGG1ju5pkoU2eTh66FKFIrR7b2xl5iEGArkKUDZc78h4l3ZsweaN9c7MiWzbh2+RVJ8klUOtHtEJYpscq/kzv0r90mISdA7FCWHWBe4juZzm/PBpjGANl/T0aNQtarOgSlZct3/OgAlGlpnQzaoRJFtHr4eICE0MFTvUJQcYF3gOrot7UZhqrJixGcEBYGNDXh66h2ZklVBe4MoWK4gzoWd9Q4lyzKdKIQQzkIItSR7sseTA6p2CiWb1l9YT7el3SgQX5WgCVtoUKMAhaxvEK+SgpTaRIDWXO0EGUgUQggbIcQrQoh1Qoi7wDkgWAhxWgjxnRCinOnDtFzuFdyxsbfhzok7eoeiWLHYxFiG/jMU56gq3PluC8MGF2DpUsiTR+/IlOwIDQwlOiTaasdPPJKREsUOoAzwMVBESllCSlkYaALsByYKIfqZMEaLZutgi0clD+4EqEShZJ2TnRPtwzZx/6etTBxbgKlTtXWuFet2w9+6B9o9kpFOva2klM+01Eopw4DlwHIhhL3RI7MiRfyKcGnzJb3DUKzQirMrOHHnBF+88AXfj65M+9rQpYveUSnGcmX7FfJ65MW9grveoWTLc0sUj5KEEOInkcZsVqklEmMSQlwVQpwUQgQIIQ6b8l5Z4Vndk8jgSKLuqtXulIxbdmYZPf/uyS8bNhMWHoerq0oSOYk0SC5vvUyZ1mUQNtY9hD4zjdmRwBohhDOAEKKNEMLfNGGlqrmU0k9KWduM98yQIn5FALh9/LbOkSjWYuHJhfRe1htu1sdm4SbuBTvpHZJiZHdO3iHqThSlW5fWO5Rsy/B4cinlp0KIV4CdQog4IAr4yGSRWZEi1ZMTRcBtyrQuo3M0iqWbGzCX11a/hrj2AqX2/8Pmf10obf2fJcpTLm+5DJAjEoWQMmMzTwohWgKfAgIoCnSSUp43YWwp730FuA9IYIaUcuZT+4cCQwE8PT1rLV682Kj3j4yMxMXFJd1j9vfaT/5q+fEd42vUe2dGRuK0BLk9zp+2HWL1le1UOP4nk766RP782au5ze3P05iMGeOJD04Qdy+OOnPqGOV6KZniWTZv3vxImjU2UsoM/QDbgcbJv1cFAoAWGT0/Oz+AV/KfhYHjQNO0jq1Vq5Y0th07djz3mIUvLZTTKk8z+r0zIyNxWoLcGueV+1eklFJeuCDlwFcNMirKONfNrc/TFIwVY3x0vPzK6Su5YdQGo1zvaaZ4lsBhmcbnaobbKKSULaSUe5J/Pwm8CHyVtdyVOVLKW8l/3gVWAnXNcd/M8PTzJORcCImxiXqHoligb3Z9S7mfK3Ag6CBly8KcPwV58+odlWIq1/dcJzE2McdURWdkwF1aPZ2CgZbpHWMMySPB8z36HWgDnDLV/bKqSPUiyCTJ3dN39Q5FsSBSSj7a9AWf7PiQxJPdeHiuht4hKWZwectlbOxt8H7BW+9QjCIjJYrtQojhQognxqALIRyABkKIucBAk0Sn8QT2CCGOAweBdVLKjSa8X5Y86vl057gaeKdopJS8teoDJu0fjwh4jd9fnE+bVrl6yFGucXnLZUo2KomDs4PeoRhFRno9XQCSgJVCiKLAA8AJsAU2A5OllAGmClBKeRmobqrrG0uB0gVwcHHgdoDqIqtoftm+gt9O/IDdkbdZ+cbPvNQhA9/LpHxy2bqnXysWL/JOJLcDbtNiQgu9QzGajCSKhlLKoUKI14GSgAcQI6V8YNLIrIywEXhW81QlCuWxioZuFNi8nA0/dqVevQx82I8dCw8ewOTJWnKQEt55B9zctH2KVbiy7QoAZdrkjPYJyFii2CSE2IdWBTQArdfRaZNGZaU8q3tycuFJpJSYsNlGsWBxiXG89vcIxrf9gNaty3KzcbfUJ/aLiflvxr+//oK1a2HXLrh9G+bNAx8faNoUfv4ZmjWDN98Eb28oVQrq14eSJVVJw0Jd2nyJPAXzUKRGEb1DMZrnJgop5XtCiNLATqAU0AmoLISIB05JKXuZNkTrUcSvCId/PczDaw9x83HTOxzFzKLio6jzY1fOxm3BM6E+kweU/S9JxMbCpk2wcyeGnbsQZ05z+td/iY4RFF+1lQLH9xGXvxgGj/zY37uJ/f0z2Bw7hcPIkRAfD0uWQFjYfzerVQsOa7PZ2MTHm//NKqmSUnJ5y2VKtyqNjW3OWe4nQyOzpZSXhRCtpJSBj7YJIVyAKiaLzAp5VtdWl7kdcFslilzmfswDqk/qwA25nypX/uTL914FtA+OiF/nk/e9t7CLjSQBO4IoznXqsX/wCmLJC5TWflJZ0iTf3/nwaeaDz7evU6qeBwUSQsDfX0se2g2o/frrULYs9O0L3btrVVWKLkLOhhBxKyJHjMZOKTNTeAQ+9ToSbZpxJZlnVU+EjeD28dtU7FJR73AUM7n18C5Vv21DmO0ZmoUuYfNPbYkdO5b91104eNQBcekCTSjDDe8myKYvULBSEQpXKMSgCu7kdc+LsBXY2NogbCD+3Y95MGsZD3DjAW7cdWnKle2SkwtPAuBWyo2qfatS47UaFACIj+dOy5aU8veH11+HYcOgVy8YMwbKl9f1ueRGj2aRzrWJQnk++7z2FCxXUDVo5zL/bnUm7IYHvYv8zdSwrRg8XyVfYhRJtk1wb/s/yr3bAJ/2X+KXXikzueHacdbP5Bs5khKTJ2sN2T9/jRwxkpA3PuHKjqtcWHuBPV/vYfdXu/Fp7kONQTUI6dOfUrNnw6FDWvvG7NnQqZOWKAwGbS1VxSwubrhIoQqFcPN20zsUo1KJwsiK+BXh5sGbeoehmMG5e+cp5upF764u5J3RkRfn98RBxnPRqTKRQ4ZTY3x/GrlncPi1EFqV0ciR//V6mjxZ2+XmhkelwnhUKkzdYXUJDwonYG4AAbMDWNl/JY6FHXEd50qNQbWwrVtX6yFVsKB23S+/1BLI5MlQLlcvRmlyMWExXNl+hQbvNdA7FKNTicLIPKt7cnrJaWIfxuKUX00dnVOtOHCAnmva08TtBfoua0/Jg+sIcqtC0pjPKD2yI7b2WViebuzYJ8dNPEoWT/Vuci3uStMxTWnycRMubbnEP+/9w7o317Hnmz00/qQxNV6rge2jUoSHB+zeDVWqwHvvaVVSzs7Ze/NKqs6vOY8h0YBvd/0mBjUVVSY1sscjtNUa2jnW1A2b6P5PC2RUPmp/48nDGw8p/OdESoUeptz7XbKWJB55ustrOl1ghY2gbNuy+E31o+/GvrgUdWHd/9bxW/XfuLJD68vPW2/B+fPQpw988w1UrKj1vlKM7uzys+QvmR+v2l56h2J0KlEY2aO1KVQ7Rc700fyFjNjXEftQb7bMcmJQQ2eGBw7H79Uauq1iJoSWMAbvG0yff/qQFJ/EvBbzWNFvBZF3IqFIEZgzR+stVawYuFv3spyWKC48jkubL+Hb3TdHjqFSVU9G5lLUBefCzgQfCdY7FMXI/llyjUnHRuMcVpUNq+2psnYGBV6wnNllhBCUf6k8pVqWYs83e/Cf5E/g2kBaf9uamkNqIho2hH37/iuljB8PrVpBw4b6Bp4DBK4LJCk+KUdWO4EqURidEIJi9YoRdCBI71AUI5FScnX3VRKHfcWbc3qw/Vo9GgXvtqgkkZJ9Hnuaj2/O/078D69aXqx9Yy2LOy/W1nR/lCQePoS5c6FJE61tJClJ15it3dnlZ3Ep6kKJBiX0DsUkVKIwgWL1ihFyNoTYB7F6h6JkU1xCIpXe7MHLXw/khltVPvu9J3W3T8fG0fJngXWv4E7/Lf1p93M7Lm2+xK/VfuXChgvazvz54dgxbZDeuHHQpQuEh+sar7WKj4rn4oaLVOxaUbfqR1NTicIEitcvDsDNQ6qbrDVasGABPj4+7Pp3H0UHNuZc0RWQpzhDDg+haDfrqqYRNoJ6I+ox5NAQnAs7s7D9QjaM2EBSfBK4umrjLqZNgw0btGoog0HvkK3OxY0XSYhOoFL3SnqHYjKqjcIEitUpBgKC9gflmBWucosFCxYwdOhQ8pKPSUGLiC5/ikZr2/Pm223J45ba7H7WwbOqJ0MODmHrR1s58PMBgo8E8/Kyl8lXNJ/WM6p8ea06Sg3Oy7Szy8+S1z0v3k1zxiJFqVH/KkzA0dURj0oe3DygShTWZsyYMRSJKUn4gAJEFwmk4dJW+B9ez5gvPtc7tGyzc7Kj3U/t6LGkB7cDbjOz1kxu7L2h7WzVSpsnCuDPP2HxYv0CtSKJcYkErg2kQpcK2Njl3I/TnPvOdFasXjGC9gehrVmuWIuIaxFMkD6U2PkaAwMGsffsFgCuX7+uc2TGU7lnZV4/8Dr2ee2Z02wOh3499N9OKWHhQnjlFZg1S78grcTlLZeJj4jP0dVOoBKFyRSvV5yY0BjuX76vdyhKBn31x1LqVW9EAFVxP/c9VZv9V21YsmTJdM60PoWrFGbIoSGUaV2G9W+tZ/3w9RgSDVqvqNWroW1bbZLBn3/WO1SLdnb5WRzzO1KqRSm9QzEplShM5FGDdtB+1U3WGvR/bxyf3XiFvXUDWZBnEQdSzPmdN29eJkyYoGN0ppGnQB56r+lNg/cacOiXQyzuspj4yHjImxdWrYJu3WDUKPjqK71DtUgJ0QmcXXGWil0qYuuQjdH4VkAlChPxqOyBvbO9aqewcAaDpMnbw5jvOpYCl2vh3+4PJv4+EW9vrWHS29ubmTNn0rdvX50jNQ0bWxvafN+G9tPbc3HDRf5s+ifhN8PB0VFbLKl/f0hM1DtMi3R66WniwuOoMbiG3qGYnOr1ZCI2tjYUq1NMJQoLlpBooNI7PbnosRyfYy3wH/UDXs38qExj+vbty86dO7l69areYZpFnTfr4ObjxrKey/ij3h/03dAXz6qe2tQfjwbpPXigFkVK4ejvR3Gv6E7JxjmrWjI1qkRhQsXqFSP4WDCJseobmSU6tSyQ66fK0mBbew6/9Q1ezfz0DklX5V4sx2t7XgMJc5rO4br/da27rBBw7pw2Tfns2XqHaRHunr7Ljb03tKlRcuDcTk+zikQhhGgnhDgvhLgohPhI73gyqnj94hgSDNwOuK13KEoKZ25dYcexHewfvZKtew6yduT7FGpTV++wLEKR6kUYtHcQzoWd+avVXwSuTV7YslQpqFkThgyBZcv0DdICHP39KLYOtlQfYJnTuBibxScKIYQtMA14EagE9BFCWEVftGL1igGqQduSrDy8j2pT69F57kDuh0vK7J9Pwe7N9Q7Lorh5u/HantcoXKUwi7ss5vi841qbxYoVUL++1nU2F09VnhCTwPF5x/Ht5kvejC5MZeUsPlEAdYGLUsrLUsp4YDHQWeeYMiRf0XzkL5lftVNYiG/XL6Hb6uYYol34fEF1+v3TF69aOW/tAGNw9nBmwPYBlGpeilUDV7Fv8j5twaN166BSJXj5ZTh7Vu8wdXF2+Vli78dSc0hNvUMxG2HpA8KEED2AdlLK15Nf9wfqSSnfTnHMUGAogKenZ63FRh5VGhkZiYuLS5bOPTP2DBHnI6i3qJ5RY0pNduI0J3PHKaXku/3L2RA/Dfvr9di2+AFObVoQNbJnuuep5wmGeANnvz5LyL8heL/qjfcAb5xCQig5fz6X3nwTg1PGV3G0hueZkRgDRgYQHxpPnXl1dJsE0BTPsnnz5keklLVT3SmltOgf4GXgjxSv+wNT0zq+Vq1a0th27NiR5XP3/rBXjmWsjLgdYbyA0pCdOM3J3HHeCEqSNq90lvle7iYv2nrJoOZ9M3Seep6apIQkuerVVXIsY+Wm9zZJg8Hw386HD6WMicnQdazheT4vxntn78mxjJW7J+42T0BpMMWzBA7LND5XraHqKQhIOcl7ceCWTrFk2qN2ClX9ZH73ou4RFB5E8WI2fHf/Va78vQ3nkiXx2jJX79Csio2dDZ1mdaLu8Lrs+2Efa99YiyHJALGx0LixNoLbwmsmjOXoH0exsbPB71U/vUMxK2tIFIeAckKIUkIIB6A3sEbnmDKsaM2i2NjZqIWMzOzE7VOU/bYubX7vSeD6QJw2biW6SHkKH92EsM3Zo2hNQdgI2v3cjsafNObo70dZNWAVSbb20Ls3LFgAOXDk+tMSYhIImBNAhc4VcPG07Co0Y7P4AXdSykQhxNvAJsAWmC2lPK1zWBlmn8cez+qeBO1VicJcVp1ez8tLepMY7UL7e9+w4ssVFKheFc/dP2Lj4qB3eFZLCEHLCS1xzOfIto+3kRCTQPeFH2B39ix8/jnUrg3t2ukdpskcmXGEmNAY6o0wfXujpbH4RAEgpVwPrNc7jqzyfsGbQ9MOkRibiJ2TVTxyqySl5MvtP/DF7tFw14+Piy1n0MzuRCU44L1yAw4qSRhF448aY5/Xno0jN7Kk61J6zv8F++PHoV8/OHoUctgEiqCVJvwn+ePTzCdHrzuRFmuoerJ6pVqUIikuiRv7bugdSo4WHBLL1+vmIs72YFajXXRf8gVlI45RYkAz3HwK6B1ejlJvRD06/t6Ri5susvDlVcTPXQjVq+fYtoqjvx8l8nYkL3zxgt6h6EJ9vTUD7ybeCFvB1R1XKdU8Z09HrIfbkbfJ55CPou7O9E/aSe+hBXFbMA2/0wu4X7UJBX/7Ru8Qc6Sar9fELo8dqwau4q9hifRdvw4nNyctWeSgaS0SYxPxn+SP9wve+DTz0TscXagShRk4ujriVduLK9uv6B1KjnP41mGq/VKHfovfQgj4/edClLixj7J/jiHWxQO3f1fnqA8tS1OtbzVeXvoytw7fYm7zuURdua1NT750qd6hGc3RP44ScSsi15YmQCUKs/Fp7sPNAze1+f4Vo/jr+F80/KMx9+7YErb2XQBCA0M59NZs7O3BccsaRAFV5WRqvt186bOmDyHnQpjXfgmJN27B4MFw6ZLeoWVbYmwieybuoWSTkrm2NAEqUZhNqRalMCQatBk5lWxJNCTy7qZ3GbBqAAmXG1Lv+GFW/ladhOgElvZYys285Uk4HYhdfTXRn7mUbVeWfpv68eBmNHPvvojBxjZHrGVxdNZRIm5qpYncMEtsWlSiMJOSjUpiY2+jqp+M4Fb4bX7dOxcODKdr5CZ2rnenQAHJv31n4H1yLd3mdyV/OU+9w8x1vJt6M2DbAEIi87DB5iXYtw8mTtQ7rCxLjEvEf6I/JRqVyPFLnT6PShRmYp/XnuL1i3N1+1W9Q7FaF8MuYpAGPByLU2nnad4uM4W/l9jj5AQBMw9SadXXtMqzh7K13PQONdcqVqcYr/77Kufy1OC0gx9JP/8CUVF6h5UleybuITwonGbjmuXq0gSoRGFWpVqUIvhoMLEPYvUOxerMPzGfqtOrMnHnz+TJA7s3FGHKFLC1hdsBt4kaNhovgrGbNws8PPQON1fzrOrJIP9B7CnWm1+iBnFxd7DeIWXa3dN32T1hN1VfqUrplqX1Dkd3KlGYkU9zH6RBcm3XNb1DsRoJSQmM2jiK/iv7Y3O7Hlt/7IuUkDev1pkpLjyO3R2+oWHSbhJeGYBNjx56h6wABUoVoO++YThV9GbxSwu4Mnq63iFlmCHJwD+v/4OjqyNtf2qrdzgWQSUKMypevzh2TnaqnSKDgiOCaTGvBT8f+BmXUyOxmb+FT0YWftzbVUrJuqGraHnrL5K8SmD/2y/6Bqw8wcXThYE7BtKq9EVKfTeMpG/XPZoB2qIdmnaIoP1BtPu5Hc4eznqHYxFUojAjO0c7SjQqwdUdV/UOxSpcDLvIsZsnyLthIfn8f2L3Tntatfpvf8CfAZxcco6gVz/DftliyJdPv2CVVDnld6L2od8Idy1GrQ2/s+G1pSQlJOkdVppib8ey7ZNtlH2xLFVfqap3OBZDJQozK9WiFHdO3CHqnnU28JmalJJ9N/YBUN+rCe7zr1HyYR/27QM/v/+Ou3f2HhuHraFUi1JU+WMkNGigT8DKc9nldybf+qXkJxz3uT+ysMNCYh9aXjudlJLAHwMRQvDSby/l+gbslFSiMDOf5j4AXN15Vdc4LFF4XDi9lvWi4eyG7L9xAHt72LDSDX9/8E4xD1tCTAIreixicMIMeja8jo2t+mds6USjhtzs1pU64hBJ2/9ldsPZ3L98X++wnnBo+iHuH7pPy29akr9kfr3DsSjqf5iZedX2wsHFQVU/PeXknZPUnlmbFWdX0DRuEgu/r4uU4OsLBQs+eeymdzdR4cwKCicF41S/hj4BK5l25fXXEW3a0GZKByJuRTCz1kwC1wbqHRYA5/85z8YRGylYvyB13qqjdzgWRyUKM7O1t8W7qTdXtqkG7Uf+Ov4X9f6oR2R8JC9c3c6ub0ZjSBKpTkR6dsVZrv+2nqY2/tC3L3ToYP6AlSxJypMHNm7E662uDD0ylAKlC7Co4yK2fbINQ6JBt7huHrzJ8t7LKVqzKJU+r6TbOtiWTCUKHZRuU5rQwFDCLobpHYpFiIyPpHaR+pTefIztfzblm29g6lSweepfZ3hQOP8MXkWPvBsQBd3gp5/0CFfJrshICkwZx6DpNak5pCZ7vtnDX23+IvJOpNlDCbsUxsKXFuLs6UyftX2wzaNWP0yNShQ6qNi5IgDnVp/TORL9nAs5x7rAdQAMrfk/Ymdu4cB2T+bNg48+enbCV0OSgZUDVuIRex2PhJuIn34Cd3fzB65kX3w8LFyI3Tsj6PhbBzrP6UzQ/iCmV57OiQUnzNaFNjokmgUvLkAaJP029st1y5tmhkoUOnDzccOzmifnV5/XOxRdbLmzhdozazNi4wgSkhKwtRV88rEt69dr88ilZu93e7m64yp+04ciAgPhlVfMG7RiPAULwnffaXNBzZ2L30A/hh4ZSqFyhVjZbyWLOi4iPCjcpCHcPn6bWQ1mEX4jnD5r+lCofCGT3s/aqUShkwqdK3DD/wbRIdF6h2I2UfFRDF49mK/PfU0tr1p8V2kXSxfbA9ClC7Runfp5Nw/eZMdnO2jQNh9+r/qBj49aY8La9e8PjRrB6NFw/z4evh68tuc12k5uy5XtV5heeToHfzlIYpzxZ589NvsYs+rPIj4qnn6b+1GiYQmj3yOnUYlCJxU6V0AapMX0+jC18Lhw6vxehz8D/qRfyX685byNV14qxsSJkJCQ9nlxEXEsf2U55QqF0mbTe4i5c80XtGI6NjYwbRqEhcFnn2mbbG2oP6o+b558E6/aXmwYvoFfyv/CkZlHSIrP/iC9hOgEVr+2mjWD11CiYQneOPYG3k1y3/rXWaEShU6K1iyKa3HXXFP95OroSpeKXdjcfzMFjn1On1521KwJO3eCvX3a520csZGHl8Po6roVihWD7t3NFrNiYtWrw2+/wciRT2wuWKYg/bf2p9+mfuTzysfaN9byS4VfOPzbYaJDM18Cj7kfw97v9zLNdxoBcwNo+llT+m1WbRKZodbM1okQgvKdynN8znESYhKwz5POp6WVuh9zn2Hrh/FBww+oUbQGE1p8zUcfaT2aunSBhQshT560zz+99DQBcwLo/eIDHDechiVL1DQdOc2QIf/9nmKtbSEEZdqUoXTr0lzceJGdX+xk3ZvrWP/2enya+eDb3ZeKnSviUtQl1RHUCdEJ3Dtzj2Ozj3F87nESohPwfsGbzn92zvVrS2SFRScKIcRYYAhwL3nTJ1LK9fpFZFwVO1fk8PTDXN56mQodK+gdjlHtvrabviv6EhwZTKvSrahRtAZCaImhU6ebLFtWDNt0eiI+vPGQtW+spUxNV8rv+wlatoSXXzZb/IoZRURobRYdO2pLqKYghKDci+Uo264swUeDObv8LGeXn2X9W+tZ/9Z67PPa41rcFdfirjgXdiYiOIKwi2FE3IwAwNbRlqqvVKXeiHoU8Suix7vLESw6USSbLKX8Xu8gTMH7BW8c8jlwfvX5HJMoEg2JjP93PBN2T6B0gdLsHbSX8i51OH5cq2n44gvYufMCtrbF0ryGIcnAyv4rMSQa6PReWcR7TloxRDVg50wuLhASAp98Aj17plpqFELgVcsLr1petJjQgntn7nF5y2Ue3nhIRFAE4UHh3Dx4E5eiLpRuVZqC5QpSsGxBSrUopWaANQJrSBQ5lp2jHeVeLEfgP4EYkgw5Ys6i34/8zpe7vuRVv1eZ0m4KEaH5aNoU7t6FS5f+W0ciPXu/38u1f6/R+c/OuL7iBz2ugYODWeJXdCAETJ4MdetqS6dOmPCcwwWFKxemcOXCZgpQEZY8P3xy1dOrQDhwGHhPSvnMTGJCiKHAUABPT89aixcvNmockZGRuLiYpuHrztY7nJtwDr+pfuSvkr2JyEwZZ3qklITFh1HIsRCJhkQO3z9M/UL1uXo1Lx99VI3wcDvGjTtNnTr3nxtnxPkIjg07hnsTdxq3eUhY3bqkW0dlQno9z8zKKXH6TpiA+65dHJw3jzhPfdY8zynPMiuaN29+REpZO9WdUkpdf4CtwKlUfjoDnoAtWu+sCcDs512vVq1a0th27Nhh9Gs+EnM/Ro63Gy83j96c7WuZMs60hESFyO5LukuvH7xkWHTY4+27dknp5iZlkSJSHjny5DlpxRkXESenlJsifyz+o4xdtkZKkPL3300Yffr0eJ5ZkWPivHZNSicnKV9/3SzxpCbHPMssAA7LND5Xda96klK2ev5RIIT4HVhr4nDMzsnNCe8XvDm/+jytJ6Ux4sxCbbm0hVdXv8q9qHt82fxLXB1dH+/79Vfw9ISNG7XxcRmxYeQGwi6GMXBrPxxHdoHSpdMeqq3kPCVLwrJlam0RC2TRleJCiKIpXnZFK2nkOBW7VCT0fCh3T93VO5QMiU+KZ/j64bSZ3wZXR1f2v76fDxt/iK2NLVHJ6zHNmgX+/hlPEqf/Pk3A7AAaf9wYn0vb4dQpmDQJHB1N9j4UC9ShgzbFh8FAqtMHK7qw6EQBfCuEOCmEOAE0B97ROyBTqNyrMjZ2Nhz785jeoWSIvY09lx9cZlS9URwdepSaRWtiMGizMTRoAOHhWjfYQhmcPufh9YesHbqWYnWL0ey9WtpI3UaN1OC63OrmTahdG1as0DsSJZlFJwopZX8pZVUpZTUpZScpZbDeMZmCs4cz5TuW5+T8kxa7nnB8Ujzjdo7j2oNrCCFY3Xs1k9tNJo99HuLjtRqi776DJk3AORO9EVN2he22sBu2t2+Bhwf88IPqDptbeXpq87p8+GH687soZmPRiSI38XvNj6i7UVxYf0HvUJ5x/PZx6v5el7H/juXvM38DYGejNW89fAjt22ujrL/+Gn75JXOdlPZ8s4dru67Rflp7CpYpCJUqwYkTUK+eKd6KYg3s7OCbb7T+1LNn6x2NgkoUFqPci+Vw9nQm4M8AvUN5LNGQyIRdE6jzex1uR95mde/VvN/w/SeOefNN+PdfmDsXPv44c4WA63uus3PsTqr0qUK1/tW0lu/wcFWSULS2ioYNYfx4iInRO5pcTyUKC2FjZ0P1AdW5sO6CLit9pWbSnkl8uuNTulfqzum3TtOpQqdnjvn2W+3zfcCAzF07JiyG5a8sx83bjZd+ewlx4wZ07qyNzlUUIbRSxa1bqlRhAVSisCB+r/lhSDRwYv4J3WJISErgxsMbAAyvN5wVPVewqPsiCuX9r2V6925tSp6kJCheXJuGKTOklKwZvIbI25H0WNIDR1dHGDdO2zl6tLHeimLtmjaFVauenDhQ0YVKFBbEw9eDYvWKEfBngNmWg0wp4HYAdf+oS/uF7Uk0JOLq6EpX365PHLNsmbbAkL8/hIZm7T63Vt3i3KpztJrYCq/aXnDuHMyZo9VjlSyZ/Tei5BydO2vTt6iusrpSicLC+L3mx73T97h1+JbZ7hmbGMuYbWOoPbM2wRHBfNn8y8eN1SlNmaLN2VarlpYoCmdhqp3bAbe59OslyrUvR/1R9bWNn3+u9adV1U5KarZsgYoVtQnDFF2oRGFhqvSugp2Tndkata89uIbfb358vedr+lXrx5lhZ+hSscszx335pba+TOfOsHVrxsdIpBQXHseyXsuwd7Wn85zOCBsB8fHaNNPvvpu1zKPkfCVKwMWLWpuFoguVKCyMU34nfLv7cnLhSRJiTNeH/FHVllc+L3w9fNnUbxNzusyhYJ6CqR7fsiWMGqVVPaW32FB691vz+hrCLoXh+6nvf1M/OzjAhg3a/OOKkpqKFeHVV2H6dG0wnmJ2KlFYoBqDahD3MI5Ti0wzY8nKsyup83sdHsQ+wN7WnpW9VtKmTJtnjnv4EObP135v2FCbCTqrE7kemHKAM3+foeXXLXHzc9M2XrwI165pv+s0Q6xiJT77TJvWY9IkvSPJlVSisEA+zX0oUqMIeybuwZBkMNp1g8KD6LqkK92WdiPRkMi9qHtpHnvzptbpZNAguHw5e/e9se8GW97fQoXOFWj4QcP/drz7rjawTo2+VZ7HxwcGDoSZM+HOHb2jyXVUorBAQgiafNKEsAthnFl2JtvXM0gDUw5ModK0Smy6uIlJrSZxaMghyhUql+rxZ85oczZdvgzr1mmTuGZV1L0olvVcRv6S+ekyp8t/6xsfPQr//ANvvw32OW+9cMUEPv0UVq5UbVk60H2acSV1vt18cfd1Z/eE3VR+ubLW8JtFAsGmS5toWKIh0ztMp3SBtD/5d++GTp3AyQl27YIaNbJ8WwyJBla8soKoe1EM3jcYJzen/3aOHw9ubjB8eNZvoOQuPj4Zn45YMSpVorBQwkbQ+OPG3D15l8C1gZk+/0HsA0ZsGMHl+5cRQrC0x1I29N2QbpIArdmgSBHYty97SQJgy+gtXN56mQ7TO1C0xn8zxrtcvAirV2ut4/mzt6qfkstIqZUsPv9c70hyFZUoLFjVPlVxK+XG7gm7MzwAzyANzA2YS/mp5Zl2aBrbr2wHwNnB+b9qn1Q8aod47TU4diz7X9yOzT7G/sn7qTuiLjUGPZlxXM+cAXd3rb+tomSGEBAUBN9/r9oqzEglCgtmY2dD448ac/PgTS5vfX6L8sXIizT9symvrn6VsgXLcnjIYV6v+Xq65xgM8MEHULkynD6tbXNySveU57ruf521/1tL6dalaftD22f23+rUCa5e1aqeFCWzxoyBuDgtWShmoRKFhas+sDr5iuVj94Tdzz12ffB6zoeeZ3an2ewZtIcaRdOvO4qLg759tf9vgwdr3dWz6+H1hyztthQ3bzd6LOmBjd1T/8SuXNH+zMyiFYqSUrly8Mor2riKe2n33FOMRyUKC2fnaEfD9xty7d9rXN9z/Yl9SYYkZh6Zyd4bewEYVGoQgW8H8lqN17AR6f/VPnwIL74IixfDxIkwdWr2hzLER8azuPNiEmMT6fNPH/IUeGpkXmAglC1L0XXrsncjRRkzRpt+fOpUvSPJFVSisAK1htbCpagLG0ZswJCojavwv+5Pnd/r8MbaN/jr+F8AuNi5UCBPgQxd89dftR5Of/2lLSSW3SUgkuKTWNJtCXdO3qH74u64V3R/9qDvvgMHB0IaNMjezRSlYkWtKNytm96R5Aqqe6wVsM9rz4tTX+TvHn+z8oeV/F3mb5acXkJx1+Is7r6YnpV7ZvhaBgPY2GjtEm3bZr9nE4A0SFa9uorLWy7TaXYnyr2YyviMW7dg3jwYPJiEgqlPE6IomfLuu3pHkGuoEoWV8O3mS4XOFZi9bjarz63m86afc27YOXpV6ZVub6aU/v0XqleHGze0aiajJAkp2fjORk4tOkXLiS2p8VoaF/3pJ0hMhPffT32/omRFYKA2Fic+Xu9IcjRVorBwSYYk5h2fRz7HfLSf1p4LlS/QKl8rRo0ZleEEAbB0KfTvr42yNhhvVhD2fLOHg1MOUv/d+jQa3Sj1gxITYdEi6NVLC+D69dSPU5TMunpVW6i9Zk2tb7diEqpEYcG2XNpCzZk1GbRmEItOLcK1mCvtvmlH+Ppwjs87nuHrTJ6sfUbXqaOtI+HtbZz4Dkw5wPYx26nWrxptvmuTduKys4NTp1R3RsX4WrfWisaTJhn3G5DyBN0ThRDiZSHEaSGEQQhR+6l9HwshLgohzgshnu2Qn0OduXeG9gva02Z+GyLiIljSYwnLXl4GQO03alOiUQk2v7uZqLtRz73WjBlaVW737to6EsZqHtj99W42jtyIbzdfOs3ulPYUI4mJ2mja/PnBy8s4N1eUR4TQemOcP6+N9ldMQvdEAZwCugG7Um4UQlQCegOVgXbAdCFErpiLOjA0kH1B+/i+9fecHXaWnpV7Pv62LmwEHWd2JC4ijtWDVj/uBZWWXr207q9LlmR/IB1obRJbP96qlST6V6PHkh7Y2qfz1zJzptYwktV1UxXlebp3hzJltH/oaslUk9A9UUgpz0opz6eyqzOwWEoZJ6W8AlwE6po3OvMIiwlj9JbRfL37awA6V+jMlZFXeK/hezjaOT5zvEclD9r91I4L6y6w9s21z0zv8eCBVoqIidEGP3/4oXGWe5AGyYbhG/Cf6E+t/9Wiy5wuzw6oSykxUatucnY2XlFGUZ5mZ6fN/9SggWrUNhGR0TmETE0IsRN4X0p5OPn1L8B+KeX85NezgA1SymWpnDsUGArg6elZa/HixUaNLTIyEhcXF6NeEyAmKYblQctZfGMx0UnRdPTqyDvl3snw+VdmXeH6/OuU7F+SUoNKERkZSXR0IT76qCo3buTlu+9O4Of3wCixJkYlcv6784T8G0LxXsUp/Ubp5zame/z7L5XHjuXUuHGENG36eLupnqexqTiNyxritIYYwTRxNm/e/IiUsnaqO6WUJv8BtqJVMT390znFMTuB2ileTwP6pXg9C+j+vHvVqlVLGtuOHTuMfs1/zv8jC39XWDIW2WlRJ3n89vFMX8NgMMjVg1fLsYyVB6cdlLNmHZTFiknp6irl1q3Gi/XOyTtyavmpcpztOOn/vb80GAwZO7FhQylLl5YyMfGJzaZ4nqag4jQuk8dpMEi5bZuUly9n+RK5+VkCh2Uan6tm6R4rpWyVhdOCgBIpXhcHbhknIn0kJCUQGR9JgTwFKJavGJU9KrOq1yoalMjaSGUhBC/99hLR96L5ddhJljj2w62QNuK6WjXjxHxi/gnWvrEWR1dHBm4fiHfTDHaZOngQ9u6Fn39Wy5wq5hESos1LM3iwNg+UYjS6t1GkYw3QWwjhKIQoBZQDDuocU5Y8GgtRcVpFRm0aBUCNojXYPnB7lpPEIzZ2NnRf1J2yNV3xiLvF12124Fs2+0uLRtyKYNXAVazsvxKv2l4MPTo040kCwM9PG4mt+rYr5uLhAf36wdy5EBamdzQ5iu6JQgjRVQgRBDQA1gkhNgFIKU8DS4EzwEZgmJQySb9IMy/RkMj8E/OpNL0SA1cNxNXRlZ6VMj7dRkZs2gR2eez5YE9nxnTbytU5u5hRcwY3D93M0vXiI+PZ8cUOppabyqnFp2j8SWMGbBtAvqL5MnchBwdthF++TJ6nKNkxahRER2u97RSj0T1RSClXSimLSykdpZSeUsq2KfZNkFKWkVJWkFJu0DPOrPjy3y/pv7I/TnZOLO+5nCNDj9ChfAejXNtggHfegXbttFHX9nnsKTe8LP239ichKoFZDWax9eOthF3M2Der8KBw9v+8nyllp7Br/C7KdyzPsLPDaDmhZfo9m1Lz3XfalB2KYm5Vq0KrVtqssqoHlNGoKTyMKD4pXitBeFSifvH6DKk1BL8ifnSu2Pm5035nRmwsDBgAf/+tLRL38sv/7SvdsjRvnnyTjSM34j/RH/+J/hSuWpiKXStSrn05HJwdMCQZkEmS+Mh4rmy/wvk157l97DYAJRqVoPeq3hSvXzxrwUVEwFdfaXXFiqKHd9/VqjwDA6FKFb2jyRFUojCCmIQYZh+bzST/SdwIv8GwOsOoX7w+xV2LU9w1ix+4abh/H7p0gV27tCEK77337DFObk50mduFZuObcW7lOc6tPMeuL3exa/yuZw8WUKJBCVpObEmFjhVw93XP1BxSz/jzTwgP14o7iqKHtm3h2jVwfHYMkpI1KlFk04zDM/hi5xfcibpDoxKNmPHSDNqVbWey+wUEwOHD2hx7vXunf6ybtxv1R9Wn/qj6RN2N4vqe6xiSDNjY2iBsBbb2tnjV8cLZw0irzSUlab2cGjSAevWMc01FySwbGy1JJCZq36w8PPSOyOqpRJEFtyNv457XHTsbO8JiwqjmWY0xTcbQ1Ltp9r6Np+PBA22UdfPm2oSZmf2371zYGd9uviaILIV16+DyZW0qBUXRk5RQvz6ULAkrVugdjdXTvTHbmpy9d5Yha4bg85MPf5/+G4APG3/I5v6becHnBZMliW3boFQpWLNGe22xX5A8PLS1jLt21TsSJbcTAlq21CYKvHFD72isnkoUzyGlJOBBAB0XdaTS9ErMPzmfV/1epW4xbdopYzZSp2bBAq1duFgx4yw0ZFINGmgB26mCqmIB3nxTK1nMmKF3JFZPJYrnkEh+uvATB4IOMPaFsVwfdZ3fXvqNMgXLmPa+Er79Vhs/1KgR7NkDJUo8/zzdrF2rvrkplsXHBzp21MZUxMXpHY1VU4niOWyEDeMrj+faqGt80ewLPJzNU++zfbs262uvXrBxo9Y+YbEiIqBvX/j4Y70jUZQnvf023Lun1qrIJlVHkAEl85Ykj30es96zRQtYtUr7QmRj6el8/nytS+zbb+sdiaI8qWVL2LJF+w+lZJmlfwTlKmFh8NJLcOKE1hbXubMVJAkp/1uzWHWJVSyNjY02Utvi/yNZNotZj8JYhBD3gGtGvqw7EGLka5qCitO4VJzGZQ1xWkOMYJo4vaWUqdat57hEYQpCiMMyrQU9LIiK07hUnMZlDXFaQ4xg/jhVeUxRFEVJl0oUiqIoSrpUosgYa5ncXsVpXCpO47KGOK0hRjBznKqNQlEURUmXKlEoiqIo6VKJQlEURUmXShQZJIT4UghxQggRIITYLITw0jum1AghvhNCnEuOdaUQwk3vmFIjhHhZCHFaCGEQQlhUd0QhRDshxHkhxEUhxEd6x5MWIcRsIcRdIcQpvWNJixCihBBihxDibPLf90i9Y0qNEMJJCHFQCHE8Oc5xeseUFiGErRDimBBirbnuqRJFxn0npawmpfQD1gKf6xxPWrYAVaSU1YBAwFInYDoFdANSWXZPP0IIW2Aa8CJQCegjhKikb1RpmgOYbpUs40gE3pNS+gL1gWEW+jzjgBZSyuqAH9BOCFFf35DSNBI4a84bqkSRQVLK8BQvnQGL7AUgpdwspUxMfrkfMO5arEYipTwrpTyvdxypqAtclFJellLGA4uBzjrHlCop5S4gTO840iOlDJZSHk3+PQLtA66YvlE9S2oik1/aJ/9Y3P9xIURxoAPwhznvqxJFJgghJgghbgB9sdwSRUqDgA16B2FligEp50sPwgI/2KyREMIHqAEc0DmUVCVX6QQAd4EtUkpLjPMnYDRgMOdNVaJIQQixVQhxKpWfzgBSyjFSyhLAAkC3qVKfF2fyMWPQiv0LLDlOC5TaMoUW983S2gghXIDlwKinSucWQ0qZlFy1XByoK4SoonNITxBCvATclVIeMfe91TTjKUgpW2Xw0IXAOuALE4aTpufFKYQYCLwEtJQ6DpTJxPO0JEFAyiWiigO3dIolRxBC2KMliQVSSotfwFpK+UAIsROt/ceSOgo0AjoJIdoDToCrEGK+lLKfqW+sShQZJIQol+JlJ+CcXrGkRwjRDvgQ6CSljNY7Hit0CCgnhCglhHAAegNrdI7JagltIflZwFkp5Y96x5MWIYTHox6CQog8QCss7P+4lPJjKWVxKaUP2r/L7eZIEqASRWZMTK42OQG0Qet5YIl+AfIBW5K78v6md0CpEUJ0FUIEAQ2AdUKITXrHBJDcEeBtYBNaw+tSKeVpfaNKnRBiEbAPqCCECBJCDNY7plQ0AvoDLZL/PQYkfyO2NEWBHcn/vw+htVGYrfuppVNTeCiKoijpUiUKRVEUJV0qUSiKoijpUolCURRFSZdKFIqiKEq6VKJQFEVR0qUShaIoipIulSgURVGUdKlEoShmkLwmQ+vk378SQkzROyZFySg115OimMcXwHghRGG0GVQ76RyPomSYGpmtKGYihPgXcAGaJa/NoChWQVU9KYoZCCGqos0nFKeShGJtVKJQFBMTQhRFWxekMxAlhGirc0iKkikqUSiKCQkh8gIr0NaNPgt8CYzVNShFySTVRqEoiqKkS5UoFEVRlHSpRKEoiqKkSyUKRVEUJV0qUSiKoijpUolCURRFSZdKFIqiKEq6VKJQFEVR0vV/SSVGpB0zKV0AAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEWCAYAAAB42tAoAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAABPTUlEQVR4nO3dd3gU5drH8e+dXkhCSeiQ0DuEKr1Js1AUCxpFbHgQFfsLVizYDyjHdjiioqCgWFBUUDAI0juEUKUGAoRQkhASUp73j9mEBJKQwCazCffnuvbK7szu7G8nydw7z8w8jxhjUEoppfLjZncApZRSrk0LhVJKqQJpoVBKKVUgLRRKKaUKpIVCKaVUgbRQKKWUKpAWCnUBEUkSkbp25yiK4sosIt1EZLuzl+tMIhImIkZEPOzOosomLRRXMBHZKyJnHBvZrFt1Y0w5Y8zuS1heTxGJuchzPheRsyKS6LhFicjrIhJ06Z8ELjVzHvmMiNTPsdwlxphGl7tcO4lIVxFZJiKnROS4iCwVkfZ25yoMx99oH7tzXOm0UKiBjo1s1u1QQU8WEXcnvOdbxpgAIAS4G+gILBUR/6IuSL9FF0xEAoG5wH+AikAN4CUg9RKWJSLidt40Xf9XAC0U6gI5v1U79gA+EpFfReQ00EtErhWRaMcewUERedKxkf8NqJ5z76Sg9zHGpBhjVgODgEpYRSMrwz0islVETojIfBEJPS/faBHZCezMmVlEOorI4ZwFTURuEJFNjvsdRGS5iJwUkVgReV9EvBzzFjtestGR/9ace0kiMlZEZp+3rt4TkcmO+0EiMtWx3IMi8mp+hbWgHDk+z79EZKdjHXwgIuKY5y4i74jIMRHZDVxXwGpu6FjXXxtjMowxZ4wxvxtjstbHeBGZnuN9czVjicgiEZkgIkuBZKBuPuv/fhHZ5dhj+Snn715E+onIdscezYci8peI3OeYV09E/hSReMfnmSEi5R3zvgRqAz87fh9PO6Z3dOwhnRSRjSLSM8d7jRCR3Y6/zT0iElHAulGFZYzR2xV6A/YCffKYboD6jvufA6eALlhfLHyAWKCbY34FoI3jfk8g5iLv+Tnwah7TvwBmOe4PAXYBTQAP4Dlg2Xn5/sD6huybR+Z/gL45nv8tMNZxvy3WHowHEAZsBR7N67Of/5mAUKyNZaDjsbtjXXR0PP4R+C/gD1QGVgEP5LMeCpNjLlAea2MZBwxwzPsXsA2o5VgHkY7ne+TxPoFAPDANuAaocN788cD0HI/Dci4LWATsB5o5snqev/6B3sAxoA3gjbX3stjx+mAgAbjR8foxQBpwn2N+faCv43UhwGLg3fz+RrH2iOKBa7H+Hvs6Hoc41nsC0Mjx3GpAM7v/z8rCTfco1I+Ob2YnReTHfJ4zxxiz1BiTaYxJwfpHbyoigcaYE8aYdU7IcQhrwwPwAPC6MWarMSYdeA0Iz7lX4Zh/3BhzJo9lfQ3cBiAiAVgbla8BjDFrjTErjDHpxpi9WBv2HoUJaIzZB6zDKmRgbSCTjTErRKQK1ob4UWPMaWPMUWASMCyfZRUmxxvGmJPGmP1YxSDcMf0WrI3pAWPMceD1AjInAF2xNu7/A+Ic3/irFOYzO3xujNniyJrmmJZz/UcAnxpj1hljUoFxQCcRCcNa91uMMd87fpeTgcM58u0yxvxhjEk1xsQBE/NYDzndAfxqjPnV8ff4B7DG8T4AmUBzEfE1xsQaY7YU4XOqfGihUEOMMeUdtyH5POfAeY+HYv1j7nM0I3RyQo4awHHH/VDgvawC5pgujufklymnr4AbRcQb65vsOsdGHhFpKCJzHc1TCVhFKLgIOb/CUYSA2x2PszJ7ArE5cv8Xa8/iAoXMcTjH/WSgnON+dXJ//n0FBXYU3BHGmJpAc8fr3y3oNefJa13nnFY9ZwZjTBLWt/wa52c1xhgg+4QHEaksIjMdTXUJwHQK/n2EAjfn+HJzEqsQVjPGnAZuxdrjihWRX0SkcRE+p8qHFgpVGLm6GDbGrDbGDMbaCP4IfJPX8wpLRMoBfYAljkkHsJpsyue4+RpjluWX6bx80VgbrmvIvTEH+Air2aaBMSYQeAarCBXWt0BPEakJ3JBj2QewDhAH58gcaIxpls9yLidHLFazU5bahQ1vjNmG1fzX3DHpNOCX4ylV83rZRaYdwtqAAyDW8apKwEFH1po55knOx1h7QwZo6VgPd5B7PZz/3geAL8/72/A3xrzh+HzzjTF9sZqdtmHtRanLpIVCFYmIeIlIhIgEOZohEoAMx+wjQCUp5KmuIuItIm2xis0J4DPHrI+BcSLSzPG8IBG5uYhRvwIeAbpjbdyzBDgyJzm+bY4673VHgHyvx3A0jyxyZN1jjNnqmB4L/A78W0QCRcTNcaA2v2aUi+UoyDfAIyJSU0QqAGPze6KINBaRJxyFDRGphbVHtMLxlA1AdxGp7fi9jStCjixfAXeLSLhjL+41YKWjSe0XoIWIDHEcIB9N7mIUACQBJ0WkBvDUecs+//cxHRgoIv0dB/V9xDrhoKaIVBGRQY5ClepYbgbqsmmhUJfiTmCvo6ngX1jfArO+rX4N7HY0C+R31tPTIpKI1aT0BbAW6OxoOsAY8wPwJjDT8R5RWHsHRfE11oHoP40xx3JMfxJrLyMR69vmrPNeNx6Y5sh/Sz7L/gprD+ir86YPB7yAaKzCNxvrm21eLpajIP8D5gMbsY6ZfF/AcxOBq4CVYp21tgJrfT4B4GjjnwVswvo9zC1CDhzLWAg8D3yHtQdRD8exGce6vxl4C6s5qinWMYWs03NfwjoIfgqrqJz/WV4HnnP8Pp40xhwABmPtgcVh7WE8hbUtc3N8rkNYf1s9gAeL+nnUhcRqMlRKqeIn1nUYMUCEMSbS7jyqcHSPQilVrBzNROUdzVJZx2JWXORlyoVooVBKFbdOWNe2HAMGYp1pl9dpzcpFadOTUkqpAukehVJKqQKVuQ69goODTVhYmFOXefr0afz9i9xfXYnTnM6lOZ2rNOQsDRmheHKuXbv2mDEmJM+ZdvQbUpy3tm3bGmeLjIx0+jKLg+Z0Ls3pXKUhZ2nIaEzx5ATWGO3rSSml1KXQQqGUUqpAWiiUUsqFLX17KUteX3LxJxYjLRRKKeWiTKZhxaQVHFpV4MCTxU4LhVJKuaj9S/eTFJtE01ua2ppDC4VSSrmo6G+jcfd2p+H1DW3NoYVCKaVckMk0bP1uKw2uaYB3gLetWbRQKKWUCzqw7ACJhxJperO9zU6ghUIppVzSlm+3WM1OA+1tdgItFEop5XJMpmHrbNdodgItFEop5XJcqdkJtFAopZTLcaVmJ9BCoZRSLiWr2an+gPou0ewEWiiUUsqlHFjuWs1OoIVCKaVcStZFdo0GNrI7SjYtFEop5SJMpiF6drTV7BToGs1OoIVCKaVcxt6/9pJ4MJHmtzW3O0ouLlUoRMRdRNaLyFzH44oi8oeI7HT8rGB3RqWUKi6bpm/Cq5yXSzU7gYsVCmAMsDXH47HAQmNMA2Ch47FSSpU56SnpbJ29lSZDm+Dp52l3nFxcplCISE3gOuCTHJMHA9Mc96cBQ0o4llJKlYgdc3eQmpBKi4gWdke5gFhjattPRGYDrwMBwJPGmOtF5KQxpnyO55wwxlzQ/CQiI4GRAFWqVGk7c+ZMp2ZLSkqiXLlyTl1mcdCczqU5nas05LQzY9TzUSRGJ9Lxm46IuxT43OLI2atXr7XGmHZ5zjTG2H4Drgc+dNzvCcx13D953vNOXGxZbdu2Nc4WGRnp9GUWB83pXJrTuUpDTrsyJscnm1e8XjHzHptXqOcXR05gjclnu+rh1JJ06boAg0TkWsAHCBSR6cAREalmjIkVkWrAUVtTKqVUMYieHU3G2QyXbHYCFzlGYYwZZ4ypaYwJA4YBfxpj7gB+Au5yPO0uYI5NEZVSqthsnrGZ4MbBVGtTze4oeXKJQlGAN4C+IrIT6Ot4rJRSZcbJfSfZt3gfLSJaIFLwsQm7uErTUzZjzCJgkeN+PHC1nXmUUqo4RX0dBUCL212z2Qlcf49CKaXKLGMMm6ZvolbnWlSo67rXE2uhUEopmxxef5i4LXG0uMN19yZAC4VSStlm/afrcfd2p/kw1+rb6XxaKJRSygZpZ9LYPGMzTW5sgm8FX7vjFEgLhVJK2WDbj9tIOZlC63tb2x3lorRQKKWUDdZPXU/5sPLU6VXH7igXpYVCKaVK2Mm9J9mzcA/hd4cjbq557UROWiiUUqqErf9sPQiEjwi3O0qhaKFQSqkSlJmRyYbPNlCvbz2CagfZHadQtFAopVQJ2rNwDwkHEgi/J9zuKIWmhUIppUrQ+k/X41vRl8ZDGtsdpdC0UCilVAlJjk9m2w/baBHRAg9vl+tqL19aKJRSqoRs/GIjGWczSsW1EzlpoVBKqRJgMg1rPlpDzU41qdqqqt1xikQLhVJKlYDdC3dzfOdx2o9ub3eUItNCUQih06bBxIlw/LjdUZRSpdTqD1bjF+xH05ua2h2lyLRQXIwxBEVFwRNPQI0acO+9sHat3amUUqXIqf2n2PHzDlrf17pUHcTOooXiYkTY9PbbsGEDDB8Os2ZBu3bw1lt2J1NKlRJrp6zFGEO7f7WzO8ol0UJRWK1awX//CwcPwuTJMHiwNX3ZMnj6adizx958SimXlJ6azrr/raPh9Q0pH1re7jiXRAtFUQUFwcMPQ6NG1uMVK6zjF/XqwXXXwa+/QkaGvRmVUi5j6/dbOX30NO0fLH0HsbNoobhcjz8Oe/fC88/DunVWsejaFYyxO5lSygWs+XANFepVoF6/enZHuWRaKJyhZk146SXYt886hnH//SBi7Vk89hisWqWFQ6kr0JFNR9j/937ajWpXKroTz48WCmfy8oJbboF77rEeb90Kn3wCV10F7dvDp59CcrK9GZVSJWbl5JV4+HiUmu7E86OFojg1b24d/H7/fThzxjq1tmZNq4Aopcq0pMNJbPpyE61GtMKvkp/dcS6LForiFhgIo0dDVBQsWgTDhkHDhta8L7+En37Sg99KlUGrPlhFRloGnR7rZHeUy6aFoqSIQI8e8OGH4O5uHbOYNMk6zbZuXXj9dYiLszulUsoJ0pLTWPPRGhoNakSlhpXsjnPZtFDYRQRWroTZs6F+fXjmGatZ6oMP7E6mlLpMG6Zt4Ez8GTo9Ufr3JkALhb08PWHoUFi4EKKj4YEHIDzcmrdjB/zvf3D6tK0RlVJFk5mRyYqJK6jevjq1u9a2O45TaKFwFU2aWFd8d+liPf72Wxg50upf6tFHYft2W+MppQpnx887OL7rOJ2f7IxI6T0lNictFK7qmWdgyRK49lrruEbjxtbxDL0eQymXtuydZQSFBtHkxiZ2R3EaLRSuSsS6wvurr2D/fnjlFWjRwppuDEyZAkeO2J1SKZVDzMoYDiw9QMdHO+LmUXY2r2Xnk5RlVavCc8/Bq69aj7dts45n1KoFt90Gf/+texpKuYBlby/DO8i71A11ejFaKEqjJk2sYxajR8Nvv0G3btCqFX7799udTKkr1tGoo2z9bisdHuqAd4C33XGcSgtFadWwoXUdxsGDVjchwcGkVK5szVu0SK/+VqqELZmwBE9/Tzo+1tHuKE7nEoVCRGqJSKSIbBWRLSIyxjG9ooj8ISI7HT8r2J3V5fj7W12D/PknmT4+1rQxY6BpU+jd27pOIy3N3oxKlXHHth0jalYUHR7qUOq768iLSxQKIB14whjTBOgIjBaRpsBYYKExpgGw0PFYXcyCBdaV3rt3w803Q1iY1V2IUqpYLHltCR4+HnR6vGxcYHc+lygUxphYY8w6x/1EYCtQAxgMTHM8bRowxJaApU1ICIwdC//8Y/Ul1bIl+Ppa844etZqm9OC3Uk5xfNdxNn+1mXaj2uFf2d/uOMXCJQpFTiISBrQGVgJVjDGxYBUToLKN0Uofd3cYONA64H3TTda0qVOhVy+rZ9sPPoCEBHszKlXKLXl9CW4ebnR+srPdUYqNGBf6Ziki5YC/gAnGmO9F5KQxpnyO+SeMMRccpxCRkcBIgCpVqrSdOXOmU3MlJSVRrlw5py6zOBQmp1tqKpX//JMaP/5IwI4dpPv6cqR/f3Y+8oh1jYaL5HQFmtO5SkPOomZMOZzCqjtWUX1Qdeo/Ur8Yk+VWHOuyV69ea40x7fKcaYxxiRvgCcwHHs8xbTtQzXG/GrD9Ystp27atcbbIyEinL7M4FDnnypXG3HWXMTfffG7aokXGpKY6M9YFyuz6tInmdJ6iZvz5gZ/NK16vmFMHThVPoHwUx7oE1ph8tqsu0fQkVocoU4GtxpiJOWb9BNzluH8XMKeks5VpHTrA559bw7cC7NljNUuFhsILL0BMjK3xlHJlx/85zvqp6wm/J5zAmoF2xylWLlEogC7AnUBvEdnguF0LvAH0FZGdQF/HY+VsWU1OtWvD3LnQtq11FXhYmNW77e7dtsZTyhVFPh+Ju5c7PV7oYXeUYudhdwAAY8zfQH4N5FeXZJYrmru71QnhtddaexcffwzTp0NWW+j27VZ3IkFB9uZUymax62KJ+jqKrs90JaBagN1xip2r7FEoV1OnDrz5ptUhYdYV3/fdB9WrW/1Mbdpkbz6lbLRw3EJ8K/rS5ekudkcpEVooVMHc3c/df/dda8zvL76AVq2s3m1/+822aErZYffC3fzz+z90e7YbPkE+dscpEVooVOG1bWtdh3HwIPz731Y351nHL06ftvY+lCrDjDEsHLuQwFqBtH+wvd1xSowWClV0FSvC449bxyxGjrSmzZhhNVcNGQJ//AGZmbZGVKo4RM+O5tCaQ/R6uRcePi5xiLdEaKFQl87NzRr3G2DAAKvbkGXLoF8/a0S+SZO0YKgyI+NsBn8++ychzUJoeWdLu+OUKC0Uyjlq14YJE+DAAetMqZAQ6/oMN8ef2IED9uZT6jKtnLyS4zuP0/etvri5X1mbzitn30mVDG9viIiwbomJ1rT4eGv8jFatYPRo3KpUsTejUkWUGJvIXy/9RYPrGtDg2gZ2xylxV1ZZVCUrwHF+ube3dartyZMwfDgdb7nFaqY6fNjWeEoV1oL/W0DG2QwGvDvA7ii20EKhil+5cvDII9aoe3/8wamWLa2zprJ6rj1xQo9lKJd1YNkBNn25iU5PdKJi/Yp2x7GFFgpVckSgTx+2vPwyxMZazVFgXcjXoAG8847VTKWUi8jMyOTXh34loEYA3Z7pZncc22ihUPYIDj53/7bboEYNeOopqFkT7r4b1q2zL5tSDus+Wcfh9Yfp904/vMp52R3HNloolP1uugkWL7a6Bbn7bvj2W/jxR2teRgacOWNrPHVlOnP8DH8++yehPUJpdmszu+PYSguFch0tWsCHH8KhQ9YFfQA//2ztZTz1lDW0q1IlZP5j80k9lco1k69BSmhQL1elhUK5nsBAKF/eul+7NvTubV28V78+XHON1RW6HvxWxWjnbzvZ+MVGuoztQpWWejq3Fgrl2tq0sZqi9u2DF1+EjRthzJhz88+etS+bKpNSE1KZ+8BcQpqG0P257nbHcQlaKFTpUKMGjB9vFYx586wrvlNSoG5dGD4cVqwAFxr/XZVeC8YuICEmgUFTB+Hhbd81ycfPHGffyX1EHY2yLUMWvTJbuYT01HTOxJ8hOT6Zs4nWXoK4iXVzF3wr+uIf4o+nvyfSwHFlbHIy3HADTJsGX34JrVvD6NHWWVR+fjZ+GlVandxwko0fbeSqR6+iZseahX6dMYbUjFRS01MJ8rEG9lp9cDVxyXEkpiaSkJpA4tlEqgdUZ1jzYQCMmjuK/Qn7c83vV7cfH13/EQCh74aSdDYJgLTn0/Bws29zrYVClRhjDMd3Hufon0eJjIzkWPQx4rbGcXLvSdJOpxVqGR4+HviF+FGhTgUqNqxIcKPbCJ4ygpr//IXvzM+Q++6DRo2ssTIyM8/1NaXUeYwxJKclk3jW2lCfOHWCP774g0Z1G9H71d78vP1nth7bSmJqIolnE0lMTaS8T3n+3f/fANzx/R38vf/v7I18emY6V9W4ihX3rQDgvp/vY9OR3AN89QrrlV0odp3YxYkzJwjwDqB2UG0CvANoXrl59nMn9puIu5s7gd72j8ethUIVq1P7T7F7wW72/LmHvZF7STxk9f+0zW0bFepWILhJMHX71MUvxA+/Sn74VvLFO9AbEcFkGowxZKZlcub4GU7HnSY5LpnTR05zYvcJts/Zzvq49dnv5Rd8Jy07p+DzZzq1UncT9u3buO3ZDQ8+CNddBx76517aZWRm4CZuiAixibHsP7U/eyOe9fPB9g8iIny9+Wvm/TMv1zf2jMwM1oxcA8AdP9zBV5u/yrV8/6v92XzNZrz8vZi6fipzts9BEAK8AwjwCqBxcOPs5zao2AB3N3cCvKx5gd6BhJYPzZ4/ddBUMjIzCPC25gV4BVDOq1z2/D/u/KPAz3p/2/udscqcQv9zlNMlH0tmyzdb2DxjMweWWb3G+lf2p07vOoT1CiPWLZYBdwxwSn/+Z06cIX57PLHrYzm06hD/rDpI3Pi/wEBnj310dl+N/+9DyKhaHbfRo5D77wftlLBEpWemk5iayOGUw0QdjaJuhbr4efqxM35nrm/kCakJJKYm8nKvlwnxD2H6pum8u+LdXPNOp53m6JNHCfEP4f1V7/Pa369d8H53t74bP08/ouOiWbR3UfZGurxPeQK9AzHGICLc0vQWWlVpRaB3IElbklj7+lpqXVWLOr3rADBtyDTc3dzx8/TDTS7cM32x54sFfu521ds5ZwW6AC0UyimMMez5cw8r313Jrnm7yEzPpHLzylz9+tU0GtSI4CbB2eeiL1q0yGmDvvhW8KVmx5pWe/Ioa1rKqRT2/72f3Quu4ovfr6Fi9N+0P7yaus8/z/5vV8AHH1KzYw2rq+gr/Pz4gqSmpxKTEHPBN/ZOtTpRO6g2249tZ8raKdb0HBvzif0n0q56O77f+j0R30eQkp5ybqErYeV9K+lQowN/7fuL+38+963Z292bQO9AHuv0GCH+Ifh6+FKlXBUaeDfI/tYe4B2Al7t1hfQdLe+gc63Oub6xB3oH4uvhC8ArvV/hld6v5Pv5BjceDEDCwQQ+HvAxPWv1pEHEuZ5hs441KC0U6jJlpmcS/V00y95aRuy6WMpVLUfHxzvSMqKlbeef+wT50PC6hjS8riEwgMTYEez8dSdzv/yTPcsOc7zbZzSoEMf17r+SOfJfBI0dhWT1dFtK5Wxv93b3poJvBc6knWHB7gUXfGPvV68f3UK7sf/Ufkb+PDK7AGQ9b1L/SQxvNZz1h9fTaWqnC97r66FfUzuoNocSD/Hftf/NbpbJ+plprGtcGlRswMMdHs6ed2jPIdq3bE+9CvUAuLnpzfSp24dA70DKeZXLLgBZhjYdytCmQ/P9zE1CmtAkpMllrbfMjEx+uPMH0s+kM3TmUKJi7T/DyBVpoVCXxGQaNn+9mcjnIzm55ySVGlVi4CcDaXlHS1tPKcxLQLUA2tzbhjb3tiE1IZWdv+4k7sNvSP77DFVf+z9S33iRY1ddR9DrYynXox0zZszg2Wef5eGHH2bEiBFMmDCBiIiIYsmWkJqQvQHP2lAH+wUTXjUcYwxvLn0ze37Wxr5/vf480O4BktOSafR+I06cPsGZxWeyN9DPdXuOV3q/QkJqAoNmDsr1foIQ5BNEt9BuuIs7J1JOEOAVQGX/ytnfyutXrA9YG/rPB3+e6xt7gHcAtQJrAdCrTi+SnknK97O1qNKCt/q+lf14Ucoiejbrmf04yCfI9m/tS99ayt7IvQz6dBDBjYIh1tY4Lsu1/qNVqRCzMoZ5Y+ZxcOVBqrWpRv+J/Wk0qBHi5vrNON6B3jQf1hyGNefM8bFse3Mmnp/9j7DlP5Da8zcmhj/PZ1tnsD91PwD79u1jpGNc8IiICNIy0khJTyHA29oD2Xh4I0dOH8m1sQ/xD+H2FrcD8Ni8x9h9cneuDX232t34ZNAnANSbXI9jycdyZby9xe3MuHEGIsIri1/hbMbZ7GaVAO8AOtToAICvhy996/blVNwpmtRtkr0xb1+jPQCV/Cqx5v41ub7x52xvrxFYg5X3rcx3XVXyq8Rd4Xc5a9W7nJgVMUQ+H0nzYc0JHxFudxyXpoWiEKZNC+W//809rU4deM1xHG3cONizJ/f8pk3hhRes+48+avWqnVObNvB//2fdHznSGpIhp65dz12AfOedF/aL17cvPPCAdf+mm6yfR482IyTEuj9wIIwYYb3ujjusaTmvR7v1Vut2/LjVy/f580eMgMGD4eBB69IEgPSUNOK2xHEqJonuFcrz4Gft8O/ciiefEvgsd74nnoDu3WHzZnj22dzz4uObM2kSdOgAq1bBK3k0I7/2mtX106JFVu/j53v3XatHj99+g/ffv3D+lCnWNXrffWeY8mkq6e6JZLgnku6eSKakMPe/V1Gxoh+f1qvBT9fdzNn03qSePkpi+jrcqrRj4/wUTnz8G94Dm5Jc5zh3bHyI4TvuI9MthYDTrUh4awMAgz4Zyf6MVbneu0JSJ25/2yoUv67azqHEQ3hkBOCeEYJHRj3WRjcFxxf9DomvsXu3wSMjAI+MQNzSAzhzoAbcaM2/Lz6eqI3eCJL9O9q7EegKIoLXb5+yZ9UJTpSvkP3+O1pBu0ng4ebBe2PbXjAKbadO5/52hw69sGf3q6+G55+37l9zjXW5Sk4DB8KTT1r3e/QgO1eWW2+1/maSk6F//3PTT50KJyjI6vfxnnvg2DEYMuTC313WpTD791s/z/f009bf5rZt1nLO99JL1v/HunXn/nZzevttaFUvkTeuX8pcj/upvKsKb3ey1m9CQhumT7f+P+fPP/c/nNPnn0OTJvD99/DGGxfOnz3b6nlm+nR4770L5//2m9V58pQp1u18f/0F/v5WrzXTp1vTVq6096Q9LRSFcPCgL/v25Z6Wmnru/o4dsGVL7vleOZpbt23jgtdXzDH+yfbtEBeX+7hqWFju1ycn557fvHnu+QCnT/tlF5y4OOtnZqaVL0vWMo4ft36mp8OuXRfOP3XK+pmWBnv3QsrJMyTEJGAy3fCvXIPe/65H+B2eREdb/9DnO33a+pmaCjExueclJXmT4ji+mZJiFaOcn81gHPOFw4lx7D5zgAyPBDI8Esn0SCTDI4EzqfcBHvx5+DtWVf01e36GRyKZ7qdJS1sPCP/Zfz9/dZia6/3d0wLJyLA+YOSJz9geNgsAt3Q/MlN8cDtei2Qy6b5rIb2rd2JpTG1SzvpRqWId3NOD8Eqplb2s693e56+labinB+CWEYBHeiDlvM4d7xiW8St/LM39+XP2sN4s5X5Onvclw9v73P3Msz6kpuSen5bjkpP0dMjIENLTz03LyDh//nnr1+S+b0zBx/RFcs/PeT/nZSpZ03NOy/l/4OFh8PICd/dz03x8Lny/rA2iSN7XTWbNd3OzxsQ6X9by3d2tbsMukJnON0O/IT3JnbptK+IVcC5wZmZ69vK9vHL/n57//r6+uX+XWbI+v58fVK584fys9VSuHFStmv/8wECoXj33NLuIKWPdHrRr186sWbPGqctctGgRPXv2dOoyi0Nx5Ew5mcKvD/3K5hmbqdGhBkO+GGK15Z4n02SSdDYpu/mldlBt/L382XNiD0v2L8nV9LJt9zY+GPYB1QKqMTt6Nu8seye7fT7reXvH7KVWUC1e+esVXlh04de6+KfjqehbkVf+eiXXAdWs5plvbvoGT3dPft7+M1FHo3I1vwR5B3F13asBOJlyEkEo51UOdzd3wsLC2Oeo6lPue4rgT75lAIfxJYXfmz1K6Ov/ouF1DV2qme1K/vssKmMMP937Exs+28DNs2+m6dCmuea7QsbCKI6cIrLWGJPnOb26R3GFS8tIIzYpNtdB1cSzibSv3p7M9ZlMHT2VRbUWUWl8JXY038HP638mYUUCE3pPoHOtzvy681du+fYWTqedzrXcv0b8RffQ7iw7sIy7fjzXzu0u7vi5+xGXHEe1gGp4uXsR5BNEzcCauQ6Y+nlaXyVvbnYzLau0zC4AOc+JB3i+x/M83+P5fD/fwEYDGdhoYL7zs5aTZcKECYwcOZLk5GQSGldhJHup7lOez8NvYuvBmiwfNJM+IRto0NyLiu88g0ebVkVc48pOq/6zig2fbaD7890vKBIqf1ooSpGs/mQSUxPxdPekvE95zmacZcHuBSSmJrI6djXrlq8jMTWRHmE96BnWk8NJh7n3p3tznQefkGpt6O9vez9b4rbQ+r+tL3iv5/yew3OcJ8kdk1nTdQ0BPgEExARkb6zTM622jrDyYYxsOzLXRj7QOzD7CtbrG17Prod3ZX+j9/Hw4a+//qJllZYADGo0iEGNBl3w/lkaBzfOdTVsccs6u+lZx4GV0NBQJkyYQN+ICK5Oz2TLt1vIfHQpFSN/xqPtN5yq2xq/F57E8/abwdOzxHKqotu9cDfzH59Po8GN6Dm+p91xShUtFCUgOS35gm/s5X3KE141HIBJyydxIuVErlMke4b15MH2D5KRmUG9yfWym22yNtBPdnqSt/u9zZm0M1z31XXn3sxxPOJleZmeYT1xF3cOJx0m0DuQWoG1sjfYWadAhpUPY+qgqee+yYsf699az+Fph2k+sDmDpw1mYuDEfD9b05CmTOyf/3xXOAWyqCIiIoiIiGDRokXs3bs3e7qbhxstbmuBGTaf/T+sJX7sO9TZOR/PERHETvyCwAXf4R/ib19wla/DGw/zzdBvCG4czA1f3uBSTYelQZELhYj4AynGmIyLPrmM2HN6Dxm7M3JdtFTepzwRLa1vn+MWjGN7/PZcbeztqrdj2pBpADR6vxExCbmP6N7Y5Ea+u+U7AF5d8mp252BZG+ymIdZusbubO1fXuRofD59czS9tq7UFIMA7gBX3riDAO4CotVH069mPcl7lsnuaDPEPYe3Itfl+tvI+5bmntXXqSNLhJGbdOIuTy0/S7/l+9BzfU/+h8iAihN7YjtAbZ3Jo1QE2P/Yh25YdJy70XbrdUpVOx+bi+cQj0LOn/UchFcf/Oc70/tPxDvAm4tcIvAO8L/4ilctFC4WIuAHDgAigPZAKeItIHPArMMUYs7NYU9rs3Z3vsmlN7l4gW1dtnV0oouKi2HNiD4Hegdnt7Y0rnWsuebHHi5zNOJurm4HqAdWz5x947AC+Hr75Drc4dfDUPKcDuIkbV9W8CoCjPkcvaHMvrPgd8XzR5wvOxJ/hpm9uotnNV/YYwYVVvUMtqi99nabbjvH3639z6MtvScucj+cvP5JRvxHuYx6yzm8OKl17VWVFYmwiX/b9ksz0TO6KvIug2vp7uBSF2aOIBBYA44AoY6zLP0WkItALeENEfjDGTC++mPYaVXcUTVs1zdVNQc6uf3++7ecCX39fm/sKnJ914NYuRzYd4ct+X2IyDXcvuZtqbarZmqc0Cm4czJBpQzjxYg8iJ9xA+rSvaLdrFTUefpjMF17E7dDBvM8FVcXmzIkzTO8/ndNHT3NX5F2ENAmxO1KpVZhC0ccYc8FgAcaY48B3wHciUqaP4jUObEz30LI5JOLBVQeZPmA6nn6eDF8wnODGeZwYrgqtQt0KXDf1Jk6N78vSt5Yy778/U/nkITJHzafrM12p9N6L1tWUN96Y+yID5VQpp1L46rqviN8ez+2/3E6N9jXsjlSqXXRUl6wiISLvSj5tI3kVEuX69v61ly+u/gLfCr7cveRuLRJOFFQriGv/cy237HsLzzGjiJoZxdRG75A07TvrcuNateC557jgsml12ZKPJfPF1V9waPUhhn49lLp96todqdQryvBfScBPjoPZiEg/EVl6kdc4hYgMEJHtIrJLRMaWxHuWdfsW72PGgBkE1Q7i7iV3U6FOhYu/SBVZQLUABkwawJg9Ywh/vBeTM0YznQgOedTGvPaadQn+b7/ZHbPMSIxN5PMenxO3JY5hc4bR5MbL611WWQp91pMx5jkRuR1YJCKpwGmg2DfaIuIOfAD0BWKA1SLykzEmurjfu6w6vOEwXw/8mvJh5blr0V16SmcJKFe1HP3e6UeX/+vC8onLmfb+anxNF/o32k/FwAZUAfjmGzh0yOpoq3x564UX619DZTu59yRf9PmC00dOE/FbBGE9w+yOVGYUulCIyNXA/VgFohpwrzFme3EFy6EDsMsYs9uRYyYwGNBCcQnid8ZbpwoGeXPH73dokShh/iH+9Hm9D52f7MyKSSuY859VpHadQcOBDRm07U38d260elGMiIBRo2DaNKtojB9vd3SXlvXl52zSWe5ccCc1r6ppd6QypdB9PYnIn8ALxpi/RaQF8CXwuDHmz2INKHITMMAYc5/j8Z3AVcaYh3I8ZyQwEqBKlSptZ86c6dQMSUlJlMur9zEXc7GcqcdS2fDwBjLOZBA+ORy/2vacbVVW1qczpCelc/D7g8R8F0N6QjoNax+hU4XN1Nq2GvfUVA527szOf/3LOqZhY05nKK6ccYvi2PbmNjzKedDi9RaUq3/p73Elr8tevXrl29cTxphLumHtVSy71NcX4X1uBj7J8fhO4D/5Pb9t27bG2SIjI52+zOJQUM4zJ86YD5t/aF4r95o5uPpgyYXKQ1lYn86WkpBi/n5jiXnb7wUznvHmC+4wRwgxmQMHGZOZaczRo8aMHWvMnj225rwczs6ZmZFpFj630IxnvPmk0ycmMTbxspd5pa5LY4wB1ph8tqsXPZhdwJlOscDVBT3HSWKAnF+nagKHivH9ypzMjExmD5vNse3HGDZnGNXbVb/4i1SJ8g7wpsv/dWVM3LNcy1yOU4mPGM1Hu/uzYdpGMhZGwltvQd26MGgQzJtn9SF/hUo5lcKsG2ex5NUlhN8Tzl2Rd1GuquvvCZRWhbrgTkS+A+YYY7JHHhARL6CTiNyFdVHe58UTkdVAAxGpAxzEukr89mJ6rzJpwdgF/DP/H66fcj11etexO47KjzF4PvM07VlDW9YRRXOWHh7EnLvn8Gf1ALo9/Q2tz67CY/rn8PPP0KABrF9vd+oSt3fRXn6860cSDiYw4L0BdHi4Q769GijnKEyhGADcA3zt2FifBHwAd+B3YJIxZkNxBTTGpIvIQ8B8x3t+aozZcpGXKYdN0zex/J3ltB/dnrb3t7U7jsqPMfDYY9aQaGPG4DZpEi0fe4wW773KP0OeYHlSHX59I4oF5crTZvj/6FzvMAFH/rGGQgP4z3+soeva5d3EXBakp6Sz8NmFrJi4gooNKnLP0nv0oHUJuWihMMakAB8CHzquwA4GzhhjThZztpwZfsXqV0oVwcHVB/npvp8I6xlG/0n9L/4CZR8R6+ymMWOsMTBFYNIkBKhfvhz1xw8ndn0sKyauYNX/NrIiLZP617Tkqnm7cEtLsi7eS0iwxpcdPRpuuaVMdRkSszKGn+79ibgtcbR7sB193+qLl79e2V5SCiwUIjIE6zjEf4wxO4x1BXZsQa9RriHpcBKzbphFuarluPnbm3H3dL/4i5S9xo/Pfd2Eo1hkPa7Wuho3fHkDfd/uy9opa1nz0RpmXDMDn+o+eD42izZeW/D+8hO46y54/HGYORP69LHv8zhBwsEEFo5byKYvNxFQPYCI3yKoP6C+3bGuOAUWCmPMjyJyD3C1iPQ3xvynhHKpy5CZkcl3t39HyokU7ll2D37B9nY6qIrg/Lb2PNrey1UtR48XetB1bFeiZ0ez8K2F/P7SShZ4uNFo0Hg6Dz9LjXU/IU0dI7j9/bc1CPqAAbkHrHZhaWfSWP7v5fz9+t9kZmTSdVxXuo7rql2E26QwxyjqGmM+EpG1gBaKUmDpW0vZG7mXQVMHUbVVHqO3qzLB3cudFre3IL56PM2rNWfd/9axcdpGtn6fjH/lq2j+1iZa3gnV3nsPmT0b6tSBf/0L7rkHgl2zX68zJ86w5uM1rHxvJaePnKbJ0Cb0fbuvdjFjs8IUinkishyo6ti72AhscRy7UC4mZkUMkc9H0uzWZoTfHW53HFVCghsF0++dflz92tXs/G0nm77cxJqPrA1uSIOudB3UmEYHFuD9f/8HL7wATz0Fr7xid+xsp/afYsV7K1g3ZR1nk85Sr389uj3TjdDuoXZHUxTuYPaTIlIXWATUAQYBzUTkLNb4FLcWb0RVWOlJ6Xx393cE1Qri+o+v11MGr0DuXu40HtyYxoMbc+bEGaJnRxP9bTRzfk0gM30AYZW70qPyVrzjPalwMgUfbwOzZlkHv/1Ktoky5WQK0d9Fs3nGZvYu2ou4Cc2HNafzU511T9jFFKqvJ2PMbhHpY4zZkTVNRMoBzYstmSoSYww7Ju3g1IFT3L3kbnzKl50zXtSl8a3gS9v729L2/racOXGGnb/sZOv3W/nq9wqkRaUh/32LLnUPcvWuKWQ8/CiZdwy3hnCtXzwHi40xxEXHsSdyD7v/2M2u33aRcTaDig0q0uPFHoSPCKd8aPlieW91eYrSe+yO8x4nASucnkhdko3TNhL3Zxy9Xu1FrU759wukrky+FXxpeUdLWt7RkoyzGcSsjGH3H7vZ/fs/TPsnjbZJq2jy8Qfw8X84XKUVO++eQPmWtQluFEzFBhWLfBA5Mz2T4/8c59jWY8RFx3Fk0xF2/L6DxScWAxBUO4h2o9rRIqIF1dtV171fF1foQqFcV0JMAvPGzCOoZRBdx3a1O45yce5e7oR2CyW0Wyi9Xu7F2dPDiV0Xy7o/NuD7/Vf47d7Cn2+sBtZQn50cohoZgZXwC/HDL9gP/xB/PP09ERHETUAgIzWD5PhkzsSfITk+mdNHT5OZdq6LkcBagVRoU4Grhl1Fnd51KF+nvBaHUkQLRSlnjOGXUb+QkZZBo6cb4eZelLGolAIvf6/swsHLg8EYnjmTxomogwT3aAZp6cRW68rO2n04YMqTEJNA2pk0MGAyDSbT4O7ljm8lX8qHlada22r4V/EnuHEwIU1CCG4cjHegN4sWLaJNzzZ2f1x1CbRQlHJRM6PYMXcHfd/py9kaZ+2Oo8oCETz9vKjcoQ6sWwsffUSNadOosT0SwsPh/fehSxe7U6oSpF8/S7HTcaeZ98g8anSoQcdHO9odR5VFTZrA5Mlw8CB8/LHVY23W6Hs7dlg3VeZpoSjF5j0yj5RTKQz6dJA2OaniVa4cPPAAbNgAzZpZ0156CRo1gr594YcfID3d1oiq+OjWpZTa/tN2omZG0f257lRuVtnuOOpKkfMA9MSJ8OqrsH073HijdeX3++/bl00VGy0UpdDZpLP88uAvVG5RWc9yUvapUsUa33v3bmuPokkTOOQYUywjA5Ytszo5VKWeHswuhZa8toTEg4nc/M3NuHuVjk7eVBnm4QFDhli3rFH35s+H666DFi3gwQfhjjvsTKguk+5RlDLHdx1n+b+X0/LOltTqrBfWKRfj5tik9OgB//uf1VvtqFFQvTr1J0+2xsxQpY4WilJm3qPzcPd2p8+bpXucAVXG+fvDfffBunWwfDkMHkzF1avPjcgXHQ1pafZmVIWmhaIU2fHLDnb+spMeL/QgoFqA3XGUujgR6NgRvvyS1Z99Zu1hnD0LvXtDWJh15lTWcQ3lsvQYRSmRnprO/EfnU6lRJa565Cq747istLQ0YmJiSEm5/F7wg4KC2Lp1qxNSFS9n5fTx8aFmzZp4eno6IdWFjIdjc+PubjVLffihNarfq6/CDTdYw7m2bFks760ujxaKUmLFpBUc33WcO+bfoQewCxATE0NAQABhYWGX3ZdQYmIiAQGuv+fmjJzGGOLj44mJiaFOnTpOSpYPd3cYONC67dplXcj36afWQW+AuDjw9obAwOLNoQpNm55KgaTDSSx+dTGNhzSmXr96dsdxaSkpKVSqVEk7nCsiEaFSpUpO2RMrkvr14Z13rCu/e/Swpr36KtSoYRWOqKiSzaPypIWiFPjrlb/ISM2g79t97Y5SKmiRuDS2rjdf33MX8w0fDkOHWnsZLVpYBeSHH+zLprRQuLrju46zbso62oxsQ8X6Fe2Oo1Txa9sWPv/c2st46y2IiYG5c8/NP3zYtmhXKi0ULu7P5/7E3cudHs/3sDuKKqTJkyfTpEkTatSowfjx47Onv/vuu3zxxRcFvnbYsGHs3LmzmBOWEpUqWWN779xpdRcCsHo11KxpdRmycKFe+V1CtFC4sENrD7Fl1hY6Pt6RclXL2R1HFdKHH37Ir7/+yoQJE7Knpaen8+mnn3L77bcX+NpRo0bx1ltvFXfE0sXNDYKCrPvVq8MTT8DixdCnz7nebZOT7c1YxmmhcGELxy7Et5IvXZ7Svv9Li3/961/s3r2bQYMGceTIEcqVswr8n3/+SZs2bfDw8CA9PZ327duzaNEiAMaNG8ezzz4LQLdu3ViwYAHp2hNr3mrUgDfftJqjpk2zujx/4YVzexanTtkar6zS02Nd1O4Fu9m9YDf9J/XHO7Bo4xUry7xH53F4w6W3Z2dkZODunvtU5KrhVRnw7oB8X/Pxxx8zb948IiMjCQ4Ozp6+dOlS2rZtC4CHhweff/45N910E5MnT2bevHmsXLkSADc3N+rXr8/GjRuzn6/y4ONjHfQePhxiY60rvo2xLu6rVMk6Y2roUOs0W3XZdI/CBZlMw4KxCwgKtQagV6VfbGwsISEh2Y+bNWvGnXfeycCBA/n000/x8vLKnle5cmUO6dXKhVetmvUzPR1GjoQjRyAiAmrXtnq3PXDA3nxlgO5RuKBtP24jdm0sQ6YNwcNbf0WXqqBv/oXhzAvufH19L7hGYfPmzZQvX54jR47kmp6SkoKvr69T3veK4ukJjz0GY8ZYB7o/+ADeeMO62vvWWyE11XqOm34/LipdYy7GGMPiVxZTqWElWkS0sDuOcpImTZqwa9eu7Mfff/898fHxLF68mEceeYSTJ09mz9uxYwfNskaRU0Xn5maNuvfjj9ZYGTfcYE1/5x1rRL6JE+HECVsjljZaKFzMjrk7OLzhMF2f6arDm5Yh11xzDYsXLwbg2LFjjB07lqlTp9KwYUMeeughxowZA8CRI0fw9fWlWlZziro8oaGQ1azXsiVUrmydNVWjxrnebdVFabuGCzHGsPjlxVSoW4EWt+veRGm1d+/eC6aFhoZSqVIldu7cSYMGDdixY0f2vEceeST7/ldffcUDDzxQEjGvPFn9S23YAB99BNOnW8czfv7Zmq9nmuVLv7K6kH/m/8OhNYfoOq4r7p7a8V9Z88YbbxAbG1vgc8qXL89dd91VQomuUOHh8N//Wld+T55sTduzB2rUoO6UKdZ9lYsWChdhjOGvl/4iqHYQrYa3sjuOKgaNGjWie/fuBT7n7rvvxsNDd/RLRPnykNVT7tmz0LUrtWbNgnr1rD2P3347N7TrFc72QiEib4vINhHZJCI/iEj5HPPGicguEdkuIv1tjFns9izcQ8yKGLqM7aLdiCtV0ho1gu++Y8XMmda4GKtXw+DBVpfncMV3FWJ7oQD+AJobY1oCO4BxACLSFBgGNAMGAB+KSJndgi5+ZTEBNQJofU9ru6ModcVKDQmBl1+G/fth0SKoUsWacc01MGKEVUCuQLYXCmPM78aYrKNIK4CajvuDgZnGmFRjzB5gF9DBjozFbd/ifexbvI8uT3fR6yaUcgVeXtC5s3U/PR3q1oXvvoMOHaB9e/jsMzhzxt6MJcj2QnGee4DfHPdrADkvqYxxTCtzlr61FL8QP9rc38buKEqp83l4WMO2HjwI778Pp0/DPfdY42VcIcSUQNubiCwAquYx61ljzBzHc54F2gE3GmOMiHwALDfGTHfMnwr8aoz5Lo/ljwRGAlSpUqXtzJkznZo/KSkpu3M3Zzu97zRrRqwhdEQoYXeFXdayijOnMxVnzqCgIOrXr++UZeXV11NhBAYG8tBDD/Haa68BVrfjSUlJPPPMM5ecZdOmTcTGxtK//4WH6i41Z1527drFqWLqWK80/H0WKqMxlN+4kcT69ckoV46qv/5KyF9/cWjIEOI7dLCGenWFnEXUq1evtcaYvPsMMsbYfgPuApYDfjmmjQPG5Xg8H+h0sWW1bdvWOFtkZKTTl5llzn1zzKs+r5qko0mXvazizOlMxZkzOjraactKSEi4pNd5e3ubsLAwExcXZ4wx5u233zYvvvjiZWX57LPPzOjRo/Ocd6k58+LM9Xe+0vD3eUkZP/nEmGrVjAFjQkONef11Y44edXa0XIpjXQJrTD7bVdubnkRkAPB/wCBjTM5O5X8ChomIt4jUARoAq+zIWFySjiSx6ctNtLqrFf4h/nbHUU7i4eHByJEjmTRp0gXz4uLiGDp0KO3bt6d9+/YsXboUgBYtWnDy5EmMMVSqVCl7gKM777yT33//nRdeeIFZs2YRHh7OrFmzOH78OEOGDKFly5b07t2bTZs2ATB+/HjuueceevbsSd26dZmcdZ2AKj733gv79sG331qn244bd67bkDLCFY6cvg94A384xuxdYYz5lzFmi4h8A0QD6cBoY0yGjTmdbvWHq8lIzaDjYx3tjlJ29ex54bRbbrG6oU5OhmuvvXD+iBEwYgQSH2+dT5+TYwyJixk9ejQtW7bk6aefzjV9zJgxPPbYY3Tt2pX9+/fTv39/tm7dSpcuXVi6dCmhoaHUrVuXJUuWMHz4cFasWMFHH33Eyy+/zJo1a3j//fcBePjhh2ndujU//vgjc+fOZfjw4WzYsAGAbdu2ERkZSWJiIo0aNWLUqFF4enoWKre6RJ6ecNNN1i06GhISrOknTlh/Q3ffDbfdBn5+9ua8RLYXCmNMvg3KxpgJwIT85pdmaWfSWPPhGhoObEhwo+CLv0CVKoGBgQwfPpzJkyfn6gl2wYIFREdHZz9OSEggMTGRbt26sXjxYkJDQxk1ahRTpkzh4MGDVKxYMc+26L///pvvvrMO1/Xo0YP4+PjsYwvXXXcd3t7eeHt7U7lyZY4cOULNmjUvWIYqJk2bnru/f781mNJ998GTT1oFY9QoaNDAvnyXwPZCcaXa+MVGko8l0/nJznZHKdsK2gPw8ytwvqlUqdB7EHl59NFHadOmDXfffXf2tMzMTJYvX35BN+Ldu3fngw8+YP/+/UyYMIEffviB2bNn061bt7yz5XESimOPHO8cg/W4u7vraHl2atUKNm2Cv/+2zpz6z3/g3Xdh715rvIxSwvZjFFcik2lYMXEF1dtVp3a30vPHooqmYsWK3HLLLUydOjV7Wr9+/bKbj4Ds5qJatWpx7Ngxdu7cSd26denatSvvvPNOdqEICAggMTEx+3Xdu3dnxowZACxZsoTg4GACAwNL4FOpIhOBbt3g66+tQZQ+//xckXj0UZgwweqc0IVpobDBjrk7iN8RT6cnO2V/C1Rl0xNPPMGxY8eyH0+ePJk1a9bQsmVLmjZtyscff5w976qrrqJhw4aANXb2wYMH6dq1KwC9evUiOjo6+2D2+PHjs5fz4osvMm3atJL9YOrSVK1qDd8KkJEB27dbXYbUqgW33w5Ll7pkdyHa9GSDlZNXElgrkKZDm178yarUSUpKyr5fpUoVkpPPncwXHBzMrFmz8nzdl19+mX2/c+fOZObokK5ixYqsPq/7iDlz5gC5R+IbP358rudERUVd2odQxc/d3ep4cNs2+Phja0/j669h0iRrT8OF6B5FCTu27Rh7Fu6h3ah2uHno6lfqite4sXXc4uBBmDLFOnMKYP58a1jXbdtsjQdaKErc6o9W4+7lTpt7tbsOpVQO/v5w//2QdYba5s3WnkaTJtaQrjbSQlGCziadZePnG2l6c1P8K+sFdkqpAjz55LmD33Xr2hpFC0UJ2vzVZlITUmn/YHu7oyilSoPKlcEFRjzUQlFCjDGs/mA1VVpVoWYnvfhJKVV6aKEoIQeWHeDIpiO0H91eT4lVSpUqWihKyJoP1+Ad6E2L21vYHUUVs7y63Bg/fjwiwq5du7KnTZo0CRFhzZo1JRlPqSLTQlECko4kseXbLbQa0Qovfy+74yibtGjRgpxjpcyePZumTfVaGuX6tFCUgPVT15OZlqkHsa9wQ4YMyb5Ibvfu3QQFBRESEmJzKqUuTq/MLmYm07B2ylrq9K6jvcTa4DJ6GSc+Xi61l/E8BQYGUqtWLaKiopgzZw633norn3322aUvUKkSonsUxWzPn3s4te8Ure9rbXcU5QKGDRvGzJkz+fHHH7mhjA1uo8ou3aMoZus/XY9PeR+a3NDE7ihXpMvoZZxKlcxl7UHkZeDAgTz11FO0a9dOe3tVpYYWimJ05sQZtn6/lTb3tcHDR1e1Al9fX958883sXmKVKg1061WMNn+1mYzUDFrfq81OV5Lk5ORcI8o9/vjjueYPGzaspCMpdVm0UBSjDZ9uoGp4Vaq1rmZ3FFWCcnYPfjGLnN22pVQx0IPZxeTwhsPErovVvQmlVKmnhaKYrP90Pe7e7noltlKq1NNCUQzSU9LZNH0TTW5ogm9FX7vjKKXUZdFCUQy2zdlGyokUwu8JtzuKUkpdNi0UxWD91PUE1Q6i7tX2DjailFLOoIXCyRIOJrB7wW5ajWiFuGl34kqp0k8LhZNFfR0FBlre0dLuKMomEyZMoFmzZrRs2ZLw8HBWrlzJu+++S3Jysq25Tp48yYcffmhrBlU6aaFwss0zNlOjQw0qNahkdxRlg+XLlzN37lzWrVvHpk2bWLBgAbVq1dJCoUo1LRROdHTLUQ5vOEyLCD0l9koVGxtLcHAw3t7eAAQHBzN79mwOHTpEr1696NWrFwC///47nTp1ok2bNtx8880kJSUBsHbtWnr06EHbtm3p378/sbGxAPTs2ZNHH32Uzp0707x5c1atWgXA6dOnefDBB2nfvj2tW7fO7sZ8y5YtdOjQgfDwcFq2bMnOnTsZO3Ys//zzD+Hh4Tz11FMlvWpUKaZXZjvR5hmbEXeh2a3N7I6iHHp+3vOCabc0u4UH2z9Icloy1864sJ/xEeEjGBE+gvgz8Qz8Lnc/44tGLCrw/fr168fLL79Mw4YN6dOnD7feeiuPPPIIEydOJDIykuDgYI4dO8arr77KggUL8Pf3580332TixImMGzeOhx9+mDlz5hASEsKsWbN49tln+fTTTwGrKCxbtozFixdzzz33EBUVxYQJE+jevTtffvklJ0+epEOHDvTp04ePP/6YMWPGEBERwdmzZ8nIyOCNN94gKiqKDRs2XOrqVFcoLRROYjINm2dspl7fepSrcuFQmOrKUK5cOdauXcuSJUuIjIzk1ltv5Y033sj1nBUrVhAdHU2XLl0AOHv2LJ06dWL79u1ERUXRt29fADIyMqhW7Vz3L7fddhsA3bt3JyEhgZMnT/L777+TnJzMBx98AEBKSgr79++nU6dOTJgwgZiYGG688UYaNGhQEh9flVFaKJxk/9L9nNp/it6v9bY7isqhoD0AP0+/AudX8q100T2IvLi7u9OzZ0969uxJixYtmDZtWq75xhj69u3L119/nWv65s2badasGcuXL89zuSJywWNjDNOnT6dNmza55jVp0oSrrrqKX375hf79+/PJJ59Qt66erq0ujR6jcJJN0zfh6edJ48GN7Y6ibLR9+3Z27tyZ/XjDhg2EhoYSEBBAYmIiAB07dmTp0qXs2rULsHqb3bFjB40aNSIuLi67UKSlpbFly5bsZc2aNQuAv//+m6CgIIKCgujfvz8ff/wxxhgA1q9fD1hDrdatW5dHHnmEQYMGsWnTplwZlCoK3aNwgvTUdKK/jabxDY3xKudldxxlo6SkJB5++GFOnjyJh4cH9evXZ8qUKXz99ddcc801VKtWjcjISD7//HNuu+02UlNTAXj11Vdp2LAhs2fP5pFHHuHUqVOkp6fz6KOP0qyZdcyrQoUKdO7cmYSEhOzjFs8//zyjR4+mZcuWGGMICwtj7ty5zJo1i+nTp+Pp6UnVqlV54YUXqFixIl26dKF58+Zcc801vP3227atJ1W6aKFwgl2/7SLlRIqe7aRo27Yty5Ytu2D6ww8/zMMPP5z9uHfv3qxevfqC54WHh7N48eI8lz106FBef/31XNN8fX157733CAgIyDV93LhxjBs37oJlfPXVV4X6HErlpE1PTrB5xmb8Qvyo17ee3VGUUsrpXKZQiMiTImJEJDjHtHEisktEtotIfzvz5SflVArbf95O82HNcfNwmdWpyphFixbRrl07u2OoK5RLND2JSC2gL7A/x7SmwDCgGVAdWCAiDY0xGfakzNv2n7aTkZpB89ua2x1FKaWKhat8BZ4EPA2YHNMGAzONManGmD3ALqCDHeEKEv1tNIG1Aql5Vc2LP1kppUoh2/coRGQQcNAYs/G888RrACtyPI5xTMtrGSOBkQBVqlRx+jjESUlJeS4zPSmdnfN2Un1wdf5a/JdT3/NS5JfT1RRnzqCgIKedApqRkVEqTid1Zs6UlJRi+92Uhr/P0pARSj5niRQKEVkAVM1j1rPAM0C/vF6WxzSTxzSMMVOAKQDt2rUzPXv2vLSg+Vi0aBF5LXPT9E2YNEP/x/tTq1Mtp77npcgvp6spzpxbt2694AygS5WYmOi0ZRUnZ+b08fGhdeviGee9NPx9loaMUPI5S6RQGGP65DVdRFoAdYCsvYmawDoR6YC1B5Fz61sTOFTMUYtkyzdbCKypzU5KqbLN1mMUxpjNxpjKxpgwY0wYVnFoY4w5DPwEDBMRbxGpAzQAVtkYN5eUUyn8M/8fmtzURAcoKsVmzJhBWFgYbm5uhIWFMWPGDLsjKeVyXOVg9gWMMVuAb4BoYB4w2pXOeNrx8w4yzmbQ7GbtKba0mjFjBiNHjmTfvn0YY9i3bx8jR450SrHo1asXf/zxBwDPPfccjzzyyGUvUym72H4wOyfHXkXOxxOACfakKVj0t9FWs1NHbXYqrZ599tkLBhNKTk7m2WefJSIi4rKW/dJLL/HCCy9w9OhR1q9fz08//XRZy1PKTi5VKEqL1IRUds3fRbtR7bTZqRTbv39/kaYXRffu3THGMHHiRBYtWoS7u3v2IENeXl707NnzsouRUiXFZZueXNn2n62L7LTZqXSrXbt2kaYXxebNm4mNjcXb2zv7jKTvv/+em266if/973+6h6FKFS0UlyD622gCagRos1MpN2HCBPz8/HJN8/PzY8KEy2vtjI2NJSIigjlz5uDv78/8+fMBiImJoVYt60Q+d3f3y3oPpUqSFooiSk1IZde8XTS9qak2O5VyERERTJkyhdDQUESE0NBQpkyZcllNQsnJydx44438+9//pkmTJjz//POMHz8egJo1axITEwNAZmamMz6CUiVCj1EU0Y5fdpCRmkHTm5vaHUU5QUREhFOPFfj5+eUaoa579+7Zj2+88UYeeughfvnlFwYOHJjfIpRyOVooimj7j9vxr+LvEldiq9LF39+fzz77zO4YShWZNj0VQXpqOjt/20mjQY202UkpdcXQQlEEeyP3cjbxLI2H6LjYSqkrhxaKItj24zY8/T2p07uO3VGUUqrEaKEoJJNp2P7Tdhpc0wAPHz2048qMybOTYXURut5UfrRQFNLB1QdJik2i0ZBGdkdRBfDx8SE+Pl43ekVkjCE+Ph4fHx+7oygXpF+NC2n7nO2Iu9Dg2gZ2R1EFyLpWIS4u7rKXlZKSUio2nM7K6ePjQ82aehGpupAWikLa9uM2wnqG4VvB1+4oqgCenp7UqeOcY0iLFi0qtkF8nKm05FSllzY9FULygWSObT1Go8Ha7KSUuvJooSiE+KXxADQerKfFKqWuPFooCuHY38eo2roqQbWD7I6ilFIlTsra2SEiEgfsc/Jig4FjTl5mcdCczqU5nas05CwNGaF4coYaY0LymlHmCkVxEJE1xph2due4GM3pXJrTuUpDztKQEUo+pzY9KaWUKpAWCqWUUgXSQlE4U+wOUEia07k0p3OVhpylISOUcE49RqGUUqpAukehlFKqQFoolFJKFUgLRSGJyCsisklENojI7yJS3e5MeRGRt0VkmyPrDyJS3u5MeRGRm0Vki4hkiohLnY4oIgNEZLuI7BKRsXbnyY+IfCoiR0Ukyu4s+RGRWiISKSJbHb/vMXZnyouI+IjIKhHZ6Mj5kt2Z8iMi7iKyXkTmltR7aqEovLeNMS2NMeHAXOAFm/Pk5w+guTGmJbADGGdznvxEATcCi+0OkpOIuAMfANcATYHbRKSpvany9TkwwO4QF5EOPGGMaQJ0BEa76PpMBXobY1oB4cAAEelob6R8jQG2luQbaqEoJGNMQo6H/oBLngVgjPndGJPueLgCcMl+o40xW40x2+3OkYcOwC5jzG5jzFlgJjDY5kx5MsYsBo7bnaMgxphYY8w6x/1ErA1cDXtTXchYkhwPPR03l/sfF5GawHXAJyX5vlooikBEJojIASAC192jyOke4De7Q5QyNYADOR7H4IIbttJIRMKA1sBKm6PkydGkswE4CvxhjHHFnO8CTwOZJfmmWihyEJEFIhKVx20wgDHmWWNMLWAG8JCr5nQ851ms3f4ZrpzTBUke01zum2VpIyLlgO+AR8/bO3cZxpgMR9NyTaCDiDS3OVIuInI9cNQYs7ak31sHLsrBGNOnkE/9CvgFeLEY4+TrYjlF5C7geuBqY+OFMkVYn64kBqiV43FN4JBNWcoEEfHEKhIzjDHf253nYowxJ0VkEdbxH1c6UaALMEhErgV8gEARmW6MuaO431j3KApJRHKOgToI2GZXloKIyADg/4BBxphku/OUQquBBiJSR0S8gGHATzZnKrVERICpwFZjzES78+RHREKyzhAUEV+gDy72P26MGWeMqWmMCcP6u/yzJIoEaKEoijcczSabgH5YZx64oveBAOAPx6m8H9sdKC8icoOIxACdgF9EZL7dmQAcJwI8BMzHOvD6jTFmi72p8iYiXwPLgUYiEiMi99qdKQ9dgDuB3o6/xw2Ob8SuphoQ6fj/Xo11jKLETj91ddqFh1JKqQLpHoVSSqkCaaFQSilVIC0USimlCqSFQimlVIG0UCillCqQFgqllFIF0kKhlFKqQFoolCoBjjEZ+jruvyoik+3OpFRhaV9PSpWMF4GXRaQyVg+qg2zOo1Sh6ZXZSpUQEfkLKAf0dIzNoFSpoE1PSpUAEWmB1Z9QqhYJVdpooVCqmIlINaxxQQYDp0Wkv82RlCoSLRRKFSMR8QO+xxo3eivwCjDe1lBKFZEeo1BKKVUg3aNQSilVIC0USimlCqSFQimlVIG0UCillCqQFgqllFIF0kKhlFKqQFoolFJKFej/AQf2crCsfMHbAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"calc_step(0,1E-2)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.2.4 Consider $x_0 = 0$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.2.4-Consider-$x_0-=-0$)",
"section": "3.6.2.4 Consider $x_0 = 0$"
}
},
"source": [
"**Discussion**\n",
"* Why does $f(x)$ increase for all of the steps?\n",
"* Explain Newton-type method in the context of root finding for $\\nabla f(x) = 0$ using the second plot."
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.2.5 Descent Properties](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.2.5-Descent-Properties)",
"section": "3.6.2.5 Descent Properties"
}
},
"source": [
"### 3.6.2.5 Descent Properties\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.6.3 Line Search](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3-Line-Search)",
"section": "3.6.3 Line Search"
}
},
"source": [
"## 3.6.3 Line Search"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.6.3 Line Search](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3-Line-Search)",
"section": "3.6.3 Line Search"
}
},
"source": [
"Excerpts from **Section 3.4** in Biegler (2010)."
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.6.3 Line Search](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3-Line-Search)",
"section": "3.6.3 Line Search"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.6.3 Line Search](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3-Line-Search)",
"section": "3.6.3 Line Search"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.6.3 Line Search](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3-Line-Search)",
"section": "3.6.3 Line Search"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.6.3 Line Search](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3-Line-Search)",
"section": "3.6.3 Line Search"
}
},
"source": [
"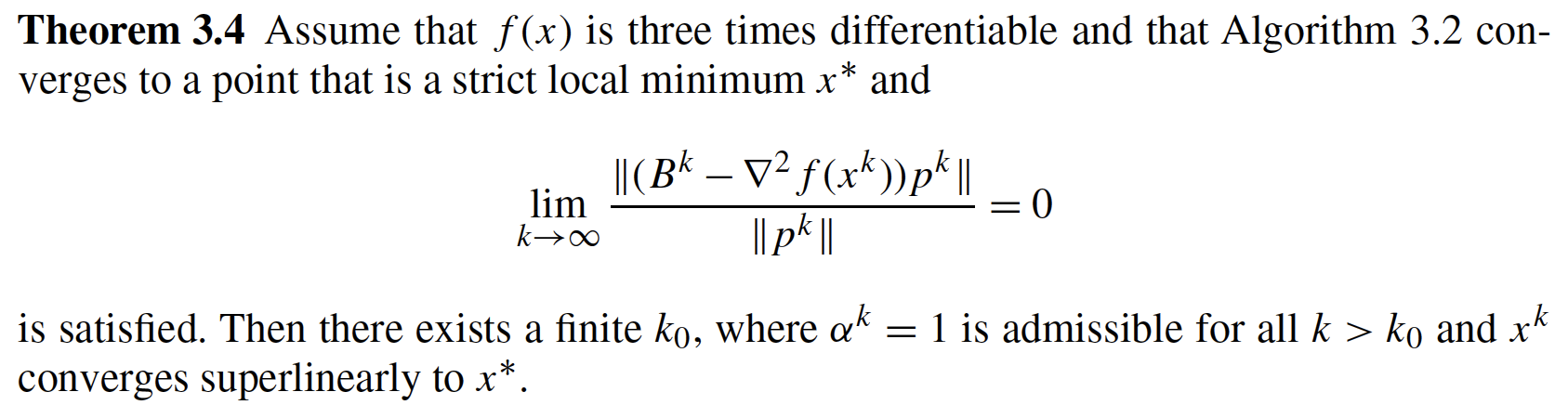"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.1 Visualization Code](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.1-Visualization-Code)",
"section": "3.6.3.1 Visualization Code"
}
},
"source": [
"### 3.6.3.1 Visualization Code"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.1 Visualization Code](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.1-Visualization-Code)",
"section": "3.6.3.1 Visualization Code"
}
},
"source": [
"**Goal**: Visualize Amijo and Goldstein conditions for an example."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.1 Visualization Code](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.1-Visualization-Code)",
"section": "3.6.3.1 Visualization Code"
}
},
"outputs": [],
"source": [
"def plot_alpha(xk,eta_ls=0.25,algorithm=\"newton\",alpha_max=1.0):\n",
" '''\n",
" Calculate step and visualize line search conditions\n",
" \n",
" Arguments:\n",
" xk : initial point (required)\n",
" eta_ls : eta in Goldstein-Armijo conditions\n",
" algorithm : either \"newton\" or \"steepest-descent\"\n",
" alpha_max : plots alpha between 0 and alpha_max\n",
" \n",
" Returns:\n",
" Nothing\n",
" \n",
" Creates:\n",
" Plot showing function value and line search conditions as a function of alpha\n",
" '''\n",
" \n",
" fxk = f(xk)\n",
" dfxk = df(xk)\n",
" \n",
" if(algorithm == \"newton\"):\n",
" pk = - dfxk / ddf(xk)\n",
" elif algorithm == \"steepest-descent\":\n",
" pk = - dfxk\n",
" else:\n",
" print(\"algorithm argument must be either 'newton' or 'steepest-descent'\")\n",
" \n",
" print(\"Considering xk =\",xk,\"and f(xk) = \",fxk)\n",
" print(\"Step with\",algorithm,\"algorithm:\")\n",
" print(\"pk = \",pk)\n",
" print(\"With full step, xk+1 =\",pk + xk,\"and f(xk+1) =\",f(xk + pk))\n",
" \n",
" n = 100\n",
" alpha = np.linspace(0,alpha_max,n)\n",
" fval = np.zeros(n)\n",
" \n",
" for i in range(0,n):\n",
" fval[i] = f(xk + alpha[i]*pk)\n",
" \n",
" fs = 18\n",
" plt.figure()\n",
" \n",
" # Evaluate f(x^{k+1}) for different alpha values\n",
" plt.plot(alpha,fval,color=\"blue\",label=r\"$f(x^{k+1})$\")\n",
" \n",
" # Armijo condition\n",
" arm = np.zeros(n)\n",
" for i in range(0,n):\n",
" arm[i] = fxk + eta_ls*alpha[i]*dfxk*pk\n",
" \n",
" plt.plot(alpha,arm,color=\"red\",label=\"Armijo\")\n",
" \n",
"\n",
" # Goldstein condition\n",
" gold = np.zeros(n)\n",
" for i in range(0,n):\n",
" gold[i] = fxk + (1-eta_ls)*alpha[i]*dfxk*pk\n",
" \n",
" plt.plot(alpha,gold,color=\"green\",label=\"Goldstein\")\n",
" \n",
" # Apply backtracking linestep (starting with alpha = alpha_max)\n",
" i = n - 1\n",
" flag = True\n",
" failed = False\n",
" while flag:\n",
" \n",
" if i < n-1 and fval[i] < gold[i]:\n",
" flag = False\n",
" print(\"Line search failed. Goldstein conditions violated. Consider increasing alpha_max.\")\n",
" failed = True\n",
" \n",
" # Armijo condition\n",
" if fval[i] < arm[i]:\n",
" flag = False\n",
" else:\n",
" i = i - 1\n",
" \n",
" if i < 0:\n",
" print(\"Line search failed. Try decreasing alpha_max.\")\n",
" failed = True\n",
" \n",
" if not failed:\n",
" print(\"alphak =\",alpha[i],\"with backtracking line search starting at alpha =\",alpha_max)\n",
" print(\"f(xk + alphak*pk) =\",fval[i])\n",
" \n",
" plt.scatter(alpha[i],fval[i],marker='x',color='black',label=r\"$a^{k}$ for line search\")\n",
" \n",
" # Labels\n",
" plt.xlabel(r\"$\\alpha^k$\",fontsize=fs)\n",
" plt.ylabel(r\"$f(x^k + \\alpha^k p^k)$\",fontsize=fs)\n",
" plt.grid()\n",
" plt.legend()\n",
" plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.2 Newton Step, $x^k = -3$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.2-Newton-Step,-$x^k-=--3$)",
"section": "3.6.3.2 Newton Step, $x^k = -3$"
}
},
"source": [
"### 3.6.3.2 Newton Step, $x^k = -3$"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.2 Newton Step, $x^k = -3$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.2-Newton-Step,-$x^k-=--3$)",
"section": "3.6.3.2 Newton Step, $x^k = -3$"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Considering xk = -3 and f(xk) = 15.0\n",
"Step with newton algorithm:\n",
"pk = 0.796875\n",
"With full step, xk+1 = -2.203125 and f(xk+1) = -8.660857647657394\n",
"alphak = 1.5 with backtracking line search starting at alpha = 1.5\n",
"f(xk + alphak*pk) = -11.1743426900357\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZYAAAESCAYAAADe2fNYAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAABQP0lEQVR4nO3dd3yN1x/A8c9JhJDYe69aGRJCxKb2KGrVaFEzqKLVomoVVVXzZ6+aNWpWadXepLaIWbWqVVI7YsT5/XESSRAybnJv4vt+vZ7Xzb3Pc5/7veHme89zzvkepbVGCCGEsBQ7awcghBAiaZHEIoQQwqIksQghhLAoSSxCCCEsShKLEEIIi5LEIoQQwqKSWTsAW5ApUyadL1++WD33/v37ODk5WTYgC7L1+MD2Y7T1+EBitARbjw9sK8aDBw/e0FpnfulOrfUbv3l5eenY2rp1a6yfmxBsPT6tbT9GW49Pa4nREmw9Pq1tK0bggI7ib6pcChNCCGFRkliEEEJYlCQWIYQQFiWJRQghhEVJYhFCCGFRkliEEEJYlCSWOJAVB4QQ4kUyQTKWgoKeUKN7DmrcKUTlq91RZctCvnyglLVDE0IIq5LEEkuXLlzknkMwQ4vvwW/9HqZ1gzzJM0OZMuDjY25Ll4a0aa0dqhBCJChJLLFU1KUgu8bepGSnr9lQ4GuK9NB8d6sgXTedxe7nn81BSoGLi0kyYZurKySTX7sQIumSPpY4SO1sz/ROFenw+CTBFyvxUaZ9VPw0C2f+8IMNG2DoUMibF9asgS5dwNMT0qWDKlWgb19YtQquXrXyuxBCCMuSr85xZGcHM77NR8lpG+g2Yx776vTGfVFFvqo6lE8H9CeZXTLTy3/+POzbB/v3m9tx4+DxY3OS3LnDL5+VKQNeXpAypXXfmBBCxJIkFgvx9VUULNiOJm1r86h6d/o97ceygGXMaTAHj2weULCg2Vq3Nk8IDobDh02iCUs2P/5o9iVLBsWLhycbHx8oVEgGBgghEgVJLBZUowbs35yN+vVXcOnoCv5o1p1SM0vRt3xfvqz0JY7JHMMPdnSEsmXNFubatfAks38/LFgAU6aYfenTg7d3eLLx9oaMGRP2DQohRDRIYrGwYsVMTmjSpAk7vq6K+2e9GbFzBCtOrmB2g9mUy10u6idnzQoNGpgNICQETp6M3KoZNgyePjX7CxWKfAmteHFInjz+36QQQryCJJZ4kCkTbNwI3btnYNZX8yjXphWXU3emwpwK9PDuwYhqI3BO7vz6E9nbg5ub2Tp0MI/dvQsHDoS3ajZuNC0bMK2gkiUjX0KTWZxCiAQmiSWeJE8OM2aY0cWfflqLYv7+fPD5F0z0m8hPZ35iRv0Z1ChYI+YnTp0aqlY1G5jEcelS5FbNlCkwdiwAZTNkgIoVw5NNqVLmHEIIEU8kscQjpaBXLzOV5b33UnPto/8xcdZ7TL7ckZoLa/Kh54eMqTmG9CnTx+1F8uY1W/Pm5rHHj+HYMdi3j5tr1pAtIMAMeQYzjM3VNfJEzmLFTOtICCEsQBJLAqhZ0zQmGjSAT5pW4LvxR/in/FeM3vMtv5z7hcl1J9O4WGPLvaCDgxmy7OXFKVdXslWpAv/9B35+pkWzbx+sWAGzZpnjU6c2VQIiJpusWS0XjxDijSKJJYEULmySS+vW0OsjRzp2/JrdXzbD99f2NFnWhCbFmjCp7iSyOWeLnwAyZIDatc0GZgDA2bPhl9D274fRo+HJE7M/b97IfTUlSpg+HCGEeA1JLAkobVpzRWrwYBgxAk6cKMHqZX788Od3DN0+lC1/bmFcrXG08WiDiu85K3Z2UKSI2dq0MY89eACHDoW3avbsgaVLzT4HB1M5IGwEmo+PmZcjc2uEEM+Rki4JzN4ehg83cyGPHQOf0g5UsuvPUd+juGZxpd2adtReVJsLty4kfHApU0L58vDppybAS5dMyZmVK+GTT8DJCb7/Hj74wAx1zpwZ6tWDr76C336DW7cSPmYhhM2RFouVNG0KRYvCu++aAV4TJhRhW5ftTDswlX6b++E2xY2R1UbS3bs7dsqK+T97dhPku++a+0+ewIkTkUeh/fJL+LDmIkUiX0Jzd5eim0K8YeQTb0VubvD77/D++9CtG+zfb8fUqd2pX7g+XX7uwse/fszSE0uZ1WAWRTMVtXa4RrJk4OFhts6dzWN37pg3Eja3Zv16mDfP7EuZ0gxxjngJLVcu68UvhIh3klisLF06+OknM6F+6FA4ehRWrszLL61/YcGxBfT6tRee0zwZXHkwfcr1wcHewdohvyhNGqhWzWxgWi8XLkQuTzNxIjx6ZPbnyGESTGjLxu7BA6uFLoSwPEksNsDOznToly5tRo15ecGCBYo29dpQq2AtPvrlI77Y8sWzopYlspewdsivphTkz2+2Fi3MYw8fmqwZ8RLaypUAVLSzM5fMIpanKVrU/GKEEIlOov3kKqXmKKX+VUr5R3gsg1Jqo1LqbOhtHGYeJry6deHgQTPSt359+PJLyJQyKz82+5EVzVfwz71/KD2zNF9s/oLgJ8HWDjdmUqQwhTN79ICFC+HcOfj3X/j5Zy62bg1ZssCSJdC+vZnAmSGDmQA0cCCsWwc3blj7HQghoinRJhZgLlD7ucf6AZu11oWAzaH3E5UCBcwo3w4dzJDkWrVM0ePGxRoT0C2ANh5tGLlrJJ7TPNl1aZe1w42b0FFlF9q3N6PK/vsPAgJgzhzT0rl+Hb7+2mTZzJnN8OZWrcxltf37TStICGFzEm1i0VrvAP577uGGQGivMfOARgkZk6WkTGkmxc+eDbt3m7mJO3ZA+pTpmdNwDr+9/xsPQx5S8fuKfLT+I+4+vGvtkC3Dzs6Ul/nwQ5g2zaxXc+cObN8O335r5tHs2AE9e5rLZmnSmNtevWDxYvjzTym6KYQNSLSJJQpZtdZ/A4TeZrFyPHHSvr3pinB2NkOSv/nGTJivUbAGx7se52Pvj5ny+xTcprqx4dwGa4cbP5ycoFIl+OwzU4bmyhW4fNnMs/n44/Bqn61ameZe1qzwzjumubd5s0lMQogEpXQi/oanlMoH/Ky1dgu9f0trnS7C/pta65f2syilOgOdAbJmzeq1ZMmSWMVw7949nJ2jUQI/Du7ft+e774qwbVsWypQJpF+/U6RLZ5Y1PnH7BKPPjOZi0EVqZq1Jt4LdSOuQNkHji6u4xqhCQnD680/SBAQ821JdvgyAVoqgPHm44+LCnWLFuFOsGEH586NjUHTzTfgdJgRbj9HW4wPbirFq1aoHtdalXrpTa51oNyAf4B/h/mkge+jP2YHT0TmPl5eXjq2tW7fG+rkx8fSp1lOmaJ0ihdY5cmi9fXv4vuDHwfrLzV/qZF8l01lGZ9HL/Jfpp0+fJmh8cREvMf73n9YbNmg9dKjWdetqnTGj1uZCmdZOTlpXrqx1375ar1yp9dWrCR+fhUmMcWfr8WltWzECB3QUf1OT2qWwn4C2oT+3BdZYMRaLUgq6djWXxpyczKWxYcPMIpMpkqVg2NvDONDpALnT5Kb58uY0WdaEv+/+be2wrSd9ejOqbNAgM6rs+nVTdHPhQnONMSjIrFnTuLGZV5MnDzRrBmPGwK5dpm6aECJWEu08FqXUYqAKkEkpdQUYDHwDLFNKdQAuAc2sF2H88PQ0Q5J9fc3fzC1bYNEi87fRI5sH+zruY9zecQzaNgiXKS50ytOJyrpy/Be1tHVKwVtvma11a/NYcLAZIBBxbs3y5WZfWIWBMmXImiaNKW1TqJDMrREiGhJtYtFat4xiV7UEDcQKUqc2X7xr1IDu3c3fv++/N6Nyk9kl47Pyn9GwaEM6re3E6DOjObzwMDPqzyB/+vzWDt22ODpC2bJmC3PtWuR1axYsoNjdu2bkRPr0Zi5OWGkab2/ImNF68Qtho+TrVyKlFLRrZ1ovOXOagVAff2y+hAMUzliYrW230rtQb/Zf2Y/bVDcm7JtAyNMQq8Zt854fVXbzJn5z5pjx302bmmrPw4eb2ayZMpmFdj74ACZPhgMHwsvWCPEGk8SSyBUtar5Y9+wJ//uf+RJ94oTZZ6fsaJCjASe6naBKvir02tCLit9XJOB6gHWDTkzs7QnKn9/MWJ0xw6x1cOuWuQY5cqRZd3rTJvjoI1OTJ00as/TAJ5+YtWwuXpS5NeKNI4klCXB0hPHjTR/1P/+YYsKTJoX/PcudNjc/t/yZhe8u5EzgGUpML8Gw7cN4HPLYqnEnWqlTm9ET/frB6tWmFXPxokkk3bub5uTUqaZ6QL58pgOsUSOTiLZuhbtJZEKrEFFItH0s4kV168Lx42bieo8eZpmUDh1MNWSlFK2Lt6ZGwRp8/MvHDNo2iOUnlzOnwRy8cnhZOfJETikzqixPHmje3Dz26JH5xwir7rx/v1k+FMwAAFfX8L6aMmVMxYEYzK0RwpZJiyWJyZrVtFz+9z9ztaZ9+9LP/p4BZHHKwpKmS1jTYg3X71/He5Y3fTf25cFjGV5rUcmTmzLV3bvD/Plw+rQppLl+vSmsmTOnqSTQsaOp7Jw+vVl24IsvTAL65x9rvwMhYk0SSxKklLnkf/AgZM78kEaNzN+viFdgGhRpQED3AD70/JBv93yLxzQPtl/YbrWY3wgZM0KdOjBkiGlOBgaahDN/vhkAcOsWjB5tLptlz24uo7VoAePGwd694SMzhLBxkliSMBcXmDLlEP37m4LBHh6wc2f4/nSO6ZjVYBabPtjEk6dPqDKvCl1/7sqdh1JfK0EoFXlU2cGDprbZrl3w3XdmJMbevWYgQLlyZmBA6dLmOueiRWbpARkYIGyQJJYkzsFB8/XXpiiwUlC5sqnnGPHLb7UC1Tje9Ti9fXoz/eB0XKe4sv7seusF/SZLmdKMKvv0U1i2zAwKuHoVVq0yjzk7m0lL779vJmyGLj2Qd948s/TArVvWfgdCSGJ5U1SoYBZw7NzZfBn28jJfkMM4JXdibK2x7OmwhzQp0lDvh3q8v/J9bgTJAltWlz175FFlt2+bf8zp06FhQ7h4kXzz5pnFe9KnN2PQ27UzI9MOH4YnT6z9DsQbRhLLG8TZ2Sxzsn69+WJbpowpCxNxTp9PLh8OdT7EoEqDWHpiKcUmF2OJ/5KwIp/CFtjbQ/Hi5lvC7Nng78+utWvNfJoRI0xLZv166NYNSpY0l9DClh5YvtwsPSBEPJLE8gaqUwf8/U3JrGHDzKX8I0fC96dIloKhVYdyqPMh8qXLR8sVLWm0tBF/3fnLajGLVwtxcgofVbZ2rSlNc/68WQCtSxd4/NisvNmsGeTObUalNW5sFlDbsQPu37f2WxBJiCSWN1T69DBvnpnfd+2a6RMePDhy68U9qzt7O+xldI3RbPxjIy5TXJh5cKa0XhIDpSB//sijyu7eNXXQJk6EKlVMFYG+fU3HW9q0psKpr6/pwzl50qwqJ0QsSGJ5wzVsaErAtGwJX31lZu3//nv4/mR2yehTrg/Huh6jZPaSdP65M9XmV+OP//6wXtAidpInf3FU2b//ws8/m5ZOliymhdO+vRlSmCGDWXpg4EBzzPXr1n4HIpGQxCLIkMFMpVi71kyt8PGBzz+PvCTJWxneYnObzUyvP52Dfx/Efao7Y/eOlaKWiV3oqDK++sqMKrt5EwICTKulRQuTTEaONIU5s2SBggXNMtATJ5pqAg8fWvsdCBskiUU8U7++ab106GDm6RUvbgYhhbFTdnT26kxAtwCqF6jOp799Srk55fD/1996QQvLsrMz5WXatTMjPQ4fNqPQtm83/TElSpg+mZ49zTeQNGnMba9eprVz/rzMrRGSWERk6dKZIr6bN5tL7G+/DZ06mS+yYXKmycmaFmtY3GQx52+ep+T0kgzdNpRHIVIyPklycnpxVNnly+bnnj3NJbYZM0xLpmDByEsPbNpkEpN4o0gRSvFSb79taigOHWpW6127FiZMMDUWlTJFLVu4taB6ger0/LUnQ7YPeVbUsnTO0tYOX8S3XLnM1qSJuf/kiRlqGFZ0c98+0y8D5j9MsWIUyZPHlLDx8TFFOJPJn5+kSlosIkqpUsGoUWYgUa5c5pJ7/fpw4UL4MZlSZWJR40WsbbmWmw9u4jPbhz6/9SHocZDV4hZWkCzZi6PK/vsPNmww307y5SPTnj1mv6enGYVWpYpZemDVKlNdQCQZkljEa5Usab6Ajh1rLrW7uprL7Y8jLOdSv3B9TnQ7QaeSnRizdwzFpxZn659boz6pSPrSpw8fVbZuHbtXr4azZ8262h06QFCQ+U/VuLGZV5Mnj5ln8913pl5akHw5SawksYhoSZYMevc2A4aqVzfTH7y8YM+e8GPSOqZlWv1pbG1rEsrb89+my9ou3A6Wa+wCc0nsrbfMzNyJE01T+M4dM8dm3DhTI+3gQdOXU7GiGRjg5WUqCIQtPSBzaxIFSSwiRvLkMcuFrF5tysKUL2++fN6IUFKsSr4qHOt6jD5l+zDr8Cxcp7iy9vRaa4UsbJmj44ujyv75x/wn69vXtHoWLoS2bU0NtIwZoXZtM5v3l1/M5TZhcySxiFhp2NC0Xj7/3HyZLFLEDAwK+0KZyiEVo2uOZl+HfWRImYEGSxrQakUrrt+XSXbiNbJmhQYNwkeV3bxpBgbMmgVNm5r+mOHDzZKpGTOGLz0waRIcOBC5fISwijglFqVUYaXUu0qpLkqpzqE/F7JUcMK2OTubzv0jR8wiiF26mC+ffn7hx5TOWZoDnQ/wVZWvWB6wnGKTi/HD8R+kLIyIPnt707HXoQPMnGlK0dy6ZSZZjRxp9m3aZCoKlC5tLqGVK2fWsQlbekD+vyWoGCcWpVQxpdQEpdRV4CSwHJgKTAv9+ZRS6qpSarxSqphlwxW2yNXVfMYXLjTTG3x8zNyXsAogye2TM7DyQA53OcxbGd6i9crWvLP4HS7fvmzdwEXilTr1i6PKLl40iaR7d9OfM3UqvPeeWYkzR47ISw9EXE5VWFy0B5IrpQoCo4B3gQfATmAv8AcQCCggA/AW4AN0BHoopVYCfbXW5y0burAlSpk+2XfeMRWTx4838+eGDoWuXcHBAVyzuLK7/W7+5/c/BmwZgOsUV76t8S2FdWFrhy8SO6VMB2DYyDIwwxaPHQufW7N/v+m7AVNhwNXVrB3h42NuQ6Q8kaXEZIZSAHAcaAes1Fq/ss62UsoJaAp8HPpcx1jGKBKRNGlMOZj27U1/bM+epu9l/Hgzmszezp5ePr1oUKQBndd2puu6rnik9eDH4j9SKKNcRRUW5OBgRpV5eZlWDJjOfj+/8EmcK1aYvhugQqpUkRONj4/p7xExFpNLYc211qW01gtel1QAtNb3tdbztNZewHuxD1EkRsWKwa+/mtFjQUFQo4bp8D971uwvkL4AGz/YyOwGszl37xzFpxVn9O7RPHkqqx2KeJQhQ+RRZYGBZhjzvHlcq1HDDH8ePdpcNsuW7cWlByKu6S2iFO0Wi9Z6TWxfJC7PFYmXUiaZ1KplWiwjRpirDz16mDlz6dIp2pdoT5p/07Do1iI+3/Q5ywKWMbvBbIpnLW7t8MWbQCkzqqxwYc7myUPOKlVMWe9Dh8Ivoe3dC0uXmuMdHMDDI7xF4+Nj6qMpZdW3YWui3WJRSsknXcSKo6PpYz1zxowKHTfOzJObPNlcBs+UIhMrm69kWdNlXLp9Ca8ZXgzaOoiHT6Qku7CClCnNBK1PPw0fVXb1qhkk8OmnZjjk3LnmP3OhQpGXHtiwIXLF1jdUTC6FLVFKpX7+QaVUEQvGI5Kw7NnNEu2HDpmS/B99ZIYp796dEVA0c21GQLcAWrq1ZNiOYZScUZJ9V/ZZO2whzH/eiKPKbt2Co0dNB2LDhib5DBliLrNlyGAmc7ZrZ0amHT5sinS+QWKSWGYCCyI+oJSqCuywaEQiyfP0NGX5wwbofPmlO1WqmJUrM6bKyPx357O+1XruPrxLudnl6P1rb+4/kjXZhQ1Jlsx8O+rUyXxb8vc3yWbjRjN5s3Bh04fTrZsptpcmjSlT06ePGS55+XKSnlsT7cSitR4HhCil+gIopdoAS4D34yk2kYQpZSZXHz8OvXqd4eRJ8PY20w7OnYM6herg380f31K+jN8/Hvep7mw+v9naYQsRtTRpzNDHAQPgp59MaZrz502pmi5dTKvlf/8zw6Hz5DElwxs3NhVdt2+H+0nny9MrE4tSqrlSqqhSz3qmPgTaK6XmAUOBt7XWG+M7SJF0OThAw4ZXOXcufGn1YsXMZbIHt9Iwpd4UtrfbTjK7ZFRfUJ2OP3XkVvAta4ctxOsp9eKosjt3zICACRPMBM9jx0xNtCpVTGJ6fumBRFp083Wjwj4B3ACllAoAjgL7gBpAFa31mXiOT7wh0qQxfZ9du5pJldOmmf7R3r2hT59KHPU9ytDtQ/luz3esP7ueqfWm0rBoQ2uHLUTMpEhhmube3uGPXb8eeW7NkiUwfbrZlzatKVMTOrfGIZH01byyxaK19gFSA17AGOAGkBUzy/6kUuqsUmpZvEcZQ0qp2kqp00qpc0qpftaOR0Rf9uwmqQQEmIE2w4dDgQIwaXxKBpX7hv0d95PFKQuNljbiveXvce3eNWuHLETcRBxV9ttvZhJnQIBptbRsaUqHjxwJ77xD+XffNR+IVq3M0gP798ND2xs9+do+Fm2c0lov0Vr301rX1lpnB3JgZtUfjPcoY0ApZQ9MBuoALkBLpZSLdaMSMVW4sJk6cOCA+XL3+edmiPL+1V7savM7w6sOZ/Wp1bhMcWHB0QVS1FIkHXZ25npwxFFlt2/Djh380aULlCgBO3aYshY+Pqa57+Nj7octPWDlz0Osqxtrra9prX/RWo+yZEAW4A2c01qf11o/wgwwkGsmiZSXlxlcs2OHmYfWvTu4FnMg65kB/N7hCEUyFqHN6jbU+6Eel25fsna4QsQPJyeoWJHLLVqYMjRXrpiRZcuXm4SSIoUpTdOqlfmgZM1qCvcNH24qP99O2MX2YlIr7AVKqaxAcyAfcA84DPymtbbmmqI5gYhlc68AZawUi7CQihVNcvntN9PJ36kTFChQjC8G7KRZzckM3PoFrlNcGVV9FL6lfLFTstSQSOJy5TJbkybm/pMnZthzWLWA/fvNaBgwAwmKFTMVA8KqBri6mmHT8UDF9hKCUqoisB5IhelzCRMIDNNaT4x7eLGKqxlQS2vdMfT+B4C31rrHc8d1BjoDZM2a1WvJkiWxer179+7h7Owct6Djka3HBzGPUWvYuzcjc+fm4+zZ1OTI8YAGbfbwe7Z+HLx1gOJpi/Np4U/JkyqPVeKzBokx7mw9Poh5jMnu3SP1yZOkCdsCAnC4cweAEEdHbnl4cPybb2IVS9WqVQ9qrUu9dKfWOlYbsB+4C7QFcgF5MK2XfcBT4IfYnjsuG1AW2BDhfn+g/6ue4+XlpWNr69atsX5uQrD1+LSOfYxPn2q9Zo3WJUpoDVrnL/BUfzjhe53um3Q6xbAUeuTOkfpxyGOrxZeQJMa4s/X4tLZAjE+fan3unNYLF2rdo4fWvr6xPhVwQEfxNzUu1wvcgHHaVDC+orW+pLVeps1Isk7Ae0qpj+Jw/tj6HSiklMqvlEoOtAB+skIcIp6FTbI8eNDMR8uYQfF9z3Y4zz1JsWT16L+5P2VmleHIP0esHaoQtkEp0wfTurUZVTZ1ary8TFwSy13gpb2lWuvZmE5z3zicP1a01k+Aj4ANmBUul2mtTyR0HCLhKGX6Kf38YN06yJ0+G0f6ryDdb8s5+89flJ5Zmi+3fEnwEyl5LkRCiEti2QrUfc3+gnE4f6xprddrrQtrrQtqrUdYIwaR8JSCunVh927YsgVKOjbh7jcB2Pm3ZsTOERSfUoI9l/dYO0whkry4JJYZQDmlVM8o9ucDrsbh/ELEilJQtaopdLlvawbqPJwLC37l3IUgys+uwIfLenLv0T1rhylEkhWXxLIZs8b9WKXUNqXU+0qpYkqpQkqpjkBPzGx9IaymTBmziqX/mlq0+M8fdaA7cwP+R7av3Ji68TdrhydEkhSXxDIMM9z4MlAJmA/4A6eA6cBp4JZSyk0pFT+DpYWIJldX+GFuai5O/R/N7+8g6I4j3fbUIme3D1m+7qa1JyoLkaTEZeb9YK11I611PkzLpRrQB1gInACKh/58FLinlDqqlFoQ1fmESAi5c8PS0RX4a+ARqtj352rmBTTb6kLe2iuZM0eWNBfCEiwyPVlrfUtrvVVrPU5r3VZrXRxwBkphhh7PxIwie8cSrydEXGXP7MjWL79mX/vfyZMxO5fLNaHDhqbkKvoPgwebpTSEELETb2vea60faa0Paa3naK17aK0raK3TxThCIeJRmbwlOPf5fr5+eyQOrj9z5wMXvvppLrnzaD74wKxqKYSIGVnzXrzxHOwd6F+xH8e7HaVMAVdo9CE5PqvNyi0X8PaGbt1KsmiRTVYnF8ImyZr3QoQqkqkI29ttZ1KdSfznvAfV3Y0mo/7Hnbt2vP++WU12wAC4JEWUhXglWfNeiAjslB3dvbvj39WfinkrsuLBx6T/pCwzV53Cxwe++casNtuwIfz6a6JdOVaIeCVr3gvxEnnT5WV9q/XMbzSfS0GX6O7vQZk+X3P63GP69jUryNapYxYfGzlSOvuFiOh1LZZPgAOY4cK/A2MJX/O+ltTgEkmZUooPPD7g+9Lf07BIQwZsGUDTDaVp2uMQly+bFS7z5oUvvjDDmJs0Ma2YkBBrRy6EdSXJNe+FsKQMyTOwrNkyVjZfybX71/Ce6c2gHf14590HbN0Kp09D795mIbI6dcylskGD4M8/rR25ENaR5Na8FyK+vFvsXQK6BdDWoy2jdo/Cc7onOy/upHBh+PZb+Osv+PFHM8t/+HAoUACqVYOFCyHImmuqCpHAkuKa90LEm/Qp0zO74Ww2frCRRyGPqDS3Et3Xdefuw7skTw5Nm8Ivv8CFC/DVV+b2gw8gWzbo2BF27kTKx4gkL9aJRSn1niUDESIxqV6gOse7Hudj74+ZemAqrlNc+eXsL8/258kDAwfC2bOwbZvpf1myBCpVMussDRpk9gmRFMWlpMvc0PpfDV+2UymVVSlVKA7nF8KmOSd3ZkKdCexuvxvn5M7U/aEubVa1ITAo8NkxdnZQuTJ8/z1cuwbz55vEMnw4FC4MPj5mIb9r16z4RoSwsLgkloLANuAHpZSfUqrWc/tbYCodC5Gklc1dlsNdDvNlxS9Z7L8Ylyku/HjiR/Rz17ycnMxlsY0b4fJl0y8THAw9e0KOHFCzpklAt25Z530IYSlxSSxBwBPgIqbY5Hql1DGl1FallB9mFNlJC8QohM1LkSwFw94exoFOB8idJjfNlzen8bLGXL378rXucuaEzz6DI0fA3x/694dz56B9e8iaFd59FxYvhrt3E/Z9CGEJcUksM4FewH+Y8viLgL+BypjhyRuAJnGMT4hExSObB/s67mNU9VH8eu5XXCa7MPvQ7BdaLxGFjSL74w/Yvx+6dQM/P2jVCrJkCe+fkSQjEou4JJZqwMTQqsVtQrdaQBXgDKYVIwUvxBsnmV0yPi//Ocd8j+GRzYOOaztSY0ENzt88/8rnKQXe3jBunLlUtnMndOoEe/ZAy5aQOTM0amT6aW7eTJj3IkRsxHU9lhemgGmtd2CSyhVgThzPL0SiVShjIba23crUelPx+8sP96nujN83npCnr5+ab2cHFSqYjv2//jJJxtcXDh6Etm1NS6ZmTZg61ewXwpbEJbFsB95XSiV/fofW+j7mUlnJOJxfiETPTtnhW8qXE91OUDVfVXpv6E2F7ytw4t/oV0MKSzLjx8PFi+ZyWZ8+5udu3SBXLujatSQjRsDx4zJPRlhfXBLLV4AHsF0pVeol+8thOveFeOPlTpubtS3XsvDdhZwNPEuJ6SUYtn0Yj0Iexeg8dnbmctnIkXDqFAQEwNdfm31ffgnFi5sZ/z16wIYNstSysI64zLw/DLTDJJf9SqnTSqmFSqkJSqltQGvMcGQhBKaoZevirTnZ/SRNXJowaNsgSs0oxe9/xW6ZSqWgWDEzomzq1ENcvQozZ4KbG8yeDbVrQ8aMpsT/9OmyjoxIOHHqY9FaLwZcgUmAA9AK6AFUAn4HPoprgEIkNZmdMrO4yWLWtFhD4INAfGb78PnGz3nw+EGczps9uykbs3YtBAbCunWmP+bYMdM/kzevGYH26afw22/SmhHxJ66d92it/9Ra99RaFwAyYhJNTq21j9b6cpwjFCKJalCkAQHdAuhQogOj94ym+LTibL+w3SLnTpkS6taFKVPg/HlzyWzMGDN/ZvJkqFUL0qc3t2PGmOQji5YJS4lzYolIa31Ta31Sa/23Jc8rRFKV1jEtM96ZweY2m3mqn1JlXhW6/tyVOw/vWOw1wi6ZffKJaan8959pzXTpAleumIEAHh6mxdOyJcyaZZKRDAIQsWXRxCKEiJ2387/NMd9jfOLzCTMOzcB1iivrzqyLl9dKlcq0ZsaPhxMnTN/L99+b4cvbtpm5MwULmnVlPvwQ5s0zI9CEiC5JLELYCKfkToypNYY97feQNkVa6i+uz/sr3+dG0I14fd3cuaFdO1iwAK5eNZfNJk2CUqXgp5/Mvnz5zNa2rRkYcOaMtGhE1CSxCGFjyuQqw6EuhxhceTDLTiyj2ORiLPFf8sqyMJYSdtmse3dYvhyuXzf9LxMngpeXWWumY0coUsSsMdOkCYwda+bWPIrZyGmRhFkksSgjz8smSwohYi65fXKGVBnCoS6HyJ8uPy1XtKTR0kb8dSdhp9nb2YG7u5kXs2KFKe9/8qQZvly7timi+emnpvx/mjRmIudnn8HKlab1I95MlmqxZMCUd6lgofMJIQC3LG7s7bCXMTXHsPGPjbhMcWHmwZkJ0np5GaWgaFHo3Nn0vfzxh0kgy5ebVk5IiGndNGliRqDlzm1+/vZbOHw4HXcsNyZB2LBkFjyXsuC5hBCh7O3s+aTsJzQs0pBOazvR+efOLPZfzMx3ZlIwQ0Frh0f27CZ5NAmtZf7woWnJ7N1rqjT7+ZkWDHjyySfmMlqpUubSWsmSUKKEae2IpMOSiUUIEY8KZijI5jabmXVoFn029sF9qjvDqg6jl08va4cWSYoUUKaM2cLcuAFz5hzl0SMPfv/djD5btCh8/1tvmQTj6WmGPnt6msXPlHxdTZQSZWJRSjUDhgDFAG+t9YEI+/oDHYAQ4GOt9QarBClEPFBK0cmrE3UL1aXruq702diHZQHL8M3uSxWqWDu8KGXKBN7eN6lSJfyxa9dMtebDh8128CD8+GP4/owZTe2z4sVNP4+bG7i4QOrUCR6+iKFYJRalVKXnHkobeltcKRWp8GRoGX1L8wcaA9Ofi8sFsySyK5AD2KSUKqy1fn2dciESkZxpcrKmxRqWnVhGj1960PlqZy46XeSLil+Q3D5xjKHJmtXMp6lbN/yxO3fMKLQjR8ztsWOm/llQUPgxefOaBOPiYkawhW3p0yf4WxBRiG2LZRvwst7DMRF+VqHH2MfyNaKktT4J5tvbcxoCS7TWD4E/lVLnAG9gr6VjEMLalFK85/Ye1QpUo+W8lgzdPpTlAcuZ03AO3jm9rR1erISNLKsQYRjQ06dw4YJZwvn4cTPPJiAAtm6NXO8sSxbTf1O0qLktVMhsBQqYy3Mi4cQ2sVR97n46YBXwGXAwLgHFUU5gX4T7V0IfEyLJypQqEwOKDaBXtV74rvOl7Oyy9CrTi2FvDyOVQyprhxdndnYmORQoAA0ahD8eEmISzqlTZgj0yZNw+jSsWmX6dMIoBXnymH6ct94KP1eBAqa6gLR0LE9ZYtiiUiojcB2orrXeEucTmnNuArK9ZNcArfWa0GO2AX3C+liUUpOBvVrrhaH3ZwPrtdYrXnL+zkBngKxZs3otWbIkVnHeu3cPZ2fnWD03Idh6fGD7Mdp6fBAe4/0n95lxfgY//f0TORxz0KdwH0qkL2Ht8ICE/T3euZOMK1dS8tdfqbh8OSVXr6bkr7/M7Z07DpGOdXJ6QrZswWTKdI+cOZ+QNWswWbM+JEuWYLJkeUj69I+ws5Gp5Lb0f7Fq1aoHtdYvW4vLdjvvtdbVY/G0K0DuCPdzAS+dpqW1ngHMAChVqpSuErFXMQa2bdtGbJ+bEGw9PrD9GG09PogcYz3qsf3Cdjqu7cgnxz6hU8lOjK4xmrSOaV99kgSM0Zpu34Y//zRzcC5cgAsXkvHnn84EBMCJE87cuxf5+GTJzJycXLnMbY4c4bfZs4dvadLE/yg2S/0OtdaRuhKevx9XNptYYukn4Ael1FhM530hwM+6IQmR8Crnq8xR36MM3jqYsfvGsu7sOqbVm8Y7Rd6xdmhWlzatGc7s6Rn58W3bDlC5chVu3oTLl01xzkuX4K+/TBXoy5fN6LWff448mCCMo6MZkBC2ZckCmTOHb5kymS1jRrMlRCJ6mSFDhnDr1i3GjRuHUgqtNb179yZdunQMGTLEIq+RKBOLUupd4H9AZmCdUuqI1rqW1vqEUmoZEIBZFrm7jAgTb6pUDqkYXXM077m9R/s17WmwpAEt3FowsfZEMjtltnZ4NkkpyJDBbB4eLz9GazN67e+/w7d//gnfrl0zSejgQfj3X3gSxQLt9vbmddKnD9/SpTNb2rThW5o0Zoh16tRw5kxqsmUDJydwdja3yWMwCFBrza1bt5gwYQIA48aNo3fv3kyYMIGePXtarOViqcTyH5Af+MdC53slrfUqzGCBl+0bAYxIiDiESAxK5SjFgc4HGLVrFMN2DGPjHxuZWGciLd1aWvTyx5tCqfA/+kWLvvrYsCR0/brZAgPNduOGWRcnbLt1yzx+7py5VHf7dlRFPb1eeCRZMrMUgpOTWeAtbHN0DN9SpDAJKEUKRbJk4yhevAkTJhxgwoR+gEkqYS0YS7BIYtFmBICs2CCEjUpun5yBlQfSuFhjOvzUgdYrW/PD8R+YWm8qudPmfv0JRKxETEJvvRWz5wYHm6R0+7a5vXsX9uw5Tr587ty/D/fvw7175rJc2PbgQfhtcLD5OTDQJKmHD8NuFY8fVwA8gAvAtxZNKpBIL4UJIWLHNYsru9vv5n9+/2PAlgG4TnFldI3RdPLqhJ2ykaFPAghvbWTJEvHRQOLadx/WpxJ2OQygd+/eFk0u8j9JiDeMvZ09vXx6cbzrcbxzeuO7zpe3573N2cCz1g5NxLOISaVnz548ffqUnj17MmHCBHr37m2xqtmSWIR4QxVIX4CNH2xkdoPZHPnnCMWnFWf07tE8eRpFb7NI9JRSpEuXLlKfyrhx4+jZsyfp0qWzrT4WIUTipJSifYn21H6rNt3Xd+fzTZ+z9MRSZjeYjUe2KIZFiURtyJAhkUZ/hSUXS/axRLvFopQqbrFXFULYlBypc7Cy+UqWNV3G5TuXKTWzFAO3DOThk4fWDk3Eg+eTiKVHB8bkUtgSpdQLBauVUkUsGI8QwkqUUjRzbUZAtwBaubdi+M7hlJhegr2XpYariJmYJJaZwIKIDyilqgLxURZfCGElGVNlZF6jeaxvtZ57j+5Rfk55ev3ai/uP7ls7NJFIRDuxaK3HASFKqb4ASqk2wBLg/XiKTQhhRXUK1eFEtxN0K92NCfsn4D7Vnc3nN1s7LJEIvDKxKKWaK6WKqvALcB8C7ZVS84ChwNta643xHaQQwjpSp0jNpLqT2NFuBw72DlRfUJ2OP3XkVvAta4cmbNjrWiyfAAeAe0qp34GxmPVOagC1tNYn4jk+IYQNqJi3Ikd9j9KvfD/mHpmLy2QXVp9abe2whI16ZWLRWvsAqTEFasYAN4CsmNUhTyqlzoYWfRRCJHGOyRwZWX0kfp38yOqclXeXvkvzH5tz7d41a4cmbMxr+1i0cUprvURr3U9rXVtrnR1Tlv5jrLtipBAigZXMXhK/jn6MeHsEa06vwWWKCwuOLrDYrG2R+MVl5n1lrfUvWutRFotGCJEoONg78EXFLzjS5QhFMxWlzeo21P2hLpduX7J2aMIGxCWx/KCU6mKxSIQQiU6xzMXY+eFOJtaeyM6LO3Gd4spkv8k81U+tHZqworgklrnAFKXUgJftVEqVVUrtjMP5hRCJgJ2yo0eZHvh386dc7nJ89MtHVJ5bmdM3Tls7NGElsU4sWuuOwLfAMKXUuLDHlVJFlFIrgV1AibiHKIRIDPKly8evrX9lbsO5nPj3BB7TPPhm1zc8Dnls7dBEAotTdWOtdX/MkOSPlVILlVLTgONAPWA6EMOlbYQQiZlSiraebQnoHkD9wvXpv7k/ZWaV4fDfh60dmkhAlqhuPBOTSFoBGjMbf6DW+rwFzm01jx8/5sqVKwQHB7/yuLRp03Ly5MkEiirmbD0+sF6Mjo6O5MqVCwcHhwR/7aQum3M2ljdfzoqAFXRf353SM0vzXq738Kngg2MyR2uHJ+JZrBOLUsoB6Ab0BzIDhwBPwAG4bIngrOnKlSukTp2afPnyvbLy5927d0md+oXanDbD1uMD68SotSYwMJArV66QP3/+BH3tN0kTlyZUzV+VT3/7lLlH5nJw2kFmN5hN+TzlrR2aiEdxuRR2FjMT/zrQQGtdCtNqaQCsV0o5WyA+qwkODiZjxowWLyctbINSiowZM762RSriLkPKDHzf8Hu+df+W4CfBVPy+Ih//8jH3Ht2zdmginsQlsdgDnQAPrfU6AK31Mkxi8QG2KqUyxT1E65GkkrTJv2/CKp2hNP7d/PnI+yMm+U3CbYobG85tsHZYIh7EJbEU0lrP0TrygHWt9W9AdSA/sCcuwQkhkhbn5M5MrDORnR/uxDGZI7UX1abd6nb89+A/a4cmLCguw42jvIagtd4PVASkl04I8YLyecpzxPcIAyoOYOGxhbhMdmFFwAprhyUsJE7DjV9Fa30SkB46K2jfvn2U+44fP86lS5HLbpw/f54OHTrQtGnT+A5NiGcckzky/O3hHOh8gBypc9D0x6Y0WdaEv+/+be3QRBzFZM37ajE9udb6cuhzq8f0uSLcp59+iouLC506daJy5cqEhIREeWxQUBBp06Zl69at9O3b94XO6YMHD3L+fOSR4AUKFGD27NmRHnv06BGVKlXiyZMnlnsjQryEZzZP/Dr58U21b1h3Zh0uU1yYe2SuFLVMxGLSYvlVKbVFKVVfKWX/uoOVUg5KqXeVUtuB9bEP8c12/vx5du/eTUBAAJ6enjRu3Bh7+6h//YcOHeLIkSOcPn2aUaNG4ehorkYGBATg6+vLvHnzGDt2LL6+vly7FnW58+TJk1OtWjWWLl1q8fckxPOS2SWjb4W+HPU9ilsWNz5c8yG1F9Xmwq0L1g5NxEJM5rF4AuOAn4AbSqmNgB/wB/AfZo2WDEAhzKiwt0Pvbwh9roih06dPU716dZ48eUKJEqY6zqpVq57tr1q1Kl988QU1atTgyy+/5M6dO+TPn58yZcrg5OQU6VwuLi5MmzaNuXPnki9fPqpUqfLa12/UqBH9+/endevWFn1fQkSlSKYibG+3nam/T6Xf5n64TXFjZLWRdPfujp2Ktyv3wsJi8i/VDOiM6TfZALyDSTRrgJ3ADmA18B1QE5OAymit62itAywY8xujSJEitG3blmHDhrF//37+/vtv8uXL92z/0KFDGTFiBIsWLeLw4cOMGzeOgIAAvv76a06dOsXOndGrARoYGIivry+HDx9m5MiRzx53c3Pj999/t/TbEuKV7JQd3b2749/Vn4p5K/Lxrx9T8fuKnLxu2xUkRLiYtFgGAWe01j8Ae5VSTYFLgAtm5r3GTJb0Bw4/Pww5MevVC44cefm+kJCUvOLKVJQ8PWH8+Ncfd/z4cRo2bMiNGzdIly5dpH2VKlVCa83YsWPZtm0b9vb2zJw5E4ARI0YAZlZ7RO3atXvhNTJmzMi0adNeeNze3p7kyZMnitn7IunJmy4v61utZ+GxhfTa0AvP6Z4MqjSIz8t/joO9lOGxZTFpsdwEUkW4vxR4S2s9V2s9Wmv9ndZ6ntb6YFJKKtZ24sQJXF1dSZky5Qsd8cePH+fvv/8mRYoU8faH/+HDh8/6aYRIaEopPvD4gIBuATQq2ogvt35J6ZmlOfT3IWuHJl4hJi0Wf6CDUuoXrfVfmD6VN8KrWhZ37z6Itz/qd+/excHBgVSpUpEqVSpCQkIIDg7G0dGRv//+m9atW7NmzRo+/vhjNmzYQK1atSz6+oGBgWTOnFmKNAqry+qclaVNl9LSrSXd1nXDe6Y3fcr1YXDlwaR0SGnt8MRzYtJiGQqUBC4ppU5hLn3VVUrVUUpljZfo3nD+/v64ubk9u1+zZk127dpFUFAQjRs3ZsyYMRQrVoyBAwcyZMgQi7/+1q1bqVu3rsXPK0RsNSraiIDuAbTzbMeo3aPwnO7JzouynqCtiXZi0VpvAdyBMUAgpsXSCvgZuKqUuqqU+lkpNSx0mHG++Aj4TVK2bFl+/PHHZ/c/+ugj5s2bR6pUqdi7dy81atQATF/L3r17Lf76P/zwA507d7b4eYWIi3SO6ZjVYBabPtjE45DHVJpbie7runP34d3XP1kkiBiN39Nan9Faf661DptR/xnQFBgJHMa0aAYAy4E/lFI3LBlsGKXUaKXUKaXUMaXUKqVUugj7+iulzimlTiulLHttyMpKlChB1apVXzlB0lIePXpEo0aNKFKkSLy/lhCxUa1ANY53PU6vMr2YemAqrlNc+eXsL9YOSxC3ki5fATu11qu01l9qretprXMAOTEVjodihiDHh42Am9a6OHAGsyYMSikXoAXgCtQGpkRnMmdi0r59+1dOkLSU5MmT06ZNm3h/HSHiwim5E+Nqj2N3+904J3em7g91abOqDYFBgdYO7Y0WlyKUQ7TWfi95/G+t9Tqt9Vda68ZxCy/K1/5Nax1Wa2QfkCv054bAEq31Q631n8A5wDs+YhBC2I6yuctyuMthBlYayGL/xbhMceHHEz9KWRgrSQpTWdsDYe3fnERevfJK6GNCiCQuRbIUfFX1Kw52PkjuNLlpvrw5jZc15urdq9YO7Y2jbDWjK6U2AdlesmuA1npN6DEDgFJAY621VkpNBvZqrReG7p8NrNdav1CPWynVGVNJgKxZs3otWbIk0v60adPy1ltvvTbOkJCQBLk0FVu2Hh9YN8Zz585x+/btVx5z7949nJ1te0FUiTGyEB3C8ivLmXNhDg7Kga4Fu1I3W91XLu4mv8OYqVq16sHQlYNfpLVOlBvQFtgLpIrwWH+gf4T7G4CyrzuXl5eXfl5AQMALj73MnTt3onWctdh6fFpbN8bo/Dtv3bo1/gOJI4nx5c7cOKMrf19ZMwRdbV41/cd/f0R5rPwOYwY4oKP4m5ooL4UppWoDfYEGWuugCLt+AloopVIopfJjCmK+0A8khHgzFMpYiC1ttzCt3jT8/vLDfao74/eNJ+Rp/I+sfJMlysQCTAJSAxuVUkeUUtMAtNYngGVAAPAr0F1rLf+DhHiD2Sk7upTqwoluJ6iaryq9N/SmwvcVCLgutXHjS6JMLFrrt7TWubXWnqGbb4R9I7TWBbXWRbTWiX5Q+6pVq1BKcerUqTidZ9q0acyfPx+AQYMGsWnTJkuEJ0SikTttbta2XMuixos4G3gWz2mefLX9Kx6FPLJ2aElOokwsb5LFixdToUIFnh9cAMRooqSvr++zeSlfffUV1avLop7izaOUopV7K052P0kTlyYM3jaYUjNK8ftfsjyEJUlisWH37t1j9+7dzJ49+1li2bZtG1WrVqVVq1a4u7uzbds2KleuTPPmzSlcuDD9+vVj0aJFeHt74+7u/mwZ4iFDhvDdd98BpnT+8uXLAdi8eTMlSpTA3d2d9u3b8/DhQ+u8WSESUGanzCxuspg1LdYQ+CAQn9k+TPtjGkGPg17/ZPFaMalu/OZ6xYIsKUNCiK8FWVavXk3t2rUpXLgwGTJk4NAhUyrcz88Pf39/8ufPz7Zt2zh69CgnT54kQ4YMFChQgI4dO+Ln58eECROYPn06U6ZMeen5g4ODadeuHZs3b6Zw4cK0adOGqVOn0qtXr5i/HyESoQZFGlA5b2U+2/gZMw/N5OC0g8x8ZyZV8lWxdmiJmrRYbNjixYtp0aIFAC1atGDx4sUAeHt7kz9//mfHlS5dmuzZs5MiRQoKFixIzZo1AXB3d+fSpUtRnv/06dPkz5+fwoULA9C2bVt27IivKjxC2Ka0jmmZ8c4MxhQfw1P9lKrzquL7sy+3g189v0lETVos0fGKlsWDeFpdMTAwkC1btuDv749SipCQEJRS1K1b94X17FOkSPHsZzs7u2f37ezsePLkCVHRNjo5VghrKJm+JMfrH2fgloGM3z+en8/8zPT606lXuJ61Q0t0pMVio5YvX06bNm24ePEiFy5c4PLly+TPn59du3ZZ7DWKFi3KhQsXOHfuHAALFiygcuXKFju/EIlNKodUjKk1hj3t95DOMR31F9en9crWXL9/3dqhJSqSWGzU4sWLeffddyM91qRJE3744QeLnF8phaOjI99//z3NmjXD3d0dOzs7fH19X/9kIZK4MrnKcKjLIYZUHsKPJ37EZYoLS/yXSCs/uqKakv8mbW9aSZf69evrLVu2WCGal5OSLnEnMcZdVPEdv3Zce8/01gxBv/PDO/rK7SsJG1gEtvQ7JKmVdBGx1759e4KCgqhQoYK1QxEiUXDL4sae9nsYU3MMm85vwmWKCzMPzpTWyytIYnnDzJkzh82bN+Pg4GDtUIRINOzt7Pmk7Ccc73ocr+xedP65M9XmV+OP//6wdmg2SRKLEEJEU8EMBdncZjMz6s/g4N8HcZ/qzpg9Y6So5XMksQghRAwopejk1YmAbgFUL1CdPhv7UHZ2Wfz/9bd2aDZDEosQQsRCzjQ5WdNiDYubLObCrQuUnF6SIduGSFFLJLEIIUSsKaVo4daCgO4BNHdtztDtQyk5vSR+f73Zy0BJYrFh165do1WrVhQoUAAvLy/Kli3LqlWrojx+27Zt1K9f/6X78uXLx40bN6J87vjx4wkKen0Bvo4dOxIQIOtYCBFRplSZWNh4IT+3/JnbD29TdnZZPt3w6Rtb1FISi43SWtOoUSMqVarE+fPnOXjwIEuWLOHKlSvx8nrRTSyzZs3CxcUlXmIQIrGrV7geJ7qdoItXF8buG4v7VHe2/LnF2mElOEksNmrLli0kT5480kz4vHnz0qNHD4KDg/nwww9xd3enRIkSbN269YXnBwYGUrNmTSpUqECXLl2ejbm/f/8+9erVw8PDAzc3N5YuXcrEiRO5evUqVatWpWrVqgD89ttvlC1blpIlS9KsWTPu3bsHQJUqVThw4AAAzs7ODBgwAA8PD3x8fLh27Vp8/1qEsHlpUqRhSr0pbGu7DTtlR7X51ei8tvMbVdRSilBGQ69fe3HknyMv3RcSEoJ9LMrme2bzZHzt8VHuP3HiBCVLlnzpvsmTJwNw/PhxTp06Rc2aNTlz5kykY4YOHUqFChXo3bs3O3bsYMaMGQD8+uuv5MiRg3Xr1gFw+/Zt0qZNy9ixY9m6dSuZMmXixo0bDB8+nE2bNuHk5MSoUaMYO3YsgwYNivQa9+/fx8fHhxEjRvD5558zc+ZMvvzyyxj/LoRIiirnq8wx32MM3jaYMXvHsO7sOqbVm8Y7Rd6xdmjxTlosiUT37t3x8PCgdOnS7Nq1iw8++AAwhSTz5s37QmLZsWMH77//PgD16tUjffr0gCmlv2nTJvr27cvOnTtJmzbtC6+1b98+AgICKF++PJ6ensybN4+LFy++cFzy5Mmf9el4eXlx4cIFS75lIRK9lA4p+bbGt+zvuJ+MKTPSYEkDWq5omeSLWkqLJRpe1bK4G09l811dXVmxYsWz+5MnT+bGjRuUKlWKnDlzRuscSqkXHitcuDAHDx5k/fr19O/fn5o1a77QEtFaU6NGjWfrv0TFwcHh2WvY29u/skS/EG+yUjlKcaDzAUbtGsXwncPZ+MdGJtSeQCv3Vi/9nCZ20mKxUW+//TbBwcFMnTr12WNhneuVKlVi0aJFAJw5c4ZLly5RpEiRSM+PeMwvv/zCzZs3Abh69SqpUqXi/fffp0+fPs9WpUydOjV3794FwMfHh927dz8rpx8UFPRCi0gIETPJ7ZMzsPJADnc5TKGMhXh/1fvUX1yfy7cvWzs0i5PEYqOUUqxevZrt27eTP39+vL29adu2LaNGjaJbt26EhITg7u7Oe++9x9y5cyMt9gUwePBgduzYQcWKFfntt9/IkycPYPplvL298fT0ZMSIEc/6RDp37kydOnWoWrUqmTNnZu7cubRs2ZLixYvj4+PDqVOnEvx3IERS5JLZhV0f7mJ8rfFsu7AN1ymuTP19Kk/1U2uHZjlRlT1+k7Y3rWy+rZGy+XEnMcadNeL7478/dLV51TRD0JW+r6TP3DjzyuNt6XeIlM0XQgjbUyB9ATZ+sJHZDWZz9J+jFJ9WnG93f8uTp4m7v1ISixBCWJFSivYl2hPQPYDab9Wm76a++Mzy4eg/R60dWqxJYhFCCBuQI3UOVjZfybKmy7h85zKlZpZi4JaBPHzy0NqhxZgkFiGEsBFKKZq5NiOgWwCt3FsxfOdwSkwvwd7Le60dWoxIYhFCCBuTMVVG5jWax/pW67n/+D7l55Sn5y89eRDywNqhRYskFiGEsFF1CtXBv6s/3Up3Y6LfRNofaM/GPzZaO6zXksQihBA2LHWK1EyqO4kd7XbgoByoubAm7de05+aDm9YOLUqSWIQQIhGomLcis0rNol/5fsw/Oh+XKS6sOhn1+kzWJIklkWrfvr21QxBCJLDkdskZWX0kfp38yOacjcbLGtPsx2b8c+8fa4cWiSSWRCgoKIi0adOydetW+vbtS3Bw8AvHTJw4kWLFitGhQ4dYv46zszMA5cqVi/U5rOXChQu4ublZOwwh4kXJ7CXx6+jH129/zdrTa3GZ7ML8o/OfrbtkbZJYEqFDhw5x5MgRTp8+zahRo3B0dHzhmClTprB+/Xpmz5792vNprXn6NOo6RXv27IlTvPHldXELkZQ52DvQv2J/jvgeoVjmYrRd3ZY6i+pw8daLS1wkNEksFvL8NwVLfXNYvnw5Pj4+eHh4UKFCBa5fv87vv/9OmTJlcHJyeulzfH19OX/+PA0aNGDSpEmMHTsWNzc33NzcGD9+PGC+0RcrVoxu3bpRsmRJLl+OusJqWMsl7DmdOnXC1dWVmjVr8uCBGf64cOHCZ8Utu3TpQkhIyAvnednqlQBLlix56XMbNWqEl5cXrq6uzxYqe1nc8+fPp3jx4nh4eDxbpwbMImwvi1WIpKRopqLs/HAnE2tPZNelXbhNdWOy32TrFrWMqoiYLW/AMOAYcAT4DcgRYV9/4BxwGqgVnfPFtQjl4MGDdc+ePfXTp0+11lo/ffpU9+zZUw8ePDha53iVGzduPPt5yJAhetKkSbpjx446JCREf/HFF3rHjh0vfV7evHn19evX9fbt27Wbm5u+d++evnv3rnZxcdGHDh3Sf/75p1ZK6b1790b52k5OTpFu//zzT21vb68PHz6stda6WbNmesGCBTogIEDXr19fP3r0SGutddeuXfW8efNeON/y5ct1x44dn92/deuWDggI0LVr137pcwMDA7XWWgcFBWlXV1d948aNF+L29/fXhQsX1tevX4/0nKhifZ4UoUw4th6jrcen9etj/PPmn7rmgpqaIegKcyroU9dPxVssJMEilKO11sW11p7Az8AgAKWUC9ACcAVqA1OUUjFfNzgGtNbcunWLCRMm0Lt3b7TW9O7dmwkTJnDr1q04t1zmzp2Lt7c3Hh4eTJkyBUdHR2bOnImdnR0jRoygYsWKr3z+3r17effdd3FycsLZ2ZnGjRuzc+dOAPLmzYuPj0+M4smfPz+enp5A+KqRmzdv5uDBg5QuXRpPT082b97M+fPnX3juy1av3Lx5M0eOHHnpcydOnIiHhwc+Pj5cvnyZs2fPvhD3li1baNq0KZkyZQIgQ4YMr4xViKQsX7p8/Nr6V+Y2nMuJf0/gMc2Db3Z9w+OQxwkaR6JcQVJrfSfCXScg7K93Q2CJ1voh8KdS6hzgDcRbPQSlFOPGjQNgwoQJTJgwAYCePXsybty4OK0ON3/+fPz8/NiyZQvOzs5UqlQJV1fXGJ3jVYktqktprxJx3Rd7e3sePHiA1pq2bdsycuTIVz73ZatXpk+fnlatWjFmzJhIx27bto1Nmzaxd+9eUqVKRZUqVZ4NUogYt9Y6yt/xy2IVIqlTStHWsy213qrFR+s/ov/m/iw7sYzZDWZTInuJBIkhsbZYUEqNUEpdBloT2mIBcgIROwuuhD4W37E8Sy5h4ppUwCzKVa5cOZydnVmxYgV79uzB3d09RucoX748q1evJigoiPv377Nq1arXtnJiqlq1aixfvpx///0XgP/++4+LF1/sQHzZ6pXVqlVj9erVLzz39u3bpE+fnlSpUnHq1Cn27dsX5WsvW7aMwMDAZ88XQkA252wsb76c5c2Wc/XuVUrPLM2AzQMIfvLiKFJLs9kWi1JqE5DtJbsGaK3XaK0HAAOUUv2Bj4DBwMv+kr/0K7tSqjPQGSBr1qxs27Yt0v60adM+W6r3VUJCQrhz5w79+vWL9Hj37t355ptv4pRcmjZtSosWLVi6dCk1a9YkX758PH36NFpxaa25d+8e7u7utGzZklKlSgHQpk0b3nrrLS5evBitc4Xtv3v3Lvfu3Yv0nIcPH/Lw4UNy587NgAEDqF69Ok+fPsXBwYHvvvsu0mUpgP379zNw4EDs7OxIliwZ48aNi/K55cuXZ9KkSbi5uVGoUCFKly5NUFDQCzHkyZOHTz75hIoVK2Jvb0/x4sWZNm1alLE+/36Dg4Nf+Ld/3r179157jLVJjHFn6/FB7GLMSEZmeMxg6h9T+XrX1yw4uIDPinyGe9qYfUmNkag6XxLLBuQF/HV4x33/CPs2AGVfd464dN7fvn1b9+zZUwPPOvCfv29NsoLkq0nnfcKx9RhtPT6t4x7jhnMbdN5xebUaonSP9T303Yd3Y30uklrnvVKqUIS7DYCwBdl/AloopVIopfIDhQC/eI6FdOnSRepTGTduHD179iRdunRxvhwmhBCWUrNgTfy7+fOR90dM8ptEyekleRTyyOKvY7OXwl7jG6VUEeApcBHwBdBan1BKLQMCgCdAd631ixMqLGzIkCGROpHDkoskFSGErXFO7szEOhNp4dYC/3/9SW6f3OKvkSgTi9a6ySv2jQBGJGA4AC8kEUkqQghbVi53Ocrljp9yTYnyUpgQQgjbJYnlFXQcJzcK2yb/vkLED0ksUXB0dCQwMFD++CRRWmsCAwNfWsBTCBE3ibKPJSHkypWLK1eucP369VceFxwcbNN/nGw9PrBejI6OjuTKlSvBX1eIpE4SSxQcHBzInz//a4/btm0bJUokTJmE2LD1+CBxxCiEiD65FCaEEMKiJLEIIYSwKEksQgghLErJqCdQSl3HzOCPjUzADQuGY2m2Hh/Yfoy2Hh9IjJZg6/GBbcWYV2ud+WU7JLHEkVLqgNa6lLXjiIqtxwe2H6OtxwcSoyXYenyQOGIEuRQmhBDCwiSxCCGEsChJLHE3w9oBvIatxwe2H6OtxwcSoyXYenyQOGKUPhYhhBCWJS0WIYQQFiWJJRqUUrWVUqeVUueUUv1esl8ppSaG7j+mlCppgzG2Do3tmFJqj1LKw9ZijHBcaaVUiFKqqa3Fp5SqopQ6opQ6oZTanpDxRSdGpVRapdRapdTR0Bg/TOD45iil/lVK+Uex36qflWjEZwufk1fGGOE4q3xOoiWqNYtl02GVje2BP4ACQHLgKODy3DF1gV8ABfgA+20wxnJA+tCf69hijBGO2wKsB5raUnxAOszqpHlC72extd8h8AUwKvTnzMB/QPIEjLESUBLwj2K/tT8rr4vPqp+T6MQY4f9Cgn9OortJi+X1vIFzWuvzWutHwBKg4XPHNATma2MfkE4pld2WYtRa79Fa3wy9uw9I6LK+0fk9AvQAVgD/JmRwRC++VsBKrfUlAK21LcaogdTKLGHqjEksTxIqQK31jtDXjIpVPyuvi88GPifR+R2C9T4n0SKJ5fVyApcj3L8S+lhMj4lPMX39DphvjQnptTEqpXIC7wLTEjCuMNH5HRYG0iultimlDiql2iRYdEZ0YpwEFAOuAseBnlrrpwkTXrRY+7MSE9b4nLyWlT8n0SJl81/vZYvXPz+ULjrHxKdov75SqirmA1MhXiN6yUu/5LHnYxwP9NVah5gv3AkqOvElA7yAakBKYK9Sap/W+kx8BxcqOjHWAo4AbwMFgY1KqZ1a6zvxHFt0WfuzEi1W/JxEx3is9zmJFkksr3cFyB3hfi7Mt8GYHhOfovX6SqniwCygjtY6MIFiCxOdGEsBS0I/LJmAukqpJ1rr1TYS3xXghtb6PnBfKbUD8AASKrFEJ8YPgW+0uRB/Tin1J1AU8EuYEF/L2p+V17Ly5yQ6rPk5iR5rd/LY+oZJvueB/IR3mLo+d0w9IndI+tlgjHmAc0A5W/09Pnf8XBK28z46v8NiwObQY1MB/oCbjcU4FRgS+nNW4C8gUwL/W+cj6s5xq35WohGfVT8n0YnxueMS9HMS3U1aLK+htX6ilPoI2IAZiTFHa31CKeUbun8aZmRGXcx/yCDMt0Zbi3EQkBGYEvpN54lOwGJ20YzRaqITn9b6pFLqV+AY8BSYpbV+5ZDQhI4RGAbMVUodx/zx7qu1TrBquEqpxUAVIJNS6gowGHCIEJ9VPyvRiM+qn5NoxmjzZOa9EEIIi5JRYUIIISxKEosQQgiLksQihBDCoiSxCCGEsChJLEIkIkqp/UqpFtaOQ4hXkcQiRCKhlLID3DDDnYWwWZJYhEg8imA+s6etHYgQryKJRYjEwxMI0FqHACileiulTimlPK0alRDPkZn3QiQensBRpVRa4HvM59dHa33LmkEJ8TxpsQiReHhiksnvwAGgoSQVYYukpIsQiYRS6p/QHzdqrT+wajBCvIK0WISwMqVUCaXUKqXUzdBtuVIqg1Iqh1IqWCnVUimVDVOtuApQUSnV1rpRCxE16WMRwoqUUi2BeZghxEMxJfE/Bi5hPp9ngaWYBbzOa61PKaXqA1uVUpe11lusE7kQUZPEIoSVKKUKAHMwKz5W0loHhz5eCqiDWZOjtdb6qVLKAzgMoLX2V0q1BpYqpSpprU9aI34hoiJ9LEJYiVJqAqZ14qO13h/h8QXA+8AhoJSWD6lIZKSPRQjraQCci5hUnjNQkopIjCSxCGEFSqkMmEtdv79kd1bghNZ6fYIGJYSFSGIRwjqyhd4GRnxQKVUJqPH840IkJpJYhLCOW6G3HmEPKKWcgemhd50SOiAhLEUSixBWoLW+Cvhh5qQsUEp1BXYAmYBfgRJKqV5KqezWjFOI2JBRYUJYiVIqLzAJM+kxGWY4cfvQ3SsAF6Co1lqqGYtERRKLEEIIi5JLYUIIISxKEosQQgiLksQihBDCoiSxCCGEsChJLEIIISxKEosQQgiLksQihBDCoiSxCCGEsChJLEIIISxKEosQQgiLksQihBDCov4P/jLkSEBeat4AAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"plot_alpha(-3,eta_ls=0.25,algorithm=\"newton\",alpha_max=1.5)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.2 Newton Step, $x^k = -3$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.2-Newton-Step,-$x^k-=--3$)",
"section": "3.6.3.2 Newton Step, $x^k = -3$"
}
},
"source": [
"**Discussion**\n",
"* Why did the backtracking line search stop at $\\alpha^k = $ `alpha_max`?\n",
"* Is it possible to find a larger improvement in $f(x)$ with $\\alpha^k > 1$?"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.3 Steepest Descent Step, $x^k = -3$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.3-Steepest-Descent-Step,-$x^k-=--3$)",
"section": "3.6.3.3 Steepest Descent Step, $x^k = -3$"
}
},
"source": [
"### 3.6.3.3 Steepest Descent Step, $x^k = -3$"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.3 Steepest Descent Step, $x^k = -3$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.3-Steepest-Descent-Step,-$x^k-=--3$)",
"section": "3.6.3.3 Steepest Descent Step, $x^k = -3$"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Considering xk = -3 and f(xk) = 15.0\n",
"Step with steepest-descent algorithm:\n",
"pk = 51\n",
"With full step, xk+1 = 48 and f(xk+1) = 2534689.5\n",
"alphak = 0.03535353535353535 with backtracking line search starting at alpha = 0.1\n",
"f(xk + alphak*pk) = -8.67145500733185\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZwAAAESCAYAAADJ+2ORAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAABQIklEQVR4nO3de3zO5f/A8de12QFzyKE5lfNpBxvDppxWkXMOERHllEORTjpHpb46EL9yCpFyKMcKEVmkkPNhDiFFqVDYMId5//647tnGhu3edu/e3s/H43ps9+d0vy+z+73r+lyf6zIiglJKKZXZPFwdgFJKqdxBE45SSqksoQlHKaVUltCEo5RSKktowlFKKZUlNOEopZTKEnlcHUB2VqxYMSlXrly6zj1z5gz58+fP2ICyOa1z7qB1zvmcre+mTZuOi0jxq7drwrmOcuXKsXHjxnSdGxUVRePGjTM2oGxO65w7aJ1zPmfra4z5LaXt2qWmlFIqS2jCUUoplSU04SillMoSmnCUUkplCU04SimlsoQmHKWUUllCE04m0VUflFIqOX0OJxM82bc9e09vJnhLf4rVj4TQUPD2dnVYSinlUppwMsF/F/7lm6q/EfLHc4zvDm1+9YZatSA83JaICChXDoxxdahKKZVltEstE3w8LYqHL8/h+Lnq3NcF2g0uzz/5BCZNggcfhAoVoEQJaNMGRoyAlSvh9GlXh62UUplKWziZ5KG7b+UR7200e2MkC8NeZ0WkH+PfHUfXy8GYDRtg/XpYtw6++sqeYAxUr25bPwmtoMBA8PR0bUWUUiqDaMLJRPXv8GL3xJdo0aM9Oyv05qEvH2FmpRZMfHACt/Xvbw/67z/4+WebfNavh4ULYepUuy9/fqhTJ3lXXMmSLquPUko5QxNOJrvtNvh5SQCPDVrDlKUfsKzpCwT8FsjbTUbyaO1H8bjlFmja1Baww9sOHEhsAa1bB6NGwcWLdv/ttycmn/Bwe28ob17XVVAppW6SJpws4OsLkyd5Um/KYAa82IYLrfoyYMkAZu+azeTWk6lctHLiwcZApUq2dO1qt8XFwZYtia2gdevgiy/svjx5ICQksRUUHg5VquiABKVUtqMJJwv16gXh4eXp9MBydm/+mPVtnqTGhBoMbzycJ+s9SR6PVH4cvr5Qr54tCf76C5LeC5oxA8aNs/tuuSV5N1zdulCkSOZXUCmlrkMTThYLCoKNPxuGDOnJpFHNKNhlIENXDOXzXZ8zpc0UQkqE3NyFEka5tWljX8fHw+7dia2g9evhtdcSn0CtXDn5gIQaNcDLK3MqqZRSKdCE4wL58sHEidCqVSl695nPmVvnsafDQGp/VJvn7nyOlxq+hE8en7Rd1NPTZrOgIOjd226LiYGNGxNbQd9+a1tCYFtNYWHJW0K33aZdcUqpTKPP4bhQ69YQvcvQofr9nBkZTYFDD/LGmjeoObEmPx3+yfk3KFAAIiPhuefs6Lc//4RDh2D2bOjf37Z+xo2DBx6AsmWhVClo2xb+9z9YtQpiY52PQSmlHLSF42JFi8KcOfDA/KI89th0jF8XjnTpy51T72RQ+CDeuOsN/Lz9MubNjLGJpWxZm2QALlyA7duTj4pbtMju8/CwzwIlHRVXvbo+G6SyjIjtLb540X5NKCLJ5ys0xv539fCw/z09PW2PsaenNtqzk1yVcIwxzYAxgCcwWUT+5+KQrmjfHu6+G154oRnjRu4iX+vnGcMYFu1dxKRWk2hSsUnmvLG3N9SubcvAgXbbiRN2QELC/aB582DyZLuvQIHEZ4MSkpC/f+bEptxOXJz97/Pvv7acPGnLqVO2nD5tS0wMnDljG9FnzsC5c4nl/Hl7nfPnbaJxdiJcb29bfHxsT7Kvr32SIG9e+6hbQvHzs/+9/fygYEEoVMh+LVwYDh4siL+/HY9TpIhOjZheuSbhGGM8gQ+BJsAR4GdjzJciEu3ayBIVKgQffggPP1yAxx//gPUbHuCvTr1p+mlTeob25N2m73JL3lsyP5CiRaF5c1vA/sbv25c4GGHdOnjnHbh0ye4vVw7CwylTrJj9ra5Z0/5WK7cnYhPGn3/C0aN2cOTatbexeDH8809iOX7cJpozZ65/vbx57Yd6wgd7wod7iRL23mbevPa/jo9PYqLw8rKj//PkSWy9GJNYElo7ly/bktAKunjRlgsXbElIYnFxcPasTW5nz9p6JSS/2FibDC9fvjryWsle5c9vE0/RorYUKwbFi9uvt96avPj7299tbWnlooQD1AX2i8hBAGPMbOA+INsknAR16sCPP8Knnzbg2Re2EVftNT6Wt/lyzxImtRlHu+rtsjYgY6BqVVu6d7fbzp6FzZsTk9CPP1Lp8GGbMb287AzZCS2g8HCoWFF/47IZETvRxe+/w2+/weHDcOSI/frHH/b7P/6wH9DJVcTHx36QJnygBgXZD9uED+AiRRJbA4UL2w/cQoVs0sjuROx/74RW2alTsHr1dm6/vQb//mv/zf791ybYhLJ5Mxw7ZpNzShL+vUqUsJOFJHwtVSrxa6lSNmnl5B5rN/jxZ5jSwOEkr48A4S6K5YY8POxne4cOvowe/SZvTevI8SY9af95e5rdfj8fd/w/SviVcF2A+fJB/fq2OPw4dy53eHomtoKmToX/+z+7s2jRa58NKlzYNbHnIjExcPAg/Pqr/XrokP3+0CGbZGJikh/v7Q2lS0OZMvZHlPBBmPDBWKIE/PLLGlq2bJBj/34wJrGbrVQpuy0u7l8aN77xuRcv2tZeQsvv778Ty19/2a8HD8Latfa4q3l62n/jhJ/B1V8TvnfXDgQjuWSlMGNMR+BeEenteP0QUFdEHr/quL5AXwB/f/+w2bNnp+v9YmNj8fPLoJv9wMmTXsz4rCSLjs0ivsHr5JG8PFJyEF0CGmOyyW/+1XU28fHkO3SIgtHRFNy9m4LR0eT7/XeM4//cmdtvJ6Z6dU4HBHC6enXOVKiAuNmfdxn9c06PmJg8HDmSlyNH8vLnn3n54w9b/vwzLydPJr/ZkC/fJUqUiKNkyTj8/ZOW89x6axyFC1/E4wZjV7NDnbNaZtT54kXDf/95c/y4N//+68Px494cP+7jKInfnzlzbbugYMGLFC9+/kq59dY4ihU7n2xb3rzX9AveNGfrGxkZuUlEal+9PTclnHrAMBG51/H6eQAReSu1c2rXri0bN25M1/tFRUXR+Gb+JEqjv/6C59/bwycne3O5zFqKn2rGuOYT6XDP7S7/i/Om6nzqlJ2sNKEVtH697YsA22oKC0v+gGrp0pketzMy6+d8tbg42L8f9u61t9MSvu7bZ7t0EhhjH6eqWDGxVKiQWG65xfmezayqc3biyjrHxNiuzYRuzqRdngnfp9RaKlz42lZS0lKqlO0GTekPDGfra4xJMeHkpi61n4HKxpjywB9AZ+BB14aUdiVKwMfvVON//6zmkXHjWJr3OTquCuS2Cf/jlRb9ebCLB/nyuTrK6yhUCO65xxawHeaHDiWfIWHMGHuXF+xvRtKuuLAw29eRA4nYD47du2HPHptU9uyx5dCh5DeyS5WyU+Z16GAnkahc2U6/V7Gi+3a3qJQVKADVqtmSmnPnrk1KCffgjhyBbdtsd97V7QsvL/uZktBlmlBOnSpJ1aoZPzl9rkk4InLJGPMYsAw7LHqqiOxycVjp5n+rB0uGPcaeo61pP60vu2s8Rp+1s3lyxGQeblWVRx6xg8WyPWOgfHlbunSx286ft78hSZPQ/Pl2n6cnBAcnH5ZdtWrKf6ZlU5cv2xv1u3dfW/79N/G4vHlt1erUgW7dEsdtVKliP4SUSpA3b+Kcv6m5eNH2kPzxhx11mJCgjh615ZdfYM2ahBZzVTp00ITjFBFZAixxdRwZqVrJsux67humb/uEQYuHcOa2EMZ9P4z/q/0UIcFePPQQdOpku1ncho+PvWNdt27itmPHEpPP+vUwa5adHwhsq6lu3eQzZhcv7prYk7h40XaDJSST6Gj7de9eOwoqQfHi9q/XDh3sc7XVq9vXt9/uVnlUZXNeXvZz4EafBefPw8KFP1GzZr3rH5gOuSrh5FTGGB4O7UGzSvfy2JLHmOfxPLc1+ZyLq6bw9NM1efppuOMO6NjRzvVZoYKrI06H4sWhVStbwDYT9u5NPkPCm28m9jtVqGBbQAmtoNDQFJ/WE5Fkgy6ufn0zTp9O7P5KSC579thkk/CoEtgEUr06NGoEAQGJiaVYsbT+YyiVeewQ7vOZ0jWrCScHKeFXgrmd5jIveh4Dlwxkb8M69Ov3LCX2vsL8z30ZMgSGDLHPTLRsadd8u/NO+x/M7Xh4JDYHHn7YbjtzBjZtSuyKi4qCmTPtPm9v28eYJAkNmzaNk6dOMXr0aIwxiAhDhgyhcOHCDBs2LNnbxcfbbrCEG/YJCWb79nrJbtjmyWO7NapXt7NHJIRYtap9yFGp3EwTTg7UIaADkeUjeWr5U0zY+hZVi85nyldTKHHxTr76yk6V9t57MHKkHRjWoEFiqVvXjW86588PDRvakuDIkeStoEmT7KAE4Km8eVl17hxLNmygxWuvMXTufMZM/JIOHZ5j0iThwAHDvn22b3v/ftvVkKBQIds6qVXrPxo1KnElsVSooNOeKJUaTTg5VJG8Rfj4vo/pEtSFvl/1pcHHDRhYZyBv9n+TJ54oQEyMbQB8+62dGPqll+x5Xl52qZy6de30aiEhtvvHbVexTnharkMH+2T9Pxf557udxH2/Dq9N6wnasYoKP/0ETZrwPww9qM66eVtYP+8jNuWJ4HylQCpV9aR5c3uzPuHG/a232vEOUVF7aNzYhQ/gKuVGNOHkcE0rNmXngJ28sPIFPtjwAV/u+5JJrSZxb6V7ad3aLpEAdmTK2rV2Sp2ff4bPPoPx4+0+Dw/bTVStmv3QrVLF/iVfrpy9AZkd/qK/cCHxye6jR+0onISROIcPJ5aYGC+gpqP0p0ABwfP8D9ThW8JZT+9ATx76fSG9YqbCJeBwfihRBzzDoXgEVA4H/wweuqNULqEJJxfw8/ZjbPOxdA7qTK8ve9Hss2b0COnBqHtHUSSvXXq6aNHkC4hevmy7kXbssKsX7Nxp718sW5a8a8kYez+/ZEnw8QmmatXE+bQKF7YTMxYokHxixoTJGBMmFUiYePHSJZs4Ll5MnGDxzBlbEmYZPnUq+VxWx46lPoeVMbYlcttttlVy9902SSas0FCunPD660MYO3YM3wLfAjH3DGb0qK/t/CNJJysdNcoGBvbuv2M0XCFvb/u92zYBlco6mnBykTtuu4Mtj27hjdVvMHLtSL7Z/w0ftviQDgEdrjnWwyOxNdMhye74eHtb5NChxJIwk/Devd6sWWMfXsystdv8/OyEkAmTQ9asaRNe8eL2AbYSJewkiaVL2+9TW0U7YYDA2LFjGDx4MKNHj2bIkCGMcdzfGT16NKZSJeja1Z4QFwdbtybeC1q/Hr74gpoATz5p+yETng2KiLBPYrp66gelshlNOLmMbx5f3rjrDe4PuJ9eX/bi/i/up121dnzY4kNKFrhxV5GnZ2ILoVGj5PuiojZdmQ7j/PnEVsnp08nXO7l0ySauhCHDHh72szlPnuRrl+TPb1tG+fLZm/R+fhk3k64xhsKFC19JNsYYRo8eDUDhwoWvHRrt65uYTBL8/Tc7Jk8m+OxZm4RmzEjsh7zlluTPBYWH2yypVC6mCSeXCi0Ryvre63nvx/d4NepVAsYFMKrpKB4OfThDJgP18UlseWRXw4YNS/bcTULSuen6+/tz4s47uTKNcHy8fQgn6Txxr7+e+GxQ5crJZ0ioUSN73ABTKotowsnF8njkYWj9obSr3o7eX/am55c9mbVzFhNbTaT8LeVdHV6WuDq5OJVsPT3tQ05BQdCrl90WEwMbNybeD/r2W/j0U7vP1xdq1Uq+btDtt2tXnMqxNOEoqhStQtTDUUzYOIGhK4YSPD6YN+9+k4F1BuLp4V7LBWQ7BQpAZKQtYEdI/P578gEJ48bZQQlgbzwlTUC1a+vEaSrH0ISjAPAwHgyoM4BWVVrx6NePMvibwczZNYfJrSdTvXh1V4eXcxiTeBOsUye77cIFOxQw6WSlCxfafR4eEBiYvCuuevWcvSykyrE04ahkbi90O0seXMKn2z/liWVPEDoxlFcavsKzdz6Ll2cqQ76Uc7y9bUumdm147DG77cQJ2LAhsRU0bx5Mnmz3FShgp5BO2hLy93dd/ErdJE046hrGGB4KeYimFZsy6JtBvLTqJb6I/oIpbaYQVirM1eHlDkWLQvPmtoDtivvll8RW0Lp18PbbiUP9ypVL3gqqWdON5yhSOZUmHJUqfz9/5tw/hy5BXRiweADhk8N5+o6nebXRq+T10gcds5QxiQ9Gde9ut507B5s3Jyahn36COXPsPi8vO0N20iRUsaIOSFAupQlH3VDbam1pVLYRz3z7DCPXjmT+7vlMbjOZhmUb3vhklXny5rXTfd95Z+K2o0eT3wv6+GP44AO7r2jR5Kun1q1rp4NQKotowlE35Za8tzC5zWS6BHWhz1d9aDStEf1r9+d/9/yPgj4FXR2eSlCyJLRrZwvYLrfo6OQzJCxdmrjWcLVqyZNQcLB9AlepTJCj/mcZY94BWgMXgAPAIyJy0hhTDtgN7HUcuk5E+rkmSvd2d4W72dF/By999xJj1o/hq31fMbHVRFpUbuHq0FRK8uSxD5jWqAF9+9ptp07ZZ4OSJqDp0+2+vHkhLCz54nVlyrgufpWj5KiEg51/8XkRuWSMGQk8Dwx17DsgIqEuiywHye+dn9HNRvNA0AP0+rIXLWe2pFuNbtzvd7+rQ1M3o1AhO5Pp3Xfb1yJ2Uryk6waNHQvvvmv3ly6drBXkce6cy0JX7i1HJRwRWZ7k5TpAPwEzUUSZCDb33cyba97kzR/e5GvPr5lQcgKdAjtlyPQ4KosYA+XL29K5s912/jxs25Z8VNz8+QA08PBIPllpeLidjtvDw4WVUO4gJ/8P6QksTfK6vDFmizHme2NMA1cFldP45PFheORwNvXdhL+vP53ndabtnLb8GfOnq0NTzvDxsYMKBg2yiyMdOGAXHPrqK37r2hWKFYNZs+CRR+wKfUWK2DXLX34ZFi8m2brbSjkYSbh56CaMMSuAlJZYfFFEFjmOeRGoDbQXETHG+AB+InLCGBMGLAQCReR0CtfvC/QF8Pf3D5s9e3a64oyNjcUvly1ifyrmFMtOLmPKoSl4GS/6V+xPixItcnRrJzf+nK/U+fJl8h0+TMHoaAru3k2B3bvxO3gQ45is9FypUpyuXv1Kia1UCXHTyUpz28/Z2fpGRkZuEpHa1+wQkRxVgB7AT0C+6xwTBdS+0bXCwsIkvVatWpXuc91VQp1/OfGLNJ7WWBiG3DX9Ljnw7wHXBpaJcvPPOUWxsSLffy8ycqRI+/YipUuL2LtEIt7eIhERIoMHi8yaJXLwoMjly1kVtlNy28/Z2foCGyWFz9QcdQ/HGNMMO0igkYicTbK9OPCviMQbYyoAlYGDLgozx6tUpBIru69k8ubJPL38aYLHB/NG5BsMCh+kk4HmdPnzQ8OGtiQ4ciT5ZKWTJoFjoTuKF09+L6hOHTuoQeVIOSrhAB8APsC3jm6chOHPDYHXjDGXgHign4j867owcz4P40HfsL60qNyCfl/348nlTzJn1xymtJlC4K2Brg5PZaUyZWxJWDr24kW7ZnnSdYO+/truM8ZOTpqQgCIi7OSlOllpjpCjEo6IVEpl+zxgXhaHo4AyBcvwVZevmL1zNoO+GUTNiTV5qeFLPFf/Obw93bM/XznJy8vO9VazJvRzPA7333+Jk5WuXw+LFsHUqXZf/vx2YtOkLaFSpVwXv0q3HJVwVPZkjKFLcBfuqXAPg78ZzKtRrzI3ei5T2kyhTuk6rg5PZQe33AL33msL2Ls+Bw4k74obPdq2jgBuuy15AgoLsw+tqmxNE47KMsXzF2dmh5l0CepC/8X9iZgSwZMRTzI8cjj5vPK5OjyVnRgDlSrZ0rWr3RYXB1u2JJ8rbu5cuy9hRoWkXXGVK+tkpdmMJhyV5VpXbU3Dsg159ttnefend1mwZwGT20ymcbnGrg5NZWe+vlCvni0J/v47eStoxgy7girYVlPduolJqG5dO4GpchmnEo4xpgoQCNwKCHAM2Ckiv2RAbCoHK+RbiImtJ9I5qDN9vupD5PRI+tbqy9tN3qaQr45SUjfJ3x/atLEFID4edu9OnoRefx0czwZRuXLyrriQEHtPSWWJNCccY0x1oB/QEUhYZjCh3SqOY/4GPgcmisjuDIhT5VCR5SPZ3n87r6x6hdHrRrP4l8VMaDWBVlVauTo05Y48PSEoyJZevey22NjEyUrXrYMVK+DTT+0+X1+oVSsxCUVE2PtD2hWXKW464RhjKgIjgXbAOWAN9gHLA8AJbNIpAlQCIoDewOPGmPnAUBHR515UivJ55ePdpu/SKbATvb7sRetZrekS1IUxzcZQPH9xV4en3J2fHzRubAvYAQmHDye/FzR+vB2UAFCiRPJWUO1rH5hX6ZOWFk40sAN4GJgvImeud7AxJj928sxBjnN1vVt1XXVL12VT3028teYtRqwZwbcHv2Vss7F0Duqco6fHUVnMGLj9dls6dbLbLl6E7duTrxu0aJHd5+FB7XLl4K67EpNQ9er6bFA6pCXhdBLHXGU3w5GQpgPTjTH3pTkylSt5e3rzauNXuT/gfnp92YsH5z/IzJ0zGd9yPGUK6rosKpN4edmh1WFhMHCg3fbvv1daQOeXLsVv3jyYPNnuK1DAzoqQtCXk75/69RWQhoSTlmSTkeeq3Cnw1kDW9lzL2PVjefG7Fwn4MIB3mrxDn7A+eJicPMm5yjaKFIHmzaF5c3Y0bkzjhg1h//7kXXHvvGNXVQUoWzb5sOyaNe09InVFWu7h1BCR7ZkZjFJJeXp4MqTeEO6rdh99vupDv8X9mL1rNh+1/ohKRVKcVEKpzOPhAVWq2NK9u9127hxs3pyYhH78EebMsfu8vCA0NPkS3hUr5uoBCWnpUpttjAkXkZikG40xVUVkb2onKeWsCrdUYMVDK5iyZcqVyUBfj3ydIRFDdDJQ5Vp588Kdd9qS4OjR5KunfvwxfPCB3Ve0aPJuuLp1oXBhl4TuCmlJOB8BM4C2CRuMMZHAbBKHRyuVKYwx9K7VmxaVW9B/cX+e+fYZPt/1OVPaTCHYP9jV4SmVqGRJaNvWFrBdbtHRyVdPXbrUjpYDqFYtsRUUHg7BwTn22aCb7gwXkdFAvDFmKIAxpjs22XTLpNiUukapAqVY+MBCZneYzaGThwibFMawqGGcv3Te1aEplbKEaXf69oUpU2DXLjtZ6YoVMGKEfRh16VIYMMAOWihUyC7v8MwzduqeI0dcXYMMc90WjjGmE7Ad2OtYVOcR4GdjTAB2yv+7RGRX5oepVCJjDA8EPcDdFe5myLIhDP9++JXJQMPLhLs6PKVurFAhuPtuW8C2dg4dSj4gYexYuHDB7i9VKvmAhLAwO4u2m7lRl9qTQBBgjDHRwDZgHdAEaCwi+zI5PqVSVSxfMWa0m0HnwM70W9yPelPq8UTEE7we+Tr5vd3vl1HlYsZA+fK2dOlit50/D9u2JV83aP58u8/T03a9JR2QULWqHdiQjV034YhIhLFP3FUFQpMUA+w2xhwEtohIp8wNU6nUtazSkl1ld/HciucYvW40i/YuYlKrSdxd4W5Xh6ZU+vn42EEFdevC44/bbceOJbaA1q+H2bNh4kS7r1Ah+2xQwhQ94eFQrJjr4k/BDQcNOLrS9jjK7ITtxhh/oBZQI9OiSyNjzDCgD3YSUYAXRGSJY9/zQC/sip+DRGSZS4JUmaKgT0HGtRxH56DO9P6yN/fMuIfeNXvzTtN3KOxb2NXhKZUxiheHVq1sATsp6d69yVtBb76ZOFlphQrJR8WFhtpE5iLpni1aRP4GljpKdjJaRN5NusFxz6kzdmbrUsAKY0wVEYl3RYAq8zQs25Bt/bYxLGoY7/70Lot/Wcz4luO5r5pOdqFyIA8PO81O9erw8MN225kzsGlTYito9WqYNcvu8/a2D6Qmnay0XLksezbI2eUJ/IFOQDkgFtgCLBeRs86HlqHuA2aLyHngV2PMfqAudvJRlcPk9crLyCYj6RjYkV5f9qLtnLY8EPgAY5uP5db8t7o6PKUyV/78dpRbw4aJ244cSb5kw0cf2UEJYFtNSVtBdTJvFd50JxxjTANgCZCPxOUJAE4YY14XkbHOBpdOjzmGbG8EnhKR/4DS2MEOCY44tqkcrHap2mzss5G3177Na6tf49uD3zKm2Ri6BnfVyUBV7lKmjC0dOtjXFy/Czp3Jk9DXX9t9xlDn9tvh88/t/aMMZCTh4aO0nmjMeiAAeAxYiX2mJwI7sq0utkXxYAbFmfR9VwAlUtj1IjapHMeuy/M6UFJEehpjPgR+EpFPHdeYAiwRkXkpXL8v0BfA398/bPbs2VcfclNiY2Px8/NL17nuKjvX+bczv/HOvnfYdXoX4UXCGVJ5CP6+zj+vnJ3rnFm0zjlTnpgYCuzZQ8HoaPLt3MnBp57ifImUPmpvLDIycpOIXLuug4ikqwBngNdS2Zdwc/6x9F7f2YLt5tvp+P554Pkk+5YB9W50jbCwMEmvVatWpftcd5Xd63wp/pKMWTdG8o3IJ35v+smHGz6U+MvxTl0zu9c5M2idcz5n6wtslBQ+U50ZtB0D/J7SDhGZgh3R1s+J66eZMaZkkpftgJ2O778EOhtjfIwx5YHKwIasjE25nqeHJ4PCB7Gz/04iykQwcMlAIqdH8ssJXRFdqazgTMJZBbS4wf6KTlw/Pd42xuwwxmwHIoEhAGJnQ/gcuxDcN8BA0RFquVb5W8qzvNtypraZyva/t1NjQg3eXvs2ly5fcnVoSuVoziScScAdxpjBqewvB/zpxPXTTEQeEpFgEakhIm1E5GiSfSNEpKKIVBWR7DaUW2UxYwyP1HyE6AHRNKvUjKErhhIxOYJtf21zdWhK5VjOJJyVQBFglDEmyhjTzRhT3RhT2RjTGxgMvJchUSqVSUoWKMn8TvP5ouMXHD59mNof1ebl717WyUCVygTOJJzXscOiD2Mn8vwEe89kDzAR2AucNMYEGWOcet5HqcxkjOH+gPuJHhDNg8EP8saaN6g5sSY/HdbHtJTKSOlOOCLyqoi0FZFy2JbO3cDTwKfALuyUN59iJ/yMNcZsM8bMcD5kpTJH0XxFmd52Oku7LuXMxTPcOfVOBi8dTOyFWFeHplSOkCFTi4rISRFZJSKjRaSHiNQA/IDa2LnNPsKOamudEe+nVGZqVqkZO/vvZECdAYzdMJbg8cF8e+BbV4ellNu76YRjjEnTJJ0ickFENovIVBF5XETqi0jhNEeolAsU8CnABy0+YM0ja/Dx9KHpp03puagn/537z9WhKeW20tLCmW2MKXD1RmNM1QyMR6lspf7t9dnabyvP3fkcn2z7hIBxASzYvcDVYSnlltKScD4Ckt2DMcZEAqszNCKlshnfPL68dc9bbOizgRJ+JWj/eXs6ftGRv2L/cnVoSrmVm044IjIaiDfGDAVwTJA5G+iWSbEpla3UKlmLDb038OZdb/LV3q8I+DCAb/76JmG6JKXUDVw34RhjOhljqpnEqXUfAXoaY6YDw4G7RETvpqpcw8vTi+cbPM/WflsJKB7AyL0jaf5Zc347+ZurQ1Mq27tRC+dJ7DT/scaYn4FR2BmZmwD3OqaMUSrXqVasGqsfWc2gSoP44fcfCBwXyAcbPuCyXHZ1aEplW9dNOCISARQAwrCzBhwH/LHr3+w2xvxijPk806NUKhvyMB60K92OXQN2Uf/2+jy+9HEafNyAPcf3uDo0pbKlG97Dccw2vUdEZovIcyLSTERKYpdqHgRsyvQolcrGyhYuy9KuS5l23zR2H9tN6IRQ3lrzFhfjL7o6NKWyFWdmGvhbRJaKyMiMDEgpd2SMoUdoD6IHRtO6amte+O4F6k6uy5ajW1wdmlLZRroTjjHmgYwMRKmcoIRfCb7o+AXzOs3jr9i/qPNRHV5Y+QJxl+JcHZpSLufM1DbTHPOj3ZfSTmOMvzGmshPXV8ptta/enugB0XQP6c5bP7xF6IRQfvj9B1eHpZRLOZNwKgJRwExjzAZjzL1X7e+MnTlaqVzplry3MPW+qSzrtoy4S3E0+LgBjy15jJjzMa4OTSmXcCbhnAUuAb9hJ+lcYozZboxZZYzZgB3VtjsDYrxpxpg5xpitjnLIGLPVsb2cMeZckn0TsjIulbs1rdiUnQN2MqjuIMb9PI6g8UF8s/8bV4elVJZzJuF8BDwB/ItdhuAz4CjQCDuMehnQwcn40kREHhCRUBEJBeYB85PsPpCwT0T6ZWVcSvl5+zGm+Rh+6PkD+bzy0fyz5vRY2IMTZ0+4OjSlsowzCeduYKxjFujujnIv0BjYh231uOQpOMfMCJ2AWa54f6VSc8dtd7Dl0S281OAlZu6YScC4AL7Y9YVOj6NyBWfXw/n16g0ishqbbI4AU528fno1AP4WkV+SbCtvjNlijPneGNPARXEphW8eX16/63U29tnIbQVvo9PcTnT4vANHY466OjSlMpVJ719WxpgFQGmgvohcSGF/P+A9EcnvXIjXXHcFUCKFXS+KyCLHMeOB/SLynuO1D+AnIieMMWHAQiBQRE6ncP2+QF8Af3//sNmzZ6crztjYWPz8/NJ1rrvSOqddvMTzxZEv+PjQx3h7eNO/Qn+al2hO4vSF2Y/+nHM+Z+sbGRm5SURqX7NDRNJVgJrAeeAnoHYK+z8BTqX3+k7ElQf4GyhznWOiUor56hIWFibptWrVqnSf6660zum37/g+afhxQ2EYcs8n98jBfw9myHUzg/6ccz5n6wtslBQ+U52ZaWAL8DAQAqw3xuw1xnxqjBljjIkCujo+2LPaPcAeETmSsMEYU9wY4+n4vgJQGTjogtiUSlHlopVZ1WMV41uOZ/2R9QSND2LMujHEX453dWhKZRin7uGIyCwgEPgA8AIeBB4HGgI/A485G2A6dObawQINge3GmG3AXKCfiPyb5ZEpdR0exoN+tfuxa8AuGpdrzBPLnqDBxw3YfSxLny5QKtM4O2gAEflVRAaLSAWgKDYBlRaRCBE57HSEaY/nYRGZcNW2eSISKCIhIlJLRL7K6riUulm3FbqNr7t8zaftPmXfiX2ETgzljdVv6GSgyu05nXCSEpH/RGS3iOhwG6WcYIyha42uRA+Mpm21try86mVqf1SbTX/q5OzKfWVowlFKZaxb89/KnPvnsOCBBRw7c4zwyeEM/XYo5y6ec3VoSqWZJhyl3EDbam2JHhjNI6GP8PaPbxMyIYTVv612dVhKpYkmHKXcRGHfwnzU5iNWPLSCS5cv0WhaIwYsHsDp89c8TqZUtpQhCcdYtxtjvDPiekqp1N1d4W529N/BkIghTNw0kaBxQSz5ZYmrw1LqhjKqhVMEO81N/Qy6nlLqOvJ752fUvaP4seePFPApQMuZLek2vxvHzx53dWhKpSoju9Sy71wcSuVQ4WXC2dx3M680fIU5u+YQ8GEAc3bO0clAVbak93CUcnM+eXwYHjmczX03U7ZwWTrP60zbOW354/Qfrg5NqWQ04SiVQwT7B/NTr594p8k7fHvgWwLHBTJ582Rt7ahsI10JxxjTMGkB7nDsqpHCPqVUFsnjkYen73ia7f23U7NkTfp81Ye7P7mbA/8ecHVoSpEnnedFASn92fReku+N4xjPdL6HUiqdKhWpxMruK5m8eTLPfPsMweODeeOuNxgcPhhPD/2VVK6R3oQTedXrwsAC4BlA595QKhvwMB70DetLi8ot6L+4P08tf4o5u+Ywpc0Ugm4NcnV4KhdKV5eaiHyftAA/OHZtTWGfUsqFyhQsw5edv2Rm+5kc/O8gtSbWYnjUcC7EX7NuolKZSgcNKJULGGPoEtyF6AHRdAzsyLDvhxE2KYyf//jZ1aGpXEQTjlK5SPH8xfms/Wd82flL/jv3HxFTInhm+TOcvXjW1aGpXEATjlK5UOuqrdk1YBd9avXh3Z/epcb4GkQdinJ1WCqHy6iE8y9QHlibQddTSmWyQr6FmNBqAqt6rAIgcnokj371KKfiTrk4MpVTZUjCEes3ETmfEde7EWNMR2PMLmPMZWNM7av2PW+M2W+M2WuMuTfJ9jBjzA7HvrHGGJ2KRymgcbnGbO+/nafrPc3kLZMJHBfI1/u+dnVYKgdy1y61nUB7INmCIMaYAKAzdpnrZsA4Y0zCQwfjgb5AZUdplmXRKpXN5fPKxztN32Fdr3UUyVuE1rNa8+C8Bzl25pirQ1M5iFsmHMcy1ntT2HUfMFtEzovIr8B+oK4xpiRQUER+EjvPxydA26yLWCn3UKd0HTb23cjwxsOZGz2X6h9WZ+aOmTo9jsoQbplwrqM0cDjJ6yOObaUd31+9XSl1FW9Pb15p9ApbHt1CpSKV6Dq/K21mt+HI6SM3Plmp60jvTAOZzhizAiiRwq4XRWRRaqelsE2usz2l9+2L7XrD39+fqKioGwebgtjY2HSf6660zjnPiIojWOC7gCn7p1B1bFUerfAojQs0ztF1TklO/zlfLdPqKyI3VYAaN3tsVhXsnG61k7x+Hng+yetlQD2gJLAnyfYuwMQbXT8sLEzSa9WqVek+111pnXOuA/8ekLum3yUMQ0JGh8i+4/tcHVKWyi0/5wTO1hfYKCl8pqalS222MabA1RuNMVXTne0y3pdAZ2OMjzGmPHZwwAYROQrEGGMiHKPTugOptZKUUlepcEsFVjy0gsmtJ7M/dj81JtTg3R/f5dLlS64OTbmRtCScj4AZSTcYYyK5aqRYVjDGtDPGHMG2XhYbY5YBiMgu4HMgGvgGGCgi8Y7T+gOTsQMJDgBLszpupdyZMYZetXoxrc407q14L898+wx3TLmDHX/vcHVoyk3cdMIRkdFAvDFmKIAxpjswG+iWSbFdL5YFIlJGRHxExF9E7k2yb4SIVBSRqiKyNMn2jSIS5Nj3mKPZp5RKo2I+xVjwwALm3D+HQycPUWtSLV5d9SrnL2XJY3jKjV034RhjOhljqiV5SPIRoKcxZjowHLhLRL7N7CCVUtmLMYZOgZ3YPXA3nYM689rq1wibFMb6I+tdHZrKxm7UwnkS2AjEGmN+BkYB64AmwL2OLiylVC5VNF9RZrSbweIHF3Pq/CnqTanHk8ue5MyFM64OTWVD1004IhIBFADCsKt5Hgf8scOMdxtjfjHGfJ7pUSqlsrUWlVuwa8Au+tXux+h1owkeH8zKgytdHZbKZm54D8cxym2PiMwWkedEpJmIlARKAYPQFT6VUkBBn4KMazmO7x/+njweebhnxj30+bIPJ+NOujo0lU04M9NAIxFZKiIjMywapZTba1i2Idv6bePZO55l6tapBHwYwKI9+hSCci7hzDTGPJphkSilcoy8XnkZ2WQk63uvp3j+4rSd05YH5j7A37F/uzo05ULOJJxp2NmYX0xppzGmnjFmjRPXV0q5udqlarOxz0Zej3ydhXsWEjAugBnbZuhkoLlUuhOOiPQG3gZeN8aMTthujKlqjJkP/ADUdD5EpZQ78/L04qWGL7H10a1ULVqV7gu703JmS34/9burQ1NZzKnZokXkeezQ6UHGmE+NMROAHUBLYCJQyfkQlVI5QfXi1VnzyBrGNBvD9799T+C4QMb9PI7LctnVoakskhGzRX+ETTAPYmdgng28LCIHM+Da2c7Fixc5cuQIcXFx1z2uUKFC7N69O4uiyh5yUp19fX0pU6YMXl5erg4lR/H08GRQ+CDaVG1D36/6MnDJQGbvnM3kNpOpUrSKq8NTmSzdCccY4wUMwM7QXBzYDIQCXiRfkyZHOXLkCAUKFKBcuXJcb5XqmJgYChS4Zq7THC2n1FlEOHHiBEeOHKF8+fKuDidHKle4HMu6LWPa1mk8ufxJaoyvwfDGw3nqjqfI45FtV01RTnKmS+0X7MwDx4A2IlIb28ppAywxxvhlQHzZTlxcHEWLFr1uslHuzRhD0aJFb9iKVc4xxvBIzUeIHhBNi8oteG7lc4RPDmfbX9tcHZrKJM4kHE+gDxAiIosBRORzbMKJAFYZY4o5H2L2o8km59OfcdYpWaAk8x+Yz9yOc/nj9B/U/qg2L333EnGXNOHnNM4knMoiMlUk+R0/EVkO3AOUB350JjilVO7RIaAD0QOj6RrclRFrRlBzYk1+PKwfITmJM8OiU/3zQ0TWAw0A3/ReXymV+xTJW4RpbafxTddvOHvxLPWn1mfw0sHEXoh1dWgqAzg1LPp6RGQ3cGdmXV+lXc+ePVPdt2PHDn7/PflzEQcPHqRXr17cf//9mR2aUsncW+ledvbfycA6A/m/Df9H0Lgglh9Y7uqwlJNuOuEYY+5O68VF5LDj3HvSeu4NYulojNlljLlsjKmdZHsTY8wmY8wOx9e7kuyLMsbsNcZsdZRbMzImV3jqqacICAigT58+NGrUiPj4+FSPPXv2LIUKFWLVqlUMHTr0mhvimzZt4uDB5CPZK1SowJQpU5Jtu3DhAg0bNuTSJV1aWGWuAj4F+L8W/8eaR9bgm8eXez+9l0cWPcJ/5/5zdWgqndLSwvnGGPOdMaaVMcbzRgcbY7wcS0F/DyxJf4gp2gm059rlrY8DrUUkGOjBVUtiA11FJNRR/sngmLLUwYMHWbt2LdHR0YSGhtK+fXs8PVP/sWzevJmtW7eyd+9eRo4cia+v7e2Mjo6mX79+TJ8+nVGjRtGvXz/+/jv1+a68vb25++67mTNnTobXSamU3Hn7nWztt5Xn6z/PjG0zCBgXwPzd810dlkqHtAx4DwVGA18Cx40x3wIbgAPAv9g1cooAlbGj1O5yvF7mODfDOLrrrhlJJCJbkrzcBfgaY3xEJEetfbt3717uueceLl26RM2advagBQsWXNkfGRnJCy+8QJMmTXjppZc4ffo05cuXJzw8nPz58ye7VkBAABMmTGDatGmUK1eOxo0b3/D927Zty/PPP0/Xrl0ztF5KpcY3jy9v3v0mHQM60uvLXnT4vAMdqnfggxYfUMKvhKvDUzcpLS2cjkBf7H2ZZUBrbAJaBKzBtjYWAu8CTbGJKVxEmotIdAbGfLM6AFuuSjYfO7rTXjZuPO61atWq9OjRg9dff53169dz9OhRypUrd2X/8OHDGTFiBJ999hlbtmxh9OjRREdH8+abb7Jnzx7WrLm5OVVPnDhBv3792LJlC2+99daV7UFBQfz8888ZXS2lbqhmyZqs772et+5+i6/3fU3AhwFM2zpNJwN1E+Zmf1DGmMtANxGZ6Xh9P/A7EICdaUCwD4HuxH7QOzVBkjFmBZDSny4visgixzFRwNMisvGqcwOxCa+piBxwbCstIn8YYwoA84BPReSTFN63Lzax4u/vHzZ79uxk+wsVKkSlSnaKuKFDfdixI+WcLQLpSWnBwZcZOfLGDbLOnTvzzDPPUKpUKVq1asWmTcnXwWvevDlnzpxh8eLFmfL0f9WqVdm4cWOya8fHx1+3W8/d7N+/n1OnTl33mNjYWPz8cuQzzqnKLnX+/ezvvLv3XXac3kHtW2rzVJWnKOGbOa2d7FLnrOJsfSMjIzc5JgNIJi1dav8B+ZK8ngM8JCLT0h3VdYhIugYaGGPKAAuA7gnJxnG9PxxfY4wxM4G6wDUJR0QmAZMAateuLVd3Me3evfvKh6y3N6T2+RoffwlPz7RP0eHtDQUKeN/wuL1791K3bl3Onz/PhQsXkn3w79ixg3/++YdixYpRqlSpNMdwMy5cuEDx4sWTzTWWU6a2SeDr63ulyzI1UVFRN9UNmZNkpzp3a96NCRsnMHTFUHpv7s1bd7/FwLoD8TAZOwA3O9U5K2RWfdPyibgT6GWMWer48M52XVLGmMLAYuB5EVmbZHseoLCIHHfMAdcKWOHs+73/fur7YmLOZdqHb0xMDF5eXuTLl498+fIRHx9PXFwcvr6+HD16lK5du7Jo0SIGDRrEsmXLuPfeezP0/U+cOHFNslHKFTyMBwPqDKBVlVY8+vWjDPpmEHN2zWFym8lUK1bN1eGpq6Tlz4DhQC3gd2PMHmwXWgtjTHNjjH+mRJcKx+i3I0A9YLExZplj12PYJRFevmr4sw+wzBizHdgK/IGd5dot7dy5k6CgoCuvmzZtyg8//MDZs2dp37497733HtWrV+fll19m2LBhGf7+q1atokWLFhl+XaXS6/ZCt7PkwSVMbzud6GPRhEwI4c01b3Ix/qKrQ1NJichNF6AKdtG1tcBlR4l3lD+Br4HXgXZAubRcOzuWsLAwuVp0dPQ121Jy+vTpmzouI2zevFm6deuWZe/Xrl072bNnzzXbs7LOWeFmftarVq3K/ECymexe579i/pL7P79fGIaETgiVzX9udvqa2b3OGc3Z+gIbJYXP1DR1dIrIPhF5VkQSZhB4BrgfeAvYgm0BvQjMBQ4YY447lw7VzahZsyaRkZHXffAzo1y4cIG2bdtStWrVTH8vpdLD38+fLzp+wbxO8/gr9i/qfFSH51c8r5OBZgPO3Fl7DVgjIgtE5CURaSkipYDS2Bmjh3Ptg5kqk/Ts2TNLRoh5e3vTvXv3TH8fpZzVvnp7ogdE0z2kO/9b+z9CJoTww+8/uDqsXM2ZyTuHiciGFLYfFZHFIvKaiLR3LjyllEq/W/LewtT7prK823IuxF+gwccNeGzJY8Scj3F1aLlSpk3eqZRS2UWTik3Y0X8Hg8MHM+7ncQSND+Kb/d+4OqxcRxOOUipX8PP24/1m77O251rye+Wn+WfN6bGwByfOnnB1aLmGJhylVK5S77Z6bHl0Cy81eImZO2YSMC6AudFzdXqcLKAJRymV6/jk8eH1u15nY5+N3FbwNjp+0ZEOn3fgaMxRV4eWo2nCUUrlWiElQljXex0j7xnJ0v1Lqf5hdaZumaqtnUyiCcdNLViwAGMMe/bsceo6EyZM4JNP7JRyr7zyCitWOD3jj1JuJY9HHp6981m29dtGSIkQen3Zi6afNuXX/351dWg5jiYcNzVr1izq16/P1bNZA2l6ALRfv35Xnqt57bXXuOeeDF2cVSm3UaVoFVb1WMW4FuNYf2Q9QeODGLNuDPGXM/+B6txCE44bio2NZe3atUyZMuVKwomKiiIyMpIHH3yQ4OBgoqKiaNSoEZ06daJKlSo899xzfPbZZ9StW5fg4GAOHLATaQ8bNox3330XgIcffpi5c+cCsHLlSmrWrElwcDA9e/bk/PkctYadUinyMB70r9OfXQN20bhcY55Y9gT1P67PoTOHXB1ajpD2+fNVoieegK1bU9yVNz4+9bULric09PrTUAMLFy6kWbNmVKlShSJFirB582YANmzYwM6dOylfvjxRUVFs27aN3bt3U6RIESpUqEDv3r3ZsGEDY8aM4f/+7/94P5X3iYuL4+GHH2blypVUqVKF7t27M378eJ544om010cpN3Rbodv4usvXzNwxk8HfDKbvH3057HeYofWH4u154+VDVMq0heOGZs2aRefOnQG7ENusWbMAqFu3LuXLl79yXJ06dShZsiQ+Pj5UrFiRpk2bAhAcHMyhQ4dSvf7evXspX748VapUAaBHjx6sXq2zFKncxRhD1xpdiR4YTYNiDXgl6hVqT6rNxj833vhklSJt4TjjOi2Rc5m0GNmJEyf47rvv2LlzJ8YY4uPjMcbQokUL8ufPn+xYHx+fK997eHhcee3h4cGlS5dSfQ8doaNUolvz38rLAS8zuORg+i/uT/jkcJ6q9xTDGw8nr1deV4fnVrSF42bmzp1L9+7d+e233zh06BCHDx+mfPny/PBDxk1KWK1aNQ4dOsT+/fsBmDFjBo0aNcqw6yvljtpUbcOuAbvoVbMX7/z4DjUm1OD7Q9+7Oiy3ognHzcyaNYt27dol29ahQwdmzpyZIdc3xuDr68vHH39Mx44dCQ4OxsPDg379+mXI9ZVyZ4V9CzOp9SRWdl/JZblM4+mN6f91f06fP+3q0NxDSovkZPcCdAR2YReAq51kezngHHZVz63AhCT7woAdwH5gLGBu9D7usgBbRmnVqpV899136T7fHet8PboAW8q0zlbs+Vh58psnxWO4h5QZVUa+3vt11geWSbLFAmzZyE6gPSmvt3NAREIdJemf5eOBvkBlR2mW+WG6j549e3L27Fnq16/v6lCUcgv5vfPz3r3v8WPPHynkU4hWs1rRbX43jp/VdSdT45YJR0R2i8jemz3eGFMSKCgiPzmy7ydA28yKzx1NnTqVlStX4uXl5epQlHIr4WXC2dR3E682epXPd31OwIcBzNk5RwffpMAtE84NlDfGbDHGfG+MaeDYVho4kuSYI45tSinlNJ88PgxrPIxNfTdRrnA5Os/rTNs5bfnj9B+uDi1bybbDoo0xK4ASKex6UUQWpXLaUeB2ETlhjAkDFhpjAgGTwrEp/vlhjOmL7XrD39+fqKioZPsLFSpETMyNVwuMj4+/qeNykpxW57i4uGt+/leLjY294TE5jdb5+t6q9BbzfOcx9ZepVB1blX4V+9GyREuMSeljKHvKtJ9xSjd23KUAUSQZNJDafqAksCfJ9i7AxBtdP7cNGnBWTquzDhpImdb55vxy4hdpPK2xMAyJnBYp+0/sz/jAMokOGrgJxpjixhhPx/cVsIMDDorIUSDGGBNh7J8Z3YHUWklKKeW0SkUqsbL7Sia2msimo5sIHh/MqJ9G5erJQN0y4Rhj2hljjgD1gMXGmGWOXQ2B7caYbcBcoJ+I/OvY1x+YjB0WfQBYmsVhZ5i///6bBx98kAoVKhAWFka9evVYsGBBqsdHRUXRqlWrFPeVK1eO48dTH1Xz/vvvc/bs2RvG1Lt3b6eXSlAqp/EwHvQN60v0gGjuqXAPTy1/ijum3sHOf3a6OjSXcMuEIyILRKSMiPiIiL+I3OvYPk9EAkUkRERqichXSc7ZKCJBIlJRRB5zNPvcjojQtm1bGjZsyMGDB9m0aROzZ8/myJEjNz45HW424UyePJlq1aplSgxKubvSBUuzqPMiZnWYxcH/DlJrYi2GRw3nQvwFV4eWpdwy4eRm3333Hd7e3sme/C9btiyPP/44cXFxPPLIIwQHB1OzZk1WrVp1zfknTpygadOm1KxZk0cfffTK0M0zZ87QsmVLQkJCCAoKYs6cOYwdO5Y///yTyMhIIiMjAVi+fDn16tWjVq1adOzYkdjYWAAaN258ZdZqPz8/XnzxRUJCQoiIiODvv//O7H8WpbI9Ywydgzqze+BuOgZ2ZNj3wwibFMbPf/zs6tCyTLYdpeYOnvjmCbb+tTXFffHx8XimY3mC0BKhvN/s/VT379q1i1q1aqW478MPPwRgx44d7Nmzh6ZNm7Jv375kxwwfPpz69evzyiuvsHjxYiZNmgTAN998Q6lSpVi8eDEAp06dolChQowaNYpVq1ZRrFgxjh8/zhtvvMGKFSvInz8/I0eOZNSoUbzyyivJ3uPMmTNEREQwYsQInn32WT766CNeeumlNP9bKJUTFctXjM/af0aXoC70+7ofEVMiGBIxhNciXyOfVz5Xh5eptIXj5gYOHEhISAh16tThhx9+4KGHHgLsBJxly5a9JuGsXr2abt26AdCyZUtuueUWwC5ZsGLFCoYOHcqaNWsoVKjQNe+1bt06oqOjufPOOwkNDWX69On89ttv1xzn7e195Z5RWFjYdZdCUCq3alWlFbsG7KJ3zd6899N71Bhfg6hDUa4OK1NpC8cJ12uJxGTS8gSBgYHMmzfvyusPP/yQ48ePU7t2bUqXvrlnWVN6HqBKlSps2rSJJUuW8Pzzz9O0adNrWi4iQpMmTa6sv5MaLy+vK+/h6el53aUQlMrNCvkWYmLriXQJ7kLvL3sTOT2SvrX68naTtynke+0ffe5OWzhu5q677iIuLo7x48df2ZZwU79hw4Z89tlnAOzbt4/ff/+dqlWrJjs/6TFLly7lv//+A+DPP/8kX758dOvWjaeffvrK/ZgCBQpceZgzIiKCtWvXXlm24OzZs9e0oJRSade4XGO299/O0/WeZvKWyQSMC+CrvV/d+EQ3ownHzRhjWLhwId9//z3ly5enbt269OjRg5EjRzJgwADi4+MJDg7mgQceYNq0ackWYQN49dVXWb16NbVq1WL58uXcfvvtgL3vU7duXUJDQxkxYsSVey59+/alefPmREZGUrx4caZNm0aXLl2oUaMGEREROhRaqQySzysf7zR9h3W91lE0b1HazG7Dg/Me5NiZY64OLeOk9DSoFp1pID1yWp11poGUaZ0z3/lL52V41HDxes1Lio4sKp9t/0wuX76cZe+vMw0opVQu4e3pzSuNXmHLo1uoVKQSXed3pfWs1hw+ddjVoTlFE45SSmVTgbcGsrbnWkY1HcWqQ6sIHBfIhI0TuCyXXR1aumjCUUqpbMzTw5Mh9Yawo/8O6pauS//F/blr+l38cuIXV4eWZppwlFLKDVS4pQLfPvQtk1tPZutfW6kxoQbvrH2HS5fd57EDTThKKeUmjDH0qtWL6IHR3FvxXp5d8Sz1ptRj+9/bXR3aTdGEo5RSbqZUgVIseGABn9//Ob+f+p2wSWG8suoVzl867+rQrksTjlJKuSFjDB0DOxI9IJrOQZ15ffXr1JxYk58O/+Tq0FKlCUcppdxY0XxFmdFuBkseXELshVjunHonT3zzBGcunHF1aNfQhJPD9OzZ09UhKKVcoHnl5uwcsJP+tfszZv0YgscHs+LgCleHlYwmnBzk7NmzFCpUiFWrVjF06FDi4uKuOWbs2LFUr16drl27pvt9/Pz8ALjjjjvSfQ1XOXToEEFBQa4OQ6lMUdCnIB+2/JDVD68mj0cemsxoQu8ve3My7qSrQwPcNOEYYzoaY3YZYy4bY2on2d7VGLM1SblsjAl17IsyxuxNsu9Wl1Ugk2zevJmtW7eyd+9eRo4cia+v7zXHjBs3jiVLllyZwPN6RITLl1N/wOzHH390Kt7McqO4lcrpGpRtwLZ+2xh651CmbZ1GwIcBLNyz0NVhuWfCAXYC7YHVSTeKyGciEioiocBDwCER2ZrkkK4J+0Xkn6wIVK5ayfrq1+k1d+5cIiIiCAkJoX79+hw7doyff/6Z8PBw8ufPn+I5/fr14+DBg7Rp04bRo0czatQogoKCCAoK4v333wdsC6B69eoMGDCAWrVqcfhw6lNpJLR0Es55/PHHCQwMpGnTppw7dw6ATz/99MqkoI8++ijx8fHXXCel1Uavd27btm0JCwsjMDDwygJyKcX9ySefUKNGDUJCQq6sEwR2cbw+ffpcE6tSOUler7z8757/sb73em7Nfyvt5rSj0xed+DvWhSvwpjTBmrsUIAqoncq+N4ERN3NsasXZyTtfffVVGTx48JVJ9y5fviyDBw+WV1999aaucT3Hjx+/8v2wYcPkgw8+kN69e0t8fLy88MILsnr16hTPK1u2rBw7dkw2btwoQUFBEhsbKzExMRIQECCbN2+WX3/9VYwx8tNPP6X63vnz50/29ddffxVPT0/54YcfRESkY8eOMmPGDImOjpZWrVrJhQsXRESkf//+Mn369GuuN3fuXOndu/eV1ydPnrzuuSdOnBARkbNnz0pgYKAcP378mrh37twpVapUkWPHjiU7JyHWLVu2JIs1JTp5Z8q0zu7nwqULMmL1CPF+3VuKjCwin2z95LqTgerknWn3AHD1SmEfO7rTXjYprUKWgUSEkydPMmbMGIYMGYKIMGTIEMaMGcPJkyedbulMmzaNunXrEhISwrhx4/D19eWjjz7Cw8ODESNG0KBBg+ue/8MPP9CuXTvy58+Pn58f7du3Z82aNQCULVuWiIiINMVTvnx5atSoASSu8rly5Uo2bdpEnTp1CA0NZeXKlRw8ePCac1NabfR6544dO5aQkBAiIiI4fPgwv/zyyzVxf/fdd9x///0UK1YMgCJFiiSLNTQ0NFmsSuVkXp5evNDgBbY+upVqxarRfWF3Ws5sye+nfs/SOLLtip/GmBVAiRR2vSgii25wbjhwVkR2JtncVUT+MMYUAOZhu9w+SeHcvkBfAH9/f6KiopLtL1So0JUFya7n8uXLvPbaa1y4cIExY8YwZswYAPr3789rr71GbGzsDa+RmpkzZ/Ljjz+yaNEi/Pz8aNasGeXKlbupuESE2NhYzp07x/nz56+cc/78eeLi4oiNjSVv3rw3vFbC/piYGGJjY/Hy8iI+Pp6YmBguXbrEmTNn8PHxoUuXLgwbNizFcxOULFmSqKgoli9fzrPPPstdd91F4cKFUzx3yZIlLFu2jOXLl5MvXz5atGjBv//+i5+fX7K4z507x4ULF655r4RYE7YnxJpSfePi4q75+V8tNjb2hsfkNFpn9/Za+ddY5LOIjw5+RLX/q0bf8n1pU6oNHiax/ZFp9U2p2eMuhVS6yYDRwAvXOe9h4IMbXT8j1sO5fPmyAFdKRqxp8fTTT8v7778vIrY7ytPTU2JjY2/q3IQutU2bNklwcLCcOXNGYmNjJTAw8EqXWmBg4HWvkVKXWmBg4JU6v/POO/Lqq6/Krl27pFKlSvL333+LiO3WOnTo0DXX++OPP+TcuXMiIrJgwQK57777Uj134cKF0qpVKxER2b17t/j4+MiqVauuiXvnzp1SuXLlK12PSbvUkh6XEGtKtEstZVrnnOHX/36VJp80EYYhDaY2kD3H9lzZp11qN8kY4wF0BGYn2ZbHGFPM8b0X0Ao78CBTiaMbLamE7jVn9OjRg7Fjx9KgQQP27dtHhQoVUh0okJpatWrx8MMPU7duXcLDw+nduzc1a9Z0Kq6rBQQE8MYbb9C0aVNq1KhBkyZNOHr06DXHpbTaaGrnNmvWjEuXLlGjRg1efvnlVLv+AgMDefHFF2nUqBEhISE8+eSTGVo3pdxducLlWNZtGR/f9zE7/tlByIQQ/vfD/zJ3MtCUslB2L0A74AhwHvgbWJZkX2Ng3VXH5wc2AduBXcAYwPNG7+NMC+fUqVMyePBgAa4MHLj6dU6jK37mDlrnnOdozFFpP6e9MAypNbGWfPTVR05dj1RaONn2Hs71iMgCYEEq+6KAiKu2nQHCMj+yRMYYChcuzODBgxk9ejTGGEaPHg1A4cKFyeQxC0opddNK+JVgXqd5zIuex8AlA3n06KOUrV6WJhWbZOj7uGXCcRfDhg1DRK4kl4Sko8lGKZUddQjoQGT5SB6f9TgNyl5/pGt65Lh7ONnN1clFk41SKjsrkrcIfSr0wTfPtTOVOEsTjlJKqSyhCScdxMlRZir705+xUhlPE04a+fr6cuLECf1AysFEhBMnTqQ4+alSKv100EAalSlThiNHjnDs2LHrHhcXF5frPrByUp19fX0pU6aMq8NQKkfRhJNGXl5elC9f/obHRUVFZfiDlNldbqyzUurmaZeaUkqpLKEJRymlVJbQhKOUUipLGB1tlTpjzDHgt3SeXgw4noHhuAOtc+6gdc75nK1vWREpfvVGTTiZxBizUURquzqOrKR1zh20zjlfZtVXu9SUUkplCU04SimlsoQmnMwzydUBuIDWOXfQOud8mVJfvYejlFIqS2gLRymlVJbQhJMOxphmxpi9xpj9xpjnUthvjDFjHfu3G2Nq3ey52VF662uMuc0Ys8oYs9sYs8sYMzjro08fZ37Gjv2expgtxpivsy5q5zj5/7qwMWauMWaP4+ddL2ujTx8n6zzE8f96pzFmljHGLSYSvIk6VzPG/GSMOW+MeTot595QSutOa0m9AJ7AAaAC4A1sAwKuOqYFsBQw2OWu19/sudmtOFnfkkAtx/cFgH3Zvb7O1jnJ/ieBmcDXrq5PVtQZmA70dnzvDRR2dZ0ys85AaeBXIK/j9efAw66uUwbV+VagDjACeDot596oaAsn7eoC+0XkoIhcAGYD9111zH3AJ2KtAwobY0re5LnZTbrrKyJHRWQzgIjEALuxv6jZnTM/Y4wxZYCWwOSsDNpJ6a6zMaYg0BCYAiAiF0TkZBbGnl5O/Zyxkx/nNcbkAfIBf2ZV4E64YZ1F5B8R+Rm4mNZzb0QTTtqVBg4neX2Eaz9EUzvmZs7Nbpyp7xXGmHJATWB9xoeY4Zyt8/vAs8DlTIovMzhT5wrAMeBjRzfiZGNM/swMNoOku84i8gfwLvA7cBQ4JSLLMzHWjOLMZ5DTn1+acNLOpLDt6qF+qR1zM+dmN87U1+40xg+YBzwhIqczMLbMku46G2NaAf+IyKaMDytTOfNzzgPUAsaLSE3gDOAO9yed+Tnfgv3rvjxQCshvjOmWwfFlBmc+g5z+/NKEk3ZHgNuSvC7DtU3p1I65mXOzG2fqizHGC5tsPhOR+ZkYZ0Zyps53Am2MMYewXQ53GWM+zbxQM4yz/6+PiEhC63UuNgFld87U+R7gVxE5JiIXgfnAHZkYa0Zx5jPI+c8vV9/EcreC/WvuIPYvm4QbZ4FXHdOS5DcaN9zsudmtOFlfA3wCvO/qemRVna86pjHuM2jAqToDa4Cqju+HAe+4uk6ZWWcgHNiFvXdjsIMmHnd1nTKizkmOHUbyQQNOf365/B/AHQt25Mo+7IiNFx3b+gH9HN8b4EPH/h1A7eudm91LeusL1Mc2ubcDWx2lhavrk9k/4yTXcJuE42ydgVBgo+NnvRC4xdX1yYI6Dwf2ADuBGYCPq+uTQXUugW3NnAZOOr4vmNq5aSk604BSSqksofdwlFJKZQlNOEoppbKEJhyllFJZQhOOUkqpLKEJR6kcwBiz3hjT2dVxKHU9mnCUcnPGGA8gCDskWalsSxOOUu6vKvZ3ea+rA1HqejThKOX+QoFoEYmHK+u07DHGhLo0KqWuksfVASilnBYKbDPGFAI+xv5eR4h7LBGgchFt4Sjl/kKxSeZn7PQy92myUdmRTm2jlJszxvzl+PZbEXnIpcEodR3awlEqmzLG1DTGLDDG/Ococ40xRYwxpYwxccaYLsaYEoA/dqLQBsaYHq6NWqnU6T0cpbIhY0wX7JT327GzEpcHBmFXmMwD/ALMAe4FDorIHsfib6uMMYdF5DvXRK5U6jThKJXNGGMqAFOxyzk0FJE4x/baQHOgHNBVRC4bY0KALQAistMY0xWYY4xpKCK7XRG/UqnRezhKZTPGmDHY1kyEJK6iiTFmBtAN2Ixdl0V/eZVb0Xs4SmU/bYD9SZPNVV7WZKPckSYcpbIRY0wRbJfZzyns9gd2iciSLA1KqQyiCUep7KWE4+uJpBuNMQ2BJldvV8qdaMJRKns56fgakrDBGOMHTHS8zJ/VASmVUTThKJWNiMifwAbsMzUzjDH9gdVAMeAboKYx5gljTElXxqlUeugoNaWyGWNMWeAD7MOcebDDnns6ds8DAoBqIqKzQyu3oglHKaVUltAuNaWUUllCE45SSqksoQlHKaVUltCEo5RSKktowlFKKZUlNOEopZTKEppwlFJKZQlNOEoppbKEJhyllFJZQhOOUkqpLKEJRymlVJb4f7Fhr4jBsHPAAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"plot_alpha(-3,eta_ls=0.25,algorithm=\"steepest-descent\",alpha_max=1E-1)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.3 Steepest Descent Step, $x^k = -3$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.3-Steepest-Descent-Step,-$x^k-=--3$)",
"section": "3.6.3.3 Steepest Descent Step, $x^k = -3$"
}
},
"source": [
"**Discussion**\n",
"* Why did the line search stop where the Armijo conditions are satisfied?\n",
"* Why not further decrease $\\alpha^k$ to achieve a greater improvement in the objective?"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.4 Newton Step, $x^k = 0$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.4-Newton-Step,-$x^k-=-0$)",
"section": "3.6.3.4 Newton Step, $x^k = 0$"
}
},
"source": [
"### 3.6.3.4 Newton Step, $x^k = 0$"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.4 Newton Step, $x^k = 0$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.4-Newton-Step,-$x^k-=-0$)",
"section": "3.6.3.4 Newton Step, $x^k = 0$"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Considering xk = 0 and f(xk) = 1.5\n",
"Step with newton algorithm:\n",
"pk = 0.75\n",
"With full step, xk+1 = 0.75 and f(xk+1) = 3.486328125\n",
"Line search failed. Goldstein conditions violated. Consider increasing alpha_max.\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZEAAAETCAYAAAD3WTuEAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAABJtElEQVR4nO3dd3gUVffA8e8lJITemxTpKEV6UwQiglIECyKgohKaUgRFEH2lKPKKStGfSBPECvpSJFIVSKRI7xA6UmIQIdQECCnn98ddIIQEUja7m+R8nmeeZGdmZ86FZE/u3GZEBKWUUiolsrg7AKWUUumXJhGllFIppklEKaVUimkSUUoplWKaRJRSSqWYJhGllFIp5rFJxBhz1Bizyxiz3RizOYHjxhjzuTHmkDFmpzGmtjviVEqpzCyruwO4Cz8ROZPIsVZARcfWAJjk+JqoQoUKSZkyZVIcTEREBDlz5kzx+9ObzFZe0DJnFlrm5NmyZcsZESmc0DFPTyJ30h74VuxoyfXGmHzGmOIicjKxN5QpU4bNm2+r1CRZUFAQzZo1S/H705vMVl7QMmcWWubkMcYcS+yYxz7OAgT4zRizxRjTM4HjJYATcV6HOPYppZRyEU+uiTwkIqHGmCLA78aYfSKyKs5xk8B7bpvDxZGAegIULVqUoKCgFAcUHh6eqvenN5mtvKBlziy0zM7jsUlEREIdX/81xswH6gNxk0gIUCrO65JAaALXmQpMBahbt66kpgqb2arAma28oGXOLLTMzuORScQYkxPIIiKXHN+3BN6Pd1oA0NcYMxvboH7hTu0hiYmKiiIkJISrV6/e9dy8efOyd+/e5N4i3UpueX19fSlZsiTe3t5pGJVSypN4ZBIBigLzjTFgY/xRRJYaY3oDiMhkYDHQGjgEXAZeScmNQkJCyJ07N2XKlMFxv0RdunSJ3Llzp+Q26VJyyisihIWFERISQtmyZdM4MqWUp/DIJCIiR4AaCeyfHOd7Afqk9l5Xr15NUgJRd2aMoWDBgpw+fdrdoSilXMiTe2e5jCYQ59B/R6UyH00iSimVgV2Ouszg3wcz468ZaXJ9TSJKKZVBBR0NosbkGnzy5ydcjL5IWqxkq0kkHevWrVuix3bt2sXx48dv2XfkyBH8/f3p0KFDWoemlHKjC1cv0Hthb/y+8UNEWNl1JQMqDkiTR86aRDzIm2++SZUqVejRowdNmzYlJiYm0XMvX75M3rx5CQwMZMiQIbd1Ud6yZQtHjhy5ZV+5cuWYPn36LfuuXbtGkyZNiI6Odl5BlFJus/DAQqp+WZVpW6fxZqM32fnqTvzK+qXZ/TSJeIgjR46wdu1agoODqVmzJk8//TReXl6Jnr9161a2b9/O/v37GTNmDL6+vgAEBwfTu3dvvvnmG8aNG0fv3r05depUotfx8fGhefPm/PTTT04vk1LKdU5HnKbL3C48MesJ8vnm489uf/Jpy0/J4Z0jTe/rkV18M5v9+/fz6KOPEh0dTa1atQCYP3/+jeN+fn688847tGjRgv/85z9cvHiRsmXL0qBBg9tm5axSpQqTJ09m5syZlClTJkkjVJ988kmGDh3K888/79RyKaXSnogwe/ds+i/tz4WrFxjRdARDHx6Kj5ePS+6vNREPULlyZV566SU++OADNmzYwMmTJ4k7Zf3IkSP58MMP+eGHH9i2bRvjx48nODiY0aNHs2/fPlavXp2k+4SFhdG7d2+2bdvGf//73xv7q1WrxqZNm5xdLKVUGvv74t+0m92OLvO6UDZfWbb22srwZsNdlkBAayK3GDAAtm9P/HhMTHbu8IQpQTVrwoQJdz9v165dtG/fnjNnzpAvX75bjjVp0gQRYdy4cQQFBeHl5cW0adMA+PDDDxO83ssvv3zbvoIFCzJ58uTb9nt5eeHj45PpRuQrlV6JCF9t/YpBvw8iKiaKsS3H8nqD1/HKkswPKCfQJOIh9uzZQ9WqVYmMjLytkXzXrl2cPHmSQoUKpdmHfGRk5I12FaWU5zp89jA9fu1B4NFA/Mr4Me2JaZQvUN5t8WgSieNuNYZLl66kyYf4pUuX8Pb2JkeOHOTIkYOYmBiuXr2Kr68vJ0+e5Pnnn2fBggX079+fZcuW8dhjjzn1/mFhYRQuXFgnTlTKg8XExjBh/QTeC3wPby9vpradSvfa3d0+U4S2iXiA3bt3U61atRuvW7ZsyZo1a7h8+TJPP/00Y8eO5f777+e9995jxIgRTr9/YGAgrVu3dvp1lVLOsevULhpNb8Sg3wfRonwLgl8LpkedHm5PIKBJxCM0atSI//3vfzde9+3bl2+++YYcOXKwbt06WrRoAdi2kXXr1jn9/j/++CM9eya0eKRSyp2uxVxjeOBwak+tzdHzR5n9zGx+ee4XSuTxnEVc9XGWB6pVqxZ+fn7ExMTccayIM1y7do0nn3ySypUrp+l9lFLJsyFkA/4B/uw5vYcXHniB8Y+Np1COQu4O6zaaRDzUnaY0cSYfHx+6du3qknsppe4u4loE7wW+x4T1EyiRpwQLOy+kTaU27g4rUZpElFLKQ6z8ayU9fu3BkXNHeLXuq3z06EfkyZbH3WHdkSYRpZRys/NXz/PWb2/x1bavqFCgAkEvBdG0TFN3h5UkmkSUUsqNFuxbwKuLXuVUxCneevAtRjYbSXbv7O4OK8k0iSillBv8G/Ev/Zf056c9P1G9SHUCOgdQ95667g4r2TSJKKWUC4kIP+z6gdeXvs6lyEu83+x9hjQe4tL5rpzJo5OIMcYL2Az8LSJt4x1rBiwA/nLsmici77s0QKWUSoYTF07Qe1FvFh9cTMOSDZnebjpVCldxd1ip4umDDV8H9t7h+GoRqenY0nUCmT9/PsYY9u3bl6rrTJ48mW+//RaAYcOGsXz5cmeEp5RKhViJZfLmyVT9sipBR4MY/9h41ryyJt0nEPDgmogxpiTQBvgQeMPN4aS5WbNm0bhxY2bPnn3b1CbJGXTYu3fvG9+//366zqtKZQgHww7S49ce/HHsDx4t9yhT206lbP6y7g7LaTy5JjIBGAzE3uGcRsaYHcaYJcaYqq4Jy/nCw8NZu3Yt06dPZ/bs2QAEBQXh5+dHly5dqF69OkFBQTRt2pSOHTtSqVIl3n77bX744Qfq169P9erVOXz4MAAjRozg008/Bex08HPmzAFgxYoV1KpVi+rVq9OtWzciIyPdU1ilMono2Gg+XvsxD0x+gB2ndjCj3Qx+e+G3DJVAwENrIsaYtsC/IrLF0faRkK3AvSISboxpDfwCVEzgWj2BngBFixYlKCjoluN58+bl0qVLAGQbMoQsu3YlGld2EaKTOeFZbPXqRI4Zc8dzZs+eTfPmzSlevDh58+Zl9erVXL58mY0bN7J+/XrKlCnD6tWr2bFjB5s2bSJ//vw88MADdO3alRUrVvDll18yduxYxowZQ2RkJN7e3ly6dImoqCiuXLnC6dOneemllwgICKBixYr07NmT8ePH06dPnzvGFRMTc+PfJqmuXr16279xehIeHp6u408JLbPzHQo/xCf7P+FA+AEaF2zMgIoDKHihIH/88Uea3fNu0qrMHplEgIeAdo7k4AvkMcZ8LyIvXD9BRC7G+X6xMeZLY0whETkT90IiMhWYClC3bl2Jv1zs3r17b07v7uPDnVadio6JIWty57Ly8cHnLtPH//LLLwwYMIDcuXPz/PPPExAQQJs2bW7UMgBy5MhBvXr1qFjR5skKFSrwxBNPkDt3burVq8e6devInTs32bJlI1u2bOTOnRtvb2+yZ89OaGgo5cqVo3bt2gB0796diRMn8vbbb98xrpQsUuXr63tjid/0KCgoKElLCmckWmbniYyOZNSqUXy07SMKZC/Azx1+pkOVDh4x225aldkjk4iIDAWGwo1eWIPiJhDH/mLAKRERY0x97KO5sFTd+C4LilxJg5X/wsLCWLlyJbt378YYQ0xMDMYYWrdufdv66dmyZbvxfZYsWW68zpIlC9HR0YneQ0ScGrNS6nbrTqyjW0A39p3ZR9caXRnXchwFcxR0d1hpzpPbRG5jjOltjLnectwB2G2M2QF8DnSSdPhpOWfOHLp27cqxY8c4evQoJ06coGzZsqxZs8Zp97jvvvs4evQohw4dAuC7776jadP0MaWCUp4u/Fo4A5YO4KEZD3E56jJLnl/CN09+kykSCHhoTSQuEQkCghzfT46z/wvgC/dE5TyzZs267bHSM888w6RJkyhfPvVLXhpj8PX15euvv+bZZ58lOjqaevXq3dKLSymVMsuPLKfHrz04ev4ofev1ZXTz0eTOljZLWHsqj08iGV1CDV39+/enf//+t+xr1qzZLc8z474v7rG43YPDwsIoUKAAAM2bN2fbtm3OClupTO3clXMM+m0QM7bPoFLBSqx+ZTWNSzd2d1huoUkkg+rWrRuXL1+mcePM+YOtVFqZv3c+ry1+jdMRp3n7obcZ3mw4vll93R2W22gSyaBmzJjh7hCUylD+Cf+Hfkv6MSd4DjWL1WRRl0XULl7b3WG5nSYRpZS6AxHh2x3fMnDZQCKiIvjwkQ9568G38PbydndoHkGTiFJKJeLY+WP0WtiLZYeX8WCpB5nebjr3FbrP3WF5FE0iSikVT6zE8uWmL3l7ue05+fnjn9Onfh+ymHQ1KsIlNIkopVQc+8/sp/uv3VlzfA0ty7dkStsplMlXxt1heSxNqx7i1KlTdOnShXLlylGnTh0aNWrE/PnzEz0/KCiItm3bJnisTJkynDlzJsFjABMmTODy5ct3jalv374EBwffPXilMoComCg+WvMRNSbXYM+/e/i6/dcsfX6pJpC70CTiAUSEJ598kiZNmnDkyBG2bNnC7NmzCQkJSZP7JTWJfPHFF1Spkv7XO1Dqbrad3EaDrxowdMVQnqj8BMF9gnm55sseMeeVp9Mk4gFWrlyJj4/PLaPI7733Xvr168fVq1d55ZVXqF69OrVq1SIwMPC294eFhdGyZUtq1apFr169bsyVFRERQZs2bahRowbVqlXjp59+4vPPPyc0NBQ/Pz/8/PwA+O2332jUqBG1a9fm2WefJTw8HIDWrVuzefNmAHLlysW7775LjRo1aNiwIadOnUrrfxal0tzV6Ku8s+Id6k2rR+ilUOZ2nMv/nv0fxXIVc3do6Ya2icQxYOkAtv+zPdHjyVkc6rqaxWoy4fEJdzxnz549N2bYjW/ixIkA7Nq1i3379tGyZUsOHDhwyzkjR46kcePGDBs2jEWLFjF16lQAli5dyj333MOiRYsAuHDhAnnz5mXcuHEEBgZSqFAhzpw5w6hRo1i+fDk5c+ZkzJgxjBs3jmHDht1yj4iICBo2bMiHH37I4MGDmTZtGv/5z3+S9W+hlCdZe3wt/gH+7A/bzys1X2Fsy7Hkz57f3WGlO5pEPFCfPn1Ys2YNPj4+lCxZkn79+gF2IsV77733tiSyatUq5s2bB0CbNm3In9/+IlSvXp1BgwYxZMgQ2rZty8MPP3zbvdavX09wcDAPPfQQANeuXaNRo0a3nefj43OjDaZOnTr8/vvvziuwUi50KfISnx/8nF/++IV7893LsheW0bJ8S3eHlW5pEonjbjWGlKyvkRRVq1Zl7ty5N15PnDiRM2fOULduXUqUKJGkayT07LZSpUps2bKFxYsXM3ToUFq2bHlbDUNEaNGiBbNmzbrj9b29vW/cw8vL645TzyvlqZYdWkavhb04fuE4/er348PmH5LLJ5e7w0rXtE3EAzzyyCNcvXqVSZMm3dh3veG7SZMm/PDDDwAcOHCA48ePU7ly5VveH/ecJUuWcO7cOQBCQ0PJkSMHL7zwAoMGDWLr1q0A5M6d+8aKhQ0bNmTt2rU3pom/fPnybTUdpdK7s1fO8tIvL/H4D4+T3Ts7n9f8nM9afaYJxAm0JuIBjDH88ssvDBw4kI8//pjChQvfaJ9o3749vXv3pnr16mTNmpWZM2fesjgVwPDhw+ncuTO1a9emadOmlC5dGrDtKG+99RZZsmTB29v7RpLq2bMnrVq1onjx4gQGBjJz5kw6d+58Y931UaNGUalSJdf+IyiVRuYEz6Hv4r6EXQnj3Yff5T9N/sP6NevdHVbGISKZZqtTp47EFxwcfNu+xFy8eDHJ52YEKSlvcv49PVFgYKC7Q3C5jFrm0Iuh8vRPTwsjkNpTasu2k9tuHMuoZb6T1JQZ2CyJfK5qTUQplaGICN/s+IaBywZyJeoKHzX/iDcffJOsWfTjLi3ov6pSKsM4ev4oPX/tye9Hfqdx6cZMbzedSgX10Wxa0iSilEr3YmJjmLhpIu+seAdjDF+2/pJedXvphIkuoEkEW/3V6Q1STxwj5ZVypb2n9+If4M+6kHW0qtCKyW0nUzpvaXeHlWlk+jTt6+tLWFiYfgCmkogQFhaGr2/mXSZUuVZUTBQfrvqQmlNqsj9sP9899R2LuizSBOJiHl0TMcZ4AZuBv0WkbbxjBvgMaA1cBl4Wka3JvUfJkiUJCQnh9OnTdz336tWrmepDMrnl9fX1pWTJkmkYkVLWltAt+Af4s+PUDp6r+hyft/qcIjmLuDusTMmjkwjwOrAXyJPAsVZARcfWAJjk+Jos3t7elC1bNknnBgUFUatWreTeIt3KbOVVnu9K1BVG/jGST//8lCI5i/DLc7/Q/r727g4rU0tVEjHGVAKqAkUAAU4Du0XkYGoDM8aUBNoAHwJvJHBKe+BbRx/m9caYfMaY4iJyMrX3Vkp5nlXHVtE9oDsHzx6ke63ufNLyE/L55nN3WJmeSW5bgDHmfqA38CxQ9Ppux9frFzsF/AxMEZG9KQrMmDnAf4HcwKAEHmctBD4SkTWO1yuAISKyOd55PYGeAEWLFq0ze/bslIQDQHh4OLlyZZ5pEjJbeUHL7IkioiOY9tc0FoQuoLhvcd6s9CZ18tdJ1TU9vcxpITVl9vPz2yIidRM8mNgoxPgbUB6YA8QA4cASYBjwPPA49vHS88Bwx7Fwx7n/A8ol9T6Oe7UFvnR83wxYmMA5i4DGcV6vAOrc6boJjVhPjsw2yjWzlVdEy+xpFh1YJKXGlRIzwsiAJQMkPDLcKdf15DKnFU8YsR4M7AJeBuaJSMSdTjbG5AQ6AP0d701Oi/RDQDtjTGvH+/IYY74XkRfinBMClIrzuiQQmox7KKU81JnLZxi4bCDf7/ye+wvdz5/+f9KwZEN3h6USkJwuvh1FpK6IfHe3BAIgIhEi8o2I1AGeS05QIjJUREqKSBmgE7AyXgIBCAC6GqshcEG0PUSpdE1E+HnPz1SZWIXZu2czrMkwtvXapgnEgyW5JiIiC1J6k9S8Ny5jTG/H9SYDi7Hdew9hu/i+4ox7KKXcI/RSKK8teo0F+xdQ9566LG+3nAeKPuDusNRdJDmJGGMeEJGdaRlMQkQkCAhyfD85zn4B+rg6HqWUc4kIM7bN4M3f3iQyJpKPH/2YgY0G6oSJ6URy/pdmG2MaiMiluDuNMZVFZL+T41JKZQJHzh2h5689WfHXCpre25Sv2n1FhQIV3B2WSobktIlMA76Lu8MY4wescmpESqkMLyY2hgnrJ1B9UnU2/r2RSW0msfKllZpA0qEkJxERGQ/EGGOGABhjugKzgfgN3koplajg08E0/roxA5cNxK+MH8F9guldt7fOuJtO3fFxljGmI7AT2O9og3gF2GSMqQI0AR4RkT1pH6ZSKr27FnONj9Z8xKhVo8iTLQ/fP/U9Xap30Rm007m7tYm8AVTDzncYDOwA1gMtgGYiciCN41NKZQCb/t6Ef4A/u/7dRedqnfns8c8onLOwu8NSTnDHJCIiDR2z5VYGasbZDLDXGHME2CYiHdM2TKVUenQ56jLDA4czbv04iuUqxoJOC2hXuZ27w1JOdNfeWY7HWPsc242Jp4wxRYHagHbkVkrdJuhoEN0DunP43GF61u7Jxy0+Jq9vXneHpZwsxR2xReQUdo6sJc4LRymV3l24eoHBvw9m6taplM9fnpVdV+JX1s/dYak0ktqp4IsCHYEy2AkXtwG/icjl1IemlEpvFh5YSO+FvTkZfpI3G73J+37vk8M7h7vDUmkoxUnEGPMwduqRHNycCh4gzBjzgYh8ntrglFLpw+mI07y+9HVm7Z5FtSLVmPfcPOqXqO/usJQLpKZj9qeOr92A0tjaSCfgMDDBGPNj6kJTSnk6EWHWrllU+bIKc4LnMLzpcLb03KIJJBNJzeOsasBYEfkmzr7jwM/GGH9gqjHmTxH5IlURKqU8UsjFEF5b9Bq/HviV+iXqM73ddKoVqebusJSLpSaJXMImjduIyHRjzCPYFRA1iSiVgcRKLF9t/Yq3fn+LqJgoxrYcy+sNXscri5e7Q1NukJokEoidiv2rOxx/OhXXV0p5mENnD9Hj1x4EHQ3ikbKPMLXtVMoXKO/usJQbpaZNZCrwoDHm9USOl0FXGlQqQ4iOjebTPz+l+qTqbD25lWlPTGP5i8s1gahU1URWANHAOGPMU9gayRbHvqbA68CQVEeolHKrXad24R/gz6bQTbSr3I4vW39JiTwl3B2W8hCpSSIfADWw06A0cWwS5/g24LwxphqwT0SiU3EvpZSLRUZHMnr1aEavGU1+3/zMfmY2Hat21AkT1S1SM2J9+PXvjTH5gFrcnFurFnY6lO+xiSXKGLMf2CkiL6Y8XKWUK2wI2YB/gD97Tu/hhQdeYPxj4ymUo5C7w1IeyCnrT4rIeWxDeuD1fcYYH2w34JrYpFILeMIZ91NKpY2IaxG8F/geE9ZPoESeEizqsojWFVu7OyzlwdJsjXURuQZsdWxKKQ+38q+V9Pi1B0fOHaF3nd6MaTGGPNnyuDss5eGS0ztrtjEmd/ydxpjKTozn+jV9jTEbjTE7jDF7jDEjEzinmTHmgjFmu2Mb5uw4lMoMwqPD6RHQg+bfNsfLeBH0UhCT2k7SBKKSJDmPs66vsf7k9R2ONdZnA0WdGxaR2FUTw40x3sAaY8wSEVkf77zVItLWyfdWKtNYsG8B/pv8ORd1jsEPDmZEsxFk987u7rBcLiYGzp+HCxfg4kW7hYff3C5fhitX7BYZCdeu2a9RUfa90dEQG2s3cXQvMsZuXl6QNavdvL3BxweyZbNb9uyQI4f9mivXzS1PHrvlzWs3Lw8ex5nkJCIi440xjY0xQ0RkjGON9U9IgzXWHWuYhDteejs2SfwdSqnk+DfiX/ot6cfPe36mXM5yLH1pKXXvqevusJwmJgZOn4aTJ+32zz/w779w6pT9euDAA4hAWBicPWuTRlJ5edkE4ONjk0LWrHZflix2u955TcRuMTF2i4qy2/UEFBub9HvmzQsFCkDBgnYrVAgKF4YiRexWrBgUL263IkVcm3Q8do11Y4wXdtxJBWCiiGxI4LRGxpgd2EGNg3S9d6XuTET4YdcPvL70dcKvhTPKbxQNohukuwQSHg5Hj8Jff8GxY3Y7fhxOnICQEAgNtR/c8eXKZT98s2XLStmycP/99sM5f3675c17sxaQO7c9P2fOm7WF7Nlt0nCG6Ghbs7l82W4REbZcly7Z7eJFWzs6f94muuvbmTNw4IBNkuHht1/Xy8smlZIloVQpu5UuDTEx+WnWzDmxx2VEEv8D3xizHsca68D1Nda9ceEa647uw/OBfiKyO87+PECs45FXa+AzEamYwPt7Aj0BihYtWmf27NnxT0my8PBwcuXKleL3pzeZrbyQsct86uopxh8cz4azG6iapypvVXqLe3Pe67FlvnIlCyEhOThxIjshITkICclOaKjdzp3zueVcb+9Yiha9SuHCkTe2QoUiKVjwGgULXqNAgWvky3cNX1/757+nljm5rl7NwvnzPpw960NY2PUtG6dPZ+PMGR/+/deXf//NRmSkF7Vq/cu4ccEpuo+fn98WEUnwL407JhGARNZYrwEUAVyyxroxZjgQISKf3uGco0BdETmT2Dl169aVzZs3pziOoKAgmqVFKvdQma28kDHLHCuxTNk8hcHLBxMrsYx+ZDR96/e9MWGiu8t86RLs2WO33bshOBj27bM1i7hKloQKFexWrhyULWu3MmXsI5zkjIF0d5ld6fpju5Ur19GxY6MUXcMYk2gS8cg11o0xhYEoETlvjMkOPAqMiXdOMeCUiIgxpj62p1mYs2NRKj07GHaQ7r92Z9WxVTxa7lGmtp1K2fxl3RKLiH3stH07bNsGO3fCjh32kdR12bPDffdB48b2UVPlynarUME+UlLJZ4xtQylSJDJNru+pa6wXB75xtItkAX4WkYXGmN6Oe08GOgCvGmOigStAJ7lbtUqpTCI6Nppx68YxPGg4vll9md5uOq/UfMVlU5aI2PaJjRth82bYsgW2brXP9ME2QFeqBPXqgb8/VK8OVavamkWW1EwLq1wuNcvjPiciPzkzmOscgxprJbB/cpzvv0DXKlHqNjv+2YF/gD9bTm7hqfueYmLriRTPXTxN7xkeDps2wbp1sH69TR6nTtlj3t42STzzDNSuDbVq2ddas8gYUtPPYKYx5h1gmIgsiH/Q8bgrj4gcTMU9lFJJFBkdyahVo/ho7UcUyF6Anzv8TIcqHdKk9nHyJKxeDWvWwNq19hHV9S6rlSvDY49Bgwa2pvHAA7ZLrMqYUpNEymOnev/RGLMHeE9ElsU53gkYB3jwMBmlMoY/T/xJ94Du7D2zl5dqvMTYlmMpmKOg065/4gQEBdlt1So4dMjuz5EDGjaEd9+FRo1s4ihQwGm3VelAapLIZezaIceAusBiRzIJA3JiG933pjpCpVSiwq+F8+6Kd/m/jf9HqbylWPL8Eh6v8Hiqr3v6NKxcCStW2K+HD9v9+fNDkybw6qvw8MNQs6Z9XKUyr9QkkWnY5W/XYad8Bzv9SQvs6PKlwBupik4plajfD/9Oz4U9OXr+KH3r9WV089Hkznbb9HZJEhlpH0v99pvdtm2z+/PkgWbNoG9f8POzbRna8K3iSk0SaQ58LiID4+40xjQBpmBrJ8kY2K+USopzV87x5m9v8vX2r6lUsBKrX1lN49KNk32do0dh8WL4/vtq7NhhR01nzQoPPQSjRsGjj0KdOs4boa0yptT+ePwVf4eIrDLG1AVWATOAh1N5D6WUw7y98+izuA+nI04ztPFQhjUdhm9W3yS9Nzoa/vwTFi6ERYvsoD6A4sVz8vLL8PjjttaRO2WVGZVJpSaJ/AG8YIyZ7Fg75AYRiTDGTAPGpio6pRQA/4T/Q9/FfZm7dy41i9VkcZfF1Cp+Wy/424SHw9KlEBBgE8fZs7YNo0kT6N4d2rSBv//egJ9fs7QugsqgUpNE3gfWA38YY/qJSPz5RB7ENrwrpVJIRPh2x7cMXDaQy1GXGf3IaAY9OAhvr8Rbs8PCbNKYP9+2b0RG2h5TbdpAu3bQsqVt67guNNQFBVEZVmpGrG8zxrwMTAc2GGMOAZuwvbNqYB9jLXRGkEplRsfOH6PXwl4sO7yMh0o9xFftvuK+QvcleO7p0zBvHsyZA4GBdgbb0qWhd2948kk7jYi2bai0kKofKxGZ5ZjpdwB2/fQucQ5vBPqm5vpKZUaxEsukTZN4e8XbiAj/1+r/eK3ea2Qxt3aLCguDuXPhf/+z3XBjY6FiRXjrLejQwY4Od9EsJyoTS/XfJiLyF/A68LoxJj9QDDgvIidTe22lMpv9Z/bT/dfurDm+hpblWzK17VTuzXfvjeOXLsGCBTBrln1UFR1tE8fQofDss3Z0uCYO5UpOreCKyDngnDOvqVRmEBUTxdh1YxkRNIIc3jmY2X4mXWt0xRhDVJRNGN9/bxPIlSt2oaGBA6FzZzvgTxOHchd9SqqUm207uQ3/AH+2/bONZ+5/hi9af0HRnMXYtg2+/RZ+/NG2eRQoAC+9BM8/Dw8+qIP+lGfQJKKUm1yNvsr7f7zPx2s/plCOQsztOJfGBZ/m+6kwcybs2mXX8X7iCXjxRWjVyr5WypNoElHKDdYeX4t/gD/7w/bT9YGXeZxxfDs0P88tsu0c9evDl1/Cc8/phIbKszkliTiW0C0F/BN/4KFS6qZLkZd4Z8U7TNw0kRK57qVz1G/83qcF3560S7wOGACvvAJVqrg7UqWSxlk1kQLYKVBaACuddE2lMpRlh5bR89eenLh4glKh/Tg+80N+is5Fq1Y3R4/rjLgqvXHm4yztH6JUAs5eOUuv+W8w5+A3ZD13HzJvDcKDjHgHunWzPa2USq+0TUSpNBIbK4z831zG7OpDZJazsPZdmmf/D30m+tK6NXjpcm0qA9AkopSThYfDFzNPMnpHHy6VnI/X2Tq8nOc3hn1Vg7Jl3R2dUs6VoiTiWDMkrryOrw8YY26ZdFFEVqXg+r7YqeSzOWKcIyLD451jgM+A1thVFl8Wka3JvZdSznL0KHz+f8LkdTO50uQNTPGrPJv/I2a89Sa5cujfaypjSulPdhB29cL44k79bhznpKTSHgk8IiLhxhhvYI0xZomIrI9zTiugomNrAExyfFXKZUTsioATJsC8wL+gbU/kseXUyPcwPz3/FZULVXJ3iEqlqZQmEb94r/MB84G3gC2pCQhARAQId7z0dmzxk1Z74FvHueuNMfmMMcV1zi7lCtHRdtbcsWNh46YYsjedSNZ+Q/HxycLHLSbSu27v2yZMVCojSlESEZE/4r42xhR0fLs9/rGUMsZ4YRNSBWCiiGyId0oJ4ESc1yGOfZpEVJqJiIAZM2DcOPv46t46eyn7gT9/Ra+jVYVWTG47mdJ5S7s7TKVcxtg/5FN5EZtETgOPiohTx4kYY/Jhazn9RGR3nP2LgP+KyBrH6xXAYBHZEu/9PYGeAEWLFq0ze/bsFMcSHh5Orly5Uvz+9CazlRcSL/P5897Mm1eCBQtKcPGiN9UeOE3RZ95nFVPI7pWdPhX60KJIC0w6nAlR/58zh9SU2c/Pb4uI1E3woIikegMKArHYdgynXDPe9YcDg+LtmwJ0jvN6P1D8TtepU6eOpEZgYGCq3p/eZLbyitxe5qNHRfr1E8meXcQYkSefFJm+ZLM8MOkBYQTS8X8d5VT4KfcE6yT6/5w5pKbMwGZJ5HPVIx/aGmMKO2ogGGOyA48C++KdFgB0NVZD4IJoe4hykn374OWXoUIFmDwZOnWCrTuvUOm1IfTc2IDTEaeZ/9x8furwE0VyFnF3uEq5jbP6HZ4FygL/OOl6xYFvHO0iWYCfRWShMaY3gIhMBhZju/cewnbxfcVJ91aZ2KFDufjiC9to7usLffrAm2/CX7Gr6BjQnYNnD9K9Vnc+afkJ+XzzuTtcpdzOKUnEUd055oxrOa63E6iVwP7J8e7Zx1n3VJnb5s3wwQcQEFCXPHnsSoEDBkC2PBd5e/nbTNo8ibL5yrL8xeU0L9fc3eEq5TF0BJTK1DZuhJEjYfFiyJ8fXn75L8aPL0u+fLD44GJ6fd+Lvy/+zYAGAxj1yChy+uR0d8hKeRSPbBNRKq1t2mRnzW3QANavhw8/tF12X3rpGNE+Z3hx/ou0+bENebLl4U//Pxn/+HhNIEolQGsiKlPZvh2GD4eAALvY0+jR0Lcv5M5teyqu/HclHSd25NzVcwxrMox3Hn6HbFmzuTtspTyWJhGVKezdC8OGwZw5kC+fbf/o3x/y5LHHQy+F8tqi11iwfwF176nL8nbLeaDoA26NWan0IMlJxBjzgKPBW6l04+hRGDECvvsOcuSA996DN96wiQRs7WP6tukM+m0QkTGR9CrXiy+e/4KsWfTvK6WSIjm/KbONMQ1E5FLcncaYyiKy38lxKZUqp07BqFEwZYpdt2PgQBgyBAoXvnnO4bOH6fFrDwKPBtL03qZ81e4rQnaGaAJRKhmS07A+Dfgu7g5jjB92ynalPMLFi7a2Ua4cTJpk1ys/dAg+/fRmAomJjWH8uvFUn1SdzaGbmdxmMitfWkmFAhXcG7xS6VCS/+QSkfHGmMbGmCEiMsYY0xX4BHgh7cJTKmmuXbMjyz/4AM6cgY4dbU2kYsVbz9vz7x78A/zZ8PcG2lRsw+S2kymZp6R7glYqA7hjEjHGdAR2Avsdg/teATYZY6oATbBzZe1J+zCVSpgI/PyzHRz411/wyCMwZgzUjTdV3LWYa3y05iNGrRpFXt+8/Pj0j3Sq1ildTpiolCe5W03kDaAadiHBYGAHsB5oATQTkQNpHJ9SiVq92k5JsmkTVK8OS5bAY49B/Lyw6e9NdAvoxu5/d9O5Wmc+e/wzCucsnPBFlVLJcsc2ERFpCOQG6mBXLTwDFMWuWrjXGHPQGPNzmkepVBwHD8LTT0OTJhAaCl9/Ddu2weOP35pALkdd5q3f3qLh9Iacu3KOgE4B/PjMj5pAlHKiu7aJOB5j7XNsNxbjMMYUBWoD2pleucS5c/D++/DFF5Atm23/eOMN23U3vqCjQXQP6M7hc4fpVacXYx4dQ17fvK4PWqkMLjV9GZuKyM/AEmcFo1RCoqNtV93hw+HsWfD3twmkWLHbz71w9QKDfx/M1K1TKZ+/PIEvBdKsTDOXx6xUZpGaJPKjMSa/iExxWjRKxbN8uZ1Nd88e8POD8eOhRo2Ez/11/6/0XtSbf8L/YVCjQYz0G0kO7wSqKUopp0nNBIwzgS+NMe8mdNAY08gYszoV11eZ2OHD8OST0KIFXL0K8+fDihUJJ5DTEafpMrcL7Wa3o2D2gqz3X88nLT/RBKKUC6S4JiIi3Y0xp4EPjDGFRGQg2BHswH+B9sAV54SpMouICDuj7tix4OMDH33kWNcjgTkQRYRZu2fRf0l/LkZeZGSzkbzd+G18vHxcHrdSHi8mJk0um6r5HURkqDHmFDDWGFMYCAe6AYJdA/391IeoMoPr4z3efBP+/htefNEmkHvuSfj8kIshvLroVRYeWEiDEg2Y3m46VYtUdW3QSnmq6GjYtQs2bLBrHWzYQNUiRaC58xdUc8YkQdOANkAXbPKYDbwnIkeccG2VCQQH2+nYAwOhVi346Sd46KGEz42VWKZtmcZbv79FjMQwruU4+jfoj1cWL9cGrZQnCQm5JWGweTNccTwIKlIEGjTgXLlypEXn9hQnEWOMN/AaMBQoDGwFagLewAlnBKcytvBwu6rghAl2PY8vv4SePe2EiQk5GHaQHr/24I9jf9C8bHOmPjGVcvnLuTRmpdwuIgK2bLmZMDZssNV3sM+Aa9e2v0gNG9pV18qUAWMIDQqiUhqEk5qayEGgFBAM+IvIIsc0Kd8Ci40xT4lIuDOCVBmLCMybZ9s6QkJsl93//vfWGXbjio6NZsL6CbwX+B7ZvLLx1RNf0a1WN52yRGV8sbGwf/+ttYxdu262b5QvD02b2mTRsKHteZJQA2IaSk0S8QJ6ADNFJBZARH42xpwH5gKBxphWInIm9WGqjOLwYfvoaulS+/P+88/QqFHi5+86tQv/AH82hW6ifeX2fNnmS+7JnUhDiVLp3enTN2sXGzbAxo1w4YI9liePTRZDh9qEUb9+4n95uVBqkkhFEbkaf6eI/GaMeRRYBPwJya9BGWNKYWs0xYBYYKqIfBbvnGbAAuAvx655IqIN+R4qMtJOxz5qFHh720dYffpA1kR+AiOjIxm9ejSj14wmv29+Zj8zm45VO2rtQ2UckZGwY8fNGsb69XDE0ZScJQs88AB06nTzsVTlyna/h0lNF9/bEkicYxuMMQ8Dy1J4+WjgTRHZaozJDWwxxvwuIsHxzlstIm1TeA/lIqtXQ69edonaZ5+1CSSxXlcA60PW4x/gT/DpYF544AUmPDaBgjkKuixepZxOxC6zGfex1Natdg0DsL8QDRvaX5QGDew01DlzujXkpEqzJdxEZK8xJpE+Nnd970ngpOP7S8aYvUAJbPuLSifOnoXBg2H6dNu2t3gxtGqV+PkR1yJ4L/A9JqyfQMk8JVnUZRGtK7Z2WbxKOc2FC3Z66euPpdavt4+qALJnt0mif/+btYyS6XdNG2PnV0zCicY0F5EVKbqJMY+KyPIUvrcMdvXEaiJyMc7+Zti2lxAgFBiU0NomxpieQE+AokWL1pk9e3b8U5IsPDycXLlypfj96U1KyysCgYFF+OKLCly44E3Hjid46aWj+PrGJvqeree2MvbAWEKvhtL+nvb0KNuDnFld/5dYZvs/Bi1zqsXEkPPoUfIEB5Nn717yBAeT4/hxjOOzNaJ0aS7dfz8XHVtEuXJIYs9x01Bqyuzn57dFROomeFBEkrQBUcBKoC3glYTzvYGngD+Aa0m9T7xr5AK2AE8ncCwPkMvxfWvg4N2uV6dOHUmNwMDAVL0/vUlJeY8dE2ndWgRE6tYV2bbtzuefu3JOui/oLoxAKn5eUf44+keKYnWWzPZ/LKJlTra//xaZN09kyBCRpk1Fcua0P/AgUrCg/QUYOVJk2TKRs2edFXKqpabMwGZJ5HM1OemwJjAeCADOGGN+BzYCh4Gz2DVGCgAVgYbAI47XyxzvTRbHOJS5wA8iMi/+cYlTKxGRxcaYLx3Tr2hvMDeIjbXjPN5+2/42jR8P/folPuYDYMG+Bby66FX+jfiXIQ8NYXjT4WT3zu66oJW6mytX7JiMuG0ZJxzD4Ly9oWZN6NbNPpJq0MB2uc1knT+Sk0SexT4WKo4dZNge6IwdpR6XAS4C84BJIrIpuUEZ2wVnOrBXRMYlck4x4JSIiDGmPnYyybDk3kul3r590L07rF1rVxacPNm2gSTmVPgp+i/tz897fqZG0Rr82vlX6txTx2XxKpWg2Fi74lnchLFzp51CBOwP9YMP2mTRqJFNIL6+7ozYIyQniQwDDojIj8A6Y0wH4DhQBTtiXYDTwG5gmzjGjqTQQ8CLwC5jzHbHvneA0gAiMhnoALxqjInGTvTYyVHtUi4SFWW77Y4YAblywbffwgsvJP6HmIjww64feH3p64RfC2eU3ygGPzQYby9vl8atFGB7fsRt+N640a58BvYHun592zPkei2jaFH3xuuhkpNEzgFx59b+CXhRRGY6NSJARNZgazR3OucL4Atn31slzY4dtha/dSt06GBXG7zT79jxC8fpvbA3Sw4toVHJRkxvN537C9/vuoBV5nbtmq1VOBJG/aAgO10C2LEX1arZH+TrCeP+++/8LFbdkJwkshvwN8YsEZG/ucuHvMqYrl2D0aPtdO0FCsCcOfDMM4mfHyuxTNk8hcHLByMifP7457xW7zWdMFGlHRHbbhF3EN/WrXZhGoBixbhcvjw5+vSxXWzr1rU1D5UiyUkiI7FL4R43xhzEPr5qbYw5B2wVkVNpEaDyHNu3w8sv21rI88/DZ59BwTuMATwQdoDuAd1ZfXw1Lcq1YOoTUymTr4yLolWZxqVLdtbauI+m/vnHHvP1hTp14LXXbs4vVaoUu//4g2bNmrk17IwiyUlERFYaY6oD3bFtFpWw0793BnCsK7IV2Hb9q4gcdXbAyvWiouwEiR98AIUKwYIF0K5d4udHx0Yz9s+xDA+yva1mtJvByzVf1ilLVOrFxNipD+I2fu/ZYxvFASpWtMthXn8sVaOG7UWl0kyyRryIyAFgMIAxJhZ4CzgC1AFqAbWxYzbEcc45ESnkzICVa+3ZA1272qcBXbrA55/fufax458ddAvoxtaTW3nqvqeY2HoixXMXd13AKmM5derWGsamTbbmAZA/v00UTz99c0LCAgXcG28mlJphk+9j567aCMy/vtMYUxybTOqQgvEhyjPExMCsWaWYORPy5oW5c+3vamKuRl9l1KpRjFk7hoLZCzLn2Tk8U+UOjSVKxXf1Kmzbdus6GUeP2mNZs9oJCV988WYto1KlTDcmwxOlZgLGEYnsP4mdwXdRSq+t3OvwYXjpJVi7tjxPPw2TJtnF0RLz54k/8Q/wZ9+ZfXSt0ZXxj42nQHb9i1DdgYj9QYv7WGr7dvvsFKB0aZso+va1tYzate2cU8rjuH4CF+WxRGDaNHjjDfuH3zvv7GXUqPsT/WMv/Fo47654l//b+H+UyluKpc8v5bEKj7k2aJU+nD9vx2HETRphjrHBOXPaHlJvvHGzlnGnaZ6VR9EkogD76Ll7d1i4EJo3h6+/hsOHT2FMwmM5fj/8Oz0X9uTo+aP0qdeH/zb/L7mz5XZx1MojRUfb1ffiPpbat88eM8aOwWjXztYwGjaEKlUSX1hGeTz9n1MsWGATSHi47bbbt68df3X48O3nnrtyjjd/e5Ovt39N5YKVWf3KahqXbuz6oJXnCAm5tYaxebOdcwrsynsNG9qpDBo0gHr1bCObyjA0iWRi4eEwcCB89RXUqgXff2//KEzMvL3z6LO4D6cjTjO08VCGNR2Gb1adOyhTiYiwExLGHcgXGmqP+fjYtouePW+OyShTRhu/MzhNIpnUxo12wODhw3bm3ZEj7WdAQv4J/4d+S/oxJ3gOtYrVYnGXxdQqXsu1ASvXi42F/ftvfSy1a5ftugd2xtpmzW4urFSjBmTL5taQletpEslkYmLgo49g+HAoUQICA6Fp04TPFRG+2f4NA5cN5HLUZUY/MppBDw7SCRMzqtOnbx+TceGCPZY3rx2HMXTozTEZhQu7N17lETSJZCInTthH06tWQadOtutuvnwJn3v0/FEG7xrM5nObaVy6MV898RWVC1V2abwqDUVG2i61GzZwf0AA+PvDkSP2WJYsUL26/SG5XsuoXNnuVyoeTSKZxNy5tvE8Ohq++caO2UroUXWsxDJx40SGrhhKbGws/9fq/3it3mtkMfoBkm6J2EF7cdsxtm2zs2kC+QoVgiZNoFcvmzTq1LHdbpVKAk0iGdzly7bxfOpU2zHmxx+hQoWEz913Zh/+Af78eeJPHiv/GC8XeplO9Tu5NmCVehcu2EdRcXtMnT5tj2XPbsdkvP76jTEZ6w4d0skIVYppEsnAdu2C556z89UNHmwnUEyo8TwqJopP/vyEkX+MJKd3Tma2n0nXGl35448/XB+0Sp7oaDvBWdy2jL17be0D4L77oE2bm4P4qlW7fULCQ4dcH7fKMDSJZEAiMGWKrYHkzQu//WYnNk3I1pNb8Q/wZ/s/2+lQpQNftPqCorl0BTePFRp6+5iMiAh7rGBBmyiee85+rV/fTlKoVBrSJJLBnD8PPXrYxaIee8y2fyS04uCVqCu8/8f7fPLnJxTOWZi5Hefy9P13mGFRud7ly3b65Li1jBMn7DFvb7vG9yuv3Bz5Xa6cjslQLqdJJAPZuNH+ERoSAmPGwKBBCXeoWXN8Df4B/hwIO8ArNV9hbMux5M+uf7G6VWwsHDx4ay1j5077uArsoL0HH7zZW6pWLbvgklJupkkkAxCBCRNgyBA7b93q1fazJr5LkZcYumIoEzdNpEy+Mvz2wm+0KJ/Icy6VtsLCbNaPO5Dv/Hl7LHdu+yhq8OCbYzLutIC9Um7kkUnEGFMK+BYoBsQCU0Xks3jnGOAz7CJYl4GXRWSrq2N1t3Pn7JK1AQHw5JMwY0bCj8GXHFxCr4W9CLkYQv/6/fmw+Yfk8tF1pV3i2jVbq4hbyzh40B7LkgWqVoVnn73Z+H3//eCla9Cr9MEjkwgQDbwpIluNMbmBLcaY30UkOM45rYCKjq0BMMnxNdPYuBE6drRtrRMmQP/+tz8SD7scxsBlA/lu53fcX+h+1nZbS6NSjdwSb6YgAseP31rD2LrVLrgEUKyYTRTX2zLq1rU1D6XSKY9MIo6FrU46vr9kjNkLlADiJpH2wLciIsB6Y0w+Y0xxx3szNBH4v/+zbR733ANr1tgnHreeI8wJnkPfJX05e+Us7zV5j3cffpdsWXVuI6e6dMn2kLpey1i/3s6rD7bNonZteO21m7WM0qW18VtlKEau9yf3UMaYMsAqoJqIXIyzfyHwkYiscbxeAQwRkc3x3t8T6AlQtGjROrNnz05xLOHh4eTK5d5HQBERXnzySWX++KMIDz54hrff3kfu3NG3nBMWGcaEgxNYE7aGSrkqMbjyYMrnKp/se3lCeV3tjmWOiSHn8ePkDg4mz9695AkOJuexY5jYWAAulyzJxfvvt1uVKkSUL4+kg3Uy9P85c0hNmf38/LaISN0ED4qIx25ALmAL8HQCxxYBjeO8XgHUudP16tSpI6kRGBiYqven1s6dIhUrinh5iXz8sUhs7K3HY2NjZfrW6ZLvo3ziO8pXPl7zsUTFRKX4fu4urzvcUuZ//hFZsEBk6FCRRx4RyZ1bxFYERfLlE3nsMZHhw0WWLBE5c8ZdIadapv9/ziRSU2ZgsyTyueqxfyYZY7yBucAPIjIvgVNCgFJxXpcEQl0Rmzt8952d2ihvXli50k51FNdf5/6i58KeLD+ynCb3NmHaE9OoVLCSe4JNj65ehW3bKPm//8Hkyfax1LFj9ljWrHaa8xdfvLlORsWK+lhKKTy0TcTR82o6sFdExiVyWgDQ1xgzG9ugfkEyYHtIZKSd5mjKFLt0w6xZtm32upjYGCZushMmehkvJrWZRM86PXXCxDsRsQupxG383r4doqKoAFCqlE0U/frZpFGnjp1zSil1G49MIsBDwIvALmPMdse+d4DSACIyGViM7d57CNvF9xXXh5m2jh2DDh1su+2QITBq1K1LUQefDqZ7QHfWhayjVYVWTGk7hVJ5SyV+wczq/Pnbx2SEhdljOXPamSnfeAMaNuTPmBgefOYZt4arVHrikUlEbGP5HZ8VOJ7T9XFNRK73++/QuTNERcEvv0D79jePRcVEMWbtGD5Y9QG5fXLz3VPf8Xz15zH6eMX+g+3adetUIfv322PG2DEY7dvfHPldteotYzKuBQW5J26l0imPTCKZmYhdefDdd+3n27x59vH7dVtCt9AtoBs7T+2kU7VOfPb4ZxTJWcR9AbtbSMitNYzNm+HKFXusSBGbKF580SaNevUgTx73xqtUBqNJxINcvGhHn8+fb2sh06bdXBvoStQVRgSN4NN1n1IsVzF+ee4X2t/X/o7Xy3AiIm4dk7Fhgx1pCXaO+9q1oWfPm7WMMmW08VupNKZJxEPs3QtPPWWXdhg/3jamX//8W3VsFd0DunPw7EG61+rOJy0/IZ9vPrfGm+ZiY2HfvlsfS+3ebReJByhfHvz8bg7iq1EDsulASqVcTZOIB/jlF+ja1Q5wXr7c9sICuBh5kbeXv82kzZMol78cK7qu4JGyj7gz1LRz5sytNYyNG+0KfWD7NdevD++8c3OdjMKF3RuvUgrQJOJWsbEwYoRdcbBePbsOeilH56rFBxfTa2EvQi+F8kbDN3jf731y+mSQda8jI22X2rhJ48gRe8zLC6pXh06dbo7JqFw54TntlVJup0nETS5csO29v/5q20EmTbI1kTOXzzBg6QB+2PUDVQpXYc6zc2hQMh3PKykCR4/eTBbr18O2bXZmW4ASJWyi6N375piMnBkkWSqVCWgScYP9+20v08OH7USKffoACD/t/pl+S/px/up5hjcdztDGQ9PfhIkXLsCmTbfWMk6ftseyZ7ez1vbvf7Pxu2RJ98arlEoVTSIutnix7Xnl42PbP5o2hdBLoby66FUC9gdQ7556TG83nepFq7s71LuLjoY9e25t/N6719Y+AO67D9q0udn4Xb36raMllVLpnv5Gu4gIfPwxDB1qOxL98guULi18tXU6g34bxLWYa3za4lMGNByAVxYPXZAoNPTWGsbmzbbbLUDBgjZRPPccNGpkG3ny5XNruEqptKdJxAWuXIHu3eHHH+1n7IwZcPLqYZp/24PAo4E0K9OMaU9Mo0KBCu4O9abLl8m7a9fNcRkbNsCJE/aYtzfUrAndut2sZZQvr2MylMqENImksb//tsvWbtkCH34Ig4fE8PnGz/jPyv/g7eXNlLZT6FG7h3unLImNtcu1xm383rmTWtfHZJQpAw89dDNh1KplewEopTI9TSJpaONGm0AuXbKPr8o13M1DX/uz8e+NPFHpCSa1mUSJPCVcH1hY2K0TEm7caBdrB7tUa716MGQIu3LmpLq/PxQt6voYlVLpgiaRNPLjj/ZpT/HisGjpNQLO/pcOUz4kr29efnz6RzpV6+Sa2se1a7Bz561tGQcP2mNZskC1anaq4OtjMu6778aEhGFBQZpAlFJ3pEnEyWJjYdgw++iqSRP4z5eb6LqqG7v/3U2X6l347PHPKJSjUNrcXASOH791QsItW+zgPrALkTRoAP7+9mvdupDJlghVSjmXJhEnioiw05fMmwcv97hMvqeG8fjc8RTPVZxfO/9K20ptnXvDS5dsw3fctoxTp+wxX187cK9Pn5tjMkqV0sZvpZRTaRJxkr//hnbt7Gwer30cxLJs3Tm88TC96vRizKNjyOubN3U3iImxYzDiPpbas8dWfcDOF9+ixc2EUaOG7UWllFJpSJOIE2zZYhPIxcgLtPx8MF+emUr5bOUJfMl2302Rf/65+UhqwwY7CvzSJXssf36bKJ5++maPqQIFnFYepZRKKk0iqTRvHrzwAuSq8ys52vbmt7B/eOvBtxjRbAQ5vHMk7SJXr9r5pOI+ljp2zB7LmtXWKq4vrNSgga116GMppZQH0CSSQiLwyScwZORpCr74OqfvmUX1PNVZ2O4X6pWod+c3Hjp061QhO3bYZV0BSpe2iaJfP5s0ate2c04ppZQH0iSSAlFR0PtVYcbGWfi80Z+LPhd5v8n7DGk8BB8vn1tPPnfOjsOI+2gqLMwey5nTjsl4882bj6WKF3d9gZRSKoU8NokYY2YAbYF/RaRaAsebAQuAvxy75onI+2kd1/nz0KZzCH/mfxWeWUitEg2Y3m46VYtUtRMSxn8stX//9YChShU7fe/1MRlVq94Yk6GUUumRxyYRYCbwBfDtHc5ZLSJO7jebuL9Dfeg8dgr/1HoLH98YxtQfRr9LVfD6ZObNCQmvXLEnFy5sk0XXrvZrvXqQJ4+rQlVKKZfw2CQiIquMMWXcHcd1cxfvoP/KVzlbdycPny3MzHmGcsMdFZ9s2ex8Uj173mz8LlNGG7+VUhmexyaRJGpkjNkBhAKDRGRPWtxk3ndzeWF/B7IVhq8WQLdLeTANGkIfRztGzZp2gRCllMpkjFxfQMgDOWoiCxNpE8kDxIpIuDGmNfCZiFRM4LyeQE+AokWL1pk9e3ay44i+eo0pM/9Dx1JNuadxY6LypnLgYDoRHh5Orkw2LYqWOXPQMiePn5/fFhGpm9CxdJtEEjj3KFBXRM4kdk7dunVl8+bNKY4nKCiIZs2apfj96U1mKy9omTMLLXPyGGMSTSJZUhOUOxljihnHNLjGmPrYsoS5NyqllMpcPLZNxBgzC2gGFDLGhADDAW8AEZkMdABeNcZEA1eATuLJ1SqllMqAPDaJiEjnuxz/AtsFWCmllJuk28dZSiml3E+TiFJKqRTTJKKUUirFNIkopZRKMU0iSimlUsyjBxs6mzHmNHAsFZcoBCQ6mDEDymzlBS1zZqFlTp57RaRwQgcyVRJJLWPM5sRGbWZEma28oGXOLLTMzqOPs5RSSqWYJhGllFIppkkkeaa6OwAXy2zlBS1zZqFldhJtE1FKKZViWhNRSimVYppE4jHGPG6M2W+MOWSMeTuB48YY87nj+E5jTG13xOlMSSjz846y7jTG/GmMqeGOOJ3pbmWOc149Y0yMMaaDK+NLC0kpszGmmTFmuzFmjzHmD1fH6GxJ+NnOa4z51Rizw1HmV9wRp7MYY2YYY/41xuxO5LjzP79ERDfHBngBh4FygA+wA6gS75zWwBLAAA2BDe6O2wVlfhDI7/i+VWYoc5zzVgKLgQ7ujtsF/8/5gGCgtON1EXfH7YIyvwOMcXxfGDgL+Lg79lSUuQlQG9idyHGnf35pTeRW9YFDInJERK4Bs4H28c5pD3wr1nognzGmuKsDdaK7lllE/hSRc46X64GSLo7R2ZLy/wzQD5gL/OvK4NJIUsrcBZgnIscBRCS9lzspZRYgt2OBu1zYJBLt2jCdR0RWYcuQGKd/fmkSuVUJ4ESc1yGOfck9Jz1Jbnn8sX/JpGd3LbMxpgTwFDDZhXGlpaT8P1cC8htjgowxW4wxXV0WXdpISpm/AO4HQoFdwOsiEuua8NzC6Z9fHrsolZuYBPbF776WlHPSkySXxxjjh00ijdM0orSXlDJPAIaISIxjFeb0LillzgrUAZoD2YF1xpj1InIgrYNLI0kp82PAduARoDzwuzFmtYhcTOPY3MXpn1+aRG4VApSK87ok9i+U5J6TniSpPMaYB4CvgFYikt7Xsk9KmesCsx0JpBDQ2hgTLSK/uCRC50vqz/YZEYkAIowxq4AaQHpNIkkp8yvAR2IbDA4ZY/4C7gM2uiZEl3P655c+zrrVJqCiMaasMcYH6AQExDsnAOjq6OXQELggIiddHagT3bXMxpjSwDzgxXT8V2lcdy2ziJQVkTIiUgaYA7yWjhMIJO1newHwsDEmqzEmB9AA2OviOJ0pKWU+jq15YYwpClQGjrg0Stdy+ueX1kTiEJFoY0xfYBm2Z8cMEdljjOntOD4Z21OnNXAIuIz9SybdSmKZhwEFgS8df5lHSzqevC6JZc5QklJmEdlrjFkK7ARiga9EJMGuoulBEv+fPwBmGmN2YR/1DBGRdDu7rzFmFtAMKGSMCQGGA96Qdp9fOmJdKaVUiunjLKWUUimmSUQppVSKaRJRSimVYppElFJKpZgmEaU8lDFmgzGmk7vjUOpONIko5YGMMVmAatjutkp5LE0iSnmmytjfz/3uDkSpO9EkopRnqgkEi0gMgDFmoDFmnzGmplujUioeHbGulGeqCewwxuQFvsb+rjYUkfPuDEqp+LQmopRnqolNHJuAzUB7TSDKE+m0J0p5IGPMP45vfxeRF90ajFJ3oDURpVzIGFPLGDPfGHPOsc0xxhQwxtxjjLlqjOlsjCkGFMVOpPewMeYl90atVOK0TUQpFzHGdAa+wXbbHQmUBfpjpyPPChwEfsIulHRERPYZY9oCgcaYEyKy0j2RK5U4TSJKuYAxphwwA7uKXhMRuerYXxdoBZQBnheRWGNMDWAbgIjsNsY8D/xkjGkiIul5fQ+VAWmbiFIuYIz5DFvraCgiG+Ls/w54AdgK1BX9hVTpjLaJKOUa7YBDcRNIPO9pAlHpkSYRpdKYMaYA9nHVpgQOFwX2iMhilwallJNoElEq7RVzfA2Lu9MY0wRoEX+/UumJJhGl0t55x9ca13cYY3IBUxwvc7o6IKWcRZOIUmlMREKBjdgxH98ZY14FVgGFgKVALWPMAGNMcXfGqVRKaO8spVzAGHMv8AV2AGFWbBfebo7Dc4EqwH0iorP2qnRFk4hSSqkU08dZSimlUkyTiFJKqRTTJKKUUirFNIkopZRKMU0iSimlUkyTiFJKqRTTJKKUUirFNIkopZRKMU0iSimlUkyTiFJKqRTTJKKUUirF/h9rfoGzHyPTkQAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"plot_alpha(0,eta_ls=0.25,algorithm=\"newton\",alpha_max=1.0)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.4 Newton Step, $x^k = 0$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.4-Newton-Step,-$x^k-=-0$)",
"section": "3.6.3.4 Newton Step, $x^k = 0$"
}
},
"source": [
"**Discussion**\n",
"* Why does the line search fail?\n",
"* How could we modify Newton's method to improve robustness?"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.5 Steepest Descent Step, $x^k = 0$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.5-Steepest-Descent-Step,-$x^k-=-0$)",
"section": "3.6.3.5 Steepest Descent Step, $x^k = 0$"
}
},
"source": [
"### 3.6.3.5 Steepest Descent Step, $x^k = 0$"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.5 Steepest Descent Step, $x^k = 0$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.5-Steepest-Descent-Step,-$x^k-=-0$)",
"section": "3.6.3.5 Steepest Descent Step, $x^k = 0$"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Considering xk = 0 and f(xk) = 1.5\n",
"Step with steepest-descent algorithm:\n",
"pk = -6\n",
"With full step, xk+1 = -6 and f(xk+1) = 685.5\n",
"alphak = 0.4191919191919192 with backtracking line search starting at alpha = 0.5\n",
"f(xk + alphak*pk) = -2.9749848430038526\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZYAAAESCAYAAADe2fNYAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAABN9ElEQVR4nO3dd1yV1R/A8c8BQUTcIq5yZCIoKm7NRebeov1sqGVmNsxMy8qGZVaWe6RpllmuEneuUnDvbaJmjqTcG3Hi+f1xkBDZ914eLnzfr9fzutx7n/E9XuF7z3OW0lojhBBC2IuL1QEIIYTIXCSxCCGEsCtJLEIIIexKEosQQgi7ksQihBDCriSxCCGEsKtsVgeQERQsWFCXLFkyTcdeu3aNnDlz2jegDC6rlTmrlRekzFmFLWXevn37Oa21d0LvSWIBSpYsybZt29J0bFhYGA0bNrRvQBlcVitzVisvSJmzClvKrJQ6nth7citMCCGEXUliEUIIYVeSWIQQQtiVtLEk4vbt20RERHDjxo0k98uTJw/h4eHpFFXGkFnK7OHhQfHixXFzc7M6FCEyFadNLEqp74BWwBmtdYWY1wYBLwJnY3Z7T2u9JC3nj4iIIFeuXJQsWRKlVKL7Xb16lVy5cqXlEk4rM5RZa8358+eJiIigVKlSVocjRKbizLfCpgLNEnh9pNa6csyWpqQCcOPGDQoUKJBkUhHOSylFgQIFkq2RCiFSz2kTi9Z6DXDBkdeQpJK5yecrhGM4bWJJwmtKqT1Kqe+UUvmsDkYIITKi4cPhq698ccSSXMqZF/pSSpUEFsdpY/EBzgEaGAwU0Vp3T+TYnkBPAB8fn6qzZs267/08efJQpkyZZGOIjo7G1dXVhlI4n8xU5sOHD3P58uUk94mMjMTLyyudIsoYpMyZX8+eVXF3v8W4cXvTdHxQUNB2rXW1BN/UWjvtBpQE9qX2vfhb1apVdXz79+9/4LWEXLlyJUX7pafnn38+0ff27Nmjjx8/ft9rf/31l+7evbsODg5O0fkzYpnTKiWfc2hoqOMDyWCkzJnb6dNag9YvvPBXms8BbNOJ/E3NVLfClFJF4jxtD+yzKhZ76tevH/7+/rz44os0aNCA6OjoRPeNiooiT548hIaGMmDAgAcap7dv386RI0fue6106dJMmTLlvtdu3bpF/fr1uXPnjv0KIoTIEH7/3TxWq3bRIed32sSilJoJbAR8lVIRSqkXgC+VUnuVUnuAIKCvpUHawZEjR1i/fj379++ncuXKdOjQIcnbUDt27GDXrl0cPHiQoUOH4uHhAcD+/fvp1asXP/zwAyNGjKBXr16cPn060fO4u7vTqFEjZs+ebfcyCSGstXw5FCgAjz561SHnd9pxLFrrpxJ4eUoCrzmtgwcP8sQTT3Dnzh0CAwMBmDdvXuz7QUFBvPfeezRu3Jj333+fK1euUKpUKWrWrPnAjKX+/v5MnDiRqVOnUrJkyRRNPNeuXTveffddnnnmGbuWSwhhHa1hxQpo3Bgc1VTqtDWWrMDX15du3boxePBgNm/ezMmTJ4k7vf/HH3/MkCFDmD59Ojt37mTkyJHs37+fzz77jAMHDrB27doUXef8+fP06tWLnTt38vnnn8e+XqFCBbZu3WrvYgkhLLRnD5w6BU2bOu4aTltjSU9vvAG7diX8XnR0jjRl/cqVYdSo5Pfbu3cvbdu25dy5c+TNm/e+9+rXr4/WmhEjRhAWFoarqyuTJ08GYMiQIQme77nnnnvgtQIFCjBx4sQHXnd1dcXd3T1TjLQXQhjLl5vHJk3g0CHHXENqLBncH3/8Qfny5cmRI8cDDfF79+7l5MmTZM+e3WF/+G/evBnbTiOEcH7Ll0NAABQt6rhrSI0lBZKqWVy9et1hf9SvXr2Km5sbnp6eeHp6Eh0dzY0bN/Dw8ODkyZM888wzLFiwgNdff53ly5fT1M512/Pnz+Pt7S2TNAqRSVy7BuvWweuvO/Y6UmPJwPbt20eFChVinzdp0oR169YRFRVFhw4dGD58OH5+fnzwwQcMGjTI7tcPDQ2lRYsWdj+vEMIaYWFw65Zj21dAEkuGVrt2bX755ZfY56+99ho//PADnp6ebNy4kcaNGwOmrWXjxo12v/6MGTPo2bOn3c8rhLDG8uWQIwfUrevY60hicSKBgYEEBQUlOUDSXm7dukW7du3w9fV1+LWEEOlj2TJo2BAc3WwqicXJdO/ePV3m6XJ3d6dr164Ov44QIn0cPgx//gnpcXdbEosQQmQBS5eaR0ksQggh7GLJEvD1hdKlHX8tSSxCCJHJRUVBaGj61FZAEosQQmR6oaFw8yY0b54+15PEIoQQmdzSpeDpCfXrp8/1JLEIIUQmpjX8+is88QRkz54+15TEksHNmzcPpRQHDhyw6TwTJ05k2rRpAHz44Yf8fm+lHyFEpnbwIBw7ln63wUDmCsvwZs6cSd26dZk1a9YD07akZu35Xr16xf78ySef2DNEIUQGtmSJeUzPxCI1lgwsMjKS9evXM2XKFGbNmgVAWFgYQUFBPP300wQEBBAWFkaDBg148sknKVu2LO+88w7Tp0+nRo0aBAQE8NdffwEwaNAghg0bBpip8+fMmQPAypUrCQwMJCAggO7du3Pz5k1rCiuEcIglS6B8eShRIv2uKTWWlEhiQZYc0dFpW4YtBQuyzJ8/n2bNmlG2bFny58/Pjh07ANiyZQv79u2jVKlShIWFsXv3bsLDw8mfPz+lS5emR48ebNmyhdGjRzN27FhGJXKdGzdu8Nxzz7Fy5UrKli1L165dmTBhAm+88UbqyyOEyHCuXIE1a8yfsPQkNZYMbObMmXTu3BmAzp07M3PmTABq1KhBqVKlYverXr06RYoUIXv27DzyyCM0adIEgICAAI4dO5bo+Q8ePEipUqUoW7YsAN26dWPNmjUOKo0QIr2tWAG3b0Pr1ul7XamxpEQSNYvrDlpd8fz586xatYp9+/ahlCI6OhqlFC1atHhgPfvscbp6uLi4xD53cXHhzp07iV5Da233uIUQGceiRZA/P9Sunb7XlRpLBjVnzhy6du3K8ePHOXbsGCdOnKBUqVKsW7fObtcoV64cx44d4/DhwwD8+OOPNGjQwG7nF0JYJzratK+0aAHZ0rkKIYklg5o5cybt27e/77Xg4GBmzJhhl/MrpfDw8OD777+nU6dOBAQE4OLicl/vMSGE89q8Gc6dg1at0v/acissgwoLC3vgtddff53X460p2rBhQxo2bJjgcXHfi9tV+fz58+TPnx+ARo0asXPnTnuFLYTIIBYtMjUVR68WmRCpsWQx3bt3JyoqirqOXkJOCGGpRYugXj3Imzf9ry01lizmu+++szoEIYSDHT0Kf/wBL7xgzfWlxiKEEJnM4sXmMb27Gd8jiUUIITKZxYvNol5lylhzfUksQgiRiVy+bNZfsaq2Ak6cWJRS3ymlziil9sV5Lb9S6jel1J8xj/msjFEIIdLb0qVmtH280QrpymkTCzAVaBbvtXeAlVrrR4GVMc+d1unTp3n66acpXbo0VatWpXbt2sybNy/R/cPCwmiVSKf1kiVLcu7cuUSPHTVqFFFRUcnG1KNHD5un8BdCOM78+VCoENSsaV0MTptYtNZrgAvxXm4L/BDz8w9Au/SMyZ601rRr14769etz5MgRtm/fzqxZs4iIiHDI9VKaWL799lvKlSvnkBiEELa5edOMtm/TJm1z49qL0yaWRPhorU8CxDwWsjieNFu1ahXu7u73jYQvUaIEvXv35saNGzz//PMEBAQQGBhIaGjoA8efP3+eJk2aEBgYyEsvvRQ7L9i1a9do2bIllSpVokKFCsyePZsxY8bw77//EhQURFBQEAArVqygdu3aVKlShU6dOhEZGQmYQZf3Zln28vJi4MCBVKpUiVq1anH69GlH/7MIIZIQFgZXr0K7dtbGkWXHsSilegI9AXx8fB4Y6Z4nTx6uXr0KwIDQAew9uzfB82itUUql+voB3gEMDRqa6Pvbt2+nQoUKsTHENXbsWG7fvs2GDRs4dOgQ7dq1Y8eOHURFRXHnzh2uXr3KwIEDqV69Ou+88w7Lli1j0qRJREZGsmzZMry9vWPXd7l8+TJ58uRh+PDhLFq0iAIFCnDs2DE+/vhj5s2bR86cORk5ciSff/4577zzDtHR0dy9e5erV69y7do1KlWqxDvvvMMHH3zAuHHjePvtt1P9b2GlGzduJDjLQVyRkZHJ7pPZSJmd09dfP4qHR2Hc3NYTFnY32f0dVebMllhOK6WKaK1PKqWKAGcS21FrPQmYBFCtWjUdd1oUgPDw8NhZi93d3RNdqTE1qzjG5e7unuSsyB4eHvft8+qrr7Ju3Trc3d0pXrw4vXv3JleuXFStWpWSJUty8uRJPD09yZYtG7ly5WLTpk3MnTuXXLly0alTJ/Lly4eXlxc1atTggw8+4NNPP6VVq1bUq1cPMHOHeXl5kStXLlavXs3Bgwdp1sw0Yd26dYvatWuTK1cuXF1dcXFxIVeuXLi7u9OpUyeUUtSuXZvffvvNITM9O5KHhweBgYFJ7hMWFkb8/x+ZnZTZ+dy9C08/beYGa9KkfoqOcVSZM1tiWQh0A76IeVxgj5OOajYq0feuOmja/PLlyxMSEhL7fPz48Zw7d45q1apRrFixFJ0joZpU2bJl2b59O0uWLOHdd9+lSZMmfPjhh/fto7WmcePGseu/JMbNzS32Gq6urklO0S+EcKytW+HkSWjb1upInLiNRSk1E9gI+CqlIpRSL2ASSmOl1J9A45jnTunxxx/nxo0bTJgwIfa1e43r9evXZ/r06QAcOnSIv//+G19f3/uOj7vP0qVLuXjxIgD//vsvnp6ePPvss/Tv3z+2vSRXrlyxt91q1arF+vXrY6fTj4qK4tChQw4srRDCVvPnmwb7li2tjsSJayxa66cSeatRugbiIEop5s+fT9++ffnyyy/x9vYmZ86cDB06lLZt29KrVy8CAgLIli0bU6dOvW+xL4CPPvqIp556iipVqtCgQQMefvhhAPbu3ctbb72Fi4sLbm5usYmrZ8+eNG/enCJFihAaGsrUqVN56qmnuHnzJgCffvpp7EqTQoiMZ/58aNgQ8mWE0Xta6yy/Va1aVce3f//+B15LyJUrV1K0X2aSmcqcks85NDTU8YFkMFJm5/LHH1qD1uPGpe44W8oMbNOJ/E112lthQgghjHvNsVaOto9LEosQQji5kBCoUweKFrU6EkMSixBCOLG//oLduyE42OpI/iOJRQghnNi922AdOlgbR1ySWIQQwomFhEC1alCypNWR/EcSixBCOKkTJ2DLlox1GwxsHMeilCoLlMdM9qiBs8A+rfWfdohNCCFEEubONY9On1iUUn5AL6AT4HPv5ZhHHbPPaeBn4Butdbgd4hRCCBFPSAgEBMCjj1odyf1SfCtMKfWIUmoOsA94AdgNfAx0BVoALWN+/iTmvR7APqXUL0qp0vYOPKvr3r271SEIISx08iSsW5fxaiuQujaW/UBJ4DnMuifNtdafaK2na62Xaa2Xxvz8sda6OaY20x0oHXOssJOoqCjy5MlDaGgoAwYM4MaNGw/sM2bMGPz8/HjmmWfSfB0vLy8A6tSpk+ZzWOXYsWNUqFDB6jCEcJg5c0BrePJJqyN5UGpuhT2ptU7xbMFa62uYVRx/UEplgPk2M48dO3awa9cufH19GTo04TVdvv76a5YuXUqpUqWSPV/sNAwuCX/P2LBhg03xOkpycQuRmc2ebW6D+flZHcmDUvwbmZqkYs9jnYWOWaExsedpNWfOHGrVqkWlSpWoW7cuZ8+eZevWrdSsWZOcOXMmeEyvXr04cuQIbdq0YeTIkYwYMYIKFSpQoUIFRo0aBZhv9H5+frzyyitUqVKFEydOJBrDvZrLvWN69+5N+fLladKkCdevXwfgp59+okaNGlSuXJmXXnqJ6OjoB86T0OqVSR3brl07qlatSvny5Zk0aVKicU+bNo2KFStSqVIlunTpEnu96OhoXnzxxQdiFcLZnTgB69fD//5ndSSJSGwSsfgbUDGl+zrbZusklB999JHu06ePvnv3rtZa67t37+o+ffrojz76KEXnSMq5c+difx40aJAeN26c7tGjh46OjtbvvfeeXrNmTYLHlShRQp89e1Zv27ZNV6hQQUdGRuqrV69qf39/vWPHDn306FGtlNIbN25M9No5c+a87/Ho0aPa1dVVr1u3TmutdadOnfSPP/6o9+/fr1u1aqVv3bqltdb65Zdf1j/88MMD55szZ47u0aNH7PNLly4leez58+e11lpHRUXp8uXL63Pnzj0Q9759+3TZsmX12bNn7zvmXqw7d+68L9b4ZBLKhEmZM7YRI8ykk4cO2XaejDAJ5Syl1AMrWimlfBPaOavQWnPp0iVGjx5N37590VrTt29fRo8ezaVLl2yuuUydOpUaNWpQqVIlvv76azw8PJg8eTIuLi4MGTIkdgXIxKxbt4727duTM2dOvLy86NChA2vXrgWgRIkS1KpVK1XxlCpViooVKwJQtWpVjh07xsqVK9m+fTvVq1encuXKrFy5kiNHjjxwbEBAAL///jsDBgxg7dq15MmTJ8ljx4wZQ6VKlahVqxYnTpzgzz//fCDuVatW0bFjRwoWLAhA/vz574u1cuXK98UqRGYwezYEBma83mD3pKaNZTLwI9Du3gtKqSBgFv91O85ylFKMHDkSgNGjRzN69GgA+vTpw8iRIxNcxTGlpk2bxpYtW1i1ahVeXl7Ur1+f8uXLp+ocSSW2xG6lJSXuui+urq5cv34drTXdunXj888/T/LYhFavzJcvX4LHhoWF8fvvv7Nx40Y8PT1p2LBhbCeFuHFrrRP9N04oViGc3bFjsHkzfJGBlzFMTRvLSCBaKTUAQCnVFZNUnnVQbE4jbnK5x9akAmZRrjp16uDl5UVISAgbNmwgICAgVeeoX78+8+fPJyoqimvXrjFv3rxkazmp1ahRI+bMmcOZM2cAuHDhAsePH39gv4RWr0zs2MuXL5MvXz48PT05cOAAmzZtSvTaP//8M+fPn489XojM7JdfzGNG7A12T5I1FqXUk8Ae4GDMPbXnga1KKX+gPvC41voPx4eZsd27/RVX3759bU4u3bp1o23btsyZM4cWLVpQunTpVNcyqlSpwnPPPUeNGjUA6NGjB4GBgXa9LeTv78+nn35KkyZNuHv3Lm5ubowfP54SJUrct19Cq1cmdmyzZs2YOHEiFStWxNfXN9FbduXLl2fgwIE0aNAAV1dXAgMDmTp1qt3KJkRGM3s2VK8OKejwaZ3EGl9ibqFsAiKBa8BW4FtMF+J/gbJJHetMmy2N95cvX9Z9+vTRQGwDfvznmY2sIJn5SZkzpj//NI32w4bZ53yOarxPssaita6lzFduX6BynE0B4UqpI8BOrXUGrpQ5llKKvHnz3temcu+2WN68eW2+HSaEEPfMmAFKZeBuxjGSbbyPyUwHYrZZ915XSvkAVYCKDovOSQwaNOi+RuR7yUWSihDCXrSG6dOhQQMoXtzqaJKW5iHLWuvT2kzjkvDQ7ywmfhKRpCKEsKft2+HQIbBhlqZ0Y+u0+T7Ak5g5xCKBncAKrXWU7aEJIYS4Z8YMcHfPmJNOxpfmxKKUqgcsATz5b9p8gPNKqcFa6zG2Bme1uLe3ROajbRy8KkR6iY6GWbOgRQvIl8/qaJJny+x9w2IeuwMPY2otnYG/gFFKqRm2hWYtDw8Pzp8/L398MimtNefPn8fDw8PqUIRIVmiomSb/6aetjiRlbLkVVgEYrrX+Ic5rfwM/K6VeACYppTZorcfZFKFFihcvTkREBGfPnk1yvxs3bmS5P06ZpcweHh4Uz+itoEJgboPlygWtWlkdScrYkliuYhLJA7TWU5RSj2NWmnTKxOLm5paiKefDwsIIDAxMh4gyjqxYZiGscuOGWSmyQwfIkcPqaFLGllthoZiVI5N6/xEbzp9mSqljSqm9SqldSqltVsQghBD2sHAhXLniHL3B7rElsUwC6iil+iTyfknMCH2rBGmtK2utq1kYgxBC2GTaNChWDB5/3OpIUs6WW2ErgTvACKVUe8x0L9tjXmsA9AEG2ByhEEJkUadPw7Jl0L8/uLpaHU3K2ZJYBgOVMFO81I/Z4nah2glcUkpVAA5ore/YcK3U0sAKpZQGvtFaT0rHawshhF3MmGG6GnftanUkqaPs0Z1WKZUXCOS/ucQCgXKYxKWB28BBYI/WukuCJ7EjpVRRrfW/SqlCwG9Ab631mnj79AR6Avj4+FSdNWtWAmdKXmRkZOzSvVlFVitzVisvSJkzih49qpEt210mTtzhkPPbUuagoKDtiTY1JDY7pa0b4I6ZS6w7MBZYB1xy1PWSiGMQ0D+pfRKa3TilnGFGVHvLamXOauXVWsqcEezaZWYyHjvWcdewZHbjuJRSFbXWe1K6v9b6FrAjZks3SqmcgIvW+mrMz02AT9IzBiGEsNW0aeDmBp07Wx1J6mXGNe99gHVKqd3AFuBXrfUyi2MSQogUu3PHzGTcsiUULGh1NKmX6da811ofwXQqEEIIp7R8uekR5myN9vfImvdCCJHBTJkC3t6mxuKMZM17IYTIQE6fhkWLoE8fM02+M0ruVtibmMkmlVJqP7Ab2AQ0BhpqrQ85OD4hhMhSfvzRtLF07251JGmX5K0wrXUtIBdQFRgOnMO0p9xb8/5PpdTPDo9SCCGyAK3NbbBatcDf3+po0k7WvBdCiAxi40Y4cAAmT7Y6EtukeUoXrfVpYGnMJoQQwkZTpkDOnPC//1kdiW3SPLuxUsrJiy6EEBnH1aswezY8+aRZ1MuZ2TJt/lSl1G6lVNuE3lRK+SilHrXh/EIIkWXMng3XrsELL1gdie1sSSyPAGHADKXUFqVU03jvd8a0ywghhEjGN9+YBvs6dayOxHa2TJsfhVl75ThQDViilPoDOA/kxDTsh9scoRBCZHLbt8O2bTBmDChldTS2syWxTAY6ABuBn2Je88GMcdHAMsw4GCGEEEn45huznn0Xhy8qkj5sSSyNgDFa675xX1RK1Qe+wdRi7tpwfiGEyPSuXDELenXuDHnzWh2NfdjSxgJwNP4L2iyoVQ2IAL6z8fxCCJGpTZ9uGu179bI6EvuxJbGsBp5VSj0wm43W+hrmVlkVG84vhBCZmtbmNlhgIFSvbnU09mNLYvkEMz39aqVUQstT1sE07gshhEjAli2weze89FLmaLS/x5aR9zuVUs8BU4DNSqnDwFZMr7BKQD1gsT2CFEKIzGj8eDMY8umnrY7EvmxpvEdrPVMptQl4A2gNxP3n2QK8Zsv5hRAiszpzxgyKfOkl5x9pH59NiQVAa30U6AP0UUrlAwoDl7TWJ209txBCZFaTJ8OtW/Dqq1ZHYn82J5a4tNYXgYv2PKcQQmQ2t2/DhAnQpAn4+lodjf3ZNbFkNTdvyTAdIUTqLVgA//xjkktmJIklja5fv0O5d3PgdzYnRyc+SkfvQHIVKw3Fi0OxYv89enpaHaoQIoMZOxZKlYIWLayOxDEksaTR6dPnqHKuDKuLHmG51zZevrONprsheBa0Pgj5bsTsmC+fSTLxE86914oXhzx5MldfQyFEovbsgTVr4KuvwNXV6mgcwy6JRSmlgIeAU1rrW/Y4Z0ZXsmRh5v0Uztz5q1m2z4Xpe0NY9PAcFpb7B1ftSqMc/nS8XYZ2J/PgHXHB1Hu3bzddQeLLmfPBhBP/Z29vcLF1ogQhhNXGjDHzgjnzmvbJsVeNJT9mepfGwCo7ndMp5M+rmfR+PcberMdP00fw6fdbOZYjhFUBIazIPY9ePi7Ur1GfYL/n6ODXgaLZC8LJkxARYbZ//rn/57Aw8xgdff+F3NxMgolf24mbhIoUgWxSCRUiozp9Gn76ySSV/PmtjsZx7PlXKEvfy8meHV7o7sLzz9VkyZKafPb5UDYe2YVHtRD+IISwY73pvbQ3tYvXpqN/R4LLB1PisccSPll0tKnZJJZ8tm83rX83btx/nIsL+PgkXuu595gjh+P/QYQQD5gwAW7ehDfesDoSx5Kvt3bm4gKtWkHLloq1awMZMiSQFR99Sp4y+6naJYQzN0Lot6If/Vb0o2qRqgT7BRPsH0zZAmX/O4mrq6l9FCmS+ARCWsPFi4knn0OHYOVKM3VqfPnzJ9zWEzcJ5c4t7T5C2NH16/D11+bvQ9myye/vzCSxOIhSUL++2bZsgcGD/Vn8kT95835A335/ka9OCIuPhPDeqvd4b9V7BBQKINgvmI7+HfH39kcl90ddKZMg8ueHihUT3y8y0iSaEyfMY/yft22Ds2cfPM7LK9Faj9epU2apu4IFpd1HiBSaPt38qr2ZBVapSlNiiVlzJa48MY8VlVL3TTwZM41+llajBixaBDt2wKBBMPKDRyhQ4G3eeuttpr30N0uPzSUkPISPV3/MoNWD8C3gG1uTCSwcmHySSYqXlxmBldQorJs3TbvPvYRzr+Zzr/azcqV5P6bdpxpAz57g7p50h4PixaFwYWn3EVme1jBiBFSuDA0bWh2N46X1Nz4Ms0pkfMPj/Kxi9kn3DnVKqWbA6Jhrf6u1/iK9Y0hIlSqwcCFs3QoffQTvvAOjRj3M+++/wcoX3+DCrVPMC59HSHgIQ9cP5bN1n1Eyb0mTZPyCqVm8Ji7KATWE7NmhZEmzJSY62rQ8RkSwb9kyKuTLd3/y2bLFPCbU7lO4cPLtPh4e9i+XEBnE8uUQHg7TpmWNO8xpTSxB8Z7nBeYBbwHbbQnIVkopV2A8podaBLBVKbVQa73fyrjiql4dliyB9evhvffgtddg2DAYPLgwLz39Mi9Xf5lzUedYeHAhIeEhjNk8huEbh1MsVzHal2tPsH8w9R6uh6tLOuZsV1coWhSKFuVcVFTCX7u0hgsXTLJJ6NbbgQPw229w9eqDxxYsmHyX69y5HV5MIRzhq69Mk+n//md1JOkjTYlFa7067nOlVIGYH3fFf88CNYDDWusjAEqpWUBbIMMklnsee8z0Lv7tN3j3XbPe9VdfwRdfQLNmBeke2J3ugd25fOMyiw8tZk74HL7d+S3jto7D29M7NskElQzCzdXN6uKYr2IFCpitUqXE97t6NfF2n4gI2LQJzp9/8LhcuZLvdFCgQNb4SiicxtatsGqV+d12f2BZxMwpM978LgaciPM8AqhpUSzJUspMRPfEE/DLLzBwoJnm4fHHzX/EKlUgj0cenqn4DM9UfIbIW5Es/XMpIeEhzNg3g0k7JpHPIx9tfNsQ7BdM40ca45Etg99WypULypUzW2Ju3IB//024x1tEhMnGJ0/C3XjztWXPnrJ2n8w65FlkOEOHmrXse/a0OpL0o7ROqKkklScxNZazwBNaa0sHSCqlOgFNtdY9Yp53AWporXvH268n0BPAx8en6qxZs9J0vcjISLy8vGwLOo7btxWLFhXlhx9KcuWKG40bn6JHj6MUKnTzgX1vRt9k28VtrDm3hvXn1nMt+ho5XHNQO39t6nvXp0b+GuRwtf+YFXuXOa1UdDRuFy6Q/exZs5079+DP587hcvv2fcdpFxdu5c/PTW/vB7eCBc1jgQLomK+XGaW86UnKbB9//52D556rwdNP/02PHkftem57sKXMQUFB27XWCa0enCkTS21gkNa6aczzdwG01p8ndky1atX0tm3b0nS9sLAwGjqgm8fly+aW2MiRplbTvz8MGGA6eSXkVvQtVh1dRcj+EOYfnM+5qHPkyJaD5o82J9gvmFZlW5E7u33aKBxVZofQGs6du7/Gk9BtuMjIB4/19obixTnn4UHBSpUSrgFlthWaYjjVZ2wnjijziy+akfbHjpmxyxmNLWVWSiWaWOx1K+wCUAo4Zafz2WIr8KhSqhTwD9CZ+1e2dAp58sDnn0OvXqb32KefwpQp5rUuXR4cPuLu6k6zMs1oVqYZE+5OYO3xtYSEhzA3fC5zw+fi7upO49KN6ejfkTa+bcifIxPPJxGXUiZBeHtDYGDi+1258mBbT8zPHgcPws8/m44J8eXOnfgUO/ce8+eXdp8s6N9/TS+wHj0yZlJxJLskFm2qPcftcS5baa3vKKVeA5Zjuht/p7X+w+Kw0qxECZg5E15/3UwD8dxzZvTu6NFQq1bCx2RzyUZQqSCCSgUxpvkYNkVsYs7+OYSEh/Drn7+a90sGEewXTLty7fDxymL/6xOSO7fZ/PweeGvbvW91168n3e6zbx+cOvVgu4+HR+LtPve2QoWk3SeTGTkS7tyBfv2sjiT9ZcbGe7TWS4AlVsdhT7Vrw8aNZvTugAHmedeupmGwcOHEj3NRLtR5qA51HqrD8CbD2X5yOyH7QwgJD6HXr714+deXqVeiHsF+wXTw60Dx3MXTr1DOJkcOeOQRsyXmzh2TXBIbbLp+vXmM1+4T2507qSUWihbNOt2KnNzZs+YLYOfOULq01dGkv0yZWDIrFxdzG6x9e/jsMxg+HObNM4MtX3/dTICcFKUU1YpWo1rRanzW6DP2ndlHSLhJMn2W9aHPsj7ULFYzdtR/6XxZ8DfCVtmy/ZcIEnP3rmn3SazL9Z498OuvEBX14LGFCiXf5TpnTseVT6TIyJGmgvv++1ZHYg1JLE7Iy8skluefN7fH+veH776DceMgKP7Q1UQopQjwCSDAJ4BBDQdx8NzB2CTz9u9v8/bvbxNYODA2yZQrmETXYJE6Li4mQRQqlHi7j9amB0diyef4cVi3zkxEGl/evEnPclC8uFmATtp9HOLCBbNC5JNPJnhnNUuQxOLEHn3UfLFdtAj69DFjX556ytRkihRJ3bl8C/ryXr33eK/eexy9eJS54Wb+svdD3+f90Pfx9/aPnVrGHj0JRTKUMgkib14oXz7x/aKiTLtP/Ftv937evdtMxRP/M8uRI/GaT7FiuF+4YGpWMsloqo0aZToZZtXaCqQisSilKmqt9zgyGJE2rVubAZZDh5ouyosXm15kr7yStvkfS+UrRb86/ehXpx//XPknNskMWTuEwWsGUyxHMZ6NfpZgv2CqFa1m2ySZwjaenlCmjNkSc/v2f4vLJZR81q41ySlOu08dMP95Emr3iftz0aLJ34PNQi5dMh1rgoOhQgWro7FOav7szFJK1dRa3zfRk1LKV2t90M5xiVTKkcPMnPzss2busT59YOpUmDjRzK6cVsVyF6N3zd70rtmbM9fOMP/AfCavn8zwjcMZun4oD+d5mA7lOhDsH0ydh+o4ZpJMYRs3N3j4YbMl5u5d0+Ic0836UGgoZXPm/K8mtGuXqRpfv37/cUr9t7hcUjMeeHo6tIgZxZgxpud6Vq6tQOoSy2TgR6DdvReUUkHALED6q2YQZcrA0qUwZ45pf6lVy9RchgwxY2NsUShnIXpW7UnZq2WpWLMiiw4uYk74HL7e9jWjNo+isFdhM3+ZXzANSjYgm4vcaXUa91Yf9fGBqlX5N29eysYfOKe1+UqeWLvPkSOwerXZJ758+ZLvcp0nj1O3+1y8aKbGb9vWTI+flaX4N19rPVIpVVcpNUBrPVQp1RX4CnjWceGJtFAKOnWCpk3NN6dx42DuXPNtKjjYPr+7+XPkp1vlbnSr3I0rN6/w66FfCQkPYequqUzYNoECOQrQrlw7gv2CaVS6Ee6u0k3W6SllEkS+fEnf57l27b/bbAndetu50yy9Hb/dJ2fO5Od58/bOsO0+w4aZ2sonn1gdifWSTCxKqSeBPcDBmEGQz2OmofcH6gOPO/Pgw8wud26TTLp0gZdeMsmmdWsYPx4eesiO18mem6cCnuKpgKeIuh3FssPLCAkP4ec/fmbKzinkyZ6H1r6tCfYLpukjTcnhZv/5y0QGkjOnWXs3qfV3b91Kut0nNNS8f+fO/ce5uf3X7pNYl+siRdJ9cbkzZ0zbyv/+l/SCrllFcv/6bwIVAKWU2g/sBjZh1jppqLU+5OD4hB1Ur27W4Ro9Gj780Kwq/Nln5haZvQd7e7p50sGvAx38OnDzzk1+O/IbIeEhLDiwgJ/2/EROt5y0LNuSYL9gWjzaAi/3rDXRoYjh7m6mlShRIvF9oqPNX+y4CSfurbedOxNv97m3uFxSNaAc9vuC88UXJoxBg+x2SqeWZGLRWtdSpsuPL1A5zqaAcKXUEWCn1vpJx4YpbJUtm5laokMHePllM6Byxgz49tuke7PaInu27LQq24pWZVtxu9Vtwo6FERIewrwD8/j5j5/xyOZB00eaEuwXTGvf1uT1yOuYQIRzcnU1tY8iRcy3o4RobRo34s/zdi8J/fmnqf1cvvzgsfnz31fTKXHrlmknipuEcudO9t5xRIQZZd+tW9IrgGclydYXY26BHYjZYueWV0r5AFUAqfg5kVKlTOP+jBmm51hgoFlk7L33zFImjuLm6kbjRxrT+JHGjG8xnvUn1jNn/xzmhs9lwcEFuLm40ah0Izr6daRtubYU9CzouGBE5qGUSRD580NAQOL7RUYm3e6zbRulzpwxXSnj8vJKttPBp4MLcveu4sMPHVpSp2LLjcgGWuufgaX2CkakD6XgmWfMAmN9+5rGxpAQM3tyzXRYEs3VxZX6JepTv0R9RjUbxdZ/tsZOktljUQ9eWvwSDUo2INgvmPbl2lMkVypHewoRn5eXqU4kUaVYvWIFDcqWTXyw6cqVpt0nOvq+40bjzqe5i1GwaxLzvBUunO7tPlaypaQzlFL5tNbf2C0aka68vc1aEU8/bRr3a9c2XZQ//TT9hh24KBdqFq9JzeI1+bLxl+w6tYuQ8BDm7J/Dq0te5bUlr1HnoTqxU8s8nCeJsRhC2EC7u0PJkmZLTHS0mckgJuF8+3EEV/dH8HLjf+BcBGzebBLRzXgL87m4JNzuE3crWtTMhJ0J2JJYpgJfK6UKaq2HxH8zZsGtL7XW9Wy4hkgHLVrAH3+YdV9GjoSFC03bS3qv86SUIrBIIIFFAhkcNJj9Z/fHzl/25oo3eXPFm1QvWj02yZTJn8RocyEcwdUVXaQIqmhRNmyAF3fDJ59oPD6I0w6jNZw//+B4n3u1n4MH4fff4erVB89fsGDyXa5z22fBPkdKc2LRWvdQSp0FBsckl75gRuIDnwNtgetJnUNkHLlzmwbIJ5+EF14wk1m+/DJ8+WXiq1Y6klKK8oXKU75QeT5s8CGHLxyOne7/nZXv8M7Kd6joUzF2/jJ/b3+ZWkY43KBBg7h06RIjRozkrbcURYpoTp0awKBBngy61yVMKZMgChaESpUSP9nVqw+2+8S9Dbd5s5kFO75cuZKe3bp4cShQwNLBpjbd9NNav6uUOg0MV0p5A5FAd0AD3wAyVMjJNGxoZm1//33TPXnpUtP28vjj1sZVJn8ZBtQdwIC6Azh+6Xjs/GWDwgbxUdhH+BbwpaN/R4L9gqlcuLIkGWF3WmsuXbrE6NGjOXw4gA0bXqBRo9l8/fVX9OnTB6116v7f5coF5cqZLTE3biS9uNxvv5l2n/iLy2XPnnBbT/x2HwexR2vSZKAlZvlfjek59oHW+ogdzi0skDOnuSXWsSN07w6NGpklkr/8MmMs8V4ibwn61u5L39p9OXn1JPMOzCMkPITP133OkLVDKJ2vdOz8ZTWK1ZD5y4RdKKUYOXIk0dGujBtXD9jPypXP0qdPH0aOHOmYLzMeHmalsKRWC7tz5752nwdqPps2mZ9v3br/OFdXqpQpAwcO2D3sNCcWpZQb8ArwLuAN7MCMcXEDTtgjOGGtxx4zcw9++KGZiv9e7SUjraBbJFcRXqn+Cq9Uf4VzUedYcGABIeEhjN48mmEbh1EsVzE6+HWgo39HHnvoMVxdMlDwwukopShRYhhmKF8LINpxSSWlsmUzNZFixRLfR2tzWy3eYNPzERE4pMVGa52mDTgGRAN7gZYxrz0J3AB+A7zSeu703qpWrarTKjQ0NM3HOpMNG7QuW1Zr0LpNmwh95YrVESXt4vWLetquabrtzLY6++DsmkHoQl8V0i8tekmvOLxC37pzK8XnyiqfcVxS5oSdOnVXu7tHaVisMXdodJ8+ffTdu3cdH6AD2PI5A9t0In9TbblH4Aq8CFTSWv8ak6R+BtoAtYBQpZSMcsskatc2tZc334RFi4pSsSKEhVkdVeLyeuSlS6UuzO88n3Nvn2N2x9k0KNGAn/b8RJOfmuAzzIfnFzzP4kOLuXnnZvInFFme1ponntjIrVvZ6Np1N3fv3qVPnz6MHj2avn37ygJ4cdjSxvKo1vpG/Be11iuUUk8AvwIbgCRmohPOJEcOc0usZMmdjBlThaAg6N3bzJOUkZfb8HL34snyT/Jk+Se5fvs6y/9abqaWCZ/H1F1TyeWeK3aSzGZlmuHploELIyyze7di377aBAauZurUd2PbXADy5s0rHUbisKW78QNJJc57m5VS9YDlaT2/yLgCAq6wa5eZCmbsWFi2zMyEUaeO1ZElL4dbDtqVa0e7cu24FX2LlUdWEhIewvwD85mxdwaebp40L9OcYL9gWpZtSe7sGX/MgHA8rc0USAULKlaubBCbRO4lF0kq93NYdxmtdTjwmKPOL6yVM6eZkn/VKtPZpF49ePtt0zvSWbi7utP80eZ82+ZbTvU/xcquK3mu0nOsP7Gep+c+jfdX3rSe2Zplp5Zx4foFq8MVFvrpJ1izxswKni/f/UlEksqDUpxYlFKNUntyrfWJmGOfSO2xwjkEBcHevWZQ5VdfQdWqsH271VGlXjaXbDxe6nHGtxzPP2/+w7rn1/Fq9VfZc3oPQw8OxWeYD01/asqk7ZM4c+2M1eGKdHTxopkZvFYt8/9cJC81NZZlSqlVSqlWSqlk+2wqpdyUUu2VUquBJWkPUWR0uXLBpEmwZIlZlbZWLbMuxe3bVkeWNi7KhccefowRTUdwrM8xJgROoF/tfhy5eISXFr9EkeFFaDi1IWM3j+WfK/9YHa5wsIEDzQwtEyZk2MUrM5zU/DNVBu4AC4GTSqnpSqk+MYmmjlLqMaVUa6XUm0qpn4GTQAgQFXOsyOSaN4d9+6BzZ/j4Y5Ng/nDy9UWVUpTLXY4vnviCQ68dYtdLuxhYbyBno87y+rLXKT6yOLWn1Gb4huEcvXjU6nCFnW3ZAhMnmk4qWX0d+9RITeN9J6AnUAQzMLIt8BSmL3dcCrgCzAUmaK232iFO4STy5YMff4T27c2MyVWrmtmS+/bNWAMr00IpRaXClahUuBKfBH3CgXMHYucv6/9bf/r/1p/AwoGxU8v4FpRVn5zZnTtmvrwiRWQd+9RKTWL5EDiktZ4BbFRKdQT+BvwxI+81cBbYh1lV8m6iZxKZXocOULeuSS5vvQULFpieY488YnVk9lOuYDkG1h/IwPoDOXLxSGySGbhqIANXDaS8d/nYJFOhUAVp5HUyo0bBjh3w889OMaFwhpKaW2EXgbgd/GcDZbTWU7XWX2mth2mtf9Bab7cqqSilBiml/lFK7YrZWlgRhzAKFYK5c2HaNNPAX6mSua2QGceRlc5Xmrcee4tNPTZxou8JxjQbQ0HPgnyy+hMqTqyI7zhf3v39Xbb9u00G0jmBw4fhgw+gXTszZ55IndQkln3AC0qpexPSZNSvXyO11pVjNuk0YDGloEsXk1hq1za3Fpo3N9MVZVbFcxend83ehD0Xxsl+J5nYciIl85bkqw1fUX1ydUqNLsWby99kw4kN3JWKfYZz9y706GEmCB4/3tLZ551WahLLx5g17v9WSh3A3PpqoZRqrpTycUh0ItN46CFYscL8oq5dCxUqwPTpmbP2EpePlw8vVXuJFV1WcOatM3zf9nsCfAIYv3U8j333GA+NfIjXlrzGqqOruHP3jtXhCswid6tXm1kmiha1OhrnpFJTLVdKlQV6YAY+1o55+d4JTmNmON5571FrfcxukaYsvkHAc5jOA9uAflrri4ns2xPTGQEfH5+qs2bNStM1IyMj8bJiJSwL2VrmiIgcfPFFOf74Iw/165+lb99D5M2bcfsmO+IzvnbnGhvPb2TNuTVsubCFm3dvksctD3UL1KW+d30C8wbi5uJm12umRlb9f33tWgFeeKE6ZcteZfjw3Zm+tmLL5xwUFLRda10twTcTm50yuQ24C/QD2gOfYuYG+zfm9eiY7Vxaz5/EdX/H3JaLv7UFfDCTY7oAQ4DvUnJOmd04dexR5jt3tP7iC63d3bUuVEjr+fNtj8tRHP0ZR96M1HP+mKM7z+msvT7z0gxC5/0ir+4yt4tecGCBvn77ukOvn5Cs+P965cpQHRSktZeX1n/9ZXU06cNRsxvbMgnlJ8BarfUWYN69F5VSRTC3zKrigPErWusUjeJXSk0GFtv7+sI+XF1hwABo0cK0wbRrB926mZ44efNaHFw6y+mek2D/YIL9g7lx5wa//fUbIeEhLDy4kB/3/IiXuxctH21JsF8wzR9tjpd71qpJpJe5c4sTGgqTJye9rpZIni2TUA5K5PWTmNrLr2k9d1oppYrEXB9MTWpfescgUicgwAxCGzwYPv8cVq6E77+HJ7LoJEAe2Txo7dua1r6tuR19m9BjoYTsD2HegXnM/mM2Htk8aFamGcF+wbQu25o8HnmsDjlT2L8fJk0qTatWMm2LPWS2CQq+VErtVUrtAYKAvlYHJJLn7m4Sy8aN4OUFjRvDK69AZKTVkVnLzdWNJo804ZvW33Cy30nCuoXxYpUX2frPVrrM64L3V960mN6CKTumcC7qnNXhOq3bt6FrV8iRI5rJk6UXmD1kqsSite6itQ7QWlfUWreJU3sRTqB6dTMg7c03zXiXSpXMjLICXF1caVCyAWOaj+Hvvn+zofsGXq/5OuHnwumxqAeFhxXmiWlPMGHrBE5FnrI6XKfy/vtm4tR+/Q5SuLDV0WQOmSqxCOd3bzGx1avN84YNzXQwUVGWhpWhuCgXaj9Um2FNhnHk9SNs77mdAY8NIOJKBK8seYWiw4tS7/t6jNo0ir8v/211uBna8uXw5ZfQqxfUry+1PnuRxCIypHr1YPduM6By1CgIDDS3ysT9lFJUKVKFIY2GEP5qOPte3sdHDT7i8o3L9F3elxKjSlBjcg2+XP8lf134y+pwM5STJ03HkQoVYMQIq6PJXCSxiAzLy8sMqPz9d7OAWN26zreYWHpSSlG+UHk+avgRe17ew8HXDvLZ459xV99lwO8DKDO2DJUnVmbw6sGEnw23OlxL3b1r2lUiI2H2bFNTFvYjiUVkeI0amSlhevQwi4kFBsLmzVZHlfGVLVCWd+u9y7ae2zja5yjDmwwnp3tOPgz7EP+v/fEf788Hqz5g16ldWW7+so8/Nl9Yxo4Ff3+ro8l8JLEIp5A7N3zzjZkW5to1qFPH1F6uX7c6MudQMm9J3qz9Juu7r+efN/9hXPNxFPYqzGfrPiPwm0DKjC3D27+9zeaIzZk+ySxebKbBf+456N7d6mgyJ0kswqk0bmwWE7u3FHJgIGzYYHVUzqVorqK8WuNVVnVbxal+p5jcejJlC5Rl5KaR1JpSi4dHPczYw2NZc3wN0XejrQ7Xrg4fhmefNf9vvv5auhY7iiQW4XRy5zZLIa9YYWosdeuaLsrScyz1vHN606NKD5Y+s5Qz/c/wQ7sfqFKkCov+XUSDqQ0oNqIYLy9+md+P/O70k2Reu2bWCXJxgZAQaVdxJEkswmndq7306gUjR0LFihAWZnVUzitfjnx0rdSVBZ0XML/OfGYGz6ReiXpM2zONxj82xmeYD90XdOfXQ79y885Nq8NNlXuN9fv2wYwZUKqU1RFlbpJYhFPLlcvc0ggNNc+DgkwX5StXrI3L2Xlm86Rzhc780ukXzr51lrlPzqV5meaEhIfQamYrCg0rxDNzn2Fe+Dyibmf8quIHH5hF54YNg2bNrI4m85PEIjKFhg1hzx5zS2zSJNPTZ9Eiq6PKHDzdPGnv156fOvzEmf5n+PXpX+no15Hlh5fT4ecOeH/lTadfOjF732yu3rxqdbgP+PFH+Owz06uwr0zylC4ksYhMw9PTjNrfuBHy5YM2baBzZzh92urIMo/s2bLT4tEWTGk7hVP9T/F7l9/pVqkb6/5eR+eQznh/5U3bWW2ZtnsaF68nuBRSulq3ziSUoCBZDTI9SWIRmU6NGmbup08+gXnzwM8Pvvsu869Wmd6yuWSjUelGfN3yayL6RrDmuTX0qtaLnSd30m1+NwoNK0Szn5oxeftkzl47m+7x7dsHrVub9pQ5c8xkpyJ9SGIRmZK7u7mvvmsXlC9vuic//jgcPGh1ZJmTq4sr9UrUY1SzURx/4zibe2zmzVpvcvjCYXou7knh4YUJ+iGIcVvG8e/Vfx0ez99/m7YUT08zH1j+/A6/pIhDEovI1Pz8zISW33wDO3eanmMffww3natTk1NRSlGjWA2GNh7Kn73/ZNdLu3iv7nucjjxN76W9KTaiGHWm1GHExhEcv3Tc7tc/fx6aNjXTtSxbBiVK2P0SIhmSWESm5+ICPXvCgQMQHAyDBpkEs3Kl1ZFlfkopKhWuxODHB7P/1f3sf2U/g4MGc/3Odfqt6EfJ0SWpNqkan6/9nEPnD9l8vUuXoEkTOHoUFi40C8mJ9CeJRWQZhQubMQzLl8OdO2aVyqefNrPcivTh5+3H+/XfZ+dLOznc+zBfPvEl2Vyy8d6q9/Ad50vAhAAGhQ1i35l9qZ5a5soVc/tr717Ttbh+fQcVQiRLEovIcpo0MQ27H35oRmCXKwejR5tkI9LPI/kf4a3H3mJTj038/cbfjGo6inwe+fhk9ScETAig3PhyvLfyPbb/uz3ZJBMZCS1bmk4bP/8MLVqkUyFEgiSxiCwpRw7T1rJvH9SqBW+8AVWqwNq1VkeWNT2U5yH61OrDmufX8G+/f5nQcgIP53mYL9d/SbXJ1Sg9pjT9lvdjw4kN3NV37zv28mVTU9mwwdRI27WzpgziP5JYRJb26KOmgXfuXPMHqn59c3ssIsLqyLKuwl6F6VWtF791+Y3T/U8zpc0U/L39GbtlLI999xgPjXyI15a8RtixME6fiaZRI7OMwsyZ0KmT1dELkMQiBEpB+/YQHv7f1B++vvDppzItv9UKeBage2B3fn36V86+dZaf2v9EzWI1+W7ndwT9EESxkUXYWbwnH/ywnHbBt6wOV8SQxCJEDE9PM6jywAFo3twkGT8/WLWqkAyuzADyeOThmYrPMPd/c1nb5izeob/A0UZkrzaTj/5shs8wH7rN78bCgwu5cUeWGbWSJBYh4ilZ0ozUXrXKTA0zeLA/jz0GmzZZHZkAMy7pifo5cTnQkU39Z3LhnbMs6LyANr5tWHhwIW1ntcX7K2+eCnmKOfvncO3WNatDznIksQiRiKAg2LYN+vc/wNGjULu2uYd/+LDVkWVdP/1kevUVLmwSfbVq4JHNgza+bfih3Q+c7n+aZc8s46kKT7HyyEo6/dIJ76+86TC7A9P3TOfyjctWFyFLkMQiRBJcXaFly1P8+acZWLl0qbk99tprcOqU1dFlHXfuQL9+0KWLSfAbNpiaZXzuru40LdOUSa0n8W+/f1nVdRXdA7uzKWITz857lkLDCtFqRiu+3/k956POp3s5sgpJLEKkgJcXfPSRqa306AETJ8Ijj8DAgWa0t3Ccc+dMd+IRI6B3b/jtN3OLMjnZXLIRVCqIcS3GEfFmBOu7r+e16q+x78w+ui/sjs8wHxr/2JiJ2yZyKlK+JdiTJBYhUqFwYZgwwTTwt21r1vkoVcr0IJPFxexv7VozvmjdOvj+exgzBtzcUn8eF+VCnYfqMLzpcI72Ocq2F7fxVp23OH7pOC//+jJFhxelz64+jN40mhOXT9i/IFmMJBYh0qBMGTMYb+dOaNDA9CArVcokGkkwtouONj30GjaE7Nlh/Xp47jn7nFspRdWiVfn8ic85+NpB9r68lw8bfMjVO1d5Y/kbPDzqYWp9W4uv1n/FkYtH7HPRLMYpE4tSqpNS6g+l1F2lVLV4772rlDqslDqolGpqVYwia6hcGebPh61bzQj+gQPNbLqDBsGFCxYH56T+/NMklI8+MoNVd+yAqlUdcy2lFBUKVWBQw0F8V+07Dr52kM8e/4w7d+/w9u9v88iYRwj8JpBP13xK+NlwxwSRCTllYgH2AR2ANXFfVEr5A52B8kAz4GullGv6hyeymmrV4NdfTS+yhg3NdDEPP2yWSj4hd1ZSJDrarABasaKZamfaNLOscK5c6RdD2QJlebfeu2zruY0jrx9hWONh5MiWgw9CP8D/a3/Kf12eD0M/ZPep3ameJDMrccrEorUO11ontGRTW2CW1vqm1voocBiokb7RiaysalWzauWePWbOqjFjoHRp6NbNLDomErZtG9SpA/37Q+PG8McfpgeYlUrlK0W/Ov3Y8MIGIvpGMLb5WArlLMSQtUOo/E1lyo4ryzu/v8PWf7ZKkonHKRNLEooBcb8fRsS8JkS6CggwYy4OH4aXXzazKAcGmrEx8+fLTMr3nD0LL75olpM+fhymT4cFC6BoUasju1+x3MV4rcZrhHYL5WS/k3zT6htK5yvN8I3DqfFtDUqOLknfZX1Z9/e6BybJzIpURs20SqnfgcIJvDVQa70gZp8woL/WelvM8/HARq31TzHPpwBLtNYhCZy/J9ATwMfHp+qsWbPSFGdkZCReXl5pOtZZZbUy26O8V69mY8mSIsybV4zTpz0oVOgGrVqdpGXLk+TPn/HmuHL0Z3z9uishIcWYNethrl93JTg4gq5dj+HlFe2wayYnLWW+evsqG85vYM25NWy9sJXb+jb53fNTt2Bd6hesT+W8lXHNwHfjbfmcg4KCtmutqyX4ptbaaTcgDKgW5/m7wLtxni8Haid3nqpVq+q0Cg0NTfOxziqrldme5b19W+t587Ru3Fhr0DpbNq3bttV64ULzXkbhqM/42jWtR4/WulAhU/42bbTet88hl0o1W8t8+cZlPWPPDB08O1h7DvHUDEIXGFpAd5/fXS85tETfvHPTPoHakS1lBrbpRP6mZktTqsq4FgIzlFIjgKLAo8AWa0MS4j/Zspm2l3btTO+nb7+FH34wt398fKBzZ3jmGdMZQCmro7WfCxdg/HjT5nTunOngMH++GUWfWeTOnpunAp7iqYCniLodxbLDywgJD+GX/b/w3a7vyJM9D619WxPsF0zTR5qSwy2H1SE7jFO2sSil2iulIoDawK9KqeUAWus/gJ+B/cAy4FWttXV1ayGS8OijMHSo6TW2YIFpvJ4wwbQ3+Pqarss7duC0MytrDVu2wAsvwEMPmRU7a9WCNWvMBJ+ZKanE5+nmSQe/DkzvMJ2zb51l8VOL6eDXgSV/LqH97PZ4f+XNk788yex9s4m8FWl1uHbnlDUWrfU8YF4i7w0BhqRvREKknZsbtGljtosXTUP/zJkm6Xz2mZkTq1Urs/Ruw4bg4WF1xEn7+2+zPPD06aYnXM6cphb2+utQoYLV0aW/7Nmy07JsS1qWbcnt6NusPr6aOfvnMO/APH7Z/wvZXbPTrEwzgv2Cae3bmrweea0O2WZOmViEyKzy5TNzkfXoYW4ZLVxoui9PmQLjxpkllevVg8cfN1tgoLm9ZiWtYe9eWLIEFi0yE0SCuZ03YYIZ5Jg7t7UxZhRurm48UfoJnij9BONbjGfDiQ3M2T+HuQfmsuDgAtxc3GhUuhHBfsG09W2Ld05vq0NOE0ksQmRQBQtC9+5mu37drEOydCmsXAnvvGP28fSE6tXNLaaqVaFSJTM5pqsDOyLdvm3Gmaxfb7Y1a+Cff8x7lSvDkCHwv/+ZOETiXF1cqVeiHvVK1GNks5Fs/WcrIeEhhISH8OKiF3lp8Us0KNGAjv4daV+uPUVyFbE65BSTxCKEE8iRw8zw26yZeX76NISFmdrBxo1mxPq9sTGenqaNpmxZ045TogQUK2a2QoUgb96kb6dFR8Ply9k4eBBOnjTjS44dM50N9u41Szjfvm32LVYM6taFpk1NbEWc529fhuKiXKhZvCY1i9dk6BND2X16NyH7Q5gTPodXl7zKa0teo85DdQj2C6aDXwdK5C1hdchJksQihBPy8TG1gv/9zzy/cQP274fdu8128KAZzf7LL3A3gfF67u4mAbm5mU1ruHnTbFFRoHXd+/ZXCooXNwM/mzc3NaM6dcy0NZmp91pGoJSicuHKVC5cmcGPD2b/2f2E7Dc1mTdXvMmbK96kWtFqBPsFE+wXzKMFHrU65AdIYhEiE/DwMNPLV6ly/+u3bplaxz//mO38ebN+zMWL5vba7dv/1XSyZzdbzpxw8eKf1Kr1KIUKmVmbH3rIvCfSn7+3P/4N/PmgwQccvnA4Nsm8u/Jd3l35LgGFAgj2C6ajf0f8vf1RGSDTS2IRIhNzdze3wkqk8s5JWNg/NGyY8b4JZ3Vl8pdhQN0BDKg7gL8v/83c8LmEhIfw8eqPGbR6EL4FfE1Nxj+YwMKBliUZpxzHIoQQWd3DeR7mjVpvsPb5tfzz5j+MbzGeYrmLMXT9UKpOqsojYx6h/4r+bIrYlO7zl0liEUIIJ1ckVxFeqf4KK7uu5FT/U3zb+lvKFSzHmM1jqD2lNg+PfJjXl77O6mOrib7r+DHjcitMCCEykYKeBXmhygu8UOUFLt24xOJDiwkJD2HyjsmM3WKm/m/n245g/2Bc7jqmbiGJRQghMqm8Hnl5tuKzPFvxWSJvRbL0z6WEhIcwY98MJu2YRBGPIkQEReCi7JtgJLEIIUQW4OXuRafynehUvhPXb1/ntyO/EbY9zO5JBSSxCCFElpPDLQdtfNuQ+6Rj5tqRxnshhBB2JYlFCCGEXUliEUIIYVeSWIQQQtiVJBYhhBB2JYlFCCGEXUliEUIIYVeSWIQQQtiV0lpbHYPllFJngeNpPLwgcM6O4TiDrFbmrFZekDJnFbaUuYTW2juhNySx2EgptU1rXc3qONJTVitzVisvSJmzCkeVWW6FCSGEsCtJLEIIIexKEovtJlkdgAWyWpmzWnlBypxVOKTM0sYihBDCrqTGIoQQwq4ksaSAUqqZUuqgUuqwUuqdBN5XSqkxMe/vUUpVsSJOe0pBmcsppTYqpW4qpfpbEaO9paDMz8R8vnuUUhuUUpWsiNOeUlDmtjHl3aWU2qaUqmtFnPaUXJnj7FddKRWtlOqYnvE5Qgo+54ZKqcsxn/MupdSHNl1Qay1bEhvgCvwFlAbcgd2Af7x9WgBLAQXUAjZbHXc6lLkQUB0YAvS3OuZ0KnMdIF/Mz82zyOfsxX+3zCsCB6yO29FljrPfKmAJ0NHquNPhc24ILLbXNaXGkrwawGGt9RGt9S1gFtA23j5tgWna2ATkVUoVSe9A7SjZMmutz2ittwK3rQjQAVJS5g1a64sxTzcBxdM5RntLSZkjdcxfHiAn4OyNsin5fQboDYQAZ9IzOAdJaZntRhJL8ooBJ+I8j4h5LbX7OJPMVp6USG2ZX8DUUp1ZisqslGqvlDoA/Ap0T6fYHCXZMiuligHtgYnpGJcjpfT/dm2l1G6l1FKlVHlbLiiJJXkqgdfif2tLyT7OJLOVJyVSXGalVBAmsQxwaESOl6Iya63naa3LAe2AwY4OysFSUuZRwACtdbTjw0kXKSnzDswULZWAscB8Wy4oiSV5EcBDcZ4XB/5Nwz7OJLOVJyVSVGalVEXgW6Ct1vp8OsXmKKn6nLXWa4BHlFIFHR2YA6WkzNWAWUqpY0BH4GulVLt0ic4xki2z1vqK1joy5uclgJstn7MkluRtBR5VSpVSSrkDnYGF8fZZCHSN6R1WC7istT6Z3oHaUUrKnNkkW2al1MPAXKCL1vqQBTHaW0rKXEYppWJ+roJp/HXmhJpsmbXWpbTWJbXWJYE5wCta6/npHqn9pORzLhznc66ByQ1p/pyz2RBslqC1vqOUeg1Yjuld8Z3W+g+lVK+Y9ydieo60AA4DUcDzVsVrDykps1KqMLANyA3cVUq9gelpcsWquG2Rws/5Q6AA5hsswB3txJMWprDMwZgvTbeB68D/4jTmO50UljlTSWGZOwIvK6XuYD7nzrZ8zjLyXgghhF3JrTAhhBB2JYlFCCGEXUliEUIIYVeSWIQQQtiVJBYhnIhSarNSqrPVcQiRFEksQjgJpZQLUAHYY3UsQiRFEosQzsMX8zt70OpAhEiKJBYhnEdlYP+9OayUUn2VUgeUUpUtjUqIeGTkvRDOozKwWymVB/ge8/tbS2t9ycqghIhPaixCOI/KmGSyFTOdTltJKiIjkildhHASSqlTMT/+prXuYmkwQiRBaixCWEwpFaiUmqeUuhizzVFK5VdKFVVK3VBKPRUz6acPZgnZekqpbtZGLUTipI1FCAsppZ4CfsB0If4YKAW8DvyN+f38E5gNNAWOaK0PKKVaAaFKqRNa61XWRC5E4iSxCGERpVRp4DtgF1Bfa30j5vVqQHOgJPCM1vquUqoSsBNAa71PKfUMMFspVV9rHW5F/EIkRtpYhLCIUmo0pnZSS2u9Oc7rPwLPYpaLrebM65+IrEnaWISwThvgcNykEs8HklSEM5LEIoQFlFL5Mbe6tibwtg/wR8za40I4HUksQlijcMzjfeuKK6XqA43jvy6EM5HEIoQ1LsU8Vrr3glLKC/gm5mnO9A5ICHuRxCKEBbTW/wJbMGNSflRKvQysAQoCy4BApdQbSqkiVsYpRFpIrzAhLKKUKgGMwwx6zIbpTtw95u0QwB8op7WW2YyFU5HEIoQQwq7kVpgQQgi7ksQihBDCriSxCCGEsCtJLEIIIexKEosQQgi7ksQihBDCriSxCCGEsCtJLEIIIexKEosQQgi7ksQihBDCriSxCCGEsKv/A6y1V7oipRKUAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"plot_alpha(0,eta_ls=0.25,algorithm=\"steepest-descent\",alpha_max=5E-1)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.5 Steepest Descent Step, $x^k = 0$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.5-Steepest-Descent-Step,-$x^k-=-0$)",
"section": "3.6.3.5 Steepest Descent Step, $x^k = 0$"
}
},
"source": [
"**Discussion**\n",
"* How does the region where the Armijo and Goldstein conditions are satisfied change for different values of `eta_ls`?"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.6.4 Trust Regions](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.4-Trust-Regions)",
"section": "3.6.4 Trust Regions"
}
},
"source": [
"## 3.6.4 Trust Regions"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.6.4 Trust Regions](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.4-Trust-Regions)",
"section": "3.6.4 Trust Regions"
}
},
"source": [
"Excerpts from **Section 3.5** in Biegler (2010)."
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.4.1 Main Idea and General Algorithm](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.4.1-Main-Idea-and-General-Algorithm)",
"section": "3.6.4.1 Main Idea and General Algorithm"
}
},
"source": [
"### 3.6.4.1 Main Idea and General Algorithm"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.4.1 Main Idea and General Algorithm](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.4.1-Main-Idea-and-General-Algorithm)",
"section": "3.6.4.1 Main Idea and General Algorithm"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.4.1 Main Idea and General Algorithm](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.4.1-Main-Idea-and-General-Algorithm)",
"section": "3.6.4.1 Main Idea and General Algorithm"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.4.2 Trust Region Variations](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.4.2-Trust-Region-Variations)",
"section": "3.6.4.2 Trust Region Variations"
}
},
"source": [
"### 3.6.4.2 Trust Region Variations"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.4.2 Trust Region Variations](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.4.2-Trust-Region-Variations)",
"section": "3.6.4.2 Trust Region Variations"
}
},
"source": [
"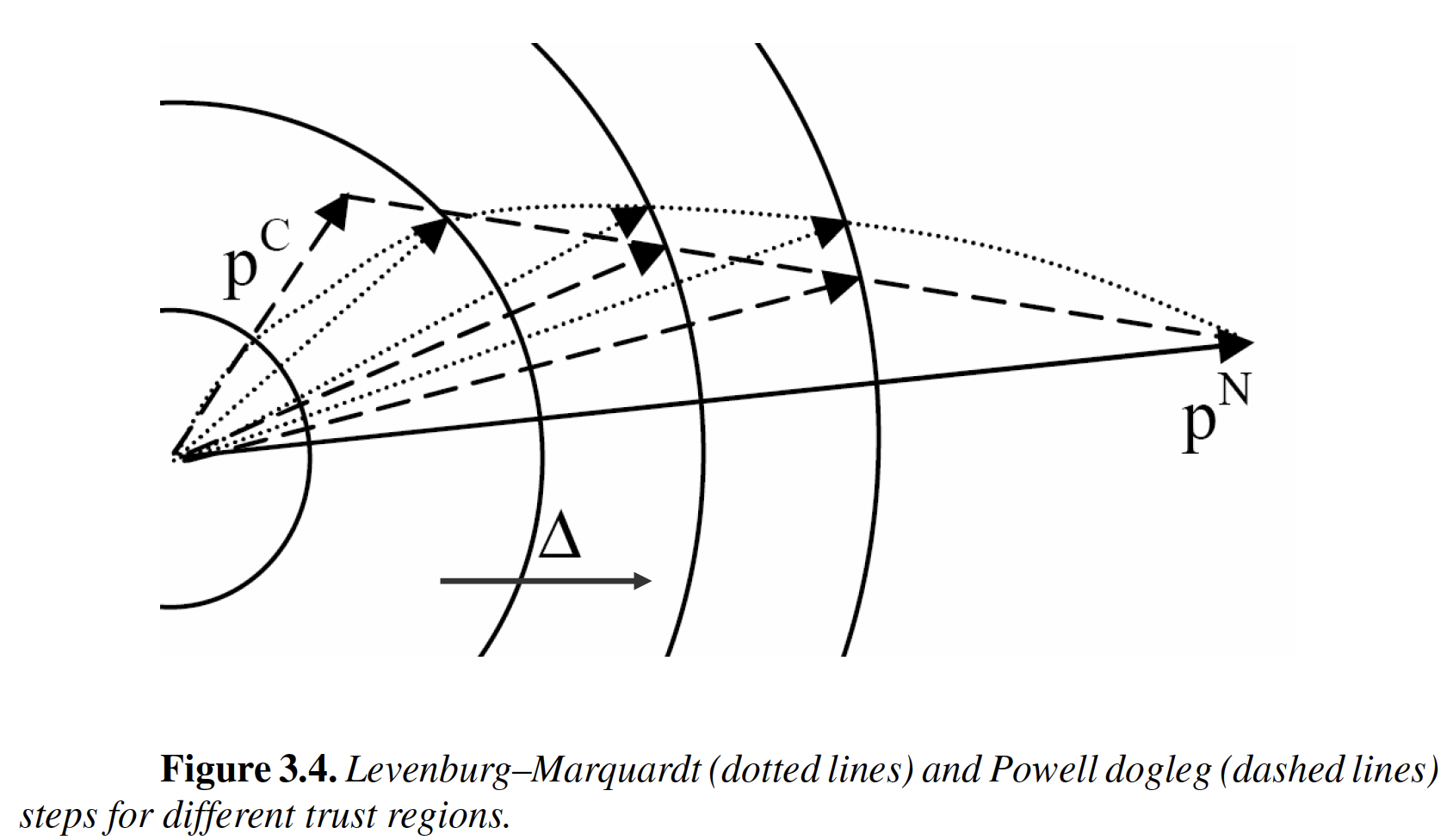"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.4.2 Trust Region Variations](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.4.2-Trust-Region-Variations)",
"section": "3.6.4.2 Trust Region Variations"
}
},
"source": [
"$p^C$: Cauchy step\n",
" \n",
"$p^N$: Newton step"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.6.4.2.1 Levenburg-Marquardt](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.4.2.1-Levenburg-Marquardt)",
"section": "3.6.4.2.1 Levenburg-Marquardt"
}
},
"source": [
"#### 3.6.4.2.1 Levenburg-Marquardt"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.6.4.2.1 Levenburg-Marquardt](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.4.2.1-Levenburg-Marquardt)",
"section": "3.6.4.2.1 Levenburg-Marquardt"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.6.4.2.2 Powell Dogleg](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.4.2.2-Powell-Dogleg)",
"section": "3.6.4.2.2 Powell Dogleg"
}
},
"source": [
"#### 3.6.4.2.2 Powell Dogleg"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.6.4.2.2 Powell Dogleg](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.4.2.2-Powell-Dogleg)",
"section": "3.6.4.2.2 Powell Dogleg"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.6.4.2.2 Powell Dogleg](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.4.2.2-Powell-Dogleg)",
"section": "3.6.4.2.2 Powell Dogleg"
}
},
"source": [
""
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.6.4.2.2 Powell Dogleg](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.4.2.2-Powell-Dogleg)",
"section": "3.6.4.2.2 Powell Dogleg"
}
},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"id": "49ad7a0a",
"metadata": {},
"source": [
"\n",
"< [3.5 Quasi-Newton Methods for Unconstrained Optimization](https://ndcbe.github.io/CBE60499/03.05-Quasi-Newton-Method.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [3.7 Algorithms Homework 1](https://ndcbe.github.io/CBE60499/03.07-Algorithms1.html) >
"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 1,
"link": "[3.6 Descent and Globalization](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6-Descent-and-Globalization)",
"section": "3.6 Descent and Globalization"
}
},
"source": [
"# 3.6 Descent and Globalization"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"nbpages": {
"level": 1,
"link": "[3.6 Descent and Globalization](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6-Descent-and-Globalization)",
"section": "3.6 Descent and Globalization"
}
},
"outputs": [],
"source": [
"import matplotlib.pyplot as plt\n",
"import numpy as np"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.6.1 Define Test Function and Derivatives](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.1-Define-Test-Function-and-Derivatives)",
"section": "3.6.1 Define Test Function and Derivatives"
}
},
"source": [
"## 3.6.1 Define Test Function and Derivatives\n",
"\n",
"Let's get started by defining a test function we will use throughout the notebook.\n",
"\n",
"Consider a scalar function $f(x): \\mathbb{R} \\rightarrow \\mathbb{R}$ to allow for easier visualization. Let\n",
"\n",
"$$f(x) = 0.5 (x-1)^4 + (x+1)^3 - 10 x^2 + 5 x$$\n",
"\n",
"$$f'(x) = 6 - 8 x - 3 x^2 + 2 x^3$$\n",
"\n",
"$$f''(x) = -8 - 6 x + 6 x^2 $$"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.6.1 Define Test Function and Derivatives](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.1-Define-Test-Function-and-Derivatives)",
"section": "3.6.1 Define Test Function and Derivatives"
}
},
"outputs": [],
"source": [
"## Define f(x)\n",
"f = lambda x : 0.5*(x-1)**4 + (x+1)**3 - 10*x**2 + 5*x\n",
"\n",
"## Define f'(x)\n",
"df = lambda x : 6 - 8*x - 3*x**2 + 2*x**3\n",
"\n",
"## Define f''(x)\n",
"ddf = lambda x : -8 - 6*x + 6*x**2"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.6.1 Define Test Function and Derivatives](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.1-Define-Test-Function-and-Derivatives)",
"section": "3.6.1 Define Test Function and Derivatives"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXkAAAEGCAYAAACAd+UpAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAABBkUlEQVR4nO3deZzN1f/A8deZzQxj3/elkC1rJBGiJEvf0CaFSouU9mjToq9UtEqWflSWdkrFV5ZIIbJm34mxjMEMZn///jgzY2jGLPd+5nPnzvv5eHwe5m6f856L9z33fM55HyMiKKWU8k8BbgeglFLKOZrklVLKj2mSV0opP6ZJXiml/JgmeaWU8mNBbgeQXpkyZaRGjRq5fv3p06cpUqSI9wJymMbrLI3XWRqvs3IS7+rVq4+JSNkMHxQRnzmaN28unli0aJFHr89rGq+zNF5nabzOykm8wCrJJK/qcI1SSvkxTfJKKeXHNMkrpZQf0ySvlFJ+TJO8Ukr5MU3ySinlxzTJK6WUH/ObJC8ixCfHux2GUkr5FJ9a8ZpbSclJdJvRjZAzIVzX8Tq3w1FKKZ/hF0k+MCCQFhVbEBMR43YoSinlU/xmuObVjq/Ss1JPt8NQSimf4jdJPtWcbXOYsnaK22EopZRP8EqSN8aUMMZ8bYzZYozZbIxpbYwpZYyZb4zZnvJnSW+0lZXxq8bz0aqPSJbkvGhOKaV8mrd68u8Cc0XkMqAxsBl4FlggIrWBBSm3HTflpiksHbCUAON3X1KUUirHPM6ExphiQDtgMoCIxIvICaAnMDXlaVOBmzxtKzvKFC5DSGAI8UnxbD22NS+aVEopn2VsKWIPTmBME2ACsAnbi18NPAr8IyIl0j0vSkT+NWRjjBkEDAIoX75885kzZ+Y6lpiYGMLDwwEY8fcINkVv4vOWnxMSEJLrczopfbz5gcbrLI3XWb4ab0RsBMsjl9OjUo/zRiByEm+HDh1Wi0iLDB/MrNB8dg+gBZAItEq5/S7wKnDigudFZXUub24asvLASpmzdY5H53OaP29i4As0XmdpvN7xwsIXpMjIInLg5IHz7vfWpiHemCd/ADggIitSbn+NHX8/bIypKCKHjDEVgSNeaCvbrqh8RdrPIoIxJi+bV0qpbHm5/cv0bdSXysUqO3J+j8fkRSQC2G+MqZty17XYoZvvgbtT7rsbmO1pW7kxbf002nzShvgkLXmglPIdUWejOH72OMYY6papm/ULcslbU1CGANOMMeuBJsDrwCigszFmO9A55XaeKx5anPCQcE7GnnSjeaWUytDj/3ucxuMbcybhjKPteKWsgYisxY7NX+hab5zfE93qdOPG2jfqcI1SyqcMbTWUNlXbUDi4sKPtFIjJ5MYYjp89zqjfRukiKaWUqyRlRmPjCo25t9m9jrdXIJI82HIHzy98nj//+dPtUJRSBdjT85/mmfnPpCV7p/lFFcrs6Hd5P1pVbuXoBQ6llLoYESE6PppAE5hnQ8gFJsmnv4K9+ehmLitzmY7TK6XylDGG8d3G5+mwcYEZrkm14sAKGn3UiE/Xfep2KEqpAuSTNZ+w8/hOgDytrVXgkvwVla/g9Wtfp+dlWnteKZU3Tsae5Kn5T/HW72/ledsFZrgmVYAJ4Ok2TwPnrnLrsI1SyknFQ4uz7oF1FA0pmudtF7iefKqos1F0+qwTn6//3O1QlFJ+LLUabpViVSgeWjzP2y+wSb5YoWKEBPpmdUqllH9Yf3g9DcY1YMLqCa7FUOCGa1IFBgTy0x0/6VCNUsox9crU47/X/pdbGtziWgwFNsnDubH4H7b+wKm4U/S9vK/LESml/EVSchLBgcE81eYpV+MosMM1qUSEd1e8y7hV4/JsBZpSyr8t27eMxuMbsy1ym9uhFOyePNje/IxeMyhWqJgO3SilvCJJkihduDQVwyu6HYr25AHKFilLoaBCxCXGsWzfMrfDUUrlc+2qt+PX/r9StFDeT5m8kCb5dJ6e/zSdP+vM4ZjDboeilMqH5u+cz3sr3st52YLjx50JCE3y5xnWdhhf3/I15cPLux2KUiof+uLvLxi/anzOdqLbuxcqVYLPPnMkpgI/Jp9ehfAKdK3dFbDLkN1YuKCUyr8mdp/IsTPHCA0Kzf6L3n8fEhOhfXtHYtKefAaW7l1KtXeqsWTvErdDUUrlA4t2L+LYmWMYYyhbpGzOXtylC4wcCVWrOhKbJvkMNK3YlF71elGzRE23Q1FK+bgzCWe45etbePDHB3N3gk6d4JlnvBtUOjpck4HwkHA+6fmJ22EopfKBwsGF+aXfL5QILZGzFyYlwahR0L8/VK7sRGiA9uQvKiY+hju/vZMvNn7hdihKKR/0z6l/ALtfa/US1XP24lmz4PnnYcUK7weWjib5iygUWIg9J/Zw4NQBt0NRSvmYlf+spNZ7tfh609e5O8HYsVCzJvR0dm8LHa65iODAYBb3X0xQgL5NSqnz1S9bn0dbPUrnWp1z/uKVK2HZMnj3XQgM9H5w6WhPPgupCX7VwVV8sPIDl6NRSrlNREhKTiI8JJzRnUfnbqr12LFQrBgMGOD9AC+gST6bxq8az9t/vM3p+NNuh6KUctGUtVO4Zso1HD+by1WqyckQFAQPPQRFnS974LVxCGNMILAK+EdEuhljSgFfADWAPcAtIhLlrfby2jtd3iEhKYEiIUXcDkUp5aLCwYUpXbg0xQvlcrFkQIBd3ZpHVW+92ZN/FNic7vazwAIRqQ0sSLmdb4WHhFMyrCTJksw3m77RssRKFVC3NryV2bfNJjAgF2Ppx47Bhg325zyqeuuVJG+MqQLcCExKd3dPYGrKz1OBm7zRlttmbZlF769688O2H9wORSmVh4YvGM53m7/z7CRjx0KTJvDPP16JKTuMN3qkxpivgf8CRYEnU4ZrTohIiXTPiRKRkhm8dhAwCKB8+fLNZ86cmes4YmJiCA8Pz/Xrs0NE+CPyD1qXbu1x/fm8iNebNF5nabzO8iTeuKQ4hq4bSqPijXjokodydY7AmBha33Ybx1u0YNOIEVk+PyfxdujQYbWItMjwQRHx6AC6AeNSfm4PzEn5+cQFz4vK6lzNmzcXTyxatMij1+dURHSEHD9zPNevz+t4PaXxOkvjdZan8cYmxEp8YnzuT/D66yIgsnp1tp6ek3iBVZJJXvXGcE0boIcxZg8wE+hojPkcOGyMqQiQ8ucRL7TlM2ITY2k5qWXu61UopXxebGIsry99nbMJZykUVIjgwODcnejMGTtU06ULNGvm3SCz4HGSF5FhIlJFRGoAtwELReRO4Hvg7pSn3Q3M9rQtXxIaFMprHV7jubbPuR2KUsoh83bM4/mFz/Pbvt88O9Fff8Hp0zB8uHcCywEnl3KOAr40xtwD7AP6ONiWK/o17pf2c3RctE9s9aWU8p6el/Vk0+BNXFbmMs9OdPXV9mJriRJeiSsnvLoYSkQWi0i3lJ8jReRaEamd8qdz+1u57L0V79FgXAOOnParESmlCqzNRzez8chGAM8T/OHDdk68CwkedMWrV7St1pYba99I0RDtySvlDx766SF6zuxJYnKiZydKSIA2bWDgQO8ElgtaecsLmlZsykfdPgIgWZIJMPrZqVR+Nv3m6ew/td/z4oSffgo7d9qLri7RbORFh2MOc9Xkq5i1ZZbboSilcmFtxFpEhIpFK9KyckvPThYXB6+8Ai1bQrdu3gkwFzTJe1Hx0OKEh4RjyJvlykop71kXsY4WE1rw4Z8feueEkyfDvn3w6qt5VsIgIzpc40WhQaHM7zff45WwSqm816h8I97t8u55s+ZyTcQO1Vx9NXTORb15L9KevJelJvivN33NXd/dRbIkuxyRUupiziac5diZYwSYAAa3HEyxQsU8P6kxsHgxTJvmai8eNMk7Zv/J/Ww/vp3ouGi3Q1FKXcSQn4fQcmJL7+0VERsL8fEQGgrVqnnnnB7QJO+QoVcOZUn/JbnbNUYplWfub34/j135mPf2inj3XahTB477xtIgTfIOMcYQHBjM2YSzPDDnATYf3Zz1i5RSeeZU3CkArqh8BUNaDfHOSU+ehNGjoX59KFXKO+f0kCZ5hx0/e5zZW2fz695f3Q5FKZVid9RuLn3vUqaunZr1k3Ni1Cjbg3/tNe+e1wM6u8ZhlYtVZsvgLTpso5QPKVekHN3rdKdNtTbeO+m+fXbRU79+eV5p8mK0J58HUhP8uoh1vLjoRd06UCmXJCYnEp8UT5GQIkzuOZlLS13qvZN/8omdSeNDvXjQJJ+nvt38LZ+s+YSjZ466HYpSBdLj8x7nus+uIy4xzvsnf+klWLnSJ2bUpKfDNXnopfYvMaTVEMoULuN2KEoVSK0qtyI8JJxCQYW8d1IRiIqyF1obNfLeeb1Ee/J5KMAEUKZwGUSEt39/m92nd7sdklIFQmrPve/lfXn92te9e/I5c6BGDVi92rvn9RJN8i6IPBvJW3+8xc8RP7sdilJ+b8PhDVz6/qWsP7He+ydPTISnn4aKFeHyy71/fi/Q4RoXlClchpX3rmT7X9vdDkUpv1citAQNyzWkYlhF7598wgTYsgVmzYLgXO7/6jDtybukavGqBJgAjp4+yrO/POv55gRKqfPEJcYhIlQtXpWf+/5M2UJlvdvA0aPw/PPQoQP06OHdc3uRJnmXzds5j3dXvMu6iHVuh6KU30hISqDHzB4MnTvUuUZ++AFiYuCDD1wvQnYxOlzjsjsvv5Nrql9D1eJV3Q5FKb8RGBBIk/JNqFO6jnONDBwInTr53JTJC2mS9wGpCX7OtjlEnonk7iZ3uxyRUvnX6fjTFAkpwhud33CmgaQkOw7foIHPJ3jQ4RqfISJ8tOojxq8eT1JyktvhKJUvfbjyQ5p83ISImAjnGpkwwc6k+esv59rwIu3J+whjDF/0/gIRITAg0O1wlMqXmlVsRttqbZ1bcHj0KAwfDu3bQ9OmzrThZdqT9yHhIeEULVSUhKQEHv7pYTYe2eh2SErlC8fP2trtrau25pOenxAU4FD/9Zln8sXF1vQ0yfugI6eP8N2W71i4e6HboSjl89YfXk+td2vx9aavnW1o4UL4v/+Dxx+HevWcbcuLdLjGB1UuVpm/H/qbEqEl3A5FKZ93SclL6F2/N22qerFscEZ27ICGDWHECGfb8TKPe/LGmKrGmEXGmM3GmL+NMY+m3F/KGDPfGLM95c+SnodbcKQm+C3HtnDdZ9dx9LRWrlQqvb0n9qaVDZ7UYxIVizqwojW9QYPsxdawMGfb8TJvDNckAk+ISD3gSmCwMaY+8CywQERqAwtSbqscOnL6CNuPb+fI6SNuh6KUz4iJj6Ht/7Xl3u/vdb6xFStg9mz7s0OlC155BaZPd+TUnid5ETkkIn+l/BwNbAYqAz2B1L21pgI3edpWQdSueju2PryVBuUaAOj0SqWwkxRe6fAKT7R+wtmGYmOhf3945BH7swP+/tsm+d9/d+T0GG/uUmSMqQEsARoC+0SkRLrHokTkX0M2xphBwCCA8uXLN585c2au24+JiSE8PDzXr89rOY33mwPfsCxyGa83fJ3QwFAHI8uYv7+/btN4s3Y8/jgn4k9QK7xWjl+bm3hrTpxI9enTWTd6NFFXXJHjNrMiAk8/fTlbthTl889XUrx4QtpjOYm3Q4cOq0WkRSaNiFcOIBxYDdyccvvEBY9HZXWO5s2biycWLVrk0evzWk7j/Xzd59Lnyz4SnxjvTEBZ8Pf3120ab9a6fN5Fqo2tJrEJsTl+bY7j/fNPkcBAkQEDctxWds2ZIwIi77zz78dyEi+wSjLJq16ZXWOMCQa+AaaJyLcpdx82xlQUkUPGmIqADip7qO/lfbmj0R0YY4iJjyHQBBIWnL8uAinliQ+7fsiBUwe8u7NTRmJj4Y47bJ34t992pIn4eDsbs25deOghR5oAvDO7xgCTgc0iMibdQ98DqUVY7gZme9qWsitjkyWZbtO7cfOXN+um4MrvHT19lI9XfQxArZK1aFe9nfONFipkywh/9hmUdGZi4LhxsG0bjBnjbCl6b/Tk2wD9gA3GmLUp9w0HRgFfGmPuAfYBfbzQlsJuIzigyQBCg0Ix+WTVnVK59cHKD3jz9ze5/tLrqVGihvMNxsXZJH/XXY41cewYvPwyXH893HCDY80AXkjyIvIbkFmmudbT86uMpa9UuergKuqWrkvRQkVdjEgpZ7x4zYv0rt87bxL8/v3QujW8/z785z+ONfPSSxAdbXvxTvfTtKxBPncy9iTXfXYdD//8sNuhKOU1e07sodeXvYg6G0VgQCCNyjdyvtGkJNt7P3ECGjnX3vr1MH48PPgg1K/vWDNp/KKsQVISfPMNlCxZ8IYuiocW5/ObP6dJhSZuh6KU1+w4voNl+5ax9+ReSobl0WL50aNh8WL45BO49FJHmkhMtHuNlCmTd9UR/KInv3gx3Hor/Pijw8uafVTX2l2pVLQSIsKo30ZxMPqg2yEplStnE84C0KlWJ3Y9uivvOi8LF9oLrbfeahc/OWTMGFi92haxLF3asWbO4xdJvmNHaNsWPv20BjExbkfjnl1Ruxi5dCSfrfvM7VCUyrE1h9ZQ671aLNq9CIDCwYXzrvHff4fLLoNJkxwbJN+6FV580Q719+7tSBMZ8oskbwy88QZERYXwzjtuR+OeS0pdwtr71/J0m6cBSJZklyNSKvtqlKhB6yqt8+YC64Wefx5WrgSHVvAmJ8O999raZh9+mLel6P0iyYO9IN6mzTFGj7bTkwqqS0pdgjGGwzGHaTGhhdakVz5v0e5FJCUnUTKsJN/e+i01S9bMu8afew6WL7c/FyniWDPjxsFvv8HYsXZ9VV7ymyQPcO+9uzh9Gl5/3e1I3JeYnEhwYDBhQboiVvmu1QdX0/HTjnz454d53/ikSTZZzJnjaDN79sCzz9o58XffneXTvc6vknyNGmfo399+Hdq71+1o3FW5WGWW37Oc1lVbA7A2Yq2ujlU+p3ml5ky/eTr3N78/bxtetgwGD4bOne2qJIckJtrruMbAxx+7s2OgXyV5sNOSjLEXOAq61NWwK/9ZSfMJzZn01ySXI1IKTsefZsDsAeyK2gXA7Y1ud74WTXrbt0OPHlC9OsyYAYGBjjX18svw6692bVX16o41c1F+l+SrVrWlnz/7DDZscDsa39CiUgvGXj+WOxrd4XYoSnEo5hA/bvuRP/b/4U4A770HAQHw88+OzmP83/9g5Ejbk3dwVmaW/C7Jgx3/Kl4cnnrK1msu6AJMAI+0eoQiIUWIT4pnyE9DOHDqgNthqQImIiYCgEtLXcqOR3bQ9/K+7gTyzjvwxx9wySWONXHwINx5p13R+qELlxvS84sVrxcqVcoO2wwdCt9+C716uR2R79h0dBNT103l6mpXc2vDW3Nxgk326+7evRARASdPQuXKMHy4fXzAAHulyRh7hIXBlVfaKWpgVxOGhUGVKvZrV+XKzpbgUz5hzaE1tP2/tnzc7WP6Xt6XYoWK5W0AycnUnDgRate2/+YcWtEKdhz+9tvh9Gn46isonIfT/TPil0ke7DWVKVPg0UfhuuugqNbuAqBJhSbseGQH5YqUA+BQ9KF/b4CcnAxbtthNi9esgTNn4KOP7GP332/nggEEBdmvTFddde61IrbOhIg9z4kTtuhTqueesx8OqYyx67wnpVwvmDYNataExo0dndKm8laj8o0Y1HwQHWp2yPvGReCxx6g+fTpcfbUtGuOgl16CJUvg00+hXj1Hm8oWv03yQUE2L111le3VO1T3P19KTfC7o3bT9OOmjGg/gqFXDrUPjh4Nb755brFBaCi0bHlu3Ovtt+14ZvXqtgDHhdMFpky5eONbt8KBAzbxpx6XXWYfi4mx33HBtlGvHrRoAf36wbVa0DS/OR1/mpd/fZkX2r1A0UJFGXP9mKxf5G0idvz2vffY37s3VR94wNHmvvjCzsq85x77z9YX+G2SBztKcN998O67dn7q5Ze7HZFvqXr4LIPjLuc/Qz6En/pC2bI2cd9wg60V0aKFTcBB6f6ZtGzpWaPFitmByozK7xUuDLt32zJ9q1fbY+5c2+a119phoPvvtzUs2reHVq10qMeH/XXoL95d8S5tqrah52U93Qni5Zdtx+XBB9nZpw9VHZzDuHSpLWJ59dW2No2v8OskD/Df/8J338EDD9hRhgC/vNScA1FRMHkyTJ9O0Jo1jDQG2rWDEyd4YcN7dO3cldYDB7oTW0AA1Khhjx497H2pwz4Ahw/bK1ovvGBvFy0KHTrY/8R167oRscrAvpP7qFa8Gm2rt2XHkB1ULV7VnUBOn7blaQcOtFl3yRLHmtqyBXr2tCONs2fbL8C+wu9TXqlSdvThjz/sNb8CKy7O/nnsGDz9tO2djxljh0sWLyaqShmmb5zOnG3Orv7LMWPOzWNu1crOi42MtP95+/aFjRvttwOAL7+Exx6zFQUTEjI/p3LM1LVTqfN+HdZGrAVwL8EnJdlrOkuXwoQJjvbuIiLsl9/gYDsrs1Qpx5rKFb/vyYP9CjV5MjzzDHTrBhUquB1RHhGBn36yn3IlS9qvNLVr25kxVc//z1cyrCSrB60mPMQWaNpx3F6czfNZENlRqhTcfLM90tu0yV6IeecdKFaMei1a2A+1Xr3cWWpYAHWv253tx7dTr4xLVxxF4LXX7FDf119DiRKONnf6tM0pR47YRU8187DsTnb5fU8ezi0pPnPGXhApEHPnFyywV527dbNj2ddcc+6xqhn3rkqEliAoIIik5CT+88V/6Da9W/4qhTBihO3lz5oFvXtTcvVqO5STmuAXL4ZTp1wM0D/9uO1H7p51NyJCqbBSvNbxtbxdwZoqOdnOm37xRceTO9h5At262QloX3xhL2H5ogKR5MFO1HjzTduxHTfO7WgcNn48dOpkZ7FMmGDntQ8dmu2XBwYEMv7G8bzW8TWMMYhI/ilbXKSIHRydPJk/vvnGLpQAu6Fmly5Qrpzt2X/5pf3UVx7bc2IP6w+vJ/JspHtBJCTYr+zvvQePP27HZoOcG6g4edIWHFu61K6u79bNsaY8VmCSPNi58zfcAE8+ab/Z+5WjR8/9Un362ClF27fb6UW5mIHSplob2lVvB8CHf35I5886czbprDcjdpwEBtpFV2CT/4IFMGiQ3SDi1lttwv/yS3eDzKc2Hd3EhpO2bshDVzzE8nuWU6ZwGfcCuuceu8biv/+Ft95ydAw+KsrWNVu5EmbOhDt8vFpIgRiTT2WM/YBv1Mhes1u+HAq58K3Sq5KTYeJEGDbMDgiuWmXrcTzyiNeaCA8Jp1RYKUIDfGjKQE4FBECbNvYYO9bOtJg589y82gUL7DWLvn3t3NuUIZ6EBDh+3A7tpx6nTtkvAalHbKz9axA5NxQYHGwX9oaG2qNIEXspoWRJe5QqBeXL588ZoCJCv+/6cfLUSR6WhzHGuDM8k97gwXaW2L33OtrM0aN2ceWmTfZLYvfujjbnHSLiM0fz5s3FE4sWLcrW877/3v53fOopj5rzWHbjzdSGDSKtWtlf5pprRDZt8kZYGUpOTpZFixbJsdPH5N7Z98rhmMOOteUt2Xl/ExNFdu4U2fTAu5IQHCoCcrDIpTK+0svSssxOMSY1dWd+BAeLFCokEhoqEhZmj6CgrF9njEi5ciJNmoh07SrSvfs/8sYbIl99JbJqlUhUlONvUY7sOr5L4hLjRERk05FN8s28b9wN6NdfRV5/PdtP9/T/2/btIvXq2b/nuXM9OlW25CReYJVkklcLVE8+Vffudk3NW2/ZcbV8uZhy+XK7IKhYMbt++s47HZ1Bklq2+Pf9vzPz75kMbjk4beVsfhERAevWnTvWr4dt2yA+HuARitKfOwp9S3/5jPsOjqBX+Cd88MJuypU3lC2ZSKlyQZQuba/pFS5sj7CwzCvVJibaXn5srL0kEBV17oiMtPEcPHju2LmzDD/8cP45ype315NSj0aNbMWHkiUdfrMusO/kPhp+1JBn2jzDi9e8SL2y9Tgccjhvg0hv/HgYMsQWGRsyxLFt+1LNnWvr0QQG2p/Tz2PwdQUyyYNdnb9kiR2a/fNP35z6lCERm8ybN7dDMk88YTNBHuletzv7hu6jZJjNMp+u+5SONTtSpViVPIshO86ehQ0birF6tf08XL7cXodOVbWqTZY33GDXUdWtC3XqFKNs2f4Y0x/276fMrl2MuMbYbH3ppXYY5667oOF12bqoFxRkc094uF1InNW/scWLf6dZs/bs3g27dsGOHbB5sz2mT7cX+1JVr27jb9oUrrjCHuUc+MyNjoumaKGiVCtejZEdR9K7fh7uQJ2RM2fsJIKJE6FrVzsO72CCF7ETNoYNg4YN7cStfJMrUmXWxffWAXQBtgI7gGcv9ty8Gq5JtW2bSMmSIg0bipw65VHTuZLjr48//mi/2x875kg8Wbkw3mOnj0n46+Ey5KchrsST3unTIr/8IvL88yJt24qEhJwbFqlZU+S220TGjBFZtEgkMjKHJz9xQmTwYJFSpewJy5cXefxxO87jRRf795CcLHLwoB0mGDVK5Pbb7dBBQMC537NaNZHevUXeflvkjz9EYmM9i+fzdZ9LqTdKyb4T+3IcryOSkkSaNbPjXMOG2bG2HMhpvNHR9n0GkVtuEYmJydHLPZYvhmuMMYHAh0Bn4ADwpzHmexHxibkttWvbyRVdutjRju++89GyB6kLPF580XbfTpxwdLOD7CpduDTrHlhHqTC7xG/n8Z2cjDtJs4rNHG9bxA65zJtnj2XL7LBLQID9kvPoo1Cs2Abuu6+R5190ihe3y+LHjIEff4SpU+1UvW7doFYtOHTINuzgNypj7AbQFSvaIcZUMTG2WOiff9pj5Uq7BgjspILmze215rZtbU2V7AzzJCQlEBwYzFVVr+KmujcRFuzyPsHJyfYNCAiw0yMrVrS1lRy0YIG9hrt3r52w88wz+Xg9XWbZ3xsH0BqYl+72MGBYZs/P6558qvfft5/Ww4Z51HyOZSve6GjbPQORO+8UOXPG8bgyk1W8fb7sI6XeKCWn40870n50tMg334j0728706k92EaNRJ54wn7ROXky+/F65OhR27MUERk6VCQwUOSGG0RmzMj135G34j10SOTbb0WefFKkdetz32qMse/V4MEiX34pcviCa+fJycly61e3Sv9Z/fM03ovasUOkQweRTz/1+FTZiffkSZH777fvV+3aIr/95nGzueatnryxjzvDGNMb6CIi96bc7ge0EpGH0z1nEDAIoHz58s1nzpyZ6/ZiYmIIz8X4nAiMGVOHOXMq8dxzm+jU6UiuY8iJ7MRb+913qfT99+y8/34O9Onjanciq3hjEmPYGbOTxiUaA7D02FKuKn0VgSb3e2hGRobw229l+P330qxZU5KEhADCwxO44oooWrY8TosWxylTJj5X8XpL4X37KD9vHuV/+YXQI0dILFyYiC5d2DFkSI7O41S8cXEBbN5clA0bSrB+fXE2bixObKz9O6le/TSNGh+jWZMYGjc+wQ+nJhESEMJtVW9Lu9ie1/ECBMTHU3XGDKpPm0ZycDDbhw7lcOfOHp3zYvGKwPLlpXnnndocO1aIPn32M2DAHgoVcm8RYE7e3w4dOqwWkYzX3GaW/b1xAH2ASelu9wPez+z5bvXkRUTi4uwsxJAQkZ9/9iiMbLtovMnJ9s9jx+xgsw/Iyfu7bN8yYQQyafWkHLezd6/I2LEibdpI2hTGSy4ReewxO6YeH+/9eL0iKUlk4UKRAQNEhqRcp0hOttP8Vq0693eaibyKNz5eZPlyO7bfutefYh6vKlRcJSBSv77IQw/ZaZxHjlz8PI7Fu3ix7UaDyK23ivzzj1dOm1m8S5eKXH21be6yy0R+/90rzXksX4zJY8fh0xdKqQIcdLjNXAkJsWPyHTvCTTfBnDm2MoArfv7Zbu/+zTd27D0fzvFsXaU1c26fQ6da9k1cuncpgqStor3QwYN2q7SZM+1MGLDTBV96yVYhaNAgH4yJBgTY0scd0u1+tHev/SWGD7czdG691R4NG7r2CwUFCXUuP0GrViV5ILY2t3/diFuvN0SsseV9pk49V/qjQQM7XbB9e7vWyNGJXJIyc+zkSfvzvHl25ZFD1q2zG5X9+KMtWjhunF04GxLiWJPuyCz7e+PATtHcBdQEQoB1QIPMnu9mTz7VsWN23DIszHYonJRhvNOn25U0TZpk3ZXKY568v9d9dp3Ufq+2JCadmxERGSkyfrxI+/bneuyNG9uO77Zt7sbrVcePi0yaJNK587npMLNm2cfi49N6+HkVb68vekm7/2snyZl8s4iPt7NzRo0S6dJFpEiRc9c/6tQRufdekalTRaZP/yOrLyfZs327SN++Ii+8cO6+uDgvnPh8ixYtkrg4kS++sMP8IFKihP09TztzGckj3urJO5rkbdt0BbYBO4HnLvZcX0jyIvaCVP369h+3kxde/hXv++/bbHfNNXbano/x5P09HX9aNh3ZJGfOiEybGS/VHh4oQVXWpH1FHjFCZPNm78Uq4kNJPr3Dh0XGjbNXkUVshrnkEpGnnpLV77+f42mB2ZGcnCwLdy1MS+pT1kyRiasnSlJyUrZen5r0R48W6d7dJsbUpF++vMh//mMfW7o0h8ly40aRgQPtReuwMJGXX87Fb5e15GTb1B137JFy5WzcNWrYzsTx44406RX5Jsnn5PCVJC9iZyjUqSNStKhdPe2E8+IdM8b+dfTsKXL2rDMNeii3729Skh1LHzDAvp+U2yABz5aWnk/PljVrROITEzLtVXrCJ5P8hWbPFrn++nN1EMqWFbnvvizH73Piu83fCSOQH7f96JXzJSWJrFsnMnToVunXz35GpSb9gAC77qR/f5EPPrCdpAzLM7z+un1BaKjIww/bRQBeFBsrMm+evTRSs2ZqbMnSo4fITz858lnqdfllTD7fqlDBbjDUqZM9Jk2yix0d06WL3aVp9GhHS6TmpS1bbBnWzz+HffvswsTevaFfv4Y0b72HYqFFMAbeWf4BU9dNZfHdiykeWtztsPNWjx72iIpi05gx1N+1y66DSB2vHzwYKlWyY9PNmmVeQyGdxOREPvrzIyoVrUSv+r3oVqcbn/3ns7TrI54KCLB13Xr2PEj79nUAu2nG8uV2r45Vq+w4d/o93a8uv537is7k0FW9KNqqPk3Cr6P2E4Zij91LocqeVa+MjrYrhFO3BV61yo63x8XZ4nCdOtl57qVK/UGfPld51FZ+5B/ZxCGVK9ttA3v3thuBb9sGr7zi5QVTy5bZzT3q1bOLbfK5yEi7gcLUqXZhTkCAzU+jRtky74ULpz7z3NSwKsWq0LRC07QEv2DXAuqXrU/FohXz/hdwS8mSHLn2Wuq/+uq5+xIT7Zu4ahU8/7wtXdmunb06mEEB81NxpyhWqBiBJpDJaybTtGJTetXvRVBAEHdefqej4Zcrd+7zCmy//tAfezg5+WtKzptBhX/+Ivmw4bk9YTz7aX2gOdAcM8bOLShXzh5ly9oFW6GhdjFXoUL2QmhcnC1VcfasrWxw9KjtE+3fbz8TUxUtaj8LBw+21787djz3b27x4oyn2vo7TfJZKFHCTnZ56CEYOdIm+qlTbWEqT1X84Qeb2D/5BAYM8PyELomPt+/Rp5/CDz/Y8ryNGtkCcHfcYRcoXkzv+r3TaqLEJsbS56s+XH/p9czoNQOwQ4pZzdn2S0FBdhnrkSN2Ceb8+XaPuR077OOHDkG/ftCiBS9V3cmE07+y9/H9hAQVYnH/xZQILZG38R4/brNu48aY5CQq3diUSidO2MI6T4whoE8fRlaqwiOHbc879YiIsL/ikSO2aFxUlE3qsbHntiY25vyicKVL2xoy7drZOkQ1akCTJnYVu0+uWneRJvlsCA62GyzVrWv3wN6+3dZFql/fg5NOnUqdsWNtkaW+fb0Wa14Rsfnn00/ttMfISNsTe/hhO6zVpEnuzhsaFMrye5enXrTnUPQh2v5fWyZ0n0DHms4uZfdZ5crZEoi3325vJyez58Qe3vllOM+fPkqZMWNoXzmB4GqQ8FYFQr74lhIdOtiE+/ffdupmlSq2e+xFxf7+247RrFljayvs2AGXXWYrqgUG2rG6yy6z7acI4Fx5hjZtsm5DxH6hCQrKB1NofZQm+Wwyxu4oVbcuDBxovxKOGmULQea45/DDDzBwIFHNmlHqm2/y1cTcnTvtB9y0afZbTWioXVfQr58dlvHG5YQ6peuk/RwVG0WtkrWoXLQyAH8d+ov5O+fzQIsHCtT4vYiw6egmwkPCqV6iOtFx0Yzf+y3XTvmK7jWuo8PGjXRYtcom22rV7It++gkeeODcScqWtd3er7+23eBff7XfEIoXt+Mixthj4ED7F/u//8GiRXbe+smTtoznkSN2xwxjqPT99/Y5NWrYcph3333+GgEv7IlnTP7cWMWnZHZF1o3Dl2bXXExEhJ1KBiIdO9oVmtl2/LhIsWIiLVrIrz/95FiM3hQRYWd31q9/Iq0GSvv2dup3Xs/0fOO3NyTstTA5FWvLhq44sEJWHFiR4eycfDG7Jp0L441PjJeI6AgREYmOi5aQV0Nk6M9D0x4/GXtSLurECZElS0SmTBF59VVblKVr13NVTP/7X8lwV5TUx4cPtzuilCkjUquWXRaarn7Ssi+/9O05iBfI7/8eLgadQul9yck2yYWH25w9alQO6lLNnSty6JBP/6M7dkxkwgSRa689t36nVq1oeeMNkX0ZV57NM0dPH037+cZpN8ol716SluSX7Vsmu6N2i0j++0+9cOHC83bcajGhhXSf3j3t9g9bf5CDp7w71VCSkuyHwZEjdg5/RMS5wmuJiRedypnf3l9/jvdiSV4vUeSSMXaSw7p19uLPs89CnTp22lhSUgYvOHHCfrUFWyu2QoU8jDZ7Dh2yG+5cd50Nb9AgO/Xxuedg40aYPHkVTz9tv/G7Kf2G0VNvmsoXvb9IuzDbf1Z/hvx8rjDYFxu/YNNRn6hs/S8x8TH8deivtNuvb3mdtv/XNu32Iy0fYVDzQWm3u9Xp5v0ZRwEBdrimbFk79l++/Lnxx8BAHQj3A5rkPVSrlh1iX7zYXkwaMMAOT375pZ1lAtjpJzffbOcQRkS4Ge55ROx1udGj7UWwypXhwQdhzx674dRff8HWrXbaaIMGbkebsdKFS9O8UvO029/d+h2vdrDTEBOSE7hr1l1MWTsFgGRJ5p7Z9/DLrl8A+y02PinvptWtP7ye15a8RlKy7QW8+uurXDnpSuIS7RSSTuU68fRVT6dddO7XuB/d6ng+rq0KNk3yXnLNNbBihU3uZ8/aGlTVqtl9PmL6P2wvYE2c6HoP/sQJmD3bXo+rUcPWyXrmGTv3+OWXbY9961Z7Ublp0/zXkWtQrgFNKjQBIMgEsWPIDh5t9SgAkWci+d+u/7ErahcAh2IOEfpaaNqHQOSZSB6b+xjrItYBdt753B1zOXr6KGB73usPrycmPgaAqLNRLNq9iBOxJwDYFrmNlxe/TESM/SCftWUWFd6qwN4TewFYdXAVLyx6gf2n9gNwV+O7+O7W79K+hbQq3Yp7mt1TMKeLKsdokvciY6BPH7vS88cf7a48h16dRPiMiXxxyXAmnLnzvH1G80JkpK2o+eST0KKFnV980012dkyzZnZq6P79dhbcCy/kk2qP2WSMoWrxqlQuZmfmlC1Slv2P7ee+ZvcBEBwQzAvtXkj7UNh/aj8T/5rI3pM2KW8+upkbpt3Anwf/BGDNoTU0Ht+YFQdWAHamT8dPO7Lh8AYAdkXtYsSvI9hzYg8AVYtVpUfdHgQY+9/s1ga3EjMshholagD2A+nGOjcSEph/Zlep/EenUDogMNBOf+9aZwcyfzDbKl/Hs/GvsOd++/jll9vHixQpTfXqtkftaWJNTrbJeutWm7BXrbLHnj328ZAQaN3aJvL27e0i23w0c9OrUnvKZYuU5eUOL6fd36RCE2KGx6QNlzQo14BlA5dxWZnLAKhXth5f9/maBuXs2FWzis1YfPdiGpVvBECnWp1IeCGBoAD736p5peZMqDQh7fxFQoo4/8spdQFN8k665BLMBx9Q5+ab2VUqkM2bbQ//p5/satDExEa88IJdin355Xa1XurS7nLl7Cr2gIDz57dFR8OxY+eOgwft4qydO8+tDgQ7DfqKK+wYe8uW0KqVd1bpFgSpHwLhIeFcVfVcrZMyhcvQq36vtNslw0pyTY1r0m6nJnelfIn+q3RCYqLtVtesCffZoQGDXSFbvz489RScPg1Tp64mKKg569fbWTrz59uaHPHZuBZojB16KV/efjh07Wr/rF3bfmD4wD7fSikfoEneCc89Bx99ZKeuZDLfsEgRqF8/mvbtz78/tbd+5IgtBSJybiGiMbaSY5kytohTNgoSKqUKOE3y3jZ3rp2TeP/9uZpQbgwUK2YPpZTylM6u8aYjR6B/fzsvcexYt6NRSintyXuNiF0Ce+KEHVzXq5xKKR+gPXlvSUiwS15Hj7bF1JVSygdoT95bQkLsyqKUOdZKKeULtCfvqdhYu8x1zRp721+Wiyql/IImeU+NGGE3YTh0yO1IlFLqXzTJe2LVKnjzTXvBtWtXt6NRSql/0SSfW/Hxdpu0ChVsjQKllPJBeuE1tyZOhA0b4PvvoUQJt6NRSqkMedSTN8a8aYzZYoxZb4z5zhhTIt1jw4wxO4wxW40x13scqa8ZNAi++Qa6d3c7EqWUypSnwzXzgYYicjmwDRgGYIypD9wGNAC6AOOMMf5RaSUx0S54Cg62uz0ppZQP8yjJi8j/RCQx5eZyoErKzz2BmSISJyK7gR1AS0/a8hnvvGNLSR486HYkSimVJW9eeB0I/Jzyc2Vgf7rHDqTcl7/t2wcvvWQLtVf08obKSinlACNZrNA0xvwCZLQx6XMiMjvlOc8BLYCbRUSMMR8Cf4jI5ymPTwZ+EpFvMjj/IGAQQPny5ZvPnDkz179MTEwM4eHhuX59VuqPGEHp5ctZOWUKcV7Yq9XpeL1N43WWxussf463Q4cOq0WkRYYPiohHB3A38AdQON19w4Bh6W7PA1pnda7mzZuLJxYtWuTR6y9q3jy7OdNrr3ntlI7G6wCN11kar7P8OV5glWSSVz2dXdMFeAboISJn0j30PXCbMaaQMaYmUBtY6Ulbrps1Cy691O6IrZRS+YSn8+Q/AAoB81P2xVwuIg+IyN/GmC+BTUAiMFhEkjxsy10ffmg3VS1UyO1IlFIq2zxK8iJy6UUeGwmM9OT8PuGff2wZ4Ro17A7bSimVj2hZg6w88gi0aAFnzmT9XKWU8jGa5C9m4UL49lt47DEoXNjtaJRSKsc0yWcmOdleZK1WDZ54wu1olFIqV7RAWWamTbMbgUybBqGhbkejlFK5oj35zGzbBq1awW23uR2JUkrlmvbkM/Pqq/DCCxCgn4NK+bqEhAQOHDhAbGxsps8pXrw4mzdvzsOoPJNRvKGhoVSpUoXg4OBsn0eT/IWOHIHdu20vPiTE7WiUUtlw4MABihYtSo0aNTCZ7LMcHR1N0aJF8ziy3LswXhEhMjKSAwcOULNmzWyfR7upF3r5Zbj6at2zVal8JDY2ltKlS2ea4P2BMYbSpUtf9NtKRjTJp7dlC3z8Mdx/v1aZVCqf8ecEnyo3v6Mm+fSef97Oh3/pJbcjUUopr9Akn2rNGrud3+OPa/kCpVSOvffee9SrV4++ffsya9YsXnnllYs+/8knn2ThwoWOx6UXXlNt3w41a9rVrUoplUPjxo3j559/pmbNmlx11VV8//33F33+kCFDuO++++jYsaOjcWmST3XLLdCrFwT6x1a0ShVUQ4fC2rX/vj8pKSzX/72bNLE7f2bmgQceYNeuXfTo0YM777yTQoUKUaZMGQB69uxJr169uOuuu/j4449ZsmQJ06ZNo3r16kRGRhIREUEFL2xClBkdrgH49VdbxkATvFIqF8aPH0+lSpVYtGgR5cqVo1mzZmmPTZgwgVdeeYWlS5fy9ttv8/7776c91qxZM5YtW+ZobNqTX7oU2reHyZNh4EC3o1FKeSizHnd09Nk8mSd/6NAhyqa7rle+fHleeeUVOnTowHfffUepUqXSHitXrhwHDx50NJ6C3ZMXsTNqKlTQ8gVKKa8ICwv711z2DRs2ULp06X8l9NjYWMLCwhyNp2An+QULYMkSGD5cSwkrpbyiXr167NixI+32ypUr+fnnn1mzZg1vvfUWu3fvTnts27ZtNGzY0NF4Cm6SF4EXX4SqVWHQILejUUr5iXbt2rFmzRpEhLi4OO677z4++eQTKlWqxNtvv83AgQMRERISEtixYwctWrRwNJ6COyZ/+LAtXTB8uO7bqpTy2J49e9J+7tSpEwsWLKBTp06sW7cu7f4ePXrQo0cPAObMmUPv3r0JCnI2DRfcJF+hgi0nrJRSXjZ8+HBWrFhx0eckJibyRB5sSFQwk/yhQ1CypG4GopRyRPny5dN67Jnp06dPnsRSMMfkH3gAmje34/JKKeXHCl6S37gRvv/ernAtAFXrlFIFW8FL8qNGQZEiMGSI25EopZTjClaS37ULZsyABx+EdKvOlFLKXxWsJD9jBgQF2XLCSinlRamlhitXrsyIESPS7n/nnXf49NNPL/ra2267je3btzsSl1eSvDHmSWOMGGPKpLtvmDFmhzFmqzHmem+047Hhw2H9et31SSnldePGjeOnn35i5MiRafclJibyySefcMcdd1z0tQ8++CCjR492JC6Pp1AaY6oCnYF96e6rD9wGNAAqAb8YY+qISJKn7eVaYqLtxdet61oISqk80r79v+4K7tHDfos/cwa6dv33a/r3t8exY9C79/mPLV580eYuLDUcHh4OwMKFC2nWrBlBQUEkJibSunVr3nzzTdq3b8+wYcMICAhg5MiRtG3blv79+5OYmOj1xVHeONtY4Glgdrr7egIzRSQO2G2M2QG0BP7wQns5FxMD9erBK6/AgAGuhKCU8l/jx49n7ty5LFq0KK2OPMCyZcto3rw5AEFBQUyZMoXevXvz3nvvMXfu3LQFUwEBAVx66aWsW7cu7fne4lGSN8b0AP4RkXUXbDBbGVie7vaBlPsyOscgYBDYBQSLs/jEvJiYmJgMX1/pu++oc+AAf505wykPzu9tmcXrqzReZ2m8uVe8eHGio6PP3fHDD/96TlJSEgmpz8ngcQCio22ZkwsfT3/uTIgIMTExFEpXJmXfvn3UqFEjLbZq1apxyy230L17d3755Rfi4uKIi4sDoGTJkuzcuZM6deqkxRudQbuxsbE5et+zTPLGmF+AjLYteQ4YDlyX0csyuC/DlUciMgGYANCiRQtpn8HXrOxavHgx/3p9UhLcdx9ceSXNBg/O9bmdkGG8PkzjdZbGm3ubN2/OslZ8dHS0o/XkjTGEh4ef10axYsUwxpx337Zt2yhRogQxMTHn3Z+UlESpUqXS7sss3tDQUJo2bZrtuLJM8iLSKZNfqBFQE0jtxVcB/jLGtMT23Kume3oVwNnK+JmZMwd27IB0F0OUUiovXFh2+NtvvyUyMpIlS5bQrVs3Vq5cSYkSJQCb/Bs0aOD1GHI9u0ZENohIORGpISI1sIm9mYhEAN8DtxljChljagK1gZVeiTinxoyBatXg5ptdaV4pVXDdcMMNLFmyBIBjx47x7LPPMnnyZOrUqcPDDz/Mo48+CsDhw4cJCwujogMz/xwpUCYifxtjvgQ2AYnAYNdm1nz4IRw8aGfWKKWUQ9KXGk5VvXp1Spcuzfbt26lduzbb0lW+feSRR9J+nj59Ovfff78jcXkt86X05tPfHgm4P0bSsKE9lFLKBaNGjeLQoUPUrl070+eUKFGCfv36OdK+/654/ecf6NsXdu50OxKlVAFWt25d2rVrd9HnDBgwwLHNQ/w3yX/wAcycCQH++ysqpVRW/DMDnj0LEyZAz55Qs6bb0SillGv8M8l/9RUcPw4PP+x2JEop5Sr/TPLjxtkaNR06uB2JUkq5yv+SfEICXHMNPPOM7vyklMozGZUaHjFiBFOmTEl7ztChQ9PmzWemU6dOREVFeS0u/0vywcHwxhtaiEwplacyKjWc3vHjx1m+fHmWM2369evHuHHjvBaXXyX5oOhomDsXkpPdDkUp5aL2U9ozZe0UABKSEmg/pT0zN80E4EzCGdpPac8XG78A4GTsSdpPac+3m78F4NiZY7Sf0p4fttoiZRExEVm2l77U8OHDh9NKDYeHhxMWFgbA119/TZcuXWybJ09St25dtm7dCsDtt9/OxIkTAejRowczZszwxtsAOLTi1S0V5s2zK1zXr4dGjdwORylVQGRWavjJJ59M+3nZsmX0TqlTX7x4cT744AP69+/Po48+SlRUFPfddx9gq1HGxcURGRnplYJq/pPkk5OpNHs2XHWVJnilCrjF/Ren/RwcGMzi/ovTyvYWDi583uPFQ4ufd7tM4TLn3a4QnlER3pw7dOgQZcuWTbvduXNnvvrqKwYPHsy6devOe265cuWIiIigRo0aHrfrP8M1CxZQ+MABeOghtyNRSql/CQsLIzY2Nu12cnIymzdvJiwsjOPHj5/33NjYWEJDQ73Srv8k+XHjiC9R4t/bdimllA+4sOzw2LFjqVevHjNmzGDgwIEkJCQAdvORiIgIqlev7pV2/SPJnz0La9dyqGtXu6uLUkr5mBtvvDFtR6dt27YxadIk3n77bdq2bUu7du147bXXAFi9ejVXXnml12rZ+MeYfFgYbN/Ovvnz8c5nn1JK5UxGpYbTa9u2LcOGDePEiRPUqVOHzZs3pz02ZsyYtJ8/++wzHvLisLN/9OQBgoJISpmqpJRSvujtt99m3759F31Ow4YNufbaa73Wpn/05JVSKh9o1apVls9JnUrpLf7Tk1dKFWgi4nYIjsvN76hJXimV74WGhhIZGenXiV5EiIyMzPHUSh2uUUrle1WqVOHAgQMcPXo00+d4c+55Xsgo3tDQUKpUqZKj82iSV0rle8HBwdTMYoOgxYsX07Rp0zyKyHPeileHa5RSyo9pkldKKT+mSV4ppfyY8aWr0caYo8BeD05RBjjmpXDygsbrLI3XWRqvs3ISb3URKZvRAz6V5D1ljFklIi3cjiO7NF5nabzO0nid5a14dbhGKaX8mCZ5pZTyY/6W5Ce4HUAOabzO0nidpfE6yyvx+tWYvFJKqfP5W09eKaVUOprklVLKj/lVkjfGvGqMWW+MWWuM+Z8xppLbMV2MMeZNY8yWlJi/M8aUcDumizHG9DHG/G2MSTbG+OxUNGNMF2PMVmPMDmPMs27HkxVjzCfGmCPGmI1ux5IdxpiqxphFxpjNKf8eHnU7posxxoQaY1YaY9alxPuy2zFlhzEm0Bizxhgzx5Pz+FWSB94UkctFpAkwB3jR5XiyMh9oKCKXA9uAYS7Hk5WNwM3AErcDyYwxJhD4ELgBqA/cboyp725UWZoCdHE7iBxIBJ4QkXrAlcBgH3+P44COItIYaAJ0McZc6W5I2fIosDnLZ2XBr5K8iJxKd7MI4NNXlUXkfyKSmHJzOZCzGqJ5TEQ2i8hWt+PIQktgh4jsEpF4YCbQ0+WYLkpElgDH3Y4ju0TkkIj8lfJzNDYRVXY3qsyJFZNyMzjl8OncYIypAtwITPL0XH6V5AGMMSONMfuBvvh+Tz69gcDPbgfhByoD+9PdPoAPJ6D8zhhTA2gKrHA5lItKGfpYCxwB5ouIT8cLvAM8DSR7eqJ8l+SNMb8YYzZmcPQEEJHnRKQqMA142N1os4435TnPYb8CT3Mv0rRYsozXx5kM7vPpXlt+ZYwJB74Bhl7wLdrniEhSyjBuFaClMaahyyFlyhjTDTgiIqu9cb58t2mIiHTK5lOnAz8CLzkYTpayitcYczfQDbhWfGDRQg7eX191AKia7nYV4KBLsfgtY0wwNsFPE5Fv3Y4nu0TkhDFmMfYaiK9e6G4D9DDGdAVCgWLGmM9F5M7cnCzf9eQvxhhTO93NHsAWt2LJDmNMF+AZoIeInHE7Hj/xJ1DbGFPTGBMC3AZ873JMfsUYY4DJwGYRGeN2PFkxxpRNnblmjAkDOuHDuUFEholIFRGpgf33uzC3CR78LMkDo1KGFtYD12GvTvuyD4CiwPyUaZ/j3Q7oYowx/zHGHABaAz8aY+a5HdOFUi5kPwzMw14Q/FJE/nY3qoszxswA/gDqGmMOGGPucTumLLQB+gEdU/7drk3pdfqqisCilLzwJ3ZM3qNpifmJljVQSik/5m89eaWUUulokldKKT+mSV4ppfyYJnmllPJjmuSVUsqPaZJXSik/pkleKaX8mCZ5pS7CGHNFSr3/UGNMkZR65D5b90SpC+liKKWyYIx5DVtDJAw4ICL/dTkkpbJNk7xSWUipgfMnEAtcJSJJLoekVLbpcI1SWSsFhGPrDIW6HItSOaI9eaWyYIz5HrvDVE2gooi4vk+BUtmV7+rJK5WXjDF3AYkiMj1l/9jfjTEdRWSh27EplR3ak1dKKT+mY/JKKeXHNMkrpZQf0ySvlFJ+TJO8Ukr5MU3ySinlxzTJK6WUH9Mkr5RSfuz/AQ/kisdVNAryAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"plt.figure()\n",
"xplt = np.arange(-3,4,0.1)\n",
"\n",
"fplt = f(xplt)\n",
"dfplt = df(xplt)\n",
"ddfplt = ddf(xplt)\n",
"\n",
"plt.plot(xplt, fplt, label=\"f(x)\", color=\"b\", linestyle=\"-\")\n",
"plt.plot(xplt, dfplt, label=\"f'(x)\", color=\"r\", linestyle=\"--\")\n",
"plt.plot(xplt, ddfplt, label=\"f''(x)\", color=\"g\", linestyle=\":\")\n",
"plt.xlabel(\"x\")\n",
"plt.legend()\n",
"plt.grid()\n",
"plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.6.2 Geometric Insights into Newton Steps](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.2-Geometric-Insights-into-Newton-Steps)",
"section": "3.6.2 Geometric Insights into Newton Steps"
}
},
"source": [
"## 3.6.2 Geometric Insights into Newton Steps"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.2.1 Motivation](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.2.1-Motivation)",
"section": "3.6.2.1 Motivation"
}
},
"source": [
"### 3.6.2.1 Motivation\n",
"\n",
"We can interpret Newton-type methods for unconstrained optimization as root finding of $\\nabla f(x) = 0$.\n",
"\n",
"At iteration $k$, we assemble an approximation to $f(x)$ using a Taylor series expansion:\n",
"\n",
"$$f(x^k + p^k) \\approx f(x^k) + \\nabla f(x^k)^T p^k + \\frac{1}{2} (p^k)^T (B^k) p^k$$\n",
"\n",
"and solve for $p^k$ such that $f(x^k + p^k)=0$. This gives:\n",
"\n",
"$$p^k = -(B^k)^{-1} \\nabla f(x^k)$$\n",
"\n",
"The choice of $B^k$ determines the algorithm classification:\n",
"* Pure **Newton Method**, $B^k = \\nabla^2 f(x^k)$\n",
"* **Steepest Descent**, $B^k = \\frac{1}{\\alpha} I$, where scalar $\\alpha$ is sometimes known as the dampening factor\n",
"* **Levenberg-Marquart**, $B^k = \\nabla^2 f(x^k) + \\delta I$, where scalar $\\delta$ is chosen to ensure $B^k$ is positive definite.\n",
"* **Broyden Methods**, $B^{k}$ is approximated using history of gradient evaluations, i.e., $\\nabla f(x^0), ... \\nabla f(x^k)$. We will study the SR1 and BFGS formulas in this family of methods.\n",
"\n",
"This section **explores how choosing $B^k$ impacts the shape of the approximation and calculated step.**"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.2.2 Compute and Plot Steps](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.2.2-Compute-and-Plot-Steps)",
"section": "3.6.2.2 Compute and Plot Steps"
}
},
"source": [
"### 3.6.2.2 Compute and Plot Steps\n",
"\n",
"Define a function that:\n",
"* Computes the i. Newton, ii. Levenberg-Marquardt and iii. Steepest Descent Step for a given starting point $x_0$\n",
"* Plots the step in terms of $f(x)$ and $f'(x)$"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.2.2 Compute and Plot Steps](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.2.2-Compute-and-Plot-Steps)",
"section": "3.6.2.2 Compute and Plot Steps"
}
},
"outputs": [],
"source": [
"def calc_step(x0, epsLM):\n",
" \n",
" # Evaluate f(x0), f'(x0) and f''(x0)\n",
" f0 = f(x0)\n",
" df0 = df(x0)\n",
" ddf0 = ddf(x0)\n",
" print(\"x0 = \",x0)\n",
" print(\"f(x0) =\",f0)\n",
" print(\"f'(x0) =\",df0)\n",
" print(\"f''(x0) =\",ddf0)\n",
" \n",
" \n",
" ### Calculate steps\n",
" \n",
" # Newtwon Step\n",
" xN = x0 - df0 / ddf0\n",
" \n",
" print(\"\\n### Newton Step ###\")\n",
" print(\"xN = \",xN)\n",
" print(\"pN = xN - x0 = \",xN - x0)\n",
" f_xN = f(xN)\n",
" print(\"f(xN) = \",f_xN)\n",
" print(\"f(xN) - f(x0) = \",f_xN - f0)\n",
" \n",
" # Levenberg-Marquardt Step\n",
" # Recall the eigenvalue of a 1x1 matrix is just that value\n",
" dffLM = np.amax([ddf0, epsLM])\n",
" xLM = x0 - df0 / dffLM\n",
" \n",
" print(\"\\n### Levenberg-Marquardt Step ###\")\n",
" print(\"xLM = \",xLM)\n",
" print(\"pLM = xLM - x0 = \",xN - x0)\n",
" f_xLM = f(xLM)\n",
" print(\"f(xLM) = \",f_xLM)\n",
" print(\"f(xLM) - f(x0) = \",f_xLM - f0)\n",
" \n",
" \n",
" # Steepest Descent Step\n",
" xSD = x0 - df0 / 1\n",
" \n",
" print(\"\\n### Steepest Descent Step ###\")\n",
" print(\"xSD = \",xSD)\n",
" print(\"pSD = xSD - x0 = \",xSD - x0)\n",
" f_xSD = f(xSD)\n",
" print(\"f(xSD) = \",f_xSD)\n",
" print(\"f(xSD) - f(x0) = \",f_xSD - f0)\n",
" \n",
" ### Plot Surrogates on x vs f(x)\n",
" \n",
" ### Plot f(x)\n",
" plt.figure()\n",
" plt.scatter(x0,f0,label=\"$x_0$\",color=\"black\")\n",
" plt.plot(xplt, fplt, label=\"f(x)\",color=\"purple\")\n",
" \n",
" ### Plot approximation for Newton's method\n",
" fN = lambda x : f0 + df0*(x - x0) + 0.5*ddf0*(x-x0)**2\n",
" plt.plot(xplt, fN(xplt),label=\"Newton\",linestyle=\"--\",color=\"red\")\n",
" plt.scatter(xN, f(xN),color=\"red\",marker=\"x\")\n",
" \n",
" \n",
" ### Plot approximation for LM\n",
" fLM = lambda x : f0 + df0*(x-x0) + 0.5*dffLM*(x-x0)**2\n",
" plt.plot(xplt, fLM(xplt),label=\"LM\",linestyle=\"--\",color=\"blue\")\n",
" plt.scatter(xLM, f(xLM),color=\"blue\",marker=\"x\")\n",
"\n",
" ### Plot approximation for SD\n",
" fSD = lambda x : f0 + df0*(x-x0) + 0.5*(x-x0)**2\n",
" plt.plot(xplt, fSD(xplt),label=\"Steepest\",linestyle=\"--\",color=\"green\")\n",
" plt.scatter(xSD, f(xSD),color=\"green\",marker=\"x\")\n",
" \n",
" #plt.plot([x0, xLM],[f0, f(xLM)],label=\"LM\",color=\"green\",marker=\"o\")\n",
" #plt.plot([x0,xSD],[f0,f(xSD)],label=\"Steepest\",color=\"blue\",marker=\"s\")\n",
" \n",
" plt.xlim((-3.5,4.5))\n",
" plt.ylim((-12.5,22.5))\n",
" plt.xlabel(\"$x$\")\n",
" plt.ylabel(\"$f(x)$\")\n",
" plt.legend()\n",
" plt.title(\"Function and Surrogates\")\n",
" plt.grid()\n",
" plt.show()\n",
" \n",
" ### Plot Surrogates on x vs f(x)\n",
" plt.figure()\n",
" plt.scatter(x0,df0,label=\"$x_0$\",color=\"black\")\n",
" plt.plot(xplt, dfplt, label=\"f'(x)\",color=\"purple\")\n",
" \n",
" \n",
" ### Plot approximation for Newton's method\n",
" dfN = lambda x : df0 + ddf0*(x-x0)\n",
" plt.plot(xplt, dfN(xplt),label=\"Newton\",linestyle=\"--\",color=\"red\")\n",
" plt.scatter(xN, df(xN),color=\"red\",marker=\"x\")\n",
" \n",
" \n",
" ### Plot approximation for LM\n",
" dfLM = lambda x : df0 + dffLM*(x-x0)\n",
" plt.plot(xplt, dfLM(xplt),label=\"LM\",linestyle=\"--\",color=\"blue\")\n",
" plt.scatter(xLM, df(xLM),color=\"blue\",marker=\"x\")\n",
"\n",
" ### Plot approximation for SD\n",
" dfSD = lambda x : df0 + (x-x0)\n",
" plt.plot(xplt, dfSD(xplt),label=\"Steepest\",linestyle=\"--\",color=\"green\")\n",
" plt.scatter(xSD, df(xSD),color=\"green\",marker=\"x\")\n",
" \n",
" \n",
" plt.xlim((-3.5,4.5))\n",
" plt.ylim((-50,50))\n",
" plt.xlabel(\"$x$\")\n",
" plt.ylabel(\"$f'(x)$\")\n",
" plt.legend()\n",
" plt.title(\"First Derivative and Surrogates\")\n",
" plt.grid()\n",
" plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.2.3 Consider $x_0 = -3$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.2.3-Consider-$x_0-=--3$)",
"section": "3.6.2.3 Consider $x_0 = -3$"
}
},
"source": [
"### 3.6.2.3 Consider $x_0 = -3$"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.2.3 Consider $x_0 = -3$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.2.3-Consider-$x_0-=--3$)",
"section": "3.6.2.3 Consider $x_0 = -3$"
},
"scrolled": false
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"x0 = -3\n",
"f(x0) = 15.0\n",
"f'(x0) = -51\n",
"f''(x0) = 64\n",
"\n",
"### Newton Step ###\n",
"xN = -2.203125\n",
"pN = xN - x0 = 0.796875\n",
"f(xN) = -8.660857647657394\n",
"f(xN) - f(x0) = -23.660857647657394\n",
"\n",
"### Levenberg-Marquardt Step ###\n",
"xLM = -2.203125\n",
"pLM = xLM - x0 = 0.796875\n",
"f(xLM) = -8.660857647657394\n",
"f(xLM) - f(x0) = -23.660857647657394\n",
"\n",
"### Steepest Descent Step ###\n",
"xSD = 48.0\n",
"pSD = xSD - x0 = 51.0\n",
"f(xSD) = 2534689.5\n",
"f(xSD) - f(x0) = 2534674.5\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEWCAYAAAB42tAoAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAABOnUlEQVR4nO3dd1wUd/7H8deHIggi3YIgxYoVezdgSUyzxDRjSeIlppe7XO7SY3LnXe6X3hPTi0Zz9mhM1Kixxk4UQRSxIShNpIm07++PRQ4NIODuzu7yfT4ePGRnZmfeOy772ZnvzPcrSik0TdM0rSZORgfQNE3TbJsuFJqmaVqtdKHQNE3TaqULhaZpmlYrXSg0TdO0WulCoWmaptVKFwrNYYjIMBFJNDrH5YjIehG5x+gcmlZXulBoZiMiR0XknIjkV/kJsuD2lIi0v/BYKbVRKdXJUtuzBhHxEZHPReSUiOSJyEER+bvRuepCRGaKyLdG59DMz8XoAJrDuVEptcboEHbsTcATiATOAh2Bbg1ZkYi4KKVKL5nmrJQqu+KUWqOijyg0i6s40hhV5XHlN08RCas4MrhTRI6LSKaIPFtlWWcReUZEDld8w94lIiEisqFikd8rjlxuE5FoEUmp8tzIitM8OSKyX0TGVpn3pYi8LyIrKta7TUTa1fIa/lvxLf+siGwQka51XZeIjBaRAxXPfQ+QWnZXP2CuUuqMUqpcKXVAKbXgkn1V+QWv6mksEblLRDaLyJsikg3MrMj2oYj8KCIFQMxl9ou/iPwgIrkiskNE/ikim6rMf1tETlTM3yUiwyqmjwGeAW6r+P/4vWK6t4h8JiJpInKyYn3OFfPai8ivFfslU0Tm17JfNAPpQqHZiqFAJ2Ak8IKIRFZM/wswCbgOaA5MBwqVUsMr5vdUSjVTSl30ISMirsAPwCqgBfAIMEdEqp6amgS8BPgCScCsWvKtBDpUrGs3MOeS+dWuS0QCgIXAc0AAcBgYUst2fgNmicjdItKhluVqMgBIrsh54fXcUfG7F7CN2vfL+0AB0Aq4s+Knqh1AFOAHzAX+KyLuSqmfgH8B8yv+P3pWLP8VUAq0B3oBVwMX2mf+UZHDFwgG3m3A69WsQBcKzdyWVHxTzRGRJfV43ktKqXNKqd+B34ELHzT3AM8ppRKVye9Kqaw6rG8g0Ax4RSlVrJRaCyzH9IF+wSKl1PaK0zNzMH0AVksp9blSKk8pdR6YCfQUEe86rOs6IF4ptUApVQK8BZyqJfcjFc9/GIgXkSQRubYOr/eCVKXUu0qpUqXUuYppS5VSm5VS5RW5qt0vFd/0JwIvKqUKlVLxmD7oq+6Hb5VSWRXrfx1ww1Tg/0BEWgLXAo8rpQqUUumYTq3dXrFICRAKBCmlipRSm6pbj2Y8XSg0cxuvlPKp+Blfj+dV/fAsxPRhBhCC6Vt4fQUBJyo+HC84BrSpwzYvUnH665WK01+5wNGKWQF1WFcQcOLCDGXqhfMENagolv9SSvUB/IHvMX1r96vpOZeobt1Vp9W2XwIxtVueqOG5iMgTIpJQcbooB/Dm4v1QVSjgCqRd+PIAfIzpSAbgb5hOw22vOAU2vQ6vTzOALhSaNRQAHlUet6rHc08ANbYd1CIVCBGRqu/xtsDJBqzrDmAcMArTB2NYxfTa2houSMNU7ExPEJGqj2ujlMrFdDrHEwjHtB+h9n1ZXXfQVafVtl8yMJ0mCq4yr2r2YcDfgVsBX6WUD6YG9wv74dJtnwDOAwFVvjw0V0p1rXh9p5RS9yqlgoD7gA+kylVsmu3QhUKzhljgdhFxFZG+wM31eO6nwD9EpIOY9BAR/4p5p4GIGp63DdMH698qthsN3AjMa0B+L0wfeFmYPqT/VY/nrgC6ishNFY3Qj1JLoRSR50Wkn4g0ERF34DEgB0hUSmVg+kCfUnGUM536F9Ea90vF1VCLMDWCe4hIZ2Baled6YSokGYCLiLyAqd3ogtNA2IUipJRKw9QG8bqINBcRJxFpJyJXVbzWW0TkQlE6g6nQ6CuybJAuFJo1PI/pA+0MpgbfufV47huYTr+sAnKBz4CmFfNmAl9VnNa4teqTlFLFwFhM58gzgQ+AaUqpAw3I/zWm0zMngXhMDc51opTKBG4BXsFUaDoAm2t7CvBFReZUYDRwvVIqv2L+vcCTFevqCmypzwupw355GNNR0yngG+A7TEUS4GdMjfoHMe2PIi4+NfXfin+zRGR3xe/TgCaY9tsZYAHQumJeP2CbiOQDy4DHlFJH6vN6NOsQPXCRpmk1EZH/AK2UUpde/aQ1IvqIQtO0SiLSueL0nohIf+BPwGKjc2nG0ndma5pWlRem001BQDrwOrDU0ESa4fSpJ03TNK1W+tSTpmmaViuHO/UUEBCgwsLCzLrOgoICPD09zbpOSzAiZ2F2EQlH3GnXsgCf4LptW+9P89I5zcceMoJlcu7atStTKRVY7UyllEP99OnTR5nbunXrzL5OSzAi55Knf1Og1I6v9tf5OXp/mpfOaT72kFEpy+QEdqoaPlf1qSftiqQkFQEQHFVTLw6aptk7XSi0K9JlYHPu77KBFl10odA0R+VwbRSadcX8pRcxfzE6haZplqQLhXZFsg5l4xPqjXMTZ6OjAFBSUkJKSgpFRUVXvC5vb28SEhLMkMqyzJXT3d2d4OBgXF1dzZBKcyS6UGhXpH+XPAa0SWDu0drG4rGelJQUvLy8CAsLw9RRa8Pl5eXh5eVlpmSWY46cSimysrJISUkhPDzcTMk0R6HbKLQGU+WKlNJWBLcoMTpKpaKiIvz9/a+4SDQ2IoK/v79ZjsQ0x6MLhdZgmYlZFONGcIhtfSjrItEwer9pNdGFQmuwlNhMAILbuRmcRNM0S9KFQmuwE3FnAQjp2vwyS2qaZs90odAarNPQQP45aj3thra+/MKNyDvvvENkZCSTJ09myZIlvPzyy7Uu/9e//pW1a9daKZ2m1Z++6klrsE7XRvDstTWNRNp4ffDBB6xcuZLw8HAGDx7MsmXLal3+kUce4d5772XEiBFWSqjZk4RFCSAQOSHSsAw2UShEJATTcJOtgHJgtlLqbRHxA+ZjGsz+KHCrUuqMUTm1ix38+QjebZrRslv1/YgZ7afHf+JU7KkGP7+srAxn54vvD2kV1Yoxb42p8Tn3338/ycnJjB07lilTpuDm5kZAgOmu9XHjxjFx4kSmTZvGxx9/zIYNG5gzZw6hoaFkZWVx6tQpWrWqcThtrZHa8toWXNxcDC0UtnLqqRR4QikVCQwEHhKRLsBTwC9KqQ7ALxWPNRsxZWIh06KPGR3Dpnz00UcEBQWxbt06WrRoQe/evSvnzZ49m5dffpmNGzfy+uuv8+6771bO6927N5s31zaUttZYZSVm4d/J39AMNnFEoZRKA9Iqfs8TkQSgDTAOiK5Y7CtgPfB3AyJq1Tha2IJeIbZ753Jt3/zr4kpvZEtLSyMw8H9HWy1btuTll18mJiaGxYsX4+fnVzmvRYsWpKamXlFezfEUZhVyLvsc/h11obiIiIQBvYBtQMuKIoJSKk1EWtTwnBnADDD9Ma5fv96smfLz882+TkuwZs7inGIy1NV4eW6s9zYtmdPb25u8vDyzrKusrKxB61JKkZ+fj4hw9uzZi9axa9cu/Pz8SE5Ovmh6bm4urVu3btD2GpqzOkVFRRb7v7GHvyNby3h2v+nKwtTzqRflsnrOmvofN+IHaAbsAm6qeJxzyfwzl1uHHo/COuJ/SFKg1JwHN9X7uZbMGR8fb7Z15ebmNuh5oaGhKiMjQ61cuVJNnjy5cvq2bdtUz5491cmTJ1X79u1VcnJy5bwbbrhBbd261ao5q2PO/Xcpe/g7srWMe77Yo2YyU2UezLxoeqMdj0JEXIGFwByl1KKKyadFpHXF/NaYBnvXbMDR3dkAhHaz/b6QjDJ8+HD27NmDUorz589z77338vnnnxMUFMTrr7/O9OnTUUpRUlJCUlISffv2NTqyZmOyDmbh5OKET5iPoTlsolCIqe+Az4AEpdQbVWYtA+6s+P1OYKm1s2nV63FdMF/du4mu14UaHcXmHD16lICAADw8PBg1ahS//PILbm5u/P7775WN22PHjmXdunWICMuXL+fmm2/GxcXmzgRrBstKzMK3nS/Orsb2zmwr78whwFRgn4jEVkx7BngF+F5E/gQcB24xJp52qTZ9WzOtr77R7nKeeeYZtm3bVusypaWlPPHEE1ZKpNmTrINZhjdkg40UCqXUJqCmHslGWjOLVje/fRpH0+au9Ly1k9FRbFrLli0ZO3Zsrcvccov+/qP9kSpXZB3Kot2YdkZHsY1CodmfP/9Z4elawJpbjU6iaY7p7PGzlJ0vs4kjCptoo9Dsz7HCQEIDCoyOoWkOK+tgFoAuFJp9KsopIq28FWEhZUZH0TSHlZlo6sY/oFOAwUl0odAa4Pi2NABC2+kzl9URkYsap1977TVmzpx5ReuMjY3lxx9/vMJkmj3JOphFE68meLb0NDqKLhRa/R3bY7qHIqy7voeiOm5ubixatIjMzEyzrVMXisYn+2A2AZ0CbGLkQV0otHrrf0d71r6+h6gJ4UZHsUkuLi7MmDGDN9988w/zMjIymDhxIv369aNfv36VHQF2796dnJwclFL4+/vz9ddfAzB16lRWrVrFCy+8wPz584mKimL+/PlkZ2czfvx4evTowYgRI9i7dy8AM2fOZPr06URHRxMREcE777xjvReumVVmYqZNtE+AvupJawDvtt7E/KWX0THqJjr6j9NuvRUefBAKC+G66/44/6674K67kKwsuPHGi+fVsX+dhx56iB49evC3v/3toumPPfYYf/7znxk6dCjHjx/nmmuuISEhgSFDhrB582ZCQ0OJiIhg48aNTJs2jd9++40PP/yQl19+mZ07d/Lee+8BpjEsevXqxZIlS1i+fDnTpk0jNjYWgAMHDrBu3Try8vLo1KkTDzzwAK6urnXKrdmGknMlnD1+Fr+7/S6/sBXoQqHV248v7cDJWRjznO5yoibNmzdn2rRpvPPOOzRt2rRy+po1a4iPj698nJubS15eHsOGDWPDhg2EhobywAMPMHv2bE6ePImfnx/NmjX7w/o3bdrEwoULAbjqqqvIysri7FlTB3LXX389bm5uuLm50aJFC06fPk1wcLCFX7FmTtlJ2aBsoyEbdKHQGuDfbzTBWRRjnjM6SR3UdgTg4VHrfOXvX+cjiOo8/vjj9O7dm7vvvrtyWnl5OVu3br2oeICpX6j333+f48ePM2vWLBYvXsyCBQsYNmxY9dlMnWRe5MK5bDc3t8ppzs7OlJaWNvg1aMawpUtjQbdRaA1wtCCQsIB8o2PYPD8/P2699VY+++yzymlXX3115ekjoPJ0UUhICJmZmRw6dIiIiAiGDh3Ka6+9VlkovLy8LupKfPjw4cyZMweAjRs3EhAQQPPmza3wqjRr0IVCs2vF+cWklrUktI3+lloXTzzxxEVXP73zzjvs3LmTHj160KVLFz766KPKeQMGDKBjx44ADBs2jJMnTzJ06FAAYmJiiI+Pr2zMnjlzZuV6XnzxRb766ivrvjDNorISs/AK8qJJsyZGRwH0qSetnlJ2nqKctoS1M7Y3S1uWn/+/o62WLVtSWFhY+TggIID58+dX+7xvvvmm8vfBgwdTXl5e+djPz48dO3ZctPzSpabOlKuOxHfp/RpxcXENexGaobIOGj/8aVX6iEKrl6O7TIfEoV3/2MCqaZp5ZCXaRq+xF+gjCq1eht7XlYM9jhLUs6PRUTTNIdnKONlV6UKh1UuTZk3oMDrM6Bia5rAqG7L1qSfNXs19aDOf373R6Bia5rCyEm3riifQhUKrp9lzPPl8obfRMTTNYV0YJ9s33NfoKJV0odDq5ViBP2H+eZdfUNO0BrkwTraTi+18PNtOEs3mlRaVcqK0NWFtSoyOYtOq63Jj5syZiAhJSUmV0958801EhJ07d1oznmbjbGWc7Kp0odDqLHXPacpwITRCv20aonv37sybN6/y8YIFC+jSpYuBiTRbU15aTtahLAI620YfTxfov3itzlL2VoxD0cX4gVTs0fjx4ytvkktOTsbb25vAwECDU2m2JPtwNmXny2jRrYXRUS6iL4/V6mzwfd0pvOUczk26Gx2lzq6gl3GysqShvYxXq3nz5oSEhBAXF8fSpUu57bbb+OKLLxq+Qs3hpMelA9hcobCZIwoR+VxE0kUkrsq0mSJyUkRiK36q+bO2nDlz5hAWFsauXbsICwur7IStMWvq19Rm+p+xR7fffjvz5s1jyZIlTJgwweg4mo1Jj0sHgYBI2zr1ZEtHFF8C7wFfXzL9TaXUa9YOM2fOHGbMmFHZT8+xY8eYMWMGAJMnT7Z2HJvwzsRfyctVPLs62ugodXYFvYzj76+u6AiiOjfeeCNPPvkkffv21b29an+QEZeBX3s/XJva1kBTNnNEoZTaAGQbneOCZ599lsLCQnrRi9PvZABQWFjIs88+a3Ay43y/2pfVO3yMjmHXmjZtyn/+859G/T7SapYel06LrrZ12gls64iiJg+LyDRgJ/CEUurMpQuIyAxgBph661xvhq+BjzzyCABLftrBq0P/w3OZL+ATZvoGaI71W0J+fr5Fsx3O70x0m9+veBuWzOnt7X3RuA1XoqysrEHrKiwspE2bNpWPH374Yc6fP4+rqyt5eXlcf/31gKnX17KyMgoKCq4oc0NzVqeoqMhi/zeWfn+ag5EZy4vLyTyYiUc/j8tmsHpOpZTN/ABhQFyVxy0BZ0xHPrOAzy+3jj59+ihzCA0NVYDq1SlaMRPVM2iQAlRoaKhZ1m8J69ats9i689LyFCj1r6uvfBuWzBkfH2+2deXm5pptXZZkzpzm3H+XsuT/u7kYmTEtNk3NZKbaN2/fZZe1RE5gp6rhc9VmTj1VRyl1WilVppQqBz4B+ltr27NmzcLDw4OCM6bTTs6+Pnh4eDBr1ixrRbAphzecBKB9V7fLLKlpWkPY6hVPYENtFNURkdZVHk4ArDYKy+TJk5k9ezZlHucBOO/vwuzZsxttQ3bWiUICJJN2fXyMjqJpDik9Lh0nVyf8O9jWXdlgQ4VCRL4DtgKdRCRFRP4E/J+I7BORvUAM8GdrZpo8eTJJRw7hlB9Avn9poy0SACOe6EVGeQC9JnU2OoqmOaSMuAwCOgXg3MT2Ro+0mcZspdSkaiZ/Vs00q4vZMZrW5/yMjmETxEmMjqBpDil9fzrBA4KNjlEtmzmisGW3ekfTPamt0TEM9UDXDbwwfL3RMTTNIRXnF5NzJIfAbrbZpYsuFHVQ5l9GottR0g+mGx3FMCsS23H0pM0cgGqaQ8mIN100Y4v3UIAuFHWytnAnn9/3ISu+XW90FEMU5RSRUtaa9qGlRkexC7NmzaJr16706NGDqKgotm3bxltvvVV5l79RcnJy+OCDDwzNoFXPlq94Al0o6qR9kOnmqZ0JBwxOYowjm06icKJdZ9vqVsAWbd26leXLl7N792727t3LmjVrCAkJ0YVCq1V6XDouTV3wCfcxOkq1dKGog679OgKQmJtmcBJjJG0zjeHbvo8eAvVy0tLSCAgIwM3NdL9JQEAACxYsIDU1lZiYGGJiYgBYtWoVgwYNonfv3txyyy3k5+cDsGvXLq666ir69OnDNddcQ1qa6T0XHR3N448/zuDBg+nWrRvbt28HoKCggAcffJB+/frRq1evym7M9+/fT//+/YmKiqJHjx4cOnSIp556isOHDxMVFcWTTz5p7V2j1SI9Lp3ALoE4OdvmR7I+6VwHrVu1hvgmnHC2ma6orEoEejVNoP3wIKOj1Fv0l9F/mHZr11t5sN+DFJYUct2cP3ZIfFfUXdwVdRdZ57K4ceHF/Yyvv2t9rdu7+uqrefnll+nYsSOjRo3itttu49FHH+WNN95g3bp1BAQEkJmZyT//+U/WrFmDp6cn//nPf3jjjTd4+umneeSRR1i6dCmBgYHMnz+fZ599ls8//xwwFYUtW7awYcMGpk+fTlxcHLNmzWL48OF888035OTk0L9/f0aNGsVHH33EY489xuTJkykuLqasrIxXXnmFuLg4YmNjG7o7NQtJj0un3dXtjI5RI10o6sBZnHE/24qMZo2zUNzwcn9ueNnoFPahWbNm7Nq1i40bN7Ju3Tpuu+02XnnllYuW+e2334iPj2fIkCEAFBcXM2jQIBITE4mLi2P06NGAqQ+n1q3/d8/ppEmmK8iHDx9Obm4uOTk5rFq1isLCQt5//33A1FfT8ePHGTRoELNmzSIlJYWbbrqJDh06WOPlaw1QmFVIflq+zbZPgC4UdTbtyERKE8uMjqHVU21HAB6uHrXO92/qf9kjiOo4OzsTHR1NdHQ03bt356uvvrpovlKK0aNH89133100fd++fXTt2pWtW7dWu14R+cNjpRTffvstvXv3vmheZGQkAwYMYMWKFVxzzTV8+umnRERE1Pu1aJaXsb/iiicbLhS2eULMBk0dehNtD/lxPve80VGsbmCzOJ4ftt7oGHYhMTGRQ4cOVT6OjY0lNDQULy+vyh5eBw4cyObNm0lKSgJMvc0ePHiQTp06kZGRUVkoSkpK2L9/f+W65s+fD8CmTZvw9vbG29uba665ho8++uhCJ5rs2bMHMA21GhERwaOPPsrYsWPZu3fvRRk025G+37aveAJdKOqswKuQPZ2OEPvDXqOjWFVJYQk7CzpT8TmkXUZ+fj533nknXbp0oUePHsTHxzNz5kxmzJjBtddeS0xMDIGBgXz55ZdMmjSJHj16MHDgQA4cOECTJk1YsGABf//73+nZsydRUVFs2bKlct2+vr4MHjyY+++/n88+M3Va8Pzzz1NaWkqPHj3o1q0bzz//PGAqKt26dSMqKooDBw4wbdo0/P39GTJkCN26ddON2TYkPS4dt+ZueLXxMjpKjfSppzrakbeHpZO+InJJFAMm9zM6jtUc25pKGaG076zfKnXRp0+fiz7cL3jkkUcqxzgBGDFiBDt27PjDclFRUWzYsKHadU+cOJF///vfF01r2rQpb7/9Nl5eF3/IPP300zz99NN/WMfcuXPr9Do068mIy6BFtxZ/OLVoS/QRRR0NGzkQgPisVIOTWFfSVtP50/a99bCdmmZuSinTpbE22nXHBfprYh1FdYuCFXBUGteVT4f3FgDQbnBLg5M0brY+MpzWMPlp+ZzLPmfT7ROgjyjqzNvdG5fC5pzy+MNIrA6tTTt3bgr6jVY9bPuNrGn2KG236YbK1r1aX2ZJY+lCUQ9euS3J8ckyOoZVjf/3ABaeHKi7F9c0C0jbnQYCraJaGR2lVvrUUz08rR7gyI/HKC4opolnE6PjWEVxfjFNmjWO16pp1pa2K42ATgE2/zemjyjq4dqY0bTM9uVMcuM4/VRWXIa3Vxn/GLne6Cia5pBSd6XSurdtn3YCXSjqJcs9izX997Pmq81GR7GKk7tOUURTWrXRbxNNM7f80/nkncyjdR9dKBxKhlcmm677Lyu27b/8wg4gaYvpjtF2PW33RiBNs1eVDdn6iMKx9O7VC4DD5Y3jEtmkPabuHtoPdtwrnubMmUNYWBhOTk6EhYUxZ84cs6w3JiaG1atXA/Dcc8/x6KOPmmW9muO4UCha9bLthmzQjdn1EtI8BMqdSfXIMTqKVSQdLMeNIoL72f43noaYM2cOM2bMqBxQ6NixY8yYMQOAyZMnX9G6X3rpJV544QXS09PZs2cPy5Ytu+K8mmNJ25WGXwc/3L3djY5yWfqIoh5cnV3xyA0ky7txNGYPH+PBMzG/4eTimG+TZ5999g+jzhUWFvLss89e8bqHDx+OUoo33niDefPm4ezsTEFBAXfeeSf33nuv2Y5cNPuVtjvNLk47gQ0VChH5XETSRSSuyjQ/EVktIocq/vU1MiOAf2ELzvmeIvdkrtFRLO6Gl/vzwtpoo2NYzPHjx+s1vT727dtHWloabm5ulf0wLVq0iJtvvplPPvlEH2E0coVZhZw9dtYuGrLBhgoF8CUw5pJpTwG/KKU6AL9UPDbUe5H/5O9fx1CUU2R0FIsqLSrl0OqjlBU77hgcbdu2rdf0ukpLS2Py5MksXboUT09Pfv75ZwBSUlIICQkBTGNWaI1X2i77acgGGyoUSqkNwKWtxOOAC6O+fAWMt2am6vQd1oemxe5kHsg0OopFJa09Tserw5jzcPWD6DiCWbNm4eHhcdE0Dw8PZs2a1eB1FhYWctNNN/H6668TGRnJ888/z8yZMwEIDg4mJSUFgPLy8gZvQ7N/9nTFE4AoGxpoQETCgOVKqW4Vj3OUUj5V5p9RSv3h9JOIzABmALRs2bLPvHnzzJorPz+fZs2aAXA86zj/99H3jMwZxoRXB5h1O1eqas4r9fvH6Tw+71a++vtC2o7xN8s6LzBnzkt5e3vTvn37Oi///fff89JLL5GSkkJwcDAvvvgit956K2AaitSc3/wLCgr461//iru7OwMHDuS2224zy3rNmTMpKYmzZ8+aZV2XsuT/u7lYK+P+mfvJP5jPgLkN+wyxRM6YmJhdSqm+1c5UStnMDxAGxFV5nHPJ/DOXW0efPn2Uua1bt67y9+0p2xUzUf16vGT27Vypqjmv1KzR6xQolXsy12zrvMCcOS8VHx9vtnXl5pr/tVuCOXOac/9dypL/7+ZirYxvR7ytvr/5+wY/3xI5gZ2qhs9Vmzn1VIPTItIaoOLfdIPzEOFrGnf4uGfhZZa0b/GHXAlxPolXkL7ZTtPM6dyZc5xJPkOr3rZ//8QFtl4olgF3Vvx+J7DUwCwA+DX1w/W8Bxk+ZykpLDE6jsUknPYj0ifN6Bia5nBO7TkFQFCfIIOT1J3NFAoR+Q7YCnQSkRQR+RPwCjBaRA4BoyseG0pECDzfknLf4+xbcMDoOBbz0l/zeOIJ3bW4pplb6i7TKJn20pANNnRntlJqUg2zRlo1SB2EeYZw2vMUyVtO0Xtad6PjWMQNL/c3OkKDKaVsevxhW6Vs6MIWR3Zq9ym823rjEeBx+YVthM0cUdiTHx5czHOf3EhQB0+jo1jEsc0prHtjD+dzzxsdpd7c3d3JysrSH3r1pJQiKysLd3fb707C3qXuSrWbG+0usJkjCnvi18oPz0BPMhMc816Khf+XxBPLosm8MRu35m5Gx6mXC/cqZGRkXPG6ioqK7OKD01w53d3dCQ4ONkMirSZFZ4vIPpRNz2k9jY5SL7pQNEBSdhKfjlxM0Ko7GGt0GAtISHQiUDLw7xBodJR6c3V1JTw83CzrWr9+Pb0qegy2ZfaSU/tfQ7Y9tU+APvXUIEopDnbeyha/JpSVOF4XF/GpPkQ2P2l0DE1zOCe2ngCgTf82BiepH10oGiDUJxRRQrFvKgdXJhsdx6xUuSIhP4TIIMfv9FDTrO3E5hP4d/K3q4Zs0IWiQZo4N8G/PBB8k9m9+IjRccwqPT6TM8qXyM66MVjTzEmVK05sOUHIkBCjo9SbbqNooPb+EWT6JnNgh2Pdoe0b5s22z/fTpntHo6NomkPJPJBJ0Zki2g65st6JjaCPKBqoT4c+NC89jxQ5VnfjTZo1of/dXWnT174a2zTN1p3YYmqfsMcjCl0oGui9697j9QP30T6k2OgoZrX8he0seMJxuxbXNKOc2HwCjwAP/Duatzdma9CF4goERAaQkXDl1+vbkrfec+H/Pm5udAxNczjHNx8nZHCIXfYaoAtFAx3OPswTvk/zT/dQkjccMzqO2cSfDSKyZeMYE1zTrKUgvYDsQ9l2edoJdKFoMC83L5J9DpDTIpU93zvGJbJnj58lrbwVkR1KjY6iaQ7FntsnQBeKBgv0CKSpkwf4JhO/zTIjgllbwirTmzmyd1ODk2iaYzm++TjOTZztqmvxqnShaCARob1/O1x8Ezl0pInRccwicVsOAF1iWhobRNMczInNJwjqG4SLu33ekaALxRWI8IvAxfcgSWcDjI5iFtM+HsLJXaeIuMo+D481zRaVFpWStiuN4MH22+GiLhRXYHDIYNrmB9DVJdHoKGYhTkJQ71Y4N3E2OoqmOYzUnamUFZfZ5Y12F+hCcQX+NuRvfBzxH4LPJ1Nyzv6HRX2i73qWPrPN6Bia5lCObz4OQMhg+z1S14XiCgVGBlKuFCe2pRgd5Yrkpebxxq5o9m0/Z3QUTXMoKVtS8Ovgh2cL+x3orN6FQkQ8RUSfmwBOnD3B1UnX8I9uHZn/zD6j41yR35eYOjfsNdR+38yaZmuUMnUEaM+nnaAOhUJEnETkDhFZISLpwAEgTUT2i8irItLB8jFtU6BnIKklJ3HziyMu0b6vfNqz1nSTXa+x9nt4rGm2JutgFoWZhXZ7/8QFdTmiWAe0A54GWimlQpRSLYBhwG/AKyIyxYIZbZa7iztBXkE09/ud+Bz7vD76gj17TaPatY7Sl8Zqmrmc2GzfN9pdUJeLekcppf7QUquUygYWAgtFxNXsyexEhG8ESYFHiS/vRElhCa4e9rkrCoqc6R94BHGyv+FPNc1WHVl7BI9ADwI62fcl9Jc9orhQJETkLamhN6vqCok5ichREdknIrEistOS26qvCN8Izvmfphg3ds9NMDpOg80/Ppgf0voZHUPTHIYqVySvSabd6HaIk/11BFhVfRqz84FlIuIJICJXi8hmy8SqVoxSKkop1deK27ys0RGjGekTzT18BMXnjY5zRez9zaxptuT0vtMUnC4gYnSE0VGuWJ0LhVLqOeA7YL2IbAKeAJ6yVDB7MaXHFL699xuCOU1pgX2OTTH/sS2M8N1DZmKW0VE0zWEkrzZ1FuoIhUKUqtvYyCIyEngOEKA1MFYpZZVbkkXkCHAGUMDHSqnZl8yfAcwAaNmyZZ958+aZdfv5+fk0a9asxvllqoyNt26hib8vgz/qZtZt18flctbkm3sKmHc4mmU//2aVu7IbmtPadE7zsoec5sy498m9nM84T78vzX9K1xL7MiYmZleNZ2yUUnX6AdYCQyt+7w7EAiPq+vwr+QGCKv5tAfwODK9p2T59+ihzW7duXY3zTuefVq4vu6q+Q2coL86qspIys2+/rmrLWZthzWPVoGZ7zRumFg3NaW06p3nZQ05zZSwuLFb/dP+nWvn4SrOs71KW2JfATlXD52p9Tj2NUEptqvh9H3At8M+G1a76UUqlVvybDiwG+ltju3UR4BGAs5MzTdqmkkdzDq4+YnSkeikvLSc2N5xeYdlGR9E0h3F803FKi0ppN7qd0VHMoi433NV0pVMaMLK2Zcyh4k5wrwu/A1cDcZbaXn05iRMRvhGUh5luWNv6rX0NYnRkwwnyaE6v3ro3F00zl+TVyTi5OhF6VajRUcyiLp8Oa0XkERG56B50EWkCDBKRr4A7LZLOpCWwSUR+B7YDK5RSP1lwe/UW4RtBbsAZXChh92/21aB97mwxV/vvpN/1LYyOomkOI3l1Mm2HtKWJp3332HBBXW64OwSUAYtFpDWQA7gDzsAq4E2lVKylAiqlkoGellq/OUT4RPDr0V/pSCL7U32NjlMv3SZ04OcJRqfQNMeRfzqfU7GnGDFrhNFRzKYuhWKwUmqGiNwDtAUCgXNKqRyLJrMjN3S8gRaeLXBu/yvNmroAg42OVGf2fDe5ptmiI7+Y2inbXe0Y7RNQt1NPP4vIVkyngKYBQUCRRVPZmdHtRvPs8GfpPjqM/ONnLlypZRcimmfw9wHrjY6haQ7j8KrDNPVrSqterYyOYjaXPaJQSj0hIhHAeiAcGAt0FZFiIE4pdZtlI9o+pRSn8k9BGJw468XWD/cw+MHeRse6rNNxGaSUBdGq9UGjozQq53PPk3Uwi6yDWZw7cw5VpigvK0eVKVw9XPEJ88EnzAfvUG+HOcfdWCilSF6dTMSoCJycHecCkTqN9K2UShaRUUqpyk8UEWkGGHd3mQ05V3qOoDeCeDzoz3zIazT/eCWDHzQ61eXtWXIMCKRXtI/RURyWUoqsg1kcWnGIwz8f5vTe0+Sfyq/z872CvAiLDiNsRBjhI8LxDbevNrDGJjMhk7zUPIe4G7uqOhUKgKpFouJxPqZuxhs9D1cPWjVrxVn/HMI5wt5kL6Mj1UnsJtMHVtSEcIOTOJ70/ens/nQ3B384yJnDpkunA7sG0n5Me/w7+ePfyZ+ATgF4BHggzoKTsxPiLBTnFZNzLIeco6af9H3pHFl7hH1zTQNj+YT70H1yd3rd3QvfCF00bM3hVYcBx+i2o6o6FwqtdhG+ERzNO0pnlyT2F3Q2Ok6d7IlvQrjLcXxC7Xv0LVuhyhWHfjzEtre3kbwmGWc3ZyJGRjDoL4PocF0HfMJ8LrsONy83vIK8CBn0v/ELlFJkHsjkyNojHFp+iE3/2sTGf24kLCaMXtN7Ud6i3IKvSquPpJVJ+HfyxyfUx+goZqULhZlE+Eaw8dhGJgSc4cdToWQfPoNfO9v+xnfj9YqhGUcwXcymNZQqV+ybu49fX/qV7KRsvNp4MeJfI+hzbx88AjyueP0iQmBkIIGRgfR/qD+5KbnEfhVL7OexLJ66GLcWbjR/qTm9pveySl9dWvXOZZ/jyNojDHpikNFRzM5xWlsMFuETwYncE7TvabriKXbxYYMTXd6UD4fwyIKrjI5h105sPcFngz4zfWA3d2PivIk8duQxhj09zCxFojrNg5sz/NnhPHLoESb/NBm3QDdWPLCCdzu8y86Pd1JWXGaR7Wq1S1yWSHlpOZETI42OYnb6iMJMJkROoJ1fO7pFduaFn1+i3YC7jI5Uq7TY05zPLyF0cBs9DkUD5J7MZfWTq4n7Lo5mrZsx7stx9Jza06r7UpyE9te0J6pJFCHFIax/cT0r7l/Btre2cd0H1xEeo9uerClhYQLebb0J6mvfwyJXRx9RmElUqyim9ZxGhyHtcQJO/37a6Ei1mv3nBCKGBZGbkmt0FLsTNz+OD7t9yIHFBxj23DAeOfgIUXdGGVZwRUwF409b/8SkHyZRVlzG1yO+ZtGUReSfrvsVVlrDnc89z+FVh4mcGIkFu74zjC4UZlKuytl+cjun3E5R5OHDv546iyq33RvvNu/1oof7IbzbehsdxW4UnS1i8dTFLLx9If6d/Ll/7/2M+McImjSzjXsdRISON3TkgbgHGP78cOL/G897nd5j1+xddnUTqD06uOIgZcVlDnnaCXShMKthXwzjk92foHx8WVowmuT1x42OVK3SolK2ZndkSPtTRkexG8c3HeejHh+x77t9XDXzKqZvmo5/B3+jY1XLtakrMS/HcP/e+wnqE8Ty+5Yzb9w8CtILjI7msBIWJtCsdbOLrlZzJLpQmImTOBHuE07ymWSiopsDsP4L2xybYu/CQ+TjxdBo3cdTXeyavYuvYr7CydWJ6ZumE/1iNE4utv+nE9ApgKmrpzLm7TEcXnWYD3t8yKGVh4yO5XCKC4pJWplE5wmdHba9z/bf7XYkwjeC5DPJ9J3WDV+y+XW9bV59snlxOgBD7nCMvvItRZUpVj66kuX3LSdiVAQzds0geGCw0bHqRZyEAY8O4N4d9+LZwpO5181l5aMr9ZVRZpT0UxIlhSV0mdjF6CgWo696MqMI3wg2n9hM8O3B9GQL29Js84P4lhciCQrfSttBjne9t7mcO3OOfU/t48zOMwz880BGvzrarvvuadm9Jfduv5c1T61h29vbSNuVxi0LbsGrtX30ImDLEhYm4BHgQehw2/x7Nwf7fefboAjfCHLP51LYpJAeXsfwkzOczz1vdKw/aNWjBRNf1UWiJmdPnOXzwZ+TE5vDjZ/eyDVvXGPXReICF3cXxrw1hpvn38yp2FPM7jObE1tOGB3LrpWeL+Xg8oN0Gt/JLk5HNpTjvjID3BR5E2unrcXT1ZMRt/gxwXsdTbxs44qYC9JiT/Puzb9yOi7D6Cg2KftwNl8M+4K81Dx6vNqD3n+y/V6A66vrrV25Z9s9uHq48mX0l+z4cIfRkexW8upkivOKHfq0E+hCYVZhPmHEhMfg5uJG8IBgzmWdI+tgltGxLrJ2dhKPLryKtP3ZRkexORnxGXwx7AuK84uZtnYaPlE+RkeymBbdWnDvjntpN7odPz74Iz8+8iPlpbrPqPpKWJiAm7cb4SMc++ZGXSjMSCnFwviFbEvZRvDAYOLowthetnVov3lDGV7k0n1Ce6Oj2JS03Wl8MfwLUHDXr3cR1Mfx7q69VFPfpty+7HYGPTGIHe/tYN74eRTn29eY70YqKSwhYVECncd3dvg+tnShMCMR4YEVD/DZns8I7BpIU6cidpzrZlPXr2863IpB/gcd/o1dH6m7Uvkq5iuaNGvC3RvvpkXXFkZHshonZyeufu1qrvvgOpJWJvHF8C/IPanv1q+L/d/v53zueXr9qZfRUSxOFwozu3CJrJOzE53bFlGKK9u/tY0R5HKOnSWuqD1DeuhuHS5I35/Ot9d8S1O/pty98W782vsZHckQ/R7ox6Tlk8g+lM2nAz7l9D7b7oLGFuz+ZDcBnQNoO9Txe1/WhcLMLhQKgB5jghDK+XVZjrGhKuz74SgAQ6/X3XaAqeH6m9Hf4NzEmalrpuId0rj3S4drO3D3prtBwZfDv+T4ZtvsWcAWpO9P58SWE/S+t7dD9u10KbsoFCIyRkQSRSRJRJ4yOk9tInwjOH72OCVlJbS/ph2RJLBpTzOjYwEw7OGe5JzIZ+h9XY2OYrjclFy+GfUNZcVlTF09Fb92jfNI4lKterZi+pbpeLbw5JtR33BwuW0cDdua3Z/sxrmJMz2n9TQ6ilXYfKEQEWfgfeBaoAswSURs9lq0CN8IylQZJ3JP0GZAG6JZx7AI22nQbh7c3GY6sTNKQUYB34z+hnPZ55jy85RG1SZRFz6hPty96W5adGvBvPHz+P3r342OZFNKzpXw+9e/E3lTpMXGHLE1Nl8ogP5AklIqWSlVDMwDxhmcqUbjO4/n0COHaOvdFq/WXnRoW0q3zsb33FlSWML1LXbw0z93Gh3FUCXnSpg3dh45R3O4Y8UdjeLqpobwDPRk2tpphMeEs+TOJWx9c6vRkWxGwsIEis4U0ftex7vHpiZi690Pi8jNwBil1D0Vj6cCA5RSD1dZZgYwA6Bly5Z95s2bZ9YM+fn5NGvWsNNH8TPjyYnLpeMzkQT0tuw58NpyHluRyV2v3cwbt3xPrweN/QZ9JfvzSqhyRfxL8WRuzKTLzC4EDg+sdXmjctaXJXOWF5eT8K8EMn/NJPSuUEKnhTb4nLw97M+6ZIx9LJbirGL6fd3PsE4ALbEvY2Jidiml+lY7Uyll0z/ALcCnVR5PBd6tafk+ffooc1u3bl29ln9v23tq6YGlSimltry+RbXlqJrQarPZc12qtpwzo9cpoUylx2dYPMfl1Hd/msuqJ1epmcxUW17fUqfljcpZX5bOWVZSppbctUTNZKb6+YmfVXl5eYPWYw/783IZMxIy1Exmqo2vbLROoBpYYl8CO1UNn6v2cOopBajayXswkGpQljp5e9vbzNk3B4A2A9rQi938cqqroTczLd/egkFecQRGBhiWwUg7PtzBlle30O+hfgz880Cj49gVJxcnxn42lv6P9Gfr61tZft9yyssa513cuz/djZOLE1F3RRkdxarsoVDsADqISLiINAFuB5YZnKlWVS+Rbd27NR0kmVy82fhhnCF5UnefYmdhF24Y1Di77Ti08hArH15Jxxs6MuatMY3ickZzEydhzNtjGPrMUHZ/spsl05ZQVtK4uiovOVdC7JexdBrXiWYtbfsUmrnZfKFQSpUCDwM/AwnA90qp/camql2EbwSHsw8DptHGwnt44s45ls3JMyRP9rE8Ynz2cOP9bQzZvpGyDmaxcNJCWvZoycTvJjp0D5+WJiKMnDWSkf8eyb65+1hw2wJKz5caHctqdn28i3NZ5xjw6ACjo1idXfzVKKV+VEp1VEq1U0rNMjrP5UT4RnCm6Axnzp0BoN3IcAaxlWVxEYaMo91tQgfWnulFtwkdrL5tI53PPc+8cfNwdnXmtiW3NfrLgs1l6FNDGfP2GA4sPsD88fMpOVdidCSLKzlXwub/bCYsOsyhx52oiV0UCnsT4RsBwPGzpjtbw0eEM5jNfPNqqtWvkijOLyb78BmrbtMWqHLFoimLyDqUxS3/vQWfUB+jIzmUAY8O4MZPbiTp5yTmXj/X4TsT3P3JbvJP5XPVi1cZHcUQulBYwHUdrqPwmUJ6tjLdtRk6LJQmzoqSM4VWz/LLG7/Tor0Xv31qTPuIUdbPXM/BHw4y5q0xhEWHGR3HIfW+pzcTvpnAsQ3H+ObqbyjKKTI6kkWUFpWy+T+bCb0qtNG+l3ShsAB3F3eaujatfOzW3I2gvkFs+eogzwxeb9UsP3x/DneKiLq58XQrnrAogQ3/2EDU9Cj6PdTP6DgOrcfkHtzy/S2k7jT1wFuQYTs9JZvL7k93k5ea12iPJkAXCot5af1LfLTzo8rHYTFhHD7hyitbh3Nqb7pVMqhyxfID7RjdOg53H3erbNNoWQezWHLXEtoMaMP1H1yvr3CygsibIpm0bBKZBzL58qovHaqb8tKiUja9som2w9o22qMJ0IXCYlYcWsGihEWVj8NHhNNapaJwYsUbiVbJsG/RIU6UteGGqx2/sRFM3ZR8f/P3ODdx5pb/3oKLm4vRkRqN9mPaM+XnKeSm5PLFsC84c8Qx2sV2f7abvJOmo4nG/KVDFwoLaefXrvJeCoC2Q9ri5lxOiJxg2c/Wufpm+WzTfYnXPd7RKtszklKKFQ+uID0unZvm3NTouww3QujwUKb9Mo2inCK+GPoF6futc+RsKaXnS9n8ymZChoQ4/FCnl6MLhYVE+ERw7OwxSstN15m7ergSMjiEYe47WX2qO+eyz1k8wx0vtOfr+zbROqqlxbdltD2f7+H3r35n+PPDaX9N42mPsTVt+rXhrl/vQinFF8O+IOW3FKMjNdimVzaRm5JL9EvRjfpoAnShsJgI3whKy0tJyf3fH0r4iHCCzx0ivEkqx7elWTxD2NBgpn401OLbMdqp2FP8+NCPRIyK4KoXGm+Do61o2b0l0zdPx8Pfg69Hfk3ST0lGR6q39P3pbJy1ke53dCdiZITRcQynC4WFRPhGEOARQEZBRuW0sJgwmlLIov+W0elay7751r8Vy9yHNlNa5Nh3zp7PPc/3N3+PR4AHN829CSdn/Za2Bb7hvty96W78O/nz3Y3fsW/uPqMj1Vl5WTk/3PMDbs3duOata4yOYxP0X5WFRIdFk/FkBv3a/O/yzOCBwbi6u3Jk7RHyT+VTUmi5RubnXnDixU/a4NzE2WLbMJpSiuX3LyfnSA4Tv5uIZ6Cn0ZG0Kpq1bMad6+6k7dC2LJq8iBPzTlzoAdqm7Xh/Bym/pTDm7TH6PVVBFwoLqe6cpoubCyFDQti/NIk2rctY+NQOi2z79+8T2ZzXgwevO2pYf/nWEPtFLHHfxRH9UjShwxpftwr2wN3bnckrJ9P1tq4kf5zM8vuW23RngkWnivjlmV9of217ut/R3eg4NkMXCgt6/KfHefaXZy+aFj4inNyjmbRwOcO7X1qmB8oPXjxNUwq5680oi6zfFmQkZPDjwz8SPiKcoU87fjuMPXNxd2Hi3Im0ndyW3Z/sZu71cyk6a3t3cSulOPjGQUSEGz66odE3YFelC4UFJWQmsDp59UXTwmLCcEKY2msfW/J6sHtOglm3efb4Wb490Ic7Ou7CN9zHrOu2FSXnSlhw6wKaNGvChG8m6HYJOyBOQvg94Yz9fCxH1x3l88GfcybZtu612PHBDs7sOMPIf4/Eu62+vLoq/RdmQRE+ERw+c/iiaUF9g2jSrAndOpXiST7vzsw06zaPbT9NaJNTPPiC4w5Q9PNffiY9Lp0JX0/AK8jL6DhaPfS6uxdTVk0hLzWP2X1mc3D5QaMjAZD4QyI/PfoTfgP96Peg7vblUrpQWFCEbwTZ57LJKcqpnObs6kzo8FBSt59kWtfdfJfUjzNHcmpcR331uLkj+89F0HtypNnWaUsSFiWw66NdDPrrINqP0fdL2KPwmHBm7JqBb4Qv3934Hb888wvlpcaNmHdy+0kW3r6Q1r1b0+WFLg7drtdQulBY0IXuxo+cOXLx9KsjyDqYxf3PBbD5myNmO0V09kA+BekFDvtGz03JZdk9y2jdpzUjZ400Oo52BXwjfJm+eTq97+3Npn9v4purvyH/dL7Vc2QfzmbuDXPxbOnJpOWTcG7quFcJXgldKCyoo39HerXqRVHpxQ13ncd1BiD/ZA59ppjvm//s55oTFZxhyOBIllZeVs7iaYspKy5j4tyJDn3Zb2Ph4u7CjbNvZNyX40j5LYUPun7A3jl7rXYJbWFmIXOunYMqV0z5aUqjG960PnShsKDuLbuz+77dDAoZdNF0nzAfWvZoSeLSRHKOneWu9ptY+sy2K9pWyo40fsoawsTejnlJ7JZXt3B03VGuffda/Dv6Gx1HM6OoO6OYsWsG/h38WTxlMd/d+B25KZbtgfbU76f4bNBn5J7IZdKySfo9dRm6UBik07hOnNh8AmdXJ349FsobH7hd0frefzQRhXDf/7UzU0LbcXL7SdY9v46ut3Yl6q4oo+NoFhAYGcjdm+7mmjev4cjaI3zQ9QO2v7fdImNy7/l8D58N/IzigmKmrJpCyOAQs2/D0ehCYWF/WvonJi2c9IfpncZ1QpUrDq86zMNjDrPhbBTLX9jeoG3Ezk/k9d8GM6HlOsKHO9ab/nzeeRbesRCvIC+u/0iPL+HInJydGPj4QB7Y9wBBfYNY+chK3uv4Hrtm76Ks+Mpv0ispLGHp3UtZ9qdlhAwO4b499+kbNetIFwoLyy/JZ2fqzj9Mb927Nc2Dm5O4NJGH5wyip3sid/8zokGDGi18Lw1/pzNMf/W8OSLblJ8e/YmcIzlM+HYCTX2bXv4Jmt3za+fH1DVTmfLzFLyCvFh+33Le6/QeOz/aSWFW/YcTPnfmHFte28L7ke8T+1Usw58fzpRVuk2iPnShsLAInwiO5hylrPzib0QiQsexHTm86jBOrk7Mne9MvvLkyfH1v678Hxujif3dCc8QD3PFtgn7v99P7JexDHt2mP7m18iICO2ubsf0LdO548c78Aj0YMUDK3it5Wt8Peprdny4g7zUvBobvksKS0jdmcqKB1fwZvCbrH5yNT7hPkxbM42Yl2P0TZr1ZNNDgInITOBe4EIXrM8opX40LlH9Ve1uPNTn4g+7zuM6s/ODnSSvSabL2E4semkHfW/pXOd17/gqHk/fJnQZ256W3QJJWG/m8AY6e+Isy+9bTpsBbRj+/HCj42gGERE6XNuB9mPak7Y7jYSFCSQsTODHB3/kxwd/xNXDlebBzWke3BzPFp7kpeWRnZRN3sk8AJzdnOl+R3cGPDqAVlGtDH419sumC0WFN5VSrxkdoqEu3EuRfCb5D4Ui9KpQmng1IXFpIp1u7MS1L5juCC0tKuXUvgyC+7Wucb15qXncdk8zmjoXsy+/HCcXx/mGVF5WzuKpiykvLeemOTfh7KovhW3sRISgPkEE9QlixKwRZMRnkLw6mbMnzpKXkkduSi4nt5+kWetmRIyKwK+DH37t/QgfEa57gDUDeygUdq1TQCfGdhpLU9c/nl93cXOhw7UdOPjDQcrLyisPh29vv4P4jBb8su10taPTnY7L4KExSRwtHcCGt+McqkgAbHltC8d+Pca4L8bh187P6DiajRERWnRtQYuuLYyO0miILfcPX3Hq6S4gF9gJPKGU+kNPYiIyA5gB0LJlyz7z5s0za478/HyaNbNMw9fpNac5MOsAUe9G4d3N1BFZ4ncZPDx7PE6UM77Nr4y7J5+gaNMH5qJHc/h039Wcx42/9F3K9a/+74PUkjnNqbaceYl57HloDwHDAoh8IdLQq5wcYX/aEnvIaQ8ZwTI5Y2Jidiml+lY7Uyll6A+wBoir5mcc0BJwxtToPgv4/HLr69OnjzK3devWXfE6SstKq51+7sw59bLLy2rV31ZdNP3QmqPq4e7rlQf5CpSa9+hmpZRSf+u/Tk2N2KgOrjpikZzWUFPO83nn1Tsd3lFvBL+hCrMLrRuqGva+P22NPeS0h4xKWSYnsFPV8Llq+KknpdSouiwnIp8Ayy0cxyImLZzEkTNH+O2e3/4wz93HndCrQklcmsjo/4yunN5+ZCjv7g3lpcNn+PSRHVz7ZG8AXtl6lUPeeQ2w8rGVZCdlc+e6O/WlsJpmQ2z65LaIVG3NnYDpSMPueLt5k5Rd8wDzncd3Jisxi/S4P95D4dfOl7/9GE3z4OYADlsk9v93P7GfxzL06aGEXRVmdBxN06qw6UIB/J+I7BORvUAM8GejAzVEhG8EWeeyOFt0ttr5XW/ripOLE3u+2GPlZLbh7PGzLJ+xnDb92xA9M9roOJqmXcKmC4VSaqpSqrtSqodSaqxSKs3oTA1R2d14zpFq53sGetLxxo7s+3afTY8nbAkXXQo7V18Kq2m2yKYLhaOoei9FTaLujqIgvYBDPx6yViybsOnfmzi24RjXvX+dvhRW02yULhRW0N6vPQ/1e4i23m1rXKbDtR3wbOlJ7Bex1gtmsOObjrN+5nq6TepGj6k9jI6jaVoNDL/qqTFo7tac9657r9ZlnFyc6DmtJ7+9+Rv5p/MdvsOyc9nnWHjHQnxCfbjhoxt0r7CaZsP0EYWVlJSVcCr/VK3LRN0dRXlpOXu/3WulVMZQSrHsT8vIP5XPzfNvxq35lY3FoWmaZelCYSVTFk9h+Be1d24XGBlImwFtiP0i1mrDQRohdUkqB5YcYNQrowjqG2R0HE3TLkMXCiupqbvxS0XdHUXG/gxSd6ZaKZl1nYo9xeEPD9Phug4MfHyg0XE0TasDXSisJMI3gpLyEk7mnax1uW63d8PF3cUhG7XP555nwW0LcG3uyrgvxznszYOa5mh0obCSulwiC+Du7U7kxEj2zd1HybkSa0SzCqUUy+5ZRvbhbCKfi9RdP2uaHdGFwkrqWigAek3vxfmz54n7zi57LKnWtne2Ef/feEb+ayQ+UT5Gx9E0rR50obCSEO8Q/j3y3/QL6nfZZcNiwmjVqxWbXtlEeVm5FdJZ1omtJ1j919V0GteJwU8ONjqOpmn1pAuFlbg4ufDU0Kfo3rL7ZZcVEYY9M4zsQ9nEL4i3QjrLKcgoYMGtC/Bu6834L8fr+yU0zQ7pQmFFp/JPsSt1V52WjbwpkoDIADbO2ogqt89LZctLy1l0xyIKMgq4ZcEtuPu4Gx1J07QG0IXCimaun8mYOWPqtKw4CUOfHkr6vnQOLj9o4WSWsfpvq0lek8z1H1xP6141j/+taZpt04XCiiJ8I8gszCT3fG6dlu8+qTs+4T5smLXhohvw7OEIY8/ne/jtzd/o/2h/ek3vZXQcTdOugC4UVlTZ3fiZ6rsbv5STixNnXAJJ3Z7K4VWHAVOR+HOfDcyMXm+pmFfs+ObjLL9/ORGjI7jm9WuMjqNp2hXShcKK6nOJLJiKQk7T1uTixZcTl1cWibdjryLnrNjkkcXZ42f5/qbv8Qn14eb5N+Pkot9immbv9F+xFdW3UIiT8OaeaFyCWuBacJYw5xO8HXsVj0X9ypu7htvcnc3F+cXMGzeP0qJSJv0wSY97rWkOQhcKK/Jx92HexHmM7zy+zs8RJ+EfibeSRzOuZSVOlNtkkSgrLmP+TfM5ve80E+dNJKBzgNGRNE0zE10orOy2brfRzq9dnZdX5Yq/DdvKj1xLa04xkK38uc8GmzrtpMoVS+5aQvLqZG785EY6XNvB6EiappmRLhRWdiDzAEsOLKnTslXbJK7umU6nsZ0YLWv5Ora7zRQLpRQ//fkn4r6LY+QrI+l1t77CSdMcjS4UVvZV7Ffc+t9bL9vdOJhOO/l4K1ObxO6ruO6D63Br5sKDzb7Bp3m5TZx+2vTvTWx/ZzsD/zKQIX8bYnQcTdMsQBcKK6trd+MXzFwfXdkm0bxNc0b9ZxSu+TmMn+5r4aSXt+2dbax9di09pvTg6lev1t1zaJqDMrxQiMgtIrJfRMpFpO8l854WkSQRSRQRh7ggv75XPgEXHTn0va8vIUNCWPWXVRSkF5g9X11t/NdGfnrsJyJvimTs52Nt4uhG0zTLMLxQAHHATcCGqhNFpAtwO9AVGAN8ICLO1o9nXg0pFFWJk3Dj7Bs5n3eepdOXUl5q3d5llVKseXqN6Uhiag9unn8zzq52/9+iaVotDC8USqkEpVRiNbPGAfOUUueVUkeAJKC/ddOZX4h3CM7i3OBCARDYJZAxb43h0IpDLH9gudXG11blipWPrGTzK5vpc38fxn85Xt9Qp2mNgFjrQ+ZyRGQ98Fel1M6Kx+8Bvymlvq14/BmwUim1oJrnzgBmALRs2bLPvHnzzJotPz+fZs2amW198bnxBLkH4dPE54rWc+SzIxz/9jhtp7YlfHq42XNWVVpQSuKriWT+mknwbcFE3BfR4DYJS+Y0J53TvOwhpz1kBMvkjImJ2aWU6lvdPBezbqkGIrIGaFXNrGeVUktrelo106qtakqp2cBsgL59+6ro6OiGxKzR+vXrMec6ozHPuq666ip+cPuBPZ/todvAbtAFs+a8ID0une/v+57sw9mMfm00g/4y6Ioars29Py1F5zQve8hpDxnB+jmtUiiUUqMa8LQUIKTK42Ag1TyJjLXj5A42Ht/IXwb95YrWIyLc8NENFGYU8uPDPxL5XCRmqkGV9n67l+X3LcetuRt3rr2T0OGh5t2Apmk2z5ZPMC8DbhcRNxEJBzoA2w3OZBZrj6zliVVP1Lm78do4uTgx8buJhAwOIeEfCax8dCUlhSVXvN681DyW3LmExVMXE9Q3iBm7Z+gioWmNlOGFQkQmiEgKMAhYISI/Ayil9gPfA/HAT8BDSqnL36VmB+rb3fjluHq4MnX1VNpMbMP2d7fzce+PObmjbvdpXKo4v5h1L67j3Q7vEjcvjqHPDGXaL9Pwau1llqyaptkfq5x6qo1SajGwuIZ5s4BZ1k1keRf6eko+k0zPVj3Nsk7Xpq60f7g9Ix4YwdK7lvLZoM8Y/ORgev+pN37t/S77/NyUXOIXxrPp35soOF1A19u6MvJfI/GNMP7GPk3TjGV4oWiMrvReilrXPTKCB/Y9wE+P/cTmVzaz+ZXNtOjegs4TOtPhug408WxCeVk5qkxRnF/MkbVHSFyWyKk9pwAIGRLC7UtuJ3hgsNmzaZpmn3ShMICPuw++7r4WKRQA7j7ujP9qPNEvR3Ng8QEOLD7Ahn9sYMPLG/64sEDIoBBGvjKSTjd2IiAyQHfFoWnaRXShMEjcg3G08Gxh0W34hPow8PGBDHx8IAXpBRzfdJzysnKcnJ0QZ8HZ1ZmgfkF4BnpaNIemafZNFwqDBHkFWXV7ni08ibwp0qrb1DTNMRh+1VNjteHYBh5c8WCduhvXNE0zki4UBknMTOTDnR+SkptidBRN07Ra6UJhEEte+aRpmmZOulAYRBcKTdPshS4UBjFHd+OapmnWoAuFQVycXIjwjeBM0Rmjo2iaptXKZsajMBcRyQCOmXm1AUCmmddpCTqneemc5mUPOe0hI1gmZ6hSKrC6GQ5XKCxBRHbWNKCHLdE5zUvnNC97yGkPGcH6OfWpJ03TNK1WulBomqZptdKFom5mGx2gjnRO89I5zcsectpDRrByTt1GoWmaptVKH1FomqZptdKFQtM0TauVLhR1JCL/EJG9IhIrIqtExLr9hNeRiLwqIgcqsi4WER+jM1VHRG4Rkf0iUi4iNnU5ooiMEZFEEUkSkaeMzlMTEflcRNJFJM7oLDURkRARWSciCRX/348Znak6IuIuIttF5PeKnC8ZnakmIuIsIntEZLm1tqkLRd29qpTqoZSKApYDLxicpyargW5KqR7AQeBpg/PUJA64Cahm2D3jiIgz8D5wLdAFmCQiXYxNVaMvgTFGh7iMUuAJpVQkMBB4yEb353lghFKqJxAFjBGRgcZGqtFjQII1N6gLRR0ppXKrPPQEbPIqAKXUKqVUacXD3wCbHPxaKZWglEo0Okc1+gNJSqlkpVQxMA8YZ3CmaimlNgDZRueojVIqTSm1u+L3PEwfcG2MTfVHyiS/4qFrxY/N/Y2LSDBwPfCpNberC0U9iMgsETkBTMZ2jyiqmg6sNDqEnWkDnKjyOAUb/GCzRyISBvQCthkcpVoVp3RigXRgtVLKFnO+BfwNKLfmRnWhqEJE1ohIXDU/4wCUUs8qpUKAOcDDtpqzYplnMR32z7HlnDZIqplmc98s7Y2INAMWAo9fcnRuM5RSZRWnloOB/iLSzeBIFxGRG4B0pdQua29bj5ldhVJqVB0XnQusAF60YJwaXS6niNwJ3ACMVAbeKFOP/WlLUoCQKo+DgVSDsjgEEXHFVCTmKKUWGZ3ncpRSOSKyHlP7jy1dKDAEGCsi1wHuQHMR+VYpNcXSG9ZHFHUkIh2qPBwLHDAqS21EZAzwd2CsUqrQ6Dx2aAfQQUTCRaQJcDuwzOBMdktEBPgMSFBKvWF0npqISOCFKwRFpCkwChv7G1dKPa2UClZKhWF6X661RpEAXSjq45WK0yZ7gasxXXlgi94DvIDVFZfyfmR0oOqIyAQRSQEGAStE5GejMwFUXAjwMPAzpobX75VS+41NVT0R+Q7YCnQSkRQR+ZPRmaoxBJgKjKh4P8ZWfCO2Na2BdRV/3zswtVFY7fJTW6e78NA0TdNqpY8oNE3TtFrpQqFpmqbVShcKTdM0rVa6UGiapmm10oVC0zRNq5UuFJqmaVqtdKHQNE3TaqULhaZZQcWYDKMrfv+niLxjdCZNqyvd15OmWceLwMsi0gJTD6pjDc6jaXWm78zWNCsRkV+BZkB0xdgMmmYX9KknTbMCEemOqT+h87pIaPZGFwpNszARaY1pXJBxQIGIXGNwJE2rF10oNM2CRMQDWIRp3OgE4B/ATENDaVo96TYKTdM0rVb6iELTNE2rlS4UmqZpWq10odA0TdNqpQuFpmmaVitdKDRN07Ra6UKhaZqm1UoXCk3TNK1W/w8H5U0wrcDPmwAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEWCAYAAAB42tAoAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAABK2ElEQVR4nO3dd3gVZdrH8e+dSjqQ0EPvLQRCr0FBQA0iiqKoiG3VVbHsurqoL7sra0dlRd1dsYKCYsGAgqKhSgsdAiR0A6EFQnp/3j/OIZtAEgKckzlJ7s915eKcmTkzvzMhc888M/OMGGNQSimlyuJmdQCllFKuTQuFUkqpcmmhUEopVS4tFEoppcqlhUIppVS5tFAopZQqlxYKdQERSReRVlbnuBTOyiwig0Rkj6Pn60gi0kJEjIh4WJ1FVU9aKGowETkoIln2jey5n8bGGH9jzP7LmF+kiCReZJqPRSRXRNLsPztE5CURCbr8bwKXm7mUfEZE2hSb70pjTPsrna+VRGSgiPwmImdF5LSIrBaRXlbnqgj7/9FhVueo6bRQqCj7Rvbcz9HyJhYRdwcs81VjTABQD5gE9AVWi4jfpc5I96LLJyKBwELgX0BdoAnwNyDnMuYlIuJ23jBd/zWAFgp1geJ71fYjgPdE5AcRyQCGisi1IhJnPyI4IiJ/sm/kfwQaFz86KW85xphsY8wGYDQQjK1onMtwj4jsEpEzIrJERJqfl++PIpIAJBTPLCJ9ReRY8YImIjeKyDb7694iskZEUkQkSUTeEREv+7gV9o9stee/tfhRkog8IyLzz1tXb4vIDPvrIBGZZZ/vERF5sazCWl6OYt/nQRFJsK+DmSIi9nHuIvK6iJwSkf3AdeWs5nb2df2FMabAGJNljPnJGHNufUwVkdnFlluiGUtElonINBFZDWQCrcpY//eLyF77Ecv3xX/3InKNiOyxH9G8KyLLReQ++7jWIvKriCTbv88cEaltH/cZ0AyItv8+nrYP72s/QkoRka0iEllsWXeLyH77/80DIjKhnHWjKsoYoz819Ac4CAwrZbgB2thffwycBQZg27GoBSQBg+zj6wA97K8jgcSLLPNj4MVShn8KzLO/HgPsBToCHsBzwG/n5fsZ2x6yTymZ9wHDi03/FfCM/XUEtiMYD6AFsAt4vLTvfv53Appj21gG2t+729dFX/v774B/A35AfWA98Icy1kNFciwEamPbWJ4ERtrHPQjsBpra10GMfXqPUpYTCCQDnwCjgDrnjZ8KzC72vkXxeQHLgMNAZ3tWz/PXP3AVcAroAXhjO3pZYf98CJAKjLV/fjKQB9xnH98GGG7/XD1gBfBWWf9HsR0RJQPXYvv/ONz+vp59vacC7e3TNgI6W/13Vh1+9IhCfWffM0sRke/KmGaBMWa1MabQGJON7Q+9k4gEGmPOGGM2OSDHUWwbHoA/AC8ZY3YZY/KBfwLhxY8q7ONPG2OySpnXF8BtACISgG2j8gWAMWajMWatMSbfGHMQ24Z9SEUCGmMOAZuwFTKwbSAzjTFrRaQBtg3x48aYDGPMCeBNYHwZ86pIjpeNMSnGmMPYikG4ffgt2DamvxtjTgMvlZM5FRiIbeP+X+CkfY+/QUW+s93Hxpid9qx59mHF1/8E4ENjzCZjTA7wLNBPRFpgW/c7jTHf2H+XM4BjxfLtNcb8bIzJMcacBKaXsh6KuwP4wRjzg/3/489ArH05AIVAFxHxMcYkGWN2XsL3VGXQQqHGGGNq23/GlDHN7+e9vwnbH+YhezNCPwfkaAKctr9uDrx9roDZh4t9mrIyFfc5MFZEvLHtyW6yb+QRkXYistDePJWKrQiFXELOz7EXIeB2+/tzmT2BpGK5/43tyOICFcxxrNjrTMDf/roxJb//ofIC2wvu3caYUKCL/fNvlfeZ85S2rosPa1w8gzEmHdtefpPzsxpjDFB0wYOI1BeRufamulRgNuX/PpoD44rt3KRgK4SNjDEZwK3YjriSRGSRiHS4hO+pyqCFQlVEiS6GjTEbjDE3YNsIfgd8Wdp0FSUi/sAwYKV90O/YmmxqF/vxMcb8Vlam8/LFYdtwjaLkxhzgPWzNNm2NMYHAX7EVoYr6CogUkVDgxmLz/h3bCeKQYpkDjTGdy5jPleRIwtbsdE6zioY3xuzG1vzXxT4oA/AtNknD0j52kWFHsW3AARDb+apg4Ig9a2ixcVL8PbajIQOE2dfDHZRcD+cv+3fgs/P+b/gZY162f78lxpjh2JqddmM7ilJXSAuFuiQi4iUiE0QkyN4MkQoU2EcfB4Klgpe6ioi3iERgKzZngI/so94HnhWRzvbpgkRk3CVG/Rx4DBiMbeN+ToA9c7p9b/Oh8z53HCjzfgx788gye9YDxphd9uFJwE/AGyISKCJu9hO1ZTWjXCxHeb4EHhORUBGpAzxT1oQi0kFEnrIXNkSkKbYjorX2SbYAg0Wkmf339uwl5Djnc2CSiITbj+L+CayzN6ktArqKyBj7CfI/UrIYBQDpQIqINAH+fN68z/99zAaiRGSE/aR+LbFdcBAqIg1EZLS9UOXY51uAumJaKNTluBM4aG8qeBDbXuC5vdUvgP32ZoGyrnp6WkTSsDUpfQpsBPrbmw4wxnwLvALMtS9jB7ajg0vxBbYT0b8aY04VG/4nbEcZadj2Nued97mpwCf2/LeUMe/PsR0BfX7e8LsALyAOW+Gbj23PtjQXy1Ge/wJLgK3Yzpl8U860aUAfYJ3Yrlpbi219PgVgb+OfB2zD9ntYeAk5sM/jF+B54GtsRxCtsZ+bsa/7ccCr2JqjOmE7p3Du8ty/YTsJfhZbUTn/u7wEPGf/ffzJGPM7cAO2I7CT2I4w/oxtW+Zm/15Hsf3fGgI8fKnfR11IbE2GSinlfGK7DyMRmGCMibE6j6oYPaJQSjmVvZmotr1Z6ty5mLUX+ZhyIVoolFLO1g/bvS2ngChsV9qVdlmzclHa9KSUUqpcekShlFKqXNWuQ6+QkBDTokULh84zIyMDP79L7q+u0mlOx9KcjlUVclaFjOCcnBs3bjxljKlX6kgr+g1x5k9ERIRxtJiYGIfP0xmcmfPJiBjz6xubHDIvXZ+OpTkdpypkNMY5OYFYo309qcu179dDTN8YybZVqVZHUUpZQAuFuqjofx0EIOqxltYGUUpZQguFuqjo5QF08t5Lq8gKdymklHKQ1a+tZuVLKy8+oRNVu5PZyrHOHj7LijNdearPamyPDnBteXl5JCYmkp2dfcXzCgoKYteuXQ5I5VyOylmrVi1CQ0Px9PR0QCrlCKbQsPbNtYT2Cb34xE6khUKV6+DaY7Ty9CJqYt2LT+wCEhMTCQgIoEWLFtg6Kr18aWlpBAQEOCiZ8zgipzGG5ORkEhMTadlSmxhdxeHVh0lPSqfTLZ0szaGFQpWr2y3t2XOLbc+mKsjOznZIkahpRITg4GBOnjxpdRRVTNxXcbh7u9Pu+naW5tBzFKpMhfmF5GXaHmgmblVnw6tF4vLoenMtptCw6+tdtB3VFu8Ab0uzaKFQZVr13nbq+2ewbtYOq6MoVeP8/tvvpB1No9M4a5udQAuFKsfCz86QYXzpOEKvdlKqsu38aqet2SnK2mYn0EKhyhG9tSmRdbcTGBpodZQqZcaMGXTs2JEmTZowderUouFvvfUWn376abmfHT9+PAkJCU5OqFydKTTsmu8azU6ghUKVIeHng+zObU3U0HSro1Q57777Lj/88APTpk0rGpafn8+HH37I7bffXu5nH3roIV599VVnR1QuzpWanUCvelJliH7nINCCqMdbWx3lsi1+fDHHthy77M8XFBTg7u5eYljD8IaMfGtkmZ958MEH2b9/P6NHj+aOO+7A398fgF9//ZUePXrg4eFBfn4+/fr147XXXiMyMpJnn30WNzc3pk2bxqBBg7j77rvJz8/Hw0P/PGsqV2p2Ai0UqgxDxzfk5dxltBgYaXWUKuX9999n8eLFxMTEEBISUjR89erVREREAODh4cHHH3/MzTffzIwZM1i8eDHr1q0DwM3NjTZt2rB169ai6VXNcq7Zqc3INi7R7ARaKFQZut/Wge63dbA6xhUpb8+/Ihx5w11SUhIdO3Yset+5c2fuvPNOoqKiWLNmDV5eXkXj6tevz9GjR7VQ1FC/r3GtZifQcxSqFJvm7GLZW1sozC+0Okq14ePjc0G3Itu3b6d27docP368xPDs7Gx8fHwqM55yIedusmsf1d7qKEW0UKgLvD7lNLc82aTK3I1dFXTs2JG9e/cWvf/mm29ITk5mxYoVPPbYY6SkpBSNi4+Pp3PnzhakVFYzhYa4+XG2ZqdA12h2Ai0U6jx5mXn8eLgz17XejbuX+8U/oCpk1KhRrFixAoBTp07xzDPPMGvWLNq1a8cjjzzC5MmTATh+/Dg+Pj40atTIyrjKIgeXHyTtSBpdbutidZQSXOochYi4A7HAEWPM9SJSF5gHtAAOArcYY85Yl7D6W/2fnaSYcKJu1B5EL9fBgwcvGNa8eXOCg4NJSEigbdu2xMfHF4177LHHil5//vnn/OEPf6iMmMoFbZu9DS9/L5dqdgLXO6KYDBTvL/kZ4BdjTFvgF/t75UTRs1PwIodrnnStPZrq4OWXXyYpKancaWrXrs3EiRMrKZFyJfnZ+eyav4uON3XE09e1dtRcplCISChwHfBBscE3AJ/YX38CjKnkWDXOyt31GBq8Hf+G/lZHqXbat2/P4MGDy51m0qRJev9EDRW/MJ6c1By6TuhqdZQLiO2Z2tYTkfnAS0AA8Cd701OKMaZ2sWnOGGPqlPLZB4AHABo0aBAxd+5ch2ZLT08vunHKlTkiZ0F2ARmJ2QS28XNQqgs5c30GBQXRpo1jHrBU2g13rsiROffu3cvZs2cdMq/zVYW/Iysz7nh+B2lxafT9si/iXn5Pvs7IOXTo0I3GmJ6ljjTGWP4DXA+8a38dCSy0v045b7ozF5tXRESEcbSYmBiHz9MZNKcxcXFxDptXamqqw+blTI7M6cj1d76q8P/TqoyZyZnmH17/MIufWFyh6Z2RE4g1ZWxXXaXpaQAwWkQOAnOBq0RkNnBcRBoB2P89YV3E6m9S25W8PXa51TGUqnHi5sdRkFvgks1O4CLnKIwxzxpjQo0xLYDxwK/GmDuA74FzZ/YmAgssiljtnd53hs/29uPkCddoiqzKRISnnnqq6P3rr79eohfZy7FlyxZ++OGHK0ymXNX2OdsJ6RBCox6ueVm0SxSKcrwMDBeRBGC4/b1ygh/fiKMAD6ImhVx8YlUub29vvvnmG06dOuWweWqhqL5SDqVwaMUhuk7o6rJPGXS5QmGMWWaMud7+OtkYc7Uxpq3939NW56uuohcK9eUkvSa6Tv8yVZWHhwcPPPAAb7755gXjTp48yU033USvXr3o1asXq1evBqBr166kpKRgjCE4OLjouRV33nknP/30Ey+88ALz5s0jPDycefPmcfr0acaMGUNYWBhXXXUV27ZtA2Dq1Kncc889REZG0qpVK2bMmFF5X1xdlh1f2J4g2fV212x2Ahe74U5ZIy8zj8W/d2Zs2224eQyyOo5jRUZeOOyWW+DhhyEzE6699sLxd98Nd9+NJCdDVFTJccuWVWixf/zjHwkLC+Ppp58uMXzy5Mk88cQTDBw4kMOHDzNixAh27drFgAEDWL16Nc2bN6dVq1asXLmSu+66i7Vr1/Lee+/x97//ndjYWN555x0AHn30Ubp37853333HwoULueuuu9iyZQsAu3fvJiYmhrS0NNq3b89DDz2Ep6drXZevbIwxbJu9jab9m1Kn1QUXdLoMLRSKlENnubb5HsbdUcvqKNVGYGAgd911FzNmzCjRwd/SpUuJi4srep+amkpaWhqDBg1ixYoVNG/enIceeoj//Oc/HDlyhLp165Z6GeSqVav4+uuvARgyZAjJyclFl7Ved911eHt74+3tTf369Tl+/DihoaFO/sbqchzbfIyTO09y7bul7LC4EC0UinodQ/j8YDU9N1HeEYCvb7njTXBwhY8gSvP444/To0cPJk2aVDSssLCQNWvWXNA77ODBg5k5cyaHDx9m2rRpfPvtt8yfP59Bg0o/wjOl3P90rn3b2/t/ncm5u7uTn59/2d9BOdfmDzfj7u1Ol/Gu3ROCy52jUJXLFBr2/XrI6hjVUt26dbnllluYNWtW0bBrrrmmqPkIKGouatq0KadOnSIhIYFWrVoxcOBAXn/99aJCERAQQFpaWtHnBg8ezJw5cwBYuXIlISEhBAbqs82rkrysPLbP2U7HsR3xqePa3cproajh9iw+QJurm/PpA6usjlItPfXUUyWufpoxYwaxsbGEhYXRqVMn3n///aJxffr0oV0726MvBw0axJEjRxg4cCAAQ4cOJS4uruhk9tSpU4vm83//93988sknqKpl93e7yU7Jpvu93a2OclHa9FTDRc88DLQiclJLq6NUG+np6UWvGzRoQGZmZtH7kJAQ5s2bV+rnPvvss6LX/fv3p7Dwfw+Oqlu3Lhs2bCgx/YIFttuKij+J7/z7NXbs2HF5X0I53eZZm6ndojYth7r+354eUdRw0avq0K3WHpr1a2J1FKVqjJSDKRz45QDhk8IRN9e8d6I4LRQ1WHLCaVandiGqZ/ldXyulHGvzR5tBIPzucKujVIgWihrsx+m7KMSdqHvqWR1FqRqjsKCQLR9tofXw1gQ1C7I6ToXoOYoa7PpnujCv1m/0vLOv1VGUqjEO/HKA1N9TGf7acKujVJgWihqsdvMgbnmzv9UxlKpRNn+4GZ+6PnQY08HqKBWmTU811MbZu3gjahmpialWR1GqxshMzmT3t7vpOqErHt5VZz9dC0UN9dkbJ5iysC/uXq7/BLeqprQuN6ZOnYqIsHfv3qJhb775JiJCbGxsZcZTFtr66VYKcguqxL0TxWmhqIFMoSF6Rwuurrcdv/rOe+SpKqlr164Uf0zv/Pnz6dRJe+utKUyhIfa9WEL7hdKwW0Or41wSLRQ10K6F+9if35yoYVlWR6lRxowZU3ST3P79+wkKCqJePb3irKbY/8t+Tiecptcfe1kd5ZJVnUYy5TDR7yUCbbj+ibZWR3G6K+hlnORkudxexksVGBhI06ZN2bFjBwsWLODWW2/lo48+uvwZqiplw8wN+Ib40unmqncUqUcUNdDRJKG33w5Ce7nmYxers/HjxzN37ly+++47brzxRqvjqEpy9vBZ4qPj6X5f9yp1EvucqpdYXbG3twwhP7tmdD19Bb2MExxsrugIojRRUVH8+c9/pmfPntrbaw2y8T8bMcbQ88GeVke5LFooapjC/ELcPNzwqKW/eiv4+PjwyiuvFPUSq6q//Jx8Nv13E+2ub0ft5rWtjnNZdGtRw9zRZg3GCF8c0hvtnCUzM7PEE+WefPLJEuPHjx9f2ZGUhXZ9s4uMExn0erjqncQ+RwtFDZKbnsvCQ10Z32GL1VGqteLdg1/MMke3bSmXE/tuLHVa16H1Na2tjnLZ9GR2DbL8ne2kEUjUzfpsbKUqw/Ftxzm86jA9H+pZJboTL4sWihok+ot0apHF1ZNd+/m8SlUX62asw6OWR5XpTrwsWihqCFNoiI5rxfAG2/AN8bU6jlLVXvqxdLZ9to1ud3fDN7hq/83pOYoaIj87n0dG7qNDhHbZoVRlWD9zPQV5BfR7op/VUa6YFooawtPXk6eiI62OoVSNkJeZR+x7sbQf3Z7gdsFWx7li2vRUQyyZFsuZAylWx1CqRtjyyRaykrPo91TVP5oALRQ1womdJxn1XA9m3LPF6ig1wrRp0+jcuTNhYWGEh4ezbt063nrrLTIzMy3NlZKSwrvvvmtphpqgsKCQtdPX0rhXY5oNbGZ1HIfQQlED/PDmHgxuRN3XwOoo1d6aNWtYuHAhmzZtYtu2bSxdupSmTZtqoahB4qPjOb33NP3/1B+RqntJbHFaKGqA6B89aOKWRPfbqs6jF6uqpKQkQkJC8Pb2BiAkJIT58+dz9OhRhg4dytChQwH46aef6NevHz169GDcuHGkp6cDsHHjRoYMGUJERAQjRowgKSkJgMjISB5//HH69+9Ply5dWL9+PQAZGRk8/PDD9OrVi+7duxd1Y75z50569+5NeHg4YWFhJCQk8Mwzz7Bv3z7Cw8P585//XNmrpsb47fXfCGoeRMexHa2O4jB6Mruay0nN4aejnZnQcTPiVvN6i438OPKCYbd0voWHez1MZl4m1865sJ/xu8Pv5u7wu0nOSibq65L9jC+7e1m5y7vmmmv4+9//Trt27Rg2bBi33norjz32GNOnTycmJoaQkBBOnTrFiy++yNKlS/Hz8+OVV15h+vTpPPvsszz66KMsWLCAevXqMW/ePKZMmcKHH34I2IrCb7/9xooVK7jnnnvYsWMH06ZNY/DgwXz22WekpKTQu3dvhg0bxvvvv8/kyZOZMGECubm5FBQU8PLLL7Njxw62bNlyuatTXUTiukR+X/07I94cgZtH9dkP10JRza35cBfphBN1i4/VUWoEf39/Nm7cyMqVK4mJieHWW2/l5ZdfLjHN2rVriYuLY8CAAQDk5ubSr18/9uzZw44dOxg+fDgABQUFNGr0v+J+2223ATB48GBSU1NJSUnhp59+IjMzk5kzZwKQnZ3N4cOH6devH9OmTSMxMZGxY8fStm31f/aIK/jttd/wDvKuco86vRgtFNVc5OPh7Ol4gGZ9ulodxRLlHQH4evqWOz7YJ/iiRxClcXd3JzIyksjISLp27conn3xSYrwxhuHDh/PFF1+UGL59+3Y6d+7MmjVrSp3v+e3dIoIxhtmzZ9OjR48S4zp27EifPn1YtGgRI0aM4IMPPqBVq1aX/F1UxZ3YcYJdX+9i0JRBeAd4Wx3HoarPsZEqU7sRLalVW/t3qgx79uwhISGh6P2WLVto3rw5AQEBpKWlAdC3b19Wr17N3r17AVtvs/Hx8bRv356TJ08WFYq8vDx27txZNK958+YBsGrVKoKCgggKCmLEiBG8//77GGMA2Lx5M2B71GqrVq147LHHGD16NNu2bSuRQTneymkr8fTzpO8Tfa2O4nAuUShEpKmIxIjILhHZKSKT7cPrisjPIpJg/7eO1Vmrkp0L9nJ7i9Xs+/WQ1VFqjPT0dCZOnEinTp0ICwsjLi6OqVOn8sADDzBq1CiGDh1KvXr1+Pjjj7ntttsICwujb9++7N69Gy8vL+bPn89f/vIXunXrRnh4OL/99lvRvOvUqUP//v158MEHmTVrFgDPP/88+fn5hIWF0aVLF55//nnAVlS6dOlCeHg4u3fv5q677iI4OJgBAwbQpUsXPZntYKd2n2LHvB30fqR3le+uo1TGGMt/gEZAD/vrACAe6AS8CjxjH/4M8MrF5hUREWEcLSYmxuHzdIbzc744LMaAMUc3H7MmUBmcuT7j4uIcNq/U1FSHzetKDRkyxGzYsKHUcY7M6cj1d76q8Hd0uRm/ufMb86LPiyb9eLpjA5XBGesSiDVlbFdd4ojCGJNkjNlkf50G7AKaADcA5xp4PwHGWBKwiopeE0Ivv500Ctf7J5RyltN7T7P98+30fKgnfvWrZ19qLncyW0RaAN2BdUADY0wS2IqJiNS3MltVcnzHSdZndOJvV62wOopyAH3Aketa+dJK3Dzc6P+n6vvUSDH2k2CuQET8geXANGPMNyKSYoypXWz8GWPMBecpROQB4AGABg0aRMydO9ehudLT0/H393foPJ2heM7Vr5zgucW3MPv5b2hyVV2Lk5XkzPUZFBREmzZtHDKvgoIC3N3dHTIvZ3Jkzr1793L27FmHzOt8VeHv6FIzZh/LZv0d62k8ujFtHnPM/7uKcMa6HDp06EZjTM9SR5bVJlXZP4AnsAR4stiwPUAj87/zGHsuNh89R2Hz8X0rTWTtTaawoNC6QGXQcxSOpecoHOdSM0b/Idr8w+sf5uzvZ50TqAw18hyF2C4QnwXsMsZMLzbqe2Ci/fVEYEFlZ6uqJv53IDFnulfpxy8q5cpO7zvN5lmbCb8nnMDQQKvjOJVLFApgAHAncJWIbLH/XAu8DAwXkQRguP29uogzB1LIz863OoZS1VrM8zG4e7kz5IUhVkdxOpc4mW2MWQWUtet7dWVmqQ6mRG0jencbDmY2wN3L9dvYlapqkjYlseOLHQz860ACGgVYHcfpXOWIQjmIKTQs3N2anvUPa5FQykl+efYXfOr6MODpAVZHqRRaKKqZrV/F83tBE6JG5FkdpUqYM2cOLVq0wM3NjRYtWjBnzhyHzHfo0KH8/PPPADz33HM89thjDpmvst7+X/az76d9DJoyiFpBNaNrHJdoelKOE/2fJIS2XPeUPnviYubMmcMDDzxQ9EChQ4cO8cADDwAwYcKEK5r33/72N1544QVOnDjB5s2b+f777684r7KeMYZfnvmFwKaB9Hq4l9VxKo0eUVQz0evq0dsvjgZd6lkdxeVNmTLlgqfOZWZmMmXKlCue9+DBgzHGMH36dObOnYu7uzsZGRlMnDiR+++/32FHLqpyxc2P42jsUYb+fSgetWrOfrYWimrmtWl5vPhCrtUxqoTDhw9f0vBLsX37dpKSkvD29iYgwHay85tvvuHmm2/mv//9rx5hVEEFuQX8OuVX6nWuR9idYVbHqVRaKKqZIZPDGfZ0j4tPqGjWrPQH35c1vKKSkpKYMGECCxYswM/PjyVLlgCQmJhI06ZNAarEHd+qpHUz1nE64TTDXx2Om3vN2nTWrG9bza1+5QTrZu2wOkaVMW3aNHx9S3YJ7evry7Rp0y57npmZmYwdO5Y33niDjh078vzzzzN16lQAQkNDSUxMBKCwsPCyl6EqX1pSGsv/tpy217Wl7bU172mBNaeRrZrLOp3FtMXXk3RkA33utTpN1XDuhPWUKVM4fPgwzZo1Y9q0aVd0ItvX17fEE+oGDx5c9H7s2LE88sgjLFq0iKioqLJmoVzQ0r8spSC3gJFvjbQ6iiW0UFQTv87YQRa9iLq1enZz7CwTJky44iucKsrPz4+PPvqoUpalHOf3335n22fbGPjsQOq2ca0ONiuLNj1VEwu/ysKfNCIfrZnPxlbKGQoLCvnhkR8IaBLAoL8OsjqOZbRQVAOm0BC9uy1DgjfhHVi9HuqulJU2fbCJY5uPcc3r1+Dl72V1HMtooagGDq85QobxYUCfE1ZHUarayDqdxa9TfqX5kOZ0vrWz1XEspecoqoHmA0I5kZ7Hsl9rWx3FJRhjsPVcry6FcaGHmLmCJU8sIedsDqNmjKrx/5/0iKKa8PT1xNPf0+oYlqtVqxbJycm60btExhiSk5OpVatm9F10MQk/JrD1060MeGYADcL0mfN6RFHFHd10jKv6ZfLuP8/iFmF1Guudu1fh5MmTVzyv7OzsKrHhdFTOWrVqERoa6oBEVVtOag4L/7CQep3qMfi5wVbHcQlaKKq4hdPj2ZM7mPqtEjiFc551XJV4enrSsmVLh8xr2bJldO/e3SHzcqaqkrOqWPrMUlITU7n3t3vx8NZNJGihqPKif65FC4/f6XxDG5avOGJ1nMuWn5NPVnIWmcmZ5KbZ+qoSN7H9uAs+dX3wq+eHp59njW8vVs6TsiWFre9tpc/jfQjtq0dX52ihqMIyT2Wy9ERX7g9bj7g1tTrORRljOJ1wmhO/niAmJoZTcac4ueskKQdTyMuo2PMzPGp54FvPlzot61C3XV1C2ocQ3C6YBmENCGoepEVEXba8zDziX4+nTqs6XPXiVVbHcSlaKKqwX97eQTa9ibrN3+ooZTp7+Cz7l+7nwK8HOBhzkLSjaQDsdttNnVZ1COkYQqthrfCt54tvsC8+wT54B3ojIphCgzGGwrxCsk5nkXEyg8yTmWQcz+DM/jPsWbCHzSc3Fy3Lt54vTXo3oUmfJjTt35RmA5rVqK6g1ZX5+S8/k3Uki3G/jMPLr+beM1Ea/Suqwuq38OWuVqsY8khvq6OUkHkqk51f7mT7nO38/tvvAPjV96PlVS1pMbQFSW5JjLxjpEM24llnskjek0zS5iSOrj/KkfVHSPghAYzt6KPZoGa0Gt6K1te0pkFYAz3iUKXaE72HDe9soMnNTWh5lWPOcVUnWiiqsD73dnGZDgCNMRz49QDr3lrH3sV7KcwvpH6X+lz90tW0H92ekI4hRRvpZcuWOWxP36eOD6F9Q23tyQ/ZhmWfzebwqsPsX7qf/T/vZ+nTS1n69FJqt6hNh7Ed6HhjR0L7hda4rqJV6VKPpLJg0gIahjek1f2trI7jkrRQVFFHNx0j/WQW7UZYu/dTmF9I3Ndx/PbqbyRtSsK/oT99n+xL2IQwy64/rxVUi3bXtaPdde0AWxfRCT8ksPvb3Wx4ZwNrp6/Fr4EfXcZ3IezOMBr1aKRHGjVUYUEh3975LflZ+dw09yZ2JGk3/aXRQlFF/fuJ3fxjxWBOxp8muG3l92hpCg3bv9hOzPMxpBxIIbh9MFEfRBF2R5jLXVIY0CiAHvf2oMe9PchJzSHhhwTivooj9r1Y1r29jpAOIYTdGUa3id0IbBJodVxViVa/upqDMQcZ/eFoQtqHQJLViVyTa/1FqwqL3tCAfgE7CG5b+Y9kTFyXyOLJizmy7giNejRixPQRtB/dHnFz/b1y70BvuozvQpfxXcg6k0XcV3Fs+2wbv075lZjnY2h3fTt6PNCDNiPbWB1VOVni2kRino+hy/guhN8dbnUcl6aFogpK3JDE5qyOvDRiWaUuNy0pjaVPL2Xb7G34N/Tnho9uoNtd3apEgSiNTx0fIh6IIOKBCE7vO83mWZvZ/OFm9ny/h8CmgdQdXpeMThn41ddnfFQ3aUlpfHnTlwQ1C+K696/TpseL0EJRBS18MwFoRNRDlXdD0M6vdrLowUXkZuQy8NmBDHx2IN4B1adL87qt63L1P68m8m+RxEfHE/t+LPs/3M+bc96k621d6f1Ybxp1b2R1TOUA+Tn5fHnTl2SnZHPvmnupFeT63bRYTQtFFbTol1q09DhMp6jWTl9Wdko2PzzyA9vnbKdJ7yaM+XSMrS23mnL3dKfj2I50HNuRRZ8sgvWw9ZOtbPl4C80GNaP/n/vT7rp2VfYoqqYzxrDooUUkrklk3Pxx2uFfBWmhqII++a0tB9Ycc/rG6kDMAb676zvSktKI/Fskg/46CDePmnNJqV9zPyInRnL1tKvZ/OFm1r29jrmj5xLSIYR+T/WznbjXG/qqlPX/Ws+Wj7Yw+PnBdLqpk9Vxqoya81dfjdRtXYeIOzo6bf7GGNa+vZbPhn+Gp58n9665lyEvDKlRRaK4WrVr0e/Jfjy27zHGfj4WDx8Pou+P5q0Wb7H61dXkpOZYHVFVwP5f9rPkySW0v6E9kVMjrY5TpejuUBUz/YZl+Pq58eDnzun+OD8nn0UPLWLLR1voMKYDYz4dU63ORVwJNw83ut7WlS7ju3Aw5iCrX1nN0r8sZdVLq+j1x170mdwHv3p64tsVHdt6jC9v+pKQDiHc+NmN2nR4iS65UIiIH5BtjClwQh5VjsL8Ql5b2JFBjffzoBPmn34snXlj55G4JpHBzw8mcmqk/kGVQkRoeVVLWl7VkqMbj7LqpVWs/OdK1kxfQ8QfIhjw5wEENA6wOqayO73vNLNHzMY7wJsJP0zQHZ/LcNFCISJuwHhgAtALyAG8ReQk8APwH2NMglNTKgA2ztnNscJORF3n+NWdHJ/Mp8M+JSs5i5u/vJnO42r2M4IrqnFEY26Zfwundp9i1UurWP+v9cS+G0v3e7sz4C8DqN28ttURa7S0pDQ+G/4ZhfmFTIyZSFCzIKsjVUkVaXSOAVoDzwINjTFNjTH1gUHAWuBlEbnDiRmVXfSsE7hRwLVPOfYk3PFtx/lo8EfkZ+czaeUkLRKXIaRDCGM+GcOj8Y/S7e5ubPpgE/9q8y++v+97zuw/Y3W8GinrTBazR8wm40QGE36cQL2O9ayOVGVVpOlpmDHmgocFGGNOA18DX4uIPqy5EkTHNqR/4A6C23Zz2DyPrD/C7JGz8fT15K6ldxHSofpe+loZ6rSqQ9S/oxj83GBWv7qaTf/dxJaPt9Dtzm4M/OtAgtsGWx2xRsg+m83n131O8p5kbl90O016NbE6UpV20SOKc0VCRN6SMm5fLK2QKMfKTsmmtncWN0Y6bu/04PKDfHr1p/jU8WHSyklaJBwoqGkQ1/7rWiYfmEzvR3uzY+4OZnaYybd3fsup3aesjletZZ7K5NOrP+XohqPc9MVNtBqmPcJeqUu53jEd+N5+MhsRuUZEVjsnVkkiMlJE9ojIXhF5pjKW6Wpq1a5FzJnuPLkg0iHzO7TiEHNGziGoWRCTVk6iTss6DpmvKimgUQAj3xzJ5AOT6ftEX3Z9s4uZnWby9W1fc2LnCavjVTtpSWl8PORjTu48yfgF4+k41nmXkdckFb7qyRjznIjcDiwTkRwgA3D6RltE3IGZwHAgEdggIt8bY+KcvWxXknkqE98QX4fM69iWY3wR9QW1W9Rm4rKJeklnJfBv6M81r1/DgL8MYM30NWx4ZwM75u2g002dGDRlEA3DG1odscpLOZjCp8M+JeO47ZxEi8gWVkeqNip8RCEiVwP3YysQ9YDHjDErnRWsmN7AXmPMfmNMLjAXuKESlusyMk5kUL9eIf+6efkVzys5Idl2qWCQN3f8dIcWiUrmV8+PYS8NY/LByQz66yD2/bSPf3f/N1+M/oIj649YHa/KOrblGB8N+ois5CzuXHqnFgkHE2NMxSYU+RV4wRizSkS6Ap8BTxpjfnVqQJGbgZHGmPvs7+8E+hhjHik2zQPAAwANGjSImDt3rkMzpKen4+9v3XOpt/7nBI9/cQv/fvAr2t1a9pUbF8uZcyqHLY9uoSCrgPAZ4fg2c8wRyqWyen1WVGXkzE/P58g3R0j8OpH81Hzq9KxDswnNCOoWVOEeTWv6+jy57CS7X9mNh78HXV/qin+by19GTV6XQ4cO3WiM6VnqSGPMZf0AjYDfLvfzl7CcccAHxd7fCfyrrOkjIiKMo8XExDh8npfinrYrTBApJjcjt9zpysuZdSbLvNvlXfNP/3+aIxuOODjhpbF6fVZUZebMTs02q15ZZV5r8JqZylTzQd8PzO4Fu01hQeFFP1tT12dhQaH55blfbOur3wcmLSntiudZU9elMcYAsaaM7epFm57KudIpCbi6vGkcJBFoWux9KHDUictzKYX5hSza155RzXbi6Xt5VyEXFhQyf/x8Tu05xfgF42ncs7GDU6or5R3gzYCnBzD5wGSuffda0o+lM/eGubwX9h5bPt5CQa52hFBc9tls5o2dx8oXVxJ+TzgTYybi39D1jwSqqgrdcCcij4pIs+IDRcQL6CcinwATnZLOZgPQVkRa2pc5HvjeictzKRs+ieN4YX2irq9YE2Fplj6zlH1L9nHtzGtpeZW1z9hW5fP08aTXQ714NOHRoj6JFkxawNst32b1q6vJTsm2OqLlDi47yPth7xO/MJ6Rb49k9AejXe7xu9VNRdbuSOAe4AsRaQmkALUAd+An4E1jzBZnBTTG5IvII8AS+zI/NMbsdNbyXE3zXvV5/fpljPpT+GV9ftvsbax5fQ29/tiLiPsjHBtOOY2bhxthd4TRdUJX9v20jzWvr2HpX5ay4h8rCJ8UTu9HehPcrmbdvJefnc8vU35h7fS11G1bl3tW30Non8p7eFdNdtFCYYzJBt4F3rXfgR0CZBljUpycrXiGH7D1K1XjNAyrz1PR9S/rs0c2HOH7+76nRWQLRrw5wsHJVGUQEdqMaEObEW1I2pzE2ulriX0/lvX/Wk+bUW3o81gfjNflH21WFYnrEvn+3u85ufMkPR/uyfBXh+Pl52V1rBqj3KYnERkjIv8SkXZguwPbGJNUmUWiJkvacpwvHv2NtKNpl/zZ9GPpzLtxHv4N/Rn31TjcPd2dkFBVpkbdG3HjZzfyxOEniPxbJMc2H2POqDmsv3M9q15eRfqxdKsjOlzqkVS+vetbZvWdRfaZbCb8OIHrZl6nRaKSlVsojDHfAc2Bq0Xk0UpJpIp888/d3P5Of45uPXlJnyssKOTr278m+0w24xeMd9iNeso1+Df0Z8gLQ3j80OOMnTMW73re/PLsL7zZ9E2+vPlLEn5IoDC/0OqYVyQvK48VL67gnXbvsPPLnQx8diB/3P1H2oxsY3W0Gqki5yhaGWPeE5GNwL+cHUj9T/SvfrT1PED7UZfWV83qV1dzMOYgo2eNpmE3veO3unL3cqfr7V1JbpxMl0Zd2PTfTWz9ZCu7vt6FX30/utzWhbA7w2jUo1GF78mwWtaZLGLfj2Xd2+vIOJ5Bx5s6Mvy14drFjMUqUigWi8gaoKGI3ANsBXbaz10oJ0k7mkZMclceiVgDVPxKpcS1icQ8H0PnWzsTPincafmUawlpH8I1r1/D1f+8moQfE9j22TZi37NtcIPbBdPhxg50uLEDTXo1ccmHUZ09fJa1b69l0382kZueS+sRrRn010E0H9zc6miKip3M/pOItAKWYdtijQY6i0gusMMYc6tzI9ZMP7+1k1z6MvrO2hX+TH56Pl9P+pqgpkFc//71VWYvUjmOu5c7HW7oQIcbOpB1Jou4+XHEfRXHmjfWsPqV1QQ0CaD96Pa0vqY1LSJbUKt2LcuyZqdkE/d1HNvnbOfgsoOIm9BlfBf6/7m/Hgm7mApdfGyM2S8iw4wx8eeGiYg/0MVpyWq4dcuzqSNnGPCHiq1iYwzxb8Zz9vezTFo5ydINgHINPnV8iLg/goj7I8g6k0XCogR2fbOLrZ9uJfa9WMRNaNyrMS2vbknTfk1p0rsJfvWd1/eXMYaTcSc5EHOA/T/vZ++PeynILaBu27oM+b8hhN8drk8EdFGX0nts/Hnv07E94U45wSvrInlyx0k8alXsV7T1k62c/PUkQ18cStN+TS/+AVWj+NTxIeyOMMLuCKMgt4DEdYns/3k/+3/ez+qXV2MKbZfY1m5Rm8a9GlOvcz2C2wUT0j6Eum3rXvJzpgvzCzm97zSndp3iZNxJjm87TvxP8aw4swKAoGZB9HyoJ10ndKVxz8Z69Ovi9HZGF9agS8Ue3ZiamMriyYsJCgti4DMDnZxKVXXuXu40H9Sc5oOaM/TvQ8nNyCVpUxJH1h/hyLojHI09Stz8OCh2e4Z3oDe+9XzxDfHFr54fnn6eiIjtfIdAQU4BmcmZZCVnkZmcScaJDArz/nflVWDTQOr0qEOf8X1oeVVLaresrcWhCtFC4YJeGbWMuHgPPk4YcNETj8YYFj20iIK8Ato/3R4390t5FpVS4OXnVVQ4zsnLyuPMvjOc2nOK5Phk0o+lk3Uqi4yTGaQmppKXlQcGTKHBFBrcvdzxCfahdovaNIpohF8DP0I6hFCvYz1COoTgHejNsmXL6BHZw8Jvqi6XFgoXNDumCfV80it0dcqOuTuIXxjP8NeHk9sktxLSqZrA08eT+l3qU7/L5fUKoKoX3f10MQdXJbIjpy1RQ85edNqMkxksfmwxTXo3oe/jfSshnVKqJtJC4WKi39oHQNSjF793YvFji8k+m83oD0drk5NSyml06+JiomP86eC1jzZXl3+j0Z7v97Bj7g4GPzeY+p21eUAp5Tx6jsLF9OqQxqh6aUDrMqfJTc9l0cOLqN+1vl7lpJRyOi0ULmba6siLTrPynytJO5LGuC/H4e6lvcIqpZxLm55cyJ4f95OfnV/uNKf3nmbNG2sIuzOMpv31xjqllPNpoXARBbkFDLwukAe7rSl3usWPL8bd251hrwyrpGRKqZpOC4WLWDtrJ6dMCNdce2FT0rnuFeIXxZOwKIHBzw8moFFAZUdUStVQWihcRPQnp/EgjxFPdC4xfGrkMp6IWEFeVh5LHl9CcPtgvpqdy9TIZdYEVUrVOFooXET0llAG19lOULOgomGm0JByVnh7yxCea/0Fp/ee5mBeE97eNpSUs1J0pKGUUs6kVz25gH2/HiIupw33j1peYri4CW9uHIyE/YTHzkR20YF5+29kcvhy23AXfACNUqr60ULhApr3b0LMm1toH9nhgnHiJgwbnMe6nQX8zHAALRJKqUqlTU8uwKOWB5GPh9MovMEF45Ljk9nw3kY20oPT1AXgiYgV2uyklKo0WigsdvbwWf7UcxkJPx+8YJwpNEzvM488PGjX2ZPCAsPk8OW8vWWIFgulVKXRQmGxJW/u5I2NkRxPSL1gXNLmJLxSTlLQoDHTtw0vOmcxOXw5tYOMNj8ppSqFnqOwWPSCQoIlmX73db5g3C/P/IJPsA9/2T2+qCgUneDWIqGUqiR6RGGh/Ox8fjjYiWtb7rqgz6b9S/ezf+l+Bj83mFq1a5UYp0VCKVWZtFBYaM0HOzlt6hJ1Q8kiYQoNS59ZSlBz2wPolVLKStr0ZKHfd6VTX04y4smSzU67v9tN0sYkxnwyBg9v/RUppaylRxQWun3mAJJygwkMDSwaZoxhxT9WENwumK4TulqYTimlbLRQWKQgtwAAN4+Sv4L4hfEc23KMgX8dqI83VUq5BN0SWWTGLStp73WA1MT/XRZrjGHF31dQp1Udut6uRxNKKdeghcIi0cuD8HTLL9HstG/JPo7GHmXgswNx99Qn1ymlXIMWCgukHDrLypQuRHU/UjTMGMPyvy0nqFkQ3e7qZmE6pZQqyfJCISKvichuEdkmIt+KSO1i454Vkb0iskdERlgY06EWv7GTfDyJuju4aNiBXw6QuDaRAc8M0OdgK6VciuWFAvgZ6GKMCQPigWcBRKQTMB7oDIwE3hWRarEFjf7eECKn6DOpU9GwFf9YQUCTALrf093CZEopdSHLC4Ux5idjTL797Vog1P76BmCuMSbHGHMA2Av0tiKjo427zYMXb4srOnI4tOIQh1YcYsDTA/S+CaWUy3G1rdI9wDz76ybYCsc5ifZhVd6Yl/qUeL/61dX41vOlx/09LEqklFJlE2Oc31W1iCwFGpYyaooxZoF9milAT2CsMcaIyExgjTFmtn38LOAHY8zXpcz/AeABgAYNGkTMnTvXofnT09Px9/d3yLz2zj9JUDNP6vWuDUDGoQxi746l+d3NaTGxxRXN25E5nUlzOpbmdJyqkBGck3Po0KEbjTGl9xlkjLH8B5gIrAF8iw17Fni22PslQL+LzSsiIsI4WkxMjMPm1c5zv7kmeEPR+wX3LTAv1nrRpJ9Iv+J5OzKnM2lOx9KcjlMVMhrjnJxArClju2r5OQoRGQn8BRhtjMksNup7YLyIeItIS6AtsN6KjI4Sv+QA8XktiRqaAUD68XS2fbaNbhO74VfPz+J0SilVOlc4R/EO4A38LCIAa40xDxpjdorIl0AckA/80RhTYGHOKxb9ziGgJVGPtwZgw7sbKMgpoO8Tfa0NppRS5bC8UBhj2pQzbhowrRLjOFX0ytp0rRVP8wHtyMvKI/bdWNpFtSOkfYjV0ZRSqkyWNz3VFBknMlh7tgNRPY4CsPXTrWSeyqT/n/pbnEwppcpn+RFFTeFX34+k/SnkZ3fBFBrWTl9L456NaTaomdXRlFKqXFooKlGdlrUB2PP9HpLjk7lp7k3Yz8sopZTL0qanSpCXmcf1DdazZFosAOtmrCOwaSCdbup0kU8qpZT1tFBUgtX/2cmiE73JTM3n1O5THPjlAD0f6nnBQ4uUUsoV6ZaqEkTPTsGLHIY/0YUN723A3cudHvdqdx1KqapBC0UliN7WnKtCtuHl78XWj7fSaVwn/OrrDXZKqapBC4WT7flxPwl5LYm6OpPtn28nJzWHXg/3sjqWUkpVmBYKJ0s7mc2QoC1c91hrNszcQINuDQjtF3rxDyqllIvQQuFkPe/qxLKUcMQUcnzbcXr9sZdeEquUqlK0UDhR5qlMzhxIASD23Vi8A73pentXa0MppdQl0kLhRN88v5l6rfyJ/XQHO7/aSbe7u+Hl52V1LKWUuiRaKJwoepEQ4naajIPJFOYV6klspVSVpIXCSXLTc1n8e2eubb2HzR9upuVVLbWXWKVUlaSFwklW/XsnqQQxqEcGZw+dpft93a2OpJRSl0ULhZNEz0nFm2x8clOoVbsWHW/saHUkpZS6LNp7rJM88noLen+9gb2z9tLjvh541NJVrZSqmvSIwklaX9Wc1p28KcgpoPu92uyklKq6dDfXCRa+sJ60M/mkrtpOw/CGNOreyOpISil12bRQOMErb3uTlhPAjTnHGPWvUVbHUUqpK6JNTw52ak8yv6V2YWDwLty93fVObKVUlaeFwsF+fHMXhbgTkrKXjjd2xKeuj9WRlFLqimihcLDoRe40kmOYzEzC7wm3Oo5SSl0xPUfhQKbQcPBMIIN8YqkTUptWV7eyOpJSSl0xPaJwIHETlu5pSofMWLrd3Q1x0+7ElVJVnxYKBzKFhh1f7MANIeyOMKvjKKWUQ2jTk4OYQkOvgF3080igW+8mBLcNtjqSUko5hB5ROEhc9D42ZnaiMDWNrhP0klilVPWhhcJBot9LBCBETtP51s4Wp1FKKcfRQuEg0b/VJUy20W5Ea/wb+FsdRymlHEYLhQOc3HWKNWld6GE20vUObXZSSlUvWigcID+ngHtCvqe513E63NDB6jhKKeVQetWTA9TrGEzbgj20HdcOL38vq+MopZRD6RHFFcpJzeHrh38h80yWXu2klKqWtFBcoeUzdzD+wxHk+tSm9fDWVsdRSimHc5lCISJ/EhEjIiHFhj0rIntFZI+IjLAyX1kWzE7Fh0z63dEKNw+XWZ1KKeUwLnGOQkSaAsOBw8WGdQLGA52BxsBSEWlnjCmwJuWFTKFh4e629GUt3Sfp406VUtWTq+wCvwk8DZhiw24A5hpjcowxB4C9QG8rwpVl+zcJHC4MpZtvAqF9Qq2Oo5RSTmH5EYWIjAaOGGO2ipTobbUJsLbY+0T7sNLm8QDwAECDBg1YtmyZQzOmp6eXOs+F/0wG2tG6XyHLVyx36DIvR1k5XY3mdCzN6ThVISNYkNMY4/QfYCmwo5SfG4B1QJB9uoNAiP31TOCOYvOYBdx0sWVFREQYR4uJiSl1eOx/Y81fedEc/u2ww5d5OcrK6Wo0p2NpTsepChmNcU5OINaUsV2tlCMKY8yw0oaLSFegJXDuaCIU2CQivbEdQTQtNnkocNTJUS9J/PfxhIT6arOTUqpas/QchTFmuzGmvjGmhTGmBbbi0MMYcwz4HhgvIt4i0hJoC6y3MG4J859cTXQ0tLm+jT6gSClVrVl+jqIsxpidIvIlEAfkA380LnTF0ycfFbKZQbw8odDqKEop5VSuctUTAPYji1PF3k8zxrQ2xrQ3xvxoZbbislOyiUnpTn+PDTTt3/TiH1BKqSrMpQpFVfHzG1vIwJ8BPbO02UkpVe1pobgM3358Fl8yuHaqS93WoZRSTuGy5yhcmUnLYLh7DG2GX2d1FKVUFZGTn0NuQS4B3gEArE1cy+ms06TlpJGWm0ZqTiqt6rRiTIcxANz93d2cyjxFem46MRNjOO8+s0qlheIS5aTm0Do7jp6P9NRmJ6WqMWMMmXmZRRvxtJw0ACIaRwDwza5v2Hd6X4nxTQKb8PehfwdgzNwxbD2+lbQc2/i8wjxGtB7B4jsWA3Dr/Fs5fPZwiWXe2OHGokKx69Qu8gvzCfQOJLcgF28P70r65hfSQnGJtny6lYKcAjqN62R1FKXUeQpNIW5ia1E/mnaUxNTEog11Wm4aOfk53B9xPwCzNs1ixeEVRXv0aTlp5GbksilyEwBRX0SxKGFRifm3rduW+EfjAZixbgbLDy1HEAK8AwjwCqBXk15F07YLbkegdyABXgG2f70DaB/cvmj83Jvm4iZuBHgHFE3n7/W/xyivu2+dc1bSZdBCcYkeftyb+m59eaGfXu2klCPkFeQVbajTctNoF9wOL3cv4k7GsS5xXYk99rTcNF4d/ir+Xv78O/bf/HfTf4s+m5qTSkZeBrnP5eLp7sk/V/6TmRtmlliWh5sH9/W4DxFh6/GtLDu4rGgjHVQryHYhvt2dYXcyqNmgoo18gFcAIb5FnVvz7a3f4unuiZ+nX6nNQq8Of7Xc792vab8rW3GVSAvFJUjccJRNBd14rHG8NjupGi87P5ujaUdLtLGn5aQxpMUQGvo3ZOuxrXy27bOi8QeOHsDzgCf/ifoPHUI68NHmj3j4h4fJzs8uMd89j+yhXXA7fkz4kT/9/Kei4d7u3gR4B/D84Ofx9/Knlkct6vvVp03dNgR4BRTtmRca271N9/e4n1FtRhVt5M/9e86MUTOYMWpGiWUX7z/p1i63lvv96/jUudxVV+VoobgEX/11M9CYkXfWszqKUpekeHu7r6cvgd6BpOWksezgsqJmmXMb9NHtR9OzcU92ndzFE0ueKDEuLSeNWaNncUOHG1h+cDkj54y8YFk/TviRkW1Gsv/Mft6Lfa9oIy25QmNpTH6hbbe9U71OPNLrkRJ77IHegTTwawDApO6TuKnTTUWf93Iv+ZjhieETmRg+sczv3K1hN7o17ObAtVhzaaG4BEtW+xPK7wx7YYDVUVQNYIwp0axy7nWjgEZ0qteJ3IJcpq+Zzvb92/k68+uivfqxHcdyR9gdHE8/Ts//9izayJ/b0359+Os81f8pktKTGD13dIllCkLTwKb0bNwTEeF01mkCvAOo71fftsH2CiA00Na3WViDMD6+4eMSG/kA7wCaBzUH4MaON5LRMaNo3suWLSMyMrLofZ/QPvQJ7VPm96/rU5e6PnUdtTrVFdBCUUFZp7NYmdWTGwN/wdN39MU/oGqk/MJ8cvJz8PPyA2Dj0Y0kZyUXNcuk5qTSNKgpYzuOBeDBhQ+SlJ5Uohhc1/Y6po+YDkDwq8FFe+DnPNzzYWZeNxNBePaXZ3HDjcCTgUVt7SnZKQD4e/kzvNXwEs0uAd4BDGhq29FpHtScDfdvKNFs4+vpW3QyuENIB9bfX3b3ao0CGpW7R6+qDy0UFXRk41Ee4HuG3KFXO1U3Ofk5JfbYC0wBPRr1ACB6TzQJpxNKtMPX96vPi1e9CMBtX9/GhiMbij6blZ/FkOZDWHb3MgBu/+Z24pPjSyxvVJtRRYVi+4ntpOemE+Bl22tvXbc1beu2BUBEeHPEm3i5e5XYY28W1AwAT3dPMv6awbpV6xg6dOgF38vPy48Pb/iwzO/t7eFNz8Y9r2zlqRpBC0UFHYo5SB33NEa8ONjqKDWeret824b0ePpxjqQdKXFVTEZuRtElkLO3zSbmQIxtQ27fmLu7ubP8btuDpm756ha+ivuqxPybBjbl8BO269tnbpjJkn1LAPDx8CHQO5DwhuFF07YIamG7xNHrf80vreu2Lhr/0Q0fYYy5oHnmnNX3rC73uz7S+5Fyx/t6+lp6I5aqGbRQVIApNES/c5AO3RvjU8fH6jhVUqEpJD03nbScNA5lHCI7P5taHrWIT45nXeK6Env0qTmp/OOqf1C7Vm0+2fIJ78W+d8EJ15S/pBDgHcBrv73GG2veuGB5k7pPwsPNg81Jm1myb0mJppdgn+Ci6cZ1Gkd4w/ASG/Hi7eJzxs7B3c0dfy9/PNwu/HN5adhL5X7v/k37X8FaU8o1aKGogAPzj/F22r287P6N1VEqXW5BLsfSj5XYY0/NSaV/0/40DmhM3Mk4PtnySYk99tScVN4e+TZdG3Rl3o553Bd9H+m56SXmGx4RTreG3fh538888uP/9prdxZ0A7wCe7PcktWvVxtPdk0DvQEIDQ/+3sfcKKGpHv6vbXQxqNuiCPXZ3cQfgjRFv8MaICwvJOeM6jyv3+wf7Bpc7XqmaQAtFBWxYIAiF3Pxid6ujXFROfg5puWl4uXsR6B1IZl4myw4uK3F5Y2pOKiPbjKRPaB/2n9nP5MWTSc1JLVEM3hn1DuM6j2PN72uI/CTyguV8e+u3jOkwhoMpB3lr3VtFJ1LPnRTNK8wDoE3dNtzf4/4SJ1QT9yfSNMh2w+JtXW9jRJsRRRv5Wh61SjSl3N71dm7venuZ3zesQRhhDcIcug6VUiVpoSjHnDlzmDJlCrWTviOcTaw9vofWtHT4cjLzMktc9ZKak0o933p0rt+ZgsICpq+ZfsHdqde1vY6J4RNJyU6h+7+7k5aTxtnss+Qvt10h8+LQF5kyeAqnMk9x3ecXdl5Yu1Zt+oT2wRjD0bSjRZc9ntvgn9uQdwjpwAdRH5Rougn0DqRlbdt6GNVmFDnP5ZT53SIaRxT1jXPOsvRlRc07egmkUq5Pzp0YrC5E5CRwyAGzqgs0p2RX7IX2eZ92wPydIQQ4ddGprKc5HUtzOk5VyAjOydncGFPq3cTVrlA4g4jEGmNc/jpCzelYmtOxqkLOqpARKj+nPrhIKaVUubRQKKWUKpcWior5j9UBKkhzOpbmdKyqkLMqZIRKzqnnKJRSSpVLjyiUUkqVSwuFUkqpcmmhqCAR+YeIbBORLSLyk4g0tjpTaUTkNRHZbc/6rYjUtjpTaURknIjsFJFCEXGpyxFFZKSI7BGRvSLyjNV5yiIiH4rICRHZYXWWsohIUxGJEZFd9t/3ZKszlUZEaonIehHZas/5N6szlUVE3EVks4gsrKxlaqGouNeMMWHGmHBgIfCCxXnK8jPQxRgTBsQDz1qcpyw7gLHACquDFCci7sBMYBTQCbhNRFy1b/mPgQsfMeda8oGnjDEdgb7AH110feYAVxljugHhwEgR6WttpDJNBnZV5gK1UFSQMSa12Fs/wCWvAjDG/GSMOfekm7VAqJV5ymKM2WWM2WN1jlL0BvYaY/YbY3KBucANFmcqlTFmBa7bSwAAxpgkY8wm++s0bBu4JtamupCxOddzpaf9x+X+xkUkFLgO+KAyl6uF4hKIyDQR+R2YgOseURR3D/Cj1SGqmCbA78XeJ+KCG7aqSERaAN2BdRZHKZW9SWcLcAL42RjjijnfAp7G1p1QpdFCUYyILBWRHaX83ABgjJlijGkKzAHKf6KMhTnt00zBdtg/x5VzuqDSngLkcnuWVY2I+ANfA4+fd3TuMowxBfam5VCgt4h0sThSCSJyPXDCGLOxspetvccWY4wZVsFJPwcWAf/nxDhlulhOEZkIXA9cbSy8UeYS1qcrSQSaFnsfChy1KEu1ICKe2IrEHGOMyz/UxRiTIiLLsJ3/caULBQYAo0XkWqAWECgis40xdzh7wXpEUUEi0rbY29HAbquylEdERgJ/AUYbYzKtzlMFbQDaikhLEfECxgPfW5ypyhLbw0VmAbuMMdOtzlMWEal37gpBEfEBhuFif+PGmGeNMaHGmBbY/l/+WhlFArRQXIqX7c0m24BrsF154IreAQKAn+2X8r5vdaDSiMiNIpII9AMWicgSqzMB2C8EeARYgu3E65fGmJ3WpiqdiHwBrAHai0iiiNxrdaZSDADuBK6y/3/cYt8jdjWNgBj73/cGbOcoKu3yU1enXXgopZQqlx5RKKWUKpcWCqWUUuXSQqGUUqpcWiiUUkqVSwuFUkqpcmmhUEopVS4tFEoppcqlhUKpSmB/JsNw++sXRWSG1ZmUqijt60mpyvF/wN9FpD62HlRHW5xHqQrTO7OVqiQishzwByLtz2ZQqkrQpielKoGIdMXWn1COFglV1WihUMrJRKQRtueC3ABkiMgIiyMpdUm0UCjlRCLiC3yD7bnRu4B/AFMtDaXUJdJzFEoppcqlRxRKKaXKpYVCKaVUubRQKKWUKpcWCqWUUuXSQqGUUqpcWiiUUkqVSwuFUkqpcv0/WmM9jql8sK4AAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"calc_step(-3,1E-2)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.2.3 Consider $x_0 = -3$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.2.3-Consider-$x_0-=--3$)",
"section": "3.6.2.3 Consider $x_0 = -3$"
}
},
"source": [
"**Discussion**\n",
"* In this case, do we expect the Newton and LM steps to be the same? Explain.\n",
"* Why does $f(x)$ increase with a steepest descent ($B^k = I$) step? I thought the main idea was that because $B^k$ is **positive definite** the step is in a **descent direction**!"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.2.4 Consider $x_0 = 0$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.2.4-Consider-$x_0-=-0$)",
"section": "3.6.2.4 Consider $x_0 = 0$"
}
},
"source": [
"### 3.6.2.4 Consider $x_0 = 0$"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.2.4 Consider $x_0 = 0$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.2.4-Consider-$x_0-=-0$)",
"section": "3.6.2.4 Consider $x_0 = 0$"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"x0 = 0\n",
"f(x0) = 1.5\n",
"f'(x0) = 6\n",
"f''(x0) = -8\n",
"\n",
"### Newton Step ###\n",
"xN = 0.75\n",
"pN = xN - x0 = 0.75\n",
"f(xN) = 3.486328125\n",
"f(xN) - f(x0) = 1.986328125\n",
"\n",
"### Levenberg-Marquardt Step ###\n",
"xLM = -600.0\n",
"pLM = xLM - x0 = 0.75\n",
"f(xLM) = 65014556401.5\n",
"f(xLM) - f(x0) = 65014556400.0\n",
"\n",
"### Steepest Descent Step ###\n",
"xSD = -6.0\n",
"pSD = xSD - x0 = -6.0\n",
"f(xSD) = 685.5\n",
"f(xSD) - f(x0) = 684.0\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEWCAYAAAB42tAoAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAABeFklEQVR4nO3dd3iN5xvA8e+TTSKCRIiR2GLG3mpTaqtRq6X016rRpUMHWi1dWkpLS1G7du1dxB6xiU2IkQTZ8zy/P97QIImMc857TvJ8riuXnHfe58W5z7OFlBJFURRFSYuN3gEoiqIolk0lCkVRFCVdKlEoiqIo6VKJQlEURUmXShSKoihKulSiUBRFUdKlEoWSYwghmgghzusdx/MIIXYKIV7XOw5FySiVKBSjEUJcFULECCEiU/x4mfB+UghR9tFrKeVuKWUFU93PHIQQbkKI2UKI20KICCFEoBDiQ73jygghxFghxHy941CMz07vAJQcp6OUcqveQVixyYAz4As8BMoDVbJyISGEnZQy8alttlLKpGxHqeQqqkShmFxySaNVitePv3kKIXySSwYDhRDXhRAhQogxKY61FUJ8IoS4lPwN+4gQooQQYlfyIceTSy69hBDNhBBBKc71Ta7meSCEOC2E6JRi3xwhxDQhxLrk6x4QQpRJ5z38nfwt/6EQYpcQonJGryWEaC2EOJd87i+ASOdx1QEWSinvSykNUspzUsplTz2rx1/wUlZjCSFeFUL4CyEmCyHCgLHJsf0qhFgvhIgCmj/nuRQSQvwjhAgXQhwSQnwlhNiTYv/PQogbyfuPCCGaJG9vB3wC9Er++zievD2/EGKWECJYCHEz+Xq2yfvKCiH+TX4uIUKIJek8F0VHKlEolqIxUAFoCXwuhPBN3v4u0AdoD7gCg4BoKWXT5P3VpZQuUsonPmSEEPbAP8BmoDAwHFgghEhZNdUHGAcUAC4CE9KJbwNQLvlaR4EFT+1P9VpCCHdgOfAp4A5cAhqlc5/9wAQhxGtCiHLpHJeWesDl5DgfvZ9Xkn/PBxwg/ecyDYgCigADk39SOgT4AQWBhcDfQggnKeVG4GtgSfLfR/Xk4+cCiUBZoAbQBnjUPvNlchwFgOLA1Cy8X8UMVKJQjG1V8jfVB0KIVZk4b5yUMkZKeRw4Djz6oHkd+FRKeV5qjkspQzNwvfqACzBRShkvpdwOrEX7QH9khZTyYHL1zAK0D8BUSSlnSykjpJRxwFiguhAifwau1R44I6VcJqVMAH4CbqcT9/Dk898GzgghLgohXszA+33klpRyqpQyUUoZk7xttZTSX0ppSI4r1eeS/E2/O/CFlDJaSnkG7YM+5XOYL6UMTb7+D4AjWoJ/hhDCE3gRGCWljJJS3kWrWuudfEgC4A14SSljpZR7UruOoj+VKBRj6yKldEv+6ZKJ81J+eEajfZgBlED7Fp5ZXsCN5A/HR64BxTJwzyckV39NTK7+CgeuJu9yz8C1vIAbj3ZIbRbOG6QhOVl+LaWsBRQClqJ9ay+Y1jlPSe3aKbel91w80Notb6RxLkKI94QQZ5Orix4A+XnyOaTkDdgDwY++PAAz0EoyAKPRquEOJleBDcrA+1N0oBKFYg5RQN4Ur4tk4twbQJptB+m4BZQQQqT8N14SuJmFa70CdAZaoX0w+iRvT6+t4ZFgtGSnnSCESPk6PVLKcLTqHGegFNpzhPSfZWrTQafclt5zuYdWTVQ8xb6UsTcBPgR6AgWklG5oDe6PnsPT974BxAHuKb48uEopKye/v9tSyiFSSi/gDWC6SNGLTbEcKlEo5hAA9BZC2AshagM9MnHuH8CXQohyQlNNCFEoed8doHQa5x1A+2AdnXzfZkBHYHEW4s+H9oEXivYh/XUmzl0HVBZCdEtuhB5BOolSCPGZEKKOEMJBCOEEjAQeAOellPfQPtD7JZdyBpH5JJrmc0nuDbUCrRE8rxCiIjAgxbn50BLJPcBOCPE5WrvRI3cAn0dJSEoZjNYG8YMQwlUIYSOEKCOEeCH5vb4shHiUlO6jJRrVI8sCqUShmMNnaB9o99EafBdm4twf0apfNgPhwCwgT/K+scDc5GqNnilPklLGA53Q6shDgOnAACnluSzEPw+teuYmcAatwTlDpJQhwMvARLREUw7wT+8U4M/kmG8BrYEOUsrI5P1DgA+Sr1UZ2JuZN5KB5/I2WqnpNvAXsAgtSQJsQmvUD0R7HrE8WTX1d/KfoUKIo8m/DwAc0J7bfWAZUDR5Xx3ggBAiElgDjJRSXsnM+1HMQ6iFixRFSYsQYhJQREr5dO8nJRdRJQpFUR4TQlRMrt4TQoi6wGBgpd5xKfpSI7MVRUkpH1p1kxdwF/gBWK1rRIruVNWToiiKki5V9aQoiqKkK8dVPbm7u0sfHx+jXjMqKgpnZ2ejXtMUVJzGpeI0LkuIMzA0kMj4SHzdfcljn+eZ/caM8c4dcHCAAgWMcrknmOJZHjlyJERK6ZHqTilljvqpVauWNLYdO3YY/ZqmoOI0LhWncekd5/zj8yVjkbOPzk7zGGPEmJQk5bvvSglSvvJKti+XKlM8S+CwTONzNceVKBRFUVLzStVXKJinIC+Wy8zUWZkTHw+vvgqLFsHbb8NPP5nsVmalEoWiKDnatQfXMEgDpQqUMnmS6NABtm6Fb76BDz8EkZFJXqyAShSKouRYcYlx9Pi7ByHRIQS+HYi9rb3J7uXgAHXqQL9+MDCHDU/MFYkiISGBoKAgYmNjs3R+/vz5OXv2rJGjMj5TxOnk5ETx4sWxtzfdfzBFMZV3Nr3D4VuHWdlrpcmSRGAgREeDnx98nZlZwKxIrkgUQUFB5MuXDx8fH0QWyoIRERHky5fPBJEZl7HjlFISGhpKUFAQpUqVMtp1FcUcFpxYwK+Hf+WDhh/QpWIXk9zjwAF46SUoWhQCAsAmhw44yKFv60mxsbEUKlQoS0kiNxNCUKhQoSyXxBRFL2funWHo2qE09W7K1y1N8zV/3Tpo0QJcXWHFipybJCCXJApAJYksUs9NsUbe+b0Z5DeIJT2WYGdj/IqT2bOhc2eoWBH27oWyOXwVjVxR9aQoSu4gpSQmMQZnB2emtjfNEtxSwrJl0LKl9qcV1EpnW64pUSiKkvN96/8tdX6vQ2h0RpZVz5ykJLh/X+vy+vff8M8/uSNJgEoUZjVlyhR8fX3p27cvq1atYvz48eke//7777N9+3YzRaco1m3b5W18sv0TqhauSsE8GV1iPGNiYqBHD2jTRhsv4eysdYfNLVTVkxlNnz6dDRs2UKpUKRo2bMiaNWvSPX748OEMGTKEFi1amClCRbFONx7eoPfy3lR0r8gfnf4wattaWBh06qS1Rfz8s/kTxNkVZ0GAb1df8944BYtIFEKIEmjLTRYBDMBMKeXPQoiCwBK0xeyvAj2llPezc6+NozZyO+B2ps5JSkrC1tY2zf1F/IrQ7qd26V7jf//7H5cvX6ZTp07069cPR0dH3N3dAejcuTPdu3dnwIABzJgxg127drFgwQK8vb0JDQ3l9u3bFCmS5jLLipKrxSbG0n1pd+IS41jeczkuDi5Gu/b169CuHVy6BEuWwMsvG+3SGbb3+73YOdrpmigspeopEXhPSukL1AeGCSEqAR8B26SU5YBtya+t0m+//YaXlxc7duygcOHC1KxZ8/G+mTNnMn78eHbv3s0PP/zA1Kn/NcLVrFkTf//0llhWlNztYexDJJK5XeZS0b2iUa/96qtw6xZs2qRPkgAIPR9KoQqF9Ll5MosoUUgpg4Hg5N8jhBBngWJAZ6BZ8mFzgZ3Ah9m51/O++afG2APZgoOD8fD4bzZfT09Pxo8fT/PmzVm5ciUFC/5Xv1q4cGFu3bpltHsrSk7j6eLJ/sH7sbVJu9SfVbNmQWQkVK1q9EtnSHRoNDFhMRQqrxLFE4QQPkAN4ADgmZxEkFIGCyEKp3HOUGAoaB+6O3fufGJ//vz5iYiIyHJMSUlJ2Tr/ESklkZGRCCF4+PDhE9c8cuQIBQsW5PLly09sDw8Pp2jRohm6v7HifFpsbOwzzzQ7IiMjjXo9U1FxGpex4zwXfo7FQYt5v/z7uNgZp7opMjKSsWNPc/BgQd5///zjQXR6Pd6Hpx8CcCvu1hPPzux/52nNP67HD+ACHAG6Jb9+8NT++8+7RmrrUZw5cybzk7OnEB4enq3zH/H29pb37t2TGzZskH379n28/cCBA7J69ery5s2bsmzZsvLy5cuP97300kty3759Zo3zadl9fk/Te12CjFJxGpcx47wTeUcW/7G49J7sLUOiQox23eHDA6UQUjZqJGVEhNEum2XH/jwmxzJWhgQ++R7NvR6FpbRRIISwB5YDC6SUK5I33xFCFE3eXxRtsXer17RpU44dO4aUkri4OIYMGcLs2bPx8vLihx9+YNCgQUgpSUhI4OLFi9SuXVvvkBXFYiQaEum1rBch0SGs6LWCQnmzXy0jJXz8MUydWo7OnWHLFnAxXpt4loUGhmJjZ4Obj5uucVhEohBaX7ZZwFkp5Y8pdq0BHk3YOxBYbe7YjOnq1au4u7uTN29eWrVqxbZt23B0dOT48eOPG7c7derEjh07EEKwdu1aevTogZ2dxdUQKopuRm8Zzc6rO5n50kxqFq35/BMyYPhwmDgROnW6ybJlkOfZVVJ1EXo+lAJlCmBrb/z2l8ywlE+gRkB/4KQQIiB52yfARGCpEGIwcB3Qqd+B8X3yySccOHAg3WMSExN57733zBSRoli+kOgQFp5cyMh6I+lfvb/Rrtu9O3h5QYMGF7C1LWa062ZXaGCo7g3ZYCGJQkq5B0hrhExLc8ZiLp6ennTq1CndY17Wqz+eolgo97zuHHvjGO553bN9rTt3tCqmfv2geXPtx5L6BEiDJPRCKGXaldE7FMuoelIURUlPSHQI3/p/S5IhiaL5imZ7EaKLF6FhQ/jf/+B25sbfms3D6w9JikuyiBKFShSKoli0R43Xn+/4nPOh57N9vUOHtCQRHg7btoGlTnoQGqhNbKgShaIoynOM3jKa7Ve289tLv1HJo1K2rrVhAzRrpvVo8veHevWME6MphJwPAcC9Qvar2bJLJQozEUI80TD9/fffM3bs2GxdMyAggPXr12czMkWxXPOOz2Py/smMqDuCV/1ezfb1Ll+GChW0Cf7Kl89+fKYUGhiKQz4HnD2d9Q5FJQpzcXR0ZMWKFYSEhBjtmipRKDnZg9gHDN8wnOY+zfm+zfdZvo6U2qR+AMOGwf79llvdlFJYYBjuFdwtYpVJlSjMxM7OjqFDhzJ58uRn9t27d4/u3btTp04d6tSp83gSwKpVq/LgwQOklBQqVIh58+YB0L9/fzZv3sznn3/OkiVL8PPzY8mSJYSFhdGlSxeqVatG/fr1OXHiBABjx45l0KBBNGvWjNKlSzNlyhTzvXFFySI3Jzc299vMkh5Lstx4nZQEb78N1atrDdhgPetIhJwPsYj2CbCQ7rFm16zZs9t69oS33oLoaGjf/oldeZKSYPBgbSrJkBBtBZOUMtinbtiwYVSrVo3Ro0c/sX3kyJG88847NG7cmOvXr9O2bVvOnj1Lo0aN8Pf3x9vbm9KlS7N7924GDBjA/v37+fXXXxk/fjyHDx/ml19+AeCNN96gRo0arFq1iu3btzNgwAACAgIAOHfuHDt27CAiIoIKFSrw5ptvYm+fvZ4jimIK8UnxbL+ynXZl21GveNYbEWJitK6vK1bABx9A6dJGDNLEEmISeHj9IQVfM+4CTFmVOxOFTlxdXRkwYABTpkwhT4qhn1u3buXMmTOPX4eHhxMREUGTJk3YtWsX3t7evPnmm8ycOZObN29SsGBBXFKZX2D//v2sXLkSgBYtWhAaGsrDh9qkYh06dMDR0RFHR0cKFy7MnTt3KF68uInfsaJkjpSSYeuG8cexPzjxvxNU9czatK1hYdC5s9Zg/dNPMHKkceM0tbCLYSAtoyEbcmuiSK8EkDfvM/tjUk4z7u6erVE5o0aNombNmrz22muPtxkMBvbt2/dE8gBtTqhp06Zx/fp1JkyYwMqVK1m2bBlNmjRJ9dravF5PelS/6ejo+Hibra0tiYmJWX4PimIq0w5N449jf/BJ40+ynCQApkyBgwdh0SLo1cuIAZqJJXWNBdVGYXYFCxakZ8+ezJo16/G2Nm3aPK4+Ah5XF5UoUYKQkBAuXLhA6dKlady4Md9///3jRJEvX74nphVv2LAhCxYsAGDnzp24u7vj6upqhnelKNm3/cp2Rm0cRcfyHfmyxZdZusaj70qffgr79llnkgCVKBTgvffee6L305QpUzh8+DDVqlWjUqVK/Pbbb4/31atXj/LJ/fiaNGnCzZs3ady4MQDNmzfnzJkzjxuzP/7448fX+eijj5g7d65535iiZFFYTBgv//0yFdwrML/bfGxE5j+a/v0XatfWRlrb2UFN48wXqIvQ86Hk88qHg4tltLznzqonHURGRj7+3dPTk+jo6Mev3d3dWbJkSarn/fXXX49/b9iwIQaD4fHrggULcujQocevIyIiWL362Ql2nx6vcerUqUzHryimVDBPQSa3nUzDEg1xdcx8KXjZMq3hunRpiI83QYBmFhqo//KnKakShaIoujFIA+dDtGk5BlQfQNmCZTN9jalTtU6LtWrBnj1QsqSxozS/0POWMWvsIypRKIqim0+3f4rfDD8uhF7I0vkzZsCIEVoPp61boaBl9CbNFktZJzslVfWkKIouFpxYwDd7vmFozaFZKkmANqTp7l345BOw1XdtH6N53JCtqp4URcnNDt48yOA1g3nB+wWmtp+aqWkqIiK0Xk1xcVCoEHz2Wc5JEqBVO4Hl9HgClSgURTGz25G36bK4C175vFjWcxkOthnv2XPnjjaxwsSJ2mC6nOjROtkFShXQO5THVNWToihm5Z7Xnf7V+tO/ev9MrVR34QK0a6d1f12zBlq0MGGQOnq0TraNneV8j7ecSHK41KbcGDt2LEIILj6arQyYPHkyQggOHz5szvAUxeQM0kBIdAh2NnZMaj2JKoWrZPjclIsN7djxzHRsOYqlrJOdkkoUOqtatSqLFy9+/HrZsmVUqpS9xVkUxRL9efVPasyowZ3IO5k+N08erdvr3r1Qt64JgrMQhkQDoRdCca9oGXM8PaIShc66dOnyeJDc5cuXyZ8/Px4eHjpHpSjGNf/EfOZfn0+7Mu0o7Fw4w+ft369Ny1GlChw+DOXKmTBICxB2KYykuCQKV8n4MzKHXNlGkclZxklKymOMWcZT5erqSokSJTh16hSrV6+mV69e/Pnnn1m/oKJYmH039jF4zWCq56/OtA7TMtTDSUqYMEHr0bRoEfTuDRawfo/J3T11F8DiEoXFlCiEELOFEHeFEKdSbBsrhLgphAhI/smRNZO9e/dm8eLFrFq1iq5du+odjqIYzdUHV+m8uDMlXEswrvK4DPVwSkrSVqL77DNtWo5u3cwQqIW4e+ouCHD3tayqJ0sqUcwBfgHmPbV9spQy6+sgpiKTs4wTERHzeJrxbM4ynqqOHTvywQcfULt2bTXbq5KjuDm50cynGV82/5LgU8HPPT4mBl55BVatgtGjtW6wuaEk8ci9U/coWLYg9nksa1Exi0kUUspdQggfveN4WtS9KKLuROFS2cVka9fmyZOHSZMmPZ4lVlGsXaIhkURDIm5Obix9eSkAwTw/UezbB2vXautJDB9u6igtz91Tdylc2bKqncCCEkU63hZCDAAOA+9JKe8/fYAQYigwFLSZWXc+9ZU/f/78T6zbkBnxMfEYYg2EPwjPVr/m6OhoihUr9vj122+/TVxcHPb29kRERNChQwdAmwE2KSmJqKioTMeclJSU5feZntjY2GeeaXZERkYa9XqmouLMup8v/MyFyAv8WP1HHGy06qb04oyPFzg4SGxsYN48J4oWjTV6yT0j9HyWhngDIYEh5K2T97kxmD1OKaXF/AA+wKkUrz0BW7S2lAnA7Oddo1atWvJpZ86ceWZbRsXcj5E3D92UcRFxWb6GuYSHh5vkutl5fqnZsWOHUa9nKirOrPl5/8+Sscj3N73/xPa04jx+XEpvbynXrzd9bM+j57MMDgiWYxkrTy4++dxjTREncFim8blqMY3ZqZFS3pFSJkkpDcDvgNl7UNs6aZPIJMappUMV5Xn+Of8P72x6hy4VuzCx1cTnHr9zJzRpAomJkNuXcLfUHk9gQb2eUiOEKJriZVfA7Cvu2DlotXOJsSpRKEp6jgYfpffy3tQsWpP5Xedja5P+TH1Ll0LbtlqC2LcPqmZ9iewc4e6pu9jY21ConGWNygYLaqMQQiwCmgHuQogg4AugmRDCD5DAVeANs8dlIxD2gqS4JHPfWlGsiouDC/WL12d+1/k4Ozine+yBA9rYiMaNYfVqKGA589/p5t6pe7hXcMfWwfKmwrWYRCGl7JPK5llmDyQVNvY2qupJUdIQmxiLo60j5QuVZ9uAbRk6p25dbdGh/v3BycnEAVqJu6fvUryeZda/WXTVk6WwcbBRJQpFSUWiIZFuS7rxxtrnF/YTEgRvvQXnz2tjI4YMUUnikfjIeB5ceYBHFcucvkcligywsbfBkGjAkGjQOxRFsRhSSoatG8aGixuo7VU73WPDw+Gjj6rx66+wfbuZArQi987cA7DIMRSgEkWGCHttoF12q58mTJhA5cqVqVatGn5+fhw4cICffvqJ6OhoY4SZZQ8ePGD69Om6xqBYn2/9v2Xm0Zl81OgjhtYamuZxwcHwwgtw/Hh+5syBN980X4zWwpJ7PIFKFBli46A9puz0fNq3bx9r167l6NGjnDhxgq1bt1KiRAmVKBSrtOTUEj7a9hG9q/RmQssJaR539aq2jsSFC/D116cYONB8MVqTu6fuYpfHDrdSbnqHkiqVKDLAxl57TNlppwgODsbd3R1HR0cA3N3dWbZsGbdu3aJ58+Y0b94cgM2bN9OgQQNq1qzJyy+/TGRkJABHjhzhhRdeoFatWrRt25bgYG06hGbNmjFq1CgaNmxIvXr1OHjwIABRUVEMGjSIOnXqUKNGjcdTmZ8+fZq6devi5+dHtWrVuHDhAh999BGXLl3Cz8+PDz74IMvvUck9CuQpQPty7fmz85/YiLQ/Rjw9oWZNbbxE3bph5gvQytw9dRePSh7Y2FrmR7LF9Hoyp2Zzmj2zrWflnrxV5y2iE6Jpv+DJSWqTkpLoUbgHAwoNICQ6hB5Ln5xnfOerO597zzZt2jB+/HjKly9Pq1at6NWrFyNGjODHH39kx44duLu7ExISwldffcXWrVtxdnZm0qRJ/Pjjj3z88ccMHz6c1atX4+HhwZIlSxgzZgyzZ88GtKSwd+9eNm7cyKBBgzh16hQTJkygRYsWzJ49mwcPHlC3bl1atWrFb7/9xsiRI+nbty/x8fEkJSUxceJETp06RUBAQFYfqZJLxCTEkMc+D23KtKFNmTZpHrdlC9SpA25usHy5ts3CZhmxKHdP3aVMmzJ6h5GmXJkossLGLns9n1xcXDhy5Ai7d+9mx44d9OrVi4kTnxy5un//fs6cOUOjRo0AiI+Pp0GDBpw/f55Tp07RunVrQEtcRYv+NxaxTx+tZ3GjRo0IDw/nwYMHbN68mTVr1vD999rEu7GxsVy/fp0GDRowYcIEgoKC6NatG+Vy+kowitHcibxDo9mN+KjxR7xe8/U0j/v9d/jf/7T1XaZONWOAVio6NJrI4EiLbZ+AXJoo0isB5LXP+8z+iIgIkkKTiH0QS5G8RTJUgkiNra0tzZo1o1mzZlStWpW5c+c+sV9KSevWrVm0aNET20+ePEnlypXZt29fqtd9elZbIQRSSpYvX06FChWe2Ofr60u9evVYt24dbdu25Y8//qB06dJZej9K7hEZH0mHhR0Ijgymumf1VI+REsaN037atYNvvjFzkFbq3unkHk8WnCgss0LMAtk62mpdZJOy1kX2/PnzXLhw4fHrgIAAvL29yZcv3+MZX+vXr4+/vz8XL14EtBlnAwMDqVChAvfu3XucKBISEjh9+vTjay1ZsgTQGszz589P/vz5adu2LVOnTn00uSLHjh0DtOVWS5cuzYgRI+jUqRMnTpx4IgZFeVqiIZFey3px7PYxlvRYQp1idZ49JlEbFzFuHLz2GqxZAy4uOgRrhe6etuweT6ASRYbZOSXP+ZTFLrKRkZEMHDiQSpUqUa1aNc6cOcPYsWMZOnQoL774Is2bN8fDw4M5c+bQp08fqlWrRv369Tl37hwODg4sW7aMDz/8kOrVq+Pn58fevXsfX7tAgQI0bNiQUaNGMWuWNpj9s88+IyEhgWrVqlGlShU+++wzQEsqVapUwc/Pj3PnzjFgwAAKFSpEo0aNqFKlimrMVp7waKzE+gvrmd5+Oi+VfynV40JDYfNm+PRTmDUL7C1r3R2LdvfUXRxdHclXLJ/eoaQpV1Y9ZYWdo/aokmKTIG/mz69Vq9YTH+6PDB8+nOEpVmhp0aIFhw4deuY4Pz8/du3aleq1u3fvzjfffENERMTjlfjy5MnDjBkznjn2448/5uOPP35m+8KFCzP8XpTcQwhBBfcKfNL4E96o/ezo6/v3wdVV69104oTWeK1kzr1T9yhcpbDJFkYzBpUoMsjWUU03ruQu4XHhuDq68m6Dd1Pdf+WKNvtrhw4webJKElkhpeTuqbv49vDVO5R0qaqnDLKxtcHG3vLmfNq5cye1a6c/fYKiZNa6wHWU+rkUh24+W7oFOHYMGjSAkBDo0SPVQ5QMiAyOJCYsxqLbJ0Alikyxc7RT61IoOd7BmwfpuawnpdxKUdG94jP7t26Fpk3B0RH8/SG5N7eSBcFHtYGzRWsUfc6R+lKJIhPsHO1U1ZOSo10IvUCHhR3wdPZk3SvryOf4ZAPrgwdaCaJUKdi7F3wtu8bE4gUfDQYBRfyK6B1KulQbRSbYOtliCNW6yFrqUHtFyaq7UXdpO78tABv7bcTTxfOZY9zctK6v1atD/vxmDjAHCj4SjHsFdxxcHPQOJV3q0y4THvd8srB2CkUxBjcnN1qXbs36V9ZTvlD5x9uTkmDkSK3bK2jVTipJGMetI7coWtOyq51AJYpMUT2flJwoNjGWkOgQHGwdmNFxxhMD6mJjoU8fmDIFzp3TMcgcKPJOJBE3IyhaSyWKHEWVKJScJsmQRP+V/Wk0uxExCTFP7HvwQJuK4++/4fvv4bvv9Ikxp3rckK1KFNZpwYIF+Pj4YGNjg4+PD0uXLgW0iQFt7LK+fnbz5s3ZsmULAJ9++ikjRowwWsyKkllSSkZsGMGyM8t4o9Yb5LHP83hfbKxWxbR3LyxcCO+9p2OgOdSjRFGkhmU3ZINqzH7GggULGDp06OPFhK5du8bw4cNxcnKib9++2DraZrmL7Lhx4/j888+5e/cux44dY82aNcYMXVEyZdy/45h+eDofNPzgmUF1Tk4wYADUqAEtW+oUYA4XfCSYguUK4pTf8hcOVyWKp4wZM+aZFediYmIYM2YMoFU/ZbXqqWnTpkgp+fHHH1m8eDG2trZERUUxcOBAhgwZwoIFC7Idv6JkxLzj8xj37zhe83uNSa0mPd6+e7c2NgLg/fdVkjCl4KPBVlHtBBaUKIQQs4UQd4UQp1JsKyiE2CKEuJD8ZwFTx3H9+vV0t9s52ZEUn4TBkPlZZE+ePElwcDCOjo6P52RasWIFPXr04Pfff1clDMVs2pVtx4eNPmRmx5mP5xhatgxat4bRo7UpwxXTiQ6N5uG1h1bRkA0WlCiAOUC7p7Z9BGyTUpYDtiW/NqmSJUumu/1Rz6fMliqCg4Pp27cvq1evxtnZmU2bNgEQFBREiRIltGvb2mY1bEXJkGPBx0hISqCwc2EmtpqInY1W+/zLL9CzJ9SqBf/8AxY8P12OEHzEehqywYIShZRyF/D0orqdgUer+8wFupg6jgkTJpA375PTw+bJk4cJE7QF5B9PN56Jdoro6Gi6devGDz/8gK+vL5999hljx44FoHjx4gQFBQFkqZSiKBm178Y+Gv/ZmNFbRj/eJiV8/DEMHw6dO2vTcxQsqGOQuYQ19XgCENKCyphCCB9grZSySvLrB1JKtxT770spn6l+EkIMBYYCeHp61lq8ePET+/Pnz0/ZsmUzHMfSpUsZN24cQUFBFC9enM8++4zevXsDIA2SyAuROLg74FjIMdPv8WlRUVG8//77ODk5Ub9+fXr16pXlayUlJZmkVHLx4kUePnxotOtFRkbiYgWr2uSkOC9FXmLU8VHkt8/PFL8pFHTQsoHBAOPHVyJ//gRGjLiAKQu11vA8zRXj6bGniQyMpN7Celk63xRxNm/e/IiUMvUZRqWUFvMD+ACnUrx+8NT++8+7Rq1ateTTzpw588y2zAgPD3/i9e3jt2XYpbBsXdMUno7TWLL7/J62Y8cOo17PVHJKnBdDL8oi3xeRxX4oJq/cvyKllDI8XMqbN7X98fFSGgymjVFK63ie5orx59I/y6U9lmb5fFPECRyWaXyuWkzVUxruCCGKAiT/eVfneACt+knNIqtYAyklPf7uQUJSApv7b8bHzYfbt+GFF6B9e216Dnt71SZhTjH3Y7h/+T5Falr++IlHLH0cxRpgIDAx+c/V+oajsctjR/S9aKSUFr0qlaIIIZjdaTaJhkQqeVQiMFAbbX3njtbLSfWfML/bx24D4FXLS+dIMs5iShRCiEXAPqCCECJICDEYLUG0FkJcAFonv9adnZMd0iBJildTeSiWKTwunHnH5wFQo2gN6hSrw/790LAhREbCzp3w4ov6xphb3TpyC7CehmywoBKFlLJPGruMMuTHmN/+U/Z8ejT/U04lLaizg5IxMQkxdFzUkb039lK3WF0quldESnj3XW2a8I0bIRN9OxQju330NvlL5ieve97nH2whcvanXDInJydCQ0MpVKiQUZKFXZ7kRBGTCDl4umUpJaGhoTg5Wf4UA4omPimeHn/3YPe13SzotoCK7hVJStKqmJYtAzs7KGzZq27meLeO3LKagXaP5IpE8Wiswr1797J0fmxs7DMflg/DHmIfa0/e+5bzrSC1OLPLycmJ4sWLG/Waimk8mgl2/YX1zHhpBr2r9GHcOG1962XLwMt6qsRzrNiHsYRdCKP6gOp6h5IpuSJR2NvbU6pUqSyfv3PnTmrUqPHEtjlvzsGQYGCQ/6Dshmc0qcWp5B67ru3i79N/813r7xhUfShDh8Iff8DAgWpKDkvxqCHbmtonIJckClNw93Xn9OLTqueTYjGal2pOwP8CKONSja5dYe1aGDMGvvxSdX+1FDf23QCgWN1iOkeSORbT68naePh6EPsglqg7UXqHouRiUkpmX5nN5kubAajmWY3evWHdOpg2Db76SiUJS3LD/waFKhSyqoZsUIkiy9x93QG4dzZr7R6KYgxf7vqSv67/xbrAdY+3ffopLF8Ob72lY2DKM6RBcmPvDUo0KqF3KJmmEkUWeVTyACDkbIjOkSi51Xf+3/HFzi9o69mW/oUn8/332vZ69aBrV31jU54Vci6E2PuxlGyU+gzVlkwliizK55UPh3wOqkSh6GLqgamM3jqaXpV70Sx8As2b2TB1Khhx7kbFyG7s1donrLFEoRqzs0gIgYevByFnVIlCMS8pJSfunKBrxa60jf6LIZ/YUrkybNgA+XPwuB5rd8P/Bnnd81KofCG9Q8k0VaLIBndfd1WiUMwqLjEOIQQzOs6g7rUlDBpoT7VqD9m1S42TsHTX/a9TomEJq+wlqRJFNrj7uhMZHEnsw1i9Q1FygUUnF1FpeiWuP7yOjbDBq4g9ffrAxIknVEnCwkXdjSLsQphVVjuBShTZohq0FXNZenop/Vb2o5hLCS4c13rcDRgACxaAg4MaTWfprLl9AlSiyBYPXy1RqOonxZSWn1nOK8tfoW7RhiT9tZaO7fISrK2kqcZIWInr/texdbC1qqnFU1KN2dngVsoNW0dbVaJQTGbr5a30Xt6b6u51uf/Lei6fdWHePChqXTNA5Ho3/G/gVdvr8czT1kaVKLLBxtaGQuULce+MKlEoplGraC26eg8m+LuNBF/Nx6ZNkLx8u2IlEmMTCT4STPGG1ju5pkoU2eTh66FKFIrR7b2xl5iEGArkKUDZc78h4l3ZsweaN9c7MiWzbh2+RVJ8klUOtHtEJYpscq/kzv0r90mISdA7FCWHWBe4juZzm/PBpjGANl/T0aNQtarOgSlZct3/OgAlGlpnQzaoRJFtHr4eICE0MFTvUJQcYF3gOrot7UZhqrJixGcEBYGNDXh66h2ZklVBe4MoWK4gzoWd9Q4lyzKdKIQQzkIItSR7sseTA6p2CiWb1l9YT7el3SgQX5WgCVtoUKMAhaxvEK+SgpTaRIDWXO0EGUgUQggbIcQrQoh1Qoi7wDkgWAhxWgjxnRCinOnDtFzuFdyxsbfhzok7eoeiWLHYxFiG/jMU56gq3PluC8MGF2DpUsiTR+/IlOwIDQwlOiTaasdPPJKREsUOoAzwMVBESllCSlkYaALsByYKIfqZMEaLZutgi0clD+4EqEShZJ2TnRPtwzZx/6etTBxbgKlTtXWuFet2w9+6B9o9kpFOva2klM+01Eopw4DlwHIhhL3RI7MiRfyKcGnzJb3DUKzQirMrOHHnBF+88AXfj65M+9rQpYveUSnGcmX7FfJ65MW9grveoWTLc0sUj5KEEOInkcZsVqklEmMSQlwVQpwUQgQIIQ6b8l5Z4Vndk8jgSKLuqtXulIxbdmYZPf/uyS8bNhMWHoerq0oSOYk0SC5vvUyZ1mUQNtY9hD4zjdmRwBohhDOAEKKNEMLfNGGlqrmU0k9KWduM98yQIn5FALh9/LbOkSjWYuHJhfRe1htu1sdm4SbuBTvpHZJiZHdO3iHqThSlW5fWO5Rsy/B4cinlp0KIV4CdQog4IAr4yGSRWZEi1ZMTRcBtyrQuo3M0iqWbGzCX11a/hrj2AqX2/8Pmf10obf2fJcpTLm+5DJAjEoWQMmMzTwohWgKfAgIoCnSSUp43YWwp730FuA9IYIaUcuZT+4cCQwE8PT1rLV682Kj3j4yMxMXFJd1j9vfaT/5q+fEd42vUe2dGRuK0BLk9zp+2HWL1le1UOP4nk766RP782au5ze3P05iMGeOJD04Qdy+OOnPqGOV6KZniWTZv3vxImjU2UsoM/QDbgcbJv1cFAoAWGT0/Oz+AV/KfhYHjQNO0jq1Vq5Y0th07djz3mIUvLZTTKk8z+r0zIyNxWoLcGueV+1eklFJeuCDlwFcNMirKONfNrc/TFIwVY3x0vPzK6Su5YdQGo1zvaaZ4lsBhmcbnaobbKKSULaSUe5J/Pwm8CHyVtdyVOVLKW8l/3gVWAnXNcd/M8PTzJORcCImxiXqHoligb3Z9S7mfK3Ag6CBly8KcPwV58+odlWIq1/dcJzE2McdURWdkwF1aPZ2CgZbpHWMMySPB8z36HWgDnDLV/bKqSPUiyCTJ3dN39Q5FsSBSSj7a9AWf7PiQxJPdeHiuht4hKWZwectlbOxt8H7BW+9QjCIjJYrtQojhQognxqALIRyABkKIucBAk0Sn8QT2CCGOAweBdVLKjSa8X5Y86vl057gaeKdopJS8teoDJu0fjwh4jd9fnE+bVrl6yFGucXnLZUo2KomDs4PeoRhFRno9XQCSgJVCiKLAA8AJsAU2A5OllAGmClBKeRmobqrrG0uB0gVwcHHgdoDqIqtoftm+gt9O/IDdkbdZ+cbPvNQhA9/LpHxy2bqnXysWL/JOJLcDbtNiQgu9QzGajCSKhlLKoUKI14GSgAcQI6V8YNLIrIywEXhW81QlCuWxioZuFNi8nA0/dqVevQx82I8dCw8ewOTJWnKQEt55B9zctH2KVbiy7QoAZdrkjPYJyFii2CSE2IdWBTQArdfRaZNGZaU8q3tycuFJpJSYsNlGsWBxiXG89vcIxrf9gNaty3KzcbfUJ/aLiflvxr+//oK1a2HXLrh9G+bNAx8faNoUfv4ZmjWDN98Eb28oVQrq14eSJVVJw0Jd2nyJPAXzUKRGEb1DMZrnJgop5XtCiNLATqAU0AmoLISIB05JKXuZNkTrUcSvCId/PczDaw9x83HTOxzFzKLio6jzY1fOxm3BM6E+kweU/S9JxMbCpk2wcyeGnbsQZ05z+td/iY4RFF+1lQLH9xGXvxgGj/zY37uJ/f0z2Bw7hcPIkRAfD0uWQFjYfzerVQsOa7PZ2MTHm//NKqmSUnJ5y2VKtyqNjW3OWe4nQyOzpZSXhRCtpJSBj7YJIVyAKiaLzAp5VtdWl7kdcFslilzmfswDqk/qwA25nypX/uTL914FtA+OiF/nk/e9t7CLjSQBO4IoznXqsX/wCmLJC5TWflJZ0iTf3/nwaeaDz7evU6qeBwUSQsDfX0se2g2o/frrULYs9O0L3btrVVWKLkLOhhBxKyJHjMZOKTNTeAQ+9ToSbZpxJZlnVU+EjeD28dtU7FJR73AUM7n18C5Vv21DmO0ZmoUuYfNPbYkdO5b91104eNQBcekCTSjDDe8myKYvULBSEQpXKMSgCu7kdc+LsBXY2NogbCD+3Y95MGsZD3DjAW7cdWnKle2SkwtPAuBWyo2qfatS47UaFACIj+dOy5aU8veH11+HYcOgVy8YMwbKl9f1ueRGj2aRzrWJQnk++7z2FCxXUDVo5zL/bnUm7IYHvYv8zdSwrRg8XyVfYhRJtk1wb/s/yr3bAJ/2X+KXXikzueHacdbP5Bs5khKTJ2sN2T9/jRwxkpA3PuHKjqtcWHuBPV/vYfdXu/Fp7kONQTUI6dOfUrNnw6FDWvvG7NnQqZOWKAwGbS1VxSwubrhIoQqFcPN20zsUo1KJwsiK+BXh5sGbeoehmMG5e+cp5upF764u5J3RkRfn98RBxnPRqTKRQ4ZTY3x/GrlncPi1EFqV0ciR//V6mjxZ2+XmhkelwnhUKkzdYXUJDwonYG4AAbMDWNl/JY6FHXEd50qNQbWwrVtX6yFVsKB23S+/1BLI5MlQLlcvRmlyMWExXNl+hQbvNdA7FKNTicLIPKt7cnrJaWIfxuKUX00dnVOtOHCAnmva08TtBfoua0/Jg+sIcqtC0pjPKD2yI7b2WViebuzYJ8dNPEoWT/Vuci3uStMxTWnycRMubbnEP+/9w7o317Hnmz00/qQxNV6rge2jUoSHB+zeDVWqwHvvaVVSzs7Ze/NKqs6vOY8h0YBvd/0mBjUVVSY1sscjtNUa2jnW1A2b6P5PC2RUPmp/48nDGw8p/OdESoUeptz7XbKWJB55ustrOl1ghY2gbNuy+E31o+/GvrgUdWHd/9bxW/XfuLJD68vPW2/B+fPQpw988w1UrKj1vlKM7uzys+QvmR+v2l56h2J0KlEY2aO1KVQ7Rc700fyFjNjXEftQb7bMcmJQQ2eGBw7H79Uauq1iJoSWMAbvG0yff/qQFJ/EvBbzWNFvBZF3IqFIEZgzR+stVawYuFv3spyWKC48jkubL+Hb3TdHjqFSVU9G5lLUBefCzgQfCdY7FMXI/llyjUnHRuMcVpUNq+2psnYGBV6wnNllhBCUf6k8pVqWYs83e/Cf5E/g2kBaf9uamkNqIho2hH37/iuljB8PrVpBw4b6Bp4DBK4LJCk+KUdWO4EqURidEIJi9YoRdCBI71AUI5FScnX3VRKHfcWbc3qw/Vo9GgXvtqgkkZJ9Hnuaj2/O/078D69aXqx9Yy2LOy/W1nR/lCQePoS5c6FJE61tJClJ15it3dnlZ3Ep6kKJBiX0DsUkVKIwgWL1ihFyNoTYB7F6h6JkU1xCIpXe7MHLXw/khltVPvu9J3W3T8fG0fJngXWv4E7/Lf1p93M7Lm2+xK/VfuXChgvazvz54dgxbZDeuHHQpQuEh+sar7WKj4rn4oaLVOxaUbfqR1NTicIEitcvDsDNQ6qbrDVasGABPj4+7Pp3H0UHNuZc0RWQpzhDDg+haDfrqqYRNoJ6I+ox5NAQnAs7s7D9QjaM2EBSfBK4umrjLqZNgw0btGoog0HvkK3OxY0XSYhOoFL3SnqHYjKqjcIEitUpBgKC9gflmBWucosFCxYwdOhQ8pKPSUGLiC5/ikZr2/Pm223J45ba7H7WwbOqJ0MODmHrR1s58PMBgo8E8/Kyl8lXNJ/WM6p8ea06Sg3Oy7Szy8+S1z0v3k1zxiJFqVH/KkzA0dURj0oe3DygShTWZsyYMRSJKUn4gAJEFwmk4dJW+B9ez5gvPtc7tGyzc7Kj3U/t6LGkB7cDbjOz1kxu7L2h7WzVSpsnCuDPP2HxYv0CtSKJcYkErg2kQpcK2Njl3I/TnPvOdFasXjGC9gehrVmuWIuIaxFMkD6U2PkaAwMGsffsFgCuX7+uc2TGU7lnZV4/8Dr2ee2Z02wOh3499N9OKWHhQnjlFZg1S78grcTlLZeJj4jP0dVOoBKFyRSvV5yY0BjuX76vdyhKBn31x1LqVW9EAFVxP/c9VZv9V21YsmTJdM60PoWrFGbIoSGUaV2G9W+tZ/3w9RgSDVqvqNWroW1bbZLBn3/WO1SLdnb5WRzzO1KqRSm9QzEplShM5FGDdtB+1U3WGvR/bxyf3XiFvXUDWZBnEQdSzPmdN29eJkyYoGN0ppGnQB56r+lNg/cacOiXQyzuspj4yHjImxdWrYJu3WDUKPjqK71DtUgJ0QmcXXGWil0qYuuQjdH4VkAlChPxqOyBvbO9aqewcAaDpMnbw5jvOpYCl2vh3+4PJv4+EW9vrWHS29ubmTNn0rdvX50jNQ0bWxvafN+G9tPbc3HDRf5s+ifhN8PB0VFbLKl/f0hM1DtMi3R66WniwuOoMbiG3qGYnOr1ZCI2tjYUq1NMJQoLlpBooNI7PbnosRyfYy3wH/UDXs38qExj+vbty86dO7l69areYZpFnTfr4ObjxrKey/ij3h/03dAXz6qe2tQfjwbpPXigFkVK4ejvR3Gv6E7JxjmrWjI1qkRhQsXqFSP4WDCJseobmSU6tSyQ66fK0mBbew6/9Q1ezfz0DklX5V4sx2t7XgMJc5rO4br/da27rBBw7pw2Tfns2XqHaRHunr7Ljb03tKlRcuDcTk+zikQhhGgnhDgvhLgohPhI73gyqnj94hgSDNwOuK13KEoKZ25dYcexHewfvZKtew6yduT7FGpTV++wLEKR6kUYtHcQzoWd+avVXwSuTV7YslQpqFkThgyBZcv0DdICHP39KLYOtlQfYJnTuBibxScKIYQtMA14EagE9BFCWEVftGL1igGqQduSrDy8j2pT69F57kDuh0vK7J9Pwe7N9Q7Lorh5u/HantcoXKUwi7ss5vi841qbxYoVUL++1nU2F09VnhCTwPF5x/Ht5kvejC5MZeUsPlEAdYGLUsrLUsp4YDHQWeeYMiRf0XzkL5lftVNYiG/XL6Hb6uYYol34fEF1+v3TF69aOW/tAGNw9nBmwPYBlGpeilUDV7Fv8j5twaN166BSJXj5ZTh7Vu8wdXF2+Vli78dSc0hNvUMxG2HpA8KEED2AdlLK15Nf9wfqSSnfTnHMUGAogKenZ63FRh5VGhkZiYuLS5bOPTP2DBHnI6i3qJ5RY0pNduI0J3PHKaXku/3L2RA/Dfvr9di2+AFObVoQNbJnuuep5wmGeANnvz5LyL8heL/qjfcAb5xCQig5fz6X3nwTg1PGV3G0hueZkRgDRgYQHxpPnXl1dJsE0BTPsnnz5keklLVT3SmltOgf4GXgjxSv+wNT0zq+Vq1a0th27NiR5XP3/rBXjmWsjLgdYbyA0pCdOM3J3HHeCEqSNq90lvle7iYv2nrJoOZ9M3Seep6apIQkuerVVXIsY+Wm9zZJg8Hw386HD6WMicnQdazheT4vxntn78mxjJW7J+42T0BpMMWzBA7LND5XraHqKQhIOcl7ceCWTrFk2qN2ClX9ZH73ou4RFB5E8WI2fHf/Va78vQ3nkiXx2jJX79Csio2dDZ1mdaLu8Lrs+2Efa99YiyHJALGx0LixNoLbwmsmjOXoH0exsbPB71U/vUMxK2tIFIeAckKIUkIIB6A3sEbnmDKsaM2i2NjZqIWMzOzE7VOU/bYubX7vSeD6QJw2biW6SHkKH92EsM3Zo2hNQdgI2v3cjsafNObo70dZNWAVSbb20Ls3LFgAOXDk+tMSYhIImBNAhc4VcPG07Co0Y7P4AXdSykQhxNvAJsAWmC2lPK1zWBlmn8cez+qeBO1VicJcVp1ez8tLepMY7UL7e9+w4ssVFKheFc/dP2Lj4qB3eFZLCEHLCS1xzOfIto+3kRCTQPeFH2B39ix8/jnUrg3t2ukdpskcmXGEmNAY6o0wfXujpbH4RAEgpVwPrNc7jqzyfsGbQ9MOkRibiJ2TVTxyqySl5MvtP/DF7tFw14+Piy1n0MzuRCU44L1yAw4qSRhF448aY5/Xno0jN7Kk61J6zv8F++PHoV8/OHoUctgEiqCVJvwn+ePTzCdHrzuRFmuoerJ6pVqUIikuiRv7bugdSo4WHBLL1+vmIs72YFajXXRf8gVlI45RYkAz3HwK6B1ejlJvRD06/t6Ri5susvDlVcTPXQjVq+fYtoqjvx8l8nYkL3zxgt6h6EJ9vTUD7ybeCFvB1R1XKdU8Z09HrIfbkbfJ55CPou7O9E/aSe+hBXFbMA2/0wu4X7UJBX/7Ru8Qc6Sar9fELo8dqwau4q9hifRdvw4nNyctWeSgaS0SYxPxn+SP9wve+DTz0TscXagShRk4ujriVduLK9uv6B1KjnP41mGq/VKHfovfQgj4/edClLixj7J/jiHWxQO3f1fnqA8tS1OtbzVeXvoytw7fYm7zuURdua1NT750qd6hGc3RP44ScSsi15YmQCUKs/Fp7sPNAze1+f4Vo/jr+F80/KMx9+7YErb2XQBCA0M59NZs7O3BccsaRAFV5WRqvt186bOmDyHnQpjXfgmJN27B4MFw6ZLeoWVbYmwieybuoWSTkrm2NAEqUZhNqRalMCQatBk5lWxJNCTy7qZ3GbBqAAmXG1Lv+GFW/ladhOgElvZYys285Uk4HYhdfTXRn7mUbVeWfpv68eBmNHPvvojBxjZHrGVxdNZRIm5qpYncMEtsWlSiMJOSjUpiY2+jqp+M4Fb4bX7dOxcODKdr5CZ2rnenQAHJv31n4H1yLd3mdyV/OU+9w8x1vJt6M2DbAEIi87DB5iXYtw8mTtQ7rCxLjEvEf6I/JRqVyPFLnT6PShRmYp/XnuL1i3N1+1W9Q7FaF8MuYpAGPByLU2nnad4uM4W/l9jj5AQBMw9SadXXtMqzh7K13PQONdcqVqcYr/77Kufy1OC0gx9JP/8CUVF6h5UleybuITwonGbjmuXq0gSoRGFWpVqUIvhoMLEPYvUOxerMPzGfqtOrMnHnz+TJA7s3FGHKFLC1hdsBt4kaNhovgrGbNws8PPQON1fzrOrJIP9B7CnWm1+iBnFxd7DeIWXa3dN32T1hN1VfqUrplqX1Dkd3KlGYkU9zH6RBcm3XNb1DsRoJSQmM2jiK/iv7Y3O7Hlt/7IuUkDev1pkpLjyO3R2+oWHSbhJeGYBNjx56h6wABUoVoO++YThV9GbxSwu4Mnq63iFlmCHJwD+v/4OjqyNtf2qrdzgWQSUKMypevzh2TnaqnSKDgiOCaTGvBT8f+BmXUyOxmb+FT0YWftzbVUrJuqGraHnrL5K8SmD/2y/6Bqw8wcXThYE7BtKq9EVKfTeMpG/XPZoB2qIdmnaIoP1BtPu5Hc4eznqHYxFUojAjO0c7SjQqwdUdV/UOxSpcDLvIsZsnyLthIfn8f2L3Tntatfpvf8CfAZxcco6gVz/DftliyJdPv2CVVDnld6L2od8Idy1GrQ2/s+G1pSQlJOkdVppib8ey7ZNtlH2xLFVfqap3OBZDJQozK9WiFHdO3CHqnnU28JmalJJ9N/YBUN+rCe7zr1HyYR/27QM/v/+Ou3f2HhuHraFUi1JU+WMkNGigT8DKc9nldybf+qXkJxz3uT+ysMNCYh9aXjudlJLAHwMRQvDSby/l+gbslFSiMDOf5j4AXN15Vdc4LFF4XDi9lvWi4eyG7L9xAHt72LDSDX9/8E4xD1tCTAIreixicMIMeja8jo2t+mds6USjhtzs1pU64hBJ2/9ldsPZ3L98X++wnnBo+iHuH7pPy29akr9kfr3DsSjqf5iZedX2wsHFQVU/PeXknZPUnlmbFWdX0DRuEgu/r4uU4OsLBQs+eeymdzdR4cwKCicF41S/hj4BK5l25fXXEW3a0GZKByJuRTCz1kwC1wbqHRYA5/85z8YRGylYvyB13qqjdzgWRyUKM7O1t8W7qTdXtqkG7Uf+Ov4X9f6oR2R8JC9c3c6ub0ZjSBKpTkR6dsVZrv+2nqY2/tC3L3ToYP6AlSxJypMHNm7E662uDD0ylAKlC7Co4yK2fbINQ6JBt7huHrzJ8t7LKVqzKJU+r6TbOtiWTCUKHZRuU5rQwFDCLobpHYpFiIyPpHaR+pTefIztfzblm29g6lSweepfZ3hQOP8MXkWPvBsQBd3gp5/0CFfJrshICkwZx6DpNak5pCZ7vtnDX23+IvJOpNlDCbsUxsKXFuLs6UyftX2wzaNWP0yNShQ6qNi5IgDnVp/TORL9nAs5x7rAdQAMrfk/Ymdu4cB2T+bNg48+enbCV0OSgZUDVuIRex2PhJuIn34Cd3fzB65kX3w8LFyI3Tsj6PhbBzrP6UzQ/iCmV57OiQUnzNaFNjokmgUvLkAaJP029st1y5tmhkoUOnDzccOzmifnV5/XOxRdbLmzhdozazNi4wgSkhKwtRV88rEt69dr88ilZu93e7m64yp+04ciAgPhlVfMG7RiPAULwnffaXNBzZ2L30A/hh4ZSqFyhVjZbyWLOi4iPCjcpCHcPn6bWQ1mEX4jnD5r+lCofCGT3s/aqUShkwqdK3DD/wbRIdF6h2I2UfFRDF49mK/PfU0tr1p8V2kXSxfbA9ClC7Runfp5Nw/eZMdnO2jQNh9+r/qBj49aY8La9e8PjRrB6NFw/z4evh68tuc12k5uy5XtV5heeToHfzlIYpzxZ589NvsYs+rPIj4qnn6b+1GiYQmj3yOnUYlCJxU6V0AapMX0+jC18Lhw6vxehz8D/qRfyX685byNV14qxsSJkJCQ9nlxEXEsf2U55QqF0mbTe4i5c80XtGI6NjYwbRqEhcFnn2mbbG2oP6o+b558E6/aXmwYvoFfyv/CkZlHSIrP/iC9hOgEVr+2mjWD11CiYQneOPYG3k1y3/rXWaEShU6K1iyKa3HXXFP95OroSpeKXdjcfzMFjn1On1521KwJO3eCvX3a520csZGHl8Po6roVihWD7t3NFrNiYtWrw2+/wciRT2wuWKYg/bf2p9+mfuTzysfaN9byS4VfOPzbYaJDM18Cj7kfw97v9zLNdxoBcwNo+llT+m1WbRKZodbM1okQgvKdynN8znESYhKwz5POp6WVuh9zn2Hrh/FBww+oUbQGE1p8zUcfaT2aunSBhQshT560zz+99DQBcwLo/eIDHDechiVL1DQdOc2QIf/9nmKtbSEEZdqUoXTr0lzceJGdX+xk3ZvrWP/2enya+eDb3ZeKnSviUtQl1RHUCdEJ3Dtzj2Ozj3F87nESohPwfsGbzn92zvVrS2SFRScKIcRYYAhwL3nTJ1LK9fpFZFwVO1fk8PTDXN56mQodK+gdjlHtvrabviv6EhwZTKvSrahRtAZCaImhU6ebLFtWDNt0eiI+vPGQtW+spUxNV8rv+wlatoSXXzZb/IoZRURobRYdO2pLqKYghKDci+Uo264swUeDObv8LGeXn2X9W+tZ/9Z67PPa41rcFdfirjgXdiYiOIKwi2FE3IwAwNbRlqqvVKXeiHoU8Suix7vLESw6USSbLKX8Xu8gTMH7BW8c8jlwfvX5HJMoEg2JjP93PBN2T6B0gdLsHbSX8i51OH5cq2n44gvYufMCtrbF0ryGIcnAyv4rMSQa6PReWcR7TloxRDVg50wuLhASAp98Aj17plpqFELgVcsLr1petJjQgntn7nF5y2Ue3nhIRFAE4UHh3Dx4E5eiLpRuVZqC5QpSsGxBSrUopWaANQJrSBQ5lp2jHeVeLEfgP4EYkgw5Ys6i34/8zpe7vuRVv1eZ0m4KEaH5aNoU7t6FS5f+W0ciPXu/38u1f6/R+c/OuL7iBz2ugYODWeJXdCAETJ4MdetqS6dOmPCcwwWFKxemcOXCZgpQEZY8P3xy1dOrQDhwGHhPSvnMTGJCiKHAUABPT89aixcvNmockZGRuLiYpuHrztY7nJtwDr+pfuSvkr2JyEwZZ3qklITFh1HIsRCJhkQO3z9M/UL1uXo1Lx99VI3wcDvGjTtNnTr3nxtnxPkIjg07hnsTdxq3eUhY3bqkW0dlQno9z8zKKXH6TpiA+65dHJw3jzhPfdY8zynPMiuaN29+REpZO9WdUkpdf4CtwKlUfjoDnoAtWu+sCcDs512vVq1a0th27Nhh9Gs+EnM/Ro63Gy83j96c7WuZMs60hESFyO5LukuvH7xkWHTY4+27dknp5iZlkSJSHjny5DlpxRkXESenlJsifyz+o4xdtkZKkPL3300Yffr0eJ5ZkWPivHZNSicnKV9/3SzxpCbHPMssAA7LND5Xda96klK2ev5RIIT4HVhr4nDMzsnNCe8XvDm/+jytJ6Ux4sxCbbm0hVdXv8q9qHt82fxLXB1dH+/79Vfw9ISNG7XxcRmxYeQGwi6GMXBrPxxHdoHSpdMeqq3kPCVLwrJlam0RC2TRleJCiKIpXnZFK2nkOBW7VCT0fCh3T93VO5QMiU+KZ/j64bSZ3wZXR1f2v76fDxt/iK2NLVHJ6zHNmgX+/hlPEqf/Pk3A7AAaf9wYn0vb4dQpmDQJHB1N9j4UC9ShgzbFh8FAqtMHK7qw6EQBfCuEOCmEOAE0B97ROyBTqNyrMjZ2Nhz785jeoWSIvY09lx9cZlS9URwdepSaRWtiMGizMTRoAOHhWjfYQhmcPufh9YesHbqWYnWL0ey9WtpI3UaN1OC63OrmTahdG1as0DsSJZlFJwopZX8pZVUpZTUpZScpZbDeMZmCs4cz5TuW5+T8kxa7nnB8Ujzjdo7j2oNrCCFY3Xs1k9tNJo99HuLjtRqi776DJk3AORO9EVN2he22sBu2t2+Bhwf88IPqDptbeXpq87p8+GH687soZmPRiSI38XvNj6i7UVxYf0HvUJ5x/PZx6v5el7H/juXvM38DYGejNW89fAjt22ujrL/+Gn75JXOdlPZ8s4dru67Rflp7CpYpCJUqwYkTUK+eKd6KYg3s7OCbb7T+1LNn6x2NgkoUFqPci+Vw9nQm4M8AvUN5LNGQyIRdE6jzex1uR95mde/VvN/w/SeOefNN+PdfmDsXPv44c4WA63uus3PsTqr0qUK1/tW0lu/wcFWSULS2ioYNYfx4iInRO5pcTyUKC2FjZ0P1AdW5sO6CLit9pWbSnkl8uuNTulfqzum3TtOpQqdnjvn2W+3zfcCAzF07JiyG5a8sx83bjZd+ewlx4wZ07qyNzlUUIbRSxa1bqlRhAVSisCB+r/lhSDRwYv4J3WJISErgxsMbAAyvN5wVPVewqPsiCuX9r2V6925tSp6kJCheXJuGKTOklKwZvIbI25H0WNIDR1dHGDdO2zl6tLHeimLtmjaFVauenDhQ0YVKFBbEw9eDYvWKEfBngNmWg0wp4HYAdf+oS/uF7Uk0JOLq6EpX365PHLNsmbbAkL8/hIZm7T63Vt3i3KpztJrYCq/aXnDuHMyZo9VjlSyZ/Tei5BydO2vTt6iusrpSicLC+L3mx73T97h1+JbZ7hmbGMuYbWOoPbM2wRHBfNn8y8eN1SlNmaLN2VarlpYoCmdhqp3bAbe59OslyrUvR/1R9bWNn3+u9adV1U5KarZsgYoVtQnDFF2oRGFhqvSugp2Tndkata89uIbfb358vedr+lXrx5lhZ+hSscszx335pba+TOfOsHVrxsdIpBQXHseyXsuwd7Wn85zOCBsB8fHaNNPvvpu1zKPkfCVKwMWLWpuFoguVKCyMU34nfLv7cnLhSRJiTNeH/FHVllc+L3w9fNnUbxNzusyhYJ6CqR7fsiWMGqVVPaW32FB691vz+hrCLoXh+6nvf1M/OzjAhg3a/OOKkpqKFeHVV2H6dG0wnmJ2KlFYoBqDahD3MI5Ti0wzY8nKsyup83sdHsQ+wN7WnpW9VtKmTJtnjnv4EObP135v2FCbCTqrE7kemHKAM3+foeXXLXHzc9M2XrwI165pv+s0Q6xiJT77TJvWY9IkvSPJlVSisEA+zX0oUqMIeybuwZBkMNp1g8KD6LqkK92WdiPRkMi9qHtpHnvzptbpZNAguHw5e/e9se8GW97fQoXOFWj4QcP/drz7rjawTo2+VZ7HxwcGDoSZM+HOHb2jyXVUorBAQgiafNKEsAthnFl2JtvXM0gDUw5ModK0Smy6uIlJrSZxaMghyhUql+rxZ85oczZdvgzr1mmTuGZV1L0olvVcRv6S+ekyp8t/6xsfPQr//ANvvw32OW+9cMUEPv0UVq5UbVk60H2acSV1vt18cfd1Z/eE3VR+ubLW8JtFAsGmS5toWKIh0ztMp3SBtD/5d++GTp3AyQl27YIaNbJ8WwyJBla8soKoe1EM3jcYJzen/3aOHw9ubjB8eNZvoOQuPj4Zn45YMSpVorBQwkbQ+OPG3D15l8C1gZk+/0HsA0ZsGMHl+5cRQrC0x1I29N2QbpIArdmgSBHYty97SQJgy+gtXN56mQ7TO1C0xn8zxrtcvAirV2ut4/mzt6qfkstIqZUsPv9c70hyFZUoLFjVPlVxK+XG7gm7MzwAzyANzA2YS/mp5Zl2aBrbr2wHwNnB+b9qn1Q8aod47TU4diz7X9yOzT7G/sn7qTuiLjUGPZlxXM+cAXd3rb+tomSGEBAUBN9/r9oqzEglCgtmY2dD448ac/PgTS5vfX6L8sXIizT9symvrn6VsgXLcnjIYV6v+Xq65xgM8MEHULkynD6tbXNySveU57ruf521/1tL6dalaftD22f23+rUCa5e1aqeFCWzxoyBuDgtWShmoRKFhas+sDr5iuVj94Tdzz12ffB6zoeeZ3an2ewZtIcaRdOvO4qLg759tf9vgwdr3dWz6+H1hyztthQ3bzd6LOmBjd1T/8SuXNH+zMyiFYqSUrly8Mor2riKe2n33FOMRyUKC2fnaEfD9xty7d9rXN9z/Yl9SYYkZh6Zyd4bewEYVGoQgW8H8lqN17AR6f/VPnwIL74IixfDxIkwdWr2hzLER8azuPNiEmMT6fNPH/IUeGpkXmAglC1L0XXrsncjRRkzRpt+fOpUvSPJFVSisAK1htbCpagLG0ZswJCojavwv+5Pnd/r8MbaN/jr+F8AuNi5UCBPgQxd89dftR5Of/2lLSSW3SUgkuKTWNJtCXdO3qH74u64V3R/9qDvvgMHB0IaNMjezRSlYkWtKNytm96R5Aqqe6wVsM9rz4tTX+TvHn+z8oeV/F3mb5acXkJx1+Is7r6YnpV7ZvhaBgPY2GjtEm3bZr9nE4A0SFa9uorLWy7TaXYnyr2YyviMW7dg3jwYPJiEgqlPE6IomfLuu3pHkGuoEoWV8O3mS4XOFZi9bjarz63m86afc27YOXpV6ZVub6aU/v0XqleHGze0aiajJAkp2fjORk4tOkXLiS2p8VoaF/3pJ0hMhPffT32/omRFYKA2Fic+Xu9IcjRVorBwSYYk5h2fRz7HfLSf1p4LlS/QKl8rRo0ZleEEAbB0KfTvr42yNhhvVhD2fLOHg1MOUv/d+jQa3Sj1gxITYdEi6NVLC+D69dSPU5TMunpVW6i9Zk2tb7diEqpEYcG2XNpCzZk1GbRmEItOLcK1mCvtvmlH+Ppwjs87nuHrTJ6sfUbXqaOtI+HtbZz4Dkw5wPYx26nWrxptvmuTduKys4NTp1R3RsX4WrfWisaTJhn3G5DyBN0ThRDiZSHEaSGEQQhR+6l9HwshLgohzgshnu2Qn0OduXeG9gva02Z+GyLiIljSYwnLXl4GQO03alOiUQk2v7uZqLtRz73WjBlaVW737to6EsZqHtj99W42jtyIbzdfOs3ulPYUI4mJ2mja/PnBy8s4N1eUR4TQemOcP6+N9ldMQvdEAZwCugG7Um4UQlQCegOVgXbAdCFErpiLOjA0kH1B+/i+9fecHXaWnpV7Pv62LmwEHWd2JC4ijtWDVj/uBZWWXr207q9LlmR/IB1obRJbP96qlST6V6PHkh7Y2qfz1zJzptYwktV1UxXlebp3hzJltH/oaslUk9A9UUgpz0opz6eyqzOwWEoZJ6W8AlwE6po3OvMIiwlj9JbRfL37awA6V+jMlZFXeK/hezjaOT5zvEclD9r91I4L6y6w9s21z0zv8eCBVoqIidEGP3/4oXGWe5AGyYbhG/Cf6E+t/9Wiy5wuzw6oSykxUatucnY2XlFGUZ5mZ6fN/9SggWrUNhGR0TmETE0IsRN4X0p5OPn1L8B+KeX85NezgA1SymWpnDsUGArg6elZa/HixUaNLTIyEhcXF6NeEyAmKYblQctZfGMx0UnRdPTqyDvl3snw+VdmXeH6/OuU7F+SUoNKERkZSXR0IT76qCo3buTlu+9O4Of3wCixJkYlcv6784T8G0LxXsUp/Ubp5zame/z7L5XHjuXUuHGENG36eLupnqexqTiNyxritIYYwTRxNm/e/IiUsnaqO6WUJv8BtqJVMT390znFMTuB2ileTwP6pXg9C+j+vHvVqlVLGtuOHTuMfs1/zv8jC39XWDIW2WlRJ3n89vFMX8NgMMjVg1fLsYyVB6cdlLNmHZTFiknp6irl1q3Gi/XOyTtyavmpcpztOOn/vb80GAwZO7FhQylLl5YyMfGJzaZ4nqag4jQuk8dpMEi5bZuUly9n+RK5+VkCh2Uan6tm6R4rpWyVhdOCgBIpXhcHbhknIn0kJCUQGR9JgTwFKJavGJU9KrOq1yoalMjaSGUhBC/99hLR96L5ddhJljj2w62QNuK6WjXjxHxi/gnWvrEWR1dHBm4fiHfTDHaZOngQ9u6Fn39Wy5wq5hESos1LM3iwNg+UYjS6t1GkYw3QWwjhKIQoBZQDDuocU5Y8GgtRcVpFRm0aBUCNojXYPnB7lpPEIzZ2NnRf1J2yNV3xiLvF12124Fs2+0uLRtyKYNXAVazsvxKv2l4MPTo040kCwM9PG4mt+rYr5uLhAf36wdy5EBamdzQ5iu6JQgjRVQgRBDQA1gkhNgFIKU8DS4EzwEZgmJQySb9IMy/RkMj8E/OpNL0SA1cNxNXRlZ6VMj7dRkZs2gR2eez5YE9nxnTbytU5u5hRcwY3D93M0vXiI+PZ8cUOppabyqnFp2j8SWMGbBtAvqL5MnchBwdthF++TJ6nKNkxahRER2u97RSj0T1RSClXSimLSykdpZSeUsq2KfZNkFKWkVJWkFJu0DPOrPjy3y/pv7I/TnZOLO+5nCNDj9ChfAejXNtggHfegXbttFHX9nnsKTe8LP239ichKoFZDWax9eOthF3M2Der8KBw9v+8nyllp7Br/C7KdyzPsLPDaDmhZfo9m1Lz3XfalB2KYm5Vq0KrVtqssqoHlNGoKTyMKD4pXitBeFSifvH6DKk1BL8ifnSu2Pm5035nRmwsDBgAf/+tLRL38sv/7SvdsjRvnnyTjSM34j/RH/+J/hSuWpiKXStSrn05HJwdMCQZkEmS+Mh4rmy/wvk157l97DYAJRqVoPeq3hSvXzxrwUVEwFdfaXXFiqKHd9/VqjwDA6FKFb2jyRFUojCCmIQYZh+bzST/SdwIv8GwOsOoX7w+xV2LU9w1ix+4abh/H7p0gV27tCEK77337DFObk50mduFZuObcW7lOc6tPMeuL3exa/yuZw8WUKJBCVpObEmFjhVw93XP1BxSz/jzTwgP14o7iqKHtm3h2jVwfHYMkpI1KlFk04zDM/hi5xfcibpDoxKNmPHSDNqVbWey+wUEwOHD2hx7vXunf6ybtxv1R9Wn/qj6RN2N4vqe6xiSDNjY2iBsBbb2tnjV8cLZw0irzSUlab2cGjSAevWMc01FySwbGy1JJCZq36w8PPSOyOqpRJEFtyNv457XHTsbO8JiwqjmWY0xTcbQ1Ltp9r6Np+PBA22UdfPm2oSZmf2371zYGd9uviaILIV16+DyZW0qBUXRk5RQvz6ULAkrVugdjdXTvTHbmpy9d5Yha4bg85MPf5/+G4APG3/I5v6becHnBZMliW3boFQpWLNGe22xX5A8PLS1jLt21TsSJbcTAlq21CYKvHFD72isnkoUzyGlJOBBAB0XdaTS9ErMPzmfV/1epW4xbdopYzZSp2bBAq1duFgx4yw0ZFINGmgB26mCqmIB3nxTK1nMmKF3JFZPJYrnkEh+uvATB4IOMPaFsVwfdZ3fXvqNMgXLmPa+Er79Vhs/1KgR7NkDJUo8/zzdrF2rvrkplsXHBzp21MZUxMXpHY1VU4niOWyEDeMrj+faqGt80ewLPJzNU++zfbs262uvXrBxo9Y+YbEiIqBvX/j4Y70jUZQnvf023Lun1qrIJlVHkAEl85Ykj30es96zRQtYtUr7QmRj6el8/nytS+zbb+sdiaI8qWVL2LJF+w+lZJmlfwTlKmFh8NJLcOKE1hbXubMVJAkp/1uzWHWJVSyNjY02Utvi/yNZNotZj8JYhBD3gGtGvqw7EGLka5qCitO4VJzGZQ1xWkOMYJo4vaWUqdat57hEYQpCiMMyrQU9LIiK07hUnMZlDXFaQ4xg/jhVeUxRFEVJl0oUiqIoSrpUosgYa5ncXsVpXCpO47KGOK0hRjBznKqNQlEURUmXKlEoiqIo6VKJQlEURUmXShQZJIT4UghxQggRIITYLITw0jum1AghvhNCnEuOdaUQwk3vmFIjhHhZCHFaCGEQQlhUd0QhRDshxHkhxEUhxEd6x5MWIcRsIcRdIcQpvWNJixCihBBihxDibPLf90i9Y0qNEMJJCHFQCHE8Oc5xeseUFiGErRDimBBirbnuqRJFxn0npawmpfQD1gKf6xxPWrYAVaSU1YBAwFInYDoFdANSWXZPP0IIW2Aa8CJQCegjhKikb1RpmgOYbpUs40gE3pNS+gL1gWEW+jzjgBZSyuqAH9BOCFFf35DSNBI4a84bqkSRQVLK8BQvnQGL7AUgpdwspUxMfrkfMO5arEYipTwrpTyvdxypqAtclFJellLGA4uBzjrHlCop5S4gTO840iOlDJZSHk3+PQLtA66YvlE9S2oik1/aJ/9Y3P9xIURxoAPwhznvqxJFJgghJgghbgB9sdwSRUqDgA16B2FligEp50sPwgI/2KyREMIHqAEc0DmUVCVX6QQAd4EtUkpLjPMnYDRgMOdNVaJIQQixVQhxKpWfzgBSyjFSyhLAAkC3qVKfF2fyMWPQiv0LLDlOC5TaMoUW983S2gghXIDlwKinSucWQ0qZlFy1XByoK4SoonNITxBCvATclVIeMfe91TTjKUgpW2Xw0IXAOuALE4aTpufFKYQYCLwEtJQ6DpTJxPO0JEFAyiWiigO3dIolRxBC2KMliQVSSotfwFpK+UAIsROt/ceSOgo0AjoJIdoDToCrEGK+lLKfqW+sShQZJIQol+JlJ+CcXrGkRwjRDvgQ6CSljNY7Hit0CCgnhCglhHAAegNrdI7JagltIflZwFkp5Y96x5MWIYTHox6CQog8QCss7P+4lPJjKWVxKaUP2r/L7eZIEqASRWZMTK42OQG0Qet5YIl+AfIBW5K78v6md0CpEUJ0FUIEAQ2AdUKITXrHBJDcEeBtYBNaw+tSKeVpfaNKnRBiEbAPqCCECBJCDNY7plQ0AvoDLZL/PQYkfyO2NEWBHcn/vw+htVGYrfuppVNTeCiKoijpUiUKRVEUJV0qUSiKoijpUolCURRFSZdKFIqiKEq6VKJQFEVR0qUShaIoipIulSgURVGUdKlEoShmkLwmQ+vk378SQkzROyZFySg115OimMcXwHghRGG0GVQ76RyPomSYGpmtKGYihPgXcAGaJa/NoChWQVU9KYoZCCGqos0nFKeShGJtVKJQFBMTQhRFWxekMxAlhGirc0iKkikqUSiKCQkh8gIr0NaNPgt8CYzVNShFySTVRqEoiqKkS5UoFEVRlHSpRKEoiqKkSyUKRVEUJV0qUSiKoijpUolCURRFSZdKFIqiKEq6VKJQFEVR0vV/SSVGpB0zKV0AAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEWCAYAAAB42tAoAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAABPTUlEQVR4nO3dd3gU5drH8e+dXkhCSeiQ0DuEKr1Js1AUCxpFbHgQFfsLVizYDyjHdjiioqCgWFBUUDAI0juEUKUGAoRQkhASUp73j9mEBJKQwCazCffnuvbK7szu7G8nydw7z8w8jxhjUEoppfLjZncApZRSrk0LhVJKqQJpoVBKKVUgLRRKKaUKpIVCKaVUgbRQKKWUKpAWCnUBEUkSkbp25yiK4sosIt1EZLuzl+tMIhImIkZEPOzOosomLRRXMBHZKyJnHBvZrFt1Y0w5Y8zuS1heTxGJuchzPheRsyKS6LhFicjrIhJ06Z8ELjVzHvmMiNTPsdwlxphGl7tcO4lIVxFZJiKnROS4iCwVkfZ25yoMx99oH7tzXOm0UKiBjo1s1u1QQU8WEXcnvOdbxpgAIAS4G+gILBUR/6IuSL9FF0xEAoG5wH+AikAN4CUg9RKWJSLidt40Xf9XAC0U6gI5v1U79gA+EpFfReQ00EtErhWRaMcewUERedKxkf8NqJ5z76Sg9zHGpBhjVgODgEpYRSMrwz0islVETojIfBEJPS/faBHZCezMmVlEOorI4ZwFTURuEJFNjvsdRGS5iJwUkVgReV9EvBzzFjtestGR/9ace0kiMlZEZp+3rt4TkcmO+0EiMtWx3IMi8mp+hbWgHDk+z79EZKdjHXwgIuKY5y4i74jIMRHZDVxXwGpu6FjXXxtjMowxZ4wxvxtjstbHeBGZnuN9czVjicgiEZkgIkuBZKBuPuv/fhHZ5dhj+Snn715E+onIdscezYci8peI3OeYV09E/hSReMfnmSEi5R3zvgRqAz87fh9PO6Z3dOwhnRSRjSLSM8d7jRCR3Y6/zT0iElHAulGFZYzR2xV6A/YCffKYboD6jvufA6eALlhfLHyAWKCbY34FoI3jfk8g5iLv+Tnwah7TvwBmOe4PAXYBTQAP4Dlg2Xn5/sD6huybR+Z/gL45nv8tMNZxvy3WHowHEAZsBR7N67Of/5mAUKyNZaDjsbtjXXR0PP4R+C/gD1QGVgEP5LMeCpNjLlAea2MZBwxwzPsXsA2o5VgHkY7ne+TxPoFAPDANuAaocN788cD0HI/Dci4LWATsB5o5snqev/6B3sAxoA3gjbX3stjx+mAgAbjR8foxQBpwn2N+faCv43UhwGLg3fz+RrH2iOKBa7H+Hvs6Hoc41nsC0Mjx3GpAM7v/z8rCTfco1I+Ob2YnReTHfJ4zxxiz1BiTaYxJwfpHbyoigcaYE8aYdU7IcQhrwwPwAPC6MWarMSYdeA0Iz7lX4Zh/3BhzJo9lfQ3cBiAiAVgbla8BjDFrjTErjDHpxpi9WBv2HoUJaIzZB6zDKmRgbSCTjTErRKQK1ob4UWPMaWPMUWASMCyfZRUmxxvGmJPGmP1YxSDcMf0WrI3pAWPMceD1AjInAF2xNu7/A+Ic3/irFOYzO3xujNniyJrmmJZz/UcAnxpj1hljUoFxQCcRCcNa91uMMd87fpeTgcM58u0yxvxhjEk1xsQBE/NYDzndAfxqjPnV8ff4B7DG8T4AmUBzEfE1xsQaY7YU4XOqfGihUEOMMeUdtyH5POfAeY+HYv1j7nM0I3RyQo4awHHH/VDgvawC5pgujufklymnr4AbRcQb65vsOsdGHhFpKCJzHc1TCVhFKLgIOb/CUYSA2x2PszJ7ArE5cv8Xa8/iAoXMcTjH/WSgnON+dXJ//n0FBXYU3BHGmJpAc8fr3y3oNefJa13nnFY9ZwZjTBLWt/wa52c1xhgg+4QHEaksIjMdTXUJwHQK/n2EAjfn+HJzEqsQVjPGnAZuxdrjihWRX0SkcRE+p8qHFgpVGLm6GDbGrDbGDMbaCP4IfJPX8wpLRMoBfYAljkkHsJpsyue4+RpjluWX6bx80VgbrmvIvTEH+Air2aaBMSYQeAarCBXWt0BPEakJ3JBj2QewDhAH58gcaIxpls9yLidHLFazU5bahQ1vjNmG1fzX3DHpNOCX4ylV83rZRaYdwtqAAyDW8apKwEFH1po55knOx1h7QwZo6VgPd5B7PZz/3geAL8/72/A3xrzh+HzzjTF9sZqdtmHtRanLpIVCFYmIeIlIhIgEOZohEoAMx+wjQCUp5KmuIuItIm2xis0J4DPHrI+BcSLSzPG8IBG5uYhRvwIeAbpjbdyzBDgyJzm+bY4673VHgHyvx3A0jyxyZN1jjNnqmB4L/A78W0QCRcTNcaA2v2aUi+UoyDfAIyJSU0QqAGPze6KINBaRJxyFDRGphbVHtMLxlA1AdxGp7fi9jStCjixfAXeLSLhjL+41YKWjSe0XoIWIDHEcIB9N7mIUACQBJ0WkBvDUecs+//cxHRgoIv0dB/V9xDrhoKaIVBGRQY5ClepYbgbqsmmhUJfiTmCvo6ngX1jfArO+rX4N7HY0C+R31tPTIpKI1aT0BbAW6OxoOsAY8wPwJjDT8R5RWHsHRfE11oHoP40xx3JMfxJrLyMR69vmrPNeNx6Y5sh/Sz7L/gprD+ir86YPB7yAaKzCNxvrm21eLpajIP8D5gMbsY6ZfF/AcxOBq4CVYp21tgJrfT4B4GjjnwVswvo9zC1CDhzLWAg8D3yHtQdRD8exGce6vxl4C6s5qinWMYWs03NfwjoIfgqrqJz/WV4HnnP8Pp40xhwABmPtgcVh7WE8hbUtc3N8rkNYf1s9gAeL+nnUhcRqMlRKqeIn1nUYMUCEMSbS7jyqcHSPQilVrBzNROUdzVJZx2JWXORlyoVooVBKFbdOWNe2HAMGYp1pl9dpzcpFadOTUkqpAukehVJKqQKVuQ69goODTVhYmFOXefr0afz9i9xfXYnTnM6lOZ2rNOQsDRmheHKuXbv2mDEmJM+ZdvQbUpy3tm3bGmeLjIx0+jKLg+Z0Ls3pXKUhZ2nIaEzx5ATWGO3rSSml1KXQQqGUUqpAWiiUUsqFLX17KUteX3LxJxYjLRRKKeWiTKZhxaQVHFpV4MCTxU4LhVJKuaj9S/eTFJtE01ua2ppDC4VSSrmo6G+jcfd2p+H1DW3NoYVCKaVckMk0bP1uKw2uaYB3gLetWbRQKKWUCzqw7ACJhxJperO9zU6ghUIppVzSlm+3WM1OA+1tdgItFEop5XJMpmHrbNdodgItFEop5XJcqdkJtFAopZTLcaVmJ9BCoZRSLiWr2an+gPou0ewEWiiUUsqlHFjuWs1OoIVCKaVcStZFdo0GNrI7SjYtFEop5SJMpiF6drTV7BToGs1OoIVCKaVcxt6/9pJ4MJHmtzW3O0ouLlUoRMRdRNaLyFzH44oi8oeI7HT8rGB3RqWUKi6bpm/Cq5yXSzU7gYsVCmAMsDXH47HAQmNMA2Ch47FSSpU56SnpbJ29lSZDm+Dp52l3nFxcplCISE3gOuCTHJMHA9Mc96cBQ0o4llJKlYgdc3eQmpBKi4gWdke5gFhjattPRGYDrwMBwJPGmOtF5KQxpnyO55wwxlzQ/CQiI4GRAFWqVGk7c+ZMp2ZLSkqiXLlyTl1mcdCczqU5nas05LQzY9TzUSRGJ9Lxm46IuxT43OLI2atXr7XGmHZ5zjTG2H4Drgc+dNzvCcx13D953vNOXGxZbdu2Nc4WGRnp9GUWB83pXJrTuUpDTrsyJscnm1e8XjHzHptXqOcXR05gjclnu+rh1JJ06boAg0TkWsAHCBSR6cAREalmjIkVkWrAUVtTKqVUMYieHU3G2QyXbHYCFzlGYYwZZ4ypaYwJA4YBfxpj7gB+Au5yPO0uYI5NEZVSqthsnrGZ4MbBVGtTze4oeXKJQlGAN4C+IrIT6Ot4rJRSZcbJfSfZt3gfLSJaIFLwsQm7uErTUzZjzCJgkeN+PHC1nXmUUqo4RX0dBUCL212z2Qlcf49CKaXKLGMMm6ZvolbnWlSo67rXE2uhUEopmxxef5i4LXG0uMN19yZAC4VSStlm/afrcfd2p/kw1+rb6XxaKJRSygZpZ9LYPGMzTW5sgm8FX7vjFEgLhVJK2WDbj9tIOZlC63tb2x3lorRQKKWUDdZPXU/5sPLU6VXH7igXpYVCKaVK2Mm9J9mzcA/hd4cjbq557UROWiiUUqqErf9sPQiEjwi3O0qhaKFQSqkSlJmRyYbPNlCvbz2CagfZHadQtFAopVQJ2rNwDwkHEgi/J9zuKIWmhUIppUrQ+k/X41vRl8ZDGtsdpdC0UCilVAlJjk9m2w/baBHRAg9vl+tqL19aKJRSqoRs/GIjGWczSsW1EzlpoVBKqRJgMg1rPlpDzU41qdqqqt1xikQLhVJKlYDdC3dzfOdx2o9ub3eUItNCUQih06bBxIlw/LjdUZRSpdTqD1bjF+xH05ua2h2lyLRQXIwxBEVFwRNPQI0acO+9sHat3amUUqXIqf2n2PHzDlrf17pUHcTOooXiYkTY9PbbsGEDDB8Os2ZBu3bw1lt2J1NKlRJrp6zFGEO7f7WzO8ol0UJRWK1awX//CwcPwuTJMHiwNX3ZMnj6adizx958SimXlJ6azrr/raPh9Q0pH1re7jiXRAtFUQUFwcMPQ6NG1uMVK6zjF/XqwXXXwa+/QkaGvRmVUi5j6/dbOX30NO0fLH0HsbNoobhcjz8Oe/fC88/DunVWsejaFYyxO5lSygWs+XANFepVoF6/enZHuWRaKJyhZk146SXYt886hnH//SBi7Vk89hisWqWFQ6kr0JFNR9j/937ajWpXKroTz48WCmfy8oJbboF77rEeb90Kn3wCV10F7dvDp59CcrK9GZVSJWbl5JV4+HiUmu7E86OFojg1b24d/H7/fThzxjq1tmZNq4Aopcq0pMNJbPpyE61GtMKvkp/dcS6LForiFhgIo0dDVBQsWgTDhkHDhta8L7+En37Sg99KlUGrPlhFRloGnR7rZHeUy6aFoqSIQI8e8OGH4O5uHbOYNMk6zbZuXXj9dYiLszulUsoJ0pLTWPPRGhoNakSlhpXsjnPZtFDYRQRWroTZs6F+fXjmGatZ6oMP7E6mlLpMG6Zt4Ez8GTo9Ufr3JkALhb08PWHoUFi4EKKj4YEHIDzcmrdjB/zvf3D6tK0RlVJFk5mRyYqJK6jevjq1u9a2O45TaKFwFU2aWFd8d+liPf72Wxg50upf6tFHYft2W+MppQpnx887OL7rOJ2f7IxI6T0lNictFK7qmWdgyRK49lrruEbjxtbxDL0eQymXtuydZQSFBtHkxiZ2R3EaLRSuSsS6wvurr2D/fnjlFWjRwppuDEyZAkeO2J1SKZVDzMoYDiw9QMdHO+LmUXY2r2Xnk5RlVavCc8/Bq69aj7dts45n1KoFt90Gf/+texpKuYBlby/DO8i71A11ejFaKEqjJk2sYxajR8Nvv0G3btCqFX7799udTKkr1tGoo2z9bisdHuqAd4C33XGcSgtFadWwoXUdxsGDVjchwcGkVK5szVu0SK/+VqqELZmwBE9/Tzo+1tHuKE7nEoVCRGqJSKSIbBWRLSIyxjG9ooj8ISI7HT8r2J3V5fj7W12D/PknmT4+1rQxY6BpU+jd27pOIy3N3oxKlXHHth0jalYUHR7qUOq768iLSxQKIB14whjTBOgIjBaRpsBYYKExpgGw0PFYXcyCBdaV3rt3w803Q1iY1V2IUqpYLHltCR4+HnR6vGxcYHc+lygUxphYY8w6x/1EYCtQAxgMTHM8bRowxJaApU1ICIwdC//8Y/Ul1bIl+Ppa844etZqm9OC3Uk5xfNdxNn+1mXaj2uFf2d/uOMXCJQpFTiISBrQGVgJVjDGxYBUToLKN0Uofd3cYONA64H3TTda0qVOhVy+rZ9sPPoCEBHszKlXKLXl9CW4ebnR+srPdUYqNGBf6Ziki5YC/gAnGmO9F5KQxpnyO+SeMMRccpxCRkcBIgCpVqrSdOXOmU3MlJSVRrlw5py6zOBQmp1tqKpX//JMaP/5IwI4dpPv6cqR/f3Y+8oh1jYaL5HQFmtO5SkPOomZMOZzCqjtWUX1Qdeo/Ur8Yk+VWHOuyV69ea40x7fKcaYxxiRvgCcwHHs8xbTtQzXG/GrD9Ystp27atcbbIyEinL7M4FDnnypXG3HWXMTfffG7aokXGpKY6M9YFyuz6tInmdJ6iZvz5gZ/NK16vmFMHThVPoHwUx7oE1ph8tqsu0fQkVocoU4GtxpiJOWb9BNzluH8XMKeks5VpHTrA559bw7cC7NljNUuFhsILL0BMjK3xlHJlx/85zvqp6wm/J5zAmoF2xylWLlEogC7AnUBvEdnguF0LvAH0FZGdQF/HY+VsWU1OtWvD3LnQtq11FXhYmNW77e7dtsZTyhVFPh+Ju5c7PV7oYXeUYudhdwAAY8zfQH4N5FeXZJYrmru71QnhtddaexcffwzTp0NWW+j27VZ3IkFB9uZUymax62KJ+jqKrs90JaBagN1xip2r7FEoV1OnDrz5ptUhYdYV3/fdB9WrW/1Mbdpkbz6lbLRw3EJ8K/rS5ekudkcpEVooVMHc3c/df/dda8zvL76AVq2s3m1/+822aErZYffC3fzz+z90e7YbPkE+dscpEVooVOG1bWtdh3HwIPz731Y351nHL06ftvY+lCrDjDEsHLuQwFqBtH+wvd1xSowWClV0FSvC449bxyxGjrSmzZhhNVcNGQJ//AGZmbZGVKo4RM+O5tCaQ/R6uRcePi5xiLdEaKFQl87NzRr3G2DAAKvbkGXLoF8/a0S+SZO0YKgyI+NsBn8++ychzUJoeWdLu+OUKC0Uyjlq14YJE+DAAetMqZAQ6/oMN8ef2IED9uZT6jKtnLyS4zuP0/etvri5X1mbzitn30mVDG9viIiwbomJ1rT4eGv8jFatYPRo3KpUsTejUkWUGJvIXy/9RYPrGtDg2gZ2xylxV1ZZVCUrwHF+ube3dartyZMwfDgdb7nFaqY6fNjWeEoV1oL/W0DG2QwGvDvA7ii20EKhil+5cvDII9aoe3/8wamWLa2zprJ6rj1xQo9lKJd1YNkBNn25iU5PdKJi/Yp2x7GFFgpVckSgTx+2vPwyxMZazVFgXcjXoAG8847VTKWUi8jMyOTXh34loEYA3Z7pZncc22ihUPYIDj53/7bboEYNeOopqFkT7r4b1q2zL5tSDus+Wcfh9Yfp904/vMp52R3HNloolP1uugkWL7a6Bbn7bvj2W/jxR2teRgacOWNrPHVlOnP8DH8++yehPUJpdmszu+PYSguFch0tWsCHH8KhQ9YFfQA//2ztZTz1lDW0q1IlZP5j80k9lco1k69BSmhQL1elhUK5nsBAKF/eul+7NvTubV28V78+XHON1RW6HvxWxWjnbzvZ+MVGuoztQpWWejq3Fgrl2tq0sZqi9u2DF1+EjRthzJhz88+etS+bKpNSE1KZ+8BcQpqG0P257nbHcQlaKFTpUKMGjB9vFYx586wrvlNSoG5dGD4cVqwAFxr/XZVeC8YuICEmgUFTB+Hhbd81ycfPHGffyX1EHY2yLUMWvTJbuYT01HTOxJ8hOT6Zs4nWXoK4iXVzF3wr+uIf4o+nvyfSwHFlbHIy3HADTJsGX34JrVvD6NHWWVR+fjZ+GlVandxwko0fbeSqR6+iZseahX6dMYbUjFRS01MJ8rEG9lp9cDVxyXEkpiaSkJpA4tlEqgdUZ1jzYQCMmjuK/Qn7c83vV7cfH13/EQCh74aSdDYJgLTn0/Bws29zrYVClRhjDMd3Hufon0eJjIzkWPQx4rbGcXLvSdJOpxVqGR4+HviF+FGhTgUqNqxIcKPbCJ4ygpr//IXvzM+Q++6DRo2ssTIyM8/1NaXUeYwxJKclk3jW2lCfOHWCP774g0Z1G9H71d78vP1nth7bSmJqIolnE0lMTaS8T3n+3f/fANzx/R38vf/v7I18emY6V9W4ihX3rQDgvp/vY9OR3AN89QrrlV0odp3YxYkzJwjwDqB2UG0CvANoXrl59nMn9puIu5s7gd72j8ethUIVq1P7T7F7wW72/LmHvZF7STxk9f+0zW0bFepWILhJMHX71MUvxA+/Sn74VvLFO9AbEcFkGowxZKZlcub4GU7HnSY5LpnTR05zYvcJts/Zzvq49dnv5Rd8Jy07p+DzZzq1UncT9u3buO3ZDQ8+CNddBx76517aZWRm4CZuiAixibHsP7U/eyOe9fPB9g8iIny9+Wvm/TMv1zf2jMwM1oxcA8AdP9zBV5u/yrV8/6v92XzNZrz8vZi6fipzts9BEAK8AwjwCqBxcOPs5zao2AB3N3cCvKx5gd6BhJYPzZ4/ddBUMjIzCPC25gV4BVDOq1z2/D/u/KPAz3p/2/udscqcQv9zlNMlH0tmyzdb2DxjMweWWb3G+lf2p07vOoT1CiPWLZYBdwxwSn/+Z06cIX57PLHrYzm06hD/rDpI3Pi/wEBnj310dl+N/+9DyKhaHbfRo5D77wftlLBEpWemk5iayOGUw0QdjaJuhbr4efqxM35nrm/kCakJJKYm8nKvlwnxD2H6pum8u+LdXPNOp53m6JNHCfEP4f1V7/Pa369d8H53t74bP08/ouOiWbR3UfZGurxPeQK9AzHGICLc0vQWWlVpRaB3IElbklj7+lpqXVWLOr3rADBtyDTc3dzx8/TDTS7cM32x54sFfu521ds5ZwW6AC0UyimMMez5cw8r313Jrnm7yEzPpHLzylz9+tU0GtSI4CbB2eeiL1q0yGmDvvhW8KVmx5pWe/Ioa1rKqRT2/72f3Quu4ovfr6Fi9N+0P7yaus8/z/5vV8AHH1KzYw2rq+gr/Pz4gqSmpxKTEHPBN/ZOtTpRO6g2249tZ8raKdb0HBvzif0n0q56O77f+j0R30eQkp5ybqErYeV9K+lQowN/7fuL+38+963Z292bQO9AHuv0GCH+Ifh6+FKlXBUaeDfI/tYe4B2Al7t1hfQdLe+gc63Oub6xB3oH4uvhC8ArvV/hld6v5Pv5BjceDEDCwQQ+HvAxPWv1pEHEuZ5hs441KC0U6jJlpmcS/V00y95aRuy6WMpVLUfHxzvSMqKlbeef+wT50PC6hjS8riEwgMTYEez8dSdzv/yTPcsOc7zbZzSoEMf17r+SOfJfBI0dhWT1dFtK5Wxv93b3poJvBc6knWHB7gUXfGPvV68f3UK7sf/Ufkb+PDK7AGQ9b1L/SQxvNZz1h9fTaWqnC97r66FfUzuoNocSD/Hftf/NbpbJ+plprGtcGlRswMMdHs6ed2jPIdq3bE+9CvUAuLnpzfSp24dA70DKeZXLLgBZhjYdytCmQ/P9zE1CmtAkpMllrbfMjEx+uPMH0s+kM3TmUKJi7T/DyBVpoVCXxGQaNn+9mcjnIzm55ySVGlVi4CcDaXlHS1tPKcxLQLUA2tzbhjb3tiE1IZWdv+4k7sNvSP77DFVf+z9S33iRY1ddR9DrYynXox0zZszg2Wef5eGHH2bEiBFMmDCBiIiIYsmWkJqQvQHP2lAH+wUTXjUcYwxvLn0ze37Wxr5/vf480O4BktOSafR+I06cPsGZxWeyN9DPdXuOV3q/QkJqAoNmDsr1foIQ5BNEt9BuuIs7J1JOEOAVQGX/ytnfyutXrA9YG/rPB3+e6xt7gHcAtQJrAdCrTi+SnknK97O1qNKCt/q+lf14Ucoiejbrmf04yCfI9m/tS99ayt7IvQz6dBDBjYIh1tY4Lsu1/qNVqRCzMoZ5Y+ZxcOVBqrWpRv+J/Wk0qBHi5vrNON6B3jQf1hyGNefM8bFse3Mmnp/9j7DlP5Da8zcmhj/PZ1tnsD91PwD79u1jpGNc8IiICNIy0khJTyHA29oD2Xh4I0dOH8m1sQ/xD+H2FrcD8Ni8x9h9cneuDX232t34ZNAnANSbXI9jycdyZby9xe3MuHEGIsIri1/hbMbZ7GaVAO8AOtToAICvhy996/blVNwpmtRtkr0xb1+jPQCV/Cqx5v41ub7x52xvrxFYg5X3rcx3XVXyq8Rd4Xc5a9W7nJgVMUQ+H0nzYc0JHxFudxyXpoWiEKZNC+W//809rU4deM1xHG3cONizJ/f8pk3hhRes+48+avWqnVObNvB//2fdHznSGpIhp65dz12AfOedF/aL17cvPPCAdf+mm6yfR482IyTEuj9wIIwYYb3ujjusaTmvR7v1Vut2/LjVy/f580eMgMGD4eBB69IEgPSUNOK2xHEqJonuFcrz4Gft8O/ciiefEvgsd74nnoDu3WHzZnj22dzz4uObM2kSdOgAq1bBK3k0I7/2mtX106JFVu/j53v3XatHj99+g/ffv3D+lCnWNXrffWeY8mkq6e6JZLgnku6eSKakMPe/V1Gxoh+f1qvBT9fdzNn03qSePkpi+jrcqrRj4/wUTnz8G94Dm5Jc5zh3bHyI4TvuI9MthYDTrUh4awMAgz4Zyf6MVbneu0JSJ25/2yoUv67azqHEQ3hkBOCeEYJHRj3WRjcFxxf9DomvsXu3wSMjAI+MQNzSAzhzoAbcaM2/Lz6eqI3eCJL9O9q7EegKIoLXb5+yZ9UJTpSvkP3+O1pBu0ng4ebBe2PbXjAKbadO5/52hw69sGf3q6+G55+37l9zjXW5Sk4DB8KTT1r3e/QgO1eWW2+1/maSk6F//3PTT50KJyjI6vfxnnvg2DEYMuTC313WpTD791s/z/f009bf5rZt1nLO99JL1v/HunXn/nZzevttaFUvkTeuX8pcj/upvKsKb3ey1m9CQhumT7f+P+fPP/c/nNPnn0OTJvD99/DGGxfOnz3b6nlm+nR4770L5//2m9V58pQp1u18f/0F/v5WrzXTp1vTVq6096Q9LRSFcPCgL/v25Z6Wmnru/o4dsGVL7vleOZpbt23jgtdXzDH+yfbtEBeX+7hqWFju1ycn557fvHnu+QCnT/tlF5y4OOtnZqaVL0vWMo4ft36mp8OuXRfOP3XK+pmWBnv3QsrJMyTEJGAy3fCvXIPe/65H+B2eREdb/9DnO33a+pmaCjExueclJXmT4ji+mZJiFaOcn81gHPOFw4lx7D5zgAyPBDI8Esn0SCTDI4EzqfcBHvx5+DtWVf01e36GRyKZ7qdJS1sPCP/Zfz9/dZia6/3d0wLJyLA+YOSJz9geNgsAt3Q/MlN8cDtei2Qy6b5rIb2rd2JpTG1SzvpRqWId3NOD8Eqplb2s693e56+labinB+CWEYBHeiDlvM4d7xiW8St/LM39+XP2sN4s5X5Onvclw9v73P3Msz6kpuSen5bjkpP0dMjIENLTz03LyDh//nnr1+S+b0zBx/RFcs/PeT/nZSpZ03NOy/l/4OFh8PICd/dz03x8Lny/rA2iSN7XTWbNd3OzxsQ6X9by3d2tbsMukJnON0O/IT3JnbptK+IVcC5wZmZ69vK9vHL/n57//r6+uX+XWbI+v58fVK584fys9VSuHFStmv/8wECoXj33NLuIKWPdHrRr186sWbPGqctctGgRPXv2dOoyi0Nx5Ew5mcKvD/3K5hmbqdGhBkO+GGK15Z4n02SSdDYpu/mldlBt/L382XNiD0v2L8nV9LJt9zY+GPYB1QKqMTt6Nu8seye7fT7reXvH7KVWUC1e+esVXlh04de6+KfjqehbkVf+eiXXAdWs5plvbvoGT3dPft7+M1FHo3I1vwR5B3F13asBOJlyEkEo51UOdzd3wsLC2Oeo6lPue4rgT75lAIfxJYXfmz1K6Ov/ouF1DV2qme1K/vssKmMMP937Exs+28DNs2+m6dCmuea7QsbCKI6cIrLWGJPnOb26R3GFS8tIIzYpNtdB1cSzibSv3p7M9ZlMHT2VRbUWUWl8JXY038HP638mYUUCE3pPoHOtzvy681du+fYWTqedzrXcv0b8RffQ7iw7sIy7fjzXzu0u7vi5+xGXHEe1gGp4uXsR5BNEzcCauQ6Y+nlaXyVvbnYzLau0zC4AOc+JB3i+x/M83+P5fD/fwEYDGdhoYL7zs5aTZcKECYwcOZLk5GQSGldhJHup7lOez8NvYuvBmiwfNJM+IRto0NyLiu88g0ebVkVc48pOq/6zig2fbaD7890vKBIqf1ooSpGs/mQSUxPxdPekvE95zmacZcHuBSSmJrI6djXrlq8jMTWRHmE96BnWk8NJh7n3p3tznQefkGpt6O9vez9b4rbQ+r+tL3iv5/yew3OcJ8kdk1nTdQ0BPgEExARkb6zTM622jrDyYYxsOzLXRj7QOzD7CtbrG17Prod3ZX+j9/Hw4a+//qJllZYADGo0iEGNBl3w/lkaBzfOdTVsccs6u+lZx4GV0NBQJkyYQN+ICK5Oz2TLt1vIfHQpFSN/xqPtN5yq2xq/F57E8/abwdOzxHKqotu9cDfzH59Po8GN6Dm+p91xShUtFCUgOS35gm/s5X3KE141HIBJyydxIuVErlMke4b15MH2D5KRmUG9yfWym22yNtBPdnqSt/u9zZm0M1z31XXn3sxxPOJleZmeYT1xF3cOJx0m0DuQWoG1sjfYWadAhpUPY+qgqee+yYsf699az+Fph2k+sDmDpw1mYuDEfD9b05CmTOyf/3xXOAWyqCIiIoiIiGDRokXs3bs3e7qbhxstbmuBGTaf/T+sJX7sO9TZOR/PERHETvyCwAXf4R/ib19wla/DGw/zzdBvCG4czA1f3uBSTYelQZELhYj4AynGmIyLPrmM2HN6Dxm7M3JdtFTepzwRLa1vn+MWjGN7/PZcbeztqrdj2pBpADR6vxExCbmP6N7Y5Ea+u+U7AF5d8mp252BZG+ymIdZusbubO1fXuRofD59czS9tq7UFIMA7gBX3riDAO4CotVH069mPcl7lsnuaDPEPYe3Itfl+tvI+5bmntXXqSNLhJGbdOIuTy0/S7/l+9BzfU/+h8iAihN7YjtAbZ3Jo1QE2P/Yh25YdJy70XbrdUpVOx+bi+cQj0LOn/UchFcf/Oc70/tPxDvAm4tcIvAO8L/4ilctFC4WIuAHDgAigPZAKeItIHPArMMUYs7NYU9rs3Z3vsmlN7l4gW1dtnV0oouKi2HNiD4Hegdnt7Y0rnWsuebHHi5zNOJurm4HqAdWz5x947AC+Hr75Drc4dfDUPKcDuIkbV9W8CoCjPkcvaHMvrPgd8XzR5wvOxJ/hpm9uotnNV/YYwYVVvUMtqi99nabbjvH3639z6MtvScucj+cvP5JRvxHuYx6yzm8OKl17VWVFYmwiX/b9ksz0TO6KvIug2vp7uBSF2aOIBBYA44AoY6zLP0WkItALeENEfjDGTC++mPYaVXcUTVs1zdVNQc6uf3++7ecCX39fm/sKnJ914NYuRzYd4ct+X2IyDXcvuZtqbarZmqc0Cm4czJBpQzjxYg8iJ9xA+rSvaLdrFTUefpjMF17E7dDBvM8FVcXmzIkzTO8/ndNHT3NX5F2ENAmxO1KpVZhC0ccYc8FgAcaY48B3wHciUqaP4jUObEz30LI5JOLBVQeZPmA6nn6eDF8wnODGeZwYrgqtQt0KXDf1Jk6N78vSt5Yy778/U/nkITJHzafrM12p9N6L1tWUN96Y+yID5VQpp1L46rqviN8ez+2/3E6N9jXsjlSqXXRUl6wiISLvSj5tI3kVEuX69v61ly+u/gLfCr7cveRuLRJOFFQriGv/cy237HsLzzGjiJoZxdRG75A07TvrcuNateC557jgsml12ZKPJfPF1V9waPUhhn49lLp96todqdQryvBfScBPjoPZiEg/EVl6kdc4hYgMEJHtIrJLRMaWxHuWdfsW72PGgBkE1Q7i7iV3U6FOhYu/SBVZQLUABkwawJg9Ywh/vBeTM0YznQgOedTGvPaadQn+b7/ZHbPMSIxN5PMenxO3JY5hc4bR5MbL611WWQp91pMx5jkRuR1YJCKpwGmg2DfaIuIOfAD0BWKA1SLykzEmurjfu6w6vOEwXw/8mvJh5blr0V16SmcJKFe1HP3e6UeX/+vC8onLmfb+anxNF/o32k/FwAZUAfjmGzh0yOpoq3x564UX619DZTu59yRf9PmC00dOE/FbBGE9w+yOVGYUulCIyNXA/VgFohpwrzFme3EFy6EDsMsYs9uRYyYwGNBCcQnid8ZbpwoGeXPH73dokShh/iH+9Hm9D52f7MyKSSuY859VpHadQcOBDRm07U38d260elGMiIBRo2DaNKtojB9vd3SXlvXl52zSWe5ccCc1r6ppd6QypdB9PYnIn8ALxpi/RaQF8CXwuDHmz2INKHITMMAYc5/j8Z3AVcaYh3I8ZyQwEqBKlSptZ86c6dQMSUlJlMur9zEXc7GcqcdS2fDwBjLOZBA+ORy/2vacbVVW1qczpCelc/D7g8R8F0N6QjoNax+hU4XN1Nq2GvfUVA527szOf/3LOqZhY05nKK6ccYvi2PbmNjzKedDi9RaUq3/p73Elr8tevXrl29cTxphLumHtVSy71NcX4X1uBj7J8fhO4D/5Pb9t27bG2SIjI52+zOJQUM4zJ86YD5t/aF4r95o5uPpgyYXKQ1lYn86WkpBi/n5jiXnb7wUznvHmC+4wRwgxmQMHGZOZaczRo8aMHWvMnj225rwczs6ZmZFpFj630IxnvPmk0ycmMTbxspd5pa5LY4wB1ph8tqsXPZhdwJlOscDVBT3HSWKAnF+nagKHivH9ypzMjExmD5vNse3HGDZnGNXbVb/4i1SJ8g7wpsv/dWVM3LNcy1yOU4mPGM1Hu/uzYdpGMhZGwltvQd26MGgQzJtn9SF/hUo5lcKsG2ex5NUlhN8Tzl2Rd1GuquvvCZRWhbrgTkS+A+YYY7JHHhARL6CTiNyFdVHe58UTkdVAAxGpAxzEukr89mJ6rzJpwdgF/DP/H66fcj11etexO47KjzF4PvM07VlDW9YRRXOWHh7EnLvn8Gf1ALo9/Q2tz67CY/rn8PPP0KABrF9vd+oSt3fRXn6860cSDiYw4L0BdHi4Q769GijnKEyhGADcA3zt2FifBHwAd+B3YJIxZkNxBTTGpIvIQ8B8x3t+aozZcpGXKYdN0zex/J3ltB/dnrb3t7U7jsqPMfDYY9aQaGPG4DZpEi0fe4wW773KP0OeYHlSHX59I4oF5crTZvj/6FzvMAFH/rGGQgP4z3+soeva5d3EXBakp6Sz8NmFrJi4gooNKnLP0nv0oHUJuWihMMakAB8CHzquwA4GzhhjThZztpwZfsXqV0oVwcHVB/npvp8I6xlG/0n9L/4CZR8R6+ymMWOsMTBFYNIkBKhfvhz1xw8ndn0sKyauYNX/NrIiLZP617Tkqnm7cEtLsi7eS0iwxpcdPRpuuaVMdRkSszKGn+79ibgtcbR7sB193+qLl79e2V5SCiwUIjIE6zjEf4wxO4x1BXZsQa9RriHpcBKzbphFuarluPnbm3H3dL/4i5S9xo/Pfd2Eo1hkPa7Wuho3fHkDfd/uy9opa1nz0RpmXDMDn+o+eD42izZeW/D+8hO46y54/HGYORP69LHv8zhBwsEEFo5byKYvNxFQPYCI3yKoP6C+3bGuOAUWCmPMjyJyD3C1iPQ3xvynhHKpy5CZkcl3t39HyokU7ll2D37B9nY6qIrg/Lb2PNrey1UtR48XetB1bFeiZ0ez8K2F/P7SShZ4uNFo0Hg6Dz9LjXU/IU0dI7j9/bc1CPqAAbkHrHZhaWfSWP7v5fz9+t9kZmTSdVxXuo7rql2E26QwxyjqGmM+EpG1gBaKUmDpW0vZG7mXQVMHUbVVHqO3qzLB3cudFre3IL56PM2rNWfd/9axcdpGtn6fjH/lq2j+1iZa3gnV3nsPmT0b6tSBf/0L7rkHgl2zX68zJ86w5uM1rHxvJaePnKbJ0Cb0fbuvdjFjs8IUinkishyo6ti72AhscRy7UC4mZkUMkc9H0uzWZoTfHW53HFVCghsF0++dflz92tXs/G0nm77cxJqPrA1uSIOudB3UmEYHFuD9f/8HL7wATz0Fr7xid+xsp/afYsV7K1g3ZR1nk85Sr389uj3TjdDuoXZHUxTuYPaTIlIXWATUAQYBzUTkLNb4FLcWb0RVWOlJ6Xx393cE1Qri+o+v11MGr0DuXu40HtyYxoMbc+bEGaJnRxP9bTRzfk0gM30AYZW70qPyVrzjPalwMgUfbwOzZlkHv/1Ktoky5WQK0d9Fs3nGZvYu2ou4Cc2HNafzU511T9jFFKqvJ2PMbhHpY4zZkTVNRMoBzYstmSoSYww7Ju3g1IFT3L3kbnzKl50zXtSl8a3gS9v729L2/racOXGGnb/sZOv3W/nq9wqkRaUh/32LLnUPcvWuKWQ8/CiZdwy3hnCtXzwHi40xxEXHsSdyD7v/2M2u33aRcTaDig0q0uPFHoSPCKd8aPlieW91eYrSe+yO8x4nASucnkhdko3TNhL3Zxy9Xu1FrU759wukrky+FXxpeUdLWt7RkoyzGcSsjGH3H7vZ/fs/TPsnjbZJq2jy8Qfw8X84XKUVO++eQPmWtQluFEzFBhWLfBA5Mz2T4/8c59jWY8RFx3Fk0xF2/L6DxScWAxBUO4h2o9rRIqIF1dtV171fF1foQqFcV0JMAvPGzCOoZRBdx3a1O45yce5e7oR2CyW0Wyi9Xu7F2dPDiV0Xy7o/NuD7/Vf47d7Cn2+sBtZQn50cohoZgZXwC/HDL9gP/xB/PP09ERHETUAgIzWD5PhkzsSfITk+mdNHT5OZdq6LkcBagVRoU4Grhl1Fnd51KF+nvBaHUkQLRSlnjOGXUb+QkZZBo6cb4eZelLGolAIvf6/swsHLg8EYnjmTxomogwT3aAZp6cRW68rO2n04YMqTEJNA2pk0MGAyDSbT4O7ljm8lX8qHlada22r4V/EnuHEwIU1CCG4cjHegN4sWLaJNzzZ2f1x1CbRQlHJRM6PYMXcHfd/py9kaZ+2Oo8oCETz9vKjcoQ6sWwsffUSNadOosT0SwsPh/fehSxe7U6oSpF8/S7HTcaeZ98g8anSoQcdHO9odR5VFTZrA5Mlw8CB8/LHVY23W6Hs7dlg3VeZpoSjF5j0yj5RTKQz6dJA2OaniVa4cPPAAbNgAzZpZ0156CRo1gr594YcfID3d1oiq+OjWpZTa/tN2omZG0f257lRuVtnuOOpKkfMA9MSJ8OqrsH073HijdeX3++/bl00VGy0UpdDZpLP88uAvVG5RWc9yUvapUsUa33v3bmuPokkTOOQYUywjA5Ytszo5VKWeHswuhZa8toTEg4nc/M3NuHuVjk7eVBnm4QFDhli3rFH35s+H666DFi3gwQfhjjvsTKguk+5RlDLHdx1n+b+X0/LOltTqrBfWKRfj5tik9OgB//uf1VvtqFFQvTr1J0+2xsxQpY4WilJm3qPzcPd2p8+bpXucAVXG+fvDfffBunWwfDkMHkzF1avPjcgXHQ1pafZmVIWmhaIU2fHLDnb+spMeL/QgoFqA3XGUujgR6NgRvvyS1Z99Zu1hnD0LvXtDWJh15lTWcQ3lsvQYRSmRnprO/EfnU6lRJa565Cq747istLQ0YmJiSEm5/F7wg4KC2Lp1qxNSFS9n5fTx8aFmzZp4eno6IdWFjIdjc+PubjVLffihNarfq6/CDTdYw7m2bFks760ujxaKUmLFpBUc33WcO+bfoQewCxATE0NAQABhYWGX3ZdQYmIiAQGuv+fmjJzGGOLj44mJiaFOnTpOSpYPd3cYONC67dplXcj36afWQW+AuDjw9obAwOLNoQpNm55KgaTDSSx+dTGNhzSmXr96dsdxaSkpKVSqVEk7nCsiEaFSpUpO2RMrkvr14Z13rCu/e/Swpr36KtSoYRWOqKiSzaPypIWiFPjrlb/ISM2g79t97Y5SKmiRuDS2rjdf33MX8w0fDkOHWnsZLVpYBeSHH+zLprRQuLrju46zbso62oxsQ8X6Fe2Oo1Txa9sWPv/c2st46y2IiYG5c8/NP3zYtmhXKi0ULu7P5/7E3cudHs/3sDuKKqTJkyfTpEkTatSowfjx47Onv/vuu3zxxRcFvnbYsGHs3LmzmBOWEpUqWWN779xpdRcCsHo11KxpdRmycKFe+V1CtFC4sENrD7Fl1hY6Pt6RclXL2R1HFdKHH37Ir7/+yoQJE7Knpaen8+mnn3L77bcX+NpRo0bx1ltvFXfE0sXNDYKCrPvVq8MTT8DixdCnz7nebZOT7c1YxmmhcGELxy7Et5IvXZ7Svv9Li3/961/s3r2bQYMGceTIEcqVswr8n3/+SZs2bfDw8CA9PZ327duzaNEiAMaNG8ezzz4LQLdu3ViwYAHp2hNr3mrUgDfftJqjpk2zujx/4YVzexanTtkar6zS02Nd1O4Fu9m9YDf9J/XHO7Bo4xUry7xH53F4w6W3Z2dkZODunvtU5KrhVRnw7oB8X/Pxxx8zb948IiMjCQ4Ozp6+dOlS2rZtC4CHhweff/45N910E5MnT2bevHmsXLkSADc3N+rXr8/GjRuzn6/y4ONjHfQePhxiY60rvo2xLu6rVMk6Y2roUOs0W3XZdI/CBZlMw4KxCwgKtQagV6VfbGwsISEh2Y+bNWvGnXfeycCBA/n000/x8vLKnle5cmUO6dXKhVetmvUzPR1GjoQjRyAiAmrXtnq3PXDA3nxlgO5RuKBtP24jdm0sQ6YNwcNbf0WXqqBv/oXhzAvufH19L7hGYfPmzZQvX54jR47kmp6SkoKvr69T3veK4ukJjz0GY8ZYB7o/+ADeeMO62vvWWyE11XqOm34/LipdYy7GGMPiVxZTqWElWkS0sDuOcpImTZqwa9eu7Mfff/898fHxLF68mEceeYSTJ09mz9uxYwfNskaRU0Xn5maNuvfjj9ZYGTfcYE1/5x1rRL6JE+HECVsjljZaKFzMjrk7OLzhMF2f6arDm5Yh11xzDYsXLwbg2LFjjB07lqlTp9KwYUMeeughxowZA8CRI0fw9fWlWlZziro8oaGQ1azXsiVUrmydNVWjxrnebdVFabuGCzHGsPjlxVSoW4EWt+veRGm1d+/eC6aFhoZSqVIldu7cSYMGDdixY0f2vEceeST7/ldffcUDDzxQEjGvPFn9S23YAB99BNOnW8czfv7Zmq9nmuVLv7K6kH/m/8OhNYfoOq4r7p7a8V9Z88YbbxAbG1vgc8qXL89dd91VQomuUOHh8N//Wld+T55sTduzB2rUoO6UKdZ9lYsWChdhjOGvl/4iqHYQrYa3sjuOKgaNGjWie/fuBT7n7rvvxsNDd/RLRPnykNVT7tmz0LUrtWbNgnr1rD2P3347N7TrFc72QiEib4vINhHZJCI/iEj5HPPGicguEdkuIv1tjFns9izcQ8yKGLqM7aLdiCtV0ho1gu++Y8XMmda4GKtXw+DBVpfncMV3FWJ7oQD+AJobY1oCO4BxACLSFBgGNAMGAB+KSJndgi5+ZTEBNQJofU9ru6ModcVKDQmBl1+G/fth0SKoUsWacc01MGKEVUCuQLYXCmPM78aYrKNIK4CajvuDgZnGmFRjzB5gF9DBjozFbd/ifexbvI8uT3fR6yaUcgVeXtC5s3U/PR3q1oXvvoMOHaB9e/jsMzhzxt6MJcj2QnGee4DfHPdrADkvqYxxTCtzlr61FL8QP9rc38buKEqp83l4WMO2HjwI778Pp0/DPfdY42VcIcSUQNubiCwAquYx61ljzBzHc54F2gE3GmOMiHwALDfGTHfMnwr8aoz5Lo/ljwRGAlSpUqXtzJkznZo/KSkpu3M3Zzu97zRrRqwhdEQoYXeFXdayijOnMxVnzqCgIOrXr++UZeXV11NhBAYG8tBDD/Haa68BVrfjSUlJPPPMM5ecZdOmTcTGxtK//4WH6i41Z1527drFqWLqWK80/H0WKqMxlN+4kcT69ckoV46qv/5KyF9/cWjIEOI7dLCGenWFnEXUq1evtcaYvPsMMsbYfgPuApYDfjmmjQPG5Xg8H+h0sWW1bdvWOFtkZKTTl5llzn1zzKs+r5qko0mXvazizOlMxZkzOjraactKSEi4pNd5e3ubsLAwExcXZ4wx5u233zYvvvjiZWX57LPPzOjRo/Ocd6k58+LM9Xe+0vD3eUkZP/nEmGrVjAFjQkONef11Y44edXa0XIpjXQJrTD7bVdubnkRkAPB/wCBjTM5O5X8ChomIt4jUARoAq+zIWFySjiSx6ctNtLqrFf4h/nbHUU7i4eHByJEjmTRp0gXz4uLiGDp0KO3bt6d9+/YsXboUgBYtWnDy5EmMMVSqVCl7gKM777yT33//nRdeeIFZs2YRHh7OrFmzOH78OEOGDKFly5b07t2bTZs2ATB+/HjuueceevbsSd26dZmcdZ2AKj733gv79sG331qn244bd67bkDLCFY6cvg94A384xuxdYYz5lzFmi4h8A0QD6cBoY0yGjTmdbvWHq8lIzaDjYx3tjlJ29ex54bRbbrG6oU5OhmuvvXD+iBEwYgQSH2+dT5+TYwyJixk9ejQtW7bk6aefzjV9zJgxPPbYY3Tt2pX9+/fTv39/tm7dSpcuXVi6dCmhoaHUrVuXJUuWMHz4cFasWMFHH33Eyy+/zJo1a3j//fcBePjhh2ndujU//vgjc+fOZfjw4WzYsAGAbdu2ERkZSWJiIo0aNWLUqFF4enoWKre6RJ6ecNNN1i06GhISrOknTlh/Q3ffDbfdBn5+9ua8RLYXCmNMvg3KxpgJwIT85pdmaWfSWPPhGhoObEhwo+CLv0CVKoGBgQwfPpzJkyfn6gl2wYIFREdHZz9OSEggMTGRbt26sXjxYkJDQxk1ahRTpkzh4MGDVKxYMc+26L///pvvvrMO1/Xo0YP4+PjsYwvXXXcd3t7eeHt7U7lyZY4cOULNmjUvWIYqJk2bnru/f781mNJ998GTT1oFY9QoaNDAvnyXwPZCcaXa+MVGko8l0/nJznZHKdsK2gPw8ytwvqlUqdB7EHl59NFHadOmDXfffXf2tMzMTJYvX35BN+Ldu3fngw8+YP/+/UyYMIEffviB2bNn061bt7yz5XESimOPHO8cg/W4u7vraHl2atUKNm2Cv/+2zpz6z3/g3Xdh715rvIxSwvZjFFcik2lYMXEF1dtVp3a30vPHooqmYsWK3HLLLUydOjV7Wr9+/bKbj4Ds5qJatWpx7Ngxdu7cSd26denatSvvvPNOdqEICAggMTEx+3Xdu3dnxowZACxZsoTg4GACAwNL4FOpIhOBbt3g66+tQZQ+//xckXj0UZgwweqc0IVpobDBjrk7iN8RT6cnO2V/C1Rl0xNPPMGxY8eyH0+ePJk1a9bQsmVLmjZtyscff5w976qrrqJhw4aANXb2wYMH6dq1KwC9evUiOjo6+2D2+PHjs5fz4osvMm3atJL9YOrSVK1qDd8KkJEB27dbXYbUqgW33w5Ll7pkdyHa9GSDlZNXElgrkKZDm178yarUSUpKyr5fpUoVkpPPncwXHBzMrFmz8nzdl19+mX2/c+fOZObokK5ixYqsPq/7iDlz5gC5R+IbP358rudERUVd2odQxc/d3ep4cNs2+Phja0/j669h0iRrT8OF6B5FCTu27Rh7Fu6h3ah2uHno6lfqite4sXXc4uBBmDLFOnMKYP58a1jXbdtsjQdaKErc6o9W4+7lTpt7tbsOpVQO/v5w//2QdYba5s3WnkaTJtaQrjbSQlGCziadZePnG2l6c1P8K+sFdkqpAjz55LmD33Xr2hpFC0UJ2vzVZlITUmn/YHu7oyilSoPKlcEFRjzUQlFCjDGs/mA1VVpVoWYnvfhJKVV6aKEoIQeWHeDIpiO0H91eT4lVSpUqWihKyJoP1+Ad6E2L21vYHUUVs7y63Bg/fjwiwq5du7KnTZo0CRFhzZo1JRlPqSLTQlECko4kseXbLbQa0Qovfy+74yibtGjRgpxjpcyePZumTfVaGuX6tFCUgPVT15OZlqkHsa9wQ4YMyb5Ibvfu3QQFBRESEmJzKqUuTq/MLmYm07B2ylrq9K6jvcTa4DJ6GSc+Xi61l/E8BQYGUqtWLaKiopgzZw633norn3322aUvUKkSonsUxWzPn3s4te8Ure9rbXcU5QKGDRvGzJkz+fHHH7mhjA1uo8ou3aMoZus/XY9PeR+a3NDE7ihXpMvoZZxKlcxl7UHkZeDAgTz11FO0a9dOe3tVpYYWimJ05sQZtn6/lTb3tcHDR1e1Al9fX958883sXmKVKg1061WMNn+1mYzUDFrfq81OV5Lk5ORcI8o9/vjjueYPGzaspCMpdVm0UBSjDZ9uoGp4Vaq1rmZ3FFWCcnYPfjGLnN22pVQx0IPZxeTwhsPErovVvQmlVKmnhaKYrP90Pe7e7noltlKq1NNCUQzSU9LZNH0TTW5ogm9FX7vjKKXUZdFCUQy2zdlGyokUwu8JtzuKUkpdNi0UxWD91PUE1Q6i7tX2DjailFLOoIXCyRIOJrB7wW5ajWiFuGl34kqp0k8LhZNFfR0FBlre0dLuKMomEyZMoFmzZrRs2ZLw8HBWrlzJu+++S3Jysq25Tp48yYcffmhrBlU6aaFwss0zNlOjQw0qNahkdxRlg+XLlzN37lzWrVvHpk2bWLBgAbVq1dJCoUo1LRROdHTLUQ5vOEyLCD0l9koVGxtLcHAw3t7eAAQHBzN79mwOHTpEr1696NWrFwC///47nTp1ok2bNtx8880kJSUBsHbtWnr06EHbtm3p378/sbGxAPTs2ZNHH32Uzp0707x5c1atWgXA6dOnefDBB2nfvj2tW7fO7sZ8y5YtdOjQgfDwcFq2bMnOnTsZO3Ys//zzD+Hh4Tz11FMlvWpUKaZXZjvR5hmbEXeh2a3N7I6iHHp+3vOCabc0u4UH2z9Icloy1864sJ/xEeEjGBE+gvgz8Qz8Lnc/44tGLCrw/fr168fLL79Mw4YN6dOnD7feeiuPPPIIEydOJDIykuDgYI4dO8arr77KggUL8Pf3580332TixImMGzeOhx9+mDlz5hASEsKsWbN49tln+fTTTwGrKCxbtozFixdzzz33EBUVxYQJE+jevTtffvklJ0+epEOHDvTp04ePP/6YMWPGEBERwdmzZ8nIyOCNN94gKiqKDRs2XOrqVFcoLRROYjINm2dspl7fepSrcuFQmOrKUK5cOdauXcuSJUuIjIzk1ltv5Y033sj1nBUrVhAdHU2XLl0AOHv2LJ06dWL79u1ERUXRt29fADIyMqhW7Vz3L7fddhsA3bt3JyEhgZMnT/L777+TnJzMBx98AEBKSgr79++nU6dOTJgwgZiYGG688UYaNGhQEh9flVFaKJxk/9L9nNp/it6v9bY7isqhoD0AP0+/AudX8q100T2IvLi7u9OzZ0969uxJixYtmDZtWq75xhj69u3L119/nWv65s2badasGcuXL89zuSJywWNjDNOnT6dNmza55jVp0oSrrrqKX375hf79+/PJJ59Qt66erq0ujR6jcJJN0zfh6edJ48GN7Y6ibLR9+3Z27tyZ/XjDhg2EhoYSEBBAYmIiAB07dmTp0qXs2rULsHqb3bFjB40aNSIuLi67UKSlpbFly5bsZc2aNQuAv//+m6CgIIKCgujfvz8ff/wxxhgA1q9fD1hDrdatW5dHHnmEQYMGsWnTplwZlCoK3aNwgvTUdKK/jabxDY3xKudldxxlo6SkJB5++GFOnjyJh4cH9evXZ8qUKXz99ddcc801VKtWjcjISD7//HNuu+02UlNTAXj11Vdp2LAhs2fP5pFHHuHUqVOkp6fz6KOP0qyZdcyrQoUKdO7cmYSEhOzjFs8//zyjR4+mZcuWGGMICwtj7ty5zJo1i+nTp+Pp6UnVqlV54YUXqFixIl26dKF58+Zcc801vP3227atJ1W6aKFwgl2/7SLlRIqe7aRo27Yty5Ytu2D6ww8/zMMPP5z9uHfv3qxevfqC54WHh7N48eI8lz106FBef/31XNN8fX157733CAgIyDV93LhxjBs37oJlfPXVV4X6HErlpE1PTrB5xmb8Qvyo17ee3VGUUsrpXKZQiMiTImJEJDjHtHEisktEtotIfzvz5SflVArbf95O82HNcfNwmdWpyphFixbRrl07u2OoK5RLND2JSC2gL7A/x7SmwDCgGVAdWCAiDY0xGfakzNv2n7aTkZpB89ua2x1FKaWKhat8BZ4EPA2YHNMGAzONManGmD3ALqCDHeEKEv1tNIG1Aql5Vc2LP1kppUoh2/coRGQQcNAYs/G888RrACtyPI5xTMtrGSOBkQBVqlRx+jjESUlJeS4zPSmdnfN2Un1wdf5a/JdT3/NS5JfT1RRnzqCgIKedApqRkVEqTid1Zs6UlJRi+92Uhr/P0pARSj5niRQKEVkAVM1j1rPAM0C/vF6WxzSTxzSMMVOAKQDt2rUzPXv2vLSg+Vi0aBF5LXPT9E2YNEP/x/tTq1Mtp77npcgvp6spzpxbt2694AygS5WYmOi0ZRUnZ+b08fGhdeviGee9NPx9loaMUPI5S6RQGGP65DVdRFoAdYCsvYmawDoR6YC1B5Fz61sTOFTMUYtkyzdbCKypzU5KqbLN1mMUxpjNxpjKxpgwY0wYVnFoY4w5DPwEDBMRbxGpAzQAVtkYN5eUUyn8M/8fmtzURAcoKsVmzJhBWFgYbm5uhIWFMWPGDLsjKeVyXOVg9gWMMVuAb4BoYB4w2pXOeNrx8w4yzmbQ7GbtKba0mjFjBiNHjmTfvn0YY9i3bx8jR450SrHo1asXf/zxBwDPPfccjzzyyGUvUym72H4wOyfHXkXOxxOACfakKVj0t9FWs1NHbXYqrZ599tkLBhNKTk7m2WefJSIi4rKW/dJLL/HCCy9w9OhR1q9fz08//XRZy1PKTi5VKEqL1IRUds3fRbtR7bTZqRTbv39/kaYXRffu3THGMHHiRBYtWoS7u3v2IENeXl707NnzsouRUiXFZZueXNn2n62L7LTZqXSrXbt2kaYXxebNm4mNjcXb2zv7jKTvv/+em266if/973+6h6FKFS0UlyD622gCagRos1MpN2HCBPz8/HJN8/PzY8KEy2vtjI2NJSIigjlz5uDv78/8+fMBiImJoVYt60Q+d3f3y3oPpUqSFooiSk1IZde8XTS9qak2O5VyERERTJkyhdDQUESE0NBQpkyZcllNQsnJydx44438+9//pkmTJjz//POMHz8egJo1axITEwNAZmamMz6CUiVCj1EU0Y5fdpCRmkHTm5vaHUU5QUREhFOPFfj5+eUaoa579+7Zj2+88UYeeughfvnlFwYOHJjfIpRyOVooimj7j9vxr+LvEldiq9LF39+fzz77zO4YShWZNj0VQXpqOjt/20mjQY202UkpdcXQQlEEeyP3cjbxLI2H6LjYSqkrhxaKItj24zY8/T2p07uO3VGUUqrEaKEoJJNp2P7Tdhpc0wAPHz2048qMybOTYXURut5UfrRQFNLB1QdJik2i0ZBGdkdRBfDx8SE+Pl43ekVkjCE+Ph4fHx+7oygXpF+NC2n7nO2Iu9Dg2gZ2R1EFyLpWIS4u7rKXlZKSUio2nM7K6ePjQ82aehGpupAWikLa9uM2wnqG4VvB1+4oqgCenp7UqeOcY0iLFi0qtkF8nKm05FSllzY9FULygWSObT1Go8Ha7KSUuvJooSiE+KXxADQerKfFKqWuPFooCuHY38eo2roqQbWD7I6ilFIlTsra2SEiEgfsc/Jig4FjTl5mcdCczqU5nas05CwNGaF4coYaY0LymlHmCkVxEJE1xph2due4GM3pXJrTuUpDztKQEUo+pzY9KaWUKpAWCqWUUgXSQlE4U+wOUEia07k0p3OVhpylISOUcE49RqGUUqpAukehlFKqQFoolFJKFUgLRSGJyCsisklENojI7yJS3e5MeRGRt0VkmyPrDyJS3u5MeRGRm0Vki4hkiohLnY4oIgNEZLuI7BKRsXbnyY+IfCoiR0Ukyu4s+RGRWiISKSJbHb/vMXZnyouI+IjIKhHZ6Mj5kt2Z8iMi7iKyXkTmltR7aqEovLeNMS2NMeHAXOAFm/Pk5w+guTGmJbADGGdznvxEATcCi+0OkpOIuAMfANcATYHbRKSpvany9TkwwO4QF5EOPGGMaQJ0BEa76PpMBXobY1oB4cAAEelob6R8jQG2luQbaqEoJGNMQo6H/oBLngVgjPndGJPueLgCcMl+o40xW40x2+3OkYcOwC5jzG5jzFlgJjDY5kx5MsYsBo7bnaMgxphYY8w6x/1ErA1cDXtTXchYkhwPPR03l/sfF5GawHXAJyX5vlooikBEJojIASAC192jyOke4De7Q5QyNYADOR7H4IIbttJIRMKA1sBKm6PkydGkswE4CvxhjHHFnO8CTwOZJfmmWihyEJEFIhKVx20wgDHmWWNMLWAG8JCr5nQ851ms3f4ZrpzTBUke01zum2VpIyLlgO+AR8/bO3cZxpgMR9NyTaCDiDS3OVIuInI9cNQYs7ak31sHLsrBGNOnkE/9CvgFeLEY4+TrYjlF5C7geuBqY+OFMkVYn64kBqiV43FN4JBNWcoEEfHEKhIzjDHf253nYowxJ0VkEdbxH1c6UaALMEhErgV8gEARmW6MuaO431j3KApJRHKOgToI2GZXloKIyADg/4BBxphku/OUQquBBiJSR0S8gGHATzZnKrVERICpwFZjzES78+RHREKyzhAUEV+gDy72P26MGWeMqWmMCcP6u/yzJIoEaKEoijcczSabgH5YZx64oveBAOAPx6m8H9sdKC8icoOIxACdgF9EZL7dmQAcJwI8BMzHOvD6jTFmi72p8iYiXwPLgUYiEiMi99qdKQ9dgDuB3o6/xw2Ob8SuphoQ6fj/Xo11jKLETj91ddqFh1JKqQLpHoVSSqkCaaFQSilVIC0USimlCqSFQimlVIG0UCillCqQFgqllFIF0kKhlFKqQFoolCoBjjEZ+jruvyoik+3OpFRhaV9PSpWMF4GXRaQyVg+qg2zOo1Sh6ZXZSpUQEfkLKAf0dIzNoFSpoE1PSpUAEWmB1Z9QqhYJVdpooVCqmIlINaxxQQYDp0Wkv82RlCoSLRRKFSMR8QO+xxo3eivwCjDe1lBKFZEeo1BKKVUg3aNQSilVIC0USimlCqSFQimlVIG0UCillCqQFgqllFIF0kKhlFKqQFoolFJKFej/AQf2crCsfMHbAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"calc_step(0,1E-2)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.2.4 Consider $x_0 = 0$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.2.4-Consider-$x_0-=-0$)",
"section": "3.6.2.4 Consider $x_0 = 0$"
}
},
"source": [
"**Discussion**\n",
"* Why does $f(x)$ increase for all of the steps?\n",
"* Explain Newton-type method in the context of root finding for $\\nabla f(x) = 0$ using the second plot."
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.2.5 Descent Properties](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.2.5-Descent-Properties)",
"section": "3.6.2.5 Descent Properties"
}
},
"source": [
"### 3.6.2.5 Descent Properties\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.6.3 Line Search](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3-Line-Search)",
"section": "3.6.3 Line Search"
}
},
"source": [
"## 3.6.3 Line Search"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.6.3 Line Search](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3-Line-Search)",
"section": "3.6.3 Line Search"
}
},
"source": [
"Excerpts from **Section 3.4** in Biegler (2010)."
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.6.3 Line Search](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3-Line-Search)",
"section": "3.6.3 Line Search"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.6.3 Line Search](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3-Line-Search)",
"section": "3.6.3 Line Search"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.6.3 Line Search](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3-Line-Search)",
"section": "3.6.3 Line Search"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.6.3 Line Search](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3-Line-Search)",
"section": "3.6.3 Line Search"
}
},
"source": [
"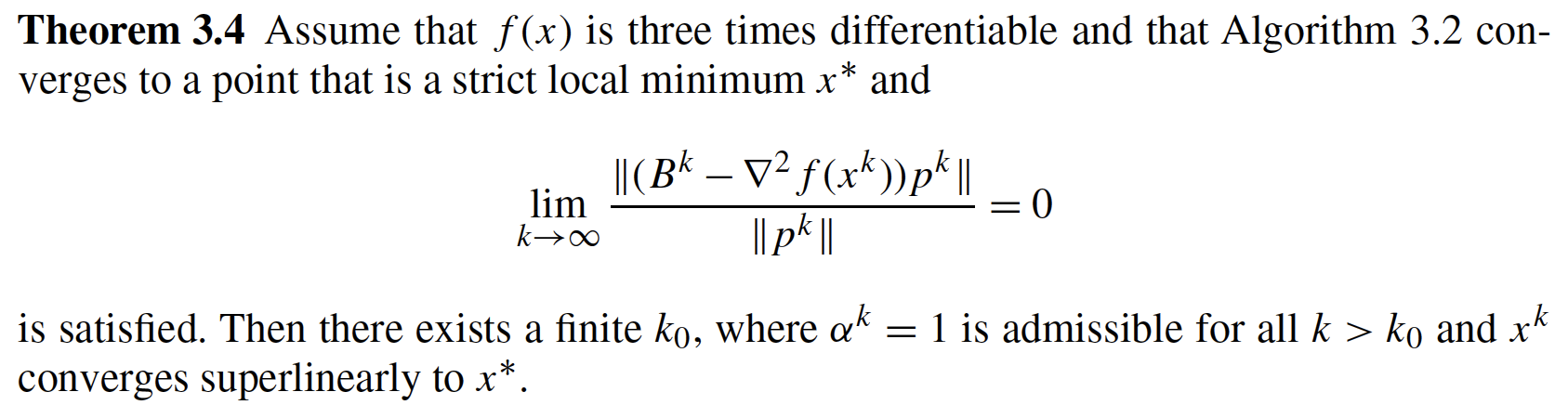"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.1 Visualization Code](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.1-Visualization-Code)",
"section": "3.6.3.1 Visualization Code"
}
},
"source": [
"### 3.6.3.1 Visualization Code"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.1 Visualization Code](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.1-Visualization-Code)",
"section": "3.6.3.1 Visualization Code"
}
},
"source": [
"**Goal**: Visualize Amijo and Goldstein conditions for an example."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.1 Visualization Code](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.1-Visualization-Code)",
"section": "3.6.3.1 Visualization Code"
}
},
"outputs": [],
"source": [
"def plot_alpha(xk,eta_ls=0.25,algorithm=\"newton\",alpha_max=1.0):\n",
" '''\n",
" Calculate step and visualize line search conditions\n",
" \n",
" Arguments:\n",
" xk : initial point (required)\n",
" eta_ls : eta in Goldstein-Armijo conditions\n",
" algorithm : either \"newton\" or \"steepest-descent\"\n",
" alpha_max : plots alpha between 0 and alpha_max\n",
" \n",
" Returns:\n",
" Nothing\n",
" \n",
" Creates:\n",
" Plot showing function value and line search conditions as a function of alpha\n",
" '''\n",
" \n",
" fxk = f(xk)\n",
" dfxk = df(xk)\n",
" \n",
" if(algorithm == \"newton\"):\n",
" pk = - dfxk / ddf(xk)\n",
" elif algorithm == \"steepest-descent\":\n",
" pk = - dfxk\n",
" else:\n",
" print(\"algorithm argument must be either 'newton' or 'steepest-descent'\")\n",
" \n",
" print(\"Considering xk =\",xk,\"and f(xk) = \",fxk)\n",
" print(\"Step with\",algorithm,\"algorithm:\")\n",
" print(\"pk = \",pk)\n",
" print(\"With full step, xk+1 =\",pk + xk,\"and f(xk+1) =\",f(xk + pk))\n",
" \n",
" n = 100\n",
" alpha = np.linspace(0,alpha_max,n)\n",
" fval = np.zeros(n)\n",
" \n",
" for i in range(0,n):\n",
" fval[i] = f(xk + alpha[i]*pk)\n",
" \n",
" fs = 18\n",
" plt.figure()\n",
" \n",
" # Evaluate f(x^{k+1}) for different alpha values\n",
" plt.plot(alpha,fval,color=\"blue\",label=r\"$f(x^{k+1})$\")\n",
" \n",
" # Armijo condition\n",
" arm = np.zeros(n)\n",
" for i in range(0,n):\n",
" arm[i] = fxk + eta_ls*alpha[i]*dfxk*pk\n",
" \n",
" plt.plot(alpha,arm,color=\"red\",label=\"Armijo\")\n",
" \n",
"\n",
" # Goldstein condition\n",
" gold = np.zeros(n)\n",
" for i in range(0,n):\n",
" gold[i] = fxk + (1-eta_ls)*alpha[i]*dfxk*pk\n",
" \n",
" plt.plot(alpha,gold,color=\"green\",label=\"Goldstein\")\n",
" \n",
" # Apply backtracking linestep (starting with alpha = alpha_max)\n",
" i = n - 1\n",
" flag = True\n",
" failed = False\n",
" while flag:\n",
" \n",
" if i < n-1 and fval[i] < gold[i]:\n",
" flag = False\n",
" print(\"Line search failed. Goldstein conditions violated. Consider increasing alpha_max.\")\n",
" failed = True\n",
" \n",
" # Armijo condition\n",
" if fval[i] < arm[i]:\n",
" flag = False\n",
" else:\n",
" i = i - 1\n",
" \n",
" if i < 0:\n",
" print(\"Line search failed. Try decreasing alpha_max.\")\n",
" failed = True\n",
" \n",
" if not failed:\n",
" print(\"alphak =\",alpha[i],\"with backtracking line search starting at alpha =\",alpha_max)\n",
" print(\"f(xk + alphak*pk) =\",fval[i])\n",
" \n",
" plt.scatter(alpha[i],fval[i],marker='x',color='black',label=r\"$a^{k}$ for line search\")\n",
" \n",
" # Labels\n",
" plt.xlabel(r\"$\\alpha^k$\",fontsize=fs)\n",
" plt.ylabel(r\"$f(x^k + \\alpha^k p^k)$\",fontsize=fs)\n",
" plt.grid()\n",
" plt.legend()\n",
" plt.show()"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.2 Newton Step, $x^k = -3$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.2-Newton-Step,-$x^k-=--3$)",
"section": "3.6.3.2 Newton Step, $x^k = -3$"
}
},
"source": [
"### 3.6.3.2 Newton Step, $x^k = -3$"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.2 Newton Step, $x^k = -3$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.2-Newton-Step,-$x^k-=--3$)",
"section": "3.6.3.2 Newton Step, $x^k = -3$"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Considering xk = -3 and f(xk) = 15.0\n",
"Step with newton algorithm:\n",
"pk = 0.796875\n",
"With full step, xk+1 = -2.203125 and f(xk+1) = -8.660857647657394\n",
"alphak = 1.5 with backtracking line search starting at alpha = 1.5\n",
"f(xk + alphak*pk) = -11.1743426900357\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZYAAAESCAYAAADe2fNYAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAABQP0lEQVR4nO3dd3yN1x/A8c9JhJDYe69aGRJCxKb2KGrVaFEzqKLVomoVVVXzZ6+aNWpWadXepLaIWbWqVVI7YsT5/XESSRAybnJv4vt+vZ7Xzb3Pc5/7veHme89zzvkepbVGCCGEsBQ7awcghBAiaZHEIoQQwqIksQghhLAoSSxCCCEsShKLEEIIi5LEIoQQwqKSWTsAW5ApUyadL1++WD33/v37ODk5WTYgC7L1+MD2Y7T1+EBitARbjw9sK8aDBw/e0FpnfulOrfUbv3l5eenY2rp1a6yfmxBsPT6tbT9GW49Pa4nREmw9Pq1tK0bggI7ib6pcChNCCGFRkliEEEJYlCQWIYQQFiWJRQghhEVJYhFCCGFRkliEEEJYlCSWOJAVB4QQ4kUyQTKWgoKeUKN7DmrcKUTlq91RZctCvnyglLVDE0IIq5LEEkuXLlzknkMwQ4vvwW/9HqZ1gzzJM0OZMuDjY25Ll4a0aa0dqhBCJChJLLFU1KUgu8bepGSnr9lQ4GuK9NB8d6sgXTedxe7nn81BSoGLi0kyYZurKySTX7sQIumSPpY4SO1sz/ROFenw+CTBFyvxUaZ9VPw0C2f+8IMNG2DoUMibF9asgS5dwNMT0qWDKlWgb19YtQquXrXyuxBCCMuSr85xZGcHM77NR8lpG+g2Yx776vTGfVFFvqo6lE8H9CeZXTLTy3/+POzbB/v3m9tx4+DxY3OS3LnDL5+VKQNeXpAypXXfmBBCxJIkFgvx9VUULNiOJm1r86h6d/o97ceygGXMaTAHj2weULCg2Vq3Nk8IDobDh02iCUs2P/5o9iVLBsWLhycbHx8oVEgGBgghEgVJLBZUowbs35yN+vVXcOnoCv5o1p1SM0vRt3xfvqz0JY7JHMMPdnSEsmXNFubatfAks38/LFgAU6aYfenTg7d3eLLx9oaMGRP2DQohRDRIYrGwYsVMTmjSpAk7vq6K+2e9GbFzBCtOrmB2g9mUy10u6idnzQoNGpgNICQETp6M3KoZNgyePjX7CxWKfAmteHFInjz+36QQQryCJJZ4kCkTbNwI3btnYNZX8yjXphWXU3emwpwK9PDuwYhqI3BO7vz6E9nbg5ub2Tp0MI/dvQsHDoS3ajZuNC0bMK2gkiUjX0KTWZxCiAQmiSWeJE8OM2aY0cWfflqLYv7+fPD5F0z0m8hPZ35iRv0Z1ChYI+YnTp0aqlY1G5jEcelS5FbNlCkwdiwAZTNkgIoVw5NNqVLmHEIIEU8kscQjpaBXLzOV5b33UnPto/8xcdZ7TL7ckZoLa/Kh54eMqTmG9CnTx+1F8uY1W/Pm5rHHj+HYMdi3j5tr1pAtIMAMeQYzjM3VNfJEzmLFTOtICCEsQBJLAqhZ0zQmGjSAT5pW4LvxR/in/FeM3vMtv5z7hcl1J9O4WGPLvaCDgxmy7OXFKVdXslWpAv/9B35+pkWzbx+sWAGzZpnjU6c2VQIiJpusWS0XjxDijSKJJYEULmySS+vW0OsjRzp2/JrdXzbD99f2NFnWhCbFmjCp7iSyOWeLnwAyZIDatc0GZgDA2bPhl9D274fRo+HJE7M/b97IfTUlSpg+HCGEeA1JLAkobVpzRWrwYBgxAk6cKMHqZX788Od3DN0+lC1/bmFcrXG08WiDiu85K3Z2UKSI2dq0MY89eACHDoW3avbsgaVLzT4HB1M5IGwEmo+PmZcjc2uEEM+Rki4JzN4ehg83cyGPHQOf0g5UsuvPUd+juGZxpd2adtReVJsLty4kfHApU0L58vDppybAS5dMyZmVK+GTT8DJCb7/Hj74wAx1zpwZ6tWDr76C336DW7cSPmYhhM2RFouVNG0KRYvCu++aAV4TJhRhW5ftTDswlX6b++E2xY2R1UbS3bs7dsqK+T97dhPku++a+0+ewIkTkUeh/fJL+LDmIkUiX0Jzd5eim0K8YeQTb0VubvD77/D++9CtG+zfb8fUqd2pX7g+XX7uwse/fszSE0uZ1WAWRTMVtXa4RrJk4OFhts6dzWN37pg3Eja3Zv16mDfP7EuZ0gxxjngJLVcu68UvhIh3klisLF06+OknM6F+6FA4ehRWrszLL61/YcGxBfT6tRee0zwZXHkwfcr1wcHewdohvyhNGqhWzWxgWi8XLkQuTzNxIjx6ZPbnyGESTGjLxu7BA6uFLoSwPEksNsDOznToly5tRo15ecGCBYo29dpQq2AtPvrlI77Y8sWzopYlspewdsivphTkz2+2Fi3MYw8fmqwZ8RLaypUAVLSzM5fMIpanKVrU/GKEEIlOov3kKqXmKKX+VUr5R3gsg1Jqo1LqbOhtHGYeJry6deHgQTPSt359+PJLyJQyKz82+5EVzVfwz71/KD2zNF9s/oLgJ8HWDjdmUqQwhTN79ICFC+HcOfj3X/j5Zy62bg1ZssCSJdC+vZnAmSGDmQA0cCCsWwc3blj7HQghoinRJhZgLlD7ucf6AZu11oWAzaH3E5UCBcwo3w4dzJDkWrVM0ePGxRoT0C2ANh5tGLlrJJ7TPNl1aZe1w42b0FFlF9q3N6PK/vsPAgJgzhzT0rl+Hb7+2mTZzJnN8OZWrcxltf37TStICGFzEm1i0VrvAP577uGGQGivMfOARgkZk6WkTGkmxc+eDbt3m7mJO3ZA+pTpmdNwDr+9/xsPQx5S8fuKfLT+I+4+vGvtkC3Dzs6Ul/nwQ5g2zaxXc+cObN8O335r5tHs2AE9e5rLZmnSmNtevWDxYvjzTym6KYQNSLSJJQpZtdZ/A4TeZrFyPHHSvr3pinB2NkOSv/nGTJivUbAGx7se52Pvj5ny+xTcprqx4dwGa4cbP5ycoFIl+OwzU4bmyhW4fNnMs/n44/Bqn61ameZe1qzwzjumubd5s0lMQogEpXQi/oanlMoH/Ky1dgu9f0trnS7C/pta65f2syilOgOdAbJmzeq1ZMmSWMVw7949nJ2jUQI/Du7ft+e774qwbVsWypQJpF+/U6RLZ5Y1PnH7BKPPjOZi0EVqZq1Jt4LdSOuQNkHji6u4xqhCQnD680/SBAQ821JdvgyAVoqgPHm44+LCnWLFuFOsGEH586NjUHTzTfgdJgRbj9HW4wPbirFq1aoHtdalXrpTa51oNyAf4B/h/mkge+jP2YHT0TmPl5eXjq2tW7fG+rkx8fSp1lOmaJ0ihdY5cmi9fXv4vuDHwfrLzV/qZF8l01lGZ9HL/Jfpp0+fJmh8cREvMf73n9YbNmg9dKjWdetqnTGj1uZCmdZOTlpXrqx1375ar1yp9dWrCR+fhUmMcWfr8WltWzECB3QUf1OT2qWwn4C2oT+3BdZYMRaLUgq6djWXxpyczKWxYcPMIpMpkqVg2NvDONDpALnT5Kb58uY0WdaEv+/+be2wrSd9ejOqbNAgM6rs+nVTdHPhQnONMSjIrFnTuLGZV5MnDzRrBmPGwK5dpm6aECJWEu08FqXUYqAKkEkpdQUYDHwDLFNKdQAuAc2sF2H88PQ0Q5J9fc3fzC1bYNEi87fRI5sH+zruY9zecQzaNgiXKS50ytOJyrpy/Be1tHVKwVtvma11a/NYcLAZIBBxbs3y5WZfWIWBMmXImiaNKW1TqJDMrREiGhJtYtFat4xiV7UEDcQKUqc2X7xr1IDu3c3fv++/N6Nyk9kl47Pyn9GwaEM6re3E6DOjObzwMDPqzyB/+vzWDt22ODpC2bJmC3PtWuR1axYsoNjdu2bkRPr0Zi5OWGkab2/ImNF68Qtho+TrVyKlFLRrZ1ovOXOagVAff2y+hAMUzliYrW230rtQb/Zf2Y/bVDcm7JtAyNMQq8Zt854fVXbzJn5z5pjx302bmmrPw4eb2ayZMpmFdj74ACZPhgMHwsvWCPEGk8SSyBUtar5Y9+wJ//uf+RJ94oTZZ6fsaJCjASe6naBKvir02tCLit9XJOB6gHWDTkzs7QnKn9/MWJ0xw6x1cOuWuQY5cqRZd3rTJvjoI1OTJ00as/TAJ5+YtWwuXpS5NeKNI4klCXB0hPHjTR/1P/+YYsKTJoX/PcudNjc/t/yZhe8u5EzgGUpML8Gw7cN4HPLYqnEnWqlTm9ET/frB6tWmFXPxokkk3bub5uTUqaZ6QL58pgOsUSOTiLZuhbtJZEKrEFFItH0s4kV168Lx42bieo8eZpmUDh1MNWSlFK2Lt6ZGwRp8/MvHDNo2iOUnlzOnwRy8cnhZOfJETikzqixPHmje3Dz26JH5xwir7rx/v1k+FMwAAFfX8L6aMmVMxYEYzK0RwpZJiyWJyZrVtFz+9z9ztaZ9+9LP/p4BZHHKwpKmS1jTYg3X71/He5Y3fTf25cFjGV5rUcmTmzLV3bvD/Plw+rQppLl+vSmsmTOnqSTQsaOp7Jw+vVl24IsvTAL65x9rvwMhYk0SSxKklLnkf/AgZM78kEaNzN+viFdgGhRpQED3AD70/JBv93yLxzQPtl/YbrWY3wgZM0KdOjBkiGlOBgaahDN/vhkAcOsWjB5tLptlz24uo7VoAePGwd694SMzhLBxkliSMBcXmDLlEP37m4LBHh6wc2f4/nSO6ZjVYBabPtjEk6dPqDKvCl1/7sqdh1JfK0EoFXlU2cGDprbZrl3w3XdmJMbevWYgQLlyZmBA6dLmOueiRWbpARkYIGyQJJYkzsFB8/XXpiiwUlC5sqnnGPHLb7UC1Tje9Ti9fXoz/eB0XKe4sv7seusF/SZLmdKMKvv0U1i2zAwKuHoVVq0yjzk7m0lL779vJmyGLj2Qd948s/TArVvWfgdCSGJ5U1SoYBZw7NzZfBn28jJfkMM4JXdibK2x7OmwhzQp0lDvh3q8v/J9bgTJAltWlz175FFlt2+bf8zp06FhQ7h4kXzz5pnFe9KnN2PQ27UzI9MOH4YnT6z9DsQbRhLLG8TZ2Sxzsn69+WJbpowpCxNxTp9PLh8OdT7EoEqDWHpiKcUmF2OJ/5KwIp/CFtjbQ/Hi5lvC7Nng78+utWvNfJoRI0xLZv166NYNSpY0l9DClh5YvtwsPSBEPJLE8gaqUwf8/U3JrGHDzKX8I0fC96dIloKhVYdyqPMh8qXLR8sVLWm0tBF/3fnLajGLVwtxcgofVbZ2rSlNc/68WQCtSxd4/NisvNmsGeTObUalNW5sFlDbsQPu37f2WxBJiCSWN1T69DBvnpnfd+2a6RMePDhy68U9qzt7O+xldI3RbPxjIy5TXJh5cKa0XhIDpSB//sijyu7eNXXQJk6EKlVMFYG+fU3HW9q0psKpr6/pwzl50qwqJ0QsSGJ5wzVsaErAtGwJX31lZu3//nv4/mR2yehTrg/Huh6jZPaSdP65M9XmV+OP//6wXtAidpInf3FU2b//ws8/m5ZOliymhdO+vRlSmCGDWXpg4EBzzPXr1n4HIpGQxCLIkMFMpVi71kyt8PGBzz+PvCTJWxneYnObzUyvP52Dfx/Efao7Y/eOlaKWiV3oqDK++sqMKrt5EwICTKulRQuTTEaONIU5s2SBggXNMtATJ5pqAg8fWvsdCBskiUU8U7++ab106GDm6RUvbgYhhbFTdnT26kxAtwCqF6jOp799Srk55fD/1996QQvLsrMz5WXatTMjPQ4fNqPQtm83/TElSpg+mZ49zTeQNGnMba9eprVz/rzMrRGSWERk6dKZIr6bN5tL7G+/DZ06mS+yYXKmycmaFmtY3GQx52+ep+T0kgzdNpRHIVIyPklycnpxVNnly+bnnj3NJbYZM0xLpmDByEsPbNpkEpN4o0gRSvFSb79taigOHWpW6127FiZMMDUWlTJFLVu4taB6ger0/LUnQ7YPeVbUsnTO0tYOX8S3XLnM1qSJuf/kiRlqGFZ0c98+0y8D5j9MsWIUyZPHlLDx8TFFOJPJn5+kSlosIkqpUsGoUWYgUa5c5pJ7/fpw4UL4MZlSZWJR40WsbbmWmw9u4jPbhz6/9SHocZDV4hZWkCzZi6PK/vsPNmww307y5SPTnj1mv6enGYVWpYpZemDVKlNdQCQZkljEa5Usab6Ajh1rLrW7uprL7Y8jLOdSv3B9TnQ7QaeSnRizdwzFpxZn659boz6pSPrSpw8fVbZuHbtXr4azZ8262h06QFCQ+U/VuLGZV5Mnj5ln8913pl5akHw5SawksYhoSZYMevc2A4aqVzfTH7y8YM+e8GPSOqZlWv1pbG1rEsrb89+my9ou3A6Wa+wCc0nsrbfMzNyJE01T+M4dM8dm3DhTI+3gQdOXU7GiGRjg5WUqCIQtPSBzaxIFSSwiRvLkMcuFrF5tysKUL2++fN6IUFKsSr4qHOt6jD5l+zDr8Cxcp7iy9vRaa4UsbJmj44ujyv75x/wn69vXtHoWLoS2bU0NtIwZoXZtM5v3l1/M5TZhcySxiFhp2NC0Xj7/3HyZLFLEDAwK+0KZyiEVo2uOZl+HfWRImYEGSxrQakUrrt+XSXbiNbJmhQYNwkeV3bxpBgbMmgVNm5r+mOHDzZKpGTOGLz0waRIcOBC5fISwijglFqVUYaXUu0qpLkqpzqE/F7JUcMK2OTubzv0jR8wiiF26mC+ffn7hx5TOWZoDnQ/wVZWvWB6wnGKTi/HD8R+kLIyIPnt707HXoQPMnGlK0dy6ZSZZjRxp9m3aZCoKlC5tLqGVK2fWsQlbekD+vyWoGCcWpVQxpdQEpdRV4CSwHJgKTAv9+ZRS6qpSarxSqphlwxW2yNXVfMYXLjTTG3x8zNyXsAogye2TM7DyQA53OcxbGd6i9crWvLP4HS7fvmzdwEXilTr1i6PKLl40iaR7d9OfM3UqvPeeWYkzR47ISw9EXE5VWFy0B5IrpQoCo4B3gQfATmAv8AcQCCggA/AW4AN0BHoopVYCfbXW5y0burAlSpk+2XfeMRWTx4838+eGDoWuXcHBAVyzuLK7/W7+5/c/BmwZgOsUV76t8S2FdWFrhy8SO6VMB2DYyDIwwxaPHQufW7N/v+m7AVNhwNXVrB3h42NuQ6Q8kaXEZIZSAHAcaAes1Fq/ss62UsoJaAp8HPpcx1jGKBKRNGlMOZj27U1/bM+epu9l/Hgzmszezp5ePr1oUKQBndd2puu6rnik9eDH4j9SKKNcRRUW5OBgRpV5eZlWDJjOfj+/8EmcK1aYvhugQqpUkRONj4/p7xExFpNLYc211qW01gtel1QAtNb3tdbztNZewHuxD1EkRsWKwa+/mtFjQUFQo4bp8D971uwvkL4AGz/YyOwGszl37xzFpxVn9O7RPHkqqx2KeJQhQ+RRZYGBZhjzvHlcq1HDDH8ePdpcNsuW7cWlByKu6S2iFO0Wi9Z6TWxfJC7PFYmXUiaZ1KplWiwjRpirDz16mDlz6dIp2pdoT5p/07Do1iI+3/Q5ywKWMbvBbIpnLW7t8MWbQCkzqqxwYc7myUPOKlVMWe9Dh8Ivoe3dC0uXmuMdHMDDI7xF4+Nj6qMpZdW3YWui3WJRSsknXcSKo6PpYz1zxowKHTfOzJObPNlcBs+UIhMrm69kWdNlXLp9Ca8ZXgzaOoiHT6Qku7CClCnNBK1PPw0fVXb1qhkk8OmnZjjk3LnmP3OhQpGXHtiwIXLF1jdUTC6FLVFKpX7+QaVUEQvGI5Kw7NnNEu2HDpmS/B99ZIYp796dEVA0c21GQLcAWrq1ZNiOYZScUZJ9V/ZZO2whzH/eiKPKbt2Co0dNB2LDhib5DBliLrNlyGAmc7ZrZ0amHT5sinS+QWKSWGYCCyI+oJSqCuywaEQiyfP0NGX5wwbofPmlO1WqmJUrM6bKyPx357O+1XruPrxLudnl6P1rb+4/kjXZhQ1Jlsx8O+rUyXxb8vc3yWbjRjN5s3Bh04fTrZsptpcmjSlT06ePGS55+XKSnlsT7cSitR4HhCil+gIopdoAS4D34yk2kYQpZSZXHz8OvXqd4eRJ8PY20w7OnYM6herg380f31K+jN8/Hvep7mw+v9naYQsRtTRpzNDHAQPgp59MaZrz502pmi5dTKvlf/8zw6Hz5DElwxs3NhVdt2+H+0nny9MrE4tSqrlSqqhSz3qmPgTaK6XmAUOBt7XWG+M7SJF0OThAw4ZXOXcufGn1YsXMZbIHt9Iwpd4UtrfbTjK7ZFRfUJ2OP3XkVvAta4ctxOsp9eKosjt3zICACRPMBM9jx0xNtCpVTGJ6fumBRFp083Wjwj4B3ACllAoAjgL7gBpAFa31mXiOT7wh0qQxfZ9du5pJldOmmf7R3r2hT59KHPU9ytDtQ/luz3esP7ueqfWm0rBoQ2uHLUTMpEhhmube3uGPXb8eeW7NkiUwfbrZlzatKVMTOrfGIZH01byyxaK19gFSA17AGOAGkBUzy/6kUuqsUmpZvEcZQ0qp2kqp00qpc0qpftaOR0Rf9uwmqQQEmIE2w4dDgQIwaXxKBpX7hv0d95PFKQuNljbiveXvce3eNWuHLETcRBxV9ttvZhJnQIBptbRsaUqHjxwJ77xD+XffNR+IVq3M0gP798ND2xs9+do+Fm2c0lov0Vr301rX1lpnB3JgZtUfjPcoY0ApZQ9MBuoALkBLpZSLdaMSMVW4sJk6cOCA+XL3+edmiPL+1V7savM7w6sOZ/Wp1bhMcWHB0QVS1FIkHXZ25npwxFFlt2/Djh380aULlCgBO3aYshY+Pqa57+Nj7octPWDlz0Osqxtrra9prX/RWo+yZEAW4A2c01qf11o/wgwwkGsmiZSXlxlcs2OHmYfWvTu4FnMg65kB/N7hCEUyFqHN6jbU+6Eel25fsna4QsQPJyeoWJHLLVqYMjRXrpiRZcuXm4SSIoUpTdOqlfmgZM1qCvcNH24qP99O2MX2YlIr7AVKqaxAcyAfcA84DPymtbbmmqI5gYhlc68AZawUi7CQihVNcvntN9PJ36kTFChQjC8G7KRZzckM3PoFrlNcGVV9FL6lfLFTstSQSOJy5TJbkybm/pMnZthzWLWA/fvNaBgwAwmKFTMVA8KqBri6mmHT8UDF9hKCUqoisB5IhelzCRMIDNNaT4x7eLGKqxlQS2vdMfT+B4C31rrHc8d1BjoDZM2a1WvJkiWxer179+7h7Owct6Djka3HBzGPUWvYuzcjc+fm4+zZ1OTI8YAGbfbwe7Z+HLx1gOJpi/Np4U/JkyqPVeKzBokx7mw9Poh5jMnu3SP1yZOkCdsCAnC4cweAEEdHbnl4cPybb2IVS9WqVQ9qrUu9dKfWOlYbsB+4C7QFcgF5MK2XfcBT4IfYnjsuG1AW2BDhfn+g/6ue4+XlpWNr69atsX5uQrD1+LSOfYxPn2q9Zo3WJUpoDVrnL/BUfzjhe53um3Q6xbAUeuTOkfpxyGOrxZeQJMa4s/X4tLZAjE+fan3unNYLF2rdo4fWvr6xPhVwQEfxNzUu1wvcgHHaVDC+orW+pLVeps1Isk7Ae0qpj+Jw/tj6HSiklMqvlEoOtAB+skIcIp6FTbI8eNDMR8uYQfF9z3Y4zz1JsWT16L+5P2VmleHIP0esHaoQtkEp0wfTurUZVTZ1ary8TFwSy13gpb2lWuvZmE5z3zicP1a01k+Aj4ANmBUul2mtTyR0HCLhKGX6Kf38YN06yJ0+G0f6ryDdb8s5+89flJ5Zmi+3fEnwEyl5LkRCiEti2QrUfc3+gnE4f6xprddrrQtrrQtqrUdYIwaR8JSCunVh927YsgVKOjbh7jcB2Pm3ZsTOERSfUoI9l/dYO0whkry4JJYZQDmlVM8o9ucDrsbh/ELEilJQtaopdLlvawbqPJwLC37l3IUgys+uwIfLenLv0T1rhylEkhWXxLIZs8b9WKXUNqXU+0qpYkqpQkqpjkBPzGx9IaymTBmziqX/mlq0+M8fdaA7cwP+R7av3Ji68TdrhydEkhSXxDIMM9z4MlAJmA/4A6eA6cBp4JZSyk0pFT+DpYWIJldX+GFuai5O/R/N7+8g6I4j3fbUIme3D1m+7qa1JyoLkaTEZeb9YK11I611PkzLpRrQB1gInACKh/58FLinlDqqlFoQ1fmESAi5c8PS0RX4a+ARqtj352rmBTTb6kLe2iuZM0eWNBfCEiwyPVlrfUtrvVVrPU5r3VZrXRxwBkphhh7PxIwie8cSrydEXGXP7MjWL79mX/vfyZMxO5fLNaHDhqbkKvoPgwebpTSEELETb2vea60faa0Paa3naK17aK0raK3TxThCIeJRmbwlOPf5fr5+eyQOrj9z5wMXvvppLrnzaD74wKxqKYSIGVnzXrzxHOwd6F+xH8e7HaVMAVdo9CE5PqvNyi0X8PaGbt1KsmiRTVYnF8ImyZr3QoQqkqkI29ttZ1KdSfznvAfV3Y0mo/7Hnbt2vP++WU12wAC4JEWUhXglWfNeiAjslB3dvbvj39WfinkrsuLBx6T/pCwzV53Cxwe++casNtuwIfz6a6JdOVaIeCVr3gvxEnnT5WV9q/XMbzSfS0GX6O7vQZk+X3P63GP69jUryNapYxYfGzlSOvuFiOh1LZZPgAOY4cK/A2MJX/O+ltTgEkmZUooPPD7g+9Lf07BIQwZsGUDTDaVp2uMQly+bFS7z5oUvvjDDmJs0Ma2YkBBrRy6EdSXJNe+FsKQMyTOwrNkyVjZfybX71/Ce6c2gHf14590HbN0Kp09D795mIbI6dcylskGD4M8/rR25ENaR5Na8FyK+vFvsXQK6BdDWoy2jdo/Cc7onOy/upHBh+PZb+Osv+PFHM8t/+HAoUACqVYOFCyHImmuqCpHAkuKa90LEm/Qp0zO74Ww2frCRRyGPqDS3Et3Xdefuw7skTw5Nm8Ivv8CFC/DVV+b2gw8gWzbo2BF27kTKx4gkL9aJRSn1niUDESIxqV6gOse7Hudj74+ZemAqrlNc+eXsL8/258kDAwfC2bOwbZvpf1myBCpVMussDRpk9gmRFMWlpMvc0PpfDV+2UymVVSlVKA7nF8KmOSd3ZkKdCexuvxvn5M7U/aEubVa1ITAo8NkxdnZQuTJ8/z1cuwbz55vEMnw4FC4MPj5mIb9r16z4RoSwsLgkloLANuAHpZSfUqrWc/tbYCodC5Gklc1dlsNdDvNlxS9Z7L8Ylyku/HjiR/Rz17ycnMxlsY0b4fJl0y8THAw9e0KOHFCzpklAt25Z530IYSlxSSxBwBPgIqbY5Hql1DGl1FallB9mFNlJC8QohM1LkSwFw94exoFOB8idJjfNlzen8bLGXL378rXucuaEzz6DI0fA3x/694dz56B9e8iaFd59FxYvhrt3E/Z9CGEJcUksM4FewH+Y8viLgL+BypjhyRuAJnGMT4hExSObB/s67mNU9VH8eu5XXCa7MPvQ7BdaLxGFjSL74w/Yvx+6dQM/P2jVCrJkCe+fkSQjEou4JJZqwMTQqsVtQrdaQBXgDKYVIwUvxBsnmV0yPi//Ocd8j+GRzYOOaztSY0ENzt88/8rnKQXe3jBunLlUtnMndOoEe/ZAy5aQOTM0amT6aW7eTJj3IkRsxHU9lhemgGmtd2CSyhVgThzPL0SiVShjIba23crUelPx+8sP96nujN83npCnr5+ab2cHFSqYjv2//jJJxtcXDh6Etm1NS6ZmTZg61ewXwpbEJbFsB95XSiV/fofW+j7mUlnJOJxfiETPTtnhW8qXE91OUDVfVXpv6E2F7ytw4t/oV0MKSzLjx8PFi+ZyWZ8+5udu3SBXLujatSQjRsDx4zJPRlhfXBLLV4AHsF0pVeol+8thOveFeOPlTpubtS3XsvDdhZwNPEuJ6SUYtn0Yj0Iexeg8dnbmctnIkXDqFAQEwNdfm31ffgnFi5sZ/z16wIYNstSysI64zLw/DLTDJJf9SqnTSqmFSqkJSqltQGvMcGQhBKaoZevirTnZ/SRNXJowaNsgSs0oxe9/xW6ZSqWgWDEzomzq1ENcvQozZ4KbG8yeDbVrQ8aMpsT/9OmyjoxIOHHqY9FaLwZcgUmAA9AK6AFUAn4HPoprgEIkNZmdMrO4yWLWtFhD4INAfGb78PnGz3nw+EGczps9uykbs3YtBAbCunWmP+bYMdM/kzevGYH26afw22/SmhHxJ66d92it/9Ra99RaFwAyYhJNTq21j9b6cpwjFCKJalCkAQHdAuhQogOj94ym+LTibL+w3SLnTpkS6taFKVPg/HlzyWzMGDN/ZvJkqFUL0qc3t2PGmOQji5YJS4lzYolIa31Ta31Sa/23Jc8rRFKV1jEtM96ZweY2m3mqn1JlXhW6/tyVOw/vWOw1wi6ZffKJaan8959pzXTpAleumIEAHh6mxdOyJcyaZZKRDAIQsWXRxCKEiJ2387/NMd9jfOLzCTMOzcB1iivrzqyLl9dKlcq0ZsaPhxMnTN/L99+b4cvbtpm5MwULmnVlPvwQ5s0zI9CEiC5JLELYCKfkToypNYY97feQNkVa6i+uz/sr3+dG0I14fd3cuaFdO1iwAK5eNZfNJk2CUqXgp5/Mvnz5zNa2rRkYcOaMtGhE1CSxCGFjyuQqw6EuhxhceTDLTiyj2ORiLPFf8sqyMJYSdtmse3dYvhyuXzf9LxMngpeXWWumY0coUsSsMdOkCYwda+bWPIrZyGmRhFkksSgjz8smSwohYi65fXKGVBnCoS6HyJ8uPy1XtKTR0kb8dSdhp9nb2YG7u5kXs2KFKe9/8qQZvly7timi+emnpvx/mjRmIudnn8HKlab1I95MlmqxZMCUd6lgofMJIQC3LG7s7bCXMTXHsPGPjbhMcWHmwZkJ0np5GaWgaFHo3Nn0vfzxh0kgy5ebVk5IiGndNGliRqDlzm1+/vZbOHw4HXcsNyZB2LBkFjyXsuC5hBCh7O3s+aTsJzQs0pBOazvR+efOLPZfzMx3ZlIwQ0Frh0f27CZ5NAmtZf7woWnJ7N1rqjT7+ZkWDHjyySfmMlqpUubSWsmSUKKEae2IpMOSiUUIEY8KZijI5jabmXVoFn029sF9qjvDqg6jl08va4cWSYoUUKaM2cLcuAFz5hzl0SMPfv/djD5btCh8/1tvmQTj6WmGPnt6msXPlHxdTZQSZWJRSjUDhgDFAG+t9YEI+/oDHYAQ4GOt9QarBClEPFBK0cmrE3UL1aXruq702diHZQHL8M3uSxWqWDu8KGXKBN7eN6lSJfyxa9dMtebDh8128CD8+GP4/owZTe2z4sVNP4+bG7i4QOrUCR6+iKFYJRalVKXnHkobeltcKRWp8GRoGX1L8wcaA9Ofi8sFsySyK5AD2KSUKqy1fn2dciESkZxpcrKmxRqWnVhGj1960PlqZy46XeSLil+Q3D5xjKHJmtXMp6lbN/yxO3fMKLQjR8ztsWOm/llQUPgxefOaBOPiYkawhW3p0yf4WxBRiG2LZRvwst7DMRF+VqHH2MfyNaKktT4J5tvbcxoCS7TWD4E/lVLnAG9gr6VjEMLalFK85/Ye1QpUo+W8lgzdPpTlAcuZ03AO3jm9rR1erISNLKsQYRjQ06dw4YJZwvn4cTPPJiAAtm6NXO8sSxbTf1O0qLktVMhsBQqYy3Mi4cQ2sVR97n46YBXwGXAwLgHFUU5gX4T7V0IfEyLJypQqEwOKDaBXtV74rvOl7Oyy9CrTi2FvDyOVQyprhxdndnYmORQoAA0ahD8eEmISzqlTZgj0yZNw+jSsWmX6dMIoBXnymH6ct94KP1eBAqa6gLR0LE9ZYtiiUiojcB2orrXeEucTmnNuArK9ZNcArfWa0GO2AX3C+liUUpOBvVrrhaH3ZwPrtdYrXnL+zkBngKxZs3otWbIkVnHeu3cPZ2fnWD03Idh6fGD7Mdp6fBAe4/0n95lxfgY//f0TORxz0KdwH0qkL2Ht8ICE/T3euZOMK1dS8tdfqbh8OSVXr6bkr7/M7Z07DpGOdXJ6QrZswWTKdI+cOZ+QNWswWbM+JEuWYLJkeUj69I+ws5Gp5Lb0f7Fq1aoHtdYvW4vLdjvvtdbVY/G0K0DuCPdzAS+dpqW1ngHMAChVqpSuErFXMQa2bdtGbJ+bEGw9PrD9GG09PogcYz3qsf3Cdjqu7cgnxz6hU8lOjK4xmrSOaV99kgSM0Zpu34Y//zRzcC5cgAsXkvHnn84EBMCJE87cuxf5+GTJzJycXLnMbY4c4bfZs4dvadLE/yg2S/0OtdaRuhKevx9XNptYYukn4Ael1FhM530hwM+6IQmR8Crnq8xR36MM3jqYsfvGsu7sOqbVm8Y7Rd6xdmhWlzatGc7s6Rn58W3bDlC5chVu3oTLl01xzkuX4K+/TBXoy5fN6LWff448mCCMo6MZkBC2ZckCmTOHb5kymS1jRrMlRCJ6mSFDhnDr1i3GjRuHUgqtNb179yZdunQMGTLEIq+RKBOLUupd4H9AZmCdUuqI1rqW1vqEUmoZEIBZFrm7jAgTb6pUDqkYXXM077m9R/s17WmwpAEt3FowsfZEMjtltnZ4NkkpyJDBbB4eLz9GazN67e+/w7d//gnfrl0zSejgQfj3X3gSxQLt9vbmddKnD9/SpTNb2rThW5o0Zoh16tRw5kxqsmUDJydwdja3yWMwCFBrza1bt5gwYQIA48aNo3fv3kyYMIGePXtarOViqcTyH5Af+MdC53slrfUqzGCBl+0bAYxIiDiESAxK5SjFgc4HGLVrFMN2DGPjHxuZWGciLd1aWvTyx5tCqfA/+kWLvvrYsCR0/brZAgPNduOGWRcnbLt1yzx+7py5VHf7dlRFPb1eeCRZMrMUgpOTWeAtbHN0DN9SpDAJKEUKRbJk4yhevAkTJhxgwoR+gEkqYS0YS7BIYtFmBICs2CCEjUpun5yBlQfSuFhjOvzUgdYrW/PD8R+YWm8qudPmfv0JRKxETEJvvRWz5wYHm6R0+7a5vXsX9uw5Tr587ty/D/fvw7175rJc2PbgQfhtcLD5OTDQJKmHD8NuFY8fVwA8gAvAtxZNKpBIL4UJIWLHNYsru9vv5n9+/2PAlgG4TnFldI3RdPLqhJ2ykaFPAghvbWTJEvHRQOLadx/WpxJ2OQygd+/eFk0u8j9JiDeMvZ09vXx6cbzrcbxzeuO7zpe3573N2cCz1g5NxLOISaVnz548ffqUnj17MmHCBHr37m2xqtmSWIR4QxVIX4CNH2xkdoPZHPnnCMWnFWf07tE8eRpFb7NI9JRSpEuXLlKfyrhx4+jZsyfp0qWzrT4WIUTipJSifYn21H6rNt3Xd+fzTZ+z9MRSZjeYjUe2KIZFiURtyJAhkUZ/hSUXS/axRLvFopQqbrFXFULYlBypc7Cy+UqWNV3G5TuXKTWzFAO3DOThk4fWDk3Eg+eTiKVHB8bkUtgSpdQLBauVUkUsGI8QwkqUUjRzbUZAtwBaubdi+M7hlJhegr2XpYariJmYJJaZwIKIDyilqgLxURZfCGElGVNlZF6jeaxvtZ57j+5Rfk55ev3ai/uP7ls7NJFIRDuxaK3HASFKqb4ASqk2wBLg/XiKTQhhRXUK1eFEtxN0K92NCfsn4D7Vnc3nN1s7LJEIvDKxKKWaK6WKqvALcB8C7ZVS84ChwNta643xHaQQwjpSp0jNpLqT2NFuBw72DlRfUJ2OP3XkVvAta4cmbNjrWiyfAAeAe0qp34GxmPVOagC1tNYn4jk+IYQNqJi3Ikd9j9KvfD/mHpmLy2QXVp9abe2whI16ZWLRWvsAqTEFasYAN4CsmNUhTyqlzoYWfRRCJHGOyRwZWX0kfp38yOqclXeXvkvzH5tz7d41a4cmbMxr+1i0cUprvURr3U9rXVtrnR1Tlv5jrLtipBAigZXMXhK/jn6MeHsEa06vwWWKCwuOLrDYrG2R+MVl5n1lrfUvWutRFotGCJEoONg78EXFLzjS5QhFMxWlzeo21P2hLpduX7J2aMIGxCWx/KCU6mKxSIQQiU6xzMXY+eFOJtaeyM6LO3Gd4spkv8k81U+tHZqworgklrnAFKXUgJftVEqVVUrtjMP5hRCJgJ2yo0eZHvh386dc7nJ89MtHVJ5bmdM3Tls7NGElsU4sWuuOwLfAMKXUuLDHlVJFlFIrgV1AibiHKIRIDPKly8evrX9lbsO5nPj3BB7TPPhm1zc8Dnls7dBEAotTdWOtdX/MkOSPlVILlVLTgONAPWA6EMOlbYQQiZlSiraebQnoHkD9wvXpv7k/ZWaV4fDfh60dmkhAlqhuPBOTSFoBGjMbf6DW+rwFzm01jx8/5sqVKwQHB7/yuLRp03Ly5MkEiirmbD0+sF6Mjo6O5MqVCwcHhwR/7aQum3M2ljdfzoqAFXRf353SM0vzXq738Kngg2MyR2uHJ+JZrBOLUsoB6Ab0BzIDhwBPwAG4bIngrOnKlSukTp2afPnyvbLy5927d0md+oXanDbD1uMD68SotSYwMJArV66QP3/+BH3tN0kTlyZUzV+VT3/7lLlH5nJw2kFmN5hN+TzlrR2aiEdxuRR2FjMT/zrQQGtdCtNqaQCsV0o5WyA+qwkODiZjxowWLyctbINSiowZM762RSriLkPKDHzf8Hu+df+W4CfBVPy+Ih//8jH3Ht2zdmginsQlsdgDnQAPrfU6AK31Mkxi8QG2KqUyxT1E65GkkrTJv2/CKp2hNP7d/PnI+yMm+U3CbYobG85tsHZYIh7EJbEU0lrP0TrygHWt9W9AdSA/sCcuwQkhkhbn5M5MrDORnR/uxDGZI7UX1abd6nb89+A/a4cmLCguw42jvIagtd4PVASkl04I8YLyecpzxPcIAyoOYOGxhbhMdmFFwAprhyUsJE7DjV9Fa30SkB46K2jfvn2U+44fP86lS5HLbpw/f54OHTrQtGnT+A5NiGcckzky/O3hHOh8gBypc9D0x6Y0WdaEv+/+be3QRBzFZM37ajE9udb6cuhzq8f0uSLcp59+iouLC506daJy5cqEhIREeWxQUBBp06Zl69at9O3b94XO6YMHD3L+fOSR4AUKFGD27NmRHnv06BGVKlXiyZMnlnsjQryEZzZP/Dr58U21b1h3Zh0uU1yYe2SuFLVMxGLSYvlVKbVFKVVfKWX/uoOVUg5KqXeVUtuB9bEP8c12/vx5du/eTUBAAJ6enjRu3Bh7+6h//YcOHeLIkSOcPn2aUaNG4ehorkYGBATg6+vLvHnzGDt2LL6+vly7FnW58+TJk1OtWjWWLl1q8fckxPOS2SWjb4W+HPU9ilsWNz5c8yG1F9Xmwq0L1g5NxEJM5rF4AuOAn4AbSqmNgB/wB/AfZo2WDEAhzKiwt0Pvbwh9roih06dPU716dZ48eUKJEqY6zqpVq57tr1q1Kl988QU1atTgyy+/5M6dO+TPn58yZcrg5OQU6VwuLi5MmzaNuXPnki9fPqpUqfLa12/UqBH9+/endevWFn1fQkSlSKYibG+3nam/T6Xf5n64TXFjZLWRdPfujp2Ktyv3wsJi8i/VDOiM6TfZALyDSTRrgJ3ADmA18B1QE5OAymit62itAywY8xujSJEitG3blmHDhrF//37+/vtv8uXL92z/0KFDGTFiBIsWLeLw4cOMGzeOgIAAvv76a06dOsXOndGrARoYGIivry+HDx9m5MiRzx53c3Pj999/t/TbEuKV7JQd3b2749/Vn4p5K/Lxrx9T8fuKnLxu2xUkRLiYtFgGAWe01j8Ae5VSTYFLgAtm5r3GTJb0Bw4/Pww5MevVC44cefm+kJCUvOLKVJQ8PWH8+Ncfd/z4cRo2bMiNGzdIly5dpH2VKlVCa83YsWPZtm0b9vb2zJw5E4ARI0YAZlZ7RO3atXvhNTJmzMi0adNeeNze3p7kyZMnitn7IunJmy4v61utZ+GxhfTa0AvP6Z4MqjSIz8t/joO9lOGxZTFpsdwEUkW4vxR4S2s9V2s9Wmv9ndZ6ntb6YFJKKtZ24sQJXF1dSZky5Qsd8cePH+fvv/8mRYoU8faH/+HDh8/6aYRIaEopPvD4gIBuATQq2ogvt35J6ZmlOfT3IWuHJl4hJi0Wf6CDUuoXrfVfmD6VN8KrWhZ37z6Itz/qd+/excHBgVSpUpEqVSpCQkIIDg7G0dGRv//+m9atW7NmzRo+/vhjNmzYQK1atSz6+oGBgWTOnFmKNAqry+qclaVNl9LSrSXd1nXDe6Y3fcr1YXDlwaR0SGnt8MRzYtJiGQqUBC4ppU5hLn3VVUrVUUpljZfo3nD+/v64ubk9u1+zZk127dpFUFAQjRs3ZsyYMRQrVoyBAwcyZMgQi7/+1q1bqVu3rsXPK0RsNSraiIDuAbTzbMeo3aPwnO7JzouynqCtiXZi0VpvAdyBMUAgpsXSCvgZuKqUuqqU+lkpNSx0mHG++Aj4TVK2bFl+/PHHZ/c/+ugj5s2bR6pUqdi7dy81atQATF/L3r17Lf76P/zwA507d7b4eYWIi3SO6ZjVYBabPtjE45DHVJpbie7runP34d3XP1kkiBiN39Nan9Faf661DptR/xnQFBgJHMa0aAYAy4E/lFI3LBlsGKXUaKXUKaXUMaXUKqVUugj7+iulzimlTiulLHttyMpKlChB1apVXzlB0lIePXpEo0aNKFKkSLy/lhCxUa1ANY53PU6vMr2YemAqrlNc+eXsL9YOSxC3ki5fATu11qu01l9qretprXMAOTEVjodihiDHh42Am9a6OHAGsyYMSikXoAXgCtQGpkRnMmdi0r59+1dOkLSU5MmT06ZNm3h/HSHiwim5E+Nqj2N3+904J3em7g91abOqDYFBgdYO7Y0WlyKUQ7TWfi95/G+t9Tqt9Vda68ZxCy/K1/5Nax1Wa2QfkCv054bAEq31Q631n8A5wDs+YhBC2I6yuctyuMthBlYayGL/xbhMceHHEz9KWRgrSQpTWdsDYe3fnERevfJK6GNCiCQuRbIUfFX1Kw52PkjuNLlpvrw5jZc15urdq9YO7Y2jbDWjK6U2AdlesmuA1npN6DEDgFJAY621VkpNBvZqrReG7p8NrNdav1CPWynVGVNJgKxZs3otWbIk0v60adPy1ltvvTbOkJCQBLk0FVu2Hh9YN8Zz585x+/btVx5z7949nJ1te0FUiTGyEB3C8ivLmXNhDg7Kga4Fu1I3W91XLu4mv8OYqVq16sHQlYNfpLVOlBvQFtgLpIrwWH+gf4T7G4CyrzuXl5eXfl5AQMALj73MnTt3onWctdh6fFpbN8bo/Dtv3bo1/gOJI4nx5c7cOKMrf19ZMwRdbV41/cd/f0R5rPwOYwY4oKP4m5ooL4UppWoDfYEGWuugCLt+AloopVIopfJjCmK+0A8khHgzFMpYiC1ttzCt3jT8/vLDfao74/eNJ+Rp/I+sfJMlysQCTAJSAxuVUkeUUtMAtNYngGVAAPAr0F1rLf+DhHiD2Sk7upTqwoluJ6iaryq9N/SmwvcVCLgutXHjS6JMLFrrt7TWubXWnqGbb4R9I7TWBbXWRbTWiX5Q+6pVq1BKcerUqTidZ9q0acyfPx+AQYMGsWnTJkuEJ0SikTttbta2XMuixos4G3gWz2mefLX9Kx6FPLJ2aElOokwsb5LFixdToUIFnh9cAMRooqSvr++zeSlfffUV1avLop7izaOUopV7K052P0kTlyYM3jaYUjNK8ftfsjyEJUlisWH37t1j9+7dzJ49+1li2bZtG1WrVqVVq1a4u7uzbds2KleuTPPmzSlcuDD9+vVj0aJFeHt74+7u/mwZ4iFDhvDdd98BpnT+8uXLAdi8eTMlSpTA3d2d9u3b8/DhQ+u8WSESUGanzCxuspg1LdYQ+CAQn9k+TPtjGkGPg17/ZPFaMalu/OZ6xYIsKUNCiK8FWVavXk3t2rUpXLgwGTJk4NAhUyrcz88Pf39/8ufPz7Zt2zh69CgnT54kQ4YMFChQgI4dO+Ln58eECROYPn06U6ZMeen5g4ODadeuHZs3b6Zw4cK0adOGqVOn0qtXr5i/HyESoQZFGlA5b2U+2/gZMw/N5OC0g8x8ZyZV8lWxdmiJmrRYbNjixYtp0aIFAC1atGDx4sUAeHt7kz9//mfHlS5dmuzZs5MiRQoKFixIzZo1AXB3d+fSpUtRnv/06dPkz5+fwoULA9C2bVt27IivKjxC2Ka0jmmZ8c4MxhQfw1P9lKrzquL7sy+3g189v0lETVos0fGKlsWDeFpdMTAwkC1btuDv749SipCQEJRS1K1b94X17FOkSPHsZzs7u2f37ezsePLkCVHRNjo5VghrKJm+JMfrH2fgloGM3z+en8/8zPT606lXuJ61Q0t0pMVio5YvX06bNm24ePEiFy5c4PLly+TPn59du3ZZ7DWKFi3KhQsXOHfuHAALFiygcuXKFju/EIlNKodUjKk1hj3t95DOMR31F9en9crWXL9/3dqhJSqSWGzU4sWLeffddyM91qRJE3744QeLnF8phaOjI99//z3NmjXD3d0dOzs7fH19X/9kIZK4MrnKcKjLIYZUHsKPJ37EZYoLS/yXSCs/uqKakv8mbW9aSZf69evrLVu2WCGal5OSLnEnMcZdVPEdv3Zce8/01gxBv/PDO/rK7SsJG1gEtvQ7JKmVdBGx1759e4KCgqhQoYK1QxEiUXDL4sae9nsYU3MMm85vwmWKCzMPzpTWyytIYnnDzJkzh82bN+Pg4GDtUIRINOzt7Pmk7Ccc73ocr+xedP65M9XmV+OP//6wdmg2SRKLEEJEU8EMBdncZjMz6s/g4N8HcZ/qzpg9Y6So5XMksQghRAwopejk1YmAbgFUL1CdPhv7UHZ2Wfz/9bd2aDZDEosQQsRCzjQ5WdNiDYubLObCrQuUnF6SIduGSFFLJLEIIUSsKaVo4daCgO4BNHdtztDtQyk5vSR+f73Zy0BJYrFh165do1WrVhQoUAAvLy/Kli3LqlWrojx+27Zt1K9f/6X78uXLx40bN6J87vjx4wkKen0Bvo4dOxIQIOtYCBFRplSZWNh4IT+3/JnbD29TdnZZPt3w6Rtb1FISi43SWtOoUSMqVarE+fPnOXjwIEuWLOHKlSvx8nrRTSyzZs3CxcUlXmIQIrGrV7geJ7qdoItXF8buG4v7VHe2/LnF2mElOEksNmrLli0kT5480kz4vHnz0qNHD4KDg/nwww9xd3enRIkSbN269YXnBwYGUrNmTSpUqECXLl2ejbm/f/8+9erVw8PDAzc3N5YuXcrEiRO5evUqVatWpWrVqgD89ttvlC1blpIlS9KsWTPu3bsHQJUqVThw4AAAzs7ODBgwAA8PD3x8fLh27Vp8/1qEsHlpUqRhSr0pbGu7DTtlR7X51ei8tvMbVdRSilBGQ69fe3HknyMv3RcSEoJ9LMrme2bzZHzt8VHuP3HiBCVLlnzpvsmTJwNw/PhxTp06Rc2aNTlz5kykY4YOHUqFChXo3bs3O3bsYMaMGQD8+uuv5MiRg3Xr1gFw+/Zt0qZNy9ixY9m6dSuZMmXixo0bDB8+nE2bNuHk5MSoUaMYO3YsgwYNivQa9+/fx8fHhxEjRvD5558zc+ZMvvzyyxj/LoRIiirnq8wx32MM3jaYMXvHsO7sOqbVm8Y7Rd6xdmjxTlosiUT37t3x8PCgdOnS7Nq1iw8++AAwhSTz5s37QmLZsWMH77//PgD16tUjffr0gCmlv2nTJvr27cvOnTtJmzbtC6+1b98+AgICKF++PJ6ensybN4+LFy++cFzy5Mmf9el4eXlx4cIFS75lIRK9lA4p+bbGt+zvuJ+MKTPSYEkDWq5omeSLWkqLJRpe1bK4G09l811dXVmxYsWz+5MnT+bGjRuUKlWKnDlzRuscSqkXHitcuDAHDx5k/fr19O/fn5o1a77QEtFaU6NGjWfrv0TFwcHh2WvY29u/skS/EG+yUjlKcaDzAUbtGsXwncPZ+MdGJtSeQCv3Vi/9nCZ20mKxUW+//TbBwcFMnTr12WNhneuVKlVi0aJFAJw5c4ZLly5RpEiRSM+PeMwvv/zCzZs3Abh69SqpUqXi/fffp0+fPs9WpUydOjV3794FwMfHh927dz8rpx8UFPRCi0gIETPJ7ZMzsPJADnc5TKGMhXh/1fvUX1yfy7cvWzs0i5PEYqOUUqxevZrt27eTP39+vL29adu2LaNGjaJbt26EhITg7u7Oe++9x9y5cyMt9gUwePBgduzYQcWKFfntt9/IkycPYPplvL298fT0ZMSIEc/6RDp37kydOnWoWrUqmTNnZu7cubRs2ZLixYvj4+PDqVOnEvx3IERS5JLZhV0f7mJ8rfFsu7AN1ymuTP19Kk/1U2uHZjlRlT1+k7Y3rWy+rZGy+XEnMcadNeL7478/dLV51TRD0JW+r6TP3DjzyuNt6XeIlM0XQgjbUyB9ATZ+sJHZDWZz9J+jFJ9WnG93f8uTp4m7v1ISixBCWJFSivYl2hPQPYDab9Wm76a++Mzy4eg/R60dWqxJYhFCCBuQI3UOVjZfybKmy7h85zKlZpZi4JaBPHzy0NqhxZgkFiGEsBFKKZq5NiOgWwCt3FsxfOdwSkwvwd7Le60dWoxIYhFCCBuTMVVG5jWax/pW67n/+D7l55Sn5y89eRDywNqhRYskFiGEsFF1CtXBv6s/3Up3Y6LfRNofaM/GPzZaO6zXksQihBA2LHWK1EyqO4kd7XbgoByoubAm7de05+aDm9YOLUqSWIQQIhGomLcis0rNol/5fsw/Oh+XKS6sOhn1+kzWJIklkWrfvr21QxBCJLDkdskZWX0kfp38yOacjcbLGtPsx2b8c+8fa4cWiSSWRCgoKIi0adOydetW+vbtS3Bw8AvHTJw4kWLFitGhQ4dYv46zszMA5cqVi/U5rOXChQu4ublZOwwh4kXJ7CXx6+jH129/zdrTa3GZ7ML8o/OfrbtkbZJYEqFDhw5x5MgRTp8+zahRo3B0dHzhmClTprB+/Xpmz5792vNprXn6NOo6RXv27IlTvPHldXELkZQ52DvQv2J/jvgeoVjmYrRd3ZY6i+pw8daLS1wkNEksFvL8NwVLfXNYvnw5Pj4+eHh4UKFCBa5fv87vv/9OmTJlcHJyeulzfH19OX/+PA0aNGDSpEmMHTsWNzc33NzcGD9+PGC+0RcrVoxu3bpRsmRJLl+OusJqWMsl7DmdOnXC1dWVmjVr8uCBGf64cOHCZ8Utu3TpQkhIyAvnednqlQBLlix56XMbNWqEl5cXrq6uzxYqe1nc8+fPp3jx4nh4eDxbpwbMImwvi1WIpKRopqLs/HAnE2tPZNelXbhNdWOy32TrFrWMqoiYLW/AMOAYcAT4DcgRYV9/4BxwGqgVnfPFtQjl4MGDdc+ePfXTp0+11lo/ffpU9+zZUw8ePDha53iVGzduPPt5yJAhetKkSbpjx446JCREf/HFF3rHjh0vfV7evHn19evX9fbt27Wbm5u+d++evnv3rnZxcdGHDh3Sf/75p1ZK6b1790b52k5OTpFu//zzT21vb68PHz6stda6WbNmesGCBTogIEDXr19fP3r0SGutddeuXfW8efNeON/y5ct1x44dn92/deuWDggI0LVr137pcwMDA7XWWgcFBWlXV1d948aNF+L29/fXhQsX1tevX4/0nKhifZ4UoUw4th6jrcen9etj/PPmn7rmgpqaIegKcyroU9dPxVssJMEilKO11sW11p7Az8AgAKWUC9ACcAVqA1OUUjFfNzgGtNbcunWLCRMm0Lt3b7TW9O7dmwkTJnDr1q04t1zmzp2Lt7c3Hh4eTJkyBUdHR2bOnImdnR0jRoygYsWKr3z+3r17effdd3FycsLZ2ZnGjRuzc+dOAPLmzYuPj0+M4smfPz+enp5A+KqRmzdv5uDBg5QuXRpPT082b97M+fPnX3juy1av3Lx5M0eOHHnpcydOnIiHhwc+Pj5cvnyZs2fPvhD3li1baNq0KZkyZQIgQ4YMr4xViKQsX7p8/Nr6V+Y2nMuJf0/gMc2Db3Z9w+OQxwkaR6JcQVJrfSfCXScg7K93Q2CJ1voh8KdS6hzgDcRbPQSlFOPGjQNgwoQJTJgwAYCePXsybty4OK0ON3/+fPz8/NiyZQvOzs5UqlQJV1fXGJ3jVYktqktprxJx3Rd7e3sePHiA1pq2bdsycuTIVz73ZatXpk+fnlatWjFmzJhIx27bto1Nmzaxd+9eUqVKRZUqVZ4NUogYt9Y6yt/xy2IVIqlTStHWsy213qrFR+s/ov/m/iw7sYzZDWZTInuJBIkhsbZYUEqNUEpdBloT2mIBcgIROwuuhD4W37E8Sy5h4ppUwCzKVa5cOZydnVmxYgV79uzB3d09RucoX748q1evJigoiPv377Nq1arXtnJiqlq1aixfvpx///0XgP/++4+LF1/sQHzZ6pXVqlVj9erVLzz39u3bpE+fnlSpUnHq1Cn27dsX5WsvW7aMwMDAZ88XQkA252wsb76c5c2Wc/XuVUrPLM2AzQMIfvLiKFJLs9kWi1JqE5DtJbsGaK3XaK0HAAOUUv2Bj4DBwMv+kr/0K7tSqjPQGSBr1qxs27Yt0v60adM+W6r3VUJCQrhz5w79+vWL9Hj37t355ptv4pRcmjZtSosWLVi6dCk1a9YkX758PH36NFpxaa25d+8e7u7utGzZklKlSgHQpk0b3nrrLS5evBitc4Xtv3v3Lvfu3Yv0nIcPH/Lw4UNy587NgAEDqF69Ok+fPsXBwYHvvvsu0mUpgP379zNw4EDs7OxIliwZ48aNi/K55cuXZ9KkSbi5uVGoUCFKly5NUFDQCzHkyZOHTz75hIoVK2Jvb0/x4sWZNm1alLE+/36Dg4Nf+Ld/3r179157jLVJjHFn6/FB7GLMSEZmeMxg6h9T+XrX1yw4uIDPinyGe9qYfUmNkag6XxLLBuQF/HV4x33/CPs2AGVfd464dN7fvn1b9+zZUwPPOvCfv29NsoLkq0nnfcKx9RhtPT6t4x7jhnMbdN5xebUaonSP9T303Yd3Y30uklrnvVKqUIS7DYCwBdl/AloopVIopfIDhQC/eI6FdOnSRepTGTduHD179iRdunRxvhwmhBCWUrNgTfy7+fOR90dM8ptEyekleRTyyOKvY7OXwl7jG6VUEeApcBHwBdBan1BKLQMCgCdAd631ixMqLGzIkCGROpHDkoskFSGErXFO7szEOhNp4dYC/3/9SW6f3OKvkSgTi9a6ySv2jQBGJGA4AC8kEUkqQghbVi53Ocrljp9yTYnyUpgQQgjbJYnlFXQcJzcK2yb/vkLED0ksUXB0dCQwMFD++CRRWmsCAwNfWsBTCBE3ibKPJSHkypWLK1eucP369VceFxwcbNN/nGw9PrBejI6OjuTKlSvBX1eIpE4SSxQcHBzInz//a4/btm0bJUokTJmE2LD1+CBxxCiEiD65FCaEEMKiJLEIIYSwKEksQgghLErJqCdQSl3HzOCPjUzADQuGY2m2Hh/Yfoy2Hh9IjJZg6/GBbcWYV2ud+WU7JLHEkVLqgNa6lLXjiIqtxwe2H6OtxwcSoyXYenyQOGIEuRQmhBDCwiSxCCGEsChJLHE3w9oBvIatxwe2H6OtxwcSoyXYenyQOGKUPhYhhBCWJS0WIYQQFiWJJRqUUrWVUqeVUueUUv1esl8ppSaG7j+mlCppgzG2Do3tmFJqj1LKw9ZijHBcaaVUiFKqqa3Fp5SqopQ6opQ6oZTanpDxRSdGpVRapdRapdTR0Bg/TOD45iil/lVK+Uex36qflWjEZwufk1fGGOE4q3xOoiWqNYtl02GVje2BP4ACQHLgKODy3DF1gV8ABfgA+20wxnJA+tCf69hijBGO2wKsB5raUnxAOszqpHlC72extd8h8AUwKvTnzMB/QPIEjLESUBLwj2K/tT8rr4vPqp+T6MQY4f9Cgn9OortJi+X1vIFzWuvzWutHwBKg4XPHNATma2MfkE4pld2WYtRa79Fa3wy9uw9I6LK+0fk9AvQAVgD/JmRwRC++VsBKrfUlAK21LcaogdTKLGHqjEksTxIqQK31jtDXjIpVPyuvi88GPifR+R2C9T4n0SKJ5fVyApcj3L8S+lhMj4lPMX39DphvjQnptTEqpXIC7wLTEjCuMNH5HRYG0iultimlDiql2iRYdEZ0YpwEFAOuAseBnlrrpwkTXrRY+7MSE9b4nLyWlT8n0SJl81/vZYvXPz+ULjrHxKdov75SqirmA1MhXiN6yUu/5LHnYxwP9NVah5gv3AkqOvElA7yAakBKYK9Sap/W+kx8BxcqOjHWAo4AbwMFgY1KqZ1a6zvxHFt0WfuzEi1W/JxEx3is9zmJFkksr3cFyB3hfi7Mt8GYHhOfovX6SqniwCygjtY6MIFiCxOdGEsBS0I/LJmAukqpJ1rr1TYS3xXghtb6PnBfKbUD8AASKrFEJ8YPgW+0uRB/Tin1J1AU8EuYEF/L2p+V17Ly5yQ6rPk5iR5rd/LY+oZJvueB/IR3mLo+d0w9IndI+tlgjHmAc0A5W/09Pnf8XBK28z46v8NiwObQY1MB/oCbjcU4FRgS+nNW4C8gUwL/W+cj6s5xq35WohGfVT8n0YnxueMS9HMS3U1aLK+htX6ilPoI2IAZiTFHa31CKeUbun8aZmRGXcx/yCDMt0Zbi3EQkBGYEvpN54lOwGJ20YzRaqITn9b6pFLqV+AY8BSYpbV+5ZDQhI4RGAbMVUodx/zx7qu1TrBquEqpxUAVIJNS6gowGHCIEJ9VPyvRiM+qn5NoxmjzZOa9EEIIi5JRYUIIISxKEosQQgiLksQihBDCoiSxCCGEsChJLEIkIkqp/UqpFtaOQ4hXkcQiRCKhlLID3DDDnYWwWZJYhEg8imA+s6etHYgQryKJRYjEwxMI0FqHACileiulTimlPK0alRDPkZn3QiQensBRpVRa4HvM59dHa33LmkEJ8TxpsQiReHhiksnvwAGgoSQVYYukpIsQiYRS6p/QHzdqrT+wajBCvIK0WISwMqVUCaXUKqXUzdBtuVIqg1Iqh1IqWCnVUimVDVOtuApQUSnV1rpRCxE16WMRwoqUUi2BeZghxEMxJfE/Bi5hPp9ngaWYBbzOa61PKaXqA1uVUpe11lusE7kQUZPEIoSVKKUKAHMwKz5W0loHhz5eCqiDWZOjtdb6qVLKAzgMoLX2V0q1BpYqpSpprU9aI34hoiJ9LEJYiVJqAqZ14qO13h/h8QXA+8AhoJSWD6lIZKSPRQjraQCci5hUnjNQkopIjCSxCGEFSqkMmEtdv79kd1bghNZ6fYIGJYSFSGIRwjqyhd4GRnxQKVUJqPH840IkJpJYhLCOW6G3HmEPKKWcgemhd50SOiAhLEUSixBWoLW+Cvhh5qQsUEp1BXYAmYBfgRJKqV5KqezWjFOI2JBRYUJYiVIqLzAJM+kxGWY4cfvQ3SsAF6Co1lqqGYtERRKLEEIIi5JLYUIIISxKEosQQgiLksQihBDCoiSxCCGEsChJLEIIISxKEosQQgiLksQihBDCoiSxCCGEsChJLEIIISxKEosQQgiLksQihBDCov4P/jLkSEBeat4AAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"plot_alpha(-3,eta_ls=0.25,algorithm=\"newton\",alpha_max=1.5)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.2 Newton Step, $x^k = -3$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.2-Newton-Step,-$x^k-=--3$)",
"section": "3.6.3.2 Newton Step, $x^k = -3$"
}
},
"source": [
"**Discussion**\n",
"* Why did the backtracking line search stop at $\\alpha^k = $ `alpha_max`?\n",
"* Is it possible to find a larger improvement in $f(x)$ with $\\alpha^k > 1$?"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.3 Steepest Descent Step, $x^k = -3$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.3-Steepest-Descent-Step,-$x^k-=--3$)",
"section": "3.6.3.3 Steepest Descent Step, $x^k = -3$"
}
},
"source": [
"### 3.6.3.3 Steepest Descent Step, $x^k = -3$"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.3 Steepest Descent Step, $x^k = -3$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.3-Steepest-Descent-Step,-$x^k-=--3$)",
"section": "3.6.3.3 Steepest Descent Step, $x^k = -3$"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Considering xk = -3 and f(xk) = 15.0\n",
"Step with steepest-descent algorithm:\n",
"pk = 51\n",
"With full step, xk+1 = 48 and f(xk+1) = 2534689.5\n",
"alphak = 0.03535353535353535 with backtracking line search starting at alpha = 0.1\n",
"f(xk + alphak*pk) = -8.67145500733185\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZwAAAESCAYAAADJ+2ORAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAABQIklEQVR4nO3de3zO5f/A8de12QFzyKE5lfNpBxvDppxWkXMOERHllEORTjpHpb46EL9yCpFyKMcKEVmkkPNhDiFFqVDYMId5//647tnGhu3edu/e3s/H43ps9+d0vy+z+73r+lyf6zIiglJKKZXZPFwdgFJKqdxBE45SSqksoQlHKaVUltCEo5RSKktowlFKKZUlNOEopZTKEnlcHUB2VqxYMSlXrly6zj1z5gz58+fP2ICyOa1z7qB1zvmcre+mTZuOi0jxq7drwrmOcuXKsXHjxnSdGxUVRePGjTM2oGxO65w7aJ1zPmfra4z5LaXt2qWmlFIqS2jCUUoplSU04SillMoSmnCUUkplCU04SimlsoQmHKWUUllCE04m0VUflFIqOX0OJxM82bc9e09vJnhLf4rVj4TQUPD2dnVYSinlUppwMsF/F/7lm6q/EfLHc4zvDm1+9YZatSA83JaICChXDoxxdahKKZVltEstE3w8LYqHL8/h+Lnq3NcF2g0uzz/5BCZNggcfhAoVoEQJaNMGRoyAlSvh9GlXh62UUplKWziZ5KG7b+UR7200e2MkC8NeZ0WkH+PfHUfXy8GYDRtg/XpYtw6++sqeYAxUr25bPwmtoMBA8PR0bUWUUiqDaMLJRPXv8GL3xJdo0aM9Oyv05qEvH2FmpRZMfHACt/Xvbw/67z/4+WebfNavh4ULYepUuy9/fqhTJ3lXXMmSLquPUko5QxNOJrvtNvh5SQCPDVrDlKUfsKzpCwT8FsjbTUbyaO1H8bjlFmja1Baww9sOHEhsAa1bB6NGwcWLdv/ttycmn/Bwe28ob17XVVAppW6SJpws4OsLkyd5Um/KYAa82IYLrfoyYMkAZu+azeTWk6lctHLiwcZApUq2dO1qt8XFwZYtia2gdevgiy/svjx5ICQksRUUHg5VquiABKVUtqMJJwv16gXh4eXp9MBydm/+mPVtnqTGhBoMbzycJ+s9SR6PVH4cvr5Qr54tCf76C5LeC5oxA8aNs/tuuSV5N1zdulCkSOZXUCmlrkMTThYLCoKNPxuGDOnJpFHNKNhlIENXDOXzXZ8zpc0UQkqE3NyFEka5tWljX8fHw+7dia2g9evhtdcSn0CtXDn5gIQaNcDLK3MqqZRSKdCE4wL58sHEidCqVSl695nPmVvnsafDQGp/VJvn7nyOlxq+hE8en7Rd1NPTZrOgIOjd226LiYGNGxNbQd9+a1tCYFtNYWHJW0K33aZdcUqpTKPP4bhQ69YQvcvQofr9nBkZTYFDD/LGmjeoObEmPx3+yfk3KFAAIiPhuefs6Lc//4RDh2D2bOjf37Z+xo2DBx6AsmWhVClo2xb+9z9YtQpiY52PQSmlHLSF42JFi8KcOfDA/KI89th0jF8XjnTpy51T72RQ+CDeuOsN/Lz9MubNjLGJpWxZm2QALlyA7duTj4pbtMju8/CwzwIlHRVXvbo+G6SyjIjtLb540X5NKCLJ5ys0xv539fCw/z09PW2PsaenNtqzk1yVcIwxzYAxgCcwWUT+5+KQrmjfHu6+G154oRnjRu4iX+vnGcMYFu1dxKRWk2hSsUnmvLG3N9SubcvAgXbbiRN2QELC/aB582DyZLuvQIHEZ4MSkpC/f+bEptxOXJz97/Pvv7acPGnLqVO2nD5tS0wMnDljG9FnzsC5c4nl/Hl7nfPnbaJxdiJcb29bfHxsT7Kvr32SIG9e+6hbQvHzs/+9/fygYEEoVMh+LVwYDh4siL+/HY9TpIhOjZheuSbhGGM8gQ+BJsAR4GdjzJciEu3ayBIVKgQffggPP1yAxx//gPUbHuCvTr1p+mlTeob25N2m73JL3lsyP5CiRaF5c1vA/sbv25c4GGHdOnjnHbh0ye4vVw7CwylTrJj9ra5Z0/5WK7cnYhPGn3/C0aN2cOTatbexeDH8809iOX7cJpozZ65/vbx57Yd6wgd7wod7iRL23mbevPa/jo9PYqLw8rKj//PkSWy9GJNYElo7ly/bktAKunjRlgsXbElIYnFxcPasTW5nz9p6JSS/2FibDC9fvjryWsle5c9vE0/RorYUKwbFi9uvt96avPj7299tbWnlooQD1AX2i8hBAGPMbOA+INsknAR16sCPP8Knnzbg2Re2EVftNT6Wt/lyzxImtRlHu+rtsjYgY6BqVVu6d7fbzp6FzZsTk9CPP1Lp8GGbMb287AzZCS2g8HCoWFF/47IZETvRxe+/w2+/weHDcOSI/frHH/b7P/6wH9DJVcTHx36QJnygBgXZD9uED+AiRRJbA4UL2w/cQoVs0sjuROx/74RW2alTsHr1dm6/vQb//mv/zf791ybYhLJ5Mxw7ZpNzShL+vUqUsJOFJHwtVSrxa6lSNmnl5B5rN/jxZ5jSwOEkr48A4S6K5YY8POxne4cOvowe/SZvTevI8SY9af95e5rdfj8fd/w/SviVcF2A+fJB/fq2OPw4dy53eHomtoKmToX/+z+7s2jRa58NKlzYNbHnIjExcPAg/Pqr/XrokP3+0CGbZGJikh/v7Q2lS0OZMvZHlPBBmPDBWKIE/PLLGlq2bJBj/34wJrGbrVQpuy0u7l8aN77xuRcv2tZeQsvv778Ty19/2a8HD8Latfa4q3l62n/jhJ/B1V8TvnfXDgQjuWSlMGNMR+BeEenteP0QUFdEHr/quL5AXwB/f/+w2bNnp+v9YmNj8fPLoJv9wMmTXsz4rCSLjs0ivsHr5JG8PFJyEF0CGmOyyW/+1XU28fHkO3SIgtHRFNy9m4LR0eT7/XeM4//cmdtvJ6Z6dU4HBHC6enXOVKiAuNmfdxn9c06PmJg8HDmSlyNH8vLnn3n54w9b/vwzLydPJr/ZkC/fJUqUiKNkyTj8/ZOW89x6axyFC1/E4wZjV7NDnbNaZtT54kXDf/95c/y4N//+68Px494cP+7jKInfnzlzbbugYMGLFC9+/kq59dY4ihU7n2xb3rzX9AveNGfrGxkZuUlEal+9PTclnHrAMBG51/H6eQAReSu1c2rXri0bN25M1/tFRUXR+Gb+JEqjv/6C59/bwycne3O5zFqKn2rGuOYT6XDP7S7/i/Om6nzqlJ2sNKEVtH697YsA22oKC0v+gGrp0pketzMy6+d8tbg42L8f9u61t9MSvu7bZ7t0EhhjH6eqWDGxVKiQWG65xfmezayqc3biyjrHxNiuzYRuzqRdngnfp9RaKlz42lZS0lKqlO0GTekPDGfra4xJMeHkpi61n4HKxpjywB9AZ+BB14aUdiVKwMfvVON//6zmkXHjWJr3OTquCuS2Cf/jlRb9ebCLB/nyuTrK6yhUCO65xxawHeaHDiWfIWHMGHuXF+xvRtKuuLAw29eRA4nYD47du2HPHptU9uyx5dCh5DeyS5WyU+Z16GAnkahc2U6/V7Gi+3a3qJQVKADVqtmSmnPnrk1KCffgjhyBbdtsd97V7QsvL/uZktBlmlBOnSpJ1aoZPzl9rkk4InLJGPMYsAw7LHqqiOxycVjp5n+rB0uGPcaeo61pP60vu2s8Rp+1s3lyxGQeblWVRx6xg8WyPWOgfHlbunSx286ft78hSZPQ/Pl2n6cnBAcnH5ZdtWrKf6ZlU5cv2xv1u3dfW/79N/G4vHlt1erUgW7dEsdtVKliP4SUSpA3b+Kcv6m5eNH2kPzxhx11mJCgjh615ZdfYM2ahBZzVTp00ITjFBFZAixxdRwZqVrJsux67humb/uEQYuHcOa2EMZ9P4z/q/0UIcFePPQQdOpku1ncho+PvWNdt27itmPHEpPP+vUwa5adHwhsq6lu3eQzZhcv7prYk7h40XaDJSST6Gj7de9eOwoqQfHi9q/XDh3sc7XVq9vXt9/uVnlUZXNeXvZz4EafBefPw8KFP1GzZr3rH5gOuSrh5FTGGB4O7UGzSvfy2JLHmOfxPLc1+ZyLq6bw9NM1efppuOMO6NjRzvVZoYKrI06H4sWhVStbwDYT9u5NPkPCm28m9jtVqGBbQAmtoNDQFJ/WE5Fkgy6ufn0zTp9O7P5KSC579thkk/CoEtgEUr06NGoEAQGJiaVYsbT+YyiVeewQ7vOZ0jWrCScHKeFXgrmd5jIveh4Dlwxkb8M69Ov3LCX2vsL8z30ZMgSGDLHPTLRsadd8u/NO+x/M7Xh4JDYHHn7YbjtzBjZtSuyKi4qCmTPtPm9v28eYJAkNmzaNk6dOMXr0aIwxiAhDhgyhcOHCDBs2LNnbxcfbbrCEG/YJCWb79nrJbtjmyWO7NapXt7NHJIRYtap9yFGp3EwTTg7UIaADkeUjeWr5U0zY+hZVi85nyldTKHHxTr76yk6V9t57MHKkHRjWoEFiqVvXjW86588PDRvakuDIkeStoEmT7KAE4Km8eVl17hxLNmygxWuvMXTufMZM/JIOHZ5j0iThwAHDvn22b3v/ftvVkKBQIds6qVXrPxo1KnElsVSooNOeKJUaTTg5VJG8Rfj4vo/pEtSFvl/1pcHHDRhYZyBv9n+TJ54oQEyMbQB8+62dGPqll+x5Xl52qZy6de30aiEhtvvHbVexTnharkMH+2T9Pxf557udxH2/Dq9N6wnasYoKP/0ETZrwPww9qM66eVtYP+8jNuWJ4HylQCpV9aR5c3uzPuHG/a232vEOUVF7aNzYhQ/gKuVGNOHkcE0rNmXngJ28sPIFPtjwAV/u+5JJrSZxb6V7ad3aLpEAdmTK2rV2Sp2ff4bPPoPx4+0+Dw/bTVStmv3QrVLF/iVfrpy9AZkd/qK/cCHxye6jR+0onISROIcPJ5aYGC+gpqP0p0ABwfP8D9ThW8JZT+9ATx76fSG9YqbCJeBwfihRBzzDoXgEVA4H/wweuqNULqEJJxfw8/ZjbPOxdA7qTK8ve9Hss2b0COnBqHtHUSSvXXq6aNHkC4hevmy7kXbssKsX7Nxp718sW5a8a8kYez+/ZEnw8QmmatXE+bQKF7YTMxYokHxixoTJGBMmFUiYePHSJZs4Ll5MnGDxzBlbEmYZPnUq+VxWx46lPoeVMbYlcttttlVy9902SSas0FCunPD660MYO3YM3wLfAjH3DGb0qK/t/CNJJysdNcoGBvbuv2M0XCFvb/u92zYBlco6mnBykTtuu4Mtj27hjdVvMHLtSL7Z/w0ftviQDgEdrjnWwyOxNdMhye74eHtb5NChxJIwk/Devd6sWWMfXsystdv8/OyEkAmTQ9asaRNe8eL2AbYSJewkiaVL2+9TW0U7YYDA2LFjGDx4MKNHj2bIkCGMcdzfGT16NKZSJeja1Z4QFwdbtybeC1q/Hr74gpoATz5p+yETng2KiLBPYrp66gelshlNOLmMbx5f3rjrDe4PuJ9eX/bi/i/up121dnzY4kNKFrhxV5GnZ2ILoVGj5PuiojZdmQ7j/PnEVsnp08nXO7l0ySauhCHDHh72szlPnuRrl+TPb1tG+fLZm/R+fhk3k64xhsKFC19JNsYYRo8eDUDhwoWvHRrt65uYTBL8/Tc7Jk8m+OxZm4RmzEjsh7zlluTPBYWH2yypVC6mCSeXCi0Ryvre63nvx/d4NepVAsYFMKrpKB4OfThDJgP18UlseWRXw4YNS/bcTULSuen6+/tz4s47uTKNcHy8fQgn6Txxr7+e+GxQ5crJZ0ioUSN73ABTKotowsnF8njkYWj9obSr3o7eX/am55c9mbVzFhNbTaT8LeVdHV6WuDq5OJVsPT3tQ05BQdCrl90WEwMbNybeD/r2W/j0U7vP1xdq1Uq+btDtt2tXnMqxNOEoqhStQtTDUUzYOIGhK4YSPD6YN+9+k4F1BuLp4V7LBWQ7BQpAZKQtYEdI/P578gEJ48bZQQlgbzwlTUC1a+vEaSrH0ISjAPAwHgyoM4BWVVrx6NePMvibwczZNYfJrSdTvXh1V4eXcxiTeBOsUye77cIFOxQw6WSlCxfafR4eEBiYvCuuevWcvSykyrE04ahkbi90O0seXMKn2z/liWVPEDoxlFcavsKzdz6Ll2cqQ76Uc7y9bUumdm147DG77cQJ2LAhsRU0bx5Mnmz3FShgp5BO2hLy93dd/ErdJE046hrGGB4KeYimFZsy6JtBvLTqJb6I/oIpbaYQVirM1eHlDkWLQvPmtoDtivvll8RW0Lp18PbbiUP9ypVL3gqqWdON5yhSOZUmHJUqfz9/5tw/hy5BXRiweADhk8N5+o6nebXRq+T10gcds5QxiQ9Gde9ut507B5s3Jyahn36COXPsPi8vO0N20iRUsaIOSFAupQlH3VDbam1pVLYRz3z7DCPXjmT+7vlMbjOZhmUb3vhklXny5rXTfd95Z+K2o0eT3wv6+GP44AO7r2jR5Kun1q1rp4NQKotowlE35Za8tzC5zWS6BHWhz1d9aDStEf1r9+d/9/yPgj4FXR2eSlCyJLRrZwvYLrfo6OQzJCxdmrjWcLVqyZNQcLB9AlepTJCj/mcZY94BWgMXgAPAIyJy0hhTDtgN7HUcuk5E+rkmSvd2d4W72dF/By999xJj1o/hq31fMbHVRFpUbuHq0FRK8uSxD5jWqAF9+9ptp07ZZ4OSJqDp0+2+vHkhLCz54nVlyrgufpWj5KiEg51/8XkRuWSMGQk8Dwx17DsgIqEuiywHye+dn9HNRvNA0AP0+rIXLWe2pFuNbtzvd7+rQ1M3o1AhO5Pp3Xfb1yJ2Uryk6waNHQvvvmv3ly6drBXkce6cy0JX7i1HJRwRWZ7k5TpAPwEzUUSZCDb33cyba97kzR/e5GvPr5lQcgKdAjtlyPQ4KosYA+XL29K5s912/jxs25Z8VNz8+QA08PBIPllpeLidjtvDw4WVUO4gJ/8P6QksTfK6vDFmizHme2NMA1cFldP45PFheORwNvXdhL+vP53ndabtnLb8GfOnq0NTzvDxsYMKBg2yiyMdOGAXHPrqK37r2hWKFYNZs+CRR+wKfUWK2DXLX34ZFi8m2brbSjkYSbh56CaMMSuAlJZYfFFEFjmOeRGoDbQXETHG+AB+InLCGBMGLAQCReR0CtfvC/QF8Pf3D5s9e3a64oyNjcUvly1ifyrmFMtOLmPKoSl4GS/6V+xPixItcnRrJzf+nK/U+fJl8h0+TMHoaAru3k2B3bvxO3gQ45is9FypUpyuXv1Kia1UCXHTyUpz28/Z2fpGRkZuEpHa1+wQkRxVgB7AT0C+6xwTBdS+0bXCwsIkvVatWpXuc91VQp1/OfGLNJ7WWBiG3DX9Ljnw7wHXBpaJcvPPOUWxsSLffy8ycqRI+/YipUuL2LtEIt7eIhERIoMHi8yaJXLwoMjly1kVtlNy28/Z2foCGyWFz9QcdQ/HGNMMO0igkYicTbK9OPCviMQbYyoAlYGDLgozx6tUpBIru69k8ubJPL38aYLHB/NG5BsMCh+kk4HmdPnzQ8OGtiQ4ciT5ZKWTJoFjoTuKF09+L6hOHTuoQeVIOSrhAB8APsC3jm6chOHPDYHXjDGXgHign4j867owcz4P40HfsL60qNyCfl/348nlTzJn1xymtJlC4K2Brg5PZaUyZWxJWDr24kW7ZnnSdYO+/truM8ZOTpqQgCIi7OSlOllpjpCjEo6IVEpl+zxgXhaHo4AyBcvwVZevmL1zNoO+GUTNiTV5qeFLPFf/Obw93bM/XznJy8vO9VazJvRzPA7333+Jk5WuXw+LFsHUqXZf/vx2YtOkLaFSpVwXv0q3HJVwVPZkjKFLcBfuqXAPg78ZzKtRrzI3ei5T2kyhTuk6rg5PZQe33AL33msL2Ls+Bw4k74obPdq2jgBuuy15AgoLsw+tqmxNE47KMsXzF2dmh5l0CepC/8X9iZgSwZMRTzI8cjj5vPK5OjyVnRgDlSrZ0rWr3RYXB1u2JJ8rbu5cuy9hRoWkXXGVK+tkpdmMJhyV5VpXbU3Dsg159ttnefend1mwZwGT20ymcbnGrg5NZWe+vlCvni0J/v47eStoxgy7girYVlPduolJqG5dO4GpchmnEo4xpgoQCNwKCHAM2Ckiv2RAbCoHK+RbiImtJ9I5qDN9vupD5PRI+tbqy9tN3qaQr45SUjfJ3x/atLEFID4edu9OnoRefx0czwZRuXLyrriQEHtPSWWJNCccY0x1oB/QEUhYZjCh3SqOY/4GPgcmisjuDIhT5VCR5SPZ3n87r6x6hdHrRrP4l8VMaDWBVlVauTo05Y48PSEoyJZevey22NjEyUrXrYMVK+DTT+0+X1+oVSsxCUVE2PtD2hWXKW464RhjKgIjgXbAOWAN9gHLA8AJbNIpAlQCIoDewOPGmPnAUBHR515UivJ55ePdpu/SKbATvb7sRetZrekS1IUxzcZQPH9xV4en3J2fHzRubAvYAQmHDye/FzR+vB2UAFCiRPJWUO1rH5hX6ZOWFk40sAN4GJgvImeud7AxJj928sxBjnN1vVt1XXVL12VT3028teYtRqwZwbcHv2Vss7F0Duqco6fHUVnMGLj9dls6dbLbLl6E7duTrxu0aJHd5+FB7XLl4K67EpNQ9er6bFA6pCXhdBLHXGU3w5GQpgPTjTH3pTkylSt5e3rzauNXuT/gfnp92YsH5z/IzJ0zGd9yPGUK6rosKpN4edmh1WFhMHCg3fbvv1daQOeXLsVv3jyYPNnuK1DAzoqQtCXk75/69RWQhoSTlmSTkeeq3Cnw1kDW9lzL2PVjefG7Fwn4MIB3mrxDn7A+eJicPMm5yjaKFIHmzaF5c3Y0bkzjhg1h//7kXXHvvGNXVQUoWzb5sOyaNe09InVFWu7h1BCR7ZkZjFJJeXp4MqTeEO6rdh99vupDv8X9mL1rNh+1/ohKRVKcVEKpzOPhAVWq2NK9u9127hxs3pyYhH78EebMsfu8vCA0NPkS3hUr5uoBCWnpUpttjAkXkZikG40xVUVkb2onKeWsCrdUYMVDK5iyZcqVyUBfj3ydIRFDdDJQ5Vp588Kdd9qS4OjR5KunfvwxfPCB3Ve0aPJuuLp1oXBhl4TuCmlJOB8BM4C2CRuMMZHAbBKHRyuVKYwx9K7VmxaVW9B/cX+e+fYZPt/1OVPaTCHYP9jV4SmVqGRJaNvWFrBdbtHRyVdPXbrUjpYDqFYtsRUUHg7BwTn22aCb7gwXkdFAvDFmKIAxpjs22XTLpNiUukapAqVY+MBCZneYzaGThwibFMawqGGcv3Te1aEplbKEaXf69oUpU2DXLjtZ6YoVMGKEfRh16VIYMMAOWihUyC7v8MwzduqeI0dcXYMMc90WjjGmE7Ad2OtYVOcR4GdjTAB2yv+7RGRX5oepVCJjDA8EPcDdFe5myLIhDP9++JXJQMPLhLs6PKVurFAhuPtuW8C2dg4dSj4gYexYuHDB7i9VKvmAhLAwO4u2m7lRl9qTQBBgjDHRwDZgHdAEaCwi+zI5PqVSVSxfMWa0m0HnwM70W9yPelPq8UTEE7we+Tr5vd3vl1HlYsZA+fK2dOlit50/D9u2JV83aP58u8/T03a9JR2QULWqHdiQjV034YhIhLFP3FUFQpMUA+w2xhwEtohIp8wNU6nUtazSkl1ld/HciucYvW40i/YuYlKrSdxd4W5Xh6ZU+vn42EEFdevC44/bbceOJbaA1q+H2bNh4kS7r1Ah+2xQwhQ94eFQrJjr4k/BDQcNOLrS9jjK7ITtxhh/oBZQI9OiSyNjzDCgD3YSUYAXRGSJY9/zQC/sip+DRGSZS4JUmaKgT0HGtRxH56DO9P6yN/fMuIfeNXvzTtN3KOxb2NXhKZUxiheHVq1sATsp6d69yVtBb76ZOFlphQrJR8WFhtpE5iLpni1aRP4GljpKdjJaRN5NusFxz6kzdmbrUsAKY0wVEYl3RYAq8zQs25Bt/bYxLGoY7/70Lot/Wcz4luO5r5pOdqFyIA8PO81O9erw8MN225kzsGlTYito9WqYNcvu8/a2D6Qmnay0XLksezbI2eUJ/IFOQDkgFtgCLBeRs86HlqHuA2aLyHngV2PMfqAudvJRlcPk9crLyCYj6RjYkV5f9qLtnLY8EPgAY5uP5db8t7o6PKUyV/78dpRbw4aJ244cSb5kw0cf2UEJYFtNSVtBdTJvFd50JxxjTANgCZCPxOUJAE4YY14XkbHOBpdOjzmGbG8EnhKR/4DS2MEOCY44tqkcrHap2mzss5G3177Na6tf49uD3zKm2Ri6BnfVyUBV7lKmjC0dOtjXFy/Czp3Jk9DXX9t9xlDn9tvh88/t/aMMZCTh4aO0nmjMeiAAeAxYiX2mJwI7sq0utkXxYAbFmfR9VwAlUtj1IjapHMeuy/M6UFJEehpjPgR+EpFPHdeYAiwRkXkpXL8v0BfA398/bPbs2VcfclNiY2Px8/NL17nuKjvX+bczv/HOvnfYdXoX4UXCGVJ5CP6+zj+vnJ3rnFm0zjlTnpgYCuzZQ8HoaPLt3MnBp57ifImUPmpvLDIycpOIXLuug4ikqwBngNdS2Zdwc/6x9F7f2YLt5tvp+P554Pkk+5YB9W50jbCwMEmvVatWpftcd5Xd63wp/pKMWTdG8o3IJ35v+smHGz6U+MvxTl0zu9c5M2idcz5n6wtslBQ+U50ZtB0D/J7SDhGZgh3R1s+J66eZMaZkkpftgJ2O778EOhtjfIwx5YHKwIasjE25nqeHJ4PCB7Gz/04iykQwcMlAIqdH8ssJXRFdqazgTMJZBbS4wf6KTlw/Pd42xuwwxmwHIoEhAGJnQ/gcuxDcN8BA0RFquVb5W8qzvNtypraZyva/t1NjQg3eXvs2ly5fcnVoSuVoziScScAdxpjBqewvB/zpxPXTTEQeEpFgEakhIm1E5GiSfSNEpKKIVBWR7DaUW2UxYwyP1HyE6AHRNKvUjKErhhIxOYJtf21zdWhK5VjOJJyVQBFglDEmyhjTzRhT3RhT2RjTGxgMvJchUSqVSUoWKMn8TvP5ouMXHD59mNof1ebl717WyUCVygTOJJzXscOiD2Mn8vwEe89kDzAR2AucNMYEGWOcet5HqcxkjOH+gPuJHhDNg8EP8saaN6g5sSY/HdbHtJTKSOlOOCLyqoi0FZFy2JbO3cDTwKfALuyUN59iJ/yMNcZsM8bMcD5kpTJH0XxFmd52Oku7LuXMxTPcOfVOBi8dTOyFWFeHplSOkCFTi4rISRFZJSKjRaSHiNQA/IDa2LnNPsKOamudEe+nVGZqVqkZO/vvZECdAYzdMJbg8cF8e+BbV4ellNu76YRjjEnTJJ0ickFENovIVBF5XETqi0jhNEeolAsU8CnABy0+YM0ja/Dx9KHpp03puagn/537z9WhKeW20tLCmW2MKXD1RmNM1QyMR6lspf7t9dnabyvP3fkcn2z7hIBxASzYvcDVYSnlltKScD4Ckt2DMcZEAqszNCKlshnfPL68dc9bbOizgRJ+JWj/eXs6ftGRv2L/cnVoSrmVm044IjIaiDfGDAVwTJA5G+iWSbEpla3UKlmLDb038OZdb/LV3q8I+DCAb/76JmG6JKXUDVw34RhjOhljqpnEqXUfAXoaY6YDw4G7RETvpqpcw8vTi+cbPM/WflsJKB7AyL0jaf5Zc347+ZurQ1Mq27tRC+dJ7DT/scaYn4FR2BmZmwD3OqaMUSrXqVasGqsfWc2gSoP44fcfCBwXyAcbPuCyXHZ1aEplW9dNOCISARQAwrCzBhwH/LHr3+w2xvxijPk806NUKhvyMB60K92OXQN2Uf/2+jy+9HEafNyAPcf3uDo0pbKlG97Dccw2vUdEZovIcyLSTERKYpdqHgRsyvQolcrGyhYuy9KuS5l23zR2H9tN6IRQ3lrzFhfjL7o6NKWyFWdmGvhbRJaKyMiMDEgpd2SMoUdoD6IHRtO6amte+O4F6k6uy5ajW1wdmlLZRroTjjHmgYwMRKmcoIRfCb7o+AXzOs3jr9i/qPNRHV5Y+QJxl+JcHZpSLufM1DbTHPOj3ZfSTmOMvzGmshPXV8ptta/enugB0XQP6c5bP7xF6IRQfvj9B1eHpZRLOZNwKgJRwExjzAZjzL1X7e+MnTlaqVzplry3MPW+qSzrtoy4S3E0+LgBjy15jJjzMa4OTSmXcCbhnAUuAb9hJ+lcYozZboxZZYzZgB3VtjsDYrxpxpg5xpitjnLIGLPVsb2cMeZckn0TsjIulbs1rdiUnQN2MqjuIMb9PI6g8UF8s/8bV4elVJZzJuF8BDwB/ItdhuAz4CjQCDuMehnQwcn40kREHhCRUBEJBeYB85PsPpCwT0T6ZWVcSvl5+zGm+Rh+6PkD+bzy0fyz5vRY2IMTZ0+4OjSlsowzCeduYKxjFujujnIv0BjYh231uOQpOMfMCJ2AWa54f6VSc8dtd7Dl0S281OAlZu6YScC4AL7Y9YVOj6NyBWfXw/n16g0ishqbbI4AU528fno1AP4WkV+SbCtvjNlijPneGNPARXEphW8eX16/63U29tnIbQVvo9PcTnT4vANHY466OjSlMpVJ719WxpgFQGmgvohcSGF/P+A9EcnvXIjXXHcFUCKFXS+KyCLHMeOB/SLynuO1D+AnIieMMWHAQiBQRE6ncP2+QF8Af3//sNmzZ6crztjYWPz8/NJ1rrvSOqddvMTzxZEv+PjQx3h7eNO/Qn+al2hO4vSF2Y/+nHM+Z+sbGRm5SURqX7NDRNJVgJrAeeAnoHYK+z8BTqX3+k7ElQf4GyhznWOiUor56hIWFibptWrVqnSf6660zum37/g+afhxQ2EYcs8n98jBfw9myHUzg/6ccz5n6wtslBQ+U52ZaWAL8DAQAqw3xuw1xnxqjBljjIkCujo+2LPaPcAeETmSsMEYU9wY4+n4vgJQGTjogtiUSlHlopVZ1WMV41uOZ/2R9QSND2LMujHEX453dWhKZRin7uGIyCwgEPgA8AIeBB4HGgI/A485G2A6dObawQINge3GmG3AXKCfiPyb5ZEpdR0exoN+tfuxa8AuGpdrzBPLnqDBxw3YfSxLny5QKtM4O2gAEflVRAaLSAWgKDYBlRaRCBE57HSEaY/nYRGZcNW2eSISKCIhIlJLRL7K6riUulm3FbqNr7t8zaftPmXfiX2ETgzljdVv6GSgyu05nXCSEpH/RGS3iOhwG6WcYIyha42uRA+Mpm21try86mVqf1SbTX/q5OzKfWVowlFKZaxb89/KnPvnsOCBBRw7c4zwyeEM/XYo5y6ec3VoSqWZJhyl3EDbam2JHhjNI6GP8PaPbxMyIYTVv612dVhKpYkmHKXcRGHfwnzU5iNWPLSCS5cv0WhaIwYsHsDp89c8TqZUtpQhCcdYtxtjvDPiekqp1N1d4W529N/BkIghTNw0kaBxQSz5ZYmrw1LqhjKqhVMEO81N/Qy6nlLqOvJ752fUvaP4seePFPApQMuZLek2vxvHzx53dWhKpSoju9Sy71wcSuVQ4WXC2dx3M680fIU5u+YQ8GEAc3bO0clAVbak93CUcnM+eXwYHjmczX03U7ZwWTrP60zbOW354/Qfrg5NqWQ04SiVQwT7B/NTr594p8k7fHvgWwLHBTJ582Rt7ahsI10JxxjTMGkB7nDsqpHCPqVUFsnjkYen73ia7f23U7NkTfp81Ye7P7mbA/8ecHVoSpEnnedFASn92fReku+N4xjPdL6HUiqdKhWpxMruK5m8eTLPfPsMweODeeOuNxgcPhhPD/2VVK6R3oQTedXrwsAC4BlA595QKhvwMB70DetLi8ot6L+4P08tf4o5u+Ywpc0Ugm4NcnV4KhdKV5eaiHyftAA/OHZtTWGfUsqFyhQsw5edv2Rm+5kc/O8gtSbWYnjUcC7EX7NuolKZSgcNKJULGGPoEtyF6AHRdAzsyLDvhxE2KYyf//jZ1aGpXEQTjlK5SPH8xfms/Wd82flL/jv3HxFTInhm+TOcvXjW1aGpXEATjlK5UOuqrdk1YBd9avXh3Z/epcb4GkQdinJ1WCqHy6iE8y9QHlibQddTSmWyQr6FmNBqAqt6rAIgcnokj371KKfiTrk4MpVTZUjCEes3ETmfEde7EWNMR2PMLmPMZWNM7av2PW+M2W+M2WuMuTfJ9jBjzA7HvrHGGJ2KRymgcbnGbO+/nafrPc3kLZMJHBfI1/u+dnVYKgdy1y61nUB7INmCIMaYAKAzdpnrZsA4Y0zCQwfjgb5AZUdplmXRKpXN5fPKxztN32Fdr3UUyVuE1rNa8+C8Bzl25pirQ1M5iFsmHMcy1ntT2HUfMFtEzovIr8B+oK4xpiRQUER+EjvPxydA26yLWCn3UKd0HTb23cjwxsOZGz2X6h9WZ+aOmTo9jsoQbplwrqM0cDjJ6yOObaUd31+9XSl1FW9Pb15p9ApbHt1CpSKV6Dq/K21mt+HI6SM3Plmp60jvTAOZzhizAiiRwq4XRWRRaqelsE2usz2l9+2L7XrD39+fqKioGwebgtjY2HSf6660zjnPiIojWOC7gCn7p1B1bFUerfAojQs0ztF1TklO/zlfLdPqKyI3VYAaN3tsVhXsnG61k7x+Hng+yetlQD2gJLAnyfYuwMQbXT8sLEzSa9WqVek+111pnXOuA/8ekLum3yUMQ0JGh8i+4/tcHVKWyi0/5wTO1hfYKCl8pqalS222MabA1RuNMVXTne0y3pdAZ2OMjzGmPHZwwAYROQrEGGMiHKPTugOptZKUUlepcEsFVjy0gsmtJ7M/dj81JtTg3R/f5dLlS64OTbmRtCScj4AZSTcYYyK5aqRYVjDGtDPGHMG2XhYbY5YBiMgu4HMgGvgGGCgi8Y7T+gOTsQMJDgBLszpupdyZMYZetXoxrc407q14L898+wx3TLmDHX/vcHVoyk3cdMIRkdFAvDFmKIAxpjswG+iWSbFdL5YFIlJGRHxExF9E7k2yb4SIVBSRqiKyNMn2jSIS5Nj3mKPZp5RKo2I+xVjwwALm3D+HQycPUWtSLV5d9SrnL2XJY3jKjV034RhjOhljqiV5SPIRoKcxZjowHLhLRL7N7CCVUtmLMYZOgZ3YPXA3nYM689rq1wibFMb6I+tdHZrKxm7UwnkS2AjEGmN+BkYB64AmwL2OLiylVC5VNF9RZrSbweIHF3Pq/CnqTanHk8ue5MyFM64OTWVD1004IhIBFADCsKt5Hgf8scOMdxtjfjHGfJ7pUSqlsrUWlVuwa8Au+tXux+h1owkeH8zKgytdHZbKZm54D8cxym2PiMwWkedEpJmIlARKAYPQFT6VUkBBn4KMazmO7x/+njweebhnxj30+bIPJ+NOujo0lU04M9NAIxFZKiIjMywapZTba1i2Idv6bePZO55l6tapBHwYwKI9+hSCci7hzDTGPJphkSilcoy8XnkZ2WQk63uvp3j+4rSd05YH5j7A37F/uzo05ULOJJxp2NmYX0xppzGmnjFmjRPXV0q5udqlarOxz0Zej3ydhXsWEjAugBnbZuhkoLlUuhOOiPQG3gZeN8aMTthujKlqjJkP/ADUdD5EpZQ78/L04qWGL7H10a1ULVqV7gu703JmS34/9burQ1NZzKnZokXkeezQ6UHGmE+NMROAHUBLYCJQyfkQlVI5QfXi1VnzyBrGNBvD9799T+C4QMb9PI7LctnVoakskhGzRX+ETTAPYmdgng28LCIHM+Da2c7Fixc5cuQIcXFx1z2uUKFC7N69O4uiyh5yUp19fX0pU6YMXl5erg4lR/H08GRQ+CDaVG1D36/6MnDJQGbvnM3kNpOpUrSKq8NTmSzdCccY4wUMwM7QXBzYDIQCXiRfkyZHOXLkCAUKFKBcuXJcb5XqmJgYChS4Zq7THC2n1FlEOHHiBEeOHKF8+fKuDidHKle4HMu6LWPa1mk8ufxJaoyvwfDGw3nqjqfI45FtV01RTnKmS+0X7MwDx4A2IlIb28ppAywxxvhlQHzZTlxcHEWLFr1uslHuzRhD0aJFb9iKVc4xxvBIzUeIHhBNi8oteG7lc4RPDmfbX9tcHZrKJM4kHE+gDxAiIosBRORzbMKJAFYZY4o5H2L2o8km59OfcdYpWaAk8x+Yz9yOc/nj9B/U/qg2L333EnGXNOHnNM4knMoiMlUk+R0/EVkO3AOUB350JjilVO7RIaAD0QOj6RrclRFrRlBzYk1+PKwfITmJM8OiU/3zQ0TWAw0A3/ReXymV+xTJW4RpbafxTddvOHvxLPWn1mfw0sHEXoh1dWgqAzg1LPp6RGQ3cGdmXV+lXc+ePVPdt2PHDn7/PflzEQcPHqRXr17cf//9mR2aUsncW+ledvbfycA6A/m/Df9H0Lgglh9Y7uqwlJNuOuEYY+5O68VF5LDj3HvSeu4NYulojNlljLlsjKmdZHsTY8wmY8wOx9e7kuyLMsbsNcZsdZRbMzImV3jqqacICAigT58+NGrUiPj4+FSPPXv2LIUKFWLVqlUMHTr0mhvimzZt4uDB5CPZK1SowJQpU5Jtu3DhAg0bNuTSJV1aWGWuAj4F+L8W/8eaR9bgm8eXez+9l0cWPcJ/5/5zdWgqndLSwvnGGPOdMaaVMcbzRgcbY7wcS0F/DyxJf4gp2gm059rlrY8DrUUkGOjBVUtiA11FJNRR/sngmLLUwYMHWbt2LdHR0YSGhtK+fXs8PVP/sWzevJmtW7eyd+9eRo4cia+v7e2Mjo6mX79+TJ8+nVGjRtGvXz/+/jv1+a68vb25++67mTNnTobXSamU3Hn7nWztt5Xn6z/PjG0zCBgXwPzd810dlkqHtAx4DwVGA18Cx40x3wIbgAPAv9g1cooAlbGj1O5yvF7mODfDOLrrrhlJJCJbkrzcBfgaY3xEJEetfbt3717uueceLl26RM2advagBQsWXNkfGRnJCy+8QJMmTXjppZc4ffo05cuXJzw8nPz58ye7VkBAABMmTGDatGmUK1eOxo0b3/D927Zty/PPP0/Xrl0ztF5KpcY3jy9v3v0mHQM60uvLXnT4vAMdqnfggxYfUMKvhKvDUzcpLS2cjkBf7H2ZZUBrbAJaBKzBtjYWAu8CTbGJKVxEmotIdAbGfLM6AFuuSjYfO7rTXjZuPO61atWq9OjRg9dff53169dz9OhRypUrd2X/8OHDGTFiBJ999hlbtmxh9OjRREdH8+abb7Jnzx7WrLm5OVVPnDhBv3792LJlC2+99daV7UFBQfz8888ZXS2lbqhmyZqs772et+5+i6/3fU3AhwFM2zpNJwN1E+Zmf1DGmMtANxGZ6Xh9P/A7EICdaUCwD4HuxH7QOzVBkjFmBZDSny4visgixzFRwNMisvGqcwOxCa+piBxwbCstIn8YYwoA84BPReSTFN63Lzax4u/vHzZ79uxk+wsVKkSlSnaKuKFDfdixI+WcLQLpSWnBwZcZOfLGDbLOnTvzzDPPUKpUKVq1asWmTcnXwWvevDlnzpxh8eLFmfL0f9WqVdm4cWOya8fHx1+3W8/d7N+/n1OnTl33mNjYWPz8cuQzzqnKLnX+/ezvvLv3XXac3kHtW2rzVJWnKOGbOa2d7FLnrOJsfSMjIzc5JgNIJi1dav8B+ZK8ngM8JCLT0h3VdYhIugYaGGPKAAuA7gnJxnG9PxxfY4wxM4G6wDUJR0QmAZMAateuLVd3Me3evfvKh6y3N6T2+RoffwlPz7RP0eHtDQUKeN/wuL1791K3bl3Onz/PhQsXkn3w79ixg3/++YdixYpRqlSpNMdwMy5cuEDx4sWTzTWWU6a2SeDr63ulyzI1UVFRN9UNmZNkpzp3a96NCRsnMHTFUHpv7s1bd7/FwLoD8TAZOwA3O9U5K2RWfdPyibgT6GWMWer48M52XVLGmMLAYuB5EVmbZHseoLCIHHfMAdcKWOHs+73/fur7YmLOZdqHb0xMDF5eXuTLl498+fIRHx9PXFwcvr6+HD16lK5du7Jo0SIGDRrEsmXLuPfeezP0/U+cOHFNslHKFTyMBwPqDKBVlVY8+vWjDPpmEHN2zWFym8lUK1bN1eGpq6Tlz4DhQC3gd2PMHmwXWgtjTHNjjH+mRJcKx+i3I0A9YLExZplj12PYJRFevmr4sw+wzBizHdgK/IGd5dot7dy5k6CgoCuvmzZtyg8//MDZs2dp37497733HtWrV+fll19m2LBhGf7+q1atokWLFhl+XaXS6/ZCt7PkwSVMbzud6GPRhEwI4c01b3Ix/qKrQ1NJichNF6AKdtG1tcBlR4l3lD+Br4HXgXZAubRcOzuWsLAwuVp0dPQ121Jy+vTpmzouI2zevFm6deuWZe/Xrl072bNnzzXbs7LOWeFmftarVq3K/ECymexe579i/pL7P79fGIaETgiVzX9udvqa2b3OGc3Z+gIbJYXP1DR1dIrIPhF5VkQSZhB4BrgfeAvYgm0BvQjMBQ4YY447lw7VzahZsyaRkZHXffAzo1y4cIG2bdtStWrVTH8vpdLD38+fLzp+wbxO8/gr9i/qfFSH51c8r5OBZgPO3Fl7DVgjIgtE5CURaSkipYDS2Bmjh3Ptg5kqk/Ts2TNLRoh5e3vTvXv3TH8fpZzVvnp7ogdE0z2kO/9b+z9CJoTww+8/uDqsXM2ZyTuHiciGFLYfFZHFIvKaiLR3LjyllEq/W/LewtT7prK823IuxF+gwccNeGzJY8Scj3F1aLlSpk3eqZRS2UWTik3Y0X8Hg8MHM+7ncQSND+Kb/d+4OqxcRxOOUipX8PP24/1m77O251rye+Wn+WfN6bGwByfOnnB1aLmGJhylVK5S77Z6bHl0Cy81eImZO2YSMC6AudFzdXqcLKAJRymV6/jk8eH1u15nY5+N3FbwNjp+0ZEOn3fgaMxRV4eWo2nCUUrlWiElQljXex0j7xnJ0v1Lqf5hdaZumaqtnUyiCcdNLViwAGMMe/bsceo6EyZM4JNP7JRyr7zyCitWOD3jj1JuJY9HHp6981m29dtGSIkQen3Zi6afNuXX/351dWg5jiYcNzVr1izq16/P1bNZA2l6ALRfv35Xnqt57bXXuOeeDF2cVSm3UaVoFVb1WMW4FuNYf2Q9QeODGLNuDPGXM/+B6txCE44bio2NZe3atUyZMuVKwomKiiIyMpIHH3yQ4OBgoqKiaNSoEZ06daJKlSo899xzfPbZZ9StW5fg4GAOHLATaQ8bNox3330XgIcffpi5c+cCsHLlSmrWrElwcDA9e/bk/PkctYadUinyMB70r9OfXQN20bhcY55Y9gT1P67PoTOHXB1ajpD2+fNVoieegK1bU9yVNz4+9bULric09PrTUAMLFy6kWbNmVKlShSJFirB582YANmzYwM6dOylfvjxRUVFs27aN3bt3U6RIESpUqEDv3r3ZsGEDY8aM4f/+7/94P5X3iYuL4+GHH2blypVUqVKF7t27M378eJ544om010cpN3Rbodv4usvXzNwxk8HfDKbvH3057HeYofWH4u154+VDVMq0heOGZs2aRefOnQG7ENusWbMAqFu3LuXLl79yXJ06dShZsiQ+Pj5UrFiRpk2bAhAcHMyhQ4dSvf7evXspX748VapUAaBHjx6sXq2zFKncxRhD1xpdiR4YTYNiDXgl6hVqT6rNxj833vhklSJt4TjjOi2Rc5m0GNmJEyf47rvv2LlzJ8YY4uPjMcbQokUL8ufPn+xYHx+fK997eHhcee3h4cGlS5dSfQ8doaNUolvz38rLAS8zuORg+i/uT/jkcJ6q9xTDGw8nr1deV4fnVrSF42bmzp1L9+7d+e233zh06BCHDx+mfPny/PBDxk1KWK1aNQ4dOsT+/fsBmDFjBo0aNcqw6yvljtpUbcOuAbvoVbMX7/z4DjUm1OD7Q9+7Oiy3ognHzcyaNYt27dol29ahQwdmzpyZIdc3xuDr68vHH39Mx44dCQ4OxsPDg379+mXI9ZVyZ4V9CzOp9SRWdl/JZblM4+mN6f91f06fP+3q0NxDSovkZPcCdAR2YReAq51kezngHHZVz63AhCT7woAdwH5gLGBu9D7usgBbRmnVqpV899136T7fHet8PboAW8q0zlbs+Vh58psnxWO4h5QZVUa+3vt11geWSbLFAmzZyE6gPSmvt3NAREIdJemf5eOBvkBlR2mW+WG6j549e3L27Fnq16/v6lCUcgv5vfPz3r3v8WPPHynkU4hWs1rRbX43jp/VdSdT45YJR0R2i8jemz3eGFMSKCgiPzmy7ydA28yKzx1NnTqVlStX4uXl5epQlHIr4WXC2dR3E682epXPd31OwIcBzNk5RwffpMAtE84NlDfGbDHGfG+MaeDYVho4kuSYI45tSinlNJ88PgxrPIxNfTdRrnA5Os/rTNs5bfnj9B+uDi1bybbDoo0xK4ASKex6UUQWpXLaUeB2ETlhjAkDFhpjAgGTwrEp/vlhjOmL7XrD39+fqKioZPsLFSpETMyNVwuMj4+/qeNykpxW57i4uGt+/leLjY294TE5jdb5+t6q9BbzfOcx9ZepVB1blX4V+9GyREuMSeljKHvKtJ9xSjd23KUAUSQZNJDafqAksCfJ9i7AxBtdP7cNGnBWTquzDhpImdb55vxy4hdpPK2xMAyJnBYp+0/sz/jAMokOGrgJxpjixhhPx/cVsIMDDorIUSDGGBNh7J8Z3YHUWklKKeW0SkUqsbL7Sia2msimo5sIHh/MqJ9G5erJQN0y4Rhj2hljjgD1gMXGmGWOXQ2B7caYbcBcoJ+I/OvY1x+YjB0WfQBYmsVhZ5i///6bBx98kAoVKhAWFka9evVYsGBBqsdHRUXRqlWrFPeVK1eO48dTH1Xz/vvvc/bs2RvG1Lt3b6eXSlAqp/EwHvQN60v0gGjuqXAPTy1/ijum3sHOf3a6OjSXcMuEIyILRKSMiPiIiL+I3OvYPk9EAkUkRERqichXSc7ZKCJBIlJRRB5zNPvcjojQtm1bGjZsyMGDB9m0aROzZ8/myJEjNz45HW424UyePJlq1aplSgxKubvSBUuzqPMiZnWYxcH/DlJrYi2GRw3nQvwFV4eWpdwy4eRm3333Hd7e3sme/C9btiyPP/44cXFxPPLIIwQHB1OzZk1WrVp1zfknTpygadOm1KxZk0cfffTK0M0zZ87QsmVLQkJCCAoKYs6cOYwdO5Y///yTyMhIIiMjAVi+fDn16tWjVq1adOzYkdjYWAAaN258ZdZqPz8/XnzxRUJCQoiIiODvv//O7H8WpbI9Ywydgzqze+BuOgZ2ZNj3wwibFMbPf/zs6tCyTLYdpeYOnvjmCbb+tTXFffHx8XimY3mC0BKhvN/s/VT379q1i1q1aqW478MPPwRgx44d7Nmzh6ZNm7Jv375kxwwfPpz69evzyiuvsHjxYiZNmgTAN998Q6lSpVi8eDEAp06dolChQowaNYpVq1ZRrFgxjh8/zhtvvMGKFSvInz8/I0eOZNSoUbzyyivJ3uPMmTNEREQwYsQInn32WT766CNeeumlNP9bKJUTFctXjM/af0aXoC70+7ofEVMiGBIxhNciXyOfVz5Xh5eptIXj5gYOHEhISAh16tThhx9+4KGHHgLsBJxly5a9JuGsXr2abt26AdCyZUtuueUWwC5ZsGLFCoYOHcqaNWsoVKjQNe+1bt06oqOjufPOOwkNDWX69On89ttv1xzn7e195Z5RWFjYdZdCUCq3alWlFbsG7KJ3zd6899N71Bhfg6hDUa4OK1NpC8cJ12uJxGTS8gSBgYHMmzfvyusPP/yQ48ePU7t2bUqXvrlnWVN6HqBKlSps2rSJJUuW8Pzzz9O0adNrWi4iQpMmTa6sv5MaLy+vK+/h6el53aUQlMrNCvkWYmLriXQJ7kLvL3sTOT2SvrX68naTtynke+0ffe5OWzhu5q677iIuLo7x48df2ZZwU79hw4Z89tlnAOzbt4/ff/+dqlWrJjs/6TFLly7lv//+A+DPP/8kX758dOvWjaeffvrK/ZgCBQpceZgzIiKCtWvXXlm24OzZs9e0oJRSade4XGO299/O0/WeZvKWyQSMC+CrvV/d+EQ3ownHzRhjWLhwId9//z3ly5enbt269OjRg5EjRzJgwADi4+MJDg7mgQceYNq0ackWYQN49dVXWb16NbVq1WL58uXcfvvtgL3vU7duXUJDQxkxYsSVey59+/alefPmREZGUrx4caZNm0aXLl2oUaMGEREROhRaqQySzysf7zR9h3W91lE0b1HazG7Dg/Me5NiZY64OLeOk9DSoFp1pID1yWp11poGUaZ0z3/lL52V41HDxes1Lio4sKp9t/0wuX76cZe+vMw0opVQu4e3pzSuNXmHLo1uoVKQSXed3pfWs1hw+ddjVoTlFE45SSmVTgbcGsrbnWkY1HcWqQ6sIHBfIhI0TuCyXXR1aumjCUUqpbMzTw5Mh9Yawo/8O6pauS//F/blr+l38cuIXV4eWZppwlFLKDVS4pQLfPvQtk1tPZutfW6kxoQbvrH2HS5fd57EDTThKKeUmjDH0qtWL6IHR3FvxXp5d8Sz1ptRj+9/bXR3aTdGEo5RSbqZUgVIseGABn9//Ob+f+p2wSWG8suoVzl867+rQrksTjlJKuSFjDB0DOxI9IJrOQZ15ffXr1JxYk58O/+Tq0FKlCUcppdxY0XxFmdFuBkseXELshVjunHonT3zzBGcunHF1aNfQhJPD9OzZ09UhKKVcoHnl5uwcsJP+tfszZv0YgscHs+LgCleHlYwmnBzk7NmzFCpUiFWrVjF06FDi4uKuOWbs2LFUr16drl27pvt9/Pz8ALjjjjvSfQ1XOXToEEFBQa4OQ6lMUdCnIB+2/JDVD68mj0cemsxoQu8ve3My7qSrQwPcNOEYYzoaY3YZYy4bY2on2d7VGLM1SblsjAl17IsyxuxNsu9Wl1Ugk2zevJmtW7eyd+9eRo4cia+v7zXHjBs3jiVLllyZwPN6RITLl1N/wOzHH390Kt7McqO4lcrpGpRtwLZ+2xh651CmbZ1GwIcBLNyz0NVhuWfCAXYC7YHVSTeKyGciEioiocBDwCER2ZrkkK4J+0Xkn6wIVK5ayfrq1+k1d+5cIiIiCAkJoX79+hw7doyff/6Z8PBw8ufPn+I5/fr14+DBg7Rp04bRo0czatQogoKCCAoK4v333wdsC6B69eoMGDCAWrVqcfhw6lNpJLR0Es55/PHHCQwMpGnTppw7dw6ATz/99MqkoI8++ijx8fHXXCel1Uavd27btm0JCwsjMDDwygJyKcX9ySefUKNGDUJCQq6sEwR2cbw+ffpcE6tSOUler7z8757/sb73em7Nfyvt5rSj0xed+DvWhSvwpjTBmrsUIAqoncq+N4ERN3NsasXZyTtfffVVGTx48JVJ9y5fviyDBw+WV1999aaucT3Hjx+/8v2wYcPkgw8+kN69e0t8fLy88MILsnr16hTPK1u2rBw7dkw2btwoQUFBEhsbKzExMRIQECCbN2+WX3/9VYwx8tNPP6X63vnz50/29ddffxVPT0/54YcfRESkY8eOMmPGDImOjpZWrVrJhQsXRESkf//+Mn369GuuN3fuXOndu/eV1ydPnrzuuSdOnBARkbNnz0pgYKAcP378mrh37twpVapUkWPHjiU7JyHWLVu2JIs1JTp5Z8q0zu7nwqULMmL1CPF+3VuKjCwin2z95LqTgerknWn3AHD1SmEfO7rTXjYprUKWgUSEkydPMmbMGIYMGYKIMGTIEMaMGcPJkyedbulMmzaNunXrEhISwrhx4/D19eWjjz7Cw8ODESNG0KBBg+ue/8MPP9CuXTvy58+Pn58f7du3Z82aNQCULVuWiIiINMVTvnx5atSoASSu8rly5Uo2bdpEnTp1CA0NZeXKlRw8ePCac1NabfR6544dO5aQkBAiIiI4fPgwv/zyyzVxf/fdd9x///0UK1YMgCJFiiSLNTQ0NFmsSuVkXp5evNDgBbY+upVqxarRfWF3Ws5sye+nfs/SOLLtip/GmBVAiRR2vSgii25wbjhwVkR2JtncVUT+MMYUAOZhu9w+SeHcvkBfAH9/f6KiopLtL1So0JUFya7n8uXLvPbaa1y4cIExY8YwZswYAPr3789rr71GbGzsDa+RmpkzZ/Ljjz+yaNEi/Pz8aNasGeXKlbupuESE2NhYzp07x/nz56+cc/78eeLi4oiNjSVv3rw3vFbC/piYGGJjY/Hy8iI+Pp6YmBguXbrEmTNn8PHxoUuXLgwbNizFcxOULFmSqKgoli9fzrPPPstdd91F4cKFUzx3yZIlLFu2jOXLl5MvXz5atGjBv//+i5+fX7K4z507x4ULF655r4RYE7YnxJpSfePi4q75+V8tNjb2hsfkNFpn9/Za+ddY5LOIjw5+RLX/q0bf8n1pU6oNHiax/ZFp9U2p2eMuhVS6yYDRwAvXOe9h4IMbXT8j1sO5fPmyAFdKRqxp8fTTT8v7778vIrY7ytPTU2JjY2/q3IQutU2bNklwcLCcOXNGYmNjJTAw8EqXWmBg4HWvkVKXWmBg4JU6v/POO/Lqq6/Krl27pFKlSvL333+LiO3WOnTo0DXX++OPP+TcuXMiIrJgwQK57777Uj134cKF0qpVKxER2b17t/j4+MiqVauuiXvnzp1SuXLlK12PSbvUkh6XEGtKtEstZVrnnOHX/36VJp80EYYhDaY2kD3H9lzZp11qN8kY4wF0BGYn2ZbHGFPM8b0X0Ao78CBTiaMbLamE7jVn9OjRg7Fjx9KgQQP27dtHhQoVUh0okJpatWrx8MMPU7duXcLDw+nduzc1a9Z0Kq6rBQQE8MYbb9C0aVNq1KhBkyZNOHr06DXHpbTaaGrnNmvWjEuXLlGjRg1efvnlVLv+AgMDefHFF2nUqBEhISE8+eSTGVo3pdxducLlWNZtGR/f9zE7/tlByIQQ/vfD/zJ3MtCUslB2L0A74AhwHvgbWJZkX2Ng3VXH5wc2AduBXcAYwPNG7+NMC+fUqVMyePBgAa4MHLj6dU6jK37mDlrnnOdozFFpP6e9MAypNbGWfPTVR05dj1RaONn2Hs71iMgCYEEq+6KAiKu2nQHCMj+yRMYYChcuzODBgxk9ejTGGEaPHg1A4cKFyeQxC0opddNK+JVgXqd5zIuex8AlA3n06KOUrV6WJhWbZOj7uGXCcRfDhg1DRK4kl4Sko8lGKZUddQjoQGT5SB6f9TgNyl5/pGt65Lh7ONnN1clFk41SKjsrkrcIfSr0wTfPtTOVOEsTjlJKqSyhCScdxMlRZir705+xUhlPE04a+fr6cuLECf1AysFEhBMnTqQ4+alSKv100EAalSlThiNHjnDs2LHrHhcXF5frPrByUp19fX0pU6aMq8NQKkfRhJNGXl5elC9f/obHRUVFZfiDlNldbqyzUurmaZeaUkqpLKEJRymlVJbQhKOUUipLGB1tlTpjzDHgt3SeXgw4noHhuAOtc+6gdc75nK1vWREpfvVGTTiZxBizUURquzqOrKR1zh20zjlfZtVXu9SUUkplCU04SimlsoQmnMwzydUBuIDWOXfQOud8mVJfvYejlFIqS2gLRymlVJbQhJMOxphmxpi9xpj9xpjnUthvjDFjHfu3G2Nq3ey52VF662uMuc0Ys8oYs9sYs8sYMzjro08fZ37Gjv2expgtxpivsy5q5zj5/7qwMWauMWaP4+ddL2ujTx8n6zzE8f96pzFmljHGLSYSvIk6VzPG/GSMOW+MeTot595QSutOa0m9AJ7AAaAC4A1sAwKuOqYFsBQw2OWu19/sudmtOFnfkkAtx/cFgH3Zvb7O1jnJ/ieBmcDXrq5PVtQZmA70dnzvDRR2dZ0ys85AaeBXIK/j9efAw66uUwbV+VagDjACeDot596oaAsn7eoC+0XkoIhcAGYD9111zH3AJ2KtAwobY0re5LnZTbrrKyJHRWQzgIjEALuxv6jZnTM/Y4wxZYCWwOSsDNpJ6a6zMaYg0BCYAiAiF0TkZBbGnl5O/Zyxkx/nNcbkAfIBf2ZV4E64YZ1F5B8R+Rm4mNZzb0QTTtqVBg4neX2Eaz9EUzvmZs7Nbpyp7xXGmHJATWB9xoeY4Zyt8/vAs8DlTIovMzhT5wrAMeBjRzfiZGNM/swMNoOku84i8gfwLvA7cBQ4JSLLMzHWjOLMZ5DTn1+acNLOpLDt6qF+qR1zM+dmN87U1+40xg+YBzwhIqczMLbMku46G2NaAf+IyKaMDytTOfNzzgPUAsaLSE3gDOAO9yed+Tnfgv3rvjxQCshvjOmWwfFlBmc+g5z+/NKEk3ZHgNuSvC7DtU3p1I65mXOzG2fqizHGC5tsPhOR+ZkYZ0Zyps53Am2MMYewXQ53GWM+zbxQM4yz/6+PiEhC63UuNgFld87U+R7gVxE5JiIXgfnAHZkYa0Zx5jPI+c8vV9/EcreC/WvuIPYvm4QbZ4FXHdOS5DcaN9zsudmtOFlfA3wCvO/qemRVna86pjHuM2jAqToDa4Cqju+HAe+4uk6ZWWcgHNiFvXdjsIMmHnd1nTKizkmOHUbyQQNOf365/B/AHQt25Mo+7IiNFx3b+gH9HN8b4EPH/h1A7eudm91LeusL1Mc2ubcDWx2lhavrk9k/4yTXcJuE42ydgVBgo+NnvRC4xdX1yYI6Dwf2ADuBGYCPq+uTQXUugW3NnAZOOr4vmNq5aSk604BSSqksofdwlFJKZQlNOEoppbKEJhyllFJZQhOOUkqpLKEJR6kcwBiz3hjT2dVxKHU9mnCUcnPGGA8gCDskWalsSxOOUu6vKvZ3ea+rA1HqejThKOX+QoFoEYmHK+u07DHGhLo0KqWuksfVASilnBYKbDPGFAI+xv5eR4h7LBGgchFt4Sjl/kKxSeZn7PQy92myUdmRTm2jlJszxvzl+PZbEXnIpcEodR3awlEqmzLG1DTGLDDG/Ococ40xRYwxpYwxccaYLsaYEoA/dqLQBsaYHq6NWqnU6T0cpbIhY0wX7JT327GzEpcHBmFXmMwD/ALMAe4FDorIHsfib6uMMYdF5DvXRK5U6jThKJXNGGMqAFOxyzk0FJE4x/baQHOgHNBVRC4bY0KALQAistMY0xWYY4xpKCK7XRG/UqnRezhKZTPGmDHY1kyEJK6iiTFmBtAN2Ixdl0V/eZVb0Xs4SmU/bYD9SZPNVV7WZKPckSYcpbIRY0wRbJfZzyns9gd2iciSLA1KqQyiCUep7KWE4+uJpBuNMQ2BJldvV8qdaMJRKns56fgakrDBGOMHTHS8zJ/VASmVUTThKJWNiMifwAbsMzUzjDH9gdVAMeAboKYx5gljTElXxqlUeugoNaWyGWNMWeAD7MOcebDDnns6ds8DAoBqIqKzQyu3oglHKaVUltAuNaWUUllCE45SSqksoQlHKaVUltCEo5RSKktowlFKKZUlNOEopZTKEppwlFJKZQlNOEoppbKEJhyllFJZQhOOUkqpLKEJRymlVJb4f7Fhr4jBsHPAAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"plot_alpha(-3,eta_ls=0.25,algorithm=\"steepest-descent\",alpha_max=1E-1)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.3 Steepest Descent Step, $x^k = -3$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.3-Steepest-Descent-Step,-$x^k-=--3$)",
"section": "3.6.3.3 Steepest Descent Step, $x^k = -3$"
}
},
"source": [
"**Discussion**\n",
"* Why did the line search stop where the Armijo conditions are satisfied?\n",
"* Why not further decrease $\\alpha^k$ to achieve a greater improvement in the objective?"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.4 Newton Step, $x^k = 0$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.4-Newton-Step,-$x^k-=-0$)",
"section": "3.6.3.4 Newton Step, $x^k = 0$"
}
},
"source": [
"### 3.6.3.4 Newton Step, $x^k = 0$"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.4 Newton Step, $x^k = 0$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.4-Newton-Step,-$x^k-=-0$)",
"section": "3.6.3.4 Newton Step, $x^k = 0$"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Considering xk = 0 and f(xk) = 1.5\n",
"Step with newton algorithm:\n",
"pk = 0.75\n",
"With full step, xk+1 = 0.75 and f(xk+1) = 3.486328125\n",
"Line search failed. Goldstein conditions violated. Consider increasing alpha_max.\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZEAAAETCAYAAAD3WTuEAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAABJtElEQVR4nO3dd3gUVffA8e8lJITemxTpKEV6UwQiglIECyKgohKaUgRFEH2lKPKKStGfSBPECvpSJFIVSKRI7xA6UmIQIdQECCnn98ddIIQEUja7m+R8nmeeZGdmZ86FZE/u3GZEBKWUUiolsrg7AKWUUumXJhGllFIppklEKaVUimkSUUoplWKaRJRSSqWYJhGllFIp5rFJxBhz1Bizyxiz3RizOYHjxhjzuTHmkDFmpzGmtjviVEqpzCyruwO4Cz8ROZPIsVZARcfWAJjk+JqoQoUKSZkyZVIcTEREBDlz5kzx+9ObzFZe0DJnFlrm5NmyZcsZESmc0DFPTyJ30h74VuxoyfXGmHzGmOIicjKxN5QpU4bNm2+r1CRZUFAQzZo1S/H705vMVl7QMmcWWubkMcYcS+yYxz7OAgT4zRizxRjTM4HjJYATcV6HOPYppZRyEU+uiTwkIqHGmCLA78aYfSKyKs5xk8B7bpvDxZGAegIULVqUoKCgFAcUHh6eqvenN5mtvKBlziy0zM7jsUlEREIdX/81xswH6gNxk0gIUCrO65JAaALXmQpMBahbt66kpgqb2arAma28oGXOLLTMzuORScQYkxPIIiKXHN+3BN6Pd1oA0NcYMxvboH7hTu0hiYmKiiIkJISrV6/e9dy8efOyd+/e5N4i3UpueX19fSlZsiTe3t5pGJVSypN4ZBIBigLzjTFgY/xRRJYaY3oDiMhkYDHQGjgEXAZeScmNQkJCyJ07N2XKlMFxv0RdunSJ3Llzp+Q26VJyyisihIWFERISQtmyZdM4MqWUp/DIJCIiR4AaCeyfHOd7Afqk9l5Xr15NUgJRd2aMoWDBgpw+fdrdoSilXMiTe2e5jCYQ59B/R6UyH00iSimVgV2Ouszg3wcz468ZaXJ9TSJKKZVBBR0NosbkGnzy5ydcjL5IWqxkq0kkHevWrVuix3bt2sXx48dv2XfkyBH8/f3p0KFDWoemlHKjC1cv0Hthb/y+8UNEWNl1JQMqDkiTR86aRDzIm2++SZUqVejRowdNmzYlJiYm0XMvX75M3rx5CQwMZMiQIbd1Ud6yZQtHjhy5ZV+5cuWYPn36LfuuXbtGkyZNiI6Odl5BlFJus/DAQqp+WZVpW6fxZqM32fnqTvzK+qXZ/TSJeIgjR46wdu1agoODqVmzJk8//TReXl6Jnr9161a2b9/O/v37GTNmDL6+vgAEBwfTu3dvvvnmG8aNG0fv3r05depUotfx8fGhefPm/PTTT04vk1LKdU5HnKbL3C48MesJ8vnm489uf/Jpy0/J4Z0jTe/rkV18M5v9+/fz6KOPEh0dTa1atQCYP3/+jeN+fn688847tGjRgv/85z9cvHiRsmXL0qBBg9tm5axSpQqTJ09m5syZlClTJkkjVJ988kmGDh3K888/79RyKaXSnogwe/ds+i/tz4WrFxjRdARDHx6Kj5ePS+6vNREPULlyZV566SU++OADNmzYwMmTJ4k7Zf3IkSP58MMP+eGHH9i2bRvjx48nODiY0aNHs2/fPlavXp2k+4SFhdG7d2+2bdvGf//73xv7q1WrxqZNm5xdLKVUGvv74t+0m92OLvO6UDZfWbb22srwZsNdlkBAayK3GDAAtm9P/HhMTHbu8IQpQTVrwoQJdz9v165dtG/fnjNnzpAvX75bjjVp0gQRYdy4cQQFBeHl5cW0adMA+PDDDxO83ssvv3zbvoIFCzJ58uTb9nt5eeHj45PpRuQrlV6JCF9t/YpBvw8iKiaKsS3H8nqD1/HKkswPKCfQJOIh9uzZQ9WqVYmMjLytkXzXrl2cPHmSQoUKpdmHfGRk5I12FaWU5zp89jA9fu1B4NFA/Mr4Me2JaZQvUN5t8WgSieNuNYZLl66kyYf4pUuX8Pb2JkeOHOTIkYOYmBiuXr2Kr68vJ0+e5Pnnn2fBggX079+fZcuW8dhjjzn1/mFhYRQuXFgnTlTKg8XExjBh/QTeC3wPby9vpradSvfa3d0+U4S2iXiA3bt3U61atRuvW7ZsyZo1a7h8+TJPP/00Y8eO5f777+e9995jxIgRTr9/YGAgrVu3dvp1lVLOsevULhpNb8Sg3wfRonwLgl8LpkedHm5PIKBJxCM0atSI//3vfzde9+3bl2+++YYcOXKwbt06WrRoAdi2kXXr1jn9/j/++CM9eya0eKRSyp2uxVxjeOBwak+tzdHzR5n9zGx+ee4XSuTxnEVc9XGWB6pVqxZ+fn7ExMTccayIM1y7do0nn3ySypUrp+l9lFLJsyFkA/4B/uw5vYcXHniB8Y+Np1COQu4O6zaaRDzUnaY0cSYfHx+6du3qknsppe4u4loE7wW+x4T1EyiRpwQLOy+kTaU27g4rUZpElFLKQ6z8ayU9fu3BkXNHeLXuq3z06EfkyZbH3WHdkSYRpZRys/NXz/PWb2/x1bavqFCgAkEvBdG0TFN3h5UkmkSUUsqNFuxbwKuLXuVUxCneevAtRjYbSXbv7O4OK8k0iSillBv8G/Ev/Zf056c9P1G9SHUCOgdQ95667g4r2TSJKKWUC4kIP+z6gdeXvs6lyEu83+x9hjQe4tL5rpzJo5OIMcYL2Az8LSJt4x1rBiwA/nLsmici77s0QKWUSoYTF07Qe1FvFh9cTMOSDZnebjpVCldxd1ip4umDDV8H9t7h+GoRqenY0nUCmT9/PsYY9u3bl6rrTJ48mW+//RaAYcOGsXz5cmeEp5RKhViJZfLmyVT9sipBR4MY/9h41ryyJt0nEPDgmogxpiTQBvgQeMPN4aS5WbNm0bhxY2bPnn3b1CbJGXTYu3fvG9+//366zqtKZQgHww7S49ce/HHsDx4t9yhT206lbP6y7g7LaTy5JjIBGAzE3uGcRsaYHcaYJcaYqq4Jy/nCw8NZu3Yt06dPZ/bs2QAEBQXh5+dHly5dqF69OkFBQTRt2pSOHTtSqVIl3n77bX744Qfq169P9erVOXz4MAAjRozg008/Bex08HPmzAFgxYoV1KpVi+rVq9OtWzciIyPdU1ilMono2Gg+XvsxD0x+gB2ndjCj3Qx+e+G3DJVAwENrIsaYtsC/IrLF0faRkK3AvSISboxpDfwCVEzgWj2BngBFixYlKCjoluN58+bl0qVLAGQbMoQsu3YlGld2EaKTOeFZbPXqRI4Zc8dzZs+eTfPmzSlevDh58+Zl9erVXL58mY0bN7J+/XrKlCnD6tWr2bFjB5s2bSJ//vw88MADdO3alRUrVvDll18yduxYxowZQ2RkJN7e3ly6dImoqCiuXLnC6dOneemllwgICKBixYr07NmT8ePH06dPnzvGFRMTc+PfJqmuXr16279xehIeHp6u408JLbPzHQo/xCf7P+FA+AEaF2zMgIoDKHihIH/88Uea3fNu0qrMHplEgIeAdo7k4AvkMcZ8LyIvXD9BRC7G+X6xMeZLY0whETkT90IiMhWYClC3bl2Jv1zs3r17b07v7uPDnVadio6JIWty57Ly8cHnLtPH//LLLwwYMIDcuXPz/PPPExAQQJs2bW7UMgBy5MhBvXr1qFjR5skKFSrwxBNPkDt3burVq8e6devInTs32bJlI1u2bOTOnRtvb2+yZ89OaGgo5cqVo3bt2gB0796diRMn8vbbb98xrpQsUuXr63tjid/0KCgoKElLCmckWmbniYyOZNSqUXy07SMKZC/Azx1+pkOVDh4x225aldkjk4iIDAWGwo1eWIPiJhDH/mLAKRERY0x97KO5sFTd+C4LilxJg5X/wsLCWLlyJbt378YYQ0xMDMYYWrdufdv66dmyZbvxfZYsWW68zpIlC9HR0YneQ0ScGrNS6nbrTqyjW0A39p3ZR9caXRnXchwFcxR0d1hpzpPbRG5jjOltjLnectwB2G2M2QF8DnSSdPhpOWfOHLp27cqxY8c4evQoJ06coGzZsqxZs8Zp97jvvvs4evQohw4dAuC7776jadP0MaWCUp4u/Fo4A5YO4KEZD3E56jJLnl/CN09+kykSCHhoTSQuEQkCghzfT46z/wvgC/dE5TyzZs267bHSM888w6RJkyhfPvVLXhpj8PX15euvv+bZZ58lOjqaevXq3dKLSymVMsuPLKfHrz04ev4ofev1ZXTz0eTOljZLWHsqj08iGV1CDV39+/enf//+t+xr1qzZLc8z474v7rG43YPDwsIoUKAAAM2bN2fbtm3OClupTO3clXMM+m0QM7bPoFLBSqx+ZTWNSzd2d1huoUkkg+rWrRuXL1+mcePM+YOtVFqZv3c+ry1+jdMRp3n7obcZ3mw4vll93R2W22gSyaBmzJjh7hCUylD+Cf+Hfkv6MSd4DjWL1WRRl0XULl7b3WG5nSYRpZS6AxHh2x3fMnDZQCKiIvjwkQ9568G38PbydndoHkGTiFJKJeLY+WP0WtiLZYeX8WCpB5nebjr3FbrP3WF5FE0iSikVT6zE8uWmL3l7ue05+fnjn9Onfh+ymHQ1KsIlNIkopVQc+8/sp/uv3VlzfA0ty7dkStsplMlXxt1heSxNqx7i1KlTdOnShXLlylGnTh0aNWrE/PnzEz0/KCiItm3bJnisTJkynDlzJsFjABMmTODy5ct3jalv374EBwffPXilMoComCg+WvMRNSbXYM+/e/i6/dcsfX6pJpC70CTiAUSEJ598kiZNmnDkyBG2bNnC7NmzCQkJSZP7JTWJfPHFF1Spkv7XO1Dqbrad3EaDrxowdMVQnqj8BMF9gnm55sseMeeVp9Mk4gFWrlyJj4/PLaPI7733Xvr168fVq1d55ZVXqF69OrVq1SIwMPC294eFhdGyZUtq1apFr169bsyVFRERQZs2bahRowbVqlXjp59+4vPPPyc0NBQ/Pz/8/PwA+O2332jUqBG1a9fm2WefJTw8HIDWrVuzefNmAHLlysW7775LjRo1aNiwIadOnUrrfxal0tzV6Ku8s+Id6k2rR+ilUOZ2nMv/nv0fxXIVc3do6Ya2icQxYOkAtv+zPdHjyVkc6rqaxWoy4fEJdzxnz549N2bYjW/ixIkA7Nq1i3379tGyZUsOHDhwyzkjR46kcePGDBs2jEWLFjF16lQAli5dyj333MOiRYsAuHDhAnnz5mXcuHEEBgZSqFAhzpw5w6hRo1i+fDk5c+ZkzJgxjBs3jmHDht1yj4iICBo2bMiHH37I4MGDmTZtGv/5z3+S9W+hlCdZe3wt/gH+7A/bzys1X2Fsy7Hkz57f3WGlO5pEPFCfPn1Ys2YNPj4+lCxZkn79+gF2IsV77733tiSyatUq5s2bB0CbNm3In9/+IlSvXp1BgwYxZMgQ2rZty8MPP3zbvdavX09wcDAPPfQQANeuXaNRo0a3nefj43OjDaZOnTr8/vvvziuwUi50KfISnx/8nF/++IV7893LsheW0bJ8S3eHlW5pEonjbjWGlKyvkRRVq1Zl7ty5N15PnDiRM2fOULduXUqUKJGkayT07LZSpUps2bKFxYsXM3ToUFq2bHlbDUNEaNGiBbNmzbrj9b29vW/cw8vL645TzyvlqZYdWkavhb04fuE4/er348PmH5LLJ5e7w0rXtE3EAzzyyCNcvXqVSZMm3dh3veG7SZMm/PDDDwAcOHCA48ePU7ly5VveH/ecJUuWcO7cOQBCQ0PJkSMHL7zwAoMGDWLr1q0A5M6d+8aKhQ0bNmTt2rU3pom/fPnybTUdpdK7s1fO8tIvL/H4D4+T3Ts7n9f8nM9afaYJxAm0JuIBjDH88ssvDBw4kI8//pjChQvfaJ9o3749vXv3pnr16mTNmpWZM2fesjgVwPDhw+ncuTO1a9emadOmlC5dGrDtKG+99RZZsmTB29v7RpLq2bMnrVq1onjx4gQGBjJz5kw6d+58Y931UaNGUalSJdf+IyiVRuYEz6Hv4r6EXQnj3Yff5T9N/sP6NevdHVbGISKZZqtTp47EFxwcfNu+xFy8eDHJ52YEKSlvcv49PVFgYKC7Q3C5jFrm0Iuh8vRPTwsjkNpTasu2k9tuHMuoZb6T1JQZ2CyJfK5qTUQplaGICN/s+IaBywZyJeoKHzX/iDcffJOsWfTjLi3ov6pSKsM4ev4oPX/tye9Hfqdx6cZMbzedSgX10Wxa0iSilEr3YmJjmLhpIu+seAdjDF+2/pJedXvphIkuoEkEW/3V6Q1STxwj5ZVypb2n9+If4M+6kHW0qtCKyW0nUzpvaXeHlWlk+jTt6+tLWFiYfgCmkogQFhaGr2/mXSZUuVZUTBQfrvqQmlNqsj9sP9899R2LuizSBOJiHl0TMcZ4AZuBv0WkbbxjBvgMaA1cBl4Wka3JvUfJkiUJCQnh9OnTdz336tWrmepDMrnl9fX1pWTJkmkYkVLWltAt+Af4s+PUDp6r+hyft/qcIjmLuDusTMmjkwjwOrAXyJPAsVZARcfWAJjk+Jos3t7elC1bNknnBgUFUatWreTeIt3KbOVVnu9K1BVG/jGST//8lCI5i/DLc7/Q/r727g4rU0tVEjHGVAKqAkUAAU4Du0XkYGoDM8aUBNoAHwJvJHBKe+BbRx/m9caYfMaY4iJyMrX3Vkp5nlXHVtE9oDsHzx6ke63ufNLyE/L55nN3WJmeSW5bgDHmfqA38CxQ9Ppux9frFzsF/AxMEZG9KQrMmDnAf4HcwKAEHmctBD4SkTWO1yuAISKyOd55PYGeAEWLFq0ze/bslIQDQHh4OLlyZZ5pEjJbeUHL7IkioiOY9tc0FoQuoLhvcd6s9CZ18tdJ1TU9vcxpITVl9vPz2yIidRM8mNgoxPgbUB6YA8QA4cASYBjwPPA49vHS88Bwx7Fwx7n/A8ol9T6Oe7UFvnR83wxYmMA5i4DGcV6vAOrc6boJjVhPjsw2yjWzlVdEy+xpFh1YJKXGlRIzwsiAJQMkPDLcKdf15DKnFU8YsR4M7AJeBuaJSMSdTjbG5AQ6AP0d701Oi/RDQDtjTGvH+/IYY74XkRfinBMClIrzuiQQmox7KKU81JnLZxi4bCDf7/ye+wvdz5/+f9KwZEN3h6USkJwuvh1FpK6IfHe3BAIgIhEi8o2I1AGeS05QIjJUREqKSBmgE7AyXgIBCAC6GqshcEG0PUSpdE1E+HnPz1SZWIXZu2czrMkwtvXapgnEgyW5JiIiC1J6k9S8Ny5jTG/H9SYDi7Hdew9hu/i+4ox7KKXcI/RSKK8teo0F+xdQ9566LG+3nAeKPuDusNRdJDmJGGMeEJGdaRlMQkQkCAhyfD85zn4B+rg6HqWUc4kIM7bN4M3f3iQyJpKPH/2YgY0G6oSJ6URy/pdmG2MaiMiluDuNMZVFZL+T41JKZQJHzh2h5689WfHXCpre25Sv2n1FhQIV3B2WSobktIlMA76Lu8MY4wescmpESqkMLyY2hgnrJ1B9UnU2/r2RSW0msfKllZpA0qEkJxERGQ/EGGOGABhjugKzgfgN3koplajg08E0/roxA5cNxK+MH8F9guldt7fOuJtO3fFxljGmI7AT2O9og3gF2GSMqQI0AR4RkT1pH6ZSKr27FnONj9Z8xKhVo8iTLQ/fP/U9Xap30Rm007m7tYm8AVTDzncYDOwA1gMtgGYiciCN41NKZQCb/t6Ef4A/u/7dRedqnfns8c8onLOwu8NSTnDHJCIiDR2z5VYGasbZDLDXGHME2CYiHdM2TKVUenQ56jLDA4czbv04iuUqxoJOC2hXuZ27w1JOdNfeWY7HWPsc242Jp4wxRYHagHbkVkrdJuhoEN0DunP43GF61u7Jxy0+Jq9vXneHpZwsxR2xReQUdo6sJc4LRymV3l24eoHBvw9m6taplM9fnpVdV+JX1s/dYak0ktqp4IsCHYEy2AkXtwG/icjl1IemlEpvFh5YSO+FvTkZfpI3G73J+37vk8M7h7vDUmkoxUnEGPMwduqRHNycCh4gzBjzgYh8ntrglFLpw+mI07y+9HVm7Z5FtSLVmPfcPOqXqO/usJQLpKZj9qeOr92A0tjaSCfgMDDBGPNj6kJTSnk6EWHWrllU+bIKc4LnMLzpcLb03KIJJBNJzeOsasBYEfkmzr7jwM/GGH9gqjHmTxH5IlURKqU8UsjFEF5b9Bq/HviV+iXqM73ddKoVqebusJSLpSaJXMImjduIyHRjzCPYFRA1iSiVgcRKLF9t/Yq3fn+LqJgoxrYcy+sNXscri5e7Q1NukJokEoidiv2rOxx/OhXXV0p5mENnD9Hj1x4EHQ3ikbKPMLXtVMoXKO/usJQbpaZNZCrwoDHm9USOl0FXGlQqQ4iOjebTPz+l+qTqbD25lWlPTGP5i8s1gahU1URWANHAOGPMU9gayRbHvqbA68CQVEeolHKrXad24R/gz6bQTbSr3I4vW39JiTwl3B2W8hCpSSIfADWw06A0cWwS5/g24LwxphqwT0SiU3EvpZSLRUZHMnr1aEavGU1+3/zMfmY2Hat21AkT1S1SM2J9+PXvjTH5gFrcnFurFnY6lO+xiSXKGLMf2CkiL6Y8XKWUK2wI2YB/gD97Tu/hhQdeYPxj4ymUo5C7w1IeyCnrT4rIeWxDeuD1fcYYH2w34JrYpFILeMIZ91NKpY2IaxG8F/geE9ZPoESeEizqsojWFVu7OyzlwdJsjXURuQZsdWxKKQ+38q+V9Pi1B0fOHaF3nd6MaTGGPNnyuDss5eGS0ztrtjEmd/ydxpjKTozn+jV9jTEbjTE7jDF7jDEjEzinmTHmgjFmu2Mb5uw4lMoMwqPD6RHQg+bfNsfLeBH0UhCT2k7SBKKSJDmPs66vsf7k9R2ONdZnA0WdGxaR2FUTw40x3sAaY8wSEVkf77zVItLWyfdWKtNYsG8B/pv8ORd1jsEPDmZEsxFk987u7rBcLiYGzp+HCxfg4kW7hYff3C5fhitX7BYZCdeu2a9RUfa90dEQG2s3cXQvMsZuXl6QNavdvL3BxweyZbNb9uyQI4f9mivXzS1PHrvlzWs3Lw8ex5nkJCIi440xjY0xQ0RkjGON9U9IgzXWHWuYhDteejs2SfwdSqnk+DfiX/ot6cfPe36mXM5yLH1pKXXvqevusJwmJgZOn4aTJ+32zz/w779w6pT9euDAA4hAWBicPWuTRlJ5edkE4ONjk0LWrHZflix2u955TcRuMTF2i4qy2/UEFBub9HvmzQsFCkDBgnYrVAgKF4YiRexWrBgUL263IkVcm3Q8do11Y4wXdtxJBWCiiGxI4LRGxpgd2EGNg3S9d6XuTET4YdcPvL70dcKvhTPKbxQNohukuwQSHg5Hj8Jff8GxY3Y7fhxOnICQEAgNtR/c8eXKZT98s2XLStmycP/99sM5f3675c17sxaQO7c9P2fOm7WF7Nlt0nCG6Ghbs7l82W4REbZcly7Z7eJFWzs6f94muuvbmTNw4IBNkuHht1/Xy8smlZIloVQpu5UuDTEx+WnWzDmxx2VEEv8D3xizHsca68D1Nda9ceEa647uw/OBfiKyO87+PECs45FXa+AzEamYwPt7Aj0BihYtWmf27NnxT0my8PBwcuXKleL3pzeZrbyQsct86uopxh8cz4azG6iapypvVXqLe3Pe67FlvnIlCyEhOThxIjshITkICclOaKjdzp3zueVcb+9Yiha9SuHCkTe2QoUiKVjwGgULXqNAgWvky3cNX1/757+nljm5rl7NwvnzPpw960NY2PUtG6dPZ+PMGR/+/deXf//NRmSkF7Vq/cu4ccEpuo+fn98WEUnwL407JhGARNZYrwEUAVyyxroxZjgQISKf3uGco0BdETmT2Dl169aVzZs3pziOoKAgmqVFKvdQma28kDHLHCuxTNk8hcHLBxMrsYx+ZDR96/e9MWGiu8t86RLs2WO33bshOBj27bM1i7hKloQKFexWrhyULWu3MmXsI5zkjIF0d5ld6fpju5Ur19GxY6MUXcMYk2gS8cg11o0xhYEoETlvjMkOPAqMiXdOMeCUiIgxpj62p1mYs2NRKj07GHaQ7r92Z9WxVTxa7lGmtp1K2fxl3RKLiH3stH07bNsGO3fCjh32kdR12bPDffdB48b2UVPlynarUME+UlLJZ4xtQylSJDJNru+pa6wXB75xtItkAX4WkYXGmN6Oe08GOgCvGmOigStAJ7lbtUqpTCI6Nppx68YxPGg4vll9md5uOq/UfMVlU5aI2PaJjRth82bYsgW2brXP9ME2QFeqBPXqgb8/VK8OVavamkWW1EwLq1wuNcvjPiciPzkzmOscgxprJbB/cpzvv0DXKlHqNjv+2YF/gD9bTm7hqfueYmLriRTPXTxN7xkeDps2wbp1sH69TR6nTtlj3t42STzzDNSuDbVq2ddas8gYUtPPYKYx5h1gmIgsiH/Q8bgrj4gcTMU9lFJJFBkdyahVo/ho7UcUyF6Anzv8TIcqHdKk9nHyJKxeDWvWwNq19hHV9S6rlSvDY49Bgwa2pvHAA7ZLrMqYUpNEymOnev/RGLMHeE9ElsU53gkYB3jwMBmlMoY/T/xJ94Du7D2zl5dqvMTYlmMpmKOg065/4gQEBdlt1So4dMjuz5EDGjaEd9+FRo1s4ihQwGm3VelAapLIZezaIceAusBiRzIJA3JiG933pjpCpVSiwq+F8+6Kd/m/jf9HqbylWPL8Eh6v8Hiqr3v6NKxcCStW2K+HD9v9+fNDkybw6qvw8MNQs6Z9XKUyr9QkkWnY5W/XYad8Bzv9SQvs6PKlwBupik4plajfD/9Oz4U9OXr+KH3r9WV089Hkznbb9HZJEhlpH0v99pvdtm2z+/PkgWbNoG9f8POzbRna8K3iSk0SaQ58LiID4+40xjQBpmBrJ8kY2K+USopzV87x5m9v8vX2r6lUsBKrX1lN49KNk32do0dh8WL4/vtq7NhhR01nzQoPPQSjRsGjj0KdOs4boa0yptT+ePwVf4eIrDLG1AVWATOAh1N5D6WUw7y98+izuA+nI04ztPFQhjUdhm9W3yS9Nzoa/vwTFi6ERYvsoD6A4sVz8vLL8PjjttaRO2WVGZVJpSaJ/AG8YIyZ7Fg75AYRiTDGTAPGpio6pRQA/4T/Q9/FfZm7dy41i9VkcZfF1Cp+Wy/424SHw9KlEBBgE8fZs7YNo0kT6N4d2rSBv//egJ9fs7QugsqgUpNE3gfWA38YY/qJSPz5RB7ENrwrpVJIRPh2x7cMXDaQy1GXGf3IaAY9OAhvr8Rbs8PCbNKYP9+2b0RG2h5TbdpAu3bQsqVt67guNNQFBVEZVmpGrG8zxrwMTAc2GGMOAZuwvbNqYB9jLXRGkEplRsfOH6PXwl4sO7yMh0o9xFftvuK+QvcleO7p0zBvHsyZA4GBdgbb0qWhd2948kk7jYi2bai0kKofKxGZ5ZjpdwB2/fQucQ5vBPqm5vpKZUaxEsukTZN4e8XbiAj/1+r/eK3ea2Qxt3aLCguDuXPhf/+z3XBjY6FiRXjrLejQwY4Od9EsJyoTS/XfJiLyF/A68LoxJj9QDDgvIidTe22lMpv9Z/bT/dfurDm+hpblWzK17VTuzXfvjeOXLsGCBTBrln1UFR1tE8fQofDss3Z0uCYO5UpOreCKyDngnDOvqVRmEBUTxdh1YxkRNIIc3jmY2X4mXWt0xRhDVJRNGN9/bxPIlSt2oaGBA6FzZzvgTxOHchd9SqqUm207uQ3/AH+2/bONZ+5/hi9af0HRnMXYtg2+/RZ+/NG2eRQoAC+9BM8/Dw8+qIP+lGfQJKKUm1yNvsr7f7zPx2s/plCOQsztOJfGBZ/m+6kwcybs2mXX8X7iCXjxRWjVyr5WypNoElHKDdYeX4t/gD/7w/bT9YGXeZxxfDs0P88tsu0c9evDl1/Cc8/phIbKszkliTiW0C0F/BN/4KFS6qZLkZd4Z8U7TNw0kRK57qVz1G/83qcF3560S7wOGACvvAJVqrg7UqWSxlk1kQLYKVBaACuddE2lMpRlh5bR89eenLh4glKh/Tg+80N+is5Fq1Y3R4/rjLgqvXHm4yztH6JUAs5eOUuv+W8w5+A3ZD13HzJvDcKDjHgHunWzPa2USq+0TUSpNBIbK4z831zG7OpDZJazsPZdmmf/D30m+tK6NXjpcm0qA9AkopSThYfDFzNPMnpHHy6VnI/X2Tq8nOc3hn1Vg7Jl3R2dUs6VoiTiWDMkrryOrw8YY26ZdFFEVqXg+r7YqeSzOWKcIyLD451jgM+A1thVFl8Wka3JvZdSznL0KHz+f8LkdTO50uQNTPGrPJv/I2a89Sa5cujfaypjSulPdhB29cL44k79bhznpKTSHgk8IiLhxhhvYI0xZomIrI9zTiugomNrAExyfFXKZUTsioATJsC8wL+gbU/kseXUyPcwPz3/FZULVXJ3iEqlqZQmEb94r/MB84G3gC2pCQhARAQId7z0dmzxk1Z74FvHueuNMfmMMcV1zi7lCtHRdtbcsWNh46YYsjedSNZ+Q/HxycLHLSbSu27v2yZMVCojSlESEZE/4r42xhR0fLs9/rGUMsZ4YRNSBWCiiGyId0oJ4ESc1yGOfZpEVJqJiIAZM2DcOPv46t46eyn7gT9/Ra+jVYVWTG47mdJ5S7s7TKVcxtg/5FN5EZtETgOPiohTx4kYY/Jhazn9RGR3nP2LgP+KyBrH6xXAYBHZEu/9PYGeAEWLFq0ze/bsFMcSHh5Orly5Uvz+9CazlRcSL/P5897Mm1eCBQtKcPGiN9UeOE3RZ95nFVPI7pWdPhX60KJIC0w6nAlR/58zh9SU2c/Pb4uI1E3woIikegMKArHYdgynXDPe9YcDg+LtmwJ0jvN6P1D8TtepU6eOpEZgYGCq3p/eZLbyitxe5qNHRfr1E8meXcQYkSefFJm+ZLM8MOkBYQTS8X8d5VT4KfcE6yT6/5w5pKbMwGZJ5HPVIx/aGmMKO2ogGGOyA48C++KdFgB0NVZD4IJoe4hykn374OWXoUIFmDwZOnWCrTuvUOm1IfTc2IDTEaeZ/9x8furwE0VyFnF3uEq5jbP6HZ4FygL/OOl6xYFvHO0iWYCfRWShMaY3gIhMBhZju/cewnbxfcVJ91aZ2KFDufjiC9to7usLffrAm2/CX7Gr6BjQnYNnD9K9Vnc+afkJ+XzzuTtcpdzOKUnEUd055oxrOa63E6iVwP7J8e7Zx1n3VJnb5s3wwQcQEFCXPHnsSoEDBkC2PBd5e/nbTNo8ibL5yrL8xeU0L9fc3eEq5TF0BJTK1DZuhJEjYfFiyJ8fXn75L8aPL0u+fLD44GJ6fd+Lvy/+zYAGAxj1yChy+uR0d8hKeRSPbBNRKq1t2mRnzW3QANavhw8/tF12X3rpGNE+Z3hx/ou0+bENebLl4U//Pxn/+HhNIEolQGsiKlPZvh2GD4eAALvY0+jR0Lcv5M5teyqu/HclHSd25NzVcwxrMox3Hn6HbFmzuTtspTyWJhGVKezdC8OGwZw5kC+fbf/o3x/y5LHHQy+F8tqi11iwfwF176nL8nbLeaDoA26NWan0IMlJxBjzgKPBW6l04+hRGDECvvsOcuSA996DN96wiQRs7WP6tukM+m0QkTGR9CrXiy+e/4KsWfTvK6WSIjm/KbONMQ1E5FLcncaYyiKy38lxKZUqp07BqFEwZYpdt2PgQBgyBAoXvnnO4bOH6fFrDwKPBtL03qZ81e4rQnaGaAJRKhmS07A+Dfgu7g5jjB92ynalPMLFi7a2Ua4cTJpk1ys/dAg+/fRmAomJjWH8uvFUn1SdzaGbmdxmMitfWkmFAhXcG7xS6VCS/+QSkfHGmMbGmCEiMsYY0xX4BHgh7cJTKmmuXbMjyz/4AM6cgY4dbU2kYsVbz9vz7x78A/zZ8PcG2lRsw+S2kymZp6R7glYqA7hjEjHGdAR2Avsdg/teATYZY6oATbBzZe1J+zCVSpgI/PyzHRz411/wyCMwZgzUjTdV3LWYa3y05iNGrRpFXt+8/Pj0j3Sq1ildTpiolCe5W03kDaAadiHBYGAHsB5oATQTkQNpHJ9SiVq92k5JsmkTVK8OS5bAY49B/Lyw6e9NdAvoxu5/d9O5Wmc+e/wzCucsnPBFlVLJcsc2ERFpCOQG6mBXLTwDFMWuWrjXGHPQGPNzmkepVBwHD8LTT0OTJhAaCl9/Ddu2weOP35pALkdd5q3f3qLh9Iacu3KOgE4B/PjMj5pAlHKiu7aJOB5j7XNsNxbjMMYUBWoD2pleucS5c/D++/DFF5Atm23/eOMN23U3vqCjQXQP6M7hc4fpVacXYx4dQ17fvK4PWqkMLjV9GZuKyM/AEmcFo1RCoqNtV93hw+HsWfD3twmkWLHbz71w9QKDfx/M1K1TKZ+/PIEvBdKsTDOXx6xUZpGaJPKjMSa/iExxWjRKxbN8uZ1Nd88e8POD8eOhRo2Ez/11/6/0XtSbf8L/YVCjQYz0G0kO7wSqKUopp0nNBIwzgS+NMe8mdNAY08gYszoV11eZ2OHD8OST0KIFXL0K8+fDihUJJ5DTEafpMrcL7Wa3o2D2gqz3X88nLT/RBKKUC6S4JiIi3Y0xp4EPjDGFRGQg2BHswH+B9sAV54SpMouICDuj7tix4OMDH33kWNcjgTkQRYRZu2fRf0l/LkZeZGSzkbzd+G18vHxcHrdSHi8mJk0um6r5HURkqDHmFDDWGFMYCAe6AYJdA/391IeoMoPr4z3efBP+/htefNEmkHvuSfj8kIshvLroVRYeWEiDEg2Y3m46VYtUdW3QSnmq6GjYtQs2bLBrHWzYQNUiRaC58xdUc8YkQdOANkAXbPKYDbwnIkeccG2VCQQH2+nYAwOhVi346Sd46KGEz42VWKZtmcZbv79FjMQwruU4+jfoj1cWL9cGrZQnCQm5JWGweTNccTwIKlIEGjTgXLlypEXn9hQnEWOMN/AaMBQoDGwFagLewAlnBKcytvBwu6rghAl2PY8vv4SePe2EiQk5GHaQHr/24I9jf9C8bHOmPjGVcvnLuTRmpdwuIgK2bLmZMDZssNV3sM+Aa9e2v0gNG9pV18qUAWMIDQqiUhqEk5qayEGgFBAM+IvIIsc0Kd8Ci40xT4lIuDOCVBmLCMybZ9s6QkJsl93//vfWGXbjio6NZsL6CbwX+B7ZvLLx1RNf0a1WN52yRGV8sbGwf/+ttYxdu262b5QvD02b2mTRsKHteZJQA2IaSk0S8QJ6ADNFJBZARH42xpwH5gKBxphWInIm9WGqjOLwYfvoaulS+/P+88/QqFHi5+86tQv/AH82hW6ifeX2fNnmS+7JnUhDiVLp3enTN2sXGzbAxo1w4YI9liePTRZDh9qEUb9+4n95uVBqkkhFEbkaf6eI/GaMeRRYBPwJya9BGWNKYWs0xYBYYKqIfBbvnGbAAuAvx655IqIN+R4qMtJOxz5qFHh720dYffpA1kR+AiOjIxm9ejSj14wmv29+Zj8zm45VO2rtQ2UckZGwY8fNGsb69XDE0ZScJQs88AB06nTzsVTlyna/h0lNF9/bEkicYxuMMQ8Dy1J4+WjgTRHZaozJDWwxxvwuIsHxzlstIm1TeA/lIqtXQ69edonaZ5+1CSSxXlcA60PW4x/gT/DpYF544AUmPDaBgjkKuixepZxOxC6zGfex1Natdg0DsL8QDRvaX5QGDew01DlzujXkpEqzJdxEZK8xJpE+Nnd970ngpOP7S8aYvUAJbPuLSifOnoXBg2H6dNu2t3gxtGqV+PkR1yJ4L/A9JqyfQMk8JVnUZRGtK7Z2WbxKOc2FC3Z66euPpdavt4+qALJnt0mif/+btYyS6XdNG2PnV0zCicY0F5EVKbqJMY+KyPIUvrcMdvXEaiJyMc7+Zti2lxAgFBiU0NomxpieQE+AokWL1pk9e3b8U5IsPDycXLlypfj96U1KyysCgYFF+OKLCly44E3Hjid46aWj+PrGJvqeree2MvbAWEKvhtL+nvb0KNuDnFld/5dYZvs/Bi1zqsXEkPPoUfIEB5Nn717yBAeT4/hxjOOzNaJ0aS7dfz8XHVtEuXJIYs9x01Bqyuzn57dFROomeFBEkrQBUcBKoC3glYTzvYGngD+Aa0m9T7xr5AK2AE8ncCwPkMvxfWvg4N2uV6dOHUmNwMDAVL0/vUlJeY8dE2ndWgRE6tYV2bbtzuefu3JOui/oLoxAKn5eUf44+keKYnWWzPZ/LKJlTra//xaZN09kyBCRpk1Fcua0P/AgUrCg/QUYOVJk2TKRs2edFXKqpabMwGZJ5HM1OemwJjAeCADOGGN+BzYCh4Gz2DVGCgAVgYbAI47XyxzvTRbHOJS5wA8iMi/+cYlTKxGRxcaYLx3Tr2hvMDeIjbXjPN5+2/42jR8P/folPuYDYMG+Bby66FX+jfiXIQ8NYXjT4WT3zu66oJW6mytX7JiMuG0ZJxzD4Ly9oWZN6NbNPpJq0MB2uc1knT+Sk0SexT4WKo4dZNge6IwdpR6XAS4C84BJIrIpuUEZ2wVnOrBXRMYlck4x4JSIiDGmPnYyybDk3kul3r590L07rF1rVxacPNm2gSTmVPgp+i/tz897fqZG0Rr82vlX6txTx2XxKpWg2Fi74lnchLFzp51CBOwP9YMP2mTRqJFNIL6+7ozYIyQniQwDDojIj8A6Y0wH4DhQBTtiXYDTwG5gmzjGjqTQQ8CLwC5jzHbHvneA0gAiMhnoALxqjInGTvTYyVHtUi4SFWW77Y4YAblywbffwgsvJP6HmIjww64feH3p64RfC2eU3ygGPzQYby9vl8atFGB7fsRt+N640a58BvYHun592zPkei2jaFH3xuuhkpNEzgFx59b+CXhRRGY6NSJARNZgazR3OucL4Atn31slzY4dtha/dSt06GBXG7zT79jxC8fpvbA3Sw4toVHJRkxvN537C9/vuoBV5nbtmq1VOBJG/aAgO10C2LEX1arZH+TrCeP+++/8LFbdkJwkshvwN8YsEZG/ucuHvMqYrl2D0aPtdO0FCsCcOfDMM4mfHyuxTNk8hcHLByMifP7457xW7zWdMFGlHRHbbhF3EN/WrXZhGoBixbhcvjw5+vSxXWzr1rU1D5UiyUkiI7FL4R43xhzEPr5qbYw5B2wVkVNpEaDyHNu3w8sv21rI88/DZ59BwTuMATwQdoDuAd1ZfXw1Lcq1YOoTUymTr4yLolWZxqVLdtbauI+m/vnHHvP1hTp14LXXbs4vVaoUu//4g2bNmrk17IwiyUlERFYaY6oD3bFtFpWw0793BnCsK7IV2Hb9q4gcdXbAyvWiouwEiR98AIUKwYIF0K5d4udHx0Yz9s+xDA+yva1mtJvByzVf1ilLVOrFxNipD+I2fu/ZYxvFASpWtMthXn8sVaOG7UWl0kyyRryIyAFgMIAxJhZ4CzgC1AFqAbWxYzbEcc45ESnkzICVa+3ZA1272qcBXbrA55/fufax458ddAvoxtaTW3nqvqeY2HoixXMXd13AKmM5derWGsamTbbmAZA/v00UTz99c0LCAgXcG28mlJphk+9j567aCMy/vtMYUxybTOqQgvEhyjPExMCsWaWYORPy5oW5c+3vamKuRl9l1KpRjFk7hoLZCzLn2Tk8U+UOjSVKxXf1Kmzbdus6GUeP2mNZs9oJCV988WYto1KlTDcmwxOlZgLGEYnsP4mdwXdRSq+t3OvwYXjpJVi7tjxPPw2TJtnF0RLz54k/8Q/wZ9+ZfXSt0ZXxj42nQHb9i1DdgYj9QYv7WGr7dvvsFKB0aZso+va1tYzate2cU8rjuH4CF+WxRGDaNHjjDfuH3zvv7GXUqPsT/WMv/Fo47654l//b+H+UyluKpc8v5bEKj7k2aJU+nD9vx2HETRphjrHBOXPaHlJvvHGzlnGnaZ6VR9EkogD76Ll7d1i4EJo3h6+/hsOHT2FMwmM5fj/8Oz0X9uTo+aP0qdeH/zb/L7mz5XZx1MojRUfb1ffiPpbat88eM8aOwWjXztYwGjaEKlUSX1hGeTz9n1MsWGATSHi47bbbt68df3X48O3nnrtyjjd/e5Ovt39N5YKVWf3KahqXbuz6oJXnCAm5tYaxebOdcwrsynsNG9qpDBo0gHr1bCObyjA0iWRi4eEwcCB89RXUqgXff2//KEzMvL3z6LO4D6cjTjO08VCGNR2Gb1adOyhTiYiwExLGHcgXGmqP+fjYtouePW+OyShTRhu/MzhNIpnUxo12wODhw3bm3ZEj7WdAQv4J/4d+S/oxJ3gOtYrVYnGXxdQqXsu1ASvXi42F/ftvfSy1a5ftugd2xtpmzW4urFSjBmTL5taQletpEslkYmLgo49g+HAoUQICA6Fp04TPFRG+2f4NA5cN5HLUZUY/MppBDw7SCRMzqtOnbx+TceGCPZY3rx2HMXTozTEZhQu7N17lETSJZCInTthH06tWQadOtutuvnwJn3v0/FEG7xrM5nObaVy6MV898RWVC1V2abwqDUVG2i61GzZwf0AA+PvDkSP2WJYsUL26/SG5XsuoXNnuVyoeTSKZxNy5tvE8Ohq++caO2UroUXWsxDJx40SGrhhKbGws/9fq/3it3mtkMfoBkm6J2EF7cdsxtm2zs2kC+QoVgiZNoFcvmzTq1LHdbpVKAk0iGdzly7bxfOpU2zHmxx+hQoWEz913Zh/+Af78eeJPHiv/GC8XeplO9Tu5NmCVehcu2EdRcXtMnT5tj2XPbsdkvP76jTEZ6w4d0skIVYppEsnAdu2C556z89UNHmwnUEyo8TwqJopP/vyEkX+MJKd3Tma2n0nXGl35448/XB+0Sp7oaDvBWdy2jL17be0D4L77oE2bm4P4qlW7fULCQ4dcH7fKMDSJZEAiMGWKrYHkzQu//WYnNk3I1pNb8Q/wZ/s/2+lQpQNftPqCorl0BTePFRp6+5iMiAh7rGBBmyiee85+rV/fTlKoVBrSJJLBnD8PPXrYxaIee8y2fyS04uCVqCu8/8f7fPLnJxTOWZi5Hefy9P13mGFRud7ly3b65Li1jBMn7DFvb7vG9yuv3Bz5Xa6cjslQLqdJJAPZuNH+ERoSAmPGwKBBCXeoWXN8Df4B/hwIO8ArNV9hbMux5M+uf7G6VWwsHDx4ay1j5077uArsoL0HH7zZW6pWLbvgklJupkkkAxCBCRNgyBA7b93q1fazJr5LkZcYumIoEzdNpEy+Mvz2wm+0KJ/Icy6VtsLCbNaPO5Dv/Hl7LHdu+yhq8OCbYzLutIC9Um7kkUnEGFMK+BYoBsQCU0Xks3jnGOAz7CJYl4GXRWSrq2N1t3Pn7JK1AQHw5JMwY0bCj8GXHFxCr4W9CLkYQv/6/fmw+Yfk8tF1pV3i2jVbq4hbyzh40B7LkgWqVoVnn73Z+H3//eCla9Cr9MEjkwgQDbwpIluNMbmBLcaY30UkOM45rYCKjq0BMMnxNdPYuBE6drRtrRMmQP/+tz8SD7scxsBlA/lu53fcX+h+1nZbS6NSjdwSb6YgAseP31rD2LrVLrgEUKyYTRTX2zLq1rU1D6XSKY9MIo6FrU46vr9kjNkLlADiJpH2wLciIsB6Y0w+Y0xxx3szNBH4v/+zbR733ANr1tgnHreeI8wJnkPfJX05e+Us7zV5j3cffpdsWXVuI6e6dMn2kLpey1i/3s6rD7bNonZteO21m7WM0qW18VtlKEau9yf3UMaYMsAqoJqIXIyzfyHwkYiscbxeAQwRkc3x3t8T6AlQtGjROrNnz05xLOHh4eTK5d5HQBERXnzySWX++KMIDz54hrff3kfu3NG3nBMWGcaEgxNYE7aGSrkqMbjyYMrnKp/se3lCeV3tjmWOiSHn8ePkDg4mz9695AkOJuexY5jYWAAulyzJxfvvt1uVKkSUL4+kg3Uy9P85c0hNmf38/LaISN0ED4qIx25ALmAL8HQCxxYBjeO8XgHUudP16tSpI6kRGBiYqven1s6dIhUrinh5iXz8sUhs7K3HY2NjZfrW6ZLvo3ziO8pXPl7zsUTFRKX4fu4urzvcUuZ//hFZsEBk6FCRRx4RyZ1bxFYERfLlE3nsMZHhw0WWLBE5c8ZdIadapv9/ziRSU2ZgsyTyueqxfyYZY7yBucAPIjIvgVNCgFJxXpcEQl0Rmzt8952d2ihvXli50k51FNdf5/6i58KeLD+ynCb3NmHaE9OoVLCSe4JNj65ehW3bKPm//8Hkyfax1LFj9ljWrHaa8xdfvLlORsWK+lhKKTy0TcTR82o6sFdExiVyWgDQ1xgzG9ugfkEyYHtIZKSd5mjKFLt0w6xZtm32upjYGCZushMmehkvJrWZRM86PXXCxDsRsQupxG383r4doqKoAFCqlE0U/frZpFGnjp1zSil1G49MIsBDwIvALmPMdse+d4DSACIyGViM7d57CNvF9xXXh5m2jh2DDh1su+2QITBq1K1LUQefDqZ7QHfWhayjVYVWTGk7hVJ5SyV+wczq/Pnbx2SEhdljOXPamSnfeAMaNuTPmBgefOYZt4arVHrikUlEbGP5HZ8VOJ7T9XFNRK73++/QuTNERcEvv0D79jePRcVEMWbtGD5Y9QG5fXLz3VPf8Xz15zH6eMX+g+3adetUIfv322PG2DEY7dvfHPldteotYzKuBQW5J26l0imPTCKZmYhdefDdd+3n27x59vH7dVtCt9AtoBs7T+2kU7VOfPb4ZxTJWcR9AbtbSMitNYzNm+HKFXusSBGbKF580SaNevUgTx73xqtUBqNJxINcvGhHn8+fb2sh06bdXBvoStQVRgSN4NN1n1IsVzF+ee4X2t/X/o7Xy3AiIm4dk7Fhgx1pCXaO+9q1oWfPm7WMMmW08VupNKZJxEPs3QtPPWWXdhg/3jamX//8W3VsFd0DunPw7EG61+rOJy0/IZ9vPrfGm+ZiY2HfvlsfS+3ebReJByhfHvz8bg7iq1EDsulASqVcTZOIB/jlF+ja1Q5wXr7c9sICuBh5kbeXv82kzZMol78cK7qu4JGyj7gz1LRz5sytNYyNG+0KfWD7NdevD++8c3OdjMKF3RuvUgrQJOJWsbEwYoRdcbBePbsOeilH56rFBxfTa2EvQi+F8kbDN3jf731y+mSQda8jI22X2rhJ48gRe8zLC6pXh06dbo7JqFw54TntlVJup0nETS5csO29v/5q20EmTbI1kTOXzzBg6QB+2PUDVQpXYc6zc2hQMh3PKykCR4/eTBbr18O2bXZmW4ASJWyi6N375piMnBkkWSqVCWgScYP9+20v08OH7USKffoACD/t/pl+S/px/up5hjcdztDGQ9PfhIkXLsCmTbfWMk6ftseyZ7ez1vbvf7Pxu2RJ98arlEoVTSIutnix7Xnl42PbP5o2hdBLoby66FUC9gdQ7556TG83nepFq7s71LuLjoY9e25t/N6719Y+AO67D9q0udn4Xb36raMllVLpnv5Gu4gIfPwxDB1qOxL98guULi18tXU6g34bxLWYa3za4lMGNByAVxYPXZAoNPTWGsbmzbbbLUDBgjZRPPccNGpkG3ny5XNruEqptKdJxAWuXIHu3eHHH+1n7IwZcPLqYZp/24PAo4E0K9OMaU9Mo0KBCu4O9abLl8m7a9fNcRkbNsCJE/aYtzfUrAndut2sZZQvr2MylMqENImksb//tsvWbtkCH34Ig4fE8PnGz/jPyv/g7eXNlLZT6FG7h3unLImNtcu1xm383rmTWtfHZJQpAw89dDNh1KplewEopTI9TSJpaONGm0AuXbKPr8o13M1DX/uz8e+NPFHpCSa1mUSJPCVcH1hY2K0TEm7caBdrB7tUa716MGQIu3LmpLq/PxQt6voYlVLpgiaRNPLjj/ZpT/HisGjpNQLO/pcOUz4kr29efnz6RzpV6+Sa2se1a7Bz561tGQcP2mNZskC1anaq4OtjMu6778aEhGFBQZpAlFJ3pEnEyWJjYdgw++iqSRP4z5eb6LqqG7v/3U2X6l347PHPKJSjUNrcXASOH791QsItW+zgPrALkTRoAP7+9mvdupDJlghVSjmXJhEnioiw05fMmwcv97hMvqeG8fjc8RTPVZxfO/9K20ptnXvDS5dsw3fctoxTp+wxX187cK9Pn5tjMkqV0sZvpZRTaRJxkr//hnbt7Gwer30cxLJs3Tm88TC96vRizKNjyOubN3U3iImxYzDiPpbas8dWfcDOF9+ixc2EUaOG7UWllFJpSJOIE2zZYhPIxcgLtPx8MF+emUr5bOUJfMl2302Rf/65+UhqwwY7CvzSJXssf36bKJ5++maPqQIFnFYepZRKKk0iqTRvHrzwAuSq8ys52vbmt7B/eOvBtxjRbAQ5vHMk7SJXr9r5pOI+ljp2zB7LmtXWKq4vrNSgga116GMppZQH0CSSQiLwyScwZORpCr74OqfvmUX1PNVZ2O4X6pWod+c3Hjp061QhO3bYZV0BSpe2iaJfP5s0ate2c04ppZQH0iSSAlFR0PtVYcbGWfi80Z+LPhd5v8n7DGk8BB8vn1tPPnfOjsOI+2gqLMwey5nTjsl4882bj6WKF3d9gZRSKoU8NokYY2YAbYF/RaRaAsebAQuAvxy75onI+2kd1/nz0KZzCH/mfxWeWUitEg2Y3m46VYtUtRMSxn8stX//9YChShU7fe/1MRlVq94Yk6GUUumRxyYRYCbwBfDtHc5ZLSJO7jebuL9Dfeg8dgr/1HoLH98YxtQfRr9LVfD6ZObNCQmvXLEnFy5sk0XXrvZrvXqQJ4+rQlVKKZfw2CQiIquMMWXcHcd1cxfvoP/KVzlbdycPny3MzHmGcsMdFZ9s2ex8Uj173mz8LlNGG7+VUhmexyaRJGpkjNkBhAKDRGRPWtxk3ndzeWF/B7IVhq8WQLdLeTANGkIfRztGzZp2gRCllMpkjFxfQMgDOWoiCxNpE8kDxIpIuDGmNfCZiFRM4LyeQE+AokWL1pk9e3ay44i+eo0pM/9Dx1JNuadxY6LypnLgYDoRHh5Orkw2LYqWOXPQMiePn5/fFhGpm9CxdJtEEjj3KFBXRM4kdk7dunVl8+bNKY4nKCiIZs2apfj96U1mKy9omTMLLXPyGGMSTSJZUhOUOxljihnHNLjGmPrYsoS5NyqllMpcPLZNxBgzC2gGFDLGhADDAW8AEZkMdABeNcZEA1eATuLJ1SqllMqAPDaJiEjnuxz/AtsFWCmllJuk28dZSiml3E+TiFJKqRTTJKKUUirFNIkopZRKMU0iSimlUsyjBxs6mzHmNHAsFZcoBCQ6mDEDymzlBS1zZqFlTp57RaRwQgcyVRJJLWPM5sRGbWZEma28oGXOLLTMzqOPs5RSSqWYJhGllFIppkkkeaa6OwAXy2zlBS1zZqFldhJtE1FKKZViWhNRSimVYppE4jHGPG6M2W+MOWSMeTuB48YY87nj+E5jTG13xOlMSSjz846y7jTG/GmMqeGOOJ3pbmWOc149Y0yMMaaDK+NLC0kpszGmmTFmuzFmjzHmD1fH6GxJ+NnOa4z51Rizw1HmV9wRp7MYY2YYY/41xuxO5LjzP79ERDfHBngBh4FygA+wA6gS75zWwBLAAA2BDe6O2wVlfhDI7/i+VWYoc5zzVgKLgQ7ujtsF/8/5gGCgtON1EXfH7YIyvwOMcXxfGDgL+Lg79lSUuQlQG9idyHGnf35pTeRW9YFDInJERK4Bs4H28c5pD3wr1nognzGmuKsDdaK7lllE/hSRc46X64GSLo7R2ZLy/wzQD5gL/OvK4NJIUsrcBZgnIscBRCS9lzspZRYgt2OBu1zYJBLt2jCdR0RWYcuQGKd/fmkSuVUJ4ESc1yGOfck9Jz1Jbnn8sX/JpGd3LbMxpgTwFDDZhXGlpaT8P1cC8htjgowxW4wxXV0WXdpISpm/AO4HQoFdwOsiEuua8NzC6Z9fHrsolZuYBPbF776WlHPSkySXxxjjh00ijdM0orSXlDJPAIaISIxjFeb0LillzgrUAZoD2YF1xpj1InIgrYNLI0kp82PAduARoDzwuzFmtYhcTOPY3MXpn1+aRG4VApSK87ok9i+U5J6TniSpPMaYB4CvgFYikt7Xsk9KmesCsx0JpBDQ2hgTLSK/uCRC50vqz/YZEYkAIowxq4AaQHpNIkkp8yvAR2IbDA4ZY/4C7gM2uiZEl3P655c+zrrVJqCiMaasMcYH6AQExDsnAOjq6OXQELggIiddHagT3bXMxpjSwDzgxXT8V2lcdy2ziJQVkTIiUgaYA7yWjhMIJO1newHwsDEmqzEmB9AA2OviOJ0pKWU+jq15YYwpClQGjrg0Stdy+ueX1kTiEJFoY0xfYBm2Z8cMEdljjOntOD4Z21OnNXAIuIz9SybdSmKZhwEFgS8df5lHSzqevC6JZc5QklJmEdlrjFkK7ARiga9EJMGuoulBEv+fPwBmGmN2YR/1DBGRdDu7rzFmFtAMKGSMCQGGA96Qdp9fOmJdKaVUiunjLKWUUimmSUQppVSKaRJRSimVYppElFJKpZgmEaU8lDFmgzGmk7vjUOpONIko5YGMMVmAatjutkp5LE0iSnmmytjfz/3uDkSpO9EkopRnqgkEi0gMgDFmoDFmnzGmplujUioeHbGulGeqCewwxuQFvsb+rjYUkfPuDEqp+LQmopRnqolNHJuAzUB7TSDKE+m0J0p5IGPMP45vfxeRF90ajFJ3oDURpVzIGFPLGDPfGHPOsc0xxhQwxtxjjLlqjOlsjCkGFMVOpPewMeYl90atVOK0TUQpFzHGdAa+wXbbHQmUBfpjpyPPChwEfsIulHRERPYZY9oCgcaYEyKy0j2RK5U4TSJKuYAxphwwA7uKXhMRuerYXxdoBZQBnheRWGNMDWAbgIjsNsY8D/xkjGkiIul5fQ+VAWmbiFIuYIz5DFvraCgiG+Ls/w54AdgK1BX9hVTpjLaJKOUa7YBDcRNIPO9pAlHpkSYRpdKYMaYA9nHVpgQOFwX2iMhilwallJNoElEq7RVzfA2Lu9MY0wRoEX+/UumJJhGl0t55x9ca13cYY3IBUxwvc7o6IKWcRZOIUmlMREKBjdgxH98ZY14FVgGFgKVALWPMAGNMcXfGqVRKaO8spVzAGHMv8AV2AGFWbBfebo7Dc4EqwH0iorP2qnRFk4hSSqkU08dZSimlUkyTiFJKqRTTJKKUUirFNIkopZRKMU0iSimlUkyTiFJKqRTTJKKUUirFNIkopZRKMU0iSimlUkyTiFJKqRTTJKKUUirF/h9rfoGzHyPTkQAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"plot_alpha(0,eta_ls=0.25,algorithm=\"newton\",alpha_max=1.0)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.4 Newton Step, $x^k = 0$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.4-Newton-Step,-$x^k-=-0$)",
"section": "3.6.3.4 Newton Step, $x^k = 0$"
}
},
"source": [
"**Discussion**\n",
"* Why does the line search fail?\n",
"* How could we modify Newton's method to improve robustness?"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.5 Steepest Descent Step, $x^k = 0$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.5-Steepest-Descent-Step,-$x^k-=-0$)",
"section": "3.6.3.5 Steepest Descent Step, $x^k = 0$"
}
},
"source": [
"### 3.6.3.5 Steepest Descent Step, $x^k = 0$"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.5 Steepest Descent Step, $x^k = 0$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.5-Steepest-Descent-Step,-$x^k-=-0$)",
"section": "3.6.3.5 Steepest Descent Step, $x^k = 0$"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Considering xk = 0 and f(xk) = 1.5\n",
"Step with steepest-descent algorithm:\n",
"pk = -6\n",
"With full step, xk+1 = -6 and f(xk+1) = 685.5\n",
"alphak = 0.4191919191919192 with backtracking line search starting at alpha = 0.5\n",
"f(xk + alphak*pk) = -2.9749848430038526\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZYAAAESCAYAAADe2fNYAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAABN9ElEQVR4nO3dd1yV1R/A8c8BQUTcIq5yZCIoKm7NRebeov1sqGVmNsxMy8qGZVaWe6RpllmuEneuUnDvbaJmjqTcG3Hi+f1xkBDZ914eLnzfr9fzutx7n/E9XuF7z3OW0lojhBBC2IuL1QEIIYTIXCSxCCGEsCtJLEIIIexKEosQQgi7ksQihBDCriSxCCGEsKtsVgeQERQsWFCXLFkyTcdeu3aNnDlz2jegDC6rlTmrlRekzFmFLWXevn37Oa21d0LvSWIBSpYsybZt29J0bFhYGA0bNrRvQBlcVitzVisvSJmzClvKrJQ6nth7citMCCGEXUliEUIIYVeSWIQQQtiVtLEk4vbt20RERHDjxo0k98uTJw/h4eHpFFXGkFnK7OHhQfHixXFzc7M6FCEyFadNLEqp74BWwBmtdYWY1wYBLwJnY3Z7T2u9JC3nj4iIIFeuXJQsWRKlVKL7Xb16lVy5cqXlEk4rM5RZa8358+eJiIigVKlSVocjRKbizLfCpgLNEnh9pNa6csyWpqQCcOPGDQoUKJBkUhHOSylFgQIFkq2RCiFSz2kTi9Z6DXDBkdeQpJK5yecrhGM4bWJJwmtKqT1Kqe+UUvmsDkYIITKi4cPhq698ccSSXMqZF/pSSpUEFsdpY/EBzgEaGAwU0Vp3T+TYnkBPAB8fn6qzZs267/08efJQpkyZZGOIjo7G1dXVhlI4n8xU5sOHD3P58uUk94mMjMTLyyudIsoYpMyZX8+eVXF3v8W4cXvTdHxQUNB2rXW1BN/UWjvtBpQE9qX2vfhb1apVdXz79+9/4LWEXLlyJUX7pafnn38+0ff27Nmjjx8/ft9rf/31l+7evbsODg5O0fkzYpnTKiWfc2hoqOMDyWCkzJnb6dNag9YvvPBXms8BbNOJ/E3NVLfClFJF4jxtD+yzKhZ76tevH/7+/rz44os0aNCA6OjoRPeNiooiT548hIaGMmDAgAcap7dv386RI0fue6106dJMmTLlvtdu3bpF/fr1uXPnjv0KIoTIEH7/3TxWq3bRIed32sSilJoJbAR8lVIRSqkXgC+VUnuVUnuAIKCvpUHawZEjR1i/fj379++ncuXKdOjQIcnbUDt27GDXrl0cPHiQoUOH4uHhAcD+/fvp1asXP/zwAyNGjKBXr16cPn060fO4u7vTqFEjZs+ebfcyCSGstXw5FCgAjz561SHnd9pxLFrrpxJ4eUoCrzmtgwcP8sQTT3Dnzh0CAwMBmDdvXuz7QUFBvPfeezRu3Jj333+fK1euUKpUKWrWrPnAjKX+/v5MnDiRqVOnUrJkyRRNPNeuXTveffddnnnmGbuWSwhhHa1hxQpo3Bgc1VTqtDWWrMDX15du3boxePBgNm/ezMmTJ4k7vf/HH3/MkCFDmD59Ojt37mTkyJHs37+fzz77jAMHDrB27doUXef8+fP06tWLnTt38vnnn8e+XqFCBbZu3WrvYgkhLLRnD5w6BU2bOu4aTltjSU9vvAG7diX8XnR0jjRl/cqVYdSo5Pfbu3cvbdu25dy5c+TNm/e+9+rXr4/WmhEjRhAWFoarqyuTJ08GYMiQIQme77nnnnvgtQIFCjBx4sQHXnd1dcXd3T1TjLQXQhjLl5vHJk3g0CHHXENqLBncH3/8Qfny5cmRI8cDDfF79+7l5MmTZM+e3WF/+G/evBnbTiOEcH7Ll0NAABQt6rhrSI0lBZKqWVy9et1hf9SvXr2Km5sbnp6eeHp6Eh0dzY0bN/Dw8ODkyZM888wzLFiwgNdff53ly5fT1M512/Pnz+Pt7S2TNAqRSVy7BuvWweuvO/Y6UmPJwPbt20eFChVinzdp0oR169YRFRVFhw4dGD58OH5+fnzwwQcMGjTI7tcPDQ2lRYsWdj+vEMIaYWFw65Zj21dAEkuGVrt2bX755ZfY56+99ho//PADnp6ebNy4kcaNGwOmrWXjxo12v/6MGTPo2bOn3c8rhLDG8uWQIwfUrevY60hicSKBgYEEBQUlOUDSXm7dukW7du3w9fV1+LWEEOlj2TJo2BAc3WwqicXJdO/ePV3m6XJ3d6dr164Ov44QIn0cPgx//gnpcXdbEosQQmQBS5eaR0ksQggh7GLJEvD1hdKlHX8tSSxCCJHJRUVBaGj61FZAEosQQmR6oaFw8yY0b54+15PEIoQQmdzSpeDpCfXrp8/1JLEIIUQmpjX8+is88QRkz54+15TEksHNmzcPpRQHDhyw6TwTJ05k2rRpAHz44Yf8fm+lHyFEpnbwIBw7ln63wUDmCsvwZs6cSd26dZk1a9YD07akZu35Xr16xf78ySef2DNEIUQGtmSJeUzPxCI1lgwsMjKS9evXM2XKFGbNmgVAWFgYQUFBPP300wQEBBAWFkaDBg148sknKVu2LO+88w7Tp0+nRo0aBAQE8NdffwEwaNAghg0bBpip8+fMmQPAypUrCQwMJCAggO7du3Pz5k1rCiuEcIglS6B8eShRIv2uKTWWlEhiQZYc0dFpW4YtBQuyzJ8/n2bNmlG2bFny58/Pjh07ANiyZQv79u2jVKlShIWFsXv3bsLDw8mfPz+lS5emR48ebNmyhdGjRzN27FhGJXKdGzdu8Nxzz7Fy5UrKli1L165dmTBhAm+88UbqyyOEyHCuXIE1a8yfsPQkNZYMbObMmXTu3BmAzp07M3PmTABq1KhBqVKlYverXr06RYoUIXv27DzyyCM0adIEgICAAI4dO5bo+Q8ePEipUqUoW7YsAN26dWPNmjUOKo0QIr2tWAG3b0Pr1ul7XamxpEQSNYvrDlpd8fz586xatYp9+/ahlCI6OhqlFC1atHhgPfvscbp6uLi4xD53cXHhzp07iV5Da233uIUQGceiRZA/P9Sunb7XlRpLBjVnzhy6du3K8ePHOXbsGCdOnKBUqVKsW7fObtcoV64cx44d4/DhwwD8+OOPNGjQwG7nF0JYJzratK+0aAHZ0rkKIYklg5o5cybt27e/77Xg4GBmzJhhl/MrpfDw8OD777+nU6dOBAQE4OLicl/vMSGE89q8Gc6dg1at0v/acissgwoLC3vgtddff53X460p2rBhQxo2bJjgcXHfi9tV+fz58+TPnx+ARo0asXPnTnuFLYTIIBYtMjUVR68WmRCpsWQx3bt3JyoqirqOXkJOCGGpRYugXj3Imzf9ry01lizmu+++szoEIYSDHT0Kf/wBL7xgzfWlxiKEEJnM4sXmMb27Gd8jiUUIITKZxYvNol5lylhzfUksQgiRiVy+bNZfsaq2Ak6cWJRS3ymlziil9sV5Lb9S6jel1J8xj/msjFEIIdLb0qVmtH280QrpymkTCzAVaBbvtXeAlVrrR4GVMc+d1unTp3n66acpXbo0VatWpXbt2sybNy/R/cPCwmiVSKf1kiVLcu7cuUSPHTVqFFFRUcnG1KNHD5un8BdCOM78+VCoENSsaV0MTptYtNZrgAvxXm4L/BDz8w9Au/SMyZ601rRr14769etz5MgRtm/fzqxZs4iIiHDI9VKaWL799lvKlSvnkBiEELa5edOMtm/TJm1z49qL0yaWRPhorU8CxDwWsjieNFu1ahXu7u73jYQvUaIEvXv35saNGzz//PMEBAQQGBhIaGjoA8efP3+eJk2aEBgYyEsvvRQ7L9i1a9do2bIllSpVokKFCsyePZsxY8bw77//EhQURFBQEAArVqygdu3aVKlShU6dOhEZGQmYQZf3Zln28vJi4MCBVKpUiVq1anH69GlH/7MIIZIQFgZXr0K7dtbGkWXHsSilegI9AXx8fB4Y6Z4nTx6uXr0KwIDQAew9uzfB82itUUql+voB3gEMDRqa6Pvbt2+nQoUKsTHENXbsWG7fvs2GDRs4dOgQ7dq1Y8eOHURFRXHnzh2uXr3KwIEDqV69Ou+88w7Lli1j0qRJREZGsmzZMry9vWPXd7l8+TJ58uRh+PDhLFq0iAIFCnDs2DE+/vhj5s2bR86cORk5ciSff/4577zzDtHR0dy9e5erV69y7do1KlWqxDvvvMMHH3zAuHHjePvtt1P9b2GlGzduJDjLQVyRkZHJ7pPZSJmd09dfP4qHR2Hc3NYTFnY32f0dVebMllhOK6WKaK1PKqWKAGcS21FrPQmYBFCtWjUdd1oUgPDw8NhZi93d3RNdqTE1qzjG5e7unuSsyB4eHvft8+qrr7Ju3Trc3d0pXrw4vXv3JleuXFStWpWSJUty8uRJPD09yZYtG7ly5WLTpk3MnTuXXLly0alTJ/Lly4eXlxc1atTggw8+4NNPP6VVq1bUq1cPMHOHeXl5kStXLlavXs3Bgwdp1sw0Yd26dYvatWuTK1cuXF1dcXFxIVeuXLi7u9OpUyeUUtSuXZvffvvNITM9O5KHhweBgYFJ7hMWFkb8/x+ZnZTZ+dy9C08/beYGa9KkfoqOcVSZM1tiWQh0A76IeVxgj5OOajYq0feuOmja/PLlyxMSEhL7fPz48Zw7d45q1apRrFixFJ0joZpU2bJl2b59O0uWLOHdd9+lSZMmfPjhh/fto7WmcePGseu/JMbNzS32Gq6urklO0S+EcKytW+HkSWjb1upInLiNRSk1E9gI+CqlIpRSL2ASSmOl1J9A45jnTunxxx/nxo0bTJgwIfa1e43r9evXZ/r06QAcOnSIv//+G19f3/uOj7vP0qVLuXjxIgD//vsvnp6ePPvss/Tv3z+2vSRXrlyxt91q1arF+vXrY6fTj4qK4tChQw4srRDCVvPnmwb7li2tjsSJayxa66cSeatRugbiIEop5s+fT9++ffnyyy/x9vYmZ86cDB06lLZt29KrVy8CAgLIli0bU6dOvW+xL4CPPvqIp556iipVqtCgQQMefvhhAPbu3ctbb72Fi4sLbm5usYmrZ8+eNG/enCJFihAaGsrUqVN56qmnuHnzJgCffvpp7EqTQoiMZ/58aNgQ8mWE0Xta6yy/Va1aVce3f//+B15LyJUrV1K0X2aSmcqcks85NDTU8YFkMFJm5/LHH1qD1uPGpe44W8oMbNOJ/E112lthQgghjHvNsVaOto9LEosQQji5kBCoUweKFrU6EkMSixBCOLG//oLduyE42OpI/iOJRQghnNi922AdOlgbR1ySWIQQwomFhEC1alCypNWR/EcSixBCOKkTJ2DLlox1GwxsHMeilCoLlMdM9qiBs8A+rfWfdohNCCFEEubONY9On1iUUn5AL6AT4HPv5ZhHHbPPaeBn4Butdbgd4hRCCBFPSAgEBMCjj1odyf1SfCtMKfWIUmoOsA94AdgNfAx0BVoALWN+/iTmvR7APqXUL0qp0vYOPKvr3r271SEIISx08iSsW5fxaiuQujaW/UBJ4DnMuifNtdafaK2na62Xaa2Xxvz8sda6OaY20x0oHXOssJOoqCjy5MlDaGgoAwYM4MaNGw/sM2bMGPz8/HjmmWfSfB0vLy8A6tSpk+ZzWOXYsWNUqFDB6jCEcJg5c0BrePJJqyN5UGpuhT2ptU7xbMFa62uYVRx/UEplgPk2M48dO3awa9cufH19GTo04TVdvv76a5YuXUqpUqWSPV/sNAwuCX/P2LBhg03xOkpycQuRmc2ebW6D+flZHcmDUvwbmZqkYs9jnYWOWaExsedpNWfOHGrVqkWlSpWoW7cuZ8+eZevWrdSsWZOcOXMmeEyvXr04cuQIbdq0YeTIkYwYMYIKFSpQoUIFRo0aBZhv9H5+frzyyitUqVKFEydOJBrDvZrLvWN69+5N+fLladKkCdevXwfgp59+okaNGlSuXJmXXnqJ6OjoB86T0OqVSR3brl07qlatSvny5Zk0aVKicU+bNo2KFStSqVIlunTpEnu96OhoXnzxxQdiFcLZnTgB69fD//5ndSSJSGwSsfgbUDGl+zrbZusklB999JHu06ePvnv3rtZa67t37+o+ffrojz76KEXnSMq5c+difx40aJAeN26c7tGjh46OjtbvvfeeXrNmTYLHlShRQp89e1Zv27ZNV6hQQUdGRuqrV69qf39/vWPHDn306FGtlNIbN25M9No5c+a87/Ho0aPa1dVVr1u3TmutdadOnfSPP/6o9+/fr1u1aqVv3bqltdb65Zdf1j/88MMD55szZ47u0aNH7PNLly4leez58+e11lpHRUXp8uXL63Pnzj0Q9759+3TZsmX12bNn7zvmXqw7d+68L9b4ZBLKhEmZM7YRI8ykk4cO2XaejDAJ5Syl1AMrWimlfBPaOavQWnPp0iVGjx5N37590VrTt29fRo8ezaVLl2yuuUydOpUaNWpQqVIlvv76azw8PJg8eTIuLi4MGTIkdgXIxKxbt4727duTM2dOvLy86NChA2vXrgWgRIkS1KpVK1XxlCpViooVKwJQtWpVjh07xsqVK9m+fTvVq1encuXKrFy5kiNHjjxwbEBAAL///jsDBgxg7dq15MmTJ8ljx4wZQ6VKlahVqxYnTpzgzz//fCDuVatW0bFjRwoWLAhA/vz574u1cuXK98UqRGYwezYEBma83mD3pKaNZTLwI9Du3gtKqSBgFv91O85ylFKMHDkSgNGjRzN69GgA+vTpw8iRIxNcxTGlpk2bxpYtW1i1ahVeXl7Ur1+f8uXLp+ocSSW2xG6lJSXuui+urq5cv34drTXdunXj888/T/LYhFavzJcvX4LHhoWF8fvvv7Nx40Y8PT1p2LBhbCeFuHFrrRP9N04oViGc3bFjsHkzfJGBlzFMTRvLSCBaKTUAQCnVFZNUnnVQbE4jbnK5x9akAmZRrjp16uDl5UVISAgbNmwgICAgVeeoX78+8+fPJyoqimvXrjFv3rxkazmp1ahRI+bMmcOZM2cAuHDhAsePH39gv4RWr0zs2MuXL5MvXz48PT05cOAAmzZtSvTaP//8M+fPn489XojM7JdfzGNG7A12T5I1FqXUk8Ae4GDMPbXnga1KKX+gPvC41voPx4eZsd27/RVX3759bU4u3bp1o23btsyZM4cWLVpQunTpVNcyqlSpwnPPPUeNGjUA6NGjB4GBgXa9LeTv78+nn35KkyZNuHv3Lm5ubowfP54SJUrct19Cq1cmdmyzZs2YOHEiFStWxNfXN9FbduXLl2fgwIE0aNAAV1dXAgMDmTp1qt3KJkRGM3s2VK8OKejwaZ3EGl9ibqFsAiKBa8BW4FtMF+J/gbJJHetMmy2N95cvX9Z9+vTRQGwDfvznmY2sIJn5SZkzpj//NI32w4bZ53yOarxPssaita6lzFduX6BynE0B4UqpI8BOrXUGrpQ5llKKvHnz3temcu+2WN68eW2+HSaEEPfMmAFKZeBuxjGSbbyPyUwHYrZZ915XSvkAVYCKDovOSQwaNOi+RuR7yUWSihDCXrSG6dOhQQMoXtzqaJKW5iHLWuvT2kzjkvDQ7ywmfhKRpCKEsKft2+HQIbBhlqZ0Y+u0+T7Ak5g5xCKBncAKrXWU7aEJIYS4Z8YMcHfPmJNOxpfmxKKUqgcsATz5b9p8gPNKqcFa6zG2Bme1uLe3ROajbRy8KkR6iY6GWbOgRQvIl8/qaJJny+x9w2IeuwMPY2otnYG/gFFKqRm2hWYtDw8Pzp8/L398MimtNefPn8fDw8PqUIRIVmiomSb/6aetjiRlbLkVVgEYrrX+Ic5rfwM/K6VeACYppTZorcfZFKFFihcvTkREBGfPnk1yvxs3bmS5P06ZpcweHh4Uz+itoEJgboPlygWtWlkdScrYkliuYhLJA7TWU5RSj2NWmnTKxOLm5paiKefDwsIIDAxMh4gyjqxYZiGscuOGWSmyQwfIkcPqaFLGllthoZiVI5N6/xEbzp9mSqljSqm9SqldSqltVsQghBD2sHAhXLniHL3B7rElsUwC6iil+iTyfknMCH2rBGmtK2utq1kYgxBC2GTaNChWDB5/3OpIUs6WW2ErgTvACKVUe8x0L9tjXmsA9AEG2ByhEEJkUadPw7Jl0L8/uLpaHU3K2ZJYBgOVMFO81I/Z4nah2glcUkpVAA5ore/YcK3U0sAKpZQGvtFaT0rHawshhF3MmGG6GnftanUkqaPs0Z1WKZUXCOS/ucQCgXKYxKWB28BBYI/WukuCJ7EjpVRRrfW/SqlCwG9Ab631mnj79AR6Avj4+FSdNWtWAmdKXmRkZOzSvVlFVitzVisvSJkzih49qpEt210mTtzhkPPbUuagoKDtiTY1JDY7pa0b4I6ZS6w7MBZYB1xy1PWSiGMQ0D+pfRKa3TilnGFGVHvLamXOauXVWsqcEezaZWYyHjvWcdewZHbjuJRSFbXWe1K6v9b6FrAjZks3SqmcgIvW+mrMz02AT9IzBiGEsNW0aeDmBp07Wx1J6mXGNe99gHVKqd3AFuBXrfUyi2MSQogUu3PHzGTcsiUULGh1NKmX6da811ofwXQqEEIIp7R8uekR5myN9vfImvdCCJHBTJkC3t6mxuKMZM17IYTIQE6fhkWLoE8fM02+M0ruVtibmMkmlVJqP7Ab2AQ0BhpqrQ85OD4hhMhSfvzRtLF07251JGmX5K0wrXUtIBdQFRgOnMO0p9xb8/5PpdTPDo9SCCGyAK3NbbBatcDf3+po0k7WvBdCiAxi40Y4cAAmT7Y6EtukeUoXrfVpYGnMJoQQwkZTpkDOnPC//1kdiW3SPLuxUsrJiy6EEBnH1aswezY8+aRZ1MuZ2TJt/lSl1G6lVNuE3lRK+SilHrXh/EIIkWXMng3XrsELL1gdie1sSSyPAGHADKXUFqVU03jvd8a0ywghhEjGN9+YBvs6dayOxHa2TJsfhVl75ThQDViilPoDOA/kxDTsh9scoRBCZHLbt8O2bTBmDChldTS2syWxTAY6ABuBn2Je88GMcdHAMsw4GCGEEEn45huznn0Xhy8qkj5sSSyNgDFa675xX1RK1Qe+wdRi7tpwfiGEyPSuXDELenXuDHnzWh2NfdjSxgJwNP4L2iyoVQ2IAL6z8fxCCJGpTZ9uGu179bI6EvuxJbGsBp5VSj0wm43W+hrmVlkVG84vhBCZmtbmNlhgIFSvbnU09mNLYvkEMz39aqVUQstT1sE07gshhEjAli2weze89FLmaLS/x5aR9zuVUs8BU4DNSqnDwFZMr7BKQD1gsT2CFEKIzGj8eDMY8umnrY7EvmxpvEdrPVMptQl4A2gNxP3n2QK8Zsv5hRAiszpzxgyKfOkl5x9pH59NiQVAa30U6AP0UUrlAwoDl7TWJ209txBCZFaTJ8OtW/Dqq1ZHYn82J5a4tNYXgYv2PKcQQmQ2t2/DhAnQpAn4+lodjf3ZNbFkNTdvyTAdIUTqLVgA//xjkktmJIklja5fv0O5d3PgdzYnRyc+SkfvQHIVKw3Fi0OxYv89enpaHaoQIoMZOxZKlYIWLayOxDEksaTR6dPnqHKuDKuLHmG51zZevrONprsheBa0Pgj5bsTsmC+fSTLxE86914oXhzx5MldfQyFEovbsgTVr4KuvwNXV6mgcwy6JRSmlgIeAU1rrW/Y4Z0ZXsmRh5v0Uztz5q1m2z4Xpe0NY9PAcFpb7B1ftSqMc/nS8XYZ2J/PgHXHB1Hu3bzddQeLLmfPBhBP/Z29vcLF1ogQhhNXGjDHzgjnzmvbJsVeNJT9mepfGwCo7ndMp5M+rmfR+PcberMdP00fw6fdbOZYjhFUBIazIPY9ePi7Ur1GfYL/n6ODXgaLZC8LJkxARYbZ//rn/57Aw8xgdff+F3NxMgolf24mbhIoUgWxSCRUiozp9Gn76ySSV/PmtjsZx7PlXKEvfy8meHV7o7sLzz9VkyZKafPb5UDYe2YVHtRD+IISwY73pvbQ3tYvXpqN/R4LLB1PisccSPll0tKnZJJZ8tm83rX83btx/nIsL+PgkXuu595gjh+P/QYQQD5gwAW7ehDfesDoSx5Kvt3bm4gKtWkHLloq1awMZMiSQFR99Sp4y+6naJYQzN0Lot6If/Vb0o2qRqgT7BRPsH0zZAmX/O4mrq6l9FCmS+ARCWsPFi4knn0OHYOVKM3VqfPnzJ9zWEzcJ5c4t7T5C2NH16/D11+bvQ9myye/vzCSxOIhSUL++2bZsgcGD/Vn8kT95835A335/ka9OCIuPhPDeqvd4b9V7BBQKINgvmI7+HfH39kcl90ddKZMg8ueHihUT3y8y0iSaEyfMY/yft22Ds2cfPM7LK9Faj9epU2apu4IFpd1HiBSaPt38qr2ZBVapSlNiiVlzJa48MY8VlVL3TTwZM41+llajBixaBDt2wKBBMPKDRyhQ4G3eeuttpr30N0uPzSUkPISPV3/MoNWD8C3gG1uTCSwcmHySSYqXlxmBldQorJs3TbvPvYRzr+Zzr/azcqV5P6bdpxpAz57g7p50h4PixaFwYWn3EVme1jBiBFSuDA0bWh2N46X1Nz4Ms0pkfMPj/Kxi9kn3DnVKqWbA6Jhrf6u1/iK9Y0hIlSqwcCFs3QoffQTvvAOjRj3M+++/wcoX3+DCrVPMC59HSHgIQ9cP5bN1n1Eyb0mTZPyCqVm8Ji7KATWE7NmhZEmzJSY62rQ8RkSwb9kyKuTLd3/y2bLFPCbU7lO4cPLtPh4e9i+XEBnE8uUQHg7TpmWNO8xpTSxB8Z7nBeYBbwHbbQnIVkopV2A8podaBLBVKbVQa73fyrjiql4dliyB9evhvffgtddg2DAYPLgwLz39Mi9Xf5lzUedYeHAhIeEhjNk8huEbh1MsVzHal2tPsH8w9R6uh6tLOuZsV1coWhSKFuVcVFTCX7u0hgsXTLJJ6NbbgQPw229w9eqDxxYsmHyX69y5HV5MIRzhq69Mk+n//md1JOkjTYlFa7067nOlVIGYH3fFf88CNYDDWusjAEqpWUBbIMMklnsee8z0Lv7tN3j3XbPe9VdfwRdfQLNmBeke2J3ugd25fOMyiw8tZk74HL7d+S3jto7D29M7NskElQzCzdXN6uKYr2IFCpitUqXE97t6NfF2n4gI2LQJzp9/8LhcuZLvdFCgQNb4SiicxtatsGqV+d12f2BZxMwpM978LgaciPM8AqhpUSzJUspMRPfEE/DLLzBwoJnm4fHHzX/EKlUgj0cenqn4DM9UfIbIW5Es/XMpIeEhzNg3g0k7JpHPIx9tfNsQ7BdM40ca45Etg99WypULypUzW2Ju3IB//024x1tEhMnGJ0/C3XjztWXPnrJ2n8w65FlkOEOHmrXse/a0OpL0o7ROqKkklScxNZazwBNaa0sHSCqlOgFNtdY9Yp53AWporXvH268n0BPAx8en6qxZs9J0vcjISLy8vGwLOo7btxWLFhXlhx9KcuWKG40bn6JHj6MUKnTzgX1vRt9k28VtrDm3hvXn1nMt+ho5XHNQO39t6nvXp0b+GuRwtf+YFXuXOa1UdDRuFy6Q/exZs5079+DP587hcvv2fcdpFxdu5c/PTW/vB7eCBc1jgQLomK+XGaW86UnKbB9//52D556rwdNP/02PHkftem57sKXMQUFB27XWCa0enCkTS21gkNa6aczzdwG01p8ndky1atX0tm3b0nS9sLAwGjqgm8fly+aW2MiRplbTvz8MGGA6eSXkVvQtVh1dRcj+EOYfnM+5qHPkyJaD5o82J9gvmFZlW5E7u33aKBxVZofQGs6du7/Gk9BtuMjIB4/19obixTnn4UHBSpUSrgFlthWaYjjVZ2wnjijziy+akfbHjpmxyxmNLWVWSiWaWOx1K+wCUAo4Zafz2WIr8KhSqhTwD9CZ+1e2dAp58sDnn0OvXqb32KefwpQp5rUuXR4cPuLu6k6zMs1oVqYZE+5OYO3xtYSEhzA3fC5zw+fi7upO49KN6ejfkTa+bcifIxPPJxGXUiZBeHtDYGDi+1258mBbT8zPHgcPws8/m44J8eXOnfgUO/ce8+eXdp8s6N9/TS+wHj0yZlJxJLskFm2qPcftcS5baa3vKKVeA5Zjuht/p7X+w+Kw0qxECZg5E15/3UwD8dxzZvTu6NFQq1bCx2RzyUZQqSCCSgUxpvkYNkVsYs7+OYSEh/Drn7+a90sGEewXTLty7fDxymL/6xOSO7fZ/PweeGvbvW91168n3e6zbx+cOvVgu4+HR+LtPve2QoWk3SeTGTkS7tyBfv2sjiT9ZcbGe7TWS4AlVsdhT7Vrw8aNZvTugAHmedeupmGwcOHEj3NRLtR5qA51HqrD8CbD2X5yOyH7QwgJD6HXr714+deXqVeiHsF+wXTw60Dx3MXTr1DOJkcOeOQRsyXmzh2TXBIbbLp+vXmM1+4T2507qSUWihbNOt2KnNzZs+YLYOfOULq01dGkv0yZWDIrFxdzG6x9e/jsMxg+HObNM4MtX3/dTICcFKUU1YpWo1rRanzW6DP2ndlHSLhJMn2W9aHPsj7ULFYzdtR/6XxZ8DfCVtmy/ZcIEnP3rmn3SazL9Z498OuvEBX14LGFCiXf5TpnTseVT6TIyJGmgvv++1ZHYg1JLE7Iy8skluefN7fH+veH776DceMgKP7Q1UQopQjwCSDAJ4BBDQdx8NzB2CTz9u9v8/bvbxNYODA2yZQrmETXYJE6Li4mQRQqlHi7j9amB0diyef4cVi3zkxEGl/evEnPclC8uFmATtp9HOLCBbNC5JNPJnhnNUuQxOLEHn3UfLFdtAj69DFjX556ytRkihRJ3bl8C/ryXr33eK/eexy9eJS54Wb+svdD3+f90Pfx9/aPnVrGHj0JRTKUMgkib14oXz7x/aKiTLtP/Ftv937evdtMxRP/M8uRI/GaT7FiuF+4YGpWMsloqo0aZToZZtXaCqQisSilKmqt9zgyGJE2rVubAZZDh5ouyosXm15kr7yStvkfS+UrRb86/ehXpx//XPknNskMWTuEwWsGUyxHMZ6NfpZgv2CqFa1m2ySZwjaenlCmjNkSc/v2f4vLJZR81q41ySlOu08dMP95Emr3iftz0aLJ34PNQi5dMh1rgoOhQgWro7FOav7szFJK1dRa3zfRk1LKV2t90M5xiVTKkcPMnPzss2busT59YOpUmDjRzK6cVsVyF6N3zd70rtmbM9fOMP/AfCavn8zwjcMZun4oD+d5mA7lOhDsH0ydh+o4ZpJMYRs3N3j4YbMl5u5d0+Ic0836UGgoZXPm/K8mtGuXqRpfv37/cUr9t7hcUjMeeHo6tIgZxZgxpud6Vq6tQOoSy2TgR6DdvReUUkHALED6q2YQZcrA0qUwZ45pf6lVy9RchgwxY2NsUShnIXpW7UnZq2WpWLMiiw4uYk74HL7e9jWjNo+isFdhM3+ZXzANSjYgm4vcaXUa91Yf9fGBqlX5N29eysYfOKe1+UqeWLvPkSOwerXZJ758+ZLvcp0nj1O3+1y8aKbGb9vWTI+flaX4N19rPVIpVVcpNUBrPVQp1RX4CnjWceGJtFAKOnWCpk3NN6dx42DuXPNtKjjYPr+7+XPkp1vlbnSr3I0rN6/w66FfCQkPYequqUzYNoECOQrQrlw7gv2CaVS6Ee6u0k3W6SllEkS+fEnf57l27b/bbAndetu50yy9Hb/dJ2fO5Od58/bOsO0+w4aZ2sonn1gdifWSTCxKqSeBPcDBmEGQz2OmofcH6gOPO/Pgw8wud26TTLp0gZdeMsmmdWsYPx4eesiO18mem6cCnuKpgKeIuh3FssPLCAkP4ec/fmbKzinkyZ6H1r6tCfYLpukjTcnhZv/5y0QGkjOnWXs3qfV3b91Kut0nNNS8f+fO/ce5uf3X7pNYl+siRdJ9cbkzZ0zbyv/+l/SCrllFcv/6bwIVAKWU2g/sBjZh1jppqLU+5OD4hB1Ur27W4Ro9Gj780Kwq/Nln5haZvQd7e7p50sGvAx38OnDzzk1+O/IbIeEhLDiwgJ/2/EROt5y0LNuSYL9gWjzaAi/3rDXRoYjh7m6mlShRIvF9oqPNX+y4CSfurbedOxNv97m3uFxSNaAc9vuC88UXJoxBg+x2SqeWZGLRWtdSpsuPL1A5zqaAcKXUEWCn1vpJx4YpbJUtm5laokMHePllM6Byxgz49tuke7PaInu27LQq24pWZVtxu9Vtwo6FERIewrwD8/j5j5/xyOZB00eaEuwXTGvf1uT1yOuYQIRzcnU1tY8iRcy3o4RobRo34s/zdi8J/fmnqf1cvvzgsfnz31fTKXHrlmknipuEcudO9t5xRIQZZd+tW9IrgGclydYXY26BHYjZYueWV0r5AFUAqfg5kVKlTOP+jBmm51hgoFlk7L33zFImjuLm6kbjRxrT+JHGjG8xnvUn1jNn/xzmhs9lwcEFuLm40ah0Izr6daRtubYU9CzouGBE5qGUSRD580NAQOL7RUYm3e6zbRulzpwxXSnj8vJKttPBp4MLcveu4sMPHVpSp2LLjcgGWuufgaX2CkakD6XgmWfMAmN9+5rGxpAQM3tyzXRYEs3VxZX6JepTv0R9RjUbxdZ/tsZOktljUQ9eWvwSDUo2INgvmPbl2lMkVypHewoRn5eXqU4kUaVYvWIFDcqWTXyw6cqVpt0nOvq+40bjzqe5i1GwaxLzvBUunO7tPlaypaQzlFL5tNbf2C0aka68vc1aEU8/bRr3a9c2XZQ//TT9hh24KBdqFq9JzeI1+bLxl+w6tYuQ8BDm7J/Dq0te5bUlr1HnoTqxU8s8nCeJsRhC2EC7u0PJkmZLTHS0mckgJuF8+3EEV/dH8HLjf+BcBGzebBLRzXgL87m4JNzuE3crWtTMhJ0J2JJYpgJfK6UKaq2HxH8zZsGtL7XW9Wy4hkgHLVrAH3+YdV9GjoSFC03bS3qv86SUIrBIIIFFAhkcNJj9Z/fHzl/25oo3eXPFm1QvWj02yZTJn8RocyEcwdUVXaQIqmhRNmyAF3fDJ59oPD6I0w6jNZw//+B4n3u1n4MH4fff4erVB89fsGDyXa5z22fBPkdKc2LRWvdQSp0FBsckl75gRuIDnwNtgetJnUNkHLlzmwbIJ5+EF14wk1m+/DJ8+WXiq1Y6klKK8oXKU75QeT5s8CGHLxyOne7/nZXv8M7Kd6joUzF2/jJ/b3+ZWkY43KBBg7h06RIjRozkrbcURYpoTp0awKBBngy61yVMKZMgChaESpUSP9nVqw+2+8S9Dbd5s5kFO75cuZKe3bp4cShQwNLBpjbd9NNav6uUOg0MV0p5A5FAd0AD3wAyVMjJNGxoZm1//33TPXnpUtP28vjj1sZVJn8ZBtQdwIC6Azh+6Xjs/GWDwgbxUdhH+BbwpaN/R4L9gqlcuLIkGWF3WmsuXbrE6NGjOXw4gA0bXqBRo9l8/fVX9OnTB6116v7f5coF5cqZLTE3biS9uNxvv5l2n/iLy2XPnnBbT/x2HwexR2vSZKAlZvlfjek59oHW+ogdzi0skDOnuSXWsSN07w6NGpklkr/8MmMs8V4ibwn61u5L39p9OXn1JPMOzCMkPITP133OkLVDKJ2vdOz8ZTWK1ZD5y4RdKKUYOXIk0dGujBtXD9jPypXP0qdPH0aOHOmYLzMeHmalsKRWC7tz5752nwdqPps2mZ9v3br/OFdXqpQpAwcO2D3sNCcWpZQb8ArwLuAN7MCMcXEDTtgjOGGtxx4zcw9++KGZiv9e7SUjraBbJFcRXqn+Cq9Uf4VzUedYcGABIeEhjN48mmEbh1EsVzE6+HWgo39HHnvoMVxdMlDwwukopShRYhhmKF8LINpxSSWlsmUzNZFixRLfR2tzWy3eYNPzERE4pMVGa52mDTgGRAN7gZYxrz0J3AB+A7zSeu703qpWrarTKjQ0NM3HOpMNG7QuW1Zr0LpNmwh95YrVESXt4vWLetquabrtzLY6++DsmkHoQl8V0i8tekmvOLxC37pzK8XnyiqfcVxS5oSdOnVXu7tHaVisMXdodJ8+ffTdu3cdH6AD2PI5A9t0In9TbblH4Aq8CFTSWv8ak6R+BtoAtYBQpZSMcsskatc2tZc334RFi4pSsSKEhVkdVeLyeuSlS6UuzO88n3Nvn2N2x9k0KNGAn/b8RJOfmuAzzIfnFzzP4kOLuXnnZvInFFme1ponntjIrVvZ6Np1N3fv3qVPnz6MHj2avn37ygJ4cdjSxvKo1vpG/Be11iuUUk8AvwIbgCRmohPOJEcOc0usZMmdjBlThaAg6N3bzJOUkZfb8HL34snyT/Jk+Se5fvs6y/9abqaWCZ/H1F1TyeWeK3aSzGZlmuHploELIyyze7di377aBAauZurUd2PbXADy5s0rHUbisKW78QNJJc57m5VS9YDlaT2/yLgCAq6wa5eZCmbsWFi2zMyEUaeO1ZElL4dbDtqVa0e7cu24FX2LlUdWEhIewvwD85mxdwaebp40L9OcYL9gWpZtSe7sGX/MgHA8rc0USAULKlaubBCbRO4lF0kq93NYdxmtdTjwmKPOL6yVM6eZkn/VKtPZpF49ePtt0zvSWbi7utP80eZ82+ZbTvU/xcquK3mu0nOsP7Gep+c+jfdX3rSe2Zplp5Zx4foFq8MVFvrpJ1izxswKni/f/UlEksqDUpxYlFKNUntyrfWJmGOfSO2xwjkEBcHevWZQ5VdfQdWqsH271VGlXjaXbDxe6nHGtxzPP2/+w7rn1/Fq9VfZc3oPQw8OxWeYD01/asqk7ZM4c+2M1eGKdHTxopkZvFYt8/9cJC81NZZlSqlVSqlWSqlk+2wqpdyUUu2VUquBJWkPUWR0uXLBpEmwZIlZlbZWLbMuxe3bVkeWNi7KhccefowRTUdwrM8xJgROoF/tfhy5eISXFr9EkeFFaDi1IWM3j+WfK/9YHa5wsIEDzQwtEyZk2MUrM5zU/DNVBu4AC4GTSqnpSqk+MYmmjlLqMaVUa6XUm0qpn4GTQAgQFXOsyOSaN4d9+6BzZ/j4Y5Ng/nDy9UWVUpTLXY4vnviCQ68dYtdLuxhYbyBno87y+rLXKT6yOLWn1Gb4huEcvXjU6nCFnW3ZAhMnmk4qWX0d+9RITeN9J6AnUAQzMLIt8BSmL3dcCrgCzAUmaK232iFO4STy5YMff4T27c2MyVWrmtmS+/bNWAMr00IpRaXClahUuBKfBH3CgXMHYucv6/9bf/r/1p/AwoGxU8v4FpRVn5zZnTtmvrwiRWQd+9RKTWL5EDiktZ4BbFRKdQT+BvwxI+81cBbYh1lV8m6iZxKZXocOULeuSS5vvQULFpieY488YnVk9lOuYDkG1h/IwPoDOXLxSGySGbhqIANXDaS8d/nYJFOhUAVp5HUyo0bBjh3w889OMaFwhpKaW2EXgbgd/GcDZbTWU7XWX2mth2mtf9Bab7cqqSilBiml/lFK7YrZWlgRhzAKFYK5c2HaNNPAX6mSua2QGceRlc5Xmrcee4tNPTZxou8JxjQbQ0HPgnyy+hMqTqyI7zhf3v39Xbb9u00G0jmBw4fhgw+gXTszZ55IndQkln3AC0qpexPSZNSvXyO11pVjNuk0YDGloEsXk1hq1za3Fpo3N9MVZVbFcxend83ehD0Xxsl+J5nYciIl85bkqw1fUX1ydUqNLsWby99kw4kN3JWKfYZz9y706GEmCB4/3tLZ551WahLLx5g17v9WSh3A3PpqoZRqrpTycUh0ItN46CFYscL8oq5dCxUqwPTpmbP2EpePlw8vVXuJFV1WcOatM3zf9nsCfAIYv3U8j333GA+NfIjXlrzGqqOruHP3jtXhCswid6tXm1kmiha1OhrnpFJTLVdKlQV6YAY+1o55+d4JTmNmON5571FrfcxukaYsvkHAc5jOA9uAflrri4ns2xPTGQEfH5+qs2bNStM1IyMj8bJiJSwL2VrmiIgcfPFFOf74Iw/165+lb99D5M2bcfsmO+IzvnbnGhvPb2TNuTVsubCFm3dvksctD3UL1KW+d30C8wbi5uJm12umRlb9f33tWgFeeKE6ZcteZfjw3Zm+tmLL5xwUFLRda10twTcTm50yuQ24C/QD2gOfYuYG+zfm9eiY7Vxaz5/EdX/H3JaLv7UFfDCTY7oAQ4DvUnJOmd04dexR5jt3tP7iC63d3bUuVEjr+fNtj8tRHP0ZR96M1HP+mKM7z+msvT7z0gxC5/0ir+4yt4tecGCBvn77ukOvn5Cs+P965cpQHRSktZeX1n/9ZXU06cNRsxvbMgnlJ8BarfUWYN69F5VSRTC3zKrigPErWusUjeJXSk0GFtv7+sI+XF1hwABo0cK0wbRrB926mZ44efNaHFw6y+mek2D/YIL9g7lx5wa//fUbIeEhLDy4kB/3/IiXuxctH21JsF8wzR9tjpd71qpJpJe5c4sTGgqTJye9rpZIni2TUA5K5PWTmNrLr2k9d1oppYrEXB9MTWpfescgUicgwAxCGzwYPv8cVq6E77+HJ7LoJEAe2Txo7dua1r6tuR19m9BjoYTsD2HegXnM/mM2Htk8aFamGcF+wbQu25o8HnmsDjlT2L8fJk0qTatWMm2LPWS2CQq+VErtVUrtAYKAvlYHJJLn7m4Sy8aN4OUFjRvDK69AZKTVkVnLzdWNJo804ZvW33Cy30nCuoXxYpUX2frPVrrM64L3V960mN6CKTumcC7qnNXhOq3bt6FrV8iRI5rJk6UXmD1kqsSite6itQ7QWlfUWreJU3sRTqB6dTMg7c03zXiXSpXMjLICXF1caVCyAWOaj+Hvvn+zofsGXq/5OuHnwumxqAeFhxXmiWlPMGHrBE5FnrI6XKfy/vtm4tR+/Q5SuLDV0WQOmSqxCOd3bzGx1avN84YNzXQwUVGWhpWhuCgXaj9Um2FNhnHk9SNs77mdAY8NIOJKBK8seYWiw4tS7/t6jNo0ir8v/211uBna8uXw5ZfQqxfUry+1PnuRxCIypHr1YPduM6By1CgIDDS3ysT9lFJUKVKFIY2GEP5qOPte3sdHDT7i8o3L9F3elxKjSlBjcg2+XP8lf134y+pwM5STJ03HkQoVYMQIq6PJXCSxiAzLy8sMqPz9d7OAWN26zreYWHpSSlG+UHk+avgRe17ew8HXDvLZ459xV99lwO8DKDO2DJUnVmbw6sGEnw23OlxL3b1r2lUiI2H2bFNTFvYjiUVkeI0amSlhevQwi4kFBsLmzVZHlfGVLVCWd+u9y7ae2zja5yjDmwwnp3tOPgz7EP+v/fEf788Hqz5g16ldWW7+so8/Nl9Yxo4Ff3+ro8l8JLEIp5A7N3zzjZkW5to1qFPH1F6uX7c6MudQMm9J3qz9Juu7r+efN/9hXPNxFPYqzGfrPiPwm0DKjC3D27+9zeaIzZk+ySxebKbBf+456N7d6mgyJ0kswqk0bmwWE7u3FHJgIGzYYHVUzqVorqK8WuNVVnVbxal+p5jcejJlC5Rl5KaR1JpSi4dHPczYw2NZc3wN0XejrQ7Xrg4fhmefNf9vvv5auhY7iiQW4XRy5zZLIa9YYWosdeuaLsrScyz1vHN606NKD5Y+s5Qz/c/wQ7sfqFKkCov+XUSDqQ0oNqIYLy9+md+P/O70k2Reu2bWCXJxgZAQaVdxJEkswmndq7306gUjR0LFihAWZnVUzitfjnx0rdSVBZ0XML/OfGYGz6ReiXpM2zONxj82xmeYD90XdOfXQ79y885Nq8NNlXuN9fv2wYwZUKqU1RFlbpJYhFPLlcvc0ggNNc+DgkwX5StXrI3L2Xlm86Rzhc780ukXzr51lrlPzqV5meaEhIfQamYrCg0rxDNzn2Fe+Dyibmf8quIHH5hF54YNg2bNrI4m85PEIjKFhg1hzx5zS2zSJNPTZ9Eiq6PKHDzdPGnv156fOvzEmf5n+PXpX+no15Hlh5fT4ecOeH/lTadfOjF732yu3rxqdbgP+PFH+Owz06uwr0zylC4ksYhMw9PTjNrfuBHy5YM2baBzZzh92urIMo/s2bLT4tEWTGk7hVP9T/F7l9/pVqkb6/5eR+eQznh/5U3bWW2ZtnsaF68nuBRSulq3ziSUoCBZDTI9SWIRmU6NGmbup08+gXnzwM8Pvvsu869Wmd6yuWSjUelGfN3yayL6RrDmuTX0qtaLnSd30m1+NwoNK0Szn5oxeftkzl47m+7x7dsHrVub9pQ5c8xkpyJ9SGIRmZK7u7mvvmsXlC9vuic//jgcPGh1ZJmTq4sr9UrUY1SzURx/4zibe2zmzVpvcvjCYXou7knh4YUJ+iGIcVvG8e/Vfx0ez99/m7YUT08zH1j+/A6/pIhDEovI1Pz8zISW33wDO3eanmMffww3natTk1NRSlGjWA2GNh7Kn73/ZNdLu3iv7nucjjxN76W9KTaiGHWm1GHExhEcv3Tc7tc/fx6aNjXTtSxbBiVK2P0SIhmSWESm5+ICPXvCgQMQHAyDBpkEs3Kl1ZFlfkopKhWuxODHB7P/1f3sf2U/g4MGc/3Odfqt6EfJ0SWpNqkan6/9nEPnD9l8vUuXoEkTOHoUFi40C8mJ9CeJRWQZhQubMQzLl8OdO2aVyqefNrPcivTh5+3H+/XfZ+dLOznc+zBfPvEl2Vyy8d6q9/Ad50vAhAAGhQ1i35l9qZ5a5soVc/tr717Ttbh+fQcVQiRLEovIcpo0MQ27H35oRmCXKwejR5tkI9LPI/kf4a3H3mJTj038/cbfjGo6inwe+fhk9ScETAig3PhyvLfyPbb/uz3ZJBMZCS1bmk4bP/8MLVqkUyFEgiSxiCwpRw7T1rJvH9SqBW+8AVWqwNq1VkeWNT2U5yH61OrDmufX8G+/f5nQcgIP53mYL9d/SbXJ1Sg9pjT9lvdjw4kN3NV37zv28mVTU9mwwdRI27WzpgziP5JYRJb26KOmgXfuXPMHqn59c3ssIsLqyLKuwl6F6VWtF791+Y3T/U8zpc0U/L39GbtlLI999xgPjXyI15a8RtixME6fiaZRI7OMwsyZ0KmT1dELkMQiBEpB+/YQHv7f1B++vvDppzItv9UKeBage2B3fn36V86+dZaf2v9EzWI1+W7ndwT9EESxkUXYWbwnH/ywnHbBt6wOV8SQxCJEDE9PM6jywAFo3twkGT8/WLWqkAyuzADyeOThmYrPMPd/c1nb5izeob/A0UZkrzaTj/5shs8wH7rN78bCgwu5cUeWGbWSJBYh4ilZ0ozUXrXKTA0zeLA/jz0GmzZZHZkAMy7pifo5cTnQkU39Z3LhnbMs6LyANr5tWHhwIW1ntcX7K2+eCnmKOfvncO3WNatDznIksQiRiKAg2LYN+vc/wNGjULu2uYd/+LDVkWVdP/1kevUVLmwSfbVq4JHNgza+bfih3Q+c7n+aZc8s46kKT7HyyEo6/dIJ76+86TC7A9P3TOfyjctWFyFLkMQiRBJcXaFly1P8+acZWLl0qbk99tprcOqU1dFlHXfuQL9+0KWLSfAbNpiaZXzuru40LdOUSa0n8W+/f1nVdRXdA7uzKWITz857lkLDCtFqRiu+3/k956POp3s5sgpJLEKkgJcXfPSRqa306AETJ8Ijj8DAgWa0t3Ccc+dMd+IRI6B3b/jtN3OLMjnZXLIRVCqIcS3GEfFmBOu7r+e16q+x78w+ui/sjs8wHxr/2JiJ2yZyKlK+JdiTJBYhUqFwYZgwwTTwt21r1vkoVcr0IJPFxexv7VozvmjdOvj+exgzBtzcUn8eF+VCnYfqMLzpcI72Ocq2F7fxVp23OH7pOC//+jJFhxelz64+jN40mhOXT9i/IFmMJBYh0qBMGTMYb+dOaNDA9CArVcokGkkwtouONj30GjaE7Nlh/Xp47jn7nFspRdWiVfn8ic85+NpB9r68lw8bfMjVO1d5Y/kbPDzqYWp9W4uv1n/FkYtH7HPRLMYpE4tSqpNS6g+l1F2lVLV4772rlDqslDqolGpqVYwia6hcGebPh61bzQj+gQPNbLqDBsGFCxYH56T+/NMklI8+MoNVd+yAqlUdcy2lFBUKVWBQw0F8V+07Dr52kM8e/4w7d+/w9u9v88iYRwj8JpBP13xK+NlwxwSRCTllYgH2AR2ANXFfVEr5A52B8kAz4GullGv6hyeymmrV4NdfTS+yhg3NdDEPP2yWSj4hd1ZSJDrarABasaKZamfaNLOscK5c6RdD2QJlebfeu2zruY0jrx9hWONh5MiWgw9CP8D/a3/Kf12eD0M/ZPep3ameJDMrccrEorUO11ontGRTW2CW1vqm1voocBiokb7RiaysalWzauWePWbOqjFjoHRp6NbNLDomErZtG9SpA/37Q+PG8McfpgeYlUrlK0W/Ov3Y8MIGIvpGMLb5WArlLMSQtUOo/E1lyo4ryzu/v8PWf7ZKkonHKRNLEooBcb8fRsS8JkS6CggwYy4OH4aXXzazKAcGmrEx8+fLTMr3nD0LL75olpM+fhymT4cFC6BoUasju1+x3MV4rcZrhHYL5WS/k3zT6htK5yvN8I3DqfFtDUqOLknfZX1Z9/e6BybJzIpURs20SqnfgcIJvDVQa70gZp8woL/WelvM8/HARq31TzHPpwBLtNYhCZy/J9ATwMfHp+qsWbPSFGdkZCReXl5pOtZZZbUy26O8V69mY8mSIsybV4zTpz0oVOgGrVqdpGXLk+TPn/HmuHL0Z3z9uishIcWYNethrl93JTg4gq5dj+HlFe2wayYnLWW+evsqG85vYM25NWy9sJXb+jb53fNTt2Bd6hesT+W8lXHNwHfjbfmcg4KCtmutqyX4ptbaaTcgDKgW5/m7wLtxni8Haid3nqpVq+q0Cg0NTfOxziqrldme5b19W+t587Ru3Fhr0DpbNq3bttV64ULzXkbhqM/42jWtR4/WulAhU/42bbTet88hl0o1W8t8+cZlPWPPDB08O1h7DvHUDEIXGFpAd5/fXS85tETfvHPTPoHakS1lBrbpRP6mZktTqsq4FgIzlFIjgKLAo8AWa0MS4j/Zspm2l3btTO+nb7+FH34wt398fKBzZ3jmGdMZQCmro7WfCxdg/HjT5nTunOngMH++GUWfWeTOnpunAp7iqYCniLodxbLDywgJD+GX/b/w3a7vyJM9D619WxPsF0zTR5qSwy2H1SE7jFO2sSil2iulIoDawK9KqeUAWus/gJ+B/cAy4FWttXV1ayGS8OijMHSo6TW2YIFpvJ4wwbQ3+Pqarss7duC0MytrDVu2wAsvwEMPmRU7a9WCNWvMBJ+ZKanE5+nmSQe/DkzvMJ2zb51l8VOL6eDXgSV/LqH97PZ4f+XNk788yex9s4m8FWl1uHbnlDUWrfU8YF4i7w0BhqRvREKknZsbtGljtosXTUP/zJkm6Xz2mZkTq1Urs/Ruw4bg4WF1xEn7+2+zPPD06aYnXM6cphb2+utQoYLV0aW/7Nmy07JsS1qWbcnt6NusPr6aOfvnMO/APH7Z/wvZXbPTrEwzgv2Cae3bmrweea0O2WZOmViEyKzy5TNzkfXoYW4ZLVxoui9PmQLjxpkllevVg8cfN1tgoLm9ZiWtYe9eWLIEFi0yE0SCuZ03YYIZ5Jg7t7UxZhRurm48UfoJnij9BONbjGfDiQ3M2T+HuQfmsuDgAtxc3GhUuhHBfsG09W2Ld05vq0NOE0ksQmRQBQtC9+5mu37drEOydCmsXAnvvGP28fSE6tXNLaaqVaFSJTM5pqsDOyLdvm3Gmaxfb7Y1a+Cff8x7lSvDkCHwv/+ZOETiXF1cqVeiHvVK1GNks5Fs/WcrIeEhhISH8OKiF3lp8Us0KNGAjv4daV+uPUVyFbE65BSTxCKEE8iRw8zw26yZeX76NISFmdrBxo1mxPq9sTGenqaNpmxZ045TogQUK2a2QoUgb96kb6dFR8Ply9k4eBBOnjTjS44dM50N9u41Szjfvm32LVYM6taFpk1NbEWc529fhuKiXKhZvCY1i9dk6BND2X16NyH7Q5gTPodXl7zKa0teo85DdQj2C6aDXwdK5C1hdchJksQihBPy8TG1gv/9zzy/cQP274fdu8128KAZzf7LL3A3gfF67u4mAbm5mU1ruHnTbFFRoHXd+/ZXCooXNwM/mzc3NaM6dcy0NZmp91pGoJSicuHKVC5cmcGPD2b/2f2E7Dc1mTdXvMmbK96kWtFqBPsFE+wXzKMFHrU65AdIYhEiE/DwMNPLV6ly/+u3bplaxz//mO38ebN+zMWL5vba7dv/1XSyZzdbzpxw8eKf1Kr1KIUKmVmbH3rIvCfSn7+3P/4N/PmgwQccvnA4Nsm8u/Jd3l35LgGFAgj2C6ajf0f8vf1RGSDTS2IRIhNzdze3wkqk8s5JWNg/NGyY8b4JZ3Vl8pdhQN0BDKg7gL8v/83c8LmEhIfw8eqPGbR6EL4FfE1Nxj+YwMKBliUZpxzHIoQQWd3DeR7mjVpvsPb5tfzz5j+MbzGeYrmLMXT9UKpOqsojYx6h/4r+bIrYlO7zl0liEUIIJ1ckVxFeqf4KK7uu5FT/U3zb+lvKFSzHmM1jqD2lNg+PfJjXl77O6mOrib7r+DHjcitMCCEykYKeBXmhygu8UOUFLt24xOJDiwkJD2HyjsmM3WKm/m/n245g/2Bc7jqmbiGJRQghMqm8Hnl5tuKzPFvxWSJvRbL0z6WEhIcwY98MJu2YRBGPIkQEReCi7JtgJLEIIUQW4OXuRafynehUvhPXb1/ntyO/EbY9zO5JBSSxCCFElpPDLQdtfNuQ+6Rj5tqRxnshhBB2JYlFCCGEXUliEUIIYVeSWIQQQtiVJBYhhBB2JYlFCCGEXUliEUIIYVeSWIQQQtiV0lpbHYPllFJngeNpPLwgcM6O4TiDrFbmrFZekDJnFbaUuYTW2juhNySx2EgptU1rXc3qONJTVitzVisvSJmzCkeVWW6FCSGEsCtJLEIIIexKEovtJlkdgAWyWpmzWnlBypxVOKTM0sYihBDCrqTGIoQQwq4ksaSAUqqZUuqgUuqwUuqdBN5XSqkxMe/vUUpVsSJOe0pBmcsppTYqpW4qpfpbEaO9paDMz8R8vnuUUhuUUpWsiNOeUlDmtjHl3aWU2qaUqmtFnPaUXJnj7FddKRWtlOqYnvE5Qgo+54ZKqcsxn/MupdSHNl1Qay1bEhvgCvwFlAbcgd2Af7x9WgBLAQXUAjZbHXc6lLkQUB0YAvS3OuZ0KnMdIF/Mz82zyOfsxX+3zCsCB6yO29FljrPfKmAJ0NHquNPhc24ILLbXNaXGkrwawGGt9RGt9S1gFtA23j5tgWna2ATkVUoVSe9A7SjZMmutz2ittwK3rQjQAVJS5g1a64sxTzcBxdM5RntLSZkjdcxfHiAn4OyNsin5fQboDYQAZ9IzOAdJaZntRhJL8ooBJ+I8j4h5LbX7OJPMVp6USG2ZX8DUUp1ZisqslGqvlDoA/Ap0T6fYHCXZMiuligHtgYnpGJcjpfT/dm2l1G6l1FKlVHlbLiiJJXkqgdfif2tLyT7OJLOVJyVSXGalVBAmsQxwaESOl6Iya63naa3LAe2AwY4OysFSUuZRwACtdbTjw0kXKSnzDswULZWAscB8Wy4oiSV5EcBDcZ4XB/5Nwz7OJLOVJyVSVGalVEXgW6Ct1vp8OsXmKKn6nLXWa4BHlFIFHR2YA6WkzNWAWUqpY0BH4GulVLt0ic4xki2z1vqK1joy5uclgJstn7MkluRtBR5VSpVSSrkDnYGF8fZZCHSN6R1WC7istT6Z3oHaUUrKnNkkW2al1MPAXKCL1vqQBTHaW0rKXEYppWJ+roJp/HXmhJpsmbXWpbTWJbXWJYE5wCta6/npHqn9pORzLhznc66ByQ1p/pyz2RBslqC1vqOUeg1Yjuld8Z3W+g+lVK+Y9ydieo60AA4DUcDzVsVrDykps1KqMLANyA3cVUq9gelpcsWquG2Rws/5Q6AA5hsswB3txJMWprDMwZgvTbeB68D/4jTmO50UljlTSWGZOwIvK6XuYD7nzrZ8zjLyXgghhF3JrTAhhBB2JYlFCCGEXUliEUIIYVeSWIQQQtiVJBYhnIhSarNSqrPVcQiRFEksQjgJpZQLUAHYY3UsQiRFEosQzsMX8zt70OpAhEiKJBYhnEdlYP+9OayUUn2VUgeUUpUtjUqIeGTkvRDOozKwWymVB/ge8/tbS2t9ycqghIhPaixCOI/KmGSyFTOdTltJKiIjkildhHASSqlTMT/+prXuYmkwQiRBaixCWEwpFaiUmqeUuhizzVFK5VdKFVVK3VBKPRUz6acPZgnZekqpbtZGLUTipI1FCAsppZ4CfsB0If4YKAW8DvyN+f38E5gNNAWOaK0PKKVaAaFKqRNa61XWRC5E4iSxCGERpVRp4DtgF1Bfa30j5vVqQHOgJPCM1vquUqoSsBNAa71PKfUMMFspVV9rHW5F/EIkRtpYhLCIUmo0pnZSS2u9Oc7rPwLPYpaLrebM65+IrEnaWISwThvgcNykEs8HklSEM5LEIoQFlFL5Mbe6tibwtg/wR8za40I4HUksQlijcMzjfeuKK6XqA43jvy6EM5HEIoQ1LsU8Vrr3glLKC/gm5mnO9A5ICHuRxCKEBbTW/wJbMGNSflRKvQysAQoCy4BApdQbSqkiVsYpRFpIrzAhLKKUKgGMwwx6zIbpTtw95u0QwB8op7WW2YyFU5HEIoQQwq7kVpgQQgi7ksQihBDCriSxCCGEsCtJLEIIIexKEosQQgi7ksQihBDCriSxCCGEsCtJLEIIIexKEosQQgi7ksQihBDCriSxCCGEsKv/A6y1V7oipRKUAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"plot_alpha(0,eta_ls=0.25,algorithm=\"steepest-descent\",alpha_max=5E-1)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.3.5 Steepest Descent Step, $x^k = 0$](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.3.5-Steepest-Descent-Step,-$x^k-=-0$)",
"section": "3.6.3.5 Steepest Descent Step, $x^k = 0$"
}
},
"source": [
"**Discussion**\n",
"* How does the region where the Armijo and Goldstein conditions are satisfied change for different values of `eta_ls`?"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.6.4 Trust Regions](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.4-Trust-Regions)",
"section": "3.6.4 Trust Regions"
}
},
"source": [
"## 3.6.4 Trust Regions"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.6.4 Trust Regions](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.4-Trust-Regions)",
"section": "3.6.4 Trust Regions"
}
},
"source": [
"Excerpts from **Section 3.5** in Biegler (2010)."
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.4.1 Main Idea and General Algorithm](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.4.1-Main-Idea-and-General-Algorithm)",
"section": "3.6.4.1 Main Idea and General Algorithm"
}
},
"source": [
"### 3.6.4.1 Main Idea and General Algorithm"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.4.1 Main Idea and General Algorithm](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.4.1-Main-Idea-and-General-Algorithm)",
"section": "3.6.4.1 Main Idea and General Algorithm"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.4.1 Main Idea and General Algorithm](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.4.1-Main-Idea-and-General-Algorithm)",
"section": "3.6.4.1 Main Idea and General Algorithm"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.4.2 Trust Region Variations](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.4.2-Trust-Region-Variations)",
"section": "3.6.4.2 Trust Region Variations"
}
},
"source": [
"### 3.6.4.2 Trust Region Variations"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.4.2 Trust Region Variations](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.4.2-Trust-Region-Variations)",
"section": "3.6.4.2 Trust Region Variations"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.6.4.2 Trust Region Variations](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.4.2-Trust-Region-Variations)",
"section": "3.6.4.2 Trust Region Variations"
}
},
"source": [
"$p^C$: Cauchy step\n",
" \n",
"$p^N$: Newton step"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.6.4.2.1 Levenburg-Marquardt](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.4.2.1-Levenburg-Marquardt)",
"section": "3.6.4.2.1 Levenburg-Marquardt"
}
},
"source": [
"#### 3.6.4.2.1 Levenburg-Marquardt"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.6.4.2.1 Levenburg-Marquardt](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.4.2.1-Levenburg-Marquardt)",
"section": "3.6.4.2.1 Levenburg-Marquardt"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.6.4.2.2 Powell Dogleg](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.4.2.2-Powell-Dogleg)",
"section": "3.6.4.2.2 Powell Dogleg"
}
},
"source": [
"#### 3.6.4.2.2 Powell Dogleg"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.6.4.2.2 Powell Dogleg](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.4.2.2-Powell-Dogleg)",
"section": "3.6.4.2.2 Powell Dogleg"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.6.4.2.2 Powell Dogleg](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.4.2.2-Powell-Dogleg)",
"section": "3.6.4.2.2 Powell Dogleg"
}
},
"source": [
""
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.6.4.2.2 Powell Dogleg](https://ndcbe.github.io/CBE60499/03.06-Globalization.html#3.6.4.2.2-Powell-Dogleg)",
"section": "3.6.4.2.2 Powell Dogleg"
}
},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"id": "49ad7a0a",
"metadata": {},
"source": [
"\n",
"< [3.5 Quasi-Newton Methods for Unconstrained Optimization](https://ndcbe.github.io/CBE60499/03.05-Quasi-Newton-Method.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [3.7 Algorithms Homework 1](https://ndcbe.github.io/CBE60499/03.07-Algorithms1.html) > 
 "
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.6"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.6"
}
},
"nbformat": 4,
"nbformat_minor": 2
}

