{
"cells": [
{
"cell_type": "markdown",
"id": "f8ee167d",
"metadata": {},
"source": [
"\n",
"*This notebook contains material from [CBE60499](https://ndcbe.github.io/CBE60499);\n",
"content is available [on Github](git@github.com:ndcbe/CBE60499.git).*\n"
]
},
{
"cell_type": "markdown",
"id": "41ce4d8c",
"metadata": {},
"source": [
"\n",
"< [3.0 Unconstrained Nonlinear Optimization: Theory and Algorithms](https://ndcbe.github.io/CBE60499/03.00-Unconstrained.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [3.2 Mathematics Primer](https://ndcbe.github.io/CBE60499/03.02-Math-Primer-2.html) > 
 "
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 1,
"link": "[3.1 Linear Algebra Review and SciPy Basics](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1-Linear-Algebra-Review-and-SciPy-Basics)",
"section": "3.1 Linear Algebra Review and SciPy Basics"
}
},
"source": [
"# 3.1 Linear Algebra Review and SciPy Basics\n",
"\n",
"Screenshots from Section **2.2 Vectors and Matrices** in Biegler (2010)\n",
"\n",
"**Recommended Links**\n",
"* [NumPy Documentation - Main Page](https://docs.scipy.org/doc/numpy-1.15.0/reference/)\n",
"* [SciPy Documentation - Main Page](https://docs.scipy.org/doc/scipy-1.1.0/reference/)\n",
"* [SciPy Linear Algebra - Tutorial](https://docs.scipy.org/doc/scipy-1.1.0/reference/tutorial/linalg.html)\n",
"* [SciPy Linear Algebra - API](https://docs.scipy.org/doc/scipy-1.1.0/reference/linalg.html)\n",
"* [SciPy Lecture Notes](http://www.scipy-lectures.org/) (Especially 1.1 - 1.6 for everyone and 2.1 - 2.2 for advanced users)\n",
"\n",
"Tip: We will mostly use SciPy for linear algebra. (It has more sophisticated capabilities than NumPy.) We will use NumPy if/when SciPy does not offer a specific command."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"nbpages": {
"level": 1,
"link": "[3.1 Linear Algebra Review and SciPy Basics](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1-Linear-Algebra-Review-and-SciPy-Basics)",
"section": "3.1 Linear Algebra Review and SciPy Basics"
}
},
"outputs": [],
"source": [
"# Load required Python libraries.\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"from scipy import linalg"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.1 Notation (for textbook)](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.1-Notation-(for-textbook))",
"section": "3.1.1 Notation (for textbook)"
}
},
"source": [
"## 3.1.1 Notation (for textbook)\n",
"* Scalar constants and variables - Greek letters\n",
"* Vectors - Lower case Roman letters\n",
"* Matrices - Upper case Roman letters\n",
"\n",
"The notation for lectures will (hopefully) be obvious from context. I sometimes use Greek letters for constants and Roman letters for variables... unless the Greek letters have engineering or scientific meaning.\n",
"\n",
"## Matrix Operations\n",
"\n",
""
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.1 Notation (for textbook)](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.1-Notation-(for-textbook))",
"section": "3.1.1 Notation (for textbook)"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Ao = \n",
"[[0.90471685 0.17317304 0.40300532]\n",
" [0.63393766 0.90146479 0.61500922]]\n",
"\n",
"Bo = \n",
"[[0.34621818 0.9393221 ]\n",
" [0.67416793 0.95718324]\n",
" [0.61310823 0.40727659]]\n",
"\n",
"Ao*Bo =\n",
"[[0.67706301 1.17971349]\n",
" [1.20428661 1.7088175 ]]\n"
]
}
],
"source": [
"# Generate random matrices\n",
"n = 2\n",
"m = 3\n",
"\n",
"Ao = np.random.rand(n,m)\n",
"Bo = np.random.rand(m,n)\n",
"\n",
"print(\"Ao = \")\n",
"print(Ao)\n",
"print(\"\\nBo = \")\n",
"print(Bo)\n",
"\n",
"\n",
"# What is the dimension of A*B? Try to answer this without the computer.\n",
"\n",
"# Calculate A*B using Python\n",
"print(\"\\nAo*Bo =\")\n",
"print(Ao.dot(Bo))"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.1 Notation (for textbook)](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.1-Notation-(for-textbook))",
"section": "3.1.1 Notation (for textbook)"
}
},
"source": [
"**Activity**\n",
"* Calculate $A_o^{T}$\n",
"* Create a square matrix and check if it is symmetric\n",
"* Create a 3x3 identity matrix"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.1 Notation (for textbook)](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.1-Notation-(for-textbook))",
"section": "3.1.1 Notation (for textbook)"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"transpose(Ao) = \n",
" [[0.90471685 0.63393766]\n",
" [0.17317304 0.90146479]\n",
" [0.40300532 0.61500922]] \n",
"\n",
"I = \n",
" [[1. 0. 0.]\n",
" [0. 1. 0.]\n",
" [0. 0. 1.]] \n",
"\n"
]
}
],
"source": [
"# Transpose\n",
"print(\"transpose(Ao) = \\n\",Ao.transpose(),\"\\n\")\n",
"\n",
"# Create a square matrix. Is it symmetric?\n",
"\n",
"# Identify matrix\n",
"print(\"I = \\n\",np.identity(3),\"\\n\")"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.2 Determinant](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.2-Determinant)",
"section": "3.1.2 Determinant"
}
},
"source": [
"## 3.1.2 Determinant\n",
""
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.2 Determinant](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.2-Determinant)",
"section": "3.1.2 Determinant"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Ad = \n",
"[[0.35144304 0.40331999]\n",
" [0.98819481 0.83989719]]\n",
"\n",
"Bd = \n",
"[[0.24359748 0.02035267]\n",
" [0.32634249 0.99856976]]\n",
"\n",
"Cd = \n",
"[[ 1 0 0]\n",
" [-2 0 0]\n",
" [ 0 1 1]]\n"
]
}
],
"source": [
"# Generate random matrices\n",
"nd = 2\n",
"\n",
"Ad = np.random.rand(nd,nd)\n",
"Bd = np.random.rand(nd,nd)\n",
"\n",
"Cd = np.array([(1, 0, 0),(-2, 0, 0),(0, 1, 1)])\n",
"\n",
"print(\"Ad = \")\n",
"print(Ad)\n",
"print(\"\\nBd = \")\n",
"print(Bd)\n",
"print(\"\\nCd = \")\n",
"print(Cd)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.2 Determinant](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.2-Determinant)",
"section": "3.1.2 Determinant"
}
},
"source": [
"**Activity**\n",
"* Verify the properties listed under *Some properties for the determinant include*\n",
"* If $A_d$, $B_d$ or $C_d$ singular?"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.2 Determinant](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.2-Determinant)",
"section": "3.1.2 Determinant"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"det(A*B) = -0.024461085784763897\n",
"det(A)*det(B) = -0.02446108578476388\n"
]
}
],
"source": [
"# Property 1\n",
"print(\"det(A*B) = \",linalg.det(Ad.dot(Bd)))\n",
"\n",
"print(\"det(A)*det(B) = \",linalg.det(Ad)*linalg.det(Bd))"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.2 Determinant](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.2-Determinant)",
"section": "3.1.2 Determinant"
}
},
"outputs": [],
"source": [
"# Property 2"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.2 Determinant](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.2-Determinant)",
"section": "3.1.2 Determinant"
}
},
"outputs": [],
"source": [
"# Property 3"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.2 Determinant](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.2-Determinant)",
"section": "3.1.2 Determinant"
}
},
"outputs": [],
"source": [
"# Property 4"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.2 Determinant](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.2-Determinant)",
"section": "3.1.2 Determinant"
}
},
"source": [
"**Another Example** (for at home)\n",
"\n",
"Below is an example from *Linear Algebra and Its Applications* by David C. Lay, 3rd edition that shows how to calculate a determinant by hand.\n",
"\n",
"\n",
"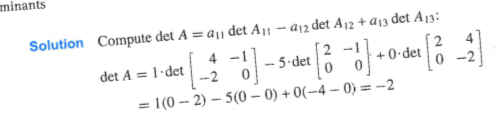"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.3 Rank](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.3-Rank)",
"section": "3.1.3 Rank"
}
},
"source": [
"## 3.1.3 Rank\n",
"\n",
"\n",
"**Activity**\n",
"* Predict the rank of $A_o^T$, $B_o^T$, $A_d$, $B_d$, $C_d$\n",
"* Calculate np.linalg.matrix_rank(). Where you correct?"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.3 Rank](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.3-Rank)",
"section": "3.1.3 Rank"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"rank(A_o) = 2 \n",
"\n"
]
}
],
"source": [
"print(\"rank(A_o) = \",np.linalg.matrix_rank(Ao),\"\\n\")\n",
"\n",
"# Fill in remainder here."
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.4 Inverse](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.4-Inverse)",
"section": "3.1.4 Inverse"
}
},
"source": [
"## 3.1.4 Inverse\n",
"\n",
"\n",
"**Activity**\n",
"1. Calculate the inverse of $A_o$ and verity that $A_o^{-1} A_o = I$\n",
"2. Verify that det($A^{-1}$) = 1/det($A$)\n",
"3. Is $Q$ an orthogonal matrix?"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.4 Inverse](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.4-Inverse)",
"section": "3.1.4 Inverse"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Q = \n",
"[[ 0.98006658 -0.19866933]\n",
" [ 0.19866933 0.98006658]]\n"
]
}
],
"source": [
"# Task 1\n",
"\n",
"# Task 2\n",
"\n",
"# Task 3\n",
"# Is this an orthogonal matrix? Yes, no, or need more information?\n",
"theta = 0.2\n",
"Q = np.array([(np.cos(theta), -np.sin(theta)),(np.sin(theta),np.cos(theta))])\n",
"\n",
"print(\"Q = \")\n",
"print(Q)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.5 Solving Linear Systems](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5-Solving-Linear-Systems)",
"section": "3.1.5 Solving Linear Systems"
}
},
"source": [
"## 3.1.5 Solving Linear Systems\n",
"Consider the linear system $A_l x = b_l$"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.5 Solving Linear Systems](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5-Solving-Linear-Systems)",
"section": "3.1.5 Solving Linear Systems"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Al = \n",
" [[4 3]\n",
" [6 3]]\n",
"\n",
"bl = \n",
" [1 0]\n"
]
}
],
"source": [
"Al = np.array([(4,3),(6,3)])\n",
"bl = np.array([1,0])\n",
"print(\"Al = \\n\",Al)\n",
"print(\"\\nbl = \\n\",bl)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.1.5.1 Explicit Inverse](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.1-Explicit-Inverse)",
"section": "3.1.5.1 Explicit Inverse"
}
},
"source": [
"### 3.1.5.1 Explicit Inverse\n",
"\n",
"Calculate $x$ by explicitly using $A_l^{-1}$. Hint: Use linalg.inv()."
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.1.5.1 Explicit Inverse](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.1-Explicit-Inverse)",
"section": "3.1.5.1 Explicit Inverse"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Ainv = \n",
" [[-0.5 0.5 ]\n",
" [ 1. -0.66666667]] \n",
"\n"
]
}
],
"source": [
"Ainv = linalg.inv(Al)\n",
"print(\"Ainv = \\n\",Ainv,\"\\n\")\n",
"\n",
"# Now calculate and print x"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.1.5.2 LU Decomposition](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.2-LU-Decomposition)",
"section": "3.1.5.2 LU Decomposition"
}
},
"source": [
"### 3.1.5.2 LU Decomposition\n",
"\n",
"Perform LU decomposition on $A_l$. What structures do the $P$, $L$, and $U$ matrices have?"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.1.5.2 LU Decomposition](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.2-LU-Decomposition)",
"section": "3.1.5.2 LU Decomposition"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"A = \n",
" [[0.68331246 0.29422836 0.22419151 0.41620186]\n",
" [0.05988483 0.58705665 0.07246852 0.45441375]\n",
" [0.6024749 0.36997327 0.13872522 0.45388322]\n",
" [0.34311843 0.47101812 0.51826738 0.25525007]] \n",
"\n",
"b = \n",
" [[0.00949348]\n",
" [0.82027783]\n",
" [0.90273651]\n",
" [0.37915841]] \n",
"\n"
]
}
],
"source": [
"# Create test linear systems\n",
"A = np.random.rand(4,4)\n",
"print(\"A = \\n\",A,\"\\n\")\n",
"\n",
"b = np.random.rand(4,1)\n",
"print(\"b = \\n\",b,\"\\n\")"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.1.5.2 LU Decomposition](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.2-LU-Decomposition)",
"section": "3.1.5.2 LU Decomposition"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"P = \n",
" [[1. 0. 0. 0.]\n",
" [0. 1. 0. 0.]\n",
" [0. 0. 0. 1.]\n",
" [0. 0. 1. 0.]]\n",
"L = \n",
" [[ 1. 0. 0. 0. ]\n",
" [ 0.08763901 1. 0. 0. ]\n",
" [ 0.50213986 0.5759686 1. 0. ]\n",
" [ 0.88169751 0.19696885 -0.18479522 1. ]]\n",
"U = \n",
" [[ 0.68331246 0.29422836 0.22419151 0.41620186]\n",
" [ 0. 0.56127076 0.05282059 0.41793823]\n",
" [ 0. 0. 0.37526888 -0.19446077]\n",
" [ 0. 0. 0. -0.03133716]]\n",
"P*L*U = \n",
" [[0.68331246 0.29422836 0.22419151 0.41620186]\n",
" [0.05988483 0.58705665 0.07246852 0.45441375]\n",
" [0.6024749 0.36997327 0.13872522 0.45388322]\n",
" [0.34311843 0.47101812 0.51826738 0.25525007]] \n",
"\n"
]
}
],
"source": [
"# Perform LU decomposition\n",
"(P, L, U) = linalg.lu(A)\n",
"\n",
"# Permutation matrix\n",
"print(\"P = \\n\",P)\n",
"\n",
"# Lower diagonal matrix\n",
"print(\"L = \\n\",L)\n",
"\n",
"# Upper diagonal matrix\n",
"print(\"U = \\n\",U)\n",
"\n",
"# Verify result\n",
"print(\"P*L*U = \\n\",P.dot(L.dot(U)),\"\\n\")"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.1.5.2.1 Is P orthogonal?](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.2.1-Is-P-orthogonal?)",
"section": "3.1.5.2.1 Is P orthogonal?"
}
},
"source": [
"#### 3.1.5.2.1 Is P orthogonal?"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.1.5.2.1 Is P orthogonal?](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.2.1-Is-P-orthogonal?)",
"section": "3.1.5.2.1 Is P orthogonal?"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"inv(P) = \n",
" [[ 1. -0. -0. 0.]\n",
" [ 0. 1. -0. 0.]\n",
" [ 0. 0. -0. 1.]\n",
" [ 0. 0. 1. 0.]] \n",
"\n",
"transpose(P) = \n",
" [[1. 0. 0. 0.]\n",
" [0. 1. 0. 0.]\n",
" [0. 0. 0. 1.]\n",
" [0. 0. 1. 0.]] \n",
"\n",
"P.T*P = \n",
" [[1. 0. 0. 0.]\n",
" [0. 1. 0. 0.]\n",
" [0. 0. 1. 0.]\n",
" [0. 0. 0. 1.]] \n",
"\n"
]
}
],
"source": [
"print(\"inv(P) = \\n\",linalg.inv(P),\"\\n\")\n",
"\n",
"print(\"transpose(P) = \\n\",P.T,\"\\n\")\n",
"\n",
"print(\"P.T*P = \\n\",np.matmul(P.T,P),\"\\n\")"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.1.5.2.1 Is P orthogonal?](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.2.1-Is-P-orthogonal?)",
"section": "3.1.5.2.1 Is P orthogonal?"
}
},
"source": [
"**Yes!** We see that $P^T = P^{-1}$ and $P^T \\cdot P = I$."
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.1.5.2.2 MATLAB](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.2.2-MATLAB)",
"section": "3.1.5.2.2 MATLAB"
}
},
"source": [
"#### 3.1.5.2.2 MATLAB\n",
"\n",
"Defines LU decomposition as follows:\n",
"\n",
"$$ P \\cdot A = L \\cdot U$$\n",
"\n",
"Consider $$A \\cdot x=b$$\n",
"\n",
"Using MATLAB LU definition\n",
"\n",
"$$P\\cdot A = L\\cdot U$$\n",
"$$P^T \\cdot P \\cdot A = P^T \\cdot L \\cdot U$$\n",
"$$A = P^T \\cdot L \\cdot U$$\n",
"\n",
"Substitute into linear system:\n",
"\n",
"$$P^T \\cdot L \\cdot U \\cdot x = b$$\n",
"$$ L \\cdot U \\cdot x = P \\cdot b$$\n",
"\n",
"Let $y = U \\cdot x$ and substitute.\n",
"\n",
"Step 1. Solve $L \\cdot y = P \\cdot b$ for $y$\n",
"\n",
"Step 2. Solve $U \\cdot x = y$ for $x$"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.1.5.2.2 MATLAB](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.2.2-MATLAB)",
"section": "3.1.5.2.2 MATLAB"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"P*b = [[0.00949348]\n",
" [0.82027783]\n",
" [0.37915841]\n",
" [0.90273651]] \n",
"\n",
"yLU = [[ 0.00949348]\n",
" [ 0.81944583]\n",
" [-0.09758371]\n",
" [ 0.71492782]] \n",
"\n",
"xLU = [[ 9.4407442 ]\n",
" [ 19.58501477]\n",
" [-12.08206663]\n",
" [-22.81406129]] \n",
"\n"
]
}
],
"source": [
"Pb = P.dot(b)\n",
"print(\"P*b = \",Pb,\"\\n\")\n",
"\n",
"yLU = linalg.solve(L,Pb)\n",
"print(\"yLU = \",yLU,\"\\n\")\n",
"\n",
"xLU = linalg.solve(U,yLU)\n",
"print(\"xLU = \",xLU,\"\\n\")"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.1.5.2.3 SciPy](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.2.3-SciPy)",
"section": "3.1.5.2.3 SciPy"
}
},
"source": [
"#### 3.1.5.2.3 SciPy\n",
"\n",
"Defines LU decomposition as:\n",
"\n",
"$$ A = P \\cdot L \\cdot U $$\n",
"\n",
"Consider $$A \\cdot x=b$$\n",
"\n",
"SciPy LU definition\n",
"\n",
"$$A = P \\cdot L\\cdot U$$\n",
"\n",
"Substitute into linear system:\n",
"\n",
"$$P \\cdot L \\cdot U \\cdot x = b$$\n",
"$$P^T \\cdot P \\cdot L \\cdot U \\cdot x = P^T \\cdot b$$\n",
"$$L \\cdot U \\cdot x = P^T \\cdot b$$\n",
"\n",
"Let $y = U \\cdot x$ and substitute.\n",
"\n",
"Step 1. Solve $L \\cdot y = P^T \\cdot b$ for $y$\n",
"\n",
"Step 2. Solve $U \\cdot x = y$ for $x$"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.1.5.2.3 SciPy](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.2.3-SciPy)",
"section": "3.1.5.2.3 SciPy"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"P.T*b = [[0.00949348]\n",
" [0.82027783]\n",
" [0.37915841]\n",
" [0.90273651]] \n",
"\n",
"yLU = [[ 0.00949348]\n",
" [ 0.81944583]\n",
" [-0.09758371]\n",
" [ 0.71492782]] \n",
"\n",
"xLU = [[ 9.4407442 ]\n",
" [ 19.58501477]\n",
" [-12.08206663]\n",
" [-22.81406129]] \n",
"\n"
]
}
],
"source": [
"## LU decomposition algorithm.\n",
"Pb = (P.T).dot(b)\n",
"print(\"P.T*b = \",Pb,\"\\n\")\n",
"\n",
"yLU = linalg.solve(L,Pb)\n",
"print(\"yLU = \",yLU,\"\\n\")\n",
"\n",
"xLU = linalg.solve(U,yLU)\n",
"print(\"xLU = \",xLU,\"\\n\")"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.1.5.2.3 SciPy](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.2.3-SciPy)",
"section": "3.1.5.2.3 SciPy"
}
},
"source": [
"**What is the difference?** A transpose.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.1.5.2.4 Verify our answer with `linalg.solve`](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.2.4-Verify-our-answer-with-`linalg.solve`)",
"section": "3.1.5.2.4 Verify our answer with `linalg.solve`"
}
},
"source": [
"#### 3.1.5.2.4 Verify our answer with `linalg.solve`\n",
"\n",
"Solve the linear system using linalg.solve"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.1.5.2.4 Verify our answer with `linalg.solve`](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.2.4-Verify-our-answer-with-`linalg.solve`)",
"section": "3.1.5.2.4 Verify our answer with `linalg.solve`"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"x = \n",
" [-0.5 1. ]\n"
]
}
],
"source": [
"x = linalg.solve(Al,bl)\n",
"print(\"x = \\n\",x)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.6 Invertable Matrix Theorem](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.6-Invertable-Matrix-Theorem)",
"section": "3.1.6 Invertable Matrix Theorem"
}
},
"source": [
"## 3.1.6 Invertable Matrix Theorem\n",
"Screenshots from *Linear Algebra and Its Applications* by David C. Lay, 3rd edition\n",
"\n",
"\n",
"\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.7 Eigenvectors and Eigenvalues](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.7-Eigenvectors-and-Eigenvalues)",
"section": "3.1.7 Eigenvectors and Eigenvalues"
}
},
"source": [
"## 3.1.7 Eigenvectors and Eigenvalues\n",
""
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.7 Eigenvectors and Eigenvalues](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.7-Eigenvectors-and-Eigenvalues)",
"section": "3.1.7 Eigenvectors and Eigenvalues"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Ae = \n",
" [[ 0 -4 -6]\n",
" [-1 0 -3]\n",
" [ 1 2 5]]\n"
]
}
],
"source": [
"Ae = np.array([(0, -4, -6), (-1, 0, -3), (1, 2, 5)])\n",
"print(\"Ae = \\n\",Ae)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.7 Eigenvectors and Eigenvalues](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.7-Eigenvectors-and-Eigenvalues)",
"section": "3.1.7 Eigenvectors and Eigenvalues"
}
},
"source": [
"**Activity**\n",
"* Do you expect this matrix to have negative eigenvalues? Choose: Yes / No / Cannot tell from inspection.\n",
"* Calculate the eigenvalues.\n",
"* Based on your calculations above, is this matrix i) positive definite, ii) positive semi definite, iii) negative definite, iv) negative semi definite, v) indefinite, or vi) cannot say without additional calculations? Write a sentence to justify your answer.\n",
"* Calculate the determinate using only the eigenvalues."
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.7 Eigenvectors and Eigenvalues](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.7-Eigenvectors-and-Eigenvalues)",
"section": "3.1.7 Eigenvectors and Eigenvalues"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Matrix = \n",
" [[4 3]\n",
" [6 3]] \n",
"\n",
"Eigenvalues = [ 7.77200187+0.j -0.77200187+0.j] \n",
"\n",
"Eigenvectors = \n",
" [[ 0.62246561 -0.53222953]\n",
" [ 0.78264715 0.8466001 ]] \n",
"\n"
]
}
],
"source": [
"# Expect negative eigenavalues?\n",
"# Yes / No / Cannot tell from inspect?\n",
"# Write a sentence to justify your answer.\n",
"\n",
"### Calculate eigenvalues\n",
"\n",
"# Matrix Al\n",
"print(\"Matrix = \\n\",Al,\"\\n\")\n",
"l, v = linalg.eig(Al)\n",
"print(\"Eigenvalues = \",l,\"\\n\")\n",
"print(\"Eigenvectors = \\n\",v,\"\\n\")"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.8 Singular Value Decomposition](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.8-Singular-Value-Decomposition)",
"section": "3.1.8 Singular Value Decomposition"
}
},
"source": [
"## 3.1.8 Singular Value Decomposition\n",
"Notes will be given in class.\n",
"\n",
"**Activity**\n",
"* Calculate singular value decomposition of $A_l$ and $C_d$\n",
"* What is the rank of each matrix?"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.8 Singular Value Decomposition](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.8-Singular-Value-Decomposition)",
"section": "3.1.8 Singular Value Decomposition"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Matrix = \n",
" [[4 3]\n",
" [6 3]] \n",
"\n",
"U = \n",
" [[-0.59581566 -0.80312122]\n",
" [-0.80312122 0.59581566]] \n",
"\n",
"S = \n",
" [8.33557912 0.71980602] \n",
"\n",
"Vh = \n",
" [[-0.86400595 -0.50348159]\n",
" [ 0.50348159 -0.86400595]] \n",
"\n"
]
}
],
"source": [
"# Matrix Al\n",
"print(\"Matrix = \\n\",Al,\"\\n\")\n",
"U,s,Vh = linalg.svd(Al)\n",
"print(\"U = \\n\",U,\"\\n\")\n",
"print(\"S = \\n\",s,\"\\n\")\n",
"print(\"Vh = \\n\",Vh,\"\\n\")\n",
"\n",
"## Rank (from inspecting singular values)?"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.9 Vector and Matrix Norms](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.9-Vector-and-Matrix-Norms)",
"section": "3.1.9 Vector and Matrix Norms"
}
},
"source": [
"## 3.1.9 Vector and Matrix Norms\n",
"\n",
""
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.9 Vector and Matrix Norms](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.9-Vector-and-Matrix-Norms)",
"section": "3.1.9 Vector and Matrix Norms"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"x = \n",
" [[0.02808233]\n",
" [0.20488865]\n",
" [0.77425602]]\n",
"y = \n",
" [[0.73113614]\n",
" [0.20737529]\n",
" [0.97754014]]\n"
]
}
],
"source": [
"x = np.random.rand(3,1)\n",
"print(\"x = \\n\",x)\n",
"\n",
"y = np.random.rand(3,1)\n",
"print(\"y = \\n\",y)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.9 Vector and Matrix Norms](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.9-Vector-and-Matrix-Norms)",
"section": "3.1.9 Vector and Matrix Norms"
}
},
"source": [
"**Activity**\n",
"* Verify the vector norm properties hold for the p-2 norm using $x$ and $y$. Hint: linalg.norm()\n",
"* Calculate $||A_l||_1$, $||A_l||_{\\infty}$ and $||A_l||_2$ using both the rules given above and SciPy"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.10 Condition Number](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.10-Condition-Number)",
"section": "3.1.10 Condition Number"
}
},
"source": [
"## 3.1.10 Condition Number\n",
"\n",
"**Activity**\n",
"* Estimate the condition number of $A_l$ by inspecting the SVD results.\n",
"* Calculate the condition number of $A_l$ using np.linalg.cond()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.10 Condition Number](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.10-Condition-Number)",
"section": "3.1.10 Condition Number"
}
},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"id": "68adbc5a",
"metadata": {},
"source": [
"\n",
"< [3.0 Unconstrained Nonlinear Optimization: Theory and Algorithms](https://ndcbe.github.io/CBE60499/03.00-Unconstrained.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [3.2 Mathematics Primer](https://ndcbe.github.io/CBE60499/03.02-Math-Primer-2.html) >
"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 1,
"link": "[3.1 Linear Algebra Review and SciPy Basics](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1-Linear-Algebra-Review-and-SciPy-Basics)",
"section": "3.1 Linear Algebra Review and SciPy Basics"
}
},
"source": [
"# 3.1 Linear Algebra Review and SciPy Basics\n",
"\n",
"Screenshots from Section **2.2 Vectors and Matrices** in Biegler (2010)\n",
"\n",
"**Recommended Links**\n",
"* [NumPy Documentation - Main Page](https://docs.scipy.org/doc/numpy-1.15.0/reference/)\n",
"* [SciPy Documentation - Main Page](https://docs.scipy.org/doc/scipy-1.1.0/reference/)\n",
"* [SciPy Linear Algebra - Tutorial](https://docs.scipy.org/doc/scipy-1.1.0/reference/tutorial/linalg.html)\n",
"* [SciPy Linear Algebra - API](https://docs.scipy.org/doc/scipy-1.1.0/reference/linalg.html)\n",
"* [SciPy Lecture Notes](http://www.scipy-lectures.org/) (Especially 1.1 - 1.6 for everyone and 2.1 - 2.2 for advanced users)\n",
"\n",
"Tip: We will mostly use SciPy for linear algebra. (It has more sophisticated capabilities than NumPy.) We will use NumPy if/when SciPy does not offer a specific command."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"nbpages": {
"level": 1,
"link": "[3.1 Linear Algebra Review and SciPy Basics](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1-Linear-Algebra-Review-and-SciPy-Basics)",
"section": "3.1 Linear Algebra Review and SciPy Basics"
}
},
"outputs": [],
"source": [
"# Load required Python libraries.\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"from scipy import linalg"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.1 Notation (for textbook)](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.1-Notation-(for-textbook))",
"section": "3.1.1 Notation (for textbook)"
}
},
"source": [
"## 3.1.1 Notation (for textbook)\n",
"* Scalar constants and variables - Greek letters\n",
"* Vectors - Lower case Roman letters\n",
"* Matrices - Upper case Roman letters\n",
"\n",
"The notation for lectures will (hopefully) be obvious from context. I sometimes use Greek letters for constants and Roman letters for variables... unless the Greek letters have engineering or scientific meaning.\n",
"\n",
"## Matrix Operations\n",
"\n",
""
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.1 Notation (for textbook)](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.1-Notation-(for-textbook))",
"section": "3.1.1 Notation (for textbook)"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Ao = \n",
"[[0.90471685 0.17317304 0.40300532]\n",
" [0.63393766 0.90146479 0.61500922]]\n",
"\n",
"Bo = \n",
"[[0.34621818 0.9393221 ]\n",
" [0.67416793 0.95718324]\n",
" [0.61310823 0.40727659]]\n",
"\n",
"Ao*Bo =\n",
"[[0.67706301 1.17971349]\n",
" [1.20428661 1.7088175 ]]\n"
]
}
],
"source": [
"# Generate random matrices\n",
"n = 2\n",
"m = 3\n",
"\n",
"Ao = np.random.rand(n,m)\n",
"Bo = np.random.rand(m,n)\n",
"\n",
"print(\"Ao = \")\n",
"print(Ao)\n",
"print(\"\\nBo = \")\n",
"print(Bo)\n",
"\n",
"\n",
"# What is the dimension of A*B? Try to answer this without the computer.\n",
"\n",
"# Calculate A*B using Python\n",
"print(\"\\nAo*Bo =\")\n",
"print(Ao.dot(Bo))"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.1 Notation (for textbook)](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.1-Notation-(for-textbook))",
"section": "3.1.1 Notation (for textbook)"
}
},
"source": [
"**Activity**\n",
"* Calculate $A_o^{T}$\n",
"* Create a square matrix and check if it is symmetric\n",
"* Create a 3x3 identity matrix"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.1 Notation (for textbook)](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.1-Notation-(for-textbook))",
"section": "3.1.1 Notation (for textbook)"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"transpose(Ao) = \n",
" [[0.90471685 0.63393766]\n",
" [0.17317304 0.90146479]\n",
" [0.40300532 0.61500922]] \n",
"\n",
"I = \n",
" [[1. 0. 0.]\n",
" [0. 1. 0.]\n",
" [0. 0. 1.]] \n",
"\n"
]
}
],
"source": [
"# Transpose\n",
"print(\"transpose(Ao) = \\n\",Ao.transpose(),\"\\n\")\n",
"\n",
"# Create a square matrix. Is it symmetric?\n",
"\n",
"# Identify matrix\n",
"print(\"I = \\n\",np.identity(3),\"\\n\")"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.2 Determinant](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.2-Determinant)",
"section": "3.1.2 Determinant"
}
},
"source": [
"## 3.1.2 Determinant\n",
""
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.2 Determinant](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.2-Determinant)",
"section": "3.1.2 Determinant"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Ad = \n",
"[[0.35144304 0.40331999]\n",
" [0.98819481 0.83989719]]\n",
"\n",
"Bd = \n",
"[[0.24359748 0.02035267]\n",
" [0.32634249 0.99856976]]\n",
"\n",
"Cd = \n",
"[[ 1 0 0]\n",
" [-2 0 0]\n",
" [ 0 1 1]]\n"
]
}
],
"source": [
"# Generate random matrices\n",
"nd = 2\n",
"\n",
"Ad = np.random.rand(nd,nd)\n",
"Bd = np.random.rand(nd,nd)\n",
"\n",
"Cd = np.array([(1, 0, 0),(-2, 0, 0),(0, 1, 1)])\n",
"\n",
"print(\"Ad = \")\n",
"print(Ad)\n",
"print(\"\\nBd = \")\n",
"print(Bd)\n",
"print(\"\\nCd = \")\n",
"print(Cd)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.2 Determinant](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.2-Determinant)",
"section": "3.1.2 Determinant"
}
},
"source": [
"**Activity**\n",
"* Verify the properties listed under *Some properties for the determinant include*\n",
"* If $A_d$, $B_d$ or $C_d$ singular?"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.2 Determinant](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.2-Determinant)",
"section": "3.1.2 Determinant"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"det(A*B) = -0.024461085784763897\n",
"det(A)*det(B) = -0.02446108578476388\n"
]
}
],
"source": [
"# Property 1\n",
"print(\"det(A*B) = \",linalg.det(Ad.dot(Bd)))\n",
"\n",
"print(\"det(A)*det(B) = \",linalg.det(Ad)*linalg.det(Bd))"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.2 Determinant](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.2-Determinant)",
"section": "3.1.2 Determinant"
}
},
"outputs": [],
"source": [
"# Property 2"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.2 Determinant](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.2-Determinant)",
"section": "3.1.2 Determinant"
}
},
"outputs": [],
"source": [
"# Property 3"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.2 Determinant](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.2-Determinant)",
"section": "3.1.2 Determinant"
}
},
"outputs": [],
"source": [
"# Property 4"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.2 Determinant](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.2-Determinant)",
"section": "3.1.2 Determinant"
}
},
"source": [
"**Another Example** (for at home)\n",
"\n",
"Below is an example from *Linear Algebra and Its Applications* by David C. Lay, 3rd edition that shows how to calculate a determinant by hand.\n",
"\n",
"\n",
"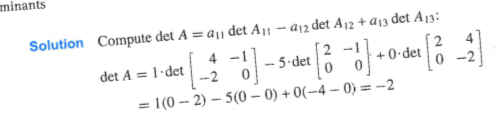"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.3 Rank](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.3-Rank)",
"section": "3.1.3 Rank"
}
},
"source": [
"## 3.1.3 Rank\n",
"\n",
"\n",
"**Activity**\n",
"* Predict the rank of $A_o^T$, $B_o^T$, $A_d$, $B_d$, $C_d$\n",
"* Calculate np.linalg.matrix_rank(). Where you correct?"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.3 Rank](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.3-Rank)",
"section": "3.1.3 Rank"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"rank(A_o) = 2 \n",
"\n"
]
}
],
"source": [
"print(\"rank(A_o) = \",np.linalg.matrix_rank(Ao),\"\\n\")\n",
"\n",
"# Fill in remainder here."
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.4 Inverse](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.4-Inverse)",
"section": "3.1.4 Inverse"
}
},
"source": [
"## 3.1.4 Inverse\n",
"\n",
"\n",
"**Activity**\n",
"1. Calculate the inverse of $A_o$ and verity that $A_o^{-1} A_o = I$\n",
"2. Verify that det($A^{-1}$) = 1/det($A$)\n",
"3. Is $Q$ an orthogonal matrix?"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.4 Inverse](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.4-Inverse)",
"section": "3.1.4 Inverse"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Q = \n",
"[[ 0.98006658 -0.19866933]\n",
" [ 0.19866933 0.98006658]]\n"
]
}
],
"source": [
"# Task 1\n",
"\n",
"# Task 2\n",
"\n",
"# Task 3\n",
"# Is this an orthogonal matrix? Yes, no, or need more information?\n",
"theta = 0.2\n",
"Q = np.array([(np.cos(theta), -np.sin(theta)),(np.sin(theta),np.cos(theta))])\n",
"\n",
"print(\"Q = \")\n",
"print(Q)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.5 Solving Linear Systems](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5-Solving-Linear-Systems)",
"section": "3.1.5 Solving Linear Systems"
}
},
"source": [
"## 3.1.5 Solving Linear Systems\n",
"Consider the linear system $A_l x = b_l$"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.5 Solving Linear Systems](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5-Solving-Linear-Systems)",
"section": "3.1.5 Solving Linear Systems"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Al = \n",
" [[4 3]\n",
" [6 3]]\n",
"\n",
"bl = \n",
" [1 0]\n"
]
}
],
"source": [
"Al = np.array([(4,3),(6,3)])\n",
"bl = np.array([1,0])\n",
"print(\"Al = \\n\",Al)\n",
"print(\"\\nbl = \\n\",bl)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.1.5.1 Explicit Inverse](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.1-Explicit-Inverse)",
"section": "3.1.5.1 Explicit Inverse"
}
},
"source": [
"### 3.1.5.1 Explicit Inverse\n",
"\n",
"Calculate $x$ by explicitly using $A_l^{-1}$. Hint: Use linalg.inv()."
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.1.5.1 Explicit Inverse](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.1-Explicit-Inverse)",
"section": "3.1.5.1 Explicit Inverse"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Ainv = \n",
" [[-0.5 0.5 ]\n",
" [ 1. -0.66666667]] \n",
"\n"
]
}
],
"source": [
"Ainv = linalg.inv(Al)\n",
"print(\"Ainv = \\n\",Ainv,\"\\n\")\n",
"\n",
"# Now calculate and print x"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.1.5.2 LU Decomposition](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.2-LU-Decomposition)",
"section": "3.1.5.2 LU Decomposition"
}
},
"source": [
"### 3.1.5.2 LU Decomposition\n",
"\n",
"Perform LU decomposition on $A_l$. What structures do the $P$, $L$, and $U$ matrices have?"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.1.5.2 LU Decomposition](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.2-LU-Decomposition)",
"section": "3.1.5.2 LU Decomposition"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"A = \n",
" [[0.68331246 0.29422836 0.22419151 0.41620186]\n",
" [0.05988483 0.58705665 0.07246852 0.45441375]\n",
" [0.6024749 0.36997327 0.13872522 0.45388322]\n",
" [0.34311843 0.47101812 0.51826738 0.25525007]] \n",
"\n",
"b = \n",
" [[0.00949348]\n",
" [0.82027783]\n",
" [0.90273651]\n",
" [0.37915841]] \n",
"\n"
]
}
],
"source": [
"# Create test linear systems\n",
"A = np.random.rand(4,4)\n",
"print(\"A = \\n\",A,\"\\n\")\n",
"\n",
"b = np.random.rand(4,1)\n",
"print(\"b = \\n\",b,\"\\n\")"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.1.5.2 LU Decomposition](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.2-LU-Decomposition)",
"section": "3.1.5.2 LU Decomposition"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"P = \n",
" [[1. 0. 0. 0.]\n",
" [0. 1. 0. 0.]\n",
" [0. 0. 0. 1.]\n",
" [0. 0. 1. 0.]]\n",
"L = \n",
" [[ 1. 0. 0. 0. ]\n",
" [ 0.08763901 1. 0. 0. ]\n",
" [ 0.50213986 0.5759686 1. 0. ]\n",
" [ 0.88169751 0.19696885 -0.18479522 1. ]]\n",
"U = \n",
" [[ 0.68331246 0.29422836 0.22419151 0.41620186]\n",
" [ 0. 0.56127076 0.05282059 0.41793823]\n",
" [ 0. 0. 0.37526888 -0.19446077]\n",
" [ 0. 0. 0. -0.03133716]]\n",
"P*L*U = \n",
" [[0.68331246 0.29422836 0.22419151 0.41620186]\n",
" [0.05988483 0.58705665 0.07246852 0.45441375]\n",
" [0.6024749 0.36997327 0.13872522 0.45388322]\n",
" [0.34311843 0.47101812 0.51826738 0.25525007]] \n",
"\n"
]
}
],
"source": [
"# Perform LU decomposition\n",
"(P, L, U) = linalg.lu(A)\n",
"\n",
"# Permutation matrix\n",
"print(\"P = \\n\",P)\n",
"\n",
"# Lower diagonal matrix\n",
"print(\"L = \\n\",L)\n",
"\n",
"# Upper diagonal matrix\n",
"print(\"U = \\n\",U)\n",
"\n",
"# Verify result\n",
"print(\"P*L*U = \\n\",P.dot(L.dot(U)),\"\\n\")"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.1.5.2.1 Is P orthogonal?](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.2.1-Is-P-orthogonal?)",
"section": "3.1.5.2.1 Is P orthogonal?"
}
},
"source": [
"#### 3.1.5.2.1 Is P orthogonal?"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.1.5.2.1 Is P orthogonal?](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.2.1-Is-P-orthogonal?)",
"section": "3.1.5.2.1 Is P orthogonal?"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"inv(P) = \n",
" [[ 1. -0. -0. 0.]\n",
" [ 0. 1. -0. 0.]\n",
" [ 0. 0. -0. 1.]\n",
" [ 0. 0. 1. 0.]] \n",
"\n",
"transpose(P) = \n",
" [[1. 0. 0. 0.]\n",
" [0. 1. 0. 0.]\n",
" [0. 0. 0. 1.]\n",
" [0. 0. 1. 0.]] \n",
"\n",
"P.T*P = \n",
" [[1. 0. 0. 0.]\n",
" [0. 1. 0. 0.]\n",
" [0. 0. 1. 0.]\n",
" [0. 0. 0. 1.]] \n",
"\n"
]
}
],
"source": [
"print(\"inv(P) = \\n\",linalg.inv(P),\"\\n\")\n",
"\n",
"print(\"transpose(P) = \\n\",P.T,\"\\n\")\n",
"\n",
"print(\"P.T*P = \\n\",np.matmul(P.T,P),\"\\n\")"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.1.5.2.1 Is P orthogonal?](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.2.1-Is-P-orthogonal?)",
"section": "3.1.5.2.1 Is P orthogonal?"
}
},
"source": [
"**Yes!** We see that $P^T = P^{-1}$ and $P^T \\cdot P = I$."
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.1.5.2.2 MATLAB](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.2.2-MATLAB)",
"section": "3.1.5.2.2 MATLAB"
}
},
"source": [
"#### 3.1.5.2.2 MATLAB\n",
"\n",
"Defines LU decomposition as follows:\n",
"\n",
"$$ P \\cdot A = L \\cdot U$$\n",
"\n",
"Consider $$A \\cdot x=b$$\n",
"\n",
"Using MATLAB LU definition\n",
"\n",
"$$P\\cdot A = L\\cdot U$$\n",
"$$P^T \\cdot P \\cdot A = P^T \\cdot L \\cdot U$$\n",
"$$A = P^T \\cdot L \\cdot U$$\n",
"\n",
"Substitute into linear system:\n",
"\n",
"$$P^T \\cdot L \\cdot U \\cdot x = b$$\n",
"$$ L \\cdot U \\cdot x = P \\cdot b$$\n",
"\n",
"Let $y = U \\cdot x$ and substitute.\n",
"\n",
"Step 1. Solve $L \\cdot y = P \\cdot b$ for $y$\n",
"\n",
"Step 2. Solve $U \\cdot x = y$ for $x$"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.1.5.2.2 MATLAB](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.2.2-MATLAB)",
"section": "3.1.5.2.2 MATLAB"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"P*b = [[0.00949348]\n",
" [0.82027783]\n",
" [0.37915841]\n",
" [0.90273651]] \n",
"\n",
"yLU = [[ 0.00949348]\n",
" [ 0.81944583]\n",
" [-0.09758371]\n",
" [ 0.71492782]] \n",
"\n",
"xLU = [[ 9.4407442 ]\n",
" [ 19.58501477]\n",
" [-12.08206663]\n",
" [-22.81406129]] \n",
"\n"
]
}
],
"source": [
"Pb = P.dot(b)\n",
"print(\"P*b = \",Pb,\"\\n\")\n",
"\n",
"yLU = linalg.solve(L,Pb)\n",
"print(\"yLU = \",yLU,\"\\n\")\n",
"\n",
"xLU = linalg.solve(U,yLU)\n",
"print(\"xLU = \",xLU,\"\\n\")"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.1.5.2.3 SciPy](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.2.3-SciPy)",
"section": "3.1.5.2.3 SciPy"
}
},
"source": [
"#### 3.1.5.2.3 SciPy\n",
"\n",
"Defines LU decomposition as:\n",
"\n",
"$$ A = P \\cdot L \\cdot U $$\n",
"\n",
"Consider $$A \\cdot x=b$$\n",
"\n",
"SciPy LU definition\n",
"\n",
"$$A = P \\cdot L\\cdot U$$\n",
"\n",
"Substitute into linear system:\n",
"\n",
"$$P \\cdot L \\cdot U \\cdot x = b$$\n",
"$$P^T \\cdot P \\cdot L \\cdot U \\cdot x = P^T \\cdot b$$\n",
"$$L \\cdot U \\cdot x = P^T \\cdot b$$\n",
"\n",
"Let $y = U \\cdot x$ and substitute.\n",
"\n",
"Step 1. Solve $L \\cdot y = P^T \\cdot b$ for $y$\n",
"\n",
"Step 2. Solve $U \\cdot x = y$ for $x$"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.1.5.2.3 SciPy](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.2.3-SciPy)",
"section": "3.1.5.2.3 SciPy"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"P.T*b = [[0.00949348]\n",
" [0.82027783]\n",
" [0.37915841]\n",
" [0.90273651]] \n",
"\n",
"yLU = [[ 0.00949348]\n",
" [ 0.81944583]\n",
" [-0.09758371]\n",
" [ 0.71492782]] \n",
"\n",
"xLU = [[ 9.4407442 ]\n",
" [ 19.58501477]\n",
" [-12.08206663]\n",
" [-22.81406129]] \n",
"\n"
]
}
],
"source": [
"## LU decomposition algorithm.\n",
"Pb = (P.T).dot(b)\n",
"print(\"P.T*b = \",Pb,\"\\n\")\n",
"\n",
"yLU = linalg.solve(L,Pb)\n",
"print(\"yLU = \",yLU,\"\\n\")\n",
"\n",
"xLU = linalg.solve(U,yLU)\n",
"print(\"xLU = \",xLU,\"\\n\")"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.1.5.2.3 SciPy](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.2.3-SciPy)",
"section": "3.1.5.2.3 SciPy"
}
},
"source": [
"**What is the difference?** A transpose.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.1.5.2.4 Verify our answer with `linalg.solve`](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.2.4-Verify-our-answer-with-`linalg.solve`)",
"section": "3.1.5.2.4 Verify our answer with `linalg.solve`"
}
},
"source": [
"#### 3.1.5.2.4 Verify our answer with `linalg.solve`\n",
"\n",
"Solve the linear system using linalg.solve"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"nbpages": {
"level": 4,
"link": "[3.1.5.2.4 Verify our answer with `linalg.solve`](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.5.2.4-Verify-our-answer-with-`linalg.solve`)",
"section": "3.1.5.2.4 Verify our answer with `linalg.solve`"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"x = \n",
" [-0.5 1. ]\n"
]
}
],
"source": [
"x = linalg.solve(Al,bl)\n",
"print(\"x = \\n\",x)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.6 Invertable Matrix Theorem](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.6-Invertable-Matrix-Theorem)",
"section": "3.1.6 Invertable Matrix Theorem"
}
},
"source": [
"## 3.1.6 Invertable Matrix Theorem\n",
"Screenshots from *Linear Algebra and Its Applications* by David C. Lay, 3rd edition\n",
"\n",
"\n",
"\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.7 Eigenvectors and Eigenvalues](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.7-Eigenvectors-and-Eigenvalues)",
"section": "3.1.7 Eigenvectors and Eigenvalues"
}
},
"source": [
"## 3.1.7 Eigenvectors and Eigenvalues\n",
""
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.7 Eigenvectors and Eigenvalues](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.7-Eigenvectors-and-Eigenvalues)",
"section": "3.1.7 Eigenvectors and Eigenvalues"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Ae = \n",
" [[ 0 -4 -6]\n",
" [-1 0 -3]\n",
" [ 1 2 5]]\n"
]
}
],
"source": [
"Ae = np.array([(0, -4, -6), (-1, 0, -3), (1, 2, 5)])\n",
"print(\"Ae = \\n\",Ae)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.7 Eigenvectors and Eigenvalues](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.7-Eigenvectors-and-Eigenvalues)",
"section": "3.1.7 Eigenvectors and Eigenvalues"
}
},
"source": [
"**Activity**\n",
"* Do you expect this matrix to have negative eigenvalues? Choose: Yes / No / Cannot tell from inspection.\n",
"* Calculate the eigenvalues.\n",
"* Based on your calculations above, is this matrix i) positive definite, ii) positive semi definite, iii) negative definite, iv) negative semi definite, v) indefinite, or vi) cannot say without additional calculations? Write a sentence to justify your answer.\n",
"* Calculate the determinate using only the eigenvalues."
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.7 Eigenvectors and Eigenvalues](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.7-Eigenvectors-and-Eigenvalues)",
"section": "3.1.7 Eigenvectors and Eigenvalues"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Matrix = \n",
" [[4 3]\n",
" [6 3]] \n",
"\n",
"Eigenvalues = [ 7.77200187+0.j -0.77200187+0.j] \n",
"\n",
"Eigenvectors = \n",
" [[ 0.62246561 -0.53222953]\n",
" [ 0.78264715 0.8466001 ]] \n",
"\n"
]
}
],
"source": [
"# Expect negative eigenavalues?\n",
"# Yes / No / Cannot tell from inspect?\n",
"# Write a sentence to justify your answer.\n",
"\n",
"### Calculate eigenvalues\n",
"\n",
"# Matrix Al\n",
"print(\"Matrix = \\n\",Al,\"\\n\")\n",
"l, v = linalg.eig(Al)\n",
"print(\"Eigenvalues = \",l,\"\\n\")\n",
"print(\"Eigenvectors = \\n\",v,\"\\n\")"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.8 Singular Value Decomposition](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.8-Singular-Value-Decomposition)",
"section": "3.1.8 Singular Value Decomposition"
}
},
"source": [
"## 3.1.8 Singular Value Decomposition\n",
"Notes will be given in class.\n",
"\n",
"**Activity**\n",
"* Calculate singular value decomposition of $A_l$ and $C_d$\n",
"* What is the rank of each matrix?"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.8 Singular Value Decomposition](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.8-Singular-Value-Decomposition)",
"section": "3.1.8 Singular Value Decomposition"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Matrix = \n",
" [[4 3]\n",
" [6 3]] \n",
"\n",
"U = \n",
" [[-0.59581566 -0.80312122]\n",
" [-0.80312122 0.59581566]] \n",
"\n",
"S = \n",
" [8.33557912 0.71980602] \n",
"\n",
"Vh = \n",
" [[-0.86400595 -0.50348159]\n",
" [ 0.50348159 -0.86400595]] \n",
"\n"
]
}
],
"source": [
"# Matrix Al\n",
"print(\"Matrix = \\n\",Al,\"\\n\")\n",
"U,s,Vh = linalg.svd(Al)\n",
"print(\"U = \\n\",U,\"\\n\")\n",
"print(\"S = \\n\",s,\"\\n\")\n",
"print(\"Vh = \\n\",Vh,\"\\n\")\n",
"\n",
"## Rank (from inspecting singular values)?"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.9 Vector and Matrix Norms](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.9-Vector-and-Matrix-Norms)",
"section": "3.1.9 Vector and Matrix Norms"
}
},
"source": [
"## 3.1.9 Vector and Matrix Norms\n",
"\n",
""
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.9 Vector and Matrix Norms](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.9-Vector-and-Matrix-Norms)",
"section": "3.1.9 Vector and Matrix Norms"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"x = \n",
" [[0.02808233]\n",
" [0.20488865]\n",
" [0.77425602]]\n",
"y = \n",
" [[0.73113614]\n",
" [0.20737529]\n",
" [0.97754014]]\n"
]
}
],
"source": [
"x = np.random.rand(3,1)\n",
"print(\"x = \\n\",x)\n",
"\n",
"y = np.random.rand(3,1)\n",
"print(\"y = \\n\",y)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.9 Vector and Matrix Norms](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.9-Vector-and-Matrix-Norms)",
"section": "3.1.9 Vector and Matrix Norms"
}
},
"source": [
"**Activity**\n",
"* Verify the vector norm properties hold for the p-2 norm using $x$ and $y$. Hint: linalg.norm()\n",
"* Calculate $||A_l||_1$, $||A_l||_{\\infty}$ and $||A_l||_2$ using both the rules given above and SciPy"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.10 Condition Number](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.10-Condition-Number)",
"section": "3.1.10 Condition Number"
}
},
"source": [
"## 3.1.10 Condition Number\n",
"\n",
"**Activity**\n",
"* Estimate the condition number of $A_l$ by inspecting the SVD results.\n",
"* Calculate the condition number of $A_l$ using np.linalg.cond()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.1.10 Condition Number](https://ndcbe.github.io/CBE60499/03.01-Math-Primer.html#3.1.10-Condition-Number)",
"section": "3.1.10 Condition Number"
}
},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"id": "68adbc5a",
"metadata": {},
"source": [
"\n",
"< [3.0 Unconstrained Nonlinear Optimization: Theory and Algorithms](https://ndcbe.github.io/CBE60499/03.00-Unconstrained.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [3.2 Mathematics Primer](https://ndcbe.github.io/CBE60499/03.02-Math-Primer-2.html) >

 "
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.3"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.3"
}
},
"nbformat": 4,
"nbformat_minor": 2
}

