{
"cells": [
{
"cell_type": "markdown",
"id": "507f5c71",
"metadata": {},
"source": [
"\n",
"*This notebook contains material from [CBE60499](https://ndcbe.github.io/CBE60499);\n",
"content is available [on Github](git@github.com:ndcbe/CBE60499.git).*\n"
]
},
{
"cell_type": "markdown",
"id": "2ad910a6",
"metadata": {},
"source": [
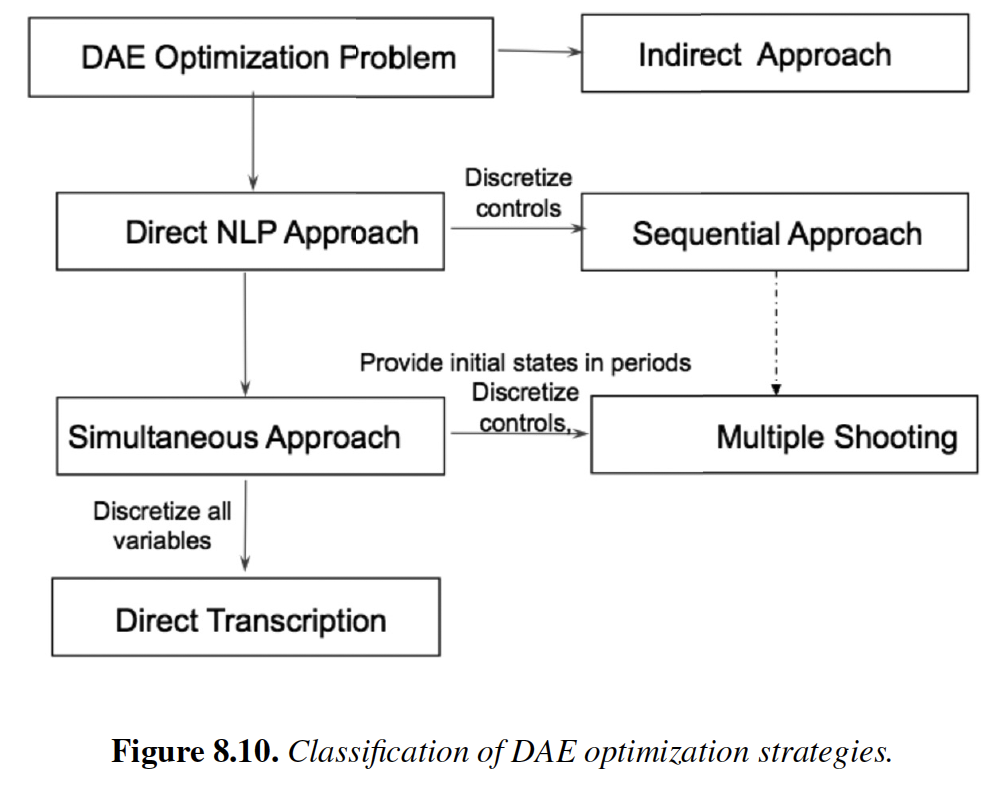
"\n",
"< [2.3 Logical Modeling and Generalized Disjunctive Programs](https://ndcbe.github.io/CBE60499/02.03-GDP.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [2.5 Numeric Integration for DAEs](https://ndcbe.github.io/CBE60499/02.05-Numeric-Integration.html) > 
 "
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 1,
"link": "[2.4 Dynamic Optimization: Differential Algebraic Equations (DAEs)](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4-Dynamic-Optimization:-Differential-Algebraic-Equations-(DAEs))",
"section": "2.4 Dynamic Optimization: Differential Algebraic Equations (DAEs)"
}
},
"source": [
"# 2.4 Dynamic Optimization: Differential Algebraic Equations (DAEs)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"nbpages": {
"level": 1,
"link": "[2.4 Dynamic Optimization: Differential Algebraic Equations (DAEs)](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4-Dynamic-Optimization:-Differential-Algebraic-Equations-(DAEs))",
"section": "2.4 Dynamic Optimization: Differential Algebraic Equations (DAEs)"
}
},
"outputs": [],
"source": [
"import sys\n",
"if \"google.colab\" in sys.modules:\n",
" !wget \"https://raw.githubusercontent.com/ndcbe/CBE60499/main/notebooks/helper.py\"\n",
" import helper\n",
" !pip install casadi\n",
" helper.install_idaes()\n",
" #helper.install_ipopt()"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.4.1 Dynamic Optimization Overview](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.1-Dynamic-Optimization-Overview)",
"section": "2.4.1 Dynamic Optimization Overview"
}
},
"source": [
"## 2.4.1 Dynamic Optimization Overview"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.4.1 Dynamic Optimization Overview](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.1-Dynamic-Optimization-Overview)",
"section": "2.4.1 Dynamic Optimization Overview"
}
},
"source": [
"**Chapter 8: Dynamic Optimization Introduction** (Biegler, 2010)\n",
"-\tChemical engineering examples\n",
"-\tClassical (variational) approaches including Hamiltonian and Euler-Lagrange equations\n",
"-\tDAE background (this notebook)\n",
"\n",
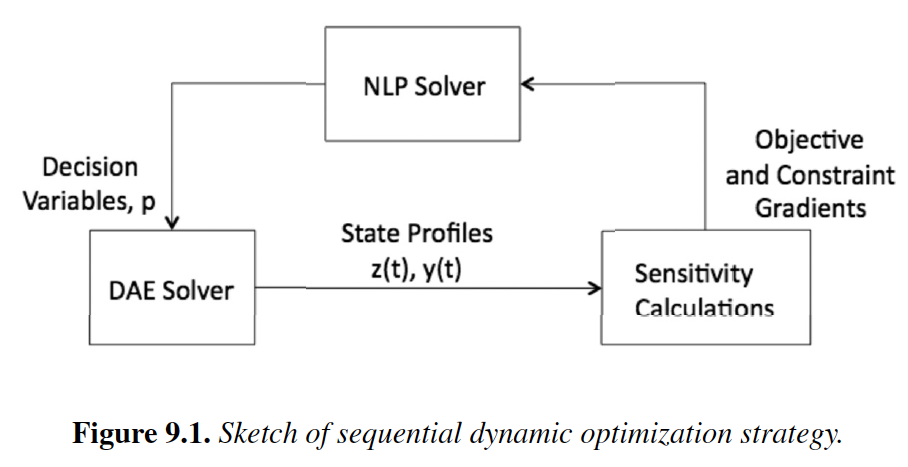
"**Chapter 9: Sequential Methods** (Biegler, 2010)\n",
"-\tDAE integration (this notebook, next notebook)\n",
"-\tSingle Shooting\n",
"-\tMultiple Shooting\n",
"\n",
"**Chapter 10: Simultaneous Methods** (Biegler, 2010)\n",
"-\tGauss quadrature (next notebook)\n",
"-\tOrthogonal collocation on finite elements (next notebook, next next notebook)\n",
"-\tExamples, benchmarks, and large-scale extensions"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.4.1 Dynamic Optimization Overview](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.1-Dynamic-Optimization-Overview)",
"section": "2.4.1 Dynamic Optimization Overview"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.4.1 Dynamic Optimization Overview](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.1-Dynamic-Optimization-Overview)",
"section": "2.4.1 Dynamic Optimization Overview"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.4.2 DAE Index Reduction](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.2-DAE-Index-Reduction)",
"section": "2.4.2 DAE Index Reduction"
}
},
"source": [
"## 2.4.2 DAE Index Reduction"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.4.2 DAE Index Reduction](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.2-DAE-Index-Reduction)",
"section": "2.4.2 DAE Index Reduction"
}
},
"source": [
"Excerpts from Chapter 8 of Biegler (2010)."
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.4.2 DAE Index Reduction](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.2-DAE-Index-Reduction)",
"section": "2.4.2 DAE Index Reduction"
}
},
"source": [
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.4.2 DAE Index Reduction](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.2-DAE-Index-Reduction)",
"section": "2.4.2 DAE Index Reduction"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.4.3 DAE Formulations for Simple Pendulum Example](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3-DAE-Formulations-for-Simple-Pendulum-Example)",
"section": "2.4.3 DAE Formulations for Simple Pendulum Example"
}
},
"source": [
"## 2.4.3 DAE Formulations for Simple Pendulum Example\n",
"\n",
"Pyomo.dae documentation:\n",
"* https://pyomo.readthedocs.io/en/latest/modeling_extensions/dae.html\n",
"\n",
"Pendulum example:\n",
"* http://apmonitor.com/wiki/index.php/Apps/PendulumMotion\n",
"* https://www.lehigh.edu/~wes1/apci/11may00.pdf\n",
"\n",
"CasADi (need to integrate DAEs):\n",
"* https://web.casadi.org/get/\n",
"* For local installation: ```pip install casadi```. Warning: installing `CasADi` with `conda` will install an \"okay\" version of Ipopt. If you really want to install `CasADi` with `conda`, you'll likely need to add `import idaes` to your notebook to load the \"good\" version of Ipopt (Linux and Windows users).\n",
"\n",
"DAE simulation example:\n",
"* https://github.com/Pyomo/pyomo/blob/master/examples/dae/simulator_dae_example.py"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.4.3 DAE Formulations for Simple Pendulum Example](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3-DAE-Formulations-for-Simple-Pendulum-Example)",
"section": "2.4.3 DAE Formulations for Simple Pendulum Example"
}
},
"outputs": [],
"source": [
"## Load libraries\n",
"from pyomo.environ import *\n",
"from pyomo.dae import *\n",
"from pyomo.dae.simulator import Simulator\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"\n",
"## Define function for plotting results\n",
"def plot_results(sim, tsim, profiles):\n",
"\n",
" '''\n",
" time = list(m.t)\n",
" x = [value(m.x[t]) for t in m.t]\n",
" y = [value(m.y[t]) for t in m.t]\n",
"\n",
" plt.plot(time, x, '-b', label='x')\n",
" plt.plot(time, y, '-r', label='y')\n",
" plt.xlabel('Time')\n",
" plt.ylabel('Position')\n",
" plt.legend(loc='best')\n",
" plt.show()\n",
" '''\n",
" \n",
" plt.figure(1)\n",
" varorder = sim.get_variable_order()\n",
" algorder = sim.get_variable_order(vartype='algebraic')\n",
"\n",
" # Create empty dictionary\n",
" results = {}\n",
" \n",
" for idx1, v in enumerate(varorder):\n",
" i = idx1\n",
" v_ = str(v)\n",
" results[v_] = profiles[:, i]\n",
" plt.plot(tsim, results[v_], label=v)\n",
"\n",
" for idx2, v in enumerate(algorder):\n",
" i = len(varorder) + idx2\n",
" v_ = str(v)\n",
" results[v_] = profiles[:, i]\n",
" plt.plot(tsim, results[v_], label=v)\n",
" \n",
" plt.xlabel('t')\n",
" plt.legend(loc='best')\n",
" \n",
" plt.show()\n",
" \n",
" plt.figure(2)\n",
" x_ = results['x[{t}]']\n",
" y_ = results['y[{t}]']\n",
" plt.plot(tsim, np.sqrt(x_**2 + y_**2), '-b', label='length')\n",
" plt.xlabel('t')\n",
" plt.ylabel('$\\sqrt{x^2 + y^2}$')\n",
" plt.show()\n",
" \n",
" #return results"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.1 Formulation 1: Index-3 DAE](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.1-Formulation-1:-Index-3-DAE)",
"section": "2.4.3.1 Formulation 1: Index-3 DAE"
}
},
"source": [
"### 2.4.3.1 Formulation 1: Index-3 DAE\n",
"\n",
"Consider the following model:\n",
"\n",
"$$\\begin{align}\n",
"\\frac{d x}{dt} &= u \\\\\n",
"\\frac{d y}{dt} &= v \\\\\n",
"\\frac{d u}{dt} &= -T x \\\\\n",
"\\frac{d v}{dt} &= g - Ty \\\\\n",
"& x^2 + y^2 = 1\n",
"\\end{align}$$\n",
"\n",
"This assumes mass and length of unity."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.1 Formulation 1: Index-3 DAE](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.1-Formulation-1:-Index-3-DAE)",
"section": "2.4.3.1 Formulation 1: Index-3 DAE"
}
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"At t = 0 and h = 1.06624e-14, the corrector convergence failed repeatedly or with |h| = hmin.\n"
]
},
{
"ename": "RuntimeError",
"evalue": ".../casadi/interfaces/sundials/idas_interface.cpp:591: IDASolve returned \"IDA_CONV_FAIL\". Consult IDAS documentation.",
"output_type": "error",
"traceback": [
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
"\u001b[0;31mRuntimeError\u001b[0m Traceback (most recent call last)",
"\u001b[0;32m\u001b[0m in \u001b[0;36m\u001b[0;34m\u001b[0m\n\u001b[1;32m 60\u001b[0m \u001b[0;31m# Solve DAEs\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 61\u001b[0m \u001b[0msim\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mSimulator\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mindex3\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mpackage\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;34m'casadi'\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m---> 62\u001b[0;31m \u001b[0mtsim\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mprofiles\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0msim\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0msimulate\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mnumpoints\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;36m100\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mintegrator\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;34m'idas'\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0mintegrator_options\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mint_ops\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 63\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 64\u001b[0m \u001b[0;31m# Plot solution\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/pyomo/dae/simulator.py\u001b[0m in \u001b[0;36msimulate\u001b[0;34m(self, numpoints, tstep, integrator, varying_inputs, initcon, integrator_options)\u001b[0m\n\u001b[1;32m 905\u001b[0m \u001b[0;32melse\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 906\u001b[0m \u001b[0mtsim\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mprofile\u001b[0m \u001b[0;34m=\u001b[0m\u001b[0;31m \u001b[0m\u001b[0;31m\\\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 907\u001b[0;31m self._simulate_with_casadi_no_inputs(initcon, tsim,\n\u001b[0m\u001b[1;32m 908\u001b[0m \u001b[0mintegrator\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 909\u001b[0m integrator_options)\n",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/pyomo/dae/simulator.py\u001b[0m in \u001b[0;36m_simulate_with_casadi_no_inputs\u001b[0;34m(self, initcon, tsim, integrator, integrator_options)\u001b[0m\n\u001b[1;32m 967\u001b[0m \u001b[0mintegrator_options\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;34m'output_t0'\u001b[0m\u001b[0;34m]\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0;32mTrue\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 968\u001b[0m \u001b[0mF\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mcasadi\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mintegrator\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m'F'\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mintegrator\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mdae\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mintegrator_options\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 969\u001b[0;31m \u001b[0msol\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mF\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mx0\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0minitcon\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 970\u001b[0m \u001b[0mprofile\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0msol\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;34m'xf'\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mfull\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mT\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 971\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/casadi/casadi.py\u001b[0m in \u001b[0;36m__call__\u001b[0;34m(self, *args, **kwargs)\u001b[0m\n\u001b[1;32m 13451\u001b[0m \u001b[0;32melse\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 13452\u001b[0m \u001b[0;31m# Named inputs -> return dictionary\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m> 13453\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mcall\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mkwargs\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 13454\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 13455\u001b[0m \u001b[0;32mdef\u001b[0m \u001b[0mbuffer\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/casadi/casadi.py\u001b[0m in \u001b[0;36mcall\u001b[0;34m(self, *args)\u001b[0m\n\u001b[1;32m 12322\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 12323\u001b[0m \"\"\"\n\u001b[0;32m> 12324\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0m_casadi\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mFunction_call\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m*\u001b[0m\u001b[0margs\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 12325\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 12326\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;31mRuntimeError\u001b[0m: .../casadi/interfaces/sundials/idas_interface.cpp:591: IDASolve returned \"IDA_CONV_FAIL\". Consult IDAS documentation."
]
}
],
"source": [
"def create_model_index3():\n",
"\n",
" m = ConcreteModel()\n",
"\n",
" # Declare time\n",
" m.t = ContinuousSet(bounds=(0.0, 1))\n",
"\n",
" # Declare parameter - acceleration due to gravity\n",
" m.g = Param(initialize=9.81) # m/s^2\n",
"\n",
" # Declare variables indexed over time\n",
" m.x = Var(m.t) # horizontal position\n",
" m.y = Var(m.t) # vertical position\n",
" m.u = Var(m.t) # horizontal velocity\n",
" m.v = Var(m.t) # vertical velocity\n",
" m.T = Var(m.t) # tension\n",
"\n",
" # Declare derivative variables\n",
" m.dx = DerivativeVar(m.x) # with respect to t is implied\n",
" m.dy = DerivativeVar(m.y)\n",
" m.du = DerivativeVar(m.u)\n",
" m.dv = DerivativeVar(m.v)\n",
"\n",
" # Declare differential equations\n",
" def _dx_eqn(m, t):\n",
" return m.dx[t] == m.u[t]\n",
" m.dx_eqn = Constraint(m.t, rule=_dx_eqn)\n",
"\n",
" def _dy_eqn(m, t):\n",
" return m.dy[t] == m.v[t]\n",
" m.dy_eqn = Constraint(m.t, rule=_dy_eqn)\n",
"\n",
" def _du_eqn(m, t):\n",
" return m.du[t] == -m.T[t]*m.x[t]\n",
" m.du_eqn = Constraint(m.t, rule=_du_eqn)\n",
"\n",
" def _dv_eqn(m, t):\n",
" return m.dv[t] == m.g -m.T[t]*m.y[t]\n",
" m.dv_eqn = Constraint(m.t, rule=_dv_eqn)\n",
"\n",
" # Declare algebraic equation\n",
" def _alg_eqn(m, t):\n",
" return m.x[t]**2 + m.y[t]**2 == 1\n",
" m.alg_eqn = Constraint(m.t, rule=_alg_eqn)\n",
"\n",
" # Specify initial conditions\n",
" m.x[0] = 0\n",
" m.y[0] = 1\n",
" m.u[0] = 1\n",
" m.v[0] = 0\n",
" m.T[0] = 1 + m.g\n",
" \n",
" return m\n",
"\n",
"index3 = create_model_index3()\n",
"\n",
"# Specify integrator options\n",
"int_ops = {'print_stats':True,\"abstol\":1E-8,\"reltol\":1E-6}\n",
"\n",
"# Solve DAEs\n",
"sim = Simulator(index3, package='casadi')\n",
"tsim, profiles = sim.simulate(numpoints=100, integrator='idas',integrator_options=int_ops)\n",
"\n",
"# Plot solution\n",
"plot_results(sim, tsim, profiles)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.1 Formulation 1: Index-3 DAE](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.1-Formulation-1:-Index-3-DAE)",
"section": "2.4.3.1 Formulation 1: Index-3 DAE"
}
},
"source": [
"**Warning**: If you run this notebook in Colab, you may get the following runtime error and your kernel may crash:\n",
"\n",
"\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.1 Formulation 1: Index-3 DAE](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.1-Formulation-1:-Index-3-DAE)",
"section": "2.4.3.1 Formulation 1: Index-3 DAE"
}
},
"source": [
"Why did the `IDAS` integrator in `SUNDIALS` fail? It is only meant for index 0 or 1 DAEs! Integrating high index DAEs is really hard!"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.2 Formulation 2: Pure ODE Model](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.2-Formulation-2:-Pure-ODE-Model)",
"section": "2.4.3.2 Formulation 2: Pure ODE Model"
}
},
"source": [
"### 2.4.3.2 Formulation 2: Pure ODE Model\n",
"\n",
"$$\\begin{align}\n",
"\\frac{d x}{dt} &= u \\\\\n",
"\\frac{d y}{dt} &= v \\\\\n",
"\\frac{d u}{dt} &= -T x \\\\\n",
"\\frac{d v}{dt} &= g - Ty \\\\\n",
"\\frac{d T}{dt} &= 4 T (x u + y v) + 3 g v\n",
"\\end{align}$$\n"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.2 Formulation 2: Pure ODE Model](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.2-Formulation-2:-Pure-ODE-Model)",
"section": "2.4.3.2 Formulation 2: Pure ODE Model"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"FORWARD INTEGRATION:\n",
"Number of steps taken by SUNDIALS: 167\n",
"Number of calls to the user’s f function: 242\n",
"Number of calls made to the linear solver setup function: 31\n",
"Number of error test failures: 7\n",
"Method order used on the last internal step: 5\n",
"Method order to be used on the next internal step: 5\n",
"Actual value of initial step size: 7.90569e-07\n",
"Step size taken on the last internal step: 0.00246466\n",
"Step size to be attempted on the next internal step: 0.00492933\n",
"Current internal time reached: 0.00492933\n",
"Number of nonlinear iterations performed: 240\n",
"Number of nonlinear convergence failures: 0\n",
"\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXAAAAEGCAYAAAB8Ys7jAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAABLaUlEQVR4nO3deXxU1d348c+ZyUwm+x6yAVkJIQkJEPZFcUfB1qV1rz5q0Vq1arVVW62tT62t1Me91r3+6oJrqyju7LIFCIRsLIHs+77NZJbz+2OSmECAkMxkMnDerxevMJM7935vztzvPffcc84VUkoURVEU96NxdQCKoijK8KgEriiK4qZUAlcURXFTKoEriqK4KZXAFUVR3JTHaG4sNDRUxsbGjuYmFUVR3N6OHTvqpZRhR74/qgk8NjaW7Ozs0dykoiiK2xNClAz2vmpCURRFcVMqgSuKorgplcAVRVHclErgiqIobkolcEVRFDelEriiKIqbUglcURTFTY1qP/DhOpxbT1N1J+ET/Qib4Ife4BZhD5ux3UxdaRuNVR34BnkSHuuPb5AnQghXh+Y0VrONhsp26krbMJusPWXtj85T6+rQnKqjxUR9eTvN1Z34hxoYFxeAt7/e1WE5lcVspbGyg/rydqxmG+Pi/AmJ9kXrcerWJ01dFjy9HJ+33CITluxtYO+6CvsLAeET/JhzSQLjJwe7NjAHkjZJ0bZqsj87TEtd11G/9/LXk7ogiunnTzylklpzbSfff3iAktwGbLaBc9MLARHxAcy9NJHIhAAXReh4NquNvA2V7PiihI5m01G/9w81kLoomoyzxp9SSa2hsp3NHx2kNL8ReURZa3UaoicFMe/SBEKifV0UoeNZuq3kfFPGzi9LWHZnpsO/x2I0H+iQlZUlhzsSs7O1m7rSNmpLWincXEVrvZGEaWHMuywR/1AvB0c6umoOtbLhvX3UHGolfKIfCdPDCZvoR0iUL20NRmpLWikvbKI4pw7fIE/mXZZI4oxwt66RdxstZH9+mN3flqH10JC6MIpxcQGETfBD56mltqSVmkP2sm5vMjF5TgRzLknAJ8DT1aGPSGl+AxvfP0BTVQdRSYHEZ4YROt6XoAgfWmo7qT7USmleA+WFTQRFeLPoyknEuHlFxdhuZtunxezdUIneoCV1YRThE/0JibHXumsOtVJ9qIWizdWYuixMXRzDrKVx6J1QYx0tUkr2b69h88cHaW8yEZ8ZxrzLEggI8x7W+oQQO6SUWUe97y4JvD+L2UrO12Xs+OIwCMEFy9OYmBoy8gBdYPe3ZWz8YD9efnrm/jiByXMiEJrBE3PlgWY2rNxHfVk7SVnhnH3DFLesobXWd/HJMzm01HadMDF3Gy3sWF1Czjel6Dy1XHTbVCITA0c3YAeQUrLlv8Xs/KIE/zAv5l+WSFxG6DFPwof31LPhvX201huZelYMCy5POub3YixrqGxn1bO76WjpJm1hFDOXxeHlO3gTkbHdzJb/HiRvYyW+gZ4svT3DLWvjVquNdW8VUfB9FaHjfVlweRLRyUEjWucplcB7tTUa+fwfe2is6OCs61NInh3hsHU7m5SSLf85yM4vS4mfFsbZP0sZUo3DZpPs/KKErZ8UMz4liAtuSXerewL15e18+mwOVrONJbemEz1paF/spuoOPv9HLu2NRs5fnkZseqiTI3Ucq9XG2v9XSOGWaqYsjGLRTyeh1Z34xGsxW9n80UH2rCknaeY4zr4+xa1O2JUHmvn8hT1odRqW/jKDsAl+Q/pc9aEWvngxF4vZxtLbM4iId5/mM7PJypcv76VkbwNZF8Yya2mcQ068p2QCB/vNgdX/2EPFvmYW/CSJjLPHO3T9zmCz2ljTc0CnLopm0ZWT0JxkIRd8X8mafxcRNt6Xpbdn4OU39m98Ve5v5rMX9qA3aFl6RwYhUSdXu+ps7WbVc7tpKG93mxO2udvKly/ZD+hZy+LIujD2pJq+pJTs/LKELf8pZkJqMBcsT3eLeyDFOXV89WoefsEGlt2RcdLNnK31XXzydA4dLSaW3JLOBDe4wja2m/n02RzqSts44+pkUhdGO2zdx0rg7nM6PwZPLw+W3pFBfGYYG9/fT96GCleHdFxSSta+XUThlmpmLYvjjKtOPnkDpMyLYsktaTRUdvDJMzl0Gy1OiNZx6krb+PS53fgE6Ln0vhknnbwBvP31/PjuaUQmBfDN6/kc2FHrhEgdx2a18dXLeynNa+DMa5KZeVHcSd+3EEIw44JYzrwmmbL8Rla/uAer1eakiB2jvLCRL1/eS0i0L5feN31Y96j8Q7249L4ZBIR789kLeygvanJCpI5j7ray6vndNFR0sOTWdIcm7+Nx+wQO4KHTcv7PU5mYFsK6d/ZxOLfe1SEd047VhynYVEXWhbHDOqD7i8sIY8kt6TRUdPDly3nYxuiB3drQxarndmPw8eBHd0/DL9gw7HXpvTxY+kv7ZfU3r+dTdbDFgZE6jpSS9Sv3czi3gUVXThrxAZ26MJrF102mrKCJtW8VMZpXziejoaKd1S/mEjjOm4vvzDhme/dQ9J6wA8K9Wf1iLo2VHQ6M1HFsNsnXr+ZRc7iVc2+aQlzGUdN2O80pkcABNFoN592cSki0D1++kkddaZurQzpK4ZYqtn5yiOTZEcxaFueQdU5MC+GMqyZRmtfAunf3jbkD29RpZtVze7CYbSy7PdMhvUg89FouvC0d3yBPPv/HHpprOx0QqWPt/LKEvPUVTD9/AmlnxDhknSnzosi6KJbC76vI/vywQ9bpSO1NJlY9txudp5alt2fg6a0b8ToNPjqW/nIqWp2GVc/tpqPl6G6XriSlZOP7+zm0u54FP0kiYVr4qG7/lEngAHqDvXZm8PFg1XO7aW8yujqkPhVFTax5s5CYyUEsvm6yQ7sApi6MZvoFE8nfUMmur0odtt6RslptrP7nXlpqO7nw1nSCo3wctm4vXz1Lb88ACaue242xw+ywdY/U/uwatvynmKSZ45jzowSHrnvW0jiSZ0ew7dNDFG2tdui6R8JssvLZC7sxdVq46PaMEV1lHck/1Iulv5xKV3s3n7+wB3O31WHrHqk9a8rJXVNO5jnjyThr9O+/nVIJHMCnp/uR2WTli5f2YjW7vlmhrdHIl6/sJSDciwtuSXdKT4I5F8eTmBXO5v8cpDSvweHrH47NHx2koqiJxddNHnE3qsEEjvPmwl+k09Zg5OvX8o4aCOQK9eXtfPdmAZEJAZz9sxSHd/0TQtj/npMCWfP/CsfElaaUkjX/LqS+vJ3zf55G2Pih9TY5GeET/TnvplRqS9tYN0aakCr2NbHpgwPEZYQy79JEl8RwyiVwgJAoX86+IYWaQ62sf2+fS2OxmK188U97l6glt6Y7ZTgtgNAIzrouhZAoX756NY/W+qNHc46mfduq2f1tGVMXxzB5TqTTthOZGMjCKyZRmtfI9lWHnLadoTB2mFn9z1z0Xh6cvzxtSF0Fh0ProeH8n6fh5afj8xf30NXe7ZTtDNXub8vYv72G2RfHMzHNeb1F4jLCmLU0jqKt1T+MzHaR9iYjX768l4AwL865YYrL+uif8BsmhHhNCFErhNjb771gIcTXQoj9PT8dX70aoYRp4X3NCvkbK10Sg5SS9e/uo7akjXNumEJQhOOaEAaj89Sy5NY0AD5/Mddll5r15e2s+X+FRCYGMO9y59dMUhdGMXleJNmfH+bQ7jqnb28w0ib55vV82huNXLA83ekjRr389Cy5NZ2uVjNfveK6G9jlRU18/9FB4jPDmHHBRKdvL2tJLLHpIWx8bz9VB5qdvr3BWM02vnhpL5Zue6XMlSNGh1JFeAO44Ij37ge+lVImAd/2vB5zZl8cz/gpwax7t4iaQ62jvv28DZV9PU7iM0fnznRAmDfn3pRKQ0U7a/9dOOqXmsYOM6tf3IOntwfn/zwNrdb5F3lCCM64chJhE/z45vV8mmtG/6bmtlWHKNnbwMKfJo3avC3hE/054+pJlBc2seU/xaOyzf7aGo189cpeAsO9OPv6lFGZ2kFoBOf8zxT8Qgx88dJel9zUXN8z7cXZN6QQHOncStmJnPDoklKuBxqPePtHwL96/v8v4MeODcsxNBrBeTem4hPgyep/5tLZOnqXmtXFLWxYuY8JqcHMXOqYHidDNTE1hNnL4tm3rYY935WP2nZtNsnXr+XR3mTiglucXwvtz0Ov5YJb0tBoNXz+Yu6o9osvzqkj+/PDTJ4XSeqi0en/2ytlXhRpi6LZ9XUp+7NrRm27RzYNjmYt1NNbx5Jb0+k2Wvjin3uxWkbv6iN/YyX5GyqZfv6EUe9xMpjhVo/GSSmrAHp+HnNPhBDLhRDZQojsurrRv7w1+NoL29Rh5suX947KIIiOFhOr/5mLb5An596YOqyBOiM144KJxGeGsenDA1SM0iCIbZ8WU5rXyMIrJrlk+LN/iBfn3ZxKc3UH371ZMCpXH03VHXzzRj7hE/0446pJLplgbMFPk4iID+C7NwtoqGh3+vaklKx/Z/SaBgcTEu3LWT9Lobq4hY3v7x+VbdYcamXdu0WMTwlitoN7Fw2X069vpZQvSSmzpJRZYWGj18G9v7Dxfpx57WQq9zfz/YcHnLotq8XGly/tpbvLwpJbp2LwGXlf2OEQGsHZ16cQGO7Fl6/spa3RuV0qi3Pq2LG6hJT5kaQujHLqto5nfEowcy9J5ODOOqd3qew2Wlj9Yi5aDw0X3JKOh841Q9zt209D7+XB5//Y4/QulXkbKin4fnSbBgeTlDWOaedOYO+6Cgq+d+59rs7Wbr54KRcff0/OuynNJZWywQw3gdcIISIBen6O7THNQPLsCKaeFcOe78rJ3+Scwu69aVl1sIWzrkshNMa1M6npvTxYcms6FrON1U5sVqgvb+urhS660jW10P4yzx1PYlY4W/5z0Gmjcm1WG1+/Zm9vP//mVIf2ex4OnwBPltySTnuTia9ecd6VZnlhY0/TYMioNw0OZs6P44mZHMS6t/dRXeycUbkWs5UvXsqlq93MklvTMfi6plI2mOEm8E+A63v+fz3wX8eE41zzLktkfEoQa98qckpf6R2rS8jfWMn0CyaSNHOcw9c/HEERPpx3Uyr15e1OaUJqazSy6tnd6A32k4WraqH9CdHTpTLGly9fyaO2xLE3sKWUbFi5n8N76ll4xdiZrzsiPsA+Z0pBk1NuYPcfJn/eTVPGRC1Uo9Vw/s1p+AR58tnzexx+A1vaJN++UUDVgRbOvj5lyDMqjpahdCN8B9gMJAshyoUQNwGPA+cKIfYD5/a8HvO0Wg0XLE8nJNqHL17a69BBEPZh8sVMmj2OOT+Kd9h6HSE2PZQzr06mNK/RofNo2IfJ78ZssrLsjgx8g1xbC+2vdzi3l4+OVc/tHvQpR8O166tS9q6vYNp5E0g/0zHD5B0lZV4UMy+KpXBzNds+dVy/+PYmo8OHyTuKwVfHsjsyEBr49Nkch3ZW2PzxQQ7sqGXupQkkZY2NSll/Q+mFcpWUMlJKqZNSxkgpX5VSNkgpz5ZSJvX8PLKXypjVOxmSZ89we0cc2KV5DX3D5M+6bnS6U52sKQt+mEdj26eHRpzEzd1WVr+YS3NNJ0tuTR+TE+/7BHiy7M4MbDbJp8/m0NU28gO7aEsVmz8+SFJWOHN/PDZuZB1p5tI4Uubb+8XvXT/yAS/Gdvt8Ns4YJu8ogeHeXHRbRt+Uw45oLtz9bRm7vi4lbVE0086d4IAoHe+UHIl5Ij6Bniy7PROr1cZHT+wYUU18//YaPnthD0FRPk4bJu8os5bGMaXnwN743v5hDz03tpv57//tomJ/M2dfnzJmmhAGExThw0W/mEp7k4kPn9gxohP27u/K+OaNAqKTAzn7eteNvjsRIQRnXJ1sn53z7SJ2flky7BN2W6ORj1bsoLmmkwtucc4weUcZF+fP+T9Po768nf88uWvYNXEpJds+LWbj+/uJywhl4RVJY7JSBqfAAx1GorGyg0+fzcHUZWHJLemMTzm5RLT72zI2vr+fyMQALvyF63qcnAxpk2z66AC7vykjYXoY5/zPlJNqt26t7+LTZ3fT1mDk3JumjIm+sEPR+3QYjVaw9PYMwif6D/mz/R+HFp8Zxrk3ndzfzFWsZhvf/CufA9m1pJ8RzYIrTm7u+YaKdj59Jgdzt42LbksnKmnMDbge1OHcer58eS/e/vYJz06mm6PNJtmwch9711UweW4Ei6+djGYUBqOdyCn7RJ6Rsk+BmUNTVSdzfpzA1LNiTliLNrab2fyfg+RvrCR+Whjn3ugeB3R/Od+UsumDA0TE+3PmNZNP2AQipeTQ7nrWvVOE1Wzjwl9MJSopcHSCdZDGqg5WPbubrg4zZ1w5ieTZx37+aK/2JhMb39/HwZ11TFkYxRlXJY+Jm3dDJW2SzR8fZNfXpUxMC2HRVZPwDzn+AxakTVKwuYrvPzyAVqfh4jszx2QT2fHUHG7ls+d3Y7NJzrou5bjPH+3VWt/Funf2UZrXwLTzJjD3koQxU/NWCfw4TJ1mvnk9n8O5DQSEezH/8iRi00OOKjyr1Ube+gq2fXqIbqOVjLPHM/eSBLc6oPvbn13DureL6O6ykLowmlnL4gZ9NFtDRTsb399vf1J6pA/n35zqdgd0r44WE6tfzKXmUCthE/xY8JPEQWuWVrONnG9LyV5dgrRKZi6NZfr5E8fMAX2ycteWs+nDAyAh4+wYpl8QO+jEar0jiGtL2oiID+DcG6cM64k6Y0FLXSef/8P+IIjoSYHMuyxx0CsvS7eVnV+WsPPLUoRWMO+ShDF3c1ol8CEo2dvApg/201TdiW+QJ2ET/Agd74fVbKW2pI260jZMnRZiJgex4CdJbpvE+jO2m9m26hB711eg0QhCon0IneCHX7CBxsoO6krbaK7pxNPbg1nL4klbFDUmLilHQtok+7bXsOU/B2lvMhEU4U1IjC+hMb50d1moOdxKbUkbZqOV+Mww5l+e6LZJrL+2RiNb/1tM0dZqPDy1hEbb99knUE99eTs1h1tpbzThE6Bn3mWJJM0c57YnrF5Wq438DZVsW3UIY7uZ0PG+hET7Ehzlg6nDTHVxK7UlrVi6bSTNHMe8SxPxDRq9KSCGSiXwIbJabRR+X0XFvmZ78qrt7ElsvoRN8CNuaigTB6mdu7vGyg4KNldRV9pGfZn9RNV7EhsX50/qgugxNYDBEczdVvLWV1C5v5n68nbaGoxotILQGF/CY/1JmBY2pm/QDldtSSuF31dRX9FOQ3k73UYr/qEGwmP9iYgPIGVeJHqD62bYcwZTl4XcNWVUHWihvqKdzpZue1mPt3+/E6eHj+kmQZXAh6nbaEGr1ThtbuexSEqJ2Wh16TSZrmDqsqD1EG53P2MkpJSYTdZTLmGfiLHDjIde4zZlfawEfnqV2jCcbl9ssHdDO92SN+C0h22MZUKI0/I77g49xobi9KlWKoqinGJUAlcURXFTKoEriqK4KZXAFUVR3JRK4IqiKG5KJXBFURQ3pRK4oiiKm1IJXFEUxU2pBK4oiuKmVAJXFEVxUyqBK4qiuCmVwBVFUdyUSuCKoihuSiVwRVEUN6USuKIoiptSCVxRFMVNjSiBCyHuFkLkCSH2CiHeEUIYHBWYoiiKcnzDTuBCiGjgTiBLSpkGaIErHRWYoiiKcnwjbULxALyEEB6AN1A58pAURVGUoRh2ApdSVgArgFKgCmiRUn515HJCiOVCiGwhRHZdXd3wI1UURVEGGEkTShDwIyAOiAJ8hBDXHrmclPIlKWWWlDIrLCxs+JEqiqIoA4ykCeUc4JCUsk5KaQY+AuY5JixFURTlREaSwEuBOUIIbyGEAM4GChwTlqIoinIiI2kD3wp8AOwEcnvW9ZKD4lIURVFOwGMkH5ZS/gH4g4NiURRFUU6CGompKIriplQCVxRFcVMqgSuKorgplcAVRVHclErgiqIobkolcEVRFDelEriiKIqbGlE/cEVRFEcwm82Ul5djNBpdHYpLGQwGYmJi0Ol0Q1peJXBFUVyuvLwcPz8/YmNjsc/McfqRUtLQ0EB5eTlxcXFD+oxqQlEUxeWMRiMhISGnbfIGEEIQEhJyUlchKoErijImnM7Ju9fJ/g1UAlcURXFTKoEriqK4KZXAFUVRBrF27VoCAgK48MILB7zf1tbG/PnzyczMxGq1AvDUU0/R2dnZt8yKFStITk7mnXfeGfDZlStXkpiYyNKlSx0So0rgiqIox7Bw4UI+//zzAe999913REdHk5OTg1arBY5O4Pfeey//+te/eOGFFwZ89oorruCVV15xWHyqG6GiKGPKHz/NI7+y1aHrnBLlzx+WpR7z99u3b+emm25i27ZtWK1WZs2axS9+8YtBl21ubiY8PLzv9TPPPENlZSWLFy8mNDSUNWvWABAREUFzc7ND9+NIqgauKMppb+bMmVx88cX8/ve/5ze/+Q3XXnstaWlpgy5rtVrRaH5InXfeeSdRUVGsWbOmL3kDaDSaviYWZ1E1cEVRxpTj1ZSd6eGHH2bmzJkYDAaeeeYZNmzYMOhyOTk5xMTEnHB9oaGh1NbW0tTURFBQkKPDBVQCVxRFAaCxsZH29nbMZvMxB9MsWLCAffv2sXPnzhOuz9vbm6uuuoq4uDhWrlzJ+eef7+iQVROKoigKwPLly3n00Ue55ppr+O1vfzvoMhs3buSmm27ipZcGPr/dz8+Ptra2Ae81NTWxcuVKysvLnZK8QSVwRVEU3nzzTTw8PLj66qu5//772b59OzabbdBlk5OTaWxsHPDe8uXLWbJkCYsXL+57r6WlhfDwcHx9fZ0Wt0rgiqKc9n72s5/x0UcfAaDVatm6deuAG5X9eXt7U1tbO+C9O+64g8LCwgE3MWtra/Hx8XFe0KgEriiKMii9Xs/evXuPGshzzjnn0NTUREZGxjF7maxYsYLly5dzxx13DHh/5cqV3HbbbQ67qSmklA5Z0VBkZWXJ7OzsUdueoijuoaCggJSUFFeHMSYM9rcQQuyQUmYduayqgSuKoripESVwIUSgEOIDIUShEKJACDHXUYEpiqIoxzfSfuBPA19IKS8XQugBbwfEpCiKogzBsGvgQgh/YBHwKoCUsltK2eyguBRFUVzqVJ+NMB6oA14XQuwSQrwihDiqz4wQYrkQIlsIkV1XVzeCzSmKooyusT4b4UgSuAcwHfiHlHIa0AHcf+RCUsqXpJRZUsqssLCwEWxOURTFOR566CGefvrpvte/+93v2LNnz6DLHm82wv4DeUZjNsKRtIGXA+VSyq09rz9gkASuKIpyUlbfD9W5jl1nRDosefyYv77pppu49NJL+dWvfoXNZuPdd9/lb3/726DLDjYb4ZNPPsmaNWsIDQ3te39Mz0YopawWQpQJIZKllEXA2UC+40JTFEUZHbGxsYSEhLBr1y5qamqYNm0aISEhgy57Ks1GeAfwVk8PlGLgf0YekqIop7Xj1JSd6eabb+aNN96gurqaG2+8cdBlTqnZCKWUOT3t21OllD+WUjY5KjBFUZTRdMkll/DFF1+wffv2YybbsTYboZoPXFEUBfvcJ4sXLyYwMLCvd8lgkpOTOXJKkN7ZCCMjI/smtBqN2QhVAlcURQFsNhtbtmzh/fffP+5yx5qN8MiJq9RshIqiKKMgPz+fxMREzj77bJKSkgA1G+FR1GyEiqIMRs1G+AM1G6GiKMppQCVwRVEUN6USuKIoiptSCVxRFMVNqQSuKIriplQCVxRFOY4zzzyT5ORkPvnkkwHvv/baayQnJ/P8888D9jlS+k8929bWRkZGBmeeeSZGo3HAZxcvXoyvr+9RA4JOlkrgiqIoJ/DWW29x8cUXD3jv2Wef5eOPP+aXv/wlcHQC9/PzY/fu3RgMBjZt2jTgs2vWrCEr66hegSdNjcRUFGVM+eu2v1LYWOjQdU4OnsxvZ/32uMscPnyYpUuXsnfvXsA+GKe9vf2Yy/efF7y7u5uHH36Yrq4uNm7cyAMPPMAVV1wBOHdecJXAFUVRhqH/vOB6vZ4//elPZGdn89xzzw1YzpnzgqsErijKmHKimvJYUF1dTUdHBwEBASdcNjo6mj179vDTn/7U4XGoNnBFURTAw8MDm83W9/rIG4+9Pv74Y5KSkli+fPlxZy3sdf311/OPf/xj7M0HriiKcqoYN24ctbW1NDQ0YDKZWLVq1aDLXXLJJZSUlPDiiy8OSPKDzQkO8Pzzz3Pvvffy5ZdfOjxmlcAVRVEAnU7Hww8/zOzZs1m6dCmTJ08+5rLBwcEEBAQMuMm5ePFi8vPzyczMZOXKlX3vNzU19c1w6GiqDVxRFKXHnXfeyZ133jngvTPPPHPQZXvnBe99kHFwcDDbt28/ajlnzguuauCKoijHERwczA033HDUQJ67776bq666qm8gz5F6B/KA/Vma/S1evJji4mJ0Ot2IYlPzgSuK4nJqPvAfqPnAFUVRTgMqgSuKorgplcAVRVHclErgiqIobmrECVwIoRVC7BJCDN7rXVEUxQ2tXbuWgICAo55K39bWxvz588nMzOyb4+Spp56is7Ozb5kVK1aQnJzMO++8M+CzK1euJDExkaVLlzokRkfUwH8FFDhgPYqiKGPKwoULB0wRC/Ddd98RHR1NTk5O31D6IxP4vffey7/+9S9eeOGFAZ+94ooreOWVVxwW34gG8gghYoCLgD8D9zgkIkVRTmvVjz2GqcCx08l6pkwm4sEHj/n73/72t0ycOJHbbrsNgEceeQQ/P79Bl+0/jSzAM888Q2VlJYsXLyY0NJQ1a9YAzp1GttdIa+BPAb8BbMdaQAixXAiRLYTIrqurG+HmFEVRHO/KK68cMPz9vffeIywsbNBl+08jC/bRm1FRUaxZs6YveYNzp5HtNewauBBiKVArpdwhhDjzWMtJKV8CXgL7QJ7hbk9RlNPD8WrKzjJt2jRqa2uprKykrq6OoKAgJkyYMOiyOTk5xMTEnHCdoaGh1NbW0tTURFBQkKNDBkbWhDIfuFgIcSFgAPyFEP+WUl7rmNAURVFGz+WXX84HH3xAdXU1V1555aDLLFiwgH379rFz584Trs/b25urrrqKuLg4Vq5cObamk5VSPiCljJFSxgJXAt+p5K0oiru68soreffdd/nggw+4/PLLB11m48aN3HTTTbz00ksD3h9sKtmmpiZWrlxJeXm5U5I3qH7giqIoAKSmptLW1kZ0dDSRkZHHXC45OZnGxsYB7y1fvpwlS5awePHivvdaWloIDw/H19fXaTE7ZDpZKeVaYK0j1qUoiuIqubm5J1ymdxrZ/u644w7uuOOOAe85cxrZXqoGriiKMgi9Xs/evXuPGshzzjnn0NTUREZGxjF7maxYsYLly5cfldRXrlzJbbfd5rCbmmo6WUVRXE5NJ/sDNZ2soijKaUAlcEVRFDelEriiKIqbUglcURTFTakErijKaa+hoYHMzEwyMzOJiIggOjqazMxMAgMD8fLyIjMzc8DyNpuNpUuXkp6eTllZGQBvvPEGlZWVfcu8/fbbJCcn8/e//33AZzds2MCUKVNIS0sbcdwqgSuKctoLCQkhJyeHnJwcbr31Vu6+++6+1wkJCeTk5AxYPjc3l9raWnJzcxk/fjxwdAK/+uqrWbduHU899dSAzw42Re1wOWQgj6IoiqNseG8f9WXtDl1n6HhfFv50ksPWd+SUsh988AHZ2dlcc801eHl5sXnzZry8vJw+payqgSuKopykI6eUvfzyy8nKyuKtt94iJycHLy+vvt85c6yNqoErijKmOLKm7CxDnVIWICgoiAMHDpCYmOjwOFQNXFEU5SRcffXVPPLII9x8881DWv6uu+4iIyOD1157zeGxqASuKIpyEt5++22eeOKJo25ODjalLMBjjz3G/v37ufHGGx0ei0rgiqIoJ2mwKWVvuOEGbr31VjIzM+nq6up732QyERUV5ZQ4VBu4oihKP4888sgJl/H29qaurg4pJUIIAC677DIuu+yyAcs5e0pZVQNXFEU5Bq1WS0tLy1EDeTIzMxk/fjyZmZl9A3mO9Pbbb3POOedw3333DXh/w4YNLFu2jNDQ0BHHp6aTVRTF5QoKCpg8eXJfbfZ0JaWksLBQTSerKIr7MBgMNDQ0OLXP9FgnpaShoQGDwTDkz6g2cEVRXC4mJoby8nLq6upcHYpLGQyGIfcvB5XAFUUZA3Q6HXFxca4Ow+2oJhRFURQ3pRK4oiiKm1IJXFEUxU2pBK4oiuKmVAJXFEVxU8NO4EKI8UKINUKIAiFEnhDiV44MTFEURTm+kXQjtAC/llLuFEL4ATuEEF9LKfMdFJuiKIpyHMOugUspq6SUO3v+3wYUANGOCkxRFEU5Poe0gQshYoFpwNZBfrdcCJEthMg+3UdZKYqiONKIE7gQwhf4ELhLStl65O+llC9JKbOklFlhYWEj3ZyiKIrSY0QJXAihw56835JSfuSYkBRFUZShGEkvFAG8ChRIKZ90XEiKoijKUIykBj4fuA44SwiR0/PvQgfFpSiKopzAsLsRSik3Aqf37OuKoigupEZiKoqiuCmVwBVFUdyUSuCKoihuSiVwRVEUN6USuKIoiptSCVxRFMVNqQSuKIriplQCVxRFcVMqgSuKoripkTzQYdQU7vuU2sZ9BHr4EqjzIVQfgLfeF7Q60OrBwxM8DPafOm/QeYGHF2jH2O5ZzWDuBHOX/afFBBaj/afVDDYzWC0gbfZ/SECA0Nj/abT2fdbowEPfs889//Te9n3X6kGMoQGyNpt9H81dYO4YuM8WE9jMmM1Gak1NtFjaaTF3YJU2AnW+BOp8CdUHYtB72/e5r6x7yru3rHVe9r/NWCHl8cvaZu4pb+uJy1qr79nv3u93z/6O1bIesM/9ytlqApsFk7mLWlMjreYOWswd2JAE6fwI0vsSqg9CrzMcUdYG0BkGHteaMVTvlNK+f737a+466vttL2sLRM8An1CHbn6MZbjBvbfzed43VfS9FlKSYDaTYexmusnE4o5O/KQ8+oNavb3g9T49P71B59Pzs+fLoDOAticpaPWg8bAfOL0HktAA0l5Q0mY/6GyWHwrGYuwpOOMPX9zeZNXdaX/d3Wl/bbM4/48lNP32sXffew74/gnPw7Nnv/U9B4zOnjT69ln07HdPgrFawNpt329Ld78vaVfP/nZBd8fA/e3utP/+CGZgs5eBLV4Gcj09ydfr6dYMnoi0UjKp20yGycQMo4lFnV14D1rWnvZ91vsOLOu+hOf1Q0LoTYpanb28j1vWPeXcV9a9+2zsKesj9tfcaf87SKsjS3Vwg5a19w+ve7/jvSf73pN/336LH8q6t5yl7Jd0jijrvu927/e73z73JrAjGIVgg5eBbV4Gcj31FOn1WI5x0vGQkimmbjJMJrKMJhZ0dqEfdEGvo4/lAWXt3a9S11PWGp29Qte7v31lbfuhrPsqUf3Kund/LV0Dy7d/uUvb0Mrrmg8h6ZwhFu7QCDnYweAkWVlZMjs7+6Q/V1u9m6qmA7R0t9Lc3UZFVy27Ww6wp7WYNksXeuHBGQFJLA1I4QzvaLQW09EHVd8fvPOHL2J3hz0p9dWCu4eeZHtrCTrD0bX/3i/UkQdW38F15Mmj/5es9+Qh6Jtqpu9LZhn4Jes72x9x8ujuhO72wZNp74nGahpYSxjKl1Dj0VP79/zhn877h9rwoInkhxNIrrmJ/7QU8FVzAc2WTjw1OlJ8xzM1IJEE32gC9f4E6PzQCkGzuZ2m7lbKOqrZ03KAPa2H6LJ146XRc07gZJYFpDDHMxxhMQ5+UHV3HpFwOodZ1qLflZ6h3373SxjHqiD0X6bvakl/RBI9QVlbuwdWFHrL+lj72/t+7wmm//4Ou6wH+34fub8/lLv0MLDdVMt/Wwr5trmQDpsJL42eNL9Y0gMSiPOJItDTnwCdLwJo6m6jsbuFko4qdrccIK+tBJPNjJ/WwPlBU/iRfwoZ+mBE/yQ6YN/7f7/7X/H0XPVYzUM7oQpNTwWu/9WtZ7/vseEYx7XXDxUlD6+BJ4++stZBaCIYAobwnRskNCF2SCmzjnrfHRL4sdikjbz6PD479BmrD62m0dhIrH8sN6bdyNL4pei0upNfqZQ9l7bWnpqYlR8ubcURB90pxGbrObglfTWT/rVxrW5Y+yylZHPlZl7Z+wrbq7dj0BpYPH4xF8VfxLyoeUMuI4vNwq7aXXxW/BlfHf6KNnMbyUHJ3Dz1Zs6dcC7a4TShSGlPlL01z8HKeiw1zTjKoGWtPeI7fvJlbZM2viv9jldzX2Vvw178dH6cM/EclsQtYWbETDw0Q7vgN1vNbKvexqriVXxb+i1dli4ywzJZPnU5C6IXIIZz7PU2a/U2Vx35/dZ4jK2mmSOckgm8P4vNwrel3/Jq7qsUNBYQ4RPBndPu5KL4i9CIsVswp7Kc2hz+tv1v5NbnEu4Vzs9Sf8blky7HR+czovWarCZWH1rNq7mvcrj1MLH+sdwz4x7OHH/m8A5uZcQ2VWxiRfYKDjQfYLzfeP4n7X+4OOFiPLWeI1pvp7mT/x78L6/vfZ2qjipSglO4b+Z9zIyY6aDI3cMpn8B7SSnZVLmJ53Y9R15DHlPDpnL/zPtJD0t36naVH1R3VPPkjidZfWg14V7h/CLzF1yccDF67aAtmsNmtVn5pvQbns95nkMth5gXNY/fzvwt8YHxDt2OcmyHWg6xInsF68vXM95vPHdMu4NzJ5475Nr2UJmtZlYVr+LF3S9S2VHJuRPP5d6se4nyjXLodsaq0yaB97JJG58c/ISndjxFg7GBK5Ov5O4Zd+Ot8x6V7Z+ObNLGu4Xv8tTOp7BJGzek3sCNaTc6/W9utplZWbiSF3JeoMvSxf+k/Q+3Ztzq8BOG8gOzzcxrua/x4p4X8dR6csvUW7gm5Rqn/82NFiOv573Oa7mvIZHcMe0Ork25dnhNaG7ktEvgvdq723ku5zneLnibKN8oHpn3CHMi54xqDKeDktYSHt70MDtrdzI/aj4PzX2IaN/oUY2h0djI37P/zicHPyExMJFH5z9KWmjaqMZwOihoKOChTQ9R1FTEBbEX8NtZvyXUy7Hd406kqr2Kx7Y9xtqytUwNm8qj8x8lPuDUvfI6bRN4r501O3n4+4cpaS3h6slXc0/WPSNun1PsTVYf7P+Av237Gzqtjt/M/A0/SviRS9ui15ev54+b/0h9Vz23TL2F5VOXO/yS/nRktVl5Pe91nt/1PIGGQH4/+/ecPfFsl8UjpeTzQ5/zl21/ocvcxT1Z93D15KtPyfsgp30CB/vl19M7n+bfBf8mKSiJJxY9QUJggsvicXfNxmYe2fwI35Z+y9zIufzvgv8l3Dvc1WEB0Nbdxl+2/oVPiz9lWvg0Hl/4+GnTXuoMNR01PLjxQbZVb+P82PN5aM5DBHgOr0uco9V31fPI94+wrnwdi2IW8ej8Rwk2BLs6LIdSCbyf9eXreWjTQ3SYO3hg1gNcmnTpKXnWdqZdtbu4b919NBgbuGv6XVw35box2dtnVfEq/nfL/6JBw5/m/4lzJjp2IMXpYH35eh7c+CDd1m4emPUAP0788Zg7XqSUvF34Nk9mP0mAZwCPL3ycWZGzXB2Ww6gEfoT6rnoe3PAgm6s2c3HCxfx+zu/x8vBydVhjnpSSN/Pf5P92/B9RvlGsOGMFU0KmuDqs4yprLeM363/D3oa9XDflOu6ecTc6zTDGCJxmLDYLz+c8zyu5rzA5eDJPLHqC2IBYV4d1XEWNRdy3/j5KWku4Y9od3Jh245isWJwslcD7MVttVDR1cbihjfcPvsH6urfx18SQor0diymUNqMFk8WK2SIx22wIQKfV4KEVeOs88PfywN+gI9Bbzzh/T8b5G4gIMDAxxJtxfgY0xxgW7u7autt4aNNDfFv6LedMOIc/zf8Tfno/V4d1XCaLlfKmLg7WN/PO/ufJblpFsHYSyZrbMBn9aDOaMVlsWKz2stYIgYdGoPfQYNBp8Tfo8PfyINhbzzh/A+H+nkQFejEx2JswP88xVxN1lPquen6z/jdsr97OZUmXcf+s+zF4GFwd1nEZzVbKGjvZX9fAG/ueoKBtPeEemSTwc4wmA21GM91HlLVOq0GvFXjpe8taR4iPnnB/A+P8PYkM8CI2xJtgH71Ly/q0TOA2m6SksZPcihaKqlspqm5nf20b5U1dWG0/7LfWZx/e0e8ihI0w4w2M85iBQadFpxV4aDUg7UnfbLXRZbbS2mWh1WimsaObzu6BQ3Q9PTRMDPFm0jg/Jkf4kRzhz9SYAMb5j+0v/4kcbD7IXWvuorytnLtm3MXPpvxsTCUvq01SXNduL+uaNvZVt7Gvpp3Kli76f8U9/HbjFfURAj0Rxp8TpkvB4KHFo19Zd/eUdWe3lTajhdYuMw0dJozmgUPQvfVaYkN8SI7ws5d3pB9TowMI8XXvm+O763Zzz5p7aO1u5aG5D3FxwsWuDmkAs9XGvpo28ipa7WVd08b+mnaqW/vPxSLRBW3BMG4VGlsgkaZfEKaPxdNDg4dGg1Yr+sq622Kjq9tKq9FMS5eZho5uui0Dy9rP04O4MB8mjfMjuaes06MDCPQena6qp0UCb+kys7O0iR2Hm9hZ2kRuRQttRvt8F1qNID7UXgBxoT5MCPFmYrA3UYFehPl50mSq5a61d5HfkM+tGbfyi4xfDOnSq91koabVSGVzFyUNnZTVtVJdUkV5VQPNDa3obFaMWh2+/r7ETQxnyuQJZMWHkB4dgEHnHn1Xvy75mt9v/D0GDwN/P+PvZEUM/B5JKbG1tGBta8PW2YU0doHWA42XAY3BgDYkBI3BsSewhnYTO0ubyS5pZFdJM3srW/pOpnqthoRwXyaN8yU2xIeJId5MCPYmIsBAmJ8n5e2H+05G9868d0g9F6SUtJks1LYaKW/qorSxk9LqFmpKKymvaqStuR2tzYpJqycwyI/4uHFMSR5PVlwIqVH+6LTucRn//r73eWzrY4zzHsfTi58mOTh5wO+llFibm7G1tWHrMv5Q1t5eaLy87GWtd2xSq2k1sqOkieye4zq/qrUvwRp0GpLC/Uga50tciP24Hh/sTWSAgVBfT/Ibc7ln7T20mlr5w7w/sDR+6Qm3J6WkpctMdb/jury6iarDVVTUNNHZ0o5W2jBq9YSEBhAfF0FacgwzYoNJifRH64QrcKckcCHEBcDTgBZ4RUr5+PGWd3QCbzWa2VrcyJbiBjYfbKCguhUp7ck6JdKPjJhApsYEkBYdQGK4L54ex0+YJquJ/93yv/znwH9YFLOIxxc+fswmApvRiLGgAGNBAaaCAkzFhzBXVGCprbXPNXEM3RoPar0CqfMJoXN8HD5pqcTPm0HGvHQMurHV1c1qs/JcznO8kvsKU8Om8vdFfye42YIxLx9jQT6mon2Yy8vorqhEdnYed13akBB0UVF4xsfhmZKCYcoUDFNS0foObVh9Y0d3XzlvKW5gf207ADqtIDUqgMzxgaRHBzA1JoC4UB97bfo42rrbeHDjg6wtW8uy+GU8PPfhYzYRWNs7MBXkYywoxFhQQHdxMebKSix1dcfdhlGro9Y7iFrfUEwT4vGfmkbi/OmkZU1Bf4Lv4mjrtnbz2NbH+HD/h8yPms/jCx/Hq6oJY34+psJCjEVFmMvKMVdVIY1HzzrYRwg8wsLQRUejj4+zl3PKFAwpk9F4De0eU22rke97ynlLcQOHG+zfLU8PTd8xnR4TQHp0ABNDfE6YMOu76vn12l+zs3Yn16Zcy6+zfn3MbqXW1laMeXn2si4soPvQYcyVlVgbGo67jU4PT2q8g6j3DaU7NoHAzHSSF85iSkaiQxK6wxO4EEIL7APOBcqB7cBVUsr8Y31mpAncbLWxq7SZDfvr2Hignt1lzdgk6D00zJgQxJz4EGbGBpExPhAfz+ElQykl7xW9x+PbHifGL4anFz9NfGA8to4OOnfsoHP7djq3Z9OVlwdmMwCagAA8kxLRR8egi47GIzwcjY8PGm8vhE6HzWhEGo1YW9toKymj/sBhTGVl+FWW4tEzI16L3ofqiZPxmD6d+PMWM3luBhoXTq7T2t3Kb9f9hkN7NnJtZwaL6kMx7dz1Q9LSatHHxaKPjUUXFYUuKgqtfwAab280Xgak1YY0dmHr7MRSX4+5ogJzRQWm/Qd+WIdGg2HKFLyzsvCeNQvvWbP6ErrRbCX7cBMbDtSx6UA9eZX2k7O3XktWbDCz44KZGRvM1JjhX8nYpI1/7vknL+S8QGpIKk8tfooInwisLS10bNtGV3Y2ndk7MBYWgtVeu9eGhOCZmIguOhpddBQeYWFovHvKWqvF1mXE1tWFra2VlsNlNBwowVxWil9NGdqeE3ujwZ/auCl4zphB0pLFJExLcWlZ13XWcfd3d9GSt5ubumcxvcoL486dWJub7QvodHgmJKCfMKGnrCPR+Pmj8fKyl7XFYt/vzg4sdXWYKyoxl5dj2r8fa1NT3zq80tLwnjnTXtZZM/quyjpMFrYeamDD/no2HahnX4395Oxv8GBWXAhz4oPJig1mSqQ/eo/h/Z3MNjMrtq/g7cK3mR0xmyfOeIIgQxCWxkY6t261H9fZOzDt309vm5vHuHH2so6Kspd1aCgab2+EwQuh1fSVtbW5maZDpTQWl2AtLcG/rhJNzzrqfIJpiJ+C18yZTPvpUsbFDq8rqzMS+FzgESnl+T2vHwCQUv7lWJ8ZbgJf99K7HNySw+ee48nxi8Gm9SBjfCALEkOZlxDKtAmBDm+O2FGxleffvoukA11c2DAefeFhsFjsX8TUVLyzZuCVmYlhyhQ8IiOH1R4szWYa8vdRtH4bLVu24bdvL6Ft9QA0eflTPykDn/lzSV12DhFx4x26f8dirqri0LefsH3VK8QdaCfIfizhERGB94wZeM2Yjld6Op5JScNuFrHU12PMz6crJ4fObdvp2rMH2d0NWi0t8ZPZPS6ZVboY8vyi0eo8mD4hyF7WiaFMjQlweHPEmgNf8ea7D5JeIjmvLgLtvsNgsyE8PfHKyLCXdUYGnikp6MKH18/dZjJRuyeffeu20b59O0H79xLY2QJAg08QDZMz8V+4gKnLziEk2vl96aWUmMvK2PfV++xe/W+Sik34ddlzgW7CBHtZT5+GV1oangkJiGE0i0gpsdTU2Mt61y57WeflgcWC1OlpSpjCjrAkPtPHsM83Ek+9BzNjg1mQGMr8xFCnNEf8d+97/OeDx5hZ7snimmDYfxgAjbc3XpmZePWUtSElBY/g4fUlt3V1UbUzl/3rt9G5fTshxfn4G9tpfmQFc6+8aFjrdEYCvxy4QEp5c8/r64DZUsrbj1huObAcYMKECTNKSkpOeluf3vYA8Wv+i0ZKbAYDXlkzCZgzC++sLAypqQjdyLuE2bq7Mebm0rljJ507sunano2tsxMp4OA40M2ewfyLf4HP9OlDvhQcjsqiQ+Sv+pbOzd8TsX8PfqYOAKqCouhMzSR0/hzSLliEb+S4EW9LSom5opKuHfaaZuf27XQfPgxAq48G79mziVm8BJ+5c9HHxIx4e0eqbTWy8UA9mwsqqd28nbiSfKbXFpHQUokGic3HF585s/GfbS9rz+RkhHbkJ2pbVxddu/fQmZ1tL+udu5AmE1YNHIgSBMxfyKylN+OdkTGsxDUUUkpKdhdR9Pm3dG/dQmTxXnzMRmwIKsMmYErPZNz8OaResAjvkJEPSpFSYi4pse9zT1mbK+wPSWn21xK04AwizzgP7zlz0I0b+XfrSOVNnWw6UM+WvHKatmwjqayA6bVFxLbVAGDzD8Bv7hx8Z8/Ce0YWnkmJCAdclVjbO+wVheztdGZn07V7D5jNmLWwP0ZL5BnnM+2in9nziIdzmjBtNhvFO/KISo7D2993WOtwRgL/CXD+EQl8lpTyjmN9Zrg1cLPVhqajnY6tW+n4/ns6t2yl+9AhexyenngmJ2NIScEwORldTAy6qCg8xkXYL2v7fQmk1YqtowNzVbX9kr68DGNhkb0d+8CBviYRfUIC3rNm4jN3LtoZGTxW8AyfHPyEs8afxZ8X/Blf/fAK4WRZLVYKNmRz+Ks1iB3biK44gKfVHmOTfwim2EQC0tOYkJmCz/hoPKKi8AgKGnBCk1Lam28aG+muqMBcXkH3oWKM+fb2e2tjIwAaPz9qE4P5LLiMrswk7r/qH0T6Rjp0f+rbTWw71HhUO3aQt455iaGckRTGgqRQwqWRzs2baf/+ezo3b+lLNBpvbzwnT8aQkoJn8iR7M0ZUFLqICITBMOAqSFos2NrbMVdV0V1ejrmsHFNRIcb8AkzFxfYmESHwTE7GZ/YsvOfOxZYxmQd3Psr68vVcmnQpv5v9u1GbEMts6mbvd1so/2YtHruyia4uRmezN9s0BI3DEpdIUEYa46dOxismBl1UJNrAwAEnNCklsqsLS0MD5vJye5PVweK+ezW2FnuNXxMURFm8L6tDKvCYOY0HfvIcgYZAh+5PdYuRrYfs9yw2FzdQ0tOOHe7nyYLEUBZNCmN+YiiBnS10bP6+77i21NbaY/TzwzB5MoYpKXhOSraXdWQEHuPGITwHdt+UZjPW9nZ7001FBeayUvtxnZ9vzxNSglaLYcqUvrLuSpnIPVseIKcuhxvTbuTOaXeO6Qmx3LoJZTCW+no6s3fQtWvXD1/Qtraj4zQYEJ6eSKMRaTId9XttcLA9+adMtl9CzZiBR1DQgGWklLxV8BYrslcw0X8iTy1+iriAOIfsx8no7DCy69stVK7/HmthASHVJUS116PhiDLUavuaN2ydnXBkGXt44JmYaN/v1FRkxmT+WP06ayrX8aOEH/HQ3IdGPE+M2WqjqLqN3IoWdpQ0saOkiUP19qsJb72WmbHBzE0IYUFiKFMi/Y/bd95cXT2grE2Fhfb96k8Ie1nr9ccsa4+wMDynpGBIScErMxPv6dPR+vsPWMYmbTy36zlezn2Z9NB0njzzSSJ8Ikb0txiO1pZ2cr76nqqNW5D7CgmvKSGys/HoBT087GVts2Hr6jqqrIVeb6/gTJmCIXUKprQEfnv4aXbW7eKG1Bv41fRfjXieGKPZSmF1G3vKm/t6i1Q02x+l52fwYHZcCHMTQliYFEpSuO8xmxullJjLy+1lnZNjv3m6bx+y64jH8mk09iSu0yG7upA9Fa8Bf5bIyJ4bqCl4TcvEOzMTjc/AG+Zmq5m/bPsL7+97n/lR8/nror+OmekBjuSMBO6B/Sbm2UAF9puYV0sp8471GWd2I5RSYqmuxlxVhbmiEkttDbbOLmzGLqSpG+Gpt99g8/ZBFzGu5yZUNNrg4CG3X2+r2sa96+7FbDPz2ILHWDxhsVP2Zahausxk55dTmFNERdEhOsoq8DJ24Gk14y8shPro8Q0KICg0gODIMMKTYglJmIg+KqqvaeBA0wHuWnsXFW0V3DfzPq6afNVJtedbrDaqWowcqu9gf207+6rbKKxpo6BfV69gHz3TJwSRFRvUd+NxJO3Y0mbDXFmFubICS1UV5ppa+w3TLnviFl4GND4+aH188IiI/OGG4xEn5uPp33VyxRkrXP4AgcaObrbvLaEoZx+V+w5jLC/H29SJ3mohQGsjxNcTv+AAAkMCCIkKIzwpjqDEWPQREX1NA/37d/9x3h+5MP7Ck4rBbLVR3tTF4foO9tW0UVTdRmF1G/tr2zBb7Xkk3M+TrNggZkwMZlZsMFOiRtaOLa1We626sgpzVRWW2lr7MW00Ic1me1dVb280Pr54REagj4lBFxOD1m/oA8w+2PcBj219jHDvcJ5a/BSTgycPO15ncVY3wguBp7B3I3xNSvnn4y0/VkZijkRVexV3r72bvIY8lk9dzm0Zt42ZSy+TxUpRdRt7ylvYU95MYbV9kEP/ASg+ei0xQd6E+3sivXPIM7+MTnjx4+j7SQnKsI841WjQagQWqw2zTdJtsdFuNNNqtNDSZaa2zURNq5GaViMVTV1Y+g2KCvHRkxzhR2qUP1N7unxNCPYeU4N+hqp38FJZWxn3zLiH66ZcN2b2o6vbSn5VK7nlzeypaKGgqo2Dde0DBqD4GTwYH+RNmL8eo+cmCs1v4usRymXRvyMhcFJfOfeWde+gljajfaBac6eZunYTta1Gqlrs//oPgAv38+wp6wAyYgKYOj6QqADDmPkbnYw9dXu4e+3dtJha+MPcP7AsYZmrQxrgtBjIM1pMVhOPbX2Mj/Z/xOzI2fx14V8J8QpxdViDstokZY2dFNe3U9LQSUlDJ6VNbRR1v02rfg22rgl0ll+DtAzt0tFHryXMz7NnqLGB8UFePQNlfEga50uom49CPFJbdxu/2/g71pSt4dyJ5/LHeX8cs9MHWKw2Djd0UlzXbh9o1NhJaVMTheY36NBvw9o+ic6KK8E2tAds+Hp6EO7nSbi/JxH+BsYHezOxZ2BUYpgvQT6n1gMz6rvquW/dfWTXZHP5pMu5f9b9Y2bKaZXAneDj/R/z561/JkAfwBNnPMH0cdNdHdIJVbVXce+6e9lTv4drU67l7ul3Y5NaWo1mOkxWe63bKrHaJB7a3rkiNPgZPPAzeJxwgMypSErJG3lv8PTOp4n2jebJM588aoTiWFTcXMw9a++huKWYX2b+kpvTb6bbAm1GM+0mCxabxGy1YbMxoKz9vTzw9Tw9y9pis/Dsrmd5be9rpASn8Pcz/s54/9Hpwns8KoE7SVFjEfesvYfy9nJuzbiVn6f/fMw+PODrkq/5w/d/wCZt/Gnenzgv9jxXh+RWdtTs4L5199FiahnTDw/o/5ANb503jy98nLlRc10dlltZV7aOBzc+iE3a+P2c33NR/PD6bzuKSuBO1N7dzp+3/plVxauYHj6dxxc+7vAueCPRae7kb9v/xof7PyQ9NJ2/LvzrmKhVuKOGrgYe/v5h1pevH5MPD2gxtfDI94/wTek3zImcw2MLHiPMO8zVYbmlyvZK7t9wP7tqd7EsfhkPzn5w1LoQH0kl8FHw6cFP+fPWPyMQ3DfzPi5JvMTlNbTs6mz+8P0fKGsr48a0G/nltF+qubBHqP/DA/z0fvx+zu/HxIMi1pat5U+b/0STsYk7p9/J9anXnxJzYbuSxWbh5T0v8+KeF4n0ieSP8/7I7MjZox6HSuCjpKytjIc3PUx2TTZzI+fyyLxHXPIor05zJ0/tfIp3Ct8h2jeaR+c/6vKucKeaosYiHtr0EAWNBZw38TwenP2gS25mt5ha+Ou2v/Jp8ackBSXx6PxHSQ1JHfU4TmW7anfx0KaHKGkt4fJJl3PPjHtG9Wa2SuCjyCZtvFf0Hk/ueBKAn6f/nJ+l/mxU7mhLKfni8Bc8ueNJqjuquSblGu6cdifeuqH1PFBOjtlm5o29b/CP3f/Ay8OL26fdzk8m/WRU7oNYbVY+3P8hz+16jrbuNm6eejPL05ej06orLGcwWoy8kPMC/8r/F6GGUO6acRcXxV80Klc5KoG7QEV7BU9sf4JvS78l2jeaX2f9mnMmnOO0ZpW8+jz+tv1v7KzdSUpwCg/MfoBp4dOcsi1loIPNB/nL1r+wtXoriYGJ3Jd1H3Oj5jqtrLdXb+dv2/9GYWMh08On8+DsB92iZ8ypILculz9v/TN5DXlMDZ3KfTPvIzM806nbVAnchbZUbeGv2/7KgeYDJAUlcXPazZwXe57Damk7anbwcu7LbKrYRJBnEHdOv5NLEi8ZMwOMThdSSr4r+44V21dQ3l5ORlgGN6XdxBnjz3BILU1KycaKjbyS+wo7a3cS4RPBr2f8mvNjz3f5vZbTjU3a+PTgpzy982nquuqYEzmHm9NvZlbELKeUhUrgLmaxWfj80Oe8mvsqxS3FxPjGcHHixSyNWzqsHiHNxma+PPwlnxR/wp66PQQbgrluynVckXzFmB1ocrrotnbz8f6PeT3vdSraK0gISOBHiT9iSdySYc2rUtdZx+eHPueTg5+wr2kfET4R3JB6A5clXTbmn1N5qus0d/Ju0bu8mfcmDcYGUkNSuTjhYs6PPd+h90NUAh8jbNLGmrI1vFXwFtnV2Ugk6aHpzIyYydSwqaSHphPqFTqgxialpLW7lYLGAnbX7mZX7S62Vm3FIi0kBiZy+aTLuTTpUrw8nDfNrXLyzDYzXxz6gncK3yG3PheBYFr4NLIispgaOpXU0FRCDCEDamw2aaPZ1Ex+Qz45tTnsrN3Jjpod2KSNtJA0fpL8E5bFL1Pt3GOMyWrivwf+yzuF73Cg+QBaoWVmxExmjJvRV9YjmShLJfAxqLqjmtWHVvNN6TfkN+Rj6Xk6j0Zo8Nf746f3o8vSRbOpue93APEB8SyMXsiyhGVMCpqkLp/dQGlrKasPrebb0m8pairCJu1zlmiFFn+9P756XzrMHbSYWrBK+zSyGqFhUtAkFsUsYmn8UpfMgKmcvP1N+1l9aDXflX5HcUsxsme20GcWPzPsCfBUAh/jTFYTBQ0F5Dfk02BsoMXUQmt3K94e3gR6BhJkCCIxMJH0sHT89f4nXqEyZnWaO8lvyKewsZBGYyOt3a20drfio/MhyDOIIEMQk4ImkR6arnoPubm27jbyG/LJrc9lWfwyxvkM72EZKoEriqK4qWMlcDVMS1EUxU2pBK4oiuKmVAJXFEVxUyqBK4qiuCmVwBVFUdyUSuCKoihuSiVwRVEUN6USuKIoipsa1YE8Qog6oGSYHw8F6h0YjjtQ+3x6UPt8ehjJPk+UUh71bLxRTeAjIYTIHmwk0qlM7fPpQe3z6cEZ+6yaUBRFUdyUSuCKoihuyp0S+EuuDsAF1D6fHtQ+nx4cvs9u0wauKIqiDORONXBFURSlH5XAFUVR3JRbJHAhxAVCiCIhxAEhxP2ujsfZhBCvCSFqhRB7XR3LaBBCjBdCrBFCFAgh8oQQv3J1TM4mhDAIIbYJIXb37PMfXR3TaBFCaIUQu4QQq1wdy2gQQhwWQuQKIXKEEA59os2YbwMXQmiBfcC5QDmwHbhKSpnv0sCcSAixCGgH3pRSprk6HmcTQkQCkVLKnUIIP2AH8ONTvIwF4COlbBdC6ICNwK+klFtcHJrTCSHuAbIAfynlUlfH42xCiMNAlpTS4QOX3KEGPgs4IKUsllJ2A+8CP3JxTE4lpVwPNLo6jtEipaySUu7s+X8bUABEuzYq55J27T0vdT3/xnZtygGEEDHARcArro7lVOAOCTwaKOv3upxT/OA+nQkhYoFpwFYXh+J0PU0JOUAt8LWU8pTfZ+Ap4DeAzcVxjCYJfCWE2CGEWO7IFbtDAheDvHfK11ROR0IIX+BD4C4pZaur43E2KaVVSpkJxACzhBCndHOZEGIpUCul3OHqWEbZfCnldGAJ8MueJlKHcIcEXg6M7/c6Bqh0USyKk/S0A38IvCWl/MjV8YwmKWUzsBa4wLWRON184OKeNuF3gbOEEP92bUjOJ6Ws7PlZC3yMvVnYIdwhgW8HkoQQcUIIPXAl8ImLY1IcqOeG3qtAgZTySVfHMxqEEGFCiMCe/3sB5wCFLg3KyaSUD0gpY6SUsdiP4++klNe6OCynEkL49NyYRwjhA5wHOKx32ZhP4FJKC3A78CX2m1vvSSnzXBuVcwkh3gE2A8lCiHIhxE2ujsnJ5gPXYa+R5fT8u9DVQTlZJLBGCLEHeyXlaynladGt7jQzDtgohNgNbAM+k1J+4aiVj/luhIqiKMrgxnwNXFEURRmcSuCKoihuSiVwRVEUN6USuKIoiptSCVxRFMVNqQSunPaEEIFCiNtcHYeinCyVwBUFAgGVwBW3oxK4osDjQELPAKInXB2MogyVGsijnPZ6ZkBcdTrMva6cWlQNXFEUxU2pBK4oiuKmVAJXFGgD/FwdhKKcLJXAldOelLIB2CSE2KtuYiruRN3EVBRFcVOqBq4oiuKmVAJXFEVxUyqBK4qiuCmVwBVFUdyUSuCKoihuSiVwRVEUN6USuKIoipv6/wzHnio6yQ5bAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYsAAAERCAYAAACKHYuuAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAAA2c0lEQVR4nO2deXxV9bX2n8UkyCAoIGMkAQmCA2qIIlStdaw4VdvqbWsHW9RqtW+r3lJf61V7b3t7O1874Vhsq61TVay2iqIEBEkCKDNEgswJgkwyZ71/rPzeHENyhj2fnOf7+eSzk5xz9lmBZD97zaKqIIQQQtLRLm4DCCGEJB+KBSGEkIxQLAghhGSEYkEIISQjFAtCCCEZoVgQQgjJSJsVCxF5WETqRGRhQOc7KCLzGz+ez+F1I0TkLRHZKyK3BWELIYREjbTVPgsRORPATgBTVPX4AM63U1W7ZXhOraoOafa9vgCOAXA5gK2q+lO/thBCSNS0Wc9CVd8EsCX1eyIyVEReFpEqEZkhIiMisKNOVecC2B/2exFCSFi0WbFohckAvqWqpwK4DcBvc3htZxGpFJHZInJ5KNYRQkhC6RC3AVEhIt0AnAHgSRFx3z6s8bHPALi3hZetU9ULGj8vUtX1IlIC4DUReVdVa0TkNwDGNT5ngIjMb/z8SVX9zzB+FkIIiZqCEQuYF/Whqo5u/oCqPgPgmXQvVtX1jcf3RGQ6gJMB1KjqTe45jTmLQ85PCCH5TsGEoVR1O4BVIvJZABDjpGxeKyK9RMR5Ib1hnsTi0IwlhJCE0ZaroR4HcDaA3gA2AbgbwGsAfgegP4COAJ5Q1ZbCT83PdQaAPwBogAnsL1X1oRae11I1VD8AlQB6NL5+J4CRjeJFCCF5QZsVC0IIIcFRMGEoQggh3mmTCe7evXvrkCFD4jaDEELyiqqqqs2q2qelx9qkWAwZMgSVlZVxm0EIIXmFiKxu7TGGoQghhGSEYkEIISQjFAtCCCEZoVgQQgjJCMWCEEJIRigWhBBCMkKxIIQQkhGKBSGE5BHbtgF/+AOwPeLpcnnTlCcitQB2ADgI4ICqlsVrESGEREdDA/Doo8CkSUBdnYnF7bdH9/55IxaNfFJVN8dtBCGERMlHHwHnngu89RYwdizQsSMwa1a0NjAMRQghCWf2bBOKn/wEmDnThGPmTCDKoeH5JBYK4F8iUiUiE5s/KCITG3dkV9bX18dgHiGEhENtrR2vvBIQAc44A6ivB2pqorMhn8RinKqeAuAiADeJyJmpD6rqZFUtU9WyPn1aHJpICCF5SW0t0K4dMGiQfX3GGXaMMhSVN2KRsgO7DsCzAMrjtYgQQqJh9Wpg4ECgUyf7euRI4IgjKBaHICJdRaS7+xzA+QAWxmsVIYREQ20tcMwxTV+3a2eJborFoRwNoEJEFgB4G8CLqvpyzDYRQtJQUwNcfz2wfn3cluQ/tbVA831uZ5wBLFwIfPhhNDbkRemsqr4H4KS47SCEZMdbbwGXXgps3gx06wb87GdxW5S/7N8PrF3bslioAnPmABdcEL4d+eJZEELyhKeeAj75SaBnT+Dss4FHHgF2747bqvxl3TpryGsuFuXlFo6KKhRFsSCEBMbjjwOf/Sxw6qnmXdx1F7B1K/Dkk3Fblr+4stnUnAUAdO8OnHgixYIQkme89Rbw1a8CZ54JTJsG9O5tHsbw4cDvfhe3dfmLE4vmngVgoajZs4GDB8O3g2JBCPFNbS1w+eXWB/D000DnzvZ9EeCGG+yCNn9+jAbmMatX27/j4MGHPjZuHLBzJ/Duu+HbQbEghPhi507gkkuAvXuBqVPNo0jly1828fj97+OxL9+prQUGDAAOO+zQx6JszqNYEEJ88cILVsL52GPAiBGHPn7kkcDVVwN/+lP0Y7XbAs17LFI55hgrJKBnQQhJPFu22PG001p/zsSJwK5dwPPPR2OTH3bsAL7+dWDBgrgtMVrqsXCIAKNGAYsWhW8HxYIQ4gvnLfTo0fpzysqA9u2BJUuisckP3/0u8NBDwK23xm0JcOBAyz0WqTixCHsCLcWCEOKL7dttv0JLMXVHx45ASQmwfHl0dnnhxReBBx6wcNobbwBvvhmvPevXm2BkEostW4BNm8K1hWJBCPHF9u3mVYikf97w4ckWi82bgeuuA044wcqA+/YF7rsvXpta67FIZdQoOy4MeVoexYIQ4gsnFpkYPhxYudK6kZOGKnDjjXaH/thjljS+7Tbg1Vet7Dcu0vVYOJxYhJ23oFgQQnyRrVgce6ytB03iYMF33rExJT/4AXBS4xS6G28EjjoqXu9i9Wo7FhW1/pyjj7aKM4oFISTR5OJZAMkMRc2YYccvf7npe926Ad/5DvCPfwCVlfHYVVsL9O/f1OTYEiLA8cdTLAghCSdXsVixIlx7vFBRYR3Szbukb77ZEvePPx6PXel6LFKJoiKKYkEI8cX27ba1LRMDB9odctI8C1XzLMaPP/SxHj0sLFVdHb1dQPoei1RGjQK2bQs3xEexIIT4Ytu27DyLdu0sb5E0sVi92i6yLYkFYBN0q6ujT8wfPAisWZO9WADhhqIoFoQQX2QbhgIsFJW0MFRFhR1bE4tTTrGfsaYmOpsAYMMGW3xEsSCE5D1799pHLmJRU2ONZklh5kyz311wm3PqqXaMOhSVTY+Fo08f+6BYEEISyY4ddsxWLI491oTCXQiTQEWFTW9t377lx0eNAjp1AqqqorVrwwY7DhyY3fPDnhGVN2IhIu1FZJ6ITI3bFkKIkc1cqFSSVhG1dat1PrcWggJMKE44IXqxcOM7+vbN7vmjRgGLF4dXEZU3YgHgVgB5MIaMkMLBq1gkJcnt9kCkEwugKckd9rC+VOrqrCig+X6Q1hg1yv4/1q4Nx568EAsRGQTgYgAPxm0LIaSJXMWid28rs02KWMycCXToAIwZk/55p54KfPghsGpVJGYBMM+id+/Ww2PNCTvJnRdiAeCXAO4A0GrxmohMFJFKEamsr6+PzDBCCplcxUIkWRVRFRUmBIcfnv55p5xixyhDUZs22SiPbCl4sRCRCQDqVDXtf5OqTlbVMlUt69OnT0TWEVLYOLHIpinPkZTps3v3Am+/nTkEBVjOomPHaCuiNm3KPl8B2Byr8ePTjwbxQ4dwThso4wBcKiKfBtAZQA8R+ZOqfjFmuwgpeLZts2O2ngVgYvGXvwB79oR3YcuG+fNNMNwe63QcdpjNX4rSs6irA04/PbfXuBlXYZB4z0JVJ6nqIFUdAuBqAK9RKAhJBrmGoQArn1WNvsmtOUuX2vGEE7J7/imnmFhEleTONQwVNokXC0JIctm+3RKwXbpk/5qkVEQtX27J7Ww6pAHLbWzZArz/fqhmAbB95bt2USw8o6rTVXVC3HYQQoxst+Slcuyxdow7yb1iBVBcbLmIbHCd3FGEonLtsYiCvBILQkiyyGUulKNHD1vWE3cX9/LlTV5ONpxwgnlRUSS56+rsSM+CENIm8CIWgIV+3Ba4OFA1z8J5OdnQpQswdGhTriNMnGdBsSCEtAm8isUxx8TrWaxfbytec/EsABOXKMJnFAtCSJvCj2dRWxvt+IxUXHLdq1iEvdvChaGS1DJGsSCEeCbbLXnNGTLE7uw3bw7cpKxw3kEuYSj3/N27w91IB5hn0bOn9XckBYoFIcQz2W7Ja44rV40rFLV8uTUEDhqU2+uiquRKWo8FQLEghPjATxgKiFcshg2zqa65QLEghJAc2b/fQjJeE9xAfBVRK1bknq8AgMGDbb9F2GJRV5esHguAYkEI8UiuW/JSOeIIi8nH4VkcOGCjRryIRfv25pHQsyCEkCzxMhcqFVcRFTWrV5tXlGty2xF2+ey+fbbBj2JBCGkT5KtYuAu9F88CMLGoqQmvfDaJ3dsAxYIQ4hG/YuEa86LutXA9Fn48i717gTVrgrMpFScWzFkQQtoEQXgWu3YBH3wQmElZsXy52ez1Yhx2RVQSu7cBigUhxCNetuSl4spno66IcpVQuUzKTYViQQghOeBlS14qcfVaLF/uPQQFAAMG2FBBigUhhGRBEGEoIFqx2LvXPBmvyW3AGvmGDQtveVNdHXD44UDXruGc3ysUC0KIJ7Zvt1CO14taz54mNFGKRU2NJdT9eBZAuOWzSeyxACgWhBCPeNmS15yoy2dXrrRjEGLx3nvW4Bc0FAsfiEhnEXlbRBaIyCIRuSdumwgpdLzOhUolarFw+7PduBGvHHusCUUYyfm6OoqFH/YCOEdVTwIwGsCFInJ6vCYRUtgEJRarV0fXa7Fmjc128rsnIsyKqE2bktdjAeSJWKixs/HLjo0fMa1NIYQAwYnFjh023iIK1qwBBg7Mfdpsc8ISi4MHgfp6eha+EJH2IjIfQB2AV1R1TrPHJ4pIpYhU1tfXx2IjIYVEEGLhwkFRhaLWrrXJsX7p1w/o1i14sfjgAxsjQrHwgaoeVNXRAAYBKBeR45s9PllVy1S1rE+SdhES0kbxuiUvlajLZ9esCUYsRKx8tqbG/7lSSepcKCCPxMKhqh8CmA7gwngtIaSw8bolL5UoxaKhAVi3LvfteK1RUhK8WLiGPOYsPCIifUSkZ+PnXQCcC2BprEYRUuAEEYbq1cvCOVGM/Kirs9HkQXgWADB0KLBqVbDTZ5PavQ3kiVgA6A/gdRF5B8BcWM5iasw2EVKwHDxoQwD9ioWIXbzDmuCainuPoMSipMR2T6xfH8z5AGDjRjv26xfcOYOiQ9wGZIOqvgPg5LjtIIQYfrbkNSefxQKwUFRQoa1Nm4DDDvOfCwqDfPEsCCEJwu9cqFSiEou1a+0Y1IV96FA7vvdeMOcDzLPo189fV3xYUCwIITkTtFhs2mRD/sJkzRqgc2egd+9gzldUZP0aYYhFEqFYEEJyJkixKCqy47p1/s+VjjVrzKsI6q69Y0eznWJBCCGtELRnATTNbQoLJxZBMnRosOWzGzcmsxIKoFgQQjzgFh8FkYh1YhF23iKo7u1USkqC8ywOHLBRH/QsCCFthjA8izDF4uBBC3OFIRb19U3VYX6or7eBihQLQkibwY2lOPJI/+c6/HA7T5hisXGjCUYYYSggGO8iyT0WAMWCEOKB1attJMXhhwdzvrDLZ13ZbBieBUCxIISQFqmtbZrrFARFReGKRdANeY4gxcKN+qBYEELaDEGLRdieRVhi0auXfQRREeU8C1ZDkYJmyZK4LSBB0dBgYaigxWLrVmDnzszP9cLatUCXLnZhD5qgKqI2brSCgaBCe0FDsSCh849/ACNHAq+8ErclJAg2brQBekGLBRCed+H2WIQxRiNIsUiqVwFQLEgEPPywHZ95Jl47SDC43RP5KBZhMHSo/ZscPOjvPEnu3gYyiIWI+PzxSaGzdSvwwgv2+fPPWx05yW+cWLiVqEEQhVgEXTbrKCmxPRmu4soreS0WABI4+5DkE3/7m4UsbrnF5v5XV8dtUX4zfz5w6qnAvHnx2eAWFQUpFgMHWogoDLE4cADYsCFczwLwH4rKd7HgfSDxxWOPWb7irrtsQufzz8dtUf5y4ABw3XUmuDffHJ+XVlsL9OkDdO0a3Dk7dbILZRhisWGDJeXDEovUvRZe2b3bRqjks1gQ4pmaGmDmTODaa20s9LhxFAs//PrXJhSf+QwwaxbwxBPx2BF02awjrPLZsMpmHYMGAR06+PMskt5jAXgQCxE5T0QeEJHRjV9PDNwq0ib4058stPCFL9jXl15qYZSwp4u2RVavNu/s4osttHfyycAddwAffRS9LWGKRRi/G0EvPWpOhw727+HHs2iTYgHgmwBuB/BFETkHwOhALSJtAlVgyhTgnHOa/kgvvdSOLuFNskMVuOkmE97f/AZo3x741a/sIviTn0RrSxg9Fg7nWQQdXlu1yo5B5liaM2wYsGKF99cnvSEP8CYW9ar6oareBuB8AGMCtukQRGSwiLwuIktEZJGI3Br2exJ/zJ5tbvmXvtT0veHDgdJShqJy5bXXgBdfBO67r+mC94lPAJ/7nIlFFCtJHW6jXRhiUVRkntLWrcGet6bGcixBTMhtjeHDgeXLvQtd0udCAd7E4kX3iap+D8CU4MxplQMAvquqxwE4HcBNIjIygvclHpk+3Y6XXPLx7196KfD6600jrklm/vUv28p2/fUf//4Pf2iJ0Wefjc6WMHosHGGVz9bUNFUshUVpKbBrl1X8ecGJRd++wdkUNDmLhao+1+zr/w3OnFbfc4OqVjd+vgPAEgADw35f4p3Zs4ERIw4dYT1hgtWkv/56PHblIxUVVi7bfAzEscdayelbb0VnS76KhatYCovSUjsuW+bt9Rs3WhFIx47B2RQ0vqqhRORVETkpKGOyfM8hAE4GMKfZ9yeKSKWIVNbX10dpEmmGqonF6acf+tiJJ9rRT3y3kNi9G5g718JOLTF2bLRiEUaPhSMMsdi3z84XtmcxfLgdly/39vqk91gA/ktn7wDwCxF5RET6B2FQOkSkG4CnAXxbVT8WyFDVyapapqplffr0CdsUkoZVq2w5Tkti0bOnfbikY9JYscLsfvvtuC0x3n7bPLF0YrF6tfUSREFtrd0BB9lj4Tj6aKssClIsamstKR+2WAwcaJ6fH8+iTYuFqlar6jkApgJ4WUTuFpEuwZj2cUSkI0wo/qyqnDKUYGbPtmNLYgEAxcXJFYs77gDmzAG+9jW7K42bigo7nnFGy4+PHWvHqLyLsMpmAavyGjy4KdQVBK6cNWyxaNfOvAuKRRpERAAsA/A7AN8CsEJEvpT+VZ7e4yEAS1T150GemwTP7Nl25zlqVMuPB7nkPkhmzAD+/nfggguARYuAn/40bovMplGjgKOOavnxU06x7ue2IBaA/W4EeSMRlVgA3sVCNfkTZwH/OYsKAOsA/AKWcP4KgLMBlIvIZL/GpTAOwJcAnCMi8xs/Ph3g+UmAzJ4NjBljIYWWKC5uCg8kBVXg9tstnPDMM8BVVwH33gusXBmfTQcPWqd2ayEoADjsMBOMKMRCNbweC0dJSTCLhBw1NRYeiuKuvbTUfq/37s3tdTt2AHv2tH3P4gYAA1X1PFW9S1WnqupKVf0WgDS/4rmhqhWqKqp6oqqObvz4R1DnJ8Gxe7cNuWstBAWYWOzd21QumASefNLCT/fdZxeXX/3KLsQ33BDfDKZ33rELSTqxACwUVVkZfths0ya7qIUtFvX19nMHgauECmOPRXNKS+0GKFexy4ceC8B/zmKhaqt/Shf7OTfJT+bNs4F3LpbeEkHuLQ6CvXuBSZOAE06wOVYAMGAA8OMfA9OmWUNcHMyYYcfx49M/b+xY+xkWLAjXnjDLZh0uXBRUKCqKHguHq4jKNRRVEGKRDlVNyKWARIlLbp92WuvPKS62Y1KS3C+9ZML1X/9lSVbHddeZd+EaDKNmxgzrai4qSv+8qJLcrmw2bM8CCOZGQtXOE5VYuF6LXMtnC0osROS8IM5D8p/Zs00M0iXrXI1+UsRizhzLr5x77se/36mTDeyLo4xW1SqhMoWgAJu9NWhQ+GIRxtKj5gQx7tuxYYOFzaISix497IKfq2exbp0d+4fefOCPoDyL/w7oPCTPaa0ZL5XOnS2RnJQwVGWlNQt27nzoY+XlQFWVhdaipKbG7jizEQsgmua8998HevUCunUL7z169bI+nCB+N6KshHJ4qYhasQI44ohDpx0kDe6zIIGxbp01VGUSCyA5vRaqJhZjWhmHWV5uw+0WL47Wrpkz7ZgpX+GIojkvzD3WqQwdmr9iUVqaexhqxQob3RJFEt4PnsWisWv7YRF5BEBR4+cPi8jDAdpH8ohMzXipJEUsVq4EPvwQKCtr+fHycjvOnRuZSQCsUKBLF5uvlQ1R5C2iEoug+nBqaqxZLlPOJ0hKS4HNm4EtW7J/zcqVJhZJx49n8SiAPzYetzZ+7j5IATJrloVyRo/O/NySEtvHkGtNetA4EWjNsxg2zMIiUectFiyw0Fhqwj0do0fbnem774Zn09q14S0QSqWkxPIjBw/6O09NjQlFp06BmJUVuQ4U3LvXwnttWixU9Q33AWBHs69JATJrll10s/njLC62EFDcW/PmzrU7+Na6zUXsZ4pSLFRNLE7KYURn585WpeR13EQmdu+2O+aoPIt9+5oSv16JsmzWketAwffes96MNi0WzUjAFB0SJ7t3WyK4tRlGzUlK+ezcuVbx1Fq3OWChqHffjW6F6dq1tgAoF7EA7K526dLwbAKiEwvAfygqDrEoLrbfpWxF201fLhixUNUsotSkLVNVZdNRx43L7vlJaMw7cACorm49BOUoL7eQyLx50djlmuu8iIWfbW3piFIs3AXez+/Gtm3ABx9ELxYdO9p75ioWw4aFZ1NQsBqKBIKr3knXuZ3KgAEWrorTs1i82DyiTGLhHo8qFOXEwu3+yJYRI2xbm9/wTUu4seFR5CwGD7ZcjR+xiKMSynHccdnnjlassHLh1gZFJgmKBQmEWbPszrZ37+ye366dxdjjFItMyW1H//52AYuqImrBAvO8unfP7XUuuRpGKCpKsejQwRr/8lUsTjvNROCDDzI/N18qoQCKBQkAVROLbPMVjuLieMNQc+daM1Q2IYDy8mg9i1xDUID/1Z7pWLPGbgS6hLKt5lD8Tp9dtMiKE+IQC1c6PmdO+ucBTT0W+UDOYiEi54nIAyIyuvHriYFbRfKKFSusUibbfIUj7l6LuXOtv6JdFn8FY8bYxSubu0U/7Npl/55exKJ/f+uuDkMsoiqbdfhtzPvnP+3/LFfvLAjGjLHfqUw9L3v2mAi3WbEA8E0AtwP4ooicA2B0oBaRvMPlK3L1LEpKrHlp27bgbcrEnj02AjxTCMoRVXPewoXmqXkRCxHLW4QVhooiue0oKbEbkO3bMz+3OR98YF7ghRcGb1c2dO1q+SbXpNoaNTX2f92WxaJeVT9U1dsAnA8gyz830laZNcvm2rgwSLbEWT67YIFVQ2UrFqeeasfq6vBsArxXQjlKS8MLQ0UtFoC3341XXrHehYsuCtamXBg71sJQ6RoL86lsFvAmFv9/ur+qfg/AlODMIfnIzJn2x5FNOCeVuMUCsC1z2dCjhw0/DKvpzbFggb2X1zHgpaXW6BhkT8iuXdb3EYdYeAlFvfSS3bxkeyMQBqefbguc0s0Uy6eyWcCDWKjqc+5zEfklgPuDNIjkF1u2AEuW5J6vAOIVi2XLLFmby9ygsO7aU3FjPrwOlXPenbsQBYHrsYgyZ+F1VHlDg+Urzj8/+1EpYeBKyNOFolautJLZXr2isckvfquhdgJ4XkS6AoCInC8iM/2b9XEaBxTWicjCoM9N/OGSeLnmKwD7I+nataksM0qWLzf3PxdvyHVIh7VmtaHB8iheQ1BA0+DBIPMW7v8nSs+iZ0/zDnL1LObPt/WvcYagAPMWjjoqfZI7nyqhAP9rVf8vgMcBTBeRCgDfBfC9IAxrxqMAYkpXkXRMnWpziby4/CJWT+82sEXJsmVNc3yyZcQIS8bX1YVjU22thS78iIUbdR2kBxSHWAAmzrmuin3pJTtecEHw9uSCiIWi0nkWBSUWIvIpAN8AsAtAHwC3qOqMIAxLRVXfBJDD0F8SBdu3A489Blx9NXD44d7OUVQU/TDBffvsjjXXhHyYTW+A/+Q20BRaC1IsXBhq4MDgzpkN48bZrpE9e7J/zUsvWTFCuk2NUTF2rIVot2499LGPPrJ/14IRCwB3ArhLVc8GcBWAvzaW00aOiEwUkUoRqayvr4/DhIJjyhRLft50k/dzxCEWq1ZZlUquYuFCPGHlLd55x+5Ijz/e33mCLp9dswbo29f2kUfJ+PEm7JWV2T1/61YL+8RVMtsc15zXUjOny8UUjFio6jmqWtH4+bsALgLwwyAM82DLZFUtU9WyPn36xGFCbGzZAtx9d9Pi9yhQBX77W+s/aG1xUDYccwxQX28zmqLCXexzDUMNHmx37mGJxaJFltj16qU5gh4oGHXZrMPlwSoqsnv+q6/GXzKbSnm5iX9LeYt8K5sFMouFiMhVIpJVH6SqbgDwKf9mkWzZswe47DLg3nuBiy8Gdu6M5n1ff91c7G9+0995XDVSlN6F2zWQq1i0a2d/3GGFoRYu9O9VACYWO3cC69f7PxcQffe2o08f85KyFYu//MVGkpx2Wrh2ZUv37vb/2ZJYuH6dfCmbBTKIhaq2AzAbwOdE5P+IyNdFJG2xoapGeI9Y2DQ0ANdea39Mt95qMe+rr7Zms7D5zW+s2uPzn/d3njjEYtkyuxB5KVkcMSIcz2LvXrvbbG0JUy4EnVuJy7MAgE98wvp4GhrSP2/VKuC554CJE9PvJoma888Hpk37eDPnhg3Ar34FTJhgs8nyhYxhKFVdq6oPqeovYJVPZSLyXRG5RUR8BCCyR0QeB/AWgFIRWSsi10Xxvknn9tuBJ58EfvpT4Je/tAv4iy8C3/pWeOWdgN1pPvcccN11Vgnlh2OOsWPUnkWu+QpHaaldmIJeB7t8uYl8EJ5FkLmVHTusAiwusRg/3nakp2tuA4D777e+Cr+ebtDceafdmHz96003cZMm2e/Pz38er225kpMGq+ouAM8AgIi0A3CGiHwbgABYBmCaqga+VVlVrwn6nPnOc8/ZL9sttwDf+Y597/rrrfzyxz+20sHLLw/nvR94wO70brjB/7kGDLDwTpTls8uWWcjOC6Wl9rOvXBmMF+BYtMiOQYjFgAGW9wiiMS+uslnH+PF2rKho/d9m507goYeAq66KvmIrE716mZBddRXwi18AZ54J/PGPwL//e37lKwB/O7gbVLVCVX/Z6HWsAPBVEblHRL6abZ6D5I4q8B//Yb9sP/vZx7t9f/hDi9s+/XQ4793QADz6KHDeeU0d2H7o2NEublF5Ftu2WdOWV88irIqohQvtzjjXPEpLuNHcfkZ8O+Lo3k6luNim6abLW/zxj/b/euut0dmVC5/5jN24/eAH5o33728eR74RSHRPREoAXALgYgANAD4AEGOzfdtm6lTrVH300UPjs+3bA5/+tD3n4MHgRx5Mn24X9v/+7+DOecwx0YmFS257FQt3MQ86yb1okZ07qPLUoUObflY/xO1ZiJh30ZpYNDQAv/61VR65UtWkIWLexciR9v88ZUo8o9P94tmzEOOHIvIWgB8B2AjgSlU9T1V/raofBmUkaULVKp9KSoB/+7eWnzNhgpXTZhqR7IVHH7Wk3GWXBXfOoqLowlBey2Yd3bubJxSGZxFkWMvtg8iUGM7EmjV2sRswIBi7vDB+vP1+tDQW5p//NFH89rcjNysnBg60BtZbbwW+8IW4rfGGnzCUAtgH4HxV/byq/oUCET4vv2xNSpMmWQinJc4/3zyOqVODfe/t24GnnrKKqyA3phUV2YXA74UtG5YvtxyJnw1qQVdEffSRhYyCyFc4hg61smq/5bOrV1vYpFOnYOzygstbuL0pjr17ge99z0JkV10VvV25cumlVoiS63TmpODX7PtUdUcglpCMOK+iqMhKZlvjiCMskRa0WDz5pDXPfeUrwZ63qAjYv99yCWGzbJnFwf1c/IIeKOjOFaRn4er3/eYtamriWU2ayokn2gbAN974+Pfvvtu63n//+9ZvnEhw+O3gDrFAkzTntdcstDRpUuaL3YQJFtqorQ3u/R991C6UQTc9ufLZKEJRfspmHaWlwQ4UXNg4SzlozwLwLxYrV8bfONahg3VlT55sFUWqlsP4yU+Ab3zDe2UbyY08dYgKk//9X6vZzubO3v0Bvfhi+udly8qV9gf61a9637XQGlE15jU0mFj4rTgKegz4okUm/kFelIuK7CLrRyx27bIGsrg9CwB45BGrKPrOd0wgvvxl8xDzrVchn6FY5Anvvw+88II192TTCDd8uJXWBhWKmjLFYq1f/GIw50slKrFYv97yA0F4FkBweYuFC02Aguw87tDBPDY/YuF2SSRBLLp2tTDonXdaT8WqVVYy261b3JYVDglqjCfp+P3v7Xj99dm/ZsIE6+reudP/H9WLL9rI6DCano44wj7CFgt3cfcrFkVFluAP0rPwsjwqE8OGmUfoFSc0cYehHO3aWR/RmDHm9bjEN4kGehZ5wN69wIMP2sXfxfezYcIEG/E8bZq/99+yBZg3Dzj3XH/nSUcU5bN+y2Yd7dqZ4CxZ4t+mHTvs5w4yX+Hw25jnhCYJnkUql13Wetk4CQ+KRR7w1FM2xjvXvRHjx1uT1wyf66hef92Sip8KcZ5wFHstli0zDyuInoGRIzPPK8oGd44gK6EcQ4faXKUtHteG1dTYatN82RFNwoVikQf89reWf8j1zr5TJ+Dkk1tevpILr75qF9nycn/nSUcUXdzLlplHEESC/rjjzF6/I+HDqIRy+C2fXbkyeV4FiQ+KRcKZNw+YNQu48UZvzTzl5UBVlb+x5dOmAWedFW4te1GR3QGHuY9j6VL/+QrHyJFN5/TDu+9a/iOIOVvNcRd6r3mLmprk5CtI/FAsEsyHH1r1Uc+e3hvhxoyxCiCv8fU1a2x6aZghKCD8iqjdu+3cQYnFccfZ0W/eYt4827kdRldvSYkdvXgW+/ZZLoWeBXFQLBLKvn3AlVfahfqZZ7zHjV3oyGsoyiXHw0xuA+HvtVixwvIurkfCL8OGWXmqn7xFQ4MNhDzllGBsak6XLpaf8SIWq1ebffQsiINikUBUbePXa69ZTfknP+n9XMOGmWcyd66317/6KtC3bzgx9VScZxFWRZQLFwXlWXTsaHkkP57Fe+/ZvK2TTw7GppYYNsybWLjX0LMgDopFwlAFvv99azi65x7gS1/yd7527YCyMm+ehap5FuecE3zXdnP697c79bA8C1c2G+TCmZEj/YnFvHl2DMuzAOxi7yVnkdSyWRIfFIss2bEj3FWlQJNQ/PjH1nx3113BnLe83Aau7c5xO/qSJcDGjeGHoADbuzFwYMtjqINg6VILdR1+eHDnPO44u6h6XbFaXW0CGUbZrGPoUBvZ8dFHub2upsb+rfr1C8cukn9QLDLgJr326GHNXD/6EbBuXTjvM2mSCcUNN1i5bFB38+Xltghp/vzcXvfqq3YMO7ntGDw4XM8iqBCUY+RIi+t7XV86b56F94JaeNQSzjNwozuyxZXNhu1RkvwhL8RCRC4UkWUislJEvhfV++7ZY4tK7r4buOIKSxZ+//t2h/rYY8G+19132/a5G26wER1BVseMGWPHXENRr79uFTVDhgRnSzrcXougUQ1HLFxFlJckt6p5FmHmKwDvvRYsmyXNSbxYiEh7AL8BcBGAkQCuEZGRYb1fQ4NdWP74R+Dss4HHHzdv4umnbZ7+8uXWGT1xYu536q3x4IPAfffZRNeghQIwkRs4MDexULVlM2eeGawt6Rg8OJwlSOvXW/9GUJVQDtfg5yVvsX69deWHma8AvI0qb2gwT4T5CpJK4sUCQDmAlar6nqruA/AEgACXejbx978DRx1lF5WvfMWE4amnbBuXc8ePPRb4299sDMJVV1kvhB9eftm8iQsuAP7wh/C2aI0Zk1tF1MqVdjELY8Bda4S1BCmoAYLNcc10XjyL6mo7hu1Z9Oplv6u57ONet87yMPQsSCr5IBYDAaQGJ9Y2fu9jiMhEEakUkcr6+npPbzR0KPDZz1q56sKFdrG88spDn9e3r41LXr3aRMVr4nv+fHu/44+384XZIV1ebrH1bOcEzZplx6jFAgg+FBV02WwqXiuiqqvtBuSkk4K3qTm5roFl2SxpiXwQi5ZSbIdcnlV1sqqWqWpZnz59PL3RCSfYNq6vfc0qVNq3b/25Z5wB/PSnwHPPeVvAsnix7cru2dPGf3fv7snkrHHNeZWV2T1/5kyzzcXlo2DwYDsGneRetsz2IYQxXv244+yuPddxKvPmWcFEFPsYRozIbSwJy2ZJS+SDWKwFMDjl60EAfK6hD4ZbbrHE96RJTWGFbFi+3CqM2rWziqMwLmLNKSuzY7Z5i1mzgLFjo10uH5ZnEeQAweaMHGkhm1WrcntddXX4+QrHiBFWAp1tyLSmxrzcwYMzP5cUDvkgFnMBHCsixSLSCcDVAJ6P2SYAdvF54AELS11zjS1kyURNjTW5HTxoHdphhEZa4ogj7MLmwkvp2Lo1vIU86ejZ0zyAoD2LIAcINsfLjKjNm00Qw85XOFxiP9tQ1NKllosJcnMfyX8SLxaqegDAzQD+CWAJgL+p6qJ4rWriqKOsjHbFCuDb307/3L//HTjtNCvJnTataXJpVIwbB7z1VuZqo9mzm54fJSLB77X46CM7X9CVUA4v5bNRdG6nkuvO8Ci9HpI/JF4sAEBV/6Gqw1V1qKr+Z9z2NOeTn7SKqQcftF6J/fs//viuXdaRfcUV1qMxc6blR6Jm3DgLRWS6sM2aZfka158RJa58NijcAMGwPIsePUzgcglDOrGIyrMoLrawUjZiUV9v4nrqqeHbRfKLvBCLfOCee4CLLzbROP54S3y/8YZttyspsXDVHXfYnX1UoafmOE9h5sz0z5s506p0oki+NidozyKsstlUzjzT/q+zrYqbO9duGo48MjybUunQwcpgsxGLqio7UixIcygWAdGxI/DCC8Dzz1s45fLLranvkUdscdD06eZ1dOoUn41Dh1p+JZ1YHDgAzJkTfQjKUVRkfRZe5y01x10ggxwg2Jyzzwbq6rK7GKsCFRXW2Bkl2VZEObFgGIo0hymsABEBLrkEuPBC4K9/NWG4+GJL2iYBEROBdGLxzjsW5486ue1wFThr1wZTujl/vglFmP8HZ59tx+nTM5cav/eeVSbFIRYvvGAh0nT9PFVV9u91xBHR2UbyA3oWIdCxo224+9znkiMUjnHjmi5YLeGEJC6xCLp8NopkbUkJMGiQiUUmZsywYxxiceBA5oGCVVUMQZGWoVgUGJnyFrNm2YXPXbSjJsjGvC1brMs+7ESyiHkX2eQtKipsBEfUlXDZVEQxuU3SQbEoME45BejcuWWx2LPHZlX52cznl0GD7BiEWERZonr22ZZrydTLUFFhgh1lsyPQlOBPJxZMbpN0UCwKjE6drCS2JbGYOtVKa/1u5/NDly6WhA8iDBXVsD7g43mL1qirMzGJOgQFWA6if//sxILJbdISFIsCZNw4u5A23542ZYqNMz/nnHjscgS1BGnePDtX797+z5WJbPIWTqA/8Ynw7WmJTBVRTG6TdFAsCpBx4yzZmTqyvK4OeOklS8ynG6AYBUEtQYqyE9nlLaZPbz1vUVFhW/HiCvM4sWjNvspKhqBI61AsChBX6TRtWtP3nnjCBCTOEJRj8GBLTPvZeb5zpw1sjKpLGsict5gxw6b/hrlGNR0jRliYsa7u0Mfq602gKRakNSgWBciRRwIXXWT7vp1gTJlid+HHHx+vbYB5Fjt3Atu2eT/HggUmNlHG39PlLXbtMk8nrhAUkL4iyuUr3HRiQppDsShQ/vIXu3hccQXw5z/bxeLaa+O2ynDls35CUVEP6wOa8hbPPHPoY3Pm2KThOJLbjmzEIkpPjOQXFIsCpWdPy1H07NmUp7jmmritMlyPh58kd3U10KePJeyjQsR2nLzyiu0pSWXGDHt87Njo7GnOoEHA4Ye3PEhy9mwmt0l6KBYFzMCB1lfRqxdw2WVWspoEgujidsntMBYepeNb3wKGDAFuu808CcC65R94wPIBPXtGa08q7dpZccOzz358s9+GDfZ7cOml8dlGkg/FosAZOdIWMk2ZErclTRx9tE1KXb3a2+v37rXlTXGEVDp3Bn70I8uZPPaYNTpecYUtlHrggejtac6NN5oIT53a9L2HHzbxuP76+OwiyYdiQdCrV7JmWLVvb95Fba231y9caBe/uJrLPv95q3q6807guussxDNlCjB6dDz2pHLJJZYTuv9++/rgQds7f+654U7mJfkPxYIkkuLi3PdaO+JIbqciAvzsZ8D69VZIcM89wJVXxmNLczp0AG64wargliyx8NP779v3CEkHR5STRFJSYgukvFBdbRvsiouDtSkXxo+3Nbv79wN33RWfHS3x9a+bgP32t+a99evHfAXJTOLFQkQ+C+A/ABwHoFxVK+O1iERBcbE1j+3cmfvGvqoq8yqiHtbXnF/8It73b42+fW18/iOPALt3A9//fvodF4QA+RGGWgjgMwDejNsQEh3OK8g1b7F/vyWX2YmcnptvtkZBAPjGN+K1heQHifcsVHUJAEjUNZAkVkpK7LhqVW5d5YsXWzUUJ6emp7zcusn79YtvdwnJLxIvFtkiIhMBTASAIv725z3Os8g1yc2dDNkhArz2WvR9KCR/SYRYiMirAPq18NCdqppVmlNVJwOYDABlZWU+RtCRJNC7t5XzZloD2pyqKqB7d5aBZkOHRPz1k3whEb8uqnpu3DaQZCHirXy2qsqa8eJObhPS1uCfFEksJSW5icWBA0xuExIWiRcLEblCRNYCGAvgRRH5Z9w2kWgoLrYwVLZ7LRYvtvEaFAtCgicRYah0qOqzAJ6N2w4SPcXFVt65ebNNkM0Ek9uEhEfiPQtSuORaEVVVZQ18w4eHZxMhhQrFgiSW1F6LbGBym5Dw4J8VSSxDhtgxm/JZJrcJCReKBUks3bpZriIbz2LJEptzxM5tQsKBYkESTbbls0xuExIuFAuSaLJtzKuuto7v0tLwbSKkEKFYkERTXGzrVd0+69aYO9eS2+3bR2MXIYUGxYIkmuJiS16vXdv6c/bvt+145eXR2UVIoUGxIIkmm/LZd9+1seRjxkRjEyGFCMWCJBrXmJeufHbuXDvSsyAkPCgWJNEMHmxNduk8i7lzgaOOinfnNiFtHYoFSTQdO5oILF7c+nPefttCUFzkQ0h4UCxI4hk3DqioaHn67K5dwKJFzFcQEjYUC5J4zjwTqKsDli499LHqaqChgfkKQsKGYkESz1ln2fGNNw59zCW36VkQEi4UC5J4hg4FBgxoXSyKioCjj47eLkIKCYoFSTwi5l288caheQuX3CaEhAvFguQFZ50FbNgArFzZ9L0PPrD+C+YrCAkfigXJC1rKWzBfQUh0JF4sROR/RGSpiLwjIs+KSM+4bSLRU1oK9O0LvPlm0/fmzrUQFceSExI+iRcLAK8AOF5VTwSwHMCkmO0hMSBiJbTOs9i1C3j2WWDECKBHj3htI6QQSLxYqOq/VPVA45ezAQyK0x4SH2edBbz/vvVbXHaZrVG99964rSKkMOgQtwE58jUAf23pARGZCGAiABQVFUVpE4kIl7f41Kcs2f3oo8BVV8VqEiEFQyLEQkReBdCvhYfuVNXnGp9zJ4ADAP7c0jlUdTKAyQBQVlbWwmAIku+MGgUceSSwfj3whz8A114bt0WEFA6JEAtVPTfd4yLyZQATAHxKtaUJQaQQaNcOuP9+O37+83FbQ0hhkQixSIeIXAjg3wGcpaofxW0PiZdrronbAkIKk8QnuAHcD6A7gFdEZL6I/D5ugwghpNBIvGehqsPitoEQQgqdfPAsCCGExAzFghBCSEYoFoQQQjJCsSCEEJIRigUhhJCMUCwIIYRkRNpiQ7SI1ANY7fHlvQFsDtCcfIA/c2HAn7kw8PMzH6OqfVp6oE2KhR9EpFJVy+K2I0r4MxcG/JkLg7B+ZoahCCGEZIRiQQghJCMUi0OZHLcBMcCfuTDgz1wYhPIzM2dBCCEkI/QsCCGEZIRiQQghJCMUixRE5EIRWSYiK0Xke3HbEzYi8rCI1InIwrhtiQoRGSwir4vIEhFZJCK3xm1T2IhIZxF5W0QWNP7M98RtUxSISHsRmSciU+O2JQpEpFZE3m3c+1MZ+PmZszBEpD2A5QDOA7AWwFwA16jq4lgNCxERORPATgBTVPX4uO2JAhHpD6C/qlaLSHcAVQAub+P/zwKgq6ruFJGOACoA3Kqqs2M2LVRE5DsAygD0UNUJcdsTNiJSC6BMVUNpQqRn0UQ5gJWq+p6q7gPwBIDLYrYpVFT1TQBb4rYjSlR1g6pWN36+A8ASAAPjtSpc1NjZ+GXHxo82fZcoIoMAXAzgwbhtaStQLJoYCGBNytdr0cYvIoWOiAwBcDKAOTGbEjqNIZn5AOoAvKKqbf1n/iWAOwA0xGxHlCiAf4lIlYhMDPrkFIsmpIXvtem7r0JGRLoBeBrAt1V1e9z2hI2qHlTV0QAGASgXkTYbdhSRCQDqVLUqblsiZpyqngLgIgA3NYaZA4Ni0cRaAINTvh4EYH1MtpAQaYzbPw3gz6r6TNz2RImqfghgOoAL47UkVMYBuLQxhv8EgHNE5E/xmhQ+qrq+8VgH4FlYaD0wKBZNzAVwrIgUi0gnAFcDeD5mm0jANCZ7HwKwRFV/Hrc9USAifUSkZ+PnXQCcC2BprEaFiKpOUtVBqjoE9nf8mqp+MWazQkVEujYWbEBEugI4H0CgVY4Ui0ZU9QCAmwH8E5b0/JuqLorXqnARkccBvAWgVETWish1cdsUAeMAfAl2tzm/8ePTcRsVMv0BvC4i78Buil5R1YIoJy0gjgZQISILALwN4EVVfTnIN2DpLCGEkIzQsyCEEJIRigUhhJCMUCwIIYRkhGJBCCEkIxQLQgghGaFYEBIRItJTRL4Ztx2EeIFiQUh09ARAsSB5CcWCkOj4MYChjY2A/xO3MYTkApvyCImIxim3UwtldwhpW9CzIIQQkhGKBSGEkIxQLAiJjh0AusdtBCFeoFgQEhGq+gGAmSKykAlukm8wwU0IISQj9CwIIYRkhGJBCCEkIxQLQgghGaFYEEIIyQjFghBCSEYoFoQQQjJCsSCEEJKR/wdXPHW5j5j9GAAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"def create_model_ode():\n",
"\n",
" m = ConcreteModel()\n",
"\n",
" # Declare time\n",
" m.t = ContinuousSet(bounds=(0.0, 5.0))\n",
"\n",
" # Declare parameter - acceleration due to gravity\n",
" m.g = Param(initialize=9.81) # m/s^2\n",
"\n",
" # Declare variables indexed over time\n",
" m.x = Var(m.t) # horizontal position\n",
" m.y = Var(m.t) # vertical position\n",
" m.u = Var(m.t) # horizontal velocity\n",
" m.v = Var(m.t) # vertical velocity\n",
" m.T = Var(m.t) # tension\n",
"\n",
" # Declare derivative variables\n",
" m.dx = DerivativeVar(m.x) # with respect to t is implied\n",
" m.dy = DerivativeVar(m.y)\n",
" m.du = DerivativeVar(m.u)\n",
" m.dv = DerivativeVar(m.v)\n",
" m.dT = DerivativeVar(m.T)\n",
"\n",
" # Declare differential equations\n",
" def _dx_eqn(m, t):\n",
" return m.dx[t] == m.u[t]\n",
" m.dx_eqn = Constraint(m.t, rule=_dx_eqn)\n",
"\n",
" def _dy_eqn(m, t):\n",
" return m.dy[t] == m.v[t]\n",
" m.dy_eqn = Constraint(m.t, rule=_dy_eqn)\n",
"\n",
" def _du_eqn(m, t):\n",
" return m.du[t] == -m.T[t]*m.x[t]\n",
" m.du_eqn = Constraint(m.t, rule=_du_eqn)\n",
"\n",
" def _dv_eqn(m, t):\n",
" return m.dv[t] == m.g -m.T[t]*m.y[t]\n",
" m.dv_eqn = Constraint(m.t, rule=_dv_eqn)\n",
"\n",
" def _dT_eqn(m, t):\n",
" return m.dT[t] == 4*m.T[t]*(m.x[t]*m.u[t] + m.y[t]*m.v[t]) + 3*m.g*m.v[t]\n",
" m.dT_eqn = Constraint(m.t, rule=_dT_eqn)\n",
"\n",
" # Specify initial conditions\n",
" m.x[0] = 0\n",
" m.y[0] = 1\n",
" m.u[0] = 1\n",
" m.v[0] = 0\n",
" m.T[0] = 1 + m.g\n",
" \n",
" return m\n",
"\n",
"ode = create_model_ode()\n",
"\n",
"# Specify integrator options\n",
"int_ops = {'print_stats':True,\"abstol\":1E-6,\"reltol\":1E-4}\n",
"\n",
"# Solve DAEs\n",
"sim = Simulator(ode, package='casadi')\n",
"tsim, profiles = sim.simulate(numpoints=100, integrator='idas',integrator_options=int_ops)\n",
"\n",
"# Plot solution\n",
"results = plot_results(sim, tsim, profiles)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.2 Formulation 2: Pure ODE Model](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.2-Formulation-2:-Pure-ODE-Model)",
"section": "2.4.3.2 Formulation 2: Pure ODE Model"
}
},
"source": [
"**Discussion**\n",
"* Are all of the algebraic constraints in the original formulation satisfied?"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.3 Formulation 3: Index-1 DAE Model](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.3-Formulation-3:-Index-1-DAE-Model)",
"section": "2.4.3.3 Formulation 3: Index-1 DAE Model"
}
},
"source": [
"### 2.4.3.3 Formulation 3: Index-1 DAE Model\n",
"\n",
"$$\\begin{align}\n",
"\\frac{d y}{dt} &= v \\\\\n",
"\\frac{d v}{dt} &= g - Ty \\\\\n",
" & x^2 + y^2 = 1 \\\\\n",
" & 2 x u + 2 y v = 0 \\\\\n",
" & (u^2 + v^2) - T (x^2 + y^2) + g y = 0\n",
"\\end{align}$$\n",
"\n",
"(This reformulation is NOT unique... could have written $\\frac{dx}{dt}$ and $\\frac{du}{dt}$ instead.)\n",
"\n",
"Consistent initial conditions:\n",
"1. Specify $y(0)$ and $v(0)$.\n",
"2. Solve for $x(0)$, $u(0)$, and $T(0)$"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.3 Formulation 3: Index-1 DAE Model](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.3-Formulation-3:-Index-1-DAE-Model)",
"section": "2.4.3.3 Formulation 3: Index-1 DAE Model"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Constraint 1:\n",
"0\n",
"\n",
"Constraint 2:\n",
"0\n",
"\n",
"Constraint 3:\n",
"0.0\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"The residual routine or the linear setup or solve routine had a recoverable error, but IDACalcIC was unable to recover.\n"
]
},
{
"ename": "RuntimeError",
"evalue": ".../casadi/interfaces/sundials/idas_interface.cpp:591: IDACalcIC returned \"IDA_NO_RECOVERY\". Consult IDAS documentation.",
"output_type": "error",
"traceback": [
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
"\u001b[0;31mRuntimeError\u001b[0m Traceback (most recent call last)",
"\u001b[0;32m\u001b[0m in \u001b[0;36m\u001b[0;34m\u001b[0m\n\u001b[1;32m 77\u001b[0m \u001b[0;31m# Solve DAEs\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 78\u001b[0m \u001b[0msim\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mSimulator\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mindex1\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mpackage\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;34m'casadi'\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m---> 79\u001b[0;31m \u001b[0mtsim\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mprofiles\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0msim\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0msimulate\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mnumpoints\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;36m100\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mintegrator\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;34m'idas'\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0mintegrator_options\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mint_ops\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 80\u001b[0m \u001b[0;31m# tsim, profiles = sim.simulate(numpoints=100, integrator='collocation')\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/pyomo/dae/simulator.py\u001b[0m in \u001b[0;36msimulate\u001b[0;34m(self, numpoints, tstep, integrator, varying_inputs, initcon, integrator_options)\u001b[0m\n\u001b[1;32m 905\u001b[0m \u001b[0;32melse\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 906\u001b[0m \u001b[0mtsim\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mprofile\u001b[0m \u001b[0;34m=\u001b[0m\u001b[0;31m \u001b[0m\u001b[0;31m\\\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 907\u001b[0;31m self._simulate_with_casadi_no_inputs(initcon, tsim,\n\u001b[0m\u001b[1;32m 908\u001b[0m \u001b[0mintegrator\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 909\u001b[0m integrator_options)\n",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/pyomo/dae/simulator.py\u001b[0m in \u001b[0;36m_simulate_with_casadi_no_inputs\u001b[0;34m(self, initcon, tsim, integrator, integrator_options)\u001b[0m\n\u001b[1;32m 967\u001b[0m \u001b[0mintegrator_options\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;34m'output_t0'\u001b[0m\u001b[0;34m]\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0;32mTrue\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 968\u001b[0m \u001b[0mF\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mcasadi\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mintegrator\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m'F'\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mintegrator\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mdae\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mintegrator_options\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 969\u001b[0;31m \u001b[0msol\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mF\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mx0\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0minitcon\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 970\u001b[0m \u001b[0mprofile\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0msol\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;34m'xf'\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mfull\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mT\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 971\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/casadi/casadi.py\u001b[0m in \u001b[0;36m__call__\u001b[0;34m(self, *args, **kwargs)\u001b[0m\n\u001b[1;32m 13451\u001b[0m \u001b[0;32melse\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 13452\u001b[0m \u001b[0;31m# Named inputs -> return dictionary\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m> 13453\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mcall\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mkwargs\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 13454\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 13455\u001b[0m \u001b[0;32mdef\u001b[0m \u001b[0mbuffer\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/casadi/casadi.py\u001b[0m in \u001b[0;36mcall\u001b[0;34m(self, *args)\u001b[0m\n\u001b[1;32m 12322\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 12323\u001b[0m \"\"\"\n\u001b[0;32m> 12324\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0m_casadi\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mFunction_call\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m*\u001b[0m\u001b[0margs\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 12325\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 12326\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;31mRuntimeError\u001b[0m: .../casadi/interfaces/sundials/idas_interface.cpp:591: IDACalcIC returned \"IDA_NO_RECOVERY\". Consult IDAS documentation."
]
}
],
"source": [
"def create_model_index1():\n",
"\n",
" m = ConcreteModel()\n",
"\n",
" # Declare time\n",
" m.t = ContinuousSet(bounds=(0, 5))\n",
"\n",
" # Declare parameter - acceleration due to gravity\n",
" m.g = Param(initialize=9.81) # m/s^2\n",
"\n",
" # Declare variables indexed over time\n",
" m.x = Var(m.t) # horizontal position\n",
" m.y = Var(m.t) # vertical position\n",
" m.u = Var(m.t) # horizontal velocity\n",
" m.v = Var(m.t) # vertical velocity\n",
" m.T = Var(m.t) # tension\n",
"\n",
" # Declare derivative variables\n",
" m.dy = DerivativeVar(m.y)\n",
" m.dv = DerivativeVar(m.v)\n",
"\n",
" # Declare differential equations\n",
" def _dy_eqn(m, t):\n",
" return m.dy[t] == m.v[t]\n",
" m.dy_eqn = Constraint(m.t, rule=_dy_eqn)\n",
"\n",
" def _dv_eqn(m, t):\n",
" return m.dv[t] == m.g - m.T[t]*m.y[t]\n",
" m.dv_eqn = Constraint(m.t, rule=_dv_eqn)\n",
"\n",
" # Declare algebraic equations\n",
" def _alg_eqn1(m, t):\n",
" return m.x[t]**2 + m.y[t]**2 == 1\n",
" m.alg_eqn1 = Constraint(m.t, rule=_alg_eqn1)\n",
"\n",
" def _alg_eqn2(m, t):\n",
" return m.x[t]*m.u[t] + m.y[t]*m.v[t] == 0\n",
" m.alg_eqn2 = Constraint(m.t, rule=_alg_eqn2)\n",
"\n",
" def _alg_eqn3(m, t):\n",
" return m.u[t]**2 + m.v[t]**2 - m.T[t]*(m.x[t]**2 + m.y[t]**2) + m.g*m.y[t] == 0\n",
" m.alg_eqn3 = Constraint(m.t, rule=_alg_eqn3)\n",
"\n",
" # Specify initial conditions\n",
" m.x[0] = 0\n",
" m.y[0] = 1\n",
" m.u[0] = 1\n",
" m.v[0] = 0\n",
" m.T[0] = 1 + m.g\n",
" \n",
" return m\n",
"\n",
"def index1_check_constraints(m):\n",
" \"\"\" Check if the three constraints are feasible.\n",
" \"\"\"\n",
" \n",
" print(\"Constraint 1:\")\n",
" r1 = m.x[0]()**2 + m.y[0]()**2 - 1\n",
" print(r1)\n",
" \n",
" print(\"\\nConstraint 2:\")\n",
" r2 = m.x[0]()*m.u[0]() + m.y[0]()*m.v[0]()\n",
" print(r2)\n",
" \n",
" print(\"\\nConstraint 3:\")\n",
" r3 = m.u[0]()**2 + m.v[0]()**2 - m.T[0]() + m.g*m.y[0]()\n",
" print(r3)\n",
"\n",
"index1 = create_model_index1()\n",
"\n",
"# Check initial condition\n",
"index1_check_constraints(index1)\n",
"\n",
"# Specify integrator options\n",
"int_ops = {'print_stats':True,\"abstol\":1E-6,\"reltol\":1E-4}\n",
"\n",
"# Solve DAEs\n",
"sim = Simulator(index1, package='casadi')\n",
"tsim, profiles = sim.simulate(numpoints=100, integrator='idas',integrator_options=int_ops)\n",
"# tsim, profiles = sim.simulate(numpoints=100, integrator='collocation')"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.3 Formulation 3: Index-1 DAE Model](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.3-Formulation-3:-Index-1-DAE-Model)",
"section": "2.4.3.3 Formulation 3: Index-1 DAE Model"
}
},
"source": [
"What happened? Point singularity at $x=0$.\n",
"\n",
"Let's try $x=0.1$ as the initial point."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.3 Formulation 3: Index-1 DAE Model](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.3-Formulation-3:-Index-1-DAE-Model)",
"section": "2.4.3.3 Formulation 3: Index-1 DAE Model"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Constraint 1:\n",
"0.010000000000000009\n",
"\n",
"Constraint 2:\n",
"0.1\n",
"\n",
"Constraint 3:\n",
"0.0\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"The residual routine or the linear setup or solve routine had a recoverable error, but IDACalcIC was unable to recover.\n"
]
},
{
"ename": "RuntimeError",
"evalue": ".../casadi/interfaces/sundials/idas_interface.cpp:591: IDACalcIC returned \"IDA_NO_RECOVERY\". Consult IDAS documentation.",
"output_type": "error",
"traceback": [
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
"\u001b[0;31mRuntimeError\u001b[0m Traceback (most recent call last)",
"\u001b[0;32m\u001b[0m in \u001b[0;36m\u001b[0;34m\u001b[0m\n\u001b[1;32m 17\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 18\u001b[0m \u001b[0;31m# Simulator\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m---> 19\u001b[0;31m \u001b[0mtsim\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mprofiles\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0msim\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0msimulate\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mnumpoints\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;36m100\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mintegrator\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;34m'idas'\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0mintegrator_options\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mint_ops\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/pyomo/dae/simulator.py\u001b[0m in \u001b[0;36msimulate\u001b[0;34m(self, numpoints, tstep, integrator, varying_inputs, initcon, integrator_options)\u001b[0m\n\u001b[1;32m 905\u001b[0m \u001b[0;32melse\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 906\u001b[0m \u001b[0mtsim\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mprofile\u001b[0m \u001b[0;34m=\u001b[0m\u001b[0;31m \u001b[0m\u001b[0;31m\\\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 907\u001b[0;31m self._simulate_with_casadi_no_inputs(initcon, tsim,\n\u001b[0m\u001b[1;32m 908\u001b[0m \u001b[0mintegrator\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 909\u001b[0m integrator_options)\n",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/pyomo/dae/simulator.py\u001b[0m in \u001b[0;36m_simulate_with_casadi_no_inputs\u001b[0;34m(self, initcon, tsim, integrator, integrator_options)\u001b[0m\n\u001b[1;32m 967\u001b[0m \u001b[0mintegrator_options\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;34m'output_t0'\u001b[0m\u001b[0;34m]\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0;32mTrue\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 968\u001b[0m \u001b[0mF\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mcasadi\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mintegrator\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m'F'\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mintegrator\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mdae\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mintegrator_options\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 969\u001b[0;31m \u001b[0msol\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mF\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mx0\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0minitcon\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 970\u001b[0m \u001b[0mprofile\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0msol\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;34m'xf'\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mfull\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mT\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 971\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/casadi/casadi.py\u001b[0m in \u001b[0;36m__call__\u001b[0;34m(self, *args, **kwargs)\u001b[0m\n\u001b[1;32m 13451\u001b[0m \u001b[0;32melse\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 13452\u001b[0m \u001b[0;31m# Named inputs -> return dictionary\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m> 13453\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mcall\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mkwargs\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 13454\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 13455\u001b[0m \u001b[0;32mdef\u001b[0m \u001b[0mbuffer\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/casadi/casadi.py\u001b[0m in \u001b[0;36mcall\u001b[0;34m(self, *args)\u001b[0m\n\u001b[1;32m 12322\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 12323\u001b[0m \"\"\"\n\u001b[0;32m> 12324\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0m_casadi\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mFunction_call\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m*\u001b[0m\u001b[0margs\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 12325\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 12326\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;31mRuntimeError\u001b[0m: .../casadi/interfaces/sundials/idas_interface.cpp:591: IDACalcIC returned \"IDA_NO_RECOVERY\". Consult IDAS documentation."
]
}
],
"source": [
"index1_again = create_model_index1()\n",
"\n",
"# Specify alternative initial conditions\n",
"small_number = 0.1\n",
"\n",
"index1_again.x[0] = small_number\n",
"index1_again.y[0] = 1\n",
"index1_again.u[0] = 1\n",
"index1_again.v[0] = 0\n",
"index1_again.T[0] = 1 + index1_again.g\n",
"\n",
"# Check initial condition\n",
"index1_check_constraints(index1_again)\n",
"\n",
"# Solve DAEs\n",
"sim = Simulator(index1_again, package='casadi')\n",
"\n",
"# Simulator\n",
"tsim, profiles = sim.simulate(numpoints=100, integrator='idas',integrator_options=int_ops)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.3 Formulation 3: Index-1 DAE Model](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.3-Formulation-3:-Index-1-DAE-Model)",
"section": "2.4.3.3 Formulation 3: Index-1 DAE Model"
}
},
"source": [
"Our initial point does not satisfy the algebraic constraints! We need a consistent initial point."
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.3 Formulation 3: Index-1 DAE Model](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.3-Formulation-3:-Index-1-DAE-Model)",
"section": "2.4.3.3 Formulation 3: Index-1 DAE Model"
}
},
"source": [
"Given $x = \\epsilon$, solve $x^2 + y^2 = 1$ for $y$:\n",
"\n",
"$$ y = \\sqrt{1^2 - \\epsilon^2}$$\n",
"\n",
"Then, assume $u = 1$ and solve $2 x u + 2 y v = 0$ for $v$:\n",
"\n",
"$$v = \\frac{-x u}{y}$$\n",
"\n",
"Finally, we can solve $(u^2 + v^2) - T (x^2 + y^2) + g y = 0$ for $T$:\n",
"\n",
"$$\n",
"T = \\frac{(u^2 + v^2) + gy}{x^2 + y^2} = \\frac{(u^2 + v^2) + gy}{1}\n",
"$$"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.3 Formulation 3: Index-1 DAE Model](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.3-Formulation-3:-Index-1-DAE-Model)",
"section": "2.4.3.3 Formulation 3: Index-1 DAE Model"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Constraint 1:\n",
"0.0\n",
"\n",
"Constraint 2:\n",
"0.0\n",
"\n",
"Constraint 3:\n",
"0.0\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"The residual routine or the linear setup or solve routine had a recoverable error, but IDACalcIC was unable to recover.\n"
]
},
{
"ename": "RuntimeError",
"evalue": ".../casadi/interfaces/sundials/idas_interface.cpp:591: IDACalcIC returned \"IDA_NO_RECOVERY\". Consult IDAS documentation.",
"output_type": "error",
"traceback": [
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
"\u001b[0;31mRuntimeError\u001b[0m Traceback (most recent call last)",
"\u001b[0;32m\u001b[0m in \u001b[0;36m\u001b[0;34m\u001b[0m\n\u001b[1;32m 22\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 23\u001b[0m \u001b[0;31m# Simulator\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m---> 24\u001b[0;31m \u001b[0mtsim\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mprofiles\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0msim\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0msimulate\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mnumpoints\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;36m20\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mintegrator\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;34m'idas'\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0mintegrator_options\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mint_ops2\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/pyomo/dae/simulator.py\u001b[0m in \u001b[0;36msimulate\u001b[0;34m(self, numpoints, tstep, integrator, varying_inputs, initcon, integrator_options)\u001b[0m\n\u001b[1;32m 905\u001b[0m \u001b[0;32melse\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 906\u001b[0m \u001b[0mtsim\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mprofile\u001b[0m \u001b[0;34m=\u001b[0m\u001b[0;31m \u001b[0m\u001b[0;31m\\\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 907\u001b[0;31m self._simulate_with_casadi_no_inputs(initcon, tsim,\n\u001b[0m\u001b[1;32m 908\u001b[0m \u001b[0mintegrator\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 909\u001b[0m integrator_options)\n",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/pyomo/dae/simulator.py\u001b[0m in \u001b[0;36m_simulate_with_casadi_no_inputs\u001b[0;34m(self, initcon, tsim, integrator, integrator_options)\u001b[0m\n\u001b[1;32m 967\u001b[0m \u001b[0mintegrator_options\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;34m'output_t0'\u001b[0m\u001b[0;34m]\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0;32mTrue\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 968\u001b[0m \u001b[0mF\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mcasadi\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mintegrator\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m'F'\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mintegrator\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mdae\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mintegrator_options\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 969\u001b[0;31m \u001b[0msol\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mF\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mx0\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0minitcon\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 970\u001b[0m \u001b[0mprofile\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0msol\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;34m'xf'\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mfull\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mT\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 971\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/casadi/casadi.py\u001b[0m in \u001b[0;36m__call__\u001b[0;34m(self, *args, **kwargs)\u001b[0m\n\u001b[1;32m 13451\u001b[0m \u001b[0;32melse\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 13452\u001b[0m \u001b[0;31m# Named inputs -> return dictionary\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m> 13453\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mcall\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mkwargs\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 13454\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 13455\u001b[0m \u001b[0;32mdef\u001b[0m \u001b[0mbuffer\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/casadi/casadi.py\u001b[0m in \u001b[0;36mcall\u001b[0;34m(self, *args)\u001b[0m\n\u001b[1;32m 12322\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 12323\u001b[0m \"\"\"\n\u001b[0;32m> 12324\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0m_casadi\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mFunction_call\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m*\u001b[0m\u001b[0margs\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 12325\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 12326\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;31mRuntimeError\u001b[0m: .../casadi/interfaces/sundials/idas_interface.cpp:591: IDACalcIC returned \"IDA_NO_RECOVERY\". Consult IDAS documentation."
]
}
],
"source": [
"index1_take_two = create_model_index1()\n",
"\n",
"# Specify alternative initial conditions\n",
"small_number = 0.1\n",
"\n",
"index1_take_two.x[0] = small_number\n",
"index1_take_two.y[0] = np.sqrt(1 - small_number**2)\n",
"index1_take_two.u[0] = 1\n",
"index1_take_two.v[0] = -index1_take_two.x[0]()*index1_take_two.u[0]()/index1_take_two.y[0]()\n",
"index1_take_two.T[0] = (index1_take_two.u[0]()**2 + index1_take_two.v[0]()**2\n",
" + index1_take_two.g*index1_take_two.y[0]())\n",
"\n",
"# Check initial condition\n",
"index1_check_constraints(index1_take_two)\n",
"\n",
"# Solve DAEs\n",
"sim = Simulator(index1_take_two, package='casadi')\n",
"\n",
"# Specify integrator options\n",
"int_ops2 = {'print_stats':True,\"abstol\":1E-6,\"reltol\":1E-4,\n",
" \"verbose\":False,\"calc_ic\":True}\n",
"\n",
"# Simulator\n",
"tsim, profiles = sim.simulate(numpoints=20, integrator='idas',integrator_options=int_ops2)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.4 Formulation 4: Index-1 DAE Model](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.4-Formulation-4:-Index-1-DAE-Model)",
"section": "2.4.3.4 Formulation 4: Index-1 DAE Model"
}
},
"source": [
"### 2.4.3.4 Formulation 4: Index-1 DAE Model\n",
"\n",
"$$\\begin{align}\n",
"\\frac{d x}{dt} &= u \\\\\n",
"\\frac{d y}{dt} &= v \\\\\n",
"\\frac{d u}{dt} &= -T x \\\\\n",
"\\frac{d v}{dt} &= g - Ty \\\\\n",
"0 &= (u^2 + v^2) - T (x^2 + y^2) + g y\n",
"\\end{align}$$\n",
"\n",
"Consistent initial conditions:\n",
"1. Specify $x(0)$, $u(0)$, $y(0)$, and $v(0)$.\n",
"2. Solve for $T(0)$"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.4 Formulation 4: Index-1 DAE Model](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.4-Formulation-4:-Index-1-DAE-Model)",
"section": "2.4.3.4 Formulation 4: Index-1 DAE Model"
}
},
"outputs": [],
"source": [
"def create_model_index1_b():\n",
"\n",
" m = ConcreteModel()\n",
" \n",
" # Declare time\n",
" m.t = ContinuousSet(bounds=(0.0, 5))\n",
"\n",
" # Declare parameter - acceleration due to gravity\n",
" m.g = Param(initialize=9.81) # m/s^2\n",
"\n",
" # Declare variables indexed over time\n",
" m.x = Var(m.t) # horizontal position\n",
" m.y = Var(m.t) # vertical position\n",
" m.u = Var(m.t) # horizontal velocity\n",
" m.v = Var(m.t) # vertical velocity\n",
" m.T = Var(m.t) # tension\n",
"\n",
" # Declare derivative variables\n",
" m.dx = DerivativeVar(m.x) # with respect to t is implied\n",
" m.dy = DerivativeVar(m.y)\n",
" m.du = DerivativeVar(m.u)\n",
" m.dv = DerivativeVar(m.v)\n",
"\n",
" # Declare differential equations\n",
" def _dx_eqn(m, t):\n",
" return m.dx[t] == m.u[t]\n",
" m.dx_eqn = Constraint(m.t, rule=_dx_eqn)\n",
"\n",
" def _dy_eqn(m, t):\n",
" return m.dy[t] == m.v[t]\n",
" m.dy_eqn = Constraint(m.t, rule=_dy_eqn)\n",
"\n",
" def _du_eqn(m, t):\n",
" return m.du[t] == -m.T[t]*m.x[t]\n",
" m.du_eqn = Constraint(m.t, rule=_du_eqn)\n",
"\n",
" def _dv_eqn(m, t):\n",
" return m.dv[t] == m.g -m.T[t]*m.y[t]\n",
" m.dv_eqn = Constraint(m.t, rule=_dv_eqn)\n",
"\n",
" def _alg_eqn3(m, t):\n",
" return m.u[t]**2 + m.v[t]**2 - m.T[t]*(m.x[t]**2 + m.y[t]**2) + m.g*m.y[t] == 0\n",
" m.alg_eqn3 = Constraint(m.t, rule=_alg_eqn3)\n",
"\n",
" # Specify initial conditions\n",
" m.x[0] = 0\n",
" m.y[0] = 1\n",
" m.u[0] = 1\n",
" m.v[0] = 0\n",
" m.T[0] = 1 + m.g\n",
" \n",
" return m"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.4 Formulation 4: Index-1 DAE Model](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.4-Formulation-4:-Index-1-DAE-Model)",
"section": "2.4.3.4 Formulation 4: Index-1 DAE Model"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"FORWARD INTEGRATION:\n",
"Number of steps taken by SUNDIALS: 379\n",
"Number of calls to the user’s f function: 485\n",
"Number of calls made to the linear solver setup function: 31\n",
"Number of error test failures: 3\n",
"Method order used on the last internal step: 5\n",
"Method order to be used on the next internal step: 5\n",
"Actual value of initial step size: 7.90569e-09\n",
"Step size taken on the last internal step: 0.0120795\n",
"Step size to be attempted on the next internal step: 0.0120795\n",
"Current internal time reached: 0.0120795\n",
"Number of nonlinear iterations performed: 483\n",
"Number of nonlinear convergence failures: 0\n",
"\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXAAAAEGCAYAAAB8Ys7jAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAABLvUlEQVR4nO3deXxU1d348c+ZLZPJvpINyAYhkJAAYQeVijvo4/JYtbW2anFfq63aam1t/WldHmvVx7q0tU9dsFZbRXFHZIcAAUIWlkD2fd9mP78/JokJBAjJTCYD5/168QozuXPv9+bM/d5zzz3nXCGlRFEURfE9Gm8HoCiKogyPSuCKoig+SiVwRVEUH6USuKIoio9SCVxRFMVH6UZzY5GRkTIxMXE0N6koiuLztm/f3iCljDry/VFN4ImJieTm5o7mJhVFUXyeEKJ0sPdVE4qiKIqPUglcURTFR6kEriiK4qNUAlcURfFRKoEriqL4KJXAFUVRfJRK4IqiKD5qVPuBD9fh3Q001XQSPTGYqAlB+Pn7RNjD1tlqob60nabqTgLD/IhODCYkyh8hhLdD8xi7zUFjZScN5e3YLI6+stb7ab0dmsdIKWlvMtNQ3kFLbRdBEUbGJQUTFG48pcvaarbTVNVJQ0UHDpuTcUnBRI0PQqs/deuTli4bfia929frE5mwbG8je9ZW9r2OmhDE/EtTGJ8e7sWo3MvplBRtrGbbJ4foaLIc9Xs/k46pC+PIuSgRg9Enim1IWmq72PCvA5TmNyKdA+emFwJikkNYcHkqMckhXorQ/RwOJ/nfVLL908N0t9uO+r0p2EDGmfHMOHcCOv2pcwKrL29n478OUFHUfNTvNDpB/KRQFlyeSmRCkBei8wy71UHel2Xs+KyM5XdkEZsa6tb1i9F8oENOTo4c7kjM7g4r9aXt1JW2UbixmrYGM8nZUSy8IpXgSH83Rzq6qg+2sm7lPurL2olJDiF1VjRRE4OIiAugvclM3eF2youaOJBbhynEwILLUpk8Z5xP19Is3XZyPz7E7jUVaPUapi2OJybJVevWGbTUlbZRe8hV1p0tFqbMj2H+pamYgg3eDn1ESvMbWf/P/bTUdpEwJYyUGVFEjg8iLMZEa303tYfaKNvbyOE9jQRH+bP4ykkkZkZ6O+wR6Wqzsvk/ByncWI3RpCfjzHiiJwYROT4IjVZQW9JGTUkrhZuqsXTZyTwrnjnLk336SltKyf5ttWz64CAdzRaSZ0Sx8PLh5yohxHYpZc5R7/tKAu/PbnOw66tycj85DMD5KzKZmBEx4vV6w47PS9n0/kECQv1YcFkKk2YfOzHXHGpl3Tv7qCttJ2VGFEuvn+qTNbTW+i4+fH4XbQ3dpC+IZd4lKcdMzFazndxPDrPrq3L0Ri0X3ZpFbIrv1callGz64CA7Py8jdJyJhVekMjEj4phlXV7YxLqV+2iu6WLa4jjOuDoNjcb3Ttj15e2s+tMuzB02Mr+XwOwLE4/ZlGDutLH5PyXsXVdJQIgfy+/IIiI+cJQjHjmHw8naN4sp3FhN1IQgFl6RSvzksBGt85RK4L3am8ysfnkPjRUdfO+6dNLmxrht3Z4mnZKN7x8g78tyUmdFs+TaKUNqGpFOyc4vytj0wUHi00K58ObpGHyoplJf1s5Hf8pDOuHCWzKHfEnZVN3JJy/tprPFwvk3+dYJ2+Fwsub/iijeXEPGGfEsunISWt2J23sddidbPixh5+dlpMyI4pzrp/lUO3FFUROfvLwHP38dy24fejKuPdTG6pd3Y7c5WXZ7lk81n9ksDj57NZ/S/EZyLkxkzrIkhBtOvKdkAgewdtv55OXdVBa3sPCKVLKXTnDr+j3B4XCy5u9FFG+pIXNJAov/e9JJF3Lx5mq++nsRkQmBLLs9yyeaFvoOaJOOi+/MJiwm4KQ+39Vm5aM/5dFU2ekzJ2ybxcGnr+RTtreRuRcnMeuCxJNu+sr7sowN7x0gYUoYF9yc6RP3QA5sr+OLv+wldJyJ5XdkERhmPKnPtzV08+Ef8+hstXDBTZlMmDb2T9jmDhsfvbCL+tI2zrg6jYwz4t227mMlcN85nR+DoefsnjIjig3vHSD/28oTf8iLpJR88w9X8p57cTKLrzz55A2QNi+WC2/JpLm6kw+fz8NqtnsgWvepPdzGxy/uJijcyOX355x08gbXzb1L751JbGoIX/6tgAPb6zwQqfs4HU4+fy2f8oJGlvxwCjkXJg3rvkX20gmc/eN0Kve18PGLu3HYnB6I1n3K9jby+et7GZcUzKU/m3nSyRsgONKfy+6fRUi0iY9f2k1F8dE3PscSu9XBxy/torGig/NvynRr8j4en0/gADq9lnNvnMbEzAi+fbuYw7sbvB3SMeV+cpiiTTXMviiRnAtPvjbWX2JmJBfcnElTVSefvZKPwzE2D+zW+m4+fnEXphADl9w9g8Awv2Gvq/eEHZMUzJd/K6CmpNWNkbqPlJJvV+7n8J5GzrhqMlMXxY1ofVPmxXL2delU7W/h638UMppXziejvqydT1/JJzwugGW3ZWEMGH7XOVOwgf+6ZwYh0SZWv7yHpqpON0bqPk6n5Iu/FFBzqI1zrp9KcvZR03Z7zCmRwAE0Wg3n3jCNyPFBfPZaPnWlbd4O6ShFm6rZ+tEhpsyLYfayJLesc8K0CM66Jo2ygia+fat4zB3Y5g4bq17YhdMp3dbUozNoufCW6QSE+vHxS7tpqetyQ6TuteOzUvZ+W8nM8yaQcWaCW9aZNjeGuRcns29LLVs/OuSWdbpTe5OZVS/uws+kY/ntWW65N2MM0LPstulo9RpWvbiLrjarGyJ1HyklG/65n5K8ehZdMYmUmdGjuv1TJoEDGIw6LrptOsZAPate3E17k9nbIfWpKG5mzf8VkTAljLN+OMWtXQCnLopj1vkTKdhQzY7PBp333SscdiefvLyb9kYzF94yfVjNJsfiH2Rg+e1ZIGHVC7swdx7dn9pb9ufWsvnfJUyaPY55l6S4dd2zLphI+oJYcj85TOHGareueySsZjurXtiF3epk2R1ZBIQO/yrrSMGR/iy7bTrd7VY+fnEXNqvDbeseqT3fVLJ7TQVZZ48n6+zxo779UyqBA67uR7dnY7c6+PTPe7DbvF/Y7U1mPns1n5Bof86/KXNIPRBO1txLkpmUE83m/5RQurfR7esfjg3/3E/1gVa+d90U4tw8gAEgdJyJC2/JpL3RzBd/2YvT6f2rj8bKDr7+eyExySGc/aN0t/RA6E8IwZk/SCNhShjfvFVE7SHvX2lKKfn6jUKaqzs5/6YMIuLc3/UvemIw51w/jbqydta+OTauNKv2N7P+n/tJnB7JwstTvRLDKZfAAcLjAlh63VTqStv59p19Xi1su811InHanVxwc6bHBicIIVhybToRcYF88fpeWuu7PbKdoSraVM2etZVkLx3P5Nme6y0SmxrK4u9PpmxvE9tWebdZwdJlY/XLezAYdZx/U4bHuvxptRrOvXEaAcF+fPrKHq83K+z8vIyDO+uZf2kq46d4bnR0cnYUc5YlUbylhvy13u2s0NFs5tNX8gmJ8mfpT6a6/UQ9VCf8hgkh/iKEqBNC5Pd7L1wI8YUQYn/Pz5H1UveA5BlRzDp/IoUbqilYX+WVGKSUfPu2a+DN2T+e6tYmhMHo/bRccHMGAKv/vMdrl5r1Ze1882Yx8WmhzL/UvU0Ig5m2OK6vWeHQrnqPb28wsudGVnujmfNXZBAQ4r4mhMH4Bxq44OZMujtsfP56Pk4v3cAuL2hi878PkpoTTfY5nm9CyLkgkcTMCNa/u5/qAy0e395gHDYnq/+cj93q2UrZUAylivA34Pwj3nsA+EpKOQn4quf1mDPn4mQmTA3n23f2eaW3wt51VRRurCbnwsRRuzMdEmXinOun0VjZwZr/Kxr1q4/uDiurX96Df5Ce827MQKP1/EWeEIIzrp5M9MQgvvxrAc01o99bYdvHhyjNb2TRlZPcPt/FsURNCOKsa9KoLG5h0wcHR2Wb/bU1dPPZ6/mExQbwvWvTR2VqB6ERLP3JVIIijHz6Sj6drUfPG+Rp367cR93hNs7+cTrhsZ6tlJ3ICY8uKeW3QNMRb18CvNHz/zeA/3JvWO6h0QjOuWEagWF+fPrnPaNa2DUlrvlNJkyLcFuPk6GamBHB3OVJ7N9Wy+6vK0Ztu65+z3vparNy/k2Z+AeN3uAinV7L+TdlotFpWP3ynlHtF39odwPbPj7MlHkxZJw5Ov1/e02ZH0vGmfHkfVnO/tzaUduuzepg9Z/3IJ1wwc2ZozprpJ9JzwU3Z2I12/n0z/k47KN39bF3XSUF66uYef5EUmaMbo+TwQy3ejROSlkN0PPzmHsihFghhMgVQuTW14/+5a0xwFXYli47n706On2lO1strP7zHgLDjZxz/VSvzGEx6/xEkrIi2fCvA1TuG51BEJv/XUJFUTNnXjOZcYnBo7LN/oLCjZz30wxa6rr56o3R6SvdUtvFl3/ZS9SEIM68Js0rE4wt+u9JxKaE8PXfC2mo6PD49qSUrH2zmIaKDs65fiqh0SaPb/NIEfGBfO9H6dSUtLL+3f2jss2aQ618u3If46eGM/fi5FHZ5ol4/PpWSvmKlDJHSpkTFTV6Hdz7i0wIYsm1U6g+0MqG9w54dFsOu5PPXsnH2m3nwpszRzSQYSSERrD0x1MJifLns1fzPd6lcn9uLTu/KCPjjHjSF4xs0MpIJKSFseCyFEp21nu8S6XVbOeTl/eg0Wk4/6YMdAbvTCym1Wk4b0UGBn8dq1/e7fEulXu+qaB4Sw1zliV5dabESTnjmHHuBPK/raRgg2fvc3W1Wfn0z/kEhPhx7vXTxszEYsNN4LVCiFiAnp9je0wzMHlODFlnj2fPmgqP3dSUUvLtO/uoPtjK965N9/pMagZ/HRfekond5mT1y3uwWTxzU7OutK2v69yiKyd5ZBsnI+vs8UyaPY7N/ynhkIdG5faOvmup6eS8G6cRHOHdKY0DQvy44KZMOpotfP76Xo9daZYVNLLhnwdInB5JzgWJHtnGyZh3STIJU8JY+3Yx1Qc9c5/LbnWw+uU9mDttXHBTJsZA71TKBjPcBP4hcF3P/68D/uOecDxrwWUpjJ8azjdvFVOa7/6+0ttXl1KwvopZ509k0uxxbl//cITFBHDu9dNoKG/ns1fd31uhraGbVS/uxj/Q4Oo654E+7ifL1aVyCtETgvj81XxqDrn3wJZSsm7lPg7vbmDRlZNJ8GDXuZMRkxzCmdekUV7QxDf/cP8N7IYK1zD5sNgAzvFi17n+NFoN592YQVCYkY9f2uX2G9jSKfnyrwXUHGpl6Y+nEjVhbD1sYijdCN8GNgFpQogKIcQNwBPAOUKI/cA5Pa/HPI1Ww/krMoiID+DTV9073L5oUzVbPixxDXe+ZGy0j/VKnB7JGVenUZrfyNq33dcv3txp46M/7cJp7xl95+GucydDb9By0W1ZmEIMfPziblpq3TfcfufnZeSvrST7nAlMX+KeYfLuMnVhHLMvSqRoU41bh9u3N5lZ9addfVPDjqUpjI2BepbfmYVGI/joT7vc2llhw/sHOLiznoWXp5I6y/s3LY80lF4oV0spY6WUeillgpTydSllo5TybCnlpJ6fR/ZSGbMMRtcX0BigY9ULu9wyj0bp3sa+YfJLrnXvMHl3yTgj3jXcfn0V2z4+POL1Wc12Pvnf3bQ1dnPhLdO93p1qMKZgA8vvyAYJH/0pzy0HdvHmajZ94Or3vGAU+rgPx+xlSaQvdPWLz1878l5I3e1WVr2wC5vFwbLbs0Y0GZmnhESZWHZ7Ft09c+9Yu0feC2nn52Xs+rKc6UsSvDJMfii8f73rBa6nfWTjdEref2r7iGri+7bV8MlLuwmLC/DYMHl3mXtJMlPmxbBt1SE2vLf/qGdQDlV3u5X//M9Oag66LivjJoW6N1A3Ch1n4qLbptPVZuX9p7aPqCa+6+tyvvxbIfFpoSy9bmw0IQxGCMFZ16QxMTOCtW/vY8dnpcO+6mpr6Ob9p3fQWt/NBTdnev2+zvFETwzm/J9m0FjZyQfP7hj2CVtKyeZ/H2Tj+wdImRnNwv+eNCYrZXAKPNBhJJprXHNpWzrtnH9TBhOmntyk8b0T7cdNCuXCWzI98tRpd3M6Jevf3c+ebyqYlBPN2ddNPakh320N3Xz4fB4dzRbOu3EaSVne6Vl0smoOtfLxi7sBuOi26cQkDf0pL64DuoQdn5WSlBXJuTdM81qPk5PhsDn56o0C9ufWkXlmPIu+P/mkek80Vnbw4fN5OGxOLrp1+qgNUBqp0vxGPn01H2OAjuV3ZJ/U1aHT4WTtW8UUbKhm6qI4zrxmbDzK7pR9Is9IdbZY+OhPu2iu7mTuJclknT3+hLVoc4eNTR8coGBDtU8+m1JKyc7PXY9li00NYckPp5xwmL+UkpKd9ax9Zx9Ou5OLbvO9Z1O21Hbx0Z/y6Gq1sujKSaQvjDvhwdnRbGb9u/s5uLOeqYvjONPHnk0pnZKNHxwk74syJmZGcObVaQSFH/8BC9IpKdxUzYb3DqD307L8ziyPTFDlSfVl7ax6YRcOu5OzfjCFlJlRJ6xFt9R2sfbtYiqKml2PQ1s+vAdweIJK4Mdh6bbz1d8KOLSrgZAofxZcnkpSVuRRhedwOMlfW8m2VYewmh1knz2eeZem+NQB3V/xlhq+fbsYu9XJtDPjmXNR0qBdpBoqOlj/z31UFrcQER/AuTdkEB439tq8h6Krzcpnr+ZTtb+FiPhAFv734BMw2W0O8r4sZ/vqw0gnzFmexIxzJ4yZA/pk7V5TwcZ/HQAB2WePZ+b5Ewd9NFvvCOK60nZiU0JYev1Ur3eRHK62hm4+6XlmbkxyCAuvSB30+ZpWs53tqw+T92U5Or2GhVdMGvEDONxNJfAhKNvbyPp/7qe5povAMD8ixwcRNT4Qu81JfVk79WXtWLrsjE8PY+F/T/K5WslgutqsbF11iIJ1lWh1GiISAokcH0RQuB+NlZ3Ul7XTUtuFX4COeRcnM3VR3KjMb+JJUkoO7qhn4/sHaG80ExxpJGp8EBEJgVi77dSVtlNX1o7d4iB5RhQLL08lONI3k1h/7U1mNv/7IPu21qI3aolMCCQyIYiAUAMN5R3UHmqjvcmMKcTAgstSmTxnnM+esHo5nZKija4eYl1tVsJiTETEBxIeF4C500btoTbqy9tx2iVT5scw/9LUMfl8WZXAh8jhcFK8uYbK4mbqy9ppru1CoxFExAcSNTGIpOmRTMyI8Pkv9pEaKzso3FBNfXk7DRUdWLvtBIT6ET0xiHFJwUxbHO+1UaWeYrc5KFhfTdX+ZhoqOmit60ar0xA5PpDoxGBSsqOITxtzE22OWO2hNoo2VdNQ0UFjZQc2i4OgcCPjkoKJSQ4hfWGsTzw4+WRYzXby11ZSfbCVpqoO2hrM6PQaoiYGEZMUQsrMaMYljf70D0OlEvgw2awONEJ4bG7nsUhKibXb7hM3Zd3JZnGg0Qm0Pn6FcTKkU2K1OLw6Jao3WM12tHqNz5T1sRL46VVqw6D3gd4G7iaEOO2SNzCqM+qNFUIjTrvkDZwyVxi+cfpRFEVRjqISuKIoio9SCVxRFMVHqQSuKIrio1QCVxRF8VEqgSuKovgolcAVRVF8lErgiqIoPkolcEVRFB+lEriiKIqPUglcURTFR6kEriiK4qNUAlcURfFRKoEriqL4KJXAFUVRfJRK4IqiKD5qRAlcCHGPEGKvECJfCPG2EOL4j7tWFEVR3GbYCVwIEQ/cCeRIKTMALXCVuwJTFEVRjm+kTSg6wF8IoQNMQNXIQ1IURVGGYtgJXEpZCTwNlAHVQKuU8vMjlxNCrBBC5Aohcuvr64cfqaIoijLASJpQwoBLgCQgDggQQvzwyOWklK9IKXOklDlRUVHDj1RRFEUZYCRNKEuBQ1LKeimlDXgfWOCesBRFUZQTGUkCLwPmCSFMQggBnA0UuicsRVEU5URG0ga+BXgP2AHs6VnXK26KS1EURTkB3Ug+LKX8NfBrN8WiKIqinAQ1ElNRFMVHqQSuKIrio1QCVxRF8VEqgSuKovgolcAVRVF8lErgiqIoPkolcEVRFB81on7giqIo7mCz2aioqMBsNns7FK8yGo0kJCSg1+uHtLxK4IqieF1FRQVBQUEkJibimpnj9COlpLGxkYqKCpKSkob0GdWEoiiK15nNZiIiIk7b5A0ghCAiIuKkrkJUAlcUZUw4nZN3r5P9G6gEriiK4qNUAlcURfFRKoEriqIM4ptvviEkJIQLL7xwwPvt7e0sXLiQ7OxsHA4HAM899xxdXV19yzz99NOkpaXx9ttvD/jsypUrSU1NZdmyZW6JUSVwRVGUY1i8eDGffPLJgPe+/vpr4uPjycvLQ6vVAkcn8Pvuu4833niDl156acBnv//97/Paa6+5LT7VjVBRlDHlNx/tpaCqza3rnBoXzK+XTzvm77dt28YNN9zA1q1bcTgczJkzh1tuuWXQZVtaWoiOju57/fzzz1NVVcWSJUuIjIxkzZo1AMTExNDS0uLW/TiSqoErinLamz17NhdffDG/+tWv+PnPf84Pf/hDMjIyBl3W4XCg0XyXOu+8807i4uJYs2ZNX/IG0Gg0fU0snqJq4IqijCnHqyl70iOPPMLs2bMxGo08//zzrFu3btDl8vLySEhIOOH6IiMjqauro7m5mbCwMHeHC6gEriiKAkBTUxMdHR3YbLZjDqZZtGgR+/btY8eOHSdcn8lk4uqrryYpKYmVK1dy3nnnuTtk1YSiKIoCsGLFCh577DF+8IMf8Itf/GLQZdavX88NN9zAK68MfH57UFAQ7e3tA95rbm5m5cqVVFRUeCR5g0rgiqIo/P3vf0en03HNNdfwwAMPsG3bNpxO56DLpqWl0dTUNOC9FStWcMEFF7BkyZK+91pbW4mOjiYwMNBjcasErijKae9HP/oR77//PgBarZYtW7YMuFHZn8lkoq6ubsB7d9xxB0VFRQNuYtbV1REQEOC5oFEJXFEUZVAGg4H8/PyjBvIsXbqU5uZmsrKyjtnL5Omnn2bFihXccccdA95fuXIlt956q9tuagoppVtWNBQ5OTkyNzd31LanKIpvKCwsJD093dthjAmD/S2EENullDlHLqtq4IqiKD5qRAlcCBEqhHhPCFEkhCgUQsx3V2CKoijK8Y20H/gfgU+llFcIIQyAyQ0xKYqiKEMw7Bq4ECIYOAN4HUBKaZVStrgpLkVRFK861WcjTAbqgb8KIXYKIV4TQhzVZ0YIsUIIkSuEyK2vrx/B5hRFUUbXWJ+NcCQJXAfMBP5XSjkD6AQeOHIhKeUrUsocKWVOVFTUCDanKIriGQ8//DB//OMf+17/8pe/ZPfu3YMue7zZCPsP5BmN2QhH0gZeAVRIKbf0vH6PQRK4oijKSVn9ANTsce86YzLhgieO+esbbriByy67jLvuugun08k777zDH/7wh0GXHWw2wmeffZY1a9YQGRnZ9/6Yno1QSlkjhCgXQqRJKYuBs4EC94WmKIoyOhITE4mIiGDnzp3U1tYyY8YMIiIiBl32VJqN8A7gzZ4eKCXAT0YekqIop7Xj1JQ96cYbb+Rvf/sbNTU1XH/99YMuc0rNRiilzOtp354upfwvKWWzuwJTFEUZTZdeeimffvop27ZtO2ayHWuzEar5wBVFUXDNfbJkyRJCQ0P7epcMJi0tjSOnBOmdjTA2NrZvQqvRmI1QJXBFURTA6XSyefNm/vnPfx53uWPNRnjkxFVqNkJFUZRRUFBQQGpqKmeffTaTJk0C1GyER1GzESqKMhg1G+F31GyEiqIopwGVwBVFUXyUSuCKoig+SiVwRVEUH6USuKIoio9SCVxRFOU4zjrrLNLS0vjwww8HvP+Xv/yFtLQ0XnzxRcA1R0r/qWfb29vJysrirLPOwmw2D/jskiVLCAwMPGpA0MlSCVxRFOUE3nzzTS6++OIB7/3pT3/igw8+4LbbbgOOTuBBQUHs2rULo9HIhg0bBnx2zZo15OQc1SvwpKmRmIqijClPbn2SoqYit65zSvgUfjHnF8dd5vDhwyxbtoz8/HzANRino6PjmMv3nxfcarXyyCOP0N3dzfr163nwwQf5/ve/D3h2XnCVwBVFUYah/7zgBoOB3/72t+Tm5vLCCy8MWM6T84KrBK4oyphyopryWFBTU0NnZychISEnXDY+Pp7du3dz5ZVXuj0O1QauKIoC6HQ6nE5n3+sjbzz2+uCDD5g0aRIrVqw47qyFva677jr+93//d+zNB64oinKqGDduHHV1dTQ2NmKxWFi1atWgy1166aWUlpby8ssvD0jyg80JDvDiiy9y33338dlnn7k9ZpXAFUVRAL1ezyOPPMLcuXNZtmwZU6ZMOeay4eHhhISEDLjJuWTJEgoKCsjOzmblypV97zc3N/fNcOhuqg1cURSlx5133smdd9454L2zzjpr0GV75wXvfZBxeHg427ZtO2o5T84LrmrgiqIoxxEeHs6Pf/zjowby3HPPPVx99dV9A3mO1DuQB1zP0uxvyZIllJSUoNfrRxSbmg9cURSvU/OBf0fNB64oinIaUAlcURTFR6kEriiK4qNUAlcURfFRI07gQgitEGKnEGLwXu+Koig+6JtvviEkJOSop9K3t7ezcOFCsrOz++Y4ee655+jq6upb5umnnyYtLY233357wGdXrlxJamoqy5Ytc0uM7qiB3wUUumE9iqIoY8rixYsHTBEL8PXXXxMfH09eXl7fUPojE/h9993HG2+8wUsvvTTgs9///vd57bXX3BbfiAbyCCESgIuA3wP3uiUiRVFOazWPP46l0L3TyfqlTyHmoYeO+ftf/OIXTJw4kVtvvRWARx99lKCgoEGX7T+NLMDzzz9PVVUVS5YsITIykjVr1gCenUa210hr4M8BPwecx1pACLFCCJErhMitr68f4eYURVHc76qrrhow/P3dd98lKipq0GX7TyMLrtGbcXFxrFmzpi95g2enke017Bq4EGIZUCel3C6EOOtYy0kpXwFeAddAnuFuT1GU08PxasqeMmPGDOrq6qiqqqK+vp6wsDAmTJgw6LJ5eXkkJCSccJ2RkZHU1dXR3NxMWFiYu0MGRtaEshC4WAhxIWAEgoUQ/5BS/tA9oSmKooyeK664gvfee4+amhquuuqqQZdZtGgR+/btY8eOHSdcn8lk4uqrryYpKYmVK1eOrelkpZQPSikTpJSJwFXA1yp5K4riq6666ireeecd3nvvPa644opBl1m/fj033HADr7zyyoD3B5tKtrm5mZUrV1JRUeGR5A2qH7iiKAoA06ZNo729nfj4eGJjY4+5XFpaGk1NTQPeW7FiBRdccAFLlizpe6+1tZXo6GgCAwM9FrNbppOVUn4DfOOOdSmKonjLnj17TrhM7zSy/d1xxx3ccccdA97z5DSyvVQNXFEUZRAGg4H8/PyjBvIsXbqU5uZmsrKyjtnL5Omnn2bFihVHJfWVK1dy6623uu2mpppOVlEUr1PTyX5HTSerKIpyGlAJXFEUxUepBK4oiuKjVAJXFEXxUSqBK4py2mtsbCQ7O5vs7GxiYmKIj48nOzub0NBQ/P39yc7OHrC80+lk2bJlZGZmUl5eDsDf/vY3qqqq+pZ56623SEtL45lnnhnw2XXr1jF16lQyMjJGHLdK4IqinPYiIiLIy8sjLy+Pm2++mXvuuafvdUpKCnl5eQOW37NnD3V1dezZs4fx48cDRyfwa665hrVr1/Lcc88N+OxgU9QOl1sG8iiKorjLunf30VDe4dZ1Ro4PZPGVk922viOnlH3vvffIzc3lBz/4Af7+/mzatAl/f3+PTymrauCKoign6cgpZa+44gpycnJ48803ycvLw9/fv+93nhxro2rgiqKMKe6sKXvKUKeUBQgLC+PAgQOkpqa6PQ5VA1cURTkJ11xzDY8++ig33njjkJa/++67ycrK4i9/+YvbY1EJXFEU5SS89dZbPPXUU0fdnBxsSlmAxx9/nP3793P99de7PRaVwBVFUU7SYFPK/vjHP+bmm28mOzub7u7uvvctFgtxcXEeiUO1gSuKovTz6KOPnnAZk8lEfX09UkqEEABcfvnlXH755QOW8/SUsqoGriiKcgxarZbW1tajBvJkZ2czfvx4srOz+wbyHOmtt95i6dKl3H///QPeX7duHcuXLycyMnLE8anpZBVF8brCwkKmTJnSV5s9XUkpKSoqUtPJKoriO4xGI42NjR7tMz3WSSlpbGzEaDQO+TOqDVxRFK9LSEigoqKC+vp6b4fiVUajccj9y0ElcEVRxgC9Xk9SUpK3w/A5qglFURTFR6kEriiK4qNUAlcURfFRKoEriqL4KJXAFUVRfNSwE7gQYrwQYo0QolAIsVcIcZc7A1MURVGObyTdCO3Az6SUO4QQQcB2IcQXUsoCN8WmKIqiHMewa+BSymop5Y6e/7cDhUC8uwJTFEVRjs8tbeBCiERgBrBlkN+tEELkCiFyT/dRVoqiKO404gQuhAgE/gXcLaVsO/L3UspXpJQ5UsqcqKiokW5OURRF6TGiBC6E0ONK3m9KKd93T0iKoijKUIykF4oAXgcKpZTPui8kRVEUZShGUgNfCFwLfE8Ikdfz70I3xaUoiqKcwLC7EUop1wOn9+zriqIoXqRGYiqKovgolcAVRVF8lErgiqIoPkolcEVRFB+lEriiKIqPUglcURTFR6kEriiK4qNUAlcURfFRKoEriqL4qJE80GHUFO37iLqmfYTqAgnVBxBpCMFkCAStHrQG0PmBzuj6qTeB3h90/qAdY7vnsIGtC2zdrp92C9jNrp8OGzht4LCDdLr+IQEBQoDQgEYLmt59NvTsc88/g8m171qDa/mxwukEe/fg+2y3gNOGzWamztJMq72DFlsnDukkTB9IqD6QSEMoRoOp3377fVfevWWt93f9bcYKKY9f1k5bT3k7BilrzXdl3fv91hr6fb979neslvWAfe5Xzg4LOO1YbWZqLY202TpptXXiRBKmDyLMEEikIQyD3nhEWRtBbxx4XGvGUL1TStf+9e6vrfuo77errO0QPwsCIt26+TGW4Qb37o4X+aelsu+1kJIUm40ss5WZFgtLOrsIkvLoD2oNroI3BPT8NIE+oOdnz5dBbwRtT1LQGkCjcx04vQeS0ADSVVDS6TronPbvCsZu7ik483dfXFs32DrB2uV6be1yvXbaPf/HEpqeL/uR+2samPB0fj37beg5YPSupNG3z6Jnv3sSjMMODqtrv+3Wfl/S3uTcDdbOgftr7XL9/gg2YJO/kS3+Rnb7+VFgMGDVDJ6ItFIy2WpjusVCjtnCGV3dmAYta7+j99cQMDDh9SaE3qSo1bvK+7hl3VPOfWXdu8/mnrI+Yn9tXa6/g3S4s1QHJzSD7K+pX3n3fMf79ru3nHvLWnxX1r0nkeOVdd93u/f73W+fexPYESwC1vn7s9VoZI/RQJHBgP0YJx2dlEy1WMnqKetFXd0YBl3Q/+hjWX+Mstb1lLVG76rQ9e5vX1k7vyvrvkpUv7Lu3V9798Dy7V/u0jm08vrBv2DS0qEtO0RCDnYweEhOTo7Mzc096c/V1eyiuvkArdY2WqztVHbXsav1ALvbSmi3d2MQOs4MmcSykHTONMWjtVuOPqj6/uBd330RrZ2uL2pfLdg6xCQrjl/77/1CHXlg9R1cR548+n/Jek8egr6pZqTTlVT6ThzWnhped78TSL+Th7ULrB2DJ9PeE43DMrCWMJQvoUbnirGvFtyzz7214UETSUDfQbXH1sy/Wwv5vKWQFnsXfho96YHjmR6SSkpgPKGGYEL0QWiFhlZbO83WNso6a9jdeoDdbYfodlrx1xg4O3QKy0OmMN9vHMJuHvygsnYdkXC63FDWxn773S9h9JWv/zH23b/f1VL/E6buGGXtdMXm6FfWveXcW9bH2t/e93tPMP33d9hlPdj3e5AKQs++S52RXEs9/2kt4qvWQjocFvw1BjKCEskMSSEpII4QQxAh+kCEEDRb22i2tlHaWc2u1gPsbS/F4rQRpDVyXthULg6eQrYhAtE/iQ7Y9/7f7/5XPD1XPQ7b0E6oQtNTget/dev33f7pjGAIHOS47il3nfE4Za2HyFQwhgzhOzdIaEJsl1LmHPW+LyTwY3FKJ3sb9vLxoY9ZfWg1TeYmEoMTuT7jepYlL0Ov1Z/8SqXsubR19NTEHHx3aSt6vthj6HLdXZzOnoNb0lcz6V8b1+qHdbkupWRT9SZe2/Ma22q2YdQaWTJ+CRclX8SCuAVDLiO7087Oup18XPIxn5d+Tru1nbSwNG6cfiPnTDgH7XDKpPek2HuCVGXNSMraKZ2sKVvDa3teI78xn0B9IEsnLuXCpAuZHTMbnWZoF/w2h42tNVtZVbKKr8q+otveTVZUFiumr2Bx/GLEcJqNepu1+l9p9N9njW5sNc0c4ZRM4P3ZnXa+KvuK1/e8TmFTITEBMdw5404uSr4IjRi7BXMqy6vL46ltT7G7YTfR/tH8aNqPuGLyFQToA0a0XqvDyupDq3ltz2scbjtMYnAi9866l7PGnzW8g1sZsY2VG3kq9ykOtBxgfNB4fpLxE5YnL8eoM45ovV22Lv5z8D/8Nf+vVHdWkx6ezn059zEndo6bIvcNp3wC7yWlZEPVBl7Y+QJ7G/cyPWo6D8x+gMyoTI9uV/lOTWcNz+14jo9LPibaP5pbsm/h4pSLMWgHbdEcNofTwVdlX/Fi3ouUtJawIG4BP5/9c1JCU9y6HeXYDrce5uncp1lbsZbxQeO5Y8YdnDPxnCHXtofK5rCxqmQVL+96marOKs6ZeA735dxHXGCcW7czVp02CbyXUzr58OCHPLf9ORrNjVyVdhX3zLoHk940Kts/HTmlk5XFK/mf7f+Dw+ngumnXcWPmjR7/m9ucNt4tfpcX816k29bNTzJ+ws1ZN7v9hKF8x+a08df8v/LyrpcxaA3cNP0mfpD+A4//zc12M3/b+zde3/M6Esnt2bdz7dRrh9eE5kNOuwTeq8PawQt5L/BW4VvEBcbx6IJHmRc7b1RjOB2UtZXxyMZH2F67nYVxC/nVvF+REJQwqjE0mZt4JvcZPjz4IamhqTy28DEyIjNGNYbTQVFTEQ9veJiipiLOSzyPB+Y8QKS/e7vHnUhNZw2Pb3mcNeVrmB45nccWPkZyaPKoxjCaTtsE3mtH7Q4e2fgIpW2lXDPlGu7NuRc/rZ9XYjmVSCn51/5/8eTWJ9Fr9Px8zs+5JOUSr7ZFr6tYx6ObHqWhu4EV01dw0/Sb3H5JfzpySid/zf8rL+x8gRC/EB6e9zBnTzzba/FIKVl9aDWPb32cbls398y6hx+k/+CUvA9y2idwcF1+/XHHH/lH4T+YFDaJp854SrWXjkCrpZVHNz7Kl2VfMj92Pr9b9DuiTdHeDguAdms7T2x9gg8PfsiM6Bk8sfiJ06a91BNqO2v55fpfsqVmC+dMPIdfz/81IX7D6xLnbg3dDfxm42/4puIbFscv5rGFjxHhH+HtsNxKJfB+vq34loc3PEynrZMH5zzIZZMuOyXP2p6UV5fHfWvvo9HcyF0z7uJH0340Jnv7fFzyMY9tfgwNGn678LcsnejegRSng3UV63ho/UNYHBYenPMg/5X6X2PueJFS8nbR2zyT+wzBfsE8ufjJU6qnikrgR2jobuChdQ+xqXoTF6dczK/m/Qp/nb+3wxrzpJT8veDvPLf9OWIDY3nqzKeYFjHN22EdV3l7OT9f+3PyG/O5duq13DPrHvSaYYwROM3YnXZeynuJV/e8SlpYGk+f+TSJIYneDuu4ipuKuf/b+yltK+X27Nu5IfOGMVmxOFkqgfdjczipaunmcGM77x74K9/Wv02wJoF07e3YLZG0m+1Y7A5sdonN6UQAeq0GvVaDv0FLsFFHsFFPqMnAuGA/xgUbiQkxMjHCxLggI5pjDAv3dR3WDh7e8DBfln3J2RPO5rGFjxFkCPJ2WMdlsTuoaO7mYEMLb+9/kdzmVYRrJ5OmuRWLOYh2sw2L3Ynd4SprjRDoNAKDToNRryXYqCfYX0e4ycC4YCPRwX7EhfozMdxEVJDfmKuJuktDdwO/+PYXbK3ZyuWTLueBOQ+MuE+3p5ltDsqbuthf38gb+5+moG0t0bpsUvgpZouRdrMN6xFlrddqMGhFz3GtJ9hfT0SAgehgI+OC/YgN8ScxwkR4gMGrZX1aJnCnU1La1MWeylaKa9oorulgf107Fc3dOJzf7bc2YB+m+HcQwkmU+ceM083CqNei1wp0Wg1IV9K3OZx02xy0ddtpM9to6rTSZR04RNdPp2FihInJ44KYEhNEWkww0xNCGBc8tr/8J3Kw5SB3r7mbivYK7p51Nz+a+qMxlbwcTklJfYerrGvb2VfTzr7aDqpau+n/FdcF7cI/7n0EBmLMPyVKn45Rp0XXr6ytPWXdZXXQbrbT1m2jsdOC2TZwCLrJoCUxIoC0mCBXeccGMT0+hIhA3745vrt+N/d8cw+tllYenvcwl6Re4u2QBrA5nOyv7SC/t6xr29lf20FNW/+5WCT60C0YYz5C4wwh1nILkfok/HSao8raanfSbXXQZrbR2m2jsdOK1T6wrIP8dCRFBTB5XBBpPWWdGR9CqGl0uqqeFgm8tdvGjrJmth9uZkdZM3sqW2k3u+a70GoEyZGuAkiKDGBChImJ4SbiQv2JCvKjyVLLPd/cQ0FjATdn3cwtWbcM6dKrw2Knts1MVUs3pY1dlNW1UlNaQ2V1Iy1NbeidDsxaPYHBgSRNjGbqlAnkJEeQGR+CUe8bfVe/KP2CX63/FUadkWfOfIacmIHfIyklztZWHO3tOLu6keZu0OrQ+BvR+PujDQ9HY3TvCayp08r20mZyS5vYWdpCflVr38nUoNWQEh3I5HGBJEYEMDHCxIRwEzEhRqKC/KjoONx3Mrpv9n1cM+WaE56MpJS0W+zUtZmpaO6mrKmLsppWasuqqKhuor2lA11PWYeGBZOc2FPWSRFMiwtGr/WNy/j39r3H41seJ9oUzXNLnmNK+JQBv5dS4mhpwdnejrPb/F1Zm/xdZR0Rgcbg3qRW12Ymt7SZ7aWu47qgqg1LT4L102mYNC6QydFBJEYGMCHcxPhwE3GhRiID/Shsyueeb+6hzdLGrxf8mmXJy064PSklrd02avod1xU1zVSX1lBZ00RnWydapwOL1kBEZAjJSTFkpCUwKzGc9NhgtB64AvdIAhdCnA/8EdACr0kpnzje8u5O4G1mG1tKmthc0simg40U1rQhpStZp8cGkZUQyvSEEDLiQ0iNDsRPd/yEaXFY+N3m3/HvA//mjIQzeGLxE8dsInCazZgLCzEXFmIpLMRScghbZSX2ujrXXBPHYNXoqPMPpT4ggq7xSQRkTCV5/iyyFmRiNIytdlmH08GLeS/y6p5XmR45nWfOfIbwZhvmgkLMhQVYivdhqyjHWlmF7Oo67rq0kZHo4+LwS0rCODUdv/R0jFOnoQ0c2rD6pk4rm0sa+/7tq+0AQK8VTIsLIXt8KJnxIUxPCCEpMsBVwzqOdms7D61/iG/Kv2F58nIemf/IMZsIHB2dWAoLMBcWYS4sxFpSgq2qCnt9/XG3YdbqqfMPoy4wAsuEZIKnZ5C6cCYZs6dhOMF3cbRZHVb+39b/x3v73mNh3EKeWPwE/lXNrnIuKsJcXIytvAJbdTXSfPSsg32EQBcVhT4+HkNyEsapUzGmT8WYPgWN/9DuMdW1mdl48LuyPtzo+m756TR9x3RmQgiZ8SFMjAg4YcJs6G7gvrX3sb12Oz9M/yE/y/nZMbuVOtraMO/d6yrrokKshw5jq6rC0dh43G106fyoNYXREBiJLTGF0KwMJi+ew9TsSW5J6G5P4EIILbAPOAeoALYBV0spC471mZEmcJvDyc6yFtbtr2f9gQZ2lbfglGDQaZg1IYx5yRHMTgwja3woAX7D6/crpeTd4nd5YusTJAQl8MclfyQ5NBlnZydd27fTtW0bXdty6d67F2w2ADQhIfhNSsUQn4A+Ph5ddDSagAA0Jn+EXo/TbEaazTja2mkvLafhwGEs5eUEVZWh65kRr80QQPXENHQzZpF87llMWZCNxouT67RZ23hg7S84tGsdP+yazuKGSMw7d+Kob3AtoNXil5yEfuJEDPHx6GJj0YaEovH3R+NvRDocOLu7cXZ14WhowFZVha2yEsv+A98lPq0WY3o6ptmzMc2ZjWn2nL6EbrY5yD3czLoD9Ww40MDeKtfJ2WTQkpMYztykcGYnhjM9YfhXMk7p5M+7/8xLeS8xLWIazy15jpiAGBxtbXRt3eoq69ztmIuKwOGq3WsjIvBLTUUfH48+Pg5dVBQaU09Z63Q4u804u7twtrXTeriMhoNl2MtKCaotR9tzYm8yBlOXlI7fzFlMuvB7pMxI92pZ13fVc+/X99CyN4/rLbOZVWPCvGMHjpYW1wJ6PX4pKRgmTEAfF4c+LhZNUPDAsu7qxtnVib2+HltlFbaKCiz79+Nobu5bh39Ghqus587BNGtW31VZp8XOlkONrNvfwIYDDX0n5yCjjrlJ4cxNiiAnMYxpcSEYdMP7O9mcNp7JfYY3C99kbsxcnjrzKcKMYdibmujasqWvrC3799Pb5qYbNw6/lBT08XHo4+LQRkaiMZnQ+PsjtNqesu7G0dJC86EymktKsZeVElxfhaZnHfWmMBpTpmHKySH7+8sZlzi8rqyeSODzgUellOf1vH4QQEr5/471meEm8LWvvMPBzXl84jeevKAEnFodWeNDWZQayYKUSGZMCHV7c8T2yi28+NbdTDrQzYWN4zEUHQa73fVFnDYNU84s/LOzMU6dii42dljtwdJmo7FgH8XfbqV1yzaCivcQ2e5KkC3GYOrTsghYOJ9py5cSkzTerft3LLbqag5/9SFbV71G0v4Owjpd7+tiYzHNmoVp1kyMGZn4TZ6Exm94bb32+nrMBQV05eXRtW0b5l27kTYbaLW0Jk9h17g0VukT2BsUj1avY+aEMFdZp0YyPSHE7c0Raw58zt9XPkTmYcm5DbFoiw+B04nw88N/+nT8c2Zhys7GLz0dXVTUsMraabFQt7uAfWu30rEtl9D9+YR1tQDQGBBG45RsghcvYvrypUTEe74vvZQSW3k5+z7/J7tW/4NJJRaCul25QD9xAqZZOZhmzsCYkYFfcjJiGM0iUkrsNTWYCwro3rmTzm3bMOfvBYcDqTfQnDKVHVGTWGVIYF9gLAa9jjlJ4X3H9dQ49zdHfJj/Tz547/fklBv4Xl0E7D8MgMZkwj87G/+cWfhnZWFMT0cXHj6sbTi7u6nesYf9326lKzeXiIN7CTZ30PLo08y/6qJhrdMTCfwK4Hwp5Y09r68F5kopbz9iuRXACoAJEybMKi0tPeltfXTrgySv+Q8aKXEajfjnzCZk3hxMOTkYp01D6Efe9OC0WjHn59OVu52u7bl0b8vF2dWFFHBwHOjnzmLhxbcQMHPmkC8Fh6Nq32EKPvqSrk0bGbd/N8EWVwatDo+jc9oMohbOJeO8MwmMHflBLqXEXlXlurLI3U7X1q1YDx8GoC1AYJo3j/FLLsQ0bz6GhPgRb+9IdW1mNhxsYFNBNXWbt5J0eC8z6vaR0lqFBokzIJCAuXMJ7ilrv7Q0hHbkJ2qn2Uz3rt105W6jKzeX7h07kRYLDg0ciBOELFzMnItuxD87y+3tub2klJTt2UfRx19h3byJ2JJ8AmxmnAiqoiZgycxm3KL5TDtvMaaI4SWSI7dnKyujKzeXrm25dG3bhq3S9ZCUlmAtoYvOIO6s8zHNnYd+nPtPIBXNXWw40MDmgkpaNm1lUrmrrBPbawFwhoQSNH8eQXPn4D9rFn6pqQg3XJU4Ojrpzsv7rqx37QabDZsW9idoiT3zXGZcdJ0rj+g8M1rX6XRSsqOAuLQkTEHDm4nTEwn8v4Hzjkjgc6SUdxzrM8OtgVvtTrRdHXRu2ULnxo10bd6C9dAhVxx+fvilpWFMT8c4JQ19QgL6uDh042Jcl7X9vgTS4cDZ2YmtugZbZSW2inLMxcWuds39B1y1QMCQkoJpzmwC5s9HOyuLxwuf58ODH/K98d/j8cWPj3g61KFy2B0Ursvl8OdrENu3El95AD+HK8bm4EgsiamETM9gYnY6pvHxrsu8sLABX0QppSs5NTVhq6zEWlGJtaSkr/2+t21PExREXWoEH4eX0ZWdyoNXv0xsYKxb96exw8KWQ9/ds9hf57pUDjXpWZgSyRmTI1k0KYpx0kzXpk10bNxI16bNfYlGYzLhN2UKxvR0/NImu5ox4uLQx8QgjMYBNWNpt+Nob8deU4O1ogJbeQWW4iLMBYVYSkpcTSJC4Dd5MgHz5mKaPx9n1hQe2vEY31Z8y2WTLuOXc385ahNi2SxW8r/eTMWX36DbmUt8TQl6pwMnguawcdiTUwmbPo3x06fgn5CAPi4WbWjogBOalBLZ3Y29sdH1/a6sxHKwBHNhAeaCQpytra6/Y1gY5SlBrA6vQDM7i4eueJEw/zC37k9Nq5kth1zlvKmkkdKeduyoID8WpbrKemFqJGFdbXRu2th3XNvr6lwxBgdjnDIFY/oU/Canuco6NgbduHEIv4HdN6XNhqOjo6/pxlpehqWoGHNBgatCIqWruW7qVALmzsE0fz7d6RP52ZaH2Fm3k59k/IS7Ztw1pifE8ukmlMHYGxroyt1O986dfcnI2d5+dJxGI8LPD2k2Iy2Wo36vDQtzJf+p6a5LqFmz0IUN/DJLKXmz8E2ezn2aicETeW7JcySFJLllP05GV6eZnV9tpurbjTiKComoKSWuowENR5ShTtfXvujs6jr6pqpOh19qqmu/p01DZk3hN7V/ZU3lWi5OuZhH5j8y4nlibA4nxTXt7KlsZXtPD4JDDa6rid527PnJESyeFMnU2ODj9p231dQMKGtLUZFrv/oTwlXWBgOyuxtptR61Hl1UFH5T0zGmu8raNHMm2uDgAcs4pZMX817kld2vkBmZybNnPUtMQMyI/hbD0dbaQd7nG6levxm5r4jo2lJiu5qOXlCnc10ROp2uv8kRx7MwGPCbPLmvrC2ZKfyi9Hl21O/kuqnXcfesu0c8T4zF7qCwup3dFS2unkGHm6lscT1Kz9WOHcH8FFdZT4oOPGYTlJQSW0WFq6zz8jAXFWIp3nf0TVONxpXE9XpXWfdUvAb8WWJje26gpuM/IxtTdjaagIEVL5vDxhNbn+Ddfe+yIG4BTy5+klBj6Ij+Fp7iiQSuw3UT82ygEtdNzGuklHuP9RlPdiPsbW+zVVdjq6zCXlvjurHSk7iF0Q+NvwlNQAD6mHF9tTdtRMSQ2zS3Vm/lvrX3YXPaeHzR4yyZsMQj+zJUrd02cgsqKMorprLoEF3lFfibOzE4bYQIBxEBBgLDQgiLDCE8JpLoSYlEpCZiiIvra9Ps3797qF3q+rM7nFS3mjnU0Mn+ug721bRTVNtOYXVbX1/aMJOeWRPDyUkM67vxOJJ2bOl0YquqxlZVib26GlttHdLcjdNsQVosaPyNCJMJbUAAupjY7244hg29lvll6Zf8cv0vMeqMPH3m08yOmT3seN2hqdPKtvxS9uUVU7XvMObySvytXfg5bIRoJeGBBoLCQgiLCCEiLoroyUmEpSa5rk56rsh21e/i3jX30mYdepe6/mwOJ5XN3Rxq7GR/bTtFNe0U17j6YdscrjwSFeTH7MQwZk0MZ05i+IjbsaXDga2iwnXVXF2Nva4Op7kbabYgbTZXV9WAADSmAHSxMRgSEtAnJKANGvoAs/5dJ//nrP8hPSJ92PF6iqe6EV4IPIerG+FfpJS/P97yY2Uk5khUd1Rzzzf3sLdxLyumr+DWrFvHzKWXxe6guKad3RWt7K5ooajn4Oo/ACXQT0dCmKvvuzTtYq/tVfTCyH/FP0B6WBZ6rQadRoNWI7A7nNicEqvdSYfZRpvZTmu3jbp2C7VtZmrbzFQ2d2PvNygqPMBA2rggpsUFM318KNPjQ5gYYRpTg36GqqSlhLvW3EV5ezn3zrqXa6deO2b2o9vqoKC6jT0VLeyubKWwup2D9R0DBqAEG3UkhJmICjZgMW6g0Pp/BOoiuDzhl6SETO4r596y7h3U0m52DVRr6bJR32Ghrs1MdavrX/8BcNFBfqTFBDEtLoSsnq598aH+Y+ZvdDL6D156ZP4jXJxysbdDGuC0GMgzWiwOC49veZz397/P3Ni5PLn4yTE7+5nDKSlv6qKkoYPSxi7XYKPmdoqtb9FmWIOzewJdFT9A2oc2s5zJoCUqyI9xQa5h5ePDTSRGmJgQHsCkcYFE+vgoxCN1WDv45fpf8nX515wz8Rx+s+A3Y3b6ALvDyeHGLkrqO1wDjZq6KGtuocj2VzoNW3F0Tqar4ipwDu0BG4F+OqKD/IjumS5ifJiJiREmEiMDSI0KJCzg1HpgRkN3A/evvZ/c2lwun3Q5D859cMxMOa0SuAd8sP8Dfr/l94QYQnjqzKeYOW6mt0M6oeqOau779j521+/mh+k/5J6Z9+CUWtrMNjrMduxOic3hxOkEnVag17rmiwgy6gky6nxmRKE7SSl5Y+8bPLfjOeID43n2rGdJC0/zdlgnVNJSws/W/oyDLQe5NftWfpr5U6x2aDfb6LAMVtYaDFoNwf46Av10JxwMdSqyO+28sPMFXs9/nfTwdJ458xnGB49OF97jUQncQ4qbirn3m3up6Kjg5qyb+WnmT8fswwO+KP2CX2/8NU7p5LcLfsu5ied6OySfsr12O/evvZ9WSyv35tx70vcLRkv/h2yY9CaeWPwE8+Pmezssn7K2fC0PrX8Ip3Tyq3m/4qLk4fXfdheVwD2ow9rB77f8nlUlq5gZPZMnFj/h9i54I9Fl6+IP2/7Av/b/i8zITJ5c/OSYqFX4osbuRh7Z+AjfVnzLGQln8NjCxwg3jryftru0Wlr5zabf8EXpF8yLncfjix4nyhTl7bB8UlVHFQ+se4CddTtZlryMX879JYGGQK/EohL4KPjo4Ef8fsvvEQjun30/l6Ze6vUa2vba7Tyy4RHK28u5PuN6bptxm5oLe4SklLxV9BbP5j5LoCGQX837FedMPMfbYbG2fC2/3fRbmsxN3DHzDn487cenxFzY3mR32nl196u8vPtlYgNivfZMXZXAR0l5ezmPbHiE3Npc5sfO59EFj3rlUV5dti7+uOOPvF30NnGBcTy28DGvd4U71RQ3FfPwhocpbCrk3Inn8tDch7xyM7vV0sqTW5/ko5KPSA1N5XeLfjfmH7Lha3bW7eThDQ9T2lbKFZOv4N5Z947qzWyVwEeRUzp5t/hdnt3+LAA/zfwpP5r2o1G5oy2l5LPDn/HM9meo6azhminXcNfMuzDph9bzQDk5NqeNN/a+wUt5L+Gv8+e27Nu4Mu3KUbkP4nA6eP/A+/xpx59ot7ZzQ+YNrJi+YtRGj55uzHYzL+W9xBsFbxBpjOTuWXdzUfJFo3KVoxK4F1R2VPLUtqf4quwr4gPj+VnOz1g6YanHmlX2NuzlD9v+wI66HUwJn8KDcx70iZ4xp4KSlhIe3/I4W2q2kBKSwv2z72dB3AKPlfW2mm08te0pCpsKmRk9kwfnPnjU3N2KZ+Q35PO7zb9jb+NepkdO5/7Z95Mdne3RbaoE7kWbqzfz5NYnOdBygElhk7gx40bOTTzXbbW07bXbeXXPq2yo3ECYXxh3zryTS1MvHTMDjE4XUkq+Lv+ap7c9TUVHBdOjpnNjxo2cOf5Mt9TSpJRsqNrAq7tfZUfdDmICYvjZrJ9xXuJ5Xr/XcrpxSicfHfyIP+74I/Xd9cyLnccNmTcwN2auR8pCJXAvszvtfHLoE17f8zolrSUkBCZwcerFLEtaNqweIS3mFj47/BkflnzI7vrdhBvDuXbqtXw/7ftjdqDJ6cLqsPLB/g/4696/UtlRSUpICpekXsIFSRcMa16V+q56Pjn0CR8e/JB9zfsYZxrHTzJ+wuWTLh/zz6k81XXZulhZvJK/F/ydhu4GpkZM5ZKUSzg38Vwi/SPdth2VwMcIp3SypnwNbxa+SW5NLhJJRkQGs2NnkxWVRWZkJpH+kQNqbFJK2qxtFDYVsqtuFzvrd7Klegt2p53U0FSumHwFl026DH+d56a5VU6e3Wnn08Of8lbhW+xp2INAMCN6BjkxOUyPnM60yGlEGAfOxeOUTlosLRQ0FpBXl8eOuh1sr92OUzqZFjGNK9OuZHnycvRa1ZNoLLE4LHx48EPeLnqb/c370QgNc2LmMGvcLDIjM8mIzCDEb2ijnQejEvgYVNNZw+pDq/my7EsKGguw9zydRyM0BBuCCTIE0W3vpsXS0vc7gOSQZBbHL2Z5ynImh01Wl88+oKytjNWHVvNV2VcUNxfjlK45S7RCS7AhmEBDIJ22TlotrTik6+k/GqFhcthkFscvZlnKMpJDkr25C8oQ7W/ez+pDq/m67GtKWkuQPbOFPr/k+WFPgKcS+BhncVgobCykoLGARnMjrZZW2qxtmHQmQv1CCTOGkRqaSmZUJsGG4BOvUBmzumxdFDQWUNRURJO5iTZrG23WNgL0AYT5hRFmDGNy2GQyIzNV7yEf125tp6CxgD0Ne1ievJxxAeOGtR6VwBVFUXzUsRK4GqalKIrio1QCVxRF8VEqgSuKovgolcAVRVF8lErgiqIoPkolcEVRFB+lEriiKIqPUglcURTFR43qQB4hRD1QOsyPRwINbgzHF6h9Pj2ofT49jGSfJ0opj3o23qgm8JEQQuQONhLpVKb2+fSg9vn04Il9Vk0oiqIoPkolcEVRFB/lSwn8FW8H4AVqn08Pap9PD27fZ59pA1cURVEG8qUauKIoitKPSuCKoig+yicSuBDifCFEsRDigBDiAW/H42lCiL8IIeqEEPnejmU0CCHGCyHWCCEKhRB7hRB3eTsmTxNCGIUQW4UQu3r2+Tfejmm0CCG0QoidQohV3o5lNAghDgsh9ggh8oQQbn2izZhvAxdCaIF9wDlABbANuFpKWeDVwDxICHEG0AH8XUqZ4e14PE0IEQvESil3CCGCgO3Af53iZSyAACllhxBCD6wH7pJSbvZyaB4nhLgXyAGCpZTLvB2PpwkhDgM5Ukq3D1zyhRr4HOCAlLJESmkF3gEu8XJMHiWl/BZo8nYco0VKWS2l3NHz/3agEIj3blSeJV06el7qe/6N7dqUGwghEoCLgNe8HcupwBcSeDxQ3u91Baf4wX06E0IkAjOALV4OxeN6mhLygDrgCynlKb/PwHPAzwGnl+MYTRL4XAixXQixwp0r9oUELgZ575SvqZyOhBCBwL+Au6WUbd6Ox9OklA4pZTaQAMwRQpzSzWVCiGVAnZRyu7djGWULpZQzgQuA23qaSN3CFxJ4BTC+3+sEoMpLsSge0tMO/C/gTSnl+96OZzRJKVuAb4DzvRuJxy0ELu5pE34H+J4Q4h/eDcnzpJRVPT/rgA9wNQu7hS8k8G3AJCFEkhDCAFwFfOjlmBQ36rmh9zpQKKV81tvxjAYhRJQQIrTn//7AUqDIq0F5mJTyQSllgpQyEddx/LWU8odeDsujhBABPTfmEUIEAOcCbutdNuYTuJTSDtwOfIbr5ta7Usq93o3Ks4QQbwObgDQhRIUQ4gZvx+RhC4FrcdXI8nr+XejtoDwsFlgjhNiNq5LyhZTytOhWd5oZB6wXQuwCtgIfSyk/ddfKx3w3QkVRFGVwY74GriiKogxOJXBFURQfpRK4oiiKj1IJXFEUxUepBK4oiuKjVAJXTntCiFAhxK3ejkNRTpZK4IoCoYBK4IrPUQlcUeAJIKVnANFT3g5GUYZKDeRRTns9MyCuOh3mXldOLaoGriiK4qNUAlcURfFRKoErCrQDQd4OQlFOlkrgymlPStkIbBBC5KubmIovUTcxFUVRfJSqgSuKovgolcAVRVF8lErgiqIoPkolcEVRFB+lEriiKIqPUglcURTFR6kEriiK4qP+PwddmBmKxYMEAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYwAAAERCAYAAABowZDXAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAAAjnElEQVR4nO3de7iVc/7/8edLhSQ0aZLSVCT6OtvCZMa5ciyUKcM4DUKGn8M4G2QI4zBGmCSHmd+vnGfSNMI4DeNQOUQSOW+hEqZMhvL+/fFZfe22Xa19Wvfaa70e17Wuvdda932v9xrX7Fef+3NSRGBmZrYyq2RdgJmZNQ0ODDMzy4sDw8zM8uLAMDOzvDgwzMwsLw4MMzPLS8kHhqQxkuZIerWBrrdE0ku5x/hanNdG0v2Spkl6XtJmyzluN0kvSHpV0u2Smq/sfEkn546fLumUKq9vKekZSa9IekDSWvX46kuvOUzSLEkhad36Xs/Mmo6SDwzgNqBfA15vUURslXvsX9MBkt6t4eVzgJciYgvgF8DvazhvFeB2YHBEbAa8Bxy+ovNzwXEM0AvYEthXUvfcOaOBsyJic+B+4Iw6fN/qngb2yNVmZmWk5AMjIp4E5ld9TdKGkh6UNFXSPyVtUoBSegL/yNX0OtBFUvtqx7QF/hsRb+SePwwctJLzNwWejYj/RMRi4AnggNw5PYAnq19LUjNJV0qanGuxHJfvl4iIFyPi3XyPN7PSUfKBsRyjgJMiYlvgdOCGWpy7uqQpkp6VNKAW570MHAggqRfwI6BTtWPmAS0kVeSeDwQ2WMn5rwI/ldRW0hrA3lXOeRVY2goaVOX1o4EvImI7YDvgGElda/FdzKwMNc+6gEKTtCbwY+BuSUtfXi333oHAxTWc9mFE9M393jkiZkvqBjwq6ZWIeEvSSKB37pj1Jb2U+/3uiPgtMAL4fe71V4AXgcVVPyQiQtJg4BpJqwEPVTmmxvMjYoaky0ktiIWkYFl6zlHAdZIuAMYDX+de7wNsIWlg7vnaQHdJ7+fOr8mRETF5Oe+ZWRlQOawlJakLMCEiNst1/M6MiA4NcN3bcte9p9rr70ZElxWcJ+AdYIuI+PcKjusD/DIiDs73fEmXApURcUO11zcG/hwRvSTdC4yKiEl5fM3l1fYuUBER8+p6DTNrWsrullTuD+w7kgZB+uMract8zs2NVFraGlmX1KJ4Lc9z15G0au7pL4EnawoLST/M/VwNOBO4aWXnVzmnM+m21dhqr68CnLf0WsAk4HhJLXLvbyypVT7fw8zKV8kHhqSxwDNAD0mVko4Gfg4cLellYDrQP8/LbQpMyZ33GDAiIvIKjNy50yW9DuwFnFylxomS1s89PUPSDGAa8EBEPLqy84F7Jb0GPACcGBGf5V4fIukN4HVgNnBr7vXRpKB7ITfc+I/keXtS0q8kVZL6T6ZJGp3n9zezJq4sbkmZmVn9lXwLw8zMGkbJjpJad911o0uXLlmXYWbWpEydOnVeRLSr6b2SDYwuXbowZcqUrMswM2tSJC13FQffkjIzs7w4MMzMLC8ODDMzy4sDw8zM8uLAMDOzvDgwzMwsLw4MMzPLS1EEhlayjWpugcDrcluDTpO0TaFrXLQIRo+GUaPg2Wfhyy8LXYGZWbaKZeLebcD1wB3LeX8voHvusT1wY+5no/vqqxQSI0bARx9997oE3bvD1lvDNtvAtttCRQWsvXYhqjIzK7yiCIyIeDK3Z8Xy9AfuiLRS4rO5pb47RMRHKzinTj79FI4/Hj75BD7+GD78MLUmdtkFxo6Fzp3h5ZfT46WXUmvjzju/O3/jjWHHHWHXXdOjc+eGrtDMLBtFERh56Ah8UOV5Ze61ZQJD0rHAsQCd6/iXetVVUxistx5suSX07QsHHJD++C/VtSsMGPDd808/halT4fnn0+OBB+D22787tndv2Gkn6NULunVbeSvkm2/SNefN++7x6aewYEF6LFwI33773fGtW0PbtunRrRv8z/+4pWNmDa+pBIZqeO1767JHxCjSft1UVFTUad321q1h5szandO2LfTpkx6Q/pi/+io89hj885/w8MPw5z9/d3ybNtCxI6yxBrRsCc2aweefp8f8+enniqyxBjTP/ZeLSAFSfZX6Tp1SUO29N/TrBz/8Ye2+k5lZdU0lMCqBDao870TaEKgorbIKbLFFepx8cvpj/tZb6RbWO++kx+zZqX9k0aL0c731YNNNU5isuy60a5d+Ln384Aep1dCqVbp+VUuWpJCZNw/efDOF1SuvwKOPpttlEuy8M5x4IvTvDy1aZPG/ipk1dU0lMMYDwySNI3V2f9EY/ReNRYKNNkqPxtCs2Xe3pHr0gH33Ta9/+226vTZhAowZA4MGpZbNr34FJ52UWjdmZvkqlmG139tGVdJQSUNzh0wE3gZmATcDJ2RUapOyyippFNf558OsWTB+PPTsCWeemTrnb701tU7MzPJRslu0VlRUhPfDqNkTT8AZZ8DkybD55nDNNbD77llXZWbFQNLUiKio6b2iaGFYYe28Mzz3XOrfWLgQ9tgj9W288UbWlZlZMXNglCkJDj4YXnsNLr88jejq2ROOOw4qK7OuzsyKkQOjzK2+Ovz612l01QknpH6NjTaC009Po67MzJZyYBgA7dvDddel21KDB6d+jW7d4MIL4d//zro6MysGDgxbRpcucNttaR5Hnz5w0UVptvpvfwtffJF1dWaWJQeG1ahnT7jnnjSSascd4bzzUphceOHKZ6KbWWlyYNgKVVSkiX9Tp6b1tC66KN2quuyyNMLKzMqHA8Pyss02cN998OKLaY2qc85JwXHppW5xmJULB4bVylZbpdV4n3km7QFy7rmwwQZpIqCH45qVNgeG1ckOO8Df/55aHPvtB1dfnTrHDz88dZibWenx0iDWIN55B669Nm1j+5//pNtWRx6ZFjxca60Vn7tkSdqsavbs9Pjww9RaqaxMG1nNnw+ffZZW9W3RIu1ZsvbaacfDjTdOy5v07ZtW8jWz+lnR0iAODGtQ8+en0BgzJu0r0rJl+oO+4Yapz6NZs7SD4YIFKRBmzUph8803y16neXNYf/00P6Rt27S8e8uW6bivv04bSr35Jrz3Xlo+vmVL2GefNIekf//v9gsxs9pxYFjBRaT1qsaOTcuPvPVW+uP+7bdpA6g110xLrW+0UQqTLl1SQCx9tG///X0/avLVV+lz7r47DQP+5JN0rTPOSC0cL+FuVjsODCsKixenEMgnCOpiyZLUIT9iRAqR9u3h4ovh6KNTy8bMVs6r1VpRaN688cICUigMGJBGcD3+eOrjOO64NCT4scca73PNyoUDw0rO0i1pn3wS7rorLWmy225w0EGpv8TM6saBYSVLSqO0Xn8dLrkEHnww7Zt+7rlpJJeZ1Y4Dw0re6qunkHjjjRQgl14KW26ZWiBmlj8HhpWNjh3hT39K/RnffptuW510Uhria2Yr58CwsrPLLjBtGpx8MowcmTrHx4xJIWJmy+fAsLLUqlWamf7cc2keyNFHp5V5n3oq68rMipcDw8radtulkBg7Nm1J+5OfwM9/npYnMbNlOTCs7ElpSZEZM+D88+Hee6FHj9Q5/tVXWVdnVjwcGGY5rVqlmeEzZsCee6aRVT17pgAp0QURzGrFgWFWTdeucP/98MgjKUQGDky7DU6dmnVlZtlyYJgtx+67p/0+brghLaBYUQGHHQbvv591ZWbZcGCYrUDz5nD88Wkp9bPOSqvibrwxnH56WmLdrJwURWBI6idppqRZks6q4f21JT0g6WVJ0yUdmUWdVr7WXhsuuyzNFh8yJO0wuOGGqWN84cKsqzMrjMwDQ1IzYCSwF9ATGCKpZ7XDTgRei4gtgV2AqyStWtBCzYDOneHWW9PEv5/+NHWMd+uWAmTRoqyrM2tcmQcG0AuYFRFvR8TXwDigf7VjAmgtScCawHxgcWHLNPvOZpvB+PFpKfUtt4TTTkvB8fvfOzisdBVDYHQEPqjyvDL3WlXXA5sCs4FXgJMj4nsLOUg6VtIUSVPmzp3bWPWa/a8ddoCHH077b2yyCZxySgqOa65JW9GalZJiCAzV8Fr1Ue99gZeA9YGtgOslrfW9kyJGRURFRFS0a9euoes0W66dd06LGj7+eJq7ceqpaavYSy9N+3GYlYJiCIxKYIMqzzuRWhJVHQncF8ks4B1gkwLVZ5a3nXeGf/wjLTey3Xapj6NzZzjnHJgzJ+vqzOqnGAJjMtBdUtdcR/ZgYHy1Y94HdgeQ1B7oAbxd0CrNaqF3b5g4MU3269Mn7TP+ox/BsGHw7rtZV2dWN5kHRkQsBoYBk4AZwF0RMV3SUElDc4cNB34s6RXgH8CZETEvm4rN8rfNNmnuxowZcMghMGoUbLRRWuDw5ZeXf96SJamVMnw43HJLmkD49deFq9usJooSXSSnoqIipkyZknUZZsuorEzLqv/xj2n+xvbbw1FHwQEHwHvvpRbJs8/C3/4G1cdttGiR9vI48EDo3x86dMjiG1ipkzQ1IipqfM+BYVZ4n32WNm269VaYPn3Z99q0gX79Uij07Zv6Pl58ESZPTkN533wzrbD7q1/BVVdBs2bZfAcrTQ4MsyIVAVOmpIUON9oItt02LX6omsYO5o5/7TW4/nq46SbYZ5+0l0fr1oWt20qXA8OsBN14Y9qTfLPNYMIE6NQp64qsFKwoMDLv9Dazujn++NTX8fbbsPfenihojc+BYdaE9e0L99yT+kGOOsobPVnjcmCYNXFL53ncdRdccUXW1Vgpc2CYlYDTT0/7kp99Njz4YNbVWKlyYJiVAAlGj4bNN0+TAr0roDUGB4ZZiWjVKvVnfPMNHHywZ4Zbw3NgmJWQ7t3ThMDnnoMzz8y6Gis1DgyzEjNwYJoFfu21cO+9WVdjpcSBYVaCrrwSevWCo4/26rjWcBwYZiVo1VVh3Lg0L+OQQ1K/hll9OTDMSlTXrmk59WeegQsvzLoaKwUODLMS9rOfpRngl10Gjz6adTXW1DkwzErcdddBjx5pfsbHH2ddjTVlDgyzEteqVVo25IsvUn/GkiVZV2RNlQPDrAxsvjnccAM89pj7M6zuHBhmZeKII+DII+GSS7zelNWNA8OsjFx/fWptHHoofPhh1tVYU+PAMCsja6wBd98NX32VOsHdn2G14cAwKzM9eqT+jCeegOHDs67GmhIHhlkZ+sUv0mP4cHj88ayrsabCgWFWpkaOTKvbHnooLFyYdTXWFDgwzMrUmmvCrbemzu/f/S7raqwpcGCYlbEdd4RBg9LqtrNnZ12NFTsHhlmZGzECFi+G887LuhIrdg4MszLXrRucdBLcdhu89FLW1VgxK4rAkNRP0kxJsySdtZxjdpH0kqTpkp4odI1mpezcc6FNGzjttLSHhllNMg8MSc2AkcBeQE9giKSe1Y5ZB7gB2D8i/gcYVOg6zUpZmzZpiO2jj8LVV2ddjRWrzAMD6AXMioi3I+JrYBzQv9oxhwD3RcT7ABExp8A1mpW844+Hgw6CM8/03AyrWTEERkfggyrPK3OvVbUx0EbS45KmSvpFTReSdKykKZKmzJ07t5HKNStNUhpm2707HHwwVFZmXZEVm2IIDNXwWvW7qM2BbYF9gL7A+ZI2/t5JEaMioiIiKtq1a9fwlZqVuNat4f77YdEiGDjQe4HbslYYGJIKsTRZJbBBleedgOojwiuBByPiy4iYBzwJbFmA2szKziabwJgx8NxzcPnlWVdjxWRlLYya/vXf0CYD3SV1lbQqMBgYX+2YvwI/kdRc0hrA9sCMAtRmVpYGDYLBg+Hii2H69KyrsWKxssBo9AF2EbEYGAZMIoXAXRExXdJQSUNzx8wAHgSmAc8DoyPi1cauzaycXXcdrL122nRp8eKsq7FioFjBoGtJSyKiWQHraTAVFRUxZcqUrMswa9LGjYMhQ9LSIaefnnU1VgiSpkZERU3v1brTW9Kekm6WtFXu+bH1rM/MitTPfgb9+8P558O0aVlXY1mryyipE4AzgEMl7QZs1aAVmVnRkOCmm+AHP4D99oNPPsm6IstSXQJjbkR8HhGnA32A7Rq4JjMrIuutB+PHw9y5cMABaXtXK091CYy/Lf0lIs4C7mi4csysGG27LdxxBzzzDBxzjNebKle1DoyI+Gu1539ouHLMrFgNHAiXXAJ//jNcemnW1VgW6jXTW9IjkjyBzqxMnHNO2tL1vPPgrruyrsYKrb5Lg/wauEbSrZI6NERBZla8JBg9Gnr3hsMPT7PBrXzUKzAi4oWI2A2YADwo6TeSWjZMaWZWjFZbLa031aFDGnL73ntZV2SFUu/FByUJmAncCJwEvCnpsPpe18yKV7t2MGEC/Pe/0LcvzJuXdUVWCPXtw3gK+BC4hrQk+RHALkAvSaPqW5yZFa+ePdNw2/feg332gYULs67IGlvzep4/FJge319f5CRJXhzQrMT95Cdw551pfsbAgfDAA9CiRdZVWWOpbx/GqzWExVL71OfaZtY07L8/jBoFkyaljvAlhdgUwTJR3xbGckXE2411bTMrLkcfDZ9+mrZ3XXttuOGGNKLKSkuDBIakPSPi4Ya4lpk1Tb/+NcyfnzZdatPGk/tKUUO1MC4HHBhmZe6yy+Czz9LPddZJIWKlo9FuSZlZ+ZHS7ah//zvdnmrVCk48MeuqrKHUOTAk3UrakU9AZ0ljlr4XEUc1QG1m1gQ1a5YWKly0CIYNS6FxxBFZV2UNoT4tjNuq/L4TcHv9SjGzUtGiRRpuu//+qUO8Zcu0GZM1bXUOjIh4YunvkhZUfW5mtnQJkb32gp//HFZdNc3XsKar3kuD5HzdQNcxsxKyxhppCZHttkstjL/9beXnWPFqkMCIiB0a4jpmVnpat4a//x023xwOOgge9njKJquhWhhmZsu1zjrw0EPQo0da4fYJ38BukhwYZlYQbdum1kXXrmmxwqefzroiqy0HhpkVzA9/CI88AuuvnzrDn38+64qsNmodGJL2lHSzpK1yz49t8KrMrGR16ACPPpr21OjbF158MeuKLF91aWGcAJwBHCppN2CrBq3IzEpep04pNNZaC/bcE155JeuKLB91CYy5EfF5RJwO9AG2a+CazKwM/OhHKTRWWw322ANefz3rimxl6hIY/zuSOiLOAu6obxGS+kmaKWmWpLNWcNx2kpZIGljfzzSz7G24YQoNCXbbDd56K+uKbEVqHRgR8delv0u6Fri+PgVIagaMBPYCegJDJPVcznGXA5Pq83lmVlx69Egd4f/9L+y+O3zwQdYV2fLUd5TUQmC8pFYAkvpIqu1guV7ArIh4OyK+BsYB/Ws47iTgXmBOfQo2s+Kz2WZpnsZnn6XbU598knVFVpP6btF6HjAWeFzSU8BpwHJvKS1HR6Dqvykqc6/9L0kdgQOAm1Z0IUnHSpoiacrcuXNrWYaZZWnbbdPSIZWV0KdPCg8rLvUKDEm7A8cAXwLtgF9FxD9re5kaXqu+T/i1wJkRscLdgiNiVERURERFu3btalmGmWVtp53gL39JHeD77ANffpl1RVZVfW9JnQucHxG7AAOBO3NDbWujEtigyvNOwOxqx1QA4yS9m/ucGyQNqEvBZlbc9twTxo6F556DAw9MfRtWHOp7S2q3iHgq9/srpI7rS2p5mclAd0ldJa0KDAbGV/ucrhHRJSK6APcAJ0TEX+pTu5kVrwMPhJtvTv0ahx0GS1Z4b8EKZWX7YSg3hHVSRCxY2cUi4qPcbaq8RcRiScNIo5+aAWMiYrqkobn3V9hvYWal6aij4PPP4bTTYN11YeTINPzWsrPCwIiIVSR1Ag6WtBawAHgoIt5fwTmLaltEREwEJlZ7rcagiIgjant9M2uaTj01jZi64gpYbz244IKsKypvK91xLyIqgVsAcsNn+0oaBHwD/CsipjRuiWZWzkaMSKHxm9+kxQuHDs26ovJVqy1aI+JL4D4ASasAP5Z0Cmmk00zgHxHhLiozazBS6s+YNw9OOCGFxoEHZl1VearPnt7fAk/lHkjqDhwpqQPwLnBPPv0eZmYr06IF3HVXmgl+yCEwaRLsvHPWVZWfBtkPQ1I3YD9gEPBjoDWpA9vMrEEs3R+8a9e0a59XuC28OrcwJAkYDuwOvA/8FTgoIj5vmNLMzJbVtm1qXey4I/TrB089lQLECqPOLYyICOBroE9E/Cwi/p/DwswaW+fOKTQWLUqT/D76KOuKykd9b0kNdz+FmRXaZpvBxInw8cdp177587OuqDzUd6Z39TWfzMwKYocd4K9/hZkz07pTCxdmXVHpa5BObzOzLOy+O9x5Jzz/PBx0kNedamwODDNr0gYMgNGj07pTv/iF151qTHUeJWVmViyOPDL1Y5x+OrRpAzfe6HWnGoMDw8xKwmmnpdngI0akobZnnpl1RaXHgWFmJePSS+Hdd+Hss2HTTWH//bOuqLS4D8PMSoYEY8ZARUVaQmTatKwrKi0ODDMrKS1bpm1e11kH9tsP5szJuqLS4cAws5Kz/vppjsacOTBoEHzzTdYVlQYHhpmVpG23hVtugSefhFNOybqa0uBObzMrWYccAi++CL/7HWy9Nfzyl1lX1LS5hWFmJW3ECOjTJ22+9MwzWVfTtDkwzKykNWsGY8fCBhuk5UO8um3dOTDMrOT94Adw//3wxRepE/zrr7OuqGlyYJhZWdhii9QJ/vTTcOqpWVfTNLnT28zKxuDBMHkyXH11mtx3xBFZV9S0uIVhZmXl8sth111h6FCYMiXrapoWB4aZlZXmzdMeGu3bwwEHeCZ4bTgwzKzstGuXOsHnzYODD/ZM8Hw5MMysLG2zDdx8MzzxhDvB81UUgSGpn6SZkmZJOquG938uaVru8S9JW2ZRp5mVlkMPhf/zf+D669OufbZimQeGpGbASGAvoCcwRFLPaoe9A+wcEVsAw4FRha3SzErVFVd8NxP8qaeyrqa4ZR4YQC9gVkS8HRFfA+OA/lUPiIh/RcRnuafPAp0KXKOZlajmzWHcOOjSJc0Ef//9rCsqXsUQGB2BD6o8r8y9tjxHA3+v6Q1Jx0qaImnK3LlzG7BEMytlbdqk5dC/+irt0rdwYdYVFadiCIyatmqPGg+UdiUFRo279UbEqIioiIiKdu3aNWCJZlbqNt0U7roLXn0VhgyBJUuyrqj4FENgVAIbVHneCZhd/SBJWwCjgf4R8WmBajOzMtK3L/zhDzBhApxxRtbVFJ9iWBpkMtBdUlfgQ2AwcEjVAyR1Bu4DDouINwpfopmVi+OPh5kz4ZprYKONUme4JZkHRkQsljQMmAQ0A8ZExHRJQ3Pv3wRcALQFbpAEsDgiKrKq2cxK21VXwdtvw0knpe1eBwzIuqLioIgauwuavIqKipjihWLMrI6+/BJ23x1efhkeeQR69866osKQNHV5/yAvhj4MM7Oi06oVPPBA2nhpv/1gxoysK8qeA8PMbDnatYMHH4RVV02T+957L+uKsuXAMDNbgW7dUmgsWAB77AEff5x1RdlxYJiZrcRWW8HEiTB7dmppzJ+fdUXZcGCYmeXhxz+Gv/wlDbnda6+0P3i5cWCYmeVpzz3TbPAXXkihsWBB1hUVlgPDzKwW+vdPO/Y9/3z5hYYDw8yslg48MK1w++yzsPfe5RMaDgwzszoYOBDGjoVnnkkd4Z9/nnVFjc+BYWZWR4MGwT33wNSpaVb4pyW+LKoDw8ysHgYMSKOnpk+HXXeFTz7JuqLG48AwM6unvfdOS6K/9Rb85Celu2ufA8PMrAHssQc89BDMmQM77QRvvpl1RQ3PgWFm1kB694bHHoNFi1JL45VXsq6oYTkwzMwa0NZbwz//Cc2bwy67QCntsuDAMDNrYJtsAk8+CWutlUZPPf101hU1DAeGmVkj6NYttTTWWy/N03jkkawrqj8HhplZI+nUKbU0NtwQ9t03jaRqyhwYZmaNqH371BG++eZwwAFw991ZV1R3Dgwzs0bWtm26JbX99jB4MNx+e9YV1Y0Dw8ysANZeGyZNSp3gRxwBI0dmXVHtOTDMzAqkVSsYPz4tkT5sGIwYkXVFtePAMDMroNVXT/0YhxwCZ58NF1wAEVlXlZ/mWRdgZlZuWrSAO+6Ali1h+HD45hu49FKQsq5sxRwYZmYZaNYMRo1KM8JHjEihceWVxR0aDgwzs4yssgrceGNqcVx1VQqNa68t3tBwYJiZZUiC665LLY1rr4XFi+EPf0hhUmwcGGZmGZPg6qtTS+PKK1No3Hhj8YVGUZQjqZ+kmZJmSTqrhvcl6brc+9MkbZNFnWZmjUWCyy9PI6dGjYJjjoFvv826qmVl3sKQ1AwYCewJVAKTJY2PiNeqHLYX0D332B64MffTzKxkSPDb36YO8UsuSYExenR6XgwyDwygFzArIt4GkDQO6A9UDYz+wB0REcCzktaR1CEiPip8uWZmjUdKQ22bNYOLLkpzNG65pThCoxgCoyPwQZXnlXy/9VDTMR2BZQJD0rHAsQCdO3du8ELNzArlwgtTH8ZvfpNaGrfemn1oFENg1DSArPq8x3yOISJGAaMAKioqmsjcSTOzml1wQQqJ885LoXH77dmGRjEERiWwQZXnnYDZdTjGzKzknHtuuk117rnp9tTtt6chuFkohsCYDHSX1BX4EBgMHFLtmPHAsFz/xvbAF+6/MLNycc456fbU2Wen8MiqpZF5YETEYknDgElAM2BMREyXNDT3/k3ARGBvYBbwH+DIrOo1M8vCWWelFsY558Aaa8Af/1j4GeGZBwZAREwkhULV126q8nsAJxa6LjOzYnL22fDll2nobatWabJfIUOjKALDzMzyM3w4LFyYlhFZa6009LZQHBhmZk2IBNdcAwsWwMUXw/rrw3HHFeazHRhmZk2MlPowPvkETjgB2reHAQMa/3OLYi0pMzOrnebN4c47YbvtYMgQePrpxv9MB4aZWRPVqhVMmACdO8P++8MbbzTu5zkwzMyasHXXhYkT0zyNffaBefMa77McGGZmTdyGG8L48fDBB9C/P3z1VeN8jgPDzKwE7Lgj/OlP8K9/weGHN85eGh4lZWZWIgYNgiuuSJP7GmNCnwPDzKyEnHFG413bt6TMzCwvDgwzM8uLA8PMzPLiwDAzs7w4MMzMLC8ODDMzy4sDw8zM8uLAMDOzvCjtflp6JM0F3qvHJdYFGnEZr6JUbt+53L4v+DuXi/p85x9FRLua3ijZwKgvSVMioiLrOgqp3L5zuX1f8HcuF431nX1LyszM8uLAMDOzvDgwlm9U1gVkoNy+c7l9X/B3LheN8p3dh2FmZnlxC8PMzPLiwDAzs7w4MKqR1E/STEmzJJ2VdT2NTdIYSXMkvZp1LYUiaQNJj0maIWm6pJOzrqmxSVpd0vOSXs5954uyrqkQJDWT9KKkCVnXUiiS3pX0iqSXJE1p0Gu7D+M7kpoBbwB7ApXAZGBIRLyWaWGNSNJPgYXAHRGxWdb1FIKkDkCHiHhBUmtgKjCgxP87C2gVEQsltQCeAk6OiGczLq1RSToVqADWioh9s66nECS9C1RERINPVnQLY1m9gFkR8XZEfA2MA/pnXFOjiogngflZ11FIEfFRRLyQ+30BMAPomG1VjSuShbmnLXKPkv7XoqROwD7A6KxrKRUOjGV1BD6o8rySEv9DUu4kdQG2Bp7LuJRGl7s98xIwB3g4Ikr9O18L/Br4NuM6Ci2AhyRNlXRsQ17YgbEs1fBaSf8rrJxJWhO4FzglIv6ddT2NLSKWRMRWQCegl6SSvQUpaV9gTkRMzbqWDPSOiG2AvYATc7edG4QDY1mVwAZVnncCZmdUizWi3H38e4H/GxH3ZV1PIUXE58DjQL9sK2lUvYH9c/fzxwG7SfpztiUVRkTMzv2cA9xPutXeIBwYy5oMdJfUVdKqwGBgfMY1WQPLdQDfAsyIiKuzrqcQJLWTtE7u95bAHsDrmRbViCLi7IjoFBFdSP8/fjQiDs24rEYnqVVuIAeSWgF9gAYbAenAqCIiFgPDgEmkjtC7ImJ6tlU1LkljgWeAHpIqJR2ddU0F0Bs4jPSvzpdyj72zLqqRdQAekzSN9A+jhyOibIaalpH2wFOSXgaeB/4WEQ821MU9rNbMzPLiFoaZmeXFgWFmZnlxYJiZWV4cGGZmlhcHhpmZ5cWBYVZAktaRdELWdZjVhQPDrLDWARwY1iQ5MMwKawSwYW6y4JVZF2NWG564Z1ZAudVxJ5TL3iNWWtzCMDOzvDgwzMwsLw4Ms8JaALTOugizunBgmBVQRHwKPC3pVXd6W1PjTm8zM8uLWxhmZpYXB4aZmeXFgWFmZnlxYJiZWV4cGGZmlhcHhpmZ5cWBYWZmefn/YDOo/riYVKsAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"index1_b = create_model_index1_b()\n",
"\n",
"# Specify integrator options\n",
"int_ops = {'print_stats':True,\"abstol\":1E-8,\"reltol\":1E-6}\n",
"\n",
"# Solve DAEs\n",
"sim = Simulator(index1_b, package='casadi')\n",
"tsim, profiles = sim.simulate(numpoints=100, integrator='idas',integrator_options=int_ops)\n",
"\n",
"# Plot solution\n",
"plot_results(sim, tsim, profiles)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.4.4 Take Away Messages](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.4-Take-Away-Messages)",
"section": "2.4.4 Take Away Messages"
}
},
"source": [
"## 2.4.4 Take Away Messages\n",
"1. Differential algebriac equations (DAEs) are really powerful modeling tools.\n",
"2. Integrating DAEs requires special care. Make sure your model is index 1.\n",
"3. Often there are many ways to reformulate the DAE model. But the numeric integrator only enforces error tolerances on the equations that are explicitly modeled. If an algebriac constraint must be satified to a specific tolerance, include it in the DAE model (as long as it is not high index!)."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.4.4 Take Away Messages](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.4-Take-Away-Messages)",
"section": "2.4.4 Take Away Messages"
}
},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"id": "8618538f",
"metadata": {},
"source": [
"\n",
"< [2.3 Logical Modeling and Generalized Disjunctive Programs](https://ndcbe.github.io/CBE60499/02.03-GDP.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [2.5 Numeric Integration for DAEs](https://ndcbe.github.io/CBE60499/02.05-Numeric-Integration.html) >
"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 1,
"link": "[2.4 Dynamic Optimization: Differential Algebraic Equations (DAEs)](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4-Dynamic-Optimization:-Differential-Algebraic-Equations-(DAEs))",
"section": "2.4 Dynamic Optimization: Differential Algebraic Equations (DAEs)"
}
},
"source": [
"# 2.4 Dynamic Optimization: Differential Algebraic Equations (DAEs)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"nbpages": {
"level": 1,
"link": "[2.4 Dynamic Optimization: Differential Algebraic Equations (DAEs)](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4-Dynamic-Optimization:-Differential-Algebraic-Equations-(DAEs))",
"section": "2.4 Dynamic Optimization: Differential Algebraic Equations (DAEs)"
}
},
"outputs": [],
"source": [
"import sys\n",
"if \"google.colab\" in sys.modules:\n",
" !wget \"https://raw.githubusercontent.com/ndcbe/CBE60499/main/notebooks/helper.py\"\n",
" import helper\n",
" !pip install casadi\n",
" helper.install_idaes()\n",
" #helper.install_ipopt()"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.4.1 Dynamic Optimization Overview](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.1-Dynamic-Optimization-Overview)",
"section": "2.4.1 Dynamic Optimization Overview"
}
},
"source": [
"## 2.4.1 Dynamic Optimization Overview"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.4.1 Dynamic Optimization Overview](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.1-Dynamic-Optimization-Overview)",
"section": "2.4.1 Dynamic Optimization Overview"
}
},
"source": [
"**Chapter 8: Dynamic Optimization Introduction** (Biegler, 2010)\n",
"-\tChemical engineering examples\n",
"-\tClassical (variational) approaches including Hamiltonian and Euler-Lagrange equations\n",
"-\tDAE background (this notebook)\n",
"\n",
"**Chapter 9: Sequential Methods** (Biegler, 2010)\n",
"-\tDAE integration (this notebook, next notebook)\n",
"-\tSingle Shooting\n",
"-\tMultiple Shooting\n",
"\n",
"**Chapter 10: Simultaneous Methods** (Biegler, 2010)\n",
"-\tGauss quadrature (next notebook)\n",
"-\tOrthogonal collocation on finite elements (next notebook, next next notebook)\n",
"-\tExamples, benchmarks, and large-scale extensions"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.4.1 Dynamic Optimization Overview](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.1-Dynamic-Optimization-Overview)",
"section": "2.4.1 Dynamic Optimization Overview"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.4.1 Dynamic Optimization Overview](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.1-Dynamic-Optimization-Overview)",
"section": "2.4.1 Dynamic Optimization Overview"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.4.2 DAE Index Reduction](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.2-DAE-Index-Reduction)",
"section": "2.4.2 DAE Index Reduction"
}
},
"source": [
"## 2.4.2 DAE Index Reduction"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.4.2 DAE Index Reduction](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.2-DAE-Index-Reduction)",
"section": "2.4.2 DAE Index Reduction"
}
},
"source": [
"Excerpts from Chapter 8 of Biegler (2010)."
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.4.2 DAE Index Reduction](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.2-DAE-Index-Reduction)",
"section": "2.4.2 DAE Index Reduction"
}
},
"source": [
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.4.2 DAE Index Reduction](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.2-DAE-Index-Reduction)",
"section": "2.4.2 DAE Index Reduction"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.4.3 DAE Formulations for Simple Pendulum Example](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3-DAE-Formulations-for-Simple-Pendulum-Example)",
"section": "2.4.3 DAE Formulations for Simple Pendulum Example"
}
},
"source": [
"## 2.4.3 DAE Formulations for Simple Pendulum Example\n",
"\n",
"Pyomo.dae documentation:\n",
"* https://pyomo.readthedocs.io/en/latest/modeling_extensions/dae.html\n",
"\n",
"Pendulum example:\n",
"* http://apmonitor.com/wiki/index.php/Apps/PendulumMotion\n",
"* https://www.lehigh.edu/~wes1/apci/11may00.pdf\n",
"\n",
"CasADi (need to integrate DAEs):\n",
"* https://web.casadi.org/get/\n",
"* For local installation: ```pip install casadi```. Warning: installing `CasADi` with `conda` will install an \"okay\" version of Ipopt. If you really want to install `CasADi` with `conda`, you'll likely need to add `import idaes` to your notebook to load the \"good\" version of Ipopt (Linux and Windows users).\n",
"\n",
"DAE simulation example:\n",
"* https://github.com/Pyomo/pyomo/blob/master/examples/dae/simulator_dae_example.py"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.4.3 DAE Formulations for Simple Pendulum Example](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3-DAE-Formulations-for-Simple-Pendulum-Example)",
"section": "2.4.3 DAE Formulations for Simple Pendulum Example"
}
},
"outputs": [],
"source": [
"## Load libraries\n",
"from pyomo.environ import *\n",
"from pyomo.dae import *\n",
"from pyomo.dae.simulator import Simulator\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"\n",
"## Define function for plotting results\n",
"def plot_results(sim, tsim, profiles):\n",
"\n",
" '''\n",
" time = list(m.t)\n",
" x = [value(m.x[t]) for t in m.t]\n",
" y = [value(m.y[t]) for t in m.t]\n",
"\n",
" plt.plot(time, x, '-b', label='x')\n",
" plt.plot(time, y, '-r', label='y')\n",
" plt.xlabel('Time')\n",
" plt.ylabel('Position')\n",
" plt.legend(loc='best')\n",
" plt.show()\n",
" '''\n",
" \n",
" plt.figure(1)\n",
" varorder = sim.get_variable_order()\n",
" algorder = sim.get_variable_order(vartype='algebraic')\n",
"\n",
" # Create empty dictionary\n",
" results = {}\n",
" \n",
" for idx1, v in enumerate(varorder):\n",
" i = idx1\n",
" v_ = str(v)\n",
" results[v_] = profiles[:, i]\n",
" plt.plot(tsim, results[v_], label=v)\n",
"\n",
" for idx2, v in enumerate(algorder):\n",
" i = len(varorder) + idx2\n",
" v_ = str(v)\n",
" results[v_] = profiles[:, i]\n",
" plt.plot(tsim, results[v_], label=v)\n",
" \n",
" plt.xlabel('t')\n",
" plt.legend(loc='best')\n",
" \n",
" plt.show()\n",
" \n",
" plt.figure(2)\n",
" x_ = results['x[{t}]']\n",
" y_ = results['y[{t}]']\n",
" plt.plot(tsim, np.sqrt(x_**2 + y_**2), '-b', label='length')\n",
" plt.xlabel('t')\n",
" plt.ylabel('$\\sqrt{x^2 + y^2}$')\n",
" plt.show()\n",
" \n",
" #return results"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.1 Formulation 1: Index-3 DAE](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.1-Formulation-1:-Index-3-DAE)",
"section": "2.4.3.1 Formulation 1: Index-3 DAE"
}
},
"source": [
"### 2.4.3.1 Formulation 1: Index-3 DAE\n",
"\n",
"Consider the following model:\n",
"\n",
"$$\\begin{align}\n",
"\\frac{d x}{dt} &= u \\\\\n",
"\\frac{d y}{dt} &= v \\\\\n",
"\\frac{d u}{dt} &= -T x \\\\\n",
"\\frac{d v}{dt} &= g - Ty \\\\\n",
"& x^2 + y^2 = 1\n",
"\\end{align}$$\n",
"\n",
"This assumes mass and length of unity."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.1 Formulation 1: Index-3 DAE](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.1-Formulation-1:-Index-3-DAE)",
"section": "2.4.3.1 Formulation 1: Index-3 DAE"
}
},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"At t = 0 and h = 1.06624e-14, the corrector convergence failed repeatedly or with |h| = hmin.\n"
]
},
{
"ename": "RuntimeError",
"evalue": ".../casadi/interfaces/sundials/idas_interface.cpp:591: IDASolve returned \"IDA_CONV_FAIL\". Consult IDAS documentation.",
"output_type": "error",
"traceback": [
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
"\u001b[0;31mRuntimeError\u001b[0m Traceback (most recent call last)",
"\u001b[0;32m\u001b[0m in \u001b[0;36m\u001b[0;34m\u001b[0m\n\u001b[1;32m 60\u001b[0m \u001b[0;31m# Solve DAEs\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 61\u001b[0m \u001b[0msim\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mSimulator\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mindex3\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mpackage\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;34m'casadi'\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m---> 62\u001b[0;31m \u001b[0mtsim\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mprofiles\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0msim\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0msimulate\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mnumpoints\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;36m100\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mintegrator\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;34m'idas'\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0mintegrator_options\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mint_ops\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 63\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 64\u001b[0m \u001b[0;31m# Plot solution\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/pyomo/dae/simulator.py\u001b[0m in \u001b[0;36msimulate\u001b[0;34m(self, numpoints, tstep, integrator, varying_inputs, initcon, integrator_options)\u001b[0m\n\u001b[1;32m 905\u001b[0m \u001b[0;32melse\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 906\u001b[0m \u001b[0mtsim\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mprofile\u001b[0m \u001b[0;34m=\u001b[0m\u001b[0;31m \u001b[0m\u001b[0;31m\\\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 907\u001b[0;31m self._simulate_with_casadi_no_inputs(initcon, tsim,\n\u001b[0m\u001b[1;32m 908\u001b[0m \u001b[0mintegrator\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 909\u001b[0m integrator_options)\n",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/pyomo/dae/simulator.py\u001b[0m in \u001b[0;36m_simulate_with_casadi_no_inputs\u001b[0;34m(self, initcon, tsim, integrator, integrator_options)\u001b[0m\n\u001b[1;32m 967\u001b[0m \u001b[0mintegrator_options\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;34m'output_t0'\u001b[0m\u001b[0;34m]\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0;32mTrue\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 968\u001b[0m \u001b[0mF\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mcasadi\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mintegrator\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m'F'\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mintegrator\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mdae\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mintegrator_options\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 969\u001b[0;31m \u001b[0msol\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mF\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mx0\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0minitcon\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 970\u001b[0m \u001b[0mprofile\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0msol\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;34m'xf'\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mfull\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mT\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 971\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/casadi/casadi.py\u001b[0m in \u001b[0;36m__call__\u001b[0;34m(self, *args, **kwargs)\u001b[0m\n\u001b[1;32m 13451\u001b[0m \u001b[0;32melse\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 13452\u001b[0m \u001b[0;31m# Named inputs -> return dictionary\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m> 13453\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mcall\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mkwargs\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 13454\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 13455\u001b[0m \u001b[0;32mdef\u001b[0m \u001b[0mbuffer\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/casadi/casadi.py\u001b[0m in \u001b[0;36mcall\u001b[0;34m(self, *args)\u001b[0m\n\u001b[1;32m 12322\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 12323\u001b[0m \"\"\"\n\u001b[0;32m> 12324\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0m_casadi\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mFunction_call\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m*\u001b[0m\u001b[0margs\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 12325\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 12326\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;31mRuntimeError\u001b[0m: .../casadi/interfaces/sundials/idas_interface.cpp:591: IDASolve returned \"IDA_CONV_FAIL\". Consult IDAS documentation."
]
}
],
"source": [
"def create_model_index3():\n",
"\n",
" m = ConcreteModel()\n",
"\n",
" # Declare time\n",
" m.t = ContinuousSet(bounds=(0.0, 1))\n",
"\n",
" # Declare parameter - acceleration due to gravity\n",
" m.g = Param(initialize=9.81) # m/s^2\n",
"\n",
" # Declare variables indexed over time\n",
" m.x = Var(m.t) # horizontal position\n",
" m.y = Var(m.t) # vertical position\n",
" m.u = Var(m.t) # horizontal velocity\n",
" m.v = Var(m.t) # vertical velocity\n",
" m.T = Var(m.t) # tension\n",
"\n",
" # Declare derivative variables\n",
" m.dx = DerivativeVar(m.x) # with respect to t is implied\n",
" m.dy = DerivativeVar(m.y)\n",
" m.du = DerivativeVar(m.u)\n",
" m.dv = DerivativeVar(m.v)\n",
"\n",
" # Declare differential equations\n",
" def _dx_eqn(m, t):\n",
" return m.dx[t] == m.u[t]\n",
" m.dx_eqn = Constraint(m.t, rule=_dx_eqn)\n",
"\n",
" def _dy_eqn(m, t):\n",
" return m.dy[t] == m.v[t]\n",
" m.dy_eqn = Constraint(m.t, rule=_dy_eqn)\n",
"\n",
" def _du_eqn(m, t):\n",
" return m.du[t] == -m.T[t]*m.x[t]\n",
" m.du_eqn = Constraint(m.t, rule=_du_eqn)\n",
"\n",
" def _dv_eqn(m, t):\n",
" return m.dv[t] == m.g -m.T[t]*m.y[t]\n",
" m.dv_eqn = Constraint(m.t, rule=_dv_eqn)\n",
"\n",
" # Declare algebraic equation\n",
" def _alg_eqn(m, t):\n",
" return m.x[t]**2 + m.y[t]**2 == 1\n",
" m.alg_eqn = Constraint(m.t, rule=_alg_eqn)\n",
"\n",
" # Specify initial conditions\n",
" m.x[0] = 0\n",
" m.y[0] = 1\n",
" m.u[0] = 1\n",
" m.v[0] = 0\n",
" m.T[0] = 1 + m.g\n",
" \n",
" return m\n",
"\n",
"index3 = create_model_index3()\n",
"\n",
"# Specify integrator options\n",
"int_ops = {'print_stats':True,\"abstol\":1E-8,\"reltol\":1E-6}\n",
"\n",
"# Solve DAEs\n",
"sim = Simulator(index3, package='casadi')\n",
"tsim, profiles = sim.simulate(numpoints=100, integrator='idas',integrator_options=int_ops)\n",
"\n",
"# Plot solution\n",
"plot_results(sim, tsim, profiles)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.1 Formulation 1: Index-3 DAE](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.1-Formulation-1:-Index-3-DAE)",
"section": "2.4.3.1 Formulation 1: Index-3 DAE"
}
},
"source": [
"**Warning**: If you run this notebook in Colab, you may get the following runtime error and your kernel may crash:\n",
"\n",
"\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.1 Formulation 1: Index-3 DAE](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.1-Formulation-1:-Index-3-DAE)",
"section": "2.4.3.1 Formulation 1: Index-3 DAE"
}
},
"source": [
"Why did the `IDAS` integrator in `SUNDIALS` fail? It is only meant for index 0 or 1 DAEs! Integrating high index DAEs is really hard!"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.2 Formulation 2: Pure ODE Model](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.2-Formulation-2:-Pure-ODE-Model)",
"section": "2.4.3.2 Formulation 2: Pure ODE Model"
}
},
"source": [
"### 2.4.3.2 Formulation 2: Pure ODE Model\n",
"\n",
"$$\\begin{align}\n",
"\\frac{d x}{dt} &= u \\\\\n",
"\\frac{d y}{dt} &= v \\\\\n",
"\\frac{d u}{dt} &= -T x \\\\\n",
"\\frac{d v}{dt} &= g - Ty \\\\\n",
"\\frac{d T}{dt} &= 4 T (x u + y v) + 3 g v\n",
"\\end{align}$$\n"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.2 Formulation 2: Pure ODE Model](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.2-Formulation-2:-Pure-ODE-Model)",
"section": "2.4.3.2 Formulation 2: Pure ODE Model"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"FORWARD INTEGRATION:\n",
"Number of steps taken by SUNDIALS: 167\n",
"Number of calls to the user’s f function: 242\n",
"Number of calls made to the linear solver setup function: 31\n",
"Number of error test failures: 7\n",
"Method order used on the last internal step: 5\n",
"Method order to be used on the next internal step: 5\n",
"Actual value of initial step size: 7.90569e-07\n",
"Step size taken on the last internal step: 0.00246466\n",
"Step size to be attempted on the next internal step: 0.00492933\n",
"Current internal time reached: 0.00492933\n",
"Number of nonlinear iterations performed: 240\n",
"Number of nonlinear convergence failures: 0\n",
"\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXAAAAEGCAYAAAB8Ys7jAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAABLaUlEQVR4nO3deXxU1d348c+ZyUwm+x6yAVkJIQkJEPZFcUfB1qV1rz5q0Vq1arVVW62tT62t1Me91r3+6oJrqyju7LIFCIRsLIHs+77NZJbz+2OSmECAkMxkMnDerxevMJM7935vztzvPffcc84VUkoURVEU96NxdQCKoijK8KgEriiK4qZUAlcURXFTKoEriqK4KZXAFUVR3JTHaG4sNDRUxsbGjuYmFUVR3N6OHTvqpZRhR74/qgk8NjaW7Ozs0dykoiiK2xNClAz2vmpCURRFcVMqgSuKorgplcAVRVHclErgiqIobkolcEVRFDelEriiKIqbUglcURTFTY1qP/DhOpxbT1N1J+ET/Qib4Ife4BZhD5ux3UxdaRuNVR34BnkSHuuPb5AnQghXh+Y0VrONhsp26krbMJusPWXtj85T6+rQnKqjxUR9eTvN1Z34hxoYFxeAt7/e1WE5lcVspbGyg/rydqxmG+Pi/AmJ9kXrcerWJ01dFjy9HJ+33CITluxtYO+6CvsLAeET/JhzSQLjJwe7NjAHkjZJ0bZqsj87TEtd11G/9/LXk7ogiunnTzylklpzbSfff3iAktwGbLaBc9MLARHxAcy9NJHIhAAXReh4NquNvA2V7PiihI5m01G/9w81kLoomoyzxp9SSa2hsp3NHx2kNL8ReURZa3UaoicFMe/SBEKifV0UoeNZuq3kfFPGzi9LWHZnpsO/x2I0H+iQlZUlhzsSs7O1m7rSNmpLWincXEVrvZGEaWHMuywR/1AvB0c6umoOtbLhvX3UHGolfKIfCdPDCZvoR0iUL20NRmpLWikvbKI4pw7fIE/mXZZI4oxwt66RdxstZH9+mN3flqH10JC6MIpxcQGETfBD56mltqSVmkP2sm5vMjF5TgRzLknAJ8DT1aGPSGl+AxvfP0BTVQdRSYHEZ4YROt6XoAgfWmo7qT7USmleA+WFTQRFeLPoyknEuHlFxdhuZtunxezdUIneoCV1YRThE/0JibHXumsOtVJ9qIWizdWYuixMXRzDrKVx6J1QYx0tUkr2b69h88cHaW8yEZ8ZxrzLEggI8x7W+oQQO6SUWUe97y4JvD+L2UrO12Xs+OIwCMEFy9OYmBoy8gBdYPe3ZWz8YD9efnrm/jiByXMiEJrBE3PlgWY2rNxHfVk7SVnhnH3DFLesobXWd/HJMzm01HadMDF3Gy3sWF1Czjel6Dy1XHTbVCITA0c3YAeQUrLlv8Xs/KIE/zAv5l+WSFxG6DFPwof31LPhvX201huZelYMCy5POub3YixrqGxn1bO76WjpJm1hFDOXxeHlO3gTkbHdzJb/HiRvYyW+gZ4svT3DLWvjVquNdW8VUfB9FaHjfVlweRLRyUEjWucplcB7tTUa+fwfe2is6OCs61NInh3hsHU7m5SSLf85yM4vS4mfFsbZP0sZUo3DZpPs/KKErZ8UMz4liAtuSXerewL15e18+mwOVrONJbemEz1paF/spuoOPv9HLu2NRs5fnkZseqiTI3Ucq9XG2v9XSOGWaqYsjGLRTyeh1Z34xGsxW9n80UH2rCknaeY4zr4+xa1O2JUHmvn8hT1odRqW/jKDsAl+Q/pc9aEWvngxF4vZxtLbM4iId5/mM7PJypcv76VkbwNZF8Yya2mcQ068p2QCB/vNgdX/2EPFvmYW/CSJjLPHO3T9zmCz2ljTc0CnLopm0ZWT0JxkIRd8X8mafxcRNt6Xpbdn4OU39m98Ve5v5rMX9qA3aFl6RwYhUSdXu+ps7WbVc7tpKG93mxO2udvKly/ZD+hZy+LIujD2pJq+pJTs/LKELf8pZkJqMBcsT3eLeyDFOXV89WoefsEGlt2RcdLNnK31XXzydA4dLSaW3JLOBDe4wja2m/n02RzqSts44+pkUhdGO2zdx0rg7nM6PwZPLw+W3pFBfGYYG9/fT96GCleHdFxSSta+XUThlmpmLYvjjKtOPnkDpMyLYsktaTRUdvDJMzl0Gy1OiNZx6krb+PS53fgE6Ln0vhknnbwBvP31/PjuaUQmBfDN6/kc2FHrhEgdx2a18dXLeynNa+DMa5KZeVHcSd+3EEIw44JYzrwmmbL8Rla/uAer1eakiB2jvLCRL1/eS0i0L5feN31Y96j8Q7249L4ZBIR789kLeygvanJCpI5j7ray6vndNFR0sOTWdIcm7+Nx+wQO4KHTcv7PU5mYFsK6d/ZxOLfe1SEd047VhynYVEXWhbHDOqD7i8sIY8kt6TRUdPDly3nYxuiB3drQxarndmPw8eBHd0/DL9gw7HXpvTxY+kv7ZfU3r+dTdbDFgZE6jpSS9Sv3czi3gUVXThrxAZ26MJrF102mrKCJtW8VMZpXziejoaKd1S/mEjjOm4vvzDhme/dQ9J6wA8K9Wf1iLo2VHQ6M1HFsNsnXr+ZRc7iVc2+aQlzGUdN2O80pkcABNFoN592cSki0D1++kkddaZurQzpK4ZYqtn5yiOTZEcxaFueQdU5MC+GMqyZRmtfAunf3jbkD29RpZtVze7CYbSy7PdMhvUg89FouvC0d3yBPPv/HHpprOx0QqWPt/LKEvPUVTD9/AmlnxDhknSnzosi6KJbC76vI/vywQ9bpSO1NJlY9txudp5alt2fg6a0b8ToNPjqW/nIqWp2GVc/tpqPl6G6XriSlZOP7+zm0u54FP0kiYVr4qG7/lEngAHqDvXZm8PFg1XO7aW8yujqkPhVFTax5s5CYyUEsvm6yQ7sApi6MZvoFE8nfUMmur0odtt6RslptrP7nXlpqO7nw1nSCo3wctm4vXz1Lb88ACaue242xw+ywdY/U/uwatvynmKSZ45jzowSHrnvW0jiSZ0ew7dNDFG2tdui6R8JssvLZC7sxdVq46PaMEV1lHck/1Iulv5xKV3s3n7+wB3O31WHrHqk9a8rJXVNO5jnjyThr9O+/nVIJHMCnp/uR2WTli5f2YjW7vlmhrdHIl6/sJSDciwtuSXdKT4I5F8eTmBXO5v8cpDSvweHrH47NHx2koqiJxddNHnE3qsEEjvPmwl+k09Zg5OvX8o4aCOQK9eXtfPdmAZEJAZz9sxSHd/0TQtj/npMCWfP/CsfElaaUkjX/LqS+vJ3zf55G2Pih9TY5GeET/TnvplRqS9tYN0aakCr2NbHpgwPEZYQy79JEl8RwyiVwgJAoX86+IYWaQ62sf2+fS2OxmK188U97l6glt6Y7ZTgtgNAIzrouhZAoX756NY/W+qNHc46mfduq2f1tGVMXxzB5TqTTthOZGMjCKyZRmtfI9lWHnLadoTB2mFn9z1z0Xh6cvzxtSF0Fh0ProeH8n6fh5afj8xf30NXe7ZTtDNXub8vYv72G2RfHMzHNeb1F4jLCmLU0jqKt1T+MzHaR9iYjX768l4AwL865YYrL+uif8BsmhHhNCFErhNjb771gIcTXQoj9PT8dX70aoYRp4X3NCvkbK10Sg5SS9e/uo7akjXNumEJQhOOaEAaj89Sy5NY0AD5/Mddll5r15e2s+X+FRCYGMO9y59dMUhdGMXleJNmfH+bQ7jqnb28w0ib55vV82huNXLA83ekjRr389Cy5NZ2uVjNfveK6G9jlRU18/9FB4jPDmHHBRKdvL2tJLLHpIWx8bz9VB5qdvr3BWM02vnhpL5Zue6XMlSNGh1JFeAO44Ij37ge+lVImAd/2vB5zZl8cz/gpwax7t4iaQ62jvv28DZV9PU7iM0fnznRAmDfn3pRKQ0U7a/9dOOqXmsYOM6tf3IOntwfn/zwNrdb5F3lCCM64chJhE/z45vV8mmtG/6bmtlWHKNnbwMKfJo3avC3hE/054+pJlBc2seU/xaOyzf7aGo189cpeAsO9OPv6lFGZ2kFoBOf8zxT8Qgx88dJel9zUXN8z7cXZN6QQHOncStmJnPDoklKuBxqPePtHwL96/v8v4MeODcsxNBrBeTem4hPgyep/5tLZOnqXmtXFLWxYuY8JqcHMXOqYHidDNTE1hNnL4tm3rYY935WP2nZtNsnXr+XR3mTiglucXwvtz0Ov5YJb0tBoNXz+Yu6o9osvzqkj+/PDTJ4XSeqi0en/2ytlXhRpi6LZ9XUp+7NrRm27RzYNjmYt1NNbx5Jb0+k2Wvjin3uxWkbv6iN/YyX5GyqZfv6EUe9xMpjhVo/GSSmrAHp+HnNPhBDLhRDZQojsurrRv7w1+NoL29Rh5suX947KIIiOFhOr/5mLb5An596YOqyBOiM144KJxGeGsenDA1SM0iCIbZ8WU5rXyMIrJrlk+LN/iBfn3ZxKc3UH371ZMCpXH03VHXzzRj7hE/0446pJLplgbMFPk4iID+C7NwtoqGh3+vaklKx/Z/SaBgcTEu3LWT9Lobq4hY3v7x+VbdYcamXdu0WMTwlitoN7Fw2X069vpZQvSSmzpJRZYWGj18G9v7Dxfpx57WQq9zfz/YcHnLotq8XGly/tpbvLwpJbp2LwGXlf2OEQGsHZ16cQGO7Fl6/spa3RuV0qi3Pq2LG6hJT5kaQujHLqto5nfEowcy9J5ODOOqd3qew2Wlj9Yi5aDw0X3JKOh841Q9zt209D7+XB5//Y4/QulXkbKin4fnSbBgeTlDWOaedOYO+6Cgq+d+59rs7Wbr54KRcff0/OuynNJZWywQw3gdcIISIBen6O7THNQPLsCKaeFcOe78rJ3+Scwu69aVl1sIWzrkshNMa1M6npvTxYcms6FrON1U5sVqgvb+urhS660jW10P4yzx1PYlY4W/5z0Gmjcm1WG1+/Zm9vP//mVIf2ex4OnwBPltySTnuTia9ecd6VZnlhY0/TYMioNw0OZs6P44mZHMS6t/dRXeycUbkWs5UvXsqlq93MklvTMfi6plI2mOEm8E+A63v+fz3wX8eE41zzLktkfEoQa98qckpf6R2rS8jfWMn0CyaSNHOcw9c/HEERPpx3Uyr15e1OaUJqazSy6tnd6A32k4WraqH9CdHTpTLGly9fyaO2xLE3sKWUbFi5n8N76ll4xdiZrzsiPsA+Z0pBk1NuYPcfJn/eTVPGRC1Uo9Vw/s1p+AR58tnzexx+A1vaJN++UUDVgRbOvj5lyDMqjpahdCN8B9gMJAshyoUQNwGPA+cKIfYD5/a8HvO0Wg0XLE8nJNqHL17a69BBEPZh8sVMmj2OOT+Kd9h6HSE2PZQzr06mNK/RofNo2IfJ78ZssrLsjgx8g1xbC+2vdzi3l4+OVc/tHvQpR8O166tS9q6vYNp5E0g/0zHD5B0lZV4UMy+KpXBzNds+dVy/+PYmo8OHyTuKwVfHsjsyEBr49Nkch3ZW2PzxQQ7sqGXupQkkZY2NSll/Q+mFcpWUMlJKqZNSxkgpX5VSNkgpz5ZSJvX8PLKXypjVOxmSZ89we0cc2KV5DX3D5M+6bnS6U52sKQt+mEdj26eHRpzEzd1WVr+YS3NNJ0tuTR+TE+/7BHiy7M4MbDbJp8/m0NU28gO7aEsVmz8+SFJWOHN/PDZuZB1p5tI4Uubb+8XvXT/yAS/Gdvt8Ns4YJu8ogeHeXHRbRt+Uw45oLtz9bRm7vi4lbVE0086d4IAoHe+UHIl5Ij6Bniy7PROr1cZHT+wYUU18//YaPnthD0FRPk4bJu8os5bGMaXnwN743v5hDz03tpv57//tomJ/M2dfnzJmmhAGExThw0W/mEp7k4kPn9gxohP27u/K+OaNAqKTAzn7eteNvjsRIQRnXJ1sn53z7SJ2flky7BN2W6ORj1bsoLmmkwtucc4weUcZF+fP+T9Po768nf88uWvYNXEpJds+LWbj+/uJywhl4RVJY7JSBqfAAx1GorGyg0+fzcHUZWHJLemMTzm5RLT72zI2vr+fyMQALvyF63qcnAxpk2z66AC7vykjYXoY5/zPlJNqt26t7+LTZ3fT1mDk3JumjIm+sEPR+3QYjVaw9PYMwif6D/mz/R+HFp8Zxrk3ndzfzFWsZhvf/CufA9m1pJ8RzYIrTm7u+YaKdj59Jgdzt42LbksnKmnMDbge1OHcer58eS/e/vYJz06mm6PNJtmwch9711UweW4Ei6+djGYUBqOdyCn7RJ6Rsk+BmUNTVSdzfpzA1LNiTliLNrab2fyfg+RvrCR+Whjn3ugeB3R/Od+UsumDA0TE+3PmNZNP2AQipeTQ7nrWvVOE1Wzjwl9MJSopcHSCdZDGqg5WPbubrg4zZ1w5ieTZx37+aK/2JhMb39/HwZ11TFkYxRlXJY+Jm3dDJW2SzR8fZNfXpUxMC2HRVZPwDzn+AxakTVKwuYrvPzyAVqfh4jszx2QT2fHUHG7ls+d3Y7NJzrou5bjPH+3VWt/Funf2UZrXwLTzJjD3koQxU/NWCfw4TJ1mvnk9n8O5DQSEezH/8iRi00OOKjyr1Ube+gq2fXqIbqOVjLPHM/eSBLc6oPvbn13DureL6O6ykLowmlnL4gZ9NFtDRTsb399vf1J6pA/n35zqdgd0r44WE6tfzKXmUCthE/xY8JPEQWuWVrONnG9LyV5dgrRKZi6NZfr5E8fMAX2ycteWs+nDAyAh4+wYpl8QO+jEar0jiGtL2oiID+DcG6cM64k6Y0FLXSef/8P+IIjoSYHMuyxx0CsvS7eVnV+WsPPLUoRWMO+ShDF3c1ol8CEo2dvApg/201TdiW+QJ2ET/Agd74fVbKW2pI260jZMnRZiJgex4CdJbpvE+jO2m9m26hB711eg0QhCon0IneCHX7CBxsoO6krbaK7pxNPbg1nL4klbFDUmLilHQtok+7bXsOU/B2lvMhEU4U1IjC+hMb50d1moOdxKbUkbZqOV+Mww5l+e6LZJrL+2RiNb/1tM0dZqPDy1hEbb99knUE99eTs1h1tpbzThE6Bn3mWJJM0c57YnrF5Wq438DZVsW3UIY7uZ0PG+hET7Ehzlg6nDTHVxK7UlrVi6bSTNHMe8SxPxDRq9KSCGSiXwIbJabRR+X0XFvmZ78qrt7ElsvoRN8CNuaigTB6mdu7vGyg4KNldRV9pGfZn9RNV7EhsX50/qgugxNYDBEczdVvLWV1C5v5n68nbaGoxotILQGF/CY/1JmBY2pm/QDldtSSuF31dRX9FOQ3k73UYr/qEGwmP9iYgPIGVeJHqD62bYcwZTl4XcNWVUHWihvqKdzpZue1mPt3+/E6eHj+kmQZXAh6nbaEGr1ThtbuexSEqJ2Wh16TSZrmDqsqD1EG53P2MkpJSYTdZTLmGfiLHDjIde4zZlfawEfnqV2jCcbl9ssHdDO92SN+C0h22MZUKI0/I77g49xobi9KlWKoqinGJUAlcURXFTKoEriqK4KZXAFUVR3JRK4IqiKG5KJXBFURQ3pRK4oiiKm1IJXFEUxU2pBK4oiuKmVAJXFEVxUyqBK4qiuCmVwBVFUdyUSuCKoihuSiVwRVEUN6USuKIoiptSCVxRFMVNjSiBCyHuFkLkCSH2CiHeEUIYHBWYoiiKcnzDTuBCiGjgTiBLSpkGaIErHRWYoiiKcnwjbULxALyEEB6AN1A58pAURVGUoRh2ApdSVgArgFKgCmiRUn515HJCiOVCiGwhRHZdXd3wI1UURVEGGEkTShDwIyAOiAJ8hBDXHrmclPIlKWWWlDIrLCxs+JEqiqIoA4ykCeUc4JCUsk5KaQY+AuY5JixFURTlREaSwEuBOUIIbyGEAM4GChwTlqIoinIiI2kD3wp8AOwEcnvW9ZKD4lIURVFOwGMkH5ZS/gH4g4NiURRFUU6CGompKIriplQCVxRFcVMqgSuKorgplcAVRVHclErgiqIobkolcEVRFDelEriiKIqbGlE/cEVRFEcwm82Ul5djNBpdHYpLGQwGYmJi0Ol0Q1peJXBFUVyuvLwcPz8/YmNjsc/McfqRUtLQ0EB5eTlxcXFD+oxqQlEUxeWMRiMhISGnbfIGEEIQEhJyUlchKoErijImnM7Ju9fJ/g1UAlcURXFTKoEriqK4KZXAFUVRBrF27VoCAgK48MILB7zf1tbG/PnzyczMxGq1AvDUU0/R2dnZt8yKFStITk7mnXfeGfDZlStXkpiYyNKlSx0So0rgiqIox7Bw4UI+//zzAe999913REdHk5OTg1arBY5O4Pfeey//+te/eOGFFwZ89oorruCVV15xWHyqG6GiKGPKHz/NI7+y1aHrnBLlzx+WpR7z99u3b+emm25i27ZtWK1WZs2axS9+8YtBl21ubiY8PLzv9TPPPENlZSWLFy8mNDSUNWvWABAREUFzc7ND9+NIqgauKMppb+bMmVx88cX8/ve/5ze/+Q3XXnstaWlpgy5rtVrRaH5InXfeeSdRUVGsWbOmL3kDaDSaviYWZ1E1cEVRxpTj1ZSd6eGHH2bmzJkYDAaeeeYZNmzYMOhyOTk5xMTEnHB9oaGh1NbW0tTURFBQkKPDBVQCVxRFAaCxsZH29nbMZvMxB9MsWLCAffv2sXPnzhOuz9vbm6uuuoq4uDhWrlzJ+eef7+iQVROKoigKwPLly3n00Ue55ppr+O1vfzvoMhs3buSmm27ipZcGPr/dz8+Ptra2Ae81NTWxcuVKysvLnZK8QSVwRVEU3nzzTTw8PLj66qu5//772b59OzabbdBlk5OTaWxsHPDe8uXLWbJkCYsXL+57r6WlhfDwcHx9fZ0Wt0rgiqKc9n72s5/x0UcfAaDVatm6deuAG5X9eXt7U1tbO+C9O+64g8LCwgE3MWtra/Hx8XFe0KgEriiKMii9Xs/evXuPGshzzjnn0NTUREZGxjF7maxYsYLly5dzxx13DHh/5cqV3HbbbQ67qSmklA5Z0VBkZWXJ7OzsUdueoijuoaCggJSUFFeHMSYM9rcQQuyQUmYduayqgSuKoripESVwIUSgEOIDIUShEKJACDHXUYEpiqIoxzfSfuBPA19IKS8XQugBbwfEpCiKogzBsGvgQgh/YBHwKoCUsltK2eyguBRFUVzqVJ+NMB6oA14XQuwSQrwihDiqz4wQYrkQIlsIkV1XVzeCzSmKooyusT4b4UgSuAcwHfiHlHIa0AHcf+RCUsqXpJRZUsqssLCwEWxOURTFOR566CGefvrpvte/+93v2LNnz6DLHm82wv4DeUZjNsKRtIGXA+VSyq09rz9gkASuKIpyUlbfD9W5jl1nRDosefyYv77pppu49NJL+dWvfoXNZuPdd9/lb3/726DLDjYb4ZNPPsmaNWsIDQ3te39Mz0YopawWQpQJIZKllEXA2UC+40JTFEUZHbGxsYSEhLBr1y5qamqYNm0aISEhgy57Ks1GeAfwVk8PlGLgf0YekqIop7Xj1JSd6eabb+aNN96gurqaG2+8cdBlTqnZCKWUOT3t21OllD+WUjY5KjBFUZTRdMkll/DFF1+wffv2YybbsTYboZoPXFEUBfvcJ4sXLyYwMLCvd8lgkpOTOXJKkN7ZCCMjI/smtBqN2QhVAlcURQFsNhtbtmzh/fffP+5yx5qN8MiJq9RshIqiKKMgPz+fxMREzj77bJKSkgA1G+FR1GyEiqIMRs1G+AM1G6GiKMppQCVwRVEUN6USuKIoiptSCVxRFMVNqQSuKIriplQCVxRFOY4zzzyT5ORkPvnkkwHvv/baayQnJ/P8888D9jlS+k8929bWRkZGBmeeeSZGo3HAZxcvXoyvr+9RA4JOlkrgiqIoJ/DWW29x8cUXD3jv2Wef5eOPP+aXv/wlcHQC9/PzY/fu3RgMBjZt2jTgs2vWrCEr66hegSdNjcRUFGVM+eu2v1LYWOjQdU4OnsxvZ/32uMscPnyYpUuXsnfvXsA+GKe9vf2Yy/efF7y7u5uHH36Yrq4uNm7cyAMPPMAVV1wBOHdecJXAFUVRhqH/vOB6vZ4//elPZGdn89xzzw1YzpnzgqsErijKmHKimvJYUF1dTUdHBwEBASdcNjo6mj179vDTn/7U4XGoNnBFURTAw8MDm83W9/rIG4+9Pv74Y5KSkli+fPlxZy3sdf311/OPf/xj7M0HriiKcqoYN24ctbW1NDQ0YDKZWLVq1aDLXXLJJZSUlPDiiy8OSPKDzQkO8Pzzz3Pvvffy5ZdfOjxmlcAVRVEAnU7Hww8/zOzZs1m6dCmTJ08+5rLBwcEEBAQMuMm5ePFi8vPzyczMZOXKlX3vNzU19c1w6GiqDVxRFKXHnXfeyZ133jngvTPPPHPQZXvnBe99kHFwcDDbt28/ajlnzguuauCKoijHERwczA033HDUQJ67776bq666qm8gz5F6B/KA/Vma/S1evJji4mJ0Ot2IYlPzgSuK4nJqPvAfqPnAFUVRTgMqgSuKorgplcAVRVHclErgiqIobmrECVwIoRVC7BJCDN7rXVEUxQ2tXbuWgICAo55K39bWxvz588nMzOyb4+Spp56is7Ozb5kVK1aQnJzMO++8M+CzK1euJDExkaVLlzokRkfUwH8FFDhgPYqiKGPKwoULB0wRC/Ddd98RHR1NTk5O31D6IxP4vffey7/+9S9eeOGFAZ+94ooreOWVVxwW34gG8gghYoCLgD8D9zgkIkVRTmvVjz2GqcCx08l6pkwm4sEHj/n73/72t0ycOJHbbrsNgEceeQQ/P79Bl+0/jSzAM888Q2VlJYsXLyY0NJQ1a9YAzp1GttdIa+BPAb8BbMdaQAixXAiRLYTIrqurG+HmFEVRHO/KK68cMPz9vffeIywsbNBl+08jC/bRm1FRUaxZs6YveYNzp5HtNewauBBiKVArpdwhhDjzWMtJKV8CXgL7QJ7hbk9RlNPD8WrKzjJt2jRqa2uprKykrq6OoKAgJkyYMOiyOTk5xMTEnHCdoaGh1NbW0tTURFBQkKNDBkbWhDIfuFgIcSFgAPyFEP+WUl7rmNAURVFGz+WXX84HH3xAdXU1V1555aDLLFiwgH379rFz584Trs/b25urrrqKuLg4Vq5cObamk5VSPiCljJFSxgJXAt+p5K0oiru68soreffdd/nggw+4/PLLB11m48aN3HTTTbz00ksD3h9sKtmmpiZWrlxJeXm5U5I3qH7giqIoAKSmptLW1kZ0dDSRkZHHXC45OZnGxsYB7y1fvpwlS5awePHivvdaWloIDw/H19fXaTE7ZDpZKeVaYK0j1qUoiuIqubm5J1ymdxrZ/u644w7uuOOOAe85cxrZXqoGriiKMgi9Xs/evXuPGshzzjnn0NTUREZGxjF7maxYsYLly5cfldRXrlzJbbfd5rCbmmo6WUVRXE5NJ/sDNZ2soijKaUAlcEVRFDelEriiKIqbUglcURTFTakErijKaa+hoYHMzEwyMzOJiIggOjqazMxMAgMD8fLyIjMzc8DyNpuNpUuXkp6eTllZGQBvvPEGlZWVfcu8/fbbJCcn8/e//33AZzds2MCUKVNIS0sbcdwqgSuKctoLCQkhJyeHnJwcbr31Vu6+++6+1wkJCeTk5AxYPjc3l9raWnJzcxk/fjxwdAK/+uqrWbduHU899dSAzw42Re1wOWQgj6IoiqNseG8f9WXtDl1n6HhfFv50ksPWd+SUsh988AHZ2dlcc801eHl5sXnzZry8vJw+payqgSuKopykI6eUvfzyy8nKyuKtt94iJycHLy+vvt85c6yNqoErijKmOLKm7CxDnVIWICgoiAMHDpCYmOjwOFQNXFEU5SRcffXVPPLII9x8881DWv6uu+4iIyOD1157zeGxqASuKIpyEt5++22eeOKJo25ODjalLMBjjz3G/v37ufHGGx0ei0rgiqIoJ2mwKWVvuOEGbr31VjIzM+nq6up732QyERUV5ZQ4VBu4oihKP4888sgJl/H29qaurg4pJUIIAC677DIuu+yyAcs5e0pZVQNXFEU5Bq1WS0tLy1EDeTIzMxk/fjyZmZl9A3mO9Pbbb3POOedw3333DXh/w4YNLFu2jNDQ0BHHp6aTVRTF5QoKCpg8eXJfbfZ0JaWksLBQTSerKIr7MBgMNDQ0OLXP9FgnpaShoQGDwTDkz6g2cEVRXC4mJoby8nLq6upcHYpLGQyGIfcvB5XAFUUZA3Q6HXFxca4Ow+2oJhRFURQ3pRK4oiiKm1IJXFEUxU2pBK4oiuKmVAJXFEVxU8NO4EKI8UKINUKIAiFEnhDiV44MTFEURTm+kXQjtAC/llLuFEL4ATuEEF9LKfMdFJuiKIpyHMOugUspq6SUO3v+3wYUANGOCkxRFEU5Poe0gQshYoFpwNZBfrdcCJEthMg+3UdZKYqiONKIE7gQwhf4ELhLStl65O+llC9JKbOklFlhYWEj3ZyiKIrSY0QJXAihw56835JSfuSYkBRFUZShGEkvFAG8ChRIKZ90XEiKoijKUIykBj4fuA44SwiR0/PvQgfFpSiKopzAsLsRSik3Aqf37OuKoigupEZiKoqiuCmVwBVFUdyUSuCKoihuSiVwRVEUN6USuKIoiptSCVxRFMVNqQSuKIriplQCVxRFcVMqgSuKoripkTzQYdQU7vuU2sZ9BHr4EqjzIVQfgLfeF7Q60OrBwxM8DPafOm/QeYGHF2jH2O5ZzWDuBHOX/afFBBaj/afVDDYzWC0gbfZ/SECA0Nj/abT2fdbowEPfs889//Te9n3X6kGMoQGyNpt9H81dYO4YuM8WE9jMmM1Gak1NtFjaaTF3YJU2AnW+BOp8CdUHYtB72/e5r6x7yru3rHVe9r/NWCHl8cvaZu4pb+uJy1qr79nv3u93z/6O1bIesM/9ytlqApsFk7mLWlMjreYOWswd2JAE6fwI0vsSqg9CrzMcUdYG0BkGHteaMVTvlNK+f737a+466vttL2sLRM8An1CHbn6MZbjBvbfzed43VfS9FlKSYDaTYexmusnE4o5O/KQ8+oNavb3g9T49P71B59Pzs+fLoDOAticpaPWg8bAfOL0HktAA0l5Q0mY/6GyWHwrGYuwpOOMPX9zeZNXdaX/d3Wl/bbM4/48lNP32sXffew74/gnPw7Nnv/U9B4zOnjT69ln07HdPgrFawNpt329Ld78vaVfP/nZBd8fA/e3utP/+CGZgs5eBLV4Gcj09ydfr6dYMnoi0UjKp20yGycQMo4lFnV14D1rWnvZ91vsOLOu+hOf1Q0LoTYpanb28j1vWPeXcV9a9+2zsKesj9tfcaf87SKsjS3Vwg5a19w+ve7/jvSf73pN/336LH8q6t5yl7Jd0jijrvu927/e73z73JrAjGIVgg5eBbV4Gcj31FOn1WI5x0vGQkimmbjJMJrKMJhZ0dqEfdEGvo4/lAWXt3a9S11PWGp29Qte7v31lbfuhrPsqUf3Kund/LV0Dy7d/uUvb0Mrrmg8h6ZwhFu7QCDnYweAkWVlZMjs7+6Q/V1u9m6qmA7R0t9Lc3UZFVy27Ww6wp7WYNksXeuHBGQFJLA1I4QzvaLQW09EHVd8fvPOHL2J3hz0p9dWCu4eeZHtrCTrD0bX/3i/UkQdW38F15Mmj/5es9+Qh6Jtqpu9LZhn4Jes72x9x8ujuhO72wZNp74nGahpYSxjKl1Dj0VP79/zhn877h9rwoInkhxNIrrmJ/7QU8FVzAc2WTjw1OlJ8xzM1IJEE32gC9f4E6PzQCkGzuZ2m7lbKOqrZ03KAPa2H6LJ146XRc07gZJYFpDDHMxxhMQ5+UHV3HpFwOodZ1qLflZ6h3373SxjHqiD0X6bvakl/RBI9QVlbuwdWFHrL+lj72/t+7wmm//4Ou6wH+34fub8/lLv0MLDdVMt/Wwr5trmQDpsJL42eNL9Y0gMSiPOJItDTnwCdLwJo6m6jsbuFko4qdrccIK+tBJPNjJ/WwPlBU/iRfwoZ+mBE/yQ6YN/7f7/7X/H0XPVYzUM7oQpNTwWu/9WtZ7/vseEYx7XXDxUlD6+BJ4++stZBaCIYAobwnRskNCF2SCmzjnrfHRL4sdikjbz6PD479BmrD62m0dhIrH8sN6bdyNL4pei0upNfqZQ9l7bWnpqYlR8ubcURB90pxGbrObglfTWT/rVxrW5Y+yylZHPlZl7Z+wrbq7dj0BpYPH4xF8VfxLyoeUMuI4vNwq7aXXxW/BlfHf6KNnMbyUHJ3Dz1Zs6dcC7a4TShSGlPlL01z8HKeiw1zTjKoGWtPeI7fvJlbZM2viv9jldzX2Vvw178dH6cM/EclsQtYWbETDw0Q7vgN1vNbKvexqriVXxb+i1dli4ywzJZPnU5C6IXIIZz7PU2a/U2Vx35/dZ4jK2mmSOckgm8P4vNwrel3/Jq7qsUNBYQ4RPBndPu5KL4i9CIsVswp7Kc2hz+tv1v5NbnEu4Vzs9Sf8blky7HR+czovWarCZWH1rNq7mvcrj1MLH+sdwz4x7OHH/m8A5uZcQ2VWxiRfYKDjQfYLzfeP4n7X+4OOFiPLWeI1pvp7mT/x78L6/vfZ2qjipSglO4b+Z9zIyY6aDI3cMpn8B7SSnZVLmJ53Y9R15DHlPDpnL/zPtJD0t36naVH1R3VPPkjidZfWg14V7h/CLzF1yccDF67aAtmsNmtVn5pvQbns95nkMth5gXNY/fzvwt8YHxDt2OcmyHWg6xInsF68vXM95vPHdMu4NzJ5475Nr2UJmtZlYVr+LF3S9S2VHJuRPP5d6se4nyjXLodsaq0yaB97JJG58c/ISndjxFg7GBK5Ov5O4Zd+Ot8x6V7Z+ObNLGu4Xv8tTOp7BJGzek3sCNaTc6/W9utplZWbiSF3JeoMvSxf+k/Q+3Ztzq8BOG8gOzzcxrua/x4p4X8dR6csvUW7gm5Rqn/82NFiOv573Oa7mvIZHcMe0Ork25dnhNaG7ktEvgvdq723ku5zneLnibKN8oHpn3CHMi54xqDKeDktYSHt70MDtrdzI/aj4PzX2IaN/oUY2h0djI37P/zicHPyExMJFH5z9KWmjaqMZwOihoKOChTQ9R1FTEBbEX8NtZvyXUy7Hd406kqr2Kx7Y9xtqytUwNm8qj8x8lPuDUvfI6bRN4r501O3n4+4cpaS3h6slXc0/WPSNun1PsTVYf7P+Av237Gzqtjt/M/A0/SviRS9ui15ev54+b/0h9Vz23TL2F5VOXO/yS/nRktVl5Pe91nt/1PIGGQH4/+/ecPfFsl8UjpeTzQ5/zl21/ocvcxT1Z93D15KtPyfsgp30CB/vl19M7n+bfBf8mKSiJJxY9QUJggsvicXfNxmYe2fwI35Z+y9zIufzvgv8l3Dvc1WEB0Nbdxl+2/oVPiz9lWvg0Hl/4+GnTXuoMNR01PLjxQbZVb+P82PN5aM5DBHgOr0uco9V31fPI94+wrnwdi2IW8ej8Rwk2BLs6LIdSCbyf9eXreWjTQ3SYO3hg1gNcmnTpKXnWdqZdtbu4b919NBgbuGv6XVw35box2dtnVfEq/nfL/6JBw5/m/4lzJjp2IMXpYH35eh7c+CDd1m4emPUAP0788Zg7XqSUvF34Nk9mP0mAZwCPL3ycWZGzXB2Ww6gEfoT6rnoe3PAgm6s2c3HCxfx+zu/x8vBydVhjnpSSN/Pf5P92/B9RvlGsOGMFU0KmuDqs4yprLeM363/D3oa9XDflOu6ecTc6zTDGCJxmLDYLz+c8zyu5rzA5eDJPLHqC2IBYV4d1XEWNRdy3/j5KWku4Y9od3Jh245isWJwslcD7MVttVDR1cbihjfcPvsH6urfx18SQor0diymUNqMFk8WK2SIx22wIQKfV4KEVeOs88PfywN+gI9Bbzzh/T8b5G4gIMDAxxJtxfgY0xxgW7u7autt4aNNDfFv6LedMOIc/zf8Tfno/V4d1XCaLlfKmLg7WN/PO/ufJblpFsHYSyZrbMBn9aDOaMVlsWKz2stYIgYdGoPfQYNBp8Tfo8PfyINhbzzh/A+H+nkQFejEx2JswP88xVxN1lPquen6z/jdsr97OZUmXcf+s+zF4GFwd1nEZzVbKGjvZX9fAG/ueoKBtPeEemSTwc4wmA21GM91HlLVOq0GvFXjpe8taR4iPnnB/A+P8PYkM8CI2xJtgH71Ly/q0TOA2m6SksZPcihaKqlspqm5nf20b5U1dWG0/7LfWZx/e0e8ihI0w4w2M85iBQadFpxV4aDUg7UnfbLXRZbbS2mWh1WimsaObzu6BQ3Q9PTRMDPFm0jg/Jkf4kRzhz9SYAMb5j+0v/4kcbD7IXWvuorytnLtm3MXPpvxsTCUvq01SXNduL+uaNvZVt7Gvpp3Kli76f8U9/HbjFfURAj0Rxp8TpkvB4KHFo19Zd/eUdWe3lTajhdYuMw0dJozmgUPQvfVaYkN8SI7ws5d3pB9TowMI8XXvm+O763Zzz5p7aO1u5aG5D3FxwsWuDmkAs9XGvpo28ipa7WVd08b+mnaqW/vPxSLRBW3BMG4VGlsgkaZfEKaPxdNDg4dGg1Yr+sq622Kjq9tKq9FMS5eZho5uui0Dy9rP04O4MB8mjfMjuaes06MDCPQena6qp0UCb+kys7O0iR2Hm9hZ2kRuRQttRvt8F1qNID7UXgBxoT5MCPFmYrA3UYFehPl50mSq5a61d5HfkM+tGbfyi4xfDOnSq91koabVSGVzFyUNnZTVtVJdUkV5VQPNDa3obFaMWh2+/r7ETQxnyuQJZMWHkB4dgEHnHn1Xvy75mt9v/D0GDwN/P+PvZEUM/B5JKbG1tGBta8PW2YU0doHWA42XAY3BgDYkBI3BsSewhnYTO0ubyS5pZFdJM3srW/pOpnqthoRwXyaN8yU2xIeJId5MCPYmIsBAmJ8n5e2H+05G9868d0g9F6SUtJks1LYaKW/qorSxk9LqFmpKKymvaqStuR2tzYpJqycwyI/4uHFMSR5PVlwIqVH+6LTucRn//r73eWzrY4zzHsfTi58mOTh5wO+llFibm7G1tWHrMv5Q1t5eaLy87GWtd2xSq2k1sqOkieye4zq/qrUvwRp0GpLC/Uga50tciP24Hh/sTWSAgVBfT/Ibc7ln7T20mlr5w7w/sDR+6Qm3J6WkpctMdb/jury6iarDVVTUNNHZ0o5W2jBq9YSEBhAfF0FacgwzYoNJifRH64QrcKckcCHEBcDTgBZ4RUr5+PGWd3QCbzWa2VrcyJbiBjYfbKCguhUp7ck6JdKPjJhApsYEkBYdQGK4L54ex0+YJquJ/93yv/znwH9YFLOIxxc+fswmApvRiLGgAGNBAaaCAkzFhzBXVGCprbXPNXEM3RoPar0CqfMJoXN8HD5pqcTPm0HGvHQMurHV1c1qs/JcznO8kvsKU8Om8vdFfye42YIxLx9jQT6mon2Yy8vorqhEdnYed13akBB0UVF4xsfhmZKCYcoUDFNS0foObVh9Y0d3XzlvKW5gf207ADqtIDUqgMzxgaRHBzA1JoC4UB97bfo42rrbeHDjg6wtW8uy+GU8PPfhYzYRWNs7MBXkYywoxFhQQHdxMebKSix1dcfdhlGro9Y7iFrfUEwT4vGfmkbi/OmkZU1Bf4Lv4mjrtnbz2NbH+HD/h8yPms/jCx/Hq6oJY34+psJCjEVFmMvKMVdVIY1HzzrYRwg8wsLQRUejj4+zl3PKFAwpk9F4De0eU22rke97ynlLcQOHG+zfLU8PTd8xnR4TQHp0ABNDfE6YMOu76vn12l+zs3Yn16Zcy6+zfn3MbqXW1laMeXn2si4soPvQYcyVlVgbGo67jU4PT2q8g6j3DaU7NoHAzHSSF85iSkaiQxK6wxO4EEIL7APOBcqB7cBVUsr8Y31mpAncbLWxq7SZDfvr2Hignt1lzdgk6D00zJgQxJz4EGbGBpExPhAfz+ElQykl7xW9x+PbHifGL4anFz9NfGA8to4OOnfsoHP7djq3Z9OVlwdmMwCagAA8kxLRR8egi47GIzwcjY8PGm8vhE6HzWhEGo1YW9toKymj/sBhTGVl+FWW4tEzI16L3ofqiZPxmD6d+PMWM3luBhoXTq7T2t3Kb9f9hkN7NnJtZwaL6kMx7dz1Q9LSatHHxaKPjUUXFYUuKgqtfwAab280Xgak1YY0dmHr7MRSX4+5ogJzRQWm/Qd+WIdGg2HKFLyzsvCeNQvvWbP6ErrRbCX7cBMbDtSx6UA9eZX2k7O3XktWbDCz44KZGRvM1JjhX8nYpI1/7vknL+S8QGpIKk8tfooInwisLS10bNtGV3Y2ndk7MBYWgtVeu9eGhOCZmIguOhpddBQeYWFovHvKWqvF1mXE1tWFra2VlsNlNBwowVxWil9NGdqeE3ujwZ/auCl4zphB0pLFJExLcWlZ13XWcfd3d9GSt5ubumcxvcoL486dWJub7QvodHgmJKCfMKGnrCPR+Pmj8fKyl7XFYt/vzg4sdXWYKyoxl5dj2r8fa1NT3zq80tLwnjnTXtZZM/quyjpMFrYeamDD/no2HahnX4395Oxv8GBWXAhz4oPJig1mSqQ/eo/h/Z3MNjMrtq/g7cK3mR0xmyfOeIIgQxCWxkY6t261H9fZOzDt309vm5vHuHH2so6Kspd1aCgab2+EwQuh1fSVtbW5maZDpTQWl2AtLcG/rhJNzzrqfIJpiJ+C18yZTPvpUsbFDq8rqzMS+FzgESnl+T2vHwCQUv7lWJ8ZbgJf99K7HNySw+ee48nxi8Gm9SBjfCALEkOZlxDKtAmBDm+O2FGxleffvoukA11c2DAefeFhsFjsX8TUVLyzZuCVmYlhyhQ8IiOH1R4szWYa8vdRtH4bLVu24bdvL6Ft9QA0eflTPykDn/lzSV12DhFx4x26f8dirqri0LefsH3VK8QdaCfIfizhERGB94wZeM2Yjld6Op5JScNuFrHU12PMz6crJ4fObdvp2rMH2d0NWi0t8ZPZPS6ZVboY8vyi0eo8mD4hyF7WiaFMjQlweHPEmgNf8ea7D5JeIjmvLgLtvsNgsyE8PfHKyLCXdUYGnikp6MKH18/dZjJRuyeffeu20b59O0H79xLY2QJAg08QDZMz8V+4gKnLziEk2vl96aWUmMvK2PfV++xe/W+Sik34ddlzgW7CBHtZT5+GV1oangkJiGE0i0gpsdTU2Mt61y57WeflgcWC1OlpSpjCjrAkPtPHsM83Ek+9BzNjg1mQGMr8xFCnNEf8d+97/OeDx5hZ7snimmDYfxgAjbc3XpmZePWUtSElBY/g4fUlt3V1UbUzl/3rt9G5fTshxfn4G9tpfmQFc6+8aFjrdEYCvxy4QEp5c8/r64DZUsrbj1huObAcYMKECTNKSkpOeluf3vYA8Wv+i0ZKbAYDXlkzCZgzC++sLAypqQjdyLuE2bq7Mebm0rljJ507sunano2tsxMp4OA40M2ewfyLf4HP9OlDvhQcjsqiQ+Sv+pbOzd8TsX8PfqYOAKqCouhMzSR0/hzSLliEb+S4EW9LSom5opKuHfaaZuf27XQfPgxAq48G79mziVm8BJ+5c9HHxIx4e0eqbTWy8UA9mwsqqd28nbiSfKbXFpHQUokGic3HF585s/GfbS9rz+RkhHbkJ2pbVxddu/fQmZ1tL+udu5AmE1YNHIgSBMxfyKylN+OdkTGsxDUUUkpKdhdR9Pm3dG/dQmTxXnzMRmwIKsMmYErPZNz8OaResAjvkJEPSpFSYi4pse9zT1mbK+wPSWn21xK04AwizzgP7zlz0I0b+XfrSOVNnWw6UM+WvHKatmwjqayA6bVFxLbVAGDzD8Bv7hx8Z8/Ce0YWnkmJCAdclVjbO+wVheztdGZn07V7D5jNmLWwP0ZL5BnnM+2in9nziIdzmjBtNhvFO/KISo7D2993WOtwRgL/CXD+EQl8lpTyjmN9Zrg1cLPVhqajnY6tW+n4/ns6t2yl+9AhexyenngmJ2NIScEwORldTAy6qCg8xkXYL2v7fQmk1YqtowNzVbX9kr68DGNhkb0d+8CBviYRfUIC3rNm4jN3LtoZGTxW8AyfHPyEs8afxZ8X/Blf/fAK4WRZLVYKNmRz+Ks1iB3biK44gKfVHmOTfwim2EQC0tOYkJmCz/hoPKKi8AgKGnBCk1Lam28aG+muqMBcXkH3oWKM+fb2e2tjIwAaPz9qE4P5LLiMrswk7r/qH0T6Rjp0f+rbTWw71HhUO3aQt455iaGckRTGgqRQwqWRzs2baf/+ezo3b+lLNBpvbzwnT8aQkoJn8iR7M0ZUFLqICITBMOAqSFos2NrbMVdV0V1ejrmsHFNRIcb8AkzFxfYmESHwTE7GZ/YsvOfOxZYxmQd3Psr68vVcmnQpv5v9u1GbEMts6mbvd1so/2YtHruyia4uRmezN9s0BI3DEpdIUEYa46dOxismBl1UJNrAwAEnNCklsqsLS0MD5vJye5PVweK+ezW2FnuNXxMURFm8L6tDKvCYOY0HfvIcgYZAh+5PdYuRrYfs9yw2FzdQ0tOOHe7nyYLEUBZNCmN+YiiBnS10bP6+77i21NbaY/TzwzB5MoYpKXhOSraXdWQEHuPGITwHdt+UZjPW9nZ7001FBeayUvtxnZ9vzxNSglaLYcqUvrLuSpnIPVseIKcuhxvTbuTOaXeO6Qmx3LoJZTCW+no6s3fQtWvXD1/Qtraj4zQYEJ6eSKMRaTId9XttcLA9+adMtl9CzZiBR1DQgGWklLxV8BYrslcw0X8iTy1+iriAOIfsx8no7DCy69stVK7/HmthASHVJUS116PhiDLUavuaN2ydnXBkGXt44JmYaN/v1FRkxmT+WP06ayrX8aOEH/HQ3IdGPE+M2WqjqLqN3IoWdpQ0saOkiUP19qsJb72WmbHBzE0IYUFiKFMi/Y/bd95cXT2grE2Fhfb96k8Ie1nr9ccsa4+wMDynpGBIScErMxPv6dPR+vsPWMYmbTy36zlezn2Z9NB0njzzSSJ8Ikb0txiO1pZ2cr76nqqNW5D7CgmvKSGys/HoBT087GVts2Hr6jqqrIVeb6/gTJmCIXUKprQEfnv4aXbW7eKG1Bv41fRfjXieGKPZSmF1G3vKm/t6i1Q02x+l52fwYHZcCHMTQliYFEpSuO8xmxullJjLy+1lnZNjv3m6bx+y64jH8mk09iSu0yG7upA9Fa8Bf5bIyJ4bqCl4TcvEOzMTjc/AG+Zmq5m/bPsL7+97n/lR8/nror+OmekBjuSMBO6B/Sbm2UAF9puYV0sp8471GWd2I5RSYqmuxlxVhbmiEkttDbbOLmzGLqSpG+Gpt99g8/ZBFzGu5yZUNNrg4CG3X2+r2sa96+7FbDPz2ILHWDxhsVP2Zahausxk55dTmFNERdEhOsoq8DJ24Gk14y8shPro8Q0KICg0gODIMMKTYglJmIg+KqqvaeBA0wHuWnsXFW0V3DfzPq6afNVJtedbrDaqWowcqu9gf207+6rbKKxpo6BfV69gHz3TJwSRFRvUd+NxJO3Y0mbDXFmFubICS1UV5ppa+w3TLnviFl4GND4+aH188IiI/OGG4xEn5uPp33VyxRkrXP4AgcaObrbvLaEoZx+V+w5jLC/H29SJ3mohQGsjxNcTv+AAAkMCCIkKIzwpjqDEWPQREX1NA/37d/9x3h+5MP7Ck4rBbLVR3tTF4foO9tW0UVTdRmF1G/tr2zBb7Xkk3M+TrNggZkwMZlZsMFOiRtaOLa1We626sgpzVRWW2lr7MW00Ic1me1dVb280Pr54REagj4lBFxOD1m/oA8w+2PcBj219jHDvcJ5a/BSTgycPO15ncVY3wguBp7B3I3xNSvnn4y0/VkZijkRVexV3r72bvIY8lk9dzm0Zt42ZSy+TxUpRdRt7ylvYU95MYbV9kEP/ASg+ei0xQd6E+3sivXPIM7+MTnjx4+j7SQnKsI841WjQagQWqw2zTdJtsdFuNNNqtNDSZaa2zURNq5GaViMVTV1Y+g2KCvHRkxzhR2qUP1N7unxNCPYeU4N+hqp38FJZWxn3zLiH66ZcN2b2o6vbSn5VK7nlzeypaKGgqo2Dde0DBqD4GTwYH+RNmL8eo+cmCs1v4usRymXRvyMhcFJfOfeWde+gljajfaBac6eZunYTta1Gqlrs//oPgAv38+wp6wAyYgKYOj6QqADDmPkbnYw9dXu4e+3dtJha+MPcP7AsYZmrQxrgtBjIM1pMVhOPbX2Mj/Z/xOzI2fx14V8J8QpxdViDstokZY2dFNe3U9LQSUlDJ6VNbRR1v02rfg22rgl0ll+DtAzt0tFHryXMz7NnqLGB8UFePQNlfEga50uom49CPFJbdxu/2/g71pSt4dyJ5/LHeX8cs9MHWKw2Djd0UlzXbh9o1NhJaVMTheY36NBvw9o+ic6KK8E2tAds+Hp6EO7nSbi/JxH+BsYHezOxZ2BUYpgvQT6n1gMz6rvquW/dfWTXZHP5pMu5f9b9Y2bKaZXAneDj/R/z561/JkAfwBNnPMH0cdNdHdIJVbVXce+6e9lTv4drU67l7ul3Y5NaWo1mOkxWe63bKrHaJB7a3rkiNPgZPPAzeJxwgMypSErJG3lv8PTOp4n2jebJM588aoTiWFTcXMw9a++huKWYX2b+kpvTb6bbAm1GM+0mCxabxGy1YbMxoKz9vTzw9Tw9y9pis/Dsrmd5be9rpASn8Pcz/s54/9Hpwns8KoE7SVFjEfesvYfy9nJuzbiVn6f/fMw+PODrkq/5w/d/wCZt/Gnenzgv9jxXh+RWdtTs4L5199FiahnTDw/o/5ANb503jy98nLlRc10dlltZV7aOBzc+iE3a+P2c33NR/PD6bzuKSuBO1N7dzp+3/plVxauYHj6dxxc+7vAueCPRae7kb9v/xof7PyQ9NJ2/LvzrmKhVuKOGrgYe/v5h1pevH5MPD2gxtfDI94/wTek3zImcw2MLHiPMO8zVYbmlyvZK7t9wP7tqd7EsfhkPzn5w1LoQH0kl8FHw6cFP+fPWPyMQ3DfzPi5JvMTlNbTs6mz+8P0fKGsr48a0G/nltF+qubBHqP/DA/z0fvx+zu/HxIMi1pat5U+b/0STsYk7p9/J9anXnxJzYbuSxWbh5T0v8+KeF4n0ieSP8/7I7MjZox6HSuCjpKytjIc3PUx2TTZzI+fyyLxHXPIor05zJ0/tfIp3Ct8h2jeaR+c/6vKucKeaosYiHtr0EAWNBZw38TwenP2gS25mt5ha+Ou2v/Jp8ackBSXx6PxHSQ1JHfU4TmW7anfx0KaHKGkt4fJJl3PPjHtG9Wa2SuCjyCZtvFf0Hk/ueBKAn6f/nJ+l/mxU7mhLKfni8Bc8ueNJqjuquSblGu6cdifeuqH1PFBOjtlm5o29b/CP3f/Ay8OL26fdzk8m/WRU7oNYbVY+3P8hz+16jrbuNm6eejPL05ej06orLGcwWoy8kPMC/8r/F6GGUO6acRcXxV80Klc5KoG7QEV7BU9sf4JvS78l2jeaX2f9mnMmnOO0ZpW8+jz+tv1v7KzdSUpwCg/MfoBp4dOcsi1loIPNB/nL1r+wtXoriYGJ3Jd1H3Oj5jqtrLdXb+dv2/9GYWMh08On8+DsB92iZ8ypILculz9v/TN5DXlMDZ3KfTPvIzM806nbVAnchbZUbeGv2/7KgeYDJAUlcXPazZwXe57Damk7anbwcu7LbKrYRJBnEHdOv5NLEi8ZMwOMThdSSr4r+44V21dQ3l5ORlgGN6XdxBnjz3BILU1KycaKjbyS+wo7a3cS4RPBr2f8mvNjz3f5vZbTjU3a+PTgpzy982nquuqYEzmHm9NvZlbELKeUhUrgLmaxWfj80Oe8mvsqxS3FxPjGcHHixSyNWzqsHiHNxma+PPwlnxR/wp66PQQbgrluynVckXzFmB1ocrrotnbz8f6PeT3vdSraK0gISOBHiT9iSdySYc2rUtdZx+eHPueTg5+wr2kfET4R3JB6A5clXTbmn1N5qus0d/Ju0bu8mfcmDcYGUkNSuTjhYs6PPd+h90NUAh8jbNLGmrI1vFXwFtnV2Ugk6aHpzIyYydSwqaSHphPqFTqgxialpLW7lYLGAnbX7mZX7S62Vm3FIi0kBiZy+aTLuTTpUrw8nDfNrXLyzDYzXxz6gncK3yG3PheBYFr4NLIispgaOpXU0FRCDCEDamw2aaPZ1Ex+Qz45tTnsrN3Jjpod2KSNtJA0fpL8E5bFL1Pt3GOMyWrivwf+yzuF73Cg+QBaoWVmxExmjJvRV9YjmShLJfAxqLqjmtWHVvNN6TfkN+Rj6Xk6j0Zo8Nf746f3o8vSRbOpue93APEB8SyMXsiyhGVMCpqkLp/dQGlrKasPrebb0m8pairCJu1zlmiFFn+9P756XzrMHbSYWrBK+zSyGqFhUtAkFsUsYmn8UpfMgKmcvP1N+1l9aDXflX5HcUsxsme20GcWPzPsCfBUAh/jTFYTBQ0F5Dfk02BsoMXUQmt3K94e3gR6BhJkCCIxMJH0sHT89f4nXqEyZnWaO8lvyKewsZBGYyOt3a20drfio/MhyDOIIEMQk4ImkR6arnoPubm27jbyG/LJrc9lWfwyxvkM72EZKoEriqK4qWMlcDVMS1EUxU2pBK4oiuKmVAJXFEVxUyqBK4qiuCmVwBVFUdyUSuCKoihuSiVwRVEUN6USuKIoipsa1YE8Qog6oGSYHw8F6h0YjjtQ+3x6UPt8ehjJPk+UUh71bLxRTeAjIYTIHmwk0qlM7fPpQe3z6cEZ+6yaUBRFUdyUSuCKoihuyp0S+EuuDsAF1D6fHtQ+nx4cvs9u0wauKIqiDORONXBFURSlH5XAFUVR3JRbJHAhxAVCiCIhxAEhxP2ujsfZhBCvCSFqhRB7XR3LaBBCjBdCrBFCFAgh8oQQv3J1TM4mhDAIIbYJIXb37PMfXR3TaBFCaIUQu4QQq1wdy2gQQhwWQuQKIXKEEA59os2YbwMXQmiBfcC5QDmwHbhKSpnv0sCcSAixCGgH3pRSprk6HmcTQkQCkVLKnUIIP2AH8ONTvIwF4COlbBdC6ICNwK+klFtcHJrTCSHuAbIAfynlUlfH42xCiMNAlpTS4QOX3KEGPgs4IKUsllJ2A+8CP3JxTE4lpVwPNLo6jtEipaySUu7s+X8bUABEuzYq55J27T0vdT3/xnZtygGEEDHARcArro7lVOAOCTwaKOv3upxT/OA+nQkhYoFpwFYXh+J0PU0JOUAt8LWU8pTfZ+Ap4DeAzcVxjCYJfCWE2CGEWO7IFbtDAheDvHfK11ROR0IIX+BD4C4pZaur43E2KaVVSpkJxACzhBCndHOZEGIpUCul3OHqWEbZfCnldGAJ8MueJlKHcIcEXg6M7/c6Bqh0USyKk/S0A38IvCWl/MjV8YwmKWUzsBa4wLWRON184OKeNuF3gbOEEP92bUjOJ6Ws7PlZC3yMvVnYIdwhgW8HkoQQcUIIPXAl8ImLY1IcqOeG3qtAgZTySVfHMxqEEGFCiMCe/3sB5wCFLg3KyaSUD0gpY6SUsdiP4++klNe6OCynEkL49NyYRwjhA5wHOKx32ZhP4FJKC3A78CX2m1vvSSnzXBuVcwkh3gE2A8lCiHIhxE2ujsnJ5gPXYa+R5fT8u9DVQTlZJLBGCLEHeyXlaynladGt7jQzDtgohNgNbAM+k1J+4aiVj/luhIqiKMrgxnwNXFEURRmcSuCKoihuSiVwRVEUN6USuKIoiptSCVxRFMVNqQSunPaEEIFCiNtcHYeinCyVwBUFAgGVwBW3oxK4osDjQELPAKInXB2MogyVGsijnPZ6ZkBcdTrMva6cWlQNXFEUxU2pBK4oiuKmVAJXFGgD/FwdhKKcLJXAldOelLIB2CSE2KtuYiruRN3EVBRFcVOqBq4oiuKmVAJXFEVxUyqBK4qiuCmVwBVFUdyUSuCKoihuSiVwRVEUN6USuKIoipv6/wzHnio6yQ5bAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYsAAAERCAYAAACKHYuuAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAAA2c0lEQVR4nO2deXxV9bX2n8UkyCAoIGMkAQmCA2qIIlStdaw4VdvqbWsHW9RqtW+r3lJf61V7b3t7O1874Vhsq61TVay2iqIEBEkCKDNEgswJgkwyZ71/rPzeHENyhj2fnOf7+eSzk5xz9lmBZD97zaKqIIQQQtLRLm4DCCGEJB+KBSGEkIxQLAghhGSEYkEIISQjFAtCCCEZoVgQQgjJSJsVCxF5WETqRGRhQOc7KCLzGz+ez+F1I0TkLRHZKyK3BWELIYREjbTVPgsRORPATgBTVPX4AM63U1W7ZXhOraoOafa9vgCOAXA5gK2q+lO/thBCSNS0Wc9CVd8EsCX1eyIyVEReFpEqEZkhIiMisKNOVecC2B/2exFCSFi0WbFohckAvqWqpwK4DcBvc3htZxGpFJHZInJ5KNYRQkhC6RC3AVEhIt0AnAHgSRFx3z6s8bHPALi3hZetU9ULGj8vUtX1IlIC4DUReVdVa0TkNwDGNT5ngIjMb/z8SVX9zzB+FkIIiZqCEQuYF/Whqo5u/oCqPgPgmXQvVtX1jcf3RGQ6gJMB1KjqTe45jTmLQ85PCCH5TsGEoVR1O4BVIvJZABDjpGxeKyK9RMR5Ib1hnsTi0IwlhJCE0ZaroR4HcDaA3gA2AbgbwGsAfgegP4COAJ5Q1ZbCT83PdQaAPwBogAnsL1X1oRae11I1VD8AlQB6NL5+J4CRjeJFCCF5QZsVC0IIIcFRMGEoQggh3mmTCe7evXvrkCFD4jaDEELyiqqqqs2q2qelx9qkWAwZMgSVlZVxm0EIIXmFiKxu7TGGoQghhGSEYkEIISQjFAtCCCEZoVgQQgjJCMWCEEJIRigWhBBCMkKxIIQQkhGKBSGE5BHbtgF/+AOwPeLpcnnTlCcitQB2ADgI4ICqlsVrESGEREdDA/Doo8CkSUBdnYnF7bdH9/55IxaNfFJVN8dtBCGERMlHHwHnngu89RYwdizQsSMwa1a0NjAMRQghCWf2bBOKn/wEmDnThGPmTCDKoeH5JBYK4F8iUiUiE5s/KCITG3dkV9bX18dgHiGEhENtrR2vvBIQAc44A6ivB2pqorMhn8RinKqeAuAiADeJyJmpD6rqZFUtU9WyPn1aHJpICCF5SW0t0K4dMGiQfX3GGXaMMhSVN2KRsgO7DsCzAMrjtYgQQqJh9Wpg4ECgUyf7euRI4IgjKBaHICJdRaS7+xzA+QAWxmsVIYREQ20tcMwxTV+3a2eJborFoRwNoEJEFgB4G8CLqvpyzDYRQtJQUwNcfz2wfn3cluQ/tbVA831uZ5wBLFwIfPhhNDbkRemsqr4H4KS47SCEZMdbbwGXXgps3gx06wb87GdxW5S/7N8PrF3bslioAnPmABdcEL4d+eJZEELyhKeeAj75SaBnT+Dss4FHHgF2747bqvxl3TpryGsuFuXlFo6KKhRFsSCEBMbjjwOf/Sxw6qnmXdx1F7B1K/Dkk3Fblr+4stnUnAUAdO8OnHgixYIQkme89Rbw1a8CZ54JTJsG9O5tHsbw4cDvfhe3dfmLE4vmngVgoajZs4GDB8O3g2JBCPFNbS1w+eXWB/D000DnzvZ9EeCGG+yCNn9+jAbmMatX27/j4MGHPjZuHLBzJ/Duu+HbQbEghPhi507gkkuAvXuBqVPNo0jly1828fj97+OxL9+prQUGDAAOO+zQx6JszqNYEEJ88cILVsL52GPAiBGHPn7kkcDVVwN/+lP0Y7XbAs17LFI55hgrJKBnQQhJPFu22PG001p/zsSJwK5dwPPPR2OTH3bsAL7+dWDBgrgtMVrqsXCIAKNGAYsWhW8HxYIQ4gvnLfTo0fpzysqA9u2BJUuisckP3/0u8NBDwK23xm0JcOBAyz0WqTixCHsCLcWCEOKL7dttv0JLMXVHx45ASQmwfHl0dnnhxReBBx6wcNobbwBvvhmvPevXm2BkEostW4BNm8K1hWJBCPHF9u3mVYikf97w4ckWi82bgeuuA044wcqA+/YF7rsvXpta67FIZdQoOy4MeVoexYIQ4gsnFpkYPhxYudK6kZOGKnDjjXaH/thjljS+7Tbg1Vet7Dcu0vVYOJxYhJ23oFgQQnyRrVgce6ytB03iYMF33rExJT/4AXBS4xS6G28EjjoqXu9i9Wo7FhW1/pyjj7aKM4oFISTR5OJZAMkMRc2YYccvf7npe926Ad/5DvCPfwCVlfHYVVsL9O/f1OTYEiLA8cdTLAghCSdXsVixIlx7vFBRYR3Szbukb77ZEvePPx6PXel6LFKJoiKKYkEI8cX27ba1LRMDB9odctI8C1XzLMaPP/SxHj0sLFVdHb1dQPoei1RGjQK2bQs3xEexIIT4Ytu27DyLdu0sb5E0sVi92i6yLYkFYBN0q6ujT8wfPAisWZO9WADhhqIoFoQQX2QbhgIsFJW0MFRFhR1bE4tTTrGfsaYmOpsAYMMGW3xEsSCE5D1799pHLmJRU2ONZklh5kyz311wm3PqqXaMOhSVTY+Fo08f+6BYEEISyY4ddsxWLI491oTCXQiTQEWFTW9t377lx0eNAjp1AqqqorVrwwY7DhyY3fPDnhGVN2IhIu1FZJ6ITI3bFkKIkc1cqFSSVhG1dat1PrcWggJMKE44IXqxcOM7+vbN7vmjRgGLF4dXEZU3YgHgVgB5MIaMkMLBq1gkJcnt9kCkEwugKckd9rC+VOrqrCig+X6Q1hg1yv4/1q4Nx568EAsRGQTgYgAPxm0LIaSJXMWid28rs02KWMycCXToAIwZk/55p54KfPghsGpVJGYBMM+id+/Ww2PNCTvJnRdiAeCXAO4A0GrxmohMFJFKEamsr6+PzDBCCplcxUIkWRVRFRUmBIcfnv55p5xixyhDUZs22SiPbCl4sRCRCQDqVDXtf5OqTlbVMlUt69OnT0TWEVLYOLHIpinPkZTps3v3Am+/nTkEBVjOomPHaCuiNm3KPl8B2Byr8ePTjwbxQ4dwThso4wBcKiKfBtAZQA8R+ZOqfjFmuwgpeLZts2O2ngVgYvGXvwB79oR3YcuG+fNNMNwe63QcdpjNX4rSs6irA04/PbfXuBlXYZB4z0JVJ6nqIFUdAuBqAK9RKAhJBrmGoQArn1WNvsmtOUuX2vGEE7J7/imnmFhEleTONQwVNokXC0JIctm+3RKwXbpk/5qkVEQtX27J7Ww6pAHLbWzZArz/fqhmAbB95bt2USw8o6rTVXVC3HYQQoxst+Slcuyxdow7yb1iBVBcbLmIbHCd3FGEonLtsYiCvBILQkiyyGUulKNHD1vWE3cX9/LlTV5ONpxwgnlRUSS56+rsSM+CENIm8CIWgIV+3Ba4OFA1z8J5OdnQpQswdGhTriNMnGdBsSCEtAm8isUxx8TrWaxfbytec/EsABOXKMJnFAtCSJvCj2dRWxvt+IxUXHLdq1iEvdvChaGS1DJGsSCEeCbbLXnNGTLE7uw3bw7cpKxw3kEuYSj3/N27w91IB5hn0bOn9XckBYoFIcQz2W7Ja44rV40rFLV8uTUEDhqU2+uiquRKWo8FQLEghPjATxgKiFcshg2zqa65QLEghJAc2b/fQjJeE9xAfBVRK1bknq8AgMGDbb9F2GJRV5esHguAYkEI8UiuW/JSOeIIi8nH4VkcOGCjRryIRfv25pHQsyCEkCzxMhcqFVcRFTWrV5tXlGty2xF2+ey+fbbBj2JBCGkT5KtYuAu9F88CMLGoqQmvfDaJ3dsAxYIQ4hG/YuEa86LutXA9Fn48i717gTVrgrMpFScWzFkQQtoEQXgWu3YBH3wQmElZsXy52ez1Yhx2RVQSu7cBigUhxCNetuSl4spno66IcpVQuUzKTYViQQghOeBlS14qcfVaLF/uPQQFAAMG2FBBigUhhGRBEGEoIFqx2LvXPBmvyW3AGvmGDQtveVNdHXD44UDXruGc3ysUC0KIJ7Zvt1CO14taz54mNFGKRU2NJdT9eBZAuOWzSeyxACgWhBCPeNmS15yoy2dXrrRjEGLx3nvW4Bc0FAsfiEhnEXlbRBaIyCIRuSdumwgpdLzOhUolarFw+7PduBGvHHusCUUYyfm6OoqFH/YCOEdVTwIwGsCFInJ6vCYRUtgEJRarV0fXa7Fmjc128rsnIsyKqE2bktdjAeSJWKixs/HLjo0fMa1NIYQAwYnFjh023iIK1qwBBg7Mfdpsc8ISi4MHgfp6eha+EJH2IjIfQB2AV1R1TrPHJ4pIpYhU1tfXx2IjIYVEEGLhwkFRhaLWrrXJsX7p1w/o1i14sfjgAxsjQrHwgaoeVNXRAAYBKBeR45s9PllVy1S1rE+SdhES0kbxuiUvlajLZ9esCUYsRKx8tqbG/7lSSepcKCCPxMKhqh8CmA7gwngtIaSw8bolL5UoxaKhAVi3LvfteK1RUhK8WLiGPOYsPCIifUSkZ+PnXQCcC2BprEYRUuAEEYbq1cvCOVGM/Kirs9HkQXgWADB0KLBqVbDTZ5PavQ3kiVgA6A/gdRF5B8BcWM5iasw2EVKwHDxoQwD9ioWIXbzDmuCainuPoMSipMR2T6xfH8z5AGDjRjv26xfcOYOiQ9wGZIOqvgPg5LjtIIQYfrbkNSefxQKwUFRQoa1Nm4DDDvOfCwqDfPEsCCEJwu9cqFSiEou1a+0Y1IV96FA7vvdeMOcDzLPo189fV3xYUCwIITkTtFhs2mRD/sJkzRqgc2egd+9gzldUZP0aYYhFEqFYEEJyJkixKCqy47p1/s+VjjVrzKsI6q69Y0eznWJBCCGtELRnATTNbQoLJxZBMnRosOWzGzcmsxIKoFgQQjzgFh8FkYh1YhF23iKo7u1USkqC8ywOHLBRH/QsCCFthjA8izDF4uBBC3OFIRb19U3VYX6or7eBihQLQkibwY2lOPJI/+c6/HA7T5hisXGjCUYYYSggGO8iyT0WAMWCEOKB1attJMXhhwdzvrDLZ13ZbBieBUCxIISQFqmtbZrrFARFReGKRdANeY4gxcKN+qBYEELaDEGLRdieRVhi0auXfQRREeU8C1ZDkYJmyZK4LSBB0dBgYaigxWLrVmDnzszP9cLatUCXLnZhD5qgKqI2brSCgaBCe0FDsSCh849/ACNHAq+8ErclJAg2brQBekGLBRCed+H2WIQxRiNIsUiqVwFQLEgEPPywHZ95Jl47SDC43RP5KBZhMHSo/ZscPOjvPEnu3gYyiIWI+PzxSaGzdSvwwgv2+fPPWx05yW+cWLiVqEEQhVgEXTbrKCmxPRmu4soreS0WABI4+5DkE3/7m4UsbrnF5v5XV8dtUX4zfz5w6qnAvHnx2eAWFQUpFgMHWogoDLE4cADYsCFczwLwH4rKd7HgfSDxxWOPWb7irrtsQufzz8dtUf5y4ABw3XUmuDffHJ+XVlsL9OkDdO0a3Dk7dbILZRhisWGDJeXDEovUvRZe2b3bRqjks1gQ4pmaGmDmTODaa20s9LhxFAs//PrXJhSf+QwwaxbwxBPx2BF02awjrPLZsMpmHYMGAR06+PMskt5jAXgQCxE5T0QeEJHRjV9PDNwq0ib4058stPCFL9jXl15qYZSwp4u2RVavNu/s4osttHfyycAddwAffRS9LWGKRRi/G0EvPWpOhw727+HHs2iTYgHgmwBuB/BFETkHwOhALSJtAlVgyhTgnHOa/kgvvdSOLuFNskMVuOkmE97f/AZo3x741a/sIviTn0RrSxg9Fg7nWQQdXlu1yo5B5liaM2wYsGKF99cnvSEP8CYW9ar6oareBuB8AGMCtukQRGSwiLwuIktEZJGI3Br2exJ/zJ5tbvmXvtT0veHDgdJShqJy5bXXgBdfBO67r+mC94lPAJ/7nIlFFCtJHW6jXRhiUVRkntLWrcGet6bGcixBTMhtjeHDgeXLvQtd0udCAd7E4kX3iap+D8CU4MxplQMAvquqxwE4HcBNIjIygvclHpk+3Y6XXPLx7196KfD6600jrklm/vUv28p2/fUf//4Pf2iJ0Wefjc6WMHosHGGVz9bUNFUshUVpKbBrl1X8ecGJRd++wdkUNDmLhao+1+zr/w3OnFbfc4OqVjd+vgPAEgADw35f4p3Zs4ERIw4dYT1hgtWkv/56PHblIxUVVi7bfAzEscdayelbb0VnS76KhatYCovSUjsuW+bt9Rs3WhFIx47B2RQ0vqqhRORVETkpKGOyfM8hAE4GMKfZ9yeKSKWIVNbX10dpEmmGqonF6acf+tiJJ9rRT3y3kNi9G5g718JOLTF2bLRiEUaPhSMMsdi3z84XtmcxfLgdly/39vqk91gA/ktn7wDwCxF5RET6B2FQOkSkG4CnAXxbVT8WyFDVyapapqplffr0CdsUkoZVq2w5Tkti0bOnfbikY9JYscLsfvvtuC0x3n7bPLF0YrF6tfUSREFtrd0BB9lj4Tj6aKssClIsamstKR+2WAwcaJ6fH8+iTYuFqlar6jkApgJ4WUTuFpEuwZj2cUSkI0wo/qyqnDKUYGbPtmNLYgEAxcXJFYs77gDmzAG+9jW7K42bigo7nnFGy4+PHWvHqLyLsMpmAavyGjy4KdQVBK6cNWyxaNfOvAuKRRpERAAsA/A7AN8CsEJEvpT+VZ7e4yEAS1T150GemwTP7Nl25zlqVMuPB7nkPkhmzAD+/nfggguARYuAn/40bovMplGjgKOOavnxU06x7ue2IBaA/W4EeSMRlVgA3sVCNfkTZwH/OYsKAOsA/AKWcP4KgLMBlIvIZL/GpTAOwJcAnCMi8xs/Ph3g+UmAzJ4NjBljIYWWKC5uCg8kBVXg9tstnPDMM8BVVwH33gusXBmfTQcPWqd2ayEoADjsMBOMKMRCNbweC0dJSTCLhBw1NRYeiuKuvbTUfq/37s3tdTt2AHv2tH3P4gYAA1X1PFW9S1WnqupKVf0WgDS/4rmhqhWqKqp6oqqObvz4R1DnJ8Gxe7cNuWstBAWYWOzd21QumASefNLCT/fdZxeXX/3KLsQ33BDfDKZ33rELSTqxACwUVVkZfths0ya7qIUtFvX19nMHgauECmOPRXNKS+0GKFexy4ceC8B/zmKhaqt/Shf7OTfJT+bNs4F3LpbeEkHuLQ6CvXuBSZOAE06wOVYAMGAA8OMfA9OmWUNcHMyYYcfx49M/b+xY+xkWLAjXnjDLZh0uXBRUKCqKHguHq4jKNRRVEGKRDlVNyKWARIlLbp92WuvPKS62Y1KS3C+9ZML1X/9lSVbHddeZd+EaDKNmxgzrai4qSv+8qJLcrmw2bM8CCOZGQtXOE5VYuF6LXMtnC0osROS8IM5D8p/Zs00M0iXrXI1+UsRizhzLr5x77se/36mTDeyLo4xW1SqhMoWgAJu9NWhQ+GIRxtKj5gQx7tuxYYOFzaISix497IKfq2exbp0d+4fefOCPoDyL/w7oPCTPaa0ZL5XOnS2RnJQwVGWlNQt27nzoY+XlQFWVhdaipKbG7jizEQsgmua8998HevUCunUL7z169bI+nCB+N6KshHJ4qYhasQI44ohDpx0kDe6zIIGxbp01VGUSCyA5vRaqJhZjWhmHWV5uw+0WL47Wrpkz7ZgpX+GIojkvzD3WqQwdmr9iUVqaexhqxQob3RJFEt4PnsWisWv7YRF5BEBR4+cPi8jDAdpH8ohMzXipJEUsVq4EPvwQKCtr+fHycjvOnRuZSQCsUKBLF5uvlQ1R5C2iEoug+nBqaqxZLlPOJ0hKS4HNm4EtW7J/zcqVJhZJx49n8SiAPzYetzZ+7j5IATJrloVyRo/O/NySEtvHkGtNetA4EWjNsxg2zMIiUectFiyw0Fhqwj0do0fbnem774Zn09q14S0QSqWkxPIjBw/6O09NjQlFp06BmJUVuQ4U3LvXwnttWixU9Q33AWBHs69JATJrll10s/njLC62EFDcW/PmzrU7+Na6zUXsZ4pSLFRNLE7KYURn585WpeR13EQmdu+2O+aoPIt9+5oSv16JsmzWketAwffes96MNi0WzUjAFB0SJ7t3WyK4tRlGzUlK+ezcuVbx1Fq3OWChqHffjW6F6dq1tgAoF7EA7K526dLwbAKiEwvAfygqDrEoLrbfpWxF201fLhixUNUsotSkLVNVZdNRx43L7vlJaMw7cACorm49BOUoL7eQyLx50djlmuu8iIWfbW3piFIs3AXez+/Gtm3ABx9ELxYdO9p75ioWw4aFZ1NQsBqKBIKr3knXuZ3KgAEWrorTs1i82DyiTGLhHo8qFOXEwu3+yJYRI2xbm9/wTUu4seFR5CwGD7ZcjR+xiKMSynHccdnnjlassHLh1gZFJgmKBQmEWbPszrZ37+ye366dxdjjFItMyW1H//52AYuqImrBAvO8unfP7XUuuRpGKCpKsejQwRr/8lUsTjvNROCDDzI/N18qoQCKBQkAVROLbPMVjuLieMNQc+daM1Q2IYDy8mg9i1xDUID/1Z7pWLPGbgS6hLKt5lD8Tp9dtMiKE+IQC1c6PmdO+ucBTT0W+UDOYiEi54nIAyIyuvHriYFbRfKKFSusUibbfIUj7l6LuXOtv6JdFn8FY8bYxSubu0U/7Npl/55exKJ/f+uuDkMsoiqbdfhtzPvnP+3/LFfvLAjGjLHfqUw9L3v2mAi3WbEA8E0AtwP4ooicA2B0oBaRvMPlK3L1LEpKrHlp27bgbcrEnj02AjxTCMoRVXPewoXmqXkRCxHLW4QVhooiue0oKbEbkO3bMz+3OR98YF7ghRcGb1c2dO1q+SbXpNoaNTX2f92WxaJeVT9U1dsAnA8gyz830laZNcvm2rgwSLbEWT67YIFVQ2UrFqeeasfq6vBsArxXQjlKS8MLQ0UtFoC3341XXrHehYsuCtamXBg71sJQ6RoL86lsFvAmFv9/ur+qfg/AlODMIfnIzJn2x5FNOCeVuMUCsC1z2dCjhw0/DKvpzbFggb2X1zHgpaXW6BhkT8iuXdb3EYdYeAlFvfSS3bxkeyMQBqefbguc0s0Uy6eyWcCDWKjqc+5zEfklgPuDNIjkF1u2AEuW5J6vAOIVi2XLLFmby9ygsO7aU3FjPrwOlXPenbsQBYHrsYgyZ+F1VHlDg+Urzj8/+1EpYeBKyNOFolautJLZXr2isckvfquhdgJ4XkS6AoCInC8iM/2b9XEaBxTWicjCoM9N/OGSeLnmKwD7I+nataksM0qWLzf3PxdvyHVIh7VmtaHB8iheQ1BA0+DBIPMW7v8nSs+iZ0/zDnL1LObPt/WvcYagAPMWjjoqfZI7nyqhAP9rVf8vgMcBTBeRCgDfBfC9IAxrxqMAYkpXkXRMnWpziby4/CJWT+82sEXJsmVNc3yyZcQIS8bX1YVjU22thS78iIUbdR2kBxSHWAAmzrmuin3pJTtecEHw9uSCiIWi0nkWBSUWIvIpAN8AsAtAHwC3qOqMIAxLRVXfBJDD0F8SBdu3A489Blx9NXD44d7OUVQU/TDBffvsjjXXhHyYTW+A/+Q20BRaC1IsXBhq4MDgzpkN48bZrpE9e7J/zUsvWTFCuk2NUTF2rIVot2499LGPPrJ/14IRCwB3ArhLVc8GcBWAvzaW00aOiEwUkUoRqayvr4/DhIJjyhRLft50k/dzxCEWq1ZZlUquYuFCPGHlLd55x+5Ijz/e33mCLp9dswbo29f2kUfJ+PEm7JWV2T1/61YL+8RVMtsc15zXUjOny8UUjFio6jmqWtH4+bsALgLwwyAM82DLZFUtU9WyPn36xGFCbGzZAtx9d9Pi9yhQBX77W+s/aG1xUDYccwxQX28zmqLCXexzDUMNHmx37mGJxaJFltj16qU5gh4oGHXZrMPlwSoqsnv+q6/GXzKbSnm5iX9LeYt8K5sFMouFiMhVIpJVH6SqbgDwKf9mkWzZswe47DLg3nuBiy8Gdu6M5n1ff91c7G9+0995XDVSlN6F2zWQq1i0a2d/3GGFoRYu9O9VACYWO3cC69f7PxcQffe2o08f85KyFYu//MVGkpx2Wrh2ZUv37vb/2ZJYuH6dfCmbBTKIhaq2AzAbwOdE5P+IyNdFJG2xoapGeI9Y2DQ0ANdea39Mt95qMe+rr7Zms7D5zW+s2uPzn/d3njjEYtkyuxB5KVkcMSIcz2LvXrvbbG0JUy4EnVuJy7MAgE98wvp4GhrSP2/VKuC554CJE9PvJoma888Hpk37eDPnhg3Ar34FTJhgs8nyhYxhKFVdq6oPqeovYJVPZSLyXRG5RUR8BCCyR0QeB/AWgFIRWSsi10Xxvknn9tuBJ58EfvpT4Je/tAv4iy8C3/pWeOWdgN1pPvcccN11Vgnlh2OOsWPUnkWu+QpHaaldmIJeB7t8uYl8EJ5FkLmVHTusAiwusRg/3nakp2tuA4D777e+Cr+ebtDceafdmHz96003cZMm2e/Pz38er225kpMGq+ouAM8AgIi0A3CGiHwbgABYBmCaqga+VVlVrwn6nPnOc8/ZL9sttwDf+Y597/rrrfzyxz+20sHLLw/nvR94wO70brjB/7kGDLDwTpTls8uWWcjOC6Wl9rOvXBmMF+BYtMiOQYjFgAGW9wiiMS+uslnH+PF2rKho/d9m507goYeAq66KvmIrE716mZBddRXwi18AZ54J/PGPwL//e37lKwB/O7gbVLVCVX/Z6HWsAPBVEblHRL6abZ6D5I4q8B//Yb9sP/vZx7t9f/hDi9s+/XQ4793QADz6KHDeeU0d2H7o2NEublF5Ftu2WdOWV88irIqohQvtzjjXPEpLuNHcfkZ8O+Lo3k6luNim6abLW/zxj/b/euut0dmVC5/5jN24/eAH5o33728eR74RSHRPREoAXALgYgANAD4AEGOzfdtm6lTrVH300UPjs+3bA5/+tD3n4MHgRx5Mn24X9v/+7+DOecwx0YmFS257FQt3MQ86yb1okZ07qPLUoUObflY/xO1ZiJh30ZpYNDQAv/61VR65UtWkIWLexciR9v88ZUo8o9P94tmzEOOHIvIWgB8B2AjgSlU9T1V/raofBmUkaULVKp9KSoB/+7eWnzNhgpXTZhqR7IVHH7Wk3GWXBXfOoqLowlBey2Yd3bubJxSGZxFkWMvtg8iUGM7EmjV2sRswIBi7vDB+vP1+tDQW5p//NFH89rcjNysnBg60BtZbbwW+8IW4rfGGnzCUAtgH4HxV/byq/oUCET4vv2xNSpMmWQinJc4/3zyOqVODfe/t24GnnrKKqyA3phUV2YXA74UtG5YvtxyJnw1qQVdEffSRhYyCyFc4hg61smq/5bOrV1vYpFOnYOzygstbuL0pjr17ge99z0JkV10VvV25cumlVoiS63TmpODX7PtUdUcglpCMOK+iqMhKZlvjiCMskRa0WDz5pDXPfeUrwZ63qAjYv99yCWGzbJnFwf1c/IIeKOjOFaRn4er3/eYtamriWU2ayokn2gbAN974+Pfvvtu63n//+9ZvnEhw+O3gDrFAkzTntdcstDRpUuaL3YQJFtqorQ3u/R991C6UQTc9ufLZKEJRfspmHaWlwQ4UXNg4SzlozwLwLxYrV8bfONahg3VlT55sFUWqlsP4yU+Ab3zDe2UbyY08dYgKk//9X6vZzubO3v0Bvfhi+udly8qV9gf61a9637XQGlE15jU0mFj4rTgKegz4okUm/kFelIuK7CLrRyx27bIGsrg9CwB45BGrKPrOd0wgvvxl8xDzrVchn6FY5Anvvw+88II192TTCDd8uJXWBhWKmjLFYq1f/GIw50slKrFYv97yA0F4FkBweYuFC02Aguw87tDBPDY/YuF2SSRBLLp2tTDonXdaT8WqVVYy261b3JYVDglqjCfp+P3v7Xj99dm/ZsIE6+reudP/H9WLL9rI6DCano44wj7CFgt3cfcrFkVFluAP0rPwsjwqE8OGmUfoFSc0cYehHO3aWR/RmDHm9bjEN4kGehZ5wN69wIMP2sXfxfezYcIEG/E8bZq/99+yBZg3Dzj3XH/nSUcU5bN+y2Yd7dqZ4CxZ4t+mHTvs5w4yX+Hw25jnhCYJnkUql13Wetk4CQ+KRR7w1FM2xjvXvRHjx1uT1wyf66hef92Sip8KcZ5wFHstli0zDyuInoGRIzPPK8oGd44gK6EcQ4faXKUtHteG1dTYatN82RFNwoVikQf89reWf8j1zr5TJ+Dkk1tevpILr75qF9nycn/nSUcUXdzLlplHEESC/rjjzF6/I+HDqIRy+C2fXbkyeV4FiQ+KRcKZNw+YNQu48UZvzTzl5UBVlb+x5dOmAWedFW4te1GR3QGHuY9j6VL/+QrHyJFN5/TDu+9a/iOIOVvNcRd6r3mLmprk5CtI/FAsEsyHH1r1Uc+e3hvhxoyxCiCv8fU1a2x6aZghKCD8iqjdu+3cQYnFccfZ0W/eYt4827kdRldvSYkdvXgW+/ZZLoWeBXFQLBLKvn3AlVfahfqZZ7zHjV3oyGsoyiXHw0xuA+HvtVixwvIurkfCL8OGWXmqn7xFQ4MNhDzllGBsak6XLpaf8SIWq1ebffQsiINikUBUbePXa69ZTfknP+n9XMOGmWcyd66317/6KtC3bzgx9VScZxFWRZQLFwXlWXTsaHkkP57Fe+/ZvK2TTw7GppYYNsybWLjX0LMgDopFwlAFvv99azi65x7gS1/yd7527YCyMm+ehap5FuecE3zXdnP697c79bA8C1c2G+TCmZEj/YnFvHl2DMuzAOxi7yVnkdSyWRIfFIss2bEj3FWlQJNQ/PjH1nx3113BnLe83Aau7c5xO/qSJcDGjeGHoADbuzFwYMtjqINg6VILdR1+eHDnPO44u6h6XbFaXW0CGUbZrGPoUBvZ8dFHub2upsb+rfr1C8cukn9QLDLgJr326GHNXD/6EbBuXTjvM2mSCcUNN1i5bFB38+Xltghp/vzcXvfqq3YMO7ntGDw4XM8iqBCUY+RIi+t7XV86b56F94JaeNQSzjNwozuyxZXNhu1RkvwhL8RCRC4UkWUislJEvhfV++7ZY4tK7r4buOIKSxZ+//t2h/rYY8G+19132/a5G26wER1BVseMGWPHXENRr79uFTVDhgRnSzrcXougUQ1HLFxFlJckt6p5FmHmKwDvvRYsmyXNSbxYiEh7AL8BcBGAkQCuEZGRYb1fQ4NdWP74R+Dss4HHHzdv4umnbZ7+8uXWGT1xYu536q3x4IPAfffZRNeghQIwkRs4MDexULVlM2eeGawt6Rg8OJwlSOvXW/9GUJVQDtfg5yVvsX69deWHma8AvI0qb2gwT4T5CpJK4sUCQDmAlar6nqruA/AEgACXejbx978DRx1lF5WvfMWE4amnbBuXc8ePPRb4299sDMJVV1kvhB9eftm8iQsuAP7wh/C2aI0Zk1tF1MqVdjELY8Bda4S1BCmoAYLNcc10XjyL6mo7hu1Z9Oplv6u57ONet87yMPQsSCr5IBYDAaQGJ9Y2fu9jiMhEEakUkcr6+npPbzR0KPDZz1q56sKFdrG88spDn9e3r41LXr3aRMVr4nv+fHu/44+384XZIV1ebrH1bOcEzZplx6jFAgg+FBV02WwqXiuiqqvtBuSkk4K3qTm5roFl2SxpiXwQi5ZSbIdcnlV1sqqWqWpZnz59PL3RCSfYNq6vfc0qVNq3b/25Z5wB/PSnwHPPeVvAsnix7cru2dPGf3fv7snkrHHNeZWV2T1/5kyzzcXlo2DwYDsGneRetsz2IYQxXv244+yuPddxKvPmWcFEFPsYRozIbSwJy2ZJS+SDWKwFMDjl60EAfK6hD4ZbbrHE96RJTWGFbFi+3CqM2rWziqMwLmLNKSuzY7Z5i1mzgLFjo10uH5ZnEeQAweaMHGkhm1WrcntddXX4+QrHiBFWAp1tyLSmxrzcwYMzP5cUDvkgFnMBHCsixSLSCcDVAJ6P2SYAdvF54AELS11zjS1kyURNjTW5HTxoHdphhEZa4ogj7MLmwkvp2Lo1vIU86ejZ0zyAoD2LIAcINsfLjKjNm00Qw85XOFxiP9tQ1NKllosJcnMfyX8SLxaqegDAzQD+CWAJgL+p6qJ4rWriqKOsjHbFCuDb307/3L//HTjtNCvJnTataXJpVIwbB7z1VuZqo9mzm54fJSLB77X46CM7X9CVUA4v5bNRdG6nkuvO8Ci9HpI/JF4sAEBV/6Gqw1V1qKr+Z9z2NOeTn7SKqQcftF6J/fs//viuXdaRfcUV1qMxc6blR6Jm3DgLRWS6sM2aZfka158RJa58NijcAMGwPIsePUzgcglDOrGIyrMoLrawUjZiUV9v4nrqqeHbRfKLvBCLfOCee4CLLzbROP54S3y/8YZttyspsXDVHXfYnX1UoafmOE9h5sz0z5s506p0oki+NidozyKsstlUzjzT/q+zrYqbO9duGo48MjybUunQwcpgsxGLqio7UixIcygWAdGxI/DCC8Dzz1s45fLLranvkUdscdD06eZ1dOoUn41Dh1p+JZ1YHDgAzJkTfQjKUVRkfRZe5y01x10ggxwg2Jyzzwbq6rK7GKsCFRXW2Bkl2VZEObFgGIo0hymsABEBLrkEuPBC4K9/NWG4+GJL2iYBEROBdGLxzjsW5486ue1wFThr1wZTujl/vglFmP8HZ59tx+nTM5cav/eeVSbFIRYvvGAh0nT9PFVV9u91xBHR2UbyA3oWIdCxo224+9znkiMUjnHjmi5YLeGEJC6xCLp8NopkbUkJMGiQiUUmZsywYxxiceBA5oGCVVUMQZGWoVgUGJnyFrNm2YXPXbSjJsjGvC1brMs+7ESyiHkX2eQtKipsBEfUlXDZVEQxuU3SQbEoME45BejcuWWx2LPHZlX52cznl0GD7BiEWERZonr22ZZrydTLUFFhgh1lsyPQlOBPJxZMbpN0UCwKjE6drCS2JbGYOtVKa/1u5/NDly6WhA8iDBXVsD7g43mL1qirMzGJOgQFWA6if//sxILJbdISFIsCZNw4u5A23542ZYqNMz/nnHjscgS1BGnePDtX797+z5WJbPIWTqA/8Ynw7WmJTBVRTG6TdFAsCpBx4yzZmTqyvK4OeOklS8ynG6AYBUEtQYqyE9nlLaZPbz1vUVFhW/HiCvM4sWjNvspKhqBI61AsChBX6TRtWtP3nnjCBCTOEJRj8GBLTPvZeb5zpw1sjKpLGsict5gxw6b/hrlGNR0jRliYsa7u0Mfq602gKRakNSgWBciRRwIXXWT7vp1gTJlid+HHHx+vbYB5Fjt3Atu2eT/HggUmNlHG39PlLXbtMk8nrhAUkL4iyuUr3HRiQppDsShQ/vIXu3hccQXw5z/bxeLaa+O2ynDls35CUVEP6wOa8hbPPHPoY3Pm2KThOJLbjmzEIkpPjOQXFIsCpWdPy1H07NmUp7jmmritMlyPh58kd3U10KePJeyjQsR2nLzyiu0pSWXGDHt87Njo7GnOoEHA4Ye3PEhy9mwmt0l6KBYFzMCB1lfRqxdw2WVWspoEgujidsntMBYepeNb3wKGDAFuu808CcC65R94wPIBPXtGa08q7dpZccOzz358s9+GDfZ7cOml8dlGkg/FosAZOdIWMk2ZErclTRx9tE1KXb3a2+v37rXlTXGEVDp3Bn70I8uZPPaYNTpecYUtlHrggejtac6NN5oIT53a9L2HHzbxuP76+OwiyYdiQdCrV7JmWLVvb95Fba231y9caBe/uJrLPv95q3q6807guussxDNlCjB6dDz2pHLJJZYTuv9++/rgQds7f+654U7mJfkPxYIkkuLi3PdaO+JIbqciAvzsZ8D69VZIcM89wJVXxmNLczp0AG64wargliyx8NP779v3CEkHR5STRFJSYgukvFBdbRvsiouDtSkXxo+3Nbv79wN33RWfHS3x9a+bgP32t+a99evHfAXJTOLFQkQ+C+A/ABwHoFxVK+O1iERBcbE1j+3cmfvGvqoq8yqiHtbXnF/8It73b42+fW18/iOPALt3A9//fvodF4QA+RGGWgjgMwDejNsQEh3OK8g1b7F/vyWX2YmcnptvtkZBAPjGN+K1heQHifcsVHUJAEjUNZAkVkpK7LhqVW5d5YsXWzUUJ6emp7zcusn79YtvdwnJLxIvFtkiIhMBTASAIv725z3Os8g1yc2dDNkhArz2WvR9KCR/SYRYiMirAPq18NCdqppVmlNVJwOYDABlZWU+RtCRJNC7t5XzZloD2pyqKqB7d5aBZkOHRPz1k3whEb8uqnpu3DaQZCHirXy2qsqa8eJObhPS1uCfFEksJSW5icWBA0xuExIWiRcLEblCRNYCGAvgRRH5Z9w2kWgoLrYwVLZ7LRYvtvEaFAtCgicRYah0qOqzAJ6N2w4SPcXFVt65ebNNkM0Ek9uEhEfiPQtSuORaEVVVZQ18w4eHZxMhhQrFgiSW1F6LbGBym5Dw4J8VSSxDhtgxm/JZJrcJCReKBUks3bpZriIbz2LJEptzxM5tQsKBYkESTbbls0xuExIuFAuSaLJtzKuuto7v0tLwbSKkEKFYkERTXGzrVd0+69aYO9eS2+3bR2MXIYUGxYIkmuJiS16vXdv6c/bvt+145eXR2UVIoUGxIIkmm/LZd9+1seRjxkRjEyGFCMWCJBrXmJeufHbuXDvSsyAkPCgWJNEMHmxNduk8i7lzgaOOinfnNiFtHYoFSTQdO5oILF7c+nPefttCUFzkQ0h4UCxI4hk3DqioaHn67K5dwKJFzFcQEjYUC5J4zjwTqKsDli499LHqaqChgfkKQsKGYkESz1ln2fGNNw59zCW36VkQEi4UC5J4hg4FBgxoXSyKioCjj47eLkIKCYoFSTwi5l288caheQuX3CaEhAvFguQFZ50FbNgArFzZ9L0PPrD+C+YrCAkfigXJC1rKWzBfQUh0JF4sROR/RGSpiLwjIs+KSM+4bSLRU1oK9O0LvPlm0/fmzrUQFceSExI+iRcLAK8AOF5VTwSwHMCkmO0hMSBiJbTOs9i1C3j2WWDECKBHj3htI6QQSLxYqOq/VPVA45ezAQyK0x4SH2edBbz/vvVbXHaZrVG99964rSKkMOgQtwE58jUAf23pARGZCGAiABQVFUVpE4kIl7f41Kcs2f3oo8BVV8VqEiEFQyLEQkReBdCvhYfuVNXnGp9zJ4ADAP7c0jlUdTKAyQBQVlbWwmAIku+MGgUceSSwfj3whz8A114bt0WEFA6JEAtVPTfd4yLyZQATAHxKtaUJQaQQaNcOuP9+O37+83FbQ0hhkQixSIeIXAjg3wGcpaofxW0PiZdrronbAkIKk8QnuAHcD6A7gFdEZL6I/D5ugwghpNBIvGehqsPitoEQQgqdfPAsCCGExAzFghBCSEYoFoQQQjJCsSCEEJIRigUhhJCMUCwIIYRkRNpiQ7SI1ANY7fHlvQFsDtCcfIA/c2HAn7kw8PMzH6OqfVp6oE2KhR9EpFJVy+K2I0r4MxcG/JkLg7B+ZoahCCGEZIRiQQghJCMUi0OZHLcBMcCfuTDgz1wYhPIzM2dBCCEkI/QsCCGEZIRiQQghJCMUixRE5EIRWSYiK0Xke3HbEzYi8rCI1InIwrhtiQoRGSwir4vIEhFZJCK3xm1T2IhIZxF5W0QWNP7M98RtUxSISHsRmSciU+O2JQpEpFZE3m3c+1MZ+PmZszBEpD2A5QDOA7AWwFwA16jq4lgNCxERORPATgBTVPX4uO2JAhHpD6C/qlaLSHcAVQAub+P/zwKgq6ruFJGOACoA3Kqqs2M2LVRE5DsAygD0UNUJcdsTNiJSC6BMVUNpQqRn0UQ5gJWq+p6q7gPwBIDLYrYpVFT1TQBb4rYjSlR1g6pWN36+A8ASAAPjtSpc1NjZ+GXHxo82fZcoIoMAXAzgwbhtaStQLJoYCGBNytdr0cYvIoWOiAwBcDKAOTGbEjqNIZn5AOoAvKKqbf1n/iWAOwA0xGxHlCiAf4lIlYhMDPrkFIsmpIXvtem7r0JGRLoBeBrAt1V1e9z2hI2qHlTV0QAGASgXkTYbdhSRCQDqVLUqblsiZpyqngLgIgA3NYaZA4Ni0cRaAINTvh4EYH1MtpAQaYzbPw3gz6r6TNz2RImqfghgOoAL47UkVMYBuLQxhv8EgHNE5E/xmhQ+qrq+8VgH4FlYaD0wKBZNzAVwrIgUi0gnAFcDeD5mm0jANCZ7HwKwRFV/Hrc9USAifUSkZ+PnXQCcC2BprEaFiKpOUtVBqjoE9nf8mqp+MWazQkVEujYWbEBEugI4H0CgVY4Ui0ZU9QCAmwH8E5b0/JuqLorXqnARkccBvAWgVETWish1cdsUAeMAfAl2tzm/8ePTcRsVMv0BvC4i78Buil5R1YIoJy0gjgZQISILALwN4EVVfTnIN2DpLCGEkIzQsyCEEJIRigUhhJCMUCwIIYRkhGJBCCEkIxQLQgghGaFYEBIRItJTRL4Ztx2EeIFiQUh09ARAsSB5CcWCkOj4MYChjY2A/xO3MYTkApvyCImIxim3UwtldwhpW9CzIIQQkhGKBSGEkIxQLAiJjh0AusdtBCFeoFgQEhGq+gGAmSKykAlukm8wwU0IISQj9CwIIYRkhGJBCCEkIxQLQgghGaFYEEIIyQjFghBCSEYoFoQQQjJCsSCEEJKR/wdXPHW5j5j9GAAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"def create_model_ode():\n",
"\n",
" m = ConcreteModel()\n",
"\n",
" # Declare time\n",
" m.t = ContinuousSet(bounds=(0.0, 5.0))\n",
"\n",
" # Declare parameter - acceleration due to gravity\n",
" m.g = Param(initialize=9.81) # m/s^2\n",
"\n",
" # Declare variables indexed over time\n",
" m.x = Var(m.t) # horizontal position\n",
" m.y = Var(m.t) # vertical position\n",
" m.u = Var(m.t) # horizontal velocity\n",
" m.v = Var(m.t) # vertical velocity\n",
" m.T = Var(m.t) # tension\n",
"\n",
" # Declare derivative variables\n",
" m.dx = DerivativeVar(m.x) # with respect to t is implied\n",
" m.dy = DerivativeVar(m.y)\n",
" m.du = DerivativeVar(m.u)\n",
" m.dv = DerivativeVar(m.v)\n",
" m.dT = DerivativeVar(m.T)\n",
"\n",
" # Declare differential equations\n",
" def _dx_eqn(m, t):\n",
" return m.dx[t] == m.u[t]\n",
" m.dx_eqn = Constraint(m.t, rule=_dx_eqn)\n",
"\n",
" def _dy_eqn(m, t):\n",
" return m.dy[t] == m.v[t]\n",
" m.dy_eqn = Constraint(m.t, rule=_dy_eqn)\n",
"\n",
" def _du_eqn(m, t):\n",
" return m.du[t] == -m.T[t]*m.x[t]\n",
" m.du_eqn = Constraint(m.t, rule=_du_eqn)\n",
"\n",
" def _dv_eqn(m, t):\n",
" return m.dv[t] == m.g -m.T[t]*m.y[t]\n",
" m.dv_eqn = Constraint(m.t, rule=_dv_eqn)\n",
"\n",
" def _dT_eqn(m, t):\n",
" return m.dT[t] == 4*m.T[t]*(m.x[t]*m.u[t] + m.y[t]*m.v[t]) + 3*m.g*m.v[t]\n",
" m.dT_eqn = Constraint(m.t, rule=_dT_eqn)\n",
"\n",
" # Specify initial conditions\n",
" m.x[0] = 0\n",
" m.y[0] = 1\n",
" m.u[0] = 1\n",
" m.v[0] = 0\n",
" m.T[0] = 1 + m.g\n",
" \n",
" return m\n",
"\n",
"ode = create_model_ode()\n",
"\n",
"# Specify integrator options\n",
"int_ops = {'print_stats':True,\"abstol\":1E-6,\"reltol\":1E-4}\n",
"\n",
"# Solve DAEs\n",
"sim = Simulator(ode, package='casadi')\n",
"tsim, profiles = sim.simulate(numpoints=100, integrator='idas',integrator_options=int_ops)\n",
"\n",
"# Plot solution\n",
"results = plot_results(sim, tsim, profiles)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.2 Formulation 2: Pure ODE Model](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.2-Formulation-2:-Pure-ODE-Model)",
"section": "2.4.3.2 Formulation 2: Pure ODE Model"
}
},
"source": [
"**Discussion**\n",
"* Are all of the algebraic constraints in the original formulation satisfied?"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.3 Formulation 3: Index-1 DAE Model](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.3-Formulation-3:-Index-1-DAE-Model)",
"section": "2.4.3.3 Formulation 3: Index-1 DAE Model"
}
},
"source": [
"### 2.4.3.3 Formulation 3: Index-1 DAE Model\n",
"\n",
"$$\\begin{align}\n",
"\\frac{d y}{dt} &= v \\\\\n",
"\\frac{d v}{dt} &= g - Ty \\\\\n",
" & x^2 + y^2 = 1 \\\\\n",
" & 2 x u + 2 y v = 0 \\\\\n",
" & (u^2 + v^2) - T (x^2 + y^2) + g y = 0\n",
"\\end{align}$$\n",
"\n",
"(This reformulation is NOT unique... could have written $\\frac{dx}{dt}$ and $\\frac{du}{dt}$ instead.)\n",
"\n",
"Consistent initial conditions:\n",
"1. Specify $y(0)$ and $v(0)$.\n",
"2. Solve for $x(0)$, $u(0)$, and $T(0)$"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.3 Formulation 3: Index-1 DAE Model](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.3-Formulation-3:-Index-1-DAE-Model)",
"section": "2.4.3.3 Formulation 3: Index-1 DAE Model"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Constraint 1:\n",
"0\n",
"\n",
"Constraint 2:\n",
"0\n",
"\n",
"Constraint 3:\n",
"0.0\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"The residual routine or the linear setup or solve routine had a recoverable error, but IDACalcIC was unable to recover.\n"
]
},
{
"ename": "RuntimeError",
"evalue": ".../casadi/interfaces/sundials/idas_interface.cpp:591: IDACalcIC returned \"IDA_NO_RECOVERY\". Consult IDAS documentation.",
"output_type": "error",
"traceback": [
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
"\u001b[0;31mRuntimeError\u001b[0m Traceback (most recent call last)",
"\u001b[0;32m\u001b[0m in \u001b[0;36m\u001b[0;34m\u001b[0m\n\u001b[1;32m 77\u001b[0m \u001b[0;31m# Solve DAEs\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 78\u001b[0m \u001b[0msim\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mSimulator\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mindex1\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mpackage\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;34m'casadi'\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m---> 79\u001b[0;31m \u001b[0mtsim\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mprofiles\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0msim\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0msimulate\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mnumpoints\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;36m100\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mintegrator\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;34m'idas'\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0mintegrator_options\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mint_ops\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 80\u001b[0m \u001b[0;31m# tsim, profiles = sim.simulate(numpoints=100, integrator='collocation')\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/pyomo/dae/simulator.py\u001b[0m in \u001b[0;36msimulate\u001b[0;34m(self, numpoints, tstep, integrator, varying_inputs, initcon, integrator_options)\u001b[0m\n\u001b[1;32m 905\u001b[0m \u001b[0;32melse\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 906\u001b[0m \u001b[0mtsim\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mprofile\u001b[0m \u001b[0;34m=\u001b[0m\u001b[0;31m \u001b[0m\u001b[0;31m\\\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 907\u001b[0;31m self._simulate_with_casadi_no_inputs(initcon, tsim,\n\u001b[0m\u001b[1;32m 908\u001b[0m \u001b[0mintegrator\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 909\u001b[0m integrator_options)\n",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/pyomo/dae/simulator.py\u001b[0m in \u001b[0;36m_simulate_with_casadi_no_inputs\u001b[0;34m(self, initcon, tsim, integrator, integrator_options)\u001b[0m\n\u001b[1;32m 967\u001b[0m \u001b[0mintegrator_options\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;34m'output_t0'\u001b[0m\u001b[0;34m]\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0;32mTrue\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 968\u001b[0m \u001b[0mF\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mcasadi\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mintegrator\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m'F'\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mintegrator\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mdae\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mintegrator_options\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 969\u001b[0;31m \u001b[0msol\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mF\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mx0\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0minitcon\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 970\u001b[0m \u001b[0mprofile\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0msol\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;34m'xf'\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mfull\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mT\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 971\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/casadi/casadi.py\u001b[0m in \u001b[0;36m__call__\u001b[0;34m(self, *args, **kwargs)\u001b[0m\n\u001b[1;32m 13451\u001b[0m \u001b[0;32melse\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 13452\u001b[0m \u001b[0;31m# Named inputs -> return dictionary\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m> 13453\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mcall\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mkwargs\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 13454\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 13455\u001b[0m \u001b[0;32mdef\u001b[0m \u001b[0mbuffer\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/casadi/casadi.py\u001b[0m in \u001b[0;36mcall\u001b[0;34m(self, *args)\u001b[0m\n\u001b[1;32m 12322\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 12323\u001b[0m \"\"\"\n\u001b[0;32m> 12324\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0m_casadi\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mFunction_call\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m*\u001b[0m\u001b[0margs\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 12325\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 12326\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;31mRuntimeError\u001b[0m: .../casadi/interfaces/sundials/idas_interface.cpp:591: IDACalcIC returned \"IDA_NO_RECOVERY\". Consult IDAS documentation."
]
}
],
"source": [
"def create_model_index1():\n",
"\n",
" m = ConcreteModel()\n",
"\n",
" # Declare time\n",
" m.t = ContinuousSet(bounds=(0, 5))\n",
"\n",
" # Declare parameter - acceleration due to gravity\n",
" m.g = Param(initialize=9.81) # m/s^2\n",
"\n",
" # Declare variables indexed over time\n",
" m.x = Var(m.t) # horizontal position\n",
" m.y = Var(m.t) # vertical position\n",
" m.u = Var(m.t) # horizontal velocity\n",
" m.v = Var(m.t) # vertical velocity\n",
" m.T = Var(m.t) # tension\n",
"\n",
" # Declare derivative variables\n",
" m.dy = DerivativeVar(m.y)\n",
" m.dv = DerivativeVar(m.v)\n",
"\n",
" # Declare differential equations\n",
" def _dy_eqn(m, t):\n",
" return m.dy[t] == m.v[t]\n",
" m.dy_eqn = Constraint(m.t, rule=_dy_eqn)\n",
"\n",
" def _dv_eqn(m, t):\n",
" return m.dv[t] == m.g - m.T[t]*m.y[t]\n",
" m.dv_eqn = Constraint(m.t, rule=_dv_eqn)\n",
"\n",
" # Declare algebraic equations\n",
" def _alg_eqn1(m, t):\n",
" return m.x[t]**2 + m.y[t]**2 == 1\n",
" m.alg_eqn1 = Constraint(m.t, rule=_alg_eqn1)\n",
"\n",
" def _alg_eqn2(m, t):\n",
" return m.x[t]*m.u[t] + m.y[t]*m.v[t] == 0\n",
" m.alg_eqn2 = Constraint(m.t, rule=_alg_eqn2)\n",
"\n",
" def _alg_eqn3(m, t):\n",
" return m.u[t]**2 + m.v[t]**2 - m.T[t]*(m.x[t]**2 + m.y[t]**2) + m.g*m.y[t] == 0\n",
" m.alg_eqn3 = Constraint(m.t, rule=_alg_eqn3)\n",
"\n",
" # Specify initial conditions\n",
" m.x[0] = 0\n",
" m.y[0] = 1\n",
" m.u[0] = 1\n",
" m.v[0] = 0\n",
" m.T[0] = 1 + m.g\n",
" \n",
" return m\n",
"\n",
"def index1_check_constraints(m):\n",
" \"\"\" Check if the three constraints are feasible.\n",
" \"\"\"\n",
" \n",
" print(\"Constraint 1:\")\n",
" r1 = m.x[0]()**2 + m.y[0]()**2 - 1\n",
" print(r1)\n",
" \n",
" print(\"\\nConstraint 2:\")\n",
" r2 = m.x[0]()*m.u[0]() + m.y[0]()*m.v[0]()\n",
" print(r2)\n",
" \n",
" print(\"\\nConstraint 3:\")\n",
" r3 = m.u[0]()**2 + m.v[0]()**2 - m.T[0]() + m.g*m.y[0]()\n",
" print(r3)\n",
"\n",
"index1 = create_model_index1()\n",
"\n",
"# Check initial condition\n",
"index1_check_constraints(index1)\n",
"\n",
"# Specify integrator options\n",
"int_ops = {'print_stats':True,\"abstol\":1E-6,\"reltol\":1E-4}\n",
"\n",
"# Solve DAEs\n",
"sim = Simulator(index1, package='casadi')\n",
"tsim, profiles = sim.simulate(numpoints=100, integrator='idas',integrator_options=int_ops)\n",
"# tsim, profiles = sim.simulate(numpoints=100, integrator='collocation')"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.3 Formulation 3: Index-1 DAE Model](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.3-Formulation-3:-Index-1-DAE-Model)",
"section": "2.4.3.3 Formulation 3: Index-1 DAE Model"
}
},
"source": [
"What happened? Point singularity at $x=0$.\n",
"\n",
"Let's try $x=0.1$ as the initial point."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.3 Formulation 3: Index-1 DAE Model](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.3-Formulation-3:-Index-1-DAE-Model)",
"section": "2.4.3.3 Formulation 3: Index-1 DAE Model"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Constraint 1:\n",
"0.010000000000000009\n",
"\n",
"Constraint 2:\n",
"0.1\n",
"\n",
"Constraint 3:\n",
"0.0\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"The residual routine or the linear setup or solve routine had a recoverable error, but IDACalcIC was unable to recover.\n"
]
},
{
"ename": "RuntimeError",
"evalue": ".../casadi/interfaces/sundials/idas_interface.cpp:591: IDACalcIC returned \"IDA_NO_RECOVERY\". Consult IDAS documentation.",
"output_type": "error",
"traceback": [
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
"\u001b[0;31mRuntimeError\u001b[0m Traceback (most recent call last)",
"\u001b[0;32m\u001b[0m in \u001b[0;36m\u001b[0;34m\u001b[0m\n\u001b[1;32m 17\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 18\u001b[0m \u001b[0;31m# Simulator\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m---> 19\u001b[0;31m \u001b[0mtsim\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mprofiles\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0msim\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0msimulate\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mnumpoints\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;36m100\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mintegrator\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;34m'idas'\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0mintegrator_options\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mint_ops\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/pyomo/dae/simulator.py\u001b[0m in \u001b[0;36msimulate\u001b[0;34m(self, numpoints, tstep, integrator, varying_inputs, initcon, integrator_options)\u001b[0m\n\u001b[1;32m 905\u001b[0m \u001b[0;32melse\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 906\u001b[0m \u001b[0mtsim\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mprofile\u001b[0m \u001b[0;34m=\u001b[0m\u001b[0;31m \u001b[0m\u001b[0;31m\\\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 907\u001b[0;31m self._simulate_with_casadi_no_inputs(initcon, tsim,\n\u001b[0m\u001b[1;32m 908\u001b[0m \u001b[0mintegrator\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 909\u001b[0m integrator_options)\n",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/pyomo/dae/simulator.py\u001b[0m in \u001b[0;36m_simulate_with_casadi_no_inputs\u001b[0;34m(self, initcon, tsim, integrator, integrator_options)\u001b[0m\n\u001b[1;32m 967\u001b[0m \u001b[0mintegrator_options\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;34m'output_t0'\u001b[0m\u001b[0;34m]\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0;32mTrue\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 968\u001b[0m \u001b[0mF\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mcasadi\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mintegrator\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m'F'\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mintegrator\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mdae\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mintegrator_options\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 969\u001b[0;31m \u001b[0msol\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mF\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mx0\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0minitcon\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 970\u001b[0m \u001b[0mprofile\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0msol\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;34m'xf'\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mfull\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mT\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 971\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/casadi/casadi.py\u001b[0m in \u001b[0;36m__call__\u001b[0;34m(self, *args, **kwargs)\u001b[0m\n\u001b[1;32m 13451\u001b[0m \u001b[0;32melse\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 13452\u001b[0m \u001b[0;31m# Named inputs -> return dictionary\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m> 13453\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mcall\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mkwargs\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 13454\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 13455\u001b[0m \u001b[0;32mdef\u001b[0m \u001b[0mbuffer\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/casadi/casadi.py\u001b[0m in \u001b[0;36mcall\u001b[0;34m(self, *args)\u001b[0m\n\u001b[1;32m 12322\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 12323\u001b[0m \"\"\"\n\u001b[0;32m> 12324\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0m_casadi\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mFunction_call\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m*\u001b[0m\u001b[0margs\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 12325\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 12326\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;31mRuntimeError\u001b[0m: .../casadi/interfaces/sundials/idas_interface.cpp:591: IDACalcIC returned \"IDA_NO_RECOVERY\". Consult IDAS documentation."
]
}
],
"source": [
"index1_again = create_model_index1()\n",
"\n",
"# Specify alternative initial conditions\n",
"small_number = 0.1\n",
"\n",
"index1_again.x[0] = small_number\n",
"index1_again.y[0] = 1\n",
"index1_again.u[0] = 1\n",
"index1_again.v[0] = 0\n",
"index1_again.T[0] = 1 + index1_again.g\n",
"\n",
"# Check initial condition\n",
"index1_check_constraints(index1_again)\n",
"\n",
"# Solve DAEs\n",
"sim = Simulator(index1_again, package='casadi')\n",
"\n",
"# Simulator\n",
"tsim, profiles = sim.simulate(numpoints=100, integrator='idas',integrator_options=int_ops)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.3 Formulation 3: Index-1 DAE Model](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.3-Formulation-3:-Index-1-DAE-Model)",
"section": "2.4.3.3 Formulation 3: Index-1 DAE Model"
}
},
"source": [
"Our initial point does not satisfy the algebraic constraints! We need a consistent initial point."
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.3 Formulation 3: Index-1 DAE Model](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.3-Formulation-3:-Index-1-DAE-Model)",
"section": "2.4.3.3 Formulation 3: Index-1 DAE Model"
}
},
"source": [
"Given $x = \\epsilon$, solve $x^2 + y^2 = 1$ for $y$:\n",
"\n",
"$$ y = \\sqrt{1^2 - \\epsilon^2}$$\n",
"\n",
"Then, assume $u = 1$ and solve $2 x u + 2 y v = 0$ for $v$:\n",
"\n",
"$$v = \\frac{-x u}{y}$$\n",
"\n",
"Finally, we can solve $(u^2 + v^2) - T (x^2 + y^2) + g y = 0$ for $T$:\n",
"\n",
"$$\n",
"T = \\frac{(u^2 + v^2) + gy}{x^2 + y^2} = \\frac{(u^2 + v^2) + gy}{1}\n",
"$$"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.3 Formulation 3: Index-1 DAE Model](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.3-Formulation-3:-Index-1-DAE-Model)",
"section": "2.4.3.3 Formulation 3: Index-1 DAE Model"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Constraint 1:\n",
"0.0\n",
"\n",
"Constraint 2:\n",
"0.0\n",
"\n",
"Constraint 3:\n",
"0.0\n"
]
},
{
"name": "stderr",
"output_type": "stream",
"text": [
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"psetup failed: .../casadi/interfaces/sundials/idas_interface.cpp:852: Linear solve failed\n",
"The residual routine or the linear setup or solve routine had a recoverable error, but IDACalcIC was unable to recover.\n"
]
},
{
"ename": "RuntimeError",
"evalue": ".../casadi/interfaces/sundials/idas_interface.cpp:591: IDACalcIC returned \"IDA_NO_RECOVERY\". Consult IDAS documentation.",
"output_type": "error",
"traceback": [
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
"\u001b[0;31mRuntimeError\u001b[0m Traceback (most recent call last)",
"\u001b[0;32m\u001b[0m in \u001b[0;36m\u001b[0;34m\u001b[0m\n\u001b[1;32m 22\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 23\u001b[0m \u001b[0;31m# Simulator\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m---> 24\u001b[0;31m \u001b[0mtsim\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mprofiles\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0msim\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0msimulate\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mnumpoints\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;36m20\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mintegrator\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0;34m'idas'\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0mintegrator_options\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mint_ops2\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/pyomo/dae/simulator.py\u001b[0m in \u001b[0;36msimulate\u001b[0;34m(self, numpoints, tstep, integrator, varying_inputs, initcon, integrator_options)\u001b[0m\n\u001b[1;32m 905\u001b[0m \u001b[0;32melse\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 906\u001b[0m \u001b[0mtsim\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mprofile\u001b[0m \u001b[0;34m=\u001b[0m\u001b[0;31m \u001b[0m\u001b[0;31m\\\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 907\u001b[0;31m self._simulate_with_casadi_no_inputs(initcon, tsim,\n\u001b[0m\u001b[1;32m 908\u001b[0m \u001b[0mintegrator\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 909\u001b[0m integrator_options)\n",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/pyomo/dae/simulator.py\u001b[0m in \u001b[0;36m_simulate_with_casadi_no_inputs\u001b[0;34m(self, initcon, tsim, integrator, integrator_options)\u001b[0m\n\u001b[1;32m 967\u001b[0m \u001b[0mintegrator_options\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;34m'output_t0'\u001b[0m\u001b[0;34m]\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0;32mTrue\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 968\u001b[0m \u001b[0mF\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mcasadi\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mintegrator\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m'F'\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mintegrator\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mdae\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mintegrator_options\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 969\u001b[0;31m \u001b[0msol\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mF\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mx0\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0minitcon\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 970\u001b[0m \u001b[0mprofile\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0msol\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;34m'xf'\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mfull\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mT\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 971\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/casadi/casadi.py\u001b[0m in \u001b[0;36m__call__\u001b[0;34m(self, *args, **kwargs)\u001b[0m\n\u001b[1;32m 13451\u001b[0m \u001b[0;32melse\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 13452\u001b[0m \u001b[0;31m# Named inputs -> return dictionary\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m> 13453\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mcall\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mkwargs\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 13454\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 13455\u001b[0m \u001b[0;32mdef\u001b[0m \u001b[0mbuffer\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;32m/anaconda3/envs/spring2021/lib/python3.8/site-packages/casadi/casadi.py\u001b[0m in \u001b[0;36mcall\u001b[0;34m(self, *args)\u001b[0m\n\u001b[1;32m 12322\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 12323\u001b[0m \"\"\"\n\u001b[0;32m> 12324\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0m_casadi\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mFunction_call\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m*\u001b[0m\u001b[0margs\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 12325\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 12326\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n",
"\u001b[0;31mRuntimeError\u001b[0m: .../casadi/interfaces/sundials/idas_interface.cpp:591: IDACalcIC returned \"IDA_NO_RECOVERY\". Consult IDAS documentation."
]
}
],
"source": [
"index1_take_two = create_model_index1()\n",
"\n",
"# Specify alternative initial conditions\n",
"small_number = 0.1\n",
"\n",
"index1_take_two.x[0] = small_number\n",
"index1_take_two.y[0] = np.sqrt(1 - small_number**2)\n",
"index1_take_two.u[0] = 1\n",
"index1_take_two.v[0] = -index1_take_two.x[0]()*index1_take_two.u[0]()/index1_take_two.y[0]()\n",
"index1_take_two.T[0] = (index1_take_two.u[0]()**2 + index1_take_two.v[0]()**2\n",
" + index1_take_two.g*index1_take_two.y[0]())\n",
"\n",
"# Check initial condition\n",
"index1_check_constraints(index1_take_two)\n",
"\n",
"# Solve DAEs\n",
"sim = Simulator(index1_take_two, package='casadi')\n",
"\n",
"# Specify integrator options\n",
"int_ops2 = {'print_stats':True,\"abstol\":1E-6,\"reltol\":1E-4,\n",
" \"verbose\":False,\"calc_ic\":True}\n",
"\n",
"# Simulator\n",
"tsim, profiles = sim.simulate(numpoints=20, integrator='idas',integrator_options=int_ops2)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.4 Formulation 4: Index-1 DAE Model](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.4-Formulation-4:-Index-1-DAE-Model)",
"section": "2.4.3.4 Formulation 4: Index-1 DAE Model"
}
},
"source": [
"### 2.4.3.4 Formulation 4: Index-1 DAE Model\n",
"\n",
"$$\\begin{align}\n",
"\\frac{d x}{dt} &= u \\\\\n",
"\\frac{d y}{dt} &= v \\\\\n",
"\\frac{d u}{dt} &= -T x \\\\\n",
"\\frac{d v}{dt} &= g - Ty \\\\\n",
"0 &= (u^2 + v^2) - T (x^2 + y^2) + g y\n",
"\\end{align}$$\n",
"\n",
"Consistent initial conditions:\n",
"1. Specify $x(0)$, $u(0)$, $y(0)$, and $v(0)$.\n",
"2. Solve for $T(0)$"
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.4 Formulation 4: Index-1 DAE Model](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.4-Formulation-4:-Index-1-DAE-Model)",
"section": "2.4.3.4 Formulation 4: Index-1 DAE Model"
}
},
"outputs": [],
"source": [
"def create_model_index1_b():\n",
"\n",
" m = ConcreteModel()\n",
" \n",
" # Declare time\n",
" m.t = ContinuousSet(bounds=(0.0, 5))\n",
"\n",
" # Declare parameter - acceleration due to gravity\n",
" m.g = Param(initialize=9.81) # m/s^2\n",
"\n",
" # Declare variables indexed over time\n",
" m.x = Var(m.t) # horizontal position\n",
" m.y = Var(m.t) # vertical position\n",
" m.u = Var(m.t) # horizontal velocity\n",
" m.v = Var(m.t) # vertical velocity\n",
" m.T = Var(m.t) # tension\n",
"\n",
" # Declare derivative variables\n",
" m.dx = DerivativeVar(m.x) # with respect to t is implied\n",
" m.dy = DerivativeVar(m.y)\n",
" m.du = DerivativeVar(m.u)\n",
" m.dv = DerivativeVar(m.v)\n",
"\n",
" # Declare differential equations\n",
" def _dx_eqn(m, t):\n",
" return m.dx[t] == m.u[t]\n",
" m.dx_eqn = Constraint(m.t, rule=_dx_eqn)\n",
"\n",
" def _dy_eqn(m, t):\n",
" return m.dy[t] == m.v[t]\n",
" m.dy_eqn = Constraint(m.t, rule=_dy_eqn)\n",
"\n",
" def _du_eqn(m, t):\n",
" return m.du[t] == -m.T[t]*m.x[t]\n",
" m.du_eqn = Constraint(m.t, rule=_du_eqn)\n",
"\n",
" def _dv_eqn(m, t):\n",
" return m.dv[t] == m.g -m.T[t]*m.y[t]\n",
" m.dv_eqn = Constraint(m.t, rule=_dv_eqn)\n",
"\n",
" def _alg_eqn3(m, t):\n",
" return m.u[t]**2 + m.v[t]**2 - m.T[t]*(m.x[t]**2 + m.y[t]**2) + m.g*m.y[t] == 0\n",
" m.alg_eqn3 = Constraint(m.t, rule=_alg_eqn3)\n",
"\n",
" # Specify initial conditions\n",
" m.x[0] = 0\n",
" m.y[0] = 1\n",
" m.u[0] = 1\n",
" m.v[0] = 0\n",
" m.T[0] = 1 + m.g\n",
" \n",
" return m"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.4.3.4 Formulation 4: Index-1 DAE Model](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.3.4-Formulation-4:-Index-1-DAE-Model)",
"section": "2.4.3.4 Formulation 4: Index-1 DAE Model"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"FORWARD INTEGRATION:\n",
"Number of steps taken by SUNDIALS: 379\n",
"Number of calls to the user’s f function: 485\n",
"Number of calls made to the linear solver setup function: 31\n",
"Number of error test failures: 3\n",
"Method order used on the last internal step: 5\n",
"Method order to be used on the next internal step: 5\n",
"Actual value of initial step size: 7.90569e-09\n",
"Step size taken on the last internal step: 0.0120795\n",
"Step size to be attempted on the next internal step: 0.0120795\n",
"Current internal time reached: 0.0120795\n",
"Number of nonlinear iterations performed: 483\n",
"Number of nonlinear convergence failures: 0\n",
"\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXAAAAEGCAYAAAB8Ys7jAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAABLvUlEQVR4nO3deXxU1d348c+ZLZPJvpINyAYhkJAAYQeVijvo4/JYtbW2anFfq63aam1t/WldHmvVx7q0tU9dsFZbRXFHZIcAAUIWlkD2fd9mP78/JokJBAjJTCYD5/168QozuXPv9+bM/d5zzz3nXCGlRFEURfE9Gm8HoCiKogyPSuCKoig+SiVwRVEUH6USuKIoio9SCVxRFMVH6UZzY5GRkTIxMXE0N6koiuLztm/f3iCljDry/VFN4ImJieTm5o7mJhVFUXyeEKJ0sPdVE4qiKIqPUglcURTFR6kEriiK4qNUAlcURfFRKoEriqL4KJXAFUVRfJRK4IqiKD5qVPuBD9fh3Q001XQSPTGYqAlB+Pn7RNjD1tlqob60nabqTgLD/IhODCYkyh8hhLdD8xi7zUFjZScN5e3YLI6+stb7ab0dmsdIKWlvMtNQ3kFLbRdBEUbGJQUTFG48pcvaarbTVNVJQ0UHDpuTcUnBRI0PQqs/deuTli4bfia929frE5mwbG8je9ZW9r2OmhDE/EtTGJ8e7sWo3MvplBRtrGbbJ4foaLIc9Xs/k46pC+PIuSgRg9Enim1IWmq72PCvA5TmNyKdA+emFwJikkNYcHkqMckhXorQ/RwOJ/nfVLL908N0t9uO+r0p2EDGmfHMOHcCOv2pcwKrL29n478OUFHUfNTvNDpB/KRQFlyeSmRCkBei8wy71UHel2Xs+KyM5XdkEZsa6tb1i9F8oENOTo4c7kjM7g4r9aXt1JW2UbixmrYGM8nZUSy8IpXgSH83Rzq6qg+2sm7lPurL2olJDiF1VjRRE4OIiAugvclM3eF2youaOJBbhynEwILLUpk8Z5xP19Is3XZyPz7E7jUVaPUapi2OJybJVevWGbTUlbZRe8hV1p0tFqbMj2H+pamYgg3eDn1ESvMbWf/P/bTUdpEwJYyUGVFEjg8iLMZEa303tYfaKNvbyOE9jQRH+bP4ykkkZkZ6O+wR6Wqzsvk/ByncWI3RpCfjzHiiJwYROT4IjVZQW9JGTUkrhZuqsXTZyTwrnjnLk336SltKyf5ttWz64CAdzRaSZ0Sx8PLh5yohxHYpZc5R7/tKAu/PbnOw66tycj85DMD5KzKZmBEx4vV6w47PS9n0/kECQv1YcFkKk2YfOzHXHGpl3Tv7qCttJ2VGFEuvn+qTNbTW+i4+fH4XbQ3dpC+IZd4lKcdMzFazndxPDrPrq3L0Ri0X3ZpFbIrv1callGz64CA7Py8jdJyJhVekMjEj4phlXV7YxLqV+2iu6WLa4jjOuDoNjcb3Ttj15e2s+tMuzB02Mr+XwOwLE4/ZlGDutLH5PyXsXVdJQIgfy+/IIiI+cJQjHjmHw8naN4sp3FhN1IQgFl6RSvzksBGt85RK4L3am8ysfnkPjRUdfO+6dNLmxrht3Z4mnZKN7x8g78tyUmdFs+TaKUNqGpFOyc4vytj0wUHi00K58ObpGHyoplJf1s5Hf8pDOuHCWzKHfEnZVN3JJy/tprPFwvk3+dYJ2+Fwsub/iijeXEPGGfEsunISWt2J23sddidbPixh5+dlpMyI4pzrp/lUO3FFUROfvLwHP38dy24fejKuPdTG6pd3Y7c5WXZ7lk81n9ksDj57NZ/S/EZyLkxkzrIkhBtOvKdkAgewdtv55OXdVBa3sPCKVLKXTnDr+j3B4XCy5u9FFG+pIXNJAov/e9JJF3Lx5mq++nsRkQmBLLs9yyeaFvoOaJOOi+/MJiwm4KQ+39Vm5aM/5dFU2ekzJ2ybxcGnr+RTtreRuRcnMeuCxJNu+sr7sowN7x0gYUoYF9yc6RP3QA5sr+OLv+wldJyJ5XdkERhmPKnPtzV08+Ef8+hstXDBTZlMmDb2T9jmDhsfvbCL+tI2zrg6jYwz4t227mMlcN85nR+DoefsnjIjig3vHSD/28oTf8iLpJR88w9X8p57cTKLrzz55A2QNi+WC2/JpLm6kw+fz8NqtnsgWvepPdzGxy/uJijcyOX355x08gbXzb1L751JbGoIX/6tgAPb6zwQqfs4HU4+fy2f8oJGlvxwCjkXJg3rvkX20gmc/eN0Kve18PGLu3HYnB6I1n3K9jby+et7GZcUzKU/m3nSyRsgONKfy+6fRUi0iY9f2k1F8dE3PscSu9XBxy/torGig/NvynRr8j4en0/gADq9lnNvnMbEzAi+fbuYw7sbvB3SMeV+cpiiTTXMviiRnAtPvjbWX2JmJBfcnElTVSefvZKPwzE2D+zW+m4+fnEXphADl9w9g8Awv2Gvq/eEHZMUzJd/K6CmpNWNkbqPlJJvV+7n8J5GzrhqMlMXxY1ofVPmxXL2delU7W/h638UMppXziejvqydT1/JJzwugGW3ZWEMGH7XOVOwgf+6ZwYh0SZWv7yHpqpON0bqPk6n5Iu/FFBzqI1zrp9KcvZR03Z7zCmRwAE0Wg3n3jCNyPFBfPZaPnWlbd4O6ShFm6rZ+tEhpsyLYfayJLesc8K0CM66Jo2ygia+fat4zB3Y5g4bq17YhdMp3dbUozNoufCW6QSE+vHxS7tpqetyQ6TuteOzUvZ+W8nM8yaQcWaCW9aZNjeGuRcns29LLVs/OuSWdbpTe5OZVS/uws+kY/ntWW65N2MM0LPstulo9RpWvbiLrjarGyJ1HyklG/65n5K8ehZdMYmUmdGjuv1TJoEDGIw6LrptOsZAPate3E17k9nbIfWpKG5mzf8VkTAljLN+OMWtXQCnLopj1vkTKdhQzY7PBp333SscdiefvLyb9kYzF94yfVjNJsfiH2Rg+e1ZIGHVC7swdx7dn9pb9ufWsvnfJUyaPY55l6S4dd2zLphI+oJYcj85TOHGareueySsZjurXtiF3epk2R1ZBIQO/yrrSMGR/iy7bTrd7VY+fnEXNqvDbeseqT3fVLJ7TQVZZ48n6+zxo779UyqBA67uR7dnY7c6+PTPe7DbvF/Y7U1mPns1n5Bof86/KXNIPRBO1txLkpmUE83m/5RQurfR7esfjg3/3E/1gVa+d90U4tw8gAEgdJyJC2/JpL3RzBd/2YvT6f2rj8bKDr7+eyExySGc/aN0t/RA6E8IwZk/SCNhShjfvFVE7SHvX2lKKfn6jUKaqzs5/6YMIuLc3/UvemIw51w/jbqydta+OTauNKv2N7P+n/tJnB7JwstTvRLDKZfAAcLjAlh63VTqStv59p19Xi1su811InHanVxwc6bHBicIIVhybToRcYF88fpeWuu7PbKdoSraVM2etZVkLx3P5Nme6y0SmxrK4u9PpmxvE9tWebdZwdJlY/XLezAYdZx/U4bHuvxptRrOvXEaAcF+fPrKHq83K+z8vIyDO+uZf2kq46d4bnR0cnYUc5YlUbylhvy13u2s0NFs5tNX8gmJ8mfpT6a6/UQ9VCf8hgkh/iKEqBNC5Pd7L1wI8YUQYn/Pz5H1UveA5BlRzDp/IoUbqilYX+WVGKSUfPu2a+DN2T+e6tYmhMHo/bRccHMGAKv/vMdrl5r1Ze1882Yx8WmhzL/UvU0Ig5m2OK6vWeHQrnqPb28wsudGVnujmfNXZBAQ4r4mhMH4Bxq44OZMujtsfP56Pk4v3cAuL2hi878PkpoTTfY5nm9CyLkgkcTMCNa/u5/qAy0e395gHDYnq/+cj93q2UrZUAylivA34Pwj3nsA+EpKOQn4quf1mDPn4mQmTA3n23f2eaW3wt51VRRurCbnwsRRuzMdEmXinOun0VjZwZr/Kxr1q4/uDiurX96Df5Ce827MQKP1/EWeEIIzrp5M9MQgvvxrAc01o99bYdvHhyjNb2TRlZPcPt/FsURNCOKsa9KoLG5h0wcHR2Wb/bU1dPPZ6/mExQbwvWvTR2VqB6ERLP3JVIIijHz6Sj6drUfPG+Rp367cR93hNs7+cTrhsZ6tlJ3ICY8uKeW3QNMRb18CvNHz/zeA/3JvWO6h0QjOuWEagWF+fPrnPaNa2DUlrvlNJkyLcFuPk6GamBHB3OVJ7N9Wy+6vK0Ztu65+z3vparNy/k2Z+AeN3uAinV7L+TdlotFpWP3ynlHtF39odwPbPj7MlHkxZJw5Ov1/e02ZH0vGmfHkfVnO/tzaUduuzepg9Z/3IJ1wwc2ZozprpJ9JzwU3Z2I12/n0z/k47KN39bF3XSUF66uYef5EUmaMbo+TwQy3ejROSlkN0PPzmHsihFghhMgVQuTW14/+5a0xwFXYli47n706On2lO1strP7zHgLDjZxz/VSvzGEx6/xEkrIi2fCvA1TuG51BEJv/XUJFUTNnXjOZcYnBo7LN/oLCjZz30wxa6rr56o3R6SvdUtvFl3/ZS9SEIM68Js0rE4wt+u9JxKaE8PXfC2mo6PD49qSUrH2zmIaKDs65fiqh0SaPb/NIEfGBfO9H6dSUtLL+3f2jss2aQ618u3If46eGM/fi5FHZ5ol4/PpWSvmKlDJHSpkTFTV6Hdz7i0wIYsm1U6g+0MqG9w54dFsOu5PPXsnH2m3nwpszRzSQYSSERrD0x1MJifLns1fzPd6lcn9uLTu/KCPjjHjSF4xs0MpIJKSFseCyFEp21nu8S6XVbOeTl/eg0Wk4/6YMdAbvTCym1Wk4b0UGBn8dq1/e7fEulXu+qaB4Sw1zliV5dabESTnjmHHuBPK/raRgg2fvc3W1Wfn0z/kEhPhx7vXTxszEYsNN4LVCiFiAnp9je0wzMHlODFlnj2fPmgqP3dSUUvLtO/uoPtjK965N9/pMagZ/HRfekond5mT1y3uwWTxzU7OutK2v69yiKyd5ZBsnI+vs8UyaPY7N/ynhkIdG5faOvmup6eS8G6cRHOHdKY0DQvy44KZMOpotfP76Xo9daZYVNLLhnwdInB5JzgWJHtnGyZh3STIJU8JY+3Yx1Qc9c5/LbnWw+uU9mDttXHBTJsZA71TKBjPcBP4hcF3P/68D/uOecDxrwWUpjJ8azjdvFVOa7/6+0ttXl1KwvopZ509k0uxxbl//cITFBHDu9dNoKG/ns1fd31uhraGbVS/uxj/Q4Oo654E+7ifL1aVyCtETgvj81XxqDrn3wJZSsm7lPg7vbmDRlZNJ8GDXuZMRkxzCmdekUV7QxDf/cP8N7IYK1zD5sNgAzvFi17n+NFoN592YQVCYkY9f2uX2G9jSKfnyrwXUHGpl6Y+nEjVhbD1sYijdCN8GNgFpQogKIcQNwBPAOUKI/cA5Pa/HPI1Ww/krMoiID+DTV9073L5oUzVbPixxDXe+ZGy0j/VKnB7JGVenUZrfyNq33dcv3txp46M/7cJp7xl95+GucydDb9By0W1ZmEIMfPziblpq3TfcfufnZeSvrST7nAlMX+KeYfLuMnVhHLMvSqRoU41bh9u3N5lZ9addfVPDjqUpjI2BepbfmYVGI/joT7vc2llhw/sHOLiznoWXp5I6y/s3LY80lF4oV0spY6WUeillgpTydSllo5TybCnlpJ6fR/ZSGbMMRtcX0BigY9ULu9wyj0bp3sa+YfJLrnXvMHl3yTgj3jXcfn0V2z4+POL1Wc12Pvnf3bQ1dnPhLdO93p1qMKZgA8vvyAYJH/0pzy0HdvHmajZ94Or3vGAU+rgPx+xlSaQvdPWLz1878l5I3e1WVr2wC5vFwbLbs0Y0GZmnhESZWHZ7Ft09c+9Yu0feC2nn52Xs+rKc6UsSvDJMfii8f73rBa6nfWTjdEref2r7iGri+7bV8MlLuwmLC/DYMHl3mXtJMlPmxbBt1SE2vLf/qGdQDlV3u5X//M9Oag66LivjJoW6N1A3Ch1n4qLbptPVZuX9p7aPqCa+6+tyvvxbIfFpoSy9bmw0IQxGCMFZ16QxMTOCtW/vY8dnpcO+6mpr6Ob9p3fQWt/NBTdnev2+zvFETwzm/J9m0FjZyQfP7hj2CVtKyeZ/H2Tj+wdImRnNwv+eNCYrZXAKPNBhJJprXHNpWzrtnH9TBhOmntyk8b0T7cdNCuXCWzI98tRpd3M6Jevf3c+ebyqYlBPN2ddNPakh320N3Xz4fB4dzRbOu3EaSVne6Vl0smoOtfLxi7sBuOi26cQkDf0pL64DuoQdn5WSlBXJuTdM81qPk5PhsDn56o0C9ufWkXlmPIu+P/mkek80Vnbw4fN5OGxOLrp1+qgNUBqp0vxGPn01H2OAjuV3ZJ/U1aHT4WTtW8UUbKhm6qI4zrxmbDzK7pR9Is9IdbZY+OhPu2iu7mTuJclknT3+hLVoc4eNTR8coGBDtU8+m1JKyc7PXY9li00NYckPp5xwmL+UkpKd9ax9Zx9Ou5OLbvO9Z1O21Hbx0Z/y6Gq1sujKSaQvjDvhwdnRbGb9u/s5uLOeqYvjONPHnk0pnZKNHxwk74syJmZGcObVaQSFH/8BC9IpKdxUzYb3DqD307L8ziyPTFDlSfVl7ax6YRcOu5OzfjCFlJlRJ6xFt9R2sfbtYiqKml2PQ1s+vAdweIJK4Mdh6bbz1d8KOLSrgZAofxZcnkpSVuRRhedwOMlfW8m2VYewmh1knz2eeZem+NQB3V/xlhq+fbsYu9XJtDPjmXNR0qBdpBoqOlj/z31UFrcQER/AuTdkEB439tq8h6Krzcpnr+ZTtb+FiPhAFv734BMw2W0O8r4sZ/vqw0gnzFmexIxzJ4yZA/pk7V5TwcZ/HQAB2WePZ+b5Ewd9NFvvCOK60nZiU0JYev1Ur3eRHK62hm4+6XlmbkxyCAuvSB30+ZpWs53tqw+T92U5Or2GhVdMGvEDONxNJfAhKNvbyPp/7qe5povAMD8ixwcRNT4Qu81JfVk79WXtWLrsjE8PY+F/T/K5WslgutqsbF11iIJ1lWh1GiISAokcH0RQuB+NlZ3Ul7XTUtuFX4COeRcnM3VR3KjMb+JJUkoO7qhn4/sHaG80ExxpJGp8EBEJgVi77dSVtlNX1o7d4iB5RhQLL08lONI3k1h/7U1mNv/7IPu21qI3aolMCCQyIYiAUAMN5R3UHmqjvcmMKcTAgstSmTxnnM+esHo5nZKija4eYl1tVsJiTETEBxIeF4C500btoTbqy9tx2iVT5scw/9LUMfl8WZXAh8jhcFK8uYbK4mbqy9ppru1CoxFExAcSNTGIpOmRTMyI8Pkv9pEaKzso3FBNfXk7DRUdWLvtBIT6ET0xiHFJwUxbHO+1UaWeYrc5KFhfTdX+ZhoqOmit60ar0xA5PpDoxGBSsqOITxtzE22OWO2hNoo2VdNQ0UFjZQc2i4OgcCPjkoKJSQ4hfWGsTzw4+WRYzXby11ZSfbCVpqoO2hrM6PQaoiYGEZMUQsrMaMYljf70D0OlEvgw2awONEJ4bG7nsUhKibXb7hM3Zd3JZnGg0Qm0Pn6FcTKkU2K1OLw6Jao3WM12tHqNz5T1sRL46VVqw6D3gd4G7iaEOO2SNzCqM+qNFUIjTrvkDZwyVxi+cfpRFEVRjqISuKIoio9SCVxRFMVHqQSuKIrio1QCVxRF8VEqgSuKovgolcAVRVF8lErgiqIoPkolcEVRFB+lEriiKIqPUglcURTFR6kEriiK4qNUAlcURfFRKoEriqL4KJXAFUVRfJRK4IqiKD5qRAlcCHGPEGKvECJfCPG2EOL4j7tWFEVR3GbYCVwIEQ/cCeRIKTMALXCVuwJTFEVRjm+kTSg6wF8IoQNMQNXIQ1IURVGGYtgJXEpZCTwNlAHVQKuU8vMjlxNCrBBC5Aohcuvr64cfqaIoijLASJpQwoBLgCQgDggQQvzwyOWklK9IKXOklDlRUVHDj1RRFEUZYCRNKEuBQ1LKeimlDXgfWOCesBRFUZQTGUkCLwPmCSFMQggBnA0UuicsRVEU5URG0ga+BXgP2AHs6VnXK26KS1EURTkB3Ug+LKX8NfBrN8WiKIqinAQ1ElNRFMVHqQSuKIrio1QCVxRF8VEqgSuKovgolcAVRVF8lErgiqIoPkolcEVRFB81on7giqIo7mCz2aioqMBsNns7FK8yGo0kJCSg1+uHtLxK4IqieF1FRQVBQUEkJibimpnj9COlpLGxkYqKCpKSkob0GdWEoiiK15nNZiIiIk7b5A0ghCAiIuKkrkJUAlcUZUw4nZN3r5P9G6gEriiK4qNUAlcURfFRKoEriqIM4ptvviEkJIQLL7xwwPvt7e0sXLiQ7OxsHA4HAM899xxdXV19yzz99NOkpaXx9ttvD/jsypUrSU1NZdmyZW6JUSVwRVGUY1i8eDGffPLJgPe+/vpr4uPjycvLQ6vVAkcn8Pvuu4833niDl156acBnv//97/Paa6+5LT7VjVBRlDHlNx/tpaCqza3rnBoXzK+XTzvm77dt28YNN9zA1q1bcTgczJkzh1tuuWXQZVtaWoiOju57/fzzz1NVVcWSJUuIjIxkzZo1AMTExNDS0uLW/TiSqoErinLamz17NhdffDG/+tWv+PnPf84Pf/hDMjIyBl3W4XCg0XyXOu+8807i4uJYs2ZNX/IG0Gg0fU0snqJq4IqijCnHqyl70iOPPMLs2bMxGo08//zzrFu3btDl8vLySEhIOOH6IiMjqauro7m5mbCwMHeHC6gEriiKAkBTUxMdHR3YbLZjDqZZtGgR+/btY8eOHSdcn8lk4uqrryYpKYmVK1dy3nnnuTtk1YSiKIoCsGLFCh577DF+8IMf8Itf/GLQZdavX88NN9zAK68MfH57UFAQ7e3tA95rbm5m5cqVVFRUeCR5g0rgiqIo/P3vf0en03HNNdfwwAMPsG3bNpxO56DLpqWl0dTUNOC9FStWcMEFF7BkyZK+91pbW4mOjiYwMNBjcasErijKae9HP/oR77//PgBarZYtW7YMuFHZn8lkoq6ubsB7d9xxB0VFRQNuYtbV1REQEOC5oFEJXFEUZVAGg4H8/PyjBvIsXbqU5uZmsrKyjtnL5Omnn2bFihXccccdA95fuXIlt956q9tuagoppVtWNBQ5OTkyNzd31LanKIpvKCwsJD093dthjAmD/S2EENullDlHLqtq4IqiKD5qRAlcCBEqhHhPCFEkhCgUQsx3V2CKoijK8Y20H/gfgU+llFcIIQyAyQ0xKYqiKEMw7Bq4ECIYOAN4HUBKaZVStrgpLkVRFK861WcjTAbqgb8KIXYKIV4TQhzVZ0YIsUIIkSuEyK2vrx/B5hRFUUbXWJ+NcCQJXAfMBP5XSjkD6AQeOHIhKeUrUsocKWVOVFTUCDanKIriGQ8//DB//OMf+17/8pe/ZPfu3YMue7zZCPsP5BmN2QhH0gZeAVRIKbf0vH6PQRK4oijKSVn9ANTsce86YzLhgieO+esbbriByy67jLvuugun08k777zDH/7wh0GXHWw2wmeffZY1a9YQGRnZ9/6Yno1QSlkjhCgXQqRJKYuBs4EC94WmKIoyOhITE4mIiGDnzp3U1tYyY8YMIiIiBl32VJqN8A7gzZ4eKCXAT0YekqIop7Xj1JQ96cYbb+Rvf/sbNTU1XH/99YMuc0rNRiilzOtp354upfwvKWWzuwJTFEUZTZdeeimffvop27ZtO2ayHWuzEar5wBVFUXDNfbJkyRJCQ0P7epcMJi0tjSOnBOmdjTA2NrZvQqvRmI1QJXBFURTA6XSyefNm/vnPfx53uWPNRnjkxFVqNkJFUZRRUFBQQGpqKmeffTaTJk0C1GyER1GzESqKMhg1G+F31GyEiqIopwGVwBVFUXyUSuCKoig+SiVwRVEUH6USuKIoio9SCVxRFOU4zjrrLNLS0vjwww8HvP+Xv/yFtLQ0XnzxRcA1R0r/qWfb29vJysrirLPOwmw2D/jskiVLCAwMPGpA0MlSCVxRFOUE3nzzTS6++OIB7/3pT3/igw8+4LbbbgOOTuBBQUHs2rULo9HIhg0bBnx2zZo15OQc1SvwpKmRmIqijClPbn2SoqYit65zSvgUfjHnF8dd5vDhwyxbtoz8/HzANRino6PjmMv3nxfcarXyyCOP0N3dzfr163nwwQf5/ve/D3h2XnCVwBVFUYah/7zgBoOB3/72t+Tm5vLCCy8MWM6T84KrBK4oyphyopryWFBTU0NnZychISEnXDY+Pp7du3dz5ZVXuj0O1QauKIoC6HQ6nE5n3+sjbzz2+uCDD5g0aRIrVqw47qyFva677jr+93//d+zNB64oinKqGDduHHV1dTQ2NmKxWFi1atWgy1166aWUlpby8ssvD0jyg80JDvDiiy9y33338dlnn7k9ZpXAFUVRAL1ezyOPPMLcuXNZtmwZU6ZMOeay4eHhhISEDLjJuWTJEgoKCsjOzmblypV97zc3N/fNcOhuqg1cURSlx5133smdd9454L2zzjpr0GV75wXvfZBxeHg427ZtO2o5T84LrmrgiqIoxxEeHs6Pf/zjowby3HPPPVx99dV9A3mO1DuQB1zP0uxvyZIllJSUoNfrRxSbmg9cURSvU/OBf0fNB64oinIaUAlcURTFR6kEriiK4qNUAlcURfFRI07gQgitEGKnEGLwXu+Koig+6JtvviEkJOSop9K3t7ezcOFCsrOz++Y4ee655+jq6upb5umnnyYtLY233357wGdXrlxJamoqy5Ytc0uM7qiB3wUUumE9iqIoY8rixYsHTBEL8PXXXxMfH09eXl7fUPojE/h9993HG2+8wUsvvTTgs9///vd57bXX3BbfiAbyCCESgIuA3wP3uiUiRVFOazWPP46l0L3TyfqlTyHmoYeO+ftf/OIXTJw4kVtvvRWARx99lKCgoEGX7T+NLMDzzz9PVVUVS5YsITIykjVr1gCenUa210hr4M8BPwecx1pACLFCCJErhMitr68f4eYURVHc76qrrhow/P3dd98lKipq0GX7TyMLrtGbcXFxrFmzpi95g2enke017Bq4EGIZUCel3C6EOOtYy0kpXwFeAddAnuFuT1GU08PxasqeMmPGDOrq6qiqqqK+vp6wsDAmTJgw6LJ5eXkkJCSccJ2RkZHU1dXR3NxMWFiYu0MGRtaEshC4WAhxIWAEgoUQ/5BS/tA9oSmKooyeK664gvfee4+amhquuuqqQZdZtGgR+/btY8eOHSdcn8lk4uqrryYpKYmVK1eOrelkpZQPSikTpJSJwFXA1yp5K4riq6666ireeecd3nvvPa644opBl1m/fj033HADr7zyyoD3B5tKtrm5mZUrV1JRUeGR5A2qH7iiKAoA06ZNo729nfj4eGJjY4+5XFpaGk1NTQPeW7FiBRdccAFLlizpe6+1tZXo6GgCAwM9FrNbppOVUn4DfOOOdSmKonjLnj17TrhM7zSy/d1xxx3ccccdA97z5DSyvVQNXFEUZRAGg4H8/PyjBvIsXbqU5uZmsrKyjtnL5Omnn2bFihVHJfWVK1dy6623uu2mpppOVlEUr1PTyX5HTSerKIpyGlAJXFEUxUepBK4oiuKjVAJXFEXxUSqBK4py2mtsbCQ7O5vs7GxiYmKIj48nOzub0NBQ/P39yc7OHrC80+lk2bJlZGZmUl5eDsDf/vY3qqqq+pZ56623SEtL45lnnhnw2XXr1jF16lQyMjJGHLdK4IqinPYiIiLIy8sjLy+Pm2++mXvuuafvdUpKCnl5eQOW37NnD3V1dezZs4fx48cDRyfwa665hrVr1/Lcc88N+OxgU9QOl1sG8iiKorjLunf30VDe4dZ1Ro4PZPGVk922viOnlH3vvffIzc3lBz/4Af7+/mzatAl/f3+PTymrauCKoign6cgpZa+44gpycnJ48803ycvLw9/fv+93nhxro2rgiqKMKe6sKXvKUKeUBQgLC+PAgQOkpqa6PQ5VA1cURTkJ11xzDY8++ig33njjkJa/++67ycrK4i9/+YvbY1EJXFEU5SS89dZbPPXUU0fdnBxsSlmAxx9/nP3793P99de7PRaVwBVFUU7SYFPK/vjHP+bmm28mOzub7u7uvvctFgtxcXEeiUO1gSuKovTz6KOPnnAZk8lEfX09UkqEEABcfvnlXH755QOW8/SUsqoGriiKcgxarZbW1tajBvJkZ2czfvx4srOz+wbyHOmtt95i6dKl3H///QPeX7duHcuXLycyMnLE8anpZBVF8brCwkKmTJnSV5s9XUkpKSoqUtPJKoriO4xGI42NjR7tMz3WSSlpbGzEaDQO+TOqDVxRFK9LSEigoqKC+vp6b4fiVUajccj9y0ElcEVRxgC9Xk9SUpK3w/A5qglFURTFR6kEriiK4qNUAlcURfFRKoEriqL4KJXAFUVRfNSwE7gQYrwQYo0QolAIsVcIcZc7A1MURVGObyTdCO3Az6SUO4QQQcB2IcQXUsoCN8WmKIqiHMewa+BSymop5Y6e/7cDhUC8uwJTFEVRjs8tbeBCiERgBrBlkN+tEELkCiFyT/dRVoqiKO404gQuhAgE/gXcLaVsO/L3UspXpJQ5UsqcqKiokW5OURRF6TGiBC6E0ONK3m9KKd93T0iKoijKUIykF4oAXgcKpZTPui8kRVEUZShGUgNfCFwLfE8Ikdfz70I3xaUoiqKcwLC7EUop1wOn9+zriqIoXqRGYiqKovgolcAVRVF8lErgiqIoPkolcEVRFB+lEriiKIqPUglcURTFR6kEriiK4qNUAlcURfFRKoEriqL4qJE80GHUFO37iLqmfYTqAgnVBxBpCMFkCAStHrQG0PmBzuj6qTeB3h90/qAdY7vnsIGtC2zdrp92C9jNrp8OGzht4LCDdLr+IQEBQoDQgEYLmt59NvTsc88/g8m171qDa/mxwukEe/fg+2y3gNOGzWamztJMq72DFlsnDukkTB9IqD6QSEMoRoOp3377fVfevWWt93f9bcYKKY9f1k5bT3k7BilrzXdl3fv91hr6fb979neslvWAfe5Xzg4LOO1YbWZqLY202TpptXXiRBKmDyLMEEikIQyD3nhEWRtBbxx4XGvGUL1TStf+9e6vrfuo77errO0QPwsCIt26+TGW4Qb37o4X+aelsu+1kJIUm40ss5WZFgtLOrsIkvLoD2oNroI3BPT8NIE+oOdnz5dBbwRtT1LQGkCjcx04vQeS0ADSVVDS6TronPbvCsZu7ik483dfXFs32DrB2uV6be1yvXbaPf/HEpqeL/uR+2samPB0fj37beg5YPSupNG3z6Jnv3sSjMMODqtrv+3Wfl/S3uTcDdbOgftr7XL9/gg2YJO/kS3+Rnb7+VFgMGDVDJ6ItFIy2WpjusVCjtnCGV3dmAYta7+j99cQMDDh9SaE3qSo1bvK+7hl3VPOfWXdu8/mnrI+Yn9tXa6/g3S4s1QHJzSD7K+pX3n3fMf79ru3nHvLWnxX1r0nkeOVdd93u/f73W+fexPYESwC1vn7s9VoZI/RQJHBgP0YJx2dlEy1WMnqKetFXd0YBl3Q/+hjWX+Mstb1lLVG76rQ9e5vX1k7vyvrvkpUv7Lu3V9798Dy7V/u0jm08vrBv2DS0qEtO0RCDnYweEhOTo7Mzc096c/V1eyiuvkArdY2WqztVHbXsav1ALvbSmi3d2MQOs4MmcSykHTONMWjtVuOPqj6/uBd330RrZ2uL2pfLdg6xCQrjl/77/1CHXlg9R1cR548+n/Jek8egr6pZqTTlVT6ThzWnhped78TSL+Th7ULrB2DJ9PeE43DMrCWMJQvoUbnirGvFtyzz7214UETSUDfQbXH1sy/Wwv5vKWQFnsXfho96YHjmR6SSkpgPKGGYEL0QWiFhlZbO83WNso6a9jdeoDdbYfodlrx1xg4O3QKy0OmMN9vHMJuHvygsnYdkXC63FDWxn773S9h9JWv/zH23b/f1VL/E6buGGXtdMXm6FfWveXcW9bH2t/e93tPMP33d9hlPdj3e5AKQs++S52RXEs9/2kt4qvWQjocFvw1BjKCEskMSSEpII4QQxAh+kCEEDRb22i2tlHaWc2u1gPsbS/F4rQRpDVyXthULg6eQrYhAtE/iQ7Y9/7f7/5XPD1XPQ7b0E6oQtNTget/dev33f7pjGAIHOS47il3nfE4Za2HyFQwhgzhOzdIaEJsl1LmHPW+LyTwY3FKJ3sb9vLxoY9ZfWg1TeYmEoMTuT7jepYlL0Ov1Z/8SqXsubR19NTEHHx3aSt6vthj6HLdXZzOnoNb0lcz6V8b1+qHdbkupWRT9SZe2/Ma22q2YdQaWTJ+CRclX8SCuAVDLiO7087Oup18XPIxn5d+Tru1nbSwNG6cfiPnTDgH7XDKpPek2HuCVGXNSMraKZ2sKVvDa3teI78xn0B9IEsnLuXCpAuZHTMbnWZoF/w2h42tNVtZVbKKr8q+otveTVZUFiumr2Bx/GLEcJqNepu1+l9p9N9njW5sNc0c4ZRM4P3ZnXa+KvuK1/e8TmFTITEBMdw5404uSr4IjRi7BXMqy6vL46ltT7G7YTfR/tH8aNqPuGLyFQToA0a0XqvDyupDq3ltz2scbjtMYnAi9866l7PGnzW8g1sZsY2VG3kq9ykOtBxgfNB4fpLxE5YnL8eoM45ovV22Lv5z8D/8Nf+vVHdWkx6ezn059zEndo6bIvcNp3wC7yWlZEPVBl7Y+QJ7G/cyPWo6D8x+gMyoTI9uV/lOTWcNz+14jo9LPibaP5pbsm/h4pSLMWgHbdEcNofTwVdlX/Fi3ouUtJawIG4BP5/9c1JCU9y6HeXYDrce5uncp1lbsZbxQeO5Y8YdnDPxnCHXtofK5rCxqmQVL+96marOKs6ZeA735dxHXGCcW7czVp02CbyXUzr58OCHPLf9ORrNjVyVdhX3zLoHk940Kts/HTmlk5XFK/mf7f+Dw+ngumnXcWPmjR7/m9ucNt4tfpcX816k29bNTzJ+ws1ZN7v9hKF8x+a08df8v/LyrpcxaA3cNP0mfpD+A4//zc12M3/b+zde3/M6Esnt2bdz7dRrh9eE5kNOuwTeq8PawQt5L/BW4VvEBcbx6IJHmRc7b1RjOB2UtZXxyMZH2F67nYVxC/nVvF+REJQwqjE0mZt4JvcZPjz4IamhqTy28DEyIjNGNYbTQVFTEQ9veJiipiLOSzyPB+Y8QKS/e7vHnUhNZw2Pb3mcNeVrmB45nccWPkZyaPKoxjCaTtsE3mtH7Q4e2fgIpW2lXDPlGu7NuRc/rZ9XYjmVSCn51/5/8eTWJ9Fr9Px8zs+5JOUSr7ZFr6tYx6ObHqWhu4EV01dw0/Sb3H5JfzpySid/zf8rL+x8gRC/EB6e9zBnTzzba/FIKVl9aDWPb32cbls398y6hx+k/+CUvA9y2idwcF1+/XHHH/lH4T+YFDaJp854SrWXjkCrpZVHNz7Kl2VfMj92Pr9b9DuiTdHeDguAdms7T2x9gg8PfsiM6Bk8sfiJ06a91BNqO2v55fpfsqVmC+dMPIdfz/81IX7D6xLnbg3dDfxm42/4puIbFscv5rGFjxHhH+HtsNxKJfB+vq34loc3PEynrZMH5zzIZZMuOyXP2p6UV5fHfWvvo9HcyF0z7uJH0340Jnv7fFzyMY9tfgwNGn678LcsnejegRSng3UV63ho/UNYHBYenPMg/5X6X2PueJFS8nbR2zyT+wzBfsE8ufjJU6qnikrgR2jobuChdQ+xqXoTF6dczK/m/Qp/nb+3wxrzpJT8veDvPLf9OWIDY3nqzKeYFjHN22EdV3l7OT9f+3PyG/O5duq13DPrHvSaYYwROM3YnXZeynuJV/e8SlpYGk+f+TSJIYneDuu4ipuKuf/b+yltK+X27Nu5IfOGMVmxOFkqgfdjczipaunmcGM77x74K9/Wv02wJoF07e3YLZG0m+1Y7A5sdonN6UQAeq0GvVaDv0FLsFFHsFFPqMnAuGA/xgUbiQkxMjHCxLggI5pjDAv3dR3WDh7e8DBfln3J2RPO5rGFjxFkCPJ2WMdlsTuoaO7mYEMLb+9/kdzmVYRrJ5OmuRWLOYh2sw2L3Ynd4SprjRDoNAKDToNRryXYqCfYX0e4ycC4YCPRwX7EhfozMdxEVJDfmKuJuktDdwO/+PYXbK3ZyuWTLueBOQ+MuE+3p5ltDsqbuthf38gb+5+moG0t0bpsUvgpZouRdrMN6xFlrddqMGhFz3GtJ9hfT0SAgehgI+OC/YgN8ScxwkR4gMGrZX1aJnCnU1La1MWeylaKa9oorulgf107Fc3dOJzf7bc2YB+m+HcQwkmU+ceM083CqNei1wp0Wg1IV9K3OZx02xy0ddtpM9to6rTSZR04RNdPp2FihInJ44KYEhNEWkww0xNCGBc8tr/8J3Kw5SB3r7mbivYK7p51Nz+a+qMxlbwcTklJfYerrGvb2VfTzr7aDqpau+n/FdcF7cI/7n0EBmLMPyVKn45Rp0XXr6ytPWXdZXXQbrbT1m2jsdOC2TZwCLrJoCUxIoC0mCBXeccGMT0+hIhA3745vrt+N/d8cw+tllYenvcwl6Re4u2QBrA5nOyv7SC/t6xr29lf20FNW/+5WCT60C0YYz5C4wwh1nILkfok/HSao8raanfSbXXQZrbR2m2jsdOK1T6wrIP8dCRFBTB5XBBpPWWdGR9CqGl0uqqeFgm8tdvGjrJmth9uZkdZM3sqW2k3u+a70GoEyZGuAkiKDGBChImJ4SbiQv2JCvKjyVLLPd/cQ0FjATdn3cwtWbcM6dKrw2Knts1MVUs3pY1dlNW1UlNaQ2V1Iy1NbeidDsxaPYHBgSRNjGbqlAnkJEeQGR+CUe8bfVe/KP2CX63/FUadkWfOfIacmIHfIyklztZWHO3tOLu6keZu0OrQ+BvR+PujDQ9HY3TvCayp08r20mZyS5vYWdpCflVr38nUoNWQEh3I5HGBJEYEMDHCxIRwEzEhRqKC/KjoONx3Mrpv9n1cM+WaE56MpJS0W+zUtZmpaO6mrKmLsppWasuqqKhuor2lA11PWYeGBZOc2FPWSRFMiwtGr/WNy/j39r3H41seJ9oUzXNLnmNK+JQBv5dS4mhpwdnejrPb/F1Zm/xdZR0Rgcbg3qRW12Ymt7SZ7aWu47qgqg1LT4L102mYNC6QydFBJEYGMCHcxPhwE3GhRiID/Shsyueeb+6hzdLGrxf8mmXJy064PSklrd02avod1xU1zVSX1lBZ00RnWydapwOL1kBEZAjJSTFkpCUwKzGc9NhgtB64AvdIAhdCnA/8EdACr0kpnzje8u5O4G1mG1tKmthc0simg40U1rQhpStZp8cGkZUQyvSEEDLiQ0iNDsRPd/yEaXFY+N3m3/HvA//mjIQzeGLxE8dsInCazZgLCzEXFmIpLMRScghbZSX2ujrXXBPHYNXoqPMPpT4ggq7xSQRkTCV5/iyyFmRiNIytdlmH08GLeS/y6p5XmR45nWfOfIbwZhvmgkLMhQVYivdhqyjHWlmF7Oo67rq0kZHo4+LwS0rCODUdv/R0jFOnoQ0c2rD6pk4rm0sa+/7tq+0AQK8VTIsLIXt8KJnxIUxPCCEpMsBVwzqOdms7D61/iG/Kv2F58nIemf/IMZsIHB2dWAoLMBcWYS4sxFpSgq2qCnt9/XG3YdbqqfMPoy4wAsuEZIKnZ5C6cCYZs6dhOMF3cbRZHVb+39b/x3v73mNh3EKeWPwE/lXNrnIuKsJcXIytvAJbdTXSfPSsg32EQBcVhT4+HkNyEsapUzGmT8WYPgWN/9DuMdW1mdl48LuyPtzo+m756TR9x3RmQgiZ8SFMjAg4YcJs6G7gvrX3sb12Oz9M/yE/y/nZMbuVOtraMO/d6yrrokKshw5jq6rC0dh43G106fyoNYXREBiJLTGF0KwMJi+ew9TsSW5J6G5P4EIILbAPOAeoALYBV0spC471mZEmcJvDyc6yFtbtr2f9gQZ2lbfglGDQaZg1IYx5yRHMTgwja3woAX7D6/crpeTd4nd5YusTJAQl8MclfyQ5NBlnZydd27fTtW0bXdty6d67F2w2ADQhIfhNSsUQn4A+Ph5ddDSagAA0Jn+EXo/TbEaazTja2mkvLafhwGEs5eUEVZWh65kRr80QQPXENHQzZpF87llMWZCNxouT67RZ23hg7S84tGsdP+yazuKGSMw7d+Kob3AtoNXil5yEfuJEDPHx6GJj0YaEovH3R+NvRDocOLu7cXZ14WhowFZVha2yEsv+A98lPq0WY3o6ptmzMc2ZjWn2nL6EbrY5yD3czLoD9Ww40MDeKtfJ2WTQkpMYztykcGYnhjM9YfhXMk7p5M+7/8xLeS8xLWIazy15jpiAGBxtbXRt3eoq69ztmIuKwOGq3WsjIvBLTUUfH48+Pg5dVBQaU09Z63Q4u804u7twtrXTeriMhoNl2MtKCaotR9tzYm8yBlOXlI7fzFlMuvB7pMxI92pZ13fVc+/X99CyN4/rLbOZVWPCvGMHjpYW1wJ6PX4pKRgmTEAfF4c+LhZNUPDAsu7qxtnVib2+HltlFbaKCiz79+Nobu5bh39Ghqus587BNGtW31VZp8XOlkONrNvfwIYDDX0n5yCjjrlJ4cxNiiAnMYxpcSEYdMP7O9mcNp7JfYY3C99kbsxcnjrzKcKMYdibmujasqWvrC3799Pb5qYbNw6/lBT08XHo4+LQRkaiMZnQ+PsjtNqesu7G0dJC86EymktKsZeVElxfhaZnHfWmMBpTpmHKySH7+8sZlzi8rqyeSODzgUellOf1vH4QQEr5/471meEm8LWvvMPBzXl84jeevKAEnFodWeNDWZQayYKUSGZMCHV7c8T2yi28+NbdTDrQzYWN4zEUHQa73fVFnDYNU84s/LOzMU6dii42dljtwdJmo7FgH8XfbqV1yzaCivcQ2e5KkC3GYOrTsghYOJ9py5cSkzTerft3LLbqag5/9SFbV71G0v4Owjpd7+tiYzHNmoVp1kyMGZn4TZ6Exm94bb32+nrMBQV05eXRtW0b5l27kTYbaLW0Jk9h17g0VukT2BsUj1avY+aEMFdZp0YyPSHE7c0Raw58zt9XPkTmYcm5DbFoiw+B04nw88N/+nT8c2Zhys7GLz0dXVTUsMraabFQt7uAfWu30rEtl9D9+YR1tQDQGBBG45RsghcvYvrypUTEe74vvZQSW3k5+z7/J7tW/4NJJRaCul25QD9xAqZZOZhmzsCYkYFfcjJiGM0iUkrsNTWYCwro3rmTzm3bMOfvBYcDqTfQnDKVHVGTWGVIYF9gLAa9jjlJ4X3H9dQ49zdHfJj/Tz547/fklBv4Xl0E7D8MgMZkwj87G/+cWfhnZWFMT0cXHj6sbTi7u6nesYf9326lKzeXiIN7CTZ30PLo08y/6qJhrdMTCfwK4Hwp5Y09r68F5kopbz9iuRXACoAJEybMKi0tPeltfXTrgySv+Q8aKXEajfjnzCZk3hxMOTkYp01D6Efe9OC0WjHn59OVu52u7bl0b8vF2dWFFHBwHOjnzmLhxbcQMHPmkC8Fh6Nq32EKPvqSrk0bGbd/N8EWVwatDo+jc9oMohbOJeO8MwmMHflBLqXEXlXlurLI3U7X1q1YDx8GoC1AYJo3j/FLLsQ0bz6GhPgRb+9IdW1mNhxsYFNBNXWbt5J0eC8z6vaR0lqFBokzIJCAuXMJ7ilrv7Q0hHbkJ2qn2Uz3rt105W6jKzeX7h07kRYLDg0ciBOELFzMnItuxD87y+3tub2klJTt2UfRx19h3byJ2JJ8AmxmnAiqoiZgycxm3KL5TDtvMaaI4SWSI7dnKyujKzeXrm25dG3bhq3S9ZCUlmAtoYvOIO6s8zHNnYd+nPtPIBXNXWw40MDmgkpaNm1lUrmrrBPbawFwhoQSNH8eQXPn4D9rFn6pqQg3XJU4Ojrpzsv7rqx37QabDZsW9idoiT3zXGZcdJ0rj+g8M1rX6XRSsqOAuLQkTEHDm4nTEwn8v4Hzjkjgc6SUdxzrM8OtgVvtTrRdHXRu2ULnxo10bd6C9dAhVxx+fvilpWFMT8c4JQ19QgL6uDh042Jcl7X9vgTS4cDZ2YmtugZbZSW2inLMxcWuds39B1y1QMCQkoJpzmwC5s9HOyuLxwuf58ODH/K98d/j8cWPj3g61KFy2B0Ursvl8OdrENu3El95AD+HK8bm4EgsiamETM9gYnY6pvHxrsu8sLABX0QppSs5NTVhq6zEWlGJtaSkr/2+t21PExREXWoEH4eX0ZWdyoNXv0xsYKxb96exw8KWQ9/ds9hf57pUDjXpWZgSyRmTI1k0KYpx0kzXpk10bNxI16bNfYlGYzLhN2UKxvR0/NImu5ox4uLQx8QgjMYBNWNpt+Nob8deU4O1ogJbeQWW4iLMBYVYSkpcTSJC4Dd5MgHz5mKaPx9n1hQe2vEY31Z8y2WTLuOXc385ahNi2SxW8r/eTMWX36DbmUt8TQl6pwMnguawcdiTUwmbPo3x06fgn5CAPi4WbWjogBOalBLZ3Y29sdH1/a6sxHKwBHNhAeaCQpytra6/Y1gY5SlBrA6vQDM7i4eueJEw/zC37k9Nq5kth1zlvKmkkdKeduyoID8WpbrKemFqJGFdbXRu2th3XNvr6lwxBgdjnDIFY/oU/Canuco6NgbduHEIv4HdN6XNhqOjo6/pxlpehqWoGHNBgatCIqWruW7qVALmzsE0fz7d6RP52ZaH2Fm3k59k/IS7Ztw1pifE8ukmlMHYGxroyt1O986dfcnI2d5+dJxGI8LPD2k2Iy2Wo36vDQtzJf+p6a5LqFmz0IUN/DJLKXmz8E2ezn2aicETeW7JcySFJLllP05GV6eZnV9tpurbjTiKComoKSWuowENR5ShTtfXvujs6jr6pqpOh19qqmu/p01DZk3hN7V/ZU3lWi5OuZhH5j8y4nlibA4nxTXt7KlsZXtPD4JDDa6rid527PnJESyeFMnU2ODj9p231dQMKGtLUZFrv/oTwlXWBgOyuxtptR61Hl1UFH5T0zGmu8raNHMm2uDgAcs4pZMX817kld2vkBmZybNnPUtMQMyI/hbD0dbaQd7nG6levxm5r4jo2lJiu5qOXlCnc10ROp2uv8kRx7MwGPCbPLmvrC2ZKfyi9Hl21O/kuqnXcfesu0c8T4zF7qCwup3dFS2unkGHm6lscT1Kz9WOHcH8FFdZT4oOPGYTlJQSW0WFq6zz8jAXFWIp3nf0TVONxpXE9XpXWfdUvAb8WWJje26gpuM/IxtTdjaagIEVL5vDxhNbn+Ddfe+yIG4BTy5+klBj6Ij+Fp7iiQSuw3UT82ygEtdNzGuklHuP9RlPdiPsbW+zVVdjq6zCXlvjurHSk7iF0Q+NvwlNQAD6mHF9tTdtRMSQ2zS3Vm/lvrX3YXPaeHzR4yyZsMQj+zJUrd02cgsqKMorprLoEF3lFfibOzE4bYQIBxEBBgLDQgiLDCE8JpLoSYlEpCZiiIvra9Ps3797qF3q+rM7nFS3mjnU0Mn+ug721bRTVNtOYXVbX1/aMJOeWRPDyUkM67vxOJJ2bOl0YquqxlZVib26GlttHdLcjdNsQVosaPyNCJMJbUAAupjY7244hg29lvll6Zf8cv0vMeqMPH3m08yOmT3seN2hqdPKtvxS9uUVU7XvMObySvytXfg5bIRoJeGBBoLCQgiLCCEiLoroyUmEpSa5rk56rsh21e/i3jX30mYdepe6/mwOJ5XN3Rxq7GR/bTtFNe0U17j6YdscrjwSFeTH7MQwZk0MZ05i+IjbsaXDga2iwnXVXF2Nva4Op7kbabYgbTZXV9WAADSmAHSxMRgSEtAnJKANGvoAs/5dJ//nrP8hPSJ92PF6iqe6EV4IPIerG+FfpJS/P97yY2Uk5khUd1Rzzzf3sLdxLyumr+DWrFvHzKWXxe6guKad3RWt7K5ooajn4Oo/ACXQT0dCmKvvuzTtYq/tVfTCyH/FP0B6WBZ6rQadRoNWI7A7nNicEqvdSYfZRpvZTmu3jbp2C7VtZmrbzFQ2d2PvNygqPMBA2rggpsUFM318KNPjQ5gYYRpTg36GqqSlhLvW3EV5ezn3zrqXa6deO2b2o9vqoKC6jT0VLeyubKWwup2D9R0DBqAEG3UkhJmICjZgMW6g0Pp/BOoiuDzhl6SETO4r596y7h3U0m52DVRr6bJR32Ghrs1MdavrX/8BcNFBfqTFBDEtLoSsnq598aH+Y+ZvdDL6D156ZP4jXJxysbdDGuC0GMgzWiwOC49veZz397/P3Ni5PLn4yTE7+5nDKSlv6qKkoYPSxi7XYKPmdoqtb9FmWIOzewJdFT9A2oc2s5zJoCUqyI9xQa5h5ePDTSRGmJgQHsCkcYFE+vgoxCN1WDv45fpf8nX515wz8Rx+s+A3Y3b6ALvDyeHGLkrqO1wDjZq6KGtuocj2VzoNW3F0Tqar4ipwDu0BG4F+OqKD/IjumS5ifJiJiREmEiMDSI0KJCzg1HpgRkN3A/evvZ/c2lwun3Q5D859cMxMOa0SuAd8sP8Dfr/l94QYQnjqzKeYOW6mt0M6oeqOau779j521+/mh+k/5J6Z9+CUWtrMNjrMduxOic3hxOkEnVag17rmiwgy6gky6nxmRKE7SSl5Y+8bPLfjOeID43n2rGdJC0/zdlgnVNJSws/W/oyDLQe5NftWfpr5U6x2aDfb6LAMVtYaDFoNwf46Av10JxwMdSqyO+28sPMFXs9/nfTwdJ458xnGB49OF97jUQncQ4qbirn3m3up6Kjg5qyb+WnmT8fswwO+KP2CX2/8NU7p5LcLfsu5ied6OySfsr12O/evvZ9WSyv35tx70vcLRkv/h2yY9CaeWPwE8+Pmezssn7K2fC0PrX8Ip3Tyq3m/4qLk4fXfdheVwD2ow9rB77f8nlUlq5gZPZMnFj/h9i54I9Fl6+IP2/7Av/b/i8zITJ5c/OSYqFX4osbuRh7Z+AjfVnzLGQln8NjCxwg3jryftru0Wlr5zabf8EXpF8yLncfjix4nyhTl7bB8UlVHFQ+se4CddTtZlryMX879JYGGQK/EohL4KPjo4Ef8fsvvEQjun30/l6Ze6vUa2vba7Tyy4RHK28u5PuN6bptxm5oLe4SklLxV9BbP5j5LoCGQX837FedMPMfbYbG2fC2/3fRbmsxN3DHzDn487cenxFzY3mR32nl196u8vPtlYgNivfZMXZXAR0l5ezmPbHiE3Npc5sfO59EFj3rlUV5dti7+uOOPvF30NnGBcTy28DGvd4U71RQ3FfPwhocpbCrk3Inn8tDch7xyM7vV0sqTW5/ko5KPSA1N5XeLfjfmH7Lha3bW7eThDQ9T2lbKFZOv4N5Z947qzWyVwEeRUzp5t/hdnt3+LAA/zfwpP5r2o1G5oy2l5LPDn/HM9meo6azhminXcNfMuzDph9bzQDk5NqeNN/a+wUt5L+Gv8+e27Nu4Mu3KUbkP4nA6eP/A+/xpx59ot7ZzQ+YNrJi+YtRGj55uzHYzL+W9xBsFbxBpjOTuWXdzUfJFo3KVoxK4F1R2VPLUtqf4quwr4gPj+VnOz1g6YanHmlX2NuzlD9v+wI66HUwJn8KDcx70iZ4xp4KSlhIe3/I4W2q2kBKSwv2z72dB3AKPlfW2mm08te0pCpsKmRk9kwfnPnjU3N2KZ+Q35PO7zb9jb+NepkdO5/7Z95Mdne3RbaoE7kWbqzfz5NYnOdBygElhk7gx40bOTTzXbbW07bXbeXXPq2yo3ECYXxh3zryTS1MvHTMDjE4XUkq+Lv+ap7c9TUVHBdOjpnNjxo2cOf5Mt9TSpJRsqNrAq7tfZUfdDmICYvjZrJ9xXuJ5Xr/XcrpxSicfHfyIP+74I/Xd9cyLnccNmTcwN2auR8pCJXAvszvtfHLoE17f8zolrSUkBCZwcerFLEtaNqweIS3mFj47/BkflnzI7vrdhBvDuXbqtXw/7ftjdqDJ6cLqsPLB/g/4696/UtlRSUpICpekXsIFSRcMa16V+q56Pjn0CR8e/JB9zfsYZxrHTzJ+wuWTLh/zz6k81XXZulhZvJK/F/ydhu4GpkZM5ZKUSzg38Vwi/SPdth2VwMcIp3SypnwNbxa+SW5NLhJJRkQGs2NnkxWVRWZkJpH+kQNqbFJK2qxtFDYVsqtuFzvrd7Klegt2p53U0FSumHwFl026DH+d56a5VU6e3Wnn08Of8lbhW+xp2INAMCN6BjkxOUyPnM60yGlEGAfOxeOUTlosLRQ0FpBXl8eOuh1sr92OUzqZFjGNK9OuZHnycvRa1ZNoLLE4LHx48EPeLnqb/c370QgNc2LmMGvcLDIjM8mIzCDEb2ijnQejEvgYVNNZw+pDq/my7EsKGguw9zydRyM0BBuCCTIE0W3vpsXS0vc7gOSQZBbHL2Z5ynImh01Wl88+oKytjNWHVvNV2VcUNxfjlK45S7RCS7AhmEBDIJ22TlotrTik6+k/GqFhcthkFscvZlnKMpJDkr25C8oQ7W/ez+pDq/m67GtKWkuQPbOFPr/k+WFPgKcS+BhncVgobCykoLGARnMjrZZW2qxtmHQmQv1CCTOGkRqaSmZUJsGG4BOvUBmzumxdFDQWUNRURJO5iTZrG23WNgL0AYT5hRFmDGNy2GQyIzNV7yEf125tp6CxgD0Ne1ievJxxAeOGtR6VwBVFUXzUsRK4GqalKIrio1QCVxRF8VEqgSuKovgolcAVRVF8lErgiqIoPkolcEVRFB+lEriiKIqPUglcURTFR43qQB4hRD1QOsyPRwINbgzHF6h9Pj2ofT49jGSfJ0opj3o23qgm8JEQQuQONhLpVKb2+fSg9vn04Il9Vk0oiqIoPkolcEVRFB/lSwn8FW8H4AVqn08Pap9PD27fZ59pA1cURVEG8qUauKIoitKPSuCKoig+yicSuBDifCFEsRDigBDiAW/H42lCiL8IIeqEEPnejmU0CCHGCyHWCCEKhRB7hRB3eTsmTxNCGIUQW4UQu3r2+Tfejmm0CCG0QoidQohV3o5lNAghDgsh9ggh8oQQbn2izZhvAxdCaIF9wDlABbANuFpKWeDVwDxICHEG0AH8XUqZ4e14PE0IEQvESil3CCGCgO3Af53iZSyAACllhxBCD6wH7pJSbvZyaB4nhLgXyAGCpZTLvB2PpwkhDgM5Ukq3D1zyhRr4HOCAlLJESmkF3gEu8XJMHiWl/BZo8nYco0VKWS2l3NHz/3agEIj3blSeJV06el7qe/6N7dqUGwghEoCLgNe8HcupwBcSeDxQ3u91Baf4wX06E0IkAjOALV4OxeN6mhLygDrgCynlKb/PwHPAzwGnl+MYTRL4XAixXQixwp0r9oUELgZ575SvqZyOhBCBwL+Au6WUbd6Ox9OklA4pZTaQAMwRQpzSzWVCiGVAnZRyu7djGWULpZQzgQuA23qaSN3CFxJ4BTC+3+sEoMpLsSge0tMO/C/gTSnl+96OZzRJKVuAb4DzvRuJxy0ELu5pE34H+J4Q4h/eDcnzpJRVPT/rgA9wNQu7hS8k8G3AJCFEkhDCAFwFfOjlmBQ36rmh9zpQKKV81tvxjAYhRJQQIrTn//7AUqDIq0F5mJTyQSllgpQyEddx/LWU8odeDsujhBABPTfmEUIEAOcCbutdNuYTuJTSDtwOfIbr5ta7Usq93o3Ks4QQbwObgDQhRIUQ4gZvx+RhC4FrcdXI8nr+XejtoDwsFlgjhNiNq5LyhZTytOhWd5oZB6wXQuwCtgIfSyk/ddfKx3w3QkVRFGVwY74GriiKogxOJXBFURQfpRK4oiiKj1IJXFEUxUepBK4oiuKjVAJXTntCiFAhxK3ejkNRTpZK4IoCoYBK4IrPUQlcUeAJIKVnANFT3g5GUYZKDeRRTns9MyCuOh3mXldOLaoGriiK4qNUAlcURfFRKoErCrQDQd4OQlFOlkrgymlPStkIbBBC5KubmIovUTcxFUVRfJSqgSuKovgolcAVRVF8lErgiqIoPkolcEVRFB+lEriiKIqPUglcURTFR6kEriiK4qP+PwddmBmKxYMEAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYwAAAERCAYAAABowZDXAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuNCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8QVMy6AAAACXBIWXMAAAsTAAALEwEAmpwYAAAjnElEQVR4nO3de7iVc/7/8edLhSQ0aZLSVCT6OtvCZMa5ciyUKcM4DUKGn8M4G2QI4zBGmCSHmd+vnGfSNMI4DeNQOUQSOW+hEqZMhvL+/fFZfe22Xa19Wvfaa70e17Wuvdda932v9xrX7Fef+3NSRGBmZrYyq2RdgJmZNQ0ODDMzy4sDw8zM8uLAMDOzvDgwzMwsLw4MMzPLS8kHhqQxkuZIerWBrrdE0ku5x/hanNdG0v2Spkl6XtJmyzluN0kvSHpV0u2Smq/sfEkn546fLumUKq9vKekZSa9IekDSWvX46kuvOUzSLEkhad36Xs/Mmo6SDwzgNqBfA15vUURslXvsX9MBkt6t4eVzgJciYgvgF8DvazhvFeB2YHBEbAa8Bxy+ovNzwXEM0AvYEthXUvfcOaOBsyJic+B+4Iw6fN/qngb2yNVmZmWk5AMjIp4E5ld9TdKGkh6UNFXSPyVtUoBSegL/yNX0OtBFUvtqx7QF/hsRb+SePwwctJLzNwWejYj/RMRi4AnggNw5PYAnq19LUjNJV0qanGuxHJfvl4iIFyPi3XyPN7PSUfKBsRyjgJMiYlvgdOCGWpy7uqQpkp6VNKAW570MHAggqRfwI6BTtWPmAS0kVeSeDwQ2WMn5rwI/ldRW0hrA3lXOeRVY2goaVOX1o4EvImI7YDvgGElda/FdzKwMNc+6gEKTtCbwY+BuSUtfXi333oHAxTWc9mFE9M393jkiZkvqBjwq6ZWIeEvSSKB37pj1Jb2U+/3uiPgtMAL4fe71V4AXgcVVPyQiQtJg4BpJqwEPVTmmxvMjYoaky0ktiIWkYFl6zlHAdZIuAMYDX+de7wNsIWlg7vnaQHdJ7+fOr8mRETF5Oe+ZWRlQOawlJakLMCEiNst1/M6MiA4NcN3bcte9p9rr70ZElxWcJ+AdYIuI+PcKjusD/DIiDs73fEmXApURcUO11zcG/hwRvSTdC4yKiEl5fM3l1fYuUBER8+p6DTNrWsrullTuD+w7kgZB+uMract8zs2NVFraGlmX1KJ4Lc9z15G0au7pL4EnawoLST/M/VwNOBO4aWXnVzmnM+m21dhqr68CnLf0WsAk4HhJLXLvbyypVT7fw8zKV8kHhqSxwDNAD0mVko4Gfg4cLellYDrQP8/LbQpMyZ33GDAiIvIKjNy50yW9DuwFnFylxomS1s89PUPSDGAa8EBEPLqy84F7Jb0GPACcGBGf5V4fIukN4HVgNnBr7vXRpKB7ITfc+I/keXtS0q8kVZL6T6ZJGp3n9zezJq4sbkmZmVn9lXwLw8zMGkbJjpJad911o0uXLlmXYWbWpEydOnVeRLSr6b2SDYwuXbowZcqUrMswM2tSJC13FQffkjIzs7w4MMzMLC8ODDMzy4sDw8zM8uLAMDOzvDgwzMwsLw4MMzPLS1EEhlayjWpugcDrcluDTpO0TaFrXLQIRo+GUaPg2Wfhyy8LXYGZWbaKZeLebcD1wB3LeX8voHvusT1wY+5no/vqqxQSI0bARx9997oE3bvD1lvDNtvAtttCRQWsvXYhqjIzK7yiCIyIeDK3Z8Xy9AfuiLRS4rO5pb47RMRHKzinTj79FI4/Hj75BD7+GD78MLUmdtkFxo6Fzp3h5ZfT46WXUmvjzju/O3/jjWHHHWHXXdOjc+eGrtDMLBtFERh56Ah8UOV5Ze61ZQJD0rHAsQCd6/iXetVVUxistx5suSX07QsHHJD++C/VtSsMGPDd808/halT4fnn0+OBB+D22787tndv2Gkn6NULunVbeSvkm2/SNefN++7x6aewYEF6LFwI33773fGtW0PbtunRrRv8z/+4pWNmDa+pBIZqeO1767JHxCjSft1UVFTUad321q1h5szandO2LfTpkx6Q/pi/+io89hj885/w8MPw5z9/d3ybNtCxI6yxBrRsCc2aweefp8f8+enniqyxBjTP/ZeLSAFSfZX6Tp1SUO29N/TrBz/8Ye2+k5lZdU0lMCqBDao870TaEKgorbIKbLFFepx8cvpj/tZb6RbWO++kx+zZqX9k0aL0c731YNNNU5isuy60a5d+Ln384Aep1dCqVbp+VUuWpJCZNw/efDOF1SuvwKOPpttlEuy8M5x4IvTvDy1aZPG/ipk1dU0lMMYDwySNI3V2f9EY/ReNRYKNNkqPxtCs2Xe3pHr0gH33Ta9/+226vTZhAowZA4MGpZbNr34FJ52UWjdmZvkqlmG139tGVdJQSUNzh0wE3gZmATcDJ2RUapOyyippFNf558OsWTB+PPTsCWeemTrnb701tU7MzPJRslu0VlRUhPfDqNkTT8AZZ8DkybD55nDNNbD77llXZWbFQNLUiKio6b2iaGFYYe28Mzz3XOrfWLgQ9tgj9W288UbWlZlZMXNglCkJDj4YXnsNLr88jejq2ROOOw4qK7OuzsyKkQOjzK2+Ovz612l01QknpH6NjTaC009Po67MzJZyYBgA7dvDddel21KDB6d+jW7d4MIL4d//zro6MysGDgxbRpcucNttaR5Hnz5w0UVptvpvfwtffJF1dWaWJQeG1ahnT7jnnjSSascd4bzzUphceOHKZ6KbWWlyYNgKVVSkiX9Tp6b1tC66KN2quuyyNMLKzMqHA8Pyss02cN998OKLaY2qc85JwXHppW5xmJULB4bVylZbpdV4n3km7QFy7rmwwQZpIqCH45qVNgeG1ckOO8Df/55aHPvtB1dfnTrHDz88dZibWenx0iDWIN55B669Nm1j+5//pNtWRx6ZFjxca60Vn7tkSdqsavbs9Pjww9RaqaxMG1nNnw+ffZZW9W3RIu1ZsvbaacfDjTdOy5v07ZtW8jWz+lnR0iAODGtQ8+en0BgzJu0r0rJl+oO+4Yapz6NZs7SD4YIFKRBmzUph8803y16neXNYf/00P6Rt27S8e8uW6bivv04bSr35Jrz3Xlo+vmVL2GefNIekf//v9gsxs9pxYFjBRaT1qsaOTcuPvPVW+uP+7bdpA6g110xLrW+0UQqTLl1SQCx9tG///X0/avLVV+lz7r47DQP+5JN0rTPOSC0cL+FuVjsODCsKixenEMgnCOpiyZLUIT9iRAqR9u3h4ovh6KNTy8bMVs6r1VpRaN688cICUigMGJBGcD3+eOrjOO64NCT4scca73PNyoUDw0rO0i1pn3wS7rorLWmy225w0EGpv8TM6saBYSVLSqO0Xn8dLrkEHnww7Zt+7rlpJJeZ1Y4Dw0re6qunkHjjjRQgl14KW26ZWiBmlj8HhpWNjh3hT39K/RnffptuW510Uhria2Yr58CwsrPLLjBtGpx8MowcmTrHx4xJIWJmy+fAsLLUqlWamf7cc2keyNFHp5V5n3oq68rMipcDw8radtulkBg7Nm1J+5OfwM9/npYnMbNlOTCs7ElpSZEZM+D88+Hee6FHj9Q5/tVXWVdnVjwcGGY5rVqlmeEzZsCee6aRVT17pgAp0QURzGrFgWFWTdeucP/98MgjKUQGDky7DU6dmnVlZtlyYJgtx+67p/0+brghLaBYUQGHHQbvv591ZWbZcGCYrUDz5nD88Wkp9bPOSqvibrwxnH56WmLdrJwURWBI6idppqRZks6q4f21JT0g6WVJ0yUdmUWdVr7WXhsuuyzNFh8yJO0wuOGGqWN84cKsqzMrjMwDQ1IzYCSwF9ATGCKpZ7XDTgRei4gtgV2AqyStWtBCzYDOneHWW9PEv5/+NHWMd+uWAmTRoqyrM2tcmQcG0AuYFRFvR8TXwDigf7VjAmgtScCawHxgcWHLNPvOZpvB+PFpKfUtt4TTTkvB8fvfOzisdBVDYHQEPqjyvDL3WlXXA5sCs4FXgJMj4nsLOUg6VtIUSVPmzp3bWPWa/a8ddoCHH077b2yyCZxySgqOa65JW9GalZJiCAzV8Fr1Ue99gZeA9YGtgOslrfW9kyJGRURFRFS0a9euoes0W66dd06LGj7+eJq7ceqpaavYSy9N+3GYlYJiCIxKYIMqzzuRWhJVHQncF8ks4B1gkwLVZ5a3nXeGf/wjLTey3Xapj6NzZzjnHJgzJ+vqzOqnGAJjMtBdUtdcR/ZgYHy1Y94HdgeQ1B7oAbxd0CrNaqF3b5g4MU3269Mn7TP+ox/BsGHw7rtZV2dWN5kHRkQsBoYBk4AZwF0RMV3SUElDc4cNB34s6RXgH8CZETEvm4rN8rfNNmnuxowZcMghMGoUbLRRWuDw5ZeXf96SJamVMnw43HJLmkD49deFq9usJooSXSSnoqIipkyZknUZZsuorEzLqv/xj2n+xvbbw1FHwQEHwHvvpRbJs8/C3/4G1cdttGiR9vI48EDo3x86dMjiG1ipkzQ1IipqfM+BYVZ4n32WNm269VaYPn3Z99q0gX79Uij07Zv6Pl58ESZPTkN533wzrbD7q1/BVVdBs2bZfAcrTQ4MsyIVAVOmpIUON9oItt02LX6omsYO5o5/7TW4/nq46SbYZ5+0l0fr1oWt20qXA8OsBN14Y9qTfLPNYMIE6NQp64qsFKwoMDLv9Dazujn++NTX8fbbsPfenihojc+BYdaE9e0L99yT+kGOOsobPVnjcmCYNXFL53ncdRdccUXW1Vgpc2CYlYDTT0/7kp99Njz4YNbVWKlyYJiVAAlGj4bNN0+TAr0roDUGB4ZZiWjVKvVnfPMNHHywZ4Zbw3NgmJWQ7t3ThMDnnoMzz8y6Gis1DgyzEjNwYJoFfu21cO+9WVdjpcSBYVaCrrwSevWCo4/26rjWcBwYZiVo1VVh3Lg0L+OQQ1K/hll9OTDMSlTXrmk59WeegQsvzLoaKwUODLMS9rOfpRngl10Gjz6adTXW1DkwzErcdddBjx5pfsbHH2ddjTVlDgyzEteqVVo25IsvUn/GkiVZV2RNlQPDrAxsvjnccAM89pj7M6zuHBhmZeKII+DII+GSS7zelNWNA8OsjFx/fWptHHoofPhh1tVYU+PAMCsja6wBd98NX32VOsHdn2G14cAwKzM9eqT+jCeegOHDs67GmhIHhlkZ+sUv0mP4cHj88ayrsabCgWFWpkaOTKvbHnooLFyYdTXWFDgwzMrUmmvCrbemzu/f/S7raqwpcGCYlbEdd4RBg9LqtrNnZ12NFTsHhlmZGzECFi+G887LuhIrdg4MszLXrRucdBLcdhu89FLW1VgxK4rAkNRP0kxJsySdtZxjdpH0kqTpkp4odI1mpezcc6FNGzjttLSHhllNMg8MSc2AkcBeQE9giKSe1Y5ZB7gB2D8i/gcYVOg6zUpZmzZpiO2jj8LVV2ddjRWrzAMD6AXMioi3I+JrYBzQv9oxhwD3RcT7ABExp8A1mpW844+Hgw6CM8/03AyrWTEERkfggyrPK3OvVbUx0EbS45KmSvpFTReSdKykKZKmzJ07t5HKNStNUhpm2707HHwwVFZmXZEVm2IIDNXwWvW7qM2BbYF9gL7A+ZI2/t5JEaMioiIiKtq1a9fwlZqVuNat4f77YdEiGDjQe4HbslYYGJIKsTRZJbBBleedgOojwiuBByPiy4iYBzwJbFmA2szKziabwJgx8NxzcPnlWVdjxWRlLYya/vXf0CYD3SV1lbQqMBgYX+2YvwI/kdRc0hrA9sCMAtRmVpYGDYLBg+Hii2H69KyrsWKxssBo9AF2EbEYGAZMIoXAXRExXdJQSUNzx8wAHgSmAc8DoyPi1cauzaycXXcdrL122nRp8eKsq7FioFjBoGtJSyKiWQHraTAVFRUxZcqUrMswa9LGjYMhQ9LSIaefnnU1VgiSpkZERU3v1brTW9Kekm6WtFXu+bH1rM/MitTPfgb9+8P558O0aVlXY1mryyipE4AzgEMl7QZs1aAVmVnRkOCmm+AHP4D99oNPPsm6IstSXQJjbkR8HhGnA32A7Rq4JjMrIuutB+PHw9y5cMABaXtXK091CYy/Lf0lIs4C7mi4csysGG27LdxxBzzzDBxzjNebKle1DoyI+Gu1539ouHLMrFgNHAiXXAJ//jNcemnW1VgW6jXTW9IjkjyBzqxMnHNO2tL1vPPgrruyrsYKrb5Lg/wauEbSrZI6NERBZla8JBg9Gnr3hsMPT7PBrXzUKzAi4oWI2A2YADwo6TeSWjZMaWZWjFZbLa031aFDGnL73ntZV2SFUu/FByUJmAncCJwEvCnpsPpe18yKV7t2MGEC/Pe/0LcvzJuXdUVWCPXtw3gK+BC4hrQk+RHALkAvSaPqW5yZFa+ePdNw2/feg332gYULs67IGlvzep4/FJge319f5CRJXhzQrMT95Cdw551pfsbAgfDAA9CiRdZVWWOpbx/GqzWExVL71OfaZtY07L8/jBoFkyaljvAlhdgUwTJR3xbGckXE2411bTMrLkcfDZ9+mrZ3XXttuOGGNKLKSkuDBIakPSPi4Ya4lpk1Tb/+NcyfnzZdatPGk/tKUUO1MC4HHBhmZe6yy+Czz9LPddZJIWKlo9FuSZlZ+ZHS7ah//zvdnmrVCk48MeuqrKHUOTAk3UrakU9AZ0ljlr4XEUc1QG1m1gQ1a5YWKly0CIYNS6FxxBFZV2UNoT4tjNuq/L4TcHv9SjGzUtGiRRpuu//+qUO8Zcu0GZM1bXUOjIh4YunvkhZUfW5mtnQJkb32gp//HFZdNc3XsKar3kuD5HzdQNcxsxKyxhppCZHttkstjL/9beXnWPFqkMCIiB0a4jpmVnpat4a//x023xwOOgge9njKJquhWhhmZsu1zjrw0EPQo0da4fYJ38BukhwYZlYQbdum1kXXrmmxwqefzroiqy0HhpkVzA9/CI88AuuvnzrDn38+64qsNmodGJL2lHSzpK1yz49t8KrMrGR16ACPPpr21OjbF158MeuKLF91aWGcAJwBHCppN2CrBq3IzEpep04pNNZaC/bcE155JeuKLB91CYy5EfF5RJwO9AG2a+CazKwM/OhHKTRWWw322ANefz3rimxl6hIY/zuSOiLOAu6obxGS+kmaKWmWpLNWcNx2kpZIGljfzzSz7G24YQoNCXbbDd56K+uKbEVqHRgR8delv0u6Fri+PgVIagaMBPYCegJDJPVcznGXA5Pq83lmVlx69Egd4f/9L+y+O3zwQdYV2fLUd5TUQmC8pFYAkvpIqu1guV7ArIh4OyK+BsYB/Ws47iTgXmBOfQo2s+Kz2WZpnsZnn6XbU598knVFVpP6btF6HjAWeFzSU8BpwHJvKS1HR6Dqvykqc6/9L0kdgQOAm1Z0IUnHSpoiacrcuXNrWYaZZWnbbdPSIZWV0KdPCg8rLvUKDEm7A8cAXwLtgF9FxD9re5kaXqu+T/i1wJkRscLdgiNiVERURERFu3btalmGmWVtp53gL39JHeD77ANffpl1RVZVfW9JnQucHxG7AAOBO3NDbWujEtigyvNOwOxqx1QA4yS9m/ucGyQNqEvBZlbc9twTxo6F556DAw9MfRtWHOp7S2q3iHgq9/srpI7rS2p5mclAd0ldJa0KDAbGV/ucrhHRJSK6APcAJ0TEX+pTu5kVrwMPhJtvTv0ahx0GS1Z4b8EKZWX7YSg3hHVSRCxY2cUi4qPcbaq8RcRiScNIo5+aAWMiYrqkobn3V9hvYWal6aij4PPP4bTTYN11YeTINPzWsrPCwIiIVSR1Ag6WtBawAHgoIt5fwTmLaltEREwEJlZ7rcagiIgjant9M2uaTj01jZi64gpYbz244IKsKypvK91xLyIqgVsAcsNn+0oaBHwD/CsipjRuiWZWzkaMSKHxm9+kxQuHDs26ovJVqy1aI+JL4D4ASasAP5Z0Cmmk00zgHxHhLiozazBS6s+YNw9OOCGFxoEHZl1VearPnt7fAk/lHkjqDhwpqQPwLnBPPv0eZmYr06IF3HVXmgl+yCEwaRLsvHPWVZWfBtkPQ1I3YD9gEPBjoDWpA9vMrEEs3R+8a9e0a59XuC28OrcwJAkYDuwOvA/8FTgoIj5vmNLMzJbVtm1qXey4I/TrB089lQLECqPOLYyICOBroE9E/Cwi/p/DwswaW+fOKTQWLUqT/D76KOuKykd9b0kNdz+FmRXaZpvBxInw8cdp177587OuqDzUd6Z39TWfzMwKYocd4K9/hZkz07pTCxdmXVHpa5BObzOzLOy+O9x5Jzz/PBx0kNedamwODDNr0gYMgNGj07pTv/iF151qTHUeJWVmViyOPDL1Y5x+OrRpAzfe6HWnGoMDw8xKwmmnpdngI0akobZnnpl1RaXHgWFmJePSS+Hdd+Hss2HTTWH//bOuqLS4D8PMSoYEY8ZARUVaQmTatKwrKi0ODDMrKS1bpm1e11kH9tsP5szJuqLS4cAws5Kz/vppjsacOTBoEHzzTdYVlQYHhpmVpG23hVtugSefhFNOybqa0uBObzMrWYccAi++CL/7HWy9Nfzyl1lX1LS5hWFmJW3ECOjTJ22+9MwzWVfTtDkwzKykNWsGY8fCBhuk5UO8um3dOTDMrOT94Adw//3wxRepE/zrr7OuqGlyYJhZWdhii9QJ/vTTcOqpWVfTNLnT28zKxuDBMHkyXH11mtx3xBFZV9S0uIVhZmXl8sth111h6FCYMiXrapoWB4aZlZXmzdMeGu3bwwEHeCZ4bTgwzKzstGuXOsHnzYODD/ZM8Hw5MMysLG2zDdx8MzzxhDvB81UUgSGpn6SZkmZJOquG938uaVru8S9JW2ZRp5mVlkMPhf/zf+D669OufbZimQeGpGbASGAvoCcwRFLPaoe9A+wcEVsAw4FRha3SzErVFVd8NxP8qaeyrqa4ZR4YQC9gVkS8HRFfA+OA/lUPiIh/RcRnuafPAp0KXKOZlajmzWHcOOjSJc0Ef//9rCsqXsUQGB2BD6o8r8y9tjxHA3+v6Q1Jx0qaImnK3LlzG7BEMytlbdqk5dC/+irt0rdwYdYVFadiCIyatmqPGg+UdiUFRo279UbEqIioiIiKdu3aNWCJZlbqNt0U7roLXn0VhgyBJUuyrqj4FENgVAIbVHneCZhd/SBJWwCjgf4R8WmBajOzMtK3L/zhDzBhApxxRtbVFJ9iWBpkMtBdUlfgQ2AwcEjVAyR1Bu4DDouINwpfopmVi+OPh5kz4ZprYKONUme4JZkHRkQsljQMmAQ0A8ZExHRJQ3Pv3wRcALQFbpAEsDgiKrKq2cxK21VXwdtvw0knpe1eBwzIuqLioIgauwuavIqKipjihWLMrI6+/BJ23x1efhkeeQR69866osKQNHV5/yAvhj4MM7Oi06oVPPBA2nhpv/1gxoysK8qeA8PMbDnatYMHH4RVV02T+957L+uKsuXAMDNbgW7dUmgsWAB77AEff5x1RdlxYJiZrcRWW8HEiTB7dmppzJ+fdUXZcGCYmeXhxz+Gv/wlDbnda6+0P3i5cWCYmeVpzz3TbPAXXkihsWBB1hUVlgPDzKwW+vdPO/Y9/3z5hYYDw8yslg48MK1w++yzsPfe5RMaDgwzszoYOBDGjoVnnkkd4Z9/nnVFjc+BYWZWR4MGwT33wNSpaVb4pyW+LKoDw8ysHgYMSKOnpk+HXXeFTz7JuqLG48AwM6unvfdOS6K/9Rb85Celu2ufA8PMrAHssQc89BDMmQM77QRvvpl1RQ3PgWFm1kB694bHHoNFi1JL45VXsq6oYTkwzMwa0NZbwz//Cc2bwy67QCntsuDAMDNrYJtsAk8+CWutlUZPPf101hU1DAeGmVkj6NYttTTWWy/N03jkkawrqj8HhplZI+nUKbU0NtwQ9t03jaRqyhwYZmaNqH371BG++eZwwAFw991ZV1R3Dgwzs0bWtm26JbX99jB4MNx+e9YV1Y0Dw8ysANZeGyZNSp3gRxwBI0dmXVHtOTDMzAqkVSsYPz4tkT5sGIwYkXVFtePAMDMroNVXT/0YhxwCZ58NF1wAEVlXlZ/mWRdgZlZuWrSAO+6Ali1h+HD45hu49FKQsq5sxRwYZmYZaNYMRo1KM8JHjEihceWVxR0aDgwzs4yssgrceGNqcVx1VQqNa68t3tBwYJiZZUiC665LLY1rr4XFi+EPf0hhUmwcGGZmGZPg6qtTS+PKK1No3Hhj8YVGUZQjqZ+kmZJmSTqrhvcl6brc+9MkbZNFnWZmjUWCyy9PI6dGjYJjjoFvv826qmVl3sKQ1AwYCewJVAKTJY2PiNeqHLYX0D332B64MffTzKxkSPDb36YO8UsuSYExenR6XgwyDwygFzArIt4GkDQO6A9UDYz+wB0REcCzktaR1CEiPip8uWZmjUdKQ22bNYOLLkpzNG65pThCoxgCoyPwQZXnlXy/9VDTMR2BZQJD0rHAsQCdO3du8ELNzArlwgtTH8ZvfpNaGrfemn1oFENg1DSArPq8x3yOISJGAaMAKioqmsjcSTOzml1wQQqJ885LoXH77dmGRjEERiWwQZXnnYDZdTjGzKzknHtuuk117rnp9tTtt6chuFkohsCYDHSX1BX4EBgMHFLtmPHAsFz/xvbAF+6/MLNycc456fbU2Wen8MiqpZF5YETEYknDgElAM2BMREyXNDT3/k3ARGBvYBbwH+DIrOo1M8vCWWelFsY558Aaa8Af/1j4GeGZBwZAREwkhULV126q8nsAJxa6LjOzYnL22fDll2nobatWabJfIUOjKALDzMzyM3w4LFyYlhFZa6009LZQHBhmZk2IBNdcAwsWwMUXw/rrw3HHFeazHRhmZk2MlPowPvkETjgB2reHAQMa/3OLYi0pMzOrnebN4c47YbvtYMgQePrpxv9MB4aZWRPVqhVMmACdO8P++8MbbzTu5zkwzMyasHXXhYkT0zyNffaBefMa77McGGZmTdyGG8L48fDBB9C/P3z1VeN8jgPDzKwE7Lgj/OlP8K9/weGHN85eGh4lZWZWIgYNgiuuSJP7GmNCnwPDzKyEnHFG413bt6TMzCwvDgwzM8uLA8PMzPLiwDAzs7w4MMzMLC8ODDMzy4sDw8zM8uLAMDOzvCjtflp6JM0F3qvHJdYFGnEZr6JUbt+53L4v+DuXi/p85x9FRLua3ijZwKgvSVMioiLrOgqp3L5zuX1f8HcuF431nX1LyszM8uLAMDOzvDgwlm9U1gVkoNy+c7l9X/B3LheN8p3dh2FmZnlxC8PMzPLiwDAzs7w4MKqR1E/STEmzJJ2VdT2NTdIYSXMkvZp1LYUiaQNJj0maIWm6pJOzrqmxSVpd0vOSXs5954uyrqkQJDWT9KKkCVnXUiiS3pX0iqSXJE1p0Gu7D+M7kpoBbwB7ApXAZGBIRLyWaWGNSNJPgYXAHRGxWdb1FIKkDkCHiHhBUmtgKjCgxP87C2gVEQsltQCeAk6OiGczLq1RSToVqADWioh9s66nECS9C1RERINPVnQLY1m9gFkR8XZEfA2MA/pnXFOjiogngflZ11FIEfFRRLyQ+30BMAPomG1VjSuShbmnLXKPkv7XoqROwD7A6KxrKRUOjGV1BD6o8rySEv9DUu4kdQG2Bp7LuJRGl7s98xIwB3g4Ikr9O18L/Br4NuM6Ci2AhyRNlXRsQ17YgbEs1fBaSf8rrJxJWhO4FzglIv6ddT2NLSKWRMRWQCegl6SSvQUpaV9gTkRMzbqWDPSOiG2AvYATc7edG4QDY1mVwAZVnncCZmdUizWi3H38e4H/GxH3ZV1PIUXE58DjQL9sK2lUvYH9c/fzxwG7SfpztiUVRkTMzv2cA9xPutXeIBwYy5oMdJfUVdKqwGBgfMY1WQPLdQDfAsyIiKuzrqcQJLWTtE7u95bAHsDrmRbViCLi7IjoFBFdSP8/fjQiDs24rEYnqVVuIAeSWgF9gAYbAenAqCIiFgPDgEmkjtC7ImJ6tlU1LkljgWeAHpIqJR2ddU0F0Bs4jPSvzpdyj72zLqqRdQAekzSN9A+jhyOibIaalpH2wFOSXgaeB/4WEQ821MU9rNbMzPLiFoaZmeXFgWFmZnlxYJiZWV4cGGZmlhcHhpmZ5cWBYVZAktaRdELWdZjVhQPDrLDWARwY1iQ5MMwKawSwYW6y4JVZF2NWG564Z1ZAudVxJ5TL3iNWWtzCMDOzvDgwzMwsLw4Ms8JaALTOugizunBgmBVQRHwKPC3pVXd6W1PjTm8zM8uLWxhmZpYXB4aZmeXFgWFmZnlxYJiZWV4cGGZmlhcHhpmZ5cWBYWZmefn/YDOo/riYVKsAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"index1_b = create_model_index1_b()\n",
"\n",
"# Specify integrator options\n",
"int_ops = {'print_stats':True,\"abstol\":1E-8,\"reltol\":1E-6}\n",
"\n",
"# Solve DAEs\n",
"sim = Simulator(index1_b, package='casadi')\n",
"tsim, profiles = sim.simulate(numpoints=100, integrator='idas',integrator_options=int_ops)\n",
"\n",
"# Plot solution\n",
"plot_results(sim, tsim, profiles)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.4.4 Take Away Messages](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.4-Take-Away-Messages)",
"section": "2.4.4 Take Away Messages"
}
},
"source": [
"## 2.4.4 Take Away Messages\n",
"1. Differential algebriac equations (DAEs) are really powerful modeling tools.\n",
"2. Integrating DAEs requires special care. Make sure your model is index 1.\n",
"3. Often there are many ways to reformulate the DAE model. But the numeric integrator only enforces error tolerances on the equations that are explicitly modeled. If an algebriac constraint must be satified to a specific tolerance, include it in the DAE model (as long as it is not high index!)."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.4.4 Take Away Messages](https://ndcbe.github.io/CBE60499/02.04-DAE-modeling.html#2.4.4-Take-Away-Messages)",
"section": "2.4.4 Take Away Messages"
}
},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"id": "8618538f",
"metadata": {},
"source": [
"\n",
"< [2.3 Logical Modeling and Generalized Disjunctive Programs](https://ndcbe.github.io/CBE60499/02.03-GDP.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [2.5 Numeric Integration for DAEs](https://ndcbe.github.io/CBE60499/02.05-Numeric-Integration.html) > 
 "
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.6"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.6"
}
},
"nbformat": 4,
"nbformat_minor": 2
}

