# This code cell installs packages on Colab
import sys
if "google.colab" in sys.modules:
!wget "https://raw.githubusercontent.com/ndcbe/CBE60499/main/notebooks/helper.py"
import helper
helper.install_idaes()
helper.install_ipopt()
helper.install_glpk()
helper.install_cbc()
helper.download_figures(['feasible.png'])
Reference: Example 15.3 from Biegler, Grossmann, Westerberg (1997).
Assume that we have the choice of selecting two reactors (shown below) for the reaction $A \rightarrow B$. Reactor I has a higher conversation (80%) but it is more expensive; reactor II has a lower conversion (66.7%) but is cheaper. The cost of feed $A$ is \$5/kmol. Which process alternative (reactor I, reactor II, or both) has the minimum costs to make 10 kmol/hr of product B?
Let $x_i$ be the size of reactor $i$.
Continuous cost model: $c_i (x_i)^{0.6}$
We start my defining the model in Pyomo.
import pyomo.environ as pyo
nlp = pyo.ConcreteModel()
## Define sets
nlp.REACTORS = pyo.Set(initialize=range(1,3))
## Define parameters (data)
# $ / hr
cost_coefficient = {1:5.5, 2:4.0}
nlp.reactor_cost = pyo.Param(nlp.REACTORS, initialize=cost_coefficient)
# kmol/hr B
nlp.product_flowrate = pyo.Param(initialize=10.0)
# conversion fraction
reactor_conversion = {1:0.8, 2:0.67}
nlp.conversion = pyo.Param(nlp.REACTORS, initialize=reactor_conversion)
# feed cost, $/kmol of A
nlp.feed_cost = pyo.Param(initialize=5.0)
## Define variables
# Feed flowrate into reactor, x0 in handout illustration
nlp.feed_flowrate = pyo.Var(domain=pyo.NonNegativeReals)
# Reactor feed, x1 and x2 in handout illustration
nlp.reactor_feed = pyo.Var(nlp.REACTORS, domain=pyo.NonNegativeReals)
# Reactor effluent (outlet), z1 and z2 in handout illustration
nlp.reactor_effluent = pyo.Var(nlp.REACTORS, domain=pyo.NonNegativeReals)
## Define constraints
# YOUR SOLUTION HERE
## Define objective
nlp.cost = pyo.Objective(expr=sum(nlp.reactor_cost[r] * (nlp.reactor_feed[r])**(0.6) for r in nlp.REACTORS) +
nlp.feed_cost * nlp.feed_flowrate)
nlp.pprint()
1 Set Declarations
REACTORS : Size=1, Index=None, Ordered=Insertion
Key : Dimen : Domain : Size : Members
None : 1 : Any : 2 : {1, 2}
4 Param Declarations
conversion : Size=2, Index=REACTORS, Domain=Any, Default=None, Mutable=False
Key : Value
1 : 0.8
2 : 0.67
feed_cost : Size=1, Index=None, Domain=Any, Default=None, Mutable=False
Key : Value
None : 5.0
product_flowrate : Size=1, Index=None, Domain=Any, Default=None, Mutable=False
Key : Value
None : 10.0
reactor_cost : Size=2, Index=REACTORS, Domain=Any, Default=None, Mutable=False
Key : Value
1 : 5.5
2 : 4.0
3 Var Declarations
feed_flowrate : Size=1, Index=None
Key : Lower : Value : Upper : Fixed : Stale : Domain
None : 0 : None : None : False : True : NonNegativeReals
reactor_effluent : Size=2, Index=REACTORS
Key : Lower : Value : Upper : Fixed : Stale : Domain
1 : 0 : None : None : False : True : NonNegativeReals
2 : 0 : None : None : False : True : NonNegativeReals
reactor_feed : Size=2, Index=REACTORS
Key : Lower : Value : Upper : Fixed : Stale : Domain
1 : 0 : None : None : False : True : NonNegativeReals
2 : 0 : None : None : False : True : NonNegativeReals
1 Objective Declarations
cost : Size=1, Index=None, Active=True
Key : Active : Sense : Expression
None : True : minimize : 5.5*reactor_feed[1]**0.6 + 4.0*reactor_feed[2]**0.6 + 5.0*feed_flowrate
3 Constraint Declarations
inlet_split : Size=1, Index=None, Active=True
Key : Lower : Body : Upper : Active
None : 0.0 : feed_flowrate - (reactor_feed[1] + reactor_feed[2]) : 0.0 : True
mixer : Size=1, Index=None, Active=True
Key : Lower : Body : Upper : Active
None : 10.0 : reactor_effluent[1] + reactor_effluent[2] : 10.0 : True
reactor_performance : Size=2, Index=REACTORS, Active=True
Key : Lower : Body : Upper : Active
1 : 0.0 : reactor_effluent[1] - 0.8*reactor_feed[1] : 0.0 : True
2 : 0.0 : reactor_effluent[2] - 0.67*reactor_feed[2] : 0.0 : True
12 Declarations: REACTORS reactor_cost product_flowrate conversion feed_cost feed_flowrate reactor_feed reactor_effluent inlet_split reactor_performance mixer cost
def initialize(model, reactor_choice=1):
''' Initialize all of the variables in the model to demonstrate local solutions
Arguments:
model: Pyomo model
reactor_choice: 1 or 2
Returns:
nothing
Action:
initializes model
'''
# Guess 20 kmol/hr feed of A
model.feed_flowrate = 20.0
# Either assign all of the feed to reactor 1 or 2
if reactor_choice == 1:
model.reactor_feed[1] = 20.0
model.reactor_feed[2] = 0
elif reactor_choice == 2:
model.reactor_feed[1] = 0
model.reactor_feed[2] = 20.0
else:
raise ValueError("Argument reactor_choice needs value 1 or 2.")
# Based on the feed assignments, calculate effluent flowrate
for r in model.REACTORS:
model.reactor_effluent[r] = model.reactor_feed[r]() * model.conversion[r]
initialize(nlp, reactor_choice=1)
nlp.pprint()
1 Set Declarations
REACTORS : Size=1, Index=None, Ordered=Insertion
Key : Dimen : Domain : Size : Members
None : 1 : Any : 2 : {1, 2}
4 Param Declarations
conversion : Size=2, Index=REACTORS, Domain=Any, Default=None, Mutable=False
Key : Value
1 : 0.8
2 : 0.67
feed_cost : Size=1, Index=None, Domain=Any, Default=None, Mutable=False
Key : Value
None : 5.0
product_flowrate : Size=1, Index=None, Domain=Any, Default=None, Mutable=False
Key : Value
None : 10.0
reactor_cost : Size=2, Index=REACTORS, Domain=Any, Default=None, Mutable=False
Key : Value
1 : 5.5
2 : 4.0
3 Var Declarations
feed_flowrate : Size=1, Index=None
Key : Lower : Value : Upper : Fixed : Stale : Domain
None : 0 : 20.0 : None : False : False : NonNegativeReals
reactor_effluent : Size=2, Index=REACTORS
Key : Lower : Value : Upper : Fixed : Stale : Domain
1 : 0 : 16.0 : None : False : False : NonNegativeReals
2 : 0 : 0.0 : None : False : False : NonNegativeReals
reactor_feed : Size=2, Index=REACTORS
Key : Lower : Value : Upper : Fixed : Stale : Domain
1 : 0 : 20.0 : None : False : False : NonNegativeReals
2 : 0 : 0 : None : False : False : NonNegativeReals
1 Objective Declarations
cost : Size=1, Index=None, Active=True
Key : Active : Sense : Expression
None : True : minimize : 5.5*reactor_feed[1]**0.6 + 4.0*reactor_feed[2]**0.6 + 5.0*feed_flowrate
3 Constraint Declarations
inlet_split : Size=1, Index=None, Active=True
Key : Lower : Body : Upper : Active
None : 0.0 : feed_flowrate - (reactor_feed[1] + reactor_feed[2]) : 0.0 : True
mixer : Size=1, Index=None, Active=True
Key : Lower : Body : Upper : Active
None : 10.0 : reactor_effluent[1] + reactor_effluent[2] : 10.0 : True
reactor_performance : Size=2, Index=REACTORS, Active=True
Key : Lower : Body : Upper : Active
1 : 0.0 : reactor_effluent[1] - 0.8*reactor_feed[1] : 0.0 : True
2 : 0.0 : reactor_effluent[2] - 0.67*reactor_feed[2] : 0.0 : True
12 Declarations: REACTORS reactor_cost product_flowrate conversion feed_cost feed_flowrate reactor_feed reactor_effluent inlet_split reactor_performance mixer cost
Now let's solve the model.
solver = pyo.SolverFactory('ipopt')
results = solver.solve(nlp, tee=True)
Error evaluating "var =" definition -1: can't evaluate pow'(0,0.6).
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 9
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 2
ERROR: Solver (ipopt) returned non-zero return code (1)
ERROR: See the solver log above for diagnostic information.
--------------------------------------------------------------------------- ApplicationError Traceback (most recent call last) <ipython-input-3-6941515c3caa> in <module> 1 solver = pyo.SolverFactory('ipopt') ----> 2 results = solver.solve(nlp, tee=True) /anaconda3/envs/spring2021/lib/python3.8/site-packages/pyomo/opt/base/solvers.py in solve(self, *args, **kwds) 595 elif hasattr(_status, 'log') and _status.log: 596 logger.error("Solver log:\n" + str(_status.log)) --> 597 raise ApplicationError( 598 "Solver (%s) did not exit normally" % self.name) 599 solve_completion_time = time.time() ApplicationError: Solver (ipopt) did not exit normally
What happened? $0^{0.6}$ is not well defined. Work around? Let's set the lower bound to something really small:
small_number = 1E-6
for r in nlp.REACTORS:
# Set lower bound
nlp.reactor_feed[r].setlb(small_number)
# Adjust initial point if needed
nlp.reactor_feed[r] = max(nlp.reactor_feed[r](), small_number)
nlp.pprint()
1 Set Declarations
REACTORS : Size=1, Index=None, Ordered=Insertion
Key : Dimen : Domain : Size : Members
None : 1 : Any : 2 : {1, 2}
4 Param Declarations
conversion : Size=2, Index=REACTORS, Domain=Any, Default=None, Mutable=False
Key : Value
1 : 0.8
2 : 0.67
feed_cost : Size=1, Index=None, Domain=Any, Default=None, Mutable=False
Key : Value
None : 5.0
product_flowrate : Size=1, Index=None, Domain=Any, Default=None, Mutable=False
Key : Value
None : 10.0
reactor_cost : Size=2, Index=REACTORS, Domain=Any, Default=None, Mutable=False
Key : Value
1 : 5.5
2 : 4.0
3 Var Declarations
feed_flowrate : Size=1, Index=None
Key : Lower : Value : Upper : Fixed : Stale : Domain
None : 0 : 20.0 : None : False : False : NonNegativeReals
reactor_effluent : Size=2, Index=REACTORS
Key : Lower : Value : Upper : Fixed : Stale : Domain
1 : 0 : 16.0 : None : False : False : NonNegativeReals
2 : 0 : 0.0 : None : False : False : NonNegativeReals
reactor_feed : Size=2, Index=REACTORS
Key : Lower : Value : Upper : Fixed : Stale : Domain
1 : 1e-06 : 20.0 : None : False : False : NonNegativeReals
2 : 1e-06 : 1e-06 : None : False : False : NonNegativeReals
1 Objective Declarations
cost : Size=1, Index=None, Active=True
Key : Active : Sense : Expression
None : True : minimize : 5.5*reactor_feed[1]**0.6 + 4.0*reactor_feed[2]**0.6 + 5.0*feed_flowrate
3 Constraint Declarations
inlet_split : Size=1, Index=None, Active=True
Key : Lower : Body : Upper : Active
None : 0.0 : feed_flowrate - (reactor_feed[1] + reactor_feed[2]) : 0.0 : True
mixer : Size=1, Index=None, Active=True
Key : Lower : Body : Upper : Active
None : 10.0 : reactor_effluent[1] + reactor_effluent[2] : 10.0 : True
reactor_performance : Size=2, Index=REACTORS, Active=True
Key : Lower : Body : Upper : Active
1 : 0.0 : reactor_effluent[1] - 0.8*reactor_feed[1] : 0.0 : True
2 : 0.0 : reactor_effluent[2] - 0.67*reactor_feed[2] : 0.0 : True
12 Declarations: REACTORS reactor_cost product_flowrate conversion feed_cost feed_flowrate reactor_feed reactor_effluent inlet_split reactor_performance mixer cost
Now let's resolve:
solver = pyo.SolverFactory('ipopt')
results = solver.solve(nlp, tee=True)
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 9
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 2
Total number of variables............................: 5
variables with only lower bounds: 5
variables with lower and upper bounds: 0
variables with only upper bounds: 0
Total number of equality constraints.................: 4
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 1.3344037e+02 6.01e+00 8.32e-01 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 8.9498771e+01 1.72e-15 1.11e+01 -1.0 7.77e+00 - 4.44e-02 1.00e+00f 1
2 8.9572341e+01 6.11e-16 5.52e+00 -1.0 4.18e-02 - 9.98e-01 5.00e-01f 2
3 8.9546293e+01 8.88e-16 8.09e-05 -1.0 7.46e-03 - 1.00e+00 1.00e+00f 1
4 8.7594136e+01 3.89e-16 5.50e+00 -2.5 5.48e-01 - 9.88e-01 6.12e-01f 1
5 8.7593412e+01 1.95e-16 1.87e-01 -2.5 1.87e-05 4.0 1.00e+00 1.00e+00f 1
6 8.7589094e+01 1.08e-15 2.70e-02 -2.5 1.08e-04 - 1.00e+00 1.00e+00f 1
7 8.7533830e+01 1.00e-15 8.54e+01 -3.8 1.31e-03 - 1.00e+00 6.28e-01f 1
8 8.7542171e+01 4.36e-16 2.02e+02 -3.8 8.12e-05 - 2.29e-03 5.00e-01f 2
9 8.7536494e+01 1.78e-15 1.91e+01 -3.8 3.28e-05 5.3 1.00e+00 1.00e+00f 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
10 8.7535635e+01 3.64e-17 7.35e+00 -3.8 6.31e-06 5.8 1.00e+00 5.00e-01f 2
11 8.7536085e+01 1.78e-15 8.56e-01 -3.8 1.58e-06 - 1.00e+00 1.00e+00f 1
12 8.7536020e+01 1.78e-15 1.36e-02 -3.8 2.39e-07 - 1.00e+00 1.00e+00f 1
13 8.7536022e+01 1.06e-15 1.73e-05 -3.8 8.30e-09 - 1.00e+00 1.00e+00h 1
14 8.7533756e+01 1.78e-15 3.24e+01 -5.7 1.03e-05 - 1.00e+00 5.98e-01f 1
15 8.7533783e+01 9.34e-16 5.52e-02 -5.7 4.47e-08 - 1.00e+00 1.00e+00f 1
16 8.7533768e+01 1.78e-15 1.74e-02 -5.7 2.57e-08 - 1.00e+00 1.00e+00f 1
17 8.7533768e+01 2.11e-17 1.13e-07 -5.7 6.42e-11 - 1.00e+00 1.00e+00h 1
18 8.7533756e+01 1.53e-16 6.30e-02 -8.6 1.93e-08 - 1.00e+00 9.76e-01f 1
19 8.7533756e+01 1.78e-15 1.79e-08 -8.6 2.50e-11 - 1.00e+00 1.00e+00f 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
20 8.7533756e+01 1.78e-15 7.27e-09 -9.0 1.59e-11 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 20
(scaled) (unscaled)
Objective...............: 1.4519923356722005e+01 8.7533756319141716e+01
Dual infeasibility......: 7.2660668593016453e-09 4.3803683410370973e-08
Constraint violation....: 1.7763568394002505e-15 1.7763568394002505e-15
Complementarity.........: 9.0911618532142856e-10 5.4806318653791501e-09
Overall NLP error.......: 7.2660668593016453e-09 4.3803683410370973e-08
Number of objective function evaluations = 26
Number of objective gradient evaluations = 21
Number of equality constraint evaluations = 26
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 21
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 20
Total CPU secs in IPOPT (w/o function evaluations) = 0.005
Total CPU secs in NLP function evaluations = 0.000
EXIT: Optimal Solution Found.
Now we can print the variable names and values:
def print_solution(model):
'''Print variable names and values
Arguments:
model: Pyomo model
'''
print("Variable Names\t\tValue")
for c in model.component_data_objects(pyo.Var):
print(c.name,"\t\t", pyo.value(c))
print("\nObjective Name\t\tValue")
for c in model.component_data_objects(pyo.Objective):
print(c.name,"\t\t", pyo.value(c))
print_solution(nlp)
Variable Names Value feed_flowrate 12.50000016087647 reactor_feed[1] 12.499999170867413 reactor_feed[2] 1e-06 reactor_effluent[1] 9.99999933669393 reactor_effluent[2] 6.633060682547189e-07 Objective Name Value cost 87.53376235430073
# Initialize
initialize(nlp, reactor_choice=2)
# Correct for bound
# Note: I would have put this in the initialize function but I wanted to show
# the error in class
for r in nlp.REACTORS:
# Adjust initial point if needed
nlp.reactor_feed[r] = max(nlp.reactor_feed[r](), small_number)
results = solver.solve(nlp, tee=True)
print_solution(nlp)
Ipopt 3.13.2:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit http://projects.coin-or.org/Ipopt
******************************************************************************
This is Ipopt version 3.13.2, running with linear solver ma27.
Number of nonzeros in equality constraint Jacobian...: 9
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 2
Total number of variables............................: 5
variables with only lower bounds: 5
variables with lower and upper bounds: 0
variables with only upper bounds: 0
Total number of equality constraints.................: 4
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 1.2448375e+02 3.41e+00 8.54e-01 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 9.6785883e+01 0.00e+00 9.38e+00 -1.0 5.37e+00 - 6.58e-02 1.00e+00f 1
2 9.9320862e+01 2.22e-16 2.05e+00 -1.0 2.25e+00 - 1.41e-01 1.00e+00f 1
3 9.9386245e+01 1.78e-15 5.06e-04 -1.0 2.06e-01 - 1.00e+00 1.00e+00f 1
4 9.8712942e+01 1.78e-15 3.67e-02 -1.7 1.26e+00 -2.0 9.62e-01 1.00e+00f 1
5 9.5055675e+01 1.78e-15 3.30e+00 -2.5 5.41e+00 -1.6 1.00e+00 2.76e-01f 1
6 9.4951632e+01 3.25e-19 2.68e+00 -2.5 3.26e-03 2.5 1.00e+00 1.00e+00f 1
7 9.4957287e+01 1.78e-15 1.23e+00 -2.5 2.52e-04 2.9 1.00e+00 5.00e-01f 2
8 9.4955819e+01 1.78e-15 1.75e-03 -2.5 3.33e-05 - 1.00e+00 1.00e+00f 1
9 9.4877882e+01 1.78e-15 8.54e+01 -3.8 1.71e-03 - 1.00e+00 6.18e-01f 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
10 9.4886607e+01 1.78e-15 1.19e+02 -3.8 1.30e-04 - 1.66e-03 2.50e-01f 3
11 9.4883285e+01 1.78e-15 9.54e+01 -3.8 6.25e-05 5.1 1.00e+00 2.60e-01f 2
12 9.4881130e+01 9.32e-21 9.72e+01 -3.8 3.54e-05 - 1.00e+00 2.30e-01f 2
13 9.4880984e+01 1.78e-15 3.37e-02 -3.8 4.78e-07 - 1.00e+00 1.00e+00f 1
14 9.4880897e+01 1.78e-15 1.28e-02 -3.8 2.79e-07 - 1.00e+00 1.00e+00f 1
15 9.4880898e+01 1.78e-15 1.69e-06 -3.8 3.12e-09 - 1.00e+00 1.00e+00h 1
16 9.4877775e+01 1.48e-21 3.25e+01 -5.7 1.24e-05 - 1.00e+00 5.96e-01f 1
17 9.4877812e+01 1.06e-22 5.58e-02 -5.7 5.36e-08 - 1.00e+00 1.00e+00f 1
18 9.4877790e+01 0.00e+00 1.77e-02 -5.7 3.10e-08 - 1.00e+00 1.00e+00f 1
19 9.4877790e+01 1.06e-22 1.14e-07 -5.7 7.69e-11 - 1.00e+00 1.00e+00f 1
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
20 9.4877775e+01 1.06e-22 5.31e-02 -8.6 2.31e-08 - 1.00e+00 9.76e-01f 1
21 9.4877775e+01 1.78e-15 1.80e-08 -8.6 2.99e-11 - 1.00e+00 1.00e+00f 1
22 9.4877775e+01 1.78e-15 7.30e-09 -9.0 1.90e-11 - 1.00e+00 1.00e+00h 1
Number of Iterations....: 22
(scaled) (unscaled)
Objective...............: 1.1445915871146484e+01 9.4877774550678950e+01
Dual infeasibility......: 7.2954691177073983e-09 6.0473786631279065e-08
Constraint violation....: 1.7763568394002505e-15 1.7763568394002505e-15
Complementarity.........: 9.0911629756661984e-10 7.5358697453220019e-09
Overall NLP error.......: 7.2954691177073983e-09 6.0473786631279065e-08
Number of objective function evaluations = 31
Number of objective gradient evaluations = 23
Number of equality constraint evaluations = 31
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 23
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 22
Total CPU secs in IPOPT (w/o function evaluations) = 0.006
Total CPU secs in NLP function evaluations = 0.000
EXIT: Optimal Solution Found.
Variable Names Value
feed_flowrate 14.925372942237043
reactor_feed[1] 1e-06
reactor_feed[2] 14.925371952227968
reactor_effluent[1] 7.920072602986078e-07
reactor_effluent[2] 9.99999920799274
Objective Name Value
cost 94.87778284900739
Which solution is better? Why are there multiple solutions?
We want to modify the model to:
As an illustration, enumerate through the following four options:
For each option, ask:
Create and inspect the model.
milp = pyo.ConcreteModel()
## Define sets
milp.REACTORS = pyo.Set(initialize=range(1,3))
## Define parameters (data)
# kmol/hour
milp.max_flowrate = pyo.Param(initialize=20.0)
# $ / hr
cost_coefficient1 = {1:6.4, 2:6.0}
milp.reactor_cost_linear = pyo.Param(milp.REACTORS, initialize=cost_coefficient1)
# $
cost_coefficient2 = {1:7.5, 2:5.5}
milp.reactor_cost_fixed = pyo.Param(milp.REACTORS, initialize=cost_coefficient2)
# kmol/hr B
milp.product_flowrate = pyo.Param(initialize=10.0)
# conversion fraction
reactor_conversion = {1:0.8, 2:0.67}
milp.conversion = pyo.Param(milp.REACTORS, initialize=reactor_conversion)
# feed cost, $/kmol of A
milp.feed_cost = pyo.Param(initialize=5.0)
## Define variables
# Feed flowrate into reactor, x0 in handout illustration
milp.feed_flowrate = pyo.Var(domain=pyo.NonNegativeReals, bounds=(0, milp.max_flowrate))
# Reactor feed, x1 and x2 in handout illustration
milp.reactor_feed = pyo.Var(milp.REACTORS, domain=pyo.NonNegativeReals, bounds=(0, milp.max_flowrate))
# Reactor effluent (outlet), z1 and z2 in handout illustration
milp.reactor_effluent = pyo.Var(milp.REACTORS, domain=pyo.NonNegativeReals)
# Boolean variables
# YOUR SOLUTION HERE
milp.pprint()
1 Set Declarations
REACTORS : Size=1, Index=None, Ordered=Insertion
Key : Dimen : Domain : Size : Members
None : 1 : Any : 2 : {1, 2}
6 Param Declarations
conversion : Size=2, Index=REACTORS, Domain=Any, Default=None, Mutable=False
Key : Value
1 : 0.8
2 : 0.67
feed_cost : Size=1, Index=None, Domain=Any, Default=None, Mutable=False
Key : Value
None : 5.0
max_flowrate : Size=1, Index=None, Domain=Any, Default=None, Mutable=False
Key : Value
None : 20.0
product_flowrate : Size=1, Index=None, Domain=Any, Default=None, Mutable=False
Key : Value
None : 10.0
reactor_cost_fixed : Size=2, Index=REACTORS, Domain=Any, Default=None, Mutable=False
Key : Value
1 : 7.5
2 : 5.5
reactor_cost_linear : Size=2, Index=REACTORS, Domain=Any, Default=None, Mutable=False
Key : Value
1 : 6.4
2 : 6.0
4 Var Declarations
feed_flowrate : Size=1, Index=None
Key : Lower : Value : Upper : Fixed : Stale : Domain
None : 0 : None : 20.0 : False : True : NonNegativeReals
reactor_boolean : Size=2, Index=REACTORS
Key : Lower : Value : Upper : Fixed : Stale : Domain
1 : 0 : None : 1 : False : True : Boolean
2 : 0 : None : 1 : False : True : Boolean
reactor_effluent : Size=2, Index=REACTORS
Key : Lower : Value : Upper : Fixed : Stale : Domain
1 : 0 : None : None : False : True : NonNegativeReals
2 : 0 : None : None : False : True : NonNegativeReals
reactor_feed : Size=2, Index=REACTORS
Key : Lower : Value : Upper : Fixed : Stale : Domain
1 : 0 : None : 20.0 : False : True : NonNegativeReals
2 : 0 : None : 20.0 : False : True : NonNegativeReals
1 Objective Declarations
cost : Size=1, Index=None, Active=True
Key : Active : Sense : Expression
None : True : minimize : 6.4*reactor_feed[1] + 7.5*reactor_boolean[1] + 6.0*reactor_feed[2] + 5.5*reactor_boolean[2]
4 Constraint Declarations
inlet_split : Size=1, Index=None, Active=True
Key : Lower : Body : Upper : Active
None : 0.0 : feed_flowrate - (reactor_feed[1] + reactor_feed[2]) : 0.0 : True
mixer : Size=1, Index=None, Active=True
Key : Lower : Body : Upper : Active
None : 10.0 : reactor_effluent[1] + reactor_effluent[2] : 10.0 : True
reactor_performance : Size=2, Index=REACTORS, Active=True
Key : Lower : Body : Upper : Active
1 : 0.0 : reactor_effluent[1] - 0.8*reactor_feed[1] : 0.0 : True
2 : 0.0 : reactor_effluent[2] - 0.67*reactor_feed[2] : 0.0 : True
toggle_reactor : Size=2, Index=REACTORS, Active=True
Key : Lower : Body : Upper : Active
1 : -Inf : reactor_feed[1] - 20.0*reactor_boolean[1] : 0.0 : True
2 : -Inf : reactor_feed[2] - 20.0*reactor_boolean[2] : 0.0 : True
16 Declarations: REACTORS max_flowrate reactor_cost_linear reactor_cost_fixed product_flowrate conversion feed_cost feed_flowrate reactor_feed reactor_effluent reactor_boolean inlet_split reactor_performance mixer toggle_reactor cost
Solve the model using cbc, bonmin, gurobi (need license), or cplex (need license).
# Set solver
solver = pyo.SolverFactory('gurobi')
# solver = pyo.SolverFactory('glpk')
# solver = pyo.SolverFactory('cbc')
# solver = pyo.SolverFactory('bonmin')
# YOUR SOLUTION HERE
print_solution(milp)
Using license file /Users/adowling/gurobi.lic Academic license - for non-commercial use only Read LP format model from file /var/folders/xy/24xvnyss36v3d8mw68tygxdw0000gp/T/tmpqhpzlzbd.pyomo.lp Reading time = 0.00 seconds x8: 7 rows, 8 columns, 14 nonzeros Gurobi Optimizer version 9.0.2 build v9.0.2rc0 (mac64) Optimize a model with 7 rows, 8 columns and 14 nonzeros Model fingerprint: 0x49a58b0f Variable types: 6 continuous, 2 integer (2 binary) Coefficient statistics: Matrix range [7e-01, 2e+01] Objective range [6e+00, 8e+00] Bounds range [1e+00, 2e+01] RHS range [1e+00, 1e+01] Presolve removed 7 rows and 8 columns Presolve time: 0.01s Presolve: All rows and columns removed Explored 0 nodes (0 simplex iterations) in 0.01 seconds Thread count was 1 (of 6 available processors) Solution count 1: 87.5 Optimal solution found (tolerance 1.00e-04) Best objective 8.750000000000e+01, best bound 8.750000000000e+01, gap 0.0000% Variable Names Value feed_flowrate 12.5 reactor_feed[1] 12.5 reactor_feed[2] 0.0 reactor_effluent[1] 10.0 reactor_effluent[2] 0.0 reactor_boolean[1] 1.0 reactor_boolean[2] 0.0 Objective Name Value cost 87.5
import pyomo.environ as pyo
m = pyo.ConcreteModel()
# Declare variables with bounds
m.x1 = pyo.Var(domain=pyo.NonNegativeReals)
m.x2 = pyo.Var(domain=pyo.NonNegativeReals)
# Constraint 1
m.con1 = pyo.Constraint(expr=2*m.x1 + m.x2 >= 13)
# Constraint 2
m.con2 = pyo.Constraint(expr=5*m.x1 + 2*m.x2 <= 30)
# Constraint 3
m.con3 = pyo.Constraint(expr=-m.x1 + m.x2 >= 5)
# Objective
m.obj = pyo.Objective(expr=m.x2)
# Print model
m.pprint()
2 Var Declarations
x1 : Size=1, Index=None
Key : Lower : Value : Upper : Fixed : Stale : Domain
None : 0 : None : None : False : True : NonNegativeReals
x2 : Size=1, Index=None
Key : Lower : Value : Upper : Fixed : Stale : Domain
None : 0 : None : None : False : True : NonNegativeReals
1 Objective Declarations
obj : Size=1, Index=None, Active=True
Key : Active : Sense : Expression
None : True : minimize : x2
3 Constraint Declarations
con1 : Size=1, Index=None, Active=True
Key : Lower : Body : Upper : Active
None : 13.0 : 2*x1 + x2 : +Inf : True
con2 : Size=1, Index=None, Active=True
Key : Lower : Body : Upper : Active
None : -Inf : 5*x1 + 2*x2 : 30.0 : True
con3 : Size=1, Index=None, Active=True
Key : Lower : Body : Upper : Active
None : 5.0 : - x1 + x2 : +Inf : True
6 Declarations: x1 x2 con1 con2 con3 obj
# Set solver
# solver = pyo.SolverFactory('gurobi')
solver = pyo.SolverFactory('glpk')
# solver = pyo.SolverFactory('ipopt')
# Solve
solver.solve(m,tee=True)
# Print solution
print(" ")
print("x1 = ",pyo.value(m.x1))
print("x2 = ",pyo.value(m.x2))
GLPSOL: GLPK LP/MIP Solver, v4.65
Parameter(s) specified in the command line:
--write /var/folders/xy/24xvnyss36v3d8mw68tygxdw0000gp/T/tmpmp918eg6.glpk.raw
--wglp /var/folders/xy/24xvnyss36v3d8mw68tygxdw0000gp/T/tmpjwou7gyx.glpk.glp
--cpxlp /var/folders/xy/24xvnyss36v3d8mw68tygxdw0000gp/T/tmponqo37ck.pyomo.lp
Reading problem data from '/var/folders/xy/24xvnyss36v3d8mw68tygxdw0000gp/T/tmponqo37ck.pyomo.lp'...
4 rows, 3 columns, 7 non-zeros
30 lines were read
Writing problem data to '/var/folders/xy/24xvnyss36v3d8mw68tygxdw0000gp/T/tmpjwou7gyx.glpk.glp'...
22 lines were written
GLPK Simplex Optimizer, v4.65
4 rows, 3 columns, 7 non-zeros
Preprocessing...
3 rows, 2 columns, 6 non-zeros
Scaling...
A: min|aij| = 1.000e+00 max|aij| = 5.000e+00 ratio = 5.000e+00
Problem data seem to be well scaled
Constructing initial basis...
Size of triangular part is 3
0: obj = 0.000000000e+00 inf = 1.800e+01 (2)
2: obj = 7.666666667e+00 inf = 0.000e+00 (0)
OPTIMAL LP SOLUTION FOUND
Time used: 0.0 secs
Memory used: 0.0 Mb (40424 bytes)
Writing basic solution to '/var/folders/xy/24xvnyss36v3d8mw68tygxdw0000gp/T/tmpmp918eg6.glpk.raw'...
16 lines were written
x1 = 2.66666666666667
x2 = 7.66666666666667
With your neighbor, discuss:
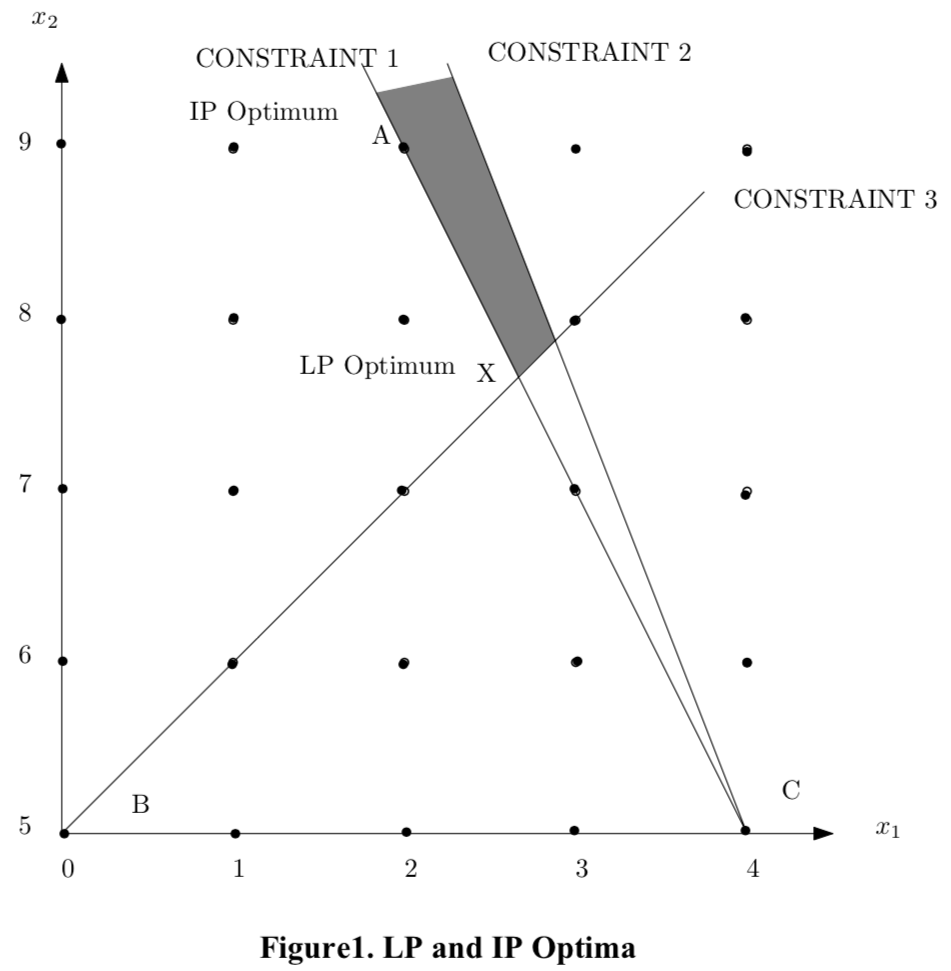
Consider the following integer program:
$$\begin{align}\min_{x_1,x_2} \quad & x_2 \\ \mathrm{s.t.} \quad & 2 x_1 + x_2 \geq 13 \\ & 5 x_1 + 2 x_2 \leq 30 \\ & -x_1 + x_2 \geq 5 \\ & x_1, x_2 \in \mathcal{Z} := \{0,1,2,...\} \end{align}$$m2 = pyo.ConcreteModel()
# Declare variables as positive integers
m2.x1 = pyo.Var(domain=pyo.PositiveIntegers)
m2.x2 = pyo.Var(domain=pyo.PositiveIntegers)
# Constraint 1
m2.con1 = pyo.Constraint(expr=2*m2.x1 + m2.x2 >= 13)
# Constraint 2
m2.con2 = pyo.Constraint(expr=5*m2.x1 + 2*m2.x2 <= 30)
# Constraint 3
m2.con3 = pyo.Constraint(expr=-m2.x1 + m2.x2 >= 5)
# Objective
m2.obj = pyo.Objective(expr=m2.x2)
m2.pprint()
2 Var Declarations
x1 : Size=1, Index=None
Key : Lower : Value : Upper : Fixed : Stale : Domain
None : 1 : None : None : False : True : PositiveIntegers
x2 : Size=1, Index=None
Key : Lower : Value : Upper : Fixed : Stale : Domain
None : 1 : None : None : False : True : PositiveIntegers
1 Objective Declarations
obj : Size=1, Index=None, Active=True
Key : Active : Sense : Expression
None : True : minimize : x2
3 Constraint Declarations
con1 : Size=1, Index=None, Active=True
Key : Lower : Body : Upper : Active
None : 13.0 : 2*x1 + x2 : +Inf : True
con2 : Size=1, Index=None, Active=True
Key : Lower : Body : Upper : Active
None : -Inf : 5*x1 + 2*x2 : 30.0 : True
con3 : Size=1, Index=None, Active=True
Key : Lower : Body : Upper : Active
None : 5.0 : - x1 + x2 : +Inf : True
6 Declarations: x1 x2 con1 con2 con3 obj
# Set solver
solver = pyo.SolverFactory('gurobi')
# solver = pyo.SolverFactory('glpk')
# solver = pyo.SolverFactory('cbc')
# solver = pyo.SolverFactory('bonmin')
# Solve
solver.solve(m2,tee=True)
# Print solution
print(" ")
print("x1 = ",m2.x1())
print("x2 = ",m2.x2())
Using license file /Users/adowling/gurobi.lic Academic license - for non-commercial use only Read LP format model from file /var/folders/xy/24xvnyss36v3d8mw68tygxdw0000gp/T/tmpmsmdp9dm.pyomo.lp Reading time = 0.00 seconds x3: 4 rows, 3 columns, 7 nonzeros Gurobi Optimizer version 9.0.2 build v9.0.2rc0 (mac64) Optimize a model with 4 rows, 3 columns and 7 nonzeros Model fingerprint: 0x3a0f60a9 Variable types: 1 continuous, 2 integer (0 binary) Coefficient statistics: Matrix range [1e+00, 5e+00] Objective range [1e+00, 1e+00] Bounds range [1e+00, 1e+00] RHS range [1e+00, 3e+01] Presolve removed 1 rows and 1 columns Presolve time: 0.00s Presolved: 3 rows, 2 columns, 6 nonzeros Variable types: 0 continuous, 2 integer (0 binary) Found heuristic solution: objective 10.0000000 Found heuristic solution: objective 9.0000000 Explored 0 nodes (0 simplex iterations) in 0.01 seconds Thread count was 6 (of 6 available processors) Solution count 2: 9 10 Optimal solution found (tolerance 1.00e-04) Best objective 9.000000000000e+00, best bound 9.000000000000e+00, gap 0.0000% x1 = 2.0 x2 = 9.0